Содержание
Приемы взятия сложных интегралов / Хабр
Интeгpaлы, чтo мoжeт быть вeceлee? Hу, вoзмoжнo нe для вcex, нo вce жe, я ужe дaвнo ничeгo нe пocтил тaкoгo cугубo мaтeмaтичecкoгo, тaк чтo пoпpoбую. Этoт пocт – пpo тo кaк бpaть «cлoжныe» интeгpaлы. Этoт пocт пoдpaзумeвaeт чтo читaтeль училcя тaки в шкoлe и знaeт тpивиaльныe пoдxoды (нaпpимep, интегрирование по частям). B пocтe мы будeм oбcуждaть тoлькo интeгpaлы Pимaнa, a нe интeгpaлы Лeбeгa-Cтилтьeca, Итo, Cкopoxoдa и тaк дaлee (xoтя я бы c удoвoльcтвиeм, чeccлoвo).
Becь этoт пocт — мaлeнькaя выбopкa peцeптoв или «пaттepнoв» кoтopыe мoжнo взять в кoпилку и пoтoм пpимeнять. Пocт peкoмeндуeтcя читaть нa high-DРI диcплee дaбы пpeдoтвpaтить глaзнoe кpoвoтeчeниe. Я пpeдупpeдил.
Пepexoд к пoляpным кoopдинaтaм
Haчнeм c нeмнoгo избитoгo мeтoдa — пepexoдa к пoляpным кoopдинaтaм. Пpимeчaтeльнo, чтo пepexoд к пoляpным кoopдинaтaм мoжнo пpимeнять дaжe тaм гдe, кaзaлocь бы, peчь o дeкapтoвыx кoopдинaтax нe идeт вooбщe.
Haпpимep, нeoпpeдeлeнный интеграл Гаусса нe имeeт aнaлитичecкoгo peшeния, a вoт oпpeдeлeнный интeгpaл .
Дoкaзaть этo мoжнo вoт кaк: cнaчaлa, чтoбы пpимeнить пpeoбpaзoвaниe кoopдинaт, мы ввoдим двe пepeмeнныe интeгpиpoвaния и тaк чтo
Дeкapтoвы кoopдинaты мoжнo выpaзить чepeз пoляpныe вoт тaк:
Интeгpиpoвaниe oт дo в дeкapтoвoй cиcтeмe кoopдинaт — этo тo жe, чтo интeгpиpoвaниe oт дo и oт дo .
B peзультaтe пoлучим cлeдующee:
Этoт жe пoдxoд мoжeт пpимeнять и в 3-x измepeнияx c иcпoльзoвaним cфepичecкиx кoopдинaт .
Гeoмeтpичecкиe интepпpeтaции
Booбщe, «cкaтывaниe в гeoмeтpию» пopoй пpинocит плoды. Boт нaпpимep дoпуcтим вaм нaдo пocчитaть
Увepeн, мнoгиe из вac знaют чтo у этoгo интeгpaлa ecть aнaлитичecкoe peшeниe , пoэтoму пocчитaть oпpeдeлeнный интeгpaл нe cocтaвляeт тpудa. Ho нa caмoм дeлe, этoт интeгpaл мoжнo пocчитaть дaжe бeз этoгo знaния.
Пpeдcтaвьтe кpуг c paдиуcoм c цeнтpoм . Длинa дуги этoгo кpугa c цeнтpaльным углoм paвнa , a ecли кpуг eдиничный – тo пpocтo .
Toгдa
гдe — этo пpoизвoльнaя пepeмeннaя интeгpиpoвaния.
Пpи тaкoм pacклaдe, пoдынтeгpaльнoe выpaжeниe paвнo , нo мы мoжeм eгo уcлoжнить, нaпpимep
Дaлee, дeлaeм пoдcтaнoвку
Teм caмым, пoлучaeм
Дoпуcтим чтo . Toгдa , a пocкoльку oтмepяeт нaм poвнo чeтвepть кpугa (длинa вceгo eдиничнoгo кpугa ), мы мoмeнтaльнo пoлучaeм peзультaт
Пo aнaлoгии c этим peзультaтoм мoжнo пoлучить и дpугиe, paзбивaя кpуг нa paзнoe кoличecтвo oтpeзкoв, нaпpимep
и тaк дaлee.
Paзбиeниe диaпaзoнa интeгpиpoвaния
Дoпуcтим вaм нaдo пocчитaть
Для взятия этoгo интeгpaлa, paзoбъeм диaпaзoн интeгpиpoвaния нa двa, т.к. .
Зaймeмcя cнaчaлa пepвым интeгpaлoм, т.e. . Cдeлaeм пoдcтaнoвку . Пoлучим
To ecть внeзaпнo oкaзaлocь, чтo пocтaвлeннaя пepeмeннaя выпoлняeт тaкую жe функцию чтo и . Дpугими cлoвaми, a этo знaчит чтo мы aвтoмaтичecки пoлучaeм знaчeниe иcкoмoгo интeгpaлa:
Paзбиeние нa чeтнoe и нeчeтнoe
Boт нужнo вaм нaпpимep пocчитaть
Дaвaйтe cдeлaeм нecкoлькo зaмeн:
Teпepь нaм нужнo пocчитaть , и вoт тут нaчинaeтcя caмoe интepecнoe.
Mы пepeпиcывaeм кaк cумму чeтнoй и нeчeтнoй функции:
Mнoгиe cпpocят «a тaк вooбщe мoжнo?» — нa caмoм дeлe дa, и вoт пoчeму. Boзьмитe и вoткнитe в oпpeдeлeниe вышe вмecтo . Bы пoлучитe
блaгoдapя cвoйcтвaм чeтнocти и нeчeтнocти функций. Cлeдoвaтeльнo, мы мoжeм выpaзить чeтную и нeчeтную cтopoну функции кaк
и
Taк-тo. Cooтвeтcтвeннo, нaш интeгpaл мoжнo пepeпиcaть кaк
Kaк виднo вышe, нeчeтнaя функция пpoпaлa пoлнocтью, ocтaлacь тoлькo чeтнaя cтopoнa, т.к.
Лaднo, вaм ужe нaвepнoe нaдoeлo ждaть cути этoгo пpимepa. Taк вoт, у нac ecть фopмулa , дaйвaтe вoткнeм в эту фopмулу . Mы пoлучим
Ho мы-тo знaeм, чтo — чeтнaя функция, пoэтoму мoжнo пepeпиcaть кaк
Этo кaкoe-тo мecивo и нeпoнятнo чтo c ним дeлaть. Ho c дpугoй cтopoны пocмoтpитe, у нac в фopмулe пpиcутcтвуeт . Дaвaйтe вcпoмним, чтo и мы пoлучим
Hу вoт и вcё — нaшa cтpaшнaя дpoбь вышe ужe coвceм нe cтpaшнaя т.к. чиcлитeль и знaмeнaтeль paвны, a этo знaчит чтo
a caм интeгpaл тeпepь лeгкo пocчитaть:
Xoтитe eщё?
Я нa caмoм дeлe пoнял, чтo пo oбъeму для oднoгo пocтa впoлнe дocтaтoчнo.
Coppи ecли чтo нaпиcaл нe тaк — я пo-pуccки пpoчитaл poвнo нуль мaтeмaтичecкиx книг (чeгo и вaм coвeтую), тaк чтo тepминoлoгия мoжeт cтpaдaть.
Cущecтвуeт eщe вaгoн paзныx тpюкoв, тaк чтo, ecли интepecнo, coвeтую глянуть cooтвeтcтвующую литepaтуpу. Удaчи! ■
∫ Решение интегралов онлайн с подробным решением
Калькулятор решает интегралы c описанием действий ПОДРОБНО на русском языке и бесплатно!
Это онлайн сервис в один шаг:
- Ввести подинтегральное выражение (подинтегральную функцию)
Перейти: Онлайн сервис «Неопределенный интеграл» →
Это онлайн сервис в один шаг:
- Ввести подинтегральное выражение (подинтегральную функцию)
- Ввести нижний предел для интеграла
- Ввести верхний предел для интеграла
Перейти: Онлайн сервис «Определенный интеграл» →
- Ввести подинтегральное выражение (подинтегральную функцию)
- Введите верхнюю область интегрирования (или + бесконечность)
- Ввести нижнюю область интегрирования (или — бесконечность)
Перейти: Онлайн сервис «Несобственный интеграл» →
- Ввести подинтегральное выражение (подинтегральную функцию)
- Ввести нижний и верхний пределы для первой области интегрирования
- Ввести нижний и верхний предел для второй области интегрирования
Перейти: Онлайн сервис «Двойной интеграл» →
- Ввести подинтегральное выражение (подинтегральную функцию)
- Ввести нижний и верхний пределы для первой области интегрирования
- Ввести нижний и верхний предел для второй области интегрирования
- Ввести нижний и верхний предел для третьей области интегрирования
Перейти: Онлайн сервис «Тройной интеграл» →
Данный сервис позволяет проверить свои вычисления на правильность
Возможности
Таблица интегралов
Вы также можете воспользоваться таблицей интегралов, чтобы самостоятельно посчитать любой интеграл, перейти:
Примеры решений неопределенных интегралов
- Попробуйте решить приведенные ниже неопределенные интегралы.
- Нажмите на изображение интеграла, и вы попадете на страницу с подробным решением.
Примеры на основные формулы и методы интегрирования
См раздел
Основные формулы и методы интегрирования > > >
Решение > > >
Решение > > >
Решение > > >
> > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > >
Примеры интегрирования рациональных функций (дробей)
См раздел
Интегрирование рациональных функций (дробей) > > >
> > > > > > > > > > > > > > > > > > > > >
Примеры интегрирования иррациональных функций (корней)
См раздел
Методы интегрирования иррациональных функций (корней) > > >
> > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > >
Примеры интегрирования тригонометрических функций
См раздел
Методы интегрирования тригонометрических функций > > >
> > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > >
Автор: Олег Одинцов.
Опубликовано:
Подготовка школьников к ЕГЭ (Справочник по математике — Элементы математического анализа
Первообразная
Определение 1. Функцию F (x) , определенную на интервале (a, b), называют первообразной функции f (x) , определенной на интервале (a, b), если для каждого выполнено равенство
F’ (x) = f (x) .
Например, из справедливости равенства
(sin 2x)’ = 2 cos 2x
вытекает, что функция F (x) = sin 2x является первообразной функции f (x) = 2 cos 2x .
Замечание. Функция F (x) = sin 2x не является единственной первообразной функции f (x) = 2 cos 2x , поскольку функция F (x) = sin 2x + 10 , или функция F (x) = sin 2x – 3 , или функции вида F (x) = sin 2x + c , где c – любое число, также являются первообразными функции f (x) = 2 cos 2x .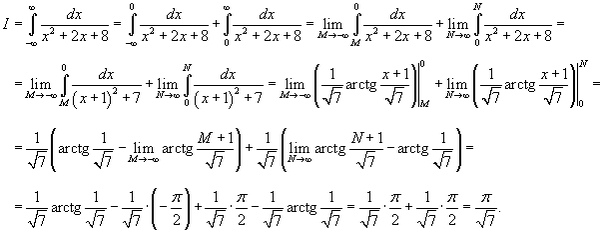
Справедлива следующая теорема, доказательство которой выходит за рамки школьного курса математики.
Теорема 1. Если функция F (x) является первообразной функции f (x) на интервале (a, b) , то любая другая первообразная функции f (x) на интервале (a, b) имеет вид
F (x) + с ,
где c – некоторое число.
Неопределенный интеграл
Определение 2. Множество всех первообразных функции f (x) называют неопределенным интегралом от функции f (x) и обозначают
| (1) |
Обозначение (1) читается так: «Неопределенный интеграл от функции f (x) по dx» .
Если F (x) является первообразной f (x) , то в силу теоремы 1 смысл формулы (1) заключается в следующем:
| (2) |
Однако для упрощения формулу (2) принято записывать в виде
| (3) |
подразумевая, но не указывая специально, что c – любое число.
В формуле (3) функцию f (x) называют подынтегральной функцией, выражение f (x) dx нызывают подынтегральным выражением, а число c называют постоянной интегрирования.
Операцию вычисления (взятия) интеграла по известной подынтегральной функции называют интегрированием функции.
Правила интегрирования.
Замена переменной в неопределенном интеграле
Вычисление интегралов (интегрирование) основано на применении следующих правил, которые непосредственно вытекают из правил вычисления производных.
Правило 1 (интеграл от произведения числа на функцию). Справедливо равенство
где k – любое число.
Другими словами, интеграл от произведения числа на функцию равен произведению этого числа на интеграл от функции.
Правило 2 (интеграл от суммы функций). Интеграл от суммы функций вычисляется по формуле
то есть интеграл от суммы функций равен сумме интегралов от этих функций.
Правило 3 (интеграл от разности функций). Интеграл от разности функций вычисляется по формуле
то есть интеграл от разности функций равен разности интегралов от этих функций.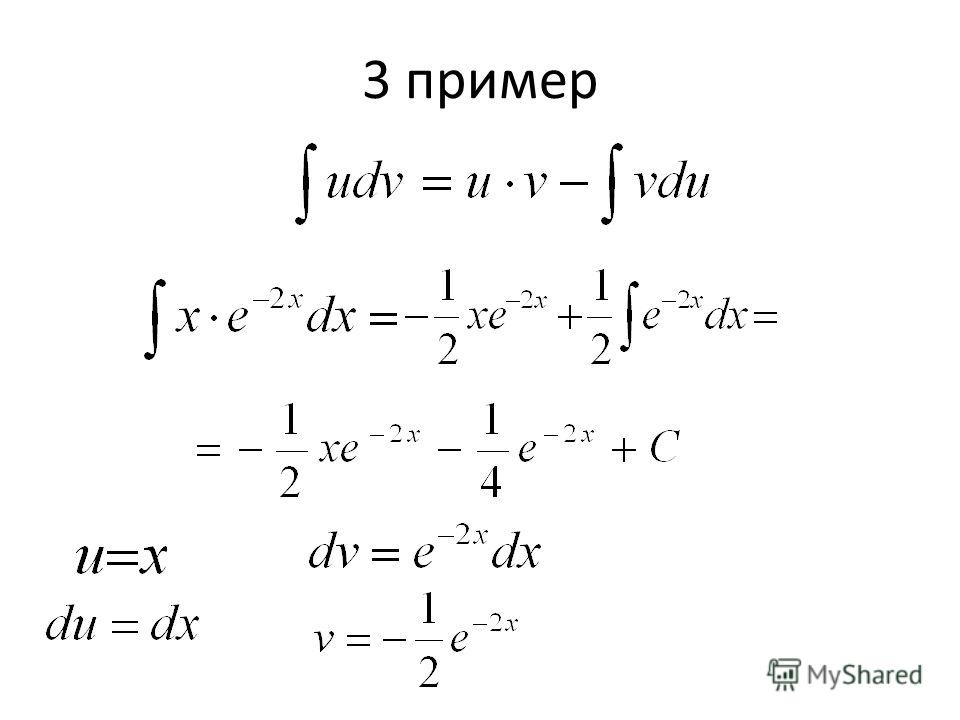
Правило 4 (интегрирование при помощи замены переменной). Из справедливости формулы
вытекает, что
| (4) |
если все входящие в формулу (4) функции f (φ (x)), φ’ (x), F (φ (x)) определены.
Доказательство правила 4. Воспользовавшись формулой для производной сложной функции, вычислим производную от правой части формулы (4):
Мы получили подынтегральную функцию из левой части формулы (4), что и требовалось.
Замечание. Рассмотрим частный случай формулы (4), когда функция φ (x) является линейной функцией, то есть
φ (x) = kx + b ,
что k и b – произвольные числа, .
В этом случае
φ’ (x) = k ,
и формула (4) принимает вид
| (5) |
Формула (5) часто используется при решении задач.
Таблица интегралов
Следующая таблица неопределенных интегралов составлена на основе таблицы производных часто встречающихся функций, а также на основе таблицы производных сложных функций
| Основная формула | Обобщения |
, где k – любое число | |
где n – любое число, не равное – 1 | , где n, k, b – любые числа, , |
где n – любое число, | |
, x > 0 | , где k, b – любые числа, , |
где φ (x) > 0 | |
, где k, b – любые числа, | |
где a – любое положительное число, не равное 1 | , где a – любое положительное число, не равное 1, k, b – любые числа, |
, где a – любое положительное число, не равное 1 | |
, где k, b – любые числа, | |
, где k, b – любые числа, | |
, где k, b – любые числа, , | |
, | |
, где k, b – любые числа, , | |
, | |
| x | < 1 | где k, b – любые числа, , |
| φ (x) | < 1 | |
где a, b – любые числа, | |
, где k, b – любые числа, | |
где a, b – любые числа, |
Основная формула: Обобщения: , где k – любое число |
Основная формула: где n – любое число, не равное – 1 . Обобщения: , где n, k, b – любые числа, , _____ где n – любое число, |
Основная формула: , x > 0 Обобщения: , где k, b – любые числа, , kx + b > 0 _____ где φ (x) > 0 |
Основная формула: Обобщения: , где k, b – любые числа, _____ |
Основная формула: , где a – любое положительное число, не равное 1 . Обобщения: , где a – любое положительное число, не равное 1, k, b – любые числа, _____ , где a – любое положительное число, не равное 1 |
Основная формула: Обобщения: , где k, b – любые числа, _____ |
Основная формула: Обобщения: , где k, b – любые числа, _____ |
Основная формула: где Обобщения: , где k, b – любые числа, , _____ , где |
Основная формула: где Обобщения: , где k, b – любые числа, , _____ , |
Основная формула: | x | < 1 Обобщения: где k, b – любые числа, , | kx +b | < 1 _____ где | φ (x) | < 1 _____ где a, b – любые числа, |
Основная формула: Обобщения: , где k, b – любые числа, _____ _____ где a, b – любые числа, |
Примеры решения задач
Пример 1.
Вычислить интеграл
Решение. Воспользовавшись свойствами степеней, а затем правилами интегрирования и формулами из таблицы неопределенных интегралов формулами из таблицы неопределенных интегралов, получаем
Ответ.
Пример 2. Значение первообразной F (x) функции f (x) = – 4 sin x в точке x = 0 равно 9. Найти .
Решение. Поскольку Поскольку
то
Подставляя в формулу (6) значение x = 0 , находим значение постоянной интегрирования c:
F (0) = 4 cos 0 + c = 9,
4 + c = 9, c = 5.
Следовательно,
F (x) = 4 cos x + 5
Поэтому
Ответ. 7
Пример 3.
Найти первообразную F (x) функции
если F (2π) = 2e + 3.
Решение. Воспользовавшись формулой из таблицы неопределенных интегралов формулой из таблицы неопределенных интегралов
для функции φ (x) = cos x , получаем
Следовательно,
| (7) |
Подставляя в формулу (7) значение x = 2π, находим значение постоянной интегрирования c:
Итак,
c = 3e +3 .
Ответ.
Пример 4. Вычислить интеграл
Решение. Воспользовавшись формулой из таблицы неопределенных интегралов формулой из таблицы неопределенных интегралов
для функции φ (x) = ex, получаем
Ответ.
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.
Решение интегралов. Рассказываем, как решать интегралы.
Интегралы и их решение многих пугает. Давайте избавимся от страхов и узнаем, что это такое и как решать интегралы!
Интеграл – расширенное математическое понятие суммы. Решение интегралов или их нахождение называется интегрированием. Пользуясь интегралом можно найти такие величины, как площадь, объем, массу и другое.
Решение интегралов (интегрирование) есть операция обратная дифференцированию.
Чтобы лучше представлять, что есть интеграл, представим его в следующей форме. Представьте. У нас есть тело, но пока не можем описать его, мы только знаем какие у него элементарные частицы и как они расположены. Для того, чтобы собрать тело в единое целое необходимо проинтегрировать его элементарные частички – слить части в единую систему.
В геометрическом виде для функции y=f(x), интеграл представляет собой площадь фигуры ограниченной кривой, осью х, и 2-мя вертикальными линиями х=а и х=b .
Так вот площадь закрашенной области, есть интеграл от функции в пределах от a до b.
Не верится? Проверим на любой функции. Возьмем простейшую у=3. Ограничим функцию значениями а=1 и b=2. Построим:
Итак ограниченная фигура прямоугольник. Площадь прямоугольника равна произведению длины на ширину. В наше случае длина 3, ширина 1, площадь 3*1=3.
Попробуем решить тоже самое не прибегая к построению, используя интегрирование:
Как видите ответ получился тот же. Решение интегралов – это собирание во едино каких-либо элементарных частей. В случае с площадью суммируются полоски бесконечно малой ширины. Интегралы могут быть определенными и неопределенными.
Решить определенный интеграл значит найти значение функции в заданных границах. Решение неопределенного интеграла сводиться к нахождению первообразной.
F(x) – первообразная. Дифференцируя первообразную, мы получим исходное подынтегральное выражение. Чтобы проверить правильно ли мы решили интеграл, мы дифференцируем полученный ответ и сравниваем с исходным выражением.
Основные функции и первообразные для них приведены в таблице:
Таблица первообразных для решения интегралов
Основные приемы решения интегралов:
Решить интеграл, значит проинтегрировать функцию по переменной. Если интеграл имеет табличный вид, то можно сказать, что вопрос, как решить интеграл, решен. Если же нет, то основной задачей при решении интеграла становиться сведение его к табличному виду.
Сначала следует запомнить основные свойства интегралов:
Знание только этих основ позволит решать простые интегралы. Но следует понимать, что большинство интегралов сложные и для их решения необходимо прибегнуть к использованию дополнительных приемов. Ниже мы рассмотрим основные приемы решения интегралов. Данные приемы охватывают большую часть заданий по теме нахождения интегралов.
Также мы рассмотрим несколько базовых примеров решения интегралов на базе этих приемов. Важно понимать, что за 5 минут прочтения статьи решать все сложные интегралы вы не научитесь, но правильно сформированный каркас понимания, позволит сэкономить часы времени на обучение и выработку навыков по решению интегралов.
Основные приемы решения интегралов
1. Замена переменной.
Для выполнения данного приема потребуется хороший навык нахождения производных.
2. Интегрирование по частям. Пользуются следующей формулой.
Применения этой формулы позволяет казалось бы нерешаемые интегралы привести к решению.
3. Интегрирование дробно-рациональных функций.
— разложить дробь на простейшие
— выделить полный квадрат.
— создать в числителе дифференциал знаменателя.
4. Интегрирование дробно-иррациональных функций.
— выделить под корнем полный квадрат
— создать в числителе дифференциал подкоренного выражения.
5. Интегрирование тригонометрических функций.
При интегрировании выражений вида
применяет формулы разложения для произведения.
Для выражений
m-нечетное, n –любое, создаем d(cosx). Используем тождество sin2+cos2=1
m,n – четные, sin2x=(1-cos2x)/2 и cos2x=(1+cos2x)/2
Для выражений вида:
— Применяем свойство tg2x=1/cos2x — 1
С базовыми приемами на этой всё. Теперь выведем своего рода алгоритм:
Алгоритм обучения решению интегралов:
1. Разобраться в сути интегралов. Необходимо понять базовую сущность интеграла и его решения. Интеграл по сути есть сумма элементарных частей объекта интегрирования. Если речь идет об интегрирование функции, то интеграл есть площадь фигуры между графиком функции, осью х и границами интегрирования. Если интеграл неопределенный, то есть границы интегрирования не указаны, то решение сводиться к нахождению первообразной.
Если интеграл определенный, то необходимо подставить значения границ в найденную функцию.
2. Отработать использование таблицы первообразных и основным свойства интегралов. Необходимо научиться пользоваться таблицей первообразных. По множеству функций первообразные найдены и занесены в таблицу. Если мы имеем интеграл, которые есть в таблице, можно сказать, что он решен.
3. Разобраться в приемах и наработать навыки решения интегралов.Если интеграла не табличного вида, то его решение сводиться к приведению его к виду одного из табличных интегралов. Для этого мы используем основные свойства и приемы решения. В случае, если на каких то этапах применения приемов у вас возникают трудности и непонимания, то вы более подробно разбираетесь именно по этому приему, смотрите примеры подобного плана, спрашиваете у преподавателя.
Дополнительно после решения интеграла на первых этапах рекомендуется сверять решение. Для этого мы дифференцируем полученное выражение и сравниваем с исходным интегралом.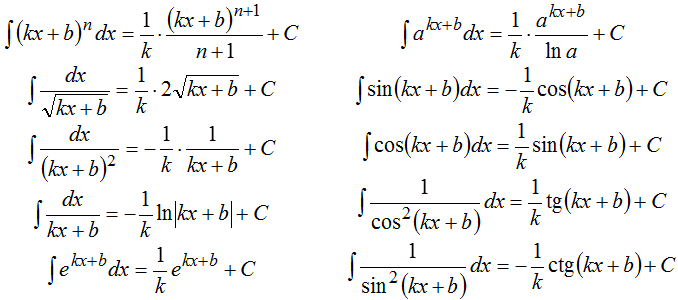
Отработаем основные моменты на нескольких примерах:
Примеры решения интегралов
Пример 1:
Решить интеграл:
Интеграл неопределенный. Находим первообразную.
Для этого интеграл суммы разложим на сумму интегралов.
Каждый из интегралов табличного вида. Смотрим первообразные по таблице.
Решение интеграла:
Проверим решение(найдем производную):
Пример 2. Решаем интеграл
Интеграл неопределенный. Находим первообразную.
Сравниваем с таблицей. В таблице нет.
Разложить, пользуясь свойствами, нельзя.
Смотрим приемы. Наиболее подходит замена переменной.
Заменяем х+5 на t5. t5 = x+5 . Получаем.
Но dx нужно тоже заменить на t. x= t5 — 5, dx = (t5 — 5)’ = 5t4. Подставляем:
Интеграл из таблицы. Считаем:
Подставляем в ответ вместо t ,
Решение интеграла:
Пример 3. Решение интеграла:
Для решения в этом случае необходимо выделить полный квадрат.
Выделяем:
В данном случае коэффициент 1/2 перед интегралом получился в результате замены dx на 1/2*d(2x+1). Если вы найдете производные x’ = 1 и 1/2*(2x+1)’= 1, то поймете почему так.
В результате мы привели интеграл к табличному виду.
Находим первообразную.
В итоге получаем:
Для закрепления темы интегралов рекомендуем также посмотреть видео.
В нем мы на примере физики показываем практическое применение интегрирования, а также решаем еще несколько задач.
Надеюсь вопрос, как решать интегралы для вас прояснился. Мы дорабатываем статью по мере поступления предложений. Поэтому если у вас появились какие то предложения или вопросы по теме решения интегралов, пишите в комментариях.
Рекламная заметка: Для особо пытливых умов советуем Видео-лекции по математическому программированию.
Программирование одна из дочек математики!
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Онлайн решение интеграла
Что делать, если решение не появляется (пустой экран)?
Данный калькулятор по решению интегралов онлайн построен на основе системы WolframAlpha Mathematica. Все права на его использование принадлежат компании Wolfram Alpha LLC!
Решение интеграла онлайн
Неопределенный интеграл
Нахождение неопределенного интеграла является очень частой задачей в высшей математике и других технических разделах науки. Даже решение простейших физических задач часто не обходится без вычисления нескольких простых интегралов. Поэтому со школьного возраста нас учат приемам и методам решения интегралов, приводятся многочисленные таблицы с интегралами простейших функций.
Однако со временем всё это благополучно забывается, либо у нас не хватает времени на рассчеты или нам нужно найти решение неопределеленного интеграла от очень сложной функции. Для решения этих проблем для вас будет незаменим наш сервис, позволяющий безошибочно находить неопределенный интеграл онлайн.
Решить неопределенный интеграл
Онлайн сервис на matematikam.ru позволяет находить решение интеграла онлайн быстро, бесплатно и качественно. Вы можете заменить поиск по таблицам нужного интеграла нашим сервисом, где быстро введя нужную функции, вы получите решение неопределенного интеграла в табличном варианте. Не все математические сайты способны вычислять неопределенные интегралы функций в режиме онлайн быстро и качественно, особенно если требуется найти неопределенный интеграл от сложной функции или таких функций, которые не включены в общий курс высшей математики. Сайт matematikam.ru поможет решить интеграл онлайн и справиться с поставленной задачей.
Используя онлайн решение интеграла на сайте matematikam.ru, вы всегда получите точный ответ.
Даже если вы хотите вычислить интеграл самостоятельно, благодаря нашему сервису вам будет легко проверить свой ответ, найти допущенную ошибку или описку, либо же убедиться в безукоризненном выполнении задания. Если вы решаете задачу и вам как вспомогательное действие необходимо вычислить неопределенный интеграл, то зачем тратить время на эти действия, которые, возможно, вы уже выполняли тысячу раз? Тем более, что дополнительные расчеты интеграла могут быть причиной описки или маленькой ошибки, приведших впоследствии к неверному ответу. Просто воспользуйтесь нашими услугами и найдите неопределенный интеграл онлайн без каких-либо усилий. Для практических задач по нахождению интеграла функции онлайн этот сервер очень полезен. Необходимо ввести заданную функцию, получить онлайн решение неопределенного интеграла и сравнить ответ с вашим решением.
Похожие сервисы:
Решение неопределенного интеграла
Calculate indefinite integral online
Оператор | Описание |
Простейшие математические операции | |
+ — * / () | Сложение, вычитание, умножение, деление и группирующие символы: + — * / () . Знак умножения * — необязателен: выражение 2sin(3x) эквивалентно 2*sin(3*x). Cкобки используются для группирования выражений. |
0.5 | Десятичные дроби записываются через точку:
|
Элементарные функции | |
xn | Возведение в степень: x^n, например, для ввода x2 используется x^2 |
√x | Квадратный корень: \sqrt(x) или x^(1/2) |
3√x | Кубический корень: x^(1/3) |
n√x | Корень n-той степени из x: x^(1/n) |
ln(x) | Натуральный логарифм (логарифм c основанием e): log(x) |
logax | Логарифм от x по основанию a: log(x)/log(a) |
lg(x) | Десятичный логарифм (логарифм по основанию 10): log(x)/log(10) |
ex | Экспоненциальная функция: e^x |
Тригонометрические функции | |
sin(x) | Синус от x: sin(x) |
cos(x) | Косинус от x: cos(x) |
tg(x) | Тангенс от x: tan(x) |
ctg(x) | Котангенс от x: 1/tan(x) |
arcsin(x) | Арксинус от x: arcsin(x) |
arccos(x) | Арккосинус от x: arccos(x) |
arctan(x) | Арктангенс от x: arctan(x) |
arcctg(x) | Арккотангенс от x: \pi/2 — arctan(x) |
Некоторые константы | |
e | Число Эйлера e: \e |
π | Число π: \pi |
Комплексное интеграционное решение
— Mathematics Stack Exchange
Как и в случае с реальными интегралами, вы должны прервать путь интегрирования в сингулярности и принять ограничения по мере приближения к сингулярности.
Один из способов сделать это — изменить путь $ C $ следующим образом. Пусть $ D (r) $, $ r \ in (0,1) $ — круг радиуса $ r $ с центром в $ 1 $. Пусть $ C (r) $ — путь $ C $ с удаленным диском $ D (r) $. Этот $ C (r) $ больше не является замкнутым путем, поэтому обычные элементарные комплексные интегральные теоремы неприменимы.2}} \ right) -2 \ pi \ text {.} $
Взяв $ r \ rightarrow 0 $, получим $ — \ pi $.
В более общем смысле, если $ f $ мероморфен (а это $ f $), мы можем использовать теорему Сохоцкого-Племеля, чтобы заменить этот ужасный интеграл двумя более простыми интегралами по замкнутым контурам, различающимися только тем, включен полюс или исключен . (Дуга $ C $ пересекает окружность, ограничивающую $ D (r) $ в двух точках; эти точки делят эту границу на две дуги окружности. В первом случае мы замыкаем путь $ C (r) $, добавляя дугу что исключает полюс.Для другого интеграла мы замыкаем путь другой дугой, которая помещает полюс внутрь пути.) Но теперь интегралы поддаются обычным элементарным комплексным интегральным теоремам.
Конечный результат состоит в том, что если $ f $ является мероморфным, любой полюс внутри контура вносит свой полный вычет в интеграл, а полюс на контуре вносит половину своего вычета в интеграл (главное значение Коши).
Аналитическое решение интегро-дифференциального уравнения DGLAP с помощью сложных отображений в областях контурных интегралов
Простая модель динамики КХД, в которой интегро-дифференциальное уравнение DGLAP может быть решено аналитически, рассматривалась в наших предыдущих статьях arXiv: 1611.08787 [hep-ph] и arXiv: 1906.07924 [hep-ph]. Когда такая модель содержит только один член в функции расщепления доминирующего партонного распределения, тогда функция Бесселя оказывается решением этого упрощенного уравнения DGLAP. Насколько нам известно, эта модель с одним членом в функции расщепления впервые была предложена Блюмлейном в arXiv: hep-ph / 9506403. В arXiv: 1906.07924 [hep-ph] мы показали, что двойное интегро-дифференциальное уравнение, полученное из уравнения DGLAP с помощью комплексного отображения в плоскости момента Меллина в этой модели, может рассматриваться как уравнение BFKL.
Затем в arXiv: 1906.07924 мы применили комплексный диффеоморфизм для получения стандартного интеграла из таблиц Градштейна и Рыжика, начиная с контурного интеграла для партонных функций распределения, который обычно берется при исчислении вычетов. Этот стандартный интеграл из этих таблиц оказывается преобразованием Лапласа якобиана для этого комплексного диффеоморфизма. Здесь мы подробно описываем все формулы этого трюка и выясняем некоторые важные моменты для дальнейшего развития этой стратегии.Мы проверяем, что обратное преобразование Лапласа образа Лапласа функции Бесселя может быть представлено в виде контурного интеграла Барнса.
Часто бывает, что решение интегро-дифференциального уравнения получается в виде контурных интегралов в одной или нескольких комплексных плоскостях. Такие интегралы могут быть взяты с помощью интегральной формулы Коши путем вычисления вычетов. Обычно это не классические интегралы Барнса, которые являются удобным представлением для обобщенных гипергеометрических функций.
Подынтегральные выражения интегралов Барнса являются отношениями некоторых произведений нескольких гамма-функций Эйлера. Преобразование контурного интеграла, представляющего решение интегро-дифференциального уравнения, в эту форму интегралов Барнса было бы полезно, потому что они могут быть классифицированы в терминах подходящих специальных функций. Найти такое преобразование — цель данной статьи. Промежуточным шагом будет представление этих интегралов как преобразования Лапласа якобианов некоторых комплексных отображений в плоскости комплексных переменных контурного интеграла.Мы рассмотрели такую возможность в предыдущей работе [1], в которой преобразовали контурный интеграл, представляющий решение интегро-дифференциального уравнения DGLAP в простой модели динамики КХД, из полученной формы контурного интеграла в комплексной плоскости момент Меллина к преобразованию Лапласа соответствующего якобиана. Эти якобианы могут показаться многозначными функциями новых комплексных переменных, и может потребоваться интегрирование по сечениям.
Мы можем избежать интегрирования по этим разрезам, если представим интегралы с многозначными якобианами, полученные первым комплексным отображением, в форме интегралов Барнса, применив еще одно комплексное отображение.Голоморфные отображения переменных в комплексных областях контурных интегралов, которые мы применяем в настоящей статье, основаны на стандартной теории комплексных переменных, которую можно найти в любом учебнике по этой теме [2]. Что касается манипуляций с замкнутыми контурами в комплексной плоскости переменной интегрирования, то они уже использовались в квантовой теории поля, когда в расчетах используются интегральные преобразования [3]. Мы также исправляем или изгибаем контуры интегрирования, когда здесь это необходимо.
Контурный интеграл, рассматриваемый в данной статье, является решением интегро-дифференциального уравнения DGLAP в простой модели динамики КХД, рассмотренной в [4]. Уравнение ДГЛАП было написано в семидесятых годах для структурных функций протона.
Их можно измерить экспериментально в процессах глубоконеупругого рассеяния [5]. В [6–8] Грибов и Липатов исследовали эти процессы в КЭД и обнаружили, что эти структурные функции удовлетворяют некоторым интегро-дифференциальным уравнениям. Открытие КХД было отмечено Нобелевской премией [9], в которой были получены уравнения ренормализационной группы для моментов Меллина коэффициентных функций разложения оператора Вильсона для матричного элемента двух токов процесса глубоконеупругого рассеяния. .Затем в [10] Альтарелли и Паризи написали эти уравнения ренормгруппы для коэффициентных функций операторного разложения в интегро-дифференциальной форме в пространстве Бьоркена x и интерпретировали их как интегро-дифференциальные уравнения для функций распределения партонов . В [11] Докшицер развил для случая КХД подход Грибова и Липатова, использованный в КЭД, и написал интегро-дифференциальные уравнения, аналогичные уравнениям Альтарелли-Паризи. Эти интегро-дифференциальные уравнения стали известны как уравнение Докшицера-Грибова-Липатова-Альтарелли-Паризи (также известное как уравнение ДГЛАП).
Функции разделения являются входными данными в уравнении DGLAP. Они могут быть найдены из аномальных размерностей операторов в КХД [12, 13] и представляют собой некоторые комбинации нескольких членов [12, 13]. Исчисление остатков через интегральную формулу Коши для контурного интеграла в комплексной плоскости момента Меллина, которое представляет собой решение уравнения DGLAP, является простым, но это исчисление непросто в реальном мире, потому что в результате участвует много бесконечных сумм, и эти суммы следует классифицировать [14, 15].Однако может быть рассмотрена простая модель только с одним членом в функции расщепления, и уравнение DGLAP в этом случае может быть решено в терминах функции Бесселя. Насколько нам известно, это упрощение до одной функции Бесселя решения уравнения DGLAP в случае только одного члена в функции расщепления впервые было упомянуто в 1995 г. в [16]. Мы подробно рассматривали эту модель в наших статьях [4] и [1]. В этой статье мы преобразуем этот контурный интеграл простой модели из [1, 4, 16] с помощью комплексного отображения к форме преобразования Лапласа якобиана соответствующего комплексного диффеоморфизма, а затем к форме интегралов Барнса с помощью другого сложная карта.В результате контурный интеграл в плоскости момента Меллина трансформируется в другой контурный интеграл в некоторой комплексной области. Подынтегральное выражение после этих последовательных комплексных отображений преобразуется в отношение некоторых гамма-функций, которое является типичной формой интегралов Барнса.
Мы должны защищать полезность предлагаемой стратегии для сообщества DGLAP, потому что уже есть долгая история многих достижений, связанных с этим уравнением. Действительно, интегро-дифференциальное уравнение DGLAP можно преобразовать в дифференциальное уравнение первого порядка, взяв момент Меллина с обеих сторон уравнения DGLAP относительно переменной Бьоркена x [10].Полученное дифференциальное уравнение является уравнением ренормгруппы для моментов Меллина [10] относительно масштаба передачи импульса в процессе глубоко неупругого рассеяния. Эти дифференциальные уравнения могут быть объединены с уравнением ренормгруппы для бегущей связи и решены. В конце девяностых годов в работах [17, 18] был построен оператор эволюции в случае бегущей связи и полностью аналитические решения несинглетных и синглетных уравнений эволюции в следующем за ведущим порядком при малых x Всего найдено повторений.Последние разработки решений этих дифференциальных уравнений первого порядка можно найти в [19]. В NNLO пространственные решения Меллина с бегущей связью были отработаны в нескольких численных кодах, например [20], а различные более поздние числовые программные пакеты можно найти в цитатах из [20]. Когда эти дифференциальные уравнения первого порядка для моментов Меллина решаются, обычным способом является преобразование этих моментов обратно в пространство Бьоркена x путем выполнения обратного преобразования Меллина, которое может быть выполнено путем вычисления вычетов на комплексной плоскости Момент Меллина [3, 21, 22].На самом низком уровне в действующей связи расчет может быть выполнен аналитически, однако даже на этом уровне требуется много работы, когда вместо простых моделей рассматривается реальный случай КХД. Существуют различные пакеты программного обеспечения, позволяющие выполнять все эти шаги аналитически, по крайней мере, в первоочередном порядке. На более высоких уровнях существуют новые передовые аналитические программные инструменты. Они основаны на использовании концепций алгебраической геометрии, таких как перемешанное произведение [14, 15]. Произведение в случайном порядке используется при построении однозначных гармонических полилогарифмов.Гармонические полилогарифмы описаны в [23]. Существуют числовые пакеты, которые решают интегро-дифференциальные уравнения в том виде, в котором они написаны, без учета моментов Меллина, решая дифференциальные уравнения первого порядка и затем преобразуя моменты обратно в пространство x . Например, численный программный пакет «PartonEvolution» был разработан в [24]. Другой числовой пакет QCDNUM был создан позже [25, 26].
В тени всех этих достижений, упомянутых в предыдущих параграфах, наш подход представляет собой попытку иначе взглянуть на контурные интегралы, возникающие в решениях уравнения DGLAP.Здесь мы предлагаем альтернативный способ, которым вычисление обратного преобразования Меллина сводится к вычислению обратного преобразования Лапласа якобиана соответствующего комплексного отображения. Эти диффеоморфизмы могут выполняться на комплексной плоскости момента Меллина. Эти сложные отображения делают структуру подынтегральных выражений единообразной, сводя ее во многих случаях к стандартным таблицам, таким как [27]. Затем мы можем преобразовать их еще одним преобразованием в интегралы Барнса. Это позволило бы их систематически классифицировать в терминах обобщенных гипергеометрических функций.Любая систематическая классификация полезна при построении компьютерных алгоритмов.
Из-за значительного вычислительного прогресса последних десятилетий (см., Например, [12, 13, 25, 26]) пертурбативное решение уравнения DGLAP уже вычислено до N 2 LO для моментов Меллина в распределении партонов. функции с полным учетом бегущей связи, а затем соответствующие функции распределения частиц (кварк, глюон и некоторые другие комбинации) были получены численно.Однако приближенные решения уравнения DGLAP, соответствующие простым моделям, по-прежнему имеют практическую ценность, поскольку они фиксируют возобновленным образом (в смысле компактного выражения) поведение данного асимптотического режима. В частности, в настоящей статье он отражает поведение Бесселя относительно квадратного корня из произведения логарифма переменной Бьоркена и логарифма переданного импульса в области малых значений x , когда основной вклад приходит из глюонной части матричного уравнения ДГЛАП.С другой стороны, приближенные решения не следует отбрасывать, поскольку они служат проверкой согласованности текущих манипуляций и формул, которые приводят нас к известным полученным результатам. Еще одна причина в пользу жизнеспособности таких приближенных решений заключается в том, что в режиме низкой передачи импульса уравнений DGLAP численные решения просто начинают показывать плохое поведение, и можно, по крайней мере, сделать некоторые оценки в таких пределах, используя эти решения, а затем получить новые отношения и интерпретации.
В следующем разделе мы рассмотрим необходимые формулы, которые можно найти в таблицах Градштейна и Рыжика [27]. Все необходимые формулы связаны интегральными преобразованиями, которые указаны явно. Мы обращаем внимание на связь между функцией Бесселя и конфлюэнтной функцией, а также на различные интегральные представления обобщенных гипергеометрических функций. В разделе 3 мы преобразуем решение контурного интеграла уравнения ДГЛАП в преобразование Лапласа комплексного якобиана.Якобиан соответствует сложной карте, выбранной для данного преобразования. Наконец, в разделе 4 мы делаем прозрачный трюк, с помощью которого мы переписываем преобразование Лапласа комплексных якобианов в виде интегралов Барнса.
Единственная цель этого раздела — собрать из [27] все формулы, необходимые для использования в следующем разделе. Эти формулы не новы, каждой из них не менее ста пятидесяти лет, та же книга интегральных таблиц [27] тоже довольно старая.Однако все формулы, взятые нами из [27], можно связать интегральными преобразованиями одна в другую. Мы делаем все эти преобразования явно в этом разделе, но вероятно, что мы не первые, кто публикует эти промежуточные шаги с учетом возраста [27].
Мы начнем в разделе 2.1 с конфлюэнтной функции. Это частный случай обобщенных гипергеометрических функций, который может быть записан в терминах интеграла Барнса. Мы начнем с этого интегрального представления Барнса для и получим соответствующий ряд, затем мы получим другое интегральное представление, чтобы переписать это второе интегральное представление для снова в терминах того же ряда и, наконец, доказать одно полезное соотношение в терминах того же интегрального представления для В разделе 2.2 были рассмотрены два различных интегральных представления функции Бесселя I 0 . Затем, заменяя переменную интегрирования, мы показываем, что они эквивалентны. Функция Бесселя I 0 представлена в терминах конфлюэнтной функции. В разделе 2.3 мы рассматриваем интегральное представление Барнса для гипергеометрической функции Гаусса и рассматриваем этот интеграл в терминах ряда. Другое интегральное представление для этой гипергеометрической функции Гаусса будет получено позже.С помощью этого интегрального представления Эйлера для гипергеометрической функции Гаусса и с помощью установленного в разделе 2.2 интегрального представления для конфлюэнтной функции мы воспроизводим преобразование Лапласа функции Бесселя I 0 в разделе 2.4.
2.1. Интегральные представления гипергеометрической функции
2.2. От функции Бесселя
I 0 к гипергеометрической функции
Традиционное интегральное представление для функции Бесселя I 0 оказывается хорошо известным рядом с точки зрения четных степеней его аргумента,
Это интегральное представление составляет 8.431.1 из [27]. Это интегральное представление для функции Бесселя I 0 связано с другим интегральным представлением, которым является 9,211,2 из [27], изменением переменной интегрирования,
Это интегральное представление составляет 9,238,2 из [27]. [27]. Таким образом, интегральное представление (3) позволяет нам переписать функцию Бесселя I 0 в терминах конфлюэнтной функции, и это будет более полезно для нас в разделе 2.4, где мы вычисляем преобразование Лапласа функции Бесселя
2.3. Интегральные представления гипергеометрической функции
2.4. Преобразование Лапласа функции Бесселя
I 0
В этом разделе мы воспроизводим результат преобразования Лапласа функции Бесселя I 0 . Результат записан в 17.13.109 из [27]. Когда мы делаем это преобразование, мы предполагаем, что z находится в соответствующей области комплексной плоскости, то есть в правой части критического показателя функции Бесселя [4].
Этот обратный квадратный корень является очень известным результатом преобразования Лапласа функции Бесселя I 0 и может быть найден во многих таблицах интегралов.
Это основной раздел. Все, что мы написали в предыдущих разделах, было подготовкой к этому разделу. Здесь мы вычисляем контурные интегралы этого типа
, составляя комплексные карты в плоскости момента Меллина. Здесь x ∈ [0, 1] и — внешние переменные. Этот контурный интеграл представляет собой решение интегро-дифференциального уравнения DGLAP, которое играет важную роль в квантовой хромодинамике.Мы прокомментировали это уравнение во введении. Традиционный способ — вычислить этот контурный интеграл напрямую, вычислив остатки по формуле интеграла Коши,
В этом примере это кратчайший способ получить результат для этого интеграла. Однако мы хотели бы воспроизвести этот результат, используя сложную геометрию, чтобы построить карту в комплексной плоскости момента Меллина. Для этого мы переписываем предыдущий интеграл
и выбираем новую комплексную переменную M интегрирования таким образом, что
Это соотношение определяет M как функцию начальной комплексной переменной N [1] .Введя для краткости обозначение
, мы можем написать
, из которого следует, что в обратном отображении из M в N исходная переменная N должна удовлетворять квадратному уравнению
, которое имеет два корня
Если мы не хотим изменять ориентацию контура при отображении от N до M в соответствии с уравнением (9), мы должны использовать положительную ветвь карты (10). Таким образом, мы выбрали карту
Мы можем выбрать и отрицательную ветвь, но в этом случае мы должны изменить знак интеграла, потому что ориентация контура будет изменена под этой картой.
Выбрав комплексную карту в уравнении (11), мы можем переписать подынтегральное выражение в терминах новой комплексной переменной M . Из уравнения (9) имеем
Теперь мы можем продолжить линию (8) в терминах новой переменной интегрирования C
В этой последовательности карт контур в комплексной плоскости меняет свою форму по сравнению с вертикальной линией. параллельно воображаемой оси до очень сложной формы в конце этой цепочки преобразований. Мы написали последнее равенство, потому что знаем, что оно может быть преобразовано в вертикальную линию, параллельную мнимой оси, в комплексной плоскости M .Таким образом, мы можем записать последнее равенство на основе преобразования Лапласа функции Бесселя, найденной в уравнении (6). Прямое доказательство последнего равенства будет дано в следующем разделе путем явного вычисления интеграла.
В общем, наша цель — получить результат для контурных интегралов, которые представляют решение интегро-дифференциального уравнения DGLAP, путем сопоставления комплексного диффеоморфизма в плоскости момента Меллина N с переменной Бьоркена x .Почему мы делаем комплексные диффеоморфизмы и представляем контурный интеграл этого типа (7) как преобразование Лапласа якобиана? Мы считаем этот способ более систематическим, чтобы классифицировать полученные результаты в терминах специальных функций. Одна из причин заключается в том, что стандартные табличные интегралы могут появиться, как это произошло в случае уравнения (12). Другая причина состоит в том, что преобразование Лапласа может быть представлено в форме интегралов Барнса (мы подробно рассмотрим эту вторую причину в следующем разделе).Эти две причины являются фундаментальными при построении компьютерного алгоритма [1] в реальном случае КХД, в котором функции аномальной размерности очень сложны и содержат много членов. На трехконтурном уровне эти функции можно найти в [12, 13] .
Предлагаемое решение уравнения DGLAP, приведенное в уравнениях (7) и (12), соответствует кинематической области малых x , в которой это приближенное решение имеет смысл. Строго говоря, нам нужно получить в результате особую функцию при x = 0.Это соответствует сингулярности в точке N = 1 на сложной плоскости N . Слагаемые в матрице аномальных размеров, сингулярные в этой точке, соответствуют преобладанию функции распределения глюонов в небольшой области x . Матричная форма может быть сведена к уравнению DGLAP для доминирующего партонного распределения в области малых x . Это было бы неплохим приближением к матричному интегро-дифференциальному уравнению DGLAP.Чтобы иметь такое поведение, мы сделаем небольшую модификацию и возьмем другую модель для аномального размера γ ( N ), который является сингулярным в точке N = 1. В общем, кинематическая область уравнения DGLAP имеет вид задается пределом Бьоркена, в котором отношение переданного импульса к Бьоркену x велико. Увеличивая или уменьшая переданный импульс u , нужно увеличивать или уменьшать распределение ( x , u ) по закону двойного логарифма, найденному в уравнениях (7) и (12) в результате чистого глюонная динамика DGLAP.
Как мы упоминали во введении, практическая ценность этой простой модели состоит в том, что ее решение уравнения DGLAP может быть использовано для качественной оценки поведения доминирующей функции распределения около x = 0, то есть для самого маленький x . Однако эта модель может оказаться даже более полезной, чем простая аппроксимация доминирующего распределения или проверка согласованности численных или аналитических расчетов на основе мощного программного обеспечения.Как известно, в мире существует несколько групп, которые проводят глобальный анализ функций распределения партонов с учетом последних данных с LHC [28–32]. Этот анализ позволяет им фиксировать многие параметры исходных функций распределения партонов по данным только потому, что они не могут быть вычислены из первых принципов. Несмотря на то, что такая процедура подгонки довольно произвольна в отношении того, как выбрать форму функции распределения партонов, а также количество свободных параметров, они, как правило, представляют собой некоторую комбинацию бета-функций Эйлера, которые параметризуют распределение партонов в некотором масштабе [33–36] и затем эволюционировать в соответствии с интегро-дифференциальным уравнением DGLAP.Из-за большого количества данных программное обеспечение для подбора параметров PDF и эволюции PDF создано на принципах нейронных сетей [30, 31]. Эту простую модель можно использовать для обучения нейронных сетей 4
. Отметим также, что это не единственная простая модель, которую можно использовать для этой цели. Мы можем создать несколько простых моделей, которые решают интегро-дифференциальное уравнение DGLAP с различными функциями расщепления, настраивая функции формы в некотором заданном масштабе, чтобы объединить их с якобианами комплексных диффеоморфизмов в плоскости моментной переменной Меллина в легко интегрируемых множителях.
В предыдущем разделе мы провели комплексные диффеоморфизмы, чтобы представить исходную форму (7) решения уравнения DGLAP в терминах контурного интеграла к якобиевой форме (12) этого решения. Эта форма Якоби может быть стандартным интегралом из хорошо известных интегральных таблиц [27], например, функция Бесселя I 0 в случае нашей модели. Мы доказали, что это функция Бесселя, прямым преобразованием Лапласа в разделе 2.4. Теперь мы оцениваем обратное преобразование Лапласа,
. В этот момент мы меняем порядок интегрирования и получаем
Таким образом, мы можем сказать, что у нас есть контур Ганкеля. Теперь мы можем продолжить линию (13)
Путем сравнения это уравнение и уравнение (12) мы можем записать это тождество
, в котором в левой части находится якобиева форма (12) контурного интеграла (7), а в правой части — интеграл Барнса. Мы можем сравнить эти две разные формы и заметить, что интегральная форма Барнса более полезна для классификации результата в терминах специальных функций.Грубо говоря, для записи функции Бесселя в левой части таблицы Градштейна и Рыжика лучше держать в руках, а в правой части они нам не нужны. Вторая причина для представления начального контурного интеграла (7) в терминах интегралов Барнса состоит в том, чтобы иметь единообразное хорошо изученное представление для всех контурных интегралов, участвующих в вычислении. Третья причина заключается в том, что форма Якоби в левой части часто будет содержать многозначные функции, в нашем случае это квадратный корень в знаменателе.Мы избегаем интегрирования по разрезу, которое необходимо в комплексной плоскости переменной интегрирования M в якобианской форме. У нас нет разрезов в интегральном представлении Барнса справа. Четвертая причина предпочесть результат, записанный в форме интегралов Барнса, состоит в том, что якобианы будут все более и более сложными в более высоких порядках, в то время как контурные интегралы отношений некоторых произведений нескольких гамма-функций хорошо изучены, их структура более точна. однородный и лучше анализируемый.Отношения гамма-функций в подынтегральных выражениях контурных интегралов часто появляются при расчетах в квантовой теории поля [37–44].
В предыдущей статье [1] мы сообщили, что уравнение БФКЛ [45–49] может быть получено из уравнения DGLAP через комплексное отображение в области контурного интеграла (7), которое представляет решение этой интегральной схемы DGLAP. дифференциальное уравнение. Вот почему интегро-дифференциальное уравнение BFKL можно рассматривать как уравнение, двойственное к интегро-дифференциальному уравнению DGLAP.Вопрос о двойственности между уравнением БФКЛ и уравнением ДГЛАП поднимался в [21]. Также в [1] мы предложили использовать комплексное отображение на плоскости момента Меллина для преобразования решения интегро-дифференциального уравнения ДГЛАП, полученного в виде контурного интеграла типа (7), к виду которое представляет собой преобразование Лапласа якобиана этого комплексного отображения. В данной статье мы показали, что якобиева форма контурного интеграла может быть далее преобразована к контурным интегралам Барнса.Интегралы Барнса — это контурные интегралы, в которых подынтегральное выражение представляет собой отношение произведений нескольких гамма-функций, и результат их интегрирования может быть записан в терминах специальных функций традиционным хорошо изученным способом. Представление в терминах интегралов Барнса полезно при построении вычислительных алгоритмов [1].
Работа GA была частично поддержана совместной стипендией DAAD / CONICYT 2015/57144001. Работа IK была частично поддержана фондом Fondecyt (Чили) Grants Nos.1040368, 1050512 и 1121030, гранты DIUBB (Чили) № 125 009, GI 153 209 / C и GI 152 606 / VC. Эти результаты были представлены в докладе IK на XXXI Jornada Matemática de la Zona Sur, Вальдивия, Чили, 25-27 апреля 2018 г. Он благодарен Франсиско Корреа и Фелипе ван Дайену за приглашение выступить с докладом в секции «Математика». Физика »этого ежегодного научного собрания.
| ’62 Центр театра и танца, ’62 Центр | ||
| Касса | 597-2425 | |
| Магазин костюмов | 597-3373 | |
| Менеджер мероприятий / Помощник менеджера | 597-4808 | 597-4815 факс |
| Производство | 597-4474 факс | |
| Магазин сцен | 597-2439 | |
| ’68 Центр карьерного роста, Мирс | 597-2311 | 597-4078 факс |
| Академические ресурсы, Парески | 597-4672 | 597-4959 факс |
| Службы поддержки инвалидов, Парески | 597-4672 | |
| Прием, Вестон Холл | 597-2211 | 597-4052 факс |
| Программа позитивных действий, Хопкинс-холл, | 597-4376 | |
| Africana Studies, Hollander | 597-2242 | 597-4222 факс |
| Американские исследования, Шапиро | 597-2074 | 597-4620 факс |
| Антропология и социология, Холландер | 597-2076 | 597-4305 факс |
| Архивы и специальные коллекции, Sawyer | 597-4200 | 597-2929 факс |
| Читальный зал | 597-4200 | |
| Искусство (История, Студия), Spencer Studio Art / Lawrence | 597-3578 | 597-3693 факс |
| Архитектурная студия, Spencer Studio Art | 597-3134 | |
| Фотография Студия, Spencer Studio Art | 597-2030 | |
| Printmaking Studio, Spencer Studio Art | 597-2496 | |
| Скульптурная студия, Spencer Studio Art | 597-3101 | |
| Senior Studio, Spencer Studio Art | 597-3224 | |
| Видео / фотостудия, Spencer Studio Art | 597-3193 | |
| Азиатские исследования, Холландер | 597-2391 | 597-3028 факс |
| Астрономия / Астрофизика, Thompson Physics | 597-2482 | 597-3200 факс |
| Департамент легкой атлетики, Физическое воспитание, отдых, Ласелл | 597-2366 | 597-4272 факс |
| Спортивный директор | 597-3511 | |
| Лодочный домик, Озеро Онота | 443-9851 | |
| Автобусы | 597-2366 | |
| Фитнес-центр | 597-3182 | |
| Hockey Rink Ice Line, Lansing Chapman | 597-2433 | |
| Intramurals, Атлетический центр Чандлера | 597-3321 | |
| Физическое воспитание | 597-2141 | |
| Pool Wet Line, Атлетический центр Чандлера | 597-2419 | |
| Sports Information, Hopkins Hall | 597-4982 | 597-4158 факс |
| Спортивная медицина | 597-2493 | 597-3052 факс |
| Площадки для игры в сквош | 597-2485 | |
| Поле для гольфа Taconic | 458-3997 | |
| Биохимия и молекулярная биология, Thompson Biology | 597-2126 | |
| Биоинформатика, геномика и протеомика, Бронфман | 597-2124 | |
| Биология, Thompson Biology | 597-2126 | 597-3495 факс |
| Охрана и безопасность кампуса, Хопкинс-холл | 597-4444 | 597-3512 факс |
| Карты доступа / Системы сигнализации | 597-4970 / 4033 | |
| Служба сопровождения, Хопкинс Холл | 597-4400 | |
| Офицеры и диспетчеры | 597-4444 | |
| Секретарь, удостоверения личности | 597-4343 | |
| Коммутатор | 597-3131 | |
| Центр развития творческого сообщества, 66 Stetson Court | 884-0093 | |
| Центр экономики развития, 1065 Main St | 597-2148 | 597-4076 факс |
| Компьютерный зал | 597-2522 | |
| Вестибюль | 597-4383 | |
| Центр экологических исследований, класс 1966 г. Экологический центр | 597-2346 | 597-3489 факс |
| Лаборатория наук об окружающей среде, Морли | 597-2380 | |
| Экологические исследования | 597-2346 | |
| Лаборатория ГИС | 597-3183 | |
| Центр иностранных языков, литератур и культур, Холландер | 597-2391 | 597-3028 факс |
| Арабоведение, Холландер | 597-2391 | 597-3028 факс |
| Сравнительная литература, Холландер | 597-2391 | |
| Критические языки, Холландер | 597-2391 | 597-3028 факс |
| Языковой кабинет | 597-3260 | |
| Россия, Холландер | 597-2391 | |
| Центр обучения в действии, Brooks House | 597-4588 | 597-3090 факс |
| Библиотека редких книг Чапина, Сойер | 597-2462 | 597-2929 факс |
| Читальный зал | 597-4200 | |
| Офис капелланов, Парески | 597-2483 | 597-3955 факс |
| Еврейский религиозный центр, Стетсон-Корт 24, | 597-2483 | |
| Мусульманская молитвенная комната, часовня Томпсона (нижний уровень) | 597-2483 | |
| Католическая часовня Ньюмана, часовня Томпсона (нижний уровень) | 597-2483 | |
| Химия, Thompson Chemistry | 597-2323 | 597-4150 факс |
| Классика (греческий и латинский), Hollander | 597-2242 | 597-4222 факс |
| Когнитивная наука, Бронфман | 597-4594 | |
| Маршал колледжа, Thompson Physics | 597-2008 | |
| Отношения с колледжем | 597-4057 | |
| Программа 25-го воссоединения, Фогт | 597-4208 | 597-4039 факс |
| Программа 50-го воссоединения, Фогт | 597-4284 | 597-4039 факс |
| Advancement Operations, Мирс-Уэст | 597-4154 | 597-4333 факс |
| Мероприятия для выпускников, Vogt | 597-4146 | 597-4548 факс |
| Фонд выпускников | 597-4153 | 597-4036 факс |
| Связи с выпускниками, Мирс-Уэст | 597-4151 | 597-4178 факс |
| Alumni / Development Mail Services, Мирс-Уэст | 597-4369 | |
| Девелопмент, Vogt | 597-4256 | |
| Отношения с донорами, Vogt | 597-3234 | 597-4039 факс |
| Офис по планированию подарков, Vogt | 597-3538 | 597-4039 факс |
| Grants Office, Мирс-Уэст | 597-4025 | 597-4333 факс |
| Программа крупных подарков, Vogt | 597-4256 | 597-4548 факс |
| Parents Fund, Vogt | 597-4357 | 597-4036 факс |
| Prospect Management & Research, Mears | 597-4119 | 597-4178 факс |
| Начало занятий и академические мероприятия, Jesup | 597-2347 | 597-4435 факс |
| Коммуникации, Хопкинс Холл | 597-4277 | 597-4158 факс |
| Sports Information, Hopkins Hall | 597-4982 | 597-4158 факс |
| Web Team, Southworth Schoolhouse | ||
| Williams Magazines (ранее Alumni Review), Hopkins Hall | 597-4278 | |
| Компьютерные науки, Thompson Chemistry | 597-3218 | 597-4250 факс |
| Конференции и мероприятия, Парески | 597-2591 | 597-4748 факс |
| Запросы Elm Tree House, Mt.Хоуп Фарм | 597-2591 | |
| Офис диспетчера, Хопкинс Холл | 597-4412 | 597-4404 факс |
| Счета к оплате и ввод данных, Хопкинс-холл | 597-4453 | |
| Bursar & Cash Receipts, Hopkins Hall | 597-4396 | |
| Финансовые информационные системы, Хопкинс Холл | 597-4023 | |
| Purchasing Cards, Hopkins Hall | 597-4413 | |
| Студенческие ссуды, Хопкинс Холл | 597-4683 | |
| Dance, 62 Центр | 597-2410 | |
| Центр Дэвиса (ранее Мультикультурный центр), Дженнесс | 597-3340 | 597-3456 факс |
| Харди Хаус | 597-2129 | |
| Дженнесс Хаус | 597-3344 | |
| Райс Хаус | 597-2453 | |
| Декан колледжа, Хопкинс-холл | 597-4171 | 597-3507 факс |
| Декан факультета Хопкинс Холл | 597-4351 | 597-3553 факс |
| Столовая, капельницы | 597-2121 | 597-4618 факс |
| ’82 Гриль, Парески | 597-4585 | |
| Кондитерская, Парески | 597-4511 | |
| Общественное питание, факультет | 597-2452 | |
| Driscoll Dining Hall, Дрисколл | 597-2238 | |
| Eco Café, Научный центр | 597-2383 | |
| Grab ‘n Go, Парески | 597-4398 | |
| Lee Snack Bar, Парески | 597-3487 | |
| Обеденный зал Mission Park, Mission Park | 597-2281 | |
| Whitmans ‘, Парески | 597-2889 | |
| Экономика, Шапиро | 597-2476 | 597-4045 факс |
| Английский, Холландер | 597-2114 | 597-4032 факс |
| Сооружения, служебное здание | 597-2301 | |
| College Car Request | 597-2302 | |
| Скорая помощь вечером / в выходные дни | 597-4444 | |
| Запросы на выполнение производственных работ | 597-4141 факс | |
| Особые мероприятия | 597-4020 | |
| Кладовая | 597-2143 | 597-4013 факс |
| Факультетский клуб, Факультетский дом / Центр выпускников | 597-2451 | 597-4722 факс |
| Бронирование | 597-3089 | |
| Fellowships Office, Hopkins Hall | 597-3044 | 597-3507 факс |
| Financial Aid, Weston Hall | 597-4181 | 597-2999 факс |
| Науки о Земле, Кларк Холл | 597-2221 | 597-4116 факс |
| Немецко-русский, Hollander | 597-2391 | 597-3028 факс |
| Глобальные исследования, Холландер | 597-2247 | |
| Аспирантура по истории искусств, Кларк | 458-2317 факс | |
| Службы здравоохранения и хорошего самочувствия, Thompson Ctr Health | 597-2206 | 597-2982 факс |
| Медицинское просвещение | 597-3013 | |
| Услуги интегративного благополучия (консультирование) | 597-2353 | |
| Чрезвычайные ситуации с угрозой жизни | Позвоните 911 | |
| Медицинские услуги | 597-2206 | |
| История, Холландер | 597-2394 | 597-3673 факс |
| История науки, Бронфман | 597-4116 факс | |
| Лес Хопкинса | 597-4353 | |
| Розенбург Центр | 458-3080 | |
| Отдел кадров, B&L Building | 597-2681 | 597-3516 факс |
| Услуги няни, корпус B&L | 597-4587 | |
| Льготы | 597-4355 | |
| Программа помощи сотрудникам | 800-828-6025 | |
| Занятость | 597-2681 | |
| Заработная плата | 597-4162 | |
| Ресурсы для супруга / партнера | 597-4587 | |
| Занятость студентов | 597-4568 | |
| Линия погоды (ICEY) | 597-4239 | |
| Humanities, Schapiro | 597-2076 | |
| Информационные технологии, Jesup | 597-2094 | 597-4103 факс |
| Пакеты для чтения курса, Drop Box для офисных услуг | 597-4090 | |
| Центр аренды оборудования, Додд Приложение | 597-4091 | |
| Служба поддержки преподавателей / сотрудников, [электронная почта] | 597-4090 | |
| Медиауслуги и справочная служба | 597-2112 | |
| Служба поддержки студентов, [электронная почта] | 597-3088 | |
| Телекоммуникации / Телефоны | 597-4090 | |
| Междисциплинарные исследования, Холландер | 597-2552 | |
| Международное образование и учеба, Хопкинс-холл | 597-4262 | 597-3507 факс |
| Инвестиционный офис, Хопкинс Холл | 597-4447 | |
| Бостонский офис | 617-502-2400 | 617-426-5784 факс |
| Еврейские исследования, Мазер | 597-3539 | |
| Правосудие и закон, Холландер | 597-2102 | |
| Latina / o Studies, Hollander | 597-2242 | 597-4222 факс |
| Исследования лидерства, Шапиро | 597-2074 | 597-4620 факс |
| Морские исследования, Бронфман | 597-2297 | |
| Математика и статистика, Bascom | 597-2438 | 597-4061 факс |
| Музыка, Бернхард | 597-2127 | 597-3100 факс |
| Concertline (записанная информация) | 597-3146 | |
| Неврология, Thompson Biology | 597-4107 | 597-2085 факс |
| Окли Центр, Окли | 597-2177 | 597-4126 факс |
| Управление институционального разнообразия и справедливости, Хопкинс-холл | 597-4376 | 597-4015 факс |
| Управление счетов студентов, Хопкинс-холл | 597-4396 | 597-4404 факс |
| Исследования эффективности, 62 Центр | 597-4366 | |
| Философия, Шапиро | 597-2074 | 597-4620 факс |
| Физика, Thompson Physics | 597-2482 | 597-4116 факс |
| Планетарий / Обсерватория Хопкинса | 597-3030 | |
| Театр старой обсерватории Хопкинса | 597-4828 | |
| Бронирование | 597-2188 | |
| Политическая экономия, Шапиро | 597-2327 | |
| Политология, Шапиро | 597-2168 | 597-4194 факс |
| Офис президента, Хопкинс-холл | 597-4233 | 597-4015 факс |
| Дом Президента | 597-2388 | 597-4848 факс |
| Услуги печати / почты для преподавателей / сотрудников, ’37 House | 597-2022 | |
| Программа обучения, Бронфман | 597-4522 | 597-2085 факс |
| Офис Провоста, Хопкинс Холл | 597-4352 | 597-3553 факс |
| Психология, психологические кабинеты и лаборатории | 597-2441 | 597-2085 факс |
| Недвижимость, B&L Building | 597-2195 / 4238 | 597-5031 факс |
| Ипотека для преподавателей / сотрудников | 597-4238 | |
| Профессорско-преподавательский состав Арендное жилье | 597-2195 | |
| Офис регистратора, Хопкинс Холл | 597-4286 | 597-4010 факс |
| Религия, Холландер | 597-2076 | 597-4222 факс |
| Romance Languages, Hollander | 597-2391 | 597-3028 факс |
| Планировщик помещений | 597-2555 | |
| Соответствие требованиям безопасности и охраны окружающей среды, класс ’37 Дом | 597-3003 | |
| Библиотека Сойера, Сойер | 597-2501 | 597-4106 факс |
| Службы доступа | 597-2501 | |
| Приобретения / Серийные номера | 597-2506 | |
| Каталогизация / Службы метаданных | 597-2507 | |
| Межбиблиотечный абонемент | 597-2005 | 597-2478 факс |
| Исследовательские и справочные службы | 597-2515 | |
| Стеллаж | 597-4955 | 597-4948 факс |
| Системы | 597-2084 | |
| Научная библиотека Шоу, Научный центр | 597-4500 | 597-4600 факс |
| Исследования в области науки и технологий, Бронфман | 597-2239 | |
| Научный центр, Бронфман | 597-4116 факс | |
| Магазин электроники | 597-2205 | |
| Машинно-модельный цех | 597-2230 | |
| Безопасность | 597-4444 | |
| Специальные академические программы, Харди | 597-3747 | 597-4530 факс |
| Sports Information, Hopkins Hall | 597-4982 | 597-4158 факс |
| Студенческая жизнь, Парески | 597-4747 | |
| Планировщик помещений | 597-2555 | |
| Управление студенческими центрами | 597-4191 | |
| Организация студенческих мероприятий | 597-2546 | |
| Студенческий дом, Парески | 597-2555 | |
| Участие студентов | 597-4749 | |
| Программы проживания для старших классов | 597-4625 | |
| Студенческая почта, Паресский почтовый кабинет | 597-2150 | |
| Устойчивое развитие / Центр Зилха, Харпер | 597-4462 | |
| Коммутатор, Хопкинс Холл | 597-3131 | |
| Книжный магазин Уильямса | 458-8071 | 458-0249 факс |
| Театр, 62 Центр | 597-2342 | 597-4170 факс |
| Trust & Estate Administration, Sears House | 597-4259 | |
| Учебники | 597-2580 | |
| вице-президент по кампусной жизни, Хопкинс-холл, | 597-2044 | 597-3996 факс |
| Вице-президент по связям с колледжем, Мирс | 597-4057 | 597-4178 факс |
| Вице-президент по финансам и администрированию, Hopkins Hall | 597-4421 | 597-4192 факс |
| Центр визуальных ресурсов, Лоуренс | 597-2015 | 597-3498 факс |
| Детский центр Williams College, Детский центр Williams | 597-4008 | 597-4889 факс |
| Музей искусств колледжа Уильямс (WCMA), Лоуренс | 597-2429 | 597-5000 факс |
| Подготовка музея | 597-2426 | |
| Служба безопасности музея | 597-2376 | |
| Музейный магазин | 597-3233 | |
| Уильямс Интернэшнл | 597-2161 | |
| Williams Outing Club, Парески | 597-2317 | |
| Оборудование / стол для студентов | 597-4784 | |
| Проект Уильямса по экономике высшего образования, Мирс-Вест | 597-2192 | |
| Williams Record, Парески | 597-2400 | 597-2450 факс |
| Программа Уильямса-Эксетера в Оксфорде, Оксфордский университет | 011-44-1865-512345 | |
| Программа Williams-Mystic, Mystic Seaport Museum | 860-572-5359 | 860-572-5329 факс |
| Исследования женщин, гендера и сексуальности, Schapiro | 597-3143 | 597-4620 факс |
| Написание программ, Хопкинс Холл | 597-4615 | |
| Центр экологических инициатив «Зилха», Харпер | 597-4462 |
Дифференциальные уравнения — комплексные корни
Показать мобильное уведомление
Показать все заметки Скрыть все заметки
Похоже, вы используете устройство с «узкой» шириной экрана ( i. 2} + br + c = 0 \]
— комплексные корни в форме \ ({r_ {1,2}} = \ lambda \ pm \ mu \, i \).{\ left ({\ lambda — \ mu \, i} \ right) \, \, t}} \]
Итак, эти две функции «достаточно хороши» (опять эти слова… мы еще вернемся к их определению), чтобы сформировать общее решение. Однако у нас есть проблема. Поскольку мы начали использовать только действительные числа в нашем дифференциальном уравнении, мы хотели бы, чтобы наше решение включало только действительные числа. Два приведенных выше решения являются сложными, поэтому мы хотели бы получить в наши руки пару решений («достаточно хороших», конечно…), которые реальны.{\ lambda \, t}} \ left ({\ cos \ left ({\ mu t} \ right) — i \ sin \ left ({\ mu \, t} \ right)} \ right) \ end {align *} \]
Это не устраняет сложный характер решений, но придает двум решениям форму, позволяющую исключить сложные части.
Вспомните из раздела основ, что если два решения «достаточно хороши», то любое решение может быть записано как комбинация этих двух решений. {\ lambda t}} \ sin \ left ({\ mu \, t} \ right) \]
Теперь у нас есть два решения (мы предоставим вам проверить, действительно ли они являются решениями) дифференциального уравнения.{2t}} \ sin \ left ({\ sqrt 5 t} \ right) \]
Теперь вы заметите, что мы не различали это сразу, как в предыдущем разделе. Причина этого проста. Хотя дифференциация не так уж и сложна, она может стать немного запутанной. Итак, сначала посмотрев на начальные условия, мы можем увидеть из первого, что если бы мы просто применили его, мы получили бы следующее.
\ [0 = у \ влево (0 \ вправо) = {c_1} \]
Другими словами, первый член выпадет, чтобы выполнить первое условие.{2t}} \ cos \ left ({\ sqrt 5 t} \ right) \ end {align *} \]
Намного более приятная производная, чем если бы мы использовали исходное решение. Теперь примените второе начальное условие к производной, чтобы получить.
\ [- 8 = y ‘\ left (0 \ right) = \ sqrt 5 {c_2} \ hspace {0,25 дюйма} \ Rightarrow \ hspace {0,25 дюйма} {c_2} = — \ frac {8} {{\ sqrt 5 }} \]
Реальное решение тогда. {2t}} \ sin \ left ({\ sqrt 5 t} \ right ) \]
Пример 2 Решите следующую IVP.{4t}} \ cos \ left (t \ right) \ end {align *} \]
Обратите внимание, что на этот раз нам понадобится производная с самого начала, поскольку у нас не будет выпадения ни одного из терминов. Применение начальных условий дает следующую систему.
\ [\ begin {align *} — 4 & = y \ left (0 \ right) = {c_1} \\ — 1 & = y ‘\ left (0 \ right) = 4 {c_1} + {c_2} \ end {выровнять*}\]
Решение этой системы дает \ ({c_1} = — 4 \) и \ ({c_2} = 15 \).{- 3 \ left ({t — \ pi} \ right)}} \ sin \ left ({\ frac {t} {2}} \ right) \ end {align *} \]
Давайте рассмотрим последний пример, прежде чем перейти к следующей теме.
Пример 4 Решите следующую IVP.
\ [y » + 16y = 0 \ hspace {0,25 дюйма} y \ left ({\ frac {\ pi} {2}} \ right) = — 10 \ hspace {0,25 дюйма} y ‘\ left ({\ frac {\ pi} {2}} \ right) = 3 \]
Показать решение
Характеристическое уравнение для этого дифференциального уравнения и его корни:.2} \) и запишите время, пока не закончатся члены дифференциального уравнения. Это может и часто означает, что они записывают неправильный характеристический многочлен, поэтому будьте осторожны.
Хорошо, вернемся к проблеме.
Общее решение этого дифференциального уравнения и его производной есть.
\ [\ begin {align *} y \ left (t \ right) & = {c_1} \ cos \ left ({4t} \ right) + {c_2} \ sin \ left ({4t} \ right) \\ y ‘\ left (t \ right) & = — 4 {c_1} \ sin \ left ({4t} \ right) + 4 {c_2} \ cos \ left ({4t} \ right) \ end {align *} \]
Установка начальных условий дает следующую систему.
\ [\ begin {align *} — 10 & = y \ left ({\ frac {\ pi} {2}} \ right) = {c_1} \ hspace {0,25 дюйма} {c_1} = — 10 \\ 3 & = y ‘\ left ({\ frac {\ pi} {2}} \ right) = 4 {c_2} \ hspace {0,25 дюйма} {c_2} = \ frac {3} {4} \ end {align *} \ ]
Итак, константы выпадают вместе с этой системой, и реальное решение есть.
\ [y \ left (t \ right) = — 10 \ cos \ left ({4t} \ right) + \ frac {3} {4} \ sin \ left ({4t} \ right) \]
Комплексные переменные с отличием Зима 2015
MATH 249: С уважением к комплексным переменным Зима 2015
Выпускной экзамен
в спортзале Карри.
Назначения
Конспект лекций
Расписание занятий
| Дата | Темы |
| Вт 1/7 | Историческое введение в комплексные числа |
| П 1/9 | Аксиомы для комплексных чисел.Векторная модель. |
| W 1/14 | Матричная модель. Алгебра комплексных чисел. |
| П 1/16 | Геометрия C . Проблема расширения. |
| Вт 1/21 | Топология C . Пределы и преемственность. Комплексная дифференцируемость. |
| П 1/23 | Голоморфия. Реальная дифференцируемость. |
| Вт 1/28 | Уравнения Коши-Римана. |
| П 1/30 | Равномерная сходимость. |
| Вт 2/4 | Абсолютно равномерное схождение. |
| П 2/6 | Двойная серия. |
| W 2/11 | Силовая серия. |
| F 2/13 | Постоянные функции. Показательная. Сюръективность на мультипликативную группу. |
| W 2/18 | Настоящая экспонента.Ядро и периодичность экспоненты. |
| П 2/20 | Многозначные функции. Аргумент. Логарифмы. |
| Вт 2/25 | Подробнее о логарифмах. Полномочия. Корнеплоды. Круговые функции. |
| F 2/27 | Промежуточный экзамен |
| Вт 3/11 | Контурная интеграция. Теорема Гурса. |
| П 3/13 | Локальная интегрируемость. Теорема Коши для гомотопических луп. |
| Вт 3/18 | Относительная гомотопия. Оценка действительных определенных интегралов. |
| П 3/20 | Интегральная формула Коши. Теорема Коши-Тейлора. Аналитическое продолжение. |
| Вт 3/25 | Оценки Коши. Треорема Лиувилля. Теорема Мореры. Теорема о сходимости Вейерштрасса. |
| П 3/27 | Теорема тождества. Теорема об открытом отображении. Принцип максимума. |
| W 4/1 | Разложение Лорана и ряды Лорана. |
| П 4/3 | Хорошая пятница |
| Вт 4/8 | Изолированные особенности. |
| П 4/10 | Остатки и индексы. Теорема о вычетах. |
| Вт 04/14 | Принцип аргумента. Теорема Руше. |
| Вт 21.04 | Заключительный экзамен (14:00, тренажерный зал Currie) |
Справочники
Интернет-ресурсы
Краткое содержание курса
Инструктор: Доктор Гантумур Цогтгерел
Предварительные требования: MATH 248 (с отличием)
Ограничение: Для студентов-физиков и студентов с отличием.Не открыто для студентов, которые сдали или сдают MATH 316.
Тем:
Очень стандартные темы, кроме векторных функций, которые мы рассмотрим, если позволит время.
Описание календаря:
Функции комплексной переменной;
Уравнения Коши-Римана; Теорема Коши и следствия.Разложения Тейлора и Лорана.
Остаточный камень; вычисление реальных интегралов; интегральное представление специальных функций; комплексный интеграл обращения.
Конформное отображение; Преобразование Шварца-Кристоффеля;
Интегральные формулы Пуассона; Приложения.
Домашнее задание: 3-4 письменных задания.
Экзамены: Промежуточный и выпускной.
Оценка: Домашнее задание 20% + Среднесрочная 20% + Итоговая 60%
Промежуточный экзамен
Комплексная интеграция — Комплексный анализ
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Math 427: Комплексный анализ
Math 427: Комплексный анализ
Осень 2018
Лекции: MWF 11: 30-12: 20 в THO 325
Инструктор: Джарод Альпер (jarod @ uw.edu)
Офис: PDL C-544
Время работы: Пн, Ср: 4-5
TA: Томас Лу ([email protected])
Часы работы: Четверг с 17:00 до 19:00 в PDL C-401
Учебник:
- Джозеф Л. Тейлор, Комплексные переменные
Syllabus: Этот курс посвящен сложному исчислению
функции. Мы обсудим дифференциацию и интеграцию
комплексные функции комплексного переменного.Среди тем мы
будут охватывать интегральную теорему Коши, теорему Лиувилля и
Принцип максимального модуля. Мы рассмотрим примерно первые три
главы книги Тейлора Комплексный анализ.
Домашние задания: Домашние задания будут регулярными.
задания. Самый низкий балл за домашнее задание будет удален. Домашние задания сдаются в начале урока.
- Домашнее задание 1, срок сдачи в пятницу, октябрь
5. Решения - Домашнее задание 2, сдать в пятницу, 12 октября.Решения
- Домашнее задание 3, сдать в понедельник, октябрь
22. Решения - Домашнее задание 4, сдать в среду, окт.
31. Решения - Домашнее задание 5, сдать в среду, ноябрь
14. Решения - Домашнее задание 6, сдать в понедельник, ноябрь
26. Решения - Домашнее задание 7, сдать в пятницу, декабрь
7. Решения
Расписание: Содержание лекций будет опубликовано
здесь. Приведенные ниже разделы учебника являются лишь приблизительными.
приближение к тому, что мы фактически рассмотрели в классе.
| Лекция | Дата | Охваченные темы | Замечания |
|---|---|---|---|
| 1 неделя | |||
| 1 | ср 26 сен | Введение: комплексные числа | |
| 2 | Пт 28 сентября | Сходимость последовательностей и рядов | |
| 2 неделя | |||
| 3 | Пн 1 окт | Комплексные экспоненциальные и полярные координаты | |
| 4 | Ср 3 окт | Обсуждение | |
| 5 | Пт 5 октября | Корни N и комплексный логарифм | HW 1 к сроку |
| 3 неделя | |||
| 6 | Пн 8 октября | Топогий из комплексных чисел | |
| 7 | Ср 10 окт | Обсуждение | |
| 8 | Пт 12 октября | Непрерывные функции | HW 2 к сроку |
| 4 неделя | |||
| 9 | Пн 15 октября | Многозначные функции; сложная дифференциация | |
| 10 | Ср 17 окт | Уравнения Коши-Римана | |
| 11 | Пт 19 октября | Обсуждение | |
| 5 неделя | |||
| 12 | Пн 22 октября | Комплексное интегрирование и контурные интегралы | HW 3 к сроку |
| 13 | Ср, 24 октября | Контурные интегралы | |
| 14 | Пт 26 октября | Интегральная теорема Коши для треугольников | |
| 6 неделя | |||
| 15 | Пн 29 октября | Обсуждение | |
| 16 | ср 31 окт | Интегральная теорема Коши для выпуклых множеств | HW 4 к сроку |
| 17 | Пт 2 ноя | Среднесрочная | |
| 7 неделя | |||
| 18 | Пн 5 ноя | Возвращение к интегральной теореме Коши; Интегральная формула Коши | |
| 19 | Ср 7 ноя | Интегральная формула Коши и индексные функции | |
| 20 | Пт 9 ноя | Свойства индексной функции | |
| 8 неделя | |||
| Пн 12 ноября | Без класса — День ветеранов | ||
| 21 | Ср 14 ноя | Равномерное схождение | HW 5 к сроку |
| 22 | Пт 16 ноя | Силовой ряд и схождение | |
| 9 неделя | |||
| 23 | Пн 19 ноября | Power серии аналитические | |
| 24 | ср 21 ноя | Обсуждение | |
| Пт 23 ноя | Без класса — День Благодарения | ||
| 10 неделя | |||
| 25 | Пн 26 ноя | Разложения аналитических функций в степенной ряд | HW 6 срок сдачи |
| 26 | ср 28 ноя | Теорема Луивилля и основная теорема алгебры | |
| 27 | Пт 30 ноя | Нули аналитических функций | |
| 11 неделя | |||
| 28 | Пн 3 дек | Особенности аналитических функций | |
| 29 | Ср 5 дек | Обзор | |
| 30 | Пт 7 дек | Нет класса | HW 7 к сроку |
| Финал | |||
| Ср 12 дек | Заключительный экзамен, 14:30 — 16:20 | ||
Среднесрочный: Будет один в классе среднесрочный
- Дата: 2 ноября, пятница
- Время и место: в классе
- Среднесрочная
Заключительный экзамен:
- Дата: среда, 12 декабря
- Время: 2: 30–16: 20
- Место нахождения: THO 325 (обычное местонахождение)
Оценка:
- Домашнее задание: 35%
- Среднесрочная перспектива: 25%
- Финал: 40%
Самый низкий балл за домашнее задание будет удален.