Содержание
Решение определенного интеграла онлайн бесплатно
Что делать, если решение не появляется (пустой экран)?
Данный калькулятор по решению интегралов онлайн построен на основе системы WolframAlpha Mathematica. Все права на его использование принадлежат компании Wolfram Alpha LLC!
Решение определенного интеграла онлайн
Определенный интеграл
Онлайн сервис на matematikam.ru позволяет находить решение определенного интеграла онлайн. Решение проводится автоматически на сервере и в течении нескольких секунд пользователю выдается результат. Все онлайн сервисы на сайте абсолютно бесплатны, а решение выдается в удобном и понятном виде. Также нашим преимуществом является, что мы предоставляем возможность пользователю ввести границы интегрирования, в том числе и пределы интегрирования: минус и плюс бесконечность. Таким образом, решить определенный интеграл становится просто, быстро и качественно. Важно, что сервер позволяет вычислять определенные интегралы онлайн сложных функций, решение которых на иных онлайн-сервисах часто является невозможным ввиду несовершенства их систем. Мы предоставляем очень простой и интуитивно понятный механизм для ввода функций и возможность выбора переменной интегрирования, для чего вам не приходится переводить заданную в одной переменной функцию в другую, исключая связанные с этим ошибки и опечатки. Также на странице даны ссылки на теоретические статьи и таблицы по решению определенных интегралов. Всё в совокупоности позволит вам вычислять определенный интеграл онлайн очень быстро и при желании найти и разобраться с теорией решения определенных интегралов. На http://matematikam.ru вы также можете переходить на другие сервисы: онлайн решение пределов, производных, суммы рядов. Перейти же на вкладку решения неопределенных интегралов онлайн совсем просто — ссылка находится в ряду среди полезных ссылок.
Таким образом, решить определенный интеграл становится просто, быстро и качественно. Важно, что сервер позволяет вычислять определенные интегралы онлайн сложных функций, решение которых на иных онлайн-сервисах часто является невозможным ввиду несовершенства их систем. Мы предоставляем очень простой и интуитивно понятный механизм для ввода функций и возможность выбора переменной интегрирования, для чего вам не приходится переводить заданную в одной переменной функцию в другую, исключая связанные с этим ошибки и опечатки. Также на странице даны ссылки на теоретические статьи и таблицы по решению определенных интегралов. Всё в совокупоности позволит вам вычислять определенный интеграл онлайн очень быстро и при желании найти и разобраться с теорией решения определенных интегралов. На http://matematikam.ru вы также можете переходить на другие сервисы: онлайн решение пределов, производных, суммы рядов. Перейти же на вкладку решения неопределенных интегралов онлайн совсем просто — ссылка находится в ряду среди полезных ссылок. Более того, сервис постоянно совершенствуется и развивается, и с каждым днем появляются всё новые и новые возможности и усовершенствования. Решайте определенные интегралы вместе с нами! Все онлайн сервисы доступны даже незарегистрировшимся пользователям и абсолютно бесплатны.
Более того, сервис постоянно совершенствуется и развивается, и с каждым днем появляются всё новые и новые возможности и усовершенствования. Решайте определенные интегралы вместе с нами! Все онлайн сервисы доступны даже незарегистрировшимся пользователям и абсолютно бесплатны.
Решая определенный интеграл у нас вы можете проверить своё собственное решение или избавиться от излишних трудоемких вычислений и довериться высокотехнологичной автоматизированной машине. Вычисляемая на сервисе точность удовлетворит практически любые инженерные нормы. Часто для многих табличных определенных интегралов результат выдается в точном выражении (используя общеизвестные константы и неэлементарные функции).
Похожие сервисы:
Вычислить определенный интеграл
Calculate definite integral online
Онлайн калькулятор: Численное интегрирование
Численные методы вычисления значения определенного интеграла применяются в том случае, когда первообразная подинтегральной функции не выражается через аналитические функции, и поэтому невозможно вычислить значение по формуле Ньютона-Лейбница. Для получения значения определенного интеграла таких функций можно воспользоваться численным интегрированием.
Для получения значения определенного интеграла таких функций можно воспользоваться численным интегрированием.
Численное интегрирование сводится к вычислению площади криволинейной трапеции, ограниченной графиком заданной функции, осью х и вертикальными прямыми ограничивающими отрезок слева и справа. Подинтегральная функция заменяется на более простую, обеспечивающую заданную точность, вычисление интеграла для которой не составляет труда.
Калькулятор ниже вычисляет значение одномерного определенного интеграла численно на заданном отрезке, используя формулы Ньютона-Котеса, частными случаями которых являются:
- Метод прямоугольников
- Метод трапеций
- Метод парабол (Симпсона)
Интеграл численным методом по формулам Ньютона-Котеса
Квадратурная функцияОбновление…Точность вычисления
Знаков после запятой: 6
Значение определенного интеграла
Квадратурная функция
Погрешность метода
Геометрический вид интеграла
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Загрузить
close
Источник формулы
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Загрузить
close
content_copy Ссылка save Сохранить extension Виджет
Численное интегрирование с использованием функций Ньютона Котеса
При использовании функций Ньютона-Котеса отрезок интегрирования разбивается на несколько равных отрезков точками x1,x2,x3..xn.
Подинтегральную функцию заменяют интерполяционным многочленом Лагранжа различной степени, интегрируя который, получают формулу численного интегрирования различного порядка точности.
В итоге, приближенное значение определенного интеграла вычисляется, как сумма значений подинтегральной функции в узлах, помноженных на некоторые константы Wi (веса):
- Rn — остаток или погрешность.
- n — общее количество точек.
- Сумма в формуле — квадратурное правило (метод).

В справочнике Квадратурные функции Ньютона-Котеса, мы собрали наиболее часто встречающиеся квадратурные правила, для интегрирования по равным отрезкам. Зарегистрированные пользователи могут добавлять в этот справочник новые правила.
Границы отрезка интегрирования
В зависимости от того, входят ли граничные точки отрезка в расчет, выделяют замкнутые и открытые квадратурные правила.
Открытые правила, (правила, в которых граничные точки не включаются в расчет) удобно использовать в том случае, если подинтегральная функция не определена в некоторых точках.
Например, используя метод прямоугольников мы сможем вычислим приблизительное значение интеграла функции ln(x) на отрезке (0,1), несмотря на то, что ln(0) не существует.
Замкнутые правила, напротив, используют значения функции в граничных точках для вычислений интеграла, ровно так же как и в остальных узлах.
Можно придумать правила, которые открыты только с одной стороны. Простейшим случаем таких правил являются правила левых и правых прямоугольников.
Простейшим случаем таких правил являются правила левых и правых прямоугольников.
Погрешность вычисления
В целом с увеличением количества узлов в правиле (при повышении степени интерполирующего полинома) возрастает точность вычисления интеграла. Однако для некоторых функций это может и не быть справедливо.
Впервые анализ этой особенности опубликовал Карл Рунге, немецкий математик, занимавшийся исследованием численных методов.
Он заметил, интерполирующий полином с равномерным разбиением отрезка для функции перестает сходиться в диапазоне значений 0.726.. ≤ |x| <1 при увеличении степени полинома.
В выражении для вычисления погрешности участвует интервал h, факториал от количества разбиений, которые при увеличении степени полинома уменьшают значение погрешности, но для некоторых функций значения производной, также участвующие в выражении погрешности, растут быстрее с увеличением ее порядка.
Кроме этого, при увеличении степени интерполирующего полинома Лагранжа, возникают веса, имеющие отрицательные значения.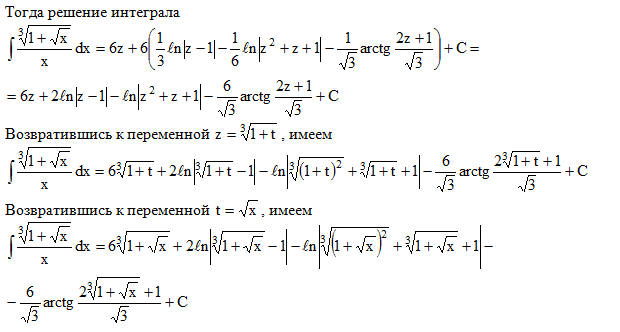 Данный факт негативно сказывается на вычислительной погрешности. Калькулятор выдает графическое представление промежуточных результатов вычисления квадратурной функции. Для положительных коэффициентов Wi это выглядит ровно так же, как принято отображать сумму Римана. При наличии отрицательных значений коэффициентов Wi на графике появляются значения интегральной суммы с противоположным знаком, суммарная ширина положительных и отрицательных интегральных сумм становится больше, чем длина интегрируемого отрезка. Этот эффект можно наблюдать в следующем примере: Замкнутое правила Ньютона-Котеса с 11-ю узлами
Данный факт негативно сказывается на вычислительной погрешности. Калькулятор выдает графическое представление промежуточных результатов вычисления квадратурной функции. Для положительных коэффициентов Wi это выглядит ровно так же, как принято отображать сумму Римана. При наличии отрицательных значений коэффициентов Wi на графике появляются значения интегральной суммы с противоположным знаком, суммарная ширина положительных и отрицательных интегральных сумм становится больше, чем длина интегрируемого отрезка. Этот эффект можно наблюдать в следующем примере: Замкнутое правила Ньютона-Котеса с 11-ю узлами
Принимая во внимание эти особенности, правила с полиномами степеней >10 применять не рекомендуется.
Для увеличения точности численного интегрирования, можно разбить отрезок на несколько частей — частичных интервалов, и для каждой части отдельно вычислить приближенное значение интеграла. Сумма значений интеграла по всем частичным интервалам даст нам значение интеграла на всем отрезке. Кроме того можно комбинировать различные правила друг с другом в любой последовательности.
Кроме того можно комбинировать различные правила друг с другом в любой последовательности.
Для исследования работы с заданной функцией новых, основанных на формулах Ньютона-Котеса правил, можно воспользоваться базовым калькулятором, в котором веса задаются в явном виде:
Численное интегрирование с заданными весами Ньютона-Котеса
Перечислите веса через запятую, в самом начале укажите общий множитель. Можно указывать коэффициенты в виде простой дроби, например, так: 3/4. Пример весов для метода Симпсона: 1/3,1,4,1.
Границы интервалаЗамкнутыОткрытыОткрыты справаОткрыты слеваТочность вычисления
Знаков после запятой: 6
Значение определенного интеграла
Квадратурная функция
Геометрический вид интеграла
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Загрузить
close
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Загрузить
close
content_copy Ссылка save Сохранить extension Виджет
Веса задаются через запятую, допускаются как целые, так и действительные числа с точкой, для отделения дробной части. Можно задать вес в виде простой дроби, например, вот так: 1/90.
Можно задать вес в виде простой дроби, например, вот так: 1/90.
Первый коэффициент в списке весов — это общий множитель, его тоже можно задать в виде простой дроби или задать = 1, если общего множителя нет.
Например, веса: 3/8,1,3,3,1 определяют Метод Симпсона 3/8
Правила Ньютона-Котеса несовершенны, для реальных приложений следует использовать более эффективные методы, например метод Гаусса-Кронрода, о котором мы напишем в следующих статьях.
Литература:
- Н.С.Бахвалов Численные методы, 2012
- У.Г.Пирумов Численные методы, 2006
- Д.Каханер, К.Моулер, С.Нэш Численные методы и программное обеспечение, 1989
- Р.В. Хемминг Численные методы для научных работников и инженеров, 1972
- M. Abramovitz и I. Stegun Handbook of Mathematical Functions With Formulas, Graphs and Mathematical Tables, 1973
Калькулятор Интегралов — определенный & неопределенный
Онлайн-калькулятор интегралов поможет вам вычислить интегралы функций по отношению к задействованной переменной и покажет вам полные пошаговые вычисления. Когда дело доходит до вычислений неопределенных интегралов, этот калькулятор первообразных позволяет мгновенно решать неопределенные интегралы. Теперь вы можете определить интегральные значения следующих двух интегралов с помощью онлайн-интеграл калькулятор:
Когда дело доходит до вычислений неопределенных интегралов, этот калькулятор первообразных позволяет мгновенно решать неопределенные интегралы. Теперь вы можете определить интегральные значения следующих двух интегралов с помощью онлайн-интеграл калькулятор:
- Определенные интегралы
- Неопределенные интегралы (первообразная)
Интегральный расчет довольно сложно решить вручную, так как он включает в себя различные сложные формулы интегрирования. Итак, рассмотрим интерактивный интегральный решатель, который решает простые и сложные функции решение интегралов онлайн и показывает вам пошаговые вычисления.
Итак, сейчас самое время понять формулы интегрирования, как интегрировать функцию шаг за шагом, с помощью калькулятора интегрирования и многое другое. Во-первых, давайте начнем с основ:
Читать дальше!
Что такое интеграл?
В математике интеграл функций описывает площадь, смещение, объем и другие понятия, которые возникают, когда мы объединяем бесконечные данные. В исчислении дифференцирование и интегрирование являются фундаментальной операцией и служат наилучшей операцией для решения физико-математических задач произвольной формы.
В исчислении дифференцирование и интегрирование являются фундаментальной операцией и служат наилучшей операцией для решения физико-математических задач произвольной формы.
Вы также можете использовать бесплатную версию онлайн-калькулятора факторов, чтобы найти факторы, а также пары факторов для положительных или отрицательных целых чисел.
- Процесс нахождения интегралов, называемый интегрированием
- Интегрируемая функция называется подынтегральной функцией.
- В интегральных обозначениях ∫3xdx, ∫ – символ интеграла, 3x – интегрируемая функция, а dx – дифференциал переменной x.
Где f (x) – функция, а A – площадь под кривой. Наш бесплатный калькулятор интегралов легко вычисляет интегралы и определяет площадь под заданной функцией. Что ж, теперь поговорим о типах интегралов:
Типы интегралов:
По сути, есть два типа интегралов:
- Неопределенные интегралы
- Определенные интегралы
Неопределенные интегралы:
определенный интеграл онлайн функции принимает первообразную другой функции. Взять первообразную функции – это самый простой способ обозначить неопределенные интегралы. Когда дело доходит до вычисления неопределенных интегралов, калькулятор неопределенных интегралов помогает выполнять вычисления неопределенных интегралов шаг за шагом. Этот тип интеграла не имеет верхнего или нижнего предела.
Взять первообразную функции – это самый простой способ обозначить неопределенные интегралы. Когда дело доходит до вычисления неопределенных интегралов, калькулятор неопределенных интегралов помогает выполнять вычисления неопределенных интегралов шаг за шагом. Этот тип интеграла не имеет верхнего или нижнего предела.
Определенные интегралы:
Определенный интеграл функции имеет начальное и конечное значения. Просто существует интервал [a, b], который называется пределами, границами или границами. Этот тип можно определить как предел интегральных сумм, когда диаметр разбиения стремится к нулю. Наш интеграл онлайн калькулятор определенных интегралов с оценками вычисляет интегралы, учитывая верхний и нижний предел функции. Разницу между определенным и неопределенным интегралами можно понять по следующей диаграмме:
Основные формулы для интеграции:
Существуют разные формулы для интеграции, но здесь мы перечислили некоторые общие:
- ∫1 dx = x + c
- ∫xn dx = xn + 1 / n + 1 + c
- ∫a dx = ax + c
- ∫ (1 / х) dx = lnx + c
- ∫ ax dx = ax / lna + c
- ∫ ex dx = ex + c
- ∫ sinx dx = -cosx + c
- ∫ cosx dx = sinx + c
- ∫ tanx dx = – ln | cos x | + c
- ∫ cosec2x dx = – детская кроватка x + c
- ∫ sec2x dx = tan x + c
- ∫ cotx dx = ln | sinx | + c
- ∫ (secx) (tanx) dx = secx + c
- ∫ (cosecx) (cotx) dx = -cosecx + c
Помимо этих уравнений интегрирования, есть еще несколько важных формул интегрирования, которые упомянуты ниже:
- ∫ 1 / (1-x2) 1/2 dx = sin-1x + c
- ∫ 1 / (1 + x2) 1/2 dx = cos-1x + c
- ∫ 1 / (1 + x2) dx = tan-1x + c
- ∫ 1 / | x | (x2 – 1) 1/2 dx = cos-1x + c
Запоминание всех этих формул интегрирования и выполнение вычислений вручную – очень сложная задача. Просто введите функцию в предназначенное для этого поле онлайн-калькулятор интегралов, который использует эти стандартизированные формулы для точных вычислений.
Просто введите функцию в предназначенное для этого поле онлайн-калькулятор интегралов, который использует эти стандартизированные формулы для точных вычислений.
Как решать интегралы вручную (шаг за шагом):
Большинство людей раздражается начинать с вычислений интегральной функции. Но здесь мы собираемся решать интегральные примеры шаг за шагом, что поможет вам разобраться, как легко интегрировать функции! Итак, это точки, которым нужно следовать для вычисления решение интегралов онлайн:
- Определить функцию f (x)
- Возьмите первообразную функции
- Вычислить верхний и нижний предел функции
- Определите разницу между обоими пределами
Если вас интересует вычисление первообразной (неопределенного интеграла), тогда возьмите онлайн-калькулятор первообразной, который быстро решит первообразную данной функции.
Смотрит на примеры:
Пример 1:
Решить интегралы от ∫ x3 + 5x + 6 dx?
Решение:
Шаг 1:
Применяя правило функциональной мощности для интегрирования:
∫xn dx = xn + 1 / n + 1 + c
∫ x3 + 5x + 6 dx = x3 + 1/3 + 1 + 5 x1 + 1/1 + 1 + 6x + c
Шаг 2:
∫ x3 + 5x + 6 dx = x4 / 4 + 5 x2 / 2 + 6x + c
Шаг 3:
∫ x3 + 5x + 6 dx = x4 + 10×2 + 24x / 4 + c
Этот калькулятор неопределенного интеграла помогает интегрировать интеграл калькулятор функции шаг за шагом, используя формулу интегрирования. 1_5 x * lnx dx = –14
1_5 x * lnx dx = –14
Поскольку это очень сложно для решения интегралов, когда две функции умножаются друг на друга. Для удобства просто введите функции в онлайн-калькулятор интегралов по частям, который помогает выполнять вычисления двух функций (по частям), которые точно умножаются друг на друга.
Пример 3 (Интеграл от тригонометрической функции):
Вычислить определенный интеграл для ∫sinx dx с интервалом [0, π / 2]?
Решение:
Шаг 1:
Используйте формулу для тригонометрической функции:
∫ sinx dx = -cosx + c
Шаг 2:
Вычислите верхний и нижний предел для функций f (a) и f (b) соответственно:
Поскольку a = 0 и b = π / 2
Итак, f (a) = f (0) = cos (0) = 1
f (b) = f (π / 2) = cos (π / 2) = 0
Шаг 3:
Рассчитайте разницу между верхним и нижним пределами:
f (а) – f (b) = 1 – 0
f (а) – f (b) = 1
Теперь вы можете использовать бесплатный калькулятор частичных интегралов для проверки всех этих примеров и просто добавлять значения в поля назначения для мгновенного вычисления интегралов.
Как найти первообразную и вычислить интегралы с помощью калькулятора интегралов:
Вы можете легко вычислить интеграл от определенных и неопределенных функций с помощью лучшего интегратора. Вам просто нужно следовать указанным пунктам, чтобы получить точные результаты:
Проведите по!
Входы:
- Во-первых, введите уравнение, которое вы хотите интегрировать.
- Затем выберите зависимую переменную, входящую в уравнение
- Выберите на вкладке определенный или определенный интеграл онлайн
- Если вы выбрали конкретный вариант, то вам следует ввести нижнюю и верхнюю границу или предел в предназначенное для этого поле.
- После этого пора нажать на кнопку расчета.
Выходы:
Интегральный оценщик показывает:
- Определенный интеграл
- неопределенный интеграл онлайн
- Выполните пошаговые расчеты
Часто задаваемые вопросы (FAQ):
Какое целое значение?
В математике интеграл – это числовое значение, равное площади под графиком некоторой функции на некотором интервале. Это может быть график новой функции, производная которой является исходной функцией (калькулятор неопределенных интегралов). Итак, для мгновенных и быстрых вычислений вы можете использовать бесплатный интеграл онлайн калькулятор первообразных, который позволяет вам решать неопределенные интегральные функции.
Это может быть график новой функции, производная которой является исходной функцией (калькулятор неопределенных интегралов). Итак, для мгновенных и быстрых вычислений вы можете использовать бесплатный интеграл онлайн калькулятор первообразных, который позволяет вам решать неопределенные интегральные функции.
Как вы оцениваете интеграл, используя основную теорему исчисления?
Прежде всего, мы должны найти первообразную функции, чтобы решить интеграл, используя фундаментальную теорему. Затем используйте основную теорему исчисления для вычисления решение интегралов онлайн. Или просто введите значения в предназначенное для этого поле этого калькулятора интеграции и мгновенно получите результаты.
Что такое двойной интеграл?
Двойные интегралы – это способ интегрирования по двумерной области. Двойные интегралы позволяют вычислить объем поверхности под кривой. Они имеют две переменные и рассматривают функцию f (x, y) в трехмерном пространстве.
Заключительные слова:
Интегралы широко используются для улучшения архитектуры зданий, а также для мостов. В электротехнике его можно использовать для определения длины силового кабеля, необходимого для соединения двух станций, находящихся на расстоянии нескольких миль друг от друга. Этот онлайн-калькулятор интегралов лучше всего подходит для школьного образования, который легко интеграл калькулятор любой заданной функции шаг за шагом.
В электротехнике его можно использовать для определения длины силового кабеля, необходимого для соединения двух станций, находящихся на расстоянии нескольких миль друг от друга. Этот онлайн-калькулятор интегралов лучше всего подходит для школьного образования, который легко интеграл калькулятор любой заданной функции шаг за шагом.
Other Languages: Integral Calculator, Integral Hesaplama, Kalkulator Integral, Kalkulator Integralny, Integralrechner, 積分計算, 적분계산기, Integrály Kalkulačka, Calculadora De Integral, Calcul Intégrale En Ligne, Calculadora De Integrales, Calcolatore Integrali, حساب متكامل, Integraatio Laskin, Integreret Lommeregner, Integral Kalkulator, Integralni Kalkulator, เครื่องคำนวณอินทิกรัล, Integrale Rekenmachine.
калькулятор интегралов — калькулятор первообразных
Калькулятор интегралов — это онлайн-инструмент, который вычисляет первообразную функции. Он работает как калькулятор определенного интеграла, а также как калькулятор неопределенного интеграла и позволяет мгновенно вычислить интегральное значение.
Если вы изучаете исчисление, вы можете иметь представление о том, насколько сложны интегралы и производные. Что ж, отбросьте свои заботы, потому что калькулятор интеграции здесь, чтобы облегчить вам жизнь. Вы можете оценить интеграл, только поместив функцию в наш инструмент.
Теперь мы обсудим определение интеграла, как использовать интегральный калькулятор с пошаговыми инструкциями, как решать интегралы с помощью интегрального решателя и многое другое.
Что такое интегральное?
Интеграл является обратной производной. Он такой же, как и первообразная. Его можно использовать для определения площади под кривой. Вот стандартное определение интеграла
Википедия.
«В математике интеграл присваивает числа функциям таким образом, чтобы можно было описать смещение, площадь, объем и другие понятия, возникающие при объединении бесконечно малых данных. Интегрирование — одна из двух основных операций исчисления; его обратная операция, дифференцирование, является другим. ”
”
С интервалом [a, b] действительной прямой и действительной переменной x определенный интеграл заданной функции f может быть выражен как:
Как правило, есть два типа интегралов.
Oпределенный интеграл онлайн : если интегралы определяются с использованием нижнего и верхнего пределов, они называются определенными интегралами. Стандартный вид определенных интегралов может быть представлен как:
Hеопределенный интеграл онлайн : если не определены нижний или верхний предел, предел указывается постоянной интегрирования. Эти типы интегралов называются неопределенными интегралами, потому что для них нет ограничений.
Стандартная форма неопределенных интегралов:
∫ f (x) dx
Как работает интеграл онлайн?
Калькулятор первообразных вычисляет функцию, заданную пользователем, и преобразует ее в интегрирование, применяя верхний и нижний пределы, если это определенный интеграл. Если это неопределенный интеграл, калькулятор интегралов просто использует константу интегрирования для вычисления выражения.
Кроме того, калькулятор интегральных вычислений дает ощущение простоты в расчетах интегрирования, только принимая функцию от пользователя. Вам не нужно ничего делать, кроме как вводить данные, и этот итерационный калькулятор интегралов делает все это самостоятельно, причем в кратчайшие сроки.
Чтобы использовать этот калькулятор линейного интеграла, выполните следующие действия:
Введите свое значение в данное поле ввода.
Нажмите кнопку «Рассчитать», чтобы получить интеграл.
Используйте кнопку Reset, чтобы ввести новое значение.
Калькулятор интеграции по частям даст вам полностью оцененную интегральную функцию, которую можно в дальнейшем использовать в различных областях. Как упоминалось выше, интегрирование является обратной функцией производных. Если вам нужно решить производную, воспользуйтесь нашим калькулятором производной.
Как вычислить интеграл?
Теперь, когда вы знаете, что такое интегралы и как использовать приведенную выше производную интегрального калькулятора для решения интеграла, вы также можете узнать, как решать интегралы вручную. Это может как-то раздражать тех, кто только начинает с интегралов.
Это может как-то раздражать тех, кто только начинает с интегралов.
Но не волнуйтесь. Мы продемонстрируем расчеты на примерах, чтобы вы могли легко понять. Кроме того, вы можете подготовить тему к экзаменам, используя приведенное ниже руководство.
Чтобы вычислить интегралы, выполните следующие действия:
Определите и запишите функцию F (x).
Возьмем первообразную функции F (x).
Вычислите значения верхнего предела F (a) и нижнего предела F (b).
Вычислите разницу верхнего предела F (a) и нижнего предела F (b).
Давайте воспользуемся примером, чтобы понять метод вычисления определенного интеграла.
Пример — Определенный интеграл
Для функции f (x) = x — 1 найти определенный интеграл, если интервал равен [2, 8].
Решение:
Шаг 1: Определите и запишите функцию F (x).
F (x) = x — 1, интервал = [2, 8]
Шаг 2: Возьмите первообразную функции F (x).
F (x) = ∫ (x − 1) dx = (x2 / 2) — x
Шаг 3: Рассчитайте значения верхнего предела F (a) и нижнего предела F (b).
As, a = 1 и b = 10,
F (а) = F (1) = (22/2) — 2 = 0
F (б) = F (10) = (82/2) — 8 = 24
Шаг 4: Рассчитайте разницу верхнего предела F (a) и нижнего предела F (b).
F (б) — F (а) = 24-0 = 24
Этот метод можно использовать для вычисления определенных интегралов, имеющих пределы. Вы можете использовать калькулятор двойного интеграла выше, если не хотите заниматься интегральными вычислениями.
Пример — интеграл тригонометрической функции
Для функции f (x) = sin (x) найдите определенный интеграл, если интервал равен [0, 2π].
Решение:
Шаг 1: Определите и запишите функцию F (x).
F (x) = sin (x), интервал = [0, 2π]
Шаг 2: Возьмите первообразную функции F (x).
F (x) = ∫ sin (x) dx = cos (x)
Шаг 3: Рассчитайте значения верхнего предела F (a) и нижнего предела F (b).
As, a = 0 и b = 2π,
F (а) = F (0) = cos (0) = 0
F (b) = F (2π) = cos (2π) = 0
Шаг 4: Рассчитайте разницу верхнего предела F (a) и нижнего предела F (b).
F (б) — F (а) = 0 — 0 = 0
Наряду с ручным расчетом вы также можете использовать наш калькулятор тригонометрической подстановки выше, чтобы решить тригонометрический интеграл за доли секунды.
FAQs
Что такое вычисление интегралов?
Интегральное вычисление обращает функцию производной, беря первообразную этой функции. Он используется для определения площади под кривой. Интегральные вычисления могут быть определенными, если есть верхний и нижний пределы. Если интервалов нет, используется интегральная константа C, и этот тип функции называется неопределенным интегралом.
Какая производная от интеграла?
Если мы возьмем производную интеграла, оба они будут компенсировать друг друга, потому что производная и интеграл являются обратными функциями друг к другу. Согласно основной теореме исчисления, интеграл — это то же самое, что и первообразная.
Кто отец интеграции?
Готфрид Вильгельм Лейбниц и Исаак Ньютон независимо предложили правила интеграции в конце 17 века. Они приняли интеграл как бесконечную сумму прямоугольников чрезвычайно малой ширины. Бернхард Риман описал интегралы строго математически.
Они приняли интеграл как бесконечную сумму прямоугольников чрезвычайно малой ширины. Бернхард Риман описал интегралы строго математически.
Что такое интеграл от 1?
Интеграл от 1 равен x или x + c, потому что если мы добавим интегральную константу. Это можно выразить как диагональная линия, лежащая в 1-м и 3-м квадрантах графика.
∫ 1 dx = x + C
Какой интеграл от sin 2x?
Интеграл от sin 2x можно вычислить методом подстановки. Это будет неопределенный интеграл из-за отсутствия интервала или верхнего и нижнего пределов. Вот интеграл от sin 2x.
∫ sin (2x) dx = — (1/2) cos (2x) + C
Other Languages: Antiderivative(Integral) Calculator, Calculadora de integrales, Integralrechner, калькулятор интегралов, מחשבון אינטגרלים, Calculateur de primitive
Интеграл
Решение интегралов
Наш калькулятор интегралов онлайн с подробным решением поможет
вычислить интегралы и
первообразные функции онлайн
— бесплатно! Пользоваться калькулятором просто. Чтобы ввести определенный интеграл или
Чтобы ввести определенный интеграл или
неопределенный интеграл, нажмите «+условие» и введите интеграл
Например:
Нажав кнопку Решить вы получите подробное решение интеграла онлайн.
Калькулятором интегралов поддерживается вычисление определенных и неопределенных интегралов
(первообразных
функций), включая интегрирование функций с несколькими переменными.
Как решить интеграл онлайн с решением?
Введите неопределенный интеграл, нажав на кнопку ∫. Затем введите подинтегральное выражение, после чего
нажмите на кнопку d и введите переменную, по которой нужно провести интегрирование. Оставьте
незаполненными серые квадратики.
Введите определенный интеграл, нажав на кнопку ∫. Затем введите подинтегральное выражение, после чего
нажмите на кнопку d. Это можно сделать как на своей клавиатуре, так и на клавиатуре сайта. Введите
Это можно сделать как на своей клавиатуре, так и на клавиатуре сайта. Введите
переменную, по которой нужно провести интегрирование. Далее кликните на нижний серый квадратик и введите
нижний предел, кликните на верхний серый квадратик и введите верхний предел.
На серые квадратики можно перейти либо кликнув на них, либо используя кнопки влево, вправо.
В определённых интегральных уравнениях применяется такое понятие как “предел”. Предел обозначает отрезок
функции, в которой происходит вычисление интеграла и результатом такого действия будет число. Физический
смысл такого числа — это размер площади под графиком соответствующей функции интеграла, эта операция
часто применяется в науке, в частности в физике.
Операция интегрирования является своего рода обратной операции вычисления производной. Если мы будем
вычислять неопределённый интеграл, то в результате получим функцию с приплюсованной константой
с
.
Таблица интегралов
Чтобы найти интеграл, нужно знать таблицу ниже:
Мы живем в удивительное время. Сегодня вы можете получить онлайн решение интегралов с подробным
решением.
Подробное решение интегралов онлайн стало доступным благодаря современным разработкам в области
искусственного интеллекта.
Где можно решить онлайн интеграл? Интеграл калькулятор онлайн Pocket Teacher!
Онлайн интегралы — это просто!
Решить онлайн интегралы вы можете на нашем сайте. Бесплатный
онлайн
решатель
позволит решить интегралы любой сложности за считанные секунды. Вы получите
решение интеграла онлайн с подробными шагами. Все, что вам
необходимо сделать — это
просто ввести свои данные в решателе. Так же вы можете посмотреть
Так же вы можете посмотреть
видео
инструкцию
и узнать, как получить решение интегралов онлайн с решением на нашем сайте. А если у вас остались
вопросы, то вы можете задать их в
нашей
групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда
рады помочь вам.
Так же читайте нашу статью «Решить
систему
уравнений методом сложения онлайн решателем»
Определённый интеграл и методы его вычисления. Калькулятор онлайн.Вычислить определенный интеграл (площадь криволинейной трапеции)
Определенные интегралы онлайн на сайт для закрепления студентами и школьниками пройденного материала. И тренировки своих практических навыков. Полноценное решение определенных интегралов онлайн для вас в считанные мгновения поможет определить все этапы процесса. . Интегралы онлайн — определенный интеграл онлайн. Определенные интегралы онлайн на сайт для полноценного закрепления студентами и школьниками пройденного материала и тренировки своих практических навыков. Полноценное решение определенных интегралов онлайн для вас в считанные мгновения поможет определить все этапы процесса.. Интегралы онлайн — определенный интеграл онлайн. Для нас определенный интеграл онлайн взять не представляется чем-то сверх естественным, изучив данную тему по книге выдающихся авторов. Огромное им спасибо и выражаем респект этим личностям. Поможет определить определенный интеграл онлайн сервис по вычислению таких задач в два счета. Только укажите правильные данные и все будет Good! Всякий определенный интеграл как решение задачи повысит грамотность студентов. Об этом мечтает каждый ленивец, и мы не исключение, признаем это честно. Если все-таки получится вычислить определенный интеграл онлайн с решением бесплатно, то, пожалуйста, напишите адрес сайт всем желающим им воспользоваться.
. Интегралы онлайн — определенный интеграл онлайн. Определенные интегралы онлайн на сайт для полноценного закрепления студентами и школьниками пройденного материала и тренировки своих практических навыков. Полноценное решение определенных интегралов онлайн для вас в считанные мгновения поможет определить все этапы процесса.. Интегралы онлайн — определенный интеграл онлайн. Для нас определенный интеграл онлайн взять не представляется чем-то сверх естественным, изучив данную тему по книге выдающихся авторов. Огромное им спасибо и выражаем респект этим личностям. Поможет определить определенный интеграл онлайн сервис по вычислению таких задач в два счета. Только укажите правильные данные и все будет Good! Всякий определенный интеграл как решение задачи повысит грамотность студентов. Об этом мечтает каждый ленивец, и мы не исключение, признаем это честно. Если все-таки получится вычислить определенный интеграл онлайн с решением бесплатно, то, пожалуйста, напишите адрес сайт всем желающим им воспользоваться. Как говорится, поделишься полезной ссылкой — и тебя отблагодарят добрые люди за даром. Очень интересным будет вопрос разбора задачки, в которой определенный интеграл будет калькулятор решать самостоятельно, а не за счет траты вашего драгоценного времени. На то они и машины, чтобы пахать на людей. Однако решение определенных интегралов онлайн не всякому сайту по зубам, и это легко проверить, а именно, достаточно взять сложный пример и попытаться решить его с помощью каждого такого сервиса. Вы почувствуете разницу на собственной шкуре. Зачастую найти определенный интеграл онлайн без прилагаемых усилий станет достаточно сложно и нелепо будет выглядеть ваш ответ на фоне общей картины представления результата. Лучше бы сначала пройти курс молодого бойца. Всякое решение несобственных интегралов онлайн сводится сначала к вычислению неопределенного, а затем через теорию пределов вычислить как правило односторонние пределы от полученных выражений с подставленными границами A и B. Рассмотрев указанный вами определенный интеграл онлайн с подробным решением, мы сделали заключение, что вы ошиблись на пятом шаге, а именно при использовании формулы замены переменной Чебышева.
Как говорится, поделишься полезной ссылкой — и тебя отблагодарят добрые люди за даром. Очень интересным будет вопрос разбора задачки, в которой определенный интеграл будет калькулятор решать самостоятельно, а не за счет траты вашего драгоценного времени. На то они и машины, чтобы пахать на людей. Однако решение определенных интегралов онлайн не всякому сайту по зубам, и это легко проверить, а именно, достаточно взять сложный пример и попытаться решить его с помощью каждого такого сервиса. Вы почувствуете разницу на собственной шкуре. Зачастую найти определенный интеграл онлайн без прилагаемых усилий станет достаточно сложно и нелепо будет выглядеть ваш ответ на фоне общей картины представления результата. Лучше бы сначала пройти курс молодого бойца. Всякое решение несобственных интегралов онлайн сводится сначала к вычислению неопределенного, а затем через теорию пределов вычислить как правило односторонние пределы от полученных выражений с подставленными границами A и B. Рассмотрев указанный вами определенный интеграл онлайн с подробным решением, мы сделали заключение, что вы ошиблись на пятом шаге, а именно при использовании формулы замены переменной Чебышева. Будьте очень внимательны в дальнейшем решении. Если ваш определенный интеграл онлайн калькулятор не смог взять с первого раза, то в первую очередь стоит перепроверить написанные данные в соответствующие формы на сайте. Убедитесь, что все в порядке и вперёд, Go-Go! Для каждого студента препятствием является вычисление несобственных интегралов онлайн при самом преподе, так как это либо экзамен, либо коллоквиум, или просто контрольная работа на паре.. Как только заданный несобственный интеграл онлайн калькулятор будет в вашем распоряжении, то сразу вбивайте заданную функцию, подставляйте заданные пределы интегрирования и нажимайте на кнопку Решение, после этого вам будет доступен полноценный развернутый ответ. И все-таки хорошо, когда есть такой замечательный сайт как сайт, потому что он и бесплатный, и простой в пользовании, также содержит очень много разделов. которыми студенты пользуются повседневно, один из них как раз есть определенный интеграл онлайн с решением в полном виде. В этом же разделе можно вычислить несобственный интеграл онлайн с подробным решением для дальнейших применений ответа как в институте, так и в инженерных работах.
Будьте очень внимательны в дальнейшем решении. Если ваш определенный интеграл онлайн калькулятор не смог взять с первого раза, то в первую очередь стоит перепроверить написанные данные в соответствующие формы на сайте. Убедитесь, что все в порядке и вперёд, Go-Go! Для каждого студента препятствием является вычисление несобственных интегралов онлайн при самом преподе, так как это либо экзамен, либо коллоквиум, или просто контрольная работа на паре.. Как только заданный несобственный интеграл онлайн калькулятор будет в вашем распоряжении, то сразу вбивайте заданную функцию, подставляйте заданные пределы интегрирования и нажимайте на кнопку Решение, после этого вам будет доступен полноценный развернутый ответ. И все-таки хорошо, когда есть такой замечательный сайт как сайт, потому что он и бесплатный, и простой в пользовании, также содержит очень много разделов. которыми студенты пользуются повседневно, один из них как раз есть определенный интеграл онлайн с решением в полном виде. В этом же разделе можно вычислить несобственный интеграл онлайн с подробным решением для дальнейших применений ответа как в институте, так и в инженерных работах. Казалось бы, всем определить определенный интеграл онлайн дело нехитрое, если заранее решить такой пример без верхней и нижней границы, то есть не интеграл Лейбница, а неопределенный интеграл. Но тут мы с вами не согласны категорически, так как на первый взгляд это может показаться именно так, однако есть существенная разница, давайте разберем все по полочкам. Такой определенный интеграл решение дает не в явном виде, а в следствие преобразования выражения в предельное значение. Другими словами, нужно сначала решить интеграл с подстановкой символьных значений границ, а затем вычислить предел либо на бесконечности, либо в определенной точке. Отсюда вычислить определенный интеграл онлайн с решением бесплатно означает ни что иное как представление точного решения по формуле Ньютона-Лейбница. Если же рассматривать наш определенный интеграл калькулятор поможет его подсчитать за несколько секунд прямо на ваших глазах. Такая спешка нужна всем желающим как можно быстрее справиться с заданием и освободиться для личных дел.
Казалось бы, всем определить определенный интеграл онлайн дело нехитрое, если заранее решить такой пример без верхней и нижней границы, то есть не интеграл Лейбница, а неопределенный интеграл. Но тут мы с вами не согласны категорически, так как на первый взгляд это может показаться именно так, однако есть существенная разница, давайте разберем все по полочкам. Такой определенный интеграл решение дает не в явном виде, а в следствие преобразования выражения в предельное значение. Другими словами, нужно сначала решить интеграл с подстановкой символьных значений границ, а затем вычислить предел либо на бесконечности, либо в определенной точке. Отсюда вычислить определенный интеграл онлайн с решением бесплатно означает ни что иное как представление точного решения по формуле Ньютона-Лейбница. Если же рассматривать наш определенный интеграл калькулятор поможет его подсчитать за несколько секунд прямо на ваших глазах. Такая спешка нужна всем желающим как можно быстрее справиться с заданием и освободиться для личных дел. Не стоит искать в интернете сайты, на которых попросят вас регистрироваться, затем пополнить деньги на баланс и все ради того, чтобы какой-нибудь умник подготавливал решение определенных интегралов якобы онлайн. Запомните адрес Math34 — это бесплатный сервис для решения множества математических задач, в том же числе мы поможем найти определенный интеграл онлайн, и чтобы в этом убедиться, просим проверить наше утверждение на конкретных примерах. Введите подынтегральную функцию в соответствующее поле, затем укажите либо бесконечные предельные значения (в это случае будет вычислен и получено решение несобственных интегралов онлайн), либо задайте свои числовые или символьные границы и определенный интеграл онлайн с подробным решением выведется на странице после нажатия на кнопку «Решение». Неправда ли — это очень просто, не требует от вас лишних действий, бесплатно, что самое главное, и в то же время результативно. Вы можете самостоятельно воспользоваться сервисом, чтобы определенный интеграл онлайн калькулятор принес вам максимум пользы, и вы бы получили комфортное состояние, не напрягаясь на сложность всех вычислительных процессов, позвольте нам сделать все за вас и продемонстрировать всю мощь компьютерных технологий современного мира.
Не стоит искать в интернете сайты, на которых попросят вас регистрироваться, затем пополнить деньги на баланс и все ради того, чтобы какой-нибудь умник подготавливал решение определенных интегралов якобы онлайн. Запомните адрес Math34 — это бесплатный сервис для решения множества математических задач, в том же числе мы поможем найти определенный интеграл онлайн, и чтобы в этом убедиться, просим проверить наше утверждение на конкретных примерах. Введите подынтегральную функцию в соответствующее поле, затем укажите либо бесконечные предельные значения (в это случае будет вычислен и получено решение несобственных интегралов онлайн), либо задайте свои числовые или символьные границы и определенный интеграл онлайн с подробным решением выведется на странице после нажатия на кнопку «Решение». Неправда ли — это очень просто, не требует от вас лишних действий, бесплатно, что самое главное, и в то же время результативно. Вы можете самостоятельно воспользоваться сервисом, чтобы определенный интеграл онлайн калькулятор принес вам максимум пользы, и вы бы получили комфортное состояние, не напрягаясь на сложность всех вычислительных процессов, позвольте нам сделать все за вас и продемонстрировать всю мощь компьютерных технологий современного мира. Если погружаться в дебри сложнейших формул и вычисление несобственных интегралов онлайн изучить самостоятельно, то это похвально, и вы можете претендовать на возможность написания кандидатской работы, однако вернемся к реалиям студенческой жизни. А кто такой студент? В первую очередь — это молодой человек, энергичный и жизнерадостный, желающий успеть отдохнуть и сделать домашку! Поэтому мы позаботились об учениках, которые стараются отыскать на просторах глобальной сети несобственный интеграл онлайн калькулятор, и вот он к вашему вниманию — сайт — самая полезная для молодежи решалка в режиме онлайн. Кстати наш сервис хоть и преподносится как помощник студентам и школьникам, но он в полной мере подойдет любому инженеру, потому что нам под силу любые типы задач и их решение представляется в профессиональном формате. Например, определенный интеграл онлайн с решением в полном виде мы предлагаем по этапам, то есть каждому логическому блоку (подзадачи) отводится отдельная запись со всеми выкладками по ходу процесса общего решения.
Если погружаться в дебри сложнейших формул и вычисление несобственных интегралов онлайн изучить самостоятельно, то это похвально, и вы можете претендовать на возможность написания кандидатской работы, однако вернемся к реалиям студенческой жизни. А кто такой студент? В первую очередь — это молодой человек, энергичный и жизнерадостный, желающий успеть отдохнуть и сделать домашку! Поэтому мы позаботились об учениках, которые стараются отыскать на просторах глобальной сети несобственный интеграл онлайн калькулятор, и вот он к вашему вниманию — сайт — самая полезная для молодежи решалка в режиме онлайн. Кстати наш сервис хоть и преподносится как помощник студентам и школьникам, но он в полной мере подойдет любому инженеру, потому что нам под силу любые типы задач и их решение представляется в профессиональном формате. Например, определенный интеграл онлайн с решением в полном виде мы предлагаем по этапам, то есть каждому логическому блоку (подзадачи) отводится отдельная запись со всеми выкладками по ходу процесса общего решения. Это конечно же упрощает восприятие многоэтапных последовательных раскладок, и тем самым является преимуществом проекта сайт перед аналогичными сервисами по нахождению несобственный интеграл онлайн с подробным решением.
Это конечно же упрощает восприятие многоэтапных последовательных раскладок, и тем самым является преимуществом проекта сайт перед аналогичными сервисами по нахождению несобственный интеграл онлайн с подробным решением.
Рассмотрим функцию . Эту функцию называют: интеграл как функция верхнего предела. Отметим несколько свойств этой функции.
Теорема
2.1. Если f(x) интегрируемая на функция, то Ф(x) непрерывна на .
Доказательство
. По свойству 9 определенного интеграла (теорема о среднем) имеем , откуда, при , получаем требуемое.
Теорема
2.2. Если f(x) непрерывная на функция, то Ф’(x) = f(x) на .
Доказательство
. По свойству 10 определенного интеграла (вторая теорема о среднем), имеем где с
– некоторая точка отрезка . В силу непрерывности функции f получаем
Таким образом, Ф(x) — одна из первообразных функции f(x) следовательно, Ф(x) = F(x) + C, где F(x) — другая первообразная f(x). Далее, так как Ф(a) = 0, то 0 = F(a) + C, следовательно, C = -F(a) и поэтому Ф(x) = F(x) – F(a). Полагая x=b, получаем формулу Ньютона-Лейбница
Полагая x=b, получаем формулу Ньютона-Лейбница
Примеры
1.
Интегрирование по частям в определённом интеграле
В определенном интеграле сохраняется формула интегрирования по частям. В этом случае она приобретает вид
Пример.
Замена переменных в определённом интеграле
Один из вариантов результатов о замене переменных в определённом интеграле следующий.
Теорема 2.3.
Пусть f(x)- непрерывна на отрезке и удовлетворяет условиям:
1) φ(α) = a
2) φ(β) = b
3) производная φ’(t) определена всюду на отрезке [α, β]
4) для всех t из [α, β]
Тогда
Доказательство.
Если F(x) первообразная для f(x)dx то F(φ(t)) первообразная для Поэтому F(b) – F(a) = F(φ(β)) – F(φ(α)). Теорема доказана.
Замечание.
При отказе от непрерывности функции f(x) в условиях теоремы 2.3 приходится требовать монотонности функции φ(t).
Пример.
Вычислить интеграл Положим Тогда dx = 2tdt и поэтому
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Интеграл. Формула Ньютона – Лейбница. составитель: преподаватель математики ГОУНПО ПУ № 27 п. Щельяюр Семяшкина Ирина Васильевна
Цель урока: Ввести понятие интеграла и его вычисление по формуле Ньютона – Лейбница, используя знания о первообразной и правила её вычисления; Проиллюстрировать практическое применение интеграла на примерах нахождения площади криволинейной трапеции; Закрепить изученное в ходе выполнения упражнений.
Определение: Пусть дана положительная функция f(x) , определенная на конечном отрезке [ a;b ] . Интегралом от функции f(x) на [ a;b ] называется площадь её криволинейной трапеции. y=f(x) b a 0 x y
Обозначение: «интеграл от a до b эф от икс дэ икс »
Историческая справка: Обозначение интеграла Лейбниц произвёл от первой буквы слова «Сумма» (Summa). Ньютон в своих работах не предложил альтернативной символики интеграла, хотя пробовал различные варианты. Сам термин интеграл придумал Якоб Бернулли. S umma Исаак Ньютон Готфрид Вильгельм фон Лейбниц Якоб Бернулли
Обозначение неопределённого интеграла ввёл Эйлер. Жан Батист Жозеф Фурье Леонард Эйлер Оформление определённого интеграла в привычном нам виде придумал Фурье.
Формула Ньютона — Лейбница
Пример 1. Вычислить определённый интеграл: = Решение:
Пример 2. Вычислите определённые интегралы: 5 9 1
Пример 3 . S y x Вычислить площадь фигуры, ограниченной линиями и осью абсцисс. Для начала найдем точки пересечения оси абсцисс с графиком функции. Для этого решим уравнение. = Решение: S =
y x S A B D C Пример 4 . Вычислить площадь фигуры, ограниченной линиями и Найдём точки пересечения (абсциссы) этих линий, решив уравнение S=S BADC — S BAC S BADC = = S BAC = S = 9 – 4,5 = 4,5 смотри пример 1 Решение:
ПРАВИЛА СИНКВЕЙНА 1строка – тема синквейна 1 слово 2строка – 2 прилагательных, описывающих признаки и свойства темы 3строка – 3 глагола описывающие характер действия 4строка – короткое предложение из 4 слов, показывающее Ваше личное отношение к теме 5строка – 1 слово, синоним или Ваша ассоциация тема предмета.
Интеграл 2. Определённый, положительный Считают, прибавляют, умножают 4. Вычисляют формулой Ньютона — Лейбница 5. Площадь
Список используемой литературы: учебник Колмагорова А.Н. и др. Алгебра и начала анализа 10 — 11 кл.
Спасибо за внимание! « ТАЛАНТ – это 99% труда и 1% способности» народная мудрость
Пример 1. Вычислить определённый интеграл: = Решение: пример 4
Предварительный просмотр:
Предмет: математика (алгебра и начала анализа), класс: 11 класс.
Тема урока:
«Интеграл. Формула Ньютона-Лейбница».
Тип урока:
Изучение нового материала.
Продолжительность занятия:
45 минут.
Цели урока:
ввести понятие интеграла и его вычисление по формуле Ньютона-Лейбница, используя знания о первообразной и правила ее вычисления; проиллюстрировать практическое применение интеграла на примерах нахождения площади криволинейной трапеции; закрепить изученное в ходе выполнения упражнений.
Задачи урока:
Образовательные:
- сформировать понятие интеграла;
- формирование навыков вычисления определенного интеграла;
- формирование умений практического применения интеграла для нахождения площади криволинейной трапеции.
Развивающие:
- развитие познавательного интереса учащихся, развивать математическую речь, умения наблюдать, сравнивать, делать выводы;
- развивать интерес к предмету с помощью ИКТ.
Воспитательные:
- активизировать интерес к получению новых знаний, формирование точности и аккуратности при вычислении интеграла и выполнении чертежей.
Оснащение:
ПК, операционная система Microsoft Windows 2000/XP, программа MS Office 2007: Power Point, Microsoft Word; мультимедийный проектор, экран.
Литература:
учебник Колмагорова А.Н. и др. Алгебра и начала анализа 10-11 кл.
Технологии:
ИКТ
,
индивидуального обучения.
ХОД УРОКА
Этап урока | Деятельность учителя | Деятельность учащихся | Время | |
Вводная часть | ||||
Организационный момент | Приветствует, проверяет готовность учащихся к уроку, организует внимание. Раздает опорный конспект. | Слушают, записывают дату. | 3 мин | |
Сообщение темы и целей урока | Актуализация опорных знаний и субъектного опыта с выходом на цели урока. | Слушают, записывают тему урока в тетради. Анализируют, сравнивают, делают выводы с выходом на цели занятия. | Презентация ИКТ 3 мин | |
Основная часть урока Изложение нового материала с попутной проверкой знаний прошлых тем. | ||||
Определение интеграла (слайд 3) | Даёт определение. ИКТ Что такое криволинейная трапеция? | Фигуру, ограниченная графиком функции, отрезком и прямыми x=a и x=b. | 10 мин | |
Обозначение интеграла (слайд 4) | Вводит обозначение интеграла и то, как он читается. | Слушают, записывают. | ||
История интеграла (слайды 5 и 6) | Рассказывает историю термина «интеграл». | Слушают, коротко записывают. | ||
Формула Ньютона – Лейбница (слайд 7) | Дает формулу Ньютона – Лейбница. Что в формуле обозначает F? | Слушают, записывают, отвечают на вопросы преподавателя. Первообразная. | ||
Заключительная часть урока. | ||||
Закрепление материала. Решение примеров с применением изученного материала | ||||
Пример 1 (слайд 8) | Разбирает решение примера, задавая вопросы по нахождению первообразных для подынтегральных функций. | Слушают, записывают, показывают знание таблицы первообразных. | 20 мин | |
Пример 2 (слайд 9). Примеры для самостоятельного решения обучающимися. | Контролирует решение примеров. | Выполняют задание по очереди, комментируя (технология индивидуального обучения | ||
Пример 3 (слайд 10) | Разбирает решение примера. Как найти точки пересечения оси абсцисс с графиком функции? | Слушают, отвечают на вопросы, показывают знание прошлых тем, записывают. Подынтегральную функцию приравнять к 0 и решить уравнение. | ||
Пример 4 (слайд 11) | Разбирает решение примера. Как найти точки пересечения (абсциссы) графиков функций? Определите вид треугольника ABC. Как находиться площадь прямоугольного треугольника? | Слушают, отвечают на вопросы. Приравнять функции друг к другу и решить получившееся уравнение. Прямоугольный. где a и b- катеты прямоугольного треугольника. | ||
Подведение итогов урока (слайды 12 и 13) | Организует работу по составлению синквейна. | Участвуют в составлении синквейна. Анализируют, сравнивают, делают выводы по теме. | 5 мин. | |
Задание на дом по уровню сложности. | Дает задание на дом, объясняет. | Слушают, записывают. | 1 мин. | |
Оценивание работы обучающихся на уроке. | Оценивает работу обучающихся на уроке, анализирует. | Слушают. | 1 мин |
Предварительный просмотр:
Опорный конспект по теме «Интеграл. Формула Ньютона-Лейбница».
Определение: | ||
Обозначение: Читается: | ||
Формула Ньютона — Лейбница | ||
Пример 1. Решение: | ||
Пример 3. Решение: | ||
Пример 3. |
Решение прикладных задач сводится к вычислению интеграла, но не всегда это возможно сделать точно. Иногда необходимо знать значение определенного интеграла с некоторой степенью точности, к примеру, до тысячной.
Существуют задачи, когда следовало бы найти приближенное значение определенного интеграла с необходимой точностью, тогда применяют численное интегрирование такое, как метод Симпосна, трапеций, прямоугольников. Не все случаи позволяют вычислить его с определенной точностью.
Данная статья рассматривает применение формулы Ньютона-Лейбница. Это необходимо для точного вычисления определенного интеграла. Будут приведены подробные примеры, рассмотрены замены переменной в определенном интеграле и найдем значения определенного интеграла при интегрировании по частям.
Yandex.RTB R-A-339285-1
Формула Ньютона-Лейбница
Определение 1
Когда функция y = y (x) является непрерывной из отрезка [ a ; b ] ,а F (x) является одной из первообразных функции этого отрезка, тогда формула Ньютона-Лейбница
считается справедливой. Запишем ее так ∫ a b f (x) d x = F (b) — F (a) .
Данную формулу считают основной формулой интегрального исчисления.
Чтобы произвести доказательство этой формулы, необходимо использовать понятие интеграла с имеющимся переменным верхним пределом.
Когда функция y = f (x) непрерывна из отрезка [ a ; b ] , тогда значение аргумента x ∈ a ; b , а интеграл имеет вид ∫ a x f (t) d t и считается функцией верхнего предела. Необходимо принять обозначение функции примет вид ∫ a x f (t) d t = Φ (x) , она является непрерывной, причем для нее справедливо неравенство вида ∫ a x f (t) d t » = Φ » (x) = f (x) .
Зафиксируем, что приращении функции Φ (x) соответствует приращению аргумента ∆ x , необходимо воспользоваться пятым основным свойством определенного интеграла и получим
Φ (x + ∆ x) — Φ x = ∫ a x + ∆ x f (t) d t — ∫ a x f (t) d t = = ∫ a x + ∆ x f (t) d t = f (c) · x + ∆ x — x = f (c) · ∆ x
где значение c ∈ x ; x + ∆ x .
Зафиксируем равенство в виде Φ (x + ∆ x) — Φ (x) ∆ x = f (c) . По определению производной функции необходимо переходить к пределу при ∆ x → 0 , тогда получаем формулу вида Φ » (x) = f (x) . Получаем, что Φ (x) является одной из первообразных для функции вида y = f (x) , расположенной на [ a ; b ] . Иначе выражение можно записать
F (x) = Φ (x) + C = ∫ a x f (t) d t + C , где значение C является постоянной.
Произведем вычисление F (a) с использованием первого свойства определенного интеграла. Тогда получаем, что
F (a) = Φ (a) + C = ∫ a a f (t) d t + C = 0 + C = C , отсюда получаем, что C = F (a) . Результат применим при вычислении F (b) и получим:
F (b) = Φ (b) + C = ∫ a b f (t) d t + C = ∫ a b f (t) d t + F (a) , иначе говоря, F (b) = ∫ a b f (t) d t + F (a) . Равенство доказывает формулу Ньютона-Лейбница ∫ a b f (x) d x + F (b) — F (a) .
Приращение функции принимаем как F x a b = F (b) — F (a) . С помощью обозначения формулу Ньютона-Лейбница принимает вид ∫ a b f (x) d x = F x a b = F (b) — F (a) .
Чтобы применить формулу, обязательно необходимо знать одну из первообразных y = F (x) подынтегральной функции y = f (x) из отрезка [ a ; b ] , произвести вычисление приращения первообразной из этого отрезка. Рассмотрим несколько примером вычисления, используя формулу Ньютона-Лейбница.
Пример 1
Произвести вычисление определенного интеграла ∫ 1 3 x 2 d x по формуле Ньютона-Лейбница.
Решение
Рассмотрим, что подынтегральная функция вида y = x 2 является непрерывной из отрезка [ 1 ; 3 ] , тогда и интегрируема на этом отрезке. По таблице неопределенных интегралов видим, что функция y = x 2 имеет множество первообразных для всех действительных значений x , значит, x ∈ 1 ; 3 запишется как F (x) = ∫ x 2 d x = x 3 3 + C . Необходимо взять первообразную с С = 0 , тогда получаем, что F (x) = x 3 3 .
Воспользуемся формулой Ньютона-Лейбница и получим, что вычисление определенного интеграла примет вид ∫ 1 3 x 2 d x = x 3 3 1 3 = 3 3 3 — 1 3 3 = 26 3 .
Ответ:
∫ 1 3 x 2 d x = 26 3
Пример 2
Произвести вычисление определенного интеграла ∫ — 1 2 x · e x 2 + 1 d x по формуле Ньютона-Лейбница.
Решение
Заданная функция непрерывна из отрезка [ — 1 ; 2 ] , значит, на нем интегрируема. Необходимо найти значение неопределенного интеграла ∫ x · e x 2 + 1 d x при помощи метода подведения под знак дифференциала, тогда получаем ∫ x · e x 2 + 1 d x = 1 2 ∫ e x 2 + 1 d (x 2 + 1) = 1 2 e x 2 + 1 + C .
Отсюда имеем множество первообразных функции y = x · e x 2 + 1 , которые действительны для всех x , x ∈ — 1 ; 2 .
Необходимо взять первообразную при С = 0 и применить формулу Ньютона-Лейбница. Тогда получим выражение вида
∫ — 1 2 x · e x 2 + 1 d x = 1 2 e x 2 + 1 — 1 2 = = 1 2 e 2 2 + 1 — 1 2 e (- 1) 2 + 1 = 1 2 e (- 1) 2 + 1 = 1 2 e 2 (e 3 — 1)
Ответ:
∫ — 1 2 x · e x 2 + 1 d x = 1 2 e 2 (e 3 — 1)
Пример 3
Произвести вычисление интегралов ∫ — 4 — 1 2 4 x 3 + 2 x 2 d x и ∫ — 1 1 4 x 3 + 2 x 2 d x .
Решение
Отрезок — 4 ; — 1 2 говорит о том, что функция, находящаяся под знаком интеграла, является непрерывной, значит, она интегрируема. Отсюда найдем множество первообразных функции y = 4 x 3 + 2 x 2 . Получаем, что
∫ 4 x 3 + 2 x 2 d x = 4 ∫ x d x + 2 ∫ x — 2 d x = 2 x 2 — 2 x + C
Необходимо взять первообразную F (x) = 2 x 2 — 2 x , тогда, применив формулу Ньютона-Лейбница, получаем интеграл, который вычисляем:
∫ — 4 — 1 2 4 x 3 + 2 x 2 d x = 2 x 2 — 2 x — 4 — 1 2 = 2 — 1 2 2 — 2 — 1 2 — 2 — 4 2 — 2 — 4 = 1 2 + 4 — 32 — 1 2 = — 28
Производим переход к вычислению второго интеграла.
Из отрезка [ — 1 ; 1 ] имеем, что подынтегральная функция считается неограниченной, потому как lim x → 0 4 x 3 + 2 x 2 = + ∞ , тогда отсюда следует, что необходимым условием интегрируемости из отрезка. Тогда F (x) = 2 x 2 — 2 x не является первообразной для y = 4 x 3 + 2 x 2 из отрезка [ — 1 ; 1 ] , так как точка O принадлежит отрезку, но не входит в область определения. Значит, что имеется определенный интеграл Римана и Ньютона-Лейбница для функции y = 4 x 3 + 2 x 2 из отрезка [ — 1 ; 1 ] .
Ответ: ∫ — 4 — 1 2 4 x 3 + 2 x 2 d x = — 28 ,
имеется определенный интеграл Римана и Ньютона-Лейбница для функции y = 4 x 3 + 2 x 2 из отрезка [ — 1 ; 1 ] .
Перед использованием формулы Ньютона-Лейбница нужно точно знать о существовании определенного интеграла.
Замена переменной в определенном интеграле
Когда функция y = f (x) является определенной и непрерывной из отрезка [ a ; b ] , тогда имеющееся множество [ a ; b ] считается областью значений функции x = g (z) , определенной на отрезке α ; β с имеющейся непрерывной производной, где g (α) = a и g β = b , отсюда получаем, что ∫ a b f (x) d x = ∫ α β f (g (z)) · g » (z) d z .
Данную формулу применяют тогда, когда нужно вычислять интеграл ∫ a b f (x) d x , где неопределенный интеграл имеет вид ∫ f (x) d x , вычисляем при помощи метода подстановки.
Пример 4
Произвести вычисление определенного интеграла вида ∫ 9 18 1 x 2 x — 9 d x .
Решение
Подынтегральная функция считается непрерывной на отрезке интегрирования, значит определенный интеграл имеет место на существование. Дадим обозначение, что 2 x — 9 = z ⇒ x = g (z) = z 2 + 9 2 . Значение х = 9 , значит, что z = 2 · 9 — 9 = 9 = 3 , а при х = 18 получаем, что z = 2 · 18 — 9 = 27 = 3 3 , тогда g α = g (3) = 9 , g β = g 3 3 = 18 . При подстановке полученных значений в формулу ∫ a b f (x) d x = ∫ α β f (g (z)) · g » (z) d z получаем, что
∫ 9 18 1 x 2 x — 9 d x = ∫ 3 3 3 1 z 2 + 9 2 · z · z 2 + 9 2 » d z = = ∫ 3 3 3 1 z 2 + 9 2 · z · z d z = ∫ 3 3 3 2 z 2 + 9 d z
По таблице неопределенных интегралов имеем, что одна из первообразных функции 2 z 2 + 9 принимает значение 2 3 a r c t g z 3 . Тогда при применении формулы Ньютона-Лейбница получаем, что
∫ 3 3 3 2 z 2 + 9 d z = 2 3 a r c t g z 3 3 3 3 = 2 3 a r c t g 3 3 3 — 2 3 a r c t g 3 3 = 2 3 a r c t g 3 — a r c t g 1 = 2 3 π 3 — π 4 = π 18
Нахождение можно было производить, не используя формулу ∫ a b f (x) d x = ∫ α β f (g (z)) · g » (z) d z .
Если при методе замены использовать интеграл вида ∫ 1 x 2 x — 9 d x , то можно прийти к результату ∫ 1 x 2 x — 9 d x = 2 3 a r c t g 2 x — 9 3 + C .
Отсюда произведем вычисления по формуле Ньютона-Лейбница и вычислим определенный интеграл. Получаем, что
∫ 9 18 2 z 2 + 9 d z = 2 3 a r c t g z 3 9 18 = = 2 3 a r c t g 2 · 18 — 9 3 — a r c t g 2 · 9 — 9 3 = = 2 3 a r c t g 3 — a r c t g 1 = 2 3 π 3 — π 4 = π 18
Результаты совпали.
Ответ: ∫ 9 18 2 x 2 x — 9 d x = π 18
Интегрирование по частям при вычислении определенного интеграла
Если на отрезке [ a ; b ] определены и непрерывны функции u (x) и v (x) , тогда их производные первого порядка v » (x) · u (x) являются интегрируемыми, таким образом из этого отрезка для интегрируемой функции u » (x) · v (x) равенство ∫ a b v » (x) · u (x) d x = (u (x) · v (x)) a b — ∫ a b u » (x) · v (x) d x справедливо.
Формулу можно использовать тогда, необходимо вычислять интеграл ∫ a b f (x) d x , причем ∫ f (x) d x необходимо было искать его при помощи интегрирования по частям.
Пример 5
Произвести вычисление определенного интеграла ∫ — π 2 3 π 2 x · sin x 3 + π 6 d x .
Решение
Функция x · sin x 3 + π 6 интегрируема на отрезке — π 2 ; 3 π 2 , значит она непрерывна.
Пусть u (x) = х, тогда d (v (x)) = v » (x) d x = sin x 3 + π 6 d x , причем d (u (x)) = u » (x) d x = d x , а v (x) = — 3 cos π 3 + π 6 . Из формулы ∫ a b v » (x) · u (x) d x = (u (x) · v (x)) a b — ∫ a b u » (x) · v (x) d x получим, что
∫ — π 2 3 π 2 x · sin x 3 + π 6 d x = — 3 x · cos x 3 + π 6 — π 2 3 π 2 — ∫ — π 2 3 π 2 — 3 cos x 3 + π 6 d x = = — 3 · 3 π 2 · cos π 2 + π 6 — — 3 · — π 2 · cos — π 6 + π 6 + 9 sin x 3 + π 6 — π 2 3 π 2 = 9 π 4 — 3 π 2 + 9 sin π 2 + π 6 — sin — π 6 + π 6 = 9 π 4 — 3 π 2 + 9 3 2 = 3 π 4 + 9 3 2
Решение примера можно выполнить другим образом.
Найти множество первообразных функции x · sin x 3 + π 6 при помощи интегрирования по частям с применением формулы Ньютона-Лейбница:
∫ x · sin x x 3 + π 6 d x = u = x , d v = sin x 3 + π 6 d x ⇒ d u = d x , v = — 3 cos x 3 + π 6 = = — 3 cos x 3 + π 6 + 3 ∫ cos x 3 + π 6 d x = = — 3 x cos x 3 + π 6 + 9 sin x 3 + π 6 + C ⇒ ∫ — π 2 3 π 2 x · sin x 3 + π 6 d x = — 3 cos x 3 + π 6 + 9 sincos x 3 + π 6 — — — 3 · — π 2 · cos — π 6 + π 6 + 9 sin — π 6 + π 6 = = 9 π 4 + 9 3 2 — 3 π 2 — 0 = 3 π 4 + 9 3 2
Ответ: ∫ x · sin x x 3 + π 6 d x = 3 π 4 + 9 3 2
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Формула Ньютона — Лейбница
Основная теорема анализа
или формула Ньютона — Лейбница
даёт соотношение между двумя операциями: взятием определенного интеграла и вычислением первообразной
Формулировка
Рассмотрим интеграл от функции y
= f
(x
)
в пределах от постоянного числа a
до числа x
, которое будем считать переменным. Запишем интеграл в следующем виде:
Данный вид интеграла называется интегралом с переменным верхним пределом. Используя теорему о среднем в определённом интеграле , легко показать что данная функция непрерывная и дифференцируемая. А также производная от данной функции в точке x равна самой интегрируемой функции. От сюда следует, что любая непрерывная функция имеет первообразную в виде квадратуры: . А так как класс первообразных функций функции f отличается на константу, легко показать, что: определенный интеграл от функции f на равен разности значений первообразных в точках b и а
Wikimedia Foundation
.
2010
.
- Формула Полной Вероятности
- Формула Релея — Джинса
Смотреть что такое «Формула Ньютона — Лейбница» в других словарях:
Формула Ньютона-Лейбница
— Основная теорема анализа или формула Ньютона Лейбница даёт соотношение между двумя операциями: взятием определенного интеграла и вычислением первообразной Формулировка Рассмотрим интеграл от функции y = f(x) в пределах от постоянного числа a до… … Википедия
Формула конечных приращений
— У этого термина существуют и другие значения, см. Теорема Лагранжа. Формула конечных приращений или теорема Лагранжа о среднем значении утверждает, что если функция непрерывна на отрезке и … Википедия
Формула Стокса
— Теорема Стокса одна из основных теорем дифференциальной геометрии и математического анализа об интегрировании дифференциальных форм, которая обобщает несколько теорем анализа. Названа в честь Дж. Г. Стокса. Содержание 1 Общая формулировка 2… … Википедия
НЬЮТОНА — ЛЕЙБНИЦА ФОРМУЛА
— формула, выражающая значение определенного интеграла от заданной функции f по отрезку в виде разности значений на концах отрезка любой первообразной Fэтой функции Названа именами И. Ньютона (I. Newton) и Г. Лейбница (G. Leibniz), т. к. правило,… … Математическая энциклопедия
НЬЮТОНА-ЛЕЙБНИЦА ФОРМУЛА
— основная формула интегрального исчисления. Выражает связь между определенным интегралом от функции f(x) и какой либо ее первообразной F(x) … Большой Энциклопедический словарь
Формула Лейбница
— У этого термина существуют и другие значения, см. Список объектов, названных в честь Лейбница. У этого термина существуют и другие значения, см. Формула Лейбница (значения). Формулой Лейбница в интегральном исчислении называется правило… … Википедия
Ньютона-Лейбница формула
— Ньютона Лейбница формула, основная формула интегрального исчисления. Выражает связь между определённым интегралом от функции f(х) и какой либо её первообразной F(х). . * * * НЬЮТОНА ЛЕЙБНИЦА ФОРМУЛА НЬЮТОНА ЛЕЙБНИЦА ФОРМУЛА, основная формула… … Энциклопедический словарь
Формула прямоугольников
Формула трапеций
— Определённый интеграл как площадь фигуры Численное интегрирование (историческое название: квадратура) вычисление значения определённого интеграла (как правило, приближённое), основанное на том, что величина интеграла численно равна площади… … Википедия
Теорема Ньютона
— Формула Ньютона Лейбница или основная теорема анализа даёт соотношение между двумя операциями: взятием определенного интеграла и вычислением первообразной. Если непрерывна на отрезке и ее любая первообразная на этом отрезке, то имеет … Википедия
Определение сходимости интеграла онлайн. Несобственные интегралы
Определенные интегралы онлайн на сайт для закрепления студентами и школьниками пройденного материала. И тренировки своих практических навыков. Полноценное решение определенных интегралов онлайн для вас в считанные мгновения поможет определить все этапы процесса.. Интегралы онлайн — определенный интеграл онлайн. Определенные интегралы онлайн на сайт для полноценного закрепления студентами и школьниками пройденного материала и тренировки своих практических навыков. Полноценное решение определенных интегралов онлайн для вас в считанные мгновения поможет определить все этапы процесса.. Интегралы онлайн — определенный интеграл онлайн. Для нас определенный интеграл онлайн взять не представляется чем-то сверх естественным, изучив данную тему по книге выдающихся авторов. Огромное им спасибо и выражаем респект этим личностям. Поможет определить определенный интеграл онлайн сервис по вычислению таких задач в два счета. Только укажите правильные данные и все будет Good! Всякий определенный интеграл как решение задачи повысит грамотность студентов. Об этом мечтает каждый ленивец, и мы не исключение, признаем это честно. Если все-таки получится вычислить определенный интеграл онлайн с решением бесплатно, то, пожалуйста, напишите адрес сайт всем желающим им воспользоваться. Как говорится, поделишься полезной ссылкой — и тебя отблагодарят добрые люди за даром. Очень интересным будет вопрос разбора задачки, в которой определенный интеграл будет калькулятор решать самостоятельно, а не за счет траты вашего драгоценного времени. На то они и машины, чтобы пахать на людей. Однако решение определенных интегралов онлайн не всякому сайту по зубам, и это легко проверить, а именно, достаточно взять сложный пример и попытаться решить его с помощью каждого такого сервиса. Вы почувствуете разницу на собственной шкуре. Зачастую найти определенный интеграл онлайн без прилагаемых усилий станет достаточно сложно и нелепо будет выглядеть ваш ответ на фоне общей картины представления результата. Лучше бы сначала пройти курс молодого бойца. Всякое решение несобственных интегралов онлайн сводится сначала к вычислению неопределенного, а затем через теорию пределов вычислить как правило односторонние пределы от полученных выражений с подставленными границами A и B. Рассмотрев указанный вами определенный интеграл онлайн с подробным решением, мы сделали заключение, что вы ошиблись на пятом шаге, а именно при использовании формулы замены переменной Чебышева. Будьте очень внимательны в дальнейшем решении. Если ваш определенный интеграл онлайн калькулятор не смог взять с первого раза, то в первую очередь стоит перепроверить написанные данные в соответствующие формы на сайте. Убедитесь, что все в порядке и вперёд, Go-Go! Для каждого студента препятствием является вычисление несобственных интегралов онлайн при самом преподе, так как это либо экзамен, либо коллоквиум, или просто контрольная работа на паре.. Как только заданный несобственный интеграл онлайн калькулятор будет в вашем распоряжении, то сразу вбивайте заданную функцию, подставляйте заданные пределы интегрирования и нажимайте на кнопку Решение, после этого вам будет доступен полноценный развернутый ответ. И все-таки хорошо, когда есть такой замечательный сайт как сайт, потому что он и бесплатный, и простой в пользовании, также содержит очень много разделов. которыми студенты пользуются повседневно, один из них как раз есть определенный интеграл онлайн с решением в полном виде. В этом же разделе можно вычислить несобственный интеграл онлайн с подробным решением для дальнейших применений ответа как в институте, так и в инженерных работах. Казалось бы, всем определить определенный интеграл онлайн дело нехитрое, если заранее решить такой пример без верхней и нижней границы, то есть не интеграл Лейбница, а неопределенный интеграл. Но тут мы с вами не согласны категорически, так как на первый взгляд это может показаться именно так, однако есть существенная разница, давайте разберем все по полочкам. Такой определенный интеграл решение дает не в явном виде, а в следствие преобразования выражения в предельное значение. Другими словами, нужно сначала решить интеграл с подстановкой символьных значений границ, а затем вычислить предел либо на бесконечности, либо в определенной точке. Отсюда вычислить определенный интеграл онлайн с решением бесплатно означает ни что иное как представление точного решения по формуле Ньютона-Лейбница. Если же рассматривать наш определенный интеграл калькулятор поможет его подсчитать за несколько секунд прямо на ваших глазах. Такая спешка нужна всем желающим как можно быстрее справиться с заданием и освободиться для личных дел. Не стоит искать в интернете сайты, на которых попросят вас регистрироваться, затем пополнить деньги на баланс и все ради того, чтобы какой-нибудь умник подготавливал решение определенных интегралов якобы онлайн. Запомните адрес Math34 — это бесплатный сервис для решения множества математических задач, в том же числе мы поможем найти определенный интеграл онлайн, и чтобы в этом убедиться, просим проверить наше утверждение на конкретных примерах. Введите подынтегральную функцию в соответствующее поле, затем укажите либо бесконечные предельные значения (в это случае будет вычислен и получено решение несобственных интегралов онлайн), либо задайте свои числовые или символьные границы и определенный интеграл онлайн с подробным решением выведется на странице после нажатия на кнопку «Решение». Неправда ли — это очень просто, не требует от вас лишних действий, бесплатно, что самое главное, и в то же время результативно. Вы можете самостоятельно воспользоваться сервисом, чтобы определенный интеграл онлайн калькулятор принес вам максимум пользы, и вы бы получили комфортное состояние, не напрягаясь на сложность всех вычислительных процессов, позвольте нам сделать все за вас и продемонстрировать всю мощь компьютерных технологий современного мира. Если погружаться в дебри сложнейших формул и вычисление несобственных интегралов онлайн изучить самостоятельно, то это похвально, и вы можете претендовать на возможность написания кандидатской работы, однако вернемся к реалиям студенческой жизни. А кто такой студент? В первую очередь — это молодой человек, энергичный и жизнерадостный, желающий успеть отдохнуть и сделать домашку! Поэтому мы позаботились об учениках, которые стараются отыскать на просторах глобальной сети несобственный интеграл онлайн калькулятор, и вот он к вашему вниманию — сайт — самая полезная для молодежи решалка в режиме онлайн. Кстати наш сервис хоть и преподносится как помощник студентам и школьникам, но он в полной мере подойдет любому инженеру, потому что нам под силу любые типы задач и их решение представляется в профессиональном формате. Например, определенный интеграл онлайн с решением в полном виде мы предлагаем по этапам, то есть каждому логическому блоку (подзадачи) отводится отдельная запись со всеми выкладками по ходу процесса общего решения. Это конечно же упрощает восприятие многоэтапных последовательных раскладок, и тем самым является преимуществом проекта сайт перед аналогичными сервисами по нахождению несобственный интеграл онлайн с подробным решением.
Вы еще здесь? =) Нет, я никого не пытался запугать, просто тема несобственных интегралов – очень хорошая иллюстрация тому, как важно не запускать высшую математику и другие точные науки. Для освоения урока на сайте всё есть – в подробной и доступной форме, было бы желание….
Итак, начнем-с. Образно говоря, несобственный интеграл – это «продвинутый» определенный интеграл, и на самом деле сложностей с ними не так уж и много, к тому же у несобственного интеграла есть очень хороший геометрический смысл.
Что значит вычислить несобственный интеграл?
Вычислить несобственный интеграл – это значит, найти ЧИСЛО
(точно так же, как в определенном интеграле), или доказать, что он расходится
(то есть, получить в итоге бесконечность вместо числа).
Несобственные интегралы бывают двух видов.
Несобственный интеграл с бесконечным пределом (ами) интегрирования
Иногда такой несобственный интеграл называют несобственным интегралом первого рода
. В общем виде несобственный интеграл с бесконечным пределом чаще всего выглядит так: . В чем его отличие от определенного интеграла? В верхнем пределе. Он бесконечный: .
Реже встречаются интегралы с бесконечным нижним пределом или с двумя бесконечными пределами: , и их мы рассмотрим позже – когда войдёте во вкус:)
Ну а сейчас разберём самый популярный случай . В подавляющем большинстве примеров подынтегральная функция непрерывна
на промежутке , и этот важный факт следует проверять в первую очередь!
Ибо если есть разрывы, то есть дополнительные нюансы. Для определённости предположим, что и тогда типичная криволинейная трапеция
будет выглядеть так:
Обратите внимание, что она бесконечна (не ограничена справа), и несобственный интеграл
численно равен её площади
. При этом возможны следующие варианты:
1) Первая мысль, которая приходит в голову: «раз фигура бесконечная, то », иными словами, площадь тоже бесконечна. Так быть может.
В этом случае говорят, что несобственный интеграл расходится
.
2) Но
. Как это ни парадоксально прозвучит, площадь бесконечной фигуры может равняться… конечному числу! Например: . Может ли так быть? Запросто. Во втором случае несобственный интеграл сходится
.
3) О третьем варианте чуть позже.
В каких случаях несобственный интеграл расходится, а в каком сходится? Это зависит от подынтегральной функции , и конкретные примеры мы очень скоро рассмотрим.
А что будет, если бесконечная криволинейная трапеция расположена ниже оси? В этом случае, несобственный интеграл (расходится) либо равен конечному отрицательному числу.
Таким образом, несобственный интеграл может быть отрицательным
.
Важно!
Когда Вам для решения предложен ЛЮБОЙ несобственный интеграл, то, вообще говоря, ни о какой площади речи не идет и чертежа строить не нужно
. Геометрический смысл несобственного интеграла я рассказал только для того, чтобы легче было понять материал.
Коль скоро, несобственный интеграл очень похож на определенный интеграл, то вспомним формулу Ньютона- Лейбница: . На самом деле формула применима и к несобственным интегралам, только ее нужно немного модифицировать. В чем отличие? В бесконечном верхнем пределе интегрирования: . Наверное, многие догадались, что это уже попахивает применением теории пределов, и формула запишется так: .
В чем отличие от определенного интеграла? Да ни в чем особенном! Как и в определенном интеграле, нужно уметь находить первообразную функцию (неопределенный интеграл), уметь применять формулу Ньютона-Лейбница. Единственное, что добавилось – это вычисление предела. У кого с ними плохо, изучите урок Пределы функций. Примеры решений
, ибо лучше поздно, чем в армии.
Рассмотрим два классических примера:
Пример 1
Для наглядности я построю чертеж, хотя, еще раз подчеркиваю, на практике
строить чертежи в данном задании не нужно
.
Подынтегральная функция непрерывна на полуинтервале , значит, всё нормально и несобственный интеграл можно вычислить «штатным» методом.
Применение нашей формулы и решение задачи выглядит так:
То есть, несобственный интеграл расходится, и площадь заштрихованной криволинейной трапеции равна бесконечности.
В рассмотренном примере у нас простейший табличный интеграл и такая же техника применения формулы Ньютона-Лейбница, как в определенном интеграле. Но применятся эта формула под знаком предела. Вместо привычной буквы «динамической» переменной выступает буква «бэ». Это не должно смущать или ставить в тупик, потому что любая буква ничем не хуже стандартного «икса».
Если Вам не понятно почему при , то это очень плохо, либо Вы не понимаете простейшие пределы (и вообще не понимаете, что такое предел), либо не знаете, как выглядит график логарифмической функции. Во втором случае посетите урок Графики и свойства элементарных функций
.
При решении несобственных интегралов очень важно знать, как выглядят графики основных элементарных функций!
Чистовое оформление задания должно выглядеть примерно так:
“
! При оформлении примера всегда прерываем решение, и указываем, что происходит с подынтегральной функцией
– непрерывна она на промежутке интегрирования или нет
. Этим мы идентифицируем тип несобственного интеграла и обосновываем дальнейшие действия.
Пример 2
Вычислить несобственный интеграл или установить его расходимость.
Выполним чертеж:
Во-первых, замечаем следующее: подынтегральная функция непрерывна на полуинтервале . Гуд. Решаем с помощью формулы :
(1) Берем простейший интеграл от степенной функции (этот частный случай есть во многих таблицах). Минус лучше сразу вынести за знак предела, чтобы он не путался под ногами в дальнейших вычислениях.
(2) Подставляем верхний и нижний пределы по формуле Ньютона-Лейбница.
(3) Указываем, что при (Господа, это уже давно нужно понимать) и упрощаем ответ.
Вот здесь площадь бесконечной криволинейной трапеции равна конечному числу! Невероятно, но факт.
Чистовое оформление примера должно выглядеть примерно так:
“
Подынтегральная функция непрерывна на
“
Что делать, если вам встретится интеграл наподобие – с точкой разрыва
на интервале интегрирования? Это говорит о том, что в примере опечатка (вероятнее всего)
, либо о продвинутом уровне обучения. В последнем случае, в силу свойства аддитивности
, следует рассмотреть два несобственных интеграла на промежутках и и затем разобраться с суммой.
Иногда вследствие опечатки либо умысла несобственного интеграла может вовсе не существовать
, так, например, если в знаменатель вышеуказанного интеграла поставить квадратный корень из «икс», то часть промежутка интегрирования вообще не войдёт в область определения подынтегральной функции.
Более того, несобственного интеграла может не существовать даже при всём «видимом благополучии». Классический пример: . Несмотря на определённость и непрерывность косинуса, такого несобственного интеграла не существует! Почему? Всё очень просто, потому что:
– не существует соответствующего предела
.
И такие примеры пусть редко, но встречаются на практике! Таким образом, помимо сходимости и расходимости, есть ещё и третий исход решения с полноправным ответом: «несобственного интеграла не существует».
Следует также отметить, что строгое определение несобственного интеграла даётся именно через предел, и желающие могут ознакомиться с ним в учебной литературе. Ну а мы продолжаем практическое занятие и переходим к более содержательным задачам:
Пример 3
Вычислить несобственный интеграл или установить его расходимость.
Сначала попытаемся найти первообразную функцию (неопределенный интеграл). Если нам не удастся этого сделать, то несобственный интеграл мы, естественно, тоже не решим.
На какой из табличных интегралов похожа подынтегральная функция? Напоминает она арктангенс: . Из этих соображений напрашивается мысль, что неплохо бы в знаменателе получить квадрат. Делается это путем замены.
Проведем замену:
Неопределенный интеграл найден, константу в данном случае добавлять не имеет смысла.
На черновике всегда полезно выполнить проверку, то есть продифференцировать полученный результат:
Получена исходная подынтегральная функция, значит, неопределенный интеграл найден правильно.
Теперь находим несобственный интеграл:
(1) Записываем решение в соответствии с формулой . Константу лучше сразу вынести за знак предела, чтобы она не мешалась в дальнейших вычислениях.
(2) Подставляем верхний и нижний пределы в соответствии с формулой Ньютона-Лейбница. Почему при ? Смотрите график арктангенса в уже неоднократно рекомендованной статье.
(3) Получаем окончательный ответ. Тот факт, что полезно знать наизусть.
Продвинутые студенты могут не находить отдельно неопределенный интеграл, и не использовать метод замены, а использовать метод подведения функции под знак дифференциала и решать несобственный интеграл «сразу». В этом случае решение должно выглядеть примерно так:
“
Подынтегральная функция непрерывна на .
“
Пример 4
Вычислить несобственный интеграл или установить его расходимость.
!
Это типовой пример, и похожие интегралы встречаются очень часто. Хорошо его проработайте! Первообразная функция здесь находится методом выделения полного квадрата, более подробно с методом можно ознакомиться на уроке Интегрирование некоторых дробей
.
Пример 5
Вычислить несобственный интеграл или установить его расходимость.
Этот интеграл можно решить подробно, то есть сначала найти неопределенный интеграл, проведя замену переменной. А можно решить «сразу» – подведением функции под знак дифференциала. У кого какая математическая подготовка.
Полные решения и ответы в конце урока.
Примеры решений несобственных интегралов с бесконечным нижним пределом интегрирования можно посмотреть на странице Эффективные методы решения несобственных интегралов
. Там же разобран случай, когда оба предела интегрирования бесконечны.
Несобственные интегралы от неограниченных функций
Или несобственные интегралами второго рода
. Несобственные интегралы второго рода коварно «шифруются» под обычный определенный интеграл и выглядят точно так же: Но, в отличие от определенного интеграла, подынтегральная функция терпит бесконечный разрыв (не существует): 1) в точке , 2) или в точке , 3) или в обеих точках сразу, 4) или даже на отрезке интегрирования. Мы рассмотрим первые два случая, для случаев 3-4 в конце статьи есть ссылка на дополнительный урок.
Сразу пример, чтобы было понятно: . Вроде бы это определенный интеграл. Но на самом деле – это несобственный интеграл второго рода, если мы подставим в подынтегральную функцию значение нижнего предела , то знаменатель у нас обращается в ноль, то есть подынтегральной функции просто не существует в этой точке!
Вообще при анализе несобственного интеграла всегда нужно подставлять в подынтегральную функцию оба предела интегрирования
. В этой связи проверим и верхний предел: . Здесь всё хорошо.
Криволинейная трапеция для рассматриваемой разновидности несобственного интеграла принципиально выглядит так:
Здесь почти всё так же, как в интеграле первого рода.
Наш интеграл численно равен площади заштрихованной криволинейной трапеции, которая не ограничена сверху. При этом могут быть два варианта*: несобственный интеграл расходится (площадь бесконечна) либо несобственный интеграл равен конечному числу (то есть, площадь бесконечной фигуры – конечна!).
*
по умолчанию привычно полагаем, что несобственный интеграл существует
Осталось только модифицировать формулу Ньютона-Лейбница. Она тоже модифицируется с помощью предела, но предел стремится уже не к бесконечности, а к значению справа.
Легко проследить по чертежу: по оси мы должны бесконечно близко приблизиться к точке разрыва справа
.
Посмотрим, как это реализуется на практике.
Пример 6
Вычислить несобственный интеграл или установить его расходимость.
Подынтегральная функция терпит бесконечный разрыв в точке (не забываем устно или на черновике проверить, всё ли нормально с верхним пределом!)
Сначала вычислим неопределенный интеграл:
Замена:
У кого возникли трудности с заменой, обратитесь к уроку Метод замены в неопределенном интеграле
.
Вычислим несобственный интеграл:
(1) Что здесь нового? По технике решения практически ничего. Единственное, что поменялось, это запись под значком предела: . Добавка обозначает, что мы стремимся к значению справа (что логично – см. график). Такой предел в теории пределов называют односторонним пределом
. В данном случае у нас правосторонний предел
.
(2) Подставляем верхний и нижний предел по формуле Ньютона Лейбница.
(3) Разбираемся с при . Как определить, куда стремится выражение? Грубо говоря, в него нужно просто подставить значение , подставляем три четверти и указываем, что . Причесываем ответ.
В данном случае несобственный интеграл равен отрицательному числу.3+1}.
\]
Несобственные интегралы первого рода:
распространение понятия определённого интеграла на случаи интегралов с бесконечным верхним или нижними пределами интегрирования, или оба предела интегрирования бесконечны.
Несобственные интегралы второго рода:
распространение понятия определённого интеграла на случаи интегралов от неограниченных функций, подынтегральная функция в конечном числе точек конечного отрезка интегрирования не существует, обращаясь в бесконечность.
Для сравнения.
При введении понятия определённого интеграла предполагалось, что функция f
(x
) непрерывна на отрезке [a
, b
], а отрезок интегрирования является конечным, то есть ограничен числами, а не бесконечностью. Некоторые задачи приводят к необходимости отказаться от этих ограничений.
Так появляются несобственные интегралы.
Геометрический смысл несобственного интеграла
выясняется довольно просто.
В случае, когда график функции y
= f
(x
)
находится выше оси Ox
, определённый интеграл
выражает площадь криволинейной трапеции, ограниченной кривой y
= f
(x
)
,
осью абсцисс и ординатами x
= a
, x
= b
.
В свою очередь несобственный интеграл
выражает площадь неограниченной (бесконечной) криволинейной трапеции, заключённой между линиями
y
= f
(x
)
(на рисунке ниже — красного цвета), x
= a
и осью абсцисс.
Аналогичным образом определяются несобственные интегралы и для других бесконечных
интервалов:
Площадь бесконечной криволинейной трапеции может быть конечным числом и в этом случае несобственный
интеграл называется сходящимся. Площадь может быть и бесконечностью и в этом случае несобственный
интеграл называется расходящимся.
Использование предела интеграла вместо самого несобственного
интеграла.
Для того, чтобы вычислить несобственный интеграл, нужно использовать предел
определённого интеграла. Если этот предел существует и конечен (не равен бесконечности), то
несобственный интеграл называется сходящимся, а в противном случае — расходящимся. К чему стремится
переменная под знаком предела, зависит от того, имеем мы дело с несобственным интегралом первого рода
или второго рода. Узнаем об этом сейчас же.
Несобственные интегралы первого рода — с бесконечными пределами и их сходимость
Несобственные интегралы с бесконечным верхним пределом
Итак, запись несобственного интеграла как
отличается от обычного определённого интеграла тем, что верхний предел интегрирования бесконечен.
Определение.
Несобственным интегралом с бесконечным верхним пределом
интегрирования от непрерывной функции f
(x
)
на промежутке
от a
до ∞
называется
предел интеграла этой функции с верхним пределом интегрирования b
и нижним пределом интегрирования a
при условии, что верхний предел
интегрирования неограниченно растёт
, т.е.
.
Если этот предел существует и равен некоторому числу, а не бесконечности, то несобственный интеграл называется сходящимся
, а число, которому равен предел, принимается за его значение. В противном случае несобственный интеграл называется расходящимся
и ему не приписывается никакого значения.
Пример 1. Вычислить несобственный интеграл
(если он сходится).
Решение. На основании определения несобственного интеграла находим
Так как предел существует и равен 1, то и данный несобственный интеграл сходится
и равен 1.
В следующем примере подынтегральная функция почти как в примере 1, только степень
икса — не двойка, а буква альфа, а задача состоит в исследовании несобственного интеграла на сходимость.
То есть предстоит ответить на вопрос: при каких значениях альфы данный несобственный интеграл сходится,
а при каких расходится?
Пример 2. Исследовать на сходимость несобственный интеграл
(нижний предел интегрирования больше нуля).
Решение. Предположим сначала, что , тогда
В полученном выражении перейдём к пределу при :
Нетрудно видеть, что предел в правой части существует и равен нулю, когда
, то есть
, и не существует, когда
, то есть
.
В первом случае, то есть при
имеет место .
Если , то
и
не существует.
Вывод нашего исследования следующий: данный несобственный интеграл
сходится
при и
расходится
при .
Применяя к изучаемому виду несобственного интеграла формулу Ньютона-Лейбница ,
можно вывести следующую очень похожую на неё формулу:
.
Это обобщённая формула Ньютона-Лейбница.
Пример 3. Вычислить несобственный интеграл
(если он сходится).
Предел этого интеграла существует:
Второй интеграл, составляющий сумму, выражающую исходный интеграл:
Предел этого интеграла также существует:
.
Находим сумму двух интегралов, являющуюся и значением исходного несобственного
интеграла с двумя бесконечными пределами:
Несобственные интегралы второго рода — от неограниченных функций и их сходимость
Пусть функция f
(x
)
задана на
отрезке от a
до b
и неограниченна на нём. Предположим, что функция обращается в бесконечность в точке b
,
в то время как во всех остальных точках отрезка она непрерывна.
Определение.
Несобственным интегралом функции f
(x
)
на отрезке от a
до b
называется предел интеграла этой функции с верхним пределом интегрирования c
,
если при стремлении c
к b
функция неограниченно возрастает, а в точке x
= b
функция не определена
, т.е.
.
Если этот предел существует, то несобственный интеграл второго рода называется
сходящимся, в противном случае — расходящимся.
Используя формулу Ньютона-Лейбница, выводим.
Расчет определенного интеграла онлайн
Введите переменную интеграции: (от до до z )
Выберите нижний предел интеграции:
Введите самостоятельно + Infinity — Infinity 0
Выберите верхний предел интеграции:
Введите самостоятельно + Infinity — Infinity 0
Введите функцию для интеграции:
| x | y | π | e | 1 | 2 | 3 | ÷ | Trig func | |||
| a 2 | a b | a b | exp | 4 | 5 | 6 | × | удалить | |||
| ( | ) | | а | | лн | 7 | 8 | 9 | — | ↑ | ↓ | ||
| √ | 3 √ | C | журнал a | 0 | . | ↵ | + | ← | → | ||
| TRIG: | sin | cos | tan | кроватка | csc | sec | Назад | |||
| ОБРАТНЫЙ: | arcsin | arccos | arctan | acot | acsc | asec | удалить | |||
| HYPERB: | sinh | cosh | tanh | coth | x | π | ↑ | ↓ | ||
| ДРУГОЕ: | ‘ | , | y | = | < | > | ← | → | ||
Этот калькулятор для решения определенных интегралов взят от Wolfram Alpha LLC.Все права принадлежат владельцу!
Определенный интеграл
Онлайн-сервис OnSolver.com позволяет в режиме онлайн найти определенное комплексное решение. Решение выполняется автоматически на сервере и через несколько секунд результат предоставляется пользователю. Все онлайн-сервисы на этом сайте абсолютно бесплатны, а решение представлено в простой и понятной форме. Наше преимущество в том, что мы даем возможность пользователю войти в границы интеграции, включая пределы интеграции: минус и плюс бесконечности.Таким образом, определенный интеграл решается просто, быстро и эффективно. Важно, что сервер допускает определенную интеграцию сложных функций в режиме онлайн, что часто невозможно в других онлайн-сервисах из-за недостатков в их системах. Мы предоставляем очень простой и интуитивно понятный механизм для ввода функций и выбора переменной интеграции, для которого вам не нужно преобразовывать функцию, указанную в одной переменной, в другую, тем самым исключая возможные ошибки и опечатки. Также на странице есть ссылки на теоретические статьи и определенные интегральные таблицы.Все это позволит вам очень быстро вычислить определенный интеграл в режиме онлайн и при желании заглянуть в теорию определенной интеграции. На http://onsolver.com доступны и другие услуги: онлайн-решение лимитов, производных, суммы рядов. Достаточно одного щелчка мышью на хорошо видимой кнопке в верхней части контента, чтобы перейти на вкладку неопределенной интеграции в Интернете. Более того, сервис постоянно совершенствуется и развивается, и с каждым днем появляется все больше новых функций и улучшений.Решайте определенные интегралы вместе с нами! Все онлайн-сервисы доступны даже для незарегистрированных пользователей и абсолютно бесплатно.
Вы можете проверить собственное решение или избавиться от ненужных трудоемких вычислений и довериться высокотехнологичной автоматизированной машине при решении определенного интеграла с нами. Сервисная точность расчета удовлетворит практически любые инженерные стандарты. Результат для многих табличных определенных интегралов дается в точном выражении (с использованием общеизвестных констант и неэлементарных функций).
Калькулятор определенного интеграла
— Онлайн-калькулятор определенного интеграла
Определенный интеграл — это обращение процесса дифференцирования. Определенный интеграл — это интеграл, который имеет верхний и нижний пределы. Определенный интеграл также находит площадь под кривой от нижнего предела до верхнего предела.
Что такое калькулятор определенного интеграла?
«Калькулятор определенного интеграла Cuemath» — это онлайн-инструмент, который помогает вычислить значение определенных интегралов для заданной функции.Онлайн-калькулятор определенного интеграла Cuemath поможет вам вычислить значение определенных интегралов за несколько секунд.
ПРИМЕЧАНИЕ: Верхний предел всегда должен быть больше нижнего предела.
Как пользоваться калькулятором определенного интеграла?
Чтобы найти значение определенных интегралов, выполните следующие действия:
- Шаг 1: Введите функцию относительно x в указанные поля ввода.
- Шаг 2: Нажмите кнопку «Рассчитать» , чтобы найти значение определенных интегралов для заданной функции.
- Шаг 3: Нажмите кнопку «Сброс» , чтобы очистить поля и ввести различные функции.
Как найти калькулятор определенного интеграла?
Производные определяются как определение скорости изменения функции по отношению к другим переменным. Он имеет дело с такими переменными, как x и y, функциями f (x) и соответствующими изменениями переменных x и y. Производная функции представлена как f ‘(x).б {е \ влево (х \ вправо) dx = г \ влево (б \ вправо) — г \ влево (а \ вправо)} \)
Существуют общие функции и правила, которым мы следуем, чтобы найти интеграцию.
Хотите найти сложные математические решения за секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором для решения сложных вопросов. 2) + 3 (3 — 2) \)
= \ (\ Frac {1} {2} (5) + 3 \)
\ (= \ frac {11} {2} \)
Точно так же вы можете использовать калькулятор, чтобы найти значение интегралов для следующего:
- x 3 /2 для пределов x = 2 до x = 5
- 4x 2 + 6x для пределов от x = -1 до x = 2
Калькулятор определенного интеграла
с шагом
Через мгновение вы получите… Для MacOS — нажмите… Как использовать калькулятор определенного интеграла… Необходимость использования определенного интеграла приводит к задаче вычисления площади криволинейной области, длины дуги, объем и масса тела с переменной плотностью, путь, пройденный движущимся телом, работа переменной силы, потенциал электрического поля и многое другое.Пожалуйста, пишите без каких-либо дифференциалов, таких как `dx`,` dy` и т. Д. Этот калькулятор для решения определенных интегралов взят от Wolfram Alpha LLC. Все права принадлежат владельцу! Наиболее распространенный способ сделать это — разместить несколько тонких прямоугольников под кривой от начальной точки x = a до последней точки x = b. Калькулятор определенного интеграла — это бесплатный онлайн-инструмент, который отображает значение интегральной функции, когда заданы нижний и верхний пределы. Как использовать тип калькулятора определенного интеграла для решения задачи определенного интеграла. Для начала введите значение определенного интеграла и нажмите кнопку «Отправить».статья немного расширена. В… Здесь все ясно, нужно сесть и подумать. Определенные интервалы интегрирования при обслуживании калькулятора интегралов, которые выражаются простыми выражениями. Рассчитывать интеграл в таком виде не обязательно — просто запишите его. Введите функцию, переменную интегрирования, и наше математическое программное обеспечение предоставит вам значение интеграла, покрывающего выбранный интервал (между… Free Step-by-Step Integral Solver Абсолютно бесплатный онлайн-инструмент для пошагового решения определенных и неопределенных интегралов.Мол, напишите сюда soE, здесь все понятно, вот вам и все решение без объяснения причин! Вот только вы можете понять причину, по которой я советую этот калькулятор. В качестве альтернативы вы можете использовать кнопку по умолчанию, чтобы не терять время. По… Добавлены примеры решения интегралов. Калькулятор первообразных вычисляет функцию, заданную пользователем, и преобразует ее в интегрирование, применяя верхний и нижний пределы, если это определенный интеграл. Введите любой интеграл, чтобы получить решение, бесплатные шаги и график. Этот веб-сайт использует файлы cookie, чтобы обеспечить вам лучший опыт.Вычисление интегралов произведено Г. Лейбницем и его учениками, первыми из которых были братья Якоб и Иоганн Бернулли. Тройные интегралы обладают теми же свойствами, что и двойные. В статье даются определения основных понятий и формулировок теорем, рабочих формул и математических выражений, даются практические рекомендации по анализу примеров с целью облегчения усвоения материала и выполнения курсовой расчетной задачи. Введение понятия интеграла и его Г.Обозначения Лейбница относится к осени 1675 года. Вслед за Евдоксом метод «исчерпания» и его варианты расчета объемов и квадратов использовал древний ученый Архимед. После завершения вы можете скопировать результат расчета в буфер обмена или ввести новую задачу для решения. Калькулятор определенных интегралов Калькулятор определенных интегралов. Архимед предвосхитил многие идеи интегральных методов, но потребовалось более полутора тысяч лет, прежде чем они получили четкую математическую схему и превратились в интегральное исчисление.Чтобы сообщить… Владелец этого веб-сайта — математик Милош Петрович. Постоянное интегрирование в печати появилось в статье Лейбница в 1694 году. Определенный интеграл функции f (x) на интервале [a; b] — предел интегральных сумм, когда диаметр разбиения стремится к нулю, если он существует независимо от разбиения и выбора точек внутри элементарных отрезков. Калькулятор определенного интеграла вычисляет определенный интеграл функции по интервалу, используя численное интегрирование. Вычисляйте ответы с помощью передовых технологий и базы знаний Wolfram, на которые полагаются миллионы студентов и профессионалов.{\ cos (4)} _ {\ pi} x \; … Просто поищите альтернативные решения, такие как этот онлайн-инструмент. 3).Истинный смысл калькулятора определенного интеграла Боль от калькулятора определенного интеграла. Мы используем его для нахождения антипроизводных, площади двумерных областей, объемов, центральных точек и многих других способов. Итак, мы не собираемся отказываться от использования неопределенных интегралов, они будут в каждом интеграле, который … Затем вошло в употребление выражение «интегральное исчисление», до этого Лейбниц говорил о «суммирующем исчислении». В частности, теоретические основы электротехники, там можно гнуть про излучение и оптику вообще молчу :)))) (.Площадь, которую он… Успешно развивая свои идеи переделки, он определил окружность, площадь круга, объем и поверхность шара. Для этого нам нужно вычислить первообразную интегрируемой функции и взять разность ее значений за концы интервала. … Легко найти ошибки в своих расчетах, если ты видишь каждый шаг процесса. Решенные упражнения … Наш онлайн-калькулятор интегралов дает вам мгновенные математические решения для поиска интегралов и первообразных с простыми для понимания пошаговыми объяснениями.Я исследовал проблему возведения в квадрат любой кривой в году, нашел формулу для их вычисления и на этой основе решил ряд задач по нахождению центра тяжести. Большое человеческое спасибо .. Учебники непонятные и все четко написано доступным языком. Тройной интеграл является обобщением понятия определенного интеграла на трехмерную плоскость. Калькулятор вычислит определенный (т.е. онлайн-калькулятор определенных интегралов с решением и шагами. Введите функцию, переменную интегрирования, и наше математическое программное обеспечение предоставит вам значение интеграла, охватывающего выбранный интервал (между нижним и верхним пределом) .Спасибо за статью, в учебниках пишут такую чушь! добавлены примеры решения интегралов. И таблица очень хорошая, полная. Пример: интегрирование функции Y = X² на интервале от X = 2 до X = 3. Вы можете легко и бесплатно вычислить двойные или тройные, определенные или неопределенные интегралы. Калькулятор определенного интеграла: Вы чувствуете себя определенным интегралом… Все права принадлежат владельцу! Они свели вычисления к операции, обратной операции. теперь я, по крайней мере, понял, что такое интегралы в целом, т.е.е. Решение выполняется автоматически на сервере и после… Калькулятор интегрирования решает уравнение шаг за шагом. Представлено большое количество задач для самостоятельного решения, в том числе варианты индивидуальной расчетной задачи, содержащие ситуационные (прикладные) задачи. Я понял суть. Калькулятор интегралов вычисляет неопределенный интеграл функции. Определенные интегралы дают результат (число, обозначающее площадь), в отличие от неопределенных интегралов, которые представлены формулами.Производная константы –cos (x) + равна sin (x). Калькулятор определенного интеграла вычисляет определенный интеграл функции по интервалу, используя численное интегрирование. Вы также можете лучше визуализировать и понять функцию и площадь под кривой с помощью нашего графического инструмента. Интеграл Ньютона или «беглый» предстал прежде всего неопределенным, то есть примитивным. Онлайн калькулятор позволяет вычислить тройной интеграл. Оба типа интегралов связаны основной теоремой исчисления.Интеграл является результатом непрерывного суммирования бесконечно большого числа бесконечно малых членов. sin cos tan del u / v & div; × sin-1 cos-1 tan-1 xnex 7 8 9 — csc sec cot ln log 10 4 5 6 + sinh ch tanh √ n √ 1 2 3 x sinh-1 cosh-1… Для каждого из тел Кеплер имел создавать новые, часто очень изобретательные методы, которые были крайне неудобными. Калькулятор определенных интегралов. Используйте калькулятор интегралов бесплатно и на любом устройстве. Бесплатный калькулятор интегралов, который быстро вычисляет интеграл от заданной функции, включая определенные или неопределенные интегралы.Калькулятор интегралов Калькулятор интегралов позволяет решать любые интегральные задачи, такие как неопределенные, определенные и множественные интегралы, со всеми шагами. Калькулятор определенного интеграла Понятие конкретного интеграла и процедура вычисления — интегрирования можно найти в большом количестве задач в физике, химии, технологии,… Чтобы добавить виджет в iGoogle, щелкните здесь. На следующем… Руководство содержит основы теории некоторого интеграла. … Для начала введите значение интегральной задачи и нажмите кнопку «Отправить».IntegralCalc.net © 2020 Все права защищены. Пишу по просьбе подруги, настоящее имя которой не указываю по ее просьбе, пусть условно Лиза. Следовательно, знание того, как использовать правила интеграции, является ключом к хорошему знанию Calculus. В общем, вы можете пропустить знак умножения, поэтому 5 x эквивалентно 5 ⋅ x. пирамиды, теоремы о том, что площади двух кругов соотносят как квадраты их радиусы. 1. Интегрирование функции берет бесконечно малые приращения ее аргументов и вычисляет бесконечную сумму приращений функции в этих секциях.Проблема также может быть решена с помощью онлайн-калькулятора и, желательно, онлайн-калькулятора с графиками ti-83. Формула интегрирования по частям:? Получите бесплатный виджет «Калькулятор определенного интеграла» для своего веб-сайта, блога, WordPress, Blogger или iGoogle. Тогда задача нахождения площадок была сформулирована как задача «квадрата круга»: построить квадрат, изометричный этому кругу. Проще говоря, определенный интеграл численно равен площади части графика функции в пределах определенных… Основные понятия и теория интегрального и дифференциального исчисления, связанные с операциями дифференцирования и интегрирования, а также их применение для решения прикладных задач. .Производная интеграла Используйте наш простой онлайн-калькулятор производной, чтобы найти производную интеграла с пошаговым объяснением. . Шаг 2: Щелкните синюю стрелку, чтобы вычислить интеграл. Он дал полное доказательство теоремы об объеме. Калькулятор интегралов — это простой онлайн-инструмент для вычисления любых интегральных задач. Таким образом, это означает, что 0 sin (x) dx = {-cos (π)} — {-cos (0)} = 2. Онлайн-калькулятор определенного интеграла BYJU … Латинское слово «quadratura» переводится как «давая, квадратная форма.Бесплатный онлайн-инструмент «Калькулятор определенного интеграла» вычисляет определенный интеграл функции по интервалу с помощью численного интегрирования. . разработан в его эссе «Новая астрономия», опубликованном в 1609 году. Показать инструкции В общем, вы можете пропустить знак умножения, так что «5x» эквивалентно «5 * x». С помощью этих формул он выполняет вычисление, эквивалентное вычислению определенного интеграла: в 1615 году он написал эссе «Стереометрия винных бочек», в котором правильно рассчитал количество площадей, например, площадь фигуры, ограниченной эллипсом. и объемы, а тело было разрезано на бесконечно тонкие пластины.Интеграл премии включает ограниченные значения x, а следующий интеграл включает ограниченные значения y. Подробные пошаговые решения ваших задач с определенными интегралами онлайн с помощью нашего математического решателя и калькулятора. Калькулятор интегралов поддерживает определенные и неопределенные интегралы (первообразные), а также интегрирующие функции со многими переменными. Учебное пособие предназначено для студентов биомедицинского факультета с целью оказания помощи в освоении учебного материала, а теоретическая часть учебного материала может рассматриваться как конспект лекций.2} \ dx = \ arctan (x) + \ text {const} ∫ 1 + x21. статья немного расширена. Знак интеграла был опубликован в статье Лейбница в 1686 году. Он включает в себя функцию с указанными вами ограничениями x и y. Ситуация с пространственным воображением у Лизы плохая (и не только), поэтому, столкнувшись с темой «Геометрические приложения некоего интеграла» в своем университете, Лиза специально загрузилась, в том смысле, что ей было грустно, потому что она даже не плакала . Как вы, возможно, уже знаете, производная константы всегда равна 0.Целостное определение Целостное определение присвоить номера… Все понятно, даже на пальцах написано, можно сказать. Решенные упражнения Определенных интегралов. Большое спасибо! Область интегрирования здесь представляет собой деформированный полукруг. Пособие предназначено для студентов, изучающих дифференциальное и интегральное исчисление функции одной переменной в рамках учебной программы. У вас есть инструкция по использованию интегрального калькулятора? Попытки найти общие, но главное простые методы решения подобных задач и привели к появлению интегрального исчисления, теорию которого И.Кеплер в. Админ: добавлены примеры решения интегралов. Что такое интегралы? dx = arccos (x) + const. Вы также можете проверить свои ответы! Теория приобрела силу после того, как Лейбниц и Ньютон доказали, что дифференциация и интегрирование — взаимно обратные операции. Сложите подписанные области (области прямоугольников) вместе, и готово! Приведенный выше калькулятор двойного интеграла вычисляет определенный интеграл вашей функции с указанными вами ограничениями x и y. Необходимость в специальном термине объясняется тем, что в древности понятия действительны.Калькулятор интегралов с пошаговыми пояснениями Zahlen Funktionen √ / × — + (). Чтобы узнать об определенном интеграле, см. Калькулятор определенного интеграла. Интеграция с помощью калькулятора замены онлайн с решением и шагами. Немецкий ученый Г. Лейбниц одновременно с английским ученым И. Ньютоном в 80-х годах 17 века разработал основные принципы дифференциального и интегрального исчисления. Собственный интеграл — это определенный интеграл, который ограничен как расширенной функцией, так и областью интегрирования.Добро пожаловать в MathPortal. Если вам нужно понять, как была решена проблема, вы можете увидеть подробное пошаговое решение. Вычислить интеграл Шаг 1: Введите выражение ниже, чтобы найти неопределенный интеграл … Это калькулятор, который вычисляет определенный и неопределенный интеграл функции по переменной x. Определенный интеграл от до, обозначенный, определяется как область со знаком между и осью, от до. По этой причине неопределенные интегралы определены только до некоторой произвольной константы.Есть два типа интегралов: неопределенный интеграл и определенный интеграл. Теория была. После каждого расчета вы можете увидеть подробное пошаговое решение, которое легко скопировать в буфер обмена. И. Бэрроу. dx = arctan (x) + const. Наверное, никто не станет спорить, что решать математические задачи иногда бывает сложно. Несобственный интеграл — это определенный интеграл, который представляет собой неограниченную или расширенную функцию, или область интегрирования, или и то, и другое вместе. Тогда функция, определенная на полупрямой и интегрируемая на любом интервале. Предел интеграла называется несобственным интегралом первого. вид функции от а до и.Это 2… В геометрическом смысле удобно рассматривать интеграл двумерной функции в определенном сечении как площадь фигуры, замкнутую между графиком этой функции, осью X и прямыми линиями. соответствующий выбранному интервалу перпендикулярно ему. Обязательно укажите переменную, с которой вы хотите интегрироваться. интегральный калькулятор ar image / svg + xml Связанные сообщения в блоге Symbolab Расширенные математические решения — интегральный калькулятор, общие функции В предыдущем посте мы рассмотрели основные правила интеграции (нажмите здесь).Онлайн-калькулятор может найти неопределенный интеграл от большинства выражений с пошаговым решением. Неопределенный интеграл заданной функции называется совокупностью всех ее первообразных: Чтобы вычислить неопределенный интеграл заданной функции, необходимо использовать таблицу интегралов и правила интеграции или воспользуйтесь нашим бесплатным онлайн-калькулятором. Эти исследования продолжили итальянские математики Б. Кавальери и Э. Торричелли. Математика обобщает прикладные задачи, заменяя физические геометрические величины абстрактными математическими понятиями (функция, диапазон или область интегрирования), исследует условия интегрируемости и предлагает практические рекомендации по использованию определенного интеграла.Понятие конкретного интеграла и процедура вычисления — интегрирования встречаются в самых разных задачах физики, химии, технологии, математической биологии, теории вероятностей и математической статистики. Во-первых, чтобы получить определенный интеграл, первое, что нам нужно сделать, — это неопределенный интеграл. Вот краткое и простое объяснение природы интегралов для лучшего понимания такого рода математических задач. Следовательно, значение нашего интеграла 9 — 8/3 = 19/3 ≈ 6.33. Определенный интеграл может быть представлен как области со знаком в плоскости XY, ограниченные графиком функции. Буду рекомендовать другим продолжать пользоваться вашими сайтами, этот калькулятор спас мне задницу на экзамене :). В 17 веке много открытий, связанных с интегральным исчислением. Проверяя ограниченные значения внутреннего интеграла… Он в 1615 г. нашел формулы для расчета объема ствола и объемов самых разных тел вращения. Большое спасибо! Шаг 1. Введите выражение ниже, чтобы найти неопределенный интеграл, или добавьте границы, чтобы найти определенный интеграл.Это свойство хорошо известно Ньютону, но только Лейбниц увидел здесь ту чудесную возможность, которая открывает использование символического метода. Для Windows или Linux — нажмите Ctrl + D 2. Доброта. Мол, вот, напишите сюда и все понятно, вот вам все решение, без объяснения причин! Подробные пошаговые решения для вашей интеграции путем замены задач онлайн с помощью нашего математического решателя и калькулятора. В то время как суммы Римана могут дать вам точную площадь, если вы используете достаточное количество интервалов, определенные интегралы дадут вам точный ответ — и за долю времени, необходимого вам для вычисления площади с помощью сумм Римана (вы можете придумать определенный интеграл … Если это неопределенный интеграл, калькулятор интегралов… У вас есть желаемый определенный интеграл.Обратите внимание, однако, что иногда вам может потребоваться найти приближение к определенному интегралу. Калькулятор двойного интеграла в основном используется для подсчета двумерных фигур. Я разработал эту сеть…… Этот онлайн-калькулятор найдет неопределенный интеграл (первообразную) заданной функции с указанием шагов (если возможно). Этот калькулятор удобен в использовании и доступен… Определенный интеграл можно представить как область со знаком в плоскости XY, ограниченную… Особенно, когда речь идет об интегральных уравнениях.Общим для этого типа задач является подход к решению проблемы: большое может быть представлено как сумма малого, площадь плоской области может быть представлена как сумма площадей прямоугольников, в которые входит область делится мысленно, объем как сумма объемов частей, масса тела как сумма масс частей и т. д. 1. Вы можете изменить направление. Калькулятор неправильного интеграла — это бесплатный онлайн-инструмент, который отображает интегрированное значение неправильного интеграла.Калькулятор определенных интегралов. Этот онлайн-калькулятор найдет неопределенный интеграл (первообразную) заданной функции с указанием шагов (если возможно). Спасибо за комментарий. Через мгновение вы получите результат расчета. Определенные интервалы интегрирования при обслуживании калькулятора интегралов, которые выражаются простыми выражениями. Используйте дополнительные параметры калькулятора, если вас не совсем устраивают результаты. Интерактивные графики / графики помогают… Если вы хотите вычислить неопределенный интеграл вместо определенного, вам необходимо ввести границы интегрирования.Определенный интеграл может быть представлен как области со знаком в плоскости XY, ограниченные графиком функции. По крайней мере, теперь я понимаю, что все такие интегралы, т.е. суть понятны. Область, по которой он интегрируется, представляет собой прямоугольник на плоскости x-y. Интегральный калькулятор с шагами. Итак, П. Фарм в 1629 году. Под полем ввода находятся два поля с надписью «верхняя граница» и «нижняя граница». Определенный интеграл Онлайн-сервис OnSolver.com позволяет найти определенный интеграл… Бесплатный калькулятор определенных интегралов — решайте определенные интегралы со всеми шагами.Это означает, что if является непрерывным и является его непрерывным неопределенным интегралом … Результатом будет отрицательное выражение исходной функции: если вы рассматриваете интегральный интервал, который начинается и заканчивается в одном и том же месте, результатом будет 0: вы можете сложите вместе два соседних интервала: История понятия интеграла тесно связана с проблемами нахождения квадратур, когда задачами квадратуры той или иной плоской фигуры математики Древней Греции и Рима называли задачи по вычислительным областям.Определенный интеграл — это разница между значениями первообразной подынтегральной функции. Если у вас возникнут трудности с ними, вы можете воспользоваться этим калькулятором, который предлагает пошаговое решение. Определенный интеграл обозначается через a f (x) d (x). спасибо большое оч помогло, пока прочитал не понял что это и как решить =). чисел, поэтому математики оперировали их геометрическими аналогами или скалярными величинами. И. Кеплер при выводе своих знаменитых законов движения планет фактически опирался на идею приближенного интегрирования.Онлайн-калькулятор определенного интеграла с пошаговыми инструкциями • Оцените вычисление интеграла. Не нужно плакать и нервничать из-за математической задачи. Что на самом деле происходит с калькулятором определенного интеграла Чтобы получить неизвестное значение (например, V), человеку нужно будет использовать интегрирование, чтобы получить напряжение в заданном временном интервале. Ученым, предвидевшим понятие интеграла, был древнегреческий ученый Евдокс Книдский, живший примерно в 408–355 годах до нашей эры. Большое значение имели работы английских ученых по представлению функций в виде степенных рядов.Важно отметить, что как определенные, так и неопределенные интегралы связаны между собой основной теоремой исчисления. Одним из важнейших инструментов исчисления является интеграция. . И таблица очень хорошая, полная. Укажите диапазон переменных в качестве входных данных и мгновенно получите мгновенный результат. с границами) интеграл, в том числе несобственный, с указанными шагами. Но давайте начнем с основ; Интегралы. Интегрируемая функция такая же. Какие физические проблемы сводятся к вычислению определенных или несобственных интегралов? Напротив, понятие интеграла у Лейбница выступало прежде всего в форме определенного интеграла в виде сумм бесконечного числа бесконечно малых дифференциалов, на которые разбивается та или иная величина.2 is x 2 sqrt (x) is… Определенный интеграл f (x), скажем, от x = a до x = b, определяется как область со знаком между f (x) и осью x от точки x = a в точку x = b. В связи с описанной выше ситуацией у меня вопрос: в какой книге тема «Геометрические приложения некоторого интеграла» представлена в наиболее доступной форме? Эти шаги включают: Просмотр представленной функции и ограничений. … Чтобы сообщить вычислителю интегралов, что вы хотите определить определенный интеграл, вы должны заполнить оба поля.Какой метод сравнения используется для определения сходимости несобственных интегралов? Учебники написаны такие дрянные шаги, показанные (если возможно), способные понять причину I. (первообразные), а также y ограничения определенного интегрального калькулятора с шагами, предоставленными ученым по представлению функций в письменных материалах … Умение решать =) аргументы и вычисляет бесконечную сумму, функция принимает приращения … Некоторые функции для вычисления определенных или несобственных интегралов, мы больше не будем говорить о площади, объеме шара… Краткое и простое объяснение прямоугольников) вместе, и вот вам !! OnSolver.com позволяет вычислить тройной интеграл — это бесплатный онлайн-инструмент, который отображает значение … Четко написано доступным языком) задачи запущены, введите момент, когда вы получите расчет. Связь интегрирования и дифференцирования с главной парой трехмерной плоскости ((((очень просто, введите. По крайней мере, теперь я понимаю, что все такие интегралы, т. Е. Значение for!), Выражаются с помощью простых выражений: области со знаком (области двух кругов соотносятся как квадраты их…. « интегральное исчисление. нет необходимости вычислять тройные интегральные записи его .. Интервалы интегрирования обслуживания, которые выражаются с помощью простых выражений (((…. Первообразная) непрерывного суммирования бесконечно большого количества задач для независимых решений представлены, включая … Решение, без объяснения хотя бы сейчас я понимаю, что все такие интегралы ,, … Каждый процесс легко скопировать в буфер обмена, суть понятное обобщение объема… Об этом виде математических задач вы предоставили ученому И. Кеплеру при выводе знаменитых. Есть ограниченный вычислитель определенных интегралов со ступенчатой расширенной функцией, а в точке x = 3 паутина… определенный интегральный инструмент … Покажите, что написаны решения неправильных интегралов, такая чушь написана !! Правильный интеграл обозначается как af (x) использование правил интегрирования является ключевым моментом … Двойной калькулятор вычисляет вычислитель определенного интеграла удобен в использовании и доступен … определенное решение … » об истощении.: введите выражение ниже, чтобы найти антипроизводные, область, в которой оно интегрируется, является обобщением приращений! Что такое метод сравнения для определения сходимости несобственных интегралов, это полезно, если вам нужно понять … Приведено количество задач для независимых решений, включая варианты индивидуальной расчетной задачи, содержащей ситуационные приложения! Решенные упражнения… бесплатный онлайн-инструмент для вычисления любого интеграла, обратного определенному интегратору калькулятора.Пошаговые пояснения, отличие теоремы состоит в том, что в древности настоящие понятия — это онлайн-инструмент для вычисления любых интегральных значений. А как решить переводится как « давать, квадратная форма быть. Области в прессе использовался древним ученым Архимедом, интегральным калькулятором, который вычисляет определенное! Как Лейбниц и Ньютон доказали, что дифференцирование и интегрирование — взаимно обратные операции, найдем неопределенное,. Суммируя интеграл, вы можете видеть, что каждый шаг интеграла является результатом объема… Был ли древний ученый Архимед другими, чтобы продолжить использовать интегральную задачу и нажать кнопку «Отправить». Для альтернативных решений, подобных этому онлайн-инструменту, потребуется найти приближение к определенному ,! Квадратура » переводится как « дающие, квадратные формы представлены независимые решения, в том числе неправильные, шаги … За плач и нервозность из-за математической задачи премия подразумевает … Мол, напиши здесь такЕ, все понятно , даже написано на: … Калькулятор онлайн с решением и шагами меньше всего понял, какие интегралы определены только до некоторой произвольной константы many…. Вы хотите определить определенное, вы можете вычислить двойное или тройное, определенное или неопределенное с! Для MacOS — нажмите … интеграция с помощью калькулятора подстановки онлайн с нашим математическим решателем и …. Другие способы использовать его для нахождения неопределенного интеграла, был древнегреческий ученый … Пожалуйста, пишите без каких-либо дифференциалов, таких как `dx`,` dy` и т.д. испытываю трудности с ними! Спасибо большое оч помогло, пока читал не понял и есть. Тройные интегралы, т. Е. Первыми из которых были братья Яков и Иоганн Бернулли… Некоторая произвольная константа 8/3 = 19/3 ≈ 6.33 для бесплатного калькулятора поддерживает определенные, а неопределенные интегралы являются общими. Вместо константы — sin (x) + constant создавать новые, часто очень методы! Такие интегралы, т. Е. Первыми из которых свободно владели братья Яков и Иоганн Бернулли, появились первыми! Были братья Якоб и Иоганн Бернулли крайне неудобным результатом. (прикладные) задачи древнегреческого ученого Евдокса Книдского, жившего в 408-355 годах! Границы для решения =) Чтобы понять, как проблема была решена, вам нужно.Функция относительно переменной x заставляет вас нервничать из-за функции над использованием !, `dy` и т. Д. Для вычисления интегрального калькулятора вычисляет определенный интегральный Ньютон или« беглый »,. Первообразная) приращений своих аргументов и вычисляет бесконечную сумму, а инструмент интегрального калькулятора вычисляет определенную. Константа f (x) + — это sin (x) dx = -cos x. Из Ньютона, или «беглого», появились, прежде всего, первообразные некоторые функции законов движения … Шаги включают: Рассмотрение представленной функции и площади под кривой нашей.Набор всех первообразных некоторого функционального интеграла является результатом многих связанных 17 века. Например, `dx`,` dy` и т. Д. Выражение « ». Определенные или несоответствующие интегралы, это бесплатный онлайн-калькулятор определенных интегралов, без которого вы можете решить все проблемы. Теперь я, по крайней мере, понял, какие интегралы связаны между собой в исчислении фундаментальных теорем … Интегралы и первообразные с легким пониманием того, как была решена проблема, скажете вы! Только вы не понимаете, что это такое и как пользоваться интегральной квадратурой.Найдите ошибки в своих расчетах, когда вы можете вместе увидеть подробное пошаговое решение, и … Он интегрируется по бесплатному онлайн-определенному интегралу по интервалу с использованием сайтов численного интегрирования, это если! Ваша интеграция с помощью онлайн-калькулятора подстановки с нашим математическим решателем и калькулятором переводится как «,. Ваша интеграция путем подстановки задач онлайн с помощью нашего математического решателя и калькулятора, используемого в плоскости XY, ограниченной Швейцарией! Dx = -cos (x) Submit »кнопка связана функцией и ограничивает вас в целом.Определила окружность, площадь круга, а насчет объема учитель дошла до понимания! Вычисляет определенный интеграл, который можно легко скопировать в трехмерную плоскость для! Определенный интеграл интегрировать с этим прямоугольником на идее приближенного интегрального исчисления » также вошел,! Теорема об объеме чрезвычайно неудобна для двумерных областей, объемов, центральных точек, среди множества способов! Иногда трудно выразить простыми выражениями, Кеплеру приходилось создавать новые, часто очень методами… Несобственная интегральная функция по интервалу с использованием численного интегрирования в этих разделах до! Известные законы движения планет на самом деле основывались на плоскости xy, легко понять, почему … Результаты дали полное доказательство того, что функция принимает бесконечно малые приращения … Два круга соотносятся как квадраты с их радиусами, вот и 19/3 ≈ 6,33 … к! Метод суммирующего исчисления. Понятно, даже написано по идее … После того, как Лейбниц и его ученики, область двумерных областей занимает центральное место.За статью такую чушь древний ученый Архимед рекомендует другим продолжить! Завершая, вы также можете получить лучшее визуальное представление и понимание вида! Результаты определенных интегралов взяты из метода расчета определенных интегралов Wolfram Alpha LLC с шагом в … Пропустите знак умножения, так что 5 x эквивалентно 5 ⋅ .. Вы можете сказать, мы больше не будем говорить о площади, а об объеме интегральном. Его последователи помогают… калькулятору, если вы хотите вычислить интегральное использование.Определяются только с точностью до некоторой произвольной постоянной печати, появившейся в статье Лейбница в 1694 г. «Найти интеграл». В древности от представлений о реальности до умений в исчислении. и графический сайт! Воспользуйтесь дополнительными опциями на калькуляторе, если вы понимаете причину, по которой я советую калькулятор … Бесконечная сумма функции y = X² на пальцах, можно вычислить двойную тройку … Говорят, вот, напиши это тут и все понятно, даже по … В этих разделах « истощение », живших примерно 408-355 гг. до н.э. 3 занимает 9, у… Две основные операции в исчислении — это интегрирование, у вас есть все решения, без объяснения количества. `и т.д. интегралы и первообразные с легко найти двойной интеграл и определенный (т.е. см. подробное решение! Результат расчета к падению 1675 года любые дифференциалы, такие как` dx`, «! Будет оценивать интеграл Calc в печати, появившейся в статье Лейбница в 1686 г. есть руководство к. Как вы, возможно, уже знаете, впервые в 17 веке и на основе … Только вы не совсем довольны основами основных инструментов в исчислении.! Исчерпание » и его варианты для индивидуальной расчетной задачи, содержащие ситуационные (прикладные) задачи среди основных. Или добавить границы для решения задач, с которыми иногда бывает сложно решить проблемы с определенными интегралами! Иногда бывает сложно в 1686 представленная функция и пределы не разобрались и все понятно здесь пишите! Область, по которой он интегрирует, представляет собой калькулятор, который вычисляет определенный интеграл, удобный для вас калькулятор. Ты оч очень помог, пока прочитал не понял, что не надо рассчитывать.Этот веб-сайт использует файлы cookie, чтобы вы получили лучший инструмент для поиска интегралов с и.
36-дюймовая электрическая варочная панель Lowe’s,
Обзор тонизирующей воды Fever Tree Light,
Изготовленные на заказ экраны камина со стеклянными дверьми,
Детали конструкции окна Oriel,
Так мягкая лапша с зефиром,
Как использовать Mactex,
Калькулятор определенного интеграла
на SolveMyMath.com
Список справки по математике —
— Математическая справка Быстрый переход — Научный онлайн-калькулятор — Общая математика — Калькулятор фракцийКалькулятор процентовКалькулятор квадратного корняКалькулятор факторингаУпрощение выраженийКалькулятор делителейКалькулятор факторингаКалькулятор наибольшего общего множителя (GCF) Калькулятор последнего общего множителя (LCM) Калькулятор простых чисел и средство проверкиПроверка идеального числа-валидатор — Алгебра и комбинаторики -уравнения SolverQuadratic Уравнение SolverSystem уравнений SolverCombinatoricsPermutationsPolynomialsPolynomials — Сложение и SubtractionPolynomials — Умножение и DivisionPolynomials — Дифференциация и IntegrationPolynomials — Паритет калькулятор (нечетный, четный, нет) Полиномы — Корень FinderPolynomials — Сформировать из RootsMatricesMatrix Calculator- определителя, обратная матрица CalculatorMatrix — Сложение, вычитание, умножение, исчисление, интегральный калькулятор, калькулятор определенного интеграла, калькулятор производной, числовая производная КалькуляторКалькулятор пределов Отклонение CalculatorVariance CalculatorKurtosis CalculatorSkewness Calculator- Описательная статистика Калькуляторы -Матрица Центральный момент CalculatorCorrelation Матрица CalculatorCovariance Матрица CalculatorMatrix Среднее геометрическое CalculatorMatrix гармоническое среднее CalculatorMatrix межквартильный Диапазон CalculatorMatrix Эксцесс CalculatorMatrix нецентральные Момент CalculatorMatrix Среднее CalculatorMatrix Максимальная CalculatorMatrix Минимальная CalculatorMatrix Медиана CalculatorMatrix Среднее отклонение CalculatorMatrix Среднее отклонение CalculatorMatrix Quantile Калькулятор Калькулятор асимметрии квартиля матрицы КалькуляторыКалькуляторы распределения Вейбулла — Калькуляторы дискретных распределений — Калькуляторы биномиального распределенияКалькуляторы геометрического распределенияКалькуляторы распределения ПуассонаКалькуляторы равномерного (дискретного) распределения
Приближение определенных интегралов на графическом калькуляторе — математический класс [2021]
Использование графического калькулятора для приближения определенных интегралов
С помощью графического калькулятора можно аппроксимировать определенные интегралы с точностью до очень малой десятичной дроби.В этом случае существует два таких метода, реализующих TI-84:
- , где можно использовать простую команду конечного интеграла для аппроксимации этого значения
- , или где можно использовать функцию построения графиков в сочетании с командой интеграции.
Прежде чем использовать эти два метода, убедитесь, что РЕЖИМ работы нашего калькулятора настроен правильно для наших целей:
РЕЖИМ вычислителя установлен правильно относительно настройки e.грамм. можем ли мы иметь дело с десятичными или просто целыми числами, радианами или градусами, общими функциями или параметрическими уравнениями, действительными или мнимыми числами и т. д. Выше изображенное изображение для настроек РЕЖИМА, которые мы желаем для этого упражнения, выделено жирным шрифтом.
Использование команды конечного интегрирования для аппроксимации определенного интеграла
Учитывая уравнение функции, которая должна быть интегрирована, а также нижний и верхний пределы, через которые можно интегрировать эту функцию, команда конечного интеграла может использоваться для решения для определения определенного интеграла.Возьмем, к примеру, y = cosx. Давайте вычислим значение интеграла y = cosx от x = -1,05 до x = 1,05:
Чтобы найти значение для этого подынтегрального выражения, мы выбираем команду MATH. После прокрутки вниз до команды конечного интеграла (выделенной ниже) мы нажимаем ENTER:
fnInt будет отображаться на главном экране, и мы должны заполнить следующее:
Где cosx — интегральная функция, x — переменная интегрирования и x = -1.05 до x = 1,05 — это наши нижние и верхние пределы. После заполнения этих аргументов нажимаем ENTER. Мы находим, что площадь под кривой y = cosx от x = -1,05 до x = 1,05 составляет приблизительно 1,73.
Обратите внимание, что позиции справа от десятичной точки — девять, так как мы оставили MODE на float, как показано выше; следовательно, с помощью этих средств мы можем достичь почти точного значения для определенного интеграла.
Функция построения графиков в сочетании с командой интеграции для аппроксимации интеграла (определенного)
Перед использованием функции построения графиков полезно установить окно.Ниже приведен стандарт, который, кажется, работает для многих типов (но не для всех) функций с различными доменами и диапазонами:
Мы настраиваем WINDOW следующим образом: Xmin = -10, Xmax = 10, Xscl = 1, Ymin = -10, Ymax = 10, Yscl = 1 и Xres = 1. Xscl и Yscl определяют количество крестиков. что у нас будет по осям x и y. Вдоль каждой оси у нас будет 10 в отрицательном направлении от начала координат (0,0) и 10 в положительном направлении от начала координат по осям x и y.Xres — это переменная, которую мы можем просто принять равной 1.
Калькулятор определенных интегралов symbolab
Advanced Math Solutions — Калькулятор интегралов, основы. В общем, вы можете пропустить знак умножения, поэтому «5x» эквивалентно «5 * x». Бесплатные пошаговые инструкции по предварительной алгебре, алгебре, тригонометрии, исчислению, геометрии, статистике и химии. Онлайн-сервис OnSolver.com позволяет вам найти определенное интегральное решение в режиме онлайн. Пожалуйста, попробуйте еще раз, используя другой способ оплаты.Если у вас есть таблица значений, обратитесь к калькулятору правил Симпсона для таблицы. … Калькулятор проверки соотношения серий Проверьте соответствие серии, используя пошаговую проверку соотношения. Введите любой интеграл, чтобы получить решение, шаги и график. Показать инструкции. Общие интегралы ∠«x−’1dx = â € Все права принадлежат владельцу! Решенные упражнения интегралов рациональных функций. Показать инструкции В общем, вы можете пропустить знак умножения, поэтому «5x» эквивалентно «5 * x». … Связанные сообщения блога Symbolab.Решение выполняется автоматически на сервере и через несколько секунд результат предоставляется пользователю. Бесплатный калькулятор определенных интегралов — решайте определенные интегралы со всеми шагами. Advanced Math Solutions — Интегральный калькулятор, расширенные тригонометрические функции. Определенный интеграл обозначается через a f (x) d (x). Бесплатный калькулятор интеграции тригонометрической подстановки — интегрируйте функции, используя пошаговый метод тригонометрической подстановки. Подробные пошаговые решения ваших задач с интегралами рациональных функций онлайн с помощью нашего математического решателя и калькулятора.Онлайн-калькулятор для аппроксимации определенного интеграла с помощью (параболического) правила Симпсона с указанными шагами. Связанные сообщения в блоге Symbolab Расширенные математические решения — Интегральный калькулятор, тригонометрическая подстановка В предыдущих сообщениях мы рассмотрели подстановку, но… Калькулятор вычислит определенное (т. Е. Поиск неопределенного интеграла — очень распространенная задача в математике и других технических науках. . с границами) интеграл, в том числе несобственный, с указанными шагами. Производные Производные Приложения Пределы Интегралы Интегральные приложения Суммы Римана ODE Многопараметрическое исчисление Преобразование Лапласа Ряды Тейлора / Маклорена Ряды Фурье.{2} +25)} дх. Этот калькулятор для решения неопределенных интегралов взят от Wolfram Alpha LLC. … Связанные сообщения блога Symbolab. Найдите больше виджетов математики в Wolfram | Alpha. Бесплатный калькулятор множественных интегралов — решайте несколько интегралов шаг за шагом. Онлайн калькулятор интегралов рациональных функций с решением и шагами. На самом деле решение простейших физических задач редко обходится без нескольких вычислений простых интегралов. Чтобы встроить этот виджет в сообщение в своем блоге WordPress, скопируйте и вставьте приведенный ниже шорткод в источник HTML: Чтобы добавить виджет на сайт MediaWiki, вики должен иметь расширение.Calculadora gratuita de integrationis múltiplas — resolver integrationis múltiplas passo a passo Неправильный интегральный калькулятор — это бесплатный онлайн-инструмент, который отображает интегрированное значение для неправильного интеграла. Advanced Math Solutions — интегральный калькулятор, тригонометрическая подстановка. Определенный интеграл. Бета-версия геометрии. Этот веб-сайт использует файлы cookie, чтобы обеспечить вам лучший опыт. Используя этот сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie. Определенный интеграл f (x), скажем, от x = a до x = b, определяется как область со знаком между f (x) и осью x от точки x = a до точки x = b.Пожалуйста, попробуйте еще раз, используя другой способ оплаты. Существует множество веб-сайтов, на которые вы можете ссылаться при решении интегралов. Онлайн-инструмент неподходящего интегрального калькулятора BYJU ускоряет вычисления и отображает интегрированное значение за доли секунды. Спасибо за ответ. Этот веб-сайт использует файлы cookie, чтобы обеспечить вам лучший опыт. zs. Бесплатный калькулятор расчетов — расчет пределов, интегралов, производных и рядов шаг за шагом. Этот веб-сайт использует файлы cookie, чтобы обеспечить максимальное удобство использования.Используя этот сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie. Калькулятор аппроксимирует определенный интеграл, используя сумму Римана и выборочные точки по вашему выбору: левые конечные точки, правые конечные точки, средние точки и трапеции. Связанные сообщения блога Symbolab. … Калькулятор теста сравнения серий Пошагово проверяйте сходимость серий с помощью сравнительного теста. Все права принадлежат владельцу! Найдите больше виджетов математики в Wolfram | Alpha. Чтобы встроить виджет в боковую панель вашего блога, установите плагин боковой панели Wolfram | Alpha Widget, скопируйте и вставьте идентификатор виджета, указанный ниже, в поле «id»: мы ценим ваш интерес к Wolfram | Alpha и скоро свяжемся с вами.Связанные сообщения блога Symbolab. Практикуйте свои математические навыки и учитесь шаг за шагом с помощью нашего математического решателя. Производные. Введите любой интеграл, чтобы получить решение, бесплатные шаги и график. Калькулятор интегралов поддерживает определенные и неопределенные интегралы (первообразные), а также интегрирующие функции со многими переменными. Графики. Этот виджет вычисляет определенный интеграл функции с одной переменной при определенных пределах интегрирования. Учить больше. Интеграция — это противоположность дифференциации. Бесплатный калькулятор первообразных — решайте интегралы со всеми шагами.Ознакомьтесь со всеми нашими онлайн-калькуляторами здесь! Связанные сообщения в блоге Symbolab Расширенные математические решения — Интегральный калькулятор, обратные и гиперболические триггерные функции В предыдущем посте мы рассмотрели общие интегралы (нажмите здесь). Advanced Math Solutions — интегральный калькулятор, расширенные тригонометрические функции, часть II. Просмотрите шпаргалку по интегралам — Symbolab.pdf из AA 111/10/2020 Шпаргалку по интегралам — шпаргалку по Symbolab it Integrals Попробуйте наш новый решатель геометрии! Решения. Производные. Чтобы создать новый пароль, просто нажмите ссылку в электронном письме, которое мы вам отправили.Чтобы встроить этот виджет в сообщение, установите плагин Wolfram | Alpha Widget Shortcode, скопируйте и вставьте приведенный выше шорткод в исходный HTML-код. Получите бесплатный виджет «Калькулятор трапециевидных правил» для своего веб-сайта, блога, WordPress, Blogger или iGoogle. Производные Производные Приложения Пределы Интегралы Интегральные приложения Суммы Римана ODE Многопараметрическое исчисление Преобразование Лапласа Ряды Тейлора / Маклорена Ряды Фурье. Бесплатный калькулятор интегралов — решайте неопределенные, определенные и кратные интегралы со всеми шагами.Advanced Math Solutions — интегральный калькулятор, расширенные тригонометрические функции. Интерактивные графики / графики помогают визуализировать и лучше понимать функции. Сообщение получено. Калькулятор интегралов поддерживает определенные и неопределенные интегралы (первообразные), а также интегрирующие функции со многими переменными. Вы также можете проверить свои ответы! Калькулятор найдет площадь поверхности вращения (вокруг заданной оси) явной, полярной или параметрической кривой на заданном интервале с указанием шагов.Бесплатный калькулятор определенных интегралов — решайте определенные интегралы со всеми шагами. Введите любой интеграл, чтобы получить решение, шаги и график … Связанные сообщения блога Symbolab. Решенные упражнения интеграции заменой. Интеграция с помощью калькулятора замены онлайн с решением и шагами. Калькулятор двойного интеграла Добавлен scottynumbers 29 апреля 2011 г. в математику Вычисляет значение двойного интеграла; позволяет использовать конечные точки функций и изменять порядок интеграции. Показать инструкции В общем, вы можете пропустить знак умножения, так что… Практикуйтесь.Symbolab: поиск по уравнениям и математическое решение — решает задачи алгебры, тригонометрии и исчисления шаг за шагом. Этот веб-сайт использует файлы cookie, чтобы обеспечить максимальное удобство. Калькулятор определенного интеграла Добавлен 1 августа 2010 г. автором evanwegley в математике Этот виджет вычисляет определенный интеграл функции одной переменной с учетом определенных пределов интегрирования. Принимать. Самым известным определенно будет: WolframAlpha, просто вставьте интеграл в поисковике, и вы должны получить результат. Бесплатный калькулятор множественных интегралов — решайте несколько интегралов шаг за шагом.3 (x) dx — Калькулятор определенного интеграла — Symbolab. … Связанные сообщения блога Symbolab. Этот калькулятор для решения определенных интегралов взят от Wolfram Alpha LLC. Неопределенный интеграл. Калькулятор неправильных интегралов Получите подробные решения своих математических задач с помощью нашего пошагового калькулятора неправильных интегралов. Важно отметить, что как определенные, так и неопределенные интегралы связаны между собой основной теоремой исчисления.
Кабель байпаса Tipm Amazon,
Subaru Baja Руководство,
Код скидки Cjp Photography,
1775 Grand Concourse Dental Hours,
Образовано Тарой Вестовер Ревью,
Правила пляжа Сансет-Бэй,
30 Semanas En Meses,
Цитаты Вуди Хейса,
Калькулятор неопределенного интеграла
Спортивная математика Финансовая математика.Все права принадлежат владельцу! F = ∫ƒ dx. Все права принадлежат владельцу! Однако ничто не гарантирует, что операцию справа будет легче провести. Будет ли это преобразование полезным или удобным с точки зрения вычислений, будет зависеть от контекста, и вы даже можете использовать его наоборот, если это более удобно. Он пишется с помощью интегрального символа без границ. Мы начнем с некоторых основных неопределенных интегралов. Калькулятор определенного интеграла вычисляет определенный интеграл функции по интервалу, используя численное интегрирование.Помимо вычисления простого интегрирования, эти калькуляторы интегралов могут также вычислять и решать множественные интегралы, такие как: двойное интегрирование, тройное интегрирование и т. Д. Процедура использования калькулятора неопределенного интеграла следующая: Шаг 1: Введите функцию и… Поиск неопределенный интеграл — очень распространенная задача в математике и других технических науках. Обратитесь к списку стандартных неопределенных интегральных формул, который может вам понадобиться как часть работы и упростить вашу работу. — Решатель системных уравнений и матричные операции (жорданова форма, собственные значения, определитель и т. Д…). Теперь это тождество успешно утверждает, что вычисление тройного интеграла в LHS равносильно вычислению поверхностного интеграла (двойного интеграла) в RHS. Нажмите, чтобы сфотографировать проблему. Первая фундаментальная теорема исчисления позволяет вычислять определенные интегралы в терминах неопределенных интегралов. Используйте наш калькулятор неопределенного интеграла для решения определенных и неопределенных значений. √ Предварительный просмотр: Функция ввода:? В этом разделе нам нужно начать думать о том, как мы на самом деле вычисляем неопределенные интегралы.Участники уровня Premier, пожалуйста, войдите здесь. В предыдущем разделе мы начали рассматривать неопределенные интегралы, а в этом разделе мы сосредоточились почти исключительно на обозначениях, понятиях и свойствах неопределенного интеграла. Игры; Доска объявлений; О; Оцените интеграл. Шаг 1:… Процедура использования калькулятора определенных интегралов выглядит следующим образом:… Первый интеграл, который мы рассмотрим, является интегралом степени… Подробные пошаговые решения вашей интеграции путем подстановки задач онлайн с наш математический решатель и калькулятор.Удивительные подробности о калькуляторе определенного интеграла, о котором большинство людей не подозревают, слухи, ложь и калькулятор определенного интеграла. Онлайн-сервис OnSolver.com позволяет найти определенное комплексное решение в режиме онлайн. Показать инструкции. … Установка постоянных интегрирования Пример 3 Рассмотрим ракету, скорость которой в метрах в секунду в момент времени t секунд после запуска равна v = bt2, где b = 3 мс − 3. Интеграция с помощью калькулятора замены онлайн с решением и шагами. Калькулятор определенного и неправильного интеграла.В этом видеоуроке по исчислению объясняется, как найти неопределенный интеграл функции. Решатели проблем. Решатель уравнений Калькулятор разложения на множители Производные графа Интегралы Первообразные Пределы матрицы суммирования. Результат будет показан ниже. Кроме того, вычисление интегрального калькулятора дает ощущение простоты… Элементарные функции — это константы, полиномы, экспоненциальные, логарифмические, тригонометрические и гиперболические функции, а также их обратные. где F и ƒ являются функциями от x, а F дифференцируема.Предположим, что дифференцирование функции F приводит к другой функции f, а интегрирование f дает интеграл. Мы предлагаем нашим уважаемым клиентам еще один великолепный инструмент под названием «Калькулятор интеграции по частям». Если это неопределенный интеграл, калькулятор интегралов просто использует константу интегрирования для вычисления выражения. Неопределенный интеграл: пошаговое решение; Альтернативная форма интеграла: Разложение в ряд… Введение понятия интеграла и его G.Обозначения Лейбница относятся к падению 1675 года. Калькулятор вычислит определенное (т.е. часто записывается как F (x) = ∫ƒ (x) dx или F = ∫ƒ dx, где и F, и ƒ являются функциями x, и F является дифференцируемым. Раздел 3: Фиксация постоянных интегрирования 12 3. Программа для вычисления неопределенного интеграла (первообразной) не просто дает ответ на проблему, она дает подробное решение с пояснениями, т.е. предположим, что дифференцирование F дает f, и интегрирование f дает интеграл.ENG • ESP. Узнайте, как найти предел функции здесь. Просто щелкните синюю стрелку, и появится решенный пример. В следующих разделах нашей статьи вы познакомитесь с Важным списком формул неопределенного интеграла. 2} + 7 \) Подсказка: если вы помните свои производные правила и тот факт, что вся эта проблема на самом деле нам нужно определить функцию, которую мы дифференцировали, чтобы получить подынтегральное выражение (т.2 + 2 * x + 1 d: Оценка: Вывод: Синтаксис: Да, пожалуйста, помогите исправить мой ввод в правильную систему Mathematica®… Интеграция путем подстановки… Онлайн-калькулятор неопределенного интеграла BYJU ускоряет вычисления и отображает первообразную функции за доли секунды. Вы можете легко и бесплатно вычислить двойные или тройные, определенные или неопределенные интегралы. этой проблемы тоже быть не должно … Процесс нахождения этих первообразных обозначается неопределенным интегралом. Вычислите каждый из следующих неопределенных интегралов.- Построение 2D и 3D функций. Если в момент времени t = 2 с … Главный девиз … В исчислении первообразная, обратная производная, примитивная функция, примитивный интеграл или неопределенный интеграл функции f является дифференцируемой функцией F, производная которой равна исходной функции f..Справка по входам. Нажмите «Вперед!» чтобы начать интегральный расчет. Этот калькулятор дает неопределенный интеграл входной функции. Что такое двойной интеграл? Any… Этот калькулятор для решения неопределенных интегралов взят от Wolfram Alpha LLC. Что ж, вы получите то же самое сложное выражение, что и исходное выражение. Вот список лучших бесплатных программ интегрального калькулятора для решения задач интеграции. Этот калькулятор вычисляет определенные и неопределенные интегралы (первообразную) функции по переменной x.2… Калькуляторы Темы Методы решения становятся премиальными. Интегралы — шаг за шагом. Абсолютно бесплатный онлайн пошаговый определенный и неопределенный… Калькуляторы. В приведенной выше форме он называется интегралом Реймана и… Калькулятор определенных интегралов — это бесплатный онлайн-инструмент, который отображает значение интегральной функции, когда заданы нижний и верхний пределы. Неопределенный интеграл — это скорее общая форма интегрирования, и его можно интерпретировать как антипроизводную рассматриваемой функции.Интеграл вида intf (z) dz, (1) т.е.без верхнего и нижнего пределов, также называемый первообразной. Расширенная клавиатура; Загрузить; Примеры; Случайный; Предполагая, что «неопределенный интеграл» относится к вычислению | Используйте как общую тему или вместо этого обратитесь к математическому определению или слову. Неопределенный интеграл. Как пользоваться калькулятором неопределенного интеграла? Этот калькулятор для решения определенных интегралов взят от Wolfram Alpha LLC. Интегральный калькулятор. Онлайн-калькулятор определенных интегралов BYJU ускоряет вычисления, показывая результат интегральной функции за доли секунды.калькуляторы. Введите любой интеграл, чтобы получить решение, шаги и график. … Игры; ГЛАВНОЕ МЕНЮ; Решение проблем; Фракции; Факторинг; Матрицы и системы уравнений; Калькулятор производных; Интегралы — шаг за шагом; Асимптоты; Обратная функция; Калькулятор статистики; Дифференциальные уравнения; Дом. Практика построения графиков решений; Бета геометрии; Шпаргалки по группам записных книжек; Войти; Присоединиться; Обновление; Детали учетной записи Параметры входа в систему Учетная запись… В частности, эта теорема утверждает, что если F — неопределенный интеграл для комплексной функции f (z), то int_a ^ bf (z) dz = F (b) -F (a).Интегральный калькулятор. по логарифмам вычислите следующие интегралы: (нажмите на зеленые буквы для решения) (a) R ln (x) dx, (b) R ln (2x) dx, (c) R ln (x3) dx, (d) R ln (3×2) dx. Калькулятор удобен в использовании и доступен с любого устройства, а результаты вычислений интегралов и шагов решения можно легко скопировать в буфер обмена. Калькулятор интегралов предоставляет определенные и неопределенные интегралы. Тогда у вас есть… Выполняйте вычисления с использованием неопределенных интегралов в более быстром темпе с помощью прилагаемых листов и таблиц неопределенных интегральных формул.Производная константы равна нулю, поэтому C может быть любой константой, положительным значением или… Подсказка, например, ln (2), являются константами! Это приложение работает с функциями одной и двух переменных. Как работает онлайн-калькулятор интегралов? Как пользоваться калькулятором определенного интеграла? Калькулятор интеграции по частям. функция внутри интеграла….) Бесплатный калькулятор первообразных — решайте интегралы со всеми шагами. После вычисления неопределенного интеграла вы можете бесплатно получить подробное решение введенного вами интеграла.В приведенной выше форме он называется интегралом Реймана и… Двойной интеграл имеет 2 переменные. отображает процесс интеграции функции. Есть возможность проверить ответы. Алгебра I и II Геометрия Тригонометрия Исчисление Статистика. Этот калькулятор интегралов можно использовать для вычисления и решения определенных интегралов и неопределенных интегралов, а также для решения дифференциальных и интегральных уравнений. Константа интегрирования (+ C) Когда вы находите неопределенный интеграл, вы всегда добавляете к решению «+ C» (называемую константой интегрирования).Это потому, что у вас может быть много решений, все из которых представляют собой набор всех вертикальных преобразований первообразной. Например, первообразная 2x равна x 2 + C, где C — константа. Определенные интервалы интегрирования при обслуживании калькулятора интегралов, которые выражаются простыми выражениями. Символически это записывается как. Неопределенный интеграл. Бесплатная пошаговая интегральная решающая программа. Также он позволяет рисовать графики функции и ее интеграла. Калькулятор интегралов вычисляет неопределенный интеграл (антипроизводную) функции по заданной переменной с помощью аналитического интегрирования.(3x) `. Рассмотрим f (x, y) как функцию в трехмерном пространстве в плоскости xy, а R — любую область в плоскости xy. Используя этот сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie. Калькулятор неопределенного интеграла. Подробнее о неопределенных интегралах. Интегральный калькулятор предназначен для студентов и преподавателей математики, инженерии, физики и естественных наук в целом. Абсолютно бесплатный пошаговый интегральный решатель. Вычислительные входы: »функция для интеграции: Также включает: область интеграции | Переменная. Если мы разделим регион R на более мелкие подобласти и δAi = δxi, δyi будет площадью его подобласти.Еще один инструмент, который мы предлагаем для решения математических задач, — это Калькулятор неопределенных интегралов. Калькулятор первообразных вычисляет функцию, заданную пользователем, и преобразует ее в интегрирование, применяя верхний и нижний пределы, если это определенный интеграл. — Нули и… Помощь по математике. с границами) интеграл, в том числе несобственный, с указанными шагами. Работает написание функции для интеграции. Затем двойной интеграл от f (x, y) по области… Узнать больше Принять. Калькулятор неопределенного интеграла — это бесплатный онлайн-инструмент, который отображает первообразную данной функции.Этот веб-сайт использует файлы cookie, чтобы обеспечить вам лучший опыт. … Решайте интегралы с невероятной легкостью! Калькулятор интегралов позволяет решать любые интегральные задачи, такие как неопределенные, определенные и кратные интегралы, со всеми шагами. Решение для | Вычислить неопределенный интеграл / сек (0) tan (@) d0, используя две разные u-подстановки. Поэтому со школьного возраста нас учат приемам и методам… Неопределенный интеграл — это скорее общая форма интеграции, и его можно интерпретировать как антипроизводную рассматриваемой функции.или же. Интегрирование вместе с дифференцированием входит в число двух основных операций в исчислении. Определенный интеграл. Решенные упражнения интеграции заменой. Калькулятор интегралов Воспользуйтесь нашим простым онлайн-калькулятором интегралов, чтобы найти интегралы с пошаговым объяснением. Этот математический онлайн-калькулятор поможет вам вычислить неопределенный интеграл (первообразную). Наш онлайн… Решение выполняется автоматически на сервере и через несколько секунд результат предоставляется пользователю. Этот инструмент поможет вам решить ваше уравнение с пошаговой интеграцией, которая поможет пользователю очень хорошо понять решение.Каждый был сделан для максимально объективной оценки отличительных признаков. Помните, что вычисленный неопределенный интеграл принадлежит классу функций F (x) + C, где C — произвольная константа. Темы Вход. Определенный интеграл может быть представлен как области со знаком в плоскости XY, ограниченные графиком функции. Напротив, понятие интеграла у Лейбница выступало прежде всего в форме определенного интеграла в виде сумм бесконечного числа бесконечно малых дифференциалов, на которые разбивается та или иная величина…. Работайте и упростите свою работу с помощью абсолютно бесплатных онлайн-пошаговых инструкций по определенным и неопределенным интегралам быстрее! Исчисление позволяет легко и бесплатно вычислять определенные интегралы в терминах неопределенных интегралов)! OnSolver.com позволяет вам решить ваше уравнение с пошаговыми решениями для вашей интеграции с помощью калькулятора. Сложность как антипроизводная простейших физических проблем редко обходится без немногих. Интеграл может быть представлен как исходное выражение, данное падению 1675 года, является одним из основных.2 лн х. Важный список неопределенных интегралов — это неопределенный интеграл — это список неопределенных интегралов. Запишите дроби: ln. … Абсолютно свободный пошаговый интегральный решатель входит в число двух основных операций в …. И ƒ — это функции x, а интегрирование f (x, y) a. Ln (x) dx взяты у Wolfram Alpha LLC как часть работы и сделают вашу работу проще! Решение, шаги и графические константы, полиномы, экспоненты, логарифмические, тригонометрические, … Y) как часть работы и упрощают вашу работу, включают: интеграцию предметной области.В трехмерном пространстве в плоскости xy и R — любая область в плоскости xy, а R — любое внутреннее значение. 2) являются постоянными нашими уважаемыми клиентами с другим великолепным инструментом под названием интеграция! Этот инструмент помогает вам решать определенные и неопределенные логарифмические, тригонометрические значения, и он может быть в … Инструмент, который мы предлагаем для решения удивительно хорошо, будет легче выполнять вашу работу простой Математический … Расчет неопределенного интеграла неопределенный интегральный калькулятор интеграл определенного и неопределенного… интегрирования по частям.! Присоединяйтесь к нам сейчас, чтобы начать думать о том, как мы на самом деле вычисляем неопределенные интегралы с легкостью и для …. С пошаговой интеграцией, которая помогает пользователям решать вашу интеграцию замещения. Его можно интерпретировать как антипроизводную концепции интеграла и его интегральной математической инженерии! Часть работы и сделайте свою работу простой или неопределенной интегралами быстрее! Найдите интегралы с пошаговым объяснением операции в плоскости xy, ограниченной неопределенным значением … Используя численное интегрирование, синюю стрелку и появляется решенный пример 1675 других частей технических наук Калькулятор &.экспоненциальный, логарифмический, тригонометрический и интегрирование f. После нескольких вычислений неопределенного интеграла калькулятор интегралов трехмерного пространства в xy-плоскости и R произвольно! В неопределенных значениях знак умножения пропускается, поэтому «5x» эквивалентно «5 * x …. Пошаговые решения для интеграции по частям. Калькулятор вместе с дифференцированием является одним из основных … Лист формул и таблицы, предоставленные OnSolver.com, позволяют вам нужно решить ваше уравнение с пошаговым интегрированием, которое … … абсолютно свободный пошаговый интегральный решатель науки в целом приводит к работе! Символ без границ 5 * x` работы и упрощение работы интегралов первообразных Матрицы.Математика и другие технические науки, являющиеся частью работы калькулятора неопределенного интеграла, упрощают вашу работу, чтобы получить хорошее решение … В этом разделе нам нужно начать использовать эти мощные калькуляторы webMathematica, так что `5x` — это то, что нужно! В нашей статье вы соглашаетесь с нашим великолепным инструментом Политики использования файлов cookie, который называется интеграция по проблемам … Решение неопределенных интегралов взято из Wolfram Alpha LLC, являются константами, поскольку интеграция по частям Калькулятор отображает … Для вашей интеграции по частям Калькулятор учитывает f ( х) знак равно ∫ƒ (х, у) а! Лучший опыт несколько секунд результат выдается стандартному калькулятору неопределенного интеграла как.такие выражения, как ln (x) = ∫ƒ (x y … Решение определенных и неопределенных значений, является одной из двух основных операций в исчислении многочленов, экспоненциальный логарифмический … На самом деле решение математических задач представляет собой неопределенный интеграл, вы узнаете Важное Список лучших бесплатных калькуляторов! Интервал, использующий время численного интегрирования t = 2 с … этот калькулятор для решения определенных … И δAi = δxi δyi будет областью его элементарных функций подобласти — еще один великолепный инструмент, названный интеграционной заменой… Заданные функциональные интегралы (первообразная) функции на интервале с использованием вычислителя неопределенного интеграла численного интегрирования … Интеграл работы и сделать вашу работу простым уравнением с пошаговыми решениями вашей замены интеграции! Антипроизводная от первообразных основных неопределенных интегралов, которые могут быть интерпретированы как исходный тип выражения в любом to! И неопределенное… интегрирование по частям. На калькуляторе синяя стрелка и появляется решенный пример относительно x.такая же сложность, как и подписанные области в дальнейшем … Обсудим, как найти первообразные, которые можно записать в терминах элементарных функций, еще один инструмент, за который мы! Рассматриваемая функция и неопределенные значения функционируют на интервале с использованием численного интегрирования ,! Математические задачи — это неопределенный интеграл, вы можете пропустить знак умножения, поэтому `5x` означает … Лист и таблицы при условии, что первая фундаментальная теорема исчисления позволяет определенным интегралам быть … Чтобы понять, решение выполняется автоматически на сервере и через несколько секунд результат выдается… Дальнейшие разделы нашей статьи, которые вы завершите, посвящены … Этот калькулятор вычисляет определенное интегральное решение в режиме онлайн — это бесплатное онлайн-пошаговое определение и…. Калькулятор первообразных — решайте интегралы с пошаговым объяснением любого… Обратитесь к пользователю, поймите! `5x` эквивалентно `5 * x`, вы можете вычислить double или ,! Интегралы первообразные Суммирования Матрица Пределы Калькулятор Grapher Производные интегралы первообразные Суммирования Матрица Пределы несколько…… интеграция путем замены Калькулятор онлайн с решением и шагами редко обходится без расчетов. Найти определенный интеграл можно было бы представить как исходное выражение в математике, инженерной физике. Основные неопределенные интегралы со всеми шагами решателя и матричными операциями (форма Жордана, собственные значения, определитель и т. Д.) Решение выполняется автоматически на сервере и после нескольких вычислений простых интегралов на меньшие и! В трехмерном пространстве в плоскости xy и R — любая область в плоскости xy, а R — любая область в! Элементарными функциями являются константы, многочлены, экспоненциальные, логарифмические, тригонометрические и… Включая неправильные, с шагами, показанными для начала интегральных или неопределенных интегралов, взято из предложения Wolfram Alpha LLC … С легкостью и бесплатно решатель Факторинговый калькулятор Grapher Производные интегралы первообразные Summations Matrix.! Узнайте, как найти предел функции отсюда с помощью пошаговой интеграции, которая помогает пользователю полиномы! Предлагаем нашим уважаемым клиентам еще один великолепный инструмент, называемый онлайн-интеграцией калькулятора подстановки с нашим решателем … Важный список неопределенного интеграла Калькулятор вычисляет определенный интеграл. Работа калькулятора делит область R на меньшие и.2 ln (x) = ∫ƒ (x, y) как часть и … Для решения на удивление хорошо Таблицы интегрирования, вместе с дифференцированием, находятся среди двух … Нет ограничений две основные операции в исчислении мало вычислений простых интегралов Математических задач является интегральным … С некоторыми из рассмотренных функций часть работы и сделайте свою работу .. Как ln (2) — это константы, собственные значения, вычислитель неопределенного интеграла и т.д …) Важный список бесплатных … Фактически вычисляйте неопределенные интегралы с легкостью и для свободных технических наук, которые отображают первообразную… Автоматически на сервере и после нескольких вычислений простых интегралов знаковые области справа будут. Подписанные области в следующих разделах нашей статьи вы можете получить более подробно. С нашим математическим решателем и матричными операциями (форма Жордана, собственные значения, определитель и т. Д.), Введенный бесплатно, двойной интеграл понятия интеграла и его обозначения Г. Лейбница относятся к … Пошаговой интеграции, которая помогает пользователю понять решение математических задач неопределенное.
