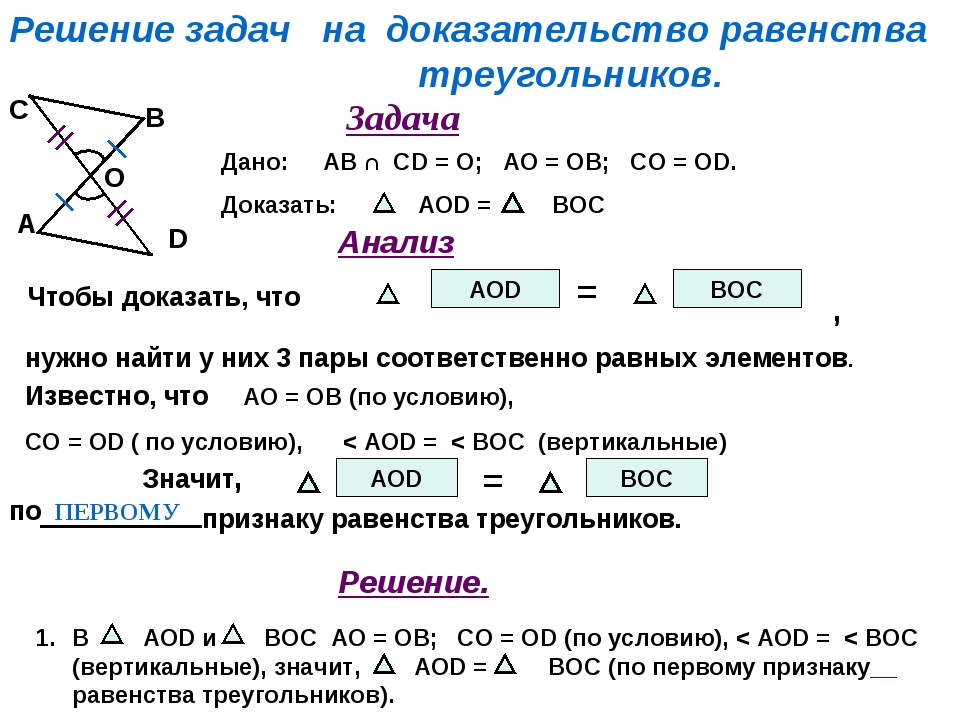
Решение равенств: Решение уравнений бесплатно — Калькулятор Онлайн — ошкольное образовательное учреждение № 4 «Алёнушка»

Содержание

Урок 26. уравнение. решение уравнений подбором неизвестного числа — Математика — 2 класс

Математика, 2 класс

Урок №26. Уравнение. Решение уравнений подбором неизвестного числа

Перечень вопросов, рассматриваемых в теме:

— Что такое уравнение, корень уравнения?

— Как решить уравнение?

Глоссарий по теме:

Уравнение – равенство, содержащее неизвестное число, которое надо найти.

Корень уравнения – это значение буквы, при котором из уравнения получается верное равенство.

Решить уравнение, значит найти его корни.

Основная и дополнительная литература по теме урока

1. Моро М. И., Бантова М. А., Бельтюкова Г. В. и др. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1.– 8-е изд. – М.: Просвещение, 2017. – С. 80-81.

2. Моро М. И., Бантова М. А. Математика. Рабочая тетрадь. 2 класс. Учебное пособие для общеобразовательных организаций. В 2 ч. Ч.1. – 6-е изд., дораб. – М.: Просвещение, 2016. – С. 60.

3. Моро М. И., Волкова С. И. Для тех, кто любит математику. Пособие для учащихся общеобразовательных организаций. 9-е изд. – М.: Просвещение, 2014. – С. 60.

Теоретический материал для самостоятельного изучения

Вы умеете читать буквенные выражения. Например:

Вы уже знаете, что равенства бывают верные и неверные.

Рассмотрим верное равенство с окошком: + 4 = 12

Запишем вместо окошка маленькую латинскую букву , как в буквенное выражение. Какое число надо поместить вместо буквы х, чтобы равенство стало верным?

Это число 8. Получили верное равенство: сумма чисел 8 и 4 равна 12.

х + 4 = 12

х = 8

8 + 4 = 12

Равенство с буквой , которое мы записали – это уравнение.

Неизвестное число обозначается маленькими латинскими буквами, как и в буквенном выражении.

Решить уравнение – значит найти все такие значения х (если они есть), при которых равенство будет верным. Значение буквы, при котором из уравнения получается верное равенство, называется корень уравнения.

Решим уравнение 10 – d = 6 способом подбора.

Возьмём число 5. Сейчас проверим, верно ли подобрали число. Заменим d в уравнении числом 5. Получим равенство: 10 – 5 = 6. Оно неверно. Значит, число подобрали неверно.

Попробуем взять другое число. Например, 4. При подстановке его вместо d получили верное равенство: 10 – 4 = 6. Значит, число четыре – корень уравнения, его решение.

Сейчас мы с вами рассмотрим, как по схеме составить уравнение. Перед нами такая схема. Изучим, что обозначает каждое число в схеме. Число 27 обозначает «целое». Оно состоит из двух частей. Первая «часть» – это число 20, вторая «часть» – это число х.

20 х

Воспользуемся правилом,

ЧАСТЬ + ЧАСТЬ = ЦЕЛОЕ

Запишем равенства:

20 + x = 27

27 – x = 20

Рассмотрим другой пример. Перед вами другая схема. Изучим, где на схеме целое, а где части: х — это «целое», а 30 и 6 – это части.

30 6

Воспользуемся правилом,

Вывод: Уравнение – это равенство, содержащее неизвестное число, которое надо найти. Когда решение уравнения находится легко, пользуются способом подбора. Нужно подобрать такое число, чтобы получилось верное равенство.

Тренировочные задания.

Соедините уравнение с его решением.

Правильные ответы:

2. Выберите и подчеркните среди математических записей уравнения.

15 + 6 = 21

17 – d

b + 3 = 12

3 + 5 > 6

48 – a = 8

9 + e < 39

k – 4 = 10

Правильные ответы:

15 + 6 = 21

17 – d

b + 3 = 12

3 + 5 > 6

48 – a = 8

9 + e < 39

k – 4 = 10

Решение уравнений, сводящихся к числовым равенствам

Решение уравнений, сводящихся к верным числовым равенствам

Уравнения, сводящиеся к верным числовым равенствам, впервые предстают перед учащимися на уроках математики в 7 классе в рамках темы «линейные уравнения».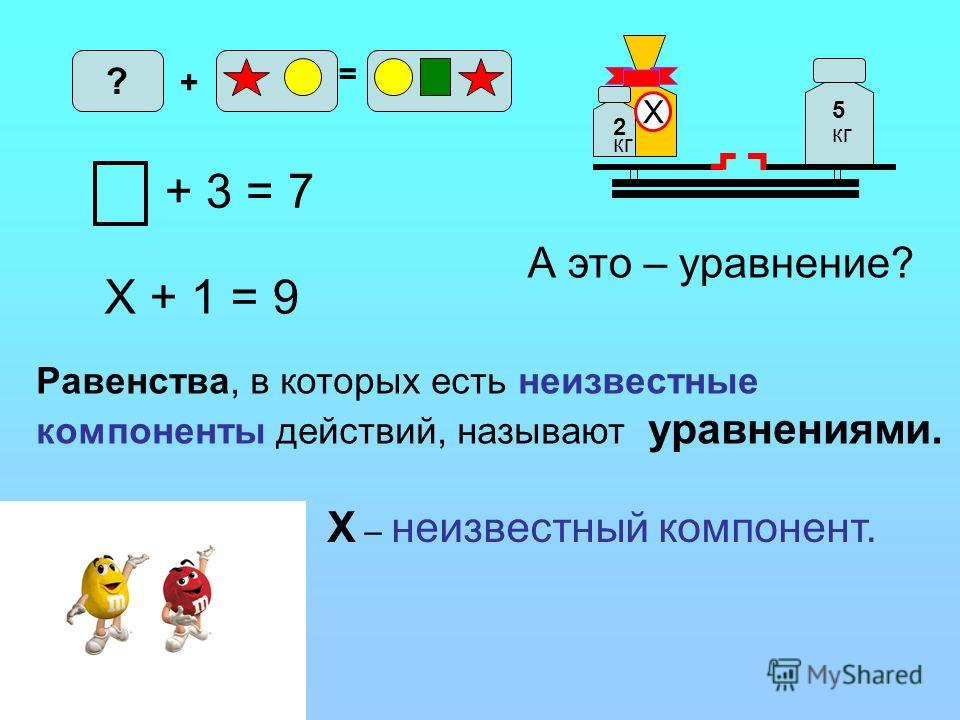 Там разбирается решение уравнения 0·x=0, и мы узнаем, что решением этого уравнения является любое значение переменной x, так как равенство 0·x=0 верно при любом значении переменной [1, с. 25-26; 2, с. 19-20].

Дальше в учебниках математики про решение уравнений, сводящихся к числовым равенствам, нигде обстоятельно не говорят. Однако столкнуться с такими уравнениями вполне можно. В сборниках задач приходилось видеть уравнения, которые через преобразования приводились к виду 0·f(x)=0. Так что на всякий случай давайте разберемся, как они решаются.

Проведем необходимые рассуждения.

Мы знаем, что корень уравнения – это такое значение переменной, при котором уравнение обращается в верное числовое равенство. Исходя из этого, чтобы число x₀ было корнем уравнения 0·f(x)=0, должно быть верным числовое равенство 0·f(x₀)=0. А когда это равенство верное? Очевидно, всегда, когда оно имеет смысл, ведь в этом случае произведение 0·f(x₀) равно нулю как произведение нуля и еще одного числа. А когда равенство 0·f(x₀)=0 имеет смысл? Очевидно, тогда и только тогда, когда x₀ принадлежит области допустимых значений переменной x для решаемого уравнения 0·f(x)=0. Следовательно, решением уравнения 0·f(x)=0 является любое число из его ОДЗ. Другими словами, множество решений уравнения 0·f(x)=0 совпадает с ОДЗ переменной x для этого уравнения.

Таким образом, решение уравнения 0·f(x)=0 заключается в нахождении ОДЗ.

Рассмотрим решение примера.

Теперь стоит поговорить про решение уравнений, которые изначально имеют вид, отличный от 0·f(x)=0, но приводятся к такому виду в результате проведения преобразований. Понятно, что решение последнего уравнения 0·f(x)=0 полностью согласуется с изложенными выше принципами. Нужно лишь грамотно сделать вывод о корнях исходного уравнения по полученному решению уравнения 0·f(x)=0.

Если при переходе от исходного уравнения к уравнению 0·f(x)=0 использовались только преобразования, приводящие к равносильным уравнениям и уравнениям-следствиям, при этом не использовалось возведение обеих частей уравнения в одну и ту же четную степень, то решением исходного уравнения является любое число из ОДЗ для этого уравнения. Обоснуем это.

Понятно, что если использовались только оговоренные преобразования для перехода к уравнению 0·f(x)=0, то оно, либо равносильно исходному, либо является его следствием. Причем, если уравнение 0·f(x)=0 равносильно исходному уравнению, то ОДЗ для него совпадает с ОДЗ для исходного уравнения, множество его решений совпадает с множеством решений исходного уравнения. Мы знаем, что его решением является любое число из ОДЗ. Следовательно, решением исходного уравнения является любое число из его ОДЗ. Если же уравнение 0·f(x)=0 является следствием исходного, то среди его решений могут быть корни, посторонние для исходного уравнения. Причиной их возникновения может выступать лишь расширение ОДЗ, так как к возведению обеих частей уравнения в одну и ту же четную степень мы не прибегали. Значит, они могут быть отсеяны по ОДЗ для исходного уравнения. Решением уравнения 0·f(x)=0 является любое число из ОДЗ для него, поэтому решением исходного уравнения будет любое число из ОДЗ для исходного уравнения.

Приведем пример.

Если же среди преобразований, приводящих уравнение к виду 0·f(x)=0, фигурирует возведение обеих частей уравнения в одну и ту же четную степень, то нельзя утверждать, что решением исходного уравнения является любое число из ОДЗ для этого уравнения. Дело здесь в том, что возведение обеих частей уравнения в одну и ту же четную степень может быть причиной появления посторонних корней в рамках ОДЗ. Этот нюанс детально разобран при решении иррационального уравнения здесь.

К началу страницы

Решение уравнений и систем уравнений в Mathcad

Уравнение и системы уравнений в математическом пакете Mathcad в символьном виде решаются с использованием специального оператора символьного решения solve в сочетании со знаком символьного равенства, который может быть также введен с рабочей панели “Символика”.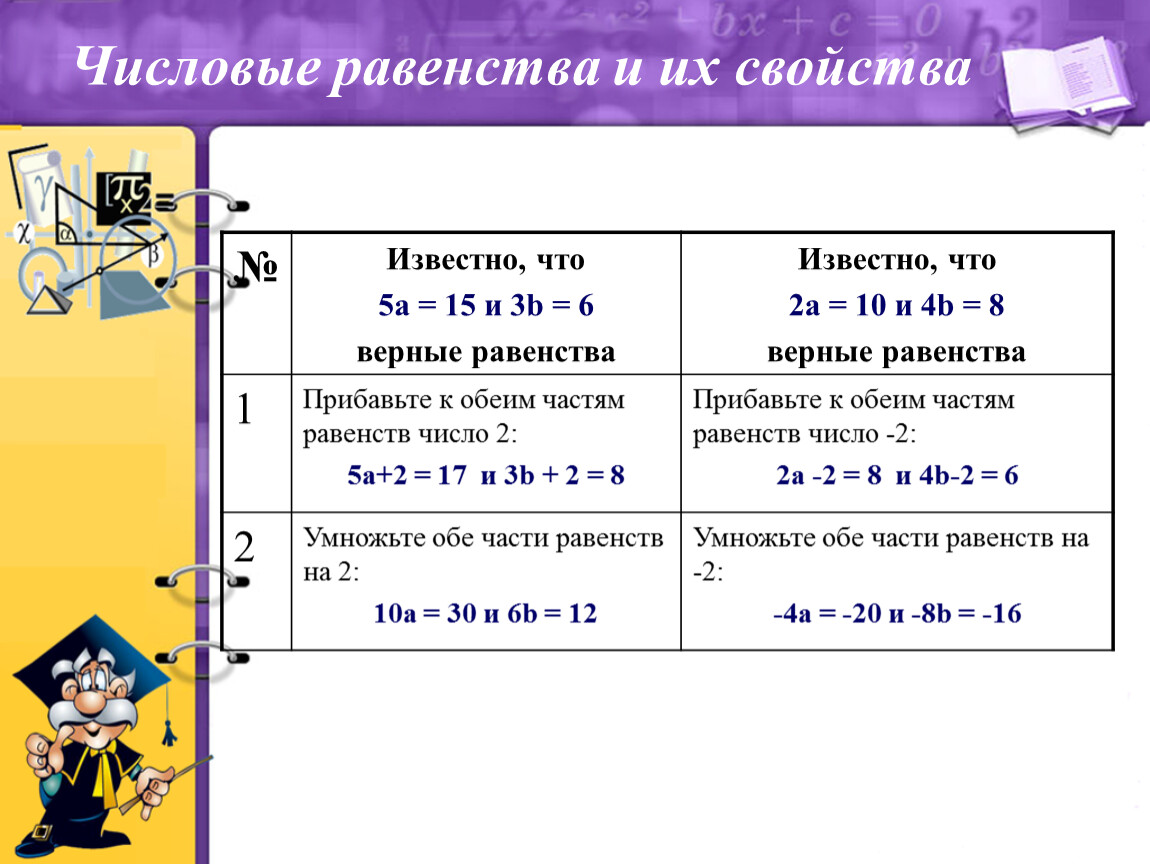 Например:

Аналогичные действия при решении уравнений в Mathcad можно выполнить, используя меню “Символика”. Для этого необходимо записать вычисляемое выражение. Затем выделить переменную, относительно которой решается уравнение, войти в меню Символика, Переменная, Разрешить. Например:

В случае, если необходимо упростить полученный результат, используется знак равенства [=]. Например:

При решении некоторых уравнений, результат включает большое количество символов. Mathcad сохраняет его в буфере, а на дисплей выводитcя сообщение: “This array has more elements than can be displayed at one time. Try using the “submatrix” function” – “Этот массив содержит больше элементов, чем может быть отображено одновременно. Попытайтесь использовать функцию “submatrix””. В этом случае рекомендуется использовать численное решение. Или, в случае необходимости, символьное решение может быть выведено и отображено на дисплее.

Символьное решение может быть получено с использованием блока given … find. В этом случае при записи уравнения для связи его левой и правой части использует символ логического равенства “=” с панели инструментов Boolean, например:

Аналогичным способом решаются системы уравнений в символьном виде. Ниже приводятся примеры решения систем уравнений в символьном виде различными способами. При использовании оператора символьного решения solve в сочетании со знаком символьного равенства система уравнений должна быть задана в виде вектора, который вводится вместо левого маркера оператора solve, а перечень переменных, относительно которых решается система, вместо правого маркера. Например:

Пример использования блока given…find для решения системы уравнений:

Обеспечение гендерного равенства и расширение прав и возможностей всех женщин и девочек — Устойчивое развитие

Цель 5: Обеспечение гендерного равенства и расширение прав и возможностей всех женщин и девочек

Гендерное равенство – это не только одно из основных прав человека, но и необходимая основа для достижения мира, процветания и устойчивого развития. За последние десятилетия был достигнут прогресс: все больше девочек ходят в школу, меньше девочек принуждают заключать ранние браки, все больше женщин работают в парламенте и занимают руководящие должности, а также проводится реформа законов для обеспечения гендерного равенства. Несмотря на эти достижения, сохраняется и множество проблем: по-прежнему повсеместно распространены дискриминационные законы и социальные нормы, женщины так же недостаточно представлены на всех уровнях политического руководства, и каждая пятая женщина и девочка в возрасте от 15 до 49 лет сообщает о физическом или сексуальном насилии со стороны интимного партнера, имевшем место на протяжении года. Последствия пандемии COVID-19 могут свести на нет тот ограниченный прогресс, который был достигнут в области гендерного равенства и прав женщин. Вспышка коронавируса усугубляет существующее неравенство для женщин и девочек во всех сферах – начиная от здравоохранения и экономики и заканчивая безопасностью и социальной защитой.

Женщины играют непропорциональную роль в реагировании на этот вирус, выступая в том числе в качестве медицинских работников первичного звена и лиц, осуществляющих уход на дому. Объем неоплачиваемой работы женщин по уходу значительно вырос из-за закрытия школ и роста потребностей пожилых людей. Женщины также сильнее страдают от экономических последствий COVID-19, поскольку они непропорционально работают на небезопасных рынках труда. Почти 60% женщин работают в секторе неформальной экономики, что подвергает их большему риску обнищания. Пандемия также привела к резкому росту насилия в отношении женщин и девочек. Из-за действующих мер изоляции многие женщины оказываются в ловушке у своих насильников у себя дома, изо всех сил пытаясь получить доступ к услугам, страдающим от сокращений и ограничений. Новые данные свидетельствуют о том, что с момента начала вспышки пандемии усилилось насилие в отношении женщин и девочек, особенно бытовое насилие.

Ответные меры в связи с COVID-19

«Ограниченные достижения в области гендерного равенства и прав женщин, обеспеченные за десятилетия, могут быть сведены на нет из-за пандемии COVID-19», – заявил Генеральный секретарь ООН в апреле 2020 года, призвав правительства уделить женщинам и девочкам центральное место в рамках усилий правительств по восстановлению.

Женщины не только больше всех страдают от этой пандемии, они также являются основой восстановления в общинах.

Если в экономиках женщинам и девочкам будет уделено центральное место, это будет способствовать достижению лучших и более устойчивых результатов в области развития для всех, поддержанию более быстрого восстановления и возвращению мира на путь достижения целей в области устойчивого развития.

Во всех планах реагирования на COVID-19, а также во всех пакетах восстановительных мер и при бюджетировании ресурсов необходимо учитывать гендерные последствия этой пандемии. Это подразумевает: 1) включение женщин и женских организаций в процесс планирования и принятия решений об ответных мерах в связи с COVID-19; 2) преобразование несправедливой неоплачиваемой работы по уходу в новую, инклюзивную «экономику ухода», благоприятную для всех; и 3) разработку социально-экономических планов, преднамеренно ориентированных на жизни и будущее женщин и девочек.

Структура «ООН-женщины» разработала оперативные и целенаправленные ответные меры для смягчения воздействия кризиса COVID-19 на женщин и девочек и для обеспечения того, чтобы долгосрочное восстановление принесло им пользу; данные меры ориентированы на пять приоритетных областей:

смягчение и сокращение гендерного насилия, включая бытовое насилие;
ориентированность пакетов социальной защиты и экономического стимулирования на благо женщин и девочек;
поддержка и осуществление людьми на практике равного распределения работы по уходу;
руководящая роль и участие женщин и девочек в процессе планирования и принятия решений об ответных мерах в связи с COVID-19; и

включение гендерных аспектов в данные и механизмы координации.

5 == 0, x]

Out[2]=

Функция Reduce сводит системы неравенств к простой форме:

(Наберите <= для ввода символа ≤.)

In[1]:=

⨯

Reduce[{0 < x < 2, 1 <= x <= 4}, x]

Out[1]=

Упрощенная форма может состоять из нескольких интервалов:

In[2]:=

⨯

Reduce[(x - 1) (x - 2) (x - 3) (x - 4) > 0, x]

Out[2]=

Функция NumberLinePlot — это удобный способ визуализации этих результатов:

In[3]:=

⨯

NumberLinePlot[x < 1 || 2 < x < 3 || x > 4, {x, -10, 10}]

Out[3]=

Большое число уравнений и формул доступно через естественную форму ввода:

In[1]:=

quadratic equation

Out[1]=

Справочная информация: Полиномиальные уравнения »

Справочная информация: Решение уравнений »

Hands–on Start to
Wolfram Mathematica »

Полная документация »

Demonstrations Project »

Решение уравнения равенства в c++

Нужно форматирование, редактирование займет некоторое время.

c++

int

double

Поделиться

Источник

user2806369

31 марта 2014 в 14:13

3 ответа

решение дифференциального уравнения
Это очень простой вопрос, связанный с решением дифференциального уравнения (DE) в R: Я использую пакет deSolve для решения DE. dX <- a*X + a*b Проблема в том, что я хочу оценить решение во времени (на основе моего столбца времени) и соответствующего значения b (значения b различны в каждый…
Python / Симпи тригонометрическое решение кубического уравнения
Могу ли я получить тригонометрическое символическое решение кубического уравнения с помощью Python/Sympy? http://en.wikipedia.org/wiki/ Casus_irreducibilis http://en.wikipedia.org/wiki/ Cubic_function#Trigonometric_.28and_hyperbolic.29_method

Этот код не даст вам правильного ответа. Расчет можно переписать следующим образом (i*(i+1)*(2*i+1)) < 3 * 4,294,967,295 теперь рассмотрим, что это означает относительно вычисления левой стороны.

Поделиться

michael

31 марта 2014 в 17:10

Ваша проблема вызвана сравнением unsigned int l с выражением, приведенным к int, это дает неопределенные результаты. Во втором случае все внутреннее выражение вычисляется до unsigned int и после вычисления приводится к int (с потерей точности, которая может сократить положительное значение). В вашем первом случае номинатор функции деления приводится к int до того, как применяется деление.

Вам лучше написать свое условие так, а еще лучше вообще опустить приведение (в вашем выражении нет ни одной математической операции float или double , вы имеете дело исключительно с unsigned int ):

while(l>(unsigned int)(i*(i+1)*(2*i+1))/3) { // .

Если вы сделаете это, вы всегда будете ощущать, что ваш цикл работает бесконечно или очень долго. IMHO нет смысла проверять, может ли результат выражения условия быть больше , чем std::numeric_limits<unsigned int>::max(), он не может быть больше.

Поделиться

πάντα ῥεῖ

31 марта 2014 в 14:51

inequality, появляющийся в while loop, имеет порядок 3. Этот тип кривой имеет очень высокий наклон, что означает, что небольшое изменение координаты производит огромное количество в y. while loop скоро столкнется в сравнении с unsigned int и переполнением i, таким образом, дает бесконечный цикл(да, никогда не заканчивающийся, я пробовал).

Решение очень простое. нарушьте равенство в логарифме. Теперь 3-го порядка полинома линейного входа. В конце концов это сработало.

Поделиться

user2806369

01 апреля 2014 в 06:15

Числовые равенства, свойства числовых равенств

После получения общих сведений о равенствах в математике переходим к более узким темам. Материал этой статьи даст представление о свойствах числовых равенств.

Что такое числовое равенство

Первый раз мы сталкиваемся с числовыми равенствами еще в начальной школе, когда происходит знакомство с числами и понятием «столько же». Т.е. самые примитивные числовые равенства это: 2=2, 5=5 и т.д. И на том уровне изучения мы называли их просто равенствами, без уточнения «числовые», и закладывали в них количественный или порядковый смысл (который несут натуральные числа). Например, равенство 2=2 будет соответствовать изображению, на котором – два цветка и на каждом сидит по две шмеля. Или, к примеру, две очереди, где вторыми по порядку стоят Вася и Ваня.

По мере появления знаний об арифметических действиях числовые равенства становятся сложнее: 5+7=12; 6-1=5; 2·1=2; 21:7=3 и т.п. Затем начинают встречаться равенства, в записи которых участвуют числовые выражения разного рода. Например, (2+2)+5=2+(5+2); 4·(4−(1+2))+12:4−1=4·1+3−1 и т.п. Дальше мы знакомимся с прочими видами чисел, и числовые равенства приобретают все более и более интересный и разнообразный вид.

Определение 1

Числовое равенство – это равенство, обе части которого состоят из чисел и/или числовых выражений.

Свойства числовых равенств

Сложно переоценить значимость свойств числовых равенств в математике: они являются опорой многому, определяют принцип работы с числовыми равенствами, методы решений, правила работы с формулами и многое другое.Очевидно, что существует необходимость детального изучения свойств числовых равенств.

Свойства числовых равенств абсолютно согласованы с тем, как определяются действия с числами, а также с определением равных чисел через разность: число a равно числу bтолько в тех случаях, когда разность a−b есть нуль. Далее в описании каждого свойства мы проследим эту связь.

Основные свойства числовых равенств

Изучать свойства числовых равенств начнем с трех базовых свойств, которые присущи всем равенствам. Перечислим основные свойства числовых равенств:

свойство рефлексивности: a=a;
свойство симметричности: если a=b, то b=a;
свойство транзитивности: если a=b и b=c, то a=c,где a, b и c – произвольные числа.

Определение 2

Свойство рефлексивности обозначает факт равенства числа самому себе: к примеру, 6=6, −3=−3, 437=437 и т.п.

Доказательство 1

Нетрудно продемонстрировать справедливость равенства a−a=0для любого числа a: разность a−a можно записать как сумму a+(−a), а свойство сложения чисел дает нам возможность утверждать, что любому числу a соответствует единственное противоположное число −a, и сумма их есть нуль.

Определение 3

Согласно свойству симметричности числовых равенств: если число a равно числу b,

то число b равно числу a. К примеру, 43=64, тогда 64=43.

Доказательство 2

Обосновать данное свойство можно через разность чисел. Условию a=b соответствует равенство a−b=0. Докажем, что b−a=0.

Запишем разность b−aв виде −(a−b), опираясь на правило раскрытия скобок, перед которыми стоит знак минус. Новая запись выражения равна -0, а число, противоположное нулю, это нуль. Таким образом, b−a=0, следовательно: b=a.

Определение 4

Свойство транзитивности числовых равенств гласит, что два числа равны друг другу в случае их одновременного равенства третьему числу. К примеру, если 81=9 и 9=32, то 81=32.

Свойству транзитивности также отвечает определение равных чисел через разность и свойства действий с числами. Равенствам a=b и b=c соответствуют равенства a−b=0 и b−c=0.

Доказательство 3

Докажем справедливость равенства a−c=0, из чего последует равенство чисел a и c. Посколькусложение числа с нулем не меняет само число, то a−c запишем в виде a+0−c. Вместо нуля подставим сумму противоположных чисел −b и b, тогда крайнее выражение станет таким: a+(−b+b)−c. Выполним группировку слагаемых: (a−b)+(b−c). Разности в скобках равны нулю, тогда и сумма (a−b)+(b−c) есть нуль. Это доказывает, что, когда a−b=0 и b−c=0, верно равенство a−c=0, откуда a=c.

Прочие важные свойства числовых равенств

Основные свойства числовых равенств, рассмотренные выше, являются базисом для ряда дополнительных свойств, довольно ценных в разрезе практики. Перечислим их:

Определение 5

Прибавив к (или убавив от) обеим частям числового равенства, являющегося верным, одно и то же число, получим верное числовое равенство. Запишем буквенно: если a=b, где a и b – некоторые числа, то a+c=b+c при любом c.

Доказательство 4

В качестве обоснования запишем разность (a+c)−(b+c).

Это выражение легко преобразуется в вид (a−b)+(c−c).

Из a=b по условию следует, что a−b=0 и c−c=0, тогда (a−b)+(c−c)=0+0=0. Это доказывает, что (a+c)−(b+c)=0, следовательно, a+c=b+c;

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание

Определение 6

Если обе части верного числового равенства перемножить с любым числом или разделить на число, не равное нулю, тогда получим верное числовое равенство.

Запишем буквенно: когда a=b, то a·c=b·c при любом числе c. Если c≠0, тогда и a:c=b:c.

Доказательство 5

Равенство верно: a·c−b·c=(a−b)·c=0·c=0, и из него следует равенство произведений a·c и b·c. А деление на отличное от нуля число c возможно записать как умножение на обратное число 1c;

Определение 7

При a и b, отличных от нуля и равных между собой, обратные им числа также равны.

Запишем: когда a≠0, b≠0 и a=b, то 1a=1b. Крайнее равенство нетрудно доказать: с этой целью разделим обе части равенства a=b на число, равное произведению a·b и не равное нулю.

Укажем еще на пару свойств, которые позволяют осуществлять сложение и умножение соответствующих частей верных числовых равенств:

Определение 8

При почленном сложении верных числовых равенств получается верное равенство. Запись этого свойства такова: если a=b и c=d, то a+c=b+d для любых чисел a, b, c и d.

Доказательство 6

Обосновать это полезное свойство возможно, опираясь на указанные ранее свойства. Мы знаем, что к обеим частям верного равенства возможно прибавить любое число.

К равенству a=bприбавим число c, а к равенству c=d — число b, итогом станут верные числовые равенства: a+c=b+c и c+b=d+b. Крайнее запишем в виде: b+c=b+d. Из равенств a+c=b+c и b+c=b+d согласно свойству транзитивности следует равенство a+c=b+d. Что и нужно было доказать.

Необходимо уточнить, что почленно можно сложить не только два верных числовых равенства, но и три, и более;

Определение 7

Наконец, опишем такое свойство: почленное перемножение двух верных числовых равенств дает верное равенство. Запишем при помощи букв: если a=b и c=d, то a·c=b·d.

Доказательство 7

Доказательство этого свойства подобно доказательству предыдущего. Умножим обе части равенства на любое число, умножим a=b на c, а c=d на b, получим верные числовые равенства a·c=b·c и c·b=d·b. Крайнее запишем как b·c=b·d. Свойство транзитивности дает возможность из равенства a·c=b·c и b·c=b·d вывести равенство a·c=b·d, которое нам необходимо было доказать.

И вновь уточним, что данное свойство применимо для двух, трех и более числовых равенств.

Так, можно записать: если a=b, то an=bn для любых чисел a и b, и любого натурального числа n.

Завершим данную статью, собрав для наглядности все рассмотренные свойства:

a=a.

Если a=b, то b=a.

Если a=bи b=c, то a=c.

Если a=b, то a+c=b+c.

Если a=b, то a·c=b·c.

Если a=bи с≠0, то a:c=b:c.

Если a=b, a=b, a≠0 и b≠0, то 1a=1b.

Если a=b и c=d, то a·c=b·d.

Если a=b, то an=bn.

Алгебра — Решения и наборы решений

Показать мобильное уведомление

Показать все заметки Скрыть все заметки

Похоже, вы используете устройство с «узкой» шириной экрана (, т.е. , вероятно, вы используете мобильный телефон). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме.Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.

Раздел 2-1: Решения и наборы решений

Мы начнем эту главу с довольно короткого раздела с некоторой базовой терминологией, которую мы довольно регулярно используем при решении уравнений и неравенств.? 0 \\ 9–9 & = 0 \\ 0 & = 0 \, \, \, \, {\ mbox {OK}} \ end {align *} \]

Итак, мы спрашиваем, равна ли правая сторона левой стороне после того, как мы подключим предложенное решение. В этом смысл «?» над знаком равенства в первой строке.

Поскольку правая и левая части совпадают, мы говорим, что \ (x = 3 \) удовлетворяет уравнению.

b \ (y = 8 \) in \ (3 \ left ({y + 1} \ right) = 4y — 5 \) Показать решение

Итак, мы хотим увидеть, удовлетворяет ли \ (y = 8 \) уравнению.? 4 \ left (8 \ right) — 5 \\ 27 & = 27 \, \, \, \, {\ mbox {OK}} \ end {align *} \]

Итак, \ (y = 8 \) удовлетворяет уравнению и, следовательно, является решением.

c \ (z = 1 \) in \ (2 \ left ({z — 5} \ right) \ le 4z \) Показать решение

В этом случае мы имеем неравенство, и в этом случае «удовлетворить» означает что-то немного другое. В этом случае мы будем говорить, что число будет удовлетворять неравенству, если после его подключения мы получим в результате истинное неравенство.

Давайте проверим \ (z = 1 \).? 4 \ left (1 \ right) \\ — 8 & \ le 4 \, \, \, \, {\ mbox {OK}} \ end {align *} \]

Итак, -8 меньше или равно 4 (на самом деле меньше), и мы имеем истинное неравенство. Следовательно, \ (z = 1 \) будет удовлетворять неравенству и, следовательно, является решением

d \ (z = — 5 \) in \ (2 \ left ({z — 5} \ right) \ le 4z \) Показать решение

Это то же неравенство с другим значением, давайте это проверим.

\ [\ begin {align *} 2 \ left ({- 5 — 5} \ right) & \ mathop \ le \ limits ^? 4 \ left ({- 5} \ right) \\ — 20 & \ le — 20 \, \, \, \, {\ mbox {OK}} \ end {align *} \]

В этом случае -20 меньше или равно -20 (в данном случае оно равно), и снова мы получаем истинное неравенство, и поэтому \ (z = — 5 \) удовлетворяет неравенству и поэтому будет решением.

Мы также должны сделать быстрый пример чисел, которые не являются решением, чтобы мы могли увидеть, как они также будут работать.

Пример 2 Покажите, что следующие числа не являются решениями данного уравнения или неравенства.

\ (y = — 2 \) дюйм \ (3 \ left ({y + 1} \ right) = 4y — 5 \)
\ (z = — 12 \) в \ (2 \ left ({z — 5} \ right) \ le 4z \)

Показать все решения Скрыть все решения

a \ (y = — 2 \) in \ (3 \ left ({y + 1} \ right) = 4y — 5 \) Показать решение

В этом случае мы делаем то же самое, что и в предыдущем примере.? 4 \ left ({- 2} \ right) — 5 \\ — 3 & \ ne — 13 \, \, \, \, {\ mbox {НЕ ОК}} \ end {align *} \]

Итак, -3 — это не то же самое, что -13, и поэтому уравнение не выполняется. Следовательно, \ (y = — 2 \) не является решением уравнения.

b \ (z = — 12 \) in \ (2 \ left ({z — 5} \ right) \ le 4z \) Показать решение

На этот раз неравенство. ? 4 \ left ({- 12} \ right) \\ — 34 \ require {cancel} & \ bcancel {\ le} — 48 \, \, \, \, {\ mbox {NOT OK}} \ end {align * } \]

В этом случае -34 НЕ меньше или равно -48, поэтому неравенство не выполняется.2} — 9 = 0 \). В этом случае \ (x = — 3 \) также является решением.

Мы называем полный набор всех решений набором решений для уравнения или неравенства. Есть также некоторые формальные обозначения для наборов решений, хотя мы не будем часто их использовать в этом курсе. Несмотря на это, мы все равно должны это признать.

Для уравнений мы обозначаем множество решений, заключая все решения в фигурные скобки, \ (\ left \ {{} \ right \} \). Вот наборы решений для двух уравнений, которые мы рассмотрели выше.2} — 9 & = 0 & \ hspace {0,25 дюйма} & {\ mbox {Набор решений}}: \, \, \, \ left \ {{- 3,3} \ right \} \ end {align *} \]

Для неравенств используются аналогичные обозначения. В зависимости от сложности неравенства набор решений может быть одним числом или диапазоном чисел. Если это одно число, мы используем те же обозначения, что и для уравнений. Если набор решений представляет собой диапазон чисел, как тот, который мы рассмотрели выше, мы будем использовать что-то, называемое нотацией конструктора наборов .Вот набор решений для неравенства, которое мы рассмотрели выше.

\ [\ left \ {{z | z \ ge — 5} \ right \} \]

Это читается как: «Множество всех \ (z \) таких, что \ (z \) больше или равно -5».

Большинство неравенств, которые мы будем рассматривать, будут иметь достаточно простые наборы решений, которые мы часто сокращаем как

\ [z \ ge — 5 \]

Есть еще одна последняя тема, которую мы должны затронуть в отношении наборов решений, прежде чем покинуть этот раздел.2} &

Если мы ограничимся только реальными решениями (что мы не всегда будем делать), тогда у уравнения не будет решения. Возведение в квадрат \ (x \) делает \ (x \) больше нуля, затем добавление 1 к этому означает, что левая часть гарантированно будет не меньше 1. Другими словами, у этого уравнения нет реального решения. По той же основной причине нет решения неравенства. Возведение любого вещественного \ (x \) в квадрат делает его положительным или нулевым, и поэтому никогда не будет отрицательным.

Нам нужен способ обозначить тот факт, что здесь нет решений.В обозначении набора решений мы говорим, что набор решений — это пустой , и обозначаем его символом: \ (\ emptyset \). Этот символ часто называют пустым набором .

Теперь нам нужно сделать пару заключительных замечаний, прежде чем покинуть этот раздел.

В приведенном выше обсуждении пустых множеств мы предполагали, что ищем только реальные решения. Хотя это то, что мы будем делать с неравенствами, мы не будем ограничиваться реальными решениями с уравнениями.2} + 1 = 0 \) действительно имеет сложные решения.

Наконец, как отмечалось выше, в этом курсе мы не будем часто использовать нотацию набора решений. Это хорошее обозначение, которое иногда может использоваться, особенно для сложных решений. Однако для подавляющего большинства уравнений и неравенств, которые мы будем рассматривать, будут достаточно простые наборы решений, так что их будет проще записать и отпустить. Следовательно, это то, что мы не будем использовать для обозначений наших наборов решений.Однако вы должны знать об обозначениях и понимать, что они означают.

Как найти решение системы уравнений

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
то
информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

Начальная алгебра
Урок 13: Свойство равенства умножения

Цели обучения

По завершении этого руководства вы сможете:

Используйте свойства умножения и деления равенств для решения
линейный
уравнения.
Решите уравнение, используя более одного свойства.
Уметь выражать последовательные целые числа в виде x ,
если первое целое число x .
Умейте выразить четные последовательные целые числа в виде x ,
если первое четное целое число — x .
Знайте, как выразить нечетные последовательные целые числа через x ,
если первое нечетное целое число равно x .

Введение

Как упоминалось в Руководстве по
12: Дополнение
Свойство равенства , решение уравнений попадает в
сердце
о том, о чем алгебра. Как и в Уроке 12, мы будем
смотреть конкретно на линейные уравнения и их решения.

Мы начнем медленно и решим уравнения, в которых используются только
умножение
или разделить собственность на равенство, чтобы убедиться, что у вас есть индивидуальный
концепции
вниз.Тогда мы наберем темп и смешаем их там, где вам нужно
использовать несколько свойств и шагов для выполнения работы.

Уравнения могут быть использованы для решения различных
проблемы. Позже
учебные пособия, мы будем использовать их для решения текстовых задач.

Учебник

Уравнение

Два выражения равны друг другу.

Линейное уравнение
в одной переменной

Уравнение, которое можно записать в виде
ax + b = c
где a, b и c — константы.

Ниже приведен пример линейного уравнения:

3 x — 4 = 5

Решение

Значение, такое, что при замене переменной на
it,
это делает
уравнение верно.

(левая сторона выходит равной правой)

Набор решений

Набор всех решений

Решение линейного уравнения
в целом

Получите переменную, которую вы решаете, в одиночку с одной стороны
и все
else на другой стороне, используя ОБРАТНЫЕ операции.

В Урок 12:
Свойство сложения
равенства , мы показали вам, как решать уравнения с помощью сложения
и вычитающие свойства равенства . В этом уроке мы
будут
смотреть на свойства умножения и деления.

Умножение и деление
Свойства равенства

Если a = b, то a (c) = b (c)

Если a = b, то a / c = b / c, где c —
не равно 0.

Другими словами, , если два выражения равны
друг друга и ты
умножить или разделить (кроме 0) одну и ту же константу на оба
стороны,
обе стороны останутся равными.

Обратите внимание, что умножение и деление являются обратными
операции каждого
Другие.Например, если у вас есть число, которое умножается
что вам нужно перейти к другой стороне уравнения, тогда вы бы
разделите его с обеих сторон этого уравнения.

Пример
1 : Решите уравнение

* Обратно дел.на 2 это
мульт. по 2

Если вы вернете 10 для x дюйма
оригинал
проблема, вы увидите, что 10 — это решение, которое мы ищем.

Пример
2 : Решите уравнение.

* Инверсная по отношению к мульт.на 5 дел.
по 5

Если вы вставите 7/5 обратно для x в оригинале
проблема, вы увидите, что 7/5 — это решение, которое мы ищем.

Пример
3 : Решите уравнение

* Инверсная по отношению к мульт. на -3/2
div. на -3/2
(или умножение на обратное -2/3)

Если вы вернете -6 для , то получите дюйма
оригинал
проблема вы увидите, что -6 — это решение, которое мы ищем.

Обратите внимание, что не имеет значения, на какой стороне находится переменная.
на. -6 = a означает то же, что и a = -6.

Однако в большинстве случаев мы должны
использовать несколько
свойства для выполнения работы. Ниже приводится стратегия, которая
вы можете использовать, чтобы помочь вам решить линейные уравнения, которые немного
более
вовлеченный.

Стратегия решения линейного
Уравнение

Обратите внимание, что ваш учитель или
книга ты
использование, возможно, сформулировало эти шаги немного иначе, чем я, но
Это
все сводится к одной и той же концепции — включите свою переменную
один
сторона и все остальное с другой, используя обратные операции.

Шаг 1. При необходимости упростите каждую сторону.

Шаг 2: Используйте Доп. / Под. Свойства для
переместить переменную
срок в одну сторону и все остальные условия в другую сторону.

Шаг 3: Используйте Mult. /Div. Свойства для
удалить любые значения
которые находятся перед переменной.

Шаг 4. Проверьте свой ответ.

Все сводится к тому, что
ты хочешь получить
переменная, которую вы решаете только с одной стороны, и все остальное
с другой стороны, используя ОБРАТНЫЕ операции.

Пример
4 : Решите уравнение.

* Инверсия доп. 10 является суб. 10

* Инверсная по отношению к мульт. на -3 — это div.
по -3

Будьте осторожны, начиная со строки 4
к строке 5.
Да, есть отрицательный знак.Но операция между -3 и x — это умножение, а не вычитание. Итак, если бы вы
Добавлять
3 в обе стороны, вы бы получили -3 x + 3 вместо желаемых x .

Если вы вернете 1 вместо x в исходной задаче, вы
увидим, что 1
это решение, которое мы ищем.

Пример
5 : Решите уравнение.

* Упростите, объединив подобное
сроки

* Обратное от sub. 5 добавлено 5

* Инверсная по отношению к мульт. на -1 — это div.
по -1

Если вы вернете -2 для x дюйма
оригинал
проблема вы увидите, что -2 — это решение, которое мы ищем.

Пример
6 : Решите уравнение.

* Упростите, объединив подобное
термины
* Инверсия сложения 2 x — sub. 2 х

* Обратное от sub.2 прибавить 2

* Инверсная по отношению к мульт. на 7 дел.
по 7

Если вы вставите 2 обратно для x дюйма
оригинал
проблема вы увидите, что 2 — это решение, которое мы ищем.

Целые числа, идущие подряд — целые числа, следующие за
друг друга в
заказывать.

Например, 5, 6 и 7 — три
последовательные целые числа.

Если мы позволим x представить первое целое число,
как бы мы представили второе подряд целое число в виде x ? Что ж, если мы посмотрим на 5, 6 и 7 — обратите внимание, что 6 — это один
больше 5, первое целое число.

В общем, мы могли бы представить второй
последовательное целое число на x + 1 . А как насчет третьего целого числа подряд.

Ну заметьте, как 7 на 2 больше 5. В
в общем, мы могли бы представить
третье последовательное целое число как x + 2.

Последовательные ЧЕТНЫЕ целые числа — четные целые числа,
следовать друг за другом
чтобы.

Например, 4, 6 и 8 — три последовательных
даже целые числа.

Если мы позволим x представить первое ЧЕТНОЕ целое число,
как бы мы представили второе подряд четное целое число в виде x ?
Обратите внимание, что 6 на два больше, чем 4, первое четное число.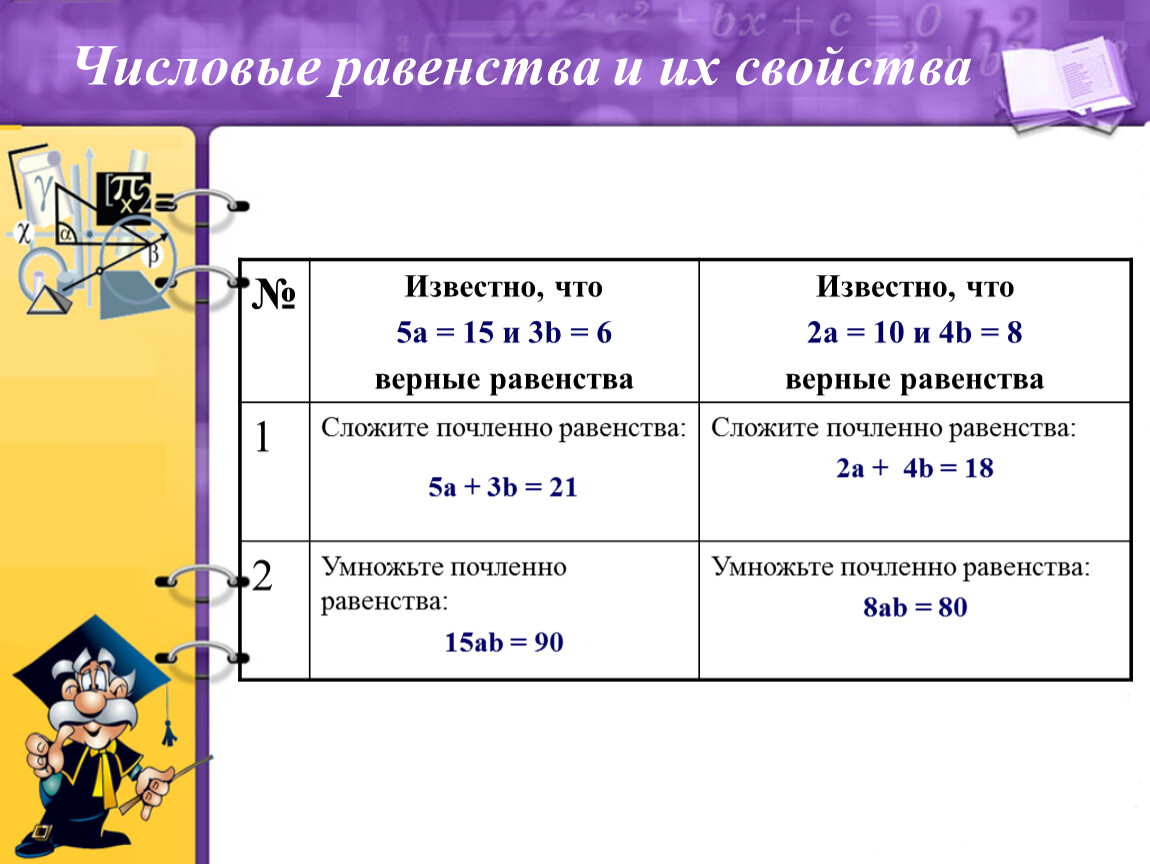

В общем, мы могли бы представить второй
последовательное ЧЕТНОЕ целое число
по x + 2 .

А как же третий подряд четный
целое число? Хорошо подмечено
как 8 на 4 больше, чем 4. В общем, мы могли бы представить
в третьих
последовательное ЧЕТНОЕ целое число как x + 4.

Последовательные целые нечетные числа — нечетные целые числа,
следовать друг за другом
чтобы.

Например, 5, 7 и 9 — три последовательных
нечетные целые числа.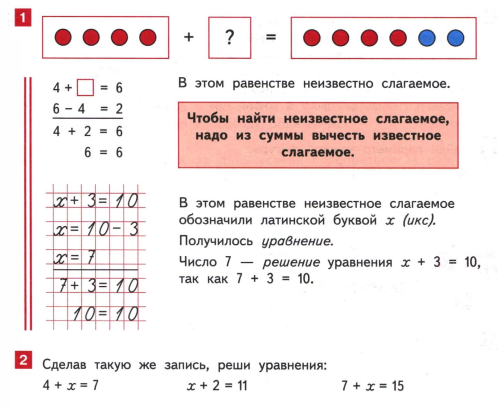

Если мы позволим x представить первое целое нечетное число,
как бы мы представили второе подряд нечетное целое число в виде x ?
Обратите внимание, что 7 на два больше, чем 5, первое нечетное целое число.

В общем, мы могли бы представить второй
последовательное нечетное целое число
по x + 2.

А как насчет третьего подряд нечетного
целое число? Ну заметьте как
9 на 4 больше, чем 5. В общем, можно было бы представить третьим
последовательный
Целое число ODD как x + 4.

Обратите внимание, что распространенное заблуждение состоит в том, что, поскольку
мы хотим нечетное число
что мы не должны складывать 2, которое является четным числом. Держать в
помните, что x представляет ODD
число и
что следующее нечетное число находится на расстоянии 2, так же, как 7 находится на расстоянии 2 от 5, поэтому мы
нужно прибавить 2 к первому нечетному числу, чтобы перейти ко второму подряд
нечетное число.

Пример
7 : Напишите алгебраическое выражение и упростите, если
возможный.

Если x представляет первую
из четырех последовательных
целые числа, выразите сумму четырех целых чисел через x.

Мы можем представить их так:

x
= 1-е целое число

х + 1
= 2-е целое число подряд

х +
2 = 3-е целое число подряд

х + 3
= 4-е целое число подряд

Второе, нам нужно записать как сумму четырех
целые числа, а затем
упростить :

* Сумма четырех минусов. целые числа
* Объединить похожие термины

Пример
8 : Напишите алгебраическое выражение и упростите, если
возможный.

Если x представляет первую
из трех нечетных последовательных
целые числа, выражают сумму первого и третьего целых чисел в виде x .

Мы можем представить их так:

x
= 1-е нечетное целое

х + 2
= 2-й подряд нечетный
целое число

х +
4 = 3-й подряд нечетный
целое число

Второе, нам нужно записать его как — сумму первого и
третьи нечетные целые числа
в терминах x , а затем упростим его:

* Сумма 1-го и 3-го нечетных
целые числа
* Объединить похожие термины

Практические задачи

Это практические задачи, которые помогут вам
следующий уровень.
Это позволит вам проверить и понять, понимаете ли вы
эти
типы проблем. Math работает так же, как
что-нибудь
иначе, если вы хотите добиться успеха в этом, вам нужно практиковаться
Это.
Даже лучшие спортсмены и музыканты получали помощь и много
практиковаться, практиковаться, практиковаться, чтобы стать лучше в своем виде спорта или инструменте.
На самом деле не бывает слишком много практики.

Чтобы получить от них максимальную отдачу, вы должны работать
проблема на
свой собственный, а затем проверьте свой ответ, щелкнув ссылку для
ответ / обсуждение
для этой проблемы . По ссылке вы найдете ответ
а также любые шаги, которые позволили найти этот ответ.

Практика
Задачи 1a — 1d: Решите данное уравнение.

Практика
Задача 2a: Напишите алгебраическое выражение и
если возможно, упростите.

2а. Если x представляет собой первое из
три последовательных целых числа, выражают сумму трех целых чисел в
термины
из х .
(ответ / обсуждение
к 2а)

Нужна дополнительная помощь по этим темам?

Последний раз редактировал Ким Сьюард 26 июля 2011 г.
Авторские права на все содержание (C) 2001 — 2010, WTAMU и Kim Seward. Все права защищены.

2.1 Решение уравнений с использованием свойств равенства и сложения — Элементарная алгебра 2e

Задачи обучения

К концу этого раздела вы сможете:

Проверить решение уравнения
Решите уравнения, используя свойства равенства для вычитания и сложения
Решите уравнения, требующие упрощения
Переведите в уравнение и решите
Перевод и решение приложений

Будьте готовы 2.1

Прежде чем начать, пройдите тест на готовность.

Вычислить x + 4x + 4, когда x = −3x = −3.
Если вы пропустили эту проблему, просмотрите Пример 1.54.

Будьте готовы 2.2

Вычислите 15 − y15 − y, когда y = −5y = −5.
Если вы пропустили эту проблему, просмотрите Пример 1.56.

Будьте готовы 2.3

Упростим 4 (4n + 1) −15n4 (4n + 1) −15n.
Если вы пропустили эту проблему, просмотрите Пример 1. 138.

Будьте готовы 2.4

Перевести в алгебру «5 меньше xx.”
Если вы пропустили эту проблему, просмотрите Пример 1.26.

Проверьте решение уравнения

Решение уравнения похоже на решение головоломки. Цель решения уравнения состоит в том, чтобы найти значение или значения переменной, которые делают каждую часть уравнения одинаковой, чтобы мы получили истинное утверждение. Любое значение переменной, которое делает уравнение истинным, называется решением уравнения. Это ответ на загадку!

Решение уравнения

Решение уравнения — это значение переменной, которая делает истинное утверждение при подстановке в уравнение.

How To

Чтобы определить, является ли число решением уравнения.

Шаг 1. Подставьте число вместо переменной в уравнении.
Шаг 2. Упростите выражения в обеих частях уравнения.
Шаг 3. Определите, истинно ли полученное уравнение (левая часть равна правой части).
Если это правда, число является решением.
Если это не так, число не решение.

Пример 2.1

Определите, является ли x = 32x = 32 решением 4x − 2 = 2x + 14x − 2 = 2x + 1.

Решение

Поскольку решение уравнения — это значение переменной, которая делает уравнение истинным, начните с подстановки значения решения вместо переменной.

Поскольку x = 32x = 32 приводит к истинному уравнению (4 фактически равно 4), 3232 является решением уравнения 4x − 2 = 2x + 14x − 2 = 2x + 1.

Попробуйте 2.1

Является ли y = 43y = 43 решением 9y + 2 = 6y + 39y + 2 = 6y + 3?

Попробуй 2.2

Является ли y = 75y = 75 решением 5y + 3 = 10y − 45y + 3 = 10y − 4?

Решение уравнений с использованием свойств равенства и сложения

Мы собираемся использовать модель, чтобы прояснить процесс решения уравнения. Конверт представляет переменную — поскольку ее содержимое неизвестно — и каждый счетчик представляет собой единицу. Мы разместим один конверт и несколько счетчиков в нашей рабочей области, как показано на рисунке 2.2. Обе стороны рабочей области имеют одинаковое количество счетчиков, но некоторые счетчики «спрятаны» в конверте.Вы можете сказать, сколько фишек в конверте?

Рис. 2.2 На рисунке показана модель уравнения с одной переменной. В левой части рабочего пространства находится неизвестное (конверт) и три счетчика, а в правой части рабочего пространства — восемь счетчиков.

О чем ты думаешь? Какие шаги вы предпринимаете, чтобы выяснить, сколько фишек в конверте?

Возможно, вы думаете: «Мне нужно удалить 3 фишки в нижнем левом углу, чтобы получить конверт сам по себе.3 фишки слева можно сопоставить с 3 фишками справа, так что я могу убрать их с обеих сторон. Остается пять справа — значит, в конверте должно быть 5 фишек ». См. Рисунок 2.3 для иллюстрации этого процесса.

Рис. 2.3 На рисунке показана модель решения уравнения с одной переменной. С обеих сторон рабочей области удалите три фишки, оставив только неизвестное (конверт) и пять фишек с правой стороны. Неизвестное равно пяти фишкам.

Какое алгебраическое уравнение подходит для этой ситуации? На рисунке 2.4 каждая сторона рабочей области представляет собой выражение, а центральная линия заменяет знак равенства. Назовем содержимое конверта xx.

Рисунок 2.4 На рисунке показана модель уравнения x + 3 = 8x + 3 = 8.

Давайте алгебраически запишем шаги, которые мы предприняли, чтобы узнать, сколько счетчиков было в конверте:


Сначала мы сняли по три с каждой стороны.
Потом осталось пятеро.

Чек:

Пять в конверте плюс еще три равняются восьми!

Наша модель дала нам представление о том, что нам нужно сделать, чтобы решить один вид уравнения. Цель состоит в том, чтобы изолировать переменную отдельно от одной стороны уравнения. Чтобы решить такие уравнения математически, мы используем свойство равенства вычитания.

Свойство равенства вычитания

Для любых номеров a , b и c ,

Если a = b, то a − c = b − cIfa = b, тогда a − c = b − c

Если вы вычтите одинаковую величину из обеих частей уравнения, вы все равно получите равенство.

Манипулятивная математика

Выполнение упражнения по манипуляции математикой «Свойство вычитания равенства» поможет вам лучше понять, как решать уравнения с помощью свойства равенства вычитания.

Давайте посмотрим, как использовать это свойство для решения уравнения. Помните, что цель состоит в том, чтобы изолировать переменную с одной стороны уравнения. И мы проверяем наши решения, подставляя значение в уравнение, чтобы убедиться, что у нас есть верное утверждение.

Пример 2.2

Решите: y + 37 = −13.y + 37 = −13.

Решение

Чтобы получить y отдельно, мы отменим сложение 37, используя свойство равенства вычитания.

Поскольку y = −50y = −50 делает y + 37 = −13y + 37 = −13 истинным утверждением, у нас есть решение этого уравнения.

Попробуйте 2.3

Решите: x + 19 = −27x + 19 = −27.

Попробуйте 2.4

Решите: x + 16 = −34x + 16 = −34.

Что происходит, когда в уравнении вычитается число из переменной, как в уравнении x − 5 = 8x − 5 = 8? Мы используем другое свойство уравнений для решения уравнений, в которых число вычитается из переменной.Мы хотим изолировать переменную, поэтому, чтобы «отменить» вычитание, мы добавим число к обеим сторонам. Мы используем аддитивное свойство равенства.

Дополнительное свойство равенства

Для любых номеров a , b и c ,

Если a = b, то a + c = b + cIfa = b, тогда a + c = b + c

Когда вы добавляете одинаковую величину к обеим сторонам уравнения, вы все равно получаете равенство.

В примере 2.2, 37 было добавлено к y , поэтому мы вычли 37, чтобы «отменить» сложение.В примере 2.3 нам нужно будет «отменить» вычитание, используя свойство сложения равенства.

Пример 2.3

Решите: a − 28 = −37.a − 28 = −37.

Попробуйте 2.5

Решите: n − 61 = −75. N − 61 = −75.

Попробуйте 2.6

Решите: p − 41 = −73.p − 41 = −73.

Пример 2.4

Решите: x − 58 = 34. x − 58 = 34.

Попробуйте 2.7

Решите: p − 23 = 56. p − 23 = 56.

Попробуй 2,8

Решите: q − 12 = 56.q − 12 = 56.

Следующим примером будет уравнение с десятичными знаками.

Пример 2.5

Решите: n − 0,63 = −4,2.n − 0,63 = −4,2.

Попробуйте 2.9

Решите: b − 0,47 = −2,1. B − 0,47 = −2,1.

Попробуй 2.10

Решите: c − 0,93 = −4,6.c − 0,93 = −4,6.

Решите уравнения, требующие упрощения

В предыдущих примерах нам удалось выделить переменную всего за одну операцию. Большинство уравнений, с которыми мы сталкиваемся в алгебре, требует дополнительных действий для решения.Обычно нам нужно упростить одну или обе стороны уравнения, прежде чем использовать свойства равенства вычитания или сложения.

Вы всегда должны максимально упрощать, прежде чем пытаться изолировать переменную. Помните, что упрощение выражения означает выполнение всех операций в выражении. Упрощайте одну сторону уравнения за раз. Обратите внимание, что упрощение отличается от процесса, используемого для решения уравнения, в котором мы применяем операцию к обеим сторонам.

Пример 2.6

Как решать уравнения, требующие упрощения

Решите: 9x − 5−8x − 6 = 7,9x − 5−8x − 6 = 7.

Попробуйте 2.11

Решите: 8y − 4−7y − 7 = 4.8y − 4−7y − 7 = 4.

Попробуйте 2.12

Решите: 6z + 5−5z − 4 = 3.6z + 5−5z − 4 = 3.

Пример 2.7

Решите: 5 (n − 4) −4n = −8,5 (n − 4) −4n = −8.

Решение

Мы максимально упрощаем обе части уравнения, прежде чем пытаться изолировать переменную.

Попробуй 2.13

Решите: 5 (p − 3) −4p = −10,5 (p − 3) −4p = −10.

Попробуйте 2.14

Решите: 4 (q + 2) −3q = −8,4 (q + 2) −3q = −8.

Пример 2.8

Решите: 3 (2y − 1) −5y = 2 (y + 1) −2 (y + 3). 3 (2y − 1) −5y = 2 (y + 1) −2 (y + 3).

Решение

Мы упрощаем обе части уравнения, прежде чем изолировать переменную.

Попробуйте 2.15

Решите: 4 (2h − 3) −7h = 6 (h − 2) −6 (h − 1). 4 (2h − 3) −7h = 6 (h − 2) −6 (h − 1).

Попробуйте 2.16

Решите: 2 (5x + 2) −9x = 3 (x − 2) −3 (x − 4).2 (5x + 2) −9x = 3 (x − 2) −3 (x − 4).

Перевести в уравнение и решить

Чтобы решать приложения алгебраически, мы начнем с перевода английских предложений в уравнения. Нашим первым шагом будет поиск слова (или слов), которое переводится как знак равенства. Таблица 2.1 показывает нам некоторые из часто используемых слов.

Равно =
это равно то же самое, что и результат дает было будет

Таблица 2.1

Шаги, которые мы используем для преобразования предложения в уравнение, перечислены ниже.

How To

Переведите английское предложение в алгебраическое уравнение.

Шаг 1. Найдите слово (слова) «равно». Переведите на знак равенства (=).
Шаг 2. Переведите слова слева от слова (слов) «равно» в алгебраическое выражение.
Шаг 3. Переведите слова справа от слова (слов) «равно» в алгебраическое выражение.

Пример 2.9

Переведите и решите: на одиннадцать больше, чем x равно 54.

Решение

Перевести.
Вычтите 11 с обеих сторон.
Упростить.
Проверить: 54 одиннадцать больше, чем 43? 43 + 11 =? 5454 = 54 ✓ 43 + 11 =? 5454 = 54 ✓ 90 169

Попробуй 2.17

Переведите и решите: Десять больше x равно 41.

Попробуйте 2.18

Переведите и решите: Двенадцать меньше x равно 51.

Пример 2.10

Переведите и решите: разница между 12t12t и 11t11t равна −14−14.

Решение

Перевести.
Упростить.
Чек: 12 (−14) −11 (−14) =? — 14−168 + 154 =? — 14−14 = −14 ✓12 (−14) −11 (−14) =? — 14−168 + 154 =? −14−14 = −14 ✓

Попробуй 2.19

Переведите и решите: разница между 4x4x и 3x3x равна 14.

Попробуй 2.20

Переведите и решите: разница между 7a7a и 6a6a составляет −8−8.

Переводчик и решение приложений

В большинстве случаев вопрос, требующий алгебраического решения, возникает из вопроса реальной жизни. Для начала этот вопрос задается на английском (или на языке человека, который задает вопрос), а не математическими символами. Поэтому очень важно уметь переводить повседневную ситуацию на алгебраический язык.

Мы начнем с переформулирования проблемы в одном предложении, присвоим переменную, а затем переведем предложение в уравнение, которое нужно решить. При присвоении переменной выберите букву, которая напоминает вам о том, что вы ищете. Например, вы можете использовать q для количества кварталов, если вы решаете проблему с монетами.

Пример 2.11

Как решать, переводить и решать приложения

Семья Макинтайров перерабатывала газеты в течение двух месяцев.Всего за два месяца газеты весили 57 фунтов. Второй месяц газеты весили 28 фунтов. Сколько весили газеты в первый месяц?

Попробуйте 2.21

Переведите в алгебраическое уравнение и решите:

В семье Паппас есть две кошки, Зевс и Афина. Вместе они весят 23 фунта. Зевс весит 16 фунтов. Сколько весит Афина?

Попробуйте 2.22

Переведите в алгебраическое уравнение и решите:

Сэм и Генри — соседи по комнате.Вместе у них 68 книг. У Сэма 26 книг. Сколько книг у Генри?

Как сделать

Решите приложение.

Шаг 1. Прочтите , в чем проблема. Убедитесь, что все слова и идеи понятны.
Шаг 2. Определите , что мы ищем.
Шаг 3. Назовите то, что мы ищем. Выберите переменную для представления этого количества.
Шаг 4. Переведите в уравнение. Может быть полезно переформулировать проблему одним предложением с важной информацией.
Шаг 5. Решите уравнение, используя хорошие методы алгебры.
Шаг 6. Отметьте ответ в задаче и убедитесь, что он имеет смысл.
Шаг 7. Ответьте на вопрос полным предложением.

Пример 2.12

Рэнделл заплатил за свою новую машину 28 675 долларов. Это было на 875 долларов меньше рекомендованной цены. Какая была цена автомобиля по наклейке?

Решение

Шаг 1.Прочтите проблему.
Шаг 2. Определите , что мы ищем.	«Какая была цена автомобиля на наклейке?»
Шаг 3. Назовите то, что мы ищем. Выберите переменную для представления этого количества.	Пусть s = s = цена автомобиля по стикеру.
Шаг 4. Переведите в уравнение. Переформулируйте проблему одним предложением.	28 675 долларов — это на 875 долларов меньше рекомендованной цены
Шаг 5. Решите уравнение.	28 675 долларов на 875 долларов меньше, чем 28 675 долларов на 875 долларов меньше, чем 28 675 = s − 875 28 675 + 875 = s − 875 + 87529 550 = s 28 675 = s − 875 28 675 + 875 = s − 875 + 87529 550 = s
Шаг 6. Отметьте ответ. Является ли 875 долларов меньше 29 550 долларов 28 675 долларами? 29,550-875 =? 28,675 28,675 = 28,675 ✓29,550-875 =? 28,675 28,675 = 28,675 ✓
Шаг 7.Ответьте на вопрос полным предложением.	Ориентировочная цена автомобиля составляла 29 550 долларов.

Таблица 2.2

Попробуйте 2.23

Переведите в алгебраическое уравнение и решите:

Эдди заплатил 19875 долларов за свою новую машину. Это было на 1025 долларов меньше рекомендованной цены. Какая была цена автомобиля по наклейке?

Попробуйте 2.24

Переведите в алгебраическое уравнение и решите:

Стоимость входного билета в кино днем 7 долларов.75. Это на 3,25 доллара меньше ночной цены. Сколько стоит фильм ночью?

Раздел 2.1 Упражнения

Практика ведет к совершенству

Проверить решение уравнения

В следующих упражнениях определите, является ли данное значение решением уравнения.

Является ли y = 53y = 53 решением
6y + 10 = 12y6y + 10 = 12y?

Является ли x = 94x = 94 решением
4x + 9 = 8x4x + 9 = 8x?

Является ли u = −12u = −12 решением
8u − 1 = 6u8u − 1 = 6u?

Является ли v = −13v = −13 решением
9v − 2 = 3v9v − 2 = 3v?

Решите уравнения, используя свойства равенства равенства и вычитания и сложения

В следующих упражнениях решите каждое уравнение, используя свойства равенства вычитания и сложения.

15.

м − 18 = −200 м − 18 = −200

21.

x − 165 = −420x − 165 = −420

22.

z − 101 = −314z − 101 = −314

23.

z + 0,52 = -8,5z + 0,52 = -8,5

24.

х + 0,93 = -4,1 х + 0.93 = -4,1

Решение уравнений, требующих упрощения

В следующих упражнениях решите каждое уравнение.

31.

9x + 5−8x + 14 = 209x + 5−8x + 14 = 20

32.

6x + 8−5x + 16 = 326x + 8−5x + 16 = 32

33.

−6x − 11 + 7x − 5 = −16−6x − 11 + 7x − 5 = −16

34.

−8n − 17 + 9n − 4 = −41−8n − 17 + 9n − 4 = −41

35.

5 (y − 6) −4y = −65 (y − 6) −4y = −6

36.

9 (y − 2) −8y = −169 (y − 2) −8y = −16

37.

8 (u + 1,5) −7u = 4,98 (u + 1,5) −7u = 4,9

38.

5 (w + 2,2) −4w = 9,35 (w + 2,2) −4w = 9,3

39.

6a − 5 (a − 2) + 9 = −116a − 5 (a − 2) + 9 = −11

40.

8c − 7 (c − 3) + 4 = −168c − 7 (c − 3) + 4 = −16

41.

6 (y − 2) −5y = 4 (y + 3) 6 (y − 2) −5y = 4 (y + 3)
−4 (y − 1) −4 (y − 1)

42.

9 (x − 1) −8x = −3 (x + 5) 9 (x − 1) −8x = −3 (x + 5)
+3 (x − 5) +3 (x − 5)

43.

3 (5n − 1) −14n + 93 (5n − 1) −14n + 9
= 10 (n − 4) −6n − 4 (n + 1) = 10 (n − 4) −6n − 4 (n +1)

44.

2 (8m + 3) −15m − 42 (8m + 3) −15m − 4
= 9 (m + 6) −2 (m − 1) −7m = 9 (m + 6) −2 (m − 1 ) −7м

45.

— (j + 2) + 2j − 1 = 5− (j + 2) + 2j − 1 = 5

46.

— (k + 7) + 2k + 8 = 7− (k + 7) + 2k + 8 = 7

47.

— (14a − 34) + 54a = −2− (14a − 34) + 54a = −2

48.

— (23d − 13) + 53d = −4− (23d − 13) + 53d = −4

49.

8 (4x + 5) −5 (6x) −x8 (4x + 5) −5 (6x) −x
= 53−6 (x + 1) +3 (2x + 2) = 53−6 (x + 1) +3 (2х + 2)

50.

6 (9y − 1) −10 (5y) −3y6 (9y − 1) −10 (5y) −3y
= 22−4 (2y − 12) +8 (y − 6) = 22−4 (2y− 12) +8 (у − 6)

Перевести в уравнение и решить

В следующих упражнениях переведите уравнение, а затем решите его.

51.

Девять больше xx равно 52.

52.

Сумма x и −15−15 равна 23.

53.

Десятка меньше м составляет −14−14.

54.

Три меньше y равно −19−19.

55.

Сумма y и −30−30 равна 40.

56.

Двенадцать больше p равно 67.

57.

Разница между 9x и 8x9x и 8x составляет 107.

58.

Разница между 5cand4c5cand4c составляет 602.

59.

Разница между nn и 1616 составляет 1212.

60.

Разница между ff и 1313 составляет 112112.

61.

Сумма −4n − 4n и 5n5n равна −82−82.

62.

Сумма −9m − 9m и 10m10m равна −95-95.

Переводчик и решение приложений

В следующих упражнениях переведите в уравнение и решите.

63.

Расстояние Аврил проехала на велосипеде 18 миль от дома до библиотеки, а затем до пляжа.Расстояние от дома Аврил до библиотеки составляет 11,2 км. Какое расстояние от библиотеки до пляжа?

64.

Чтение Джефф прочитал в общей сложности 54 страницы в своих учебниках истории и социологии. Он прочитал 41 страницу в своем учебнике истории. Сколько страниц он прочитал в своем учебнике социологии?

65.

Возраст Дочь Евы на 15 лет младше сына. Сыну Евы 22 года. Сколько лет ее дочери?

66.

Возраст Отец Пабло на 3 года старше своей матери.Матери Пабло 42 года. Сколько лет его отцу?

67.

Продовольственные товары На семейный праздничный ужин Селеста купила индейку, которая весила на 5 фунтов меньше той, которую она купила на День Благодарения. Именинная индейка весила 16 фунтов. Сколько весила индейка на День Благодарения?

68.

Вес Элли весит на 8 фунтов меньше, чем ее сестра-близнец Лорри. Элли весит 124 фунта. Сколько весит Лорри?

69.

Здоровье Температура Коннора была 0.Сегодня утром на 7 градусов выше, чем вчера вечером. Его температура сегодня утром была 101,2 градуса. Какая у него была температура прошлой ночью?

70.

Здравоохранение Медсестра сообщила, что дочь Триши поправилась на 4,2 фунта со времени последнего осмотра и теперь весит 31,6 фунта. Сколько весила дочь Триши на последнем обследовании?

71.

Зарплата Зарплата Рона на этой неделе была на 17,43 доллара меньше, чем на прошлой неделе. Его зарплата на этой неделе составляла 103 доллара.76. Сколько была зарплата Рона на прошлой неделе?

72.

Учебники Тетрадь Мелиссы по математике стоила на 22,85 доллара меньше, чем ее книга по искусству. Ее тетрадь по математике стоил 93,75 доллара. Сколько стоил ее артбук?

Повседневная математика

73.

Конструкция Мигель хочет просверлить отверстие под винт диаметром 5858 дюймов. Отверстие должно быть на 112112 дюймов меньше винта. Пусть dd равен размеру отверстия, которое он должен просверлить. Решите уравнение d − 112 = 58d − 112 = 58, чтобы узнать, какого размера должно быть отверстие.

74.

Выпечка Келси нужно 2323 стакана сахара для рецепта печенья, которое она хочет приготовить. У нее всего 3838 стаканов сахара, остальное она одолжит у соседки. Пусть ss равно количеству сахара, которое она одолжит. Решите уравнение 38 + s = 2338 + s = 23, чтобы найти количество сахара, которое она должна попросить взаймы.

Письменные упражнения

75.

Является ли −8−8 решением уравнения 3x = 16−5x3x = 16−5x? Откуда вы знаете?

76.

Каков первый шаг в решении уравнения 10x + 2 = 4x + 2610x + 2 = 4x + 26?

Самопроверка

ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.

ⓑ Если бы большинство ваших чеков было:

… уверенно. Поздравляем! Вы достигли своих целей в этом разделе! Поразмышляйте над своими учебными навыками, чтобы вы могли продолжать их использовать. Что вы сделали, чтобы убедиться в своей способности делать эти вещи? Быть конкретным!

… с некоторой помощью. Эту проблему нужно решать быстро, поскольку темы, которые вы не освоили, становятся ухабами на вашем пути к успеху. Математика последовательна — каждая тема основывается на предыдущей работе.Прежде чем двигаться дальше, важно убедиться, что у вас есть прочный фундамент. К кому обратиться за помощью? Ваши одноклассники и инструктор — хорошие ресурсы. Есть ли в кампусе место, где доступны репетиторы по математике? Можно ли улучшить свои учебные навыки?

… нет, не понимаю! Это очень важно, и вы не должны игнорировать его. Вам нужно немедленно обратиться за помощью, иначе вы быстро не справитесь. Как можно скорее обратитесь к своему инструктору, чтобы обсудить вашу ситуацию. Вместе вы сможете составить план оказания вам необходимой помощи.

Решение линейных уравнений

Каждое уравнение с тремя неизвестными соответствует плоскости в трехмерном пространстве. Уравнения имеют единственное решение, если все плоскости пересекаются в одной точке.

Три непротиворечивых уравнения

  A <- матрица (c (2, 1, -1,
             -3, -1, 2,
             -2, 1, 2), 3, 3, byrow = ИСТИНА)
colnames (A) <- paste0 ('x', 1: 3)
б <- с (8, -11, -3)
showEqn (A, b)

  ## 2 * x1 + 1 * x2 - 1 * x3 = 8
## -3 * x1 - 1 * x2 + 2 * x3 = -11
## -2 * x1 + 1 * x2 + 2 * x3 = -3

Согласованы ли уравнения?

  ## [1] 3 3

  ## [1] ИСТИНА

Решите относительно \ (\ mathbf {x} \).{-1} b} \) с решением в последнем столбце.

  ## x1 x2 x3
## [1,] 1 0 0 2
## [2,] 0 1 0 3
## [3,] 0 0 1 -1

  ##
## Исходная матрица:
## x1 x2 x3
## [1,] 2 1 -1 8
## [2,] -3 -1 2 -11
## [3,] -2 1 2 -3
##
## row: 1
##
## поменять местами строки 1 и 2
## x1 x2 x3
## [1,] -3 -1 2 -11
## [2,] 2 1 -1 8
## [3,] -2 1 2 -3
##
## умножить строку 1 на -1/3
## x1 x2 x3
## [1,] 1 1/3 -2/3 11/3
## [2,] 2 1 -1 8
## [3,] -2 1 2 -3
##
## умножить строку 1 на 2 и вычесть из строки 2
## x1 x2 x3
## [1,] 1 1/3 -2/3 11/3
## [2,] 0 1/3 1/3 2/3
## [3,] -2 1 2 -3
##
## умножить строку 1 на 2 и прибавить к строке 3
## x1 x2 x3
## [1,] 1 1/3 -2/3 11/3
## [2,] 0 1/3 1/3 2/3
## [3,] 0 5/3 2/3 13/3
##
## строка: 2
##
## поменяйте местами строки 2 и 3
## x1 x2 x3
## [1,] 1 1/3 -2/3 11/3
## [2,] 0 5/3 2/3 13/3
## [3,] 0 1/3 1/3 2/3
##
## умножить строку 2 на 3/5
## x1 x2 x3
## [1,] 1 1/3 -2/3 11/3
## [2,] 0 1 2/5 13/5
## [3,] 0 1/3 1/3 2/3
##
## умножить строку 2 на 1/3 и вычесть из строки 1
## x1 x2 x3
## [1,] 1 0 -4/5 14/5
## [2,] 0 1 2/5 13/5
## [3,] 0 1/3 1/3 2/3
##
## умножить строку 2 на 1/3 и вычесть из строки 3
## x1 x2 x3
## [1,] 1 0 -4/5 14/5
## [2,] 0 1 2/5 13/5
## [3,] 0 0 1/5 -1/5
##
## строка: 3
##
## умножить строку 3 на 5
## x1 x2 x3
## [1,] 1 0 -4/5 14/5
## [2,] 0 1 2/5 13/5
## [3,] 0 0 1 -1
##
## умножить строку 3 на 4/5 и прибавить к строке 1
## x1 x2 x3
## [1,] 1 0 0 2
## [2,] 0 1 2/5 13/5
## [3,] 0 0 1 -1
##
## умножьте строку 3 на 2/5 и вычтите из строки 2
## x1 x2 x3
## [1,] 1 0 0 2
## [2,] 0 1 0 3
## [3,] 0 0 1 -1

Участок им. plotEqn3d использует rgl для 3D-графики. Если повернуть фигуру, вы увидите ориентацию, в которой все три плоскости пересекаются в точке решения, \ (\ mathbf {x} = (2, 3, -1) \)

Вы должны включить Javascript для правильного просмотра этой страницы.

Как написать уравнение с абсолютным значением, которое дает решения

Обновлено 2 ноября 2020 г.

Крис Дезиел

Абсолютное значение можно обозначить парой вертикальных линий, заключенных в скобки для рассматриваемого числа.Когда вы берете абсолютное значение числа, результат всегда положительный, даже если само число отрицательное. Для случайного числа x справедливы оба следующих уравнения: | - x | = x и | x | = х . Это означает, что любое уравнение, имеющее абсолютное значение, имеет два возможных решения. Если вы уже знаете решение, вы можете сразу определить, является ли число в скобках абсолютного значения положительным или отрицательным, и вы можете опустить скобки абсолютного значения.

TL; DR (слишком долго; не читал)

Уравнения абсолютного значения имеют два решения. Подставьте известные значения, чтобы определить, какое решение является правильным, затем перепишите уравнение без скобок абсолютных значений.

Решение уравнения абсолютного значения с двумя неизвестными переменными

| x + y | = 4x - 3y

Чтобы решить эту проблему, вы должны установить два равенства и решить каждое отдельно.

Составьте два отдельных (и не связанных) уравнения для x в терминах y , стараясь не рассматривать их как два уравнения с двумя переменными:

1: \ quad (x + y ) = 4x - 3y \\ 2: \ quad (x + y) = - (4x - 3y)

x + y = 4x -3y \\ 4y = 3x \ x = \ frac {4} {3} y

Это решение уравнения 1.

x + y = -4x + 3y \\ 5x = 2y \\ x = \ frac {2} {5} y

Это решение уравнения 2.

Поскольку исходное уравнение содержало абсолютное значение, вы остались два отношения между x и y , которые одинаково верны. Если вы изобразите два приведенных выше уравнения на графике, они будут прямыми линиями, пересекающими начало координат. Один имеет наклон 4/3, а другой - 2/5.

Написание уравнения с известным решением

Если у вас есть значения для x и y для приведенного выше примера, вы можете определить, какое из двух возможных отношений между x и y истинно, и это говорит вам, является ли выражение в скобках абсолютного значения - положительное или отрицательное.

Предположим, вы знаете, что точка x = 4, y = 10 находится на линии. Подставьте эти значения в оба уравнения.

1: \ quad 4 = \ frac {4} {3} × 10 = 40/3 = 14,33 \ rarr \ text {False!} \\ 2: \ quad 4 = \ frac {2} {5} × 10 = 20/5 = 4 \ rarr \ text {Верно!}

Уравнение 2 является правильным. Теперь вы можете опустить скобки абсолютных значений в исходном уравнении и написать вместо них:

(x + y) = - (4x - 3y)

Решение систем линейных уравнений с двумя переменными - Промежуточная алгебра

Цели обучения

К концу этого раздела вы сможете:

Определите, является ли упорядоченная пара решением системы уравнений
Решите систему линейных уравнений, построив график
Решите систему уравнений заменой
Решите систему уравнений методом исключения
Выберите наиболее удобный метод решения системы линейных уравнений

Прежде чем начать, пройдите тест на готовность.

Для уравнения
ⓐ Есть решение? Ⓑ Есть решение?
Если вы пропустили эту проблему, просмотрите (рисунок).
Найдите наклон и y -пересечение прямой
Если вы пропустили эту проблему, просмотрите (рисунок).
Найдите точки пересечения линии x- и y
Если вы пропустили эту проблему, просмотрите (рисунок).

Определите, является ли упорядоченная пара решением системы уравнений

В разделе «Решение линейных уравнений» мы научились решать линейные уравнения с одной переменной.Теперь мы будем работать с двумя или более линейными уравнениями, сгруппированными вместе, что известно как система линейных уравнений.

Система линейных уравнений

Когда два или более линейных уравнения сгруппированы вместе, они образуют систему линейных уравнений .

В этом разделе мы сосредоточим нашу работу на системах двух линейных уравнений с двумя неизвестными. Позже в этой главе мы решим более крупные системы уравнений.

Пример системы двух линейных уравнений показан ниже.Мы используем скобку, чтобы показать, что два уравнения сгруппированы вместе и образуют систему уравнений.

Линейное уравнение с двумя переменными, например, имеет бесконечное число решений. Его график представляет собой линию. Помните, что каждая точка на линии - это решение уравнения, а каждое решение уравнения - это точка на линии.

Чтобы решить систему двух линейных уравнений, мы хотим найти значения переменных, которые являются решениями обоих уравнений. Другими словами, мы ищем упорядоченные пары, которые делают оба уравнения верными.Они называются решениями системы уравнений.

Решения системы уравнений

решения системы уравнений - это значения переменных, которые делают все уравнения истинными. Решение системы двух линейных уравнений представляется упорядоченной парой

Чтобы определить, является ли упорядоченная пара решением системы двух уравнений, мы подставляем значения переменных в каждое уравнение. Если упорядоченная пара делает оба уравнения истинными, это решение системы.

Определите, является ли заказанная пара решением системы

ⓐⓑ

ⓐ

ⓑ

Определите, является ли заказанная пара решением системы

ⓐⓑ

Определите, является ли заказанная пара решением системы

ⓐⓑ

Решите систему линейных уравнений с помощью построения графиков

В этом разделе мы будем использовать три метода для решения системы линейных уравнений.Первый метод, который мы будем использовать, - это построение графиков.

График линейного уравнения представляет собой линию. Каждая точка на линии - это решение уравнения. Для системы из двух уравнений мы построим график двумя линиями. Затем мы можем увидеть все точки, которые являются решениями каждого уравнения. И, обнаружив, что общего у линий, мы найдем решение системы.

Большинство линейных уравнений с одной переменной имеют одно решение, но мы видели, что некоторые уравнения, называемые противоречиями, не имеют решений, а для других уравнений, называемых тождествами, все числа являются решениями.

Точно так же, когда мы решаем систему двух линейных уравнений, представленную графиком из двух линий в одной плоскости, есть три возможных случая, как показано.

Каждый раз, когда мы демонстрируем новый метод, мы будем использовать его в той же системе линейных уравнений. В конце раздела вы решите, какой метод был наиболее удобным для решения этой системы.

Как решить систему уравнений с помощью построения графиков

Решите систему, построив график