Содержание
Методы решения тригонометрических уравнений. Тригонометрические уравнения — формулы, решения, примеры Разложение на множители тригонометрических уравнений примеры
Методы решения тригонометрических уравнений.
Решение тригонометрического уравнения состоит из двух этапов: преобразование уравнения
для получения его простейшего
вида (см. выше
)
и
решение
полученного простейшего
тригонометрического уравнения.
Существует семь
основных методов решения тригонометрических уравнений.
1. Алгебраический метод.
(метод замены переменной и подстановки).
2. Разложение на множители.
П р и м е р 1. Решить уравнение:
sin
x
+
cos
x
= 1 .
Р е ш е н и е. Перенесём все члены уравнения влево:
Sin x
+ cos x
– 1 = 0 ,
Преобразуем и разложим на множители выражение в
Левой части уравнения:
П р и м е р 2. Решить уравнение:
cos
2
x
+
sin
x
·
cos
x
= 1.
Р е ш е н и е.
cos
2
x
+ sin x
· cos x
–
sin
2
x
–
cos
2
x
= 0 ,
Sin x
· cos x
–
sin
2
x
= 0 ,
Sin x
· (cos x
–
sin
x
) = 0 ,
П р и м е р 3. Решить уравнение:
cos
2
x
–
cos
8
x
+
cos
6
x
= 1.
Р е ш е н и е.
cos
2
x
+
cos
6
x
= 1 +
cos
8
x
,
2 cos 4x
cos 2x
= 2 cos
²
4x
,
Cos 4x
·
(cos 2x
– cos 4x
) = 0 ,
Cos 4x
· 2 sin 3x
· sin x
= 0 ,
1). cos 4x
= 0 , 2). sin 3x
= 0 , 3). sin x
= 0 ,
3. Приведение |
4.
 Переход к половинному углу.
Переход к половинному углу.
Рассмотрим этот метод на примере:
П р и м е р. Решить уравнение: 3
sin
x
– 5
cos
x
= 7.
Р е ш е н и е.
6 sin (x
/ 2) · cos (x
/ 2) – 5 cos ²
(x
/ 2) + 5 sin ²
(x
/ 2) =
7 sin ²
(x
/ 2) + 7 cos ²
(x
/ 2) ,
2 sin ²
(x
/ 2) – 6 sin (x
/ 2) · cos (x
/ 2) + 12 cos ²
(x
/ 2) = 0 ,
tan ²
(x
/ 2) – 3 tan (x
/ 2) + 6 = 0 ,
. . . . . . . . . .
5. Введение вспомогательного угла.
Рассмотрим уравнение вида
:
a
sin x
+ b
cos x
= c
,
Где
a
,
b
,
c
– коэффициенты;
x
– неизвестное.
Теперь
коэффициенты
уравнения
обладают
свойствами
синуса
и
косинуса
, а именно
: модуль ( абсолютное
значение
)
каждого
из
них не больше
1,
а сумма их квадратов равна 1
.
Тогда можно
обозначить
их соответственно
как
cos
и
sin
(здесь
— так называемый вспомогательный угол
), и
наше уравнение прини
Основными методами решения тригонометрических уравнений являются: сведение уравнений к простейшим (с использованием тригонометрических формул), введение новых переменных, разложение на множители. Рассмотрим их применение на примерах. Обратите внимание на оформление записи решений тригонометрических уравнений.
Рассмотрим их применение на примерах. Обратите внимание на оформление записи решений тригонометрических уравнений.
Необходимым условием успешного решения тригонометрических уравнений является знание тригонометрических формул (тема 13 работы 6).
Примеры.
1. Уравнения, сводящиеся к простейшим.
1) Решить уравнение
Решение:
Ответ:
2) Найти корни уравнения
(sinx + cosx) 2 = 1 – sinxcosx, принадлежащие отрезку .
Решение:
Ответ:
2. Уравнения, сводящиеся к квадратным.
1) Решить уравнение 2 sin 2 x – cosx –1 = 0.
Решение:
Используя формулу sin 2 x = 1 – cos 2 x, получаем
Ответ:
2) Решить уравнение cos 2x = 1 + 4 cosx.
Решение:
Используя формулу cos 2x = 2 cos 2 x – 1, получаем
Ответ:
3) Решить уравнение tgx – 2ctgx + 1 = 0
Решение:
Ответ:
3. Однородные уравнения
1) Решить уравнение 2sinx – 3cosx = 0
Решение: Пусть cosx = 0, тогда 2sinx = 0 и sinx = 0 – противоречие с тем, что sin 2 x + cos 2 x = 1. Значит cosx ≠ 0 и можно поделить уравнение на cosx. Получим
Значит cosx ≠ 0 и можно поделить уравнение на cosx. Получим
Ответ:
2) Решить уравнение 1 + 7 cos 2 x = 3 sin 2x
Решение:
Используем формулы 1 = sin 2 x + cos 2 x и sin 2x = 2 sinxcosx, получим
sin 2 x + cos 2 x + 7cos 2 x = 6sinxcosx
sin 2 x – 6sinxcosx+ 8cos 2 x = 0
Пусть cosx = 0, тогда sin 2 x = 0 и sinx = 0 – противоречие с тем, что sin 2 x + cos 2 x = 1.
Значит cosx ≠ 0 и можно поделить уравнение на cos 2 x.
Получим
tg 2 x – 6 tgx + 8 = 0
Обозначим tgx = y
y 2 – 6 y + 8 = 0
y 1 = 4; y 2 = 2
а) tgx = 4, x= arctg4 + 2 k
, k
б) tgx = 2, x= arctg2 + 2 k
, k
.
Ответ:
arctg4 + 2 k
, arctg2 + 2 k, k
4. Уравнения вида a
sinx + b
cosx = с, с
≠ 0.
1) Решить уравнение .
Решение:
Ответ:
5. Уравнения, решаемые разложением на множители.
1) Решить уравнение sin2x – sinx = 0. n arcsin a + \pi n, n \in Z`
n arcsin a + \pi n, n \in Z`
2. Уравнение `cos x=a`
При `|a|>1` — как и в случае с синусом, решений среди действительных чисел не имеет.
При `|a| \leq 1` имеет бесконечное множество решений.
Формула корней: `x=\pm arccos a + 2\pi n, n \in Z`
Частные случаи для синуса и косинуса в графиках.
3. Уравнение `tg x=a`
Имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arctg a + \pi n, n \in Z`
4. Уравнение `ctg x=a`
Также имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arcctg a + \pi n, n \in Z`
Формулы корней тригонометрических уравнений в таблице
Для синуса:
Для косинуса:
Для тангенса и котангенса:
Формулы решения уравнений, содержащих обратные тригонометрические функции:
Методы решения тригонометрических уравнений
Решение любого тригонометрического уравнения состоит из двух этапов:
- с помощью преобразовать его до простейшего;
- решить полученное простейшее уравнение, используя выше написанные формулы корней и таблицы.
 2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.
2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.- `sin x=0`, `x=\pi n`, `n \in Z`
- `1-sin x=0`, `sin x=-1`, `x=\pi /2+2\pi n, n \in Z`.
Учитывая, что ` x \ne \pi+2\pi n, n \in Z`, решениями будут `x=2\pi n, n \in Z` и `x=\pi /2+2\pi n`, `n \in Z`.
Ответ. `x=2\pi n`, `n \in Z`, `x=\pi /2+2\pi n`, `n \in Z`.
Тригонометрия, и тригонометрические уравнения в частности, применяются почти во всех сферах геометрии, физики, инженерии. Начинается изучение в 10 классе, обязательно присутствуют задания на ЕГЭ, поэтому постарайтесь запомнить все формулы тригонометрических уравнений — они вам точно пригодятся!
Впрочем, даже запоминать их не нужно, главное понять суть, и уметь вывести. Это не так и сложно, как кажется. Убедитесь сами, просмотрев видео.
Тема:
«Методы решения тригонометрических уравнений».Цели урока:
образовательные:
Сформировать навыки различать виды тригонометрических уравнений;
Углубление понимания методов решения тригонометрических уравнений;
воспитательные:
Воспитание познавательного интереса к учебному процессу;
Формирование умения анализировать поставленную задачу;
развивающие:
Формировать навык проводить анализ ситуации с последующим выбором наиболее рационального выхода из нее.

Оборудование:
плакат с основными тригонометрическими формулами, компьютер, проектор, экран.Начнем урок с повторения основного приема решения любого уравнения: сведение его к стандартному виду. Путем преобразований линейные уравнения сводят к виду ах = в, квадратные – к виду ax 2 +
bx +
c =0.
В случае тригонометрических уравнений необходимо свести их к простейшим, вида: sinx = a , cosx = a , tgx = a , которые легко можно решить.В первую очередь, конечно, для этого необходимо использовать основные тригонометрические формулы, которые представлены на плакате: формулы сложения, формулы двойного угла, понижения кратности уравнения. Мы уже умеем решать такие уравнения. Повторим некоторые из них:
Вместе с тем существуют уравнения, решение которых требует знаний некоторых специальных приемов.
Темой нашего урока является рассмотрение этих приемов и систематизация методов решения тригонометрических уравнений.
Методы решения тригонометрических уравнений.

1. Преобразование к квадратному уравнению относительно какой-либо тригонометрической функции с последующей заменой переменной.
Рассмотрим каждый из перечисленных методов на примерах, но более подробно остановимся на двух последних, так как два первых мы уже использовали при решении уравнений.
1. Преобразование к квадратному уравнению относительно какой-либо тригонометрической функции.
2. Решение уравнений методом разложения на множители.
3. Решение однородных уравнений.
Однородными уравнениями первой и второй степени называются уравнения вида:
соответственно (а ≠ 0, b ≠ 0, с ≠ 0).
При решении однородных уравнений почленно делят обе части уравнения на cosx для (1) уравнения и на cos 2 x для (2). Такое деление возможно, так как sinx и cosx не равны нулю одновременно – они обращаются в нуль в разных точках. Рассмотрим примеры решения однородных уравнений первой и второй степени.
Запомним это уравнение: при рассмотрении следующего метода – введение вспомогательного аргумента, решим его другим способом.

4. Введение вспомогательного аргумента.
Рассмотрим уже решенное предыдущим методом уравнение:
Как видим, получается тот же результат.
Рассмотрим еще один пример:
В рассмотренных примерах было, в общем, понятно, на что требуется разделить исходное уравнение, чтобы ввести вспомогательный аргумент. Но может случиться, что не очевидно, какой делитель выбрать. Для этого существует специальная методика, которую мы сейчас и рассмотрим в общем виде. Пусть дано уравнение.
Формулы для решения простейших тригонометрических уравнений
Прежде чем решать тригонометрические уравнения, вы должны хорошо разбираться в тригонометрическом круге.
Все тригонометрические уравнения, какими они не были – простыми или сложными, в итоге сводятся к решению четырех типов простейших тригонометрических уравнений.
Вы просто обязаны уметь решать уравнения вида
Формулы–алгоритмы будут разбросаны по трем статьям,
здесь же они собраны все вместе =>
+ показать
Давайте разбираться.
 В этой статье мы рассмотрим решение уравнения вида . Решение остальных типов простейших уравнений смотрим здесь: часть 2 (), часть 3 (, )
В этой статье мы рассмотрим решение уравнения вида . Решение остальных типов простейших уравнений смотрим здесь: часть 2 (), часть 3 (, )Уравнение вида
Решим уравнение
Мы должны подобрать такие значения аргумента , то есть такие значения углов, косинус которых равнялся бы .
Смотрим на тригонометрический круг, на оси косинусов находим :
Выстраиваем через эту точку вертикаль, получаем две точки на круге:
Но надо понимать, что за этими точками скрывается бесконечно много других точек, – таких, косинус в которых также равен . Мы об этом подробно говорили в предыдущей статье, когда знакомились с тригонометрическим кругом.
На координатной прямой подходящие нам точки располагаются так:
А с графической точки зрения решение уравнения выглядело бы так:
Как все точки взять в ответ?
Нам поможет счетчик . Возьмем , то есть
Решением уравнения будет
Возьмите, поперебирайте различные значения подставьте в вышеуказанную формулу.

Вы получите как раз точки при ,
при ,
при и т.д.
То что нам нужно!
Если бы мы решали, например, уравнение , то решением бы было
.
Я думаю, вы уже увидели общий принцип формирования ответа.
Давайте дадим формулу, которой можно руководствоваться, решая уравнения
, где – из
(в противном случае, когда – не из – решений нет)
Но вам формула будет понятна, если вы уже знакомы с понятием «арккосинус».
Если нам попадается уравнение с нетабличным значением косинуса, вроде этого , то решение будет следующее:
Частные случаи решения уравнения
1)
Мы должны бы записать так:
.
Но можно записать решение иначе (ведь в данном случае между точками расстояние – полкруга, значит нам можно использовать полукруговой счетчик ):
2)
У нас только одна серия корней:
то есть
3)
Аналогично решению примера 2, решение такое:
Формула решения косинусов частные случаи.
 Тригонометрические уравнения. Разложение на множители
Тригонометрические уравнения. Разложение на множителиПростейшие тригонометрические уравнения решаются, как правило, по формулам. Напомню, что простейшими называются вот такие тригонометрические уравнения:
sinx = а
cosx = а
tgx = а
ctgx = а
х — угол, который нужно найти,
а — любое число.
А вот и формулы, с помощью которых можно сразу записать решения этих простейших уравнений.
Для синуса:
Для косинуса:
х = ± arccos a + 2π
n, n ∈ Z
Для тангенса:
х = arctg a + π
n, n ∈ Z
Для котангенса:
х = arcctg a + π
n, n ∈ Z
Собственно, это и есть теоретическая часть решения простейших тригонометрических уравнений. Причём, вся!) Совсем ничего. Однако, количество ошибок по этой теме просто зашкаливает. Особенно, при незначительном отклонении примера от шаблона.
 Почему?
Почему?Да потому, что масса народу записывает эти буковки, не понимая их смысла совершенно!
С опаской записывает, как бы чего не вышло…) С этим надо разобраться. Тригонометрия для людей, или люди для тригонометрии, в конце концов!?)Разберёмся?
Один угол у нас будет равен arccos a,
второй: -arccos a.
И так будет получаться всегда.
При любом а.
Если не верите, наведите курсор мышки на картинку, или коснитесь рисунка на планшете.) Я изменил число а
на какое-то отрицательное. Всё равно, один угол у нас получился arccos a,
второй: -arccos a.
Следовательно, ответ можно всегда записать в виде двух серий корней:
х 1 = arccos a + 2π
n, n ∈ Z
х 2 = — arccos a + 2π
n, n ∈ Z
Объединяем эти две серии в одну:
х= ± arccos а + 2π
n, n ∈ Z
И все дела. Получили общую формулу для решения простейшего тригонометрического уравнения с косинусом.

Если вы понимаете, что это не какая-то сверхнаучная мудрость, а просто сокращённая запись двух серий ответов,
вам и задания «С» будут по плечу. С неравенствами, с отбором корней из заданного интервала… Там ответ с плюсом/минусом не катит. А если отнестись к ответу делово, да разбить его на два отдельных ответа, всё и решается.) Собственно, для этого и разбираемся. Что, как и откуда.В простейшем тригонометрическом уравнении
sinx = а
тоже получается две серии корней. Всегда. И эти две серии тоже можно записать одной строчкой.
Только эта строчка похитрее будет:х = (-1) n arcsin a + π
n, n ∈ Z
Но суть остаётся прежней. Математики просто сконструировали формулу, чтобы вместо двух записей серий корней, сделать одну. И всё!
Проверим математиков? А то мало ли…)
В предыдущем уроке подробно разобрано решение (безо всяких формул) тригонометрического уравнения с синусом:
В ответе получились две серии корней:
х 1 = π
/6 + 2π
n, n ∈ Z
х 2 = 5π
/6 + 2π
n, n ∈ Z
Если мы будем решать это же уравнение по формуле, получим ответ:
х = (-1) n arcsin 0,5 + π
n, n ∈ Z
Вообще-то, это недоделанный ответ.
 ) Ученик обязан знать, что
) Ученик обязан знать, что
arcsin 0,5 = π
/6.
Полноценный ответ будет:х = (-1) n π
/6
+ π
n, n ∈ Z
Тут возникает интересный вопрос. Ответ через х 1 ; х 2
(это правильный ответ!) и через одинокий х
(и это правильный ответ!) — одно и то же, или нет? Сейчас узнаем.)Подставляем в ответ с х 1
значения n
=0; 1; 2; и т.д., считаем, получаем серию корней:х 1 = π/6; 13π/6; 25π/6
и так далее.При такой же подстановке в ответ с х 2
, получаем:х 2 = 5π/6; 17π/6; 29π/6
и так далее.А теперь подставляем значения n
(0; 1; 2; 3; 4…) в общую формулу для одинокого х
. Т.е возводим минус один в нулевую степень, затем в первую, вторую, и т.д. Ну и, разумеется, во второе слагаемое подставляем 0; 1; 2 3; 4 и т.д. И считаем. Получаем серию:х = π/6; 5π/6; 13π/6; 17π/6; 25π/6
и так далее.
Вот всё и видно.) Общая формула выдаёт нам точно такие же результаты,
что и два ответа по отдельности. Только все сразу, по порядочку. Не обманули математики.)Формулы для решения тригонометрических уравнений с тангенсом и котангенсом тоже можно проверить. Но не будем.) Они и так простенькие.
Я расписал всю эту подстановку и проверку специально. Здесь важно понять одну простую вещь: формулы для решения элементарных тригонометрических уравнений есть, всего лишь, краткая запись ответов.
Для этой краткости пришлось вставить плюс/минус в решение для косинуса и (-1) n в решение для синуса.Эти вставки никак не мешают в заданиях, где нужно просто записать ответ элементарного уравнения. Но если надо решать неравенство, или далее нужно что-то делать с ответом: отбирать корни на интервале, проверять на ОДЗ и т.п, эти вставочки могут запросто выбить человека из колеи.
И что делать? Да либо расписать ответ через две серии, либо решать уравнение/неравенство по тригонометрическому кругу.
 Тогда исчезают эти вставочки и жизнь становится легче.)
Тогда исчезают эти вставочки и жизнь становится легче.)Можно подвести итоги.
Для решения простейших тригонометрических уравнений существуют готовые формулы ответов. Четыре штуки. Они хороши для мгновенной записи решения уравнения. Например, надо решить уравнения:
sinx = 0,3
Легко: х = (-1) n arcsin 0,3 + π
n, n ∈ Z
cosx = 0,2
Без проблем: х = ± arccos 0,2 + 2π
n, n ∈ Z
tgx = 1,2
Запросто: х = arctg 1,2 + π
n, n ∈ Z
ctgx = 3,7
Одной левой: x= arcctg3,7 + π
n, n ∈ Z
cos x = 1,8
Если вы, блистая знаниями, мгновенно пишете ответ:
х= ± arccos 1,8 + 2π
n, n ∈ Z
то блистаете вы уже, это… того… из лужи.) Правильный ответ: решений нет.
Не понимаете, почему? Прочитайте, что такое арккосинус. Кроме того, если в правой части исходного уравнения стоят табличные значения синуса, косинуса, тангенса, котангенса, — 1; 0; √3; 1/2; √3/2
и т. п. — ответ через арки будет недоделанным. Арки нужно обязательно перевести в радианы.
п. — ответ через арки будет недоделанным. Арки нужно обязательно перевести в радианы.А если уж вам попалось неравенство, типа
то ответ в виде:
х πn, n ∈ Z
есть редкая ахинея, да…) Тут надо по тригонометрическому кругу решать. Чем мы и займёмся в соответствующей теме.
Для тех, кто героически дочитал до этих строк. Я просто не могу не оценить ваши титанические усилия. Вам бонус.)
Бонус:
При записи формул в тревожной боевой обстановке, даже закалённые учёбой ботаны частенько путаются, где πn,
а где 2π
n.
Вот вам простой приёмчик. Во всех
формулах стоит πn.
Кроме единственной формулы с арккосинусом. Там стоит 2πn.
Два
пиэн. Ключевое слово — два.
В этой же единственной формуле стоят два
знака в начале. Плюс и минус. И там, и там — два.
Так что, если вы написали два
знака перед арккосинусом, легче вспомнить, что в конце будет два
пиэн. А ещё наоборот бывает. Пропустит человек знак ±
А ещё наоборот бывает. Пропустит человек знак ±
, доберётся до конца, напишет правильно два
пиэн, да и спохватится. Впереди-то два
знака! Вернётся человек к началу, да ошибку-то и исправит! Вот так.)Если Вам нравится этот сайт…
Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Простейшими тригонометрическими уравнениями называют уравнения
Cos (x) = a, sin (x) = a, tg (x) = a, ctg (x) =a
Уравнение cos (x) = a
Объяснение и обоснование
- Корни уравнения cosx = а. При | a | > 1 уравнение не имеет корней, по-скольку | cosx | 1 или при а
Пусть | а |
у = cos х. На промежутке функция y = cos x убы-вает от 1 до -1. Но убывающая функция принимает каждое свое значение только в одной точке ее области определения, поэтому уравнение cos x = а имеет на этом промежутке только один корень, который по опреде-лению арккосинуса равен: x 1 = arccos а (и для этого корня cos x = а).

Косинус — четная функция, поэтому на промежутке [-п; 0] уравнение cos x = а также имеет только один корень — число, противоположное x 1 , то есть
x 2 = -arccos а.
Таким образом, на промежутке [-п; п] (длиной 2п) уравнение cos x = а при | а |
Функция y = cos x периодическая с периодом 2п, поэтому все остальные корни отличаются от найденных на 2пп (n € Z). Получаем следующую фор-мулу корней уравнения cos x = а при
x = ±arccos а + 2пп, n £ Z.
- Частные случаи решения уравнения cosx = а.
Полезно помнить специальные записи корней уравнения cos x = а при
а = 0, а = -1, а = 1, которые можно легко получить, используя как ори-ентир единичную окружность.
Поскольку косинус равен абсциссе соответствующей точки единичной окружности, получаем, что cos x = 0 тогда и только тогда, когда соответ-ствующей точкой единичной окружности является точка A или точка B.
Аналогично cos x = 1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка C, следовательно,
x = 2πп, k € Z.

Также cos х = —1 тогда и только тогда, когда соответствующей точкой единичной окружности является точка D, таким образом, х = п + 2пn,
Уравнение sin (x) = a
Объяснение и обоснование
- Корни уравнения sinx = а. При | а | > 1 уравнение не имеет корней, по-скольку | sinx | 1 или при а
Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!
Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.
Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ.
 Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.
Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.
Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.

- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.

- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Основными методами решения тригонометрических уравнений являются: сведение уравнений к простейшим (с использованием тригонометрических формул), введение новых переменных, разложение на множители. Рассмотрим их применение на примерах.
 Обратите внимание на оформление записи решений тригонометрических уравнений.
Обратите внимание на оформление записи решений тригонометрических уравнений.Необходимым условием успешного решения тригонометрических уравнений является знание тригонометрических формул (тема 13 работы 6).
Примеры.
1. Уравнения, сводящиеся к простейшим.
1) Решить уравнение
Решение:
Ответ:
2) Найти корни уравнения
(sinx + cosx) 2 = 1 – sinxcosx, принадлежащие отрезку .
Решение:
Ответ:
2. Уравнения, сводящиеся к квадратным.
1) Решить уравнение 2 sin 2 x – cosx –1 = 0.
Решение:
Используя формулу sin 2 x = 1 – cos 2 x, получаемОтвет:
2) Решить уравнение cos 2x = 1 + 4 cosx.
Решение:
Используя формулу cos 2x = 2 cos 2 x – 1, получаемОтвет:
3) Решить уравнение tgx – 2ctgx + 1 = 0
Решение:
Ответ:
3. Однородные уравнения
1) Решить уравнение 2sinx – 3cosx = 0
Решение: Пусть cosx = 0, тогда 2sinx = 0 и sinx = 0 – противоречие с тем, что sin 2 x + cos 2 x = 1.
 Значит cosx ≠ 0 и можно поделить уравнение на cosx. Получим
Значит cosx ≠ 0 и можно поделить уравнение на cosx. ПолучимОтвет:
2) Решить уравнение 1 + 7 cos 2 x = 3 sin 2x
Решение:
Используем формулы 1 = sin 2 x + cos 2 x и sin 2x = 2 sinxcosx, получим
sin 2 x + cos 2 x + 7cos 2 x = 6sinxcosx
sin 2 x – 6sinxcosx+ 8cos 2 x = 0Пусть cosx = 0, тогда sin 2 x = 0 и sinx = 0 – противоречие с тем, что sin 2 x + cos 2 x = 1.
Значит cosx ≠ 0 и можно поделить уравнение на cos 2 x.
Получимtg 2 x – 6 tgx + 8 = 0
Обозначим tgx = y
y 2 – 6 y + 8 = 0
y 1 = 4; y 2 = 2
а) tgx = 4, x= arctg4 + 2 k
, k
б) tgx = 2, x= arctg2 + 2 k
, k
.Ответ:
arctg4 + 2 k
, arctg2 + 2 k, k
4. Уравнения вида a
sinx + b
cosx = с, с
≠ 0.1) Решить уравнение .
Решение:
Ответ:
5. Уравнения, решаемые разложением на множители.
1) Решить уравнение sin2x – sinx = 0.
 2+3t-4=0\). Корнями являются \(t_1=-4, \ t_2=1\). Сделаем обратную замену:
2+3t-4=0\). Корнями являются \(t_1=-4, \ t_2=1\). Сделаем обратную замену:\(\left[\begin{gathered} \begin{aligned}
&\mathrm{tg}\,x=1\\&\mathrm{tg}\,x=-4
\end{aligned}\end{gathered}\right. \Rightarrow
\left[\begin{gathered} \begin{aligned} &x=\dfrac{\pi}4+\pi
n\\[1ex]&x=-\mathrm{arctg}\,4+\pi n
\end{aligned}\end{gathered}\right. \ \ n\in\mathbb{Z}\)\(\blacktriangleright\) Однородные тригонометрические уравнения первой степени: \[II.\quad {\Large{a\sin x+b\cos x=0}}, a\ne0, b\ne 0\]
Заметим, что в данном уравнении никогда не являются решениями те значения \(x\), при которых \(\cos x=0\) или \(\sin x=0\). Действительно, если \(\cos x=0\), то, подставив вместо косинуса ноль в уравнение, получим: \(a\sin x=0\), откуда следует, что и \(\sin x=0\). Но это противоречит основному тригонометрическому тождеству, т.к. оно говорит о том, что если \(\cos x=0\), то \(\sin x=\pm 1\).
Аналогично и \(\sin x=0\) не является решением такого уравнения.

Значит, данное уравнение можно делить на \(\cos x\) или на \(\sin
x\). Разделим, например, на \(\cos x\):\(a \ \dfrac{\sin x}{\cos x}+b \ \dfrac{\cos x}{\cos x}=0\), откуда имеем \(a\mathrm{tg}\, x+b=0 \Rightarrow \mathrm{tg}\, x=-\dfrac
ba\)Пример 6. Решить уравнение \(\sin x+\cos x=0\)
Разделим правую и левую части уравнения на \(\sin x\):
\(1+\mathrm{ctg}\, x=0 \Rightarrow \mathrm{ctg}\, x=-1 \Rightarrow
x=-\dfrac{\pi}4+\pi n, n\in\mathbb{Z}\)\(\blacktriangleright\) Неоднородные тригонометрические уравнения первой степени: \[II.\quad {\Large{a\sin x+b\cos x=c}}, a\ne0, b\ne 0, c\ne 0\]
Существует несколько способов решения подобных уравнений. Рассмотрим те из них, которые можно использовать для любого такого уравнения:
1 СПОСОБ: при помощи формул двойного угла для синуса и косинуса и основного тригонометрического тождества:
\({\large{\sin x=2\sin{\dfrac x2}\cos{\dfrac x2}, \qquad \cos
x=\cos^2 {\dfrac x2}-\sin^2 {\dfrac x2},\qquad c=c\cdot \Big(\sin^2
{\dfrac
x2}+\cos^2 {\dfrac x2}\Big)}}\)
данное уравнение сведется к уравнению \(I\):Пример 7.
 2}=2\):
2}=2\):\(\dfrac12\sin 2x-\dfrac{\sqrt3}2\cos 2x=-\dfrac12\)
Заметим, что числа \(\dfrac12\) и \(\dfrac{\sqrt3}2\) получились табличные. Можно, например, взять за \(\dfrac12=\cos \dfrac{\pi}3, \
\dfrac{\sqrt3}2=\sin \dfrac{\pi}3\). Тогда уравнение примет вид:\(\sin 2x\cos \dfrac{\pi}3-\sin \dfrac{\pi}3\cos 2x=-\dfrac12
\Rightarrow \sin\left(2x-\dfrac{\pi}3\right)=-\dfrac12\)Решениями данного уравнения являются:
\(\left[ \begin{gathered} \begin{aligned}
&2x-\dfrac{\pi}3=-\dfrac{\pi}6+2\pi n\\[1.5ex]
&2x-\dfrac{\pi}3=-\dfrac{5\pi}6+2\pi n
\end{aligned}
\end{gathered} \right. \Rightarrow
\left[ \begin{gathered} \begin{aligned}
&x=\dfrac{\pi}{12}+\pi n\\[1.5ex]
&x=-\dfrac{\pi}4+\pi n
\end{aligned}
\end{gathered} \right. \ \ n\in\mathbb{Z}\)Заметим, что при решении уравнения третьим способом мы добились “более красивого” ответа (хотя ответы, естественно, одинаковы), чем при решении первым или вторым способом (которые, по сути, приводят уравнение к одному и тому же виду).
 2-3t-2=0\] Корнями данного уравнения являются \(t_1=2, t_2=-\dfrac12\).
2-3t-2=0\] Корнями данного уравнения являются \(t_1=2, t_2=-\dfrac12\).По формулам вспомогательного аргумента \(\sin2x+\cos
2x=\sqrt2\sin\left(2x+\dfrac{\pi}4\right)\), следовательно, сделав обратную замену: \[\left[ \begin{gathered} \begin{aligned}
&\sqrt2\sin\left(2x+\dfrac{\pi}4\right)=2\\[1ex]
&\sqrt2\sin\left(2x+\dfrac{\pi}4\right)=-\dfrac12 \end{aligned}
\end{gathered} \right. \Rightarrow
\left[ \begin{gathered} \begin{aligned}
&\sin\left(2x+\dfrac{\pi}4\right)=\sqrt2\\[1ex]
&\sin\left(2x+\dfrac{\pi}4\right)=-\dfrac1{2\sqrt2} \end{aligned}
\end{gathered} \right.\] Первое уравнение корней не имеет, т.к. область значений синуса находится в пределах от \(-1\) до \(1\). Значит: \(\sin\left(2x+\dfrac{\pi}4\right)=-\dfrac1{2\sqrt2} \Rightarrow
\left[ \begin{gathered} \begin{aligned}
&2x+\dfrac{\pi}4=-\arcsin {\dfrac1{2\sqrt2}}+2\pi n\\[1ex]
&2x+\dfrac{\pi}4=\pi+\arcsin {\dfrac1{2\sqrt2}}+2\pi n
\end{aligned}
\end{gathered} \right. \Rightarrow \)
\(\Rightarrow \left[ \begin{gathered} \begin{aligned}
&x=-\dfrac12\arcsin {\dfrac1{2\sqrt2}}-\dfrac{\pi}8+\pi n\\[1ex]
&x=\dfrac{3\pi}8+\dfrac12\arcsin {\dfrac1{2\sqrt2}}+\pi n
\end{aligned}
\end{gathered} \right. 2=(\sin
2=(\sin
x\pm \cos x)(1\pm \sin 2x)\) (по первой формуле)Простейшие тригонометрические уравнения и их решение
К простейшим тригонометрическим уравнениям относятся уравнения вида
Решение простейших тригонометрических уравнений
Рассмотрим подробнее каждое из этих уравнений и их решение.
Уравнение вида . Так как для любого x, то при и уравнение не имеет корней. При , корни этого уравнения находятся по формуле
Особые случаи
Примеры решения задач
Уравнение вида . Так как для любого x, то при и уравнение корней не имеет. При , корни этого уравнения находятся по формуле
Особые случаи:
ПРИМЕР 4
Задание Решить уравнение — Решение Косинус – функция ограниченная и лежит в пределах , поэтому данное равенство не имеет смысла. 
Ответ Решений нет. Простейшие тригонометрические уравнения с тангенсами и котангенсами
Уравнение вида . Для любого действительного a на промежутке существует единственный угол , для которого . Это угол . Учитывая периодичность функции , получим формулы для нахождения корней уравнения :
ПРИМЕР 5
Задание Решить уравнение Решение Выразим из этого равенства тангенс В последнем равенстве положив , получим простейшее тригонометрическое уравнение , корни которого вычисляются по формуле
Тогда
Сделаем обратную замену
и выразим из полученного уравнения x:
поделим обе части последнего равенства на 2, тогда окончательно получим
Ответ Уравнение вида .
 Для любого действительного a на промежутке существует единственный угол , для которого . Это угол . Учитывая периодичность функции , получим формулы для нахождения корней уравнения :
Для любого действительного a на промежутке существует единственный угол , для которого . Это угол . Учитывая периодичность функции , получим формулы для нахождения корней уравнения :ПРИМЕР 6
Задание Решить уравнение Решение Ведем замену , тогда исходное уравнение преобразуется в простейшее тригонометрическое уравнение , корни которого вычисляются по формуле Тогда
Сделаем обратную замену
и выразим из полученного уравнения x:
поделим обе части последнего равенства на 5, тогда окончательно получим
Ответ Приведение тригонометрических уравнений к простейшим
Примеры тригонометрических уравнений, которые приводятся к простейшим тригонометрическим уравнениям с помощью элементарных преобразований или тригонометрических формул.

ПРИМЕР 8
Задание Решить уравнение Решение Применим к правой части заданного уравнения формулу суммы синусов: или
Последнее равенство равносильно совокупности простейших уравнений
Ответ
Понравился сайт? Расскажи друзьям!
Урок 47. методы решения тригонометрических уравнений — Алгебра и начала математического анализа — 10 класс
Алгебра и начала математического анализа, 10 класс
Урок №47.
 Методы решения тригонометрических уравнений.
Методы решения тригонометрических уравнений.Перечень вопросов, рассматриваемых в теме:
- Формирование системы знаний и умений решать тригонометрические уравнения различными методами;
- Применение метода разложения на множители при решении тригонометрических уравнений;
- Применение метода оценки при решении тригонометрических уравнений;
- Прием домножения левой и правой частей уравнения на тригонометрическую функцию при решении тригонометрических уравнений.
Глоссарий по теме
Теорема — основа метода разложения на множители
Уравнение равносильно на своей области определения совокупности .
Теорема — основа метода замены переменной
Уравнение равносильно на ОДЗ совокупности уравнений
.
Основная литература:
Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е., Шабунин М.И. под ред. Жижченко А.Б. Алгебра и начала математического анализа. 10 класс: учеб. для общеобразоват.
 учреждений: базовый и профил. Уровни – 2-е изд. – М.: Просвещение, 2011. – 368 с.: ил. – ISBN 978-5-09-025401-4, сс.327-332
учреждений: базовый и профил. Уровни – 2-е изд. – М.: Просвещение, 2011. – 368 с.: ил. – ISBN 978-5-09-025401-4, сс.327-332Дополнительная литература:
Шахмейстер А.Х. Тригонометрия. М.: Издательство МЦНМО : СПб.: «Петроглиф» : «Виктория плюс», 2013. – 752 с.: илл. ISBN 978-5-4439-0050-6, сс.219-221, 245-262
Открытые электронные ресурсы:
Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/
Теоретический материал для самостоятельного изучения
На этом уроке мы продолжаем заниматься решением тригонометрических уравнений. И здесь мы рассмотрим такие методы как разложение на множители, метод оценки, а также продолжим решать тригонометрические уравнения методом замены переменной. Кроме того, мы узнаем, как использовать домножение правой и левой частей уравнений для получения более простого уравнения, как использовать тригонометрические формулы для решения уравнений.
Сейчас выполните несколько заданий.

Задание 1.
Представьте в виде произведения:
Решение:
Используем формулы приведения, затем формулу преобразования суммы косинусов в произведение:
.
(На последнем шаге мы фактически использовали формулу двойного аргумента:
.
Ответ: .
Задание 2.
Вычислите:
Решение:
Воспользуемся формулой понижения степени и формулой преобразования произведения косинусов в сумму косинусов. Появившийся при этом общий множитель вынесем за скобки:
Воспользуемся тем, что косинус – функция четная и известным значением косинуса. В результате получим:
Ответ: 0,25
Задание 3.
Проверьте равенство:
Решение:
При выполнении этого задания будем использовать прием домножения о деления левой части на одно и то же тригонометрическое выражение.
Но сначала заметим, что .
Теперь запишем левую часть: .
теперь домножим и разделим это выражение на : .

Теперь воспользуемся формулой синуса двойного аргумента и получим:
. Теперь еще раз воспользуемся формулой двойного аргумента, предварительно домножив числитель и знаменатель на 2:
Учитывая, что , получаем: .
То есть исходное равенство верно.
Объяснение новой темы
1. Рассмотрим метод разложения на множители
Теоретической основой метода разложения на множители является теорема:
Теорема
Уравнение равносильно на своей области определения совокупности .
Для того чтобы применить эту теоремы, нужно исходное уравнение привести к виду , используя разные приемы.
Пример 1.
Решить уравнение:
Решение:
Перенесем правую часть уравнения в левую и преобразуем:
, .
Ответ: .
В этом случае мы использовали метод группировки для разложения на множители тригонометрического выражения.
Часто для преобразования выражения в произведение нужно использовать тригонометрические формулы.
 Рассмотрим такой пример:
Рассмотрим такой пример:Пример 2.
Решить уравнение:
Решение:
Преобразуем разность синусов в произведение:
Теперь вынесем за скобку общий множитель:
И решим каждое из двух уравнений: .
. Заметим, что вторая серия решений включается в первую. Поэтому мы можем оставить в ответе только первую серию.
Ответ: .
2. Замена переменной
Еще один метод решения тригонометрических уравнений — это метод разложения на множители. Мы уже знакомились с ним, когда решали уравнения, сводимые к квадратному или другому алгебраическому уравнению, когда решали однородные уравнения, а также знакомились с универсальной тригонометрической подстановкой. На этом уроке мы познакомимся еще с одной заменой, которая позволяет решать тригонометрические уравнения.
Рассмотрим уравнение вида:
или .
Для его решения введем новую переменную .
Тогда .
Выразим отсюда (или ).
Пример3.
Решите уравнение
Решение:
Сделаем замену .
 Тогда .
Тогда .Вспомогательное уравнение имеет вид:
.
.
Вернемся к исходной переменной:
.
Решим каждое из этих уравнений с помощью формулы введения вспомогательного угла:
, .
Так как , то оба уравнения имеют решения:
, .
Ответ: .
3. Теперь рассмотрим метод оценки
Часто этот метод применяют в том случае, когда уравнение включает в себя функции разного типа, например, тригонометрические и показательные, и обычные преобразования на приводят к результату. Но мы рассмотрим метод оценки при решении тригонометрических уравнений. Он основан на свойстве ограниченности тригонометрических выражений.
Рассмотрим пример.
Пример 4.
Решить уравнение: .
Мы знаем, что . С другой стороны, для того чтобы произведение двух различных чисел было равно 1, то они должны быть взаимно обратными, то есть если одно из них меньше 1,то другое больше 1. Но так как косинус больше 1 быть не может, то равенство может выполняться только в двух случаях:
или .

или .
или .
Вторая система ни при каких значениях k и n не имеет решений.
Первая система имеет решения при n=3m, k=2m, поэтому ее решения, а значит, и решение уравнения:
Ответ:
Рассмотрим еще один пример, в котором метод оценки применяется для решения уравнения, правая и левая части которого являются функциями разного типа.
Пример 5.
Решите уравнение:
Решение:
Рассмотрим левую часть уравнения и преобразуем его:
.
Поэтому
Теперь рассмотрим правую часть: .
Поэтому данное уравнение решений не имеет.
Ответ: решений нет
Рассмотрим несколько задач.
Решите уравнение:
Решение:
Домножим уравнение на 2 и воспользуемся формулой понижения степени:
Теперь воспользуемся формулой преобразования суммы косинусов с произведение:
.
Теперь перенесем правую часть в левую и вынесем за скобку общий множитель:
Теперь используем формулу преобразования разности косинусов в произведение:
Теперь решим три простейших тригонометрических уравнения:
, .

В этом случае достаточно оставить первые две серии решений, так как числа вида при нечетных значениях m попадают в первую серию решений, а при четных — во вторую.
Таким образом, получаем ответ:
Ответ:
Решите уравнение:
Используя метод вспомогательного угла, оценим выражение, стоящее в левой части уравнения.
То есть будем рассматривать левую часть уравнения как выражение вида:
, где .
Получим, что
Мы знаем, что , поэтому
Поэтому уравнение решений не имеет.
Ответ: решений нет.
Рассмотрим решение более сложного уравнения методом оценки.
Решите уравнение
Запишем уравнение в виде
Преобразуем левую часть:
Так как , то
и .
Так как и , то
Равенство возможно только при одновременном выполнении условий:
.
,
.
.
, .
Решая эту систему, получим, что, .
Ответ: , .
Рассмотрим еще один прием, который применяется при решении тригонометрических уравнений.

Домножение левой и правой части на тригонометрическую функцию
Рассмотрим решение уравнения:
Решение:
Домножим обе части уравнения на :
.
Заметим, что домножая обе части уравнения на выражение с переменной, мы можем получить новые корни. Проверим те значения переменной, при которой :
не являются решением исходного уравнения, поэтому мы должны будем удалить эти числа из полученного решения.
Теперь с помощью формулы синуса двойного аргумента преобразуем полученное уравнение:
Теперь перенесем правую часть в левую и преобразуем по формуле преобразования разности синусов в произведение:
, .
Учитывая, что , получим: .
Ответ: .
Примеры и разборы решений заданий тренировочного модуля
Пример 1.
A=1
подсказка
B=2
замена
C=6
Период
Ответ:
Пример 2.
Решите уравнение. Найдите коэффициенты a, b, c
Ответ:
Представим левую и правую части уравнения в виде произведения.
 Затем перенесём всё в левую часть и разложим на множители
Затем перенесём всё в левую часть и разложим на множителиa=1 ВАРИАНТ
b=7 МНОЖИТЕЛЬ
c=7 СЛАГАЕМОЕ
Ответ:
Тригонометрия — Математика — Теория, тесты, формулы и задачи
Оглавление:
Основные теоретические сведения
Некоторые рекомендации к выполнению тригонометрических преобразований
К оглавлению…
При выполнении тригонометрических преобразований следуйте следующим советам:
- Не пытайтесь сразу придумать схему решения примера от начала до конца.
- Не пытайтесь преобразовывать сразу весь пример. Продвигайтесь вперёд маленькими шагами.
- Помните, что кроме тригонометрических формул в тригонометрии можно по-прежнему применять все справедливые алгебраические преобразования (вынесение за скобку, сокращение дробей, формулы сокращённого умножения и так далее).
- Верьте, что всё будет хорошо.
Основные тригонометрические формулы
К оглавлению.
 ..
..Большинство формул в тригонометрии часто применяется как справа налево, так и слева направо, поэтому учить эти формулы нужно так хорошо, чтобы Вы легко смогли применить некоторую формулу в обоих направлениях. Запишем для начала определения тригонометрических функций. Пусть имеется прямоугольный треугольник:
Тогда, определение синуса:
Определение косинуса:
Определение тангенса:
Определение котангенса:
Основное тригонометрическое тождество:
Простейшие следствия из основного тригонометрического тождества:
Формулы двойного угла. Синус двойного угла:
Косинус двойного угла:
Тангенс двойного угла:
Котангенс двойного угла:
Дополнительные тригонометрические формулы
К оглавлению…
Тригонометрические формулы сложения. Синус суммы:
Синус разности:
Косинус суммы:
Косинус разности:
Тангенс суммы:
Тангенс разности:
Котангенс суммы:
Котангенс разности:
Тригонометрические формулы преобразования суммы в произведение.
 Сумма синусов:
Сумма синусов:Разность синусов:
Сумма косинусов:
Разность косинусов:
Сумма тангенсов:
Разность тангенсов:
Сумма котангенсов:
Разность котангенсов:
Тригонометрические формулы преобразования произведения в сумму. Произведение синусов:
Произведение синуса и косинуса:
Произведение косинусов:
Формулы понижения степени. Формула понижения степени для синуса:
Формула понижения степени для косинуса:
Формула понижения степени для тангенса:
Формула понижения степени для котангенса:
Формулы половинного угла. Формула половинного угла для тангенса:
Формула половинного угла для котангенса:
Тригонометрические формулы приведения
К оглавлению…
Функцию косинус называют кофункцией функции синус и наоборот.
 Аналогично функции тангенс и котангенс являются кофункциями. Формулы приведения можно сформулировать в виде следующего правила:
Аналогично функции тангенс и котангенс являются кофункциями. Формулы приведения можно сформулировать в виде следующего правила:- Если в формуле приведения угол вычитается (прибавляется) из 90 градусов или 270 градусов, то приводимая функция меняется на кофункцию;
- Если же в формуле приведения угол вычитается (прибавляется) из 180 градусов или 360 градусов, то название приводимой функции сохраняется;
- При этом перед приведенной функцией ставится тот знак, который имеет приводимая (т.е. исходная) функция в соответствующей четверти, если считать вычитаемый (прибавляемый) угол острым.
Формулы приведения задаются в виде таблицы:
Тригонометрическая окружность
К оглавлению…
По тригонометрической окружности легко определять табличные значения тригонометрических функций:
Тригонометрические уравнения
К оглавлению…
Для решения некоторого тригонометрического уравнения его нужно свести к одному из простейших тригонометрических уравнений, которые будут рассмотрены ниже.
 Для этого:
Для этого:- Можно применять тригонометрические формулы приведенные выше. При этом не нужно пытаться преобразовать сразу весь пример, а нужно двигаться вперед маленькими шагами.
- Нужно не забывать о возможности преобразовать некоторое выражение и с помощью алгебраических методов, т.е. например, вынести что-нибудь за скобку или, наоборот, раскрыть скобки, сократить дробь, применить формулу сокращенного умножения, привести дроби к общему знаменателю и так далее.
- При решении тригонометрических уравнений можно применять метод группировки. При этом нужно помнить, что для того чтобы произведение нескольких множителей было равно нолю, достаточно чтобы любой из них был равен нолю, а остальные существовали.
- Применяя метод замены переменной, как обычно, уравнение после введения замены должно стать проще и не содержать первоначальной переменной. Также нужно не забыть выполнить обратную замену.
- Помните, что однородные уравнения часто встречаются и в тригонометрии.

- Раскрывая модули или решая иррациональные уравнения с тригонометрическими функциями нужно помнить и учитывать все тонкости решения соответствующих уравнений с обычными функциями.
- Помните про ОДЗ (в тригонометрических уравнениях ограничения на ОДЗ в основном сводятся к тому, что делить на ноль нельзя, но не забываем и о других ограничениях, особенно о положительности выражений в рациональных степенях и под корнями четных степеней). Также помните, что значения синуса и косинуса могут лежать только в пределах от минус единицы до плюс единицы включительно.
Главное, если не знаете, что делать, делайте хоть что-нибудь, при этом главное правильно использовать тригонометрические формулы. Если то, что Вы при этом получаете становиться все лучше и лучше, значит продолжайте решение, а если становиться хуже, значит вернитесь к началу и попробуйте применить другие формулы, так поступайте пока не наткнетесь на правильный ход решения.
Формулы решений простейших тригонометрических уравнений.
 Для синуса существует две равнозначные формы записи решения:
Для синуса существует две равнозначные формы записи решения:Для остальных тригонометрических функций запись однозначна. Для косинуса:
Для тангенса:
Для котангенса:
Решение тригонометрических уравнений в некоторых частных случаях:
Тригонометрических уравнений и их решений — Учебный материал для IIT JEE
Тригонометрическое уравнение
Уравнение, включающее одно или несколько тригонометрических отношений неизвестных углов, называется тригонометрическим уравнением. Тригонометрическое уравнение можно записать как Q 1 (sin θ, cos θ, tan θ, cot θ, sec θ, cosec θ) = Q 2 (sin θ, cos θ, tan θ, cot θ, sec θ , cosec θ), где Q 1 и Q 2 — рациональные функции.
Пример: Рассмотрим уравнение cos 2 x — 4 sin x = 1.
Это тригонометрическое уравнение, а не тождество, поскольку оно не выполняется для всех значений x, например. уравнение не выполняется при (2n + 1) π / 4.
Решение тригонометрического уравнения:
Все возможные значения неизвестного, которые удовлетворяют данному уравнению, называются решением данного уравнения.
Для полного решения должны быть получены «все возможные значения», удовлетворяющие уравнению.
Когда мы пытаемся решить тригонометрическое уравнение, мы пытаемся найти все наборы значений θ, которые удовлетворяют данному уравнению.Иногда в простых уравнениях и когда легко нарисовать график уравнения, можно найти решение, просто просмотрев график.
Период функции:
Функция f (x) называется периодической, если существует T> 0 такое, что f (x + T) = f (x) для всех x в области определения f (x). Если T — наименьшее положительное действительное число такое, что f (x + T) = f (x), то оно называется периодом f (x).
Тригонометрические функции, такие как sin, cos и tan, являются периодическими функциями.
Иллюстрация: Мы пытаемся найти решения уравнения sin θ = 0, отличные от θ = 0. Увидев уравнение, можно сразу прийти к выводу, что θ = 0 — единственное решение. Но в случае тригонометрических уравнений важно исключить все возможности, чтобы найти правильное решение.
Пусть OX будет начальной строкой
Пусть ∠POX = θ и OP = r
от ΔPOL,
sin θ = PL / OP = y / r.
Теперь sin θ = 0
⇒ y / r = 0; ⇒ y = 0.
Это возможно только тогда, когда OP совпадает с OX или OX ’.
Когда OP совпадает с OX, θ = 0, ± 2π, ± 4π и ± 6π ……… (1)
И когда OP совпадает с OX ’, θ = ± π, ± 3π, ± 5π ……… (2)
Таким образом, из (1) и (2) следует, что при sin θ = 0
θ = nπ, где n = 0, ± 1, ± 2, ………
Мы называем θ = nπ общим решением тригонометрического уравнения sin θ = 0, потому что для всех значений n это решение удовлетворяет данному уравнению.
Иллюстрация: Общее решение cos θ = 0
cos θ = 0 ⇒ x = π / 2.
Это возможно только тогда, когда OP совпадает с OY или OY ’
Когда OP совпадает с OY,
θ = π / 2, 5π / 2, 9π / 2 или, -3π / 2, -7π / 2 .. ……… (1)
, когда OP совпадает с OY ’
θ = -3π / 2, -7π / 2 или, -π / 2, -5π / 2 ………… (2)
Таким образом, из (1) и (2) следует, что общее решение cos θ = 0 есть θ (2n + 1) π / 2, где n = 0, ± 1, ± 2 ………
Подробнее о тригонометрических уравнениях см. В видео ниже:
Общее решение уравнения sin θ = k.
Мы знаем, что когда sin θ = k, k должно быть таким, что –1 ≤ k ≤ 1
Всегда можно найти α ∈ [–π / 2, π / 2]
Так как sin (-π) / 2 = -1 & sin π / 2 = 1, так что sin θ = k, т.е. α = sin-1k
, т.е. sin θ = sin α, α ∈ [–π / 2, π / 2]
⇒ грех θ — грех α = 0
⇒ 2 sin {(θ — α) / 2} cos {θ + α) / 2} = 0
из приведенного выше уравнения, либо sin {(θ — α) / 2) = 0
и, следовательно, ((θ — α) / 2) = целое кратное π
∴ θ — α = 2nπ
и.е. θ = 2nπ + α
θ = 2nπ + (–1) 2n α, где n = 0, ± 1, ± 2… (1)
или, cos {(θ + α) / 2} = 0
, т.е. {(θ + α) / 2} = любое нечетное кратное π / 2
, т.е. {(θ + α) / 2} = (2n + 1) π / 2
, т.е. θ = (2n + 1) π — α
⇒ θ = (2n +1) π + (–1) 2n + 1 α… (2)
Из (1) и (2) заключаем, что
θ = nπ + (–1) n α, где n — целое кратное, является общим решением уравнения sin θ = k
Тригонометрические уравнения и их общие решения:
Тригонометрическое уравнение
Общее решение
грех θ = 0
Тогда θ = nπ
cos θ = 0
θ = (nπ + π / 2)
тангенс угла θ = 0
θ = nπ
грех θ = 1
θ = (2nπ + π / 2) = (4n + 1) π / 2
cos θ = 1
θ = 2nπ
грех θ = грех α
θ = nπ + (-1) nα, где α ∈ [-π / 2, π / 2]
cos θ = cos α
θ = 2nπ ± α, где α ∈ (0, π]
тангенс угла θ = тангенс угла α
θ = nπ + α, где α ∈ (-π / 2, π / 2]
sin2 θ = sin2 α
θ = nπ ± α
cos2 θ = cos2 α
θ = nπ ± α
tan2 θ = tan2 α
θ = nπ ± α
Если предполагается, что α является наименьшим положительным значением θ, которое удовлетворяет двум данным тригонометрическим уравнениям, то общее значение θ будет 2nπ + α.
Иллюстрация: Найдите общее решение уравнения sin θ = 1/2
Решение: Мы знаем, что sin θ = 1/2 = sin π / 6.
Итак, общее решение данного уравнения: θ = nπ + (–1) nπ / 6, n ∈ 0, ± 1, ± 2
Иллюстрация: Решите уравнение sin 6x + sin 4x = 0.
Решение: Применение формул для суммы синусов, т.е.
грех А + грех В = грех (А + В) / 2. cos (A-B) / 2, имеем
sin 5x cos x = 0 ……… (1)
Если «x» является решением уравнения, то верно хотя бы одно из следующих уравнений:
sin 5x = 0 или cos x = 0 ……… (2)
И наоборот, если x является решением одного из уравнений (2), то это также решение уравнения (1).Таким образом, уравнение (1) эквивалентно уравнению (2). Решения уравнения (2) даются формулой
x = nπ / 5, x = (2n + 1) π / 2, где n = 0, ± 1, ± 2 ……
Все эти значения x и только эти значения являются решениями исходного уравнения.
Иллюстрация: Найдите наиболее общее значение θ, где sin θ = — √3 / 2 и tan θ = √3.
Решение: Знаки имеют большое значение в случае тригонометрических функций. Студенты обычно склонны упоминать общие решения sin и tan θ, что неверно, поскольку это не дает нам полного решения.
sin θ отрицателен в 3-м и 4-м квадрантах, а tan θ положителен в 1-м и 3-м квадрантах.
Таким образом, обычным является 3-й квадрант, и при θ = 4π / 3 удовлетворяются оба.
∴ Общее решение — 2nπ + 4π / 3.
Это потому, что в интервале [0, 2π] оно выполняется только при 4π / 3. Снова в [2π, 4π] это выполняется при 2π + 4π / 3 и так далее.
Следовательно, общее решение уравнения равно 2nπ + 4π / 3.
Иллюстрация: Найдите общее решение для cos 3θ = sin 2θ.
Решение: Эту проблему можно решить двумя способами.
Метод 1: Мы можем записать данное уравнение как
cos 3θ = cos (π / 2 — 2θ)
⇒ 3θ = 2nπ + (π / 2 — 2θ), где n = 0, ± 1, ± 2 ……
или 5θ = 2nπ + π / 2, а также θ = 2nπ — π / 2
или θ = (4n + 1) π / 10 и
θ = (4n – 1) π / 2, где n ∈ I …… (A)
Метод 2: sin 2θ = sin (π / 2 — 3θ)
2θ = nπ + (–1) n (π / 2 — 3θ).
Случай I: Когда n четное, n = 2m, где m = 0, ± 1, ± 2 ……
2θ = 2mπ + π / 2 — 3θ
θ = (4m + 1) π / 10, где m ∈ I ……. (В)
Случай II: Если n нечетное, n = (2m + 1)
2θ = (2m + 1) π — (π / 2 — 3θ)
θ = — (4m + 1) π / 2, где m = 0, ± 1, ± 2 …… (B)
Примечание: Без сомнения, решения, полученные обоими методами для нечетных значений n, различны, но, как показано на диаграмме ниже, вы можете видеть, что все возможные значения θ могут быть получены обоими данными решениями:
из B
от A
для m = 0, θ = — π / 2,
для n = 0, θ = — π / 2
для m = 1, θ = — 5π / 2,
для n = 1, θ = + 3π / 2
для m = 2, θ = — 9π / 2,
для n = 2, θ = + 7π / 2
для m = –1, θ = — 3π / 2,
для m = –1, θ = — 5π / 2
для m = –2, θ = 7π / 2
для m = –2, θ = — 9π / 2
Общее решение sin 2 θ = k, где k ∈ [0, 1]
Учитывая, что sin 2 θ = k, k ∈ [0, 1]
Мы можем найти такое α, что
⇒ sin 2 θ = sin 2 α, где α = sin -1 √k
и.е. (грех θ — грех α) (грех θ + грех α) = 0
либо sin θ — sin α = 0
θ = nπ + (–1) n α, где n = 0, ± 1, ± 2 ……… (1)
или, sin θ + sin α = 0
sin θ = — sin α
θ = nπ — (–1) n α, где n = 0, ± 1, ± 2 …… .. (2)
Из (1) и (2) получаем общее решение уравнения для данного
θ = nπ ± α, где n = 0, ± 1, ± 2 …… и α = sin -1 √k
Иллюстрация: Решите уравнение 7tan 2 θ — 9 = 3 секунды 2 θ
Решение: Дано, 7tan 2 θ — 9 = 3 секунды 2 θ
или, 7tan 2 θ — 9 = 3 (1 + tan 2 θ)
или, 4tan 2 θ = 12
или, tan 2 θ = 3
или, tan 2 θ = (tan π / 3) 2
⇒ θ = nπ + π / 3, где n = 0, ± 1, ± 2 …………Примечание : Мы не можем определить уникальный метод решения тригонометрических уравнений.В каждом случае успех решения тригонометрического уравнения зависит, в частности, от знания и умения применять тригонометрические формулы, а также от практики решения задач. Многие тригонометрические формулы являются истинными равенствами для всех значений переменных, входящих в них.
Иллюстрация: Решите уравнение: cos θ = 0
Решение: Мы можем решить его, чтобы получить две формы
cos θ = 0 ⇒ θ = (2n + 1) π / 2cos θ = cos π / 2 ⇒ θ = 2nπ + π / 2
или θ = (4n + 1) π / 2.Важно: Следующие советы и шаги помогут вам систематически решать тригонометрические уравнения.
1. Попытайтесь сократить уравнение в терминах одного единственного тригонометрического отношения, предпочтительно sin θ или cos θ.
Если у нас есть выбор преобразовать задачу в синус или косинус, тогда форма косинуса удобнее по сравнению с формой синуса. Это связано с тем, что в общем решении синуса нам придется иметь дело с (–1) n , что неудобно по сравнению с рассмотрением +, полученного в форме косинуса.
2. Факторизуйте многочлен в терминах этих отношений.
3. Чтобы LHS был равен нулю, решите для каждого фактора. И запишите общее решение для каждого фактора на основе стандартных результатов, полученных ранее в этом разделе.например sin θ — k 1 = 0 ⇒ θ = nπ + (–1) n sin -1 k 1
cos θ — k 2 = 0 ⇒ θ = 2nπ + cos –1 k 2 .
Внимание: Вы должны проверить, что k 1 , k 2 ∈ [–1, 1].Не пишите вслепую, как есть, иначе будет абсурдно, если они не принадлежат [–1, 1].
Иллюстрация: Решите уравнение 5sin θ — 2 cos 2 θ — 1 = 0
Решение: Дано, 5 sin θ — 2 cos 2 θ — 1 = 0
или, 5 sin θ — 2 (1 — sin 2 θ) — 1 = 0
или, 2 sin 2 θ + 5 sin θ — 3 = 0
или, (sin θ + 3) (2 sin θ — 1) = 0
∴ sin θ = -3 или sin θ = ½Сначала рассмотрим случай, когда sin θ = -3.
Но этот случай невозможен, так как диапазон синуса составляет [-1, 1].
Когда sin θ = ½
Тогда sin θ = sin π / 6.
⇒ θ = nπ + (–1) n π / 6, где n = 0, ± 1, ± 2 ………
Примечание: Никогда не делите на любое нулевое выражение. например Если данное уравнение (sin θ — cos θ) (A) = (B), где A и B обозначают тригонометрические уравнения, то вы можете разделить на (sin θ — cos θ) только тогда, когда θ ≠ nπ + π / 4
Иллюстрация: Решите уравнение tan θ + sec θ = √3
Решение: тангенс угла θ + сек θ = √3 …… (1)
Тогда (sin θ) / (cos θ) + 1 / (cos θ) = √3 …… (2)
или, cos (θ + π / 6) = cos π / 3
Общее решение θ + π / 6 = 2nπ ± π / 3, n ∈ I
Принимая положительный знак, θ + π / 6 = 2nπ + π / 3
⇒ θ = 2nπ + π / 6
Принимая отрицательный знак, θ + π / 6 = 2nπ — π / 3
⇒ θ = 2nπ — π / 2
и.е. θ = (4n — 1) π / 2.
Но полученное решение является правильным, только если, cos θ ≠ 0, иначе (2) не определено.
то есть θ ≠ нечетное кратное π / 2
⇒ θ ≠ (4n — 1) π / 2.
Следовательно, общее решение будет θ = 2nπ + π / 6 только тогда, когда n = 0, ± 1, ± 2 ……
Примечание: Домен уравнения не должен изменяться. В случае его изменения необходимо внести необходимые изменения в общее решение.
Иллюстрация: Решите уравнение tan 5θ = tan 3θ
Решение: Теперь tan 5θ = tan 3θ
⇒ 5θ = nπ + 3θ
или, 2θ = nπ
θ = nπ / 2, где n = 0, ± 1, ± 2 ……
положить n = 0 дает θ = 0, исходное уравнение выполнено
положив n = 1, получаем θ = π / 2, уравнение принимает вид tan 5π / 2 = tan 3π / 2.
Уравнение не определено для нечетного числа, кратного π / 2.
Отсюда заключаем, что θ = 2nπ, где n = 0, ± 1, ± 2 ………
Некоторые ключевые моменты, на которые следует обратить внимание:
1. Если в уравнении участвует tan θ или sec θ, θ нечетное число, кратное π / 2.
2. Если в уравнении участвует cot θ или cosec θ, θ ≠ кратно π или 0.
Тригонометрия полна формул, и студентам рекомендуется изучить все тригонометрические формулы, включая основы тригонометрии, чтобы оставаться конкурентоспособными на экзаменах JEE и других инженерных экзаменах.Студенты должны практиковать различные задачи тригонометрии, основанные на тригонометрических соотношениях и основах тригонометрии, чтобы познакомиться с темой.
Вы можете сослаться на некоторые из связанных ресурсов, перечисленных ниже:
Чтобы узнать больше, купите учебные материалы по Тригонометрия , включающие учебные заметки, заметки о пересмотре, видеолекции, решенные вопросы за предыдущий год и т. Д. Также дополнительные учебные материалы по математике можно найти здесь .
Как найти общее решение тригонометрических уравнений?
Как найти общее решение тригонометрических уравнений?
Тригонометрические уравнения
Определение:
Уравнение, включающее одно или несколько тригонометрических соотношений неизвестного угла, называется тригонометрическим уравнениемТригонометрическое уравнение отличается от тригонометрических тождеств. Идентичность выполняется для каждого значения неизвестного угла e.g ., cos 2 x = 1 — sin 2 x истинно ∀ x ∈ R, в то время как тригонометрическое уравнение выполняется для некоторых конкретных значений неизвестного угла.
(1) Корни тригонометрического уравнения: Значение неизвестного угла (переменная величина), которое удовлетворяет данному уравнению, называется корнем уравнения, например, ., Cos θ = ½, корень равен θ = 60 ° или θ = 300 °, потому что уравнение выполняется, если мы положим θ = 60 ° или θ = 300 °.
(2) Решение тригонометрических уравнений: Значение неизвестного угла, удовлетворяющее тригонометрическому уравнению, называется его решением.
Поскольку все тригонометрические отношения периодичны по своей природе, обычно тригонометрическое уравнение имеет более одного решения или бесконечное количество решений. В основном есть три типа решений:- Частное решение: Определенное значение неизвестного угла, удовлетворяющее уравнению.
- Главное решение: Наименьшее числовое значение неизвестного угла, удовлетворяющее уравнению (Наименьшее числовое частное решение).
- Общее решение: Полный набор значений неизвестного угла, удовлетворяющий уравнению.Он содержит все частные решения, а также основные решения.
Тригонометрические уравнения и их общее решение
Тригонометрическое уравнение Общее решение грех θ = 0 θ = nπ cos θ = 0 θ = nπ + π / 2 тангенс угла θ = 0 θ = nπ грех θ = 1 θ = 2nπ + π / 2 cos θ = 1 θ = 2nπ грех θ = грех α θ = nπ + (−1) n α cos θ = cos α θ = 2nπ ± α tan θ = tan α θ = nπ ± α sin 2 θ = sin 2 α θ = nπ ± α tan 2 θ = tan 2 α θ = nπ ± α cos 2 θ = cos 2 α θ = nπ ± α sin θ = sin α
cos θ = cos αθ = nπ + α sin θ = sin α
tan θ = tan αθ = nπ + α tan θ = tan α
cos θ = cos αθ = nπ + α Общее решение вида a cos θ + b sin θ = c
Метод определения главного значения
Предположим, нам нужно найти главное значение sin θ = −½, удовлетворяющее уравнению.
Поскольку sin θ отрицателен, θ будет в квадранте 3 rd или 4 th . Мы можем подойти к 3-му или 4-му квадранту с двух сторон. Если мы возьмем направление против часовой стрелки, числовое значение угла будет больше π. Если подойти к нему по часовой стрелке, угол будет численно меньше π. За главное значение мы должны взять численно наименьший угол. Итак, для главного значения.
(1) Если угол находится в 1-м или 2-м квадранте, мы должны выбрать направление против часовой стрелки, а если угол находится в квадранте 3 rd или 4 th , мы должны выбрать направление по часовой стрелке.
(2) Главное значение никогда не может быть численно больше π.
(3) Главное значение всегда находится в первом круге (т.е. в первом повороте). По вышеуказанным критериям θ будет -π / 6 или -5π / 6. Между этими двумя -π / 6 имеет наименьшее числовое значение. Следовательно, −π / 6 — это главное значение θ, удовлетворяющее уравнению sin θ = −½.
Из приведенного выше обсуждения метод нахождения главного значения можно резюмировать следующим образом:- Сначала нарисуйте тригонометрический круг и отметьте квадрант, в котором может лежать угол.
- Выберите направление против часовой стрелки для квадрантов 1 -й и 2 -й и выберите направление по часовой стрелке для квадрантов 3 -й и 4 -й .
- Найдите угол при первом повороте.
- Выберите численно наименьший угол. Найденный таким образом угол будет главной величиной.
- В случае, если два угла, один с положительным знаком, а другой с отрицательным знаком, соответствуют численно наименьшему углу, тогда принято выбирать угол с положительным знаком в качестве главного значения.
Тригонометрические уравнения Задачи с решениями
1.
Решение:
2.
Решение:
3.
Решение:
4.
5.Решение:
6.
Решение:
7.
Решение:
8.
Решение:
9.
Решение:
Основные тригонометрические уравнения :
Когда просят решить 2x — 1 = 0, мы можем легко получить 2x = 1 и x = в качестве ответа.
Когда просят решить 2 sin x — 1 = 0, мы действуем аналогичным образом. Сначала мы смотрим на sin x как на переменную уравнения и решаем, как в первом примере.
2 sin x — 1 = 0
2 sin x = 1
sin x = 1/2Знаки и квадранты :
Решения тригонометрических уравнений также можно найти, изучив знак значения триггера и определив соответствующий квадрант (квадранты) для этого значения.
Решение простых (и средней сложности) триггерных уравнений
Purplemath
При решении тригонометрических уравнений используются как исходные углы, так и тригонометрические тождества, которые вы запомнили, а также большая часть изученной вами алгебры. Будьте готовы к тому, что для решения этих уравнений потребуется думать .
Далее предполагается, что вы хорошо разбираетесь в значениях триггерного отношения в первом квадранте, как работает единичный круг, соотношение между радианами и градусами и как выглядят кривые различных триггерных функций на минимум по первому периоду.Если вы не уверены в себе, вернитесь и сначала просмотрите эти темы.
MathHelp.com
Решить sin (
x ) + 2 = 3 в интервале 0 ° & leq; x <360 °
Как и в случае с линейными уравнениями, я сначала выделю член, содержащий переменную:
грех ( x ) + 2 = 3
грех ( x ) = 1
Теперь я буду использовать запомненные углы отсчета, чтобы получить окончательный ответ.
Примечание. В инструкциях указан интервал в градусах, что означает, что я должен давать свой ответ в градусах. Да, синус в первом периоде принимает значение 1 при
π / 2 радиан, но это не тот тип угловой меры, который они хотят, и использование этого в качестве моего ответа, вероятно, приведет к моему как минимум проигрышу. несколько моментов по этому вопросу.
Итак, в градусах мой ответ:
Решить tan
2 (θ) + 3 = 0 на интервале 0 ° & leq; θ <360 ° 9 10 30
Есть соблазн быстро вспомнить, что тангенс 60 ° включает квадратный корень из 3, и получить ответ, но это уравнение на самом деле не имеет решения.Я вижу это, когда замедляюсь и делаю шаги. Мой первый шаг:
Может ли любой квадрат (касательной или любой другой триггерной функции) быть отрицательным ? Нет! Итак, мой ответ:
Решить в интервале 0 ° & leq;
x <360 °
Левая часть этого уравнения множится.Я привык делать простой факторинг, например:
2 y 2 + 3 y = 0
y (2 y + 3) = 0
… и затем решить каждый из факторов. То же самое и здесь. Чтобы решить уравнение, которое они мне дали, я начну с факторинга:
Я занимался алгеброй; то есть, я произвел факторинг, а затем решил каждое из двух уравнений, связанных с факторами.Это создало два тригонометрических уравнения. Итак, теперь я могу сделать триггер; а именно решение этих двух результирующих тригонометрических уравнений, используя то, что я запомнил о косинусоиде. Из первого уравнения я получаю:
Из второго уравнения я получаю:
Соединяя эти два набора решений вместе, я получаю решение для исходного уравнения как:
x = 30 °, 90 °, 270 °, 330 °
Решить sin
2 (θ) — sin (θ) = 2 на интервале 0 & leq; θ <2π 9 · 1030
Во-первых, перенесу все по одну сторону от знака «равно»:
sin 2 (θ) — sin (θ) — 2 = 0
Это уравнение является «квадратичным по синусу»; то есть форма уравнения — это формат квадратного уравнения:
В случае уравнения, которое они хотят, чтобы я решил, X = sin (θ), a = 1, b = –1 и c = –2.
Поскольку это квадратичная форма, я могу применить некоторые методы квадратного уравнения. В случае этого уравнения я могу разложить на множители квадратичный:
sin 2 (θ) — sin (θ) — 2 = 0
(грех (θ) — 2) (грех (θ) + 1) = 0
Первый фактор дает мне соответствующее тригонометрическое уравнение:
Но синус никогда не бывает больше 1, поэтому это уравнение не разрешимо; у него нет решения.
Другой фактор дает мне второе связанное тригонометрическое уравнение:
грех (θ) + 1 = 0
sin (θ) = –1
θ = (3/2) π
Тогда мой ответ:
(Если в своем классе вы выполняете решения только для степеней, указанное выше значение решения равно «270 °».)
Решите cos
2 (α) + cos (α) = sin 2 (α) на интервале 0 ° & leq; x <360 °
Я могу использовать триггерное тождество, чтобы получить квадратичный косинус:
cos 2 (α) + cos (α) = sin 2 (α)
cos 2 (α) + cos (α) = 1 — cos 2 (α)
2cos 2 (α) + cos (α) — 1 = 0
(2cos (α) — 1) (cos (α) + 1) = 0
cos (α) = 1/2, cos (α) = –1
Первое тригонометрическое уравнение, cos (α) = 1/2, дает мне α = 60 ° и α = 300 °.Второе уравнение дает мне α = 180 °. Итак, мое полное решение:
Решить sin (β) = sin (2β) на интервале 0 ° & leq; β
<360 ° 9 10 30
Я могу использовать обозначение с двумя углами в правой части, а также переставлять и упрощать; тогда я фактор:
sin (β) = 2sin (β) cos (β)
sin (β) — 2sin (β) cos (β) = 0
sin (β) (1-2cos (β)) = 0
sin (β) = 0, cos (β) = 1/2
Синусоида (из первого триггерного уравнения) равна нулю при 0 °, 180 ° и 360 °.Но в исходном упражнении 360 ° не включены, поэтому последнее значение решения не учитывается в данном конкретном случае.
Косинус (из второго тригонометрического уравнения) равен
1/2 при 60 ° и, следовательно, также при 360 ° — 60 ° = 300 °. Итак, полное решение:
β = 0 °, 60 °, 180 °, 300 °
Решить sin (
x ) + cos ( x ) = 1 на интервале 0 ° & leq; x <360 °
Хм… Я действительно ничего здесь не вижу. Было бы неплохо, если бы одно из этих триггерных выражений было возведено в квадрат …
Хорошо, почему бы мне не возвести обе стороны в квадрат и посмотреть, что произойдет?
(sin ( x ) + cos ( x )) 2 = (1) 2
sin 2 ( x ) + 2sin ( x ) cos ( x ) + cos 2 ( x ) = 1
[sin 2 ( x + cos 2 ( x )] + 2sin ( x ) cos ( x ) = 1
1 + 2sin ( x ) cos ( x ) = 1
2sin ( x ) cos ( x ) = 0
sin ( x ) cos ( x ) = 0
Ха; иди и подумай: я возведен в квадрат и получил кое-что, с чем я мог бы работать с .Хороший!
Из последней строки выше либо синус равен нулю, либо косинус равен нулю, поэтому мое решение выглядит следующим образом:
x = 0 °, 90 °, 180 °, 270 °
Однако (и это важно!), Чтобы получить это решение, я возведен в квадрат, а возведение в квадрат — это «необратимый» процесс.
(Почему? Если вы возведете что-то в квадрат, вы не сможете просто извлечь квадратный корень, чтобы вернуться к тому, с чего начали, потому что возведение в квадрат могло где-то поменять знак.)
Итак, чтобы быть уверенным в своих результатах, мне нужно проверить свои ответы в исходном уравнении , чтобы убедиться, что я случайно не создал решения, которые на самом деле не учитываются. Подключаю обратно, вижу:
sin (0 °) + cos (0 °) = 0 + 1 = 1
… поэтому решение « x = 0 °» работает
sin (90 °) + cos (90 °) = 1 + 0 = 1
…поэтому решение « x = 90 °» тоже работает
sin (180 °) + cos (180 °) = 0 + (–1) = –1
… ну ладно, значит « x = 180 °» НЕ работает
sin (270 °) + cos (270 °) = (–1) + 0 = –1
… так что « x = 270 °» тоже не работает,
Хорошо, что я проверил свои решения, потому что два из них на самом деле не работают.Они были созданы путем возведения в квадрат.
Мое фактическое решение :
Примечание. В приведенном выше описании я мог бы остановиться на этой строке:
… и использовал тождество с двойным углом для синуса, наоборот, вместо разделения 2 в предпоследней строке в моих вычислениях. Ответ был бы таким же, но мне нужно было бы учесть интервал решения:
2sin ( x ) cos ( x ) = sin (2 x ) = 0
Тогда 2 x = 0 °, 180 °, 360 °, 540 ° и т. Д., И разделение 2 из x даст мне x = 0 °, 90 °, 180 °, 270 °, это то же самое почти решение, что и раньше.После выполнения необходимой проверки (из-за возведения в квадрат) и отбрасывания посторонних решений мой окончательный ответ был бы таким же, как и раньше.
Уловка возведения в квадрат в последнем примере выше встречается нечасто, но если ничего не работает, возможно, стоит попробовать. Имейте это в виду для следующего теста.
URL: https://www.purplemath.com/modules/solvtrig.htm
6. \ circ \)).\ circ k \ quad \ text {для \ (k = 0 \), \ (\ pm \, 1 \), \ (\ pm \, 2 \), \ (… \)}
\]
Это является наиболее общим решением уравнения. Часто часть, в которой говорится «для \ (k = 0 \), \ (\ pm \, 1 \), \ (\ pm \, 2 \), \ (… \)», опускается, поскольку обычно понял, что \ (k \) изменяется для всех целых чисел. Общее решение в радианах будет:
\ [\ nonumber
A ~ = ~ 0.6435 \; + \; \ pi k \ quad \ text {для \ (k = 0 \), \ (\ pm \, 1 \), \ (\ pm \, 2 \), \ (… \)}
\]Пример 6.1
Решите уравнение \ (\; 2 \, \ sin \; \ theta \; + \; 1 ~ = ~ 0 \).2 \; \ theta ~ = ~ \ frac {1} {2} \ quad \ Rightarrow \ quad \ cos \; \ theta ~ = ~ \ pm \, \ frac {1} {\ sqrt {2}}
\ quad \ Rightarrow \ quad \ theta ~ = ~ \ frac {\ pi} {4} \ ;, ~ \ frac {3 \ pi} {4} \ ;, ~ \ frac {5 \ pi} {4} \ ;, ~
\ frac {7 \ pi} {4} ~,
\]
и поскольку период косинуса равен \ (2 \ pi \), мы бы добавили \ (2 \ pi k \) к каждому из этих углов, чтобы получить общее решение. Но обратите внимание, что указанные выше углы различаются кратно \ (\ frac {\ pi} {2} \). Итак, поскольку каждое кратное \ (2 \ pi \) также кратно \ (\ frac {\ pi} {2} \), мы можем объединить эти четыре отдельных ответа в один:
\ [\ nonumber
\ boxed { \ theta ~ = ~ \ frac {\ pi} {4} \; + \; \ frac {\ pi} {2} \, k}
\ qquad \ text {для \ (k = 0 \), \ (\ pm \, 1 \), \ (\ pm \, 2 \), \ ( … \)}
\]Пример 6.3
Решите уравнение \ (\; 2 \, \ sec \; \ theta ~ = ~ 1 \).
Решение:
Изоляция \ (\; \ sec \; \ theta \) дает нам
\ [\ nonumber
\ sec \; \ theta ~ = ~ \ frac {1} {2} \ quad \ Rightarrow \ quad \ cos \; \ theta ~ = ~ \ frac {1} {\ sec \; \ theta} ~ = ~ 2 ~,
\]
, что невозможно. Таким образом, существует \ (\ fbox {no solution} \).Пример 6.4
Решите уравнение \ (\; \ cos \; \ theta ~ = ~ \ tan \; \ theta \).
Решение:
Идея состоит в том, чтобы использовать идентификаторы, чтобы выразить все в терминах единой тригонометрической функции:
\ [\ nonumber \ begin {align *}
\ cos \; \ theta ~ & = ~ \ tan \; \ theta \\ \ nonumber
\ cos \; \ theta ~ & = ~ \ frac {\ sin \; \ theta} {\ cos \; \ theta} \\ \ nonumber
\ cos ^ 2 \; \ theta ~ & = ~ \ sin \; \ theta \\ \ nonumber
1 \; — \; \ sin ^ 2 \; \ theta ~ & = ~ \ sin \; \ theta \\ \ nonumber
0 ~ & = ~ \ sin ^ 2 \; \ theta \; + \; \ sin \; \ theta \; — \; 1
\ end {align *} \]
Последнее уравнение выглядит более сложным, чем исходное уравнение, но обратите внимание, что на самом деле это квадратное уравнение : выполняя замену \ (x = \ sin \; \ theta \), у нас есть
\ [\ nonumber
x ^ 2 \; + \; Икс \;-\; 1 ~ = ~ 0 \ quad \ Rightarrow \ quad x ~ = ~ \ frac {-1 \; \ pm \; \ sqrt {1 — (4) \, (- 1)}} {
2 \, (1)} ~ = ~ \ frac {-1 \; \ pm \; \ sqrt {5}} {2} ~ = ~ -1.618 \ ;, ~ 0.618
\]
по формуле корней квадратного уравнения из элементарной алгебры. Но \ (- 1.618 <-1 \), поэтому невозможно, чтобы \ (\; \ sin \ theta = x = -1.618 \). Таким образом, мы должны иметь \ (\; \ sin \; \ theta = x = 0,618 \). Следовательно, есть два возможных решения: \ (\ theta = 0,666 \) рад в QI и его отражение \ (\ pi - \ theta = 2,475 \) рад вокруг оси \ (y \) - в QII. Добавление к ним кратных \ (2 \ pi \) дает нам общее решение:
\ [\ nonumber
\ boxed {\ theta ~ = ~ 0.666 \; + \; 2 \ пи к \ квад \ текст {и} \ квад 2.475 \; + \; 2 \ pi k}
\ qquad \ text {для \ (k = 0 \), \ (\ pm \, 1 \), \ (\ pm \, 2 \), \ (… \)}
\ ]Пример 6.5
Решите уравнение \ (\; \ sin \; \ theta ~ = ~ \ tan \; \ theta \).
Решение:
Используя тот же метод, что и в предыдущем примере, мы получаем
\ [\ nonumber \ begin {align *}
\ sin \; \ theta ~ & = ~ \ tan \; \ theta \\ \ nonumber
\ sin \; \ theta ~ & = ~ \ frac {\ sin \; \ theta} {\ cos \; \ theta} \\ \ nonumber
\ sin \; \ theta ~ \ cos \; \ theta ~ & = ~ \ sin \; \ theta \\ \ nonumber
\ sin \; \ theta ~ \ cos \; \ theta \; — \; \ sin \; \ theta ~ & = ~ 0 \\ \ nonumber
\ sin \; \ theta ~ (\ cos \; \ theta \; — \; 1) ~ & = ~ 0 \\ \ nonumber
& \ Rightarrow \ quad \ sin \; \ theta ~ = ~ 0 \ quad \ text {или} \ quad \ cos \; \ theta ~ = ~ 1 \\ \ nonumber
& \ Rightarrow \ quad \ theta ~ = ~ 0 \ ;, ~ \ pi \ quad \ text {или} \ quad \ theta ~ = ~ 0 \\ \ nonumber
& \ Rightarrow \ quad \ theta ~ = ~ 0 \ ;, ~ \ pi ~,
\ end {align *} \ ]
плюс число, кратное \ (2 \ pi \).Итак, поскольку указанные выше углы кратны \ (\ pi \), а каждое кратное \ (2 \ pi \) кратно \ (\ pi \), мы можем объединить два ответа в один для общего решения:
\ [\ nonumber
\ boxed {\ theta ~ = ~ \ pi k} \ qquad \ text {для \ (k = 0 \), \ (\ pm \, 1 \), \ (\ pm \, 2 \ ), \ (… \)}
\]Пример 6.6
Решите уравнение \ (\; \ cos \; 3 \ theta ~ = ~ \ frac {1} {2} \).
Решение:
Идея состоит в том, чтобы сначала решить для \ (3 \ theta \), используя наиболее общее решение, а затем разделить это решение на \ (3 \).{-1} \ frac {1} {2} = \ frac {\ pi} {3} \), есть два возможных решения для \ (3 \ theta \): \ (3 \ theta = \ frac {\ pi } {3} \) в QI и его отражение \ (- 3 \ theta = — \ frac {\ pi} {3} \) вокруг оси \ (x \) — в QIV. Добавление к ним кратных \ (2 \ pi \) дает нам:
\ [\ nonumber
3 \ theta ~ = ~ \ pm \, \ frac {\ pi} {3} \; + \; 2 \ pi k \ qquad \ text {для \ (k = 0 \), \ (\ pm \, 1 \), \ (\ pm \, 2 \), \ (… \)}
\]
Таким образом, разделив все на \ (3 \), мы получим общее решение для \ (\ theta \):
\ [\ nonumber
\ boxed {\ theta ~ = ~ \ pm \, \ frac {\ pi} {9} \ ; + \; \ frac {2 \ pi} {3} k}
\ qquad \ text {для \ (k = 0 \), \ (\ pm \, 1 \), \ (\ pm \, 2 \), \ (… \)}
\]Пример 6.7
Решите уравнение \ (\; \ sin \; 2 \ theta ~ = ~ \ sin \; \ theta \).
Решение:
Здесь мы используем формулу двойного угла для синуса:
\ [\ nonumber \ begin {align *}
\ sin \; 2 \ theta ~ & = ~ \ sin \; \ theta \\ \ nonumber
2 \, \ sin \ theta ~ \ cos \; \ theta ~ & = ~ \ sin \; \ theta \\ \ nonumber
\ sin \; \ theta ~ (2 \, \ cos \; \ theta \ ; — \; 1) ~ & = ~ 0 \\ \ nonumber
& \ Rightarrow \ quad \ sin \; \ theta ~ = ~ 0 \ quad \ text {или} \ quad \ cos \; \ theta ~ = ~ \ frac {1} {2} \\ \ nonumber
& \ Rightarrow \ quad \ theta ~ = ~ 0 \ ;, ~ \ pi \ quad \ text {или} \ quad \ theta ~ = ~ \ pm \, \ frac { \ pi} {3} \\ \ nonumber
& \ Rightarrow \ quad \ boxed {\ theta ~ = ~ \ pi k \ quad \ text {и} \ quad \ pm \, \ frac {\ pi} {3} \ ; + \; 2 \ pi k}
\ qquad \ text {для \ (k = 0 \), \ (\ pm \, 1 \), \ (\ pm \, 2 \), \ (… \)}
\ end {align *}
\]Рисунок 6.1.1
Решение:
Мы будем использовать метод, который мы обсуждали в главе 5, для нахождения амплитуды комбинации синусоидальных и косинусных функций. Возьмите коэффициенты \ (2 \) и \ (3 \) при \ (\; \ sin \; \ theta \) и \ (\; — \ cos \; \ theta \), соответственно, в приведенном выше уравнении и сделайте им ноги прямоугольного треугольника, как на рисунке 6.1.1. Пусть \ (\ phi \) будет углом, показанным в прямоугольном треугольнике. Нога с длиной \ (3> 0 \) означает, что угол \ (\ phi \) находится выше оси \ (x \) -, а нога с длиной \ (2> 0 \) означает, что \ (\ phi \) находится справа от оси \ (y \).Следовательно, \ (\ phi \) должен находиться в QI. Гипотенуза имеет длину \ (\ sqrt {13} \) по теореме Пифагора, и, следовательно, \ (\; \ cos \; \ phi = \ frac {2} {\ sqrt {13}} \) и \ (\; \ sin \; \ theta = \ frac {3} {\ sqrt {13}} \). Мы можем использовать это, чтобы преобразовать уравнение для решения следующим образом:\ [\ nonumber \ begin {align *}
2 \, \ sin \; \ theta \; — \; 3 \, \ cos \; \ theta ~ & = ~ 1 \\ \ nonumber
\ sqrt {13} \, \ left (\ tfrac {2} {\ sqrt {13}} \, \ sin \; \ theta \ ; — \; \ tfrac {3} {\ sqrt {13}} \, \ cos \; \ theta
\ right) ~ & = ~ 1 \\ \ nonumber
\ sqrt {13} \, (\ cos \; \ phi \; \ sin \; \ theta \; — \; \ sin \; \ phi \; \ cos \; \ theta) ~ & = ~ 1 \\ \ nonumber
\ sqrt {13} \, \ sin \ ; (\ theta — \ phi) ~ & = ~ 1 \ quad \ text {(по формуле вычитания синуса)} \\ \ nonumber
\ sin \; (\ theta — \ phi) ~ & = ~ \ tfrac {1 } {\ sqrt {13}} \\ \ nonumber
& \ Rightarrow \ quad \ theta — \ phi ~ = ~ 0.281 \ quad \ text {или} \ quad \ theta — \ phi ~ = ~ \ pi — 0,281 = 2,861 \\ \ nonumber
& \ Rightarrow \ quad \ theta ~ = ~ \ phi \; + \; 0.281 \ quad \ text {или} \ quad \ theta ~ = ~ \ phi \; + \; 2.861
\ end {align *} \]Теперь, поскольку \ (\; \ cos \; \ phi = \ frac {2} {\ sqrt {13}} \) и \ (\ phi \) находится в QI , наиболее общим решением для \ (\ phi \) является \ (\ phi = 0.983 + 2 \ pi k \) для \ (k = 0 \), \ (\ pm \, 1 \), \ (\ pm \ , 2 \), \ (… \). Итак, поскольку нам нужно было добавить кратные \ (2 \ pi \) к решениям \ (0.281 \) и \ (2.861 \) в любом случае, наиболее общее решение для \ (\ theta \):
\ [\ begin {align *}
\ theta ~ & = ~ 0.983 \; + \; 0,281 \; + \; 2 \ пи к \ квад \ текст {и} \ квад 0,983 \; + \; 2,861 \; + \; 2 \ pi k \\
& \ Rightarrow \ quad \ boxed {\ theta ~ = ~ 1.264 \; + \; 2 \ пи к \ квад \ текст {и} \ квад 3.844 \; + \; 2 \ pi k}
\ quad \ text {для \ (k = 0 \), \ (\ pm \, 1 \), \ (\ pm \, 2 \), \ (… \)}
\ конец {выравнивание *} \]Примечание: в примере 6.8, если бы уравнение было \ (\; 2 \, \ sin \; \ theta \; + \; 3 \, \ cos \; \ theta ~ = ~ 1 \), то мы все равно использовали бы прямоугольный треугольник с катетами длины \ (2 \) и \ (3 \), но мы бы использовали формулу сложения синуса вместо формулы вычитания.
Авторы и авторство
Решение тригонометрических уравнений | Precalculus II
Решение линейных тригонометрических уравнений с синусом и косинусом
Тригонометрические уравнения, как следует из названия, включают в себя тригонометрические функции. Во многом аналогично решению полиномиальных или рациональных уравнений, только определенные значения переменной будут решениями, если решения вообще есть. Часто мы решаем тригонометрическое уравнение на заданном интервале.Однако так же часто нас просят найти все возможные решения, и, поскольку тригонометрические функции являются периодическими, решения повторяются в течение каждого периода. Другими словами, тригонометрические уравнения могут иметь бесконечное количество решений. Кроме того, как и в случае с рациональными уравнениями, область определения функции должна быть рассмотрена, прежде чем мы предполагаем, что какое-либо решение действительно. Период как синусоидальной, так и косинусной функции равен [latex] 2 \ pi [/ latex]. Другими словами, каждые [latex] 2 \ pi [/ latex] единицы, значения y- повторяются.Если нам нужно найти все возможные решения, мы должны добавить [latex] 2 \ pi k [/ latex], где [latex] k [/ latex] — целое число, к начальному решению. Вспомните правило, которое дает формат для указания всех возможных решений для функции, в которой период равен [latex] 2 \ pi: [/ latex]
[латекс] \ sin \ theta = \ sin \ left (\ theta \ pm 2k \ pi \ right) [/ latex]
Существуют аналогичные правила для указания всех возможных решений для других тригонометрических функций. Решение тригонометрических уравнений требует тех же методов, что и решение алгебраических уравнений.Мы читаем уравнение слева направо по горизонтали, как предложение. Мы ищем известные закономерности, множители, находим общие знаменатели и заменяем определенные выражения на переменные, чтобы упростить процесс решения. Однако с тригонометрическими уравнениями у нас также есть преимущество использования тождеств, которые мы разработали в предыдущих разделах.
Пример 1. Решение линейного тригонометрического уравнения с использованием функции косинуса
Найдите все возможные точные решения уравнения [latex] \ cos \ theta = \ frac {1} {2} [/ latex].
Решение
Из единичной окружности мы знаем, что
[латекс] \ begin {array} {l} \ cos \ theta = \ frac {1} {2} \ hfill \\ \ text {} \ theta = \ frac {\ pi} {3}, \ frac {5 \ pi} {3} \ hfill \ end {array} [/ latex]
Это решения в интервале [латекс] \ left [0,2 \ pi \ right] [/ latex]. Все возможные решения приведены в
[латекс] \ theta = \ frac {\ pi} {3} \ pm 2k \ pi \ text {и} \ theta = \ frac {5 \ pi} {3} \ pm 2k \ pi [/ latex]
где [латекс] k [/ latex] — целое число.
Пример 2: Решение линейного уравнения с использованием функции синуса
Найдите все возможные точные решения уравнения [latex] \ sin t = \ frac {1} {2} [/ latex].
Решение
Решение для всех возможных значений t означает, что решения включают углы за пределами периода [латекс] 2 \ pi [/ латекс]. Из единичного круга мы видим, что решениями являются [latex] t = \ frac {\ pi} {6} [/ latex] и [latex] t = \ frac {5 \ pi} {6} [/ latex] . Но проблема в том, чтобы указать все возможные значения, которые решают уравнение.Следовательно, ответ
[латекс] t = \ frac {\ pi} {6} \ pm 2 \ pi k \ text {и} t = \ frac {5 \ pi} {6} \ pm 2 \ pi k [/ latex]
где [латекс] k [/ latex] — целое число.
Как: решить тригонометрическое уравнение с помощью алгебры.
- Найдите шаблон, который предлагает алгебраическое свойство, такое как разность квадратов или возможность разложения на множители.
- Замените тригонометрическое выражение одной переменной, например [latex] x [/ latex] или [latex] u [/ latex].
- Решите уравнение так же, как и алгебраическое уравнение.
- Подставьте тригонометрическое выражение обратно вместо переменной в результирующих выражениях.
- Найдите угол.
Пример 3: Решите тригонометрическое уравнение в линейной форме
Точно решите уравнение: [латекс] 2 \ cos \ theta -3 = -5,0 \ le \ theta <2 \ pi [/ latex].
Решение
Используйте алгебраические методы для решения уравнения.
[латекс] \ begin {array} {l} 2 \ cos \ theta -3 = -5 \ hfill \\ \ text {} 2 \ cos \ theta = -2 \ hfill \\ \ text {} \ cos \ theta = -1 \ hfill \\ \ text {} \ theta = \ pi \ hfill \ end {array} [/ latex]
Попробуй 1
Решите в точности следующее линейное уравнение на интервале [латекс] \ left [0,2 \ pi \ right): 2 \ sin x + 1 = 0 [/ latex].
Решение
Решение тригонометрических уравнений с помощью калькулятора
Не все функции могут быть решены точно с использованием только единичной окружности. Когда мы должны решить уравнение с углом, отличным от одного из специальных углов, нам понадобится калькулятор. Убедитесь, что он установлен на правильный режим, градусы или радианы, в зависимости от критериев данной проблемы.
Пример 8: Использование калькулятора для решения тригонометрического уравнения, содержащего синус
Воспользуйтесь калькулятором, чтобы решить уравнение [латекс] \ sin \ theta = 0.{\ circ} \ hfill \ end {array} [/ latex]
Анализ решения
Обратите внимание, что калькулятор возвращает только угол в квадрантах I или IV для функции синуса, поскольку это диапазон обратного синуса. Другой угол получается с помощью [латекса] \ pi — \ theta [/ latex].
Пример 9: Использование калькулятора для решения тригонометрического уравнения, содержащего секущую
Воспользуйтесь калькулятором, чтобы решить уравнение [латекс] \ сек \ тета = -4 [/ латекс], получив ответ в радианах.{-1} \ left (- \ frac {1} {4} \ right) \ приблизительно 1.8235 \ hfill \\ \ text {} \ theta \ приблизительно 1.8235 + 2 \ pi k \ hfill \ end {array} [/ latex ]
Поскольку [латекс] \ frac {\ pi} {2} \ приблизительно 1,57 [/ латекс] и [латекс] \ pi \ приблизительно 3,14 [/ латекс], 1,8235 находится между этими двумя числами, таким образом [латекс] \ тета \ приблизительно \ text {1} \ text {.8235} [/ latex] находится во втором квадранте. Косинус также отрицателен в квадранте III. Обратите внимание, что калькулятор возвращает только угол в квадрантах I или II для функции косинуса, поскольку это диапазон обратного косинуса.
Рисунок 2.
Итак, нам также нужно найти меру угла в квадранте III. В квадранте III опорный угол составляет [латекс] \ theta \ text {} \ text {} \ text {‘} \ приблизительно \ pi — \ text {1} \ text {.8235} \ приблизительно \ text {1} \ text {.3181} \ text {.} [/ latex] Другое решение в квадранте III — [latex] \ theta \ text {} \ text {} \ text {‘} \ приблизительно \ pi + \ text {1} \ текст {.3181} \ приблизительно \ текст {4} \ text {.4597} \ text {.} [/ latex]
Растворы: [латекс] \ theta \ приблизительно 1.8235 \ pm 2 \ pi k [/ latex] и [латекс] \ theta \ приблизительно 4.4597 \ pm 2 \ pi k [/ латекс].
Попробуй 3
Решите [латекс] \ cos \ theta = -0.2 [/ latex].
Решение
Решение уравнений, содержащих одну тригонометрическую функцию
Когда нам задают уравнения, которые включают только одну из шести тригонометрических функций, их решения требуют использования алгебраических методов и единичного круга. Когда уравнение включает тригонометрические функции, отличные от синуса и косинуса, необходимо учитывать несколько факторов. Проблемы, связанные с величинами, обратными первичным тригонометрическим функциям, необходимо рассматривать с алгебраической точки зрения.Другими словами, мы напишем обратную функцию и найдем углы, используя эту функцию. Кроме того, уравнение, включающее функцию тангенса, немного отличается от уравнения, содержащего функцию синуса или косинуса. Во-первых, как мы знаем, период касательной равен [латекс] \ пи [/ латекс], а не [латекс] 2 \ пи [/ латекс]. Кроме того, область касательной — это все действительные числа, за исключением нечетных целых кратных [latex] \ frac {\ pi} {2} [/ latex], если, конечно, проблема не накладывает свои собственные ограничения на область.{2} \ theta} = \ pm \ sqrt {\ frac {1} {2}} \ hfill \\ \ text {} \ sin \ theta = \ pm \ frac {1} {\ sqrt {2}} = \ pm \ frac {\ sqrt {2}} {2} \ hfill \\ \ text {} \ theta = \ frac {\ pi} {4}, \ frac {3 \ pi} {4}, \ frac {5 \ pi} {4}, \ frac {7 \ pi} {4} \ hfill \ end {array} [/ latex]
Пример 5: Решение тригонометрического уравнения с использованием косеканса
Точно решите следующее уравнение: [latex] \ csc \ theta = -2,0 \ le \ theta <4 \ pi [/ latex].
Решение
Нам нужны все значения [latex] \ theta [/ latex], для которых [latex] \ csc \ theta = -2 [/ latex] в интервале [latex] 0 \ le \ theta <4 \ pi [/ latex] .
[латекс] \ begin {array} {l} \ csc \ theta = -2 \ hfill \\ \ frac {1} {\ sin \ theta} = — 2 \ hfill \\ \ sin \ theta = — \ frac { 1} {2} \ hfill \\ \ text {} \ theta = \ frac {7 \ pi} {6}, \ frac {11 \ pi} {6}, \ frac {19 \ pi} {6}, \ гидроразрыв {23 \ pi} {6} \ hfill \ end {array} [/ latex]
Анализ решения
Как [latex] \ sin \ theta = — \ frac {1} {2} [/ latex], обратите внимание, что все четыре решения находятся в третьем и четвертом квадрантах.
Пример 6: Решение уравнения с касательной
Точно решите уравнение: [латекс] \ tan \ left (\ theta — \ frac {\ pi} {2} \ right) = 1,0 \ le \ theta <2 \ pi [/ latex].
Решение
Напомним, что тангенциальная функция имеет период [латекс] \ пи [/ латекс]. На интервале [latex] \ left [0, \ pi \ right) [/ latex] и под углом [latex] \ frac {\ pi} {4} [/ latex] тангенс имеет значение 1 . Однако нам нужен угол [латекс] \ left (\ theta — \ frac {\ pi} {2} \ right) [/ latex]. Таким образом, если [latex] \ tan \ left (\ frac {\ pi} {4} \ right) = 1 [/ latex], то
[латекс] \ begin {array} {c} \ theta — \ frac {\ pi} {2} = \ frac {\ pi} {4} \\ \ theta = \ frac {3 \ pi} {4} \ pm k \ pi \ end {array} [/ latex]
В интервале [латекс] \ left [0,2 \ pi \ right) [/ latex] у нас есть два решения:
[латекс] \ theta = \ frac {3 \ pi} {4} \ text {и} \ theta = \ frac {3 \ pi} {4} + \ pi = \ frac {7 \ pi} {4} [ / латекс]
Попробуй 2
Найдите все решения для [латекс] \ tan x = \ sqrt {3} [/ latex].
Решение
Пример 7: Определите все решения уравнения, содержащего касательную
Определите все точные решения уравнения [латекс] 2 \ left (\ tan x + 3 \ right) = 5 + \ tan x, 0 \ le x <2 \ pi [/ latex].
Решение
Мы можем решить это уравнение, используя только алгебру. Выделите выражение [latex] \ tan x [/ latex] слева от знака равенства.
[латекс] \ begin {array} {cc} \ hfill 2 \ left (\ tan x \ right) +2 \ left (3 \ right) & = 5 + \ tan x \ hfill \\ \ hfill 2 \ tan x + 6 & = 5 + \ tan x \ hfill \\ \ hfill \ text {} 2 \ tan x- \ tan x & = 5-6 \ hfill \\ \ hfill \ tan x & = -1 \ hfill \ end {array} [ / латекс]
На единичной окружности есть два угла, значение касательной которых равно [latex] -1: \ theta = \ frac {3 \ pi} {4} [/ latex] и [latex] \ theta = \ frac {7 \ пи} {4} [/ латекс].
Решение тригонометрических уравнений в квадратичной форме
Решение квадратного уравнения может быть более сложным, но, опять же, мы можем использовать алгебру, как и любое квадратное уравнение. Посмотрите на схему уравнения. Есть ли в уравнении более одной тригонометрической функции или только одна? Какая тригонометрическая функция возводится в квадрат? Если представлена только одна функция и один из членов возведен в квадрат, подумайте о стандартной форме квадратичной функции.{2} \ theta -5 \ sin \ theta + 3 = 0 \ hfill \\ \ left (2 \ sin \ theta -3 \ right) \ left (\ sin \ theta -1 \ right) = 0 \ hfill \ end {array} \\ [/ latex]
Теперь установите каждый коэффициент равным нулю.
[латекс] \ begin {array} {l} 2 \ sin \ theta -3 = 0 \ hfill \\ \ text {} 2 \ sin \ theta = 3 \ hfill \\ \ text {} \ sin \ theta = \ frac {3} {2} \ hfill \\ \ hfill \\ \ hfill \\ \ text {} \ sin \ theta -1 = 0 \ hfill \\ \ text {} \ sin \ theta = 1 \ hfill \ end { массив} \\ [/ latex]
Затем решите для [latex] \ theta: \ sin \ theta \ ne \ frac {3} {2} \\ [/ latex], так как диапазон синусоидальной функции равен [latex] \ left [-1,1 \ справа] \\ [/ латекс].{2} + x = 0 \ hfill \\ x \ left (2x + 1 \ right) = 0 \ hfill \ end {array} \\ [/ latex]
Установите каждый коэффициент равным нулю.
[латекс] \ begin {массив} {l} \ text {} x = 0 \ text {} \ hfill \\ \ left (2x + 1 \ right) = 0 \ hfill \\ \ text {} x = — \ гидроразрыв {1} {2} \ hfill \ end {array} \\ [/ latex]
Затем снова подставьте в уравнение исходное выражение [latex] \ sin \ theta \\ [/ latex] вместо [latex] x \\ [/ latex]. Таким образом,
[латекс] \ begin {array} {l} \ sin \ theta = 0 \ hfill \\ \ text {} \ theta = 0, \ pi \ hfill \\ \ hfill \\ \ sin \ theta = — \ frac { 1} {2} \ hfill \\ \ text {} \ theta = \ frac {7 \ pi} {6}, \ frac {11 \ pi} {6} \ hfill \ end {array} \\ [/ latex]
Решения в домене [latex] 0 \ le \ theta <2 \ pi \\ [/ latex]: [latex] \ theta = 0, \ pi, \ frac {7 \ pi} {6}, \ frac { 11 \ pi} {6} \\ [/ латекс].{2} \ theta + \ sin \ theta = 0 \ hfill \\ \ sin \ theta \ left (2 \ sin \ theta +1 \ right) = 0 \ hfill \\ \ text {} \ sin \ theta = 0 \ hfill \\ \ text {} \ theta = 0, \ pi \ hfill \\ \ hfill \\ \ text {} 2 \ sin \ theta + 1 = 0 \ hfill \\ \ text {} 2 \ sin \ theta = - 1 \ hfill \\ \ text {} \ sin \ theta = - \ frac {1} {2} \ hfill \\ \ text {} \ theta = \ frac {7 \ pi} {6}, \ frac {11 \ pi} {6} \ hfill \ end {array} \\ [/ latex]
Анализ решения
Мы можем видеть решения на графике на Рисунке 3. {2} \ theta + \ cos \ theta = 0 \\ [/ latex].
Решение
Решение тригонометрических уравнений с использованием фундаментальных тождеств
Хотя алгебру можно использовать для решения ряда тригонометрических уравнений, мы также можем использовать фундаментальные тождества, потому что они упрощают решение уравнений. Помните, что методы, которые мы используем для решения проблем, не совпадают с методами проверки личности. Здесь применяются основные правила алгебры, а не переписывание одной стороны идентичности для соответствия другой стороне. В следующем примере мы используем два тождества, чтобы упростить уравнение.
Пример 14: Использование идентичностей для решения уравнения
Используйте тождества, чтобы точно решить тригонометрическое уравнение в интервале [латекс] 0 \ le x <2 \ pi [/ latex].
[латекс] \ cos x \ cos \ left (2x \ right) + \ sin x \ sin \ left (2x \ right) = \ frac {\ sqrt {3}} {2} [/ latex]
Решение
Обратите внимание, что левая часть уравнения — это формула разности для косинуса.
[латекс] \ begin {array} {ll} \ hfill & \ hfill \\ \ cos x \ cos \ left (2x \ right) + \ sin x \ sin \ left (2x \ right) = \ frac {\ sqrt {3}} {2} \ hfill & \ hfill \\ \ text {} \ cos \ left (x — 2x \ right) = \ frac {\ sqrt {3}} {2} \ begin {array} {cccc} & & & \ end {array} \ hfill & \ text {Формула разности для косинуса} \ hfill \\ \ text {} \ cos \ left (-x \ right) = \ frac {\ sqrt {3}} {2} \ hfill & \ text {Использовать тождество отрицательного угла}.\ hfill \\ \ text {} \ cos x = \ frac {\ sqrt {3}} {2} \ hfill & \ hfill \ end {array} [/ latex]
Из единичного круга в суммах и различиях идентичностей мы видим, что [latex] \ cos x = \ frac {\ sqrt {3}} {2} [/ latex], когда [latex] x = \ frac {\ pi} { 6}, \ frac {11 \ pi} {6} [/ latex].
Пример 15: Решение уравнения с использованием формулы двойного угла
Точно решите уравнение, используя формулу двойного угла: [latex] \ cos \ left (2 \ theta \ right) = \ cos \ theta [/ latex].
Решение
У нас есть три варианта выражения для замены двойного угла косинуса.{2} \ theta — \ cos \ theta -1 = 0 \ hfill \\ \ left (2 \ cos \ theta +1 \ right) \ left (\ cos \ theta -1 \ right) = 0 \ hfill \\ \ текст {} 2 \ cos \ theta + 1 = 0 \ hfill \\ \ text {} \ cos \ theta = — \ frac {1} {2} \ hfill \\ \ hfill \\ \ text {} \ cos \ theta -1 = 0 \ hfill \\ \ text {} \ cos \ theta = 1 \ hfill \ end {array} [/ latex]
Итак, если [latex] \ cos \ theta = — \ frac {1} {2} [/ latex], то [latex] \ theta = \ frac {2 \ pi} {3} \ pm 2 \ pi k [ / latex] и [latex] \ theta = \ frac {4 \ pi} {3} \ pm 2 \ pi k [/ latex]; если [латекс] \ cos \ theta = 1 [/ latex], то [latex] \ theta = 0 \ pm 2 \ pi k [/ latex].{2} \ theta +3 cos \ theta + 1 & = 0 \ hfill \\ \ hfill \ left (2 cos \ theta +1 \ right) \ left (\ cos \ theta +1 \ right) & = 0 \ hfill \ \ \ hfill 2 cos \ theta + 1 & = 0 \ hfill \\ \ hfill \ cos \ theta & = — \ frac {1} {2} \ hfill \\ \ hfill \ theta & = \ frac {2 \ pi} { 3}, \ frac {4 \ pi} {3} \ hfill \\ \ hfill \ cos \ theta + 1 & = 0 \ hfill \\ \ hfill \ cos \ theta & = -1 \ hfill \\ \ hfill \ theta & = \ pi \ hfill \ end {array} [/ latex]
Наши решения: [latex] \ theta = \ frac {2 \ pi} {3}, \ frac {4 \ pi} {3}, \ pi [/ latex].
Решение тригонометрических уравнений с несколькими углами
Иногда невозможно решить тригонометрическое уравнение с тождествами, которые имеют несколько углов, например [латекс] \ sin \ left (2x \ right) [/ latex] или [латекс] \ cos \ left (3x \ right) [/латекс].Столкнувшись с этими уравнениями, вспомните, что [latex] y = \ sin \ left (2x \ right) [/ latex] представляет собой горизонтальное сжатие с коэффициентом 2 от функции [latex] y = \ sin x [/ латекс]. На интервале [latex] 2 \ pi [/ latex] мы можем построить график двух периодов [latex] y = \ sin \ left (2x \ right) [/ latex], в отличие от одного цикла [latex] y = \ sin x [/ латекс]. Такое сжатие графика приводит нас к мысли, что может быть вдвое больше x -перехватов или решений для [latex] \ sin \ left (2x \ right) = 0 [/ latex] по сравнению с [latex] \ sin x = 0 [/ латекс].Эта информация поможет нам решить уравнение.
Пример 17: Решение многоугольного тригонометрического уравнения
Точное решение: [латекс] \ cos \ left (2x \ right) = \ frac {1} {2} [/ latex] на [латексе] \ left [0,2 \ pi \ right) [/ latex]. {- 1} \ frac {1} {2} [/ latex] дает решения только в квадрантах I и II, мы понимаем, что решения уравнения [latex] \ cos \ theta = \ frac {1} {2} [/ latex] будет в квадрантах I и IV.
Следовательно, возможные углы: [latex] \ theta = \ frac {\ pi} {3} [/ latex] и [latex] \ theta = \ frac {5 \ pi} {3} [/ latex]. Итак, [latex] 2x = \ frac {\ pi} {3} [/ latex] или [latex] 2x = \ frac {5 \ pi} {3} [/ latex], что означает, что [latex] x = \ frac {\ pi} {6} [/ latex] или [latex] x = \ frac {5 \ pi} {6} [/ latex]. Имеет ли это смысл? Да, потому что [латекс] \ cos \ left (2 \ left (\ frac {\ pi} {6} \ right) \ right) = \ cos \ left (\ frac {\ pi} {3} \ right) = \ гидроразрыв {1} {2} [/ latex].
Есть ли другие возможные ответы? Вернемся к нашему первому шагу.
В квадранте I [latex] 2x = \ frac {\ pi} {3} [/ latex], поэтому [latex] x = \ frac {\ pi} {6} [/ latex], как указано. Давайте снова начнем вращаться по кругу:
[латекс] \ begin {array} {l} \ hfill \\ 2x = \ frac {\ pi} {3} +2 \ pi \ hfill \\ \ text {} = \ frac {\ pi} {3} + \ frac {6 \ pi} {3} \ hfill \\ \ text {} = \ frac {7 \ pi} {3} \ hfill \ end {array} [/ latex]
так [латекс] x = \ frac {7 \ pi} {6} [/ latex].
Еще один оборот дает
[латекс] \ begin {массив} {l} \ begin {array} {l} \\ 2x = \ frac {\ pi} {3} +4 \ pi \ end {array} \ hfill \\ \ text {} = \ frac {\ pi} {3} + \ frac {12 \ pi} {3} \ hfill \\ \ text {} = \ frac {13 \ pi} {3} \ hfill \ end {array} [/ latex ]
[latex] x = \ frac {13 \ pi} {6}> 2 \ pi [/ latex], поэтому это значение для [latex] x [/ latex] больше, чем [latex] 2 \ pi [/ latex] , так что это не решение для [латекса] \ left [0,2 \ pi \ right) [/ latex].
В квадранте IV [latex] 2x = \ frac {5 \ pi} {3} [/ latex], поэтому [latex] x = \ frac {5 \ pi} {6} [/ latex], как указано. Давайте снова начнем вращаться по кругу:
[латекс] \ begin {array} {l} 2x = \ frac {5 \ pi} {3} +2 \ pi \ hfill \\ \ text {} = \ frac {5 \ pi} {3} + \ frac {6 \ pi} {3} \ hfill \\ \ text {} = \ frac {11 \ pi} {3} \ hfill \ end {array} [/ latex]
так [латекс] x = \ frac {11 \ pi} {6} [/ latex].
Еще один оборот дает
[латекс] \ begin {array} {l} 2x = \ frac {5 \ pi} {3} +4 \ pi \ hfill \\ \ text {} = \ frac {5 \ pi} {3} + \ frac {12 \ pi} {3} \ hfill \\ \ text {} = \ frac {17 \ pi} {3} \ hfill \ end {array} [/ latex]
[latex] x = \ frac {17 \ pi} {6}> 2 \ pi [/ latex], поэтому это значение для [latex] x [/ latex] больше, чем [latex] 2 \ pi [/ latex] , так что это не решение для [латекса] \ left [0,2 \ pi \ right) [/ latex].
Наши решения: [latex] x = \ frac {\ pi} {6}, \ frac {5 \ pi} {6}, \ frac {7 \ pi} {6}, \ text {и} \ frac {11 \ pi} {6} [/ латекс]. Обратите внимание, что всякий раз, когда мы решаем задачу в форме [латекс] \ sin \ left (nx \ right) = c [/ latex], мы должны обойти единичный круг [латекс] n [/ латекс] раз.
Решение задач прямоугольного треугольника
Теперь мы можем использовать все изученные нами методы для решения задач, связанных с применением свойств прямоугольных треугольников и теоремы Пифагора .{2} [/ latex] и смоделируйте уравнение в соответствии с ситуацией.
Пример 18: Использование теоремы Пифагора для моделирования уравнения
Используйте теорему Пифагора и свойства прямоугольных треугольников, чтобы смоделировать уравнение, которое соответствует задаче.
Один из тросов, которыми центр колеса обозрения London Eye крепится к земле, необходимо заменить. Центр колеса обозрения находится на высоте 69,5 метра над землей, а второй якорь на земле находится в 23 метрах от основания колеса обозрения.{\ circ} [/ latex], а длина кабеля составляет 73,2 метра.
Пример 19: Использование теоремы Пифагора для моделирования абстрактной задачи
Правила безопасности OSHA требуют, чтобы основание лестницы располагалось на расстоянии 1 фута от стены на каждые 4 фута длины лестницы. Найдите угол, под которым лестница любой длины образует с землей, и высоту, на которой лестница касается стены.
Решение
Для лестницы любой длины основание должно находиться на расстоянии от стены, равном одной четвертой длины лестницы.{2} \ hfill \\ \ text {} b = \ sqrt {15} a \ hfill \ end {array} [/ latex]
Таким образом, лестница касается стены на [латексном] \ sqrt {15} [/ латексном] футе от земли.
- При решении линейных тригонометрических уравнений мы можем использовать алгебраические методы так же, как при решении алгебраических уравнений. Ищите закономерности, такие как разница квадратов, квадратичная форма или выражение, которое хорошо поддается замене.
- Уравнения, содержащие одну тригонометрическую функцию, можно решить или проверить с помощью единичной окружности.
- Мы также можем решать тригонометрические уравнения с помощью графического калькулятора.
- Многие уравнения имеют квадратичную форму. Мы можем использовать подстановку, чтобы уравнение выглядело проще, а затем использовать те же методы, которые мы используем при решении алгебраической квадратичной системы: разложение на множители, квадратичная формула и т. Д.
- Мы также можем использовать тождества для решения тригонометрических уравнений.
- Мы можем использовать подстановку для решения многоугольного тригонометрического уравнения, которое является сжатием стандартной тригонометрической функции.Нам нужно будет учесть сжатие и убедиться, что мы нашли все решения на заданном интервале.
- Реальные сценарии можно моделировать и решать с помощью теоремы Пифагора и тригонометрических функций.
Упражнения по разделам
1. Всегда ли будут решения уравнений тригонометрических функций? Если нет, опишите уравнение, у которого не было бы решения. Объясните, почему да или почему нет.
2. При решении тригонометрического уравнения, включающего более одной тригонометрической функции, всегда ли мы хотим попытаться переписать уравнение так, чтобы оно выражалось в терминах одной тригонометрической функции? Почему или почему нет?
3.Решая линейные тригонометрические уравнения только с помощью синуса или косинуса, как мы узнаем, будут ли решения?
Для следующих упражнений найдите все решения точно на интервале [latex] 0 \ le \ theta <2 \ pi [/ latex].
4. [латекс] 2 \ sin \ theta = — \ sqrt {2} [/ латекс]
5. [латекс] 2 \ sin \ theta = \ sqrt {3} [/ латекс]
6. [латекс] 2 \ cos \ theta = 1 [/ латекс]
7. [латекс] 2 \ cos \ theta = — \ sqrt {2} [/ латекс]
8. [латекс] \ tan \ theta = -1 [/ латекс]
9.{2} x — 4 = 0 [/ латекс]
Для следующих упражнений решите точно на [латексе] \ левом [0,2 \ пи \ правом) [/ латексе].
13. [латекс] 2 \ cos \ theta = \ sqrt {2} [/ латекс]
14. [латекс] 2 \ cos \ theta = -1 [/ латекс]
15. [латекс] 2 \ sin \ theta = -1 [/ латекс]
16. [латекс] 2 \ sin \ theta = — \ sqrt {3} [/ латекс]
17. [латекс] 2 \ sin \ left (3 \ theta \ right) = 1 [/ латекс]
18. [латекс] 2 \ sin \ left (2 \ theta \ right) = \ sqrt {3} [/ latex]
19. [латекс] 2 \ cos \ left (3 \ theta \ right) = — \ sqrt {2} [/ latex]
20.[латекс] \ cos \ left (2 \ theta \ right) = — \ frac {\ sqrt {3}} {2} [/ latex]
21. [латекс] 2 \ sin \ left (\ pi \ theta \ right) = 1 [/ латекс]
22. [латекс] 2 \ cos \ left (\ frac {\ pi} {5} \ theta \ right) = \ sqrt {3} [/ latex]
Для следующих упражнений найдите все точные решения на [latex] \ left [0,2 \ pi \ right) [/ latex].
23. [латекс] \ sec \ left (x \ right) \ sin \ left (x \ right) -2 \ sin \ left (x \ right) = 0 [/ латекс]
24. [латекс] \ tan \ left (x \ right) -2 \ sin \ left (x \ right) \ tan \ left (x \ right) = 0 [/ латекс]
25.{5} \ left (x \ right) = \ tan \ left (x \ right) [/ латекс]
Для следующих упражнений решайте методами, показанными в этом разделе, точно в интервале [латекс] \ left [0,2 \ pi \ right) [/ latex].
33. [латекс] \ sin \ left (3x \ right) \ cos \ left (6x \ right) — \ cos \ left (3x \ right) \ sin \ left (6x \ right) = — 0,9 [/ латекс]
34. [латекс] \ sin \ left (6x \ right) \ cos \ left (11x \ right) — \ cos \ left (6x \ right) \ sin \ left (11x \ right) = — 0,1 [/ латекс]
35. [латекс] \ cos \ left (2x \ right) \ cos x + \ sin \ left (2x \ right) \ sin x = 1 [/ latex]
36.{2} x + 69 \ tan x — 130 = 0 [/ латекс]
Для следующих упражнений используйте калькулятор, чтобы найти все решения до четырех знаков после запятой.
73. [латекс] \ sin x = 0,27 [/ латекс]
74. [латекс] \ sin x = -0,55 [/ латекс]
75. [латекс] \ tan x = -0,34 [/ латекс]
76. [латекс] \ cos x = 0,71 [/ латекс]
Для следующих упражнений решите уравнения алгебраически, а затем с помощью калькулятора найдите значения в интервале [латекс] \ left [0,2 \ pi \ right) [/ latex]. Округлить до четырех знаков после запятой.{2} x = 4 [/ латекс]
93. У самолета достаточно бензина, чтобы долететь до города в 200 милях к северо-востоку от его текущего местоположения. Если пилот знает, что город находится в 25 милях к северу, на сколько градусов к северу от востока должен лететь самолет?
94. Если погрузочная рампа расположена рядом с грузовиком на высоте 4 фута, а ее длина составляет 15 футов, то какой угол образует аппарель с землей?
95. Если погрузочная рампа расположена рядом с грузовиком на высоте 2 фута, а ее длина составляет 20 футов, то какой угол образует аппарель с землей?
96.Женщина наблюдает за запущенной ракетой, которая сейчас находится на высоте 11 миль. Если она стоит в 4 милях от стартовой площадки, под каким углом она смотрит вверх из горизонтали?
97. Космонавт находится в запущенной ракете, которая сейчас находится на высоте 15 миль. Если мужчина стоит в 2 милях от стартовой площадки, под каким углом она смотрит на него сверху вниз из горизонтали? (Подсказка: это называется углом депрессии.)
98. Женщина стоит в 8 метрах от 10-метрового здания. Под каким углом она смотрит на вершину здания?
99.Мужчина стоит в 10 метрах от 6-метрового дома. Кто-то наверху здания смотрит на него сверху вниз. Под каким углом смотрит на него человек?
100. У 20-футового здания есть тень длиной 55 футов. Какой угол подъема солнца?
101. У здания высотой 90 футов есть тень длиной 2 фута. Какой угол подъема солнца?
102. Прожектор на земле в 3 метрах от человека ростом 2 метра отбрасывает 6-метровую тень на стену в 6 метрах от человека.Под каким углом свет?
103. Прожектор на земле в 3 футах от женщины ростом 5 футов отбрасывает тень высотой 15 футов на стену в 6 футах от женщины. Под каким углом свет?
Для следующих упражнений найдите решение следующей задачи со словами алгебраически. Затем воспользуйтесь калькулятором, чтобы проверить результат. Ответ округлите до десятых долей градуса.
104. Человек выполняет стойку на руках, касаясь ногами стены, а его руки находятся на расстоянии 1,5 фута от стены.Если рост человека 6 футов, какой угол у его ступни со стеной?
105. Человек выполняет стойку на руках, при этом ноги касаются стены, а руки находятся на расстоянии 3 футов от стены. Если рост человека 5 футов, какой угол у его ступни со стеной?
106. Рядом с домом стоит 23-футовая лестница. Если лестница соскользнет на расстоянии 7 футов от дома при недостаточном сцеплении с землей, какой угол должна быть сделана лестницей по отношению к земле, чтобы не поскользнуться?
3.8 Решение тригонометрических уравнений | Precalculus
Цели обучения
В этом разделе вы:
- Решите линейные тригонометрические уравнения с синусом и косинусом.
- Решите уравнения, содержащие одну тригонометрическую функцию.
- Решите тригонометрические уравнения с помощью калькулятора.
- Решите тригонометрические уравнения квадратичной формы.
- Решите тригонометрические уравнения, используя фундаментальные тождества.
- Решайте тригонометрические уравнения с несколькими углами.
Египетские пирамиды возле современного города. (кредит: Ойсин Малвихилл)
Фалес Милетский (около 625–547 гг. До н.э.) известен как основоположник геометрии. Легенда гласит, что он рассчитал высоту Великой пирамиды Гизы в Египте, используя теорию подобных треугольников , которую он разработал, измерив тень своего посоха. Эта теория, основанная на пропорциях, находит применение во многих областях, включая фрактальную геометрию, инженерию и архитектуру.Часто угол подъема и угол депрессии находят с помощью одинаковых треугольников.
В предыдущих разделах этой главы мы рассматривали тригонометрические тождества. Тождества верны для всех значений в домене переменной. В этом разделе мы начинаем изучение тригонометрических уравнений для изучения реальных сценариев, таких как определение размеров пирамид.
Решение линейных тригонометрических уравнений с синусом и косинусом
Тригонометрические уравнения, как следует из названия, включают в себя тригонометрические функции.Во многом аналогично решению полиномиальных или рациональных уравнений, только определенные значения переменной будут решениями, если решения вообще есть. Кроме того, как и в случае с рациональными уравнениями, область определения функции должна быть рассмотрена, прежде чем мы предполагаем, что какое-либо решение действительно.
Часто мы решаем тригонометрическое уравнение на заданном интервале. Однако так же часто нас просят найти все возможные решения, и, поскольку тригонометрические функции являются периодическими, решения повторяются в течение каждого периода.Другими словами, тригонометрические уравнения могут иметь бесконечное количество решений. Период функции синуса и косинуса равен [latex] 2 \ pi. [/ Latex] Другими словами, каждые [latex] 2 \ pi [/ latex] единицы, значения y- повторяются, поэтому [ латекс] \ mathrm {sin} \ left (\ theta \ right) = \ mathrm {sin} \ left (\ theta \ pm2k \ pi \ right) [/ latex]. Если нам нужно найти все возможные решения, мы должны добавить [latex] 2 \ pi k, [/ latex], где [latex] k [/ latex] — целое число, к начальному решению.
Существуют аналогичные правила для указания всех возможных решений для других тригонометрических функций.Решение тригонометрических уравнений требует тех же методов, что и решение алгебраических уравнений. Мы читаем уравнение слева направо по горизонтали, как предложение. Мы ищем известные закономерности, множители, находим общие знаменатели и заменяем определенные выражения на переменные, чтобы упростить процесс решения. Однако с тригонометрическими уравнениями у нас также есть преимущество использования тождеств, которые мы разработали в предыдущих разделах.
Пример 1. Решение линейного тригонометрического уравнения с использованием функции косинуса
Найдите все возможные точные решения уравнения [latex] \ mathrm {cos} \ left (\ theta \ right) = \ frac {1} {2}.[/ латекс]
Показать решение
Из единичной окружности мы знаем, что будут два угла, где [latex] \ mathrm {cos} \ left (\ theta \ right) = \ frac {1} {2} [/ latex] за один полный оборот, т. Е. [latex] 0 \ le \ theta \ le {2 \ pi}. [/ latex] Они будут находиться в первом и четвертом квадрантах. Мы распознаем [latex] \ frac {1} {2} [/ latex] как значение одного из наших специальных прямоугольных треугольников. Мы можем определить острый угол как [латекс] \ frac {\ pi} {3}. [/ Latex] Затем мы можем использовать его в качестве опорного угла, чтобы найти угол в четвертом квадранте, вычислив [латекс] 2 \ pi- \ frac {\ pi} {3}.[/ латекс]
[латекс] \ begin {align *} \ mathrm {cos} \ left (\ theta \ right) & = \ frac {1} {2} \\ \ theta & = \ frac {\ pi} {3}, \ frac {5 \ pi} {3} \ end {align *} [/ latex] [latex] \\ [/ latex]
Это решения в интервале [latex] \ left [0,2 \ pi \ right]. [/ Latex] Все возможные решения даются как [latex] \ frac {\ pi} {3} \ pm2k \ pi [ / latex] и [latex] \ frac {5 \ pi} {3} \ pm2k \ pi [/ latex], где [latex] k [/ latex] — целое число.
Пример 2: Решение линейного уравнения с использованием синусоидальной функции
Найдите все возможные точные решения уравнения [latex] \ mathrm {sin} \ left (t \ right) = \ frac {1} {2}.[/ латекс]
Показать решение
Решение для всех возможных значений t означает, что решения включают углы за пределами периода [латекс] 2 \ pi. [/ Latex] Из предыдущей работы с единичной окружностью мы знаем, что есть два решения за один оборот. Поскольку значение положительное, мы знаем, что эти решения находятся в первом и втором квадрантах. Из наших специальных прямоугольных треугольников мы знаем, что угол в первом квадранте равен [латекс] \ frac {\ pi} {6} [/ latex], и, используя его в качестве опорного угла, решение во втором квадранте — [латекс] \ frac {5 \ pi} {6}.[/ latex] Но проблема в том, чтобы задать все возможные значения, которые решают уравнение.
Следовательно, ответ — [латекс] \ frac {\ pi} {6} \ pm2 \ pi k [/ latex] и [латекс] \ frac {5 \ pi} {6} \ pm2 \ pi k [/ latex] где [латекс] k [/ latex] — целое число.
Пример 3: Решите тригонометрическое уравнение в линейной форме
Точно решите уравнение: [латекс] 2 \ text {} \ mathrm {cos} \ left (\ theta \ right) -3 = -5, \ text {} \ text {} 0 \ le \ theta <2 \ pi . [/ латекс]
Показать решение
Используйте алгебраические методы для решения уравнения.
[латекс] \ begin {align *} 2 \ text {} \ mathrm {cos} \ left (\ theta \ right) -3 & = — 5 \\ 2 \ mathrm {cos} \ left (\ theta \ right) & = -2 && \ text {Добавлено по 3 с обеих сторон. } \\ \ mathrm {cos} \ left (\ theta \ right) & = — 1 && \ text {Обе стороны разделены на 2.} \\ \ theta & = \ pi \ end {align *} [/ latex]
Думая об единичной окружности, мы видим, что есть только одно место, где значение косинуса равно -1 за один полный оборот.
Попробуй # 1
Решите в точности следующее линейное уравнение на интервале [латекс] \ left [0,2 \ pi \ right): \ text {} 2 \ text {} \ mathrm {sin} \ left (x \ right) + 1 = 0 .[/ латекс]
Показать решение
[латекс] x = \ frac {7 \ pi} {6}, \ text {} \ frac {11 \ pi} {6} [/ latex]
Решение уравнений, содержащих одну тригонометрическую функцию
Когда нам задают уравнения, которые включают только одну из шести тригонометрических функций, их решения требуют использования алгебраических методов и информации, которую мы знаем из единичного круга. Когда уравнение включает тригонометрические функции, отличные от синуса и косинуса, необходимо учитывать несколько факторов. Проблемы, связанные с величинами, обратными первичным тригонометрическим функциям, необходимо рассматривать с алгебраической точки зрения.Другими словами, мы запишем уравнение в терминах обратной функции и решим углы, используя функции, с которыми мы наиболее знакомы. Кроме того, уравнение, включающее функцию тангенса, немного отличается от уравнения, содержащего функцию синуса или косинуса. Во-первых, как мы знаем, период касательной равен [латекс] \ пи, [/ латекс], а не [латекс] 2 \ пи. [/ Латекс] Кроме того, область касательной — это все действительные числа, за исключением нечетных целых кратных of [latex] \ frac {\ pi} {2}, [/ latex], если, конечно, проблема не накладывает свои собственные ограничения на домен.
Пример 4: Решение тригонометрического уравнения с использованием косеканса
Точно решите следующее уравнение: [latex] \ mathrm {csc} \ left (\ theta \ right) = -2, \ text {} 0 \ le \ theta <4 \ pi. [/ Latex]
Показать решение
Нам нужны все значения [latex] \ theta [/ latex], для которых [latex] \ mathrm {csc} \ left (\ theta \ right) = -2 [/ latex] в интервале [latex] 0 \ le \ тета <4 \ пи. [/ латекс]
[латекс] \ begin {align *} \ mathrm {csc} \ left (\ theta \ right) & = — 2 \\ \ frac {1} {\ mathrm {sin} \ left (\ theta \ right)} & = -2 \\ \ mathrm {sin} \ left (\ theta \ right) & = — \ frac {1} {2} \\ & = \ frac {7 \ pi} {6}, \ text {} \ frac {11 \ pi} {6}, \ text {} \ frac {19 \ pi} {6}, \ text {} \ frac {23 \ pi} {6} \ end {align *} [/ latex] [латекс ] \\ [/ латекс]
Поскольку [latex] \ mathrm {sin} \ left (\ theta \ right) = — \ frac {1} {2}, [/ latex] обратите внимание, что все четыре решения находятся в третьем и четвертом квадрантах.
Пример 5: Решение уравнения с касательной
Точно решите уравнение: [latex] \ mathrm {tan} \ left (\ theta — \ frac {\ pi} {2} \ right) = 1, \ text {} 0 \ le \ theta <2 \ pi. [ / латекс]
Показать решение
Напомним, что тангенциальная функция имеет период [латекс] \ pi. [/ Latex] на интервале [латекс] \ left [0, \ pi \ right), [/ latex] и под углом [латекс] \ frac {\ pi} {4}, [/ latex] тангенс имеет значение 1. Однако нам нужен угол [latex] \ left (\ theta — \ frac {\ pi} {2} \ right).[/ latex] Таким образом, если [latex] \ mathrm {tan} \ left (\ frac {\ pi} {4} \ right) = 1, [/ latex], то
[латекс] \ begin {align *} \ theta — \ frac {\ pi} {2} & = \ frac {\ pi} {4} \\ \ theta & = \ frac {3 \ pi} {4} \ pm k \ pi \ end {align *} [/ латекс] [латекс] \\ [/ латекс]
В интервале [латекс] \ left [0,2 \ pi \ right), [/ latex] у нас есть два решения:
[латекс] \ frac {3 \ pi} {4} [/ latex] и [латекс] \ frac {3 \ pi} {4} + \ pi = \ frac {7 \ pi} {4} [/ latex]
Попробуй # 2
Найдите все решения для [latex] \ mathrm {tan} \ left (x \ right) = \ sqrt [\ leftroot {1} \ uproot {2}] {3}.[/ латекс]
Показать решение
[латекс] \ frac {\ pi} {3} \ pm \ pi k [/ латекс]
Пример 6: Определите все решения уравнения, содержащего касательную
Определите все точные решения уравнения [латекс] 2 \ left (\ mathrm {tan} \ left (x \ right) +3 \ right) = 5 + \ mathrm {tan} \ left (x \ right), \ text {} 0 \ le x <2 \ pi. [/ Latex]
Показать решение
Мы можем решить это уравнение, используя только алгебру. Выделите выражение [latex] \ mathrm {tan} \ left (x \ right) [/ latex] слева от знака равенства.
[латекс] \ begin {align *} 2 \ text {} \ left (\ mathrm {tan} \ left (x \ right) \ right) +2 \ text {} \ left (3 \ right) & = 5 + \ mathrm {tan} \ left (x \ right) && \ text {Распределите 2 на левой стороне. } \\ 2 \ text {} \ mathrm {tan} \ left (x \ right) + 6 & = 5 + \ mathrm {tan} \ left (x \ right) \\ 2 \ text {} \ mathrm {tan} \ left (x \ right) — \ mathrm {tan} \ left (x \ right) & = 5-6 && \ text {Изолировать касательную с одной стороны.} \\ \ mathrm {tan} \ left (x \ right) & = -1 \ end {align *} [/ latex] [latex] \\ [/ latex]
На единичной окружности есть два угла, значение касательной которых равно [latex] -1: \ theta = \ frac {3 \ pi} {4} [/ latex] и [latex] \ theta = \ frac {7 \ пи} {4}.[/ латекс]
Решение тригонометрических уравнений с помощью калькулятора
Не все функции могут быть решены точно с использованием только единичной окружности. Когда мы должны решить уравнение с углом, отличным от одного из специальных углов, нам понадобится калькулятор. Убедитесь, что он установлен на правильный режим, градусы или радианы, в зависимости от критериев данной проблемы.
Пример 7: Использование калькулятора для решения тригонометрического уравнения, содержащего синус
Воспользуйтесь калькулятором, чтобы решить уравнение [латекс] \ mathrm {sin} \ left (\ theta \ right) = 0.{-1} \ влево (0,8 \ вправо) \ приблизительно 0,9273 [/ латекс]
Раствор [латекс] 0,9273 \ pm2 \ pi k. [/ Latex]
Имейте в виду, что калькулятор будет возвращать только угол в квадрантах I или IV для функции синуса, поскольку это диапазон обратного синуса. Поскольку значение синуса положительное, в квадранте 2 будет другое решение. Другой угол получается с помощью [latex] \ pi — \ theta. [/ Latex]
Это дает нам второй набор значений в виде [латекс] 2.2143 \ pm2 \ pi k. [/ Latex]
Угловые измерения в градусах основаны на углах первого вращения
[латекс] \ тета \ приблизительно {53.{\ circ} [/ латекс]
Пример 8: Использование калькулятора для решения тригонометрического уравнения, содержащего секущую
Воспользуйтесь калькулятором, чтобы решить уравнение [latex] \ mathrm {sec} \ left (\ theta \ right) = -4, [/ latex], давая ответ в радианах.
Показать решение
Мы можем начать с некоторой алгебры.
[латекс] \ begin {align *} \ mathrm {sec} \ left (\ theta \ right) & = — 4 \\ \ frac {1} {\ mathrm {cos} \ left (\ theta \ right)} & = -4 \\\ mathrm {cos} \ left (\ theta \ right) & = — \ frac {1} {4} \ end {align *} [/ latex]
Убедитесь, что РЕЖИМ установлен в радианах.{-1} \ left (- \ frac {1} {4} \ right) & \ приблизительно 1.8235 \\ \ theta & \ приблизительно 1.8235 + 2 \ pi k \\ \ end {align *} [/ latex] [латекс] \\ [/ латекс]
Поскольку [латекс] \ frac {\ pi} {2} \ приблизительно 1,57 [/ латекс] и [латекс] \ pi \ приблизительно 3,14, [/ latex], мы знаем, что 1,8235 находится между этими двумя числами, таким образом [латекс] \ theta \ приблизительно \ text {1} \ text {.8235} [/ latex] находится во втором квадранте. Косинус также отрицателен в квадранте III. Обратите внимание, что калькулятор возвращает только угол в квадрантах I или II для функции косинуса, поскольку это диапазон обратного косинуса.{\ prime} \ приблизительно \ pi — \ text {1} \ text {.8235} \ приблизительно \ text {1} \ text {.3181} \ text {.} [/ latex] Другое решение в квадранте III — [ латекс] \ pi + \ text {1} \ text {.3181} \ приблизительно \ text {4} \ text {.4597.} [/ latex]
Растворы: [латекс] 1.8235 \ pm2 \ pi k [/ latex] и [латекс] 4.4597 \ pm2 \ pi k. [/ Latex]
Попробуй # 3
Решите [латекс] \ mathrm {csc} \ left (\ theta \ right) = 3. [/ Latex]
Показать решение
[латекс] \ theta \ приблизительно 0,33984 \ pm2 \ pi k [/ латекс] и [латекс] \ theta \ приблизительно 2.80176 \ pm2 \ pi k [/ латекс]
Решение тригонометрических уравнений в квадратичной форме
Решение квадратного уравнения может быть более сложным, но, опять же, мы можем использовать алгебру, как и любое квадратное уравнение. Посмотрите на схему уравнения. Есть ли в уравнении более одной тригонометрической функции или только одна? Какая тригонометрическая функция возводится в квадрат? Если представлена только одна функция и один из членов возведен в квадрат, подумайте о стандартной форме квадратичной функции.Замените тригонометрическую функцию переменной, такой как [latex] x [/ latex] или [latex] u. [/ Latex] Если после подстановки уравнение выглядит как квадратное уравнение, то мы можем использовать те же методы для решения квадратичных уравнений для решения тригонометрические уравнения.
Как сделать
Для данного тригонометрического уравнения решите с помощью алгебры .
- Найдите образец, который предлагает алгебраическое свойство, такое как разность квадратов или возможность разложения на множители.
- Замените тригонометрическое выражение одной переменной, например [latex] x [/ latex] или [latex] u.{2} \ left (\ theta \ right)} & = \ pm \ sqrt {\ frac {1} {2}} && \ text {Учитывайте как положительные, так и отрицательные значения квадратного корня. {2} \ left (\ theta \ right) +3 \ mathrm {cos} \ left (\ theta \ right) -1 = 0, \ text {} 0 \ ле \ тета <2 \ пи.2-5u + 3 = 0 \\ \ left (2 \ text {} \ mathrm {sin} \ left (\ theta \ right) -3 \ right) \ left (\ mathrm {sin} \ left (\ theta \ right ) -1 \ right) & = 0 &&& \ left (2u-3 \ right) \ left (u-1 \ right) \ end {align *} [/ latex] [latex] \ text {} [/ latex] [ латекс] \ [/ латекс]
Теперь установите каждый коэффициент равным нулю и решите два уравнения [latex] 2 \ text {} \ mathrm {sin} \ left (\ theta \ right) -3 = 0 [/ latex] и [latex] \ mathrm {sin } \ left (\ theta \ right) -1 = 0. [/ latex]
Для первого уравнения
[латекс] \ begin {align *} 2 \ text {} \ mathrm {sin} \ left (\ theta \ right) -3 & = 0 \\ 2 \ text {} \ mathrm {sin} \ left (\ theta \ right) & = 3 && \ textrm {Добавьте 3 с обеих сторон.} \\ \ mathrm {sin} \ left (\ theta \ right) & = \ frac {3} {2} && \ textrm {Разделите обе стороны на 2.} \\ \ mathrm {sin} \ left (\ theta \ справа) & \ ne \ frac {3} {2} && \ frac {3} {2} \ textrm {не входит в домен функции синуса.} \ end {align *} [/ latex] [latex] \ текст {} [/ latex] [latex] \\ [/ latex]
Первое уравнение не имело решения. Чтобы решить второе уравнение,
[латекс] \ begin {align *} \ mathrm {sin} \ left (\ theta \ right) -1 & = 0 \\ \ mathrm {sin} \ left (\ theta \ right) & = 1 && \ textrm {Добавить 1 в обе стороны.} \\\ theta & = \ frac {\ pi} {2} && \ textrm {Синус равен единице только для квадрантного угла.} \ end {align *} [/ latex] [latex] \ text {} [/ latex] [латекс] \ [/ латекс]
Единственное решение для этого уравнения — [latex] \ theta = \ frac {\ pi} {2}. [/ Latex]
Анализ
Обязательно проверьте все решения в данном домене, так как некоторые факторы не имеют решения. Это потому, что диапазон синусоидальной функции [latex] \ left [-1,1 \ right]. [/ Latex]
Пример 12: Решение уравнения с использованием идентификатора
Точно решите уравнение, используя тождество: [латекс] 3 \ text {} \ mathrm {cos} \ left (\ theta \ right) + 3 = 2 \ text {} {\ mathrm {sin}} ^ {2} \ влево (\ theta \ right), \ text {} 0 \ le \ theta <2 \ pi. 2 + 3u + 1 = 0 \\ \ left (2 \ mathrm {cos} \ left (\ theta \ right) +1 \ right) \ left (\ mathrm {cos} \ left (\ theta \ right) +1 \ right) & = 0 && \ left (2u + 1 \ right) \ left (u + 1 \ right) = 0 \ end {align *} [/ latex] [латекс] \ [/ латекс]
Работая с множителями с помощью косинуса, установите каждый множитель равным нулю и решите.[латекс] \ [/ латекс]
[латекс] \ begin {align *} 2 \ mathrm {cos} \ left (\ theta \ right) + 1 & = 0 & \ mathrm {cos} \ left (\ theta \ right) + 1 & = 0 \\ \ mathrm {cos} \ left (\ theta \ right) & = — \ frac {1} {2} & \ mathrm {cos} \ left (\ theta \ right) & = — 1 \\\ theta & = \ frac {2 \ pi} {3}, \ text {} \ frac {4 \ pi} {3} \ text {} \ text {} \ text {} \ text {} \ text {} & \ theta & = \ pi \ end {align *} [/ latex] [latex] \\ [/ latex]
Опять же, помните, что есть два квадранта, где [latex] \ mathrm {cos} \ left (\ theta \ right) = — \ frac {1} {2}.{2} \ left (\ theta \ right) + \ mathrm {cos} \ left (\ theta \ right) = 0. [/ Latex]
Показать решение
[латекс] \ frac {\ pi} {2}, \ text {} \ frac {2 \ pi} {3}, \ text {} \ frac {4 \ pi} {3}, \ text {} \ frac {3 \ pi} {2} [/ латекс]
Решение тригонометрических уравнений с использованием основных тождеств
Хотя алгебру можно использовать для решения ряда тригонометрических уравнений, мы также можем использовать фундаментальные тождества, потому что они упрощают решение уравнений. Помните, что методы, которые мы используем для решения проблем, не совпадают с методами проверки личности.Здесь применяются основные правила алгебры, а не переписывание одной стороны идентичности для соответствия другой стороне. В следующем примере мы используем два тождества, чтобы упростить уравнение.
В этом разделе нам нужно будет использовать несколько новых идентификаторов. Их называют двойными углами . Мы не будем тратить время, чтобы показать, откуда взялись следующие личности. Имейте в виду, что есть другие тригонометрические тождества, которые мы не рассмотрели в этом материале. {2 } \ left (\ theta \ right) -1 & = \ mathrm {cos} \ left (\ theta \ right) && \ text {Замените левую часть идентичностью.{2} \ left (\ theta \ right) — \ mathrm {cos} \ left (\ theta \ right) -1 & = 0 && \ text {Переместить все термины в одну сторону.} \\ \ left (2 \ mathrm {cos } \ left (\ theta \ right) +1 \ right) \ left (\ mathrm {cos} \ left (\ theta \ right) -1 \ right) & = 0 && \ text {Разложите на множители левую часть.} \ end {align *} [/ латекс]
[латекс] \ [/ латекс]
Установите множители равными нулю и решите.
[латекс] \ begin {align *} 2 \ mathrm {cos} \ left (\ theta \ right) + 1 & = 0 & \ mathrm {cos} \ left (\ theta \ right) -1 & = 0 \\\ mathrm { cos} \ left (\ theta \ right) & = — \ frac {1} {2} & \ mathrm {cos} \ left (\ theta \ right) & = 1 \\\ theta & = \ frac {2 \ pi} {3} \ pm2 \ pi k & \ theta & = 0 \ pm2 \ pi k \\\ theta & = \ frac {4 \ pi} {3} \ pm2 \ pi k \ end {align *} [/ latex]
Решение тригонометрических уравнений с несколькими углами
Иногда невозможно решить тригонометрическое уравнение с тождествами, имеющими несколько углов, например [latex] \ mathrm {sin} \ left (2x \ right) [/ latex] или [latex] \ mathrm {cos} \ влево (3x \ вправо).[/ latex] Столкнувшись с этими уравнениями, вспомните, что [latex] y = \ mathrm {sin} \ left (2x \ right) [/ latex] — это горизонтальное сжатие с коэффициентом 2 от функции [latex] y = \ mathrm {sin} \ left (x \ right). [/ latex] На интервале [latex] 2 \ pi, [/ latex] мы можем построить график двух периодов [latex] y = \ mathrm {sin} \ left (2x \ right), [/ latex] в отличие от одного цикла [latex] y = \ mathrm {sin} \ left (x \ right). [/ Latex] Такое сжатие графика заставляет нас думать, что может быть вдвое больше x -перехватов или решений для [latex] \ mathrm {sin} \ left (2x \ right) = 0 [/ latex] по сравнению с [latex] \ mathrm {sin} \ left (x \ right) = 0.[/ latex] Эта информация поможет нам решить уравнение аналогичного типа, показанное в примере.
Пример 14: Решение многоугольного тригонометрического уравнения
Точное решение: [latex] \ mathrm {cos} \ left (2x \ right) = \ frac {1} {2} [/ latex] на [latex] \ left [0,2 \ pi \ right). [/ латекс]
Показать решение
Мы видим, что это уравнение является стандартным уравнением с углом, кратным углу. Если [латекс] \ mathrm {cos} \ left (\ theta \ right) = \ frac {1} {2}, [/ latex], мы знаем, что [latex] \ theta [/ latex] находится в квадрантах I и IV.{-1} \ left (\ frac {1} {2} \ right) [/ latex] даст решения только в квадрантах I и II из-за диапазона функции обратного косинуса, мы понимаем, что решения уравнения [ latex] \ mathrm {cos} \ left (\ theta \ right) = \ frac {1} {2} [/ latex] будет в квадрантах I и IV, используя идеи из нашего единичного круга.
Следовательно, возможные углы: [latex] \ theta = \ frac {\ pi} {3} [/ latex] и [latex] \ theta = \ frac {5 \ pi} {3}. [/ Latex] Итак, [latex] 2x = \ frac {\ pi} {3} [/ latex] или [latex] 2x = \ frac {5 \ pi} {3}, [/ latex], что означает, что [latex] x = \ frac { \ pi} {6} [/ latex] или [latex] x = \ frac {5 \ pi} {6}.[/ latex] [latex] \\ [/ latex] Есть ли в этом смысл? Да, потому что [латекс] \ mathrm {cos} \ left (2 \ left (\ frac {\ pi} {6} \ right) \ right) = \ mathrm {cos} \ left (\ frac {\ pi} {3 } \ right) = \ frac {1} {2}. [/ latex]
Есть ли другие возможные ответы? Вернемся к нашему первому шагу.
В квадранте I [latex] 2x = \ frac {\ pi} {3}, [/ latex], поэтому [latex] x = \ frac {\ pi} {6} [/ latex], как указано. Давайте снова начнем вращаться по кругу:
[латекс] \ begin {align *} 2x & = \ frac {\ pi} {3} +2 \ pi \\ 2x & = \ frac {\ pi} {3} + \ frac {6 \ pi} {3} \ \ 2x & = \ frac {7 \ pi} {3} \\ x & = \ frac {7 \ pi} {6} \ end {align *} [/ latex] [latex] \\ [/ latex]
Еще один оборот дает
[латекс] \ begin {align *} 2x & = \ frac {\ pi} {3} +4 \ pi \\ 2x & = \ frac {\ pi} {3} + \ frac {12 \ pi} {3} \ \ 2x & = \ frac {13 \ pi} {3} \\ x & = \ frac {13 \ pi} {6} \ end {align *} [/ latex] [latex] \\ [/ latex]
[latex] x = \ frac {13 \ pi} {6}> 2 \ pi, [/ latex], поэтому это значение для [latex] x [/ latex] больше, чем [latex] 2 \ pi, [/ latex ] так что это не решение для [латекса] \ left [0,2 \ pi \ right).[/ латекс]
В квадранте IV [латекс] 2x = \ frac {5 \ pi} {3}, [/ latex], поэтому [латекс] x = \ frac {5 \ pi} {6} [/ latex], как указано. Давайте снова начнем вращаться по кругу:
[латекс] \ begin {align *} 2x & = \ frac {5 \ pi} {3} +2 \ pi \\ 2x & = \ frac {5 \ pi} {3} + \ frac {6 \ pi} {3 } \\ 2x & = \ frac {11 \ pi} {3} \\ x & = \ frac {11 \ pi} {6} \ end {align *} [/ latex] [latex] \\ [/ latex]
Еще один оборот дает
[латекс] \ begin {align *} 2x & = \ frac {5 \ pi} {3} +4 \ pi \\ 2x & = \ frac {5 \ pi} {3} + \ frac {12 \ pi} {3 } \\ 2x & = \ frac {17 \ pi} {3} \\ x & = \ frac {17 \ pi} {6} \ end {align *} [/ latex] [latex] \\ [/ latex]
[latex] x = \ frac {17 \ pi} {6}> 2 \ pi, [/ latex], поэтому это значение для [latex] x [/ latex] больше, чем [latex] 2 \ pi, [/ latex ], что означает, что это не решение для [латекса] \ left [0,2 \ pi \ right).[/ латекс]
Наши решения: [latex] \ frac {\ pi} {6}, \ text {} \ frac {5 \ pi} {6}, \ text {} \ frac {7 \ pi} {6}, [/ latex ] и [latex] \ frac {11 \ pi} {6}. [/ latex] Обратите внимание, что всякий раз, когда мы решаем задачу в форме [latex] \ mathrm {sin} \ left (nx \ right) = c [/ latex] или [latex] \ mathrm {cos} \ left (nx \ right) = c, [/ latex] мы должны обойти единичный круг [латекс] {n} [/ latex] раз.
В этом легко убедиться, если мы сначала напишем решение для [latex] 2x [/ latex] в общем виде. Одно из этих уравнений показано ниже:
[латекс] \ begin {align *} 2x & = \ frac {\ pi} {3} +2 \ pi \ cdot k \\ x & = \ frac {\ pi} {6} + \ pi \ cdot k && \ text { Разделите обе стороны на 2.} \ end {align *} [/ latex] [латекс] \\ [/ latex]
Теперь мы видим, что добавление [latex] \ pi [/ latex] к [latex] \ frac {\ pi} {6} [/ latex] дает нам [latex] \ frac {7 \ pi} {6} [/ latex] и что добавление [latex] 2 \ cdot \ pi [/ latex] даст нам [latex] \ frac {13 \ pi} {6} [/ latex], который больше, чем [latex] 2 \ pi. [/ латекс]
Ключевые понятия
- При решении линейных тригонометрических уравнений мы можем использовать алгебраические методы так же, как при решении алгебраических уравнений. Ищите закономерности, такие как разница квадратов, квадратичная форма или выражение, которое хорошо поддается замене.
- Уравнения, содержащие одну тригонометрическую функцию, можно решить или проверить с помощью единичной окружности.
- Мы также можем решать тригонометрические уравнения с помощью графического калькулятора.
- Многие уравнения имеют квадратичную форму. Мы можем использовать подстановку, чтобы уравнение выглядело проще, а затем использовать те же методы, которые мы используем при решении алгебраической квадратичной системы: разложение на множители, квадратичная формула и т. Д.
- Мы также можем использовать тождества для решения тригонометрических уравнений.
- Мы можем использовать подстановку для решения многоугольного тригонометрического уравнения, которое является сжатием стандартной тригонометрической функции. Нам нужно будет учесть сжатие и убедиться, что мы нашли все решения на заданном интервале.
Решение тригонометрических уравнений и идентичностей
Говорят, что шпионы и другие гнусные персонажи будут иметь при себе множество паспортов, что позволит им мгновенно претендовать на другую личность. Несмотря на множество идентичностей, мы знаем, что все эти паспорта являются псевдонимами одного и того же человека.
Тригонометрические идентичности — это разные способы представления одного и того же выражения. Они используются для решения тригонометрического уравнения применительно к заданному сценарию.
Когда преступник находится в бегах, он выбирает итальянский паспорт, чтобы скрыть римское удостоверение личности для целей путешествия. Идентификатор выбирается и применяется к выражению для решения тригонометрического уравнения.
Давайте исследуем основные тождества, прежде чем проверять их для решения тригонометрических уравнений.
Тригонометрические уравнения и их проверенные фундаментальные тождества
Идентичности — это инструменты, упрощающие сложные тригонометрические выражения или уравнения. Они являются жизненно важными инструментами при решении тригонометрических уравнений. Тригонометрические тождества работают вместе с факторингом, нахождением специальных формул и использованием общих знаменателей.
Подобно алгебраическим уравнениям, тригонометрические уравнения состоят из основных формул и свойств алгебры. Полный квадрат и разность квадратов упрощают работу с выражениями и тригонометрическими уравнениями.Как известно, все тригонометрические функции тесно связаны. Это потому, что все они являются определениями единичного круга, и их идентичности можно записать несколькими способами.
Решение тригонометрических тождеств
Для решения тригонометрических тождеств необходимо начать с более сложной части уравнения. Вам придется существенно переписать тригонометрическое выражение, пока оно не будет преобразовано, чтобы оно стало похоже на другую часть уравнения.
Для получения желаемых результатов вам может потребоваться развернуть или разложить выражения на множители при нахождении общих знаменателей.Вы также можете использовать любую другую алгебраическую стратегию для преобразования выражения.
Изучение алгебраических методов решения сложных тригонометрических уравнений
Рассмотрим эту функцию : f (x) = 2x² + x.
Решите f (x) = 0.
Вы уже знаете, что решение функции требует простой алгебры. Это будет работать так:
2x² + x = 0
x (2x + 1) = 0
x = 0 или
x = — ½
Дан тот же сценарий с g (t) = sin (t) и предлагается решить g (t) = 0.Вы можете найти решение для этой функции, используя значения единичного круга.
Они могут включать sin (t) = 0 для t = 0, π, 2π, и другие.
Используя аналогичные концепции, теперь вы можете рассмотреть следующие функции и их состав.
f (g (t)) = 2 (sin (t)) ² + (sin (t)) = 2sin² (t) + sin (t)
Созданное уравнение называется полиномиально-тригонометрической функцией. Чтобы решить тригонометрические уравнения с использованием подобных функций, используйте тождества, квадратную формулу и алгебраические методы, такие как разложение на множители.
Основные квадратичные формулы
Существует шесть или более соотношений, которые могут выводить тригонометрические элементы. Они известны как тригонометрические функции. Это синус, косинус, секанс, косеканс, касательная и касательная.
Идентичности и функции тригонометрии выводятся с использованием прямоугольного треугольника в качестве ориентира. Они выглядят как;
- Sin θ: равно противоположной стороне, деленной на гипотенузу
- Cos θ: равняется прилегающей стороне, деленной на гипотенузу
- Желто-коричневый θ: равняется противоположной стороне, деленной на прилегающую сторону
- сек θ: равняется гипотенузе, деленной на прилегающую сторону
- Cosec θ: равняется гипотенузе, деленной на противоположную сторону
- Детская кроватка θ: равна смежной стороне, разделенной на противоположную сторону
Взаимные идентичности
В некоторых случаях одно тригонометрическое уравнение будет использовать множество взаимных тождеств.Они представлены как;
- sin θ = 1 разделить на cosec θ
- детская кроватка θ = 1, разделенная на тангенс угла θ
- загар θ = 1 разделить на кроватку θ
- косекунд θ = 1 разделить на грех θ
- cos θ = 1, деленное на секунды θ
- сек θ = 1, деленная на cos θ
Взаимные идентичности возникают из прямоугольного треугольника. Когда заданы основание и высота, вы можете найти значения sin, cos, tan, sec, cos и cot с помощью тригонометрических формул.
Используя тригонометрические функции, можно также вывести взаимные тригонометрические тождества.
Идентичности периодичности
Формулы периодичности, также называемые ко-функциональными тождествами, используются для сдвига углов на π / 2, π, 2π и так далее.
Формулы периодичности полезны при вычислении сложной геометрии, оценке тригонометрических функций и доказательстве других тождеств. Первые два; sin (90 ° −x) = cos x и cos (90 ° −x) = sin x, и являются наиболее часто используемыми.
Поскольку тригонометрические тождества цикличны, они повторяются после константы периодичности.Для различных тригонометрических тождеств радианная постоянная периодичности отличается.
Tan 45 ° = tan 225 °, то же самое применимо для cos 45 ° = cos 225 °.
Тождества сопредельных функций
Вы также можете представить совместную функцию периодических тождеств в градусах. К ним относятся sin (90 ° −x) = cos x, cos (90 ° −x) = sin x, tan (90 ° −x) = cot x, cot (90 ° −x) = tan x и т. Д. .
Кофункциональные или периодические тождества относятся к сопарам тригонометрических функций в точках x и π / 2.Например, sin (π / 2 — x) = cos (x), cos (π / 2 — x) = sin (x), tan (π / 2 — x) = cot (x) и cot (π / 2 — х) = загар (х).
Идентификаторы двойные
Формула сложения углов позволяет получить двойные угловые тождества. Их принципиально не сложно запомнить, и они обычно пригодятся во многих тригонометрических уравнениях.
Вы можете использовать тождества с двойным углом, чтобы найти косинус и синус 2x в терминах косинусов и синусов x, следующих из формулы суммы углов.
Идентификаторы суммы углов
Формула площади синуса для треугольника : A = ½ ab sin C . Тождества суммы углов говорят, как найти синус и косинус x + y , когда заданы косинусы и синусы x и y.
Идентификаторы половинчатые
Это может показаться устрашающим, но получить их просто. Формула двойного угла может дополнительно генерировать тождества с половинным углом.
Вы можете использовать полуугловые тождества, чтобы найти синус и косинус x / 2.Это в терминах косинусов или синусов, заданных для x, следующих после формул с двойным углом.
Идентификаторы отрицательного угла
Тождества с отрицательным углом основаны на единичной окружности и часто называются нечетными или четными идентичностями. Вы можете найти тригонометрические функции в –x, когда тождества x относятся к значениям под противоположными углами –x и x.
Например;
sin (−t) = −sin (t) cos (−t) = cos (t) tan (−t) = −tan (t) csc (−t) = −csc (t) sec (−t) = sec (t) детская кроватка (−t) = −cot (t)
Помимо взаимных тождеств, вы можете использовать их для решения одного уравнения.
Пример
Вам дано тригонометрическое уравнение, которое очень похоже на квадратное уравнение.
2sin2 (t) + sin (t) = 0
Задача требует всех решений с 0≤t <2π. Его также называют квадратным синусоидальным уравнением из-за sin (t) вместо квадратичной переменной.
Используйте квадратную формулу или методы разложения на множители, как и во всех квадратных уравнениях. Если вычесть общий коэффициент sin (t), выражение хорошо множится.
sin (t) (2sin (t) +1) = 0
Если любой из множителей равен нулю, вы знаете, что произведение слева равно нулю. Ее также называют теоремой о нулевом произведении, и она позволяет разбить уравнение на два выражения.
sin (t) = 0 или,
2sin (t) + 1 = 0
Эти уравнения затем можно решить независимо.
sin (t) = 0t = 0 или,
т = π
2sin (t) +1 = 0sin (t) = −12t = 7π6 или,
11π6
Это даст вам четыре решения для уравнения 0≤t <2π: t = 0, π, 7π6, 11π6 .Чтобы проверить, разумны ли ответы, вы можете сравнить нули после построения графика функции.
Заключение
Для решения тригонометрических уравнений вам необходимо использовать тождества и исходные углы, чтобы запоминать их вместе с алгеброй.


 2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.
2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.


 В этой статье мы рассмотрим решение уравнения вида . Решение остальных типов простейших уравнений смотрим здесь: часть 2 (), часть 3 (, )
В этой статье мы рассмотрим решение уравнения вида . Решение остальных типов простейших уравнений смотрим здесь: часть 2 (), часть 3 (, )
 Тригонометрические уравнения. Разложение на множители
Тригонометрические уравнения. Разложение на множители Почему?
Почему?
 ) Ученик обязан знать, что
) Ученик обязан знать, что
 Тогда исчезают эти вставочки и жизнь становится легче.)
Тогда исчезают эти вставочки и жизнь становится легче.) п. — ответ через арки будет недоделанным. Арки нужно обязательно перевести в радианы.
п. — ответ через арки будет недоделанным. Арки нужно обязательно перевести в радианы. А ещё наоборот бывает. Пропустит человек знак ±
А ещё наоборот бывает. Пропустит человек знак ±

 Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.
Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.


 Обратите внимание на оформление записи решений тригонометрических уравнений.
Обратите внимание на оформление записи решений тригонометрических уравнений. Значит cosx ≠ 0 и можно поделить уравнение на cosx. Получим
Значит cosx ≠ 0 и можно поделить уравнение на cosx. Получим 2+3t-4=0\). Корнями являются \(t_1=-4, \ t_2=1\). Сделаем обратную замену:
2+3t-4=0\). Корнями являются \(t_1=-4, \ t_2=1\). Сделаем обратную замену:
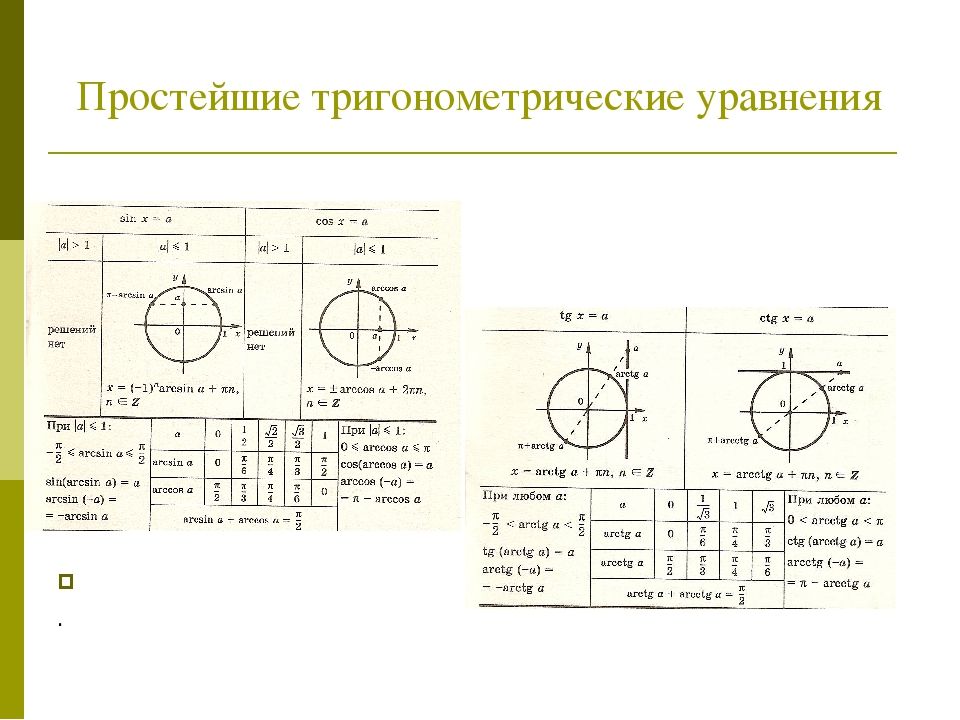 2}=2\):
2}=2\): 2-3t-2=0\] Корнями данного уравнения являются \(t_1=2, t_2=-\dfrac12\).
2-3t-2=0\] Корнями данного уравнения являются \(t_1=2, t_2=-\dfrac12\). 2=(\sin
2=(\sin
 Для любого действительного a на промежутке существует единственный угол , для которого . Это угол . Учитывая периодичность функции , получим формулы для нахождения корней уравнения :
Для любого действительного a на промежутке существует единственный угол , для которого . Это угол . Учитывая периодичность функции , получим формулы для нахождения корней уравнения :
 Методы решения тригонометрических уравнений.
Методы решения тригонометрических уравнений. учреждений: базовый и профил. Уровни – 2-е изд. – М.: Просвещение, 2011. – 368 с.: ил. – ISBN 978-5-09-025401-4, сс.327-332
учреждений: базовый и профил. Уровни – 2-е изд. – М.: Просвещение, 2011. – 368 с.: ил. – ISBN 978-5-09-025401-4, сс.327-332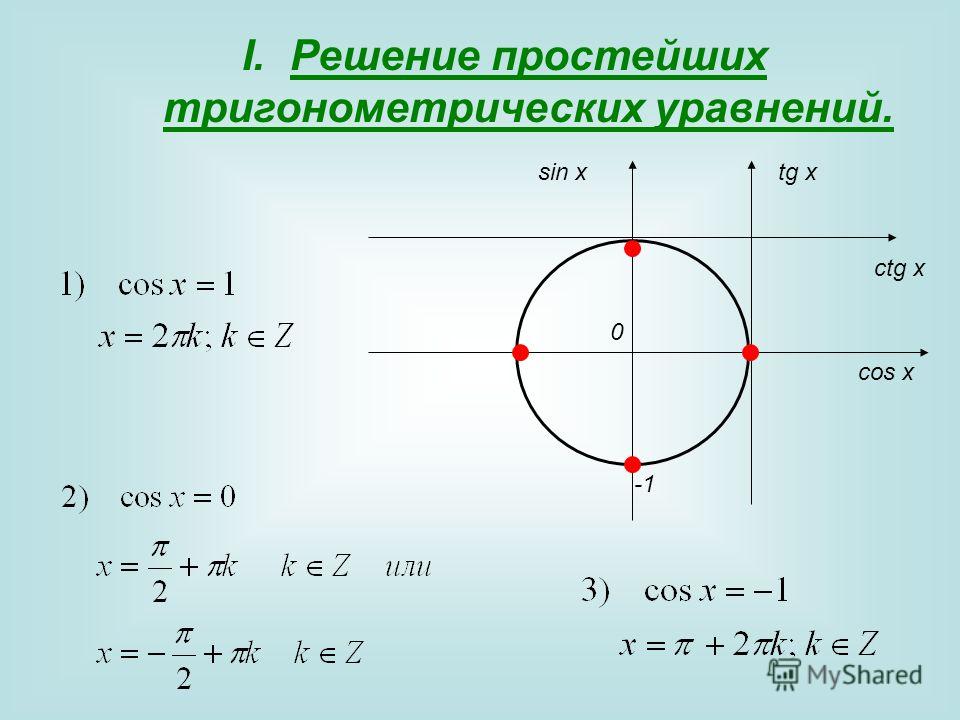

 Рассмотрим такой пример:
Рассмотрим такой пример: Тогда .
Тогда .


 Затем перенесём всё в левую часть и разложим на множители
Затем перенесём всё в левую часть и разложим на множители ..
.. Сумма синусов:
Сумма синусов: Аналогично функции тангенс и котангенс являются кофункциями. Формулы приведения можно сформулировать в виде следующего правила:
Аналогично функции тангенс и котангенс являются кофункциями. Формулы приведения можно сформулировать в виде следующего правила: Для этого:
Для этого:
 Для синуса существует две равнозначные формы записи решения:
Для синуса существует две равнозначные формы записи решения: