Содержание
Базовые методы решения уравнений и неравенств — Математика — Теория, тесты, формулы и задачи
Знание базовых методов решения уравнений и неравенств является основой для успешной подготовки и сдачи различных экзаменов, в том числе и ЦТ или ЕГЭ по математике. Базовые методы решения уравнений и неравенств, которые надежно усвоены и отработаны учеником — это один из основных инструментов, которым он должен оперировать при решении математических задач. На этой странице сайта представлены примеры применения базовых методов решения уравнений и неравенств из школьной математики.
Изучать базовые методы решения уравнений и неравенств из школьной математики онлайн:
Как успешно подготовиться к ЦТ по физике и математике?
Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:
- Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте.
 Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.
Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач. - Выучить все формулы и законы в физике, и формулы и методы в математике. На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами.
- Посетить все три этапа репетиционного тестирования по физике и математике.
 Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Успешное, старательное и ответственное выполнение этих трех пунктов, а также ответственная проработка итоговых тренировочных тестов, позволит Вам показать на ЦТ отличный результат, максимальный из того, на что Вы способны.
Нашли ошибку?
Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на электронную почту (адрес электронной почты здесь). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка.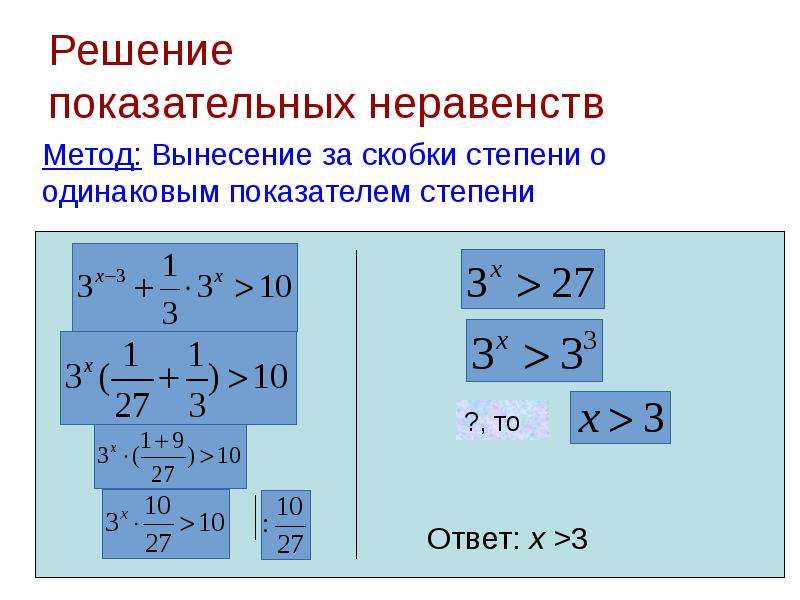 Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
Рациональные уравнения и неравенства | LAMPA
Рациональное уравнение
Уравнение вида A(x)B(x)=0\frac{A(x)}{B(x)}=0B(x)A(x)=0, где A,BA,BA,B — , называется рациональным уравнением.
- — вся ось, кроме точек, в которых B(x)=0B(x)=0B(x)=0;
- Решения уравнения в области определения совпадают с решениями уравнения A(x)=0A(x)=0A(x)=0.
2x+33x+2=0⇔{2x+3=03x+2≠0⇔x=−32.\frac{2 x+ 3}{3x+2}=0 \,\,\,\, \Leftrightarrow \,\,\,\, \left\{\begin{array}{lr} 2x+3=0 \\ 3x+2\neq 0 \end{array}\right. \,\,\,\,\Leftrightarrow \,\,\,\, x=-\frac{3}{2} .3x+22x+3=0⇔{2x+3=03x+2≠0⇔x=−23.
Рациональное неравенство
Неравенство вида A(x)B(x)≤0\frac{A(x)}{B(x)}\le 0B(x)A(x)≤0, где A,BA,BA,B — , называется рациональным неравенством.
Как решать?
- Найдите корни уравнений A(x)=0A(x)=0A(x)=0 и B(x)=0B(x)=0B(x)=0.
- Отметьте корни обоих уравнений на числовой прямой.
- Примените .
- Обратите внимание на то, что при B(x)=0B(x)=0B(x)=0 левая часть неравенства не определена, поэтому корни уравнения B(x)=0B(x)=0B(x)=0 не включаются в решение.
2x+33x+2≤0.\frac{2 x+ 3}{3x+2}\le 0.3x+22x+3≤0. Корень уравнения 2x+3=02x+3=02x+3=0 равен x=−32x=-\frac{3}{2}x=−23.
Корень уравнения 3x+2=03x+2=03x+2=0 равен x=−23x=-\frac{2}{3}x=−32.
Применим метод интервалов. Неравенство выполняется при значениях xxx, лежащих между корнями двух уравнений: −32≤x<−23-\frac{3}{2}\le x\lt -\frac{2}{3}−23≤x<−32 или x∈[−32;−23)x\in[-\frac{3}{2};-\frac{2}{3})x∈[−23;−32).
Обратите внимание на то, что корень −23-\frac{2}{3}−32 не включен в решение неравенства.
Методическая разработка «Уравнения и неравенства»
Методическая разработка по теме
«Уравнения и неравенства»
(практическая часть)
для студентов СПО.
Составитель:
Восковская Н.И.
Преподаватель математики
ГБПОУ ВО «ВЮТ»
Воронеж 2020
СОДЕРЖАНИЕ
РАЗДЕЛ 1. Рациональные, иррациональные, показательные, логарифмические и тригонометрические уравнения и системы уравнений……………………………………………………………….…….3-16
Практическая работа №1: «Решение рациональных, иррациональных уравнений и систем»…..………………………………………………………3-6
Практическая работа №2: «Решение показательных уравнений и систем»……………………………………………………………………….…6-9
Практическая работа №3: «Решение тригонометрических уравнений и систем»………………………………………………………………………. ..9-13
..9-13
Практическая работа №4: «Решение логарифмических уравнений и систем»……………………………………………………………………….13-16
РАЗДЕЛ 2. Рациональные, иррациональные, показательные, логарифмические и тригонометрические неравенства и системы неравенств……………………………………………..…………………….17-28
Практическая работа №1: «Решение рациональных, иррациональных неравенств»…..………………………………………………………………17-20
Практическая работа №2: «Решение показательных неравенств»….21-23
Практическая работа №3: «Решение тригонометрических нер-тв»…23-26
Практическая работа №4: «Решение логарифмических нер-тв»……26-28
РАЗДЕЛ 3. Использование графиков функций при решении уравнений, неравенств и систем с одной и двумя переменными…….29-35
Практическая работа №1: «Решение уравнений графическим методом»…. .……………………………………………………………….…29-31
.……………………………………………………………….…29-31
Практическая работа №2: «Решение неравенств и систем неравенств с двумя переменными»………………………………………………………31-35
ПРОВЕРОЧНАЯ РАБОТА: «Уравнения и неравенства»………36-37
СПИСОК ЛИТЕРАТУРЫ………………………………….…………..38
РАЗДЕЛ 1. Рациональные, иррациональные, показательные, логарифмические и тригонометрические уравнения и системы уравнений.
Практическая работа №1: «Решение рациональных, иррациональных уравнений и систем».
Рациональные уравнения.
Рациональное уравнение — это такой вид уравнения в которой левая и правая части рациональные выражения. В записи уравнения имеются только сложение, вычитание, умножение, деление, а также возведение в целую степень.
Рассмотрим примеры решения таких уравнений
№32 (6). Решить уравнение
Решить уравнение
На первом этапе раскроем в уравнении все скобки, получим
Теперь оставим в левой части уравнения все неизвестные, а все числа перенесем в правую часть. Не забываем, что при переносе переменных или чисел через знак равенства знак необходимо поменять на противоположный, получим
Приведем подобные слагаемые слева и справа, получим
Получили неверное равенство (0 не равен 11), следовательно
Ответ: корней нет.
№33 (2). Решить уравнение
Так как здесь присутствует неизвестная переменная в знаменателе, то на первом этапе необходимо выделить область допустимых значений. Так как в знаменателе не должен находиться ноль, то получим следующее
Итого, ОДЗ:
Теперь перейдем к непосредственному решению уравнения. Приведем левую часть уравнения к общему знаменателю
Получим в левой и правой части дроби можем применить правило пропорции, получим
Раскроем скобки
Ответ: .
Иррациональные уравнения
Иррациональное уравнение — это такой вид уравнения, содержащее неизвестное под знаком корня. или возведённое в степень, которую нельзя свести к целому числу.
Рассмотрим пример
№70 (3). Решить уравнение
Так как в уравнении присутствует квадратный корень, то вначале необходимо найти область допустимых значений. Мы знаем, что в корне четной степени должно быть неотрицательное число, то есть
С другой стороны, значение корня также не может быть отрицательным числом, то есть правая часть уравнения также должна быть неотрицательной
В итоге, получаем следующее ОДЗ:
Перейдем к непосредственному решению уравнения. Для того, чтобы избавиться от корня возведем обе части уравнения в квадрат
Перенесем все в левую часть уравнения
Получили квадратное уравнение. Решим его с помощью дискриминанта
Решим его с помощью дискриминанта
Ответ:
Задание для самостоятельного решения:
Решаем из сборника задач Богомолова следующие номера:
№32 (пункт 7), №33 (пункт 3) – всего два уравнения.Изучаем видео-урок и решаем №45 (пункт 1) (https://www.youtube.com/watch?v=8mbiYVE6kYY)
Задание по вариантам:
Примечание: Вариант выбирается по первой букве вашей фамилии следующим образом: Буквы А-Д 1 вариант, Буквы Е-М – 2 вариант,
Буквы Н-Р – 3 вариант, Буквы С-Я – 4 вариант.
Вариант 1.
1. Решите уравнение
Вариант 2.
1. Решите уравнение
Вариант 3.
1. Решите уравнение
Вариант 4.
1. Решите уравнение
Система оценивания (5-ти бальная): за каждый правильно решенный пример получаем 1 предварительный балл. Всего можно получить 13 баллов. Таблица перевода баллов в оценку:
Всего можно получить 13 баллов. Таблица перевода баллов в оценку:
Практическая работа №2: «Решение показательных уравнений и систем».
Показательное уравнение — это любое уравнение, содержащее в себе показательную функцию, т.е. выражение вида . Помимо указанной функции подобные уравнения могут содержать в себе любые другие алгебраические конструкции — многочлены, корни, тригонометрию, логарифмы и т.д.
Рассмотрим примеры решения таких уравнений
№93 (2). Решить уравнение
На первом этапе приведем все к одному показателю степени. Так как у нас есть выражение , то, применяя свойство степени разности получим , что , Подставим
Избавимся от знаменателя, для этого обе части уравнения умножим на 4, получим
Разделим обе части уравнения на 3, получим
Так как показатель степени и справа и слева одинаков (2), то приравняем степени, получим
Ответ: 2.
№94 (1). Решить уравнение
Используя свойства степеней, выражение можно переписать следующим образом: . Подставим уравнение
Сделаем замену, пусть тогда уравнение примет вид
Используя теорему Виета или формулу дискриминанта, получим следующие корни
Вернемся к замене:
, тогда
тогда
Ответ: и .
Рассмотрим теперь пример решения системы показательных уравнений.
№95 (6). Решить систему уравнений
Для решения данной системы уравнения воспользуемся методом сложения. Для этого умножим второе уравнение на 2 и сложим уравнения между собой
Разделим обе части уравнения на 5
Так как показатель степени и справа и слева одинаков (2), то приравняем степени, получим
Чтобы найти вторую переменную подставим во второе уравнение, получим
Так как показатель степени и справа и слева одинаков (2), то приравняем степени, получим
Ответ: (-2;0).
Задание для самостоятельного решения:
Решаем из сборника задач Богомолова следующие номера:
№90 (пункт 2), №93 (пункт 4) и №95 (пункт 4)– всего три примера.
Задание по вариантам:
Примечание: Вариант выбирается по первой букве вашей фамилии следующим образом: Буквы А-В — 1 вариант, Буквы Г-Ж – 2 вариант, Буквы З-Л – 3 вариант, Буквы М-О – 4 вариант, Буквы П-С – 5 вариант, Буквы Т-Я – 6 вариант
Решить следующие уравнения:
а)
б)
Решить следующие уравнения:
а)
б)
Вариант 3.
Вариант 4.
Решить следующие уравнения:
а)
б)
Решить следующие уравнения:
а)
б)
Вариант 5.
Вариант 6.
Решить следующие уравнения:
а)
б)
Решить следующие уравнения:
а) ;
б)
Система оценивания (5-ти бальная): за каждый правильно решенный пример получаем 1 предварительный балл. Всего можно получить 13 баллов. Таблица перевода баллов в оценку:
Практическая работа №3: «Решение тригонометрических уравнений и систем».
Теоретические сведения.
Тригонометрическое уравнение — это уравнение, содержащее в себе одну или несколько тригонометрических функций.
Напомним формулы для решения простейших тригонометрических уравнений
Также пригодится таблица значений тригонометрических функций
Разбор примеров.
С примерами решений простейших тригонометрических
уравнений можно ознакомиться в следующем видео-уроке: https://www. youtube.com/watch?v=o082MVvD59o
youtube.com/watch?v=o082MVvD59o
Рассмотрим примеры решения более сложных тригонометрических уравнений
№155 (1). Решить уравнение
Сначала нужно привести уравнение к однородному, то есть к такому, в котором только один вид тригонометрической функции. Из основного тригонометрического тождества можно вывести следующую формулу . Подставим ее в уравнение
Обе части уравнения умножим на -1, получим
Сделаем замену , получим
Получили квадратное уравнение, решая его через дискриминант, получим
Вернемся к замене. Получаем два простейших тригонометрических уравнения:
Ответ: и .
№156 (1). Решить уравнение
Сначала нужно привести уравнение к однородному. Для этого разделим обе части уравнения на , получим
Используя тригонометрическое свойство , получим
Сделаем замену, пусть тогда уравнение примет вид
Используя теорему Виета или формулу дискриминанта, получим следующие корни
Вернемся к замене. Получаем два простейших тригонометрических уравнения:
Получаем два простейших тригонометрических уравнения:
Ответ: и .
Рассмотрим теперь пример решения системы тригонометрических уравнений.
Задача. Решить систему уравнений
Выразим из первого уравнения через
Подставим во второе уравнение системы
Воспользовавшись формулой синуса суммы, получим
Разделим обе части уравнения на
Чтобы найти вторую переменную подставим найденный в выражение
:
Ответ: .
Задание для самостоятельного решения:
Решаем из сборника задач Богомолова следующие номера:
№155 (пункты 2-4) – всего три примера.
Задание по вариантам:
Примечание: Вариант выбирается по первой букве вашей фамилии следующим образом: Буквы А-В — 1 вариант, Буквы Г-Ж – 2 вариант, Буквы З-Л – 3 вариант, Буквы М-О – 4 вариант, Буквы П-С – 5 вариант, Буквы Т-Я – 6 вариант
Решить следующие уравнения:
а)
б)
Решить следующие уравнения:
а)
б)
Вариант 3.
Вариант 4.
Решить следующие уравнения:
а)
б)
Решить следующие уравнения:
а)
б)
Вариант 5.
Вариант 6.
Решить следующие уравнения:
а)
б)
Решить следующие уравнения:
а)
б)
Система оценивания (5-ти бальная): за каждый правильно решенный пример получаем 1 предварительный балл. Всего можно получить 13 баллов. Таблица перевода баллов в оценку:
Практическая работа №4: «Решение логарифмических уравнений и систем».
Логарифмическое уравнение — это любое уравнение, содержащее в себе Логарифмическую функцию. Помимо указанной функции подобные уравнения могут содержать в себе любые другие алгебраические конструкции — многочлены, корни, тригонометрию и т.д.
Рассмотрим примеры решения таких уравнений
№98 (5). Решить уравнение
Решить уравнение
Как мы знаем логарифмическая функция имеет свою область определения – логарифмируемое выражение должно быть больше нуля. Найдем область определения
Перейдем к непосредственному решению уравнения. На первом этапе приведем все к одному основанию логарифма. Применяя свойство логарифма можем переписать число 2 следующим образом
Подставим в уравнение
Так как основания логарифмов слева и справа одинаковые, то можем приравнять логарифмируемые выражения
Ответ: 15.
№98 (1). Решить уравнение
Найдем область определения
Применяя свойство логарифма разности, получим
Так как основания логарифмов слева и справа одинаковые, то можем приравнять логарифмируемые выражения
Ответ: 4.
Рассмотрим теперь пример решения системы показательных уравнений.
№101 (1). Решить систему уравнений
Отметим вначале область определения:
На первом этапе из второго уравнения системы выразим через :
Подставим в первое уравнение системы:
Решим данное уравнение по алгоритму предыдущего примера
Чтобы найти вторую переменную подставим в выражение
Ответ: (1;10).
Задание для самостоятельного решения:
Решаем из сборника задач Богомолова следующие номера:
№98 (пункты 2-3), №101 (пункт 4) – всего три примера.
Задание по вариантам:
Примечание: Вариант выбирается по первой букве вашей фамилии следующим образом: Буквы А-В — 1 вариант, Буквы Г-Ж – 2 вариант, Буквы З-Л – 3 вариант, Буквы М-О – 4 вариант, Буквы П-С – 5 вариант, Буквы Т-Я – 6 вариант
Решить следующие уравнения:
а) ;
б)
Решить следующие уравнения:
а) ;
б)
Вариант 3.
Вариант 4.
Решить следующие уравнения:
а) ;
б)
Решить следующие уравнения:
а) ;
б)
Вариант 5.
Вариант 6.
Решить следующие уравнения:
а) ;
б)
Решить следующие уравнения:
а) ;
б)
Система оценивания (5-ти бальная): за каждый правильно решенный пример получаем 1 предварительный балл. Всего можно получить 13 баллов. Таблица перевода баллов в оценку:
РАЗДЕЛ 2. Рациональные, иррациональные, показательные, логарифмические и тригонометрические неравенства и системы неравенств.
Практическая работа №1: «Решение рациональных, иррациональных неравенств и систем».
Рациональные неравенства.
Рациональное неравенство — это такой вид неравенства в котором левая и правая части рациональные выражения. В записи имеются только сложение, вычитание, умножение, деление, а также возведение в целую степень.
Рассмотрим примеры решения таких неравенств
№40 (1). Решить неравенство
Рациональные неравенства такого типа решаются следующем образом. На первом этапе раскрываем скобки (если они имеются) и переносим все неизвестные переменные влево, а числа вправо
Приведем подобные слагаемые слева и справа, получим
Разделим все на 4. Так как 4 положительное число, то знак неравенства не меняется. Если же мы будем умножать на число, меньше нуля, то знак неравенства необходимо менять на противоположный В нашем случае получим:
Ответ: .
Рассмотрим пример решения системы рациональных неравенств.
№41 (2). Решить систему неравенств
Вначале будем по отдельности (по такому же принципу, как в предыдущем примере) находить решения каждого из входящих в систему неравенств, получим:
Отметим оба получившихся решения на одной прямой
В ответ записываем ту часть числовой прямой где сошлись оба решения вместе.
Ответ: .
Иррациональные неравенства.
Иррациональное неравенство — это такой вид неравенства, содержащее неизвестное под знаком корня. или возведённое в степень, которую нельзя свести к целому числу.
Рассмотрим несколько примеров.
№74 (2). Решить неравенство
Так как в неравенстве присутствует квадратный корень, то вначале необходимо найти область допустимых значений.
Переходим к решению неравенства. Будем решать его методом интервалов. Для этого выполняем следующее:
Вместо знака неравенства запишем знак равенства и решим полученное уравнение
Так как у нас слева корень четной степени, то здесь получается дополнительная область определения
Возведем обе части уравнения в квадрат, получим
Находим корни по теореме Виета
Отмечаем корни, полученные в первом пункте (в нашем случае это 1) на числовой прямой вместе с областью определения неравенства и расставляем знаки на полученных промежутков (проверяем выполнение на промежутке неравенства, если неравенство выполнено ставим плюс, если нет – минус).
Записываем ответ.
Ответ:
№76 (2). Решить неравенство
Так как в неравенстве присутствует квадратный корень, то вначале необходимо найти область допустимых значений.
ОДЗ: .
Переходим к решению неравенства. Будем решать его методом интервалов. Для этого выполняем следующее:
Вместо знака неравенства запишем знак равенства и решим полученное уравнение
Возведем обе части уравнения в квадрат, получим
Отмечаем корни на числовой прямой вместе с ОДЗ и расставляем знаки на получившихся интервалах
Записываем ответ.
Ответ:
Задание для самостоятельного решения:
Решаем из сборника задач Богомолова следующие номера:
№40 (пункты 2, 3), №41 (пункт 1) – всего три примера.
Задание по вариантам:
Примечание: Вариант выбирается по первой букве вашей фамилии следующим образом: Буквы А-Д 1 вариант, Буквы Е-М – 2 вариант, Буквы Н-Р – 3 вариант, Буквы С-Я – 4 вариант.
Вариант 1.
1. Решите неравенство
2. Решите неравенство
Вариант 2.
1. Решите неравенство
2. Решите неравенство
Вариант 3.
1. Решите неравенство
2. Решите неравенство
Вариант 4.
1. Решите неравенство
2. Решите неравенство
Система оценивания (5-ти бальная): за каждый правильно решенный пример получаем 1 предварительный балл. Всего можно получить 13 баллов. Таблица перевода баллов в оценку:
Практическая работа №2: «Решение показательных неравенств».
Показательное неравенство — это любое неравенство, содержащее в себе показательную функцию, т.е. выражение вида .
Рассмотрим примеры решения таких неравенств
№96 (2). Решить неравенство
Для решения такого вида неравенства вначале необходимо и левую и правую часть привести к одному основанию степени. Так как 27 это 3 в кубе, то получим
Далее необходимо воспользоваться следующим правилом: если основания степени больше 1, то знак неравенства остается неизменным, если же меньше 1, то знак неравенства необходимо поменять на противоположный.
В нашем случае основание – число 3, больше единицы, следовательно можем «отбросить» основания без изменения знака неравенства, получим
Ответ: .
№96 (6). Решить неравенство
Так как 8 это 2 в кубе, то получим
Воспользуемся правилом, так как 2 больше единицы, следовательно можем «отбросить» основания без изменения знака неравенства, получим
Решим неравенство методом интервалов. Приравняем к нулю:
По теореме Виета, получаем корни
Отметим корни на числовой прямой и расставим знаки
Ответ: .
№97 (2). Решить неравенство
Для начала преобразуем неравенство, используя следующие 3 свойства: , получим
Переходим к решению неравенства. Будем решать его методом интервалов. Для этого выполняем следующее:
Вместо знака неравенства запишем знак равенства и решим полученное уравнение
Сделаем замену . Получим
Находим корни по теореме Виета
Возвращаясь к замене, получим
Отмечаем корни, полученные в первом пункте (в нашем случае это 1) на числовой прямой и расставляем знаки на полученных промежутков (проверяем выполнение на промежутке неравенства, если неравенство выполнено ставим плюс, если нет – минус).
Записываем ответ.
Ответ:
Задание для самостоятельного решения:
Решаем из сборника задач Богомолова следующие номера:
№96 (пункты 2-4), №97 (пункт 4) – всего 4 примера.
Задание по вариантам:
Примечание: Вариант выбирается по первой букве вашей фамилии следующим образом: Буквы А-В — 1 вариант, Буквы Г-Ж – 2 вариант, Буквы З-Л – 3 вариант, Буквы М-О – 4 вариант, Буквы П-С – 5 вариант, Буквы Т-Я – 6 вариант
Решить неравенство
Решить неравенство
Вариант 3.
Вариант 4.
Решить неравенство
Решить неравенство
Вариант 5.
Вариант 6.
Решить неравенство
Решить неравенство
Система оценивания (5-ти бальная): за каждый правильно решенный пример получаем 1 предварительный балл. Всего можно получить 13 баллов. Таблица перевода баллов в оценку:
Практическая работа №3: «Решение тригонометрических неравенств».
Решение простейших тригонометрических неравенств.
Для решения простейших тригонометрических неравенств нам вначале необходимо решить соответствующее уравнение, а затем, используя тригонометрическую окружность, найти решение неравенства. Рассмотрим решения простейших тригонометрических неравенств на примерах.
Пример 1:
Найдем решение тригонометрического неравенства
Отметим решение на тригонометрической окружности
Так как неравенство имеет знак «больше или равно», то решение лежит на верхней дуге окружности (относительно решения уравнения).
Ответ: .
Пример 2:
Найдем решение тригонометрического неравенства
Отметим решение на тригонометрической окружности
Так как неравенство имеет знак «меньше», то решение лежит на дуге окружности, расположенной слева (относительно решения уравнения).
Ответ: .
Пример 3:
Найдем решение тригонометрического неравенства
Здесь также нам понадобится область определения. Как мы помним у функции тангенса
Отметим решение на тригонометрической окружности
Так как неравенство имеет знак «меньше или равно», то решение лежит на дугах окружности, отмеченных синим на рисунке 3.
Ответ:
Пример 4:
Найдем решение тригонометрического неравенства
Здесь также нам понадобится область определения. Как мы помним у функции тангенса
Отметим решение на тригонометрической окружности
Так как неравенство имеет знак «больше», то решение лежит на дугах окружности, отмеченных синим на рисунке 4.
Ответ:
Задание для самостоятельного решения:
Решаем из сборника задач Богомолова №152 – всего 4 примера.
Практическая работа №4: «Решение логарифмических неравенств»,
Логарифмическое неравенство — это любое неравенство, содержащее в себе логарифмическую функцию.
Рассмотрим примеры решения таких неравенств
№103 (4). Решить неравенство
Как мы знаем логарифмическая функция имеет свою область определения – логарифмируемое выражение должно быть больше нуля. Найдем область определения
Разделим на -5. Так как делим на отрицательное число, то знак неравенства нужно изменить на противоположный
Переходим к непосредственному решению неравенства. Для решения такого вида неравенства вначале необходимо и левую и правую часть привести к одному основанию логарифма. Число -2 можем представить через логарифм по основанию следующим образом
Подставим
Далее необходимо воспользоваться следующим правилом: если основания логарифма больше 1, то знак неравенства остается неизменным, если же меньше 1, то знак неравенства необходимо поменять на противоположный.
В нашем случае основание – число , меньше единицы, следовательно можем «отбросить» основания, но при этом изменив знак неравенства на противоположный, получим
Разделим на -5. Так как делим на отрицательное число, то знак неравенства нужно изменить на противоположный
С учетом ОДЗ, Ответ: .
Пример 2: Решить неравенство
Вначале найдем область определения:
Единицу можем представить следующим образом
Подставим
Применяя свойство суммы логарифмов, получим
Так как основание логарифма 3 больше 1, то знак неравенства не меняем
С учетом ОДЗ, Ответ: .
Задание для самостоятельного решения:
Решаем из сборника задач Богомолова следующие номера:
103 (пункты 2-3), №104 (пункт 1) – всего 3 примера.
Задание по вариантам:
Примечание: Вариант выбирается по первой букве вашей фамилии следующим образом: Буквы А-В — 1 вариант, Буквы Г-Ж – 2 вариант, Буквы З-Л – 3 вариант, Буквы М-О – 4 вариант, Буквы П-С – 5 вариант, Буквы Т-Я – 6 вариант
Решить неравенства:
а) ;
б)
Решить неравенства:
а) ;
б)
Вариант 3.
Вариант 4.
Решить неравенства:
а) ;
б)
Решить неравенства:
а) ;
б)
Вариант 5.
Вариант 6.
Решить неравенства:
а) ;
б)
Решить неравенства:
а) ;
б)
Система оценивания (5-ти бальная): за каждый правильно решенный пример получаем 1 предварительный балл. Всего можно получить 13 баллов. Таблица перевода баллов в оценку:
РАЗДЕЛ 3. Использование графиков функций при решении уравнений, неравенств и систем с одной и двумя переменными.
Практическая работа №1: «Решение уравнений графическим методом»
Графический метод решения уравнений заключатся в следующем:
Приводим уравнение к такому виду, чтобы справа и слева были простейшие функции;
Строим эти две функции на одном графике;
Переменная по оси абсцисс точек пересечения графиков и есть решение уравнения.
Рассмотрим несколько примеров.
Пример №1. Решить графически следующее уравнение
Здесь мы сразу видим, какие две функции нам надо построить:
— показательная функция. Точки для построения
прямая, достаточно две точки
- Построим обе функции на одном графике
Видим, что графики пересекаются в точке
Ответ: .
Пример №2. Решить графически уравнение
Преобразуем для начала наше уравнение. Так как мы знаем график квадратичной функции , то слева оставим , а остальное перенесем вправо
Теперь видим, какие две функции нам надо построить:
— парабола. Точки для построения
прямая, достаточно две точки
- Построим обе функции на одном графике
Видим, что графики пересекаются в точке .
Ответ: .
Задание по вариантам:
Примечание: Вариант выбирается по первой букве вашей фамилии следующим образом: Буквы А-В — 1 вариант, Буквы Г-Ж – 2 вариант, Буквы З-Л – 3 вариант, Буквы М-О – 4 вариант, Буквы П-С – 5 вариант, Буквы Т-Я – 6 вариант
Решить графически уравнения:
а)
б)
Решить графически уравнения
а)
б)
Вариант 3.
Вариант 4.
Решить графически уравнения
а)
б)
Решить графически уравнения
а)
б)
Вариант 5.
Вариант 6.
Решить графически уравнения
а)
б)
Решить графически уравнения
а)
б)
Система оценивания (5-ти бальная): за каждый правильно решенный пример получаем 1 предварительный балл. Всего можно получить 13 баллов. Таблица перевода баллов в оценку:
Практическая работа №2: «Решение неравенств и систем неравенств с двумя переменными»
Линейные неравенства с двумя переменными.
Определение 1: Неравенства вида или , где – неизвестные переменные, а – некоторые числа, причем отличны от нуля называются линейными неравенствами с двумя переменными.
Пример : – линейное неравенство с двумя переменными.
Определение 2: Пара чисел называется решением линейного неравенства с двумя переменными, если при их подстановке в уравнение получается верное равенство.
Свойства линейных неравенств с двумя переменными:
К неравенству можно прибавлять с обоих сторон и вычитать из обоих сторон одно и тоже число.
Неравенство можно умножать и делить с обоих сторон на одно и тоже, отличное от нуля, число, причем при умножении (делении на положительное число уравнение не меняет знак, а при умножение (деление) на отрицательное число меняет знак на противоположный.
Определение 3: Графиком линейного неравенства с двумя переменными является множество всех точек, которые является решением данного линейного неравенства.
Задача 1: Решить неравенство
Решение.
Выражаем через :
Изобразим график уравнения – прямая, достаточно две точки:
- Так как последнее неравенство имеет знак «больше», получим решение, изображенное на рисунке ниже (серым цветом). Заметим, что прямая не входит в решение, так как в неравенстве не присутствует знак равенства.
Задача 2: Решить неравенство
Решение.
Выражаем через :
Изобразим график уравнения — прямая, достаточно две точки
- Так как последнее неравенство имеет знак «больше или равно», получим решение, изображенное на рисунке (серым цветом). Заметим, что прямая входит в решение, так как в неравенстве присутствует знак равенства.
Системы линейных неравенств с двумя переменными.
Определение 4: Системой линейных неравенств с двумя переменными называется такая система неравенств, которая в своем составе имеет два и более линейных неравенств с двумя переменными.
Определение 5: Решением системы линейных неравенств называется такая пара чисел, которая является решением всех неравенств, входящих в данную систему.
Решением системы неравенств является пересечение графических решений каждого неравенства по отдельности.
Задача 3: Решить систему неравенств
Решение.
Решим для начала оба неравенства отдельно также, как в задачах 1 и 2.
Красным цветом – решение первого неравенства , зеленым – решение второго неравенства .
Там, где сошлись вместе оба решения (сошлись красные и зеленые штриховки), та область и является решением всей системы неравенств
Задача 4: Решить систему неравенств
Решение.
Решим для начала два этих неравенства по отдельности
– окружность с центром в точке и радиусом 2. Изобразим график неравенства. Так как знак больше, то это область за пределами окружности (оранжевая)
– окружность с центром в точке и радиусом 3. Изобразим график неравенства. Так как знак меньше, то это область внутри окружности (желтая)
Нанесем оба решения на один рисунок, там где оба решения сошлись, та область и является решением нашей системы:
Задание по вариантам:
Примечание: Вариант выбирается по первой букве вашей фамилии следующим образом: Буквы А-В — 1 вариант, Буквы Г-Ж – 2 вариант, Буквы З-Л – 3 вариант, Буквы М-О – 4 вариант, Буквы П-С – 5 вариант, Буквы Т-Я – 6 вариант
изобразить решение неравенства:
изобразить решение системы неравенств:
а)
б)
изобразить решение неравенства:
изобразить решение системы неравенств:
а)
б)
Вариант 3.
Вариант 4.
изобразить решение неравенства:
изобразить решение системы неравенств:
а)
б)
изобразить решение неравенства:
изобразить решение системы неравенств:
а)
б)
Вариант 5.
Вариант 6.
изобразить решение неравенства:
изобразить решение системы неравенств:
а)
б)
изобразить решение неравенства:
изобразить решение системы неравенств:
а)
б)
Система оценивания (5-ти бальная): за каждый правильно решенный пример получаем 1 предварительный балл. Всего можно получить 13 баллов. Таблица перевода баллов в оценку:
ПРОВЕРОЧНАЯ РАБОТА: «Уравнения и неравенства»
Примечание: Вариант выбирается по первой букве вашей фамилии следующим образом: Буквы А-В — 1 вариант, Буквы Г-Ж – 2 вариант, Буквы З-Л – 3 вариант, Буквы М-О – 4 вариант, Буквы П-С – 5 вариант, Буквы Т-Я – 6 вариант
Решить линейное неравенство
Решить иррациональное уравнение
Решить показательное неравенство
Решить логарифмическое уравнение
Изобразить на плоскости решение системы неравенств с двумя переменными
Решить линейное неравенство
Решить иррациональное уравнение
Решить показательное неравенство
Решить логарифмическое уравнение
Изобразить на плоскости решение системы неравенств с двумя переменными
Вариант 3.
Вариант 4.
Решить линейное неравенство
Решить иррациональное уравнение
Решить показательное неравенство
Решить логарифмическое уравнение
Изобразить на плоскости решение системы неравенств с двумя переменными
Решить линейное неравенство
Решить иррациональное уравнение
Решить показательное неравенство
Решить логарифмическое уравнение
Изобразить на плоскости решение системы неравенств с двумя переменными
Вариант 5.
Вариант 6.
Решить линейное неравенство
Решить иррациональное уравнение
Решить показательное неравенство
Решить логарифмическое уравнение
Изобразить на плоскости решение системы неравенств с двумя переменными
Решить линейное неравенство
Решить иррациональное уравнение
Решить показательное неравенство
Решить логарифмическое уравнение
Изобразить на плоскости решение системы неравенств с двумя переменными
Система оценивания (5-ти бальная): за каждый правильно решенный пример получаем 1 предварительный балл. Всего можно получить 13 баллов. Таблица перевода баллов в оценку:
СПИСОК ЛИТЕРАТУРЫ
1. Богомолов Н.В. /Математика: учебник для прикладного бакалавриата / Н.В. Богомолов, П.И. Самойленко. – 5-е изд. перераб. и доп. -М.: Издательство Юрайт, 2016. — 396с. – Серия: Бакалавр. Прикладной курс.
2. Богомолов, Н.В./ Практические занятия по математике: учеб. пособие для СПО / Н.В. Богомолов. — 1-е изд. перераб. и доп, — М: Издательство Юрайт, 2016. — 495с. Серия:Профессиональное образование.
3. Григорьев С.Г. /Математика: учебник для студ. образоват. учреждений сред. проф. образования. / Григорьев С.Г. под ред. В.А.Гусева.- 11-е изд., стер.- М.: Издательский центр “Академия”, 2014. – 416 с.
4. Алимов, Ш.А. / Алгебра и начала математического анализа. 10 -11 классы : учеб. для общеобразоват. организаций: базовый и углубл. уровни / Ш.А.Алимов, Ю.М. Колягин, М.В. Ткачеваи др. — 3-е изд. – М. Просвещение, 2016. – 463 с.
5. Колмогоров А.Н./ Алгебра и начала математического анализа 10-11классы: учеб пособие для общеобразоват.организаций /Колмогоров А.Н., А.М.Абрамов, Ю.П.Дудницын и др. под ред. А.Н.Колмогорова.-26-е изд. – М.: Просвещение, 2018. – 384 с.
- Так как последнее неравенство имеет знак «больше или равно», получим решение, изображенное на рисунке (серым цветом). Заметим, что прямая входит в решение, так как в неравенстве присутствует знак равенства.
- Построим обе функции на одном графике
- Построим обе функции на одном графике
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра
Линейные уравнения
Линейным уравнением относительно переменной x называется уравнение первой степени
где k и b – произвольные вещественные числа.
В случае уравнение (1) имеет единственное решение при любом значении b :
В случае, когда уравнение (1) решений не имеет.
В случае, когда k = 0, b = 0, решением уравнения (1) является любое число
Линейные неравенства
Линейным неравенством относительно переменной x называется неравенство, принадлежащее к одному из следующих типов:
где k и b – произвольные вещественные числа.
Решая линейные, да и не только линейные, неравенства, следует помнить, что
| при умножении или делении неравенства на положительное число знак неравенства сохраняется, |
а
| при умножении или делении неравенства на отрицательное число знак неравенства меняется на противоположный. |
В соответствии с этим решение линейных неравенств, в зависимости от значений коэффициентов k и b, представлено в следующей Таблице 1.
Таблица 1. – Решение неравенств первой степени (линейных неравенств)
| k > 0 Знак неравенства сохраняется |
Неравенство: Решение неравенства: |
Неравенство: kx + b > 0 Решение неравенства: |
Неравенство: Решение неравенства: |
Неравенство: kx + b < 0 Решение неравенства: |
| k = 0, b < 0 |
Неравенство: Решение неравенства: |
Неравенство: kx + b > 0 Решение неравенства: |
Неравенство: Решение неравенства: |
Неравенство: kx + b < 0 Решение неравенства: |
| k = 0, b = 0 |
Неравенство: Решение неравенства: |
Неравенство: kx + b > 0 Решение неравенства: |
Неравенство: Решение неравенства: |
Неравенство: kx + b < 0 Решение неравенства: |
| k = 0, b > 0 |
Неравенство: Решение неравенства: |
Неравенство: kx + b > 0 Решение неравенства: |
Неравенство: Решение неравенства: |
Неравенство: kx + b < 0 Решение неравенства: |
| k < 0 Знак неравенства меняется на противоположный |
Неравенство: Решение неравенства: |
Неравенство: kx + b > 0 Решение неравенства: |
Неравенство: Решение неравенства: |
Неравенство: kx + b < 0 Решение неравенства: |
Системы линейных неравенств
Рассмотрим решение систем линейных неравенств на примерах.
Пример 1. Решить систему неравенств
Решение. Решим каждое из неравенств системы:
Изобразив на одной координатной прямой (рис. 1) оба точечных множества, составляющих последнюю систему, получаем ответ примера.
Рис.1
Ответ:
Пример 2. Решить систему неравенств
Решение. Решим каждое из неравенств системы:
Изобразив на одной координатной прямой (рис. 2) оба точечных множества, составляющих последнюю систему, получаем ответ примера.
Рис.2
Ответ:
Пример 3. Решить систему неравенств
Решение. Решим каждое из неравенств системы:
Изобразив на одной координатной прямой (рис. 3) оба точечных множества, составляющих последнюю систему, получаем ответ примера
Рис.3
Ответ:
На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Решение уравнений и неравенств с параметрами
1. Основные определения
Неравенство
f(a, b, c, …, k, x)>j(a, b, c, …, k, x), (1)
где a, b, c, …, k – параметры, а x – действительная переменная величина, называется неравенством с одним неизвестным, содержащим параметры.
Любая система значений параметров а = а0, b = b0, c = c0, …, k = k0, при некоторой функции
f(a, b, c, …, k, x) и
j(a, b, c, …, k, x
имеют смысл в области действительных чисел, называется системой допустимых значений параметров.
называется допустимым значением х, если
f(a, b, c, …, k, x) и
j(a, b, c, …, k, x
принимают действительные значения при любой допустимой системе значений параметров.
Множество всех допустимых значений х называется областью определения неравенства (1).
Действительное число х0 называется частным решением неравенства (1), если неравенство
f(a, b, c, …, k, x0)>j(a, b, c, …, k, x0)
верно при любой системе допустимых значений параметров.
Совокупность всех частных решений неравенства (1) называется общим решением этого неравенства.
Решить неравенство (1) – значит указать, при каких значениях параметров существует общее решение и каково оно.
Два неравенства
f(a, b, c, …, k, x)>j(a, b, c, …, k, x) и (1)
z(a, b, c, …, k, x)>y(a, b, c, …, k, x) (2)
называются равносильными, если они имеют одинаковые общие решения при одном и том же множестве систем допустимых значений параметров.
2. Алгоритм решения.
1.
Находим область определения данного неравенства.
2.
Сводим неравенство к уравнению.
3.
Выражаем а как функцию от х.
4.
В системе координат хОа строим графики функций а =f (х) для тех значений х, которые входят в область определения данного неравенства.
5.
Находим множества точек, удовлетворяющих данному неравенству.
6.
Исследуем влияние параметра на результат.
·
найдём абсциссы точек пересечения графиков.
·
зададим прямую а=соnst и будем сдвигать её от -∞ до +∞
7.
Записываем ответ.
Это всего лишь один из алгоритмов решения неравенств с параметрами, с использованием системы координат хОа. Возможны и другие методы решения, с использованием стандартной системы координат хОy.
3. Примеры
I. Для всех допустимых значений параметра а решить неравенство
Решение.
В области определения параметра а, определённого системой неравенств
данное неравенство равносильно системе неравенств
Если
, то решения исходного неравенства заполняют отрезок
.
Ответ:
, .
II. При каких значениях параметра а имеет решение система
Решение.
Найдем корни трехчлена левой части неравенства –
(*)
Прямые, заданные равенствами (*), разбивают координатную плоскость аОх на четыре области, в каждой из которых квадратный трехчлен
сохраняет постоянный знак. Уравнение (2) задает окружность радиуса 2 с центром в начале координат. Тогда решением исходной системы будет пересечение заштрихован
ной области с окружностью, где
, а значения
и находятся из системы
а значения
и находятся из системы
Решая эти системы, получаем, что
Ответ:
III. Решить неравенство
на
в зависимости от значений параметра а.
Решение.
Находим область допустимых значений –
Построим график функции в системе координат хОу.
·
при
неравенство решений не имеет.
·
при
для
решение х удовлетворяет соотношению
, где
Ответ: Решения неравенства существуют при
, где
, причем при
решения
; при
решения
.
IV. Решить неравенство
Решение.
Находим ОДЗ или линии разрыва (асимптоты)
Найдем уравнения функций, графики которых нужно построить в ПСК; для чего перейдем к равенству :
Разложим числитель на множители.
т. к.
то
Разделим обе части равенства на
при
. Но
является решением : левая часть уравнения равна правой части и равна нулю при
.
3. Строим в ПСК хОа графики функций
и нумеруем образовавшиеся области (оси роли не играют). Получилось девять областей.
4. Ищем, какая из областей подходит для данного неравенства, для чего берем точку из области и подставляем в неравенство.
Для наглядности составим таблицу.
? | точка | неравенство:
| вывод |
1 |
|
| — |
2 |
|
| + |
3 |
|
| — |
4 |
|
| + |
5 |
|
| — |
6 |
|
| + |
7 |
|
| — |
8 |
|
| + |
9 |
|
| — |
5. Найдем точки пересечения графиков
6. Зададим прямую а=сonst и будем сдвигать её от -∞ до +
∞.
Ответ.
при
при
при
при
решений нет
при
Курс «Уравнения и неравенства в школьном курсе математики»
К решению уравнений и неравенств сводятся многие математические задачи, — не случайно на протяжении долгого времени считалось, что алгебра, — это, прежде всего, наука о решении уравнений.
Обучение методам решения уравнений и неравенств традиционно является важнейшей частью школьного курса математики.
Каковы же результаты обучения? Окончившие среднюю школу обычно неплохо владеют техническими навыками решения уравнений и неравенств, однако, нередко можно видеть, что даже получив верный ответ, учащийся не уверен, что решил то или иное уравнение правильно. Связано это с тем, что при решении уравнений и неравенств помимо технических приходится преодолевать и логические трудности и в частности отвечать на вопрос, почему выполненные преобразования не приводят к потере корней или приобретению посторонних корней.
Предлагаемый курс лекций помимо теоретических сведений, необходимых для решения уравнений и неравенств, содержит интересные и красивые задачи, доступные школьникам. Взяты они из материалов разных вступительных экзаменов в высшие учебные заведения.
Освоение материалов учебного курса позволит учителю организовать учебный процесс в соответствии с требованиями ФГОС. В частности, формировать навыки владения приемами решения рациональных и иррациональных, показательных, степенных, тригонометрических уравнений и неравенств, их систем.
Курс предназначен для учителей, которые ведут преподавание в старших классах средней школы.
Дистанционный
Курс входит в ШЦВ
Возможность заказа печатной версии
Срок прохождения курса:
от 2 недель до 6 месяцев с момента оплаты.
Примечание: Курсы, полученные в рамках ШЦВ, доступны для прохождения только до окончания подписки, в которой они были выбраны.
Решение неравенств любого вида. Онлайн калькулятор с примерами
Решение неравенств онлайн
Перед тем как решать неравенства, необходимо хорошо усвоить как решаются уравнения.
Не важно каким является неравенство – строгим () или нестрогим (≤, ≥), первым делом приступают к решению уравнения, заменив знак неравенства на равенство (=).
Поясним что означает решить неравенство?
После изучения уравнений в голове у школьника складывается следующая картина: нужно найти такие значения переменной, при которых обе части уравнения принимают одинаковые значения. Другими словами, найти все точки, в которых выполняется равенство. Всё правильно!
Когда говорят о неравенствах, имеют в виду нахождение интервалов (отрезков), на которых выполняется неравенство. Если в неравенстве две переменные, то решением будут уже не интервалы, а какие-то площади на плоскости. Догадайтесь сами, что будет решением неравенства от трех переменных?
Как решать неравенства?
Универсальным способом решения неравенств считают метод интервалов (он же метод промежутков), который заключается в определении всех интервалов, в границах которых будет выполняться заданное неравенство.
Не вдаваясь в тип неравенства, в данном случае это не суть, требуется решить соответствующее уравнение и определить его корни с последующим обозначением этих решений на числовой оси.
Можно сказать на этом полдела сделано. Далее, взяв любую точку на каждом интервале, осталось определить выполняется ли само неравенство? Если выполняется, то он входит в решение неравенства. Ели нет, то пропускаем его.
Как правильно записывать решение неравенства?
Когда вы определили интервалы решений неравенства, нужно грамотно выписать само решение. Есть важный нюанс – входят ли границы интервалов в решение?
Тут всё просто. Если решение уравнения удовлетворяет ОДЗ и неравенство является нестрогим, то граница интервала входит в решение неравенства. В противном случае – нет.
Рассматривая каждый интервал, решением неравенства может оказаться сам интервал, либо полуинтервал (когда одна из его границ удовлетворяет неравенству), либо отрезок – интервал вместе с его границами.
Важный момент
Не думайте, что решением неравенства могут быть только интервалы, полуинтервалы и отрезки. Нет, в решение могут входить и отдельно взятые точки.
Например, у неравенства |x|≤0 всего одно решение – это точка 0.
А у неравенства |x|
Для чего нужен калькулятор неравенств?
Калькулятор неравенств выдает правильный итоговый ответ. При этом в большинстве случаев приводится иллюстрация числовой оси или плоскости. Видно, входят ли границы интервалов в решение или нет – точки отображаются закрашенными или проколотыми.
Благодаря онлайн калькулятору неравенств можно проверить правильно ли вы нашли корни уравнения, отметили их на числовой оси и проверили на интервалах (и границах) выполнение условия неравенства?
Если ваш ответ расходится с ответом калькулятора, то однозначно нужно перепроверить свое решение и выявить допущенную ошибку.
Решение уравнений и неравенств | Texas Gateway
Мы собираемся узнать, как преобразовать уравнение или неравенство в эквивалентное уравнение или неравенство. Это включает в себя перестановку значений неравенства или уравнения с помощью обратных операций. Давайте исследуем различные способы преобразования линейных уравнений из одного представления в другое.
Наиболее распространенное преобразование линейного уравнения, которое вам нужно знать, — это взять уравнение в стандартной форме (A x + B y = C) и переписать его в форме пересечения наклона ( y = м х + б) или наоборот.Это преобразование важно, потому что две разные формы быстро раскрывают разные типы информации.
В таблице ниже представлена важная информация в каждой форме.
| Форма линейного уравнения | Важная информация | Где вы увидите эту форму |
Форма пересечения уклона y = m x + b | Уклон м. Координата точки пересечения и точки пересечения и равна b. | Задачи, включающие начальную точку (b) и скорость изменения. |
Стандартная форма A x + B y = C | Координата x точки пересечения x — это C / A. Координата точки пересечения и точки пересечения и — это C / B. | Задачи, включающие комбинацию чисел, кратных x и y. |
Для преобразования стандартной формы в форму с пересечением откосов обычно требуется два шага.
Шаг 1 . Добавьте или вычтите член x с обеих сторон.
Шаг 2 . Разделите все слагаемые на коэффициент на .
Пример 1
Преобразуйте уравнение в форму с угловым пересечением: 2y + 3x = 12
2y + 3x = 12 -3x -3x2y = -3x + 122y2 = -3×2 + 122y = -32x + 6
Для преобразования формы с пересечением откоса в стандартную форму обычно требуется не более четырех шагов.
Шаг 1 . Добавьте или вычтите член x с обеих сторон.
Шаг 2 . Если коэффициент x отрицательный (член A), умножьте все члены на -1.
Шаг 3 . Если есть дробь, умножьте все члены на знаменатель, чтобы исключить дроби.
Шаг 4 . Если есть десятичная дробь, умножьте все члены на степень 10, чтобы исключить десятичные дроби.
Пример 2
Преобразуйте уравнение в стандартную форму: y = 34x — 9
y = 34x — 9-34x -34x-34x + y = -9-1 (-34x + y = -9) 34x-y = 94 (34x-y = 9) 3x-4y = 36
Проверьте свое понимание, выполнив следующие запросы.
Решение неравенств очень похоже на решение уравнений.
Применяется тот же общий метод.
Вот метод решения уравнений:
Что бы вы ни делали с одной стороной уравнения, вы должны делать с другой, чтобы сохранить равенство
Методика решения неравенств:
Что бы вы ни делали с одной стороной неравенства, вы должны делать с другой, чтобы сохранить неравенство.
техники такие же.
Техника означает:
Если вы прибавляете или вычитаете число к одной стороне уравнения или неравенства, вы должны прибавлять или вычитать это же число на другой стороне уравнения или неравенства.
Если вы умножите или разделите одну сторону уравнения или неравенства на то же число, вам придется умножить или разделить другую сторону уравнения или неравенства на то же число.
Разница между решением уравнений и решением неравенств:
Если вы умножите или разделите неравенство на отрицательное число, неравенство изменится на противоположное.!!!!!
Следующие примеры продемонстрируют это правило в действии.
Первым примером будет умножение.
Второй пример — деление.
Первый пример начинается с:
7 больше 5.
Умножьте обе части неравенства на -5, и вы получите:
7 * -5 = -35 в левой части неравенства.
5 * -5 = -25 в правой части неравенства.
Результат -35 меньше -25.
Неравенство вначале было больше чем, а стало меньше, потому что вы умножали обе стороны неравенства на отрицательное число.
Ясно видно, что 7 действительно больше 5.
Также ясно, что -35 меньше -25.
Второй пример просто противоположен первому и начинается с:
-35 меньше -25.
разделите обе части этого неравенства на -5, и вы получите:
-35 / -5 = 7 в левой части неравенства.
-25 / -5 = 5 в правой части неравенства.
Результат 7 больше 5.
Неравенство вначале было меньше, а стало больше, потому что вы делили обе стороны неравенства на отрицательное число.
Это нужно было сделать для сохранения неравенства.
С этими числами ясно, что изменение неравенства необходимо, когда вы увеличиваете обе стороны неравенства или делите обе стороны неравенства на отрицательное число.
В противном случае вы получите неправильный ответ, о чем вы узнаете, когда подтвердите результаты своего решения.
Чтобы показать вам, что это означает, мы решим равенство и неравенство, используя правила решения уравнений и решения неравенств.
Сначала уравнение.
-8x = 72
Чтобы решить эту проблему, мы хотим разделить обе части этого уравнения на -8.
Получаем:
-8x / -8 = 72 / -8
Мы упрощаем это, чтобы получить:
Фрироллы.«Фриролл» — это любое игровое соревнование или мероприятие с призовым фондом, но без дополнительных расходов. Фрироллы в покерном мире, как правило, проводятся регулярно, особенно в регионах онлайн-покера. Очевидно, что призовой фонд невелик, но, поскольку вы не рискуете наличными, это, несомненно, вдохновляющая ставка. Тем не менее, казино дополнительно предлагают соревнования, которые дают возможность играть в бесплатные игры казино, особенно соревнования на игровых автоматах. Как правило, вы должны быть представителем клуба игроков в казино, чтобы вас пригласили принять участие в одном из этих соревнований.Несколько баров также предлагают бесплатные игры казино, и вы можете найти их на веб-сайте казино http://pontst.com/bondibet-casino-review/, где вы узнаете, какие игры может предложить это казино. Раньше я постоянно играл в бесплатный блэкджек у Дэйва и Бастера. Однако я не помню, были ли у них какие-то деньги на победу. В наши дни более нормальным является открывать для себя бесплатные покерные соревнования в барах. Значительное их количество контролируется Лигой любителей покера. В дополнение к тому факту, что вы получаете шанс на 20 или 50 долларов, вы также накапливаете фокусы, которые можно обменять на разделы в более крупных соревнованиях.Это невероятный способ репетировать и попасть в реальную жизнь. Наконец, многие онлайн-казино предлагают бесплатные очереди игровых автоматов, когда вы присоединяетесь. Это тоже, можно сказать, фрироллы. Просто помните, что у суммы, которую вы можете выиграть за эти подарки, есть ограничение. Кроме того, вам, скорее всего, потребуется отложить взнос или что-то подобное, прежде чем вы сможете обналичить любые деньги, которые вы выиграли на этих бесплатных ходах игрового автомата.
х = -9
Как мы узнаем, что операция была успешно завершена?
Мы знаем это, потому что, когда мы заменяем x в исходном уравнении на решение, исходное уравнение становится истинным утверждением.
Исходное уравнение:
-8x = 72
Заменим x на -9, чтобы получить:
-8 * -9 = 72
Упрощаем, чтобы получить:
72 = 72
Это верное утверждение, поэтому мы можем предположить, что наше решение хорошее.
Теперь решим ту же задачу, что и неравенство.
-8x> = 72
Это означает, что -8x больше или равно 72.
Чтобы решить эту проблему, мы хотим разделить обе части этого уравнения на -8.
Получаем:
-8x / -8 <= 72 / -8
Неравенство пришлось отменить, потому что мы делили обе части уравнения на отрицательное число !!!!!
Мы начали с -8x больше или равно 72 и закончили с -8x / -8 меньше или равно 72 / -8
Мы упрощаем это, чтобы получить:
х <= -9
Как мы узнаем, что операция была успешно завершена?
Мы знаем это, потому что, когда мы заменяем x в исходном уравнении решением, исходное уравнение становится истинным утверждением.
В этом случае решение — не одно число, а множество чисел.
Решение: x <= -9.
Это означает, что x может быть равно -9, или -10, или -11 и т. Д.
, пока x <= -9, у нас есть решение.
Чтобы проверить это неравенство, нам нужно сделать две вещи.
Во-первых, нужно проверить, является ли неравенство ложным, если мы нарушаем правила решения.
Для этого мы выбираем число больше -9 и используем его для решения неравенства.
Мы попробуем x = 0, потому что это просто и нарушает правила решения, потому что 0 не меньше -9.
Уравнение -8x> = 72 становится -8 * 0> = 72, что становится 0> = 72, что является ложным утверждением, поскольку 0 не больше или не равно 72.
Поскольку при замене x на 0 неравенство ложно, решение x = 0 не является хорошим.
Это то, что мы ожидаем, поскольку 0 не меньше -9.
Далее мы хотим попробовать условия, в которых решение действительно следует правилам.
В этом случае мы ожидаем, что уравнение будет верным.
Правила решения таковы, что x <= -9
Выбираем x = -9
Исходное неравенство -8x> = 72 становится -8 * -9> = 72, что становится 72> = 72, что верно, потому что 72 равно 72.
Это подтверждает, что, когда x = -9, исходное неравенство истинно, поэтому решение подтверждается как хорошее.
Затем мы выбираем x <-9
Мы выберем -10, потому что -10 меньше -9 и это легко вычислить.
Исходное неравенство -8x> = 72 становится -8 * -10> = 72, которое становится 80> = 72, что верно, потому что 80 больше 72.
Это подтверждает, что, когда x = -10, исходное неравенство истинно, поэтому решение подтверждается как хорошее.
Мы проверили три условия для этого неравенства.
x> -9 (ложь)
x = -9 (верно)
x <-9 (верно)
Исходное уравнение -8x> = 72 было ложным, когда x> -9, как мы и ожидали..
Исходное уравнение -8x> = 72 было истинным, когда x = -9, как мы и ожидали.
Исходное уравнение -8x> = 72 было истинным, когда x <-9, как мы и ожидали.
Наше решение x <= -9 было подтверждено как хорошее.
Когда мы говорим, что неравенство сохраняется, мы имеем в виду, что исходное неравенство сохраняется.
Исходное неравенство было -8x> = 72
Чтобы сохранить это неравенство, мы должны были следовать правилам решения неравенств.
В процессе решения промежуточное неравенство было отменено, но исходное неравенство сохранилось.
Если вы прибавите или вычтите одно и то же положительное или отрицательное число к обеим сторонам неравенства или уравнения, неравенство останется прежним.
Если вы умножите или разделите обе части неравенства или уравнения на одно и то же положительное число, неравенство останется прежним.
Единственная разница:
Если вы умножите или разделите обе части уравнения на одно и то же отрицательное число, уравнение останется тем же, но если вы умножите или разделите обе стороны неравенства на одно и то же отрицательное число, неравенство изменится на противоположное.!!!!!
Помните об этом, и у вас будет намного меньше проблем с устранением неравенства.
Урок 2.3 — Решите и изобразите уравнения и неравенства с переменными с обеих сторон.
- Должное
15 сентября 2017 г.
23:59 - Точки
15 - Отправка
поле для ввода текста или медиа-запись
Отправить — Ответы на следующие вопросы:
- Что конкретно вы увидите в подобных проблемах?
- Каким будет ваш ответ на этот конкретный тип проблемы?
- Какую особую вещь вы хотите помнить при решении подобных задач?
- Какой у вас балл IXL за практику (и)?
Урок:
.
Практика:
Дж.6 Решите уравнения с переменными с обеих сторон
J.7 Решение уравнений: завершите решение
K.10 Решение сложных линейных неравенств
J.8 Найдите количество решений
J.9 Создание уравнений без решений или бесконечного числа решений
J.11 Решение линейных уравнений: смешанный обзор
Дополнительные ресурсы:
Академия Хана:
На бумаге (скачать и распечатать):
1505534399
15.09.2017
23:59
Рубрика
правда
10070
Невозможно изменить рубрику после того, как вы начали ее использовать.
Алгебра I Урок 2.3 Рубрика
Вы уже оценивали студентов по этой рубрике. Любые серьезные изменения могут повлиять на результаты их оценки.
| Критерии | Рейтинги | Очки | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
AI.3 Линейные уравнения, неравенства и функции Линейные уравнения, неравенства и функции включает следующие стандарты: порог: |
Эта область будет использоваться оценщиком, чтобы оставлять комментарии, относящиеся к этому критерию. | баллы / 10 баллов — | |||||||||
PS.2 Рассуждают абстрактно и количественно. порог: |
Эта область будет использоваться оценщиком, чтобы оставлять комментарии, относящиеся к этому критерию. | баллы / 5 баллов — | |||||||||
Описание критерия порог: | Эта область будет использоваться оценщиком, чтобы оставлять комментарии, относящиеся к этому критерию. | баллы / 5 баллов — | |||||||||
Общее количество очков: 15 из 15 | |||||||||||
Описание
длинное описание
Отмена
Критерий обновления
Рубрика
Невозможно изменить рубрику после того, как вы начали ее использовать.
Заголовок
Вы уже оценивали студентов по этой рубрике. Любые серьезные изменения могут повлиять на результаты их оценки.
| Критерии | Рейтинги | Очки | |
|---|---|---|---|
Описание критерия порог: | Эта область будет использоваться оценщиком, чтобы оставлять комментарии, относящиеся к этому критерию. | баллы / 5 баллов — | |
Общее количество очков: 5 из 5 | |||
Неравенство
Неравенство
В этом разделе вы узнаете, как решить проблему неравенства.»Решение»
неравенство означает нахождение всех его решений. «Решение»
неравенство — это число, которое при замене переменной делает
неравенство верное утверждение.
Вот пример: Рассмотрим неравенство
Когда мы подставляем 8 вместо x, неравенство становится 8-2> 5.
Таким образом, x = 8 является решением неравенства.
С другой стороны, замена -2 на x дает ложное утверждение.
(-2) -2> 5.
Таким образом, x = -2 НЕ является решением неравенства.Неравенства
обычно есть много решений.
Как и в случае с решением уравнений, есть определенные манипуляции
неравенства, не меняющие решений. Вот список
«допустимых» манипуляций:
- Правило 1. Сложение / вычитание одного и того же числа с обеих сторон.
Пример: Неравенство x -2> 5 имеет те же решения, что и
неравенство x > 7. (Второе неравенство получено из
первый, добавив 2 с обеих сторон.) - Правило 2. Переключение сторон и изменение ориентации
знак неравенства.Пример: Неравенство 5- x > 4 имеет те же решения, что и
неравенство 4 <5 - x . (Мы перешли на другую сторону и повернули «> »
в « <'').
И последнее, но не менее важное: операция, лежащая в основе всех
проблемы с неравенством:
- Правило 3а. Умножение / деление на одно и то же ПОЛОЖИТЕЛЬНОЕ число с обеих сторон.
- Правило 3b. Умножение / деление на одно и то же ОТРИЦАТЕЛЬНОЕ число на обоих
стороны И изменение ориентации знака неравенства.Примеры: Звучит достаточно безобидно. Неравенство имеет те же решения, что и неравенство. (Мы разделили на +2 с обеих сторон).
Неравенство -2 x > 4 имеет те же решения, что и
неравенство х <-2. (Мы разделили на (-2) с обеих сторон и поменяли местами от "> » до» <''.)Но Правило 3 запрещает более причудливые ходы: неравенство ДЕЙСТВИТЕЛЬНО.
НЕ имеет тех же решений, что и неравенство x > 1.(Мы были
планируем разделить обе стороны на x , но мы не можем, потому что мы не
теперь знайте, будет ли x положительным или отрицательным!) На самом деле,
легко проверить, что x = -2 решает первое неравенство, но делает
не решить второе неравенство.
Только « легкие » неравенства решаются с помощью этих трех правил; наиболее
неравенство устраняется с помощью различных методов.
Решим некоторые неравенства:
Пример 1:
Рассмотрим неравенство
Основная стратегия для неравенств и уравнений такая же: изолировать x с одной стороны, а «другие вещи» — с другой.Следуя этой стратегии, переместим +5 вправо. Мы достигаем этого путем вычитания 5 с обеих сторон (Правило 1), чтобы получить
после упрощения получаем
После деления на +2 с обеих сторон (Правило 3a) нам удалось выделить x слева:
или упрощенно,
Все действительные числа меньше единицы решают неравенство. Мы говорим, что
«множество решений» неравенства состоит из всех действительных чисел за вычетом
чем 1.В обозначении интервала набором решений является интервал.
Пример 2:
Найти все решения неравенства
Начнем с того, что переместим цифру 5 вправо, вычтя 5 с обеих сторон (Правило 1):
или упрощенно,
Как избавиться от знака « — » перед x ?
Просто умножьте на (-1) с обеих сторон (Правило 3b), по ходу меняя «» на «»:
или упрощенное
Все действительные числа больше или равные
-1 удовлетворяют неравенству.Множество решений неравенства — интервал.
Пример 3:
Решите неравенство
Давайте сначала упростим:
Есть несколько маршрутов, по которым нужно двигаться; возьмем вот это: вычтем 2 x с обеих сторон (Правило 1).
и упростить:
Затем вычтите 9 с обеих сторон (Правило 1):
упростить, чтобы получить
Затем разделите на 4 (Правило 3а):
и еще раз упростим:
Приятнее будет, если поменяться стороной (Правило 2).
В интервальной записи набор решений выглядит так:
.
Упражнение 1:
Найдите все решения неравенства
Ответ.
Упражнение 2:
Решите неравенство
Ответ.
Упражнение 3:
Решите неравенство
Ответ.
Упражнение 4:
Найдите все решения неравенства
Ответ.
[Назад]
[Следующий]
[Алгебра]
[Тригонометрия]
[Комплексные переменные]
[Исчисление]
[Дифференциальные уравнения]
[Матричная алгебра] С.Домашняя страница O.S MATHematics
Вам нужна дополнительная помощь? Пожалуйста, разместите свой вопрос на нашем
S.O.S. Математика CyberBoard.
Copyright 1999-2021 MathMedics, LLC. Все права защищены.
Свяжитесь с нами
Math Medics, LLC. — П.О. Box 12395 — El Paso TX 79913 — США
пользователей онлайн за последний час
Уравнений и неравенств, проверяющих решения уравнений
Как проверить, является ли значение решением уравнения?
Уравнение работает следующим образом:
(выражение в левой части) = (выражение в правой части)
Следовательно, уравнение верно только в том случае, если выражение в левой части действительно совпадает с выражением в правой части .Взгляни на свои руки. Они точно такие же?
Если это не так, это нормально. Во всяком случае, в основном. Гм, может быть, мы вернемся к этой аргументации позже.
Чтобы проверить, является ли данное значение решением уравнения:
- Вычислите выражение в левой части для данного значения, чтобы получить число.
- Вычислите выражение в правой части при заданном значении, чтобы получить число.
- Посмотрите, совпадают ли числа.
Эй, он совпадает! Вы делаете это с носками каждый день.Иногда не , а , но, по крайней мере, процесс смутно знакомый.
Если числа, полученные при вычислении двух выражений, совпадают, то данное значение является решением уравнения (делает уравнение истинным). Если числа не совпадают, данное значение не является решением уравнения (делает уравнение ложным). Возьмите те ценности, которые не являются решениями, и выбросьте их прямо в корзину, потому что они нам больше не понадобятся. На самом деле, может быть, промойте их и вместо этого отправьте на переработку.Мы стараемся быть зелеными.
Пример задачи
Является ли x = 5 решением уравнения
Не очень удивительный способ (он же неправильный путь)
Если первое, что мы делаем, это записываем, мы предъявляем претензию без выполнив работу, чтобы убедиться, что утверждение верно. Ох, хватит.
Утверждение, что левая и правая части равны, должно появиться после оценки левой части, оценки правой части и сравнения ответов.Если бы мы были юристами, мы бы назвали это нашей «должной осмотрительностью». К счастью, это Алгебра Шмупа, и мы мужественно сопротивляемся желанию отпускать ужасные шутки про адвокатов прямо сейчас.
The Super Awesome Way (также известный как The Right Way):
Сначала оцените левую часть для x = 5:
Затем оцените правую часть для x = 5:
Поскольку 2 = 2, мы можем сказать, что x = 5 является решением уравнения.Держу пари, зная, что это поможет тебе лучше спать сегодня вечером.
Линейные уравнения и неравенства
Равномерное движение означает движение с неизменной скоростью или скоростью. Мы можем определить пройденное расстояние, умножив среднюю скорость на время, пройденное с этой скоростью, по формуле D = r⋅t. Приложения, связанные с равномерным движением, обычно содержат много данных, поэтому помогает сначала организовать данные в виде диаграммы, а затем создать алгебраическое уравнение, моделирующее проблему.
Пример 14: Два поезда покидают станцию одновременно, двигаясь в противоположных направлениях.Один движется со скоростью 70 миль в час, а другой — со скоростью 60 миль в час. Сколько времени нужно, чтобы расстояние между ними достигло 390 миль?
Решение: Сначала определите неизвестное количество и систематизируйте данные.
Данная информация представлена в следующей таблице. Время на каждый поезд одинаковое.
Чтобы не вводить еще две переменные, используйте формулу D = r⋅t для заполнения неизвестных расстояний, пройденных каждым поездом.
Теперь мы можем полностью заполнить график.
Алгебраическая установка определяется столбцом расстояния. Задача спрашивает, сколько времени требуется, чтобы общее расстояние достигло 390 миль.
Решить для т .
Пример 15: Поезд, идущий без остановок к месту назначения, может двигаться со средней скоростью 72 мили в час. На обратном пути поезд делает несколько остановок и может развивать скорость только 48 миль в час. Если обратный путь занимает на 2 часа дольше, чем первоначальный путь к месту назначения, то какое время в пути в каждую сторону?
Решение: Сначала определите неизвестное количество и систематизируйте данные.
Используйте формулу D = r⋅t для заполнения неизвестных расстояний.
Используйте эти выражения для заполнения диаграммы.
Алгебраическая установка снова определяется столбцом расстояния. В этом случае расстояние до пункта назначения и обратно одинаково, и уравнение:
Решить для t .
Обратный путь занимает t + 2 = 4 + 2 = 6 часов.
Ответ: Прибытие в пункт назначения занимает 4 часа, а возвращение — 6 часов.
Попробуй! Мэри отправляется в школу на велосипеде со средней скоростью 6 миль в час.Ее сестра Кейт, опаздывая, уезжает через 15 минут и ездит вдвое быстрее. Сколько времени понадобится Кейт, чтобы догнать Мэри? Будь осторожен! Обратите внимание на единицы, указанные в задаче.
Ответ: Кейт наверстывает упущенное.
Тематические упражнения
Часть A: Перевести
Переведите следующее в алгебраические уравнения.
1. Сумма числа и 6 составляет 37.
2.Когда из удвоенного числа вычитается 12, получается 6.
3. Четырнадцать меньше, чем 5 умноженное на число 1.
4. Из 30 вычитается дважды какое-то число, и получается 50.
5. Пять умноженное на 6, а некоторое число равно 20.
6. 5 умноженное на некоторое число и 6 равно 20.
7. Когда сумма числа и 3 вычитается из 10, получается 5.
8.Сумма трех и пяти одинаковых чисел равна 24.
9. Десять вычитается из удвоенного числа, и в результате получается сумма числа и 2.
10. На шесть меньше некоторого числа — это в десять раз больше суммы этого числа и 5.
Часть B: Проблемы с номерами
Составьте алгебраическое уравнение и решите его.
11. Большое целое число на 1 больше, чем удвоенное другое целое число.Если сумма целых чисел равна 25, найдите целые числа.
12. Если большее целое число на 2 больше, чем в 4 раза больше другого целого числа, и их разница равна 32, найдите целые числа.
13. Одно целое число на 30 больше другого целого числа. Если разница между большим и удвоенным меньшим равна 8, найдите целые числа.
14. Частное числа и 4 равно 22. Найдите число.
15. Восемь раз число уменьшается в три раза на то же число, что дает разницу в 20.Какой номер?
16. Одно целое число на две единицы меньше другого. Если их сумма равна −22, найдите два целых числа.
17. Сумма двух последовательных целых чисел равна 139. Найдите целые числа.
18. Сумма трех последовательных целых чисел равна 63. Найдите целые числа.
19. Сумма трех последовательных целых чисел равна 279. Найдите целые числа.
20. Разница в два раза меньшего из двух последовательных целых чисел и большего — 39.Найдите целые числа.
21. Если меньшее из двух последовательных целых чисел вычесть из двукратного большего, то получится 17. Найдите целые числа.
22. Сумма двух последовательных четных целых чисел равна 46. Найдите целые числа.
23. Сумма двух последовательных четных целых чисел равна 238. Найдите целые числа.
24. Сумма трех последовательных четных целых чисел равна 96. Найдите целые числа.
25. Если меньшее из двух последовательных четных целых чисел вычитается из 3-х кратного большего, результат будет 42.Найдите целые числа.
26. Сумма трех последовательных четных целых чисел равна 90. Найдите целые числа.
27. Сумма двух подряд идущих нечетных целых чисел равна 68. Найдите целые числа.
28. Сумма двух подряд идущих нечетных целых чисел равна 180. Найдите целые числа.
29. Сумма трех последовательных нечетных целых чисел равна 57. Найдите целые числа.
30. Если меньшее из двух последовательных нечетных целых чисел вычитается из удвоенного большего, получается 23.Найдите целые числа.
31. Дважды сумма двух подряд идущих нечетных целых чисел равна 32. Найдите целые числа.
32. Разница между удвоенным большим из двух подряд идущих нечетных чисел и меньшим составляет 59. Найдите целые числа.
Часть C: Проблемы геометрии
Составьте алгебраическое уравнение и решите его.
33. Если периметр квадрата 48 дюймов, найдите длину каждой стороны.
34. Длина прямоугольника на 2 дюйма больше его ширины. Если периметр 36 дюймов, найдите длину и ширину.
35. Длина прямоугольника на 2 фута меньше его ширины в два раза. Если периметр составляет 26 футов, найдите длину и ширину.
36. Ширина прямоугольника на 2 сантиметра меньше половины его длины. Если периметр 56 сантиметров, найдите длину и ширину.
37. Длина прямоугольника на 3 фута меньше его ширины в два раза.Если периметр составляет 54 фута, найдите размеры прямоугольника.
38. Если длина прямоугольника вдвое больше ширины, а его периметр составляет 72 дюйма, найдите размеры прямоугольника.
39. Периметр равностороннего треугольника составляет 63 сантиметра. Найдите длину каждой стороны.
40. Равнобедренный треугольник, основание которого составляет половину длины двух других равных сторон, имеет периметр 25 сантиметров.Найдите длину каждой стороны.
41. Каждая из двух равных катетов равнобедренного треугольника в два раза длиннее основания. Если периметр составляет 105 сантиметров, то какой длины каждая ножка?
42. Треугольник имеет стороны, размеры которых являются последовательными четными целыми числами. Если периметр составляет 42 дюйма, найдите размер каждой стороны.
43. У треугольника есть стороны, размеры которых являются последовательными нечетными целыми числами. Если периметр составляет 21 дюйм, найдите размер каждой стороны.
44. У треугольника есть стороны, размеры которых являются последовательными целыми числами. Если периметр составляет 102 дюйма, найдите размер каждой стороны.
45. Длина окружности составляет 50π единиц. Найдите радиус.
46. Длина окружности составляет 10π единиц. Найдите радиус.
47. Окружность круга составляет 100 сантиметров. Определите радиус с точностью до десятых долей.
48.Окружность круга составляет 20 сантиметров. Найдите диаметр, округленный до сотых.
49. Диаметр круга 5 дюймов. Определите длину окружности с точностью до десятых долей.
50. Диаметр круга 13 футов. Рассчитайте точное значение окружности.
Часть D. Проблемы с процентами и деньгами
Составьте алгебраическое уравнение и решите его.
51.Подсчитайте простой процент, полученный от двухлетних инвестиций в размере 1550 долларов США по ставке 8¾% годовых.
52. Рассчитайте простой процент, полученный по годовой инвестиции в размере 500 долларов США при годовой процентной ставке 6%.
53. На сколько лет необходимо инвестировать 10 000 долларов под 8½% годовых, чтобы получить 4250 долларов в виде простых процентов?
54. На сколько лет необходимо инвестировать 1000 долларов под 7,75% годовых, чтобы получить 503,75 долларов в виде простых процентов?
55.По какой годовой процентной ставке нужно инвестировать 2500 долларов на 3 года, чтобы получить 412,50 долларов в виде простых процентов?
56. По какой годовой процентной ставке необходимо инвестировать 500 долларов на 2 года, чтобы получить 93,50 долларов в виде простых процентов?
57. Если простой процент, полученный за 1 год, составлял 47,25 доллара, а годовая ставка составляла 6,3%, то какой был основной процент?
58. Если простые проценты, заработанные за 2 года, составляли 369,60 долларов, а годовая ставка составляла 5%, каков был основной процент?
59.Джо вложил прошлогоднюю налоговую декларацию в размере 2500 долларов в два разных счета. Он положил большую часть денег на счет денежного рынка, получая 5% простых процентов. Остальное он вложил в компакт-диск, получив 8% простых процентов. Сколько он положил на каждый счет, если общая сумма процентов за год составила 138,50 долларов?
60. Джеймс вложил 1600 долларов в два счета. Один счет приносит 4,25% простых процентов, а другой — 8,5%. Если через год процентная ставка составила 85 долларов, сколько он вложил в каждую учетную запись?
61.Джейн вложила свои сбережения в размере 5 400 долларов в два счета. Часть этих денег она хранит на компакт-диске под 3% годовых, а остальная часть — на сберегательном счете, который приносит 2% годовых. Если простые проценты, полученные с обоих счетов, составляют 140 долларов в год, то сколько у нее есть на каждом счете?
62. Марти поместил прошлогодний бонус в размере 2400 долларов на два счета. Он вложил часть в компакт-диск с годовой процентной ставкой 2,5%, а остальную часть — в фонд денежного рынка с годовой процентной ставкой 1,3%. Его общая сумма процентов за год составила 42 доллара.00. Сколько он вложил в каждый счет?
63. Алиса кладет деньги на два счета, один с годовой процентной ставкой 2%, а другой — с годовой процентной ставкой 3%. Она инвестирует в 3 раза больше в счет с более высокой доходностью, чем в счет с более низкой доходностью. Если ее общий процент за год составляет 27,50 долларов, сколько она инвестировала в каждую учетную запись?
64. Джим вложил наследство в два отдельных банка. Один банк предложил ставку 5,5% годовых, другой — 6¼%.Он вложил в более доходный банковский счет вдвое больше, чем в другой. Если его общая простая процентная ставка за 1 год составляла 4860 долларов, то какова была сумма его наследства?
65. Если рекламируемый товар стоит 29,99 долларов плюс налог 9,25%, какова общая стоимость?
66. Если рекламируется товар, стоимость которого составляет 32,98 доллара США плюс 8¾% налог, какова его общая стоимость?
67. Товар, включая налог в размере 8,75%, стоил 46,49 долларов. Какова первоначальная стоимость товара до вычета налогов?
68.Товар, включая налог в размере 5,48%, стоил 17,82 доллара. Какова первоначальная стоимость товара до вычета налогов?
69. Если еда стоит 32,75 доллара, какова сумма после добавления 15% чаевых?
70. Сколько чаевых составляет 15% от счета в ресторане на сумму 33,33 доллара?
71. У Рэя есть пригоршня десятицентовиков стоимостью 3,05 доллара. У него на 5 центов больше, чем у него. Сколько у него каждой монеты?
72. У Джилл на 3 полдоллара меньше, чем у нее четвертей.Стоимость всех 27 ее монет составляет 9,75 доллара. Сколько каждой монеты у Джилл?
73. Кэти должна внести пяти- и десятидолларовые банкноты на 410 долларов. У нее 1 меньше, чем в три раза больше десятков, чем у нее пятидолларовых купюр. Сколько денег от каждого счета она должна внести?
74. У Билли есть стопка четвертаков, десятицентовиков и никелей стоимостью 3,75 доллара. У него на 3 центов больше, чем четвертей, и на 5 центов больше, чем четвертей. Сколько каждой монеты у Билли?
75.У Мэри есть банка с однодолларовыми банкнотами, полдолларовыми монетами и четвертаками стоимостью 14 долларов. У нее в два раза больше четвертаков, чем у нее полудолларовых монет, и столько же полудолларовых монет, как у однодолларовых банкнот. Сколько у нее каждого?
76. У Чада есть пачка одно-, пяти- и десятидолларовых банкнот на общую сумму 118 долларов. У него в 2 раза больше, чем в 3 раза больше, чем у него пятидолларовых банкнот, и на 1 банкнот меньше десяти, чем пяти долларов. Сколько каждой банкноты есть у Чада?
Часть D: Равномерное движение (проблемы расстояния)
Составьте алгебраическое уравнение и решите его.
77. Две машины выезжают с места, двигаясь в противоположных направлениях. Если одна машина развивает в среднем 55 миль в час, а другая — 65 миль в час, то сколько времени им потребуется, чтобы преодолеть расстояние в 300 миль?
78. Из аэропорта одновременно вылетают два самолета в противоположных направлениях. Средняя скорость самолетов составляет 450 миль в час и 395 миль в час. Сколько времени потребуется самолетам, чтобы преодолеть расстояние в 1478 единиц.75 миль друг от друга?
79. Билл и Тед мчатся по стране. Билл уезжает на час раньше, чем Тед, и едет со средней скоростью 60 миль в час. Если Тед намеревается наверстать упущенное со скоростью 70 миль в час, то сколько времени это займет?
80. Два брата уезжают из одного и того же места, один на машине, а другой на велосипеде, чтобы встретиться в доме своей бабушки за ужином. Если один из братьев в среднем проезжает 30 миль в час в машине, а другой — 12 миль в час на велосипеде, тогда у брата на велосипеде на 1 час меньше, чем в 3 раза дольше, чем у другого в машине.Сколько времени нужно каждому из них, чтобы совершить путешествие?
81. Пилот коммерческой авиакомпании летел со средней скоростью 350 миль в час, прежде чем был проинформирован о том, что аэродром его назначения может быть закрыт из-за плохих погодных условий. Пытаясь прибыть перед бурей, он увеличил скорость до 400 миль в час и летел еще 3 часа. Если общее расстояние полета составило 2950 миль, то сколько времени длилось путешествие?
82. Два брата проехали 2793 мили от Лос-Анджелеса до Нью-Йорка.Один из братьев, управляя автомобилем днем, мог развивать скорость в среднем 70 миль в час, а другой, двигаясь ночью, мог развивать скорость в среднем 53 мили в час. Если брат, ехавший ночью, ехал на 3 часа меньше, чем брат, ехавший днем, то сколько часов каждый из них ехал?
83. Джо и Эллен живут в 21 миле друг от друга. Отправляясь одновременно, они едут навстречу друг другу. Если у Джо в среднем 8 миль в час, а у Эллен — 6 миль в час, сколько времени у них уйдет на встречу?
84.Если дорога до автомастерской занимает 6 минут со средней скоростью 30 миль в час, то сколько времени потребуется, чтобы вернуться обратно со средней скоростью 4 мили в час?
85. Хайме и Алекс покидают то же место и едут в противоположных направлениях. Условия движения позволили Алексу в среднем разгоняться на 14 миль в час, чем Хайме. Через полтора часа их разделяет 159 миль. Найдите скорость, с которой каждый мог двигаться.
86. Джейн и Холли живут в 51 миле друг от друга и уезжают, путешествуя навстречу друг другу, чтобы встретиться за обедом.Джейн ехала по автостраде со скоростью вдвое большей, чем Холли. Они смогли встретиться через полчаса. С какой скоростью путешествовал каждый?
Часть F: Темы дискуссионной доски
87. Обсудите в уме идеи для расчета налогов и чаевых.
88. Изучите исторические методы представления неизвестных.
89. Изучите и сравните простые и сложные проценты. В чем разница?
90.Обсудите, почему алгебра — обязательный предмет.
91. Изучите способы показать, что повторяющаяся десятичная дробь рациональна. Поделитесь своими выводами на доске обсуждений.
Уравнения / Неравенства — Алгебра 1
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
то
информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
.
