Содержание
Урок по математике 3 класс. Тема «Решение уравнений. Составление равенств, неравенств.»
Математика
Дата «___»_______ ____ г Класс 3- «__»
(1 четверть)
Урок 4
Тема урока: Решение уравнений. Составление равенств, неравенств.
Цели урока:
1.
уточнить знания учащихся об уравнениях, равенствах и неравенствах; совершенствовать умение решать уравнения на основе знаний о взаимосвязи компонентов действий сложения и вычитания.
2.
Закреплять мышление, речь, внимание.
3.
Воспитывать познавательную активность, умение работать в коллективе, умение оценивать себя и одноклассников
Тип урока: урок повторения и закрепления знаний;
Оборудование, наглядность, ТСО: ____________________________________________________________________________________________________________________________________________________
Этапы и структура урока.
1.
Организационный момент. Эмоциональный настрой. Мотивация.
Громко прозвенел звонок,
Начинается урок.
Наши ушки на макушке,
Глазки широко открыты,
Слушаем, запоминаем,
Ни минуты не теряем!
2.
Актуализация знаний
Для организации устного счета предназначено упражнение №1.
Можно провести игру «Шифровальщики». Цель игры: совершенствовать навыки устных вычислений в пределах 100.
Расшифруй тему урока.
а
164-8
е
58 + 9
У
160 + 40
и
100-5
н
90-2
Р
48 + 9
с
102 + 18
т
52-3
в
26 + 7
200
57
156
33
88
67
88
95
67
57
156
33
67
88
120
49
33
156
Можно провести упражнение, направленное на формирование у ребенка умений наблюдать, сравнивать, производить анализ и синтез, обобщать, выделять главное, умение делать вывод.
G, Q, S — «сказочные» цифры.
Eсли G > Q, то Q < G.
Если Q = S, то S = Q.
Если G < Q, то Q … G.
Если S > G, G > Q, то S … Q.
Если Q = S, S > G, то Q … G.
3.
Постановка проблемы
— На какие три группы можно разделить записанные на доске выражения?
274 4- х = 594 320 + 40 = 470 — 110 415 = 400 + 15
200 + 3 = 3 + 200 35 — 15 < 15 + 6 17 > 872 — 864
524 — х = 244 22 > 87 — 67 47 < 15 + 37
х — 251 = 522
— Чем отличаются уравнения от равенств, неравенств?
4.
Решение уравнений
По заданию №2 учащиеся составляют уравнения и решают их. Можно предложить для решения у доски 1 и 3-й столбики. Остальные уравнения учащиеся составляют и решают самостоятельно.
5.
Первичное закрепление
Для повторения знаний о равенствах и неравенствах предназначено упражнение №4. Это упражнение можно выполнить по времени.
Это упражнение можно выполнить по времени.
Упражнения №3 и №5 выполняются под руководством учителя.
№4
54 + 4 > 54 — 5
35 — 15 < 8 + 16
87 + 13 = 13 + 87
45 + 45 < 45 + 54
56 — 42 < 56 — 24
31 + 8 < 31 + 80
100 — 20 > 100 — 23
250 — 30 = 210 + 10
900 — 750 = 80 + 70
№ 5
78 + х = 125 + 68
78 + x = 193
x = 193 – 78
x = 115
а — 750 = 1000 – 920
a – 750 = 80
a = 750 + 80
a = 830
952 — b = 120 + 325
952 – b = 445
b = 952 – 445
b = 507
Динамическая пауза
6.
Самостоятельная работа.
Для самостоятельной работы предназначена задача №6 (а). Учитель предлагает детям записать решение задачи по действиям и выражениям. Задачу №6 (б) учащиеся решают самостоятельно с последующей проверкой.
245 + 55 = 300 (б) – на вечерний спектакль
245 + 300 = 545 (б)
210 + 120 = 330 (б) – продали
560 – 330 = 230 (б) – осталось.
Динамическая пауза.
Задание №7 является подготовительным к знакомству с темой «Умножение и деление». Желательно выполнить рисунок, иллюстрирующий условие задачи.
7.
Повторение
Что такое уравнение?
Логическое задание №8 знакомит с применением слов «все» и «некоторые».
8.
Рефлексия
Учитель предлагает проанализировать урок тем детям, кто был пассивным на уроке, по следующему плану:
1. Тема урока.
2. Какие упражнения помогли повторить тему?
3. Кто из ребят был активным и правильно отвечал?
4. Кто из ребят мешал проведению урока?
5. Кто затруднялся в ответах?
Учитель по своему выбору может предложить детям дома выполнить упражнение №3 или решить задачу №6 (б). Ход решения можно обсудить в классе.
Ход решения можно обсудить в классе.
I. Мотивационный этап. | карточки (Обложки от тетрадок) карточка на доске | Тренинг «Мне нравится…» Цель: создание атмосферы принятия, понимания, развитие навыков общения, активного слушания, эмпатии. Каллиграфическая минутка Цель: формирование каллиграфического почерка Взаимотренаж – таблица умножения Цель: формирование навыков устного счёта Актуализация знаний. УС ТУ на 3 Сообщение темы и цели урока. С. 23 № 10 – на доске Равенства и неравенства Я узнаю… Я смогу… Я научусь | Дети садятся в круг. В центр круга садится кто-либо по желанию. Каждый по очереди называет, что ему нравится в этом ребенке. Прописывают цифры Записывают число, классная работа Работа в парах сменного состава индивидуально фронтальная работа Высказывания детей | Взаимооценка Самооценка «Сигналы рукой» Самооценка Взаимооценка | НП ОдО КМ УиЛ ВО ТиО ИКТ | II. Операционный этап. | ТТ карточка учебник учебник | «Автобусная остановка» Решение примеров 90-51 34+42 9*3 4*3+8*3 80-32 82-57 24 :8 40 — 16:2 Решение задач а) Библиотекарь разложила 27 книг на 3 полки. Сколько книг на каждой полке? б) В третьих классах 28 мальчиков, а во вторых в 4 раза мальчиков меньше. Сколько мальчиков во всех классах? Решение уравнений Х + 12= 27 +8 Нахождение периметра Начерти прямоугольник и найди его периметр. Физминутка | Работа в группах – выброс на доску | Взаимооценка Самооценка «Сигналы рукой» | НП ОдО КМ УиЛ ВО ТиО ИКТ | III. Рефлексия. | Карточки стикеры | Контроль Цель: проверить уровень сформированности знаний за текущий урок А — Реши примеры 98-43 54+25 7*3 9*2+8*4 74-38 79-36 24:4 60 — 18:3 В — Реши уравнение а – 8 = 22 — 7 С – Реши задачу В детский сад привезли 5 кг яблок, а груш в 4 раза больше. Сколько всего кг фруктов привезли? «Закончи предложение.» Д/З с.22 № 6 | Индивидуальная работа Ученики по желанию высказываются, что им на уроке понравилось, и чему они научились. | Формативное оценивание Оценивание стикерами своей работы | НП ОдО КМ УиЛ ВО ТиО ИКТ |
Слайд | Деятельность учителя. | Деятельность учащихся | Формируемые УУД. | ||||||||||||||||||||||||||||
1.Организационный этап ( 1-2 мин) | |||||||||||||||||||||||||||||||
Слайд №1 Девиз урока. | – Сегодня на уроке у нас присутствуют гости. Поприветствуйте их. – Пожелайте друг другу удачи на сегодняшний урок. Все знания, которые у вас есть, вам сегодня очень пригодятся. – Давайте вместе прочитаем девиз нашего урока: Где есть желание, найдётся и путь! – Как вы понимаете эти слова? Мы обязательно справимся со всеми заданиями | Проверяют наличие на столах учебников, тетрадей, индивидуальной карты урока, пенала, дневника. | Регулятивные: Прогнозирование своей деятельности. Коммуникативные, личностные: Умение слушать и вступать в диалог | ||||||||||||||||||||||||||||
2. Актуализация знаний (5-7 мин). | |||||||||||||||||||||||||||||||
Слайд № 2 Тема Слайд проверка | А) У детей на партах рабочие листы урока У каждого из вас на столах индивидуальная карта урока. Рассмотрите их и скажите, с чем мы сегодня будем работать. Да, основная тема нашего урока – решение уравнений. Мы обязательно справимся со всеми заданиями. Мы уже не в первый раз решаем уравнения. Давайте все вместе подумаем, какие знания нам требуются для того, чтобы решить уравнение. Итак, рассмотрите первое задание. Как вы думаете, что мы повторим, выполняя его. Задание 1. ( 2 мин) Заполнить таблицу. Рассмотрите первую таблицы. Что нужно найти в каждой таблице. Вспомните соответствующие правила
8, 32, 2, 128 Проверьте. Оцените своё умение находить неизвестный компонент деления. Поставьте + около задания, если решили правильно. +- если есть ошибки. Давайте рассмотрим получившуюся таблицу. Что интересного заметили? Что происходит с делимым? А как изменяется частное? | Участвуют в беседе с учителем, отвечают на поставленные вопросы. Вспоминают взаимосвязь между компонентами и результатом действий умножения и деления. Выполняют самопроверку | Познавательные :Поиск и выделение необходимой информации. Структурирование знаний. Развитие способности к прогнозированию. Регулятивные : самоконтроль. Коммуникативные, личностные: Умение слушать и вступать в диалог, умение проводить самооценку собственной деятельности. Познавательные Регулятивные самооценка, самоконтроль | ||||||||||||||||||||||||||||
Слайд № 3 Таблица множитель Множитель произведение | 2 мин. Рассмотрите вторую таблицу. Назовите соответствующие правила.
200, 4, 70, 80 Проверьте по эталону. Оцените своё умение находить неизвестный компонент умножения Поставьте + около задания, если решили правильно. Рассмотрите получившуюся таблицу. Что интересного заметили? На сколько увеличивается первый множитель? А второй? Почему множитель увеличивается только на 10, а произведение сразу на 40? А теперь скажите, какое же знание нам необходимо для нашего урока. (Знание правил нахождения неизвестных компонентов действий). В) Задание 2 на рабочих листах.(1 мин.) Вспомним остальные правила. В следующем задании вам необходимо соединить линиями соответствующие части математических правил
Проверка по эталону на доске. Поставьте + если всё выполнено верно. Поднимите руку, кто правильно нашёл части правил. У кого ошибки – исправьте и постарайтесь правила не забывать. | Участвуют в беседе с учителем, отвечают на поставленные вопросы. Вспоминают взаимосвязь между компонентами и результатом действий умножения и деления Выполняют самопроверку | |||||||||||||||||||||||||||||
Слайд № 4 устная работа Слайд 5 только равенства | (3 мин. На какие группы можно разбить записи? ( Равенства и неравенства). Найдите и прочитайте только равенства. 92-X=86 85 – X > 70 125+75=200 Y +75 99:X=251-248 X * 5 = 445 27 + a = 70*3 -Что можно сказать о равенствах? (Верные, неверные; числовые, равенства с переменной – уравнения) Найдите уравнение, в котором неизвестно вычитаемое,слагаемое. Какой компонент неизвестен в уравнении 99: Х =251-248 Закончите определение: уравнение – это …( равенство, содержащее переменную) корень уравнения – это …( значение переменной, при котором равенство будет верным) решить уравнение – значит …( найти все его корни или доказать, что их нет) Итак, какое же знание нам необходимо ещё. ( Мы должны знать, что такое уравнение и что значит решить уравнение и найти его корень) У себя на листочках оцените свои знания. 1.Я знаю правила и умею находить неизвестные компоненты действий. Я знаю, что такое уравнение и что значит решить уравнение. | Участвуют в беседе с учителем. Закрепляют понятия «Равенства», «Уравнения, корень уравнения. Повторяют необходимые правила. Выдвигают предположения о теме урока | |||||||||||||||||||||||||||||
Слайд 6 уравнения Картинка древний Вавилон. Слайд 7 Эталон. Решённые уравнения. | 2). Уравнения – это одна из самых важных тем в математике. Вычисления площади земли, дома, квартиры, финансовые расчёты, многие работы военного характера связаны с решением уравнений. Не зря уравнения решали уже в древнем Вавилоне больше 4 тысяч лет тому назад. А сейчас проверим себя, как мы решаем уравнения. Самостоятельная работа. Самостоятельно решите уравнения. (Первые два уравнения могут быть разными по уровню сложности.) 19 · х = 76 127 + a = 60*3 Х=4 х= 53 Проверка по эталону после решения. Найдите то уравнение, которое решали и проверьте. Оцените своё умение решать уравнения. Поставьте + за каждое правильно решённое уравнение. У кого были ошибки? С чем связаны. | Слушают учителя, решают уравнения известным им способом. | |||||||||||||||||||||||||||||
3. Постановка проблемы (3 мин). | |||||||||||||||||||||||||||||||
Слайд 8 Уравнение Слайд 10 тема и задачи урока. | Рассмотрите следующее уравнение. Попробуйте его решить. (у — 14) · 3= 54 Почему не получилось? У нас возникла проблема. Какая? ( Мы не умеем решать такие уравнения) Какую цель мы поставим себе на нашем уроке? ( Научиться решать уравнения нового вида) – Подходит ли для решения этого уравнения известный нам алгоритм? (Нет) – Почему? (Неизвестный компонент является выражением, а мы такие уравнения ещё не решали). – Какую же ещё задачу мы можем поставить на этом уроке? (Вывести алгоритм решения уравнений нового вида.) Итак, поставлены две задачи. Будем их решать по порядку. | Дети пробуют решить уравнение. Фиксируют затруднение. Определяют точную тему и задачи урока. | Познавательные учатся ставить цель работы. Регулятивные учатся отделять известное от неизвестного. Коммуникативные; слушают учителя, взаимодействуют друг с другом | ||||||||||||||||||||||||||||
4. “Открытие” детьми нового знания (10 мин). | |||||||||||||||||||||||||||||||
Решение уравнения с записью на доске. Слайд 11. с блок – схемой. | (у — 14) ·3=54 – Кто догадался, как решить такое уравнение? (Предположения детей). – На какое из известных нам уравнений похоже данное? – Сколько действий в левой части? Расставьте порядок действий. – Какое действие последнее? – Назовите компоненты при умножении. Найдём множители в нашем уравнении. Подчеркните их по линейке. – В каком из этих компонентов стоит переменная? – Закроем компонент (у-14) карточкой Х – Что заметили? (Получили простое уравнение на нахождение неизвестного множителя). – Решите полученное уравнение: Х · 3 = 54 Х = 54 : 3 Х = 18. – Убираем карточку Х.Что же получилось? Можем ли мы теперь решить уравнение? ( (да) Решим уравнение до конца: (у-14) · 3=54 у-14 =54:3 у-14 = 18 у =14 + 18 y =32 .– Выполним проверку: (32- 14) · 3=54 54=54 – Проверка показывает, что корень уравнения найден верно. Решение такого уравнения напоминает спуск по лесенке. Каждая ступенька – это шажок к нахождению корня уравнения. Корень уравнения – это самая последняя площадка на лесенке – А что вам напоминает решение уравнений? –Мы видим, что уравнение может содержать несколькоступенек. – Давайте составим алгоритм решения таких уравнений. Что мы делали сначала? ( находили последнее действие). Что делаем потом ( определяли неизвестный компонент). Назовите следующий шаг ( вспоминаем правило, применяем его, вычисляем и проверяем) Проблема разрешена. Я каждому из вас приготовила подробный алгоритм. Возьмите листочки и прочитайте ещё раз, как решать уравнение. | Дети совместно с учителем решают уравнения, участвуют в составлении алгоритма | Познавательные Уметь ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя; добывать новые знания: находить ответы на вопросы. Коммуникативные. Уметь оформлять свои мысли в устной форме; слушать и понимать речь других; | ||||||||||||||||||||||||||||
5. | |||||||||||||||||||||||||||||||
А сейчас мы будем решать уравнения все вместе, проговаривая ход решения вслух. ( 1 ученик на доске) а) (47+ а) : 2 = 27 – неизвестно делимое 47 + а (последнее действие деление 47 + а= 27 * 2 – чтобы его найти, надо частное умножить на делитель 47 + а = 54 – теперь неизвестно слагаемое а= 54- 47 , – чтобы его найти, надо из суммы вычесть слагаемое а = 7. – корень уравнения равен 7 ( 47 + 7) : 2 =27 – проверка: подставим в уравнение вместо а число 7 и сосчитаем 27=27.(и) – получили верное равенство уравнение решено правильно. Пишу ответ. б) 3· а – 7=14 – подробное комментирование по цепочке. Неизвестно уменьшаемое ( последнее действие вычитание) 3 * а =14 +7 3*а = 21 а= 21 : 3 а=7 3 *7 – 7 = 14 14 =14 | Проговаривают решение, записывают решение с комментированием на доске и в тетради. | Коммуникативные, регулятивные. | |||||||||||||||||||||||||||||
6. Самостоятельная работа с самопроверкой по эталону (5 мин). | |||||||||||||||||||||||||||||||
Слайд 12 . Эталон. проверка | А) Работа в парах (с проговариванием) ( 180 –х) * 4 = 360 – Какая пара быстрее справилась с заданием? – Проверка по эталону. У кого так? Поставьте плюс, если ваша пара справилась с заданием. Б) Выберите любое уравнение, решите его самостоятельно. ( х – 29) :3 = 17 х= 80 8 * х +37 = 93 х= 7 – Проверка по эталону. Оцените себя. Кто решил правильно, поставьте себе +, – Кто выполнил без ошибок? – Кто допустил ошибки? С чем это связано? – Чему мы научились? (Научились решать уравнения нового вида) – Зачем нужен алгоритм? (Чтобы правильно решать задачи и уравнения) – Проговорите ещё раз алгоритм решения составных уравнений. – Для тех, кто хочет проверить свои силы – решите дома уравнения по карточкам Решите столько уравнений, сколько сможете. | Работают в парах и самостоятельно в тетрадях. Проверяют решение по эталону. Выполняют самооценку. | Регулятивные, клммуникативные. | ||||||||||||||||||||||||||||
7. Повторение. Решение геометрической задачи. (5-10мин). | |||||||||||||||||||||||||||||||
Слайд 13 чертёж Слайд 14 ширина увеличилась в 2 раза. Слайд 15. Длина уменьшилась в 3 раза | – А теперь я предлагаю вам решить геометрические задачи. 6м ? м
– Какая фигура изображена? – Что такое прямоугольник? -Составьте задачу по рисунку. Обратите внимание на размеры прямоугольника .Где в жизни мы можем встретиться с такими размерами?( комната в квартире) — Что известно в этой задаче? Что нужно узнать? — При помощи какой формулы можно установить взаимосвязь между длиной, шириной и площадью прямоугольника? a ∙ b = S — Какое уравнение можно составить с этими данными? 6 ∙ х = 18 Найдите устно, чему равна ширина этого прямоугольника. -. Изменится ли площадь комнаты, если ширина увеличится в 2 раза? Докажите. ( 3*2=6 м – ширина. 6 * 6 = 36 м2) Сравните с площадью предыдущего прямоугольника .Что заметили?( ширина увеличилась в 2 раза и площадь тоже увеличилась в 2 раза) А если длина уменьшится в 3 раза, а ширина останется прежней? ( 6:3=2(м) –длина. 2*3=6м2-площадь) Сравните с площадью 1 прямоугольника ( было 18м2. Стало 6 м2) Что заметили? ( Длина уменьшилась в 3 раза и площадь тоже уменьшилась в 3 раза) А если длина уменьшится в 2 раза, а ширина увеличится в 2 раза, что произойдёт с площадью тогда? (6:2=3м-длина, 3 * 2= 6м – ширина, 3*6= 18 м2- площадь. Площадь не изменилась.) | Дети составляют задачу, выявляют практическую значимость умения составлять уравнение, наблюдают закономерности | Коммуникативные, познавательные. | ||||||||||||||||||||||||||||
8. | |||||||||||||||||||||||||||||||
Слайд 16 рефлексия | – Что нового узнали на уроке? Чему научились? – К какому выводу пришли? (Составные уравнения решаются в 2 этапа). – Оцените свою работу на уроке. Посчитайте, сколько плюсов получили .
– Помог ли нам девиз урока? | Дети проводят рефлексию деятельности на уроке. самооценку | Регулятивные, коммуникативные | ||||||||||||||||||||||||||||
9. Домашнее задание. | |||||||||||||||||||||||||||||||
Слайд 17 д.з. |
| ||||||||||||||||||||||||||||||
Урок 11. равенство. неравенство. знаки «>», «
Математика, 1 класс
Урок 11. Равенство. Неравенство. Знаки «>», «<», «=»
Перечень вопросов, рассматриваемых на уроке:
1. Определять место знаков больше, меньше, равно
2. Писать знаки >,<,=
3. Называть равенство, неравенство.
Глоссарий
Равенство – это когда одно количество равно другому.
Неравенство – это когда одна сторона выражения не равна второй.
Если носик галочки смотрит направо — это знак больше (>).
Если носик галочки смотри налево – это знак меньше (<).
Знак равенства (=) в математике, в логике и других точных науках — символ, который пишется между двумя одинаковыми по своему значению выражениями.
Ключевые слова
Знак >; знак <; знак =
Основная литература:
1.Моро М. И., Волкова С. И., Степанова С. В. Математика. Учебник. 1 кл. В 2 ч. М.: Просвещение, 2017.
Дополнительная литература:
1. Моро М. И., Волкова С. И. Математика. Рабочая тетрадь. 1 кл. В 2 ч. пособие для общеобразовательных организаций. — М.: Просвещение, 201 с.
Основное содержание урока
1. Сегодня мы отправляемся в магазин, чтобы купить Оле и Ане к уроку технологии все учебные принадлежности.
Для урока понадобится 1 пачка пластилина и две пачки картона.
По сколько пачек пластилина получили девочки? ( по одной пачке)
Можно сказать, что девочки получили одинаковое количество пластилина.
2. Для технологии необходимо две пачки картона.
По сколько пачек картона получили девочки? (по две пачки)
Можно сказать, что девочки получили одинаковое количество картона.
3. В математике используется специальный значок, чтобы записать, что число предметов одинаковое.
Можно записать цифрами и использовать для слов «одинаково», «равно» специальный значок «=»,1 = 1
=
2 = 2 (аналогично)
Две палочки напишут дети,
И что получится в ответе,
Ведь каждый выучил давно,
Как пишется тот знак: РАВНО!
Такие записи называются равенствами.
Это равенства. Записать равенства можно с помощью знака «=».
Докажем, что одинаковое количество предметов с помощью стрелочек образует пары.
На схеме каждый предмет обозначим кружочком и образуем пары. Покажем стрелочкой.
Оля Аня
Лишних фигур не осталось. Значит, поровну, одинаково.
Можно записать 1 = 1
6. 2 + 1 = 3
Как можно прочитать эту запись?
(Числовое равенство)
Под этим высказыванием понимают два числовых выражения, которые стоят по обе стороны от знака « =».
Обе части записи равны между собой.
- В каком количестве нужно было для урока картона? А пластилина?
Чтобы узнать, каких предметов потребовалось больше или меньше, используют специальные значки «>», « <».
Если с какой- то стороны больше или меньше, то запись будет называться «неравенство».
Два больше одного.
Картон Пластилин
Если слева больше число, чем справа, то используют знак «>».
2 > 1
- А если число слева меньше, чем справа, то ставим знак меньше «<».
1 < 2
- Такие записи называются неравенства:
4 > 3, 4 < 5
Разбор типового тренировочного задания
Выберите нужный знак и распределите на две группы.
Дополните каждую группу своими записями.
6 (=, >, <) 9
1 (=, >, <) 3
2 (=, >, <) 2
3 (=, >, <) 3
Правильный ответ:
Равенства: 2 = 2, 3 = 3
Неравенства: 6 < 9, 1 < 3
Конспект урока по математике в 3 классе по теме «Решение уравнений»
Конспект урока математики в 3 классе по теме :«Решение уравнений»
УМК «Школа России»(учебник математики М.Моро,3класс,2 часть)
Рябых Елена Викторовна,учитель начальных классов,МАОУ Константиновская СОШ Московская область
Цели:
— закрепление умения решать уравнения на умножение и деление;
— совершенствование вычислительных навыков, умения решать задачи;
— закрепление знания названий компонентов уравнений и правил их нахождения;
— развитие умения сравнивать, обобщать, систематизировать знания при установлении взаимосвязи между математическими понятиями;
— развитие логического мышления, памяти, внимания учащихся, математической речи;
— воспитание любви и интереса к предмету;
— воспитание уважения к другим людям через взаимопомощь при выполнении совместных видов деятельности.
Планируемые результаты:
Предметные:
Понимать, что такое «уравнение», «решить уравнение». Знать способ решения уравнения (на основе взаимосвязи между компонентами).
Уметь решать простые уравнения. Уметь решать задачи способом составления уравнения, читать математические выражения, неравенства, равенства.
Личностные:
Уметь проводить самооценку на основе критерия успешности учебной деятельности.
Метапредметные:
Уметь определять и формулировать цель на уроке с помощью учителя; проговаривать последовательность действий на уроке; работать по коллективно составленному плану; оценивать правильность выполнения действия на уровне адекватной ретроспективной оценки; планировать своё действие в соответствии с поставленной задачей; вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок; высказывать своё предположение (Регулятивные УУД).
Уметь оформлять свои мысли в устной форме; слушать и понимать речь других; совместно договариваться о правилах поведения и общения в школе и следовать им (Коммуникативные УУД).
Уметь ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя; добывать новые знания: находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке (Познавательные УУД
Ход урока:
I.Сообщение темы и целей.
Запишите число, «Классная работа».
Сегодня мы будем закреплять умение решать уравнения, находить компоненты уравнений , применяя изученные правила.
II.Устный счёт.
— Давайте ребята учиться считать,
Делить, прибавлять, умножать, вычитать,
Запомните все, что без устного счёта,
Не сдвинется с места любая работа.
-Математический диктант
1. Найдите частное чисел 36 и 6.
2.Один множитель 9, другой 7. Найдите произведение.
3. Делимое 40, делитель 5. Найдите частное.
4. Во сколько раз 7 меньше 21?
5.Во сколько раз 16 больше 4?
6. На сколько 36 больше 9?
7. От пристани отплыли 6 лодок. В каждой лодке было по 4 весла. Сколько вёсел было в этих лодках?
8. В течение недели Витя читал книгу по 9 страниц в день. За это же время Коля прочитал на 15 страниц больше Вити. Сколько страниц прочитал Коля за неделю?
9. В классе 30 учеников, 2 ученика больны. Остальные дети разделились на группы по 4 человека для работы на уроке. Сколько групп получилось?
Ответы: 6, 63, 8, 3, 4, 27, 24, 78,7.
( Ответы записаны на карточках )
8 | 3 | 63 | 6 | 27 | 24 | 4 | 7 | 78 |
Н | У | И | А | Н | Е | Р | В | Я |
— Расположите ответы в порядке возрастания ( 1 ученик работает у доски, все остальные – в тетрадях). Что получилось?
( Уравнения)
—Что же такое уравнение?( Уравнение-это равенство, в котором есть неизвестное число, которое надо найти.
—Прочитайте равенство:
Ух7=63
—Как называются числа при умножении? (первый множитель, второй множитель, произведение)
—Как найти неизвестный множитель? (Нужно произведение разделить на известный множитель)
—Прочитайте равенства:
Х:5=15 36:Х=12
— Как называются числа при делении? (делимое, делитель, частное)
— Как найти делимое? (нужно частное умножить на делитель)
—Как найти делитель? (нужно делимое разделить на частное)
—Молодцы! Я думаю, мы готовы к выполнению следующих заданий.
.
III. Работа по учебнику.
№ 1, стр. 20 Три ученика по очереди у доски с комментированием, остальные решают в тетрадях.
18:х=54 х:16=48 57:х==1
2. № 2, стр.20 – самостоятельная работа с самопроверкой(учитель оценивает работы первых выполнивших)
IV. Физкультминутка.
Скачут, скачут во лесочке (прыжки на месте)
Зайцы — серые клубочки.(руки возле груди, как лапки у зайцев, прыжки)
Прыг — скок, прыг – скок – (прыжки вперед-назад, вперед-назад)
Стал зайчонок на пенёк.(встать прямо, руки на пояс)
Всех построил по порядку, (повернули туловище вправо, правую руку в сторону, затем влево и левую руку в сторону)
Стал показывать зарядку.
Раз! Шагают все на месте.(шаги на месте)
Два! Руками машут вместе, (руки перед собой, выполняем движение “ножницы”)
Три! Присели, дружно встали.(присесть, встать)
Все за ушком почесали.(почесать за ухом)
На “четыре” потянулись.(руки вверх, затем на пояс)
Пять! Прогнулись и нагнулись.(прогнуться, наклониться вперед)
Шесть! Все встали снова в ряд, (встать прямо, руки опустить)
Зашагали как отряд.(шаги на месте)
VI. Решение задачи. № 5, стр. 20.
Самостоятельное чтение текста задачи.
— О чём задача?
— Сколько человек пошли в поход?
— Что они купили? Какие? Сколько?
— Как вы понимаете «по 2 банки», «по 3 банки»?
— Что нужно узнать в задаче?
— Запишем условие в таблицу.
На доске:
Кол-во банок на человека | Кол-во туристов | Кол-во всех банок | |
Мясные консервы | 2 б. | 19 чел. | }? |
Овощные консервы | 3 б. | 19 чел. |
Анализ решения задачи:
I способ.
— Сколько банок куплено на человека?
— Мог ли каждый турист купить себе консервы?
— Сколько банок он тогда должен купить?
— Как в таком случае узнать, сколько всего банок купили на 19 человек?
II способ.
— По сколько мясных консервов купили?
— Как узнать, сколько нужно банок на 19 человек?
— По сколько овощных консервов купили?
— Как узнать, сколько нужно банок на 19 человек?
— Как узнать, сколько купили всего банок?
Запишите решение.
(2 ученика записывают разными способами на доске
Iспособ.
(3+2)х19=95(шт.)-консервов купили туристы
Ответ: 95 консервов всего
II способ.
1) 19∙2=38 (шт.) мясных консервов у всех туристов
2) 19∙3=57 (шт.) овощных консервов у всех туристов
3) 57+38= 95 (шт.) консервов всего
Ответ: 95 консервов всего
VI.
Игра «Я задумала число…» (Устно)
— Я задумала число. Если это число разделить на 7, то в результате получиться 6. Какое число я задумала.
Я задумала число. Если 8 умножить на это число, то в результате получиться 96. Какое число я задумала?
VII. Итог урока.
Как найти неизвестный множитель?
Как найти неизвестное делимое?
Как найти неизвестный делитель?
VIII. Домашнее задание.№ 8,9, стр.20.
УРОК МАТЕМАТИКИ. 3 КЛАСС. ТЕХНОЛОГИЯ СИСТЕМНО- ДЕЯТЕЛЬНОСТНОГО ПОДХОДА (ТДМ). ТЕМА УРОКА: «РЕШЕНИЕ СОСТАВНЫХ УРАВНЕНИЙ»
Тема: «Сложение дробей с одинаковыми
Урок по математике. 4 класс. Программа «Школа 2100». по учебнику Л.Г.Петерсон (4 класс, 2 часть, урок 3) Тема: «Сложение дробей с знаменателями». Урок открытия новых знаний. Подготовила: Моисеева Е.Р.
Подробнее
Урок 22. Тип урока: ОНЗ
Тип урока: ОНЗ Урок 22 Тема: «Сравнение долей». Автор: Калинина Л. В., МОУ гимназия 9 г. Королёва. Основные цели: ) сформировать способность к изображению долей точками числового луча и сравнению долей;
Подробнее
Предмет математика класс 2 г
Предмет математика класс 2 г Тема урока Место урока по теме (в разделе/главе) Закрепление изученного по теме «Умножение и деление» «Умножение и деление» 18 из 20 Тип урока Форма урока, форма учебной деятельности,
Подробнее
Технологическая карта урока
Технологическая карта урока Учитель: Кривцовой О. И. Класс: 2 «Б» УМК: «Школа России» Предмет: математика. Тема урока: Периметр прямоугольника. Вычисление периметра. урока: урок открытия новых знаний Место
Подробнее
Конспект открытого урока
Конспект открытого урока Учитель: Иванова Елена Александровна Тип урока: ОНЗ. Тема: «Развёрнутый угол. межные углы». Основные цели: 1) формировать у учащихся представление о развернутом и смежных углах;
Подробнее
КОНСПЕКТ УРОКА МАТЕМАТИКИ
КОНСПЕКТ УРОКА МАТЕМАТИКИ Учитель: Вихрова О.Н. Класс: 4 Тема: «Встречное движение». Дата проведения: 04.02.16 г. Основные цели: 1) Сформировать умение фиксировать индивидуальное затруднение, его причину,
Подробнее
Логвина Ирина Сергеевна
Тема: Что такое суффикс? (3 класс. «Школа России») Тип урока: ОНЗ Логвина Ирина Сергеевна Основные цели: формировать представление о суффиксе, как новой значимой части слова; формировать умение строить
Подробнее
Технологическая карта урока математики
АДМИНИСТРАЦИЯ ГОРОДСКОГО ОКРУГА ПОДОЛЬСК КОМИТЕТ ПО ОБРАЗОВАНИЮ Муниципальное общеобразовательное учреждение «Лицей 1» (МОУ «Лицей 1») Технологическая карта урока математики Урок математики в 6 классе
Подробнее
Пояснительная записка
Пояснительная записка Данный урок является уроком открытия нового знания по теме «Свойства степени с натуральным показателем», расширяющий кругозор учащихся. Урок может быть проведён учителем, работающим
Подробнее
НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ
Государственное автономное учреждение дополнительного профессионального образования «БРЯНСКИЙ ИНСТИТУТ ПОВЫШЕНИЯ КВАЛИФИКАЦИИ РАБОТНИКОВ ОБРАЗОВАНИЯ» Татьяна Сергеевна Дьякович НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ
Подробнее
Технологическая карта урока математики
Технологическая карта урока математики Изучаемая тема: Устные и письменные приемы вычисления вида 32-5, 51-27 Место урока в изучаемой теме: 5 Дата проведения: 14.04.2017 г. Класс: 2 Программа: УМК «Перспектива»
Подробнее
Технологическая карта урока по геометрии
Технологическая карта урока по геометрии Автор: Турукина Светлана Ивановна, учитель математики, МБОУ «СОШ 6» города Обнинска Предмет: Геометрия Класс: 9 класс Тип урока: урок «открытия нового знания» Тема:
Подробнее
Сложение и вычитание смешанных чисел
Предмет: Математика Класс: 5 «Б» класс Сложение и вычитание смешанных чисел Учебник: Математика: 5 класс: учебник для учащихся общеобразовательных учреждений / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир.
Подробнее
«Порядок выполнения действий.»
МОУ «Новомичуринская средняя общеобразовательная школа 2» «Порядок выполнения действий.» Васина Марина Евгеньевна учитель начальных классов Урок математики во 2 классе Тема урока: «Порядок выполнения действий»
Подробнее
«Встречное движение».
1 Школа молодого учителя Открытый урок по математике на тему: «Встречное движение». Учитель высшей категории МБОУ НОШ 9 Занегина Г.В. г. Сергиев Посад 19.02.2015 г. 2 Урок математики Тема. Встречное движение.
Подробнее
Технологическая карта ученика
Технологическая карта ученика ФИ Класс 5 Дата Дорогой друг! Внимательно читай технологическую карту и работай согласно предложенному алгоритму. Будь настойчив, проявляй инициативу. Если учитель работает
Подробнее
Технологическая карта урока
Технологическая карта урока ФИО Попенкова Татьяна Сергеевна КЛАСС 3 УМК «Начальная школа XXI век» ПРЕДМЕТ Математика ТЕМА Умножение многозначного числа на двузначное. ТИП Урок открытия нового знания. ЦЕЛЬ
Подробнее
Урок математики в 1 «А» классе??????
Урок математики в 1 «А» классе?????? Художник Тюбик решил нарисовать портреты малышей. Для этого он купил несколько баночек с синей и жёлтой краской. Тюбик купил баночек с синей краской и с желтой. Сколько
Подробнее
Урок математики в 3 «б» классе
Урок математики в 3 «б» классе Тема: Переменная. Запись выражений и предложений с помощью переменной Цели: 1. Дать понятие о переменной, как букве, обозначающей меняющиеся (переменные) значения элементов
Подробнее
y 12 = 2y 7,5 y 2y = 12 7,5 -y = 4,5 y = — 4,5
Муниципальное бюджетное общеобразовательное учреждениесредняя общеобразовательная школа 7г. Белгорода Разработка урока по теме «Решение уравнений» (6 класс) Подготовила учитель математики Гриценко Т.Г.
Подробнее
Решение уравнений. Составление равенств, неравенств
Математика
Дата «___»_______ ____ г Класс 3- «Б»
(1 четверть)
Урок 7
Тема урока: Решение уравнений. Составление равенств, неравенств
Цель: Повторить изученный материал и выявить индивидуальные затруднения, провести коррекцию умения составлять, читать выражения, равенства, неравенства, решать уравнения.
Задачи урока:
1. уточнить знания учащихся об уравнениях, равенствах и неравенствах; совершенствовать умение ре¬шать уравнения на основе знаний о взаимосвязи компонен¬тов действий сложения и вычитания.
2. Закреплять мышление, речь, внимание.
3. Воспитывать познавательную активность, умение работать в коллективе, умение оценивать себя и одноклассников
Тип урока: Ознакомительное занятие
Этапы и структура урока.
1. Организационный момент. Эмоциональный настрой. Мотивация.
Громко прозвенел звонок,
Начинается урок.
Наши ушки на макушке,
Глазки широко открыты,
Слушаем, запоминаем,
Ни минуты не теряем!
2. Актуализация знаний
Для организации устного счета предназначено упражнение.
Или №4 стр. 12
4*8 36:4
7*4 27:9
9*4 20:4
3. Постановка проблемы
— На какие три группы можно разделить записанные на до¬ске выражения?
274 4- х = 594 320 + 40 = 470 — 110 415 = 400 + 15
200 + 3 = 3 + 200 35 — 15 < 15 + 6 17 > 872 — 864
524 — х = 244 22 > 87 — 67 47 < 15 + 37
х — 251 = 522
— Чем отличаются уравнения от равенств, неравенств?
4. Решение уравнений
По заданию №1 учащиеся составляют уравнения и решают их. Можно предложить для решения у доски. Остальные уравнения учащиеся составляют и решают само-стоятельно.
5. Первичное закрепление
Для повторения знаний о равенствах и неравенствах предна¬значено упражнение №4. Это упражнение можно выполнить по времени.
Упражнения №3 и №5 выполняются под руководством учи¬теля. И
№3
54 + 4 > 54 — 5
35 — 15 < 8 + 16
87 + 13 = 13 + 87
45 + 45 < 45 + 54
56 — 42 < 56 — 24
31 + 8 < 31 + 80
100 — 20 > 100 — 23
250 — 30 = 210 + 10
900 — 750 = 80 + 70
Задание №2
78 + х = 125 + 68
78 + x = 193
x = 193 – 78
x = 115
а — 750 = 1000 – 920
a – 750 = 80
a = 750 + 80
a = 830
952 — b = 120 + 325
952 – b = 445
b = 952 – 445
b = 507
Динамическая пауза
6. Самостоятельная работа.
Для самостоятельной работы предназначена задача №5(а). Учитель предлагает детям записать решение задачи по действи¬ям и выражениям. Задачу №5 (б) учащиеся решают самостоя¬тельно с последующей проверкой.
1) 245 + 55 = 300 (б) – на вечерний спектакль
2) 245 + 300 = 545 (б)
1) 210 + 120 = 330 (б) – продали
2) 560 – 330 = 230 (б) – осталось.
Динамическая пауза.
Задание №6 является подготовительным к знакомству с те¬мой «Умножение и деление». Желательно выполнить рисунок, иллюстрирующий условие задачи.
7. Повторение
Что такое уравнение?
Логическое задание №7
8. Рефлексия
Учитель предлагает проанализировать урок тем детям, кто был пассивным на уроке, по следующему плану:
1. Тема урока.
2. Какие упражнения помогли повторить тему?
3. Кто из ребят был активным и правильно отвечал?
4. Кто из ребят мешал проведению урока?
5. Кто затруднялся в ответах?
Д\З стр.12 №4Тема урока: Решение уравнений. Составление равенств, неравенств
Цель: Повторить изученный материал и выявить индивидуальные затруднения, провести коррекцию умения составлять, читать выражения, равенства, неравенства, решать уравнения.
Скачать файл
Устранение неравенств — объяснения и примеры
Что такое неравенство в математике?
Слово неравенство означает математическое выражение, в котором стороны не равны друг другу. По сути, неравенство сравнивает любые два значения и показывает, что одно значение меньше, больше или равно значению на другой стороне уравнения.
Как правило, для представления уравнений неравенства используются пять символов неравенства.
Символы неравенства
Эти символы неравенства: меньше ( <), больше (> ), меньше или равно ( ≤ ), больше или равно ( ≥ ) и символ неравенства ( ≠ ) .
Неравенства используются для сравнения чисел и определения диапазона или диапазонов значений, которые удовлетворяют условиям данной переменной.
Операции с неравенствами
Операции с линейными неравенствами включают сложение, вычитание, умножение и деление. Общие правила этих операций показаны ниже.
Хотя мы использовали символ <для иллюстрации, следует отметить, что те же правила применяются к>, ≤ и ≥.
- Символ неравенства не меняется при добавлении одного и того же числа к обеим сторонам неравенства.Например, если a
- Вычитание обеих частей неравенства на одно и то же число не меняет знака неравенства. Например, если a
- Умножение обеих сторон неравенства на положительное число не меняет знака неравенства. Например, если a
- Разделение обеих сторон неравенства на положительное число не меняет знака неравенства. Если a
- Умножение обеих сторон уравнения неравенства на отрицательное число изменяет направление символа неравенства.Например, если a b *
- Аналогичным образом, разделение обеих сторон уравнения неравенства на отрицательное число изменяет символ неравенства. Если a b / c
- Вычитание обеих частей неравенства на одно и то же число не меняет знака неравенства. Например, если a
Как решить неравенства?
Подобно линейным уравнениям, неравенства можно решить, применяя аналогичные правила и шаги за некоторыми исключениями. Единственная разница при решении линейных уравнений — это операция умножения или деления на отрицательное число.Умножение или деление неравенства на отрицательное число изменяет символ неравенства.
Линейные неравенства могут быть решены с помощью следующих операций:
- Сложение
- Вычитание
- Умножение
- Деление
- Распределение собственности
Решение линейных неравенств с добавлением
Давайте посмотрим на несколько примеров ниже, чтобы понять это понятие.
Пример 1
Решите 3x — 5 ≤ 3 — x.
Решение
Начнем с добавления обеих сторон неравенства на 5
3x — 5 + 5 ≤ 3 + 5 — x
3x ≤ 8 — x
Затем сложим обе стороны на x.
3x + x ≤ 8 — x + x
4x ≤ 8
Наконец, разделите обе части неравенства на 4, чтобы получить;
x ≤ 2
Пример 2
Вычислите диапазон значений y, который удовлетворяет неравенству: y — 4 <2y + 5.
Решение
Сложите обе части неравенства на 4.
y — 4 + 4 <2y + 5 + 4
y <2y + 9
Вычтите обе стороны на 2y.
y — 2y <2y - 2y + 9
Y <9 Умножьте обе части неравенства на -1 и измените направление символа неравенства. y> — 9
Решение линейных неравенств с вычитанием
Давайте рассмотрим несколько примеров ниже, чтобы понять эту концепцию.
Пример 3
Решите x + 8> 5.
Решение
Изолируйте переменную x, вычтя 8 из обеих сторон неравенства.
x + 8-8> 5-8 => x> −3
Следовательно, x> −3.
Пример 4
Решите 5x + 10> 3x + 24.
Решение
Вычтите 10 из обеих сторон неравенства.
5x + 10-10> 3x + 24-10
5x> 3x + 14.
Теперь вычтем обе части неравенства на 3x.
5x — 3x> 3x — 3x + 14
2x> 14
x> 7
Решение линейных неравенств с умножением
Давайте рассмотрим несколько примеров ниже, чтобы понять эту концепцию.
Пример 5
Решить x / 4> 5
Решение:
Умножить обе стороны неравенства на знаменатель дроби
4 (x / 4)> 5 x 4
x> 20
Пример 6
Решите -x / 4 ≥ 10
Решение:
Умножьте обе стороны неравенства на 4.
4 (-x / 4) ≥ 10 x 4
-x ≥ 40
Умножьте обе стороны неравенства на -1 и измените направление символа неравенства на противоположное.
x ≤ — 40
Решение линейных неравенств с делением
Давайте рассмотрим несколько примеров ниже, чтобы понять эту концепцию.
Пример 7
Решите неравенство: 8x — 2> 0.
Решение
Прежде всего, сложите обе стороны неравенства на 2
8x — 2 + 2> 0 + 2
8x> 2
Теперь решите, разделив обе части неравенства на 8, чтобы получить;
x> 2/8
x> 1/4
Пример 8
Решите следующее неравенство:
−5x> 100
Решение
Разделите оба сторон неравенства на -5 и измените направление символа неравенства
= −5x / -5 <100 / -5
= x <- 20
Решение линейных неравенств с использованием свойства распределения
Давайте посмотрим на несколько примеров ниже, чтобы понять эту концепцию.
Пример 9
Решить: 2 (x — 4) ≥ 3x — 5
Решение
2 (x — 4) ≥ 3x — 5
Примените свойство распределения, чтобы удалить скобки.
⟹ 2x — 8 ≥ 3x — 5
Сложить обе стороны на 8.
⟹ 2x — 8 + 8 ≥ 3x — 5 + 8
⟹ 2x ≥ 3x + 3
Вычесть обе стороны на 3.
⟹ 2x — 3x ≥ 3x + 3 — 3x
⟹ -x ≥ 3
⟹ x ≤ — 3
Пример 10
Студент набрал 60 баллов за первый тест и 45 баллов во втором тесте заключительного экзамена.Сколько минимальных баллов должен набрать ученик в третьем тесте, получив в среднем не менее 62 баллов?
Решение
Пусть в третьем тесте будет набрано x баллов.
(60 + 45 + x) / 3 ≥ 62
105 + x ≥ 196
x ≥ 93
Следовательно, учащийся должен набрать 93 балла, чтобы поддерживать среднее значение не менее 62 баллов.
Пример 11
Джастину требуется не менее 500 долларов для празднования своего дня рождения.Если он уже накопил 150 долларов, до этой даты осталось 7 месяцев. Какую минимальную сумму он должен откладывать ежемесячно?
Решение
Пусть минимальная ежемесячная экономия = x
150 + 7x ≥ 500
Решить для x
150-150 + 7x ≥ 500-150
x ≥ 50
Следовательно, Джастин должен экономить 50 долларов и более
Пример 12
Найдите два последовательных нечетных числа, которые больше 10 и имеют сумму меньше 40.
Решение
Пусть меньшее нечетное число = x
Следовательно, следующее число будет x + 2
x> 10 ………. больше 10
x + (x + 2) <40 …… сумма меньше 40
Решите уравнения.
2x + 2 <40
x + 1 <20
x <19
Объедините два выражения.
10 Следовательно, последовательные нечетные числа — 11 и 13, 13 и 15, 15 и 17, 17 и 19. Лучшим инструментом для представления и визуализации чисел является числовая линия. Числовая линия определяется как прямая горизонтальная линия с числами, расположенными на равных отрезках или интервалах. У числовой прямой есть нейтральная точка в середине, известная как начало координат. Справа от начала координат на числовой прямой находятся положительные числа, а слева от начала координат — отрицательные числа. Линейные уравнения также можно решить графическим методом с использованием числовой прямой.Например, чтобы построить x> 1 на числовой прямой, вы обведите цифру 1 на числовой прямой и проведете линию, идущую от круга в направлении чисел, удовлетворяющих условию неравенства. Пример 13 Если символ неравенства больше или равен или меньше или равен знаку (≥ или ≤), нарисуйте круг над числовым числом и заполните или заштрихуйте круг.Наконец, проведите линию, идущую от заштрихованного круга в направлении чисел, которая удовлетворяет уравнению неравенства. Пример 14 x ≥ 1 Неравенства и числовая линия
Та же процедура используется для решения уравнений, включающих интервалы.
Пример 15
–2 < x <2
Пример 16
–1 ≤ x ≤ 2
047
Пример 17
–1 < x ≤ 2
Практические вопросы
Решите следующие неравенства и представьте свой ответ в числовой строке.
- 2x> 9
- x + 5> 13
- −3x <4
- 7x + 11> 2x + 5
- 2 (x + 3)
- — 5 ≤ 2x — 7 ≤ 1
- 4x — 8 ≤ 12
Ответы
- x> 9/2
- x> 8
- x> −4/3
- x> −6/5
- x <−5.
- 1 ≤ x ≤ 4.
- x ≤ 5
Предыдущий урок | Главная страница | Следующий урок
Устранение неравенств
Иногда нам нужно решить такие неравенства:
Обозначение | слов | Пример |
|---|---|---|
| > | больше | х + 3 > 2 |
| < | менее | 7x < 28 |
| ≥ | больше или равно | 5 ≥ x — 1 |
| ≤ | меньше или равно | 2 года + 1 ≤ 7 |
Решение
Наша цель — иметь x (или другую переменную) самостоятельно слева от знака неравенства:
| Примерно так: | х <5 | |
| или: | лет ≥ 11 |
Мы называем это «решенным».
Пример: x + 2> 12
Вычтем 2 с обеих сторон:
х + 2 — 2> 12 — 2
Упростить:
x> 10
Решено!
Как решить
Решение неравенств очень похоже на решение уравнений … мы делаем почти то же самое …
… но мы также должны обратить внимание на направление неравенства .
Направление: куда «указывает» стрелка
Некоторые вещи могут изменить направление !
<становится>
> становится <
≤ становится ≥
≥ становится ≤
Безопасные дела
Эти вещи не влияют на направление неравенства:
- Сложить (или вычесть) число с обеих сторон
- Умножьте (или разделите) обе стороны на положительное число
- Упростить сторону
Пример: 3x
<7 + 3
Мы можем упростить 7 + 3, не влияя на неравенство:
3x <10
Но эти вещи действительно изменяют направление неравенства (например, «<" становится ">«):
Пример: 2y + 7
<12
Когда мы меняем местами левую и правую части, мы также должны изменить направление неравенства :
12 > 2 года + 7
Вот подробности:
Сложение или вычитание значения
Часто мы можем решить неравенства, добавляя (или вычитая) число с обеих сторон (точно так же, как во Введении в алгебру), например:
Пример: x + 3
<7
Если вычесть 3 с обеих сторон, получим:
х + 3 — 3 <7 — 3
х <4
И вот наше решение: x <4
Другими словами, x может быть любым значением меньше 4.
Что мы сделали?
Мы пошли от этого: Кому: | х + 3 <7 х <4 | |||
И это хорошо работает для , прибавляя и вычитая , потому что, если мы прибавляем (или вычитаем) одинаковую сумму с обеих сторон, это не влияет на неравенство
Пример: У Алекса больше монет, чем у Билли.Если и Алекс, и Билли получат по три монеты больше, у Алекс все равно будет больше монет, чем у Билли.
Что, если я решу, но «x» справа?
Неважно, просто поменяйте местами стороны, но поменяет знак на противоположное, чтобы он все еще «указывал» на правильное значение!
Пример: 12
Если вычесть 5 с обеих сторон, получим: 12 -5 7 <х Вот и решение! Но ставить «x» слева — это нормально… … так давайте обратим внимание (и знак неравенства!): x> 7 Вы видите, как знак неравенства все еще «указывает» на меньшее значение (7)? И вот наше решение: x> 7 Примечание: «x» может быть справа, но людям обычно нравится видеть его слева. Также мы умножаем или делим обе части на значение (как в алгебре — умножение). Но нам нужно быть немного осторожнее (как вы увидите). Положительные значения Все нормально, если мы хотим умножить или разделить на положительное число : <15 Если мы разделим обе стороны на 3, получим: 3 года /3 <15 /3 г <5 И вот наше решение: y <5 Отрицательные значения Почему? Ну, посмотрите на числовую строку! Например, от 3 до 7 это увеличение , Видите, как меняет знак неравенства (с <на>)? Давайте попробуем пример: <−8 Разделим обе части на −2… и отменяют неравенство ! −2y <−8 −2y / −2 > −8 / −2 г> 4 И это правильное решение: y> 4 (Обратите внимание, что я перевернул неравенство в той же строке , которую я разделил на отрицательное число.) Итак, запомните: При умножении или делении на отрицательное число отменяет неравенство Вот еще один (хитрый!) Пример: <3b Кажется легко просто разделить обе стороны на b , что дает нам: x <3 … но подождите … если b является отрицательным , нам нужно изменить неравенство следующим образом: x> 3 Но мы не знаем, положительное или отрицательное значение b, поэтому мы не можем ответить на этот вопрос ! Чтобы помочь вам понять, представьте, что замените b на 1 или −1 в примере bx <3b : Ответ может быть x <3 или x> 3 , и мы не можем выбрать, потому что не знаем b . Так: Не пытайтесь делить на переменную, чтобы решить неравенство (если вы не знаете, что переменная всегда положительна или всегда отрицательна). x − 3 2 <−5 Во-первых, давайте очистим «/ 2», умножив обе стороны на 2. Поскольку мы умножаем на положительное число, неравенства не изменятся. x − 3 2 × 2 <−5 × 2 х − 3 <−10 Теперь прибавьте 3 к обеим сторонам: х − 3 + 3 <−10 + 3 х <−7 И вот наше решение: x <−7 Как решить задачу сразу с двумя неравенствами? Умножение или деление на значение
Пример: 3y
Когда мы умножаем или делим на отрицательное число
, мы должны отменить неравенство.
, но от -3 до -7 это уменьшение. −7 <−3 7> 3 Пример: −2y
Умножение или деление на переменные
Пример: bx
Пример побольше
Пример:
Два неравенства сразу!
Пример:
−2 < 6−2x 3 <4
Во-первых, давайте очистим «/ 3», умножив каждую часть на 3.
Поскольку мы умножаем на положительное число, неравенства не меняются:
−6 <6−2x <12
Теперь вычтите 6 из каждой части:
−12 <−2x <6
Теперь разделите каждую часть на 2 (положительное число, чтобы неравенства снова не изменились):
−6 <−x <3
Теперь умножьте каждую часть на -1. Поскольку мы умножаем на отрицательное число , неравенства меняют направление .
6> х> −3
И это решение!
Но для наглядности лучше иметь меньшее число слева, большее — справа. Так что давайте поменяем их местами (и убедимся, что неравенства указывают правильно):
−3 <х <6
Сводка
- Многие простые неравенства могут быть решены путем сложения, вычитания, умножения или деления обеих сторон, пока не останется переменная сама по себе.
- Но эти вещи изменят направление неравенства:
- Умножение или деление обеих сторон на отрицательное число
- Замена левой и правой сторон
- Не умножайте и не делите на переменную (если вы не знаете, что она всегда положительна или всегда отрицательна)
Графические системы линейных неравенств
Чтобы построить линейный
неравенство
в двух переменных (скажем,
Икс
а также
у
), сначала получите
у
один на одной стороне.Затем рассмотрим соответствующее уравнение, полученное заменой знака неравенства на знак равенства. График этого уравнения представляет собой линию.
Если неравенство строгое (
< или же >
), начертите штриховой линией. Если неравенство не строгое
(
≤
или же
≥
), начертите сплошной линией.
Наконец, выберите одну точку, которая не находится ни на одной строке (
(
0
,
0
)
обычно самый простой) и решите, удовлетворяют ли эти координаты неравенству или нет.Если это так, заштрихуйте полуплоскость, содержащую эту точку. Если нет, закройте другую полуплоскость.
Аналогичным образом изобразите каждое из неравенств в системе. Решение
система неравенства
— область пересечения всех решений в системе.
Пример 1:
Решите систему неравенств, построив графики:
у
≤
Икс
—
2
у
>
—
3
Икс
+
5
Сначала изобразим неравенство
у
≤
Икс
—
2
.Связанное уравнение
у
знак равно
Икс
—
2
.
Поскольку неравенство
≤
, не строгий, граница сплошная.
Постройте прямую линию.
Рассмотрим точку, которая не находится на линии — скажем,
(
0
,
0
)
— и подставляем в неравенство
у
≤
Икс
—
2
.
0
≤
0
—
2
0
≤
—
2
Это неправда.Итак, решение не содержит точки
(
0
,
0
)
. Заштрихуйте нижнюю половину линии.
Аналогичным образом нарисуйте пунктирную линию для соответствующего уравнения второго неравенства
у
>
—
3
Икс
+
5
которое имеет строгое неравенство. Точка
(
0
,
0
)
не удовлетворяет неравенству, поэтому заштрихуйте половину, не содержащую точки
(
0
,
0
)
.
Решение системы неравенств — это область пересечения решений двух неравенств.
Пример 2:
Решите систему неравенств, построив графики:
2
Икс
+
3
у
≥
12
8
Икс
—
4
у
>
1
Икс
< 4
Перепишем первые два неравенства с
у
один на одной стороне.
3
у
≥
—
2
Икс
+
12
у
≥
—
2
3
Икс
+
4
—
4
у
>
—
8
Икс
+
1
у
< 2 Икс - 1 4
Теперь изобразим неравенство
у
≥
—
2
3
Икс
+
4
.Связанное уравнение
у
знак равно
—
2
3
Икс
+
4
.
Поскольку неравенство
≥
, не строгий, граница сплошная.
Постройте прямую линию.
Рассмотрим точку, которая не находится на линии — скажем,
(
0
,
0
)
— и подставляем в неравенство.
0
≥
—
2
3
(
0
)
+
4
0
≥
4
Это неправда.Итак, решение не содержит точки
(
0
,
0
)
. Заштрихуйте верхнюю половину линии.
Аналогичным образом проведем пунктирную линию соответствующего уравнения второго неравенства
у
< 2 Икс - 1 4 которое имеет строгое неравенство. Точка ( 0 , 0 ) не удовлетворяет неравенству, поэтому заштрихуйте половину, не содержащую точки ( 0 , 0 ) .
Нарисуйте пунктирную вертикальную линию
Икс
знак равно
4
которое является родственным уравнением третьего неравенства.
Здесь точка
(
0
,
0
)
удовлетворяет неравенству, поэтому заштрихуйте половину, содержащую точку.
Решение системы неравенств — это область пересечения решений трех неравенств.
Решение линейных неравенств (алгебра 1, линейные неравенства) — Mathplanet
График линейного неравенства по одной переменной представляет собой числовую прямую.Используйте открытый кружок для <и> и замкнутый кружок для ≤ и ≥.
График для x> -3
График для x ≥ 2
Неравенства, имеющие одно и то же решение, называются эквивалентными. Есть свойства неравенств, а также свойства равенства. Все перечисленные ниже свойства верны и для неравенств, содержащих ≥ и ≤.
Свойство сложения неравенства гласит, что добавление одного и того же числа к каждой стороне неравенства дает эквивалентное неравенство
$$ Если \: x> y, \: то \: x + z> y + z $$
$$ Если \: x Свойство неравенства вычитания говорит нам, что вычитание одного и того же числа из обеих частей неравенства дает эквивалентное неравенство. $$ Если \: x> y, \: то \: x-z> y-z $$ $$ Если \: x Свойство неравенства умножения говорит нам, что умножение обеих сторон неравенства на положительное число дает эквивалентное неравенство. $$ Если \: x> y \: и \: z> 0, \: то \: xz> yz $$ $$ Если \: x С другой стороны, умножение каждой стороны неравенства на отрицательное число не приводит к эквивалентному неравенству, если мы также не изменим направление символа неравенства $$ Если \: x> y \: и \: z <0, \: то \: xz $$ Если \: x То же самое и со свойством деления неравенства. Деление обеих частей неравенства на положительное число дает эквивалентное неравенство. $$ Если \: x> y \: и \: z> 0, \: то \: \ frac {x} {z}> \ frac {y} {z} $$ $$ Если \: x И деление на обе стороны неравенства с отрицательным числом дает эквивалентное неравенство, если знак неравенства перевернут. $$ Если \: x> y \: и \: z <0, \: then \: \ frac {x} {z} <\ frac {y} {z} $$ $$ Если \: x Чтобы решить многоступенчатое неравенство, вы делаете то же самое, что и при решении многоступенчатых уравнений.Возьмите что-то одно, желательно начать с изоляции переменной от констант. При решении многоступенчатых неравенств важно не забывать обращать знак неравенства при умножении или делении на отрицательные числа. Пример Решите неравенство $$ — 2 \ влево (x + 3 \ вправо) <10 $$ $$ — 2x-6 <10 $$ $$ — 2x-6 \, {\ color {green} {+ \, 6} <10 \,} {\ color {green} {+ \, 6}} $$ $$ — 2x <16 $$ $$ \ frac {-2x} {{\ color {green} {-2}}} \: {\ color {blue} {>}} \: \ frac {16} {{\ color {green} {- 2}}} $$ $$ x> -8 $$ Видеоурок Решите линейное неравенство $$ -2 \ влево (x + 2 \ вправо)> 4 — x $$ В этом видео мы научимся решать линейные неравенства.После того, как вы закончите этот урок, просмотрите все наши уроки Алгебры 1 и попрактикуйтесь. Например: Сначала разделим неравенства: Сначала разделим неравенства: Узнайте, как решать неравенства и построить график на числовой прямой
Пример 1
Пример 2
5x + 3 \ leq18
Сначала вычтите 3 с обеих сторон
5x + 3-3 \ leq18-3
5x \ leq15
Затем разделите 5 с обеих сторон, чтобы выделить x
\ dfrac {5x} {5} \ leq \ dfrac {15} {5}
x \ leq 3
Стенограмма видеоурока
В этом уроке мы рассмотрим решение линейных неравенств.
Это очень похоже на решение линейных уравнений, за исключением одного:
Если мы умножаем или делим на отрицательное число, мы должны перевернуть знак неравенства.
Значит, такой знак можно перевернуть в другую сторону и стать этим.
Давайте посмотрим на пример:
Итак, давайте просто будем рассматривать знак неравенства как обычный знак равенства при решении.
Во-первых, добавим с обеих сторон.
Отсюда мы должны разделить на, чтобы изолировать.
И в итоге получаем
Это наш ответ.
Итак, если нам нужно построить график, давайте нарисуем числовую линию и нарисуем открытый круг в точке. Открытый круг, потому что не равен. Затем сделайте стрелку, идущую влево.
Далее у нас
Опять же, при решении мы будем рассматривать его как обычное уравнение.
Первое, что нам нужно сделать, это избавиться от него, поэтому мы вычитаем с обеих сторон.
Тогда давайте решим делением на.
И поскольку мы делим на, мы должны обратить знак неравенства.
Наш ответ:
Помните, когда мы делим на отрицательное число, нам всегда приходится менять знак.
Не имеет значения, положительный или отрицательный дивиденд. Все, что нас волнует, — это когда делитель отрицательный, это время, когда мы меняем знак.
Если мы построим график ответа, давайте проведем числовую линию.
Нарисуйте открытый круг под номером. Это не закрашенный кружок, потому что он не равен.
Поскольку больше, проведите линию вправо.
Опять же, решение неравенств очень похоже на решение обычных уравнений, за исключением того, что если мы умножаем или делим на отрицательное число, мы должны менять знак.
Еще одно отличие состоит в том, что у нас не будет явного ответа или явного решения для. Это будет диапазон чисел.
У нас не будет равно числу.
Наш ответ: любое число меньше или больше числа. Вплоть до бесконечности.
Здесь более сложное неравенство.
У нас два разных условия.
и
Мы должны разделить это на два разных неравенства.
и
Давайте сначала решим неравенство слева.
Добавим с обеих сторон.
Затем решите, разделив на.
Теперь решим другое неравенство.
Начнем с добавления с обеих сторон.
Затем решите для, разделив обе части на.
Давайте нарисуем числовую линию, чтобы обозначить эти два неравенства, начиная с и заканчивая.
Для, мы должны нарисовать открытый круг под номером. Открытый круг, потому что он не равен. А так как оно больше чем, проведите линию вправо.
А теперь давайте нарисуем заштрихованный кружок в точке, поскольку он также равен ей. Затем проведите линию, идущую влево.
Далее проведите линию к другому кругу.
Теперь этот отрезок представляет наше решение.
Наш ответ также можно записать как:
Обратите внимание, что две конечные точки также являются конечными числами — и.
И находится где-то между этими двумя числами, но также может быть равным.
Возьмем еще одно сложное неравенство.
Разобьем это на два простых неравенства.
и
Давайте поработаем над первым неравенством, сложив с обеих сторон.
Для решения разделите обе стороны на.
Теперь решим другое неравенство.
Начнем с добавления с обеих сторон.
Чтобы найти, разделим обе стороны на.
Итак, теперь мы изобразим это, нарисовав числовую линию.
Нарисуйте открытый круг в, поскольку он не равен. Затем проведите линию вправо, поскольку больше чем.
Затем нарисуйте заштрихованный круг в точке, равной ей. Затем проведите линию влево, поскольку меньше чем.
Две стрелки указывают в разных направлениях.
Теперь мы можем записать наше решение как
или
не сможет удовлетворить оба, поэтому мы пишем «или».
Решение линейных неравенств | Уравнения и неравенства
4.7 Решение линейных неравенств (EMA3H)
Линейное неравенство похоже на линейное уравнение в том, что наибольший показатель степени переменной равен \ (\ text {1} \). Ниже приведены примеры линейных неравенств.
\ begin {align *}
2x + 2 & \ le 1 \\
\ frac {2 — x} {3x + 1} & \ ge 2 \\
\ frac {4} {3} x — 6 & <7x + 2
\ end {выровнять *}
Методы, используемые для решения линейных неравенств, аналогичны тем, которые используются для решения линейных уравнений.Единственная разница возникает при умножении или делении со знаком минус. Например, мы знаем, что \ (8> 6 \). Если обе части неравенства разделить на \ (- \ text {2} \), то мы получим \ (- 4> -3 \), что неверно. Следовательно, знак неравенства нужно поменять местами, давая \ (- 4 <-3 \).
Чтобы сравнить неравенство с нормальным уравнением, мы сначала решим уравнение.
Решить \ (2x + 2 = 1 \):
\ begin {align *}
2х + 2 & = 1 \\
2x & = 1-2 \\
2x & = -1 \\
х & = — \ frac {1} {2}
\ end {выровнять *}
Если представить этот ответ в числовой строке, получим:
Теперь решим относительно \ (x \) в неравенстве \ (2x + 2 \ le 1 \):
\ begin {align *}
2x + 2 & \ le 1 \\
2x & \ le 1 — 2 \\
2x & \ le -1 \\
х & \ le — \ frac {1} {2}
\ end {выровнять *}
Если представить этот ответ в числовой строке, получим:
Мы видим, что для уравнения существует только одно значение \ (x \), для которого уравнение верно.Однако для неравенства существует диапазон значений, для которых неравенство верно. В этом главное отличие уравнения от неравенства.
Помните: , когда мы делим или умножаем обе стороны неравенства на отрицательное число, направление неравенства меняется. Например, если \ (x <1 \), то \ (- x> -1 \). Также обратите внимание, что мы не можем делить или умножать на переменную.
Следующее видео знакомит с линейными неравенствами.
Видео: 2FGH
Обозначение интервалов (EMA3J)
Примеры:
\ (\ left (4; 12 \ right) \) | Круглые скобки указывают на то, что номер не включен. Этот интервал включает все действительные числа, большие, но не равные \ (\ text {4} \) и меньшие, но не равные \ (\ text {12} \). |
\ (\ left (- \ infty; -1 \ right) \) | Круглые скобки всегда используются для положительной и отрицательной бесконечности.Этот интервал включает все действительные числа, меньшие, но не равные \ (- \ text {1} \). |
\ (\ left [1; 13 \ right) \) | Квадратная скобка означает, что номер включен. Этот интервал включает все действительные числа, большие или равные \ (\ text {1} \) и меньшие, но не равные \ (\ text {13} \). |
Важно отметить, что это обозначение может использоваться только для представления интервала действительных чисел.
Мы представляем приведенный выше ответ в обозначении интервалов как \ (\ left (- \ infty; — \ frac {1} {2} \ right] \)
Рабочий пример 17: Решение линейных неравенств
Решить относительно \ (r \):
\ [6 — r> 2 \]
Представьте ответ в числовой строке и в виде интервалов.
Переставьте и решите для \ (r \)
\ begin {align *}
-r &> 2-6 \\
-r &> -4
\ end {align *}
Умножить на \ (- \ text {1} \) и отменить знак неравенства
\ [г <4 \]
Изобразите ответ на числовой строке
Представьте ответ в виде интервалов
\ [\ влево (- \ infty; 4 \ вправо) \]
Рабочий пример 18: Решение линейных неравенств
Решите относительно \ (q \):
\ [4q + 3
Представьте ответ в числовой строке и в интервальной записи.
Раскладной кронштейн
\ begin {align *}
4q + 3 & <2 (q + 3) \\
4q + 3 & <2q + 6
\ end {align *}
Переставьте и решите для \ (q \)
\ begin {align *}
4q + 3 & <2q + 6 \\
4q - 2q & <6 - 3 \\
2q & <3
\ end {align *}
Разделите обе стороны на \ (\ text {2} \)
\ begin {align *}
2q & <3 \\
q & <\ frac {3} {2}
\ end {align *}
Представьте ответ в числовой строке
Представьте ответ в виде интервалов
\ (\ left (- \ infty; \ frac {3} {2} \ right) \)
Рабочий пример 19: Решение сложных линейных неравенств
Решить относительно \ (x \):
\ [5 \ le x + 3
Представьте ответ в числовой строке и в интервальной записи.
Вычтем \ (\ text {3} \) из всех частей неравенства
\ [\ begin {array} {ccccc}
5 — 3 & \ le & x + 3 — 3 & <& 8 - 3 \\
2 & \ le & x & <& 5
\ конец {массив} \]
Изобразите ответ на числовой строке
Представьте ответ в виде интервалов
\ (\ left [2; 5 \ right) \)
Зарегистрируйтесь, чтобы получить стипендию и возможности карьерного роста.Используйте практику Сиявулы, чтобы получить наилучшие возможные оценки.
Зарегистрируйтесь, чтобы разблокировать свое будущее
Упражнение 4.6
\ (x <-1 \ text {и} x \ ge 6; x \ in \ mathbb {R} \)
\ (3 <х <6; х \ в \ mathbb {R} \)
\ (x \ neq 3; x \ neq 6; x \ in \ mathbb {R} \)
\ (х> -10; х \ в \ mathbb {R} \)
\ begin {align *}
3х + 4 &> 5х + 8 \\
3х — 5х &> 8 — 4 \\
-2x> 4 \\
2x
Обозначается в числовой строке:
В интервальном обозначении: \ ((- \ infty; -2) \)
\ (3 (x — 1) — 2 \ le 6x + 4 \)
\ begin {align *}
3 (x — 1) — 2 & \ le 6x + 4 \\
3x — 5 & \ le 6x + 4 \\
3х — 6х & \ ле 4 + 5 \\
-3x \ le 9 \\
х \ ge — \ frac {9} {3} \\
х \ ge -3
\ end {выровнять *}
Обозначается в числовой строке:
В интервальном обозначении: \ ([- 3; \ infty) \)
\ (\ dfrac {x — 7} {3}> \ dfrac {2x — 3} {2} \)
\ begin {align *}
\ frac {x — 7} {3} &> \ frac {2x — 3} {2} \\
2 (х — 7) &> 3 (2x — 3) \\
2х — 14> 6х — 9 \\
-4x> 5 \\
x
Обозначается в числовой строке:
В интервальном обозначении: \ ((- \ infty; — \ frac {5} {4}) \)
\ begin {align *}
-4 (x — 1) & \ frac {2} {5}
\ end {выровнять *}
Обозначается в числовой строке:
В интервальном обозначении: \ ((\ frac {2} {5}; \ infty) \)
\ (\ dfrac {1} {2} x + \ dfrac {1} {3} (x — 1) \ ge \ dfrac {5} {6} x — \ dfrac {1} {3} \)
\ begin {align *}
\ frac {1} {2} x + \ frac {1} {3} (x — 1) & \ ge \ frac {5} {6} x — \ frac {1} {3} \\
\ frac {1} {2} x + \ frac {1} {3} x — \ frac {1} {3} & \ ge \ frac {5} {6} x — \ frac {1} {3} \ \
\ frac {1} {2} x + \ frac {1} {3} x — \ frac {5} {6} x & \ ge \ frac {1} {3} — \ frac {1} {3} \ \
\ frac {3} {6} x + \ frac {2} {6} x — \ frac {5} {6} x & \ ge 0 \\
0x \ ge 0
\ end {выровнять *}
Неравенство верно для всех действительных значений \ (x \).
\ [\ begin {array} {ccccc}
-2 & \ le & x — 1 &
Обозначается числовой строкой:
В интервальном обозначении: \ ([- 1; 4) \)
\ [\ begin {array} {ccccc}
-5 и
Обозначается в числовой строке:
В интервальном обозначении: \ ((- 1; 5] \)
\ (7 (3x + 2) — 5 (2x — 3)> 7 \)
\ begin {align *}
7 (3x + 2) — 5 (2x — 3) &> 7 \\
21х + 14 — 10х + 15 &> 7 \\
11x &> -22 \\
х &> -2
\ end {выровнять *}
Обозначается в числовой строке:
В интервальном обозначении: \ ((- 2; \ infty) \)
\ (\ dfrac {5x — 1} {- 6} \ ge \ dfrac {1 — 2x} {3} \)
\ begin {align *}
\ frac {5x — 1} {- 6} & \ ge \ frac {1 — 2x} {3} \\
5x — 1 & \ ge -2 (1-2x) \\
5x — 1 & \ ge -2 + 4x \\
5x — 4x & \ ge -1 \\
х & \ ge -1
\ end {выровнять *}
Обозначается в числовой строке:
В интервальном обозначении: \ ([- 1; \ infty) \)
\ [\ begin {array} {ccccc}
3 & \ le & 4 — х & \ le & 16 \\
-1 & \ le & -x & \ le & 12 \\
1 & \ ge & x & \ ge & -12
\ конец {массив} \]
Обозначается в числовой строке:
В интервальном обозначении: \ ([1; 12] \)
\ (\ dfrac {-7y} {3} — 5> -7 \)
\ begin {align *}
\ frac {-7y} {3} — 5 &> -7 \\
-7л — 15 &> -21 \\
-7лет &> -6 \\
y &
Обозначается в числовой строке:
В интервальном обозначении: \ ((- \ infty; \ frac {6} {7}) \)
\ [\ begin {array} {ccccc}
1 & \ le & 1-2y & & -4 \\
-4 и
Обозначается в числовой строке:
В интервальном обозначении: \ ((- 4; 0] \)
\ (- 2 <\ dfrac {x - 1} {- 3} <7 \)
\ [\ begin {array} {ccccc}
-2 & & x — 1 &> & -21 \\
7 &> & x &> & -20 \\
-20 и
Обозначается в числовой строке:
В интервальном обозначении: \ ((- 20; 7) \)
\ begin {align *}
2 х -1 & <3 (х +11) \\
2 х -1 & <3 х +33 \\
2 х -3 х & <33 +1 \\
-1 х & <34 \\
\ поэтому x &> -34
\ end {align *}
\ [\ влево (-34; \ infty \ вправо) \]
\ begin {align *}
х -1 & <-4 (х -6) \\
х -1 & <-4 х +24 \\
х +4 х & <24 +1 \\
5 х & <25 \\
\ поэтому x & <5
\ end {align *}
\ [\ влево (- \ infty; 5 \ вправо) \]
\ (\ dfrac {x-1} {8} \ leq \ dfrac {2 (x-2)} {3} \)
\ begin {align *}
\ frac {x-1} {8} & \ leq \ frac {2 (x-2)} {3} \\
3 (х-1) & \ leq 16 (х-2) \\
3х-3 & \ leq 16х-32 \\
3х -16х & \ leq -32 +3 \\
-13x & \ leq -29 \\
\ поэтому x & \ geq \ frac {29} {13}
\ end {выровнять *}
\ (\; x \ in \ left [\ frac {29} {13}; \ infty \ right) \).
\ (\ dfrac {x + 2} {4} \ leq \ dfrac {-2 (x-4)} {7} \)
\ begin {align *}
\ frac {x + 2} {4} & \ leq \ frac {-2 (x-4)} {7} \\
7 (х + 2) & \ leq -8 (х-4) \\
7x + 14 & \ leq -8x + 32 \\
7x + 8x & \ leq 32-14 \\
15x & \ leq 18 \\
\ поэтому x & \ leq \ frac {6} {5}
\ end {выровнять *}
\ (\; x \ in \ left (- \ infty; \ frac {6} {5} \ right] \).
\ (\ dfrac {1} {5} x — \ dfrac {5} {4} (x + 2)> \ dfrac {1} {4} x + 3 \)
\ begin {align *}
\ frac {1} {5} x — \ frac {5} {4} (x + 2) &> \ frac {1} {4} x +3 \\
4х — 25 (х + 2) &> 5х +60 \\
4х — 25 х-50 &> 5х +60 \\
4х — 25 х -5х &> 60 + 50 \\
-26x &> 110 \\
\ поэтому x & <- \ frac {55} {13}
\ end {align *}
Интервал:
\ [\ left (- \ infty; — \ frac {55} {13} \ right) \]
\ (\ dfrac {1} {5} x — \ dfrac {2} {5} (x + 3) \ geq \ dfrac {4} {2} x +3 \)
\ begin {align *}
\ frac {1} {5} x — \ frac {2} {5} (x + 3) & \ geq \ frac {4} {2} x +3 \\
2x — 4 (x + 3) & \ geq 20x +30 \\
2х — 4 х-12 & \ geq 20x +30 \\
2х — 4 х -20х & \ geq 30 + 12 \\
-22x & \ geq 42 \\
\ поэтому x & \ leq — \ frac {21} {11}
\ end {align *}
Интервал:
\ [\ left (- \ infty; — \ frac {21} {11} \ right] \]
\ (4x +3 <-3 \ quad \ text {или} \ quad 4x +3> 5 \)
Решите неравенство:
\ [\ begin {array} {rclcrcl}
4x +3 & <& -3 & \ text {или} & 4x +3 &> & 5 \\
4x & <& -3-3 & \ text {or} & 4x &> & 5-3 \\
x & <& \ frac {-3-3} {4} & \ text {или} & x &> & \ frac {5-3} {4} \\
x & <& - \ frac {3} {2} & \ text {или} & x &> & \ frac {1} {2} \\
\ end {array} \]
\ [\ left (- \ infty; — \ frac {3} {2} \ right) \ cup \ left (\ frac {1} {2}; \ infty \ right) \]
Решите неравенство:
\ [\ begin {array} {rcccl}
4 & \ ge & -6x -6 & \ ge & -3 \\
4 + 6 & \ ge & -6x & \ ge & -3 + 6 \\
\ frac {4 + 6} {- 6} & \ le & x & \ le & \ frac {-3 + 6} {- 6} \\
— \ frac {5} {3} & \ le & x & \ le & — \ frac {1} {2} \\
\ end {array} \]
\ [\ left [- \ frac {5} {3}; — \ frac {1} {2} \ right] \]
\ (6b — 3> b + 2, ~ b \ in \ mathbb {Z} \)
\ begin {align *}
6b — 3> b + 2, ~ b \ in \ mathbb {Z} \\
5b> 5 \\
b> 1
\ end {выровнять *}
\ (3a — 1 <4a + 6, ~ a \ in \ mathbb {N} \)
\ begin {align *}
3а — 1-7
\ end {выровнять *}
Однако нам говорят, что \ (a \ in \ mathbb {N} \) и поэтому \ (a> 0 \).
\ (\ dfrac {b-3} {2} + 1 <\ dfrac {b} {4} - 4, ~ b \ in \ mathbb {R} \)
\ begin {align *}
\ frac {b-3} {2} + 1
\ (\ dfrac {4a +7} {3} — 5> a — \ dfrac {2} {3}, ~ a \ in \ mathbb {N} \)
\ begin {align *}
\ frac {4a +7} {3} — 5> a — \ frac {2} {3} \\
4а + 7-15> 3а — 2 \\
а> 6
\ end {выровнять *}
Весы как модель уравнения
В этой статье обсуждается, как использовать весы для моделирования простых линейных уравнений в предалгебре или алгебре 1.На этой странице мы имеем дело только с положительными целыми числами; часть 2 объясняет, как использовать баланс с уравнениями, которые включают отрицательные целые числа.
Уравнение в основном говорит, что две вещи (точнее, выражения) РАВНЫ. Поскольку в сбалансированной ситуации обе стороны весов имеют равный вес, мы можем моделировать простые уравнения с помощью весов.
На рисунках ниже каждый кружок представляет один, а блок представляет неизвестное x . Узнать, сколько весит блок, можно
Таким образом, обе стороны будут поддерживать баланс или «равенство».
х + 3 = 5 | Если это сбалансированная ситуация … |
x = 2 | … так оно и есть! (Мы сняли три круга с ОБЕИХ сторон.) |
3 x + 2 = 2x + 6 | Уберите два блока (два x ) с обоих стороны. Баланс остается сбалансированным. |
x + 2 = 6 | Уберите по 2 круга с обеих сторон. Баланс остается сбалансированным. |
x = 4 | Вот решение! |
Без масштабной модели процесс решения выглядит следующим образом:
| 3x + 2 -2x | = | 2x + 6 -2x | (уберите 2х с обеих сторон) | |
| х + 2 -2 | = | 6 -2 | (снимаем по 2 с двух сторон) | |
| x | = | 4 |
Деление
В некоторых ситуациях вам нужно разделить обе части уравнения на одно и то же число.Когда это? Это удачная ситуация, когда на одной стороне ТОЛЬКО x (блоков), но их больше одного.
2 x = 8 | Если забрать половину вещей на левая сторона, и аналогично половина вещей на правой стороне, баланс останется сбалансированным . |
x = 4 |
3 x = 9 | Подумай об этом! Если это уравновешенная ситуация… |
x = 3 | … как и другой (и наоборот)! Мы просто разделили обе стороны на 3. |
Объединение операций
Разрешенные операции:
- Добавьте одинаковое количество к обеим сторонам ( x или единицам)
- Вычтите одинаковое количество с обеих сторон ( x или единиц)
- Умножьте обе стороны на одинаковое число (но не на ноль)
- Разделите обе стороны на одинаковое число (но не на ноль)
(Есть и другие, но они не нужны в простых уравнениях.)
Цель состоит в том, чтобы ПЕРВЫЙ сложить и вычесть , пока у нас не будет ТОЛЬКО блоки (блоки) x с одной стороны и ТОЛЬКО блоки (кружки) с другой. Затем, если у вас более одного блока, вам нужно разделить , чтобы прийти к ситуации, когда только один блок с одной стороны, что является решенным уравнением!
Умножение с обеих сторон может произойти, если у вас есть дробный блок ( минус , чем один блок) с одной стороны.Например, уравнение 1 / 4x = 13 решается путем умножения обеих частей на 4. Попробуйте позволить своим ученикам смоделировать уравнение 1 / 2x + 14 = 20, используя весы; они могут решить это с его помощью. Более продвинутые студенты могут подумать, что делать с уравнением 2 / 3x = 12.
Пример вычитания и деления
В этом примере мы используем все вышеперечисленные операции: снятие с
обе стороны уравнения и разделив уравнение на одно и то же число.
4 x + 2 = 2 x + 5 | Сначала избавляемся от блоков с правой стороны убрав по два квартала с обеих сторон. |
2 x + 2 = 5 | Затем убираем кружочки с левой стороны убрав по 2 круга с обеих сторон. |
2 x = 3 | Теперь только блоки с одной стороны и только круги с другой. Узнать, что за 1 блок весит, берем половину с обеих сторон. |
x = 1 1/2 | Решение состоит в том, что 1 блок весит 1 1/2 круга. |
Попробуйте подставить это значение x = 1 1/2 в исходное уравнение 4 x + 2 = 2 x + 5 и проверьте, выполняется ли уравнение!
Пример упражнений
Эти уравнения достаточно просты, чтобы их можно было решить с помощью модели баланса. ВСЕГДА проверяйте свое решение, подставляя его в исходное уравнение.
- 2 x + 3 = 5
- 2 x + 5 = x + 9
- 3 x + 2 = 2 x + 4
- 3 x + 3 = 5 + x
- 5 x + 4 = 3 x + 6
- 6 x + 2 = 3 x + 6
- 6 x + 3 = 2 x + 5
Перейти к отрицательным членам в уравнении

 Таким образом, в кругу должны побывать все желающие.
Таким образом, в кругу должны побывать все желающие. Длина прямоугольника 6см, а ширина 2 см.
Длина прямоугольника 6см, а ширина 2 см.
 Настраиваются на работу.
Настраиваются на работу. (Числовой материал может быть разного уровня)
(Числовой материал может быть разного уровня)


 ) А сейчас поработаем устно. Посмотрите на слайд.
) А сейчас поработаем устно. Посмотрите на слайд. Поставьте плюсы или плюс с минусом у соответствующих высказываний.
Поставьте плюсы или плюс с минусом у соответствующих высказываний. Задание 2 на рабочих листах.
Задание 2 на рабочих листах.

 Это зависит от того, сколько действий в выражении с переменной. Поэтому в решении уравнения может быть большее число шагов.
Это зависит от того, сколько действий в выражении с переменной. Поэтому в решении уравнения может быть большее число шагов. Первичное закрепление (5 мин). Проговаривание в громкой речи.
Первичное закрепление (5 мин). Проговаривание в громкой речи.

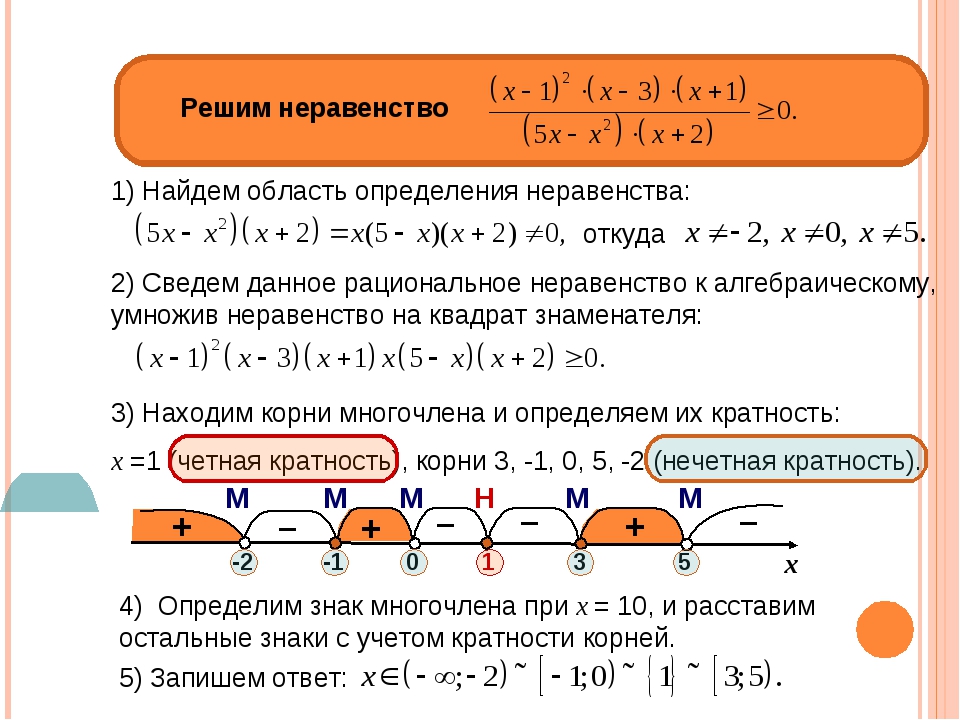 (х= 3м)
(х= 3м) Итог урока. Рефлексия деятельности (2-3мин).
Итог урока. Рефлексия деятельности (2-3мин).