Содержание
Урок 31. задачи в 3 действия — Математика — 3 класс
Математика, 3 класс
Урок № 31. Задачи в 3 действия
Перечень вопросов, рассматриваемых в теме:
— как решать текстовые задачи в 3 действия арифметическим способом?
— какие наиболее эффективные способы используются для решения задач?
Глоссарий по теме:
Задача – это текст, содержащий численные компоненты
Задача – это сформулированный словами вопрос, ответ на который может быть получен с помощью арифметических действий.
Условие – это часть задачи, в которой рассказывается о том, что неизвестно, содержит числовые данные.
Вопрос – это часть задачи, в которой сообщается о том, что нужно узнать.
Основная и дополнительная литература по теме урока:
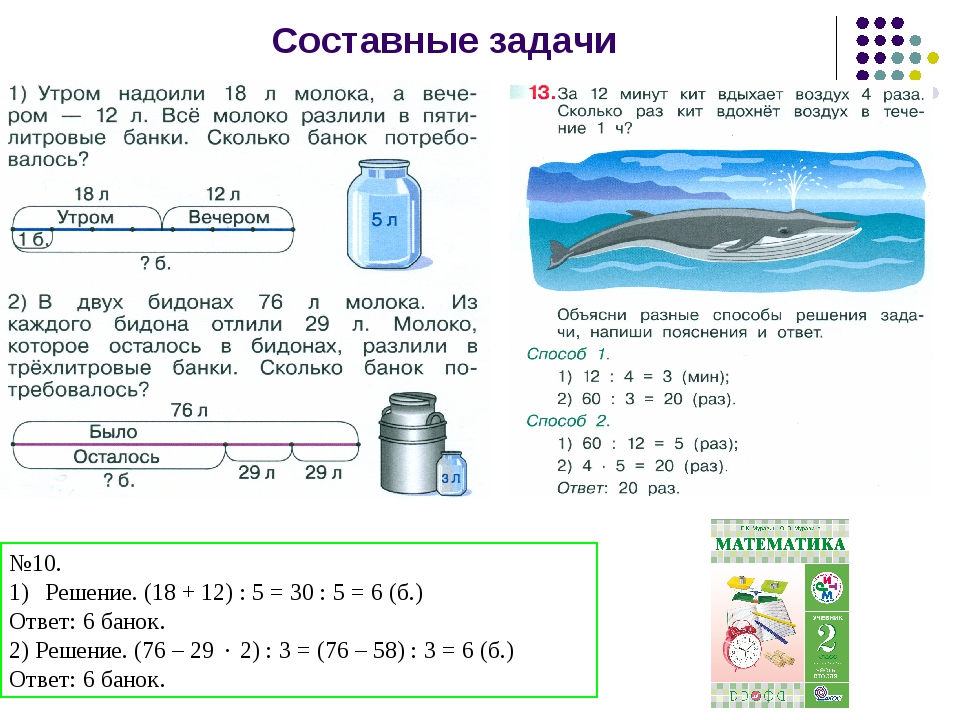
1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017. – с. 86.
2. Гребнева Ю. А. Тематические тестовые работы по математике для 3 класса М.: Ювента, 2015, с. 4-6.
Гребнева Ю. А. Тематические тестовые работы по математике для 3 класса М.: Ювента, 2015, с. 4-6.
Теоретический материал для самостоятельного изучения
Математика – самая древняя из наук, она была и остаётся необходимой людям. Слово «математика» греческого происхождения. Оно означает «наука», «размышление».
В Древнем Вавилоне математика зародилась задолго до нашей эры. Вавилонские памятники в виде глиняных плиток (всего около 500 000, причем из них примерно лишь 150 с текстами математических задач и 200 с числовыми таблицами) с клинописными надписями хранятся в различных музеях мира.
В этих текстах мы находим достаточно удобные способы решения ряда практических задач, связанных с земледелием, строительством и торговлей.
В Древнем Египте, «стране пирамид» за много тысяч лет до нашей эры возводились гигантские сооружения в виде храмов и пирамид. Некоторые из этих памятников сохранились до настоящего времени. Различные строительные работы, а также земледелие, основанное на искусственном орошении, рано вызвали потребность в математических познаниях и особенно в геометрии.
Математические правила, нужные для земледелия, астрономии и строительных работ, древние египтяне записывали на стенах храмов или на «папирусах», лентообразных свитках из особого писчего материала растительного происхождения.
В Британском музее хранится так называемый «папирус Райнда». Рукопись относится к периоду 2000—1700 лет до нашей эры. В ней содержится 84 задачи, причем большинство из них арифметического характера.
Решение задач является неотъемлемой частью жизни человека. Начиная с древних времен и до наших дней, люди используют разные виды и способы решения задач. У одной задачи бывает только один способ решения, а у другой — их несколько.
Рассмотрим решение задачи.
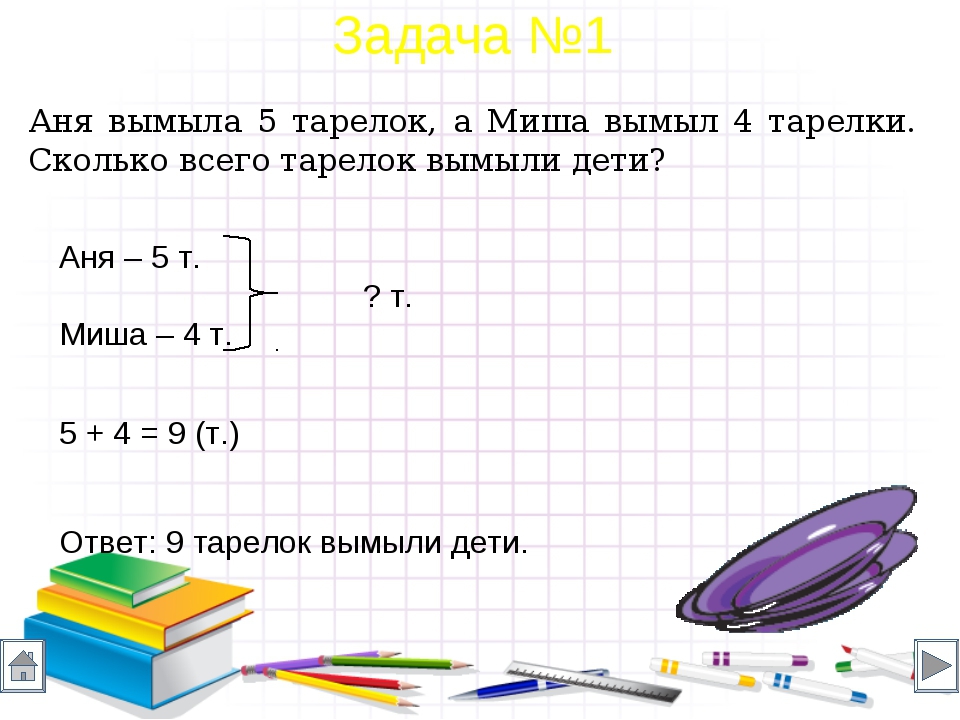
В детский сад привезли 4 коробки конфет по 9 кг в каждой, и 3 коробки печенья по 8 кг в каждой коробке. Сколько всего кг конфет и печенья привезли в детский сад?
Составим текстовую краткую запись задачи.
Конфеты — 4 кор. по 9 кг
Печенье — 3 кор. по 8 кг
? кг
Составим план решения этой задачи:
Первым действием надо узнать, сколько кг конфет привезли в детский сад (выполнить умножение).
Вторым действием узнаем, сколько кг печенья привезли в детский сад
(выполнить умножение).
Третьим действием узнаем, сколько конфет и печенья привезли в детский сад (выполнить сложение).
Запишем решение:
1) 9 ∙ 4 = 36 кг – конфеты
2) 8 ∙ 3 = 24 кг – печенье
3) 36 + 24 = 60 кг – всего
Ответ: 60 кг печенья и конфет привезли в детский сад.
Можно эту запись сократить и записать одним действием.
9 ∙ 4 + 8 ∙ 3 = 60 кг
Задания тренировочного модуля:
1. К каждому вопросу задачи подберите соответствующее выражение.
У продавца были воздушные шарики 3 цветов по 6 штук каждого цвета. Он продал по 4 шарика 2 цветов. Сколько шариков у него осталось?
Сколько шариков было? | 6 ∙ 3 — 4 ∙ 2 |
Сколько продал шариков? | 6 ∙ 3 |
Сколько шариков осталось? | 4 ∙ 2 |
Правильный ответ:
Сколько шариков было? | 6 ∙ 3 |
Сколько продал шариков? | 4 ∙ 2 |
Сколько шариков осталось? | 6 ∙ 3 — 4 ∙ 2 |
2. Выделите цветом верное решение задачи.
Выделите цветом верное решение задачи.
У Вали 5 конвертов с открытками по 7 открыток в каждом конверте. Она подарила 3 конверта по 4 открытки в каждом конверте. Сколько открыток у Вали осталось?
7 ∙ 5 + 4 ∙ 3;
7 ∙ 5 — 4 ∙ 3.
Правильный ответ:
7 ∙ 5 — 4 ∙ 3
Страница не найдена — Бесплатная электронная библиотека для детей и родителей
Начальная школа, 1-4 классы
О.В. Узорова, Е.А. Нефедова Тренинговая тетрадь содержит 49 задач трёх уровней сложности. В конце
Начальная школа, 1-4 классы
О. И. Крупенчук Эта книга поможет вашим детям научиться читать быстро тексты любой сложности. В
И. Крупенчук Эта книга поможет вашим детям научиться читать быстро тексты любой сложности. В
Начальная школа, 1-4 классы
М. В. Беденко Учебное пособие содержит более 500 задач по программе 1 класса. Эти
Начальная школа, 1-4 классы
А. В. Ефимова, М.Р. Гринштейн Данное пособие содержит разноуровневые задания по всем программным темам 3
В. Ефимова, М.Р. Гринштейн Данное пособие содержит разноуровневые задания по всем программным темам 3
Начальная школа, 1-4 классы
В.Н. Рудницкая Данное пособие содержит тематические тестовые задания, которые позволят оценить успешность освоения программы
Начальная школа, 1-4 классы
А. В. Ефимова, М.Р. Гринштейн В данной рабочей тетради представлены упражнения для повторения и закрепления
В. Ефимова, М.Р. Гринштейн В данной рабочей тетради представлены упражнения для повторения и закрепления
Викторина по математике для 3 класса.
Автор:
Ковалева Наталья Михайловна,
учитель начальных классов
МОУ «СОШ № 61»
Цели:
Развитие логического, образного и творческого мышлении у обучающихся.
Задачи:
1. Вызвать интерес к предлагаемым вопросам, таким образом расширить кругозор учащихся
2. Формировать и развивать у учащихся умения и навыки работы в группе
3. Развивать мышление и творческую инициативу ребят
Форма работы: групповая.
Регламент: 30 минут или по окончанию решения всех задач, какой-либо группой.
Условия викторины:
За каждой командой закреплён судья. Командам предлагается одинаковый набор из 21 задач разных типов. Задачи представлены в виде экзаменационных билетов, выбор той или иной задачи зависит от выбора командира. Командир берёт задачу у судьи, возвращается к группе, сообща решается задача, командир возвращается к судье с решением. Присуждение баллов: за каждую решенную верно задачу, группа получает 1 балл, на нерешенную задачу — 0 баллов, за отказ от решения — (-1) балл. Викторина заканчивается по истечению регламента или по окончанию решения всех задач, какой-либо группой. Нарушение условий викторины штрафуется — 1 баллом.
Командир берёт задачу у судьи, возвращается к группе, сообща решается задача, командир возвращается к судье с решением. Присуждение баллов: за каждую решенную верно задачу, группа получает 1 балл, на нерешенную задачу — 0 баллов, за отказ от решения — (-1) балл. Викторина заканчивается по истечению регламента или по окончанию решения всех задач, какой-либо группой. Нарушение условий викторины штрафуется — 1 баллом.
Победителем становится та команда, которая наберёт наибольшее количество баллов.
ХОД ВИКТОРИНЫ
| Этапы | Содержание урока | Время | Дополнения |
| I | Организационный момент. 1. Деление на группы в форме жеребьёвки (цветные фигурки). 2. Ознакомление с условиями викторины. 3. Работа в группе (придумывание название группы; выбор командира) | 4 мин | 1. Разлиновать доску; Разлиновать доску;2. Подготовить жетоны для жеребьёвки; 3. Распечатать условия викторины. |
| II | Решение задач. | 30 мин | 1. Подготовить тексты задачи для команд на листах разного цвета. 2. Подготовить листы-контролеры для судей. 3. Подготовить для судей «ключи» к задачам |
| III | Рефлексия: — Что особенно понравилось? — В чём возникли трудности? Почему? Что надо знать и уметь, чтобы не попадать в затруднения? — Что можете сказать своим партнёрам по групповой работе? — Что можете сказать своим соперникам? — Что можете пожелать всем участникам викторины? | 5 мин | _ |
| IV | Д/З. Подумайте над решением задач, при решении которых возникли затруднения. Мы эти задачки разберём на логике.  | 1мин | _ |
ЗАДАНИЯ ДЛЯ ГРУПП
Задача 1.
Сколько домов находится между домами № 26 и № 56, расположенными на одной стороне улицы?
Задача 2.
Сколько всего чётных чисел от 4 до 16, включая и названные числа?
Задача 3.
Сколько получиться, если из числа, выраженного тремя единицами второго разряда, вычесть число, выраженное пятью единицами первого разряда?
Задача 4.
Сколько квадратов изображено на рисунке?
Задача 5.
На прямой отметили 4 точки. Сколько всего получилось отрезков, концами которых являются эти точки?
A B C D
____________________________________________
Задача 6.
Вставьте пропущенные цифры в пример на сложение:
* 6 *
* 7
____________
* * 2 4
Задача 7.
Вставьте пропущенное число, найдя закономерность числового ряда.
3 5 7 9
9 25 49 ?
Задача 8.
Чтобы разгадать ребус, нужно каждую букву заменить цифрой. Одинаковым буквам соответствуют одинаковые цифры. Разгадайте ребус.
F F + K = K R R
Задача 9.
Решите задачу.
Три котёнка — Касьянка, Том и Плут -съели плотвичку, окуня и карася. Касьянка не ел ни плотвичку, ни окуня. Том не ел плотвичку. Какую рыбу съел каждый котёнок?
Задача 10.
Решите задачу.
В школе 400 учеников. Верно ли утверждение, что хотя бы два ученика этой школы отмечают свой день рождения в один и тот же день года?
Задача 11.
Решите задачу.
У моего отца только один сын. А всего детей в семье трое. Как такое может быть, ведь у меня нет братьев?
Задача 12.
Решите задачу.
Гном разложил свои сокровища в три сундука разного цвета, стоящих у стены: в один — драгоценные камни, в другой — золотые монеты, в третий — магические книги. Он помнит, что красный сундук находится правее, чем сундук с камнями, и что сундук с книгами — правее красного сундука. В каком сундуке лежат книги, если зелёный сундук стоит левее синего, а зелёный и синий сундуки — крайние.
Задача 13.
Расставьте в клетках квадрата числа 1, 4, 6,7,8,9 так, чтобы во всех вертикальных и горизонтальных рядах, а также по диагоналям в сумме получилось 15.
| ___ | ___ | ___ |
| ___ | _5_ | _3_ |
| _2_ | ___ | ___ |
Задача 14.
Решите задачу.
Машина за 40 минут проехала 40 км, а катер за 30 минут прошёл 35 км. Чья скорость больше?
Задача 15.
Решите задачу.
Белая мышка бежала от сарая к дому, а серая — от дома к сараю. Выбежали они одновременно. Через пять минут белая мышка была ближе к дому, чем серая к сараю. Какая мышка бежала медленнее?
Задача 16.
Решите задачу.
Как увеличить площадь бассейна вдвое, сохранив деревья и не изменив квадратную форму бассейна?
Задача 17.
Мы часто используем слово «километр». «Метр» в переводе с французского языка означает «мера», а что означает слово «кило»?
Выбери правильный вариант: мясо; тысяча; длина.
Задача 18.
Сколько получится, если из наименьшего четырёхзначного числа вычесть наибольшее однозначное?
Задача 19.
Решите задачу.
В магазин привезли 4 одинаковые полные коробки: в одной — апельсины, в другой — яблоки, в третий — мандарины, а в четвёртой — вишни. В какой коробке наибольшее число плодов?
Задача 20.
Решите задачу.
У семи братьев по одной сестре. Сколько детей в семье?
Задача 21.
Решите задачу.
На руках 10 пальцев. Сколько пальцев на 10 руках?
КЛЮЧИ К ЗАДАЧАМ
Тема 1. Нумерация.
Задача 1. (56 — 26) : 2 — 1= 14 домов
Задача 2. 7 чисел (4, 6, 8, 10, 12, 14, 16)
Задача 3. 30 — 5 = 25
Тема 2. Геометрические задачи.
Задача 4. 14 квадратов (9 маленьких, 4 средних, 1 большой)
Задача 5. 6 отрезков (AB, AC, AD, BC, BD, CD)
Тема 3. Арифметические действия, числовые и буквенные ребусы.
Задача 6.
9 6 7
5 7
____________
1 0 2 4
Задача 7. Пропущено число 81 (9х9)
Задача 8. 99 + 1 = 100 (F = 9; K = 1; R = 0)
Тема 4. Логические задачи.
Задача 9. Ответ: Касьянка съел карася, Том — окуня, Плут — плотвичку.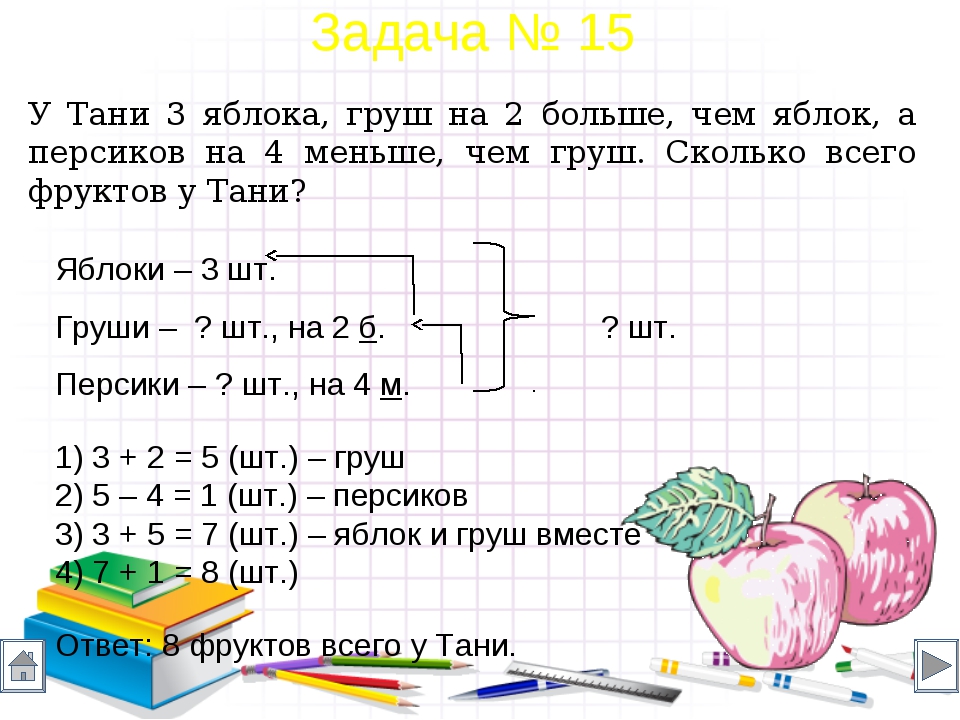
Задача 10. Ответ: Да, т.к. в году 366 дней, соответственно минимум 34 пары учеников родились в один день.
Задача 11. Ответ: в семье — один сын и две дочери.
Задача 12. Ответ: книги лежат в синем сундуке. Решение: По условию сундук с камнями стоит левее красного, а сундук с книгами — правее красного. Значит, красный сундук стоит по середине, и в нём лежат золотые монеты. Так как зелёный и синий сундуки — крайние, и зелёный стоит левее синего, то зелёный — крайний слева, а синий — крайний справа. Вспомнив, что сундук с камнями находится левее, а сундук с книгами — правее красного сундука, приходим к выводу, что камни лежат в зелёном, а книги — в синем сундуке.
Тема 5. Магические квадраты.
Задача 13.
| _6_ | _1_ | _8_ |
| _7_ | _5_ | _3_ |
| _2_ | _9_ | _4_ |
Тема 6. Задачи на движение.
Задачи на движение.
Задача 14. Ответ: скорость катера была больше.
Задача 15. Ответ: медленнее бежала серая мышка.
Тема 7. Площадь фигур.
Задача 16. Изменить площадь бассейна вдвое, не изменив квадратную форму, можно так, как показано на схеме.
Тема 8. Величины.
Задача 17. Слово «кило» означает «тысяча»
Тема 9. Задачи на смекалку.
Задача 18. 1000 — 9 = 991
Задача 19. Ответ: плодов больше в коробке с вишнями.
Задача 20. Ответ: в семье 8 детей (7 сыновей и одна дочь)
Задача 21. Ответ: на десяти руках 50 пальцев.
Кемерово, 2010
Моро. 1, 2 часть учебника
ГДЗ по математике для 3 класса Моро – это онлайн-решебник готовых домашних заданий, составленный на основе учебника по арифметике от авторитетных российских ученых – М.И. Моро, М.А. Бантовой, Г.В. Бельтюковой и др. На него опираются в своей работе многие центральные и региональные школы России.
Структура ГДЗ по учебнику математики третьего класса от Моро
Третий класс знакомит школьников с такими базовыми темами математики, как решение простых уравнений, периметр и площадь простых геометрических фигур, приемами письменных и устных вычислений. Ученикам приходится работать с числами от 1 до 100, решать с ними задачи и примеры в несколько действий.
ГДЗ по математике 3 класса Моро, составленные на основе учебника 2015 года в его 5-м издании, включают в себя примеры и задачи на такие темы:
- решение уравнений;
- обозначение геометрических фигур буквами;
- порядок выполнения действий;
- площадь и единицы площади;
- умножение и деление на 1 и 0;
- окружность и круг;
- единицы массы;
- приёмы устных и письменных вычислений;
- виды треугольников.
В классе школьник усваивает теорию по арифметике, а дома должен попробовать применять формулы и правила на практике. Чтобы научиться решать задачки и примеры, необходимо понимать их внутренние алгоритмы.
ГДЗ от Путина по Моро для 3 класса раскрывают весь процесс решения подробно и пошагово. Такой подход удобен для учеников и их родителей. Готовые домашние задания – эффективная и бесплатная альтернатива репетиторам.
Готовые решения от ГДЗ Путина по математике 3 класса к Моро
Ученики и их родители часто ищут решения домашних задач и примеров в сети. Самые свежие и правильные решения, оформленные по стандартам Министерства образования России размещены на сайте ГДЗ Путина. В чем их польза для третьеклассников и их родителей?
- каждое задание имеет несколько вариантов решения;
- ответы формируются на базе самых свежих учебников российских школ;
- все задания открыты пользователям бесплатно и без регистрации.
Достойным дополнением этих свойств выступает доступ к ГДЗ по математике 3 класса к учебнику Моро с любого устройства – будь то планшет, смартфон или компьютер. Родители, которые зачастую делают уроки вместе с младшими школьниками, могут зайти на портал в удобное время и найти нужное решение.
Готовые примеры и уравнения, чертежи и задачи облегчают подготовку домашней работы. Детальные алгоритмы позволяют ученикам глубоко вникать в задания, постигать новые горизонты в изучении предмета, создавать базу для дальнейшего изучения математики и смежных дисциплин.
ГДЗ Математика 3 класс Моро, Бантова, Бельтюкова на Решалка
В 3 классе закладываются основы для дальнейших математических дисциплин в школьной программе. Современный учебник под авторством Моро, Бантовой и Бельтюковой выделяется необычной подачей материала. Дети точно не заскучают на занятии, а вот пропущенные темы поможет подтянуть решебник для 3 класса. Закрепление пройденной информации происходит с помощью практических упражнений. Третьеклассникам не всегда удается самостоятельно выполнить все задания, усвоить тему и систематизировать нужные понятия.
Готовая домашка по пособию Бельтюковой, Бантовой
В 3 классе повторяются пройденные раннее действия с двухзначными числами, постепенно увеличивается их диапазон. Позже изучаются геометрические фигуры, понятия площади и ее вычисления, долей, единиц массы, виды треугольников. Ученики обучаются приемам устного и письменного счета.
Позже изучаются геометрические фигуры, понятия площади и ее вычисления, долей, единиц массы, виды треугольников. Ученики обучаются приемам устного и письменного счета.
Математика способствует развитию аналитических способностей, креативного мышления. А что делать, если ребенок не может разобраться сам, а родителям не хватает терпения пошагово разъяснить все правила согласно требованиям действующей школьной программы? Это тот случай, когда стоит проверить домашнее задание по решебнику.
Грамотный задачник легко решается по ГДЗ по математике за 3 класс, подготовленным авторами: Моро, Бантова, Бельтюкова. Он соответствует требованиям ФГОС для действующей программы начальной школы.
Готовые ответы для третьего класса
Сейчас нет сложностей с получением необходимых знаний. Внешние бесплатные ресурсы позволяют смело заниматься дома. Чтобы не запутаться в решении практических упражнений, стоит воспользоваться вспомогательными сервисами.
Изучение необходимого материала с нашим решебником поможет быстрее выполнять домашку, улучшить успеваемость, стать увереннее в своих силах и активнее. Эффективный способ самообучения — готовое решение упражнения с разъяснением, схематическим описанием в онлайн-сервисе «Решалке». Благодаря свободному доступу воспользоваться сервисом ГДЗ по математике (3 класс) можно везде, где есть Интернет.
Эффективный способ самообучения — готовое решение упражнения с разъяснением, схематическим описанием в онлайн-сервисе «Решалке». Благодаря свободному доступу воспользоваться сервисом ГДЗ по математике (3 класс) можно везде, где есть Интернет.
Математика, 3 класс: уроки, тесты, задания
«На» и «в»
-
Увеличить на… Увеличить в… Уменьшить на… Уменьшить в…
-
Больше на… Больше в… Меньше на… Меньше в…
Таблица умножения на 6, 7, 8, 9
-
Умножение на 6 (таблица)
-
Умножение на 7 (таблица)
-
Умножение на 8 (таблица)
-
Умножение на 9 (таблица)
Уравнения
-
Нахождение неизвестного множителя
-
Нахождение неизвестного делимого
-
Нахождение неизвестного делителя
Ломаная.
 Треугольники
Треугольники
-
Свойства ломаной линии
-
Треугольники. Виды треугольников
Умножение и деление (1, 0 и 10). Умножение и деление круглых чисел (числа до 100)
-
Умножение и деление на 0, 1, 10. Деление числа на само себя
Деление числа на само себя
-
Выполняем умножение и деление круглого числа на однозначное число
-
Правила деления круглого числа на круглое число
Умножение (числа до 100)
-
Умножаем сумму на число
-
Умножаем двузначное число на однозначное число
Деление (числа до 100)
-
Правила деления суммы на число
-
Правила деления двузначного числа на однозначное
-
Правила деления двузначного числа на двузначное
-
Правила деления с остатком
Доли
-
Находим долю от числа
-
Сравниваем доли
-
Находим число по доле
Трёхзначные числа, числа до тысячи
-
Трёхзначные числа.Нумерация
-
Сложение и вычитание трёхзначных чисел
-
Выполняем умножение и деление трёхзначного числа на однозначное число
-
Связь между величинами
Календарь
Многозначные числа (числа больше 1000)
-
Нумерация
-
Правила сложения и вычитания многозначных чисел
-
Правила сочетательного закона умножения
-
Умножаем и делим числа на 10, 100, 1000
-
Круглые числа (умножение и деление)
Единицы измерения
-
Единицы измерения времени (час, минута, сутки)
-
Миллиметр
-
Километр
Площадь
-
Нахождение площади фигуры, прямоугольника
-
Единицы измерения площади
ГДЗ по математике 3 класс Моро, Бантова Учебник Решебник
На изучение арифметики, первейшего раздела математики, отводится время начальной школы. Ученикам предстоит освоить таблицу умножения, научиться совершать операции (сложение, вычитание, деление, поиск целочисленного остатка, умножение) с натуральными числами, решать несложные практические задачи трех типов, а также понять, как работать с разрядами в десятичной системе счисления. Именно от успешности освоения данной дисциплины будет зависеть качество общего образования, на которое сможет претендовать ребенок. Школьники с разными способностями к точным наукам требуют особого подхода и различного уровня педагогического внимания.
Ученикам предстоит освоить таблицу умножения, научиться совершать операции (сложение, вычитание, деление, поиск целочисленного остатка, умножение) с натуральными числами, решать несложные практические задачи трех типов, а также понять, как работать с разрядами в десятичной системе счисления. Именно от успешности освоения данной дисциплины будет зависеть качество общего образования, на которое сможет претендовать ребенок. Школьники с разными способностями к точным наукам требуют особого подхода и различного уровня педагогического внимания.
Моро М.И., Бантова М.А. и Бельтюкова Г.В. являются авторами решебника для 3 класса. Издательство «Просвещение» отвечает за подготовку к печати и распространение данного пособия в 2019 году. Онлайн-сборник соответствует ФГОС. Он рекомендуется всем без исключения общеобразовательным организациям Российской Федерации для использования в начальной школе.
Почему третьеклассники любят ГДЗ Моро по математике?
На самом деле тут всё очень просто.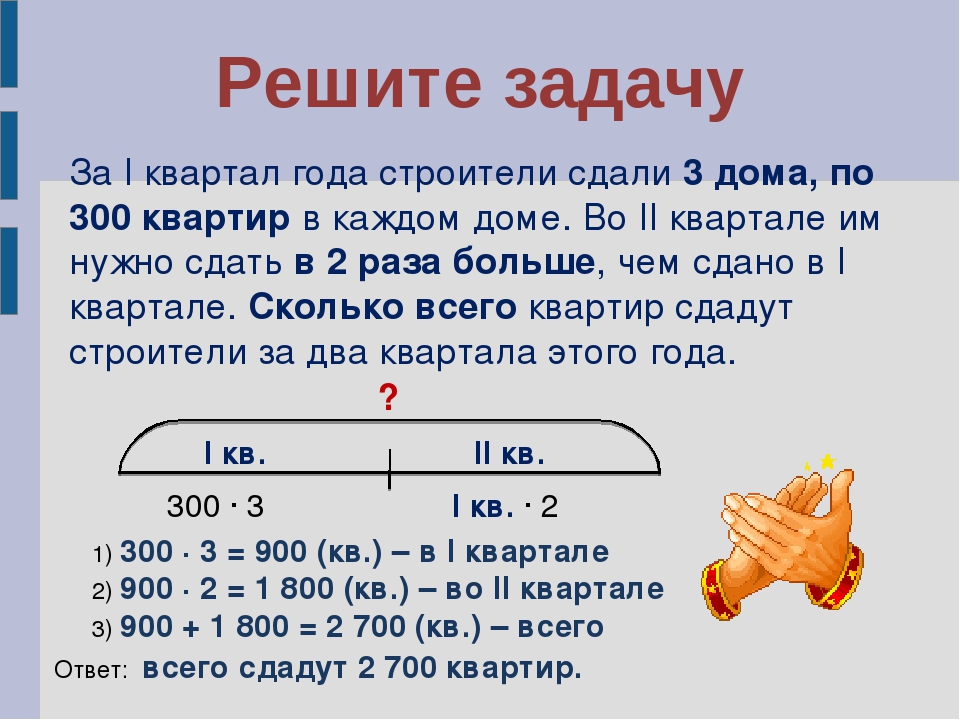 По сборнику задач с готовыми ответами легко заниматься. Благодаря удачно подобранным и хорошо отсортированным заданиям это практически не составляет труда. Достаточно включить компьютер, телефон или планшет, чтобы подключиться к нашему сайту. По табличному указателю можно запросто найти номер нужного упражнения и ознакомиться с его верным выполнением. После этого требуется закрепить полученные ценные умения и навыки. Пособие по математике Моро, Бантовой, Бельтюковой на сайте имеет следующие преимущества:
По сборнику задач с готовыми ответами легко заниматься. Благодаря удачно подобранным и хорошо отсортированным заданиям это практически не составляет труда. Достаточно включить компьютер, телефон или планшет, чтобы подключиться к нашему сайту. По табличному указателю можно запросто найти номер нужного упражнения и ознакомиться с его верным выполнением. После этого требуется закрепить полученные ценные умения и навыки. Пособие по математике Моро, Бантовой, Бельтюковой на сайте имеет следующие преимущества:
- номера легко находить по указателю;
- представлены самые актуальные версии учебников;
- материалы постоянно обновляются;
- страница с ответами доступны в любое время суток.
С ГДЗ легко готовиться к контрольным и проверочным работам, выполнять тесты, повторить забытую тему. Систематические занятия приведут к повышению успеваемости и большей уверенности в собственных силах.
Почему решебник для 3 класса Моро и Бантовой сродни репетитору?
Не стоит мучить ребенка дополнительными индивидуальными занятиями с частными педагогами или бесконечными посещениями курсов. С помощью ГДЗ вы можете стать для своего ребёнка личным репетитором, причем достигнутый результат может оказаться даже лучше. Все знают, что приятнее заниматься с мамой или папой, чем с незнакомой тетей. Используя сайт, вы получаете знания о действиях с числами, о единицах измерения, геометрических фигурах, выполнении операций в столбик. Все упражнения решены согласно действующим на данный момент требованиям и правилам. В третьем классе для ученика основными будут являться следующие темы:
С помощью ГДЗ вы можете стать для своего ребёнка личным репетитором, причем достигнутый результат может оказаться даже лучше. Все знают, что приятнее заниматься с мамой или папой, чем с незнакомой тетей. Используя сайт, вы получаете знания о действиях с числами, о единицах измерения, геометрических фигурах, выполнении операций в столбик. Все упражнения решены согласно действующим на данный момент требованиям и правилам. В третьем классе для ученика основными будут являться следующие темы:
- представление о натуральных числах;
- приемы сложения и вычитания;
- равенство и неравенство. Задачи на сравнение двух чисел;
- луч, прямая линия, отрезок. Работа с линейкой;
Онлайн-сборник в 2-х частях – это не источник для простого списывания домашних заданий. Наоборот, это инструмент для более глубокого понимания предмета и развития своих умений.
Word Стратегии решения задач для учащихся K – 4 классов [Бесплатные шаблоны]
Стратегии решения математических задач должны начинаться уже в детском саду или в первом классе! Поскольку в последние годы чтению научной литературы уделяется больше внимания, мы можем рассматривать текстовые задачи как часть жанра научной литературы. Загрузки для сегодняшней публикации включают несколько шаблонов или графических органайзеров, которые помогут студентам найти связь между задачами со словами и уравнениями, которые представляют эти проблемы.
Загрузки для сегодняшней публикации включают несколько шаблонов или графических органайзеров, которые помогут студентам найти связь между задачами со словами и уравнениями, которые представляют эти проблемы.
Как учитель математики, я много раз слышал, что «мы все учителя чтения», и этот пост покажет, как связаны эти две области, как математика, так и чтение, поскольку ученики создают представления, которые помогают им перейти от слов к уравнениям и наоборот.Кроме того, возьмите мои загружаемые шаблоны для нескольких представлений ниже! Используя эти шаблоны для разработки уроков, вы можете соответствовать многим Стандартам математической практики, которые лежат в основе стратегий решения математических задач.
- SMP 1: разбираться в проблемах и настойчиво их решать
- SMP 2: Обоснование абстрактно и количественно
- SMP 4: Модель с математикой
- SMP 7: Найдите и используйте структуру
Манипулятивное и визуальное представление математических словесных задач тесно связаны. Эти представления представляют собой стратегии решения математических задач, которые могут использовать учащиеся. Я надеюсь, что вы терпите меня, когда я расскажу немного об истории того, что я узнал об обучении студентов с помощью манипуляций и репрезентаций. В 1960-х Джером Брунер ввел термины активный, иконический и символический, чтобы описать, как ученики продвигаются от использования манипуляторов к созданию рисунков, основанных на манипуляциях, к использованию только чисел и символов. Сегодня мы можем назвать эти шаги конкретными, репрезентативными (полубетонными) и абстрактными.Сингапурская математика использует термины конкретный, графический и абстрактный. Все эти три набора терминов относятся к одной и той же основной стратегии мастерского использования манипуляторов для демонстрации математической идеи, затем ученики излагают эту идею с помощью бумаги и карандаша (повторно представляют ее) и, наконец, используют для обозначения только числа и символы. представляют это.
Эти представления представляют собой стратегии решения математических задач, которые могут использовать учащиеся. Я надеюсь, что вы терпите меня, когда я расскажу немного об истории того, что я узнал об обучении студентов с помощью манипуляций и репрезентаций. В 1960-х Джером Брунер ввел термины активный, иконический и символический, чтобы описать, как ученики продвигаются от использования манипуляторов к созданию рисунков, основанных на манипуляциях, к использованию только чисел и символов. Сегодня мы можем назвать эти шаги конкретными, репрезентативными (полубетонными) и абстрактными.Сингапурская математика использует термины конкретный, графический и абстрактный. Все эти три набора терминов относятся к одной и той же основной стратегии мастерского использования манипуляторов для демонстрации математической идеи, затем ученики излагают эту идею с помощью бумаги и карандаша (повторно представляют ее) и, наконец, используют для обозначения только числа и символы. представляют это.
Я бы посоветовал студентам сначала поработать с такими манипуляторами, как счетчики плюшевых мишек, маленькие кубики или даже бобы. Они помогают показать взаимосвязь между ситуациями, о которых учащиеся читают в словесной задаче.Лучше всего, чтобы они использовали шаблон для представления своей идеи, используя десятикратную рамку, числовую связь, массив или модель области и ленточную диаграмму (полубетонные, графические или пиктограммы). Наконец, они поймут значение уравнения (абстрактное или символическое представление), когда они его напишут.
Они помогают показать взаимосвязь между ситуациями, о которых учащиеся читают в словесной задаче.Лучше всего, чтобы они использовали шаблон для представления своей идеи, используя десятикратную рамку, числовую связь, массив или модель области и ленточную диаграмму (полубетонные, графические или пиктограммы). Наконец, они поймут значение уравнения (абстрактное или символическое представление), когда они его напишут.
Если вы ищете стратегии решения задач по математике в детском саду до 4-го класса, вы найдете нижеприведенные загружаемые шаблоны очень полезными. Используя шаблоны, вы можете дать учащимся стратегии для чтения текстовых задач и создания представлений для их решения или даже дать им представление и предложить им создать текстовые задачи.Используйте эти загружаемые шаблоны, чтобы дать учащимся стратегии решения математических задач, включающие сложение, вычитание, умножение и деление. Распечатайте их и используйте сегодня в своем классе!
Детский сад и 1 класс — добавление
Ожидается, что в младших классах учащиеся только прибавят. Типичная проблема со словами может быть такой: «У Криса три апельсина и два яблока. Сколько фруктов у Криса вместе? » Студенты могут смоделировать задачу, используя кубики разного цвета.В загружаемом шаблоне есть место для вопроса, после чего учащиеся могут нарисовать рисунок на основе своих манипуляций. Ключевые полуабстрактные представления для этих студентов — десять рамок и числовые связи. В частности, с числовыми связями учащиеся должны думать о частях и итогах. Наконец, студенты пишут дополнительное предложение.
Типичная проблема со словами может быть такой: «У Криса три апельсина и два яблока. Сколько фруктов у Криса вместе? » Студенты могут смоделировать задачу, используя кубики разного цвета.В загружаемом шаблоне есть место для вопроса, после чего учащиеся могут нарисовать рисунок на основе своих манипуляций. Ключевые полуабстрактные представления для этих студентов — десять рамок и числовые связи. В частности, с числовыми связями учащиеся должны думать о частях и итогах. Наконец, студенты пишут дополнительное предложение.
Для добавления доступны два шаблона. В первом есть один десятифрейм, предназначенный для детского сада, где ученики добавляют только в пределах десяти. Во втором есть две десятичные рамки, ориентированные на первый класс, где ученики складывают в пределах двадцати.Продвинутых студентов можно было бы подтолкнуть к представлению своих дополнительных предложений с помощью числовой линии, но это не входит в эту загрузку.
1 и 2 классы — Сложение и вычитание
По мере того, как учащиеся переходят в 1-й и 2-й классы, они узнают о взаимосвязи между сложением и вычитанием. Концептуально это отличается от ранней работы с простым добавлением. Стратегии решения проблем со сложением слов с двумя слагаемыми могут быть шаблонными. Два числа в словарной задаче необходимо сложить, но когда учащиеся сталкиваются с текстовыми задачами с отсутствующей частью, у них должны быть стратегии и представления, чтобы думать о частях и целых.
Концептуально это отличается от ранней работы с простым добавлением. Стратегии решения проблем со сложением слов с двумя слагаемыми могут быть шаблонными. Два числа в словарной задаче необходимо сложить, но когда учащиеся сталкиваются с текстовыми задачами с отсутствующей частью, у них должны быть стратегии и представления, чтобы думать о частях и целых.
В шаблоне для сложения и вычитания вы найдете числовые связи и ленточную диаграмму. Каждый шаблон имеет рамку с двумя числовыми связями, одна с удаленной «целиком», а другая — с одной из «частей». Студенты должны прочитать задачу и решить, является ли проблема типом отсутствующей части или отсутствующей целой. Здесь нам нужно связать чтение с математикой. Точно так же учащиеся должны заполнить ленточную диаграмму, используя идеи части и целого, но на этот раз используя знак «?» или буква как переменная, обозначающая неизвестное.
Наконец, учащиеся должны написать хотя бы одно предложение сложения или вычитания, чтобы представить проблему с помощью знака «?» или переменная для неизвестного. Затем они могут написать числовое предложение, показывающее «решение», вместо вопросительного знака или переменной. Студентов продвинутого уровня можно заставить представлять свои числовые предложения с помощью числовой линии, но это не входит в эту загрузку.
Затем они могут написать числовое предложение, показывающее «решение», вместо вопросительного знака или переменной. Студентов продвинутого уровня можно заставить представлять свои числовые предложения с помощью числовой линии, но это не входит в эту загрузку.
3-й и 4-й классы — умножение и деление
Опираясь на работу во втором классе, учащиеся 3 и 4 классов должны применять стратегии решения словесных задач, включающие умножение и деление.Эти задачи требуют другого представления, чем стратегии математических задач со словами, включающие сложение и вычитание.
Загружаемый шаблон для классов 3 и 4 включает место для модели массива, модели области и ленточной диаграммы. Для ясности: учащиеся могут представлять задачи умножения и деления слов, используя любое из этих трех представлений:
Вы можете видеть, что эта серия абстрактных представлений умножения и деления переходит от более конкретных (полуабстрактных) версий, где вы можете считать точки или квадраты, к более абстрактным версиям, где студенты переходят от счета к поиску решений. Это также помогает учащимся на начальном этапе использовать переменные для представления неизвестных, поскольку они могут маркировать отсутствующие части модели области или массива буквой.
Это также помогает учащимся на начальном этапе использовать переменные для представления неизвестных, поскольку они могут маркировать отсутствующие части модели области или массива буквой.
В последнем поле загружаемого шаблона учащихся просят написать уравнение, используя переменную или вопросительный знак для неизвестного, а затем «решить» его. Под решением я подразумеваю не использование алгебраических шагов (т. Е. Деление обеих сторон на три), а вместо этого просто написать «x = 7» в случае примера, приведенного непосредственно выше.Учащиеся могли использовать любую форму рассуждений, в том числе вернуться к использованию физических счетчиков и разделить их на равные группы.
Как стандарты математической практики соотносятся с использованием шаблонов
Я хочу поделиться некоторыми мыслями о том, как эти загружаемые шаблоны можно использовать для разработки стратегий учащихся по решению математических словесных задач и использования Стандартов математической практики (SMP).
SMP 1: разбираться в проблемах и настойчиво их решать.
Когда студентов просят составить схему, они должны четко понимать, что такое части и целое. Предоставление им представлений, таких как числовые связи, модели площадей и массивов или ленточные диаграммы, помогает им понять проблемы и взаимосвязи элементов, которые они обнаруживают при чтении слова «проблема».
SMP 2: Размышляйте абстрактно и количественно.
Когда учащиеся создают представление, такое как в Загрузке 4 (3 прямоугольника «x» равны 21), это абстрактное представление.Он ничего не говорит о том, в чем проблема. Когда ученики читают задачу о количестве (три игрушки общей стоимостью 21 доллар) и составляют ленточную диаграмму, они переходят от количеств к абстракциям. Еще один способ использования этих шаблонов — заполнить ленточную диаграмму (или модель массива или области) и попросить учащихся заполнить остальные поля. Другими словами, ученики будут создавать свои собственные задачи с текстом из ленточной диаграммы. Они начинают с абстрактного представления и приходят к количественной идее (это может быть 21 яблоко и три человека или 21 шоколад и три коробки и т. Д.).
Они начинают с абстрактного представления и приходят к количественной идее (это может быть 21 яблоко и три человека или 21 шоколад и три коробки и т. Д.).
SMP 4: Модель с математикой.
Такие модели, такие как модели с областями и ленточные диаграммы, если они будут внедрены на раннем этапе, помогут учащимся, когда они используют модели областей в старших классах для моделирования более сложных задач.
SMP 7: Ищите и используйте структуру.
Чтение задач со словами, а затем создание представлений с использованием шаблонов поможет учащимся искать ключевые слова и их отношение к структуре частей и целых, строк и столбцов, факторов, итогов и делителей.Просмотр общих базовых структур с использованием числовых связей, десяти рамок, моделей площадей и массивов, а также ленточных диаграмм помогает укрепить общие базовые структуры, которые появляются в различных текстовых задачах.
Резюме
Загрузите и используйте мои бесплатные шаблоны, чтобы помочь студентам установить связь между задачами со словами и уравнениями, которые представляют эти проблемы. Когда вы это сделаете, вы научите учащихся использовать «Стандарты математической практики», описанные выше, давая им возможность представить себе в голове проблемы со словами и создать представления, показывающие взаимосвязь задействованных количеств.
Когда вы это сделаете, вы научите учащихся использовать «Стандарты математической практики», описанные выше, давая им возможность представить себе в голове проблемы со словами и создать представления, показывающие взаимосвязь задействованных количеств.
Иллюстративная математика
Иллюстративная математика
Класс 3
-
Пока нет задач, иллюстрирующих этот стандарт.
-
Пока нет задач, иллюстрирующих этот стандарт.
3.OA. 3 класс — Операции и алгебраическое мышление
3. О.А.А. Представляйте и решайте задачи, связанные с умножением и делением.
3.OA.A.1. Интерпретируйте произведения целых чисел, например, интерпретируйте $ 5 \ times 7 $ как общее количество объектов в 5 группах по 7 объектов в каждой. Например, опишите контекст, в котором общее количество объектов может быть выражено как $ 5 \ times 7 $.
3.OA.A.2. Интерпретируйте целочисленные частные целых чисел, например, интерпретируйте $ 56 \ div 8 $ как количество объектов в каждой доле, когда 56 объектов разделены поровну на 8 долей, или как количество долей, когда 56 объектов разделены на равные доли По 8 предметов.
 Например, опишите контекст, в котором количество акций или групп может быть выражено как $ 56 \ div 8 $.
Например, опишите контекст, в котором количество акций или групп может быть выражено как $ 56 \ div 8 $.
3.OA.A.3. Используйте умножение и деление в пределах 100 для решения задач со словами в ситуациях, связанных с равными группами, массивами и измеряемыми величинами, например, используя рисунки и уравнения с символом неизвестного числа, чтобы представить проблему.
3.OA.A.4. Определите неизвестное целое число в уравнении умножения или деления, связывающего три целых числа. Например, определить неизвестное число, которое делает уравнение истинным в каждом из уравнений $ 8 \ times? = 48 $, $ 5 = \ boxvoid \ div 3 $, $ 6 \ times 6 =? $
3.О.А.Б. Поймите свойства умножения и взаимосвязь между умножением и делением.
3.OA.B.5. Применяйте свойства операций как стратегии умножения и деления. Примеры: Если известно $ 6 \ times 4 = 24 $, то известно также $ 4 \ times 6 = 24 $. (Коммутативное свойство умножения.
 ) $ 3 \ times 5 \ times 2 $ можно найти по $ 3 \ times 5 = 15 $, затем $ 15 \ times 2 = 30 $, или по $ 5 \ times 2 = 10 $, затем $ 3 \ times 10 = 30 $. (Ассоциативное свойство умножения.) Зная, что $ 8 \ times 5 = 40 $ и $ 8 \ times 2 = 16 $, можно найти $ 8 \ times 7 $ как $ 8 \ times (5 + 2) = (8 \ times 5) + (8 \ раз 2) = 40 + 16 = 56 $.(Распределительное свойство.)
) $ 3 \ times 5 \ times 2 $ можно найти по $ 3 \ times 5 = 15 $, затем $ 15 \ times 2 = 30 $, или по $ 5 \ times 2 = 10 $, затем $ 3 \ times 10 = 30 $. (Ассоциативное свойство умножения.) Зная, что $ 8 \ times 5 = 40 $ и $ 8 \ times 2 = 16 $, можно найти $ 8 \ times 7 $ как $ 8 \ times (5 + 2) = (8 \ times 5) + (8 \ раз 2) = 40 + 16 = 56 $.(Распределительное свойство.)
3.OA.B.6. Поймите разделение как проблему с неизвестным фактором. Например, найдите $ 32 \ div 8 $, найдя число, которое дает 32 $ при умножении на 8 $.
3.OA.C. Умножаем и делим в пределах 100.
3.OA.C.7. Плавно умножайте и делите в пределах 100, используя такие стратегии, как взаимосвязь между умножением и делением (например,g., зная, что $ 8 \ times 5 = 40 $, человек знает $ 40 \ div 5 = 8 $) или свойства операций. К концу 3 класса выучить по памяти все произведения двух однозначных чисел.

3.OA.D. Решайте задачи, связанные с четырьмя операциями, а также выявляйте и объясняйте закономерности в арифметике.
3.OA.D.8. Решите двухэтапные задачи со словами, используя четыре операции. Представьте эти проблемы, используя уравнения с буквой, обозначающей неизвестную величину. Оцените разумность ответов с помощью мысленных вычислений и стратегий оценки, включая округление.
3.OA.D.9. Определите арифметические шаблоны (включая шаблоны в таблице сложения или таблице умножения) и объясните их, используя свойства операций. Например, заметьте, что четырехкратное число всегда четно, и объясните, почему четырехкратное число можно разложить на два равных слагаемых.
3.NBT. 3 класс — Число и операции в десятичной системе счисления
3.NBT.A. Используйте понимание разрядов и свойства операций для выполнения многозначной арифметики.
3.NBT.A.1. Используйте расстановку знаков для округления целых чисел до ближайших 10 или 100.

3.NBT.A.2. Свободно складывайте и вычитайте в пределах 1000, используя стратегии и алгоритмы, основанные на разряде, свойствах операций и / или взаимосвязи между сложением и вычитанием.
3.NBT.A.3. Умножайте однозначные целые числа на кратные 10 в диапазоне 10–90 (например, $ 9 \ times 80 $, $ 5 \ times 60 $), используя стратегии, основанные на разрядах и свойствах операций.
-
Пока нет задач, иллюстрирующих этот стандарт.
-
Пока нет задач, иллюстрирующих этот стандарт.
-
Пока нет задач, иллюстрирующих этот стандарт.
3. Н.Ф. 3 класс — Число и операции — Дроби
3. Н.Ф.А. Развивайте понимание дробей как чисел.
3.NF.A.1. Под дробью $ 1 / b $ понимается количество, образованное 1 частью, когда целое делится на $ b $ равных частей; Под дробью $ a / b $ понимается количество, образованное частями $ a $ размером $ 1 / b $.
3.NF.A.2. Дробь следует понимать как число на числовой прямой; представляют дроби на числовой линейной диаграмме.
3.NF.A.2.a. Изобразите дробь $ 1 / b $ на числовой линейной диаграмме, определив интервал от 0 до 1 как целое и разделив его на равные части $ b $.
 Помните, что каждая часть имеет размер $ 1 / b $ и что конечная точка части, основанная на 0, определяет местонахождение числа $ 1 / b $ в числовой строке.
Помните, что каждая часть имеет размер $ 1 / b $ и что конечная точка части, основанная на 0, определяет местонахождение числа $ 1 / b $ в числовой строке.
3.NF.A.2.b. Изобразите дробь $ a / b $ на числовой линейной диаграмме, отметив $ a $ lengths $ 1 / b $ от 0.Помните, что результирующий интервал имеет размер $ a / b $ и что его конечная точка находит число $ a / b $ в числовой строке.
3.NF.A.3. Объясните эквивалентность дробей в особых случаях и сравните дроби, рассуждая об их размере.
3.NF.A.3.a. Считайте две дроби эквивалентными (равными), если они имеют одинаковый размер или одну и ту же точку на числовой прямой.
3.NF.A.3.b. Распознавайте и генерируйте простые эквивалентные дроби, например, $ 1/2 = 2/4 $, $ 4/6 = 2/3 $. Объясните, почему дроби эквивалентны, например, используя визуальную модель дробей.
3.NF.A.3.c. Выражайте целые числа как дроби и распознавайте дроби, которые эквивалентны целым числам. Примеры: Выразите $ 3 $ в форме $ 3 = 3/1 $; признать, что $ 6/1 = 6 $; поместите $ 4/4 $ и $ 1 $ в одну и ту же точку числовой линейной диаграммы.
3.NF.A.3.d. Сравните две дроби с одним и тем же числителем или одним знаменателем, рассуждая об их размере. Признайте, что сравнения действительны только тогда, когда две дроби относятся к одному и тому же целому. Запишите результаты сравнений с помощью символов $> $, = или $
<$ и обоснуйте выводы, например, используя модель визуальной дроби.
-
Пока нет задач, иллюстрирующих этот стандарт.
-
Пока нет задач, иллюстрирующих этот стандарт.
-
Пока нет задач, иллюстрирующих этот стандарт. -
Пока нет задач, иллюстрирующих этот стандарт.
-
Пока нет задач, иллюстрирующих этот стандарт.
-
Пока нет задач, иллюстрирующих этот стандарт.
-
Пока нет задач, иллюстрирующих этот стандарт.
3.MD. Уровень 3 — Измерения и данные
3.MD.A. Решайте задачи, связанные с измерением и оценкой интервалов времени, объемов жидкости и масс объектов.
3.MD.A.1. Назовите и запишите время с точностью до минуты и измерьте интервалы времени в минутах. Решайте задачи со словами, включая сложение и вычитание временных интервалов в минутах, например, представляя задачу на числовой диаграмме.
3.MD.A.2. Измеряйте и оценивайте объемы жидкости и массу объектов, используя стандартные единицы: граммы (г), килограммы (кг) и литры (л).Сложите, вычтите, умножьте или разделите, чтобы решить одностадийные задачи со словами, включающие массы или объемы, указанные в одних и тех же единицах, например, используя чертежи (например, стакан с измерительной шкалой) для представления проблемы.
3.MD.B. Представляйте и интерпретируйте данные.
3.MD.B.3. Нарисуйте масштабированный графический график и масштабированную гистограмму, чтобы представить набор данных с несколькими категориями. Решайте одно- и двухэтапные задачи «на сколько больше» и «на сколько меньше», используя информацию, представленную в виде масштабированных гистограмм.Например, нарисуйте гистограмму, в которой каждый квадрат гистограммы может представлять 5 домашних животных.
3.MD.B.4. Генерируйте данные измерений, измеряя длину с помощью линейки, отмеченной половинками и четвертью дюйма. Покажите данные, построив линейный график, на котором горизонтальная шкала обозначена соответствующими единицами — целыми числами, половинками или четвертями.
3.MD.C.Геометрические измерения: понять понятия площади и соотнести площадь с умножением и сложением.
3.MD.C.5. Распознайте площадь как атрибут плоских фигур и поймите концепции измерения площади.
3.MD.C.5.a. Квадрат со стороной 1 единица, называемый «единичный квадрат», считается имеющим «одну квадратную единицу» площади и может использоваться для измерения площади.
3.MD.C.5.b. Плоская фигура, которую можно покрыть без промежутков или перекрытий на $ n $ единиц квадратов, называется площадью $ n $ квадратных единиц.
3.MD.C.6. Измерьте площади, считая единичные квадраты (квадратные сантиметры, квадратные метры, квадратные дюймы, квадратные футы и импровизированные единицы).
3.MD.C.7. Отнесите область к операциям умножения и сложения.
3.MD.C.7.a. Найдите площадь прямоугольника с целыми числами сторон, выложив его мозаикой, и покажите, что площадь такая же, как и при умножении длин сторон.
3.MD.C.7.b. Умножьте длины сторон, чтобы найти площади прямоугольников с целочисленными длинами сторон в контексте решения реальных и математических задач, и представьте целочисленные произведения в виде прямоугольных областей в математических рассуждениях.
3.MD.C.7.c. Используйте мозаику, чтобы показать в конкретном случае, что площадь прямоугольника с целочисленными длинами сторон $ a $ и $ b + c $ равна сумме $ a \ times b $ и $ a \ times c $. Используйте модели площади, чтобы представить свойство распределения в математических рассуждениях.
3.MD.C.7.d. Распознайте область как добавочную. Найдите области прямолинейных фигур, разложив их на неперекрывающиеся прямоугольники и добавив области неперекрывающихся частей, применяя эту технику для решения реальных проблем.
3. MD.D. Геометрические измерения: распознать периметр как атрибут плоских фигур и различать линейные измерения и измерения площади.
3.MD.D.8. Решение реальных и математических задач, связанных с периметрами многоугольников, включая поиск периметра с учетом длины сторон, поиск неизвестной длины стороны и отображение прямоугольников с одинаковым периметром и разными областями или с одинаковой площадью и разными периметрами.
-
Пока нет задач, иллюстрирующих этот стандарт.
3.G. 3 класс — Геометрия
3.Г.А. Размышляйте с формами и их атрибутами.
3.G.A.1. Поймите, что формы в разных категориях (например, ромбы, прямоугольники и другие) могут иметь общие атрибуты (например, иметь четыре стороны), и что общие атрибуты могут определять более крупную категорию (например, четырехугольники). Считайте ромбы, прямоугольники и квадраты примерами четырехугольников и нарисуйте примеры четырехугольников, которые не принадлежат ни к одной из этих подкатегорий.
3.G.A.2. Разделите фигуры на части равной площади. Выразите площадь каждой части как единичную долю от целого. Например, разделите фигуру на 4 части с равной площадью и опишите площадь каждой части как 1/4 площади фигуры.
Обучение навыкам решения задач по математике в третьем классе
Классная комната крупным планом: математика для 3-го класса: настойчивость в решении проблем с
Дженнифер Сол
[01: 00: 07; 10]
Дженнифер: «Можно ли ошибаться?
Все: «ДА!»
Дженнифер: «Итак, вы просто исправляете их и учитесь у них.Ошибки легко исправить ».
Очень важно создать сильную классную культуру. Вы должны нормализовать ошибку. Они должны знать, что пытаться, пытаться и пробовать снова — это нормально. Мы хотим, чтобы они боролись с проблемой и оставались с ней. Итак, мы придумали «Найди три пути».
Надеюсь, это занятие поможет им взять на себя ответственность за собственное обучение.
«Хорошо, мне нужна дополнительная помощь».
Итак, вначале я представляю им проблему и действительно обращаюсь к их чувству сочувствия.
«Мне нужна твоя помощь, чтобы разобраться с четырьмя голодными учителями, хватит ли моих 20 долларов на покупку четырех буррито и, если этого хватит, есть ли у меня что-нибудь, чтобы, может быть, купить газировку? Ты попробуешь найти три разных способа решить проблему.»
Как только проблема записана на доске, их отправляют обратно на свои места вместе со своим регистрационным листом. У одной стороны есть области, в которых они могут работать, и идеи для использования стратегий. И задняя сторона намеренно оставлена пустой. Итак, у них много свободы.
«Помните, что наша первоначальная попытка решить эту проблему — это самостоятельная работа».
У них есть четыре минуты, чтобы самостоятельно разобраться с проблемой и попытаться решить ее всеми возможными способами.
«Что ты делал? О, со своего стола?»
Если они смогут решить ее тремя способами и трижды прийти к одному и тому же ответу, это повысит их уровень уверенности. Они могут убедить себя, и им не нужно ждать, пока учитель подойдет и скажет: «Ага, вы поняли.«
«Хорошо … обсудим со своим столом».
А затем мы делаем то, что называется «Головами вместе, встаем!» Мы хотим, чтобы их головы были вместе, показывая друг другу, в чем они преуспели, возможно, другие, кто нуждается в поддержке или не знает, что с ней делать, смогут получить представление.
Сара: «Как ты получила этот ответ? Я получила его, добавив это».
Лизетта: «Я получила это, сложив четыре и четыре и добавив двенадцать и двенадцать».
Сара: «Хорошо.»
Дженнифер: Им разрешено копировать записи друг друга, пока они обсуждают, почему что-то было сделано определенным образом.Для них это шанс попрактиковаться в использовании языка и обсудить то, что они делают.
Все это время я стараюсь вращаться по комнате, предлагать поддержку. И поэтому я буду иметь в виду, кого бы я хотел вывести из класса и поделиться своей работой.
«Покажите мне, пожалуйста, позиции для обучения».
Они поворачиваются к передней части комнаты, и вызывают троих студентов, я использую свою документ-камеру, и они могут показать и объяснить свою работу.
Карлос: «Затем я добавил единицы, 1,2,3,4.«
Эстаблан: «Затем я умножил четыре на четыре, получилось 16.»
Сара: «Сначала я сделала таблицу. В первые две коробки я поместила учителей и сумму».
Дженнифер: Решение, ориентированное на учеников, повышает нашу культуру обучения в классе. Я не говорю, как им добиться определенного результата. Это позволяет им выбирать свой собственный путь, но также открывает двери для консультаций друг с другом и сотрудничества, которые являются жизненными навыками, которые нужны каждому.
Учебные материалы, рабочие листы и задания по решению проблем
Выберите ваше местоположение
Выбор страны и штата поможет нам предоставить вам наиболее подходящие учебные ресурсы для ваших учеников.
Страна Австралия Соединенные Штаты Соединенное Королевство Афганистан Иландские острова Албания Алжир Американское Самоа Андорра Ангола Ангилья Антарктика Антигуа и Барбуда Аргентина Армения Аруба Австралия Австрия Азербайджан Багамы Бахрейн Бангладеш Барбадос Беларусь Бельгия Белиз Бенин Бермуды Бутан Боливия, Многонациональное Государство Сабациона и Герцеговина Бонавия Остров Буве Бразилия Британская территория в Индийском океане Бруней-Даруссалам Болгария Буркина-Фасо Бурунди Камбоджа Камерун Канада Кабо-Верде Каймановы острова Центральноафриканская Республика Чад Чили Китай Остров Рождества Кокосовые (Килинг) острова Колумбия Коморские острова Конго Конго, Демократическая Республика Острова Кука Коста-Рика Кот д’Ивуар Хорватия Куба Кюрасао Кипр Чешская Республика Дания Джибути Доминика Доминиканская Республика Эквадор Египет Сальвадор Экваториальная Гвинея Эритрея Эстония Эфиопия Фолклендские (Мальвинские) острова Фарерские острова Фиджи Финляндия Франция Французская Гвиана Французская Полинезия Французские южные территории страны Габон Гамбия Грузия Германия Гана Гибралтар Греция Гренландия Гренада Гваделупа Гуам Гватемала Гернси Гвинея Гвинея-Бисау Гайана Гаити Остров Херд и острова Макдональд Святой Престол (государство-город Ватикан) Гондурас Гонконг Венгрия Исландия Индия Индонезия Иран, Исламская Республика Ирак Ирландия Остров Мэн Израиль Италия Ямайка Япония Джерси Иордания Казахстан Кения Кирибати Корея, Корейская Народно-Демократическая Республика, Республика Кувейт Кыргызстан Лаосская Народно-Демократическая Республика Латвия Ливан Лесото Либерия Ливия Лихтенштейн Литва Люксембург Макао Македония, бывшая югославская Республика Мадагаскар Малави Малайзия Мальдивы Мали Мальта Маршалловы острова Мартиник Мавритания Маврикий Майотта Мексика Микронезия, Федеративные Штаты Молдовы, Республика Монако Монголия Черногория Монтсеррат Марокко Мозамбик Мьянма Намибия Науру Непал Нидерланды Новая Каледония Новая Зеландия Никарагуа Нигер Нигерия Ниуэ Остров Норфолк Северные Марианские острова Норвегия Оман Пакистан Палау Палестина , Государство Панама Папуа-Новая Гвинея Парагвай Перу Филиппины Питкэрн Польша Португалия Пуэрто-Рико Катар Румыния Российская Федерация Руанда Сен-Бартелеми Остров Святой Елены, Вознесения и Тристан-да-Кунья Сент-Китс и Невис Сент-Люсия Сен-Мартен (французская часть) Сен-Пьер и Микелон Сент-Винсент и Гренадины Самоа Сан-Марино Сан-Томе и Принсипи Саудовская Аравия Сенегал Сербия Сейшельские острова Сьерра-Леоне Сингапур Синт-Мартен (голландская часть) Словакия Соломоновы острова Сомали Южная Африка Южная Джорджия и Южные Сандвичевы острова Южный Судан Испания Шри-Ланка Судан Суринам Свальбард и Ян-Майен Свазил Швеция Швейцария Сирийская Арабская Республика Тайвань, провинция Китая Таджикистан Танзания, Объединенная Республика Таиланд Тимор-Лешти Того Токелау Тонга Тринидад и Тобаго Тунис Турция Туркменистан Острова Теркс и Кайкос Тувалу Уганда Украина Объединенные Арабские Эмираты Соединенное Королевство Соединенные Штаты Малые отдаленные острова США Уругвай Узбекистан Вануату Венесуэла, Бол ivarian Республика Вьетнам Виргинские острова, Британские Виргинские острова, U.С. Уоллис и Футуна Западная Сахара Йемен Замбия ZimbabweState Австралийская столичная TerritoryNew Южная WalesNorthern TerritoryQueenslandSouth AustraliaTasmaniaVictoriaWestern AustraliaAlabamaAlaskaAmerican SamoaArizonaArkansasCaliforniaColoradoConnecticutDelawareDistrict Из ColumbiaFederated Штатов MicronesiaFloridaGeorgiaGuamHawaiiIdahoIllinoisIndianaIowaKansasKentuckyLouisianaMaineMarshall IslandsMarylandMassachusettsMichiganMinnesotaMississippiMissouriMontanaNebraskaNevadaNew HampshireNew JerseyNew MexicoNew YorkNorth CarolinaNorth DakotaNorthern Mariana IslandsOhioOklahomaOregonPalauPennsylvaniaPuerto RicoRhode IslandSouth CarolinaSouth DakotaTennesseeTexasUtahVermontVirgin IslandsVirginiaWashingtonWest VirginiaWisconsinWyoming
3 Стратегии властвуй Math Слово Проблемы
Гостевая почта Кэди Дюпре
Вот вам задача со словом:
Класс мисс Фрайдей решает ежедневную задачу со словами.Десять ее учеников отлично справляются со словесными задачами, связанными с сложением, и только 7, кажется, понимают задачи на вычитание слов. Пятерым ее ученикам наскучили простые задачи. Тринадцать учеников все еще не могут усвоить основные математические факты, а трое вообще не могут читать задачи со словами. Сколько ее учеников занимаются и учатся?
Вот лучший вопрос: «Как вырастить уверенных и эффективных лиц, решающих проблемы?»
рассмотрение проблемы со словом приводит к тревоге.Никто не может ясно мыслить с ощущением страха или страха перед неудачей!
Проблема № 2: Гибкое мышление
Многих детей учат решать задачи со словами методически, с помощью подробного пошагового плана с использованием ключевых слов, которые не всегда работают. Планы хороши, но не тогда, когда ученики используют их как костыль, а не как инструмент. Сегодняшние стандартизированные тесты и реальные приложения требуют творческого мышления и гибкости в стратегиях.
Проблема № 3: Дифференциация
Учителя хотят, чтобы учащиеся быстро преуспели, и часто работают слишком быстро, слишком быстро.В случае проблем со словами вы должны действовать медленно, чтобы идти быстро. Как и в случае с управляемым чтением, вам нужно много практиковаться с «правильными» задачами и проводить управляемую практику с задачами чуть выше уровня учеников.
3 стратегии решения проблем
Решение состоит в том, чтобы преодолеть математические словесные проблемы с помощью классных стратегий, которые противодействуют вышеуказанным проблемам!
1. Обучите рутинному решению проблем
Дети (и взрослые) известны своей импульсивностью в решении проблем.Многие студенты видят проблему со словами и хотят сразу же выхватить эти числа и «что-то с ними сделать». Когда я учился в начальной школе, это была довольно надежная стратегия! Но сегодня детей просят решать гораздо более сложные задачи, часто с помощью сложных формулировок или намеренных отвлекающих факторов.
Развивайте гибких мыслителей и укрепляйте уверенность в себе, обучая рутине. Процедура решения проблем просто побуждает студентов замедлиться и подумать до и после решения. Я видел много эффективных процедур, но мои любимые всегда включают в себя образ мышления «до, во время и после».
Чтобы сделать повседневное решение проблем значимым и эффективным:
- Используйте его часто (если возможно, ежедневно)
- Включите «Повернись и научи» (учащиеся устно объясняют свое мышление и процесс партнеру.)
- Разрешить «Стратегию» Поделиться »после решения (Отобранные ученики объясняют свой метод и образ мышления.)
2. Различия словесных задач
Нет, это не означает, что каждому ученику нужно писать разные словесные задачи! Это может быть так же просто, как корректировка чисел в задаче или удаление отвлекающих факторов для испытывающих трудности учащихся.Построение строительных лесов для задач со словами повысит уверенность в себе и улучшит навыки решения проблем за счет постепенного повышения уровня сложности по мере того, как ребенок будет к этому готов. Это особенно эффективно, когда вы пытаетесь научить студентов разным структурам текстовых задач для выполнения определенной операции.
Например, некоторым ученикам очень сложно решать задачи на вычитание сравнения. Начав с простой версии, вы позволите студентам сосредоточиться на самой проблеме, а не испугаться или разочароваться.
Я добился больших успехов в использовании задач с каркасом в моих математических группах. Решив более простую задачу, ученики понимают, что это не так уж сложно, и готовы браться за более сложные!
3. Сопоставьте задачи бок о бок
Для развития гибкого мышления нет ничего более мощного, чем анализ и сравнение текстовых задач. Начните с задач, которые имеют похожие истории и номера, но разную структуру. Поощряйте разговор, используйте визуальные представления и попросите учащихся объяснить разницу в структуре и действиях.Вот пример, показывающий работу студентов над двумя похожими проблемами об обезьянах. Щелкните здесь, чтобы загрузить пустую копию этих проблем. Моя халява включает в себя несколько вариантов, которые помогут вам отличиться.
Используйте эти три стратегии, чтобы заставить детей думать и говорить о своих стратегиях решения проблем, в то же время укрепляя эту «о-о-очень важную» уверенность, и вы МОЖЕТЕ победить математические словесные задачи!
Кэди Дюпре работала классным руководителем, инструктором и учителем интервенции в начальных классах.Ей нравится создавать учебные ресурсы для студентов и учителей. Она ведет Teacher Trap, блог, цель которого — поделиться своими проблемами, успехами и идеями как учителя.
Строгое решение математических задач? Учти это!
Мы все слышали слово «строгий» в отношении инструкций по математике и математических задач. Что такое математическая строгость и как мы можем ее поощрять?
Что говорит NCTM?
Национальный совет учителей математики дает несколько советов по этому поводу.Посмотрите, что вы думаете.
- Математические задачи требуют усилий . Подумайте, что именно представляет собой это «правильное» усилие — достаточно, чтобы бросить вызов студентам с достаточным разочарованием для участия, но недостаточно, чтобы разочароваться.
- Задачи должны быть богатыми и иметь несколько точек входа и возможности для расширения и обогащения.
- Решения могут быть «беспорядочными» и иметь нескольких решений . На самом деле решение менее важно, чем сам процесс решения проблемы.
- Строгие математические задачи содержат математические материалы, актуальные для учащихся , и развивают связи между математическими понятиями.
- Качественные математические задания развивают стратегическое и гибкое мышление . Учащиеся, занятые этими задачами, используют свои рассуждения и чувство числа, чтобы помочь им продолжить.
- Тщательный математический опыт предполагает активное обучение, а — это ВСЕ студенты, , а не только самые одаренные.
- Наконец-то сотрудничают ! Решение проблем не должно быть уединенным занятием! Поощряйте партнеров и команды работать вместе, говорить о математике и добиваться успеха вместе.
Мой вопрос к вам: дает ли ваша математическая серия такой математический опыт? У меня, конечно, нет.
Открытые испытания для 2–3 классов
Здесь я знал, что могу помочь своим ученикам и другим учителям. Я знал, какие задачи нужны моим ученикам, и решил их создавать.
Как вы знаете, разработка сложных математических задач теперь стала одной из моих страстей, и я просто хотел сообщить вам, что я закончил свою коллекцию из четырех открытых наборов задач (4 набора по 3 задачи ) Последний набор летних испытаний (идеально подходит для решения проблем в теплую погоду — задания включают костры, посещение фестиваля, поездку на пляж), и его можно найти, щелкнув СПРАВО ЗДЕСЬ.Цена НАБОРНЫЙ ресурс сэкономит вам кучу денег, если вы хотите, чтобы задачи выполнялись круглый год.
Этот набор организован по сезонам, потому что я знаю, что многие учителя любят выполнять задания в течение года, но ни одно из этих заданий НЕ НУЖНО выполнять в течение «назначенного» сезона. Зимой я выполнял задание по бейсболу, потому что сказал своим ученикам, что скучаю по бейсболу!
Этот набор задач идеально подходит для вашего класса, если…
- Вы преподаете 2 или 3 классы и хотите, чтобы ваши ученики могли бросить вызов и развить у них стратегии решения проблем и настойчивость.
- Или вы преподаете 4 или 5 классы, а ваши ученики — неопытные решатели задач, которым нужен опыт решения сложных задач с менее сложными вычислениями.
- Вы хотите, чтобы ваши ученики познакомились со Стандартами математической практики.
- Может быть, вам нужны качественные математические задания для математических станций или центров.
- Ваша математическая серия лишила возможности «мышления» решения проблем, когда учащимся не нужно применять несколько стратегий или навыков в рамках одной задачи.
- Вам нужны готовые к печати, не требующие особой подготовки математические задания, которые помогут быстро завершить работу, которые будут значимыми и увлекательными.
- Вы хотите иметь ЦИФРОВОЙ ДОСТУП к задачам в дополнение к печатным версиям!
- И многое другое!
Так для какого уровня он ДЕЙСТВИТЕЛЬНО предназначен?
Это всегда такой непростой вопрос. Я преподаю в четвертом классе, и я использовал эти задания для 2-3 классов со своим классом, потому что я много учил с более сложными задачами, но я хотел, чтобы они выполняли задачи ПОЛНОСТЬЮ самостоятельно.Я хочу, чтобы они взялись за этот стандарт «разбираться в проблемах и упорствовать». Этот стандарт часто игнорируется. Мы думаем ЗА наших учеников и слишком много руководим ими. Не поймите меня неправильно — есть время и место для этих инструкций, но я хочу убедиться, что мои ученики тоже могут работать независимо. Они идеальны!
Учителя третьего класса сочтут их идеальными для этого «управляемого» обучения. Это будет варьироваться в зависимости от класса (или группы учеников), потому что мы все знаем, что все третьеклассники не созданы равными! Знайте, что большинству третьеклассников потребуется какое-то введение в задачу.Некоторым может потребоваться помощь с чтением (хотя я много работал, чтобы язык оставался простым, а структура предложений ясной). Другим учащимся может потребоваться помощь в понимании организации задач, поскольку они являются многоэтапными. Я сознательно разбил задания на разделы, чтобы помочь студентам точно знать, что им делать. Другим ученикам может потребоваться поддержка со стратегиями и советами по решению. Может, им нужны манипуляторы. Возможно, вы захотите предложить калькуляторы для проверки работы. Вы делаете то, что нужно ВАШИМ СТУДЕНТАМ!
Наконец, этот ресурс может быть идеальным для обогащения способных учеников-математиков или дополнительных групп во 2-м классе.Другие учителя 2-го класса также могут посчитать эти задания идеальными для совместного решения проблем. В зависимости от вашей группы, вам может потребоваться вести группы по пути, или вам может просто потребоваться быстрое введение и отправка их в путь! Это также отличный способ отличиться. Дайте каждой группе именно то, что им нужно.
Так что вы думаете? Заинтересованы? НАЖМИТЕ ЗДЕСЬ, чтобы получить этот набор! Знайте, что он был обновлен, чтобы иметь полный цифровой доступ!
Возможно, вас заинтересует аналогичный ресурс, который больше ориентирован на учащиеся 3–5 классов — просто НАЖМИТЕ ЗДЕСЬ, чтобы увидеть эти задачи! Эти проблемы также включали цифровой доступ для всех задач.
Приколоть на потом?
Добро пожаловать в Space Math @ NASA!
Дроби и смешанные числа
Задача 546: Относительные размеры планет и других объектов
Учащиеся используют пропорциональную информацию для определения относительных масштабов планет и больших лун в Солнечной системе.[Оценка: 3-5 | Темы: масштаб; пропорция]
[Кликните сюда]
Задача 493: Развлечение с шестеренками и дробями
Учащиеся узнают, как простые дроби используются для описания шестерен и зубчатых передач, которые уменьшают или увеличивают скорость.
[Оценка: 4-7 | Темы: умножение простых дробей]
[Нажмите здесь]
Задача 465: Сравнение планет, вращающихся вокруг других звезд
Студенты используют простую арифметику дробей для определения относительных размеров нескольких новых планет, недавно открытых миссией Кеплера,
и сравните эти размеры с размерами Юпитера и Земли.[Оценка: 3-5 | Темы: масштабные модели; пропорции; дроби]
[Кликните сюда]
Задача 464: Большие Луны и Малые планеты
Учащиеся работают с масштабным рисунком 26 больших лун Солнечной системы и вместе с упражнением используют простые
фракций, исследуйте относительные размеры лун по сравнению с Землей.
[Оценка: 3-5 | Темы: масштабные модели; пропорции; дроби]
[Кликните сюда]
Задача 347: Еще больше молекулярного безумия!
Учащиеся подсчитывают количество атомов в молекуле ципрофлоаксцина, чтобы определить его химическую формулу и массу.[Оценка: 3-5 | Темы: Подсчет; умножение]
[Кликните сюда]
Задача 297: Атомы — какие они сладкие!
Простое действие счета основано на атомах в молекуле сахара. Студенты
рассчитывать соотношения и проценты
различных типов атомов в молекуле.
[Оценка: 4-8 | Темы: Подсчет; Коэффициенты; процент] [Нажмите здесь]
Задача 242: Подсчет атомов в молекулах
Учащиеся подсчитывают количество атомов в простой молекуле и определяют основные доли, проценты и массы.они также завершают
химическая формула соединения.
[Оценка: 3-6 | Темы: целые числа; подсчет похожих вещей; фракции; проценты] [Нажмите здесь]
Задача 230: Расстояния галактик и смешанные фракции-
Учащиеся используют относительные расстояния до ближайших галактик, выраженные смешанными числами, для определения расстояний между выбранными галактиками.
[Оценка: 3-5 | Темы: Основы математики дробей.] [Щелкните здесь]
Задача 229: Атомные числа и умножение дробей-
Учащиеся используют отрывок из Периодической таблицы элементов, чтобы выяснить идентичность атомов на основе числовых подсказок, выраженных в виде смешанных чисел.[Оценка: 3-5 | Темы: Основы математики дробей; смешанные числа.] [Нажмите здесь]
Задача 217: Фракции и химия-
Студенты изучают простые химические уравнения, используя простые пропорции и смешанные числа.
[Оценка: 3-6 | Темы: Основы математики дробей; соотношения.] [Щелкните здесь]
Задача 216: Атомные доли-
Студенты изучают энергетические лестницы атома и определяют, используя разницу между смешанными числами, полученную энергию.
или теряется электроном при движении вверх и вниз по лестнице.[Оценка: 3-6 | Темы: Основы математики дробей] [Нажмите здесь]
Задача 215: Больше атомных фракций-
Студенты изучают энергетические лестницы атома и определяют, используя разницу между смешанными числами, полученную энергию.
или теряется электроном при движении вверх и вниз по лестнице.
[Оценка: 3-6 | Темы: Основы математики дробей.] [Щелкните здесь]
Задача 214: Атомные фракции III-
Студенты изучают энергетические лестницы атома и определяют, используя разницу между смешанными числами, полученную энергию.
или теряется электроном при движении вверх и вниз по лестнице.[Оценка: 3-6 | Темы: Основы математики дробей.] [Щелкните здесь]
Задача 180: Планеты, дроби и весы-
Учащиеся работают с относительными сравнениями планет, чтобы определить фактические размеры планет с учетом диаметра Земли.
[Оценка: 4-6 | Темы: масштабные модели; десятичные дроби; дроби] [Нажмите здесь]
Задача 165: Дроби в пространстве —
Учащиеся исследуют множество способов, которыми простые дроби возникают при изучении движения планет.[Оценка: 3-5 | Темы: работа с дробями; расчет времени] [Нажмите здесь]
Задача 166: Доллары и центы исследований —
Студенты работают с суммами в долларах, почасовой ставкой заработной платы, процентами, чтобы исследовать различные модели стоимости научных исследований с точки зрения отдельного ученого.
[Оценка: 4-6 | Темы: проценты, десятичная математика, простые ставки (например, доллары / час)] [Нажмите здесь]
.
