>>> from sympy import cos, Symbol, nsolve
 >>> x = Symbol('x')
 >>> consts = [random. 2 ==...
Использование python 2.7.10 fsolve для нахождения корня одного переменного нелинейного уравнения с заданной константой
 Извините, я новенькая Я хотел бы найти корень уравнения f (x) = exp (x)*erfc(sqrt(x)) - (1/(1+y)) где y-константа, переданная в уравнение. Я написал следующее в Python 2.7.10 1 from scipy.optimize...
Решение уравнения с python
 У меня есть проблема с решением этого уравнения: ra = (1.5 * (ca - (ra/2))/(1 + 0.8 * (ca - (ra/2)))) Я должен ввести переменную  ca в качестве поплавка, а затем python должен найти мне значение ra ...
Найти весь корень уравнения между заданным диапазоном
 Я пытаюсь найти весь корень между диапазоном уравнения как: def f(x): return np.tan(x) - 3*x from scipy.optimize import fsolve In [14]: fsolve(f,0) Out[14]: array([ 0.]) # one of the root of the eqn...
Python. Найти уравнение квадратные уравнения, учитывая его корни
 Пожалуйста, помогите мне написать простую программу python, которая берет два корня квадратного уравнения в качестве функций и возвращает полную квадратику equation. .Sort обратного квадратного...
Python решения уравнения угломерные
 Я использую Python. У меня есть формулы типа sin(a)=v1 и cos(a)=v2 . В математике я бы сделал arcsin(v1) и arccos(v2) , чтобы найти решение этого уравнения. Есть ли какой-нибудь хороший способ...
Как найти кубический корень в Python?
 Я пытался найти кубический корень в Python, но понятия не имею, как его найти. Там была 1 строка кода, который работал, но он не дал мне полный номер. Пример: math.pow(64, 1/3) Это дает мне не 4...
Эффективное нахождение корня уравнения в python
 Мне нужно найти корень уравнения в python для другого набора параметров, и я не уверен, что это самый эффективный способ сделать это. Вот пример того, что мне нужно (и пробовал до сих пор). import...
Используйте sympy для решения трансцендентного уравнения
 Опыт работы с Python. Новичок в симпатии. У меня есть трансцендентное уравнение, f(x) = sin (x) - x. Если y = f (x), я хочу решить для x, зная y. Я думаю, что симпатия может это сделать, но у меня...
Как найти наибольший корень уравнения. Корень уравнения
В математике встречаются разнообразные уравнения. Их всегда нужно решать, то есть искать все числа, которые сделают его верным равенством. Пути поиска решений определяются первоначальным видом уравнения. От него же будет зависеть и количество верных значений переменной, которые обозначаются, как корень уравнения. Это число может варьироваться от нуля до бесконечности.
Что подразумевается под уравнением и его корнем?
Из названия понятно, что оно приравнивает две величины, которые могут быть представлены числовыми или буквенными выражениями. Кроме того, они содержат еще неизвестные величины. Самое простое уравнение имеет только одну.
Видов уравнений большое количество, но понятие корня для них всегда одно и то же. Корень уравнения — это такое значение неизвестного числа, при котором уравнение принимает становится верным равенством. Бывают ситуации, когда таких чисел несколько, тогда неизвестная называется переменной.
 Поиск всех возможных корней уравнения является его решением. То есть нужно выполнить ряд математических действий, которые его упрощают. А потом приводят к равенству, в котором содержится только неизвестная и какое-либо число.
В алгебре при решении уравнений можно прийти к такой ситуации, что корней не будет совсем. Тогда говорят о том, что оно неразрешимо. А в ответе такого уравнения нужно записать, что решений нет.
Но иногда бывает и противоположное. То есть в процессе многочисленных преобразований появляются посторонние корни. Они не дадут верного равенства при подстановке. Поэтому числа всегда нужно проверять, чтобы избежать ситуации с лишними корнями в ответе. Иначе уравнение не будет считаться решенным.
О линейном уравнении
Оно всегда может быть преобразовано в запись следующего вида: а * х + в = 0. В нем «а» всегда не равно нулю. Чтобы понять сколько корней имеет уравнение, его потребуется решить в общем виде.
Алгоритм преобразований:
перенести в правую часть равенства слагаемое «в», заменив его знак на противоположный;
разделить обе части получившегося равенства на коэффициент «а».
 Общий вид решения такой:
х = -в/а
 .
Из него ясно, что ответом будет одно число. То есть всего один корень.
Квадратное уравнение
Его общий вид: а * х 2 + в * х + с = 0
 . Здесь коэффициенты являются любыми числами, кроме первого, «а», которое не может быть равным нулю. Ведь тогда оно автоматически превратится в линейное. Ответ на вопрос, сколько корней имеет уравнение, уже не будет столь однозначным, как это было в предыдущем случае.
Все будет зависеть от значения дискриминанта. Он вычисляется по формуле Д = в 2 - 4 а * с
 . После расчетов «Д» может получиться больше, меньше или равным нулю. В первом случае корней уравнения будет два, во втором ответом будет «корней нет», а третья ситуация даст только одно значение неизвестной.
Формулы, которые используют для нахождения корней квадратного уравнения, и содержащие дискриминант
В общем случае, когда «Д» положительное число, не равное нулю, нужно использовать такую формулу:
х 1,2 = (-в ± √Д) / (2 * а)
 .
 Здесь всегда получится два ответа. Это связано с тем, что в исходной формуле стоит знак «плюс/минус». Он существенно изменяет значение неизвестной.
При равенстве «Д» нулю корень уравнения — это единственное число. Просто потому что квадратный корень из нуля равен нулю. А значит, прибавлять и вычитать нужно будет ноль. От этого число не изменится. Поэтому формулу корня уравнения можно записать без упоминания "Д":
х = (-в) / (2 * а).
 
При отрицательном значении дискриминанта извлечь из него квадратный корень не представляется возможным. Поэтому корней у такого уравнения не будет.
Замечание. Это верно для курса школьной программы, в которой не изучаются комплексные числа. Когда они вводятся, то получается, что и в этой ситуации ответов будет два.
 
Формулы для расчета корней квадратного уравнения, не использующие дискриминант
Речь идет о теореме Виета. Она действительна в случае, когда квадратное уравнение записывается в несколько другом виде:
х 2 + в * х + с = 0.
 
Тогда формула корней квадратного уравнения сводится к тому, чтобы выполнить решение двух линейных:
х 1 + х 2 = -в
 
и
х 1 * х 2 = с.
 
Оно решается за счет того, что из первого выводится выражение для одного из корней. И это значение нужно подставить во второе. Так будет найден второй корень, а потом первый.
К этому варианту всегда можно прийти от общего вида квадратного уравнения.
Достаточно только разделить все коэффициенты на «а».
Как быть, если нужно узнать наименьшее значение корня?
Решать уравнение и находить все возможные числа, которые подойдут для ответа. А потом выбрать самое малое. Это и будет наименьший корень уравнения.
Чаще всего такие вопросы встречаются в заданиях, которые имеют степень большую, чем 2, или содержат тригонометрические функции. Примером, когда нужно найти наименьший корень, может служить такое равенство:
2 х 5 + 2 х 4 - 3 х 3 - 3 х 2 + х + 1 = 0.
Чтобы найти каждое значение, которое можно назвать "корень уравнения", это равенство нужно преобразовать. Первое действие: сгруппировать его члены попарно: первый со вторым и так далее. Потом из каждой пары вынести общий множитель.
В каждой скобке останется (х + 1). Общим множителем в первой из пар будет 2 х 4 , во второй 3 х 2 . Теперь снова нужно выполнить вынесение общего множителя, которым будет являться одинаковая скобка.
После множителя (х + 1) будет стоять (2 х 4 - 3 х 2 + 1). Произведение двух множителей равняется нулю, только если один из них принимает значение, равное нулю.
Первая скобка равна нулю при х = -1. Это будет одним из корней уравнения.
Другие будут получены из уравнения, образованного второй скобкой, приравненной к нулю. Оно биквадратное. Для его решения нужно ввести обозначение: х 2 = у. Тогда уравнение существенно преобразится и примет привычный вид квадратного уравнения.
Его дискриминант равен Д = 1. Он больше нуля, значит корней будет два. Первый корень оказывается равным 1, второй будет 0,5. Но это значения для «у».
Нужно вернуться к введенному обозначению. х 1,2 = ± 1, х 3,4 = ± √0,5. Все корни уравнения: -1; 1; -√0,5; √0,5. Наименьший из них — -1. Это ответ.
В качестве заключения
Напоминание: все уравнения нужно проверять на то, подходит ли корень. Может быть, он посторонний? Стоит выполнить проверку предложенного примера.
Если подставить в изначально данное уравнение вместо "х" единицу, то получается, что 0 = 0. Этот корень верный.
Если х = -1, то получается такой же результат. Корень тоже подходящий.
Аналогично, при значениях "х" равных -√0,5 и √0,5 опять выходит верное равенство. Все корни подходят.
Этот пример не дал посторонних корней. Такое бывает не всегда. Вполне могло оказаться, что самое маленькое значение не подходило бы при проверке. Тогда пришлось бы выбирать из оставшихся.
Вывод: надо помнить о проверке и внимательно подходить к решению.
Сегодня мы будем тренировать навык решения задания 5 ЕГЭ — найдите корень уравнения. Будем искать корень уравнения. Рассмотрим примеры решения такого рода заданий. Но для начала, давайте вспомним — что значит — найти корень уравнения?
Это значит найти такое, зашифрованное под х число, которое мы подставим вместо x и наше уравнение будет верным равенством.
Например, 3x=9 — это уравнение, а 3 . 3=9 — это уже верное равенство. То есть в данном случае, мы вместо x подставили число 3 — получили верное выражение или равенство, это означает, что мы решили уравнение, то есть нашли данное число x=3, которое превращает уравнение в верное равенство.
Вот этим мы и займемся — будем находить корень уравнения.
Задание 1 — найдите корень уравнения 2 1-4x =32
Это показательное уравнение. Оно решается следующим образом — нужно чтобы и слева, и справа от знака «равно» была степень с одинаковым основанием.
Слева у нас основание степени 2, а справа — степени нет вовсе. Но мы знаем, что 32 — это 2 в пятой степени. То есть, 32=2 5
Таким образом, наше уравнение будет выглядеть так: 2 1-4х =2 5
Слева и справа у нас основания степени одинаковы, значит, чтобы у нас было равенство, должны быть равны и показатели степени:
Получаем обыкновенное уравнение. Решаем обычным способом — все неизвестные оставляем слева, а известные переносим вправо, получим:
Делаем проверку: 2 1-4(-1) =32
Мы нашли корень уравнение. Ответ: х=-1.
Самостоятельно найдите корень уравнения в следующих заданиях:
б) 2 1-3х =128
Задание 2 — найдите корень уравнения
Уравнение решаем аналогично — путем приведения левой и правой частей уравнения к одному основанию степени. В нашем случае — к основанию степени 2.
Используем следующее свойство степени:
По этому свойству мы получим для правой части нашего уравнения:
Если равны основания степени, значит, равны и показатели степени:
Ответ: х=9.
Сделаем проверку — подставим найденное значение х в исходное уравнение — если мы получим верное равенство, значит, мы решили уравнение правильно.
Мы нашли корень уравнения правильно.
Задание 3 — найдите корень уравнения 
Заметим, что справа у нас стоит 1/8, а 1/8 — это
Тогда наше уравнение запишется в виде:
Если основания степени равны, значит, равны и показатели степени, получим простое уравнение:
Ответ: х=5. Проверку сделайте самостоятельно.
Задание 4 — найдите корень уравнения log 3 (15-х)=log 3 2
Это уравнение решается также как и показательное. Нам нужно, чтобы основания логарифмов слева и справа от знака «равно» были одинаковыми. Сейчас они одинаковы, значит, приравниваем те выражения, которые стоят под знаком логарифмов:
Ответ: х=13
Задание 5 — найдите корень уравнения log 3 (3-x)=3
Число 3 — это log 3 27. Чтобы было понятно внизу нижним индексом под знаком логарифма стоит число которое возводится в степень, в нашем случае 3, под знаком логарифма стоит число, которое получилось при возведении в степень — это 27, а сам логарифм — это показатель степени, в которую нужно возвести 3, чтобы получить 27.
Смотрите на картинке:
Таким образом, любое число можно записать в виде логарифма. В данном случае очень удобно записать число 3 в виде логарифма с основанием 3. Получим:
log 3 (3-x)=log 3 27
Основания логарифмов равны, значит, равны и числа, стоящие под знаком логарифма:
Сделаем проверку:
log 3 (3-(-24))=log 3 27
log 3 (3+24)= log 3 27
log 3 27=log 3 27
Ответ: x=-24.
Найдите корень уравнения. Задание 6.
log 2 (x+3)=log 2 (3x-15)
Проверка: log 2 (9+3)=log 2 (27-15)
log 2 12=log 2 12
Ответ: x=9.
Найдите корень уравнения. Задание 7.
log 2 (14-2x)=2log 2 3
log 2 (14-2x)=log 2 3 2
Проверка: log 2 (14-5)=2log 2 3
log 2 9=2log 2 3
log 2 3 2 =2log 2 3
2log 2 3=2log 2 3
Ответ: x=2,5
Подготовьтесь к ЕГЭ и к ОГЭ -посмотрите предыдущие темы и .
Получив общее представление о равенствах , и познакомившись с одним из их видов - числовыми равенствами , можно начать разговор еще об одном очень важном с практической точки зрения виде равенств - об уравнениях. В этой статье мы разберем, что такое уравнение
 , и что называют корнем уравнения. Здесь мы дадим соответствующие определения, а также приведем разнообразные примеры уравнений и их корней.
Навигация по странице.
Что такое уравнение?
Целенаправленное знакомство с уравнениями обычно начинается на уроках математики во 2 классе. В это время дается следующее определение уравнения
 :
Определение.
 Уравнение
  – это равенство, содержащее неизвестное число, которое надо найти.
Неизвестные числа в уравнениях принято обозначать с помощью маленьких латинских букв, например, p
 , t
 , u
 и т.п., но наиболее часто используются буквы x
 , y
 и z
 .
Таким образом, уравнение определяется с позиции формы записи. Иными словами, равенство является уравнением, когда подчиняется указанным правилам записи – содержит букву, значение которой нужно найти.
Приведем примеры самых первых и самых простых уравнений. Начнем с уравнений вида x=8
 , y=3
 и т. п. Чуть сложнее выглядят уравнения, содержащие вместе с числами и буквами знаки арифметических действий, например, x+2=3
 , z−2=5
 , 3·t=9
 , 8:x=2
 .
Разнообразие уравнений растет после знакомства со – начинают появляться уравнения со скобками, например, 2·(x−1)=18
 и x+3·(x+2·(x−2))=3
 . Неизвестная буква в уравнении может присутствовать несколько раз, к примеру, x+3+3·x−2−x=9
 , также буквы могут быть в левой части уравнения, в его правой части, или в обеих частях уравнения, например, x·(3+1)−4=8
 , 7−3=z+1
 или 3·x−4=2·(x+12)
 .
Дальше после изучения натуральных чисел происходит знакомство с целыми, рациональными, действительными числами, изучаются новые математические объекты: степени, корни, логарифмы и т.д., при этом появляются все новые и новые виды уравнений, содержащие эти вещи. Их примеры можно посмотреть в статье основные виды уравнений
 , изучающиеся в школе.
В 7 классе наряду с буквами, под которыми подразумевают некоторые конкретные числа, начинают рассматривать буквы, которые могут принимать различные значения, их называют переменными (смотрите статью ). При этом в определение уравнения внедряется слово «переменная», и оно становится таким:
Определение.
 Уравнением
  называют равенство, содержащее переменную, значение которой нужно найти.
Например, уравнение x+3=6·x+7
 – уравнение с переменной x
 , а 3·z−1+z=0
 – уравнение с переменной z
 .
На уроках алгебры в том же 7 классе происходит встреча с уравнениями, содержащими в своей записи не одну, а две различные неизвестные переменные. Их называют уравнениями с двумя переменными. В дальнейшем допускают присутствие в записи уравнений трех и большего количества переменных.
Определение.
 Уравнения с одной, двумя, тремя и т.д. переменными
  – это уравнения, содержащие в своей записи одну, две, три, … неизвестные переменные соответственно.
Например, уравнение 3,2·x+0,5=1
 – это уравнение с одной переменной x
 , в свою очередь уравнение вида x−y=3
 – это уравнение с двумя переменными x
 и y
 . И еще один пример: x 2 +(y−1) 2 +(z+0,5) 2 =27
 . Понятно, что такое уравнение – это уравнение с тремя неизвестными переменными x
 , y
 и z
 .
Что такое корень уравнения?
С определением уравнения непосредственно связано определение корня этого уравнения. Проведем некоторые рассуждения, которые нам помогут понять, что такое корень уравнения.
Допустим, перед нами находится уравнение с одной буквой (переменной). Если вместо буквы, входящей в запись этого уравнения, подставить некоторое число, то уравнение обратиться в числовое равенство. Причем, полученное равенство может быть как верным, так и неверным. Например, если вместо буквы a
 в уравнение a+1=5
 подставить число 2
 , то получится неверное числовое равенство 2+1=5
 . Если же мы в это уравнение подставим вместо a
 число 4
 , то получится верное равенство 4+1=5
 .
На практике в подавляющем большинстве случаев интерес представляют такие значения переменной, подстановка которых в уравнение дает верное равенство, эти значения называют корнями или решениями данного уравнения.
Определение.
 Корень уравнения
  – это такое значение буквы (переменной), при подстановке которого уравнение обращается в верное числовое равенство.
Отметим, что корень уравнения с одной переменной также называют решением уравнения. Другими словами, решение уравнения и корень уравнения – это одно и то же.
Поясним это определение на примере. Для этого вернемся к записанному выше уравнению a+1=5
 . Согласно озвученному определению корня уравнения, число 4
 есть корень этого уравнения, так как при подстановке этого числа вместо буквы a получаем верное равенство 4+1=5
 , а число 2
 не является его корнем, так как ему отвечает неверное равенство вида 2+1=5
 .
На этот момент возникает ряд естественных вопросов: «Любое ли уравнение имеет корень, и сколько корней имеет заданное уравнение»? Ответим на них.
Существуют как уравнения, имеющие корни, так и уравнения, не имеющие корней. Например, уравнение x+1=5
 имеет корень 4
 , а уравнение 0·x=5
 не имеет корней, так как какое бы число мы не подставили в это уравнение вместо переменной x
 , мы получим неверное равенство 0=5
 .
Что касается числа корней уравнения, то существуют как уравнения, имеющие некоторое конечное число корней (один, два, три и т.д.), так и уравнения, имеющие бесконечно много корней. Например, уравнение x−2=4
 имеет единственный корень 6
 , корнями уравнения x 2 =9
 являются два числа −3
 и 3
 , уравнение x·(x−1)·(x−2)=0
 имеет три корня 0
 , 1
 и 2
 , а решением уравнения x=x
 является любое число, то есть, оно имеет бесконечное множество корней.
Пару слов стоит сказать о принятой записи корней уравнения. Если уравнение не имеет корней, то обычно так и пишут «уравнение не имеет корней», или применяют знак пустого множества ∅. Если уравнение имеет корни, то их записывают через запятую, или записывают как элементы множества
  в фигурных скобках. Например, если корнями уравнения являются числа −1
 , 2
 и 4
 , то пишут −1
 , 2
 , 4
 или {−1, 2, 4}
 . Допустимо также записывать корни уравнения в виде простейших равенств. Например, если в уравнение входит буква x
 , и корнями этого уравнения являются числа 3
 и 5
 , то можно записать x=3
 , x=5
 , также переменной часто добавляют нижние индексы x 1 =3
 , x 2 =5
 , как бы указывая номера корней уравнения. Бесконечное множество корней уравнения обычно записывают в виде , также при возможности используют обозначения множеств натуральных чисел N
 , целых чисел Z
 , действительных чисел R
 . Например, если корнем уравнения с переменной x
 является любое целое число, то пишут , а если корнями уравнения с переменной y
 является любое действительное число от 1
 до 9
 включительно, то записывают .
Для уравнений с двумя, тремя и большим количеством переменных, как правило, не применяют термин «корень уравнения», в этих случаях говорят «решение уравнения». Что же называют решением уравнений с несколькими переменными? Дадим соответствующее определение.
Определение.
 Решением уравнения с двумя, тремя и т.д. переменными
  называют пару, тройку и т.д. значений переменных, обращающую это уравнение в верное числовое равенство.
Покажем поясняющие примеры. Рассмотрим уравнение с двумя переменными x+y=7
 . Подставим в него вместо x
 число 1
 , а вместо y
 число 2
 , при этом имеем равенство 1+2=7
 . Очевидно, оно неверное, поэтому, пара значений x=1
 , y=2
 не является решением записанного уравнения. Если же взять пару значений x=4
 , y=3
 , то после подстановки в уравнение мы придем к верному равенству 4+3=7
 , следовательно, эта пара значений переменных по определению является решением уравнения x+y=7
 .
Уравнения с несколькими переменными, как и уравнения с одной переменной, могут не иметь корней, могут иметь конечное число корней, а могут иметь и бесконечно много корней.
Пары, тройки, четверки и т.д. значений переменных часто записывают кратко, перечисляя их значения через запятую в круглых скобках. При этом записанные числа в скобках соответствуют переменным в алфавитном порядке. Поясним этот момент, вернувшись к предыдущему уравнению x+y=7
 . Решение этого уравнения x=4
 , y=3
 кратко можно записать как (4, 3)
 .
Наибольшее внимание в школьном курсе математики, алгебры и начал анализа уделяется нахождению корней уравнений с одной переменной. Правила этого процесса мы очень подробно разберем в статье решение уравнений
 .
Список литературы.
Математика
 . 2 кл. Учеб. для общеобразоват. учреждений с прил. на электрон. носителе. В 2 ч. Ч. 1 / [М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др.] - 3-е изд. - М.: Просведение, 2012. - 96 с.: ил. - (Школа России). - ISBN 978-5-09-028297-0.
Алгебра:
  учеб. для 7 кл. общеобразоват. учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. - 17-е изд. - М. : Просвещение, 2008. - 240 с. : ил. - ISBN 978-5-09-019315-3.
Алгебра:
  9 класс: учеб. для общеобразоват. учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. - 16-е изд. - М. : Просвещение, 2009. - 271 с. : ил. - ISBN 978-5-09-021134-5.
 \(2x+1=x+4\) находим ответ: \(x=3\). Если подставить тройку вместо икса, получатся одинаковые значения слева и справа:
\(2x+1=x+4\)
\(2\cdot3+1=3+4\)
\(7=7\)
И никакое другое число, кроме тройки такого равенства нам не даст. {2}+15\cdot(-2)+22=0\)
 \(2\cdot4-30+22=0\)
 \(0=0\) - сошлось, значит \(-2\) - корень уравнения
Очевидно, что решать уравнения перебором всех возможных значений – безумие, ведь чисел бесконечно много. Потому были разработаны специальные методы нахождения корней. Так, например, для
 достаточно одних только
 , для
 – уже используются формулы
 и т.д. Каждому типу уравнений – свой метод.
Ответы на часто задаваемые вопросы
Вопрос:
 
  Может ли корень уравнения быть равен нулю?
Ответ:
 
  Да, конечно. Например, уравнение \(3x=0\) имеет единственный корень - ноль. Можете проверить подстановкой.
Вопрос:
 
  Когда в уравнении нет корней?
Ответ:
 
  В уравнении может не быть корней, если нет таких значений для икса, которые сделают уравнение верным равенством. Яркий примером тут может быть уравнение \(0\cdot x=5\). 2-5x-6=0\) имеет два корня: \(x_1=-1\) и \(x_2=6\). Меньший из корней: \(-1\). Вот его и надо будет записать в ответ. Если бы спрашивали про больший корень, то надо было бы записать \(6\).
Самые простые способы решения линейных уравнений
Уравнение – это самое распространенное задание в математике. И не только в математике: вспомните физику, химию, биологию, экономику и многие другие предметы! Даже филологи и философы любят рассуждать об уравнениях с множеством неизвестных!
Но поговорим все же о математических уравнениях. Увидев даже самое простое уравнение, ребята часто попадают в ступор: «как же решать уравнение?», «что такое решение уравнения?», «с какой стороны подойти к решению уравнения?»…
В этой статье я расскажу о том, какие бывают уравнения, как их отличить друг от друга (как расклассифицировать их). Кроме того, вы узнаете о самых простых способах решения каждого вида уравнений. И на конкретных примерах вы убедитесь, что найти корень линейного уравнения – это совершенно не сложное задание. И если вам придется искать решение уравнения по физике или химии, то вы уже без труда найдете любые корни.
Итак, давайте разберемся, что вообще значит «решение уравнения», и «линейное уравнение».
Определение
Линейным уравнением называется выражение вида
где a, b – некоторые числа, а  – переменная, то есть тот самый неизвестный элемент в уравнении, который нужно найти. Процесс нахождения x называется решением уравнения, а результат, чему равен  – корнем уравнения.  Если  a  ≠ 0, то линейное уравнение называют также уравнением первой степени.
Чтобы решить уравнение   нужно все, что с  (иксами) оставить в левой стороне от равно, а все что без  – перенести в правую сторону, при этом не забывая поменять знак на противоположный (с «–» на «+», с «+» на «–»):
Затем разделим обе стороны на коэффициент перед  x, то есть на  получим
Например, дано вот такое уравнение:
Перенесем (–6 ) вправо от знака равно, не забудем поменять знак ‘–’ на ‘+’, получим:
разделим обе части уравнения на 2:
При , данное выражение превращается в верное тождество (то есть верное равенство). Подставив число 3 вместо  в наше уравнение, получим:
– это выражение называется верным тождеством.
Геометрический смысл линейного уравнения
Иногда, чтобы хорошо понять какую-либо задачу, нужно ее нарисовать. Поэтому давайте попробуем линейное уравнение изобразить на рисунке.
Итак, какой визуальный смысл заложен в выражении вида
Возьмем левую часть равенства
и попробуем отобразить это выражение на рисунке. Для этого будем рассматривать функцию
– это линейная функция, а графиком линейной функции является прямая. Так как уравнение равно нулю, то  нам нужно найти в какой точке наша прямая пересекает ось абсцисс (то есть ось Ох). Это будет точка  – корень уравнения.
На координатной плоскости, к примеру, функция
будет выглядеть вот так:
обратите внимание, прямая пересекает ось Ох в точке , а это и есть наш корень уравнения,
или еще говорят, что 3 – есть решение уравнения
Количество решений линейного уравнения
Может быть три случая:
Если , то количество решений линейного уравнения одно (единственный корень )
Если  и , то получим верное тождество   для любых , то есть – бесконечное множество решений.
Если  и , то получаем неверное тождество  значит, решений нет.
Cхематично это можно представить так:
количество корней линейного уравнения
Рассмотрим примеры.
Уравнение, где корень единственный мы уже рассмотрели, поэтому рассмотрим 2 и 3 случаи.
Перенесем  в левую сторону от знака равно, поменяем знак,   также перенесем меняя знак на противоположный в правую сторону от равно, получим:
Посчитаем сколько  получилось в левой части и что получилось в правой части:
Так как получилось верное равенство, то в этой ситуации  — любое число.
И еще пример,
Разделим переменные, то есть перенесем все что с  в левую сторону, без  — в правую сторону:
Приведем подобные, получим:
Так как при умножении на 0 всегда получается 0, то получаем ,  а такого не может быть. Значит, делаем вывод: решений нет, или математически можно сказать  – пустое множество.
Как отличить линейное уравнение от любого другого уравнения
Надо сказать, не всегда линейное уравнение выглядит так, как в определении:
Чаще линейное уравнение необходимо сначала преобразовать и привести к исходному виду. А как же отличить линейное уравнение от другого уравнения?
В первую очередь надо помнить, что в линейном уравнении переменная  всегда первой степени, то есть если над  нет никакой степени, то уравнение линейное. Но обязательно при этом нужно посмотреть, не умножается ли переменная еще на одну или несколько таких же переменных. Или не возводиться ли все выражение с переменной в степень.
Кроме того, если в уравнении есть дроби, необходимо посмотреть: переменная находится в числителе или нет. Если переменная в знаменателе – это уже не линейное уравнение.
Например, в уравнении ,  умножается на скобку, где есть тоже переменная , раскрыв скобки, мы получим  значит, данное уравнение уже не линейное.
Или  — выражение возводится в степень, значит, после раскрытия скобок переменная снова будет в степени и уравнение будет не линейное.
А в уравнении
  находится в знаменателе, хоть и в первой степени, и уравнение тоже не линейное.
А вот уравнения линейные, не смотря на скобки и дроби:
Разбор решений различных видов конкретных уравнений
Давайте теперь разберем, как решать уравнения, на конкретных примерах.
Раскроем скобки:
получим
теперь все что с  соберем в левой части равенства, а все свободные члены выражения перенесем в правую часть равенства, не забывая менять знак, перенося слагаемые с одной части в другую:
Приведем подобные, то есть сложим количество в левой части и числа в правой части равенства
разделим на коэффициент перед , то есть на 4:
выделим целую часть дроби:
В принципе это уже и есть корень искомого уравнения, но иногда просят записать ответ в виде десятичной дроби, поэтому переведем обыкновенную смешанную дробь в десятичную:
В данном уравнении все действия аналогичны предыдущему:
Раскрываем скобки;
Разделяем переменные и свободные слагаемые по разные стороны от равно;
Приводим подобные;
Делим на коэффициент перед
В этом уравнении в глаза бросаются дроби, десятичная 0,1 и простая . Здесь сначала нужно дроби сделать одинаковыми: либо десятичными, либо обыкновенными. Так как обыкновенная дробь  легко переводится в десятичную, именно ее я поменяю
. И сразу буду раскрывать скобки:
Приведем подобные и разделим переменные с числовыми значениями:
В итоге получаем 0=18, что противоречит истине, поэтому , или решений нет.
Так как в данном уравнении дроби, нужно приводить к общему знаменателю или избавится от него. Поскольку в знаменателе только числа, я пойду вторым путем. Умножим обе стороны уравнения на наибольший знаменатель, то есть на 4, получим:
Раскроем скобки
В первом слагаемом  сократим 4 и 2, получим , во втором слагаемом
тоже сокращаем 4 и 4, в итоге получим уравнение
Далее также как и в предыдущих примерах раскрываем скобки, разделяем переменные с числовыми значениями по разные стороны от равно, приводим подобные:
Избавимся от минуса перед , для этого умножим обе части равенства на , получим
Использование уравнений при решении текстовых задач, составление уравнений
Самый главный вопрос, который мучает всех ребят: для чего же нужны эти линейные уравнения? Приведу простой пример, когда можно использовать уравнения.
Допустим, мама купила на рынке картошку и морковку, всего овощей получилось 15 кг.  Она хочет посчитать, не обманул ли ее продавец, называя сумму покупки. Но не помнит, сколько же килограмм она купила картошки, а сколько морковки? Но помнит, что разница была 3 кг, причем картошки по ощущениям больше.
Итак, как же найти, сколько мама купила картошки, а сколько морковки?
Можно пойти путем подбора: если картошки на 3 кг больше, чем морковки, а всего овощей 15 кг, то разложив 15, на пары слагаемых получим:
Так как разница была 3 кг, то из этих пар нам подходит 9+6. Получаем, что 9 кг картошки и 6 кг морковки.
Когда числа простые и к тому же не большие, то найти решение подбором просто, но если овощей 40кг или 50кг… Мне бы было лень, раскладывать такие большие числа на пары, и я бы пошла другим путем: составила уравнение.
Итак, если в задаче слишком много неизвестных, и известна только зависимость составляющих между собой, то такую задачу легче всего решать с помощью уравнения.
В нашем случае,
картошки — ?
морковки — ?, но на 3кг меньше, чем картошки.
И известно, что картошки + морковки = 15.
Введем неизвестную переменную .
Пусть  кг – картошки, тогда морковки – кг, и т.к. овощей всего 15кг, то получим уравнение:
Значит, картошки 9 кг, морковки  кг.
В итоге, мама помнит, что картошка стоила 50 р за кг, а морковка – 70 р за кг. И стоимость покупки составляет:  р. А продавец посчитал  р. Тем самым мама переплатила 60 р. Вывод: не доверяйте подсчетам продавца, он всегда ошибается в свою пользу.
Вот другой пример из жизни. Дед взял своего маленького внука на рыбалку. К месту рыбалки они плыли на моторной лодке целых 2 часа, плыли по течению реки. Обратно их путь занял 3 часа. У внука появилось ряд вопросов:
Почему обратно плыли дольше? Сколько километров они проплыли всего? С какой скоростью они плыли?
На первые два вопроса дед ответил быстро, а с последним пришлось поразмышлять и даже решить математическую задачу.
Итак, что же ответил дед своему любознательному малышу?
Обратно плыли дольше потому, что пришлось плыть против течения реки, оно замедляло собственную скорость лодки.
Посмотрев на приборы лодки, дедушка увидел, что проплыли всего 47 км. А вот с какой скоростью плыла лодка, дед не смотрел, когда плыли, и чтобы ответить на вопрос внука, пришлось составить уравнение. Дед знал, что скорость реки 3 км/час. А собственную скорость лодки он обозначил через . Так как по течению они плыли 2 часа, а лодке помогала река, то за 2 часа он проплыли  км. Обратно плыли 3 часа, и река мешала лодке, тогда проплыли  км.
Так как всего путь составил 47 км. То получилось уравнение:
Решив его, дед нашел скорость лодки. Надеюсь, вы уже тоже научились решать такие уравнения. Напишите, пожалуйста, в комментариях какова была собственная скорость моторной лодки. И какие вопросы возникли у вас после прочтения этой статьи?
 
 
Найдите корень уравнения - задание 5 из ЕГЭ


 Автор Ольга Викторовна            На чтение 4 мин. Просмотров 479            Опубликовано 12.11.2015
Сегодня мы будем тренировать навык решения задания 5 ЕГЭ — найдите корень уравнения. Будем искать корень уравнения. Рассмотрим примеры решения такого рода заданий. Но для начала, давайте вспомним — что значит — найти корень уравнения?
Это значит найти такое, зашифрованное под х число, которое мы подставим вместо x и наше уравнение будет верным равенством.
Например, 3x=9 — это уравнение, а 3.3=9 — это уже верное равенство. То есть в данном случае, мы вместо x подставили число 3 — получили верное выражение или равенство, это означает, что мы решили уравнение, то есть нашли данное число x=3, которое превращает уравнение в верное равенство.
Вот этим мы и займемся  — будем находить корень уравнения.
Задание 1 — найдите корень уравнения 2
1-4x=32
Это показательное уравнение. Оно решается следующим образом — нужно чтобы и слева, и справа от знака «равно» была степень с одинаковым основанием.
Слева у нас основание степени 2, а справа — степени нет вовсе. Но мы знаем, что 32 — это 2 в пятой степени. То есть, 32=25
Таким образом, наше уравнение будет выглядеть так: 21-4х=25
Слева и справа у нас основания степени одинаковы, значит, чтобы у нас было равенство, должны быть равны и показатели степени:
1-4х=5
Получаем обыкновенное уравнение. Решаем обычным способом — все неизвестные оставляем слева, а известные переносим вправо, получим:
-4х=5-1
-4х=4
х=-1.
Делаем проверку: 21-4(-1)=32
25=32
32=32
Мы нашли корень уравнение. Ответ: х=-1.
Самостоятельно найдите корень уравнения в следующих заданиях:
а) 25-х=64
б) 21-3х=128
Задание 2 — найдите корень уравнения 2
5-x = 1/16
Уравнение решаем аналогично — путем приведения левой и правой частей уравнения к одному основанию степени. В нашем случае — к основанию степени 2.
Используем следующее свойство степени:
По этому свойству мы получим для правой части нашего уравнения:
Тогда наше уравнение запишется в виде:
Если равны основания степени, значит, равны и показатели степени:
5-х=-4
-х=-4-5
х=9
Ответ: х=9.
Сделаем проверку — подставим найденное значение х в исходное уравнение — если мы получим верное равенство, значит, мы решили уравнение правильно.
25-9=1/16
2-4=1/16
1/16=1/16
Мы нашли корень уравнения правильно.
Задание 3 — найдите корень уравнения 
Заметим, что справа у нас стоит 1/8, а 1/8 — это
Тогда наше уравнение запишется в виде:
Если основания степени равны, значит, равны и показатели степени, получим простое уравнение:
3х-12=3
3х=15
х=5
Ответ: х=5. Проверку сделайте самостоятельно.
Задание 4 — найдите корень уравнения log
3(15-х)=log32
Это уравнение решается также как и показательное. Нам нужно, чтобы основания логарифмов слева и справа от знака «равно» были одинаковыми. Сейчас они одинаковы, значит, приравниваем те выражения, которые стоят под знаком логарифмов:
15-х=2
-х=2-15
-х=-13
х=13
Ответ: х=13
Задание 5 — найдите корень уравнения log
3(3-x)=3
Число 3 — это log327. Чтобы было понятно внизу нижним индексом под знаком логарифма стоит число которое возводится в степень, в нашем случае 3, под знаком логарифма стоит число, которое получилось при возведении в степень — это 27, а сам логарифм — это показатель степени, в которую нужно возвести 3, чтобы получить 27.
Смотрите на картинке:
Таким образом, любое число можно записать в виде логарифма. В данном случае очень удобно записать число 3 в виде логарифма с основанием 3. Получим:
log3(3-x)=log327
Основания логарифмов равны, значит, равны и числа, стоящие под знаком логарифма:
3-х=27
Получим,
-х=27-3
-х=24
х=-24
Сделаем проверку:
log3(3-(-24))=log327
log3(3+24)= log327
log327=log327
3=3
Ответ: x=-24.
Задание 6. Найдите корень уравнения log(x+3)=log
2(3x-15).
log2(x+3)=log2(3x-15)
Решение:
x+3=3x-15
x-3x=-3-15
-2x=-18
x=9
Проверка: log2(9+3)=log2(27-15)
log212=log212
Ответ: x=9.
Задание 7. Найдите корень уравнения log
2(14-2x)=2log23
log2(14-2x)=2log23
log2(14-2x)=log232
14-2x=32
14-2x=9
-2x=9-14
-2x=-5
x=2,5
Проверка: log2(14-5)=2log23
log29=2log23
log232=2log23
2log23=2log23
Ответ: x=2,5
Подготовьтесь к ЕГЭ и к ОГЭ -посмотрите предыдущие темы Найдите значение выражения и Как решать неравенства .
Найти корень уравнения пример | Геометрия
Найти корень уравнения пример  | Геометрия - просто!
Добрый день!
 Сегодня мы разберём примеры задания 5 ЕГЭ — найти корень уравнения.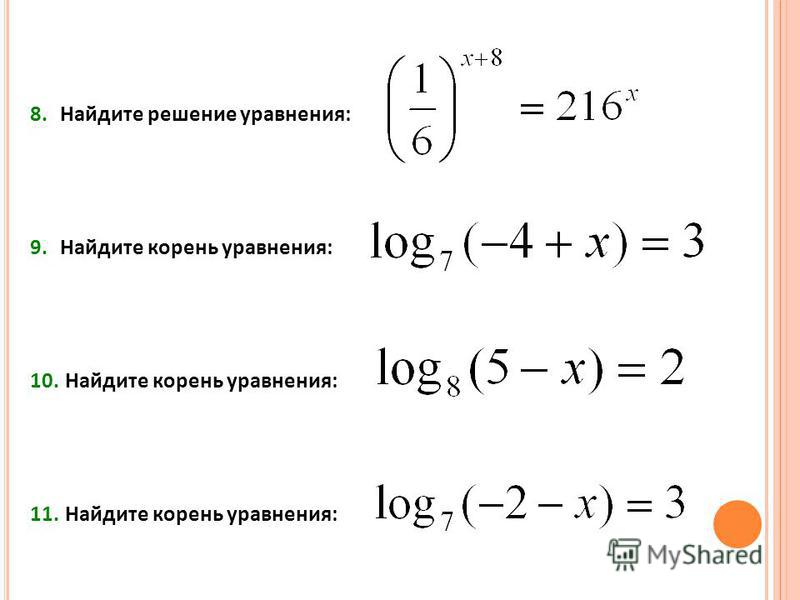 
 В этом задании собраны разнообразные уравнения — линейные, квадратные, иррациональные, показательные, логарифмические, тригонометрические.
 Каждое из них решается по своей методике
и по своим правилам.
 Решим некоторые из них.
Задание 1. найти корень уравнения √(2х + 31) = 9
 Решение: чтобы найти корень данного уравнения,
обе части его возводим в степень 2.
 При этом, обязательным условием должна быть
неотрицательность правой части уравнения.
 У нас справа стоит число 9, значит можно возвести
правую и левую часть в квадрат.
 2х + 31 = 81
 2х = 81 — 31
 2х = 50
 х = 25.
 Ответ: корень уравнения х = 25.
Задание 2. найти корень уравнения √(4х + 5) = 5
 Решение: закрепим изученное ещё одним примером.
 4х + 5 = 25
 4х = 25 — 5
 4х = 20
 х = 5.
 Ответ: корень уравнения х = 5.
Задание 3. Найти корень уравнения log
6 (8 – x) = log36 9
Решение: Число 36 можно представить,  как 62, а 9 как 32. 
Перепишем наше уравнение:
log6 (8 – x) = log62 32
 По свойству логарифма степени выносим перед логарифмом:
log6 (8 – x) = 2/2log6 3
 log6 (8 – x) = log6 3
 Логарифмы равны, основания тоже равны,
значит равны и выражения, стоящие под знаком логарифма.
 8 – x = 3
 8 – х >0  О.Д.З.
 х <8
 х = 5
 Ответ: корень уравнения х = 5
Задание 4. Найти корень уравнения  log
4 (х + 7) = 2
 Решение: здесь мы просто воспользуемся свойством логарифма:
 log4 (х + 7) = 2
 х + 7 = 4²
 х = 16 — 7
 х = 9
 Ответ: корень уравнения х = 9.
Задание 5.  Найти  корень уравнения  (х+11)² = 44х
Решение: В левой части уравнения квадрат суммы двух чисел.
Раскрываем скобки:
х² + 22х + 121 = 44х  Переносим 44х влево с противоположным знаком.
х² — 22х + 121 = 0    А это, в свою очередь, квадрат разности двух чисел. 
(х-11)² = 0.
Корень у этого уравнения один и он равен 11.
Ответ: корень уравнения 11.
Задание 6. Найдите корень уравнения:   3
5+3х = 92х
Решение:  В левой части показательного уравнения в основании стоит 3, 
а в правой — 9.
9 можно представить, как 3².
Значит, правую часть уравнения можно представить как   (32)2х
При возведении степени в степень,  показатели степеней перемножаются.
Получим    (32)2х = 34х
А теперь можно решить уравнение.
35+3х = 92х
35+3х = 34х
Поскольку степени равны, основания тоже равны,
значит, равны показатели степеней.
5+3х = 4х
5 = 4х — 3х
х=5
Ответ: корень уравнения 5.
На сегодня всё. 
Успехов и до новых задач!
 
Вам так же будет интересно:
Оставить комментарий


 

 
 В поисках корней - Алгебра II 
 Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно
 или несколько ваших авторских прав, сообщите нам об этом, отправив письменное уведомление («Уведомление о нарушении»), содержащее
 в
 информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на
 ан
 Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
 средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
 Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
 в виде
 ChillingEffects.org.
 Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно
 искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится
 на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
 Чтобы отправить уведомление, выполните следующие действия:
 Вы должны включить следующее:
 Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
 Идентификация авторских прав, которые, как утверждается, были нарушены;
 Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
 достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
 а
 ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
 к какой конкретной части вопроса - изображению, ссылке, тексту и т. д. - относится ваша жалоба;
 Ваше имя, адрес, номер телефона и адрес электронной почты; а также
 Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
 ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
 информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
 либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
 Отправьте жалобу нашему уполномоченному агенту по адресу:
 Чарльз Кон
 Varsity Tutors LLC 
 101 S. Hanley Rd, Suite 300 
 St. Louis, MO 63105
 Или заполните форму ниже:
 решений или корней квадратных уравнений 
 решений или корней квадратных уравнений
 Рассмотрим квадратное уравнение
 Действительное число  x  будет называться решением или корнем, если оно удовлетворяет уравнению, то есть.Легко видеть, что корни - это в точности точки пересечения по оси x квадратичной функции, то есть точки пересечения графика квадратичной функции с осью x.
  а <0 
  a> 0 
  Пример 1:  Найдите корни уравнения
  Решение.  Это уравнение эквивалентно
 Поскольку 1 имеет два квадратных корня, решениями этого уравнения являются
  Пример 2:  Найдите корни уравнения
  Решение. Этот пример несколько сложнее предыдущего, но мы увидим, как с ним работать в общем случае. Сначала обратите внимание, что у нас есть
 Следовательно, уравнение эквивалентно
 который совпадает с
 Поскольку 3 имеет два квадратных корня, получаем
 которые дают решения уравнения
 Тогда мы можем задаться вопросом, можно ли свести какое-либо квадратное уравнение к
 самые простые, описанные в предыдущих примерах.Ответ несколько сложнее, но он был известен очень давно (вавилонянам около 2000 г. до н. Э.). Их идея была основана в основном на том, что  завершает квадрат , что мы и сделали при решении второго примера.
[Алгебра]
 [Комплексные переменные]
[Геометрия]
 [Тригонометрия]
[Исчисление]
 [Дифференциальные уравнения]
 [Матричная алгебра]
 Домашняя страница S.O.S MATHematics
 Вам нужна дополнительная помощь? Пожалуйста, разместите свой вопрос на нашем
S.O.S. Математика CyberBoard.
 
Автор: Мохамед
 Амин Хамси 
 
Авторские права 1999-2021 MathMedics, LLC.Все права защищены.
 
 Свяжитесь с нами
 
 Math Medics, LLC. - П.О. Box 12395 - El Paso TX 79913 - США
 
 пользователя онлайн за последний час
 Как использовать квадратичную формулу для поиска корней уравнений - Видео и стенограмма урока 
 Квадратичная формула 
 Квадратичная формула   - это формула, которую мы можем использовать для нахождения корней квадратного уравнения  a   x  2 +  b   x  +  c  = 0.
 Чтобы использовать квадратную формулу для нахождения корней квадратного уравнения, все, что нам нужно сделать, это получить квадратное уравнение в форме  a   x  2 +  b   x  +  c  = 0; идентифицировать  a ,  b  и  c ; а затем подключите их к формуле.Чтобы идентифицировать эти значения, мы просто помним, что  a  находится перед  x  2,  b  находится перед  x , а  c  - это само по себе число.
 Например, в нашем уравнении -  x  2 + 4  x  + 5 = 0, число перед  x  2 равно -1, поэтому  a  = -1. Число перед  x  равно 4, поэтому  b  = 4. Наконец, само число равно 5, поэтому  c  = 5. Мы почти у цели! Все, что нам нужно сделать, это подставить эти значения в нашу формулу корней квадратного уравнения, и тогда мы сможем найти значения  x , которые делают наше уравнение истинным.Тогда мы узнаем, сколько времени нужно, чтобы мяч коснулся земли. Приступим к подключению!
 Мы видим, что мяч находится на высоте 0, когда  x  = -1 и когда  x  = 5. В нашем случае мы можем игнорировать  x  = -1. Хотя верно, что  x  = -1 является корнем уравнения, мы знаем, что  x  представляет время, и у нас не может быть -1 секунды. Единственная причина, по которой это выглядит таким образом, заключается в том, что, когда мы изначально бросали мяч на 0 секунде, мы находились на высоте 5 футов над землей.
 Поскольку мы отказались от ответа  x  = -1, остается  x  = 5 в качестве решения нашей конкретной проблемы. Это говорит нам о том, что мяч ударился о землю через 5 секунд после того, как мы его бросили, поэтому он находился в воздухе 5 секунд. Разве это не здорово, что мы могли это выяснить, используя нашу формулу корней квадратного уравнения?
 Другой пример 
 Рассмотрим еще один пример. Допустим, мы делаем каркасную поделку. На основе имеющихся у нас материалов площадь кадра может быть представлена ​​уравнением  A  =  x  2 + 2  x , где  A  - это площадь кадра, а  x  - это площадь кадра. ширина рамки.Мы хотим, чтобы наша область была 24 на 2, поэтому нам просто нужно найти ширину, которая делает это так.
 Для этого мы подключаем 24 к  A , чтобы получить
  x  2 + 2  x  = 24
 Мы вычитаем 24 с обеих сторон, чтобы получить наше уравнение в правильной форме:
  x  2 + 2  x  - 24 = 0
 Теперь мы хотим идентифицировать  a ,  b  и  c  на основе чисел перед  x  2,  x  и отдельно , соответственно.Таким образом, мы имеем  a  = 1,  b  = 2 и  c  = -24. Все, что нам нужно сделать сейчас, это подставить их в нашу квадратную формулу:
 Мы видим, что ширина равна 4 или -6. Поскольку у нас не может быть отрицательной ширины, она должна быть равна 4, чтобы иметь площадь 24 дюйма2.
 Резюме урока 
 Квадратное уравнение   - это уравнение, в котором наивысший показатель любой переменной равен 2.Решения квадратных уравнений называются  корнями . Квадратные уравнения имеют 2 корня. Мы можем найти корни квадратного уравнения, используя формулу корней квадратного уравнения:
 Чтобы использовать это, мы записываем уравнение в виде  a   x  2 +  b   x  +  c  = 0; идентифицировать  a ,  b  и  c ; а затем подставьте эти значения в формулу.
 Квадратные уравнения постоянно используются для моделирования явлений реального мира, поэтому очень полезно знать, как решать эти уравнения.Квадратичная формула - обязательный инструмент, который нужно добавить в свой математический инструментарий!
 Формула суммы и произведения корней квадратного уравнения 
 Формулы 
  сумма корней : $$ \ frac {-b} {a} $$
  продукт корней : $$ \ frac {c} {a} $$
 Как видно из работы ниже, когда вы пытаетесь решить квадратное уравнение в виде $$ ax ^ 2 + bx + c $$.2 + 5x +6 $$. Как видите, сумма корней действительно равна $$ \ color {Red} {\ frac {-b} {a}} $$, а произведение корней составляет $$ \ color {Red} {\ frac { c} {a}} $$.
 Пример 2 
 Пример ниже показывает, как эта формула применяется к квадратному уравнению x  2  - 2x - 8. Опять же, обе формулы - для суммы и произведения сводятся к -b / a и c / a, соответственно.
 Практика  Задачи
 Задача 1 
 Не решая, найти сумму и произведение корней уравнения: 2x  2  -3x -2 = 0
 Покажи ответ
 Определите коэффициенты: 
 a = 2 
 b = -3 
 c = -2
 Теперь подставим эти значения в формулы
  Сумма корней 
 $$ \ color {Красный} {\ frac {-b} {a}} = \ frac {- (- 3)} {2} = \ frac {3} {2} $$
  Продукт корней 
 $$ \ color {Красный} {\ frac {c} {a}} = \ frac {-2} {2} = -1 $$
 Задача 2 
 Не решая, найдите сумму и произведение корней следующего уравнения: -9x  2  -8x = 15
 Покажи ответ
 Сначала вычтите 15 с обеих сторон, чтобы уравнение имело вид 0 = ax  2  + bx + c переписать уравнение: -9x  2  -8x - 15 = 0
 Определите коэффициенты: 
 a = -9 
 b = -8 
 c = -15
 Теперь подставьте эти значения в формулы
  Сумма корней 
 $$ \ color {Красный} {\ frac {-b} {a}} = \ frac {- (- 8)} {- 9} = \ frac {-8} {9} $$
  Продукт корней 
 $$ \ color {Красный} {\ frac {c} {a}} = \ frac {-15} {9} = \ frac {-5} {3} $$
 Задача 3 
 Запишите квадратное уравнение с учетом следующих корней: 4 и 2
 Покажи ответ
 Есть несколько способов решить эту проблему. Вы можете создать два бинома (x-4) и (x-2) и умножить их.
 Однако, поскольку эта страница посвящена использованию наших формул, давайте воспользуемся ими, чтобы ответить на это уравнение.
 Сумма корней = 4 + 2 = 6 
 Произведение корней = 4 * 2 = 8
 Мы можем использовать наши формулы, чтобы составить следующие два уравнения
  Сумма корней 
 $$ \ frac {-b} {a} = 6 = \ frac {6} {1} $$
  Продукт корней 
 $$ \ frac {c} {a} = 8 = \ frac {8} {1} $$
 Теперь мы знаем значения всех трех коэффициентов: 
 a = 1 
 b = -6 
 c = 8
 Итак, наше окончательное квадратное уравнение y = 1x  2  - 6x + 8
 Вы можете дважды проверить свою работу, помешав биномам (x -4) (x-2) получить то же уравнение
 Задача 4 
 Если один корень приведенного ниже уравнения равен 3, каков другой корень? х  2  -5x +  к  = 0
 Покажи ответ
 Запишите то, что вы знаете: 
 a = 1 
 b = -5 
 r  1  = 3
 Теперь подставьте эти значения в формулу суммы корней
  Сумма корней 
 r  1  + r  2  = -b / a
 3 + г  2  = - (- 5) / 1
 3 + г  2  = 5
 г  2  = 2
 Следовательно, отсутствует корень 2.2-4 (6) (- 1))) / (2 (6)) `
 `= (6 + -кв (36 + 24)) / 12`
 `= (6 + -sqrt60) / 12`
 `= (6-2sqrt15) / 12 или (6 + 2sqrt15) / 12`
 `= (3-sqrt15) / 6 или (3 + sqrt15) / 6`
 Так
 `r = -0,145 или 1,145`
 Графическое определение корня уравнения в Excel 
 Есть несколько способов найти корень уравнения в Excel. Самый простой способ - сделать это графически, используя точечную диаграмму.
 В этом примере мы попытаемся найти корень уравнения Коулбрука.Это уравнение используется для определения коэффициента трения Дарси Вейсбаха для потока в трубе без необходимости искать его на диаграмме Moody.
 Входными данными в уравнение являются число Рейнольдса (Re), гидравлический диаметр (D  h ) и шероховатость стенки (ε).
 Проблема с этим уравнением в том, что оно неявно. Если вы хотите найти коэффициент трения f, нет способа составить уравнение так, чтобы f находилось с одной стороны, а все другие переменные - с другой.
 К счастью, мы можем использовать Excel, чтобы найти решение, используя несколько различных методов. В этой статье я продемонстрирую, как найти корень уравнения графически.
 Если мы изменим это уравнение так, чтобы все было по одну сторону от знака равенства, значение коэффициента трения, которое приводит к тому, что это уравнение становится равным нулю, должно быть решением.
 Учитывая некоторые входные значения для Re, D  h  и ε, мы можем ввести диапазон предположений для f и вычислить левую часть приведенного выше уравнения.
 Для начала введите значения 0,01 и 0,02 в столбец для f. Выделите эти ячейки, затем перетащите маркер заполнения вниз. Это заполнит значения для f от 0,01 до 0,1:
.
 Выберите значения f, затем назовите массив f, используя поле имени слева от строки формул. Другим переменным уже присвоены имена: eps для шероховатости, DH для гидравлического диаметра и Re для числа Рейнольдса. Мы можем использовать эти имена переменных в формуле массива. В верхней ячейке столбца результатов введите формулу:
  = 1 / КОРЕНЬ (f) + 2 * ЖУРНАЛ10 (eps / (3.7 * DH) + 2,51 / (Re * SQRT (f))) 
 
 Используйте Ctrl-Shift-Enter, чтобы ввести формулу, чтобы она применялась ко всему массиву. Выберите все данные и вставьте точечную диаграмму XY для отображения данных. Результаты в электронной таблице говорят нам, что значение «f» находится где-то в этом диапазоне, потому что числа меняются с положительного на отрицательный. На графике еще проще увидеть, что линия пересекает ноль где-то между 0,04 и 0,05:
 Мы можем использовать все более детальные предположения для f, чтобы найти решение уравнения.Сотрите значения для f и введите 0,041 в первое поле. Во втором поле введите 0,042. Выделите эти ячейки и дважды щелкните маркер заполнения, чтобы заполнить таблицу.
 Из данных слева мы видим, что линия пересекает ноль где-то между f = 0,043 и f = 0,044. Введите новый диапазон, начиная с 0,0431 и 0,0432, используя дескриптор заполнения, чтобы заполнить таблицу. Затем данные показывают, что линия пересекает ноль где-то между 0,0439 и 0,044. Для следующего раунда используйте 0.04391 в качестве начального значения предположения и 0,04392 в качестве следующего. Заполните оставшуюся часть столбца.
 На графике видно, что линия пересекает 0,04396. Если мы исследуем таблицу данных, то ошибка этого значения составит -1,9 x 10-5, что довольно мало. Это хорошая точность, поэтому мы можем остановиться на этом.
 Вы могли заметить, что могли бы выполнить это упражнение без диаграммы, изучив значения в таблице. Диаграмма является необязательной, но ее можно быстро добавить, и она дает визуальное представление, которое можно интерпретировать с первого взгляда.
 Нахождение корней математических уравнений с помощью Python | Бикаш Покхарел 
 Фото Антуана Даутри на Unsplash
 Согласно Википедии
 Уравнение   - это утверждение, которое утверждает равенство двух выражений.
 Основное действие, связанное с математическими уравнениями, - это поиск решения. Решение может различаться в зависимости от природы уравнений. В математике есть различные типы уравнений, такие как: линейные, квадратичные, кубические, полиномиальные и многие другие.Для лучшего понимания этих уравнений (если вы забыли) выполните следующее, прежде чем переходить к решению на Python:
 Уравнения являются корнем Data Science. Он превращает данные в полезную информацию, разрабатывая математические выражения. В математике решения уравнения называются корнями. Корни могут быть символьными (3/5, (√2 / 3),…) или числовыми (2.5,8.9,1.0,10,…). Для числовых мы используем пакет fsolve от Scientific Python (SciPy), а для символьных мы используем пакет  sympy  (сын numpy).
 Уравнение одного типа 
 Методы одного уравнения могут применяться к временным рядам, поперечным сечениям или к панельным данным. Давайте возьмем уравнение по одному из этих критериев. Функция равна  𝑓  ( 𝑥 ) =  𝑥  2 + 2  𝑥  −10 и не равна нулю, когда значение   не соответствует правильному решению. Первоначальное предположение  2  или  -3  дает другое решение, потому что мы начинаем близко к одному или другому.
 Если мы продолжаем изменять значение y, мы получим разные решения.
  Уравнение двойного типа 
 Уравнение двойного типа - это утверждение, которое утверждает качество двух выражений типа double. Возьмем два уравнения (квадратное и прямое), и нам нужно найти для них корень.
  𝑓  ( 𝑥 ) = x² + 5  𝑥  −10 и 𝑥 = 2𝑦
 Функция возвращает остаток ошибки для каждого уравнения в виде списка. Требуются две исходные догадки.Этот же метод распространяется и на другие уравнения. Решатели уравнений могут найти решения проблем с тысячами или миллионами переменных.
  Уравнение тройного типа 
 Основная цель состоит в том, чтобы исключить по одной переменной за раз для достижения обратной подстановки. Решение системы трех уравнений с тремя переменными (x, y, z) называется упорядоченным тройным упорядочением. Уравнение с тремя переменными генерируется трехмерным графиком.
 Трехмерная плоскость
 Возьмем три уравнения (одно квадратное и две прямые из трехмерной плоскости), и мы должны найти для них корень.Их решение вручную может занять более 5 минут (для эксперта), поскольку, используя библиотеку fsolve python, мы можем решить эту проблему за полсекунды.
 x² + y² + z² = 1
  𝑥  −5  𝑦  +6  𝑧  = 0,9
  𝑥  +  𝑦  +  𝑧  = 0
 Для решения требуется тихое время их вручную, так как с помощью библиотеки python fsolve мы можем решить их за полсекунды.
 Теперь перейдем к символьному уравнению
  Символьное решение 
 Для нахождения символьного решения имеет место взаимодействие IPython.IPython создает и отображает символьное решение линейных, квадратичных ,  и многих других типов уравнений. Возьмем два уравнения (прямая линия и уравнение кривой):
 Конечные корни отображаются в виде символа
  Оптимизация уравнения 
 Когда переменных больше, чем уравнений, проблема не определена и не может быть решена. решается с помощью программы для решения уравнений, такой как  fsolve . Дополнительная информация необходима для выбора дополнительных переменных.Целевая функция  𝐽  ( 𝑥 ) - это один из способов указать проблему так, чтобы существовало единственное решение.
 Цель этого типа - минимизировать  𝑥  1  𝑥  4 ( 𝑥  1+  𝑥  2+  𝑥  3) +  𝑥  3. Два уравнения определяют выбор двух переменных с неравенство ( 𝑥  1  𝑥  2  𝑥  3  𝑥  4≥25) и равенство ( 𝑥  21+  𝑥  22+  𝑥  23+  𝑥  24 = 40)
 ограничений.Все четыре переменные должны находиться в диапазоне от  1  (нижняя граница) до  5  (верхняя граница).
 Волшебное выполнение показано ниже:
 Итак, это демонстрация кода Python для поиска корней для различных уравнений. В этом блоге также кратко показан процесс оптимизации уравнений.
  Если вы хотите связаться со мной, вы можете найти меня по телефону   http://bikashpokharel.