Содержание
Решение системы линейных уравнений методом подстановки: алгоритм, правило, примеры
Алгоритм решения системы линейных уравнений методом подстановки
- Из любого уравнения системы выразить одну переменную через другую.
- Подставить во второе уравнение системы вместо переменной выражение, полученное на первом шаге.
- Решить второе уравнение относительно выраженной переменной.
- Подставить найденное значение переменной в выражение, полученное на первом шаге.
- Найти значение второй переменой.
- Записать ответ в виде упорядоченной пары найденных значений переменных.
Например: ${\left\{ \begin{array}{c} 3x+y = 5 \\ y-x = 1 \end{array} \right.}$
Шаг 1
Из второго уравнения выражаем y:
y = x+1
Шаг 2
Подставляем выражение для y в первое уравнение:
3x+(x+1) = 5
Шаг 3 Решаем первое уравнение:
4x = 5-1
x = 1
Шаг 4
Подставляем значение x в выражение для y:
y = 1+1
Шаг 5
Находим y:
y = 2
Шаг 6
Записываем ответ:
(1;2)
В последовательной записи:
$$ {\left\{ \begin{array}{c} 3x+y = 5 \\ y-x = 1 \end{array} \right.
} \Rightarrow {\left\{ \begin{array}{c} 3x+y = 5 \\ y = x+1 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 3x+(x+1) = 5 \\ y = x+1 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 4x = 5-1 \\ y = x+1 \end{array} \right.} \Rightarrow $$ $$ \Rightarrow {\left\{ \begin{array}{c} x = 1 \\ y = x+1 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} x = 1 \\ y = 2\end{array} \right.} $$
Ответ: (1;2)
Примеры
Пример 1. Решите систему уравнений методом подстановки:
$ а) {\left\{ \begin{array}{c} 5x-4y = 3 \\ 2x-3y = 4 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 5x-4y = 3 \\ x = \frac{3y+4}{2} = 1,5y+2 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 5(1,5y+2)-4y = 3 \\ x = 1,5y+2 \end{array} \right.} \Rightarrow $
$ \Rightarrow {\left\{ \begin{array}{c} 7,5y+10-4y = 3 \\ x=1,5y+2 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 3,5y = -7 \\ x = 1,5y+2 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} y = -2 \\ x = 1,5y+2 \end{array} \right.
} \Rightarrow {\left\{ \begin{array}{c} x = -1 \\ y = -2\end{array} \right.} $
Ответ: (-1;-2)
$ б) {\left\{ \begin{array}{c} 4x-3y = 7 \\ 3x-4y = 0 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 4x-3y = 7 \\ y = \frac{3}{4} x \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 4x-3\cdot \frac{3}{4} x = 7 \\ y = \frac{3}{4} x \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} (4- \frac{9}{4})x = 7 \\ y = \frac{3}{4} x \end{array} \right.} \Rightarrow $
$\Rightarrow {\left\{ \begin{array}{c} x = 7 \cdot \frac{4}{7} = 4 \\ y = \frac{3}{4} x = \frac{3}{4} \cdot 4 = 3 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c}x = 4 \\ y = 3 \end{array} \right.} $
Ответ: (4;3)
$ в) {\left\{ \begin{array}{c} 5a-4b = 9 \\ 2a+3b = -1 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 5a-4b = 9 \\ a = \frac{-3b-1}{2} = -1,5b-0,5 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 5(-1,5b-0,5)-4b = 9 \\ a = -1,5b-0,5 \end{array} \right.
} \Rightarrow $
$ \Rightarrow {\left\{ \begin{array}{c} -7,5b-2,5-4b = 9 \\ a = -1,5b-0,5 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c}-11,5b = 11,5 \\ a = -1,5b-0,5 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} a = 1 \\ b = -1 \end{array} \right.} $
Ответ: (1;-1)
$ г) {\left\{ \begin{array}{c} 7a+4b = 5 \\ 3a+2b = 1 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 7a+4b = 5 \\ b = \frac{-3a+1}{2} = -1,5a+0,5 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 7a+4(-1,5a+0,5) = 5 \\ b = -1,5a+0,5 \end{array} \right.} \Rightarrow $
$ \Rightarrow {\left\{ \begin{array}{c} 7a-6a+2 = 5 \\ b = -1,5a+0,5 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} a = 3 \\ b = -1,5\cdot3+0,5 = -4 \end{array} \right.} $
Ответ: (3;-4)
Пример 2. Найдите решение системы уравнений:
$а) {\left\{ \begin{array}{c} \frac{x}{4}-y = 7 | \times 4 \\ 3x+ \frac{y}{2} = 9 | \times 2\end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} x-4y = 28 \\ 6x+y = 18 \end{array} \right.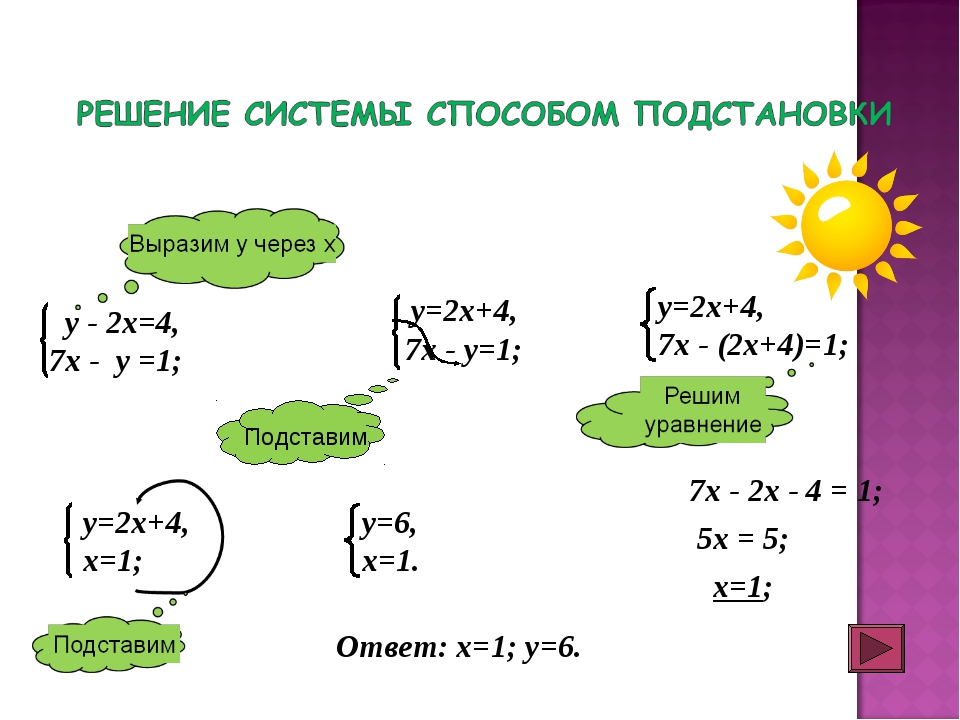
} \Rightarrow {\left\{ \begin{array}{c} x = 4y+28 = 4(y+7) \\ 6 \cdot 4(y+7)+y = 18 \end{array} \right.} \Rightarrow $
$\Rightarrow {\left\{ \begin{array}{c} x = 4(y+7) \\ 24y+168+y = 18 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} x = 4(y+7) \\ 25y = -150 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c}x = 4(-6+7) = 4 \\ y = -6 \end{array} \right.}$
Ответ: (4;-6)
$б) {\left\{ \begin{array}{c} \frac{x}{2}+ \frac{y}{3} = \frac{1}{6} |\times 6 \\ \frac{x}{3}+ \frac{y}{2} = -\frac{1}{6}| \times 6 \end{array} \right.}\Rightarrow {\left\{ \begin{array}{c} 3x+2y = 1 \\ 2x+3y = -1 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} y = \frac{-3x+1}{2} = -1,5x+0,5 \\ 2x+3(-1,5x+0,5) = -1\end{array} \right.} \Rightarrow$
$ \Rightarrow {\left\{ \begin{array}{c} y = -1,5x+0,5 \\ 2x-4,5x+1,5 = -1\end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} y = -1,5x+0,5 \\ -2,5x = -2,5 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} x = 1 \\ y = -1 \end{array} \right.
} $
Ответ: (1;-1)
$ в) {\left\{ \begin{array}{c} 3(5x-y)+14 = 5(x+y) \\ 2(x-y)+9 = 3(x+2y)-16 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 15x-3y+14 = 5x+5y \\ 2x-2y+9 = 3x+6y-16 \end{array} \right.} \Rightarrow $
$ \Rightarrow {\left\{ \begin{array}{c} 10x-8y = -14 |:2 \\ x+8y = 25 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 5x-4y = -7 \\ x = -8y+25 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 5(-8y+25)-4y = -7 \\ x = -8y+25 \end{array} \right.} \Rightarrow $
$ \Rightarrow {\left\{ \begin{array}{c} -40y+125-4y = -7 \\ x = -8y+25 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} -44y = -132 \\ x = -8y+25 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} x = 1 \\ y = 3 \end{array} \right.} $
Ответ: (1;3)
$ г) {\left\{ \begin{array}{c} 5-3(2x+7y) = x+y-52 \\ 4+3(7x+2y) = 23x \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 5-6x-21y = x+y-52 \\ 4+21x+6y = 23x \end{array} \right.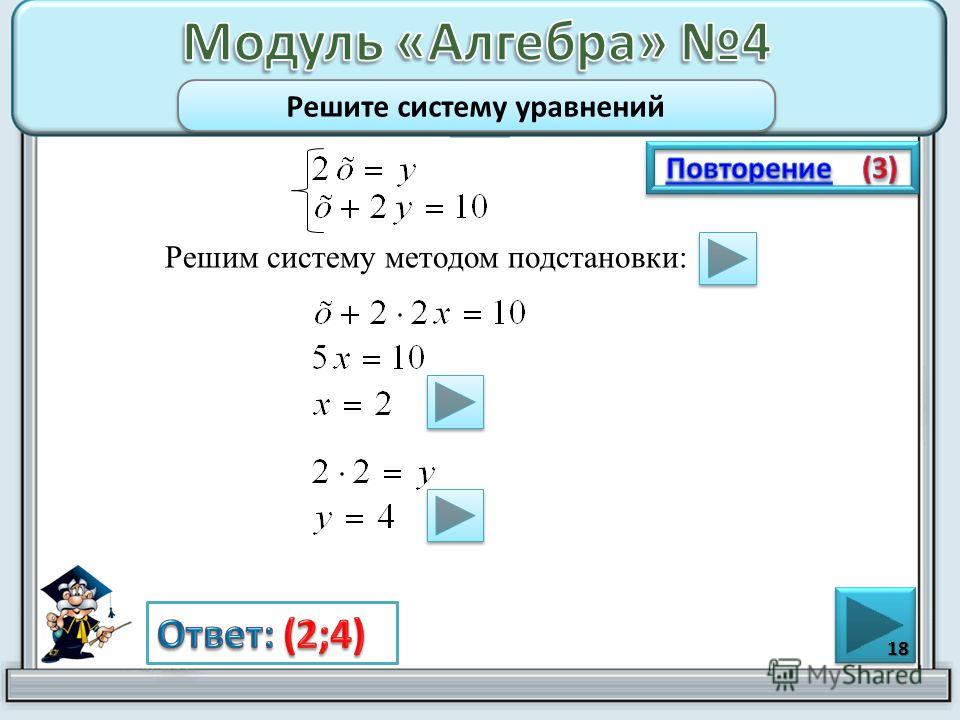
} \Rightarrow {\left\{ \begin{array}{c} 7x+22y = 57 \\ 2x-6y = 4 |:2 \end{array} \right.}$
$$ \Rightarrow {\left\{ \begin{array}{c} 7x+22y = 57 \\ x-3y = 2 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 7x+22y = 57 \\ x = 3y+2 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 7(3y+2)+22y = 57 \\ x = 3y+2 \end{array} \right.} \Rightarrow $$
$$ \Rightarrow {\left\{ \begin{array}{c} 21y+14+22y = 57 \\ x = 3y+2 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 43y = 43 \\ x = 3y+2 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} x = 5 \\ y = 1 \end{array} \right.}$$
Ответ: (5;1)
Пример 3*. Найдите решение системы уравнений:
$ {\left\{ \begin{array}{c} \frac{3}{2x-5y} + \frac{8}{x+y} = 5 \\ \frac{12}{x+y} — \frac{1}{2x-5y} = 2 \end{array} \right.} $
Введём новые переменные: $ {\left\{ \begin{array}{c} a = \frac{1}{2x-5y} \\ b = \frac{1}{x+y} \end{array} \right.} $
Перепишем систему и найдём решение для новых переменных:
$$ {\left\{ \begin{array}{c} 3a+8b = 5 \\ 12b-a = 2 \end{array} \right.
} \Rightarrow {\left\{ \begin{array}{c} 3(12b-2)+8b = 5 \\ a = 12b-2 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 36b-6+8b = 5 \\ a = 12b-2 \end{array} \right.} \Rightarrow $$
$$ \Rightarrow {\left\{ \begin{array}{c} 44b = 11 \\ a = 12b-2 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} a = 1 \\ b = \frac{1}{4} \end{array} \right.} $$
Получаем:
$$ {\left\{ \begin{array}{c} 2x-5y = \frac{1}{a} = 1 \\ x+y = \frac{1}{b} = 4 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 2x-5(4-x) = 1 \\ y = 4-x \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 2x-20+5x = 1 \\ y = 4-x \end{array} \right.} \Rightarrow $$
$$ \Rightarrow {\left\{ \begin{array}{c} 7x = 21 \\ y = 4-x \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} x = 3 \\ y = 1 \end{array} \right.} $$
Ответ: (3;1)
Система линейных уравнений с двумя переменными. Методы решения систем уравнений.
Решением системы линейных уравнений двух переменных является любая упорядоченная пара, удовлетворяющая каждому уравнению независимо.
Мы можем проверить решение, подставив значения в каждое уравнение, чтобы увидеть, удовлетворяет ли упорядоченная пара обоим уравнениям.
Как можно решить систему уравнений с двумя переменными?
Системы уравнений с двумя переменными можно решить методом подстановки:
Системы уравнений с двумя переменными можно решить методом сложения:
Пример. Решить систему методом сложения: \(\begin{equation*} \begin{cases} x-y-4=0 \\ 3x+y-8=0 \end{cases} \end{equation*}\).
Решение:
Система уравнений состоящее из двух переменных должно удовлетворять всем решениям одновременно. Система линейных уравнений из двух переменных рассматривается одновременно. Чтобы найти единственное решение системы линейных уравнений, мы должны найти численное значение для каждой переменной в системе, которая будет удовлетворять всем уравнениям системы одновременно. Некоторые линейные системы могут не иметь решения, и это будет их решением, другие системы могут иметь бесконечное число решений.
Для того чтобы линейная система имела единственное решение, должно быть не меньше уравнений, чем переменных. Тем не менее, это не гарантирует уникальное решение.
Выводы:
- Система линейных уравнений из двух переменных решается совместно методом подстановки или методом сложения.
- Чтобы найти решение системы линейных уравнений, мы должны найти численное значение для каждой переменной в системе, которая будет удовлетворять всем уравнениям в системе одновременно.
- Для того чтобы линейная система имела единственное решение, должно быть не меньше уравнений, чем переменных.
- Решить систему уравнений это значит найти численное значение для каждой переменной в системе либо доказать что решений нет.
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
«Решение линейных систем уравнения методом подстановки»
Дата публикации: .
Что такое система уравнений?
Система уравнений – это два линейных уравнения, для которых существуют пара чисел, удовлетворяющая обоим уравнениям. Система уравнений записываются следующим образом:
$\begin{cases}a_1x + b_1y +c = 0\\a_2x +b_2y +c = 0\end{cases}$
Решить систему уравнений – значит найти такие числа х и у, при которой оба уравнения превращаются в верное равенство или установить, что решения для данной системы уравнений нет.
Установить эту пару чисел можно графически, если построить для каждого уравнения системы график. Решением системы будет точка пересечения этих графиков.
Этот метод не очень удобен, т.к. требует построение графиков.
Метод подстановки
Еще один способ решения системы линейных уравнений – метода подстановки.
Пример.
Найдите два числа, разность которых равна 12, а сумма – 36.
Решение.
Обозначим через х и у числа, которые необходимо найти и составим систему линейных уравнений.
$\begin{cases}x — y = 12\\x + y = 36\end{cases}$
Представим первое уравнение, как y = x — 12, а второе уравнение представим, как y = 36 — x.
Тогда систему уравнений можно записать, как $\begin{cases}y = x — 12\\y = 36 — x\end{cases}$
Соединим оба уравнения.
x — 12 = 36 — х
2x = 48
x = 24
Тогда, у = 12.
Ответ: x = 24, у = 12.
Мы получили пару чисел, которая является решением системы уравнения, без построения графика.
Запишем алгоритм решения системы уравнений с двумя переменными, используя метод подстановки:
1. В первом уравнении системы выразим у через х.
2. Во второе уравнение вместо у подставим выражение, которое мы получили на первом шаге.
3. Решаем второе уравнение и находим х.
4. Найденное значение х подставим в первое уравнение системы.
5. Записываем ответ в виде пары чисел (х, у).
5.2 Решение систем уравнений подстановкой — элементарная алгебра 2e
Задачи обучения
К концу этого раздела вы сможете:
- Решите систему уравнений заменой
- Решите приложения систем уравнений заменой
Будьте готовы 5,4
Перед тем, как начать, пройдите тест на готовность.
Упростим −5 (3 − x) −5 (3 − x).
Если вы пропустили эту проблему, просмотрите Пример 1.136.
Будьте готовы 5.5
Упростим 4−2 (n + 5) 4−2 (n + 5).
Если вы пропустили эту проблему, просмотрите Пример 1.123.
Будьте готовы 5,6
Решить для гг. 8y − 8 = 32−2y8y − 8 = 32−2y
Если вы пропустили эту проблему, просмотрите Пример 2.34.
Будьте готовы 5,7
Решить относительно xx. 3x − 9y = −33x − 9y = −3
Если вы пропустили эту проблему, просмотрите Пример 2.65.
Решение систем линейных уравнений с помощью графиков — хороший способ визуализировать типы решений, которые могут возникнуть.Однако во многих случаях решение системы с помощью построения графиков неудобно или неточно. Если графики выходят за пределы небольшой сетки с x и y как между -10, так и 10, построение линий может быть громоздким. И если решения системы не являются целыми числами, может быть трудно точно прочитать их значения с графика.
В этом разделе мы будем решать системы линейных уравнений методом подстановки.
Решите систему уравнений подстановкой
Мы будем использовать ту же систему, которую мы использовали вначале для построения графиков.
{2x + y = 7x − 2y = 6 {2x + y = 7x − 2y = 6
Сначала мы решим одно из уравнений для x или y . Мы можем выбрать любое уравнение и решить любую переменную, но мы постараемся сделать выбор, который упростит работу.
Затем мы подставляем это выражение в другое уравнение. В результате получается уравнение с одной переменной — и мы знаем, как его решить!
После того, как мы найдем значение одной переменной, мы подставим это значение в одно из исходных уравнений и решим для другой переменной.Наконец, мы проверяем наше решение и убеждаемся, что оно выполняет оба уравнения.
Теперь мы выполним все эти шаги в примере 5.13.
Пример 5.
13
Как решить систему уравнений подстановкой
Решите систему заменой. {2x + y = 7x − 2y = 6 {2x + y = 7x − 2y = 6
Попробовать 5.25
Решите систему заменой. {−2x + y = −11x + 3y = 9 {−2x + y = −11x + 3y = 9
Попробовать 5.26
Решите систему заменой.{x + 3y = 104x + y = 18 {x + 3y = 104x + y = 18
How To
Решите систему уравнений путем подстановки.
- Шаг 1. Решите одно из уравнений для любой переменной.
- Шаг 2. Подставьте выражение из шага 1 в другое уравнение.
- Шаг 3. Решите полученное уравнение.
- Шаг 4. Подставьте решение шага 3 в одно из исходных уравнений, чтобы найти другую переменную.
- Шаг 5. Запишите решение в виде упорядоченной пары.
- Шаг 6. Убедитесь, что упорядоченная пара является решением обоих исходных уравнений.
Если одно из уравнений системы задано в форме углового пересечения, шаг 1 уже выполнен! Мы увидим это в примере 5.14.
Пример 5.14
Решите систему заменой.
{x + y = −1y = x + 5 {x + y = −1y = x + 5
Решение
Второе уравнение уже решено для y . Мы подставим выражение вместо на в первое уравнение.
Попробовать 5.27
Решите систему заменой. {x + y = 6y = 3x − 2 {x + y = 6y = 3x − 2
Попробовать 5.28
Решите систему заменой. {2x − y = 1y = −3x − 6 {2x − y = 1y = −3x − 6
Если уравнения представлены в стандартной форме, нам нужно будет начать с решения для одной из переменных. В следующем примере мы решим первое уравнение относительно y .
Пример 5.15
Решите систему заменой. {3x + y = 52x + 4y = −10 {3x + y = 52x + 4y = −10
Решение
Нам нужно решить одно уравнение для одной переменной.
Затем мы подставим это выражение в другое уравнение.
Попробовать 5.29
Решите систему заменой. {4x + y = 23x + 2y = −1 {4x + y = 23x + 2y = −1
Попробуй 5.30
Решите систему заменой. {−x + y = 44x − y = 2 {−x + y = 44x − y = 2
В примере 5.15 проще всего было решить для y в первом уравнении, потому что оно имело коэффициент 1. В примере 5.16 будет легче решить для x .
Пример 5.16
Решите систему заменой. {x − 2y = −23x + 2y = 34 {x − 2y = −23x + 2y = 34
Решение
Мы решим первое уравнение относительно xx, а затем подставим выражение во второе уравнение.
Попробуйте 5,31
Решите систему заменой. {x − 5y = 134x − 3y = 1 {x − 5y = 134x − 3y = 1
Попробуйте 5,32
Решите систему заменой. {x − 6y = −62x − 4y = 4 {x − 6y = −62x − 4y = 4
Когда оба уравнения уже решены для одной и той же переменной, их легко заменить!
Пример 5.
17
Решите систему заменой. {y = −2x + 5y = 12x {y = −2x + 5y = 12x
Решение
Поскольку оба уравнения решаются относительно y , мы можем подставить одно в другое.
Попробуйте 5,33
Решите систему заменой. {y = 3x − 16y = 13x {y = 3x − 16y = 13x
Попробуйте 5,34
Решите систему заменой. {y = −x + 10y = 14x {y = −x + 10y = 14x
Будьте очень осторожны со знаками в следующем примере.
Пример 5.18
Решите систему заменой. {4x + 2y = 46x − y = 8 {4x + 2y = 46x − y = 8
Решение
Нам нужно решить одно уравнение для одной переменной. Решим первое уравнение относительно y .
Попробуйте 5,35
Решите систему заменой. {x − 4y = −4−3x + 4y = 0 {x − 4y = −4−3x + 4y = 0
Попробовать 5,36
Решите систему заменой. {4x − y = 02x − 3y = 5 {4x − y = 02x − 3y = 5
В примере 5.
19, потребуется немного больше работы, чтобы решить одно уравнение для x или y .
Пример 5.19
Решите систему заменой. {4x − 3y = 615y − 20x = −30 {4x − 3y = 615y − 20x = −30
Решение
Нам нужно решить одно уравнение для одной переменной. Решим первое уравнение относительно x .
Поскольку 0 = 0 — истинное утверждение, система непротиворечива. Уравнения зависимы. Графики этих двух уравнений дадут одну и ту же линию.У системы бесконечно много решений.
Попробовать 5,37
Решите систему заменой. {2x − 3y = 12−12y + 8x = 48 {2x − 3y = 12−12y + 8x = 48
Попробовать 5,38
Решите систему заменой. {5x + 2y = 12−4y − 10x = −24 {5x + 2y = 12−4y − 10x = −24
Вернитесь к уравнениям в примере 5.19. Есть ли способ распознать, что это одна линия?
Давайте посмотрим, что происходит в следующем примере.
Пример 5.20
Решите систему заменой.{5x − 2y = −10y = 52x {5x − 2y = −10y = 52x
Решение
Второе уравнение уже решено для y , поэтому мы можем заменить y в первом уравнении.
| Замените x на y в первом уравнении. | |
| Заменить y на 52x.52x. | |
| Решите для x . | |
Поскольку 0 = −10 — ложное утверждение, уравнения несовместимы.Графики двух уравнений будут параллельными линиями.
В системе нет решений.
Попробовать 5,39
Решите систему заменой. {3x + 2y = 9y = −32x + 1 {3x + 2y = 9y = −32x + 1
Попробовать 5,40
Решите систему заменой. {5x − 3y = 2y = 53x − 4 {5x − 3y = 2y = 53x − 4
Решите приложения систем уравнений подстановкой
Мы скопируем сюда стратегию решения проблем, которую мы использовали в разделе «Решение систем уравнений с помощью графического представления» для решения систем уравнений.Теперь, когда мы знаем, как решать системы с помощью подстановки, это то, что мы сделаем на шаге 5.
How To
Как использовать стратегию решения задач для систем линейных уравнений.
- Шаг 1. Прочтите о проблеме. Убедитесь, что все слова и идеи понятны.
- Шаг 2. Определите , что мы ищем.
- Шаг 3. Назовите то, что мы ищем. Выберите переменные для представления этих величин.
- Шаг 4. Переведите в систему уравнений.
- Шаг 5. Решите систему уравнений, используя хорошие методы алгебры.
- Шаг 6. Отметьте ответ в задаче и убедитесь, что он имеет смысл.
- Шаг 7. Ответьте на вопрос полным предложением.
Выберите переменные для представления этих величин.Некоторым людям проще создать текстовые задачи с двумя переменными, чем с одной переменной. Выбирать имена переменных проще, когда все, что вам нужно сделать, это написать две буквы.Подумайте об этом в следующем примере — как бы вы сделали это с помощью только одной переменной?
Пример 5.21
Сумма двух чисел равна нулю. Одно число на девять меньше другого. Найдите числа.
Попробовать 5.41
Сумма двух чисел равна 10. Одно число на 4 меньше другого. Найдите числа.
Попробовать 5.
42
Сумма двух чисел равна −6. Одно число на 10 меньше другого. Найдите числа.
В Примере 5.22 воспользуемся формулой для периметра прямоугольника: P = 2 L + 2 W .
Пример 5.22
Периметр прямоугольника равен 88. Длина в пять раз больше ширины в два раза. Найдите длину и ширину.
Попробовать 5.43
Периметр прямоугольника равен 40. Длина на 4 раза больше ширины. Найдите длину и ширину прямоугольника.
Попробовать 5.44
Периметр прямоугольника равен 58.Длина в 5 раз больше ширины более чем в три раза. Найдите длину и ширину прямоугольника.
Для примера 5.23 нам нужно помнить, что сумма углов треугольника равна 180 градусам, а у прямоугольного треугольника один угол 90 градусов.
Пример 5.23
Размер одного из малых углов прямоугольного треугольника в десять раз больше, чем в три раза больше другого малого угла.
Найдите размеры обоих углов.
Решение
Нарисуем и обозначим фигуру.
Попробовать 5,45
Размер одного из малых углов прямоугольного треугольника в 2 раза больше, чем в 3 раза больше другого малого угла. Найдите размер обоих углов.
Попробовать 5,46
Размер одного из малых углов прямоугольного треугольника на 18 меньше, чем удвоение размера другого малого угла. Найдите размер обоих углов.
Пример 5.24
Хизер предложили два варианта заработной платы тренера в спортзале.Вариант А платит ей 25 000 долларов плюс 15 долларов за каждую тренировку. Вариант Б платит ей 10 000 + 40 долларов за каждую тренировку. Сколько тренировок уравняло бы варианты заработной платы?
Попробовать 5,47
Джеральдин предложили вакансии в двух страховых компаниях. Первая компания выплачивает заработную плату в размере 12 000 долларов плюс комиссия в размере 100 долларов за каждый проданный полис.
Второй платит зарплату в размере 20 000 долларов плюс комиссию в размере 50 долларов за каждый проданный полис. Сколько полисов нужно продать, чтобы общая сумма была такой же?
Попробуй 5.48
Кеннет в настоящее время продает костюмы для компании А с зарплатой 22 000 долларов плюс 10 долларов комиссионных за каждый проданный костюм. Компания B предлагает ему должность с окладом в 28000 долларов плюс комиссия в размере 4 долларов за каждый проданный костюм. Сколько костюмов нужно продать Кеннету, чтобы варианты были равны?
Раздел 5.2. Упражнения
Практика ведет к совершенству
Решите систему уравнений подстановкой
В следующих упражнениях решите системы уравнений путем подстановки.
71.
{2x + y = −43x − 2y = −6 {2x + y = −43x − 2y = −6
72.
{2x + y = −23x − y = 7 {2x + y = −23x − y = 7
73.
{x − 2y = −52x − 3y = −4 {x − 2y = −52x − 3y = −4
74.
{x − 3y = −92x + 5y = 4 {x − 3y = −92x + 5y = 4
75.
{5x − 2y = −6y = 3x + 3 {5x − 2y = −6y = 3x + 3
76.
{−2x + 2y = 6y = −3x + 1 {−2x + 2y = 6y = −3x + 1
77.
{2x + 3y = 3y = −x + 3 {2x + 3y = 3y = −x + 3
78.
{2x + 5y = −14y = −2x + 2 {2x + 5y = −14y = −2x + 2
79.
{2x + 5y = 1y = 13x − 2 {2x + 5y = 1y = 13x − 2
80.
{3x + 4y = 1y = −25x + 2 {3x + 4y = 1y = −25x + 2
81.
{3x − 2y = 6y = 23x + 2 {3x − 2y = 6y = 23x + 2
82.
{−3x − 5y = 3y = 12x − 5 {−3x − 5y = 3y = 12x − 5
83.
{2x + y = 10 − x + y = −5 {2x + y = 10 − x + y = −5
84.
{−2x + y = 10 − x + 2y = 16 {−2x + y = 10 − x + 2y = 16
85.
{3x + y = 1−4x + y = 15 {3x + y = 1−4x + y = 15
86.
{x + y = 02x + 3y = −4 {x + y = 02x + 3y = −4
87.
{x + 3y = 13x + 5y = −5 {x + 3y = 13x + 5y = −5
88.
{x + 2y = −12x + 3y = 1 {x + 2y = −12x + 3y = 1
89.
{2x + y = 5x − 2y = −15 {2x + y = 5x − 2y = −15
90.
{4x + y = 10x − 2y = −20 {4x + y = 10x − 2y = −20
91.
{y = −2x − 1y = −13x + 4 {y = −2x − 1y = −13x + 4
92.
{y = x − 6y = −32x + 4 {y = x − 6y = −32x + 4
93.
{y = 2x − 8y = 35x + 6 {y = 2x − 8y = 35x + 6
94.
{y = −x − 1y = x + 7 {y = −x − 1y = x + 7
95.
{4x + 2y = 88x − y = 1 {4x + 2y = 88x − y = 1
96.
{−x − 12y = −12x − 8y = −6 {−x − 12y = −12x − 8y = −6
97.
{15x + 2y = 6−5x + 2y = −4 {15x + 2y = 6−5x + 2y = −4
98.
{2x − 15y = 712x + 2y = −4 {2x − 15y = 712x + 2y = −4
99.
{y = 3x6x − 2y = 0 {y = 3x6x − 2y = 0
100.
{x = 2y4x − 8y = 0 {x = 2y4x − 8y = 0
101.
{2x + 16y = 8 − x − 8y = −4 {2x + 16y = 8 − x − 8y = −4
102.
{15x + 4y = 6−30x − 8y = −12 {15x + 4y = 6−30x − 8y = −12
103.
{y = −4x4x + y = 1 {y = −4x4x + y = 1
104.
{y = −14xx + 4y = 8 {y = −14xx + 4y = 8
105.
{y = 78x + 4−7x + 8y = 6 {y = 78x + 4−7x + 8y = 6
106.
{y = −23x + 52x + 3y = 11 {y = −23x + 52x + 3y = 11
Решите приложения систем уравнений подстановкой
В следующих упражнениях переведите в систему уравнений и решите.
107.
Сумма двух чисел равна 15. Одно число на 3 меньше другого. Найдите числа.
108.
Сумма двух чисел равна 30. Одно число на 4 меньше другого. Найдите числа.
109.
Сумма двух чисел равна −26. Одно число на 12 меньше другого. Найдите числа.
110.
Периметр прямоугольника равен 50. Длина на 5 больше ширины. Найдите длину и ширину.
111.
Периметр прямоугольника равен 60. Длина на 10 больше ширины.Найдите длину и ширину.
112.
Периметр прямоугольника равен 58. Его длина в 5 раз больше ширины. Найдите длину и ширину.
113.
Периметр прямоугольника равен 84. Длина в 10 раз больше ширины более чем в три раза. Найдите длину и ширину.
114.
Размер одного из малых углов прямоугольного треугольника в 14 раз больше, чем в 3 раза больше другого малого угла.
Найдите размер обоих углов.
115.
Размер одного из малых углов прямоугольного треугольника в 26 более чем в 3 раза превышает размер другого малого угла.Найдите размер обоих углов.
116.
Размер одного из малых углов прямоугольного треугольника на 15 меньше, чем удвоение размера другого малого угла. Найдите размер обоих углов.
117.
Размер одного из малых углов прямоугольного треугольника на 45 меньше, чем удвоение размера другого малого угла. Найдите размер обоих углов.
118.
Максиму предложили вакансии два автосалона. Первая компания платит зарплату в размере 10 000 долларов плюс комиссионные в размере 1 000 долларов за каждую проданную машину.Второй платит зарплату в размере 20 000 долларов плюс комиссию в размере 500 долларов за каждую проданную машину. Сколько автомобилей нужно продать, чтобы общая сумма была такой же?
119.
Джеки предложили должности две кабельные компании. Первая компания платит зарплату в размере 14 000 долларов плюс комиссию в размере 100 долларов за каждый проданный пакет кабеля.
Второй платит зарплату в размере 20 000 долларов плюс комиссию в размере 25 долларов за каждый проданный пакет кабеля. Сколько пакетов кабеля нужно продать, чтобы общая сумма была такой же?
120.
Амара в настоящее время продает телевизоры для компании А с зарплатой 17 000 долларов плюс комиссия 100 долларов за каждый проданный телевизор. Компания B предлагает ей должность с окладом в 29 000 долларов плюс 20 долларов комиссионных за каждый проданный телевизор. Какие телевизоры нужно будет продавать Amara, чтобы возможности были равными?
121.
В настоящее время Митчелл продает печи компании А с зарплатой в 12 000 долларов плюс 150 долларов комиссионных за каждую проданную печь. Компания B предлагает ему должность с зарплатой в размере 24 000 долларов плюс комиссия в размере 50 долларов за каждую проданную печь.Сколько печей нужно продать Митчеллу, чтобы варианты были равны?
Повседневная математика
122.
Когда Глория провела 15 минут на эллиптическом тренажере, а затем 30 минут выполняла круговые тренировки, ее фитнес-приложение показало, что она сожгла 435 калорий. Когда она потратила 30 минут на эллиптический тренажер и 40 минут на круговые тренировки, она сожгла 690 калорий. Решите систему {15e + 30c = 43530e + 40c = 690 {15e + 30c = 43530e + 40c = 690 для ee, количество калорий, которые она сжигает за каждую минуту на эллиптическом тренажере, и cc, количество калорий, которые она сжигает для каждую минуту круговой тренировки.
123.
Стефани выехала из Риверсайда, Калифорния, на своем автодоме на север по межштатной автомагистрали 15 в сторону Солт-Лейк-Сити со скоростью 56 миль в час. Через полчаса Тина выехала из Риверсайда на своей машине по тому же маршруту, что и Стефани, со скоростью 70 миль в час. Решите систему {56s = 70ts = t + 12 {56s = 70ts = t + 12.
- ⓐ для tt, чтобы узнать, сколько времени потребуется Тине, чтобы догнать Стефани.
- ⓑ какова стоимость ss, сколько часов Стефани будет проехать, прежде чем Тина ее догонит?
Письменные упражнения
124.
Решите систему уравнений
{x + y = 10x − y = 6 {x + y = 10x − y = 6
ⓐ по графику.
Ⓑ заменой.
Ⓒ Какой метод вы предпочитаете? Почему?
125.
Решите систему уравнений
{3x + y = 12x = y − 8 {3x + y = 12x = y − 8 путем подстановки и объясните все свои шаги словами.
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.
ⓑ Что вы сделаете, изучив этот контрольный список, чтобы стать уверенным в достижении всех целей?
Решение систем линейных уравнений с использованием подстановки
Системы линейных уравнений:
А
система
линейные уравнения
представляет собой просто набор из двух или более линейных уравнений.
В двух переменных
(
Икс
а также
y
)
, график системы двух уравнений представляет собой пару прямых на плоскости.
Есть три возможности:
- Линии пересекаются в нулевых точках. (Линии параллельны.)
- Линии пересекаются ровно в одной точке. (Большинство случаев.)
- Прямые пересекаются в бесконечном множестве точек.(Два уравнения представляют собой одну и ту же линию.)
Как решить систему с помощью
Метод замены
-
Шаг1
:
Сначала решите одно линейное уравнение относительноy
с точки зрения
Икс
.
-
Шаг2
:
Затем замените это выражение наy
в другом линейном уравнении.Вы получите уравнение в
Икс
.
-
Шаг3
:
Решите это, и у вас будетИкс
-координата перекрестка.
-
Шаг4
:
Затем подключитеИкс
к любому уравнению, чтобы найти соответствующее
y
-координат.
Примечание
1
:
Если это проще, вы можете начать с решения уравнения для
Икс
с точки зрения
y
, и — такая же разница!
Пример:
Решите систему
{
3
Икс
+
2
y
знак равно
16
7
Икс
+
y
знак равно
19
Решите второе уравнение относительно
y
.
y
знак равно
19
—
7
Икс
Заменять
19
—
7
Икс
для
y
в первом уравнении и решите относительно
Икс
.
3
Икс
+
2
(
19
—
7
Икс
)
знак равно
16
3
Икс
+
38
—
14
Икс
знак равно
16
—
11
Икс
знак равно
—
22
Икс
знак равно
2
Заменять
2
для
Икс
в
y
знак равно
19
—
7
Икс
и решить для
y
.
y
знак равно
19
—
7
(
2
)
y
знак равно
5
Решение
(
2
,
5
)
.
Примечание
2
:
Если линии параллельны, ваш
Икс
-условия будут отменены в шаге
2
, и вы получите невозможное уравнение, что-то вроде
0
знак равно
3
.
Примечание
3
:
Если два уравнения представляют одну и ту же строку, все будет отменено на шаге
2
, и вы получите избыточное уравнение,
0
знак равно
0
.
Как решить линейные уравнения с помощью подстановки
Как решить систему уравнений:
Прежде чем мы перейдем к решению систем линейных уравнений с помощью метода подстановки, давайте сначала рассмотрим и поймем, что значит «решить» систему уравнений.Когда мы говорим «решить» применительно к линейному, квадратичному, экспоненциальному или любому другому типу уравнения, на самом деле мы имеем в виду, что мы пытаемся найти значения «x» — зависимой переменной — которые удовлетворяют «y» — независимая переменная.
Возьмем, к примеру, следующее простое уравнение: y = 2x = 2
В этом примере уравнения мы знаем, что y равно 2x и также равно 2. С этим знанием, поскольку y равно как 2x, так и 2, мы можем сказать, что 2x = 2. Тогда следующим естественным шагом будет решить это уравнение с помощью алгебры, дав нам «решение», что x = 1.
В случае систем уравнений процесс не так уж и отличается. При решении систем уравнений мы пытаемся найти значения x и y, которые делают два различных уравнения равными друг другу — эффективно «решая» оба уравнения. Дополнительную информацию о системе уравнений можно найти в другом уроке. В системе уравнений есть несколько результатов, которые могут произойти в зависимости от количества решений. У нас есть конкретные уроки о том, как определять количество решений линейных уравнений и системы линейно-квадратных уравнений.У нас также есть графические системы уравнений и неравенств!
Для этого существует два основных метода: решение систем путем подстановки и решение систем путем исключения. В этой статье мы сосредоточимся на подстановке, которая, возможно, немного проще, чем другой метод — устранение. Для устранения, пожалуйста, посмотрите видео и статьи, посвященные именно этому методу. Чтобы убедиться, что вы готовы к исключению, важно научиться складывать и вычитать многочлены, а также складывать и вычитать рациональные выражения.
Теперь, когда мы рассмотрели основы, давайте решим системы с помощью подстановки!
Решение систем уравнений подстановкой:
Прежде чем мы перейдем к использованию метода подстановки, убедитесь, что вы хорошо разбираетесь в алгебре, просмотрев урок о решении линейных уравнений с переменными с обеих сторон.
Основная процедура решения систем с помощью подстановки проста: имея два линейных уравнения, все, что нам нужно сделать, это «подставить» одно из пары уравнений в другое, переставив переменные.Эту процедуру лучше описать ниже на общем примере:
Рассмотрим следующие уравнения, где (x, y) — координаты, а все остальное — константы.
1) ty = axty = axty = ax
2) zy = x + bzy = x + bzy = x + b
Шаг 1. Измените одно из уравнений так, чтобы получить «y» само по себе
1) y = axty = \ frac {ax} {t} y = налог
2) zy = x + bzy = x + bzy = x + b
Шаг 2: подставьте преобразованное уравнение в его партнера
zy = x + bzy = x + bzy = x + b
z (axt) = x + bz (\ frac {ax} {t}) = x + bz (налог) = x + b
Шаг 3: Решите относительно x
Так как это всего лишь общий случай, мы не можем решить для x.Но обратите внимание, что все, что нам нужно сделать, это получить x само по себе.
Шаг 4. Подставьте решение для x в любое из изначально заданных уравнений, чтобы найти y
Получив значение x, мы можем подставить его в любое из двух уравнений, чтобы найти решение для y.
Шаг 5. Окончательный ответ запишите точкой
Следовательно, наше решение (x, y)
Еще раз, это просто общий случай. Также обратите внимание, что в этом примере мы решили сначала решить для x.Неважно, какую переменную вы решите в первую очередь, просто обратите внимание, что x часто легче решить для первой, так как это часто требует меньших изменений в исходных уравнениях. Лучший способ научиться и научиться решать с помощью замены — это выполнять некоторые практические задачи.
Пример 1:
Возьмите следующие одновременные уравнения и решите.
6x — 1y = 7
-9x + 2y = 7
Шаг 1. Измените одно из уравнений так, чтобы получить «y» само по себе
Давайте воспользуемся первым уравнением и изменим его так, чтобы у нас было y само по себе.Конечно, мы могли бы взять второе уравнение, но это потребует дополнительной работы.
6x — 1y = 7
6x — 7 = y
Шаг 2: подставьте преобразованное уравнение в его партнера
Теперь мы собираемся заменить наше недавно преобразованное уравнение 6x — 7 = y в -9x + 2y = 7.
-9x + 2 (6x — 7) = 7
Шаг 3: Решите относительно x
Теперь, когда мы успешно выполнили замену, давайте решим относительно x.
-9x + 12x — 14 = 7
3x = 21
х = 7
Шаг 4. Подставьте решение для x в любое из изначально заданных уравнений, чтобы найти y
Теперь, когда у нас есть x, мы можем положить x = 7 в любое из уравнений, чтобы найти y.Выберем первое уравнение, потому что оно более простое.
6 (7) — 1у = 7
42 — у = 7
у = 35
Шаг 5. Окончательный ответ запишите точкой
Окончательный ответ: (7, 35)
На следующем изображении ниже показана работа, которую мы только что проделали:
Решите линейное уравнение с заменой
Пример 2:
Решите следующую линейную систему.
3 (х + 2) — (у + 7) = 4
5 (х + 1) + 4 (у + 3) = 31
В некоторых случаях нам может потребоваться некоторое упрощение обоих уравнений, прежде чем мы сможем продолжить замену и решение.В этом случае мы должны сначала расширить и упростить оба уравнения:
3 (х + 2) — (у + 7) = 4
3х + 6 — у — 7 = 4
3х — у = 5
&
5 (х + 1) + 4 (у + 3) = 31
5х + 5 + 4у + 12 = 31
5х + 4у = 14
Шаг 1. Измените одно из уравнений так, чтобы получить «y» само по себе
Как и в первом примере, давайте воспользуемся первым уравнением и изменим его так, чтобы у нас было y само по себе. Конечно, мы могли бы взять второе уравнение, но это потребует дополнительной работы.
3х — у = 5
3х — 5 = у
Шаг 2: Подставьте преобразованное уравнение в его партнер и решите относительно x
Теперь мы собираемся заменить наше недавно преобразованное уравнение 3x — 5 = y в 5x + 4y = 14 и решить относительно x.
5x + 4 (3x — 5) = 14
5x + 12x — 20 = 14
17x = 34
х = 2
Шаг 3. Подставьте решение для x в любое из изначально заданных уравнений, чтобы найти y
Теперь, когда у нас есть x, мы можем положить x = 2 в любое из уравнений, чтобы найти y. Выберем первое уравнение, потому что оно более простое.
3х — у = 5
3 (2) — у = 5
у = 1
Шаг 4. Окончательный ответ запишите точкой
Окончательный ответ: (2, 1)
Вот и все! Теперь убедитесь, что вы выполняете много практических задач, чтобы вам было удобнее использовать этот метод.Также просмотрите эту отличную ссылку, которая позволит вам легко проверить свою работу.
Как решить систему уравнений с помощью подстановки.
После того, как вы закончите этот урок, просмотрите все наши уроки предварительной алгебры и практические задачи.
Как решить систему уравнений с помощью подстановки
В этом видео показано, как решить с помощью подстановки.
Чтобы решить с помощью подстановки, приравняйте оба уравнения друг к другу, если они оба равны y.
Это можно сделать, только если у вас есть одно уравнение в виде переменной.
Имея уравнение, равное переменной, вы можете подставить другое уравнение в терминах этой переменной и решить.
Если уравнение уже НЕ равно переменной, тогда вам придется выделить переменную для уравнения (й), чтобы ее можно было вставить в другое уравнение.
После этого вы решаете отсутствующую переменную и вставляете ее обратно в одно из исходных уравнений, чтобы получить значение второй переменной.
Значения x и y — это координаты точки пересечения двух линий.
Чтобы проверить это, подставьте значения x и y в исходное уравнение и упростите его, чтобы проверить, верно ли оно.
Например:
Перепишите это после подключения 2x-1, где мы видим y в первом уравнении. Итак:
После решения находим x = 2.
Затем подставьте 2 вместо x в любое уравнение, чтобы найти значение y.
Следовательно, решение (2,3).
Примеры решения системы уравнений подстановкой
Пример 1
Уравнение уже имеет значение для.
Итак, давайте просто возьмем значение в этом уравнении и подставим его в это
У нас будет
Распределить по каждому члену внутри круглых скобок
Объединить похожие термины
Теперь давайте выделим, добавив с обеих сторон .
Затем разделите обе стороны на,
И у нас получится
Затем давайте подставим значение в одно уравнение, чтобы получить значение.
Итак, наш ответ:
Пример 2
Давайте решим одну из переменных в одном из уравнений, а затем воспользуемся этим для замены в другое.
Теперь решите значение, используя нижнее уравнение.
Чтобы найти, добавим обе части уравнения.
Давайте решим значение, подставив значение в нижнее уравнение.
Распределить по каждому термину внутри круглых скобок
Объединить похожие термины
Теперь давайте изолируем, добавив с обеих сторон.
Затем разделите обе стороны на,
И у нас получится
Затем давайте подставим значение в одно уравнение, чтобы получить значение.
Итак, наш ответ:
Стенограмма видеоурока
В этом уроке вы научитесь решать систему уравнений алгебраически.
Мы собираемся использовать алгебру, чтобы найти одну из переменных. После этого найдите другую переменную.
Но проблема в том, что у нас есть два уравнения с двумя пропущенными переменными одновременно.
Итак, чтобы решить эту проблему, мы должны найти способ объединить два уравнения только с одной переменной.
Например,
Итак, мы собираемся получить одно значение и подставить его в другое уравнение.Таким образом мы можем исключить одну недостающую переменную.
Давайте возьмем значение во втором уравнении и подставим его в первое уравнение.
Давайте решим это.
У нас есть
, но поскольку мы также знаем, что
, мы получим это уравнение
Опять же, мы просто получаем значение в одном уравнении и подставляем его во второе уравнение.
Этот процесс называется «замещением».
Возвращаясь назад, давайте сначала решим уравнение, вычтя обе части уравнения.
У нас будет
Затем, чтобы изолировать, мы должны сложить обе части уравнения.
Итак, у нас есть
Но значение не является окончательным ответом.
Нам также нужно знать, какова стоимость.
Чтобы решить эту проблему, возьмем одно уравнение и подставим значение.
Давайте возьмем
, затем подставим значение.
Давайте сделаем это
И у нас будет
Итак, наш окончательный ответ —
Чтобы проверить это, давайте возьмем другое уравнение и подставим значение и.
Это чек.
Итак, здесь вы узнали, как решить систему уравнений алгебраически с помощью подстановки.
Вкратце, мы получаем значение в одном уравнении и подставляем его в другое уравнение, чтобы найти его.
Затем мы подставляем значение в одно уравнение, чтобы найти значение.
Мы также проверяем, получили ли мы правильный ответ, получая уравнение и подставляя значение и.
Итак, давайте рассмотрим еще один пример.
Итак, наш ответ:
Поскольку мы использовали верхнее уравнение для решения, давайте воспользуемся нижним уравнением для проверки.
Затем выделите путем вычитания с обеих сторон.
Как решать системы линейных уравнений подстановкой, примеры, рисунки, практика. Шаг к ..
Видео о решении заменой
Пример замены 1
Давайте еще раз рассмотрим систему, изображенную выше.
$
\ red {y} = 2x + 1 \ text {и} \ red {y} = 4x -1
$
Шаг 1
Мы собираемся использовать подстановку, как в примере 2 обзора выше.
Теперь у нас есть 1 уравнение и 1 неизвестное, мы можем решить эту проблему, как показано в работе ниже.
Последний шаг — снова использовать подстановку, в этом случае мы знаем, что x = 1, но чтобы найти значение y решения, мы просто подставляем x = 1 в любое уравнение.
$$
у = 2х + 1
\\
y = 2 \ cdot \ red {1} + 1 = 2 + 1 = 3
\\
\\ \ boxed {\ text {или вы используете другое уравнение}}
\\
у = 4х -1
\\
у = 4 \ cdot \ red {1} — 1
\\
у = 4 — 1 = 3
\\
\ boxed {(1,3)}
$$
Пример замены 2
Каково решение системы уравнений ниже:
$
у = 2х + 1
\\
2у = 3х — 2
$
Шаг 1
Определите лучшее уравнение для замены, а затем подставьте его в другое уравнение.
Шаг 2
Решить относительно x
Шаг 3
Подставьте значение x (в данном случае -4) в любое уравнение.
$$
у = 2х + 1
\\
y = 2 \ cdot \ red {-4} + 1 = -8 + 1 = -7
\\
2у = 3х — 2 \\
2у = 3 \ cdot-4 -2
\\
\ boxed {\ text {или вы используете другое уравнение}}
\\
2у = 3х -2
\\
2у = 3 (\ красный {-4}) -2
\\
2у = -12-2
\\
2у = -14
\ frac {1} {2} \ cdot2y = \ frac {1} {2} \ cdot-14
\\
у = -7
$$
$$ \ boxed {(-4, -7)}
$$
Показать график
Проблемы практики замены
Задача 1
Решите приведенную ниже систему, используя замену
$$
у = х + 1
\\
у = 2х +2
$$
Покажи ответ
Решением этой системы является точка пересечения: (-1, 0).
$$
y = x + 1 \ quad y = 2x + 2
\\
\ hspace {1,2 см} \ downarrow \ hspace {1,4 см} \ downarrow
\\
\ hspace {6mm} x + 1 = 2x + 2
\\
\ hspace {7mm} \ text {-} x \ hspace {1.4см} \ текст {-} х
\\
\ hspace {7 мм} \ rule {3,2 см} {0,25 мм}
\\
\ hspace {1,7 см} 1 = x + 2
\\
\ hspace {1,6 см} \ text {-} 2 \ hspace {1,4 см} \ text {-} 2
\\
\ hspace {7 мм} \ rule {3,2 см} {0,25 мм}
\\
\ hspace {1.2 см} -1 = х
\\
\ hspace {1,6 см} \ downarrow
\\
\ hspace {5mm} y = 2x + 2
\\
\ hspace {7mm} y = 2 * (-1) + 2 = 0
\\ [5 мм]
\ text {Решение:} \ hspace {3mm} (-1, 0)
$$
Задача 2
Используйте подстановку для решения следующей системы линейных уравнений:
- Строка 1: y = 3x — 1
- Строка 2: y = x — 5
Отвечать
Шаг 1
Установите два уравнения, равных друг другу, затем решите относительно x
Следующий шаг
Шаг 2
Подставьте значение x, -2, в значение x для любого уравнения, чтобы определить координату y решения
Следующий шаг
$$
у = \ красный {х} -5
\\
у = \ красный {-2} -5 = -7
$$
Решение — точка (-2, -7)
Задача 3
Используйте метод подстановки, чтобы решить систему:
- Строка 1: y = 5x — 1
- Строка 2: 2y = 3x + 12
Покажи ответ
Эта система линий имеет решение в точке (2, 9).
Задача 4
Используйте замену, чтобы решить систему:
- Строка 1: y = 3x + 1
- Строка 2: 4y = 12x + 4
Покажи ответ
Задача 5
Решите систему линейных уравнений заменой
- Строка 1: y = x + 2
- Строка 2: y = x + 8
Покажи ответ
Задача 6
Используйте метод подстановки, чтобы решить систему:
- Строка 1: y = x + 1
- Строка 2: 2y = 3x
Покажи ответ
Решение этой системы — (1, 3).
Проблема 7
Используйте замену, чтобы решить систему:
- Строка 1: y = 3x + 1
- Строка 2: 4y = 12x + 3
Покажи ответ
Всякий раз, когда вы приходите к противоречию, например, 3 = 4, ваша система линейных уравнений не имеет решений.
Когда вы используете эти методы (подстановка, построение графиков или исключение), чтобы найти решение, вы действительно спрашиваете, в чем
У этой системы нет решений.
Проблема 8
Решите систему, используя замену.
- Строка 1: y = x + 5
- Строка 2: y = 2x + 2
Покажи ответ
Решением этой системы является точка пересечения: (3, 8).
Калькулятор метода подстановки
с шагами
Это калькулятор метода подстановки Omni , который помогает вам решить систему уравнений с помощью метода подстановки . Какой метод замены? , спросите вы. А как пользоваться методом подстановки?
Продолжайте читать! Мы дадим определение метода подстановки, перечислим шаги метода подстановки, и проведет вас через несколько примеров систем, решаемых с помощью метода подстановки, шаг за шагом (с ответами!). Мы также объясним, как использовать метод замены, когда система оказывается непротиворечивой или зависимой.
Что такое системы линейных уравнений?
Мы говорим, что хотим решить систему линейных уравнений , если у нас есть несколько уравнений, и мы хотим найти числа, которые решают все эти уравнения одновременно.
Напомним, что уравнение является линейным , если все переменные в этом уравнении находятся в первой степени. Это означает, что они не могут быть возведены в квадрат, ни в кубе, ни под каким-либо корнем (в частности, под квадратным корнем или кубическим корнем).Они также не могут быть знаменателями дробей.
Этот калькулятор метода подстановки работает для систем двух линейных уравнений с двумя переменными . Это самые распространенные системы при выполнении домашних заданий! 😉 Они имеют следующий вид:
a 1 x + b 1 y = c 1
a 2 x + b 2 y = c 2
где:
-
xиy— переменные; -
a 1 , b 1 , c 1— коэффициенты первого уравнения; и -
a 2 , b 2 , c 2— коэффициенты второго уравнения.
Какой метод замены?
Метод подстановки — это метод решения системы линейных уравнений . Основная идея решения систем с помощью метода подстановки состоит в том, чтобы выбрать одно из уравнений, решить его для одной из переменных и вставить результат в другое уравнение. Таким образом, мы получаем уравнение с одной переменной , которое мы можем легко решить. Как только мы нашли значение одной переменной, мы используем его для поиска другой переменной.Вот как мы используем метод подстановки для решения системы уравнений. Перейдите к следующему разделу, чтобы узнать больше об этапах метода замены.
Знаете ли вы, что существует других методов решения систем линейных уравнений ? Вас не заставляют решать методом подстановки! Вы можете использовать метод исключения (также известный как метод линейной комбинации) или метод исключения по Гауссу, или, как только вы освоите детерминанты матрицы, правило Крамера.
Как использовать наш калькулятор метода замены?
Эта система инструментов метода подстановки уравнений проста в использовании:
- Введите коэффициенты системы линейных уравнений в соответствующие поля.
- Полное решение методом замещения отображается под калькулятором метода замещения!
- Здесь находятся все шагов метода замены на тот случай, если они вам понадобятся.
- Если вам нужно, чтобы система была решена с точностью более высокой (количество значащих цифр), чем шесть фиг, которые этот калькулятор метода замены использует по умолчанию, просто нажмите кнопку расширенного режима
и установите желаемую точность.
Пошаговый метод замены
Мы уже объяснили, что такое метод замены и в чем его основная идея.Теперь давайте подробно обсудим, как сделать метод подстановки:
Выберите одно из уравнений.
В выбранном уравнении выбирает одну из переменных .
Решите это уравнение для этой переменной.
Подставьте результат в другое уравнение (то, которое вы не выбрали на шаге 1). В этом суть решения систем методом подстановки!
Вы получили уравнение с одной переменной - решите его!
Замените значение, полученное на шаге 5, в одно из исходных уравнений.
Решите это новое уравнение с одной переменной.
Вот и все! Вы решили систему уравнений методом подстановки. Если хотите, вы можете протестировать свое решение. : подставьте полученные значения в систему и посмотрите, все ли в порядке.
⚠️ Иногда может случиться так, что вы пытаетесь решить систему, и внезапно обе переменные исчезают 😱 Сохраняйте спокойствие! Переменных больше нет, но вы пришли к некоторому утверждению о числах.Все, что вам нужно сделать, это сделать выводы о системе в зависимости от того, является ли полученное вами утверждение истинным (например, 0 = 0 или 17 = 17 ) или ложным (например, 0 = 1 или 15 = 17 ):
|
Примеры методов замены с ответами
В этом разделе мы шаг за шагом покажем вам, как решить несколько систем с использованием метода подстановки, чтобы вы могли увидеть, как применить метод подстановки на практике.
Используйте метод подстановки для решения системы уравнений :
3x - 4y = 6-x + 4y = 2Решите второе уравнение относительно
x:x = 4y - 2Подставьте
4y - 2вместоxв первое уравнение:3 (4 года - 2) - 4 года = 6Решите указанное выше уравнение для
y:12лет - 6–4 года = 68y = 12у = 1.5Подставляем
y = 1,5во второе уравнение:-x + 4 * 1,5 = 2-x + 6 = 2Решить для
x:х = 6 - 2х = 4Решение:
x = 4, y = 1,5Проверить решение:
3 * 4 - 4 * 1,5 = 12 - 6 = 6 9 1089Мы видим, что первое уравнение в порядке.
-4 + 4 * 1,5 = -4 + 6 = 2И второе уравнение тоже в порядке.
Решить методом подстановки :
2x + 3y = 52x + 7y = -3Решите первое уравнение относительно
x:x = -1,5y + 2,5Подставляем
x = -1,5y + 2,5во второе уравнение:2 * (- 1.5лет + 2,5) + 7у = -3Решите указанное выше уравнение для
y:-3y + 5 + 7y = -34y = -8y = -2Подставляем
y = -2в первое уравнение:2x + 3 * (- 2) = 5Решить для
x:2x = 11х = 5,5Решение:
x = 5.5, у = -2
Теперь мы увидим, как решить следующую систему линейных уравнений, используя метод подстановки :
6x - 3y = 122x - y = 4Решите второе уравнение относительно
y:y = 2x - 4Подставляем
y = 2x - 4в первое уравнение:6x - 3 * (2x - 4) = 12Решите указанное выше уравнение для
x:6x - 6x - 12 = 120 = 0Мы исключили обе переменные и получили истинное утверждение .Следовательно, эта система уравнений имеет бесконечно много решений !
Решение систем уравнений с помощью подстановки - Задача 1
Если два уравнения находятся в форме пересечения наклона, вы можете легко использовать подстановку для решения системы, положив одно значение y равным другому значению y (поскольку в обоих уравнениях y равно чему-то). Оттуда используйте обратные операции, чтобы найти x. Получив значение x, вставьте его в любое из двух исходных уравнений системы, чтобы найти значение y.Значения x и y составляют координатную точку решения системы. Проверьте свой ответ, подставив значения x и y в оба уравнения, чтобы убедиться, что они оба верны.
Эта задача с использованием подстановки будет не слишком сложной, потому что у меня есть 2 уравнения, которые уже решены для y. Поскольку я знаю, что y равно выражению 3x плюс 1, а y также равно выражению 2x минус 3, математически имеет смысл написать 3x плюс 1 равно 2x минус 3.Этот парень равен y, и этот парень тоже равен y, поэтому я просто подставляю эти два уравнения, чтобы они выглядели как одно уравнение с одной переменной.
Теперь это проблема прямого решения. Я найду x, а затем вернусь и найду свое значение y. Итак, если я хочу найти x, я вычту 2 X с обеих сторон, так что теперь у меня x плюс 1 равно -3. Теперь мне нужно получить x сам по себе, вычитая 1 с обеих сторон, x равно -4. Имейте в виду, что это будет только половина моего ответа.Я собираюсь заключить это в рамку, как если бы я держал в уме весь свой ответ, мне все еще нужно найти, что это за значение y.
Чтобы найти y, я возьму x равным -4 и подставлю его в любое исходное уравнение, таким образом я получу свое значение y, а через секунду вернусь и проверим. Я просто собираюсь использовать первое уравнение. Я мог бы также использовать второй, и я все равно получу тот же ответ для y. Y равно 3-кратному моему количеству x плюс 1, поэтому y равно -11 ой, это +1 прямо здесь, плюс 1 хорошо.Y равно -11. Я почти уверен, что это мой ответ, я почти уверен, что именно здесь пересекаются эти линии, хотя я их не рисовал.
Чтобы проверить свою работу, я собираюсь вернуться и вставить -4 для x и -11 для y в оба исходных уравнения и убедиться, что я получаю равенства. Итак, вот мой чек, сначала я собираюсь проверить его в первом уравнении, правда ли, что мое количество y равно 3-кратному количеству x плюс 1? Давайте посмотрим, что -11 равно -12 плюс 1, да, это правда. Хорошо, я на полпути, думаю, это правильно.Мне также нужно проверить это во втором уравнении.
Мое количество y, я надеюсь, в 2 раза больше моего количества x take away 3. -8 take away 3 yap хорошо. Вот откуда я знаю, что решил эту проблему правильно. Даже если ваш учебник не просил вас проверять свою работу, всегда полезно выполнить этот процесс, это займет всего минуту, а может и меньше, и таким образом вы убедитесь, что получаете положительные оценки за домашнее задание, а также на ваших тестах.