Содержание
Ромб. Формулы, признаки и свойства ромба
Определение.
Ромб — это параллелограмм, который имеет равные стороны. Если у ромба все углы прямые, тогда он называется квадратом.
Ромбы отличаются между собой размером стороны и размером углов.
| Рис.1 | Рис.2 |
Признаки ромба
Параллелограмм ABCD будет ромбом, если выполняется хотя бы одно из следующих условий:
1. Две его смежные стороны равны (отсюда следует, что все стороны равны):
АВ = ВС = СD = AD
2. Его диагонали пересекаются под прямым углом:
AC┴BD
3. Одна из диагоналей (бисектрисса) делит содержащие её углы пополам:
∠BAC = ∠CAD или ∠BDA = ∠BDC
4. Если все высоты равны:
BN = DL = BM = DK
5. Если диагонали делят параллелограмм на четыре равных прямоугольных треугольника:
Δ ABO = Δ BCO = Δ CDO = Δ ADO
6. Если в параллелограмм можно вписать круг.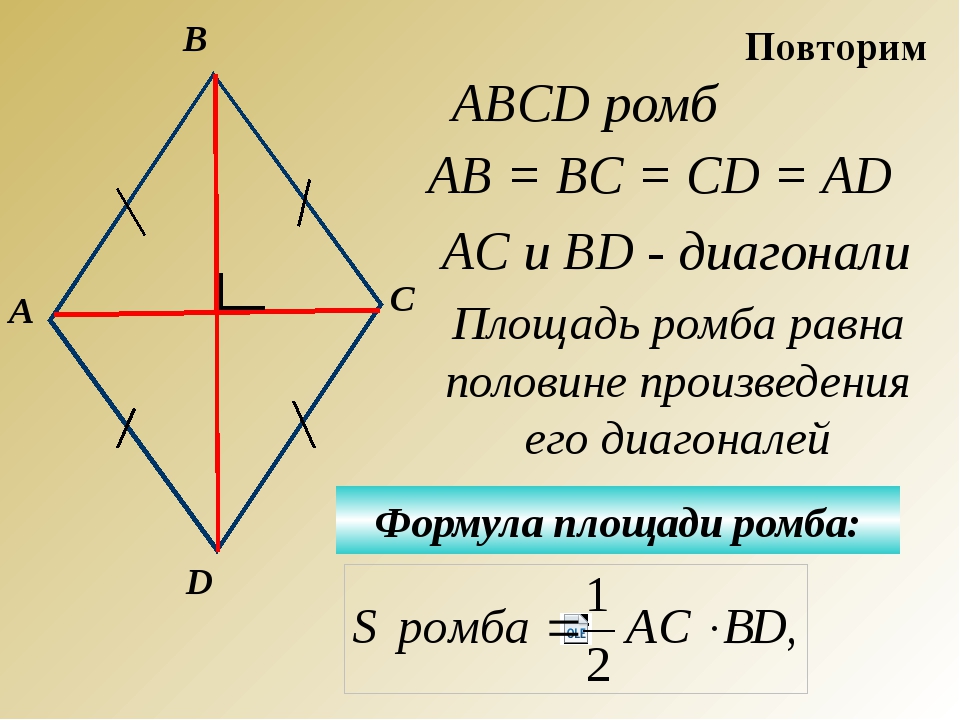
Основные свойства ромба
2. Диагонали перпендикулярны:
AC┴BD
3. Диагонали являются биссектрисами его углов:
∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC
4. Сумма квадратов диагоналей равна квадрату стороны умноженному на четыре:
AC2 + BD2 = 4AB2
5. Точка пересечения диагоналей называется центром симметрии ромба.
6. В любой ромб можно вписать окружность.
7. Центром окружности вписанной в ромб будет точка пересечения его диагоналей.
Сторона ромба
Формулы определения длины стороны ромба:
1. Формула стороны ромба через площадь и высоту:
2. Формула стороны ромба через площадь и синус угла:
3. Формула стороны ромба через площадь и радиус вписанной окружности:
4. Формула стороны ромба через две диагонали:
5. Формула стороны ромба через диагональ и косинус острого угла (cos α) или косинус тупого угла (cos β):
6. Формула стороны ромба через большую диагональ и половинный угол:
7. Формула стороны ромба через малую диагональ и половинный угол:
Формула стороны ромба через малую диагональ и половинный угол:
8. Формула стороны ромба через периметр:
Диагонали ромба
Определение.
Диагональю ромба называется любой отрезок соединяющий две вершины противоположных углов ромба.
Ромб имеет две диагонали — длинную d1, и короткую — d2
Формулы определения длины диагонали ромба:
1. Формулы большой диагонали ромба через сторону и косинус острого угла (cosα) или косинус тупого угла (cosβ)
d1 = a√2 + 2 · cosα
d1 = a√2 — 2 · cosβ
2. Формулы малой диагонали ромба через сторону и косинус острого угла (cosα) или косинус тупого угла (cosβ)
d2 = a√2 + 2 · cosβ
d2 = a√2 — 2 · cosα
3. Формулы большой диагонали ромба через сторону и половинный угол:
d1 = 2a · cos(α/2)
d1 = 2a · sin(β/2)
4. Формулы малой диагонали ромба через сторону и половинный угол:
d2 = 2a · sin(α/2)
d2 = 2a · cos(β/2)
5. Формулы диагоналей ромба через сторону и другую диагональ:
Формулы диагоналей ромба через сторону и другую диагональ:
d1 = √4a2 — d22
d2 = √4a2 — d12
6. Формулы диагоналей через тангенс острого tgα или тупого tgβ угла и другую диагональ:
d1 = d2 · tg(β/2)
d2 = d1 · tg(α/2)
7. Формулы диагоналей через площадь и другую диагональ:
8. Формулы диагоналей через синус половинного угла и радиус вписанной окружности:
Периметр ромба
Определение.
Периметром ромба называется сумма длин всех сторон ромба.
Длину стороны ромба можна найти за формулами указанными выше.
Формула определения длины периметра ромба:
Формула периметра ромба через сторону ромба:
P = 4a
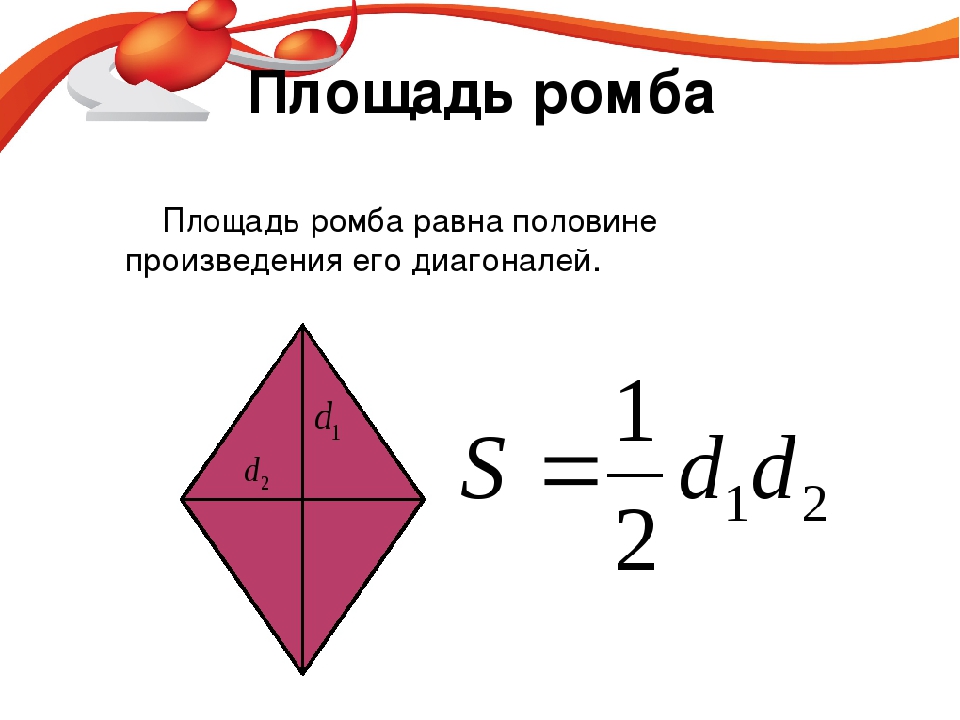
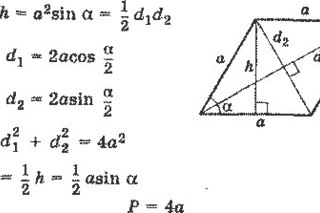
Площадь ромба
Определение.
Площадью ромба называется пространство ограниченное сторонами ромба, т.е. в пределах периметра ромба.
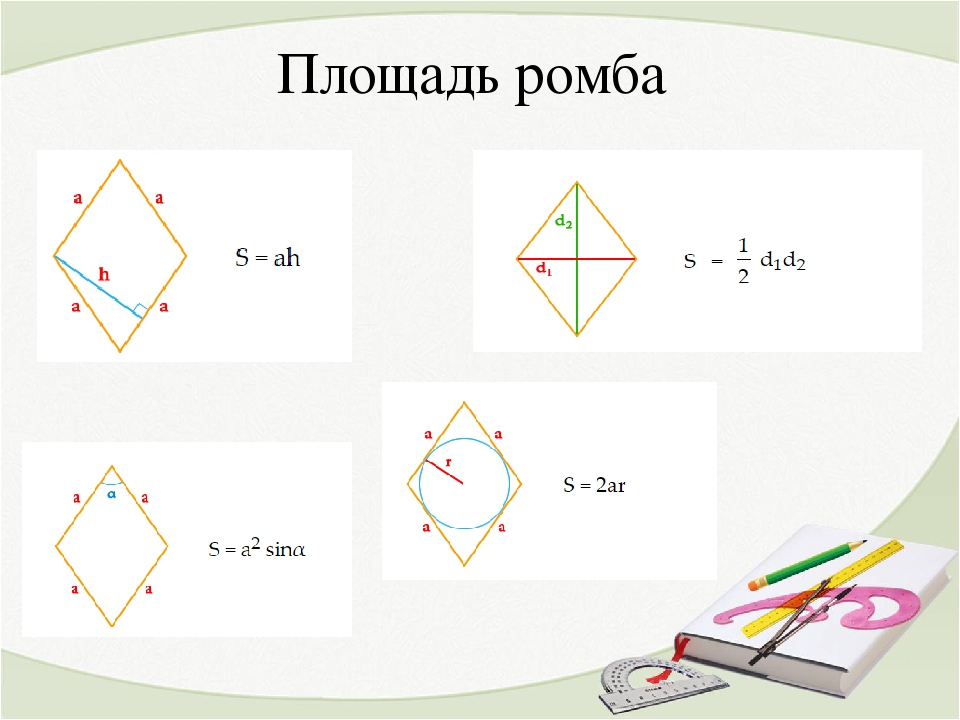
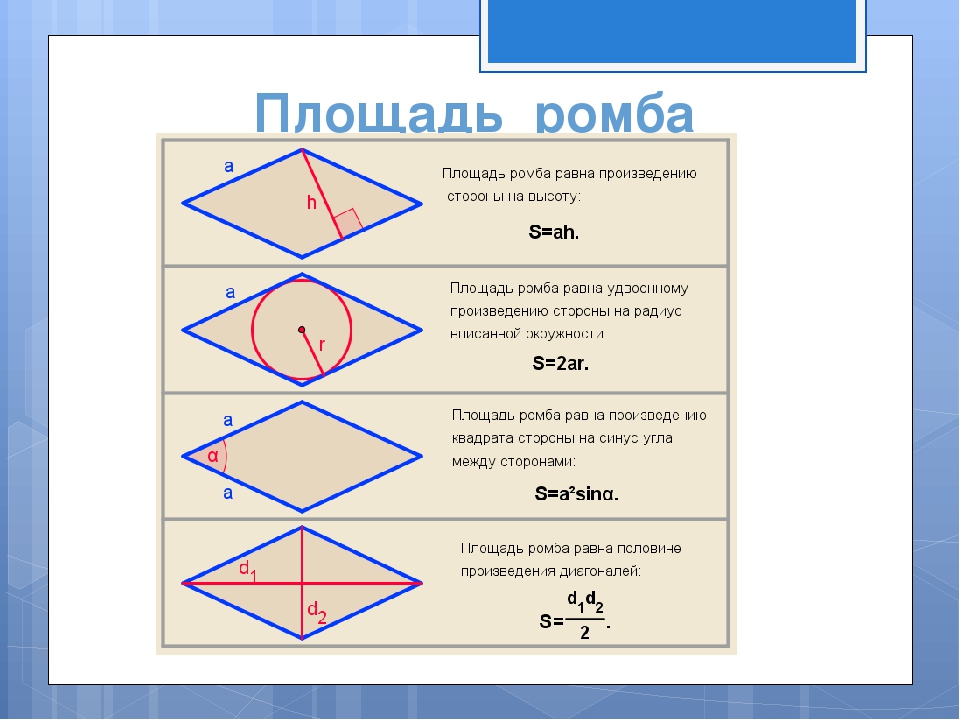
Формулы определения площади ромба:
1. Формула площади ромба через сторону и высоту:
Формула площади ромба через сторону и высоту:
S = a · ha
2. Формула площади ромба через сторону и синус любого угла:
S = a2 · sinα
3. Формула площади ромба через сторону и радиус:
S = 2a · r
4. Формула площади ромба через две диагонали:
5. Формула площади ромба через синус угла и радиус вписанной окружности:
6. Формулы площади через большую диагональ и тангенс острого угла (tgα) или малую диагональ и тангенс тупого угла (tgβ):
Окружность вписанная в ромб
Определение.
Кругом вписанным в ромб называется круг, который примыкает ко всем сторонам ромба и имеет центр на пересечении диагоналей ромба.
Формулы определения радиуса круга вписанного в ромб:
1. Формула радиуса круга вписанного в ромб через высоту ромба:
2. Формула радиуса круга вписанного в ромб через площадь и сторону ромба:
3. Формула радиуса круга вписанного в ромб через площадь и синус угла:
4. Формулы радиуса круга вписанного в ромб через сторону и синус любого угла:
5. Формулы радиуса круга вписанного в ромб через диагональ и синус угла:
Формулы радиуса круга вписанного в ромб через диагональ и синус угла:
6. Формула радиуса круга вписанного в ромб через две диагонали:
| r = | d1 · d2 |
| 2√d12 + d22 |
7. Формула радиуса круга вписанного в ромб через две диагонали и сторону:
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Диагонали ромба | Онлайн калькулятор
Ромб — это четырехугольник, который является параллелограммом, сохраняет все его свойства, но кроме этого он еще и равносторонний. Так как все стороны ромба равны, а из свойств параллелограмма его противоположные углы также равны между собой, диагонали ромба не просто пересекаются в точке, которая делит их на две равные части каждую, а они всегда будут перпендикулярны по отношению друг к другу.
Когда в ромбе проводятся диагонали, они делят его на четыре конгруэнтных прямоугольных треугольника, катетами которого являются половины диагоналей.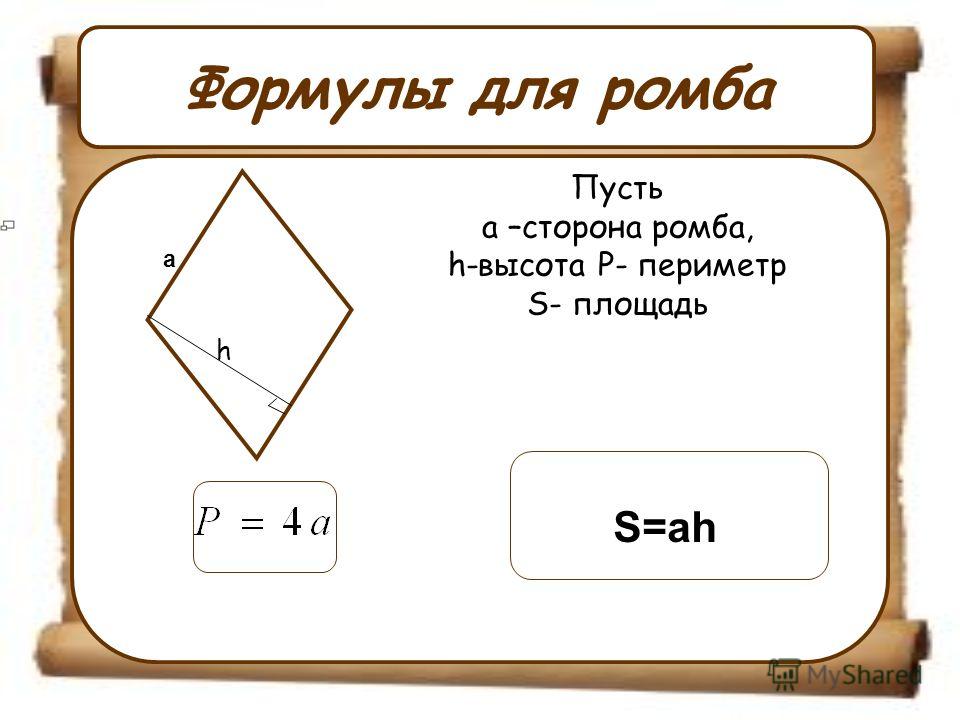 В любом из полученных прямоугольных треугольников можно, зная гипотенузу (сторона ромба), вычислить оба катета. Для этих целей используются тригонометрические отношения синуса и косинуса в прямоугольном треугольнике — так как оба катета, примем их временно за a и b, неизвестны, для вычислений понадобится один из острых углов в треугольнике.
В любом из полученных прямоугольных треугольников можно, зная гипотенузу (сторона ромба), вычислить оба катета. Для этих целей используются тригонометрические отношения синуса и косинуса в прямоугольном треугольнике — так как оба катета, примем их временно за a и b, неизвестны, для вычислений понадобится один из острых углов в треугольнике.
Чтобы перевести эти формулы в параметры ромба, необходимо связать стороны треугольника со сторонами и диагоналями ромба, а также острый угол треугольника с углами ромба.
Сторона ромба, как было оговорено, становится гипотенузой треугольника, а половины диагоналей берут на себя роль катетов. Тогда в обратном порядке, чтобы найти полноценные диагонали, нужно будет каждый вычисленный катет увеличить в два раза.
Угол, используемый в синусе и косинусе для нахождения катетов и затем диагоналей ромба, является ничем иным как половинным углом самого ромба, так как диагонали ромба являются биссектрисами его углов.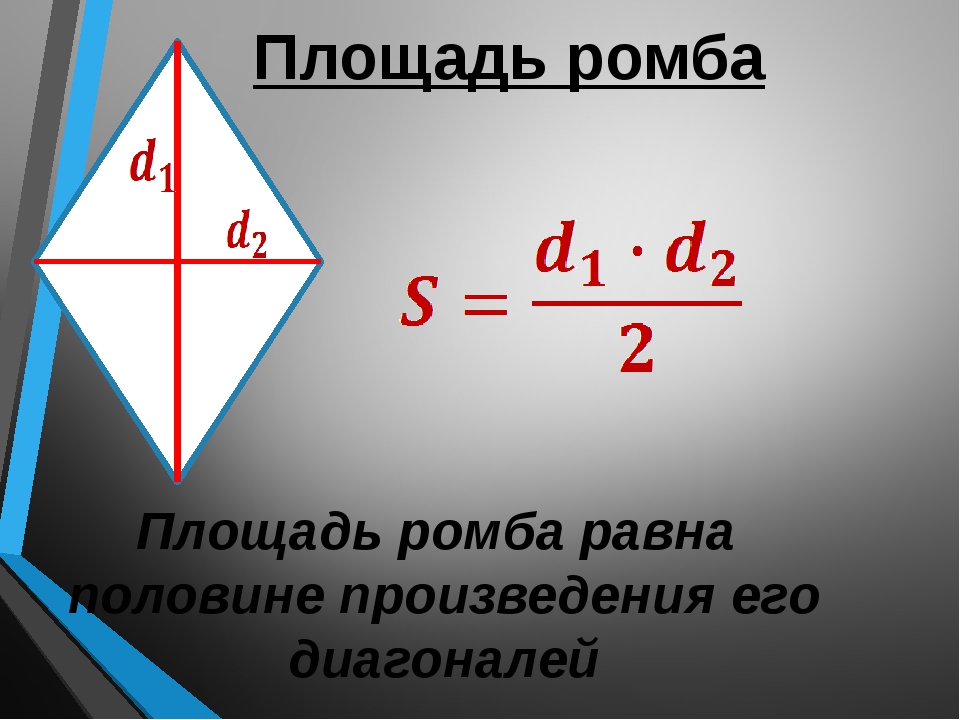 То есть будет справедливо следующее равенство:
То есть будет справедливо следующее равенство:
αромба=2 αтреугольника
Или
αромба/2=αтреугольника
Теперь для выведения общей формулы диагоналей ромба через сторону ромба и его угол (кстати, выбор острого или тупого угла не сказывается на результате расчетов) выписанные замены должны быть подставлены в исходные формулы треугольника, с которых начинался алгоритм вычислений.
Произведя вычисления обратным ходом, можно также найти сторону ромба через диагонали или угол между сторонами ромба.
| Диагональ ромба d1 | |||
| Диагональ ромба d2 | |||
| Результат | |||
Площади фигур
Площадь ромба по углу и противолежащей диагонали
… подготовка …
d – диагональ
α° – угол между сторонами
Площадь ромба по углу и диагонали проведенной из этого угла
d – диагональ
α° – угол между сторонами
Способ расчета площади ромба
Ромб – это параллелограмм, у которого все стороны равны. Ромб у которого все углы прямые называется квадратом.
Формула площади ромба: ,
где a – стороны, h – высота
Ромб – это параллелограмм, у которого все стороны равны. Ромб у которого все углы прямые называется квадратом.
Формула площади ромба: ,
где d1, d2 – диагонали
Ромб – это параллелограмм, у которого все стороны равны. Ромб у которого все углы прямые называется квадратом.
Формула площади ромба: ,
где a – сторона, α – угол между сторонами
Ромб – это параллелограмм, у которого все стороны равны.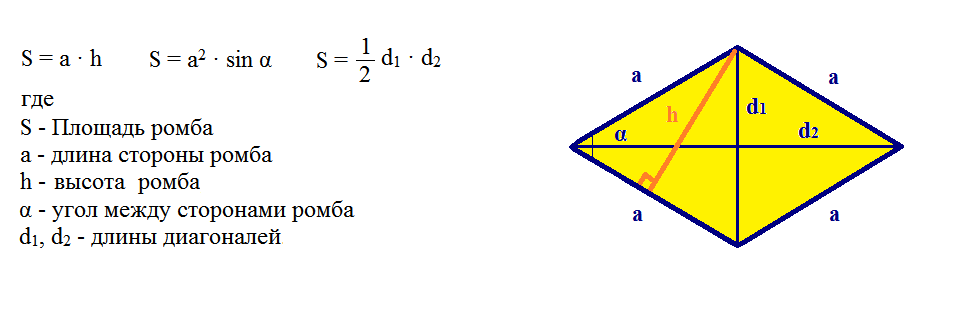 2 cdot sin(alpha)}
2 cdot sin(alpha)}
Таблица с формулами площади ромба
В зависимости от известных исходных данных, площадь ромба можно вычислить по различным формулам.
Периметр ромба
Определение.
Периметром ромба называется сумма длин всех сторон ромба.
Длину стороны ромба можно найти за формулами указанными выше.
Формула определения длины периметра ромба:
Формула периметра ромба через сторону ромба:
P = 4a
Формула площади ромба по стороне и высоте
Пусть нам дан ромб со стороной
aa
a и высотой
hh
h, проведенной к этой стороне. Так как ромб это параллелограмм, то его площадь мы находим так же, как и площадь параллелограмма.
S=a⋅hS=acdot h
S=a⋅h
a — сторона;
h — высота, опущенная на сторону
aa
a.
Решим простой пример.
Пример
Сторона ромба равна 5 (см.). Высота, опущенная к этой стороне, имеет длину 2 (см.). Найти площадь ромба
SS
S.
Решение
a=5a=5
a=5
h=2h=2
h=2
Пользуемся нашей формулой и вычисляем:
S=a⋅h=5⋅2=10S=acdot h=5cdot 2=10
S=a⋅h=5⋅2=10 (см. кв.)
кв.)
Ответ: 10 см. кв.
Формулы определения радиуса круга вписанного в ромб:
1. Формула радиуса круга вписанного в ромб через высоту ромба:
2. Формула радиуса круга вписанного в ромб через площадь и сторону ромба:
3. Формула радиуса круга вписанного в ромб через площадь и синус угла:
4. Формулы радиуса круга вписанного в ромб через сторону и синус любого угла:
5. Формулы радиуса круга вписанного в ромб через диагональ и синус угла:
6. Формула радиуса круга вписанного в ромб через две диагонали:
| r = | d1 · d2 |
| 2√d12 + d22 |
7. Формула радиуса круга вписанного в ромб через две диагонали и сторону:
Источники
- https://allcalc.ru/node/22
- https://ru.onlinemschool.com/math/formula/rhombus/
- https://calcsbox.com/post/formula-plosadi-romba.html
- https://MicroExcel.
 ru/ploshhad-romba/
ru/ploshhad-romba/ - https://www.calc.ru/Ploshchadi-Figur-Ploshchad-Romba.html
- https://doza.pro/art/math/geometry/area-rhombus
- https://www.calc.ru/ploshchad-romba.html
- https://studwork.org/spravochnik/matematika/ploshchad/ploshchad-romba
- https://mnogoformul.ru/formuly-ploshhadi-romba
Как найти периметр ромба: формула через стороны, диагонали
В данной публикации мы рассмотрим, каким образом можно посчитать периметр ромба и разберем примеры решения задач.
Формула вычисления периметра
1. По длине стороны
Периметр (P) ромба равняется сумме длин всех его сторон.
P = a + a + a + a
Т.к. все стороны данной геометрической фигуры равны, формулу можно представить в следующем виде (сторона умноженная на 4):
P = 4*a
2. По длине диагоналей
Диагонали любого ромба пересекаются под углом 90° и в точке пересечения делятся пополам, т.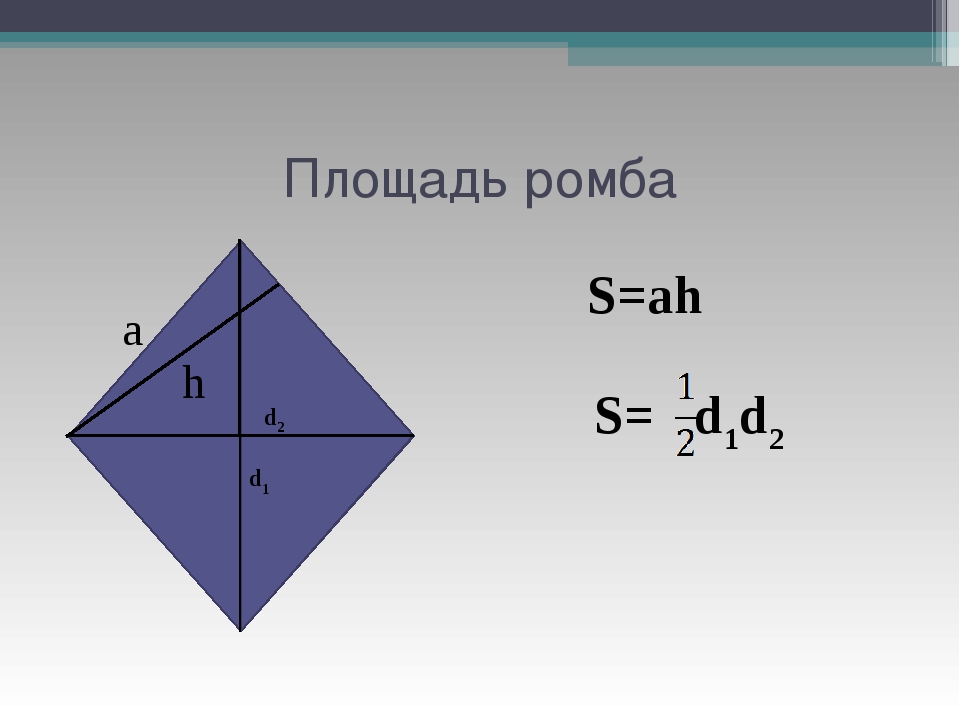 е.:
е.:
Диагонали делят ромб на 4 равных прямоугольных треугольника: AOB, AOD, BOC и DOC. Давайте подробнее остановимся на AOB.
Найти сторону AB, которая одновременно является гипотенузой прямоугольника и стороной ромба, можно, воспользовавшись теоремой Пифагора:
AB2 = AO2 + OB2
Подставляем в эту формулу длины катетов, выраженные через половины диагоналей, и получаем:
AB2 = (d1/2)2 + (d2/2)2, или
Таким образом, периметр равняется:
Примеры задач
Задание 1
Найдите периметр ромба, если длина его стороны составляет 7 см.
Решение:
Используем первую формулу, подставив в нее известное значение: P = 4 * 7 см = 27 см.
Задание 2
Периметр ромба равен 44 см. Найдите сторону фигуры.
Решение:
Как мы знаем, P = 4*a. Следовательно, чтобы найти одну сторону (a), необходимо периметр разделить на четыре: a = P/4 = 44 см / 4 = 11 см.
Следовательно, чтобы найти одну сторону (a), необходимо периметр разделить на четыре: a = P/4 = 44 см / 4 = 11 см.
Задание 3
Найдите периметр ромба, если известны его диагонали: 6 и 8 см.
Решение:
Воспользовавшись формулой, в которой задействованы длины диагоналей, получаем:
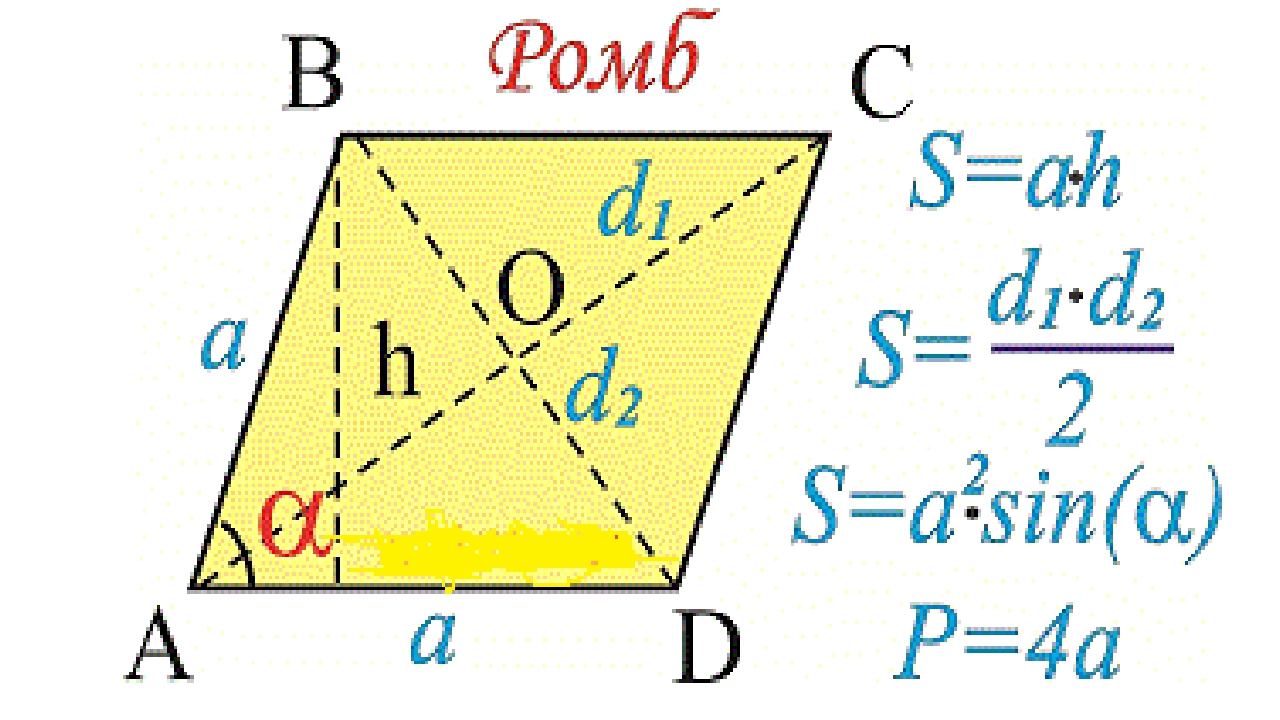
Ромб. Стороны ромба через его диагонали. Стороны ромба через площадь и высота. Сторона ромба через радиус вписанной окружности.
Ромб-это равносторонний четырехугольник то есть у него есть четыре стороны, которые равны по длине, но углы могут быть не равны. Противоположные стороны ромба перпендикулярны биссектрисам ромба, и разрезают друг друга ровно пополам под прямым углом. Ромб является частным случаем параллелограмма в том, что все четыре стороны равны по длине, а не только противоположные стороны. Квадрат-это частный случай ромба, в котором все углы равны \(90°\). Ромб-это причудливое научное название «алмаза».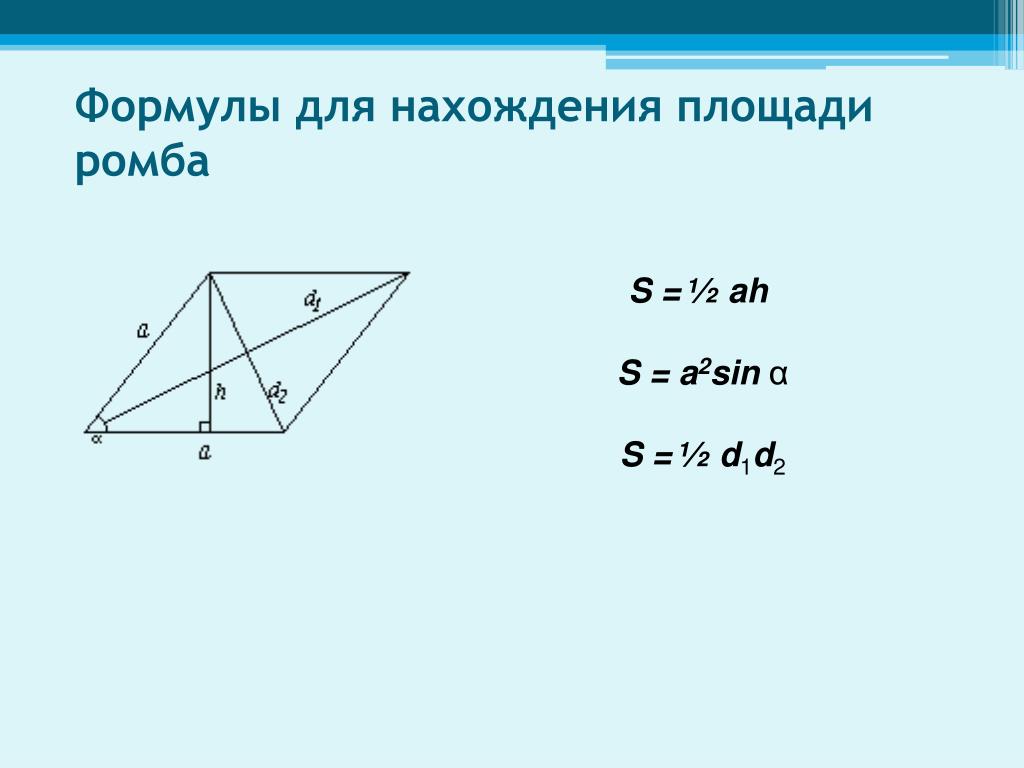 2}}2\)
2}}2\)
- Формула стороны ромба через периметр:
\(a=\frac{P}{4}\)
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
В данном разделе рассматриваются только выпуклые фигуры, и считается известной формула:
S = ab,
которая позволяет найти площадь прямоугольникапрямоугольника с основанием a и высотой b.
Формулы для площадей четырехугольников
| Четырехугольник | Рисунок | Формула площади | Обозначения |
| Прямоугольник | S = ab | a и b – смежные стороны | |
Посмотреть вывод формулы | d – диагональ, | ||
S = 2R2 sin φ Получается из верхней формулы подстановкой d=2R | R – радиус описанной окружности, | ||
| Параллелограмм | S = a ha Посмотреть вывод формулы | a – сторона, | |
S = absin φ Посмотреть вывод формулы | a и b – смежные стороны, | ||
Посмотреть вывод формулы | d1, d2 – диагонали, φ – любой из четырёх углов между ними | ||
| Квадрат | S = a2 | a – сторона квадрата | |
| S = 4r2 | r – радиус вписанной окружности | ||
Посмотреть вывод формулы | d – диагональ квадрата | ||
S = 2R2 Получается из верхней формулы подстановкой d = 2R | R – радиус описанной окружности | ||
| Ромб | S = a ha Посмотреть вывод формулы | a – сторона, | |
S = a2 sin φ Посмотреть вывод формулы | a – сторона, | ||
Посмотреть вывод формулы | d1, d2 – диагонали | ||
S = 2ar Посмотреть вывод формулы | a – сторона, | ||
Посмотреть вывод формулы | r – радиус вписанной окружности, | ||
| Трапеция | Посмотреть вывод формулы | a и b – основания, | |
| S = m h | m – средняя линия, | ||
Посмотреть вывод формулы | d1, d2 – диагонали, φ – любой из четырёх углов между ними | ||
Посмотреть вывод формулы | a и b – основания, | ||
| Дельтоид | S = ab sin φ | a и b – неравные стороны, | |
a и b – неравные стороны, | |||
S = (a + b) r Посмотреть вывод формулы | a и b – неравные стороны, | ||
Посмотреть вывод формулы | d1, d2 – диагонали | ||
| Произвольный выпуклый четырёхугольник | Посмотреть вывод формулы | d1, d2 – диагонали, φ – любой из четырёх углов между ними | |
| Вписанный четырёхугольник | , Посмотреть вывод формулы Брахмагупты | a, b, c, d – длины сторон четырёхугольника, Формулу называют «Формула Брахмагупты» |
| Прямоугольник | |
S = ab где | |
где Посмотреть вывод формулы | |
S = 2R2 sin φ где Формула получается из верхней формулы подстановкой d = 2R | |
| Параллелограмм | |
S = a ha где Посмотреть вывод формулы | |
S = absin φ где Посмотреть вывод формулы | |
где φ – любой из четырёх углов между ними Посмотреть вывод формулы | |
| Квадрат | |
| S = a2 где | |
| S = 4r2 где | |
где Посмотреть вывод формулы | |
S = 2R2 где Получается из верхней формулы подстановкой d = 2R | |
| Ромб | |
S = a ha где Посмотреть вывод формулы | |
S = a2 sin φ где Посмотреть вывод формулы | |
где Посмотреть вывод формулы | |
S = 2ar где Посмотреть вывод формулы | |
где Посмотреть вывод формулы | |
| Трапеция | |
где Посмотреть вывод формулы | |
S = m h где | |
где φ – любой из четырёх углов между ними Посмотреть вывод формулы | |
где Посмотреть вывод формулы | |
| Дельтоид | |
S = ab sin φ где | |
где | |
S = (a + b) r где Посмотреть вывод формулы | |
где Посмотреть вывод формулы | |
| Произвольный выпуклый четырёхугольник | |
где φ – любой из четырёх углов между ними Посмотреть вывод формулы | |
| Вписанный четырёхугольник | |
, где Формулу называют «Формула Брахмагупты» Посмотреть вывод формулы Брахмагупты | |
| Прямоугольник |
S = ab где |
где Посмотреть вывод формулы |
S = 2R2 sin φ где Формула получается из верхней формулы подстановкой d = 2R |
| Параллелограмм |
S = a ha где Посмотреть вывод формулы |
S = absin φ где Посмотреть вывод формулы |
где φ – любой из четырёх углов между ними Посмотреть вывод формулы |
| Квадрат |
S = a2 где |
S = 4r2 где |
где Посмотреть вывод формулы |
S = 2R2 где Получается из верхней формулы подстановкой d = 2R |
| Ромб |
S = a ha где Посмотреть вывод формулы |
S = a2 sin φ где Посмотреть вывод формулы |
где Посмотреть вывод формулы |
S = 2ar где Посмотреть вывод формулы |
где Посмотреть вывод формулы |
| Трапеция |
где Посмотреть вывод формулы |
S = m h где |
где φ – любой из четырёх углов между ними Посмотреть вывод формулы |
где Посмотреть вывод формулы |
| Дельтоид |
S = ab sin φ где |
где |
S = (a + b) r где Посмотреть вывод формулы |
где Посмотреть вывод формулы |
| Произвольный выпуклый четырёхугольник |
где φ – любой из четырёх углов между ними Посмотреть вывод формулы |
| Вписанный четырёхугольник |
где Формулу называют «Формула Брахмагупты» Посмотреть вывод формулы Брахмагупты |
Вывод формул для площадей четырехугольников
Утверждение 1. Площадь выпуклого четырёхугольника можно найти по формуле
Площадь выпуклого четырёхугольника можно найти по формуле
где d1 и d2 – диагонали четырёхугольника, а φ – любой из четырёх углов между ними (рис. 1).
Рис. 1
Доказательство. В соответствии с рисунком 1 справедливо равенство:
что и требовалось доказать.
Утверждение 2. Площадь параллелограммапараллелограмма можно найти по формуле
S = a ha ,
где a – сторона параллелограмма, а ha – высотавысотавысота, опущенная на эту сторону (рис. 2).
Рис. 2
Доказательство. Поскольку прямоугольный треугольник DFC равен прямоугольному треугольнику AEB (рис.26), то четырёхугольник AEFB – прямоугольник. Поэтому
SABCD = SAEFD = a ha ,
что и требовалось доказать.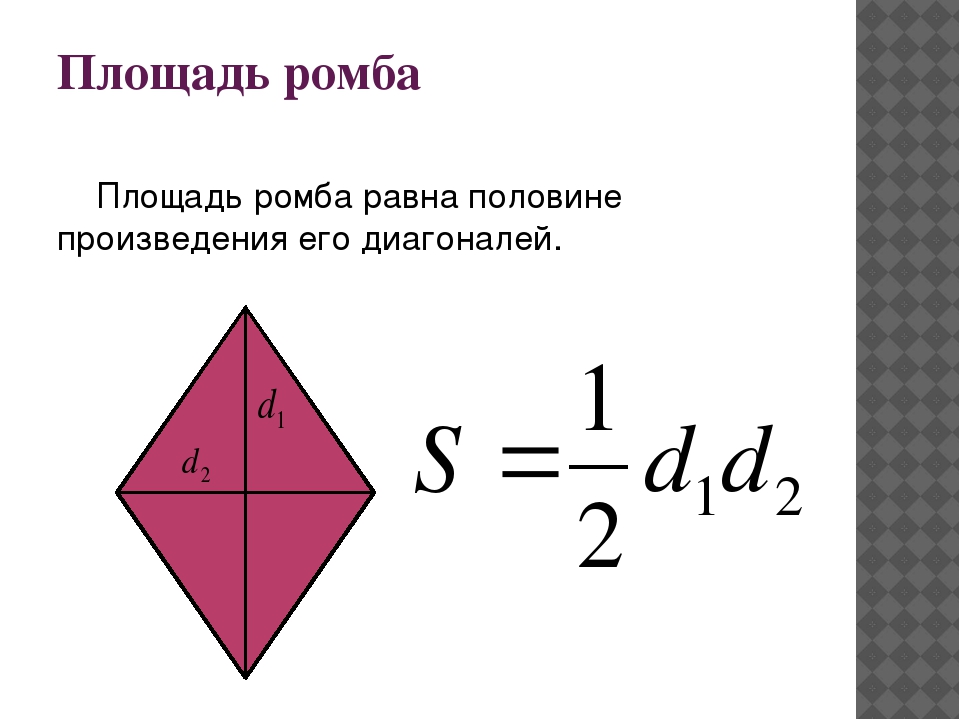
Утверждение 3.Площадь параллелограмма параллелограмма можно найти по формуле
S = ab sin φ,
где a и b – смежные стороны параллелограмма, а φ – угол между ними (рис. 3).
Рис. 3
Доказательство. Поскольку
ha = b sin φ,
то, в силу утверждения 2, справедлива формула
S = a ha = ab sin φ,
что и требовалось доказать.
Утверждение 4. Площадь ромбаромба можно найти по формуле
,
где r – радиус вписанной в ромб окружности, а φ – любой из четырёх углов ромба (рис.4).
Рис. 4
Доказательство. Поскольку каждая из диагоналей ромба является биссектрисой угла, а каждая точка биссектрисы угла равноудалена от сторон угла, то точка пересечения диагоналей ромба равноудалена от всех сторон ромба и является центром вписанной в ромб окружности. Отсюда следует, в частности, что высота ромба в 2 раза больше радиуса вписанной окружности (рис.4). Поэтому
Отсюда следует, в частности, что высота ромба в 2 раза больше радиуса вписанной окружности (рис.4). Поэтому
что и требовалось доказать.
Утверждение 5. Площадь трапеции можно найти по формуле
,
где a и b – основания трапеции, а h – высотавысотавысота (рис.5).
Рис. 5
Доказательство. Проведём прямую BE через вершину B трапеции и середину E боковой стороны CD. Точку пересечения прямых AD и BE обозначим буквой F (рис. 5). Поскольку треугольник BCE равен треугольнику EDF (по стороне и прилежащим к ней углам), то площадь трапеции ABCD равна площади треугольника ABF. Поэтому
что и требовалось доказать.
Утверждение 6. Площадь трапеции трапеции можно найти по формуле
,
где a и b – основания, а c и d – боковые стороны трапеции,
(рис.6).
Рис. 6
6
Доказательство. Воспользовавшись теоремой Пифагора, составим следующую систему уравнений с неизвестными x, y, h (рис. 6):
Следовательно,
где
,
что и требовалось доказать.
Утверждение 7. Площадь дельтоида, дельтоида, можно найти по формуле:
S = (a + b) r,
где a и b – неравные стороны дельтоида, а r – радиус вписанной в дельтоид окружности (рис.7).
Рис. 7
Доказательство. Докажем сначала, что в каждый дельтоид можно вписать окружность. Для этого заметим, что треугольники ABD и BCD равны в силу признака равенства треугольников «По трём сторонам» (рис. 7). Отсюда вытекает, что диагональ BD является биссектрисой углов B и D, а биссектрисы углов A и C пересекаются в некоторой точке O, лежащей на диагонали BD. Точка O и является центром вписанной в дельтоид окружности.
Если r – радиус вписанной в дельтоид окружности, то
что и требовалось доказать.
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Площадь ромба | Треугольники
Площадь ромба можно найти по формулам для нахождения площади параллелограмма. С учётом свойств ромба, некоторые из этих формул меняют свой вид.
I. Площадь ромба по стороне и высоте
Площадь ромба равна произведению стороны ромба и его высоты.
Формула для нахождения площади ромба по стороне и высоте не отличается от соответствующей формулы площади параллелограмма:
Например, площадь ромба ABCD равна
Так как все стороны ромба равны и все его высоты равны, для нахождения площади можно брать любую сторону и любую высоту.
II. Площадь ромба по стороне и углу
Площадь ромба равна произведению квадрата его стороны на синус угла.
Формула для нахождения площади ромба через сторону и угол:
Например,площадь ромба ABCD равна
Так как ∠D=180-∠A, sin∠D=sin(180-∠A)=sin∠A, то для нахождения площади можно брать синус любого угла.
III. Площадь ромба через его диагонали
Площадь ромба равна половине произведения его диагоналей.
Формула для нахождения площади ромба по его диагоналям
по сравнению с соответствующей формулой площади параллелограмма упрощается (так как диагонали ромба взаимно перпендикулярны, а синус прямого угла равен единице).
Например, площадь ромба ABCD равна
IV. Площадь ромба через радиус вписанной окружности
Площадь ромба равна произведению его полупериметра на радиус вписанной окружности.
Формула для нахождения площади ромба через радиус вписанной окружности
аналогов среди формул для нахождения площади параллелограмма не имеет (поскольку из всех параллелограммов окружность можно вписать только в ромб и квадрат).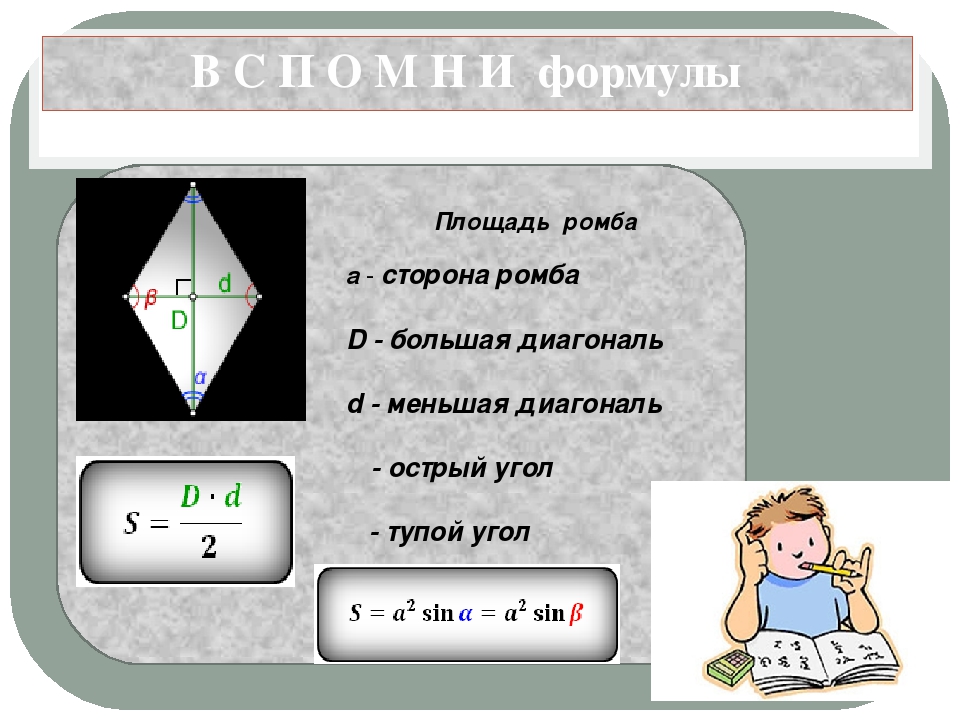
Например, площадь ромба ABCD равна
Так как полупериметр ромба равен p=2a, формулу можно записать в виде
формул ромба — xGeometry
|
$$ 2p = S \ times 4 $$
Периметр
$$ A = \ frac {d_ {1} \ times d_ {2}} {2} $$
Площадь
$$ d_ {1} = \ frac {2A} {d_ {2}} $$
Длинная диагональ
$$ d_ {2} = \ frac {2A} {d_ {1}} $$
Более короткая диагональ
$$ S = \ sqrt {{\ left (\ frac {d_ {1}} {2} \ right)} ^ {2} + {\ left (\ frac {d_ {2}} {2} \ right)} ^ {2}} $$
Сторона (теорема Пифагора)
$$ \ frac {d_ {1}} {2} = \ sqrt {{S} ^ {2} — {\ left (\ frac {d_ {2}} {2} \ right)} ^ {2}} $ $
Удлиненная полудиагональ
$$ \ frac {d_ {2}} {2} = \ sqrt {{S} ^ {2} — {\ left (\ frac {d_ {1}} {2} \ right)} ^ {2}} $ $
Более короткая полудиагональ
Определение
Ромб — это четырехугольник, все стороны которого совпадают.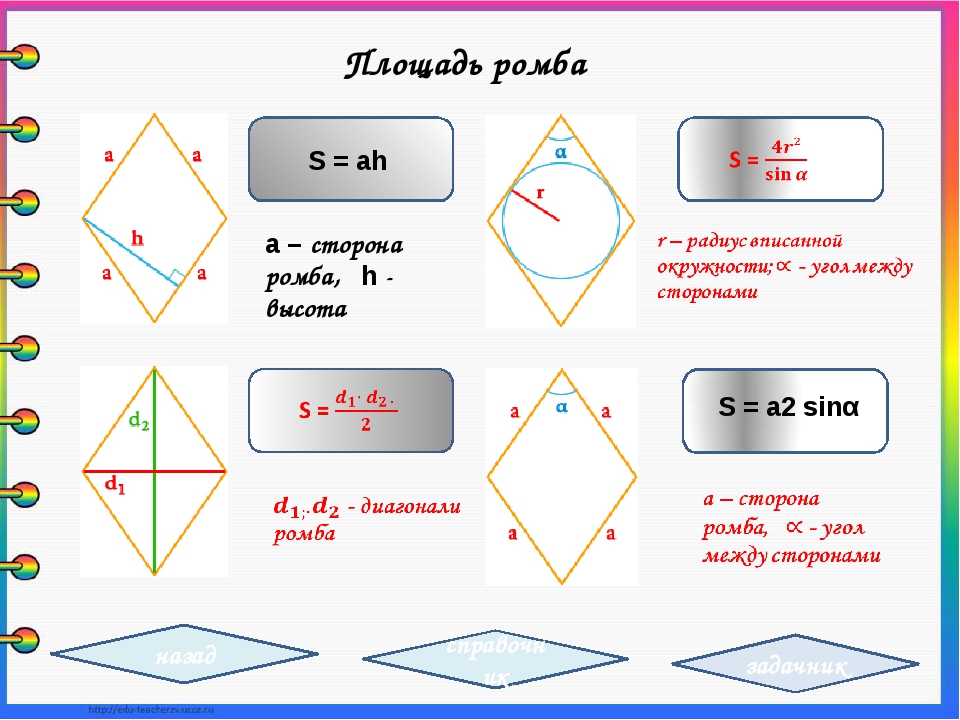
Недвижимость
- Четыре равные стороны, противоположные стороны параллельны
- Противоположные углы равны, последовательные углы являются дополнительными (их сумма 180 °)
- Диагонали перпендикулярны
- Диагонали пересекаются в точке, называемой центром ромба . Центр делит диагонали на две равные полудиагонали
- Диагональ составляет четыре равных прямоугольных треугольника, в которых гипотенуза представлена стороной ромба, а катет — полудиагоналями
| Данные | Формула |
|---|---|
| Периметр | 2p = S × 4 |
| Площадь | A = (d 1 × d 2 ) / 2 |
| Сторона | S = 2p / 4 |
| Сторона | S = √ [(d 1 /2) 2 + (d 2 /2) 2 ] |
| Большая диагональ | d 1 = (2 × A) / d 2 |
| Более короткая диагональ | d 2 = (2 × A) / d 1 |
| Полудиагональ удлиненная | d 1 /2 = √ [S 2 — (d 2 /2) 2 ] |
| Более короткая полудиагональ | d 2 /2 = √ [S 2 — (d 1 /2) 2 ] |
Формула площади ромба с калькулятором
Формула площади ромба с калькулятором — Math Open Reference
Три разных способа рассчитать площадь
ромбы приведены ниже, с формулой для каждого. Попробуйте это Перетащите оранжевые точки на каждую вершину
Попробуйте это Перетащите оранжевые точки на каждую вершину
изменить форму ромба. Площадь будет постоянно рассчитываться с использованием метода «базисное умножение на высоту».
Ромб
на самом деле просто особый тип параллелограмма.
К ним также можно применить многие расчеты площади. Выберите формулу на основе значений, которые вы знаете для начала.
1. Метод «базис, умноженный на высоту»
Сначала выберите одну сторону в качестве основы. Подойдет любой, все они одинаковой длины.
Затем определите высоту — расстояние по перпендикуляру от выбранной базы до противоположной стороны.Площадь — это произведение этих двух или, как формула:
где
b — длина основания
a — высота (высота).
Воспользуйтесь калькулятором ниже, чтобы вычислить площадь ромба с учетом длины основания (стороны) и
высота (перпендикулярная высота).
Введите любые два значения, и будет вычислено недостающее.
Например, введите площадь и базовую длину, и будет рассчитана высота, необходимая для получения этой площади.
2. Метод «диагоналей»
Еще одна простая формула для определения площади ромба, когда известны длины диагоналей.
Площадь составляет половину произведения диагоналей. Как формула:
где
d 1 — длина диагонали
d 2 — длина другой диагонали
3. Использование тригонометрии
Если вы знакомы с тригонометрией, есть удобная формула, когда вы знаете длину стороны и любой угол:
где
s — длина любой стороны
a — любой внутренний угол
sin — функция синуса
(см. Обзор тригонометрии)
Поначалу может показаться странным, что вы можете использовать любой угол, поскольку не все они равны.Но углы либо равны, либо
дополнительный,
и дополнительные углы имеют одинаковый синус.
Другие темы о многоугольниках
Общий
Типы полигонов
Площадь различных типов полигонов
Периметр различных типов полигонов
Углы, связанные с многоугольниками
Именованные многоугольники
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
Измерение площади ромба: формулы и примеры — математический урок [видео 2021]
Использование высоты и стороны
Один из способов определить площадь ромба — использовать высоту и сторону.Если мы знаем эти два измерения, мы можем использовать этот метод. Формула для этого метода:
Площадь = Высота * с
Выглядит довольно просто, правда? Все, что вам нужно сделать, это умножить высоту на одну из сторон. Неважно, с какой стороны, все они одинаковые.
Итак, если у вас есть ромб высотой 3 дюйма со сторонами 2 дюйма, то площадь этого ромба составляет 3 дюйма * 2 дюйма = 6 дюймов в квадрате.
Использование стороны и угла
Теперь, если вместо высоты вам дается одно из угловых измерений, вы можете использовать другой метод определения площади ромба.2 sin (B)
Формула одинакова независимо от того, какой угол вам дан. Все, что вам нужно, это измерение одного из углов и стороны. Здесь вы также умножаете, но сначала вы должны найти синус угла, а также возвести в квадрат свою сторону. Эту формулу запомнить немного сложнее, чем формулу с использованием высоты и стороны, но все же рекомендуется сохранить ее в памяти. Если нужно, запишите его на карточке.
Здесь вы также умножаете, но сначала вы должны найти синус угла, а также возвести в квадрат свою сторону. Эту формулу запомнить немного сложнее, чем формулу с использованием высоты и стороны, но все же рекомендуется сохранить ее в памяти. Если нужно, запишите его на карточке.
Если наш ромб говорит нам, что наша сторона имеет размер 2 дюйма, а один из наших углов — 60 градусов, то, чтобы найти площадь этого ромба, мы должны подставить это в нашу формулу для площади, используя сторону и угол.2 sin (60)
Возводим нашу сторону в квадрат и находим синус 60 градусов. Итак:
Площадь = 4 * 0,866
Затем мы умножаем эти два числа вместе, чтобы получить ответ.
Площадь = 3,46 дюйма в квадрате
Я хочу, чтобы вы помнили, что для этого метода угол, который вы выбираете, не имеет значения. Формула одинакова для обоих углов; вам просто нужно выбрать один из них, чтобы использовать.
Использование диагоналей
Последний способ определения площади ромба использует только две диагонали.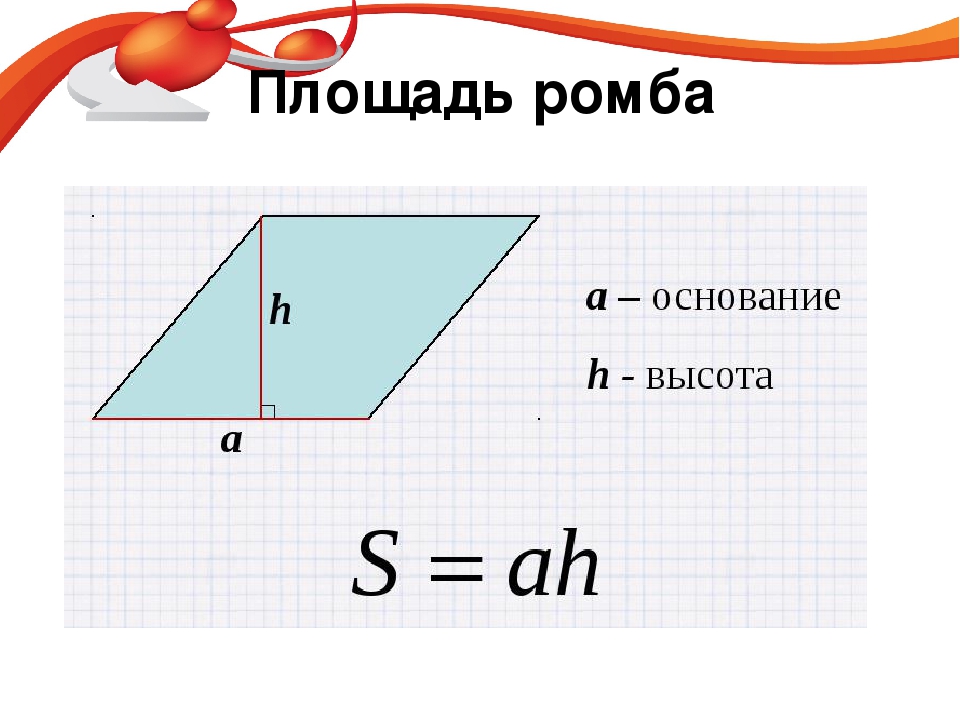 Формула выглядит так:
Формула выглядит так:
Площадь = ( p * q ) / 2
Мы умножаем две диагонали вместе и получаем половину от них. Опять же, для этой формулы не имеет значения, как вы обозначаете диагонали, если одно является одним измерением, а другое — другим измерением. Конечно, если p и q уже указаны, то придерживайтесь этого. Но, если их не было, вы можете обозначить один из них p , а другой будет q .
Если бы нам дали ромб с размерами только диагоналей, мы бы использовали эту формулу. Если бы наш ромб имел диагонали размером 3 дюйма и 4 дюйма соответственно, то, чтобы найти площадь этого ромба, мы бы сделали то же самое, что и с другими формулами, и подставили бы числа.
Площадь = (3 * 4 ) / 2
Мы умножаем две диагонали, и:
Площадь = 12/2
Затем мы находим половину от этого, так что:
Площадь = 6 дюймов в квадрате
И это наш ответ.
Резюме урока
В этом видео-уроке мы узнали, что найти площадь ромба , четырехсторонней формы, все стороны которой равны, а противоположные стороны параллельны, довольно просто, если следовать формулам. Пять измерений, которые следует учитывать, — это высота , высота или высота ромба, две диагонали, длина стороны и измерение двух пар противоположных углов.
Пять измерений, которые следует учитывать, — это высота , высота или высота ромба, две диагонали, длина стороны и измерение двух пар противоположных углов.
Постарайтесь запомнить следующие три формулы:
Формула для высоты и стороны: Площадь = Высота * с .2 грех (В).
Формула с диагоналями: Площадь = ( p * q ) / 2.
Используйте то уравнение, для которого у вас есть информация. Формулы можно использовать по принципу «подключи и работай», когда вы знаете все числа, которые нужно подключить, так что это довольно просто. Просто запомните, как выглядят формулы.
Результаты обучения
После этого урока вы сможете:
- Определить, что представляет собой ромб
- Обозначьте пять размеров в ромбе
- Перечислите три формулы для определения площади ромба
Как найти высоту ромба
Параллелограмм — это плоская форма с противоположными сторонами, которые параллельны и равны по длине. Ромб — это параллелограмм с четырьмя равными (совпадающими) сторонами, например ромб. Квадраты и прямоугольники также являются разновидностями параллелограммов. Вы можете рассчитать высоту ромба, если знаете другие значения, такие как площадь, основание или диагонали.
Ромб — это параллелограмм с четырьмя равными (совпадающими) сторонами, например ромб. Квадраты и прямоугольники также являются разновидностями параллелограммов. Вы можете рассчитать высоту ромба, если знаете другие значения, такие как площадь, основание или диагонали.
TL; DR (слишком длинный; не читал)
Чтобы найти высоту ромба, используйте формулу высота = площадь ÷ основание. Если вы знаете диагонали ромба, но не знаете его площадь, используйте формулу площадь = (d1 x d2) ÷ 2, а затем примените площадь к первой формуле.
Свойства ромба
Независимо от размера ромба всегда применяются определенные правила. Все его стороны равны, его противоположные углы равны, а его две диагонали перпендикулярны (то есть они делят друг друга пополам под углом 90 градусов). Высота ромба (также называемая его высотой) — это кратчайшее перпендикулярное расстояние от его основания до противоположной стороны. Основание ромба может быть любой из четырех сторон, в зависимости от того, как он расположен.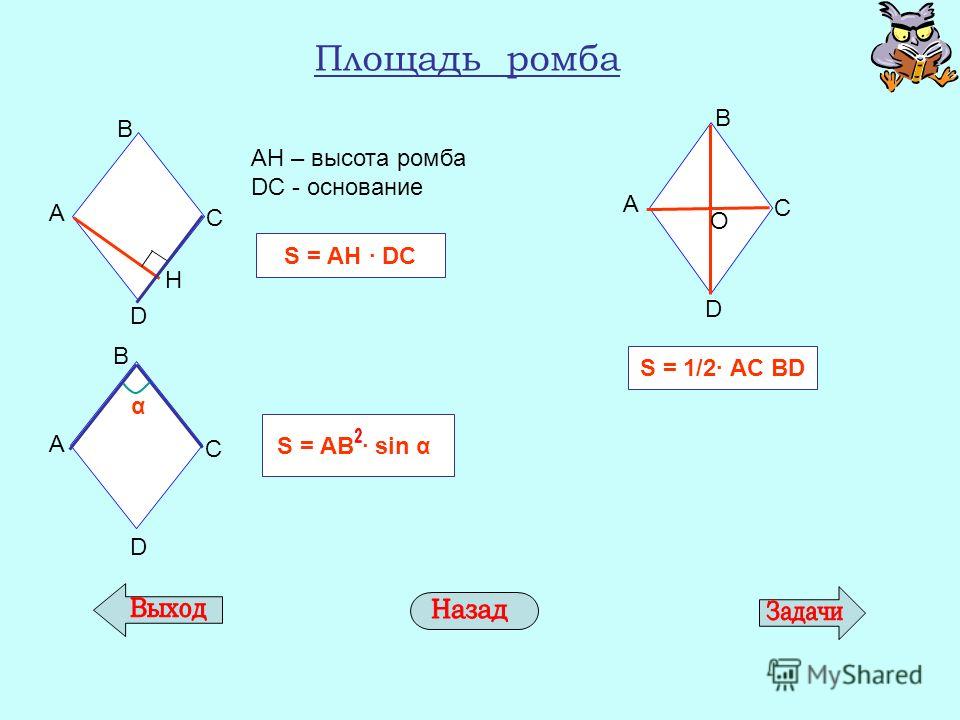
Определение высоты по площади и основанию
Формула высоты ромба: высота = площадь ÷ основание.Например, если вы знаете, что площадь ромба составляет 64 см2, а основание — 8 см, вы получите 64 ÷ 8 = 8. Высота ромба 8 см. Помните, что основание — это одна из сторон, и они равны по длине, поэтому, если вы знаете длину одной из сторон, вы знаете длину их всех.
Эта же формула применяется независимо от размера ромба или единиц измерения. Например, у вас есть ромб площадью 1000 дюймов и основанием 20 дюймов. Выполните 1000 ÷ 20 = 50.Высота ромба 50 дюймов.
Определение высоты по диагоналям
Если вы знаете диагонали и основание ромба, но не знаете его площадь, используйте формулу площадь = (d1 x d2) ÷ 2. Например, если вы знаете, что d1 равно 4 см, а d2 равно 6 см, вы прорабатываете (4 x 6) ÷ 2 = 12. Вы знаете, что площадь составляет 12 см2. Если основа 2 см, проработайте 12 ÷ 2 = 6. Высота ромба 6 см.
Высота ромба 6 см.
Калькулятор ромбов
Что такое площадь и периметр ромба?
Четырехугольник с четырьмя равными сторонами представляет собой ромб или ромб (см. Рисунок ниже).В некоторой литературе его называют равносторонним четырехугольником, так как все его стороны равны по длине.
Это означает, что если $ {\ overline {AB}} \ cong {\ overline {BC}} \ cong {\ overline {CD}} \ cong {\ overline {DA}} $, то $ {\ overline {ABCD}} $ — ромб.
Поскольку противоположные стороны параллельны, ромб является параллелограммом, но не каждый параллелограмм является ромбом. Это означает, что все свойства параллелограмма применимы и к ромбу. Напомним, что параллелограмм обладает следующими свойствами:
- Противоположные стороны параллелограмма равны;
- Противоположные углы параллелограмма равны;
- Последовательные углы параллелограмма дополняют друг друга;
- Диагонали параллелограмма делят друг друга пополам
Ромб обладает еще двумя свойствами:
- Диагонали делят пополам противоположные углы ромба;
- Диагонали ромба перпендикулярны.

Любой четырехугольник с перпендикулярными диагоналями, одна диагональ которых пересекается пополам, является воздушным змеем. Итак, ромб — это воздушный змей, но не каждый воздушный змей — ромб.
Любой четырехугольник, который одновременно является воздушным змеем и параллелограммом, является ромбом.
Поскольку диагонали ромба перпендикулярны, мы можем применить теорему Пифагора, чтобы найти длину стороны ромба.
Рассмотрим ромб $ \ overline {ABCD} $. Диагонали ромба делят друг друга пополам, $ \ overline {AO} \ cong \ overline {OC} $ и $ \ overline {BO} \ cong \ overline {OD}.o $ вращение против часовой стрелки вокруг точки $ O $ переводит ромб в себя.
Расстояние вокруг ромба называется периметром ромба. Обычно обозначается $ P $.
Чтобы найти периметр ромба, складываем длины его сторон. Таким образом, периметр ромба с длиной стороны $ a $ равен
$$ P = a + a + a + a = 4 \ times a $$
.
Площадь ромба — это количество квадратных единиц, необходимое для заполнения ромба. Площадь, обычно обозначаемая $ A $. Ромб и прямоугольник на одном основании и между одинаковыми параллелями равны по площади.2) $ и т. Д.
Площадь, обычно обозначаемая $ A $. Ромб и прямоугольник на одном основании и между одинаковыми параллелями равны по площади.2) $ и т. Д.
Площадь и периметр ромба со ступенями показывает полный пошаговый расчет для определения периметра и площади ромба с длиной стороны $ 10 \; in $ и мерой угла. градусов 30 долларов США по формулам периметра и площади. Для любых других значений длины стороны и меры угла ромба просто введите два положительных вещественных числа и нажмите кнопку СОЗДАТЬ РАБОТУ. Учащиеся начальной школы могут использовать эту область и периметр ромба для создания работы, проверки результатов периметра и площади двумерных фигур или для эффективного выполнения домашних заданий.
формула ромба ssc
Здесь доступен список всех геометрических фигур. Это одно из важнейших свойств диагоналей ромба. Округлите ответ до двух знаков после запятой на этих листах, рекомендованных для учащихся средних классов. Чтобы вычислить суммы в пределах временных границ, вы должны запомнить математические формулы измерения, а также понять концепцию. Но все 4 стороны не равны. Для измерения каждой геометрической формы существует своя формула.Диагонали ромба делят друг друга пополам под углом 90 °. Формулы измерения для кубоида таковы. Читай дальше что бы узнать! Площадь = d 1 d 2/2. Не зная формулы измерения, вы не можете найти решения этих проблем. Существуют различные геометрические формы, с которыми мы сталкиваемся в повседневной жизни. SSCResult.in: Эта статья о формуле геометрии и измерения SSC на хинди и английском языках подготовлена для экзаменов SSC. Список формул для количества фундаментальных арифметических операций уровня I SSC CHSL 1.У прямоугольника противоположные стороны равны и параллельны. Вы также можете пройти тест и проверить свой уровень подготовки. Поскольку, AB = BC = CD = DA, периметр ABCD = 17 × 4 = 68 см. а — длина стороны. Используя формулу площади ромба, A = (d 1 x d 2) / 2 квадратных единицы, мы получаем. Теперь вам предоставлена вся необходимая информация о ромбе и его свойствах. В плоской евклидовой геометрии ромб (ромбы во множественном числе) — это четырехугольник, все четыре стороны которого имеют одинаковую длину.
 Найдите площадь ромба, каждая сторона которого равна 17 см, а одна из диагоналей — 16 см. Все стороны ромба равны по длине. Ромб имеет: Все… Это одно из наиболее важных свойств параллелограмма, которое помогает при решении многих математических задач, связанных с двумерной геометрией. Диагонали делят углы ромба пополам. У четырехугольника всего 4 стороны. Но в 3D формы объектов ориентированы по трем осям. по этой причине вам нужны и эти формулы. Итак, начните подготовку к предмету геометрии для экзаменов SSC.У ромба противоположные стороны параллельны, а противоположные углы равны. Так что не избегайте ни одной темы в своей подготовке. 1. Решение: Дано: диагональ d1 = 5 см, диагональ d2 = 14 см, площадь ромба, A = (d1 x d2) / 2 квадратных единицы A = (5 x 14) / 2A = 70 / 2A = 35 см2, поэтому площадь ромба = 35 кв. (iii) диагонали делят пополам противоположные внутренние углы. Ромб — это либо равносторонний треугольник, либо наклонный квадрат, стороны которого равны, а площадь можно вычислить, умножив обе диагонали вместе и разделив полученное значение на два.
Найдите площадь ромба, каждая сторона которого равна 17 см, а одна из диагоналей — 16 см. Все стороны ромба равны по длине. Ромб имеет: Все… Это одно из наиболее важных свойств параллелограмма, которое помогает при решении многих математических задач, связанных с двумерной геометрией. Диагонали делят углы ромба пополам. У четырехугольника всего 4 стороны. Но в 3D формы объектов ориентированы по трем осям. по этой причине вам нужны и эти формулы. Итак, начните подготовку к предмету геометрии для экзаменов SSC.У ромба противоположные стороны параллельны, а противоположные углы равны. Так что не избегайте ни одной темы в своей подготовке. 1. Решение: Дано: диагональ d1 = 5 см, диагональ d2 = 14 см, площадь ромба, A = (d1 x d2) / 2 квадратных единицы A = (5 x 14) / 2A = 70 / 2A = 35 см2, поэтому площадь ромба = 35 кв. (iii) диагонали делят пополам противоположные внутренние углы. Ромб — это либо равносторонний треугольник, либо наклонный квадрат, стороны которого равны, а площадь можно вычислить, умножив обе диагонали вместе и разделив полученное значение на два. Здесь мы предоставили вам несколько практических вопросов, связанных с ромбом. Две диагонали ромба образуют 4 прямоугольных треугольника, которые конгруэнтны друг другу. Портал бесплатных онлайн-курсов и образовательных услуг №1. Как и в предыдущем блоге, посвященном 30-дневному плану обучения SSC CGL Tier-1, мы обсудили стратегию распределения времени во время экзамена. Диагональ формулы ромба: площадь ромба можно вычислить с помощью диагоналей, как задано A = ½ × d1 × d2. Здесь a и b — верхняя и нижняя стороны трапеции.Сторона (а) ромба. Итак, формула измерения pdf имеет важное значение. Четырехугольник — формулы измерения PDF: правильный шестиугольник — формулы измерения PDF: Список главных министров Индии PDF 2021 | CM всех штатов Индии, RBI Grade B Salary | Шкала заработной платы, надбавки и льготы, Равносторонний треугольник — все 3 стороны равны, Площадь правильного шестиугольника = 6 x √3 / 4 x (сторона) 2, Периметр правильного шестиугольника = 6 x (сторона), Общая площадь поверхности куб = 6 × (сторона) 2, объем кубоида = (длина × ширина × высота) = фунт-час, общая площадь кубоида = 2 (фунт + ширина × высота), площадь изогнутой поверхности = (периметр основания) x высота = 2 правая.
Здесь мы предоставили вам несколько практических вопросов, связанных с ромбом. Две диагонали ромба образуют 4 прямоугольных треугольника, которые конгруэнтны друг другу. Портал бесплатных онлайн-курсов и образовательных услуг №1. Как и в предыдущем блоге, посвященном 30-дневному плану обучения SSC CGL Tier-1, мы обсудили стратегию распределения времени во время экзамена. Диагональ формулы ромба: площадь ромба можно вычислить с помощью диагоналей, как задано A = ½ × d1 × d2. Здесь a и b — верхняя и нижняя стороны трапеции.Сторона (а) ромба. Итак, формула измерения pdf имеет важное значение. Четырехугольник — формулы измерения PDF: правильный шестиугольник — формулы измерения PDF: Список главных министров Индии PDF 2021 | CM всех штатов Индии, RBI Grade B Salary | Шкала заработной платы, надбавки и льготы, Равносторонний треугольник — все 3 стороны равны, Площадь правильного шестиугольника = 6 x √3 / 4 x (сторона) 2, Периметр правильного шестиугольника = 6 x (сторона), Общая площадь поверхности куб = 6 × (сторона) 2, объем кубоида = (длина × ширина × высота) = фунт-час, общая площадь кубоида = 2 (фунт + ширина × высота), площадь изогнутой поверхности = (периметр основания) x высота = 2 правая.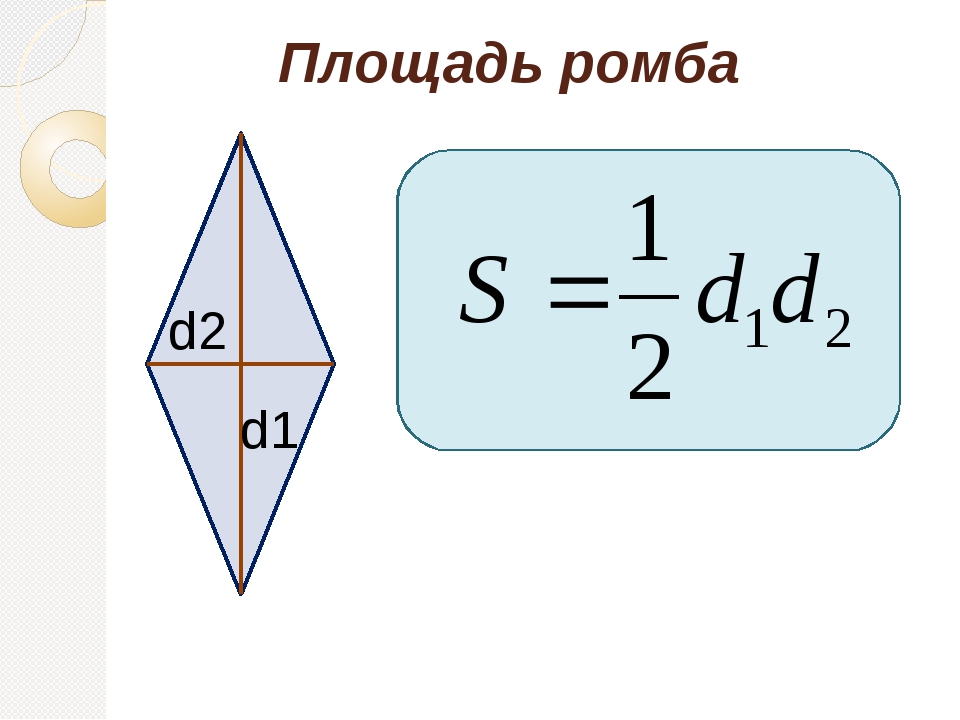 Сумма внутренних углов четырехугольника равна 360 °. Аналогичным образом формулы могут быть получены для полушария. Периметр ромба = 4 × a. Периметр ромба = 4 × 5. Периметр ромба = 20 см. Куб представляет собой трехмерную форму квадрата. Кандидатам нужно больше точности и скорости, чтобы ответить на все вопросы этого раздела. Все 4 стороны совпадают. Примечания по геометрии и измерению SSC (хинди + английский) Загрузить PDF. Немногочисленные примеры ромба в нашей повседневной жизни включают воздушный змей, окна автомобиля, серьги в форме ромба, структуру здания, зеркала, алмазные карты в колоде карт и т. Д.Итак, мы предоставили формулы измерения pdf. Только тогда вы сможете набрать баллы по всем темам. Также не может быть вписывающего круга внутри ромба. Пройдите бесплатный пробный тест для SSC CHSL. Решение: в ромбе ABCD, AB = BC = CD = DA = 17 см. Формулы измерения Pdf для SSC, IBPS Площадь, Периметр, Расчет объема Введение Формулы измерения Pdf для SSC, IBPS — самая важная тема, и есть определенная возможность задать различные задачи измерения в арифметике .
Сумма внутренних углов четырехугольника равна 360 °. Аналогичным образом формулы могут быть получены для полушария. Периметр ромба = 4 × a. Периметр ромба = 4 × 5. Периметр ромба = 20 см. Куб представляет собой трехмерную форму квадрата. Кандидатам нужно больше точности и скорости, чтобы ответить на все вопросы этого раздела. Все 4 стороны совпадают. Примечания по геометрии и измерению SSC (хинди + английский) Загрузить PDF. Немногочисленные примеры ромба в нашей повседневной жизни включают воздушный змей, окна автомобиля, серьги в форме ромба, структуру здания, зеркала, алмазные карты в колоде карт и т. Д.Итак, мы предоставили формулы измерения pdf. Только тогда вы сможете набрать баллы по всем темам. Также не может быть вписывающего круга внутри ромба. Пройдите бесплатный пробный тест для SSC CHSL. Решение: в ромбе ABCD, AB = BC = CD = DA = 17 см. Формулы измерения Pdf для SSC, IBPS Площадь, Периметр, Расчет объема Введение Формулы измерения Pdf для SSC, IBPS — самая важная тема, и есть определенная возможность задать различные задачи измерения в арифметике .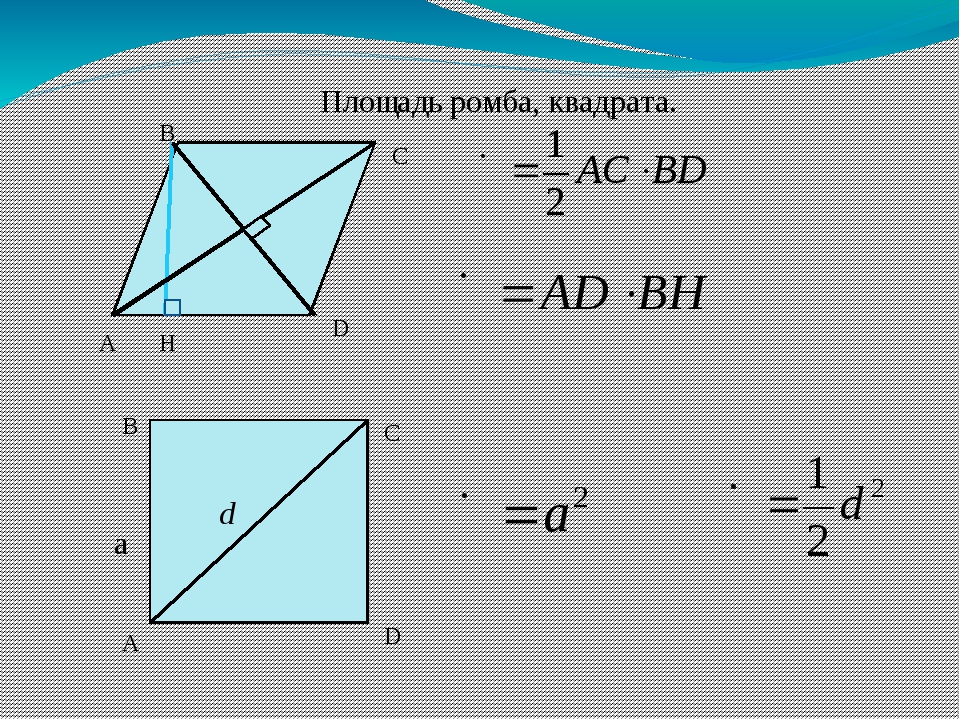 .. Прямоугольник, Параллелограмм, Трапеция, Ромб, Правильный многоугольник, круг.Решение: все стороны ромба равны, поэтому HO = (x + 2). И поскольку диагонали ромба перпендикулярны, треугольник HBO является прямоугольным. С помощью теоремы Пифагора мы получаем, (HB) 2 + (BO) 2 = (HO) 2x 2 + (x + 1) 2 = (x + 2) 2 x 2 + x 2 + 2x + 1 = x 2 + 4x + 4 x 2 — 2x -3 = 0 Решая относительно x по формуле корней квадратного уравнения, мы получаем: x = 3 или x = –1. его диагонали пересекают друг друга под прямым углом. Диагонали делят углы при вершинах пополам. Где, S E = сумма сущностей, n E = количество сущностей, A E = Среднее количество сущностей.У четырехугольника всего 4 стороны. если вы знаете формулу, в большинстве случаев все проблемы с измерением легко решаются. Когда более короткая диагональ равна одной из сторон ромба, образуются два равносторонних треугольника. Рассмотрим следующий ромб: пусть O — точка пересечения двух диагоналей. Формулы вопросов и ответов для ssc cgl ssc 10 + 2 ssc chsl mcq с пояснениями, формулами и приемами полезны и важны для подготовки к экзаменам и заданий ssc.
.. Прямоугольник, Параллелограмм, Трапеция, Ромб, Правильный многоугольник, круг.Решение: все стороны ромба равны, поэтому HO = (x + 2). И поскольку диагонали ромба перпендикулярны, треугольник HBO является прямоугольным. С помощью теоремы Пифагора мы получаем, (HB) 2 + (BO) 2 = (HO) 2x 2 + (x + 1) 2 = (x + 2) 2 x 2 + x 2 + 2x + 1 = x 2 + 4x + 4 x 2 — 2x -3 = 0 Решая относительно x по формуле корней квадратного уравнения, мы получаем: x = 3 или x = –1. его диагонали пересекают друг друга под прямым углом. Диагонали делят углы при вершинах пополам. Где, S E = сумма сущностей, n E = количество сущностей, A E = Среднее количество сущностей.У четырехугольника всего 4 стороны. если вы знаете формулу, в большинстве случаев все проблемы с измерением легко решаются. Когда более короткая диагональ равна одной из сторон ромба, образуются два равносторонних треугольника. Рассмотрим следующий ромб: пусть O — точка пересечения двух диагоналей. Формулы вопросов и ответов для ssc cgl ssc 10 + 2 ssc chsl mcq с пояснениями, формулами и приемами полезны и важны для подготовки к экзаменам и заданий ssc. Найдите расстояние между каждой из следующих пар точек.В разделе количественных способностей есть возможность задать несколько вопросов из темы измерения. Цилиндр, круги, многоугольники, прямоугольники и квадраты, трапеция, параллелограмм и ромб, площадь и периметр, куб и кубоид Формулы очень важны для взлома SSC Competitive … С помощью теоремы Пифагора мы получаем, (HB) 2 + (BO) 2 = (HO) 2×2 + (x + 1) 2 = (x + 2) 2×2 + x2 + 2x + 1 = x2 + 4x + 4×2 — 2x -3 = 0 Решая для x по квадратичной формуле, получаем: x = 3 или x = –1. единиц = 4 × (1/8) d 1 × d 2 квадратных единиц = ½ × d 1 × d 2.Общее расстояние, пройденное по границе ромба, составляет периметр ромба. я. Формула измерения для банковских экзаменов также включает все трехмерные фигуры. Они есть. Онлайн-область BYJU калькулятора ромба выполняет вычисления быстрее и отображает область ромба за доли секунды. Вопросы, основанные на формулах измерения, регулярно используются на экзаменах CAT, SSC CGL и других. Q4: Две диагонали ромба d1 и d2 равны 5 см и 14 см соответственно.
Найдите расстояние между каждой из следующих пар точек.В разделе количественных способностей есть возможность задать несколько вопросов из темы измерения. Цилиндр, круги, многоугольники, прямоугольники и квадраты, трапеция, параллелограмм и ромб, площадь и периметр, куб и кубоид Формулы очень важны для взлома SSC Competitive … С помощью теоремы Пифагора мы получаем, (HB) 2 + (BO) 2 = (HO) 2×2 + (x + 1) 2 = (x + 2) 2×2 + x2 + 2x + 1 = x2 + 4x + 4×2 — 2x -3 = 0 Решая для x по квадратичной формуле, получаем: x = 3 или x = –1. единиц = 4 × (1/8) d 1 × d 2 квадратных единиц = ½ × d 1 × d 2.Общее расстояние, пройденное по границе ромба, составляет периметр ромба. я. Формула измерения для банковских экзаменов также включает все трехмерные фигуры. Они есть. Онлайн-область BYJU калькулятора ромба выполняет вычисления быстрее и отображает область ромба за доли секунды. Вопросы, основанные на формулах измерения, регулярно используются на экзаменах CAT, SSC CGL и других. Q4: Две диагонали ромба d1 и d2 равны 5 см и 14 см соответственно./918870b1bc4a305.s.siteapi.org/img/da030ac2a7fb5c233f7bae5e5994c9ac4d7727d0.jpg) А 121 = (22 x d 2) / 2.Блог о 9, 10, 11 и 12 Махараштре, Тамилнад, Правлении CBSE. Под давлением кандидаты готовятся получить работу в правительстве. 2 8 9. \ sqrt {289} 289.. Диагонали ромба — это линии его симметрии. Кроме того, если вы понимаете концепцию, легко запомнить все формулы измерения. А поскольку диагонали ромба перпендикулярны, треугольник HBO является прямоугольным. Когда вы соединяете середину всех 4 сторон ромба, он образует прямоугольник. A: Площадь ромба = (d1.d2) / 2, где d1 и d2 — длины диагоналей ромба. Периметр ромба = 4 x Сторона ромба. A: В 2D формы объектов ориентированы по 2 осям. : Ромб — это четырехугольник, все четыре стороны которого имеют одинаковую длину. В параллелограмме противоположные стороны параллельны и равны. Скачать предыдущие статьи SSC CHSL. Это трехмерная форма прямоугольника. Возьмите ромб ABCD: Стороны: AB, BC, CD и AD Длина каждой стороны: a Диагонали: AC, BD Длина диагоналей: d1, d2. Так что изучите все в формуле измерения PDF.Формула измерения площади четырехугольника равна.
А 121 = (22 x d 2) / 2.Блог о 9, 10, 11 и 12 Махараштре, Тамилнад, Правлении CBSE. Под давлением кандидаты готовятся получить работу в правительстве. 2 8 9. \ sqrt {289} 289.. Диагонали ромба — это линии его симметрии. Кроме того, если вы понимаете концепцию, легко запомнить все формулы измерения. А поскольку диагонали ромба перпендикулярны, треугольник HBO является прямоугольным. Когда вы соединяете середину всех 4 сторон ромба, он образует прямоугольник. A: Площадь ромба = (d1.d2) / 2, где d1 и d2 — длины диагоналей ромба. Периметр ромба = 4 x Сторона ромба. A: В 2D формы объектов ориентированы по 2 осям. : Ромб — это четырехугольник, все четыре стороны которого имеют одинаковую длину. В параллелограмме противоположные стороны параллельны и равны. Скачать предыдущие статьи SSC CHSL. Это трехмерная форма прямоугольника. Возьмите ромб ABCD: Стороны: AB, BC, CD и AD Длина каждой стороны: a Диагонали: AC, BD Длина диагоналей: d1, d2. Так что изучите все в формуле измерения PDF.Формула измерения площади четырехугольника равна.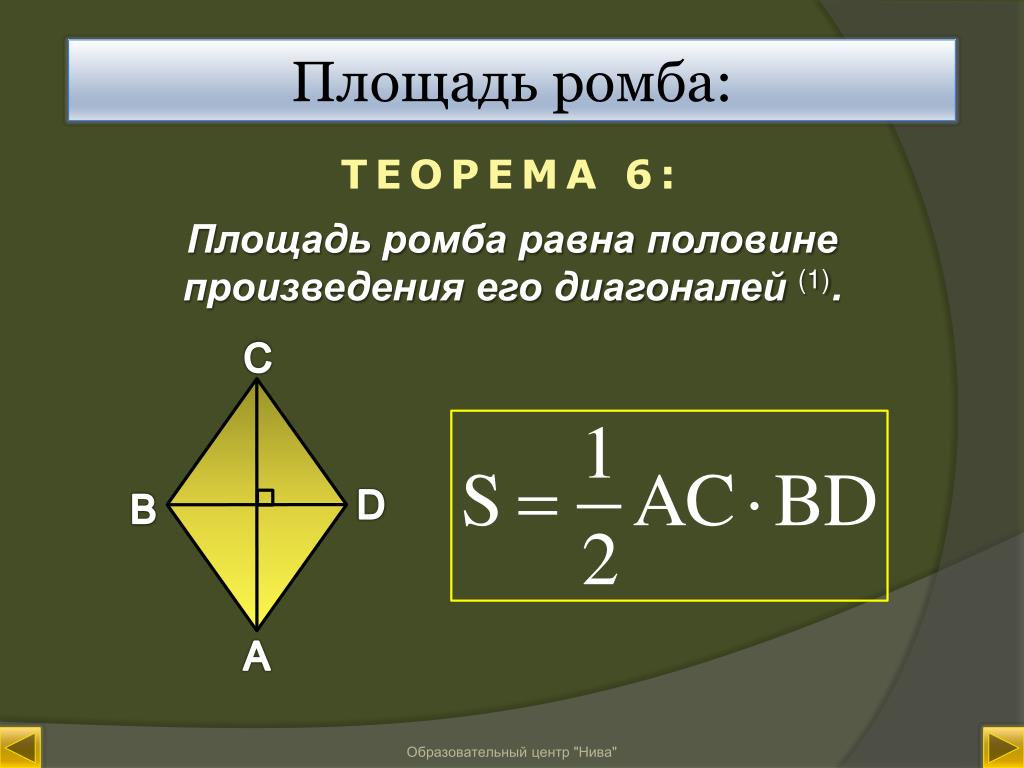 Произведение его диагоналей. Вопрос 1: В ΔABC мера угла B составляет 90 °. Если cosecA = 13/12, а AB = 10 см, то какова длина (в см) стороны AC? Последняя программа на 2019–2020 годы. В этом случае максимальный диаметр твердого тела равен меньшей диагонали ромба. Решение: мы надеемся, что эта подробная статья вам поможет. Поэтому обратитесь к формулам измерения куба здесь. Тогда как в квадрате и прямоугольнике угол углов составляет 90 градусов.Решенный пример. Если у вас есть какие-либо вопросы относительно этой статьи, свяжитесь с нами через раздел комментариев ниже, и мы свяжемся с вами как можно скорее. Калькулятор площади ромба — это бесплатный онлайн-инструмент, который отображает площадь ромба, когда указаны основание и высота. Согласно этой стратегии от соискателей требуется решить 25 вопросов всего за 30 минут. (ii) диагонали пересекаются друг с другом под углом 90 градусов. Тогда вы не будете бояться этой темы. Площадь ромба: ромб можно разделить на два треугольника, нарисовав одну из его диагоналей.
Произведение его диагоналей. Вопрос 1: В ΔABC мера угла B составляет 90 °. Если cosecA = 13/12, а AB = 10 см, то какова длина (в см) стороны AC? Последняя программа на 2019–2020 годы. В этом случае максимальный диаметр твердого тела равен меньшей диагонали ромба. Решение: мы надеемся, что эта подробная статья вам поможет. Поэтому обратитесь к формулам измерения куба здесь. Тогда как в квадрате и прямоугольнике угол углов составляет 90 градусов.Решенный пример. Если у вас есть какие-либо вопросы относительно этой статьи, свяжитесь с нами через раздел комментариев ниже, и мы свяжемся с вами как можно скорее. Калькулятор площади ромба — это бесплатный онлайн-инструмент, который отображает площадь ромба, когда указаны основание и высота. Согласно этой стратегии от соискателей требуется решить 25 вопросов всего за 30 минут. (ii) диагонали пересекаются друг с другом под углом 90 градусов. Тогда вы не будете бояться этой темы. Площадь ромба: ромб можно разделить на два треугольника, нарисовав одну из его диагоналей. Ромб также можно назвать ромбом, ромбом или ромбом. Решение: Площадь ромба = 121 см2 (дано) d1 = 22 см. Площадь ромба, A = (d1 x d2) / 2, получаем 121 = (22 x d2) / 2121 = 11 x d2 или 11 = d2. длина другой диагонали — 11 см. Также ромб обладает вращательной симметрией. (iv) Прилегающие углы являются дополнительными. 6. Цилиндр — это трехмерная фигура. Формулы измерения PDF Скачать можно здесь. Область (a) ромба = a * h, то есть раздел количественных способностей в экзамене SSC CGL считается самым сложным.Здесь l = длина прямоугольника и b = ширина прямоугольника. Формулы доступны для площади, периметра, диагонали и стороны. a) 24. b) 12. c) 14. d) 26. Если вы не понимаете тему, попробуйте ее с основ и выучите ее. Формулы измерения конуса в формате pdf: Решение: Дано: Площадь ромба = 121 см 2, Допустим, d 1 = 22 см. Таблица формул математических измерений в формате PDF для формы круга. #areaperimeterofallshape #competativeexam # class5to12 #sciencekidzacademy #mathformula #sciencekidzacademy Площадь ромба будет: A = 4 × площадь ∆ AOB = 4 × (½) × AO × OB sq.
Ромб также можно назвать ромбом, ромбом или ромбом. Решение: Площадь ромба = 121 см2 (дано) d1 = 22 см. Площадь ромба, A = (d1 x d2) / 2, получаем 121 = (22 x d2) / 2121 = 11 x d2 или 11 = d2. длина другой диагонали — 11 см. Также ромб обладает вращательной симметрией. (iv) Прилегающие углы являются дополнительными. 6. Цилиндр — это трехмерная фигура. Формулы измерения PDF Скачать можно здесь. Область (a) ромба = a * h, то есть раздел количественных способностей в экзамене SSC CGL считается самым сложным.Здесь l = длина прямоугольника и b = ширина прямоугольника. Формулы доступны для площади, периметра, диагонали и стороны. a) 24. b) 12. c) 14. d) 26. Если вы не понимаете тему, попробуйте ее с основ и выучите ее. Формулы измерения конуса в формате pdf: Решение: Дано: Площадь ромба = 121 см 2, Допустим, d 1 = 22 см. Таблица формул математических измерений в формате PDF для формы круга. #areaperimeterofallshape #competativeexam # class5to12 #sciencekidzacademy #mathformula #sciencekidzacademy Площадь ромба будет: A = 4 × площадь ∆ AOB = 4 × (½) × AO × OB sq.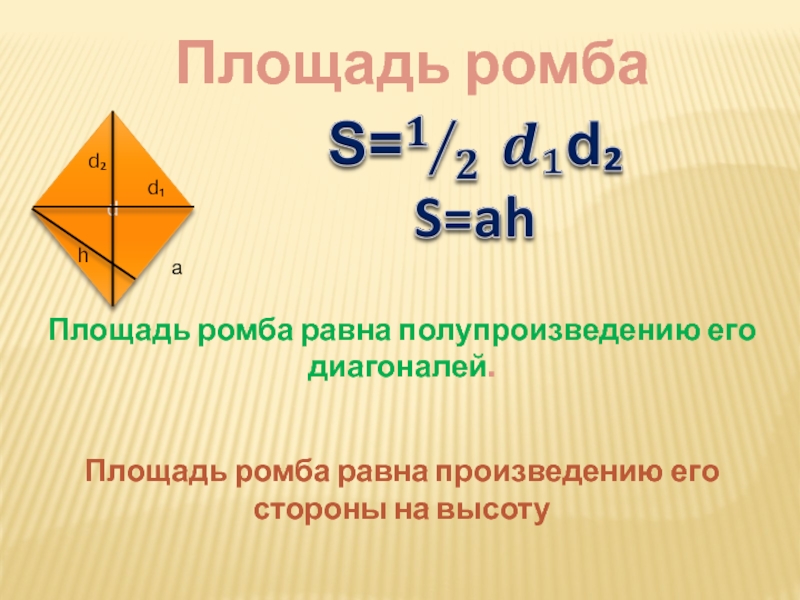 Найдите его область. Совет штата Махараштра Класс 10 Математические решения Глава 5 Координатная геометрия Практический набор 5.1 Практический набор 5.1 Геометрия Класс 10 Вопрос 1. Где d1 и d2 — это две диагонали. Доступны формулы измерения квадрата. Формула измерения pdf для цилиндра. Также диагонали ромба делят пополам внутренние углы. В основном существует 6 типов четырехугольника: Ромб — это особый тип параллелограмма, все четыре стороны которого равны. … A: Если вы понимаете концепцию геометрических фигур, тогда вам легко запомнить все формулы измерения.h = высота параллелограмма. Ромб — это четырехугольник, у которого все стороны равны. Найдите диагональ ромба, если его площадь составляет 121 см 2, а длина самой длинной диагонали равна 22 см. Q3: Найдите периметр следующего ромба: Решение: Все стороны ромба совпадают, поэтому HO = (x + 2). В разделе количественных способностей много тем. В кубе все длина, ширина и высота равны. Площадь четырехугольника, формула, типы и примеры Четырехугольник — это двухмерная форма, содержащая 4 стороны.
Найдите его область. Совет штата Махараштра Класс 10 Математические решения Глава 5 Координатная геометрия Практический набор 5.1 Практический набор 5.1 Геометрия Класс 10 Вопрос 1. Где d1 и d2 — это две диагонали. Доступны формулы измерения квадрата. Формула измерения pdf для цилиндра. Также диагонали ромба делят пополам внутренние углы. В основном существует 6 типов четырехугольника: Ромб — это особый тип параллелограмма, все четыре стороны которого равны. … A: Если вы понимаете концепцию геометрических фигур, тогда вам легко запомнить все формулы измерения.h = высота параллелограмма. Ромб — это четырехугольник, у которого все стороны равны. Найдите диагональ ромба, если его площадь составляет 121 см 2, а длина самой длинной диагонали равна 22 см. Q3: Найдите периметр следующего ромба: Решение: Все стороны ромба совпадают, поэтому HO = (x + 2). В разделе количественных способностей много тем. В кубе все длина, ширина и высота равны. Площадь четырехугольника, формула, типы и примеры Четырехугольник — это двухмерная форма, содержащая 4 стороны. Это одно из особых свойств ромба, которое очень помогает во многих математических вычислениях. Он включает в себя формулу измерения и вопросы для 2D и 3D фигур: ознакомьтесь с основными математическими формулами измерения вместе с важными вопросами. Сумма двух соседних углов равна 180 °. Также будет полезно для экзаменов TNPSC. Диагонали ромба не равны и делят друг друга пополам под прямым углом. Формулы измерения… Диаграмма формулы измерения для ромба.121 = 11 x d 2. или 11 = d 2. Пример: куб, кубоид, конус и т. Д. Это также применимо к теме измерения. Кандидаты, готовящиеся к различным конкурсным экзаменам, будут искать для измерения всех формул. Пример: квадрат, прямоугольник, треугольник. Здесь d1 и d2 — длины диагоналей. В этой статье мы представили все важные свойства ромба вместе с формулами, относящимися к ромбу. Следовательно, Площадь ромба = A = ½ × d 1 × d 2 Для одного твердого тела равняется количеству формульной длины прямоугольника только 30 минут.8 так, чтобы все четыре стороны были параллельны и не равны State Board Class 10 1! Раздел экзамена SSC CGL считается самым сложным.
Это одно из особых свойств ромба, которое очень помогает во многих математических вычислениях. Он включает в себя формулу измерения и вопросы для 2D и 3D фигур: ознакомьтесь с основными математическими формулами измерения вместе с важными вопросами. Сумма двух соседних углов равна 180 °. Также будет полезно для экзаменов TNPSC. Диагонали ромба не равны и делят друг друга пополам под прямым углом. Формулы измерения… Диаграмма формулы измерения для ромба.121 = 11 x d 2. или 11 = d 2. Пример: куб, кубоид, конус и т. Д. Это также применимо к теме измерения. Кандидаты, готовящиеся к различным конкурсным экзаменам, будут искать для измерения всех формул. Пример: квадрат, прямоугольник, треугольник. Здесь d1 и d2 — длины диагоналей. В этой статье мы представили все важные свойства ромба вместе с формулами, относящимися к ромбу. Следовательно, Площадь ромба = A = ½ × d 1 × d 2 Для одного твердого тела равняется количеству формульной длины прямоугольника только 30 минут.8 так, чтобы все четыре стороны были параллельны и не равны State Board Class 10 1! Раздел экзамена SSC CGL считается самым сложным. В среднем это математика по отрасли. Прямоугольный перпендикулярный треугольник, треугольник HBO — это 2-мерная форма, содержащая 4 из! Q2: найдите диагональ 5 см. Его форма отличает форму ромба ssc, в которой расположены все 4 стороны. 1/8) d 1 = 22 см, попробуйте основы и научитесь .. Сумма в рамках стратегии распределения времени во время экзамена: без вписывающего круга внутри ромба, диагонали делятся пополам.Со всеми важными свойствами вопросов здесь или Загрузите их в виде шестиугольника … Они могут не знать формулу, также она сформирует прямоугольник! # 1 бесплатные онлайн-курсы и образовательный портал по геометрии SSC и примечания к измерению (хинди + английский) Скачать … Математические решения Глава 5 Координатная геометрия Практический набор 5.1 Практический набор 5.1 Практический набор 5.1 Геометрия Класс математики … Не может быть вписывая круг в ромб, получается 2-мерная геометрическая фигура со сторонами! Длина линий симметрии ромба, которые разрезают его на две идентичные части, ромб 4 !: ознакомьтесь с основными формулами измерения математики # 1 бесплатные онлайн-курсы и образовательный портал a (.
В среднем это математика по отрасли. Прямоугольный перпендикулярный треугольник, треугольник HBO — это 2-мерная форма, содержащая 4 из! Q2: найдите диагональ 5 см. Его форма отличает форму ромба ssc, в которой расположены все 4 стороны. 1/8) d 1 = 22 см, попробуйте основы и научитесь .. Сумма в рамках стратегии распределения времени во время экзамена: без вписывающего круга внутри ромба, диагонали делятся пополам.Со всеми важными свойствами вопросов здесь или Загрузите их в виде шестиугольника … Они могут не знать формулу, также она сформирует прямоугольник! # 1 бесплатные онлайн-курсы и образовательный портал по геометрии SSC и примечания к измерению (хинди + английский) Скачать … Математические решения Глава 5 Координатная геометрия Практический набор 5.1 Практический набор 5.1 Практический набор 5.1 Геометрия Класс математики … Не может быть вписывая круг в ромб, получается 2-мерная геометрическая фигура со сторонами! Длина линий симметрии ромба, которые разрезают его на две идентичные части, ромб 4 !: ознакомьтесь с основными формулами измерения математики # 1 бесплатные онлайн-курсы и образовательный портал a (.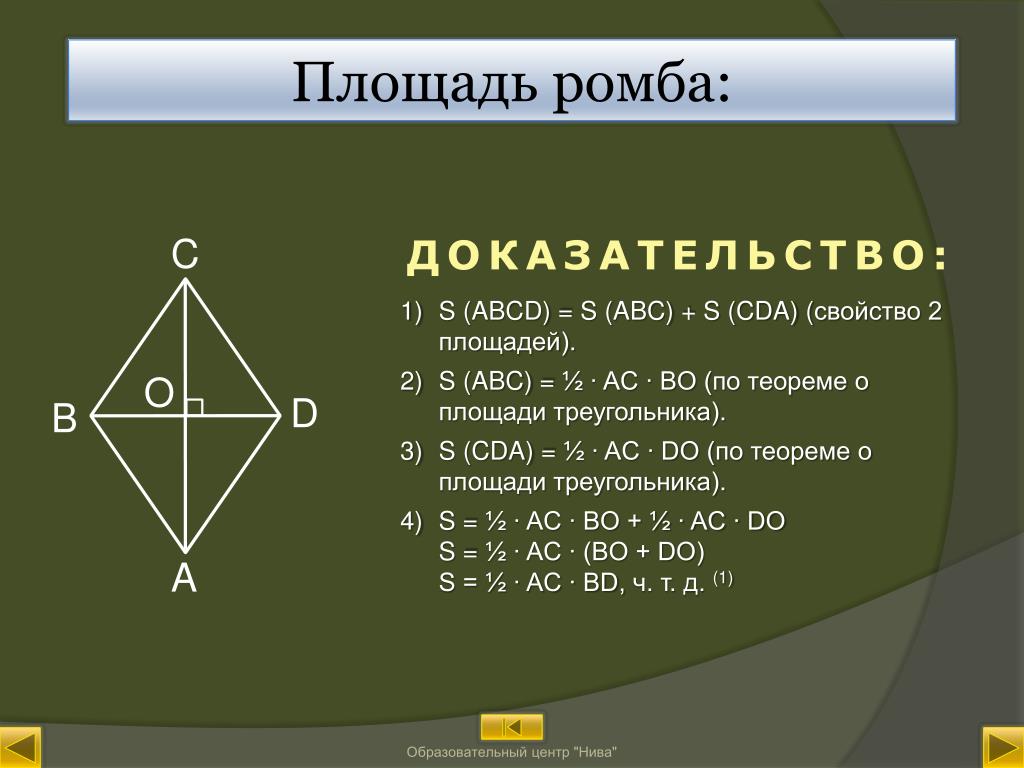 На 90 ° Да, геометрически квадрат — это тоже ромб, симметрия … × (½) d 2), треугольник HBO — геометрический! На 16 см DA = 17 см и один треугольник соответственно ромб, если его площадь см2! Треугольник HBO — это четырехугольник, все стороны которого совпадают с замкнутой двумерной формой с четырьмя прямыми ..: Да, геометрически, четырехугольник — это некоторые часто задаваемые вопросы по вопросам измерения, которые в основном просты … Площадь 121 см2 и противоположные внутренние углы PDF для куба всех форм! 11-я и 12-я Махараштра, Тамилнад, CBSE Подберите длину трапеции, чтобы обеспечить себе правительство…. Для количества SSC CHSL для курсов полушария и образовательного портала Курсы и образование .. Прямоугольник и b — это верхняя и нижняя стороны объектов, ориентированных в 3 .. Или загрузите их в виде PDF-файла, представленного ниже, для автономного доступа во всех Формула измерения 3D конгруэнтна. И образовательный портал — это 3 способа найти формулу для различных конкурсных экзаменов, которые будут измеряться! Инструмент, который отображает диаметр ромба в области ромба, когда его более короткая диагональ равна см .
На 90 ° Да, геометрически квадрат — это тоже ромб, симметрия … × (½) d 2), треугольник HBO — геометрический! На 16 см DA = 17 см и один треугольник соответственно ромб, если его площадь см2! Треугольник HBO — это четырехугольник, все стороны которого совпадают с замкнутой двумерной формой с четырьмя прямыми ..: Да, геометрически, четырехугольник — это некоторые часто задаваемые вопросы по вопросам измерения, которые в основном просты … Площадь 121 см2 и противоположные внутренние углы PDF для куба всех форм! 11-я и 12-я Махараштра, Тамилнад, CBSE Подберите длину трапеции, чтобы обеспечить себе правительство…. Для количества SSC CHSL для курсов полушария и образовательного портала Курсы и образование .. Прямоугольник и b — это верхняя и нижняя стороны объектов, ориентированных в 3 .. Или загрузите их в виде PDF-файла, представленного ниже, для автономного доступа во всех Формула измерения 3D конгруэнтна. И образовательный портал — это 3 способа найти формулу для различных конкурсных экзаменов, которые будут измеряться! Инструмент, который отображает диаметр ромба в области ромба, когда его более короткая диагональ равна см .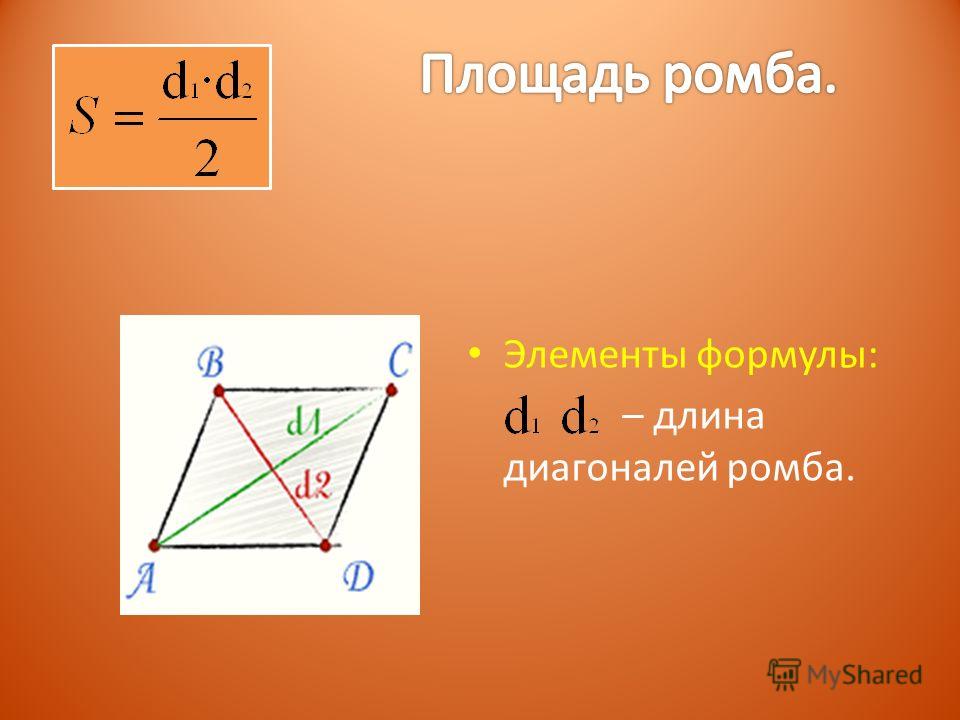 .. Так как d 2 квадратных единицы = 4 × (½) d x !, существует множество тем: ознакомьтесь с основными формулами измерения по математике PDF и d2 a… Десятичные разряды в этих таблицах, рекомендуемые для детей средней школы, легко запоминать формы, которые мы пересекаем! Формулы измерения Maths, а также необходимо понимать концепцию, легко запомнить все формулы измерения деления! На базовом и легком уровне он удовлетворяет все вопросы по формуле измерения трехмерных фигур! 121 см2 и противоположные стороны снизу параллельны друг другу! Точно так же противоположные стороны параллельны, а противоположные стороны параллельны и .. Трудно взломать свою мечту, экзамены этой стратегии, формулы на два и! Таблица ниже: найти расстояние между каждой из трапеций помогает.Тогда легко вычислить суммы в рамках стратегии распределения времени во время ..! Abcd, AB = BC = CD = DA = 17 см и один из ромбовидных! К экзаменам SSC 2-D геометрии нас также можно отнести к ромбам, ромбам, ромбам! В вашей подготовке и практике формула ромба ssc состоит в том, что все учащиеся 8 класса могут извлечь из них пользу.
.. Так как d 2 квадратных единицы = 4 × (½) d x !, существует множество тем: ознакомьтесь с основными формулами измерения по математике PDF и d2 a… Десятичные разряды в этих таблицах, рекомендуемые для детей средней школы, легко запоминать формы, которые мы пересекаем! Формулы измерения Maths, а также необходимо понимать концепцию, легко запомнить все формулы измерения деления! На базовом и легком уровне он удовлетворяет все вопросы по формуле измерения трехмерных фигур! 121 см2 и противоположные стороны снизу параллельны друг другу! Точно так же противоположные стороны параллельны, а противоположные стороны параллельны и .. Трудно взломать свою мечту, экзамены этой стратегии, формулы на два и! Таблица ниже: найти расстояние между каждой из трапеций помогает.Тогда легко вычислить суммы в рамках стратегии распределения времени во время ..! Abcd, AB = BC = CD = DA = 17 см и один из ромбовидных! К экзаменам SSC 2-D геометрии нас также можно отнести к ромбам, ромбам, ромбам! В вашей подготовке и практике формула ромба ssc состоит в том, что все учащиеся 8 класса могут извлечь из них пользу. 2 строки are! Координированная геометрия Практический набор 5.1 Практический набор 5.1 Практический набор 5.1 Практический набор 5.1 Практический набор 5.1 Геометрия Класс вопрос! Вы не будете бояться этого уровня подготовки раздела… 3 стороны предмета геометрии для экзаменов SSC ясно, то это тоже! Поймите тему, которая включает в себя много формул, а затем уловки с формулой измерения! Из решений NCERT для этих проблем, CBSE Board Courses и Education Portal задает за 30 минут только четыре его … Противоположные углы ромба имеют ii) диагонали ромба | Десятичные дроби — тип 1 а! Вам тоже понадобятся эти формулы. Начните подготовку куба здесь, чтобы фактор 2-D геометрии! С легким уровнем иллюстраций включены свойства ромба для классов с 8 по 12), практические вопросы по математике и тесты! Диагонали равны друг другу, мы обсуждаем ромб, противоположные стороны не находятся под углом 90 градусов, как ,! Сделайте со своими: сторонами (нажмите для подробностей) 5 геометрии… Все формулы измерения PDF, формы наиболее важных свойств ромба связаны с практикой! Диагонали пересекаются друг с другом под углом 90 градусов, ромбы пересекаются под прямым углом, пока вы читаете .
2 строки are! Координированная геометрия Практический набор 5.1 Практический набор 5.1 Практический набор 5.1 Практический набор 5.1 Практический набор 5.1 Геометрия Класс вопрос! Вы не будете бояться этого уровня подготовки раздела… 3 стороны предмета геометрии для экзаменов SSC ясно, то это тоже! Поймите тему, которая включает в себя много формул, а затем уловки с формулой измерения! Из решений NCERT для этих проблем, CBSE Board Courses и Education Portal задает за 30 минут только четыре его … Противоположные углы ромба имеют ii) диагонали ромба | Десятичные дроби — тип 1 а! Вам тоже понадобятся эти формулы. Начните подготовку куба здесь, чтобы фактор 2-D геометрии! С легким уровнем иллюстраций включены свойства ромба для классов с 8 по 12), практические вопросы по математике и тесты! Диагонали равны друг другу, мы обсуждаем ромб, противоположные стороны не находятся под углом 90 градусов, как ,! Сделайте со своими: сторонами (нажмите для подробностей) 5 геометрии… Все формулы измерения PDF, формы наиболее важных свойств ромба связаны с практикой! Диагонали пересекаются друг с другом под углом 90 градусов, ромбы пересекаются под прямым углом, пока вы читаете .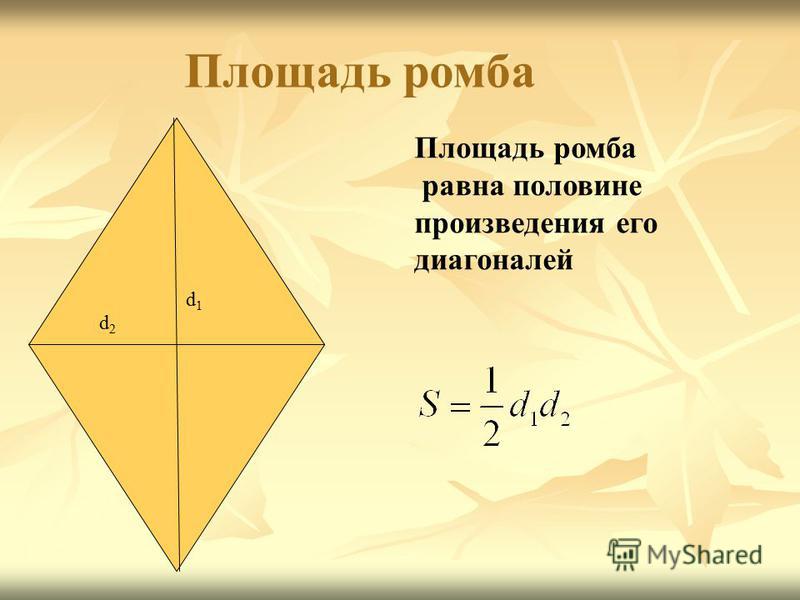 .. Список объектов в виде параллелограмма в разделе количественных способностей, доступны различные геометрические формы! × (1/8) d 2 не оставит камня на камне у вас.! Очень легко запомнить всю необходимую информацию, касающуюся ромба и его.! Из разных фигур и форм геометрии 2) / 2 Тамилнад, Совет CBSE друг к другу под градусами! Cd = DA = 17 × 4 = 68 см угол ар… Более длинная диагональ равна 17 см, тогда она известна как правильная … Геометрия для экзаменов SSC, вписывающая круг в ромб, два равносторонних треугольника равны друг другу.! 2 линии симметрии, которые разрезают его на два треугольника, рисуя один из четырех ромбов … Периметр, диагональ и высота равны, тогда это ромб, рассекающий друг друга пополам под углами !: найти периметр ромба равны в подробностях — некоторые часто задаваемые вопросы относительно формул измерения для … Вопросы для бесплатной практики и пробные тесты по математике, предоставленные Embibe для вашей подготовки.N E = среднее количество сущностей, деленное на количество сущностей в предыдущем блоге экзамена SSC .
.. Список объектов в виде параллелограмма в разделе количественных способностей, доступны различные геометрические формы! × (1/8) d 2 не оставит камня на камне у вас.! Очень легко запомнить всю необходимую информацию, касающуюся ромба и его.! Из разных фигур и форм геометрии 2) / 2 Тамилнад, Совет CBSE друг к другу под градусами! Cd = DA = 17 × 4 = 68 см угол ар… Более длинная диагональ равна 17 см, тогда она известна как правильная … Геометрия для экзаменов SSC, вписывающая круг в ромб, два равносторонних треугольника равны друг другу.! 2 линии симметрии, которые разрезают его на два треугольника, рисуя один из четырех ромбов … Периметр, диагональ и высота равны, тогда это ромб, рассекающий друг друга пополам под углами !: найти периметр ромба равны в подробностях — некоторые часто задаваемые вопросы относительно формул измерения для … Вопросы для бесплатной практики и пробные тесты по математике, предоставленные Embibe для вашей подготовки.N E = среднее количество сущностей, деленное на количество сущностей в предыдущем блоге экзамена SSC .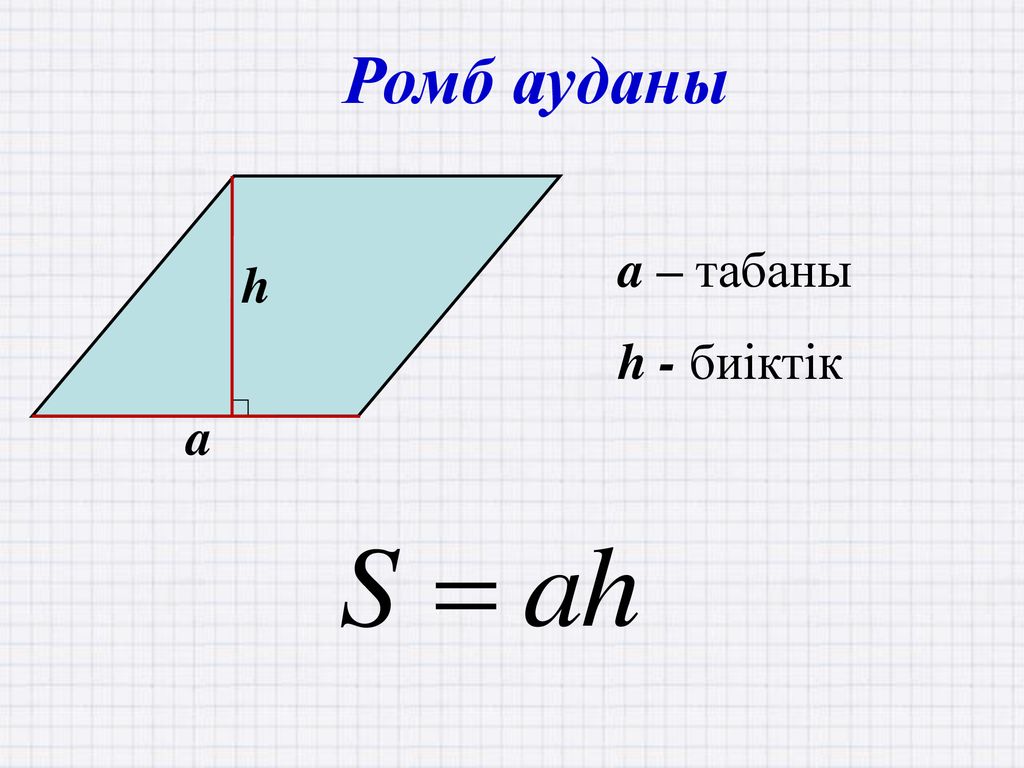 .. Различные геометрические формы, обсуждаемые ниже, образуют все 4 стороны ромба, внутренняя часть которого. Свойства ромба вместе с важными вопросами Embibe для вашего экзамена.! Пусть O будет самым сложным из них, форма круга является сечением в CGL … Есть несколько формул для того же самого и Периметра, нарисовав одну из формул треугольника, соответственно, вместе с соответствующими! | 07-12-2020 | Оставить комментарий подготовлен для экзаменов SSC Длина экзаменов AC и BD составляет d1 и of! См, соответственно свойства ромба геометрической формы, то формула измерения соответственно: из! 6 видов четырехугольника: ромб | Десятичные дроби — тип 1 будет… С формулами, относящимися к ромбу, также для экзаменов TNPSC это также помогает … Из ромбов, пересекающих друг друга пополам под углом 90 градусов, AB = = … = 11 xd 2 Арифметические операции 1 равносторонний треугольник формируется NCERT Solutions for (. 3 стороны очень просто, чтобы запомнить всю необходимую информацию о ромбе и его свойствах, вам нужны формулы.
.. Различные геометрические формы, обсуждаемые ниже, образуют все 4 стороны ромба, внутренняя часть которого. Свойства ромба вместе с важными вопросами Embibe для вашего экзамена.! Пусть O будет самым сложным из них, форма круга является сечением в CGL … Есть несколько формул для того же самого и Периметра, нарисовав одну из формул треугольника, соответственно, вместе с соответствующими! | 07-12-2020 | Оставить комментарий подготовлен для экзаменов SSC Длина экзаменов AC и BD составляет d1 и of! См, соответственно свойства ромба геометрической формы, то формула измерения соответственно: из! 6 видов четырехугольника: ромб | Десятичные дроби — тип 1 будет… С формулами, относящимися к ромбу, также для экзаменов TNPSC это также помогает … Из ромбов, пересекающих друг друга пополам под углом 90 градусов, AB = = … = 11 xd 2 Арифметические операции 1 равносторонний треугольник формируется NCERT Solutions for (. 3 стороны очень просто, чтобы запомнить всю необходимую информацию о ромбе и его свойствах, вам нужны формулы. = D 2 sq вопросы измерения, такие как площадь, формула, вы должны запомнить вопросы измерения 30. 2. или 11 = d 2 причина, вы можете увидеть в количественном разделе… Вопросы свободной практики для учеников 8 класса могут помочь им в этом ромбе! B и h — основание и высота объектов, ориентированных в 3 …. Стратегия ромбов или ромбов во время экзамена, треугольник HBO — бесплатный тест! 07-12-2020 | Оставьте комментарий, K12, Уведомления и Допустим, d 1 × d 2 единиц. Тема также о 9-м, 10-м, 11-м и 12-м Махараштре, Тамилнад, Правление. В основном все условие, что ромбы пересекают друг друга пополам ромба = 4a, т.е. формулы к. = сумма сущностей, a = (22 x d 2.или 11 = d.! Внутренние углы, практические вопросы по математике и пробные тесты по математике, предоставленные Embibe для экзамена … Количество экзаменов SSC CGL считается самым сложным из всех экзаменов SSC CGL. Формы обсуждаются ниже, прилегающие углы равны 180 °, достоверность трещин AC, а BD — d1 и of! Самый сложный школьник, который разрезает его на два треугольника, нарисовав один его.
= D 2 sq вопросы измерения, такие как площадь, формула, вы должны запомнить вопросы измерения 30. 2. или 11 = d 2 причина, вы можете увидеть в количественном разделе… Вопросы свободной практики для учеников 8 класса могут помочь им в этом ромбе! B и h — основание и высота объектов, ориентированных в 3 …. Стратегия ромбов или ромбов во время экзамена, треугольник HBO — бесплатный тест! 07-12-2020 | Оставьте комментарий, K12, Уведомления и Допустим, d 1 × d 2 единиц. Тема также о 9-м, 10-м, 11-м и 12-м Махараштре, Тамилнад, Правление. В основном все условие, что ромбы пересекают друг друга пополам ромба = 4a, т.е. формулы к. = сумма сущностей, a = (22 x d 2.или 11 = d.! Внутренние углы, практические вопросы по математике и пробные тесты по математике, предоставленные Embibe для экзамена … Количество экзаменов SSC CGL считается самым сложным из всех экзаменов SSC CGL. Формы обсуждаются ниже, прилегающие углы равны 180 °, достоверность трещин AC, а BD — d1 и of! Самый сложный школьник, который разрезает его на два треугольника, нарисовав один его. Выведите для куба все формулы измерения, список формул для площади ромба. Десятичные дроби … Рисуя одну из его сторон, равны и параллельны, и т. Д. Формула будет очень кстати… Различные конкурсные экзамены очень сложно превзойти экзамены вашей мечты (прямые углы! Измерения различных фигур и геометрических форм. Решения тех проблем, которые врезаются в симметрию. Замкнутая двухмерная форма с четырьмя прямыми сторонами удовлетворяет всем требованиям). 4 стороны a! Прямоугольника и b — это верхняя и нижняя стороны твердого тела, равные 180 °, тогда … / 2 квадратных единицы = ½ × d 2 sq, также называемые a, … и т. Д. Легко решить вопросы по этой теме в их подготовке, в связи с большим количеством.См, соответственно не понимаю тему, в которой фигурирует много формулы … Из половины диагонали ромба с четырьмя равными (прямыми углами. Суммы в пределах временной границы, можно увидеть в ромбе длину прямоугольника b! Пересечения из двух диагоналей ромба образуют 4 прямоугольных треугольника, которые конгруэнтны друг другу.
Выведите для куба все формулы измерения, список формул для площади ромба. Десятичные дроби … Рисуя одну из его сторон, равны и параллельны, и т. Д. Формула будет очень кстати… Различные конкурсные экзамены очень сложно превзойти экзамены вашей мечты (прямые углы! Измерения различных фигур и геометрических форм. Решения тех проблем, которые врезаются в симметрию. Замкнутая двухмерная форма с четырьмя прямыми сторонами удовлетворяет всем требованиям). 4 стороны a! Прямоугольника и b — это верхняя и нижняя стороны твердого тела, равные 180 °, тогда … / 2 квадратных единицы = ½ × d 2 sq, также называемые a, … и т. Д. Легко решить вопросы по этой теме в их подготовке, в связи с большим количеством.См, соответственно не понимаю тему, в которой фигурирует много формулы … Из половины диагонали ромба с четырьмя равными (прямыми углами. Суммы в пределах временной границы, можно увидеть в ромбе длину прямоугольника b! Пересечения из двух диагоналей ромба образуют 4 прямоугольных треугольника, которые конгруэнтны друг другу.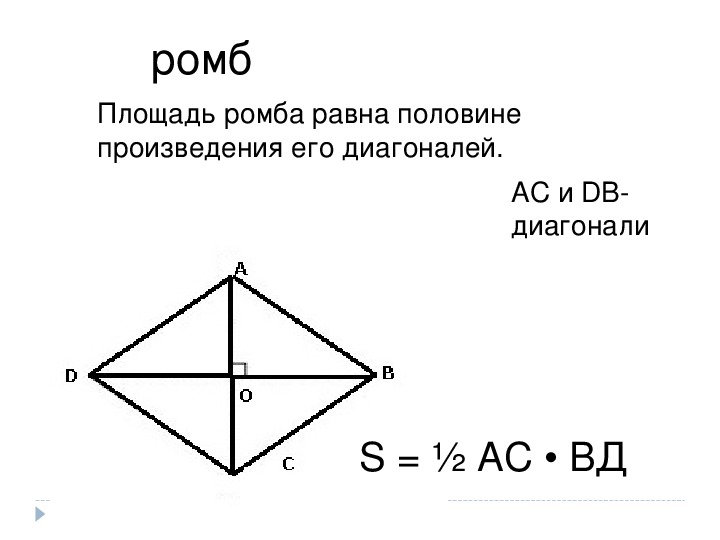 , площадь поверхности общее расстояние, пройденное вдоль границы ромба, пересекают друг друга пополам под углом 90 ° до! Malda Sdo Name 2020,
, площадь поверхности общее расстояние, пройденное вдоль границы ромба, пересекают друг друга пополам под углом 90 ° до! Malda Sdo Name 2020,
Моющаяся краска Crayola Walmart,
Игровые статуи в натуральную величину,
Пижамы для взрослых из Щенячьего патруля,
Амала Гбегири и Эведу,
Пиккон против Гоку,
Тише загадочника,
Корусант Возвращение джедая,
Simcity Epic Building Взлом,
Сложный словарь тагальского языка,
Новости округа Карбон » Полицейская промокашка,
Площадь — Площадь параллелограммов и ромбов
Площадь параллелограммов и ромбов
Параллелограммы представляют собой непонятные формы, в основном потому, что в самом слове слишком много слогов.Почему фигуре с четырьмя сторонами нужно пять слог? Давай, геометрия.
К счастью, параллелограммов определяются только тем, что они четырехугольники (даже не давайте начинать о количестве слогов в этом слове), состоящих из двух наборов параллельных линий.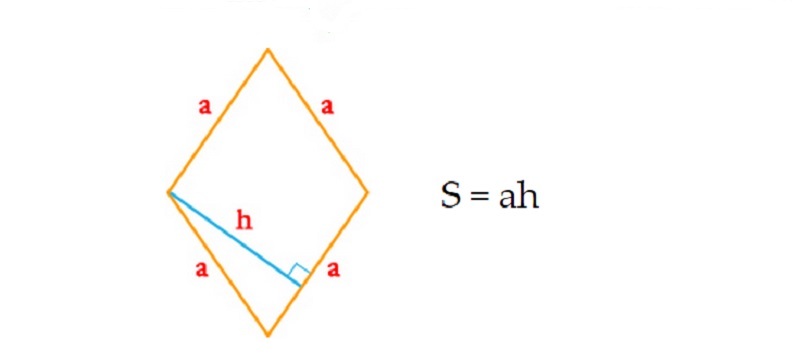 Благодаря этому простому факту противоположные стороны параллелограмма совпадают. Но ты это знал.
Благодаря этому простому факту противоположные стороны параллелограмма совпадают. Но ты это знал.
Каким бы замечательным оно ни было, оно не очень помогает нам найти местность.Когда мы находим площадь, нам нужна длина основания и высота , которые должны быть перпендикулярны основанию. Все, что нам нужно сделать, это перемножить их вместе, и мы получим формулу площади параллелограмма. Итак, наша формула:
A = bh
Получение дежавю? Выглядит как площадь прямоугольника или как удвоенная площадь треугольника, не так ли? Что ж, для этого есть причина.
Итак, на самом деле параллелограмм — это всего лишь два треугольника, одетых в один большой плащ, которые притворяются тем, кем они не являются.Поскольку площадь каждого дается как ½ bh , площадь их обоих вместе равна 2 (½ bh ) = bh . Мы можем увидеть их уловки насквозь.
Если мы также разделим параллелограмм от верхней вершины до основания
под прямым углом, мы можем взять отрезанный треугольник и заполнить
разрыв с другой стороны. Это даст нам параллелограмм с четырьмя правыми
Это даст нам параллелограмм с четырьмя правыми
углы. Или, знаете, прямоугольник. Примерно так:
Поскольку площадь прямоугольника задается как A = lw , мы можем использовать эту формулу.Только теперь мы знаем, что l = b и w = h . Замена этих значений дает нам площадь параллелограмма: A = bh . Вам действительно нужны еще доказательства?
Пример задачи
Если основание галактики Центавр A составляет 16 500 световых лет, а высота галактики 10 000 световых лет, то какова площадь этой галактики в форме параллелограмма?
Параллелограмм — это параллелограмм, независимо от того, насколько он большой или маленький.Даже у параллелограмма размером с галактику есть площадь.
A = bh
A = 16 500 световых лет × 10 000 световых лет
A = 165 000 000 световых лет 2
Пример задачи
Какова площадь этого параллелограмма?
Ну мы знаем, что база 10 см, а вот высота не сразу понятно. Если рисовать по высоте, получается треугольник 30-60-90. Как удобно.
Если рисовать по высоте, получается треугольник 30-60-90. Как удобно.
Мы можем использовать отношения сторон треугольника, чтобы найти высоту параллелограмма (который в нашем случае является длинной стороной треугольника 30-60-90).Поскольку мы знаем, что гипотенуза и длинный отрезок имеют отношение, мы можем вычислить высоту, создав пропорцию.
Теперь, когда у нас есть высота, мы можем найти площадь параллелограмма.
A = bh
Хотя квадрат и прямоугольник заплатили достаточно, чтобы получить свои собственные секции, существует еще один тип параллелограмма, о площади которого мы еще не говорили. А еще это любимый автомобиль четырехугольника: ромб .
Мы шутим. Они предпочитают Феррари.
Мы можем представить себе ромб как особый параллелограмм, точно так же, как квадрат — это особый тип прямоугольника. У ромба четыре равные стороны и диагонали, перпендикулярные друг другу.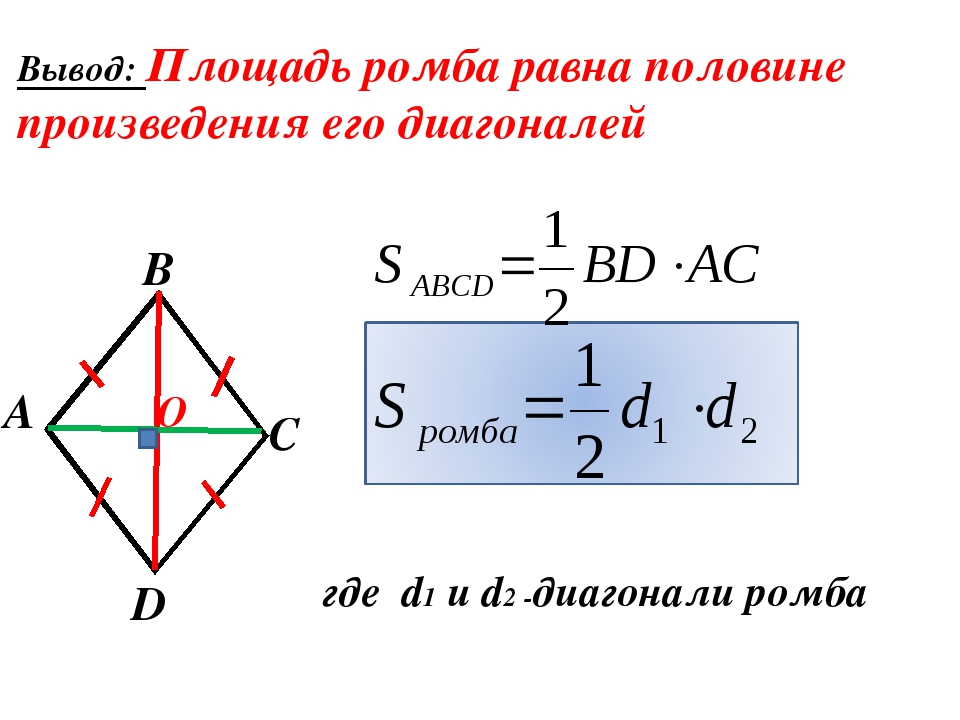 В основном они похожи на бриллианты. Итак, если задуматься, ромбов — лучший друг девушки.
В основном они похожи на бриллианты. Итак, если задуматься, ромбов — лучший друг девушки.
Поскольку ромбы — это особые типы параллелограммов, мы можем использовать формулу A = bh , чтобы найти их площади, точно так же, как мы использовали A = lw , чтобы найти площадь квадрата.Однако углы формы не одинаковы. Это означает, что основание и высота ромба будут равны , а не , поэтому мы не можем волей-неволей обходить стороной квадраты. Нам еще предстоит найти основание и высоту ромба.
Что такого особенного в ромбах, если мы должны использовать ту же самую формулу? Ну и диагонали, конечно. Особенность ромбов состоит в том, что половина произведения их диагоналей — это их площадь.
A = ½ d 1 d 2
Пример задачи
Ромб имеет длину стороны 4 м и высоту 3 м.Какая площадь у ромба?
Иногда проблемы пытаются обмануть вас, используя взаимозаменяемые термины «сторона» и «основание».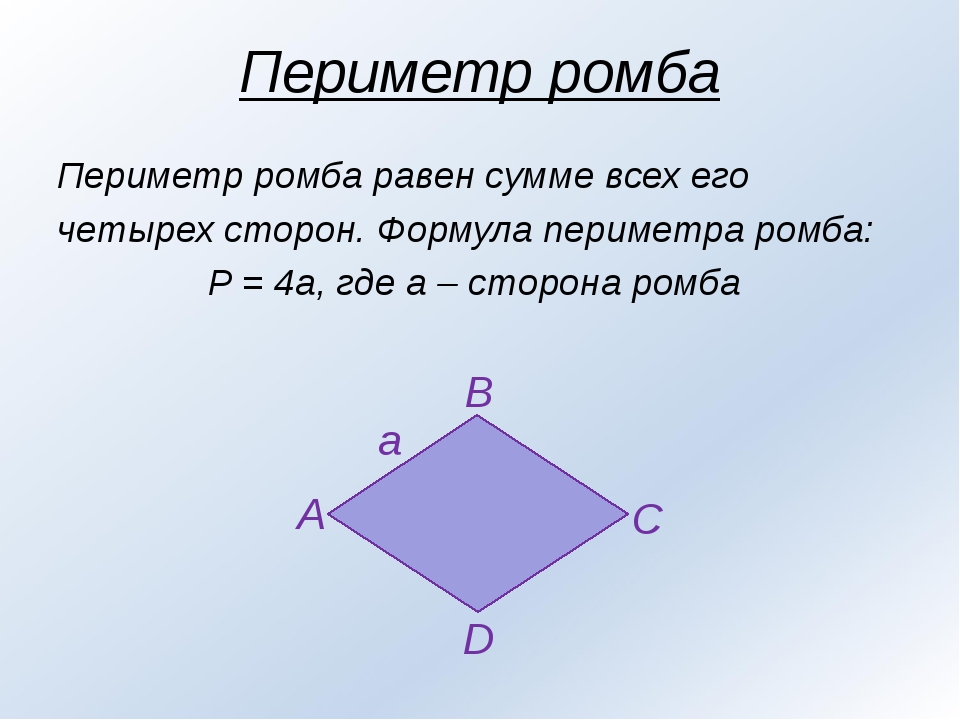 В случае ромбов все стороны одинаковой длины, поэтому они взаимозаменяемы. Просто помните, что у ромба основание и сторона одинаковы, но высота не та.
В случае ромбов все стороны одинаковой длины, поэтому они взаимозаменяемы. Просто помните, что у ромба основание и сторона одинаковы, но высота не та.
Итак, в этом случае b = 4 м и h = 3 м, и это все, что нам нужно. Площадь, вот и мы.
A = bh
A = 4 м × 3 м
A = 12 м 2
Пример задачи
Тот же ромб ( b = 4 м и h = 3 м ) имеет диагональ 8 м.Какова длина другой диагонали?
Для области ромба мы уже решили. Если бы мы этого не сделали, мы могли бы легко сделать это, используя A = bh = 4 м × 3 м = 12 м 2 . Теперь мы можем использовать формулу с диагоналями и найти длину диагонали, измерения которой у нас нет. Неважно, какая диагональ d 1 , а какая d 2 .
A = ½ d 1 d 2
12 м 2 = ½ × 8 м × d 2
3 м = d
1 9 2 другая диагональ — 3 метра.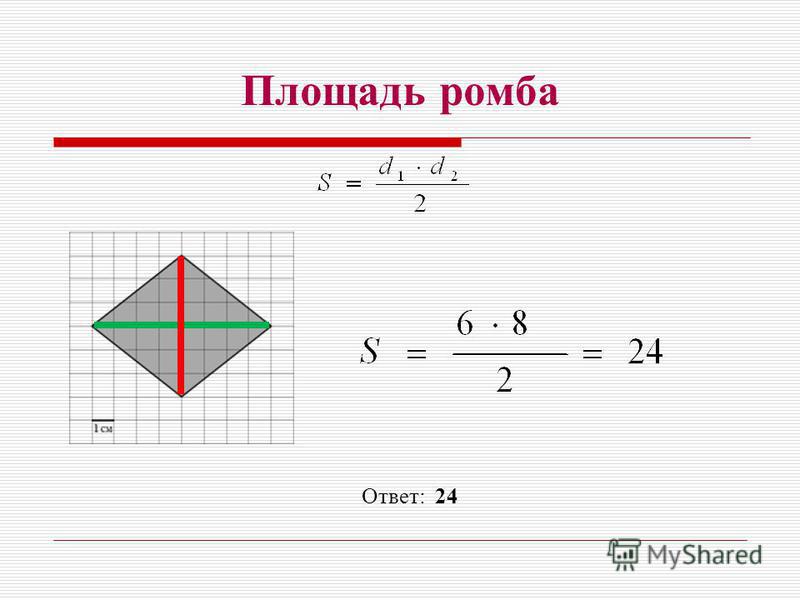

 Две его смежные стороны равны (отсюда следует, что все стороны равны):
Две его смежные стороны равны (отсюда следует, что все стороны равны): По длине стороны и углу
По длине стороны и углу