Содержание
Объёмные геометрические фигуры и их названия. Геометрические фигуры. Играем в геометрическое лото
Геометрические фигуры представляют собой комплекс точек, линий, тел или поверхностей. Эти элементы могут располагаться как на плоскости, так и в пространстве, формируя конечное количество прямых.
Термин «фигура» подразумевает под собой несколько множеств точек. Они должны располагаться на одной или нескольких плоскостях и одновременно ограничиваться конкретным числом оконченных линий.
Основными геометрическими фигурами считаются точка и прямая. Они располагаются на плоскости. Кроме них, среди простых фигур выделяют луч, ломаную линию и отрезок.
Точка
Это одна из главных фигур геометрии. Она очень маленькая, но ее всегда используют для построения различных форм на плоскости. Точка — это основная фигура для абсолютно всех построений, даже самой высокой сложности. В геометрии ее принято обозначать буквой латинской алфавита, к примеру, A, B, K, L.
С точки зрения математики точка — это абстрактный пространственный объект, не обладающий такими характеристиками, как площадь, объем, но при этом остающийся фундаментальным понятием в геометрии. Этот нульмерный объект просто не имеет определения.
Этот нульмерный объект просто не имеет определения.
Прямая
Это фигура полностью размещается в одной плоскости. У прямой нет конкретного математического определения, так как она состоит из огромного количества точек, располагающихся на одной бесконечной линии, у которой нет предела и границ.
Существует еще и отрезок. Это тоже прямая, но она начинается и заканчивается с точки, а значит, имеет геометрические ограничения.
Также линия может превратиться в направленный луч. Такое происходит, когда прямая начинается с точки, но четкого окончания не имеет. Если же поставить точку посредине линии, то она разобьется на два луча (дополнительных), причем противоположно направленных друг к другу.
Несколько отрезков, которые последовательно соединяются друг с другом концами в общей точке и располагаются не на одной прямой, принято называть ломаной линией.
Угол
Геометрические фигуры, названия которых мы рассмотрели выше, считают ключевыми элементами, использующимися при построении более сложных моделей.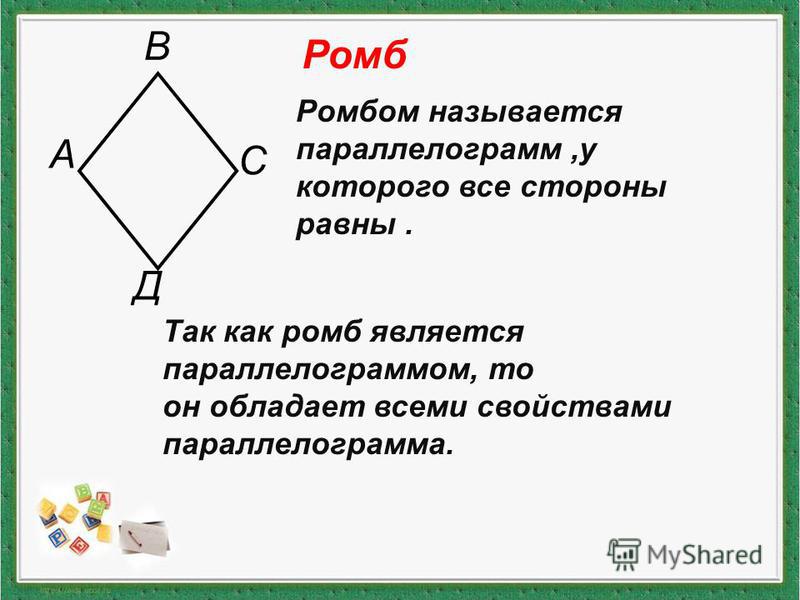
Угол — это конструкция, состоящая из вершины и двух лучей, которые выходят из нее. То есть стороны этой фигуры соединяются в одной точке.
Плоскость
Рассмотрим еще одно первичное понятие. Плоскость — это фигура, у которой нет ни конца, ни начала, равно как и прямой, и точки. Во время рассмотрения этого геометрического элемента во внимание берется лишь его часть, ограниченная контурами ломаной замкнутой линии.
Любую гладкую ограниченную поверхность можно считать плоскостью. Это может быть гладильная доска, лист бумаги или даже дверь.
Четырехугольники
Параллелограмм — это геометрическая фигура, противоположные стороны которой параллельны друг другу попарно. Среди частных видов этой конструкции выделяют ромб, прямоугольник и квадрат.
Прямоугольник — это параллелограмм, у которого все стороны соприкасаются под прямым углом.
Квадрат — это четырехугольник с равными сторонами и углами.
Ромб — это фигура, у которой все грани равны.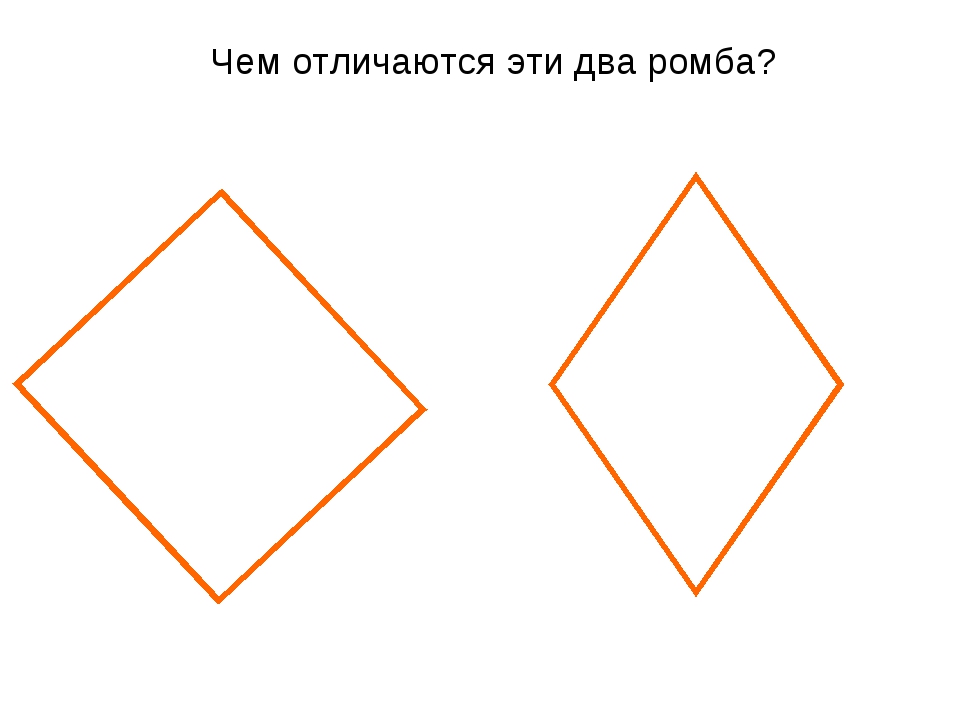 При этом углы могут быть совершенно разными, но попарно. Каждый квадрат считается ромбом. Но в противоположном направлении это правило действует не всегда. Далеко не каждый ромб является квадратом.
При этом углы могут быть совершенно разными, но попарно. Каждый квадрат считается ромбом. Но в противоположном направлении это правило действует не всегда. Далеко не каждый ромб является квадратом.
Трапеция
Геометрические фигуры бывают совершенно разными и причудливыми. Каждая из них имеет своеобразную форму и свойства.
Трапеция — это фигура, которая чем-то схожа с четырехугольником. Она имеет две параллельные противоположные стороны и при этом считается криволинейной.
Круг
Эта геометрическая фигура подразумевает расположение на одной плоскости точек, равноудаленных от ее центра. При этом заданный ненулевой отрезок принято называть радиусом.
Треугольник
Это простая геометрическая фигура, которая очень часто встречается и изучается.
Треугольник считается подвидом многоугольника, расположенным на одной плоскости и ограниченным тремя гранями и тремя точками соприкосновения. Эти элементы попарно соединены между собой.
Многоугольник
Вершинами многоугольников называют точки, соединяющие отрезки. А последние, в свою очередь, принято считать сторонами.
А последние, в свою очередь, принято считать сторонами.
Объемные геометрические фигуры
- призма;
- сфера;
- конус;
- цилиндр;
- пирамида;
Эти тела имеют нечто общее. Все они ограничиваются замкнутой поверхностью, внутри которой находится множество точек.
Объемные тела изучают не только в геометрии, но и в кристаллографии.
Любопытные факты
Наверняка вам будет интересно ознакомиться с информацией, предоставленной ниже.
- Геометрия сформировалась как наука еще в давние века. Это явление принято связывать с развитием искусства и разнообразных ремесел. А названия геометрических фигур свидетельствуют об использовании принципов определения подобия и схожести.
- В переводе с древнегреческого термин «трапеция» обозначает столик для трапезы.
- Если вы возьмете различные фигуры, периметр которых будет одинаковым, то наибольшая площадь гарантированно будет у круга.
- В переводе с греческого языка термин «конус» обозначает сосновую шишку.

- Существует известная картина Каземира Малевича, которая начиная с прошлого века притягивает к себе взгляды многих живописцев. Работа «Черный квадрат» всегда была мистической и загадочной. Геометрическая фигура на белом полотне восхищает и поражает одновременно.
Существует большое количество геометрических фигур. Все они отличаются параметрами, а порой даже удивляют формами.
Чукур Людмила Васильевна
Геометрические фигуры. Особенности восприятия детьми формы предметов и геометрических фигур
«ГЕОМЕТРИЧЕСКАЯ ФИГУРА
.
ОСОБЕННОСТИ ВОСПРИЯТИЯ ДЕТЬМИ
Подготовила
: ст. воспитатель Чукур Л
. В.
1. Понятие «геометрическая фигура
»
. Особенности развития представлений о форме предметов
у детей дошкольного возраста
Одним из свойств окружающих предметов является их форма
. Форма предметов
получила обобщенное отражение в геометрических фигурах
.
Фигура — латинское слово
, означает «образ»
, «вид»
, «начертание»
; это часть плоскости, ограниченная замкнутой линией, или часть пространства, ограниченная замкнутой поверхностью. Этот термин вошел в общее употребление в XII в. До этого чаще употреблялось другое латинское слово — «форма
Этот термин вошел в общее употребление в XII в. До этого чаще употреблялось другое латинское слово — «форма
»
, также означающее «наружный вид»
, «внешнее очертание предмета
»
.
Наблюдая за предметами окружающего мира
, люди заметили, что есть некоторое общее свойство, позволяющее объединить предметы в одну группу
. Это свойство было названо геометрической фигурой
. Геометрическая фигура – это эталон для определения формы предмета
, всякое непустое множество точек; обобщенное абстрактное понятие.
Само определение понятия геометрической фигуры дали древние греки
. Они определили
, что геометрической фигурой
является внутренняя область, ограниченная замкнутой линией на плоскости. Активно это понятие применял в своей работе Евклид. Древние греки классифицировали все геометрические фигуры и дали им названия
.
Упоминание о первых геометрических фигурах
встречается и у древних египтян и древних шумеров. Учеными-археологами был найден папирусный свиток с геометрическими задачами
Учеными-археологами был найден папирусный свиток с геометрическими задачами
, в которых упоминались геометрические фигуры
. И каждая из них называлась каким-то определенным словом
.
Таким образом, представление о геометрии
и изучаемых этой наукой фигурах
имели люди с давних времен, но название, «геометрическая фигура
»
и названия всем геометрическим фигурам
дали древнегреческие ученые.
В наше время знакомство с геометрическими фигурами
начинается с раннего детства и продолжается на всём пути обучения. Дошкольники, познавая окружающий мир, сталкиваются с разнообразием форм предметов
, учатся называть и различать их, а затем знакомятся и со свойствами геометрических фигур
.
Форма
– это внешнее очертание предмета
. Множество форм бесконечно
.
Представления о форме предметов
возникают у детей достаточно рано. В исследованиях Л. А. Венгера выясняется, возможно ли различение формы предметов детьми
, у которых еще не сформировался акт хватания
. В качестве индикатора он использовал ориентировочную реакцию ребенка в возрасте 3-4 месяцев.
В качестве индикатора он использовал ориентировочную реакцию ребенка в возрасте 3-4 месяцев.
Детям предъявлялись
два объемных тела одинакового стального цвета и размера (призма и шар, одно из них подвешивалась над манежем, чтобы угасить ориентировочную реакцию; затем снова подвешивалась пара фигур
. На одну из них (призма)
реакция угашена, другая (шар)
— новая. Малыши обращали взор на новую фигуру
и фиксировали ее взглядом в течение более длительного времени, чем старую.
Л. А. Венгер заметил также, что что на геометрической фигуре
с изменением пространственной ориентации возникает такое же зрительное сосредоточение, как и на новой геометрической фигуре
.
Исследования М. Денисовой и Н. Фигурина показали
, что грудной ребенок по форме на ощупь определяет бутылочку
, соску, материнскую грудь. Зрительно дети начинают различать форму предметов с 5 месяцев
. При этом индикатором различения являются движения рук, корпуса по направлению к экспериментальному объекту и схватывание его (при пищевом подкреплении)
.
В других исследованиях выявлено, что, если предметы отличаются цветом
, то ребенок 3-х лет выделяет их форму только в том случае
, если предмет
знаком ребенку из практического опыта (опыт манипуляций, действий)
.
Это доказывает и тот факт, что ребенок одинаково узнает прямые и перевернутые изображения (может рассматривать и понимать знакомые картинки, держа книжку «вверх ногами»
, предметы
, окрашенные в несвойственные цвета (черное яблоко, но квадрат, повернутый на угол, т. е. в виде ромба, не узнает, так как исчезает непосредственное сходство формы предмета
, которого нет в опыте.
2. Особенности восприятия детьми
дошкольного возраста формы предметов и геометрических фигур
Одним из ведущих познавательных процессов детей дошкольного возраста является восприятие
. Восприятие
помогает отличить один предмет от другого
, выделить какие-то предметы
или явления из других похожих на него.
Первичное овладение формой предмета
Форма предмета
, как таковая, не предмета
предшествовать
практическим действиям. Действия детей с предметами
на разных этапах различны.
Исследования психолога С. Н. Шабалина показывают, что геометрическая фигура воспринимается
дошкольниками своеобразно. Если взрослый воспринимает
ведро или стакан как предметы
, имеющие цилиндрическую форму
, то в его восприятие включается знание геометрических форм
. У дошкольника происходит обратное явление.
В 3-4 года дети опредмечивают геометрические фигуры
, так как они в их опыте представлена нераздельно с предметами
, не абстрагированы. Геометрическая фигура воспринимается детьми как картинка
, как некоторый предмет
: квадрат — это платочек, кармашек; треугольник — крыша, круг — колесо, мячик, два круга рядом — очки, несколько кругов рядом — бусы и т. п.
В 4 года опредмечивание геометрической фигуры
возникает только при столкновении ребенка с незнакомой фигурой
: цилиндр — это ведро, стаканчик.
В 4-5 лет ребенок начинает сравнивать геометрическую фигуру с предметом
: про квадрат говорит «это как платочек»
.
В результате организованного обучения дети начинают выделять в окружающих предметах знакомую геометрическую фигуру
, сравнивать предмет с фигурой
(стаканчик как цилиндр, крыша как треугольник, учится давать правильное название геометрической фигуры и формы предмета
, в их речи появляются слова «квадрат»
, «круг»
, «квадратный»
, «круглый»
и т. п.
Проблему знакомства детей с геометрическими фигурами
и их свойствами следует рассматривать в двух аспектах
:
В плане сенсорного восприятия форм геометрических фигур
и использования их как эталонов в познании форм окружающих предметов
;
В смысле познания особенностей их структуры
, свойств, основных свя-зей и закономерностей в их построении, т. е. собственно геометри-ческого материала
.
Контур предмета это общее начало
, которое является исходным как для зрительного, так и для осязательного восприятия
. Однако вопрос о роли контура в восприятии формы и формировании
Однако вопрос о роли контура в восприятии формы и формировании
целостного образа требует еще дальнейшей разработки.
Первичное овладение формой предмета
осуществляется в действиях с ним. Форма предмета
, как таковая, не воспринимается отдельно от предмета
, она является его неотъемлемым признаком. Специфические зрительные реакции прослеживания контура предмета
появляются в конце второго года жизни и начинают предшествовать
практическим действиям.
Действия детей с предметами
на разных этапах различны. Малыши стремятся, прежде всего, захватить предмет
руками и начать манипулировать им. Дети 2,5 лет, прежде чем действовать, довольно подробно зрительно и осязательно — двигательно знакомятся с предметами
. Значение практических действий остается главным. Отсюда следует вывод о необходимости руководить развитием перцептивных действий двухлетних детей. В зависимости от педагогического руководства характер перцептивных действий детей постепенно достигает познавательного уровня. Ребенка начинают интересовать различные признаки предмета
Ребенка начинают интересовать различные признаки предмета
, в том числе и форма
. Однако он еще долго не может выделить и обобщить тот или иной признак, в том числе и форму разных предметов
.
Сенсорное восприятие формы предмета
должно быть направлено не только на то, чтобы видеть
, узнавать формы
, наряду с другими его признаками, но уметь, абстрагируя форму от вещи
, видеть ее и в других вещах
. Такому восприятию формы предметов и ее обобщению и способствует знание детьми эталонов — геометрических фигур
. Поэтому задачей сенсорного развития является формирование
у ребенка умений узнавать в соответствии с эталоном (той или иной геометрической фигурой
)
форму разных предметов
.
Экспериментальные данные Л. А. Венгера показали, что возможностью различать геометрические фигуры
обладают дети 3-4 месяцев. Сосредоточение взгляда на новой фигуре
— свидетельство этому.
Уже на втором году жизни дети свободно выбирают фигуру
по образцу из таких пар
: квадрат и полукруг, прямоугольник и треугольник. Но различать прямоугольник и квадрат, квадрат и треугольник дети могут лишь после 2,5 лет. Отбор же по образцу фигур более сложной формы
Но различать прямоугольник и квадрат, квадрат и треугольник дети могут лишь после 2,5 лет. Отбор же по образцу фигур более сложной формы
доступен примерно на рубеже 4-5 лет, а воспроизведение сложной фигуры
осуществляют дети пятого и шестого года жизни.
Под обучающим воздействием взрослых восприятие геометрических фигур
постепенно перестраивается. Геометрические фигуры начинают восприниматься детьми как эталоны
, с помощью которых познание структуры предмета
, его формы
и размера осуществляется не только в процессе восприятия той или иной формы зрением
, но и путем активного осязания, ощупывания ее под контролем зрения и обозначения словом.
Совместная работа всех анализаторов способствует более точному восприятию формы предметов
. Чтобы лучше познать предмет
, дети стремятся коснуться его рукой, взять в руки, повернуть; причем рассматривание и ощупывание различны в зависимости от формы
и конструкции познаваемого объекта.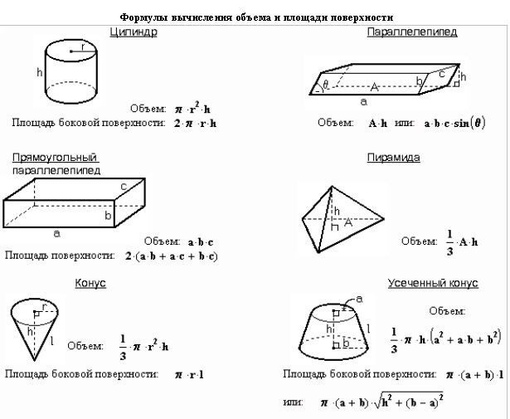 Поэтому основную роль в восприятии предмета и определении его формы имеет обследование
Поэтому основную роль в восприятии предмета и определении его формы имеет обследование
, осуществляемое одновременно зрительным и двигательно-осязательным анализаторами с последующим обозначением словом. Однако у дошкольников наблюдается весьма низкий уровень обследования формы предметов
; чаще всего они ограничиваются беглым зрительным восприятием
и поэтому не различают близкие по сходству фигуры
(овал и круг, прямоугольник и квадрат, разные треугольники)
.
В перцептивной деятельности детей осязательно-двигательные и зрительные приемы постепенно становятся основным способом рас-познавания формы
. Обследование фигур
не только обеспечивает целостное их восприятие
, но и позволяет ощутить их особенности
(характер, направления линий и их сочетания, образующиеся углы и вершины, ребенок учится чувственно выделять в любой фигуре
образ в целом и его части. Это дает возможность в дальнейшем сосредоточить внимание ребенка на осмысленном анализе фигуры
, сознательно выделяя в ней структурные элементы (стороны, углы, вершины)
. Дети уже осознанно начинают понимать и такие свойства, как устойчивость, неустойчивость и др., понимать, как образуются вершины, углы и т. д. Сопоставляя объемные и плоские фигуры
Дети уже осознанно начинают понимать и такие свойства, как устойчивость, неустойчивость и др., понимать, как образуются вершины, углы и т. д. Сопоставляя объемные и плоские фигуры
, дети находят уже общность между ними («У куба есть квадраты»
, «У бруса — прямоугольники, у цилиндра — круги»
и т. д.).
Сравнение фигуры с формой того или иного предмета
помогает детям понять, что с геометрическими фигурами
можно сравнивать разные предметы или их части
. Так, постепенно геометрическая фигура
становится эталоном определения формы предметов
.
3. Особенности
обследования и этапы обучения обследованию детьми
дошкольного возраста формы предметов и геометрических фигур
Известно, что в основе познания всегда лежит сенсорное обследование, опосредованное мышлением и речью. В исследованиях Л. Венгера с детьми
2-3 лет индикатором зрительного различения формы предметов служили предметные действия ребенка
.
По исследованиям С. Якобсон, В. Зинченко, А. Рузской дети 2-4 лет лучше узнавали предметы по форме
, когда предлагалось сначала ощупать предмет
, а потом найти такой же. Более низкие результаты наблюдались тогда, когда предмет воспринимался зрительно
.
Исследования Т. Гиневской раскрывают особенности
движений рук при обследовании предметов по форме
. Детям завязывали глаза и предлагали ознакомиться с предметом путем осязания
.
В 3-4 года – движения исполнительные (катают, стучат, возят)
. Движения немногочисленны, внутри фигуры
, иногда (однократно)
по осевой линии, много ошибочных ответов, смешение разных фигур
. В 4-5 лет – движения установочные (зажимают в руке)
. Количество движений увеличивается в два раза; судя по траектории, ориентированы на размер и площадь; крупные, размашистые, обнаруживаются группы близко расположенных фиксаций, относящихся к наиболее характерным признакам фигуры
; дают более высокие результаты. В 5-6лет – движения обследовательские (прослеживание контура, проверка на упругость)
В 5-6лет – движения обследовательские (прослеживание контура, проверка на упругость)
. Появляются движения, прослеживающие контур, однако они охватывают наиболее характерную часть контура, другие части оказываются необследованными; движения внутри контура, количество то же, высокие результаты; как и в предыдущий период
, наблюдается смешение близких фигур
. В 6-7 лет – движения по контуру, пересечение поля фигуры
, причем движения сосредотачиваются на наиболее информативных признаках
, наблюдаются отличные результаты не только при узнавании, но и при воспроизведении
.
Таким образом, для того, чтобы ребенок выделил существенные признаки геометрических фигур
, необходимо их зрительное и двигательное обследование. Движения рук организовывают движения глаз и этому детей необходимо научить.
Этапы обучения обследованию
Задача первого этапа обучения детей 3-4 лет — это сенсорное восприятие формы предметов и геометрических фигур
.
Второй этап обучения детей 5-6 лет должен быть посвящен формированию системных знаний о геометрических фигурах
и развитию у них начальных приемов и способов
«геометрического мышления
»
.
«Геометрическое мышление
»
вполне возможно развить еще в дошкольном возрасте. В развитии «геометрических знаний
»
у детей прослеживается несколько различных уровней.
Первый уровень характеризуется тем, что фигура воспринимается детьми как целое
, ребенок еще не умеет выделять в ней отдельные элементы, не замечает сходства и различия между фигурами
, каждую из них воспринимает обособленно
.
На втором уровне ребенок уже выделяет элементы в фигуре
и устанавливает отношения как между ними, так и между отдельными фигурами
, однако еще не осознает общности между фигурами
.
На третьем уровне ребенок в состоянии устанавливать связи между свойствами и структурой фигур
, связи между самими свойствами. Переход от одного уровня к другому не является самопроизвольным, идущим параллельно биологическому развитию человека и зависящим от возраста. Он протекает под влиянием целенаправленного обучения, которое содействует ускорению перехода к более высокому уровню. Отсутствие же обучения тормозит развитие. Обучение поэтому следует организовывать так, чтобы в связи с усвоением знаний о геометрических фигурах
Переход от одного уровня к другому не является самопроизвольным, идущим параллельно биологическому развитию человека и зависящим от возраста. Он протекает под влиянием целенаправленного обучения, которое содействует ускорению перехода к более высокому уровню. Отсутствие же обучения тормозит развитие. Обучение поэтому следует организовывать так, чтобы в связи с усвоением знаний о геометрических фигурах
у детей развивалось и элементарное геометрическое мышление
.
Познание геометрических фигур
, их свойств и отношений расширяет кругозор детей, позволяет им более точно и разносторонне воспринимать форму окружающих предметов
, что положительно отражается на их продуктивной деятельности (например, рисовании, лепке)
.
Большое значение в развитии геометрического
мышления и про-странственных представлений
имеют действия по преобразованию фигур
(из двух треугольников составить квадрат или из пяти палочек сложить два треугольника).
Все эти разновидности упражнений развивают пространственные представления и начала геометрического мышления детей
, формируют
у них умения наблюдать, анализировать, обобщать, выделять главное, существенное и одновременно с этим воспитывают
такие качества личности, как целенаправленность, настойчивость.
Итак, в дошкольном возрасте происходит овладение перцептивной и интеллектуальной систематизацией форм геометрических фигур
. Перцептивная деятельность в познании фигур
опережает развитие интеллектуальной систематизации.
Библиографический список
1. Белошистая А. В. Знакомство с геометрическими понятиями / А
. Белошистая // Дошкольное воспитание
. — 2008. — № 9. — с. 41- 51
2. Венгер Л. А. Воспитание
сенсорной культуры ребенка / Л. А. Венгер Э. Г. Пилюгина, Н. Б. Венгер. — М.
: Просвещение, 1988.- 144с.
3. Воспитание
и обучение детей пятого года жизни
: книга для воспитателя детского сада /
(А. Н. Давидчук, Т. И. Осокина, Л. А. Парамонова и др.)
Н. Давидчук, Т. И. Осокина, Л. А. Парамонова и др.)
; под ред. В. В. Холмовской. — М.
: Просвещение, 1986. — 144 с.
4. Габова М. А. Знакомство детей с геометрическими фигурами / М
. А. Габова // Дошкольное воспитание
. — 2002. — № 9. — с. 2- 17.
5. Дидактические игры и упражнения по сенсорному воспитанию дошкольников
: (пособие для воспитателя
детского сада / под ред. Л. А. Венгера). — М.
: Просвещение, 1978. — 203 с.
6. Кербс Е. В. Математические досуги / Е. В. Кербс // Ребёнок в детском саду. — 2008. — № 3. — с. 21- 23.
7.Математика в детском саду
: (пособие для воспитателя дет
. сада / составитель Г. М. Лямина). — М.
: Просвещение, 1977. — С. 224 — 228.
8. Метлина Л. С.Математика в детском саду
: (пособие для воспитателя дет
. сада)
/ Л. С. Метлина. — М.
: Просвещение, 1994. — 256 с.
Геометрические фигуры представляют собой комплекс точек, линий, тел или поверхностей.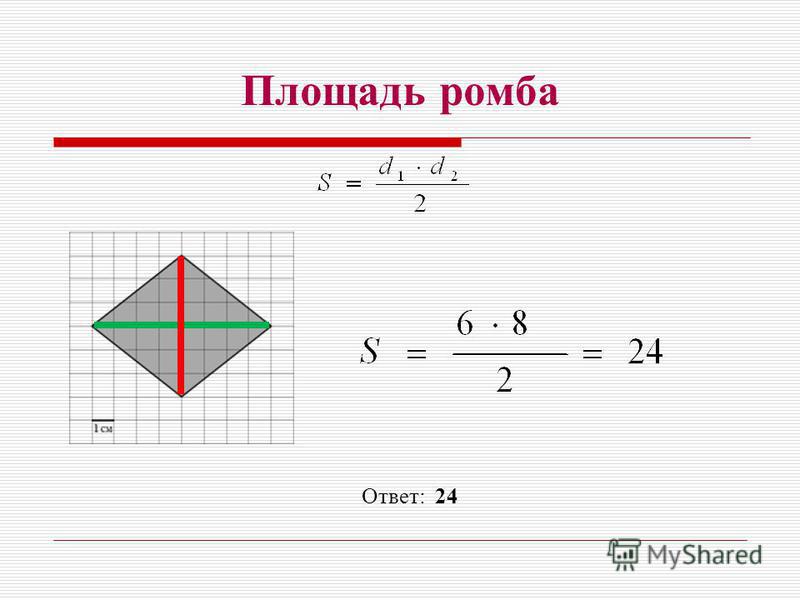 Эти элементы могут располагаться как на плоскости, так и в пространстве, формируя конечное количество прямых.
Эти элементы могут располагаться как на плоскости, так и в пространстве, формируя конечное количество прямых.
Термин «фигура» подразумевает под собой несколько множеств точек. Они должны располагаться на одной или нескольких плоскостях и одновременно ограничиваться конкретным числом оконченных линий.
Основными геометрическими фигурами считаются точка и прямая. Они располагаются на плоскости. Кроме них, среди простых фигур выделяют луч, ломаную линию и отрезок.
Точка
Это одна из главных фигур геометрии. Она очень маленькая, но ее всегда используют для построения различных форм на плоскости. Точка — это основная фигура для абсолютно всех построений, даже самой высокой сложности. В геометрии ее принято обозначать буквой латинской алфавита, к примеру, A, B, K, L.
С точки зрения математики точка — это абстрактный пространственный объект, не обладающий такими характеристиками, как площадь, объем, но при этом остающийся фундаментальным понятием в геометрии. Этот нульмерный объект просто не имеет определения.
Прямая
Это фигура полностью размещается в одной плоскости. У прямой нет конкретного математического определения, так как она состоит из огромного количества точек, располагающихся на одной бесконечной линии, у которой нет предела и границ.
Существует еще и отрезок. Это тоже прямая, но она начинается и заканчивается с точки, а значит, имеет геометрические ограничения.
Также линия может превратиться в направленный луч. Такое происходит, когда прямая начинается с точки, но четкого окончания не имеет. Если же поставить точку посредине линии, то она разобьется на два луча (дополнительных), причем противоположно направленных друг к другу.
Несколько отрезков, которые последовательно соединяются друг с другом концами в общей точке и располагаются не на одной прямой, принято называть ломаной линией.
Угол
Геометрические фигуры, названия которых мы рассмотрели выше, считают ключевыми элементами, использующимися при построении более сложных моделей.
Угол — это конструкция, состоящая из вершины и двух лучей, которые выходят из нее. То есть стороны этой фигуры соединяются в одной точке.
Плоскость
Рассмотрим еще одно первичное понятие. Плоскость — это фигура, у которой нет ни конца, ни начала, равно как и прямой, и точки. Во время рассмотрения этого геометрического элемента во внимание берется лишь его часть, ограниченная контурами ломаной замкнутой линии.
Любую гладкую ограниченную поверхность можно считать плоскостью. Это может быть гладильная доска, лист бумаги или даже дверь.
Четырехугольники
Параллелограмм — это геометрическая фигура, противоположные стороны которой параллельны друг другу попарно. Среди частных видов этой конструкции выделяют ромб, прямоугольник и квадрат.
Прямоугольник — это параллелограмм, у которого все стороны соприкасаются под прямым углом.
Квадрат — это четырехугольник с равными сторонами и углами.
Ромб — это фигура, у которой все грани равны. При этом углы могут быть совершенно разными, но попарно. Каждый квадрат считается ромбом. Но в противоположном направлении это правило действует не всегда. Далеко не каждый ромб является квадратом.
Трапеция
Геометрические фигуры бывают совершенно разными и причудливыми. Каждая из них имеет своеобразную форму и свойства.
Трапеция — это фигура, которая чем-то схожа с четырехугольником. Она имеет две параллельные противоположные стороны и при этом считается криволинейной.
Круг
Эта геометрическая фигура подразумевает расположение на одной плоскости точек, равноудаленных от ее центра. При этом заданный ненулевой отрезок принято называть радиусом.
Треугольник
Это простая геометрическая фигура, которая очень часто встречается и изучается.
Треугольник считается подвидом многоугольника, расположенным на одной плоскости и ограниченным тремя гранями и тремя точками соприкосновения. Эти элементы попарно соединены между собой.
Многоугольник
Вершинами многоугольников называют точки, соединяющие отрезки. А последние, в свою очередь, принято считать сторонами.
Объемные геометрические фигуры
- призма;
- сфера;
- конус;
- цилиндр;
- пирамида;
Эти тела имеют нечто общее. Все они ограничиваются замкнутой поверхностью, внутри которой находится множество точек.
Объемные тела изучают не только в геометрии, но и в кристаллографии.
Любопытные факты
Наверняка вам будет интересно ознакомиться с информацией, предоставленной ниже.
- Геометрия сформировалась как наука еще в давние века. Это явление принято связывать с развитием искусства и разнообразных ремесел. А названия геометрических фигур свидетельствуют об использовании принципов определения подобия и схожести.
- В переводе с древнегреческого термин «трапеция» обозначает столик для трапезы.
- Если вы возьмете различные фигуры, периметр которых будет одинаковым, то наибольшая площадь гарантированно будет у круга.
- В переводе с греческого языка термин «конус» обозначает сосновую шишку.
- Существует известная картина Каземира Малевича, которая начиная с прошлого века притягивает к себе взгляды многих живописцев. Работа «Черный квадрат» всегда была мистической и загадочной. Геометрическая фигура на белом полотне восхищает и поражает одновременно.
Существует большое количество геометрических фигур. Все они отличаются параметрами, а порой даже удивляют формами.
Маленькие детки готовы учиться везде и всегда. Их юный мозг способен улавливать, анализировать и запоминать столько информации, сколько трудно даже взрослому человеку. То, чему родители должны научить малышей, имеет общепринятые возрастные рамки.
Основные геометрические фигуры и их названия дети должны узнать в возрасте от 3 до 5 лет.
Поскольку все дети разнообучаемы, то эти границы лишь условно приняты в нашей стране.
Геометрия – это наука о формах, размерах и расположении фигур в пространстве. Может создаться впечатление, что это сложно для малышей. Однако предметы изучения этой науки находятся повсюду вокруг нас. Вот почему иметь основные познания в этой области важно и для детей, и для старших.
Чтобы увлечь детей изучением геометрии, можно прибегнуть к веселым картинкам. Дополнительно хорошо бы иметь пособия, которые ребенок сможет потрогать, ощупать, обвести, раскрасить, узнать с закрытыми глазами. Основной принцип любых занятий с детьми – удержание их внимание и развития тяги к предмету с использованием игровых приемов и непринужденной веселой обстановки.
Сочетание нескольких средств восприятия сделает свое дело очень быстро. Воспользуйтесь нашей мини-методичкой, чтобы научить ребенка отличать геометрические фигуры, знать их названия.
Круг – самая первая из всех фигур. В природе вокруг нас многое имеет круглую форму: наша планета, солнце, луна, сердцевина цветка, многие фрукты и овощи, зрачки глаз. Объемный круг – это шар (мячик, клубок)
Начать изучение формы круга с ребенком лучше, рассматривая рисунки, а потом уже подкрепить теорию практикой, дав ребенку подержать что-нибудь круглое в руках.
Квадрат – это фигура, у которой все стороны имеют одинаковую высоту и ширину. Квадратные предметы – кубики, коробки, дом, окно, подушка, табурет и т. п.
Строить из квадратных кубиков всякие домики очень просто. Рисунок квадрата проще сделать на листочке в клетку.
Прямоугольник – родственник квадрата, который отличается тем, что имеет одинаковые противоположные стороны. Так же, как и у квадрата, у прямоугольника все равны 90 градусам.
Можно найти множество предметов, имеющих форму прямоугольника: шкафы, бытовая техника, двери, мебель.
В природе форму треугольника имеют горы и некоторые деревья. Из ближайшего окружения малышей можно привести в пример треугольную крышу дома, различные дорожные знаки.
В форме треугольника были построены некоторые древние сооружения, например храмы и пирамиды.
Овал – это круг, вытянутый с двух сторон. Формой овала обладают, например: яйцо, орехи, многие овощи и фрукты, человеческое лицо, галактики т. д.
Овал в объеме называется эллипсом. Даже Земля сплюснута с полюсов – эллипсовидная.
Ромб
Ромб – тот же квадрат, только вытянутый, т. е. имеет два тупых угла и пару острых.
Изучать ромб можно с помощью наглядных пособий – нарисованной картинки или объемного предмета.
Приемы запоминания
Геометрические фигуры по названиям запомнить несложно. В игру их изучение для детей можно превратить, применив следующие идеи:
- Купите детскую книжку с картинками, в которой будут веселые и красочные рисунки фигур и их аналогии из окружающего мира.
- Нарежьте из разноцветного картона побольше всяких фигурок, заламинируйте их скотчем и используйте как конструктор – очень много интересных сочетаний можно выложить, комбинируя разные фигурки.
- Купите линейку с отверстиями в форме круга, квадрата, треугольника и других – для детей, которые уже дружат с карандашами, рисунки с помощью такой линейки – интереснейшее занятие.
Можно придумать много возможностей научить малышей знать названия геометрических фигур. Все способы хороши: рисунки, игрушки, наблюдения за окружающими предметами. Начните с малого, постепенно усложняя информацию и задания. Вы не ощутите, как пролетит время, а малыш обязательно порадует вас успехами в скором.
Геометрические объемные фигуры — это твердые тела, которые занимают ненулевой объем в евклидовом (трехмерном) пространстве. Эти фигуры изучает раздел математики, который носит название «пространственная геометрия». Знания о свойствах объемных фигур применяются в инженерии и в науках о природе. Рассмотрим в статье вопрос, геометрические объемные фигуры и их названия.
Геометрические объемные тела
Поскольку эти тела имеют конечную размерность в трех пространственных направлениях, то для их описания в геометрии используют систему из трех координатных осей. Эти оси обладают следующими свойствами:
- Они ортогональны друг другу, то есть перпендикулярны.
- Эти оси нормализированы, то есть базисные вектора каждой оси имеют одинаковую длину.
- Любая из осей координат — это результат векторного произведения двух других.
Говоря о геометрических объемных фигурах и их названиях, следует отметить, что все они принадлежат к одному из 2-х больших классов:
- Класс полиэдров. Эти фигуры, исходя из названия класса, имеют прямые ребра и плоские грани. Грань — это плоскость, которая ограничивает фигуру. Место соединения двух граней называется ребром, а точка соединения трех граней — это вершина. К полиэдрам относятся геометрическая фигура куб, тетраэдры, призмы, пирамиды. Для этих фигур справедлива теорема Эйлера, которая устанавливает связь между числом сторон (С), ребер (Р) и вершин (В) для каждого полиэдра. Математически эта теорема записывается так: С + В = Р + 2.
- Класс круглых тел или тел вращения. Эти фигуры имеют хотя бы одну поверхность, образующую их, изогнутой формы. Например, шар, конус, цилиндр, тор.
Что касается свойств объемных фигур, то следует выделить два самых важных из них:
- Наличие определенного объема, который фигура занимает в пространстве.
- Наличие у каждой объемной фигуры площади поверхности.
Оба свойства для каждой фигуры описываются конкретными математическими формулами.
Рассмотрим ниже самые простые геометрические объемные фигуры и их названия: куб, пирамиду, призму, тетраэдр и шар.
Фигура куб: описание
Под геометрической фигурой куб понимают объемное тело, которое образовано 6-тью квадратными плоскостями или поверхностями. Также эту фигуру называют правильный гексаэдр, поскольку она имеет 6 сторон, или прямоугольный параллелепипед, так как он состоит из 3-х пар параллельных сторон, которые взаимно перпендикулярны друг другу. Называют куб и у которой основание является квадратом, а высота равна стороне основания.
Поскольку куб является многогранником или полиэдром, то для него можно применить теорему Эйлера, чтобы определить число его ребер. Зная, что число сторон равно 6, а вершин у куба 8, число ребер равно: Р = С + В — 2 = 6 + 8 — 2 = 12.
Если обозначить буквой «a» длину стороны куба, тогда формулы для его объема и площади поверхности будут иметь вид: V = a 3 и S = 6*a 2 , соответственно.
Фигура пирамида
Пирамида — это полиэдр, который состоит из простого многогранника (основание пирамиды) и треугольников, которые соединяются с основанием и имеют одну общую вершину (вершина пирамиды). Треугольники называются боковыми гранями пирамиды.
Геометрические характеристики пирамиды зависят от того, какой многоугольник лежит в ее основании, а также от того, является ли пирамида прямой или косой. Под прямой пирамидой понимают такую пирамиду, для которой перпендикулярная основанию прямая, проведенная через вершину пирамиды, пересекает основание в ее геометрическом центре.
Одной из простых пирамид является четырехугольная прямая пирамида, в основании которой лежит квадрат со стороной «a», высота этой пирамиды «h». Для этой фигуры пирамиды объем и площадь поверхности будут равны: V = a 2 *h/3 и S = 2*a*√(h 2 +a 2 /4) + a 2 , соответственно. Применяя теорему Эйлера для нее, с учетом того, что число граней равно 5, и число вершин равно 5, получаем количество ребер: Р = 5 + 5 — 2 = 8.
Фигура тетраэдр: описание
Под геометрической фигурой тетраэдр понимают объемное тело, образованное 4-мя гранями. Исходя из свойств пространства, такие грани могут представлять только треугольники. Таким образом, тетраэдр является частным случаем пирамиды, у которой в основании лежит треугольник.
Если все 4-ре треугольника, образующие грани тетраэдра, являются равносторонними и равными между собой, то такой тетраэдр называется правильным. Этот тетраэдр имеет 4 грани и 4 вершины, число ребер составляет 4 + 4 — 2 = 6. Применяя стандартные формулы из плоской геометрии для рассматриваемой фигуры, получаем: V = a 3 * √2/12 и S = √3*a 2 , где a — длина стороны равностороннего треугольника.
Интересно отметить, что в природе некоторые молекулы имеют форму правильного тетраэдра. Например, молекула метана CH 4 , в которой атомы водорода расположены в вершинах тетраэдра, и соединены с атомом углерода ковалентными химическими связями. Атом углерода находится в геометрическом центре тетраэдра.
Простая в изготовлении форма фигуры тетраэдр используется также в инженерии. Например, тетраэдрическую форму используют при изготовлении якорей для кораблей. Отметим, что космический зонд НАСА, Mars Pathfinder, который совершил посадку на поверхность Марса 4 июля 1997 года, также имел форму тетраэдра.
Фигура призма
Эту геометрическую фигуру можно получить, если взять два многогранника, расположить их параллельно друг другу в разных плоскостях пространства, и соединить их вершины соответствующим образом между собой. В итоге получится призма, два многогранника называются ее основаниями, а поверхности, соединяющие эти многогранники, будут иметь форму параллелограммов. Призма называется прямой, если ее боковые стороны (параллелограммы) являются прямоугольниками.
Призма — это полиэдр, поэтому для нее верна Например, если в основании призмы лежит шестиугольник, тогда, количество сторон у призмы равно 8, а количество вершин — 12. Число ребер будет равно: Р = 8 + 12 — 2 = 18. Для прямой призмы высотой h, в основании которой лежит правильный шестиугольник со стороной a, объем равен: V = a 2 *h*√3/4, площадь поверхности равна: S = 3*a*(a*√3 + 2*h).
Говоря о простых геометрических объемных фигурах и их названиях, следует упомянуть шар. Под объемным телом под названием шар понимают тело, которое ограничено сферой. В свою очередь, сфера — это совокупность точек пространства, равноудаленных от одной точки, которая называется центром сферы.
Поскольку шар относится к классу круглых тел, то для него не существует понятия о сторонах, ребрах и вершинах. сферы, ограничивающей шар, находится по формуле: S = 4*pi*r 2 , а объем шара можно вычислить по формуле: V = 4*pi*r 3 /3, где pi — число пи (3,14), r — радиус сферы (шара).
Установка межкомнатной двери Profil 2.78XN Капучино Ромб
Настоящая Политика конфиденциальности регулирует порядок обработки и использования персональных и иных данных администратором сайтов https://belkist.ru (далее — Оператор). Передавая Оператору персональные и иные данные посредством Сайта, Пользователь подтверждает свое согласие на использование указанных данных на условиях, изложенных в настоящей Политике конфиденциальности. Если Пользователь не согласен с условиями настоящей Политики конфиденциальности, он обязан прекратить использование Сайта. Безусловным акцептом настоящей Политики конфиденциальности является начало использования Сайта Пользователем.
1. ТЕРМИНЫ
1.1. Сайт — сайты, расположенные в сети Интернет по адресам https://belkist.ru. Все исключительные права на Сайт и его отдельные элементы (включая программное обеспечение, дизайн) принадлежат Оператору в полном объеме. Передача исключительных прав Пользователю не является предметом настоящей Политики конфиденциальности.
1.2. Пользователь — лицо использующее Сайт.
1.3. Законодательство — действующее законодательство Российской Федерации.
1.4. Персональные данные — персональные данные Пользователя, которые
Пользователь предоставляет о себе самостоятельно при Регистрации или в процессе использования функционала Сайта.
1.5. Данные — иные данные о Пользователе (не входящие в понятие Персональных данных).
1.6. Регистрация — заполнение Пользователем Регистрационной формы, расположенной на Сайте, путем указания необходимых сведений и выбора Логина и пароля.
1.7. Регистрационная форма — форма, расположенная на Сайте, которую Пользователь должен заполнить для прохождения Регистрации на Сайте.
1.8. Услуга(и) — услуги, предоставляемые Оператором на основании Лицензионного соглашения.
2. СБОР И ОБРАБОТКА ПЕРСОНАЛЬНЫХ ДАННЫХ
2.1. Оператор собирает и хранит только те Персональные данные, которые необходимы для оказания Услуг Оператором и взаимодействия с Пользователем.
2.2. Персональные данные могут использоваться в следующих целях:
2.2.1 оказание Услуг Пользователю;
2.2.2 идентификация Пользователя;
2.2.3 взаимодействие с Пользователем;
2.2.4 направление Пользователю рекламных материалов, информации и запросов;
2.2.5 проведение статистических и иных исследований;
2.2.6 обработка платежей Пользователя;
2.2.7 мониторинг операций Пользователя в целях предотвращения мошенничества, противоправных ставок, отмывания денег.
2.3. Оператор в том числе обрабатывает следующие данные:
2.3.1 фамилия, имя и отчество;
2.3.2 адрес электронной почты;
2.3.3 номер мобильного телефона.
2.4. Пользователю запрещается указывать на Сайте персональные данные третьих лиц.
3. ПОРЯДОК ОБРАБОТКИ ПЕРСОНАЛЬНЫХ И ИНЫХ ДАННЫХ
3.1. Оператор обязуется использовать Персональные данные в соответствии с Федеральным Законом «О персональных данных» № 152-ФЗ от 27 июля 2006 г. и внутренними документами Оператора.
3.2. В отношении Персональных данных и иных Данных Пользователя сохраняется их конфиденциальность, кроме случаев, когда указанные данные являются общедоступными.
3.3. Оператор имеет право сохранять архивную копию Персональных данных и Данных, в том числе после удаления аккаунта Пользователя.
Оператор имеет право хранить Персональные данные и Данные на серверах вне территории Российской Федерации.
3.4. Оператор имеет право передавать Персональные данные и Данные Пользователя без согласия Пользователя следующим лицам:
3.4.1 государственным органам, в том числе органам дознания и следствия, и органам местного самоуправления по их мотивированному запросу
3.4.2 партнерам Оператора;
3.4.3 в иных случаях, прямо предусмотренных действующим законодательством РФ.
3.5. Оператор имеет право передавать Персональные данные и Данные третьим лицам, не указанным в п. 3.4. настоящей Политики конфиденциальности, в следующих случаях:
3.5.1 Пользователь выразил свое согласие на такие действия;
3.5.2 передача необходима в рамках использования Пользователем Сайта или оказания Услуг Пользователю;
3.5.3 передача происходит в рамках продажи или иной передачи бизнеса (полностью или в части), при этом к приобретателю переходят все обязательства по соблюдению условий настоящей Политики.
3.6. Оператор осуществляет автоматизированную обработку Персональных данных и Данных.
4. ИЗМЕНЕНИЕ ПЕРСОНАЛЬНЫХ ДАННЫХ
4.1. Пользователь может в любой момент изменить (обновить, дополнить) Персональные данные посредством Личного кабинета либо путем направления письменного заявления Оператору.
4.2. Пользователь в любой момент имеет право удалить Персональные данные.
4.3. Пользователь гарантирует, что все Персональные данные являются актуальными и не относятся к третьим лицам.
5. ЗАЩИТА ПЕРСОНАЛЬНЫХ ДАННЫХ
5.1. Оператор осуществляет надлежащую защиту Персональных и иных данных в соответствии с Законодательством и принимает необходимые и достаточные организационные и технические меры для защиты Персональных данных.
5.2. Применяемые меры защиты в том числе позволяют защитить Персональные данные от неправомерного или случайного доступа, уничтожения, изменения, блокирования, копирования, распространения, а также от иных неправомерных действий с ними третьих лиц.
6. ПЕРСОНАЛЬНЫЕ ДАННЫЕ ТРЕТЬИХ ЛИЦ ИСПОЛЬЗУЕМЫЕ ПОЛЬЗОВАТЕЛЯМИ
6.1. Используя Сайт Пользователь имеет право заносить данные третьих лиц для последующего использования.
6.2. Пользователь обязуется получить согласие субъекта персональных данных на использование посредством Сайта.
6.3. Оператор не использует персональные данные третьих лиц занесенные Пользователем.
6.4. Оператор обязуется предпринять необходимые меры для обеспечения сохранности персональных данных третьих лиц, занесенных Пользователем.
7. ИНЫЕ ПОЛОЖЕНИЯ
7.1. К настоящей Политике конфиденциальности и отношениям между Пользователем и Оператором, возникающим в связи с применением Политики конфиденциальности, подлежит применению право Российской Федерации.
7.2. Все возможные споры, вытекающие из настоящего Соглашения, подлежат разрешению в соответствии с действующим законодательством по месту регистрации Оператора. Перед обращением в суд Пользователь должен соблюсти обязательный досудебный порядок и направить Оператору соответствующую претензию в письменном виде. Срок ответа на претензию составляет 30 (тридцать) рабочих дней.
7.3. Если по тем или иным причинам одно или несколько положений Политики конфиденциальности будут признаны недействительными или не имеющими юридической силы, это не оказывает влияния на действительность или применимость остальных положений Политики конфиденциальности.
7.4. Оператор имеет право в любой момент изменять Политику конфиденциальности (полностью или в части) в одностороннем порядке без предварительного согласования с Пользователем. Все изменения вступают в силу на следующий день после размещения на Сайте.
7.5. Пользователь обязуется самостоятельно следить за изменениями Политики конфиденциальности путем ознакомления с актуальной редакцией.
7.6. Данный сайт носит исключительно информационный характер и ни при каких условиях не является публичной офертой, определяемой положениями Статьи 437 (2) Гражданского кодекса Российской Федерации. Все права защищены ООО «Служба Сервиса».
Ромб в основании призмы
Задача.
Основание прямой призмы — ромб с углом 120 градусов. БОльшая диагональ призмы равна 8см и составляет с боковым ребром угол 60 градусов. Найти сторону ромба и меньшую диагональ призмы.
Решение.
Поскольку диагональ AC1 образует с ребром AA1 угол 60 градусов, призма является прямой, то угол C1AC равен 90 — 60 = 30 градусов.
Исходя из этого cos 30 = AC / AC1 = √3 / 2
AC / AC1 = √3 / 2
AC / 8 = √3 / 2
2AC = 8√3
AC = 4√3
Поскольку угол ADC равен 120 градусам, то угол BAD равен 60 градусам. (Сумма углов выпуклого четырехугольника равна 180(n-2) = 360 градусам, углы ромба попарно равны).
Исходя из того, что угол BAD равен 60 градусам, треугольники ABD и BDC- равносторонние. (Так как ABCD — ромб, то они равнобедренные, следовательно углы при основании равны, значит они равны ( 180 — 60 ) / 2 = 60 градусов. Треугольник, у которого все углы равны — равносторонний).
Диагонали параллелограмма в точке пересечения делятся пополам. Таким образом, AO = AC / 2 = 4√3 / 2 = 2√3
Поскольку треугольник ABD правильный, то AO является одновременно высотой и биссектрисой. Учтем, что высота правильного треугольника равна
h = а √3 / 2, тогда
а √3 / 2 = 2√3
а = 4
Зная, что BD = 4 см, DD1 = 4 см, по теореме Пифагора найдем меньшую диагональ:
BD12 = 4 + 4
Таким образом, сторона ромба равна 4 см, а, так как треугольники ABD и BDC- равносторонние, то и меньшая диагональ ромба равна 4 см.
Для того, чтобы найти длину ребра призмы, учтем, что диагональ AC1 = 8 см, а угол C1AC = 30 градусам. Тогда sin 30 = C1C / AC1 = 1/2
C1C / 8 = 1/2
C1C = 4 см
Зная что BD = 4 см (меньшая диагональ ромба), D1D = 4 см (ребро призмы), длину меньшей диагонали призмы найдем по теореме Пифагора:
BD12 = DD12 + BD2
BD12 = 42 + 42
BD12 = 32
BD1 = 4√2
Ответ: Сторона ромба — 4 см, меньшая диагональ призмы с ромбом в основании равна 4√2 см.
Параллелограмм в основании призмы |
Описание курса
| Пирамида. Решение задач
свойства, формулы и задачи репетитора по математике — Колпаков Александр Николаевич
Параллелепипедом называется четырехугольная призма, в основаниях которой лежат параллелограммы. Высотой параллелепипеда называют расстояние между плоскостями его основаниями. На рисунке высота показана отрезком . Различают два вида параллелепипедов: прямой и наклонный. Как правило, репетитор по математике сначала дает соответствующие определения для призмы, а затем переносит их на параллелепипед. Мы сделаем также.
Напомню, что призма называется прямой, если ее боковые ребра перпендикулярны основаниям, если перпендикулярности нет – призму называют наклонной. Эту терминологию наследует и параллелепипед. Прямой параллелепипед – ни что иное, как разновидность прямой призмы, боковое ребро которой совпадает с высотой. Сохраняются определения таких понятий, как грань, ребро и вершина, являющиеся общими для всего семейства многогранников. Появляются понятие противоположные грани. У параллелепипеда 3 пары противоположных граней, 8 вершин ти 12 ребер.
Диагональ параллелепипеда (диагональ призмы) — отрезок, соединяющий две вершины многогранника и не лежащий ни в одной из его граней.
Диагональное сечение – сечение параллелепипеда, проходящее через его диагональ и диагональ его основания.
Свойства наклонного параллелепипеда:
1) Все его грани – параллелограммы, а противоположные грани — равные параллелограммы.
2) Диагонали параллелепипеда пересекаются в одной точке и делятся в этой точки пополам.
3) Каждый параллелепипед состоит из шести равных по объему треугольных пирамид. Чтобы показать их ученику репетитор по математике должен отрезать от параллелепепеда половинку его диагональным сечением и разбить ее отдельно на 3 пирамиды. Их основания должны лежать в разных гранях исходного паралеллепипеда. Репетитор математики найдет применение этого свойства в аналитической геометрии. Оно используется для вывода объема пирамиды через смешанное произведение векторов.
Формулы объема параллелепипеда:
1) , где — площадь основания, h – высота.
2) Объем параллелепипеда равен произведению площади поперечного сечения на боковое ребро .
Репетитору по математике: Как известно, формула является общей для всех призм и если репетитор уже доказал ее, нет смысла повторять тоже самое для параллелепипеда. Однако в работе со учеником среднего уровня (слабому формула не пригодиться) преподавателю желательно действовать с точностью до наоборот. Призму оставить в покое, а для параллелепипеда провести аккуратное доказательство.
3) , где –объем одной из шести треугольных пирамиды из которых состоит параллелепипед.
4) Если , то
Площадью боковой поверхности параллелепипеда называется сумма площадей всех его граней:
Полная поверхность параллелепипеда – это сумма площадей всех его граней, то есть площадь + две площади основания: .
О работе репетитора с наклонным параллелепипедом:
Задачами на наклонный параллелепипед репетитор по математике занимается не часто. Вероятность их появления на ЕГЭ достаточно мала, а дидактика неприлично бедная. Более-менее приличная задача на объем наклонного параллелепипеда вызывает серьезные проблемы, связанные с пределением расположения точки Н — основания его высоты. В этом случае репетитору по математике можно посоветовать обрезать параллелепипед до одной из шести его пирамид (о которых идет речь в свойстве №3), попробовать найти ее объем и умножить его на 6.
Если боковое ребро параллелепипеда имеет равные углы со сторонами основания, то Н лежит на биссектрисе угла A основания ABCD. И если, например, ABCD — ромб, то
Задачи репетитора по математике:
1) Грани параллелепипеда равные роибы со стороной 2см и острым углом . Найти объем параллелепипеда.
2) В наклонном параллелепипеде боковое ребро равно 5см. Сечение, перпендикулярное ему, является четырехугольником со взаимно перпендикулярными диагоналями, имеющими длины 6см и 8 см. Вычислить объем паралеллепипеда.
3) В наклонном параллелепипеде известно, что , а в онованием ABCD является ромб со стороной 2см и уголом . Определите объем параллелепипеда.
Репетитор по математике, Александр Колпаков
Площадь и объем
Периметр
Периметр = расстояние по краю.
Можно было пройтись по периметру.
Все размеры должны иметь одинаковые единицы измерения!
Не смешивайте cm с m.
Периметр имеет простые блоки.
Пример
P = 5 + 2 + 2 + 3 + 9 + 3 + 2 + 2 см
P = 28 см
Площадь
Площадь = занимаемая площадь
Вы можете закрасить область.
Все размеры должны иметь одинаковые единицы измерения!
Не смешивайте см, 2 с м 2
1 м 2 = 100 см x 100 см
= 10000 см 2
Площадь насчитывает единицы
2 .
Площадь квадрата
Пример
Посчитаем площадь квадрата
Площадь прямоугольника
Примеры
Вычислить площадь прямоугольников
Площадь треугольника
Площадь треугольника = ½ x основание x высота перпендикуляра
Примеры
Найдите площадь треугольника ниже:
Какая длина основания
треугольник, если он имеет площадь 45 см 2 ?
Площадь круга
Площадь воздушного змея
Пример
Рассчитайте площадь следующего воздушного змея:
Площадь трапеции
Площадь трапеции = ½ x среднее значение основания x высота перпендикуляра
Пример
Какова площадь этой трапеции?
(Каждый квадрат соответствует 1 см 2 )
Площадь параллелограмма
Пример
Вычислить площадь параллелограмма:
Площадь ромба
Пример
Посчитаем площадь ромба:
(Размеры указаны по полной диагонали)
Объем
Объем = вместимость
Вы можете заполнить том
Все размеры должны иметь одинаковые единицы измерения!
Не смешивайте cm с m.
Объем в единицах
3
Обратите внимание, что для кубоида
Пример
Рассчитайте объем кубоида ниже:
Пример
Преобразование 1 м 3 в литры
Сначала преобразуйте единицы
Но 1 см 3 = 1 мл и 1000 мл = 1 литр
Для литров разделите 3 в см на 1000.
Так 1000000 см 3 = 1000 литров
1 м 3 = 1000 литров
Объем сферы
Объем сферы
Где r — радиус сферы.
Примеры
Вычислите объем следующей сферы.
Дайте правильный ответ на 1 dp, а также на 2 sig.
Рассчитайте объем следующей сферы.
Дайте правильный ответ на 1 сигн. Рис.
Вычислите диаметр сферы объемом 700 см 3 .
Дайте правильный ответ с точностью до 1 дп.
Объем конуса
Конус имеет объем
Где r — радиус круговой части конуса, а h — высота перпендикуляра конуса.
Пример
Вычислите объем рожка мороженого диаметром 4 см и высотой 6 см. Дайте правильный ответ с точностью до 1 дп.
Сколько таких рожков можно налить из 1 литра мороженого?
1000 см 3 = 1 л
1000 ÷ 25,1 = 39,84
Таким образом, из одного литра мороженого можно наполнить 39 рожков.
Пример
Вычислите высоту рожка мороженого диаметром 4 см и объемом 35 мл.Дайте правильный ответ с точностью до 1 дп.
Конус высотой 8,4 см.
Пример
Вычислите диаметр рожка мороженого высотой 8 см и объемом 90 мл. Дайте правильный ответ с точностью до 1 дп.
Объем призмы
Для призмы V = Ah
Таким образом, объем = площадь x высота (или площадь x длина в положении лежа)
Пример
Какой объем призмы?
который имеет площадь 37 см 2
а высотой 4 см?
Объем цилиндра
Цилиндр представляет собой круговую призму,
Пример
Вычислите объем консервной банки высотой 0.8м и диаметром 10 см. Дайте правильный ответ на 1 сигфиг.
Пример
Вычислите диаметр консервной банки высотой 8 см и объемом 90 мл. Дайте правильный ответ с точностью до 1 дп.
Объем пирамиды
Объем любой пирамиды равен
.
где A — площадь основания пирамиды, а h — ее высота.
Примеры
Каков объем этой квадратной пирамиды?
Каков объем этой прямоугольной пирамиды?
Каков объем этой треугольной пирамиды?
Площадь
Площадь — это общая внешняя площадь
формы.
Пример
Найдите площадь поверхности кубоида:
У этой формы 6 граней
2 грани размером 6 см x 4 см
2 лица имеют площадь 6см x 2см
2 лица имеют площадь 2 см x 4 см
2 x 6 см x 4 см = 48 см 2
2 x 6 см x 2 см = 24 см 2
2 x 2 см x 4 см = 16 см 2
Площадь поверхности = 88 см 2
Площадь ≠ Объем
Общая площадь
Нарезать удобные формы
Найти недостающие размеры
Рассчитать отдельные площади
Подсчитать итого
Помните
все размеры должны иметь одинаковые единицы измерения!
Пример
Форма A = A 1 + A 2
A 1 = 5×2 = 10 см 2
A 2 = 3×9 = 27 см 2
Форма = 37 см 2
Составной том
Нарезать удобные формы
Найти недостающие размеры
Рассчитать отдельные площади
Подсчитать итого
Пример
© Александр Форрест
РАЗ МОДУЛЬ M11 — Площадь, объем и площадь поверхности
Проект «Улучшение математического образования в школах» (TIMES)
вернуться к индексу
Площадь, объем и площадь
Измерение и геометрия: Модуль 11 Год: 8-10
июнь 2011
PDF Версия модуля
Предполагаемые знания
- Знание площадей прямоугольников, треугольников, окружностей и составных фигур.
- Определения параллелограмма и ромба.
- Знакомство с основными свойствами параллельных прямых.
- Знакомство с объемом прямоугольной призмы.
- Базовые знания о совпадении и сходстве.
- Поскольку будут задействованы некоторые формулы, студентам потребуется некоторый опыт в замещении, а также в распределительном законе.
Мотивация
Площадь плоской фигуры — это мера пространства внутри нее.Расчет площадей — важный навык, используемый многими людьми в повседневной работе. Строителям и торговцам часто необходимо определить площади и размеры строящихся конструкций, а также архитекторам, дизайнерам и инженерам.
В то время как прямоугольники, квадраты и треугольники обычно встречаются в окружающем нас мире, встречаются и другие формы, такие как параллелограмм, ромб и трапеция. Рассмотрим, например, этот вид крыши с воздуха.
Вид состоит из двух трапеций и двух треугольников.
Точно так же часто встречаются твердые тела, отличные от прямоугольной призмы. Пакет Toblerone ©
(с основанием на конце) представляет собой пример треугольной призмы, а бочка с маслом
имеет форму цилиндра. Важно уметь определить объем таких твердых частиц.
Медицинские специалисты измеряют такие параметры, как скорость кровотока (которая определяется скоростью жидкости и площадью поперечного сечения потока), а также размер опухолей и новообразований.
В физике область под графиком скорость-время показывает пройденное расстояние.
В этом модуле мы будем использовать простые идеи для создания ряда фундаментальных формул
для площадей и объемов. Студенты должны понять, почему формулы верны, и запомнить их.
Содержимое
Площадь параллелограмма
Параллелограмм — это четырехугольник, противоположные стороны которого равны и параллельны.
Мы можем легко найти площадь параллелограмма по основанию b и высоте h.
На схеме ниже мы рисуем диагональ BD и делим фигуру на два треугольника, каждый с длиной основания b и высотой h. Поскольку площадь каждого треугольника равна bh, общая площадь A равна
.
A = bh.
Обратите внимание, что два треугольника на диаграмме не только имеют одинаковую площадь, но и являются конгруэнтными треугольниками.
Некоторые учителя могут предпочесть составить формулу площади для параллелограмма без использования формулы площади треугольника, чтобы они могли вычислить площадь треугольника, используя формулу площади для параллелограмма.
Это можно сделать, показав, что треугольник справа на левой диаграмме ниже можно расположить слева, чтобы сформировать прямоугольник, основание и высота которого такие же, как у
, у параллелограмма, так что, опять же, площадь равна к ч.
Площадь трапеции
Трапеция — это четырехугольник, у которого одна пара противоположных сторон параллельна. (Название происходит от греческого слова «стол».)
Мы можем найти площадь трапеции, если знаем длины двух параллельных сторон и перпендикулярное расстояние между этими двумя сторонами.
Так же, как и с параллелограммом, рисуем одну из диагоналей. Затем у нас есть два треугольника, оба с высотой h, один с основанием a, один с основанием b.
Таким образом, площадь А трапеции равна
.
Таким образом, формула для площади трапеции с параллельными сторонами a и b и перпендикулярным расстоянием h между ними составляет
А = ч (а + б).
Это можно представить как «высоту, умноженную на среднее значение параллельных сторон».
Упражнение 1
Вот еще один вывод формулы площади трапеции. Предположим, ABCD
— это трапеция.
Возьмите F за середину CD и проведите через нее линию EG, параллельную AB.
a Объясните, почему треугольники CFG и DFE совпадают.
b Что это говорит нам о КГ и ЭД?
cОбъясните, почему AE = (BC + AD).
d Используйте формулу площади параллелограмма, чтобы получить формулу площади трапеции.
Упражнение 2
(В этом упражнении используются похожие треугольники).
На схеме ABCD представляет собой трапецию с AB, параллельной DC, и расстоянием между ними h. Точки E и F являются серединами AD и BC соответственно. AG перпендикулярно DC в G и пересекает EF в H. Пусть a = AB, b = DC и = EF.
a Покажите, что EF параллелен DC.
b Рассмотрение треугольников AEH и ADG показывает, что AH = HG =.
c Сравнивая площади трех образованных трапеций или иным образом,
показывает, что площадь трапеции ABCD равна h.
Площадь ромба и воздушного змея
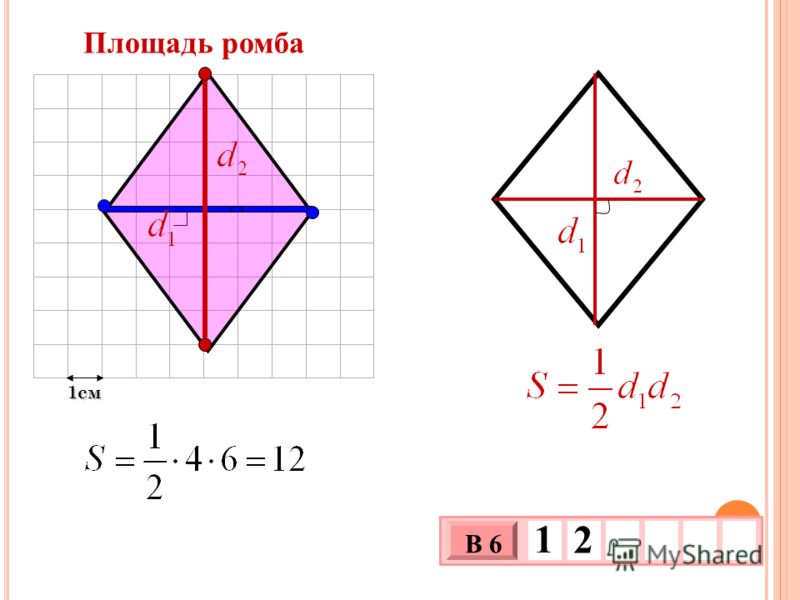
Ромб — это четырехугольник, у которого все стороны равны. В модуле Rhombuses, Kites and Trapezia , используя простые геометрические аргументы, мы показали
- противоположные стороны параллельны
- диагонали делят друг друга пополам под прямым углом
Таким образом, ромб — это параллелограмм, и мы можем вычислить площадь ромба, используя формулу для площади параллелограмма.
Теперь возьмем ромб с диагоналями длины x и y.
Установив ромб в одном углу, мы видим, что две диагонали разрезают ромб на четыре прямоугольных треугольника, которые могут быть завершены, чтобы образовать четыре прямоугольника внутри
большего прямоугольника.
Поскольку восемь треугольников имеют одинаковую площадь (действительно, все они совпадают), площадь ромба составляет половину площади большого прямоугольника, который равен xy.
Следовательно, если x и y — длины диагоналей ромба, то
Площадь ромба = xy.
Площадь ромба равна половине произведения длин диагоналей.
Упражнение 3
Предположим, что ABCD — это ромб с одной диагональю 8 см и одной стороной 5 см, как показано.
a Используйте теорему Пифагора, чтобы найти
длину другой диагонали.
bОтсюда найдите площадь ромба.
Упражнение 4
Воздушный змей — это четырехугольник, у которого две пары смежных сторон равны.
a Используйте конгруэнтность и два равнобедренных треугольника, чтобы показать, что диагонали воздушного змея перпендикулярны.
b Ясно, что мы можем закончить кайт, чтобы сформировать прямоугольник
, площадь которого вдвое больше, чем у воздушного змея,
, поэтому
Площадь воздушного змея = xy,
где x и y — длины диагоналей воздушного змея.
Площадь полигонов
Любой многоугольник можно разрезать на треугольники.Следовательно, площадь любого многоугольника определяется и может быть вычислена путем вычисления площади каждого треугольника.
Объем призмы
Многогранник — это твердое тело, ограниченное многоугольниками. Правая призма — это многогранник, у которого есть две совпадающие и параллельные грани (называемые основанием и вершиной), а все его остальные грани являются прямоугольниками. Это означает, что когда правая призма стоит на ее основании, все стены представляют собой вертикальные прямоугольники. Обычно мы говорим «призма», когда на самом деле имеем в виду «прямую призму».Призма имеет равномерное поперечное сечение. Это означает, что когда вы делаете срезы через твердое тело параллельно основанию, вы получаете многоугольники, совпадающие с основанием. Таким образом, площадь каждого среза всегда одинакова. В прямоугольной призме поперечное сечение всегда прямоугольное.
В модуле Введение в измерение мы увидели, что объем прямоугольной призмы определяется как площадь основания, умноженная на высоту, или
.
Объем = lwh, где l и w — длина и ширина призмы, а h — высота.
Треугольные призмы
В треугольной призме каждое поперечное сечение, параллельное треугольному основанию, представляет собой треугольник, конгруэнтный основанию.
Предположим, у нас есть треугольная призма, длина которой составляет 4 см, как показано на диаграмме.
Можно разрезать призму на слои длиной 1 см каждый.
Ранее мы видели, что из остроугольного треугольника можно образовать прямоугольник с удвоенной площадью.
Аналогичным образом мы можем завершить треугольную призму, чтобы сформировать прямоугольную призму. Объем каждого из слоев толщиной 1 см составляет половину объема соответствующей прямоугольной призмы, т.е.
.
Объем каждого слоя = × 3 × 2 см3.
Отсюда объем треугольной призмы | = × 3 × 2 × 4 |
Таким образом, объем треугольной призмы равен
.
Объем = площадь треугольного поперечного сечения × высота перпендикуляра = Ah.
Поскольку любой многоугольник можно разрезать на треугольники, объем любой призмы с многоугольным основанием равен площади A многоугольного основания, умноженной на высоту h, то есть
Объем = Ач
, где A — площадь многоугольного основания, а h — высота, когда призма находится на своем основании.
Пример
Найдите объем призмы, показанной на диаграмме.
Решение
Поперечное сечение представляет собой переднюю грань призмы и состоит из треугольника и прямоугольника.
А | = × 8 × 4 + (8 × 6) | |
= 64 см2. | ||
Объем | = Ач | |
= 64 × 5 | ||
= 320 см3. |
Упражнение 5
Большой постамент имеет форму призмы, передняя грань которой представляет собой трапецию.
a Найдите площадь лицевой стороны.
b Найдите объем пьедестала.
Объем цилиндра
Цилиндры повсеместно используются в повседневной жизни. Например, консервы обычно выпускаются в банках цилиндрической формы.
Если мы разрежем цилиндр параллельно его основанию, то каждое поперечное сечение будет кругом того же размера, что и основание.
Таким образом, цилиндр имеет то же основное свойство, что и призма, и мы возьмем формулу для объема цилиндра, равную площади круглого основания, умноженной на высоту. Мы не можем строго доказать эту формулу на данном этапе, потому что доказательство включает построение цилиндра как предела призм.
Если основная окружность цилиндра имеет радиус r, то мы знаем, что площадь круга равна
A = π r2.Если высота цилиндра h, то его объем
Объем = π r2 × h = π r2h.
Пример
Для цилиндра радиусом 7 см и высотой 3 см найдите:
a — точный объем, выраженный в π.
b приблизительное значение объема с использованием π.
Решение
а | В | = π r2h | б | В | = π r2h | |||
= π × 49 × 3 | ≈ × 49 × 3 | |||||||
= 147π см3 | = 462 см3. |
Упражнение 6
Термос высотой 30 см имеет форму двух цилиндров, расположенных один внутри другого. Он имеет внутренний радиус 8 см и внешний радиус 10 см. Какой объем между двумя цилиндрами?
Площадь призмы
Предположим, мы берем прямоугольную призму размером 3 см на 4 см на 5 см и открываем ее, как показано ниже.
Мы можем найти площадь плоской прямоугольной призмы, сложив площади шести прямоугольников.Есть три пары равных прямоугольников, поэтому общая площадь составляет
.
A = 2 × (3 × 4 + 3 × 5 + 4 × 5) = 94 см2.
Это называется площадью поверхности призмы.
Таким образом, площадь поверхности призмы — это сумма площадей ее граней. Действительно, площадь поверхности многогранника также является суммой площадей всех его граней.
Пример
Найдите площадь поверхности треугольной призмы
, показанной напротив.
Решение
Площадь фасада = × 12 × 16 = 96 см2.
Площадь спинки = 96 см2.
Площадь трех прямоугольных граней | = (9 × 20) + (9 × 12) + (9 × 16) |
= 432 см2. |
Общая площадь | = 96 + 96 + 432 |
= 624 см2. |
Длина кромки
Длина кромки призмы — это сумма длин всех ее граней.
Упражнение 7
Найдите общую длину ребра призмы в приведенном выше примере.
Упражнение 8
Палатка, сделанная из бязи, включая грунтовку
, имеет форму треугольной призмы с размерами, как показано.Сколько бязи нужно для изготовления палатки?
Ссылки вперед
Площади
Теперь мы можем найти площади основных геометрических фигур. Мы также видели в модуле на кругах, что площадь круга задается как A = π r2, где r — радиус. Чтобы понять площадь фигуры, которая не ограничена ни прямыми линиями, ни дугами окружностей, нам понадобится интегральное исчисление. Хотя эти идеи восходят к Архимеду и Евдоксу, систематическое развитие интегрального исчисления принадлежит Ньютону и Лейбницу.
Мы можем использовать тригонометрию, чтобы найти площади различных фигур, имея достаточно информации об их сторонах и углах.
Объемы: пирамиды и призмы
Можно показать, что объем квадратной пирамиды составляет одну треть объема соответствующей правой призмы той же высоты и основания.
Объем пирамиды = Ah,
, где A — площадь основания
, а h — перпендикулярная высота
, измеренная от основания.
Эта формула верна для пирамид с многоугольным основанием площадью A.
Поперечные сечения конуса (или сферы) представляют собой окружности, но радиусы поперечных сечений различаются. Объем конуса равен одной трети объема соответствующего цилиндра той же высоты и радиуса.
Объем конуса = π r2h,
, где r — радиус основания
, а h — высота.
Наконец, объем сферы равен
.
Объем сферы = π r3,
где r радиус сферы.
Это завершает формулы объема для основных твердых веществ. Твердые тела с нерегулярными границами можно рассматривать с помощью интегрального исчисления. Все они рассматриваются в модуле Конусы, Пирамиды и Сферы .
Площадь
Точно так же, как мы «разрезаем» призму, чтобы найти площадь поверхности, мы можем «разрезать» цилиндр радиуса r и высоты h, чтобы показать, что площадь изогнутой поверхности равна 2π rh. Складывая два круглых конца, мы получаем формулу A = 2π rh + 2π r2 для общей площади поверхности цилиндра.Формула площади поверхности для конуса: A = π r2 + π rl, где r — радиус, а l — высота наклона. Наконец, площадь поверхности сферы равна A = 4π r2, где r — радиус сферы.
История и приложения
Многие названия фигур и твердых тел, площадь и объем которых мы нашли, происходят от греческого языка. Например, трапеция (несмотря на латинское окончание) происходит от греческого слова, обозначающего стол, в то время как призма происходит от греческого слова, означающего пилу (поскольку поперечные сечения или разрезы совпадают), также слово цилиндр происходит от Греческое слово, означающее катиться.Древние греки были первыми, кто систематически исследовал площади и объемы плоских фигур и твердых тел.
В эллинистический период великий математик Архимед (ок. 287 — 212 г. до н.э.) аппроксимировал площадь круга, используя вписанные многоугольники, и нашел очень хорошее приближение к π. Он также вывел формулы для объема и площади поверхности сферы. Архимед разработал технику поиска областей и томов, названную «методом исчерпания», которая была близка к идеям, используемым в современном математическом анализе.
До разработки интегрального исчисления, которое вывело области и объемы на новый уровень абстракции, итальянский математик Бонавентура Франческо Кавальери (1598-1647) разработал результат, известный как принцип Кавальери, который гласит, что два объекта имеют одинаковый объем, если площади соответствующих им поперечных сечений во всех случаях равны. (Тот же принцип был ранее открыт Цзу Гэнчжи (480-525) в Китае.) Умное использование этого метода показывает, что объем полусферы радиусом r равен объему твердого тела, полученного путем удаления конуса радиус r и высота r от цилиндра такой же высоты и радиуса, таким образом показывая, что объем полусферы равен π r3.
Принцип
Кавальери можно использовать для определения объема наклонных твердых тел (в отличие от правильных твердых тел). Таким образом, наклонная призма имеет параллельное горизонтальное основание и вершину, но стороны не вертикальны. Такое твердое тело называется параллелепипедом (другое греческое слово, означающее параллельные плоскости).
Используя принцип Кавальери, можно показать, что формула объема такая же, как и формула
для призмы, а именно:
Объем = площадь основания × высота по перпендикуляру.
Следующим большим достижением стало интегральное исчисление, когда можно было понять понятие площади под кривой, используя идеи предела. Хотя Ферма и Декарт добились в этом большого прогресса, именно (независимая) работа Ньютона и Лейбница привела к современной теории интеграции.
Существуют приблизительные методы определения площади фигуры с неровной границей. Одно довольно точное правило называется Правило Симпсона, которое было известно Кавальери, переоткрыто Грегори (1638–1675) и приписано Томасу Симпсону (1710–1761).Это правило позволяет нам найти приблизительное значение площади неправильной фигуры, производя измерения поперек фигуры в различных точках вдоль некоторой оси. Сегодня кардиологи используют его для измерения, например, объема правого желудочка (ПЖ), связанного с кровотоком в сердце.
Ответы к упражнениям
Упражнение 1
| а | CF = DF | (F — середина CD) | |
CFG = DFE | (вертикально противоположные углы) | ||
GCF = EDF | (альтернативные углы) | ||
Треугольник CFG соответствует треугольнику DFE (SAS) | |||
b CG = ED (совпадающие стороны равных треугольников)
c | 2AE = AE + BG | = AD — ED + CG + BG | |
| = AD + BG | |||
| AE = ( AD + BG ) |
d Площадь трапеции = площадь параллелограмма
= AE × h
= ( AD + BG ) × h
Упражнение 2
a Сдвиньте треугольники ADG и BCK вместе, чтобы получился треугольник ACD
( B и A совпадают). E и F являются средними точками AC и AD соответственно. Треугольник AFE аналогичен треугольнику ACD и, таким образом, EF параллелен DC (соответствующие углы равны).
b Треугольник AEH аналогичен треугольнику ADG (AAA)
AH = HG =
с | Площадь | = (AB + CD) | |
= (2 (HJ + EH + JF)) | |||
= гл |
Упражнение 3
a 6 см
b 24 см2
Упражнение 4
| а | Треугольник CBA соответствует CDA (SSS) | |
| Треугольник BCE конгруэнтен треугольнику DCE (SAS) | ||
| CEB = CED = 90 ° | ||
б | Площадь прямоугольника = xy . | |
Упражнение 5
a 31,5 м2 b 94,5 м3
Упражнение 6
1080π см3
Упражнение 7
123 см
Упражнение 8
60 м2
Проект «Улучшение математического образования в школах» (TIMES) на 2009–2011 годы финансировался Министерством образования, занятости и трудовых отношений правительства Австралии.
Мнения, выраженные здесь, принадлежат автору и не обязательно отражают точку зрения Департамента образования, занятости и трудовых отношений австралийского правительства.
© Мельбурнский университет от имени Международного центра передового опыта в области образования в области математики (ICE-EM), образовательного подразделения Австралийского института математических наук (AMSI), 2010 г. (если не указано иное). Эта работа находится под лицензией Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Непортированная лицензия.
https://creativecommons.org/licenses/by-nc-nd/3.0/
Формула площади ромба с калькулятором
Формула площади ромба с калькулятором — Math Open Reference
Три разных способа рассчитать площадь
ромбы приведены ниже, с формулой для каждого.
Попробуйте это Перетащите оранжевые точки на каждую вершину
изменить форму ромба. Площадь будет постоянно рассчитываться с использованием метода «базисное умножение на высоту».
Ромб
на самом деле это просто особый тип параллелограмма.
К ним также можно применить многие расчеты площади. Выберите формулу на основе значений, которые вы знаете для начала.
1. Метод «базис, умноженный на высоту»
Сначала выберите одну сторону в качестве основы. Подойдет любой, все они одинаковой длины.
Затем определите высоту — расстояние по перпендикуляру от выбранной базы до противоположной стороны.
Площадь является произведением этих двух или, как формула:
где
b — длина основания
a — высота (высота).
Воспользуйтесь калькулятором ниже, чтобы вычислить площадь ромба с учетом длины основания (стороны) и
высота (перпендикулярная высота).
Введите любые два значения, и будет вычислено недостающее.
Например, введите площадь и базовую длину, и будет рассчитана высота, необходимая для получения этой площади.
2. Метод «диагоналей»
Еще одна простая формула для определения площади ромба, когда известны длины диагоналей.
Площадь составляет половину произведения диагоналей.Как формула:
где
d 1 — длина диагонали
d 2 — длина другой диагонали
3. Использование тригонометрии
Если вы знакомы с тригонометрией, есть удобная формула, когда вы знаете длину стороны и любой угол:
где
s — длина любой стороны
a — любой внутренний угол
sin — синусоидальная функция
(см. Обзор тригонометрии)
Поначалу может показаться странным, что вы можете использовать любой угол, поскольку не все они равны.Но углы либо равны, либо
дополнительный,
и дополнительные углы имеют одинаковый синус.
Другие полигоны
Общие
Типы полигонов
Площадь различных типов полигонов
Периметр различных типов полигонов
Углы, связанные с многоугольниками
Именованные полигоны
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
Калькулятор ромбов
Что такое площадь и периметр ромба?
Четырехугольник с четырьмя равными сторонами — это ромб или ромб (см. Рисунок ниже).В некоторой литературе его называют равносторонним четырехугольником, так как все его стороны равны по длине.
Это означает, что если $ {\ overline {AB}} \ cong {\ overline {BC}} \ cong {\ overline {CD}} \ cong {\ overline {DA}} $, то $ {\ overline {ABCD}} $ — ромб.
Поскольку противоположные стороны параллельны, ромб является параллелограммом, но не каждый параллелограмм является ромбом. Это означает, что все свойства параллелограмма применимы и к ромбу. Напомним, что параллелограмм обладает следующими свойствами:
- Противоположные стороны параллелограмма равны;
- Противоположные углы параллелограмма равны;
- Последовательные углы параллелограмма дополняют друг друга;
- Диагонали параллелограмма делят друг друга пополам
Ромб обладает еще двумя свойствами:
- Диагонали делят пополам противоположные углы ромба;
- Диагонали ромба перпендикулярны.
Любой четырехугольник с перпендикулярными диагоналями, одна диагональ которых пересекается пополам, является воздушным змеем. Итак, ромб — это воздушный змей, но не каждый воздушный змей — ромб.
Любой четырехугольник, который одновременно является воздушным змеем и параллелограммом, является ромбом.
Поскольку диагонали ромба перпендикулярны, мы можем применить теорему Пифагора, чтобы найти длину стороны ромба.
Рассмотрим ромб $ \ overline {ABCD} $. Диагонали ромба делят друг друга пополам, $ \ overline {AO} \ cong \ overline {OC} $ и $ \ overline {BO} \ cong \ overline {OD}.o $ вращение против часовой стрелки вокруг точки $ O $ переводит ромб в себя.
Расстояние вокруг ромба называется периметром ромба. Обычно обозначается $ P $.
Чтобы найти периметр ромба, складываем длины его сторон. Таким образом, периметр ромба с длиной стороны $ a $ равен
$$ P = a + a + a + a = 4 \ times a $$
.
Площадь ромба — это количество квадратных единиц, необходимое для заполнения ромба. Площадь, обычно обозначаемая $ A $. Ромб и прямоугольник на одном основании и между одинаковыми параллелями равны по площади.2) $ и т. Д.
Площадь и периметр ромба со ступенями показывает полный пошаговый расчет для определения периметра и площади ромба с длиной стороны $ 10 \; in $ и мерой угла. $ 30 $ градусов по формулам периметра и площади. Для любых других значений длины стороны и меры угла ромба просто введите два положительных вещественных числа и нажмите кнопку СОЗДАТЬ РАБОТУ. Учащиеся начальной школы могут использовать эту область и периметр ромба для создания работы, проверки результатов периметра и площади двумерных фигур или для эффективного выполнения домашних заданий.
Калькулятор площади ромба
Калькулятор площади ромба — отличный инструмент для определения площади ромба, а также его периметра и других характеристик: диагоналей, углов, длины стороны и высоты. Взгляните на множество способов найти область ромба: по диагоналям ромба, используя основание и высоту, сторону и любой выбранный угол … Вы все еще не знаете, как найти площадь ромба или периметра ромба? Проверьте формулы площади ромба ниже или просто поэкспериментируйте с инструментом.
Ромб и его свойства
Ромб — это простой четырехугольник, у которого все стороны равны. Другие названия — равносторонний четырехугольник или ромб (как на игральных картах ♢).
Основные свойства ромба:
- Две диагонали ромба перпендикулярны и делят друг друга пополам,
- Его диагонали делят пополам противоположные углы,
- Противоположные углы имеют одинаковую меру.
Каждый ромб представляет собой параллелограмм и воздушный змей.
Формула площади ромба
Есть три полезные формулы для вычисления площади ромба:
- Зная основание и высоту
площадь = основание * высота
- Зная диагонали ромба
площадь = (e * f) / 2
- Знающая сторона и любой (!) Угол
площадь = s² * sin (угол)
Почему мы можем использовать любой угол в формуле площади последнего ромба? Потому что мы знаем, что два соседних угла являются дополнительными, и sin (угол) = sin (180 ° — угол) .
Существуют и другие варианты этих уравнений (например, вычисление площади с учетом высоты и угла), но они представляют собой всего лишь простые тригонометрические преобразования этих трех самых популярных формул площади ромба.
Ромб по периметру
Найти периметр ромба тривиально, если мы знаем длину стороны — это 4 * . Но что, если мы знаем только диагонали ромба? Проверим:
- Мы знаем, что диагонали перпендикулярны и делят друг друга пополам.Итак, ромб — это не что иное, как четыре равных треугольника с катетами, равными e / 2 и f / 2.
- Все, что нам нужно сделать, это найти гипотенузу треугольника. Вы можете использовать здесь калькулятор прямоугольного треугольника или калькулятор теорем Пифагора.
- Умножьте полученное значение гипотенузы на 4. Это ваш ромбовидный периметр!
Также вы можете использовать эту формулу:
-
периметр = 4 * √ (e / 2) ²- (f / 2) ²)
Или просто введите длину диагоналей в калькулятор площади ромба !
Как найти площадь ромба?
Вы все еще не знаете, как пользоваться калькулятором? Покажем его потенциал на простом примере:
- Введите первое значение, которое у вас есть .Предположим, это сторона = 10 дюймов
- Введите второе заданное значение . Например, угол, равный 30 °.
- Вау! Калькулятор площади ромба отображает все остальные значения — площадь, высоту, периметр, угол и диагонали . Впечатляет, правда?
Наш инструмент действительно гибкий — если есть возможность посчитать, он это сделает. Обычно двух заданных значений достаточно, попробуйте!
Квадрат — это ромб? Или ромб — это параллелограмм?
Ответ: да на оба вопроса. Каждый квадрат представляет собой ромб , так как для ромба единственное необходимое условие — это то, что все стороны должны быть одинаковой длины. Как вы прекрасно знаете, у квадрата должны быть равны все стороны и все четыре равных угла, поэтому он удовлетворяет условиям, чтобы быть ромбом.
Точно так же ромб — это параллелограмм , так как любая фигура должна иметь две пары параллельных сторон, чтобы быть параллелограммом, а у ромба они есть. Таким образом, ромб всегда является параллелограммом, но параллелограмм является ромбом только в частном случае — для параллелограмма с четырьмя сторонами одинаковой длины.
Как определить высоту ромба
Параллелограмм — это плоская форма с противоположными сторонами, которые параллельны и равны по длине. Ромб — это параллелограмм с четырьмя равными (совпадающими) сторонами, например ромб. Квадраты и прямоугольники также являются разновидностями параллелограммов. Вы можете рассчитать высоту ромба, если знаете другие значения, такие как площадь, основание или диагонали.
TL; DR (слишком долго; не читал)
Чтобы найти высоту ромба, используйте формулу высота = площадь ÷ основание.Если вы знаете диагонали ромба, но не знаете его площадь, используйте формулу площадь = (d1 x d2) ÷ 2, а затем примените площадь к первой формуле.
Свойства ромба
Независимо от размера ромба всегда применяются определенные правила. Все его стороны равны, его противоположные углы равны, а его две диагонали перпендикулярны (то есть они делят друг друга пополам под углом 90 градусов). Высота ромба (также называемая его высотой) — это кратчайшее перпендикулярное расстояние от его основания до противоположной стороны.Основание ромба может быть любой из четырех сторон, в зависимости от того, как он расположен.
Определение высоты по площади и основанию
Формула высоты ромба: высота = площадь ÷ основание. Например, если вы знаете, что площадь ромба составляет 64 см2, а основание — 8 см, вы получите 64 ÷ 8 = 8. Высота ромба 8 см. Помните, что основание — это одна из сторон, и они равны по длине, поэтому, если вы знаете длину одной из сторон, вы знаете длину их всех.
Эта же формула применяется независимо от размера ромба или единиц измерения. Например, у вас есть ромб площадью 1000 дюймов и основанием 20 дюймов. Выполните 1000 ÷ 20 = 50. Высота ромба 50 дюймов.
Определение высоты по диагоналям
Если вам известны диагонали и основание ромба, но не площадь, используйте формулу площадь = (d1 x d2) ÷ 2. Например, если вы знаете, что d1 равно 4 см, а d2 равно 6 см, вы прорабатываете (4 х 6) ÷ 2 = 12.Вы знаете, что это площадь 12 см2. Если основа 2 см, проработайте 12 ÷ 2 = 6. Высота ромба 6 см.
Площадь любого треугольника Площадь параллелограмма Площадь воздушного змея и ромба Объем твердых тел Площадь трапеции Составная площадь Объем и площадь поверхности Площадь поверхности.
Презентация на тему: «Площадь любого треугольника, площадь параллелограмма, площадь воздушного змея и ромб, объем твердых тел, площадь трапеции, составная площадь, площадь, площадь поверхности, площадь поверхности.»- стенограмма презентации:
ins [data-ad-slot = «4502451947»] {display: none! important;}}
@media (max-width: 800px) {# place_14> ins: not ([data-ad-slot = «4502451947»]) {display: none! important;}}
@media (max-width: 800px) {# place_14 {width: 250px;}}
@media (max-width: 500 пикселей) {# place_14 {width: 120px;}}
]]>
1
Площадь любого треугольника Площадь параллелограмма Площадь воздушного змея и ромба Объем твердых тел Площадь трапециевидной композитной площади Объем и площадь поверхности Площадь поверхности цилиндра Объем цилиндра Составной объем Тип исследования Вопросы
2
2 Простое определение областей: Площадь — это «сколько места занимает форма» Несколько типов особых областей Трапеция, ромб и воздушный змей, параллелограмм Любой тип треугольника
3
3 Критерии успеха учебного намерения 1.Знать формулу площади ЛЮБОГО треугольника. 1. Разработать формулу площади ЛЮБОГО треугольника. 2. Используйте формулу для решения проблем. 2. Правильно применяйте формулу. (показывает работу) (показывает работу) 3. Ответ, содержащий соответствующие единицы соответствующие единицы Любая область треугольника
4
4 h b Иногда называется высотой h = высота по вертикали.
5
5 Площадь любого треугольника 10 см 4 см Пример 2: Найдите площадь треугольника.На этот раз высота h вне треугольника.
6
6 Площадь любого треугольника 5 см 8 см Пример 3: Найдите площадь равнобедренного треугольника. www.mathsrevision.com Подсказка: сначала используйте теорему Пифагора! 4см
7
7 Площадь параллелограмма b Важное ПРИМЕЧАНИЕ h = высота по вертикали h
8
Критерии успеха учебного намерения 1.Знать формулу площади ЛЮБОГО ромба и воздушного змея. 1. Разработать единую формулу для площади ЛЮБОГО ромба и воздушного змея. 2. Используйте формулу для решения проблем. 2. Правильно применяйте формулы. (показывает работу) (показывает работу) 3.Ответ, содержащий соответствующие единицы соответствующие единицы Ромб и область змейки
9
9 Площадь ромба D d Эта часть ромба составляет половину маленького прямоугольника.
10
10 Площадь воздушного змея D d Точно такой же процесс, как у ромба
11
11 Площадь ромба и воздушного змея Пример 2: Найдите площадь V-образного воздушного змея.7см 4см
12
12 Критерии успеха в обучении 1. Знать формулу площади трапеции. 1. Разработать формулу площади трапеции. 2. Используйте формулу для решения проблем. 2. Правильно применяйте формулу. (показаны рабочие) (показаны рабочие) 3. Ответ, содержащий соответствующие единицы соответствующие единицы Трапеция Площадь
13
13 Площадь трапеции W X Y Z 1 2 a cm b cm h cm Два треугольника WXY и WYZ
14
14 Площадь трапеции Пример 1: Найдите площадь трапеции.6см 4см 5см
15
15 Критерии успеха в обучении 1. Знать термин «составной». 1. Показать, как мы можем применять основные формулы площади для решения более сложных форм. 2. Применять базовые формулы для решения составных фигур. 3. Ответ, содержащий соответствующие единицы соответствующие единицы Составные области
16
16 Составные области Мы можем использовать наши знания в основных областях для создания более сложных форм.4см 3см 5см 6см Пример 1: Найдите область стрелки.
17
17 Составные области Пример 2: Найдите область заштрихованной области. 11см 10см 8см 4см
18
Сводка Площади Трапеция Ромб и воздушный змей Параллелограмм Треугольник любого типа
19
Критерии успеха учебного намерения 1.Знать формулу объема любой призмы. 1. Понять формулу призмы для вычисления объема. 2.Разработка объемов для различных призм. 3. Ответьте, чтобы содержать соответствующие блоки и рабочие. соответствующие агрегаты и рабочие. Объем призм твердых тел
20
Определение: призма представляет собой твердую форму с однородным поперечным сечением Цилиндр (круглая призма) Пятиугольная призма Треугольная призма Гексагональная призма Объем = Площадь поперечного сечения x длина Объем твердых тел
21 год
Определение: призма — это сплошная форма с однородным поперечным сечением. Треугольная призма. Объем = Площадь x длина Q.Найдите объем треугольной призмы. 20 см 2 10 см = 20 x 10 = 200 см 3
22
www.mathsrevision.com Определение: призма — это твердое тело с однородным поперечным сечением. Объем = Площадь x длина Q. Найдите объем шестиугольной призмы. 43,2 см 2 20 см = 43,2 x 20 = 864 см 3 Гексагональная призма Объем твердых тел
23
Back Front Это СЕТЬ для треугольной призмы.5 граней 3 конгруэнтных прямоугольника 2 конгруэнтных треугольника 10 см 4 см Нетто и площадь поверхности Треугольная призма 4 см 10 см Низ 4 см FT BT
24
= 2 x3 = 6 см 2 Пример Найдите площадь поверхности прямоугольной призмы Рабочий прямоугольник 1 Площадь = lxb = 3 x10 = 30 см 2 Прямоугольник 2 Площадь = lxb = 4 x 10 = 40 см 2 Общая площадь = 6 + 6 + 30 + 40 +50 = 132 см 2 2 треугольника одинаковые 1 прямоугольник 3 см на 10 см 1 прямоугольник 4 см на 10 см 3 см 4 см 10 см 1 прямоугольник 5 см на 10 см Площадь треугольника = прямоугольник 3 Площадь = lxb = 5 x 10 = 50 см 2 5 см
25
Bottom Top LS Back RS Front Это сетка для кубовидной сетки и площади поверхности Кубоид 6 граней Конгруэнтны верху и низу Передняя и задняя конгруэнтные Левая и правая конгруэнтны 5см 4см 3см 5см 3см 4см 3см 4см
26
Передняя площадь = lxb = 5 x 4 = 20 см 2 Пример Найдите площадь поверхности кубовидной формы Рабочий 5 см 4 см 3 см Верхняя область = lxb = 5 x 3 = 15 см 2 Боковая площадь = lxb = 3 x 4 = 12 см 2 Общая площадь = 20+ 20 + 15 + 15 + 12 + 12 = 94 см 2 Передняя и задняя части одинаковы Верхняя и нижняя части одинаковы Правая и левая одинаковы
27
Критерии успеха учебного намерения 1.Узнать разделить баллон. 1. Объяснить, как рассчитать площадь поверхности цилиндра, используя базовую площадь. 2. Рассчитайте площадь поверхности цилиндра. Площадь поверхности цилиндра
28 год
Общая площадь поверхности = 2πr 2 + 2πrh Площадь поверхности цилиндра состоит из двух основных форм, можете вы их назвать. Изогнутая область = 2πrh цилиндр (круговая призма) h Площадь поверхности цилиндра Сторона кривой раската 2πr Верхняя область = πr 2 Нижняя область = πr 2
29
Пример: Найдите площадь поверхности цилиндра ниже: = 2π (3) 2 + 2π x 3 x 10 3 см Цилиндр (круговая призма) 10 см = 18π + 60π Площадь поверхности цилиндра Площадь = 2πr 2 + 2πrh = 78π см
30
Пример: сетка цилиндра приведена ниже.Найдите диаметр банки и общую площадь поверхности. 2r = Площадь поверхности цилиндра 2πr = 25 25 см 9 см 25 π Диаметр = 2r Площадь поверхности = 2πr 2 + 2πrh = 2π (25 / 2π) 2 + 2π (25 / 2π) x 9 = 625 / 2π + 25 x 9 = 324,5 см
31 год
Объем = Площадь x высота. Объем цилиндра можно представить как набор кругов, уложенных друг на друга. = πr 2 Объем цилиндра Цилиндр (круговая призма) x h h = πr 2 h
32
V = πr 2 h Пример: Найдите объем цилиндра ниже.= π (5) 2 x 10 5 см Цилиндр (круговая призма) 10 см = 250π см Объем цилиндра
33
Другие простые тома Составной том — это просто тома, состоящие из основных томов. r D r h Цилиндр = πr 2 h Цилиндр (круговая призма) h r
34
Критерии успеха учебного намерения 1. Знать, что такое составной том.1. рассчитать объемы для составных форм, используя знания из предыдущих разделов. 2. Составьте составные объемы, используя предыдущие знания об основных призмах. 3. Ответьте, чтобы содержать соответствующие блоки и рабочие. соответствующие агрегаты и рабочие. Объем призм твердых тел
35 год
Другие простые тома Составной том — это просто тома, состоящие из основных томов. r D r h Цилиндр = πr 2 h Цилиндр (круговая призма) h r
36
Объем твердого тела Q.Найдите объем составной формы. Составной том — это просто тома, состоящие из основных томов. Объем = Цилиндр + полусфера h = 6м r 2м
37
Объем твердой буквы Q. Эта детская игрушка сделана из двух одинаковых конусов. Рассчитайте общий объем. Составные тома — это просто тома, состоящие из основных томов. Объем = 2 x конус r = 10 см h = 60 см
38
39
.
