Содержание
Группа предметов, обладающих общим признаком, 5 (пять) букв
Экономический словарь терминов
Значение слова в словаре Экономический словарь терминов
совокупность ценных бумаг, банковских билетов, выпущенных под одним идентификатором; группа однородных товаров, предметов.
Энциклопедический словарь, 1998 г.
Значение слова в словаре Энциклопедический словарь, 1998 г.
СЕРИЯ (от лат. series — ряд) группа или ряд предметов, однородных или обладающих общим признаком. Разряд, категория ценных бумаг (напр., серия облигаций), документов (напр., серия паспорта), обозначаемых цифрами. Часть фильма, демонстрируемая самостоятельно….
Часть фильма, демонстрируемая самостоятельно….
Толковый словарь русского языка. С.И.Ожегов, Н.Ю.Шведова.
Значение слова в словаре Толковый словарь русского языка. С.И.Ожегов, Н.Ю.Шведова.
-и, ас. Последовательный ряд чего-н., что обладает общим признаком, объединено общим назначением, составляет одну группу. С. популярных брошюр. С. опытов. Изделие выпускается малыми сериями. Разряд, категория ценных бумаг, документов. С. и номер паспорта….
Толковый словарь русского языка. Д.Н. Ушаков
Значение слова в словаре Толковый словарь русского языка. Д.Н. Ушаков
серии, ж. (от латин. series). Группа или ряд предметов совершенно однородных или обладающих общим, объединяющим их признаком. Эти моторы выпускаются сериями. Паровоз серии «Л». Заем выпущен в 50 сериях по 100 облигаций в каждой. Серия научно-популярных…
(от латин. series). Группа или ряд предметов совершенно однородных или обладающих общим, объединяющим их признаком. Эти моторы выпускаются сериями. Паровоз серии «Л». Заем выпущен в 50 сериях по 100 облигаций в каждой. Серия научно-популярных…
Первая оскароносная актриса из италии 7 букв
- М – первая буква
- А – вторая буква
- Н – третья буква
- Ь – четвёртая буква
- Я – пятая буква
- Н – шестая буква
- И – седьмая буква
Летающий изумруд 7 букв
«Сосновая шишка» в евклидовом пространстве 5 букв
первый
I м. разг.
1) Тот, кто или что начинает ряд однородных предметов, явлений.
2) Тот, кто или что упомянут, назван раньше.
3) Тот, кто или что произошел или стал объектом какого-либо действия раньше всех остальных.
II м.
Тот, кто лучше всех.
III прил.
1) поряд. от числ. один; предшествующий второму при счете ряда однородных предметов, явлений.
один; предшествующий второму при счете ряда однородных предметов, явлений.
2) Тот, что упомянут, назван раньше.
3) Тот, что произошел или стал объектом какого-либо действия раньше всех остальных.
IV прил.
1) Первоначальный, самый ранний.
отт. Происходящий, действующий ранее всех остальных.
отт. Ближайший из предстоящих, из будущих.
2) Ранее не бывавший, впервые услышанный, испытанный.
отт. Ранее не существовавший, впервые созданный.
отт. Только что появившийся, свежий, ранний (обычно о явлениях природы).
3. перен.
Наиболее важный, самый значительный, первенствующий.
отт. Главный.
отт. Ведущий основную мелодию, верхний (о голосе, музыкальном инструменте).
4. перен.
Лучший из всех в каком-либо отношении; отличный.
5) Такой, который явился источником или объектом действия раньше всех остальных (обычно стоит после существительного или местоимения, к которому относится, и несет на себе главное ударение в предложении).
6.
Случайно попавшийся, встретившийся; любой, какой угодно.
первый
1. -ая, -ое.; числ. порядк.
к один 1)
2. прил.
1) Первоначальный, самый ранний; происходящий, действующий раньше других.
П-ое впечатление.
Первый посетитель.
П-ая встреча.
Первый рейс.
П-ое время (сначала)
Не первой молодости (не молод)
Первый удар (упреждающая бомбардировка военных объектов противника)
П-ая волна эмиграции (о массовом выезде из нашей страны в годы гражданской войны)
2) Лучший из всех в каком-л. отношении; отличный.
Первый ученик в классе.
Первый сорт сорт товара, следующий за высшим; также: о ком-, чём-л. самом хорошем
Первый среди равных. (книжн.)
П-ое лицо (руководитель какого-л. предприятия, учреждения)
П-ая леди страны (о супруге главы государства)
– первое апреля
– первым делом
– первым долгом
– из первых рук
– первое лицо
Ответы на кроссворд АиФ 44 2018 (31 10 2018)
- 1 С чем связан главный цветочный фестиваль Японии? (загаданное слово из 10 букв).
- 5 Князь, участвовавший в убийстве Григория Распутина (загаданное слово из 6 букв).
- 9 Вклад «вдовы Клико» в производство шампанского (загаданное слово из 6 букв).
- 10 «Раскладушка от дождя» (загаданное слово из 6 букв).
- 11 Специалист по «отношениям в обществе» (загаданное слово из 8 букв).
- 14 Какую княжну русский император Александр II намерен был короновать? (загаданное слово из 11 букв).
- 16 Какая коралловая рыбка попала на почтовые марки Гонконга? (загаданное слово из 4 букв).
- 18 «Хорошее … для парковки всегда на другой стороне улицы» (загаданное слово из 5 букв).
- 19 Пискля, жаждущий крови (загаданное слово из 5 букв).
- 20 Где родился Альберт Эйнштейн? (загаданное слово из 4 букв).
- 23 Отжатая лузга (загаданное слово из 4 букв).
- 28 «Игра в наслаждение праздностью» для Агаты Кристи (загаданное слово из 8 букв).
- 29 Любимый фасон меховой шапки у Михаила Горбачева (загаданное слово из 10 букв).

- 30 Капитан с лицом Дастина Хоффмана (загаданное слово из 4 букв).
- 31 Где построили первый в России завод по производству сгущенки? (загаданное слово из 8 букв).
- 32 Похмельный синдром снимает (загаданное слово из 6 букв).
- 33 Аналог нашего КГБ в ГДР (загаданное слово из 5 букв).
- 34 Чем пахал оратай когда-то? (загаданное слово из 4 букв).
- 40 «Просветитель переломов» (загаданное слово из 7 букв).
- 42 Бабушка, воспитавшая Михаила Лермонтова (загаданное слово из 9 букв).
- 43 «Аура святого» (загаданное слово из 4 букв).
- 44 Игрок на гуслях для морского царя (загаданное слово из 5 букв).
- 45 Бани древнеримского звучания (загаданное слово из 5 букв).
- 46 Из чего Янко Марнавич в пушкинских «Песнях западных славян» застрелил брата Кирилу? (загаданное слово из 7 букв).
- 47 «Отбойник бейсболиста» (загаданное слово из 4 букв).
- 48 «Холодная красавица» из рассказа «Столетник» Александра Куприна (загаданное слово из 7 букв).
- 49 «Красна девица, а сердце каменное» (русская загадка) (загаданное слово из 5 букв).
- 50 Секс-символ, ставший носить высокие каблуки с подачи Гая Ричи (загаданное слово из 5 букв).
- 51 Чей Дом моды в 50-х годах был самым большим в Париже? (загаданное слово из 5 букв).
- 52 Одна спальня на всех воспитанников (загаданное слово из 7 букв).
- 1 Работа секундомера (загаданное слово из 11 букв).
- 2 Ради чего приезжает на дачу Митя из фильма «Утомленные солнцем»? (загаданное слово из 5 букв).
- 3 Волнительное отношение (загаданное слово из 15 букв).
- 4 «Трудотерапия для уголовников» (загаданное слово из 7 букв).
- 6 Туман смерти (загаданное слово из 4 букв).
- 7 Русский император, чью историю написал Вольтер (загаданное слово из 4 букв).
- 8 Предохранитель глаза (загаданное слово из 4 букв).
- 10 Кто вечно скачет на Торнадо туда, где надо защитить обиженных и угнетенных? (загаданное слово из 5 букв).

- 12 «Тубус» из кондитер ской (загаданное слово из 5 букв).
- 13 Чеховская экранизация «… запоздалые» (загаданное слово из 5 букв).
- 15 Языческий идол (загаданное слово из 7 букв).
- 17 Летающий изумруд (загаданное слово из 7 букв).
- 18 Первая оскароносная актриса из Италии (загаданное слово из 7 букв).
- 21 «Сосновая шишка» в евклидовом простран стве (загаданное слово из 5 букв).
- 22 Пчелиный корм (загаданное слово из 5 букв).
- 24 У какой звезды в 16 лет случился бурный роман с режиссером Анд жеем Жулавским? (загаданное слово из 5 букв).
- 25 «Лучевое оружие» Вишну (загаданное слово из 5 букв).
- 26 Материальное … (загаданное слово из 11 букв).
- 27 Весь спектр товаров (загаданное слово из 11 букв).
- 31 «Колыбель Несси» (загаданное слово из 5 букв).
- 34 О каком мореходе нам Шахерезада поведала? (загаданное слово из 7 букв).
- 35 Агрессивность мещанства (загаданное слово из 7 букв).
- 36 «Суетится, как … перед заутреней» (загаданное слово из 3 букв).
- 37 Пассия Майка из мультфильма «Корпорация монстров» (загаданное слово из 5 букв).
- 38 В какой азиатской стране загар полагают уделом плебеев, а потому люди модные и зажиточные тщательно скрывают свою кожу от палящего солнца? (загаданное слово из 7 букв).
- 39 Кто оттоптал ноги всем своим партнершам по танцам? (загаданное слово из 7 букв).
- 41 Олимпийская столица на острове Хонсю (загаданное слово из 6 букв).
- 42 «Иностранная примесь» в речи (загаданное слово из 6 букв).
- 46 Оружие для корриды (загаданное слово из 4 букв).
Ответы на кроссворд из Аргументы и Факты 44 2018 (31 10 2018):
Ответы на кроссворд АиФ 44 2018 (31 10 2018)
1 С чем связан главный цветочный фестиваль Японии? (слово из 10 букв).
5 Князь, участвовавший в убийстве Григория Распутина (слово из 6 букв).
9 Вклад «вдовы Клико» в производство шампанского (слово из 6 букв).
10 «Раскладушка от дождя» (слово из 6 букв).
11 Специалист по «отношениям в обществе» (слово из 8 букв).
14 Какую княжну русский император Александр II намерен был короновать? (слово из 11 букв).
16 Какая коралловая рыбка попала на почтовые марки Гонконга? (слово из 4 букв).
18 «Хорошее … для парковки всегда на другой стороне улицы» (слово из 5 букв).
19 Пискля, жаждущий крови (слово из 5 букв).
20 Где родился Альберт Эйнштейн? (слово из 4 букв).
23 Отжатая лузга (слово из 4 букв).
28 «Игра в наслаждение праздностью» для Агаты Кристи (слово из 8 букв).
29 Любимый фасон меховой шапки у Михаила Горбачева (слово из 10 букв).
30 Капитан с лицом Дастина Хоффмана (слово из 4 букв).
31 Где построили первый в России завод по производству сгущенки? (слово из 8 букв).
32 Похмельный синдром снимает (слово из 6 букв).
33 Аналог нашего КГБ в ГДР (слово из 5 букв).
34 Чем пахал оратай когда-то? (слово из 4 букв).
40 «Просветитель переломов» (слово из 7 букв).
42 Бабушка, воспитавшая Михаила Лермонтова (слово из 9 букв).
43 «Аура святого» (слово из 4 букв).
44 Игрок на гуслях для морского царя (слово из 5 букв).
45 Бани древнеримского звучания (слово из 5 букв).
46 Из чего Янко Марнавич в пушкинских «Песнях западных славян» застрелил брата Кирилу? (слово из 7 букв).
47 «Отбойник бейсболиста» (слово из 4 букв).
48 «Холодная красавица» из рассказа «Столетник» Александра Куприна (слово из 7 букв).
49 «Красна девица, а сердце каменное» (русская загадка) (слово из 5 букв).
50 Секс-символ, ставший носить высокие каблуки с подачи Гая Ричи (слово из 5 букв).
51 Чей Дом моды в 50-х годах был самым большим в Париже? (слово из 5 букв).
52 Одна спальня на всех воспитанников (слово из 7 букв).
1 Работа секундомера (слово из 11 букв).
2 Ради чего приезжает на дачу Митя из фильма «Утомленные солнцем»? (слово из 5 букв).
3 Волнительное отношение (слово из 15 букв).
4 «Трудотерапия для уголовников» (слово из 7 букв).
6 Туман смерти (слово из 4 букв).
7 Русский император, чью историю написал Вольтер (слово из 4 букв).
8 Предохранитель глаза (слово из 4 букв).
10 Кто вечно скачет на Торнадо туда, где надо защитить обиженных и угнетенных? (слово из 5 букв).
12 «Тубус» из кондитер ской (слово из 5 букв).
13 Чеховская экранизация «… запоздалые» (слово из 5 букв).
15 Языческий идол (слово из 7 букв).
17 Летающий изумруд (слово из 7 букв).
18 Первая оскароносная актриса из Италии (слово из 7 букв).
21 «Сосновая шишка» в евклидовом простран стве (слово из 5 букв).
22 Пчелиный корм (слово из 5 букв).
24 У какой звезды в 16 лет случился бурный роман с режиссером Анд жеем Жулавским? (слово из 5 букв).
25 «Лучевое оружие» Вишну (слово из 5 букв).
26 Материальное … (слово из 11 букв).
27 Весь спектр товаров (слово из 11 букв).
31 «Колыбель Несси» (слово из 5 букв).
34 О каком мореходе нам Шахерезада поведала? (слово из 7 букв).
35 Агрессивность мещанства (слово из 7 букв).
36 «Суетится, как … перед заутреней» (слово из 3 букв).
37 Пассия Майка из мультфильма «Корпорация монстров» (слово из 5 букв).
38 В какой азиатской стране загар полагают уделом плебеев, а потому люди модные и зажиточные тщательно скрывают свою кожу от палящего солнца? (слово из 7 букв).
39 Кто оттоптал ноги всем своим партнершам по танцам? (слово из 7 букв).
41 Олимпийская столица на острове Хонсю (слово из 6 букв).
42 «Иностранная примесь» в речи (слово из 6 букв).
46 Оружие для корриды (слово из 4 букв).
По горизонтали: 1. Хризантема 5. Юсупов 9. Ремюаж 10. Зонтик 11. Социолог 14. Долгорукова 16. Скар 18. Место 19. Комар 20. Ульм 23. Жмых 28. Билбоке 29. Амбассадор 30. Крюк 31. Оренбург 32. Рассол 33. Штази 34. Соха 40. Рентген 42. Арсеньева 43. Нимб 44. Садко 45. Термы 46. Пистоль 47. Бита 48. Камелия 49. Вишня 50. Дауни 51. Диор 52. Дортаур.
Камелия 49. Вишня 50. Дауни 51. Диор 52. Дортаур.
По вертикали: 1. Хронометраж 2. Аресть 3. Эмоциональность 4. Каторга 6. Смог 7. Петр 8. Веко 10. Зорро 12. Эклер 13. Цветы 15. Истукан 17. Колибри 18. Маньяни 21. Конус 22. Перга 24. Марсо 25. Хакра 26. Обеспечение 27. Ассортимент 31. Озеро 34. Синдбад 35. Хамство 36. Бес 37. Селия 38. Вьетнам 39. Увалень 41. Нагано 42. Акцент 46. Пика.
Вскопанная полоса земля, 5 букв, 1 буква «Г», сканворд
Слово из 5 букв, первая буква — «Г», вторая буква — «Р», третья буква — «Я», четвертая буква — «Д», пятая буква — «А», слово на букву «Г», последняя «А». Если Вы не знаете слово из кроссворда или сканворда, то наш сайт поможет Вам найти самые сложные и незнакомые слова.
Отгадайте загадку:
Мужчина вёл большой грузовик. Огни на машине не были зажжены. Луны тоже не было. Женщина стала переходить дорогу перед машиной. Как удалось водителю разглядеть её? Показать ответ>>
Мужчина зашёл в тёмную комнату, что-то задел, стекло разбилось, и Люси умерла. Что произошло? Показать ответ>>
Что произошло? Показать ответ>>
Мчат колёса по дороге, Над дорогой мчатся ноги. Это еду я бегом. Это я бегу верхом! Я и сидя бегу, И сижу на бегу! И машину качу, И качусь, куда хочу! Показать ответ>>
Другие значения этого слова:
- «караван» гор
- Вереница горных вершин
- Вскопанная полоса земля
- Вскопанная полоса земля.
- вскопанная полоса на плантации
- Вытянутая в длину возвышенность; ряд, цепь небольших гор, холмов и т. п
- Вытянутая в длину возвышенность; ряд, цепь небольших гор, холмов; цепь подводных камней
- Вытянутая в длину возвышенность; ряд, цепь небольших гор, холмов; цепь подводных камней.
- Горный кряж
- Горный кряж, гребень
- общее название положительно вытянутых форм рельефа различных размеров, высоты и происхождения
- Положительная, вытянутая форма рельефа
- Полоса вскопанной земли
- Полоса вскопанной земли в огороде, на плантации
- Полоса вскопанной земли в огороде, цветнике, на плантации
- Полоса вскопанной земли в огороде, цветнике, на плантации.

- Полоса земли в огороде
- Полоса, ряд однородных предметов
- река в Московской области России, правый приток реки Озерны
- Русловая или огородная
- Ряд барханов
- Ряд гор, цепь холмов
- Ряд небольших гор, цепь холмов
- Узкая полоса вспаханной или вскопанной земли в огороде, цветнике
- Цепочка гор
- Цепь небольших гор
- Цепь подводных камней
- Цепь холмов
- Цепь холмов, невысоких гор
- что такое сельга
- Что такое сельга?
- Шест, перекладина под потолком от печи до противоположной стены в крестьянской избе
Случайная загадка:
Стоит Антошка На деревянной ножке. Руки из палки, В руках мочалки.
Показать ответ>>
Случайный анекдот:
Расстроенный Березовский подходит к Президенту:
— Попрощаемся, Владимир Владимирович, за границу уезжаю.
— Борис Абрамович, а присесть на дорожку?
Ещё анекдоты>>
Слово Гряда: Значение слова Гряда
Значение слова гряда
Новый толково-словообразовательный словарь русского языка. Автор Т. Ф. Ефремова.
Автор Т. Ф. Ефремова.
гряда ж. 1) а) Вытянутая в длину возвышенность; ряд, цепь небольших гор, холмов и т.п. б) Цепь подводных камней. 2) Узкая полоса вспаханной или вскопанной земли в огороде, цветнике. 3) Полоса, ряд однородных предметов.
Орфографический словарь
Балтийская гряда Балт`ийская гряд`а (возвы-шенность)
Толковый словарь под ред. C. И. Ожегова и Н.Ю.Шведовой
ГРЯДА, -ы, мн. -ы, -ам и -ы, -ам, ж. 1. (-ы, -ам). Полоса вскопаннойземли в огороде, цветнике, на плантации. 2. (-ы, -ам). Ряд последовательнорасположенных друг за другом или медленно движущихся предметов, обычнодалеких, крупных, бесфор-менных. Гряды волн. Г. дюн, барханов. Г. облаков,клубов дыма. II уменью, грядка, -и, ж. (к 1 знач.). II прил. грядковый, -ая,-ое (к 1 знач.; спец.), грядной, -ая, -ое (к 1 знач.; спец.), грядовой, -ая,-ое (к 1 знач.
) и грядовый, -ая, -ое (ко 2 знач.; спец.). Грядковые илигрядные культуры. Грядовые пески (в пустыне).
Толковый словарь В.И.Даля
ГРЯДА ж. ряд, цепь, полоса, вдольное возвышение, гребень; горный кряж, хребтик, грива по материку, веретье; коса по воде или перекат под водою. Булыжник грядами лежит. Этим болотом гряда пролегла. | Взрытая полоса земли в саду, в огороде, для посева. Дай курице гряду, изроет весь огородн. Доселе Макар гряды копал, а ныне Макар в воеводы попал. Паровые гряды, парниковые, парник, крытые стеклами. | Лежачая жердь или слега; переводина, перекладина. Грядка умалит. гряда, в различных знач. | Шест, слега, жердь, подвешенная или приделанная лежмя; всякая жердь из стены в стену. Платье на грядке, а дурак на руке. | Две жерди в черной избе, над челом печи, для сушки дров, лучины и пр. | Перм. полица, полка вровень с полатями, у печи, от стамика до стены; арх. полка вкруг избы, полавочник. | Сиб. брус или две толстые доски от печи (стамика) к стене противной дверям, воронец; под воронцом, сиб.
под грядками, идет перегородка, или приделан пересовец с занавесом, для отдела кути от избы. На грядки кладут также запас луку в мешках или плетенках, отчего и загадка: Сидит баба на грядках, вся в заплатках, кто на нее ни взглянет, всяк заплачет; а в сказке о бабе яге: Сама на печи, груди на грядке. | Подвесная жердь или жерди над кутью, для одежи. | Ниж. очеп для зыбки. | Грядки в телеге, две продольные жерди, сверху и снизу, образующие боковые края кузова и соединенные с концов вязками; в грядки вдалбливаются дуги. Грядки в ручной или переносной лестнице, ступени. | Иногда то же что нахлестка. Грядки сохи, казачки, рукояти. | Астрх. плот, на котором выделывают икру. | Грядкасмол. крупный лес по грядам, по гребням болот. Грядица тамб. перекладинка, нахлестка на концы тележных грядок. Грядочка умалит. грядка огородная и | перекладинка. Грядушка умалит. ряз. грядочка, особенно гряда скошенного сена, валок; | кур. перекладина, связь, нахлестка; | грядка повозки, облук, облучек. Грядовка ж.
твер. рожь из-под цепа, невейка, вороховая рожь. Грядной, грядочный или грядковый, до грядки или грядок относящийся. Грядистый, грядчатый, состоящий из грядок; имеющий вид грядок. Грядник м. увалистая местность из мелких, продольных холмов. Грядочник м. -ница ж. работник для копания и устройства огородных грядок. Грядиль ж. гра(е)диль, плужное дышло, вал, дрога, укрепляемая в комле рукоятей и связываемая с полозом или подошвой стояком. Грядовье ср. пск. прибороздка, тропа меж двух грядок.
Толковый словарь русского языка под ред. Д. Н. Ушакова
ГРЯДА гряды, мн. гряды, грядам, ж. 1. Узкая полоса вскопанной земли в огороде или цветнике. Засеять три гряды огурцов. 2. Ряд небольших гор, цепь холмов (книжн.). Урало-Карпатская гряда. 3. Ряд подводных камней, лежащих в одном направлении (книжн.). 4. Вереница однородных предметов (книжн. поэт.). Редеет облаков летучая гряда. Пушкин.
Современный толковый словарь
ГРЯДА , общее название положительно вытянутых форм рельефа различных размеров, высоты и происхождения.
Cловарь синонимов Н. Абрамова
гряда см. гора, ряд
5 букв в слове «гряда»: а г д р я.
Слова, образованные из 5 букв слова гряда:
а ад ар ард га гад гая гра град да даг дар дра дяга ра рад рд рда ря ряд ряда яга ягра яд яда яр ярд ярда
Слова из слова гряда, по длине
Слова, связанные со словом гряда:
Слова, начинающиеся на гряда
Слова, содержащие гряда
Слова, оканчивающиеся на гряда
Слова из слова гряда, если изменить одну букву
Слова на гр
Слова заканчивающиеся на да
Слова начинающиеся на гря
Слова с яда в конце
Слова из 5 букв, слова на букву г
Худрук театра Глобус | Кроссворды, Сканворды
1. Наводчик домушника.
2. Защита рулевой колонки.
3. Напиток, полученный перегонкой сидра.
4. Худрук театра «Глобус».
5. Штат со столицей Топика.
6. Порт на Каспийском море.
7. Экс-супруга Тома Круза Кэти ….
8. Часы, напоминающие семье о прадеде.
9. Жених Сюзанны.
10. Информация, расстроившая слушателя.
11. Перегородка под легкими.
12. Разница между приходом и расходом.
13. Полезная для здоровья прогулка.
14. Пейзаж художника, влюбленного в море.
15. Лилльский профи, нанятый Атосом.
16. Жаркий спор ученных заседателей.
17. Выходка «из ряда вон» эпатажного типа.
18. «Посыльный» с государственным поручением.
19. Образец для антигероя.
20. «Самогонка» из сосновой смолы.
21. «Хвост» свадебного платья.
22. Самая верхняя точка синусоиды.
23. И абрикотин, и «Бейлис».
24. Забитый в трубку паслен.
25. Псовые из отряда хищных.
26. Максимальное значение функции.
27. «Серп» в коленке.
28. Благоговейное уважение.
29. «Клей» из рыбных хрящей.
30. Суд, рассматривающий тяжбы.
31. «Подсказчик» биатлониста на трассе.
32. «Засевший» в голове шаблон поведения.
33. Бесхребетная каракатица.
34. Достопримечательность с Пражскими курантами.
35. Художник, создававший «пейзажи настроения».
36. Одержимость Наполеона в пижаме.
37. Группа однородных предметов или явлений.
38. «Битье по рукам» для профилактики.
39. «Камнепад» на экране компьютера.
40. Гигант у орнитологов.
41. Куст, обломанный перед Пасхой.
42. Наука, изучающая гербовую символику.
43. Страх, мешающий жить.
Ответы:
1. Сообщник. 2. Кожух. 3. Кальвадос. 4. Шекспир. 5. Канзас. 6. Астрахань. 7. Холмс. 8. Реликвия. 9. Фигаро. 10. Негатив. 11. Диафрагма. 12. Сальдо. 13. Моцион. 14. Марина. 15. Палач. 16. Полемика. 17. Эксцесс. 18. Эмиссар. 19. Прототип. 20. Скипидар. 21. Шлейф. 22. Максимум. 23. Ликер. 24. Табак. 25. Семейство. 26. Экстремум. 27. Мениск. 28. Пиетет. 29. Желатин. 30. Арбитраж. 31. Тренер. 32. Стереотип. 33. Моллюск. 34. Ратуша. 35. Левитан. 36. Мания. 37. Категория. 38. Острастка. 39. Тетрис. 40. Страус. 41. Верба. 42. Геральдика. 43. Фобия.
38. Острастка. 39. Тетрис. 40. Страус. 41. Верба. 42. Геральдика. 43. Фобия.
https://krosswordscanword.ru/otvety-na-skanwordy/xudruk-teatra-globus.htmlХудрук театра ГлобусadminОтветы на сканвордысканворд1. Наводчик домушника.
2. Защита рулевой колонки.
3. Напиток, полученный перегонкой сидра.
4. Худрук театра ‘Глобус’.
5. Штат со столицей Топика.
6. Порт на Каспийском море.
7. Экс-супруга Тома Круза Кэти ….
8. Часы, напоминающие семье о прадеде.
9. Жених Сюзанны.
10. Информация, расстроившая слушателя.
11. Перегородка под легкими.
12. Разница между приходом и расходом.
13. Полезная для здоровья прогулка.
14. Пейзаж…admin
AdministratorКроссворды, Сканворды
Часть концерта, 5 букв, первая буква Н — кроссворды и сканворды
номер
Слово «номер» состоит из 5 букв:
— первая буква Н
— вторая буква О
— третья буква М
— четвертая буква Е
— пятая буква Р
Посмотреть значние слова «номер» в словаре.
Альтернативные варианты определений к слову «номер», всего найдено — 61 вариант:
- «Этот … не пройдет»
- Боец орудийного, пулеметного, минометного расчета
- Визитка на спине футболиста
- Визитка трамвая и футболиста
- Выступление в концерте
- Гостиничная «квартира»
- Гостиничная комната
- Гостиничный …
- Девятка на футболке
- Дохлый или коронный
- Его может снять гаишник при нарушении правил дорожного движения
- Его можно увидеть на трамвае, в цирке, на спине футболиста
- Есть и у авто, и у телефона
- Забронированный в гостиннице
- Заказан в гостинице
- Знак, любящий расставлять цифры по порядку
- И коронный, и пустой
- И порядковый, и смертельный
- Идеальное помещение в гостинице
- Инвентарный .
 ..
.. - Индивидуальный у налогоплательщика
- ИНН
- Иногда его отбывают
- Коронный …
- Место, на котором становится охотник при облаве в результате жеребьевки
- На трамвае или на спине игрока
- Пара к серии в паспорте
- Пара к серии на лотерейном билете
- Планка, ярлык, бляха, кусок бумаги и т. п. с изображением цифры (как документ, знак регистрации, инвентарной описи учреждения и т. п.)
- Помещение в отеле
- Порядковая цифра
- Порядковое число
- Порядковое число предмета в ряду других однородных
- Порядковый …
- Порядковый … страницы
- Порядковый … химического элемента в таблице Менделеева равен числу протонов в атомном ядре
- После серии в паспорте и на купюре
- Самостоятельный эпизод в музыке
- Семерка на футболке Роналду
- Смертельный в цирке
- Солдат, сержант, выполняющий определенные обязанности в обслуживании орудия
- Твой телефонный .
 ..
.. - Телефонные цифры
- Телефонный адрес
- Трюк
- Уличная визитка здания
- Уличное «имя» дома
- Фильм Альфреда Хичкока «… 13»
- Цифра на бильярдном шаре
- Цифра на двери квартиры
- Цифровая визитка автомобиля
- Цифровой позывной телефона
- Цифры в паспорте
- Цифры на автобусе
- Что бронируют в отеле?
- Что выкидывают, но только фигурально?
- Что можно отколоть?
- Что на майке футболиста
- Что определяет АОН?
- Элемент концертного представления
- Эстрадное или цирковое выступление
%d1%80%d1%8f%d0%b4%20%d0%be%d0%b4%d0%bd%d0%be%d1%80%d0%be%d0%b4%d0%bd%d1%8b%d1%85%20%d1%87%d0%bb%d0%b5%d0%bd%d0%be%d0%b2 — со всех языков на все языки
Все языкиАнглийскийРусскийКитайскийНемецкийФранцузскийИспанскийШведскийИтальянскийЛатинскийФинскийКазахскийГреческийУзбекскийВаллийскийАрабскийБелорусскийСуахилиИвритНорвежскийПортугальскийВенгерскийТурецкийИндонезийскийПольскийКомиЭстонскийЛатышскийНидерландскийДатскийАлбанскийХорватскийНауатльАрмянскийУкраинскийЯпонскийСанскритТайскийИрландскийТатарскийСловацкийСловенскийТувинскийУрдуФарерскийИдишМакедонскийКаталанскийБашкирскийЧешскийКорейскийГрузинскийРумынский, МолдавскийЯкутскийКиргизскийТибетскийИсландскийБолгарскийСербскийВьетнамскийАзербайджанскийБаскскийХиндиМаориКечуаАканАймараГаитянскийМонгольскийПалиМайяЛитовскийШорскийКрымскотатарскийЭсперантоИнгушскийСеверносаамскийВерхнелужицкийЧеченскийШумерскийГэльскийОсетинскийЧеркесскийАдыгейскийПерсидскийАйнский языкКхмерскийДревнерусский языкЦерковнославянский (Старославянский)МикенскийКвеньяЮпийскийАфрикаансПапьяментоПенджабскийТагальскийМокшанскийКриВарайскийКурдскийЭльзасскийАбхазскийАрагонскийАрумынскийАстурийскийЭрзянскийКомиМарийскийЧувашскийСефардскийУдмурдскийВепсскийАлтайскийДолганскийКарачаевскийКумыкскийНогайскийОсманскийТофаларскийТуркменскийУйгурскийУрумскийМаньчжурскийБурятскийОрокскийЭвенкийскийГуараниТаджикскийИнупиакМалайскийТвиЛингалаБагобоЙорубаСилезскийЛюксембургскийЧерокиШайенскогоКлингонский
Все языкиРусскийАнглийскийДатскийТатарскийНемецкийЛатинскийКазахскийУкраинскийВенгерскийТурецкийТаджикскийПерсидскийИспанскийИвритНорвежскийКитайскийФранцузскийИтальянскийПортугальскийАрабскийПольскийСуахилиНидерландскийХорватскийКаталанскийГалисийскийГрузинскийБелорусскийАлбанскийКурдскийГреческийСловенскийИндонезийскийБолгарскийВьетнамскийМаориТагальскийУрдуИсландскийХиндиИрландскийФарерскийЛатышскийЛитовскийФинскийМонгольскийШведскийТайскийПалиЯпонскийМакедонскийКорейскийЭстонскийРумынский, МолдавскийЧеченскийКарачаевскийСловацкийЧешскийСербскийАрмянскийАзербайджанскийУзбекскийКечуаГаитянскийМайяАймараШорскийЭсперантоКрымскотатарскийОсетинскийАдыгейскийЯкутскийАйнский языкКхмерскийДревнерусский языкЦерковнославянский (Старославянский)ТамильскийКвеньяАварскийАфрикаансПапьяментоМокшанскийЙорубаЭльзасскийИдишАбхазскийЭрзянскийИнгушскийИжорскийМарийскийЧувашскийУдмурдскийВодскийВепсскийАлтайскийКумыкскийТуркменскийУйгурскийУрумскийЭвенкийскийЛожбанБашкирскийМалайскийМальтийскийЛингалаПенджабскийЧерокиЧаморроКлингонскийБаскскийПушту
Матрицы
— Руководство GeoGebra
GeoGebra поддерживает реальные матрицы, которые представлены в виде списка списков, содержащих строки матрицы.
Пример: В GeoGebra, {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}} представляет матрицу 3×3 \ begin {pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \ конец {pmatrix}
Чтобы отобразить матрицу с использованием форматирования LaTeX в графическом представлении, используйте команду FormulaText или перетащите определение матрицы из Algebra View в Graphics View .
Пример: В строке ввода введите FormulaText [{{1, 2, 3}, {4, 5, 6}, {7, 8, 9}}] для отображения матрицы с использованием форматирования LaTeX.
Доступ к элементам матриц
Для доступа к определенным элементам матрицы вы можете использовать команду элемента или упрощенный синтаксис, показанный в примере ниже:
Пример: Пусть матрица = {{1, 2}, {3, 4}} , тогда:
-
matrix (1, 1)возвращает первый элемент в первой строке: 1 -
matrix (2, 2),matrix (-1,2),matrix (2, -1)иmatrix (-1, -1)все возвращают второй элемент второй строки: 4 .
- Как правило, матрица
( i , j ), где i и j являются целыми числами, возвращает элемент матрицы, занимающий i-ю строку и j-ю строку столбец.
Матричные операции
Матричные операции — это операции со списками , поэтому следующие синтаксисы дают описанные результаты.
Примечание: Некоторые синтаксисы могут представлять операции, которые не определены таким же образом в наборе матриц.
Сложение и вычитание
-
Matrix1 + Matrix2: складывает соответствующие элементы двух совместимых матриц. -
Матрица1 - Матрица2: вычитает соответствующие элементы двух совместимых матриц.
Умножение и деление
-
Матрица * Число: умножает каждый элемент Матрицы на данное Число . -
Матрица1 * Матрица2: использует умножение матриц для вычисления результирующей матрицы.
Примечание: Строки первой и столбцы второй матрицы должны иметь одинаковое количество элементов.
Пример: {{1, 2}, {3, 4}, {5, 6}} * {{1, 2, 3}, {4, 5, 6}} дает матрицу {{9, 12, 15}, {19, 26, 33}, {29, 40, 51}}.
-
Матрица 2x2 * Точка (или вектор): умножает матрицу на заданную точку / вектор и дает точку.
Пример: {{1, 2}, {3, 4}} * (3, 4) дает точку A = (11, 25).
-
Матрица 3x3 * Точка (или вектор): умножает матрицу на заданную точку / вектор и дает точку.
Пример: {{1, 2, 3}, {4, 5, 6}, {0, 0, 1}} * (1, 2) дает вам точку A = (8, 20 ).
Примечание: Это особый случай аффинных преобразований, когда используются однородные координаты: (x, y, 1) для точки и (x, y, 0) для вектора.(-1) .
Прочие операции
Раздел Matrix Commands содержит список всех доступных команд, связанных с матрицами, таких как:
- Определитель [Матрица]: вычисляет определитель для данной матрицы.

- Инвертировать [Матрица]: инвертирует данную матрицу.
- Transpose [Matrix]: транспонирует данную матрицу.
- ApplyMatrix [Matrix, Object]: применить аффинное преобразование, заданное матрицей, к объекту.
- ReducedRowEchelonForm [Matrix]: преобразует матрицу в сокращенную форму строки-эшелона.
преобразований аффинных изображений в Python с помощью Numpy, Pillow и OpenCV
В этой статье я опишу, что значит применить аффинное преобразование к изображению и как это сделать в Python.Сначала я продемонстрирую низкоуровневые операции в Numpy, чтобы дать подробную геометрическую реализацию. Затем я перейду к более практическому использованию библиотек Python Pillow и OpenCV.
Эта статья была написана с использованием записной книжки Jupyter, и исходный код можно найти в моем репозитории GitHub, поэтому, пожалуйста, не стесняйтесь клонировать / форкнуть ее и экспериментировать с кодом.
Что такое аффинное преобразование
Согласно Википедии, аффинное преобразование — это функциональное отображение между двумя геометрическими (аффинными) пространствами, которые сохраняют точки, прямые и параллельные линии, а также отношения между точками. Все, что сводится к математической абстрактной формулировке, — это, грубо говоря, линейное преобразование, которое приводит, по крайней мере, в контексте обработки изображений, к одной или нескольким манипуляциям, таким как поворот, отражение, масштабирование или сдвиг, путем применения матрицы преобразования.
Все, что сводится к математической абстрактной формулировке, — это, грубо говоря, линейное преобразование, которое приводит, по крайней мере, в контексте обработки изображений, к одной или нескольким манипуляциям, таким как поворот, отражение, масштабирование или сдвиг, путем применения матрицы преобразования.
Хорошо то, что, поскольку это, по сути, двухмерная геометрическая операция, мы можем ее визуализировать. Позвольте мне начать с таблицы аффинных преобразований, описывающих каждый тип геометрической манипуляции.
| Тип преобразования | Матрица преобразования | Уравнение сопоставления пикселей |
|---|---|---|
| Личность | $$ \ begin {bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 и 0 и 1 \ end {bmatrix} $$ | $$ x ^ {‘} = x $$ $$ y ^ {‘} = y $$ |
| Масштабирование | $$ \ begin {bmatrix} c_ {x} & 0 & 0 \\ 0 & c_ {y} & 0 \\ 0 и 0 и 1 \ end {bmatrix} $$ | $$ x ^ {‘} = c_ {x} * x $$ $$ y ^ {‘} = c_ {y} * y $$ |
| Вращение * | $$ \ begin {bmatrix} cos \ Theta & sin \ Theta & 0 \\ -sin \ Theta & cos \ Theta & 0 \\ 0 и 0 и 1 \ end {bmatrix} $$ | $$ x ^ {‘} = x * cos \ Theta — y * sin \ Theta $$ $$ y ^ {‘} = x * cos \ Theta + y * sin \ Theta $$ |
| Перевод | $$ \ begin {bmatrix} 1 & 0 & t_ {x} \\ 0 & 1 & t_ {y} \\ 0 и 0 и 1 \ end {bmatrix} $$ | $$ x ^ {‘} = x + t_ {x} $$ $$ y ^ {‘} = y + t_ {y} $$ |
| Горизонтальные ножницы | $$ \ begin {bmatrix} 1 & s_ {h} & 0 \\ 0 & 1 & 0 \\ 0 и 0 и 1 \ end {bmatrix} $$ | $$ x ^ {‘} = x + s_ {v} * y $$ $$ y ^ {‘} = y $$ |
| Вертикальные ножницы | $$ \ begin {bmatrix} 1 & 0 & 0 \\ s_ {v} & 1 & 0 \\ 0 и 0 и 1 \ end {bmatrix} $$ | $$ x ^ {‘} = x $$ $$ y ^ {‘} = x * s_ {h} + y $$ |
* Аффинное преобразование использует угол поворота по часовой стрелке, что в отличие от типичного геометрического единичного круга углов, измеряемых при вращении против часовой стрелки с 0, начиная с положительной оси X, поэтому вы увидите, что отрицательное значение угол часто применяется.
'Обозначение здесь просто относится к преобразованной выходной координате x или y, а не к обозначению исчисления для производной
Для простой демонстрации я применю пару преобразований для управления координатами x и y следующих точек, которые имеют трехмерные компоненты x, y и индекс символа ascii, аналогично тому, как пиксель изображения имеет трехмерные компоненты x, y и частота (или интенсивность).
a = (0, 1, 0)
b = (1, 0, 1)
c = (0, -1, 2)
d = (-1, 0, 3)
Преобразованиями для этого примера будут масштабирование на 2 во всех направлениях и поворот на 90 градусов по часовой стрелке.Сначала я выполню трансформации индивидуально, чтобы показать прямой эффект, который каждая из них оказывает на перемещение точек, затем я объединю трансформации и применю их за одно действие.
Для начала я хочу построить массив Numpy (некоторые могут назвать это матрицей) с каждой строкой, представляющей точку, где первый столбец — это x, второй — y, а третий — индекс его буквы в символе ascii. установить аналогично приведенной ниже таблице. Затем я использую Matplotlib для построения точек (после применения неизменного преобразования Identity), чтобы дать базовое представление о том, где мы находимся.
установить аналогично приведенной ниже таблице. Затем я использую Matplotlib для построения точек (после применения неизменного преобразования Identity), чтобы дать базовое представление о том, где мы находимся.
| Точка | x (строка) | y (столбец) | индекс ascii |
|---|---|---|---|
| a | 0 | 1 | 0 |
| 1 1 | |||
| c | 0 | -1 | 2 |
| d | -1 | 0 | 3 |
import matplotlib.pyplot
импортировать numpy как np
строка импорта
# точки a, b и, c
a, b, c, d = (0, 1, 0), (1, 0, 1), (0, -1, 2), (-1, 0, 3)
# матрица с векторами-строками точек
А = np.массив ([a, b, c, d])
# 3x3 Матрица преобразования идентичности
I = np.eye (3)
color_lut = 'rgbc'
fig = plt.figure ()
топор = plt.gca ()
xs = []
ys = []
для строки в A:
output_row = I @ строка
x, y, i = output_row
xs. append (x)
ys.append (y)
i = int (i) # преобразовать float в int для индексации
c = color_lut [i]
plt.scatter (x, y, color = c)
plt.text (x + 0,15, y, f "{string.ascii_letters [i]}")
xs.append (xs [0])
ys.append (ys [0])
plt.plot (xs, ys, color = "серый", linestyle = 'dotted')
топор.set_xticks (np.arange (-2,5; 3; 0,5))
ax.set_yticks (np.arange (-2.5, 3, 0.5))
plt.grid ()
plt.show ()
append (x)
ys.append (y)
i = int (i) # преобразовать float в int для индексации
c = color_lut [i]
plt.scatter (x, y, color = c)
plt.text (x + 0,15, y, f "{string.ascii_letters [i]}")
xs.append (xs [0])
ys.append (ys [0])
plt.plot (xs, ys, color = "серый", linestyle = 'dotted')
топор.set_xticks (np.arange (-2,5; 3; 0,5))
ax.set_yticks (np.arange (-2.5, 3, 0.5))
plt.grid ()
plt.show ()
Три точки a, b и c нанесены на сетку после применения к ним преобразования идентичности с помощью простого скалярного произведения векторной матрицы, оставляя их неизменными.
Теперь я перейду к созданию матрицы преобразования масштабирования \ (T_s \), как показано ниже, которая масштабирует размещение точек во всех направлениях.
$$
T_s = \ begin {bmatrix}
2 & 0 & 0 \\
0 и 2 и 0 \\
0 и 0 и 1
\ end {bmatrix}
$$
Теперь я перейду к построению преобразованных точек, аналогичных тому, что было сделано с исходными точками, не измененными преобразованием идентичности, но на этот раз я буду применять матрицу преобразования масштабирования, определенную выше. Для лучшей визуализации я рисую пунктирную линию, соединяющую точки.
Для лучшей визуализации я рисую пунктирную линию, соединяющую точки.
# создать матрицу преобразования масштабирования
T_s = np.array ([[2, 0, 0], [0, 2, 0], [0, 0, 1]])
fig = plt.figure ()
топор = plt.gca ()
xs_s = []
ys_s = []
для строки в A:
output_row = T_s @ строка
x, y, i = строка
x_s, y_s, i_s = output_row
xs_s.append (x_s)
ys_s.append (y_s)
i, i_s = int (i), int (i_s) # преобразовать float в int для индексации
c, c_s = color_lut [i], color_lut [i_s] # это то же самое, но лучше быть явным
plt.разброс (x, y, color = c)
plt.scatter (x_s, y_s, color = c_s)
plt.text (x + 0,15, y, f "{string.ascii_letters [int (i)]}")
plt.text (x_s + 0.15, y_s, f "{string.ascii_letters [int (i_s)]} '")
xs_s.append (xs_s [0])
ys_s.append (ys_s [0])
plt.plot (xs, ys, color = "серый", linestyle = 'dotted')
plt.plot (xs_s, ys_s, color = "серый", linestyle = 'dotted')
ax.set_xticks (np.arange (-2.5, 3, 0.5))
ax.set_yticks (np.arange (-2.5, 3, 0.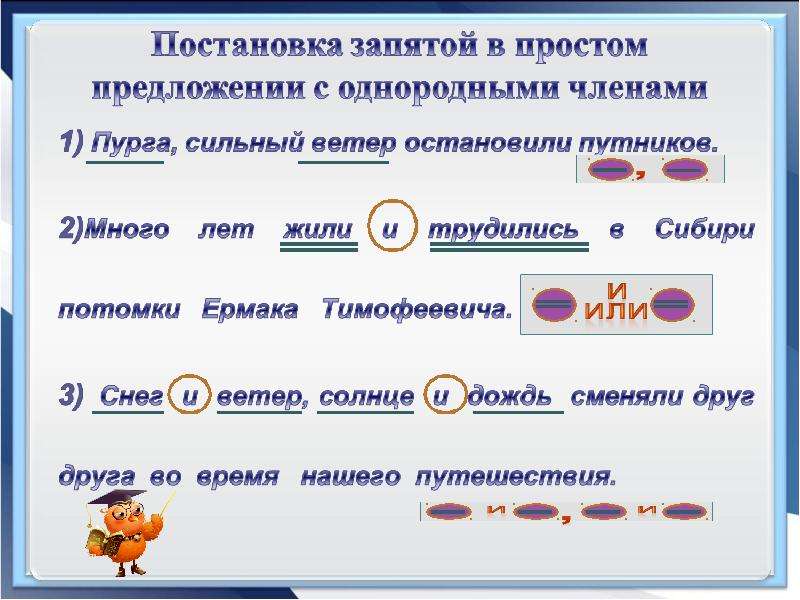 5))
plt.grid ()
plt.show ()
5))
plt.grid ()
plt.show ()
Из приведенного выше графика должно быть очень ясно, что измерения x и y были просто увеличены в два раза, в то время как третье измерение, отвечающее за буквенный индекс ASCII, осталось неизменным.Фактически, те, кто знаком с матричной алгеброй, заметят, что для всех аффинных преобразований, перечисленных в первой таблице, значение, представленное в третьем измерении, всегда остается неизменным, как указано всеми нулями и одним единственным значением в третьем измерении. индекс последнего столбца.
Теперь позвольте мне описать, как интерпретировать преобразование вращения. Я начну с решения двух тригонометрических функций для желаемого угла поворота 90 градусов, а затем просто вставлю их в матрицу преобразования поворота, указанную в предыдущей таблице.{o}) = 0
$$
$$
T_r = \ begin {bmatrix}
0 & 1 & 0 \\
-1 & 0 & 0 \\
0 и 0 и 1
\ end {bmatrix}
$$
Теперь все, что мне нужно сделать, это применить ту же логику для преобразования и построения точек, например:
# создать матрицу преобразования вращения
T_r = np. array ([[0, 1, 0], [-1, 0, 0], [0, 0, 1]])
fig = plt.figure ()
топор = plt.gca ()
для строки в A:
output_row = T_r @ строка
x_r, y_r, i_r = output_row
i_r = int (i_r) # преобразовать float в int для индексации
c_r = color_lut [i_r] # это то же самое, но лучше быть явным
letter_r = строка.ascii_letters [i_r]
plt.scatter (x_r, y_r, color = c_r)
plt.text (x_r + 0,15, y_r, f "{letter_r} '")
plt.plot (xs, ys, color = "серый", linestyle = 'dotted')
ax.set_xticks (np.arange (-2.5, 3, 0.5))
ax.set_yticks (np.arange (-2.5, 3, 0.5))
plt.grid ()
plt.show ()
array ([[0, 1, 0], [-1, 0, 0], [0, 0, 1]])
fig = plt.figure ()
топор = plt.gca ()
для строки в A:
output_row = T_r @ строка
x_r, y_r, i_r = output_row
i_r = int (i_r) # преобразовать float в int для индексации
c_r = color_lut [i_r] # это то же самое, но лучше быть явным
letter_r = строка.ascii_letters [i_r]
plt.scatter (x_r, y_r, color = c_r)
plt.text (x_r + 0,15, y_r, f "{letter_r} '")
plt.plot (xs, ys, color = "серый", linestyle = 'dotted')
ax.set_xticks (np.arange (-2.5, 3, 0.5))
ax.set_yticks (np.arange (-2.5, 3, 0.5))
plt.grid ()
plt.show ()
Надеюсь, вы можете сказать по графику, что все точки были повернуты на 90 градусов вокруг оси вращения в начале координат.
Отличная особенность аффинных преобразований, являющихся по существу линейными преобразованиями, заключается в том, что вы можете комбинировать преобразования и применять их за один шаг.Чтобы продемонстрировать это, я буду применять точечное произведение (матричное умножение) двух моих матриц преобразования, например:
$$
T_ {comb} = \ begin {bmatrix}
0 & 1 & 0 \\
-1 & 0 & 0 \\
0 и 0 и 1
\ end {bmatrix} *
\ begin {bmatrix}
2 & 0 & 0 \\
0 и 2 и 0 \\
0 и 0 и 1
\ end {bmatrix} =
\ begin {bmatrix}
0 и 2 и 0 \\
-2 & 0 & 0 \\
0 и 0 и 1
\ end {bmatrix}
$$
Теперь я могу применить эту комбинированную матрицу преобразования к точкам и перестроить их, чтобы показать комбинацию масштабирования на два и поворота на 90 градусов.
# создать комбинированную матрицу преобразования
T = T_s @ T_r
fig = plt.figure ()
топор = plt.gca ()
xs_comb = []
ys_comb = []
для строки в A:
output_row = T @ строка
x, y, i = строка
x_comb, y_comb, i_comb = output_row
xs_comb.append (x_comb)
ys_comb.append (y_comb)
i, i_comb = int (i), int (i_comb) # преобразовать float в int для индексации
c, c_comb = color_lut [i], color_lut [i_comb] # это то же самое, но лучше быть явным
буква, буква_комб = строка.ascii_letters [i], строка.ascii_letters [i_comb]
plt.scatter (x, y, color = c)
plt.scatter (x_comb, y_comb, color = c_comb)
plt.text (x + 0,15, y, f "{буква}")
plt.text (x_comb + 0.15, y_comb, f "{letter_comb} '")
xs_comb.append (xs_comb [0])
ys_comb.append (ys_comb [0])
plt.plot (xs, ys, color = "серый", linestyle = 'dotted')
plt.plot (xs_comb, ys_comb, color = "серый", linestyle = 'dotted')
ax.set_xticks (np.arange (-2.5, 3, 0.5))
ax.set_yticks (np.arange (-2.5, 3, 0. 5))
plt.grid ()
plt.show ()
5))
plt.grid ()
plt.show ()
Работа с изображением
К настоящему моменту я надеюсь, что смог сформировать некоторую интуицию о том, как аффинные преобразования используются для простого перемещения точек в 2D-пространстве, так что с учетом этого я хотел бы начать работу с некоторыми данными реального изображения. чтобы дать более конкретную демонстрацию того, как все это работает.
Это также позволяет мне затронуть другую важную тему аффинных преобразований, которая имеет дело с третьим измерением. Третье измерение данных в изображении представляет собой фактическое значение пикселя или иногда его называют областью интенсивности, тогда как физическое 2D-расположение пикселей в двух других измерениях называется пространственной областью.
Для начала я прочту и покажу изображение, используя matplotlib, которая представляет собой просто большую заглавную букву R.
img = plt.imread ('letterR.jpg')
img.shape # (1000, 1000, 4)
Используя метод imread (., я могу прочитать изображение JPG, представляющее заглавную букву R, в numpy ndarray. Затем я отображаю размеры массива, которые составляют 1000 строк на 1000 столбцов, вместе составляя 1000000 точек в пространственной области. Затем данные отдельных пикселей представлены в виде массива из 4 целых чисел без знака, представляющих красный, зеленый, синий и альфа-канал (или образец), которые вместе обеспечивают данные интенсивности каждого пикселя. ..)
..)
plt. Рисунок (figsize = (5, 5))
plt.imshow (img)
Затем я хотел бы применить предыдущий масштаб и поворот к пространственной области данных изображения, таким образом преобразовав местоположения пикселей, аналогично тому, что я продемонстрировал ранее с данными точек. Однако мне нужно использовать несколько иной подход, потому что данные изображения организованы иначе, чем строки точек данных, с которыми я работал ранее. С данными изображения мне нужно сопоставить индексы для каждого пикселя входных данных с преобразованными выходными индексами, используя матрицу преобразования T, определенную ранее.
# 2x для масштабирования требуется массив преобразованного изображения, вдвое превышающий исходное изображение
img_transformed = np.empty ((2000, 2000, 4), dtype = np.uint8)
для i строка в enumerate (img):
для j, столбец в перечислении (строка):
pixel_data = img [i, j,:]
input_coords = np.array ([i, j, 1])
i_out, j_out, _ = T @ input_coords
img_transformed [i_out, j_out,:] = pixel_data
plt.figure (figsize = (5, 5))
plt.imshow (img_transformed)
Построение изображения после применения преобразования ясно показывает, что исходное изображение было повернуто на 90 градусов по часовой стрелке и увеличено в 2 раза.Однако результат теперь явно ухудшился, так как вы можете легко увидеть неравномерность интенсивности пикселей.
Чтобы понять причину этого, я снова воспользуюсь простой сеткой для демонстрации. Рассмотрим график из 4 квадратов в сетке 2×2, аналогичный пространственной области изображения 2×2.
def plot_box (plt, x0, y0, txt, w = 1, h = 1):
plt.scatter (x0, y0)
plt.scatter (x0, y0 + h)
plt.scatter (x0 + w, y0 + h)
plt.scatter (x0 + w, y0)
plt.plot ([x0, x0, x0 + w, x0 + w, x0], [y0, y0 + h, y0 + h, y0, y0], цвет = "серый", стиль линии = 'пунктирный')
plt.текст (x0 + (.33 * w), y0 + (.5 * h), txt)
# x0, y0, буква
а = np.array ((0, 1, 0))
b = np.array ((1, 1, 1))
c = np.array ((0, 0, 2))
d = np.array ((1, 0, 3))
A = np.array ([a, b, c, d])
fig = plt.figure ()
топор = plt.gca ()
для точки в A:
x0, y0, i = I @ pt
x0, y0, я = int (x0), int (y0), int (i)
plot_box (plt, x0, y0, f "{string.ascii_letters [int (i)]} ({x0}, {y0})")
ax.set_xticks (np.arange (-1, 5, 1))
ax.set_yticks (np.arange (-1, 5, 1))
plt.grid ()
plt.show ()
Теперь посмотрите, что происходит, когда я применяю 2-кратное масштабное преобразование, как показано ниже.Напомним, что:
$$
T_s = \ begin {bmatrix}
2 & 0 & 0 \\
0 и 2 и 0 \\
0 и 0 и 1
\ end {bmatrix}
$$
Вы заметите, что такое пространственное преобразование приводит к . .. ну, «пробелам», выражаясь простым языком, что я сделал очевидным, нанеся вопросительные знаки вместе с координатами. Сетка 2×2 преобразуется в сетку 3×3 с изменением положения исходных квадратов на основе примененного линейного преобразования.Это означает, что (0,0) * \ (T_s \) остается (0,0) из-за своих свойств как вектора 0, но все остальные масштабируются на два, например (1,1) * \ (T_s \) -> (2,2).
.. ну, «пробелам», выражаясь простым языком, что я сделал очевидным, нанеся вопросительные знаки вместе с координатами. Сетка 2×2 преобразуется в сетку 3×3 с изменением положения исходных квадратов на основе примененного линейного преобразования.Это означает, что (0,0) * \ (T_s \) остается (0,0) из-за своих свойств как вектора 0, но все остальные масштабируются на два, например (1,1) * \ (T_s \) -> (2,2).
fig = plt.figure ()
топор = plt.gca ()
для точки в A:
xt, yt, i = T_s @ pt
xt, yt, я = int (xt), int (yt), int (я)
plot_box (plt, xt, yt, f "{string.ascii_letters [i]} '({xt}, {yt})")
delta_w, delta_h = 0,33, 0,5
plt.text (0 + delta_w, 1 + delta_h, "? (0, 1)")
plt.text (1 + delta_w, 0 + delta_h, "? (1, 0)")
plt.text (1 + delta_w, 1 + delta_h, "? (1, 1)")
plt.текст (1 + delta_w, 2 + delta_h, "? (1, 2)")
plt.text (2 + delta_w, 1 + delta_h, "? (2, 1)")
ax.set_xticks (np.arange (-1, 5, 1))
ax.set_yticks (np.arange (-1, 5, 1))
plt.grid ()
plt.show ()
Остается вопрос, что делать с теми пробелами, которые были внесены? Интуитивно понятная мысль — просто посмотреть на исходное изображение для ответа. Так уж получилось, что если мы применим обратное преобразование к координате на выходе, я получу соответствующее местоположение исходного ввода.{-1} * (2, 1, 1) = (1, 1/2, 1)
Так уж получилось, что если мы применим обратное преобразование к координате на выходе, я получу соответствующее местоположение исходного ввода.{-1} * (2, 1, 1) = (1, 1/2, 1)
$$
В этом случае я округлю y ‘= 1/2 до 0 и скажу, что это соответствует (1, 0). В общем смысле этот метод выбора значения в исходной сетке 2×2 для помещения в промежутки преобразованной сетки 3×3 известен как интерполяция, и в этом конкретном примере я использую упрощенную версию метода интерполяции ближайшего соседа.
Хорошо, теперь вернемся к данным изображения. Должно быть достаточно ясно, что нужно сделать сейчас, чтобы исправить эти пробелы в увеличенной и повернутой версии буквы R.Я должен разработать реализацию интерполяции ближайшего соседа на основе обратного сопоставления с использованием обратной матрицы преобразования T координат пикселей в преобразованном изображении, чтобы найти либо точное совпадение, либо ближайшего соседа в исходном изображении.
T_inv = np.linalg. inv (T)
# интерполяция ближайших соседей
def ближайший_седей (i, j, M, T_inv):
x_max, y_max = M.shape [0] - 1, M.shape [1] - 1
x, y, _ = T_inv @ np.array ([i, j, 1])
если np.floor (x) == x и np.этаж (y) == y:
х, у = int (х), int (у)
вернуть M [x, y]
если np.abs (np.floor (x) - x)
inv (T)
# интерполяция ближайших соседей
def ближайший_седей (i, j, M, T_inv):
x_max, y_max = M.shape [0] - 1, M.shape [1] - 1
x, y, _ = T_inv @ np.array ([i, j, 1])
если np.floor (x) == x и np.этаж (y) == y:
х, у = int (х), int (у)
вернуть M [x, y]
если np.abs (np.floor (x) - x) x_max:
x = x_max
если y> y_max:
y = y_max
вернуть M [x, y,]
img_nn = np.empty ((2000, 2000, 4), dtype = np.uint8)
для i строка в перечислении (img_transformed):
для j, столбец в перечислении (строка):
img_nn [i, j,:] = ближайшие_соседи (i, j, img, T_inv)
plt.рисунок (figsize = (5, 5))
plt.imshow (img_nn)
Не так уж и плохо, правда?
Следует отметить, что в большинстве случаев метода ближайшего соседа недостаточно.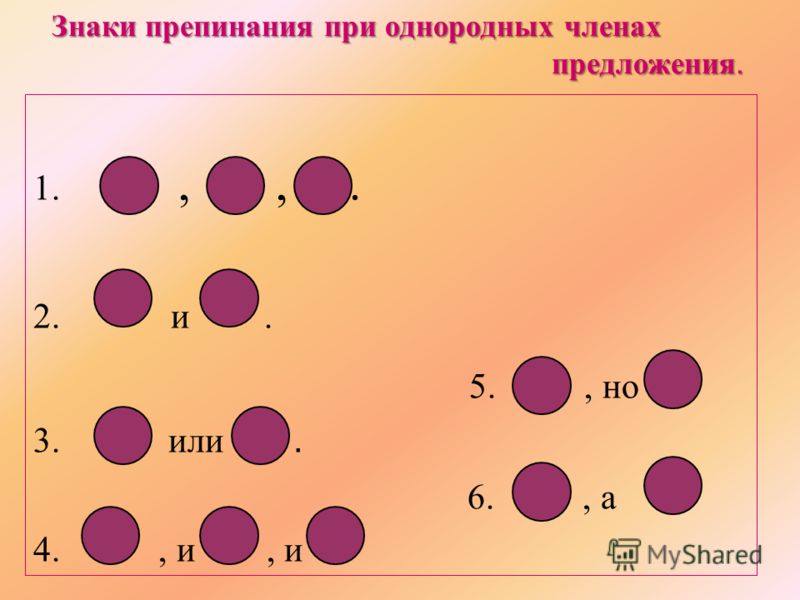 Есть два других более распространенных метода интерполяции, известных как билинейная и бикубическая интерполяция, которые обычно обеспечивают гораздо лучшие результаты. Я расскажу больше об этих других алгоритмах интерполяции при представлении библиотек Pillow и OpenCV в последних разделах. Цель этого раздела — просто создать интуитивное понимание того, как все работает.
Есть два других более распространенных метода интерполяции, известных как билинейная и бикубическая интерполяция, которые обычно обеспечивают гораздо лучшие результаты. Я расскажу больше об этих других алгоритмах интерполяции при представлении библиотек Pillow и OpenCV в последних разделах. Цель этого раздела — просто создать интуитивное понимание того, как все работает.
Аффинные преобразования с подушкой
В этом разделе я кратко расскажу, как использовать отличную библиотеку обработки изображений Python Pillow для выполнения аффинных преобразований.
Во-первых, необходимо установить подушку. Я использовал pip для этого, например:
$ pip install подушка
Теперь первый шаг — импортировать класс Image из модуля PIL (PIL — это имя модуля Python, связанного с Pillow) и прочитать его в моем изображении.
из изображения импорта PIL
Чтобы прочитать имя файла образца изображения «letterR. jpg», я вызываю метод класса
jpg», я вызываю метод класса Image.open (...) , передавая ему имя файла, который возвращает экземпляр класса Image , который я затем конвертирую в массив numpy и отобразить с помощью matplotlib.
img = Image.open ('letterR.jpg')
plt.figure (figsize = (5, 5))
plt.imshow (np.asarray (img))
Класс Pillow Image имеет удобный метод, называемый преобразованием (...) , который позволяет выполнять мелкозернистые аффинные преобразования, но есть несколько странностей, которые я должен обсудить в первую очередь, прежде чем приступить к его демонстрации. Метод преобразования (...) начинается с двух обязательных параметров, представляющих размер в виде кортежа высоты и ширины, за которым следует применяемый метод преобразования , которым в данном случае будет Image. .
Остальные параметры являются необязательными ключевыми аргументами, которые управляют выполнением преобразования. В случае этого примера я буду использовать параметр
В случае этого примера я буду использовать параметр data , который принимает первые две строки матрицы аффинного преобразования.
Например, матрица преобразования 2-кратного масштабирования, с которой я работал, урезанная до первых двух строк, выглядит так:
$$
T_s = \ begin {bmatrix}
2 & 0 & 0 \\
0 и 2 и 0
\ end {bmatrix}
$$
Последний параметр, который я буду использовать с преобразованием (...) Метод - это передискретизация , который используется для указания типа применяемого алгоритма интерполяции пикселей из возможных вариантов: Image.NEAREST (ближайший сосед), Image.BILINEAR или Image.BICUBIC . Этот выбор часто будет варьироваться в зависимости от применяемого преобразования. Однако билинейный и бикубический обычно дают лучшие результаты, чем ближайший сосед, но, как уже было продемонстрировано в этом примере, ближайший сосед работает довольно хорошо.
Есть несколько особенностей, которые послужили для меня настоящей ловушкой, когда я впервые использовал Image.transform (...) , особенно в отношении построения матрицы аффинного преобразования со странно обрезанной последней строкой. Таким образом, я хотел бы потратить некоторое время на то, чтобы понять, почему все работает именно так, потому что это своего рода процесс.
Первое, что должно произойти, - это преобразовать изображение так, чтобы начало координат (0, 0) находилось в середине изображения. В случае изображения 1000 x 1000 буквы R в этом примере это означает перевод -500 в координатах x и y.
Ниже я показываю общую матрицу преобразования трансляции \ (T_ {translate} \) и ту, которую я буду использовать в примере \ (T_ {neg500} \).
$$
T_ {translate} = \ begin {bmatrix}
1 & 0 & t_x \\
0 & 1 & t_y \\
0 и 0 и 1
\ end {bmatrix}
$$
$$
T_ {neg500} = \ begin {bmatrix}
1 & 0 & -500 \
0 & 1 & -500 \
0 & 0 & 1
\ end {bmatrix}
$$
Затем есть матрицы масштабирования 2X \ (T_ {scale} \) и поворота на 90 градусов \ (T_ {rotate} \) из предыдущих.Однако библиотека Pillow фактически решила использовать стандартные геометрические углы (то есть против часовой стрелки), а не вращение по часовой стрелке, которое я описал ранее, поэтому знаки функций sin меняются местами. Ниже приведены результирующие отдельные матрицы преобразования.
$$
T_ {rotate} = \ begin {bmatrix}
0 & -1 & 0 \\
1 & 0 & 0 \\
0 и 0 и 1
\ end {bmatrix}
$$
$$
T_ {scale} = \ begin {bmatrix}
2 & 0 & 0 \
0 & 2 & 0 \
0 & 0 & 1
\ end {bmatrix}
$$
Затем необходимо применить другую матрицу трансляции, которая действует для изменения положения пространственной области пикселей, по существу, отрицая первую, которая центрировала начало координат.В этом случае мне нужен положительный перевод 1000 по осям x и y, где 1000 происходит от удвоенного значения оригинала, потому что он был увеличен на два.
$$
T_ {pos1000} = \ begin {bmatrix}
1 & 0 & 1000 \\
0 и 1 и 1000 \\
0 и 0 и 1
\ end {bmatrix}
$$
Они составляют отдельные шаги преобразования, которые требуются, поэтому все, что остается, - это перемножить матрицы по порядку (т.е. справа налево), например:
$$
T = T_ {pos1000} * T_ {поворот} * T_ {масштаб} * T_ {neg500}
$$
Хорошо, есть еще одна странность.{-1}
$$
В коде это все работает следующим образом:
# рецентрированное результирующее изображение
T_pos1000 = np.array ([
[1, 0, 1000],
[0, 1, 1000],
[0, 0, 1]])
# поворот - противоположный угол
T_rotate = np.array ([
[0, -1, 0],
[1, 0, 0],
[0, 0, 1]])
# шкала
T_scale = np.array ([
[2, 0, 0],
[0, 2, 0],
[0, 0, 1]])
# центрировать оригинал до 0,0
T_neg500 = np.array ([
[1, 0, -500],
[0, 1, -500],
[0, 0, 1]])
T = T_pos1000 @ T_rotate @ T_scale @ T_neg500
T_inv = np.linalg.inv (T)
img_transformed = img.transform ((2000, 2000), Image.AFFINE, data = T_inv.flatten () [: 6], resample = Image.NEAREST)
plt.imshow (np.asarray (img_transformed))
Аффинные преобразования с OpenCV2
Продолжая, я хотел бы вкратце описать, как выполнять эти аффинные преобразования с помощью популярной библиотеки обработки изображений и компьютерного зрения OpenCV. Я использую здесь слово «краткое», потому что оно во многом совпадает с тем, что требуется в предыдущей демонстрации использования подушки.
Перво-наперво, вы должны установить так:
$ pip установить opencv-python
Как я уже упоминал выше, методология Pillow и использование OpenCV существенно пересекаются. Например, вы по-прежнему создаете матрицу преобразования, которая сначала центрирует массив пикселей относительно начала координат, и вы используете только первые две строки матрицы преобразования. Основное отличие состоит в том, что с OpenCV вы даете ему стандартную матрицу, а не обратную.
Итак, с изложенным выше пониманием я перейду к коду, начиная с импорта модуля opencv-python, который называется cv2 .
импорт CV2
Чтение изображения так же просто, как вызов метода cv2.imread (...) с передачей имени файла в качестве аргумента. Это возвращает данные изображения в форме трехмерного массива numpy, аналогично тому, как работает matplotlib, но данные пикселей в 3-м измерении состоят из массива каналов в следующем порядке: синий, зеленый, красный вместо красного, зеленого, синий, альфа, как и в случае чтения с помощью matplotlib.
Таким образом, для построения нескольких данных изображения, происходящих из библиотеки OpenCV, необходимо изменить порядок каналов пикселей. К счастью, OpenCV предоставляет убедительный метод cvtColor (...) , который можно использовать для этого, как показано ниже (хотя многие пуристы, вероятно, знают, что img [:,:, :: - 1] сделает одно и тоже).
img = cv2.imread ('letterR.jpg')
plt.imshow (cv2.cvtColor (img, cv2.COLOR_BGR2RGB))
Несколько последних элементов, которые следует упомянуть, это то, что OpenCV требует, чтобы данные в матрице преобразования имели тип 32-битного числа с плавающей запятой, а не 64-битное число с плавающей запятой по умолчанию, поэтому не забудьте преобразовать его до 32-битного с помощью numpy.float32 (...) . Кроме того, API для cv2.warpAffine (...) не предоставляет возможности указать, какой тип алгоритма интерполяции пикселей применять, и я не мог определить из документации, что используется. Если вы знаете или узнаете, напишите в комментариях ниже.
T_opencv = np.float32 (T.flatten () [: 6] .reshape (2,3))
img_transformed = cv2.warpAffine (img, T_opencv, (2000, 2000))
plt.imshow (cv2.cvtColor (img_transformed, cv2.COLOR_BGR2RGB))
Заключение
В этой статье я рассказал, что такое аффинное преобразование и как его можно применить к обработке изображений с помощью Python.Чистые numpy и matplotlib использовались, чтобы дать низкоуровневое интуитивное описание того, как работают аффинные преобразования. В заключение я продемонстрировал, как то же самое можно сделать с помощью двух популярных библиотек Python, Pillow и OpenCV.
Спасибо за чтение и, как всегда, не стесняйтесь комментировать или критиковать ниже.
ресурса
Описание вращения и перемещения в 2D
Теперь перенесем на картинку перевод. Система координат A, система координат B, которая перемещается и вращается относительно системы координат A и точки P.Мы можем представить точку P вектором относительно кадра B, и этот вектор можно описать в терминах его компонентов по осям XB и YB.
Теперь мы можем повернуть этот вектор в новый кадр, система координат V и система координат V имеет оси, параллельные системе координат A. Мы уже говорили о том, как повернуть вектор из одной системы координат в другую, используя вращение. матрица. И в качестве проверки правильности написания этого выражения мы заметили, что эти две B находятся рядом друг с другом.Это хорошая вещь.
Теперь давайте опишем начало системы координат V относительно системы координат A, и мы сделаем это с помощью вектора. Это вектор от A до V. Теперь нам разрешено добавлять векторы, чтобы мы могли добавить этот вектор ATV к вектору VP, чтобы получить вектор, который описывает точку P относительно системы координат A. Мы можем это сделать, потому что эти два векторы описываются относительно систем координат, оси которых параллельны друг другу. Я могу подставить одно уравнение в другое и написать это.И снова, поскольку эти две системы координат параллельны, я могу написать это.
Давайте расширим векторы и матрицу в этом выражении и запишем их в терминах их элементов. Теперь я могу немного потренироваться и написать это так. Если вы не уверены в этой глубине, разверните матрицу и убедитесь, что они точно такие же.
Теперь это выражение имеет двухэлементный вектор и трехэлементный вектор. Давайте сделаем вещи немного более симметричными и напишем это так.То, что мы сейчас опустили, это добавление нулей и единиц в нижнюю строку матрицы. Раньше у нас была матрица вращения 2x2. Теперь мы видим, что это встроено в верхний левый угол матрицы 3x3. И наши векторы, которые должны иметь 2 элемента, теперь имеют три элемента. Мы можем записать это еще лаконичнее в этой форме. Обозначение тильда над маленькой буквой p указывает на то, что это однородный фактор. В нем три элемента, а не два, и мы поговорим об этом чуть позже. Точка описывается относительно системы координат A однородным вектором, который мы можем получить из однородного вектора точки относительно системы координат B, умноженного на эту матрицу.
Элементы матрицы включают матрицу вращения, которая является функцией ориентации; Тета и перенос между началом системы координат A и системой координат B. У нас есть знакомое представление вектора в 2-мерной плоскости, два числа A и B. Однородный вектор содержит три элемента. У него есть A и B, а также дополнительный элемент, для которого установлено значение 1. Это мы называем однородным преобразованием. Это матрица 3x3. Однородная матрица преобразования T содержит матрицу вращения, которая равна 2x2, и вектор переноса, который представляет собой матрицу 2x1, дополненную парой нулей и единицей.
Эта матрица описывает относительную позу. Он описывает позу B относительно позы A. Все это закодировано в этой единственной матрице 3x3. Математик сказал бы, что однородное преобразование принадлежит специальной евклидовой группе размерности 2. Символически мы бы сказали, что матрица T принадлежит множеству SE (2).
Наконец-то пришло время воплотить эти абстрактные концепции в реальность. Поза - это просто матрица. Там, где у нас был символ ksi до того, как мы могли заменить эту однородную матрицу преобразования 3x3.Когда мы говорим о сложении или соединении двух поз вместе с помощью оператора O +, это в точности то же самое, что и умножение этих двух однородных преобразований. Мы используем O-оператор для обозначения отрицания относительной позы, а это просто обратная сторона однородной матрицы преобразования. Я упоминал ранее, что инверсия матрицы вращения равна ее транспонированию. Это не относится к однородной матрице преобразования. Вам нужно выполнить правильную инверсию матрицы: инвертировать матрицу 3x3.
Мы ввели оператор точки, который преобразует вектор из одной системы координат в другую. И это просто продукт однородной матрицы преобразования и вектора, представленного в однородной форме. Помните, что однородный вектор получается из исходного вектора P, двух векторов, и мы увеличиваем или добавляем один элемент к этому, чтобы сформировать трехэлементный вектор.
Здесь мы находимся в MATLAB и собираемся поэкспериментировать с этими двумерными однородными матрицами преобразования.Итак, что я собираюсь сделать, так это представить функцию под названием transl2, которая создает однородное преобразование, представляющее чистый перевод, то есть перевод 1 в направлении x и 2 в направлении y.
Ранее мы видели, как создать 2-мерную матрицу вращения, например, поворот на 30 градусов создается таким образом. Мы видим, что эта матрица вращения составляет всего 2x2 по сравнению с однородной матрицей преобразования 3x3. Таким образом, я могу создать однородную матрицу преобразования, эквивалентную этому вращению, поставив перед ней букву T.Эта функция возвращает однородную матрицу преобразования 3x3. Мы видим часть матрицы вращения вверху в верхнем левом углу. Мы видим, что трансляционная часть этой матрицы равна нулю. Эта однородная матрица преобразования представляет собой чистое вращение. Теперь мы можем перемножить эти два. transl2, умножьте на часть поворота - 30 градусов. И теперь у меня есть однородная трансформация, представляющая позу. У него есть вращательная составляющая и трансляционная составляющая.Теперь в наборе инструментов есть сокращенная функция для достижения этой цели. Я разбираю трансляционные части x и y; вращающаяся часть и возможность указать, что этот угол указывается в градусах. У нас здесь точно такая же матрица.
Теперь давайте нарисуем эту конкретную позу и посмотрим, как она выглядит. И для этого я собираюсь создать ось для построения графика, где x будет варьироваться от 0 до 5, а y будет от 0 до 5. Мне нужно установить соотношение сторон, чтобы все выглядело разумно, поэтому я собираюсь установить ось так, чтобы соотношение сторон было квадратным.Я собираюсь подождать, потому что собираюсь нарисовать несколько поз. Первую позу, которую я собираюсь построить, я помещаю в переменную рабочего пространства T1, и это поза, которую я смотрел только что назад: 1 по оси x, 2 по оси y и поворот на 30 градусов. . Имеется однородная матрица преобразования. Теперь я собираюсь это построить.
Для построения графика я использую функцию trplot2. Суффикс 2 означает, что это для двухмерных поз. Разбор в позе представлен однородной трансформацией.Я собираюсь изобразить его как кадр с именем 1, и я собираюсь нарисовать его синим цветом. Вариантов там довольно много. И вот мы видим нанесенную позу. Мы видим, что в нем действительно есть трансляционный компонент; 1 по оси x, 2 по оси y. И он повернут относительно мировой системы координат.
Я могу легко создать другую позу. Я могу создать позу со смещением 2 по оси x. 1 в направлении y и без вращения. Так выглядит однородное преобразование.Теперь я собираюсь это построить. Я собираюсь снова использовать функцию trplot2, проанализировать однородную матрицу преобразования, и я собираюсь изобразить ее как кадр с меткой 2. Чтобы отличаться, я собираюсь изобразить его как рамку красного цвета, а здесь мы видим вторую позу. У него нет ротации. В нем есть переводческая составляющая.
Теперь я могу составить 2 из этих поз. Я собираюсь сказать, что поза 3 равна позе 1 в сочетании с позой 2. Вот как выглядит матрица трансформации. Я могу это построить.Я собираюсь нанести на график этот, trplot2, синтаксический анализ в матрице, там будет кадр, названный 3, и я собираюсь покрасить его в зеленый цвет. Итак, если я объединю эти две позы, я получу позу, показанную здесь как 3. Мы можем думать об этом так: мы переместились из кадра мира 2 из кадра 1, который вращается, а затем в кадре 1 мы переместили 2 в в направлении x и 1 в направлении y. Но направление X и Y - это кадр 1, а не в мировом кадре, и это приводит нас к кадру, помеченному как кадр 3.
Я мог бы составить позы в обратном порядке.Я собираюсь создать новую позу T4, и это будет поза 2, смешанная с позой 1. Мы видим, как выглядит однородная матрица преобразования, и она отличается от T3. Я могу это построить. Я могу разбирать в Т4. Я могу изобразить его как рамку с меткой 4, и я собираюсь нарисовать ее в голубом цвете. Здесь мы видим кадр 4, полученный в результате объединения позы 2 с постом 1. Теперь я собираюсь ввести точку в сюжет. Я собираюсь ввести точку в координате 3, 2. Мне нужно транспонировать ее так, чтобы она стала вектором-столбцом.Вот оно. Я могу это построить. Отметьте точку P, которую я собираюсь построить, - это звездочка. Вот мы и видим это на нашем рисунке. Если я хочу определить координату точки относительно кадра 1, то мне нужно использовать инверсию относительной позы 1, которая есть таковая, и умножить ее на координату точек в однородной форме. Я возьму пункт P и добавлю к нему 1. Теперь у меня есть однородная координата звездочки относительно системы координат 1.
коэффициентов корреляции
коэффициентов корреляции
Вернуться к содержанию
Прикладная статистика - Урок 5
Обзор урока
Корреляция
Распространенное использование слова корреляция относится к
отношения между двумя или более объектами (идеи, переменные...).
В статистике слово корреляция относится к соотношению
между двумя переменными.
Мы хотим иметь возможность количественно определить эту взаимосвязь, измерить ее
сила, разработайте уравнение для прогнозирования оценок, и в конечном итоге
дает проверяемый вывод о родительской популяции.
Этот урок посвящен измерению его силы,
с уравнением из следующего урока,
и проверка выводов намного позже.
Примеры: одна переменная может быть количеством
охотники в регионе, а другой переменной может быть популяция оленей.Возможно, с увеличением числа охотников популяция оленей уменьшается.
Это пример отрицательной корреляции : как одна переменная
увеличивается, другой уменьшается. Положительная корреляция - это то место, где
две переменные реагируют одинаково, увеличиваясь или уменьшаясь вместе.
Температура в градусах Цельсия и Фаренгейта имеет положительную корреляцию.
Pearson Product Moment
Как узнать, есть ли корреляция?
Наблюдая за графиками, человек может определить, есть ли корреляция, по тому, как
данные напоминают линию.Если точки разбросаны, то
может быть без корреляции . Если точки будут точно соответствовать
квадратное или экспоненциальное уравнение, и т. д. ,
тогда они имеют нелинейную корреляцию .
В этом курсе мы ограничимся линейными корреляциями
и, следовательно, линейная регрессия.
Поскольку данные почти линейны, их можно заключить в эллипс.
Большая ось (длина) эллипса относительно малой оси (ширина) эллипса,
являются показателем степени корреляции.
Как при осмотре определить тип корреляции?
Если график переменных представляет собой линию с положительным наклоном, то
существует положительная корреляция ( x увеличивается по мере увеличения y ).
Если наклон линии отрицательный, значит, имеется отрицательная корреляция.
(при увеличении x y уменьшается).
Важным аспектом корреляции является то, насколько это сильный .
Сила корреляции измеряется корреляцией .
коэффициент r .Другое название для r - корреляция момента произведения Пирсона .
коэффициент в честь Карла Пирсона, который разработал его около 1900 года.
Обычно используются как минимум три разные формулы
чтобы вычислить это число и эти разные формулы
несколько представляют разные подходы к проблеме.
Однако такое же значение для r получается
с помощью любой из различных процедур.
Сначала мы приводим формулу оценки .
n имеет обычное значение того, сколько упорядоченных пар
находятся в нашей выборке. Также важно распознать
разница между суммой квадратов
и квадраты сумм!
Далее мы представляем формулу оценки отклонения .
Эта формула ближе к истории развития
поскольку он дает среднее перекрестное произведение
стандартные оценки двух переменных, но в
в вычислительном отношении более простой формат.
| r = xy sqrt ( x 2 y 2 ) |
Нам нужно сделать несколько замечаний относительно обозначений, поскольку
Переменные x и y в приведенной выше формуле
были преобразованы из исходных переменных
вычитая их средства.
Наконец, мы представляем ковариационную формулу ,
что является еще одним подходом.Ковариации обычно
дается между двумя переменными, и это одна из причин, почему.
(Следует отметить, что размер ковариации зависит от
об единицах измерения, используемых для каждой переменной.
Однако коэффициента корреляции нет.)
| r = s xy с x с y |
r часто обозначается как r xy
чтобы выделить две рассматриваемые переменные.Для выборок коэффициент корреляции представлен как r
а коэффициент корреляции для популяций обозначен
греческой буквой ро (которая может выглядеть как p ).
Имейте в виду, что коэффициент корреляции Спирмена ро
также использует греческую букву ро, но обычно применяется
выборкам и данным ранжируются (порядковые данные).
Чем ближе r к +1, тем сильнее положительная корреляция.
Чем ближе значение r к -1, тем сильнее отрицательная корреляция.Если | r | = 1 точно, две переменные отлично коррелируют !
Температура в градусах Цельсия и Фаренгейта прекрасно коррелирует.
Формальная проверка гипотез может быть применена к r
чтобы определить, насколько значим результат.
Это тема Хинкля главы 17 и
этот урок 12.
Распределение Student t с
n -2 степени свободы.
| Помните, что корреляция не подразумевает причинно-следственной связи. |
Нулевое значение для r не означает, что
корреляции нет, может быть нелинейная корреляция.
Смешивающие переменные также могут быть задействованы. Предположим, вы
обнаруживают, что у майнеров скорость выше среднего
рак легких. У вас может возникнуть соблазн немедленно заключить
что их занятие является причиной, в то время как, возможно,
регион имеет большое количество утечек радиоактивного газа радона
из субземных регионов и все люди в этой области затронуты.А может, они заядлые курильщики ....
r 2 часто используется и называется
Коэффициент детерминации .
Это доля вариации значений y
это объясняется регрессией наименьших квадратов y на x .
Об этом мы поговорим подробнее в уроке 6.
после введения наименьших квадратов.
Коэффициенты корреляции, величина которых находится в диапазоне от 0.9 и 1.0
укажите переменные, которые можно считать очень сильно коррелированными.
Коэффициенты корреляции от 0,7 до 0,9
указать переменные, которые можно считать сильно коррелированными.
Коэффициенты корреляции от 0,5 до 0,7
указать переменные, которые можно считать умеренно коррелированными.
Коэффициенты корреляции от 0,3 до 0,5
указывают переменные, которые имеют низкую корреляцию .
Коэффициенты корреляции, величина которых меньше 0,3
имеют небольшую (линейную) корреляцию.
Мы легко видим, что
0,9 < | r | <1.0 соответствует
0,81 < r 2 <1,00;
0,7 < | r | <0,9 соответствует
0,49 < r 2 <0,81;
0,5 < | r | <0,7 соответствует
0,25 < r 2 <0.49;
0,3 < | r | <0,5 соответствует
0,09 < r 2 <0,25; а также
0,0 < | r | <0,3 соответствует
0,0 < r 2 <0,09.
Spearman Rho для ранжированных / порядковых данных
Часто бывает так, что данные, которые мы хотим измерить, корреляцию
для не является интервалом или уровнем отношения измерения.
Был разработан коэффициент корреляции Спирмена ро.
чтобы справиться с этой ситуацией.Это досадное исключение из общего правила, что
Греческие буквы являются показателем численности населения! Есть и другие.
Формула для расчета ро Спирмена
коэффициент корреляции следующий.
| rho (p) = 1- 6 d 2 n ( n 2 -1) |
n - количество парных рангов и
d - разница между парными рядами.Если нет равных баллов, коэффициент корреляции Спирмена ро
будет еще ближе к коэффициенту корреляции момента произведения Пирсона.
Также обратите внимание, что эту формулу можно легко понять, когда
Вы понимаете, что сумма квадратов от 1 до n
может быть выражено как n ( n + 1) (2 n + 1) / 6.
Отсюда можно реализовать наименьшую сумму d 2
равно нулю, а наибольшая сумма d 2 равна
удвоенная сумма квадратов нечетных целых чисел до
n /2, а затем масштабирует такую сумму от -1 до +1.
Пример: Предположим, у нас есть результаты тестов.
из 110, 107, 100, 96, 89, 78, 67, 66 и 49.
Они соответствуют рангам с 1 по 9.
Если бы были дубликаты, то пришлось бы
найти средний рейтинг для дубликатов и
замените это значение на наши ряды.
Соответствующие итоговые оценки первой страницы были:
29, 32, 27, 29, 25, 25, 21, 26, 22.
Таким образом, эти ранги следующие:
2,5, 1, 4, 2,5, 6,5, 6,5, 9, 5, 8.
(Обратите внимание, что если мы изменили порядок, присвоение рангов
от низкого к высокому вместо высокого к низкому, в результате
Коэффициент корреляции Спирмена Ро изменил бы знак на противоположный.)
На основе информации, представленной выше, мы составили таблицу ниже.
Мы добавили дополнительные столбцы d и d 2
для простоты вычисления Spearman rho.
Используя формулу Спирмена ро, получаем 1-6 (24) / (9 (80)) = 0,80.
| Всего ( x ) | страница 1 ( y ) | x ранг | y ранг | d | d 2 | 9002 x 9002 | x 2 | y 2 |
|---|---|---|---|---|---|---|---|---|
| 110 | 29 | 1 | 2.5 | -1,5 | 2,25 | 3190 | 12100 | 841 |
| 107 | 32 | 2 | 1 | 1 | 1 | 3424 | 11449 | 1024 |
| 100 | 27 | 3 | 4 | -1 | 1 | 2700 | 10000 | 729 |
| 96 | 29 | 4 | 2.5 | 1,5 | 2,25 | 2784 | 9216 | 841 |
| 89 | 25 | 5 | 6,5 | -1,5 | 2,25 | 2225 | 7921 | 625 |
| 78 | 25 | 6 | 6,5 | -0,5 | 0,25 | 1950 | 6084 | 625 |
| 67 | 21 | 7 | 9 | -2 | 4 | 1407 | 4489 | 441 |
| 66 | 26 | 8 | 5 | 3 | 9 | 1716 | 4356 | 676 |
| 49 | 22 | 9 | 8 | 1 | 1 | 1078 | 2401 | 484 |
| --- | --- | ----- | ---- | ----- | ----- | ---- | ||
| 762 | 236 | : суммы: | 0 | 24 | 20474 | 68016 | 6286 | |
Мы добавили дополнительные столбцы xy , x 2 ,
и y 2 , чтобы упростить расчет
коэффициент корреляции момента произведения Пирсона.Использование формулы необработанной оценки для момента произведения Пирсона
коэффициент корреляции получаем (9 × 20474-762 × 236) / sqrt ((9 × 68016-762 2 ) (9 × 6286-236 2 )
= 0,843. r 2 = 0,71
что означает 71% отклонения от до
объясняется изменением в x .
Также верно и, возможно, более полезно знать, что та же самая корреляция
Коэффициент получается при обмене x и y .Однако в результате получится другое уравнение.
Возможно, имеет смысл использовать результаты первой страницы
чтобы предсказать окончательный результат теста, а не наоборот!
Факторы, влияющие на размер
r
Мы рассмотрели теперь, как рассчитать r ,
что означают разные значения, но это тоже важно
понять, какие факторы на это влияют.
Во-первых, помните, имеет смысл только вычислить
коэффициент корреляции, если данные
парных наблюдений измерений на интервале
или шкала соотношения.Далее, поскольку здесь мы имеем дело только с линейными
корреляция, момент произведения Пирсона
коэффициент корреляции недооценивает
отношения, если есть криволинейные отношения.
Перед
вычисление любых коэффициентов корреляции, а затем
продолжайте, только если корреляция достаточно сильна.
По мере того, как однородность группы увеличивается,
дисперсия уменьшается, а величина
коэффициент корреляции стремится к нулю.Таким образом, исследователь должен убедиться, что
достаточно неоднородности (вариации), чтобы
отношения могут проявиться.
В общем, коэффициент корреляции равен
не зависит от размера группы.
scale () - CSS: каскадные таблицы стилей
Функция CSS scale () определяет преобразование, которое изменяет размер элемента в 2D
самолет. Поскольку величина масштабирования определяется вектором, он может изменять размер по горизонтали и вертикали на
разные масштабы.Его результатом является тип данных .
Это масштабное преобразование характеризуется двумерным вектором. Его координаты определяют степень масштабирования.
сделано в каждом направлении. Если обе координаты равны, масштабирование будет равномерным ( изотропный ) и аспект
соотношение элемента сохраняется (это гомотетическое преобразование).
Когда значение координаты выходит за пределы диапазона [-1, 1], элемент увеличивается по этому измерению; когда внутри, это
сжимается.Если он отрицательный, результатом будет точечное отражение.
в этом измерении. Значение 1 не действует.
Примечание: Функция scale () масштабируется только в 2D. Для масштабирования в 3D используйте
scale3d () вместо этого.
Функция scale () задается одним или двумя значениями, которые представляют величину масштабирования.
для применения в каждом направлении.
шкала (sx)
масштаб (sx, sy)
Значения
-
sx - A
<число>, представляющее абсциссу вектора масштабирования. -
сы -
<число>, представляющее ординату вектора масштабирования. Если не определено, его значение по умолчанию
-sx, что приводит к равномерному масштабированию, сохраняющему соотношение сторон элемента.
| Декартовы координаты на ℝ 2 | Однородные координаты на ℝℙ 2 | Декартовы координаты на 3 | Однородные координаты на ℝℙ 3 |
|---|---|---|---|
| sx00sy | sx000sy0001 | sx000sy0001 | sx0000sy0000100001 |
[sx 0 0 sy 0 0] |
Масштабирование / масштабирование анимаций проблематично для доступности, поскольку они являются обычным триггером для определенных типов
мигрень.Если вам нужно включить такие анимации на свой веб-сайт, вы должны предоставить элемент управления, позволяющий пользователям включать
отключение анимации, желательно для всего сайта.
Также рассмотрите возможность использования медиа-функции Prefers-Reduced Motion
- используйте его для написания медиа-запроса, который отключит анимацию, если
пользователь уменьшил анимацию, указанную в их системных настройках.
Подробнее:
Масштабирование размеров X и Y вместе
HTML
Нормальный
В масштабе CSS
div {
ширина: 80 пикселей;
высота: 80 пикселей;
цвет фона: голубой;
}
.scaled {
преобразовать: масштаб (0,7);
цвет фона: розовый;
}
Результат
Масштабирование размеров X и Y отдельно, и
перевод происхождения
HTML
Нормальный
В масштабе CSS
div {
ширина: 80 пикселей;
высота: 80 пикселей;
цвет фона: голубой;
}
.scaled {
преобразовать: масштаб (2, 0,5);
трансформация происхождения: слева;
цвет фона: розовый;
}
Результат
таблицы BCD загружаются только в браузере
20.Словари - Как думать как компьютерный ученый: обучение с Python 3
Все составные типы данных, которые мы изучили до сих пор, - строки,
списки и кортежи - это типы последовательностей, которые используют целые числа в качестве индексов для доступа
ценности, которые они содержат в себе.
Словари - это еще один вид составного типа. Это Python
встроенное отображение типа . Они отображают ключей , которые могут быть любого неизменяемого типа,
к значениям, которые могут быть любого типа (разнородными), как и элементы
списка или кортежа.В других языках они называются ассоциативными.
массивы, поскольку они связывают ключ со значением.
В качестве примера мы создадим словарь для перевода английских слов на
Испанский. Для этого словаря ключи - это строки.
Один из способов создать словарь - начать с пустого словаря и добавить
ключ: пары значений . Пустой словарь обозначается {}:
>>> eng2sp = {}
>>> eng2sp ["один"] = "уно"
>>> eng2sp ["два"] = "дос"
Первое присвоение создает словарь с именем eng2sp; другой
присваивания добавляют в словарь новые пары ключ: значение.Мы можем распечатать текущий
значение словаря обычным способом:
>>> печать (eng2sp)
{"два": "дос", "один": "уно"}
Пары ключ: значение словаря разделяются запятыми. Каждая пара
содержит ключ и значение, разделенные двоеточием.
Хеширование
Порядок пар может отличаться от ожидаемого. Python использует
сложные алгоритмы, предназначенные для очень быстрого доступа, для определения
где пары ключ: значение хранятся в словаре.За наших
Мы можем думать об этом порядке как о непредсказуемом.
Вы также можете задаться вопросом, зачем мы вообще пользуемся словарями, когда
концепция сопоставления ключа со значением может быть реализована с использованием
список кортежей:
>>> {"яблоки": 430, "бананы": 312, "апельсины": 525, "груши": 217}
{"груши": 217, "яблоки": 430, "апельсины": 525, "бананы": 312}
>>> [('яблоки', 430), ('бананы', 312), ('апельсины', 525), ('груши', 217)]
[('яблоки', 430), ('бананы', 312), ('апельсины', 525), ('груши', 217)]
Причина в том, что словари очень быстрые, реализованы с использованием
метод, называемый хешированием, который позволяет нам получить доступ к значению очень
быстро.Напротив, реализация списка кортежей выполняется медленно. Если
мы хотели найти значение, связанное с ключом, нам нужно было бы
перебирать каждый кортеж, проверяя 0-й элемент. Что делать, если ключ
не было даже в списке? Мы должны дойти до конца, чтобы
выяснить.
Другой способ создать словарь - предоставить список пар ключ: значение.
используя тот же синтаксис, что и предыдущий вывод:
>>> eng2sp = {"one": "uno", "two": "dos", "three": "tres"}
Не имеет значения, в каком порядке мы пишем пары.Значения в словаре
доступ осуществляется с помощью ключей, а не индексов, поэтому нет необходимости беспокоиться о
заказ.
Вот как мы используем ключ для поиска соответствующего значения:
>>> print (eng2sp ["два"]) 'dos'
Клавиша «два» дает значение «дос».
Списки, кортежи и строки были названы последовательностями , потому что их элементы
происходят по порядку. Словарь - это первый составной тип, который мы
видно, что это не последовательность, поэтому мы не можем индексировать или разрезать словарь.
20,1. Словарные операции
Оператор del удаляет пару ключ: значение из словаря. Например,
следующий словарь содержит названия различных фруктов и количество
каждого фрукта на складе:
>>> inventory = {"яблоки": 430, "бананы": 312, "апельсины": 525, "груши": 217}
>>> распечатать (инвентарь)
{"груши": 217, "яблоки": 430, "апельсины": 525, "бананы": 312}
Если кто-то купит все груши, мы можем удалить запись из словаря:
>>> del inventory ["груши"]
>>> распечатать (инвентарь)
{'яблоки': 430, 'апельсины': 525, 'бананы': 312}
Или, если мы скоро ожидаем больше груш, мы можем просто изменить значение
связано с грушами:
>>> инвентарь ["груши"] = 0
>>> распечатать (инвентарь)
{'груши': 0, 'яблоки': 430, 'апельсины': 525, 'бананы': 312}
С поступающей новой партией бананов можно обращаться следующим образом:
>>> инвентарь ["бананы"] + = 200
>>> распечатать (инвентарь)
{'груши': 0, 'яблоки': 430, 'апельсины': 525, 'бананы': 512}
Функция len также работает со словарями; он возвращает число
пар ключ: значение:
20.2. Словарные методы
Словари
имеют ряд полезных встроенных методов.
Метод keys возвращает то, что Python 3 называет представлением его базовых ключей.
Объект представления имеет некоторое сходство с объектом диапазона, который мы видели ранее -
это ленивое обещание доставлять элементы, когда они нужны
остальная часть программы. Мы можем перебрать представление или превратить его в
список вроде этого:
для k в eng2sp.keys (): # Порядок k не определен print ("Получил ключ", k, "который соответствует значению", eng2sp [k]) ks = список (eng2sp.keys ()) печать (ks)
Это дает следующий результат:
Получил третий ключ, который соответствует значению tres Есть второй ключ, который соответствует значению dos. Получил ключ, который соответствует значению uno ['три, два, один']
Перебор ключей в словаре настолько распространен, что мы можем
опустить вызов метода ключей в цикле for - итерация по
словарь неявно перебирает свои ключи:
для k в eng2sp: print ("Получил ключ", k)
Метод значений аналогичен; он возвращает объект просмотра, который можно повернуть
в список:
>>> список (eng2sp.значения()) ['tres', 'dos', 'uno']
Метод items также возвращает представление, которое обещает список кортежей - один
кортеж для каждой пары ключ: значение:
>>> список (eng2sp.items ())
[('три', 'трэс'), ('два', 'дос'), ('один', 'уно')]
Кортежи часто полезны для получения и ключа, и значения одновременно.
время в цикле:
для (k, v) в eng2sp.items (): print ("Получил", k, "что соответствует", v)
Это дает:
Получил три, которые соответствуют tres Есть два, которые соответствуют досу Получил тот, который соответствует uno
Операторы in и not in могут проверить, есть ли ключ в словаре:
>>> "один" в eng2sp Правда >>> "шестерка" в eng2sp Ложь >>> "tres" in eng2sp # Обратите внимание, что in проверяет ключи, а не значения.Ложь
Этот метод может быть очень полезным, поскольку поиск несуществующего ключа в
словарь вызывает ошибку времени выполнения:
>>> eng2esp ["собака"] Отслеживание (последний вызов последний): ... KeyError: 'собака'
20,3. Псевдоним и копирование
Как и в случае со списками, поскольку словари изменяемы, мы должны быть
знает о наложении имен. В любое время
две переменные относятся к одному и тому же объекту, изменения одной влияют на другую.
Если мы хотим изменить словарь и сохранить копию оригинала, используйте
метод копирования.Например, противоположности - это словарь, содержащий пары
противоположностей:
>>> opposites = {"вверх": "вниз", "правильно": "неправильно", "да": "нет"}
>>> псевдоним = противоположности
>>> copy = opposites.copy () # Мелкая копия
псевдоним и противоположности относятся к одному и тому же объекту; копия относится к
свежая копия того же словаря. Если мы изменим псевдоним, противоположность будет
также изменилось:
>>> псевдоним ["right"] = "left" >>> Противоположности ["правильные"] 'оставил'
Если мы модифицируем копию, противоположности не меняются:
>>> copy ["right"] = "привилегия" >>> Противоположности ["правильные"] 'оставил'
20.4. Разреженные матрицы
Ранее мы использовали список списков для представления матрицы. Это хороший выбор
для матрицы с в основном ненулевыми значениями, но рассмотрим разреженную матрицу, подобную этой:
Представление списка содержит много нулей:
матрица = [[0, 0, 0, 1, 0],
[0, 0, 0, 0, 0],
[0, 2, 0, 0, 0],
[0, 0, 0, 0, 0],
[0, 0, 0, 3, 0]]
Альтернативой является использование словаря. Для ключей мы можем использовать кортежи, которые
содержат номера строк и столбцов.Вот словарное представление
та же матрица:
>>> matrix = {(0, 3): 1, (2, 1): 2, (4, 3): 3}
Нам нужны только три пары ключ: значение, по одной на каждый ненулевой элемент матрицы.
Каждый ключ - это кортеж, а каждое значение - целое число.
Чтобы получить доступ к элементу матрицы, мы могли бы использовать оператор []:
Обратите внимание, что синтаксис словарного представления отличается от синтаксиса
синтаксис для представления вложенного списка.Вместо двух целочисленных индексов мы
используйте один индекс, который представляет собой набор целых чисел.
Есть одна проблема. Если мы укажем нулевой элемент, мы получим ошибку,
потому что в словаре нет записи с этим ключом:
>>> матрица [(1, 3)] KeyError: (1, 3)
Эту проблему решает метод get:
>>> matrix.get ((0, 3), 0) 1
Первый аргумент - это ключ; второй аргумент - это значение, которое должно получить
вернуть, если ключа нет в словаре:
>>> матрица.получить ((1, 3), 0) 0
get определенно улучшает семантику доступа к разреженной матрице. Стыд
по поводу синтаксиса.
20,5. Воспоминание
Если вы поигрались с функцией fibo из главы о рекурсии, вы
могли заметить, что чем больше аргумент вы приводите, тем дольше
функция запускается. Кроме того, время работы увеличивается очень быстро. На одной
наших машин fib (20) завершается мгновенно, fib (30) принимает
около секунды, а fib (40) занимает примерно вечность.
Чтобы понять почему, рассмотрим график вызовов для fib с
п = 4:
График вызовов показывает некоторые функциональные фреймы (случаи, когда функция
был вызван), с линиями, соединяющими каждый кадр с
кадры функций, которые он вызывает. Вверху графика fib
с n = 4 вызывает fib с n = 3 и n = 2. В свою очередь,
fib с n = 3 вызывает fib с n = 2 и n = 1.
И так далее.
Посчитайте, сколько раз вызывается fib (0) и fib (1). Это
неэффективное решение проблемы, и оно становится еще хуже, поскольку аргумент
становится больше.
Хорошее решение - отслеживать значения, которые уже были вычислены
сохраняя их в словаре. Ранее вычисленное значение, которое сохраняется для
более позднее использование называется памяткой . Вот реализация fib
с использованием служебных записок:
уже известно = {0: 0, 1: 1} def fib (n): если n не в уже известном: новое_значение = fib (n-1) + fib (n-2) уже известно [n] = новое_значение вернуть уже известно [n]
Словарь с именем "уже известно" отслеживает числа Фибоначчи, которые мы
уже знаем.Начнем только с двух пар: 0 соответствует 1; и 1 карта на 1.
Каждый раз, когда вызывается fib, он проверяет словарь, чтобы определить,
содержит результат. Если он там есть, функция может немедленно вернуться без
делать больше рекурсивных вызовов. Если нет, он должен вычислить новое значение. В
новое значение добавляется в словарь перед возвратом функции.
Используя эту версию fib, наши машины могут вычислять
fib (100) в мгновение ока.
>>> фиб (100) 3542248481792615
20.6. Подсчет букв
В упражнениях в главе 8 (Строки) мы написали функцию, которая подсчитывала количество вхождений
буква в строке. Более общий вариант этой проблемы состоит в том, чтобы сформировать
частотная таблица букв в строке, то есть сколько раз каждая буква
появляется.
Такая таблица частот может быть полезна для сжатия текстового файла. Потому что разные
буквы появляются с разной частотой, мы можем сжать файл, используя
более короткие коды для общих букв и более длинные коды для букв, которые отображаются меньше
часто.
Словари
предоставляют элегантный способ создания таблицы частот:
>>> letter_counts = {}
>>> для письма в "Миссисипи":
... letter_counts [письмо] = letter_counts.get (письмо, 0) + 1
...
>>> letter_counts
{'M': 1, 's': 4, 'p': 2, 'i': 4}
Начнем с пустого словаря. Для каждой буквы в строке мы находим
текущий счетчик (возможно, ноль) и увеличить его. В конце словарь
содержит пары букв и их частоты.
Было бы более привлекательно отображать частотную таблицу в алфавитном порядке. Мы
можно сделать это с помощью элементов и методов сортировки:
>>> letter_items = список (letter_counts.items ())
>>> letter_items.sort ()
>>> print (letter_items)
[('M', 1), ('i', 4), ('p', 2), ('s', 4)]
Обратите внимание, что в первой строке мы должны были вызвать список функций преобразования типов.
Это превращает обещание, которое мы получаем от элементов, в список, шаг, который
необходимо, прежде чем мы сможем использовать метод сортировки списка.
20,7. Глоссарий
- график звонков
- Граф, состоящий из узлов, которые представляют функциональные фреймы (или вызовы),
и направленные края (линии со стрелками), показывающие, какие кадры дали
подняться на другие кадры. - словарь
- Набор пар ключ: значение, отображающий ключи в значения. Ключи
может быть любым неизменяемым значением, а связанное значение может быть любого типа. - неизменное значение данных
- Значение данных, которое нельзя изменить.Присвоения элементам или
срезы (части) неизменяемых значений вызывают ошибку времени выполнения. - ключ
- Элемент данных, который является , сопоставлен со значением в словаре. Ключи используются
искать значения в словаре. Каждый ключ должен быть уникальным
по словарю. - ключ: пара значений
- Одна из пар словаря. Значения ищутся в
словарь по ключу. - тип отображения
- Тип отображения - это тип данных, состоящий из набора ключей и
связанные значения.Единственный встроенный тип сопоставления Python - это
Словарь. Словари реализуют
ассоциативный массив
абстрактный тип данных. - записка
- Временное хранилище предварительно вычисленных значений, чтобы избежать дублирования одного и того же вычисления.
- значение изменяемых данных
- Значение данных, которое можно изменить. Типы всех изменяемых значений
являются составными типами. Списки и словари изменяемы; струны
а кортежи - нет.
20,8. Упражнения
Напишите программу, которая читает строку и возвращает
таблица букв алфавита в алфавитном порядке, которые встречаются в
строка вместе с количеством повторений каждой буквы.Дело должно
игнорировать. Пример вывода программы, когда пользователь вводит данные
«ThiS - строка с прописными и строчными буквами» будет выглядеть так:а 2 c 1 d 1 e 5 г 1 ч 2 я 4 l 2 п 2 o 1 п 2 r 4 с 5 т 5 u 1 w 2
Дайте ответ интерпретатора Python на каждое из следующих из
непрерывная сессия переводчика:>>> d = {"яблоки": 15, "бананы": 35, "виноград": 12} >>> d ["бананы"]>>> d ["апельсины"] = 20 >>> len (d)
>>> фрукты = список (г.ключи ()) >>> fruit.sort () >>> печать (фрукты)
>>> del d ["яблоки"] >>> "яблоки" в д
Убедитесь, что вы понимаете, почему вы получаете каждый результат. Затем примените то, что вы
научились заполнять тело функции ниже:def add_fruit (инвентарь, фрукты, количество = 0): возвращаться # Заставить эти тесты работать ... new_inventory = {} add_fruit (новый_инвентарь, «клубника», 10) тест ("клубника" в новом_инвентаре) тест (новый_инвентарь ["клубника"] == 10) add_fruit (новый_инвентарь, «клубника», 25) тест (новый_инвентарь ["клубника"] == 35)Напишите программу под названием alice_words.py, который создает текстовый файл с именем
alice_words.txt, содержащий алфавитный список всех слов, и
количество раз, которое каждое встречается в текстовой версии Приключения Алисы в стране чудес .
(Вы можете получить бесплатную текстовую версию книги, а также многие другие, по адресу
http://www.gutenberg.org.) Первые 10 строк вашего выходного файла должны выглядеть
примерно так:Word Count ======================= а 631 а-часть 1 соблюдать 1 в состоянии 1 около 94 выше 3 отсутствие 1 абсурд 2
Сколько раз слово алиса встречается в книге?
Какое самое длинное слово в Алисе в стране чудес? Сколько в нем персонажей?
Массив структур - MATLAB
Начиная с R2019a, размеры расширенного массива структур согласованы
назначаете ли вы значение отдельному полю, используя точечную нотацию или назначаете все
структура в массив.Раньше выходные размеры были другими, когда вы
не указали индексы по всем параметрам. Присвоение полю с использованием точечной записи
теперь соответствует предыдущему поведению при назначении структуры, которое согласуется с
общее расширение массива. Например:
Если
S- 1 на 2 на 3 на 4, то
S (5,2) = struct ('a', 3)и
S (5,2) .a = 3оба расширяютSдо
5 на 2 на 3 на 4.РанееS (5,2) .a = 3приводило к
Массив 5 на 24.Если
S- 0 на 5 или 5 на 0, то
S (3) = struct ('a', 2)иS (3) .a = 2
оба расширяютSдо 1 на 3. Ранее,
S (3) .a = 1привело к массиву 1 на 5, когда
Sбыло 0 на 5 и в массиве 3 на 1, когда
Sбыло 5 на 0.Если
Sравно 0 на 2 на 3, тоS (3) =и
struct ('a', 2)S (3) .a = 2приводят к ошибкам
потому что неясно, какое измерение расширять. Ранее,
S (3) .a = 2привел к массиву 1 на 6.Если
S- 1 на 1 на 3 с двумя полями, то
S (5) = struct ('a', 7, 'b', [])и
S (5).

