Нахождение значения выражения: правила, примеры, решения

В данной статье рассмотрено, как находить значения математических выражений. Начнем с простых числовых выражений и далее будем рассматривать случаи по мере возрастания их сложности. В конце приведем выражение, содержащее буквенные обозначения, скобки, корни, специальные математические знаки, степени, функции и т.д. Всю теорию, по традиции, снабдим обильными и подробными примерами.

Как найти значение числового выражения?

Числовые выражения, помимо прочего, помогают описывать условие задачи математическим языком. Вообще математические выражения могут быть как очень простыми, состоящими из пары чисел и арифметических знаков, так и очень сложными, содержащими функции, степени, корни, скобки и т.д. В рамках задачи часто необходимо найти значение того или иного выражения. О том, как это делать, и пойдет речь ниже.

Простейшие случаи

Это случаи, когда выражение не содержит ничего, кроме чисел и арифметических действий. Для успешного нахождения значений таких выражений понадобятся знания порядка выполнения арифметических действий без скобок, а также умение выполнять действия с различными числами. 

Если в выражении есть только числа и арифметические знаки «+», «·», «-«, «÷», то действия выполняются слева направо в следующем порядке: сначала умножение и деление, затем сложение и вычитание. Приведем примеры.

Пример 1. Значение числового выражения

Пусть нужно найти значения выражения 14-2·15÷6-3.

Выполним сначала умножение и деление. Получаем:

14-2·15÷6-3=14-30÷6-3=14-5-3.

Теперь проводим вычитание и получаем окончательный результат:

14-5-3=9-3=6.

Пример 2. Значение числового выражения

Вычислим: 0,5-2·-7+23÷234·1112.

Сначала выполняем преобразование дробей, деление и умножение:

0,5-2·-7+23÷234·1112=12-(-14)+23÷114·1112

12-(-14)+23÷114·1112=12-(-14)+23·411·1112=12-(-14)+29.

Теперь займемся сложением и вычитанием. Сгруппируем дроби и приведем их к общему знаменателю:

12-(-14)+29=12+14+29=14+1318=141318.

Искомое значение найдено.

Выражения со скобками

Если выражение содержит скобки, то они определяют порядок действий в этом выражении. Сначала выполняются действия в скобках, а потом уже все остальные. Покажем это на примере.

Пример 3. Значение числового выражения

Найдем значение выражения 0,5·(0,76-0,06).

В выражении присутствуют скобки, поэтому сначала выполняем операцию вычитания в скобках, а уже потом — умножение.

0,5·(0,76-0,06)=0,5·0,7=0,35.

Значение выражений, содержащих скобки в скобках, находится по такому же принципу.

Пример 4. Значение числового выражения

Вычислим значение 1+2·1+2·1+2·1-14.

Выполнять действия будем начиная с самых внутренних скобок, переходя к внешним. 

1+2·1+2·1+2·1-14=1+2·1+2·1+2·34

1+2·1+2·1+2·34=1+2·1+2·2,5=1+2·6=13.

В нахождении значений выражений со скобками главное — соблюдать последовательность действий.

Выражения с корнями

Математические выражения, значения которых нам нужно найти, могут содержать знаки корня. Причем, само выражение может быть под знаком корня. Как быть в таком случае? Сначала нужно найти значение выражения под корнем, а затем извлечь корень из числа, полученного в результате. По возможности от корней в числовых выражениях нужно лучше избавляться, заменяя из на числовые значения.

Пример 5. Значение числового выражения

Вычислим значение выражения с корнями -2·3-1+60÷43+3·2,2+0,1·0,5.

Сначала вычисляем подкоренные выражения.

-2·3-1+60÷43=-6-1+153=83=2

2,2+0,1·0,5=2,2+0,05=2,25=1,5.

Теперь можно вычислить значение всего выражения.

-2·3-1+60÷43+3·2,2+0,1·0,5=2+3·1,5=6,5

Часто найти значение выражения с корнями часто нужно сначала провести преобразование исходного выражения. Поясним это на еще одном примере.

Пример 6. Значение числового выражения

Сколько будет 3+13-1-1

Как видим, у нас нет возможности заменить корень точным значением, что усложняет процесс счета. Однако, в данном случае можно применить формулу сокращенного умножения.

3+13-1=3-1.

Таким образом:

3+13-1-1=3-1-1=1.

Выражения со степенями

Если в выражении имеются степени, их значения нужно вычислить прежде, чем приступать ко всем остальным действиям. Бывает так, что сам показатель или основание степени являются выражениями. В таком случае, сначала вычисляют значение этих выражений, а затем уже значение степени.

Пример 7. Значение числового выражения

Найдем значение выражения 23·4-10+161-123,5-2·14.

Начинаем вычислять по порядку.

23·4-10=212-10=22=4

16·1-123,5-2·14=16*0,53=16·18=2.

Осталось только провести операцию сложение и узнать значение выражения:

23·4-10+161-123,5-2·14=4+2=6.

Также часто целесообразно бывает провести упрощение выражения  с использованием свойств степени.

Пример 8. Значение числового выражения

Вычислим значение следующего выражения: 2-25·45-1+3136.

Показатели степеней опять таковы, что их точные числовые значения получить не удастся. Упростим исходное выражение, чтобы найти его значение.

2-25·45-1+3136=2-25·225-1+313·6

2-25·225-1+313·6=2-25·22·5-2+32=22·5-2-25+32

22·5-2-25+32=2-2+3=14+3=314

Выражения с дробями

Если выражение содержит дроби, то при вычислении такого выражения все дроби в нем нужно представить в виде обыкновенных дробей и вычислить их значения. 

Если в числителе и знаменателе дроби присутствуют выражения, то сначала вычисляются значения этих выражений, и записывается финальное значение самой дроби. Арифметические действия выполняются в стандартном порядке. Рассмотрим решение примера.

Пример 9. Значение числового выражения

Найдем значение выражения, содержащего дроби: 3,22-3·7-2·36÷1+2+39-6÷2.

Как видим, в исходном выражении есть три дроби. Вычислим сначала их значения.

3,22=3,2÷2=1,6

7-2·36=7-66=16

1+2+39-6÷2=1+2+39-3=66=1.

Перепишем наше выражение и вычислим его значение:

1,6-3·16÷1=1,6-0,5÷1=1,1

Часто при нахождении значений выражений удобно бывает проводить сокращение дробей. Существует негласное правило: любое выражение перед нахождением его значения лучше всего упростить по максимуму, сводя все вычисления к простейшим случаям.

Пример 10. Значение числового выражения

Вычислим выражение 25-1-25-74-3.

Мы не можем нацело извлечь корень из пяти, однако можем упростить исходное выражение путем преобразований.

25-1=25+15-15+1=25+15-1=25+24

Исходное выражение принимает вид:

25-1-25-74-3=25+24-25-74-3.

Вычислим значение этого выражения:

25+24-25-74-3=25+2-25+74-3=94-3=-34.

Выражения с логарифмами

Когда в выражении присутствуют логарифмы, их значение, если это возможно, вычисляется с самого начала. К примеру, в выражении log24+2·4 можно сразу вместо log24 записать значение этого логарифма, а потом выполнить все действия. Получим: log24+2·4=2+2·4=2+8=10.

Под самим знаком логарифма и в его основании также могут находится числовые выражения. В таком случае, первым делом находятся их значения. Возьмем выражение log5-6÷352+2+7. Имеем:

log5-6÷352+2+7=log327+7=3+7=10.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание

Если же вычислить точное значение логарифма невозможно, упрощение выражения помогает найти его значение.

Пример 11. Значение числового выражения

Найдем значение выражения log2log2256+log62+log63+log5729log0,227.

log2log2256=log28=3.

По свойству логарифмов:

log62+log63=log6(2·3)=log66=1.

Вновь применяя свойства логарифмов, для последней дроби в выражении получим:

log5729log0,227=log5729log1527=log5729-log527=-log27729=-log27272=-2.

Теперь можно переходить к вычислению значения исходного выражения.

log2log2256+log62+log63+log5729log0,227=3+1+-2=2.

Выражения с тригонометрическими функциями

Бывает, что в выражении есть тригонометрические функции синуса, косинуса, тангенса и котангенса, а также функции, обратные им. Из значения вычисляются перед выполнением всех остальных арифметических действий. В противном случае, выражение упрощается.

Пример 12. Значение числового выражения

Найдите значение выражения: tg24π3-sin-5π2+cosπ.

Сначала вычисляем значения тригонометрических функций, входящих в выражение.

tg4π3=3

sin-5π2=-1

cosπ=-1.

Подставляем значения в выражение и вычисляем его значение:

tg24π3-sin-5π2+cosπ=32-(-1)+(-1)=3+1-1=3.

Значение выражения найдено.

Часто для того, чтобы найти значение выражения с тригонометрическими функциями, его предварительно нужно преобразовать. Поясним на примере.

Пример 13. Значение числового выражения

Нужно найти значение выражения cos2π8-sin2π8cos5π36cosπ9-sin5π36sinπ9-1.

Для преобразования будем использовать тригонометрические формулы косинуса двойного угла и косинуса суммы.

cos2π8-sin2π8cos5π36cosπ9-sin5π36sinπ9-1=cos2π8cos5π36+π9-1=cosπ4cosπ4-1=1-1=0.

Общий случай числового выражения

В общем случае тригонометрическое выражение может содержать все вышеописанные элементы: скобки, степени, корни, логарифмы, функции. Сформулируем общее правило нахождения значений таких выражений.

Как найти значение выражения

1. Корни, степени, логарифмы и т.д. заменяются их значениями.
2. Выполняются действия в скобках.
3. Оставшиеся действия выполняются по порядку слева направо. Сначала — умножение и деление, затем — сложение и вычитание.

Разберем пример.

Пример 14. Значение числового выражения

Вычислим, чему равно значение выражения -2·sinπ6+2·2π5+3π5+3 lne2+1+39.

Выражение довольно сложное и громоздкое. Мы не случайно выбрали именно такой пример, постаравшись уместить в него все описанные выше случаи. Как найти значение такого выражения?

Известно, что при вычислении значения сложного дробного вида, сначала отдельно находятся значения числителя и знаменателя дроби соответственно. Будем последовательно преобразовывать и упрощать данное выражение. 

Первым делом вычислим значение подкоренного выражения 2·sinπ6+2·2π5+3π5+3. Чтобы сделать это, нужно найти значение синуса, и выражения, которое является аргументом тригонометрической функции.  

π6+2·2π5+3π5=π6+2·2π+3π5=π6+2·5π5=π6+2π

Теперь можно узнать значение синуса:

sinπ6+2·2π5+3π5=sinπ6+2π=sinπ6=12.

Вычисляем значение подкоренного выражения:

2·sinπ6+2·2π5+3π5+3=2·12+3=4

Отсюда:

2·sinπ6+2·2π5+3π5+3=4=2.

Со знаменателем дроби все проще:

lne2=2.

Теперь мы можем записать значение всей дроби:

2·sinπ6+2·2π5+3π5+3 lne2=22=1.

С учетом этого, запишем все выражение:

-1+1+39=-1+1+33=-1+1+27=27.

Окончательный результат:

-2·sinπ6+2·2π5+3π5+3 lne2+1+39=27.

В данном случае мы смогли вычислить точные значения корней, логарифмов, синусов и т.д. Если такой возможности нет, можно попробовать избавиться от них путем математических преобразований.

Вычисление значений выражений рациональными способами

Вычислять значения числовых нужно последовательно и аккуратно. Данный процесс можно рационализировать и ускорить, используя различные свойства действий с числами. К примеру, известно, что произведение равно нулю, если нулю равен хотя бы один из множителей. С учетом этого свойства, можно сразу сказать, что выражение 2·386+5+58941-sin3π4·0 равно нулю. При этом, вовсе не обязательно выполнять действия по порядку, описанному в статье выше.

Также удобно использовать свойство вычитания равных чисел. Не выполняя никаких действий, можно заказать, что значение выражения 56+8-3,789lne2-56+8-3,789lne2 также равно нулю.

Еще один прием, позволяющий ускорить процесс — использование тождественных преобразований таких как группировка слагаемых и множителей и вынесение общего множителя за скобки. Рациональный подход к вычислению выражений с дробями — сокращение одинаковых выражений в числителе и знаменателе. 

Например, возьмем выражение 23-15+3·289·343·23-15+3·289·34. Не выполняя действий в скобках, а сокращая дробь, можно сказать, что значение выражения равно 13.

Нахождение значений выражений с переменными

Значение буквенного выражения и выражения с переменными находится для конкретных заданных значений букв и переменных.  

Нахождение значений выражений с переменными

Чтобы найти значение буквенного выражения и выражения с переменными, нужно в исходное выражение подставить заданные значения букв и переменных, после чего вычислить значение полученного числового выражения.

Пример 15. Значение выражения с переменными

Вычислить значение выражения 0,5x-y при заданных x=2,4 и y=5.

Подставляем значения переменных в выражение и вычисляем:

0,5x-y=0,5·2,4-5=1,2-5=-3,8.

Иногда можно так преобразовать выражение, чтобы получить его значение независимо от значений входящих в него букв и переменных. Для этого от букв и переменных в выражении нужно по возможности избавиться, используя тождественные преобразования, свойства арифметических действий и все возможные другие способы.

Например, выражение х+3-х, очевидно, имеет значение 3, и для вычисления этого значения совсем необязательно знать значение переменной икс. Значение данного выражения равно трем для всех значений переменной икс из ее области допустимых значений.  

Еще один пример. Значение выражения xx равно единице для всех положительных иксов. 

Вычисление значения выражения «на коленке» / Хабр

Тема навеяна недавними постами Компилятор выражений и Вычисление значения выражения. Рассмотрены два подхода — построение семантического дерева выражения для быстрого вычисления и вычисление самого выражения на ходу при помощи двух своих стеков. Я же хочу показать довольно простой способ реализации, по сути алгоритма из первой статьи, но на базе рекурсии. Иногда бывает уместно переложить часть работы со стеком на комплиятор, благо современные ОС дают нам большой стек и возможность разумного использования рекурсии.

Итак, что такое арифметическое выражение? Как было написано в первой упомянутой статье, структуру выражения можно задать следующими правилами:

выражение ::= слагаемое [«+» или «-» слагаемое] *
слагаемое ::= множитель [«*» или «/» множитель] *
множитель ::= число | переменная | (выражение) | +множитель | -множитель

На заметку: такая форма описания грамматик часто используется в технической документации. В теории она называется БНФ, желающие могут почитать более детально например в википедии.

Проблему анализа текста согласно некой формальной грамматике, как правило решают двумя способами: явное построение конечного автомата (об этом как-то потом) и простенький рекурсивный разбор, который мы сейчас и будем реализовывать.

Руководствуясь приведенной схемой, можно легко записать следующий псведокод для анализа первого правила:

вычислить_выражение()
	результат = вычислить_слагаемое()
	пока есть символы
		если текущий_символ = "+"
			результат = результат + вычислить_слагаемое()
		или если текущий_символ = "-"
			результат = результат - вычислить_слагаемое()
		иначе
			ошибка
	вернуть результат

Абсолютно аналогично пишется разбор операций умножения, а на самом нижнем уровне разбора мы приходим к рекурсии — для вычисления значения в скобках мы просто вызываем вычислить_выражение().

вычислить_множитель()
	результат = 0
	если текущий_символ цифра
		результат = прочитать_число()
	или если текущий_символ буква
		результат = вычислить_переменную()
	или если текущий_символ = "("
		результат = вычислить_выражение()
		если текущий символ != ")"
			ошибка
	или если текущий_символ = "+"
		результат = вычислить_множитель()
	или если текущий_символ = "-"
		результат = -вычислить_множитель()
	иначе
		ошибка
	вернуть результат

Да, в приведенном псевдокоде не учтены пробелы, но для общего ознакомления с идеей этого достаточно. Желающим ознакомиться с рабочей реализацией такого подхода на С++ могу предложить почитать мой код в плагине Popup Plus для миранды: formula.h и formula.cpp.

P.S. если есть желающие почитать о том, как можно использовать грамматики и конечные автоматы для рабора других тектсов, могу написать о простеньком XPath парсере внутри Jabber модуля из той же миранды. Или о том, как разбирать XML.

Практическое руководство. Вычисление числовых значений — Visual Basic

• 
  07/20/2015
• Чтение занимает 2 мин

В этой статье

Числовые значения можно вычислить с помощью числовых выражений. Числовое выражение представляет собой выражение, которое содержит литералы, константы и переменные, представляющие числовые значения, и операторы, действующие на эти значения.

Вычисление числовых значений

Вычисление числового значения

• Объедините один или несколько числовых литералов, констант и переменных в числовое выражение. В следующем примере показаны некоторые допустимые числовые выражения.

  93.217

  System.Math.PI

  counter

  4 * (67 + i)

  Первые три строки показывают литерал, константу и переменную. Каждый из них формирует допустимое числовое выражение самим собой. В последней строке показано сочетание переменной с двумя литералами.

  Обратите внимание, что числовое выражение не формирует полную инструкцию Visual Basic сам по себе. Выражение необходимо использовать как часть полной инструкции.

Сохранение числового значения

• Оператор присваивания можно использовать для назначения переменной значения, представленного числовым выражением, как показано в следующем примере.

  Dim i As Integer = 2
  Dim j As Integer
  j = 4 * (67 + i)
  

  В предыдущем примере значение выражения в правой части оператора равенства ( = ) присваивается переменной j в левой части оператора, поэтому j результатом вычисления будет 276.

  Дополнительные сведения см. в разделе Инструкции.

Несколько операторов

Если числовое выражение содержит более одного оператора, порядок их вычисления определяется правилами приоритета операторов. Чтобы переопределить правила приоритета операторов, заключите выражения в круглые скобки, как в приведенном выше примере. выражения, заключенные в кавычки, оцениваются первыми.

Переопределение приоритета обычного оператора

• Используйте круглые скобки, чтобы заключать операции, которые необходимо выполнить первыми. В следующем примере показаны два разных результата с одинаковыми операндами и операторами.

  Dim i As Integer = 2
  Dim j, k As Integer
  j = 4 * (67 + i)
  k = 4 * 67 + i
  

  В предыдущем примере вычисление для j выполняет оператор сложения ( + ) сначала, так как круглые скобки (67 + i) обопределяют нормальный приоритет, а присваиваемое значение j — 276 (4 раза 69). Вычисление для k выполняет операторы в нормальном порядке ( * до + ), а присваиваемое ему значение k равно 270 (268 плюс 2).

  Дополнительные сведения см. в разделе приоритет операторов в Visual Basic.

См. также раздел

Битрикс24: вычисление значений выражений в параметрах действий при помощи специальных операторов

Вычислительные операции со значениями выражений через параметры действий

В системе имеется возможность вычислять значения выражений в параметрах действий, для этого необходимо поставить знак = в поле перед операциями.

К примеру: В поле имеется возможность применения (всего может быть использовано) только одного единственного выражения. При подобном стечении обстоятельств с целью осуществления добавления каких-либо дополнительных данных вам необходимо прибегнуть к использованию оператора конкатенации (&, а  сам текст писать в специальных кавычках («). » — возведение в определённую степень;

Возможеные варианты написания: year, y, years, month, m, months, day, d, days, hour, h, hours, min, i, minute, minutes, second, s, seconds.

На момент написания у вас имеется возможность использования верхнего или нижнего регистра.

• «if» — условие.
• «intval» — возвращает целое значение переменной;
• «substr» — возвращает подстроку.

Внимание! При осуществлении ввода  заранее не правильного синтаксиса выражения , то введённые символы будут отображены в виде текста.

У вас появились какие-либо вопросы при прочтении?

По всем вопросам и всему, что вам не понятно по теме Битрикс24 обращаетесь сюда:

Так же у вас имеется возможность отправить запрос и получить консультацию БЕСПЛАТНО! По нашей акции:

Подробнее ознакомиться с Битрикс24 и Terrasoft можно здесь:

Лабораторная работа №13. Математический редактор mathcad. Вычисление выражений.

1

Цель.
Научиться вычислять простые выражения
и алгебраические выражения.

1. Простые
   вычисления.

Простейшие
вычисления можно выполнить, используя
знак вывода результатов вычислений «=»
(равенство). Достаточно просто ввести
с клавиатуры необходимое выражение,
используя стандартную математическую
запись и нажать на клавишу со знаком
«=».

Знак
«=», введенный с клавиатуры, заставляет
программу вычислить значение выражения,
стоящего слева от курсора, и распечатать
его значение на экране.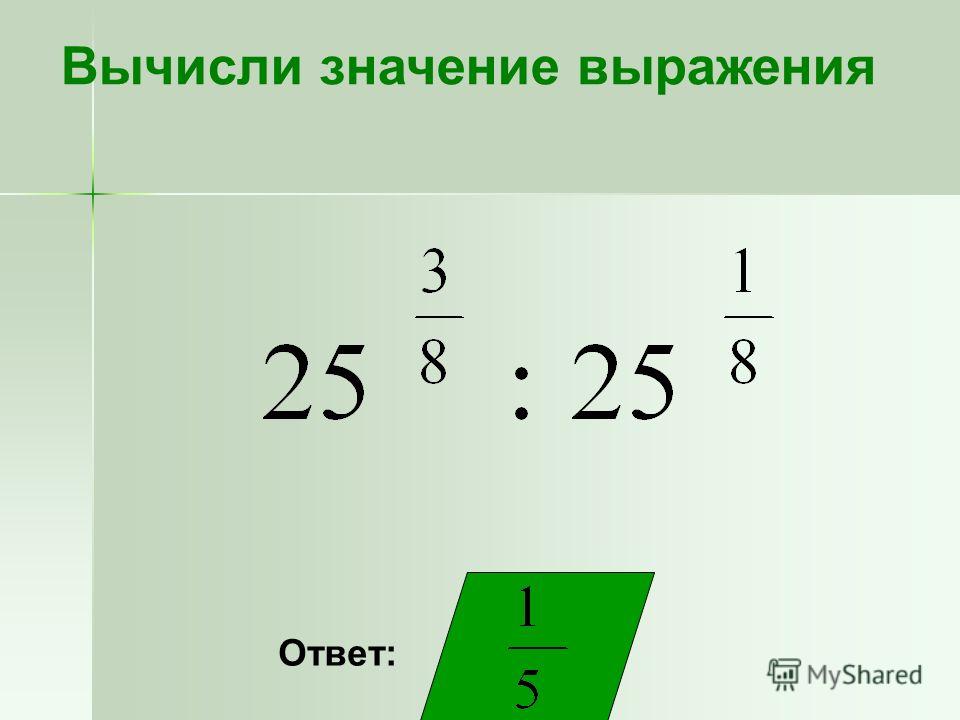 При этом курсор
изменяет свой вид со знака «=» на знак
«_». Если курсор имеет вид «_», то это
значит, что курсор находится в поле
вычисляемого выражения.

При
работе с вычисляемыми выражениями
возможно использование математических
операторов. В нижеприведенной таблице
показаны операторы вычислений.

*
Программа приводит текст, введенный с
клавиатуры, к математически верному
виду (этажность формул, надстрочные и
подстрочные индексы и т. п.), поэтому
знаки, отображаемые на экране, отличаются
от введенных с клавиатуры.

1.1.
Вычислить:
15-8/104,5.

После
щелчка в любом месте рабочего документа
появляется курсор. Весь ввод с клавиатуры
будет размещаться теперь в рабочем
документе, начиная с места расположения
курсора. После набора знака «=», Mathcad
автоматически вычисляет выражение и
выводит результат.

На
экране должно получиться:

1.2. Вычислить выражение

1.3. Вычислить
сумму на интервале предварительно
определив диапазон изменения переменной,
по которой вычисляется сумма

2. Вычисление
   алгебраических выражений

Mathcad
позволяет также вычислять значения
выражений, содержащих переменные. Любые
переменные, используемые в этом выражении,
должны быть определены заранее. В
качестве оператора определения (оператора
«присвоить значение») используют символ
оператора присваивания – « := ». Для
ввода его с клавиатуры используется
знак « : ».(Вводится по нажатию комбинации
клавиш «SHIFT
+ ;»).

Для
определения переменной необходимо
ввести с клавиатуры ее имя, знак « : » и
присваемое значение. После ввода знака
« : », Mathcad
показывает двоеточие, сопровождаемое
символом присваивания «:=».

2.1. Вычислить значение выражения:

при с=2, d=1/4

Определим переменные:

И вычислим:

Задания
для самостоятельного выполнения.

Задание
1.

Вычислить.

1. 2)
   3)4.

5)
6)7.8)

9)
10)

Задание
2.
Найти
значение выражения.

1. при
   a=4.8,
   b=1.2.

2. при
   a=0.75,
   b=4/3.

3. при
   a=1.2, b=3/5.

4. при
   x=-3.

5. при
   x=1,
   y=0.

6. при
   х=-2.

7. при
   а=54, b=6.

8. при

   ,

   и c=3.2.

9. при
   a=0.2,
   b=-1.05
   и c=1.07

10. при

    .

Задание
3.
Найти
значение выражения.

1. _{,
   а=1..10, b=5}

2. _{,
   а=1..100,
   b=15,c=2}

3. _{,
   а=1..20,
   b=5,
   c=9}

4. _{,
   а=3,
   b=5..9,
   c=8}

5. _{,
   x=2..50}

6. _{,
   x=10. .60, y=18}

7. _{,
   x=12..50}

8. _{,
   а=1..20,
   b=5}

9. _{,
   а=10..20,
   b=18}

10. _{,
    а=1..100,
    b=8}

найти значение выражения | интернет проект BeginnerSchool.ru

Продолжаем рубрику  «основные содержательные линии курса математики начальной школы». В предыдущих статьях мы уже рассмотрели такие содержательные линии как нумерация, величины и вычислительные навыки. Сегодня мы рассмотрим тему «найти значение выражения», в которой выясним значения, каких выражений учатся находить ученики начальной школы.

Начнем с первого класса.  Изучая темы «сумма» и «разность», дети впервые сталкиваются с понятием «выражение» и «значение выражения». Здесь осваиваются такие правила, как переместительный закон сложения, сложение и вычитание с числом 0. Все арифметические выражения сейчас осваиваются пока без скобок. В качестве рациональных приемов вычислений, здесь используется группировка слагаемых.

Во втором классе, помимо сложения и вычитания  изучают умножение и деление, а так же названия компонентов арифметических действий. Осваиваются такие правила, как переместительный закон умножения, сочетательные законы сложения и умножения, умножение и деление с числами 0 и 1, порядок действий и нахождение значения выражения со скобками. В качестве рациональных приемов вычислений используется группировка множителей. Дети учатся сами контролировать результаты своих вычислений: вычитание контролируется сложением, а деление – умножением.

В третьем классе изучается распределительный закон. Здесь используются такие приемы вычислений, как вычитание числа из суммы и суммы из числа, умножение и деление суммы на число, а также признаки делимости на 2, 3, 4, 5, 6, 9. Контролировать себя ученика помогает определение последней цифры результата вычислений и определение числа сотен в ответе.

И наконец, в четвертом классе изучаются числовые выражения, происходит знакомство с буквенными выражениями, но без использования терминов. Дети учатся находить значения выражения с переменной. Используются такие рациональные приемы, как разложение на удобные слагаемые при сложении и вычитании, а также разложение на удобные множители при умножении и делении. Проверяют себя дети путем оценки результатов вычислений и определения числа цифр в ответе.

Следующую тему – «решение текстовых задач» читайте в следующей статье. Спасибо, что вы с нами.

Понравилась статья — поделитесь с друзьями:

Оставляйте пожалуйста комментарии в форме ниже

Вычисление значения выражений, используя приём округления.2 класс

Тема урока: Вычисление значения выражений, используя приём округления. Оборудование: конспект, учебник по математике 2-го класса (часть 1), рабочая тетрадь к учебнику.

Цель и задачи урока:

Предметные:

• познакомить учащихся с приемом округления при сложении;

• формировать умение решать текстовые задачи.

Метапредметные:

Регулятивные:

• самостоятельно организовывать свое рабочее место в соответствии с целью выполнения заданий;

• определять правильность выполнения заданий;

• самостоятельно оценивать свою работу на уроке.

Познавательные:

• ориентироваться в учебнике, определять область своего незнания, планировать свою работу по изучению нового;

• извлекать информацию, представленную в форме текста, иллюстрации и т.д.;

• анализировать, делать выводы.

Коммуникативные:

• участвовать в диалоге, слушать и понимать других, оформлять свои мысли в устной и письменной речи;

• сотрудничать с учителем и одноклассниками.

Личностные:

Ход урока:

Этапы

Деятельность учителя

Деятельность учеников

Орг. момент

Здравствуйте.

Прозвенел звонок и смолк –

Начинается урок.

Все за парты тихо сели,

На меня все посмотрели.

Слушайте, запоминайте,

Ни минуты не теряйте.

Проверьте готовность к уроку, посмотрите готово ли ваше рабочее место, сядьте за парту правильно, выпрямите спинки, ручки положите на парту, глазки поднимаем и смотрим на меня, ушки внимательно слушают.

Здороваются с учителем, проверяют готовность к уроку.

Актуализация знаний

Откройте свои тетради и запишите сегодняшнее число. По середине строки пишем «Классная работа». Обратите внимание на удвоенную букву «с».

Перед тем как приступить к новой теме проведем устный счет.

1. Устный счет

На доске представлены нужно назвать пропущенные в них числа, чтобы

57+…=60

Сколько не хватает единиц 57 до 60?

65+…=70 19+…=20 38+…=40 46+…=50

2.Повторение изученного

Каким словом можно назвать числа 60, 70, 20, 40, 50.

Что называется круглым числом?

3.Сравнение вычислений

На доске представлены выражения, перепишите их себе в тетрадь и найдите значение выражений.

45+5= 45+7= 45+9=

Чем похожи выражения?

Чем отличаются?

Проследим, как изменяется сумма.

Почему сумма увеличивается на 2, ведь число, к которому прибавляем 45, не изменяется?

Открывают рабочие тетради и записывают число и «Классная работа».

Ответ: 57 не хватает 3 единицы до 60. Ответ: 5, 1, 2, 4.

Ответ: круглые числа. Ответ: круглое число – это

Ответ:50, 52, 54.

Определение темы урока

Запишите себе в тетрадь выражение.

46+38=

Вычислите значение выражения.

Я заметила, что вы решили это выражение разными способами. Я вынесла их на доску.

Посмотрите какими 2-я способами ученики решили это выражение.

1 сп. 46+38=(40+30)+(6+8)=84 2 сп. 46+38=50+(38-4)=84

Объясните способы вычисления значения выражения.

Действительно, чтобы вычислить значение выражения 2-с способом сначала увеличим слагаемое 46 на 4 единицы, т.е. округлим его до 50.

Потом будем складывать 50 и 38. Получим 88. Но нужно принять во внимание, что от увеличения одного из слагаемых на несколько единиц сумма увеличивается на столько же единиц. Поэтому для получения искомой суммы мы должны из 38 вычесть 4. Получим в ответе 84.

Запишем. 46+38=(46+4)+(38-4)=50+34

Как рациональнее находить значение выражения?

Что мы сделали первым действием?

Сформулируйте тему урока.

Тема урока: прием округления при сложении.

Записывают выражение в тетрадь и находят его значение.

Ответ: 1 сп. Ученик сначала нашел количество десятков и единиц, потом полученные суммы сложил и нашел значение выражения.

2 сп. Ученик сначала округлил 1-е слагаемое до круглого числа, взяв несколько единиц из 2-го слагаемого, потом прибавил оставшиеся единицы 2-го слагаемого.

Ответ: округлили первое слагаемое.

Формулируют тему урока.

Постановка целей и задач урока

Откройте учебники на странице 38, 39 рассмотрите задания и определите цель и задачи урока, т.е. чем сегодня будем заниматься.

Ответ: сегодня на уроке мы познакомимся с приемом округления при сложении, будем решать примеры и задачи, используя этот прием.

Практическая деятельность учащихся

Обратите внимание на синюю рамочку на странице 39.

… прочитает текст рамочки вслух, остальные следят за чтением текста рамочки по учебнику.

Что нового узнали?

Объясните по выражению на доске как это сделать.

26+47+18= (корректирую)

Читают текст рамочки.

Ответ: узнали, что прием округления можно использовать и в случае, когда нужно найти сумму более чем двух слагаемых.

Физминутка

А сейчас встаем из-за парт и немного отдохнем. Включаю видеофизминутку.

Выполняют физминутку.

Практическая деятельность учащихся

Тихонечко сел за столы 1-й ряд, 2-й, 3-й.

А мы переходим к выполнению заданий по новой теме.

1. Найти значение выражений с помощью приема округления при сложении.

Прочитайте упражнение №1 на странице 52.

Что нужно сделать в упражнении?

Это задание мы выполним устно.

Первое выражение разберем вместе.

Что нужно сделать?

Правильно.

Запишите значение выражения так же, как на доске.

Следующие 3 значения выражений проговариваете же, а записывать будем кратко, т.е. только число ответа.

Все думают, кто готов, поднимает руку.

29+18=30+(18-1)=47 67+15=82 46+25=71 58+27=85

Молодцы.

Кто готов попробовать объяснить, как найти значение 5-го выражения? Запишите себе в тетради так, как я записала значение выражения на доске.

36+17+28=40+20+(28-4-3)=81 Значение 6-го выражения проговариваете же, а записывать будем кратко.

18+45+16=79

С заданием справились.

Что делали в 1-м задании?

Переходим к следующему заданию.

Прочитайте упражнение №5 на странице 53.

… прочитай вслух.

Что нужно сделать в этом упражнении?

… пойдет к доске, остальные работают в своих тетрадях.

(28+45)+9=82 64-(17+18)=29 (55+36)-20=71 14+(18+56)=88 72-(3*6)=54

Кто согласен с … поднимите руку.

Кто не согласен? Почему?

Что повторили, выполняя упражнение?

Выполним упражнение № 7.

Анализ текста задачи.

Прочитайте задачу про себя.

… прочитает вслух.

О чем говориться в задаче?

Что показывает число 9?

Прочитайте вопрос задачи.

Поиск решения.

Можем сразу ответить на вопрос задачи? (нет).

Почему? (не знаем общую массу ягод).

Можем узнать массу ягод? (Да).

Каким действием? (Сложением).

Почему сложением? (Нужно узнать, сколько всего ягод).

Узнав, сколько всего ягод и зная, во сколько раз уменьшилась масса ягод после того, как их высушили, можем ответить на вопрос задачи? (Да).

Каким действием? (Делением).

Почему делением? (Потому что нужно узнать ВО СКОЛЬКО РАЗ УМЕНЬШИЛАСЬ масса ягод).

Ответили мы на вопрос задачи? (Да.)

Оформление решения задачи.

… выйдет к доске и выполнит решение задачи выражением, остальные работают в тетрадях.

(9+7):4=4 (кг.)

Кто считает, что … выполнил решение задачи, правильно поднимите руку?

Кто не согласен? Почему?

Формулировка и запись ответа.

Сформулируйте и запишите ответ.Ответ: 4 килограмма масса сушеных ягод.

… садись за свой стол.

Чем сейчас занимались?

Переходим к следующему заданию.

Прочитайте задание упражнения №3.

Что нужно сделать?

Как найти периметр 4-угольника?

Мы выполним это упражнение только под цифрой 2.

Каковы значения сторон 4-хугольника?

Можем ли мы сразу найти периметр 4-хугольника? Почему?

К какому значению будем приводить величины сторон?

Записываем в тетрадь в столбик значение сторон.

Значение каких сторон будем переводить?

Напротив каждой из этих величин напротив запишите значение сторон в см.

3 дм.=30см.

27 см.

2 дм.=20 см.

1 дм. 9 см.=19 см.

… что у тебя получилось?

Кто согласен с…?

Кто не согласен? Почему?

Теперь, когда мы привели значение всех сторон в одну величину, можем найти периметр 4-хугольника?

… найдет периметр 4-хугольника у доски, остальные в тетрадях.

Р=30+27+20+19=96 (см.)

… что у тебя получилось?

Кто согласен с…?

Кто не согласен? Почему?

Что делали, выполняя это упражнение?

Садятся за столы.

Ответ: увеличим слагаемое 29 на 1 единицу, т.е. округлим его до 30. К полученной сумме прибавим 18 без 1, т.е. 17=47.

Ответ: находили значение выражений, используя прием округления.

Читают задание.

Ответ: составить числовое выражение и вычислить его значение.

Проводят взаимопроверку.

Ответ: счет в пределах 100.

Читают текст задачи.

Ответ: о малине и ежевике.

Сколько кг. малины собрали.

Сколько кг. ежевики собрали.

Во сколько раз уменьшилась масса ягод, после того, как их просушили.

Отвечают на вопросы.

1 ученик записывает у доски, остальные в тетрадях.

Взаимопроверка.

Формулируют и записывают ответ.

Ответ: решали задачу.

Читают задание.

Вычислить периметр четырехугольника.

Ответ: сложить значение всех сторон.

Ответ: 3 дм., 27 см., 2 дм., 1 дм. 9 см.

Ответ: нет, потому что величины выражены в разных значениях.

Ответ: см.

Ответ: 1 и 3 и 4.

Взаимопроверка.

Ответ: находили периметр 4-хугольника.

Подведение итогов урока

Подводя итог, я задам вам несколько вопросов.

Что такое круглые числа?

С каким приемом при сложении сегодня знакомились?

Расскажите суть этого приема.

Все ли достигнуты задачи, которые ставили на урок?

Поднимите руку те, кто считает, что хорошо поработал на уроке. Умнички. Теперь поднимите те, кто не считает, что был не достаточно активным на уроке. Я думаю, у вас еще все получится.

Выставляю отметки.

Отвечают на вопросы.

Домашнее задание

Откройте дневники и запишите домашнее задание.

Дома вам нужно выполнить в учебнике № 6 стр. 53. И в рабочей тетради № 1,2 на стр. 40.

Записывают домашнее задание

Основы алгебры — Вычисление выражений

ср
узнали, что в алгебраическом выражении буквы могут обозначать числа.
Вот шаги для вычисления выражения:

1. Заменить
   каждая буква в выражении с присвоенным значением.
   Сначала замените каждую букву в выражении значением, которое было
   назначенный на это. Чтобы ваши расчеты были понятными и не ошибались, всегда
   заключите числа, которые вы заменяете, в круглые скобки.Значение, которое
   присвоенный переменной остается неизменным на протяжении всей задачи, даже если
   буква встречается в выражении более одного раза.

   Однако
   поскольку переменные «различаются», значение, присвоенное конкретной переменной
   может меняться от проблемы к проблеме, но не в рамках одной проблемы.

2. Выполнить
   операции в выражении с использованием правильного порядка операций.
   После того, как вы подставили значение для буквы, выполните операции, чтобы найти
   значение выражения. Не забывайте использовать правильный порядок действий:
   сначала выполните какие-либо операции с показателями, затем выполните умножение и
   деление и, наконец, сложение и вычитание!

Вот
пример. Оценим выражение 2x ³ — x ²
+ y для x = 3 и y = –2.

назад
наверх

Вычислительные выражения

Алгебраические выражения — это комбинации

переменные

, числа и хотя бы одну арифметическую операцию.

Чтобы оценить алгебраическое выражение, замените переменную или переменные известными значениями, а затем используйте

Порядок операций

.

Для вашего удобства вы можете использовать круглые скобки, когда вставляете отрицательные значения в переменные.

Пример 1:

Оцените выражение. Используйте значения

п

знак равно

—

4

, а также

п

знак равно

14

.

3

(

п

+

п

)

Чтобы оценить выражение, сначала подставьте

—

4

для

п

а также

14

для

п

в выражении.

3

(

п

+

п

)

знак равно

3

(

(

—

4

)

+

14

)

Для упрощения используйте порядок операций.Сначала проделайте операцию внутри скобок.

Сложите числа

—

4

а также

14

.

знак равно

3

(

10

)

Теперь умножьте

3

а также

10

.

3

(

10

)

знак равно

30

Так когда

п

является

—

4

а также

п

является

14

, значение данного выражения равно

30

.

Пример 2:

Оцените каждое выражение, если

Икс

знак равно

7

, а также

y

знак равно

3

.

Икс

y

3

+

2

Чтобы оценить выражение, замените

Икс

с участием

7

а также

y

с участием

3

.

Икс

y

3

+

2

знак равно

7

⋅

3

3

+

2

Используйте порядок операций и упростите выражение.

Произведите умножение и деление слева направо.

знак равно

21 год

3

+

2

знак равно

7

+

2

Добавлять

7

а также

2

.

знак равно

9

Следовательно, для данных значений

Икс

а также

y

, значение выражения равно

9

.

Оценка

: оценка выражений и многочленов

Purplemath

«Оценка» в основном означает «упрощение выражения до одного числового значения».Иногда вам будет предложено числовое выражение, и все, что вам нужно сделать, это упростить; это скорее вопрос порядка действий. В этом уроке я сконцентрируюсь на аспекте оценки «включил и нажал»: вставлял значения для переменных и «пробирался» к упрощенному ответу.

(Кстати, да, «plug-n-chug» — это довольно стандартная терминология. Это не «технический» термин, поэтому вы, вероятно, не увидите его в своем учебнике, но наверняка услышите его от других студенты, а также, возможно, ваш инструктор.)

MathHelp.com

Обычно единственной сложной задачей при оценке является отслеживание знаков «минус».Я настоятельно рекомендую вам широко использовать круглые скобки, особенно когда вы только начинаете.

• Вычислить

  a ² b для a = –2, b = 3, c = –4 и d = 4.

Чтобы найти ответ, я просто вставляю указанные значения, стараясь использовать круглые скобки, особенно вокруг знаков «минус».Если я только начинаю, сначала может быть полезно нарисовать круглые скобки:

а ² б

() ² ()

(–2) ² (3)

(4) (3)

12

Обратите внимание, как использование круглых скобок помогло мне отследить знак «минус» на значении a .Это было важно, потому что в противном случае я мог бы возвести в квадрат только 2, получив в итоге –4, что было бы неправильно.

Кстати, оказалось, что нам не нужны значения переменных c и d . Когда вам дается большой набор выражений для оценки, вы должны ожидать, что часто будут те или иные переменные, которые не будут включены в какое-либо конкретное упражнение из набора.

• Вычислить

  a — cd для a = –2, b = 3, c = –4 и d = 4.

В этом упражнении они дали мне дополнительную информацию. В выражении, которое они хотят, чтобы я оценил, нет b , поэтому я могу игнорировать это значение в своей работе:

(–2) — (–4) (4)

–2 — (–16)

–2 + 16

16–2

14

• Вычислить (

  b + d ) ² для a = –2, b = 3, c = –4 и d = 4.

Я должен позаботиться о том, чтобы не пытаться «распределить» показатель степени через круглые скобки. Экспоненты НЕ распределяются сверх сложения! Я никогда не должен пытаться сказать, что ( b + d ) ² совпадает с b ² + d ² . Это НЕ одно и то же! Я должен оценить выражение в его нынешнем виде:

• Вычислить

  b ² + d ² для a = –2, b = 3, c = –4 и d = 4.

В этом выражении возведение в квадрат выполняется отдельно для каждой из переменных.

Обратите внимание, что этот последний ответ выше не совпадает с ответом на предыдущую оценку. Это прямо демонстрирует тот факт, что показатели не распределяются сверх сложения, как это происходит при умножении.

Вы должны ожидать хотя бы упражнения, аналогичные двум предыдущим, на следующем тесте, а также на заключительном экзамене.Эта тенденция пытаться распределить показатель степени (а не умножение) над сложением — распространенная ошибка студентов, и ваш преподаватель почти наверняка захочет напоминать вам — часто! — разницы между возведением суммы в квадрат и суммированием двух квадратов. Не путайте их!

• Вычислить

  bc ³ — ad для a = –2, b = 3, c = –4 и d = 4.

В этом упражнении мне нужно использовать значения всех четырех переменных. Но мне нужно быть осторожным при размещении, потому что это выражение не использует переменные в алфавитном порядке.

(3) (- 4) ³ — (–2) (4)

(3) (- 64) — (–8)

–192 + 8

–184

Партнер

Самым распространенным типом «выражения», которое вам, вероятно, потребуется вычислить, будут полиномы.Чтобы оценить многочлен, вы берете этот многочлен и подставляете в качестве переменной (обычно x ) любое число, которое они вам дали.

• Вычислить

  x ⁴ + 3 x ³ — x ² + 6 для x = –3.

Это мой первый многочлен для оценки, поэтому я начну снова с пустых скобок, показывая мне, где нужно поместить значение переменной.

x ⁴ + 3 x ³ — x ² + 6

() ⁴ + 3 () ³ — () ² + 6

(–3) ⁴ + 3 (–3) ³ — (–3) ² + 6

81 + 3 (–27) — (9) + 6

81 — 81 — 9 + 6

–3

• Вычислить 3

  x ² — 12 x + 4 для x = –2.

Я рад, что попрактиковался в использовании скобок, чтобы мои замены были понятны. В этом случае эти скобки помогут мне отслеживать знаки «минус».

3 (–2) ² — 12 (–2) + 4

3 (4) + 24 + 4

12 + 24 + 4

40

• Вычислить

  y = 4 x — 3 при x = –1.

Это другое. Они дали мне уравнение с двумя переменными, но дали мне значение только для одной из переменных. Думаю, они хотят, чтобы я подключил x и вычислил результирующее значение для y .

Тогда мой ответ — уравнение:

Примечание. В этом последнем упражнении выше мы подставляли значение для одной из переменных и упрощали поиск значения другой переменной.Кроме того, для той части, к которой мы подключались, было присвоено имя y . Из-за этого мы не просто оценивали выражение; мы фактически вычисляли полиномиальную функцию. Результат нашего plug-n-chug означает, что точка ( x , y ) = (–1, –7) находится на линии y = 4 x — 3; то есть эта точка находится на графике полиномиальной функции.

Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в вычислении выражений для заданных значений переменных.Попробуйте выполнить указанное упражнение или введите свое собственное. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway. (Или перейдите к следующей странице этого урока.)

(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления.)

URL: https://www.purplemath.com/modules/evaluate.htm

Вычисление алгебраических выражений | MATH 1314: Колледжская алгебра

До сих пор в математических выражениях, которые мы видели, использовались только действительные числа.{2}} [/ латекс]. В выражении [latex] x + 5 [/ latex] 5 называется константой , потому что она не меняется, а x называется переменной , потому что это так. (При именовании переменной игнорируйте любые экспоненты или радикалы, содержащие переменную.) Алгебраическое выражение — это набор констант и переменных, объединенных вместе алгебраическими операциями сложения, вычитания, умножения и деления.

Мы уже видели несколько реальных числовых примеров экспоненциальной записи, сокращенного метода записи продуктов того же множителя.{3} = \ left (yz \ right) \ cdot \ left (yz \ right) \ cdot \ left (yz \ right) \ end {array} [/ latex]

В каждом случае показатель степени говорит нам, сколько факторов базы использовать, независимо от того, состоит ли база из констант или переменных.

Любая переменная в алгебраическом выражении может принимать или иметь разные значения. Когда это происходит, значение алгебраического выражения меняется. Вычислить алгебраическое выражение означает определить значение выражения для данного значения каждой переменной в выражении.{3} + у [/ латекс]

Решение

Пример 9: Вычисление алгебраического выражения при различных значениях

Вычислите выражение [латекс] 2x — 7 [/ latex] для каждого значения x.

1. [латекс] x = 0 [/ латекс]
2. [латекс] x = 1 [/ латекс]
3. [латекс] x = \ frac {1} {2} [/ латекс]
4. [латекс] x = -4 [/ латекс]

Решение

1. Заменить 0 на [латекс] x [/ латекс].

   [латекс] \ begin {array} \ text {} 2x-7 \ hfill & = 2 \ left (0 \ right) -7 \\ \ hfill & = 0-7 \\ \ hfill & = -7 \ end {array} [ / латекс]

2. Заменить 1 на [латекс] x [/ латекс].

   [латекс] \ begin {array} \ text {} 2x-7 \ hfill & = 2 \ left (1 \ right) -7 \\ \ hfill & = 2-7 ​​\\ \ hfill & = -5 \ end {array} [ / латекс]

3. Замените [латекс] \ frac {1} {2} [/ latex] на [latex] x [/ latex].

   [латекс] \ begin {array} \ text {} 2x-7 \ hfill & = 2 \ left (\ frac {1} {2} \ right) -7 \\ \ hfill & = 1-7 \\ \ hfill & = — 6 \ end {array} [/ latex]

4. Заменить [латекс] -4 [/ латекс] на [латекс] x [/ латекс].

   [латекс] \ begin {array} \ text {} 2x-7 \ hfill & = 2 \ left (-4 \ right) -7 \\ \ hfill & = -8-7 \\ \ hfill & = -15 \ end {массив } [/ латекс]

Попробуй 9

Вычислите выражение [латекс] 11 — 3y [/ latex] для каждого значения y.{2}} [/ latex] для [латекса] m = 2, n = 3 [/ latex]

Решение

1. Заменить [латекс] -5 [/ латекс] на [латекс] x [/ латекс].

   [латекс] \ begin {array} \ text {} x + 5 \ hfill & = \ left (-5 \ right) +5 \\ \ hfill & = 0 \ end {array} [/ latex]

2. Заменить 10 на [латекс] т [/ латекс].

   [латекс] \ begin {array} \ text {} \ frac {t} {2t-1} \ hfill & = \ frac {\ left (10 \ right)} {2 \ left (10 \ right) -1} \ \ \ hfill & = \ frac {10} {20-1} \\ \ hfill & = \ frac {10} {19} \ end {array} [/ latex]

3. Заменить 5 на [латекс] r [/ латекс].{3} [/ latex] for [latex] p = -2, q = 3 [/ latex]
   e. [латекс] 4 \ left (mn \ right) -5 \ left (nm \ right) [/ latex] для [латекса] m = \ frac {2} {3}, n = \ frac {1} {3} [ / латекс]

   Решение

   Оценка выражения с переменной

   Оценка выражения с переменной

   Переменная — это буква, например x, y или z, которая представляет собой неопределенное число.

   6 + x = 12

   Чтобы оценить алгебраическое выражение, вы должны подставить число для каждой переменной и выполнить арифметические операции.В приведенном выше примере переменная x равна 6, поскольку 6 + 6 = 12.

   Если мы знаем значения наших переменных, мы можем заменить переменные их значениями, а затем оценить выражение.

   Вычисление выражения с одной переменной

   В математическом выражении переменная может быть частью выражения. Если x = 3, выражение 7x + 4 становится 7 * 3 + 4, что равно 21 + 4 или 25. Чтобы оценить выражение с переменной, просто подставьте значение переменной в выражение и упростите.

   Вычисление выражения с двумя переменными

   Математическое выражение может содержать переменные как часть выражения. Если x = 3 и y = 5, выражение 7x + y — 4 становится 7 * 3 +5-4, что равно 21 + 5-4 или 22. Чтобы оценить выражение с двумя или более переменными, подставьте значение переменных в выражение и упростить.

   Объяснение

   Вот шаги для оценки выражения:

   Замените каждую букву в выражении на присвоенное значение.

   Сначала замените каждую букву в выражении на присвоенное ей значение. Чтобы сделать расчеты ясными и избежать ошибок, всегда заключайте подставляемые числа в круглые скобки. Значение, присвоенное переменной, остается неизменным на протяжении всей задачи, даже если буква встречается в выражении более одного раза.

   Однако, поскольку переменные «различаются», значение, присвоенное конкретной переменной, может меняться от проблемы к проблеме, но не в рамках одной проблемы.

   Выполните операции в выражении в правильном порядке.

   После того, как вы подставили значение для буквы, выполните действия, чтобы найти значение выражения. Не забывайте использовать правильный порядок операций: сначала выполняйте любые операции, связанные с показателями, затем выполняйте умножение и деление и, наконец, выполняйте сложение и вычитание!

   Вот пример. Давайте вычислим выражение 2x ³ — x ² + y для x = 3 и y = –2.

   2 (3) ³ — (3) ² + (-2)

   = 2 (27) — 9 + (-2)

   = 54 — 9 + (- 2) = 43

   Обычно единственная сложная задача при оценке — это отслеживать знаки минус. Я настоятельно рекомендую вам свободно использовать круглые скобки, особенно когда вы только начинаете.

   Оцените a ² b для a = –2, b = 3, c = –4 и d = 4.

   Чтобы найти мой ответ, вы просто вставляете данные значения, стараясь использовать круглые скобки, особенно вокруг знаков минус:

   (–2) 2 (3) = (4) (3) = 12

   Источник информации:

   AAAKnow

   • AAAnow имеет полный набор из тысяч
     интерактивные уроки арифметики .
   • не требует затрат или регистрации требуется для практики вашего
     математика на сайте AAAKnow.com.
   • Неограниченная практика доступно по каждой теме, что позволяет
     доскональное владение концепциями.
   • Широкий выбор уроков (от детского сада до восьмого класса).
     level) позволяет обучению или обзору происходить на текущем уровне каждого человека.
   • Немедленная обратная связь предотвращает неправильную практику и обучение
     методы, что является обычным результатом традиционных домашних заданий и рабочих листов.
     Практика может продолжаться сколько угодно долго в безопасном формате,
     помогает повысить самооценку и уверенность в себе.
   • Попробуйте уроки , нажав на один из
     оценки вверху или в области темы в левой части страницы.
   • Не забудьте добавить сайт в «Любимые места» и рассказать другим о
     сайт. Это отличный способ выучить или повторить по математике.

   Что нового в AAA Know?

   Веб-сайт AAAMath.com начал свою работу в 2000 году и предлагал бесплатные интерактивные уроки математики по основам арифметики и связанным с ней темам математики для K-8.Мы считали, что этот подход лучше, чем традиционные рабочие листы, потому что он обеспечивает немедленную обратную связь, тогда как рабочие листы позволяют студентам неоднократно практиковать неправильные методы, прежде чем они будут оценены.

   AAAKnow.com был зеркалом AAAMath.com, который использовался для обработки высоких нагрузок трафика. По сути, они были одинаковыми. Когда переписывание AAAMath.com в современный формат было завершено, мы решили разместить его на сайте AAAKnow.com. Таким образом люди все еще могли использовать AAAMath.com, если они предпочитают его, и могут опробовать и использовать новый формат, если они предпочитают его.

   AAAMath.com

   1. Использует старый веб-формат.
   2. Оригинальные уроки
   3. Не работает с мобильными устройствами
   4. В основном для настольных компьютеров
   5. Новые уроки будут ссылками на AAAKnow.com
   6. Все уроки старого формата будут доступны.
   7. Интерактивные уроки математики
   8. Бесплатно или без регистрации
   9. Безлимитная практика
   10. Немедленная обратная связь предотвращает отработку неправильных методов.
   11. Отличный способ выучить математику
   12. Может быть изменен на новый формат в будущем

   AAA Сейчас.com

   1. Использует современный веб-формат.
   2. Практически идентичные уроки
   3. Хорошо работает с мобильными устройствами
   4. Для любого типа компьютера
   5. На сайте будут разработаны новые уроки
   6. Все уроки старого формата будут доступны.
   7. Интерактивные уроки математики
   8. Бесплатно или без регистрации
   9. Безлимитная практика
   10. Немедленная обратная связь предотвращает отработку неправильных методов.
   11. Отличный способ выучить математику
   12. Будет и дальше развиваться

   Пожалуйста, дайте нам знать, если у вас есть какие-либо предложения или комментарии о веб-сайте AAAKnow.com, используя форму обратной связи для анонимных комментариев.

   Оценка

   Иногда вместо чисел используются переменные. Возможно, что в некоторых выражениях переменная могла быть заменена другими значениями.

   Когда мы заменяем переменную значением, мы называем это вычислением. Посмотрите несколько примеров:

   Пример 1: 32 + x, где x = 8

   Здесь мы перепишем выражение, но заменим x на 8 и выполним операцию.

   32 + x

   32 + 8

   40

   Пример 2: 32x, где x = 8

   Столкнувшись с примером, в котором числа рядом с буквами, не попадайтесь в ловушку простой замены x с цифрой 8 и вызывая ответ 328!

   Это распространенная ошибка.Вместо этого, когда мы видим числа рядом с переменными, нам нужно умножать.

   32x

   32 (8)

   256

   Пример 3: 5x + 7y, где x = 3 и y = 9

   В этой задаче нам нужно заменить две разные переменные. Обязательно осторожно замените значение x на 3, а значение y на 9. Кроме того, вам нужно использовать правильный порядок операций при упрощении.

   5x + 7y Заменить переменные заданными значениями.

   5 (3) + 7 (9) Далее умножим.

   15 + 63 Последние шаги — добавить.

   78

   Вычисление может стать более трудным, если добавить экспоненты, целые числа и другие дополнительные символы. Давайте рассмотрим еще несколько примеров различных типов, с которыми вы можете столкнуться.

   Пример 3: | 5m — 11 |, где m = -13

   Обратите внимание, что в этом примере у нас есть полосы абсолютных значений вокруг выражения.

   Для начала мы сначала оценим выражение внутри столбцов абсолютных значений.

   | 5 (-13) — 11 |

   | -65 — 11 |

   | -76 |

   Далее мы возьмем абсолютное значение выражения. Помните, что абсолютное значение — это расстояние от нуля, а расстояния положительны.

   | -76 | = 76

   Пример 4: 3g ² + 8h, где g = -4 и h = 12

   Помните, что после замены переменных заданными значениями необходимо использовать порядок операций, чтобы завершить процесс.

   3g ² + 8h

   3 (-4) ² + 8 (12)

   3 (16) + 8 (12)

   48 + 96

   144

   Пример 5: 11 + k (3j — 7), где k = -2 и j = 5

   И снова мы начнем с замены переменных значениями.

   11 + k (3j — 7) Начните с замены переменных заданными значениями.

   11 + -2 (3 (5) — 7) Далее мы будем умножать в скобках.