Содержание
Уроки информатики в школе — Тема 1.2. Графическое решение системы уравнений
Тема 1.2. Программные средства обучения математики.
Занятие 7 часть 2
Тема. Графическое решение системы уравнений.
Алгоритм решения:
1. Построить графики каждого из уравнений системы.
2. Отметить на координатной плоскости точки пересечения построенных графиков.
3. Указать координаты отмеченных точек.
Пример.
Решить систему уравнений графическим способом.
Шаги выполнения:
1. Запустить программу GRAN1.
2. Выбрать в окне «Список объектов» тип зависимости Неявная: 0=G(X,Y).
3. Выбрать в меню Объект команду Создать.
4. Ввести в поле окна диалога «Ввод выражения зависимости» выражение: x+3*y-9 .
5. Выбрать в меню График команду Построить.
6. Выбрать в окне «Список объектов» тип зависимости : Неявна: 0=G(X,Y).
7. Выбрать в меню Объект команду Создать.
8. Ввести в поле окна диалога «Ввод выражения зависимости» выражение: 2*х-y-4.
9. Выбрать в меню График команду Построить.
10. Выполнить График — Метки. Перейти в окно диалога «Метки на графике« и выбрать кн «Метка с экрана«.
11. В окне «График» выбрать указателем точку пересечения графиков функций (определить координаты точки пересечения графиков в окне «График») и щелкнуть кн.ОК. Результат будет сохранен в окне «Метки на графике»
(проверка: Ответ: (3.005; 2.016).)
12. Сохранить файл урок7_ч2.grn1.
Выполните задание.
назад
Графический способ решения систем линейных уравнений с двумя переменными.
Данная разработка предназначена для учеников 7 класса и для тех, кто, в своё время, пропустил эту тему. В теоретической части изложена суть графического способа решения систем, алгоритм этого способа, приведены примеры с графиками. В практической части содержатся задания для закрепления знаний и умений.
Просмотр содержимого документа
«Графический способ решения систем линейных уравнений с двумя переменными.»
Графический способ решения систем линейных уравнений с двумя переменными.
Приступаем к рассмотрению способов решения линейных уравнений с двумя переменными.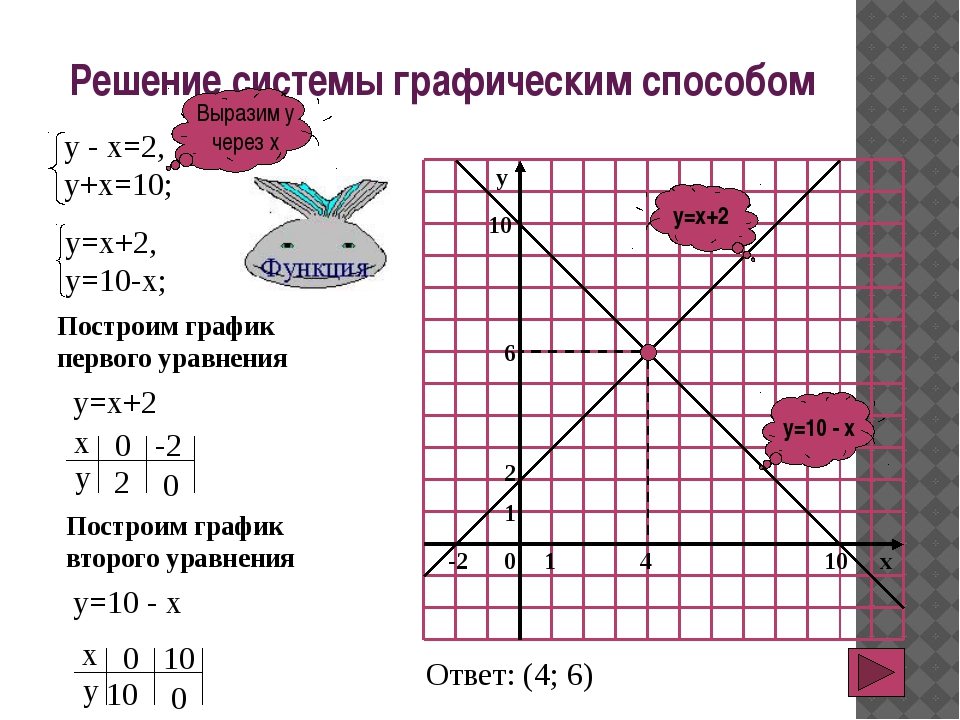 В школьном курсе алгебры изучаются три способа решения систем.
В школьном курсе алгебры изучаются три способа решения систем.
Графический способ (с помощью графиков).
Способ подстановки.
Способ сложения.
Разбираем каждый из них подробно. В этой теме внимание уделено графическому способу. Название говорит само за себя: нужно строить графики. Мы уже выяснили, что линейное уравнение с двумя переменными легко преобразуется в линейную функцию путём выражения переменной у через переменную х (используя правила переноса и деления/умножения на одно и то же число). Преобразовав таким образом каждое уравнение, входящее в систему, и, построив графики, можно визуально определить решение системы, т.е. точку пересечения этих графиков. Останется только лишь как можно более точно выяснить координаты этой точки. Это и есть решение системы.
При решении системы линейных уравнений с двумя переменными графическим способом, необходимо:
в каждом уравнении выразить переменную у через переменную х;
на одной системе координат построить график каждой полученной функции;
найти общие точки построенных прямых;
определить, если это возможно, координаты общих точек прямых. Они и есть решение системы.
Они и есть решение системы.
Например, решить графическим способом систему
Выразим переменную у через переменную х.
Описываем функции.
– линейная функция, графиком является прямая, проходящая через точки
– линейная функция, графиком является прямая, проходящая через точки
На одной системе координат строим графики описанных функций.
Находим координаты точки А – точки пересечения прямых. .
Значит, система имеет единственное решение
У графического способа решения систем есть существенный недостаток. Найденное решение не всегда бывает точным, т.к. на системе координат иногда невозможно выбрать такой единичный отрезок, чтобы чётко определить координаты точки пересечения. Зачастую решение является приближённым.
Зачастую решение является приближённым.
Решить систему уравнений графическим способом:
Составьте системы уравнений, графики которых изображены на рисунках, и найдите по рисунку их решения.
а) б) в)
г) д) е)
ж) з) и)
Используя графический способ, определите, имеет ли решения система уравнений:
Решить графически систему уравнений. Выяснить, проходит ли третья прямая через точку пересечения первых двух.
Выяснить, проходит ли третья прямая через точку пересечения первых двух.
Решить графически систему уравнений:
3
Графический метод решения системы уравнений с двумя переменными
Математика уступает
Свои крепости лишь
Сильным и смелым
А.П. Конфорович
‘Графический метод решения
системы уравнений с двумя
переменными’
2. Цель урока: Научить решать систему уравнений с двумя переменными графическим методом. Рассмотреть частные случаи решения
системы линейных уравнений.
3. Что называют системой уравнений? Рассмотрим два линейных уравнения: 1) y – 2x = – 3 2) x + y = 3
Системой уравнений называется некоторое
количество уравнений, объединенных фигурной
скобкой. Фигурная скобка означает, что все
Фигурная скобка означает, что все
уравнения должны выполняться одновременно.
a1 x b1 y c1 ,
a2 x b2 y c2 .
y – 2x = – 3
x+y=3
Каждая пара значений переменных, которая
одновременно является решением всех
уравнений системы, называется решением
системы.
Решением системы уравнений с двумя
переменными называется пара значений
переменных, обращающая каждое уравнение
системы в верное равенство.
Решить систему уравнений — значит найти все её
решения или установить, что их нет.
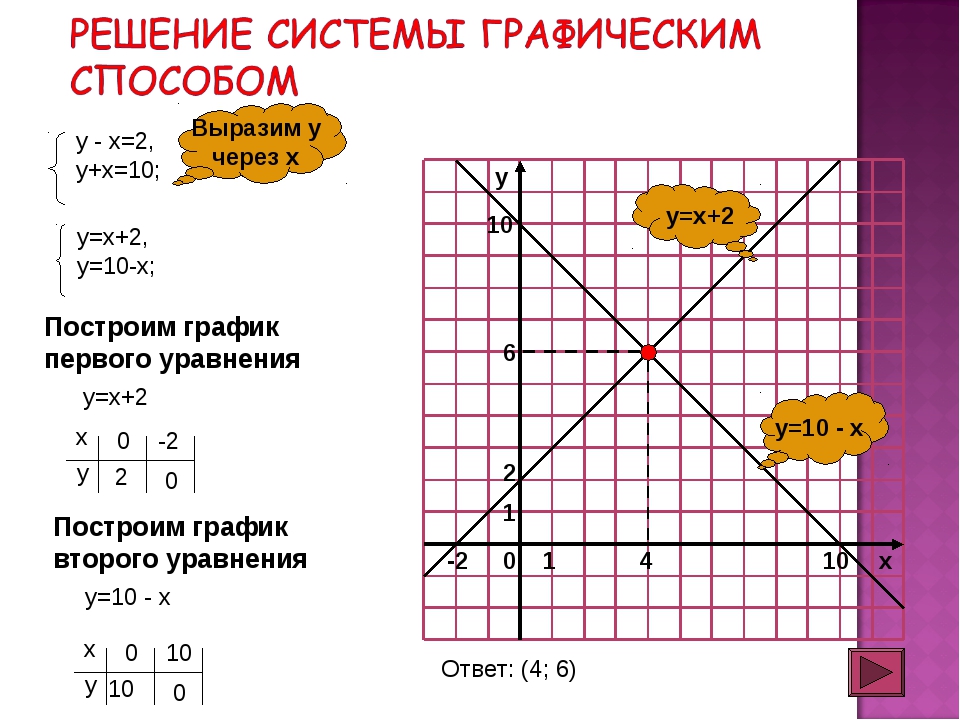
Решение системы графическим способом
у – х = 2,
у + х = 10;
Выразим у
через х
y
y=x+2
10
у = х + 2,
у = 10 – х;
Построим график первого уравнения
6
у=х+2
х 0 -2
у 2 0
y=10 — x
2
1
Построим график второго уравнения
у = 10 – х
х 0 10
у 10 0
-2
0
1
Ответ: (4; 6)
4
10
x
6. Алгоритм решения системы уравнений графическим способом
1. Приводим оба уравнения к виду линейной функции
Приводим оба уравнения к виду линейной функции
y = k x + m.
2. Составляем расчётные таблицы для каждой функции.
3. Строим графики функций в одной координатной плоскости.
4. Определяем число решений:
Если прямые пересекаются, то одно решение пара чисел (х ; у) –
координаты точки пересечения;
Если прямые параллельны, то нет решений;
Если прямые совпадают, то бесконечно много решений.
5. Записываем ответ.
7. Графический метод решения системы x + y = 3 y – 2x = – 3
Графический метод решения системы
у =3–x
x
y
0
3
3
0
A(0;3)
M(2;1)
у =1
у = 2x – 3
D(3;3)
B(3;0)
X=2
x
y
0
3
–3
3
C(0; – 3)
Ответ: (2; 1)
x+y=3
y – 2x = – 3
Решим
систему
уравнений:
Y= 0,5x+2
Y= 0,5x-1
Y=0,5x+2
x y
0
2
2
3
B(2;3)
A(0;2)
D(2;0)
Y=0,5x-1
x y
0 -1
2 0
C(0;-1)
Графики функций
параллельны и не
пересекаются.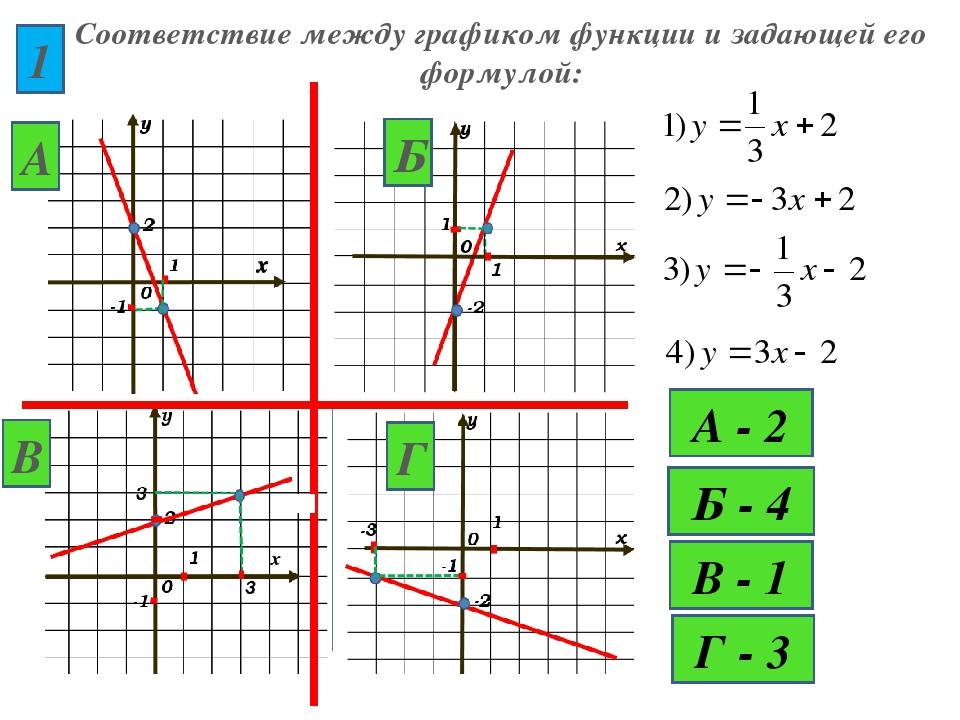
Ответ: Система не имеет решений.
Y=x+3
x
y
0
3
-3
0
D(1;4)
Система
Y=x+3
A(0;3)
Y=x+3
C(-1;2)
B(-3;0)
Y=x+3
x y
1
4
-1
2
Графики функций
совпадают.
Ответ: система имеет бесконечное множество решений
Если графиками уравнений, входящих в систему линейных уравнений,
являются прямые, то количество решений этой системы зависит от
взаимного расположения двух прямых на плоскости:
Прямые
Общие точки
Система
имеет
О системе говорят
Пересекаются
Одна общая точка Одно решение
Имеет решение
Параллельны
Нет общих точек
Не имеет
решений
Несовместна
Совпадают
Много общих
точек
Много решений Неопределена
Частные случаи пересечения графиков линейных
функций (памятка)
2) Решите систему уравнений:
х у 1,
2 х у 4.
у
1) х – у = -1,
у=х+1
х у
0 1
2 3
2) 2х + у = 4,
у = 4 — 2х
х у
0 4
2 0
Ответ: х = 1, у = 2.
4
3
2
1
1
1
2
3
х
1) Решите систему уравнений:
1) 3х +2у = 7,
2у = 7 — 3х,
у = (7 — 3х):2,
у = 3,5 -1,5х,
у = -1,5х + 3,5.
у х
1 2
3 -1
Ответ: х = 3, у = -1.
3х 2 у 7,
2 х 4 у 2.
2) 2х + 4у = 2,
4у = 2 — 2х,
у = (2 — 2х):4,
у = 0,5 – 0,5х.
х
1
3
у
0
-1
у
4
3
2
1
1
1
2
3
х
14. Решите систему уравнений графическим способом
1 вариант
у = 2х — 3
у=-х+3
2 вариант
у = 3х — 4
у = 0,5х + 1
Проверь себя!
Правильное решение систем уравнений графическим способом:
.
у
.
.
. А(2;1)
.
у
х
Ответ: А ( 2; 1)
.
.
.
.
.В(2;2)
х
Ответ: В ( 2; 2)
16. Домашнее задание:
§ 26, выучить материал со слайдов
3, 4, 6,10 (переписать в рабочую
тетрадь)
№ 1008, 1010(1)
Графический способ решения систем уравнений с двумя переменными | План-конспект урока по алгебре (9 класс):
АДМИНИСТРАЦИЯ ГОРОДА НИЖНЕГО НОВГОРОДА
Департамент образования
Муниципальное бюджетное общеобразовательное учреждение
«Школа № 115»
План-конспект урока
по алгебре в 9 классе на тему:
«Графический способ решения системы уравнений с двумя переменными. »
»
Подготовила
учитель математики
Ускова М.Н.
Технологическая карта урока математики
по теме « Системы уравнений с двумя переменными.»
Дата проведения: 23.01.2020
Учитель: Ускова М.Н.
Количество часов по теме: 6
Место урока в данной теме: 1
Формы работы: групповая, фронтальная, индивидуальная
Тип урока: урок изучения нового материала.
Цели урока: создать условия для решения и определения количества решений систем линейных уравнений с двумя переменными графическим методом.
Задачи урока:
- Создать условия для актуализации опорных знаний.
- Организовать формулировку темы урока.
- Организовать постановку учебной цели и учебных задач учащимися.
- Способствовать развитию исследовательских способностей учащихся, умению делать выводы, самоконтроля, речи, логического мышления.
- Продолжить работу по формированию ответственности учащихся за свою деятельность на уроке, умений самостоятельно добывать знания, овладению способами и критериями самоконтроля и самооценки.
Планируемые результаты:
Познавательные УУД:
Регулятивные УУД:
Коммуникативные УУД:
Личностные УУД:
— способствовать строить речевые высказывания, упражнять обучающихся в выполнении мыслительных операций: анализ, обобщение.
— формировать умение планировать свою работу с учетом конечного результата.
— формировать умение работать в группах, умение принимать участие в коллективном обсуждении проблем.
— создать условия для формирования интереса к познавательной деятельности.
Ход урока:
Основные этапы урока | Задачи этапа | Деятельность учителя | Деятельность ученика | Методы обучения | Прогнозируемый результат | Учебно-метододич. обеспечение | План. время |
1.Организационный этап | Психолог. подготовка к общению | Обеспечивает благоприятный настрой. | Настраиваются на работу, | Словесные | Психологическая готовность | Организация внимания | 2 |
2. Проверка домашнего задания. | Проверить уровень усвоения учащимися изучаемого материала, | Контролирует правильность выполнения заданий, организует устранение пробелов в знаниях учащихся | Проверяют домашнее задание | Фронтальный опрос | Правильно выполненное домашнее задание, коррекция ошибок | Фронтальный опрос | 3 |
3. | Создать ситуацию, успеха, повторив весь материал, касающийся графиков различных функций. | Организует работу по актуализации опорных знаний | Запись решения по вариантам | практический | Быстрая проверка опорных знаний | Запись на доске и в тетрадях | 5 |
4.Определение совместной цели деятельности | Обеспечить деятельность по определению целей урока | Создает проблемную ситуацию, объясняет учебную задачу, наблюдает консультирует. | Отвечают на вопросы, формулируют цель урока | Словесные | отвечают верно | беседа | 2 |
5. | способствовать деятельности учащихся по самостоятельному выводу алгоритма решения систем уравнений графическим методом | Организует работу учащихся по выводу алгоритма решения систем уравнений графическим методом | Отвечают на вопросы, записывают алгоритм | словесные | Верное составление алгоритма решения систем уравнений графическим методом в рабочих тетрадях | беседа | 13 |
6. Первичное применение знаний | Установить правильность составленного алгоритма и осознанность изученного | Предлагает выполнить задания | Выполняют задания | практические | Выполнят верно | Выполняют задания на доске и в тетрадях | 10 |
7. | Выявить качество усвоения материала | Предлагает проверить задания | Проверяют задания | самоконтроль | Выполнили верно | Проверяют задания | 5 |
8. Подведение итогов. Рефлексия | Дать оценку работы класса | Подводит итоги урока, ставит задачи на следующий урок | Заполняют листы самоконтроля | самооценка | Осмысление результатов своей работы | Листы самоконтроля | 3 |
9. | Обеспечить понимание содержания домашнего задания | Поясняет домашнее задание | Записывают дом. задание | словесные | 2 |
Актуализация опорных знаний и умений
1.Установите соответствие между функциями и их графиками.
2) 1) Является ли пара чисел (2;0) решением уравнения:
а) xy-4=-4 б) 3(x+Y)=5 В) x/y=0
Усвоение новых знаний
Объяснение учителя:
Если поставлена задача найти все общие решения двух (и более) уравнений с двумя переменными, то говорят, что нужно решить систему уравнений с двумя переменными.
{p(х,у)=0,
q(x,y)=0
Пару чисел (х,у),которая одновременно является решением и первого и второго уравнения системы, называют решением системы уравнений.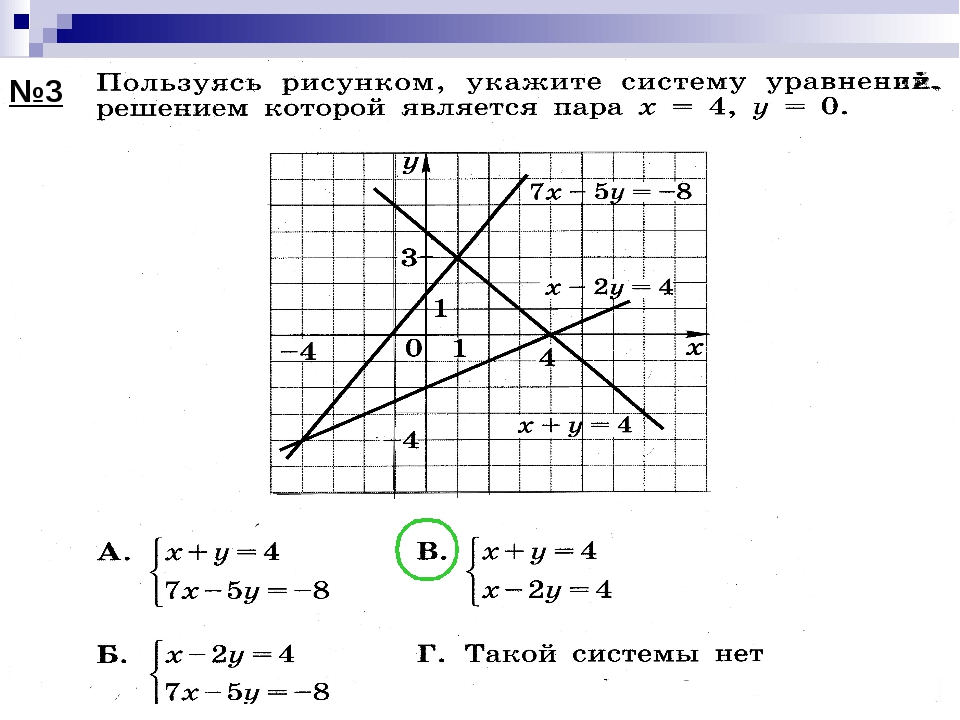
Например: пара (2 ; 3) является решением системы уравнений {
a+b=5
Так как а=2 и b=3 является решением каждого из уравнений системы.
Есть ли еще решения у этой системы уравнений?
Решить систему уравнений с двумя переменными значит найти все ее решения или доказать, что их нет.
Если система не имеет решений, ее называют несовместимой.
Иногда удается решить систему уравнений графическим методом.
Как вы думаете в чем он заключается?
Пример: { 2×2-y=0,
xy=2.
Эта система является «удобной» для графического метода: координаты точек пересечения графиков оказались целыми числами. Такая ситуация встречается не всегда. Поэтому графический метод эффективен тогда, когда нужно определить количество решений или достаточно найти приближенные значения.
Физминутка.
Мы пускаем пузыри, разноцветные они.
Смотрим влево, смотрим вправо,
Вверх глядим на пузыри, снизу тоже есть они.
Закрываем крепко глазки, открываем быстро их –
Пузыри уже пропали, глазки наши не устали.
Закрепление новых знаний.
Работа в группах, с последующей проверкой.
Определите графически количество решений системы уравнений:
1 гр.{|y|=x,
x2+4x=1.
2 гр.
{xy=4,
x2-4x+y=1.
3 гр.
{x2+y2=3,
x=y.
Итог урока. Рефлексия.
-Что называется решением системы уравнений с двумя переменными?
— Что значит решить систему уравнений с двумя переменными?
-С каким способом решение систем уравнений с двумя переменными вы познакомились?
-Дает ли данный способ точные результаты?
— Когда графический метод эффективен?
-В каком случае система уравнений не будет иметь решений?
Отвечают на вопросы, анализируют свою работу на уроке.
Домашнее задание.
П.13,№450,454
«сильным» ученикам №471,473.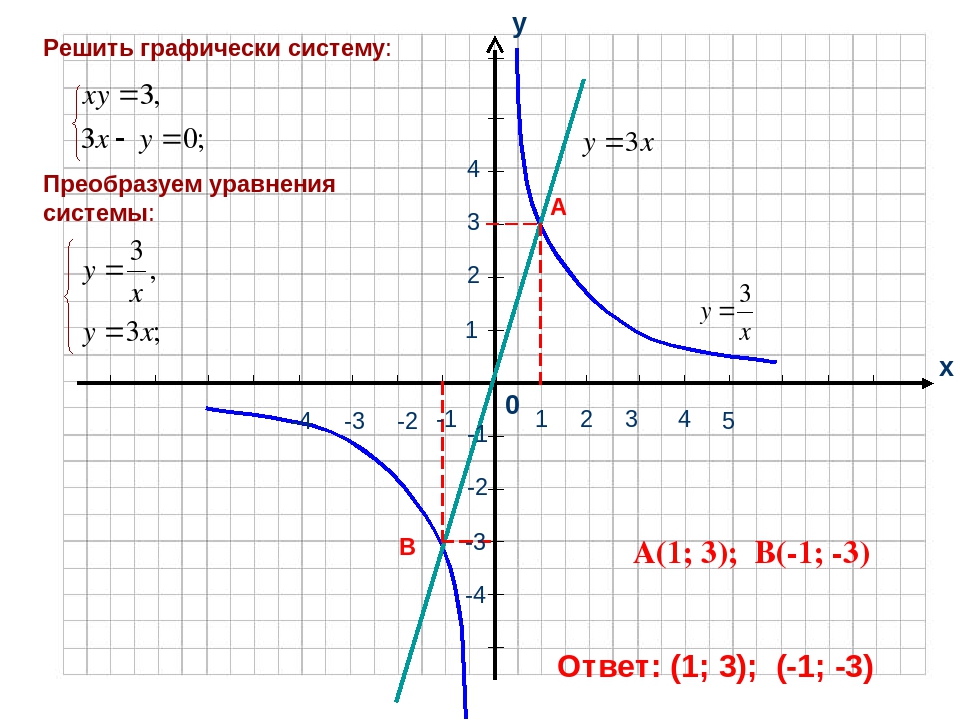
Графический способ решения систем уравнения. Графическое решение уравнений
Видеоурок «Графический способ решения систем уравнений» представляет учебный материал для освоения данной темы. Материал содержит общее понятие о решении системы уравнений, а также подробное объяснение на примере, каким образом решается система уравнений графическим способом.
Наглядное пособие использует анимацию для более удобного и понятного выполнения построений, а также разные способы выделения важных понятий и деталей для углубленного понимания материала, лучшего его запоминания.
Видеоурок начинается с представления темы. Ученикам напоминается, что такое система уравнений, и с какими системами уравнений им уже пришлось ознакомиться в 7 классе. Ранее ученикам приходилось решать системы уравнений вида ах+by=c. Углубляя понятие о решении систем уравнений и с целью формирования умения их решать в данном видеоуроке рассматривается решение системы, состоящей из двух уравнений второй степени, а также из одного уравнения второй степени, а второго — первой степени. Напоминается о том, что такое решение системы уравнений. Определение решения системы как пары значений переменных, обращающих ее уравнения при подстановке в верное равенство, выводится на экран. В соответствии с определением решения системы, конкретизируется задача. На экран выведено для запоминания, что решить систему — означает, найти подходящие решения или доказать их отсутствие.
Напоминается о том, что такое решение системы уравнений. Определение решения системы как пары значений переменных, обращающих ее уравнения при подстановке в верное равенство, выводится на экран. В соответствии с определением решения системы, конкретизируется задача. На экран выведено для запоминания, что решить систему — означает, найти подходящие решения или доказать их отсутствие.
Предлагается освоить графический способ решения некоторой системы уравнений. Применение данного способа рассматривается на примере решения системы, состоящей из уравнений х 2 +у 2 =16 и у=-х 2 +2х+4. Графическое решение системы начинается с построения графика каждого из данных уравнений. Очевидно, графиком уравнения х 2 +у 2 =16 будет окружность. Точки, принадлежащие данной окружности, являются решением уравнения. Рядом с уравнением строится на координатной плоскости окружность радиусом 4 с центром О в начале координат. График второго уравнения представляет собой параболу, ветви которой опущены вниз. На координатной плоскости построена данная парабола, соответствующая графику уравнения. Любая точка, принадлежащая параболе, представляет собой решение уравнения у=-х 2 +2х+4. Объясняется, что решение системы уравнений — точки на графиках, принадлежащие одновременно графикам обоих уравнений. Это значит, что точки пересечения построенных графиков будут являться решениями системы уравнений.
На координатной плоскости построена данная парабола, соответствующая графику уравнения. Любая точка, принадлежащая параболе, представляет собой решение уравнения у=-х 2 +2х+4. Объясняется, что решение системы уравнений — точки на графиках, принадлежащие одновременно графикам обоих уравнений. Это значит, что точки пересечения построенных графиков будут являться решениями системы уравнений.
Отмечается, что графический метод состоит в нахождении приближенного значения координат точек, находящихся на пересечении двух графиков, которые отражают множество решений каждого уравнения системы. На рисунке отмечаются координат найденных точек пересечения двух графиков: А, B, C, D[-2;-3,5]. Данные точки — решения системы уравнений, найденные графическим способом. Проверить их правильность можно, подставив в уравнение и получив справедливое равенство. После подстановки точек в уравнение, видно, что часть точек дает точное значение решения, а часть представляет приближенное значение решения уравнения: х 1 =0, у 1 =4; х 2 =2, у 2 ≈3,5; х 3 ≈3,5, у 3 =-2; х 4 =-2, у 4 ≈-3,5.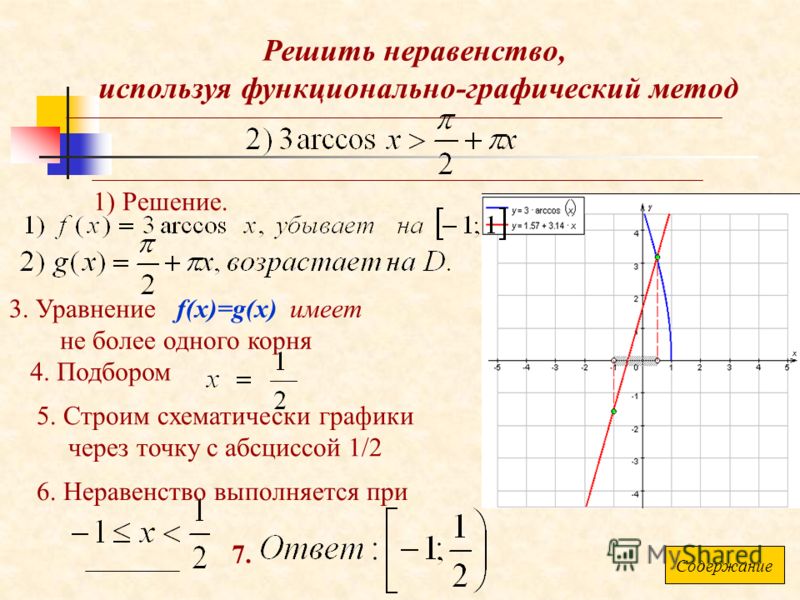
Видеоурок подробно объясняет суть и применение графического способа решения системы уравнений. Это дает возможность использовать его в качестве видеопособия на уроке алгебры в школе при изучении данной темы. Также материал будет полезен при самостоятельном изучении учениками и может помочь объяснить тему при дистанционном обучении.
Рассмотрим следующие уравнения:
1. 2*x + 3*y = 15;
2. x 2 + y 2 = 4;
4. 5*x 3 + y 2 = 8.
Каждое из представленных выше уравнений является уравнением с двумя переменными. Множество точек координатной плоскости, координаты которых обращают уравнение в верное числовое равенство, называется графиком уравнения с двумя неизвестными
.
График уравнения с двумя переменными
Уравнения с двумя переменными имеют большое многообразие графиков. Например, для уравнения 2*x + 3*y = 15 графиком будет прямая линия, для уравнения x 2 + y 2 = 4 графиком будет являться окружность с радиусом 2, графиком уравнения y*x = 1 будет являться гипербола и т. д.
д.
У целых уравнений с двумя переменными тоже существует такое понятие, как степень. Определяется эта степень, так же как для целого уравнения с одной переменной. Для этого приводят уравнение к виду, когда левая часть есть многочлен стандартного вида, а правая — нуль. Это осуществляется путем равносильных преобразований.
Графический способ решения систем уравнения
Разберемся, как решать системы уравнений, которые будут состоять из двух уравнений с двумя переменными. Рассмотрим графический способ решения таких систем.
Пример 1. Решить систему уравнений:
{ x 2 + y 2 = 25
{y = -x 2 + 2*x + 5.
Построим графики первого и второго уравнений в одной системе координат. Графиком первого уравнения будет окружность с центром в начале координат и радиусом 5. Графиком второго уравнения будет являться парабола с ветвями, опущенными вниз.
Все точки графиков будут удовлетворять каждый своему уравнению. Нам же необходимо найти такие точки, которые будут удовлетворять как первому, так и второму уравнению. Очевидно, что это будут точки, в которых эти два графика пересекаются.
Очевидно, что это будут точки, в которых эти два графика пересекаются.
Используя наш рисунок находим приблизительные значения координат, в которых эти точки пересекаются. Получаем следующие результаты:
A(-2,2;-4,5), B(0;5), C(2,2;4,5), D(4,-3).
Значит, наша система уравнений имеет четыре решения.
x1 ≈ -2,2; y1 ≈ -4,5;
x2 ≈ 0; y2 ≈ 5;
x3 ≈ 2,2; y3 ≈ 4,5;
x4 ≈ 4,y4 ≈ -3.
Если подставить данные значения в уравнения нашей системы, то можно увидеть, что первое и третье решение являются приближенными, а второе и четвертое — точными. Графический метод часто используется, чтобы оценить количество корней и примерные их границы. Решения получаются чаще приближенными, чем точными.
На этом уроке мы будем рассматривать решение систем двух уравнений с двумя переменными. Вначале рассмотрим графическое решение системы двух линейных уравнений, специфику совокупности их графиков. Далее решим несколько систем графическим методом.
Тема: Системы уравнений
Урок: Графический метод решения системы уравнений
Рассмотрим систему
Пару чисел которая одновременно является решением и первого и второго уравнения системы, называют решением системы уравнений
.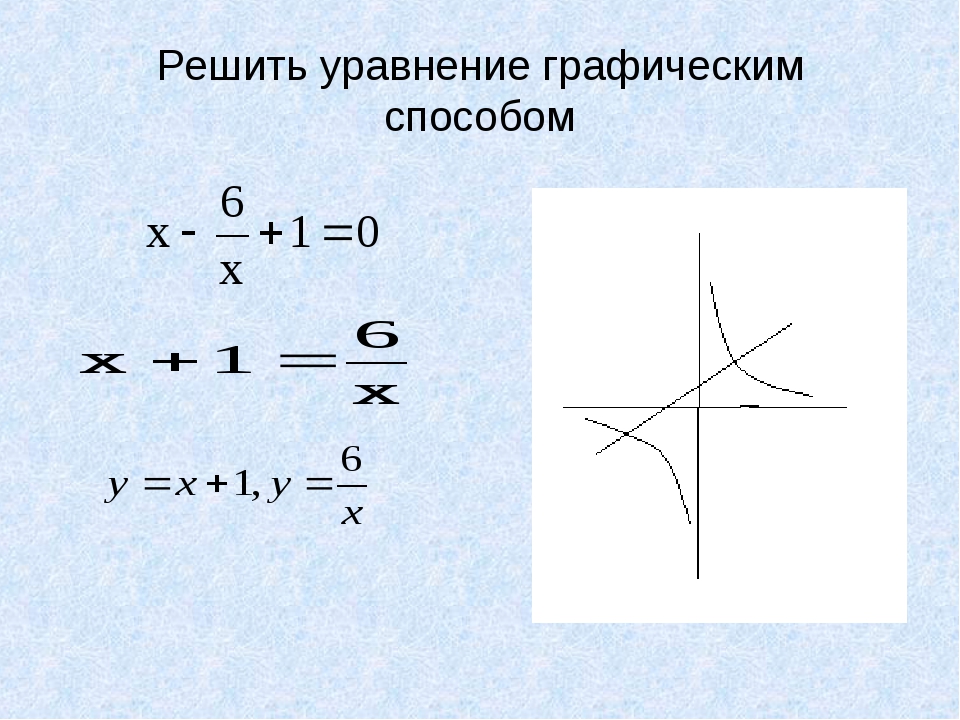
Решить систему уравнений — это значит найти все её решения, или установить, что решений нет. Мы рассмотрели графики основных уравнений, перейдем к рассмотрению систем.
Пример 1. Решить систему
Решение:
Это линейные уравнения, графиком каждого из них является прямая. График первого уравнения проходит через точки (0; 1) и (-1; 0). График второго уравнения проходит через точки (0; -1) и (-1; 0). Прямые пересекаются в точке (-1; 0), это и есть решение системы уравнений (Рис. 1).
Решением системы является пара чисел Подставив эту пару чисел в каждое уравнение, получим верное равенство.
Мы получили единственное решение линейной системы.
Вспомним, что при решении линейной системы возможны следующие случаи:
cистема имеет единственное решение — прямые пересекаются,
система не имеет решений — прямые параллельны,
система имеет бесчисленное множество решений — прямые совпадают.
Мы рассмотрели частный случай системы, когда p(x; y) и q(x; y) — линейные выражения от x и y.
Пример 2. Решить систему уравнений
Решение:
График первого уравнения — прямая, график второго уравнения — окружность. Построим первый график по точкам (Рис. 2).
Центр окружности в точке О(0; 0), радиус равен 1.
Графики пересекаются в т. А(0; 1) и т. В(-1; 0).
Пример 3. Решить систему графически
Решение: Построим график первого уравнения — это окружность с центром в т.О(0; 0) и радиусом 2. График второго уравнения — парабола. Она сдвинута относительно начала координат на 2 вверх, т.е. ее вершина — точка (0; 2) (Рис. 3).
Графики имеют одну общую точку — т. А(0; 2). Она и является решением системы. Подставим пару чисел в уравнение, чтобы проверить правильность.
Пример 4. Решить систему
Решение: Построим график первого уравнения — это окружность с центром в т.О(0; 0) и радиусом 1 (Рис. 4).
Построим график функции Это ломаная (Рис. 5).
Теперь сдвинем ее на 1 вниз по оси oy.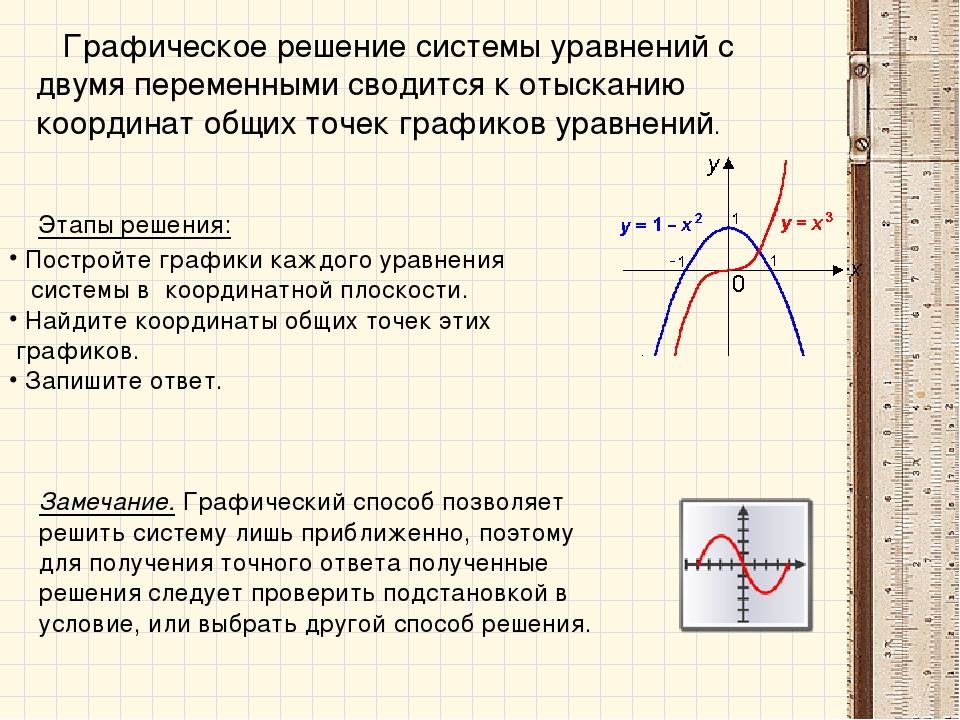 Это и будет график функции
Это и будет график функции
Поместим оба графика в одну систему координат (Рис. 6).
Получаем три точки пересечения — т. А(1; 0), т. В(-1; 0), т. С(0; -1).
Мы рассмотрели графический метод решения систем. Если можно построить график каждого уравнения и найти координаты точек пересечения, то этого метода вполне достаточно.
Но часто графический метод даёт возможность найти только приближенное решение системы или ответить на вопрос о количестве решений. Поэтому нужны и другие методы, более точные, и ими мы займемся на следующих уроках.
1. Мордкович А.Г. и др. Алгебра 9 кл.: Учеб. Для общеобразоват. Учреждений.- 4-е изд. — М.: Мнемозина, 2002.-192 с.: ил.
2. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М.: Мнемозина, 2002.-143 с.: ил.
3. Макарычев Ю. Н. Алгебра. 9 класс: учеб. для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 7-е изд., испр. и доп. — М.: Мнемозина, 2008.
4. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. Алгебра. 9 класс. 16-е изд. — М., 2011. — 287 с.
5. Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 12-е изд., стер. — М.: 2010. — 224 с.: ил.
6. Алгебра. 9 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина и др.; Под ред. А. Г. Мордковича. — 12-е изд., испр. — М.: 2010.-223 с.: ил.
1. Раздел College.ru по математике ().
2. Интернет-проект «Задачи» ().
3. Образовательный портал «РЕШУ ЕГЭ» ().
1. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М. : Мнемозина, 2002.-143 с.: ил. № 105, 107, 114, 115.
Системы уравнений с двумя переменными. Графический способ решения систем уравнений с двумя переменными — АЛГЕБРА — Уроки для 9 классов — конспекты уроков — План урока — Конспект урока — Планы уроков
УРОК № 29
Тема. Системы уравнений с двумя переменными. Графический способ решения систем уравнений с двумя переменными
Цель урока: добиться усвоения учащимися содержания: понятие «что значит решить систему уравнений с двумя переменными»; понятие решения системы уравнений с двумя переменными; схемы действий (алгоритма) для отыскания решения системы уравнений с двумя переменными графическим способом.
Выработать умения: воспроизводить содержание изученных понятий и алгоритмов; применять их для решения упражнений на построение графиков уравнений с двумя переменными графическое решение систем уравнений с двумя переменными.
Тип урока: формирования знаний, выработки умений.
Наглядность и оборудование: опорный конспект № 19.
Ход урока
И. Организационный этап
Учитель проверяет готовность учащихся к уроку, настраивает их на работу.
II. Проверка домашнего задания
Учитель организует работу учащихся по проверке выполнения упражнений домашнего задания по образцу (особое внимание обращаем на упражнения на повторение: комментируя действия, которые были сделаны учениками при их выполнении, проводим не только актуализацию опорных знаний, но и создаем мотивацию для учебной деятельности учащихся).
III. Формулировка цели и задач урока.
Мотивация учебной деятельности учащихся
После проведенной проверки выполнения упражнений домашнего задания учитель направляет мысль учащихся на размышления по поводу того, что в 7 классе, рассмотрев вопрос о содержании понятия «линейное уравнение с двумя переменными», ученики исследовали вопрос не только о построение графика линейного уравнения с двумя переменными, но и рассмотрели понятие системы линейных уравнений 3 двумя переменными и изучили способы решения таких систем. После этих рассуждений вполне логично будет сформулировать вопрос! а можно, изучив вопрос о существовании нелинейных уравнений с двумя переменными, рассматриваемая вопрос о существовании и решения систем таких уравнений? Если это возможно, то на данном уроке следует рассмотреть вопрос о системы нелинейных уравнений и способ решения таких систем с помощью графиков уравнений с двумя переменными. Последнее утверждение выражает основную дидактическую цель данного и следующего уроков.
IV. Актуализация опорных знаний и умений учащихся
Устные упражнения
1. Является ли пара чисел (2; 0) решением уравнения:
1) х2 + у = 1;
2) ху + 3 = х;
3) у(х + 2) = 0?
2. Укажите какие-нибудь два решения уравнения:
1) ху = 6;
2) (x — 3)(y + 2) = 0;
3) х2 — у2 = 0;
4) (x2 — 1)2 + (y + 2)2 = 0;
5) 4х2 — 12ху + 9у2 = -1.
3. Выразите одну переменную через другую из уравнения:
1) 2х — 4у = 8;
2) 5х — у = 2;
3) ху = -8;
4) х2 — у + 3 = 0;
5) х + 3у + ху = 2.
4. Постройте схематично (опишите вид) график функции:
1) у = 5х; 2) у = ; 3) у = 5х2; 4) у = х2 — 5.
V. Формирование знаний
План изучения нового материала
1. Понятие системы уравнений с двумя переменными и ее решения. Что значит «решить систему уравнений с двумя переменными».
2. Как решить систему уравнений с двумя переменными графическим способом.
Опорный конспект № 19
Системы уравнений с двумя переменными |
Если ставится задача найти все общие решения двух (и более) уравнений с двумя переменными, то говорят, что надо решить систему уравнений с двумя переменными. |
Решением системы уравнений с двумя переменными х и у называется такая пара значений переменных (х; у), которая является решением каждого из уравнений системы. |
Например, пара (2; 3) является решением системы уравнений ибо х = 2 и у = 3 является решением каждого из уравнений системы. |
Решить систему уравнений с двумя переменными означает найти все ее решения или доказать, что их нет. ! Если система не имеет решений, ее называют несовместимой. |
Как решить систему уравнений с двумя переменными х и у
графическим способом |
1. Строим графики каждого из уравнений системы в той самой прямоугольной системе координат.
2. Находим все точки пересечения построенных графиков и определяем их координаты. Эти координаты являются решениями данной системы уравнений. |
Методический комментарий
Решение систем уравнений с помощью построения графиков уравнений с двумя переменными позволяет наглядно обосновать количество решений системы уравнений. Материал этого и следующего уроков дает возможность повторить широкий круг вопросов курса алгебры девятилетней школы и некоторые вопросы курса геометрии. Успешному протеканию этой работы будет способствовать подготовительная работа с повторения основных понятий предыдущего урока и вопросов, рассмотренных в 7 классе при изучении систем линейных уравнений с двумя переменными, проведенная на этапе актуализации опорных знаний и умений учащихся.
VI. Формирование умений
Устные упражнения
1. Является ли решением системы уравнений пара чисел:
1) х = -1, у = 4; 2) (1; 4)?
2. Известно, что система уравнений имеет три решения. Сколько точек пересечения имеют графики этих уравнений?
3. По рисунку найдите решения системы уравнений:
1) 2) 3)
Письменные упражнения
Для письменного решения на уроке предлагаются упражнения следующего содержания:
1) решить графически систему нелинейных уравнений с двумя переменными;
2) по графикам найти количество решений системы нелинейных уравнений с двумя переменными;
3) на повторение: упражнения на применение различных способов решения систем линейных уравнений с двумя переменными и способов решения квадратных уравнений, а также уравнений, сводящиеся к квадратным (например, путем введения новой переменной).
Методический комментарий
Решения как письменных, так и устных упражнений урока, кроме выработка умений выполнять действия согласно алгоритма решения системы уравнений графическим способом, дает возможность повторить большое количество вопросов, изученных в 7-9 классах (графики функций, преобразование выражений, а также геометрические преобразования графиков функций). Для того чтобы это повторение было более эффективным, следует постоянно требовать от учащихся устных комментариев всех построений.
VII. Итоги урока
Контрольные вопросы
1. Что называют решением системы уравнений с двумя переменными?
2. Как найти решения системы уравнений с двумя переменными, используя графики этих уравнений?
3. Какую из приведенных систем уравнений можно решать с помощью данного рисунка? Сколько решений имеет эта система?
1)
2)
3)
4)
VIII. Домашнее задание
1. Изучить содержание понятий и алгоритмов урока (см. опорный конспект № 19).
2. Решить упражнения на применение изученного материала (аналогичные упражнениям классной работы).
3. На повторение: решить системы линейных уравнений с одной переменной (разными способами).
ГДЗ по Алгебре 7 класс Мордкович Задачник Решебник Базовый
Чтобы успевать по алгебре и получать хорошие оценки, необходимо проводить много времени за уроками. В зависимости от врожденных способностей к точным наукам у разных школьников изучение математики продвигается по-разному. Некоторым ученикам необходима дополнительная тренировка. Ее может обеспечить частный преподаватель (репетитор), но можно прибегнуть и к практике самостоятельных занятий по решебнику. В предлагаемой здесь книге приведены верные алгоритмы выполнения. Правильное оформление уже показано опытными методистами и снабжено подробными комментариями.
Пособие по алгебре с содержанием правильных ответов подготовлен автором Мордковичем А.Г. Он упрощает занятия ребенка, подготовку к контрольным, проверочным диагностическим работам, а также тестам, поскольку содержит грамотно оформленные объяснения и указания. Таблица, приведенная на странице сайта, представляет все доступные номера, с которыми рекомендуется ознакомиться и проверить собственное выполнение на их примере. Пособие «Математика, 7 класс» издается издательством «Мнемозина» с 2013 по 2019 годы. Сейчас актуальным является 17 издание.
Чем решебник Мордковича помогает семикласснику?
Автор использовал модель готовых домашних заданий (ГДЗ). Не представляет труда находить нужные номера и смотреть на способы решения, которые были предложены. Систематическое использование рекомендуется любому школьнику по следующим причинам:
- каждая задача имеет индивидуальный номер в оглавлении;
- решения полностью соответствуют порядку в учебнике, который выдается в библиотеке;
- легкий доступ к ответам. Достаточно использовать смартфон, планшет или компьютер с выходом в сеть;
- во многих случаях приведено несколько вариантов решения. Таким образом, можно выбрать наиболее подходящий и понятный метод.
Из ГДЗ нельзя просто списывать. Их нужно внимательно анализировать и запоминать самую важную информацию. Полезно, чтобы фундаментальные навыки были своевременно доведены ребенком до автоматизма.
Рабочая программа с ГДЗ по математике за 7 класс Мордковича
В первый год изучения алгебры (до этого в школьной программе присутствует курс математики) вводятся важнейшие понятия. Их необходимо твердо усвоить, чтобы и в дальнейшем эффективно продвигаться по школьному курсу данного предмета:
- линейная функция. Определение, график, способы записи. Зависимая и независимая переменные. Определение точек пересечения;
- системы двух линейных уравнений с двумя переменными, а также способы их систематического решения. Выполнение проверки результатов;
- одночлены и многочлены, арифметические операции с ними;
- парабола, графическое изображение графика функции. Ее аналитическая запись, ветви. Ось симметрии указанной фигуры. Функциональная запись выражений.
Программа регламентирована федеральными государственными образовательными стандартами (ФГОС). Она подходит для любой школы Российской Федерации и отлично соответствует заданиям и тестам, которые ежегодно предлагаются на внешних проверочных работах.
Решение линейных систем с помощью построения графиков
Системы в этом разделе будут состоять из двух линейных уравнений и двух неизвестных. Учитывая линейные уравнения, нас просят выяснить, есть ли у них одновременные решения. Другими словами, где пересекаются две линии? Этот вопрос вызывает три случая:
Большую часть времени линейная система будет иметь общую точку ( x , y ). Точка их пересечения — это решение системы.
Однако не все линейные системы имеют упорядоченное парное решение; у некоторых нет общих точек, а у других их бесконечно много.Представьте, что вас попросили решить систему, состоящую из двух параллельных прямых, где они пересекаются? В этом случае одновременного решения нет и система двух параллельных линий несовместима. В случае, когда система состоит из двух линий, которые оказываются одной и той же прямой, имеется бесконечно много общих точек. Эта система является зависимой, и решения могут быть представлены в форме ( x , y ), где x может быть любым действительным числом, а y = mx + b .
Решите системы по графику :
Является ли заказанная пара решением проблемы системы?
В следующем примере показано, как найти общую точку, точку пересечения двух линий, если нам дана линейная система в стандартной форме.
Решите систему :
Шаг 1 : Поместите линейные уравнения в форму пересечения наклона.
Шаг 2 : Постройте линии и используйте график, чтобы найти общую точку.
Шаг 3 : Проверьте свой ответ и представьте его как упорядоченную пару.
Здесь важна точность, используйте миллиметровую бумагу и линейку при использовании метода построения графиков для решения линейных систем.
Решите систему, используя метод построения графиков :
Постройте линии, используя форму пересечения наклона.
Решите систему, используя метод построения графиков :
Постройте линии, используя форму пересечения наклона.
Будьте особенно внимательны с масштабом при построении графика, чтобы найти пересечение.Убедитесь, что все ваши отметки одинакового размера. Это сделает ваши графики более точными и удобными для чтения. Убедитесь, что ваш ответ работает для ОБОИХ уравнений.
Решите систему, используя метод построения графиков :
Разместите линии в форме пересечения откосов.
И затем изобразите их.
Решите систему, используя метод построения графиков :
Разместите линии в форме пересечения наклона и затем нанесите их на график.
Зависимые системы, кажется, доставляют больше всего проблем начинающим изучающим алгебру.Помните, что мы ищем точки пересечения двух линий. Если линии такие же, что ж, тогда они будут пересекаться в бесконечном количестве точек. Из-за этого мы должны использовать специальные обозначения для обозначения бесконечного множества. Обратите внимание, что мы уже поместили строку в форму перехвата y , y = mx + b , поэтому записать окончательные упорядоченные парные решения в форме ( x , м x + b ).
Вы можете увидеть другие обозначения в других текстах, например,
Примеры видео на YouTube :
Ползунки используются для изменения значений коэффициентов a1, b1, c1, a2, b2 и c2, чтобы исследовать различные системы уравнений.Здесь используется графическая интерпретация, чтобы дать полную картину решения систем уравнений существующими алгебраическими методами (исключение, правило Крамера, …). Также на этом сайте есть руководство по решению линейных систем с использованием аналитических методов. Интерактивное учебное пособиеНажмите «нарисовать», чтобы начать. Начальные (значения по умолчанию) коэффициенты: a1 = 1, b1 = 3, c1 = 5 и a2 = 2, b2 = -2, c2 = 2, что дает систему уравнений: х + 3у = 5 Какова связь между пересечением линий, представляющих два уравнения системы, и решениями системы? Легко проверить, что точка пересечения (2, 1) двух прямых является решением системы уравнений, составленной из уравнений прямых.
Дополнительные ссылки и ссылки на системы линейных уравнений Калькулятор и решатель систем уравнений. |
Иллюстративная математика
Задача
Без построения графиков постройте систему из двух линейных уравнений, где $ (- 2,3) $ — решение первого уравнения, но не второго уравнения, и где $ (5, -2) $ — решение вашей системы. .
После того, как вы создали свою систему уравнений, нанесите ее на график. Объясните, как ваш график показывает, что ваша система удовлетворяет требуемым условиям.
Комментарий IM
Цель этого задания — побудить студентов критически осмыслить как алгебраическую, так и графическую интерпретацию систем линейных уравнений. Ожидается, что они воспользуются тем, что знают о решении систем линейных уравнений, а затем обратят обычный процесс. Это также дает хорошую возможность убедиться, что учащиеся понимают разницу между одним уравнением и системой, в которой мы рассматриваем два уравнения вместе, и, в частности, фразу «решение системы уравнений».«
Есть два существенно разных способа найти возможное второе уравнение после того, как мы нашли первое, и поэтому каждый из этих двух методов описан ниже (помечены (а) и (b)). Обратите внимание, что линия $ x = c $ не упоминается в решении, хотя это вполне жизнеспособное уравнение для рассмотрения.
Это задание можно использовать как дальнейшую практику и для углубления понимания после того, как материал уже был представлен, или как задание для оценки.
Кроме того, в этом задании учащимся предлагается сначала составить систему линейных уравнений, удовлетворяющую заданным условиям, без построения графиков, а затем рассмотреть свои графики.Более простой вариант — избавиться от этого ограничения. и позволить учащимся сначала нарисовать график в качестве помощи в поиске уравнений, соответствующих требованиям. Это позволит учащимся использовать навыки, которые они уже усвоили и с которыми они могут чувствовать себя более комфортно.
Аналогичный вводный вариант см. В 8.EE.8 «Пересечение двух линий».
Решение
Поскольку мы ищем два линейных уравнения в $ x $ и $ y $, мы знаем, что сможем записать наши два уравнения в форме $ y = mx + b $, где $ m $ — наклон линия, а $ b $ — $ y $ -перехват.
Поскольку мы хотим, чтобы $ (5, -2) $ было решением нашей системы уравнений, мы знаем, что это решение обоих уравнений. Поскольку $ (- 2,3) $ также является решением первого уравнения, теперь мы знаем, что наша первая строка содержит точки $ (5, -2) $ и $ (- 2,3) $. Мы можем использовать эти две точки, чтобы найти наклон линии, взяв разницу в координатах $ y $ и разделив на разницу в координатах $ x $:
$$ m = \ displaystyle \ frac {3 — (- 2)} {(- 2) -5} = — \ frac {5} {7} $$
Чтобы найти $ b $, мы используем это значение $ m $ и одну из точек, которую мы хотим решить, например, $ (- 2,3) $.Подставляя эти известные значения в нашу общую форму $ y = mx + b $, мы получаем
$$ 3 = — \ frac {5} {7} (- 2) + b $$
$$ 3 = \ frac {10} {7} + b $$
$$ \ frac {21} {7} — \ frac {10} {7} = b $$
$$ \ frac {11} {7} = b. $$
Итак, наше первое уравнение: $ \ displaystyle y = — \ frac {5} {7} x + \ frac {11} {7} $.
Есть много способов найти уравнение для завершения системы, удовлетворяющей заданным условиям: (a) Выберите любую точку, которая не лежит на прямой $ y = -5 / 7x + 11/7 $, и найдите уравнение прямой через эту точку и $ (5, -2) $, или (b) Выберите любой наклон, отличный от $ -5 / 7 $, и найдите линию с этим наклоном, которая также проходит через точку $ (- 5,2) $.Оба метода приведены ниже.
Рассмотрим точку $ (0,0) $. С
$$ 0 \ neq — \ frac {5} {7} (0) + \ frac {11} {7} = \ frac {11} {7}, $$
$ (0,0) $ не является решением нашего первого уравнения. Следовательно, если мы найдем уравнение прямой через $ (0,0) $ и $ (5, -2) $, мы найдем второе уравнение, которое соответствует критериям для нашей системы. Мы используем эти две точки, чтобы найти наклон линии:
$$ м = \ Displaystyle \ гидроразрыва {(- 2) -0} {5-0} = — \ гидроразрыва {2} {5} $$
Чтобы найти $ b $, мы используем это значение $ m $ и одну из точек, которая должна быть решением уравнения, например, $ (0,0) $.Подставляя эти известные значения в нашу общую форму $ y = mx + b $, мы имеем
$$ 0 = — \ frac {2} {5} (0) + b $$
$$ 0 = b $$
Мы также могли увидеть это, потому что выбрали точку $ (0,0) $, и поэтому значение $ y $ при $ x = 0 $ равно 0.Итак, наше второе уравнение $ \ displaystyle y = — \ frac {2} {5} x $, а наша система уравнений
$$ \ begin {case} y = — \ frac {5} {7} x + \ frac {11} {7} \\ y = — \ frac {2} {5} x \ end {cases} $$
и мы можем проверить, что $ (- 2,3) $ является решением первого уравнения, но не второго уравнения, а $ (5, -2) $ является решением системы.Затем мы можем изобразить эти два уравнения на одном и том же наборе осей:
Этот график соответствует нашей системе, потому что мы видим, что две прямые пересекаются в точке $ (5, -2) $, и что первое уравнение также проходит через точку $ (- 2,3) $, но второе уравнение не.
Примечание: здесь была выбрана точка $ (0,0) $, но подойдет любая другая точка, не лежащая в первой строке, поэтому разных ответов может быть бесконечно много!
Мы можем выбрать любой уклон, кроме $ -5 / 7 $, и поэтому давайте выберем наклон $ 7/5 $, и это даст нам линию, перпендикулярную $ \ displaystyle y = — \ frac {5} {7} x + \ frac {11} {7} $.
Используя это значение $ m $ и тот факт, что мы хотим, чтобы $ (5, -2) $ было решением, мы можем заменить эти известные значения в нашу общую форму $ y = mx + b $, и мы имеем
$$ — 2 = \ frac {7} {5} (5) + b $$
$$ — 2 = 7 + b $$
$$ — 9 = b $$Итак, наше второе уравнение $ \ displaystyle y = \ frac {7} {5} x-9 $, а наша система уравнений
$$ \ begin {case} y = — \ frac {5} {7} x + \ frac {11} {7} \\ y = \ frac {7} {5} x-9 \ end {cases} $$
и мы можем проверить, что $ (- 2,3) $ является решением первого уравнения, но не второго уравнения, а $ (5, -2) $ является решением системы.Затем мы можем изобразить эти два уравнения на одном и том же наборе осей:
Этот график соответствует нашей системе, потому что мы видим, что две прямые пересекаются в точке $ (5, -2) $, и что первое уравнение также проходит через точку $ (- 2,3) $, но второе уравнение не.
5.1. Решать системы уравнений с помощью построения графиков — Элементарная алгебра 2e
Задачи обучения
К концу этого раздела вы сможете:
- Определить, является ли упорядоченная пара решением системы уравнений
- Решите систему линейных уравнений, построив график
- Определить количество решений линейной системы
- Решение приложений систем уравнений с помощью построения графиков
Будьте готовы 5.1
Прежде чем начать, пройдите тест на готовность.
Для уравнения y = 23x − 4y = 23x − 4
Ⓐ является ли (6,0) (6,0) решением? Ⓑ является (−3, −2) (- 3, −2) решением?
Если вы пропустили эту проблему, просмотрите Пример 2.1.
Будьте готовы 5.2
Найдите наклон и пересечение y прямой 3x − y = 123x − y = 12.
Если вы пропустили эту проблему, просмотрите Пример 4.42.
Будьте готовы 5,3
Найдите точки пересечения x и y прямой 2x − 3y = 122x − 3y = 12.
Если вы пропустили эту проблему, просмотрите Пример 4.21.
Определить, является ли упорядоченная пара решением системы уравнений
В разделе «Решение линейных уравнений и неравенств» мы научились решать линейные уравнения с одной переменной. Помните, что решение уравнения — это значение переменной, которое делает истинное утверждение при подстановке в уравнение.
Теперь мы будем работать с системами линейных уравнений, двумя или более линейными уравнениями, сгруппированными вместе.
Система линейных уравнений
Когда два или более линейных уравнения группируются вместе, они образуют систему линейных уравнений.
Мы сосредоточим нашу работу здесь на системах двух линейных уравнений с двумя неизвестными. Позже вы сможете решать более крупные системы уравнений.
Пример системы двух линейных уравнений показан ниже. Мы используем скобку, чтобы показать, что два уравнения сгруппированы вместе и образуют систему уравнений.
{2x + y = 7x − 2y = 6 {2x + y = 7x − 2y = 6
Линейное уравнение с двумя переменными, например 2 x + y = 7, имеет бесконечное количество решений.Его график представляет собой линию. Помните, что каждая точка на линии — это решение уравнения, а каждое решение уравнения — это точка на линии.
Чтобы решить систему двух линейных уравнений, мы хотим найти значения переменных, которые являются решениями обоих уравнений. Другими словами, мы ищем упорядоченные пары ( x , y ), которые делают оба уравнения истинными. Они называются решениями системы уравнений.
Решения системы уравнений
Решения системы уравнений — это значения переменных, которые делают все уравнения истинными.Решение системы двух линейных уравнений представляется упорядоченной парой ( x , y ).
Чтобы определить, является ли упорядоченная пара решением системы двух уравнений, мы подставляем значения переменных в каждое уравнение. Если упорядоченная пара делает оба уравнения истинными, это решение системы.
Рассмотрим систему ниже:
{3x − y = 7x − 2y = 4 {3x − y = 7x − 2y = 4
Является ли упорядоченная пара (2, −1) (2, −1) решением?
Упорядоченная пара (2, −1) сделала оба уравнения верными.Следовательно, (2, −1) является решением этой системы.
Попробуем еще одну заказанную пару. Является ли упорядоченная пара (3, 2) решением?
Упорядоченная пара (3, 2) сделала одно уравнение истинным, а другое — ложным. Поскольку это не решение обоих уравнений , оно не является решением этой системы.
Пример 5.1
Определите, является ли упорядоченная пара решением системы: {x − y = −12x − y = −5 {x − y = −12x − y = −5
ⓐ (−2, −1) (- 2, −1) ⓑ (−4, −3) (- 4, −3)
Решение
- ⓐ
(−2, −1) не делает оба уравнения верными.(−2, −1) не является решением.
Ⓑ
(−4, −3) не делает оба уравнения верными. (−4, −3) — решение.
Попробуйте 5.1
Определите, является ли упорядоченная пара решением системы: {3x + y = 0x + 2y = −5. {3x + y = 0x + 2y = −5.
ⓐ (1, −3) (1, −3) ⓑ (0,0) (0,0)
Попробовать 5.2
Определите, является ли упорядоченная пара решением системы: {x − 3y = −8−3x − y = 4. {X − 3y = −8−3x − y = 4.
ⓐ (2, −2) (2, −2) ⓑ (−2,2) (- 2,2)
Решите систему линейных уравнений с помощью построения графиков
В этой главе мы будем использовать три метода для решения системы линейных уравнений.Первый метод, который мы будем использовать, — это построение графиков.
График линейного уравнения представляет собой линию. Каждая точка на линии — это решение уравнения. Для системы двух уравнений мы построим график двумя линиями. Затем мы можем увидеть все точки, которые являются решениями каждого уравнения. И, обнаружив, что общего у линий, мы найдем решение системы.
Большинство линейных уравнений с одной переменной имеют одно решение, но мы видели, что некоторые уравнения, называемые противоречиями, не имеют решений, а для других уравнений, называемых тождествами, все числа являются решениями.
Точно так же, когда мы решаем систему двух линейных уравнений, представленную графиком из двух линий в одной плоскости, есть три возможных случая, как показано на рисунке 5.2:
Рисунок 5.2
Для первого примера решения системы линейных уравнений в этом разделе и в следующих двух разделах мы будем решать одну и ту же систему двух линейных уравнений. Но в каждом разделе мы будем использовать разные методы. Увидев третий метод, вы решите, какой метод был наиболее удобным для решения этой системы.
Пример 5.2
Как решить систему линейных уравнений с помощью построения графиков
Решите систему, построив график: {2x + y = 7x − 2y = 6. {2x + y = 7x − 2y = 6.
Попробовать 5,3
Решите систему, построив график: {x − 3y = −3x + y = 5. {X − 3y = −3x + y = 5.
Попробовать 5.4
Решите систему, построив график: {−x + y = 13x + 2y = 12. {- x + y = 13x + 2y = 12.
Шаги, которые необходимо использовать для решения системы линейных уравнений с помощью построения графиков, показаны ниже.
How To
Чтобы решить систему линейных уравнений с помощью построения графиков.
- Шаг 1. Постройте первое уравнение.
- Шаг 2. Постройте второе уравнение в той же прямоугольной системе координат.
- Шаг 3. Определите, пересекаются ли линии, параллельны или совпадают.
- Шаг 4. Определите решение системы.
- Если линии пересекаются, укажите точку пересечения. Убедитесь, что это решение обоих уравнений. Это решение системы.
- Если линии параллельны, у системы нет решения.
- Если линии совпадают, система имеет бесконечное количество решений.
Пример 5.3
Решите систему, построив график: {y = 2x + 1y = 4x − 1. {Y = 2x + 1y = 4x − 1.
Решение
Оба уравнения в этой системе имеют форму пересечения наклона, поэтому мы будем использовать их наклоны и точки пересечения y , чтобы построить их график. {y = 2x + 1y = 4x − 1 {y = 2x + 1y = 4x − 1
| Найдите наклон и точку пересечения y первого уравнения . | |
| Найдите наклон и точку пересечения y первого уравнения . | |
| Постройте график двух линий. | |
| Определите точку пересечения. | Прямые пересекаются в точках (1, 3). |
| Проверьте решение в обоих уравнениях. | y = 2x + 13 =? 2 · 1 + 13 = 3 ✓y = 4x − 13 =? 4 · 1−13 = 3 ✓y = 2x + 13 =? 2 · 1 + 13 = 3 ✓y = 4x− 13 =? 4 · 1−13 = 3 ✓ |
| Решение (1, 3). |
Попробуй 5.5
Решите каждую систему, построив график: {y = 2x + 2y = −x − 4. {Y = 2x + 2y = −x − 4.
Попробовать 5.6
Решите каждую систему, построив график: {y = 3x + 3y = −x + 7. {Y = 3x + 3y = −x + 7.
Оба уравнения в Примере 5.3 были даны в форме углового пересечения. Это облегчило нам быстрое построение линий. В следующем примере мы сначала перепишем уравнения в форме углового пересечения.
Пример 5.4
Решите систему, построив график: {3x + y = −12x + y = 0.{3x + y = −12x + y = 0.
Решение
Мы решим оба этих уравнения относительно yy, чтобы мы могли легко построить их график, используя их наклоны и y -перехваты. {3x + y = −12x + y = 0 {3x + y = −12x + y = 0
| Решите первое уравнение относительно y . Найдите наклон и точку пересечения y . Решите второе уравнение относительно и . Найдите наклон и точку пересечения y . | 3x + y = −1y = −3x − 1m = −3b = −12x + y = 0y = −2xm = −2b = 03x + y = −1y = −3x − 1m = −3b = −12x + y = 0y = −2xm = −2b = 0 |
| Постройте линии. | |
| Определите точку пересечения. | Прямые пересекаются в точке (−1, 2). |
| Проверьте решение в обоих уравнениях. | 3x + y = −13 (−1) +2 =? — 1−1 = −1 ✓ 2x + y = 02 (−1) + 2 =? 00 = 0 ✓ 3x + y = −13 (−1) +2 =? — 1−1 = −1 ✓ 2x + y = 02 (−1) + 2 =? 00 = 0 ✓ |
| Решение (−1, 2). |
Попробовать 5,7
Решите каждую систему, построив график: {−x + y = 12x + y = 10. {- x + y = 12x + y = 10.
Попробуйте 5.8
Решите каждую систему, построив график: {2x + y = 6x + y = 1. {2x + y = 6x + y = 1.
Обычно, когда уравнения даются в стандартной форме, наиболее удобный способ построения графиков — использование точек пересечения. Мы сделаем это в примере 5.5.
Пример 5.5
Решите систему, построив график: {x + y = 2x − y = 4. {X + y = 2x − y = 4.
Решение
Мы найдем точки пересечения x и y обоих уравнений и будем использовать их для построения графиков линий.
Попробовать 5.9
Решите каждую систему, построив график: {x + y = 6x − y = 2. {X + y = 6x − y = 2.
Попробуйте 5.10
Решите каждую систему, построив график: {x + y = 2x − y = −8. {X + y = 2x − y = −8.
Вы помните, как построить линейное уравнение с одной переменной? Это будет либо вертикальная, либо горизонтальная линия.
Пример 5.6
Решите систему, построив график: {y = 62x + 3y = 12. {Y = 62x + 3y = 12.
Попробуйте 5.11
Решите каждую систему, построив график: {y = −1x + 3y = 6.{у = −1x + 3y = 6.
Попробуйте 5.12
Решите каждую систему, построив график: {x = 43x − 2y = 24. {X = 43x − 2y = 24.
До сих пор во всех системах линейных уравнений линии пересекались, и решение было одной точкой. В следующих двух примерах мы рассмотрим систему уравнений, не имеющую решения, и систему уравнений, которая имеет бесконечное число решений.
Пример 5.7
Решите систему, построив график: {y = 12x − 3x − 2y = 4. {Y = 12x − 3x − 2y = 4.
Попробовать 5.13
Решите каждую систему, построив график: {y = −14x + 2x + 4y = −8. {Y = −14x + 2x + 4y = −8.
Попробуй 5.14
Решите каждую систему, построив график: {y = 3x − 16x − 2y = 6. {Y = 3x − 16x − 2y = 6.
Пример 5.8
Решите систему, построив график: {y = 2x − 3−6x + 3y = −9. {Y = 2x − 3−6x + 3y = −9.
Попробуй 5.15
Решите каждую систему, построив график: {y = −3x − 66x + 2y = −12. {Y = −3x − 66x + 2y = −12.
Попробуйте 5.16
Решите каждую систему, построив график: {y = 12x − 42x − 4y = 16.{у = 12х − 42х − 4у = 16.
Если вы запишете второе уравнение в примере 5.8 в форме пересечения наклона, вы можете заметить, что уравнения имеют одинаковый наклон и одинаковую точку пересечения y .
Когда мы нарисовали вторую линию в последнем примере, мы нарисовали ее прямо над первой линией. Мы говорим, что две линии совпадают. Совпадающие линии имеют одинаковый наклон и одинаковое пересечение и .
Совпадающие линии
Совпадающие линии имеют одинаковый наклон и пересечение y .
Определите количество решений линейной системы
Будут моменты, когда мы захотим узнать, сколько решений будет у системы линейных уравнений, но нам, возможно, на самом деле не придется искать решение. Будет полезно определить это без построения графиков.
Мы видели, что две прямые в одной плоскости должны либо пересекаться, либо быть параллельны. Все системы уравнений в примерах 5.2–5.6 имели две пересекающиеся линии.У каждой системы было одно решение.
Система с параллельными линиями, подобная примеру 5.7, не имеет решения. Что произошло в примере 5.8? Уравнения имеют совпадающие линии, поэтому система имела бесконечно много решений.
Мы систематизируем эти результаты на Рисунке 5.3 ниже:
Рисунок 5.3
Параллельные прямые имеют одинаковый наклон, но разные точки пересечения и . Итак, если мы запишем оба уравнения в системе линейных уравнений в форме наклон-пересечение, мы сможем увидеть, сколько решений будет без графического представления! Посмотрите на систему, которую мы решили в примере 5.7.
{y = 12x − 3x − 2y = 4 Первая линия находится в форме углового пересечения. Если мы решим второе уравнение относительно y, мы получим y = 12x − 3x − 2y = 4−2y = −x + 4y = 12x − 2m = 12 , b = −3m = 12, b = −2 {y = 12x − 3x − 2y = 4 Первая линия находится в форме углового пересечения. Если мы решим второе уравнение относительно y, мы получим y = 12x − 3x − 2y = 4− 2y = −x + 4y = 12x − 2m = 12, b = −3m = 12, b = −2
Две линии имеют одинаковый наклон, но разные точки пересечения и . Это параллельные линии.
На рис. 5.4 показано, как определить количество решений линейной системы по наклонам и пересечениям.
Рисунок 5.4
Давайте еще раз посмотрим на наши уравнения в примере 5.7, которые дали нам параллельные линии.
{y = 12x − 3x − 2y = 4 {y = 12x − 3x − 2y = 4
Когда обе линии были в форме пересечения склона, у нас было:
y = 12x − 3y = 12x − 2y = 12x − 3y = 12x − 2
Вы понимаете, что невозможно иметь одну упорядоченную пару (x, y) (x, y), которая является решением обоих этих уравнений?
Мы называем такую систему уравнений несовместимой. У него нет решения.
Система уравнений, имеющая хотя бы одно решение, называется согласованной системой.
Согласованные и несовместимые системы
Непротиворечивая система уравнений — это система уравнений, имеющая по крайней мере одно решение.
Несогласованная система уравнений — это система уравнений, не имеющая решения.
Мы также классифицируем уравнения в системе уравнений, называя уравнения независимыми или зависимыми . Если два уравнения являются независимыми уравнениями, каждое из них имеет собственный набор решений. Пересекающиеся линии и параллельные линии независимы.
Если два уравнения зависимы, все решения одного уравнения также являются решениями другого уравнения. Когда мы строим график двух зависимых уравнений, мы получаем совпадающие линии.
Независимые и зависимые уравнения
Два уравнения независимы, если они имеют разные решения.
Два уравнения являются зависимыми, если все решения одного уравнения являются решениями другого уравнения.
Подведем итог, посмотрев на графики трех типов систем.См. Рисунок 5.5 и Рисунок 5.6.
Рисунок 5.5
Рисунок 5.6
Пример 5.9
Без построения графиков определите количество решений, а затем классифицируйте систему уравнений: {y = 3x − 16x − 2y = 12. {Y = 3x − 16x − 2y = 12.
Решение
| Мы сравним наклоны и пересечения двух линий. | {y = 3x − 16x − 2y = 12. {Y = 3x − 16x − 2y = 12. |
| Первое уравнение уже имеет форму пересечения наклона. | y = 3x − 1y = 3x − 1 |
| Запишите второе уравнение в форме углового пересечения. | 6x − 2y = 12−2y = −6x + 12−2y − 2 = −6x + 12−2y = 3x − 66x − 2y = 12−2y = −6x + 12−2y − 2 = −6x + 12−2y = 3х − 6 |
| Найдите наклон и точку пересечения каждой прямой. | y = 3x − 1y = 3x − 6m = 3m = 3b = −1b = −6y = 3x − 1y = 3x − 6m = 3m = 3b = −1b = −6 |
| Поскольку наклоны одинаковые, а точки пересечения yy разные, линии параллельны. |
Система уравнений, графики которой представляют собой параллельные прямые, не имеет решения, несовместима и независима.
Попробуй 5.17
Без построения графиков определите количество решений, а затем классифицируйте систему уравнений.
{y = −2x − 44x + 2y = 9 {y = −2x − 44x + 2y = 9
Попробуй 5.18
Без построения графиков определите количество решений, а затем классифицируйте систему уравнений.
{y = 13x − 5x − 3y = 6 {y = 13x − 5x − 3y = 6
Пример 5.10
Без построения графиков определите количество решений и затем классифицируйте систему уравнений: {2x + y = −3x − 5y = 5.{2x + y = −3x − 5y = 5.
Решение
| Мы сравним наклон и пересечения двух линий. | {2x + y = −3x − 5y = 5 {2x + y = −3x − 5y = 5 | |
| Запишите оба уравнения в форме пересечения наклона. | 2x + y = −3y = −2x − 32x + y = −3y = −2x − 3 | x − 5y = 5 = 5−5y = −x + 5−5y − 5 = −x + 5−5y = 15x − 1x − 5y = 5 = 5−5y = −x + 5−5y − 5 = −x + 5−5у = 15x − 1 |
| Найдите наклон и точку пересечения каждой прямой. | y = −2x − 3m = −2b = −3y = −2x − 3m = −2b = −3 | y = 15x − 1m = 15b = −1y = 15x − 1m = 15b = −1 |
| Поскольку уклоны разные, линии пересекаются. | ||
Система уравнений, графики которой пересекаются, имеет одно решение, непротиворечива и независима.
Попробуй 5.19
Без построения графиков определите количество решений, а затем классифицируйте систему уравнений.
{3x + 2y = 22x + y = 1 {3x + 2y = 22x + y = 1
Попробуйте 5.20
Без построения графиков определите количество решений, а затем классифицируйте систему уравнений.
{x + 4y = 12 − x + y = 3 {x + 4y = 12 − x + y = 3
Пример 5.11
Без построения графиков определите количество решений, а затем классифицируйте систему уравнений. {3x − 2y = 4y = 32x − 2 {3x − 2y = 4y = 32x − 2
Решение
| Мы сравним наклоны и пересечения двух линий. | {3x − 2y = 4y = 32x − 2 {3x − 2y = 4y = 32x − 2 |
| Запишите первое уравнение в форме углового пересечения. | 3x − 2y = 4−2y = −3x + 4−2y − 2 = −3x + 4−2y = 32x − 23x − 2y = 4−2y = −3x + 4−2y − 2 = −3x + 4−2y = 32x − 2 |
| Второе уравнение уже имеет форму пересечения наклона. | y = 32x − 2y = 32x − 2 |
| Поскольку наклоны одинаковы, они имеют одинаковый наклон и одинаковую точку пересечения yy, поэтому линии совпадают. |
Система уравнений, графики которой представляют собой совпадающие линии, имеет бесконечно много решений, непротиворечива и зависима.
Попробуйте 5.21
Без построения графиков определите количество решений, а затем классифицируйте систему уравнений.
{4x − 5y = 20y = 45x − 4 {4x − 5y = 20y = 45x − 4
Попробовать 5.22
Без построения графиков определите количество решений, а затем классифицируйте систему уравнений.
{−2x − 4y = 8y = −12x − 2 {−2x − 4y = 8y = −12x − 2
Решение приложений систем уравнений с помощью построения графиков
Мы будем использовать ту же стратегию решения задач, которую мы использовали в математических моделях, для создания и решения приложений систем линейных уравнений. Мы немного изменим стратегию, чтобы сделать ее подходящей для систем уравнений.
How To
Используйте стратегию решения проблем для систем линейных уравнений.
- Шаг 1. Прочтите проблему. Убедитесь, что все слова и идеи понятны.
- Шаг 2. Определите то, что мы ищем.
- Шаг 3. Назовите то, что мы ищем. Выберите переменные для представления этих величин.
- Шаг 4. Переведите в систему уравнений.
- Шаг 5. Решите систему уравнений, используя хорошие методы алгебры.
- Шаг 6. Отметьте ответ в задаче и убедитесь, что он имеет смысл.
- Шаг 7. Ответьте на вопрос полным предложением.
Шаг 5 — это место, где мы будем использовать метод, представленный в этом разделе. Мы построим графики уравнений и найдем решение.
Пример 5.12
Сондра делает 10 литров пунша из фруктового сока и содовой. Количество литров фруктового сока в 4 раза больше количества квартов содовой. Сколько литров фруктового сока и сколько литров газированной воды нужно Сондре?
Решение
Шаг 1.Прочтите задачу.
Шаг 2. Определите то, что мы ищем.
Мы ищем количество литров фруктового сока и количество литров клубной газировки, которые потребуются Сондре.
Шаг 3. Назовите то, что мы ищем. Выберите переменные для представления этих величин.
Пусть f = f = количество литров фруктового сока.
c = c = количество литров клубной соды
Шаг 4. Переведите в систему уравнений.
Теперь у нас есть система. {f + c = 10f = 4c {f + c = 10f = 4c
Шаг 5. Решите систему уравнений, используя хорошие методы алгебры.
Точка пересечения (2, 8) и есть решение. Это означает, что Сондре нужно 2 литра содовой и 8 литров фруктового сока.
Шаг 6. Найдите ответ в проблеме и убедитесь, что он имеет смысл.
Есть ли в этом смысл в проблеме?
Да, количество квартов фруктового сока, 8, в 4 раза больше количества квартов содовой, 2.
Да, 10 литров пунша — это 8 литров фруктового сока плюс 2 литра содовой.
Шаг 7. Ответьте на вопрос полным предложением.
Сондре нужно 8 литров фруктового сока и 2 литра газировки.
Попробовать 5.23
Мэнни делает 12 литров апельсинового сока из концентрата и воды. Количество литров воды в 3 раза превышает количество литров концентрата. Сколько литров концентрата и сколько литров воды нужно Мэнни?
Попробовать 5.24
Алиша готовит кофейный напиток объемом 18 унций из сваренного кофе и молока. Количество унций сваренного кофе в 5 раз больше, чем количество унций молока. Сколько унций кофе и сколько унций молока нужно Алише?
Раздел 5.1 Упражнения
Практика ведет к совершенству
Определите, является ли упорядоченная пара решением системы уравнений . В следующих упражнениях определите, являются ли следующие точки решениями данной системы уравнений.
1.
{2x − 6y = 03x − 4y = 5 {2x − 6y = 03x − 4y = 5
ⓐ (3,1) (3,1) ⓑ (−3,4) (- 3,4)
2.
{7x − 4y = −1−3x − 2y = 1 {7x − 4y = −1−3x − 2y = 1
ⓐ (1,2) (1,2) ⓑ (1, −2) (1, −2)
3.
{2x + y = 5x + y = 1 {2x + y = 5x + y = 1
ⓐ (4, −3) (4, −3) ⓑ (2,0) (2,0)
4.
{−3x + y = 8 − x + 2y = −9 {−3x + y = 8 − x + 2y = −9
ⓐ (−5, −7) (- 5, −7) ⓑ (−5,7) (- 5,7)
5.
{x + y = 2y = 34x {x + y = 2y = 34x
ⓐ (87,67) (87,67) ⓑ (1,34) (1,34)
6.
{x + y = 1y = 25x {x + y = 1y = 25x
ⓐ (57,27) (57,27) ⓑ (5,2) (5,2)
7.
{x + 5y = 10y = 35x + 1 {x + 5y = 10y = 35x + 1
ⓐ (−10,4) (- 10,4) ⓑ (54,74) (54,74)
8.
{x + 3y = 9y = 23x − 2 {x + 3y = 9y = 23x − 2
ⓐ (−6,5) (- 6,5) ⓑ (5,43) (5,43)
Решите систему линейных уравнений с помощью построения графиков В следующих упражнениях решите следующие системы уравнений с помощью построения графиков.
9.
{3x + y = −32x + 3y = 5 {3x + y = −32x + 3y = 5
10.
{−x + y = 22x + y = −4 {−x + y = 22x + y = −4
11.
{−3x + y = −12x + y = 4 {−3x + y = −12x + y = 4
12.
{−2x + 3y = −3x + y = 4 {−2x + 3y = −3x + y = 4
13.
{y = x + 2y = −2x + 2 {y = x + 2y = −2x + 2
14.
{y = x − 2y = −3x + 2 {y = x − 2y = −3x + 2
15.
{y = 32x + 1y = −12x + 5 {y = 32x + 1y = −12x + 5
16.
{y = 23x − 2y = −13x − 5 {y = 23x − 2y = −13x − 5
17.
{−x + y = −34x + 4y = 4 {−x + y = −34x + 4y = 4
18.
{x − y = 32x − y = 4 {x − y = 32x − y = 4
19.
{−3x + y = −12x + y = 4 {−3x + y = −12x + y = 4
20.
{−3x + y = −24x − 2y = 6 {−3x + y = −24x − 2y = 6
21.
{x + y = 52x − y = 4 {x + y = 52x − y = 4
22.
{x − y = 22x − y = 6 {x − y = 22x − y = 6
23.
{x + y = 2x − y = 0 {x + y = 2x − y = 0
24.
{x + y = 6x − y = −8 {x + y = 6x − y = −8
25.
{x + y = −5x − y = 3 {x + y = −5x − y = 3
26.
{x + y = 4x − y = 0 {x + y = 4x − y = 0
27.
{x + y = −4 − x + 2y = −2 {x + y = −4 − x + 2y = −2
28.
{−x + 3y = 3x + 3y = 3 {−x + 3y = 3x + 3y = 3
29.
{−2x + 3y = 3x + 3y = 12 {−2x + 3y = 3x + 3y = 12
30.
{2x − y = 42x + 3y = 12 {2x − y = 42x + 3y = 12
31.
{2x + 3y = 6y = −2 {2x + 3y = 6y = −2
32.
{−2x + y = 2y = 4 {−2x + y = 2y = 4
33.
{x − 3y = −3y = 2 {x − 3y = −3y = 2
34.
{2x − 2y = 8y = −3 {2x − 2y = 8y = −3
35.
{2x − y = −1x = 1 {2x − y = −1x = 1
36.
{x + 2y = 2x = −2 {x + 2y = 2x = −2
37.
{x − 3y = −6x = −3 {x − 3y = −6x = −3
39.
{4x − 3y = 88x − 6y = 14 {4x − 3y = 88x − 6y = 14
40.
{x + 3y = 4−2x − 6y = 3 {x + 3y = 4−2x − 6y = 3
41.
{−2x + 4y = 4y = 12x {−2x + 4y = 4y = 12x
42.
{3x + 5y = 10y = −35x + 1 {3x + 5y = 10y = −35x + 1
43.
{x = −3y + 42x + 6y = 8 {x = −3y + 42x + 6y = 8
44.
{4x = 3y + 78x − 6y = 14 {4x = 3y + 78x − 6y = 14
45.
{2x + y = 6−8x − 4y = −24 {2x + y = 6−8x − 4y = −24
46.
{5x + 2y = 7−10x − 4y = −14 {5x + 2y = 7−10x − 4y = −14
47.
{x + 3y = −64y = −43x − 8 {x + 3y = −64y = −43x − 8
48.
{−x + 2y = −6y = −12x − 1 {−x + 2y = −6y = −12x − 1
49.
{−3x + 2y = −2y = −x + 4 {−3x + 2y = −2y = −x + 4
50.
{−x + 2y = −2y = −x − 1 {−x + 2y = −2y = −x − 1
Определите количество решений линейной системы Не графически отображая следующие системы уравнений, определите количество решений и затем классифицируйте систему уравнений.
51.
{y = 23x + 1−2x + 3y = 5 {y = 23x + 1−2x + 3y = 5
52.
{y = 13x + 2x − 3y = 9 {y = 13x + 2x − 3y = 9
53.
{y = −2x + 14x + 2y = 8 {y = −2x + 14x + 2y = 8
54.
{y = 3x + 49x − 3y = 18 {y = 3x + 49x − 3y = 18
55.
{y = 23x + 12x − 3y = 7 {y = 23x + 12x − 3y = 7
56.
{3x + 4y = 12y = −3x − 1 {3x + 4y = 12y = −3x − 1
57.
{4x + 2y = 104x − 2y = −6 {4x + 2y = 104x − 2y = −6
58.
{5x + 3y = 42x − 3y = 5 {5x + 3y = 42x − 3y = 5
59.
{y = −12x + 5x + 2y = 10 {y = −12x + 5x + 2y = 10
60.
{y = x + 1 − x + y = 1 {y = x + 1 − x + y = 1
61.
{y = 2x + 32x − y = −3 {y = 2x + 32x − y = −3
62.
{5x − 2y = 10y = 52x − 5 {5x − 2y = 10y = 52x − 5
Решение приложений систем уравнений с помощью построения графиков В следующих упражнениях решите.
63.
Молли делает воду, настоянную на клубнике. На каждую унцию клубничного сока она использует в три раза больше унций воды. Сколько унций клубничного сока и сколько унций воды ей нужно, чтобы приготовить 64 унции воды, настоянной на клубнике?
64.
Джамал делает закуску, которая содержит только крендели и орехи.На каждую унцию орехов он будет использовать 2 унции кренделя. Сколько унций кренделей и сколько унций орехов ему нужно, чтобы приготовить 45 унций закуски?
65.
Энрике готовит коктейль для вечеринок, содержащий изюм и орехи. На каждую унцию орехов он использует вдвое больше изюма. Сколько унций орехов и сколько унций изюма ему нужно, чтобы приготовить 24 унции смеси для вечеринок?
66.
Оуэн делает лимонад из концентрата. Количество литров воды, которое ему нужно, в 4 раза превышает количество литров концентрата.Сколько литров воды и сколько литров концентрата нужно Оуэну для приготовления 100 литров лимонада?
Повседневная математика
67.
Лев планирует свой весенний цветочный сад. Он хочет посадить луковицы тюльпанов и нарциссов. Он посадит в 6 раз больше луковиц нарциссов, чем луковиц тюльпанов. Если он хочет посадить 350 луковиц, сколько луковиц тюльпанов и сколько луковиц нарциссов ему следует посадить?
68.
Маркетинговая компания опрашивает 1 200 человек. Они обследовали в два раза больше женщин, чем мужчин.Сколько мужчин и женщин они опросили?
Письменные упражнения
69.
В системе линейных уравнений два уравнения имеют одинаковый наклон. Опишите возможные решения системы.
70.
В системе линейных уравнений два уравнения имеют одинаковые точки пересечения. Опишите возможные решения системы.
Самопроверка
После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.
Если большая часть ваших чеков была:
… уверенно. Поздравляем! Вы достигли целей в этом разделе. Поразмышляйте над своими учебными навыками, чтобы вы могли продолжать их использовать. Что вы сделали, чтобы убедиться в своей способности делать эти вещи? Быть конкретным.
… с некоторой помощью. Эту проблему нужно решать быстро, потому что темы, которые вы не осваиваете, становятся ухабами на вашем пути к успеху. В математике каждая тема основывается на предыдущей работе.Прежде чем двигаться дальше, важно убедиться, что у вас есть прочная основа. К кому обратиться за помощью? Ваши одноклассники и инструктор — хорошие ресурсы. Есть ли в кампусе место, где доступны репетиторы по математике? Можно ли улучшить свои учебные навыки?
… нет, я не понимаю! Это предупреждающий знак, игнорировать его нельзя. Вам следует немедленно обратиться за помощью, иначе вы быстро не справитесь. Как можно скорее обратитесь к своему инструктору, чтобы обсудить вашу ситуацию. Вместе вы сможете составить план оказания вам необходимой помощи.
Плюсы и минусы методов решения систем уравнений
Система линейных уравнений включает две взаимосвязи с двумя переменными в каждой взаимосвязи. Решая систему, вы обнаруживаете, где одновременно выполняются две взаимосвязи, другими словами, точка пересечения двух линий. Методы решения систем включают замену, исключение и построение графиков. Каждый из них даст правильный ответ, но более или менее полезен в зависимости от проблемы и ситуации.
Замена
Этот метод включает в себя вставку выражения из одного уравнения в переменную в другом. Чтобы использовать этот метод, необходимо изолировать хотя бы одну переменную в одном из уравнений. Вот почему подстановка наиболее полезна, когда проблема уже содержит изолированную переменную или если есть хотя бы переменная с коэффициентом, равным единице. Если вы можете очень быстро решить основные алгебраические уравнения, подстановка будет хорошим выбором. Однако это создает проблемы для тех, кто склонен делать арифметические ошибки.
Исключение
Чтобы использовать исключение, вы должны выровнять оба уравнения по вертикали с переменными с одной стороны и константами с другой. Затем нижнее уравнение вычитается из верхнего, чтобы сократить переменную. Это делает исключение эффективным, когда константы обоих уравнений уже изолированы. Кроме того, если коэффициенты X или Y в обоих уравнениях одинаковы, исключение быстро даст решение с минимальными шагами. С другой стороны, иногда одно или оба целых уравнения нужно умножить на число, чтобы переменная сократилась.Из-за этого работа может занять больше времени, и исключение в данном сценарии — не лучший выбор.
Построение графиков вручную
Если в уравнениях не используются дроби или десятичные дроби и у вас есть хорошее визуальное представление о линейных уравнениях, хорошим вариантом будет построение графиков на координатной плоскости. Этот метод включает визуальный поиск точки на графике, где две линии пересекаются, чтобы получить решения для X и Y. Поскольку это помогает вам быстро построить график, наличие обоих уравнений в форме Y = делает этот метод полезным.Напротив, если ни одно из уравнений не имеет изолированного Y, вам лучше использовать замену или исключение.
Построение графиков на калькуляторе
Использование графического калькулятора для ввода обоих уравнений и нахождения точки пересечения удобно, когда в них используются десятичные дроби или дроби. Это также хороший выбор, когда учитель разрешает такие калькуляторы на тестах или викторинах. Однако, как и при построении графиков вручную, этот метод работает лучше всего, когда Y в обоих уравнениях уже изолированы.
Графическая интерпретация систем линейных уравнений — видео и стенограмма урока
Построение графика системы
Итак, перейдем к графическому изображению наших двух уравнений.Вот что мы получаем. Красная линия соответствует уравнению y = 2 x — 3, а синяя линия соответствует уравнению y = -3 x + 2. Чтобы построить график этих двух линий, мы начнем с нашего y. Перехват , последнее число в нашем уравнении. Для y = 2 x — 3 это -3. Для y = -3 x + 2 это будет 2. Пересечение y — это место, где эти линии пересекают ось y .
После того, как у нас есть эта точка, мы находим следующую точку, глядя на наклон уравнения.Для y = 2 x — 3 наклон равен 2, что означает, что наша следующая точка находится на 2 вверх и одна справа от точки пересечения y . Проделаем ту же процедуру для другого уравнения.
Поиск решения
Чтобы найти решение этой системы линейных уравнений, мы посмотрим, пересекаются ли линии. Если да, то точка пересечения — это решение. Если линии не пересекаются, значит, решения нет. Но если вы видите только одну строку, значит, у вас бесконечное количество решений.
Глядя на наш график, мы видим, что две наши линии пересекаются, у нас есть решение. Что это?
Поскольку мы изобразили наши уравнения в виде графика, мы можем легко найти ответ, посмотрев на график. Где пересекаются две наши линии на графике?
Наше двухстрочное насекомое в (1, -1), это наш ответ. На данный момент наши x = 1 и наши y = -1. Мы можем проверить, правильно ли это, подставив эти значения x и y в наши исходные уравнения.Если они выходят правильно, то это правильный ответ.
В большинстве случаев, если вы правильно изобразили свои уравнения, то ответ, который вы видите, верен.
Пример
Рассмотрим другой пример. Найдите решение этой линейной системы, построив ее график: -4 x + 2 y = 6, y = x .
Глядя на эти два уравнения, мы видим, что первое уравнение записано в стандартной форме. В то время как второй находится в нашей форме пересечения наклона.Нам нужно перестроить первое уравнение так, чтобы оно было в форме пересечения наклона, чтобы мы могли легко построить его график.
Для этого мы прибавляем 4 x к обеим сторонам, а затем делим обе стороны на 2. Мы получаем 2 y = 6 + 4 x после прибавления 4 x к обеим сторонам. Теперь разделив обе стороны на 2, мы получим y = 3 + 2 x . Форма пересечения наклона: y = 2 x + 3.
Теперь, сопоставив их на графике с уравнениями, мы получим следующее.Красная линия — это первое уравнение, y = 2 x + 3, а синяя линия — второе уравнение, y = x . Эти две линии пересекаются?
Да, есть. У нас есть решение!
Что это?
Это (-3, -3). это означает, что наши x равны -3, а наши y равны -3. И мы закончили.
Итоги урока
Давайте рассмотрим. Линейная система уравнений — это набор линейных уравнений.У вас будет одно уравнение для каждой переменной в вашей системе. Если ваша система имеет две переменные, у вас будет два уравнения. Если в вашей системе три переменных, то у вас будет три уравнения. В линейной системе показателей нет. Для системы с двумя переменными вы захотите, чтобы ваши уравнения были в форме пересечения наклона, которая составляет y = m x + b , чтобы вы могли легко построить их график. После того, как вы изобразили свои уравнения, вы посмотрите, пересекаются ли они. Если они пересекаются, у вас есть решение.Если они не пересекаются, у вас нет решения. Если есть только одна линия, то есть это одна и та же линия, то у вас есть бесконечное количество решений.
11.1: Системы линейных уравнений — две переменные
Производитель скейтбордов представляет новую линейку досок. Производитель отслеживает свои затраты, то есть сумму, которую он тратит на производство плат, и свой доход, который представляет собой сумму, которую он зарабатывает от продажи своих плат. Как компания может определить, получает ли она прибыль от своей новой линии? Сколько скейтбордов необходимо произвести и продать, чтобы можно было получить прибыль? В этом разделе мы рассмотрим линейные уравнения с двумя переменными, чтобы ответить на эти и подобные вопросы.
Введение в системы уравнений
Чтобы исследовать такие ситуации, как ситуация с производителем скейтборда, нам необходимо признать, что мы имеем дело с более чем одной переменной и, вероятно, более чем с одним уравнением. Система линейных уравнений состоит из двух или более линейных уравнений, состоящих из двух или более переменных, так что все уравнения в системе рассматриваются одновременно. Чтобы найти единственное решение системы линейных уравнений, мы должны найти числовое значение для каждой переменной в системе, которое будет удовлетворять всем уравнениям в системе одновременно.Некоторые линейные системы могут не иметь решения, а другие могут иметь бесконечное количество решений. Чтобы линейная система имела единственное решение, должно быть по крайней мере столько же уравнений, сколько переменных. Даже в этом случае это не гарантирует уникального решения.
В этом разделе мы рассмотрим системы линейных уравнений с двумя переменными, которые состоят из двух уравнений, содержащих две разные переменные. Например, рассмотрим следующую систему линейных уравнений с двумя переменными.
\ [\ begin {align *} 2x + y & = 15 \\ 3x – y & = 5 \ end {align *} \]
Решение системы линейных уравнений с двумя переменными — это любая упорядоченная пара, которая удовлетворяет каждому уравнению независимо. В этом примере упорядоченная пара \ ((4,7) \) является решением системы линейных уравнений. Мы можем проверить решение, подставив значения в каждое уравнение, чтобы увидеть, удовлетворяет ли упорядоченная пара обоим уравнениям. Вскоре мы исследуем способы нахождения такого решения, если оно существует.
\ [\ begin {align *} 2 (4) + (7) & = 15 \ text {True} \\ 3 (4) — (7) & = 5 \ text {True} \ end {align *} \ ]
Помимо учета количества уравнений и переменных, мы можем классифицировать системы линейных уравнений по количеству решений. Непротиворечивая система уравнений имеет по крайней мере одно решение. Согласованной системой считается независимая система , если она имеет единственное решение, такое как пример, который мы только что исследовали. Две линии имеют разные уклоны и пересекаются в одной точке на плоскости.Согласованной системой считается зависимая система , если уравнения имеют одинаковый наклон и одинаковые перехваты y . Другими словами, линии совпадают, поэтому уравнения представляют одну и ту же линию. Каждая точка на линии представляет пару координат, удовлетворяющую системе. Таким образом, существует бесконечное количество решений.
Другой тип системы линейных уравнений — это несовместимая система , в которой уравнения представляют собой две параллельные линии.Линии имеют одинаковый наклон и разные точки пересечения y- . Для обеих линий нет общих точек; следовательно, у системы нет решения.
ВИДЫ ЛИНЕЙНЫХ СИСТЕМ
Существует три типа систем линейных уравнений с двумя переменными и три типа решений.
- Независимая система имеет ровно одну пару решений \ ((x, y) \). Точка пересечения двух линий — единственное решение.
- Непоследовательная система не имеет решения.Обратите внимание, что две линии параллельны и никогда не пересекутся.
- У зависимой системы бесконечно много решений. Линии совпадают. Это одна и та же линия, поэтому каждая пара координат на линии является решением обоих уравнений.
На рисунке \ (\ PageIndex {2} \) сравниваются графические представления каждого типа системы.
Рисунок \ (\ PageIndex {2} \)
Для системы линейных уравнений и упорядоченной пары определите, является ли упорядоченная пара решением.
- Подставьте упорядоченную пару в каждое уравнение системы.
- Определите, являются ли истинные утверждения результатом подстановки в обоих уравнениях; в таком случае заказанная пара является решением.
Пример \ (\ PageIndex {1} \): определение того, является ли упорядоченная пара решением системы уравнений
Определите, является ли упорядоченная пара \ ((5,1) \) решением данной системы уравнений.
\ [\ begin {align *} x + 3y & = 8 \\ 2x − 9 & = y \ end {align *} \]
Решение
Подставляем упорядоченную пару \ ((5,1) \) в оба уравнения.
\ [\ begin {align *} (5) +3 (1) & = 8 \\ 8 & = 8 \ text {True} \\ 2 (5) −9 & = (1) \\ 1 & = 1 \ text {True} \ end {align *} \]
Упорядоченная пара \ ((5,1) \) удовлетворяет обоим уравнениям, поэтому она является решением системы.
Анализ
Мы можем ясно увидеть решение, построив график каждого уравнения. Поскольку решение представляет собой упорядоченную пару, удовлетворяющую обоим уравнениям, это точка на обеих прямых и, следовательно, точка пересечения двух прямых.См. Рисунок \ (\ PageIndex {3} \).
Рисунок \ (\ PageIndex {3} \)
Упражнение \ (\ PageIndex {1} \)
Определите, является ли упорядоченная пара \ ((8,5) \) решением следующей системы.
\ [\ begin {align *} 5x − 4y & = 20 \\ 2x + 1 & = 3y \ end {align *} \]
- Ответ
Не выход.
Решение систем уравнений с помощью построения графиков
Существует несколько методов решения систем линейных уравнений.Для системы линейных уравнений с двумя переменными мы можем определить как тип системы, так и решение, построив систему уравнений на одном и том же наборе осей.
Пример \ (\ PageIndex {2} \): решение системы уравнений с двумя переменными с помощью построения графика
Решите следующую систему уравнений, построив график. Определите тип системы.
\ [\ begin {align *} 2x + y & = −8 \\ x − y & = −1 \ end {align *} \]
Решение
Решите первое уравнение относительно \ (y \).
\ [\ begin {align *} 2x + y & = −8 \\ y & = −2x − 8 \ end {align *} \]
Решите второе уравнение относительно \ (y \).
\ [\ begin {align *} x − y & = −1 \\ y & = x + 1 \ end {align *} \]
Изобразите оба уравнения на том же наборе осей, как на рисунке \ (\ PageIndex {4} \).
Рисунок \ (\ PageIndex {4} \)
Кажется, что линии пересекаются в точке \ ((- 3, −2) \). Мы можем убедиться, что это решение системы, подставив упорядоченную пару в оба уравнения.
\ [\ begin {align *} 2 (−3) + (- 2) & = −8 \\ −8 & = −8 \ text {True} \\ (−3) — (- 2) & = — 1 \\ −1 & = −1 \ text {True} \ end {align *} \]
Решением системы является упорядоченная пара \ ((- 3, −2) \), поэтому система независима.
Упражнение \ (\ PageIndex {2} \)
Решите следующую систему уравнений, построив график.
\ [\ begin {align *} 2x − 5y & = −25 \\ −4x + 5y & = 35 \ end {align *} \]
- Ответ
Решением системы является упорядоченная пара \ ((- 5,3) \).
Рисунок \ (\ PageIndex {5} \)
Вопросы и ответы
Можно ли использовать построение графиков, если система несовместима или зависима?
Да, в обоих случаях мы можем построить график системы для определения типа системы и решения. Если две линии параллельны, система не имеет решения и непоследовательна. Если две линии идентичны, система имеет бесконечное количество решений и является зависимой системой.
Решение систем уравнений подстановкой
Решение линейной системы с двумя переменными с помощью построения графиков хорошо работает, когда решение состоит из целых значений, но если наше решение содержит десятичные дроби или дроби, это не самый точный метод.Мы рассмотрим еще два метода решения системы линейных уравнений , которые более точны, чем построение графиков. Одним из таких методов является решение системы уравнений методом подстановки , в котором мы решаем одно из уравнений для одной переменной, а затем подставляем результат во второе уравнение, чтобы найти вторую переменную. Напомним, что мы можем решать только одну переменную за раз, поэтому метод подстановки является одновременно ценным и практичным.
Как: решить систему двух уравнений с двумя переменными, используя метод подстановки.
- Решите одно из двух уравнений относительно одной из переменных через другую.
- Подставьте выражение для этой переменной во второе уравнение, затем найдите оставшуюся переменную.
- Подставьте это решение в любое из исходных уравнений, чтобы найти значение первой переменной. Если возможно, запишите решение в виде упорядоченной пары.
- Проверьте решение в обоих уравнениях.
Пример \ (\ PageIndex {3} \): решение системы уравнений с двумя переменными подстановкой
Решите следующую систему уравнений путем подстановки.
\ [\ begin {align *} −x + y & = −5 \\ 2x − 5y & = 1 \ end {align *} \]
Решение
Сначала мы решим первое уравнение относительно \ (y \).
\ [\ begin {align *} −x + y & = — 5 \\ y & = x − 5 \ end {align *} \]
Теперь мы можем подставить выражение \ (x − 5 \) вместо \ (y \) во втором уравнении.
\ [\ begin {align *} 2x − 5y & = 1 \\ 2x − 5 (x − 5) & = 1 \\ 2x − 5x + 25 & = 1 \\ −3x & = −24 \\ x & = 8 \ end {align *} \]
Теперь мы подставляем \ (x = 8 \) в первое уравнение и решаем относительно \ (y \).
\ [\ begin {align *} — (8) + y & = −5 \\ y & = 3 \ end {align *} \]
Наше решение — \ ((8,3) \).
Проверьте решение, подставив \ ((8,3) \) в оба уравнения.
\ [\ begin {align *} −x + y & = −5 \\ - (8) + (3) & = −5 \ text {True} \\ 2x − 5y & = 1 \\ 2 (8) −5 (3) & = 1 \ text {True} \ end {align *} \]
Упражнение \ (\ PageIndex {3} \)
Решите следующую систему уравнений путем подстановки.
\ [\ begin {align *} x & = y + 3 \\ 4 & = 3x − 2y \ end {align *} \]
- Ответ
\ ((- 2, −5) \)
Вопросы и ответы
Можно ли методом подстановки решить любую линейную систему с двумя переменными?
Да, но этот метод работает лучше всего, если одно из уравнений содержит коэффициент \ (1 \) или \ (- 1 \), чтобы нам не приходилось иметь дело с дробями.
Решение систем уравнений с двумя переменными методом сложения
Третий метод решения систем линейных уравнений — метод сложения. В этом методе мы складываем два члена с одинаковой переменной, но с противоположными коэффициентами, так что сумма равна нулю. Конечно, не все системы созданы с двумя членами одной переменной, имеющими противоположные коэффициенты. Часто нам приходится корректировать одно или оба уравнения путем умножения, чтобы одна переменная была исключена сложением.
Как: решить систему уравнений, используя метод сложения.
- Запишите оба уравнения с переменными x и y слева от знака равенства и константами справа.
- Напишите одно уравнение над другим, выстроив соответствующие переменные. Если одна из переменных в верхнем уравнении имеет коэффициент, противоположный той же переменной в нижнем уравнении, сложите уравнения вместе, исключив одну переменную.Если нет, используйте умножение на ненулевое число, чтобы одна из переменных в верхнем уравнении имела коэффициент, противоположный той же переменной в нижнем уравнении, затем добавьте уравнения, чтобы исключить переменную.
- Решите полученное уравнение для оставшейся переменной.
- Подставьте это значение в одно из исходных уравнений и решите для второй переменной.
- Проверьте решение, подставив значения в другое уравнение.
Пример \ (\ PageIndex {4} \): решение системы методом сложения
Решите данную систему уравнений сложением.
\ [\ begin {align *} x + 2y & = −1 \\ −x + y & = 3 \ end {align *} \]
Решение
Оба уравнения уже установлены равными константе. Обратите внимание, что коэффициент при \ (x \) во втором уравнении, \ (- 1 \), противоположен коэффициенту при \ (x \) в первом уравнении, \ (1 \). Мы можем сложить два уравнения, чтобы исключить \ (x \), не умножая его на константу.
Теперь, когда мы исключили \ (x \), мы можем решить полученное уравнение для \ (y \).
\ [\ begin {align *} 3y & = 2 \\ y & = \ dfrac {2} {3} \ end {align *} \]
Затем мы подставляем это значение вместо \ (y \) в одно из исходных уравнений и решаем относительно \ (x \).
\ [\ begin {align *} −x + y & = 3 \\ −x + \ dfrac {2} {3} & = 3 \\ −x & = 3− \ dfrac {2} {3} \\ — x & = \ dfrac {7} {3} \\ x & = — \ dfrac {7} {3} \ end {align *} \]
Решение этой системы — \ (\ left (- \ dfrac {7} {3}, \ dfrac {2} {3} \ right) \).
Проверьте решение в первом уравнении.
\ [\ begin {align *} x + 2y & = −1 \\ \ left (- \ dfrac {7} {3} \ right) +2 \ left (\ dfrac {2} {3} \ right) & = \\ — \ dfrac {7} {3} + \ dfrac {4} {3} & = — \ dfrac {3} {3} \\ −1 & = −1 \; \; \; \; \; \; \; \; \ text {True} \ end {align *} \]
Анализ
Мы получаем важное представление о системах уравнений, глядя на графическое представление. См. Рисунок \ (\ PageIndex {6} \), чтобы увидеть, что уравнения пересекаются в решении. Нам не нужно спрашивать, может ли быть второе решение, потому что наблюдение за графиком подтверждает, что система имеет ровно одно решение.
Рисунок \ (\ PageIndex {6} \)
Пример \ (\ PageIndex {5} \): Использование метода сложения, когда требуется умножение одного уравнения
Решите данную систему уравнений методом сложения.
\ [\ begin {align *} 3x + 5y & = −11 \\ x − 2y & = 11 \ end {align *} \]
Решение
Добавление этих уравнений в представленном виде не устраняет переменную. Однако мы видим, что в первом уравнении есть \ (3x \), а во втором уравнении есть \ (x \).Таким образом, если мы умножим второе уравнение на \ (- 3 \), элементы x прибавятся к нулю.
\ [\ begin {align *} x − 2y & = 11 \\ −3 (x − 2y) & = — 3 (11) \; \; \; \; \; \; \; \; \ text {Умножаем обе части на} −3. \\ −3x + 6y & = −33 \; \; \; \; \; \; \; \; \; \ text {Используйте свойство дистрибутива.} \ end {align *} \]
А теперь добавим их.
\ [\ begin {align *} 3x + 5y & = -11 \\ \ underline {-3x + 6y} & = \ underline {-33} \\ 11y & = -44 \\ y & = -4 \ end {align *} \]
На последнем этапе мы подставляем \ (y = −4 \) в одно из исходных уравнений и решаем относительно \ (x \).
\ [\ begin {align *} 3x + 5y & = −11 \\ 3x + 5 (−4) & = −11 \\ 3x − 20 & = −11 \\ 3x & = 9 \\ x & = 3 \ end {align *} \]
Наше решение — упорядоченная пара \ ((3, −4) \). См. Рисунок \ (\ PageIndex {7} \). Проверьте решение в исходном втором уравнении.
\ [\ begin {align *} x − 2y & = 11 \\ (3) −2 (−4) & = 3 + 8 \\ & = 11 \; \; \; \; \; \; \; \; \; \; \ text {True} \ end {align *} \]
Рисунок \ (\ PageIndex {7} \)
Упражнение \ (\ PageIndex {4} \)
Решите систему уравнений сложением.
\ [\ begin {align *} 2x − 7y & = 2 \\ 3x + y & = −20 \ end {align *} \]
- Ответ
\ ((- 6, −2) \)
Пример \ (\ PageIndex {6} \): Использование метода сложения, когда требуется умножение обоих уравнений
Решите данную систему уравнений с двумя переменными сложением.
\ [\ begin {align *} 2x + 3y & = −16 \\ 5x − 10y & = 30 \ end {align *} \]
Решение
Одно уравнение имеет \ (2x \), а другое — \ (5x \).Наименьшее общее кратное — \ (10x \), поэтому нам придется умножить оба уравнения на константу, чтобы исключить одну переменную. Удалим \ (x \), умножив первое уравнение на \ (- 5 \), а второе уравнение на \ (2 \).
\ [\ begin {align *} −5 (2x + 3y) & = −5 (−16) \\ −10x − 15y & = 80 \\ 2 (5x − 10y) & = 2 (30) \\ 10x −20y & = 60 \ end {align *} \]
Затем мы складываем два уравнения.
Подставляем \ (y = −4 \) в исходное первое уравнение.
\ [\ begin {align *} 2x + 3 (−4) & = — 16 \\ 2x − 12 & = −16 \\ 2x & = −4 \\ x & = — 2 \ end {align *} \ ]
Решение: \ ((- 2, −4) \).Проверьте это в другом уравнении.
\ [\ begin {align *} 5x − 10y & = 30 \\ 5 (−2) −10 (−4) & = 30 \\ −10 + 40 & = 30 \\ 30 & = 30 \ end {align *} \]
См. Рисунок \ (\ PageIndex {8} \).
Рисунок \ (\ PageIndex {8} \)
Пример \ (\ PageIndex {7} \): Использование метода сложения в системах уравнений, содержащих дроби
Решите данную систему уравнений с двумя переменными сложением.
\ [\ begin {align *} \ dfrac {x} {3} + \ dfrac {y} {6} & = 3 \\ \ dfrac {x} {2} — \ dfrac {y} {4} & = 1 \ end {align *} \]
Решение
Сначала очистите каждое уравнение от дробей, умножив обе части уравнения на наименьший общий знаменатель.
\ [\ begin {align *} 6 \ left (\ dfrac {x} {3} + \ dfrac {y} {6} \ right) & = 6 (3) \\ 2x + y & = 18 \\ 4 \ left (\ dfrac {x} {2} — \ dfrac {y} {4} \ right) & = 4 (1) \\ 2x − y & = 4 \ end {align *} \]
Теперь умножьте второе уравнение на \ (- 1 \), чтобы мы могли исключить переменную x .
\ [\ begin {align *} −1 (2x − y) & = −1 (4) \\ −2x + y & = −4 \ end {align *} \]
Добавьте два уравнения, чтобы исключить переменную \ (x \), и решить полученное уравнение.
\ [\ begin {align *} 2x + y & = 18 \\ −2x + y & = −4 \\ 2y & = 14 \\ y & = 7 \ end {align *} \]
Подставим \ (y = 7 \) в первое уравнение.
\ [\ begin {align *} 2x + (7) & = 18 \\ 2x & = 11 \\ x & = \ dfrac {11} {2} \\ & = 7.5 \ end {align *} \]
Решение: \ (\ left (\ dfrac {11} {2}, 7 \ right) \). Проверьте это в другом уравнении.
\ [\ begin {align *} \ dfrac {x} {2} — \ dfrac {y} {4} & = 1 \\ \ dfrac {\ dfrac {11} {2}} {2} — \ dfrac { 7} {4} & = 1 \\ \ dfrac {11} {4} — \ dfrac {7} {4} & = 1 \\ \ dfrac {4} {4} & = 1 \ end {align *} \ ]
Упражнение \ (\ PageIndex {5} \)
Решите систему уравнений сложением.
\ [\ begin {align *} 2x + 3y & = 8 \\ 3x + 5y & = 10 \ end {align *} \]
- Ответ
\ ((10, −4) \)
Выявление несовместимых систем уравнений, содержащих две переменные
Теперь, когда у нас есть несколько методов решения систем уравнений, мы можем использовать эти методы для идентификации несовместимых систем. Напомним, что противоречивая система состоит из параллельных линий с одинаковым наклоном, но с разными точками пересечения по оси Y.Они никогда не пересекутся. При поиске решения несовместимой системы мы получим ложное утверждение, например \ (12 = 0 \).
Пример \ (\ PageIndex {8} \): решение несовместимой системы уравнений
Решите следующую систему уравнений.
\ [\ begin {align *} x & = 9−2y \\ x + 2y & = 13 \ end {align *} \]
Решение
Мы можем подойти к этой проблеме двумя способами. Поскольку одно уравнение для \ (x \) уже решено, наиболее очевидным шагом является использование подстановки.
\ [\ begin {align *} x + 2y & = 13 \\ (9−2y) + 2y & = 13 \\ 9 + 0y & = 13 \\ 9 & = 13 \ end {align *} \]
Ясно, что это утверждение противоречит тому, что \ (9 ≠ 13 \). Следовательно, у системы нет решения.
Второй подход заключается в том, чтобы сначала манипулировать уравнениями так, чтобы они оба были в форме пересечения наклона. Мы манипулируем первым уравнением следующим образом.
\ [\ begin {align *} x & = 9−2y \\ 2y & = −x + 9 \\ y & = — \ dfrac {1} {2} x + \ dfrac {9} {2} \ end { выровнять *} \]
Затем мы преобразуем второе уравнение в форму пересечения наклона.
\ [\ begin {align *} x + 2y & = 13 \\ 2y & = −x + 13 \\ y & = — \ dfrac {1} {2} x + \ dfrac {13} {2} \ end { выровнять *} \]
Сравнивая уравнения, мы видим, что они имеют одинаковый наклон, но разные \ (y \) — точки пересечения. Следовательно, линии параллельны и не пересекаются.
\ [\ begin {align *} y & = — \ dfrac {1} {2} x + \ dfrac {9} {2} \\ y & = — \ dfrac {1} {2} x + \ dfrac {13} {2} \ end {align *} \]
Анализ
Запись уравнений в форме пересечения наклона подтверждает, что система несовместима, потому что все линии в конечном итоге будут пересекаться, если они не параллельны.Параллельные линии никогда не пересекаются; таким образом, у этих двух линий нет общих точек. Графики уравнений в этом примере показаны на рисунке \ (\ PageIndex {9} \).
Рисунок \ (\ PageIndex {9} \)
Упражнение \ (\ PageIndex {6} \)
Решите следующую систему уравнений с двумя переменными.
\ [\ begin {align *} 2y − 2x & = 2 \\ 2y − 2x & = 6 \ end {align *} \]
- Ответ
Нет решения. Это противоречивая система.
Выражение решения системы зависимых уравнений, содержащих две переменные
Напомним, что зависимая система уравнений с двумя переменными — это система, в которой два уравнения представляют одну и ту же линию. Зависимые системы имеют бесконечное количество решений, потому что все точки на одной линии также находятся на другой линии. После использования замены или добавления результирующее уравнение будет тождественным, например \ (0 = 0 \).
Пример \ (\ PageIndex {9} \): поиск решения зависимой системы линейных уравнений
Найдите решение системы уравнений с помощью метода сложения .
\ [\ begin {align *} x + 3y & = 2 \\ 3x + 9y & = 6 \ end {align *} \]
Решение
С помощью метода сложения мы хотим исключить одну из переменных, добавив уравнения. В этом случае давайте сосредоточимся на удалении \ (x \). Если мы умножим обе части первого уравнения на \ (- 3 \), то мы сможем исключить переменную x.
\ [\ begin {align *} x + 3y & = 2 \\ (−3) (x + 3y) & = (−3) (2) \\ −3x − 9y & = −6 \ end {align * } \]
Теперь сложите уравнения.
Мы видим, что будет бесконечное количество решений, удовлетворяющих обоим уравнениям.
Анализ
Если бы мы переписали оба уравнения в форме пересечения наклона, мы могли бы знать, как будет выглядеть решение перед добавлением. Давайте посмотрим, что происходит, когда мы преобразуем систему в форму с пересечением наклона.
\ [\ begin {align *} x + 3y & = 2 \\ 3y & = −x + 2 \\ y & = — \ dfrac {1} {3} x + \ dfrac {2} {3} \\ 3x + 9y & = 6 \\ 9y & = — 3x + 6 \\ y & = — \ dfrac {3} {9} x + \ dfrac {6} {9} \\ y & = — \ dfrac {1} {3 } x + \ dfrac {2} {3} \ end {align *} \]
См. Рисунок \ (\ PageIndex {10} \).Обратите внимание, что результаты такие же. Общее решение системы: \ (\ left (x, — \ dfrac {1} {3} x + \ dfrac {2} {3} \ right) \).
Рисунок \ (\ PageIndex {10} \)
Упражнение \ (\ PageIndex {7} \)
Решите следующую систему уравнений с двумя переменными.
\ [\ begin {align *} y − 2x & = 5 \\ −3y + 6x & = −15 \ end {align *} \]
- Ответ
Система зависима, поэтому существует бесконечное число решений вида \ ((x, 2x + 5) \).
Использование систем уравнений для исследования прибыли
Используя то, что мы узнали о системах уравнений, мы можем вернуться к проблеме производства скейтбордов в начале раздела.Функция дохода производителя скейтборда — это функция, используемая для расчета суммы денег, поступающей в бизнес. Его можно представить уравнением \ (R = xp \), где \ (x \) = количество и \ (p \) = цена. Функция дохода показана оранжевым цветом на рисунке \ (\ PageIndex {11} \).
Функция затрат — это функция, используемая для расчета затрат на ведение бизнеса. Он включает постоянные затраты, такие как аренда и заработная плата, и переменные затраты, такие как коммунальные услуги. Функция стоимости показана синим цветом на рисунке \ (\ PageIndex {11} \).Ось \ (x \) представляет количество в сотнях единиц. Ось \ (y \) представляет затраты или доход в сотнях долларов.
Рисунок \ (\ PageIndex {11} \)
Точка пересечения двух линий называется точкой безубыточности. Из графика видно, что если произведено \ (700 \) единиц, то стоимость составит \ (3300 долларов США \), а выручка также составит \ (3300 долларов США \). Другими словами, компания разоряется, даже если они производят и продают \ (700 \) единиц. Они не зарабатывают и не теряют деньги.
Заштрихованная область справа от точки безубыточности представляет объемы, от которых компания получает прибыль.Заштрихованная область слева представляет объемы, по которым компания терпит убытки. Функция прибыли — это функция дохода за вычетом функции затрат, записываемая как \ (P (x) = R (x) −C (x) \). Очевидно, что знание количества, при котором затраты равны выручке, имеет большое значение для бизнеса.
Пример \ (\ PageIndex {10} \): поиск точки безубыточности и функции прибыли с помощью замены
Учитывая функцию затрат \ (C (x) = 0,85x + 35,000 \) и функцию дохода \ (R (x) = 1.55x \), найдите точку безубыточности и функцию прибыли.
Решение
Запишите систему уравнений, используя \ (y \) вместо обозначения функций.
\ [\ begin {align *} y & = 0,85x + 35,000 \\ y & = 1,55x \ end {align *} \]
Подставьте выражение \ (0.85x + 35,000 \) из первого уравнения во второе уравнение и решите относительно \ (x \).
\ [\ begin {align *} 0,85x + 35,000 & = 1,55x \\ 35,000 & = 0,7x \\ 50,000 & = x \ end {align *} \]
Затем мы подставляем \ (x = 50 000 \) либо в функцию затрат, либо в функцию дохода.
\ (1,55 (50 000) = 77 500 \)
Точка безубыточности равна \ ((50,000,77,500) \).
Функция прибыли находится по формуле \ (P (x) = R (x) −C (x) \).
\ [\ begin {align *} P (x) & = 1,55x- (0,85x + 35,000) \\ & = 0,7x-35,000 \ end {align *} \]
Функция прибыли равна \ (P (x) = 0,7x − 35,000 \).
Анализ
Стоимость производства \ (50 000 \) единиц составляет \ (77 500 долларов США \), а выручка от продажи \ (50 000 \) единиц также составляет \ (77 500 долларов США \).Чтобы получить прибыль, бизнес должен произвести и продать более \ (50 000 \) единиц. См. Рисунок \ (\ PageIndex {12} \).
Рисунок \ (\ PageIndex {12} \)
Из графика на рисунке \ (\ PageIndex {13} \) видно, что функция прибыли имеет отрицательное значение до тех пор, пока \ (x = 50,000 \) не пересечет график \ (x \) — ось. Затем график переходит в положительные \ (y \) — значения и продолжает движение по этому пути, поскольку функция прибыли представляет собой прямую линию. Это показывает, что точка безубыточности для предприятий наступает, когда функция прибыли равна \ (0 \).Область слева от точки безубыточности представляет собой убыточную операцию.
Рисунок \ (\ PageIndex {13} \)
Пример \ (\ PageIndex {11} \): запись и решение системы уравнений с двумя переменными
Стоимость билета в цирк составляет \ (25 долларов США) для детей и \ (50 долларов США) для взрослых. В определенный день посещаемость цирка составляет \ (2,000 \), а общий доход от ворот составляет \ (70,000 $ \). Сколько детей и сколько взрослых купили билеты?
Решение
Пусть \ (c \) = количество детей и \ (a \) = количество присутствующих взрослых.
Общее количество человек \ (2,000 \). Мы можем использовать это, чтобы написать уравнение количества людей в цирке в тот день.
\ (с + а = 2,000 \)
Доход от всех детей можно найти, умножив \ (25,00 $ \) на количество детей \ (25c \). Доход от всех взрослых можно найти, умножив \ (50,00 $ \) на количество взрослых \ (50a \). Общий доход составляет \ (70 000 долларов США). Мы можем использовать это, чтобы написать уравнение дохода.
\ (25c + 50a = 70,000 \)
Теперь у нас есть система линейных уравнений с двумя переменными.
\ (с + а = 2,000 \)
\ (25c + 50a = 70,000 \)
В первом уравнении коэффициент при обеих переменных равен \ (1 \). Мы можем быстро решить первое уравнение для \ (c \) или \ (a \). Будем решать относительно \ (a \).
\ [\ begin {align *} c + a & = 2,000 \\ a & = 2,000 − c \ end {align *} \]
Подставьте выражение \ (2,000 − c \) во второе уравнение для a и решите относительно \ (c \).
\ [\ begin {align *} 25c + 50 (2,000-c) & = 70,000 \\ 25c + 100,000-50c & = 70,000 \\ -25c & = -30,000 \\ c & = 1,200 \ end {align *} \]
Подставьте \ (c = 1,200 \) в первое уравнение, чтобы найти \ (a \).
\ [\ begin {align *} 1,200 + a & = 2,000 \\ a & = 800 \ end {align *} \]
Мы обнаружили, что \ (1200 \) детей и \ (800 \) взрослых купили билеты в цирк в тот день.
Упражнение \ (\ PageIndex {8} \)
Билеты в цирк стоят \ ($ 4.00 \) для детей и \ ($ 12.00 \) для взрослых. Если было куплено \ (1650 \) билетов на питание на общую сумму \ (14 200 долларов \), сколько детей и сколько взрослых купили билеты на питание?
- Ответ
\ (700 \) детей, \ (950 \) взрослых
Медиа
Получите доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики с системами линейных уравнений.
Ключевые понятия
- Система линейных уравнений состоит из двух или более уравнений, состоящих из двух или более переменных, так что все уравнения в системе рассматриваются одновременно.
- Решением системы линейных уравнений с двумя переменными является любая упорядоченная пара, которая удовлетворяет каждому уравнению независимо. См. Пример \ (\ PageIndex {1} \).
- Системы уравнений классифицируются как независимые с одним решением, зависимые с бесконечным числом решений или несовместимые с отсутствием решения.
- Один из методов решения системы линейных уравнений с двумя переменными — построение графиков. В этом методе мы строим уравнения на одном и том же наборе осей. См. Пример \ (\ PageIndex {2} \).
- Другой метод решения системы линейных уравнений — подстановка. В этом методе мы решаем одну переменную в одном уравнении и подставляем результат во второе уравнение. См. Пример \ (\ PageIndex {3} \).
- Третий метод решения системы линейных уравнений — это сложение, в котором мы можем исключить переменную, добавив противоположные коэффициенты соответствующих переменных.См. Пример \ (\ PageIndex {4} \).
- Часто необходимо умножить одно или оба уравнения на константу, чтобы упростить исключение переменной при сложении двух уравнений. См. Пример \ (\ PageIndex {5} \), Пример \ (\ PageIndex {6} \) и Пример \ (\ PageIndex {7} \).
- Любой метод решения системы уравнений приводит к ложному утверждению для несовместимых систем, потому что они состоят из параллельных линий, которые никогда не пересекаются.

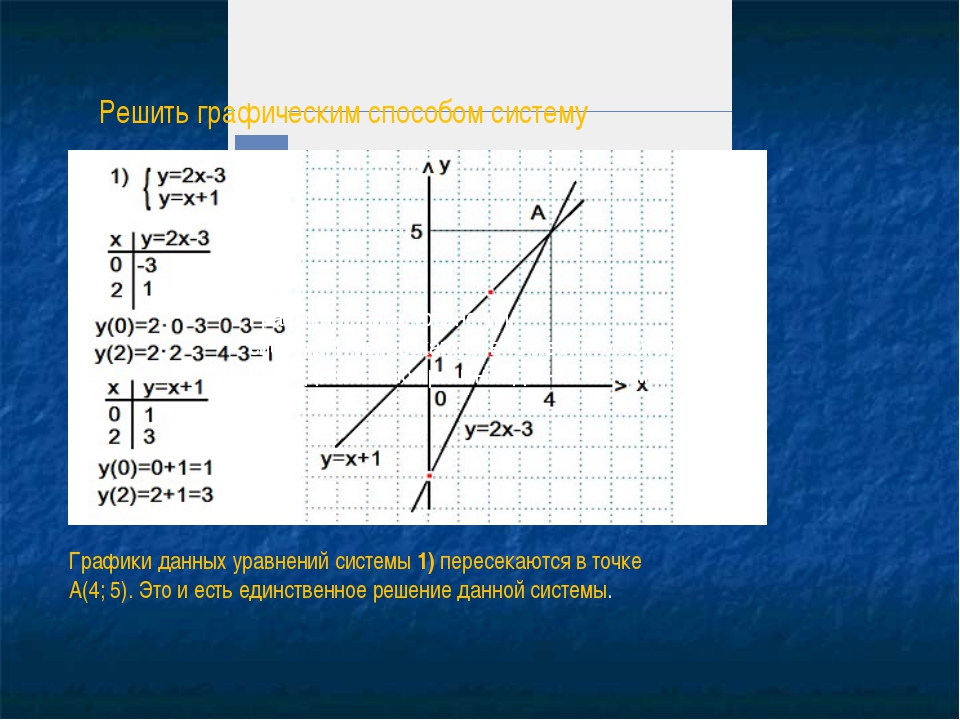
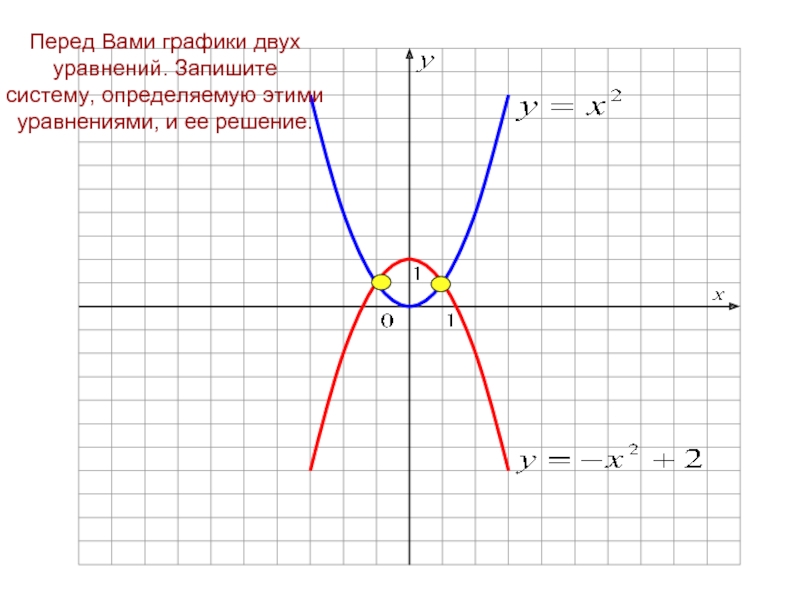 Актулизация опорных знаний
Актулизация опорных знаний Изучение нового материала
Изучение нового материала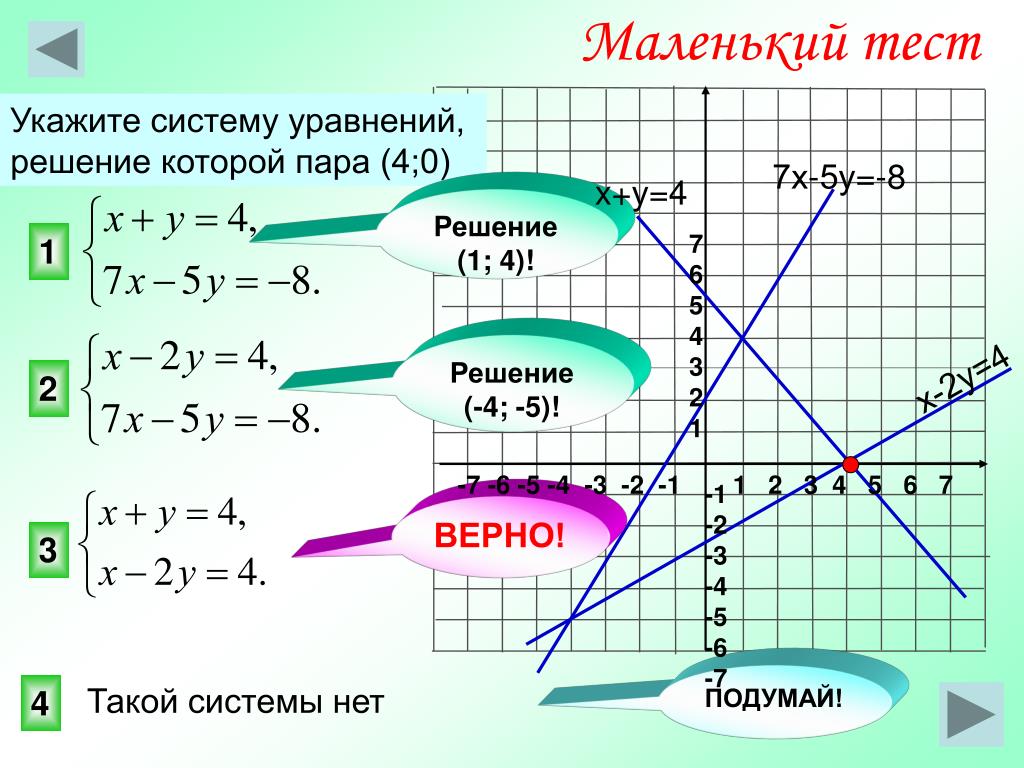 Контроль и самопроверка знаний
Контроль и самопроверка знаний информация о дом. задании
информация о дом. задании