Содержание
Установление соответствия между формулой и названием графика
1. Установите соответствие между формулой и названием графика
1) у = х2 + 4х − 3;
2) у = −6х
3) у =
10
;
х
4) у = 3х − 4;
5) у = х;
6) у = 6
А) Прямая;
Б) Ветвь параболы;
В) Гипербола;
Г) Парабола;
Д) Прямая, проходящая
через начало координат
Запишите название каждой функции
2. Самопроверка
1) у = х2 + 4х − 3;
2) у = −6х
3) у =
10
;
х
4) у = 3х − 4;
5) у = х;
6) у = 6
1) Квадратичная
функция
2) Прямая
пропорциональность;
3) Обратная
пропорциональность;
4) Линейная функция;
5) Квадратный корень
из х;
6) Линейная функция
3. Рефлексия
Начало урока Конец урока
1. Я знаю формулу
А)Квадратичной функции
Б) Обратной пропорциональности
В) Линейной функции
2. Я отличаю график данной функции от других
А)Квадратичной функции
Б) Обратной пропорциональности
В) Линейной функции
3. Я умею установить соответствие между знаками
Я умею установить соответствие между знаками
коэффициентов и графиками функций для
А)Квадратичной функции
Б) Обратной пропорциональности
В) Линейной функции
4. Установление соответствия между графиком функции и ее формулой
8 класс. Подготовка к ОГЭ
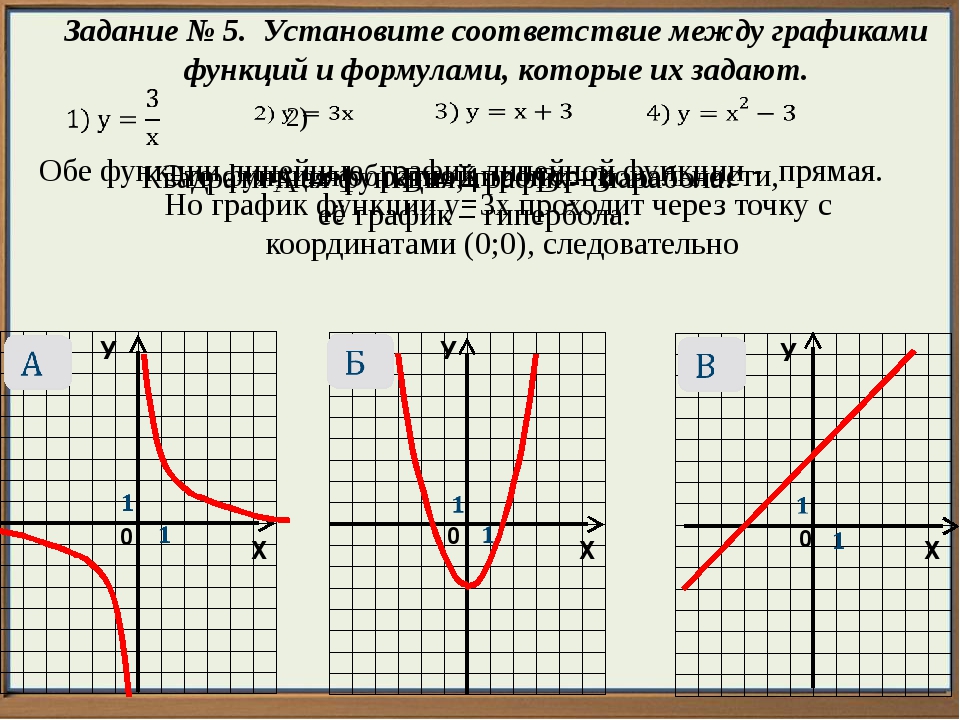
5. №1. Установите соответствие между графиками функций и формулами
А
Б
В
3 1 2
6. №2. Установите соответствие между функциями и их графиками
А
Б
В
2 3 1
7. №3. Установите соответствие между формулами и графиками
ФУНКЦИИ
А)у = 0,5х + 3
Б)у = −0,5х + 3
В)у = 0,5х − 3
А
Б
В
1 3 2
8. №4 .Установите соответствие между графиками функций и знаками коэффициентов а и с.
КОЭФФИЦИЕНТЫ
1)а > 0, с
2) а> 0; с > 0
3)а 0
А
Б
В
1 3 2
9. №5. Установите соответствие между графиками функций и знаками коэффициентов k и b
Коэффициенты
1)k0;
2) k>0,b>0;
3) k>0,b
А
Б
В
2 1 3
10.
 №6. Для каждого графика укажите соответствующее ему значение коэффициента а и дискриминанта D
№6. Для каждого графика укажите соответствующее ему значение коэффициента а и дискриминанта D
ЗНАКИ ЧИСЕЛ
1) а>0; D>0
2) а>0; D
3) а0
4) а
А
Б
В
Г
1 4 2 3
11. №7.Установите соответствие между функциями и их графиками.
А)
ФОРМУЛЫ
1) у = −3х2 − 6х + 3
2) у = −3х2 + 6х + 3
3) у = 3х2 + 6х − 3
Б)
В)
А
Б
В
1 3 2
12. Итоги работы
«5» – за 23 и более балла;
«4» – за 20-23 балла;
«3» – за 17-19 баллов;
13. Рефлексия
Начало урока Конец урока
1. Я знаю формулу
А)Квадратичной функции
Б) Обратной пропорциональности
В) Линейной функции
2. Я отличаю график данной функции от других
А)Квадратичной функции
Б) Обратной пропорциональности
В) Линейной функции
3. Я умею установить соответствие между знаками
коэффициентов и графиками функций для
А)Квадратичной функции
Б) Обратной пропорциональности
В) Линейной функции
Взаимное расположение графиков линейных функций
Презентация поможет учителю систематизировать знания учащихся по теме: «Линейная функция» и «Взаимное расположение графиков линейных функций». В работе предложены задания, соответствующие 5-у заданию ГИА за 9 класс. В работе представлены графики линейных функций и формул — надо найти соответствие между ними; а так же математический диктант на знание формулы, графика, углового коэффициента линейной функции и условий взаимного расположения линейных функций.
В работе предложены задания, соответствующие 5-у заданию ГИА за 9 класс. В работе представлены графики линейных функций и формул — надо найти соответствие между ними; а так же математический диктант на знание формулы, графика, углового коэффициента линейной функции и условий взаимного расположения линейных функций.
Просмотр содержимого документа
«Взаимное расположение графиков линейных функций»
7 класс
Каждую прямую, построенную на координатной плоскости соотнисите с её уравнением.
А. у = х
Б. х = 2
В. у = 2
Г. у = -2
0, b 0 Б. k 0, b В. k 0 «
На рисунке изображены графики функций вида у = кх + b .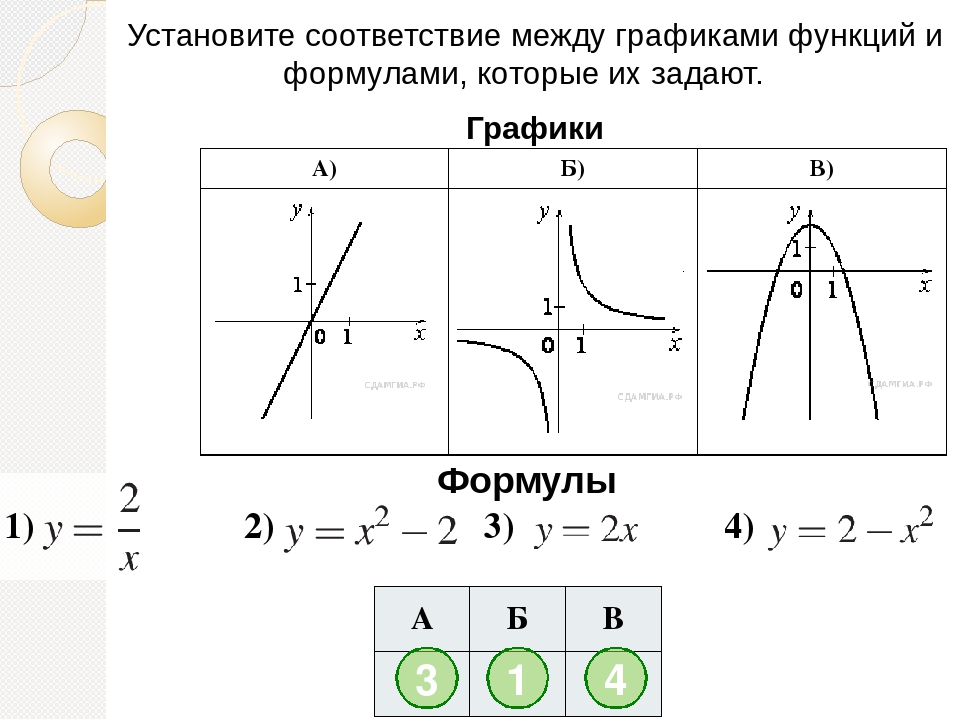 Установите соответствие между графиками и знаками коэффициентов к и b.
Установите соответствие между графиками и знаками коэффициентов к и b.
А. k 0, b 0
Б. k 0, b
В. k 0
На рисунке изображены графики функций вида у = кх + b . Установите соответствие между графиками и знаками коэффициентов к и b.
А. k1 = k2, b1 = b2
Б. k1 = k2, b1 = b2
В. k1 = k2
Среди функций, заданных формулами у = х + 0,5; у = -0,5х + 4; у = 5х – 1; у = 1 + 0,5х; у = 1/2х, выделите те, графики, которые параллельны графику функции у = 0,5х + 4
Какая из следующих прямых отсутствует на рисунке?
А. у = 2х + 3
Б. у = 2х – 3
В. у = -2х + 3
Г. у = -2х — 3
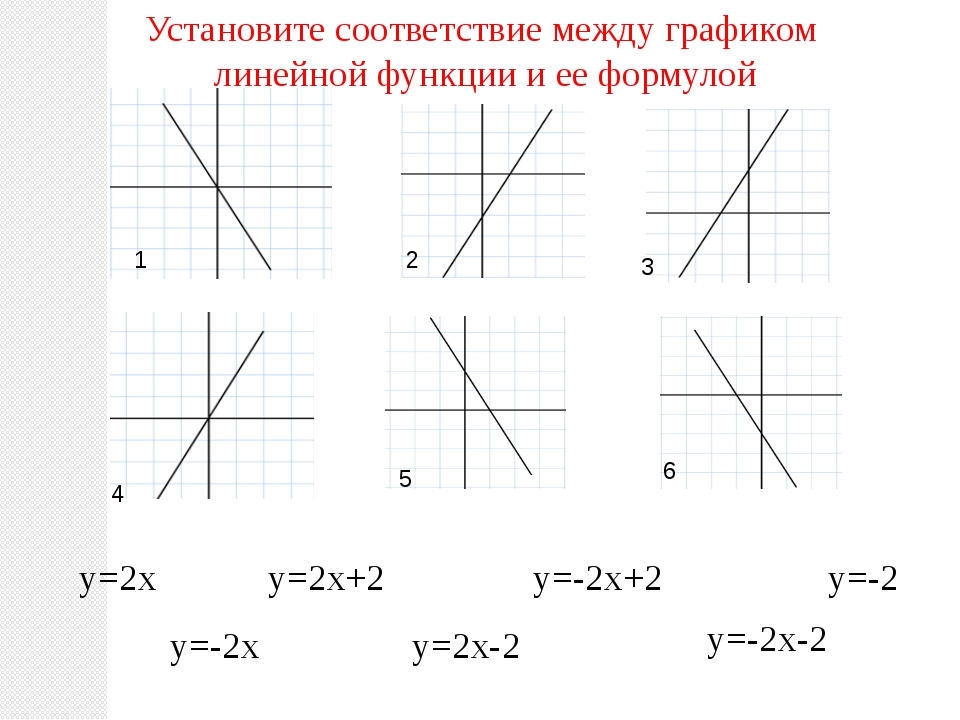
График какой функции изображён на рисунке? А. у = 2х Б. у = 2х + 2 В. у = 2х Г. у = 2х + 2
2
2
Установите соответствие между графиками функций и формулами, задающими эти функции.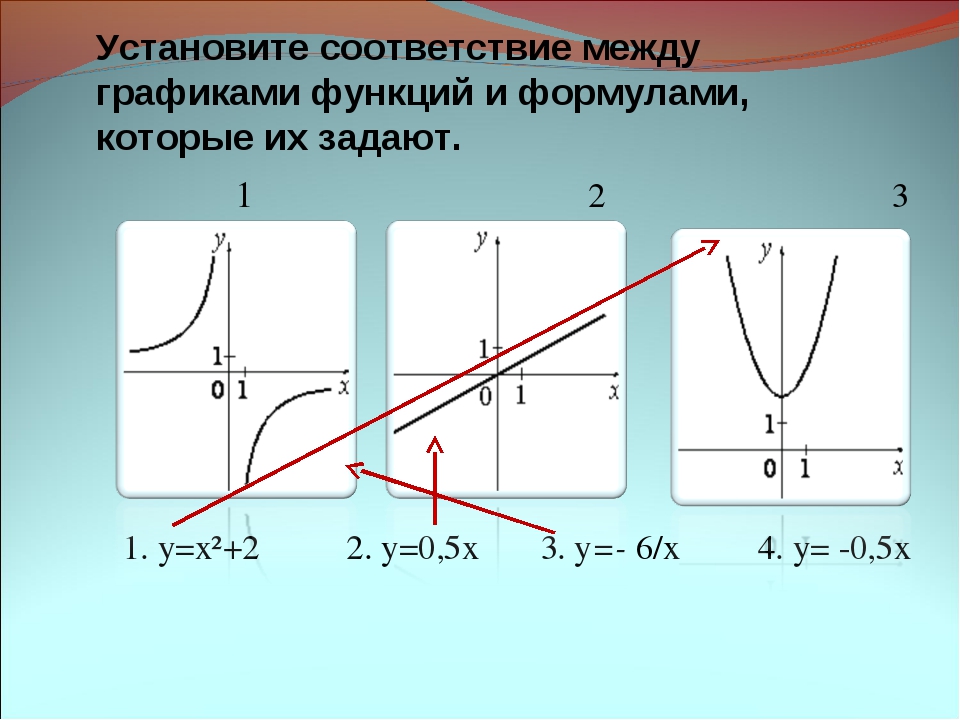
А. у = 2х
Б. у = -2х — 3
В. у = -2х
Г. у = 2х — 3
Как располагаются графики функций?
- у = 3х + 5
- у = 0,5х + 5
- у = -2х + 5
- у = -4,2х + 5
Как располагаются графики функций?
Математический диктант
I вариант II вариант
- Как называется функция и что является графиком данной функции?
у = -3х + 2 у = 1/3х
- Для функции запишите, чему равны k и b :
у = 2 – 7х у = -7 + 2х
3 . Запишите формулу, задающую какую-нибудь линейную функцию, график которой параллелен прямой
у = -5х у = 3х
Математический диктант
4 . Запишите уравнение какой-нибудь прямой с угловым коэффициентом к и уравнение прямой, график которой будет совпадать с графиком данной функции.
к = -1/7 к = -2
5 . Пересекаются ли графики функций:
у = 2 – 7х и у = -7х – 3 у = 2х + 5 и у = 3 – 4х
у = -2/5х + 4 и у = 17х + 4
у = 6х – 2 и у = 6 + 6х
Проверочная работа по теме Графики функций, 9 класс
Проверочная работа по теме «Функции и графики»,вариант 1.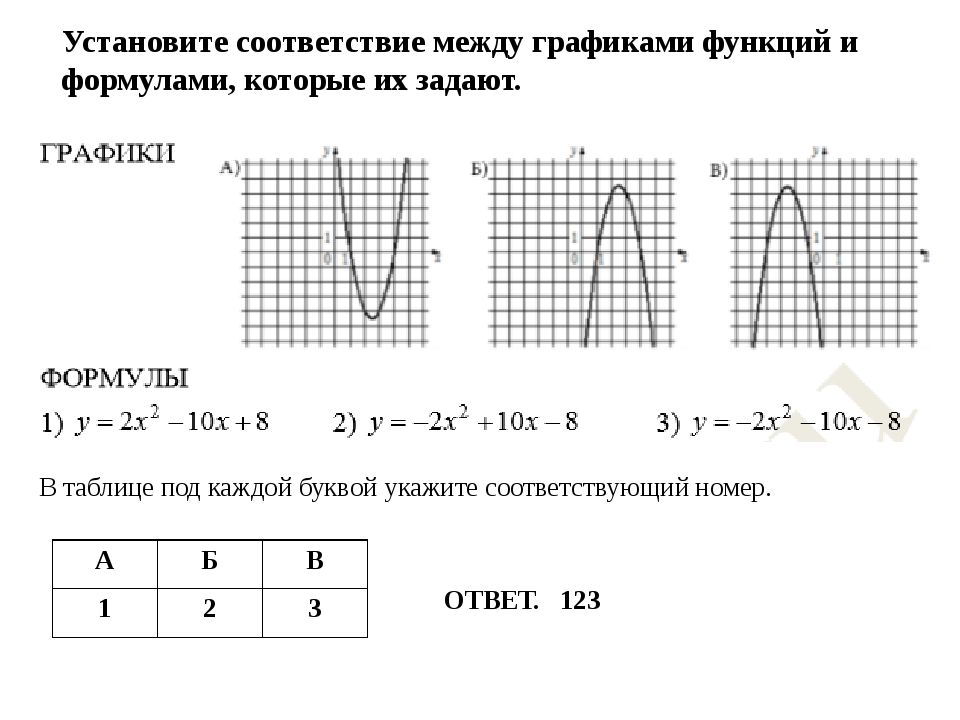
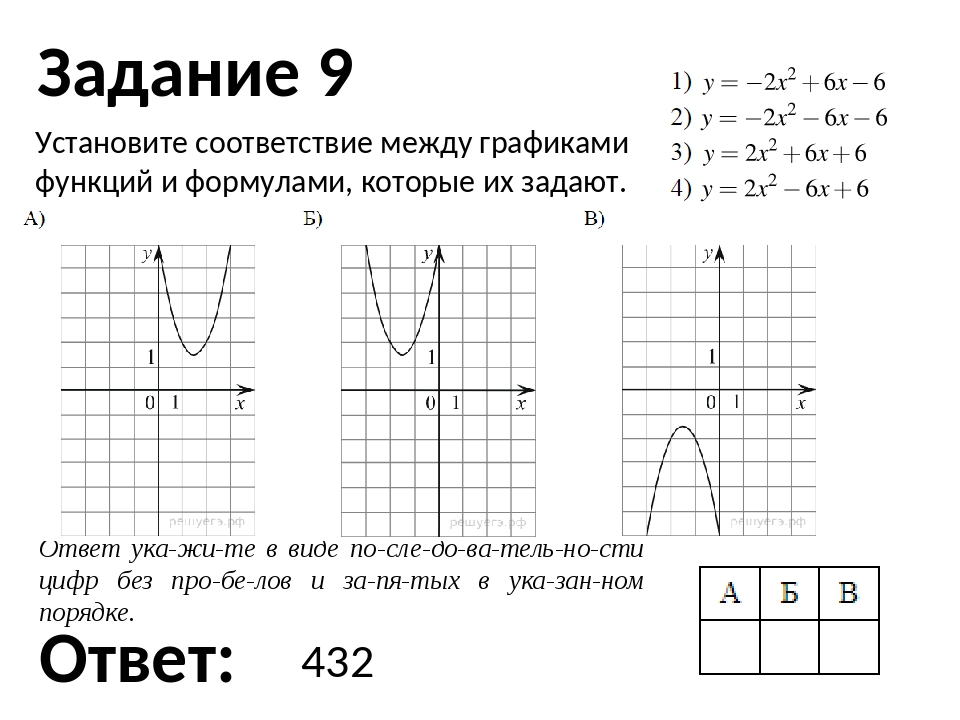
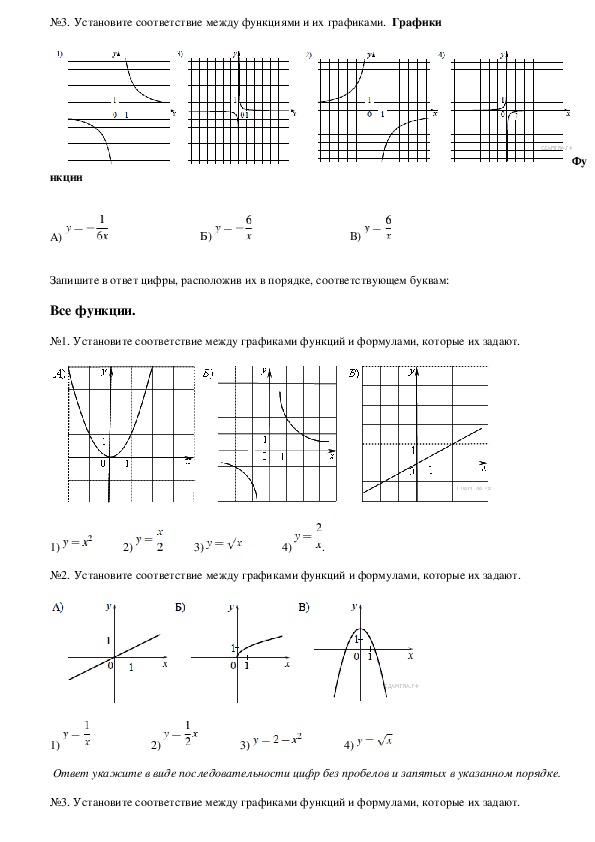
1. Установите соответствие между графиками функций и формулами, которые их задают.
1) 2) 3) 4)
2.Н а рисунке изображён график квадратичной функции y=f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) f( −2) = f(2)
2) f(x)>0 при x<−4 и при x>2
3) Наименьшее значение функции равно −9
3. Установите соответствие между функциями и их графиками.
ФУНКЦИИ
А) Б) В)
ГРАФИКИ
4. Найдите значение по графику функции изображенному на рисунке.
5. На рисунках изображены графики функций вида . Установите соответствие между знаками коэффициентов и и графиками функций.
КОЭФФИЦИЕНТЫ
А) Б) В)
ГРАФИКИ
В таблице под каждой буквой укажите соответствующий номер.
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
6. На рисунке изображён график функции Установите соответствие между утверждениями и промежутками, на которых эти утверждения удовлетворяются.
УТВЕРЖДЕНИЯ |
| ПРОМЕЖУТКИ |
А) Функция возрастает на промежутке Б) Функция убывает на промежутке |
| 1) [0; 3] 2) [− 1; 1] 3) [2; 4] 4) [1; 4] |
7. На рисунке изображены графики функций вида y = ax2 + bx + c. Установите соответствие между графиками функций и знаками коэффициентов a и c.
КОЭФФИЦИЕНТЫ
А) Б) В)
ГРАФИКИ
8.Построить график функциии определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.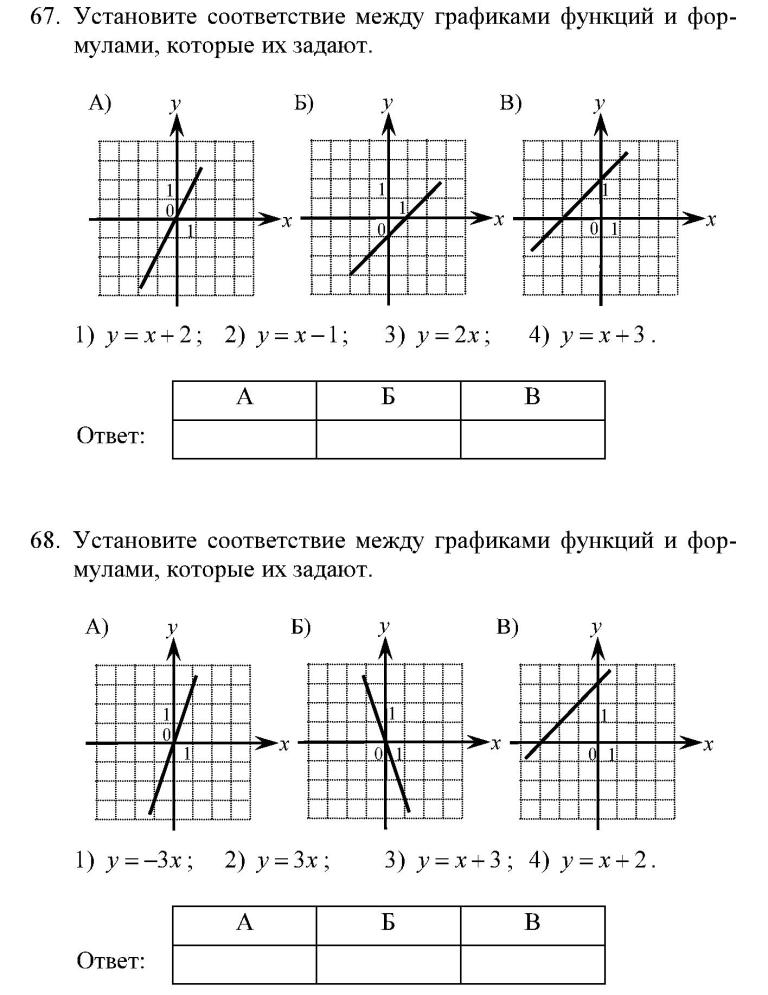
9. Постройте график функции и определите, при каких значениях прямая имеет c графиком ровно одну общую точку.
10. Найдите область определения функции
А) б) y=
Проверочная работа по теме «Функции и графики»,вариант 2.
1. На рисунке изображены графики функций вида y = ax2 + bx + c. Установите соответствие между графиками функций и знаками коэффициентов a и c.
КОЭФФИЦИЕНТЫ
А) Б) В)
ГРАФИКИ
2.
На рисунке изображён график квадратичной функции y = f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) Функция убывает на промежутке [−1; +∞).
2) f(−3)<f(0).
3) f(x)<0 при −4<x<2.
3. На рисунке изображены графики функций вида y = kx + b.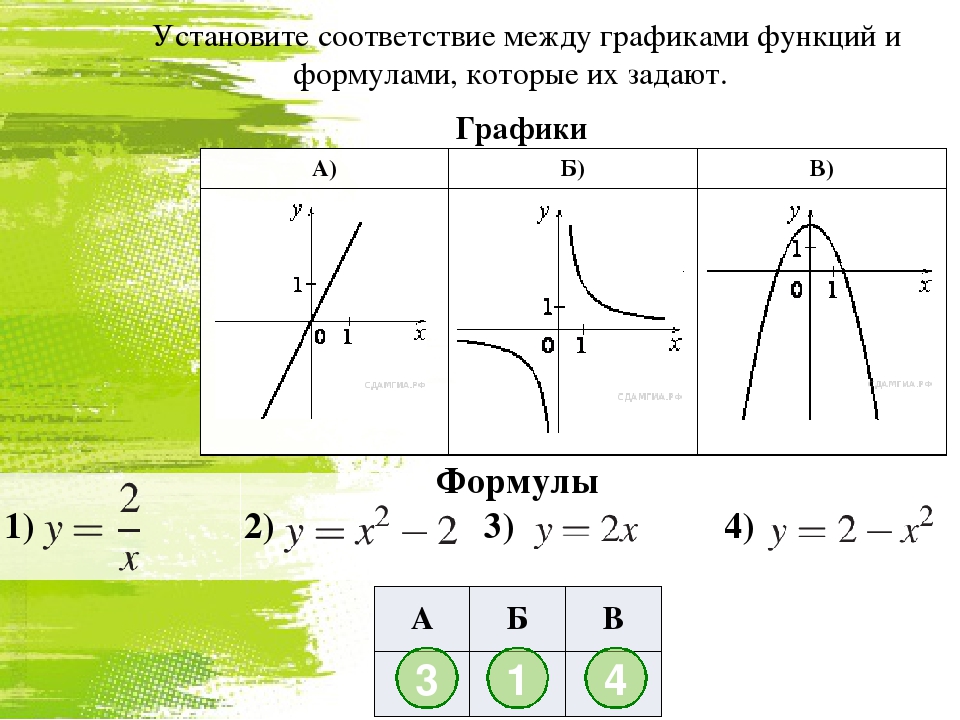 Установите соответствие между знаками коэффициентов k и b и графиками функций.
Установите соответствие между знаками коэффициентов k и b и графиками функций.
Графики
Коэффициенты
1) k < 0, b < 0 | 2) k < 0, b>0 | 3) k > 0, b>0 | 4) k > 0, b<0 |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
4. На рисунке изображён график функции y = ax2 + bx + c . Установите соответствие между утверждениями и промежутками, на которых эти утверждения выполняются.
8 класс Повторение. Функции и их графики
Тема урока: «Функции и их графики»
8 класс
(Вступительное слово учителя)
Идея функциональной зависимости восходит к древности, она содержится уже в первых формулах для нахождения объемов и площадей фигур (4-5 тысяч лет назад).
Начиная с 17 века понятие «функция» становится одним из важнейших. Функция сыграла и поныне играет большую роль в познании реального мира.
Функция сыграла и поныне играет большую роль в познании реального мира.
Функция – это математическая модель, позволяющая изучать и описывать разнообразные зависимости между реальными величинами.
Умение анализировать эти зависимости сделает вас в дальнейшем успешными в своем поле деятельности.
В настоящее время построение графиков функций, использование свойств функций при решении уравнений необходимо для успешной сдачи экзаменов.
Сегодня на уроке мы повторим все ранее изученные функции, их графики и некоторые свойства.
I. Устная работа (задания проектируются на экран):
1) Установите соответствие между графиками функций и формулами, задающими эти функции: (ученик должен сказать название функции и графика)
II. (Задание выполняет весь класс. Нужно выписать буквы, соответствующие верным ответам. Получится слово «Лейбниц». Учитель контролирует выполнение задания, при необходимости оказывает помощь.)
Установите соответствие между графиками функций и формулами.
III. (Сообщение учителя. На экран проектируется портрет Вильгельма Лейбница.)
На экран проектируется портрет Вильгельма Лейбница.)
Вильгельм Лейбниц – выдающийся немецкий математик, физик, философ, языковед в 1673 году ввел слово «функция», от латинского function – совершение, выполнение.
IV. (Работа в парах. Учащиеся, по желанию, решение выполняют на листочках, чтобы сдать на проверку. Правильность выполнения задания проверяется с помощью проектора.)
Изобразив схематически графики функций, выясните, имеет ли корни уравнение, и сколько?
1) 2) 3)
V. (Задание учащиеся выполняют по вариантам. Два ученика решают уравнения с обратной стороны доски. Правильность выполнения и оформления проверяется с помощью проектора. Учитель контролирует выполнение задания, при необходимости помогает учащимся.)
Решите графически уравнение:
I вариант II вариант
VI. Минута отдыха.
(Задание выполняется устно.)
Установите соответствие между пословицами и графиками функций:
Учитель комментирует все ответы.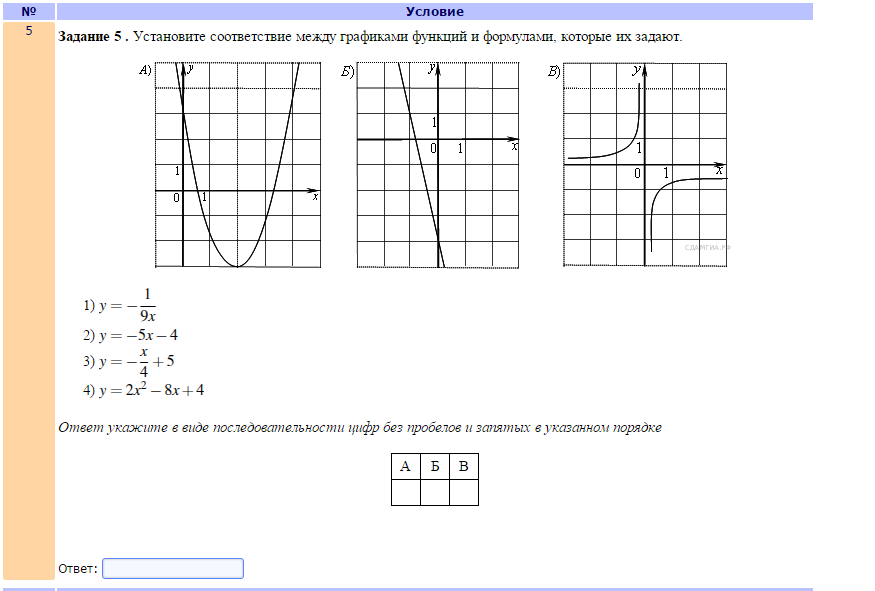 ( 1)По оси абсцисс – дела, по оси ординат – слава: если дела и поступки положительные, то и слава о человеке идет добрая.
( 1)По оси абсцисс – дела, по оси ординат – слава: если дела и поступки положительные, то и слава о человеке идет добрая.
3) По оси абсцисс – семена, по оси ординат – урожай. Для получения высокого урожая необходимо посеять оптимальное количество семян.)
VII. (Тест учащиеся выполняют по вариантам. Учащиеся, по желанию, сдают ответы на листочках. Учитель контролирует выполнение задания. Проверка осуществляется после выполнения задания большинством. Задания, где больше всего встречалось ошибок, разбираются вместе с классом.)
II вариант
Выберите верный ответ:
1)На рисунке изображен график функции вида у=kx+m.
Определите знаки k и m.
А) k>0; m>0 Б) k<0; m<0 В) k<0; m>0
2)Укажите график функции убывающей на
3)Укажите график функции ограниченной снизу.
4)Дан график функции . Какие из утверждений верны?
Какие из утверждений верны?
1.Функция ограничена сверху.
2.
3.Выпукла вверх.
4.Непрерывна.
I вариант
Выберите букву, соответствующую верному ответу:
1) На рисунке изображен график функции вида у=kх+m.
Определите знаки к и m.
А) k>0; m>0 Б) k>0; m<0 В) k<0; m>0
2)Укажите график функции возрастающей на .
3)Укажите график функции ограниченной сверху.
4)Дан график функции у= .Какие из утверждений верны:
1. Функция ограничена снизу.
Функция ограничена снизу.
2.
3.Функция непрерывна.
4.Выпукла вниз.
А) 1 и 2 Б) 2 и 3 В) 1 и 3
Ответы
I вариант II вариант
Б А Б В Б Б В А
VIII. (Задание повышенной сложности. Выполняет весь класс. Ученик решает у доски с подробными комментариями.)
Постройте график функции:
IX. Дополнительное задание. ( Для тех, кто быстро справился с основными заданиями. Проверяем с помощью пректора.)
Постройте графики функций:
а) ; б)
ХI.Домашнее задание.
Составьте уравнения, имеющие три, два, одно решение и не имеющее решения. Подтвердите ваши предположения, схематически изобразив графики.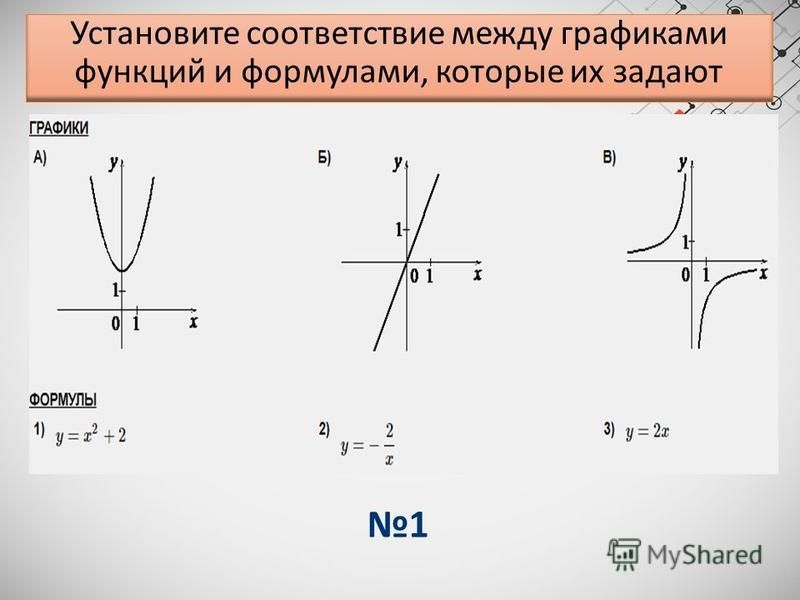
XII. Итог урока подводит учитель.
Сегодня на уроке мы повторили все ранее изученные функции, их графики и некоторые свойства. На следующих уроках будем изучать более сложные функции, графики которых получаются из данных путем сдвига вдоль оси х и оси у.
(На экране пример квадратичной функции, которая получается из графика функции у=х с помощью : а) параллельного переноса вдоль оси х; б) параллельного переноса вдоль оси х и оси у.)
Подведение итогов урока, заполнение учащимися листа самооценки.
Степень сложности урока Степень освоенности материала
Легко Обычно Сложно
Усвоен
полностью Усвоен частично Неусвоен
Степень интереса познания
Интересно Не очень интересно Скучно
I вариант
I. Cхематически изобразив графики функций, выясните, имеет ли уравнение корни, и сколько?
1) 2) 3)
II.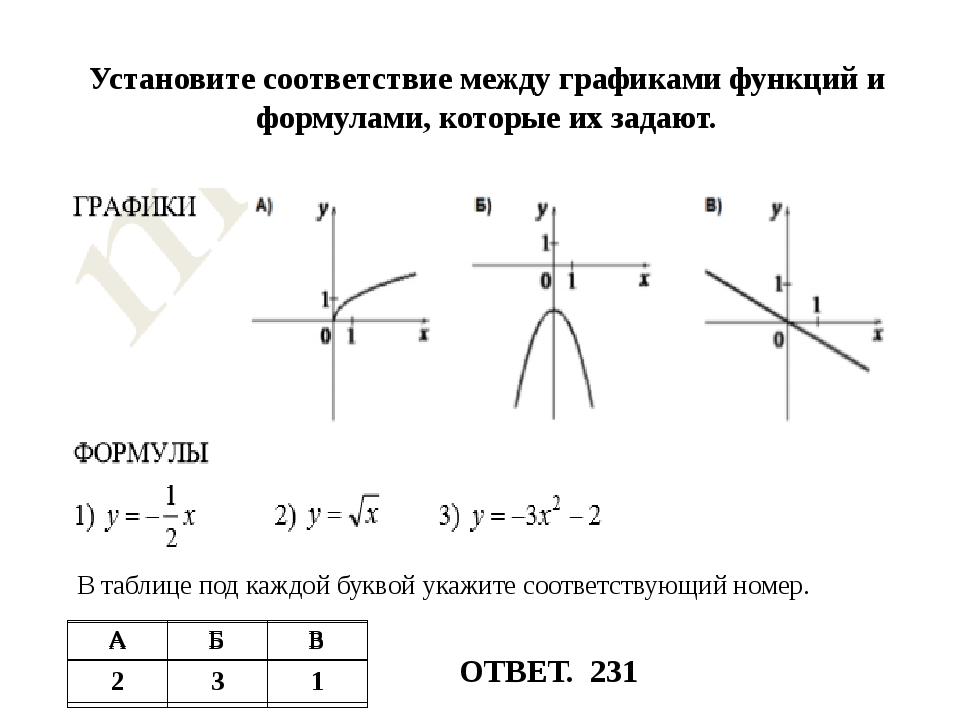 Решите графически уравнение:
Решите графически уравнение:
III. Выберите букву, соответствующую верному ответу:
1) На рисунке изображен график функции вида у=kх+m.
Определите знаки к и m.
А) k>0; m>0 Б) k>0; m<0 В) k<0; m>0
2)Укажите график функции возрастающей на .
3)Укажите график функции ограниченной сверху.
4)Дан график функции у= .Какие из утверждений верны:
1.Функция ограничена снизу.
2.
3.Функция непрерывна.
4.Выпукла вниз.
А) 1 и 2 Б) 2 и 3 В) 1 и 3
IV. Постройте график функции:
Дополнительные задания:
V.Дана функция у=f(х), где f(х)= . Решите уравнение
f(x-1)-f(x+1)=1.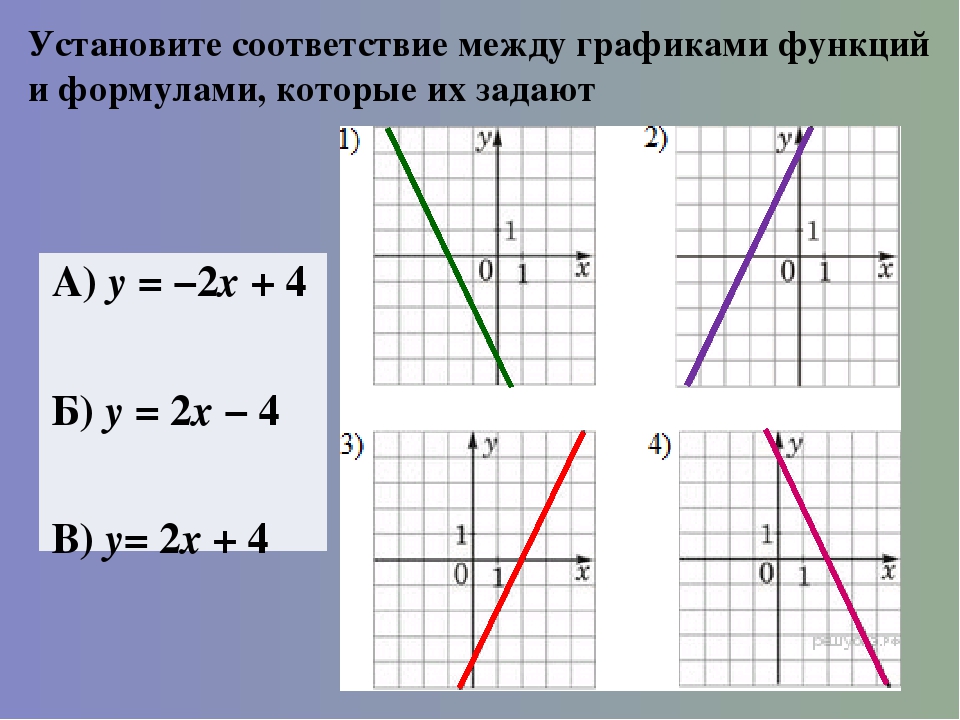
VI.Постройте графики функций:
а) ;
б)
II вариант
I. Cхематически изобразив графики функций, выясните, имеет ли уравнение корни, и сколько?
1) 2) 3)
II.Решите графически уравнение:
III. Выберите верный ответ:
1)На рисунке изображен график функции вида у=kx+m.
Определите знаки k и m.
А) k>0; m>0 Б) k<0; m<0 В) k<0; m>0
2)Укажите график функции убывающей на
3)Укажите график функции ограниченной снизу.
4)Дан график функции . Какие из утверждений верны?
1.Функция ограничена сверху.
2.
3.Выпукла вверх.
4. Непрерывна.
Непрерывна.
IV. Постройте график функции:
Дополнительные задания:
V. Дана функция у=f(х), где f(х)= . Решите уравнение
f(x-1)-f(x+1)=1.
VI. Постройте графики функций:
а) ;
б)
Функции. Графики функций. — Математика
На этом занятии мы повторим теорию по теме «Функции». Рассмотрим линейную, квадратичная функции, обратную пропорциональность, функцию y = √x . Рассмотрим правила построения графиков различных функций. Повторим определение свойств функции по ее графику (промежутки возрастания, убывания, промежутки знакопостоянства, наибольшее и наименьшее значения).
Задания по теме для самостоятельного решения
Задание 1
(2 балла)
На рисунке изображены графики функций вида y = kx + b. Установите соответствие между знаками коэффициентов k и b и графиками функций. Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Установите соответствие между знаками коэффициентов k и b и графиками функций. Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Задание 2
(2 балла)
Задание 3
(2 балла)
Проверить правильность выполнения заданий вы можете в автоматическом режиме в разделе домашние задания на странице с курсом «Математика Подготовка к ОГЭ 2016»
Понятие функции.
 Способы задания функции
Способы задания функции
Понятие функции является одним из важнейших понятий математики и её
приложений. С помощью различных функций могут быть описаны многие процессы и явления
реального мира.
Пусть X и Y —
какие-то множества. Имеет место функция, определённая на множестве X
со значениями на множестве Y, если в силу
некоторого закона f каждому элементу
x∈X ставится в соответствие один и
только один элемент y∈Y.
Это записывается в виде
y = f(x).
Другими словами, с помощью функции y = f(x)
множество X отображается в множество
Y. Поэтому функцию называют также отображением.
Например, авиапассажиры сидят в креслах салона пассажирского самолёта.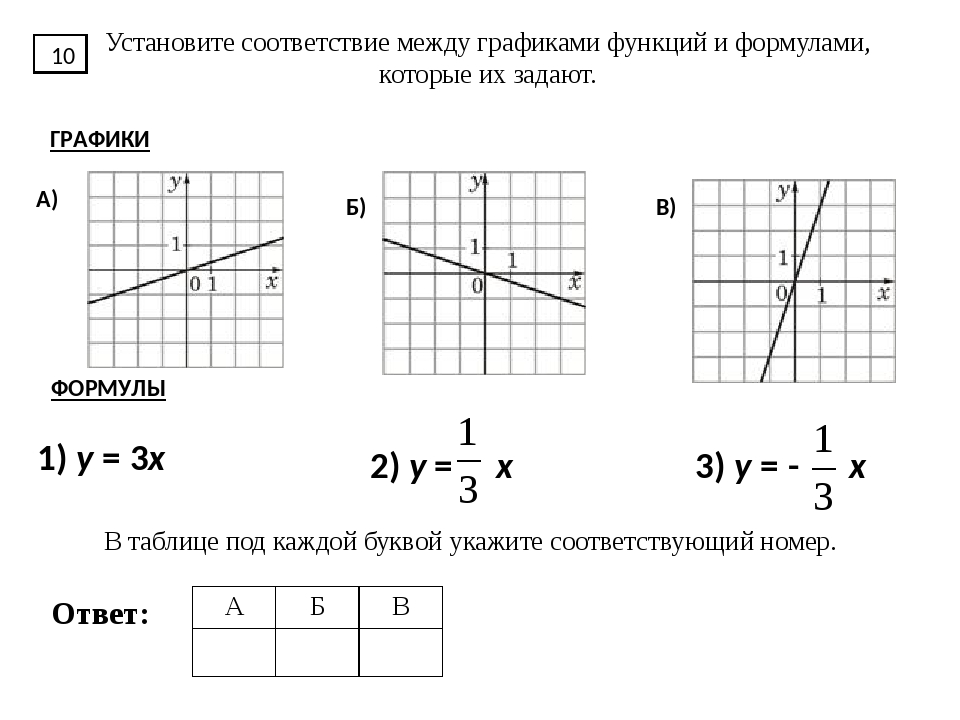
Пусть X — множество пассажиров, а Y —
множество кресел салона. Тогда возникает соответствие f :
каждому пассажиру x∈X сопоставляется
то кресло y = f(x),
в котором он сидит.
Наблюдается, таким образом, простой пример функции, областью
определения которой является множество X пассажиров,
а областью значений — множество f(X)
занимаемых ими кресел. Если заполнены не все кресла Y,
то множество значений функции будет подмножеством Y,
не совпадающим со всем множеством Y.
Если, однако, какому-то пассажиру
удастся сесть сразу в два кресла и
, то
нарушится принцип однозначной определённости значений функции, поэтому такая ситуация
не является функциональной в смысле данного выше определения функций, поскольку требуется,
чтобы каждому значению x аргумента соответствовало
бы одно определённое значение y = f(x)
функции.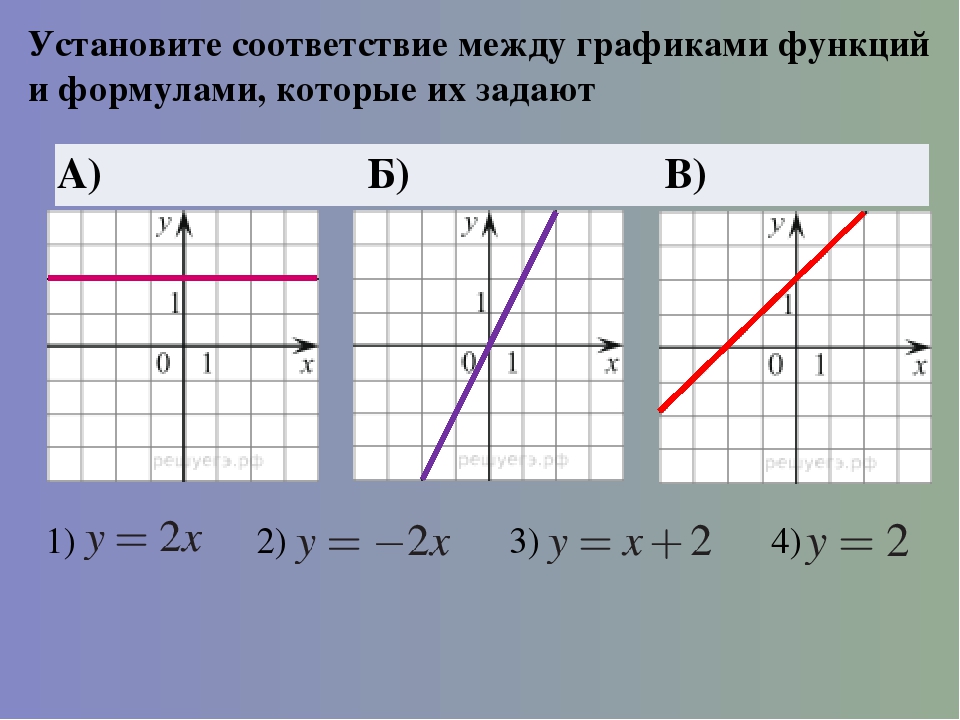
В математическом анализе часто X
обозначают как D (область определения функции), а Y
как E (область значений функции) и при этом
D и E называют
подмножествами R (множества действительных чисел).
На сайте есть урок Как найти область определения функции.
Как нетрудно догадаться по названию нашего сайта, он назван так в честь функции от
икса или f(x). И это неслучайно. Функции составляют бОльшую
часть предметов рассмотрения не только математического анализа, но и дискретной математики, а также
широко используются в программировании, где от профессионалов требуется выделять однотипные вычисления
в функции.
Пример 1. Даны множества A = {a, b, c, d, e} и
L = {l, m, n}.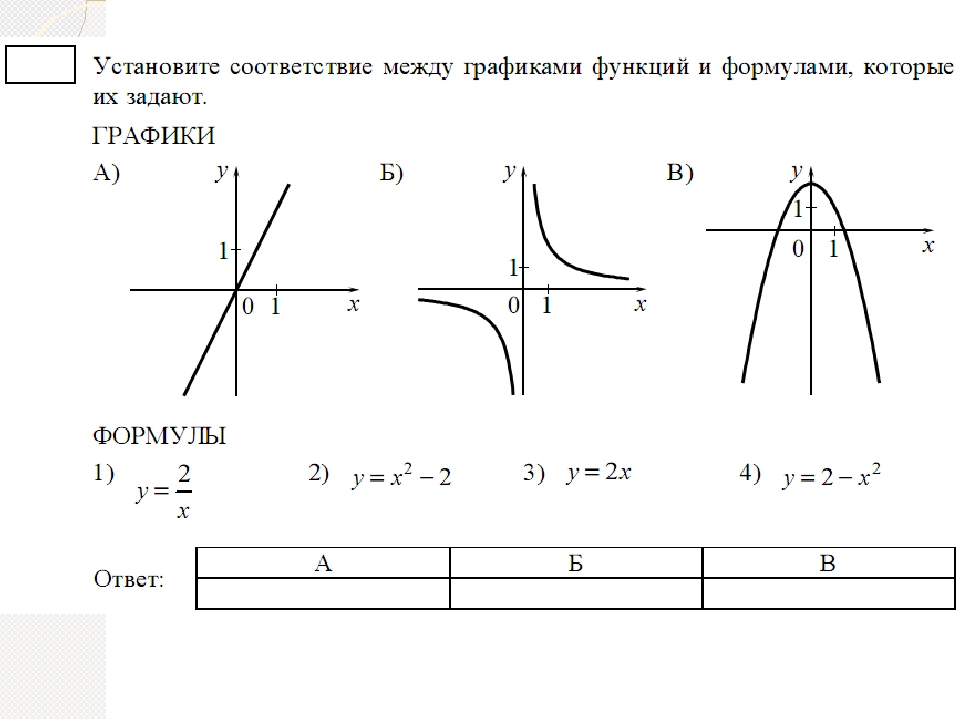
Можно ли между элементами этих множеств установить такое соответствие, чтобы оно было
функцией? Если да, то записать это соответствие, указав стрелками, какой элемент какому
соответствует.
Решение. Итак, множество A содержит
5 элементов, а множество L — 3 элемента. Если мы
поставим стрелки, ведущие от каждого элемента множества L к
элементам множества A, то некоторым элементам L
будут соответствовать более одного элемента A. Такое
соответствие не является функцией по определению. Но если мы проведём стрелки от элементов
A к элементам L,
то некоторым элементам A будут соответствовать одни и те
же элементы L, но при этом каждому элементу A
будет соответствовать не более одного элемента L. Такое
соответствие не противоречит определение функции, следовательно, ответ на вопрос задания —
положительный.
Можно задать, например, такое соответствите между элементами данных
множеств, которое будет функцией:
Пример 2. Даны множества A = {70, 140, 30, 48} и
В = {35, 15, 12}. Установить
между элементами множеств соответствие, заданное правилом «элемент A
можно нацело поделить на элемент В«. Будет ли
такое соответствие функцией?
Решение. Между элементами множеств A и
В устанавливается следующее соответствие:
Это соответствие является функцией, так как каждому элементу из множества
A соответствует не более одного элемента из множества
В.
Аналитическое задание функции.
Функция задана аналитически, если функциональная зависимость выражена
в виде формулы, которая указывает совокупность тех математических операций, которые
должны быть выполнены, чтобы по данному значению аргумента найти соответствующее значение
функции.
При аналитическом задании функции указывают область определения, либо
не указывают. В первом случае функция задаётся в виде
y = f(x), x∈D,
где D — область определения функции, во втором случае —
в виде y = f(x).
Во втором случае областью определения функции считается наибольшее множество, на котором
имеет смысл формула, которой задана функция, то есть наибольшее множество аргумента, которое
приводит к действительным значениям функции.
Важно, что функцию не следует отождествлять с формулой, с помощью
которой она задана. Например, функции y = x², x∈]-∞,+∞[ и
y = x², x∈[2, 4],
выраженные одной и той же формулой y = x²,
так как они имеют разные области определения.
Наоборот, одна и та же функция может быть задана разными формулами на
различных участках области определения. Пусть, например,
Пусть, например,
Здесь две формулы задают одну функцию, определённую на всей числовой
прямой. При x≤0 значения этой функции
определяются по первой формуле, а при x>0 — по
второй.
Аналитический способ задания функции удобен тем, что значения функции
можно вычислить при любых значениях аргумента. Недостатком этого способа задания функции
является его малая наглядность.
Графический способ задания функции
График функции даёт наглядное представление о её свойствах. Например,
график линейной функции y = kx + b
— прямая линия, график квадратичной функции y = ax² + bx + c —
парабола и т. д. При этом строятся графики функций, заданных геометрически, т. е. в виде
формул или уравнений. Таким образом, под графиком функции понимается множество точек
плоскости, декартовы координаты которых удовлетворяют заданному уравнению.
Графический способ задания функции помимо геометрического изображения
функции, заданной уравнением, удобен тогда, когда функцию трудно задать аналитически.
Задать функцию графически — это значит построить её график. Это часто делают самопишущие
приборы. Например, в медицине электрокардиограф строит электрокардиограмму — кривую
изменения электрических импульсов сердечной мышцы.
Графиком числовой функции y = f(x)
называется множество точек плоскости с координатами (x; f(x)),
абсциссы которых — числа из области определения функции, а ординаты — соответствующие значения
функции.
Не всякое множество точек координатной плоскости, даже не всякая линия
может служить графиком функции. Линия только в том случае задаёт функцию, если любая прямая,
параллельная оси 0y, пересекает её не более чем в
одной точке.
Пример 4. На рисунке ниже — график параболы,
заданной уравнением y² = 2x.
Является ли этот график графиком функции?
Решение. График параболы, заданной уравнением y² = 2x,
не является графиком функции, поскольку прямая, параллельная оси 0y,
пересекает его в двух точках при всех значениях x,
кроме x = 0. Заданное уравнение
эквивалентно двум уравнениям ,
каждое из которых определяет функцию. Графиком функции
служит верхняя половина параболы, а графиком функции —
её нижняя половина.
Табличный способ задания функции
При табличном способе задания функции рядом с числовым значением аргумента
записывается соответствующее значение функции. Широко известных таблицы квадратов и кубов
чисел, квадратных корней, то есть таблицы функций ,
,
.
Недостатком табличного способа задания функции является то, что в
таблице могут быть указаны не все, а лишь отдельные значения аргумента и функции. Особенности
Особенности
изменения функции при этом могут быть искажены или утрачены.
Если функция y зависит от переменной u, то есть
y = f(u), а
u, в свою очередь, является какой-либо функцией от
независимой переменной x, то есть u = g(x),
то переменная y называется функцией от функции или
сложной функцией от x.
Это записывается в виде
y = f(u), u = g(x)
или
y = f[g(x)].
Таким образом, сложной называется функция, аргументом которой является
не независимая переменная, а некоторая функция от неё.
Область определения сложной функции — это множество тех значений x
из X, для которых соответствующие значения
u принадлежат области определения U
функции y = f(u). Ни для
Ни для
каких других значений x сложная функция не имеет смысла.
Из определения следует, что сложная функция y = f[g(x)]
может быть представлена в виде цепочки простых функций y = f(u), u = g(x).
Переменную u принято называть промежуточным аргументом
в отличие от независимой переменной x. Цепочка,
составляющая сложную функцию, может состоять не только из двух, но и из большего числа
звеньев.
Например, функция
состоит из трёх звеньев: ,
, .
Пример 5. Представить сложную функцию
в виде
звеньев — простых функций.
Решение. Цепочка, составляющая данную функцию, состоит из следующих
звеньев:
Пример 6. Представить сложную функцию
в виде
звеньев — простых функций.
Решение. Цепочка, составляющая данную функцию, состоит из следующих
звеньев:
Если функция y задана уравнением
вида f(x, y) =0, не
разрешённым относительно y, то она называется
неявной функцией аргумента x (Что такое разрешить
уравнение относительно одной из переменных — в примере 8).
Пусть задана некоторая функция y = f(x),
т. е. некоторое соответствие между множествами D(f)
(область определения) и E(f)
(множество значений). Если обратное соответствие есть функция,
т. е. каждому значению y∈E(f)
соответствует одно единственное значение x∈E(f),
то её называют обратной функцией по отношению к функции f(x).
В этом случае уравнение y = f(x)
определяет x как неявную функцию от y.
Если это уравнение разрешимо относительно x, то
получим явное выражение обратной функции: x = g(y).
Пример 7. Будет ли функцией соответствие, обратное
функции
? А
соответствие, обратное функции ?
Решение. Соответствие, обратное функции, заданной в первом условии,
также является функцией:
.
Соответствие, обратное функции, заданной во втором условии,
не является функцией, так как ,
то есть значениям икса, кроме нуля, соответствуют два значения игрека.
Весь раздел «Исследование функций»
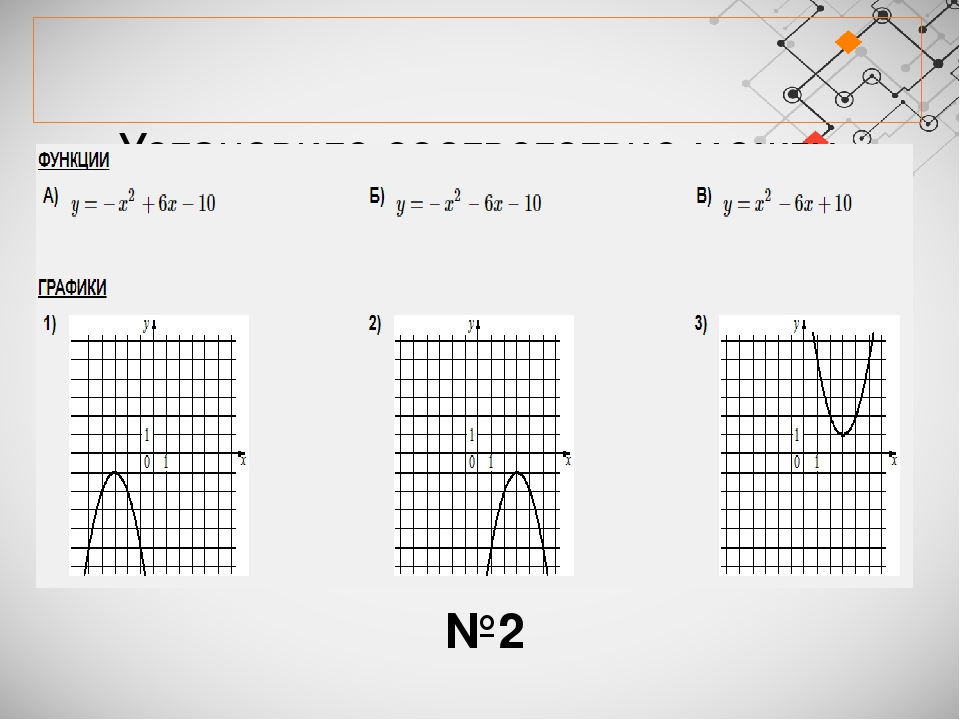
1) y=-x 2 +7x-14 2) y=x 2-7x+14 3) y=x 2 +7x+14 4) y=-x 2-7x-14
Степенная функция.
 Функция вида y=x k, где k>0 постоянная, называется степенной функцией. Если k=1, то y=x линейная функция, ее график прямая линия.
Функция вида y=x k, где k>0 постоянная, называется степенной функцией. Если k=1, то y=x линейная функция, ее график прямая линия.
Степенная функция Функция вида y=x k, где k>0 постоянная, называется степенной функцией. Если k=1, то y=x линейная функция, ее график прямая линия. Если k=2, то y=x 2 квадратичная функция, ее график парабола.
Подробнее
Квадратичная функция
Квадратичная функция Функция вида y=ax +bx+c, где а 0, называется квадратичной. Значения х, при которых функция принимает значение, равное 0, называют нулями функции. Если b=c=0, то функция принимает вид
Подробнее
Параметры и квадратный трёхчлен. 2
И. В. Яковлев Материалы по математике MathUs.ru Параметры и квадратный трёхчлен. 2 Данная статья посвящена вопросам расположения корней квадратного трёхчлена в зависимости от параметра.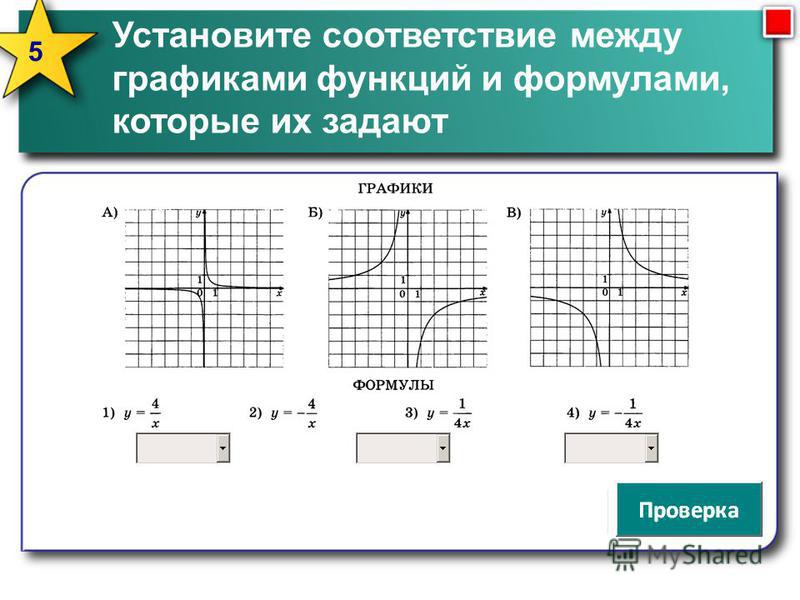 Вычисление корней
Вычисление корней
Подробнее
11.1. Функции Базовый уровень.
111 Функции Базовый уровень Оглавление 11101 Системы координат 1110 Понятие функции 7 1110 Область определения функции 10 11104 Область (множество) значений функции 1 11105 Возрастание и убывание функции
Подробнее
Тема 9 «Функция. Свойства функций»
Тема 9 «Функция. Свойства функций» Пусть X некоторое непустое множество действительных чисел. И пусть указан закон f, по которому каждому числу х ϵ X ставится в соответствие единственное число y ϵ Y, обозначаемое
Подробнее
Задание 18. Задачи с параметром
Линейное уравнение a x = b имеет: единственное решение, при a 0; бесконечное множество решений, при a = 0, b = 0; не имеет решений, при a = 0, b 0. Квадратное уравнение ax 2 + bx + c = 0 имеет: два различных
Подробнее
Пусть задано числовое множество D
Пусть задано числовое множество D R.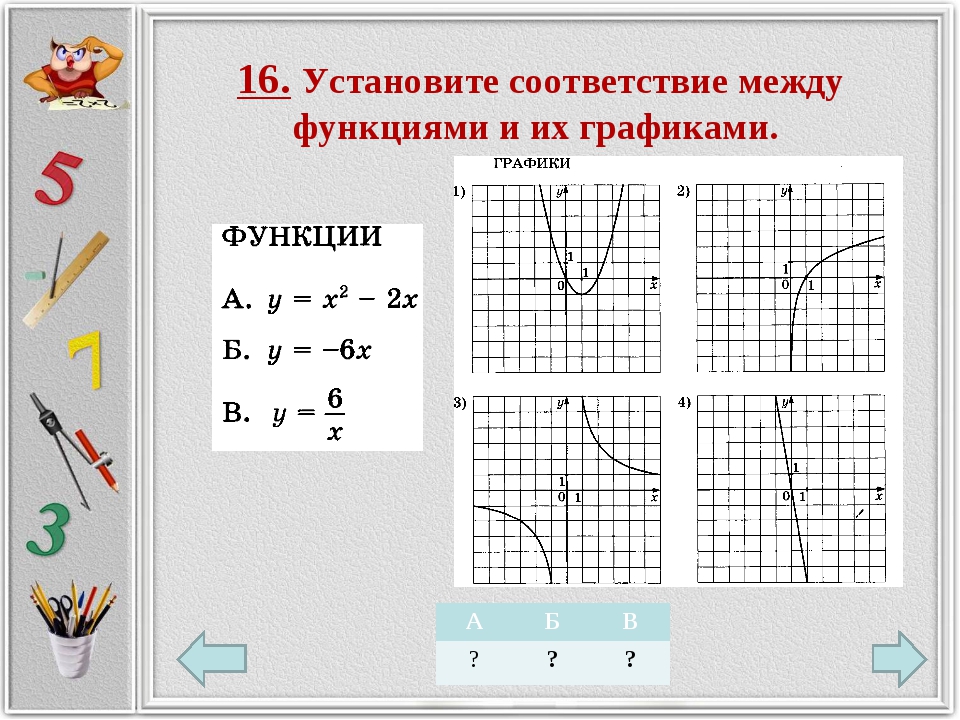 Если каждому числу x D поставлено в соответствие единственное число y, то говорят, что на множестве D задана числовая функция: y = f (x), x D. Множество D, называется
Если каждому числу x D поставлено в соответствие единственное число y, то говорят, что на множестве D задана числовая функция: y = f (x), x D. Множество D, называется
Подробнее
Критерии оценки заданий 18
Задание 18 Критерии оценки заданий 18 Содержание критерия Балл ы Обоснованно получен правильный ответ. 4 С помощью верного рассуждения получено множество значений а, отличающееся от искомого конечным числом
Подробнее
Геометрический смысл производной
Геометрический смысл производной Рассмотрим график функции y=f(x) и касательную в точке P 0 (x 0 ; f(x 0 )). Найдем угловой коэффициент касательной к графику в этой точке. Угол наклона касательной Р 0
Подробнее
Глава 11 ТЕСТОВЫЕ ЗАДАНИЯ
Глава ТЕСТОВЫЕ ЗАДАНИЯ Т-0 Исследование функции по графику Т-0 Соответствие между графиком рациональной функции и формулой Т-0 Построение графика по свойствам Т-04 Параллельный перенос графика Т-05 Симметричное
Подробнее
= 1 е) f(9) = 27; f(1) = 3
Глава 8 ФУНКЦИИ И ГРАФИКИ Алгоритмы А- Задание стандартных функций А- Понятие функции.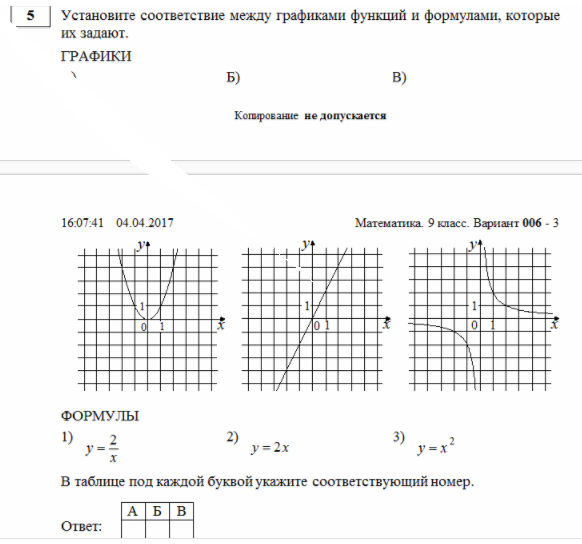 График функции А-3 Каноническая запись зависимостей А- Задание стандартных функций. К стандартным функциям отнесем
График функции А-3 Каноническая запись зависимостей А- Задание стандартных функций. К стандартным функциям отнесем
Подробнее
ТЕСТОВЫЕ ЗАДАНИЯ И ДИКТАНТЫ
М- 8 класс Рабочая тетрадь 8 глава стр. 1 Глава 8 ТЕСТОВЫЕ ЗАДАНИЯ И ДИКТАНТЫ Т-801 Установление вида зависимостей в физических формулах и законах Т-80 Выражение одной переменной через другие Т-803 Вычисление
Подробнее
ГЛАВА II. Квадратный трехчлен
ГЛАВА II. Квадратный трехчлен Справочный материал Квадратным трехчленом называют выражение a + b + c, где abc,, и a 0. График квадратного трехчлена парабола. Прямая b = ее ось симметрии. Точка ( в; в)
Подробнее
РАЗДЕЛ 14. ЗАДАЧИ С ПАРАМЕТРАМИ
РАЗДЕЛ ЗАДАЧИ С ПАРАМЕТРАМИ Комментарий Задачи с параметрами традиционно являются сложными заданиями в структуре ЕГЭ, требующими от абитуриента не только владения всеми методами и приемам решения различных
Подробнее
и x 1x 2, в частности сумму одинаковых
Тема Квадратное уравнение Формулы Виета Два алгебраических выражения, соединенных знаком «=», образуют равенство Равенство, справедливое при всех допустимых значениях входящих в него переменных, называется
Подробнее
Примеры решений контрольных работ
Примеры решений контрольных работ Л. И. Терехина, И.И. Фикс 1 Контрольная работа 3. Аналитическая геометрия на плоскости 1. Составить уравнения прямых, проходящих через точку A(4; 1) a) параллельно прямой
И. Терехина, И.И. Фикс 1 Контрольная работа 3. Аналитическая геометрия на плоскости 1. Составить уравнения прямых, проходящих через точку A(4; 1) a) параллельно прямой
Подробнее
16.2.Н. Производная.
6..Н. Производная 6..Н. Производная. Оглавление 6..0.Н. Производная Введение…. 6..0.Н. Производная сложной функции…. 5 6..0.Н. Производные от функций с модулями…. 7 6..0.Н. Возрастание и убывание
Подробнее
Учебный центр «Резольвента»
ООО «Резольвента», www.resolventa.ru, [email protected], (495) 509-8-0 Учебный центр «Резольвента» Доктор физико-математических наук, профессор К. Л. САМАРОВ КВАДРАТНЫЙ ТРЕХЧЛЕН Учебно-методическое пособие
Подробнее
Элементы высшей математики
Кафедра математики и информатики Элементы высшей математики Учебно-методический комплекс для студентов СПО, обучающихся с применением дистанционных технологий Модуль Дифференциальное исчисление Составитель:
Подробнее
1 Корни и их количество
1 Функции, их графики и связанные с ними доказательства Оглавление 1 Корни и их количество.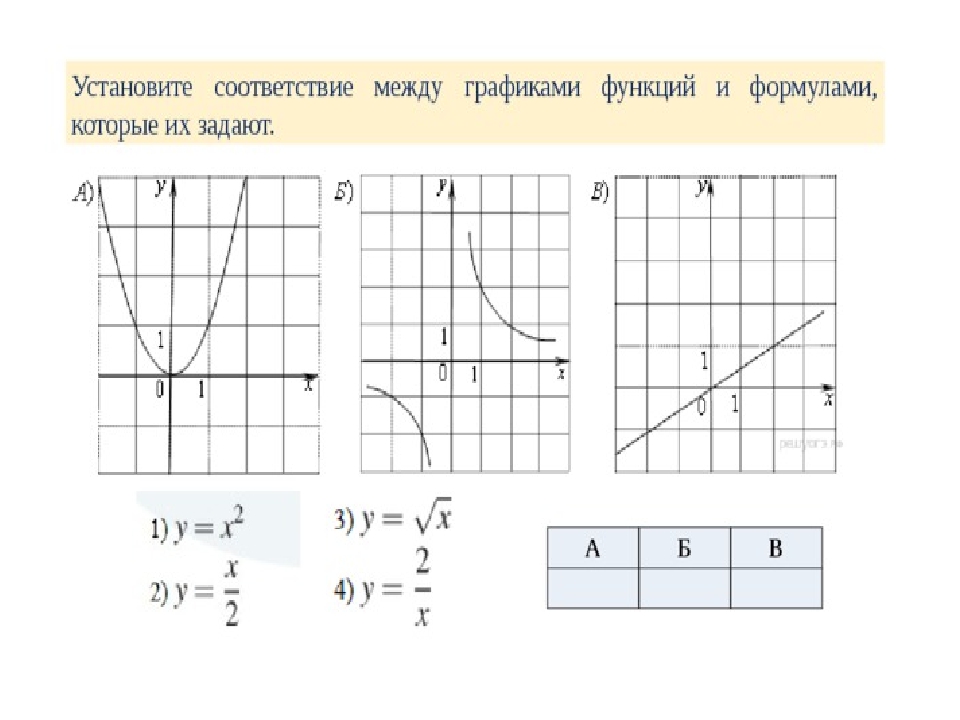 ..1 1.1 Корни уравнения…1 1.1.a Корни уравнения…1 1. Число корней… 1. Число корней… 1.4 Функциональное
..1 1.1 Корни уравнения…1 1.1.a Корни уравнения…1 1. Число корней… 1. Число корней… 1.4 Функциональное
Подробнее
ИНСТРУКЦИЯ К ДОМАШНЕМУ ЗАДАНИЮ 3
ИНСТРУКЦИЯ К ДОМАШНЕМУ ЗАДАНИЮ Для выполнения домашнего задания необходимо пользуясь табл. заполнить первую строку табл. затем выписать соответствующие вашему номеру варианта данные из табл.. Например
Подробнее
1. Решите графически систему уравнений: ( )
Представляю разбор контрольных работ из сборника «Л.А. Александрова. Алгебра 9 класс. Контрольные работы» Иногда трудно самостоятельно разобраться со всеми заданиями, предлагаемыми на контрольных, особенно
Подробнее
Домашняя работа по алгебре за 9 класс
ВЕ Бачурин Домашняя работа по алгебре за 9 класс к учебнику «Алгебра: Учеб для 9 кл общеобразоват учреждений / ЮН Макарычев, НГ Миндюк, КИ Нешков, СБ Суворова; Под ред СА Теляковского 0-е изд М: Просвещение,
Подробнее
Инструкция по выполнению работы
Проект Экзаменационная работа для проведения государственной итоговой аттестации выпускников IX классов общеобразовательных учреждений 009 года (в новой форме) по АЛГЕБРЕ Демонстрационный вариант 009 года
Подробнее
Чтение графиков функций
Материалы для выполнения внеаудиторной (домашней самостоятельной работы) нацеленные на устранение пробелов знаний и умений по дисциплине «Математика: алгебра и начала математического анализа, геометрия»
Подробнее
Переписок
А переписка
f между
X и Y
является тройкой (X, Y, Γ)
где Γ — подмножество декартова произведения
X × Y.
- Пре-домен из f
это X. - Ко-домен из f
Y. - Γ — это график функции f.
(Обратите внимание, что Γ — бинарное отношение.) - Домен из ф
(написано Dom (f))
является
{x∈X |
∃y∈Y
((x, y) ∈Γ)}. - Диапазон f
(написано Im (f))
является
{y∈Y |
∃x∈X
((x, y) ∈Γ)}. - y∈Y есть
изображение из
x∈X
если
(x, y) ∈Γ. - Изображение из
W⊆X — это
{y∈Y |
∃x∈W
((x, y) ∈Γ)}. - x∈X — это
изображение из
y∈Y
если
(y, x) ∈Γ. - Предварительный образ из
V⊆Y — это
{x∈X |
∃y∈V
((x, y) ∈Γ)}. - конвертирует f,
написано f -1
это соответствие, график которого
{(y, x) |
(x, y) ∈Γ}
График соответствия не ограничен
по количеству ребер внутри или вне каждого элемента:
изображение элемента домена может быть пустым,
синглтон, или
больше,
как и прообраз элемента диапазона.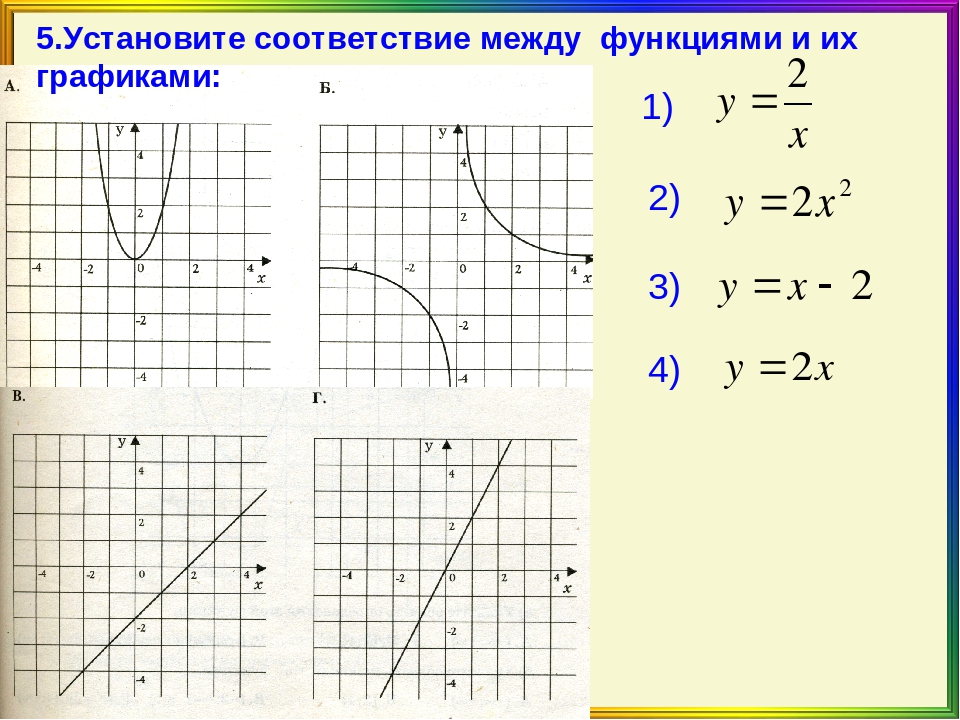
A функция
е: X → Y
является соответствием (X, Y, Γ)
который назначает не более одного элемента диапазона каждому элементу
его домен.Эквивалентно,
изображение каждого элемента в области f
это синглтон.
Отображение — это функция
чей домен — это весь его пре-домен.
Отображение
е: X → Y
является:
| на | или | сюръективный | если каждый y∈Y имеет | не менее | одно изображение в f |
| индивидуально | впрыск | не более | |||
| индивидуально и на | биектив | ровно |
Пре-домен и ко-домен не имеют отношения к отношениям,
поскольку отношение — это просто набор кортежей.
Отношение
р
то есть подмножество X × Y
является:
| функциональный | если каждый x∈X сопоставляется с | максимум один | y∈Y |
| впрыск | если каждый y∈Y отображается на | x∈X |
Отношения, графики и функции
Графики, отношения, домен и диапазон
Прямоугольная система координат Система с двумя числовыми линиями под прямым углом, определяющими точки на плоскости с помощью упорядоченных пар ( x , y ).состоит из двух вещественных числовых линий, пересекающихся под прямым углом. Горизонтальная числовая линия называется осью x Горизонтальная числовая линия, используемая в качестве опорной в прямоугольной системе координат, а вертикальная числовая линия называется осью y Вертикальная числовая линия, используемая в качестве опорной в прямоугольной системе координат. Эти две числовые линии определяют плоскую поверхность, называемую плоскостью Плоская поверхность, определяемая осями x и y , и каждая точка на этой плоскости связана с упорядоченной парой пар ( x , y ), которые определить положение относительно начала координат на прямоугольной координатной плоскости.действительных чисел ( x , y ). Первое число называется координатой x , а второе число называется координатой y . Пересечение двух осей известно как начало координат Точка пересечения осей x и y , обозначенная (0, 0)., Что соответствует точке (0, 0).
Эти две числовые линии определяют плоскую поверхность, называемую плоскостью Плоская поверхность, определяемая осями x и y , и каждая точка на этой плоскости связана с упорядоченной парой пар ( x , y ), которые определить положение относительно начала координат на прямоугольной координатной плоскости.действительных чисел ( x , y ). Первое число называется координатой x , а второе число называется координатой y . Пересечение двух осей известно как начало координат Точка пересечения осей x и y , обозначенная (0, 0)., Что соответствует точке (0, 0).
Оси x и y разбивают плоскость на четыре области, называемые квадрантами Четыре области прямоугольной координатной плоскости, частично ограниченные осями x и y и пронумерованные римскими цифрами I, II , III и IV., названные римскими цифрами I, II, III и IV, как показано на рисунке. Упорядоченная пара ( x , y ) представляет положение точек относительно начала координат. Например, упорядоченная пара (-4, 3) представляет позицию на 4 единицы слева от начала координат и на 3 единицы выше во втором квадранте.
Например, упорядоченная пара (-4, 3) представляет позицию на 4 единицы слева от начала координат и на 3 единицы выше во втором квадранте.
Эту систему часто называют декартовой системой координат. Термин используется в честь Рене Декарта при обращении к прямоугольной системе координат., названный в честь французского математика Рене Декарта (1596–1650).
Рисунок 2.1
Рене Декарт Википедия
Далее мы определяем RelationshipAny набор упорядоченных пар. как любой набор упорядоченных пар. В контексте алгебры интересующие нас отношения представляют собой наборы упорядоченных пар ( x , y ) в прямоугольной координатной плоскости. Обычно координаты связаны правилом, выраженным с помощью алгебраического уравнения.Например, оба алгебраических уравнения y = | x | −2 и x = | y | +1 определяют отношения между x и y . Ниже приведены некоторые целые числа, удовлетворяющие обоим уравнениям:
Здесь получены два соотношения, состоящие из семи упорядоченных парных решений:
y = | x | −2 имеет решения {(−3,1), (- 2,0), (- 1, −1), (0, −2), (1, −1), (2, 0), (3,1)} и x = | y | +1 имеет решения {(4, −3), (3, −2), (2, −1), (1,0), (2,1 ), (3,2), (4,3)}
Мы можем визуально отобразить любое отношение этого типа на координатной плоскости, нанеся точки.
Наборы решений каждого уравнения образуют отношение, состоящее из бесконечного числа упорядоченных пар. Мы можем использовать данные решения для упорядоченных пар, чтобы оценить все остальные упорядоченные пары, проведя линию через данные точки. Здесь мы помещаем стрелки на концах наших линий, чтобы указать, что этот набор упорядоченных пар продолжается без ограничений.
Представление отношения на прямоугольной координатной плоскости, как показано выше, называется графом. Визуальное представление отношения на прямоугольной координатной плоскости.. Любая кривая, построенная на прямоугольной координатной плоскости, представляет собой набор упорядоченных пар и, таким образом, определяет отношение.
Набор, состоящий из всех первых компонентов отношения, в данном случае значений x , называется доменом. Набор, состоящий из всех первых компонентов отношения. Для отношений, состоящих из точек на плоскости, доменом является набор всех значений x . . А набор, состоящий из всех вторых компонентов отношения, в данном случае значений y , называется диапазоном. состоящий из всех вторых компонентов отношения.Для отношений, состоящих из точек на плоскости, диапазон представляет собой набор всех значений y . (или codomain Используется при ссылке на диапазон.). Часто мы можем определить область и диапазон отношения, если нам дан его график.
. А набор, состоящий из всех вторых компонентов отношения, в данном случае значений y , называется диапазоном. состоящий из всех вторых компонентов отношения.Для отношений, состоящих из точек на плоскости, диапазон представляет собой набор всех значений y . (или codomain Используется при ссылке на диапазон.). Часто мы можем определить область и диапазон отношения, если нам дан его график.
Здесь мы видим, что график y = | x | −2 имеет область, состоящую из всех действительных чисел, ℝ = (- ∞, ∞), и диапазон всех y -значений, больших или равных — 2, [−2, ∞). Область графика x = | y | +1 состоит из всех x -значений, больших или равных 1, [1, ∞), а диапазон состоит из всех действительных чисел, ℝ = (- ∞, ∞ ).
Пример 1
Определите область и диапазон следующего отношения:
Решение:
Минимальное значение x , представленное на графике, равно −8, все остальные больше. Следовательно, область состоит из всех значений x в интервале [−8, ∞). Минимальное значение y , представленное на графике, равно 0; таким образом, диапазон равен [0, ∞).
Следовательно, область состоит из всех значений x в интервале [−8, ∞). Минимальное значение y , представленное на графике, равно 0; таким образом, диапазон равен [0, ∞).
Ответ: Домен: [−8, ∞); диапазон: [0, ∞)
Функции
Особый интерес представляют отношения, в которых каждое значение x соответствует ровно одному значению y .Отношение с этим свойством называется отношением functionA, где каждый элемент в домене соответствует ровно одному элементу в диапазоне ..
Пример 2
Определите область и диапазон следующего отношения и укажите, является ли оно функцией или нет: {(−1, 4), (0, 7), (2, 3), (3, 3), (4, — 2)}
Решение:
Здесь мы разделяем область ( значений x ) и диапазон ( значений y ) и изображаем соответствие между значениями стрелками.
Отношение является функцией, потому что каждое значение x соответствует ровно одному значению y .
Ответ: Домен {−1, 0, 2, 3, 4}, а диапазон — {−2, 3, 4, 7}. Отношение — это функция.
Пример 3
Определите область и диапазон следующего отношения и укажите, является ли оно функцией или нет: {(−4, −3), (−2, 6), (0, 3), (3, 5), (3 , 7)}
Решение:
Данное отношение не является функцией, поскольку значение 3 x соответствует двум значениям y .Мы также можем распознавать функции как отношения, в которых не повторяются значения x .
Ответ: Домен {−4, −2, 0, 3}, а диапазон — {−3, 3, 5, 6, 7}. Это отношение не является функцией.
Рассмотрим отношения, состоящие из семи упорядоченных парных решений y = | x | −2 и x = | y | +1. Соответствие между доменом и диапазоном каждого из них можно изобразить следующим образом:
Соответствие между доменом и диапазоном каждого из них можно изобразить следующим образом:
Обратите внимание, что каждый элемент в области набора решений y = | x | −2 соответствует только одному элементу в диапазоне; это функция.С другой стороны, решения x = | y | +1 имеют значения в области, которые соответствуют двум элементам в диапазоне. В частности, значение 4 x соответствует двум значениям y −3 и 3. Следовательно, x = | y | +1 не определяет функцию.
Мы можем визуально идентифицировать функции по их графикам с помощью теста вертикальной линии. Если какая-либо вертикальная линия пересекает график более одного раза, тогда график не представляет функцию. Если какая-либо вертикальная линия пересекает график более одного раза, тогда график не представляют функцию.
Вертикальная линия представляет значение в домене, а количество пересечений с графиком представляет количество значений, которым оно соответствует. Как мы видим, любая вертикальная линия пересечет график y = | x | −2 только один раз; следовательно, это функция. Вертикальная линия может пересекать график x = | y | +1 более одного раза; следовательно, это не функция. Как показано на рисунке, значение 3 x соответствует более чем одному значению y .
Как мы видим, любая вертикальная линия пересечет график y = | x | −2 только один раз; следовательно, это функция. Вертикальная линия может пересекать график x = | y | +1 более одного раза; следовательно, это не функция. Как показано на рисунке, значение 3 x соответствует более чем одному значению y .
Пример 4
Для данного графика укажите домен и диапазон и определите, представляет ли он функцию:
Решение:
Из графика видно, что минимальное значение x равно -1, а максимальное значение x равно 5.Следовательно, область состоит из всех действительных чисел из набора [−1,5]. Максимальное значение y равно 3, а минимальное –3; следовательно, диапазон состоит из y -значений в интервале [−3,3].
Кроме того, поскольку мы можем найти вертикальную линию, пересекающую график более одного раза, мы заключаем, что график не является функцией. В домене много значений x , которые соответствуют двум значениям y .
В домене много значений x , которые соответствуют двум значениям y .
Ответ: Домен: [−1,5]; диапазон: [−3,3]; функция: нет
Попробуй! Учитывая график, определите домен и диапазон и укажите, является ли это функцией:
Ответ: Домен: (−∞, 15]; диапазон: ℝ; функция: нет
Обозначение функций
Определение функции сопровождается специальными обозначениями.Если мы рассматриваем каждое значение x как вход, который производит ровно один выход, тогда мы можем использовать обозначение функции Обозначение f (x) = y, которое читается как « f из x равно y . ” Для данной функции y, и f (x) могут использоваться как взаимозаменяемые:
f (x) = y
Обозначение f (x) читается как « f из x », и его не следует путать с умножением. Алгебра часто включает функции, поэтому обозначения становятся полезными при выполнении общих задач.Здесь f — это имя функции, а f (x) обозначает значение в диапазоне, связанном со значением x в домене. Функции часто называют разными буквами; некоторые общие названия функций: f , g , h , C и R . Мы определили, что множество решений y = | x | −2 является функцией; следовательно, используя обозначение функций, мы можем написать:
Алгебра часто включает функции, поэтому обозначения становятся полезными при выполнении общих задач.Здесь f — это имя функции, а f (x) обозначает значение в диапазоне, связанном со значением x в домене. Функции часто называют разными буквами; некоторые общие названия функций: f , g , h , C и R . Мы определили, что множество решений y = | x | −2 является функцией; следовательно, используя обозначение функций, мы можем написать:
y = | x | −2 ↓ f (x) = | x | −2
Важно отметить, что y, и f (x) взаимозаменяемы.Это обозначение используется следующим образом:
f (x) = | х | −2 ↓ ↓ f (−5) = | −5 | −2 = 5−2 = 3
Здесь компактное обозначение f (−5) = 3 указывает, что где x = −5 ( вход ), функция приводит к y = 3 ( выход ). Другими словами, замените переменную значением, указанным в круглых скобках.
Функции компактно определяются алгебраическим уравнением, например f (x) = | x | −2. Учитывая значения x в домене, мы можем быстро вычислить соответствующие значения в диапазоне.Как мы видели, функции также выражаются с помощью графиков. В этом случае мы интерпретируем f (−5) = 3 следующим образом:
Учитывая значения x в домене, мы можем быстро вычислить соответствующие значения в диапазоне.Как мы видели, функции также выражаются с помощью графиков. В этом случае мы интерпретируем f (−5) = 3 следующим образом:
Функциональная нотация упрощает задачу оценки. Например, используйте функцию h , определенную как h (x) = 12x − 3, чтобы оценить x -значений в наборе {−2, 0, 7}.
h (−2) = 12 (−2) −3 = −1−3 = −4 h (0) = 12 (0) −3 = 0−3 = −3h (7) = 12 (7) −3 = 72−3 = 12
Для любой функции, определенной как h (x) = y, значение x называется аргументом функции Значение или алгебраическое выражение, используемое в качестве входных данных при использовании обозначения функции.. Аргументом может быть любое алгебраическое выражение. Например:
h (4a3) = 12 (4a3) −3 = 2a3−3h (2x − 1) = 12 (2x − 1) −3 = x − 12−3 = x − 72
Пример 5
Дано g (x) = x2, найти g (−2), g (12) и g (x + h).
Решение:
Напомним, что при оценке рекомендуется начинать с замены переменных круглыми скобками, а затем подставлять соответствующие значения. Это помогает упорядочить операции при упрощении выражений.
г (−2) = (- 2) 2 = 4g (12) = (12) 2 = 14g (x + h) = (x + h) 2 = x2 + 2xh + h3
Ответ: g (−2) = 4, g (12) = 14, g (x + h) = x2 + 2xh + h3
Здесь важно отметить, что в общем случае f (x + h) ≠ f (x) + f (h). Предыдущий пример, где g (x) = x2, прекрасно это иллюстрирует.
г (x + h) ≠ g (x) + g (h) (x + h) 2 ≠ x2 + h3
Пример 6
Дано f (x) = 2x + 4, найти f (−2), f (0) и f (12a2−2).
Решение:
f (−2) = 2 (−2) + 4 = −4 + 4 = 0 = 0f (0) = 2 (0) + 4 = 0 + 4 = 4 = 2f (12a2−2) = 2 (12a2 −2) + 4 = a2−4 + 4 = a2 = | a |
Ответ: f (−2) = 0, f (0) = 2, f (12a2−2) = | a |
Пример 7
Дан график функции g (x), найдите g (−8), g (0) и g (8).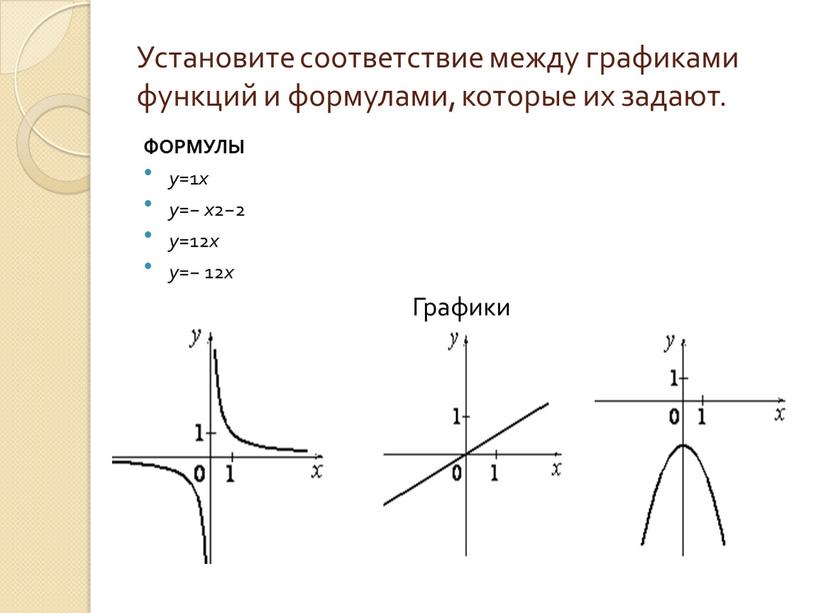
Решение:
Используйте график, чтобы найти соответствующие значения y , где x = −8, 0 и 8.
Ответ: g (−8) = — 2, g (0) = 0, g (8) = 2
Иногда выдается результат, и нас просят найти вход.
Пример 8
Дано f (x) = 5x + 7, найдите x , где f (x) = 27.
Решение:
В этом примере дан выход, и нас просят найти вход. Заменим f (x) на 27 и решим.
f (x) = 5x + 7 ↓ 27 = 5x + 720 = 5×4 = x
Следовательно, f (4) = 27. В качестве проверки мы можем вычислить f (4) = 5 (4) + 7 = 27.
Ответ: x = 4
Пример 9
По графику g найдите x , где g (x) = 2.
Решение:
Здесь нас просят найти значение x для конкретного значения y . Мы начинаем с 2 на оси y и затем считываем соответствующее значение x .
Мы начинаем с 2 на оси y и затем считываем соответствующее значение x .
Мы видим, что g (x) = 2, где x = −5; другими словами, g (−5) = 2.
Ответ: x = −5
Попробуй! По графику h найдите x , где h (x) = — 4.
Ответ: x = −5 и x = 15
Основные выводы
- Отношение — это любой набор упорядоченных пар.Однако в этом курсе мы будем работать с наборами упорядоченных пар ( x , y ) в прямоугольной системе координат. Набор значений x определяет домен, а набор значений y определяет диапазон.
- Особые отношения, в которых каждое значение x (вход) соответствует ровно одному значению y (выход), называются функциями.
- Мы можем легко определить, представляет ли уравнение функцию, выполнив тест вертикальной линии на его графике.Если какая-либо вертикальная линия пересекает график более одного раза, то график не представляет функцию.
- Если алгебраическое уравнение определяет функцию, то мы можем использовать обозначение f (x) = y. Обозначение f (x) читается как « f из x », и его не следует путать с умножением. При работе с функциями важно помнить, что y, и f (x) взаимозаменяемы.
- Если вас попросят найти f (a), мы подставляем аргумент a in вместо переменной, а затем упрощаем.Аргумент может быть алгебраическим выражением.
- Если вас попросят найти x, где f (x) = a, мы устанавливаем функцию равной a, а затем решаем относительно x.
Тематические упражнения
{(3, 1), (5, 2), (7, 3), (9, 4), (12, 4)}
{(2, 0), (4, 3), (6, 6), (8, 6), (10, 9)}
{(7, 5), (8, 6), (10, 7), (10, 8), (15, 9)}
{(1, 1), (2, 1), (3, 1), (4, 1), (5, 1)}
{(5, 0), (5, 2), (5, 4), (5, 6), (5, 8)}
{(−3, 1), (−2, 2), (−1, 3), (0, 4), (0, 5)}
Часть A: Взаимосвязи и функции
Определите домен и диапазон и укажите, является ли отношение функцией или нет.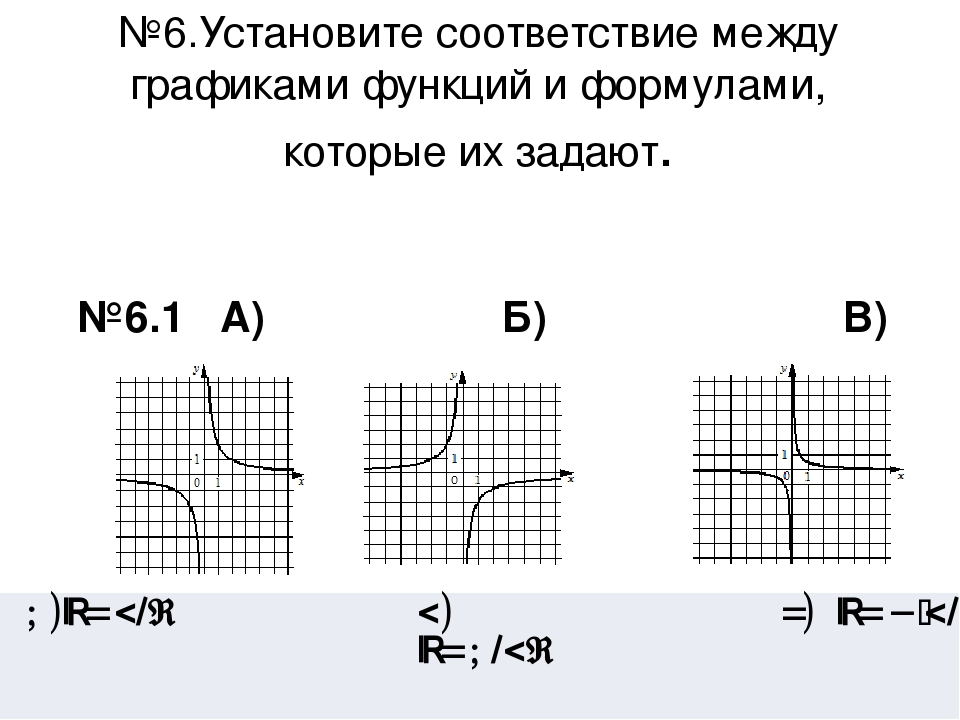
г (x) = | x − 5 | найти g (−5), g (0) и g (5).
г (х) = | х | −5; найти g (−5), g (0) и g (5).
г (х) = | 2х − 3 |; найти g (−1), g (0) и g (32).
г (х) = 3− | 2x |; найти g (−3), g (0) и g (3).
f (x) = 2x − 3; найти f (−2), f (0) и f (x − 3).
f (x) = 5x − 1; найти f (−2), f (0) и f (x + 1).
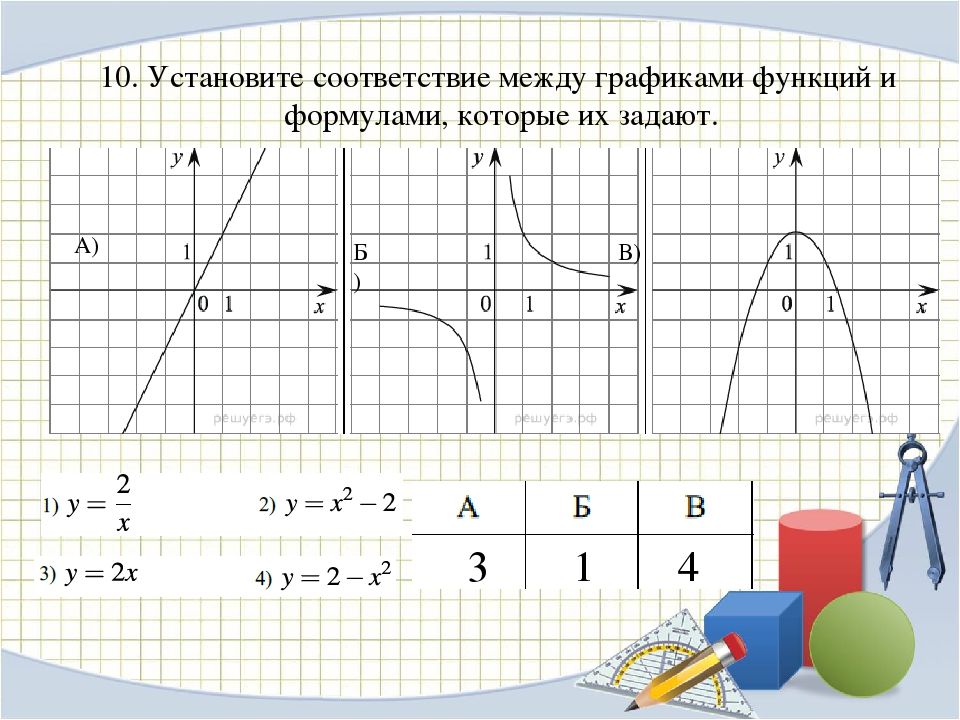
г (х) = 23х + 1; найти g (−3), g (0) и f (9x + 6).
г (x) = — 34x − 12; найти g (−4), g (0) и g (6x − 2).
г (х) = х2; найти g (−5), g (3) и g (x − 5).
г (х) = х2 + 1; найти g (−1), g (6) и g (2x − 1).
f (x) = x2 − x − 2; найти f (0), f (2) и f (x + 2).
f (x) = — 2×2 + x − 4; найти f (−2), f (12) и f (x − 3).
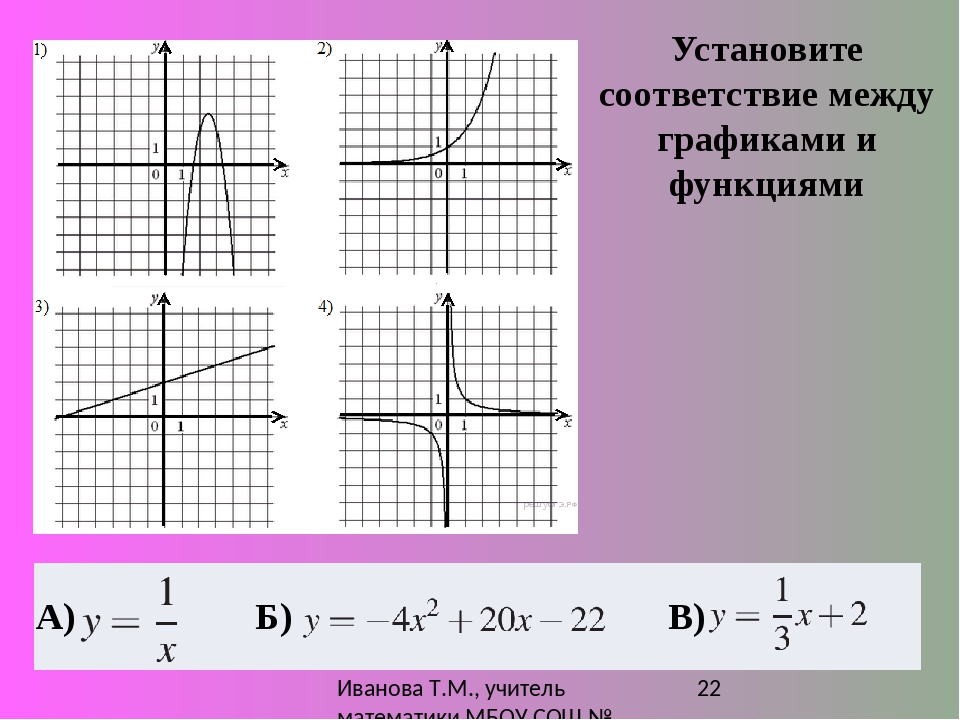
ч (т) = — 16т2 + 32; найти h (14), h (12) и h (2a − 1).
ч (т) = — 16т2 + 32; найти h (0), h (2), h (2a + 1).
f (x) = x + 1−2 найти f (−1), f (0), f (x − 1).
f (x) = x − 3 + 1; найти f (12), f (3), f (x + 3).
г (х) = х + 8; найти g (0), g (−8) и g (x − 8).
г (x) = 3x − 1; найти g (13), g (53) и g (13a2 + 13).
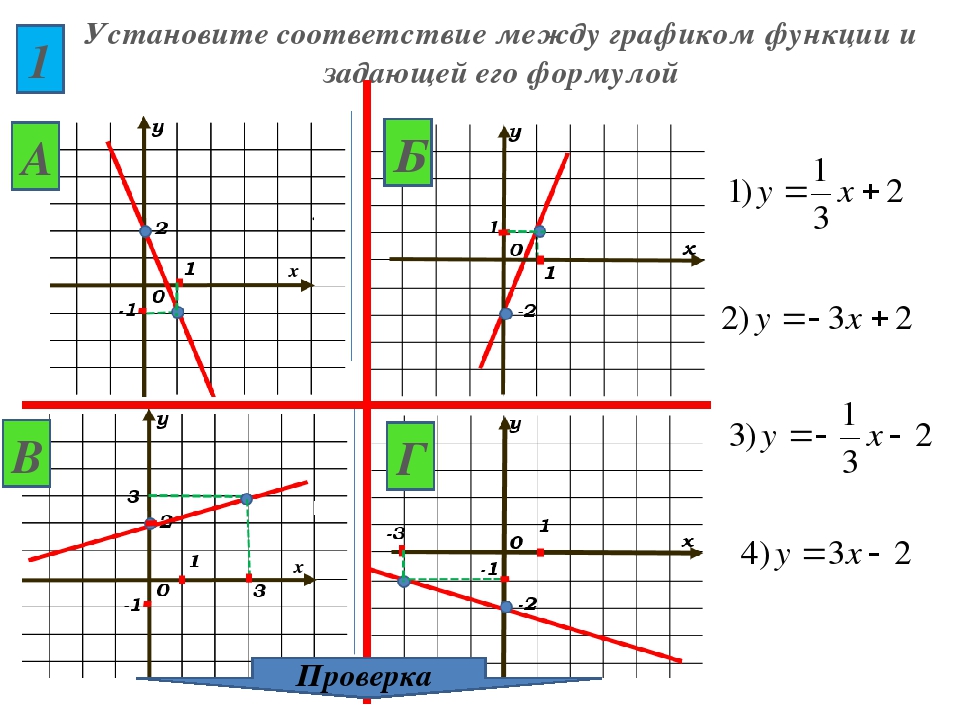
f (x) = x3 + 1; найти f (−1), f (0), f (a2).
f (x) = x3−8; найти f (2), f (0), f (a3).
f (x) = 2x − 3; найдите x , где f (x) = 25.
f (x) = 7−3x; найти x , где f (x) = — 27.
f (x) = 2x + 5; найти x , где f (x) = 0
f (x) = — 2x + 1; найти x , где f (x) = 0
г (х) = 6х + 2; найдите x , где g (x) = 5.
г (х) = 4х + 5; найдите x , где g (x) = 2.
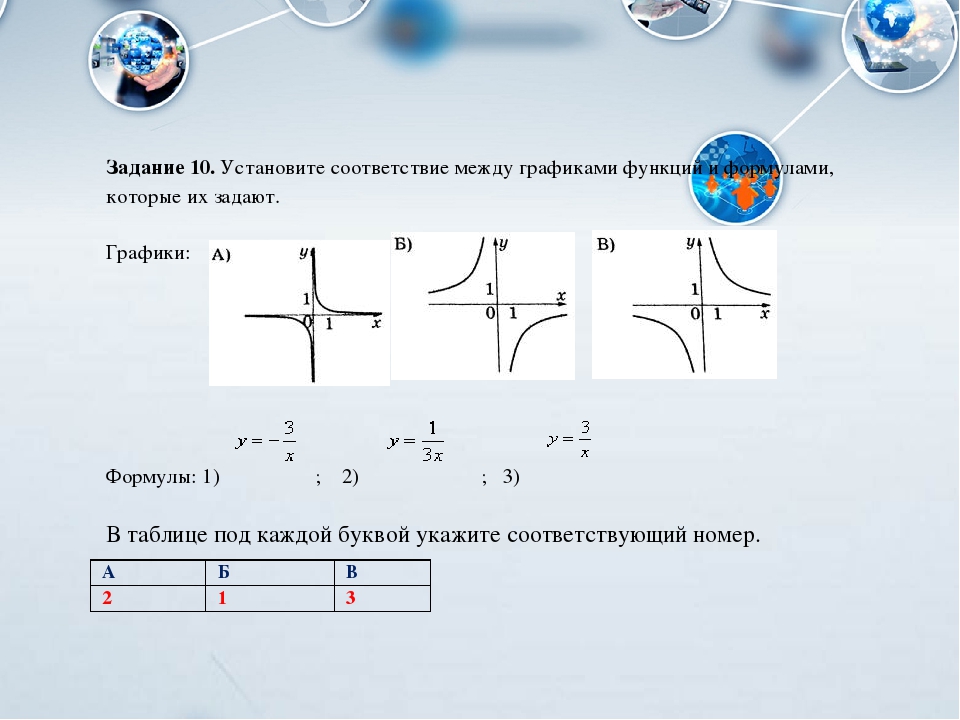
h (x) = 23x − 12; найдите x , где h (x) = 16.
h (x) = 54x + 13; найдите x , где h (x) = 12.
Стоимость нового автомобиля в долларах определяется функцией V (t) = — 1,800 т + 22,000, где т. — возраст автомобиля в годах. Воспользуйтесь функцией, чтобы определить стоимость автомобиля, когда ему исполнилось 4 года. Сколько стоила новая машина?
Ежемесячный доход продавца автомобилей в долларах определяется функцией I (n) = 350n + 1,450, где n представляет количество автомобилей, проданных в месяц.
 Используйте функцию, чтобы определить доход продавца, если он продаст 3 машины в этом месяце. Каков его доход, если он не продаст машины в течение одного месяца?
Используйте функцию, чтобы определить доход продавца, если он продаст 3 машины в этом месяце. Каков его доход, если он не продаст машины в течение одного месяца?Найдите f (0), f (2) и f (4).
Найдите f (−1), f (0) и f (1).
Найдите f (0), f (2) и f (4).
Найдите f (−3), f (0) и f (3).

Найдите f (−4), f (0) и f (2).
Найдите f (−6), f (0) и f (6).
Найдите f (−2), f (2) и f (7).
Найдите f (0), f (5) и f (9).
Найдите f (−8), f (0) и f (8).
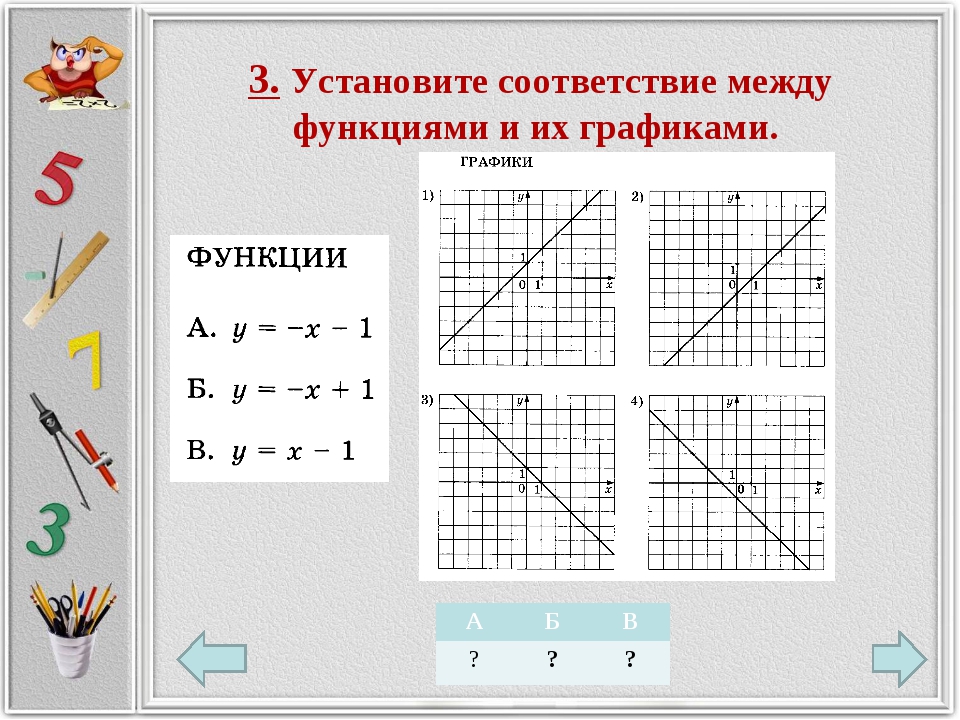
Найдите f (−12), f (0) и f (12).
Найдите x , где g (x) = 3, g (x) = 0 и g (x) = — 2.
Найдите x , где g (x) = 0, g (x) = 1 и g (x) = 4.
Найдите x , где g (x) = — 5, g (x) = 0 и g (x) = 10.

Найдите x , где g (x) = 0, g (x) = 10 и g (x) = 15.
Найдите x , где g (x) = — 5, g (x) = — 4 и g (x) = 4.
Найдите x , где g (x) = 1, g (x) = 0 и g (x) = — 3.
Найдите x , где g (x) = — 4, g (x) = 3 и g (x) = 4.
Найдите x , где g (x) = — 5, g (x) = — 4 и g (x) = 4.
Найдите x , где g (x) = — 10 и g (x) = 5.
Найдите x , где g (x) = 2.
Какова была стоимость автомобиля, когда он был новым в 1970 году?
В каком году стоимость автомобиля была минимальной?
Сколько стоила машина в 2005 году?
В какие годы автомобиль оценивался в 4000 долларов?
f (x + h) −f (x)
f (x + h) −f (x) h
Упростим c (x + h) −c (x) h, если c (x) = 3x + 1.
Упростим p (x + h) −p (x) h, задав p (x) = 7x − 3.
Упростим g (x + h) −g (x) h, задав g (x) = mx + b.

Упростим q (x + h) −q (x) h, если q (x) = ax.
Часть B: Обозначение функций
Оценить.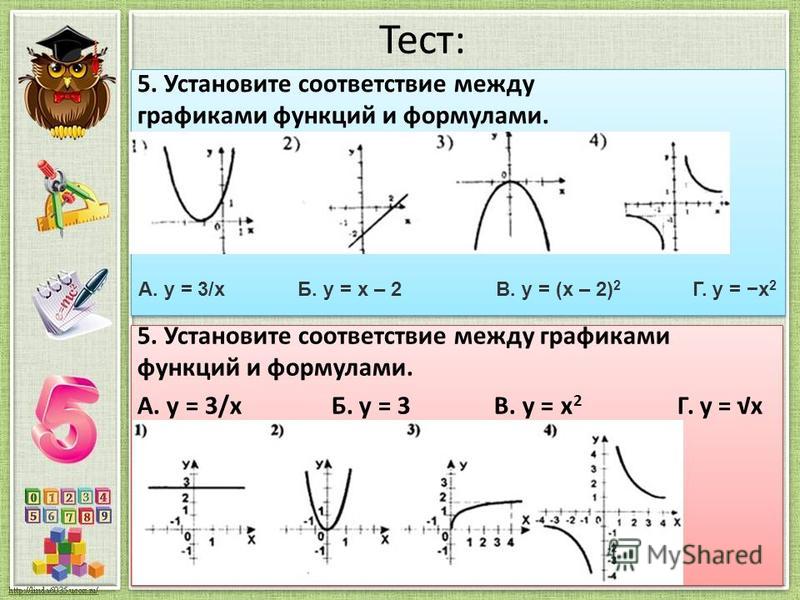
По заданной функции найти f (x + h).
Найдите x по заданной функции.
По графику функции f найдите значения функции.
По графику функции g найдите значения x- .
Стоимость определенного автомобиля в долларах зависит от количества лет, прошедших с момента его приобретения в 1970 году, согласно следующей функции:
Учитывая линейную функцию, определяемую как f (x) = 2x − 5, упрощает следующее.
Кому приписывают введение обозначения y = f (x)? Кратко опишите его жизнь и достижения.
Объясните начинающему студенту-алгебру, что такое тест по вертикальной линии и почему он работает.
Изучите и обсудите жизнь и вклад Рене Декарта.
Выполните поиск в Интернете по тесту вертикальной линии, функциям и оценочным функциям.
 Поделитесь ссылкой на страницу, которая, по вашему мнению, может оказаться полезной для других.
Поделитесь ссылкой на страницу, которая, по вашему мнению, может оказаться полезной для других.
Часть C: Обсуждение
ответов
Домен: {3, 5, 7, 9, 12}; диапазон: {1, 2, 3, 4}; функция: есть
Домен: {7, 8, 10, 15}; диапазон: {5, 6, 7, 8, 9}; функция: нет
Домен: {5}; диапазон: {0, 2, 4, 6, 8}; функция: нет
Домен: {−4, −1, 0, 2, 3}; диапазон: {1, 2, 3}; функция: есть
Домен: {−1, 0, 1, 2}; диапазон: {0, 1, 2, 3, 4}; функция: нет
Домен: {−2}; диапазон: {−4, −2, 0, 2, 4}; функция: нет
Домен: ℝ; диапазон: [−2, ∞); функция: есть
Домен: (−∞, −1]; диапазон: ℝ; функция: нет
Домен: (−∞, 0]; диапазон: [−1, ∞); функция: есть
Домен: ℝ; диапазон: (−∞, 3]; функция: да
Домен: ℝ; диапазон: ℝ; функция: есть
Домен: [−5, −1]; диапазон: [−2,2]; функция: нет
Домен: ℝ; диапазон: [0, ∞]; функция: есть
Домен: ℝ; диапазон: ℝ; функция: есть
Домен: ℝ; диапазон: [-1,1]; функция: есть
Домен: [−8,8]; диапазон: [−3,3]; функция: нет
Домен: ℝ; диапазон: [−8, ∞]; функция: есть
г (−5) = 10, г (0) = 5, г (5) = 0
г (-1) = 5, г (0) = 3, г (32) = 0
f (−2) = — 7, f (0) = — 3, f (x − 3) = 2x − 9
г (−3) = — 1, г (0) = 1, г (9x + 6) = 6x + 5
г (−5) = 25, г (3) = 3, г (x − 5) = x2−10x + 25
f (0) = — 2, f (2) = 0, f (x + 2) = x2 + 3x
h (14) = 31, h (12) = 28, h (2a − 1) = — 64a2 + 64a + 16
f (−1) = — 2, f (0) = — 1, f (x − 1) = x − 2
g (0) = 22, g (−8) = 0, g (a2−8) = | a |
f (-1) = 0, f (0) = 1, f (a2) = a6 + 1
f (x + h) = x2 + 2xh + h3 + x + h + 1.

f (x + h) = x3 + 3hx2 + 3h3x + h4
х = 14
х = -52
х = 12
х = 1
Новый: 22 000 долларов США; 4 года: 14 800 долларов США
f (−4) = 3, f (0) = 3, f (2) = 3
f (−2) = 1, f (2) = 3, f (7) = 4
f (−8) = 10, f (0) = 0, f (8) = 10
г (−4) = 3, g (2) = 0 и g (6) = — 2.
г (10) = — 5, г (5) = 0 и г (15) = 0, г (-5) = 10 и г (25) = 10
г (−2) = — 5, g (−3) = — 4 и g (−1) = — 4, g (−5) = 4 и g (1) = 4
г (−2) = — 4, г (−1) = 3, г (0) = 4
г (−10) = — 10 и g (5) = — 10; g (−5) = 5 и g (10) = 5
Индивидуальная функция — объяснение и примеры
Вы знаете, что изучаете функции, когда слышите «один к одному» чаще, чем когда-либо.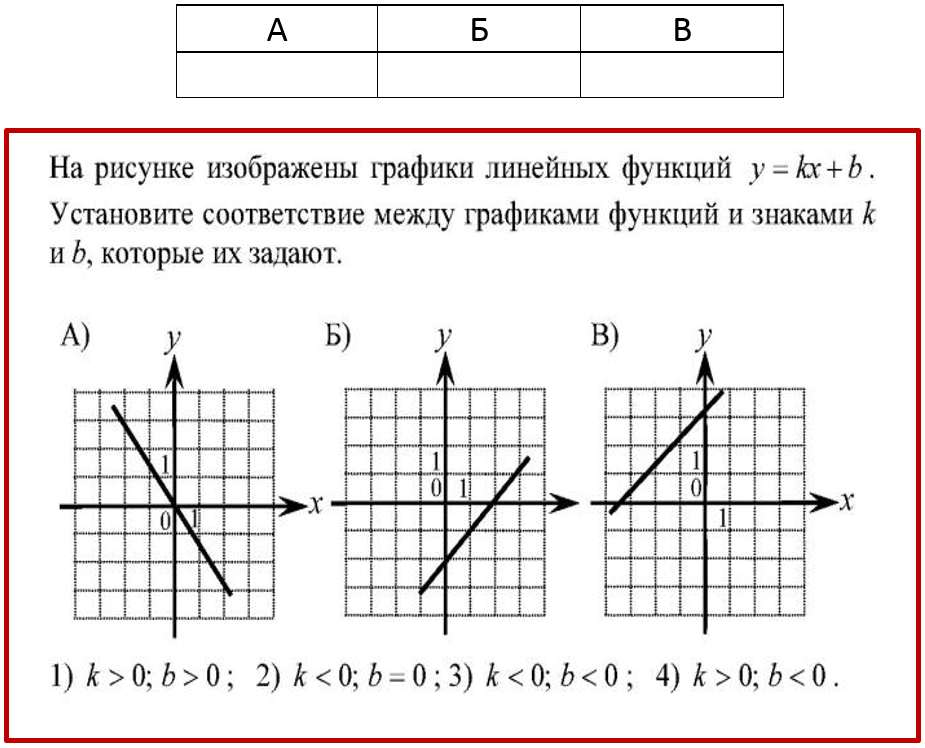 Хотите узнать, что делает индивидуальными функциями особенными? Эта статья поможет вам узнать об их свойствах и оценить эти функции. Давайте начнем с этого быстрого определения индивидуальных функций:
Хотите узнать, что делает индивидуальными функциями особенными? Эта статья поможет вам узнать об их свойствах и оценить эти функции. Давайте начнем с этого быстрого определения индивидуальных функций:
Индивидуальные функции — это функции, которые возвращают уникальный диапазон для каждого элемента в своем домене.
Поскольку индивидуальные функции — это особые типы функций, лучше всего проверить наши знания о функциях, их предметной области и их диапазоне.
Эта статья поможет нам понять свойства взаимно однозначной функции . Мы также узнаем, как определять индивидуальные функции на основе их выражений и графиков.
Давайте продолжим и начнем с определения и свойств взаимно однозначных функций.
Что такое функция «один к одному»?
Чтобы легко вспомнить, что такое взаимно однозначные функции, попробуйте вспомнить следующее утверждение: «для каждого y существует уникальный x». Следующие два раздела покажут вам, почему эта фраза помогает нам запомнить основную концепцию индивидуальных функций.
Следующие два раздела покажут вам, почему эта фраза помогает нам запомнить основную концепцию индивидуальных функций.
Индивидуальное определение функции
Функция f (x), является функцией один к одному, когда один уникальный элемент из ее домена будет возвращать каждый элемент своего диапазона. Это означает, что для каждого значения x будет уникальное значение y или f (x).
Почему бы нам не визуализировать это, отображая две пары значений для сравнения функций, которые не находятся в однозначном соответствии?
Давайте сначала посмотрим на g (x), g (4) и g (-4) имеют общее значение y, равное 16.Это также верно для g (-2) и g (2). Вы правильно угадали; g (x) — функция, не имеющая взаимно однозначного соответствия.
Теперь обратите внимание на f (x). Обратите внимание, как для каждого значения f (x) существует только одно уникальное значение x? Когда вы наблюдаете функции, имеющие это соответствие, мы вызываем эти функции один к одному.
Индивидуальный график функций
Чтобы лучше понять концепцию взаимно однозначных функций, давайте изучим индивидуальный график функции. Помните, что для функций «один к одному» каждый x должен иметь уникальное значение y.
Поскольку каждый x будет иметь уникальное значение для y, функции один к одному никогда не будут иметь упорядоченных пар с одной и той же координатой y.
Теперь, когда мы изучили определение взаимно однозначных функций, понимаете ли вы, почему выражение «для каждого y есть уникальный x» полезно запомнить?
Индивидуальные свойства функций
Какие еще важные свойства взаимно однозначных функций мы должны помнить? Вот некоторые свойства, которые могут помочь вам понять различные типы функций с взаимно однозначным соответствием:
- Если две функции, f (x) и g (x), равны один к одному, то f ◦ g взаимно однозначно. функции.
- Если функция является взаимно однозначной, ее график будет либо всегда увеличиваться, либо всегда уменьшаться.

- Если g ◦ f взаимно однозначная функция, то f (x) также гарантированно будет взаимно однозначной функцией.
Попробуйте самостоятельно изучить две пары графиков и посмотреть, сможете ли вы подтвердить эти свойства. Конечно, прежде чем мы сможем применить эти свойства, нам будет важно узнать, как мы можем подтвердить, является ли данная функция взаимно однозначной функцией или нет.
Как определить, взаимно однозначна функция?
Следующие два раздела покажут вам, как мы можем протестировать однозначное соответствие функций.Иногда нам дают выражение или график функции, поэтому мы должны научиться определять однозначные функции алгебраически и геометрически. Давайте начнем с последнего!
Тестирование функций один к одному с геометрической точки зрения
Помните, что функции должны быть взаимно однозначными. Каждая координата x должна иметь уникальную координату y? Мы можем проверить взаимно однозначные функции с помощью теста горизонтальной линии .
- Когда задана функция, рисует горизонтальные линии вместе с системой координат.
- Проверьте, могут ли горизонтальные линии проходить через две точки.
- Если горизонтальные линии проходят только через одну точку на графике, функция является взаимно однозначной функцией .
Что делать, если он проходит две или более точки функции? Тогда, как вы уже догадались, они не считаются однозначными функциями.
Чтобы лучше понять процесс, давайте продолжим и изучим эти два графика, показанные ниже.
Известно, что обратная функция f (x) = 1 / x является взаимно однозначной функцией.Мы также можем проверить это, проведя горизонтальные линии на его графике.
Посмотрите, как каждая горизонтальная линия каждый раз проходит через уникальную упорядоченную пару? Когда это происходит, мы можем подтвердить, что данная функция является функцией один к одному.
Что происходит, если функция не является взаимно однозначной? Например, квадратичная функция f (x) = x 2 не является взаимно однозначной функцией. Давайте посмотрим на его график, показанный ниже, чтобы увидеть, как тест горизонтальной линии применяется к таким функциям.
Давайте посмотрим на его график, показанный ниже, чтобы увидеть, как тест горизонтальной линии применяется к таким функциям.
Как видите, каждая горизонтальная линия, проведенная через график f (x) = x 2 , проходит через две упорядоченные пары. Это еще раз подтверждает, что квадратичная функция не является взаимно однозначной функцией.
Алгебраическое тестирование индивидуальных функций
Давайте освежим нашу память о том, как мы определяем индивидуальные функции. Напомним, что функции являются взаимно однозначными, если:
- f (x 1 ) = f (x 2 ) тогда и только тогда, когда x 1 = x 2
- f (x 1 ) ≠ f (x 2 ) тогда и только тогда, когда x 1 ≠ x 2
Мы будем использовать это алгебраическое определение, чтобы проверить, является ли функция взаимно однозначной.Как же тогда это сделать?
- Используйте заданную функцию и найдите выражение для f (x 1 ).
- Примените тот же процесс и найдите выражение для f (x 2 ).
- Приравняйте оба выражения и покажите, что x 1 = x 2 .
Почему бы нам не попытаться доказать, что f (x) = 1 / x является взаимно однозначной функцией, используя этот метод?
Сначала подставим в выражение x 1 и x 2 . У нас будет f (x 1 ) = 1 / x 1 и f (x 2 ) = 1 / x 2 .Чтобы подтвердить взаимно однозначное соответствие функции, приравняем f (x 1 ) и f (x 2 ).
1 / x 1 = 1 / x 2
Перемножьте обе части уравнения, чтобы упростить уравнение.
x 2 = x 1
x 1 = x 2
Мы только что показали, что x 1 = x 2 , когда f (x 1 ) = f ( x 2 ), следовательно, обратная функция является взаимно однозначной.
Пример 1
Заполните пропуски иногда , всегда или никогда , чтобы следующие утверждения были верными.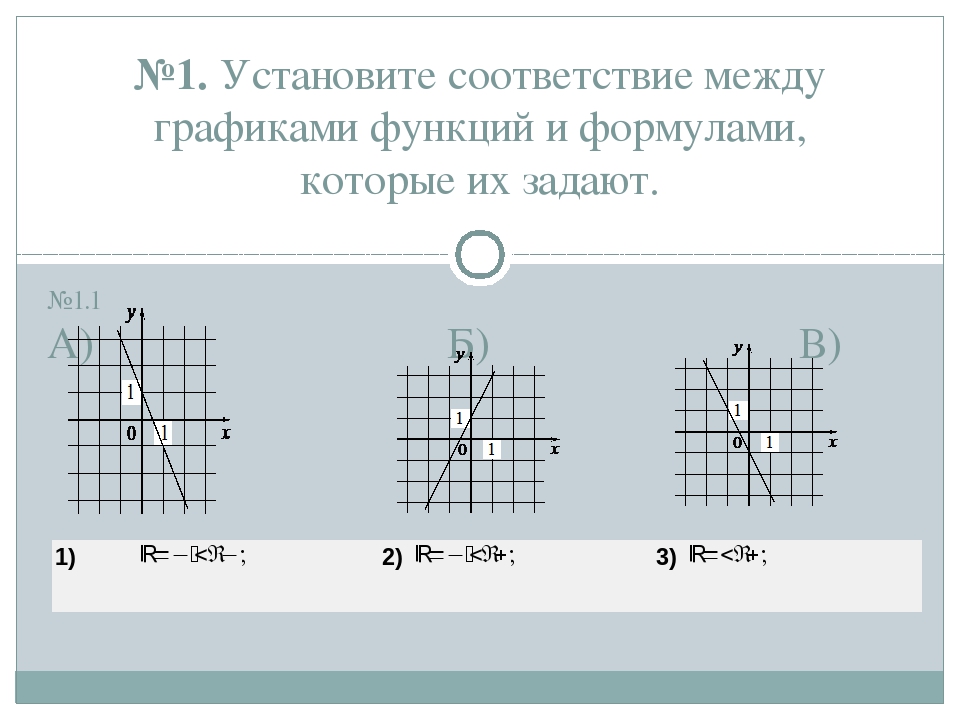
- Отношения могут _______________ быть взаимно однозначными.
- Индивидуальные функции — это ______________ функции.
- Когда горизонтальная линия проходит через функцию, которая не является взаимно однозначной, она ____________ будет проходить через две упорядоченные пары.
Решение
Отвечая на подобные вопросы, всегда возвращайтесь к определениям и свойствам, которые мы только что изучили.
- Отношения иногда могут быть функциями и, следовательно, иногда могут представлять функцию один к одному.
- Поскольку функции «один к одному» представляют собой особый тип функций, они будут всегда в первую очередь функциями.
- В нашем примере горизонтальные линии могут проходить через график f (x) = x 2 дважды, но горизонтальные линии могут проходить через большее количество точек. Следовательно, иногда проходит через две упорядоченные пары.
Пример 2
Пусть A = {2, 4, 8, 10} и B = {w, x, y, z}. Какой из следующих наборов упорядоченных пар представляет собой функцию один к одному?
- {(2, w), (2, x), (2, y), (2, z)}
- {(4, w), (2, x), (10, z), ( 8, y)}
- {(4, w), (2, x), (8, x), (10, y)}
Решение
Чтобы функция была взаимно однозначной функцией , каждый элемент из A должен объединяться с уникальным элементом из B.
- Первый вариант имеет одно и то же значение x для каждого значения y, поэтому это не функция и, следовательно, не взаимно однозначная функция. .
- Третий вариант имеет разные значения x для каждой упорядоченной пары, но 2 и 8 имеют один и тот же диапазон x. Следовательно, он не представляет собой функцию «один к одному».
- Второй вариант использует уникальный элемент из A для каждого уникального элемента из B, представляя взаимно однозначную функцию.
Это означает, что {(4, w), (2, x), (10, z), (8, y)} представляют собой взаимно однозначную функцию .
Пример 3
Какой из следующих наборов значений представляет функцию один к одному?
Решение
Всегда возвращайтесь к утверждению «для каждого y есть уникальный x.»Для каждого набора давайте проверим, сочетается ли каждый элемент справа с уникальным значением слева.
- Для первого набора, f (x), мы можем видеть, что каждый элемент с правой стороны объединен в пару с уникальным элементом слева. Следовательно, , f (x) является взаимно однозначной функцией .
- Набор g (x) показывает разное количество элементов с каждой стороны. Одно это уже говорит нам о том, что функция не является взаимно однозначной.
- Некоторые значения с левой стороны соответствуют одному и тому же элементу справа, поэтому m (x) также не является взаимно однозначной функцией.
- Каждый из элементов в первом наборе соответствует уникальному элементу в следующем, поэтому n (x) представляет собой взаимно однозначную функцию.
Пример 4
График f (x) = | x | + 1 и определить, является ли функция f (x) взаимно однозначной.
Решение
Создайте таблицу значений для f (x) и постройте сгенерированные упорядоченные пары. Соединил эти точки с графиком f (x).
Таблица уже сама по себе может дать вам представление о том, является ли f (x) взаимно однозначной функцией [ Подсказка: f (1) = 2 и f (-1) = 2 ].Но давайте продолжим и построим эти точки на плоскости xy и графике f (x).
После того, как мы построили график f (x) = | x | +1, проведите горизонтальные линии поперек графика и посмотрите, проходит ли он через одну или несколько точек.
На графике мы видим, что построенные нами горизонтальные линии проходят через две точки каждая, поэтому функция не является взаимно однозначной функцией .
Пример 5
Определите, является ли f (x) = -2x 3 — 1 взаимно однозначной функцией, используя алгебраический подход.
Решение
Напомним, что для того, чтобы функция была взаимно однозначной, f (x 1 ) = f (x 2 ) тогда и только тогда, когда x 1 = x 2 . Чтобы проверить, является ли функция f (x) взаимно однозначной, давайте сначала найдем соответствующие выражения для x 1 и x 2 .
f (x 1 ) = -2 x 1 3 — 1
f (x 2 ) = -2 x 2 3 — 1
Приравняйте оба выражения и посмотрите, если он уменьшается до x 1 = x 2 .
-2 x 1 3 — 1 = -2 x 2 3 — 1
-2 x 1 3 = -2 x 2 3
(x 1 ) 3 = (x 2 ) 3
Извлечение кубического корня из обеих частей уравнения приведет нас к x 1 = x 2 . Следовательно, f (x) = -2x 3 — 1 является взаимно однозначной функцией.
Пример 6
Покажите, что f (x) = -5x 2 + 1 не является взаимно однозначной функцией.
Решение
Еще одно важное свойство взаимно однозначных функций состоит в том, что когда x 1 ≠ x 2 , f (x 1 ) не должно быть равно f (x 2 ).
Быстрый способ доказать, что f (x) не является взаимно однозначной функцией, — это подумать о контрпримере, показывающем два значения x, где они возвращают одно и то же значение для f (x).
Давайте посмотрим, что произойдет, если x 1 = -4 и x 2 = 4.
f (x 1 ) = -5 (-4) 2 + 1 = -80 + 1 = -79 | f (x 2 ) = -5 (4) 2 + 1 = -80 + 1 = -79 |
ср. можно видеть, что даже когда x 1 не равно x 2 , он все равно возвращает то же значение для f (x). Это показывает, что функция f (x) = -5x 2 + 1 не является взаимно однозначной функцией.
Это показывает, что функция f (x) = -5x 2 + 1 не является взаимно однозначной функцией.
Пример 7
Учитывая, что a и b не равны 0, показывают, что все линейные функции являются взаимно однозначными функциями.
Решение
Помните, что общий вид линейных функций может быть выражен как ax + b, где a и b ненулевые константы.
Мы применяем тот же процесс, подставляя x 1 и x 2 в общее выражение для линейных функций.
f (x 1 ) = ax 1 + b
f (x 2 ) = ax 2 + b
Приравняйте оба уравнения и посмотрите, можно ли их уменьшить до x 1 = x 2 . Поскольку b представляет собой константу, мы можем вычесть b из обеих частей уравнения.
ax 1 + b = ax 2 + b
ax 1 = ax 2
Разделим обе части уравнения на a, и мы получим x 1 = x 2 .Отсюда можно сделать вывод, что все линейные функции взаимно однозначны.
Практические вопросы
- Заполните пропуски иногда , всегда или никогда сделайте следующие утверждения верными.
- Косинусные функции могут _______________ быть взаимно однозначными функциями.
- Если функция f (x) взаимно однозначна, ее домен ______________ будет иметь такое же количество элементов, как и диапазон.
- Когда горизонтальная линия проходит через функцию, которая является функцией один к одному, она ____________ будет проходить через две упорядоченные пары.
- Пусть M = {3, 6, 9, 12} и N = {a, b, c, d}. Какой из следующих наборов упорядоченных пар представляет собой функцию один к одному?
- {(6, a), (6, b), (6, c), (6, d)}
- {(9, d), (12, b), (6, b), (3, c)}
- {(6, d), (9, c), (12, b), (3, a)}
- Какой из следующих наборов значений представляет собой взаимно однозначную функцию ?
- Изобразите следующие функции и определите, являются ли они взаимно однозначными или нет.
- f (x) = x 2 — 4
- g (x) = -4x + 1
- h (x) = e x
- Убедитесь, что следующие функции однозначны используя алгебраический подход.
- f (x) = 2x — 1
- g (x) = 1 / x 2
- h (x) = | x | + 4
- Покажите, что g (x) = | x | — 4 не является однозначной функцией.
- Покажите, что все квадратичные выражения не являются взаимно однозначными функциями.
Изображения / математические рисунки создаются с помощью GeoGebra.
Предыдущий урок | Главная страница | Следующий урок
1.1: Четыре способа представления функции
Цели обучения
- Определите, представляет ли отношение функцию.
- Найдите значение функции.
- Определите, является ли функция взаимно однозначной.
- Используйте тест вертикальной линии для определения функций.
- Изобразите функции, перечисленные в библиотеке функций.
Авиалайнер меняет высоту по мере увеличения расстояния от точки старта полета. Вес подрастающего ребенка со временем увеличивается. В каждом случае одно количество зависит от другого. Между двумя величинами существует взаимосвязь, которую мы можем описывать, анализировать и использовать для прогнозирования.В этом разделе мы разберем такие отношения.
Определение того, представляет ли отношение функцию
Отношение — это набор упорядоченных пар. Набор первых компонентов каждой упорядоченной пары называется областью, а набор вторых компонентов каждой упорядоченной пары называется диапазоном. Рассмотрим следующий набор упорядоченных пар. Первые числа в каждой паре — это первые пять натуральных чисел. Второе число в каждой паре вдвое больше первого.
\ [\ {(1, 2), (2, 4), (3, 6), (4, 8), (5, 10) \} \ tag {1.1.1} \]
Домен \ (\ {1, 2, 3, 4, 5 \} \). Диапазон равен \ (\ {2, 4, 6, 8, 10 \} \).
Обратите внимание, что каждое значение в домене также известно как входное значение или независимая переменная и часто обозначается строчной буквой \ (x \). Каждое значение в диапазоне также известно как выходное значение или зависимая переменная и часто обозначается строчной буквой \ (y \).
Функция \ (f \) — это отношение, которое присваивает одно значение в диапазоне каждому значению в домене.Другими словами, никакие \ (x \) — значения не повторяются. В нашем примере, который связывает первые пять натуральных чисел с числами, удваивающими их значения, это отношение является функцией, потому что каждый элемент в домене, {1, 2, 3, 4, 5}, связан ровно с одним элементом в диапазон, \ (\ {2, 4, 6, 8, 10 \} \).
Теперь давайте рассмотрим набор упорядоченных пар, который связывает термины «четный» и «нечетный» с первыми пятью натуральными числами. Будет отображаться как
\ [\ mathrm {\ {(нечетное, 1), (четное, 2), (нечетное, 3), (четное, 4), (нечетное, 5) \}} \ tag {1.1.2} \]
Обратите внимание, что каждый элемент в домене {четный, нечетный} не связан ровно с одним элементом в диапазоне \ (\ {1, 2, 3, 4, 5 \} \). Например, термин «нечетный» соответствует трем значениям из области \ (\ {1, 3, 5 \} \), а термин «четный» соответствует двум значениям из диапазона \ (\ {2, 4 \} \). Это нарушает определение функции, поэтому это отношение не является функцией.
На рисунке \ (\ PageIndex {1} \) сравниваются отношения, которые являются функциями, а не функциями.
Рисунок \ (\ PageIndex {1} \): (a) Это отношение является функцией, потому что каждый вход связан с одним выходом.Обратите внимание, что входные \ (q \) и \ (r \) оба дают выход \ (n \). (б) Эта взаимосвязь также является функцией. В этом случае каждый вход связан с одним выходом. (c) Это отношение не является функцией, потому что вход \ (q \) связан с двумя разными выходами.
Функция
Функция — это отношение, в котором каждое возможное входное значение приводит ровно к одному выходному значению. Мы говорим: «Выход — это функция входа».
Входные значения составляют область , а выходные значения составляют диапазон .
Как сделать: учитывая связь между двумя величинами, определите, является ли связь функцией
- Определите входные значения.
- Определите выходные значения.
- Если каждое входное значение приводит только к одному выходному значению, классифицируйте отношение как функцию. Если какое-либо входное значение приводит к двум или более выходам, не классифицируйте отношение как функцию.
Пример \ (\ PageIndex {1} \): определение того, являются ли прайс-листы меню функциями
Меню кофейни, показанное на рисунке \ (\ PageIndex {2} \), состоит из предметов и их цен.
- Цена зависит от товара?
- Товар зависит от цены?
Рисунок \ (\ PageIndex {2} \): меню с ценами на пончики из кафе, где простой пончик стоит 1,49 доллара, а пончик с желе и шоколадный пончик — 1,99 доллара.
Решение
- Начнем с рассмотрения ввода как пунктов меню. Выходные значения — это цены. См. Рисунок \ (\ PageIndex {3} \).
Рисунок \ (\ PageIndex {3} \): меню с ценами на пончики из кафе, где простой пончик стоит 1 доллар.49, пончик с желе и шоколадный пончик — 1,99 доллара.
У каждого элемента в меню есть только одна цена, поэтому цена зависит от элемента.
- Два пункта меню имеют одинаковую цену. Если мы рассматриваем цены как входные значения, а товары как выходные, то с одним и тем же входным значением может быть связано несколько выходных данных. См. Рисунок \ (\ PageIndex {4} \).
Рисунок \ (\ PageIndex {4} \): Связь цен с пончиками.
Следовательно, товар не зависит от цены.
Пример \ (\ PageIndex {2} \): определение того, являются ли правила оценки класса функциями
В конкретном математическом классе общая процентная оценка соответствует среднему баллу. Является ли средний балл функцией процентной оценки? Является ли процентная оценка функцией среднего балла? В таблице \ (\ PageIndex {1} \) показано возможное правило назначения оценок.
| Процентное содержание | 0–56 | 57–61 | 62–66 | 67–71 | 72–77 | 78–86 | 87–91 | 92–100 |
| Средний балл | 0.0 | 1,0 | 1,5 | 2,0 | 2,5 | 3,0 | 3,5 | 4,0 |
Раствор
Для любой процентной оценки существует связанный средний балл, поэтому средний балл является функцией процентной оценки. Другими словами, если мы введем процентную оценку, на выходе получится конкретный средний балл.
В данной системе оценок существует диапазон процентных оценок, соответствующих одному и тому же среднему баллу. Например, учащиеся, получившие средний балл 3,0, могут иметь различные процентные оценки от 78 до 86. Таким образом, процентная оценка не является функцией среднего балла.
Упражнение \ (\ PageIndex {2} \)
Таблица \ (\ PageIndex {2} \) перечисляет пять величайших бейсболистов всех времен в порядке рангов.
| Игрок | Рейтинг |
|---|---|
| Бейб Рут | 1 |
| Вилли Мейс | 2 |
| Тай Кобб | 3 |
| Уолтер Джонсон | 4 |
| Хэнк Аарон | 5 |
- Является ли ранг функцией имени игрока?
- Имя игрока зависит от ранга?
- Ответьте на
Есть
- Ответ б
да.(Примечание: если бы два игрока были разделены, скажем, за 4-е место, то имя не зависело бы от ранга.)
Использование обозначения функций
Как только мы определим, что отношение является функцией, нам нужно отобразить и определить функциональные отношения, чтобы мы могли понять и использовать их, а иногда также, чтобы мы могли программировать их в компьютерах. Есть разные способы представления функций. Стандартные обозначения функций — это одно из представлений, облегчающих работу с функциями.
Чтобы представить «рост является функцией возраста», мы начинаем с определения описательных переменных \ (h \) для роста и \ (a \) для возраста. Буквы \ (f \), \ (g \) и \ (h \) часто используются для обозначения функций точно так же, как мы используем \ (x \), \ (y \) и \ (z \) для обозначения числа и \ (A \), \ (B \) и \ (C \) для представления множеств.
\ [\ begin {array} {ll} h \ text {is} f \ text {of} a \; \; \; \; \; \; & \ text {Назовем функцию} f \ text {; высота является функцией возраста.} \\ h = f (a) & \ text {Мы используем круглые скобки для обозначения ввода функции.} \\ f (a) & \ text {Мы называем функцию} f \ text {; выражение читается как «} f \ text {of} a \ text {.»} \ end {array} \]
Помните, мы можем использовать любую букву для названия функции; обозначение \ (h (a) \) показывает нам, что \ (h \) зависит от \ (a \). Значение \ (a \) необходимо поместить в функцию \ (h \), чтобы получить результат. Скобки указывают, что возраст вводится в функцию; они не указывают на умножение.
Мы также можем дать алгебраическое выражение в качестве входных данных для функции.Например, \ (f (a + b) \) означает «сначала сложите \ (a \) и \ (b \), и результат будет входом для функции \ (f \)». Для получения правильного результата операции необходимо выполнять именно в таком порядке.
Обозначение функций
Запись \ (y = f (x) \) определяет функцию с именем \ (f \). Это читается как «\ (y \) является функцией \ (x \)». Буква \ (x \) представляет входное значение или независимую переменную. Буква \ (y \) или \ (f (x) \) представляет выходное значение или зависимую переменную.
Пример \ (\ PageIndex {3} \): использование обозначения функций для дней в месяце
Используйте обозначение функции для представления функции, вход которой является названием месяца, а выход — количеством дней в этом месяце.
Решение
Использование обозначения функций для дней в месяце
Используйте обозначение функции для представления функции, вход которой является названием месяца, а выход — количеством дней в этом месяце.
Количество дней в месяце является функцией названия месяца, поэтому, если мы назовем функцию \ (f \), мы напишем \ (\ text {days} = f (\ text {month}) \) или \ (d = f (m) \). Название месяца — это вход в «правило», которое связывает определенное число (выход) с каждым входом.
Рисунок \ (\ PageIndex {5} \): функция \ (31 = f (январь) \), где 31 — результат, f — правило, а январь — вход.
Например, \ (f (\ text {March}) = 31 \), потому что в марте 31 день. Обозначение \ (d = f (m) \) напоминает нам, что количество дней, \ (d \) (выход), зависит от названия месяца \ (m \) (вход).
Анализ
Обратите внимание, что входные данные функции не обязательно должны быть числами; входные данные функции могут быть именами людей, метками геометрических объектов или любым другим элементом, определяющим какой-либо вид вывода.Однако большинство функций, с которыми мы будем работать в этой книге, будут иметь числа как входы и выходы.
Пример \ (\ PageIndex {3B} \): интерпретация обозначения функции
Функция \ (N = f (y) \) дает количество полицейских \ (N \) в городе в году \ (y \). Что означает \ (f (2005) = 300 \)?
Решение
Когда мы читаем \ (f (2005) = 300 \), мы видим, что входной год — 2005. Выходное значение, количество полицейских \ ((N) \), равно 300.Помните, \ (N = f (y) \). Утверждение \ (f (2005) = 300 \) говорит нам, что в 2005 году в городе было 300 полицейских.
Упражнение \ (\ PageIndex {3} \)
Используйте обозначение функции, чтобы выразить вес свиньи в фунтах как функцию ее возраста в днях \ (d \).
- Ответ
\ (ш = е (г) \)
Вопросы и ответы
Вместо обозначения, такого как \ (y = f (x) \), можем ли мы использовать тот же символ для вывода, что и для функции, например, \ (y = y (x) \), означающий «\ (y \) является функцией \ (x \)? »
Да, это часто делается, особенно по прикладным предметам, использующим высшую математику, например физике и инженерии.Однако, исследуя математику, нам нравится проводить различие между такой функцией, как \ (f \) , которая является правилом или процедурой, и выходом y, который мы получаем, применяя \ (f \) к конкретному ввод \ (x \) . Вот почему мы обычно используем такие обозначения, как \ (y = f (x), P = W (d) \) и т. Д.
Представление функций с помощью таблиц
Общий метод представления функций — в виде таблицы. Строки или столбцы таблицы отображают соответствующие входные и выходные значения.В некоторых случаях эти значения представляют все, что мы знаем об отношениях; в других случаях таблица предоставляет несколько избранных примеров из более полных отношений.
Таблица \ (\ PageIndex {3} \) перечисляет входное число каждого месяца (\ (\ text {Январь} = 1 \), \ (\ text {Февраль} = 2 \) и т. Д.) И вывод значение количества дней в этом месяце. Эта информация представляет все, что мы знаем о месяцах и днях для данного года (который не является високосным). Обратите внимание, что в этой таблице мы определяем функцию дней в месяце \ (f \), где \ (D = f (m) \) идентифицирует месяцы целым числом, а не именем.
Номер месяца, \ (м \) (ввод) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Дней в месяце, \ (D \) (вывод) | 31 | 28 | 31 | 30 | 31 | 30 | 31 | 31 | 30 | 31 | 30 | 31 |
Таблица \ (\ PageIndex {4} \) определяет функцию \ (Q = g (n) \). Помните, это обозначение говорит нам, что \ (g \) — это имя функции, которая принимает входные данные \ (n \) и дает результат \ (Q \).
\ (п \) | 1 | 2 | 3 | 4 | 5 |
| \ (Q \) | 8 | 6 | 7 | 6 | 8 |
Таблица \ (\ PageIndex {5} \) отображает возраст детей в годах и соответствующий им рост.В этой таблице показаны лишь некоторые из имеющихся данных о росте и возрасте детей. Сразу видно, что эта таблица не представляет функцию, потому что одно и то же входное значение, 5 лет, имеет два разных выходных значения, 40 дюймов и 42 дюйма.
Возраст в годах, \ (a \) (ввод) | 5 | 5 | 6 | 7 | 8 | 9 | 10 |
| Высота в дюймах, \ (h \) (выход) | 40 | 42 | 44 | 47 | 50 | 52 | 54 |
Как: по таблице входных и выходных значений определить, представляет ли таблица функцию
- Определите входные и выходные значения.
- Проверьте, сопряжено ли каждое входное значение только с одним выходным значением. Если это так, таблица представляет функцию.
Пример \ (\ PageIndex {5} \): определение таблиц, представляющих функции
Какая таблица, Таблица \ (\ PageIndex {6} \), Таблица \ (\ PageIndex {7} \) или Таблица \ (\ PageIndex {8} \), представляет функцию (если есть)?
| Ввод | Выход |
|---|---|
| 2 | 1 |
| 5 | 3 |
| 8 | 6 |
| Ввод | Выход |
|---|---|
| -3 | 5 |
| 0 | 1 |
| 4 | 5 |
| Ввод | Выход |
|---|---|
| 1 | 0 |
| 5 | 2 |
| 5 | 4 |
Раствор
Таблица \ (\ PageIndex {6} \) и Таблица \ (\ PageIndex {7} \) определяют функции.В обоих случаях каждое входное значение соответствует ровно одному выходному значению. Таблица \ (\ PageIndex {8} \) не определяет функцию, потому что входное значение 5 соответствует двум различным выходным значениям.
Когда таблица представляет функцию, соответствующие входные и выходные значения также могут быть указаны с использованием обозначения функции.
Функция, представленная таблицей \ (\ PageIndex {6} \), может быть представлена записью
\ [f (2) = 1 \ text {,} f (5) = 3 \ text {и} f (8) = 6 \ nonumber \]
Аналогично выписки
\ [g (−3) = 5 \ text {,} g (0) = 1 \ text {и} g (4) = 5 \ nonumber \]
представляют функцию в таблице \ (\ PageIndex {7} \).
Таблица \ (\ PageIndex {8} \) не может быть выражена аналогичным образом, потому что она не представляет функцию.
Упражнение \ (\ PageIndex {5} \)
Представляет ли таблица \ (\ PageIndex {9} \) функцию?
| Ввод | Выход |
|---|---|
| 1 | 10 |
| 2 | 100 |
| 3 | 1000 |
- Ответ
да
Поиск входных и выходных значений функции
Когда мы знаем входное значение и хотим определить соответствующее выходное значение для функции, мы оцениваем функцию.Оценка всегда дает один результат, потому что каждое входное значение функции соответствует ровно одному выходному значению.
Когда мы знаем выходное значение и хотим определить входные значения, которые будут производить это выходное значение, мы устанавливаем выход равным формуле функции и решаем для входа. Решение может дать более одного решения, потому что разные входные значения могут давать одно и то же выходное значение.
Вычисление функций в алгебраических формах
Когда у нас есть функция в форме формулы, вычислить ее обычно несложно.2 + 2p − 3 = 0 & \ text {Вычтите по 3 с каждой стороны.} \\ (p + 3) (p − 1) = 0 & \ text {Factor.} \ End {array} \ nonumber \]
Если \ ((p + 3) (p − 1) = 0 \), либо \ ((p + 3) = 0 \), либо \ ((p − 1) = 0 \) (или оба они равны \ (0 \)). Мы установим каждый множитель равным \ (0 \) и решим относительно \ (p \) в каждом случае.
\ [(p + 3) = 0, \; p = −3 \ nonumber \]
\ [(p − 1) = 0, \, p = 1 \ nonumber \]
Это дает нам два решения. Выход \ (h (p) = 3 \), когда вход либо \ (p = 1 \), либо \ (p = −3 \). Мы также можем проверить, построив график, как на рисунке \ (\ PageIndex {6} \).2 + 2п \)
Упражнение \ (\ PageIndex {7} \)
Дана функция \ (g (m) = \ sqrt {m − 4} \), решить \ (g (m) = 2 \).
- Ответ
\ (м = 8 \)
Вычисление функций, выраженных в формулах
Некоторые функции определяются математическими правилами или процедурами, выраженными в форме уравнения . Если можно выразить выход функции с помощью формулы, включающей входную величину, то мы можем определить функцию в алгебраической форме.Например, уравнение \ (2n + 6p = 12 \) выражает функциональную связь между \ (n \) и \ (p \). Мы можем переписать его, чтобы решить, является ли \ (p \) функцией \ (n \).
Как: Для данной функции в форме уравнения напишите ее алгебраическую формулу.
- Решите уравнение, чтобы изолировать выходную переменную с одной стороны от знака равенства с другой стороной как выражение, которое включает только входную переменную.
- Используйте все обычные алгебраические методы для решения уравнений, такие как сложение или вычитание одной и той же величины с обеих сторон или от них, или умножение или деление обеих сторон уравнения на одинаковую величину.
Пример \ (\ PageIndex {8A} \): поиск уравнения функции
Выразите отношение \ (2n + 6p = 12 \) как функцию \ (p = f (n) \), если это возможно.
Решение
Чтобы выразить отношение в этой форме, нам нужно иметь возможность записать отношение, где \ (p \) является функцией \ (n \), что означает запись его как \ (p = [\ text {выражение с участием} п] \).
\ [\ begin {align *} 2n + 6p & = 12 \\ 6p & = 12−2n && \ text {Вычтите 2n с обеих сторон.} \\ p & = \ dfrac {12−2n} {6} & & \ text {Разделите обе стороны на 6 и упростите.} \\ p & = \ frac {12} {6} — \ frac {2n} {6} \\ p & = 2− \ frac {1} {3} n \ end {align *} \]
Следовательно, \ (p \) как функция от \ (n \) записывается как
\ [p = f (n) = 2− \ frac {1} {3} n \ nonumber \]
Анализ
Важно отметить, что не все отношения, выраженные уравнением, можно также выразить как функцию с формулой. 2 = 1 \) функцию с \ (x \) на входе и \ (y \) на выходе? Если это так, выразите отношение как функцию \ (y = f (x) \).y \), если мы хотим выразить y как функцию от x, не существует простой алгебраической формулы, включающей только \ (x \), которая равна \ (y \). Однако каждый \ (x \) определяет уникальное значение для \ (y \), и существуют математические процедуры, с помощью которых \ (y \) может быть найден с любой желаемой точностью. В этом случае мы говорим, что уравнение дает неявное (подразумеваемое) правило для \ (y \) как функции \ (x \), даже если формулу нельзя записать явно.
Оценка функции, заданной в табличной форме
Как мы видели выше, мы можем представлять функции в виде таблиц.И наоборот, мы можем использовать информацию в таблицах для написания функций, и мы можем оценивать функции с помощью таблиц. Например, насколько хорошо наши питомцы вспоминают теплые воспоминания, которыми мы с ними делимся? Существует городская легенда, что у золотой рыбки память 3 секунды, но это всего лишь миф. Золотая рыбка может помнить до 3 месяцев, в то время как бета-рыба имеет память до 5 месяцев. И хотя продолжительность памяти щенка не превышает 30 секунд, взрослая собака может запоминать 5 минут. Это скудно по сравнению с кошкой, у которой объем памяти составляет 16 часов.
Функция, которая связывает тип питомца с продолжительностью его памяти, легче визуализировать с помощью таблицы (Table \ (\ PageIndex {10} \)).
Память для домашних животных | пролет в часах |
|---|---|
| Щенок | 0,008 |
| Взрослая собака | 0.083 |
| Кот | 3 |
| Золотая рыбка | 2160 |
| Бета Рыба | 3600 |
Иногда оценка функции в табличной форме может быть более полезной, чем использование уравнений. Здесь вызовем функцию \ (P \). Область функции — это тип домашнего животного, а диапазон — это действительное число, представляющее количество часов, в течение которых хранится память питомца.Мы можем оценить функцию \ (P \) при входном значении «золотая рыбка». Мы бы написали \ (P (золотая рыбка) = 2160 \). Обратите внимание, что для оценки функции в табличной форме мы идентифицируем входное значение и соответствующее выходное значение из соответствующей строки таблицы. Табличная форма для функции P кажется идеально подходящей для этой функции, больше, чем запись ее в форме абзаца или функции.
Как сделать: для данной функции, представленной в виде таблицы, определить конкретные выходные и входные значения
1.Найдите данный вход в строке (или столбце) входных значений.
2. Определите соответствующее выходное значение в паре с этим входным значением.
3. Найдите заданные выходные значения в строке (или столбце) выходных значений, отмечая каждый раз, когда это выходное значение появляется.
4. Определите входные значения, соответствующие заданному выходному значению.
Пример \ (\ PageIndex {9} \): Вычисление и решение табличной функции
Использование таблицы \ (\ PageIndex {11} \),
а. Оцените \ (g (3) \).
г. Решите \ (g (n) = 6 \).
\ (п \) | 1 | 2 | 3 | 4 | 5 |
| \ (г (п) \) | 8 | 6 | 7 | 6 | 8 |
Раствор
а.Вычисление \ (g (3) \) означает определение выходного значения функции \ (g \) для входного значения \ (n = 3 \). Выходное значение таблицы, соответствующее \ (n = 3 \), равно 7, поэтому \ (g (3) = 7 \).
г. Решение \ (g (n) = 6 \) означает определение входных значений n, которые производят выходное значение 6. Таблица \ (\ PageIndex {12} \) показывает два решения: 2 и 4.
\ (п \) | 1 | 2 | 3 | 4 | 5 |
| \ (г (п) \) | 8 | 6 | 7 | 6 | 8 |
Когда мы вводим 2 в функцию \ (g \), на выходе получаем 6.Когда мы вводим 4 в функцию \ (g \), наш результат также равен 6.
Упражнение \ (\ PageIndex {1} \)
Используя Table \ (\ PageIndex {12} \), вычислите \ (g (1) \).
- Ответ
\ (г (1) = 8 \)
Поиск значений функций из графика
Оценка функции с помощью графика также требует нахождения соответствующего выходного значения для данного входного значения, только в этом случае мы находим выходное значение, глядя на график.Решение функционального уравнения с использованием графика требует нахождения всех экземпляров данного выходного значения на графике и наблюдения за соответствующими входными значениями.
Пример \ (\ PageIndex {10} \): чтение значений функций из графика
Учитывая график на рисунке \ (\ PageIndex {7} \),
- Оценить \ (f (2) \).
- Решите \ (f (x) = 4 \).
Рисунок \ (\ PageIndex {7} \): График положительной параболы с центром в \ ((1, 0) \).
Решение
Чтобы оценить \ (f (2) \), найдите точку на кривой, где \ (x = 2 \), затем прочтите координату y этой точки.Точка имеет координаты \ ((2,1) \), поэтому \ (f (2) = 1 \). См. Рисунок \ (\ PageIndex {8} \).
\ (\ PageIndex {8} \): график положительной параболы с центром в \ ((1, 0) \) с отмеченной точкой \ ((2, 1) \), где \ (f (2) = 1 \) .
Чтобы решить \ (f (x) = 4 \), мы находим выходное значение 4 на вертикальной оси. Двигаясь горизонтально по прямой \ (y = 4 \), мы обнаруживаем две точки кривой с выходным значением 4: \ ((- 1,4) \) и \ ((3,4) \). Эти точки представляют два решения \ (f (x) = 4 \): −1 или 3. Это означает \ (f (−1) = 4 \) и \ (f (3) = 4 \), или когда вход — -1 или 3, выход — 4.См. Рисунок \ (\ PageIndex {9} \).
Рисунок \ (\ PageIndex {9} \): График обращенной вверх параболы с вершиной в \ ((0,1) \) и помеченными точками в \ ((- 1, 4) \) и \ ((3 , 4) \). Прямая в точке \ (y = 4 \) пересекает параболу в отмеченных точках.
Упражнение \ (\ PageIndex {10} \)
Учитывая график на рисунке \ (\ PageIndex {7} \), решите \ (f (x) = 1 \).
- Ответ
\ (x = 0 \) или \ (x = 2 \)
Определение того, является ли функция взаимно однозначной
Некоторые функции имеют заданное выходное значение, соответствующее двум или более входным значениям.Например, на биржевой диаграмме, показанной на рисунке в начале этой главы, цена акции составляла 1000 долларов в пять разных дат, что означает, что было пять различных входных значений, которые все привели к одному и тому же выходному значению в 1000 долларов.
Однако некоторые функции имеют только одно входное значение для каждого выходного значения, а также имеют только один выход для каждого входа. Мы называем эти функции взаимно однозначными функциями. В качестве примера рассмотрим школу, в которой используются только буквенные оценки и десятичные эквиваленты, как указано в Таблице \ (\ PageIndex {13} \).
| Letter Grade | Средний балл |
|---|---|
| А | 4,0 |
| B | 3,0 |
| С | 2,0 |
| D | 1,0 |
Эта система оценок представляет собой функцию «один-к-одному», поскольку каждая вводимая буква дает один конкретный выходной средний балл, а каждый средний балл соответствует одной вводимой букве.
Чтобы визуализировать эту концепцию, давайте еще раз посмотрим на две простые функции, изображенные на рисунках \ (\ PageIndex {1a} \) и \ (\ PageIndex {1b} \). Функция в части (a) показывает взаимосвязь, которая не является взаимно однозначной, потому что входы \ (q \) и \ (r \) оба дают выход \ (n \). Функция в части (b) показывает взаимосвязь, которая является функцией «один-к-одному», потому что каждый вход связан с одним выходом.
Индивидуальные функции
Однозначная функция — это функция, в которой каждое выходное значение соответствует ровно одному входному значению.2 \). Поскольку площади и радиусы являются положительными числами, существует ровно одно решение: \ (\ sqrt {\ frac {A} {\ pi}} \). Таким образом, площадь круга однозначно зависит от радиуса круга.
Упражнение \ (\ PageIndex {11A} \)
- Является ли остаток функцией номера банковского счета?
- Является ли номер банковского счета функцией баланса?
- Является ли баланс однозначной функцией номера банковского счета?
- Ответ
а.да, потому что на каждом банковском счете в любой момент времени имеется единый баланс;
г. нет, потому что несколько номеров банковских счетов могут иметь одинаковый баланс;
г. нет, потому что один и тот же выход может соответствовать более чем одному входу.
Упражнение \ (\ PageIndex {11B} \)
Оцените следующее:
- Если каждая процентная оценка, полученная на курсе, переводится в одну буквенную оценку, является ли буквенная оценка функцией процентной оценки?
- Если да, то функция взаимно однозначная?
- Ответ
а.Да, буквенная оценка является функцией процентной оценки;
г. Нет, не один на один. Мы могли бы получить 100 различных процентных чисел, но только около пяти возможных буквенных оценок, поэтому не может быть только одного процентного числа, соответствующего каждой буквенной оценке.
Использование теста вертикальной линии
Как мы видели в некоторых примерах выше, мы можем представить функцию с помощью графика. Графики отображают огромное количество пар ввода-вывода на небольшом пространстве. Предоставляемая ими визуальная информация часто упрощает понимание взаимоотношений.Обычно графики строятся с входными значениями по горизонтальной оси и выходными значениями по вертикальной оси.
Наиболее распространенные графики называют входное значение \ (x \) и выходное значение \ (y \), и мы говорим, что \ (y \) является функцией \ (x \), или \ (y = f (x) \), когда функция названа \ (f \). График функции — это совокупность всех точек \ ((x, y) \) на плоскости, которая удовлетворяет уравнению \ (y = f (x) \). Если функция определена только для нескольких входных значений, то график функции представляет собой только несколько точек, где координата x каждой точки является входным значением, а координата y каждой точки является соответствующим выходным значением.Например, черные точки на графике на рисунке \ (\ PageIndex {10} \) говорят нам, что \ (f (0) = 2 \) и \ (f (6) = 1 \). Однако множество всех точек \ ((x, y) \), удовлетворяющих \ (y = f (x) \), является кривой. Показанная кривая включает \ ((0,2) \) и \ ((6,1) \), потому что кривая проходит через эти точки
.
Рисунок \ (\ PageIndex {10} \): График многочлена.
Тест вертикальной линии можно использовать для определения того, представляет ли график функцию. Если мы можем нарисовать любую вертикальную линию, которая пересекает график более одного раза, тогда график не определяет функцию, потому что функция имеет только одно выходное значение для каждого входного значения.См. Рисунок \ (\ PageIndex {11} \) .
Рисунок \ (\ PageIndex {11} \): три графика, наглядно демонстрирующие, что является функцией, а что нет.
Практическое руководство. Имея график, используйте тест вертикальной линии, чтобы определить, представляет ли график функцию
- Проверьте график, чтобы увидеть, пересекает ли нарисованная вертикальная линия кривую более одного раза.
- Если такая линия есть, определите, что график не представляет функцию.
Пример \ (\ PageIndex {12} \): Применение теста вертикальной линии
Какой из графиков на рисунке \ (\ PageIndex {12} \) представляет (ы) функцию \ (y = f (x) \)?
Рисунок \ (\ PageIndex {12} \): график полинома (a), наклонной вниз прямой (b) и круга (c).
Решение
Если какая-либо вертикальная линия пересекает график более одного раза, отношение, представленное на графике, не является функцией. Обратите внимание, что любая вертикальная линия будет проходить только через одну точку двух графиков, показанных в частях (a) и (b) рисунка \ (\ PageIndex {12} \). Из этого можно сделать вывод, что эти два графика представляют функции. Третий график не представляет функцию, потому что не более чем значений x вертикальная линия пересекает график более чем в одной точке, как показано на рисунке \ (\ PageIndex {13} \).
Рисунок \ (\ PageIndex {13} \): График круга.
Упражнение \ (\ PageIndex {12} \)
Представляет ли график на рисунке \ (\ PageIndex {14} \) функцию?
Рисунок \ (\ PageIndex {14} \): График функции абсолютного значения.
- Ответ
да
Использование теста горизонтальной линии
После того, как мы определили, что график определяет функцию, простой способ определить, является ли он взаимно однозначной функцией, — это использовать тест горизонтальной линии .Проведите через график горизонтальные линии. Если какая-либо горизонтальная линия пересекает график более одного раза, то график не представляет собой взаимно однозначную функцию.
Практическое руководство. Имея график функции, используйте тест горизонтальной линии, чтобы определить, представляет ли график однозначную функцию
- Проверьте график, чтобы увидеть, пересекает ли нарисованная горизонтальная линия кривую более одного раза.
- Если такая линия есть, определите, что функция не является взаимно однозначной.
Пример \ (\ PageIndex {13} \): применение теста горизонтальной линии
Рассмотрим функции, показанные на рисунке \ (\ PageIndex {12a} \) и рисунке \ (\ PageIndex {12b} \). Являются ли какие-либо функции взаимно однозначными?
Решение
Функция на рисунке \ (\ PageIndex {12a} \) не является взаимно однозначной. Горизонтальная линия, показанная на рисунке \ (\ PageIndex {15} \), пересекает график функции в двух точках (и мы даже можем найти горизонтальные линии, которые пересекают его в трех точках.)
Рисунок \ (\ PageIndex {15} \): График многочлена с горизонтальной линией, пересекающей 2 точки
Функция на рисунке \ (\ PageIndex {12b} \) взаимно однозначна. Любая горизонтальная линия будет пересекать диагональную линию не более одного раза.
Упражнение \ (\ PageIndex {13} \)
Является ли график, показанный на рисунке \ (\ PageIndex {13} \), взаимно однозначным?
- Ответ
Нет, потому что он не проходит тест горизонтальной линии.
В этом тексте мы будем исследовать функции — формы их графиков, их уникальные характеристики, их алгебраические формулы и способы решения с ними проблем.Когда учимся читать, мы начинаем с алфавита. Когда мы учимся арифметике, мы начинаем с чисел. При работе с функциями также полезно иметь базовый набор стандартных элементов. Мы называем их «функциями набора инструментов», которые образуют набор основных именованных функций, для которых нам известны график, формула и специальные свойства. 2} \)
Ключевые понятия
- Отношение — это набор упорядоченных пар.Функция — это особый тип отношения, в котором каждое значение домена или вход приводит ровно к одному значению диапазона или выходу.
- Функциональная нотация — это сокращенный метод соотнесения ввода и вывода в форме \ (y = f (x) \).
- В табличной форме функция может быть представлена строками или столбцами, которые относятся к входным и выходным значениям.
- Чтобы оценить функцию, мы определяем выходное значение для соответствующего входного значения. Алгебраические формы функции можно оценить, заменив входную переменную заданным значением.
- Чтобы найти конкретное значение функции, мы определяем входные значения, которые дают конкретное выходное значение.
- Алгебраическая форма функции может быть записана из уравнения.
- Входные и выходные значения функции можно определить по таблице.
- Связь входных значений с выходными значениями на графике — еще один способ оценить функцию.
- Функция взаимно однозначна, если каждое выходное значение соответствует только одному входному значению.
- График представляет функцию, если любая вертикальная линия, проведенная на графике, пересекает график не более чем в одной точке.
- График функции «один к одному» проходит проверку горизонтальной линии.
Глоссарий
зависимая переменная
выходная переменная
домен
набор всех возможных входных значений для отношения
функция
отношение, в котором каждое входное значение дает уникальное выходное значение
Проверка горизонтальной линии
Метод проверки взаимно однозначности функции путем определения того, пересекает ли какая-либо горизонтальная линия график более одного раза
независимая переменная
входная переменная
введите
каждый объект или значение в домене, который относится к другому объекту или значению посредством отношения, известного как функция
взаимно однозначная функция
функция, для которой каждое значение вывода связано с уникальным значением ввода
вывод
каждый объект или значение в диапазоне, который создается, когда входное значение вводится в функцию
диапазон
набор выходных значений, которые являются результатом входных значений в отношении
отношение
набор заказанных пар
проверка вертикальной линии
метод проверки того, представляет ли график функцию путем определения того, пересекает ли вертикальная линия график не более одного раза
Авторы и авторство
Отношения и функции — ChiliMath
Начнем с того, что отношение — это просто набор или совокупность упорядоченных пар.Ничего особенного в этом нет. Упорядоченная пара, обычно известная как точка, имеет два компонента, которые являются координатами x и y.
Это пример упорядоченной пары.
Основные идеи и способы записи или представления отношений
Пока числа идут парами, это становится отношением. Если вы можете написать кучу точек (упорядоченных пар), то вы уже знаете, как выглядит отношение. Например, здесь у нас есть отношение с пятью упорядоченными парами.Записав это в обозначении набора с помощью фигурных скобок,
Отношение в обозначении набора :
Однако, помимо обозначения набора, есть и другие способы записать это отношение. Мы можем отобразить это в таблице, нанести на ось xy и выразить с помощью диаграммы сопоставления.
- Связь в диаграмме отображения
Мы также можем описать область и диапазон данного отношения.
- Область — это набор всех x или входных значений.Мы можем описать его как набор первых значений в упорядоченных парах.
- Диапазон — это набор всех y или выходных значений. Мы можем описать это как набор вторых значений в упорядоченных парах.
Итак, в отношении ниже
наш домен и диапазон следующие:
При перечислении элементов домена и диапазона избавьтесь от дубликатов и запишите их в порядке возрастания.
Что делает отношение функцией?
С другой стороны, функция на самом деле является «особым» видом отношения, потому что она следует дополнительному правилу.Как и отношение, функция — это также набор упорядоченных пар; однако каждое значение x должно быть связано только с одним значением y.
Предположим, у нас есть два отношения, записанные в таблицах,
- Отношение, которое не является функцией
Поскольку у нас есть повторения или дубликаты значений x с разными значениями y, это отношение перестает быть функцией.
- Отношение, которое является функцией
Это отношение определенно является функцией, потому что каждое значение x уникально и связано только с одним значением y.
Итак, для краткого обзора, если вы видите какие-либо дубликаты или повторы в значениях x, отношение не является функцией. А как насчет этого примера? Разве это не функция, потому что у нас есть повторяющиеся записи в x?
Будьте здесь очень осторожны. Да, у нас есть повторяющиеся значения x, но они связаны с одним и тем же значением y. Точка (1,5) появляется дважды, а точка (3, -8) записывается трижды. Эту таблицу можно очистить, написав единственную копию повторяющихся упорядоченных пар.
Теперь отношение явно является функцией!
Примеры того, как определить, является ли отношение также функцией
Давайте рассмотрим еще несколько примеров, определив, является ли данное отношение функцией или нет.
Пример 1: Является ли отношение, выраженное на диаграмме отображения, функцией?
Каждый элемент домена отслеживается до одного-единственного элемента в диапазоне. Однако это нормально, если два или более значений в домене имеют общее значение в диапазоне.То есть, даже несмотря на то, что элементы 5 и 10 в домене имеют одинаковое значение 2 в диапазоне, это отношение по-прежнему является функцией.
Пример 2: Является ли отношение, выраженное на диаграмме отображения, функцией?
Как вы думаете? Каждое значение в домене указывает на одно значение в диапазоне? Абсолютно! Нет ничего плохого в том, что четыре элемента из домена имеют общее значение в диапазоне. Это также отличный пример функции.
Пример 3: Является ли отношение, выраженное на диаграмме отображения, функцией?
Грязный? Да! Сбивает с толку? Не совсем. Единственное, что мне нужно, это наблюдать, является ли элемент в домене «жадным», желая быть спаренным с более чем одним элементом в диапазоне. Элемент 15 имеет две стрелки, указывающие как на 7, так и на 9. Это явное нарушение требования быть функцией. Функция хорошо работает, то есть каждый элемент в домене должен указывать на один элемент в диапазоне.Следовательно, это отношение , а не функция .
Пример 4: Является ли отношение, выраженное на диаграмме отображения, функцией?
Если вы считаете, что пример 3 «плохой», это «еще хуже». Один элемент в домене соединяется с четырьмя элементами в диапазоне. Помните, что если элемент в домене связан с более чем одним элементом в диапазоне, отношение автоматически дисквалифицируется как функция. Таким образом, это отношение является абсолютно , а не функцией .
Пример 5: Является ли диаграмма сопоставления отношением или функцией?
Позвольте мне показать вам этот пример, чтобы выделить очень важную идею о функции, которая обычно игнорируется. Ваш учитель может дать вам что-то подобное, чтобы проверить, обращаете ли вы внимание на детали определения функции.
Пока все нормально выглядит. Но есть небольшая проблема. Элемент «2» в домене не связан ни с одним элементом в диапазоне.
Вот сделка! Каждый элемент в домене должен иметь какое-то соответствие элементам в диапазоне, по крайней мере, чтобы он считался отношением.Поскольку это не отношение, отсюда следует, что оно не может быть функцией.
Итак, окончательный ответ: ни отношение, ни функция.
5.1 — Введение в функции
5.1 — Введение в функции
5.1 — Знакомство с функциями
| Определение: Функция — это соответствие или отображение из первого набора чисел, называемого доменом функции, ко второму набору чисел, называемому диапазоном функции, таким образом, что для каждого члена домена есть ровно один член диапазон, как показано на этом рисунке: |
Функциональная концепция станка и функциональные обозначения
Полезно думать о функции как о машине с числом из домена в качестве входных данных и
соответствующий номер диапазона в качестве вывода.Функция получает имя вроде f
(сокращение от слова «функция»), и если номер, вводимый в машину, будет
вызывается x , затем соответствующий номер возвращается или выходит из машины
обозначается f ( x ). Вот изображение:
Функциональное обозначение f ( x ) буквально означает
« функция x ».
Способы выражения функции
Функцию можно выразить по-разному:
Аргумент и значение функции
Значение домена, которое входит в функциональную машину, также называется
аргумент функции и значение диапазона, выходящего из
Функциональный автомат также называется значением функции.Например, предположим, что f (5) = 15. Тогда мы говорим, что
аргумент функции f равен 5, а значение f равно 15.
Определение области и диапазона функции
Домен и диапазон функции не всегда представляют собой набор всех действительных чисел.
Если функция представлена в виде списка или графика, вы можете определить
домена и диапазона, просто взглянув на список или график. Но если
функция выражается в форме формулы, тогда вы должны сделать следующее:
- Подставьте возможные значения домена в формулу и убедитесь, что
что они не вызывают неопределенную операцию (например, деление
нулем или квадратным корнем из отрицательного числа).Если они это сделают, то они
не в домене. - Как только домен известен, вы можете найти диапазон, подставив
различное значение домена в формулу.
Пример: Рассмотрим функцию
. Домен
должно быть потому что
в противном случае мы пытаемся извлечь квадратный корень из отрицательного числа.
Тогда, если подставить в формулу различные значения области,
мы видим, что диапазон есть.
Вот график этой функции, который подтверждает наши выводы:
Тест вертикальной линии для функции
Определение функции гласит, что для каждого члена домена существует
может быть только один член диапазона.Таким образом, график функции не может
выглядят так:
где есть значение x , для которого есть два или более соответствующих
и значений. Если график не проходит эту так называемую вертикальную линию
test , то это не график функции.
Вместо этого мы говорим, что это график отношения
от x до y .
Функции один-к-одному и многие-к-одному
Функция называется взаимно однозначной , если каждое значение y имеет точно
одно значение x , сопоставленное с ним, и многие-к-одному , если есть
y значений, которым сопоставлено более одного значения x .На этом графике показана функция «многие к одному». Три точки обозначают три x
значения, которые отображаются на одно и то же значение y .
Одна из сложностей с функцией «многие к одному» заключается в том, что она не может иметь
обратная функция. Если бы это было возможно, обратное
будет один ко многим, и это нарушит
определение функции.
Подстановка выражений в функции
Часто, особенно в математике, мы используем формулу функции
и мы позволяем аргументу быть выражением вместо
просто число.Единственная сложность в этом случае заключается в том, что обычно мы должны
заключите аргумент в скобки, чтобы сохранить правильный порядок операций.
Это потому, что формула — это всего лишь рецепт того, что
сделать с вводом (аргумент), чтобы получить вывод (значение функции).
Например, функциональное обозначение:
f ( x ) = x 2 -2 x
означает, что значение функции получается возведением в квадрат аргумента
и дважды вычитая из него аргумент.На самом деле это не имеет значения
какую букву мы используем для аргумента; это , как работает функция , что
это важно.
Таким образом, следующие допустимые замены:
- f (4) = 4 2 — 2 · 4
- f ( т ) = т 2 -2 т
- f ( x + h ) = ( x + h ) 2 -2 ( x + h )
- f ( a x ) = ( a x ) 2 — 2 ( a x )
Предупреждение: Не путайте скобки.В левой части каждого примера в скобках указаны функциональные обозначения. Таким образом:
f ( независимо от )
означает, что у нас есть функция с именем f и ее аргумент
все равно . Мы не умножаем f на независимо от !
С правой стороны мы используем скобки, чтобы сохранить порядок операций.
Функциональный состав
Так же, как мы можем подставить выражение в функцию, мы можем
заменяет другую функцию на функцию .Например в предыдущем
В разделе мы определили функцию:
f ( x ) = x 2 -2 x
Если подставить в эту функцию другую функцию g ( x )
тогда получаем:
Например, если г ( x ) = x + 3, то:
Мы также можем изменить порядок и заменить f на g ,
как это:
Обратите внимание, что результат совершенно другой.Если мы подумаем о f и g как о машинах, то подставив
f в g означает, что выход
f — это ввод g , как показано здесь:
Состав функций важен, потому что этот метод можно использовать
создавать сложные функции из простых компонентов.
Обратная функция
Предположим, что функция f отображает x на y и что
другая функция g отображает y обратно на исходные x , как показано здесь:
Тогда функция g называется функцией , обратной функции f .
и композиция f и g не имеет общего эффекта.Обратите внимание, что функция f должна быть взаимно однозначной, чтобы она имела инверсию.
Один из способов вывести обратную функцию g для любой функции f таков:
- Установить f ( x ) равным y .
- Решите уравнение y = f ( x ) для x .
Если существует ровно одно решение, то существует обратное; в противном случае — нет. - В найденном уравнении переименуйте x в g ( y ).
Пример: Найти обратную функцию g функции
f ( x ) = 2 x + 3.
Установить f ( x ) равным y Решить для x
Переименовать x как g ( y ).Это наоборот.
Обратите внимание, что функция f принимает свой аргумент, умножает его на 2, а затем добавляет 3.
Обратная функция, г ,
выполняет прямо противоположные шаги в обратном порядке .
Он берет свой аргумент, сначала вычитает 3, а затем делит на 2.
Это именно то, что вы ожидаете от обратного.
Пример: Попробуйте найти функцию, обратную функции.
f ( x ) = x 2 .
Установите f ( x ) равным y Решите для x . Есть два решения, поэтому обратного не существует.
Обратите внимание, что f отображает две точки на каждую точку. Например
f (2) = 4 и f (−2) = 4. Таким образом, обратное значение должно быть
отобразите точку 4 обратно в обе точки 2 и −2. Но это нарушает
определение функции, чтобы не было обратного.
Если вы нашли эту страницу в ходе веб-поиска, вы не увидите
Оглавление в рамке слева.
Щелкните здесь, чтобы отобразить его.
Переписка — Математическая энциклопедия
связь
Обобщение понятия бинарного отношения (обычно) между двумя наборами или математическими структурами одного типа. Соответствия широко используются в математике, а также в различных прикладных дисциплинах, таких как теоретическое программирование, теория графов, теория систем и математическая лингвистика.
Соответствие двух наборов $ A $
и $ B $
есть любое подмножество $ R $
декартова произведения $ A \ times B $.
Другими словами, соответствие между $ A $
и $ B $
состоит из определенных упорядоченных пар $ (a, b) $,
где $ a \ in A $
и $ b \ in B $.
Как правило, соответствие обозначается тройкой $ (R, A, B) $
и можно написать $ a R b $
или $ R (a, b) $
вместо $ (a, b) \ in R $.
Вместо «соответствия» иногда используется термин «бинарное отношение» или «отношение между множествами» (в общем случае, когда $ A $
и $ B $
не обязательно совпадать).
Для конечных множеств обычно используются матричное и графическое представления соответствия. Предположим, что $ A $
и $ B $
иметь $ n $
и $ млн.
элементов соответственно, и пусть $ (R, A, B) $
Будет какая-то переписка. Это можно описать с помощью $ n \ times m $
матрица, строки и столбцы которой помечены элементами $ A $
и $ B $,
соответственно, а пересечение $ a $ —
-я строка с $ b $ —
-й столбец содержит 1, если $ (a, b) \ in R $,
и $ 0 $
иначе.Наоборот, каждые $ (n \ times m) $ —
матрица, состоящая из нулей и единиц, описывает однозначное соответствие между $ A $
и $ B $.
В графическом представлении элементы $ A $
и $ B $
представлены точками на плоскости. Эти точки обычно обозначаются теми же символами, что и соответствующие элементы. Тогда $ a $
и $ b $
соединены стрелкой (дугой) из $ a $
в $ b $
если $ (a, b) \ in R $.
Таким образом, соответствие представляется ориентированным графом.
Множество всех соответствий между двумя множествами $ A $
и $ B $
образует полную булеву алгебру, нулем которой является пустое соответствие, а единицей является так называемое полное соответствие, состоящее из всех пар $ (a, b) $,
$ a \ in A $,
$ b \ in B $.
Пусть $ R \ substeq A \ times B $.
Набор
$$
\ mathop {\ rm Dom} R = \
\ {{a \ in A}: {\ существует b (a, b) \ in R} \}
$$
называется областью определения $ R $,
и набор
$$
\ mathop {\ rm Ran} R = \
\ {{b \ in B}: {\ существует a (a, b) \ in R} \}
$$
называется диапазоном или изображением $ R $.Переписка $ R $
всюду определено, если $ \ mathop {\ rm Dom} R = A $,
и сюръективно, если $ \ mathop {\ rm Ran} R = B $.
Для каждого $ a \ in A $
набор
$$
\ mathop {\ rm Im} _ {R} a = \
\ {{b \ in B}: {(a, b) \ in R} \}
$$
называется изображением $ a $
относительно $ R $,
и для каждого $ b \ in B $
набор
$$
\ mathop {\ rm Coim} _ {R} b = \
\ {{a \ in A}: {(a, b) \ in R} \}
$$
называется совместным изображением (или прообразом) $ b $.
относительно $ R $.{\ #} R $.
Любое дифункциональное соответствие индуцирует отношения эквивалентности в области и на изображении, фактормножества которых имеют одинаковую мощность. Это справедливо только для дифункциональных соответствий.
Пусть $ \ mathfrak A $
— класс математических структур того же типа, замкнутый относительно конечных декартовых произведений. По соответствию двух структур $ A, B \ in \ mathfrak A $,
один означает подструктуру $ R $
из $ A \ times B $.
Таким образом, у одного есть групповые соответствия, соответствия модулей, кольцевые соответствия и другие.Такие соответствия часто имеют полезные описания их структуры. Например, пусть $ A $
и $ B $
— группы и пусть $ R $
— подгруппа прямого произведения $ A \ times B $.
Наборы
$$
\ mathop {\ rm Ker} R = \
\ {{a \ in A}: {(a, b) \ in R} \}
, \ I _ {R} = \
\ {{b \ in B}: {(1, b) \ in R} \}
$$
и
называются ядром и неопределенностью $ R $,
соответственно. $ \ mathop {\ rm Ker} R $
нормальная подгруппа в $ \ mathop {\ rm Dom} R $,
$ I _ {R} $
нормальная подгруппа в $ \ mathop {\ rm Ran} R $,
и фактор-группы $ (\ mathop {\ rm Dom} R) / \ mathop {\ rm Ker} R $
и $ (\ mathop {\ rm Ran} R) / I _ {R} $
изоморфны.Отсюда, в частности, следует, что все групповые соответствия дифункциональны.
Список литературы
| [1] | А.Г. Курош, «Лекции по общей алгебре», Челси (1963) MR0158000 Zbl 0121.25901 |
| [2] | A.I. Мальцев, «Алгебраические системы», Springer (1973) Zbl 0266.08001 |
| [3] | М.Ш. [М.Ш. Цаленко] Каленко, «Классификация категорий соответствия и типов закономерностей для категорий» Пер.Московская математика. Soc. , 1 (1982) с. 239–282 Труды Моск. Мат. Общ. , 41 (1980) стр. 241–285 |
В алгебраической геометрии соответствия широко используются, [a1], гл. 2, 3. Они определяются как следующая немного более техническая концепция. Переписка $ Z $
между двумя (проективными) многообразиями $ X $
и $ Y $
определяется замкнутым алгебраическим подмножеством $ Z \ subset X \ times Y $.
Он называется рациональным отображением, если $ Z $
неприводимо и существует открытое по Зарисскому подмножество $ X _ {0} \ subset X $
такое, что каждый $ x \ in X _ {0} $
связано соотношением $ Z $
до одной и только одной точки $ Y $ (
я.{\ #} $
являются рациональными отображениями.
Список литературы
Как цитировать эту запись:
Корреспонденция.
