Содержание
Примеры решения способом сложения | Алгебра
Рассмотрим конкретные примеры решения систем линейных уравнений способом сложения.
Ищем наибольший общий делитель коэффициентов при каждой из переменных (коэффициенты берем со знаком «+»).
Наименьшее общее кратное коэффициентов при x — НОК(5;2)=10, при y — НОК(3;3)=3.
Проще работать с y, поскольку для получения перед y противоположных чисел достаточно умножить любое из уравнений на -1. Проще умножить на -1 второе уравнение системы (в этом случае после сложения уравнений коэффициент при x — положительное число).
Теперь подставим x=3 в любое из уравнений системы, например, во второе:
Решаем это уравнение:
6-3y=21
-3y=21-6
-3y=15
y= -5.
Ответ записываем в круглых скобках через точку с запятой в алфавитном порядке.
Ответ: (3; -5).
НОК(6; 4)=12, НОК(13; 5)=65. Проще работать с коэффициентами перед x.
Проще работать с коэффициентами перед x.
Чтобы получить перед иксами противоположные числа, первую систему умножим на -2, вторую — на 3
и сложим почленно левые и правые части уравнений:
Подставляем y= -1 в первое уравнение системы и находим x:
Ответ: (-2; -1).
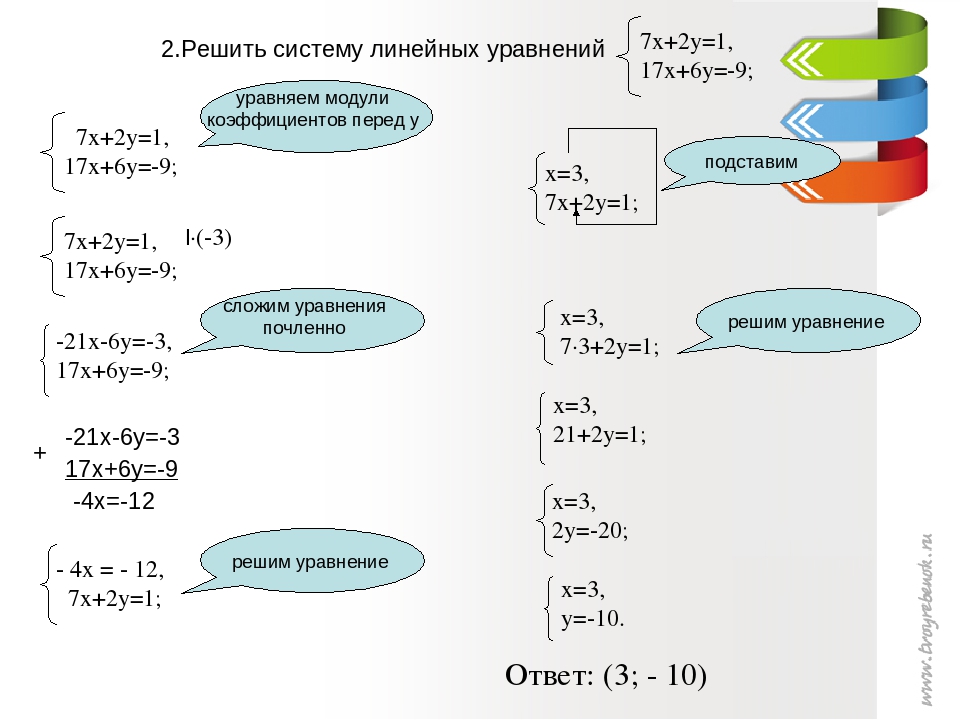
НОК(3; 5)=15, НОК(5; 7)=35. Проще получить противоположные числа перед x.
Для этого умножим первое уравнение системы на 5, второе — на -3:
и сложим почленное левые и правые части полученных уравнений:
Подставляем y=2 в первое уравнение системы и находим x:
Ответ: (-7; 2).
Прежде чем применить способ сложения, данную систему следует упростить. Умножим первое уравнение на наименьший общий знаменатель дробей, во втором раскроем скобки:
Получили систему линейных уравнений с двумя переменными. Для решения её способом сложения достаточно умножить второе уравнение на -1 и сложить почленно левые и правые части уравнений:
Для решения её способом сложения достаточно умножить второе уравнение на -1 и сложить почленно левые и правые части уравнений:
Подставляем найденное значение b в первое уравнение системы (линейных уравнений):
Ответ: (-3; 10).
Систему линейных уравнений с тремя переменными можно решить, сначала исключив одно из неизвестных, а затем — другое.
В данной системе проще всего исключить переменную z.
К первому уравнению прибавим третье, умноженное на -3:
Ко второму уравнению прибавим третье, умноженное на 2:
Получили систему линейных уравнений с двумя переменными:
НОК(8;10)=40, НОК(13; 7)=91. Проще работать с x:
Подставив полученные значение y во второе уравнение системы с двумя переменными, найдём x:
Подставив значения y и x в третье уравнение системы с тремя переменными, найдём z:
Ответ: (2; 0; -1).
Решение систем линейных уравнений способом сложения
Вопросы
занятия:
·
показать еще один способ решения систем линейных уравнений – способ сложения.
Материал
урока
Мы
с вами уже познакомились с двумя способами решения систем линейных уравнений с
двумя переменными, а именно, с графическим способом и способом подстановки.
На
этом уроке мы познакомимся с ещё одним способом решения систем линейных
уравнений, который называют способом сложения.
Рассмотрим
следующую систему
Обратите
внимание, что в уравнениях системы коэффициенты при переменной игрек –
противоположные числа. Сложим почленно левые и правые
части уравнений
Приведём
подобные слагаемые в обеих частях получившегося уравнения
Видим,
что получили уравнение с одной переменной.
Затем,
чтобы найти значение переменной игрек, мы подставим х = 3 в любое уравнение
системы, например, в первое. Снова получили уравнение с одной переменной у.
Снова получили уравнение с одной переменной у.
Решим его.
Убедиться
в этом вы можете, подставив эти значения в каждое уравнение системы.
Пример.
Пример.
Пример.
Можем
сделать вывод: чтобы решить систему линейных уравнений способом сложения, надо:
1)
умножить
почленно уравнения системы, подбирая множители так,
чтобы коэффициенты при одной из переменных стали противоположными числами;
2)
сложить
почленно левые и правые части уравнений системы;
3)
решить
получившееся уравнение с одной переменной;
4)
найти
соответствующее значение второй переменной.
При
этом следует помнить, что если коэффициенты при одной из переменных являются
противоположными числами, то решение системы сразу начинают с почленного сложения уравнений.
Урок на тему » Алгоритм решения систем линейных уравнений методом сложения»
Урок №
ТЕМА: Алгоритм решения систем
линейных уравнений способом сложения
Задачи: создать условия для развития умения решать системы двух линейных уравнений с двумя переменными методом сложения | ||
Планируемые результаты | ||
Предметные: познакомятся с алгоритмом решения системы двух линейных уравнений с двумя переменными методом сложения; научатся решать системы двух линейных уравнений с двумя переменными методом сложения | Метапредметные: познавательные ‒ ориентироваться на разнообразие способов решения задач; регулятивные ‒ учитывать правило в планировании и контроле способа решения; коммуникативные ‒ учитывать разные мнения и стремиться | Личностные: формировать интерес к изучению темы |
Образовательные ресурсы: 1) Видеоуроки. | ||
Ход урока
I. Устная работа.
1. Является ли пара чисел (4; –1) решением системы уравнений:
а) б) в)
2. Являются ли данные системы уравнений равносильными:
и
II. Объяснение нового материала.
Объяснение проводить согласно пункту 44 учебника в несколько этапов:
1. На примере 1 выявить суть способа сложения решения систем линейных уравнений.
2. Рассмотреть вопрос о равносильности систем уравнений и его геометрическую интерпретацию.
3. Рассмотреть пример 2 из учебника.
4. Вывести алгоритм решения систем линейных уравнений способом сложения.
Так же, как был записан алгоритм решения систем уравнений способом подстановки, учащиеся должны занести в тетради новый алгоритм вместе с примером.
Алгоритм
1-й шаг.
Умножить почленно уравнения системы на такие множители, чтобы коэффициенты при одной
из переменных стали противоположными
2-й шаг.
Сложить почленно левые и правые части
уравнений системы
3-й шаг.
Решить получившееся уравнение с одной
переменной
–х = –1,
х = 1.
4-й шаг.
Найти соответствующее значение второй
переменной
3·1+2у=–1,
2у=–4,
у=–2.
Ответ: (1; –2)
Системы, в которых нужно подбирать множители к обоим уравнениям, на этом уроке решать не нужно, поэтому пример 3 также лучше разобрать на следующем уроке.
III. Формирование умений и навыков.
В течение урока учащиеся должны запомнить алгоритм решения систем линейных уравнений способом сложения.
1. Умножьте одно из уравнений системы на какое-нибудь число так, чтобы с помощью сложения можно было исключить одну из переменных.
а) б) в)
2. № 1082.
Для решения каждой системы следует вызывать к доске по одному учащемуся. Требовать, чтобы они вслух комментировали все шаги решения.
Необходимо показать учащимся вариант оформления решения системы уравнений способом сложения.
Решение:
в)
2у = 60;
у = 30;
4х – 5 · 30 = 90;
4х = 240;
х = 60.
Ответ: (60; 30).
3. № 1084 (а, б, в).
Этот номер несколько сложнее предыдущего.
Учащимся придётся подбирать множитель, который сделает коэффициенты противоположными. Множитель лучше не «держать в уме», а записывать справа от уравнения.
Множитель лучше не «держать в уме», а записывать справа от уравнения.
Решение:
а)
15у = 0;
у = 0;
20х – 7 · 0 = 5;
20х = 5;
х = .
Ответ: .
IV. Итоги урока.
– Какие существуют способы решения систем уравнений?
– Сформулируйте алгоритм решения систем линейных уравнений способом сложения.
– Сколько решений может иметь система линейных уравнений?
Домашнее задание: № 1083; № 1085 (а, б).
Решение системы линейных уравнений методом сложения: алгоритм, примеры
Алгоритм решения системы линейных уравнений методом сложения
- Умножить обе части одного или обоих уравнений так, чтобы коэффициенты при одной из переменных стали противоположными (или равными) числами.

- Сложить (или отнять) уравнения, чтобы избавиться от одной из переменных.
- Решить второе уравнение относительно выраженной переменной.
- Решить полученное уравнение с одной переменной.
- Найти вторую переменную.
- Записать ответ в виде упорядоченной пары найденных значений переменных.
Например: $ {\left\{ \begin{array}{c} 3x+y = 5 \\ x+2y = 5 \end{array} \right.}$
Шаг 1
Умножаем первое уравнение на 2
${\left\{ \begin{array}{c} 6x+2y = 10 \\ x+2y = 5 \end{array} \right.}$
Шаг 2
Отнимаем от первого уравнения второе:
5x = 5
Шаг 3
Находим x:
x = 1
Шаг 4
Находим y из первого уравнения:
y = 5-3x = 2
Шаг 5
Ответ: (1;2)
В последовательной записи:
$$ {\left\{ \begin{array}{c} 3x+y = 5 | \times 2 \\ x+2y = 5 \end{array} \right.} \Rightarrow (-) {\left\{ \begin{array}{c} 6x+2y = 10 \\ x+2y = 5 \end{array} \right. } \Rightarrow {\left\{ \begin{array}{c} 5x = 5 \\ x+2y = 5 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} x = 1 \\ y = 5-3x = 2 \end{array} \right.} $$
} \Rightarrow {\left\{ \begin{array}{c} 5x = 5 \\ x+2y = 5 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} x = 1 \\ y = 5-3x = 2 \end{array} \right.} $$
Ответ: (1;2)
Примеры
Пример 1. Решите систему уравнений методом сложения:
$ а) {\left\{ \begin{array}{c} 5x-4y = 3 | \times 2 \\ 2x-3y = 4 | \times 5 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 10x-8y = 6 \\ 10x-15y = 20 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 7y = -14 \\ 2x-3y = 4 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} x = \frac{3y+4}{2} = -1 \\ y=-2 \end{array} \right.} $
Ответ: (-1;-2)
$ б) {\left\{ \begin{array}{c} 4x-3y = 7 | \times 3 \\ 3x-4y = 0 | \times 4 \end{array} \right.} \Rightarrow (-) {\left\{ \begin{array}{c} 12x-9y = 21 \\ 12x-16y = 0 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 7y = 21 \\ x = \frac{4}{3} y \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} x = 4 \\ y = 3 \end{array} \right. } $
} $
Ответ: (4;3)
$ в) {\left\{ \begin{array}{c} 5a-4b = 9 | \times 2 \\ 2a+3b = -1 | \times 5 \end{array} \right.} \Rightarrow (-) {\left\{ \begin{array}{c} 10a-8b = 18 \\ 10a+15b = -5 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} -23b = 23 \\ a = \frac{-3b-1}{2} \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} a = 1 \\ b = -1 \end{array} \right.} $
Ответ: (1;-1)
$ г) {\left\{ \begin{array}{c} 7a+4b = 5 \\ 3a+2b = 1 | \times (-2) \end{array} \right.} \Rightarrow (+) {\left\{ \begin{array}{c} 7a+4b = 5 \\ -6a-4b = -2 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} a = 3 \\ b = \frac{1-3a}{2} \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} a = 3 \\ b = -4 \end{array} \right.}$
Ответ: (3;-4)
Пример 2. Найдите решение системы уравнений:
$$а) {\left\{ \begin{array}{c} \frac{x}{4}-y = 7 \\ 3x+ \frac{y}{2} = 9 | \times 2\end{array} \right.} \Rightarrow (+) {\left\{ \begin{array}{c} \frac{x}{4} -y = 7 \\ 6x+y = 18 \end{array} \right. } \Rightarrow {\left\{ \begin{array}{c} 6 \frac{1}{4} x = 25 \\ y = 18-6x\end{array} \right.} \Rightarrow $$
} \Rightarrow {\left\{ \begin{array}{c} 6 \frac{1}{4} x = 25 \\ y = 18-6x\end{array} \right.} \Rightarrow $$
$$\Rightarrow {\left\{ \begin{array}{c} x = 25: \frac{25}{4} = 25 \cdot \frac{4}{25} = 4 \\ y = 18-6 \cdot 4 = -6 \end{array} \right.} $$
Ответ: (4;-6)
$б) {\left\{ \begin{array}{c} \frac{x}{2}+ \frac{y}{3} = \frac{1}{6} |\times 2 \\ \frac{x}{3}+ \frac{y}{2} = -\frac{1}{6}| \times 3 \end{array} \right.}\Rightarrow (-) {\left\{ \begin{array}{c} x+ \frac{2}{3} y = \frac{1}{3} \\ x+ \frac{3}{2} y = — \frac{1}{2} \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} \left( \frac{2}{3}- \frac{3}{2}\right) y = \frac{1}{3}+ \frac{1}{2} \\ x = \frac{1}{3}- \frac{2}{3} y\end{array} \right.} \Rightarrow$
$$ \Rightarrow {\left\{ \begin{array}{c} y = \frac{5}{6}:\left(-\frac{5}{6}\right) = -1 \\ x = \frac{1}{3}+ \frac{2}{3} = 1\end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} x = 1 \\ y = -1 \end{array} \right.} $$
Ответ: (1;-1)
$ в) {\left\{ \begin{array}{c} 3(5x-y)+14 = 5(x+y) \\ 2(x-y)+9 = 3(x+2y)-16 \end{array} \right. } \Rightarrow {\left\{ \begin{array}{c} 15x-3y+14 = 5x+5y \\ 2x-2y+9 = 3x+6y-16 \end{array} \right.} \Rightarrow $
} \Rightarrow {\left\{ \begin{array}{c} 15x-3y+14 = 5x+5y \\ 2x-2y+9 = 3x+6y-16 \end{array} \right.} \Rightarrow $
$$ \Rightarrow (+) {\left\{ \begin{array}{c} 10x-8y = -14 \\ x+8y = 25 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 11x = 11 \\ y = \frac{25-x}{8} \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} x = 1 \\ y = 3 \end{array} \right.}$$
Ответ: (1;3)
$ г) {\left\{ \begin{array}{c} 5-3(2x+7y) = x+y-52 \\ 4+3(7x+2y) = 23x \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 5-6x-21y = x+y-52 \\ 4+21x+6y = 23x \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 7x+22y = 57 \\ 2x-6y = 4 |:2 \end{array} \right.}$
$$ \Rightarrow {\left\{ \begin{array}{c} 7x+22y = 57 \\ x-3y = 2 | \times 7 \end{array} \right.} \Rightarrow (-) {\left\{ \begin{array}{c} 7x+22y = 57 \\ 7x-21y = 14 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 43y = 43 \\ x = 3y+2 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} x = 5 \\ y = 1 \end{array} \right. }$$
}$$
Ответ: (5;1)
Пример 3*. Найдите решение системы уравнений:
$ {\left\{ \begin{array}{c} \frac{2}{x} + \frac{3}{y} = 1 \\ \frac{3}{x} — \frac{5}{y} = 11 \end{array} \right.} $
Введём новые переменные: $ {\left\{ \begin{array}{c} a = \frac{1}{x} \\ b = \frac{1}{y} \end{array} \right.} $
Перепишем систему и найдём решение для новых переменных:
$$ {\left\{ \begin{array}{c}2a+3b = 1| \times 3 \\ 3a-5b = 11 | \times 2 \end{array} \right.} \Rightarrow (-) {\left\{ \begin{array}{c} 6a+9b = 3 \\ 6a-10b = 22 \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} 19b = -19 \\ a = \frac{1-3b}{2} \end{array} \right.} \Rightarrow {\left\{ \begin{array}{c} a = 2 \\ b = -1 \end{array} \right.} $$
Исходные переменные:
$$ {\left\{ \begin{array}{c} x = \frac{1}{a} = \frac{1}{2} \\ y = \frac{1}{b} = -1 \end{array} \right.} $$
Ответ:$ \left(\frac{1}{2} ;-1 \right)$
9 класс. Алгебра. Системы уравнений. — Решение систем уравнений методом сложения.

Комментарии преподавателя
На этом уроке мы продолжим изучение метод решения систем уравнений, а именно: метода алгебраического сложения. Вначале рассмотрим применение этого метода на примере линейных уравнений и его суть. Также вспомним, как уравнивать коэффициенты в уравнениях. И решим ряд задач на применение этого метода.
Тема: Системы уравнений
Урок: Метод алгебраического сложения
Рассмотрим метод алгебраического сложения на примере линейных систем.
Пример 1. Решить систему
Решение:
Если мы сложим эти два уравнения, то y взаимно уничтожатся, и останется уравнение относительно x.
Если же вычтем из первого уравнения второе, взаимно уничтожатся x, и мы получим уравнение относительно y. В этом и заключается смысл метода алгебраического сложения.
Ответ:
Мы решили систему и вспомнили метод алгебраического сложения. Повторим его суть: мы можем складывать и вычитать уравнения, но при этом необходимо обеспечить, чтобы получилось уравнение только с одним неизвестным.
Пример 2. Решить систему
Решение:
Член присутствует в обоих уравнениях, поэтому удобен метод алгебраического сложения. Вычтем из первого уравнения второе.
Ответ: (2; -1).
Таким образом, проанализировав систему уравнений, можно увидеть, что она удобна для метода алгебраического сложения, и применить его.
Рассмотрим еще одну линейную систему.
Пример 3. Решить систему
Решение:
Мы хотим избавиться от y, но в двух уравнениях коэффициенты при y разные. Уравняем их, для этого умножим первое уравнение на 3, второе – на 4.
Ответ:
Пример 4. Решить систему
Решить систему
Решение:
Уравняем коэффициенты при x
Можно сделать иначе – уравнять коэффициенты при y.
Ответ:
Мы решили систему, дважды применив метод алгебраического сложения.
Метод алгебраического сложения применим и при решении нелинейных систем.
Пример 5. Решить систему
Решение:
Сложим эти уравнения, и мы избавимся от y.
Эту же систему можно решить, дважды применив метод алгебраического сложения. Сложим и вычтем из одного уравнения другое.
Ответ:
Пример 6. Решить систему
Решение:
Ответ:
Пример 7. Решить систему
Решение:
Методом алгебраического сложения избавимся от члена xy. Умножим первое уравнение на .
Первое уравнение остается без изменений, вместо второго записываем алгебраическую сумму.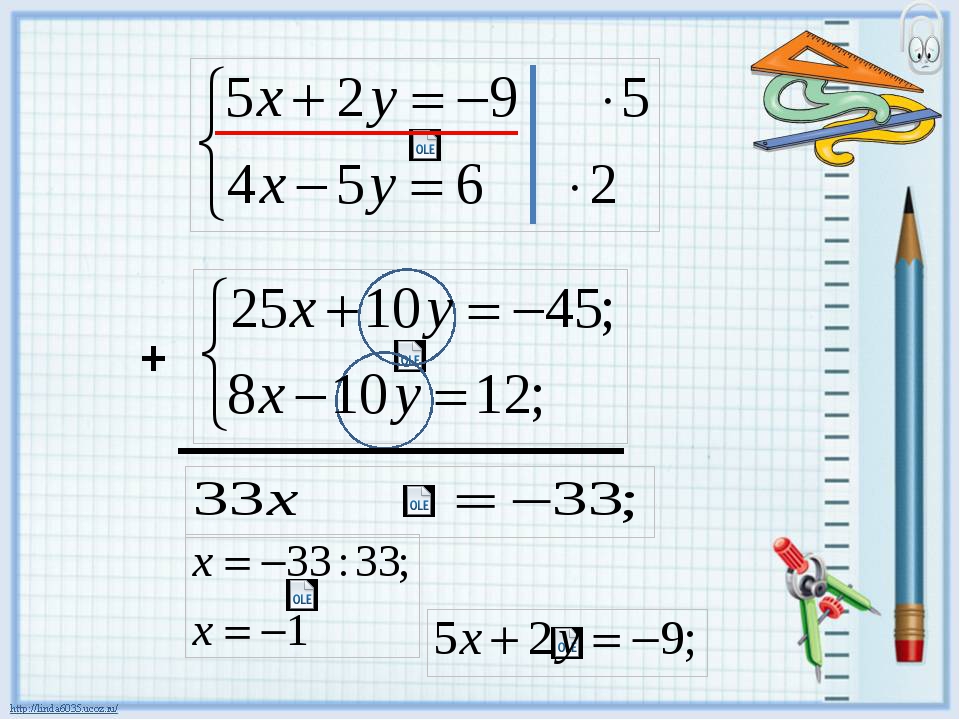
Далее применяем метод подстановки.
Ответ:
Пример 8. Решить систему
Решение:
Умножим второе уравнение на 2, чтобы выделить полный квадрат.
Наша задача свелась к решению четырех простейших систем.
Ответ:
Источник видео: http://interneturok.ru/ru/school/algebra/9-klass/sistemy-uravneniy/metod-algebraicheskogo-slozheniya-2?konspekt&chapter_id=26
Источник видео: http://www.youtube.com/watch?v=JMxiXlG_FzM
Файлы
Нет дополнительных материалов для этого занятия.
Решение систем линейных уравнений. 7 класс
1. Решение систем линейных уравнений
Алгебра (7 класс)
Решение систем
линейных уравнений
Учитель математики
Васютина Е.Г.
Лицей 126
Санкт-Петербург, 2014
2. Способ сложения при решении систем линейных уравнений
3.
 Способ сложения
Способ сложения
Этот способ используют
тогда, когда нет
коэффициентов при x или y
равных 1 или -1.
4. Способ сложения
Задача 1. Решить систему уравнений
7 x 2 y 27, (1)
5 x 2 y 33. (2)
В тех случаях, когда в обоих линейных уравнениях
системы при каком-либо из неизвестных
коэффициентами являются противоположные числа,
удобно применять способ алгебраического сложения
уравнений.
5. Способ сложения
Задача 1. Решить систему уравнений
7 x 2 y 27, (1)
5 x 2 y 33. (2)
Сложим эти
равенства почленно.
В результате
получим тоже
верное равенство,
так как к равному
прибавляли равное.
Предположим, что числа x
и y ─ решения системы,
при которых оба равенства
системы равны.
7 x 2 y 27,
+
5 x 2 y 33.
12 x 60
x 5
Откуда
6. Способ сложения
Задача 1. Решить систему уравнений
Вернемся в систему, записав
одно из исходных уравнений и
полученное значение x.
7 x 2 y 27, (1)
5 x 2 y 33. (2)
x 5, (1)
5 x 2 y 33. (2)
5 5 2 y 33,
2 y 33 25,
2 y 8; y 4.
Подставим найденное значение
x во второе уравнение, найдем
вторую неизвестную.
Тогда пара чисел (5; 4) и будет
решением системы.
Ответ: x 5, y 4
7. Способ сложения
Задача 2. Решить систему уравнений
1) Выберем неизвестную
(1) (например x),
2 x 5 y 1,
3 x 4 y 5. ( 2)
уравняем коэффициенты
при умножением на
соответствующие числа.
2 x 5 y 1, 3
2
3
x
4
y
5
8. Способ сложения
Задача 2. Решить систему уравнений
1) Выберем неизвестную
(1) (например x),
2 x 5 y 1,
3 x 4 y 5. ( 2)
уравняем коэффициенты
при умножением на
соответствующие числа.
2) Вычтем одно
уравнение из другого.
─
6 x 15 y 3,
6 x 8 y 10.
9. Способ сложения
Задача 2. Решить систему уравнений
1) Выберем неизвестную
(1) (например x),
2 x 5 1,
3x 4 y 5. (2)
(2)
уравняем коэффициенты
при умножением на
соответствующие числа.
2) Вычтем одно
уравнение из другого.
6 x 15 y 3,
6 x 8 y 10.
7y 7
10. Способ сложения
2) Вычтем одно
уравнение из другого.
6 x 15 y 3,
6 x 8 y 10.
3) Решим полученное
уравнение с одним
неизвестным
4) Вернемся в систему,
записав одно из исходных
уравнений и полученное
значение y
7y 7
7 y 7,
y 1
2 x 5 y 1, (1)
y 1. ( 2)
11. Способ сложения
4) Вернемся в систему,
записав одно из исходных
уравнений и полученное
значение y
2 x 5 y 1, (1)
y 1. ( 2)
5) Подставим найденное
2 x 5 1 1,
значение y в первое
2 x 6,
x 3.
уравнение, найдем
вторую неизвестную.
Тогда пара чисел (-3; 1) и будет решением системы.
Ответ: x 3, y 1
12. Способ сложения (алгоритм)
Уравнять модули коэффициентов при
какой-нибудь переменной
Сложить почленно уравнения системы
Составить новую систему: одно уравнение
новое, другое — одно из старых
Решить новое уравнение и найти значение
одной переменной
Подставить значение найденной
переменной в старое уравнение и найти
значение другой переменной
Записать ответ: х =…; у =… .
Разберем вместе решение
следующих систем:
5 x 3 y 29,
1.
5 x 4 y 8.
4 x 3 y 14,
3.
x 2 y 2.
3 x 2 y 10,
2.
5 x 3 y 12.
3 x 5 y 2,
4.
7 x 15 y 8.
Решите следующие системы
методом сложения:
2 x 5 y 15, (1)
1.
3x 2 y 6. (2)
4 x 5 y 3, (1)
3.
3x 2 y 11. (2)
2 x 4 y 6, (1)
2.
3 x 2 y 25. ( 2)
5 x 6 y 13, (1)
4.
7 x 18 y 1. (2)
15. Способ сложения при решении систем линейных уравнений
Домашнее задание:
§35 № 633-636 (1,3)
16. Урок закончен.
Спасибо.
До встречи на
следующем уроке!
Решение уравнений методом сложения. Калькулятор онлайн
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.

- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
ОГБОУ «Центр образования для детей с особыми образовательными потребностями г. Смоленска»
Центр дистанционного образования
Урок алгебры в 7 классе
Тема урока: Метод алгебраического сложения.
- Тип урока: Урок первичного предъявления новых знаний.
Цель урока: контроль уровня усвоения знаний и умений решения систем уравнений способом подстановки; формирование умений и навыков решения систем уравнений способом сложения.
Задачи урока:
Предметные: научиться выполнять решения систем уравнений с двумя переменными методом сложения.
Метапредметные: Познавательные УУД
: анализировать (выделять главное), определять понятия, обобщать, делать выводы. Регулятивные УУД
: определять цель, проблему в учебной деятельности. Коммуникативные УУД
: излагать своё мнение, аргументируя его. Личностные УУД: ф
ормировать положительную мотивацию к обучению, создавать позитивное эмоциональное отношение обучающегося к уроку и предмету.
Форма работы: индивидуальная
Этапы урока:
1) Организационный этап.
организовать работу обучающейся по теме через создание установки на целостность мышления и понимание данной темы.
2. Опрос обучающейся по заданному на дом материалу, актуализация знаний.
Цель: проверить знания обучающейся, полученные в ходе выполнения домашней работы, выявить ошибки, сделать работу над ошибками. Повторить материал прошлого урока.
3. Изучение нового материала.
1). формировать умение решать системы линейных уравнений способом сложения;
2). развивать и совершенствовать имеющиеся знания в новых ситуациях;
3). воспитывать навыки контроля и самоконтроля, развивать самостоятельность.
http://zhakulina20090612.blogspot.ru/2011/06/blog-post_25.html
Цель: сохранение зрения, снятие усталости с глазво время работы на уроке.
5. Закрепление изученного материала
Цель: проверить знания, умения и навыки, полученные на уроке
6. Итог урока, информация о домашнем задании, рефлексия.
Ход урока (работа в электронном документе Google):
1. Сегодня урок я хотела начать с философской загадки Вальтера.
Что самое быстрое, но и самое медленное, самое большое, но и самое маленькое, самое продолжительное и короткое, самое дорогое, но и дешево ценимое нами?
Время
Вспомним основные понятия по теме:
Перед нами система двух уравнений.
Вспомним, как мы решали системы уравнений на прошлом уроке.
Методом подстановки
Еще раз обрати внимание на решенную систему и скажи, почему мы не можем решить каждое уравнение системы не прибегая к методу подстановки?
Потому что это — уравнения системы с двумя переменными. Мы умеем решать уравнение только с одной переменной.
Только получив уравнение с одной переменной нам удалось решить систему уравнений.
3. Мы приступаем к решению следующей системы:
Выберем уравнение, в котором удобно одну переменную выразить через другую.
Такого уравнения нет.
Т.е. в данной ситуации нам не подходит изученный ранее метод. Какой выход из данной ситуации?
Найти новый метод.
Попытаемся сформулировать цель урока.
Научиться решать системы новым методом.
Что нам необходимо сделать, чтобы научиться решать системы новым методом?
знать правила (алгоритм) решения системы уравнения, выполнить практические задания
Приступим к выведению нового метода.
Обрати внимание на вывод, который мы сделали после решения первой системы. Решить систему удалось только после того, как мы получили линейное уравнение с одной переменной.
Посмотри на систему уравнений и подумай, как из двух данных уравнений получить одно уравнение с одной переменной.
Сложить уравнения.
Что значит сложить уравнения?
По отдельности составить сумму левых частей, сумму правых частей уравнений и полученные суммы приравнять.
Попробуем. Работаем вместе со мной.
13x+14x+17y-17y=43+11
Получили линейное уравнение с одной переменной.
Решили систему уравнений?
Решение системы — пара чисел.
Как найти у?
Найденное значение х подставить в уравнение системы.
Имеет значение, в какое уравнение подставим значение х?
Значит найденное значение х можно подставить в…
любое уравнение системы.
Мы познакомились с новым методом — методом алгебраического сложения.
Решая систему, мы проговорили алгоритм решения системы данным методом.
Алгоритм мы рассмотрели. Теперь применим его к решению задач.
Умение решать системы уравнений может пригодится в практике.
Рассмотрим задачу:
В хозяйстве имеются куры и овцы. Сколько тех и других, если у них вместе 19 голов и 46 ног?
Зная, что всего кур и овец 19, составим первое уравнение: х + у =19
4х — число ног у овец
2у — число ног у кур
Зная, что всего 46 ног, составим второе уравнение: 4х + 2у =46
Составим систему уравнений:
Решим систему уравнений, применяя алгоритм решения методом сложения.
Проблема! Коэффициенты перед х и у — не равные и не противоположные! Что же делать?
Рассмотрим ещё один пример!
Добавим в наш алгоритм ещё один шаг и поставим его на первое место: Если коэффициенты перед переменными- не одинаковые и не противоположные, то надо уравнять модули при какой-нибудь переменной! А далее уже будем действовать по алгоритму.
4. Электронная физкультминутка для глаз: http://zhakulina20090612.blogspot.ru/2011/06/blog-post_25.html
5. Дорешаем задачу методом алгебраического сложения, закрепив новый материал и узнаем, сколько же кур и овец было в хозяйстве.
Дополнительные задания:
6.
Рефлексия.
Я за свою работу на уроке ставлю оценку — …
6. Использованные ресурсы-интернет:
сервисы Google для образования
Учитель математики Соколова Н. Н.
Системой линейных уравнений с двумя неизвестными — это два или несколько линейных уравнений, для которых необходимо найти все их общие решения. Мы будем рассматривать системы из двух линейных уравнений с двумя неизвестными. Общий вид системы из двух линейных уравнений с двумя неизвестными представлен на рисунке ниже:
{ a1*x + b1*y = c1,
{ a2*x + b2*y = c2
Здесь х и у неизвестные переменные, a1,a2,b1,b2,с1,с2 — некоторые вещественные числа. Решением системы двух линейных уравнений с двумя неизвестными называют пару чисел (x,y) такую, что если подставить эти числа в уравнения системы, то каждое из уравнений системы обращается в верное равенство. Существует несколько способов решения системы линейных уравнений. Рассмотрим один из способов решения системы линейных уравнений, а именно способ сложения.
Алгоритм решения способом сложения
Алгоритм решения системы линейных уравнений с двумя неизвестными способом сложения.
1. Если требуется, путем равносильных преобразований уравнять коэффициенты при одной из неизвестных переменных в обоих уравнениях.
2. Складывая или вычитая полученные уравнения получить линейное уравнение с одним неизвестным
3. Решить полученное уравнение с одним неизвестным и найти одну из переменных.
4. Подставить полученное выражение в любое из двух уравнений системы и решить это уравнение, получив, таким образом, вторую переменную.
5. Сделать проверку решения.
Пример решения способом сложения
Для большей наглядности решим способом сложения следующую систему линейных уравнений с двумя неизвестными:
{3*x + 2*y = 10;
{5*x + 3*y = 12;
Так как, одинаковых коэффициентов нет ни у одной из переменных, уравняем коэффициенты у переменной у. Для этого умножим первое уравнение на три, а второе уравнение на два.
{3*x+2*y=10 |*3
{5*x + 3*y = 12 |*2
Получим следующую систему уравнений:
{9*x+6*y = 30;
{10*x+6*y=24;
Теперь из второго уравнения вычитаем первое. Приводим подобные слагаемые и решаем полученное линейное уравнение.
10*x+6*y — (9*x+6*y) = 24-30; x=-6;
Полученное значение подставляем в первое уравнение из нашей исходной системы и решаем получившееся уравнение.
{3*(-6) + 2*y =10;
{2*y=28; y =14;
Получилась пара чисел x=6 и y=14. Проводим проверку. Делаем подстановку.
{3*x + 2*y = 10;
{5*x + 3*y = 12;
{3*(-6) + 2*(14) = 10;
{5*(-6) + 3*(14) = 12;
{10 = 10;
{12=12;
Как видите, получились два верных равенства, следовательно, мы нашли верное решение.
Методом сложения, уравнения системы почленно складывают, при этом 1-но либо оба (несколько) уравнений можно умножить на любое число. В результате приходят к равнозначной СЛУ , где в одном из уравнений есть лишь одна переменная.
Для решения системы способом почленного сложения (вычитания)
следуйте следующим шагам:
1. Выбираем переменную, у которой будут делаться одинаковые коэффициенты.
2. Теперь нужно сложить либо вычесть уравнения и получим уравнение с одной переменной.
Решение системы
— это точки пересечения графиков функции.
Рассмотрим на примерах.
Пример 1.
Дана система:
Проанализировав эту систему можно заметить, что коэффициенты при переменной равны по модулю и разные по знаку (-1 и 1). В таком случае уравнения легко сложить почленно:
Действия, которые обведены красным цветом, выполняем в уме.
Результатом почленного сложения стало исчезновение переменной y
. Именно в этом и В этом, собственно, и заключается смысл метода — избавиться от 1-ой из переменных.
-4 —
y
+ 5 = 0 →
y
= 1,
В виде системы решение выглядит где-то так:
Ответ: x
=
-4
,
y
=
1.
Пример 2.
Дана система:
В этом примере можете пользоваться «школьным» методом, но в нем есть немаленький минус — когда вы будете выражать любую переменную из любого уравнения, то получите решение в обыкновенных дробях . А решение дробей занимает достаточно времени и вероятность допущения ошибок увеличивается.
Поэтому лучше пользоваться почленным сложением (вычитанием) уравнений. Проанализируем коэффициенты у соответствующих переменных:
Нужно подобрать число, которое можно поделить и на 3
и на 4
, при этом нужно, что бы это число было минимально возможным. Это наименьшее общее кратное
. Если вам тяжело подобрать подходящее число, то можете перемножить коэффициенты: .
Следующий шаг:
1-е уравнение умножаем на ,
3-е уравнение умножаем на ,
Системы уравнений получили широкое применение в экономической отрасли при математическом моделировании различных процессов. Например, при решении задач управления и планирования производства, логистических маршрутов (транспортная задача) или размещения оборудования.
Системы уравнения используются не только в области математики, но и физики, химии и биологии, при решении задач по нахождению численности популяции.
Системой линейных уравнений называют два и более уравнения с несколькими переменными, для которых необходимо найти общее решение. Такую последовательность чисел, при которых все уравнения станут верными равенствами или доказать, что последовательности не существует.
Линейное уравнение
Уравнения вида ax+by=c называют линейными. Обозначения x, y — это неизвестные, значение которых надо найти, b, a — коэффициенты при переменных, c — свободный член уравнения.
Решение уравнение путем построение его графика будет иметь вид прямой, все точки которой являются решением многочлена.
Виды систем линейных уравнений
Наиболее простыми считаются примеры систем линейных уравнений с двумя переменными X и Y.
F1(x, y) = 0 и F2(x, y) = 0, где F1,2 — функции, а (x, y) — переменные функций.
Решить систему уравнений —
это значит найти такие значения (x, y), при которых система превращается в верное равенство или установить, что подходящих значений x и y не существует.
Пара значений (x, y), записанная в виде координат точки, называется решением системы линейных уравнений.
Если системы имеют одно общее решение или решения не существует их называют равносильными.
Однородными системами линейных уравнений являются системы правая часть которых равна нулю. Если правая после знака «равенство» часть имеет значение или выражена функцией, такая система неоднородна.
Количество переменных может быть гораздо больше двух, тогда следует говорить о примере системы линейных уравнений с тремя переменными или более.
Сталкиваясь с системами школьники предполагают, что количество уравнений обязательно должно совпадать с количеством неизвестных, но это не так. Количество уравнений в системе не зависит от переменных, их может быть сколь угодно много.
Простые и сложные методы решения систем уравнений
Не существует общего аналитического способа решения подобных систем, все методы основаны на численных решениях. В школьном курсе математики подробно описаны такие методы как перестановка, алгебраическое сложение, подстановка, а так же графический и матричный способ, решение методом Гаусса.
Основная задача при обучении способам решения — это научить правильно анализировать систему и находить оптимальный алгоритм решения для каждого примера. Главное не вызубрить систему правил и действий для каждого способа, а понять принципы применения того или иного метода
Решение примеров систем линейных уравнений 7 класса программы общеобразовательной школы довольно простое и объяснено очень подробно. В любом учебнике математике этому разделу отводится достаточно внимания. Решение примеров систем линейных уравнений методом Гаусса и Крамера более подробно изучают на первых курсах высших учебных заведений.
Решение систем методом подстановки
Действия метода подстановки направлены на выражение значения одной переменной через вторую. Выражение подставляется в оставшееся уравнение, затем его приводят к виду с одной переменной. Действие повторяется в зависимости от количества неизвестных в системе
Приведем решение примера системы линейных уравнений 7 класса методом подстановки:
Как видно из примера, переменная x была выражена через F(X) = 7 + Y. Полученное выражение, подставленное во 2-е уравнение системы на место X, помогло получить одну переменную Y во 2-е уравнении. Решение данного примера не вызывает трудностей и позволяет получить значение Y. Последний шаг это проверка полученных значений.
Решить пример системы линейных уравнений подстановкой не всегда возможно. Уравнения могут быть сложными и выражение переменной через вторую неизвестную окажется слишком громоздким для дальнейших вычислений. Когда неизвестных в системе больше 3-х решение подстановкой также нецелесообразно.
Решение примера системы линейных неоднородных уравнений:
Решение с помощью алгебраического сложения
При поиске решении систем методом сложения производят почленное сложение и умножение уравнений на различные числа. Конечной целью математических действий является уравнение с одной переменной.
Для применений данного метода необходима практика и наблюдательность. Решить систему линейных уравнений методом сложения при количестве переменных 3 и более непросто. Алгебраическое сложение удобно применять когда в уравнениях присутствуют дроби и десятичные числа.
Алгоритм действий решения:
- Умножить обе части уравнения на некое число. В результате арифметического действия один из коэффициентов при переменной должен стать равным 1.
- Почленно сложить полученное выражение и найти одно из неизвестных.
- Подставить полученное значение во 2-е уравнение системы для поиска оставшейся переменной.
Способ решения введением новой переменной
Новую переменную можно вводить, если в системе требуется найти решение не более чем для двух уравнений, количество неизвестных тоже должно быть не больше двух.
Способ используется, чтобы упростить одно из уравнений, вводом новой переменной. Новое уравнение решается относительно введенной неизвестной, а полученное значение используется для определения первоначальной переменной.
Из примера видно, что введя новую переменную t удалось свести 1-е уравнение системы к стандартному квадратному трехчлену. Решить многочлен можно отыскав дискриминант.
Необходимо найти значение дискриминанта по известной формуле: D = b2 — 4*a*c, где D — искомый дискриминант, b, a, c — множители многочлена. В заданном примере a=1, b=16, c=39, следовательно, D=100. Если дискриминант больше нуля, то решений два: t = -b±√D / 2*a, если дискриминант меньше нуля, то решение одно: x= -b / 2*a.
Решение для полученных в итоге системы находят методом сложения.
Наглядный метод решения систем
Подходит для систем с 3-мя уравнениями. Метод заключается в построении на координатной оси графиков каждого уравнения, входящего в систему. Координаты точек пересечения кривых и будут общим решением системы.
Графический способ имеет ряд нюансов. Рассмотрим несколько примеров решения систем линейных уравнений наглядным способом.
Как видно из примера, для каждой прямой было построено две точки, значения переменной x были выбраны произвольно: 0 и 3. Исходя из значений x, найдены значения для y: 3 и 0. Точки с координатами (0, 3) и (3, 0) были отмечены на графике и соединены линией.
Действия необходимо повторить для второго уравнения. Точка пересечения прямых является решением системы.
В следующем примере требуется найти графическое решение системы линейных уравнений: 0,5x-y+2=0 и 0,5x-y-1=0.
Как видно из примера, система не имеет решения, потому что графики параллельны и не пересекаются на всем своем протяжении.
Системы из примеров 2 и 3 похожи, но при построении становится очевидно, что их решения разные. Следует помнить, что не всегда можно сказать имеет ли система решение или нет, всегда необходимо построить график.
Матрица и ее разновидности
Матрицы используются для краткой записи системы линейных уравнений. Матрицей называют таблицу специального вида, заполненную числами. n*m имеет n — строк и m — столбцов.
Матрица является квадратной, когда количество столбцов и строк равно между собой. Матрицей — вектором называется матрица из одного столбца с бесконечно возможным количеством строк. Матрица с единицами по одной из диагоналей и прочими нулевыми элементами называется единичной.
Обратная матрица — это такая матрица при умножении на которую исходная превращается в единичную, такая матрица существует только для исходной квадратной.
Правила преобразования системы уравнений в матрицу
Применительно к системам уравнений в качестве чисел матрицы записывают коэффициенты и свободные члены уравнений, одно уравнение — одна строка матрицы.
Строка матрицы называется ненулевой, если хотя бы один элемент строки не равен нулю. Поэтому если в каком-либо из уравнений количество переменных разнится, то необходимо на месте отсутствующей неизвестной вписать нуль.
Столбцы матрицы должны строго соответствовать переменным. Это означает что коэффициенты переменной x могут быть записаны только в один столбец, например первый, коэффициент неизвестной y — только во второй.
При умножении матрицы все элементы матрицы последовательно умножаются на число.
Варианты нахождения обратной матрицы
Формула нахождения обратной матрицы довольно проста: K -1 = 1 / |K|, где K -1 — обратная матрица, а |K| — определитель матрицы. |K| не должен быть равен нулю, тогда система имеет решение.
Определитель легко вычисляется для матрицы «два на два», необходимо лишь помножить друг на друга элементы по диагонали. Для варианта «три на три» существует формула |K|=a 1 b 2 c 3 + a 1 b 3 c 2 + a 3 b 1 c 2 + a 2 b 3 c 1 + a 2 b 1 c 3 + a 3 b 2 c 1 . Можно воспользоваться формулой, а можно запомнить что необходимо взять по одному элементу из каждой строки и каждого столбца так, чтобы в произведении не повторялись номера столбцов и строк элементов.
Решение примеров систем линейных уравнений матричным методом
Матричный способ поиска решения позволяет сократить громоздкие записи при решении систем с большим количеством переменных и уравнений.
В примере a nm — коэффициенты уравнений, матрица — вектор x n — переменные, а b n — свободные члены.
Решение систем методом Гаусса
В высшей математике способ Гаусса изучают совместно с методом Крамера, а процесс поиска решения систем так и называется метод решения Гаусса — Крамера. Данные способы используют при нахождении переменных систем с большим количеством линейных уравнений.
Метод Гаусса очень похож на решения с помощью подстановок и алгебраического сложения, но более систематичен. В школьном курсе решение способом Гаусса применяется для систем из 3 и 4 уравнений. Цель метода состоит в приведении системы к виду перевернутой трапеции. Путем алгебраических преобразований и подстановок находится значение одной переменной в одном из уравнении системы. Второе уравнение представляет собой выражение с 2-мя неизвестными, ну а 3 и 4 — соответственно с 3-мя и 4-мя переменными.
После приведения системы к описанному виду, дальнейшее решение сводится к последовательной подстановке известных переменных в уравнения системы.
В школьных учебниках для 7 класса пример решения методом Гаусса описан следующим образом:
Как видно из примера, на шаге (3) было получено два уравнения 3x 3 -2x 4 =11 и 3x 3 +2x 4 =7. Решение любого из уравнений позволит узнать одну из переменных x n .
Теорема 5, о которой упоминается в тексте, гласит что если одно из уравнений системы заменить равносильным, то полученная система будет также равносильна исходной.
Метод Гаусса труден для восприятия учеников средней школы, но является одним из наиболее интересных способов для развития смекалки детей, обучающихся по программе углубленного изучения в математических и физических классах.
Для простоты записи вычислений принято делать следующим образом:
Коэффициенты уравнений и свободные члены записываются в виде матрицы, где каждая строка матрицы соотносится с одним из уравнений системы. отделяет левую часть уравнения от правой. Римскими цифрами обозначаются номера уравнений в системе.
Сначала записывают матрицу, с которой предстоит работать, затем все действия проводимые с одной из строк. Полученную матрицу записывают после знака «стрелка» и продолжают выполнять необходимые алгебраические действия до достижения результата.
В итоге должна получиться матрица в которой по одной из диагоналей стоят 1, а все другие коэффициенты равны нулю, то есть матрицу приводят к единичному виду. Нельзя забывать производить вычисления с цифрами обеих частей уравнения.
Данный способ записи менее громоздкий и позволяет не отвлекаться на перечисление многочисленных неизвестных.
Свободное применение любого способа решения потребует внимательности и определенного опыта. Не все методы имеют прикладной характер. Какие-то способы поиска решений более предпочтительны в той иной области деятельности людей, а другие существуют в целях обучения.
TEMAX Система складных дверей с полным доступом на 180 градусов TM034 —
| Цена: | 119 долларов.98 +2,79 $ |
- Убедитесь, что это подходит
введя номер вашей модели. - Имя: 180-градусная складная дверная система с полным доступом
- Att: Свяжитесь с нами перед покупкой!
- Материал: 201 нержавеющая сталь + латунь
- Максимальный вес двери: 40 кг на комплект
- Размер: полностью открытый / закрытый Длина: 690 мм Половина открытого размера: L 484 мм, W 314 мм
›
См. Дополнительные сведения о продукте
| Если это наружное или тяжелое применение, пожалуйста, свяжитесь с нами или ознакомьтесь с другими нашими страницами | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Наружное смещение Сгибание конца | Центральная складка | Двери штабелирования | Внешний центр Фальцовка с подвесом | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Best for Exterior Лучшие погодные уплотнения | Лучше всего для перегородки | Лучшее в качестве разделителя помещения Применение для тяжелых дверей | Лучшее для патио Уплотнение для защиты от погодных условий | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3-дверная система от 2500 $ | 3-дверная направляющая и ролики от 500 $.00 | 3-дверная направляющая и ролики от 2200 $ | 3-дверная направляющая и ролики от 2200 $ | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Нижний направляющий канал Требуется | Нижний направляющий канал Рекомендуется | Нижний направляющий канал Рекомендуется | Нижний направляющий канал Требуется | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
J200 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 125 # Макс.вес створки двери | 2 дверных компонента | Максимальная ширина двери 36 дюймов | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1 — 200 Гусеница Требуются стандартные стыковые петли, но не входят в комплект Инструкции | 2-дверная система 4 ‘направляющая 80 $.00 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4-дверная система 94 «направляющая $ 160,00 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
J100 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 75 # Макс.вес створки двери | 2 дверных компонента | Максимальная ширина двери 24 дюйма | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1 — 100 Направляющая Инструкции | 2-дверная система — 4 ‘направляющая 50 $.00 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4-дверная система 94 «направляющая $ 100,00 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
J111 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Максимальный вес створки двери 50 # | 2 дверных компонента | Максимальная ширина двери 24 дюйма | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1 –111 Направляющая Инструкции | 2-дверная система 4 ‘направляющая 30 $.00 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4-дверная система 4 ‘направляющая $ 60,00 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
KT 15Комплект гусеницы с двойным складыванием | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 60 # Макс.вес створки двери | 2 дверных компонента | Максимальная ширина двери 24 дюйма | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1 Гусеница KT 40 Петли в комплект не входят | 2-дверная система 4 ‘направляющая $ 75 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4-дверная система 94 «направляющая 150 долл. США.00 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 165 # Макс.вес створки двери | 2 дверных компонента | Максимальная ширина двери 36 дюймов | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 600A Алюминиевая гусеница 1 Комплект шарнира 21B / P 1 Ролик 21B / 4 1 21N / 94 нижняя направляющая 1 94A нижний направляющий канал | 2-дверная система 1 6-дюймовая гусеница $ 466 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 дверных элемента | | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2 Алюминиевая гусеница 600A 6 футов Петли и болты с утолщением в комплект не входят | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Pacer System Страница | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
301HКомплект гусеницы с двойным складыванием | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 150 # Максимальный вес створки двери | 2 дверных компонента | Максимальная ширина двери 36 дюймов | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1 PC 301H Гусеница из оцинкованной стали Требуются стандартные стыковые петли, но не входят в комплект 301 Информационный лист Endfold Промышленная гусеница Страница | 2-дверная система 1 6 ‘трек 425 $.00
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4-дверная система (2) 6-дюймовая направляющая $ 850,00 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Flexirol | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 275 # Максимальный вес створки двери | 2 дверных компонента | Макс.ширина двери 48 дюймов | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1 шт. 550 направляющая Дверная система Flexirol Страница Требуются стандартные стыковые петли, но не входят в комплект | 2-дверная система (1) направляющая 6 футов 925 $.00 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4-дверная система (2) 6-дюймовая направляющая $ 1850,00 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Система складывания с касательным смещением | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Система смещения с 65 петлями для поверхностного монтажа | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Крепление на поверхность 65 петель используются Размеры |
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Детали системы складывания с касательным смещением | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Дополнительная информация | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Требования — Folding @ home
Новое программное обеспечение V7 имеет те же базовые требования к оборудованию и операционной системе, что и предыдущие клиенты.Однако некоторые требования к программному обеспечению были изменены для поддержки новых функций. Размещено по типу слота:
- Требования к разъему процессора
- Windows XP SP3 или новее, 32 или 64 бит
- Процессор Intel P4 1,4 ГГц или новее или эквивалент AMD (рекомендуются современные многоядерные процессоры)
- Для одноядерных процессоров доступен ограниченный выбор проектов, поскольку в августе 2013 года было объявлено о завершении срока службы одноядерных проектов.
Для проектов с большим количеством ядер может потребоваться 64-разрядная версия и более короткие сроки, обычно требующие, чтобы клиент работал на или около 24/7
- Широкополосное подключение к Интернету или более быстрое
- Windows XP SP3 или новее, 32 или 64 бит
Примечание. Хотя Pande Group еще не предоставила список необходимого программного обеспечения, доноры сообщили о трех проблемах.Во-первых, Microsoft .NET Framework требуется для V7 FAHControl в Windows, а Windows XP не включает .NET Framework по умолчанию. Для поддержки программного обеспечения V7 в Windows XP необходимо установить Microsoft .NET 2.0 или новее. Все новые версии Windows по умолчанию уже включают поддерживаемую версию .NET. Кроме того, для работы FAHClient Windows XP требуется распространяемый компонент C ++ 2008 (32-разрядная версия). И в зависимости от конфигурации вашей сети, IPv4 может потребоваться отдать приоритет IPv6 с помощью этого инструмента Microsoft Fix It.
- Требования к слоту для графического процессора
- Windows XP SP3 или новее для графических процессоров NVIDA, 32- или 64-битная (поддержка Windows XP и 32-битная поддержка ограничены, используйте Windows 7 или новее и 64-битную операционную систему для полной поддержки всех типов FAHCore)
- Windows Vista SP2 или новее для графических процессоров AMD, 32- или 64-разрядная (поддержка 32-разрядной версии ограничена, для полной поддержки используйте 64-разрядную версию)
- FAH Клиент работает больше, чем неполный рабочий день, чтобы уложиться в короткие сроки
- Широкополосное подключение к Интернету или более быстрое
- 1 или более поддерживаемых видеокарт с графическим процессором
- ATI / AMD
- (GPU3 — OpenCL — FAHCore_17)
- OpenCL-совместимый графический процессор, серия 5xxx или новее *, см. Полный список
- 13.6 Драйвер устройства AMD или новее (14.4+ повышает скорость)
- (GPU3 — OpenCL — FAHCore_18)
- OpenCL-совместимый графический процессор, серия 5xxx или новее *, см. Полный список
- 14.9 Драйвер устройства AMD или новее
- (GPU3 — OpenCL — FAHCore_21)
- OpenCL-совместимый графический процессор, серия 5xxx или новее *, см. Полный список
- 15.1 драйвер устройства AMD или новее
- (GPU3 — OpenCL — FAHCore_17)
- NVIDIA
- (GPU3 — OpenMM — fahcore_15) — конец жизни объявлен ноябрь.2013
- GPU с поддержкой CUDA (серия 8xxx и выше), см. Полный список
- 327.xx Драйвер устройства NV или новее
- Для свертывания этих проектов необходимы специальные настройки клиента. Задайте вопрос на форуме поддержки складных устройств.
- (GPU3 — OpenCL — fahcore_17)
- OpenCL-совместимый графический процессор, серия 4xx и выше (Fermi, Kepler, Maxwell или новее *)
- 361.xx Драйвер устройства NV (CUDA 8) или новее (327.xx — известная стабильная версия для старых графических процессоров)
- (GPU3 — OpenCL — fahcore_18)
- OpenCL-совместимый графический процессор, серия 4xx и выше (Fermi, Kepler, Maxwell или новее *)
- 361.xx драйвер устройства NV (CUDA 8) или новее (327.xx — известная стабильная версия для старых графических процессоров)
- (GPU3 — OpenCL — fahcore_21)
- OpenCL-совместимый графический процессор, серия 4xx и выше (Fermi, Kepler, Maxwell или новее *)
- 361.xx Драйвер устройства NV (CUDA 8) или новее (327.xx — известная стабильная версия для старых графических процессоров)
- (GPU3 — OpenMM — fahcore_15) — конец жизни объявлен ноябрь.2013
Примечание. Драйверы, модели, функции и поддержка графических процессоров разрабатываются очень быстро. Обратите внимание на эти конкретные проблемы.
- Драйвер устройства AMD v11.12 — последняя версия, поддерживающая OpenCL в Windows XP. Для плат серии 7xxx и новее потребуется Windows Vista SP2 или новее.
- Автоматическое обновление файла GPUs.txt теперь поддерживается в V7.3.x и новее. Требуется перезапуск FAHClient.exe.
- В последней версии драйвера NVidia, 361.xx или выше, были решены несколько проблем со скоростью fahcore. Однако поддержка старых графических процессоров Tesla и более старых в этом новом драйвере была прекращена.
- В последней версии драйвера AMD 15.x или выше. Однако поддержка старых графических процессоров в новом драйвере была прекращена.
- См. Раздел «Новые графические процессоры» (белый / черный список) на форуме поддержки складывания для получения дополнительной информации о сером списке аппаратного обеспечения графических процессоров (список поддерживаемых аппаратных средств) с новыми графическими процессорами.
- Об окончании поддержки серии ATI / AMD 4xxx и ниже было объявлено в марте 2011 года и должно было закончиться в сентябре 2011 года. Последнее из рабочих модулей AMD Fahcore_11 (GPU2) фактически продлилось до июня 2012 года, более чем через год после оригинальное объявление.
- Об окончании поддержки серии NVidia 8xxx (G80, G84, G86, G92, G98) было объявлено в августе 2013 года и планируется завершить примерно через год. Последний из рабочих блоков NVidia Fahcore_11 (GPU2) закончился, когда этот старый рабочий сервер вышел из строя в сентябре 2014 года, более чем через год после первоначального объявления.
- * Новые модели графических процессоров с новой архитектурой микросхем могут не поддерживаться текущим программным обеспечением. Для полной поддержки могут потребоваться новые ошибки и / или новые драйверы с обновленной оптимизацией.Новые fahcore будут доступны только через некоторое время после того, как новое оборудование будет продано широкой публике. Затем могут быть обновлены, протестированы и проверены fahcores и драйверы перед выпуском для складывания.
Примечание. В Windows антивирусное программное обеспечение может мешать работе файлов клиента Folding @ home и вызывать ошибки. Мы предлагаем настроить антивирусное программное обеспечение, чтобы исключить клиентский каталог FAH и особенно рабочий каталог из списка антивирусного сканирования. Это можно сделать, перейдя в панель списка исключений, которая должна быть у каждого антивируса.Подкаталог work содержит полуслучайные двоичные данные и может запутать чрезмерно агрессивное эвристическое сканирование на вирусы.
Что нужно знать о складных и раздвижных дверях для патио?
Вы наверняка их видели — большие складывающиеся или подъемно-раздвижные двери патио, которые открывают дом и стирают грань между внутренней и внешней частью. Вы, наверное, думали, что такая система будет хорошо смотреться в одном из ваших домов, но указать дверь не так просто, как вы думаете. Есть над чем подумать.
Двустворчатые и раздвижные дверные системы в закрытом состоянии выглядят как обычные двери для патио, но они складываются или отодвигаются, создавая большие драматические проемы.Панели имеют ширину до 5 футов в некоторых случаях и 16 футов в высоту у некоторых производителей.
История гласит, что двери возникли в Австралии, а затем распространились по Европе, Южной Америке и Северной Америке. Кто знает, правда ли эта история, но что можно сказать наверняка, так это популярность систем, которые можно найти в домах в холодном климате, в теплых регионах или даже в районах, подверженных ураганам.
Итак, что вам нужно знать, чтобы указать на одного из этих плохих парней в ваших домах? Какие соображения? А каких ошибок следует избегать? Мы попросили совета у экспертов:
Журнал «ПРОДУКТЫ»: Что следует знать профессиональным торговцам о раздвижных и раздвижных дверях для террас и где их можно использовать?
«Людям, которым нужны большие проемы, также нужны минималистичные дорожки, которые плавно переходят из помещения в улицу, эффективно расширяя их жизненное пространство.С более низким порогом возникает необходимость в управлении водными ресурсами. Для этого требуется продуманное планирование защиты от атмосферных воздействий, поддоны под дверями, разработанные для подрядчика архитектором, водостоки и, во многих случаях, выступ для защиты проема ». — Венди Канчола, региональный менеджер, Западные штаты, Weather Shield Windows and Doors
«Имея такой большой проем, вы хотите быть уверены, что пассажиры будут чувствовать себя комфортно даже в зимние месяцы.Без стекла и рамок с высокими эксплуатационными характеристиками сквозняки будут проблемой. Zola всегда рекомендует использовать стекло со значением U не более 0,2 (R-5 или выше) и как минимум два компрессионных уплотнения для обеспечения надлежащей герметичности ». — Флориан Шпейер, вице-президент и основатель Zola Windows
Euro-Wall, euro-wall.com
«Если вы можете вписать карманы в свой дизайн, подумайте о том, чтобы положить эти двери в карманы. Настоящая красота продукта в том, что проем полностью очищен, а дверцы красиво спрятаны в кармане.Обязательно просмотрите свои производственные чертежи и проверьте свои расчеты, чтобы убедиться, что вы ожидали достаточной глубины и ширины этих карманов »- Джон Кукк, AIA, Kukk Architecture & Design (для Weiland / Andersen)
«Они должны знать и понимать, что эти типы дверных систем предназначены для изменения пространства и облегчения жизни внутри и снаружи. Если их правильно объединить, они могут превратить обычное пространство во что-то динамичное ». — Эндрю Дарр, вице-президент по индивидуальным продажам Western Window Systems
«Складные и раздвижные двери для патио — это не просто точка доступа к дому.Эти двери теперь представляют собой значительно улучшенные технологические решения, которые повышают комфорт в доме, а также обеспечивают прекрасную эстетику, повышенное естественное освещение и улучшенную вентиляцию практически в любой комнате ». — Элизабет Содерс, директор по управлению продуктами для окон, Джелд-Вен
Компания Folding Sliding Door Co., foldslidingdoors.com
«Складные и многопозиционные системы эволюционировали и теперь включают в себя функциональные и эстетические возможности, которые позволяют использовать их в любой среде и в любом приложении.Независимо от того, используются ли системы для открытия большой двери в патио или для прохода через служебное окно, системы приносят свежий воздух и естественный свет в дом и создают открытые пространства, идеально подходящие для развлечений или просто наслаждения окружающей средой, не выходя из дома ». — Тим Келтинг, вице-президент по продажам и маркетингу, LaCantina Doors
«Настаивать на размерах и конфигурациях без гарантии неразумно. Я бы посоветовал им использовать опыт производителей и не выходить за рамки, которые мы предоставляем.»- Деби Димитриу, менеджер по продажам, Weiland / Andersen
«Строители и архитекторы должны исследовать и понимать характеристики этих дверей индивидуально. Производительность каждого типа в конечном итоге будет определять, где и как их следует использовать в проекте. Эти двери можно использовать как снаружи, так и в качестве креативных перегородок между двумя внутренними зонами ». — Ланс Премо, менеджер по продуктам и рынку, Kolbe
Джельд-Вен, джельд-вен.com
Журнал ПРОДУКЦИЯ: Какие типичные ошибки допускают строители при выборе складных и раздвижных дверей для террас?
«Одна из наиболее распространенных проблем, с которыми мы сталкиваемся, — это когда строители не учитывают пороговое значение перехода. Выбор порога влияет на общие характеристики двери и может существенно повлиять на окончательный эстетический вид помещения. Правильный переход порога создает ощущение бесшовности между внутренним и внешним пространством.”- Элизабет Содерс, Джелд-Вен
«Отсутствие надлежащего углубления для рельсового пути и внутренней дренажной системы». — Джон Кукк, Kukk Architecture & Design
Марвин, marvin.com
«Распространенные ошибки включают непонимание стоимости заблаговременно и включение ее в бюджет, знание инженерной и технической поддержки, необходимой для больших проемов, а также знание глубины косяка, необходимой для многодвижных дверей с несколькими панелями.”- Wendy Canchola, Weather Shield Windows & Doors
«Дверцы верхней загрузки свешиваются с жатки. Это означает, что жатка должна быть спроектирована так, чтобы выдерживать этот вес наряду с другими нагрузками на здание. Он не должен слишком сильно прогибаться или отклоняться, так как это может привести к заклиниванию двери. Для раздвижных дверей патио строители должны понимать глубину стены, необходимую для поддержки количества напольных направляющих для каждой конфигурации. Чем больше панелей в вашей системе, тем больше может потребоваться напольных направляющих.Важно помнить, что с каждым дополнительным напольным покрытием требуемая глубина стены также увеличивается. Двери патио не всегда подходят для замены. Если структурная целостность не способна поддерживать складные и раздвижные двери, продукты не будут устанавливаться и работать должным образом ». — Ярон Вос, менеджер по профессиональным услугам, архитектурные услуги и технические публикации, Pella Windows & Doors
Зола, золавокна.com
«При выборе складных дверей строители должны принять во внимание одно важное соображение — это поворот этих дверей и место, в котором они в конечном итоге будут складываться в полностью открытом положении. Требуется некоторое обдумывание и планирование, чтобы понять, как эти двери будут взаимодействовать с планировкой проекта, видами и расположением мебели ». — Lance Premeau, Kolbe
«К нам в Zola Windows приходило несколько строителей, которые хотели указать складывающиеся двери в условиях горного или другого холодного климата, не принимая во внимание, сколько времени они будут закрыты.Для такого климата, как правило, намного лучше использовать подъемные раздвижные двери, которые могут нести стеклянные панели в два-три раза больше и будут иметь меньше перегородок, мешающих обзору при закрытии. Для более теплого климата, где дверь будет открыта в течение большей части года, складные двери — отличный вариант »- Флориан Шпейер, Zola Windows
«Я думаю, что самая большая ошибка происходит, когда строитель определяет, какой продукт лучше всего подходит для рассматриваемого открытия.Например, иногда лучше всего использовать несколько слайдов. Или, возможно, для дебюта лучше всего подойдет двойная складка. Понимая, как будет использоваться и занято жилое пространство, строитель сможет принять более обоснованное решение о том, какой продукт использовать ». — Эндрю Дарр, Western Window Systems
WeatherShield, weathershield.com
«Строители часто упускают из виду переход порога, который имеет решающее значение для создания бесшовных внутренних жилых помещений на открытом воздухе.Важно не только понимать требования к характеристикам и соответствующий выбор порога для конкретного применения, но также и то, как порог будет интегрирован в состояние пола. Углубление внутренней части устойчивых к погодным условиям порогов позволяет плавно переходить в наружное пространство и помогает стереть границу между внутренним и внешним пространством. Другими ключевыми моментами являются требования к конфигурации двери и заголовку »- Тим Келтинг, LaCantina Doors
Журнал «ПРОДУКТЫ»: Что нельзя делать строителям и архитекторам, когда дело касается раздвижных и двустворчатых дверей для террас?
«Строителям и архитекторам не следует думать, что складные и раздвижные двери для террасы можно устанавливать так же, как и другие двери для террас.Складные двери, многоскатные двери и подъемно-сдвижные двери — все они имеют уникальные особенности, которые полезны только при правильной установке »- Lance Premeau, Kolbe
Не думайте, что вы сэкономите деньги, выбрав стандартные размеры. Для такой заказной европейской компании, как Zola Windows, большая часть затрат приходится на современное оборудование и рабочую силу, которые остаются неизменными вне зависимости от размера устройства. Это означает, что двери большего размера, как правило, более рентабельны на квадратный фут, а огромные раздвижные двери с подъемником могут действительно иметь большую ценность.”- Флориан Шпайер, Zola Windows
«Не откладывайте решение о системах складных и раздвижных дверей на последний момент. Фактически, мы поощряем строителей и архитекторов включать эти стеновые системы на самых ранних этапах планирования. Подумайте о том, какое влияние дизайн и стиль оказывают эти большие стеклянные панели на общий вид комнаты. Домовладельцы могут наслаждаться гораздо более бесшовным и красивым пространством, если эти двери встроены с самого начала.”- Элизабет Содерс, Джелд-Вен
Weiland, автор — Андерсен, weilandslidingdoors.com
«[Они не должны] строить конструктивную оболочку или завершать кладку проемов без утвержденных рабочих чертежей и размеров. Истинное впечатление от дверей заключается в их плавном переходе из помещения в помещение. Предвидите напольное покрытие, указанное как внутри, так и снаружи, и то, как он будет соответствовать минимальному количеству дверных проемов. В идеальном состоянии один и тот же этаж может работать как внутри помещения, так и снаружи.”- Джон Кукк, Kukk Architecture & Design
«Строители не должны пытаться формировать бюджет задом наперед, отказываясь от функций и деталей, которые действительно нужны клиенту». — Венди Канчола, Weather Shield Windows & Doors
Журнал ПРОДУКЦИЯ: Что делать строителям и архитекторам , а не ?
«Очень важно, чтобы строители и архитекторы понимали уровень производительности выбранной двери и среду, в которой дверь будет установлена.Если дверь используется в среде и применении, которые превышают уровень производительности двери, это может привести к проблемам с конструктивными характеристиками, а также к проникновению воды. Строители всегда должны проверять уровни производительности продукта, прежде чем выбирать его для конкретного приложения или среды »- Джарон Вос, Pella Windows & Doors
«Они не должны идти в одиночку. Существует множество недоразумений, связанных с большими дверными системами, включая структурные потребности, детали пола, условия карманов и т. Д.Вместо того, чтобы гадать, строитель или архитектор должны поговорить с представителем производителя, чтобы помочь в планировании и координации. Такие компании, как наша, живут, чтобы помочь архитектору реализовать его или ее замысел. Позвольте нам помочь вам! »- Эндрю Дарр, Western Window Systems
Western Window Systems, westernwindowsystems.com
«Строителям и архитекторам не следует забывать о складных и многослайдных системах. Складные системы и системы Multi Slide являются неотъемлемой частью современного дома и должны быть ведущим элементом дизайна.Принимая во внимание то, как конечный пользователь будет взаимодействовать с системами складывания и мультислайда, а также пространства, которые они создают, с самого начала этапа проектирования будет максимально увеличено влияние этих систем и, в конечном итоге, уровень удовольствия, которое они доставляют конечному пользователю. Тим Келтинг, LaCantina Doors
NanaWall, nanawall.com
Kolbe Windows & Doors, kolbe-kolbe.com
Складные двери для коммерческих помещений | Подъездные системы ASSA ABLOY US
Продукты /
Автоматические двери /
Складные двери /
Складной
Автоматическая складывающаяся дверь ASSA ABLOY SW200i
Автоматическая складывающаяся дверь ASSA ABLOY SW200i
Система автоматических складных дверей для коммерческих помещений ASSA ABLOY SW200i-Fold — удобство для небольших подъездов
Когда пространство ограничено, обратите внимание на коммерческие автоматические складывающиеся двери для максимального открывания двери.Независимо от того, выберете ли вы складывающуюся дверь с двумя или четырьмя створками, вы получите автоматический входной пакет, обеспечивающий удобство и доступность в самых ограниченных условиях.
ASSA ABLOY SW200i – Fold представляет собой превосходный шаг вперед в технологии складных дверей для коммерческого использования. Он обеспечивает безбарьерное двустороннее движение, занимая лишь небольшую часть пространства, необходимого для автоматической раздвижной или распашной двери. С помощью этих автоматических складывающихся дверей вы можете добиться максимального комфорта даже в самом тесном коридоре.Система автоматических складных дверей ASSA ABLOY SW200i-Fold идеально подходит для проектов модернизации или нового строительства и имеет неограниченные возможности применения.
Техническое описание
ASSA ABLOY SW200i-Складная дверь для профессионального использования
- Безбарьерное двустороннее движение для самых узких участков
- Конфигурация с двумя или четырьмя панелями
- Доступны складывания наружу или внутрь
- Аварийный выход
- Использование мощного привода ASSA ABLOY SW200i
Загрузки
Брошюра по продукту
BR_AA_SW200iFold_0318.pdf
(.pdf, 357 КБ)
Характеристики продукта
084229.xx_Swinging Automatic Entrances_specifiernotes_v2r1.doc
(.doc, 64 КБ)
084229.13_SW200i-Складывающаяся двустворчатая дверь_v4.dot
(.dot, 97 кБ)
Чертежи продукции (.pdf)
1010757 SW200i-Fold with Doors 2-панельная система складных дверей для поверхностного монтажа Rev 3.0.pdf
(.pdf, 207 КБ)
1010756 SW200i-Fold with Doors 4-х панельная система скрытых складных дверей Rev 3.0.pdf
(.pdf, 228 КБ)
1010758 SW200i-Fold with Doors 4-панельная система складных дверей для поверхностного монтажа, ред. 3.0.pdf
(.pdf, 217 КБ)
1010755.SW200i-Fold with Doors 2-х панельная система скрытых складных дверей Rev 3.0.pdf
(.pdf, 209 КБ)
Чертежи продукции (.dwg)
1010756 SW200i-Fold with Door 4 Скрытая складывающаяся дверная система Rev 3.0.dwg
(.dwg, 316 КБ)
1010755.SW200i-Fold with Doors 2-х панельная система скрытых складных дверей Rev 3.0.dwg
(.dwg, 296 КБ)
1010757 SW200i-Fold with Doors 2-панельная система складных дверей для поверхностного монтажа Rev 3.0.dwg
(.dwg, 305 кБ)
1010758 SW200i-Fold with Doors 4-панельная система складных дверей для поверхностного монтажа, версия 3.0.dwg
(.dwg, 278 КБ)
Чертежи продукции (.dxf)
1010758 SW200i-Fold with Doors 4-панельная система складных дверей для поверхностного монтажа, версия 3.0.dxf
(.dxf, 545 КБ)
1010755.SW200i-Fold with Doors 2-х панельная система скрытых складных дверей Rev 3.0.dxf
(.dxf, 578 КБ)
1010756 SW200i-Fold with Door 4 Скрытая складывающаяся дверная система Rev 3.0.dxf
(.dxf, 631 кБ)
1010757 SW200i-Fold with Doors 2-панельная система складных дверей для поверхностного монтажа, версия 3.0.dxf
(.dxf, 600 КБ)
FARRIER FOLDING SYSTEM ™ — Farrier International
Система складывания Farrier ™ означает меньшее проникновение в кабину и отсутствие открытых «ловушек для ног» на палубе.
Одним из ключей к успеху тримаранов Farrier является легкость передвижения, которая стала возможной благодаря уникальной системе складывания Farrier ™.
Система Farrier — это самая конструктивно прочная система складывания тримарана из имеющихся, с без петель, в балках или критическом соединении балки с плавающей точкой, в то время как проволока, подверженная коррозии, никогда не используется в конструктивно критических областях. Общий луч может быть изменен за секунды одним человеком в любом месте.
После 33 лет использования по всему миру система Farrier хорошо зарекомендовала себя, она является самой успешной системой складывания и используется большим количеством тримаранов, чем что-либо еще.Поэтому на всякий случай обязательно используйте настоящую систему складывания Farrier Folding System ™ с двумя распорками. Он существенно отличается от всех остальных, и многие преимущества можно резюмировать следующим образом:
- Складывается для легальной буксировки по дорогам за считанные минуты без какой-либо тяжелой сборки.
- Система складывания с двумя стойками дает полный контроль над движением
- Нет необходимости в воде для поддержки поплавков при складывании — двойные распорки позволяют легко складывать в любом месте
- Правильная геометрия складывающейся стойки означает, что складывание может выполнять один человек в любом месте.
- Двойные распорки означают, что поплавок не упадет на землю при складывании из воды на прицепе
- Абсолютно Отсутствуют слабые точки шарнира в реальных балках, при этом сильно напряженное соединение балки с поплавком является твердым
- Абсолютно без скользящих частей, которые могут заедать или заклинивать
- Подверженная коррозии проволока не используется в критических конструктивных областях, где внезапная поломка может угрожать судну.
- Конструктивно критически важные нижние стойки представляют собой прочную алюминиевую балку 6061 T6 без стыковых швов.
- Изготовленные на заказ втулки из армированного ацеталем (пластика) изолируют алюминиевые стойки от осей шарниров из нержавеющей стали.
- Нет необходимости полагаться на буровую установку в качестве опоры конструкции, если произойдет обратная нагрузка на поплавок
- Балки конструктивно прочны независимо от нагрузки, в том числе даже после опрокидывания
- Доказанный послужной список: 33 года разработки, шесть переходов через Атлантический океан и мировые рекорды / победы в гонках.
- Сейчас используется более чем 3000 лодок по всему миру
Складные дверные, стеновые и оконные системы
Складные дверные, стеновые и оконные системы
для любого стиля и обстановки.
Купить сейчас
ПРЕИМУЩЕСТВО EZ-FOLD-A-DOOR *
• Нестандартные размеры
• 30-дневная гарантия возврата
• Пожизненная гарантия на оборудование
• Круглосуточная служба поддержки клиентов
• Простая установка
* применяются условия
ЭКСТРЕМАЛЬНАЯ ПОГОДНАЯ СЕРИЯ: AZ57
AZ57 поставляется с термически сломанной рамой, которая поддерживает наружную температуру и внутреннюю температуру внутри.
Он также поставляется с высокотехнологичным термобарьером внутри из AZON ™ ️ для дополнительной изоляции.
Учить больше
Нужна дополнительная помощь?
Поговорите с одним из наших представителей и получите рекомендации, помощь в оформлении заказа и все, что вам нужно.
Хотите узнать больше?
Загрузите наш каталог сегодня и просмотрите все наши различные варианты складывания, стили, цвета и многое другое!
×
Какая серия вас интересует?
Используйте стрелки влево / вправо для навигации по слайд-шоу или проведите пальцем влево / вправо при использовании мобильного устройства
.

 URL: http://interneturok.ru/ 2) Школьный помощник. URL: http://school-assistant.ru/
URL: http://interneturok.ru/ 2) Школьный помощник. URL: http://school-assistant.ru/