{200} $
Содержание
7.1. Степень с натуральным показателем.
Автор Татьяна Андрющенко На чтение 3 мин. Просмотров 181 Опубликовано
I. Произведение n сомножителей, каждый из которых равен а называется n-й степенью числа а и обозначается аn.
Примеры. Записать произведение в виде степени.
1) mmmm; 2) aaabb; 3) 5·5·5·5·ccc; 4) ppkk+pppk-ppkkk.
Решение.
1) mmmm=m4, так как, по определению степени, произведение четырех сомножителей, каждый из которых равен m, будет четвертой степенью числа m.
2) aaabb=a3b2; 3) 5·5·5·5·ccc=54c3; 4) ppkk+pppk-ppkkk=p2k2+p3k-p2k3.
II. Действие, посредством которого находится произведение нескольких равных сомножителей, называется возведением в степень. Число, которое возводится в степень, называется основанием степени. Число, которое показывает, в какую степень возводится основание, называется показателем степени. Так, аn – степень, а – основание степени, n – показатель степени. Например:
23 — это степень. Число 2 — основание степени, показатель степени равен 3. Значение степени 23равно 8, так как 23=2·2·2=8.
Примеры. Написать следующие выражения без показателя степени.
5) 43; 6) a3b2c3; 7) a3-b3; 8 ) 2a4+3b2.
Решение.
5) 43=4·4·4; 6) a3b2c3=aaabbccc; 7) a3-b3=aaa-bbb; 8) 2a4+3b2=2aaaa+3bb.
III. а0=1 Любое число (кроме нуля) в нулевой степени равно единице. Например, 250=1.
IV. а1=а Любое число в первой степени равно самому себе.
V. am∙an=am+n При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели складывают.
Примеры. Упростить:
Упростить:
9) a·a3·a7; 10) b0+b2·b3; 11) c2·c0·c·c4.
Решение.
9) a·a3·a7=a1+3+7=a11; 10) b0+b2·b3=1+b2+3=1+b5;
11) c2·c0·c·c4=1·c2·c·c4=c2+1+4=c7.
VI. am:an=am— n При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя.
Примеры. Упростить:
Упростить:
12) a8:a3; 13) m11:m4; 14) 56:54.
12) a8:a3=a8-3=a5; 13) m11:m4=m11-4=m7; 14) 56:54=52=5·5=25.
VII. (am)n=amn При возведении степени в степень основание оставляют прежним, а показатели перемножают.
Примеры. Упростить:
15) (a3)4; 16) (c5)2.
15) (a3)4=a3·4=a12; 16) (c5)2=c5·2=c10.
Обратите внимание, что, так как от перестановки множителей произведение не меняется, то:
15) (a3)4=(a4)3; 16) (c5)2=(c2)5.
VIII. (a∙b)n=an∙bn При возведении произведения в степень возводят в эту степень каждый из множителей.
Примеры. Упростить:
17) (2a2)5; 18) 0,26·56; 19) 0,252·402.
Решение.
17) (2a2)5=25·a2·5=32a10; 18) 0,26·56=(0,2·5)6=16=1;
19) 0,252·402=(0,25·40)2=102=100.
IX. При возведении в степень дроби возводят в эту степень и числитель и знаменатель дроби.
Примеры. Упростить:
Решение.
Алгебра 7-9 классы. 3. Степень с натуральным показателем. Свойства степени
Алгебра 7-9 классы. 3. Степень с натуральным показателем. Свойства степени
- Подробности
- Категория: Алгебра 7-9 классы
СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ
ОПРЕДЕЛЕНИЕ СТЕПЕНИ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ
Произведение нескольких одинаковых множителей можно записать в виде степени. Например,
Например,
Выражение 57 читают по-разному: «Пять в седьмой степени», «Седьмая степень числа пять», «Степень числа пять с показателем семь».
Определение. Степенью числа а с натуральным показателем n, большим 1, называется произведение n множителей, каждый из которых равен а. Степенью числа а с показателем 1 называется само число а.
Степень числа а с показателем n обозначают так: аn. Выражение аn называют степенью, число а — основанием степени, число n — показателем степени.
По определению степени:
Вообще,
Нахождение значения степени называют возведением в степень. Приведем примеры возведения в степень:
При возведении в степень отрицательного числа может получиться как положительное число, так и отрицательное. Например,
Степень отрицательного числа с четным показателем есть число положительное, так как произведение четного числа отрицательных множителей положительно. Степень отрицательного числа с нечетным показателем есть число отрицательное, так как произведение нечетного числа отрицательных множителей отрицательно.
Степень отрицательного числа с нечетным показателем есть число отрицательное, так как произведение нечетного числа отрицательных множителей отрицательно.
Квадрат любого числа есть число положительное или нуль, т. е. при любом а.
Вычислим значения нескольких выражений, содержащих степени.
Пример 1. Найдем значение выражения :
Значит,
Пример 2. Найдем значение выражения
Значит,
УМНОЖЕНИЕ И ДЕЛЕНИЕ СТЕПЕНЕЙ
Выражение а2а3 представляет собой произведение двух степеней с одинаковыми основаниями. Это произведение можно записать в виде степени с тем же основанием:
Значит,
Мы видим, что произведение а2а3 равно степени с тем же основанием и показателем, равным сумме показателей перемножаемых степеней.
Докажем, что для любого числа а и произвольных натуральных чисел m и n
Для этого, используя определение степени и свойства умножения, представим выражение аmаn сначала в виде произведения множителей, каждый из которых равен а, а затем в виде степени:
Таким образом,
Доказанное равенство выражает свойство произведения степеней. Его называют основным свойством степени. Оно распространяется на произведение трех и более степеней.
Например,
Отсюда следует правило умножения степеней: при умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели степеней складывают.
Приведем примеры:
Выражение а7:а3 является частным двух степеней с одинаковыми основаниями. Это частное при можно представить в виде степени с тем же основанием. Действительно, так как , то по определению частного
Действительно, так как , то по определению частного
Мы видим, что частное а7:а3 равно степени с тем же основанием и показателем, равным разности показателей делимого и делителя.
Докажем, что для любого числа и произвольных натуральных чисел тип, таких, что ,
Покажем, что .
Действительно, по основному свойству степени
Значит, по определению частного
Итак, при делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя.
Приведем примеры:
Мы вывели правило деления ат на аm для случая, когда . Если это правило применить к частному an:an, то получится
Степень с нулевым показателем не была определена. Так как при всяком и любом натуральном n
то считают, что при
Определение. Всякое число (кроме нуля) в нулевой степени равно единице.
Всякое число (кроме нуля) в нулевой степени равно единице.
Например, 2° — 1, (— 3,5)° =1. Выражение 0° не имеет смысла.
Теперь, после введения нулевой степени, мы можем применять формулу и в том случае, когда m = 0 или n = 0 (при ). Точно так же формула справедлива и тогда, когда или .
ВОЗВЕДЕНИЕ В СТЕПЕНЬ ПРОИЗВЕДЕНИЯ И СТЕПЕНИ
Выражение является степенью произведения множителей а и b. Это выражение можно представить в виде произведения степеней а и b:
Значит,
Мы видим, что четвертая степень произведения аb равна произведению четвертых степеней множителей а и b.
Докажем, что для любых а и b и произвольного натурального числа n
По определению степени
Сгруппировав отдельно множители а и множители b, получим :
Воспользовавшись определением степени, находим:
Следовательно,
Свойство степени произведения, выраженное равенством , распространяется на степень произведения трех и более множителей. Например,
Например,
Отсюда следует правило: (пpu возведении в степень произведения возводят в эту степень каждый множитель и результаты перемножают.
Выражение есть степень, основание которой само является степенью. Это выражение можно представить в виде степени с основанием а:
В результате возведения степени а5 в третью степень мы получили степень с тем же основанием и показателем, равным произведению показателей 5 и 3.
Докажем, что для любого числа а и произвольных натуральных чисел m и n
По определению степени
Согласно основному свойству степени
Заменим сумму произведением mn.
Тогда получим:
Следовательно,
Из равенства следует правило: при возведении степени в степень основание оставляют тем же, а показатели перемножают.
Свойства степеней, выраженные формулами и , имеют место и для степеней с нулевым показателем (если основания отличны от нуля).
«Свойства степени с натуральным показателем»
библиотека
материалов
Содержание слайдов
Номер слайда 1
§6. Свойства степени с натуральным показателем
Номер слайда 2
Сравните значения выражений22∙23 25 42∙41 43 (33)2 36 53∙23 (5∙2)3
Номер слайда 3
𝑎2∙𝑎3= 𝑎∙𝑎∙𝑎∙𝑎∙𝑎= 𝑎∙𝑎∙𝑎∙𝑎∙𝑎= =𝑎5= 𝑎2+3 𝒂𝟐∙𝒂𝟑= 𝒂𝟐+𝟑 Для любого числа a и любых натуральных чисел m и n справедливо равенство: 𝒂𝒎∙𝒂𝒏=𝒂𝒎+𝒏 Теорема 6. 1Основное свойство степени
1Основное свойство степени
Номер слайда 4
32∙33∙37= 32+3+7= 312 𝑚5∙𝑚4= 𝑚9 𝑥 ∙𝑥7= 𝑥8 𝑎3∙𝑎3= 𝑎6 68∙63= 611 Итак, при умножении степеней с одинаковыми основаниями показатели складывают, а основание оставляют прежним
Номер слайда 5
204. Представьте в виде степени произведение:𝑦3∙𝑦5∙𝑦9= 𝑦17 𝑐8∙𝑐9∙𝑐= 𝑐18 𝑏−𝑐10∙𝑏−𝑐6 = (𝑏−𝑐)16 112∙114∙116= 1112 𝑥4∙𝑥∙𝑥11∙𝑥2= 𝑥18 𝑎𝑏5∙𝑎𝑏15 = (𝑎𝑏)20 2𝑥+3𝑦6∙2𝑥+3𝑦14 = (2𝑥+3𝑦)20 −𝑥𝑦2∙−𝑥𝑦7∙−𝑥𝑦9 = (−𝑥𝑦)18 №205 (на дом)
Представьте в виде степени произведение:𝑦3∙𝑦5∙𝑦9= 𝑦17 𝑐8∙𝑐9∙𝑐= 𝑐18 𝑏−𝑐10∙𝑏−𝑐6 = (𝑏−𝑐)16 112∙114∙116= 1112 𝑥4∙𝑥∙𝑥11∙𝑥2= 𝑥18 𝑎𝑏5∙𝑎𝑏15 = (𝑎𝑏)20 2𝑥+3𝑦6∙2𝑥+3𝑦14 = (2𝑥+3𝑦)20 −𝑥𝑦2∙−𝑥𝑦7∙−𝑥𝑦9 = (−𝑥𝑦)18 №205 (на дом)
Номер слайда 6
206. Замените * степенью с основанием a, чтобы выполнялось равенство :𝑎6∙ =𝑎14 ∙𝑎6=𝑎7 𝑎10∙ ∙𝑎2=𝑎18 ∗ ∗ ∗ 𝑎6 𝑎7 𝑎8 𝑎9 𝑎10 𝑎5 𝑎4 𝑎3 𝑎2 𝑎 №207 (на дом)style.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.colorfillcolorfill. typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.type
typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.type
Номер слайда 7
Рассмотрим выражение 𝒂𝟗:𝒂𝟒, где 𝒂≠𝟎: 𝒂𝟗:𝒂𝟒= 𝒂𝟗𝒂𝟒= 𝒂∙𝒂∙𝒂∙𝒂∙𝒂∙𝒂∙𝒂∙𝒂∙𝒂𝒂∙𝒂∙𝒂∙𝒂= =𝒂𝟓𝟏= 𝒂𝟓= 𝒂𝟗−𝟒 𝒂𝟗:𝒂𝟒= 𝒂𝟗−𝟒 Для любого числа a≠𝟎 и любых натуральных чисел m и n (𝑚>𝑛)справедливо равенство: 𝒂𝒎:𝒂𝒏=𝒂𝒎−𝒏 Теорема 6.2
Номер слайда 8
𝑎12:𝑎3= 𝑎9 𝑏6 :𝑏= 𝑏5 𝑐7:𝑐6= 𝑐1=𝑐 (𝑎+𝑏)8:(𝑎+𝑏)4= (𝑎−𝑏)4 При делении степеней с одинаковыми основаниями из показателя степени делимого вычитают показатель степени делителя, а основание оставляют прежним208. Представьте в виде степени частное:
Представьте в виде степени частное:
Номер слайда 9
77:75= 72=49 1018 :1014= 104=10000 0,69:0,66= 0,63=0,216 −1185:−1183= −1182=−982=8164=11764 209. Найдите значение выражения:№210 (на дом)
Номер слайда 10
Рассмотрим выражение 𝒂𝟑𝟒 𝑎34= 𝑎3∙𝑎3∙𝑎3∙𝑎3= 𝑎3+3+3+3= 𝑎12= 𝑎3∙4 𝑎34= 𝑎3∙4 Для любого числа a и любых натуральных чисел m и n справедливо равенство: (𝒂𝒎)𝒏=𝒂𝒎∙𝒏 Теорема 6. 3
3
Номер слайда 11
372= 37∙2= 314 𝑥𝑘3= 𝑥𝑘∙3= 𝑥3∙𝑘 При возведении степени в степень показатели перемножают, а основание оставляют прежним𝑚53= 𝑚15 𝑚34= 312 𝑚246= 𝑚48 𝑚72∙(𝑚4)9= 𝑚14∙𝑚36=𝑚50 №212 (на дом)
Номер слайда 12
Рассмотрим выражение 𝒂𝒃𝟑 𝑎𝑏3= (𝑎𝑏)∙(𝑎𝑏)∙(𝑎𝑏)= (𝑎𝑎𝑎)∙(𝑏𝑏𝑏)= 𝑎3∙𝑏3 𝑎𝑏3= 𝑎3∙𝑏3 Для любых чисел a и b и любого натурального числа n справедливо равенство: (𝒂𝒃)𝒏=𝒂𝒏∙𝒃𝒏 Теорема 6. 4При возведении произведения в степень каждый множитель возводят в степень и полученные результаты перемножают
4При возведении произведения в степень каждый множитель возводят в степень и полученные результаты перемножают
Номер слайда 13
Пример 1. Упростите выражение:1) 𝑎52∙𝑎67= 2) −𝑎49= 3) −𝑎48= 𝑎10∙𝑎42= 𝑎52 −1∙𝑎49= −19∙ 𝑎49= −𝑎36 −1∙𝑎48= −18∙ 𝑎48= 𝑎32
Номер слайда 14
Пример 2. Представьте в виде степени выражение: 216𝑎3𝑏6= 63∙𝑎3∙𝑏23= (6𝑎𝑏2)3
Представьте в виде степени выражение: 216𝑎3𝑏6= 63∙𝑎3∙𝑏23= (6𝑎𝑏2)3
Номер слайда 15
Пример 3. Найдите значение выражения:1137∙349= 437∙349= 437∙347∙342= =43∙347∙342= 342= 916
Номер слайда 16
Пример 4. Сравните значения выражений:1) −1114∙−113 −1116 2) −1219 −1215 3) 530 920 4) 163 652 >𝟎 𝟎 > > 423 =432= =642 642 652
Сравните значения выражений:1) −1114∙−113 −1116 2) −1219 −1215 3) 530 920 4) 163 652 >𝟎 𝟎 > > 423 =432= =642 642 652
Номер слайда 17
Пример 5. Какой цифрой оканчивается значение выражения2100= 2425= 1625 Поскольку 6∙6=36, то произведение любых чисел, оканчивающихся на 6, является числом, последняя цифра которого равна 6. Поэтому если число оканчивается цифрой 6, то любая его степень оканчивается цифрой 6.
Номер слайда 18
12345 Тождество, выражающее основное свойство степени. Как умножить степени с одинаковыми основаниями?Как разделить степени с одинаковыми основаниями?Как возвести степень в степень?Как возвести произведение в степень?
Как умножить степени с одинаковыми основаниями?Как разделить степени с одинаковыми основаниями?Как возвести степень в степень?Как возвести произведение в степень?
Номер слайда 19
213. Представьте степень в виде произведения степеней:1) 𝑎𝑏6= 2) 𝑚𝑛𝑝5= 3) 3𝑐7= 5) −0,2𝑐𝑑4= 4) −8𝑥𝑦3= 6) 37𝑘𝑡9= №214 (на дом)𝑎6∙𝑏6 𝑚5∙𝑚5∙𝑚5 37∙𝑐7 (−8)3∙𝑥3∙𝑦3 (−0,2)4∙𝑐4∙𝑑4 379∙𝑘9∙𝑡9
Номер слайда 20
215. Упростите выражение:1) −𝑥∙𝑥2= 2) −𝑥2∙𝑥= 3) −𝑥∙−𝑥2= 4) (−𝑥)∙−𝑥2∙(−𝑥)= −𝑥3 𝑥2∙𝑥= 𝑥3 −𝑥∙𝑥2= −𝑥3 𝑥∙𝑥2∙𝑥= 𝑥4 №216 (на дом)
Упростите выражение:1) −𝑥∙𝑥2= 2) −𝑥2∙𝑥= 3) −𝑥∙−𝑥2= 4) (−𝑥)∙−𝑥2∙(−𝑥)= −𝑥3 𝑥2∙𝑥= 𝑥3 −𝑥∙𝑥2= −𝑥3 𝑥∙𝑥2∙𝑥= 𝑥4 №216 (на дом)
Номер слайда 21
217. Упростите выражение:№218 (на дом)1) −𝑎52= 2) −𝑎33= 3) −𝑎47∙−𝑎26=
Номер слайда 22
№220 (на дом)219. Представьте в виде степени выражение:1) 𝑎3∙𝑏3= 2) −𝑚7= 3) 9𝑚2𝑛2= 4) 64𝑥3∙𝑦3= 5) −27334𝑐3∙𝑑3= 6) 0,0001𝑘4𝑝4=
Представьте в виде степени выражение:1) 𝑎3∙𝑏3= 2) −𝑚7= 3) 9𝑚2𝑛2= 4) 64𝑥3∙𝑦3= 5) −27334𝑐3∙𝑑3= 6) 0,0001𝑘4𝑝4=
Номер слайда 23
221. Представьте в виде степени выражение и вычислите:1) 23∙24= 2) 323= 3) 0,2∙0,22∙0,23= 4) 0,512∙212=
Номер слайда 24
№222 (на дом)221. Представьте в виде степени выражение и вычислите:5) 212:28= 6) 345∙319= 7) 139∙99= 8) 2,55∙405=
Представьте в виде степени выражение и вычислите:5) 212:28= 6) 345∙319= 7) 139∙99= 8) 2,55∙405=
Номер слайда 25
223. Найдите ошибки:1) 𝑎4𝑎3=𝑎12 2) 𝑎∙𝑎=2𝑎 3) 𝑎32=𝑎9 4) 32∙52=154 5) 22∙73=145 6) 2𝑎4=8𝑎4 7) 3∙43=123 8) 𝑎7𝑏7=(𝑎𝑏)14 9) 𝑎3𝑏2=(𝑎𝑏)6
Номер слайда 26
224. Вместо * запишите такое выражение, чтобы выполнялось равенство n – натуральное число:1) ∗4=с20 2) ∗2=с14 3) ∗𝑛=с8𝑛 4) ∗7=с7𝑛
Вместо * запишите такое выражение, чтобы выполнялось равенство n – натуральное число:1) ∗4=с20 2) ∗2=с14 3) ∗𝑛=с8𝑛 4) ∗7=с7𝑛
7 класс. Алгебра. Степень с натуральным показателем и ее свойства. — Степень с натуральным показателем.
Комментарии преподавателя
На этом уроке мы начнем изучение степени с натуральным показателем. Вначале обсудим, зачем математикам понадобилось вводить понятие степени, дадим определение степени с натуральным показателем, рассмотрим ряд примеров на степень. Далее дадим определение степени с единичным показателем и в конце решим несколько примеров на вычисление степени.
Тема: Степень с натуральным показателем и ее свойства
Урок: Что такое степень с натуральным показателем
Откуда появилась степень.
Выражение а+а+а в математике можно заменить на а+а+а=3а.
Выражение а+а+а+а+а можно представить в виде а+а+а+а+а=5а.
То есть, если в выражении n одинаковых слагаемых, каждое из которых а, то его можно кратко записать na.
А умножение , можно кратко записать так: а3, читается: а в кубе или третья степень числа а.
– а в пятой степени или пятая степень числа а.
А если в выражение n одинаковых сомножителей, каждый из которых а, то мы будем писать:
= an – n-ная степень числа а.
Определение. Степенью an называется произведение n одинаковых сомножителей, , где n— натуральное числоn={2,3,…..}; а – любое число.
Терминология: an
а – основание степени,
n – показатель степени,
an– степень, или а в n-ой степени, или n-ая степень числа а.
Пример 1: Записать произведение в виде степени, назвать основание и показатель степени, вычислить, если возможно.
1. – это по определению 4 в кубе или третья степень числа 4, 4— основание степени, 3— показатель степени. Результат:
Ответ: 64
2. – по определению, это x в четвертой степени, x – основание степени, 4 – показатель степени. Дальше вычислять нельзя, потому что x нужно присвоить конкретное значение.
Ответ:
3.
Это в пятой степени, – это основание степени, 5 – показатель степени, он показывает сколько раз основание умножается на себя. Замечание: от переменных мест сомножителей произведение не меняется, запишем это выражение по-другому:
Замечание: от переменных мест сомножителей произведение не меняется, запишем это выражение по-другому:
Значит, выражение .
Ответ: .
4. – это в кубе, 3 – это показатель степени, – основание степени.
Ответ:
5.
– вторая степень числа 13 , – вторая степень числа 5.
Ответ: 4225
6.
– третья степень числа 2, – вторая степень числа 3.
Ответ: 72
В степени an может отдельно меняться показатель степени или основание степени.
Пример 2: Вычислить , если
a) n=2
b) n=3
c) n=4
Решение:
a) так как стоит четная степень, минус пропадает.
b)
c) – так как стоит четная степень, минус пропадает.
Ответ: a) 25; b)-125; c)625;
В этом примере менялся показатель степени, а основание не менялось. Рассмотрим пример, когда меняется основание.
Пример 3: Вычислить: b4, где
a) b=1
b) b=-3
c) b=
d) b=
Ответ:
a)
b)
c)
Вспомним, что натуральные числа — это 1,2,3 и так далее.
n={1,2,3,…..}
По нашему определению:
an = , (1)
n={2,3,…..}
Нужно еще одно определение для случая n=1. Что же такое а1?
a1=a (2)
Пример.
()1=)
(-2)1=-2
31=3.
Итак, теперь мы знаем, что такое an, ,где n={1,2,3,…..} – любое натуральное число.
Рассмотрим геометрические задачи, в которых участвуют степени.
Задача: вычислить площадь квадрата, сторона которого равна а, где
a) а=3 см
b) а=7 см
c) а=1,5 см
Замечание. Если у нас есть квадрат со стороной а, то его площадь равна а2 или вторая степень числа а.
S=a2
Ответ:
S=32=9 см2
S=72=49 см2
S=1,52=2,25 см2
Итак, геометрическая задача потребовала от нас знание степени.
И в заключение, несколько примеров на вычисление. Задач много, но ключ к решению – первое и второе определение.
Вычислить:
a)
Как видим, вычисления могут быть разные, но ключ к решению одинаковый.
b) Вычислить при а=1 следующее выражение:
а2=12=1
а3=13=1
При а=-1 будет чуть посложнее:
а2=(-1)2=1
а3=(-13)=-1
а4=(-1)4=1
и т.д. -1 будет мерцать то 1, то -1 в зависимости от того четный или нечетный показатель.
Итак, наша задача была рассмотреть, что такое степень с натуральным показателем. Мы рассмотрели 2 основных определения (1) и (2), выучили терминологию аn, где n – это показатель степени, а – основание степени, n – натуральное число, а – любое число. Затем мы выполнили ряд задач. Далее мы будем изучать свойства степени с натуральным показателем.
Источник конспекта: http://interneturok.ru/ru/school/algebra/7-klass/stepen-s-naturalnym-pokazatelem-i-eyo-svojstva/chto-takoe-stepen-s-naturalnym-pokazatelem?konspekt&chapter_id=2
Источник видео: http://www. youtube.com/watch?v=0COo_2nOsz4
youtube.com/watch?v=0COo_2nOsz4
Конспект урока «Свойства степени с натуральным показателем»
Конспект урока.
«Свойства степени с натуральным показателем»
Учитель
Патракова Л. В.
2018г.
1. ФИО | Патракова Лариса Васильевна |
2. Место работы | МБОУ школа № 5 г.о. Кинешма |
3. Должность | Учитель |
4. Предмет | Алгебра |
5. Класс | 7 |
6. | «Свойства степени с натуральным показателем». 1 урок |
7. Базовый учебник | Г.В. Дорофеев, С.Б. Суворова и др. Алгебра 7 класс, «Просвещение», 2017г. |
Цели урока: познакомить учащихся со свойствами степени с натуральным показателем; владеть правилами выполнения действий над степенями; обеспечить условия для развития умений работы с источниками учебной информации, выделять главное и второстепенное.
Задачи:
Образовательные (формирование познавательных УУД): изучить свойства степени (умножение, деление, возведение степени в степень) с натуральным показателем; научить выполнять действия на применение правил; совершенствование вычислительных навыков.
Развивающие (формирование регулятивных УУД): развивать умения наблюдать, сравнивать, анализировать, делать выводы, развивать устную математическую речь.
Воспитательные (формирование коммуникативных и личностных УУД): формировать трудолюбие, внимательность, активность, умение слушать мнения других, участвовать в коллективном обсуждении проблем, воспитывать самостоятельность.
Тип урока: Урок «открытия» нового знания.
Формы работы учащихся: фронтальная, индивидуальная, групповая.
Используемые технологии: проблемное обучение, обучение в сотрудничестве, личностно-ориентированное обучение, коммуникативные и здоровьесберегающие технологии.
Необходимое оборудование: компьютер, проектор, экран, учебники по алгебре, карточки.
Сценарий урока.
1.Организационный момент.
Здравствуйте, ребята!
Начинаем наш урок, тему которого узнаем чуть позже.
Перед тем, как приступить к работе вспомним: какие правила мы должны соблюдать на уроке? Ответы детей. Учитель выслушивает ответы учеников: (Слушать, слышать друг друга, дополнять, исправлять, помогать)
-Запишем в тетрадях число, «Классная работа».
— Скажите, что нового вы узнали на предыдущих уроках? (ответы учеников)
Сегодня эпиграфом нашего урока станут слова М.В.Ломоносова
«Пусть кто-нибудь попробует вычеркнуть из математики степени, и он увидит, что без них далеко не уедешь»
-Где особенно часто используют степени, в каких науках? (Проверка домашнего задания найти дополнительный материал)
2.Актуализация опорных знаний.
Устная работа. (Слайд)
-Что называют степенью числа?
-Привести примеры.
-Назвать основание и показатель степени (Слайд)
-Любым ли числом может быть основание? Привести примеры.
-Всегда ли степень с отрицательным основанием, есть число отрицательное? -Сформулируйте определение. Приведите примеры.
— Что называют степенью числа с показателем 1?
Выполним вычисления и узнаем тему нашего урока (карточка 1 и 2)
ме | ой | ре | пе | св | к | да | ни | ва | нет | ра | ст | ро | см | сте | с | нь |
-36 | 25 | 12 | 81 | 16 | 8 | 4,5 | 7,9 | 10 | 7 | -6 | 9 | 6 | -9 | -8 | 36 | 1 |
|
сте | зате | нату | лем | пени | раль | ный | с | пока | ным |
-12 | 103 | 16 384 | 3026 | 10 609 | 59 049 | 177147 | 36 | 121 | 531 441 |
Запишем в тетради тему нашего урока: «Свойства степени».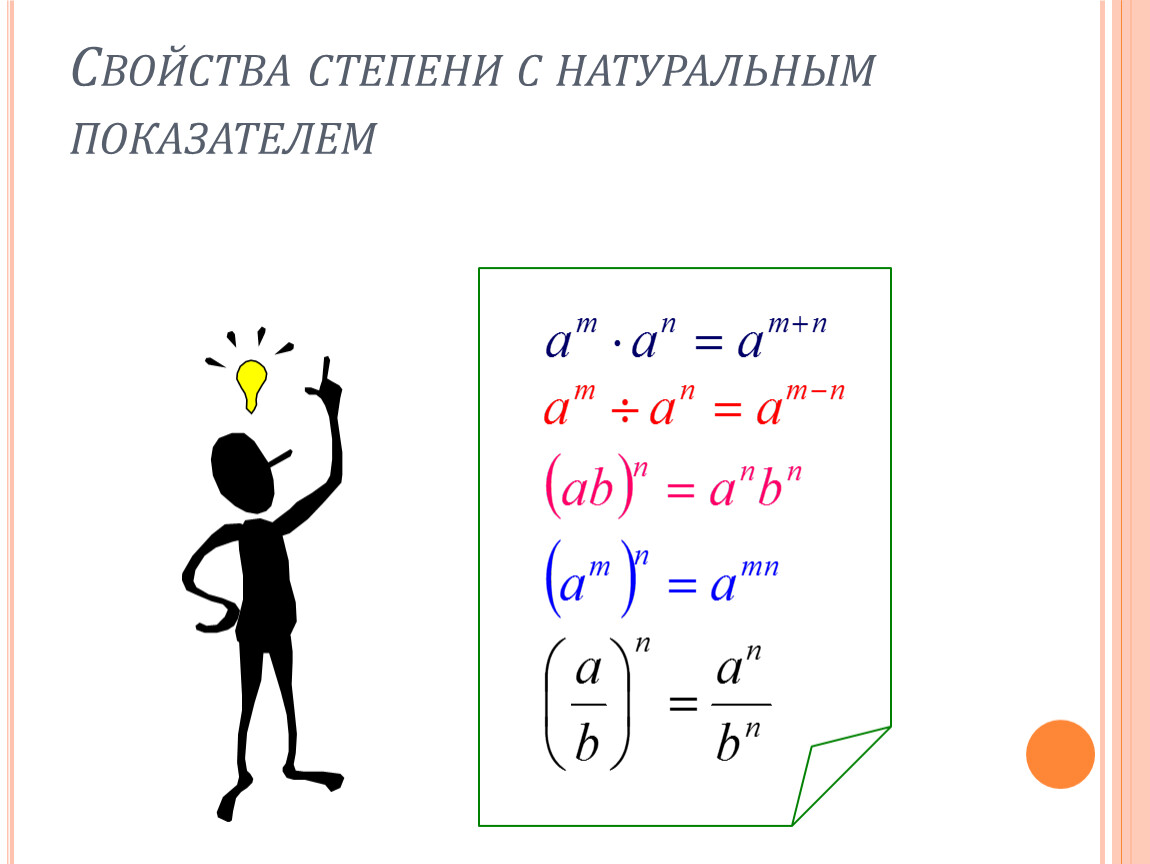 Название целей и задач урока.
Название целей и задач урока.
3. Освоение нового учебного материала.
Скажите, в чем возникла трудность при выполнении заданий второй части?
Работа в группах.
Карточка 3. ( см приложение)
-Вам сейчас предстоит изучить карточки, проанализировать, обобщить материал, сделать выводы, и после этого вы сможете вычислить примеры в которых у вас возникли затруднения. (См Инструкцию к карточке №3.)
-Посмотрите на образец решения примеров.
-Сформулируйте свойства степеней.
Работа с учебником.
Что написано в учебнике про деление степеней (какая неточность написана в карточке), Что надо запомнить и как исправить? Обязательно ли чтобы основание ≠0? Как вы думаете, почему?
Докажите, на примере почему
Запишите формулы в тетрадь.
4. Закрепление учебного материала.
Устная работа на применение формул по цепочке. Выполните номера из учебника и дайте определение, которое использовали при решение примеров 524,530,557, 540.
Физкультминутка. https://www.youtube.com/watch ?v=SAWr-KZhD0E
Проговаривание свойств степеней.
Карточка 4. ( см приложение)
Выполните задание №1, №2, №3.
Те ученики, которые быстро справились с заданием выполняют №4.
Запишите ответы в тетрадь. После того, как задание выполнено, ученики меняются тетрадями и проверяют тетради одноклассников, отмечая правильно решенные примеры знаком «+» (проверяя решения по слайду)
Объяснение трудных моментов, повторение правил, работа в группах.
Обратимся к таблицам и попробуем решить задание, с которым мы не смогли справиться в начале урока.
; ; ; ; ; .
Степень числа «3» мы можем найти в учебнике? Кто уже видел этот номер, подскажите остальным (№549)?
-Мы можем полностью озвучить тему нашего урока.
-Как она будет звучать?
-Что значит натуральная степень?
-Натуральное число?
-Какие свойства мы выучили?
-Сформулируйте свойства степеней.
Можно ли умножать или делить степени с разными основаниями?
Какое обязательное условие?
Выполним устно: , , ? (Слайд)
— Что надо сделать, чтобы применить выученные правила?
Выполнить на доске и в тетрадях №549, 548.
5.Задание на дом.
1.В тетрадь «Справочный материал» записать формулы и свойства степеней (опорные сигналы), выписать степени чисел «2», «3» с показателями от 1 до 15. (П 6.1, 6.2 )
2.Зашифровать фразу или слово, используя выражения со степенями + №537
или выполнить №№ 525, 529, 537, 536.
6. Подведение итогов урока. Рефлексия.
-Что мы изучали сегодня на уроке?
-Какие свойства степени мы выучили?
— Сформулируйте свойства степеней.
— Можно ли умножать или делить степени с разными основаниями?
Оцени свою работу:
— Я работал(а) отлично, в полную силу своих возможностей, чувствовал(а) себя уверенно.
— Я работал(а) хорошо, но не в полную силу, испытывал(а) чувство неуверенности, боязни, что отвечу неправильно.
— У меня не было желания работать. Сегодня не мой день.
Приложение
карточка 3.
Инструкция к карточке №3.
1.Повтори определение степени, вспомни, где записывается основание степени и показатель степени. (если забыл, можешь использовать карточки 1.1 и 1.2)
2. Внимательно прочитай определение 1. «Как умножать степени с одинаковым основанием», посмотри на схему- рисунок и запомни, что нужно сделать.
3. Посмотри на решение примеров. Выясни, как получается ответ.
4. Внимательно читай определение 2. Изучив схему-рисунок дополни определение необходимыми словами.
5. Посмотри на решение примеров. Выясни, как получается ответ, и проверь все ли так ты сформулировал в определении. Повтори определение еще раз.
6. Внимательно читай начало определения 3, изучив схему-рисунок дополни определение необходимыми словами.
7. Посмотри на решение примеров. Выясни, как получается ответ, и проверь все ли так ты сформулировал в определении. Повтори определение еще раз.
8. Повтори все определения еще раз.
9.Обрати внимания на перечеркнутые свойства, сделай вывод, проверь на примерах. Возьми основание равное 2, а затем 3.
Карточка 4.
В работе использован учебник Г.В. Дорофеева «Алгебра-7»
В работе использованы картинки.
https://www.google.ru/search ?q=картинка+по+математике&newwindow=1&client=opera&hs=V8e&tbm=isch&source=iu&ictx=1&fir=5JGazRRLNnZdYM%253A%252Cvah4VtVAveIjVM%252C_&usg=AFrqEzeGdgAmLzGNYLSmBYzj5dVFgJaK3w&sa=X&ved=2ahUKEwjcqMzv8_PcAhXFYpoKHRyMDKAQ9QEwAnoECAYQCA#imgrc=bDOXOOLse5BjdM:
https://www.google.ru/search?q=картинка+по+математике&newwindow=1&client=opera&hs=V8e&tbm=isch&source=iu&ictx=1&fir=5JGazRRLNnZdYM%253A%252Cvah4VtVAveIjVM%252C_&usg=AFrqEzeGdgAmLzGNYLSmBYzj5dVFgJaK3w&sa=X&ved=2ahUKEwjcqMzv8_PcAhXFYpoKHRyMDKAQ9QEwAnoECAYQCA#imgdii=KD3ROdzdl3-zpM:&imgrc=5JGazRRLNnZdYM:
https://www.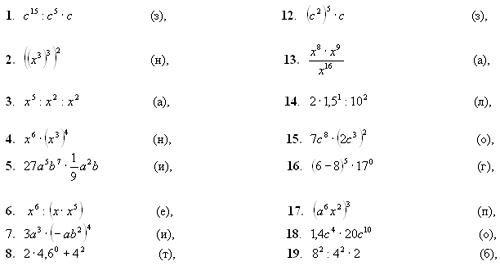 google.ru/search?q=картинка+по+математике&newwindow=1&client=opera&hs=V8e&tbm=isch&source=iu&ictx=1&fir=5JGazRRLNnZdYM%253A%252Cvah4VtVAveIjVM%252C_&usg=AFrqEzeGdgAmLzGNYLSmBYzj5dVFgJaK3w&sa=X&ved=2ahUKEwjcqMzv8_PcAhXFYpoKHRyMDKAQ9QEwAnoECAYQCA#imgrc=5JGazRRLNnZdYM:
google.ru/search?q=картинка+по+математике&newwindow=1&client=opera&hs=V8e&tbm=isch&source=iu&ictx=1&fir=5JGazRRLNnZdYM%253A%252Cvah4VtVAveIjVM%252C_&usg=AFrqEzeGdgAmLzGNYLSmBYzj5dVFgJaK3w&sa=X&ved=2ahUKEwjcqMzv8_PcAhXFYpoKHRyMDKAQ9QEwAnoECAYQCA#imgrc=5JGazRRLNnZdYM:
Карточка1
Карточка №2
Карточка №4
Карточка №5
Карточка №6
Карточка №3
Карточка 7.
Карточка №1.1
Карточка №1.2
Инструкция к карточке №3
DOCX / 11.98 Кб
Пояснительная записка к карточкам
DOCX / 13.12 Кб
Урок по алгебре в 7 классе на тему «Свойства степеней с натуральным показателем»
Тема: Свойства степени с натуральным показателем.
Цели:
Образовательные: изучить свойства степени с натуральным показателем, их формулировки и символическую запись, выработать у учащихся практические умения и навыки по применению изученных свойств.
Развивающие: способность дальнейшему развитию математически грамотной речи, внимания, наблюдательности, самоконтроля, исследовательских навыков учащихся, математического и логического мышления, активизация познавательной деятельности.
Воспитательная: воспитывать аккуратность и дисциплинированность школьников, умение работать в группе, помогать товарищам.
Место урока в системе урока по теме: первый урок по теме Свойства степени с натуральным показателем
Тип урока: комбинированный.
Формы урока: фронтальные, индивидуальные, групповые.
Оборудование: проектор, ПК, презентация, пазлы, маркеры, карточки для групп, карточки с проверочной работой, доска, мел.
Структура урока:
Организационный момент
Актуализация знаний
Сообщение новой темы, мотивация новой темы
Работа с группами, открытие знаний.
Презентация сделанных открытий
Физкультминутка
Закрепление изученного материала
Проверочная работа
Домашнее задание
Рефлексия.
 Подведение уроков.
Подведение уроков.
«Истина не рождается и не находится в голове отдельного человека, она рождается между людьми, совместно ищущими истину в процессе их диалогического общения»
Бахтин М. М.
Ход урока:
I Организационный момент.
Здравствуйте! Садитесь, пожалуйста! Начать урок хотелось бы словами великого ученого, но для того, чтобы их прочитать, необходимо решить устные примеры!
II Устный счет:
На слайде:
Каждый пример скрывает высказывание великого ученого, чтобы прочитать высказывание необходимо решить примеры.
В процессе решения примеров осуществляется повтор определения степени числа с натуральным показателем, продолжение формирования знаний и умений находить значение числовых выражений, содержащих степени.
Осуществляется фронтальная работа. В результате правильного решения примеров, перед учащимися появляются высказывания великого ученого Михаила Васильевича Ломоносова «Пусть кто-нибудь попробует выкинуть из математики степени, и он увидит, что без них далеко не уедешь»
III Сообщение новой темы и мотивация её изучения
На прошлом уроке мы с вами находили значения числовых выражений, содержащих степени. Предлагаю вычислить устно:
Предлагаю вычислить устно:
У учащихся возникают затруднения, что является следствием недостатка знаний.
Для того, чтобы выполнять такие вычисления устно, нам необходимо узнать больше про степени, изучить их свойства.
Запишем тему урока:
Свойства степени с натуральным показателем
Перед нами мозаика в ней формулы скрыты.
Чтобы пазл компоновкой в картину сложить
Вам придется в командах всерьёз потрудиться
И свойства степени получить
Для этого мы разобьемся на 5 команд.
IV Изучение нового материала
Каждая команда получает карточку с заданием
Карточка 1
Записать произведение в виде степени
А)
Б)
В)
2) Проанализируйте, что происходит с основанием степени, что происходит с показателем степени при умножении степеней с одинаковыми основаниями. Сделайте вывод.
3) Запиши полученное правило в буквенном виде.
4) Придумай несколько своих примеров.
5) Оформи пазл (буквенная запись свойства + простой пример, иллюстрирующий правило)
Карточка 2
Записать частное в виде степени:
А)
Б)
В)
2) Проанализируйте, что происходит с основанием степени, что происходит с показателем степени при умножении степеней с одинаковыми основаниями. Сделайте вывод.
3) Запиши полученное правило в буквенном виде.
4) Придумай несколько своих примеров.
5) Оформи пазл (буквенная запись свойства + простой пример, иллюстрирующий правило)
Карточка 3
Записать в виде степени:
А) с основанием 4
Б) С основанием 6
В) с основанием -17
2) Проанализируйте, что происходит с основанием степени, что происходит с показателем степени при умножении степеней с одинаковыми основаниями. Сделайте вывод.
3) Запиши полученное правило в буквенном виде.
4) Придумай несколько своих примеров.
5) Оформи пазл (буквенная запись свойства + простой пример, иллюстрирующий правило)
Карточка 4
Запиши в виде произведения степеней:
А)
Б)
В)
2) Проанализируйте, что происходит с каждым множителем при возведении в степень произведение. Сделай вывод.
3) Запиши полученное правило в буквенном виде.
4) Придумай несколько своих примеров.
5) Оформи пазл (буквенная запись свойства + простой пример, иллюстрирующий правило)
Карточка 5
Возведи в степень дробь
А)
Б)
В)
2) Проанализируйте, что происходит с числителем и знаменателем дроби при возведении дроби в степень. Сделайте вывод.
3) Запишите полученное правило в буквенном виде.
4) Придумайте несколько своих примеров.
5) Оформи пазл (буквенная запись свойства + простой пример, иллюстрирующий правило)
Учитель во время работы учащихся в группах, при необходимости помогает им формулировать выводы.
В случае возникновения трудностей при выполнении 1-го задания, учитель может давать подсказки: Карточка 1 – воспользоваться определением степени числа с натуральным показателем., Карточка 2 – заменить знак деления дробной чертой, воспользоваться определением степени с натуральным показателем и сократить дробь; Карточка 3 – определение степени числа с натуральным показателем; Карточка 4 – определение степени с натуральным показателем, применить переместительное и сочетательное свойства умножения; Карточка 5 – определение степени с натуральным показателем и правило умножения обыкновенных дробей.
V Презентация сделанных открытий.
По одному представителю от каждой группы выходят к доске и рассказывают свое свойство и приводят примеры.
Остальные учащиеся записывают свойства с примерами в тетрадь.
— Итак, мы с вами сложили мозаику! Нашли все недостающие элементы! Этой мозаикой будем пользоваться при решении примеров.
— Как решить пример, который заставил нас изучить степени и их свойства?
Каким свойством можно воспользоваться, чтобы вычисления стали устными? (уч-ся рассказывают свои версии решения примеров)
VI Физкультминутка.
Давайте теперь немного отдохнем. Встанем все и внимательно меня слушаем! Если говорю верное утверждение, то руки поднимаем вверх, если ложное в стороны!
8,
5) При делении степеней с одинаковыми основаниями выполняется деление и оснований и степеней.
6) При возведении в степень дроби в эту степень возводится числитель и знаменатель.
7) При возведении в степень произведения, в эту степень возводится только второй множитель, а первый остается без изменения.
МОЛОДЦЫ! ПРОДОЛЖИМ РАБОТУ!
VII Закрепление изученного материала.
Решение заданий на доске и в тетрадях:
№1 Упростить, воспользовавшись свойствами:
А)
Б)
В)
Г)
Д)
Е)
№2 Вычислите
А)
Б)
В)
Г)
Д)
VIII Проверочная работа
Вариант 1.
Представить выражение в виде степени
Возвести степень в степень
Представить в виде произведения степеней
Записать в виде степени выражение
Представить в виде степени числа 15
Число а отрицательно, Каков знак числа
Вариант 2.
Представить выражение в виде степени
Возвести степень в степень
Представить в виде произведения степеней
Записать в виде степени выражение
Представить в виде степени числа 8
Число а отрицательно, Каков знак числа
IX Домашнее задание
Выучить свойства: п.20
№429, 436, 438, 450(а,в)
X Рефлексия
Ребята по кругу высказываются одним предложением, выбирая начало фразы из рефлексивного экрана на доске:
Сегодня я узнал …
Было интересно…
Было трудно…
Я выполнил задание…
Я понял, что …
Теперь я могу…
Я почувствовал, что….
Я приобрел….
Я научился…
У меня получилось….
Я смог…
Я попробую…
Меня удивило…
Урок дал мне для жизни…
Подводя итоги, хочется заметить, что
Мы часто видим лиши детали,
Но чтоб из этих пазлов целое сложить,
Порой бывает нужно, чтоб нас поддержали,
Чтоб было с кем проблемы и заботы разделить.
Вы сегодня плодотворно поработали в командах!
Спасибо за урок!
3). В верхней части (или числителе) мы имеем x умноженное на x умноженное на x умноженное на x . Внизу (или знаменателе) мы имеем x , умноженное на x , умноженное на x . Надеюсь, вы помните, что x , разделенное на x , равно 1, поэтому x отменяются. Итак, x , разделенное на x , равно 1, x , разделенное на x , равно 1, а x , разделенное на x , равно 1. 1 или просто x .3), что в основном распределяет 3 на x и y .
Итоги урока
Давайте в последнюю минуту рассмотрим пять свойств.
- Произведение степени : когда вы умножаете экспоненты с одинаковым основанием, вы складываете их показатели (или степени).
- Степень в силу : Когда у вас есть сила в силу, вы умножаете степень (или степень).
- Коэффициент степеней : когда вы делите экспоненты с одинаковым основанием, вы вычитаете экспоненты (или степени).
- Степень произведения : Когда у вас есть произведение степени, вы даете каждой базе ее собственный показатель степени (или распределяете показатель степени по каждой основе).
- Степень частного : Когда у вас есть частное к степени, вы даете каждой базе свой собственный показатель степени.
Цели урока
К концу этого урока вы узнаете пять основных свойств экспоненты и разберетесь с примерами их применения.
11 правил естественного журнала, которые необходимо знать
Если вы посещаете математический класс в средней школе или колледже, вы, скорее всего, будете учиться натуральному логарифму. Но что такое натуральные бревна? Что такое ln? Почему продолжает появляться буква е?
Естественный журнал может показаться сложным, но как только вы поймете несколько ключевых правил естественного журнала, вы сможете легко решать даже очень сложные на вид проблемы. В этом руководстве мы объясним четыре наиболее важных правила натурального логарифма, обсудим другие свойства натурального логарифма, которые вам следует знать, рассмотрим несколько примеров различной сложности и объясним, чем натуральные логарифмы отличаются от других логарифмов.
Что такое ln?
Натуральный логарифм, или ln, является обратной величиной e . Буква « e » представляет математическую константу, также известную как естественный показатель степени. Как и π, e является математической константой и имеет заданное значение. Значение e равно примерно 2,71828.
e встречается во многих случаях в математике, в том числе в сценариях, касающихся сложных процентов, уравнений роста и уравнений распада. ln ( x ) — это время, необходимое для роста до x , а e x — это величина роста, произошедшая по прошествии времени x .
Поскольку e так часто используется в математике и экономике, и людям в этих областях часто требуется логарифм с основанием e числа, чтобы решить уравнение или найти значение, натуральный логарифм был создан как Быстрый способ записи и расчета базы журнала e . Натуральный логарифм просто позволяет людям, читающим задачу, знать, что вы берете логарифм числа с основанием e . Таким образом, ln ( x ) = log e ( x ).Например, ln ( 5 ) = log e ( 5 ) = 1,609.
4 основных правила естественного журнала
Есть четыре основных правила, которые вам нужно знать при работе с естественным логарифмом, и вы будете встречать каждое из них снова и снова в своих математических задачах. Хорошо знайте их, потому что они могут сбить с толку, когда вы их впервые увидите, и вы хотите убедиться, что у вас есть такие базовые правила, прежде чем переходить к более сложным темам логарифмирования.
Правило продукта
- ln (x) (y) = ln (x) + ln (y)
- Натуральный логарифм умножения x и y — это сумма ln x и ln y.
- Пример: ln (8) (6) = ln (8) + ln (6)
Правило частного
- ln (x / y) = ln (x) — ln (y)
- Натуральный логарифм деления x и y — это разность ln x и ln y.
- Пример: ln (7/4) = ln (7) — ln (4)
Взаимное правило
- ln (1 / x) = −ln (x)
- Натуральный логарифм обратной величины x противоположен ln x.
- Пример: ln (⅓) = -ln (3)
Правило мощности
- ln ( x y ) = y * ln (x)
- Натуральный логарифм числа x в степени y равен y, умноженному на ln числа x.
- Пример: ln (5 2 ) = 2 * ln (5)
Ключевые свойства натурального бревна
В дополнение к четырем правилам натурального логарифма, описанным выше, есть еще несколько свойств ln, которые вам необходимо знать, если вы изучаете натуральные логарифмы. Запомните их, чтобы вы могли быстро перейти к следующему этапу решения, не тратя время на попытки запомнить общие свойства ln.
Сценарий | ln Недвижимость |
ln отрицательного числа | Длина отрицательного числа не определена |
пер 0 | ln (0) не определено |
пер 1 | ln (1) = 0 |
Линия бесконечности | ln (∞) = ∞ |
пер. Е | лн (эл.) = 1 |
ln e повышен до x мощности | ln ( e x ) = x |
e повышен до мощности | e ln (x) = x |
Как видно из последних трех строк, ln ( e ) = 1, и это верно, даже если одна возведена в степень другой.Это потому, что ln и e являются обратными функциями друг друга.
Задачи выборки натурального журнала
Теперь пришло время проверить свои навыки и убедиться, что вы понимаете правила ln, применяя их к примерам задач. Ниже приведены три примера проблем. Попытайтесь решить их самостоятельно, прежде чем читать объяснение.
Задача 1
Оценить ln (7 2 /5)
Сначала мы используем правило частного, чтобы получить: ln (7 2 ) — ln (5).
Затем мы используем правило мощности, чтобы получить: 2ln (7) -ln (5).
Если у вас нет калькулятора, вы можете оставить уравнение в таком виде или вычислить значения натурального логарифма: 2 (1,946) — 1,609 = 3,891 — 1,609 = 2,283.
Задача 2
Оценить ln ( e ) / 7
Для этой задачи нам нужно помнить, что ln ( e ) = 1
Это означает, что задача упрощается до 1/7, что и является нашим ответом.
Задача 3
Решить ln (5 x -6) = 2
Когда у вас есть несколько переменных в скобках ln, вы хотите сделать e основанием, а все остальное — показателем степени e . Тогда вы получите ln и e рядом друг с другом и, как мы знаем из правил естественного журнала, e ln (x) = x.
Итак, уравнение принимает вид e ln (5x-6) = e 2
Начиная с e ln (x) = x , e ln (5x-6) = 5x-6
Следовательно 5 x -6 = e 2
Поскольку e является константой, вы можете вычислить значение e 2 , либо используя клавишу e на вашем калькуляторе, либо используя оценочное значение e, равное 2.718.
5 x -6 = 7,389
Теперь добавим 6 к обеим сторонам
5 x = 13,389
Наконец, мы разделим обе стороны на 5.
x = 2,678
Чем натуральные логарифмы отличаются от других логарифмов?
Напоминаем, что логарифм — это противоположность степени. Если вы возьмете журнал числа, вы отмените экспоненту. Основное различие между натуральным логарифмом и другими логарифмами заключается в используемом основании.В логарифмах обычно используется основание 10 (хотя это может быть другое значение, которое будет указано), тогда как в натуральных логарифмах всегда используется основание e .
Это означает, что ln (x) = log e ( x )
Если вам нужно преобразовать логарифм в натуральный логарифм, используйте следующие два уравнения:
- журнал 10 ( x ) = ln (x) / ln (10)
- ln (x) = log 10 ( x ) / log 10 ( e )
За исключением разницы в основании (которая является большой разницей) правила логарифмирования и правила натурального логарифма одинаковы:
Правила логарифмирования | Правила |
журнал (xy) = журнал (x) + журнал (y) | ln (x) (y) = ln (x) + ln (y) |
журнал (x / y) = журнал (x) −log (y) | ln (x / y) = ln (x) −ln (y) |
журнал (x a ) = a журнал ( x ) | лин (x a ) = a ln ( x ) |
журнал (10 x ) = x | ln ( e x ) = x |
10 журнал (x) = x | e ln (x) = x |
Резюме: Правила естественного журнала
Натуральный логарифм или ln — это величина, обратная e. Правила естественного журнала могут сначала показаться нелогичными, но как только вы их изучите, их довольно просто запомнить и применить к практическим задачам.
Четыре основных правила ln:
- ln (x) (y) = ln (x) + ln (y)
- ln (x / y) = ln (x) — ln (y)
- лин (1 / x) = — ln (x)
- n ( x y ) = y * ln (x)
Ключевое различие между натуральным логарифмом и другими логарифмами заключается в используемом основании.
Что дальше?
Пишете исследовательскую работу для школы, но не знаете, о чем писать? В нашем справочнике по темам исследовательских работ более 100 тем в десяти категориях, поэтому вы можете быть уверены, что найдете идеальную тему для себя.
Хотите узнать о самых быстрых и простых способах конвертации между градусами Фаренгейта и Цельсия? Мы вас прикрыли! Ознакомьтесь с нашим руководством по лучшим способам преобразования Цельсия в градусы Фаренгейта (или наоборот).
Сдаете SAT или ACT? Студенты часто испытывают трудности с математическим разделом этих тестов, но ознакомьтесь с нашими подробными руководствами по SAT Math и ACT Math, где вы найдете все, что вам нужно знать, чтобы сдать эти вопросы по математике.
10 законов экспонент | Sciencing
Обновлено 15 декабря 2020 г.
Автор: Кэтрин Уайт
Одна из сложнейших концепций алгебры включает манипуляции с показателями степени или степенями.Часто задачи потребуют от вас использования законов экспонент для упрощения переменных с показателями, или вам придется упростить уравнение с показателями для его решения. Чтобы работать с показателями экспоненты, вам необходимо знать основные правила экспоненты.
Структура экспоненты
Примеры экспоненты выглядят как 2 3 , что будет читаться как два в третьей степени или как два в кубе, или 7 6 , что будет читаться как семь в шестой степени. 2)
нельзя было дополнительно упростить (объединить), потому что X s и Y S имеют разные полномочия в каждом термине.4
Правило первой степени экспоненты
Все, что возведено в первую степень, остается неизменным. Например, 7 1 будет просто 7 и ( x 2 r 3 ) 1 упростится до x 2 r 3 .
Показатели нуля
Все, что возведено в степень 0, становится числом 1. Неважно, насколько сложен или велик этот член.4} \ bigg) \\ & = \ bigg (\ frac {1} {64} \ bigg) ÷ \ bigg (\ frac {1} {16} \ bigg) \\ & = \ bigg (\ frac {1} {64} \ bigg) × (16) \\ & = 4 \ end {align}
Логарифм
| Правила, примеры и формулы
Логарифм , показатель степени или степень, до которой необходимо возвести основание, чтобы получить заданное число. Выражаясь математически, x — это логарифм от n до основания b , если b x = n , и в этом случае записывается x = log b n .Например, 2 3 = 8; следовательно, 3 — это логарифм 8 по основанию 2, или 3 = log 2 8. Таким же образом, поскольку 10 2 = 100, тогда 2 = log 10 100. Логарифмы последнего вида (что То есть логарифмы с основанием 10) называются обычными, или бриггсовскими, логарифмами и записываются просто log n .
Логарифмы, изобретенные в 17 веке для ускорения вычислений, значительно сократили время, необходимое для умножения чисел на многозначные числа.Они были основой численной работы более 300 лет, пока совершенствование механических вычислительных машин в конце 19 века и компьютеров в 20 веке не сделало их устаревшими для крупномасштабных вычислений. Натуральный логарифм (с основанием e ≅ 2,71828 и записанным ln n ), тем не менее, продолжает оставаться одной из наиболее полезных функций в математике с приложениями к математическим моделям во всех физических и биологических науках.
Свойства логарифмов
Логарифмы
были быстро приняты учеными из-за различных полезных свойств, которые упростили долгие и утомительные вычисления.В частности, ученые могли найти произведение двух чисел m и n , просмотрев логарифм каждого числа в специальной таблице, сложив логарифмы вместе, а затем снова просмотрев таблицу, чтобы найти число с вычисленным логарифмом (известным как его антилогарифм). Выраженное в терминах десятичных логарифмов, это соотношение определяется как log m n = log m + log n . Например, 100 × 1000 можно вычислить, найдя логарифмы 100 (2) и 1000 (3), сложив логарифмы вместе (5), а затем найдя его антилогарифм (100000) в таблице.Аналогичным образом задачи деления преобразуются в задачи вычитания с помощью логарифмов: log m / n = log m — log n . Это еще не все; вычисление степеней и корней можно упростить с помощью логарифмов. Логарифмы также могут быть преобразованы между любыми положительными основаниями (за исключением того, что 1 не может использоваться в качестве основания, поскольку все его степени равны 1), как показано в таблице логарифмических законов.
В таблицы логарифмов обычно включались только логарифмы для чисел от 0 до 10.Чтобы получить логарифм некоторого числа за пределами этого диапазона, число сначала было записано в экспоненциальной форме как произведение его значащих цифр и его экспоненциальной степени — например, 358 будет записано как 3,58 × 10 2 , а 0,0046 будет можно записать как 4,6 × 10 −3 . Тогда логарифм значащих цифр — десятичная дробь от 0 до 1, известная как мантисса, — будет найден в таблице. Например, чтобы найти логарифм 358, нужно найти log 3,58 0.55388. Следовательно, журнал 358 = журнал 3,58 + журнал 100 = 0,55388 + 2 = 2,55388. В примере числа с отрицательной экспонентой, например 0,0046, можно найти log 4,6 0,66276. Следовательно, log 0,0046 = log 4,6 + log 0,001 = 0,66276 — 3 = −2,33724.
Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту.
Подпишитесь сейчас
История логарифмов
Изобретение логарифмов было предсказано сравнением арифметических и геометрических последовательностей. В геометрической последовательности каждый член образует постоянное отношение со своим последователем; Например,
… 1/1000, 1/100, 1/10, 1, 10, 100, 1000…
имеет общий коэффициент 10.В арифметической последовательности каждый последующий член отличается константой, известной как общая разница; Например,
… −3, −2, −1, 0, 1, 2, 3…
имеет общее различие 1. Обратите внимание, что геометрическая последовательность может быть записана в терминах ее общего отношения; для примера геометрической последовательности, приведенной выше:
… 10 −3 , 10 −2 , 10 −1 , 10 0 , 10 1 , 10 2 , 10 3 ….
Умножение двух чисел в геометрической последовательности, скажем 1/10 и 100, равносильно сложению соответствующих показателей общего отношения, -1 и 2, чтобы получить 10 1 = 10.Таким образом, умножение превращается в сложение. Первоначальное сравнение двух серий, однако, не было основано на явном использовании экспоненциальной записи; это было более позднее развитие. В 1620 году швейцарский математик Йост Бюрги опубликовал в Праге первую таблицу, основанную на концепции взаимосвязи геометрической и арифметической последовательностей.
Шотландский математик Джон Напьер опубликовал свое открытие логарифмов в 1614 году. Его цель заключалась в том, чтобы помочь в умножении величин, которые тогда назывались синусами.Полный синус был величиной стороны прямоугольного треугольника с большой гипотенузой. (Первоначальная гипотенуза Нэпьера была 10 7 .) Его определение было дано в терминах относительных скоростей.
Логарифм, следовательно, любого синуса — это число, очень точно выражающее линию, которая одинаково увеличивалась за определенное время, в то время как линия всего синуса пропорционально уменьшалась до этого синуса, причем оба движения равны по времени и начало одинаково сдвигается.
В сотрудничестве с английским математиком Генри Бриггсом Нэпьер привел свой логарифм в его современную форму.Для логарифма Напериана сравнение будет происходить между точками, движущимися по градуированной прямой, точка L (для логарифма) равномерно перемещается от минус бесконечности к плюс бесконечности, точка X (для синуса) движется от нуля до бесконечность со скоростью, пропорциональной ее расстоянию от нуля. Кроме того, L равно нулю, когда X равно единице и их скорость в этот момент равна. Суть открытия Напьера состоит в том, что оно представляет собой обобщение отношения между арифметическим и геометрическим рядами; я.е. умножение и возведение в степень значений точки X соответствуют сложению и умножению значений точки L соответственно. На практике удобно ограничить движение L, и X требованием, чтобы L = 1 при X = 10 в дополнение к условию, что X = 1 при L = 0. Это изменение произвело бриггсианский, или обыкновенный, логарифм.
Нэпир умер в 1617 году, и Бриггс продолжал работать в одиночку, опубликовав в 1624 году таблицу логарифмов, рассчитанных до 14 десятичных знаков для чисел от 1 до 20 000 и от 90 000 до 100 000.В 1628 году голландский издатель Адриан Влак выпустил 10-местную таблицу для значений от 1 до 100 000, добавив недостающие 70 000 значений. И Бриггс, и Влакк занимались настройкой тригонометрических таблиц журнала. Такие ранние таблицы были либо с точностью до одной сотой градуса, либо до одной угловой минуты. В 18 веке таблицы публиковались с интервалом в 10 секунд, что было удобно для таблиц с семью знаками после запятой. Как правило, более мелкие интервалы требуются для вычисления логарифмических функций меньших чисел — например, при вычислении функций log sin x и log tan x .
Наличие логарифмов сильно повлияло на форму плоской и сферической тригонометрии. Процедуры тригонометрии были переработаны для создания формул, в которых все операции, зависящие от логарифмов, выполняются одновременно. Тогда обращение к таблицам состояло всего из двух шагов: получения логарифмов и, после выполнения вычислений с логарифмами, получения антилогарифмов.
Фрэнсис Дж. Мюррей
Узнайте больше в этих связанных статьях Britannica:
экспоненциальных и логарифмических моделей | Колледж алгебры
Результаты обучения
- График функций экспоненциального роста и убывания.
- Решает проблемы, связанные с радиоактивным распадом, датированием углерода и периодом полураспада.
- Используйте закон охлаждения Ньютона.
- Используйте модель логистического роста.
- Выберите подходящую модель для данных.
- Используйте графическую утилиту для создания экспоненциальной регрессии из набора данных.
Мы уже исследовали некоторые основные приложения экспоненциальных и логарифмических функций. В этом разделе мы более подробно исследуем некоторые важные приложения, включая радиоактивные изотопы и закон охлаждения Ньютона.
Ядерный исследовательский реактор в Центре ядерных исследований Нили в кампусе Технологического института Джорджии. (Источник: Технологический научно-исследовательский институт Джорджии)
Экспоненциальный рост и спад
В реальных приложениях нам нужно моделировать поведение функции. {kt} [/ latex]
, где [latex] {A} _ {0} [/ latex] равно значению в нулевой момент времени, e — постоянная Эйлера, а k — положительная константа, определяющая скорость (процент) роста.Мы можем использовать функцию экспоненциального роста в приложениях, включающих время удвоения , время, необходимое для удвоения количества. Такие явления, как популяции диких животных, финансовые вложения, биологические образцы и природные ресурсы, могут демонстрировать рост, основанный на времени удвоения. Однако в некоторых приложениях, как мы увидим при обсуждении логистического уравнения, логистическая модель иногда лучше соответствует данным, чем экспоненциальная модель.
С другой стороны, если величина быстро падает к нулю, никогда не достигая нуля, то мы, вероятно, должны выбрать модель экспоненциального затухания .{-kt} [/ latex], где [latex] {A} _ {0} [/ latex] — начальное значение, а e — константа Эйлера. Теперь k — отрицательная константа, определяющая скорость распада. Мы можем использовать модель экспоненциального распада, когда мы рассчитываем период полураспада , или время, которое требуется веществу, чтобы экспоненциально распадаться до половины своего первоначального количества. Мы используем период полураспада в приложениях, связанных с радиоактивными изотопами.
При выборе функции в качестве математической модели мы часто используем точки данных, собранные путем тщательного наблюдения и измерения, для построения точек на графике и надеемся, что сможем распознать форму графика.{-2x} [/ латекс].
Экспоненциальный рост и спад часто связаны с очень большими или очень маленькими числами. Чтобы описать эти числа, мы часто используем порядки величины. Порядок — это степень десяти, когда число выражается в экспоненциальном представлении с одной цифрой слева от десятичной дроби. Например, расстояние до ближайшей звезды Proxima Centauri , измеренное в километрах, составляет 40 113 497 200 000 километров. В научных обозначениях это [латекс] 4.{kt} [/ latex] имеет следующие характеристики:
- индивидуальная функция
- горизонтальная асимптота: y = 0
- домен: [латекс] \ left (- \ infty, \ infty \ right) [/ latex]
- диапазон: [латекс] \ left (0, \ infty \ right) [/ latex]
- x перехват: нет
- Y-перехват: [латекс] \ left (0, {A} _ {0} \ right) [/ latex]
- увеличивается, если k > 0
- уменьшается, если k <0
Экспоненциальная функция моделирует экспоненциальный рост, когда k> 0, и экспоненциальный спад, когда k <0.
Пример: график экспоненциального роста
Популяция бактерий удваивается каждый час. Если культивирование началось с 10 бактерий, изобразите популяцию как функцию времени.
Показать решение
Когда сумма растет на фиксированный процент в единицу времени, рост является экспоненциальным. Чтобы найти [латекс] {A} _ {0} [/ latex], мы используем тот факт, что [latex] {A} _ {0} [/ latex] — это количество в нулевой момент времени, поэтому [latex] {A} _ {0} = 10 [/ латекс]. Чтобы найти k , используйте тот факт, что через час [latex] \ left (t = 1 \ right) [/ latex] популяция удваивается с 10 до 20.{kt} \ hfill & \ text {Разделите обе стороны на} {A} _ {0}. \ hfill \\ \ mathrm {ln} 2 = kt \ hfill & \ text {Возьмите натуральный логарифм обеих сторон}. \ hfill \\ t = \ frac {\ mathrm {ln} 2} {k} \ hfill & \ text {Разделить на коэффициент} t. \ hfill \ end {array} [/ latex]
Таким образом, время удвоения составляет
[латекс] t = \ frac {\ mathrm {ln} 2} {k} [/ latex]
Пример: поиск функции, описывающей экспоненциальный рост
Согласно закону Мура, время удвоения количества транзисторов, которые можно установить на компьютерный чип, составляет примерно два года.{\ frac {\ mathrm {ln} 2} {3} t} [/ латекс]
Период полураспада
Теперь обратимся к экспоненциальному убыванию . Одним из общих терминов, связанных с экспоненциальным распадом, как указано выше, является период полураспада , промежуток времени, который требуется экспоненциально убывающей величине, чтобы уменьшиться до половины от ее первоначального количества. {kt} [/ latex]
Мы обнаружили, что период полураспада зависит только от константы k , а не от исходного количества [латекс] {A} _ {0} [/ latex].{kt} \ hfill & \ text {Разделите обе стороны на} {A} _ {0}. \ hfill \\ \ mathrm {ln} \ left (\ frac {1} {2} \ right) = kt \ hfill & \ text {Возьмите натуральный логарифм с обеих сторон}. \ hfill \\ — \ mathrm {ln} \ left (2 \ right) = kt \ hfill & \ text {Применить свойства логарифмов}. \ hfill \\ — \ frac {\ mathrm {ln} \ left (2 \ right)} {k} = t \ hfill & \ text {Разделить на} k. \ hfill \ end {array} [/ latex]
Поскольку t , время положительное, значение k , как и ожидалось, должно быть отрицательным. Это дает нам формулу полураспада
[латекс] t = — \ frac {\ mathrm {ln} \ left (2 \ right)} {k} [/ latex]
В предыдущих разделах мы изучили свойства и правила как для экспоненциальных, так и для логарифмических функций.Мы видели, что любую экспоненциальную функцию можно записать в виде логарифмической функции и наоборот. Мы использовали показатели для решения логарифмических уравнений и логарифмы для решения экспоненциальных уравнений. Теперь мы готовы объединить наши навыки для решения уравнений, которые моделируют реальные ситуации, независимо от того, находится ли неизвестное в экспоненте или в логарифме.
Одно из таких приложений — в науке, для расчета времени, необходимого для распада половины нестабильного материала в образце радиоактивного вещества, называемого периодом полураспада .В таблице ниже перечислены периоды полураспада некоторых наиболее распространенных радиоактивных веществ.
| Вещество | Использовать | Период полураспада |
|---|---|---|
| галлий-67 | ядерная медицина | 80 часов |
| кобальт-60 | производство | 5,3 года |
| технеций-99m | ядерная медицина | 6 часов |
| америций-241 | строительство | 432 года |
| углерод-14 | Археологическая датировка | 5715 лет |
| уран-235 | атомная мощь | 703 800 000 лет |
Мы видим, насколько сильно различаются периоды полураспада этих веществ.{kt} [/ латекс].
Примечание: Также можно найти скорость распада, используя [латекс] k = — \ frac {\ mathrm {ln} \ left (2 \ right)} {t} [/ latex].
Пример: использование формулы радиоактивного распада для определения количества вещества
Сколько времени потребуется для распада 10% 1000-граммовой пробы урана-235?
Показать решение
[латекс] \ begin {array} {l} \ text {} y = \ text {1000} e \ frac {\ mathrm {ln} \ left (0.{M} \ right) = M \ hfill \\ \ text {} \ text {} t = \ text {703 800 000} \ times \ frac {\ mathrm {ln} \ left (0.9 \ right)} {\ mathrm {ln } \ left (0.5 \ right)} \ text {years} \ hfill & \ text {Решить для} t. \ hfill \\ \ text {} \ text {} t \ приблизительно \ text {106 979 777 лет} \ hfill & \ hfill \ end {array} [/ latex]
Анализ решения
Десять процентов от 1000 граммов составляют 100 граммов. Если 100 граммов распадаются, количество оставшегося урана-235 составляет 900 граммов.
Попробуй
Сколько времени пройдет, прежде чем двадцать процентов нашей 1000-граммовой пробы урана-235 распадутся?
Показать решение
[латекс] t = 703 800 000 \ times \ frac {\ mathrm {ln} \ left (0.{\ left (\ frac {\ mathrm {ln} \ left (0.5 \ right)} {5730} \ right) t} [/ latex]. Мы замечаем, что коэффициент t , [латекс] \ frac {\ mathrm {ln} \ left (0.5 \ right)} {5730} \ приблизительно -1,2097 [/ latex] отрицателен, как и ожидалось в случае экспоненциальной разлагаться.
Попробуй
Период полураспада плутония-244 составляет 80 000 000 лет. {- 0.0000000087t} [/ латекс]
Радиоуглеродное датирование
Формула радиоактивного распада важна для радиоуглеродного датирования , которое используется для расчета приблизительной даты смерти растения или животного. Радиоуглеродное датирование было открыто в 1949 году Уиллардом Либби, получившим Нобелевскую премию за свое открытие. Он сравнивает разницу между соотношением двух изотопов углерода в органическом артефакте или ископаемом веществе и соотношением этих двух изотопов в воздухе. Считается, что это точность с точностью до 1% для растений или животных, умерших в течение последних 60 000 лет.
Углерод-14 — это радиоактивный изотоп углерода с периодом полураспада 5730 лет. В небольших количествах он содержится в двуокиси углерода в воздухе, которым мы дышим. Большая часть углерода на Земле — это углерод-12, который имеет атомный вес 12 и не является радиоактивным. Ученые определили соотношение углерода-14 к углероду-12 в воздухе за последние 60 000 лет, используя годичные кольца деревьев и другие образцы органических веществ с известными датами, хотя соотношение несколько изменилось за столетия.
Пока живо растение или животное, соотношение двух изотопов углерода в его теле близко к соотношению в атмосфере.{\ left (\ frac {\ mathrm {ln} \ left (0.5 \ right)} {5730} \ right) t} \ hfill & \ text {Заменить} r \ text {в формуле непрерывного роста}. \ hfill \ end {array} [/ latex]
Чтобы определить возраст объекта, мы решаем это уравнение для t :
[латекс] t = \ frac {\ mathrm {ln} \ left (\ frac {A} {{A} _ {0}} \ right)} {- 0,000121} [/ латекс]
По необходимости мы пренебрегаем многими деталями, которые учёные принимают во внимание при датировании по углероду-14, и рассматриваем только основную формулу.{-0.000121t} [/ латекс]. Решаем это уравнение для t , получаем
[латекс] t = \ frac {\ mathrm {ln} \ left (r \ right)} {- 0,000121} [/ латекс]
Как сделать: учитывая процентное содержание углерода-14 в объекте, определить его возраст
- Выразите данное процентное содержание углерода-14 в виде десятичного эквивалента r .
- Замените r в уравнении [латекс] t = \ frac {\ mathrm {ln} \ left (r \ right)} {- 0,000121} [/ latex] и решите для возраста, t .
Пример: определение возраста кости
Обнаружен фрагмент кости, содержащий 20% исходного углерода-14. Сколько лет кости в ближайший год?
Показать решение
Мы подставляем 20% = 0,20 вместо r в уравнение и решаем относительно t :
[латекс] \ begin {array} {l} t = \ frac {\ mathrm {ln} \ left (r \ right)} {- 0.000121} \ hfill & \ text {Используйте общую форму уравнения}. \ hfill \\ = \ frac {\ mathrm {ln} \ left (0.20 \ right)} {- 0.000121} \ hfill & \ text {Заменить} r.\ hfill \\ \ приблизительно 13301 \ hfill & \ text {Округлить до ближайшего года}. \ hfill \ end {array} [/ latex]
Обломку кости около 13 301 года.
Анализ решения
Приборы, измеряющие процентное содержание углерода-14, чрезвычайно чувствительны, и, как мы упоминали выше, ученый должен будет проделать гораздо больше работы, чем мы, чтобы получить удовлетворение. Тем не менее, углеродное датирование дает точность только около 1%, поэтому этот возраст следует указывать как [латекс] \ text {13 301 год} \ pm \ text {1% или 13 301 год} \ pm \ text {133 года} [/ латекс].
Попробуй
Цезий-137 имеет период полураспада около 30 лет. Если мы начнем с 200 мг цезия-137, пройдет ли больше или меньше 230 лет, пока останется только 1 миллиграмм?
Показать решение
менее 230 лет; 229.3157 а точнее
Ограниченный рост и упадок
Использование закона охлаждения Ньютона
Экспоненциальное затухание также может применяться к температуре. Когда горячий объект остается в окружающем воздухе с более низкой температурой, температура объекта будет экспоненциально снижаться, выравниваясь по мере приближения к температуре окружающего воздуха.На графике температурной функции выравнивание будет соответствовать горизонтальной асимптоте температуры окружающего воздуха. Если комнатная температура не равна нулю, это будет соответствовать вертикальному сдвигу на стандартной функции экспоненциального затухания . {ct} \ right)} + {T} _ {s} \ hfill & \ text {Свойства логарифмов}.{kt} + {T} _ {s} [/ latex]
, где
- t время
- A — разница между начальной температурой объекта и окружающей среды
- k — постоянная, непрерывная скорость охлаждения объекта
Практическое руководство. При заданном наборе условий применить закон охлаждения Ньютона.
- Задайте [латекс] {T} _ {s} [/ latex] равным y -координате горизонтальной асимптоты (обычно температуре окружающей среды).\ circ \ text {F} [/ латекс].
Попробуй
Кувшин с водой с температурой 40 градусов по Фаренгейту помещен в комнату с температурой 70 градусов. Через час температура поднялась до 45 градусов. Сколько времени потребуется, чтобы температура поднялась до 60 градусов?
Показать решение
6.026 часов
Экспоненциальный рост не может продолжаться вечно. Экспоненциальные модели, хотя они могут быть полезны в краткосрочной перспективе, имеют тенденцию разваливаться по мере их продолжения. Представьте себе начинающего писателя, который пишет одну строку в первый день и планирует удвоить количество строк, которые она пишет каждый день в течение месяца.К концу месяца она должна написать более 17 миллиардов строк или полмиллиарда страниц. Для кого-то непрактично, если вообще возможно, написать столько за такой короткий промежуток времени. В конце концов экспоненциальная модель должна начать приближаться к некоторому предельному значению, и тогда рост будет вынужден замедлиться. По этой причине часто лучше использовать модель с верхней границей вместо модели экспоненциального роста , хотя модель экспоненциального роста все еще полезна в краткосрочной перспективе, прежде чем приблизиться к предельному значению.{-bx}} [/ латекс]
где
- [latex] \ frac {c} {1 + a} [/ latex] — начальное значение
- c — допустимая нагрузка или предельное значение
- b — константа, определяемая скоростью роста.
Пример: использование модели логистического роста
Эпидемия гриппа быстро распространяется среди населения со скоростью, которая зависит от двух факторов. Чем больше людей болеют гриппом, тем быстрее он распространяется, а также чем больше неинфицированных людей, тем быстрее он распространяется.Эти два фактора делают логистическую модель удобной для изучения распространения инфекционных заболеваний. И, очевидно, есть максимальное значение для количества инфицированных: все население.
Например, в момент времени t = 0 в сообществе из 1000 человек есть один человек, болеющий гриппом. Таким образом, в этом сообществе гриппом может заразиться не более 1000 человек. Исследователи обнаружили, что для этого конкретного штамма гриппа константа логистического роста составляет b = 0,6030. Оцените количество людей в этом сообществе, которые переболели этим гриппом через десять дней.{-0,6030x}} \ приблизительно 293,8 [/ латекс]. Поскольку фактическое число должно быть целым числом (человек либо болел гриппом, либо нет), мы округляем до 294. В долгосрочной перспективе количество людей, которые заразятся гриппом, является предельным значением, c = 1000.
Анализ решения
Помните, что поскольку мы имеем дело с вирусом, мы не можем с уверенностью предсказать количество инфицированных людей. Модель лишь приближает количество инфицированных людей и не дает нам точных или фактических значений.{-0.6030x}} [/ латекс].
Попробуй
Используя модель из предыдущего примера, оцените количество случаев гриппа на 15 день.
Выбор подходящей модели
Теперь, когда мы обсудили различные математические модели, нам нужно научиться выбирать подходящую модель для имеющихся у нас необработанных данных. На выбор математической модели влияют многие факторы, среди которых опыт, научные законы и закономерности в самих данных. Не все данные можно описать элементарными функциями.Иногда выбирается функция, которая аппроксимирует данные в заданном интервале. Например, предположим, что были собраны данные о количестве домов, купленных в Соединенных Штатах с 1960 по 2013 годы. После нанесения этих данных на диаграмму рассеяния мы замечаем, что форма данных за период с 2000 по 2013 год следует логарифмической шкале. изгиб. Мы могли бы ограничить интервал с 2000 по 2010 год, применить регрессионный анализ с использованием логарифмической модели и использовать его для прогнозирования количества покупателей жилья на 2015 год.
В математических моделях часто используются три вида функций: линейные, экспоненциальные и логарифмические. Если данные лежат на прямой линии или кажется, что они лежат приблизительно вдоль прямой линии, лучше всего подойдет линейная модель. Если данные нелинейны, мы часто рассматриваем экспоненциальную или логарифмическую модель, хотя можно также рассмотреть другие модели, такие как квадратичные модели.
Выбирая между экспоненциальной и логарифмической моделями, мы смотрим на кривую кривых данных.Это называется вогнутостью. Если мы проводим линию между двумя точками данных, и все (или большая часть) данных между этими двумя точками лежит выше этой линии, мы говорим, что кривая вогнута вниз. Мы можем думать об этом как о чаше, которая наклоняется вниз и поэтому не может удерживать воду. Если все (или большая часть) данных между этими двумя точками лежит ниже линии, мы говорим, что кривая вогнута вверх. В этом случае мы можем представить себе чашу, которая изгибается вверх и, следовательно, может удерживать воду. Экспоненциальная кривая, восходящая или падающая, будь то рост или спад, всегда вогнута вверх от своей горизонтальной асимптоты.Логарифмическая кривая всегда вогнута вниз от своей вертикальной асимптоты. В случае положительных данных, что является наиболее распространенным случаем, экспоненциальная кривая всегда вогнута вверх, а логарифмическая кривая всегда вогнута вниз.
Логистическая кривая изменяет вогнутость. Он начинается с вогнутости вверх, а затем изменяется на вогнутость вниз за определенной точкой, называемой точкой перегиба.
После использования графика, который поможет нам выбрать тип функции для использования в качестве модели, мы подставляем точки и решаем, чтобы найти параметры.Мы уменьшаем ошибку округления, выбирая точки как можно дальше друг от друга.
Пример: выбор математической модели
Что лучше всего соответствует приведенным ниже значениям: линейная, экспоненциальная, логарифмическая или логистическая? Найдите модель и используйте график, чтобы проверить свой выбор.
x 1 2 3 4 5 6 7 8 9 y 0 1.386 2,197 2,773 3,219 3,584 3.892 4,159 4,394 Показать решение
Сначала нанесите данные на график, как на графике ниже. Для построения графика округлите данные до двух значащих цифр.
Очевидно, что точки не лежат на прямой, поэтому мы отвергаем линейную модель. Если мы проведем линию между любыми двумя точками, большая часть или все точки между этими двумя точками будут находиться над линией, поэтому график будет вогнутым вниз, что предполагает логарифмическую модель.Мы можем попробовать [latex] y = a \ mathrm {ln} \ left (bx \ right) [/ latex]. Вставка первой точки, [latex] \ left (\ text {1,0} \ right) [/ latex], дает [latex] 0 = a \ mathrm {ln} b [/ latex]. Мы отвергаем случай, когда a = 0 (если бы это было так, все выходы были бы 0), поэтому мы знаем
[латекс] \ mathrm {ln} \ left (b \ right) = 0 [/ latex]. Таким образом, b = 1 и [латекс] y = a \ mathrm {ln} \ left (\ text {x} \ right) [/ latex]. Затем мы можем использовать точку [latex] \ left (\ text {9,4} \ text {.394} \ right) [/ latex], чтобы найти a :
[latex] \ begin {array} {l } y = a \ mathrm {ln} \ left (x \ right) \ hfill \\ 4.394 = a \ mathrm {ln} \ left (9 \ right) \ hfill \\ a = \ frac {4.394} {\ mathrm {ln} \ left (9 \ right)} \ hfill \ end {array} [/ latex ]Поскольку [latex] a = \ frac {4.394} {\ mathrm {ln} \ left (9 \ right)} \ приблизительно 2 [/ latex], подходящей моделью для данных является [latex] y = 2 \ mathrm { ln} \ left (x \ right) [/ латекс].
Чтобы проверить точность модели, мы строим график функции вместе с заданными точками.
График [латекс] y = 2 \ mathrm {ln} x [/ latex].
Можно сделать вывод, что модель хорошо соответствует данным.{2} \ right) [/ latex] может иметь отрицательные значения домена.
Попробуй
Что лучше всего соответствует данным в таблице: линейная, экспоненциальная или логарифмическая? Найдите модель.
x 1 2 3 4 5 6 7 8 9 y 3,297 5,437 8.{\ left (\ mathrm {ln} 0,5 \ right) x} [/ латекс] Экспоненциальная регрессия
Как мы узнали, существует множество ситуаций, которые можно моделировать экспоненциальными функциями, например рост инвестиций, радиоактивный распад, изменения атмосферного давления и температуры охлаждаемого объекта. Что общего у этих явлений? Во-первых, все модели либо увеличиваются, либо уменьшаются с течением времени. Но это еще не все. Именно способ увеличения или уменьшения данных помогает нам определить, лучше ли моделировать его экспоненциальной функцией.{x} [/ latex] (предположим, что a > 0):
- b должно быть больше нуля и не равно единице.
- Начальная стоимость модели — a .
- Если b > 1, функция моделирует экспоненциальный рост. По мере увеличения x результаты модели сначала увеличиваются медленно, но затем увеличиваются все более и более быстро, без ограничений.
- Если 0 < b <1, функция моделирует экспоненциальный спад .{2} [/ latex] вместо r , но чем ближе любое значение к 1, тем лучше уравнение регрессии аппроксимирует данные.
Общее примечание: экспоненциальная регрессия
Экспоненциальная регрессия используется для моделирования ситуаций, в которых рост начинается медленно, а затем быстро неограниченно ускоряется, или когда спад начинается быстро, а затем замедляется, приближаясь к нулю. Мы используем команду «ExpReg» в графической утилите, чтобы подогнать экспоненциальную функцию к набору точек данных.{x} [/ латекс].
Обратите внимание:
- b не должно быть отрицательным.
- Когда b > 1, мы имеем модель экспоненциального роста.
- Когда 0 < b <1, мы имеем модель экспоненциального распада.
Пример: использование экспоненциальной регрессии для подгонки модели к данным
В 2007 году было опубликовано университетское исследование риска ДТП из-за вождения в состоянии алкогольного опьянения. Данные о 2871 авариях были использованы для измерения связи уровня алкоголя в крови человека (BAC) с риском попасть в аварию.В таблице ниже показаны результаты исследования. Относительный риск — это показатель того, во сколько раз вероятность аварии для человека выше. Так, например, у человека с BAC 0,09 вероятность аварии в 3,54 раза выше, чем у человека, который не употреблял алкоголь.
ВАС 0 0,01 0,03 0,05 0,07 0,09 Относительный риск сбоя 1 1.03 1.06 1,38 2,09 3,54 ВАС 0,11 0,13 0,15 0,17 0,19 0,21 Относительный риск сбоя 6,41 12,6 22,1 39,05 65,32 99,78 - Пусть x представляет уровень BAC, а y представляет соответствующий относительный риск.Используйте экспоненциальную регрессию, чтобы подогнать модель под эти данные.
- После 6 порций алкоголь у человека весом 160 фунтов будет BAC около 0,16. Во сколько раз больше вероятность аварии для человека с таким весом, если он садится за руль, выпив 6 банок пива? Округлить до ближайшей сотой.
Показать решение
1. Используя меню STAT, затем EDIT в графической утилите, перечислите значения BAC в L1 и значения относительного риска в L2. Затем используйте функцию СТАТИЧЕСКИЙ ПЛАН, чтобы убедиться, что диаграмма рассеяния следует экспоненциальному шаблону, показанному ниже:
Используйте команду «ExpReg» из меню STAT, затем CALC, чтобы получить экспоненциальную модель,
[latex] y = 0.{x} [/ латекс]Обратите внимание, что [латекс] r2 \ приблизительно 0,97 [/ латекс], что указывает на то, что модель хорошо соответствует данным. Чтобы увидеть это, изобразите модель в том же окне, что и диаграмма рассеяния, чтобы убедиться, что она подходит, как показано ниже:
2. Используйте модель для оценки риска, связанного с BAC 0,16. Замените 0,16 на x в модели и решите для y . {x} \ hfill & \ text {Используйте модель регрессии, найденную в части (a )}\текст{.{0.16} \ hfill & \ text {Заменить 0} \ text {.16 вместо} x \ text {.} \ Hfill \\ \ hfill & \ приблизительно \ text {26} \ text {.35} \ hfill & \ text {Округлить до сотых долей} \ text {.} \ Hfill \ end {array} [/ latex]
Если 160-фунтовый человек водит машину после того, как выпил 6 порций рюмки, вероятность аварии у него примерно в 26,35 раз выше, чем при вождении в трезвом виде.
Попробуй
В таблице ниже показан баланс кредитной карты недавнего выпускника за каждый месяц после выпуска.
Месяц 1 2 3 4 5 6 7 8 Долг ($) 620.00 761,88 899,80 1039.93 1270,63 1589,04 1851,31 2154,92 - Используйте экспоненциальную регрессию, чтобы подогнать модель под эти данные.
- Если расходы продолжатся такими темпами, какой будет долг выпускника по кредитной карте через год после окончания учебы?
Показать решение
а.
Модель экспоненциальной регрессии, которая соответствует этим данным, имеет вид [latex] y = 522,88585984 {\ left (1.{x} [/ латекс].
г.
Если расходы продолжатся такими темпами, долг выпускника по кредитной карте через год составит 4 499,38 долларов.
Вопросы и ответы
Разумно ли предположить, что модель экспоненциальной регрессии будет представлять ситуацию бесконечно?
Нет. Помните, что модели формируются на основе реальных данных, собранных для регрессии. Обычно целесообразно делать оценки в пределах интервала исходного наблюдения (интерполяции).{kt} [/ latex], k <0, период полураспада равен [latex] t = - \ frac {\ mathrm {ln} \ left (2 \ right)} {k} [/ latex].
Углерод-14 датировка [латекс] t = \ frac {\ mathrm {ln} \ left (\ frac {A} {{A} _ {0}} \ right)} {- 0. {kt} + {T} _ {s} [/ latex], где [latex] {T} _ {s} [/ latex] — это температура окружающей среды, [латекс] A = T \ left (0 \ right) — {T} _ {s} [/ latex], а k — непрерывная скорость охлаждения.{kx} [/ latex], где [latex] {A} _ {0} [/ latex] — начальное значение. Если [latex] {A} _ {0} [/ latex] положительно, то мы имеем экспоненциальный рост, когда k > 0, и экспоненциальный спад, когда k <0. - Обычно мы решаем задачи, связанные с экспоненциальным ростом или спадом, в два этапа. Сначала мы настраиваем модель и используем модель для нахождения параметров. Затем мы используем формулу с этими параметрами для прогнозирования роста и распада.
- Мы можем определить возраст органического артефакта t , измерив количество k углерода-14, остающегося в артефакте, и используя формулу [latex] t = \ frac {\ mathrm {ln} \ left (k \ right)} {- 0.000121} [/ latex] решить для т .
- Учитывая время удвоения или период полураспада вещества, мы можем найти функцию, которая представляет его экспоненциальный рост или распад.
- Мы можем использовать закон охлаждения Ньютона, чтобы определить, сколько времени потребуется охлаждающему объекту, чтобы достичь желаемой температуры, или чтобы определить, какой температуре объект будет через заданное время.
- Мы можем использовать функции логистического роста для моделирования реальных ситуаций, в которых скорость роста меняется с течением времени, таких как рост населения, распространение болезней и распространение слухов.{kx} [/ latex], где [latex] k = \ mathrm {ln} b [/ latex].
- Экспоненциальная регрессия используется для моделирования ситуаций, когда рост начинается медленно, а затем быстро неограниченно ускоряется или когда спад начинается быстро, а затем замедляется, приближаясь к нулю.
Глоссарий
- грузоподъемность
- в логистической модели, предельное значение выпуска
- время удвоения
- время, необходимое для удвоения количества
- период полураспада
- время, необходимое веществу, чтобы экспоненциально распадаться до половины своего первоначального количества
- модель логистического роста
- функция вида [латекс] f \ left (x \ right) = \ frac {c} {1 + a {e} ^ {- bx}} [/ latex], где [latex] \ frac {c} { 1 + a} [/ latex] — начальное значение, c — допустимая нагрузка или предельное значение, а b — константа, определяемая скоростью роста
- Закон охлаждения Ньютона
- научная формула зависимости температуры от времени, когда температура объекта уравнивается с температурой окружающей среды
- по порядку величины
- степень десяти, когда число выражается в экспоненциальном представлении с одной ненулевой цифрой слева от десятичной дроби
College Algebra
Урок 47: Экспоненциальный рост и спадЦели обучения
После изучения этого руководства вы сможете: - Решите задачи экспоненциального роста.
- Решите проблемы экспоненциального затухания.
Введение
В этом уроке я расскажу, как решить
проблемы, связанные с экспоненциальным ростом и распадом. Эти
проблемы
потребует от вас знать, как оценивать экспоненциальные выражения и
решать экспоненциальные уравнения.
Если вам нужен обзор по этим темам, не стесняйтесь идти
to Учебное пособие
42: Экспоненциальные функции и Учебное пособие
45: Экспоненциальные уравнения .На старт, внимание, марш!!!!!Учебник
Экспоненциальный рост , ( к > 0)
A представляет собой сумму в данный момент времени т . A или представляет собой начальную сумму
растущее лицо. Обратите внимание, что это сумма, когда т = 0.k — константа, которая представляет скорость роста. ПОЛОЖИТЕЛЬНО
если говорить об экспоненциальном росте.t — это количество прошедшего времени.
Если информация о времени дана в датах, вам необходимо преобразовать ее
к тому, сколько времени прошло с первоначального времени.Например, если
модель настроена на начальный 2000 год, и вам нужно узнать
каково значение в 2010 году, т будет 2010 — 2000 = 10
годы.Вы можете использовать эту формулу, чтобы найти любую из ее переменных, в зависимости от
предоставленная информация и то, что запрашивается в проблеме. Для
Например, вам могут быть заданы значения для A o и t , и вам нужно найти сумму A по истечении заданного времени.Или вам могут дать окончательную сумму A и начальную сумму A o, и вам нужно будет найти время t .Некоторыми примерами экспоненциального роста являются рост населения и финансовая
рост. Найденная информация может помочь предсказать, какое население
для города или колонии будет в будущем или какова ценность вашего
дом через десять лет. Или вы можете использовать его, чтобы узнать, как долго он
потребуется, чтобы добраться до определенного населения или стоимости вашего дома.На диаграмме ниже показан экспоненциальный рост:
Пример
1 : Модель экспоненциального роста описывает
население города в США, в тысячах, t лет после
1994. Используйте эту модель, чтобы решить следующее:A) Каково было население города в 1994 году?
Б) На какой процент ежегодно увеличивается население города?
В) Какое будет население города в 2005 году?
Г) Когда в городе будет 60 тысяч жителей?А) Каково было население города в 1994 году?
Поскольку мы ищем население, то какая переменная
мы ищем? Если вы сказали A , вы правы !!!!То, как сформулирована проблема, 1994 — это то, что мы называем нашей начальной
год.0 упрощается до 1При составлении окончательного ответа имейте в виду, что
Проблема сказала, что население исчисляется тысячами.Население в 1994 году составило бы 30 000 человек.
Другой способ, которым мы могли бы подойти к этой проблеме, заключался в том, чтобы отметить, что
это был 1994 год, это наш начальный год, так что в основном это было
запрашивая у нас начальную популяцию, которая составляет A o в
формула.Это число перед e , которое в этой задаче равно 30.Причина, по которой я показал вам использование формулы, заключалась в том, чтобы научить вас
Это. Просто обратите внимание, что когда это начальный год, т равно 0,
Таким образом, у вас будет e , возведенное в степень 0, что означает, что он будет
упростите до 1, и вы останетесь со значением A o.Б) На какой процент населения приходится население города?
увеличение
каждый год?Как упоминалось выше, в общей формуле роста k — это константа, которая представляет скорость роста. k — это
коэффициент t в экспоненте e .Итак, каков был бы наш ответ в процентах?
Ну, k = 0,0198026, поэтому преобразовав это в проценты, мы получим 1,98026%
за наш ответ .В) Каково будет население города в 2005 г.?
Так как мы ищем население, то какая переменная
мы находим? Если вы сказали A , дайте себе пять.Что мы собираемся подключить к т в этой задаче?
Нашим начальным годом является 1994, а с т представляет годы после
1994, мы можем получить т с 2005 по 1994 год, что было бы 11.Подключив 11 для т и решив для A , мы получим:
* Заменить t на 11 * e ^.2178286 это
ок. 1,243373935
Опять же, записывая окончательный ответ, имейте в виду
что проблема говорит, что население исчисляется тысячами.Население в 2005 г. будет примерно 37 301.
Г) Когда население города составит 60 тысяч человек?
Похоже, у нас тут небольшой поворот.Сейчас мы
даны численность населения, и нам нужно сначала найти т , чтобы найти
сколько лет после 1994 года мы говорим, а затем конвертируем
эти знания в фактический год.Мы по-прежнему будем использовать ту же формулу, что и для ответов на вопросы.
выше, мы просто будем использовать его, чтобы найти другую переменную.Вставляя 60 для A и решая для t , получаем:
Это означает, что через 35 лет после 1994 г.
Население составит 60 тысяч.Итак, наш ответ — в течение 2029 года.
Пример 2 : Дом приобретен за 150 000 долларов в
2002. Стоимость дома определяется моделью экспоненциального роста. Находить
когда дом будет стоить 200000 долларов.Поскольку мы ищем, когда, какую переменную мы
нужно найти? Если вы сказали т , дайте себе кайф
пять.Что мы собираемся подключить к A в этой задаче? Если
Вы сказали 200000, вы правы!Вставляем 200000 на А в модели получаем:
Округляя 4,46 до ближайшего целого числа, получаем т = 4. Так как т измеряется в годах с 2002 года, модель показывает
что население достигнет 200000 в 2002 году + 4 = 2006.Экспоненциальное затухание , ( к <0)
A представляет собой сумму в данный момент времени т . A или представляет собой начальную сумму
растущее лицо. Обратите внимание, что это сумма, когда т = 0.k — константа, которая представляет скорость роста. Это ОТРИЦАТЕЛЬНО
если говорить с точки зрения экспоненциального РАСПАДА.т — это количество прошедшего времени.
Если
информация о времени дана в датах, вам нужно преобразовать ее в то, как
много времени прошло с первоначального времени. Например, если
модель
установлен в начальном 2000 году, и вам нужно выяснить, что
значение в 2010 году, т будет 2010 — 2000 = 10 лет.Вы можете использовать эту формулу, чтобы найти любую из ее переменных, в зависимости от
предоставленная информация и то, что запрашивается в проблеме. Для
пример,
вам могут быть предоставлены значения для A o и t , и вам нужно будет найти сумму A по истечении заданного времени. Или вам могут дать окончательную сумму A и начальную сумму A o, и вам нужно будет найти время t .Примеры экспоненциального распада: радиоактивный распад и популяция.
снижаться.Найденная информация может помочь предсказать, что
период полураспада радиоактивного материала или численность населения
для города или колонии в будущем. В
период полураспада данного вещества — это время, необходимое для половины этого
вещество разлагаться или распадаться.На диаграмме ниже показано экспоненциальное затухание:
Пример 3 : Артефакт изначально имел 12 граммов
углерода-14 присутствует.Модель распада описывает
количество углерода-14, присутствующего через t лет. Сколько грамм
углерод-14 будет присутствовать в этом артефакте через 10 000 лет?Если мы ищем количество граммов углерода-14
представьте, какую переменную нам нужно найти? Если вы сказали A дайте
Дай пять себе.Что мы собираемся подключить к т в этой задаче?
Поскольку т представляет собой количество лет, похоже, что мы
будет вставка 10,000 за т .Вставляя 10000 для т и решая для A , получаем:
Углерод-14 будет примерно 3,58 грамма.
присутствует через 10 000 лет.Пример 4 : Определенный радиоактивный изотопный элемент
экспоненциально затухает согласно модели, где A —
количество граммов изотопа в конце t дней, а Ао —
количество граммов, присутствующих изначально.Каков период полураспада этого
изотоп?Если мы ищем период полураспада этого изотопа,
какую переменную мы ищем? Если вы сказали t , вы
верный!!!!Похоже, у нас нет значений для подключения к A или A o.
Однако проблема говорила, что нас интересует ПОЛОВИНА-жизнь,
что означало бы, что ½ первоначальной суммы ( A o) будет
присутствует в конце ( A ) того времени.Это означает, что A может быть
заменен на .5 A o.Заменяя A на .5 A o и решая для t , получаем:
Период полураспада этого изотопа составляет приблизительно 2,77
дней.Пример 5 : Доисторические наскальные рисунки
обнаружен в пещере в Египте.Краска содержала 20%
оригинальный карбон-14. Используя модель экспоненциального распада для
углерод-14« оцените возраст картин.Так как мы ищем возраст картин, какой
переменную мы ищем? Если вы сказали t , вы
верный!!!!Похоже, у нас нет значений для подключения к A или A o.
Однако проблема говорила о том, что найденные картины
содержал 20% исходного углерода-14. Это означает, что A может
заменить на .2 A o (20% от оригинала).Заменяя A на .2 A o и решая для t , получаем:
Возраст картин примерно 13301 год.
годы.Практические задачи
Это практические задачи, которые помогут вам перейти на следующий уровень.
Это позволит вам проверить и понять, понимаете ли вы эти
типы проблем. Математика работает как и все
в противном случае, если вы хотите добиться успеха в этом, вам нужно практиковать это.
Даже лучшие спортсмены и музыканты получали помощь и много
практиковаться, практиковаться, практиковаться, чтобы стать лучше в своем виде спорта или инструменте.
На самом деле не бывает слишком много практики.Чтобы получить максимальную отдачу от них, вы должны решить проблему на
свой, а затем проверьте свой ответ, щелкнув ссылку для ответа / обсуждения
для этой проблемы . По ссылке вы найдете ответ
а также любые шаги, которые позволили найти этот ответ.Практические задачи 1a — 1b: Решите заданную экспоненту
проблема роста или распада.1а. Стоимость недвижимости в конкретном
блок следует модели экспоненциального роста. В 2001 году
ваша компания приобрела недвижимость в этом квартале. В
стоимость недвижимости в тысячах долларов через t лет после 2001 г.
дается моделью экспоненциального роста.Используйте эту модель для решения следующей задачи:
A) Сколько ваша компания заплатила за недвижимость?
Б) В каком процентном соотношении цена недвижимости в этом блоке
увеличивается в год?
C) Сколько будет стоить недвижимость в 2010 году?
Г) Когда недвижимость будет стоить 750 тысяч долларов?(ответ / обсуждение
к 1а)1б.В артефакте изначально было 10 граммов углерода-14.
настоящее время. Модель распада описывает
количество углерода-14, присутствующего через t лет.Используйте эту модель, чтобы решить следующее:
A) Сколько граммов углерода-14 будет присутствовать в этом артефакте после
25000 лет?
Б) Каков период полураспада углерода-14?(ответ / обсуждение
к 1b)Нужна дополнительная помощь по этим темам?
Последний раз редактировал Ким Сьюард 25 марта 2011 г.
Авторские права на все содержание (C) 2002 — 2011, WTAMU и Kim Seward. Все права защищены.Доказательство того, что число в нулевой степени равно единице
Вы здесь: Главная → Статьи → Доказательство нулевой степени
Почему (-3) 0 = 1? Как это доказано?
Как в уроке про минус и ноль
экспоненты, вы можете посмотреть
следующую последовательность и спросите, что логически будет дальше:(-3) 4 = 81
(-3) 3 = -27
(-3) 2 = 9
(-3) 1 = -3
(-3) 0 = ????Вы можете использовать тот же шаблон для других номеров.Как только ваш ребенок обнаружит, что правило этой последовательности состоит в том, что на каждом шаге вы делите на -3, следующим логическим шагом будет то, что (-3) 0 = 1.
Видео ниже демонстрирует ту же идею: обучение нулевой экспоненты, начиная с шаблона. Это оправдывает правило и делает его логичным, а не просто кусок «анонсированной» математики без доказательств. В видео также показана идея доказательства, объясненная ниже: мы можем умножить степени одного и того же основания и сделать вывод из этого, каким должно быть число в степени нуля.
Другая идея доказательства — сначала обратить внимание на следующее правило умножения ( n — любое
целое число):n 3 · n 4 = ( n · n · n )
· (n · n · n · n)
= n 7n 6 · n 2 = ( n · n · n · n · n · 0005 n) · n · n) = n 8
Вы заметили ярлык? Для любых экспонентов целых чисел x и y вы можете просто добавить
показатели:n x · n y = ( n · n · n
·… · n · n · n)
· (n · … · n)
= п х + уМатематика логична, и ее правила работают во всех случаях (теоремы применяются «для любого целого n » или «для всех целых чисел»). Итак, предположим, мы не знаем, что такое (-3) 0 . Что бы ни было (-3) 0 , если оно подчиняется приведенному выше правилу, тогда
(-3) 7 · (-3) 0 = (-3) 7 + 0 Другими словами,
(-3) 7 · (-3) 0 = (-3) 7
(-3) 3 · (-3) 0 = (-3) 3 + 0 Другими словами,
(-3) 3 · (-3) 0 = (-3) 3
(-3) 15 · (-3) 0 = (-3) 15 +
0Другими словами,
(-3) 15 · (-3) 0 = (-3) 15
…и так далее для всевозможных возможных показателей. Фактически, мы можем написать, что (-3) x · (-3) 0 = (-3) x , где x — любое целое число.
Поскольку мы предполагаем, что еще не знаем, что такое (-3) 0 , давайте заменим его P. Теперь посмотрим на уравнения, которые мы нашли выше. Зная то, что вы знаете о свойствах умножения, , что за число может быть P?
(-3) 7 · P = (-3) 7 (-3) 3 · P = (-3) 3 (-3) 15 · P = (-3) 15 Другими словами… какое единственное число, когда вы умножаете на него, ничего не меняется? 🙂
Вопрос. Какая разница между -1 в нулевой степени и (-1) в
нулевая мощность? Будет ли ответ 1 для обоих?Пример 1: -1 0 = ____
Пример 2: (-1) 0 = ___Ответ: Как уже объяснялось, ответ на (-1) 0 равен 1, поскольку мы возводим число -1 (отрицательная 1) в степень нуля.Однако в случае -1 0 отрицательный знак не означает отрицательное число, а вместо этого означает напротив числа следующего. Итак, сначала мы вычисляем 1 0 , а затем принимаем обратное, что дает -1.
Другой пример: в выражении — (- 3) 2 первый отрицательный знак означает, что вы взяли противоположность остальной части выражения. Итак, поскольку (-3) 2 = 9, то — (- 3) 2 = -9.
Вопрос. Почему при нулевом показателе экспоненты возникает ошибка ?? Пожалуйста, объясните, почему его не существует. Другими словами, что такое 0 0 ?
Ответ: Степень от нуля до нуля часто называют «неопределенной формой», потому что она может иметь несколько различных значений.
Поскольку x 0 равно 1 для всех чисел x, кроме 0, было бы логично определить, что 0 0 = 1.
Но мы могли бы также подумать о 0 0 , имеющем значение 0, потому что ноль для любой степени (кроме нулевой степени) равен нулю.
Кроме того, логарифм 0 0 будет равен 0 · бесконечность, что само по себе является неопределенной формой.

 Тема урока
Тема урока