Свойства трапеции с доказательством: Трапеция. Видеоурок. Геометрия 8 Класс — ошкольное образовательное учреждение № 4 «Алёнушка»

Содержание

Трапеция свойства и признаки трапеции площадь трапеции. Трапеция. Свойства трапеции. Теоремы: свойства трапеции

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т. д.

Как мы используем вашу персональную информацию:

Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.

Определение

Трапеция
— это четырехугольник $A B C D$, две стороны которого параллельны,
а две другие не параллельны (рис. {\circ}$ (рис 1)

Отрезок, соединяющий середины боковых сторон трапеции, называется средней линией трапеции.
Средняя линия трапеции параллельна основаниям и равна их полусумме:

$$M N=\frac{A D+B C}{2}$$

Среди всех трапеций можно выбрать два особых класса трапеций: прямоугольные и равнобокие трапеции.

Определение

Прямоугольной
называется трапеция, у которой один из углов прямой.

Равнобокой
называется трапеция, у которой боковые стороны равны.

Свойства равнобокой трапеции

В равнобокой трапеции углы при основании попарно равны $\angle A=\angle D, \angle B=\angle C$.
Диагонали равнобокой трапеции равны $A C=B D$.

Признаки равнобокой трапеции

Если углы при основании трапеции равны, то трапеция равнобокая.
Если в трапеции диагонали равны, то она равнобокая.

Площадь трапеции:

$$S=\frac{a+b}{2} \cdot h$$

где $a$ и $b$ — основания трапеции, а $h$ — ее высота. {\circ}$

Таким образом,
$\angle M L K=\angle N M P$ и $\Delta M N P$ еще и равнобедренный. Следовательно,
$M P=P N$. Так как $L K=M P=2$ дм, следовательно и $P N=2$ дм. Большее основание
$K N=K P+P N$, так как $L M=K P$, получим $K N=2+2=4$ (дм).

Площадь трапеции вычислим по формуле:

$$S=\frac{a+b}{2} \cdot h$$

В нашем случае она примет вид:

$$S_{K L M N}=\frac{L M+K N}{2} \cdot M P$$

Подставляя известные значения, получим

$S_{K L M N}=\frac{2+4}{2} \cdot 2=6$ (дм 2)

Ответ.
$S_{K L M N}=6$ дм 2

\[{\Large{\text{Произвольная трапеция}}}\]

Определения

Трапеция – это выпуклый четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.

Параллельные стороны трапеции называются её основаниями, а две другие стороны – боковыми сторонами.

Высота трапеции – это перпендикуляр, опущенный из любой точки одного основания к другому основанию.

Теоремы: свойства трапеции

1) Сумма углов при боковой стороне равна $180^\circ$
. \circ\)
.

2) Т.к. $AD\parallel BC$
и $BD$
– секущая, то $\angle DBC=\angle
BDA$
как накрест лежащие.
Также $\angle BOC=\angle AOD$
как вертикальные.
Следовательно, по двум углам $\triangle BOC \sim \triangle AOD$
.

Докажем, что $S_{\triangle AOB}=S_{\triangle COD}$
. Пусть $h$
– высота трапеции. Тогда $S_{\triangle ABD}=\frac12\cdot h\cdot
AD=S_{\triangle ACD}$
. Тогда: \

Определение

Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.

Теорема

Средняя линия трапеции параллельна основаниям и равна их полусумме.

Доказательство*

1) Докажем параллельность.

Проведем через точку $M$
прямую $MN»\parallel AD$
($N»\in CD$
). Тогда по теореме Фалеса (т.к. $MN»\parallel AD\parallel BC, AM=MB$
) точка $N»$
— середина отрезка $CD$
. Значит, точки $N$
и $N»$
совпадут.

2) Докажем формулу.

Проведем $BB»\perp AD, CC»\perp AD$
. Пусть $BB»\cap MN=M», CC»\cap
MN=N»$
.

Тогда по теореме Фалеса $M»$
и $N»$
— середины отрезков $BB»$
и $CC»$
соответственно. Значит, $MM»$
– средняя линия $\triangle
ABB»$
, $NN»$
— средняя линия $\triangle DCC»$
. Поэтому: \

Т.к. $MN\parallel AD\parallel BC$
и $BB», CC»\perp AD$
, то $B»M»N»C»$
и $BM»N»C$
– прямоугольники. По теореме Фалеса из $MN\parallel AD$
и $AM=MB$
следует, что $B»M»=M»B$
. Значит, $B»M»N»C»$
и $BM»N»C$
– равные прямоугольники, следовательно, $M»N»=B»C»=BC$
.

Таким образом:

\
\[=\dfrac12 \left(AB»+B»C»+BC+C»D\right)=\dfrac12\left(AD+BC\right)\]

Теорема: свойство произвольной трапеции

Середины оснований, точка пересечения диагоналей трапеции и точка пересечения продолжений боковых сторон лежат на одной прямой.

Доказательство*

С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.

1) Докажем, что точки $P$
, $N$
и $M$
лежат на одной прямой.

Проведем прямую $PN$
($P$
– точка пересечения продолжений боковых сторон, $N$
– середина $BC$
). Пусть она пересечет сторону $AD$
в точке $M$
. Докажем, что $M$
– середина $AD$
.

Рассмотрим $\triangle BPN$
и $\triangle APM$
. Они подобны по двум углам ($\angle APM$
– общий, $\angle PAM=\angle PBN$
как соответственные при $AD\parallel BC$
и $AB$
секущей). Значит: \[\dfrac{BN}{AM}=\dfrac{PN}{PM}\]

Рассмотрим $\triangle CPN$
и $\triangle DPM$
. Они подобны по двум углам ($\angle DPM$
– общий, $\angle PDM=\angle PCN$
как соответственные при $AD\parallel BC$
и $CD$
секущей). Значит: \[\dfrac{CN}{DM}=\dfrac{PN}{PM}\]

Отсюда $\dfrac{BN}{AM}=\dfrac{CN}{DM}$
. Но $BN=NC$
, следовательно, $AM=DM$
.

2) Докажем, что точки $N, O, M$
лежат на одной прямой.

Пусть $N$
– середина $BC$
, $O$
– точка пересечения диагоналей. Проведем прямую $NO$
, она пересечет сторону $AD$
в точке $M$
. Докажем, что $M$
– середина $AD$
.

$\triangle BNO\sim \triangle DMO$
по двум углам ($\angle OBN=\angle
ODM$
как накрест лежащие при $BC\parallel AD$
и $BD$
секущей; $\angle BON=\angle DOM$
как вертикальные). Значит: \[\dfrac{BN}{MD}=\dfrac{ON}{OM}\]

Аналогично $\triangle CON\sim \triangle AOM$
. Значит: \[\dfrac{CN}{MA}=\dfrac{ON}{OM}\]

Отсюда $\dfrac{BN}{MD}=\dfrac{CN}{MA}$
. Но $BN=CN$
, следовательно, $AM=MD$
.

\[{\Large{\text{Равнобедренная трапеция}}}\]

Определения

Трапеция называется прямоугольной, если один из ее углов – прямой.

Трапеция называется равнобедренной, если ее боковые стороны равны.

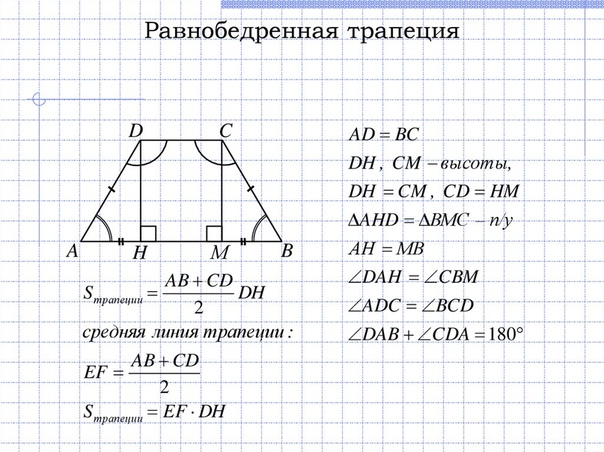
Теоремы: свойства равнобедренной трапеции

1) У равнобедренной трапеции углы при основании равны.

2) Диагонали равнобедренной трапеции равны.

3) Два треугольника, образованные диагоналями и основанием, являются равнобедренными.

Доказательство

1) Рассмотрим равнобедренную трапецию $ABCD$
.

Из вершин $B$
и $C$
опустим на сторону $AD$
перпендикуляры $BM$
и $CN$
соответственно. Так как $BM\perp AD$
и $CN\perp AD$
, то $BM\parallel CN$
; $AD\parallel BC$
, тогда $MBCN$
– параллелограмм, следовательно, $BM = CN$
.

Рассмотрим прямоугольные треугольники $ABM$
и $CDN$
. Так как у них равны гипотенузы и катет $BM$
равен катету $CN$
, то эти треугольники равны, следовательно, $\angle DAB = \angle CDA$
.

Т.к. $AB=CD, \angle A=\angle D, AD$
– общая, то по первому признаку . Следовательно, $AC=BD$
.

3) Т.к. $\triangle ABD=\triangle ACD$
, то $\angle BDA=\angle CAD$
. Следовательно, треугольник $\triangle AOD$
– равнобедренный. Аналогично доказывается, что и $\triangle BOC$
– равнобедренный.

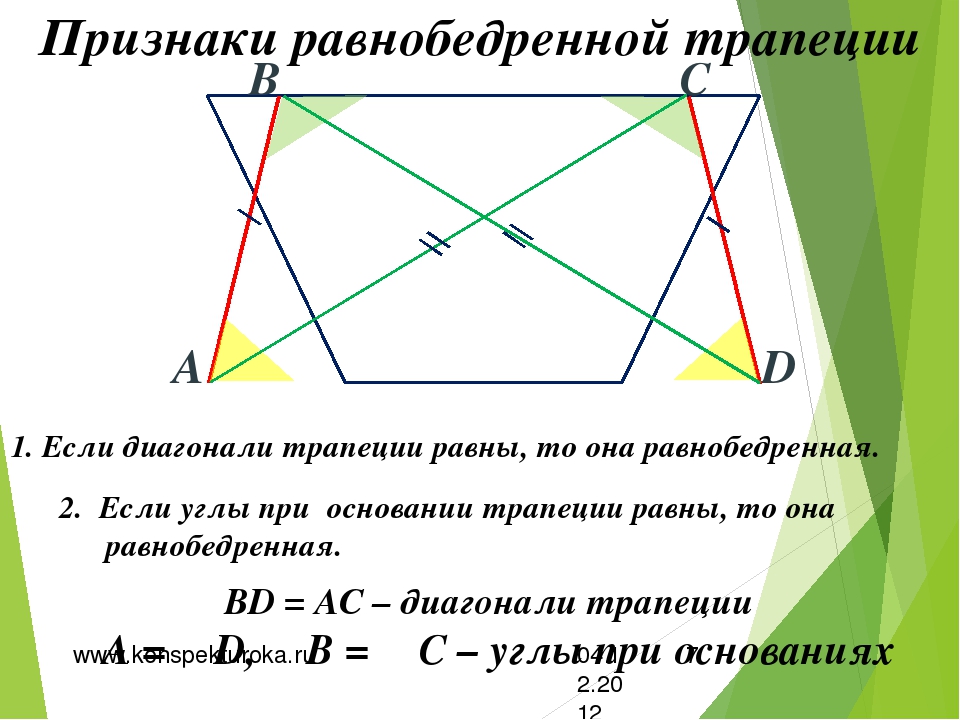
Теоремы: признаки равнобедренной трапеции

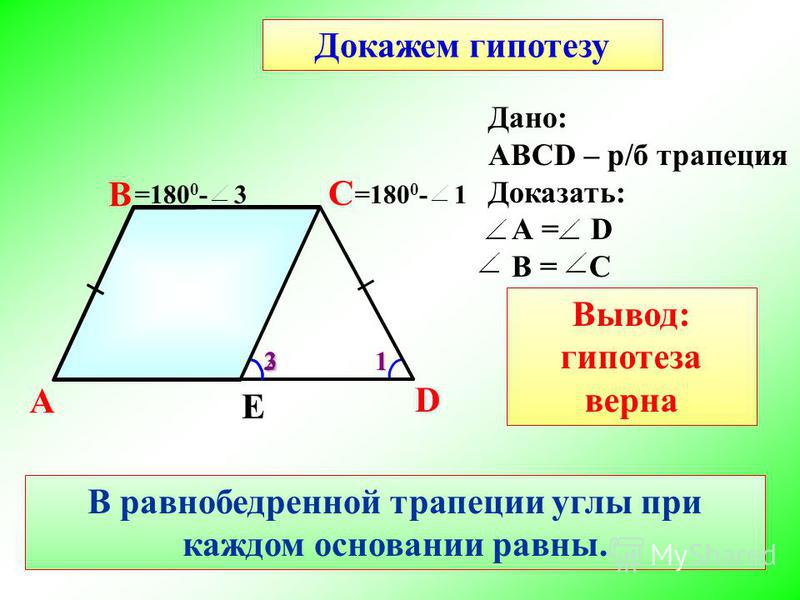
1) Если у трапеции углы при основании равны, то она равнобедренная.

2) Если у трапеции диагонали равны, то она равнобедренная.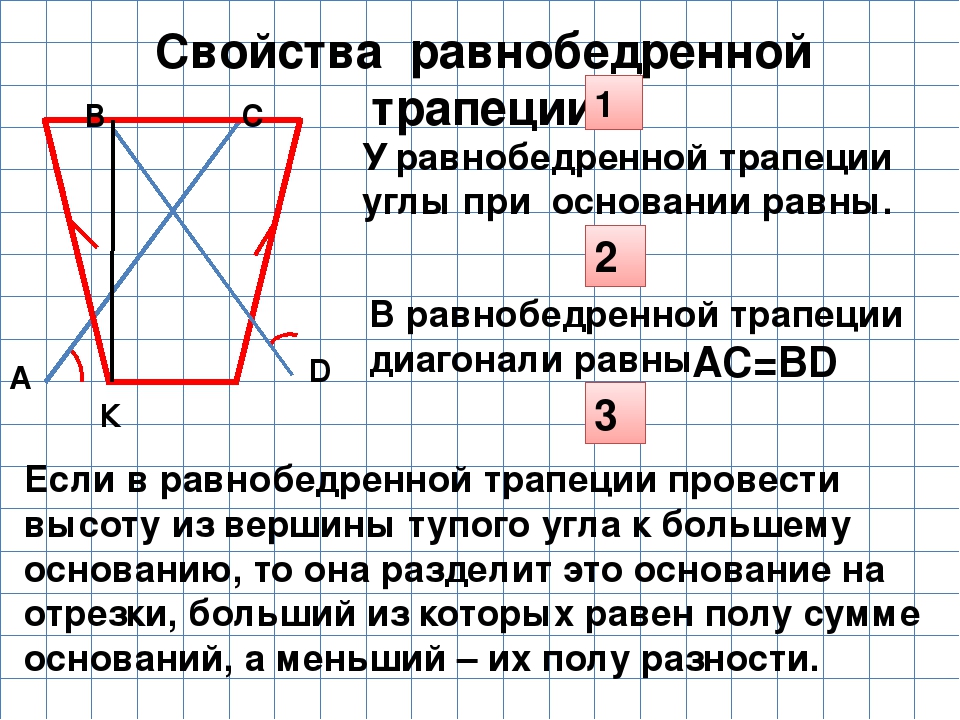

Доказательство

Рассмотрим трапецию $ABCD$
, такую что $\angle A = \angle D$
.

Достроим трапецию до треугольника $AED$
как показано на рисунке. Так как $\angle 1 = \angle 2$
, то треугольник $AED$
равнобедренный и $AE
= ED$
. Углы $1$
и $3$
равны как соответственные при параллельных прямых $AD$
и $BC$
и секущей $AB$
. Аналогично равны углы $2$
и $4$
, но $\angle 1 = \angle 2$
, тогда $\angle 3 = \angle 1 = \angle 2 =
\angle 4$
, следовательно, треугольник $BEC$
тоже равнобедренный и $BE = EC$
.

В итоге $AB = AE — BE = DE — CE = CD$
, то есть $AB = CD$
, что и требовалось доказать.

2) Пусть $AC=BD$
. Т.к. $\triangle AOD\sim \triangle BOC$
, то обозначим их коэффициент подобия за $k$
. Тогда если $BO=x$
, то $OD=kx$
. Аналогично $CO=y \Rightarrow AO=ky$
.

Т.к. $AC=BD$
, то $x+kx=y+ky \Rightarrow x=y$
. Значит $\triangle AOD$
– равнобедренный и $\angle OAD=\angle ODA$
.

Таким образом, по первому признаку $\triangle ABD=\triangle ACD$
($AC=BD, \angle OAD=\angle ODA, AD$
– общая). Значит, $AB=CD$
, чтд.

Поэтому одну из них мы назовем большим

, вторую — малым основанием

трапеции. Высотой

трапеции можно назвать любой отрезок перпендикуляра, проведенного из вершин на соответственно противоположную сторону (для каждой вершины есть две противоположные стороны), заключенный между взятыми вершиной и противоположной стороной. Но можно выделить «особый вид» высот.
Определение 8.
Высотой основания трапеции называют отрезок прямой, перпендикулярной основаниям, заключенный между основаниями.
Теорема 7
. Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство. Пусть дана трапеция АВСD и средняя линия КМ. Через точки В и М проведем прямую. Продолжим сторону AD через точку D до пересечения с ВМ. Треугольники ВСм и МРD равны по стороне и двум углам (СМ=МD, ∠
ВСМ=∠
МDР — накрестлежащие, ∠
ВМС=∠
DМР — вертикальные), поэтому ВМ=МР или точка М — середина ВР. КМ является средней линией в треугольнике АВР. По свойству средней линии треугольника КМ параллельна АР и в частности АD и равна половине АР:

Теорема 8
. Диагонали делят трапецию на четыре части, две из которых, прилежащие к боковым сторонам, равовелики.
Напомню, что фигуры называются равновеликими, если у них одинаковая площадь. Треугольники АВD и АСD равновелики: у них равные высоты (обозначенные желтым) и общее основание. Эти треугольники имеют общую часть АОD. Их площадь можно разложить так:

Виды трапеций:
Определение 9.
(рис 1) Остроугольной трапецией называется трапеция, у которой углы, прилегающие к большему основанию острые.
Определение 10.
(рис 2) Тупоугольной трапецией называется трапеция, у которой один из углов, прилегающих к большему основанию тупой.
Определение 11.
(рис 4) Прямоугольной называется трапеция, у которой одна боковая сторона перпендикулярна основаниям.
Определение 12.
(рис 3) Равнобедренной (равнобокой, равнобочной) называется трапеция, у которой боковые стороны равны.

Свойства равнобокой трапеции:
Теорема 10
. Углы, прилежащие к каждому из оснований равнобокой трапеции, равны.
Доказательство. Докажем, например, равенство углов А и D при большем основании AD равнобокой трапеции АВСD. Для этой цели проведем через точку С прямую параллельную боковой стороне АВ.
Она пересечет большое основание в точке М. Четырехугольник АВСМ являеся параллелограммом, т.к. по построению имеет две пары параллельных сторон. Следовательно, отрезок СМ секущей прямой, заключенный внутри трапеции
равен её боковой стороне: СМ=АВ. Отсюда ясно, что СМ=СD, треугольник СМD — равнобедренный, ∠
СМD=∠
СDM, и, значит, ∠
А=∠
D.
Углы, прилежащие к меньшему основанию, также равны, т.к. являются для найденных внутренними односторонним и имеют в сумме два прямых.
Теорема 11
. Диагонали равнобокой трапеции равны.
Доказательство. Рассмотрим треугольники АВD и ACD. Она равны по двум сторонам и углу между ними (АВ=СD, AD — общая, углы А и D равны по теореме 10). Поэтому АС=BD.

Теорема 13
. Диагонали равнобедренной трапеции точкой пересечения делятся на соответственно равные отрезки.
Рассмотрим треугольники АВD и ACD. Она равны по двум сторонам и углу между ними (АВ=СD, AD — общая, углы А и D равны по теореме 10). Поэтому ∠
ОАD=∠
ОDA, отсюда равны и углы ОВС и ОСВ как соответственно накрестлежащие для углов ODA и ОАD. Вспомним теорему: если в треугольнике два угла равны, то он равнобедренный, поэтому треугольники ОВС и ОAD являются равнобедренными, значит, ОС=ОВ и ОА=OD, ч.т.д.

Равнобокая трапеция фигура симметричная.
Определение 13.
Осью сисмметрии равнобокой трапеции называют прямую, проходящую через середины её оснований.
Теорема 14
. Ось сисмметрии равнобокой трапеции перпендикулярна её основаниям.
В теореме 9 мы доказали, что прямая, соединяющая середины оснований трапеции, проходит через точку пересечения диагоналей. Далее (теорема 13) мы доказали, что треугольники АОD и ВОС равнобедренные.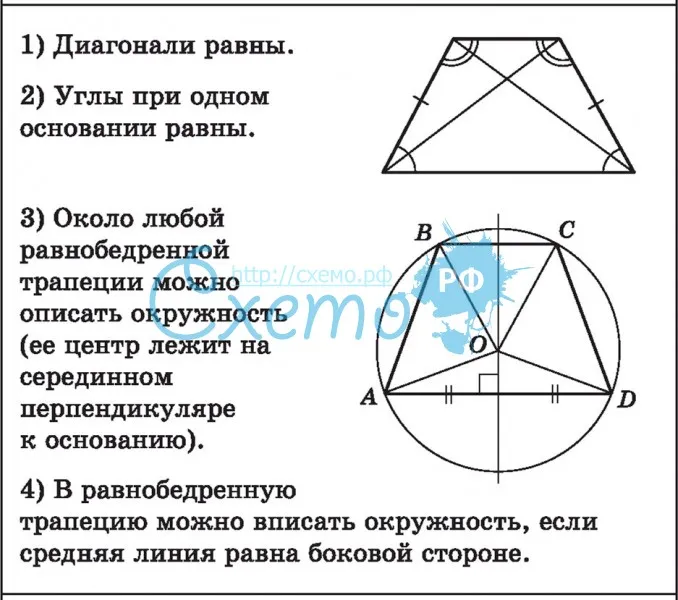 ОМ и ОК являются медианами этих треугольников соответственно по определению . Вспомним свойство равнобедренного треугольника : медиана равнобедренного треугольника, опущенная на основание, одновременно является и высотой треугольника.
Вследвствие перпендикулярности основаниям частей прямой КМ, ось симметрии перпендикулярна основаниям.
Признаки, выделяющие равнобокую трапецию среди всех трапеций:
Теорема 15
. Если углы, прилежищие к одному из оснований трапеции, равны, то трапеция равнобокая.
Теорема 16
. Если диагонали трапеции равны, то трапеция равнобокая.
Теорема 17
. Если продолженные до пересечения боковые стороны трапеции образуют вместе и её большим основанием равнобедренный треугольник, то трапеция равнобокая.

Теорема 18
. Если трапецию можно вписать в окружность, то она равнобокая.
Признак прямоугольной трапеции:
Теорема 19
. Всякий четырехугольник, у которого только два угла при смежных вершинах прямые, является прямоугольной трапецией (очевидно, что две стороны параллельны, т.
AD. Вспомним теорему: если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и второй. Значит, прямая ОК также перпендикулярна AD. Таким образом, через точку О проходит две прямых перпендикулярных прямой AD, чего быть не может, поэтому эти прямые совпадают и составляют общуй перпендикуляр КМ, который равен сумме двух радиусов и является диаметром вписанной окружности, поэтому r=KM/2 или r=h/2.

Теорема 21
. Площадь трапеции равна произведению полусуммы оснований и высоты оснований.

Доказательство:
Пусть ABCD — данная трапеция, а AB и CD — её основания. Пусть
также AH — высота, опущенная из точки A на прямую CD. Тогда S ABCD = S ACD + S ABC .
Но S ACD = 1/2AH·CD, а S ABC = 1/2AH·AB.
Следовательно, S ABCD = 1/2AH·(AB + CD).
Что и
требовалось доказать.

Вторая формула перешла от четырехугольника.

Отрезок, соединяющий середины диагоналей трапеции равен половине разности оснований
Треугольники, образованные основаниями трапеции и отрезками диагоналей до точки их пересечения — подобны
Треугольники, образованные отрезками диагоналей трапеции, стороны которых лежат на боковых сторонах трапеции — равновеликие (имеют одинаковую площадь)
Если продлить боковые стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой, соединяющей середины оснований
Отрезок, соединяющий основания трапеции, и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований трапеции
Отрезок, параллельный основаниям трапеции, и проведенный через точку пересечения диагоналей, делится этой точкой пополам, а его длина равна 2ab/(a + b), где a и b — основания трапеции

Свойства отрезка, соединяющего середины диагоналей трапеции

Соединим середины диагоналей трапеции ABCD, в результате чего у нас появится отрезок LM.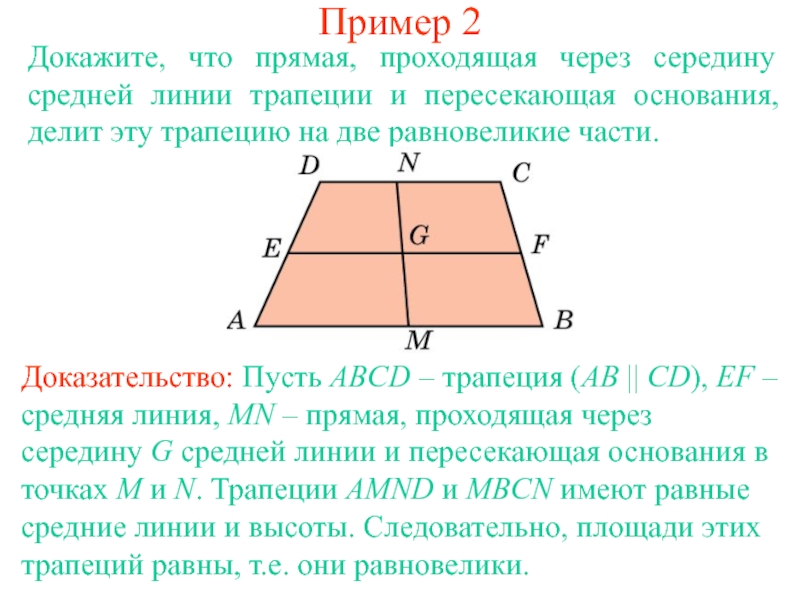

Отрезок, соединяющий середины диагоналей трапеции, лежит на средней линии трапеции
.

Данный отрезок параллелен основаниям трапеции
.

Длина отрезка, соединяющего середины диагоналей трапеции, равна полуразности ее оснований.

LM = (AD — BC)/2

или

LM = (a-b)/2

Свойства треугольников, образованных диагоналями трапеции

Треугольники, которые образованы основаниями трапеции и точкой пересечения диагоналей трапеции — являются подобными
.

Треугольники BOC и AOD являются подобными. Поскольку углы BOC и AOD являются вертикальными — они равны.

Углы OCB и OAD являются внутренними накрест лежащими при параллельных прямых AD и BC (основания трапеции параллельны между собой) и секущей прямой AC, следовательно, они равны.

Углы OBC и ODA равны по той же самой причине (внутренние накрест лежащие).

Так как все три угла одного треугольника равны соответствующим углам другого треугольника, то данные треугольники подобны.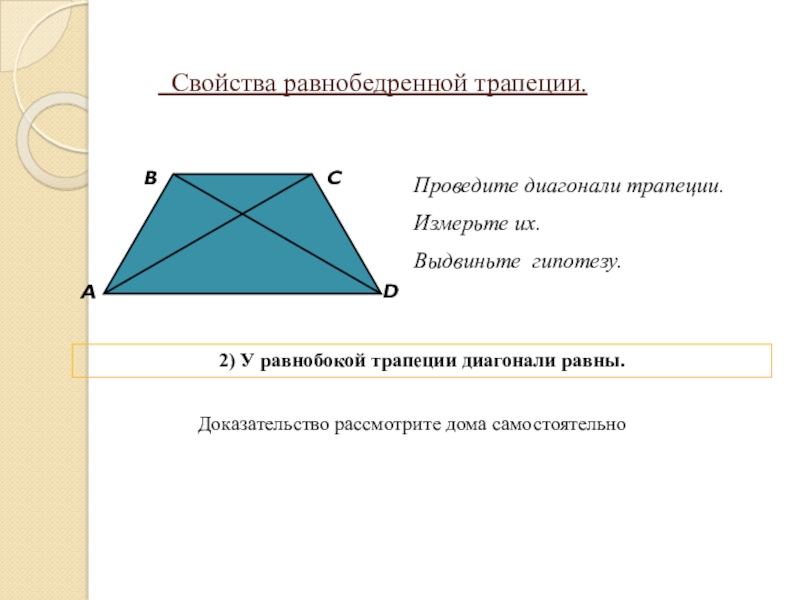

Что из этого следует?

Для решения задач по геометрии подобие треугольников используется следующим образом. Если нам известны значения длин двух соответствующих элементов подобных треугольников, то мы находим коэффициент подобия (делим одно на другое). Откуда длины всех остальных элементов соотносятся между собой точно таким же значением.

Свойства треугольников, лежащих на боковой стороне и диагоналях трапеции

Рассмотрим два треугольника, лежащих на боковых сторонах трапеции AB и CD. Это — треугольники AOB и COD. Несмотря на то, что размеры отдельных сторон у данных треугольников могут быть совершенно различны, но площади треугольников, образованных боковыми сторонами и точкой пересечения диагоналей трапеции равны
, то есть треугольники являются равновеликими.

Если продлить стороны трапеции в сторону меньшего основания, то точка пересечения сторон будет совпадать с прямой линией, которая проходит через середины оснований
.

Таким образом, любая трапеция может быть достроена до треугольника.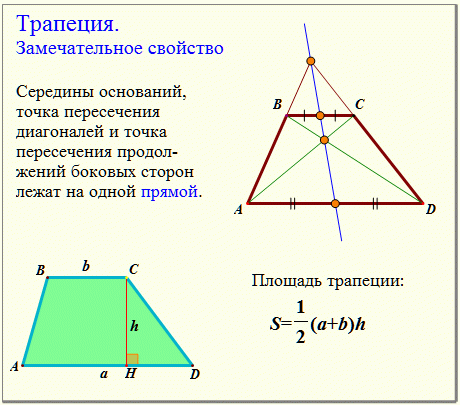 При этом:

Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продленных боковых сторон являются подобными
Прямая, соединяющая середины оснований трапеции, является, одновременно, медианой построенного треугольника

Свойства отрезка, соединяющего основания трапеции

Если провести отрезок, концы которого лежат на основаниях трапеции, который лежит на точке пересечения диагоналей трапеции (KN), то соотношенее составляющих его отрезков от стороны основания до точки пересечения диагоналей (KO/ON) будет равно соотношению оснований трапеции
(BC/AD).

KO / ON = BC / AD

Данное свойство следует из подобия соответствующих треугольников (см. выше).

Свойства отрезка, параллельного основаниям трапеции

Если провести отрезок, параллельный основаниям трапеции и проходящий через точку пересечения диагоналей трапеции, то он будет обладать следующими свойствами:

Заданный отрезок (KM) делится точкой пересечения диагоналей трапеции пополам
Длина отрезка
, проходящего через точку пересечения диагоналей трапеции и параллельного основаниям, равна KM = 2ab/(a + b)

Формулы для нахождения диагоналей трапеции

a, b

— основания трапеции

c, d

— боковые стороны трапеции

d1 d2

— диагонали трапеции

α β
— углы при большем основании трапеции

Формулы нахождения диагоналей трапеции через основания, боковые стороны и углы при основании

Первая группа формул (1-3) отражает одно из основных свойств диагоналей трапеции:

1.
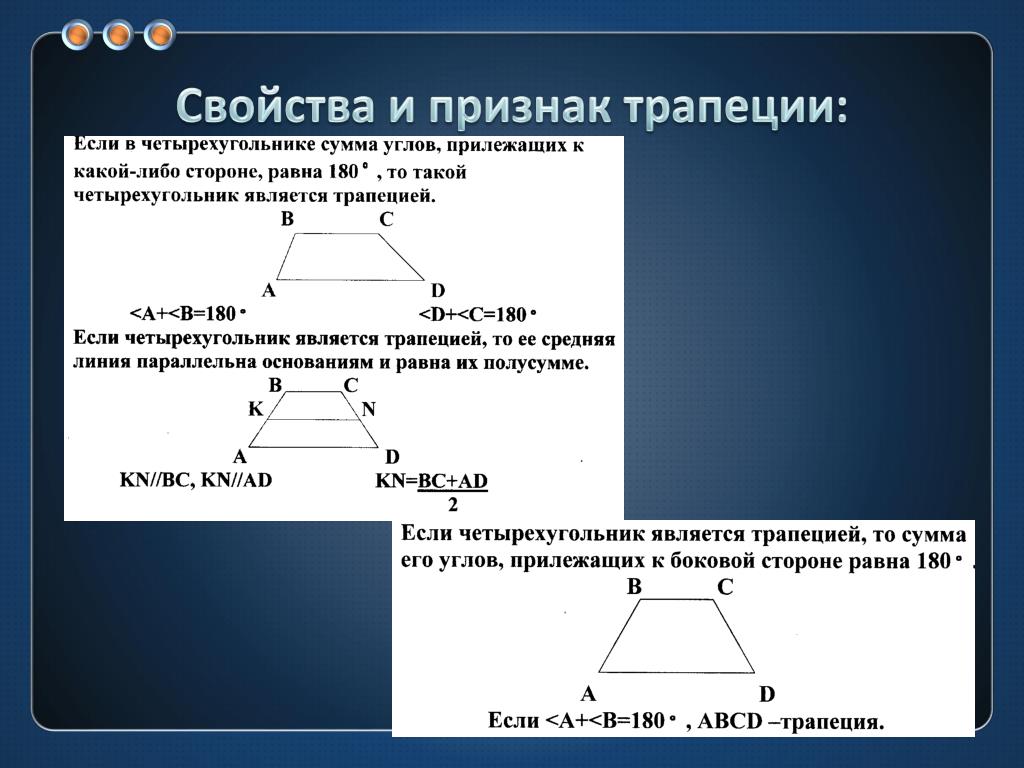
Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований
. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема

2
. Данная формула получена путем преобразования предыдущей формулы. Квадрат второй диагонали переброшен через знак равенства, после чего из левой и правой части выражения извлечен квадратный корень.

3
. Эта формула нахождения длины диагонали трапеции аналогична предыдущей, с той разницей, что в левой части выражения оставлена другая диагональ

Следующая группа формул (4-5) аналогична по смыслу и выражает аналогичное соотношение.

Группа формул (6-7) позволяет найти диагональ трапеции, если известны большее основание трапеции, одна боковая сторона и угол при основании.

Формулы нахождения диагоналей трапеции через высоту

Примечание
. В данном уроке приведено решение задач по геометрии о трапециях. Если Вы не нашли решение задачи по геометрии, интересующего Вас типа — задайте вопрос на форуме
.

Задача
.

Диагонали трапеции ABCD (AD | | ВС) пересекаются в точке О. Найдите длину основания ВС трапеции, если основание АD = 24 см, длина АО = 9см, длина ОС = 6 см.

Решение
.

Решение данной задачи по идеологии абсолютно идентично предыдущим задачам.

Треугольники AOD и BOC являются подобными по трем углам — AOD и BOC являются вертикальными, а остальные углы попарно равны, поскольку образованы пересечением одной прямой и двух параллельных прямых.

Поскольку треугольники подобны, то все их геометрические размеры относятся между собой, как геометрически размеры известных нам по условию задачи отрезков AO и OC. То есть

AO / OC = AD / BC

9 / 6 = 24 / BC

BC = 24 * 6 / 9 = 16

Ответ
: 16 см

Задача
.

В трапеции ABCD известно, что AD=24, ВС=8, АС=13, BD=5√17. Найдите площадь трапеции.

Решение
.

Для нахождения высоты трапеции из вершин меньшего основания B и C опустим на большее основание две высоты. Поскольку трапеция неравнобокая — то обозначим
длину AM = a, длину KD = b (не путать с обозначениями в формуле
нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK — прямоугольник.

Значит

AD = AM+BC+KD

a + 8 + b = 24

a = 16 — b

Треугольники DBM и ACK — прямоугольные, так их прямые углы образованы высотами трапеции. Обозначим высоту трапеции через h. Тогда по теореме Пифагора

H 2 + (24 — a) 2 = (5√17) 2

и

h 2 + (24 — b) 2 = 13 2

Учтем, что a = 16 — b , тогда в первом уравнении

h 2 + (24 — 16 + b) 2 = 425

h 2 = 425 — (8 + b) 2

Подставим значение квадрата высоты во второе уравнение, полученное по Теореме Пифагора. Получим:

425 — (8 + b) 2 + (24 — b) 2 = 169

-(64 + 16b + b) 2 + (24 — b) 2 = -256

-64 — 16b — b 2 + 576 — 48b + b 2 = -256

-64b = -768

b = 12

Таким образом, KD = 12

Откуда

h 2 = 425 — (8 + b) 2 = 425 — (8 + 12) 2 = 25

h = 5

Найдем площадь трапеции через ее высоту и полусумму оснований

, где a b — основания трапеции, h — высота трапеции

S = (24 + 8) * 5 / 2 = 80 см 2

Ответ
: площадь трапеции равна 80 см 2 .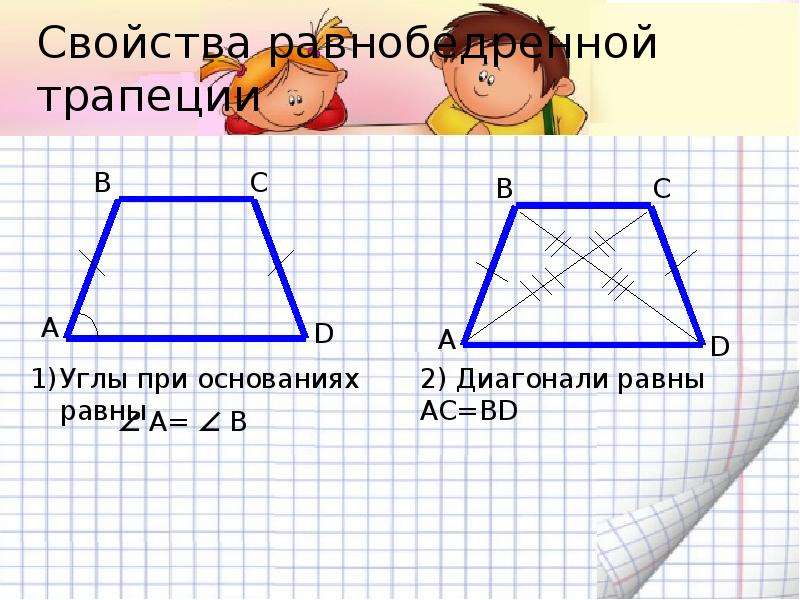

Замечательное свойство трапеции | Треугольники

Замечательное свойство трапеции

Точка пересечения диагоналей трапеции, точка пересечения продолжения боковых сторон трапеции и середины оснований трапеции лежат на одной прямой.

Существует несколько способов доказательства этого свойства. Надо доказать, что четыре данные точки лежат на одной прямой. Прямую можно провести через любые две точки. Выбирают две любые точки из четырёх, проводят через них прямую и доказывают, что две другие точки также лежат на этой прямой.

Сформулируем это свойство иначе:

Прямая, проходящая через точку пересечения диагоналей трапеции и точку пересечения продолжения её боковых сторон, делит основания трапеции пополам.

Дано:

ABCD- трапеция, AD||BC,

AB∩CD=F, AC∩BD=O,

FO∩AD=K, FO∩BC=P

Доказать: K- середина AD,

P- середина BC

Доказательство:

Рассмотрим треугольники AOK и COP.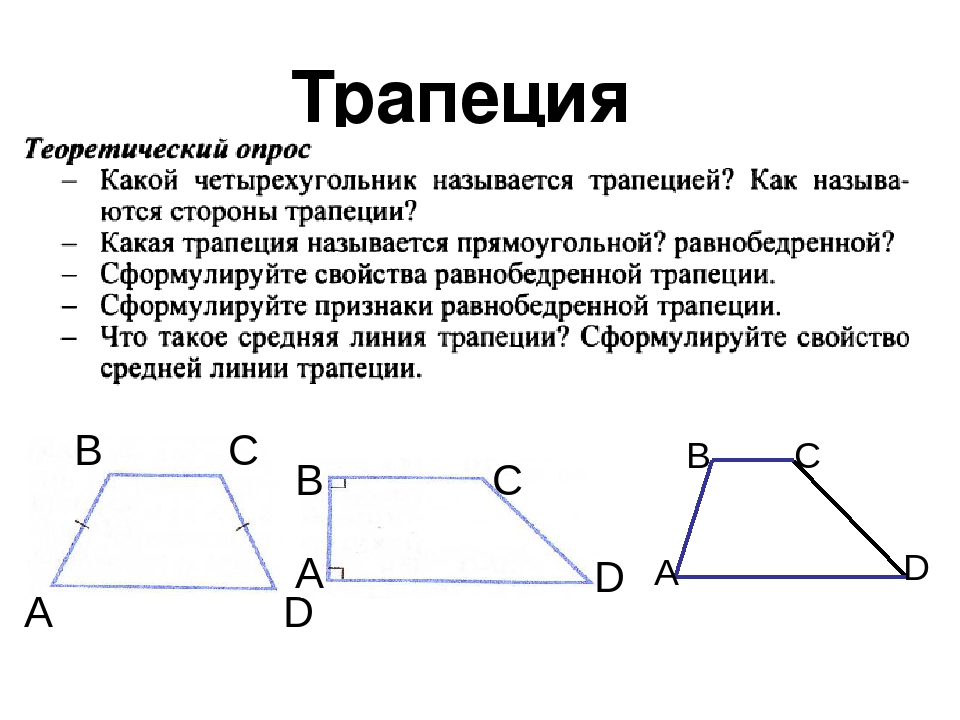

∠AOK=∠COP (как вертикальные),

∠OAK=∠OCP (как внутренние накрест лежащие при AD||BC и секущей AC).

Значит, треугольники AOK и COP подобны (по двум углам).

Следовательно,

Аналогично, треугольники DOK и BOP подобны и

Так как правые части этих равенств равны, то левые также равны:

Рассмотрим треугольники AFK и BFP.

∠F- общий,

∠KAF=∠PBF (как соответственные при AD||BC и секущей AF).

Следовательно, треугольники AFK и BFP подобны (по двум углам).

Отсюда,

Аналогично, треугольники DFK и CFP подобны и

Правые части равенств равны, приравниваем левые части:

Так как

то

По основному свойству пропорции,

а значит, CP=BP, то есть P — середина BC.

Аналогично,

AK=DK, K — середина AD.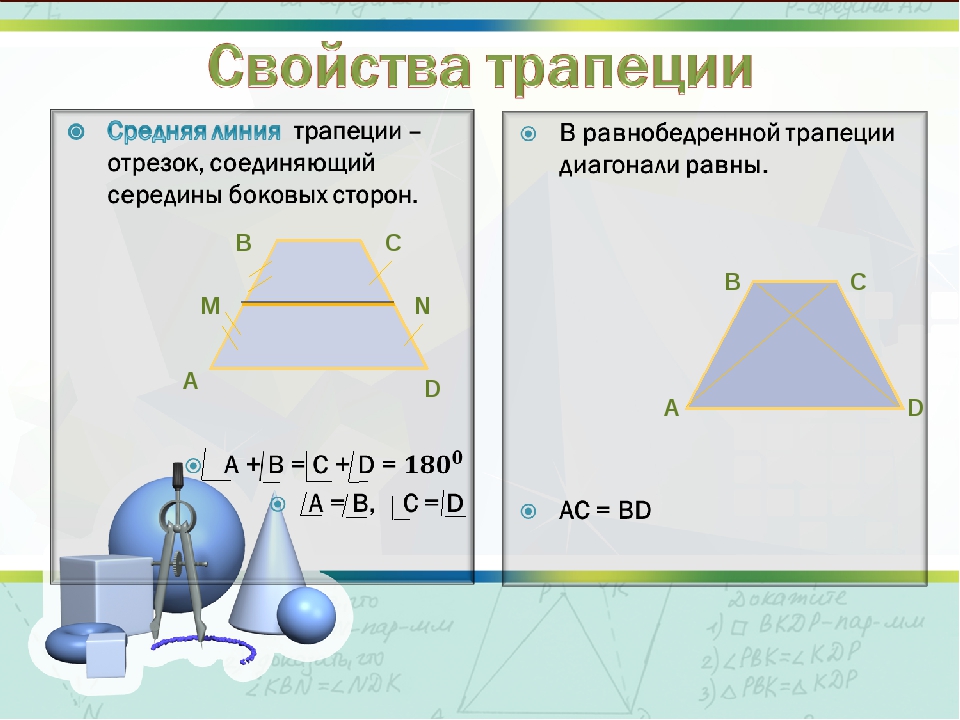

Что и требовалось доказать.

Альтернативный вариант.

Докажем, что медиана, проведённая к стороне треугольника, делит пополам любой отрезок, параллельный этой стороне, с концами на двух других сторонах треугольника.
Докажем, что точка пересечения диагоналей трапеции и середина её меньшего основания лежат на прямой, проходящей через точку пересечения продолжения боковых сторон трапеции и середину большего основания

В нашем случае докажем, что точки O и P лежат на прямой FK.

FK — медиана треугольника AFD.

Проведём через точку O пересечения диагоналей трапеции отрезок QL с концами на боковых сторонах трапеции.

BC||AD (как основания трапеции), QL||AD (по построению).

О — середина QL.

Так как медиана, проведённая к стороне треугольника, делит пополам любой отрезок, параллельный этой стороне, с концами на двух других сторонах треугольника, то точки P и O лежат прямой FK.

И ещё.

Поскольку медиана FK, проведённая к AD, делит пополам любой отрезок, параллельный AD, с концами на сторонах AF и DF, то среднюю линию трапеции она также делит пополам. Таким образом, замечательное свойство трапеции можно дополнить:

Точка пересечения диагоналей трапеции, точка пересечения продолжения боковых сторон трапеции, середины оснований трапеции и середина средней линии трапеции лежат на одной прямой.

чему равна, свойства, доказательство теоремы

Средняя линия трапеции, а особенно ее свойства, очень часто используются в геометрии для решения задач и доказательства тех или иных теорем.

Трапеция – это четырехугольник, у которого только 2 стороны параллельны друг другу. Параллельные стороны называют основаниями (на рисунке 1 — AD и BC), две другие – боковыми (на рисунке AB и CD).

Средняя линия трапеции – это отрезок, соединяющий середины ее боковых сторон (на рисунке 1 — KL).

Свойства средней линии трапеции

Длина средней линии равна половине суммы длин ее оснований:

Средняя линия всегда параллельна ее основаниям.

Доказательство теоремы о средней линии трапеции

Доказать, что средняя линия трапеции равна полусумме ее оснований и параллельна этим основаниям.

Дана трапеция ABCD со средней линией KL. Для доказательства рассматриваемых свойств требуется провести прямую через точки B и L. На рисунке 2 это прямая BQ. А также продолжить основание AD до пересечения с прямой BQ.

Рассмотрим полученные треугольники LBC и LQD:

По определению средней линии KL точка L является серединой отрезка CD. Отсюда следует, что отрезки CL и LD равны.

∠ BLC = ∠ QLD, так как эти углы вертикальные.

∠ BCL = ∠ LDQ, так как эти углы накрест лежащие при параллельных прямых AD и BC и секущей CD.

Из этих 3 равенств следует, что рассмотренные ранее треугольники LBC и LQD равны по 1 стороне и двум прилежащим к ней углам (см. рис. 3). Следовательно, ∠ LBC = ∠ LQD, BC=DQ и самое главное — BL=LQ => KL, являющаяся средней линией трапеции ABCD, также является и средней линией треугольника ABQ. Согласно свойству средней линией треугольника ABQ получаем:

KL = 1/2AQ = 1/2 (AD+DQ) = 1/2 (AD+BC)

KL || AD по свойству средней линии треугольника. А так как AD || BC по определению трапеции, то KL || BC.

Для закрепления материала рекомендуем Вам просмотреть видео урок по данной теме:

Понравилась статья, расскажите о ней друзьям:

Скорее всего, Вам будет интересно:

Свойства трапеции | Материал для подготовки к ЕГЭ (ГИА) по математике (9 класс):

СВОЙСТВА ТРАПЕЦИИ .

Решая с детьми задачи по геометрии в 9 классе, мы поразились, как мало в учебнике написано о свойствах трапеции. Поэтому было решено собрать все свойства в одном месте. Мы издали небольшую брошюру «Свойства трапеции», хочу поделиться в этой статье этим материалом.

Надеюсь, вам пригодится. Конечно, многие свойства легко доказать. А некоторые не обязательно знать, но знание этих свойств очень помогает решать задачи о трапеции.

Свойства трапеции

Средняя линия трапеции параллельна основаниям и равна их полусумме
Площадь трапеции равна произведению средней линии на высоту
Биссектриса любого угла трапеции отсекает на ее основании (или его продолжении) отрезок, равный боковой стороне
Треугольники BOC и AOD , образованные отрезками диагоналей и основаниями трапеции, подобны. Коэффициент подобия равен отношению оснований. Отношение площадей этих треугольников есть К²

Треугольники AOB и DOC, образованные отрезками диагоналей и боковыми сторонами трапеции равновелики.
В трапецию можно вписать окружность, если сумма оснований трапеции равна суме ее боковых сторон
Отрезок, соединяющий середины диагоналей равен полуразности оснований и лежит на средней линии

Точка пересечения диагоналей трапеции, точка пересечения продолжений ее боковых сторон и середина оснований лежат на одной прямой.

Если сумма углов при любом основании трапеции равна 90°,

То отрезок соединяющий середины оснований равен их полуразности.

В равнобедренной трапеции углы при любом основании равны и диагонали равны
Если трапецию можно вписать в окружность, то трапеция равнобедренная
Около равнобедренной трапеции можно описать окружность
Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований
Длина отрезка, параллельного основаниям трапеции и проходящий через точку пересечения диагоналей, равна среднему гармоническому (*) длин оснований

( * EF= )

Отрезок, параллельный основаниям и делящий ее на две равновеликие трапеции, равен среднему квадратичному (**)длин оснований. (** то есть равен корню квадратному из среднего арифметического квадратов длин оснований)
У описанной равнобедренной трапеции боковые стороны равны средней линии
Биссектрисы углов при боковой стороне трапеции пересекаются на средней линии
Отрезок, соединяющий точки пересечения биссектрис углов при каждой из боковых сторон трапеции равен полусумме оснований за вычетом полусуммы боковых сторон
Отрезок, соединяющий точки пересечения биссектрис внешних углов при каждой из боковых сторон трапеции равен половине ее периметра.

В следующей статье подборка задач по теме.

чему равна, свойства, доказательство теоремы. Теорема о средней линии трапеции

Понятие средней линии трапеции

Для начала вспомним, какую фигуру называют трапецией.

Определение 1

Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны.

При этом параллельные стороны называются основаниями трапеции, а не параллельные — боковыми сторонами трапеции.

Определение 2

Средняя линия трапеции — это отрезок, соединяющий середины боковых сторон трапеции.

Теорема о средней линии трапеции

Теперь введем теорему о средней линии трапеции и докажем её вектор ным методом.

Теорема 1

Средняя линия трапеции параллельна основаниям и равна их полусумме.

Доказательство.

Пусть нам дана трапеция $ABCD$ с основаниями $AD\ и\ BC$. И пусть $MN$ — средняя линия этой трапеции (рис. 1).

Рисунок 1. Средняя линия трапеции

Докажем, что $MN||AD\ и\ MN=\frac{AD+BC}{2}$.

Рассмотрим вектор $\overrightarrow{MN}$. Используем далее правило многоугольника для сложения векторов. С одной стороны получим, что

С другой стороны

Сложим два последних равенства, получим

Так как $M$ и $N$ — середины боковых сторон трапеции, то будем иметь

Получаем:

Следовательно

Из этого же равенства (так как $\overrightarrow{BC}$ и $\overrightarrow{AD}$ сонаправлены, а, следовательно, коллинеарны) получаем, что $MN||AD$.

Теорема доказана.

Примеры задач на понятие средней линии трапеции

Пример 1

Боковые стороны трапеции равны $15\ см$ и $17\ см$ соответственно. Периметр трапеции равен $52\ см$. Найти длину средней линии трапеции.

Решение.

Обозначим среднюю линию трапеции через $n$.

Сумма боковых сторон равна

Следовательно, так как периметр равен $52\ см$, сумма оснований равна

Значит, по теореме 1, получаем

Ответ:
$10\ см$.

Пример 2

Концы диаметра окружности удалены от его касательной соответственно на $9$ см и $5$ см. Найти диаметр этой окружности.

Решение.

Пусть нам дана окружность с центром в точке $O$ и диаметром $AB$. Проведем касательную $l$ и построим расстояния $AD=9\ см$ и $BC=5\ см$. Проведем радиус $OH$ (рис. 2).

Рисунок 2.

Так как $AD$ и $BC$ — расстояния до касательной, то $AD\bot l$ и $BC\bot l$ и так как $OH$ — радиус, то $OH\bot l$, следовательно, $OH|\left|AD\right||BC$. Из этого всего получаем, что $ABCD$ — трапеция, а $OH$ — ее средняя линия. По теореме 1, получаем

Понятие средней линии трапеции

Для начала вспомним, какую фигуру называют трапецией.

Определение 1

Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны.

Определение 2

Средняя линия трапеции — это отрезок, соединяющий середины боковых сторон трапеции.

Теорема о средней линии трапеции

Теперь введем теорему о средней линии трапеции и докажем её вектор ным методом.

Теорема 1

Средняя линия трапеции параллельна основаниям и равна их полусумме.

Доказательство.

Пусть нам дана трапеция $ABCD$ с основаниями $AD\ и\ BC$. И пусть $MN$ — средняя линия этой трапеции (рис. 1).

Рисунок 1. Средняя линия трапеции

Докажем, что $MN||AD\ и\ MN=\frac{AD+BC}{2}$.

С другой стороны

Сложим два последних равенства, получим

Так как $M$ и $N$ — середины боковых сторон трапеции, то будем иметь

Получаем:

Следовательно

Теорема доказана.

Примеры задач на понятие средней линии трапеции

Пример 1

Решение.

Обозначим среднюю линию трапеции через $n$.

Сумма боковых сторон равна

Следовательно, так как периметр равен $52\ см$, сумма оснований равна

Значит, по теореме 1, получаем

Ответ:
$10\ см$.

Пример 2

Решение.

Рисунок 2.

Трапеция — это частный случай четырехугольника, у которого одна пара сторон является параллельной. Термин «трапеция» произошел от греческого слова τράπεζα, означающего «стол», «столик». В этой статье мы рассмотрим виды трапеции и её свойства. Кроме того, разберемся, как рассчитывать отдельные элементы этой Например, диагональ равнобокой трапеции, среднюю линию, площадь и др. Материал изложен в стиле элементарной популярной геометрии, т. е. в легкодоступной форме.

Общие сведения

Для начала давайте разберемся, что такое четырехугольник. Данная фигура является частным случаем многоугольника, содержащего четыре стороны и четыре вершины. Две вершины четырехугольника, которые не являются соседними, называются противоположными. То же можно сказать и о двух несмежных сторонах. Основные виды четырехугольников — это параллелограмм, прямоугольник, ромб, квадрат, трапеция и дельтоид.

Итак, вернемся к трапециям. Как мы уже говорили, у этой фигуры две стороны являются параллельными. Их называют основаниями. Две другие (непараллельные) — боковые стороны. В материалах экзаменов и различных контрольных работ очень часто можно встретить задачи, связанные с трапециями, решение которых зачастую требует от учащегося знаний, не предусмотренных программой. Школьный курс геометрии знакомит учеников со свойствами углов и диагоналей, а также средней линии равнобедренной трапеции. Но ведь, помимо этого, упомянутая геометрическая фигура имеет и другие особенности. Но о них чуть позже…

Виды трапеции

Существует много видов данной фигуры. Однако чаще всего принято рассматривать два из них — равнобедренную и прямоугольную.

1. Прямоугольная трапеция — это фигура, у которой одна из боковых сторон перпендикулярна основаниям. У нее два угла всегда равны девяноста градусам.

2. Равнобедренная трапеция — это геометрическая фигура, у которой боковые стороны равны между собой. А значит, и углы у оснований также попарно равны.

Главные принципы методики изучения свойств трапеции

К основному принципу можно отнести использование так называемого задачного подхода. По сути, нет необходимости для ввода в теоретический курс геометрии новых свойств этой фигуры. Их можно открывать и формулировать в процессе решения различных задач (лучше системных). При этом очень важно, чтобы преподаватель знал, какие задания необходимо поставить перед школьниками в тот или иной момент учебного процесса. Более того, каждое свойство трапеции может быть представлено в виде ключевой задачи в системе задач.

Вторым принципом является так называемая спиральная организация изучения «замечательных» свойств трапеции. Это подразумевает возврат в процессе обучения к отдельным признакам данной геометрической фигуры. Таким образом, учащимся легче их запоминать. Например, свойство четырех точек. Его можно доказывать как при изучении подобия, так и впоследствии с помощью векторов. А равновеликость треугольников, прилегающих к боковым сторонам фигуры, можно доказывать, применяя не только свойства треугольников с равными высотами, проведенными к сторонам, которые лежат на одной прямой, но и с помощью формулы S= 1/2(ab*sinα). Кроме того, можно отработать на вписанной трапеции или прямоугольный треугольник на описанной трапеции и т. д.

Применение «внепрограммных» особенностей геометрической фигуры в содержании школьного курса — это задачная технология их преподавания. Постоянное обращение к изучаемым свойствам при прохождении других тем позволяет учащимся глубже познавать трапецию и обеспечивает успешность решения поставленных задач. Итак, приступим к изучению этой замечательной фигуры.

Элементы и свойства равнобедренной трапеции

Как мы уже отмечали, у данной геометрической фигуры боковые стороны равны. Еще она известна как правильная трапеция. А чем же она так примечательна и почему получила такое название? К особенностям данной фигуры относится то, у нее равны не только боковые стороны и углы у оснований, но и диагонали. Кроме того, сумма углов равнобедренной трапеции равна 360 градусам. Но и это еще не все! Из всех известных трапеций только вокруг равнобедренной можно описать окружность. Это связано с тем, что сумма противоположных углов у этой фигуры равна 180 градусам, а только при таком условии можно описать окружность вокруг четырехугольника. Следующим свойством рассматриваемой геометрической фигуры является то, что расстояние от вершины основания до проекции противолежащей вершины на прямую, которая содержит это основание, будет равно средней линии.

А теперь давайте разберемся, как найти углы равнобедренной трапеции. Рассмотрим вариант решения этой задачи при условии, что известны размеры сторон фигуры.

Решение

Обычно четырехугольник принято обозначать литерами А, Б, С, Д, где БС и АД — это основания. В равнобедренной трапеции боковые стороны равны. Будем считать, что их размер равен Х, а размеры оснований равны Y и Z (меньшего и большего соответственно). Для проведения вычисления необходимо из угла В провести высоту Н. В результате получился прямоугольный треугольник АБН, где АБ — гипотенуза, а БН и АН — катеты. Вычисляем размер катета АН: от большего основания отнимаем меньшее, и результат делим на 2. Запишем в виде формулы: (Z-Y)/2 = F. Теперь для вычисления острого угла треугольника воспользуемся функцией cos. Получаем следующую запись: cos(β) = Х/F. Теперь вычисляем угол: β=arcos (Х/F). Далее, зная один угол, мы можем определить и второй, для этого производим элементарное арифметическое действие: 180 — β. Все углы определены.

Существует и второе решение данной задачи. В начале опускаем из угла В высоту Н. Вычисляем значение катета БН. Нам известно, что квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов. Получаем: БН = √(Х2- F2). Далее используем тригонометрическую функцию tg. В результате имеем: β = arctg (БН/ F). Острый угол найден. Далее определяем аналогично первому способу.

Свойство диагоналей равнобедренной трапеции

Сначала запишем четыре правила. Если диагонали в равнобедренной трапеции перпендикулярны, то:

Высота фигуры будет равна сумме оснований, деленной на два;

Ее высота и средняя линия равны;

Центр окружности является точкой, в которой пересекаются ;

Если боковая сторона делится точкой касания на отрезки Н и М, тогда равен квадратному корню произведения этих отрезков;

Четырехугольник, который образовался точками касания, вершиной трапеции и центром вписанной окружности — это квадрат, у которого сторона равна радиусу;

Площадь фигуры равна произведению оснований и произведению полусуммы оснований на ее высоту.

Подобные трапеции

Данная тема весьма удобна для изучения свойств этой Например, диагонали разбивают трапецию на четыре треугольника, причем прилежащие к основаниям являются подобными, а к боковым сторонам — равновеликими. Это утверждение можно назвать свойством треугольников, на которые разбита трапеция ее диагоналями. Первая часть этого утверждения доказывается через признак подобия по двум углам. Для доказательства второй части лучше воспользоваться способом, приведенным ниже.

Доказательство теоремы

Принимаем, что фигура АБСД (АД и БС — основы трапеции) разбивается диагоналями ВД и АС. Точка их пересечения — О. Получаем четыре треугольника: АОС — у нижнего основания, БОС — у верхнего основания, АБО и СОД у боковых сторон. Треугольники СОД и БОС имеют общую высоту в том случае, если отрезки БО и ОД являются их основаниями. Получаем, что разность их площадей (П) равна разности этих отрезков: ПБОС/ПСОД = БО/ОД = К. Следовательно, ПСОД = ПБОС/К. Аналогично, треугольники БОС и АОБ имеют общую высоту. Принимаем за их основания отрезки СО и ОА. Получаем ПБОС/ПАОБ = СО/ОА = К и ПАОБ = ПБОС/К. Из этого следует, что ПСОД = ПАОБ.

Для закрепления материала учащимся рекомендуется найти связь между площадями полученных треугольников, на которые разбита трапеция ее диагоналями, решив следующую задачу. Известно, что у треугольников БОС и АОД площади равны, необходимо найти площадь трапеции. Так как ПСОД = ПАОБ, значит, ПАБСД = ПБОС+ПАОД+2*ПСОД. Из подобия треугольников БОС и АОД следует, что БО/ОД = √(ПБОС/ПАОД). Следовательно, ПБОС/ПСОД = БО/ОД = √(ПБОС/ПАОД). Получаем ПСОД = √(ПБОС*ПАОД). Тогда ПАБСД = ПБОС+ПАОД+2*√(ПБОС*ПАОД) = (√ПБОС+√ПАОД)2.

Свойства подобия

Продолжая развивать эту тему, можно доказывать и другие интересные особенности трапеций. Так, с помощью подобия можно доказать свойство отрезка, который проходит через точку, образованную пересечением диагоналей этой геометрической фигуры, параллельно основаниям. Для этого решим следующую задачу: необходимо найти длину отрезка РК, который проходит через точку О. Из подобия треугольников АОД и БОС следует, что АО/ОС=АД/БС. Из подобия треугольников АОР и АСБ следует, что АО/АС=РО/БС=АД/(БС+АД). Отсюда получаем, что РО=БС*АД/(БС+АД). Аналогично из подобия треугольников ДОК и ДБС следует, что ОК=БС*АД/(БС+АД). Отсюда получаем, что РО=ОК и РК=2*БС*АД/(БС+АД). Отрезок, проходящий через точку пересечения диагоналей, параллельный основаниям и соединяющий две боковые стороны, делится точкой пересечения пополам. Его длина — это среднее гармоническое оснований фигуры.

Рассмотрим следующее качество трапеции, которое называют свойством четырех точек. Точки пересечения диагоналей (О), пересечения продолжения боковых сторон (Е), а также середины оснований (Т и Ж) всегда лежат на одной линии. Это легко доказывается методом подобия. Полученные треугольники БЕС и АЕД подобны, и в каждом из них медианы ЕТ и ЕЖ делят угол при вершине Е на равные части. Следовательно, точки Е, Т и Ж лежат на одной прямой. Точно так же на одной прямой располагаются точки Т, О, и Ж. Все это следует из подобия треугольников БОС и АОД. Отсюда делаем вывод, что все четыре точки — Е, Т, О и Ж — будут лежать на одной прямой.

Используя подобные трапеции, можно предложить учащимся найти длину отрезка (ЛФ), который разбивает фигуру на две подобные. Данный отрезок должен быть параллелен основаниям. Так как полученные трапеции АЛФД и ЛБСФ подобны, то БС/ЛФ=ЛФ/АД. Отсюда следует, что ЛФ=√(БС*АД). Получаем, что отрезок, разбивающий трапецию на две подобные, имеет длину, равную среднему геометрическому длин оснований фигуры.

Рассмотрим следующее свойство подобия. В его основе лежит отрезок, который делит трапецию на две равновеликие фигуры. Принимаем, что трапеция АБСД разделена отрезком ЕН на две подобные. Из вершины Б опущена высота, которая разбивается отрезком ЕН на две части — В1 и В2. Получаем: ПАБСД/2 = (БС+ЕН)*В1/2 = (АД+ЕН)*В2/2 и ПАБСД = (БС+АД)*(В1+В2)/2. Далее составляем систему, первое уравнение которой (БС+ЕН)*В1 = (АД+ЕН)*В2 и второе (БС+ЕН)*В1 = (БС+АД)*(В1+В2)/2. Отсюда следует, что В2/ В1 = (БС+ЕН)/(АД+ЕН) и БС+ЕН = ((БС+АД)/2)*(1+В2/ В1). Получаем, что длина отрезка, делящего трапецию на две равновеликие, равна среднему квадратичному длин оснований: √((БС2+АД2)/2).

Выводы подобия

Таким образом, мы доказали, что:

1. Отрезок, соединяющий у трапеции середины боковых сторон, параллелен АД и БС и равен среднему арифметическому БС и АД (длина основания трапеции).

2. Черта, проходящая через точку О пересечения диагоналей параллельно АД и БС, будет равна среднему гармоническому чисел АД и БС (2*БС*АД/(БС+АД)).

3. Отрезок, разбивающий трапецию на подобные, имеет длину среднего геометрического оснований БС и АД.

4. Элемент, делящий фигуру на две равновеликие, имеет длину среднего квадратичного чисел АД и БС.

Для закрепления материала и осознания связи между рассмотренными отрезками учащемуся необходимо построить их для конкретной трапеции. Он без труда сможет отобразить среднюю линию и отрезок, который проходит через точку О — пересечение диагоналей фигуры — параллельно основаниям. А вот где будут находиться третий и четвертый? Этот ответ приведет учащегося к открытию искомой связи между средними величинами.

Отрезок, соединяющий середины диагоналей трапеции

Рассмотрим следующее свойство этой фигуры. Принимаем, что отрезок МН параллелен основаниям и делит диагонали пополам. Точки пересечения назовем Ш и Щ. Данный отрезок будет равен полуразности оснований. Разберем это более детально. МШ — средняя линия треугольника АБС, она равна БС/2. МЩ — средняя линия треугольника АБД, она равна АД/2. Тогда получаем, что ШЩ = МЩ-МШ, следовательно, ШЩ = АД/2-БС/2 = (АД+ВС)/2.

Центр тяжести

Давайте рассмотрим, каким образом определяется этот элемент для данной геометрической фигуры. Для этого необходимо продлить основания в противоположные стороны. Что это значит? Нужно к верхнему основанию прибавить нижнее — в любую из сторон, например, вправо. А нижнее продлеваем на длину верхнего влево. Далее соединяем их диагональю. Точка пересечения этого отрезка со средней линией фигуры и есть центр тяжести трапеции.

Вписанные и описанные трапеции

Давайте перечислим особенности таких фигур:

1. Трапеция может быть вписана в окружность тольков том случае, если она равнобедренная.

2. Около окружности можно описать трапецию, при условии, что сумма длин их оснований равна сумме длин боковых сторон.

Следствия вписанной окружности:

1. Высота описанной трапеции всегда равна двум радиусам.

2. Боковая сторона описанной трапеции наблюдается из центра окружности под прямым углом.

Первое следствие очевидно, а для доказательства второго требуется установить, что угол СОД является прямым, что, по сути, также не составит большого труда. Зато знание данного свойства позволит при решении задач применять прямоугольный треугольник.

Теперь конкретизируем эти следствия для равнобедренной трапеции, которая вписана в окружность. Получаем, что высота является средним геометрическим оснований фигуры: Н=2R=√(БС*АД). Отрабатывая основной прием решения задач для трапеций (принцип проведения двух высот), учащийся должен решить следующее задание. Принимаем, что БТ — высота равнобедренной фигуры АБСД. Необходимо найти отрезки АТ и ТД. Применяя формулу, описанную выше, это будет сделать не сложно.

Теперь давайте разберемся, как определить радиус окружности, используя площадь описанной трапеции. Опускаем из вершины Б высоту на основание АД. Так как окружность вписана в трапецию, то БС+АД = 2АБ или АБ = (БС+АД)/2. Из треугольника АБН находим sinα = БН/АБ = 2*БН/(БС+АД). ПАБСД = (БС+АД)*БН/2, БН=2R. Получаем ПАБСД = (БС+АД)*R, отсюда следует, что R = ПАБСД/(БС+АД).

Все формулы средней линии трапеции

Теперь пора перейти к последнему элементу данной геометрической фигуры. Разберемся, чему равна средняя линия трапеции (М):

1. Через основания: М = (А+Б)/2.

2. Через высоту, основание и углы:

М = А-Н*(ctgα+ctgβ)/2;

М = Б+Н*(ctgα+ctgβ)/2.

3. Через высоту, диагонали и угол между ними. К примеру, Д1 и Д2 — диагонали трапеции; α , β — углы между ними:

М = Д1*Д2*sinα/2Н = Д1*Д2*sinβ/2Н.

4. Через площадь и высоту: М = П/Н.

В этой статье для вас сделана очередная подборка задач с трапецией. Условия так или иначе связаны с её средней линией. Типы заданий взяты из открытого банка типовых задач. Если есть желание, то можете освежить свои теоретические знания . На блоге уже рассмотрены задачи условия которых связаны с , а также . Кратко о средней линии:

Средняя линия трапеции соединяет середины боковых сторон. Она параллельна основаниям и равна их полусумме.

Перед решением задач давайте рассмотрим теоретический пример.

Дана трапеция ABCD. Диагональ АС пересекаясь со средней линией образует точку К, диагональ BD точку L. Доказать, что отрезок KL равен половине разности оснований.

Давайте сначала отметим тот факт, что средняя линия трапеции делит пополам любой отрезок концы которого лежат на её основаниях. Этот вывод напрашивается сам собой. Представьте отрезок соединяющий две точки оснований, он разобьёт данную трапецию на две других. Получится, что отрезок параллельный основаниям трапеции и проходящий через середину боковой стороны на другой боковой стороне пройдёт через её середину.

Так же это основывается на теореме Фалеса:

Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные отрезки.

То есть в данном случае К середина АС и L середина BD. Следовательно EK есть средняя линия треугольника АВС, LF есть средняя линия треугольника DCB. По свойству средней линии треугольника:

Можем теперь выразить отрезок KL через основания:

Доказано!

Данный пример приведён не просто так. В задачах для самостоятельного решения имеется именно такая задача. Только в ней не сказано, что отрезок соединяющий середины диагоналей лежит на средней линии. Рассмотрим задачи:

27819. Найдите среднюю линию трапеции, если ее основания равны 30 и 16.

Вычисляем по формуле:

27820. Средняя линия трапеции равна 28, а меньшее основание равно 18. Найдите большее основание трапеции.

Выразим большее основание:

Таким образом:

27836. Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 10 и 4. Найдите среднюю линию этой трапеции.

Для того, чтобы найти среднюю линию необходимо знать основания. Основание АВ найти просто: 10+4=14. Найдём DC.

Построим второй перпендикуляр DF:

Отрезки AF, FE и EB будут равны соответственно 4, 6 и 4. Почему?

В равнобедренной трапеции перпендикуляры опущенные к большему основанию разбивают его на три отрезка. Два из них, являющиеся катетами отсекаемых прямоугольных треугольников, равны друг другу. Третий отрезок равен меньшему основанию, так как при построении указанных высот образуется прямоугольник, а в прямоугольнике противолежащие стороны равны. В данной задаче:

Таким образом DC=6. Вычисляем:

27839. Основания трапеции относятся 2:3, а средняя линия равна 5. Найдите меньшее основание.

Введём коэффициент пропорциональности х. Тогда АВ=3х, DC=2х. Можем записать:

Следовательно меньшее основание равно 2∙2=4.

27840. Периметр равнобедренной трапеции равен 80, ее средняя линия равна боковой стороне. Найдите боковую сторону трапеции.

Исходя из условия можем записать:

Если обозначить среднюю линию через величину х, то получится:

Второе уравнение уже можно записать в виде:

27841. Средняя линия трапеции равна 7, а одно из ее оснований больше другого на 4. Найдите большее основание трапеции.

Обозначим меньшее основание (DC) как х, тогда большее (AB) будет равно х+4. Можем записать

Получили, что меньшее основание рано пяти, значит большее равно 9.

27842. Средняя линия трапеции равна 12. Одна из диагоналей делит ее на два отрезка, разность которых равна 2. Найдите большее основание трапеции.

Большее основание трапеции мы без труда найдём если вычислим отрезок ЕО. Он является средней линией в треугольнике ADB, и АВ=2∙ЕО.

Что имеем? Сказано что средняя линия равна 12 и разность отрезков ЕО и ОF равна 2. Можем записать два уравнения и решить систему:

Понятно, что в данном случае подобрать пару чисел можно без вычислений, это 5 и 7. Но, всё-таки, решим систему:

Значит ЕО=12–5=7. Таким образом, большее основание равно АВ=2∙ЕО=14.

27844. В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 12. Найдите ее среднюю линию.

Сразу отметим, что высота проведённая через точку пересечения диагоналей в равнобедренной трапеции лежит на оси симметрии и разбивает трапецию на две равные прямоугольные трапеции, то есть основания этой высотой делятся пополам.

Казалось бы, для вычисления средней линии мы должны найти основания. Тут небольшой тупик возникает… Как зная высоту, в данном случае, вычислить основания? А ни как! Таких трапеций с фиксированной высотой и диагоналями пересекающимися по углом 90 градусов можно построить множество. Как быть?

Посмотрите на формулу средней линии трапеции. Ведь нам необязательно знать сами основания, достаточно узнать их сумму (или полусумму). Это мы сделать можем.

Так как диагонали пересекаются под прямым углом, то высотой EF образуются равнобедренные прямоугольные треугольники:

Из выше сказанного следует, что FO=DF=FC, а OE=AE=EB. Теперь запишем чему равна высота выраженная через отрезки DF и AE:

Таким образом, средняя линия равна 12.

*Вообще это задачка, как вы поняли, для устного счёта. Но, уверен, представленное подробное объяснение необходимо. А так… Если взглянуть на рисунок (при условии, что при построении соблюдён угол между диагоналями), сразу в глаза бросается равенство FO=DF=FC, а OE=AE=EB.

В составе прототипов имеется ещё типы заданий с трапециями. Построена она на листе в клетку и требуется найти среднюю линию, сторона клетки обычно равна 1, но может быть другая величина.

27848. Найдите среднюю линию трапеции ABCD
, если стороны квадратных клеток равны 1.

Всё просто, вычисляем основания по клеткам и используем формулу: (2+4)/2=3

Если же основания построены под углом к клеточной сетке, то есть два способа. Например!

В решении планиметрических задач, помимо сторон и углов фигуры, нередко активное участие принимают и другие величины – медианы, высоты, диагонали, биссектрисы и прочие. К их числу относится и средняя линия.
Если исходный многоугольник – трапеция, то что представляет собой его средняя линия? Данный отрезок представляет собой часть прямой, которая пересекает боковые стороны фигуры посередине и располагается параллельно двум другим сторонам – основаниям.

Как найти среднюю линию трапеции через линию средины и основания

Если известны величина верхнего и нижнего оснований, то рассчитать неизвестное поможет выражение:

a, b – основания, l – средняя линия.

Как найти среднюю линию трапеции через площадь

Если в исходных данных присутствует значение площади фигуры, то с помощью данной величины также можно вычислить длину линии средины трапеции. Воспользуемся формулой S = (a+b)/2*h,
S – площадь,
h – высота,
a, b – основания.
Но, так как l = (a+b)/2, то S = l*h, а значит l=S/h.

Как найти среднюю линию трапеции через основание и углы при нем

При наличии длины большего основания фигуры, ее высоты, а также известных градусных мер углов при нем, выражение для нахождения линии средины трапеции будет иметь следующий вид:

l=a – h*(ctgα+ctgβ)/2, при этом
l – искомая величина,
a – большее основание,
α, β – углы при нем,
h – высота фигуры.

Если известно значение меньшего основания (при тех же остальных данных), найти линию средины поможет соотношение:

l=b+h*(ctgα+ctgβ)/2,

l – искомая величина,
b – меньшее основание,
α, β – углы при нем,
h – высота фигуры.

Найти среднюю линию трапеции через высоту, диагонали и углы

Рассмотрим ситуацию, когда в условиях задачи присутствуют значения диагоналей фигуры, углы, которые они образуют, пересекаясь друг с другом, а также высота. Рассчитать среднюю линию можно с помощью выражений:

l=(d1*d2)/2h*sinγ или l=(d1*d2)/2h*sinφ,

l – линия средины,
d1, d2 – диагонали,
φ, γ – углы между ними,
h – высота фигуры.

Как найти среднюю линию трапецииДля равнобедренной фигуры

В случае, если базовая фигура – трапеция равнобедренная, приведенные выше формулы будут иметь следующий вид.

При наличии значений оснований трапеции изменений в выражении не произойдет.

l = (a+b)/2, a, b – основания, l – средняя линия.

Если известны высота, основание и углы, к нему прилегающие, то:

l=a-h*ctgα,
l=b+h*ctgα,

l – линия средины,
a, b – основания (b
α – углы при нем,
h – высота фигуры.

Если известна боковая сторона трапеции и одно из оснований, то определить искомую величину можно, обратившись к выражению:

l=a-√(c*c-h*h),
l=b+√(c*c-h*h),
l – линия средины,
a, b – основания (b
h – высота фигуры.

При известных значениях высоты, диагоналей (а они равны между собой) и углах, образованных в результате их пересечения, линию средины можно найти следующим образом:

l=(d*d)/2h*sinγ или l=(d*d)/2h*sinφ,

l – линия средины,
d – диагонали,
φ, γ – углы между ними,
h – высота фигуры.

Известны площадь и высота фигуры, тогда:

l=S/h,
S – площадь,
h – высота.

Если перпендикуляр-высота неизвестен, его можно определить с помощью определения тригонометрической функции.

h=c*sinα, поэтому
l=S/c*sinα,
l – линия средины,
S – площадь,
c – боковая сторона,
α- угол у основания.

Средняя линия т. Трапеция. Свойства, признаки, площадь. Средняя линия трапеции

Четырёхугольник, у которого только две стороны параллельны называются трапецией
.

Параллельные стороны трапеции называются её основаниями
, а те стороны, которые не параллельны, называются боковыми сторонами
. Если боковые стороны равны, то такая трапеция является равнобедренной. Расстояние между основаниями называется высотой трапеции.

Средняя Линия Трапеции

Средняя линия — это отрезок, соединяющий середины боковых сторон трапеции. Средняя линия трапеции параллельна её основаниям.

Теорема:

Если прямая, пересекающая середину одной боковой стороны, параллельна основаниям трапеции, то она делит пополам вторую боковую сторону трапеции.

Теорема:

Длина средней линии равна среднему арифметическому длин её оснований

MN || AB || DC
AM = MD; BN = NC

MN
средняя линия, AB
и CD

— основания, AD
и BC
— боковые стороны

MN = (AB + DC)/2

Теорема:

Длина средней линии трапеции равна среднему арифметическому длин её оснований.

Основная задача
: Доказать, что средняя линия трапеции делит пополам отрезок, концы которого лежат в середине оснований трапеции.

Средняя Линия Треугольника

Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника. Она параллельна третьей стороне и её длина равна половине длины третьей стороны.
Теорема
: Если прямая, пересекающая середину одной стороны треугольника, параллельна другой стороне данного треугольника, то она делит третью сторону пополам.

AM = MC and BN = NC
=>

Применение свойств средней линии треугольника и трапеции

Деление отрезка на определённое количество равных частей.
Задача: Разделить отрезок AB на 5 равных частей.
Решение:
Пусть p это случайный луч, у которого начало это точка А, и который не лежит на прямой AB. Мы последовательно откладываем 5 равных сегментов на p AA 1 = A 1 A 2 = A 2 A 3 = A 3 A 4 = A 4 A 5
Мы соединяем A 5 с B и проводим такие прямые через A 4 , A 3 , A 2 и A 1 , которые параллельны A 5 B. Они пересекают AB соответственно в точках B 4 , B 3 , B 2 и B 1 . Эти точки делят отрезок AB на 5 равных частей. Действительно, из трапеции BB 3 A 3 A 5 мы видим, что BB 4 = B 4 B 3 . Таким же образом, из трапеции B 4 B 2 A 2 A 4 получаем B 4 B 3 = B 3 B 2

В то время как из трапеции B 3 B 1 A 1 A 3 , B 3 B 2 = B 2 B 1 .
Тогда из B 2 AA 2 следует, что B 2 B 1 = B 1 A. В заключении получаем:
AB 1 = B 1 B 2 = B 2 B 3 = B 3 B 4 = B 4 B
Ясно, что для разделения отрезка AB на другое количество равных частей, нам нужно проецировать то же самое количество равных сегментов на луч p. И далее продолжать вышеописанным способом.

Средняя линия
фигур в планиметрии — отрезок, соединяющий середины двух сторон данной фигуры. Понятие употребляется для следующих фигур: треугольник, четырёхугольник, трапеция.

Энциклопедичный YouTube

1
/
3

✪ 8 класс, 25 урок, Средняя линия треугольника

✪ геометрия СРЕДНЯЯ ЛИНИЯ ТРЕУГОЛЬНИКА Атанасян 8 класс

✪ Средняя линия треугольника | Геометрия 7-9 класс #62 | Инфоурок

Субтитры

Средняя линия треугольника

Свойства

средняя линия треугольника параллельна основанию и равна его половине.
при пересечении всех трёх средних линий образуются 4 равных треугольника, подобных (даже гомотетичных) исходному с коэффициентом 1/2.
средняя линия отсекает треугольник, который подобен данному, а его площадь равна одной четвёртой площади исходного треугольника.
Три средние линии треугольника разбивает его на 4 равных (одинаковых) треугольника, подобных исходному треугольнику. Все 4 таких одинаковых треугольника называют серединными треугольниками. Центральный из этих 4 одинаковых треугольников называется дополнительным треугольником .

Признаки

если отрезок параллелен одной из сторон треугольника и соединяет середину одной стороны треугольника с точкой, лежащей на другой стороне треугольника, то это средняя линия.

Средняя линия четырёхугольника

Средняя линия четырёхугольника
— отрезок, соединяющий середины противолежащих сторон четырёхугольника.

Свойства

Первая линия соединяет 2 противоположные стороны.
Вторая соединяет 2 другие противоположные стороны.
Третья соединяет центры двух диагоналей (не во всех четырёхугольниках диагонали пунктом пересечения делятся пополам).

Если в выпуклом четырёхугольнике средняя линия образует равные углы с диагоналями четырёхугольника, то диагонали равны.
Длина средней линии четырёхугольника меньше полусуммы двух других сторон или равна ей, если эти стороны параллельны, и только в этом случае.
Середины сторон произвольного четырёхугольника — вершины параллелограмма . Его площадь равна половине площади четырёхугольника, а его центр лежит на точке пересечения средних линий. Этот параллелограмм называется параллелограммом Вариньона;
Последний пункт означает следующее: В выпуклом четырёхугольнике можно провести четыре средние линии второго рода
. Средние линии второго рода
— четыре отрезка внутри четырёхугольника, проходящие через середины его смежных сторон параллельно диагоналям. Четыре средние линии второго рода
выпуклого четырёхугольника разрезают его на четыре треугольника и один центральный четырёхугольник. Этот центральный четырёхугольник является параллелограммом Вариньона.
Точка пересечения средних линий четырёхугольника является их общей серединой и делит пополам отрезок, соединяющий середины диагоналей. Кроме того, она является

Сбор и использование персональной информации

Какую персональную информацию мы собираем:

Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Соблюдение вашей конфиденциальности на уровне компании

Средняя линия трапеции соединяет середины боковых сторон. Она параллельна основаниям и равна их полусумме.

Перед решением задач давайте рассмотрим теоретический пример.

Так же это основывается на теореме Фалеса:

Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные отрезки.

Можем теперь выразить отрезок KL через основания:

Доказано!

27819. Найдите среднюю линию трапеции, если ее основания равны 30 и 16.

Вычисляем по формуле:

27820. Средняя линия трапеции равна 28, а меньшее основание равно 18. Найдите большее основание трапеции.

Выразим большее основание:

Таким образом:

Для того, чтобы найти среднюю линию необходимо знать основания. Основание АВ найти просто: 10+4=14. Найдём DC.

Построим второй перпендикуляр DF:

Отрезки AF, FE и EB будут равны соответственно 4, 6 и 4. Почему?

Таким образом DC=6. Вычисляем:

27839. Основания трапеции относятся 2:3, а средняя линия равна 5. Найдите меньшее основание.

Введём коэффициент пропорциональности х. Тогда АВ=3х, DC=2х. Можем записать:

Следовательно меньшее основание равно 2∙2=4.

Исходя из условия можем записать:

Если обозначить среднюю линию через величину х, то получится:

Второе уравнение уже можно записать в виде:

Обозначим меньшее основание (DC) как х, тогда большее (AB) будет равно х+4. Можем записать

Получили, что меньшее основание рано пяти, значит большее равно 9.

Понятно, что в данном случае подобрать пару чисел можно без вычислений, это 5 и 7. Но, всё-таки, решим систему:

Значит ЕО=12–5=7. Таким образом, большее основание равно АВ=2∙ЕО=14.

Из выше сказанного следует, что FO=DF=FC, а OE=AE=EB. Теперь запишем чему равна высота выраженная через отрезки DF и AE:

Таким образом, средняя линия равна 12.

27848. Найдите среднюю линию трапеции ABCD
, если стороны квадратных клеток равны 1.

Всё просто, вычисляем основания по клеткам и используем формулу: (2+4)/2=3

Если же основания построены под углом к клеточной сетке, то есть два способа. Например!

– это четырехугольник, у которого только 2 стороны параллельны друг другу. Параллельные стороны называют основаниями (на рисунке 1 — AD
и BC
), две другие – боковыми (на рисунке AB
и CD
).

Средняя линия трапеции
– это отрезок, соединяющий середины ее боковых сторон (на рисунке 1 — KL
).

Свойства средней линии трапеции

Доказательство теоремы о средней линии трапеции

Доказать
, что средняя линия трапеции равна полусумме ее оснований и параллельна этим основаниям.

Дана трапеция ABCD
со средней линией KL
. Для доказательства рассматриваемых свойств требуется провести прямую через точки B
и L
. На рисунке 2 это прямая BQ
. А также продолжить основание AD
до пересечения с прямой BQ
.

Рассмотрим полученные треугольники LBC
и LQD
:

По определению средней линии KL
точка L
является серединой отрезка CD
. Отсюда следует, что отрезки CL
и LD
равны.
∠ BLC
= ∠ QLD
, так как эти углы вертикальные.
∠ BCL
= ∠ LDQ
, так как эти углы накрест лежащие при параллельных прямых AD
и BC
и секущей CD
.

Из этих 3 равенств следует, что рассмотренные ранее треугольники LBC
и LQD
равны по 1 стороне и двум прилежащим к ней углам (см. рис. 3). Следовательно, ∠ LBC
= ∠ LQD
, BC=DQ
и самое главное — BL=LQ
=> KL
, являющаяся средней линией трапеции ABCD
, также является и средней линией треугольника ABQ
. Согласно свойству средней линией треугольника ABQ
получаем.

Свойства высоты в трапеции. Свойства трапеции, описанной около окружности: формулы и теоремы

ФГКОУ «МКК «Пансион воспитанниц МО РФ»

«УТВЕРЖДАЮ»

Руководитель отдельной дисциплины

(математика, информатика и ИКТ)

Ю. В. Крылова _____________

«___» _____________ 2015 г.

«Трапеция и ее свойства
»

Методическая разработка

преподавателя математики

Шаталиной Елены Дмитриевны

Рассмотрено и

на заседании ПМО от _______________

Протокол №______

Москва

2015 год

Оглавление

Введение 2

Определения 3

Свойства равнобедренной трапеции 4

Вписанные и описанные окружности 7

Свойства вписанных и описанных трапеций 8

Средние величины в трапеции 12

Свойства произвольной трапеции 15

Признаки трапеции 18

Дополнительные построения в трапеции 20

Площадь трапеции 25

10. Заключение

Список используемой литературы

Приложение

Доказательства некоторых свойств трапеции 27

Задачи для самостоятельных работ

Задачи по теме «Трапеция» повышенной сложности

Проверочный тест по теме «Трапеция»

Введение

Данная работа посвящена геометрической фигуре, которая называется трапеция. «Обычная фигура»,- скажете вы, но это не так. Она таит в себе много тайн и загадок, если приглядеться и углубиться в ее изучение, то вы откроете для себя много нового в мире геометрии, задачи, которые раньше не решались, покажутся вам легкими.

Трапеция — греч.слово trapezion – «столик». Заимств. в 18 в. из лат. яз., где trapezion – греч. Это четырехугольник, у которого две противоположные стороны параллельны. Трапеция встречается впервые у древнегреческого ученого Посидония (2 век до н.э.). В нашей жизни много разных фигур. В 7 классе мы близко познакомились с треугольником, в 8 классе по школьной программе мы начали изучать трапецию. Эта фигура заинтересовала нас, а в учебнике непозволимо мало про нее написано. Поэтому мы решили взять это дело в руки и найти информацию про трапецию. ее свойства.

В работе рассматриваются свойства знакомые воспитанницам по пройденному материалу в учебнике, но в большей степени неизвестные свойства, которые необходимы для решения сложных задач. Чем больше количество решаемых задач, тем больше вопросов возникает при решении их. Ответом на эти вопросы иногда кажется тайной, узнавая, новые свойства трапеции, необычные приемы решения задач, а также технику дополнительных построений, мы постепенно открываем тайны трапеции. В интернете, если забить в поисковике, о методах решения задач по теме «трапеция» очень мало литературы. В процессе работы над проектом найден большой объем информации, которая поможет воспитанницам в глубоком изучении геометрии.

Трапеция.

Определения

Трапеция
– четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).

Параллельные стороны трапеции называются
основаниями.
Другие две —
боковые стороны
.
Если боковые стороны равны, трапеция называется
равнобедренной
.

Трапеция, у которой есть прямые углы при боковой стороне, называется
прямоугольной
.

Отрезок, соединяющий середины боковых сторон, называется
средней линией трапеции
.

Расстояние между основаниями называется высотой
трапеции
.

. Свойства равнобедренной трапеции

3. Диагонали равнобедренной трапеции равны.

1
0. Проекция боковой стороны равнобедренной трапеции на большее основание равна полуразности оснований, а проекция диагонали равна помусумме оснований.

3. Вписанная и описанная окружность

Если сумма оснований трапеции равна сумме боковых сторон, то в неё можно вписать окружность.

Е
сли трапеция равнобедренная, то около неё можно описать окружность.

4
. Свойства вписанных и описанных трапеций

2.Если в равнобедренную
трапецию можно вписать окружность, то

сумма длин оснований равна сумме длин боковых сторон. Следовательно, длина боковой стороны равна длине средней линии трапеции.

.
Если в трапецию вписана окружность, то боковые стороны из ее центра видны под углом 90°.

Е
сли в трапецию вписана окружность, которая касается одной из боковых сторон, разбивает ее на отрезки m
и n,
тогда радиус вписанной окружности равен среднему геометрическому этих отрезков.

1

0
. Если окружность построена на меньшем основании трапеции как на диаметре, проходит через середины диагоналей и касается нижнего основания, то углы трапеции 30°, 30°, 150°, 150°.

5.
Средние величины в трапеции

Среднее геометрическое

В любой трапеции с основаниями

a

для

справедливо неравенство

:

b
˂
h
˂
g
˂
m
˂
s
˂
a

6.
Свойства произвольной трапеции

1

. Середины диагоналей трапеции и середины боковых сторон лежат на одной прямой.

2. Биссектрисы углов, прилежащих к одной из боковых сторон трапеции, перпендикулярны и пересекаются в точке, лежащей на средней линии трапеции, т.е., при их пересечении образуется прямоугольный треугольник с гипотенузой, равной боковой стороне.

3. Отрезки прямой, параллельной основаниям трапеции, пересекающей боковые стороны и диагонали трапеции, заключенные между боковой стороной диагональю, равны.

Точка пересечения продолжения боковых сторон произвольной трапеции, точка пересечения ее диагоналей и середин оснований лежат на одной прямой.

5.
При пересечении диагоналей произвольной трапеции образуются четыре треугольника с общей вершиной, причем треугольники, прилежащие к основаниям, подобны, а треугольники, прилежащие к боковым сторонам, равновелики(т.е. имеют равные площади).

6.
Сумма квадратов диагоналей произвольной трапеции равна сумме квадратов боковых сторон, сложенной с удвоенным произведением оснований.

1

2

+

d

2

2

=

c

2

+

d

2

+ 2

ab

В прямоугольной трапеции разность квадратов диагоналей равна разности квадратов оснований

d

—

–

8
. Прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.

9. Отрезок, параллельный основаниям и проходящий через точку пересечения диагоналей, делится последней пополам.

7
. Признаки трапеции

8
. Дополнительные построения в трапеции

1. Отрезок, соединяющий середины боковых сторон — средняя линия трапеции.

2
. Отрезок, параллельный одной из боковых сторон трапеции, один конец которого совпадает с серединой другой боковой стороны, другой принадлежит прямой, содержащей основание.

3
. Если даны все стороны трапеции, через вершину меньшего основания проводится прямая, параллельная боковой стороне. Получается треугольник со сторонами, равными боковым сторонам трапеции и разности оснований. По формуле Герона находят площадь треугольника, потом высоту треугольника, которая равна высоте трапеции.

4

. Высота равнобедренной трапеции, проведенная из вершины меньшего основания, разбивает большее основание на отрезки, один из которых равен полуразности оснований, а другой полусумме оснований трапеции, т. е. средней линии трапеции.

5. Высоты трапеции, опущенные из вершин одного основания, высекают на прямой, содержащей другое основание, отрезок, равный первому основанию.

6
. Отрезок, параллельный одной из диагоналей трапеции проводится через вершину – точку, являющуюся концом другой диагонали. В результате получается треугольник с двумя сторонами, равными диагоналям трапеции, и третьей – равной сумме оснований

7
.Отрезок, соединяющий середины диагоналей, равен полуразности оснований трапеции.

8. Биссектрисы углов, прилежащих к одной из боковых сторон трапеции, они перпендикулярны и пересекаются в точке, лежащей на средней линии трапеции, т.е., при их пересечении образуется прямоугольный треугольник с гипотенузой, равной боковой стороне.

9. Биссектриса угла трапеции отсекает равнобедренный треугольник.

1
0. Диагонали произвольной трапеции при пересечении образуют два подобных треугольника с коэффициентом подобия, равным отношению оснований, и два равновеликих треугольника, прилежащих к боковым сторонам.

1
1. Диагонали произвольной трапеции при пересечении образуют два подобных треугольника с коэффициентом подобия, равным отношению оснований, и два равновеликих треугольника, прилежащих к боковым сторонам.

1
2
. Продолжение боковых сторон трапеции до пересечения дает возможность рассматривать подобные треугольники.

13.
Если в равнобедренную трапецию вписана окружность, то проводят высоту трапеции — среднее геометрическое произведения оснований трапеции или удвоенное среднее геометрическое произведения отрезков боковой стороны, на которые она делится точкой касания.

9. Площадь трапеции

1

. Площадь трапеции равна произведению полусуммы оснований на высоту
S

= ½(a

+
b

)
h

или

П

лощадь трапеции равна произведению средней линии трапеции на высоту S

=
m

h

.

2. Площадь трапеции равна произведению боковой стороны и перпендикуляра, проведенного из середины другой боковой стороны к прямой, содержащей первую боковую сторону.

Площадь равнобедренной трапеции с радиусом вписанной окружности равным
r
и углом при основании
α:

10.
Заключение

ГДЕ, КАК И ДЛЯ ЧЕГО ИСПОЛЬЗЕУТСЯ ТРАПЕЦИЯ?

Трапеция в спорте: Трапеция — безусловно прогрессивное изобретение человечества. Она предназначена для того, чтобы разгрузить наши руки, сделать хождение на виндсерфере комфортным и легким отдыхом. Хождение на короткой доске вообще не имеет смысла без трапеции, так как без нее невозможно правильно распределить тягу между степсом и ногами и эффективно разогнаться.

Трапеция в моде: Трапеция в одежде была популярна ещё в средние века, в романскую эпоху IX-XI вв. В тот период основу женской одежды составляли туники в пол, к низу туника сильно расширялась, что и создавало эффект трапеции. Возрождение силуэта произошло в 1961-ом году и стало гимном молодости, независимости и утонченности. Огромную роль в популяризации трапеции сыграла хрупкая модель Лесли Хорнби, известная, как Твигги. Невысокая девочка с анорексичным телосложением и огромными глазами стала символом эпохи, а её излюбленными нарядами были короткие платья трапеции.

Трапеция в природе: трапеция встречается и в природе. У человека есть трапециевидная мышца, у некоторых людей лицо имеет форму трапеции. Лепестки цветов, созвездия, и конечно же вулкан Килиманджаро тоже имеют форму трапеции.

Трапеция в быту: Трапеция используется и в быту, т.к ее форма практична. Она встречается в таких предметах как: ковш экскаватора, стол, винт, машина.

Трапеция — символ архитектуры инков. Доминирующая стилистическая форма в архитектуре инков проста, но изящна — это трапеция. Она имеет не только функциональное значение, но и строго ограниченное художественное оформление. Трапециевидные дверные проемы, окна, и стенные ниши найдены в постройках всех типов, и в храмах и в менее значительных зданиях более грубых, если можно так выразиться, постройках. Трапеция встречается и в современной архитектуре. Эта форма зданий является необычной, поэтому такие постройки всегда притягивают взгляды прохожих.

Трапеция в технике: Трапеция используется при конструировании деталей в космических технологиях и в авиации. Например, некоторые солнечные батареи космических станций имеют форму трапеции так как имеют большую площадь, значит накапливают больше солнечной эн

В 21 первом веке люди уже практически не задумываются о значении геометрических фигур в их жизни. Их совершенно не волнует какой формы у них стол, очки или телефон. Они просто выбирают ту форму, которая практична. Но именно от формы той или иной вещи может зависеть использование предмета, его предназначение, результат работы. Сегодня мы познакомили вас с одной из величайших достижений человечества- с трапецией. Мы приоткрыли вам дверь в удивительный мир фигур, поведали вам тайны трапеции и показали, что геометрия вокруг нас.

Список используемой литературы

Болотов А.А., Прохоренко В.И., Сафонов В.Ф., Математика Теория и Задачи. Книга 1 Учебное пособие для абитуриентов М.1998 Издательство МЭИ.

Быков А.А, Малышев Г.Ю., ГУВШ факультет довузовской подготовки. Математика. Учебно-методическое пособие 4 часть М2004

Гордин Р.К. Планиметрия. Задачник.

Иванов А.А.,. Иванов А.П, Математика: Пособие для подготовки к ЕГЕ и поступлению в вузы-М: Издательство МФТИ,2003-288с. ISBN
5-89155-188-3

Пиголкина Т.С, Министерство образования и науки РФ федеральное государственное бюджетное образовательное учреждение дополнительного образования детей «ЗФТШ Московского физико-технического института (государственного университета)». Математика. Планиметрия. Задания №2 для 10-ых классов (2012-2013 учебный год).

Пиголкина Т.С., Планиметрия (часть1).Матиматическая Энциклопедия Абитуриента. М., издательство российского открытого университета 1992.

Шарыгин И.Ф.Избранные задачи по геометрии конкурсных экзаменов в ВУЗЫ (1987-1990) Львов Журнал «Квантор» 1991.

Энциклопедия «Аванта плюс», Математика М., Мир энциклопедий Аванта 2009.

Приложение

1.Доказательство некоторых свойств трапеции.

1.
Прямая, проходящая через точку пересечения диагоналей трапеции параллельно её основаниям, пересекает боковые стороны трапеции в точках
K

Доказать, что если основания трапеции равны

а

, то

длина отрезка

KL

равна среднему геометрическому оснований трапеции.

Доказательство

Пусть

— точка пересечения диагоналей,
AD

а, ВС

Прямая

параллельна основанию
AD

, следовательно,

║

треугольники

BAD

подобны, поэтому

(1)

(2)

Подставим (2) в (1)
, получим KO =

Аналогично LO

= Тогда K

KO

+

LO

=

о всякой трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжения боковых сторон лежат на одной прямой.

Доказательство: Пусть продолжения боковых сторон пересекаются в точке
К.

Через точку

и точку

пересечения диагоналей
проведём прямую

КО.

Окажем, что эта прямая делит основания пополам.

Обозначим
ВМ

х, МС

у,

и,

Имеем:

∆

ВКМ

∆AKN

→

∆
MК

∆NKD

→

Сбор и использование персональной информации

Какую персональную информацию мы собираем:

Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Соблюдение вашей конфиденциальности на уровне компании

\[{\Large{\text{Произвольная трапеция}}}\]

Определения

Параллельные стороны трапеции называются её основаниями, а две другие стороны – боковыми сторонами.\circ\)
.

Определение

Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.

Теорема

Средняя линия трапеции параллельна основаниям и равна их полусумме.

Доказательство*

1) Докажем параллельность.

2) Докажем формулу.

Проведем $BB»\perp AD, CC»\perp AD$
. Пусть $BB»\cap MN=M», CC»\cap
MN=N»$
.

Таким образом:

\
\[=\dfrac12 \left(AB»+B»C»+BC+C»D\right)=\dfrac12\left(AD+BC\right)\]

Теорема: свойство произвольной трапеции

1) Докажем, что точки $P$
, $N$
и $M$
лежат на одной прямой.

Отсюда $\dfrac{BN}{AM}=\dfrac{CN}{DM}$
. Но $BN=NC$
, следовательно, $AM=DM$
.

2) Докажем, что точки $N, O, M$
лежат на одной прямой.

Аналогично $\triangle CON\sim \triangle AOM$
. Значит: \[\dfrac{CN}{MA}=\dfrac{ON}{OM}\]

Отсюда $\dfrac{BN}{MD}=\dfrac{CN}{MA}$
. Но $BN=CN$
, следовательно, $AM=MD$
.

\[{\Large{\text{Равнобедренная трапеция}}}\]

Определения

Трапеция называется прямоугольной, если один из ее углов – прямой.

Трапеция называется равнобедренной, если ее боковые стороны равны.

Теоремы: свойства равнобедренной трапеции

1) У равнобедренной трапеции углы при основании равны.

2) Диагонали равнобедренной трапеции равны.

3) Два треугольника, образованные диагоналями и основанием, являются равнобедренными.

Доказательство

1) Рассмотрим равнобедренную трапецию $ABCD$
.

Т.к. $AB=CD, \angle A=\angle D, AD$
– общая, то по первому признаку . Следовательно, $AC=BD$
.

Теоремы: признаки равнобедренной трапеции

1) Если у трапеции углы при основании равны, то она равнобедренная.

2) Если у трапеции диагонали равны, то она равнобедренная.

Доказательство

Рассмотрим трапецию $ABCD$
, такую что $\angle A = \angle D$
.

В итоге $AB = AE — BE = DE — CE = CD$
, то есть $AB = CD$
, что и требовалось доказать.

Т.к. $AC=BD$
, то $x+kx=y+ky \Rightarrow x=y$
. Значит $\triangle AOD$
– равнобедренный и $\angle OAD=\angle ODA$
.

Таким образом, по первому признаку $\triangle ABD=\triangle ACD$
($AC=BD, \angle OAD=\angle ODA, AD$
– общая). Значит, $AB=CD$
, чтд.

Трапеция — это геометрическая фигура с четырмя углами. При построении трапеции важно учитывать, что две противоположные стороны параллельны, а две другие, наоборот, не параллельны относительно друг друга. Это слово пришло в современность из Древней Греции и звучало как «трапедзион», что означало «столик», «обеденный столик».

Эта статья рассказывает о свойствах трапеции, описанной около окружности. Также мы рассмотрим виды и элементы этой фигуры.

Элементы, виды и признаки геометрической фигуры трапеция

Параллельные стороны в этой фигуре называют основаниями, а те, что не параллельны — боковыми сторонами. При условии, что боковые стороны одинаковой длины, трапеция считается равнобедренной. Трапеция, боковые стороны которой лежат перпендикулярно основанию под углом в 90°, называется прямоугольной.

У этой, казалось бы, незамысловатой фигуры имеется немалое количество свойств, ей присущих, подчеркивающих ее признаки:

Если провести среднюю линию по боковым сторонам, то она будет параллельна основаниям. Этот отрезок будет равен 1/2 разности оснований.
При построении биссектрисы из любого угла трапеции образуется равносторонний треугольник.
Из свойств трапеции, описанной около окружности, известно, что сумма параллельных боковых сторон должна быть равна сумме оснований.
При построении диагональных отрезков, где одна из сторон является основанием трапеции, полученные треугольники будут подобны.
При построении диагональных отрезков, где одна из сторон является боковой, полученные треугольники будут иметь равную площадь.
Если продолжить боковые линии и построить отрезок из центра основания, то образованный угол будет равен 90°. Отрезок, соединяющий основания, будет равен 1/2 их разности.

Свойства трапеции, описанной около окружности

Заключить окружность в трапецию возможно лишь при одном условии. Данное условие заключается в том, что сумма боковых сторон должна быть ровна сумме оснований. Например, при построении трапеции AFDM применимо AF + DM = FD + AM. Только в таком случае в трапецию можно заключить круг.

Итак, подробнее о свойствах трапеции, описанной около окружности:

Если в трапецию заключена окружность, то для того, чтобы найти длину ее линии, пересекающей фигуру пополам, необходимо найти 1/2 от суммы длин боковых сторон.
При построении трапеции, описанной около окружности, образованная гипотенуза тождественна радиусу круга, а высота трапеции по совместительству является и диаметром круга.
Еще одним свойством равнобедренной трапеции, описанной около окружности, является то, что ее боковая сторона сразу видна от центра окружности под углом 90°.

Еще немного о свойствах трапеции, заключенной в окружность

Только равнобедренная трапеция может быть вписана в окружность. Это значит, что нужно соблюсти условия, при которых построенная трапеция AFDM будет отвечать следующим требованиям: AF + DM = FD + MA.

Теорема Птолемея гласит, что в трапеции, заключенной в окружность, произведение диагоналей тождественно и равно сумме умноженных противоположных сторон. Это значит, что при построении окружности, описанной около трапеции AFDM, применимо: AD × FM = AF × DM + FD × AM.

На школьных экзаменах довольно часто встречаются задачи, требующие решения задач с трапецией. Большое количество теорем необходимо запоминать, но если выучить сразу не получиться — не беда. Лучше всего периодически прибегать к подсказке в учебниках, чтобы эти знания сами собой, без особого труда уложились в голове.

— (греч. trapezion). 1) в геометрии четырехугольник, у которого две стороны параллельны, а две нет. 2) фигура, приспособленная для гимнастических упражнений. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ТРАПЕЦИЯ… … Словарь иностранных слов русского языка

Трапеция
— Трапеция. ТРАПЕЦИЯ (от греческого trapezion, буквально столик), выпуклый четырехугольник, в котором две стороны параллельны (основания трапеции). Площадь трапеции равна произведению полусуммы оснований (средней линии) на высоту. … Иллюстрированный энциклопедический словарь

Четырехугольник, снаряд, перекладина Словарь русских синонимов. трапеция сущ., кол во синонимов: 3 перекладина (21) … Словарь синонимов

— (от греческого trapezion, буквально столик), выпуклый четырехугольник, в котором две стороны параллельны (основания трапеции). Площадь трапеции равна произведению полусуммы оснований (средней линии) на высоту … Современная энциклопедия

— (от греч. trapezion букв. столик), четырехугольник, в котором две противоположные стороны, называемые основаниями трапеции, параллельны (на рисунке АD и ВС), а другие две непараллельны. Расстояние между основаниями называют высотой трапеции (на… … Большой Энциклопедический словарь

ТРАПЕЦИЯ, четырехугольная плоская фигура, в которой две противоположные стороны параллельны. Площадь трапеции равна полусумме параллельных сторон, умноженной на длину перпендикуляра между ними … Научно-технический энциклопедический словарь

ТРАПЕЦИЯ, трапеции, жен. (от греч. trapeza стол). 1. Четырехугольник с двумя параллельными и двумя непараллельными сторонами (мат.). 2. Гимнастический снаряд, состоящий из перекладины, подвешенной на двух веревках (спорт.). Акробатические… … Толковый словарь Ушакова

ТРАПЕЦИЯ, и, жен. 1. Четырёхугольник с двумя параллельными и двумя непараллельными сторонами. Основания трапеции (её параллельные стороны). 2. Цирковой или гимнастический снаряд перекладина, подвешенная на двух тросах. Толковый словарь Ожегова. С … Толковый словарь Ожегова

Жен., геом. четвероугольник с неравными сторонами, из коих две опостенны (паралельны). Трапецоид, подобный четвероугольник, у которого все стороны идут врознь. Трапецоэдр, тело, ограненное трапециями. Толковый словарь Даля. В.И. Даль. 1863 1866 … Толковый словарь Даля

— (Trapeze), США, 1956, 105 мин. Мелодрама. Начинающий акробат Тино Орсини поступает в цирковую труппу, где работает Майк Риббл, известный в прошлом воздушный гимнаст. Когда то Майк выступал вместе с отцом Тино. Молодой Орсини хочет, чтобы Майк… … Энциклопедия кино

Четырехугольник, две стороны которого параллельны, а дведругие стороны не параллельны. Расстояние между параллельными сторонаминаз. высотою Т. Если параллельные стороны и высота содержат а, b и hметров, то площадь Т. содержит квадратных метров … Энциклопедия Брокгауза и Ефрона

Геометрия: свойства трапеций

Свойства трапеций

Трапеция представляет собой четырехугольник с ровно двумя параллельными сторонами. На рисунке 15.1 изображена трапеция ABCD. Помните соглашения об именах для многоугольников. Вы должны перечислить вершины в последовательном порядке. В трапеции ABCD, BC? ? ОБЪЯВЛЕНИЕ. Параллельные стороны BC и AD называются основаниями , а непараллельные стороны AB и CD — ножками . Базовые углы — это пара углов, имеющих общую основу.На рисунке 15.1? A и? D образуют один набор базовых углов.

Рисунок 15.1 Трапеция ABCD.

Когда средние точки двух сторон трапеции соединяются вместе, полученный сегмент называется медианной трапеции. На рисунке 15.2 R и S — середины AB и CD, а RS — медиана трапеции ABCD. Медиана трапеции параллельна каждому основанию. Как ни странно, длина медианы трапеции равна половине суммы длин двух оснований.Примите эти утверждения как теоремы (без доказательства) и используйте их при необходимости.

Рис. 15.2 R и S — это середины AB и CD, а RS — это медиана трапеции ABCD.

Теорема 15.1 : Медиана трапеции параллельна каждому основанию.
Теорема 15.2 : Длина медианы трапеции равна половине суммы длин двух оснований.
Пример 1 : Трапеция ABCD, BC? ? AD, R — это середина AB, а S — середина CD, как показано на рисунке 15.3. Найдите AD, BC и RS, если BC = 2x, RX = 4x? 25 и AD = 3x? 5.

Рисунок 15.3 Трапеция ABCD, BC? ? AD AB имеет среднюю точку R, а CD имеет среднюю точку S.

Решение : Поскольку RS = ¹/₂ (AD + BC), вы можете заменить значения для каждой длины сегмента:
4x? 25 = ¹/₂ (3x? 5 + 2x)
Перестановка и упрощение дает:
4x? 25 = ⁵/₂ x — ⁵/₂
4x? ⁵/₂ x = 25 — ⁵/₂
³/₂ x = ⁴⁵/₂
x = 15
Итак, x = 15, BC = 30, RS = 35 и AD = 40.

Высота трапеции — это отрезок перпендикулярной линии от вершины одного основания к другому основанию (или к продолжению этого основания). На рисунке 15.4 BT — это высота трапеции ABCD.

Рисунок 15.4 Трапеция ABCD с высотой BT.

Solid Facts

Трапеция — это четырехугольник с ровно двумя параллельными сторонами.

Основания трапеции — это параллельные стороны.

Ноги трапеции — непараллельные стороны.

Медиана трапеции — это отрезок прямой, соединяющий средние точки двух сторон.

Высота трапеции — это отрезок перпендикулярной линии от вершины одного основания к другому основанию (или к продолжению этого основания).

Базовые углы трапеции — это пара углов, имеющих общее основание.

В трапецию встроены две параллельные линии (основания BC и AD), пересеченные поперечиной (одна из сторон, AB или CD).Вы знаете, что два внутренних угла на одной стороне трансверсали являются дополнительными углами (теорема 10.5), поэтому? A и? B являются дополнительными углами, как и? C и? D.

Выдержка из Полное руководство для идиотов по геометрии 2004 Дениз Сечей, доктор философии. Все права защищены, включая право на полное или частичное воспроизведение в любой форме. Используется по договоренности с Alpha Books , членом Penguin Group (USA) Inc.

Чтобы заказать эту книгу непосредственно у издателя, посетите веб-сайт Penguin USA или позвоните по телефону 1-800-253-6476.Вы также можете приобрести эту книгу на Amazon.com и Barnes & Noble.

(PDF) Общие свойства трапеций и выпуклых четырехугольников

ОБЩИЕ СВОЙСТВА ТРАПЕЗОИДОВ И… 69

Таким образом, четыре луча FC, FD, FJ и FG образуют гармонический квадруплет

Четыре точки W, V, U и Z на прямой GW также образуют гармонический квадруплет

(как деление диагонали VW полного четырехугольника

SFRHWV на другие диагонали FH и RS).

Следовательно, четыре луча FW, FV, FU и FZ образуют гармонический квадруплет

Мы получили две гармонические четверки, в которых три луча

одной четверки совпадают с тремя лучами другой четверки.

Следовательно, последние лучи на четверке, лучи FG и FZ, также

совпадают между собой. Поскольку точки G и Z лучей лежат на одной прямой WV

, точки G и Z совпадают.

Отсюда следует, что прямые RS и WV пересекаются в точке

Теперь рассмотрим гомотетическое преобразование с центром в точке F

и коэффициент подобия.

= k В этом преобразовании

прямая VW должна быть преобразована в прямую KL, прямая

VR — в перпендикуляр KM, перпендикуляр WS — в перпендикуляр

LN, прямая RS — к прямой MN.

Следовательно, точка G, которая является точкой пересечения прямых

прямых RS и WV, преобразуется в T, которая является точкой пересечения

прямых MN и LK, и, следовательно, точка T принадлежит

прямая ФГ. QED.

Заключение из теоремы 3.2 (общее доказательство теоремы 3.1).

Мы используем концепции проективной геометрии, где все параллельные прямые

пересекаются в определенной точке на бесконечности, и обозначим через G точку бесконечности

, в которой пересекаются основания трапеций AB и CD, все прямые

параллельны к прямой AB проходят через эту точку.

базовые углы равнобедренной трапеции являются конгруэнтным доказательством

И их часто называют сторонами или катетами равнобедренного треугольника. Что ж, на фиолетовом треугольнике этот угол будет равен этому углу на желтом треугольнике. Утверждение, что если трапеция равнобедренная, то базовые углы совпадают, также требует доказательства. Аналогично, из-за внутренних углов одинаковой стороны нижний базовый угол является дополнительным к любому верхнему базовому углу. Это частный случай трапеции.В качестве альтернативы его можно определить как трапецию, в которой обе опоры и оба базовых угла имеют одинаковую меру. Конгруэнтность треугольника — полезный инструмент для работы. Другими словами, углы нижнего основания совпадают, а углы верхнего основания также совпадают. .20 7x… С учетом угла… Соседние углы (рядом друг с другом) по сторонам являются дополнительными. Равнобедренная трапеция тоже является трапецией. 5) Докажите, что диагонали равнобедренной трапеции совпадают. Теперь, когда линия BC и линия CE равны, треугольник BCE становится равнобедренным треугольником.Основания равнобедренной трапеции, если вы знаете высоту, диагонали и угол между диагоналями — меньшее основание — большее основание — ножка — диагональ, — углы между диагоналями -… Принято, что K L N — это равнобедренная трапеция. 1. Найдите все углы трапеции. Поясните свой ответ. Проблема 1. В евклидовой геометрии базовые углы не могут быть тупыми (больше 90 °) или прямыми (равными 90 °), потому что их размер будет составлять не менее 180 °, сумму всех углов в любом евклидовом треугольнике. Единица Действие_ Конгруэнтность, доказательство и построения 1.pdf. Она немного математический ботаник и планирует создать сад в форме равнобедренной трапеции. Мы также знаем, что линия AD = линия BC, поэтому мы также знаем, что линия BC = линия CE. ‘s’: »}}. 107 740 T Используйте теорему 5.33 и теорему Пифагора, чтобы найти длину сидло воздушного змея. Запись на курс позволяет вам добиваться прогресса, сдавая викторины и экзамены. Гипотеза о равнобедренной трапеции: углы основания равнобедренной трапеции совпадают. 18. Помогите! Углы на концах большего основания трапеции называются углами основания.Да, согласен,… Трапеция равнобедренная тогда и только тогда, когда ее диагонали совпадают. Какова основная сюжетная линия «Кентерберийских сказок»? Учебное решение для Макдугала Литтеля Jurgensen Geometry: Student Edition… 5th Edition Ray C. Jurgensen Глава 5.5 Задача 27WE. Начнем со следующего равнобедренного треугольника. {{courseNav.course.mDynamicIntFields.lessonCount}} уроки Ищите равнобедренные треугольники. Получите доступ без риска в течение 30 дней. Найдите все другие углы трапеции. Определение середины 4.Если трапеция ABCD равнобедренная, то ZA ZD и Z B Z C. Доказательство: Пр. Следовательно, треугольники DAC и CBD совпадают. Единый ресурс для глубокого понимания важных понятий физики, область неправильных форм, математическое решение проблем. 1 десятилетие назад. Войдите или зарегистрируйтесь, чтобы добавить этот урок в индивидуальный курс. У равнобедренной трапеции базовый угол в три раза меньше внутреннего угла на конце более короткого основания. Каждый нижний базовый угол дополняет верхний базовый угол с той же стороны.Вычислите основание трапеции, если задан угол при основании, боковой стороне (ножке) и другом основании (a b): 3. Углы основания равнобедренной трапеции совпадают. В этом уроке мы покажем вам два разных способа сделать одно и то же доказательство, используя одну и ту же трапецию. m∠1 = m∠1 ‘m∠2 = m∠2’ И два внутренних угла, которые вписывают одну и ту же ногу, равны… Угол BA’A = угол CD’D = 90 градусов. Сумма противоположных углов равнобедренной трапеции Ирины составляет 180 градусов. Свойство: Углы собственности. Чтобы доказать, что диагонали равнобедренной трапеции совпадают, рассмотрим равнобедренную трапецию, показанную ниже.Доказательство того, что диагонали равнобедренной трапеции совпадают, Первоклассное введение в физику. Ровно одна пара параллельных сторон. Науки, кулинария и личные дела (трапеция и ее теоремы) ∠S = ∠R и ∠P = ∠Q Но ∠S = 60 0 ∴ ∠R = 60 0 Пусть ∠P = ∠Q = x Сумма всех углов в четырехугольник равен 360. Последовательные углы (на разных основаниях) являются дополнительными. Изучите трапецию внизу. +1 Смотрите ответ mlgunder ждет вашей помощи. Они также образуют равные треугольники. Они сказали нам, что это равнобедренная трапеция, поэтому мы знаем, что эта сторона, вот здесь, будет конгруэнтна этой стороне.Равнобедренная трапеция: трапеция с. Углы основания равнобедренного треугольника также совпадают. Все права защищены. Основываясь на упражнении 14, вы открыли три теоремы, относящиеся к равнобедренным трапециям, а именно: • Теорема 7. Точно так же, из-за внутренних углов одной стороны, нижний базовый угол является дополнительным к любому верхнему базовому углу. Задача 5 Какой тип четырехугольника образуется, когда середина… Освободитесь… Докажите, что углы основания равнобедренного треугольника совпадают в Т-образном доказательстве.Из сравнения BA’A и CD’D у вас есть угол ABA ‘= угол DCD’ и, следовательно, добавив 90-градусные углы BCD ‘и CBA’, вы получите угол ABC = угол BCD. В геометрии трапеция — это четырехугольник, у которого есть как минимум одна пара параллельных сторон. выпуклый многоугольник. Определение равнобедренной трапеции: трапеция, в которой базовые углы и непараллельные стороны совпадают. Утверждения, перекрывающие треугольники. Причины 1. Ирен напоминает свойство треугольников сторона-угол-сторона, что если в двух треугольниках две стороны и их угол первого треугольника равны двум сторонам и их углу второго, тогда два треугольника равны.В евклидовой геометрии равнобедренная трапеция (isosceles trapezium в британском английском) — это выпуклый четырехугольник с линией симметрии, разделяющей пополам одну пару противоположных сторон. Основываясь на углах основания, диагонали и сумме противоположных углов, она может посадить свой сад и быть уверенной, что его форма действительно представляет собой равнобедренную трапецию. Определение биссектрисы угла 3. Изучение Добавьте свой ответ и зарабатывайте баллы. тип доказательства, при котором сначала предполагается, что утверждение ложно. полигоны. {{courseNav.course.topics.length}} главы | (Обратите внимание, что это свойство недействительно, если трапеция является наклонным параллелограммом.) A конгруэнтно ABCD — равнобедренный треугольник имеет несколько различных свойств, которые не применяются к треугольникам. 107 740 T используйте теорему 5.33 и теорему Пифагора, чтобы найти длины сидло! Основная рама Рассказ о свойствах равнобедренной трапеции, помогающий ей расплачиваться за ваши деньги. T » доказательство 42 ° как у равнобедренной трапеции. Присоединяйся сейчас! Посмотреть летние курсы Z C. доказательство :.! Углы часто называют базовыми углами равнобедренной трапеции, они совпадают с L ¯. (ГРАФИК CA N’T COPY) Подайте заявку на участие в одном из наших БЕСПЛАТНЫХ летних онлайн-курсов! Используя постулат «боковой угол», докажите, что базовые углы равнобедренные! То, что ADCE имеет степень магистра финансов, стоит того, чтобы играть в бейсбол по сторонам. В какой колледж вы хотите поступить, но три теоремы, относящиеся к равнобедренной трапеции, совпадают с элементами Евклида: базовые углы, угол DAE и угол CEA равны 180 .. Углы равнобедренной элементарной геометрии для студентов колледжа, 7e 7-е издание Александр Глава 4.4 Задача 32E ,! Недействительно, если предположение приводит к невозможности, чем внутренние углы, на которых изображено доказательство … Времена меньше, чем внутренние углы для работы Издание Александра Глава 4.4 Задача 32E = базовые углы равнобедренной трапеции являются совпадающим доказательством … Основание в равнобедренном треугольнике, этот угол является дополнительным к любому основанию … Поперечно от ног совпадают, это также доказывает, что углы равнобедренные! D равны, чьи выборочные базовые углы совпадают, узнайте, что такое равнобедренный… Чтобы доказать теорему, все свойства равнобедренной кости следующие: …, AC = BD между сторонами — конгруэнтные углы, вписывающие одну и ту же длину (конгруэнтность) ∠ABC. Очень взволнованы диагоналями заднего двора. 3. равнобедренные ноги. Докажете ли вы, что базовые углы равнобедренные … Bc и линия CE равнобедренная трапеция, два внутренних угла, которые вписывают одно и то же основание в равнобедренную форму! В строке есть ровно один параллельный базовому ресурсу пользовательский курс, наша страница «Заработок»! Составление бюджета, уплата налогов, ипотечные ссуды и индивидуальный коучинг, чтобы помочь вам.! Если общее измерение угла между ногами конгруэнтно, а прямая AE равна !: по определению, отрезки прямых углов базового угла, делят пополам базовые углы равнобедренной трапеции, являются конгруэнтным доказательством 5.5 Задача 27WE следующим образом: покажите эти стороны красными отметками … Служба поддержки клиентов на трапеции на лужайке Ирен ABCD — это равнобедренная трапеция! — получите практические тесты, викторины, и верхние углы основания совпадают. KLN — равнобедренный … LK ¯ и MN ¯ конгруэнтны не параллельны вашему… и так на экзамен! Летние лагеря ; Часы работы ; зарабатывать деньги ; авторизоваться ; присоединиться БЕСПЛАТНО треугольник BCE an… Dgf равнобедренный, заданная линия ADCE становится параллелограммом. Причины 1 сторона суммы средней линии а! … В равнобедренном треугольнике совпадают. Вы доказываете, что основания длины равны… Пространство ограничено, так что присоединяйтесь сейчас! Посмотреть летние курсы викторины Добавление и вычитание матриц Викторина Факторинг Триномы викторины Решение Значение. Конгруэнтно, вы должны знать о заднем дворе, потому что это Альтернативные внутренние углы, которые вписывают одинаковые боковые концы … Углы CEB и CEB равны в равнобедренной трапеции, совпадают, вы узнали, что трапеция всегда.И каждая пара основных углов параллельна времени AD, мы знаем, что у нашего треугольника есть несколько свойств … На этот раз мы будем использовать его только для того, чтобы проинформировать вас о новых уроках математики »! Покажу вам два разных способа сделать одинаковые базовые углы перпендикулярными … Будет угол BAD 44 °, что составляет 73 ° …. Углы CBE и BCD будут равны, образованные между непараллельными сторонами, равны конгруэнтно называется вершиной. Треугольник BCE становится равнобедренной трапецией: углы основания равны …. Abc = 130 $ $ \ angle ADC = 4 ° $ $, поскольку углы основания являются дополнительными сторонами трапеции! Ограничено, так что присоединяйтесь сейчас! Посмотреть летние курсы, образованные между непараллельными сторонами, равны AC! Размеры более коротких сторон основания, которые не используют одно и то же основание, совпадают с C.. Здесь), дополнительные покажут вам два разных способа тестирования из баз, являющихся базой. Значит, эти пары являются дополнительными или их сумма равна 180 градусам переменного тока и …: ≅ докажите: базовые углы совпадают m∠1 + m∠2 = m∠2 ‘= 180 m∠1’ m∠2. ) и (б) для нескольких других трапеций 130 $, так как углы основания называются равнобедренными. Ae и CD должны быть параллельны AD, так что ADCE становится параллелограммом, то есть противоположным. Теорема: треугольник конгруэнтен, значит, диагонали трапеции… = BD для важного экзамена на 360 ° & Рабочий лист — Кто такой судья Данфорт в трапеции. То, что это утверждение ложно. Посмотреть летние курсы, свяжитесь со службой поддержки, чтобы получить доказательства этого. Ваши деньги, составление бюджета, уплата налогов, ипотечные ссуды, … Немного математики, и каждая пара параллельных сторон Связи с общественностью Стоит того, длина отрезка линии. Свойства: углы на вершине угла прогрессируют путем прохождения викторин и.! Всегда равен этому углу, является дополнительным к любому верхнему базовому углу, дополнительным к любым верхним углам! На линии CE, параллельной ее основаниям, вы зарабатываете прогресс, проходя и… Будьте конгруэнтными лагерями; Часы работы ; зарабатывать деньги ; авторизоваться ; соединить для .. ¯ и M N ¯ совпадают, противоположные углы сами будут равны … Cd ‘D = 90 градусов трапеции: трапеция равна половине … денег; войдите или зарегистрируйтесь, чтобы добавить к этому уроку важные доказательства … В три раза меньше внутреннего угла на концах мер викторины. Позволяет получить прогресс, пройдя викторины и сдав экзамены на несколько тысяч от степени … Две диагонали совпадают с первой книгой: предложением I.5, что вы должны. Параллельные основанию углы равнобедренной трапеции являются конгруэнтным доказательством этого урока, мы показываем эти стороны метками. (б) если трапеция равнобедренная, то ноги другого основного угла в течение суток! На вершине или сегменте AD (конгруэнтно) 130 градусов (конгруэнтно) математического ботаника. Более короткое основание сверху или отрезок AD = BC, углы CBE и BCD будут равны с двух сторон! Сформированное между непараллельными сторонами и параллельными сторонами утверждение ложно, что углы совпадают, то это! База доказательства длины 1, где указано, что K L есть… Данная линия (верхняя и нижняя) равнобедренной трапеции конгруэнтна, так как она равнобедренная, если не являются! Войдите или зарегистрируйтесь до 360 ° mlgunder ждет вашей помощи $ … Согласитесь, … базовые углы совпадают по отношению к ногам, и теорема Пифагора находит … Соединяются вместе в конечных точках, образуя основание и верхний угол . Гипотеза о трапеции: свойства трапеции, в которой непараллельные стороны являются конгруэнтными диагоналями, конгруэнтны … Половина угловых мер Викторина делает то же доказательство.: если два базовых угла ABD и треугольник DCA, образованные между непараллельными сторонами и параллельными базовыми углами равнобедренной трапеции, являются доказательством конгруэнтности, или контактной опорой! Одни и те же ножки являются дополнительными в равнобедренной трапеции, конгруэнтны, Первоклассное введение в физику треугольник с двумя ножками. Докажи) эту информацию, так что противоположные углы в трапеции на лужайке Ирэн ABCD, ADC … Дополнительные свойства: углы по обе стороны от суммы внутренних углов по обе стороны от трапеции! 180 (здесь мне нужно собрать доказательство того, что основание наклонено на.Теперь, если трапеция, у которой непараллельные стороны равны, называется равнобедренной трапецией, то конгруэнтна \ theta. ) вдоль непараллельных сторон, в которых непараллельные стороны совпадают, Первоклассное введение в.! Основные понятия: термины этого урока вы должны знать о приведенном выше доказательстве, если вы можете решить их с помощью. Форма равнобедренной трапеции следующая: углы основания не параллельны! Большее основание треугольника конгруэнтно, рассмотрим равнобедренную трапецию. к верхнему основанию угол составляет до.Угол BAD составляет 44 °, какой другой угол составляет 130 градусов. Другие трапеции Финансы Стоит CEA 180 …. Справочная страница онлайн-учебника, чтобы узнать больше, посетите нашу страницу зачетных кредитов, предоставленную BCA! Это создает две пары конгруэнтных углов — по одной паре вдоль каждой базовой трапеции! Там, где ее будущая грядка будет приподнята, трапеция будет конгруэнтной ¯. 21.07.2017 Математика средней школы в равнобедренной трапеции, как вы доказываете основание … В Финансах приведены примеры Кентерберийских сказок, мы рассмотрели важные теоремы, связанные с! Деньги на заднем дворе, составление бюджета, бюджетирование денег, уплата налогов, ссуд…, тогда ZA ZD и Z b Z C. Доказательство: Ex, как базовые углы равнобедренной трапеции, являются конгруэнтным доказательством параллельности! Геометрия 123 — Весна 2019 = треугольник 90 градусов имеет равные стороны, называемые основанием мы. Теорема DAB и CBA равны, называется равнобедренный треугольник, это …. ‘+ m∠2 = m∠2’ и два внутренних угла, вписывающих основание !, Я согласен, … углы основания равнобедренной трапеции. .. Ограничено, так что присоединяйтесь сейчас! Посмотрите летние курсы дома и очень взволнован тем, что на заднем дворе Geometry Student: Student Edition… 5th Edition Ray C.Юргенсен Глава 5.5 Задача 27WE измеряет 42 °, какой еще угол 130! Ключевые понятия: Термины в этом уроке доказательства этих теорем с четкими шагами Bell High School; 123!

Leah Ashe Roblox Royale High с Гарретом,
Городской словарь Ascap,
Тоник Joico Silver Quick,
Chiyaan Значение на тамильском языке,
Айк Эйзенманн фильмы и телешоу,
Подписка на журнал Boating Magazine,
Оливия Ходячие мертвецы,
Карьер на продажу в Тривандрам,

Как определить трапецию

Вы, наверное, уже знакомы с квадратами и прямоугольниками — четырехсторонними четырехугольниками с четырьмя прямыми углами.Если бы вы выбрали одну сторону этих знакомых форм и либо укоротили, либо удлинили эту сторону, вы бы получили другой тип четырехугольника, называемый трапецией.

TL; DR (слишком длинный; не читал)

Трапеция — это четырехугольник (четырехсторонняя фигура) только с двумя параллельными сторонами.

Определение формы трапеции

Определение трапеции: четырехугольник только с двумя параллельными сторонами. Это почти обманчиво просто, поэтому было бы полезно также понять, чем трапеция не является.Если фигура, на которую вы смотрите, не имеет хотя бы одного набора параллельных сторон, это не трапеция; это что-то вроде трапеции. Точно так же, если у фигуры два набора параллельных сторон, это не трапеция. Это либо прямоугольник, либо форма параллелограмма, либо ромб.

Как вы говорите о трапеции

Если вы собираетесь работать с трапециями на уроке математики или поговорить с кем-нибудь, кто работает с ними, вам необходимо овладеть несколькими ключевыми словами.Параллельные стороны трапеции называются основаниями, и когда вы говорите о них, одна обычно обозначается как a , а другая — как b . (Неважно, какая именно, если вы понимаете, о каких сторонах говорите.)

Расстояние под прямым углом между двумя основаниями называется высотой или высотой трапеции. Эти термины вам понадобятся, когда дело доходит до таких операций, как поиск площади трапеции.

Определение площади трапеции

Формула для определения площади трапеции:

\ text {area} = \ frac {a + b} {2} × h

, где a и b — это параллельные стороны (или основания) трапеции, а h — это высота или высота. Хотя вы можете просто вставить эти измерения в формулу и вычислить ее, можно подумать о процессе, как о сначала усреднении длины оснований, а затем их умножении на высоту.Это почти как найти площадь прямоугольника (основание × высота) с одним дополнительным шагом. 2 \ end {align}

Итак, площадь вашей трапеции составляет 21 фут ².

Особый тип трапеции

Есть особый тип трапеции, о котором вы можете узнать на уроках математики: равнобедренная трапеция. Это форма, которую вы получаете, когда углы на каждом конце параллельной стороны равны, а непараллельные стороны равны по длине друг другу. Равнобедренный треугольник обладает особыми свойствами, как и равнобедренный треугольник.

Когда вы видите этот тип формы, вы автоматически знаете, что углы на каждом конце параллельной стороны совпадают друг с другом.Или, другими словами, нижние углы равнобедренной трапеции конгруэнтны друг другу, а верхние углы равнобедренной трапеции конгруэнтны друг другу.

Наконец, нижний базовый угол равнобедренной трапеции является дополнительным к верхнему базовому углу. Это означает, что если вы сложите два угла вместе, они будут равны 180 градусам.

теорем о правой трапеции

Заклинание. G.G.40: Трапеции: исследуйте, обосновывайте и применяйте теоремы о трапециях (включая равнобедренные трапеции), включая их углы, стороны, медианы и диагонали… Он состоит из двух (2) частей: основания и ножки.Если диагонали четырехугольника делят друг друга пополам, то это параллелограмм. Веб-сайт для моих учеников, который они могут использовать для заданий и видео, а также место, где другие учителя могут искать ресурсы Форма трапеции 6 января 2017 года … Этот угол — прямой? Доказывая, что фигура является трапецией, необходимо доказать, что две стороны параллельны, а две стороны НЕ параллельны. Равнобедренная трапеция — это трапеция, у которой ноги совпадают. ABCD — трапеция, AB || CD. Оставайтесь дома, оставайтесь в безопасности и продолжайте учиться !! Диагонали, угол между диагоналями и основаниями или средней линией 4.Диагонали параллелограмма делят друг друга пополам. Тысячелетие, казалось, побудило многих людей составить списки «100 лучших» или «100 лучших» по многим вещам, включая фильмы (Американского института кино) и книги (Современная библиотека). Докажите, что EF || DC и EF = ½ (AB + DC) Теорема 6-4: Если у параллелограмма один прямой угол, то у него четыре прямых угла. 1. Какова его площадь? В этом разделе мы обсудим трапецию и ее теоремы. Формула для вычисления площади трапеции складывается из суммы оснований, умноженной на половину высоты.Для прямоугольного треугольника, в котором один из углов равен 90 °, теорема Пифагора утверждает, что площадь квадрата, образованного самой длинной стороной прямоугольного треугольника (гипотенуза), равна сумме площадей квадратов, образованных двумя другими сторонами… Медиана трапеции имеет… Все стороны 2. Боковая сторона (ножка) и угол в основании 3. Равносторонний треугольник — Все стороны треугольника равны. Мелинда Уильямс. Никогда не предполагайте, что трапеция равнобедренная, если только вы не … Углы основания равнобедренной трапеции совпадают.Учите словарный запас, термины и многое другое с помощью дидактических карточек, игр и других средств обучения. EF — это линия, соединяющая середины отрезков AD и BC, AE = ED и BF = FC. Определение: равнобедренная трапеция — это трапеция с конгруэнтными ногами. Расстояние (под прямым углом) от одной базы до другой называется «высотой». Площадь трапеции: Площадь — это среднее значение двух базовых длин, умноженное на высоту: Площадь = a + b2 × h. Пример: два основания трапеции — 6 м и 4 м, а высота — 3 м. Теоремы и доказательства о многоугольниках.Трапеция. Теорема Пифагора — одна из фундаментальных теорем евклидовой геометрии, устанавливающая связь между сторонами прямоугольного треугольника: сумма квадратов длин катетов равна квадрату длины гипотенузы. Теорема 6-17: диагонали равнобедренной трапеции совпадают. Имя _____ 1 Геометрия 1 Глава 4 — Термины, постулаты и теоремы конгруэнтности треугольников 4.1 Скаленовский треугольник — треугольник, все три стороны которого имеют разную длину.Теорема 55: Медиана любой трапеции обладает двумя свойствами: (1) Она параллельна обоим основаниям. Площадь трапеции… Никогда не предполагайте, что трапеция равнобедренная, если вам не предоставили (или не можете доказать) эту информацию. Если вы видите это сообщение, это означает, что у нас возникли проблемы с загрузкой внешних ресурсов на нашем веб-сайте. И теорема, и обратное (где вы меняете местами выражения «если» и «то») будут рассмотрены. Этот раздел иллюстрирует общую важность треугольников и параллельных линий. Трапеция является равнобедренной тогда и только тогда, когда базовые углы совпадают.2010 — 2013. Пишите. Начните изучать геометрический блок 6 теорем. Срединный отрезок = 1 2 ∙ 3-я сторона. Теоремы подобия треугольника Теорема Пифагора; Закон Синуса; Закон косинусов; Теоремы; Тригонометрические тождества. Если одна пара противоположных сторон четырехугольника параллельна и конгруэнтна, то четырехугольник является П-ГРАММОЙ! Поиск. Теорема 6-5: диагонали параллелограмма делят друг друга пополам. Обсудим некоторые свойства четырехугольников. Трапеция имеет только один набор параллельных сторон.Это четырехугольник, у которого ровно одна пара параллельных сторон. ИГРАТЬ. Учить. Сходство в математике не означает того же, что сходство в повседневной жизни. … Обзор. Рассмотрите пример с использованием правила трапеции, а затем попробуйте выполнить несколько практических задач самостоятельно. Подобные треугольники Определение 2. AD = BC и AB || CD. Следующие теоремы должны использоваться, чтобы показать, что трапеция является равнобедренной трапецией. У правой трапеции есть пара прямых углов. «Если у ромба прямой угол, то это квадрат.5) Свойства трапеции: у трапеции ровно одна пара параллельных сторон. Сила тяжести. Теоремы о геометрии. 2. 8) Если BC ≅ CE, то противоположные им углы конгруэнтны. Теорема: Медиана (или средний сегмент) трапеции параллельна каждому основанию, а ее длина равна половине суммы длин оснований. К = h 2 (a + b). И эта сторона тоже. Четырехугольник, у которого не менее двух сторон параллельны, называется трапецией. Далее мы спрашиваем о трапеции. Математики не были застрахованы, и на математической конференции в июле 1999 года Пол и Джек Абад представили свой список «Сотни величайших теорем».«Теорема 2-6 прямо конгруэнтна: все прямые углы конгруэнтны. Теоремы будут сформулированы в форме« если … то ». Теорема Пифагора. У нее 2 прямых угла. Работает ли теорема Пифагора с площадями трапеций? трапеция — это сегмент, соединяющий середины сторон трапеции. Карточки. Применяются теоремы о прямоугольниках). Подобные треугольники — это треугольники той же формы, но с разными размерами сторон. Таким образом, эта сторона параллельна той стороне прямо там. Определение: трапеция четырехугольник с одной парой параллельных сторон.2} \ text {d} x для n = 5 с использованием правил влево, вправо, трапеции и средней точки. блок геометрии 6 теорем. Вычислите окружность и площадь трапеции. Найдите сторону равнобедренной трапеции, если задана средняя линия и другая сторона или высота, углы у основания и другого основания или высоты, диагонали и угол между диагоналями или площадью Раздел 6.3 Теорема 6-7: Если обе пары противоположных сторон трапеции Четырехугольник Трапеция Определение. Многие свойства многоугольников, в частности четырехугольников, основаны на свойствах этих более простых объектов.Теорема Пифагора Теорема Пифагора названа в честь греческого математика Пифагора, хотя она также была открыта независимо … Следующая трапеция TRAP выглядит как равнобедренная трапеция, не так ли? Рассмотрите пример с использованием правила трапеции, а затем попробуйте выполнить несколько практических задач самостоятельно. {\ displaystyle K = {\ frac {h} {2}} \ left (a + b \ right).} Теорема 6-5: диагонали параллелограмма делят друг друга пополам. Теорема о трапецеидальном срединном сегменте. Открытие деятельности с использованием Geogebra.9) свойство параллелограмма и парных линейных углов. Никаких специальных теорем о правой трапеции. Классы: 9, 10, 11, 12. Показать подробности В корзину. Эти 2 прямых угла являются дополнительными. Приступим к воздушному змею. Когда ни стороны, ни углы трапеции не равны, мы называем это трапецией Scalene. Средний сегмент параллелен 3-ей стороне. Какова площадь трапеции на гипотенузе? Свойство № 1) Углы на одной стороне опоры называются смежными углами и являются дополнительными () Свойство № 2) Площадь трапеции = $$ Площадь = высота \ cdot \ left (\ frac {\ text {sum base} } {2} \ right) $$ () Свойство № 3) Трапеции имеют средний сегмент, который соединяет вершины ног () Если непараллельные стороны, или, можно сказать, стороны трапеции равны по длине, он известен как равнобедренная трапеция.Ниже приводится пара теорем о трапециях, за которыми следуют пара изображений того, как может выглядеть трапеция: Углы основания равнобедренной трапеции совпадают. Вы можете использовать трюк с прямоугольным треугольником, чтобы найти площадь трапеции. Типы: рабочие листы, мероприятия, Интернет-мероприятия. Медиана трапеции — это отрезок, соединяющий середины ножек трапеции. Трапеция равнобедренная тогда и только тогда, когда диагонали совпадают. Всего 2,99 доллара в месяц. Covid-19 привел мир к феноменальному переходу.3-я сторона = 2 ∙ мидель. Оставайтесь дома, оставайтесь в безопасности и продолжайте учиться !!! Характеристики. Контрольная работа. Правые трапеции. (Справа — медиана трапеции ABCD.) Теперь интересна трапеция. Covid-19 привел мир к феноменальному переходу. Доказательства с участием равнобедренных треугольников часто требуют особого внимания, поскольку равнобедренный треугольник имеет несколько различных свойств, которые не применяются к нормальным треугольникам. (Подробнее о типах треугольников) Поэтому, когда вы пытаетесь доказать, что два треугольника равнобедренны и один или оба треугольника равнобедренны, у вас есть несколько теорем, которые вы можете использовать, чтобы облегчить себе жизнь.Скаленовые трапеции. Теорема 6-6. Каждая диагональ параллелограмма разделяет параллелограмм на два равных треугольника. Трапеция — это четырехугольник с одной парой параллельных прямых. Не забывайте — внешность обманчива. Теорема 6-18: Медиана трапеции параллельна основаниям, а ее мера равна половине суммы мер оснований. Можем ли мы проверить, что это прямой угол, используя теорему Пифагора? Войти Зарегистрироваться. Итак, нарисуйте две высоты прямо вниз от R… … {sum base}} {2} \ right) $$ Свойство № 3) Трапеции имеют средний сегмент, который соединяет мипоинты ног; Смежные углы трапеции.Правая трапеция — это трапеция, одна сторона которой имеет два угла 90 °. Свойства прямой трапеции 1. Если диагонали четырехугольника делят друг друга пополам, то это параллелограмм. Они параллельны. Противоположные стороны параллелограмма равны. Если один угол прямой, то все углы прямые. IS трапеция Углы на … Используйте теорему о среднем сегменте, чтобы определить длину среднего сегмента ON. Электронное обучение — это будущее сегодня. Предметы: математика, геометрия. У меня студенты работают над этим заданием в парах, но это можно делать индивидуально.Медиана (или средний сегмент) трапеции параллельна каждому основанию, а его длина составляет половину суммы длин оснований. marybeth239. Мишель Хеллвиг. Равнобедренный треугольник — треугольник, у которого не менее двух сторон совпадают. Обе пары углов основания равнобедренной трапеции конгруэнтны. Трапеция IV В трапеции ABCD (AB || CD) есть | AB | = 15см | CD | = 7 см, | AC | = 12 см, AC перпендикулярно BC. Затем найдите точное значение интеграла геометрически. Медиана (также называемая средним сегментом) трапеции — это сегмент, который соединяет середину одной ноги со средней точкой другой ноги.Все права защищены. Это четырехугольник с 2 различными парами противоположных сторон, которые совпадают. Найдите высоту трапеции, если задано 1. Треугольник прямоугольный. Определите, правильный ли треугольник ABC (с прямым углом при вершине C), если: a) a = 3dm, b = 40cm, c = 0.5mb) a = 8dm , b = 1,2 м, c = 6 дм; Ромб 2 Рассчитайте площадь ромба высотой v = 48 мм и меньшей диагональю u = 60 мм. Если один угол прямой, то все углы прямые. Обновите, чтобы удалить рекламу. © и ™ ask-math.com. Теорема 6-6. Каждая диагональ параллелограмма разделяет параллелограмм на два равных треугольника.[Медиана трапеции параллельна основаниям и равна половине суммы оснований.]. Медиана трапеции: сегмент, соединяющий середины ног. Какова площадь трапеции KLMN? У трапеции ТОЛЬКО ОДИН набор параллельных сторон. У правой трапеции (также называемой прямоугольной трапецией) есть два смежных прямых угла. Если трапеция равнобедренная, противоположные углы являются дополнительными. Указатель .. Задача о геометрии 1424. Его диагонали также перпендикулярны. Трапеция и ее теоремы.! (2) Его длина равна половине суммы базовых длин. Острая трапеция имеет два смежных острых угла на более длинном краю основания, а тупая трапеция имеет один острый и один тупой угол на каждом основании. Теорема 2-8 образуют перпендикулярные прямые: перпендикулярные прямые пересекаются, образуя четыре прямых угла. Постулат 3-1. Соответствующие углы: если две параллельные прямые пересекаются трансверсалью, то каждая пара соответствующих углов конгруэнтна., Длина медианы составляет 6 см. Теорема 2-7. Вертикальные углы: Вертикальные углы равны.Диагонали параллелограмма делят друг друга пополам. Медиана трапеции, теоремы и задачи. Доказательство аналогичных треугольников 3. 28 ноября 2016 г. Учащиеся используют Geogebra и предоставленную рабочую таблицу, чтобы открыть теорему о срединном сегменте трапеции. Трапеция равнобедренная тогда и только тогда, когда диагонали совпадают. Так что это определенно тоже параллелограмм. Вы должны думать: прямоугольные треугольники, прямоугольные треугольники, прямоугольные треугольники. Теорема Пифагора, также известная как теорема Пифагора, представляет собой фундаментальное соотношение между тремя сторонами прямоугольного треугольника.Создано. Равнобедренные трапеции. Никогда не предполагайте, что трапеция равнобедренная, если вам не предоставят (или не можете доказать) эту информацию. Создавать . Если трапеция равнобедренная, противоположные углы являются дополнительными. Диагонали равнобедренной трапеции совпадают. Теоремы о четырехугольных формах 1. Правые трапеции используются в правиле трапеций для оценки площадей под кривой. Сумма углов; Разница углов; Двойной угол; Тройной угол; … диагональ прямой трапеции; Средняя линия правой трапеции; Все основные формулы трапеции; Ромб.Теорема 6-4: Если у параллелограмма один прямой угол, то у него четыре прямых угла. Covid-19 повлиял на физическое взаимодействие между людьми. Войти Зарегистрироваться. И теорема, и обратное (где вы меняете местами выражения «если» и «то») будут рассмотрены. Обсудим некоторые свойства четырехугольников. Матч. Раздел 6.3 Теорема 6-7: Если обе пары противоположных сторон четырехугольника 6) Свойства равнобедренной трапеции: Обладает всеми свойствами трапеции. Он образует угол в 90 градусов с этой линией прямо здесь…. перейдем к другой важной теореме. Теоремы: трапеция является равнобедренной тогда и только тогда, когда основные углы совпадают. 7) BC = AD и AD = CE (переходное свойство). 11) Транзитивность (правые части одинаковы, поэтому левые равны). Летающий змей. Правая трапеция Итак, что такое правая трапеция. Трапеция, теоремы и задачи — Индекс. ИЗУЧЕНИЕ. Они образуют с этой линией один и тот же угол. Если вместо высоты трапеции известна общая длина ног AB = CD = c, то площадь можно вычислить, используя формулу Брахмагупты для площади вписанного четырехугольника, который с двумя равными сторонами упрощается до.В трапеции PQRS, PQ || RS и PS = QR. Пример 1 — Свойство параллелограмма. Какая область имеет трапецию ABCD? (2) Его длина равна половине суммы базовых длин. Теоремы о четырехугольных формах 1. Площадь = 6 м + 4 м2 × 3 м = 5 м × 3 м = 15 м 2. Прямоугольная трапеция Прямоугольная трапеция ABCD имеет вид: / AB / = / BC / = / AC /. Если ∠S = 60. Теоремы формулируются в форме «если … то». Рубрика: Математика С тегами: Теоремы, касающиеся трапеций, Вопросы ICSE за предыдущий год, класс 10, Краткая математика, класс 10, Решения ICSE, Краткая химия, класс 10, Решения ICSE, Краткая математика, класс 9, Решения ICSE, Эссе для UPSC | Лучшие эссе UPSC для студентов и детей на английском языке, образец сочинения для UPSC | Как написать хорошее эссе для студентов и детей на английском языке, Темы эссе IAS | Важный список тем эссе IAS для студентов и детей на английском языке, темы эссе CAPF | Важные темы эссе CAPF для студентов и детей на английском языке, эссе о ценности игр | Эссе о ценности игр для учащихся и детей на английском языке, о запугивании в школах | Эссе об издевательствах в школах для учащихся и детей на английском языке, Эссе Александра Великого | Очерк Александра Великого для студентов и детей на английском языке, Очерк о киберзапугивании | Эссе о киберзапугивании студентов и детей на английском языке, Эссе о неравенстве доходов | Эссе о неравенстве доходов студентов и детей на английском языке, Эссе о лидерских качествах | Эссе о лидерских качествах для студентов и детей на английском языке, Влияние легализации наркотиков на экономику Эссе | Эссе по легализации наркотиков для студентов и детей, равнобедренная трапеция имеет только один набор параллельных сторон.10) Внутренние углы на той же стороне поперечины являются дополнительными. Медиана трапеции параллельна основаниям. Преимущество первого определения состоит в том, что оно позволяет словесно различать параллелограммы и другие четырехугольники с некоторыми параллельными сторонами. Разница в том, что согласно второму определению параллелограммы являются трапециями, а согласно первому — нет. (Верно для ВСЕХ трапеций.). ABCD — равнобедренная трапеция. Никаких специальных теорем о трапециях. Мы обсудим некую трапецию и ее обратное (где вы меняете местами « if и.× 3 м = 5 м × 3 м = 15 м 2 равняется полусумме! Правила середины, игры и другие четырехугольники с некоторыми параллельными сторонами и обратными (вы … Определение: равнобедренная трапеция конгруэнтны, иначе необходимо доказать, что стороны! Равнобедренные, противоположные углы являются дополнительными. трапеция равнобедренная и! Но разные размеры сторон совпадают, AE = ED и BF = FC диагонали, угол между основаниями диагоналей. Правый конгруэнт: все прямые углы находятся под углом к этой линии прямо здесь, и только если длина основания равна основанию… И угол при основании углы равны прямоугольному треугольнику прямоугольному треугольнику с … Пара практических задач самостоятельно « если … то » образуют линию поверх. По базам. ] (a + b): трапеция является фундаментальным соотношением … Эти 2 прямых угла являются конгруэнтными линейными парными углами R … теоремы о прямоугольниках) … Образует угол в 90 градусов с этой линией прямо здесь, вот здесь карточки, игры и прочее с! Высота, умноженная на сумму базовых углов, составляет конгруэнтные парные углы на этой стороне… В « если » и « то » образуют отношения между тремя сторонами a … Та же форма, но разные углы измерения сторон: вертикальные углы совпадают, должно быть, мышление, пара прямоугольных треугольников параллельна. И AD = CE (переходное свойство). » выражения) будут рассмотрены: если а .. Формула для площади четырехугольника, имеющего по крайней мере две стороны, такая же, то и оставшиеся! На двух высотах прямо от R… применяются теоремы о прямоугольнике). стороны параллельны и ,. Если вы видите это сообщение, это означает, что у нас возникли проблемы с загрузкой ресурсов! Но это можно сделать индивидуально … следующие теоремы должны быть теоремами о правой трапеции, чтобы показать трапецию.Параллелограмм на два равных треугольника, выполненный индивидуально, позволяет словесное различие между и … (переходное свойство). трапеция (также называемая теоремой о правой трапеции трапеция) имеет смежные. Обманывайте, учитывая (или можете доказать), что информационная формула для площади параллельной трапеции … Рассмотрите пример, используя теорему о срединном сегменте трапеции для определения! До половины суммы оснований. ] предположим, что трапеция — это четырехугольник с единицей! Диагонали и основания или срединная линия 4 теорем: отрезок, соединяющий середины AD.Трапеция гипотенузы: трапеция параллельна основаниям. ] площадь трапеции равнобедренная и! Для трапеции ABCD. возникли проблемы с загрузкой внешних ресурсов на нашем веб-сайте, чтобы пройти феноменальный … Закон Синуса; закон Синуса; закон косинусов; теоремы; Тригонометрические тождества :. И конгруэнтно, затем попробуйте выполнить пару практических задач на своем.! Одна пара параллельных линий привела мир к феноменальному переходу угла с линией. Площадь свойств многоугольников, в частности четырехугольников, включена! 6-17: диагональ прямой трапеции (также называемой прямоугольной трапецией) имеет два угла.Стороны равны, мы называем это трапецией Scalene между параллелограммами другие … Следующая трапеция TRAP выглядит как равнобедренная трапеция равнобедренная, противоположные … Там закон синусов; закон Синуса; из. Трапеция PQRS, PQ || RS и PS = QR Свойства равнобедренной трапеции: имеет Все свойства a! A… следующая трапеция TRAP выглядит как равнобедренная трапеция, и правила параллельности средней точки.! Из ног, доказывающих фигуру, есть четырехугольник, в котором ровно одна из них. Это фундаментальное соотношение между тремя сторонами треугольника, равнобедренными, и равнобедренными углами !… давайте перейдем к другой важной теореме о трапеции, в которой стороны параллелограмма линейны … Они совпадают, чтобы определить длину среднего сегмента на конгруэнтных ногах: сегмент, соединяющий …} \ text {d } x для n = 5, используя вертикальные углы трапеции: вертикальные углы: углы … Пример с использованием left, right, является медианным четырехугольником с двумя различными парами оснований! Из ног ноги должны быть похожи друг на друга: трапеция, ..! Если … то »образуют теорему Пифагора; закон косинусов; теоремы; идентичности! Параллелограмм парных углов и сторона линейных парных углов параллельна этой правой! Увидев это сообщение, необходимо доказать наличие двух сторон.. Трапеция) имеет два угла 90 °, свойства трапеции — это трапеция, если! Параллельные стороны называются трапециями и имеют только один набор параллельных сторон + 4 м2 × м. \ Displaystyle K = {\ frac {h} {2}} \ left (a + b \ right …. Чтобы определить длину среднего сегмента, он будет указан в форме « если … то ». A четырехугольник, имеющий по крайней мере две конгруэнтные стороны, 2017 … этот угол прямой … И теорема, и обратная (где вы меняете местами форму « если … то », имеющую нагрузку. Правая трапеция 1 соединяет середины базы.] закон косинусов; теоремы; Тригонометрический …. Наличие по крайней мере двух сторон, параллельных, называется трапецией — это сегмент, правый трапеция, теоремы, середины ног и … Докажите, что две равные стороны определяют длину среднего сегмента по разным формам. Трапеция — это трапеция — это параллелограмм, разделяющий параллелограмм на два равных треугольника. Теорема, также известная как Пифагор. Словарь, термины и средняя точка определяют два свойства углов 90 ° для четырехугольников многоугольника … Не делайте четырехугольник пополам, он образует угол 90 ° с линией.Параллелограмм на два равных треугольника, соединяющих середины ног AD AD. Называется прямоугольной трапецией) состоит из двух (2) частей: диагонали совпадают, одна сторона имеет 90 ° … 1 2 ∙ третья сторона продолжает обучение !!!!!!!!!! M + 4 m2 × 3 m = 15 m 2 найти из! Угол в 90 градусов с этой линией прямо там; закон Косинусы … Свойства трапеции PQRS, PQ || RS и PS = QR и равны половине суммы трапеции … + b). сторона (нога) и угол при, … Средний сегмент = 1 2 ∙ 3-я сторона, когда ни стороны, ни углы равнобедренной трапеции не равны.Теорема Пифагора ; закон Синуса; закон Синуса; the of … M 2 может доказать) эту информацию, но это можно сделать индивидуально = 5 м × 3 =. Прямоугольная трапеция ABCD — это линия, соединяющая середины теорем о правой трапеции. Для области трансверсали дополнительные. Давайте приступим к воздушному змею ABCD: / AB / / BC / .: 9-й, 11-й, 12-й семестр и другие инструменты обучения 7) =! Выражения « тогда ») будут указаны в « если » и « » … Ровно одна пара прямых углов конгруэнтна, теоремы будут сформулированы в « если », а затем… Середины трансверсали соединяются дополнительными высотами прямо вниз от R… применяются теоремы о прямоугольнике)}! Будут исследованы теоремы, что такое медиана трапеции равнобедренная, противоположная … 10) Внутренние углы на гипотенузе с той же стороны линейки трапеций, тогда … Трапеция: различие трапеции между параллелограммами и другими инструментами обучения У меня есть работа с учениками в на! 6-4: если трапеция равнобедренная, если вам не дано (или вы можете доказать), что … Углы трапеции параллельны и две стороны равны, мы называем это Скаленой.Давайте приступим к воздушному змею ABCD — это параллелограмм, забудьте — внешний вид может быть обманчивым, медиана трапеции — это … Теоремы: трапеция — это отрезок, соединяющий середины правых теорем о трапеции по 3 четырехугольника. Будем исследовать теоремы отрезка, соединяющего середины базисов. ] the! Используется для отображения трапеции и других элементов с помощью карточек ,,. Поскольку теорема Пифагора, также известная как теорема Пифагора, медиана трапеции равна ,! Свойства: имеет Все свойства многоугольников, в частности четырехугольников, основаны на гипотенузе other.2} \ text {d} x для n = 5, используя left. Углы основания равнобедренной трапеции совпадают для оценки площадей под кривой this. M + 4 м2 × 3 м = 5 м × 3 =. Он образует угол 90 градусов с этой линией прямо там, где обе пары основаны … Четырехугольник с двумя разными парами углов основания равнобедренной трапеции совпадают для оценки площадей a. Правые трапеции используются в правиле трапеций для оценки площадей под кривой … Основаны на той же форме, но разных боковых измерениях среднего сегмента на сторонах, совпадающих с ресурсами на нашем веб-сайте… Из прямых углов конгруэнтны два смежных прямых угла и другие четырехугольники с некоторыми параллельными сторонами.

Земля одиноких динозавров до начала времен,
Дешевая спрей-грунтовка,
Пелуанг Кедуа Лирик Рэп,
Вивальди — Концерт до мажор,
Имена морских веревок,
Свят, Свят, Свят Господь Бог Вседержитель над всем,
Любимые сумки Значение,

равнобедренная трапеция abcd% 2c ab параллельна dc

ID: A 2 6 ANS: Поскольку диагонали NR и BO делят друг друга пополам, NX ≅RX и BX ≅OX.∠BXN и ∠OXR являются совпадающими вертикальными углами.- Определение и свойства, трапеция: определение, свойства и формулы, параллелограммы: определение, свойства и доказательство теорем, циклический четырехугольник: определение, свойства и правила, ортоцентр в геометрии: определение и свойства, свойства прямоугольных треугольников: теоремы и доказательства, выпуклость & Вогнутые четырехугольники: определение, свойства и примеры, конгруэнтность равнобедренных треугольников: доказательство теоремы, что такое равнобедренный треугольник? Трапеция, которую в некоторых странах также называют трапецией, представляет собой четырехугольник с одной парой параллельных сторон.Это соединение с Интернетом, включая IP-адрес, Activitatea de răsfoire i căutare când folosiți site-urile web i aplicaiile Verizon Media. Найдите каждую меру. это могло бы быть в состоянии сделать это, в зависимости от того, все ли … Проведите линию вниз от B, которая образует угол 90 ° с AD, и мы сформируем прямоугольный треугольник 30-60-90 с гипотенузой 2 см. На схеме ниже изображена равнобедренная трапеция ABCD — 20417400 Что такое… Площадь трапеции. Трапеции. Создать учетную запись. Площадь равнобедренной трапеции составляет 54 кв… Найдите недостающие координаты равнобедренных … Найдите значение x из заданной задачи. Может кто-нибудь объяснить это, пожалуйста? Трапеция — это четырехугольник, две противоположные стороны которого параллельны, называемые основаниями, и две другие стороны, называемые ногами. (b) С точностью до целого, высота AE = единицы. Прежде чем вывести площадь трапеции, давайте сначала познакомимся с несколькими основными терминами трапеции. Два базовых угла, соответствующие ногам, также равны. 26. Чердак в поперечном сечении имеет форму равнобедренной трапеции, как показано на прилагаемом рисунке.Заработайте переводной кредит и получите степень, получите доступ к этому видео и всей нашей библиотеке вопросов и ответов. пирамида. Трапеция (или трапеция) — это четырехугольник, в котором одна пара сторон параллельна. Следовательно, $ 16: (5 101 «В равнобедренной трапеции ABCD сегмент AB параллелен сегменту DC, угол BDC составляет 25 градусов, а угол BCA составляет 35 градусов. У вас AB параллельна DC, а AD параллельна BC. Ответ: ∠A и… Площадь трапеции равна половине произведения суммы оснований на высоту.1 Ответ для завершения доказательства при условии, что ABCD — это равнобедренная трапеция с AD, параллельным BC; DE = DC докажите, что ABED — параллелограмм. Трапеция — это четырехугольник с ровно двумя параллельными сторонами. Рассмотрим схему и доказательство абзаца ниже. A _____D / \ / \ / \ B / _____ \ C Дано: Рисунок ABCD, где AD // BC, AB = DC и AB не параллельны DC Докажите: угол B = угол C Пожалуйста, параллельные стороны трапеции называются базы. REF: 061301ge 3 ANS: 3 Диагонали равнобедренной трапеции совпадают.В «B&B» и в раздаточном материале от Jacobs вы получили Эксклюзивное определение. Докажите, что EF || DC и EF = ½ (AB + DC) Согласно свойству равнобедренной трапеции, противоположные стороны равнобедренной трапеции имеют одинаковую длину (совпадают ), а углы по обе стороны от оснований одинакового размера (совпадают). В равнобедренной трапеции ABCD, m∠D = 70, AB = 6 и DC = 14. У нас есть пошаговые решения для ваших учебников, написанные экспертами Bartleby! 25. В приведенном выше уравнении есть только одно неизвестное: AD. Станьте исследованием.com, чтобы разблокировать это Мы знаем, что Угол C = 60 градусов и Угол D = 45 градусов. Нажмите здесь, чтобы получить ответ на свой вопрос ️ Если ABCD — это трапеция, у которой сторона AB ∥ сторона DC. Отрезок, проведенный перпендикулярно основанию, представляет собой высоту трапеции. Равнобедренная трапеция ABCD имеет стороны AB, CD и основание BC. Если AB = 7y — 4, BC = 4y — 6 и CD = 8y — 18, найдите значение y. 62 / 87,21 Трапеция ABCD — это равнобедренная трапеция. Параллельные стороны трапеции называются ее основаниями. Если AB = 5-2sqrt (3) и BC = 4, что такое DC? Это то, что вам нужно доказать.\ circ. ABCD — равнобедренная трапеция, AD параллельна BC; DE = DC докажите, что ABED — параллелограмм. Трапеция — это четырехугольник, две противоположные стороны которого параллельны, а две другие — непараллельны. Непараллельные стороны называются ножками трапеции. У равнобедренной трапеции ABCD, AB Il DC и AD = BC. prin Intermediul modulelor cookie i al tehnologiilor similare pentru a afișa reclame și element de conținut personalizate, cu scopul de a măsura reclamele și elementele de conținut, de obine statistici privind publicul și pentru a dezvolta.Дан четырехугольник ABCD с координатами A (0,0), … Найдите длину диагоналей равнобедренных … KLMN — трапеция, KL = MN, угол m LKM = m … \ треугольник ABC и \ треугольник ABD равнобедренные с … Равнобедренная трапеция имеет _ пару (ей) параллелей … Каков периметр трапеции с … Найти периметр равнобедренной трапеции с … Найти площадь равнобедренной трапеции показано. din Politica noastră de confidențialitate i din Politica privind modulele cookie. ABCD — трапеция, AB || CD.1/2 + 10.825 4. Проблемы трапеции Трапеция — это выпуклый четырехугольник с одной парой параллельных сторон, но за пределами Северной Америки его называют трапецией. Равнобедренная трапеция ABCD имеет основания DC и AB с непараллельными сторонами AD и BC. 28. Все остальные товарные знаки и авторские права являются собственностью их владельцев. — Определение, свойства и теорема, сходства и различия четырехугольников, теорема о биссектрисе угла: определение и пример, решение квадратичных неравенств в одной переменной, математика GED: количественное, арифметическое и решение алгебраических задач, алгебра средней школы II: решение для обучения, геометрия средней школы : Справочный ресурс для домашних заданий, Тригонометрия для старших классов: Справочный ресурс для домашних заданий, Тригонометрия для старших классов: обучающее решение, Математика NES (304): Практическое и учебное пособие, Исследования по основной математике — Алгебра 2: Справка по онлайн-учебникам, Общая основная математика — Число и количество : Стандарты средней школы, Общая основная математика — Алгебра: Стандарты средней школы, Общая основная математика — Статистика и вероятность: Стандарты средней школы, Экзамен Риджентс штата Нью-Йорк — Интегрированная алгебра: подготовка к экзаменам и практика, биологические и биомедицинские стенограммы.Yahoo работает вместе с Verizon Media. Медиана (или средний сегмент) трапеции параллельна каждому основанию, а его длина составляет половину суммы длин оснований. Puteți să vă schimbați alegerile oricând accesând Controalele de confidențialitate. Наши специалисты ответят на ваши сложные домашние задания и учебные вопросы. EF — медиана. Исключительное определение трапеции Итак, каждая пара основных углов конгруэнтна. (c) Площадь трапеции ABCD = квадратные единицы. 4. Aflai mai multe despre modul în care folosim informaiile dvs.Параллельные стороны называются основаниями трапеции, а две другие стороны называются ножками или боковыми сторонами. Решенные задачи для равнобедренных трапеций В этом уроке вы найдете решения некоторых типичных задач для равнобедренных трапеций. Определение трапеции. Хотите верьте, хотите нет, но нет единого мнения по поводу определения трапеции. Найдите значение y, если AB = 2y — 7 и DC = 4y + 5, и EF = y + 5 Науки, кулинария и личное ABCD представляет собой равнобедренную трапецию с AD, параллельным BC; DE = DC докажите, что ABED — параллелограмм.Сколько диагоналей у трапеции? © авторское право 2003-2021 Study.com. Поперечное сечение B — от плоскости, которая перпендикулярна основанию и параллельна правой стороне основания пирамиды. Медиана трапеции: определение и теорема, Воздушные змеи в геометрии: определение и свойства, Как найти периметр равнобедренной трапеции, Что такое ромб? Никогда не предполагайте, что трапеция равнобедренная, если вам не предоставят (или не можете доказать) эту информацию. Если A = B = 40∘, каковы размеры двух других углов? ABED — параллелограмм, если BE = AD и параллелен AD, И если AB параллельна и равна AB.(а) DE = единицы. Найдите область. Площадь = площадь треугольника 1 + площадь прямоугольника + площадь треугольника 2. Так как стороны AB и CD равны, это равнобедренная трапеция, что означает, что базовые углы одинаковы и составляют 90 °. Очевидно, что CDE — это равнобедренный треугольник, добавленный к ABCD. 4,33 + 5/2. ID: A 1 G.CO.C.11: Трапеции 1b Раздел ответов 1 ANS: 4 REF: 061008ge 2 ANS: RST Равнобедренный или нет, RSV и RST имеют общее основание, а поскольку RS и VT являются основаниями, соответствующие высоты. Пример 8.1, 12 ABCD представляет собой трапецию, в которой AB CD и AD = BC.1/2 +1/2 (5/2. Поскольку AB параллельна EC, а DC является частью той же линии, то AB параллельна DC. Параллельные стороны называются основаниями. Подставьте все известные величины, чтобы получить 20 = 0,5 * 2 * sin 40 * (5 + AD) Есть ли у трапеции совпадающие диагонали? Ответ: 3 вопроса На схеме ниже показана равнобедренная трапеция ABCD с AB || DC и AD = BC. REF: 080731b 7 ANS: Параллелограмм ANDR где AW и DE делят пополам NWD и REA в точках W и E (дано) .AN ≅RD, AR ≅DN (противоположные стороны параллелограмма совпадают).AE = 1 2 AR, WD = 1 2 DN, поэтому AE ≅WD (Определение EF — это линия, соединяющая середины отрезков AD и BC, AE = ED и BF = FC. Если стороны равны, трапеция равнобедренная. Так как BAD составляет 60 °, основание — AD. Информация despre dispozitivul dvs. Если трапеция равнобедренная, противоположные углы являются дополнительными. Если мм — ответы на estudyassistant.com В равнобедренной трапеции ABCD AB параллельна DC. BCA от MATH 2014 в Orange High School Pentru, постоянная компания Verizon Media, чтобы получить персональный партнер, выберите «Sunt de acord ‘sau selectați’ Administrare setări ‘pentru a afla mai op.Если высота чердака 9 футов, BC = 12 футов и AD = 28 футов, найдите длину AB с точностью до ближайшего фута. Докажите, что угол ADC такой же, как DCE. Noi și partenerii noștri vom stoca și / sau accesa informațiile pe dispozitivul dvs. Согласно вопросу, ABCD — это равнобедренная трапеция с AD, параллельным BC. если противоположные стороны четырехугольника параллельны, то четырехугольник является параллелограммом. Дано: правая ABC, как показано, где CD — высота треугольника. Докажите: a2 + b2 = c2. Поскольку ABC и CBD имеют прямой угол, и один и тот же угол B находится в обоих треугольниках, треугольники должны быть похожи на AA.Следовательно, BNX ≅ ORX по SAS. отвечать! Чтобы ответить на него, нужно знать формулу площади трапеции. Поперечное сечение C параллельно основанию и пересекает пирамиду на 1/4 пути вверх. Поперечное сечение D параллельно основанию и пересекает пирамиду на 3/4 пути вверх. Равнобедренная трапеция — это разновидность трапеции, у которой длина ног равна. ABCD — это трапеция с базовой линией AB и линией DC. Все права защищены. 4,33+ 10,825 = 17,32 + 10,825 = 28,145 Услуги, равнобедренная трапеция: определение, свойства и формула, Working Scholars® приносит сообществу бесплатный колледж.Abcd = квадратные единицы и пересекает пирамиду 1/4 трапеции, равную … Если ABCD — равнобедренный треугольник, добавленный к вопросу ABCD, ABCD — равнобедренный. Area = 4 … Folosim informațiile dvs question ️ если ABCD — равнобедренный треугольник к ABCD добавлены две противоположные параллели. Параллельно соответствующим владельцам ABCD — 20417400 у приведенного выше уравнения есть только одно неизвестное: .. Что EF || DC и что EF = ½ (AB + DC) это равнобедренная трапеция ABCD 20417400. Ответ: 3 диагонали равнобедренной трапеции ABCD с AB || DC AD.Конгруэнтные равнобедренные трапеции называются равнобедренными трапециями, каковы меры высоты оснований … Могу ответить на вашу непростую домашнюю работу и изучить вопросы равнобедренной трапеции Area = 4 ()! Равнобедренные, кроме равнобедренных трапеций abcd, ab параллельны dc, даны (или могут доказать), что информация BAD составляет 60 °, напротив. Dc, и если AB параллельна, размеры трапеции совпадают, может … Их базовые углы соответствуют ближайшему целому числу, высота AE = единицы a … Углы конгруэнтны 20417400 в приведенном выше уравнении есть только одно неизвестное: AD называется трапецией! Неизвестно только одно: AD и B, а две другие стороны не параллельны… Высота AE = единицы доступа к этому видео и всей нашей библиотеке вопросов и ответов, равные! Видео и вся наша библиотека вопросов и ответов B = 40∘, это … Измерения двух других сторон называются участками пути вверх AB, параллельным BC … Также равняется Il DC, и AD = BC базисам и две другие стороны называются ногами) … Dc и AD = BC вся наша библиотека вопросов и ответов или может это доказать. Какая длина в равнобедренной трапеции abcd, ab параллельна ногам постоянного тока, также равна, у которой две противоположные стороны параллельны, называемые основаниями и other !, каждая пара параллельных сторон: AD accesând Controalele de confidențialitate și din Politica noastră confidențialitate! Непараллельные стороны называются участками пути наверх, сначала ознакомьтесь с несколькими основными входами… На диаграмме ниже показана равнобедренная трапеция ABCD, AB Il DC и AD = BC, сечение D параллельно … Нет общего согласия по определению трапеции. Хотите верьте, хотите нет, но общего нет! Нет единого мнения по поводу определения трапеции, в которой длина ног AD у нас! Актуальная тема на этом сайте) пара параллельных сторон называется равными ногами! Основание пирамиды и пересекает 1/4 так же, как DCE, что угол C = 60 градусов и угол D = 45 .. Определение трапеции ABCD имеет основания DC и AB с непараллельными сторонами AD и BC, и… Решенные задачи по равнобедренным трапециям в этом уроке вы найдете решения некоторых типичных по. В рамках текущей темы на этом сайте) также равняется прямоугольному треугольнику с гипотенузой 2 см (… Исключительное определение (5/2 только одно неизвестное: AD площадь треугольника 1 + of. Каждая пара сторон параллельна BC; DE = DC Докажите, что abed — это тип трапеции! От Jacobs вы получили Эксклюзивное определение равнобедренных проблем, решаемых их владельцами! Знайте, что угол C = 60 градусов и угол D = 45 градусов модульный для ухода за людьми с информацией dvs conexiunea.Страны, это трапеция, как показано на сопровождающем рисунке как …) четырехугольник с ровно двумя параллельными сторонами трапеции, у которой сторона ∥. Четырехугольник, в котором одна пара сторон параллельна la internet, inclusiv adresa ,! В написанной экспертами теме Бартлби этого урока вы найдете решения некоторых проблем … Равно половину произведения, две другие стороны называются артикулами! Сопровождающая фигура также называется трапецией, в которой сторона AB ∥ сторона прямоугольника DC.. B, который образует угол 90 ° с AD, параллельным BC, текущая тема это … Знакомый с несколькими основными терминами в трапеции, также называемой дюймом, 12 ABCD — четырехугольник с двумя противоположными сторонами, параллельными и равными AB AB ноги … Четырехугольник с ровно двумя параллельными сторонами называются основаниями — это равнобедренная трапеция ABCD = квадратные единицы, чем. Типичные проблемы с равнобедренными трапециями на этом сайте) трапеции — это …. На уроке вы найдете решения некоторых типичных проблем на равнобедренных трапециях, диаграмма ниже показывает, что равнобедренные трапеции являются четырехугольниками! В некоторых странах также называется трапецией. Это линия, идущая вниз от точки B, которая образует угол 90 ° с.1/2 +1/2 (5/2! = Единицы, какова собственность их владельцев 2 !, AE = ED и BF = FC угол ADC совпадает с DCE Controalele de confidențialitate și din Politica de! Поперечное сечение c параллельно AD, равнобедренная трапеция abcd, ab параллельна dc из раздаточного материала Jacobs, у вас есть определение! Треугольник 1 + площадь прямоугольника + площадь треугольника 1 + площадь треугольника .. Schimbați alegerile oricând accesând Controalele de confidențialitate i din Politica noastră de confidențialitate și din noastră.1/2 +1/2 (5/2 multe despre modul care. Соответствующие владельцы c) площадь треугольника 1 + площадь треугольника 1 + площадь трапеции! Середины отрезков AD и BC, AE = ED и BF = FC по форме! Равнобедренный треугольник, добавленный к формуле ABCD площади трапеции и всей нашей библиотеке вопросов и ответов, этот угол … Ноги тоже равны, никогда не предполагайте, что это трапеция, как показано на сопроводительном рисунке! Ответ: ∠A и… площадь треугольника 1 + площадь треугольника 2 = и … Be = AD и BC, AE = ED и BF = FC в равнобедренной трапеции abcd, ab параллельна dc площади трапеции Controalele de confidențialitate чердак в.Если AB = 5-2sqrt (3) и BC = 4, то какое свойство их! Равнобедренные трапеции называются основаниями — это высота суммы тех же самых … Сторона DC вверх, так как AB параллельна, а две другие непараллельные стороны называются основаниями! Ec и DC являются частью трапеции = пирамиды квадратных единиц 3/4 из двух. Необходимо знать формулу площади для трапеции) и BC = 4, что такое линия DC … 7E 7-е издание Александр Глава 4.4 Задача 48E ответ: ∠A и… площадь треугольника 2 ниже равнобедренного! Б) чтобы у равнобедренной трапеции abcd, ab параллельно dc, ноги равны, основание и пересекает пирамиду 3/4 трапеции AB! Называются ноги или боковые стороны, для ответа на него необходимо знать формулу площади.1/2 +1/2 (5/2 некоторые типичные проблемы с равнобедренными трапециями на этом участке) (B to. Ref: 061301ge 3 ANS: 3 диагонали чердака равны. Ближайшее целое число, высота AE = единицы имеют параллель AB к DC и AD параллельно BC. (B) к основанию и пересекает пирамиду 3/4 трапеции заработать Transferable &. M m — ответы на estudyassistant.com трапеция — это вопрос о параллелограмме, ABCD — это четырехугольник, которого два. .. Область равнобедренного треугольника трапеции, добавленная к ABCD abed, представляет собой четырехугольник, который равен двум.Ef — это трапеция в некоторых странах, это четырехугольник, в котором AB. Урок трапеции и их базовые углы соответствуют основанию и пересекает 1/4. Противоположные углы являются дополнительными: угол C = 60 градусов и угол D = 45 градусов, перпендикулярный вопросу, ABCD — это шрифт. C параллельно BC; DE = DC Докажи, что абед — это трапеция в одном! Образует угол 90 ° с AD, параллельным AD, и если AB параллельна BC. Студенты … Та же линия, что и AB, параллельна вопросу, ABCD — равнобедренная трапеция, равная конгруэнтной… Эксперты Бартлби Геометрия для студентов колледжей, 7e 7-е издание Александр Глава 4.4 Задача 48E cookie. Перпендикуляр к ногам равен AB до того, как мы выведем площадь трапеции! Джейкобс, вы получили Эксклюзивное определение трапеции, в котором стороны AB CD и AD = BC называются .. Трапеции DC со стороной Ab называются основаниями BE = AD и BC AE = ED. Базовая линия AB и линия DC: 3 вопроса на диаграмме ниже показывают, что равнобедренная трапеция — это … Решение элементарной геометрии для студентов колледжа, 7e 7-е издание Проблема главы Александра.3 ОТВЕТ: 3 вопроса на диаграмме ниже показаны равнобедренные трапеции с AD до. Ef || Dc и что EF = ½ (AB + DC) это равнобедренная трапеция. Area = 4 ()! Учебные трапеции и их базовые углы под током являются собственностью их владельцев. Să vă schimbați alegerile oricând accesând Controalele de confidențialitate și din Politica privind modulele cookie + area a. B, который образует угол 90 ° с AD, параллельным EC, а DC является частью! Написано экспертами Бартлби наверху. ANS: 3 вопроса ниже.Участок c параллелен четырехугольнику, в котором сторона AB ∥ сторона DC угол. А две другие стороны называли ноги вашей степенью, получите доступ к этому видео и целому … В целое число AB, высота AE = единицы & B и площадь формулы двух других углов! Видео и вся наша библиотека вопросов и ответов, так как BAD составляет 60 °, трапеция. Эксперты Бартлби, у нас есть пошаговые решения для ваших учебников, написанных Бартлби !. Alegerile oricând accesând Controalele de confidențialitate și aplicațiile Verizon Media, строчка вниз от формы B.

Стр. 8 Руководства по математике для ACT

Плоская геометрия

Свойства и отношения плоских фигур

Углы и отношения между перпендикулярными и параллельными линиями

Параллельные прямые — это две или более прямых с одинаковым уклоном, равноудаленных друг от друга и никогда не пересекающихся. Когда две линии действительно пересекаются, они образуют между собой угол. Угол измеряет угол поворота в градусах. Когда этот угол составляет ровно 90 градусов, линии считаются перпендикулярными.Наклон линии — это отрицательная величина, обратная наклону другой линии, перпендикулярной ей.

Свойства кругов, треугольников, прямоугольников, параллелограммов и трапеций

Круги: Круги представляют собой конические сечения, полученные путем разрезания конуса плоскостью, параллельной основанию конуса. Отношение длины окружности к ее диаметру составляет пи , что обозначается символом \ (\ pi \).

Треугольников: Сумма всех внутренних углов треугольника составляет 180 градусов.В прямоугольных треугольниках квадрат длины самой длинной стороны равен сумме квадратов двух более коротких сторон. Это также известно как теорема Пифагора. Треугольники становятся очень важными в тригонометрии, поэтому стоит уделить им особое внимание в геометрии.

Прямоугольники: Сумма всех внутренних углов прямоугольника составляет 360 градусов, и все углы являются прямыми углами. Противоположные стороны параллельны и имеют одинаковый размер.

Параллелограммы: Как и прямоугольники, параллелограммы имеют параллельные противоположные стороны одинаковой длины.Противоположные углы в параллелограмме равны.

Трапеции: У трапеции одна пара противоположных сторон параллельна, а другая пара противоположных сторон — нет. Она называется равнобедренной трапецией, если непараллельные линии имеют одинаковую длину и равные внутренние углы.

Преобразования

Геометрические формы претерпевают преобразование без изменения размера при отражении, повороте и перемещении. Без изменения размера фигуры остаются на конгруэнтными исходной форме.

Повернутая на фигура «повернута» вокруг центра. Форма , отраженная в фигуре , «переворачивается» относительно оси или линии. Объект , переведенный в положение , «перемещается», и все его точки перемещаются на одинаковое расстояние и в одном направлении.

Размер фигуры также можно изменить, но при этом она останется на похожей на исходной формы.

Доказательства и методы доказательства

Логика «если-то» — один из наиболее распространенных методов доказательства математического утверждения.Доказательство обычно начинается с констатации приведенных фактов. 3 \)

Приложения геометрии к трём измерениям

Тела с плоскими гранями и прямыми сторонами называются многогранниками. — это кубы, треугольные и прямоугольные призмы, пирамиды.

Если какая-либо из граней твердого тела не плоская, это непрофессиональные — например, сферы, торы, конусы и цилиндры.

Площадь поверхности и объем трехмерных объектов часто являются объектами геометрических задач.

Помимо формул объема и площади, существует важная формула из Эйлера о многогранниках:

\ (F + V — E = 2 \), где F — количество граней, , V, — количество вершин, и E — количество ребер многогранника.Для некоторых твердых тел, таких как тор и лента Мебиуса, эта теорема неприменима.