Содержание
Формулировка теоремы Фалеса по геометрии 8 класса: обобщенная, обратная
В данной публикации мы рассмотрим одну из основных теорем по геометрии 8 класса – теорему Фалеса, которая получила такое название в честь греческого математика и философа Фалеса Милетского. Также разберем пример решения задачи для закрепления изложенного материала.
Формулировка теоремы
Если на одной из двух прямых отмерить равные отрезки и через их концы провести параллельные прямые, то пересекая вторую прямую они отсекут на ней равные между собой отрезки.
- A1A2 = A2A3 …
- B1B2 = B2B3 …
Примечание: Взаимное пересечение секущих не играет роли, т.е. теорема верна и для пересекающихся прямых, и для параллельных. Расположение отрезков на секущих, также, не важно.
Обобщенная формулировка
Теорема Фалеса является частным случаем теоремы о пропорциональных отрезках*: параллельные прямые отсекают на секущих пропорциональные отрезки.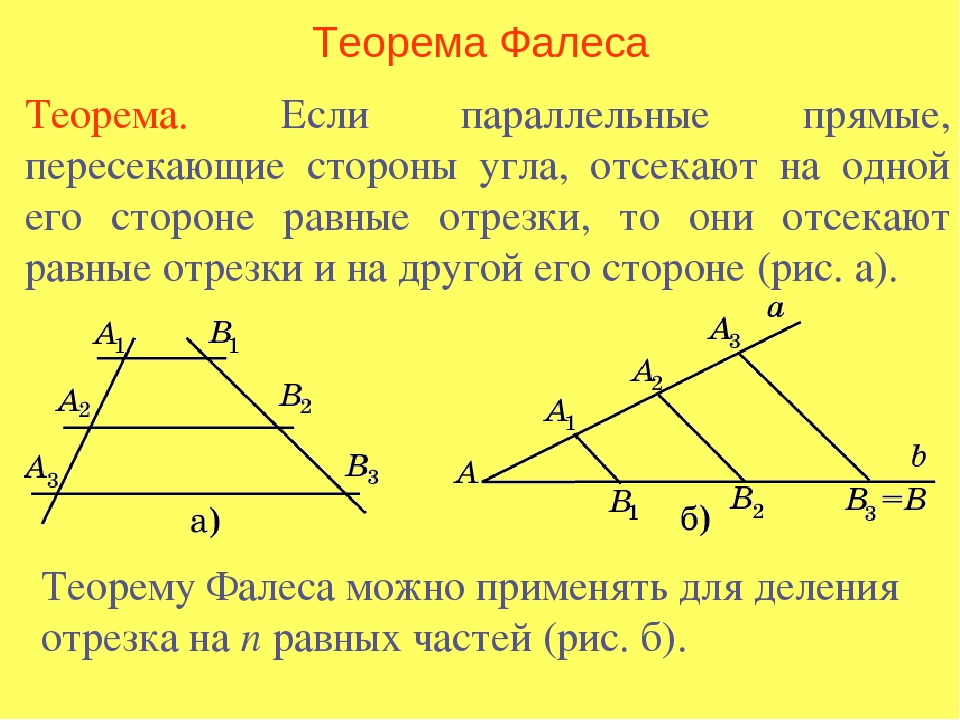
В соответствии с этим для нашего чертежа выше справедливо следующее равенство:
* т.к. равные отрезки, в т.ч., являются пропорциональными с коэффициентом пропорциональности, равным единице.
Обратная теорема Фалеса
1. Для пересекающихся секущих
Если прямые пересекают две другие прямые (параллельные или нет) и отсекают на них равные или пропорциональные отрезки, начиная от вершины, значит эти прямые являются параллельными.
Из обратной теоремы следует:
Обязательное условие: равные отрезки должны начинаться от вершины.
2. Для параллельных секущих
Отрезки на обеих секущих должны быть равны между собой. Только в этом случае теорема применима.
- a || b
- A1A2 = B1B2 = A2A3 = B2B3 …
Пример задачи
Дан отрезок AB на плоскости. Разделите его на 3 равные части.
Разделите его на 3 равные части.
Решение
Проведем из точки A прямую a и отметим на ней три подряд идущих равных отрезка: AC, CD и DE.
Крайнюю точку E на прямой a соединяем с точкой B на отрезке. После этого через оставшиеся точки C и D параллельно BE проведем две прямые, пересекающие отрезок AB.
Образованные таким образом точки пересечения на отрезке AB делят его на три части, равные между собой (согласно теореме Фалеса).
Теорема Фалеса
Одна из основополагающих теорем (теорема Фалеса) в геометрии говорит о том, что проведенные через концы одинаковых отрезков прямой параллельные линии отсекают на другой прямой тоже одинаковые по длине отрезки. Причем происходит это независимо от угла между прямыми. Это достаточно произвольная формулировка теоремы Фалеса, но достаточно емко описывающая ее суть. Разные учебники приводят разные формулировки, но суть остается неизменной.
Разные учебники приводят разные формулировки, но суть остается неизменной.
Ключевые слова в теореме (при любой формулировке) — прямые, отрезки, равные, пропорциональные, параллельные. Это говорит о том, что теорема Фалеса касается только планиметрии, то есть изображения линий на плоскости. Она очень важна для картографии и навигации, широко используется в архитектуре и живописи, строительстве и проектировании.
Классической формулировки, единой в своем роде нет. Например, формулировку можно услышать в такой редакции:
Если на одной из двух прямых отложить последовательно несколько отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой пропорциональные отрезки.
А можно и в такой:
Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.
Рис 2.
Если внимательно присмотреться, то можно увидеть, что одно утверждение не противоречит другому, а рисунки практически идентичны. Если продолжить прямые на первом рисунке по получим тот же угол.
Кроме прямых, которые проходят под углом, такая же картина происходит при пересечении параллельных прямых. Разница состоит в том, что на пересекающихся прямых отрезки АВ и А1В1 могут быть как одинаковыми, так и пропорциональными, в зависимости от угла наклона секущих. А для случая параллельных — только одинаковыми. Если обобщить два случая, то обобщенная теорема Фалеса звучит так: Параллельные прямые отсекают на секущих пропорциональные отрезки.
A1A2/B1B2=A2A3/B2B3=A1A3/B1B3
Для иллюстрации можно воспользоваться рисунком 1.
Теорема Фалеса это не только теоретическое утверждение, доказанное методами математики, но и практический инструмент для построения различных фигур. Простейшая задача — разделить на равные части произвольный отрезок ВА. Пусть этих частей будет 7.
Простейшая задача — разделить на равные части произвольный отрезок ВА. Пусть этих частей будет 7.
Для решения задачи нарисуем отрезок ВС, образующий с данным ВА угол. Как видим, отрезок ВС проходит вдоль клеток на бумаге, что позволяет выбрать на нем равные отрезки. В нашем случае, это:
BD=DE=EF=FG=GH=HJ=JC.
Начиная от крайних точек А и С проведем параллельные линии, пересекающие отрезок ВА. На нем тоже получиться семь равных отрезков: BR=RP=PN=NM=ML=LK=KA.
С таким же успехом мы можем разделить отрезок на 5, 6, 4 или любое другое количество равных частей. Суть метода состоит в том, что длину отрезка ВС мы заведомо выбираем такой, чтобы его можно было легко разделить на заданное количество частей. Например, длина отрезка ВА 37 см, а его нужно разделить на 5 частей. Выбираем длину отрезка ВС в 25 см, отмечаем точки и выполняем построение по теореме Фалеса.
Не менее широко используется и теорема, названная обратной. То есть, доказательства требует не равность или пропорциональность отрезков, а параллельность прямых. Формулируется обратная теорема Фалеса так:
То есть, доказательства требует не равность или пропорциональность отрезков, а параллельность прямых. Формулируется обратная теорема Фалеса так:
Если две или более прямых (a, b, c) отсекают от двух других прямых (d, f) равные или пропорциональные отрезки, то они параллельные.
Утверждение справедливо, независимо от того, параллельные d, f или пересекаются.
Математика, тем более, геометрия, наука точная. Каждое утверждение, кроме аксиом, требует доказательства. В геометрии под термином «теорема» подразумевается утверждение, которое доказано на базе ранее полученных знаний в виде аксиом и других теорем.
Теорема Фалеса с доказательством приведена в большинстве учебников. В отличие от теоремы Пифагора, доказательств у нее меньше, но все они четкие, понятные и аргументированные. Покажем одно из них.
Не будем повторять формулировок, продемонстрируем только ход мыслей и выполним необходимые построения:
Выберем точку В2 и проведем прямую, параллельную стороне угла ОС. При этом отмечаем, что А1А3 || EF. Рассматривая четырехугольник
При этом отмечаем, что А1А3 || EF. Рассматривая четырехугольник
А1FЕА3 замечаем, что А1F и ЕА3 параллельны по определению, а А1А3 и FВ3 параллельны по построению. Отсюда вытекает, что А1 FЕА 3 — параллелограм и А1А3 = EF.
Аналогичным образом доказываем равенство других сторон и получаем, что по равенству вертикальных и внутренних углов ∠B1B2F=∠B3B2E и ∠B2FB1=∠B2EB3 треугольники B2B1F и B2B3E равны, откуда вытекает, что B1B2=B2B3.
Именно это и требовалось доказать.
По легенде, впервые на практике использовал теорему греческий философ Фалес Милетский. Он применил ее для измерения высоты пирамиды Хеопса, пользуясь падающей на песок тенью. Для сравнения длины отрезков использовалась воткнутая рядом палка.
Для сравнения длины отрезков использовалась воткнутая рядом палка.
Но доказательство теоремы, самое давнее из известных, зафиксированных в письменных источниках, дано в книге «Элементы» другого философа и математика — Эвклида. Тем не менее, утверждение получило имя Фалеса, под которым известно до сих пор.
Теорема Фалеса. Средняя линия треугольника [wiki.eduVdom.com]
Теорема 1. Теорема Фалеса1). Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.
Доказательство. Пусть А1, А2, А3 — точки пересечения параллельных прямых с одной из сторон угла и А2 лежит между А1 и А3 (рис.1).
Рис.1
Пусть B1 В2, В3 — соответствующие точки пересечения этих прямых с другой стороной угла. Докажем, что если А1А2 = A2A3, то В1В2 = В2В3.
Докажем, что если А1А2 = A2A3, то В1В2 = В2В3.
Проведем через точку В2 прямую EF, параллельную прямой А1А3. По свойству параллелограмма А1А2 = FB2 , A2A3 = B2E .
И так как А1А2 = A2A3, то FB2 = В2Е.
Треугольники B2B1F и В2В3Е равны по второму признаку. У них B2F = В2Е по доказанному. Углы при вершине В2 равны как вертикальные, а углы B2FB1 и B2EB3 равны как внутренние накрест лежащие при параллельных А1В1 и A3B3 и секущей EF. Из равенства треугольников следует равенство сторон: В1В2 = В2В3 . Теорема доказана.
С использованием теоремы Фалеса устанавливается следующая теорема.
Теорема 2. Средняя линия треугольника параллельна третьей стороне и равна ее половине.
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. На рисунке 2 отрезок ED — средняя линия треугольника ABC.
ED — средняя линия треугольника ABC
Рис.2
Пример 1. Разделить данный отрезок на четыре равные части.
Решение. Пусть АВ — данный отрезок (рис.3), который надо разделить на 4 равные части.
Деление отрезка на четыре равные части
Рис.3
Для этого через точку А проведем произвольную полупрямую а и отложим на ней последовательно четыре равных между собой отрезка AC, CD, DE, ЕК.
Соединим точки В и К отрезком.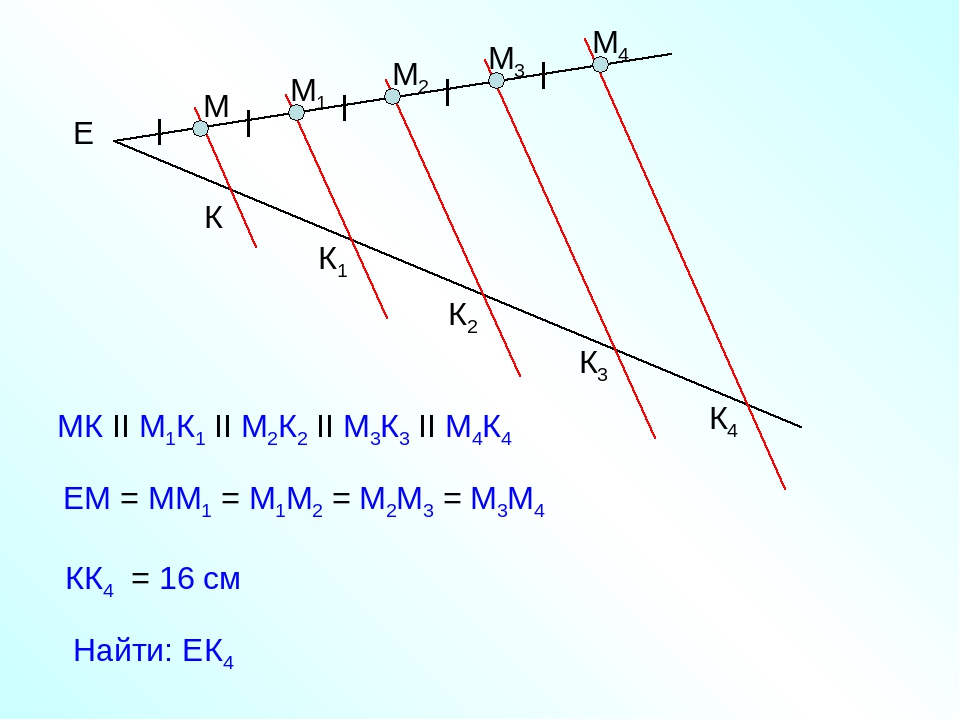 Проведем через оставшиеся точки С, D, Е прямые, параллельные прямой ВК, так, чтобы они пересекли отрезок АВ.
Проведем через оставшиеся точки С, D, Е прямые, параллельные прямой ВК, так, чтобы они пересекли отрезок АВ.
Согласно теореме Фалеса отрезок АВ разделится на четыре равные части.
Пример 2. Диагональ прямоугольника равна а. Чему равен периметр четырехугольника, вершины которого являются серединами сторон прямоугольника?
Решение. Пусть условию задачи отвечает рисунок 4.
Рис.4
Тогда EF — средняя линия треугольника ABC и, значит, по теореме 2.
$$ EF = \frac{1}{2}AC = \frac{a}{2} $$
Аналогично $$
HG = \frac{1}{2}AC = \frac{a}{2} , EH = \frac{1}{2}BD = \frac{a}{2} , FG = \frac{1}{2}BD = \frac{a}{2}
$$ и, следовательно, периметр четырехугольника EFGH равен 2a.
Пример 3. Стороны треугольника равны 2 см, 3 см и 4 см, а вершины его — середины сторон другого треугольника. Найти периметр большого треугольника.
Решение. Пусть условию задачи отвечает рисунок 5.
Рис.5
Отрезки АВ, ВС, АС — средние линии треугольника DEF. Следовательно, согласно теореме 2 $$
AB = \frac{1}{2}EF\ \ ,\ \ BC = \frac{1}{2}DE\ \ ,\ \ AC = \frac{1}{2}DF
$$ или $$
2 = \frac{1}{2}EF\ \ ,\ \ 3 = \frac{1}{2}DE\ \ ,\ \ 4 = \frac{1}{2}DF
$$ откуда $$
EF = 4\ \ ,\ \ DE = 6\ \ ,\ \ DF = 8
$$ и, значит, периметр треугольника DEF равен 18 см.
Пример 4. В прямоугольном треугольнике через середину его гипотенузы проведены прямые, параллельные его катетам. Найти периметр образовавшегося прямоугольника, если катеты треугольника равны 10 см и 8 см.
Решение. В треугольнике ABC (рис.6)
Рис.6
∠ А прямой, АВ = 10 см, АС = 8 см, KD и MD — средние линии
треугольника ABC, откуда $$
KD = \frac{1}{2}AC = 4 см.
\\
MD = \frac{1}{2}AB = 5 см.
$$ Периметр прямоугольника К DMА равен 18 см.
Математика. Основы геометрии: Теорема Фалеса. Разбиение отрезка на заданное число равных частей
Главная >
Образование >
Математика >
МАТЕМАТИКА «С НУЛЯ» (учебник) >
<< Назад | Оглавление | Далее >>
Теорема Фалеса
Пусть две произвольные прямые x и y пересекаются тремя параллельными прямыми n1, n2 и n3 в точках X1, X2, X3 и Y1, Y2, Y3, как показано на рисунке:
Пусть, далее, про точки X1, X2 и X3, расположенные на прямой x, известно, что они следуют друг за другом через равные расстояния, так что |X1X2| = |X2X3|.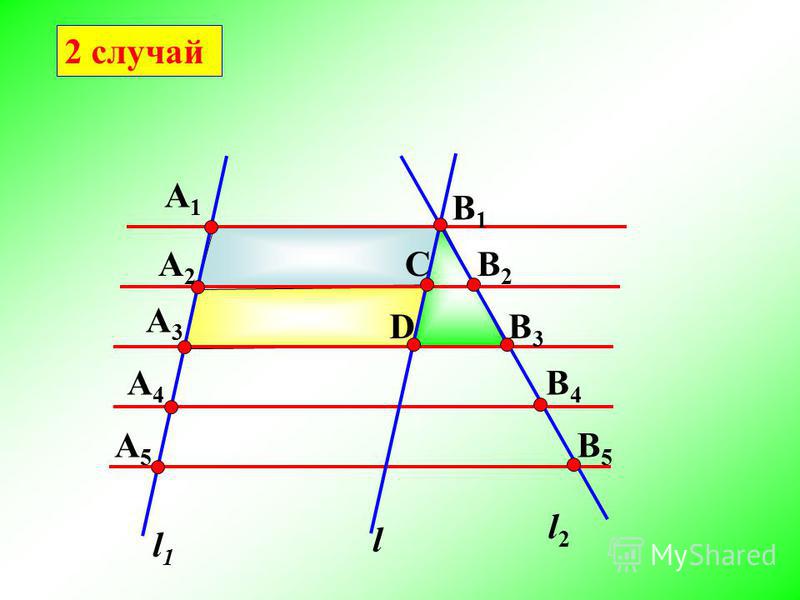 Мы собираемся теперь доказать, что точки Y1, Y2 и Y3, расположенные на прямой y, также следуют друг за другом через равные расстояния: |Y1Y2| = |Y2Y3|. Это утверждение известно как теорема Фалеса. (Под теоремами математики понимают важные утверждения, которые можно доказать на основании ранее установленных фактов. Некоторые из теорем называются именами выдающихся математиков — как в данном случае.)
Мы собираемся теперь доказать, что точки Y1, Y2 и Y3, расположенные на прямой y, также следуют друг за другом через равные расстояния: |Y1Y2| = |Y2Y3|. Это утверждение известно как теорема Фалеса. (Под теоремами математики понимают важные утверждения, которые можно доказать на основании ранее установленных фактов. Некоторые из теорем называются именами выдающихся математиков — как в данном случае.)
Приступаем к доказательству. Для этого через точку Y2 проведем прямую x1, параллельную прямой x. У нас образовалось два параллелограмма с общей стороной X2Y2.
Обозначим точки пересечения прямой x1 с прямыми n1 и n3 как N1 и N3, соответственно. Теперь мы можем обозначить параллелограммы по их вершинам как X1X2Y2N1 и X2X3N3Y2. Поскольку у параллелограммов противоположные стороны равны между собой, то
Теперь мы можем обозначить параллелограммы по их вершинам как X1X2Y2N1 и X2X3N3Y2. Поскольку у параллелограммов противоположные стороны равны между собой, то
|X1X2| = |N1Y2|,
|X2X3| = |Y2N3|
и потому
|N1Y2| = |Y2N3|.
Таким образом, точка Y2 является серединой отрезка N1N3, а значит,
параллельные прямые n1 и n3 симметричны относительно точки Y2.
Прямая y также симметрична относительно точки Y2, поскольку она проходит через эту точку.
Следовательно, Y1 и Y3 — точки пересечения прямых n1 и n3 со стороной y — симметричны относительно Y2.
Отсюда заключаем, что |Y1Y2| = |Y2Y3|. Что и требовалось доказать.
Разбиение отрезка на заданное число равных частей
Допустим нам требуется разбить некоторый отрезок OX на три равные части. Теорема Фалеса дает нам возможность сделать это легко и изящно.
Проведем от точки O произвольный луч, который образует с отрезком OX любой угол, кроме нуля и 180° (на практике, однако, удобно брать угол в пределах приблизительно от 30° до 90°).
Отметим на этом луче три точки Y1 Y2 и Y3 с одинаковым шагом, начиная от точки O, так чтобы выполнялось соотношение
|OY1| = |Y1Y2| = |Y2Y3|.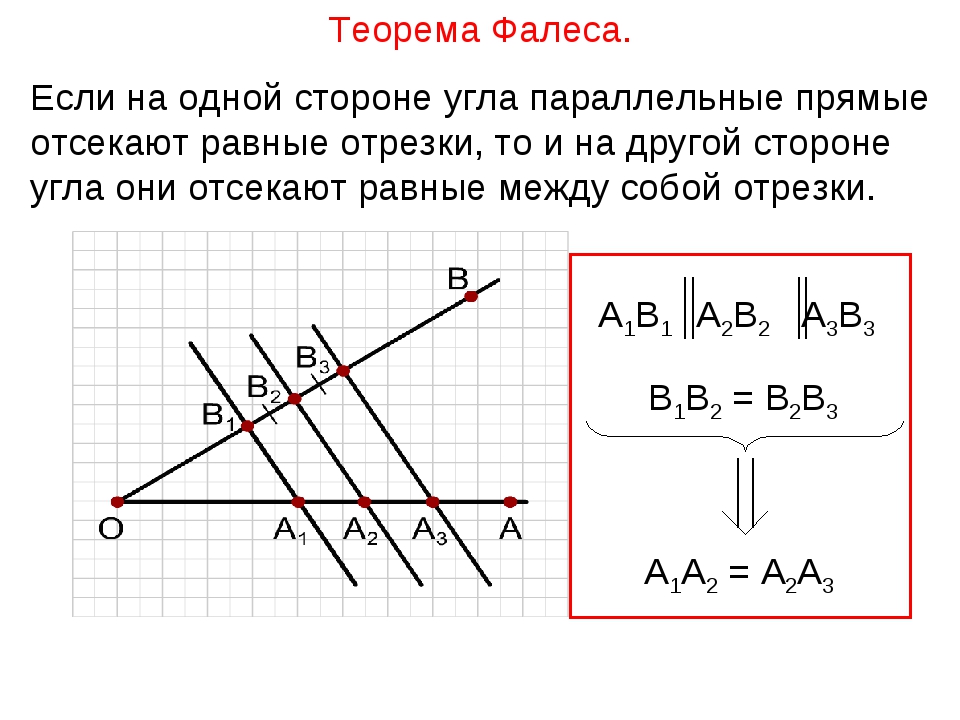
(Длина шага принципиальной роли не играет и выбирается из соображения удобства. Например, мы можем приставить к лучу линейку и сделать на нем три засечки через каждый сантиметр. Другая возможность заключается в том, чтобы делать шаги циркулем с фиксированным расстоянием между концами.)
Через точку Y3 и второй конец исходного отрезка — точку X — проведем прямую m.
Через остальные точки, отмеченные на луче, проведем прямые, параллельные прямой m. Согласно теореме Фалеса, эти прямые, пересекая отрезок OX, разобьют его на три равные части.
Подобным же образом, произвольный отрезок можно разбить на любое другое число равных частей.
Еще один способ построения параллельных прямых
Пусть дан угол X1OY1 (не равный нулю и не равный 180°) с вершиной в точке O и со сторонами, проходящими через некоторые точки X1 и Y1.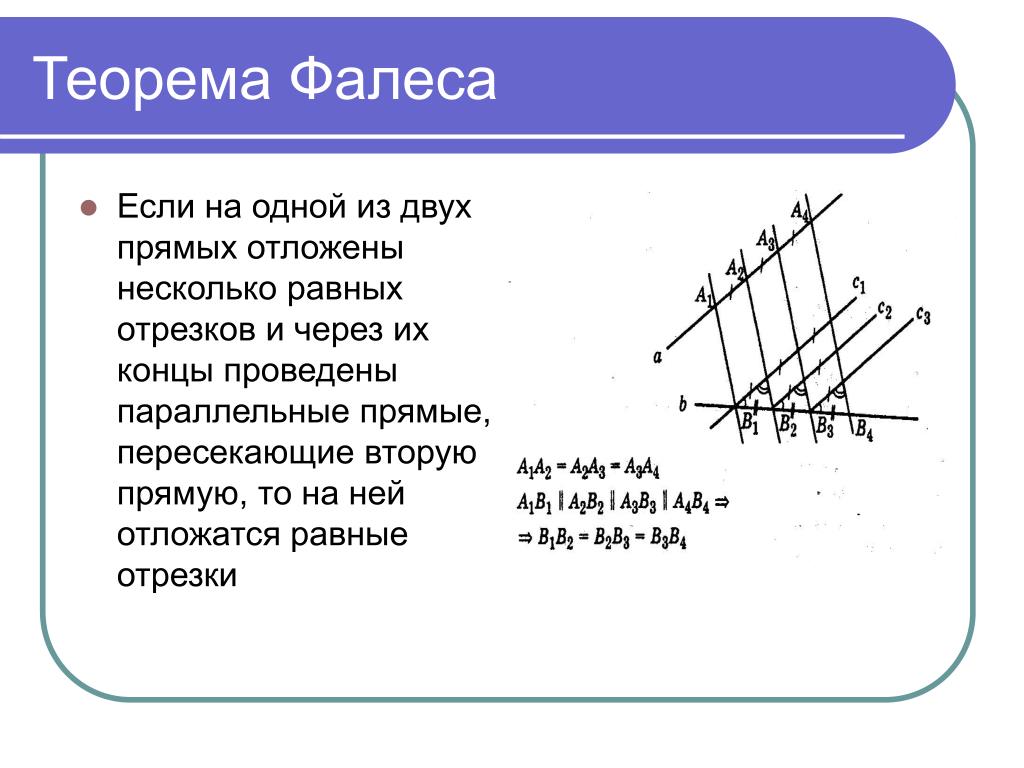
На стороне OX1 отметим точки X2 и X3, следующие с равным шагом за точкой X1:
|OX1| = |X1X2| = |X2X3|.
На стороне OY1 отметим точки Y2 и Y3, следующие с равным шагом за точкой Y1:
|OY1| = |Y1Y2| = |Y2Y3|.
Построим теперь прямые X1Y1, X2Y2 и X3Y3 и докажем, что они параллельны друг другу.
Действительно, через точку Y2 проведем прямую m2, параллельную прямой X1Y1. По теореме Фалеса, она пересекает сторону OX1 в точке X2, то есть она совпадает с прямой X2Y2. Следовательно, прямая X2Y2 параллельна прямой X1Y1. Точно таким же образом доказывается, что прямая X3Y3 параллельна прямой X2Y2.
По теореме Фалеса, она пересекает сторону OX1 в точке X2, то есть она совпадает с прямой X2Y2. Следовательно, прямая X2Y2 параллельна прямой X1Y1. Точно таким же образом доказывается, что прямая X3Y3 параллельна прямой X2Y2.
Очевидно, что в этом геометрическом построении ряды точек можно продолжить, соблюдая выбранный шаг, так что:
|X2X3| = |X3X4| = |X5X6| и так далее,
|Y2Y3| = |Y3Y4| = |Y5Y6| и так далее.
Рассуждая, как раньше, можно доказать, что все прямые, проходящие через точки X и Y с одинаковыми индексами, параллельны между собой.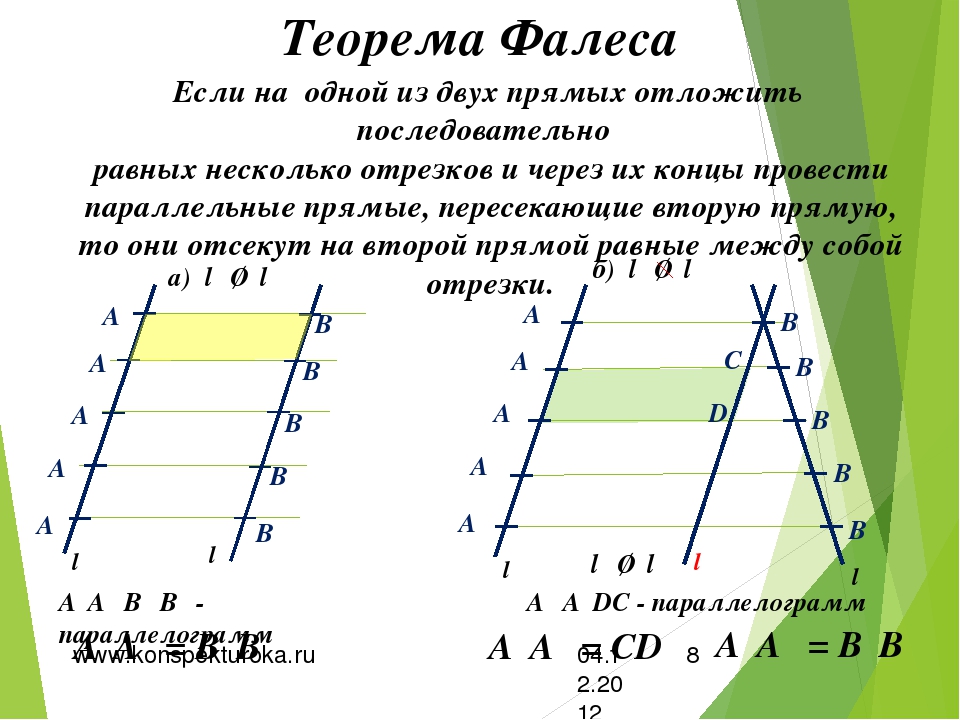
Конспект
Теорема Фалеса: Если три параллельные прямые отсекают на некоторой четвертой прямой два равных по длине отрезка, то при пересечении с какой-либо пятой прямой они также отсекут два отрезка равной длины.
Разбиение отрезка OX на n равных частей:
Строим произвольный луч с началом в точке O.
Вдоль луча от точки O делаем n шагов равной длины, делая засечку на каждом шагу.
Последнюю засечку соединяем прямой m с точкой X.
Через остальные засечки проводим прямые, параллельные m. Эти прямые делят отрезок OX на n равных частей.
Построение параллельных прямых: Пусть по двум сторонам угла, начиная от вершины, прошлись равномерным шагом два разных существа, оставляя точечные следы. Тогда все прямые, соединяющие следы с одинаковым порядковым номером, параллельны между собой.
Задачи
4. 5.1. Дана геометрическая конструкция:
5.1. Дана геометрическая конструкция:
Известно, что |X1X2| = |X2X3| и |Y1Y2| = |Y2Y3|. Можно ли утверждать, что прямые n1, n2 и n3 параллельны между собой?
4.5.2. Рассмотрим ту же геометрическую конструкцию:
Известно, что |X1X2| = |X2X3| и |Y1Y2| = |Y2Y3|. Кроме того, дано, что прямые n1 и n2 параллельны. Можно ли утверждать, что прямая n3 параллельна прямым n1 и n2?
4.5.3. Пусть дана конструкция:
Здесь прямые n1, n2 и n3 параллельны друг другу, причем |X1X2| = |X2X3|.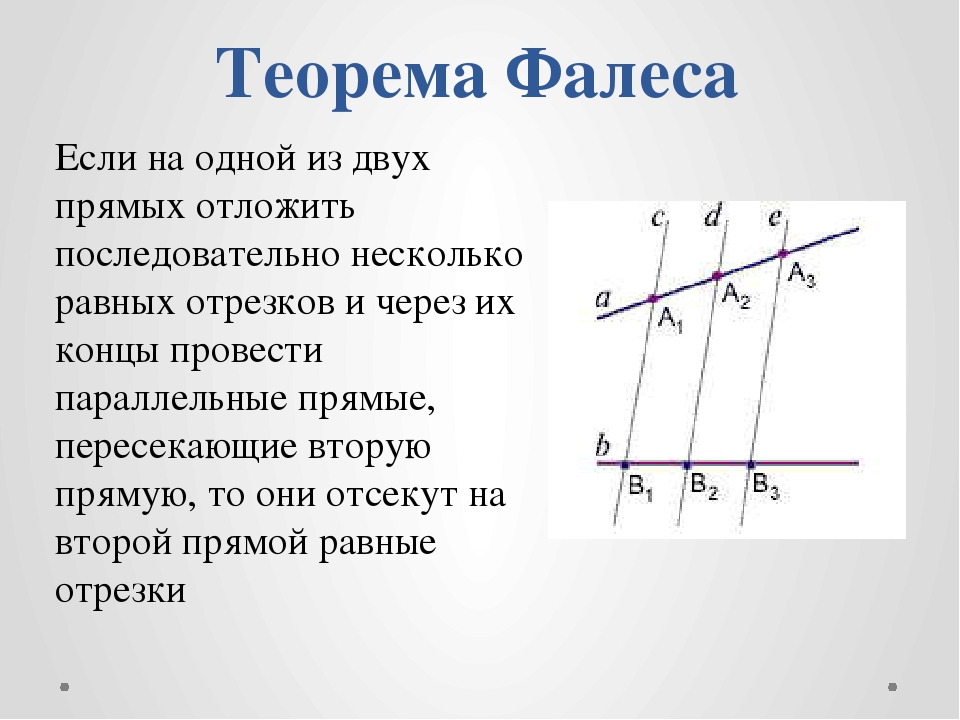 Верна ли в этом случае теорема Фалеса?
Верна ли в этом случае теорема Фалеса?
4.5.4. Рассмотрим конструкцию:
Известно, что прямые A1B1 и A2B2 параллельны, при этом |OA1| = 1,5 см; |OA2| = 3,0 см; |A1B1| = 1,0 см. Чему равна длина отрезка A2B2?
4.5.5. Дан единичный отрезок. С помощью циркуля и линейки без делений построить отрезки длиной (1) 2/3 и (2) 12/5.
4.5.6. Дана прямая и не лежащая на ней точка. Как с помощью линейки с делениями провести через эту точку прямую, параллельную данной?
Интегрированный урок (математика + информатика) по теме: «Теорема Фалеса»
Цели урока:
Образовательная: доказать теорему
Фалеса, научить применять её при решении задач по
математике и информатике.
Развивающая: развивать у учащихся
познавательный интерес к учебным дисциплинам,
умение применять свои знания на практике.
Воспитательная: воспитывать
внимание, аккуратность, расширять кругозор
учеников.
Оборудование и материалы:
Компьютер, экран, проектор.
Проектная работа “Теорема Фалеса”.
Программа “Живая геометрия”.
Плакат с рисунками 1,2,3.
Задачи учителей:
Показать практическое применение
теоретических знаний учащихся при решении задач
по геометрии и информатике.
Выявить глубокие связи между
математикой и информатикой.
Ход урока:
Урок начинает учитель математики.
Приветствие и вступительное слово о целях урока.
Фронтальный опрос учащихся:
1. Какие отрезки называются равными?
2. Какие прямые называются
параллельными? На рис. 1 покажите параллельные
прямые.
3. Какие углы называются вертикальными,
внутренними накрест лежащими? Покажите их на
рис.2
4. Сформулируйте теорему о свойстве
параллельных прямых, пересечённых третьей
прямой.
5. Сформулируйте признаки равенства
треугольников. По каким признакам равны
треугольники на рис 3?
Объяснение нового материала
Учитель математики объясняет новую
тему с помощью просмотра проектной работы
“Теорема Фалеса”.
(Приложение 1)
Сегодня мы докажем теорему, носящую
имя древнегреческого учёного Фалеса, который жил
в 624-547г.г. до н.э.
- Великий учёный Фалес Милетский основал одну из
прекраснейших наук — геометрию. Известно, что
Известно, что
Фалес Милетский имел титул одного из семи
мудрецов Греции, что он был поистине первым
философом, первым математиком, астрономом и
вообще первым по всем наукам в Греции. Короче: он
был то же для Греции, что Ломоносов для России
.
Карьеру он начинал как купец и ещё в
молодости попал в Египет. В Египте Фалес застрял
на много лет, изучая науки в Фивах и Мемфисе.
Считается, что геометрию и астрономию в Грецию
привёз он.
Фалес — математик. Он измерил по
тени высоту пирамиды; установил, что окружность
диаметром делится пополам, что углы при
основании равнобедренного треугольника равны.
Ему же принадлежит теорема, что вписанный угол,
опирающийся на диаметр окружности- прямой.
Фалес доказал теорему: “Если
параллельные прямые, пересекающие стороны угла,
отсекают на одной его стороне равные отрезки, то
они отсекают равные отрезки и на другой его
стороне”.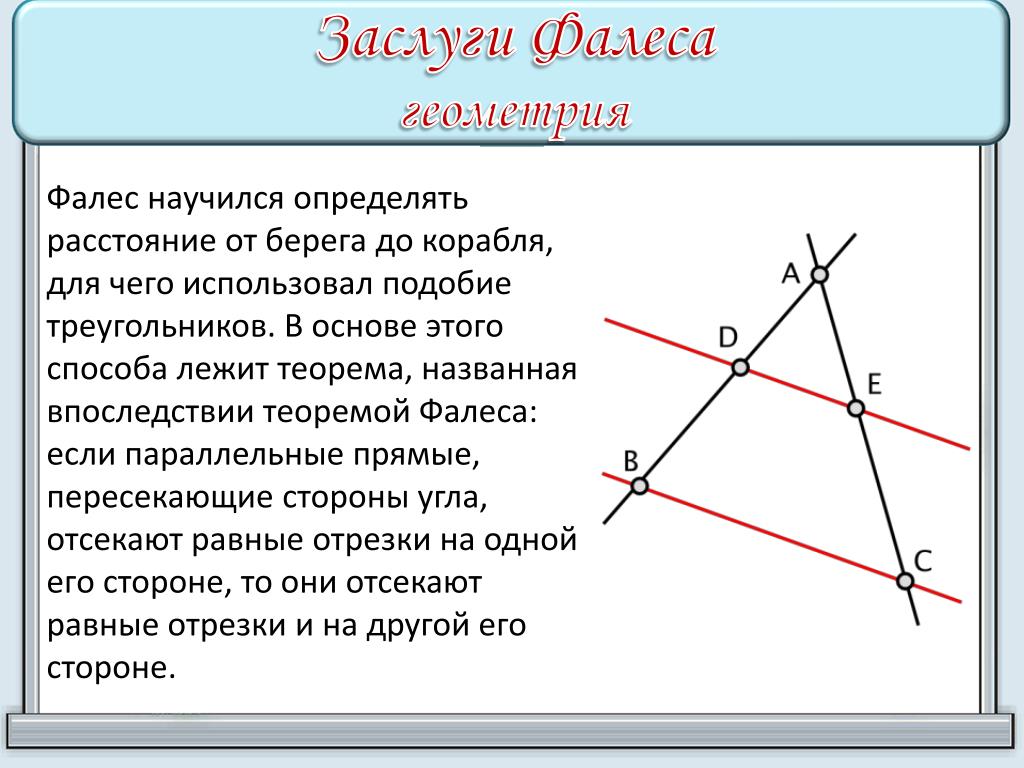
При активном участии учащихся
разбирается доказательство теоремы с
последовательным показом на экране каждого
этапа построения чертежа и доказательства
теоремы.
Из условия теоремы Фалеса делается
вывод, что вместо сторон угла можно взять любые
две прямые.
Затем ученики выполняют в тетрадях
практическую задачу на деление отрезка длиной в
7см. на 6 равных частей.
Греческие ученые открыли множество
геометрических свойств и создали стройную
систему геометрических знаний. В ее основу они
положили простейшие геометрические свойства,
подсказанные опытом. Остальные свойства
выводились из простейших с помощью рассуждений.
Все этапы решения задачи учащиеся
видят на экране. Это способствует зрительному
запоминанию алгоритма решения данной задачи.
Показ проектной работы сопровождается
музыкой- игрой на гитаре, что создаёт спокойную
рабочую обстановку.
Вторую часть урока ведёт учитель
информатики. С помощью программы “Живая
геометрия” ученики вместе с учителем на
компьютерах делят отрезок на три равные части.
Выполнение практического задания
Разделить данный отрезок на 3-равные части на
компьютере с помощью программы “Живая
геометрия”.
Используемые ИНСТРУМЕНТЫ “Живой геометрии”:
• стрелка;
• линейка (отрезок, луч).
Используемые КОМАНДЫ “Живой геометрии”:
• построения;
• правка;
Порядок работы:
1 .Построим данный
отрезок АВ.
2.Проведем из т. А полупрямую а, не
лежащую на прямой АВ.
3.Отложим на полупрямой а 3 равных
отрезка.
Для этого используем
команду ПОСТРОЕНИЯ— “окружность
по центру и радиусу”; зададим произвольный радиус СО и
построим на полупрямой а 3 окружности.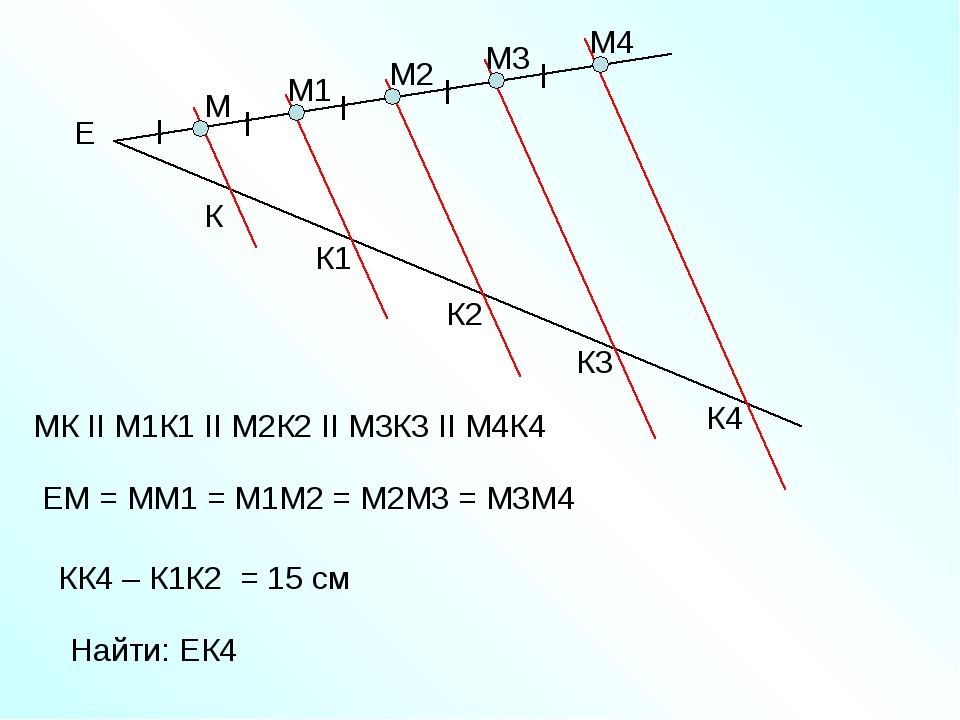
Они отсекают на полупрямой а равные отрезки АЕ=ЕР=РО.
4.Соединим точки В и О.
5. Проведем через точки Е и
Р прямые, параллельные прямой ВО.
6. Они пересекают отрезок АВ в точках Н и I , которые делят
отрезок АВ на 3 равные части; т.к. по теореме Фалеса:
Если параллельные прямые,
пересекающие стороны угла, отсекают на одной его
стороне равные отрезки, то они отсекают равные
отрезки и на другой его стороне.
Домашнее задание.
Задача: Разделить отрезок длиной 5 см.
на 7 равных частей. Выучить теорему Фалеса.
Подведение итогов урока.
Приложение
Теорема Фалеса и ее применение для решения задач
Из элементарной геометрии — из вестна теорема Фалеса: если на одной стороне угла отложить -рав ные или пропорциональные отрезки и через засечки провести — па раллельные прямые, то и другая сторона угла разделится на равные или пропорциональные отрезки.
Задача: разделить проекции прямой АВ в отношении 2:4, предварительно построив недостающую профильную проекцию.
Используя свойства эпюра Монжа, строим профильную проекцию прямой, для чего откладываем от оси OZ ординаты, замеренные на горизонтальной проекции прямой. Далее на любой проекции прямой, например на горизонтальной, проводим произвольную вспомогательную прямую m.
Откладываем на вспомогательной | |
прямой 6 равных отрезков произ- | |
вольной длины. Конец последнего | |
отрезка | соединяем с точкойВ/. |
На вспомогательной прямой -бе | |
рем точку F0 и из нее параллельно | |
отрезку | В0В/ проводим линию |
связи, которая делит А/В/, а затем | |
и другие проекции в заданном | |
отношении. | |
Определение видимости скрещивающихся прямых
При рассмотрении | пространствен- | |||
ного | чертежа | двух | скрещиваю- | |
щихся | прямых | можно | сделать | |
вывод: | на горизонтальной | проек- | ||
ции будет видна та прямая, кото- | ||||
рая имеет бóльшую аппликату в | ||||
конкурирующем месте. На фрон- | ||||
тальной проекции будет видна та | ||||
прямая, | которая имеет бóльшую | |||
ординату. На профильной проекции | ||||
будет видна прямая, имеющая бóль- | ||||
шую абсциссу. |
|
|
| |
|
| |||
Для определения видимости пря- | ||||
мых на проекциях необходимо: | ||||
-отметить конкурирующее место;
-провести через него линию связи;
-вдоль линии связи сравнить -ап пликаты скрещивающихся прямых, если определяется видимость на горизонтальной проекции;
-на рассматриваемой проекции будет видна та прямая, у которой больше аппликата (АВ).
На фронтальной проекции будет видна также прямая АВ, так как в конкурирующем месте у нее больше ордината. Метод определения видимости скрещивающихся прямых получил название метод конкурирующих точек, или метод конкурирующих прямых.
Теорема прямого угла
Прямой угол может быть спро- | |||
ецирован | в натуральную | вели- | |
чину, если его плоскость будет | |||
параллельна | плоскости | проек- | |
ций. | |||
теоремой | прямой | угол | также |
проецируется без искажения, ес- | |||
ли один из его катетов парал- | |||
лелен плоскости проекций. Эта | |||
теорема получила название тео- | |||
ремы прямого угла и широко ис- | |||
пользуется в геометрических -за | |||
дачах. |
|
|
|
На эпюре | показано использова- |
ние теоремы прямого угла для | |
построения проекций двух пере- | |
секающихся | перпендикулярных |
прямых, одна из которых явля- | |
ется фронталью. | |
Теорема прямого угла распространяется не только на пересекающиеся перпендикулярные прямые, но и на скрещивающиеся перпендикулярные прямые.
Плоскости общего и частного положения
Плоскость общего положения – это плоскость, не параллельная и не перпендикулярная ни одной из плоскостей проекций. Признак плоскости общего положения на эпюре – ни одна проекция плоскости (ни один след) не параллельна, не перпендикулярна осям проекций и ни на одной проекции плоскость не «выродилась» в прямую.
Плоскости, параллельные или перпендикулярные плоскостям проекций, называются плоскостями частного положения. Горизонтальная плоскость параллельна плоскости H. Главный признак плоскости на эпюре – фронтальная проекция «вырождается» в линию, параллельную оси ОХ.
Фронтальная | плоскость | парал- |
лельна плоскости V. На эпюре | ее | |
горизонтальная | проекция «вы- | |
рождается» в | линию, параллель- | |
ную ОХ. | ||
фронтальной | плоскостей | парал- |
лельны оси ОХ. |
|
|
Плоскости, перпендикулярные плоскостям проекций, называются проецирующими. По аналогии с прямой различают горизонтально-, фронтально- и профильно-проецирую- щие плоскости. Главный признак проецирующих плоскостей на эпюре – на одной из проекций плоскость «вырождается» в линию. Проецирующие следы перпендикулярны соответствующим осям.
8 класс. Геометрия. Четырехугольники. Трапеция. — Трапеция.
Комментарии преподавателя
Трапеция
Определение
Трапеция – это четырёхугольник, у которого две стороны параллельны, а две другие – нет.
На Рис. 1. изображена произвольная трапеция. – это боковые стороны (те, которые не параллельны). – основания (параллельные стороны).
– основания (параллельные стороны).
Рис. 1. Трапеция
Если сравнивать трапецию с параллелограммом, то у параллелограмма две пары параллельных сторон. То есть параллелограмм не является частным случаем трапеции, так как в определении трапеции чётко сказано, что две стороны трапеции не параллельны.
Выделим некоторые виды трапеции (частные случаи):
- равнобедренная (равнобокая) трапеция: боковые стороны равны;
- прямоугольная трапеция: один из углов равен (из определения трапеции и свойства параллельных прямых следует, что два угла будут по ).
Определение
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.
На Рис. 2. изображена трапеция со средней линией .
Рис. 2. Средняя линия трапеции
Свойства средней линии трапеции:
1. Средняя линия трапеции параллельна основаниям трапеции.
Средняя линия трапеции параллельна основаниям трапеции.
Доказательство:
Пусть середина боковой стороны трапеции – точка . Проведём через эту точку прямую, параллельную основаниям. Эта прямая пересечёт вторую боковую сторону трапеции в точке .
По построению: . По теореме Фалеса из этого следует: . Значит, – середина стороны . Значит, – средняя линия.
Доказано.
2. Средняя линия трапеции равна полусумме оснований трапеции: .
Доказательство:
Проведём среднюю линию трапеции и одну из диагоналей: например, (см. Рис. 3).
Рис. 3
По теореме Фалеса параллельные прямые отсекают на сторонах угла пропорциональные отрезки. Так как равны отрезки: . Значит, отрезок является средней линией треугольника , а отрезок – средней линией треугольника .
Значит, .
Примечание: это следует из свойства средней линии треугольника: средняя линия треугольника параллельна основанию и равна его половине.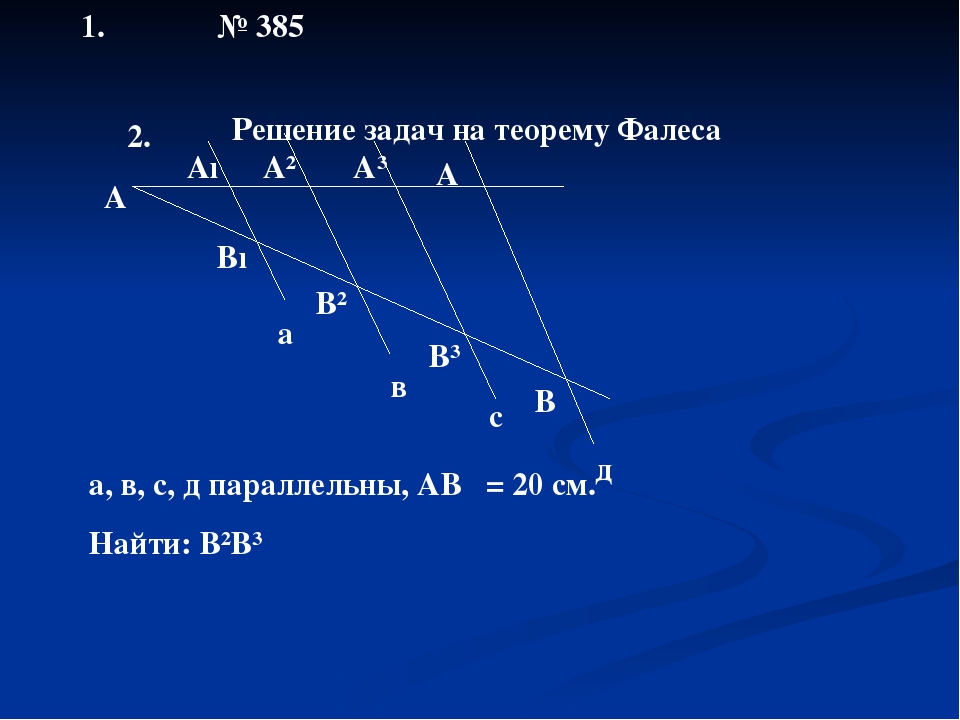 Первая часть этого свойства доказывается аналогично с доказательством первого свойства средней линии трапеции, а вторую часть можно доказать (к примеру, для средней линии треугольника ), проведя через точку прямую, параллельную . Из теоремы Фалеса будет следовать, что эта прямая будет являться средней линией, а образованный четырёхугольник – параллелограммом (две пары попарно параллельных сторон). Отсюда уже несложно получить требуемое свойство.
Первая часть этого свойства доказывается аналогично с доказательством первого свойства средней линии трапеции, а вторую часть можно доказать (к примеру, для средней линии треугольника ), проведя через точку прямую, параллельную . Из теоремы Фалеса будет следовать, что эта прямая будет являться средней линией, а образованный четырёхугольник – параллелограммом (две пары попарно параллельных сторон). Отсюда уже несложно получить требуемое свойство.
Получаем: .
Доказано.
Рассмотрим теперь подробнее основные виды трапеции и их свойства.
Напомним, что равнобедренная трапеция – трапеция, у которой боковые стороны равны. Рассмотрим свойства боковой трапеции.
1. Углы при основании равнобедренной трапеции равны.
Доказательство:
Выполним стандартное дополнительное построение, которое очень часто используется при решении различных задач на трапецию: проведём прямую параллельно боковой стороне (см. Рис. 4).
Рис. 4).
Рис. 4
– параллелограмм.
Отсюда следует, что: . Значит, треугольник – равнобедренный. А значит, углы при его основании равны, то есть: (последние два угла равны, как соответственные при параллельных прямых ).
Доказано.
2. Диагонали равнобедренной трапеции равны.
Доказательство:
Для доказательства этого свойства воспользуемся предыдущим. Действительно, рассмотрим треугольники: и (см. Рис. 5.).
Рис. 5
(по первому признаку равенства треугольников: две стороны и угол между ними).
Из этого равенства сразу следует, что: .
Доказано.
Оказывается, что, как и в случае с параллелограммом, у равнобедренной трапеции свойства одновременно являются и признаками. Сформулируем и докажем эти признаки.
Признаки равнобедренной трапеции
1. Дано: – трапеция; .
Дано: – трапеция; .
Доказать:
Доказательство:
Доказательство данного признака абсолютно аналогично доказательству соответствующего свойства. Проведём в трапеции прямую параллельно стороне (см. Рис. 6).
– параллелограмм (две пары попарно параллельных сторон).
(соответственные углы при параллельных прямых). Откуда, пользуясь условием, получаем: – равнобедренный
Рис. 6
(равны углы при основании). Значит: (у параллелограмма противоположные стороны равны).
Доказано.
2. Дано: – трапеция; .
Доказать: .
Доказательство:
Выполним ещё одно стандартное дополнительное построение при решении задач с трапецией: проведём через вершину прямую параллельно диагонали (см. Рис. 7).
Рис. 7
– параллелограмм (две пары попарно параллельных сторон).
(соответственные углы при параллельных прямых). Кроме того, – равнобедренный ( – по условию; – по свойству параллелограмма). А значит: .
Доказано.
Рассмотрим несколько примеров решения задач с трапецией.
Пример 1.
Дано: – трапеция; .
Найти:
Решение:
Сумма углов при боковой стороне трапеции равна – свойство внутренних односторонних углов при параллельных прямых. Из этого факта можно получить два равенства:
Ответ: .
Пример 2.
Дано: – трапеция; . .
Найти:
Решение:
Рис. 8
Проведём высоту . Получаем четырёхугольник , в котором противоположные стороны попарно параллельны, а два углы равны по . Значит, – параллелограмм, а точнее, прямоугольник.
Из этого следует, что . Откуда: .
Рассмотрим прямоугольный треугольник .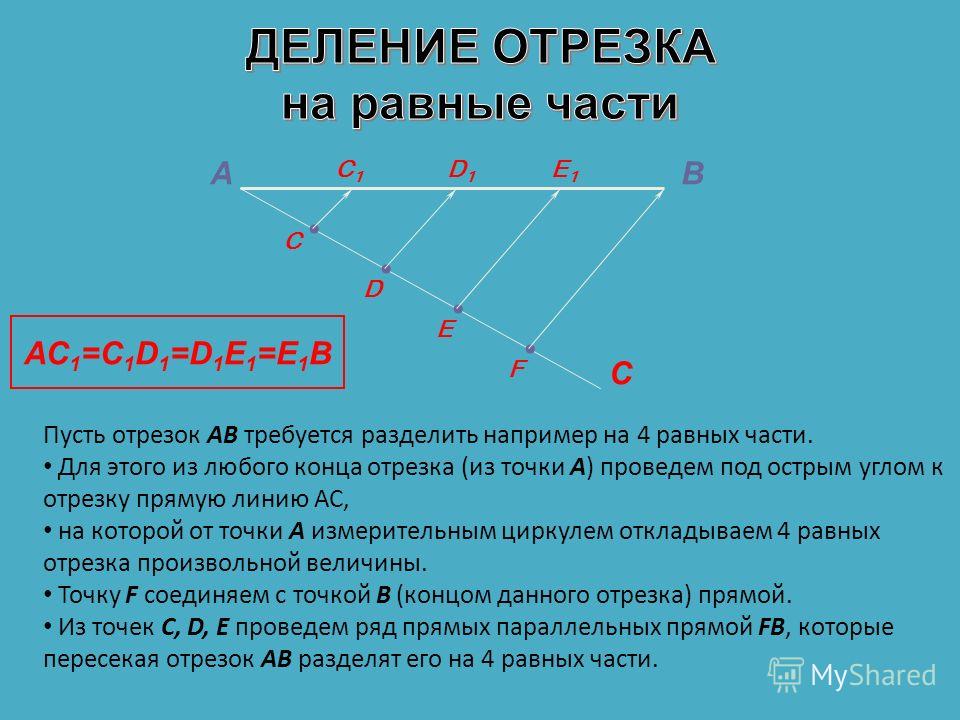 В нём один из острых углов, по условию, равен . Значит, второй равен , то есть: . Воспользуемся свойством катета, лежащего против угла : он в два раза меньше гипотенузы.
В нём один из острых углов, по условию, равен . Значит, второй равен , то есть: . Воспользуемся свойством катета, лежащего против угла : он в два раза меньше гипотенузы.
.
Ответ: .
На этом уроке мы рассмотрели понятие трапеции и её свойства, изучили виды трапеции, а также решили несколько примеров типовых задач.
ИСТОЧНИК
http://interneturok.ru/ru/school/geometry/8-klass/chyotyrehugolniki/trapetsiya
http://www.youtube.com/watch?v=Yqw5oZ3iFAI
http://www.youtube.com/watch?v=1tY3omQhTuk
http://img3.proshkolu.ru/content/media/pic/std/1000000/983000/982960-b6b4e8f6a4e7b336.jpg
http://static.wixstatic.com/media/13679f_7ac2889143594b059462e77b25eda7c6.jpg
http://delaem-uroki.narod.ru/img/102/792/KZqhOMb.gif
Трапеция. Задача на среднюю линию трапеции.
http://cs323223.vk.me/v323223595/5e51/Gi2qlTPgLVo.jpg
http://dok. opredelim.com/pars_docs/refs/47/46420/img2.jpg
opredelim.com/pars_docs/refs/47/46420/img2.jpg
Теорема Фалеса — объяснение и примеры
После того, как мы изучили теорему о вписанном угле, пришло время изучить другую связанную теорему, которая представляет собой частный случай теоремы о вписанном угле м, , называемую теоремой Фалеса . Как и теорема о вписанном угле, ее определение также основано на диаметре и углах внутри круга.
Из этой статьи вы узнаете:
- Теорема Фалеса,
- Как решить теорему Фалеса; и
- Как решить теорему Фалеса только с одной стороной
Что такое теорема Фалеса?
Теорема Фалеса утверждает, что:
Если три точки A, B и C лежат на окружности круга, при этом прямая AC является диаметром круга, то угол ∠ ABC — прямой угол (90 °).
В качестве альтернативы мы можем сформулировать теорему Фалеса как:
Диаметр круга всегда образует прямой угол с любой точкой на окружности.
Вы заметили, что теорема Фалеса является частным случаем теоремы о вписанном угле (центральный угол = удвоенный вписанный угол).
Теорема Фалеса приписывается Фалесу, греческому математику и философу, жившему в Милете.Фалес первым инициировал и сформулировал теоретическое изучение геометрии, чтобы сделать астрономию более точной наукой.
Есть различных способов доказать теорему Фалеса . Мы можем использовать методы геометрии и алгебры, чтобы доказать эту теорему. Поскольку это тема геометрии, давайте рассмотрим самый простой метод ниже.
Как решить теорему Фалеса?
- Чтобы доказать теорему Фалеса, нарисуйте серединный перпендикуляр к ∠
- Пусть точка M будет средней точкой прямой AC.
- Также пусть ∠ MBA = ∠ BAM = β и ∠ MBC = ∠ BCM = α
- Линия AM = MB = MC = радиус окружности.

- Δ AMB и Δ MCB — равнобедренные треугольники.
По теореме о сумме треугольников
∠ BAC + ∠ ACB + ∠ CBA = 180 °
β + β + α + α = 180 °
Разложите уравнение на множители.
2 β + 2 α = 180 °
2 (β + α) = 180 °
Разделим обе стороны на 2.
β + α = 90 °.
Следовательно, ABC = 90 °, следовательно, доказано
Давайте решим несколько примеров задач, связанных с теоремой Фалеса.
Пример 1
Учитывая, что точка O является центром окружности, показанной ниже, найдите значение x.
Решение
Учитывая, что прямая XY является диаметром окружности, то по теореме Фалеса
∠ XYZ = 90 °.
Сумма внутренних углов треугольника = 180 °
90 ° + 50 ° + x = 180 °
Упростить.
140 ° + x = 180 °
Вычтите 140 ° с обеих сторон.
x = 180 ° — 140 °
x = 40 °.
Итак, значение x равно 40 градусам.
Пример 2
Если точка D является центром окружности, показанной ниже, вычислите диаметр окружности.
Решение
По теореме Фалеса треугольник ABC является прямоугольным, где ∠ ACB = 90 °.
Чтобы найти диаметр круга, примените теорему Пифагора.
CB 2 + AC 2 = AB 2
8 2 + 6 2 = AB 2
64 + 36 = AB 2
10019 2 2 2 2 2
AB = 10
Следовательно, диаметр круга равен 10 см
Пример 3
Найдите угол PQR в круге, показанном ниже.Предположим, что точка R является центром круга.
Решение
Треугольник RQS и PQR — равнобедренные треугольники.
∠ RQS = ∠ RSQ = 64 °
По теореме Фалеса, ∠ PQS = 90 °
Итак, ∠ PQR = 90 ° — 64
= 26 °
Следовательно, величина угла PQR равна 26 °.
Пример 4
Какое из следующих утверждений верно относительно определения теоремы Фалеса?
A. Центральный угол в два раза больше вписанного угла
B. Угол, вписанный в полукруг, будет прямым углом.
C. Диаметр круга — самая длинная хорда.
D. Диаметр окружности в два раза больше радиуса.
Решение
Правильный ответ:
B.Угол, вписанный в полукруг, будет прямым.
Пример 5
В круге, показанном ниже, линия AB — это диаметр круга с центром C .
- Найдите размер ∠ до н.э.
- ∠ DCA
- ∠ ACE
- ∠ DCB
Решение
Заданный треугольник ACE — равнобедренный треугольник,
∠ CA 33 °
Итак, ACE = 180 ° — (33 ° + 33 °)
∠ ACE = 114 °
Но углы на прямой = 180 °
Следовательно, ∠ BCE = 180 ° — 114 °
= 66 °
Треугольник ADC — равнобедренный треугольник, поэтому ∠ DAC = 20 °
По теореме суммы треугольников DCA = 180 ° — (20 ° + 20 °)
∠ DCA = 140 °
∠ DCB = 180 ° — 140 °
= 40 °
Пример 6
Какой размер ∠ ABC ?
Решение
Теорема Фалеса утверждает, что BAC = 90 °
И по теореме суммы треугольников
∠ ABC + 40 ° + 90 ° = 180 °
∠ ABC = 180 ° — 130 °
= 50 °
Пример 7
Найдите длину AB в круге, показанном ниже.
Решение
Треугольник ABC — это прямоугольный треугольник.
Примените теорему Пифагора, чтобы найти длину AB .
AB 2 + 12 2 = 18 2
AB 2 + 144 = 324
AB 2 = 324–144
= 180
AB = 13,4
Следовательно, длина AB равна 13.4 см.
Приложения теоремы Фалеса
В геометрии ни одна из тем не обходится без реального использования. Следовательно, теорема Фалеса также имеет некоторые приложения:
- Мы можем точно провести касательную к окружности, используя теорему Фалеса. Для этого можно использовать установленный угольник.
- Мы можем точно найти центр круга, используя теорему Фалеса. Инструменты, используемые для этого приложения, представляют собой квадрат и лист бумаги. Во-первых, вы должны разместить угол на окружности — пересечение двух точек с окружностью определяет диаметр.
 Вы можете повторить это, используя другую пару точек, что даст вам другой диаметр. Пересечение диаметров даст вам центр круга.
Вы можете повторить это, используя другую пару точек, что даст вам другой диаметр. Пересечение диаметров даст вам центр круга.
Предыдущий урок | Главная страница | Следующий урок
Теорема Фалеса: доказательство | Справка по геометрии
На сегодняшнем уроке мы докажем теорему Фалеса — вписанный угол, который образует диаметр окружности, всегда является прямым углом, используя сумму углов в треугольнике.
Фалес Милетский был греческим математиком, чья работа предшествовала работе Евклида и Пифагора.
С его именем связан ряд теорем. Одна из них — это теорема о пересечении для соотношений между линейными сегментами, созданными, когда две параллельные линии пересекаются двумя пересекающимися линиями, и здесь мы докажем другую, связанную с вписанными углами.
Теорема утверждает, что любой вписанный угол в окружность, которая образует диаметр, является прямым углом.
Задача
CB — диаметр окружности с центром O, а A — точка на окружности окружности.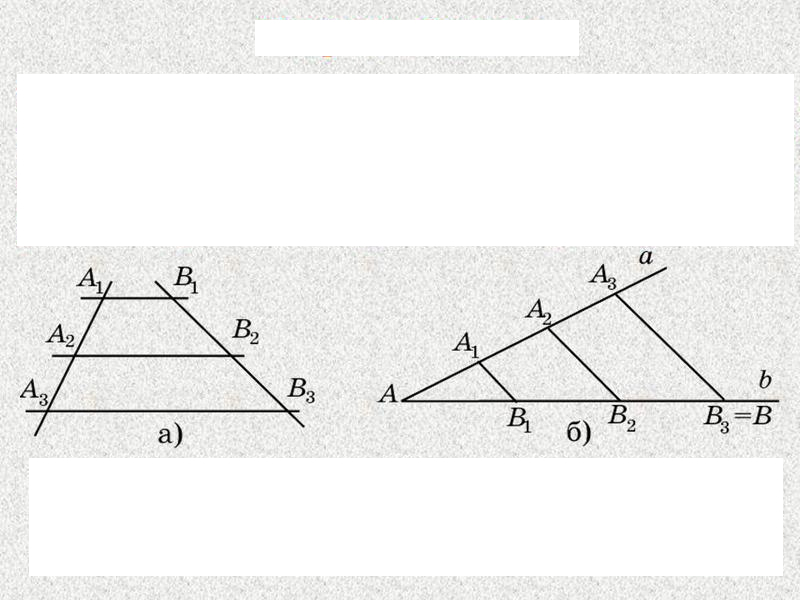 Покажите, что m∠CAB = 90 °
Покажите, что m∠CAB = 90 °
Стратегия
Один из способов доказать это — рассматривать это как частный случай теоремы о вписанных углах: центральный угол равен удвоенному вписанному углу, который образует ту же дугу; диаметр разделяет круг (который по определению равен 360 °) на две равные половины, поэтому его центральная угловая мера составляет 180 °, а вписанный угол, который образует его, должен составлять половину этого, или 90 °.
Но поскольку работа Фалеса предшествовала Евклиду (который доказал общую теорему для вписанных углов), давайте докажем ее напрямую, не полагаясь на теорему о вписанных углах.
Соедините центр O с точкой A. OA — это радиус, а также OB и OC. Все радиусы равны, поэтому два созданных нами треугольника — ΔOAC и ΔOAB — являются равнобедренными треугольниками. И, согласно теореме о базовом угле, их базовые углы равны. Обозначим базовые углы ΔOAB как ‘α’, а углы ΔOAC ‘β’.
Сумма углов в треугольнике равна 180 °. Итак, α + α + β + β = 180 °, 2 * (α + β) = 180 °, поэтому α + β = 90 °.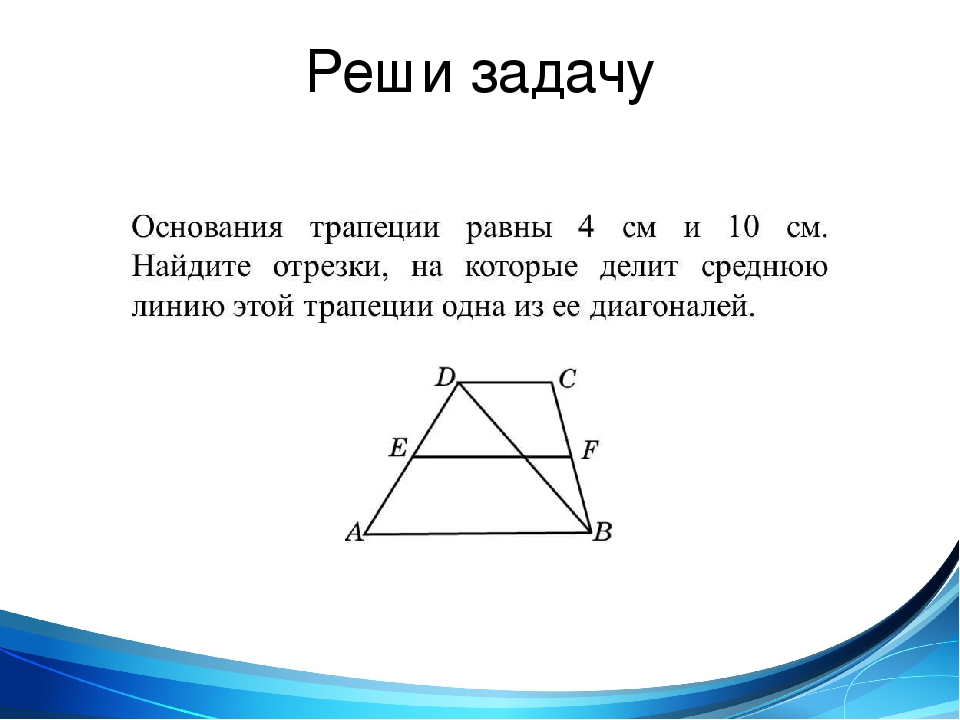 А поскольку ∠CAB = α + β, это прямой угол.
А поскольку ∠CAB = α + β, это прямой угол.
Доказательство
(1) OA = OB = OC = r // все радиусы равны
(2) ∠OCA≅∠OAC = β // Теорема об основном угле
(3) ∠OBA≅∠OAB = α // Теорема об основных углах
(4) α + α + β + β = 180 ° // сумма углов в треугольнике
(5) 2 * (α + β) = 180 ° // (4), распределительное свойство умножения
(6) α + β = 90 ° // (5), разделить на 2
(7) ∠CAB = mα + β // постулат сложения углов
(8) m∠CAB = 90 °
Теорема Фалеса — математическая Путь
Есть несколько теорем, которые приписываются Фалесу Милетскому , мы сосредоточимся особенно на двух из них:
Теорема Фалеса
Теорема Фалеса — это частный случай теоремы о вписанном угле, она относится к прямоугольным треугольникам, вписанным в окружность.
Теорема
Фалеса утверждает, что если A , B и C являются разными точками на окружности с центром O ( центр описанной окружности ), где линия AC является диаметром, то треугольник Δ ABC имеет прямой угол (90) в точке B . Таким образом, Δ ABC — прямоугольный треугольник.
Другими словами, диаметр круга всегда образует прямой угол с любой точкой на окружности.
Доказательство теоремы Фалеса
Если мы соединим центр описанной окружности O с точкой B , мы создадим два треугольника Δ ABO и Δ OBC , которые являются равнобедренными треугольниками, потому что все радиусы r равны ( OA , OB и OC равны).И, согласно теореме о базовом угле, их базовые углы равны. Обозначим базовые углы Δ ABO ‘α’ и Δ ABO ‘β’.
Поскольку это равнобедренные треугольники, каждый из них имеет два равных угла: α и β (см. Рисунок выше).
Как и в любом треугольнике, внутренние углы треугольника Δ ABC в сумме составляют 180 °:
Делим равенство на 2:
Поскольку α + β — это угол Δ ABC в точке B , Теорема Фалеса доказана .
Теорема о перехвате
Теорема о перехвате гласит, что если две пересекающиеся прямые разрезаются параллельными линиями, сегменты линии, вырезанные параллельными линиями из одной из линий, пропорциональны соответствующим сегментам линии, вырезанным ими из другой линии.
Если любые две линии (на изображении: m и n ) разрезаны серией параллельных линий (на изображении: r , s и t ), образующиеся отрезки в одной из них пропорциональны соответствующим отрезкам, образованным в другой линии.
Применяя теорему о перехвате , верно, что:
Где r — отношение.
Теорема о перехвате связана с подобием. Фактически, это эквивалентно понятию подобных треугольников. Применяя теорему о перехвате к треугольникам, мы можем утверждать, что если в данном треугольнике мы проведем линию, параллельную одной из его трех сторон, новый сгенерированный треугольник будет похож на первый. То есть мы создадим два равных треугольника, которые будут в Thales в позиции .
См. Рисунок выше.
В Δ ABC рисуем отрезок A’C ’, параллельный стороне AC . Появляется новый Δ A’BC ’, похожий на первый. У них три равных угла, а их стороны пропорциональны.
Согласно теореме о перехвате верно, что:
Это соотношение сохраняется между двумя сторонами одного и того же треугольника, а также между соответствующими сторонами другого треугольника:
Знаете ли вы , что Фалес Милетский (родился на Ионическом острове Милет в 7 веке до нашей эры) считался одним из семи мудрецов Греции? Он преуспел в философии, астрономии, геометрии, инженерии и … даже в политике).
Под влиянием египетских и вавилонских знаний было сказано (поддержанное, среди прочего, Плутархом), что на основе своей первой теоремы и путем измерения теней он определил высоту пирамид Гизы.
Основная теорема о пропорциональности | Теорема Фалеса | Заявление и доказательство
Основная теорема пропорциональности была предложена известным греческим математиком Фалесом, поэтому ее также называют теоремой Фалеса . По словам известного математика, для любых двух равноугольных треугольников отношение любых двух соответствующих сторон данных треугольников всегда одинаково.На основе этой концепции была предложена основная теорема пропорциональности (BPT). Он показывает отношения между сторонами любых двух равносторонних треугольников.
Понятие теоремы Фалеса было введено в подобных треугольниках. Если данные два треугольника похожи друг на друга, то
- Соответствующие углы обоих треугольников равны
- Соответствующие стороны обоих треугольников пропорциональны друг другу
Таким образом, теорема также помогает нам лучше понять концепцию подобных треугольников.Теперь давайте попробуем понять основную теорему о пропорциональности.
Формулировка основной теоремы о пропорциональности
Основная теорема пропорциональности, также известная как теорема Фалеса, гласит, что «линия, проведенная параллельно одной стороне треугольника и пересекающая две другие стороны, делит две другие стороны в равной пропорции». Например, на данном рисунке линия DE проведена параллельно стороне BC, так что она соединяет две другие стороны, AB и AC.Согласно основной теореме пропорциональности, можно заключить, что AD / DB = AE / EC.
Доказательство основной теоремы о пропорциональности
Давайте теперь попробуем доказать утверждение основной теоремы пропорциональности (BPT).
Заявление: Линия, проведенная параллельно одной стороне треугольника и пересекающая две другие стороны, делит две другие стороны в равной пропорции.
Дано: Рассмотрим треугольник ΔABC, как показано на данном рисунке.В этом треугольнике проведем прямую DE, параллельную стороне BC треугольника ABC и пересекающую стороны AB и AC в точках D и E соответственно.
Конструкция: На приведенной выше диаграмме создайте воображаемые линии, где вы можете соединить C с D и B с E. Нарисуйте перпендикуляр DP, перпендикулярный AE, и EQ, перпендикулярный AD.
Доказательство:
Рассмотрим треугольники ADE и BDE. Оба этих треугольника находятся на одном основании AB и имеют одинаковую высоту EQ.
(Область ADE) / (Область BDE) = (1/2 × AD × EQ) / (1/2 × BD × EQ)
(Площадь ADE) / (Площадь BDE) = AD / BD
Теперь рассмотрим треугольники CDE и ADE. Оба этих треугольника находятся на одном основании AC и имеют одинаковую высоту DP.
(Площадь ADE) / (Площадь CDE) = (1/2 × AE × DP) / (1/2 × CE × DP)
(Площадь ADE) / (Площадь CDE) = AE / CE
Оба треугольника BDE и CDE находятся между одним и тем же набором параллельных прямых.
Площадь треугольника BDE = Площадь треугольника CDE
Применяя это, мы имеем (Площадь треугольника ADE) / (Площадь треугольника BDE) = (Площадь треугольника ADE) / (Площадь треугольника CDE)
AD / BD = AE / CE
Следствие:
Приведенное выше доказательство также полезно для доказательства другой важной теоремы, называемой теоремой о средней точке.Теорема о средней точке утверждает, что отрезок линии, проведенный параллельно одной стороне треугольника, и половина этой стороны делит две другие стороны в средних точках.
Заключение:
Таким образом, мы доказываем основную теорему о пропорциональности. Следовательно, прямая DE, проведенная параллельно стороне BC треугольника ABC, делит две другие стороны AB, AC в равной пропорции. Кроме того, верно и обратное утверждение теоремы о средней точке. В нем говорится, что линия, проведенная через середину стороны треугольника, параллельной другой стороне, делит третью сторону треугольника пополам.
Обращение к основной теореме о пропорциональности
Согласно обратной теореме о пропорциональности: «Если отрезок прямой рассекает две стороны треугольника в равной пропорции, то он параллелен третьей стороне».
Дано:
ABC представляет собой треугольник, и прямая DE разрезает стороны AB и AC в равной пропорции. AD / BD = AE / CE
Доказательство:
Считайте, что DE не параллельна BC.Поэтому проведем другую линию DF, параллельную BC. Применяя основную теорему о пропорциональности, получаем: AD / BD = AF / CF. Но уже дано, что: AD / BD = AE / CE. Наблюдая за левыми частями двух приведенных выше утверждений, мы получаем следующее утверждение: AE / CE = AF / CF. Добавьте 1 с обеих сторон этого утверждения.
(AE / CE) + 1 = (AF / CF) + 1
(AE + CE) / CE = (AF + CF) / CF
AC / CE = AC / CF
∴ CE = CF
Для приведенного выше утверждения точки E и F — это одни и те же точки, и они совпадают.Следовательно, прямая DE параллельна BC, и это доказывает обратное к основной теореме пропорциональности.
Важные примечания
- Основная теорема пропорциональности — линия, проведенная параллельно одной стороне треугольника и пересекающая две другие стороны, делит две другие стороны в равной пропорции.
- Обратное к основной теореме пропорциональности — линия, разделенная на две стороны треугольника в равной пропорции, параллельна третьей стороне.
- Теорема о средней точке — линия, проведенная параллельно одной стороне треугольника и половине этой стороны, разделяет две другие стороны в его средней точке.
Сложные вопросы
- Диагонали четырехугольника PQRS пересекаются в точке O, так что PO / QO = RO / SO. Докажите, что PQRS — это трапеция.
Часто задаваемые вопросы по основной теореме пропорциональности
Что такое теорема Фалеса?
Теорема Фалеса, которую также называют основной теоремой пропорциональности, утверждает, что линия, проведенная параллельно одной стороне треугольника и пересекающая две другие стороны, делит эти две стороны в равной пропорции.
Каковы приложения основной теоремы о пропорциональности?
Основная теорема пропорциональности помогает найти длины, на которых две стороны треугольника разделены линией, проведенной параллельно третьей стороне. Кроме того, у него есть приложения для нахождения взаимосвязи между двумя равноугольными треугольниками.
Что такое история теоремы Фалеса?
Теорема Фалеса была предложена Фалесом, греческим математиком и философом около 625 г. до н.э.Теперь это называется основной теоремой пропорциональности, и она помогает найти соотношение между сторонами двух равноугольных треугольников.
Какова формула основной теоремы о пропорциональности?
Базисная формула теоремы пропорциональности для треугольника ABC с точкой D на AB, точкой E на AC и DE // BC выглядит следующим образом.
AD / DB = AE / EC
Что вы имеете в виду под основной теоремой пропорциональности?
Основная теорема пропорциональности утверждает, что если линия проводится параллельно одной стороне треугольника и пересекает две другие стороны, то она делит две другие стороны в равной пропорции.
Как доказать основную теорему о пропорциональности вырезанием из бумаги?
Чтобы показать основную теорему пропорциональности, вырежьте из цветной бумаги треугольник и отметьте его вершины как ABC. Поместите его на бумагу в линейку так, чтобы одна сторона ВС совпадала с линией на бумаге в линейку. Теперь отметьте точки D на AB и E на AC так, чтобы DE была параллельна стороне BC. Теперь измерьте длины AD, BD, AE и CE и проверьте, пропорциональны ли они.
AD / DB = AE / EC
Как решить теорему Фалеса?
Теорема Фалеса аналогична основной теореме пропорциональности.Чтобы решить эту проблему, мы должны доказать, что линия, проведенная параллельно одной стороне треугольника, делит две другие стороны в равной пропорции.
Основная теорема соразмерности
Covid-19 привел мир к феноменальному переходу.
Электронное обучение — это будущее уже сегодня.
Оставайтесь дома, оставайтесь в безопасности и продолжайте учиться !!!
Основная теорема пропорциональности (теорема Фалеса): Если линия проводится параллельно одной стороне треугольника, пересекающей две другие стороны, то она делит две стороны в одинаковом соотношении.
| In ∆ABC, если DE || BC и пересекает AB в D и AC в E, тогда AD AE —- = —— DB EC |
Доказательство теоремы Фалеса:
Если линия проведена параллельно одной сторона треугольника, и он пересекает две другие стороны в двух разных точках, затем он делит две стороны в том же соотношении.
Дано: In ∆ABC, DE || BC и пересекает AB в D и AC в E. Докажите, что: AD / DB = AE / EC Построение: Присоединитесь к BC, CD и нарисуйте EF ┴ BA и DG ┴ CA.
| Заявления | Причины |
| 1) EF ┴ BA | 1) Конструкция |
| 2) EF — высота ∆ADE и ∆DBE 2) Определение | |
| 3) Площадь (∆ADE) = (AD .EF) / 2 | 3) Площадь = (Базовая высота) / 2 |
| 4) Площадь (∆DBE) = (DB.EF) / 2 | 4) Площадь = (Базовая высота) / 2 |
| 5) (Площадь (∆ADE)) / (Площадь (∆DBE)) = AD / DB | 5) Разделить (4) на (5) |
| 6) (Площадь (∆ADE)) / (Площадь (∆DEC)) = AE / EC | 6) То же, что и выше |
| 7) ∆DBE ~ ∆DEC | 7) Оба значения ∆ s находятся на одной базе и между одинаковыми || линий. |
| 8) Площадь (∆DBE) = площадь (∆DEC) | 8) Если два треугольника похожи, их площади равны |
| 9) AD / DB = AE / EC | 9) От (5), (6) и (7) |
Некоторые решенные примеры:
1) На данном рисунке PQ || MN. Если КП / ПМ = 4/13 и КН = 20,4 см.
Найдите KQ.
Решение:
In Δ KMN,
PQ || MN
∴ KP / PM = KQ / QN (по теореме BPT)
⇒ KP / PM = KQ / (KN — KQ)
⇒ 4/13 = KQ / (20.4 — KQ)
⇒ 4 (20,4 — KQ) = 13 KQ (перекрестное умножение)
⇒ 81,6 — 4KQ = 13 KQ
⇒ 17KQ = 81,6
⇒ KQ = 81,6 / 17
∴
KQ = 4,8 см.
———————————————— ——————
2) На рисунке ниже DE || BC. Если AD = x см, DB = x-2 см,
AE = x-1 см, найдите значение x.
Решение:
В треугольнике ABC,
DE || BC
AD / DB = AE / EC (по основной теореме пропорциональности)
⇒ x / (x — 2) = (x + 2) / (x — 1)
⇒ x (x — 1) = (x — 2) (x + 2) (перекрестным умножением)
⇒ x
2 — x = x 2 — 4
⇒ -x = -4
∴ x = 4
Сходство в треугольниках
• Сходство в геометрии
• Свойства подобных треугольников
• Основная теорема пропорциональности (теорема Фалеса)
• Обратное к основной теореме пропорциональности
• Теорема о биссектрисе внутреннего угла
• Теорема о биссектрисе внешнего угла
• Доказательства базовой пропорциональности
• Критерии Сходство треугольников
• Среднее геометрическое количество похожих треугольников
• Области двух похожих треугольников
Домашняя страница
Covid-19 повлиял на физическое взаимодействие между людьми.
Не позволяйте этому влиять на ваше обучение.
теорема Фалеса — zxc.wiki
Теорема Фалеса — это набор геометрии и частный случай набора углов окружности. Проще говоря: Все углы полукруглой дуги — прямые .
Первое доказательство приписывается древнегреческому математику и философу Фалесу Милетскому. Формулировка приговора уже была известна в Египте и Вавилонии.
Формулировка приговора и его изменение
Полукруг с прямоугольными треугольниками
Точная формулировка: если вы построите треугольник из двух конечных точек диаметра полукруга ( круг Фалеса ) и другой точки этого полукруга, вы всегда получите прямоугольный треугольник.
Или: если точка C треугольника ABC лежит на полукруге над отрезком AB, то треугольник в точке C всегда имеет прямой угол.
Верно и обратное предложение: центр окружности прямоугольного треугольника всегда находится в середине гипотенузы, т.е.е. самая длинная сторона треугольника, противоположная прямому углу.
Или: Если треугольник ABC имеет прямой угол в C, то C лежит на окружности с гипотенузой AB в качестве диаметра.
проб
Евклид выводит предложение Фалеса в третьем томе своих элементов с помощью следующих предложений, которые также приписываются Фалесу и содержатся в первом томе:
- В любом равнобедренном треугольнике углы при основании одинаковые.
- Сумма внутренних углов в треугольнике равна 180 °.
Полукруг с треугольником и центром M
Пусть ABC будет треугольником внутри круга с диаметром окружности [AB] и радиусом r . Тогда центр M отрезка [AB] также является центром окружности. Таким образом, длины маршрута [AM], [BM] и [CM] равны радиусу r .
Отрезок [CM] делит треугольник ABC на два равнобедренных треугольника AMC и BCM.{\ circ}}.
Это показывает, что угол с вершиной C является прямым.
α + β {\ Displaystyle \ альфа + \ бета}
Обратное к теореме Фалеса восходит к утверждению, что диагонали прямоугольника равны по длине и делят друг друга пополам.
Еще одно доказательство можно найти здесь: Wikibooks: Evidence Archive.
Приложения
Построение касательной к окружности
Важным применением теоремы Фалеса является, среди прочего, построение двух касательных к окружности k через точку P вне этой окружности.
Построение касательных к окружности
Дан радиус r окружности k с центром O и расстояние между точками P и O. Мы знаем только, что точка T должна лежать на круговой прямой где-то в первой четверти круга k. Если бы только это условие было учтено, можно было бы нарисовать бесконечное количество треугольников OPT.
Поскольку верхняя касательная t, проходящая через точку P, касается окружности k точно в точке T, треугольник OPT должен иметь прямой угол в точке T (основное свойство касательной к окружности), или, другими словами: прямая [OT] должна быть перпендикулярно касательной t.
Чтобы найти треугольник OPT, который также является прямоугольным, мы определяем центр H линии [OP] с помощью перпендикуляра, рисуем круг с радиусом [HO] вокруг центра H и используем принцип круга Фалеса: Все треугольники со стороной основания [OP], третья угловая точка которых лежит на окружности Фалеса, являются прямоугольными. Конечно, это относится и к треугольнику OPT.
Точка контакта T, следовательно, может быть только пересечением круга k со светло-серым кругом.Теперь, соединив P с T, можно получить желаемую касательную t (красный цвет на чертеже).
В нижней половине круга есть второе, симметричное решение. Касательная t ‘(также нарисованная красным) также касается окружности, а именно в точке T’.
Квадратурный прямоугольник
Еще одно приложение — квадрат прямоугольника.
Построение действительных квадратных корней
С помощью теоремы Фалеса можно построить следующие квадратные корни:
Число больше 1
Число больше 1: построение с помощью циркуля и линейки q {\ displaystyle {\ sqrt {q}}} c {\ displaystyle {\ sqrt {c}}}
Если квадратный корень из числа, большего, чем нужно найти без предварительного деления числа на части — и -, подходит метод, показанный на рисунке рядом.В принципе, квадратные корни из чисел меньше, чем можно вообразить.
1 {\ displaystyle 1} п {\ displaystyle p} q {\ displaystyle q} 1 {\ displaystyle 1}
Начинается с построения маршрута, длина которого по прямой, здесь не указана. Если заданное число является целым числом, произведение из точки наносится на прямую линию; то есть z. Б. число, расстояние нанесено восемь раз. Получившееся пересечение приносит гипотенузу получившегося треугольника B.D. ¯ {\ displaystyle {\ overline {BD}}} 1 (= p) {\ displaystyle 1 \; (= p)} q {\ displaystyle q} q⋅BD¯ {\ displaystyle q \ cdot {\ overline {BD}}} D. {\ displaystyle D} q = 8th {\ displaystyle q = 8} BD¯ {\ displaystyle {\ overline {BD}}} A. {\ displaystyle A} c = p + q {\ displaystyle c = p + q} ABC. {\ displaystyle ABC.}
— это десятичное число (например, B.) и т. Д. Также возможно с использованием третьего набора лучей для построения.
q {\ displaystyle q} 8-е, 6-е {\ displaystyle 8 {,} 6} q {\ displaystyle q}
Далее следует вертикальная линия в точке и деление стороны пополам в. Наконец, обводится круг Фалеса.{2} = 1 \ cdot c,}
- , таким образом, длина стороны прямоугольного треугольника равна квадратному корню из .a {\ displaystyle a} A.B.C. {\ Displaystyle ABC} c {\ displaystyle c}
Число меньше 1
Число меньше 1: построение с помощью циркуля и линейки p⋅q, q {\ displaystyle {\ sqrt {p \ cdot q}}, \; {\ sqrt {q}}} п {\ displaystyle {\ sqrt {p}}}
Если квадратный корень из числа меньше искомого, подходит метод, показанный на рисунке рядом.1 {\ displaystyle 1}
Начинается с точки (значения) с полупрямой. Затем определяются маршрут с длиной и маршрут с длиной. В результате получается гипотенуза получившегося треугольника. Если данное десятичное число имеет только один десятичный разряд , произведение отображается от точки; то есть z. Б. Маршрут удаляется восемь раз. Полученное пересечение приводит к A. {\ displaystyle A} 0 {\ displaystyle 0} A.B. ¯ {\ displaystyle {\ overline {AB}}} 1 {\ displaystyle 1} A.Е. ¯ {\ displaystyle {\ overline {AE}}} 0,1 {\ displaystyle 0 {,} 1} c {\ displaystyle c} ABC. {\ Displaystyle ABC.} Q {\ displaystyle q} q⋅ AE¯ {\ displaystyle q \ cdot {\ overline {AE}}} A. {\ Displaystyle A} q = 0,8th {\ displaystyle q = 0 {,} 8} AE¯ {\ displaystyle {\ overline {AE} }} D. {\ Displaystyle D} c = p + q. {\ Displaystyle c = p + q.}
Если данное десятичное число имеет на более одного разряда после десятичной точки (например), можно, как уже указывалось выше в числе больше 1 , построить с помощью третьей теоремы о лучах.q {\ displaystyle q} q = 0,86 {\ displaystyle q = 0 {,} 86} q {\ displaystyle q}
Затем следует вертикальная линия на линии в точке и деление стороны пополам в. Наконец, обводится круг (радиус) Фалеса.
AB ¯ {\ displaystyle {\ overline {AB}}} D. {\ Displaystyle D} c {\ displaystyle c} M .. {\ displaystyle M.} = 0,5 {\ displaystyle = 0 {,} 5} M . {\ displaystyle M}
- Согласно теореме Евклида о высоте h3 = p⋅q, {\ displaystyle h ^ {2} = p \ cdot q,}
- , таким образом, высота прямоугольного треугольника равна квадратному корню из H {\ displaystyle h} A.{2} \ Rightarrow}
- b = q, {\ displaystyle b = {\ sqrt {q}},}
- , таким образом, длина стороны прямоугольного треугольника равна квадратному корню из b {\ displaystyle b} A.B.C. {\ Displaystyle ABC} q. {\ Displaystyle q.}
- Для длины стороны a: {\ displaystyle a:}
- При соответствующих значениях длины стороны результат аналогичен длине стороныha {\ displaystyle a} b: {\ displaystyle b:}
- a = p, {\ displaystyle a = {\ sqrt {p}},}
- , таким образом, длина стороны прямоугольного треугольника равна квадратному корню из a {\ displaystyle a} A.Прокл. В: Евклид: Элементы. I, 250.20
Первые доказательства: Фалес и начало геометрии
Podcast: Download
Доказательная геометрия началась с Thales. Приписываемые ему теоремы заключают в себе два способа выполнения математических вычислений, предполагая, что идея доказательства могла исходить из любого из двух источников: внимания к шаблонам и отношениям, возникающим в результате исследовательского конструирования и игры, или осознания того, что «очевидные» вещи могут быть продемонстрировано с использованием формальных определений и доказательства от противного.
Выписка
Как начались доказательства? Это похоже на головоломку с курицей или яйцом. Зачем кому-то садиться и говорить себе: «Я собираюсь доказать некоторые теоремы сегодня», если никто никогда не делал ничего подобного раньше? Как эта идея могла так неожиданно прийти в голову кому-то?
На самом деле, мы вроде как знаем ответ. Греческая традиция говорит нам, у кого был этот момент лампочки: у Фалеса. Примерно в году -600 или около того. За сотни лет до того, как у нас появились какие-либо прямые исторические источники по греческой геометрии.Но мы все еще более или менее знаем, что доказал Фалес. Более поздние источники рассказывают нам о Фалесе. История, возможно, смешана с легендами в подобных отчетах, но ключевые аспекты, вероятно, будут довольно надежными. Больше фактов, чем выдумок. Давайте проанализируем этот вопрос, вопрос о достоверности, более подробно позже, но сначала давайте примем истории за чистую монету и посмотрим, как мы можем пережить создание дедуктивной геометрии, как это передано в этих греческих историях.
Итак, поехали: какая первая теорема была доказана? Что стало той искрой, которая зажгла пожар аксиоматико-дедуктивной математики? Лучшее предположение, основанное на исторических свидетельствах, звучит так.Момент любви с первого взгляда, та теорема, открывшая нам глаза на силу математического доказательства, заключалась в следующем: диаметр разрезает круг пополам.
Довольно разочаровывающе, не правда ли? Какая неубедительная теорема. Это даже не теорема. Как можно влюбиться в геометрию, доказывая что-то столь тривиальное и очевидное?
Но не отчаивайтесь. Вообще-то, это приятно. Дело не в теореме, а в доказательстве.
Вот как это доказать. Предположим, что нет. Это будет доказательство от противного.Предположим, диаметр не делит круг на две равные половины. Хорошо, у нас есть линия, проходящая через середину круга, и она разрезана на две части. И мы предполагаем, что эти две части не совпадают. Возьмите один из кусочков и переверните его на другой. Как вы складываете омлет или креп. Мы предположили, что части не равны, поэтому, когда вы кладете одну на другую, они не совпадают. Так что должно быть какое-то место, где одна из двух частей выступает над другой.Теперь нарисуйте радиус в этом направлении от середины круга до места по периметру, где две половины не совпадают. Тогда один радиус длиннее другого. Но это означает, что дело было не в круге с самого начала. Круг — это фигура, одинаково удаленная от середины во всех направлениях. Вот что значит быть кругом.
Итак, мы доказали, что две вещи несовместимы друг с другом: нельзя одновременно быть кругом и иметь несовпадающие половинки. Потому что, если у вас есть несовпадающие половинки, у вас также есть «неравные радиусы», а это значит, что вы не круг.
Итак, у круга должны быть равные половины. Бам. Теорема. Скучный результат, но великолепное доказательство. Или убедительное доказательство. Это доказательство, намекающее на новый мир.
Фалес, должно быть, чувствовал себя волшебником, который только что обнаружил, что обладает сверхспособностями. «Ого, ты можешь это сделать ?!» С помощью чистого рассуждения, вычеркивая последствия определения, можно без тени сомнения доказать, что определенные утверждения не могут быть неправильными? Это вещь? Это то, что можно сделать? Ух ты. Давайте сделаем это со всем! Верно?
Так вот как Фалес открыл доказательство.Насколько мы можем догадаться.
Несколько других теорем также приписываются Фалесу. Я хочу особо остановиться на одном, который, как мне кажется, также является своего рода архетипом того, что из себя представляет математика.
Теорема, которую мы только что рассмотрели, о диаметре, разделяющем окружность пополам, идеально воплощает один из прототипов математических рассуждений. Вы могли бы назвать это парадигмой чистой математики. Логические следствия определений, доказательства от противного. Такие вещи. Доказательство Фалеса действительно поражает своей эстетикой.С тех пор мы делаем одно и то же снова и снова. Например, современный курс теории групп — это всего лишь идея доказательства Фалеса, примененная, по сути, пятьсот раз.
Теперь я хочу взять еще один результат, приписываемый Фалесу, и я хочу утверждать, что он символизирует другой способ математической мысли. Это второй путь к доказательствам. Этот второй способ основан больше на игре, исследовании, открытии, чем на логике и определениях.
Пример, который я хочу использовать, чтобы показать это, — это то, что на самом деле часто называют просто «теоремой Фалеса».Который утверждает, что любой треугольник, возвышающийся на диаметре круга, имеет прямой угол. Другими словами, изобразите круг. Разрежьте его пополам диаметром. Теперь поднимите треугольник, используя этот диаметр как одну из его сторон, и третья вершина треугольника находится где-то на окружности. Так что это похоже на палатку, торчащую из диаметра. И это может быть асимметричная палатка, которая больше направлена в ту или иную сторону. Независимо от того, как вы устанавливаете эту палатку, до тех пор, пока ее кончик находится в любой точке круга, тогда угол между двумя стенами палатки в этой точке, на вершине, будет прямым углом, 90 градусов. .Это теорема Фалеса.
Как мог Фалес доказать эту теорему? К сожалению, мы не знаем этого, основываясь на исторических данных. Но давайте рассмотрим одну гипотезу, которая имеет смысл с точки зрения контекста.
Мы должны представить, что Фалес каким-то образом наткнулся на доказательство. Мы не пытаемся объяснить, как кто-то может думать о доказательстве этой теоремы как таковой. Это неправильная точка зрения, потому что считается само собой разумеющимся, что в математике кто-то пытается что-то доказать. Нам нужно объяснить, откуда взялось это видение, чтобы доказать все в геометрии.Как мог кто-то случайно натолкнуться на теорему Фалеса и благодаря этой случайности осознать идею дедуктивной геометрии?
Действительно, теорема Фалеса сама по себе не слишком интересна или важна. Если бы у вас было видение систематического доказательства всей геометрии, почему бы вам начать с этой теоремы или сделать ее центральной частью, как якобы сделал Фалес? Ты бы не стал.
Теорема Фалеса интересна не в том, что это был один из первых результатов, к которому математики применили дедуктивное доказательство.Скорее, интересно то, что математики случайно наткнулись на саму идею доказательства.
Есть история о Фалесе, который упал в колодец, потому что он настолько увлекся астрономическими рассуждениями, что забыл о своем окружении. У Платона записано: «Когда он изучал звезды и смотрел вверх, он упал в яму. Поскольку ему так хотелось познать вещи в небе, он не мог видеть того, что было перед ним у самых его ног.”
Возможно, это легенда, но открытие теоремы Фалеса, должно быть, было чем-то вроде этого. Обнаружение математического доказательства должно было быть похоже на падение в яму. Вы смотрите в одном направлении и бум! Вы внезапно обнаруживаете, что сначала случайно врезались лицом в эту совершенно не связанную новую вещь, о существовании которой вы даже не подозревали.
Как могла быть теорема Фалеса такой? Что из всех мировых теорем делает теорему Фалеса особенно благоприятной для такого рода случайного открытия доказательства?
Вот моя гипотеза.В этот век невинности, прежде чем кто-либо знал что-либо о доказательствах, людям все еще нравились формы. У них были линейка и компас. Они использовали эти инструменты для измерения полей и прочего, но им также нравилась его эстетика.
Они игрались с линейкой и компасом. Играем с фигурами. После пяти минут игры с компасом вы узнаете, как нарисовать правильный шестиугольник. Помнить? Вы, наверное, делали это в детстве. Нарисуйте круг, а затем, не меняя отверстия компаса, проведите циркулем по окружности.Умещается ровно шесть раз. Очень приятная форма.
Мы точно знаем, что люди делали это до Фалеса. В мозаиках Месопотамии есть шестиугольные мозаичные узоры, датируемые примерно -700 годом.
Додекаэдры — еще одна из таких вещей. Додекаэдр похож на те двенадцатигранные кости, которые вы используете в Dungeons and Dragons и тому подобное. До-дека-эдр, буквально: двухсторонний. Другими словами, так двенадцать сторон. Двенадцать граней, каждое из которых представляет собой правильный пятиугольник.Эти вещи есть в археологической летописи. Люди делали их из камня и бронзы. Было обнаружено несколько десятков древних додекаэдров, самые старые из них были найдены еще до Фалеса. Возможно, они использовались для пророческих целей, например, карты Таро или что-то в этом роде. А может, для настольных игр, кто знает?
В любом случае, я хочу сказать, что люди интересовались геометрическими рисунками для различных целей: художественных, культурных и так далее. Не только для измерения полей в налоговых целях. И они явно работали с такими инструментами, как линейка и компас, чтобы делать эти вещи.
К теореме Фалеса легко прийти, просто играя с линейкой и циркулем, пытаясь нарисовать красивые вещи. Начните с прямоугольника. Нарисуйте его диагонали. Поместите стрелку циркуля в место пересечения, прямо в середину прямоугольника. Установите перо циркуля в один из углов прямоугольника. Теперь крутите его. У вас получится круг, который идеально и плотно прилегает к прямоугольнику.
Но посмотрите, что получилось. Диагональ прямоугольника становится диаметром круга.А выступающие из него прямоугольники — это как раз те треугольники-шатры, о которых говорит Теорема Фалеса. Это внезапно делает теорему очевидной.
Почему теорема Фалеса верна? Почему любая из этих «палаток», поднятых на диаметре круга, имеет прямой угол? Потому что он исходит из прямоугольника. Любая такая палатка представляет собой половину прямоугольника. Это мощный сдвиг в перспективе. Глядя на треугольник таким образом, мы обнаруживаем скрытые отношения, скрытый порядок в природе вещей.Определенные углы всегда должны быть прямыми в силу своего рода метафизической необходимости. Наши глаза были открыты, возможно, впервые, на существование такого рода потребностей, этих видов скрытых отношений, которые существует, чтобы мыслящий человек мог раскрыть.
Итак, ключ к этому сдвигу перспективы, что треугольник «на самом деле» является половиной прямоугольника. Предположим вместо этого, что мы застряли в точке зрения, что мы смотрим на треугольник, вписанный в круг.Тогда те ассоциации и идеи, которые нам напрашиваются, не так полезны для доказательства этой теоремы. С этой точки зрения, если бы вы искали доказательства, что бы вы сделали? Может быть, вы, например, соедините середину круга с концом треугольника. Итак, теперь у вас есть два меньших треугольника. Что ты собираешься с ними делать? Что-нибудь с суммами углов и так далее? Или, может быть, у вас возникнет соблазн опустить перпендикуляр вместо вершины треугольника, а затем вы можете использовать теорему Пифагора о двух маленьких треугольниках, которые вы получите.
Такие вещи не то, что мы хотим. Подобные подходы быстро становятся слишком техническими. Помните, это должно было быть началом геометрии. Вы не должны использовать кучу предыдущих результатов для доказательства. Это должно быть доказательство из первых принципов. Доказательство перед всеми другими доказательствами.
Идея о том, что треугольник «на самом деле» является половиной прямоугольника, отличается. Это меняет то, как мы смотрим на диаграмму. Это меняет акценты. Это меняет то, что мы считаем основным.Теперь прямоугольник идет первым, треугольник — вторым, а круг — последним. С этой точки зрения теорема на самом деле вовсе не касается кругов, так сказать. Круг — это своего рода вторичный артефакт.
В этом доказательстве мы как художники. Мы отошли от холста, наклонили голову и увидели это прозрение. И прозрение стало возможным благодаря тому, как мы раньше играли с этими идеями. Мы просто играли с линейкой и циркулем, мы исследовали треугольники, прямоугольники и круги с непредубежденной любовью.Из этой пьесы рождаются такие прозрения, как теорема Фалеса. В этом контексте естественно приходит вдохновение.
В отличие от других скучных доказательств, на которые я ссылался, которые были основаны на разрезании треугольника и бросании в него книги: суммы углов, теорема Пифагора, все, что мы можем придумать. Это скучный подход, подход грубой силы. Ему не хватает того эстетического вдохновения, этого прозрения, раскрывающего истинную природу треугольника и его второй половины, с которой ему было суждено воссоединиться.
Геометрия не могла начаться с такого рода практических доказательств, потому что они имеют смысл только после того, как для начала есть книга по геометрии. Но геометрия могла начаться с доказательства типа прозрения. Таким образом, кто-то вроде Фалеса мог прийти к идее доказательства, играя с линейкой и компасом.
Возможно, вы знакомы с «Плачом Локкарта»: отличным эссе о том, что не так с математическим образованием. Иди и прочитай, он доступен в Интернете.Интересно, что Локхарт использует именно этот пример, чтобы доказать свою точку зрения. Он описывает, как его ученики открыли теорему Фалеса, в основном так, как я говорю, что Фалес мог это сделать. Он также красноречиво показывает, насколько это удовлетворяет гораздо больше, чем сухое доказательство, записанное в книге.
Недаром в этом вопросе история и образование идут рука об руку. Доказательство должно было начаться с убедительного эстетического опыта или вау-момента. В то время другого пути не было. Заставить Фалеса запоминать факты для экзамена было некому.Открытие заставило его ценить математику. Если мы хотим развить внутреннюю мотивацию у наших студентов, неплохо было бы в первую очередь подумать, что заставило людей полюбить эти идеи. Первая любовь всегда чистейшая и невинная. Современные учебники похожи на браки по договоренности, навязанные студентам. Но в истории всегда есть настоящая история любви.
Тем не менее, несмотря на все это, вы все равно можете подумать, что теорема Фалеса немного скучна. Что-то всегда есть под прямым углом.Ну и что? Какая разница?
Как я пытался утверждать, Фалеса и его современников, вероятно, впечатлила не сама по себе теорема, а, скорее, идея о том, что теоремы и доказательства вообще существуют. Есть скрытые истины, которые можно раскрыть с помощью рассуждений. Замечательный.
Но на самом деле интересна и сама теорема. Позвольте мне показать вам кое-что интересное, что вы можете сделать с помощью теоремы Фалеса.
Существует древняя легенда о царице Дидоне.Дочь царя Тира, крупного города в древности. Вы все еще можете увидеть руины этого древнего города на территории современного Ливана. В какой-то момент Дидоне пришлось бежать из-за придворных интриг. Убийства и предательства и так далее. Поэтому она берет с прикроватной тумбочки пару диадем, может быть, сундук с золотом, который отложила на дождливый день, и торопливо уходит в ночь. С едва ли в мире остался друг.
Ей нужно пройти весь путь до нынешнего Туниса, находящегося за тысячи километров, и попытаться как-то начать все сначала, как приличествует королевской семье.Используя свой сундук с сокровищами, она заключает сделку, чтобы купить землю. Как гласит легенда, столько земли, сколько она может покрыть шкурой быка. Она разрезала бычью шкуру на тонкие полоски и связала их вместе, и что теперь? Итак, теперь у нее есть длинная веревка, которую она может использовать как своего рода забор, чтобы изолировать желаемую землю.
Но какой формы сделать? Квадрат, прямоугольник, треугольник? Нет. Дидоне виднее. Возможно, ее королевское образование включало математику. Сделайте это круглым. Это лучший способ.Круг имеет максимальную площадь среди всех фигур с заданным периметром. Или в данном случае, поскольку она была у океана: полукруг, с другой стороны береговой линией, естественной границей.
Давай докажем это. Что полукруг — лучший выбор. Я собираюсь доказать это с помощью противоречия: предположим, что кто-то построил забор на участке, который не является полукругом; Затем я могу показать, как это сделать лучше: как переместить забор так, чтобы площадь стала еще больше, без добавления забора.
Хорошо, у вас есть береговая линия, это прямая линия. И из одной точки на берегу, идя вглубь, у вас есть этот забор, который затем снова спускается и снова встречается с берегом в какой-то другой точке. Так что вместе с береговой линией он закрывает определенную территорию.
Предположим, эта форма не является полукругом. Если бы это был полукруг, применима теорема Фалеса. И он сказал бы вам, что этот угол, то, что я назвал углом палатки, в любой точке вдоль забора будет прямым углом.Итак, если фигура не является полукругом, на заборе должна быть точка, где этот угол не является прямым.
Я говорю, что если сделать этот угол прямым, то увеличится площадь покрытия. Вы можете представить это так. Итак, у вас есть форма, окруженная забором: представьте, что у вас есть вырез из картона. А по периметру у вас есть отмеченная точка, где угол палатки не является прямым ангелочком. Итак, на вашем картоне нарисован этот треугольник: треугольник, состоящий из прямой береговой линии с одной стороны и двух линий от его концов, идущих вверх, чтобы встретиться в точке палатки по периметру.
Давайте вырежем этот треугольник из картона. Итак, у вас остались две части: любые части, которые торчали из сторон треугольника. Теперь переместите эти две части так, чтобы угол палатки получился прямым. Это означает перемещение конечных точек вдоль береговой линии. Перемещая две точки на береговой линии, вы меняете угол, под которым встречаются две картонные части. Две картонные части встречаются в одной точке, точке палатки, и это похоже на петлю, которая может открываться или закрываться на больший или меньший угол.Таким образом, вы перемещаете эти штуки, пока угол поворота не станет 90 градусов.
Обратите внимание, что вы не меняли периметр таким образом. Вы только что переместили такое же количество забора.
Но вы действительно увеличили огражденную площадь. Потому что, если у вас есть две палки фиксированной длины, и вы хотите сделать из них самый большой треугольник, лучший способ — сделать угол между ними прямым. Это интуитивно понятно. Вы знаете, что площадь треугольника равна основанию, умноженному на высоту, больше двух.Итак, если одна из ваших палочек является основанием, то для увеличения площади вы хотите максимизировать высоту, то есть перпендикулярную высоту, идущую вверх от основания, что, очевидно, достигается путем направления другой палки вверх под прямым углом.
Итак, это доказывает, что для любого ограждения, не являющегося полукругом, вы можете сделать лучший. Вы можете передвинуть забор и увеличить площадь. Так что полукруг — лучшее решение, а все остальные менее хороши.
Не знаю, сможете ли вы все это представить себе.Но, может быть, позже попытайтесь реконструировать этот аргумент для себя. Это действительно очень интуитивно понятно и красиво.
Так в чем же тогда мораль этой истории? Математически это ответ на вопрос «ну и что?» вопрос относительно теоремы Фалеса. Это могло показаться достаточно скучной теоремой, но здесь мы видим ее в действии красивым и неожиданным образом, как ключевой ингредиент в этом доказательстве о том, как оградить землю. Кто бы мог предвидеть это?
Это говорит о том, что у математики есть своего рода «снежный ком» или аспект самооплодотворения.Теорема Фалеса, в чем дело? Просто скучное наблюдение о треугольнике в круге. Может показаться, что это не так уж и много. Но одно ведет к другому. Когда вам становится понятна теорема Фалеса, вы начинаете видеть ее в других, неожиданных местах. Как эта проблема о районе. Вы бы не подумали, что это связано, но чем больше вы занимаетесь математикой, тем больше связей вы обнаруживаете.
Выберите любую теорему, какой бы скучной она ни была, например, теорема Фалеса, и вы сможете найти эти удивительные вещи, в которых скучная теорема на самом деле является ключевым моментом, открывающим совершенно новые способы осмысления, казалось бы, несвязанных проблем.Это для вас математика. Неудивительно, что греки прижились как жук, как только они сдвинулись с мертвой точки. В один момент вы наталкиваетесь на какой-то случайный результат, например, теорему Фалеса, а в следующий момент вы знаете, что видите математику повсюду.
Такова математическая мораль истории. Теперь мы должны вернуться и сказать кое-что об исторической стороне всего этого. Что мы действительно знаем о Фалесе и его теоремах, королеве Дидоне и всем остальном? Сколько истории и сколько легенд?
Если мы начнем с Дидоны, эта история используется в основном через Вергилия.Энеида, знаменитая эпическая поэма. Это было написано во времена Римской империи, примерно в -20 году. Но это относится к историческим или якобы историческим событиям, которые произошли еще до Фалеса, может быть, за два столетия до Фалеса, то есть примерно 800-х годов. У нас есть версия Верджила, это то, что до нас дошло, но он просто крадет старую историю. Эти вещи существовали веками в греческой культуре, в различных литературных и исторических пересказах, которые сейчас утеряны.
Совершенно правдоподобно, что действительно существовала такая историческая королева, которая действительно покинула свой королевский дом в Тире и действительно приземлилась на северных берегах Африки, где она основала это новое поселение, которое должно было стать великим городом Карфаген. .Может быть, она даже сделала полукруглыми городские стены, кто знает? Совершенно очевидно, что она могла хотеть минимизировать периметр по какой-либо причине, и что она могла знать, что полукруглая форма была оптимальной для этой цели.
Но в то время не было бы никаких математических доказательств этого, подобных тому, которое я набросал выше. Приведенное мной доказательство принадлежит Якобу Штайнеру в начале 19 века. Со времен Греции у нас есть другое доказательство этого результата.Таким образом, они, конечно, очень хорошо знали результат, что полукруг является оптимальным, если, возможно, не то конкретное доказательство, которое я предложил.
Если история царицы Дидоны говорит что-либо об истории математики, она, вероятно, больше всего не освещает ни время, когда произошли события, около -800, ни время, когда были написаны источники, которые у нас есть, около года 0. Но, может быть, это так. что-то говорит о промежуточных веках, когда история могла бы быть передана и переработана.
История была как бы маринована в греческой культуре.Возможно, они были теми, кто придал этому математический оттенок. Подходит для обуви: греки ценили мудрых, аристократических, хорошо образованных правителей, которые разрабатывают рациональную политику для общего блага, основанную на разуме и математике. Может быть, они позволили этим идеалам окрасить то, как они пересказывают историю королевы Дидоны и ее круглого города.
С этой точки зрения мы также можем предположить, что к тому времени, когда Вергилий придет и напишет римскую версию истории, это понимание математики уже не то, чем было раньше.В самом деле, Верджил не раскрывает математический аспект оптимизации истории. Дидона — всего лишь второстепенный персонаж. Его эпос об Энее, который находится в поисках, которые в конечном итоге приведут к основанию Рима.
Эней терпит кораблекрушение и выносится на берег в Карфагене, круглом городе Дидоны. Дидона влюбляется в него, но он не отвечает на ее любовь. Он уплывает, и Дидона убивает себя из-за разбитого сердца. Моррис Клайн завершает рассказ: «Итак, неблагодарный и невосприимчивый человек с жестким умом стал причиной потери потенциального математика.Это был первый удар по математике, нанесенный римлянами ». Конечно, есть еще много всего, откуда это взялось.
Можно рассматривать эту историю как символ этого перехода от мудрых философов-королей (или в данном случае королев) греческого мира, которые лелеяли математику и использовали ее для улучшения мира. Переход от этого к бессердечному римлянину, который думает только о себе и не заботится о теореме Фалеса. В греческом мире ботаники-математики считались привлекательными, но каким-то образом эти невежественные римляне явно не думали, что королева-геометрист вообще может быть подружкой.
Итак, история о Дидоне и круглом городе, о доказательстве оптимизации и всем остальном очень интересна с точки зрения более широких математических и культурных точек, с которыми она связана, но сама по себе она не является историей как таковой.
С Thales все иначе. Это больше факт, чем легенда. Насколько мы можем определить, Фалес действительно доказал, что диаметр делит окружность пополам, скорее всего, с помощью доказательства, обсужденного выше.
Источники, которые у нас есть для этого, далеки от совершенства.В первую очередь Прокл, писавший примерно в 450 году, то есть через тысячу лет после жизни Фалеса. Такого рода запоздалые источники попадают в заблуждение. У них нет авторитета сами по себе. Прокл был никем. Его собственное понимание истории и математики очень плохо. Посредственный мыслитель, посредственный ученый, живущий в посредственном возрасте.
Таковы источники, которые у нас есть. По сути, столь же авторитетный, как факт, который вы читаете на обратной стороне коробки с хлопьями или чего-то подобного.
Но есть надежда.Во времена своей славы Греция была просто выдающейся интеллектуальной культурой. И кое-что, например, о Фалесе, можно проследить до тех пор, что делает его весьма достоверным. Ученик Аристотеля Евдем написал историю геометрии. Увы, этого уже нет. Возраст невежества игнорировал это, и теперь его нет. Но что это была бы за работа.
Эти люди знали, что делают. Более поздние люди, подобные Проклу, похожи на некоторых онлайн-рандомов, которые публикуют недоработанные идеи в блоге или плохо информированные комментарии в Facebook.Вот насколько они заслуживают доверия.
Но люди вроде Евдема — совсем другая история. Это больше похоже на первоклассного ученого в исследовательском учреждении со всей инфраструктурой, о которой можно только мечтать: библиотеки, чрезвычайно знающие и умные коллеги с широким спектром знаний, широкая финансовая и культурная поддержка со стороны общественности и политиков и т. Д. . «История геометрии» Евдема могла бы стать настоящей книгой «University Press», отрецензированной до зубов и с красивой аннотацией Аристотеля в суперобложке.
Такие люди, как Евдем, не занимались распространением случайных сплетен и непроверенных фактоидов, потому что они звучат круто. Они были настоящими учеными и интеллектуалами.
И действительно, многие сведения о Фалесе можно проследить до этого потерянного источника. Когда Прокл говорит, что Фалес был первым, кто доказал, что круг делится пополам по его диаметру, источником этого является Евдем. Следовательно, это очень достоверно. Это случилось с Фалесом на самом деле. На самом деле часть о диаметре, разделяющем окружность пополам, более определена, чем часть о теореме Фалеса.Была ли теорема Фалеса на самом деле теоремой Фалеса? Может быть. Но мы не можем проследить конкретно эту часть до лучших источников. В отличие от диаметра пополам одной и некоторых других деталей. Но с точки зрения контекста это имеет смысл.
Истории Фалеса и происхождения геометрии, очевидно, были хорошо известны не только специализированным ученым, но и широкой афинской публике. Драматург Аристофан несколько раз в своих пьесах использует имя Фалеса как символ геометрии. Так же, как сегодня, можно использовать имя Эйнштейна, например, чтобы вызвать образ ученого.У Аристофана один говорящий в диалоге говорит: «Этот человек — Фалес». Это означает, что человек — геометр. Очевидно, можно было ожидать, что театральная публика в классических Афинах поймет это упоминание. Каждый образованный человек знал бы о Фалесе и истоках геометрии.
На самом деле, общественное уважение к геометрии и ее истории было очевидно настолько велико, что Аристофан даже заставил одного из своих персонажей оплакивать ее как чрезмерную, говоря: «Почему мы продолжаем восхищаться старым Фалесом?» Какое время было бы жить.Когда драматургам приходилось решать такие проблемы, как чрезмерное уважение и интерес к математике среди широкой публики. «Привет, ребята, может быть, нам нужно охладить это тем, насколько мы любим геометрию». Какая проблема с роскошью. Едва ли та, с которой сегодня приходится бороться голливудским блокбастерам.
В любом случае, нам, возможно, не стоит слишком углубляться в эти отдельные цитаты.

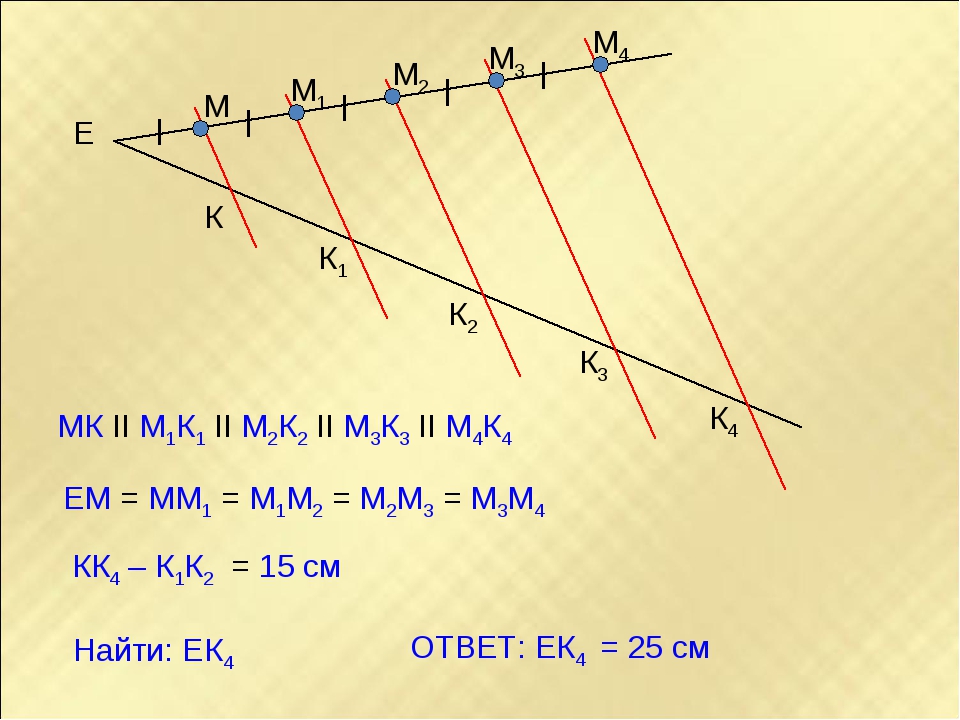
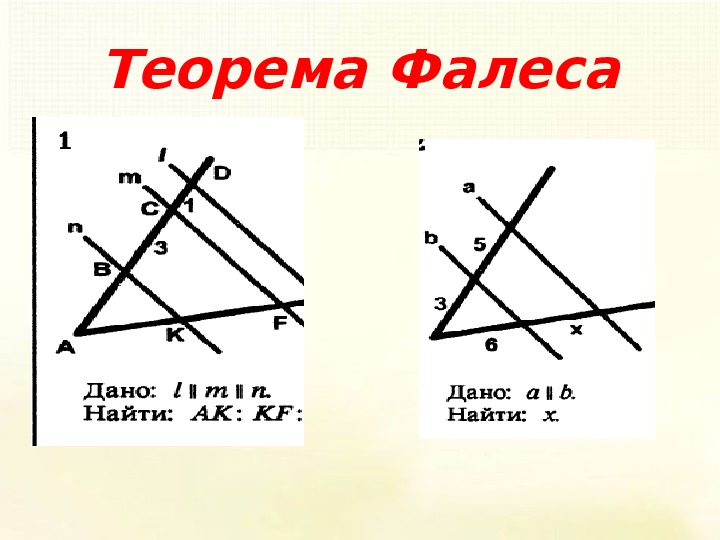 Однако в соответствии с
Однако в соответствии с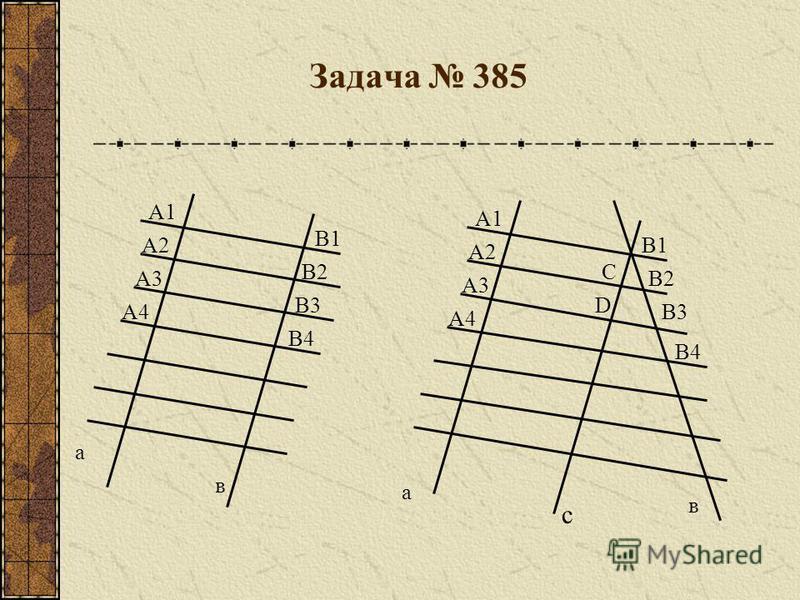
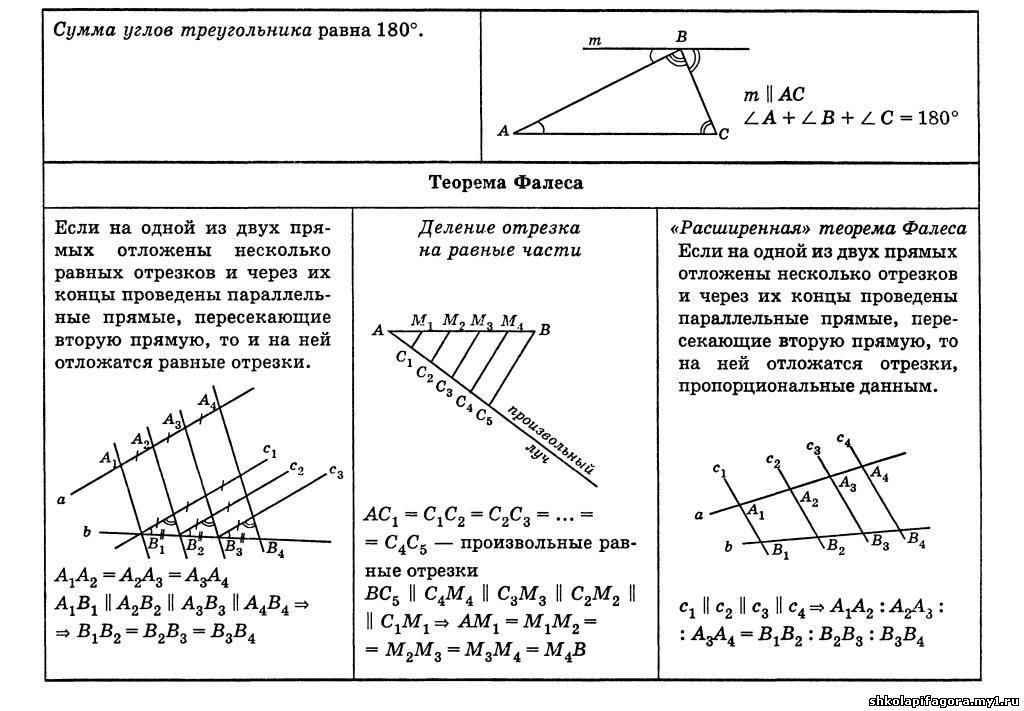 Следы горизонтальной и
Следы горизонтальной и