Содержание
Теорема пифагора и обратная ей. Урок «теорема, обратная теореме пифагора». Обратная теорема Пифагора
Теорема Пифагора
— одна из основополагающих теорем евклидовой геометрии, устанавливающая соотношение
между сторонами прямоугольного треугольника .
Считается, что доказана греческим математиком Пифагором, в честь которого и названа.
Геометрическая формулировка теоремы Пифагора.
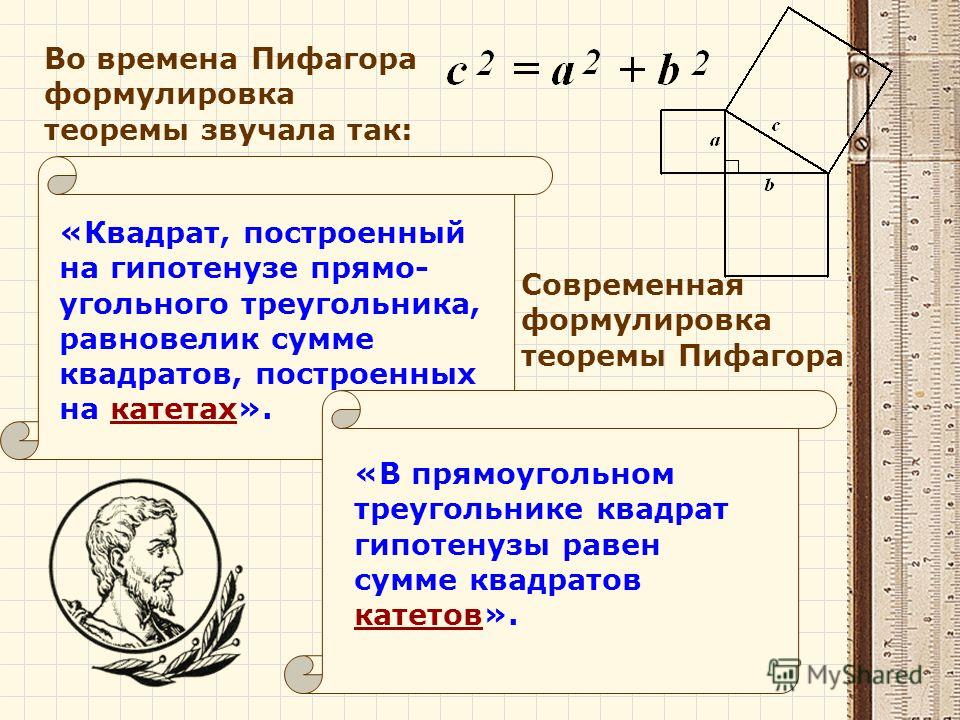
Изначально теорема была сформулирована следующим образом:
В прямоугольном треугольнике площадь квадрата , построенного на гипотенузе , равна сумме площадей квадратов ,
построенных на катетах.
Алгебраическая формулировка теоремы Пифагора.
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
То есть, обозначив длину гипотенузы треугольника через c
, а длины катетов через a
и b
:
Обе формулировки теоремы Пифагора
эквивалентны, но вторая формулировка более элементарна, она не
требует понятия площади.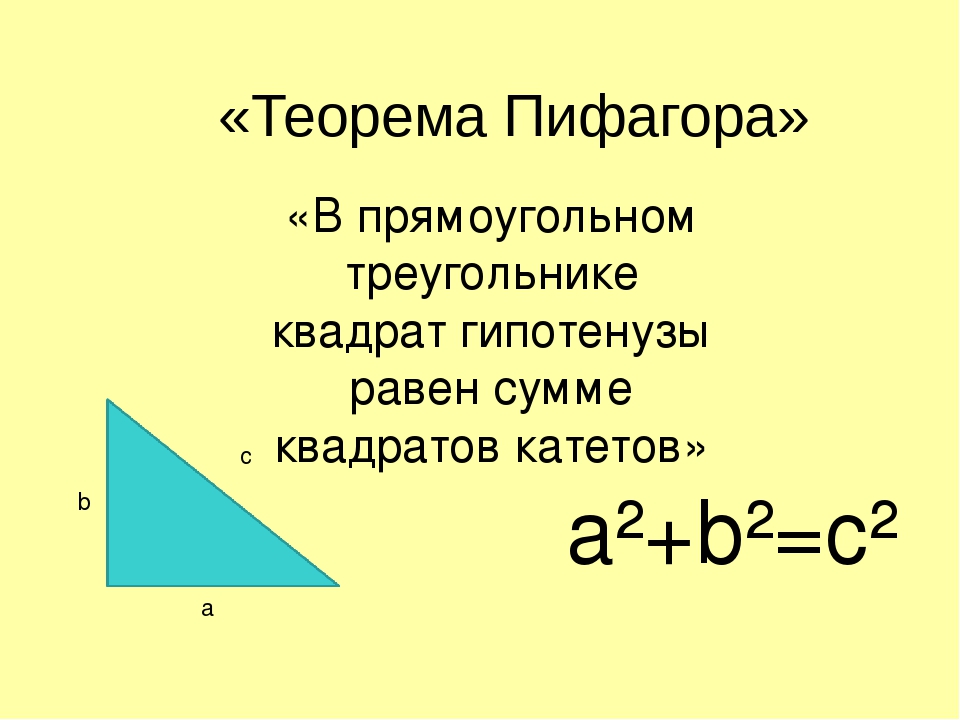 То есть второе утверждение можно проверить, ничего не зная о площади и
То есть второе утверждение можно проверить, ничего не зная о площади и
измерив только длины сторон прямоугольного треугольника .
Обратная теорема Пифагора.
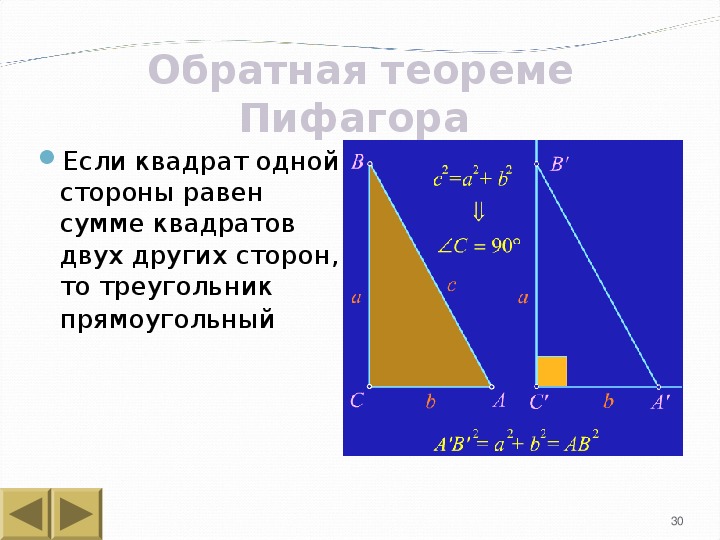
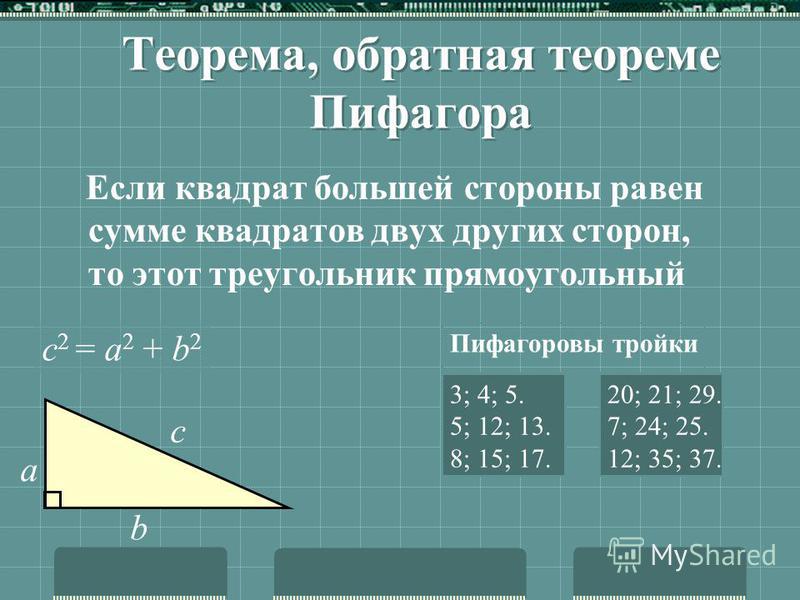
Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то
треугольник прямоугольный.
Или, иными словами:
Для всякой тройки положительных чисел a
, b
и c
, такой, что
существует прямоугольный треугольник с катетами a
и b
и гипотенузой c
.
Теорема Пифагора для равнобедренного треугольника.
Теорема Пифагора для равностороннего треугольника.
Доказательства теоремы Пифагора.
На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы. Вероятно, теорема
Пифагора является единственной теоремой со столь внушительным числом доказательств. Такое многообразие
можно объяснить лишь фундаментальным значением теоремы для геометрии.
Разумеется, концептуально все их можно разбить на малое число классов. Самые известные из них:
доказательства методом площадей
, аксиоматические
и экзотические доказательства
(например,
с помощью дифференциальных уравнений
).
1. Доказательство теоремы Пифагора через подобные треугольники.
Следующее доказательство алгебраической формулировки — наиболее простое из доказательств, строящихся
напрямую из аксиом. В частности, оно не использует понятие площади фигуры.
Пусть ABC
есть прямоугольный треугольник с прямым углом C
. Проведём высоту из C
и обозначим
её основание через H
.
Треугольник ACH
подобен треугольнику AB
C по двум углам. Аналогично, треугольник CBH
подобен ABC
.
Введя обозначения:
получаем:
,
что соответствует —
Сложив a
2 и b
2 , получаем:
или , что и требовалось доказать.
2. Доказательство теоремы Пифагора методом площадей.
Ниже приведённые доказательства, несмотря на их кажущуюся простоту, вовсе не такие простые. Все они
используют свойства площади, доказательства которых сложнее доказательства самой теоремы Пифагора.
- Доказательство через равнодополняемость.
Расположим четыре равных прямоугольных
треугольника так, как показано на рисунке
справа.
Четырёхугольник со сторонами c
— квадратом,
так как сумма двух острых углов 90°, а
развёрнутый угол — 180°.
Площадь всей фигуры равна, с одной стороны,
площади квадрата со стороной (a+b
), а с другой стороны, сумме площадей четырёх треугольников и
Что и требовалось доказать.
3. Доказательство теоремы Пифагора методом бесконечно малых.
Рассматривая чертёж, показанный на рисунке, и
наблюдая изменение стороны
a
, мы можем
записать следующее соотношение для бесконечно
малых
приращений сторон
с
и
a
(используя подобие
треугольников):
Используя метод разделения переменных, находим:
Более общее выражение для изменения гипотенузы в случае приращений обоих катетов:
Интегрируя данное уравнение и используя начальные условия, получаем:
Таким образом, мы приходим к желаемому ответу:
Как нетрудно видеть, квадратичная зависимость в окончательной формуле появляется благодаря линейной
пропорциональности между сторонами треугольника и приращениями, тогда как сумма связана с независимыми
вкладами от приращения разных катетов.
Более простое доказательство можно получить, если считать, что один из катетов не испытывает приращения
(в данном случае катет b
). Тогда для константы интегрирования получим:
Замечательно, что свойство указанное в теореме Пифагора, является характеристическим свойством прямоугольного треугольника. Это следует из теоремы, обратной теореме Пифагора.
Теорема: Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный.
Выведем формулу, выражающую плоскость треугольника через длины его сторон. Эту формулу связывают с именем Герона александрийского — древнегреческого математика и механика, жившего, вероятно в 1 в.н.э. Герон много уделял внимания практическим приложениям геометрии.
Теорема. Площадь S треугольника, стороны которого равны a , b , c , вычисляется по формуле S=, где p — полупериметр треугольника.
Доказательство.
Дано: ?ABC, АВ= с, ВС= а, АС= b.Углы А и В, острые.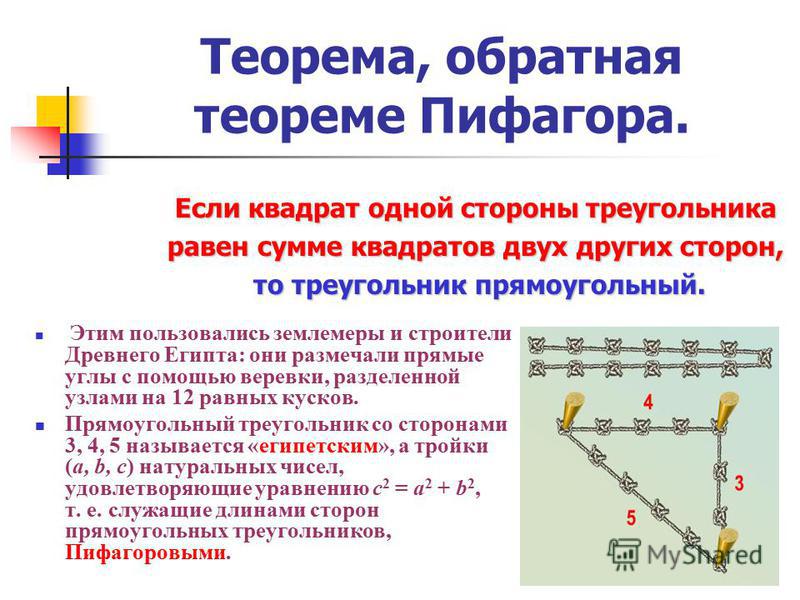 СН — высота.
СН — высота.
Доказать:
Доказательсво:
Рассмотрим треугольник ABC, в котором AB=c , BC=a, AC=b. Во всяком треугольнике, по крайней мере, два угла острые. Пусть А и В — острые углы треугольника АВС. Tогда основание H высоты CH треугольника лежит на стороне AB. Введем обозначения: CH = h, AH=y, HB=x. по теореме Пифагора a 2 — x 2 = h 2 =b 2 -y 2 , откуда
Y 2 — x 2 = b 2 — a 2 , или (y — x) (y + x) = b 2 — a 2 , а так как y + x = c, то y- x = (b2 — a2).
Складывая два последних равенства, п олучаем:
2y = +c, откуда
y=,и, значит, h 2 = b 2 -y 2 =(b — y)(b+y)=
Следовательно, h = .
Цели урока:
общеобразовательные:
- проверить теоретические знания учащихся
(свойства прямоугольного треугольника, теорема
Пифагора), умение использовать их при решении
задач; - создав проблемную ситуацию, подвести учащихся к
“открытию” обратной теоремы Пифагора.
развивающие:
- развитие умений применять теоретические знания
на практике; - развитие умения формулировать выводы при
наблюдениях; - развитие памяти, внимания, наблюдательности:
- развитие мотивации учения через эмоциональное
удовлетворение от открытий, через введение
элементов истории развития математических
понятий.
воспитательные:
- воспитывать устойчивый интерес к предмету
через изучение жизнедеятельности Пифагора; - воспитание взаимопомощи и объективного
оценивания знаний одноклассников через
взаимопроверку.
Форма урока: классно-урочная.
План урока:
- Организационный момент.
- Проверка домашнего задания. Актуализация
знаний. - Решение практических задач с использованием
теоремы Пифагора. - Новая тема.
- Первичное закрепление знаний.
- Домашнее задание.
- Итоги урока.
- Самостоятельная работа (по индивидуальным
карточкам с отгадыванием афоризмов Пифагора).
Ход урока.
Организационный момент.
Проверка домашнего задания. Актуализация
знаний.
Учитель:
Какое задание вы
выполняли дома?
Ученики:
По двум данным
сторонам прямоугольного треугольника найти
третью сторону, ответы оформить в виде таблицы.
Повторить свойства ромба и прямоугольника.
Повторить, что называется условием, а что
заключением теоремы. Подготовить сообщения о
жизни и деятельности Пифагора. Принести веревку
с 12-ю завязанными на ней узлами.
Учитель:
Ответы к домашнему
заданию проверьте по таблице
(черным цветом выделены данные,
красным – ответы).
Учитель:
На доске
записаны утверждения. Если вы согласны с ними на
листочках напротив соответствующего номера
вопроса поставьте “+”, если не согласны, то
поставьте “–”.
На доске заранее написаны
утверждения.
- Гипотенуза больше катета.
- Сумма острых углов прямоугольного треугольника
равна 180 0 . - Площадь прямоугольного треугольника с катетами
а
и в
вычисляется по формуле S=ab/2
. - Теорема Пифагора верна для всех равнобедренных
треугольников. - В прямоугольном треугольнике катет, лежащий
напротив угла 30 0 , равен половине
гипотенузы.
- Сумма квадратов катетов равна квадрату
гипотенузы. - Квадрат катета равен разности квадратов
гипотенузы и второго катета. - Сторона треугольника равна сумме двух других
сторон.
Проверяются работы с помощью
взаимопроверки. Утверждения, вызвавшие споры, –
обсуждаются.
Ключ к теоретическим вопросам.
Учащиеся ставят друг другу оценки по следующей
системе:
8 правильных ответов “5”;
6-7 правильных ответов “4”;
4-5 правильных ответов “3”;
меньше 4 правильных ответов “2”.
Учитель:
О чем мы говорили на
прошлом уроке?
Ученик:
О Пифагоре и его теореме.
Учитель:
Сформулируйте
теорему Пифагора. (Несколько учеников читают
формулировку, в это время 2-3 ученика доказывают
ее у доски, 6 учеников – за первыми партами на
листочках).
На магнитной доске на карточках
написаны математические формулы. Выберите те из
них, которые отражают смысл теоремы Пифагора, где
а
и в
– катеты, с
–
гипотенуза.
| 1) с 2 = а 2 + в 2 | 2) с = а + в | 3) а 2 = с 2 – в 2 |
| 4) с 2 = а 2 – в 2 | 5) в 2 = с 2 – а 2 | 6) а 2 = с 2 + в 2 |
Пока учащиеся, доказывающие теорему у
доски и на местах, не готовы, слово
предоставляется тем, кто подготовил сообщения о
жизни и деятельности Пифагора.
Школьники, работающие на местах, сдают
листочки и слушают доказательства тех, кто
работал у доски.
Решение практических задач с использованием
теоремы Пифагора.
Учитель:
предлагаю вам
практические задачи с применением изучаемой
теоремы. Побываем сначала в лесу, после бури,
потом на загородном участке.
Задача 1
. После бури сломалась ель.
Высота оставшейся части 4,2 м. Расстояние от
основания до упавшей макушки 5,6 м. Найти высоту
ели до бури.
Задача 2
. Высота дома 4,4 м Ширина
Высота дома 4,4 м Ширина
газона вокруг дома 1,4 м. Какой длины надо
изготовить лестницу, чтобы она не заступала на
газон и доставала до крыши дома?
Новая тема.
Учитель:
(звучит музыка)
Закройте глаза, на несколько минут мы окунемся в
историю. Мы с вами в Древнем Египте. Вот на верфях
египтяне строят свои знаменитые корабли. А вот
землемеры, они измеряют участки земли, границы
которых смылись после разлива Нила. Строители
строят грандиозные пирамиды, которые до сих пор
поражают нас своим великолепием. Во всех этих
видах деятельности египтянам необходимо было
использовать прямые углы. Они умели строить их с
помощью веревки с 12 ю завязанными на
одинаковом расстоянии друг от друга узелками.
Попробуйте и вы, рассуждая как древние египтяне,
построить с помощью своих веревок прямоугольные
треугольники. (Решая эту проблему, ребята
работают в группах по 4 человека. Через некоторое
время на планшете у доски кто-то показывает
построение треугольника).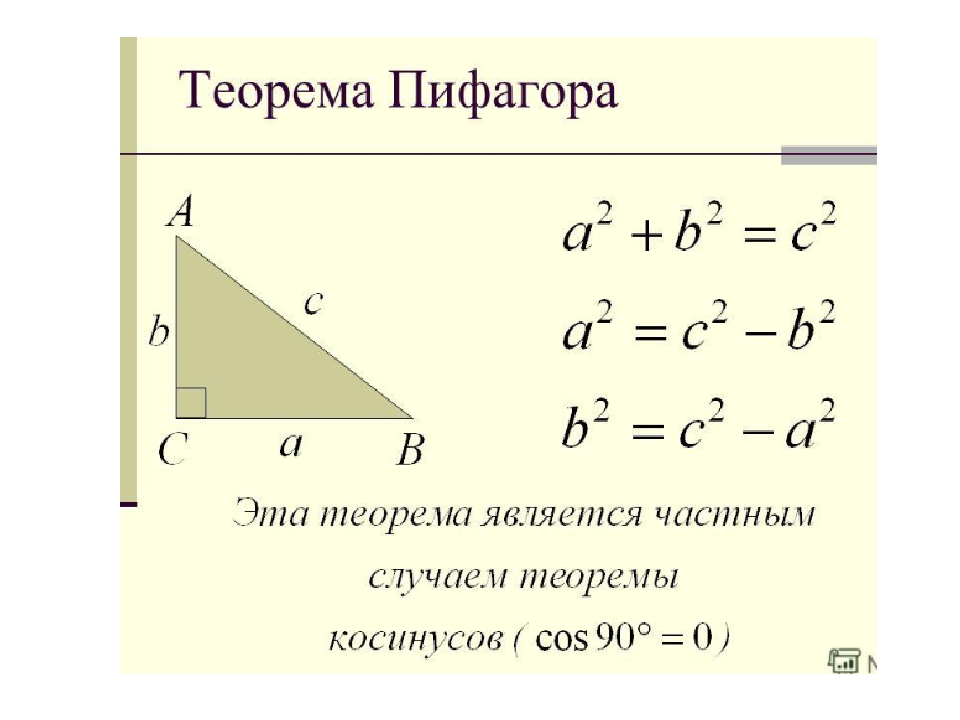
Стороны полученного треугольника 3, 4 и
5. Если между этими узлами завязать еще по одному
узлу, то его стороны станут 6, 8 и 10. Если по два – 9,
12 и 15. Все эти треугольники являются
прямоугольными т. к.
5 2 = 3 2 + 4 2 , 10 2
= 6 2 + 8 2 , 15 2 = 9 2 + 12 2
и т.д.
Каким свойством должен обладать
треугольник, чтобы быть прямоугольным? (Учащиеся
пытаются сами сформулировать обратную теорему
Пифагора, наконец, у кого-то это получается).
Чем эта теорема отличается от теоремы
Пифагора?
Ученик:
Условие и
заключение поменялись местами.
Учитель:
Дома вы повторяли,
как называются такие теоремы. Так с чем мы сейчас
познакомились?
Ученик:
С обратной
теоремой Пифагора.
Учитель:
Запишем в
тетради тему урока. Откройте учебники на стр. 127
прочитайте еще раз это утверждение, запишите его
себе в тетрадь и разберите доказательство.
(После нескольких минут
самостоятельной работы с учебником по желанию
один человек у доски приводит доказательство
теоремы).
- Как называется треугольник со сторонами 3, 4 и 5?
Почему? - Какие треугольники называются пифагоровыми?
- С какими треугольниками вы работали в домашнем
задании? А в задачах с сосной и лестницей?
Первичное закрепление знаний
.
Эта теорема помогает решать задачи, в
которых надо выяснить, будут ли треугольники
прямоугольными.
Задания:
1) Выясните, является ли треугольник
прямоугольным, если его стороны равны:
а) 12,37 и 35; б) 21, 29 и 24.
2) Вычислите высоты треугольника со сторонами 6,
8 и 10 см.
Домашнее задание
.
Стр.127:обратная теорема Пифагора. № 498(а,б,в) № 497.
Итоги урока.
Что нового узнали на уроке?
Пифагора?
Самостоятельная работа (проводится по
индивидуальным карточкам).
Учитель:
Дома вы повторяли
свойства ромба и прямоугольника. Перечислите их
(идет беседа с классом). На прошлом уроке мы
говорили о том, что Пифагор был разносторонней
личностью. Он занимался и медициной, и музыкой, и
астрономией, а так же был спортсменом и
участвовал в олимпийских играх. А еще Пифагор был
философом. Многие его афоризмы и сегодня
актуальны для нас. Сейчас вы будете выполнять
самостоятельную работу. К каждому заданию дано
несколько вариантов ответов, рядом с которыми
записаны фрагменты афоризмов Пифагора. Ваша
задача – решив все задания, составить из
полученных фрагментов высказывание и записать
его.
Тема:
Теорема, обратная теореме Пифагора.
Цели урока:
1) рассмотреть теорему, обратную теореме Пифагора; ее применение в процессе решения задач; закрепить теорему Пифагора и совершенствовать навыки решения задач на ее применение;
2) развивать логическое мышление, творческий поиск, познавательный интерес;
3) воспитывать у учащихся ответственного отношения к учению, культуры математической речи.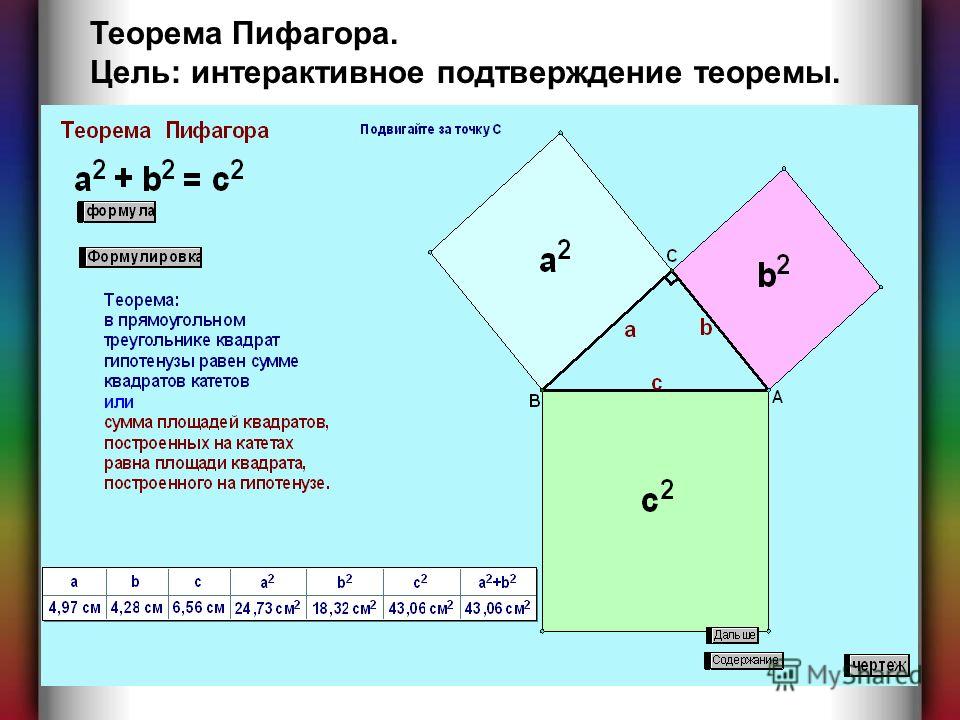
Тип урока.
Урок усвоения новых знаний.
Ход урока
І.
Организационный момент
ІІ.
Актуализация
знаний
Урок мне
бы
хотелось
начать с четверостишья.
Да, путь познания не гладок
Но знаем мы со школьных лет,
Загадок больше, чем разгадок,
И поискам предела нет!
Итак, на прошлом уроке вы выучили теорему Пифагора. Вопросы:
Теорема Пифагора справедлива для какой фигуры?
Какой треугольник называют прямоугольным?
Сформулируйте теорему Пифагора.
Как запишется теорема Пифагора для каждого треугольника?
Какие треугольники называются равными?
Сформулируйте признаки равенства треугольников?
А теперь проведем небольшую самостоятельную работу:
Решение задач по чертежам.
№1
(1 б.) Найти: АВ.
№2
(1 б.) Найти: ВС.
№3
(
2
б.)
Найти: АС
№4
(1 б.)
Найти: АС
№5
Дано: АВС
D
ромб
(2 б.) АВ = 13 см
АС = 10 см
Найти: В
D
Самопроверка №1. 5
№2. 5
№3. 16
№4. 13
№5. 24
ІІІ.
Изучение
нового
материала.
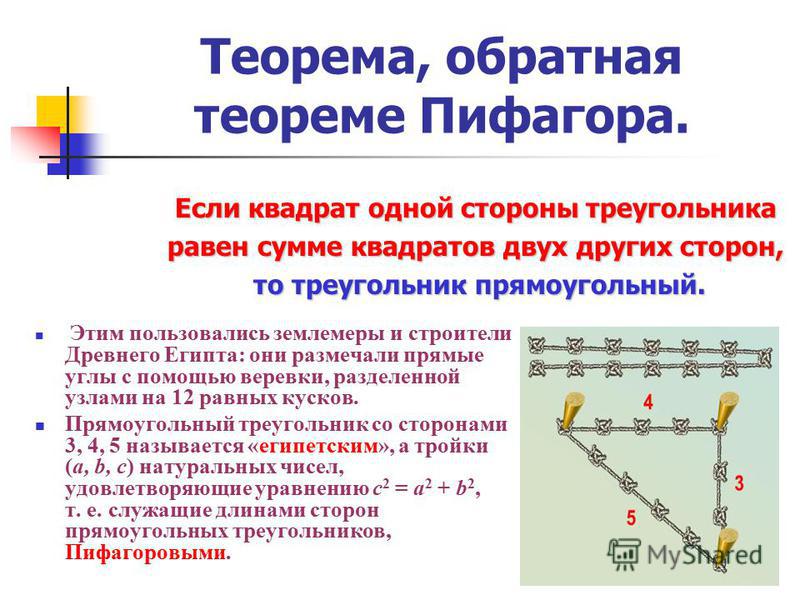
Древние египтяне строили прямые углы на местности таким образом: делили узлами веревку на 12 равных частей, связывали ее концы, после чего веревку растягивали так на земле, чтобы образовался треугольник со сторонами 3, 4 и 5 делений. Угол треугольника, который лежал против стороны с 5 делениями, был прямой.
Можете ли вы объяснить правильность этого суждения?
В результате поиска ответа на вопрос учащиеся должны понять, что с математической точки зрения вопрос ставится: будет ли треугольник прямоугольным.
Ставим проблему: как, не делая измерений, определить, будет ли треугольник с заданными сторонами прямоугольным. Решение этой проблемы и есть цель урока.
Решение этой проблемы и есть цель урока.
Запишите тему урока.
Теорема. Если сумма квадратов двух сторон треугольника равна квадрату третьей стороны, то такой треугольник прямоугольный.
Самостоятельно доказывают теорему (составляют план доказательства по учебнику).
Из этой теоремы следует, что треугольник со сторонами 3, 4, 5 – прямоугольный (египетский).
Вообще, числа, для которых выполняется равенство
, называют пифагоровыми тройками. А треугольники, длины сторон которых выражаются пифагоровыми тройками (6, 8, 10), — пифагоровы треугольники.
Закрепление.
Т.к.
, то треугольник со сторонами 12, 13, 5 не является прямоугольным.
Т.к.
, то треугольник со сторонами 1, 5, 6 является прямоугольным.
№ 430 (а, б, в)
(
— не является)
По мнению Ван-дер-Вардена , очень вероятно, что соотношение в общем виде было известно в Вавилоне уже около XVIII века до н. э.
Приблизительно в 400 году до н. {2}}
{2}}
, существует прямоугольный треугольник с катетами
a
{\displaystyle a}
и
b
{\displaystyle b}
и гипотенузой
c
{\displaystyle c}
.
Доказательства
В научной литературе зафиксировано не менее 400 доказательств теоремы Пифагора , что объясняется как фундаментальным значением для геометрии, так и элементарностью результата. Основные направления доказательств: алгебраическое использование соотношений элементов треугольника (таков, например, популярный метод подобия ), метод площадей , существуют также различные экзотические доказательства (например, с помощью дифференциальных уравнений).
Через подобные треугольники
Классическое доказательство Евклида направлено на установление равенства площадей между прямоугольниками, образованными из рассечения квадрата над гипотенузой высотой из прямого угла с квадратами над катетами.
Конструкция, используемая для доказательства следующая: для прямоугольного треугольника с прямым углом
C
{\displaystyle C}
, квадратов над катетами и и квадрата над гипотенузой
A
B
I
K
{\displaystyle ABIK}
строится высота
C
H
{\displaystyle CH}
и продолжающий её луч
s
{\displaystyle s}
, разбивающий квадрат над гипотенузой на два прямоугольника и . Доказательство нацелено на установление равенства площадей прямоугольника
Доказательство нацелено на установление равенства площадей прямоугольника
A
H
J
K
{\displaystyle AHJK}
с квадратом над катетом
A
C
{\displaystyle AC}
; равенство площадей второго прямоугольника, составляющего квадрат над гипотенузой, и прямоугольника над другим катетом устанавливается аналогичным образом.
Равенство площадей прямоугольника
A
H
J
K
{\displaystyle AHJK}
и
A
C
E
D
{\displaystyle ACED}
устанавливается через конгруэнтность треугольников
△
A
C
K
{\displaystyle \triangle ACK}
и
△
A
B
D
{\displaystyle \triangle ABD}
, площадь каждого из которых равна половине площади квадратов
A
H
J
K
{\displaystyle AHJK}
и
A
C
E
D
{\displaystyle ACED}
соответственно в связи со следующим свойством: площадь треугольника равна половине площади прямоугольника, если у фигур есть общая сторона, а высота треугольника к общей стороне является другой стороной прямоугольника. Конгруэнтность треугольников следует из равенства двух сторон (стороны квадратов) и углу между ними (составленного из прямой угла и угла при
A
{\displaystyle A}
.
Таким образом, доказательством устанавливается, что площадь квадрата над гипотенузой, составленного из прямоугольников
A
H
J
K
{\displaystyle AHJK}
и
B
H
J
I
{\displaystyle BHJI}
, равна сумме площадей квадратов над катетами.
Доказательство Леонардо да Винчи
К методу площадей относится также доказательство, найденное Леонардо да Винчи . Пусть дан прямоугольный треугольник
△
A
B
C
{\displaystyle \triangle ABC}
с прямым углом
C
{\displaystyle C}
и квадраты
A
C
E
D
{\displaystyle ACED}
,
B
C
F
G
{\displaystyle BCFG}
и
A
B
H
J
{\displaystyle ABHJ}
(см. рисунок). В этом доказательстве на стороне
H
J
{\displaystyle HJ}
последнего во внешнюю сторону строится треугольник, конгруэнтный
△
A
B
C
{\displaystyle \triangle ABC}
, притом отражённый как относительно гипотенузы, так и относительно высоты к ней (то есть
J
I
=
B
C
{\displaystyle JI=BC}
и
H
I
=
A
C
{\displaystyle HI=AC}
). Прямая
C
I
{\displaystyle CI}
разбивает квадрат, построенный на гипотенузе на две равные части, поскольку треугольники
△
A
B
C
{\displaystyle \triangle ABC}
и
△
J
H
I
{\displaystyle \triangle JHI}
равны по построению. Доказательство устанавливает конгруэнтность четырёхугольников
Доказательство устанавливает конгруэнтность четырёхугольников
C
A
J
I
{\displaystyle CAJI}
и
D
A
B
G
{\displaystyle DABG}
, площадь каждого из которых, оказывается, с одной стороны, равной сумме половин площадей квадратов на катетах и площади исходного треугольника, с другой стороны — половине площади квадрата на гипотенузе плюс площадь исходного треугольника. Итого, половина суммы площадей квадратов над катетами равна половине площади квадрата над гипотенузой, что равносильно геометрической формулировке теоремы Пифагора.
Доказательство методом бесконечно малых
Существует несколько доказательств, прибегающих к технике дифференциальных уравнений . В частности, Харди приписывается доказательство, использующее бесконечно малые приращения катетов
a
{\displaystyle a}
и
b
{\displaystyle b}
и гипотенузы
c
{\displaystyle c}
, и сохраняющие подобие с исходным прямоугольником, то есть, обеспечивающие выполнение следующих дифференциальных соотношений:
d
a
d
c
=
c
a
{\displaystyle {\frac {da}{dc}}={\frac {c}{a}}}
,
d
b
d
c
=
c
b
{\displaystyle {\frac {db}{dc}}={\frac {c}{b}}}
. {2}+\mathrm {Const} }
{2}+\mathrm {Const} }
. Применение начальных условий
a
=
b
=
c
=
0
{\displaystyle a=b=c=0}
определяет константу как 0, что в результате даёт утверждение теоремы.
Квадратичная зависимость в окончательной формуле появляется благодаря линейной пропорциональности между сторонами треугольника и приращениями, тогда как сумма связана с независимыми вкладами от приращения разных катетов.
Вариации и обобщения
Подобные геометрические фигуры на трёх сторонах
Важное геометрическое обобщение теоремы Пифагора дал Евклид в «Началах », перейдя от площадей квадратов на сторонах к площадям произвольных подобных геометрических фигур : сумма площадей таких фигур, построенных на катетах, будет равна площади подобной им фигуры, построенной на гипотенузе.
Главная идея этого обобщения заключается в том, что площадь подобной геометрической фигуры пропорциональна квадрату любого своего линейного размера и в частности квадрату длины любой стороны. Следовательно, для подобных фигур с площадями
A
{\displaystyle A}
,
B
{\displaystyle B}
и
C
{\displaystyle C}
, построенных на катетах с длинами
a
{\displaystyle a}
и
b
{\displaystyle b}
и гипотенузе
c
{\displaystyle c}
соответственно, имеет место соотношение:
A
a
2
=
B
b
2
=
C
c
2
⇒
A
+
B
=
a
2
c
2
C
+
b
2
c
2
C
{\displaystyle {\frac {A}{a^{2}}}={\frac {B}{b^{2}}}={\frac {C}{c^{2}}}\,\Rightarrow \,A+B={\frac {a^{2}}{c^{2}}}C+{\frac {b^{2}}{c^{2}}}C}
. {2}}
{2}}
, то выполнено .
Кроме того, если возможно доказать без привлечения теоремы Пифагора, что для площадей трёх подобных геометрических фигур на сторонах прямоугольного треугольника выполнено соотношение
A
+
B
=
C
{\displaystyle A+B=C}
, то с использованием обратного хода доказательства обобщения Евклида можно вывести доказательство теоремы Пифагора. Например, если на гипотенузе построить конгруэтный начальному прямоугольный треугольник площадью
C
{\displaystyle C}
, а на катетах — два подобных ему прямоугольных треугольника с площадями
A
{\displaystyle A}
и
B
{\displaystyle B}
, то оказывается, что треугольники на катетах образуются в результате деления начального треугольника его высотой, то есть сумма двух меньших площадей треугольников равна площади третьего, таким образом
A
+
B
=
C
{\displaystyle A+B=C}
и, применяя соотношение для подобных фигур, выводится теорема Пифагора.
Теорема косинусов
Теорема Пифагора — это частный случай более общей теоремы косинусов, которая связывает длины сторон в произвольном треугольнике :
a
2
+
b
2
−
2
a
b
cos
θ
=
c
2
{\displaystyle a^{2}+b^{2}-2ab\cos {\theta }=c^{2}}
,
где — угол между сторонами
a
{\displaystyle a}
и
b
{\displaystyle b}
. Если угол равен 90°, то
Если угол равен 90°, то
cos
θ
=
0
{\displaystyle \cos \theta =0}
, и формула упрощается до обычной теоремы Пифагора.
Произвольный треугольник
Существует обобщение теоремы Пифагора на произвольный треугольник, оперирующее исключительно соотношением длин сторон, считается, что оно впервые было установлено сабийским астрономом Сабитом ибн Куррой . В нём для произвольного треугольника со сторонами в него вписывается равнобедренный треугольник с основанием на стороне
c
{\displaystyle c}
, вершиной, совпадающей с вершиной исходного треугольника, противолежащей стороне
c
{\displaystyle c}
и углами при основании, равными углу
θ
{\displaystyle \theta }
, противолежащему стороне
c
{\displaystyle c}
. В результате образуются два треугольника, подобных исходному: первый — со сторонами
a
{\displaystyle a}
, дальней от неё боковой стороной вписанного равнобедренного треугольника, и
r
{\displaystyle r}
— части стороны
c
{\displaystyle c}
; второй — симметрично к нему от стороны
b
{\displaystyle b}
со стороной
s
{\displaystyle s}
— соответствующей частью стороны
c
{\displaystyle c}
. {2}}
{2}}
.
Теорема Паппа о площадях
Неевклидова геометрия
Теорема Пифагора выводится из аксиом евклидовой геометрии и недействительна для неевклидовой геометрии — выполнение теоремы Пифагора равносильно постулату Евклида о параллельности .
В неевклидовой геометрии соотношение между сторонами прямоугольного треугольника обязательно будет в форме, отличной от теоремы Пифагора. Например, в сферической геометрии все три стороны прямоугольного треугольника, которые ограничивают собой октант единичной сферы, имеют длину
π
/
2
{\displaystyle \pi /2}
, что противоречит теореме Пифагора.
При этом теорема Пифагора справедлива в гиперболической и эллиптической геометрии, если требование о прямоугольности треугольника заменить условием, что сумма двух углов треугольника должна равняться третьему .
Сферическая геометрия
Для любого прямоугольного треугольника на сфере радиусом
R
{\displaystyle R}
(например, если угол в треугольнике прямой) со сторонами
a
,
b
,
c
{\displaystyle a,b,c}
соотношение между сторонами имеет вид :
cos
(c
R)
=
cos
(a
R)
⋅
cos
(b
R)
{\displaystyle \cos \left({\frac {c}{R}}\right)=\cos \left({\frac {a}{R}}\right)\cdot \cos \left({\frac {b}{R}}\right)}
.
Это равенство может быть выведено как особый случай сферической теоремы косинусов , которая справедлива для всех сферических треугольников:
cos
(c
R)
=
cos
(a
R)
⋅
cos
(b
R)
+
sin
(a
R)
⋅
sin
(b
R)
⋅
cos
γ
{\displaystyle \cos \left({\frac {c}{R}}\right)=\cos \left({\frac {a}{R}}\right)\cdot \cos \left({\frac {b}{R}}\right)+\sin \left({\frac {a}{R}}\right)\cdot \sin \left({\frac {b}{R}}\right)\cdot \cos \gamma }
.
ch
c
=
ch
a
⋅
ch
b
{\displaystyle \operatorname {ch} c=\operatorname {ch} a\cdot \operatorname {ch} b}
,
где
ch
{\displaystyle \operatorname {ch} }
— гиперболический косинус . Эта формула является частным случаем гиперболической теоремы косинусов, которая справедлива для всех треугольников :
ch
c
=
ch
a
⋅
ch
b
−
sh
a
⋅
sh
b
⋅
cos
γ
{\displaystyle \operatorname {ch} c=\operatorname {ch} a\cdot \operatorname {ch} b-\operatorname {sh} a\cdot \operatorname {sh} b\cdot \cos \gamma }
,
где
γ
{\displaystyle \gamma }
— угол, вершина которого противоположна стороне
c
{\displaystyle c}
. {2}}}}
{2}}}}
.
Для комплексных чисел теорема Пифагора даёт естественную формулу для нахождения модуля комплексного числа — для
z
=
x
+
y
i
{\displaystyle z=x+yi}
он равен длине
Теорема, обратная теореме Пифагора
На предыдущем уроке мы с вами познакомились с теоремой
Пифагора, которая звучит следующим образом: в прямоугольном треугольнике
квадрат гипотенузы равен сумме квадратов катетов.
На этом уроке мы сформулируем и докажем теорему,
обратную теореме Пифагора.
Теорема. Если квадрат
одной стороны треугольника равен сумме квадратов двух других сторон, то этот
треугольник – прямоугольный.
Доказательство.
Пусть ABC
– треугольник, для которого справедливо равенство: .
,
Докажем, что –
прямой.
–
прямоугольный.
–
прямой, ,.
,
.
Следовательно, ,то
есть,.
по
третьему признаку.
Тогда .
Значит, –
прямоугольный.
Что и требовалось доказать.
Прямоугольные треугольники, у которых длины сторон
выражаются целыми числами, называются пифагоровыми треугольниками. Так
каждый из приведённых треугольников является пифагоровым.
В Древнем Египте для построения прямого угла строили
прямоугольный треугольник при помощи кольев и натянутых на них верёвок длиной
три, четыре и пять единиц.
Тогда угол между сторонами, равными трём и четырём,
получался прямым.
Задача. Выясните,
является ли треугольник прямоугольным, если его стороны выражаются числами: а) ,
,
;
б) ,
,
;
в) ,
,
.
Решение.
Задача. Найдите площадь
треугольника, если его стороны равны см,
см
и см.
Решение.
,
тогда –
прямоугольный, .
,
(см2).
Ответ: см2.
Задача. В равнобедренном
треугольнике длина
боковой стороны равна
см,
а основание –
см.
Найдите .
Решение.
см.
,следовательно,
–
прямоугольный, .
Так как –
равнобедренный, то .
,тогда
.
Ответ: .
Итак, на этом уроке мы вспомнили теорему Пифагора и
познакомились с обратной ей: если квадрат одной стороны треугольника равен
сумме квадратов двух других сторон, то этот треугольник – прямоугольный.
Отметили, что прямоугольные треугольники, у которых
длины сторон выражаются целыми числами, называются пифагоровыми треугольниками.
А также мы поговорили о египетском треугольнике,
который представляет собой треугольник со сторонами три, четыре, пять. При этом
если пропорционально увеличивать стороны такого треугольника, то полученные
треугольники, например, со сторонами шесть, восемь, десять; девять, двенадцать,
пятнадцать и так далее также будут прямоугольными.
Презентация по геометрии (8 класс) на тему «Теорема, обратная теореме Пифагора»
Теорема, обратная теореме Пифагора.
Вопросы и задания.
1. Сформулируйте теорему Пифагора.
2. Постройте прямоугольный треугольник АВС с прямым углом С. Запишите формулу, выражающую теорему Пифагора, используя обозначения сторон АВ, ВС и АС.
3. Докажите теорему Пифагора по рисунку (устно у доски).
Выполните задания по готовым чертежам.
1.
2.
3.
4.
5.
Мы познакомились с теоремой Пифагора. Рассмотрим внимательно содержание этой теоремы.
1. О какой фигуре идет речь в теореме?
О какой фигуре идет речь в теореме?
Прямоугольный треугольник.
2. Будет ли выполняться теорема Пифагора в остроугольном или тупоугольном треугольниках?
Не будет.
3. Чем является фраза «В прямоугольном треугольнике» в теореме?
Необходимым условием теоремы.
4. Чем является фраза «квадрат гипотенузы равен сумме квадратов катетов» в теореме?
Вывод или следствие из условия теоремы.
5. Можно ли утверждать обратное теореме Пифагора? Сформулируйте это утверждение.
Запишите теорему, обратную теореме Пифагора.
Теорема. Если квадрат одной стороны равен сумме квадратов двух других сторон, то треугольник прямоугольный.
Дано: ∆АВС,
АВ2 = ВС2 + АС2
Доказать: ∆АВС прямоугольный
Доказательство:
1. Достроим ∆ВСD так, чтобы ВD = АС, а угол СВD прямой. ∆АВС. Соединим точки А и D отрезком.
Достроим ∆ВСD так, чтобы ВD = АС, а угол СВD прямой. ∆АВС. Соединим точки А и D отрезком.
2. ∆ВСD прямоугольный по построению, СD – гипотенуза. Тогда по теореме Пифагора CD2 = ВС2 + BD2. По условию АВ2 = ВС2 + АС2. ВD = АС по построению. Значит,
CD2 = ВС2 + BD2 = ВС2 + АС2 = АВ2.
3. Так как CD2 = АВ2, то CD = АВ.
4. ВD = АС (по построению), ВD – общая, CD = АВ (по доказанному), = > ∆ВСD = ∆АВС (по 3 признаку). Из равенства треугольников следует, что АСВ = СВD = 90°, то есть ∆АВС прямоугольный.
Что и требовалось доказать.
Прямоугольные треугольники, длины сторон которых выражаются целыми числами, называются пифагоровыми треугольниками.
Египтяне использовали треугольник со сторонами 3, 4 и 5 метров для построения прямых углов на местности, поэтому такой треугольник называют египетским.
В классе: №№ 498 (а,б,в) устно, 499 (а)
Домашнее задание:
п. 56, № 498 (г-ж), 499 (б)
Задание в прикрепленном файле
На альбомном листе с помощью циркуля и линейки постройте треугольник со сторонами 3 см, 4 см и 5 см. Проверьте чертежным угольником (с прямым углом) является ли прямым углом наибольший угол треугольника.
ФИО | Козлова Лидия Николаевна | ||
Место работы | Тенистовская СОШ | ||
Должность | Учитель математики | ||
Предмет | География | ||
Класс | 8 | ||
Тема и номер урока | Теорема обратная теореме Пифагора. | ||
Базовый учебник | Геометрия 8: учебник для 8 кл. образоват. организаций с приложением на электронном носителе /Л.С. Анатасян, В.Ф.Бутузов, С.Б.Кадомцев, Э.Г.Позняк, И.И.Юдина.– М.: Просвещение, 2013. | ||
а) разности гипотенузы и катета | б) сумме квадратов гипотенузы и катета | в) разности квадратов гипотенузы и катета | г) нет правильного ответа |
2. | |||
а) острого угла | б) прямого угла | в) тупого угла | г) нет правильного ответа |
3.Квадрат гипотенузы равен сумме квадратов катетов в треугольнике с углами ………….. | |||
а) 60º и 60º | б) 37º и 53º | в) 45º и 50º | г) нет правильного ответа |
4. Какой из треугольников с указанными сторонами – прямоугольный? | |||
а) 5; 4; 2 | б) 8; 8; 8 | в) 12; 5; 13 | г) нет правильного ответа |
5. Угол А в треугольнике АВС равен В А С 2 | |||
60º | б) 45º | в) 30º | г) нет правильного ответа | 2. |
3. | 4. При построении | 2. Найти: АС | |
3. Дано: ABCD – квадрат Найти: АО. | 4. Дано: АВСD – ромб; АС = 2; DВ = 4. Найти: ВС. | 1. Диагонали ромба равны 14 и 28 см. Найдите сторону ромба. 2. В треугольнике два угла равны 45º и 90º, а большая сторона – 20 см. Найдите две другие стороны треугольника. | |
«4» | 1. Найдите диагональ ромба, если вторая диагональ и сторона ромба соответственно равны 12 и 10 см. 2. Основания равнобокой трапеции равны 4 и 12 см, а боковая сторона равна 5. Найдите высоту и диагональ трапеции. | ||
«5» | 1. Найдите диагонали равнобокой трапеции, если ее высота равна 6 см, а средняя линия, равна 8 см. 2. В параллелограмме ABCD BD = 2 см, АС= 26 см, АD= 16 см. Через точку О – точку пересечения диагоналей параллелограмма проведена прямая, перпендикулярная стороне ВС. Найдите отрезки, на которые эта прямая разделила сторону АD. | ||
Деятельность учителя. | Деятельность учеников. | Презентация. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
( Предлагается учащимся совместно составить план работы на урок.) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
— Здравствуйте, ребята. Давайте улыбнемся друг другу и начнем сегодняшний урок. А начнем его с замечательных слов Иоганна Кеплера «Геометрия владеет двумя сокровищами: одно из них – это теорема Пифагора» — Сегодня на уроке геометрии мы побываем в роли открывателей новых знаний. Чтобы окунуться в раскрытие загадок геометрии, нам потребуется план работы. Давайте его составим вместе! — Вспомните, какие виды работ мы выполняем на уроках изучения нового материала. Посовещайтесь с соседом — Вы неплохо поработали, теперь сравним мой план урока и ваш. | Приветствуют друг друга, садятся на свои места. Обсуждают пункты плана, записывают на предложенных листах бумаги свои варианты. По окончанию времени поднимают руки и озвучивают свои наработки. Сравнивают. | Слайд № 2. Эпиграф. Воспитание интереса к геометрии. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
План урока:
| Слайд № 3. План урока. Подготовка к исследовательской деятельности. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
— Приступим к реализации запланированной работы на урок. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(Работа с классом проводится фронтально, в форме подводящего диалога) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
— На прошлых уроках мы изучили площади многоугольников. Давайте вспомним их. Чему равна площадь квадрата. — Площадь прямоугольного треугольника. — Площадь произвольного треугольника. — Верно. | — Площадь квадрата со стороной а, равна квадрату стороны. — Площадь прямоугольного треугольника равна половине произведения его катетов. — Площадь треугольника равна половине произведения его основания на высоту. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Слайд № 4. Устная работа. Повторение полученных ранее знаний. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
— Молодцы, все верно. Как вы думаете, мы закончили работу по первому пункту? Решим задачу. Дан прямоугольный треугольник АВС, катет АВ равен 3 см, катет АС равен 4 см. Найдите площадь треугольника и его гипотенузу. | — Площадь квадрата равна 16, площадь прямоугольного треугольника равна 7.5, площадь произвольного треугольника равна 6. — Да. Можно приступать к выполнению следующего. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Слайд № 5. Задача. Создание проблемной ситуации. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
— Что требуется найти? — Что известно? -Каким будет первое действие? | — Площадь треугольника АВС и его гипотенузу. — Длины катетов треугольника АВС. — Найдем площадь треугольника АВС, она равна половине произведения катетов, т.е. 6 см2. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
— Верно. Нам известны длины катетов треугольника АВС, еще мы нашли его площадь. Осталось найти гипотенузу, как будем ее искать? С помощью чего? — Как вы думаете, есть ли взаимосвязь между катетами и гипотенузой прямоугольного треугольника? — Верно, она существует, но на данном этапе изучения геометрии эта взаимосвязь нам не известна. | Ученики в затруднении. — Может быть существует. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(Задача ставится учениками.) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
— Как вы считаете, чему следует посвятить урок? — Чем является данное утверждение для этого урока? — Верно. Продолжим нашу работу «открывателей». | — Найти взаимосвязь между катетами и гипотенузой прямоугольного треугольника. — Мы сформулировали учебную задачу, значит, выполнили еще один пункт нашего плана! | Слайд № 6. Учебная задача. Переход по ссылке «План урока». Слайд № 3. План урока. Переход по ссылке «Т.П.». | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(Совместно в ходе подводящего диалога.) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
— Такую взаимосвязь знали древние египтяне. С помощью веревки, разделенной узлами на 12 равных частей, они строили треугольник со сторонами длиной 3, 4, 5 частей. И точно знали, что угол, лежащий между сторонами в 3 и 4 части, есть прямой. — Как называются стороны в прямоугольном треугольнике, между которыми лежит прямой угол? — Длины катетов в египетском треугольнике чему равны? — А наш треугольник АВС случайно не египетский? — Давайте рассмотрим катеты и гипотенузу треугольника АВС. На доске записано равенство, слева знака равно катеты, справа-гипотенуза. — Нам нужно заменить звездочки, поставить тот знак, при котором равенство будет верно. Какое действие здесь выполняется? — Давайте попробуем каждое число возвести в квадрат. Получаем такое равенство. — Может, в этом равенстве какое-то действие будет выполняться? — Итак, мы получили: 42+32=52. Вернемся к катетам и гипотенузе прямоугольного треугольника, какой вывод можно сделать, исходя из полученного равенства? — Верно. Сейчас вы сформулировали важнейшую теорему геометрии, теорему Пифагора. Итак, запишите в тетради тему нашего урока: «Теорема Пифагора и ей обратная» и саму теорему: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. — Давайте обратимся к нашему плану урока и посмотрим, какой на этот раз мы выполнили пункт. — Молодцы! А сейчас один из ваших одноклассников расскажет нам интересные факты из истории о данной теореме. | — Катеты. — 3 и 4 частям. — Да, треугольник АВС египетский. Значит, его гипотенуза равна 5. — Ни вычитание, ни сложение, ни умножение, ни деление здесь не может быть, иначе равенство неверно. Обдумывают решение возникшей проблемы. — Это равенство верно при сложении. — Мы получили, что квадрат гипотенузы равен сумме квадратов катетов. Открывают тетради, записывают число, тему урока. Также ученики пишут в своих тетрадях «открытое» утверждение. — Выполнен третий пункт! | Слайд № 7. Теорема Пифагора. Ознакомление с текстом теоремы. Переход по ссылке «План урока». Слайд № 3. План урока. Переход по ссылке «И.Т.П.». | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(Один из учеников делает сообщение, подготовленное дома заранее. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Пифагор-это известный древнегреческий философ, математик, астроном.Он жил в VI веке до н. э. Его в математику очень велик. Одна из его заслуг, это теорема Пифагора. Точнее, ее доказательство. Эту теорему знали задолго до Пифагора. За 12 веков в Древнем Вавилоне и за 22 века в Древнем Китае. Эта теорема была впервые доказана Пифагором, поэтому ее так назвали. Теорема Пифагора – это важнейшее утверждение в геометрии, значение ее огромно. Она имеет множество других названий, например «теорема невесты», «теорема бабочки», «теорема ста быков», «бегство убогих». У математиков арабского востока эта теорема получила название «теорема невесты». Дело в том, что в некоторых списках «Начал» Эвклида эта теорема названа «теорема нимфы» за сходство чертежа с пчелкой (по-гречески – нимфа). Но словом «нимфа» греки называли еще и некоторых богинь, молодых женщин и невест. При переводе с греческого арабский переводчик, не обратив внимание на чертеж, перевел слово «нимфа» как «невеста», а не как «бабочка». | Слайд №8. История теоремы Пифагора. Запоминание портретов ученого. Переход по ссылке «План урока». | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
— Спасибо за такое интересное сообщение, садимся на свое место. Ребята, вернемся к плану урока и отметим, какой пункт был выполнен сейчас. — Приступим к доказательству «теоремы невест». | — Мы ознакомились с историей теоремы Пифагора, значит, четвертый пункт выполнен. | Слайд № 3. План урока. Переход по ссылке «Док.Т.П.». | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(Совместно с учащимися в ходе подводящего диалога. При доказательстве используются синтетический метод и метод площадей.) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
— Итак, мы имеем теорему, которую следует доказать. Поиск доказательства будем проводить синтетическим методом. Т.е. будем идти от условия теоремы к ее заключению. — Рассмотрим прямоугольный треугольник с катетами a и b, гипотенузой с. | Слушают, готовятся к поиску доказательства. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Слайд № 9. Доказательство теоремы Пифагора. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
— Из каких многоугольников состоит этот квадрат? — В каком отношении находятся эти треугольники? — Сравните остальные элементы этих треугольников. — Давайте равные стороны отметим буквой с. Теперь определите вид четырехугольника со сторонами с. — Рассмотрим углы этого четырехугольника. Чему они равны? — Чем же является четырехугольник со сторонами с? — Верно. Вернемся к квадрату со сторонами a+b. Чему равна площадь этого квадрата? — С другой стороны этот квадрат состоит из пяти фигур. Чему равна площадь квадрата со сторонами a+b? — И что же мы получаем? — Поиск доказательства теоремы на этом заканчивается, и нам нужно оформить наши рассуждения на доске и в тетрадях. Но сначала перенесите чертежи в свои тетради. | — Из четырех прямоугольных треугольников и четырехугольника. — Они равны по двум катетам. — Из равенства треугольников следует, что их соответствующие стороны и углы равны. — Это либо квадрат, либо ромб. — Каждый из углов четырехугольника равен разности 180 градусов и, например, суммы углов 2 и 3. Сумма углов 2 и 3 равна 90 градусов по свойству углов треугольника. Значит и каждый из углов четырехугольника равен 90 градусов. — Четырехугольник, у которого стороны равны и углы прямые, является квадратом. — Квадрату стороны a+b. — Площадь этого квадрата равна сумме площадей четырех равных прямоугольных треугольников и площади квадрата со стороной с. — Мы можем приравнять полученные площади квадрата со сторонами a+b. Ученики в своих тетрадях чертят прямоугольный треугольник и квадрат, состоящий из четырех прямоугольных треугольников и квадрата со стороной с. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Дано: Прямоугольный треугольник, a,b-катеты, с-гипотенуза. Доказать: a2+b2=c2 | Доказательство:
| Слайд № 10. Оформление доказательства. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
— Сейчас мы провели доказательство теоремы Пифагора. Чтобы осознать, каким образом мы это сделали, нам потребуется сделать «взгляд назад», т.е. проанализировать, что мы использовали при доказательстве, записать маршрут конкретных действий, которые мы выполняли. — Какие известные нам формулы мы применяли? -Верно. Такой метод доказательства называется методом площадей. Если в задаче или в теореме речь о площади не идет, то в ходе решения задачи и поиска доказательства теоремы вводятся в рассмотрение площади фигур, то говорят, что использовали метод площадей. Вот и в теореме Пифагора не говорится о площади, а доказательство ведется с помощью такого метода. — Составьте план доказательства теоремы самостоятельно в парах. — Вы все верно сделали. Посмотрите на слайд и вы заметите, что у нас одинаковые планы доказательства. — Молодцы!Посмотрите на план урока и скажите, по какому пункту мы закончили работать. — Прежде чем приступить к выполнению следующего пункта, нам необходимо вспомнить взаимосвязь теорем. Я вам подскажу, если есть прямое утверждение, то можно составить обратное ему. Обсудите данный вопрос в парах и дайте ответ. | — Мы пользовались формулами площадей прямоугольного треугольника и квадрата. Учащиеся в течение двух минут обсуждают доказательство, составляя его план. Пара, выполнившая задание первая, представляет свой план доказательства у доски: — Первым шагом доказательства было нахождение площади квадрата со сторонами a+b по известной формуле. Вторым – нахождение площади прямоугольного треугольника. Третьим – нахождение площади квадрата со стороной с. Четвертым –нахождение площади квадрата со сторонами a+b, используя площади фигур, из которых он состоит. — В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. — Доказали «открытое» нами утверждение. Теперь будем учиться друг у друга. Задумались. После подсказки начинают формулировать обратное утверждение в парах. Идет обсуждение. | Слайд № 11. План доказательства. Формирование строить логические цепочки, делать умозаключения. Переход по ссылке «План урока». Слайд № 3. План урока. Переход по ссылке «Т.О.Т.П.». | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(Используя ранее полученные сведения о обратных теоремах, ученики сами формулируют данное утверждение.) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
— Кто-то готов нам озвучить свои предложения? — Верно. Это утверждение является обратной теоремой теореме Пифагора. — Доказательство данной теоремы с вами проведет тьютор. | -Если квадрат одной стороны равен сумме квадратов двух других сторон, то такой треугольник прямоугольный. Записывают теорему. | Слайд № 12. Теорема обратная теореме Пифагора. Ознакомление с текстом теоремы. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(Проводит один из учеников.) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Рисуй глазами треугольник Рисуй глазами треугольник. Теперь его переверни Вершиной вниз. И вновь глазами ты по периметру веди. Рисуй восьмерку вертикально. Ты головою не крути, А лишь глазами осторожно Ты вдоль по линиям води. И на бочок ее клади. Теперь следи горизонтально, И в центре ты остановись. Зажмурься крепко, не ленись. Глаза открываем мы, наконец. Зарядка окончилась. Ты – молодец! | Слайд № 13. Физкультминутка. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(Проводит ученик-тьютор, заранее изучивший данное доказательство, в виде подводящего диалога, используя синтетический метод доказательства.) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
— Проведем поиск доказательства этой теоремы. На доске изображен произвольный и прямоугольный треугольники. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Дано: АВС- произвольный треугольник, АВ2=АС2+ВС2, А1В1С1- прямоугольный треугольник, А1С1=АС, В1С1=ВС, С1- прямой угол. Доказать: С прямой. | Слайд № 14. Доказательство теоремы обратной теореме Пифагора. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
— Итак, у нас есть два треугольника. Давайте сначала рассмотрим прямоугольный треугольник А1В1С1. Мы уже знаем теорему Пифагора, как можно применить ее к треугольнику А1В1С1? — Верно. А если мы посмотрим на условие, то как еще можно записать полученную формулу? — Мы получили новое равенство, а вы не заметили, что правая часть этого равенства равна квадрату совершенно другого отрезка? — И что же следует из этого равенства? — Верно. — Как вы думаете, каким методом на этот раз пользовались? Почему вы так считаете? — Сейчас каждый из вас самостоятельно оформит доказательство в своей тетради. | — Треугольник А1В1С1 прямоугольный, значит, квадрат гипотенузы равен сумме квадратов катетов. Т.е. А1В12=А1С12+В1С12. — Т.к. А1С1=АС, а В1С1=ВС, то получим, что А1В12= АС2+ВС2. — Да, сумма квадратов сторон АС и ВС равна квадрату стороны АВ треугольника АВС. Значит, А1В12=АВ2. — Что А1В1=АВ. Мы получили, что треугольники А1В1С1 и АВС равны по трем сторонам, это: А1В1=АВ, А1С1=АС, В1С1=ВС. Если треугольник А1В1С1 прямоугольный, то и треугольник АВС тоже будет прямоугольным, т.е. угол С равен углу С1 и равен 90 градусов, как соответственные углы в равных треугольниках. Думают, анализируют ход рассуждений. Обсуждение в парах. — Мы использовали синтетический метод доказательства, так как рассуждения велись по той же схеме, как и предыдущие. Самостоятельная работа в тетрадях. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Доказательство:
А1В12=А1С12+В1С12 (теорема Пифагора)
А1В12= АС2+ВС2
А1В12=АВ2, А1В1=АВ,
А1В1=АВ (п.3), А1С1=АС (по условию), В1С1=ВС (по условию),
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
— Закончили, обменялись с соседом своими работами. Проверьте оформление доказательства, сверяя его с тем, что вы видите на слайде. Оцените работу соседа. Если имеется 1, 2 недочета ставим 5, если имеем 3,4 – ставим 4, более 4 недочетов – ставим 3. — По данному доказательству нам осталось выполнить еще один этап, который называется «взгляд назад». Давайте вспомним, какие теоремы, свойства, признаки мы использовали при доказательстве? — Сформулируйте доказанное утверждение. — Какой пункт плана мы выполнили? — Что осталось сделать? | Меняются тетрадями, проводится взаимопроверка. Оценивают друг друга. — Теорему Пифагора, третий признак равенства треугольников, т.е. по трем сторонам, свойство равных треугольников, что в равных треугольниках против соответственно равных сторон лежат равные углы. — Если квадрат одной стороны равен сумме квадратов двух других сторон, то такой треугольник прямоугольный. — Седьмой пункт. Учились друг у друга. — Подвести итог урока. | Слайд № 15. Оформление доказательства. Взаимопроверка. Переход по ссылке «План урока». Слайд № 3. План урока. Переход по ссылке «Итог». | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(Работа производится фронтально с помощью карточек.) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
— Какая задача была поставлена на уроке? — Как мы решили поставленную задачу? — Еще какую теорему вы узнали на этом уроке? — Для решения каких задач можно использовать доказанную теорему Пифагора? — Сформулируйте теорему Пифагора. — Верно. Назовите основную идею, прием доказательства этой теоремы. — А теперь с помощью карточек оцените свою деятельность на уроке. Я буду задавать вопросы, вы поднимаете ту карточку, которая «отражает» ваш ответ. — Получилось ли у тебя «открыть» теорему Пифагора? — Возникали трудности во время урока? — Тыусвоил новый материал? — Интересно тебе было на уроке? — Ты бы хотел быть тьютором? — Ты бы сделал что-нибудь по-другому, будь ты учеником-тьютором? — Судя по вашей самооценке можно сделать вывод, что новые знания усвоены, но кем-то лучше, кем-то хуже. | — Найти взаимосвязь между катетами и гипотенузой прямоугольного треугольника. — Изучили теорему Пифагора, которая объясняет эту взаимосвязь. — Теорему обратную теореме Пифагора. — Для нахождения гипотенузы в прямоугольном треугольнике, неизвестного катета, если известны другой катет и гипотенуза. — Условие теоремы – это «в прямоугольном треугольнике», а заключение – «квадрат гипотенузы равен сумме квадратов катетов». — В доказательстве применялся метод площадей, также при рассуждении пользовались синтетическим методом. У ребят на партах находятся карточки со знаками «+» и « — ». используя эти карточки учащиеся отвечают на вопросы учителя, тем самым проводится самооценка каждого. | Слайд № 16. Подведение итогов урока. Слайд № 17. Оценка деятельности каждого ученика на уроке. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(Домашнюю работу ученики выбирают по мере понимания материала на уроке.) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
— Чтобы знания усвоили все , необходимо дома выполнить такие задания: к следующему уроку знать формулировки теоремы Пифагора и ей обратной. На следующем уроке состоится тестовая работа на проверку того, как вы усвоили новый материал. — Кто считает, что полностью разобрался и понял новый материал, решает дома задачи под номерами 484(а, б), 498(а, б). — У кого возникли вопросы на некоторых этапах нашего урока, решает дома задачи под номерами 483(а, б), 484(а, б). Обратная теорема Пифагора: Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный. То есть для всякой тройки положительных чисел a, b a 2 + b 2 = c 2 существует прямоугольный треугольник с катетами a Теорема Пифагора Значение теоремы Дополнительный материал: Теорема Пифагора между сторонами прямоугольного треугольника . Считается, что доказана греческим математиком Пифагором, в честь которого и названа. Геометрическая формулировка теоремы Пифагора.Изначально теорема была сформулирована следующим образом: В прямоугольном треугольнике площадь квадрата , построенного на гипотенузе , равна сумме площадей квадратов , построенных на катетах. Алгебраическая формулировка теоремы Пифагора.В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. То есть, обозначив длину гипотенузы треугольника через c Обе формулировки теоремы Пифагора требует понятия площади. То есть второе утверждение можно проверить, ничего не зная о площади и измерив только длины сторон прямоугольного треугольника . Обратная теорема Пифагора.Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный. Или, иными словами: Для всякой тройки положительных чисел a существует прямоугольный треугольник с катетами a Теорема Пифагора для равнобедренного треугольника.Теорема Пифагора для равностороннего треугольника.Доказательства теоремы Пифагора.На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы. Вероятно, теорема Пифагора является единственной теоремой со столь внушительным числом доказательств. Такое многообразие можно объяснить лишь фундаментальным значением теоремы для геометрии. Разумеется, концептуально все их можно разбить на малое число классов. Самые известные из них: доказательства методом площадей с помощью дифференциальных уравнений 1. Доказательство теоремы Пифагора через подобные треугольники. Следующее доказательство алгебраической формулировки — наиболее простое из доказательств, строящихся напрямую из аксиом. Пусть ABC её основание через H Треугольник ACH Введя обозначения: получаем: , что соответствует — Сложив a или , что и требовалось доказать. 2. Доказательство теоремы Пифагора методом площадей. Ниже приведённые доказательства, несмотря на их кажущуюся простоту, вовсе не такие простые. Все они используют свойства площади, доказательства которых сложнее доказательства самой теоремы Пифагора.
Расположим четыре равных прямоугольных треугольника так, как показано на рисунке справа. Четырёхугольник со сторонами c так как сумма двух острых углов 90°, а развёрнутый угол — 180°. Площадь всей фигуры равна, с одной стороны, площади квадрата со стороной (a+b Что и требовалось доказать. 3. Доказательство теоремы Пифагора методом бесконечно малых. Рассматривая чертёж, показанный на рисунке, и наблюдая изменение стороны записать следующее соотношение для бесконечно малых треугольников): Используя метод разделения переменных, находим: Более общее выражение для изменения гипотенузы в случае приращений обоих катетов: Интегрируя данное уравнение и используя начальные условия, получаем: Таким образом, мы приходим к желаемому ответу: Как нетрудно видеть, квадратичная зависимость в окончательной формуле появляется благодаря линейной пропорциональности между сторонами треугольника и приращениями, тогда как сумма связана с независимыми вкладами от приращения разных катетов. Более простое доказательство можно получить, если считать, что один из катетов не испытывает приращения (в данном случае катет b Цели урока: общеобразовательные:
развивающие:
воспитательные:
Форма урока: классно-урочная. План урока:
Ход урока. Организационный момент.Проверка домашнего задания. Актуализация | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1) с 2 = а 2 + в 2 | 2) с = а + в | 3) а 2 = с 2 – в 2 |
| 4) с 2 = а 2 – в 2 | 5) в 2 = с 2 – а 2 | 6) а 2 = с 2 + в 2 |
Пока учащиеся, доказывающие теорему у
доски и на местах, не готовы, слово
предоставляется тем, кто подготовил сообщения о
жизни и деятельности Пифагора.
Школьники, работающие на местах, сдают
листочки и слушают доказательства тех, кто
работал у доски.
Решение практических задач с использованием
теоремы Пифагора.
Учитель:
предлагаю вам
практические задачи с применением изучаемой
теоремы. Побываем сначала в лесу, после бури,
потом на загородном участке.
Задача 1
. После бури сломалась ель.
Высота оставшейся части 4,2 м. Расстояние от
основания до упавшей макушки 5,6 м. Найти высоту
ели до бури.
Задача 2
. Высота дома 4,4 м Ширина
газона вокруг дома 1,4 м. Какой длины надо
изготовить лестницу, чтобы она не заступала на
газон и доставала до крыши дома?
Новая тема.
Учитель:
(звучит музыка)
Закройте глаза, на несколько минут мы окунемся в
историю. Мы с вами в Древнем Египте. Вот на верфях
египтяне строят свои знаменитые корабли. А вот
землемеры, они измеряют участки земли, границы
которых смылись после разлива Нила. Строители
строят грандиозные пирамиды, которые до сих пор
поражают нас своим великолепием. Во всех этих
Во всех этих
видах деятельности египтянам необходимо было
использовать прямые углы. Они умели строить их с
помощью веревки с 12 ю завязанными на
одинаковом расстоянии друг от друга узелками.
Попробуйте и вы, рассуждая как древние египтяне,
построить с помощью своих веревок прямоугольные
треугольники. (Решая эту проблему, ребята
работают в группах по 4 человека. Через некоторое
время на планшете у доски кто-то показывает
построение треугольника).
Стороны полученного треугольника 3, 4 и
5. Если между этими узлами завязать еще по одному
узлу, то его стороны станут 6, 8 и 10. Если по два – 9,
12 и 15. Все эти треугольники являются
прямоугольными т. к.
5 2 = 3 2 + 4 2 , 10 2
= 6 2 + 8 2 , 15 2 = 9 2 + 12 2
и т.д.
Каким свойством должен обладать
треугольник, чтобы быть прямоугольным? (Учащиеся
пытаются сами сформулировать обратную теорему
Пифагора, наконец, у кого-то это получается).
Чем эта теорема отличается от теоремы
Пифагора?
Ученик:
Условие и
заключение поменялись местами.
Учитель:
Дома вы повторяли,
как называются такие теоремы. Так с чем мы сейчас
познакомились?
Ученик:
С обратной
теоремой Пифагора.
Учитель:
Запишем в
тетради тему урока. Откройте учебники на стр. 127
прочитайте еще раз это утверждение, запишите его
себе в тетрадь и разберите доказательство.
(После нескольких минут
самостоятельной работы с учебником по желанию
один человек у доски приводит доказательство
теоремы).
- Как называется треугольник со сторонами 3, 4 и 5?
Почему? - Какие треугольники называются пифагоровыми?
- С какими треугольниками вы работали в домашнем
задании? А в задачах с сосной и лестницей?
Первичное закрепление знаний
.
Эта теорема помогает решать задачи, в
которых надо выяснить, будут ли треугольники
прямоугольными.
Задания:
1) Выясните, является ли треугольник
прямоугольным, если его стороны равны:
а) 12,37 и 35; б) 21, 29 и 24.
2) Вычислите высоты треугольника со сторонами 6,
8 и 10 см.
Домашнее задание
.
Стр.127:обратная теорема Пифагора. № 498(а,б,в) № 497.
Итоги урока.
Что нового узнали на уроке?
Пифагора?
Самостоятельная работа (проводится по
индивидуальным карточкам).
Учитель:
Дома вы повторяли
свойства ромба и прямоугольника. Перечислите их
(идет беседа с классом). На прошлом уроке мы
говорили о том, что Пифагор был разносторонней
личностью. Он занимался и медициной, и музыкой, и
астрономией, а так же был спортсменом и
участвовал в олимпийских играх. А еще Пифагор был
философом. Многие его афоризмы и сегодня
актуальны для нас. Сейчас вы будете выполнять
самостоятельную работу. К каждому заданию дано
несколько вариантов ответов, рядом с которыми
записаны фрагменты афоризмов Пифагора. Ваша
Ваша
задача – решив все задания, составить из
полученных фрагментов высказывание и записать
его.
Тема:
Теорема, обратная теореме Пифагора.
Цели урока:
1) рассмотреть теорему, обратную теореме Пифагора; ее применение в процессе решения задач; закрепить теорему Пифагора и совершенствовать навыки решения задач на ее применение;
2) развивать логическое мышление, творческий поиск, познавательный интерес;
3) воспитывать у учащихся ответственного отношения к учению, культуры математической речи.
Тип урока.
Урок усвоения новых знаний.
Ход урока
І.
Организационный момент
ІІ.
Актуализация
знаний
Урок мне
бы
хотелось
начать с четверостишья.
Да, путь познания не гладок
Но знаем мы со школьных лет,
Загадок больше, чем разгадок,
И поискам предела нет!
Итак, на прошлом уроке вы выучили теорему Пифагора. Вопросы:
Вопросы:
Теорема Пифагора справедлива для какой фигуры?
Какой треугольник называют прямоугольным?
Сформулируйте теорему Пифагора.
Как запишется теорема Пифагора для каждого треугольника?
Какие треугольники называются равными?
Сформулируйте признаки равенства треугольников?
А теперь проведем небольшую самостоятельную работу:
Решение задач по чертежам.
№1
(1 б.) Найти: АВ.
№2
(1 б.) Найти: ВС.
№3
(
2
б.)
Найти: АС
№4
(1 б.)
Найти: АС
№5
Дано: АВС
D
ромб
(2 б.) АВ = 13 см
АС = 10 см
Найти: В
D
Самопроверка №1. 5
№2. 5
№3. 16
№4. 13
№5. 24
ІІІ.
Изучение
нового
материала.
Древние египтяне строили прямые углы на местности таким образом: делили узлами веревку на 12 равных частей, связывали ее концы, после чего веревку растягивали так на земле, чтобы образовался треугольник со сторонами 3, 4 и 5 делений. Угол треугольника, который лежал против стороны с 5 делениями, был прямой.
Угол треугольника, который лежал против стороны с 5 делениями, был прямой.
Можете ли вы объяснить правильность этого суждения?
В результате поиска ответа на вопрос учащиеся должны понять, что с математической точки зрения вопрос ставится: будет ли треугольник прямоугольным.
Ставим проблему: как, не делая измерений, определить, будет ли треугольник с заданными сторонами прямоугольным. Решение этой проблемы и есть цель урока.
Запишите тему урока.
Теорема. Если сумма квадратов двух сторон треугольника равна квадрату третьей стороны, то такой треугольник прямоугольный.
Самостоятельно доказывают теорему (составляют план доказательства по учебнику).
Из этой теоремы следует, что треугольник со сторонами 3, 4, 5 – прямоугольный (египетский).
Вообще, числа, для которых выполняется равенство
, называют пифагоровыми тройками. А треугольники, длины сторон которых выражаются пифагоровыми тройками (6, 8, 10), — пифагоровы треугольники.
Закрепление.
Т.к.
, то треугольник со сторонами 12, 13, 5 не является прямоугольным.
Т.к.
, то треугольник со сторонами 1, 5, 6 является прямоугольным.
№ 430 (а, б, в)
(
— не является)
Замечательно, что свойство указанное в теореме Пифагора, является характеристическим свойством прямоугольного треугольника. Это следует из теоремы, обратной теореме Пифагора.
Теорема: Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный.
Выведем формулу, выражающую плоскость треугольника через длины его сторон. Эту формулу связывают с именем Герона александрийского — древнегреческого математика и механика, жившего, вероятно в 1 в.н.э. Герон много уделял внимания практическим приложениям геометрии.
Теорема. Площадь S треугольника, стороны которого равны a , b , c , вычисляется по формуле S=, где p — полупериметр треугольника.
Доказательство.
Дано: ?ABC, АВ= с, ВС= а, АС= b.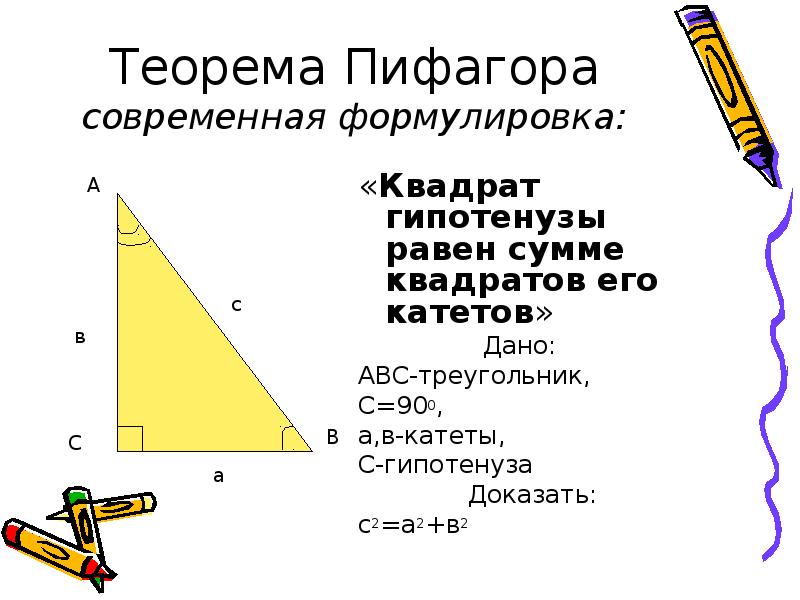 Углы А и В, острые. СН — высота.
Углы А и В, острые. СН — высота.
Доказать:
Доказательсво:
Рассмотрим треугольник ABC, в котором AB=c , BC=a, AC=b. Во всяком треугольнике, по крайней мере, два угла острые. Пусть А и В — острые углы треугольника АВС. Tогда основание H высоты CH треугольника лежит на стороне AB. Введем обозначения: CH = h, AH=y, HB=x. по теореме Пифагора a 2 — x 2 = h 2 =b 2 -y 2 , откуда
Y 2 — x 2 = b 2 — a 2 , или (y — x) (y + x) = b 2 — a 2 , а так как y + x = c, то y- x = (b2 — a2).
Складывая два последних равенства, п олучаем:
2y = +c, откуда
y=,и, значит, h 2 = b 2 -y 2 =(b — y)(b+y)=
Следовательно, h = .
Технологическая карта по теме «Теорема, обратная теореме Пифагора»
Автор: Мартынова Вера Аркадьевна- учитель математики ГОУ РК «Республиканский центр образования»
Технологическая карта урока
Ф.И.О. Мартынова Вера Аркадьевна
Предмет: Математика (геометрия). Учебник под редакцией Л.С. Атанасяна. Геометрия 7 – 9.
Учебник под редакцией Л.С. Атанасяна. Геометрия 7 – 9.
Класс: 8
Тип урока: Урок по изучению и первичному закреплению новых знаний и способов деятельности
Тема | Теорема, обратная теореме Пифагора. |
Цель урока | Создание условий по введению теоремы, обратной теореме Пифагора и её применения при решении задач. |
Задачи | Образовательные: организовать деятельность учащихся по восприятию, осмыслению и первичному закреплению новых знаний и способов деятельности Развивающие: — создать у школьников положительную мотивацию к предмету; — повысить общую культуру учащихся; -расширить умственный кругозор учащихся, — помочь школьникам лучше понять роль геометрии в жизни; -воспитывать у школьников ответственность и аккуратность, умение работать в парах. |
УУД | Личностные УУД: воспитание интереса к математике, самостоятельности, аккуратности и трудолюбия. Регулятивные УУД: умение действовать в соответствие с действующим алгоритмом. Коммуникативные УУД: сотрудничество и восприятие разных мнений. Познавательные УУД: умение видеть математическую задачу. |
Планируемые результаты | Предметные: Знать формулировку обратной теоремы Пифагора Уметь владеть геометрическим языком, использовать его для описания предметов окружающего мира Личностные: целостное мировоззрение в современной науке. |
Основные понятия | Прямоугольный треугольник, катеты, гипотенуза. |
Межпредметные связи | Подготовка к изучению технологии и физики. |
Ресурсы: основные дополнительные | Учебник, опорный конспект, исторические сведения о применении теоремы Пифагора, компьютер, презентация. Транспортир, линейка, карандаш. |
Формы урока | Ф — фронтальная, И – индивидуальная, П – парная |
Технология | Компетентно – ориентированная технология. |
I этап. | ||
Цель деятельности | Деятельность учителя | Деятельность ученика |
Проверить знание теоремы Пифагора Время: 4 мин | Читает стихотворение о теореме Пифагора. ( Ресурсный материал) | (И) Рассказывают теорему Пифагора. |
II этап. Мотивация деятельности. | ||
Подвести учащихся к теореме, обратной теореме Пифагора Время: 6 мин | Постановка учебной задачи | |
Сформулируйте утверждения, обратные данным, и выясните, верны ли они: 1. 2. Вертикальные углы равны. 3.В прямоугольном треугольнике Квадрат гипотенузы равен сумме квадратов катетов. | (Ф)1.Если диагонали взаимно перпендикулярны, то это ромб. 2. Если углы равны, то они вертикальны. 3. Если квадрат гипотезы равен сумме квадратов катетов, то треугольник прямоугольный. | |
III этап. Изучение нового материала. | ||
Рассмотреть доказательство теоремы по учебнику. Время:15 мин | Объясняет доказательство теоремы, обратной теореме Пифагора. Постройте прямоугольный треугольник, длины катетов 4см. и 3см. Измерьте гипотенузу. Проверьте теорему Пифагора. А как называется прямоугольный треугольник со сторонами 3см, 4см, 5см? Ученик подготовил презентацию «Пифагоровы треугольники». Являются ли пифагоровыми треугольники: а) С катетом 15 и гипотенузой 25? б) С катетом 6 и гипотенузой 10? | (Ф) Включены в разбор теоремы, обратной теореме Пифагора. (И) Чертят прямоугольный треугольник с данными сторонами и измеряют гипотенузу – 5 см. 32 + 42 = 52. Верно. (П) Работа по учебнику. Египетский треугольник. (И). Выступление сопровождается презентацией по этой теме. Прямоугольные треугольники, длины сторон которых выражаются целыми числами, называются пифагоровыми треугольниками. (П/И) Решают задачи. |
IVэтап. Закрепление изученного материала | ||
Закрепить изученные теоремы при решении простейших задач Время:10 мин | 1. Решить № 498(а,б,в) устно. 2. Решить задачу № 499(а) 3. Решить самостоятельно задачу: Определите углы треугольника со сторонами 1, 1,2 | (Ф/И) Решают. Один учащийся выхолит к доске, остальные работают в тетради. (П) Ответ: 450 , 450, 900. |
Vэтап. Итоги урока. Рефлексия. | ||
Рефлексия Время: 5 мин | Итак, на этом уроке мы вспомнили теорему Пифагора и познакомились с обратной ей: если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то этот треугольник – прямоугольный. 1.Теперь я узнал, что… 2. Теперь я могу… 3. Раньше я не понимал, как… 4. Раньше я не знал, что… 5. Теперь я знаю, что… Оценивание. | Учащиеся продолжают фразы… Самооценка. |
Ресурсный материал.
1. http://chto-takoe- lyubov.net/stikhi-o-lyubvi/kollektsii-stikhov/12816-stixi-o-teoreme-pifagora
Если дан нам треугольник
И притом с прямым углом,
То квадрат гипотенузы
Мы всегда легко найдем:
Катеты в квадрат возводим,
Сумму степеней находим
И таким простым путем
К результату мы придем.
Дырченко И.
2. http://www.bolshoyvopros.ru/questions/2353224-kakie-treugolniki-nazyvajutsja-pifagorovymi.html
Пифагоровы треугольники — это целая большая теория. Общее название теории — пифагоровы тройки. Это такие наборы натуральных чисел, которые удовлетворяют уравнению x2+y2=z2. Из любой пифагоровой тройки (кстати, по обратной теореме Пифагора) можно построить прямоугольный треугольник, который и будет называться пифагоровым. Есть много способов решения этого уравнения. А сами пифагоровы треугольники обладают многими интересными геометрическими свойствами.
Несколько примеров пифагоровых троек: (3,4,5), (6,8,10), (5,12,13), (9,12,15), (8,15,17), (12,16,20), (15,20,25), (7,24,25), (10,24,26), (20,21,29), (18,24,30), (16,30,34), (21,28,35), (12,35,37), (15,36,39), (24,32,40), (9,40,41), (14,48,50), (30,40,50)
Любой из этих треугольников можно построить обычным способом построения треугольника по трём сторонам с помощью циркуля и линейки.
Пифагоров треугольник со сторонами 3, 4, 5 известен с глубокой древности. Он называется египетским, и использовался для построения прямого угла на местности. Вместо вычерчивания применялась верёвка, разделённая 12 узлами на равные части, которая натягивалась на колышки.
3. https://videouroki.net/video/15-tieoriema-obratnaia-tieoriemie-pifaghora.html
В Древнем Египте для построения прямого угла строили прямоугольный треугольник при помощи кольев и натянутых на них верёвок длиной три, четыре и пять единиц.
В Древнем Египте для построения прямого угла строили прямоугольный треугольник при помощи кольев и натянутых на них верёвок длиной три, четыре и пять единиц.
Тогда угол между сторонами, равными трём и четырём, получался прямым.
Задачи:
Решение.
Что такое обратная теорема Пифагора?
Уже поздний вечер, на самом деле уже за полночь, поэтому текст поста буду кратким.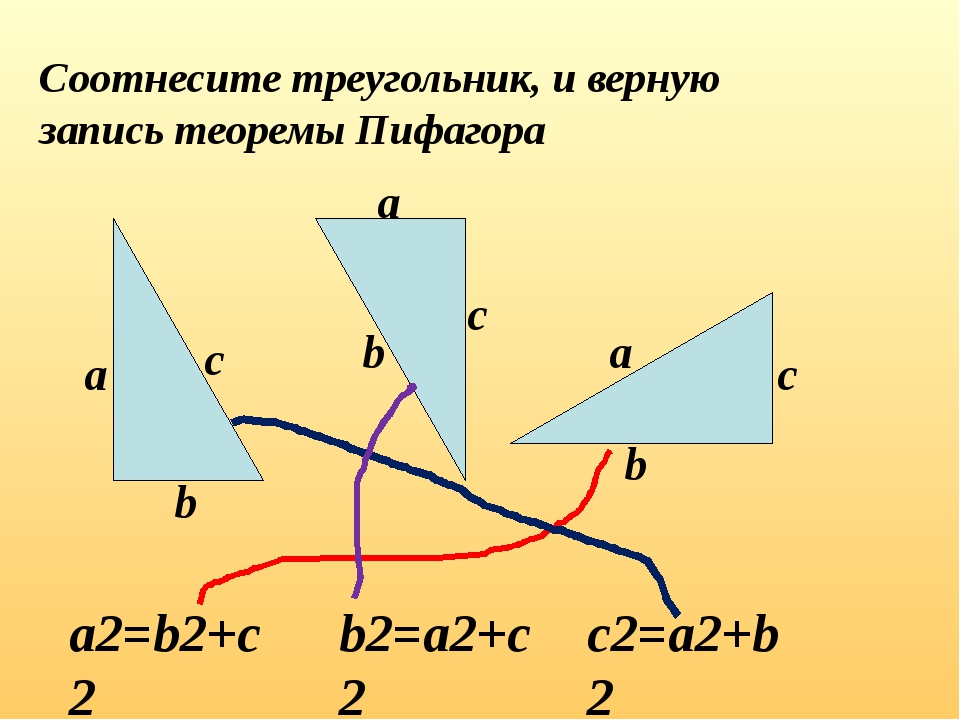 Сегодня был хороший день, и сегодня вечером я сварил 23-ю партию пива, известную как «Спин-полпиво». (Я назвал его так, потому что он содержит только половину темного солода, который я использую в пиве, известного как темная материя…;), поэтому он не имеет ничего общего с электронами).
Сегодня был хороший день, и сегодня вечером я сварил 23-ю партию пива, известную как «Спин-полпиво». (Я назвал его так, потому что он содержит только половину темного солода, который я использую в пиве, известного как темная материя…;), поэтому он не имеет ничего общего с электронами).
Это очень простой пост о некоторой «обратной теореме Пифагора», пролетевшей в каком-то математическом видео.Я был довольно удивлен, что не видел этого раньше, но существует так много теорем, использующих эту старомодную евклидову геометрию, что я, возможно, совсем забыл об этом.
В течение 10 минут у меня было хорошее доказательство 2D-версии этой «обратной теоремы Пифагора». Вы можете найти его на первой картинке ниже.
Однажды спустя, когда я немного катался, я попытался найти более многомерный аналог этого простого для понимания 2D утверждения или теоремы. И поэтому мне пришла в голову важная роль, которую число расстояния d сыграло в моем доказательстве общей теоремы Пифагора, которая действует на симплексы, которые являются более высокоразмерным аналогом двумерных треугольников.
Придя домой, было легко записать детали, но для меня все было настолько просто, что заслуживает ли этот материал названия «теорема»? Что ж, принимайте собственные решения по этому поводу, но если это не очень сложная теорема, это все равно хороший и милый результат …
Этот пост состоит из шести изображений (все 550 × 775 пикселей, кроме последнего, которое потребовало немного расширения, потому что математика не подошла должным образом, поэтому одно изображение имеет размер 600 × 775 пикселей).
Иногда это может показаться трудным, но это только потому, что в общих настройках, когда дело доходит до количества измерений, основная идея — это все простые вещи, такие как взятие внутреннего продукта с нормализованным вектором нормали.
Вот шесть картинок:
Это прекрасный результат, но для меня вектор нормали такой же милый, но только немного сложнее для написания, потому что эта часть имеет дело с общими настройками, где размерность n не фиксирована.
На этом пост пока заканчивается. Увидимся, мой дорогой читатель.
__________
Приложение, добавленное 30 марта 2018 г .: В предыдущем посте я забыл разместить ссылку на доказательство общей теоремы Пифагора, которое я когда-то создавал давным-давно.
Перед этой ссылкой я хотел бы еще раз показать вам, как доказать общую теорему Пифагора для трехмерного случая, используя только двумерную теорему.
В конце концов, это первый основной шаг в моем доказательстве общей теоремы Пифагора…
Вот два дополнительных изображения, показывающих, как проходит этот основной шаг от двухмерной плоскости к трехмерному пространству:
Вот ссылка на доказательство общей теоремы Пифагора:
Общая теорема Пифагора (второй и последний пост).
Общая теорема Пифагора (второй и последний пост).
Ладно, до обновлений.
Теорема Пифагора и обратная ей.
 Урок «Теорема противоположна теореме Пифагора». III. Вступительное слово учителя, историческая справка
Урок «Теорема противоположна теореме Пифагора». III. Вступительное слово учителя, историческая справка
Согласно ван дер Вардену, весьма вероятно, что это соотношение в общих чертах было известно в Вавилоне уже примерно в 18 веке до нашей эры. е.
Около 400 г. до н. Э. е., согласно Проклу, Платон дал метод нахождения пифагоровых троек, объединив алгебру и геометрию.Около 300 г. до н. Э. е. Самое старое аксиоматическое доказательство теоремы Пифагора появилось в «Элементах» Евклида.
Формулировка
Основная формулировка содержит алгебраические действия — в прямоугольном треугольнике длины катетов равны a (\ displaystyle a) и b (\ displaystyle b), а длина гипотенузы равна c (\ displaystyle c) соотношение выполняется:
.
Возможна и эквивалентная геометрическая формулировка, прибегая к понятию площади фигуры: в прямоугольном треугольнике площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на ножках.(2)) имеется прямоугольный треугольник с катетами a (\ displaystyle a) и b (\ displaystyle b) и гипотенуза c (\ displaystyle c).
Доказательство
В научной литературе зафиксировано не менее 400 доказательств теоремы Пифагора, что объясняется как фундаментальной важностью для геометрии, так и элементарностью результата. Основные направления доказательств: алгебраическое использование соотношений элементов треугольника (такого, например, популярный метод подобия), метод площадей, также существуют различные экзотические доказательства (например, с помощью дифференциальных уравнений).
По аналогичным треугольникам
Классическое доказательство Евклида направлено на установление равенства площадей прямоугольников, образованных разрезом квадрата над гипотенузой, с высотой от прямого угла с квадратами над катетами.
Для доказательства используется следующая конструкция: для прямоугольного треугольника с прямым углом C (\ displaystyle C) квадраты над катетами и квадраты над гипотенузой ABIK (\ displaystyle ABIK) высота построения CH (\ \ displaystyle CH) и его продолжающийся луч s (\ displaystyle s), разделяющий квадрат над гипотенузой на два прямоугольника и.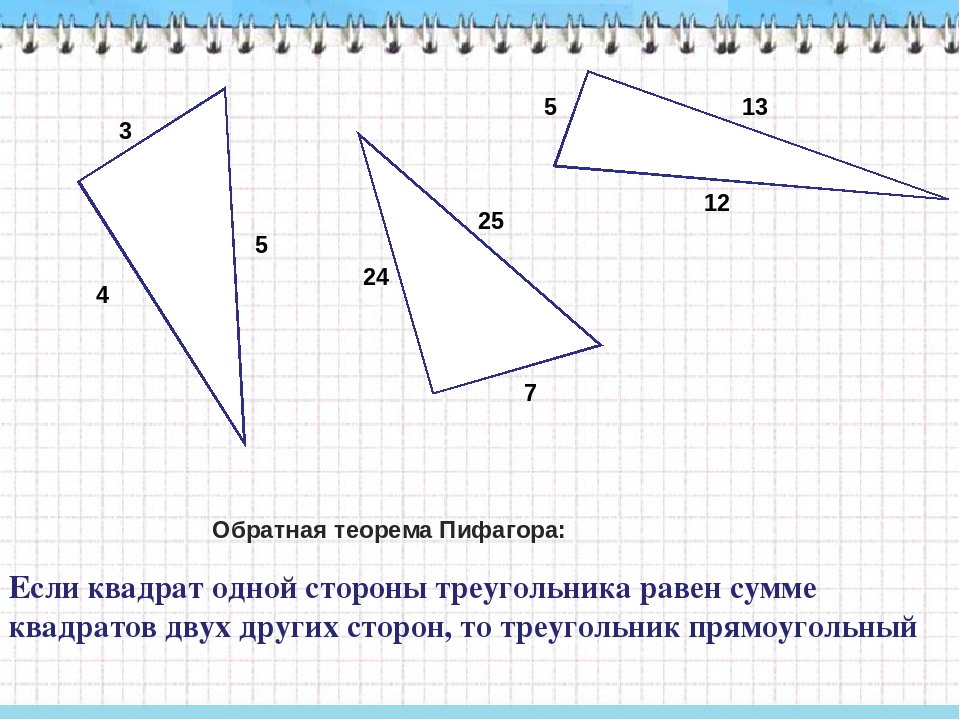 Доказательство направлено на установление равенства площадей прямоугольника A H J K (\ displaystyle AHJK) квадрату над ножкой A C (\ displaystyle AC); Таким же образом устанавливается равенство площадей второго прямоугольника, составляющего квадрат над гипотенузой, и прямоугольника над другим катетом.
Доказательство направлено на установление равенства площадей прямоугольника A H J K (\ displaystyle AHJK) квадрату над ножкой A C (\ displaystyle AC); Таким же образом устанавливается равенство площадей второго прямоугольника, составляющего квадрат над гипотенузой, и прямоугольника над другим катетом.
Equal Rectangle Areas AHJK (\ displaystyle AHJK) и ACED (\ displaystyle ACED) устанавливается через конгруэнтность треугольников △ ACK (\ displaystyle \ треугольник ACK) и △ ABD (\ displaystyle \ треугольник ABD), площадь каждого из которых равна половине площади квадратов AHJK (\ displaystyle AHJK) и ACED (\ displaystyle ACED) соответственно, в связи со следующим свойством: площадь треугольника равна половине площади прямоугольника, если фигуры имеют общую сторону, а высота треугольника до общей стороны — это другая сторона прямоугольника.Конгруэнтность треугольников следует из равенства двух сторон (сторон квадратов) и угла между ними (состоящего из прямого угла и угла при A (\ displaystyle A).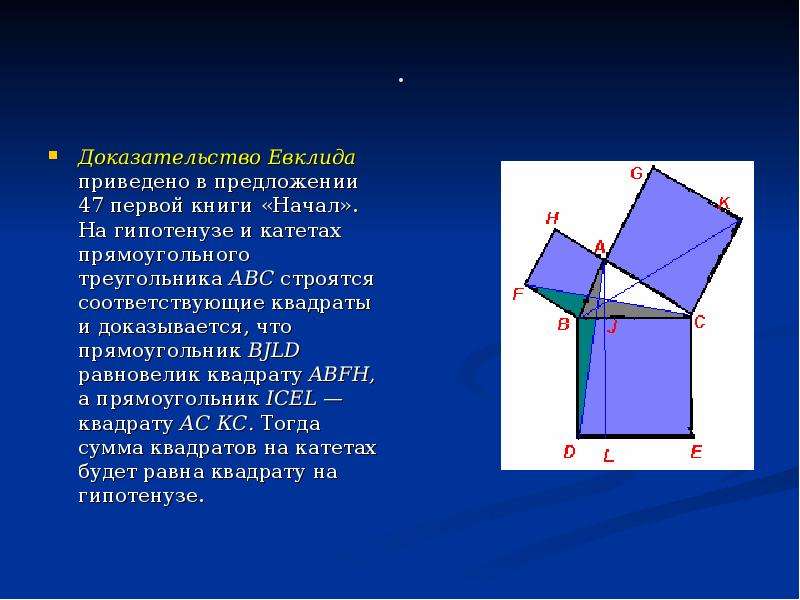
Таким образом, доказательство устанавливает, что Площадь квадрата над гипотенузой, составленного из прямоугольников AHJK (\ displaystyle AHJK) и BHJI (\ displaystyle BHJI), равна сумме площадей квадратов над катетами.
Доказательство Леонардо да Винчи
Метод площадей также включает доказательство, найденное Леонардо да Винчи.Дан прямоугольный треугольник △ ABC (\ displaystyle \ треугольник ABC), прямой угол C (\ displaystyle C) и квадраты ACED (\ displaystyle ACED), BCFG (\ displaystyle BCFG) и ABHJ (\ displaystyle ABHJ ) (см. рисунок). В этом доказательстве на стороне HJ (\ displaystyle HJ) последнего построен треугольник, конгруэнтный △ ABC (\ displaystyle \ треугольник ABC), причем отраженный как относительно гипотенузы, так и относительно высоты до он (т.е. JI = BC (\ displaystyle JI = BC) и HI = AC (\ displaystyle HI = AC)).Прямой CI (\ displaystyle CI) разбивает квадрат, построенный на гипотенузе, на две равные части, поскольку треугольники △ ABC (\ displaystyle \ треугольник ABC) и △ JHI (\ displaystyle \ треугольник JHI) равны по построению.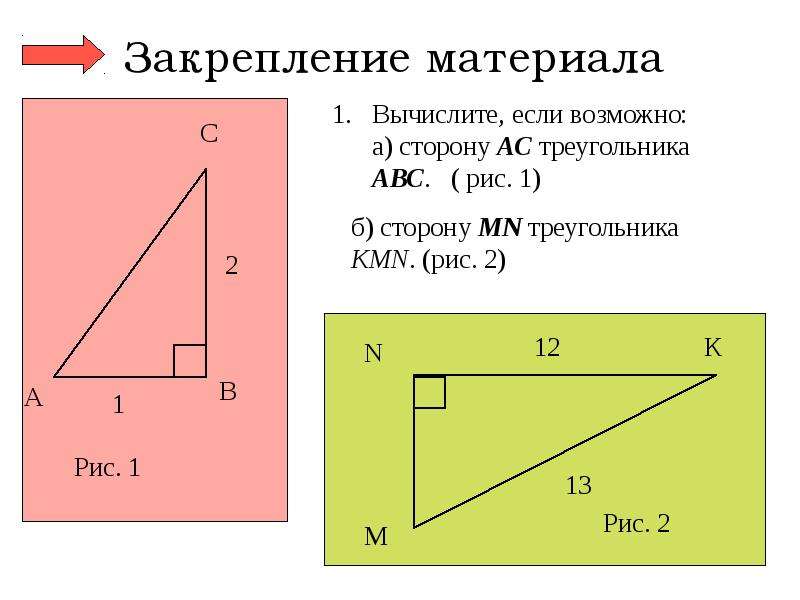 . Доказательство устанавливает соответствие четырехугольников CAJI (\ displaystyle CAJI) и DABG (\ displaystyle DABG), площадь каждого из которых оказывается, с одной стороны, равной сумме половины площади квадратов на катетах и площадь исходного треугольника, с другой стороны, половина площади квадрата на гипотенузе плюс площадь исходного треугольника.Всего половина суммы площадей квадратов над катетами равна половине площади квадрата над гипотенузой, что эквивалентно геометрической формулировке теоремы Пифагора.
. Доказательство устанавливает соответствие четырехугольников CAJI (\ displaystyle CAJI) и DABG (\ displaystyle DABG), площадь каждого из которых оказывается, с одной стороны, равной сумме половины площади квадратов на катетах и площадь исходного треугольника, с другой стороны, половина площади квадрата на гипотенузе плюс площадь исходного треугольника.Всего половина суммы площадей квадратов над катетами равна половине площади квадрата над гипотенузой, что эквивалентно геометрической формулировке теоремы Пифагора.
Доказательство методом бесконечно малых
Есть несколько доказательств, использующих технику дифференциальных уравнений. В частности, Харди приписывают доказательство, использующее бесконечно малые приращения отрезков a (\ displaystyle a) и b (\ displaystyle b) и гипотенузу c (\ displaystyle c) и сохраняющее сходство с исходным прямоугольником, что есть, обеспечивая выполнение следующих дифференциальных соотношений:
dadc = ca (\ displaystyle (\ frac (da) (dc)) = (\ frac (c) (a))), dbdc = cb (\ displaystyle (\ frac (db) ( dc)) = (\ frac (c) (b))).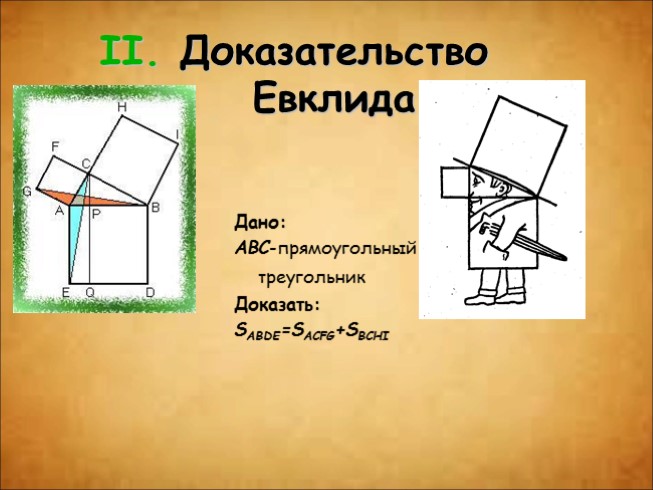 (2) + \ mathrm (Const)) … Применение начальных условий a = b = c = 0 (\ displaystyle a = b = c = 0) определяет константу как 0, которая приводит к формулировке теоремы.
(2) + \ mathrm (Const)) … Применение начальных условий a = b = c = 0 (\ displaystyle a = b = c = 0) определяет константу как 0, которая приводит к формулировке теоремы.
Квадратичная зависимость в окончательной формуле возникает из-за линейной пропорциональности между сторонами треугольника и приращениями, в то время как сумма связана с независимыми вкладами приращений различных катетов.
Варианты и обобщения
Схожие геометрические фигуры с трех сторон
Важное геометрическое обобщение теоремы Пифагора было дано Евклидом в «Элементах», переходя от площадей квадратов по сторонам к площадям произвольных одинаковых геометрических фигур: сумма площадей таких фигур, построенных на ногах, будет равна площади аналогичной фигуры, построенной на гипотенузе.
Основная идея этого обобщения состоит в том, что площадь такой геометрической фигуры пропорциональна квадрату любого из ее линейных размеров, а в частности квадрату длины любой стороны. Следовательно, для подобных фигур с областями A (\ displaystyle A), B (\ displaystyle B) и C (\ displaystyle C), построенных на ножках с длинами a (\ displaystyle a) и b (\ displaystyle b) и гипотенуза c (\ displaystyle c) соответственно, выполняется соотношение:
A a 2 = B b 2 = C c 2 ⇒ A + B = a 2 c 2 C + b 2 c 2 C (\ displaystyle (\ frac (A) (a ^ (2))) \ u003d (\ frac (B) (b ^ (2))) = (\ frac (C) (c ^ (2))) \, \ Rightarrow \, A + B = (\\ гидроразрыва (a ^ (2)) (c ^ (2))) C + (\\ frac (b ^ (2)) (c ^ (2))) C).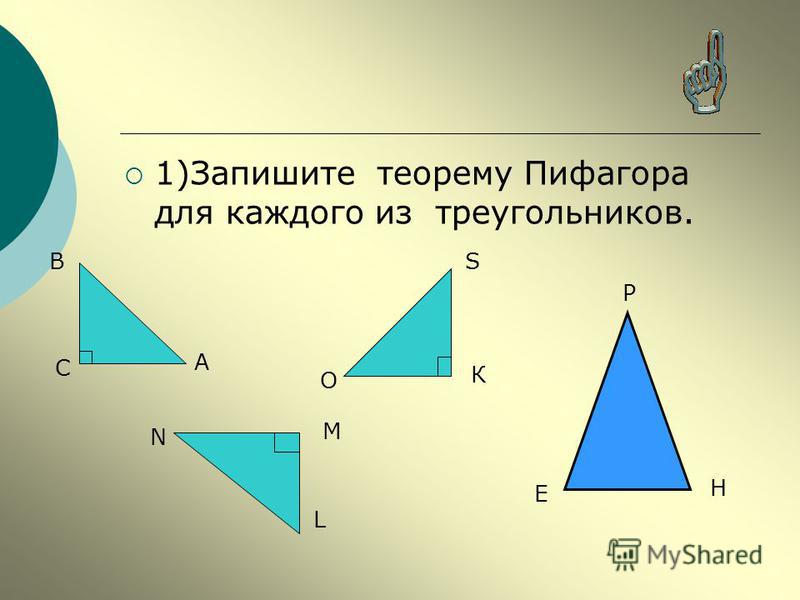 (2)), то удовлетворяется.
(2)), то удовлетворяется.
Кроме того, если можно доказать без обращения к теореме Пифагора, что для площадей трех одинаковых геометрических фигур на сторонах прямоугольного треугольника соотношение A + B = C (\ displaystyle A + B = C), то, используя обратный ход доказательства обобщения Евклида, можно вывести доказательство теоремы Пифагора. Например, если на гипотенузе построить равный исходному прямоугольный треугольник с площадью C (\ displaystyle C), а на катетах — два подобных прямоугольных треугольника с площадями A (\ displaystyle A) и B (\ displaystyle B), то получается, что треугольники на ногах образуются в результате деления исходного треугольника на его высоту, то есть сумма двух меньших площадей треугольников равна площадь третьего, таким образом, A + B = C (\ displaystyle A + B = C) и, применяя соотношение для подобных фигур, выводится теорема Пифагора.(2)),
где — угол между сторонами a (\ displaystyle a) и b (\ displaystyle b) … Если угол равен 90 °, то cos \ u2061 θ = 0 (\ displaystyle \ cos \\ theta = 0), а формула упрощается до обычной теоремы Пифагора.
Произвольный треугольник
Существует обобщение теоремы Пифагора на произвольный треугольник, основанное исключительно на соотношении длин сторон; считается, что оно было впервые установлено сабианским астрономом Сабитом ибн Куррой.В нем для произвольного треугольника со сторонами в него вписывается равнобедренный треугольник с основанием на стороне c (\ displaystyle c), вершина которого совпадает с вершиной исходного треугольника, противоположной стороне c (\ displaystyle в) и углы при основании равны углу θ (\ displaystyle \ theta), противоположной стороне c (\ displaystyle c) … В результате образуются два треугольника, аналогичные исходному: первый — со сторонами a (\ displaystyle a), наиболее удаленной от него боковой стороной вписанного равнобедренного треугольника, и r (\ displaystyle r) — боковыми частями c (\ displaystyle c); второй — симметрично ему со стороны b (\ displaystyle b) со стороной s (\ displaystyle s) — соответствующей части стороны c (\ displaystyle c). (2)).
(2)).
Теорема Паппа об площади
Неевклидова геометрия
Теорема Пифагора выведена из аксиом евклидовой геометрии и недействительна для неевклидовой геометрии — выполнение теоремы Пифагора эквивалентно постулату Евклида о параллелизме.
В неевклидовой геометрии соотношение сторон прямоугольного треугольника обязательно будет отличаться от теоремы Пифагора. Например, в сферической геометрии все три стороны прямоугольного треугольника, ограничивающие октант единичной сферы, имеют длину π / 2 (\ displaystyle \ pi / 2), что противоречит теореме Пифагора.
В этом случае теорема Пифагора верна в гиперболической и эллиптической геометрии, если требование прямоугольности треугольника заменить условием, что сумма двух углов треугольника должна равняться третьему.
Сферическая геометрия
Для любого прямоугольного треугольника на сфере радиуса R (\ displaystyle R) (например, если угол в треугольнике — прямая линия) со сторонами a, b, c (\ displaystyle a, b, c ) отношения между сторонами составляет:
соз \ u2061 (с R) = соз \ u2061 (a R) ⋅ соз \ u2061 (b R) (\ displaystyle \ cos \ left ((\\ frac (c) (R)) \ right) = \ cos \ left ((\ frac (a) (R)) \ right) \ cdot \ cos \ left ((\\ frac (b) (R)) \ right)) .
Это равенство может быть получено как частный случай теоремы о сферических косинусах, которая справедлива для всех сферических треугольников:
соз \ u2061 (c R) = соз \ u2061 (a R) ⋅ соз \ u2061 (b R) + sin \ u2061 (a R) ⋅ sin \ u2061 (b R) ⋅ cos \ u2061 γ (\ displaystyle \ \ cos \ left ((\\ frac (c) (R)) \ right) = \\ cos \ left ((\\ frac (a) (R)) \ right) \ cdot \ cos \ left ((\ frac (b) (R)) \ right) + \ ch \ u2061 c = ch \ u2061 a ⋅ ch \ u2061 b (\ displaystyle \ operatorname (ch) c \ u003d \ имя оператора (ch) a \ cdot \ имя оператора (ch) b).Где,
ch (\ displaystyle \ operatorname (ch)) — гиперболический косинус. Эта формула является частным случаем теоремы о гиперболическом косинусе, которая справедлива для всех треугольников: {! LANG-8dff69348cdd052375bb7ffde3dcad11!}
ch \ u2061 c = ch \ u2061 a ⋅ ch \ u2061 b — sh \ u2061 a ⋅ sh \ u2061 b ⋅ cos \ u2061 γ (\ displaystyle \ operatorname (ch) c = \ operatorname (ch) a \\ cdot \\ OperatorName (ch) b- \\ Operatorname (sh) a \\ cdot \\ Operatorname (sh) b \\ cdot \\ cos \\ gamma),
ch (\ displaystyle \ operatorname (ch)) γ (\ displaystyle \ gamma) — угол, вершина которого противоположна стороне c (\ displaystyle c). (2)))).
(2)))).
Для комплексных чисел теорема Пифагора дает естественную формулу для нахождения модуля комплексного числа — при z = x + y i (\ displaystyle z = x + yi) он равен длине
Задачи урока:
общеобразовательная:
- проверка теоретических знаний учащихся (свойства прямоугольного треугольника, теорема Пифагора), умение использовать их при решении задач;
- , создав проблемную ситуацию, приводит студентов к «открытию» обратной теоремы Пифагора.
развивающиеся:
- развитие навыков применения теоретических знаний на практике;
- развитие умения формулировать выводы в ходе наблюдений;
- развитие памяти, внимания, наблюдения:
- Развитие мотивации к обучению через эмоциональное удовлетворение от открытий, через введение элементов истории развития математических понятий.
образовательный:
- воспитать устойчивый интерес к предмету через изучение жизни Пифагора;
- воспитание взаимопомощи и объективной оценки знаний одноклассников путем взаимного экзамена.

Форма урока: аудиторное занятие.
План урока:
- Организация времени.
- Проверка домашнего задания. Обновление знаний.
- Решение практических задач с помощью теоремы Пифагора.
- Новая тема.
- Первичное закрепление знаний.
- Домашнее задание.
- Краткое содержание урока.
- Самостоятельная работа (по отдельным карточкам с отгадыванием афоризмов Пифагора).
Во время занятий.
Организация времени.
Проверка домашнего задания. Обновление знаний.
Учитель: Какое задание вы выполняли дома?
Ученики: Найдите третью сторону на заданных двух сторонах прямоугольного треугольника и расположите ответы в виде таблицы. Повторите свойства ромба и прямоугольника. Повторите то, что называется условием, и каков вывод теоремы. Подготовьте сообщения о жизни и творчестве Пифагора.Возьмите веревку с завязанными на ней 12 узлами.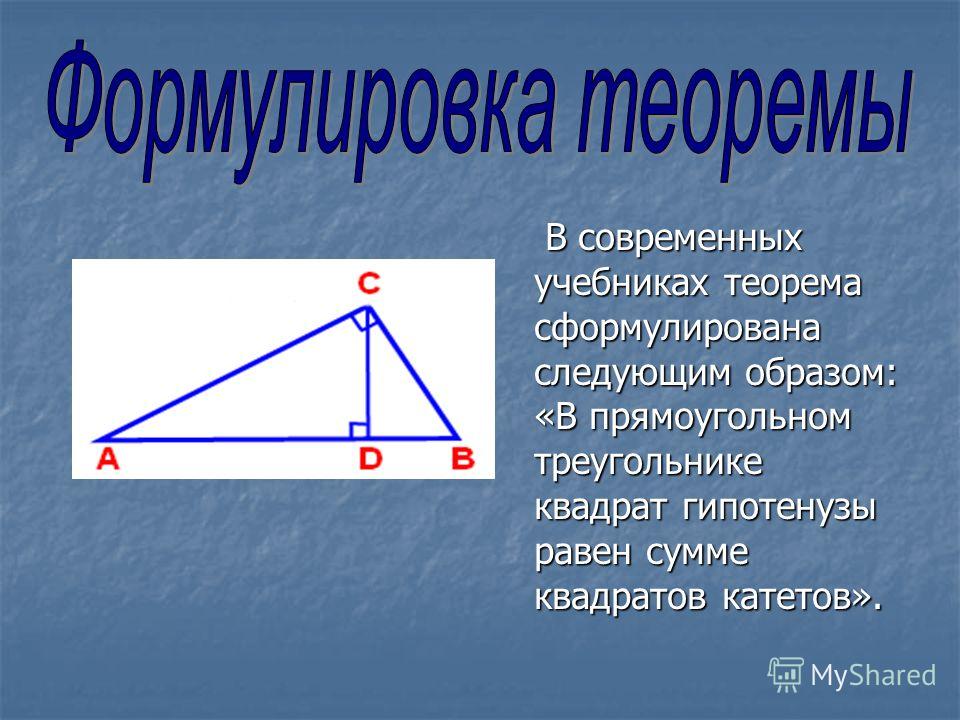
Учитель: Отметьте ответы к домашнему заданию в таблице
(данные выделены черным цветом, ответы — красным).
Учитель:
Выписки написаны на доске. Если вы согласны с ними на листках бумаги, поставьте «+» перед номером соответствующего вопроса, если вы не согласны, поставьте «-».
Выписки пишутся на доске заранее.
- Гипотенуза больше катета.
- Сумма острых углов прямоугольного треугольника равна 180 0.
- Площадь прямоугольного треугольника с катетами на и на рассчитывается по формуле S = ab / 2 .
- Теорема Пифагора верна для всех равнобедренных треугольников.
- В прямоугольном треугольнике катет, противоположный углу 30 0, равен половине гипотенузы.
- Сумма квадратов катетов равна квадрату гипотенузы.
- Квадрат катета равен разности квадратов гипотенузы и второго катета.
- Сторона треугольника равна сумме двух других сторон.
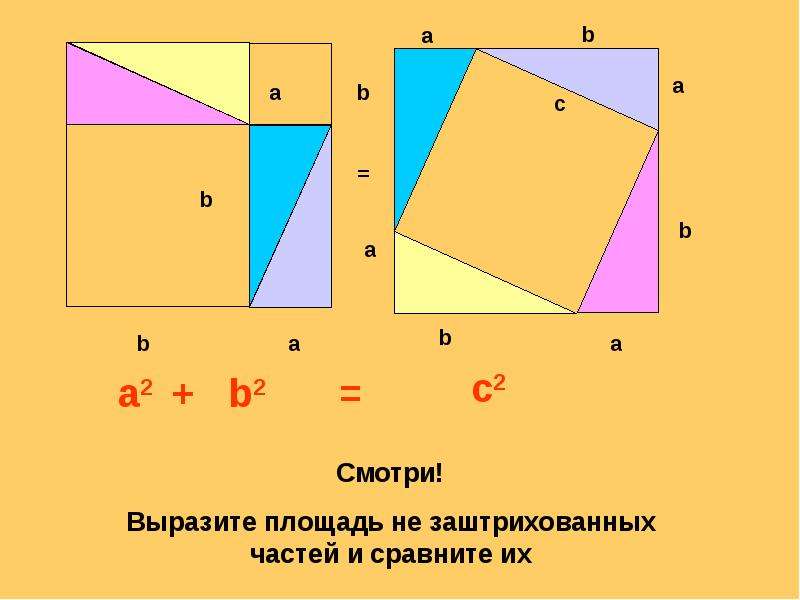
Проверка работ осуществляется взаимным контролем. Спорные утверждения обсуждаются.
Ключ к теоретическим вопросам.
Ученики выставляют друг другу оценки по следующей системе:
8 правильных ответов «5»;
6-7 правильных ответов «4»;
4-5 правильных ответов «3»;
менее 4 правильных ответов «2».
Учитель: О чем мы говорили на прошлом уроке?
Ученик: О Пифагоре и его теореме.
Учитель: Сформулируйте теорему Пифагора. (Несколько студентов читают формулировку, в это время 2-3 студента доказывают это у доски, 6 студентов за первыми партами на листках бумаги).
Математические формулы записаны на магнитной доске на карточках. Выберите те, которые отражают смысл теоремы Пифагора, где a
и в
— ножки, из
— гипотенуза.
| 1) c 2 = a 2 + b 2 | 2) c = a + b | 3) а 2 = с 2 — в 2 |
| 4) с 2 = 2 — в 2 | 5) с 2 = с 2 — а 2 | 6) а 2 = с 2 + б 2 |
Пока студенты, доказывающие теорему у доски и в поле, не будут готовы, слово предоставляется тем, кто подготовил сообщения о жизни и творчестве Пифагора.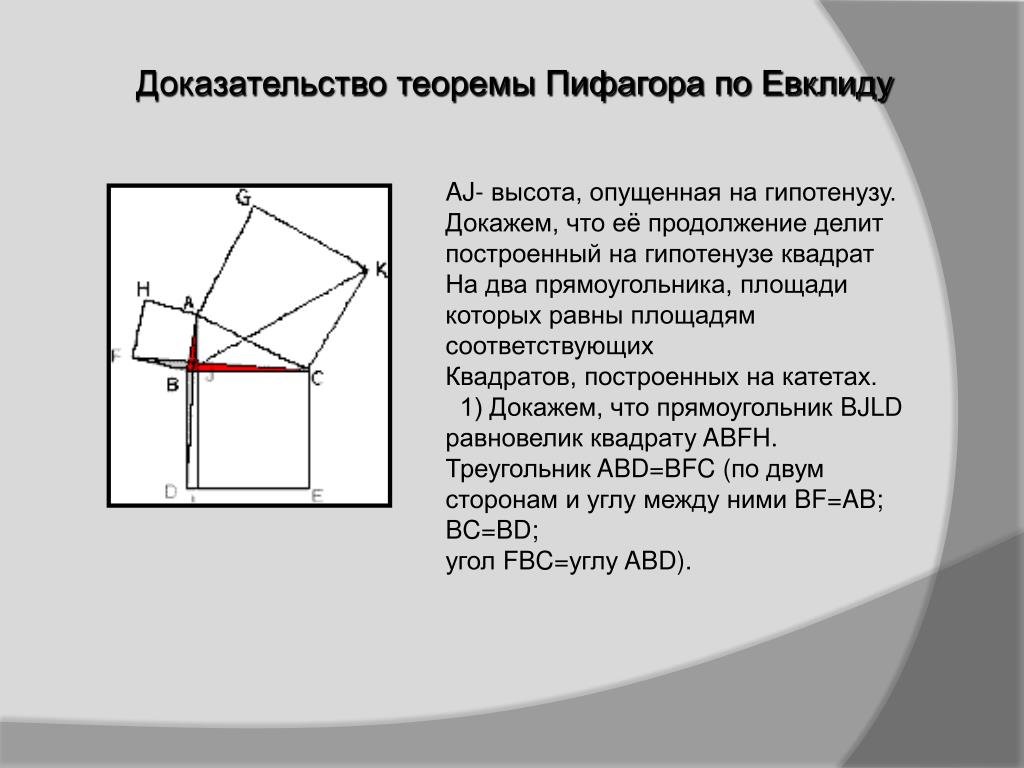
Школьники, работающие в поле, сдают бумаги и слушают свидетельства тех, кто работал у доски.
Решение практических задач с помощью теоремы Пифагора.
Учитель: Предлагаю вам практические задачи по изучаемой теореме. Мы побываем сначала в лесу, после бури, потом на дачном участке.
Задача 1 … После грозы лопнула ель. Высота оставшейся части — 4,2 м. Расстояние от основания до упавшей кроны — 5,6 м. Найдите высоту ели перед грозой.
Задача 2 … Высота дома 4,4 м. Ширина лужайки вокруг дома 1,4 м. Какой длины должна быть сделана лестница, чтобы она не ступала на лужайку и не доходила до крыши дома?
Новая тема.
Учитель: (звучит музыка) Закрой глаза, на несколько минут окунемся в историю. Мы с вами в Древнем Египте. Здесь, на верфях, египтяне строят свои знаменитые корабли.Но геодезисты измеряют землю, границы которой размыло после разлива Нила.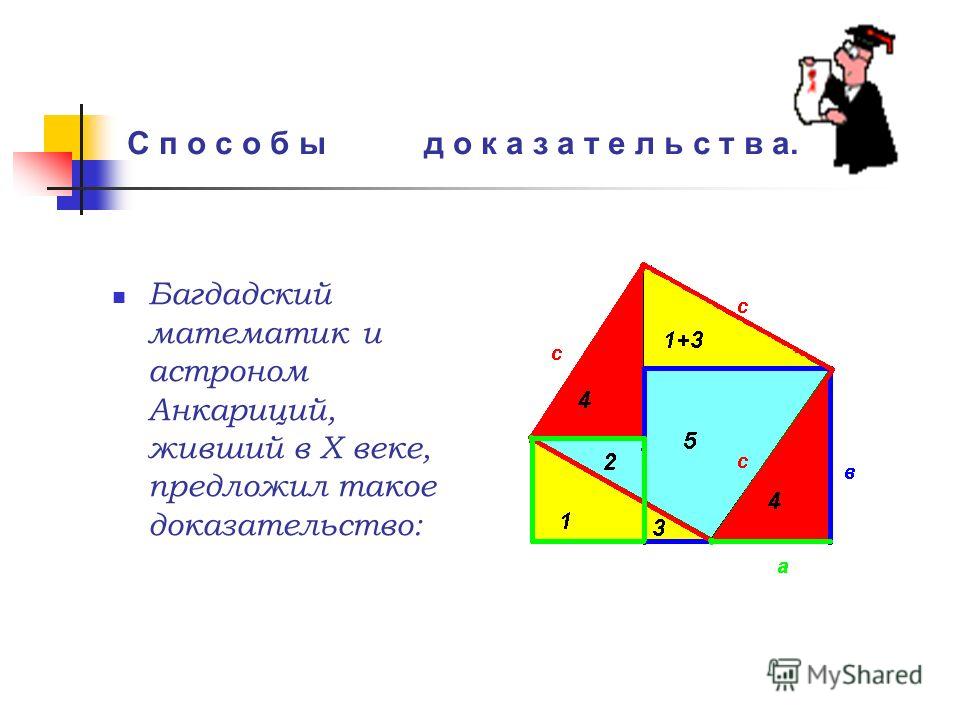 Строители строят грандиозные пирамиды, которые до сих пор поражают своим великолепием. Во всех этих действиях египтянам нужно было использовать прямые углы. Они умели строить их, используя веревку с 12 узлами, завязанными на одинаковом расстоянии друг от друга. Попробуйте, и вы, рассуждая, как древние египтяне, построите из веревок прямоугольные треугольники. (Решая эту задачу, ребята работают группами по 4 человека.Через некоторое время на планшете возле доски кто-то показывает построение треугольника).
Строители строят грандиозные пирамиды, которые до сих пор поражают своим великолепием. Во всех этих действиях египтянам нужно было использовать прямые углы. Они умели строить их, используя веревку с 12 узлами, завязанными на одинаковом расстоянии друг от друга. Попробуйте, и вы, рассуждая, как древние египтяне, построите из веревок прямоугольные треугольники. (Решая эту задачу, ребята работают группами по 4 человека.Через некоторое время на планшете возле доски кто-то показывает построение треугольника).
Стороны полученного треугольника равны 3, 4 и 5. Если между этими узлами завязать еще один узел, то его стороны станут 6, 8 и 10. Если два — 9, 12 и 15. Все эти треугольники прямоугольные, поскольку .
5 2 = 3 2 + 4 2, 10 2 = 6 2 + 8 2, 15 2 = 9 2 + 12 2 и т. Д.
Какое свойство должно быть у треугольника, чтобы он был прямоугольным? (Студенты сами пытаются сформулировать обратную теорему Пифагора, наконец-то кому-то это удается).
Чем эта теорема отличается от теоремы Пифагора?
Ученик: Условие и заключение поменялись местами.
Учитель: Дома вы повторили то, что называется этими теоремами. Итак, что мы встретили сейчас?
Ученик:
С обратной теоремой Пифагора.
Учитель:
Запишем тему урока в тетрадь.Откройте учебники на странице 127, прочтите это утверждение еще раз, запишите его в тетрадь и просмотрите доказательство.
(После нескольких минут самостоятельной работы с учебником один человек у доски по желанию дает доказательство теоремы).
- Как называется треугольник со сторонами 3, 4 и 5? Почему?
- Какие треугольники называются треугольниками Пифагора?
- С какими треугольниками вы работали в домашней работе? А в проблемах с сосной и лестницей?
Первичное закрепление знаний
.
Эта теорема помогает решать задачи, в которых необходимо выяснить, являются ли треугольники прямоугольными.
Задач:
1) Определить, является ли треугольник прямоугольным, если его стороны равны:
а) 12. 37 и 35; б) 21, 29 и 24.
37 и 35; б) 21, 29 и 24.
2) Вычислите высоту треугольника со сторонами 6, 8 и 10 см.
Домашнее задание
.
Page 127: Обратная теорема Пифагора. № 498 (а, б, в) № 497.
Краткое содержание урока.
Что нового вы узнали на уроке?
Самостоятельная работа (выполняется по индивидуальным картам).
Учитель: Дома вы повторили свойства ромба и прямоугольника. Перечислите их (говорит класс). В прошлом уроке мы говорили о том, что Пифагор был разносторонним человеком.Он изучал медицину, музыку и астрономию, а также был спортсменом и участвовал в Олимпийских играх. И Пифагор тоже был философом. Многие из его афоризмов актуальны для нас и сегодня. Теперь вы будете заниматься самостоятельной работой. Для каждого задания дано несколько вариантов ответа, рядом с которыми написаны фрагменты афоризмов Пифагора. Ваша задача решить все поставленные задачи, составить из полученных фрагментов выписку и записать ее.
Для каждого задания дано несколько вариантов ответа, рядом с которыми написаны фрагменты афоризмов Пифагора. Ваша задача решить все поставленные задачи, составить из полученных фрагментов выписку и записать ее.
Теорема Пифагора утверждает:
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы:
a 2 + b 2 = c 2 ,
- a и b — ноги, образующие прямой угол.(2)
Доказательство теоремы Пифагора
Площадь прямоугольного треугольника вычисляется по формуле:
S = \ frac (1) (2) ab
Для вычисления площади Для произвольного треугольника формула площади:
- p — полупериметр. p = \ frac (1) (2) (a + b + c),
- r — это радиус вписанной окружности. Для прямоугольника r = \ frac (1) (2) (a + b-c).
Затем приравниваем правые части обеих формул к площади треугольника:
\ frac (1) (2) ab = \ frac (1) (2) (a + b + c ) \ frac (1) (2) (a + bc)
2 ab = (a + b + c) (a + bc)
2 ab = \ left ((a + b) ^ ( 2) -c ^ (2) \ right)
2 ab = a ^ (2) + 2ab + b ^ (2) -c ^ (2)
0 = a ^ (2) + b ^ (2) -c ^ (2)
c ^ (2) = a ^ (2) + b ^ (2)
Обратная теорема Пифагора:
Если квадрат одной стороны треугольника равен равна сумме квадратов двух других сторон, то треугольник будет прямоугольным.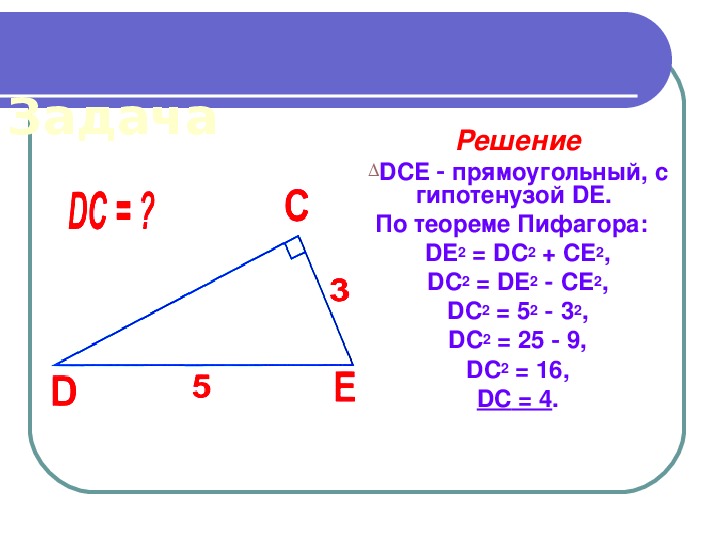 То есть для любой тройки положительных чисел a, b и c такой, что
То есть для любой тройки положительных чисел a, b и c такой, что
a 2 + b 2 = c 2 ,
существует прямоугольный треугольник с катетами a, и . b и гипотенуза c .
Теорема Пифагора — одна из фундаментальных теорем евклидовой геометрии, устанавливающая связь между сторонами прямоугольного треугольника. Это доказал ученый математик и философ Пифагор.
Смысл теоремы в том, что ее можно использовать для доказательства других теорем и решения задач.
Дополнительный материал:
Тема:
Теорема, противоположная теореме Пифагора.
Цели урока:
1) рассмотрим теорему, обратную теореме Пифагора; его применение в процессе решения проблем; закрепить теорему Пифагора и улучшить навыки решения задач для ее применения;
2) развивать логическое мышление, творческий поиск, познавательный интерес;
3) привить учащимся ответственное отношение к учебе, культуру математической речи.
Тип урока.
Урок усвоения новых знаний.
На занятиях
І.
Время на организацию
ІІ.
Обновление
знания
Урок мне хотелось начать с катрена.
Да, путь познания не гладкий
Но мы знаем еще со школьных лет
Загадок больше, чем разгадок
И нет предела поиску!
Итак, на последнем уроке вы узнали теорему Пифагора.Вопросы:
Теорема Пифагора верна для какого числа?
Какой треугольник называется прямоугольным?
Сформулируйте теорему Пифагора.
Как теорема Пифагора записывается для каждого треугольника?
Какие треугольники называются равными?
Каковы критерии равенства треугольников?
А теперь займемся небольшой самостоятельной работой:
Решение задач по чертежам.
№1
(1 шт.) Найдите: AB.
№2
(1 шт.) Находим: ВС.
№3
(
2
б.) Находим: АС
№4
(1 шт.) Находим: АС
№5
Дано: ABCD ромб
(2 б.) AB = 13 см
AC = 10 см
Найдите inD
Самопроверка №1. 5
№2. 5
№3. 16
№4. 13
№5. 24
ІІІ.
Этюд
новый
материал.
Древние египтяне так строили на земле прямые углы: они делили веревку узлами на 12 равных частей, связывали ее концы, после чего веревку натягивали на земле так, чтобы получился треугольник со сторонами 3, 4 и Было сформировано 5 дивизий. Угол треугольника, лежащий напротив стороны с пятью делениями, был прямым.
Вы можете объяснить правильность этого суждения?
В результате поиска ответа на вопрос учащиеся должны понять, что с математической точки зрения вопрос заключается в следующем: будет ли треугольник прямоугольным.
Ставим задачу: как без измерений определить, будет ли треугольник с заданными сторонами прямоугольным. Решение этой проблемы — цель урока.
Запишите тему урока.
Теорема. Если сумма квадратов двух сторон треугольника равна квадрату третьей стороны, то такой треугольник является прямоугольным.
Докажите теорему самостоятельно (составьте план доказательства по учебнику).
Из этой теоремы следует, что треугольник со сторонами 3, 4, 5 является прямоугольным (египетским).
Вообще числа, для которых выполняется равенство, называются тройками Пифагора. А треугольники, длины сторон которых выражены тройками Пифагора (6, 8, 10), являются треугольниками Пифагора.
Анкеровка.
Потому что, тогда треугольник со сторонами 12, 13, 5 не прямоугольный.
Потому что, тогда треугольник со сторонами 1, 5, 6 будет прямоугольным.
№ 430 (а, б, в)
(
— нет)
Примечательно, что свойство, указанное в теореме Пифагора, является характерным свойством прямоугольного треугольника. Это следует из теоремы, обратной теореме Пифагора.
Теорема: Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный.
Выведем формулу, выражающую плоскость треугольника через длины его сторон.Эта формула связана с именем Герона Александрийского, древнегреческого математика и механика, который, вероятно, жил в I веке нашей эры. Герон уделял много внимания практическим приложениям геометрии.
Теорема. Площадь S треугольника со сторонами, равными a, b, c вычисляется по формуле S =, где p — полупериметр треугольника.
Доказательства.
Дано 😕 ABC, AB = c, BC = a, AC = b. Углы A и B острые. СН — высота.
Доказательство:
Обоснование:
Рассмотрим треугольник ABC, в котором AB = c, BC = a, AC = b. У каждого треугольника есть как минимум два острых угла. Пусть A и B — острые углы треугольника ABC. Тогда основание H высоты CH треугольника лежит на стороне AB. Введем обозначения: CH = h, AH = y, HB = x. по теореме Пифагора a 2 — x 2 = h 2 = b 2 -y 2, откуда
Y 2 — x 2 = b 2 — a 2, или (y — x) (y + x) = b 2 — a 2, а так как y + x = c, то y- x = (b2 — а2).
Складывая последние два равенства, получаем:
2y = + c, откуда
y =, а значит, h 2 = b 2 -y 2 = (b — y) (b + y) =
Jeopardy Review Глава 8 Геометрические средние, теорема Пифагора и обратная ей, специальные треугольники, тригонометрия и углы возвышения и падения.
Презентация на тему: «Jeopardy Review Глава 8» Геометрические средние, теорема Пифагора и обратная ей, специальные треугольники, тригонометрия и углы возвышения и падения «.»- стенограмма презентации:
ins [data-ad-slot = «4502451947»] {display: none! important;}}
@media (max-width: 800px) {# place_14> ins: not ([data-ad-slot = «4502451947»]) {display: none! important;}}
@media (max-width: 800px) {# place_14 {width: 250px;}}
@media (max-width: 500 пикселей) {# place_14 {width: 120px;}}
]]>
1
Jeopardy Review Глава 8 Геометрические средние, теорема Пифагора и обратная ей, специальные треугольники, тригонометрия и углы возвышения и понижения
2
Пожалуйста, выберите команду.10 A. Команда 1 B.Команда 2 C.Команда 3 D.Команда 4 E.Команда 5 F.Команда 6 G.Команда 7 H.Команда 8
3
Треугольники, триггеры и углы 200400600800 1000200400600800 1000200400600800 1000200400600800 1000200400600800 1000 Теорема Пифагора геометрических средних и ее обратные углы возвышения и понижения Тригонометрия Специальные треугольники
4
C1-200: Найдите среднее геометрическое от 7 до 11.10 А. 7 Б. √77 ≈ 8,8 В. 11 Д. 77
5
Самые быстрые респонденты (в секундах) 0 Участник 1 0 Участник 2 0 Участник 3 0 Участник 4 0 Участник 5 0 Участник 6 0 Участник 7 0 Участник 8
6
0Команда 1 0Команда 2 0Команда 3 0Команда 4 0Команда 5 0Команда 6 0Команда 7 0Команда 8 ГЛАВНАЯ Команда Результаты
7
C1-400: Найдите среднее геометрическое между 12 и 9.10 A.6√3 ≈ 10,4 B.12 C.9 D.108
8
Самые быстрые респонденты (в секундах) 0 Участник 1 0 Участник 2 0 Участник 3 0 Участник 4 0 Участник 5 0 Участник 6 0 Участник 7 0 Участник 8
9
0Команда 1 0Команда 2 0Команда 3 0Команда 4 0Команда 5 0Команда 6 0Команда 7 0Команда 8 ГЛАВНАЯ Очки команд ГЛАВНАЯ
10
10
11
Самые быстрые респонденты (в секундах) 0 Участник 1 0 Участник 2 0 Участник 3 0 Участник 4 0 Участник 5 0 Участник 6 0 Участник 7 0 Участник 8
12
0Команда 1 0Команда 2 0Команда 3 0Команда 4 0Команда 5 0Команда 6 0Команда 7 0Команда 8 ГЛАВНАЯ Очки команд ГЛАВНАЯ
13
C1-800: Найдите на диаграмме x, y и z.10 х 9 4 y z x
14
Самые быстрые респонденты (в секундах) 0 Участник 1 0 Участник 2 0 Участник 3 0 Участник 4 0 Участник 5 0 Участник 6 0 Участник 7 0 Участник 8
15
0Команда 1 0Команда 2 0Команда 3 0Команда 4 0Команда 5 0Команда 6 0Команда 7 0Команда 8 ГЛАВНАЯ Очки команд ГЛАВНАЯ
16
C1-1000: Блейк устанавливает свою палатку на ярмарке эпохи Возрождения.Если палатка 8 футов высотой, а привязь может быть привязана не более чем в двух футах от палатки, какой длины должна быть привязь? 10 A. 8,2 фута B. 16 футов C. 10 футов D. 7 футов x 2 фута 8 футов
17
Самые быстрые респонденты (в секундах) 0 Участник 1 0 Участник 2 0 Участник 3 0 Участник 4 0 Участник 5 0 Участник 6 0 Участник 7 0 Участник 8
18
0Команда 1 0Команда 2 0Команда 3 0Команда 4 0Команда 5 0Команда 6 0Команда 7 0Команда 8 ГЛАВНАЯ Очки команд ГЛАВНАЯ
19
C2-200: Найдите x.10
20
Самые быстрые респонденты (в секундах) 0 Участник 1 0 Участник 2 0 Участник 3 0 Участник 4 0 Участник 5 0 Участник 6 0 Участник 7 0 Участник 8
21 год
0Команда 1 0Команда 2 0Команда 3 0Команда 4 0Команда 5 0Команда 6 0Команда 7 0Команда 8 ГЛАВНАЯ Очки команд ГЛАВНАЯ
22
C2-400: Найдите x и y: 10
23
Самые быстрые респонденты (в секундах) 0 Участник 1 0 Участник 2 0 Участник 3 0 Участник 4 0 Участник 5 0 Участник 6 0 Участник 7 0 Участник 8
24
Очки команд 0Команда 1 0Команда 2 0Команда 3 0Команда 4 0Команда 5 0Команда 6 0Команда 7 0Команда 8 ГЛАВНАЯ
25
C2-600: Учитывая длину 104, 106 и 10, может ли это быть прямоугольный треугольник? 10 А.Да Б. Нет В. Возможно, если бы мы знали больше D. Недостаточно информации
26 год
Самые быстрые респонденты (в секундах) 0 Участник 1 0 Участник 2 0 Участник 3 0 Участник 4 0 Участник 5 0 Участник 6 0 Участник 7 0 Участник 8
27
0Команда 1 0Команда 2 0Команда 3 0Команда 4 0Команда 5 0Команда 6 0Команда 7 0Команда 8 ГЛАВНАЯ Очки команд ГЛАВНАЯ
28 год
C2-800: Учитывая, что у треугольника обе стороны равны 3 дюймам.Это прямоугольный треугольник? Если да, укажите недостающую длину 10 A. Нет B. Да, 9 C. Недостаточно информации D. Да, 4,2
29
Самые быстрые респонденты (в секундах) 0 Участник 1 0 Участник 2 0 Участник 3 0 Участник 4 0 Участник 5 0 Участник 6 0 Участник 7 0 Участник 8
30
0Команда 1 0Команда 2 0Команда 3 0Команда 4 0Команда 5 0Команда 6 0Команда 7 0Команда 8 ГЛАВНАЯ Очки команд ГЛАВНАЯ
31 год
C2-1000: Используйте тройку Пифагора, чтобы найти x, если длины сторон прямоугольного треугольника составляют 45 футов и 24 футов.10 А. 36 Б. 51 В. 12 Д. 13
32
Самые быстрые респонденты (в секундах) 0 Участник 1 0 Участник 2 0 Участник 3 0 Участник 4 0 Участник 5 0 Участник 6 0 Участник 7 0 Участник 8
33
0Команда 1 0Команда 2 0Команда 3 0Команда 4 0Команда 5 0Команда 6 0Команда 7 0Команда 8 ГЛАВНАЯ Очки команд ГЛАВНАЯ
34
C3-200: Учитывая две стороны прямоугольного треугольника, какое тригонометрическое соотношение мы можем использовать, чтобы найти угол? 10 А.sin -1 B. cos -1 C. загар D. загар -1
35 год
Самые быстрые респонденты (в секундах) 0 Участник 1 0 Участник 2 0 Участник 3 0 Участник 4 0 Участник 5 0 Участник 6 0 Участник 7 0 Участник 8
36
0Команда 1 0Команда 2 0Команда 3 0Команда 4 0Команда 5 0Команда 6 0Команда 7 0Команда 8 ГЛАВНАЯ Очки команд ГЛАВНАЯ
37
10 А.3/5 Б. 4/5 В. 4/3 Д. 3/4 3 4 5
38
Самые быстрые респонденты (в секундах) 0 Участник 1 0 Участник 2 0 Участник 3 0 Участник 4 0 Участник 5 0 Участник 6 0 Участник 7 0 Участник 8
39
0Команда 1 0Команда 2 0Команда 3 0Команда 4 0Команда 5 0Команда 6 0Команда 7 0Команда 8 ГЛАВНАЯ Очки команд ГЛАВНАЯ
40
10 А.5/13 Б. 12/5 В. 13/12 Д. 5/12 5 12
41 год
Самые быстрые респонденты (в секундах) 0 Участник 1 0 Участник 2 0 Участник 3 0 Участник 4 0 Участник 5 0 Участник 6 0 Участник 7 0 Участник 8
42
0Команда 1 0Команда 2 0Команда 3 0Команда 4 0Команда 5 0Команда 6 0Команда 7 0Команда 8 ГЛАВНАЯ Очки команд ГЛАВНАЯ
43 год
10 А.60 градусов B. 60.3 градусов C. 45 градусов D. 30 градусов 8 14
44 год
Самые быстрые респонденты (в секундах) 0 Участник 1 0 Участник 2 0 Участник 3 0 Участник 4 0 Участник 5 0 Участник 6 0 Участник 7 0 Участник 8
45
0Команда 1 0Команда 2 0Команда 3 0Команда 4 0Команда 5 0Команда 6 0Команда 7 0Команда 8 ГЛАВНАЯ Очки команд ГЛАВНАЯ
46
C3-1000: Учитывая отношение противоположной стороны к соседней, как мы можем получить гипотенузу, используя тригонометрию вместо теоремы Пифагора? 10
47
Самые быстрые респонденты (в секундах) 0 Участник 1 0 Участник 2 0 Участник 3 0 Участник 4 0 Участник 5 0 Участник 6 0 Участник 7 0 Участник 8
48
0Команда 1 0Команда 2 0Команда 3 0Команда 4 0Команда 5 0Команда 6 0Команда 7 0Команда 8 ГЛАВНАЯ Очки команд ГЛАВНАЯ
49
C4-200: Найдите недостающие размеры углов в треугольнике ниже.10 A.90˚ B.45˚ C.30˚ D.60˚ 90˚ 45˚x
50
Самые быстрые респонденты (в секундах) 0 Участник 1 0 Участник 2 0 Участник 3 0 Участник 4 0 Участник 5 0 Участник 6 0 Участник 7 0 Участник 8
51
0Команда 1 0Команда 2 0Команда 3 0Команда 4 0Команда 5 0Команда 6 0Команда 7 0Команда 8 ГЛАВНАЯ Очки команд ГЛАВНАЯ
52
C4-400: Найдите недостающие размеры углов в треугольнике ниже.10 A.60˚ B.30˚ C.90˚ D.45˚ 30˚ 60˚ x
53
Самые быстрые респонденты (в секундах) 0 Участник 1 0 Участник 2 0 Участник 3 0 Участник 4 0 Участник 5 0 Участник 6 0 Участник 7 0 Участник 8
54
0Команда 1 0Команда 2 0Команда 3 0Команда 4 0Команда 5 0Команда 6 0Команда 7 0Команда 8 ГЛАВНАЯ Очки команд ГЛАВНАЯ
55
C4-600: Найдите x в треугольнике ниже.10 30˚ 60˚ 90˚ х 6
56
Самые быстрые респонденты (в секундах) 0 Участник 1 0 Участник 2 0 Участник 3 0 Участник 4 0 Участник 5 0 Участник 6 0 Участник 7 0 Участник 8
57
0Команда 1 0Команда 2 0Команда 3 0Команда 4 0Команда 5 0Команда 6 0Команда 7 0Команда 8 ГЛАВНАЯ Очки команд ГЛАВНАЯ
58
C4-800: Найдите недостающие размеры углов в треугольнике ниже.10 A.80˚ B.35˚ C.45˚ D.50˚ 90˚ x˚ 33
59
Самые быстрые респонденты (в секундах) 0 Участник 1 0 Участник 2 0 Участник 3 0 Участник 4 0 Участник 5 0 Участник 6 0 Участник 7 0 Участник 8
60
0Команда 1 0Команда 2 0Команда 3 0Команда 4 0Команда 5 0Команда 6 0Команда 7 0Команда 8 ГЛАВНАЯ Очки команд ГЛАВНАЯ
61
C4-1000: Найдите длину гипотенузы треугольника 45-45-90 с длиной катета 77 сантиметров.10
62
Самые быстрые респонденты (в секундах) 0 Участник 1 0 Участник 2 0 Участник 3 0 Участник 4 0 Участник 5 0 Участник 6 0 Участник 7 0 Участник 8
63
0Команда 1 0Команда 2 0Команда 3 0Команда 4 0Команда 5 0Команда 6 0Команда 7 0Команда 8 ГЛАВНАЯ Очки команд ГЛАВНАЯ
64
C5-200: Это угол, образованный ГОРИЗОНТАЛЬНОЙ линией (прямой видимостью) к объекту НАД горизонталью.10 A. Угол возвышения B. Угол депрессии
65
Самые быстрые респонденты (в секундах) 0 Участник 1 0 Участник 2 0 Участник 3 0 Участник 4 0 Участник 5 0 Участник 6 0 Участник 7 0 Участник 8
66
0Команда 1 0Команда 2 0Команда 3 0Команда 4 0Команда 5 0Команда 6 0Команда 7 0Команда 8 ГЛАВНАЯ Очки команд ГЛАВНАЯ
67
C5-400: Что мы можем использовать по углам возвышения и падения? 10 А.Уровень моря B.Кофе C. Высота D. Расстояние между 2 объектами
68
Самые быстрые респонденты (в секундах) 0 Участник 1 0 Участник 2 0 Участник 3 0 Участник 4 0 Участник 5 0 Участник 6 0 Участник 7 0 Участник 8
69
0Команда 1 0Команда 2 0Команда 3 0Команда 4 0Команда 5 0Команда 6 0Команда 7 0Команда 8 ГЛАВНАЯ Очки команд ГЛАВНАЯ
70
C5-600: Горизонтальные линии параллельны, поэтому угол подъема и угол наклона на диаграмме равны _____________ по теореме об альтернативных внутренних углах.10 A. Дополнительный B. напротив C. conongruent D. аналогичный ———————————— Линия зрения
71
Самые быстрые респонденты (в секундах) 0 Участник 1 0 Участник 2 0 Участник 3 0 Участник 4 0 Участник 5 0 Участник 6 0 Участник 7 0 Участник 8
72
0Команда 1 0Команда 2 0Команда 3 0Команда 4 0Команда 5 0Команда 6 0Команда 7 0Команда 8 ГЛАВНАЯ Очки команд ГЛАВНАЯ
73
C5-800: Кровельщик прислоняет лестницу к стене так, чтобы ее верхушка достигала 30-футовой крыши.Если угол подъема от низа лестницы до крыши составляет 55 градусов, как далеко лестница находится от основания стены? 10 A.21ft B.43ft C.17ft D.25ft ———————————— Линия зрения
74
Самые быстрые респонденты (в секундах) 0 Участник 1 0 Участник 2 0 Участник 3 0 Участник 4 0 Участник 5 0 Участник 6 0 Участник 7 0 Участник 8
75
0Команда 1 0Команда 2 0Команда 3 0Команда 4 0Команда 5 0Команда 6 0Команда 7 0Команда 8 ГЛАВНАЯ Очки команд ГЛАВНАЯ
76
C5-1000: Если Джиан хочет ударить по мячу хотя бы на один фут выше стойки ворот, которая находится на высоте 10 футов и на расстоянии 25 ярдов, то каков будет наименьший угол, под которым он может ударить по мячу.10 A.11˚ B.25˚ C.8˚ D.5˚
77
Самые быстрые респонденты (в секундах) 0 Участник 1 0 Участник 2 0 Участник 3 0 Участник 4 0 Участник 5 0 Участник 6 0 Участник 7 0 Участник 8
78
0Команда 1 0Команда 2 0Команда 3 0Команда 4 0Команда 5 0Команда 6 0Команда 7 0Команда 8 ГЛАВНАЯ Очки команд ГЛАВНАЯ
79
Г-жа Usry Creekside High HOME http: // www.tinytips.org [email protected]
Jeopardy Review Глава 8 Геометрические средние, теорема Пифагора и обратная ей, специальные треугольники, тригонометрия и углы возвышения и падения.
Jeopardy Review
Jeopardy Review Глава 8 Геометрические средние, теорема Пифагора и ее обратные, специальные треугольники, тригонометрия и углы возвышения и падения
C1-200: Найдите среднее геометрическое между 7 и 11.
10 7 77 8.8 11 77C1-400: Найдите среднее геометрическое между 12 и 9.
1063 10.4129108
10 Самые быстрые респондеры (в секундах) 0Участник 10Участник 20Участник 30Участник 40Участник 50Участник 60Участник 70Участник 80Команда 30Команда 20-200Участник .
10
Самые быстрые респондеры (в секундах) 0Участник 10Участник 20Участник 30Участник 40Участник 50Участник 60Участник 70Участник 8C2-600: Может ли это быть прямоугольный треугольник с длинами 104, 106 и 10?
10 Да Нет Возможно, если бы мы знали больше Недостаточно информации C2-800: Учитывая, что длина сторон треугольника равна 3 дюймам.Это прямоугольный треугольник? Если да, укажите недостающую длину
10 Нет Да, 9 Недостаточно информации Да, 4.2C2-1000: Используйте тройку Пифагора, чтобы найти x, при заданных длинах сторон прямоугольного треугольника 45 футов и 24 фута.
10 36 51 12 13C3-200: Учитывая две стороны прямоугольного треугольника, какое тригонометрическое соотношение мы можем использовать, чтобы найти угол?
10 sin-1 cos-1 tan tan-1
10 3/5 4/5 4/3 3/4 345
10 5/13 12/5 13/12 5/12512
10 60 градусов 60,3 градусов 45 градусов 30deg814C3-1000: Учитывая отношение противоположной стороны к соседней, как мы можем получить гипотенузу, используя тригонометрию вместо теоремы Пифагора?
10C4-200: Найдите недостающие размеры углов в треугольнике ниже.
10
0609045xC4-400: Найдите недостающие размеры углов в треугольнике ниже.
106030
060xC4-600: Найдите x в треугольнике ниже.
10306090x6C4-800: Найдите недостающие размеры углов в треугольнике ниже.
108035455090xx33C4-1000: Найдите длину гипотенузы треугольника 45-45-90 с длиной катета 77 сантиметров.
10C5-200: Это угол, образованный ГОРИЗОНТАЛЬНОЙ линией (прямой видимостью) к объекту НАД горизонталью.
10Угол возвышения Угол впадения C5-400: Что мы можем использовать для определения углов возвышения и понижения?
10 Морской уровень Высота кофе Расстояние между двумя объектами C5-600: Горизонтальные линии параллельны, поэтому угол подъема и угол наклона на диаграмме равны _____________ по теореме об альтернативных внутренних углах.
10 дополнительных противоположных конгруэнтных аналога ———————————————— ————————- Линия прямой видимости C5-800: кровельщик подпирает лестницу о стену так, чтобы верх лестницы достигал 30- футов крыши. Если угол подъема от низа лестницы до крыши составляет 55 градусов, как далеко лестница находится от основания стены?
1021ft43ft17ft25ft ———————————— Прямая видимость C5-1000: Если Джиан хочет пнуть футбольный мяч находится на высоте не менее одного фута над стойкой ворот, которая находится на высоте 10 футов и на расстоянии 25 ярдов, то есть каков наименьший угол, под которым он может ударить по мячу.
10112585
0Team 10Team 20Team 30Team 40Team 50Team 60Team 70Team 8HOMETeam ScoresHOMEFastest ответчики (в секундах) 0Participant 10Participant 20Participant 30Participant 40Participant 50Participant 60Participant 70Participant 80Team 10Team 20Team 30Team 40Team 50Team 60Team 70Team 8HOMETeam ScoresHOMEFastest ответчики (в секундах) 0Participant 10Participant 20Participant 30Participant 40Participant 50Participant 60Participant 70Participant 80Team 10Team 20Team 30Team 40Team 50Team 60Team 70Team 8HOMETeam ScoresHOMEFastest ответчики (в секундах) 0Participant 10Participant 20Participant 30Participant 40Participant 50Participant 60Participant 70Participant 80Team 10Team 20Team 30Team 40Team 50Team 60Team 70Team 8HOMETeam ScoresHOMEFastest ответчики (в секундах) 0Participant 10Participant 20Participant 30Participant 40Participant 50Participant 60Participant 70Participant 80Team 10Team 20Team 30Команда 40Команда 50Команда 60Команда 70Команда 8ГОМА Результаты команд (В секундах) 0Participant 10Participant 20Participant 30Participant 40Participant 50Participant 60Participant 70Participant 80Team 10Team 20Team 30Team 40Team 50Team 60Team 70Team 8HOMETeam ScoresHOMEFastest ответчики (в секундах) 0Participant 10Participant 20Participant 30Participant 40Participant 50Participant 60Participant 70Participant 80Team 10Team 20Team 30Team 40Team 50Team 60Team 70Team 8HOMETeam ScoresHOMEFastest ответчики (в секундах) 0Participant 10Participant 20Participant 30Participant 40Participant 50Participant 60Participant 70Participant 80Team 10Team 20Team 30Team 40Team 50Team 60Team 70Team 8HOMETeam ScoresHOMEFastest ответчики (в секундах) 0Participant 10Participant 20Participant 30Participant 40Participant 50Participant 60Participant 70Participant 80Team 10Team 20Team 30Team 40Team 50Team 60Team 70Team 8HOMETeam ScoresHOMEFastest ответчики (в секундах) 0Participant 10Participant 20Participant 30Participant 40Участник 50Участник 60Участник 70Участник 80Те утра 10Team 20Team 30Team 40Team 50Team 60Team 70Team 8HOMETeam ScoresHOMEFastest ответчики (в секундах) 0Participant 10Participant 20Participant 30Participant 40Participant 50Participant 60Participant 70Participant 80Team 10Team 20Team 30Team 40Team 50Team 60Team 70Team 8HOMETeam ScoresHOMEFastest ответчики (в секундах) 0Participant 10Participant 20Participant 30Participant 40Participant 50Participant 60Participant 70Participant 80Team 10Team 20Team 30Team 40Team 50Team 60Team 70Team 8HOMETeam ScoresHOMEFastest ответчики (в секундах) 0Participant 10Participant 20Participant 30Participant 40Participant 50Participant 60Participant 70Participant 80Team 10Team 20Team 30Team 40Team 50Team 60Team 70Team 8HOMETeam ScoresHOMEFastest ответчики (в секундах) 0Participant 10Participant 20Participant 30Participant 40Participant 50Participant 60Participant 70Participant 80Team 10Team 20Team 30Team 40Team 50Team 60Team 70Team 8HOMETОценки командыHOMFastest Responders (в секундах) 0Участник 10Участник т 20Participant 30Participant 40Participant 50Participant 60Participant 70Participant 80Team 10Team 20Team 30Team 40Team 50Team 60Team 70Team 8HOMETeam ScoresHOMEFastest ответчики (в секундах) 0Participant 10Participant 20Participant 30Participant 40Participant 50Participant 60Participant 70Participant 80Team 10Team 20Team 30Team 40Team 50Team 60Team 70Team 8HOMETeam ScoresHOMEFastest ответчики (в секундах) 0Participant 10Participant 20Participant 30Participant 40Participant 50Participant 60Participant 70Participant 80Team 10Team 20Team 30Team 40Team 50Team 60Team 70Team 8HOMETeam ScoresHOMEFastest ответчики (в секундах) 0Participant 10Participant 20Participant 30Participant 40Participant 50Participant 60Participant 70Participant 80Team 10Team 20Team 30Team 40Team 50Team 60Team 70Team 8HOMETeam ScoresHOME
HOMEMs UsryCreekside HighHOMEhttp: // WWW. {2}} [/ latex].
Ключевые термины
- ножки : стороны, смежные с прямым углом в прямоугольном треугольнике.
- прямоугольный треугольник : форма [латекс] 3 [/ латекс], где один угол имеет значение [латекс] 90 [/ латекс] градусов
- гипотенуза : сторона, противоположная прямому углу треугольника, и самая длинная сторона прямоугольного треугольника.
- Теорема Пифагора : Сумма площадей двух квадратов на ножках ([латекс] a [/ латекс] и [латекс] b [/ латекс]) равна площади квадрата на гипотенузе ([ латекс] с [/ латекс]).\ circ [/ latex]). Прямоугольный треугольник — это треугольник, в котором один угол является прямым. Соотношение сторон и углов прямоугольного треугольника является основой тригонометрии.
Сторона, противоположная прямому углу, называется гипотенузой (на рисунке сторона [латекс] c [/ латекс]). Боковые стороны, прилегающие к прямому углу, называются ножками (стороны [латекс] a [/ латекс] и [латекс] b [/ латекс]). Сторона [латекс] a [/ латекс] может быть идентифицирована как сторона, прилегающая к углу [латекс] B [/ латекс] и противоположная (или противоположная) углу [латекс] A [/ латекс].Сторона [латекс] b [/ латекс] — это сторона, прилегающая к уголку [латекс] A [/ латекс] и противоположная уголку [латекс] B [/ латекс].
Прямой треугольник: С помощью теоремы Пифагора можно найти значение длины недостающей стороны в прямоугольном треугольнике.
Если длины всех трех сторон прямоугольного треугольника являются целыми числами, треугольник называется треугольником Пифагора, а длины его сторон в совокупности известны как тройка Пифагора.
Теорема Пифагора
Теорема Пифагора, также известная как теорема Пифагора, является фундаментальным соотношением в евклидовой геометрии.{2}} [/ латекс]
В этом уравнении [латекс] c [/ латекс] представляет длину гипотенузы, а [латекс] a [/ латекс] и [латекс] b [/ латекс] — длины двух других сторон треугольника. {\ circ} [/ latex]) Три тригонометрические функции, которые наиболее часто используются для поиска недостающей стороны прямоугольного треугольника, следующие: [латекс ] \ Displaystyle {\ грех {т} = \ гидроразрыва {противоположный} {гипотенуза}} [/ латекс], [латекс] \ displaystyle {\ соз {т} = \ гидроразрыва {прилегающий} {гипотенуза}} [/ латекс], и [латекс] \ Displaystyle {\ загар {т} = \ гидроразрыва {противоположный} {смежный}} [/ латекс]
Тригонометрические функции
Мы можем определить тригонометрические функции через угол [латекс] t [/ латекс] и длины сторон треугольника.Соседняя сторона — это сторона, ближайшая к углу. («Соседний» означает «рядом».) Противоположная сторона — это сторона, противоположная углу. Гипотенуза — это сторона треугольника, противоположная прямому углу, и она самая длинная.
Прямой треугольник: Стороны прямоугольного треугольника по отношению к углу [латекс] t [/ латекс].
При поиске недостающей стороны прямоугольного треугольника, но единственной информацией, которая дается, является измерение острого угла и длина стороны, используйте тригонометрические функции, перечисленные ниже:
- Синус [латекс] \ displaystyle {\ sin {t} = \ frac {напротив} {гипотенуза}} [/ латекс]
- Косинус [латекс] \ displaystyle {\ cos {t} = \ frac {соседний} {гипотенуза}} [/ латекс]
- Касательная [латекс] \ Displaystyle {\ tan {t} = \ frac {напротив} {смежный}} [/ латекс]
Тригонометрические функции равны отношениям, которые связывают определенные длины сторон прямоугольного треугольника.При поиске отсутствующей стороны первым делом необходимо определить, какие стороны и под каким углом даны, а затем выбрать соответствующую функцию, которая будет использоваться для решения проблемы.
Вычисление тригонометрической функции прямоугольного треугольника
Иногда вы знаете длину одной стороны треугольника и угол, и вам нужно найти другие измерения. Используйте одну из тригонометрических функций ([latex] \ sin {} [/ latex], [latex] \ cos {} [/ latex], [latex] \ tan {} [/ latex]), определите стороны и заданный угол , составьте уравнение и воспользуйтесь калькулятором и алгеброй, чтобы найти недостающую длину стороны.{\ circ} [/ latex] и длина гипотенузы [latex] 25 [/ latex] футов, найдите длину стороны, противоположной острому углу (округлите до ближайшей десятой):
Правый треугольник: Для прямоугольного треугольника с острым углом [латекс] 34 [/ латекс] градуса и длиной гипотенузы [латекс] 25 [/ латекс] футов найдите длину противоположной стороны.
Глядя на рисунок, решите для стороны, противоположной острому углу [латекса] 34 [/ латекса] градуса. Соотношение сторон будет равно противоположной стороне и гипотенузе .{\ circ} [/ latex] и длина гипотенузы [latex] 300 [/ latex] футов, найдите длину гипотенузы (округлите до десятых):
Прямой треугольник: Для прямоугольного треугольника с острым углом [латекс] 83 [/ латекс] градуса и длиной гипотенузы [латекс] 300 [/ латекс] футов найдите длину гипотенузы.
Глядя на рисунок, решите гипотенузу острого угла [латекс] 83 [/ латекс] градуса. Соотношение сторон будет равняться смежной стороне и гипотенузе .{\ circ} \ right)}} \\ x & = \ frac {300} {\ left (0,1218 \ dots \ right)} \\ x & = 2461,7 ~ \ mathrm {feet} \ end {align}} [/ латекс]
Синус, косинус и тангенс
Мнемоника
SohCahToa может использоваться для определения длины стороны прямоугольного треугольника.
Цели обучения
Используйте аббревиатуру SohCahToa для определения синуса, косинуса и тангенса в терминах прямоугольных треугольников.
Основные выводы
Ключевые моменты
- Общая мнемоника для запоминания отношений между функциями синуса, косинуса и тангенса — SohCahToa.
- SohCahToa образован из первых букв « S ine is o pposite более h ypotenuse ( Soh ), C osine a djacent over h ypotenuse ypotenuse ), Касательная противоположна соседней ( Тоа ) ».
Определения тригонометрических функций
Для прямоугольного треугольника с острым углом [латекс] t [/ латекс] первые три тригонометрические функции:
- Синус [латекс] \ displaystyle {\ sin {t} = \ frac {напротив} {гипотенуза}} [/ латекс]
- Косинус [латекс] \ displaystyle {\ cos {t} = \ frac {соседний} {гипотенуза}} [/ латекс]
- Касательная [латекс] \ Displaystyle {\ tan {t} = \ frac {напротив} {смежный}} [/ латекс]
Распространенным мнемоническим символом для запоминания этих отношений является SohCahToa , образованный из первых букв « S In is o pposite в течение часов. более ч гипотенуза ( Cah ), касательная противоположна соседней ( Тоа ).{\ circ} [/ latex] и прилегающую сторону [latex] 45 [/ latex] ножек, решите для длины противоположной стороны. (округляем до десятых)
Правый треугольник: Дан прямоугольный треугольник с острым углом [латекс] 62 [/ латекс] градуса и прилегающей стороной [латекс] 45 [/ латекс] ступней, решите для длины противоположной стороны.
Во-первых, определите, какую тригонометрическую функцию использовать при заданной соседней стороне, и вам нужно найти противоположную сторону. Всегда определяйте, какая сторона дана, а какая неизвестна под острым углом ([латекс] 62 [/ латекс] градуса).\ circ [/ latex], гипотенуза составляет 30 футов, а длина отсутствующей стороны — это противоположная ножка, [latex] x [/ latex] футов.
Определите, какую тригонометрическую функцию использовать при заданной гипотенузе, и вам нужно найти противоположную сторону. Вспоминая мнемонику « S ohCahToa», указанные стороны представляют собой гипотенузу и противоположные «h» и «o», что означает использование «S» или тригонометрической функции синуса. {\ circ} \ right)} \\ x & = 30 \ cdot \ left (0.5299 \ dots \ right) \\ x & = 15.9 ~ \ mathrm {feet} \ end {align}} [/ latex]
Нахождение углов по соотношениям: обратные тригонометрические функции
Обратные тригонометрические функции можно использовать для определения острого угла прямоугольного треугольника.
Цели обучения
Использование обратных тригонометрических функций при решении задач с прямоугольными треугольниками
Основные выводы
Ключевые моменты
- Отсутствующее значение острого угла прямоугольного треугольника можно найти, если заданы две длины сторон.{-1} [/ латекс].
Использование тригонометрических функций для поиска отсутствующей стороны при заданном остром угле так же просто, как определение сторон относительно острого угла, выбор правильной функции, создание уравнения и решение. Так же просто найти недостающий острый угол при наличии двух сторон прямоугольного треугольника. {- 1} [/ latex] на калькуляторе) для определения угла ([latex] A [/ latex]) с двух сторон.\ circ [/ latex] с противоположной длиной стороны [латекс] 12 ~ \ mathrm {feet} [/ latex], найдите острый угол с точностью до градуса:
Прямой треугольник: Найдите угол [латекс] A [/ латекс], если задана противоположная сторона и гипотенуза.
От угла [латекс] A [/ латекс] даны стороны напротив и гипотенузы . Поэтому используйте тригонометрическую функцию синуса. ( Soh от SohCahToa) Напишите уравнение и решите его, используя обратный ключ для синуса.{\ circ} \ end {align}} [/ латекс]
Теорема Пифагора
Давным-давно, когда правила философия и Сократ пил болиголов, умник по имени Пифагор доказал, что для прямоугольных треугольников:
a 2 + b 2 = c 2
Последующие поклонники а люди, занимающиеся прямоугольным углом, знают это уравнение как теорема Пифагора . Стороны a и b — это ноги, а сторона c — гипотенуза (противоположная прямому углу).
Это означает, что если мы знаем длину двух сторон прямоугольного треугольника, у нас есть третья сторона в сумке. Просто помните, как использовать квадраты и квадратные корни, и все готово.
Пример задачи
Какова длина стороны c в следующем треугольнике?
Сначала запишите теорему Пифагора.
a 2 + b 2 = c 2
Мы ищем гипотенузу, что означает, что мы знаем a и b .Затем подключите 4 для a и 3 для b .
4 2 + 3 2 = c 2
Продолжайте.
16 + 9 = c 2
c 2 = 25
Извлеките квадратный корень из обеих частей. (Мы болеем за вас.)
c = 5
Ну вот. Недостающая сторона = найдена.
Пример задачи
Какова длина стороны a в этом треугольнике?
Переставьте теорему Пифагора, чтобы найти a 2 .
a 2 + b 2 = c 2
a 2 2 = c 2 — b 9106 2 0 b 9106 0
a 2 = 10 2 — 6 2 03 = 64 = 64 Для последнего штриха извлеките квадратный корень из обеих сторон. a = 8
a 2 = 100 — 36
a 2
Пример задачи
Какова длина стороны b в этом треугольнике?
Упорядочите теорему Пифагора в терминах b 2 .
a 2 + b 2 = c 2
b 2 2 = c 2 — em in 9102 03 2 9107 03 , затем решите для b с помощью умного извлечения квадратного корня. b 2 = 13 2 — 12 2
b 2 = 169 — 144
b 2 = 25
b = 502: 5
02 Производные от обратных функций
В этом разделе мы исследуем взаимосвязь между производной функции и производной ее обратной. Для функций, производные которых мы уже знаем, мы можем использовать это соотношение, чтобы найти производные от обратных без необходимости использовать предельное определение производной.В частности, мы применим формулу для производных обратных функций к тригонометрическим функциям. Эта формула также может использоваться для распространения правила мощности на рациональные показатели.
Производная обратной функции
Начнем с рассмотрения функции и ее обратной. Если \ (f (x) \) и обратимо, и дифференцируемо, кажется разумным, что обратное к \ (f (x) \) также дифференцируемо. На рисунке \ (\ PageIndex {1} \) показана связь между функцией \ (f (x) \) и ее обратной \ (f ^ {- 1} (x) \).{−1} (x) \ big)}. \ Label {inverse1} \]
В качестве альтернативы, если \ (y = g (x) \) является обратным \ (f (x) \), то
\ [g ‘(x) = \ dfrac {1} {f ′ \ big (g (x) \ big)}. \ label {inverse2} \]
Пример \ (\ PageIndex {1} \): применение теоремы об обратной функции
Используйте теорему об обратной функции, чтобы найти производную от \ (g (x) = \ dfrac {x + 2} {x} \). Сравните полученную производную с производной, полученной прямым дифференцированием функции.
Решение
Обратным к \ (g (x) = \ dfrac {x + 2} {x} \) является \ (f (x) = \ dfrac {2} {x − 1} \).{−1/3} \ nonumber \]
и
\ [\ dfrac {dy} {dx} \ Bigg | _ {x = 8} = \ frac {1} {3} \ nonumber \]
наклон касательной к графику в точке \ (x = 8 \) равен \ (\ frac {1} {3} \).
Подставляя \ (x = 8 \) в исходную функцию, мы получаем \ (y = 4 \). Таким образом, касательная проходит через точку \ ((8,4) \). Подставляя в формулу угла наклона прямой, получаем касательную
\ [y = \ tfrac {1} {3} x + \ tfrac {4} {3}. \ nonumber \]
Упражнение \ (\ PageIndex {3} \)
Найдите производную от \ (s (t) = \ sqrt {2t + 1} \).{−1/2} \)
Производные обратных тригонометрических функций
Теперь обратимся к нахождению производных от обратных тригонометрических функций. Эти производные окажутся неоценимыми при изучении интеграции далее в этом тексте. Производные от обратных тригонометрических функций весьма удивительны тем, что их производные на самом деле являются алгебраическими функциями. Ранее было доказано, что производные алгебраических функций являются алгебраическими функциями, а производные тригонометрических функций — тригонометрическими функциями.2−1}} \)
.

 Решение задач
Решение задач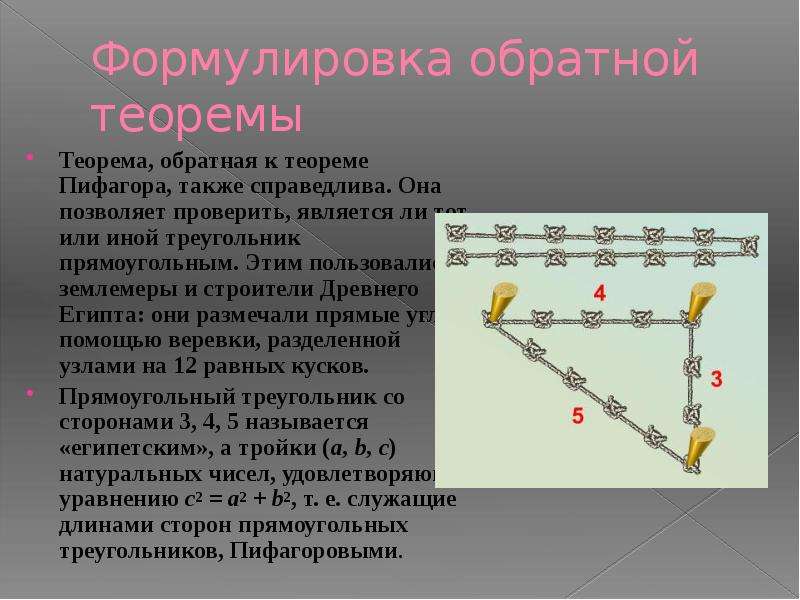 Если в треугольнике квадрат одной стороны равен разности квадратов двух других сторон, то эта сторона лежит напротив……………………………………………………………
Если в треугольнике квадрат одной стороны равен разности квадратов двух других сторон, то эта сторона лежит напротив……………………………………………………………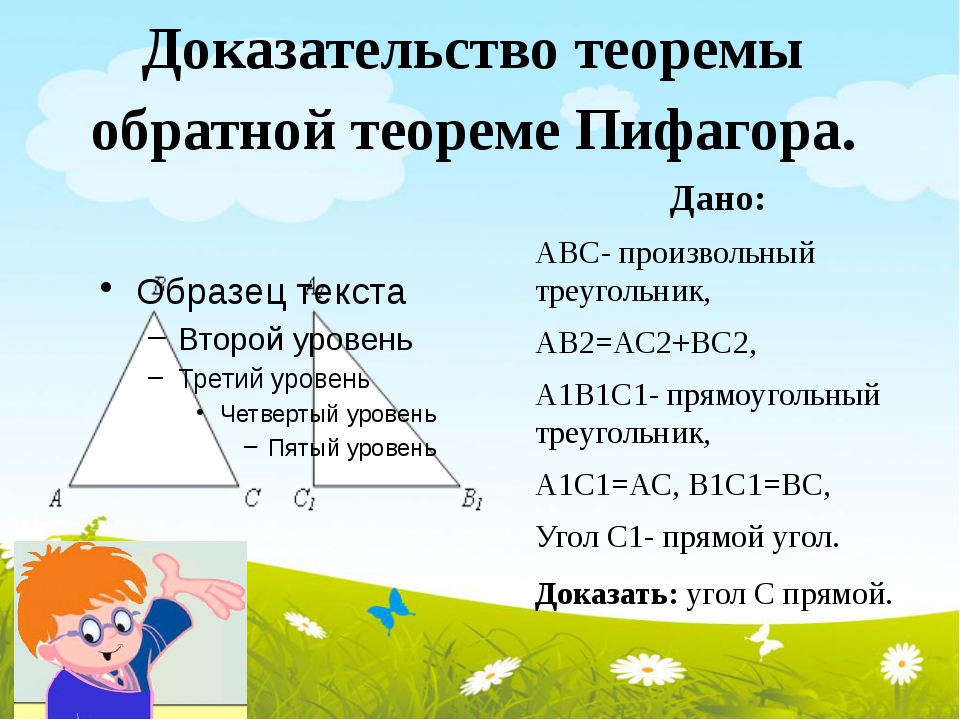
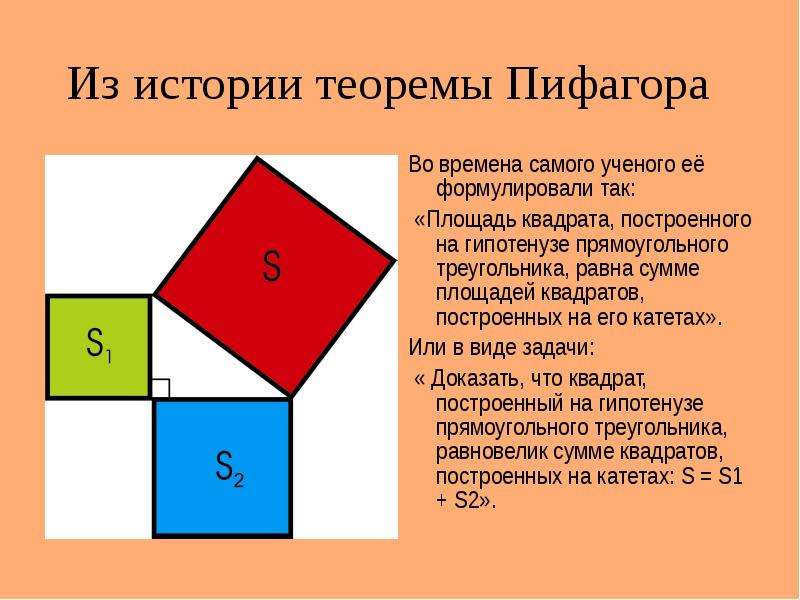

 (5 минут)
(5 минут)
 На слайде изображены фигуры, найдите их площадь.
На слайде изображены фигуры, найдите их площадь.
 (1 минута)
(1 минута) Такой треугольник называется египетским. Попробуем и мы найти эту взаимосвязь.
Такой треугольник называется египетским. Попробуем и мы найти эту взаимосвязь.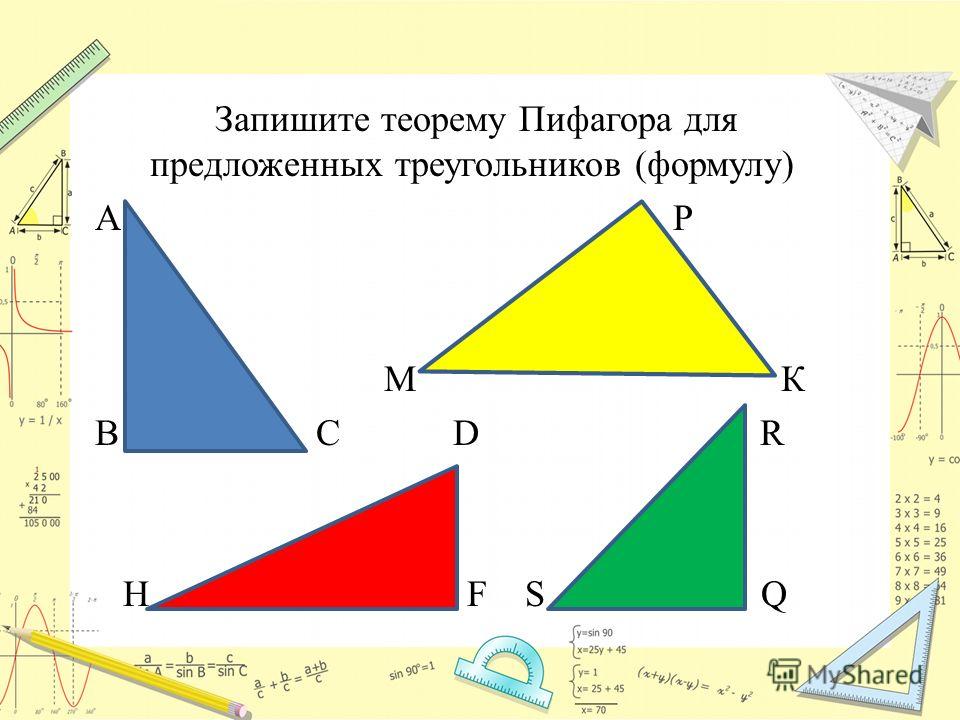
 )
)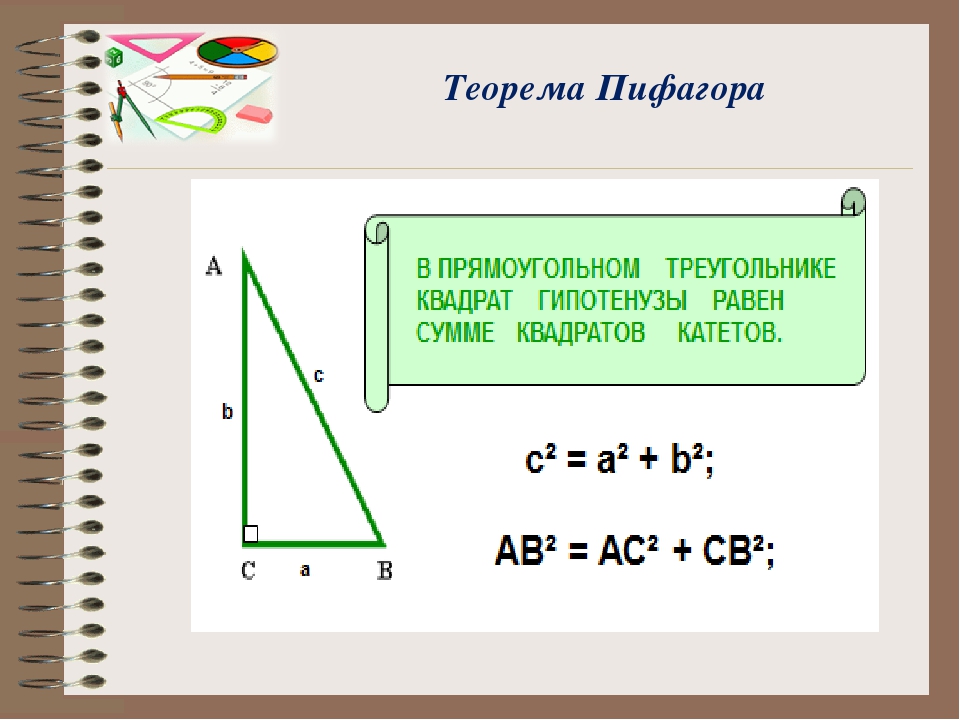 Так появилось ласковое название знаменитой теоремы Пифагора.
Так появилось ласковое название знаменитой теоремы Пифагора. Достроим прямоугольный треугольник до квадрата со стороной a+b.
Достроим прямоугольный треугольник до квадрата со стороной a+b.
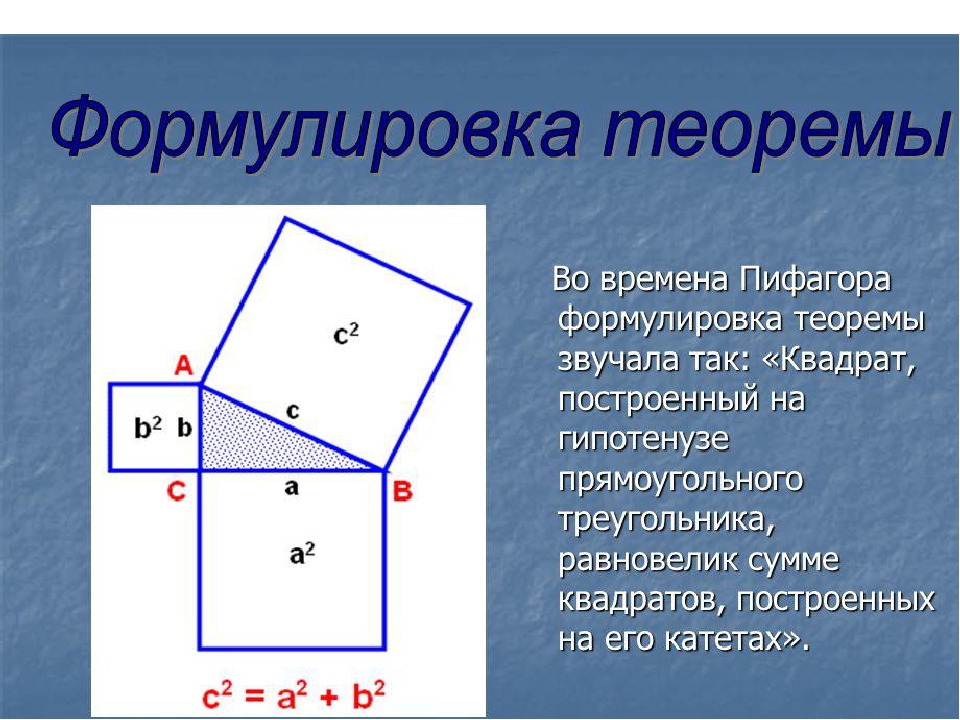
 На этом закончилась наша работа с данной теоремой. Повторите ее словесно, чтобы мы помнили, какое утверждение доказывали.
На этом закончилась наша работа с данной теоремой. Повторите ее словесно, чтобы мы помнили, какое утверждение доказывали. Последний шаг заключался в том, что мы приравняли найденные площади квадрата со сторонами a+b и упростили выражение. Итогом доказательства является полученная формула
Последний шаг заключался в том, что мы приравняли найденные площади квадрата со сторонами a+b и упростили выражение. Итогом доказательства является полученная формула 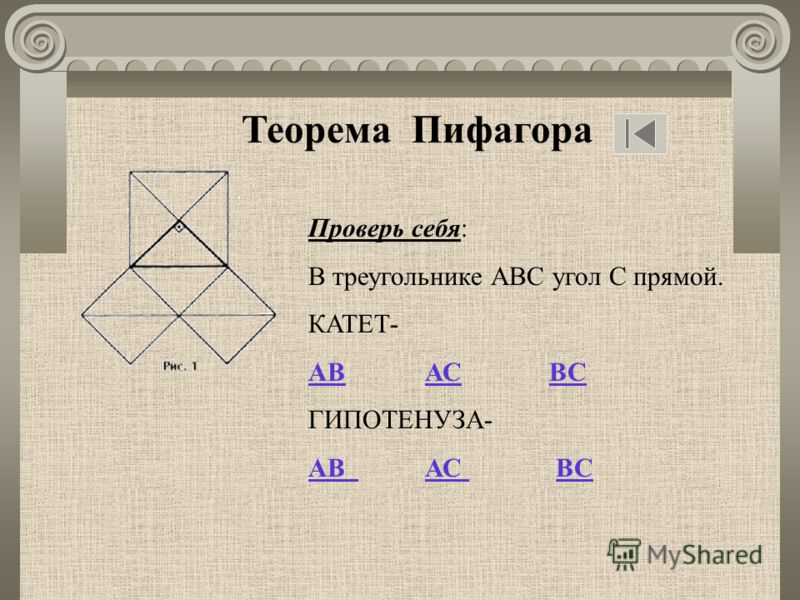 Запишите его в свои тетради.
Запишите его в свои тетради.
 Мы доказали теорему обратную теореме Пифагора. Значит, поиск доказательства закончен.
Мы доказали теорему обратную теореме Пифагора. Значит, поиск доказательства закончен.

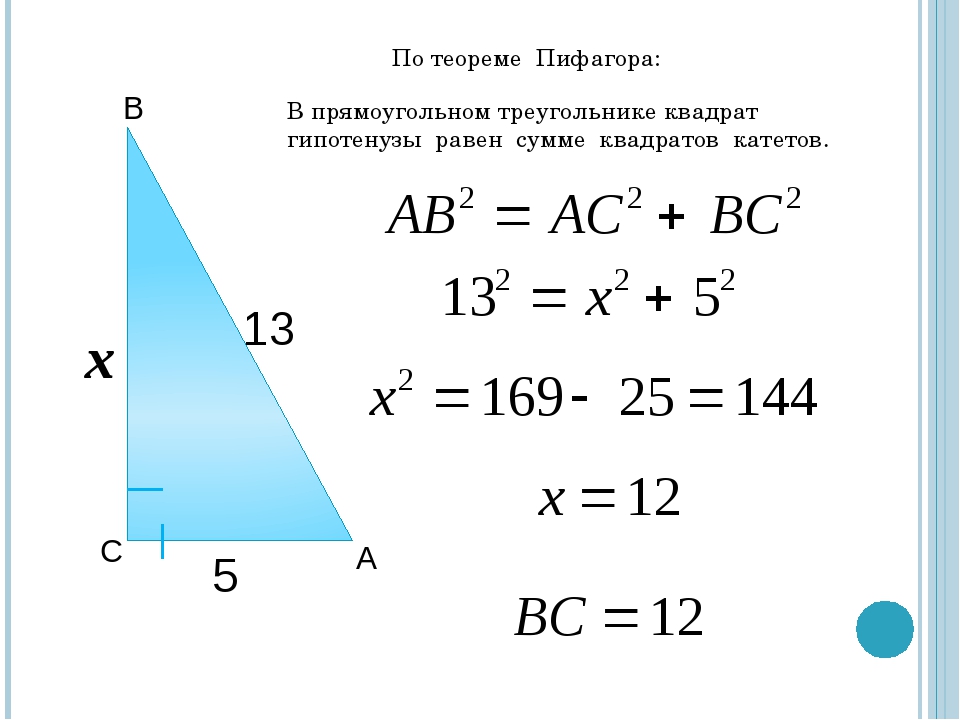 Выделите условие, заключение.
Выделите условие, заключение.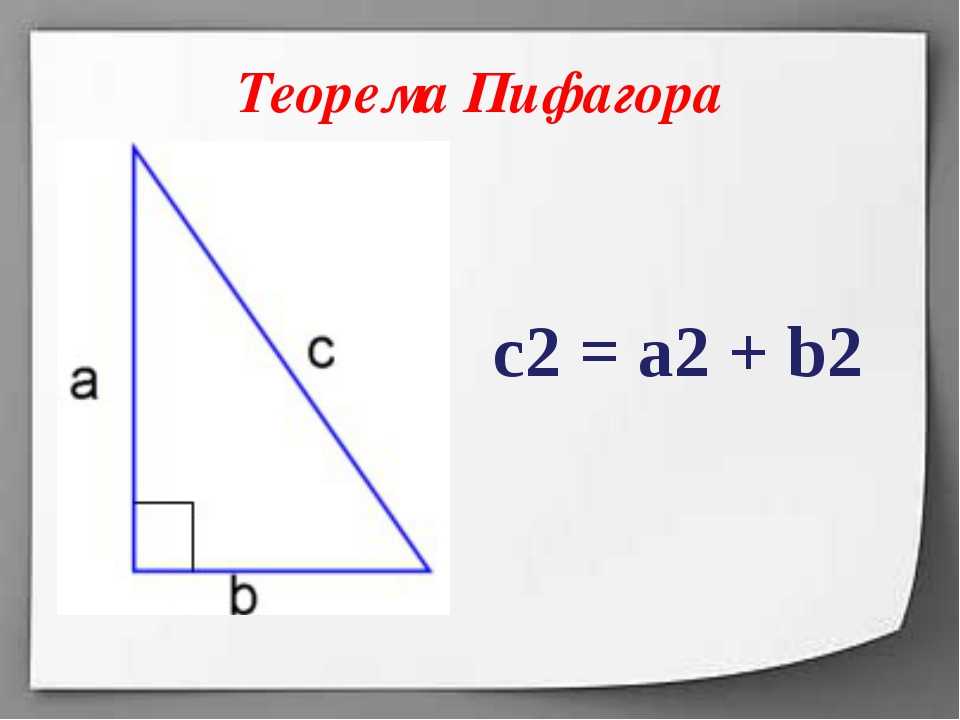
 {2}
{2}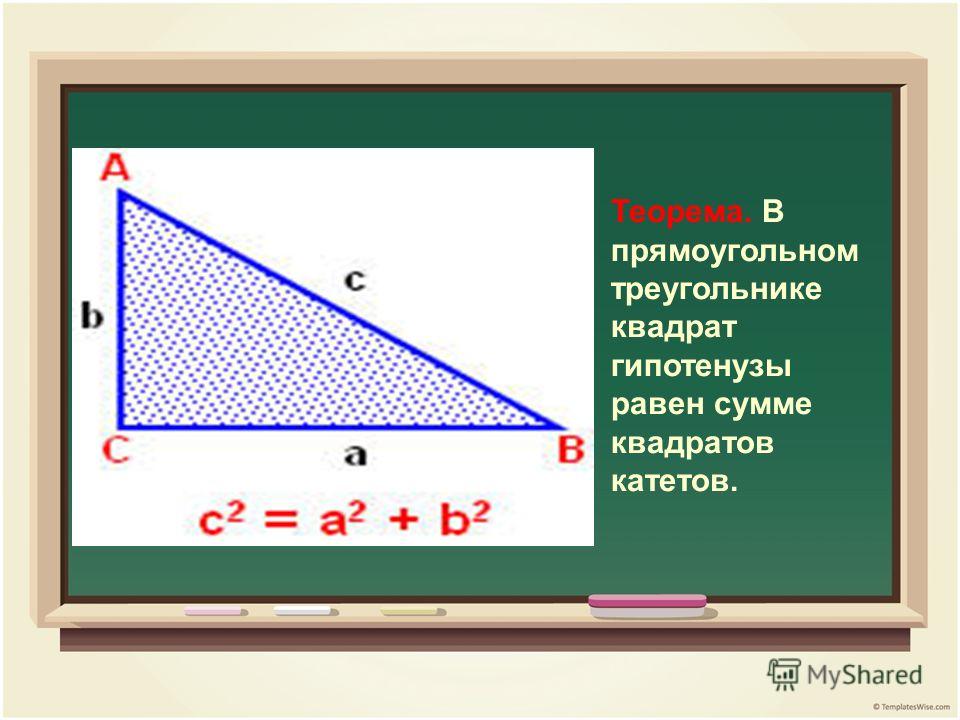

 В частности, оно не использует понятие площади фигуры.
В частности, оно не использует понятие площади фигуры.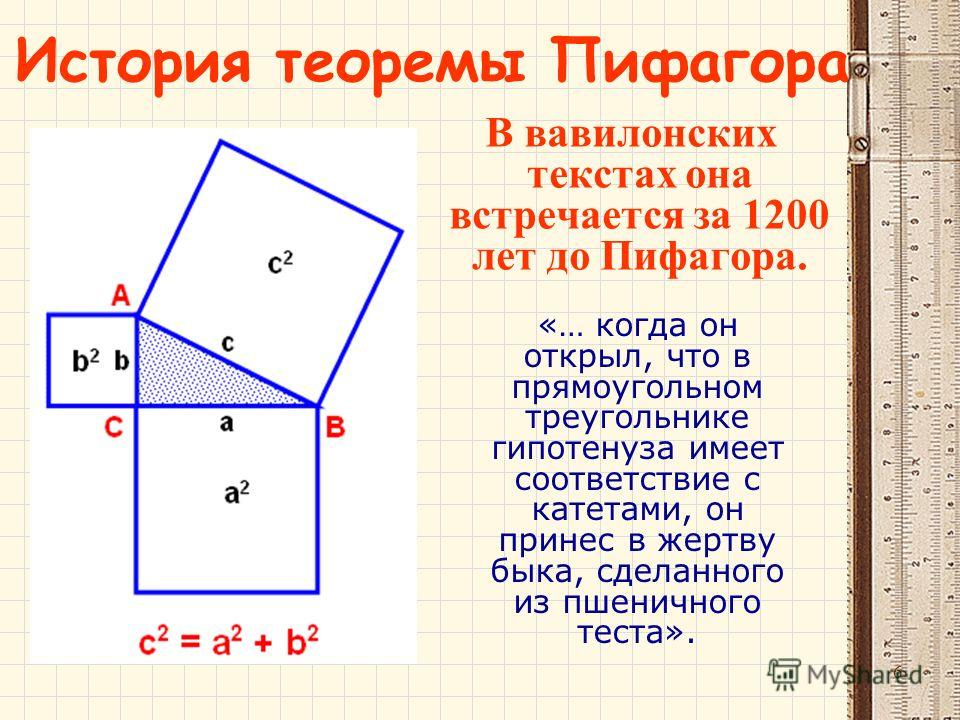



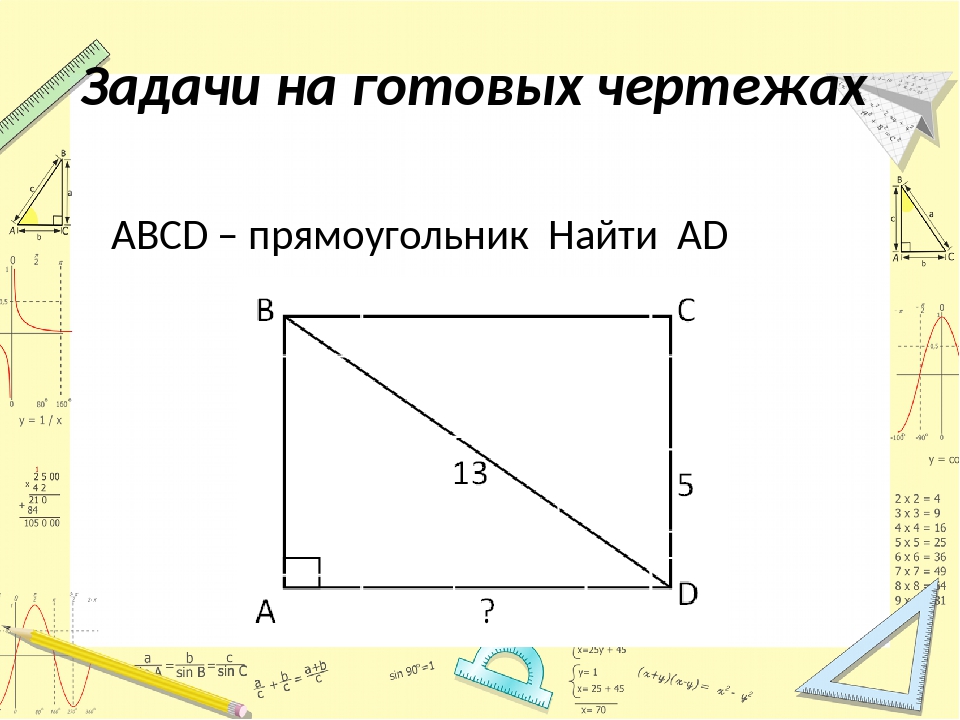
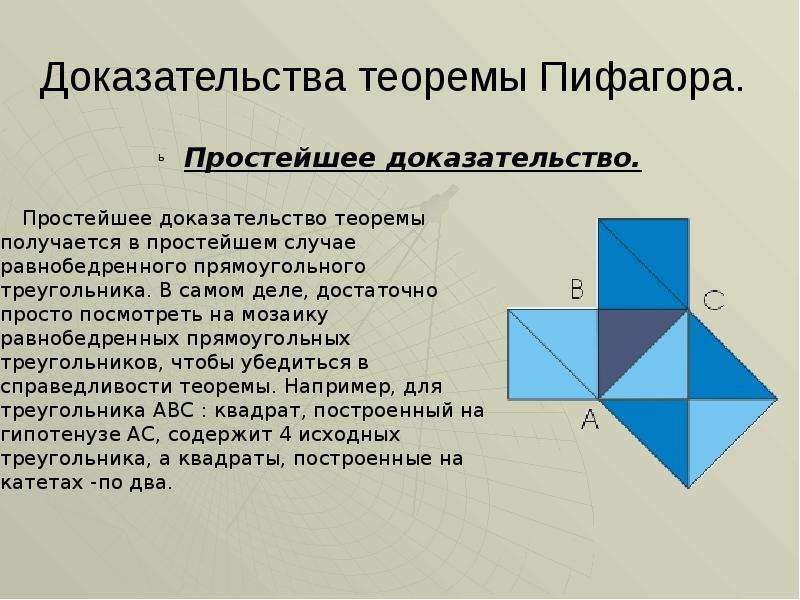
 Актуализация опорных знаний.
Актуализация опорных знаний. Диагонали ромба взаимно перпендикулярны.
Диагонали ромба взаимно перпендикулярны.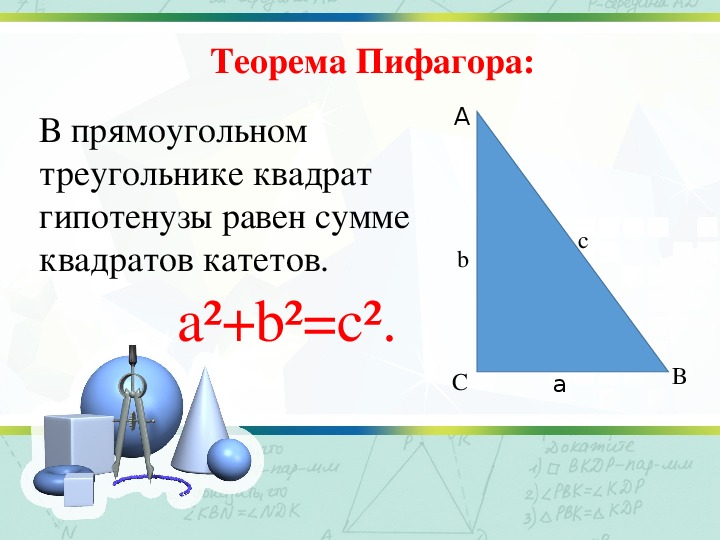
 Например: 26, 24 и 10.
Например: 26, 24 и 10.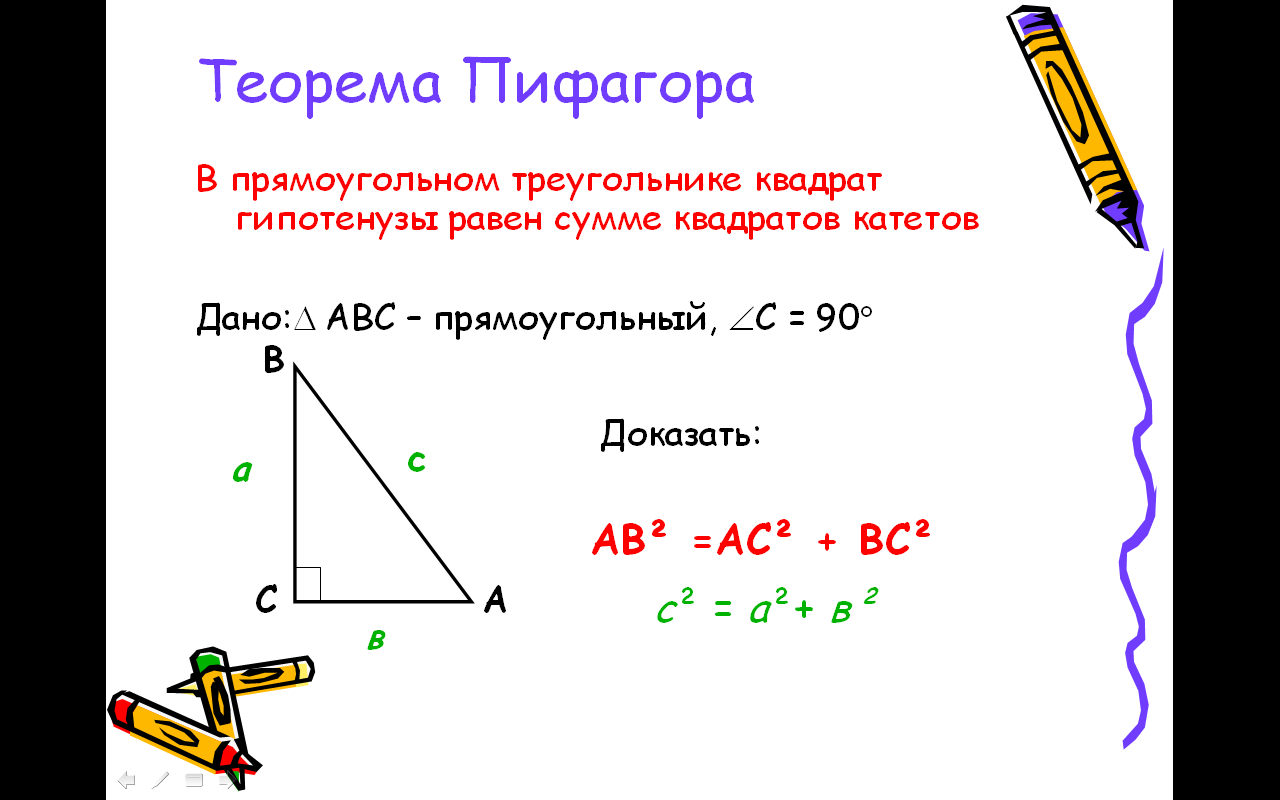 Отметили, что прямоугольные треугольники, у которых длины сторон выражаются целыми числами, называются пифагоровыми треугольниками.
Отметили, что прямоугольные треугольники, у которых длины сторон выражаются целыми числами, называются пифагоровыми треугольниками.