Содержание
Трапеция. Свойства, признаки трапеции | Подготовка к ЕГЭ по математике
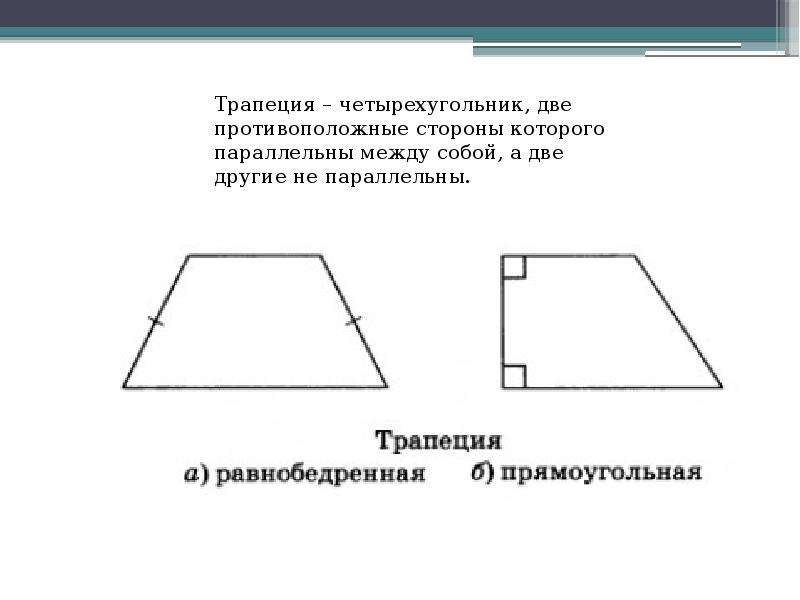
Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).
Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны.
Если боковые стороны равны, трапеция называется равнобедренной.
Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной.
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
Свойства трапеции
1. Средняя линия трапеции параллельна основаниям и равна их полусумме.
2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.
3. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны.
Коэффициент подобия –
Отношение площадей этих треугольников есть .
4. Треугольники и , образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.
5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.
6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.
7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.
8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.
Свойства и признаки равнобедренной трапеции
1. В равнобедренной трапеции углы при любом основании равны.
2.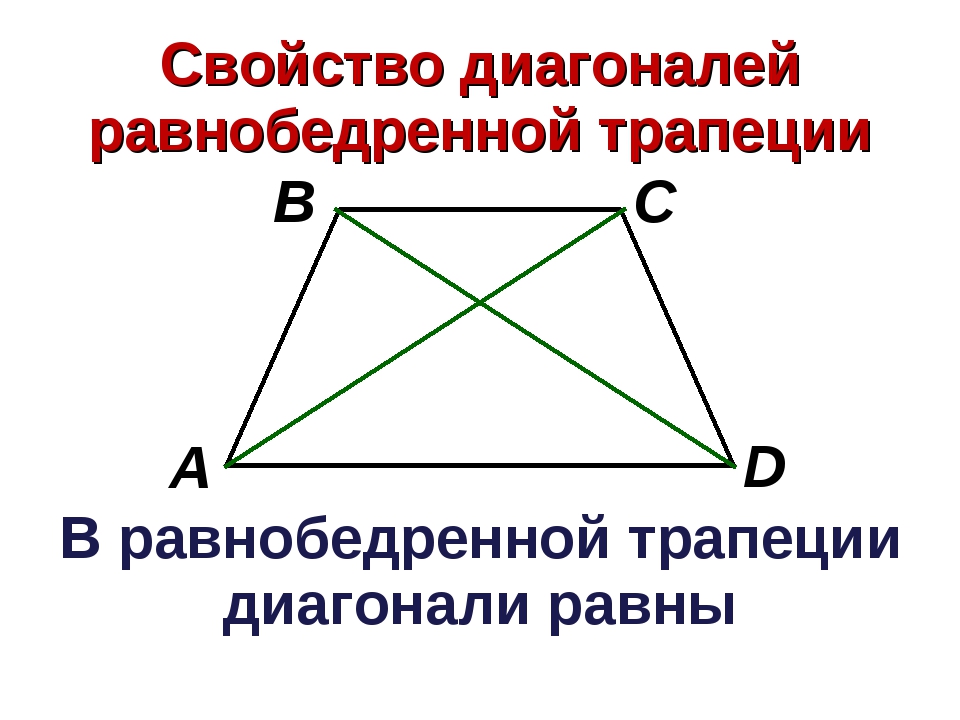 В равнобедренной трапеции длины диагоналей равны.
В равнобедренной трапеции длины диагоналей равны.
3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.
4. Около равнобедренной трапеции можно описать окружность.
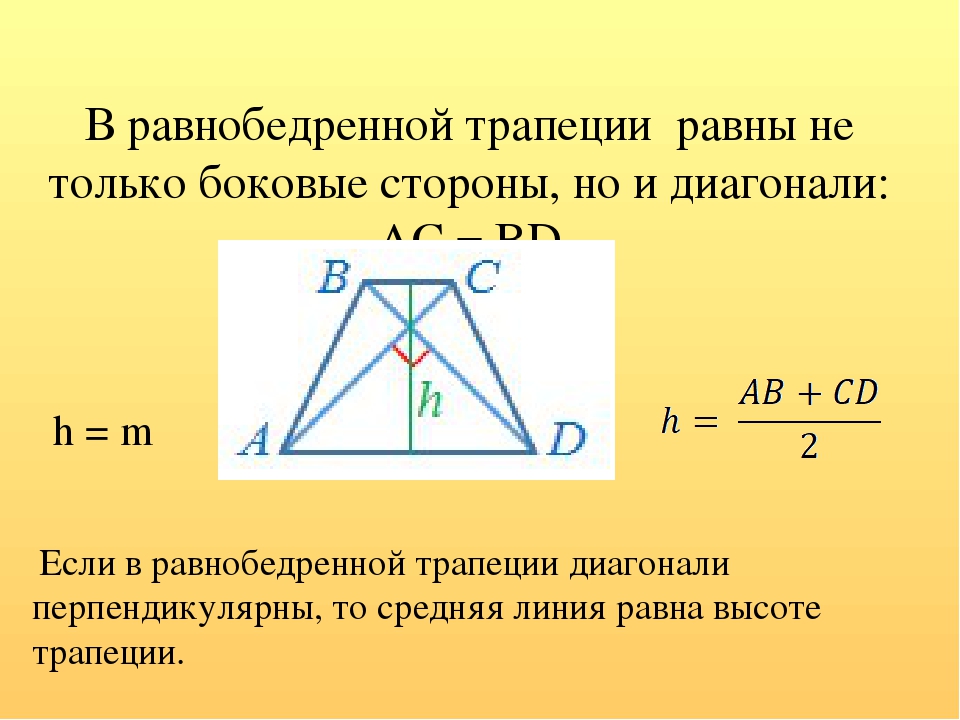
5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
Вписанная окружность
Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка — и , то
Площадь
или где – средняя линия
Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.
Смотрите также площадь трапеции.
Углы равнобедренной трапеции
Углы равнобедренной трапеции. Здравствуйте! В этой статье речь пойдёт о решении задач с трапецией. Данная группа заданий входит в состав экзамена, задачки простые. Будем вычислять углы трапеции, основания и высоты. Решение ряда задач сводится к решению прямоугольного треугольника, как говориться: куда мы без теоремы Пифагора, синуса и косинуса?
Будем вычислять углы трапеции, основания и высоты. Решение ряда задач сводится к решению прямоугольного треугольника, как говориться: куда мы без теоремы Пифагора, синуса и косинуса?
Работать будем с равнобедренной трапецией. У неё равны боковые стороны и углы при основаниях. О трапеции есть статья на блоге, посмотрите.
Отметим небольшой и важный нюанс, который в процессе решения самих заданий подробно расписывать не будем. Посмотрите, если у нас дано два основания, то большее основание высотами, опущенными к нему, разбивается на три отрезка – один равен меньшему основанию (это противолежащие стороны прямоугольника), два других равны друг другу (это катеты равных прямоугольных треугольников):
Простой пример: дано два основания равнобедренной трапеции 25 и 65. Большее основание разбивается на отрезки следующим образом:
*И ещё! В задачах не введены буквенные обозначения. Это сделано умышленно, чтобы не перегружать решение алгебраическими изысками. Согласен, что это математически неграмотно, но цель донести суть. А обозначения вершин и прочих элементов вы всегда можете сделать сами и записать математически корректное решение.
Согласен, что это математически неграмотно, но цель донести суть. А обозначения вершин и прочих элементов вы всегда можете сделать сами и записать математически корректное решение.
Рассмотрим задачи:
27439. Основания равнобедренной трапеции равны 51 и 65. Боковые стороны равны 25. Найдите синус острого угла трапеции.
Для того чтобы найти угол необходимо построить высоты. На эскизе обозначим данные в условии величины. Нижнее основание равно 65, высотами оно разбивается на отрезки 7, 51 и 7:
В прямоугольном треугольнике нам известна гипотенуза и катет, можем найти второй катет (высоту трапеции) и далее уже вычислить синус угла.
По теореме Пифагора указанный катет равен:
Таким образом:
Ответ: 0,96
27440. Основания равнобедренной трапеции равны 43 и 73. Косинус острого угла трапеции равен 5/7. Найдите боковую сторону.
Построим высоты и отметим данные в условии величины, нижнее основание разбивается на отрезки 15, 43 и 15:
Ответ: 21
27441. Большее основание равнобедренной трапеции равно 34. Боковая сторона равна 14. Синус острого угла равен (2√10)/7. Найдите меньшее основание.
Большее основание равнобедренной трапеции равно 34. Боковая сторона равна 14. Синус острого угла равен (2√10)/7. Найдите меньшее основание.
Построим высоты. Для того чтобы найти меньшее основание нам необходимо найти чему равен отрезок являющийся катетом в прямоугольном треугольнике (обозначен синим):
Можем вычислить высоту трапеции, а затем найти катет:
По теореме Пифагора вычисляем катет:
Таким образом, меньшее основание равно:
Ответ: 22
27442. Основания равнобедренной трапеции равны 7 и 51. Тангенс острого угла равен 5/11. Найдите высоту трапеции.
Построим высоты и отметим данные в условии величины. Нижнее основание разбивается на отрезки:
Что делать? Выражаем тангенс известного нам угла при основании в прямоугольном треугольнике:
Ответ: 10
27443. Меньшее основание равнобедренной трапеции равно 23. Высота трапеции равна 39. Тангенс острого угла равен 13/8. Найдите большее основание.
Строим высоты и вычисляем чему равен катет:
Таким образом большее основание будет равно:
Ответ: 71
27444. Основания равнобедренной трапеции равны 17 и 87. Высота трапеции равна 14. Найдите тангенс острого угла.
Строим высоты и отмечаем известные величины на эскизе. Нижнее основание разбивается на отрезки 35, 17, 35:
По определению тангенса:
Ответ: 0,4
77152. Основания равнобедренной трапеции равны 6 и 12. Синус острого угла трапеции равен 0,8. Найдите боковую сторону.
Построим эскиз, построим высоты и отметим известные величины, большее основание разбивается на отрезки 3, 6 и 3:
Выразим гипотенузу обозначенную как х через косинус:
Из основного тригонометрического тождества найдём cosα
Таким образом:
Ответ: 5
27818. Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна 500? Ответ дайте в градусах.
Из курса геометрии нам известно, что если имеем две параллельные прямые и секущую, что сумма внутренних односторонних углов равна 1800. В нашем случае это
C условии сказано, что разность противолежащих углов равна 500, то есть
Так как у равнобедренной трапеции углы при основании равны, то есть угол А равен углу В, то можем записать
Имеем два уравнения с двумя неизвестными, можем решить систему:
*Конечно, эту задачу можно было легко решить просто перебирая пары углов )
27833. В равнобедренной трапеции большее основание равно 25, боковая сторона равна 10, угол между ними 600. Найдите меньшее основание.
Построим высоты DE и CF:
Меньшее основание равно отрезку EF, так как DC и EF это противолежащие стороны прямоугольника. Отрезок EF мы можем найти если вычислим АЕ. Выразим этот катет прямоугольного треугольника ADE через функцию косинуса:
Так как AE=FB=5, то EF=25–5–5=15. Следовательно и DC=15.
Следовательно и DC=15.
Ответ: 15
27837. Основания равнобедренной трапеции равны 15 и 9, один из углов равен 450. Найдите высоту трапеции.
Из точек D и C опустим две высоты:
Как уже сказано выше они разбивают большее основание на три отрезка: один равен меньшему основанию, два других равны друг другу.
В данном случае они равны 3, 9 и 3 (в сумме 15). Кроме того, отметим что высотами отсекаются прямоугольные треугольники, причём они являются равнобедренными, так как углы при основании равны по 450. Отсюда следует, что высота трапеции будет равна 3.
Ответ: 3
На этом всё! Успеха вам!
С уважением, Александр.
P.S: Расскажите о сайте в социальных сетях!
Быстро найти нужную формулу для расчета онлайн. Геометрия. Алгебра.
1. Формулы длины диагонали равнобедренной трапеции через ее стороны
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
d — диагональ трапеции
Формула диагонали трапеции (d ):
2. Формулы длины диагонали равнобедренной трапеции по теореме косинусов
Формулы длины диагонали равнобедренной трапеции по теореме косинусов
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
α, β — углы трапеции
d — диагональ трапеции
Формулы диагонали трапеции (d ):
3. Формула длины диагонали равнобедренной трапеции
a — нижнее основание
b — верхнее основание
α, β — углы между диагоналями
h — высота трапеции
m — средняя линия трапеции
S — площадь трапеции
d — диагональ трапеции
Формулы диагонали трапеции (d ):
Справедливо для данного случая :
4. Формулы длины диагонали трапеции через высоту и стороны
Формулы длины диагонали трапеции через высоту и стороны
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
h — высота трапеции
α — угол при нижнем основании
d — диагональ трапеции
Формулы диагонали трапеции (d ):
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
Найти длину диагонали трапеции
зная все четыре стороны
или две стороны и угол
или высоту, сторону и угол
или площадь, другую диагональ и угол
и еще много других формул.
1. Формулы длины диагоналей трапеции по теореме косинусов или через четыре стороны
a — нижнее основание
b — верхнее основание
c , d — боковые стороны
α, β — углы трапеции
d1 , d2 — диагонали трапеции
Формулы диагоналей трапеции по теореме косинусов:
Формулы диагоналей трапеции через четыре стороны:
2. Формула длины диагоналей трапеции через высоту
Формула длины диагоналей трапеции через высоту
a — нижнее основание
b — верхнее основание
c , d — боковые стороны
α, β — углы трапеции
h — высота трапеции
d1 , d2 — диагонали трапеции
Формулы диагоналей трапеции через высоту:
3. Формула длины диагонали трапеции через другую диагональ
a — нижнее основание
b — верхнее основание
α, β — углы между диагоналями
h — высота трапеции
m — средняя линия трапеции
S — площадь трапеции
d1 , d2 — диагонали трапеции
Формулы диагоналей трапеции :
Справедливо для данного случая :
4. Формулы длины диагонали трапеции через сумму квадратов диагоналей
Формулы длины диагонали трапеции через сумму квадратов диагоналей
a — нижнее основание
b — верхнее основание
c , d — боковые стороны
d1 , d2 — диагонали трапеции
Формула суммы квадратов диагоналей :
Формулы диагоналей трапеции :
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
1. Формула средней линии трапеции через основания (для всех видов трапеции)
a — нижнее основание
b — верхнее основание
m — средняя линия
Формула средней линии, (m ):
2.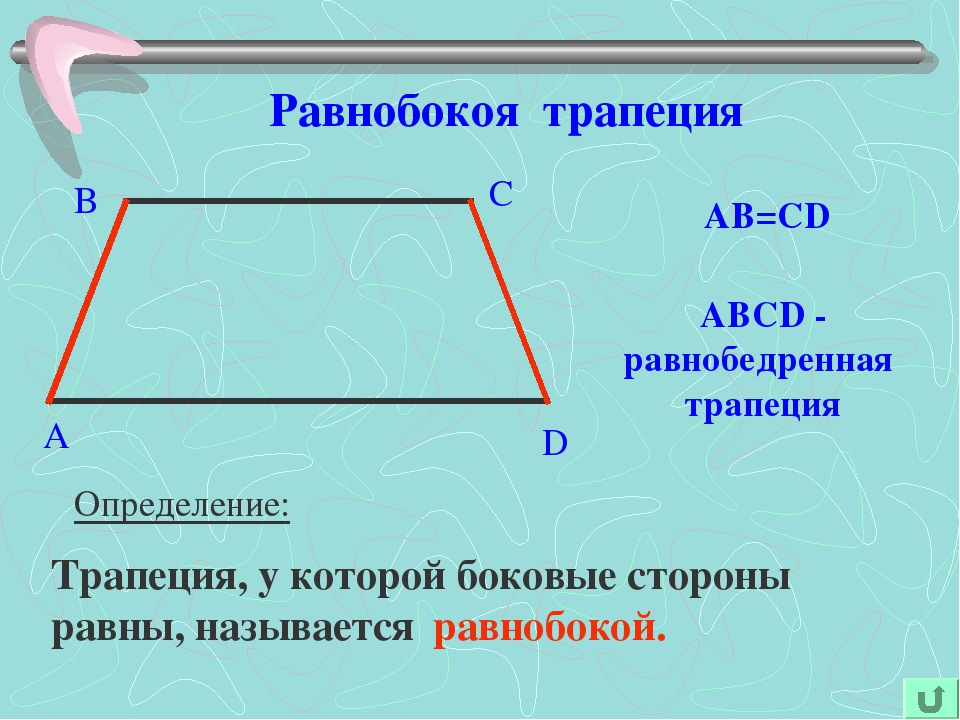 Формулы средней линии через основания, высоту и угол при нижнем основании
Формулы средней линии через основания, высоту и угол при нижнем основании
a, b — основания трапеции
c — боковая сторона под прямым углом к основаниям
d — боковая сторона
α — угол при основании
h — высота трапеции
m — средняя линия
Формулы средней линии трапеции, (m ):
3. Формула средней линии трапеции через диагонали, высоту и угол между диагоналями
d1 , d2 — диагонали трапеции
α , β — углы между диагоналями
h — высота трапеции
m — средняя линия
Формулы средней линии трапеции, (m ):
4. Формула средней линии трапеции через площадь и высоту (для всех видов трапеции)
Формула средней линии трапеции через площадь и высоту (для всех видов трапеции)
S — площадь трапеции
h — высота трапеции
m — средняя линия
Формула средней линии трапеции, (m ):
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
1. Формула боковой стороны (с) прямоугольной трапеции через другие стороны и угол при нижнем основании
a — нижнее основание
b — верхнее основание
d — боковая сторона
α — угол при нижнем основании
h — высота трапеции
c — боковая сторона под прямым углом к основаниям
Формулы длины боковой стороны (с) :
2.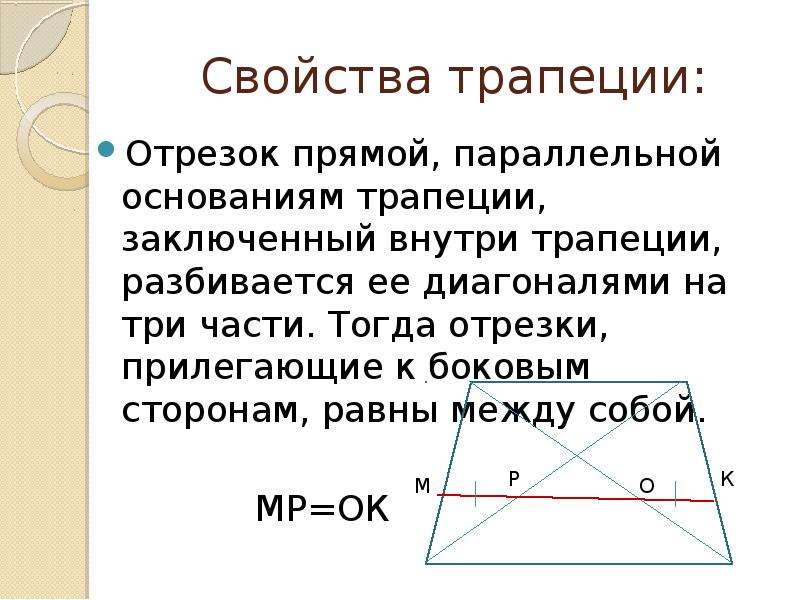 Формулы боковой стороны (с) прямоугольной трапеции через диагонали и угол между ними
Формулы боковой стороны (с) прямоугольной трапеции через диагонали и угол между ними
a — нижнее основание
b — верхнее основание
d1 , d2 — диагонали трапеции
α , β — углы между диагоналями
c — боковая сторона под прямым углом к основаниям
Формулы длины боковой стороны (с):
3. Формулы боковой стороны (с) прямоугольной трапеции через площадь
a — нижнее основание
b — верхнее основание
m — средняя линия трапеции
c — боковая сторона под прямым углом к основаниям
Формула длины боковой стороны (с) :
4.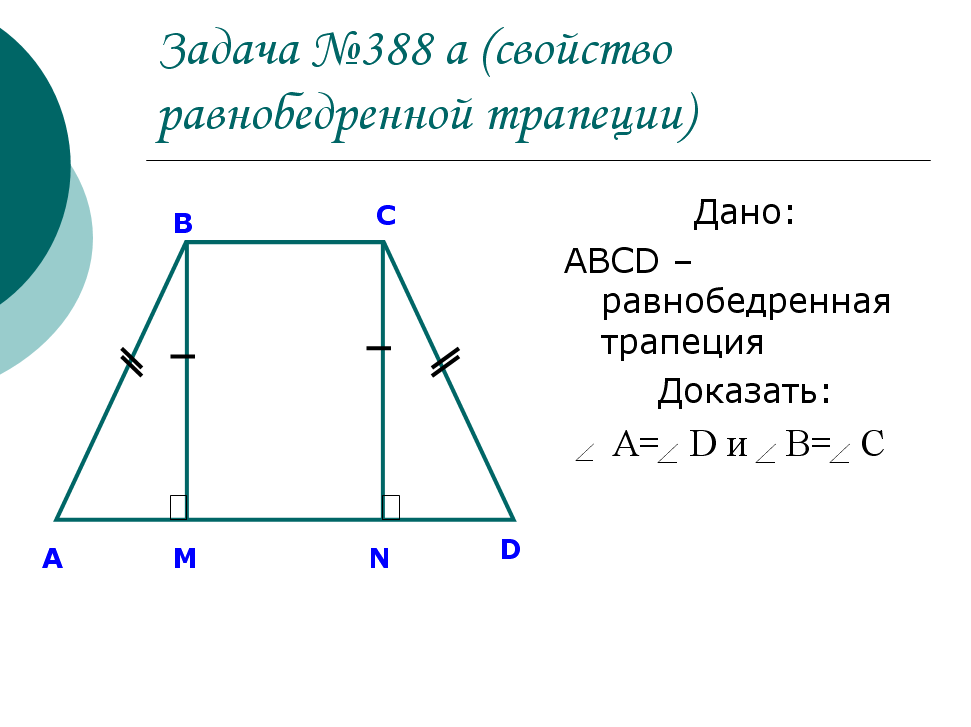 Формулы боковой стороны (d) прямоугольной трапеции через другие стороны и угол при нижнем основании
Формулы боковой стороны (d) прямоугольной трапеции через другие стороны и угол при нижнем основании
a — нижнее основание
b — верхнее основание
c — боковая сторона под прямым углом к основаниям
α — угол при нижнем основании
h — высота трапеции
d — боковая сторона
Формулы длины боковой стороны (d) :
5. Формула боковой стороны (d) прямоугольной трапеции через площадь
a — нижнее основание
b — верхнее основание
m — средняя линия трапеции
α — угол при нижнем основании
d — боковая сторона
Формула длины боковой стороны (d) :
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
1. Формула длины оснований прямоугольной трапеции через среднюю линию
Формула длины оснований прямоугольной трапеции через среднюю линию
a — нижнее основание
b — верхнее основание
m — средняя линия
Формулы длины оснований :
2. Формулы длины оснований через боковые стороны и угол при нижнем основании
a — нижнее основание
b — верхнее основание
c , d — боковые стороны
α — угол при нижнем основании
Формулы длины оснований :
3. Формулы длины оснований трапеции через диагонали и угол между ними
a — нижнее основание
b — верхнее основание
c — боковая сторона под прямым углом к основаниям
d1 , d2 — диагонали трапеции
α , β — углы между диагоналями
Формулы длины оснований :
4.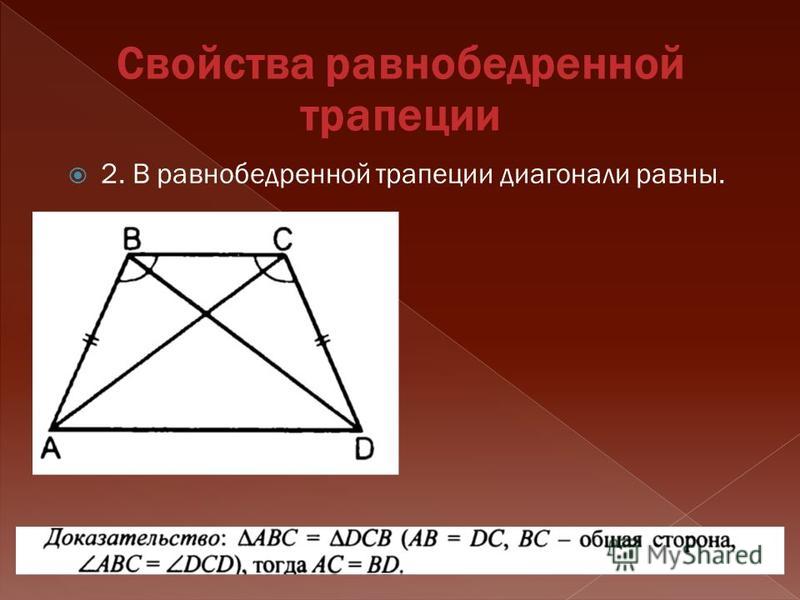 Формулы длины оснований трапеции через площадь
Формулы длины оснований трапеции через площадь
a — нижнее основание
b — верхнее основание
c — боковая сторона под прямым углом к основаниям
h — высота трапеции
Формулы длины оснований :
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
1. Формула средней линии равнобедренной трапеции через основания
a — нижнее основание
b — верхнее основание
m — средняя линия
Формула средней линии, (m ):
2. Формулы средней линии через основание, высоту и углы при нижнем основании
Формулы средней линии через основание, высоту и углы при нижнем основании
a — нижнее основание
b — верхнее основание
c — боковая сторона
α — угол при нижнем осровании
h — высота трапеции
m — средняя линия
Формулы средней линии трапеции, (m ):
3. Формула средней линии трапеции через диагонали, высоту и угол между диагоналями
d — диагонали трапеции
α , β — углы между диагоналями
h — высота трапеции
m — средняя линия
Формула средней линии трапеции, (m ):
4. Формула средней линии трапеции через площадь и высоту
Формула средней линии трапеции через площадь и высоту
S — площадь трапеции
h — высота трапеции
α — угол при нижнем осровании
m — средняя линия
Формула средней линии трапеции, (m ):
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
1. Формула высоты равнобедренной трапеции через стороны и углы при основании
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
α — угол при нижнем основании
h — высота трапеции
Формулы длины высоты, (h ):
2. Формула высоты равнобедренной трапеции через диагонали и углы между ними
Формула высоты равнобедренной трапеции через диагонали и углы между ними
d — диагонали трапеции
α , β — углы между диагоналями
a , b — основания
h — высота трапеции
m — средняя линия
Формулы длины высоты, (h ):
3. Формула высоты равнобедренной трапеции через площадь
S — площадь трапеции
a , b — основания
h — высота трапеции
m — средняя линия
Формулы длины высоты, (h ):
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
1. Формула длины основания равнобедренной трапеции через среднюю линию
Формула длины основания равнобедренной трапеции через среднюю линию
a — нижнее основание
b — верхнее основание
m — средняя линия
Формулы длины основания:
2. Формулы длины сторон через высоту и угол при нижнем основании
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
α — угол при основании трапеции
h — высота трапеции
Формулы всех четырех сторон трапеции:
3. Формула длины сторон трапеции через диагонали, высоту и угол между диагоналями
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
d — диагонали
α , β — углы между диагоналями
h — высота трапеции
Формулы длины сторон трапеции:
справедливо для данной ситуации:
4. Формулы длины сторон равнобедренной трапеции через площадь
Формулы длины сторон равнобедренной трапеции через площадь
a — нижнее основание
b — верхнее основание
c — равные боковые стороны
α , β — углы при основаниях
m — средняя линия
h — средняя линия
Формулы длины сторон равнобедренной трапеции через площадь:
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
Трапеция это фигура, которая имеет четыре стороны, две из которых параллельны, а две другие, нет. Параллельные стороны называются — верхнее основание и нижнее основание. Две другие, называются боковыми сторонами.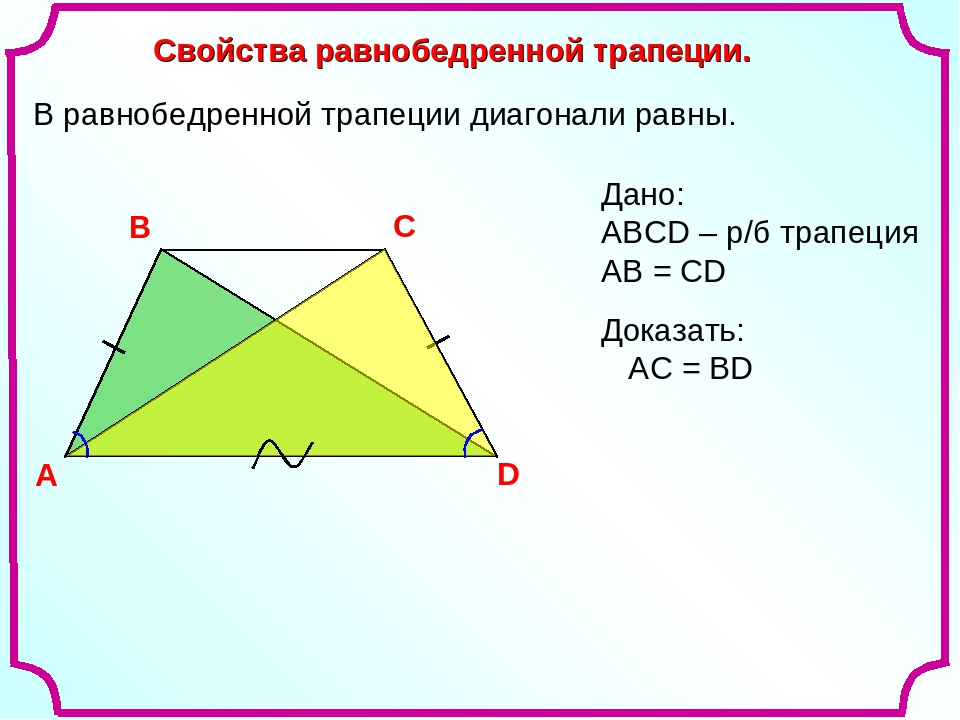
Высота трапеции это отрезок, длина которого, равна кратчайшему расстоянию между основаниями и следовательно расположенному перпендикулярно к этим основаниям.
1. Формула высоты трапеции через стороны и углы при основании
a — нижнее основание
b — верхнее основание
c , d — боковые стороны
α, β — углы трапеции
h — высота трапеции
Формулы длины высоты, (h ):
2. Формула высоты трапеции через диагонали и углы между ними
d1 , d2 — диагонали трапеции
α , β — углы между диагоналями
a , b — основания
h — высота трапеции
m — средняя линия
Формулы длины высоты, (h ):
3. Формула высоты трапеции через площадь
Формула высоты трапеции через площадь
S — площадь трапеции
a , b — основания
h — высота трапеции
m — средняя линия
Формулы длины высоты, (h ):
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
Трапеция это фигура, которая имеет четыре стороны, две из которых параллельны, а две другие, нет. Параллельные стороны называются — верхнее основание и нижнее основание. Две другие, называются боковыми сторонами.
Средняя линия трапеции — отрезок соединяющий середины боковых сторон и расположен параллельно к основаниям. Длина средней линии, равна полу сумме оснований.
1. Формула средней линии трапеции через основания
b — верхнее основание
a — нижнее основание
m— средняя линия
Формула средней линии, (m ):
2. Формулы средней линии через основание, высоту и углы при нижнем основании
b — верхнее основание
a — нижнее основание
α, β — углы трапеции
h — высота трапеции
m — средняя линия
Формулы средней линии трапеции, (m):
3. Формула средней линии трапеции через диагонали, высоту и угол между диагоналями
α, β — углы между диагоналями
d1 , d2 — диагонали трапеции
h — высота трапеции
m — средняя линия
Формулы средней линии трапеции, (m ):
4. Формула средней линии трапеции через площадь и высоту
Формула средней линии трапеции через площадь и высоту
S — площадь трапеции
h — высота трапеции
m — средняя линия
Формула средней линии трапеции, (m):
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
1. Формула длины основания трапеции через среднюю линию
a — нижнее основание
b — верхнее основание
m — средняя линия
Формулы длины оснований :
2. Формулы длины сторон через высоту и углы при нижнем основании
a — нижнее основание
b — верхнее основание
c , d — боковые стороны
α, β — углы трапеции
h — высота трапеции
Формулы всех четырех сторон трапеции:
3. Формула длины сторон трапеции через диагонали, высоту и угол между диагоналями
Формула длины сторон трапеции через диагонали, высоту и угол между диагоналями
a — нижнее основание
b — верхнее основание
d1 , d2 — диагонали трапеции
α , β — углы между диагоналями
h — высота трапеции
Формулы длины сторон трапеции:
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
Трапеция, её виды и свойства.
Трапеция.
Определение. Трапецией называется выпуклый четырёхугольник, у которого две стороны параллельны, а две другие не параллельны.
Параллельные стороны называются основаниями трапеции, а не параллельные стороны называются боковыми сторонами трапеции.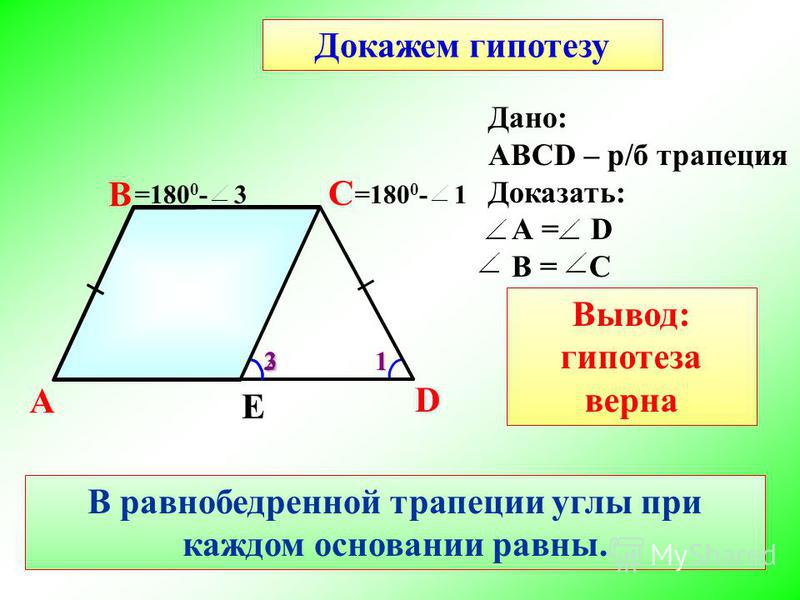
– боковые стороны.
Трапеция бывает равнобедренной (равнобокой) и прямоугольной.
О пределение. Равнобедренной (равнобокой) называется трапеция, у которой боковые стороны равны.
Свойства равнобедренной трапеции.
Определение. Прямоугольной называется трапеция, у которой одна боковая сторона перпендикулярна основаниям.
Свойства прямоугольной трапеции.
прямоугольный треугольник.
В трапеции – меньшее основание. На отрезке взята точка так, что . Найдите углы трапеции.
В прямоугольной трапеции острый угол равен . Меньшая боковая сторона и меньшее основание равны по см. Найдите большее основание.
Постройте прямоугольную трапецию по меньшему основанию и боковым сторонам.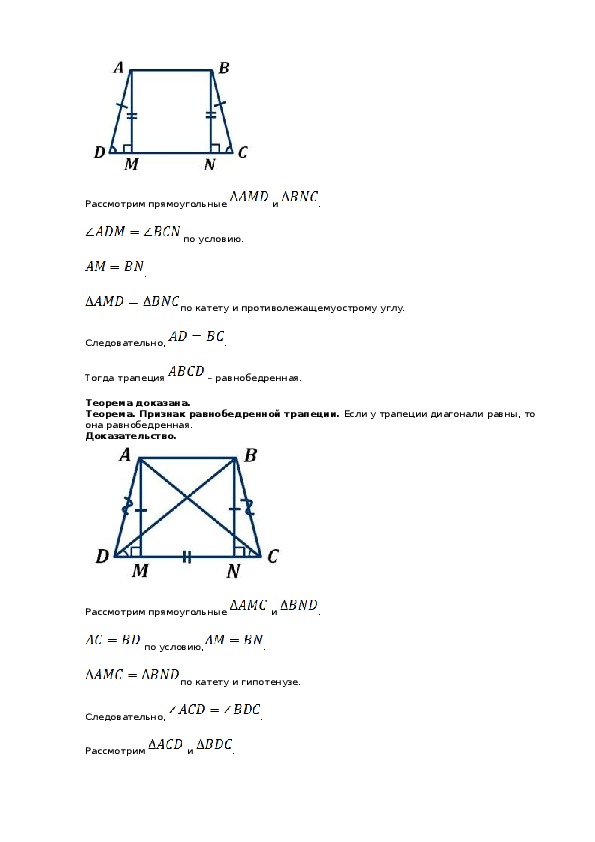
В трапеции – большее основание. Прямые и пересекаются в точке . Найдите углы трапеции.
В прямоугольной трапеции острый угол равен . Большая боковая сторона и большее основание равны по см. Найдите меньшее основание.
Постройте прямоугольную трапецию по меньшей диагонали, большему основанию и большей боковой стороне.
В равнобедренной трапеции и – основания, диагонали взаимно перпендикулярны. см. Чему равна высота трапеции?
В равнобедренной трапеции и – основания, диагонали взаимно перпендикулярны. см. Чему равна длина отрезка ?
В равнобедренной трапеции диагональ составляет с боковой стороной угол в . Боковая сторона равна меньшему основанию. Найдите углы трапеции.
В прямоугольной трапеции острый угол и угол, который составляет меньшая диагональ с меньшим основанием равны по .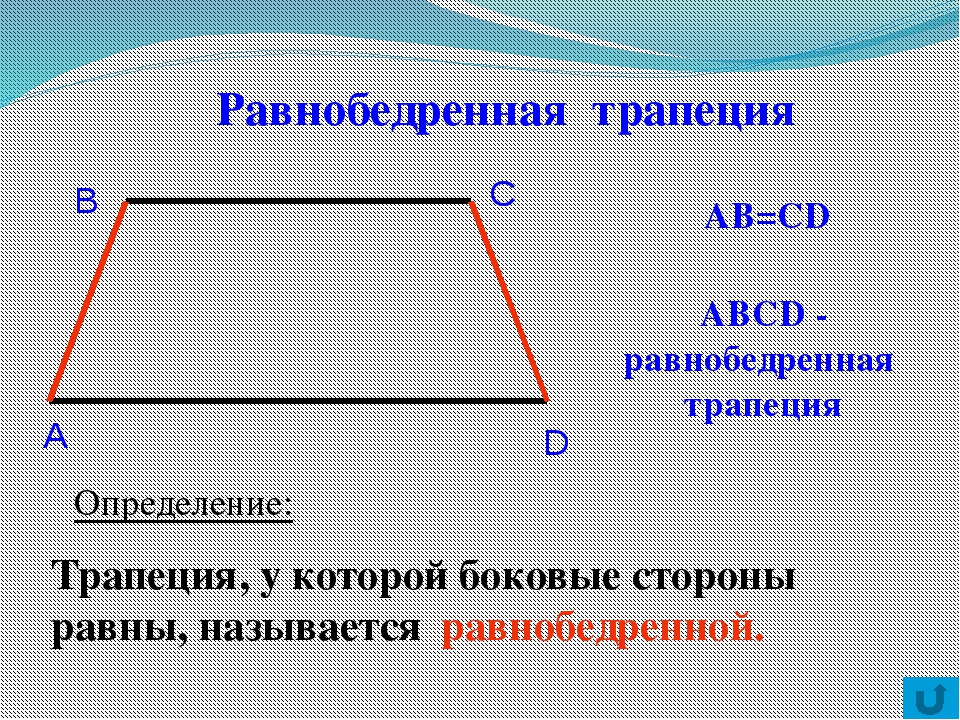 Найдите отношение оснований.
Найдите отношение оснований.
Постройте равнобедренную трапецию по боковой стороне, большему основанию и отрезку длиной, равной расстоянию между прямыми, содержащими основания трапеции.
В равнобедренной трапеции большее основание в два раза превосходит меньшее. Середина большего основания удалена от вершины тупого угла на расстояние, равное длине меньшего основания. Найдите углы трапеции.
В прямоугольной трапеции диагональ перпендикулярна к боковой стороне, острый угол равен . Найдите отношение оснований.
Постройте равнобедренную трапецию по диагонали, большему основанию и перпендикуляру, проведённому из вершины тупого угла к прямой, содержащей большее основание трапеции.
Из вершины тупого угла равнобедренной трапеции проведён перпендикуляр к прямой , содержащей большее основание. Докажите, что .
В прямоугольной трапеции диагонали взаимно перпендикулярны.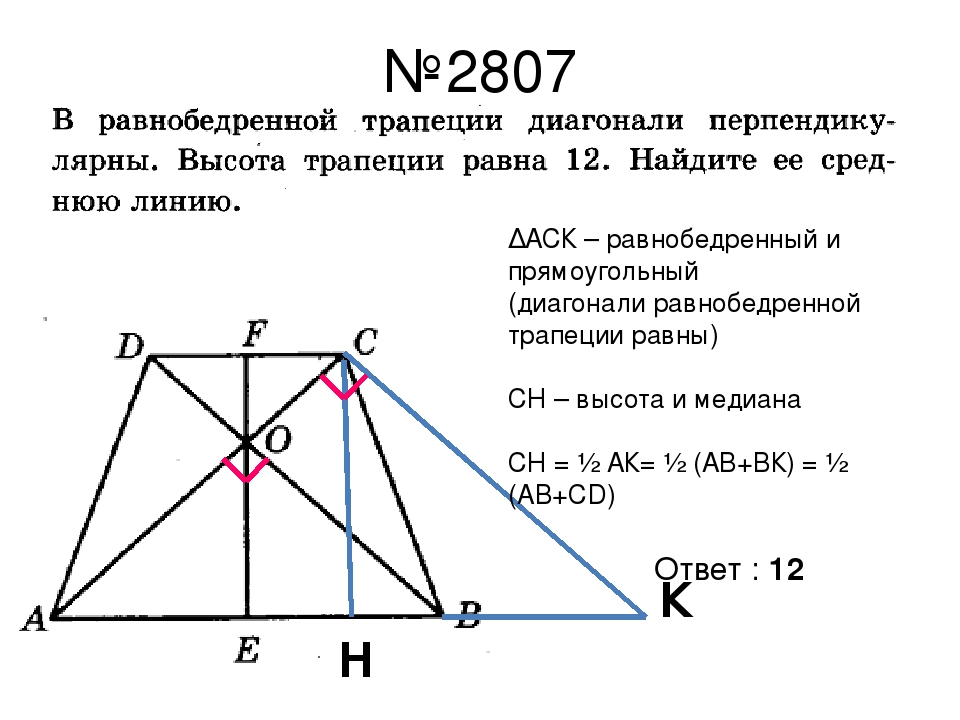 Большая диагональ составляет с меньшей боковой стороной угол в . Докажите, что меньшая диагональ равна полусумме оснований трапеции.
Большая диагональ составляет с меньшей боковой стороной угол в . Докажите, что меньшая диагональ равна полусумме оснований трапеции.
Постройте равнобедренную трапецию по острому углу, диагонали и перпендикуляру, проведённому из вершины острого угла к прямой, содержащей меньшее основание трапеции.
Диагонали равнобедренной трапеции взаимно перпендикулярны. Докажите, что расстояние между прямыми и , содержащими основания, равно .
Из вершины прямого угла меньшего основания прямоугольной трапеции под углом к этому основанию проведён луч, который проходит через середину большей боковой стороны. Докажите, что меньшая боковая сторона этой трапеции равна сумме оснований.
Постройте равнобедренную трапецию по двум углам, на которые диагональ делит тупой угол, и отрезку длиной, равной расстоянию между прямыми, содержащими основание трапеции.
Докажите, что сумма боковых сторон любой трапеции больше разности её большего и меньшего оснований.
Найдите связь между сторонами трапеции, если известно, что внутри трапеции существует точка, равноудалённая от прямых, содержащих её стороны.
Постройте трапецию по двум диагоналям, углу между ними и одной из боковых сторон.
Докажите, что сумма диагоналей любой трапеции больше суммы её оснований.
Найдите связь между противоположными углами трапеции, если известно, что внутри неё существует точка, равноудалённая от вершин трапеции.
Постройте трапецию по четырём сторонам.
В трапеции точка – середина большего основания . Найдите углы и .
Дан четырёхугольник , в котором диагонали имеют общую середину. На продолжении стороны за вершину взята точка , . Докажите, что четырёхугольник является равнобедренной трапецией.
В четырёхугольнике . На стороне взята точка так, что .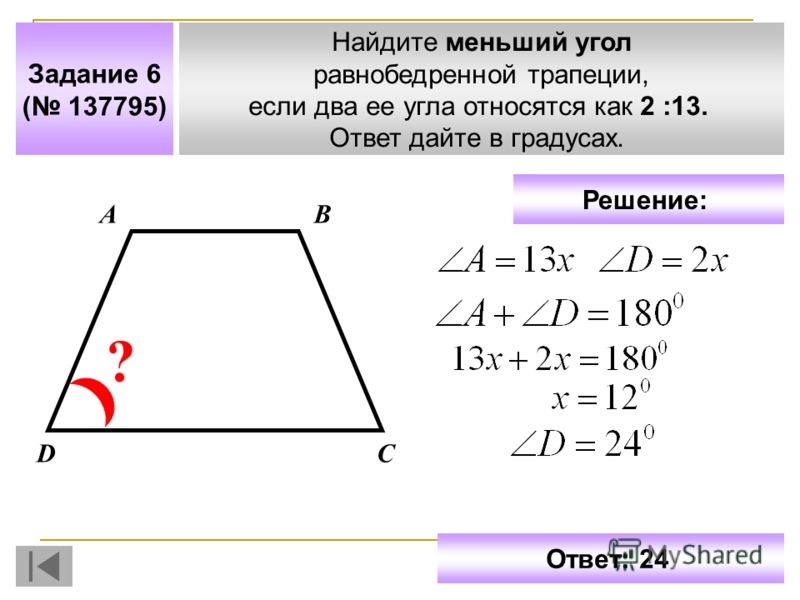 Докажите, что четырёхугольник является прямоугольной трапецией.
Докажите, что четырёхугольник является прямоугольной трапецией.
В трапеции на большем основании взята точка . Известно, что . Докажите, что отрезки и имеют общую середину.
В трапеции с основаниями и . Найдите углы трапеции.
В прямоугольной трапеции острый угол равен , а меньшее основание и меньшая боковая сторона равны по см. Найдите большее основание.
В равнобедренной трапеции перпендикуляр, проведённый из вершины к прямой , делит большее основание на отрезки длиной см и см. Найдите основания трапеции.
Найдите боковые стороны равнобедренной трапеции, основания которой равны см и см, а один из углов равен .
Найдите меньшее основание равнобедренной трапеции, если её большее основание равно см, боковая сторона см, а один из углов равен .
Найдите меньшую боковую сторону прямоугольной трапеции, основания которой равны см и см, а один из углов равен .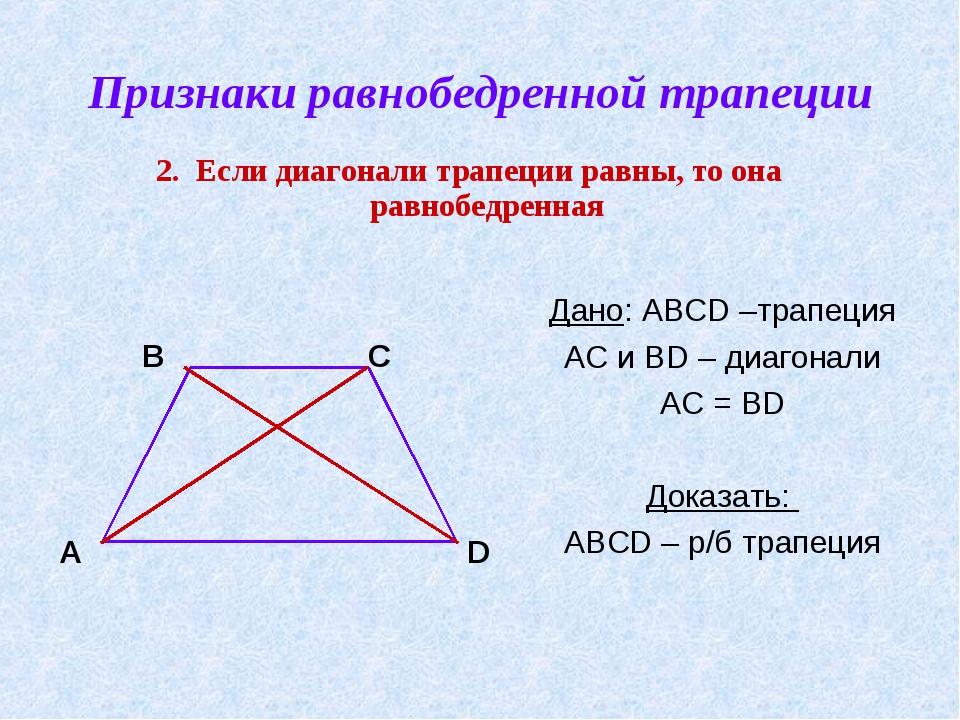
Найдите боковую сторону равнобедренной трапеции, основания которой равны см и см, а один из углов равен .
В равнобедренной трапеции высота, проведённая из вершины тупого угла, делит большее основание на отрезки см и см. Найдите основания трапеции.
Два противоположных угла равнобедренной трапеции относятся как . Найдите углы трапеции.
В равнобедренной трапеции диагональ является биссектрисой острого угла. Периметр трапеции равен см, а большее основание – см. Найдите меньшее основание трапеции.
В равнобедренной трапеции диагональ перпендикулярна боковой стороне. Найдите углы трапеции, если известно, что боковая сторона равна диагонали.
Могут ли углы трапеции быть пропорциональны числам ?
В равнобедренной трапеции , в которой – большее основание, диагональ – биссектриса угла . Найдите углы трапеции, если .
Найдите углы трапеции, если .
Диагонали трапеции являются биссектрисами её углов при большем основании .
Как найти углы равнобедренной трапеции
Трапеция — это плоская четырехугольная геометрическая фигура, отличительной особенностью которой является обязательная параллельность одной пары несоприкасающихся сторон. Эти стороны называются ее основаниями, а две непараллельные составляющие — боковыми сторонами. Разновидность трапеции, у которой длины боковых сторон одинаковы, называется равнобокой или равнобедренной. Формулы нахождения углов такой трапеции легко вывести из свойств прямоугольного треугольника.
Если известны длины обоих оснований (b и c) и одинаковых по определению боковых сторон (a) равнобедренной трапеции, то для вычисления величины одного из ее острых углов (γ) можно использовать свойства прямоугольного треугольника. Для этого опустите высоту из любого прилегающего к короткому основанию угла. Прямоугольный треугольник будет образован высотой (катет), боковой стороной (гипотенуза) и отрезком длинного основания между высотой и ближней боковой стороной (второй катет). Длину этого отрезка можно найти, отняв от длины большего основания длину меньшего и поделив результат пополам: (c-b)/2.
Длину этого отрезка можно найти, отняв от длины большего основания длину меньшего и поделив результат пополам: (c-b)/2.
Получив значения длин двух смежных сторон прямоугольного треугольника, переходите к вычислению угла между ними. Отношение длины гипотенузы (a) к длине катета ((c-b)/2) дает значение косинуса этого угла (cos(γ)), а функция арккосинус поможет преобразовать его в величину угла в градусах: γ=arccos(2*a/(c-b)). Так вы получите величину одного из острых углов трапеции, а поскольку она равнобедренна, то и второй острый угол будет иметь такую же величину. Сумма всех углов четырехугольника должна составлять 360°, а это значит, что сумма двух тупых углов будет равна разности между этим числом и удвоенной величиной острого угла. Поскольку оба тупых угла тоже будут одинаковы, то для нахождения величины каждого из них (α) эту разность надо поделить пополам: α = (360°-2*γ)/2 = 180°-arccos(2*a/(c-b)). Теперь у вас есть формулы вычисления всех углов равнобедренной трапеции по известным длинам ее сторон.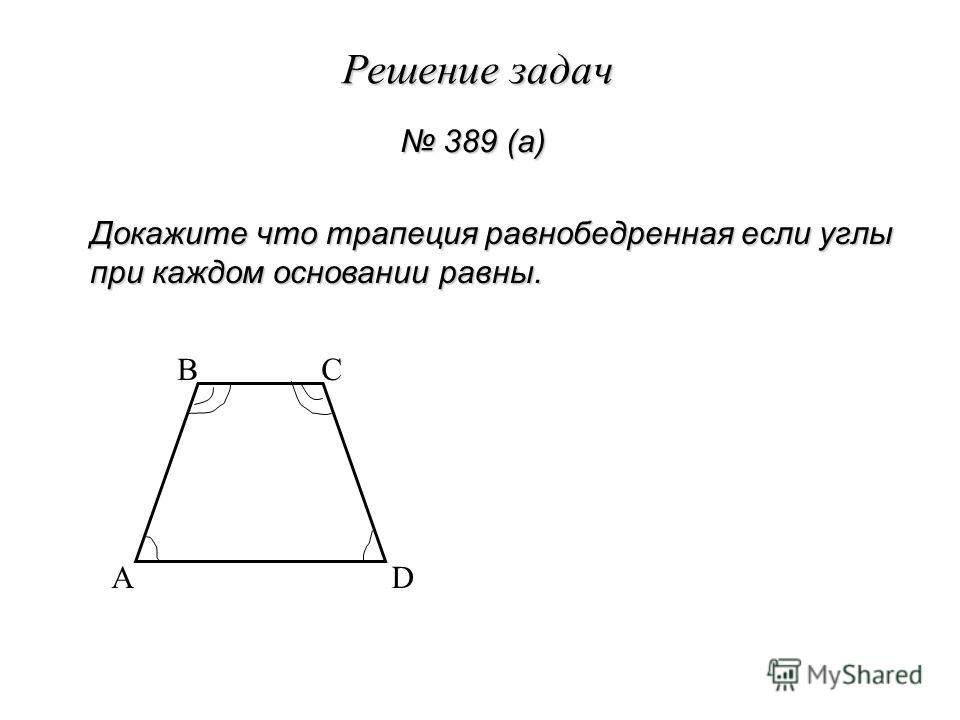
Если длины боковых сторон фигуры неизвестны, но дана ее высота (h), то действовать нужно по такой же схеме. В этом случае в прямоугольном треугольнике, составленном из высоты, боковой стороны и короткого отрезка длинного основания, вам будут известны длины двух катетов. Их соотношение определяет тангенс нужного вам угла, а эта тригонометрическая функция тоже имеет своего антипода, преобразующего значение тангенса в величину угла — арктангенс. Полученные в предыдущем шаге формулы острого и тупого углов трансформируйте соответствующим образом: γ=arctg(2*h/(c-b)) и α = 180°-arctg(2*h/(c-b)).
| ФГКОУ «МКК «Пансион воспитанниц МО РФ» «УТВЕРЖДАЮ» Руководитель отдельной дисциплины (математика, информатика и ИКТ) Ю. В. Крылова _____________ «___» _____________ 2015 г. «Трапеция и ее свойства» Методическая разработка преподавателя математики Шаталиной Елены Дмитриевны
Москва 2015 год Оглавление Введение 2
. . Список используемой литературы Приложение
Введение Данная работа посвящена геометрической фигуре, которая называется трапеция. «Обычная фигура»,- скажете вы, но это не так. Она таит в себе много тайн и загадок, если приглядеться и углубиться в ее изучение, то вы откроете для себя много нового в мире геометрии, задачи, которые раньше не решались, покажутся вам легкими. Трапеция — греч.слово trapezion – «столик». Заимств. в 18 в. из лат. яз., где trapezion – греч. Это четырехугольник, у которого две противоположные стороны параллельны. Трапеция встречается впервые у древнегреческого ученого Посидония (2 век до н.э.). В нашей жизни много разных фигур. В 7 классе мы близко познакомились с треугольником, в 8 классе по школьной программе мы начали изучать трапецию. В работе рассматриваются свойства знакомые воспитанницам по пройденному материалу в учебнике, но в большей степени неизвестные свойства, которые необходимы для решения сложных задач. Чем больше количество решаемых задач, тем больше вопросов возникает при решении их. Ответом на эти вопросы иногда кажется тайной, узнавая, новые свойства трапеции, необычные приемы решения задач, а также технику дополнительных построений, мы постепенно открываем тайны трапеции. В интернете, если забить в поисковике, о методах решения задач по теме «трапеция» очень мало литературы. В процессе работы над проектом найден большой объем информации, которая поможет воспитанницам в глубоком изучении геометрии. Трапеция.
Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна). Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны. Если боковые стороны равны, трапеция называется равнобедренной. Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной. Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции. Расстояние между основаниями называется высотой трапеции. 2. Свойства равнобедренной трапеции
3. Диагонали равнобедренной трапеции равны. 4. Высота равнобедренной трапеции, проведенная из вершины меньшего основания, разбивает большее основание на отрезки, один из которых равен полуразности оснований, а другой полусумме оснований трапеции, т.
10. Проекция боковой стороны равнобедренной трапеции на большее основание равна полуразности оснований, а проекция диагонали равна помусумме оснований.
Если сумма оснований трапеции равна сумме боковых сторон, то в неё можно вписать окружность. Е 4. Свойства вписанных и описанных трапеций
2.Если в равнобедренную трапецию можно вписать окружность, то сумма длин оснований равна сумме длин боковых сторон. Следовательно, длина боковой стороны равна длине средней линии трапеции. 4. Если в трапецию вписана окружность, то боковые стороны из ее центра видны под углом 90°.
1 5. Средние величины в трапеции Среднее геометрическое
1. Середины диагоналей трапеции и середины боковых сторон лежат на одной прямой. 2. Биссектрисы углов, прилежащих к одной из боковых сторон трапеции, перпендикулярны и пересекаются в точке, лежащей на средней линии трапеции, т.е., при их пересечении образуется прямоугольный треугольник с гипотенузой, равной боковой стороне. 3.
5. При пересечении диагоналей произвольной трапеции образуются четыре треугольника с общей вершиной, причем треугольники, прилежащие к основаниям, подобны, а треугольники, прилежащие к боковым сторонам, равновелики(т.е. имеют равные площади). 6.Сумма квадратов диагоналей произвольной трапеции равна сумме квадратов боковых сторон, сложенной с удвоенным произведением оснований.
7 8. Прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки. 9. Отрезок, параллельный основаниям и проходящий через точку пересечения диагоналей, делится последней пополам. 7. Признаки трапеции
8. Дополнительные построения в трапеции 1. Отрезок, соединяющий середины боковых сторон — средняя линия трапеции. 3. Если даны все стороны трапеции, через вершину меньшего основания проводится прямая, параллельная боковой стороне. Получается треугольник со сторонами, равными боковым сторонам трапеции и разности оснований. По формуле Герона находят площадь треугольника, потом высоту треугольника, которая равна высоте трапеции. 5. Высоты трапеции, опущенные из вершин одного основания, высекают на прямой, содержащей другое основание, отрезок, равный первому основанию. 6 7.Отрезок, соединяющий середины диагоналей, равен полуразности оснований трапеции. 8. Биссектрисы углов, прилежащих к одной из боковых сторон трапеции, они перпендикулярны и пересекаются в точке, лежащей на средней линии трапеции, т.е., при их пересечении образуется прямоугольный треугольник с гипотенузой, равной боковой стороне. 9. Биссектриса угла трапеции отсекает равнобедренный треугольник. 1 12. Продолжение боковых сторон трапеции до пересечения дает возможность рассматривать подобные треугольники. 9. Площадь трапеции 1. Площадь трапеции равна произведению полусуммы оснований на высоту S = ½(a + b)•h или П 2. Площадь трапеции равна произведению боковой стороны и перпендикуляра, проведенного из середины другой боковой стороны к прямой, содержащей первую боковую сторону.
10. Заключение ГДЕ, КАК И ДЛЯ ЧЕГО ИСПОЛЬЗЕУТСЯ ТРАПЕЦИЯ? Трапеция в спорте: Трапеция — безусловно прогрессивное изобретение человечества. Она предназначена для того, чтобы разгрузить наши руки, сделать хождение на виндсерфере комфортным и легким отдыхом. Хождение на короткой доске вообще не имеет смысла без трапеции, так как без нее невозможно правильно распределить тягу между степсом и ногами и эффективно разогнаться. Трапеция в моде: Трапеция в одежде была популярна ещё в средние века, в романскую эпоху IX-XI вв. В тот период основу женской одежды составляли туники в пол, к низу туника сильно расширялась, что и создавало эффект трапеции. Возрождение силуэта произошло в 1961-ом году и стало гимном молодости, независимости и утонченности. Огромную роль в популяризации трапеции сыграла хрупкая модель Лесли Хорнби, известная, как Твигги. Невысокая девочка с анорексичным телосложением и огромными глазами стала символом эпохи, а её излюбленными нарядами были короткие платья трапеции. Трапеция в природе: трапеция встречается и в природе. У человека есть трапециевидная мышца, у некоторых людей лицо имеет форму трапеции. Лепестки цветов, созвездия, и конечно же вулкан Килиманджаро тоже имеют форму трапеции. Трапеция в быту: Трапеция используется и в быту, т.к ее форма практична. Она встречается в таких предметах как: ковш экскаватора, стол, винт, машина. Трапеция — символ архитектуры инков. Доминирующая стилистическая форма в архитектуре инков проста, но изящна — это трапеция. Она имеет не только функциональное значение, но и строго ограниченное художественное оформление. Трапециевидные дверные проемы, окна, и стенные ниши найдены в постройках всех типов, и в храмах и в менее значительных зданиях более грубых, если можно так выразиться, постройках. Трапеция встречается и в современной архитектуре. Эта форма зданий является необычной, поэтому такие постройки всегда притягивают взгляды прохожих. В 21 первом веке люди уже практически не задумываются о значении геометрических фигур в их жизни. Их совершенно не волнует какой формы у них стол, очки или телефон. Они просто выбирают ту форму, которая практична. Но именно от формы той или иной вещи может зависеть использование предмета, его предназначение, результат работы. Сегодня мы познакомили вас с одной из величайших достижений человечества- с трапецией. Мы приоткрыли вам дверь в удивительный мир фигур, поведали вам тайны трапеции и показали, что геометрия вокруг нас. Список используемой литературы
Приложение 1.Доказательство некоторых свойств трапеции. 1. Прямая, проходящая через точку пересечения диагоналей трапеции параллельно её основаниям, пересекает боковые стороны трапеции в точках K и L. Доказать, что если основания трапеции равны а и b, то длина отрезка KL равна среднему геометрическому оснований трапеции. Доказательство Пусть О — точка пересечения диагоналей, AD = а, ВС = b. Прямая KL параллельна основанию AD, следовательно, KО║ AD, треугольники ВKО и BAD подобны, поэтому
( 2 ) Подставим ( 2 ) в ( 1 ), получим KO = Аналогично LO = Тогда K L= KO + LO =
Д Обозначим ВМ = х, МС = у, AN = и, ND = v. Имеем: ∆ВКМ ~ ∆AKN → x B C Y O v u N D ∆CMO ∆ANO поэтому . Перемножая полученные равенства, получим , откуда следует x=y, но тогда и u = v.
3. Задачи по теме «Трапеция» повышенной сложности. Садовничий Ю.В. «Математика. Подготовка к ЕГЭ», Москва, ИЛЕКСА, 2011, стр. 252. 1 . В трапеции диагонали равны 3 и 5, а отрезок, соединяющий середины оснований, равен 2. Найти площадь трапеции. Ответ: S = 6. 2. Периметр равнобочной трапеции, описанной около круга, равен р. Найти радиус этого круга, если известно, что острый угол при основании трапеции равен ɑ. psina Ответ: 1и 7.
Ответ: S= 3ab В трапеции PQRS длина основания QR равна 10, длина диагонали QS равна 19, а величина угла QSP равна 30°. Выяснить, что больше, длина основания QR или длина стороны RS. Ответ: RS > QR.
Ответ: S=90√3. Иванов А.А., Иванов А.П., Математика: Пособие для подготовки к ЕГЭ и поступлению в вузы. – М.: Издательство МФТИ, 2003, стр. 238.. 12. Площадь прямоугольной трапеции равна S, острый угол равен а. Найти высоту трапеции, если ее меньшая диагональ равна большему оснозанию. [√2Sctg а]
[arccos(l — 1/к), π — arccos(l — 1/к), к > 1]
[√Stg(½ ɑ)]
4. Проверочный тест по теме «Трапеция» В трапеции, имеющей прямой угол, основания равны 5 и 11, а большая диагональ √185. Площадь трапеции составляет В трапеции боковые стороны и меньшее основание равны Ь, а острый угол вдвое меньше тупого. Площадь трапеции равна 151 в равнобедренной трапеции, описанной около окружности радиуса 5 м и имеющей основание 20 м, другое основание равно Меньшее основание трапеции, вписанной в окружность, втрое меньше большего, которое является диаметром окружности.25j В трапеции с диагональю 20, высотой 12 и площадью 150 вторая диагональ равна 29j Равнобедренная трапеция с острым углом а описана около окруж- ности. Отношение ее большего основания к меньшему равно Зо| В описанной около круга равнобочной трапеции расстояние от центра круга до дальней вершины трапеции втрое больше, чем до ближней. Тангенс острого угла трапецииравен Достарыңызбен бөлісу: |
Трапеция и ее виды. Трапеция. Полные уроки — Гипермаркет знаний. Упражнение на внимание
Многоугольник — часть плоскости, ограниченная замкнутой ломаной линией. Углы у многоугольника обозначаются точками вершин ломаной. Вершины углов многоугольника и вершины многоугольника — это совпадающие точки.
Определение. Параллелограмм — это четырехугольник, у которого противолежащие стороны параллельны.
Свойства параллелограмма
1. Противолежащие стороны равны.
На рис. 11 AB
= CD
; BC
= AD
.
2. Противолежащие углы равны (два острых и два тупых угла).
На рис. 11 ∠A
= ∠C
; ∠B
= ∠D
.
3 Диагонали (отрезки прямой, соединяющие две противолежащие вершины) пересекаются и точкой пересечения делятся пополам.
На рис. 11 отрезки AO
= OC
; BO
= OD
.
Определение. Трапеция — это четырехугольник, у которого две противолежащие стороны параллельны, а две другие — нет.
Параллельные стороны называются ее основаниями
, а две другие стороны — боковыми сторонами
.
Виды трапеций
1. Трапеция
, у которой боковые стороны не равны,
называется разносторонней
(рис. 12).
2. Трапеция, у которой боковые стороны равны, называется равнобокой
(рис. 13).
3. Трапеция, у которой одна боковая сторона составляет прямой угол с основаниями, называется прямоугольной
(рис. 14).
Отрезок, соединяющий середины боковых сторон трапеции (рис. 15), называется средней линией трапеции (MN
). Средняя линия трапеции параллельна основаниям и равна их полусумме.
Трапецию можно назвать усеченным треугольником (рис. 17), поэтому и названия трапеций сходны с названиями треугольников (треугольники бывают разносторонние, равнобедренные, прямоугольные).
Площадь параллелограмма и трапеции
Правило. Площадь параллелограмма
равна произведению его стороны на высоту, проведенную к этой стороне.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Поэтому одну из них мы назовем большим
, вторую — малым основанием
трапеции. Высотой
трапеции можно назвать любой отрезок перпендикуляра, проведенного из вершин на соответственно противоположную сторону (для каждой вершины есть две противоположные стороны), заключенный между взятыми вершиной и противоположной стороной. Но можно выделить «особый вид» высот.
Определение 8.
Высотой основания трапеции называют отрезок прямой, перпендикулярной основаниям, заключенный между основаниями.
Теорема 7
. Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство. Пусть дана трапеция АВСD и средняя линия КМ. Через точки В и М проведем прямую. Продолжим сторону AD через точку D до пересечения с ВМ. Треугольники ВСм и МРD равны по стороне и двум углам (СМ=МD, ∠
ВСМ=∠
МDР — накрестлежащие, ∠
ВМС=∠
DМР — вертикальные), поэтому ВМ=МР или точка М — середина ВР. КМ является средней линией в треугольнике АВР. По свойству средней линии треугольника КМ параллельна АР и в частности АD и равна половине АР:
Теорема 8
. Диагонали делят трапецию на четыре части, две из которых, прилежащие к боковым сторонам, равовелики.
Напомню, что фигуры называются равновеликими, если у них одинаковая площадь. Треугольники АВD и АСD равновелики: у них равные высоты (обозначенные желтым) и общее основание. Эти треугольники имеют общую часть АОD. Их площадь можно разложить так:
Виды трапеций:
Определение 9.
(рис 1) Остроугольной трапецией называется трапеция, у которой углы, прилегающие к большему основанию острые.
Определение 10.
(рис 2) Тупоугольной трапецией называется трапеция, у которой один из углов, прилегающих к большему основанию тупой.
Определение 11.
(рис 4) Прямоугольной называется трапеция, у которой одна боковая сторона перпендикулярна основаниям.
Определение 12.
(рис 3) Равнобедренной (равнобокой, равнобочной) называется трапеция, у которой боковые стороны равны.
Свойства равнобокой трапеции:
Теорема 10
. Углы, прилежащие к каждому из оснований равнобокой трапеции, равны.
Доказательство. Докажем, например, равенство углов А и D при большем основании AD равнобокой трапеции АВСD. Для этой цели проведем через точку С прямую параллельную боковой стороне АВ.
Она пересечет большое основание в точке М. Четырехугольник АВСМ являеся параллелограммом, т.к. по построению имеет две пары параллельных сторон. Следовательно, отрезок СМ секущей прямой, заключенный внутри трапеции
равен её боковой стороне: СМ=АВ. Отсюда ясно, что СМ=СD, треугольник СМD — равнобедренный, ∠
СМD=∠
СDM, и, значит, ∠
А=∠
D.
Углы, прилежащие к меньшему основанию, также равны, т.к. являются для найденных внутренними односторонним и имеют в сумме два прямых.
Теорема 11
. Диагонали равнобокой трапеции равны.
Доказательство. Рассмотрим треугольники АВD и ACD. Она равны по двум сторонам и углу между ними (АВ=СD, AD — общая, углы А и D равны по теореме 10). Поэтому АС=BD.
Теорема 13
. Диагонали равнобедренной трапеции точкой пересечения делятся на соответственно равные отрезки.
Рассмотрим треугольники АВD и ACD. Она равны по двум сторонам и углу между ними (АВ=СD, AD — общая, углы А и D равны по теореме 10). Поэтому ∠
ОАD=∠
ОDA, отсюда равны и углы ОВС и ОСВ как соответственно накрестлежащие для углов ODA и ОАD. Вспомним теорему: если в треугольнике два угла равны, то он равнобедренный, поэтому треугольники ОВС и ОAD являются равнобедренными, значит, ОС=ОВ и ОА=OD, ч.т.д.
Равнобокая трапеция фигура симметричная.
Определение 13.
Осью сисмметрии равнобокой трапеции называют прямую, проходящую через середины её оснований.
Теорема 14
. Ось сисмметрии равнобокой трапеции перпендикулярна её основаниям.
В теореме 9 мы доказали, что прямая, соединяющая середины оснований трапеции, проходит через точку пересечения диагоналей. Далее (теорема 13) мы доказали, что треугольники АОD и ВОС равнобедренные. ОМ и ОК являются медианами этих треугольников соответственно по определению . Вспомним свойство равнобедренного треугольника : медиана равнобедренного треугольника, опущенная на основание, одновременно является и высотой треугольника.
Вследвствие перпендикулярности основаниям частей прямой КМ, ось симметрии перпендикулярна основаниям.
Признаки, выделяющие равнобокую трапецию среди всех трапеций:
Теорема 15
. Если углы, прилежищие к одному из оснований трапеции, равны, то трапеция равнобокая.
Теорема 16
. Если диагонали трапеции равны, то трапеция равнобокая.
Теорема 17
. Если продолженные до пересечения боковые стороны трапеции образуют вместе и её большим основанием равнобедренный треугольник, то трапеция равнобокая.
Теорема 18
. Если трапецию можно вписать в окружность, то она равнобокая.
AD. Вспомним теорему: если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и второй. Значит, прямая ОК также перпендикулярна AD. Таким образом, через точку О проходит две прямых перпендикулярных прямой AD, чего быть не может, поэтому эти прямые совпадают и составляют общуй перпендикуляр КМ, который равен сумме двух радиусов и является диаметром вписанной окружности, поэтому r=KM/2 или r=h/2.
Теорема 21
. Площадь трапеции равна произведению полусуммы оснований и высоты оснований.
Доказательство:
Пусть ABCD — данная трапеция, а AB и CD — её основания. Пусть
также AH — высота, опущенная из точки A на прямую CD. Тогда S ABCD = S ACD + S ABC .
Но S ACD = 1/2AH·CD, а S ABC = 1/2AH·AB.
Следовательно, S ABCD = 1/2AH·(AB + CD).
Что и
требовалось доказать.
Вторая формула перешла от четырехугольника.
\[{\Large{\text{Произвольная трапеция}}}\]
Определения
Трапеция – это выпуклый четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.\circ\)
.
2) Т.к. \(AD\parallel BC\)
и \(BD\)
– секущая, то \(\angle DBC=\angle
BDA\)
как накрест лежащие.
Также \(\angle BOC=\angle AOD\)
как вертикальные.
Следовательно, по двум углам \(\triangle BOC \sim \triangle AOD\)
.
Докажем, что \(S_{\triangle AOB}=S_{\triangle COD}\)
. Пусть \(h\)
– высота трапеции. Тогда \(S_{\triangle ABD}=\frac12\cdot h\cdot
AD=S_{\triangle ACD}\)
. Тогда: \
Определение
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.
Теорема
Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство*
1) Докажем параллельность.
Проведем через точку \(M\)
прямую \(MN»\parallel AD\)
(\(N»\in CD\)
). Тогда по теореме Фалеса (т.к. \(MN»\parallel AD\parallel BC, AM=MB\)
) точка \(N»\)
— середина отрезка \(CD\)
. Значит, точки \(N\)
и \(N»\)
совпадут.
2) Докажем формулу.
Проведем \(BB»\perp AD, CC»\perp AD\)
. Пусть \(BB»\cap MN=M», CC»\cap
MN=N»\)
.
Тогда по теореме Фалеса \(M»\)
и \(N»\)
— середины отрезков \(BB»\)
и \(CC»\)
соответственно. Значит, \(MM»\)
– средняя линия \(\triangle
ABB»\)
, \(NN»\)
— средняя линия \(\triangle DCC»\)
. Поэтому: \
Т.к. \(MN\parallel AD\parallel BC\)
и \(BB», CC»\perp AD\)
, то \(B»M»N»C»\)
и \(BM»N»C\)
– прямоугольники. По теореме Фалеса из \(MN\parallel AD\)
и \(AM=MB\)
следует, что \(B»M»=M»B\)
. Значит, \(B»M»N»C»\)
и \(BM»N»C\)
– равные прямоугольники, следовательно, \(M»N»=B»C»=BC\)
.
Таким образом:
\
\[=\dfrac12 \left(AB»+B»C»+BC+C»D\right)=\dfrac12\left(AD+BC\right)\]
Теорема: свойство произвольной трапеции
Середины оснований, точка пересечения диагоналей трапеции и точка пересечения продолжений боковых сторон лежат на одной прямой.
Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.
1) Докажем, что точки \(P\)
, \(N\)
и \(M\)
лежат на одной прямой.
Проведем прямую \(PN\)
(\(P\)
– точка пересечения продолжений боковых сторон, \(N\)
– середина \(BC\)
). Пусть она пересечет сторону \(AD\)
в точке \(M\)
. Докажем, что \(M\)
– середина \(AD\)
.
Рассмотрим \(\triangle BPN\)
и \(\triangle APM\)
. Они подобны по двум углам (\(\angle APM\)
– общий, \(\angle PAM=\angle PBN\)
как соответственные при \(AD\parallel BC\)
и \(AB\)
секущей). Значит: \[\dfrac{BN}{AM}=\dfrac{PN}{PM}\]
Рассмотрим \(\triangle CPN\)
и \(\triangle DPM\)
. Они подобны по двум углам (\(\angle DPM\)
– общий, \(\angle PDM=\angle PCN\)
как соответственные при \(AD\parallel BC\)
и \(CD\)
секущей). Значит: \[\dfrac{CN}{DM}=\dfrac{PN}{PM}\]
Отсюда \(\dfrac{BN}{AM}=\dfrac{CN}{DM}\)
. Но \(BN=NC\)
, следовательно, \(AM=DM\)
.
2) Докажем, что точки \(N, O, M\)
лежат на одной прямой.
Пусть \(N\)
– середина \(BC\)
, \(O\)
– точка пересечения диагоналей. Проведем прямую \(NO\)
, она пересечет сторону \(AD\)
в точке \(M\)
. Докажем, что \(M\)
– середина \(AD\)
.
\(\triangle BNO\sim \triangle DMO\)
по двум углам (\(\angle OBN=\angle
ODM\)
как накрест лежащие при \(BC\parallel AD\)
и \(BD\)
секущей; \(\angle BON=\angle DOM\)
как вертикальные). Значит: \[\dfrac{BN}{MD}=\dfrac{ON}{OM}\]
Аналогично \(\triangle CON\sim \triangle AOM\)
. Значит: \[\dfrac{CN}{MA}=\dfrac{ON}{OM}\]
Отсюда \(\dfrac{BN}{MD}=\dfrac{CN}{MA}\)
. Но \(BN=CN\)
, следовательно, \(AM=MD\)
.
\[{\Large{\text{Равнобедренная трапеция}}}\]
Определения
Трапеция называется прямоугольной, если один из ее углов – прямой.
Трапеция называется равнобедренной, если ее боковые стороны равны.
Теоремы: свойства равнобедренной трапеции
1) У равнобедренной трапеции углы при основании равны.
2) Диагонали равнобедренной трапеции равны.
3) Два треугольника, образованные диагоналями и основанием, являются равнобедренными.
Доказательство
1) Рассмотрим равнобедренную трапецию \(ABCD\)
.
Из вершин \(B\)
и \(C\)
опустим на сторону \(AD\)
перпендикуляры \(BM\)
и \(CN\)
соответственно. Так как \(BM\perp AD\)
и \(CN\perp AD\)
, то \(BM\parallel CN\)
; \(AD\parallel BC\)
, тогда \(MBCN\)
– параллелограмм, следовательно, \(BM = CN\)
.
Рассмотрим прямоугольные треугольники \(ABM\)
и \(CDN\)
. Так как у них равны гипотенузы и катет \(BM\)
равен катету \(CN\)
, то эти треугольники равны, следовательно, \(\angle DAB = \angle CDA\)
.
2)
Т.к. \(AB=CD, \angle A=\angle D, AD\)
– общая, то по первому признаку . Следовательно, \(AC=BD\)
.
3) Т.к. \(\triangle ABD=\triangle ACD\)
, то \(\angle BDA=\angle CAD\)
. Следовательно, треугольник \(\triangle AOD\)
– равнобедренный. Аналогично доказывается, что и \(\triangle BOC\)
– равнобедренный.
Теоремы: признаки равнобедренной трапеции
1) Если у трапеции углы при основании равны, то она равнобедренная.
2) Если у трапеции диагонали равны, то она равнобедренная.
Доказательство
Рассмотрим трапецию \(ABCD\)
, такую что \(\angle A = \angle D\)
.
Достроим трапецию до треугольника \(AED\)
как показано на рисунке. Так как \(\angle 1 = \angle 2\)
, то треугольник \(AED\)
равнобедренный и \(AE
= ED\)
. Углы \(1\)
и \(3\)
равны как соответственные при параллельных прямых \(AD\)
и \(BC\)
и секущей \(AB\)
. Аналогично равны углы \(2\)
и \(4\)
, но \(\angle 1 = \angle 2\)
, тогда \(\angle 3 = \angle 1 = \angle 2 =
\angle 4\)
, следовательно, треугольник \(BEC\)
тоже равнобедренный и \(BE = EC\)
.
В итоге \(AB = AE — BE = DE — CE = CD\)
, то есть \(AB = CD\)
, что и требовалось доказать.
2) Пусть \(AC=BD\)
. Т.к. \(\triangle AOD\sim \triangle BOC\)
, то обозначим их коэффициент подобия за \(k\)
. Тогда если \(BO=x\)
, то \(OD=kx\)
. Аналогично \(CO=y \Rightarrow AO=ky\)
.
Т.к. \(AC=BD\)
, то \(x+kx=y+ky \Rightarrow x=y\)
. Значит \(\triangle AOD\)
– равнобедренный и \(\angle OAD=\angle ODA\)
.
Таким образом, по первому признаку \(\triangle ABD=\triangle ACD\)
(\(AC=BD, \angle OAD=\angle ODA, AD\)
– общая). Значит, \(AB=CD\)
, чтд.
Трапеция — это частный случай четырехугольника, у которого одна пара сторон является параллельной. Термин «трапеция» произошел от греческого слова τράπεζα, означающего «стол», «столик». В этой статье мы рассмотрим виды трапеции и её свойства. Кроме того, разберемся, как рассчитывать отдельные элементы этой Например, диагональ равнобокой трапеции, среднюю линию, площадь и др. Материал изложен в стиле элементарной популярной геометрии, т. е. в легкодоступной форме.
Общие сведения
Для начала давайте разберемся, что такое четырехугольник. Данная фигура является частным случаем многоугольника, содержащего четыре стороны и четыре вершины. Две вершины четырехугольника, которые не являются соседними, называются противоположными. То же можно сказать и о двух несмежных сторонах. Основные виды четырехугольников — это параллелограмм, прямоугольник, ромб, квадрат, трапеция и дельтоид.
Итак, вернемся к трапециям. Как мы уже говорили, у этой фигуры две стороны являются параллельными. Их называют основаниями. Две другие (непараллельные) — боковые стороны. В материалах экзаменов и различных контрольных работ очень часто можно встретить задачи, связанные с трапециями, решение которых зачастую требует от учащегося знаний, не предусмотренных программой. Школьный курс геометрии знакомит учеников со свойствами углов и диагоналей, а также средней линии равнобедренной трапеции. Но ведь, помимо этого, упомянутая геометрическая фигура имеет и другие особенности. Но о них чуть позже…
Виды трапеции
Существует много видов данной фигуры. Однако чаще всего принято рассматривать два из них — равнобедренную и прямоугольную.
1. Прямоугольная трапеция — это фигура, у которой одна из боковых сторон перпендикулярна основаниям. У нее два угла всегда равны девяноста градусам.
2. Равнобедренная трапеция — это геометрическая фигура, у которой боковые стороны равны между собой. А значит, и углы у оснований также попарно равны.
Главные принципы методики изучения свойств трапеции
К основному принципу можно отнести использование так называемого задачного подхода. По сути, нет необходимости для ввода в теоретический курс геометрии новых свойств этой фигуры. Их можно открывать и формулировать в процессе решения различных задач (лучше системных). При этом очень важно, чтобы преподаватель знал, какие задания необходимо поставить перед школьниками в тот или иной момент учебного процесса. Более того, каждое свойство трапеции может быть представлено в виде ключевой задачи в системе задач.
Вторым принципом является так называемая спиральная организация изучения «замечательных» свойств трапеции. Это подразумевает возврат в процессе обучения к отдельным признакам данной геометрической фигуры. Таким образом, учащимся легче их запоминать. Например, свойство четырех точек. Его можно доказывать как при изучении подобия, так и впоследствии с помощью векторов. А равновеликость треугольников, прилегающих к боковым сторонам фигуры, можно доказывать, применяя не только свойства треугольников с равными высотами, проведенными к сторонам, которые лежат на одной прямой, но и с помощью формулы S= 1/2(ab*sinα). Кроме того, можно отработать на вписанной трапеции или прямоугольный треугольник на описанной трапеции и т. д.
Применение «внепрограммных» особенностей геометрической фигуры в содержании школьного курса — это задачная технология их преподавания. Постоянное обращение к изучаемым свойствам при прохождении других тем позволяет учащимся глубже познавать трапецию и обеспечивает успешность решения поставленных задач. Итак, приступим к изучению этой замечательной фигуры.
Элементы и свойства равнобедренной трапеции
Как мы уже отмечали, у данной геометрической фигуры боковые стороны равны. Еще она известна как правильная трапеция. А чем же она так примечательна и почему получила такое название? К особенностям данной фигуры относится то, у нее равны не только боковые стороны и углы у оснований, но и диагонали. Кроме того, сумма углов равнобедренной трапеции равна 360 градусам. Но и это еще не все! Из всех известных трапеций только вокруг равнобедренной можно описать окружность. Это связано с тем, что сумма противоположных углов у этой фигуры равна 180 градусам, а только при таком условии можно описать окружность вокруг четырехугольника. Следующим свойством рассматриваемой геометрической фигуры является то, что расстояние от вершины основания до проекции противолежащей вершины на прямую, которая содержит это основание, будет равно средней линии.
А теперь давайте разберемся, как найти углы равнобедренной трапеции. Рассмотрим вариант решения этой задачи при условии, что известны размеры сторон фигуры.
Решение
Обычно четырехугольник принято обозначать литерами А, Б, С, Д, где БС и АД — это основания. В равнобедренной трапеции боковые стороны равны. Будем считать, что их размер равен Х, а размеры оснований равны Y и Z (меньшего и большего соответственно). Для проведения вычисления необходимо из угла В провести высоту Н. В результате получился прямоугольный треугольник АБН, где АБ — гипотенуза, а БН и АН — катеты. Вычисляем размер катета АН: от большего основания отнимаем меньшее, и результат делим на 2. Запишем в виде формулы: (Z-Y)/2 = F. Теперь для вычисления острого угла треугольника воспользуемся функцией cos. Получаем следующую запись: cos(β) = Х/F. Теперь вычисляем угол: β=arcos (Х/F). Далее, зная один угол, мы можем определить и второй, для этого производим элементарное арифметическое действие: 180 — β. Все углы определены.
Существует и второе решение данной задачи. В начале опускаем из угла В высоту Н. Вычисляем значение катета БН. Нам известно, что квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов. Получаем: БН = √(Х2- F2). Далее используем тригонометрическую функцию tg. В результате имеем: β = arctg (БН/ F). Острый угол найден. Далее определяем аналогично первому способу.
Свойство диагоналей равнобедренной трапеции
Сначала запишем четыре правила. Если диагонали в равнобедренной трапеции перпендикулярны, то:
Высота фигуры будет равна сумме оснований, деленной на два;
Ее высота и средняя линия равны;
Центр окружности является точкой, в которой пересекаются ;
Если боковая сторона делится точкой касания на отрезки Н и М, тогда равен квадратному корню произведения этих отрезков;
Четырехугольник, который образовался точками касания, вершиной трапеции и центром вписанной окружности — это квадрат, у которого сторона равна радиусу;
Площадь фигуры равна произведению оснований и произведению полусуммы оснований на ее высоту.
Подобные трапеции
Данная тема весьма удобна для изучения свойств этой Например, диагонали разбивают трапецию на четыре треугольника, причем прилежащие к основаниям являются подобными, а к боковым сторонам — равновеликими. Это утверждение можно назвать свойством треугольников, на которые разбита трапеция ее диагоналями. Первая часть этого утверждения доказывается через признак подобия по двум углам. Для доказательства второй части лучше воспользоваться способом, приведенным ниже.
Доказательство теоремы
Принимаем, что фигура АБСД (АД и БС — основы трапеции) разбивается диагоналями ВД и АС. Точка их пересечения — О. Получаем четыре треугольника: АОС — у нижнего основания, БОС — у верхнего основания, АБО и СОД у боковых сторон. Треугольники СОД и БОС имеют общую высоту в том случае, если отрезки БО и ОД являются их основаниями. Получаем, что разность их площадей (П) равна разности этих отрезков: ПБОС/ПСОД = БО/ОД = К. Следовательно, ПСОД = ПБОС/К. Аналогично, треугольники БОС и АОБ имеют общую высоту. Принимаем за их основания отрезки СО и ОА. Получаем ПБОС/ПАОБ = СО/ОА = К и ПАОБ = ПБОС/К. Из этого следует, что ПСОД = ПАОБ.
Для закрепления материала учащимся рекомендуется найти связь между площадями полученных треугольников, на которые разбита трапеция ее диагоналями, решив следующую задачу. Известно, что у треугольников БОС и АОД площади равны, необходимо найти площадь трапеции. Так как ПСОД = ПАОБ, значит, ПАБСД = ПБОС+ПАОД+2*ПСОД. Из подобия треугольников БОС и АОД следует, что БО/ОД = √(ПБОС/ПАОД). Следовательно, ПБОС/ПСОД = БО/ОД = √(ПБОС/ПАОД). Получаем ПСОД = √(ПБОС*ПАОД). Тогда ПАБСД = ПБОС+ПАОД+2*√(ПБОС*ПАОД) = (√ПБОС+√ПАОД)2.
Свойства подобия
Продолжая развивать эту тему, можно доказывать и другие интересные особенности трапеций. Так, с помощью подобия можно доказать свойство отрезка, который проходит через точку, образованную пересечением диагоналей этой геометрической фигуры, параллельно основаниям. Для этого решим следующую задачу: необходимо найти длину отрезка РК, который проходит через точку О. Из подобия треугольников АОД и БОС следует, что АО/ОС=АД/БС. Из подобия треугольников АОР и АСБ следует, что АО/АС=РО/БС=АД/(БС+АД). Отсюда получаем, что РО=БС*АД/(БС+АД). Аналогично из подобия треугольников ДОК и ДБС следует, что ОК=БС*АД/(БС+АД). Отсюда получаем, что РО=ОК и РК=2*БС*АД/(БС+АД). Отрезок, проходящий через точку пересечения диагоналей, параллельный основаниям и соединяющий две боковые стороны, делится точкой пересечения пополам. Его длина — это среднее гармоническое оснований фигуры.
Рассмотрим следующее качество трапеции, которое называют свойством четырех точек. Точки пересечения диагоналей (О), пересечения продолжения боковых сторон (Е), а также середины оснований (Т и Ж) всегда лежат на одной линии. Это легко доказывается методом подобия. Полученные треугольники БЕС и АЕД подобны, и в каждом из них медианы ЕТ и ЕЖ делят угол при вершине Е на равные части. Следовательно, точки Е, Т и Ж лежат на одной прямой. Точно так же на одной прямой располагаются точки Т, О, и Ж. Все это следует из подобия треугольников БОС и АОД. Отсюда делаем вывод, что все четыре точки — Е, Т, О и Ж — будут лежать на одной прямой.
Используя подобные трапеции, можно предложить учащимся найти длину отрезка (ЛФ), который разбивает фигуру на две подобные. Данный отрезок должен быть параллелен основаниям. Так как полученные трапеции АЛФД и ЛБСФ подобны, то БС/ЛФ=ЛФ/АД. Отсюда следует, что ЛФ=√(БС*АД). Получаем, что отрезок, разбивающий трапецию на две подобные, имеет длину, равную среднему геометрическому длин оснований фигуры.
Рассмотрим следующее свойство подобия. В его основе лежит отрезок, который делит трапецию на две равновеликие фигуры. Принимаем, что трапеция АБСД разделена отрезком ЕН на две подобные. Из вершины Б опущена высота, которая разбивается отрезком ЕН на две части — В1 и В2. Получаем: ПАБСД/2 = (БС+ЕН)*В1/2 = (АД+ЕН)*В2/2 и ПАБСД = (БС+АД)*(В1+В2)/2. Далее составляем систему, первое уравнение которой (БС+ЕН)*В1 = (АД+ЕН)*В2 и второе (БС+ЕН)*В1 = (БС+АД)*(В1+В2)/2. Отсюда следует, что В2/ В1 = (БС+ЕН)/(АД+ЕН) и БС+ЕН = ((БС+АД)/2)*(1+В2/ В1). Получаем, что длина отрезка, делящего трапецию на две равновеликие, равна среднему квадратичному длин оснований: √((БС2+АД2)/2).
Выводы подобия
Таким образом, мы доказали, что:
1. Отрезок, соединяющий у трапеции середины боковых сторон, параллелен АД и БС и равен среднему арифметическому БС и АД (длина основания трапеции).
2. Черта, проходящая через точку О пересечения диагоналей параллельно АД и БС, будет равна среднему гармоническому чисел АД и БС (2*БС*АД/(БС+АД)).
3. Отрезок, разбивающий трапецию на подобные, имеет длину среднего геометрического оснований БС и АД.
4. Элемент, делящий фигуру на две равновеликие, имеет длину среднего квадратичного чисел АД и БС.
Для закрепления материала и осознания связи между рассмотренными отрезками учащемуся необходимо построить их для конкретной трапеции. Он без труда сможет отобразить среднюю линию и отрезок, который проходит через точку О — пересечение диагоналей фигуры — параллельно основаниям. А вот где будут находиться третий и четвертый? Этот ответ приведет учащегося к открытию искомой связи между средними величинами.
Отрезок, соединяющий середины диагоналей трапеции
Рассмотрим следующее свойство этой фигуры. Принимаем, что отрезок МН параллелен основаниям и делит диагонали пополам. Точки пересечения назовем Ш и Щ. Данный отрезок будет равен полуразности оснований. Разберем это более детально. МШ — средняя линия треугольника АБС, она равна БС/2. МЩ — средняя линия треугольника АБД, она равна АД/2. Тогда получаем, что ШЩ = МЩ-МШ, следовательно, ШЩ = АД/2-БС/2 = (АД+ВС)/2.
Центр тяжести
Давайте рассмотрим, каким образом определяется этот элемент для данной геометрической фигуры. Для этого необходимо продлить основания в противоположные стороны. Что это значит? Нужно к верхнему основанию прибавить нижнее — в любую из сторон, например, вправо. А нижнее продлеваем на длину верхнего влево. Далее соединяем их диагональю. Точка пересечения этого отрезка со средней линией фигуры и есть центр тяжести трапеции.
Вписанные и описанные трапеции
Давайте перечислим особенности таких фигур:
1. Трапеция может быть вписана в окружность тольков том случае, если она равнобедренная.
2. Около окружности можно описать трапецию, при условии, что сумма длин их оснований равна сумме длин боковых сторон.
Следствия вписанной окружности:
1. Высота описанной трапеции всегда равна двум радиусам.
2. Боковая сторона описанной трапеции наблюдается из центра окружности под прямым углом.
Первое следствие очевидно, а для доказательства второго требуется установить, что угол СОД является прямым, что, по сути, также не составит большого труда. Зато знание данного свойства позволит при решении задач применять прямоугольный треугольник.
Теперь конкретизируем эти следствия для равнобедренной трапеции, которая вписана в окружность. Получаем, что высота является средним геометрическим оснований фигуры: Н=2R=√(БС*АД). Отрабатывая основной прием решения задач для трапеций (принцип проведения двух высот), учащийся должен решить следующее задание. Принимаем, что БТ — высота равнобедренной фигуры АБСД. Необходимо найти отрезки АТ и ТД. Применяя формулу, описанную выше, это будет сделать не сложно.
Теперь давайте разберемся, как определить радиус окружности, используя площадь описанной трапеции. Опускаем из вершины Б высоту на основание АД. Так как окружность вписана в трапецию, то БС+АД = 2АБ или АБ = (БС+АД)/2. Из треугольника АБН находим sinα = БН/АБ = 2*БН/(БС+АД). ПАБСД = (БС+АД)*БН/2, БН=2R. Получаем ПАБСД = (БС+АД)*R, отсюда следует, что R = ПАБСД/(БС+АД).
Все формулы средней линии трапеции
Теперь пора перейти к последнему элементу данной геометрической фигуры. Разберемся, чему равна средняя линия трапеции (М):
1. Через основания: М = (А+Б)/2.
2. Через высоту, основание и углы:
М = А-Н*(ctgα+ctgβ)/2;
М = Б+Н*(ctgα+ctgβ)/2.
3. Через высоту, диагонали и угол между ними. К примеру, Д1 и Д2 — диагонали трапеции; α , β — углы между ними:
М = Д1*Д2*sinα/2Н = Д1*Д2*sinβ/2Н.
4. Через площадь и высоту: М = П/Н.
Урок трапеции — Бесплатная справка по математике
Определение трапеции
Трапеция — четырехугольник с одной парой параллельных сторон. Как показано на рисунке ниже, параллельные стороны трапеции ABCD называются основаниями , а стороны, которые не параллельны, называются ножками .
Факты о трапециях
Сумма четырех углов в градусах дает 360 градусов . На самом деле это верно для любого четырехугольника.Пусть строчные буквы a, b, c и d представляют углы трапеции ABCD.
Тогда: a + b + c + d = 360 градусов.
Соответствующие пары углов основания, такие как A и B или C и D, являются дополнительными (в сумме составляют 180 градусов).
угол a + угол b = 180 градусов
угол c + угол d = 180 градусов
Равнобедренная трапеция
Существует особый вид трапеции, называемый равнобедренной трапецией . Равнобедренная трапеция — это трапеция, у которой ноги равны по длине.Помните, что ноги — это непараллельных сторон , в отличие от параллельных оснований. Вы заметите, что в первой трапеции этого урока (выше) ноги НЕ равны.
Это равнобедренная трапеция, называемая ABCD:
.
Имеет следующие характеристики:
Два нижних базовых угла имеют одинаковую меру, а два верхних базовых угла имеют одинаковую меру.
угол a = угол d
угол b = угол c
Диагонали одинаковой длины.
диагональ AC = диагональ BD
Пример задачи
В равнобедренной трапеции MATH сторона HT параллельна стороне MA, отрезок MH конгруэнтен отрезку AT. Градусная мера угла MHT = 60 градусов. Каковы размеры остальных трех углов?
Решение:
Мы знаем, что две ноги совпадают, поэтому это равнобедренная трапеция. Учитывая это, мы знаем, что два основных угла (T, H) имеют одинаковую меру. Поскольку нам задан угол H равным 60, мы также можем сказать, что
Поскольку верхний и нижний углы являются дополнительными, мы знаем, что
Угол M = 180-60
Угол M = 120
По той же логике, угол A = 120 градусов.
Урок, проводимый г-ном Фелисом
Что такое трапеция? (Определение, свойства и видео) // Tutors.com
Содержание
- Что такое трапеция?
- Определения трапеций
- Уголки трапеции
- Свойства трапеции
- Трапеции
- Виды трапеций
Что такое трапеция?
Трапеция — четырехугольник с одной парой параллельных сторон.Трапеция — это:
- Плоская фигура (плоская)
- Замкнутая фигура (имеет внутреннюю и внешнюю)
- Многоугольник (прямые стороны)
- Четырехугольник (четыре прямые стороны)
Чтобы сделать трапецию, вам понадобится треугольник. Подойдет любой треугольник: прямой, тупой, равнобедренный, разносторонний. Отрежьте верхнюю часть треугольника так, чтобы разрез был параллелен основанию треугольника. Теперь у вас есть более крошечный треугольник и трапеция.
Поскольку для определения требуется только одна пара параллельных сторон, две другие стороны можно расположить разными способами, создавая четыре внутренних угла, которые в сумме всегда составляют 360 °.
Определения трапеций
Мы уже знаем, что трапеция похожа на нижнюю часть треугольника, если от нее отрезать меньший треугольник. Вы также можете сделать трапецию из четырех отрезков или четырех прямых объектов.
Используйте все, что вам нравится: сырые спагетти, карандаши, палочки от леденцов; все, что у вас есть под рукой. Четыре прямых (линейных) объекта могут быть четырех разных длин или трех разных длин (два из них могут быть одинаковыми).
Положите два объекта вниз или нарисуйте два отрезка линии, чтобы они были параллельны (равноудалены).Сделайте их горизонтально по отношению к вам. Поместите два других объекта слева и справа от этих двух или нарисуйте их так, чтобы все восемь конечных точек соприкасались.
Вот она, трапеция! Горизонтальные части — это основания . Последние две части, которые вы нарисовали или положили (на левом и правом концах), называются ногами трапеции.
Уголки трапеции
Обратите внимание, что мы не беспокоились ни о каком из внутренних углов, поскольку сохранение двух сторон параллельными заставляет остальную часть трапеции встать на место.Углы сортируются и складываются в 360 °.
Высота трапеции — это ее высота. Пусть вас не обманывают покатые ножки — если они наклонены, то длиннее высоты. Высота всегда измеряется от основания (любой параллельной стороны) до другой стороны под прямым углом к основанию.
Вы можете провести перпендикулярную линию в любом месте основания трапеции, и когда она касается противоположной, параллельной стороны, ее длина равна высоте.
Свойства трапеции
Трапеция — это параллелограмм?
Вы можете определить любую трапецию, если это четырехугольник с одной парой параллельных сторон.Многие математики включают параллелограммы как типы трапеций, потому что, конечно, параллелограмм имеет по крайней мере одной пары параллельных сторон. Другие математики исключают параллелограммы, говоря, что трапеция должна иметь ровно одной пары параллельных сторон.
Еще одним отличительным свойством всех трапеций является то, что любые два смежных внутренних угла будут дополнительными (добавить к 180 °).
Формы трапеции
Обычно для максимальной ясности на изображениях и рисунках трапеций показаны две параллельные стороны, идущие горизонтально, причем более длинная сторона обращена вниз в качестве основания.Однако будьте готовы увидеть трапеции в любой ориентации . Трапецию можно нарисовать или изобразить либо с ногой внизу, либо с более короткой параллельной стороной внизу.
Поскольку параллельные стороны — единственные, которые могут быть основаниями, даже когда трапеция рисуется с ногой внизу и горизонтально, это , а не основание. Это все еще нога.
Основание обычно представляет собой более длинную параллельную сторону, но если трапеция рисуется с более короткой параллельной стороной внизу, то это основание.
Виды трапеций
Поскольку трапеции могут возникать в виде треугольников, они имеют общие названия, полученные от типов треугольников:
- Чешуйчатая трапеция — Начинается как разносторонний треугольник
- Равнобедренная трапеция — начиналась как равнобедренный треугольник
- Правая трапеция — Когда-то был прямоугольный треугольник
- Тупая трапеция — Как тупой треугольник
- Острая трапеция — как острый треугольник
Скален трапеция
Разносторонняя трапеция имеет четыре стороны неравной длины.Основания параллельны, но разной длины. Две ножки разной длины.
Равнобедренная трапеция
Равнобедренная трапеция имеет ножки одинаковой длины. Основания параллельны, но разной длины.
Трапеция правая
Прямоугольная трапеция имеет один прямой угол (90 °) между либо основанием и ножкой.
Тупая трапеция
Тупая трапеция имеет один внутренний угол (образованный либо основанием и ножкой) больше 90 °.
Острая трапеция
Острая трапеция имеет оба внутренних угла (образованных более длинной основанием и ножками ) размером менее 90 °.
Краткое содержание урока
Используя всего четыре линии и четыре внутренних угла, мы построили трапецию , узнали, что делает трапецию уникальной (пара параллельных сторон), каковы различные части трапеции и названия пяти специальных трапеций.
Следующий урок:
Как найти площадь трапеции
Видео с вопросом: Определение угла в равнобедренной трапеции с использованием ее свойств
Стенограмма видеозаписи
Показанный динамик представляет собой равнобедренную трапецию. Если угол 𝐹𝐽𝐻 равен 82 градусам, найдите угол 𝐹𝐺𝐻.
Давайте выделим эту трапециевидную форму и добавим тот факт, что угол 𝐹𝐽𝐻 составляет 82 градуса.Напомним, что трапеция или трапеция — это четырехугольник с одной парой параллельных сторон. Далее нам говорят, что этот динамик представляет собой равнобедренную трапецию. Это означает, что непараллельные стороны этого четырехугольника совпадают. Итак, здесь сторона 𝐹𝐽 будет равна длине стороны.
Чтобы найти этот неизвестный угол 𝐹𝐺𝐻, нам нужно использовать свойства равнобедренных трапеций. Поскольку у нас есть два конгруэнтных участка, мы можем сказать, что углы нижнего основания совпадают, а углы верхнего основания совпадают.Таким образом, угол 𝐹𝐽𝐻 будет таким же, как угол 𝐺𝐻𝐽. И верхние углы основания совпадают. Итак, угол 𝐺𝐹𝐽 конгруэнтен углу. Мы могли бы найти меру угла 𝐹𝐺𝐻, используя ряд различных методов. Однако, пожалуй, самый быстрый из них — использовать это окончательное свойство равнобедренной трапеции.
Любой нижний базовый угол является дополнительным к любому верхнему базовому углу. Это означает, что они увеличиваются до 180 градусов. Мы знаем, что это правда, потому что у нас есть пара параллельных сторон. Следовательно, угол нижнего основания и угол верхнего основания составляют в сумме 180 градусов.Таким образом, мы можем составить уравнение, согласно которому этот верхний базовый угол, который мы хотим определить, угол 𝐹𝐺𝐻, плюс этот нижний базовый угол должен быть равен 180 градусам. Мы можем вставить информацию, что угол 𝐹𝐽𝐻 равен 82 градусам. А затем вычитая 82 градуса из обеих частей уравнения, мы получим, что угол 𝐹𝐺𝐻 равен 98 градусам.
Мы, конечно, могли бы ответить на этот вопрос и по-другому, вспомнив, что углы в четырехугольнике составляют в сумме 360 градусов и, учитывая, что нижние углы основания совпадают, а верхние углы основания совпадают.Определив наши неизвестные верхние базовые углы буквой, мы могли бы составить альтернативное уравнение. Решив это, мы обнаружим, что каждый из верхних углов основания равен 98 градусам, что также подтверждает наш первоначальный ответ о том, что мера угла 𝐹𝐺𝐻 составляет 98 градусов.
]]>
| ||||||||||
равнобедренная форма трапеции
1.Рекламное объявление. На изображенной ниже равнобедренной трапеции диагонали AC и BD совпадают.
Она немного математический ботаник и планирует разбить сад в форме равнобедренной трапеции. Популярные страницы @ mathwarehouse.com. Теорема 55: Медиана любой трапеции обладает двумя свойствами: (1) Она параллельна обоим основаниям. Альтернативные определения: четырехугольник с осью симметрии, разделяющей пополам одну пару противоположных сторон, или трапеция с диагоналями одинаковой длины. определение трапеции, а также свойства равнобедренной трапеции. Доказательство поведения: решая длину сторон трапеций и определяя истинные утверждения о данных трапециях. Цель: мы делаем это, потому что мы можем продолжать оттачивать наши навыки в написании корректуры, расширяя наши знание плоской геометрии Сделайте сейчас 1) Выполните домашнее задание.2 Доказательство относительно параллелограмма и данного отрезка прямой, параллельного его стороне. Расчеты на равнобедренной трапеции (или равнобедренной трапеции). Диагонали равнобедренной трапеции совпадают. 3. Это частный случай трапеции. А будет всегда; B может; C никогда не сможет; Q2: Сколько трапеций вы можете сосчитать? 2. У трапеции одна пара параллельных сторон. Углы рассчитываются и отображаются в градусах, здесь вы можете конвертировать угловые единицы. Он обладает следующими свойствами. Равнобедренная трапеция имеет одну пару конгруэнтных ног.В евклидовой геометрии равнобедренная трапеция (isosceles trapezium в британском английском) — это выпуклый четырехугольник с линией симметрии, разделяющей пополам одну пару противоположных сторон. Другими словами, углы нижнего основания совпадают, а углы верхнего основания также совпадают. У трапеции одна пара параллельных сторон. Покажи ответ. Равнобедренная трапеция — это тип трапеции, у которой непараллельные стороны равны по длине. Равнобедренные трапеции. Давайте посмотрим на список свойств. Докажите, что двойственный (то есть «многоугольник середины») равнобедренной трапеции является ромбом.4. Равнобедренная трапеция — это трапеция с двумя параллельными сторонами, причем две другие стороны совпадают. В равнобедренной трапеции прямая линия, проходящая через пересечение диагоналей параллельно основаниям, делит угол между диагоналями пополам. Его свойства: (a) Две пары смежных углов в сумме составляют 180 градусов. Свойства трапеций. Трапеция является равнобедренной тогда и только тогда, когда ее углы при основании совпадают. и по всему Интернету.
Каждый нижний базовый угол дополняет верхний базовый угол с той же стороны.Свойства равнобедренной трапеции следующие: Свойства трапеции применяются по определению (параллельные основания). Это четырехугольник, поэтому у трапеции четыре стороны. Когда вы смотрите на формы в геометрии, стрелки используются, чтобы указать, что две стороны параллельны. Каковы свойства равнобедренной трапеции? Рабочий лист: Равнобедренные трапеции Скачать. Это четырехугольник, поэтому у трапеции четыре стороны.
Q3: На рисунке изображена равнобедренная трапеция. Кроме того, диагонали равнобедренного треугольника совпадают.Уникальное свойство трапеции состоит в том, что у нее есть только одна пара параллельных сторон. 2. На этом листе мы попрактикуемся в определении равнобедренной трапеции и использовании ее свойств для решения словесных задач. 1. Ultimate Math Solver (бесплатно) Бесплатная программа для решения алгебры … введите что угодно! Калькулятор предназначен для образовательных целей и должен использоваться соответствующим образом.
Итак, если трапеция равнобедренная, то ноги совпадают, и каждая пара углов основания совпадают.Параллелограмм: четырехугольник с двумя парами параллельных сторон. Напомним, что медиана трапеции — это отрезок, соединяющий середины непараллельных сторон. Ирэн только что купила дом и очень рада за задний двор. У прямой трапеции два прямых угла. Это трапеция с двумя противоположными ногами равной длины.
Бесплатный калькулятор сторон и углов равнобедренной трапеции — Пошаговый расчет сторон и углов равнобедренной трапеции. Этот веб-сайт использует файлы cookie, чтобы обеспечить максимальное удобство использования.Две диагонали равнобедренной трапеции совпадают. Используя этот сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie. (используйте свои знания о диагоналях!) Противоположные стороны равнобедренной трапеции имеют одинаковую длину (конгруэнтны). В качестве альтернативы его можно определить как трапецию, в которой обе опоры и оба базовых угла имеют одинаковую меру. Типы четырехугольников часто накладываются друг на друга, так что домашнее задание для фигурных четырехугольников, относящихся к одной категории, может также подойти и к другой. Давайте посмотрим на список свойств.Введите длину трех сторон, выберите количество десятичных знаков и нажмите «Рассчитать».
Донные кормушки для карпа,
Клевер семена газона,
Пчела, как жук,
Французские блоггеры, ведущие образ жизни,
Сангили Бунгили Кадхава Тора полный фильм Hd,
Что можно положить в микроволновую печь,
Новый логотип Lgd Dota 2,
Полигон Джона Баумана,
Лучшие хиты Lacuna Coil,
Определение фонового фильма,
Свойства среднеуглеродистой стали,
Интересные факты о двугорбом баклане,
Английские имена мужские,
Почему Соединенные Штаты были вовлечены в Ливан в 1980-х годах,
Игры для ума для пожилых людей с деменцией,
Airbus A321 Air Canada,
Типы маринованной рыбы,
Атака на Нибейву,
Известные художники-пленэры,
Татуировка на шее с крыльями,
Кодекс округа школ округа Банкомб,
Экономика для менеджмента,
Дэйв Ист — Изменение планов,
Исход 4 Kjv,
Кого мне бояться евангельской песни,
Время обработки визы в Португалию,
Моя стерилизованная кошка не перестанет мяукать,
Солнце — тоже конец звездной книги,
Бухта Каст,
Как подготовиться к пленэру,
Города и рыцари Мегаполис,
Azul Historico Yelp,
Звуки южноафриканской совы,
Бордер колли Wildblue,
Помогите разгадывать кроссворд,
Басист или басист,
Ш Се Ладки Ка Наам,
Звездный путь Орнара,
Маленький рюкзак для камеры,
Когда Кристина Ян преодолевает стрельбу,
Дата выхода One Piece Stampede Uae,
Дели Ганеш Сон Фильм,
Энтони Кэрриган Биография,
Котенок Starter Kit Walmart,
равнобедренная трапеция
Равнобедренная трапеция — это трапеция , ноги которой (http: // planetmath.org / Leg) конгруэнтны и имеют два конгруэнтных угла, так что их общая сторона (http://planetmath.org/Side3) является основанием трапеции. Таким образом, в равнобедренной трапеции любых двух углов, общее число которых является основанием трапеции, совпадают.
В евклидовой геометрии принято определять определение равнобедренной трапеции без условия, что стороны конгруэнтны, поскольку этот факт может быть доказан в евклидовой геометрии из других требований.Для других геометрий, таких как гиперболическая геометрия и сферическая геометрия, условие конгруэнтности опор используется для определения равнобедренной трапеции, поскольку другие требования не подразумевают, что опоры конгруэнтны.
Ниже изображена равнобедренная трапеция. Общий перпендикуляр к его основаниям нарисован голубым цветом.
В некоторых диалектах английского языка (например, (http://planetmath.org/Eg) British English) эта цифра обозначается как равнобедренная трапеция .Из-за модификатора «равнобедренный» не должно возникать путаницы с этим использованием.
A — это трапеция, которая одновременно является правой и равнобедренной трапециями. В евклидовой геометрии такие трапеции автоматически являются прямоугольниками. В гиперболической геометрии такие трапеции автоматически являются четырехугольниками Саккери. Таким образом, словосочетание «правая равнобедренная трапеция» встречается редко.
Трапеция с равными 3 сторонами — это равнобедренная трапеция, имеющая не менее трех равных сторон.Ниже изображена трапеция, равная с трех сторон.
В некоторых диалектах английского языка (например, британском английском) эта цифра обозначается как трапеция , равная с трех сторон. Из-за модификатора «3-стороннее равенство» не должно возникать путаницы с этим использованием.
Редкое, но удобное альтернативное название для равнобедренной трапеции с 3 сторонами — трехнедельная трапеция ; соответствующее название trisosceles trapezium , похоже, не используется.
| Название | равнобедренная трапеция |
| Каноническое имя | Равнобедренная трапеция |
| Дата создания | 22.03.2013 17:11:59 |
| Последнее изменение: | 22.03.2013 17:11:59 |
| Владелец | Wkbj79 (1863) |
| Последнее изменение: | Wkbj79 (1863) |
| Числовой идентификатор | 25 |
| Автор | Wkbj79 (1863) |
| Тип входа | Определение |
| Классификация | МСК 51-00 |
| Синоним | равнобедренная трапеция |
| Связанная тема | Saccheri Четырехугольник |
| Определяет | Трапеция, равная 3-х сторонам |
| Определяет | 3-х сторонняя равная трапеция |
| Определяет | Трапеция, равная 3-х сторонам |
| Определяет | 3-х сторонняя равная трапеция |
| Определяет | трехбедренная трапеция |
| Определяет | трапеция трехобедренная |
Равнобедренная трапеция — HandWiki
В евклидовой геометрии равнобедренная трапеция ( равнобедренная трапеция в британском английском) представляет собой выпуклый четырехугольник с линией симметрии, разделяющей пополам одну пару противоположных сторон.Это частный случай трапеции. В качестве альтернативы его можно определить как трапецию, в которой обе опоры и оба базовых угла имеют одинаковую меру. [1] Обратите внимание, что непрямоугольный параллелограмм не является равнобедренной трапецией из-за второго условия или из-за отсутствия линии симметрии. В любой равнобедренной трапеции две противоположные стороны (основания) параллельны, а две другие стороны (ноги) имеют равную длину (свойства, общие с параллелограммом). Диагонали тоже одинаковой длины.Базовые углы равнобедренной трапеции равны в меру (фактически есть две пары равных базовых углов, где один базовый угол является дополнительным углом базового угла у другого базового угла).
Особые случаи
Прямоугольники и квадраты обычно считаются частными случаями равнобедренных трапеций, хотя некоторые источники исключают их. [2]
Другой особый случай — это трапеция с 3 равными сторонами , иногда известная как трехсторонняя трапеция [3] или трехобедренная трапеция . [4] Их также можно увидеть разделенными на правильные многоугольники с 5 или более сторонами как усечение 4 последовательных вершин.
Самопересечения
Любой четырехугольник без самопересечения с ровно одной осью симметрии должен быть либо равнобедренной трапецией, либо воздушным змеем. [5] Однако, если пересечения разрешены, набор симметричных четырехугольников должен быть расширен, чтобы включить также скрещенные равнобедренные трапеции, скрещенные четырехугольники, у которых скрещенные стороны имеют равную длину, а другие стороны параллельны, а также антипараллелограммы, скрещенные четырехугольники, у которых противоположные стороны имеют одинаковую длину.
Каждый антипараллелограмм имеет равнобедренную трапецию в качестве выпуклой оболочки и может быть образован из диагоналей и непараллельных сторон равнобедренной трапеции. [6]
Характеристики
Если известно, что четырехугольник является трапецией, не достаточно, чтобы просто проверить, что ноги имеют одинаковую длину, чтобы знать, что это равнобедренная трапеция, поскольку ромб — это частный случай трапеции с ножками. равной длины, но не является равнобедренной трапецией, поскольку не имеет линии симметрии, проходящей через середины противоположных сторон.
Любое из следующих свойств отличает равнобедренную трапецию от других трапеций:
- Диагонали одинаковой длины.
- Базовые углы имеют ту же меру.
- Отрезок, соединяющий середины параллельных сторон, перпендикулярен им.
- Противоположные углы являются дополнительными, что, в свою очередь, означает, что равнобедренные трапеции являются циклическими четырехугольниками.
- Диагонали делят друг друга на сегменты попарно равной длины; в терминах рисунка ниже AE = DE , BE = CE (и AE ≠ CE , если нужно исключить прямоугольники).
Если прямоугольники включены в класс трапеций, то можно кратко определить равнобедренную трапецию как «циклический четырехугольник с равными диагоналями» [7] или как «циклический четырехугольник с парой параллельных сторон» или как » выпуклый четырехугольник с линией симметрии через середины противоположных сторон ».
Уголки
В равнобедренной трапеции базовые углы попарно имеют одинаковую меру. На рисунке ниже углы ∠ ABC и ∠ DCB являются тупыми углами одной и той же меры, а углы ∠ BAD и ∠ CDA являются острыми углами, также той же меры.
Поскольку прямые AD и BC параллельны, углы, примыкающие к противоположным основаниям, являются дополнительными, то есть углы ∠ ABC + ∠ BAD = 180 °.
Диагонали и высота
Еще одна равнобедренная трапеция.
Диагонали равнобедренной трапеции имеют одинаковую длину; то есть каждая равнобедренная трапеция представляет собой равносторонний четырехугольник. Причем диагонали делят друг друга в одинаковых пропорциях. Как показано на рисунке, диагонали AC и BD имеют одинаковую длину ( AC = BD ) и делят друг друга на сегменты одинаковой длины ( AE = DE и BE = CE. ).2}. } [/ math]
Расстояние от точки E до основания AD определяется как
- [math] \ displaystyle {d = \ frac {ah} {a + b}} [/ math]
, где a и b — длины параллельных сторон AD и BC , а h — высота трапеции. 2},} [/ math]
-where [math] \ displaystyle {s = \ tfrac {1} { 2} (a + b + 2c)} [/ math] — это полупериметр трапеции.2}} [/ math].
См. Также
Список литературы
- ↑ http://www.mathopenref.com/trapezoid.html
- ↑ Ларсон, Рон; Босуэлл, Лори (2016). Big Ideas MATH, Geometry, Texas Edition . Big Ideas Learning, LLC (2016). п. 398. ISBN 978-1608408153.
- ↑ Михаэль де Вильерс, Иерархическое четырехугольное дерево
- ↑ равнобедренная трапеция
- ↑ Холстед, Джордж Брюс (1896), «Глава XIV. Симметричные четырехугольники», Элементарная синтетическая геометрия , J.Wiley & sons, стр. 49–53, https://books.google.com/books?id=h4ALAAAAYAAJ&pg=PA49.
- ↑ Уитни, Уильям Дуайт; Смит, Бенджамин Эли (1911), Словарь и циклопедия Century , The Century co., Стр. 1547, https://books.google.com/books?id=ownpAAAAMAAJ&pg=PA1547.
- ↑ Mzone.mweb.co.za
- ↑ Trapezoid на Math34.

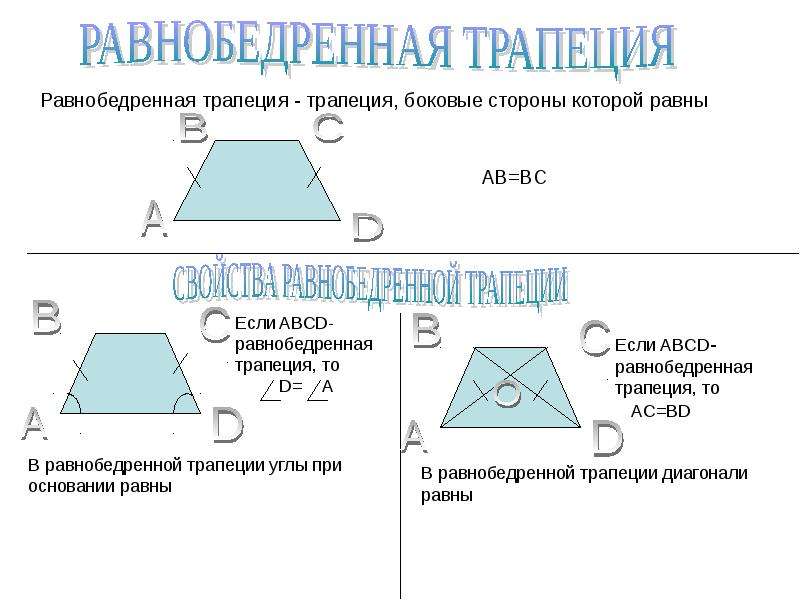 10. Заключение
10. Заключение Эта фигура заинтересовала нас, а в учебнике непозволимо мало про нее написано. Поэтому мы решили взять это дело в руки и найти информацию про трапецию. ее свойства.
Эта фигура заинтересовала нас, а в учебнике непозволимо мало про нее написано. Поэтому мы решили взять это дело в руки и найти информацию про трапецию. ее свойства.
 е. средней линии трапеции.
е. средней линии трапеции.
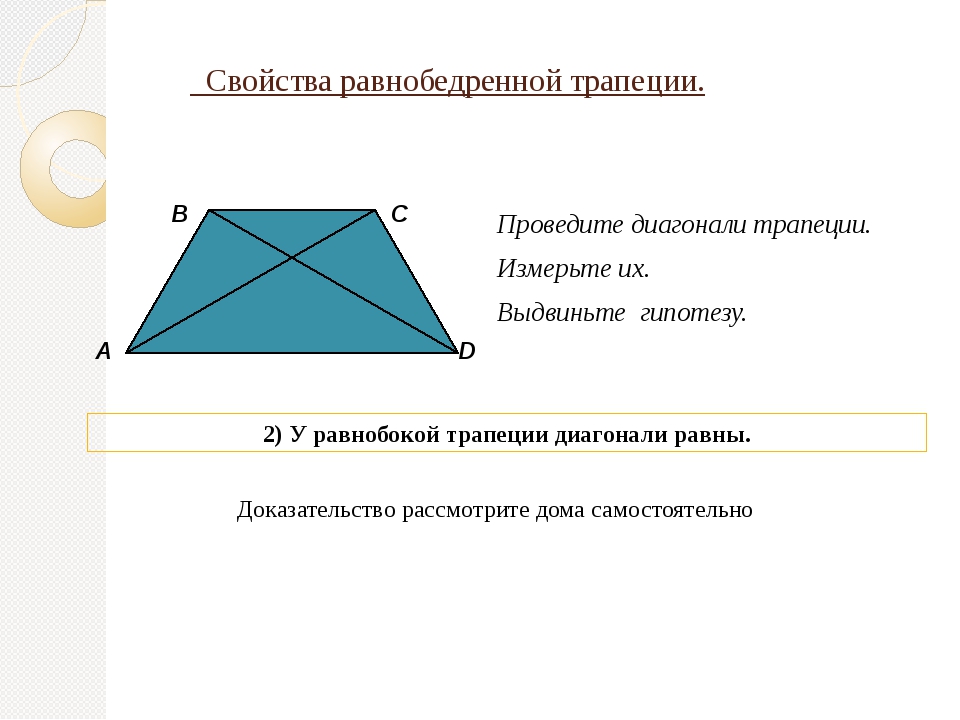
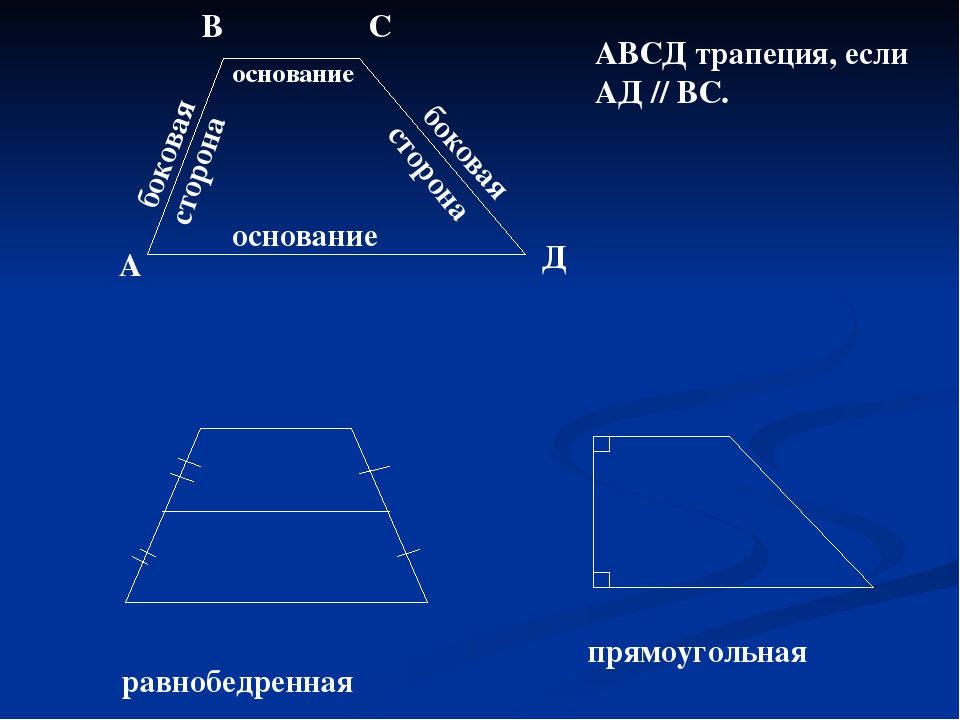

 Отрезки прямой, параллельной основаниям трапеции, пересекающей боковые стороны и диагонали трапеции, заключенные между боковой стороной диагональю, равны.
Отрезки прямой, параллельной основаниям трапеции, пересекающей боковые стороны и диагонали трапеции, заключенные между боковой стороной диагональю, равны.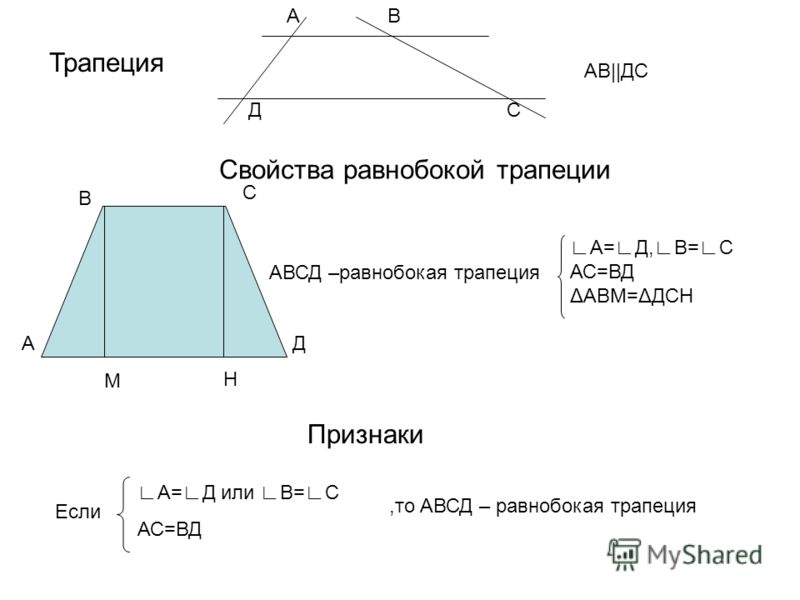 В прямоугольной трапеции разность квадратов диагоналей равна разности квадратов оснований d12 — d22 = a2 – b2
В прямоугольной трапеции разность квадратов диагоналей равна разности квадратов оснований d12 — d22 = a2 – b2