Уравнение с корнем 12: составьте уравнение с корнем -12 — ошкольное образовательное учреждение № 4 «Алёнушка»

Содержание

уравнение с корнем 12

Вы искали уравнение с корнем 12? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и уравнения с корнем 12, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «уравнение с корнем 12».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как уравнение с корнем 12,уравнения с корнем 12. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и уравнение с корнем 12. Просто введите задачу в окошко и нажмите
«решить» здесь (например, уравнение с корнем 12).

Где можно решить любую задачу по математике, а так же уравнение с корнем 12 Онлайн?

Решить задачу уравнение с корнем 12 вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора.

Пример решения иррационального уравнения методом разложения на множители

Решить иррациональное уравнение

Очевидно, уравнение имеет вид f₁(x)*f₂(x)*f₃(x)=0, где f₁(x)=x-2, f₂(x)=x²-x-12, .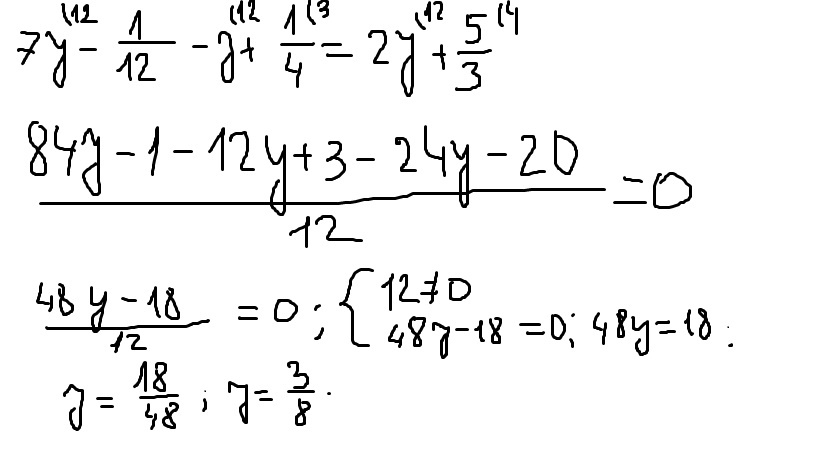 Произведение в левой части уравнения и нуль в правой подсказывают, что следует проводить решение уравнения методом разложения на множители. Согласно выбранному методу решения нам нужно:

Перейти от исходного уравнения f₁(x)*f₂(x)*f₃(x)=0 к совокупности уравнений f₁(x)=0, f₂(x)=0, …, f_n(x)=0,

Решить составленную совокупность,

Если совокупность, решенная на предыдущем шаге, не имеет корней, то сделать вывод об отсутствии корней у исходного уравнения. Если же на предыдущем шаге были найдены корни, то провести отсеивание посторонних корней.

В нашем случае в левой части уравнения три множителя f₁(x)=x-2, f₂(x)=x²-x-12, , поэтому совокупность будет состоять из трех уравнений f₁(x)=0, f₂(x)=0, f₃(x)=0, что в нашем случае есть x-2=0, x²-x-12=0, . То есть, имеем совокупность уравнений следующего вида .

Теперь нам нужно решить совокупность уравнений. Для этого решим отдельно каждое из ее уравнений, и объединим полученные решения. Уравнение x-2=0 – это линейное уравнение. Его корнем является x=2. Уравнение x²-x-12=0 – это квадратное уравнение. Его дискриминант D равен (-1)²-4*1*(-12)=49, он положительный, значит, уравнение имеет два корня. Находим их: и . Последнее уравнение совокупности — это простейшее иррациональное уравнение. Его удобно решать по определению корня: . Таким образом, совокупность имеет четыре корня x₁=2, x₂=-3, x₃=4 и x₄=1.

Остается провести отсеивание посторонних корней. Обычно при решении уравнения методом разложения на множители отсеивание осуществляют либо по ОДЗ, либо по условиям ОДЗ, либо через непосредственную подстановку корней в исходное уравнение. Как правило, выбирают самый удобный и простой способ для данного случая. В нашем случае эти способы примерно равносильны по трудозатратам, поэтому, можно воспользоваться любым из них. Для общего представления мы проведем отсеивание посторонних корней всеми тремя способами.

Отсеивание посторонних корней по ОДЗ

Чтобы отсеять посторонние корни по ОДЗ, нам, естественно, нужно найти ОДЗ переменной x для исходного уравнения . Здесь ОДЗ определяется условием x-1≥0, из которого находим x≥1. Таким образом, ОДЗ есть числовое множество [1, +∞). Теперь смотрим, какие из найденных на предыдущем шаге корней x₁=2, x₂=-3, x₃=4 и x₄=1 принадлежат этому множеству, а какие – нет. Очевидно, x₁=2, x₃=4 и x₄=1 – принадлежат ОДЗ, поэтому, являются корнями исходного иррационального уравнения, а x₂=-3 – не принадлежит ОДЗ, то есть, это посторонний корень.

Понятно, что данный способ удобен тогда, когда довольно просто найти ОДЗ в виде числового множества. Если же нахождение ОДЗ в виде числового множества затруднительно, то целесообразно обратиться к другим способам отсеивания посторонних корней, например, к следующему.

Отсеивание посторонних корней по условиям ОДЗ

При данном способе проверки, в отличие от предыдущего, мы не находим ОДЗ переменной x для исходного уравнения в виде числового множества, а просто записываем условия, определяющие ОДЗ, после чего смотрим, удовлетворяют ли этим условиям найденные на предыдущем шаге корни. Если корень удовлетворяет всем условиям ОДЗ, то он принадлежит ОДЗ и является корнем исходного уравнения. Если же корень не удовлетворяет хотя бы одному из условий ОДЗ, то он не принадлежит ОДЗ, значит, это посторонний корень, и он не является корнем исходного уравнения.

В нашем случае ОДЗ определяется одним условием x-1≥0. Остается по очереди подставить в это условие наши корни x₁=2, x₂=-3, x₃=4 и x₄=1 и посмотреть, какие из них ему удовлетворяют. Сделаем это:

Отсеивание посторонних корней путем подстановки в исходное уравнение

Здесь все просто: по очереди подставляем найденные на предыдущем шаге корни в исходное уравнение. Те значения, которые обращают исходное уравнение в верное равенство являются корнями, а те, которые обращают исходное уравнение в выражение, не имеющее смысла, являются посторонними корнями для исходного уравнения.

Осуществим подстановку найденных корней x₁=2, x₂=-3, x₃=4 и x₄=1 в исходное уравнение :

Заметим, что этот способ отсеивания посторонних корней по сути очень схож с предыдущим. Действительно, при подстановке корней в исходное уравнение лишить смысла получаемое при этом выражение могут лишь фрагменты исходного уравнения, по которым записываются условия, определяющие ОДЗ. В нашем случае определяющее ОДЗ условие x-1≥0 нам диктует корень . При подстановке в исходное уравнение x₂=-3 именно этот корень и лишает смысла все выражение .

Плюс этого способа в том, что при нем осуществляется и проверка найденных корней, что позволяет убедиться, что мы не сделали вычислительных ошибок в процессе решения.

Как видите, все три способа привели нас к такому результату: уравнение имеет три корня x₁=2, x₃=4, x₄=1, а x₂=-3 — посторонний корень для исходного иррационального уравнения.

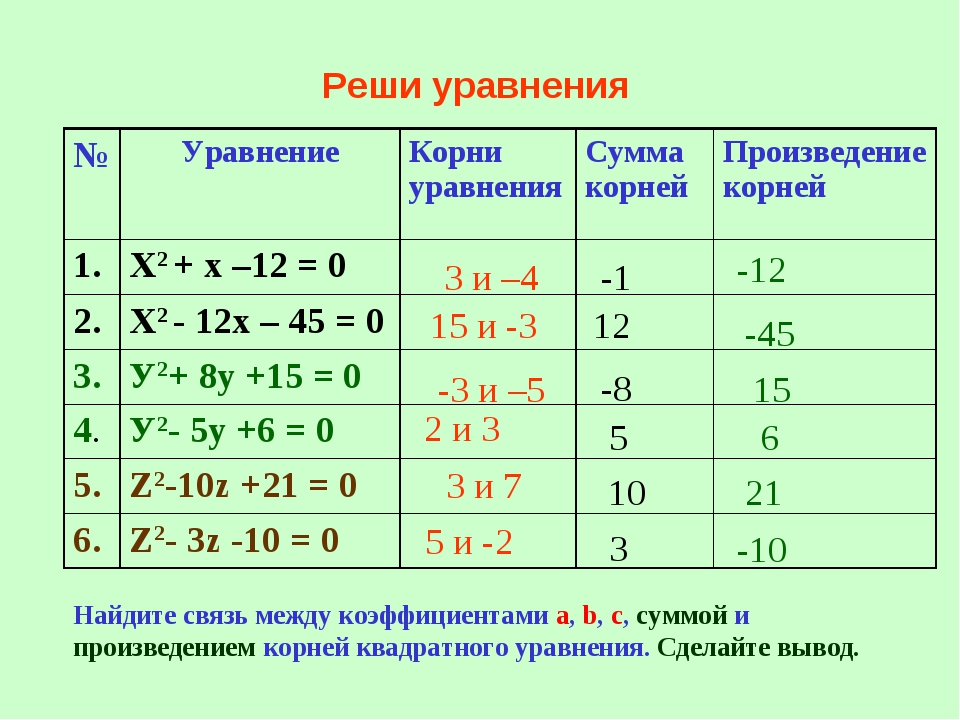
Уравнение и его корни с примерами

п.1. Определение уравнения и его корня

Уравнением с одной переменной x называют равенство f(x)=g(x), для которого поставлена задача найти все значения переменной x, которые обращают это равенство в истинное числовое равенство.

Значение переменной, при котором выражения f(x) и g(x) принимают равные числовые значения, называют корнем уравнения f(x)=g(x).

Например, для уравнения 15x+8=23 корнем является значение x=1.

В уравнении x(x + 5)(x — 3) = 0 три корня, $x_1 = 0,x_2 = -5,x_3 = 3$. 2 = -1$ действительных корней не имеет.

В уравнении 5(x + 3)=5x + 15 бесконечное количество корней, т.к. оно превращается в истинное равенство при любом $x \in \Bbb R$, т.е. является тождеством.

Решить уравнение означает найти все его корни или доказать, что их нет.

п.2. Примеры

Пример 1. Решите уравнение и выполните проверку x — (3 — 2x) = 9

Решение:

x-(3-2x)=9 $\iff$ x-3+2x=9 $\iff$ x+2x=9+3 $\iff$ 3x=12 $\iff$ x=4

Проверка:

$4 -(3 — 2 \cdot 4)=9 \implies 4 — 3 + 8 = 9 \implies 9 \equiv 9$

Ответ: x = 4

Пример 2. Решите уравнение и выполните проверку 7(x + 3) = 56

Решение:

7(x + 3)=56 |:7 $\iff$ x + 3 = 8 $\iff$ x = 8 — 3 $\iff$ x=5

Проверка:

$7(5 + 3) = 56 \implies 7 \cdot 8 = 56 \implies 56 \equiv 56$

Ответ: x = 5

Пример 3. Решите уравнение и выполните проверку (3x + 4) : 2 = 14

Решение:

(3x + 4) : 2=14 |$\times$2 $\iff$ 3x + 4 = 28 $\iff$ 3x = 28 — 4 $\iff$ 3x = 24 $\iff$ x=8

Проверка:

$(3 \cdot 8 + 4) : 2 = 14 \implies (24 + 4) : 2 = 14 \implies 28 : 2 = 14 \implies 14 \equiv 14$

Ответ: x = 8

Пример 4. Решите уравнение $ \frac{3x-7}{3} — \frac {5x-11}{5} = 0$

Решение:

$\frac {3x-7}{3} — \frac {5x-11}{5} = 0 | \times 15 \iff5(3x-7)-3(5x-11)=0 \iff$

$ \iff 15x-35-15x+33=0 \iff 0x=2 \iff x \in \varnothing $

Решений нет.

Ответ: $x \in \varnothing $

Пример 5. Решите уравнение $\frac {2x — 7}{2} = \frac {3x+6}{3}$

Решение:

$\frac {2x-7}{2}=\frac {x+6}{3} | \times 6 \iff 3(2x-7)=2(x+6) \iff 6x-21=2x+12 \iff $

$\iff 6x-2x=12+21 \iff 4x=33 \iff x= \frac {33}{4} =8 \frac 14$

Ответ: $8 \frac 14$

Пример 6. Решите уравнение |x+1|=5

Решение:

$$|x+1|=5 \iff \left[ \begin{array}{cc} {x+1=-5}\\ {x+1=5} \end{array} \right. \iff \left[ \begin{array}{cc} {x=-5-1}\\ {x=5-1} \end{array} \right. \iff \left[ \begin{array}{cc} {x_1=-6}\\ {x_2=4} \end{array} \right. $$

Ответ: $ x_1=-6, x_2=4$

Пример 7*. Решите уравнение и выполните проверку |x + 1| = x + 3

Решение:

$$ |x + 1| = x + 3 \iff \left[ \begin{array}{cc} {\left\{ \begin{array}{c} x+1 \ge 0 \\ x+1=x+3 \end{array} \right. }\\ {\left\{ \begin{array}{c} x+1<0 \\ -(x+1)=x+3 \end{array} \right.} \end{array} \right. \iff \left[ \begin{array}{cc} {\left\{ \begin{array}{c} x \ge -1 \\ 1=3 \end{array} \right.}\\ {\left\{ \begin{array}{c} x<-1 \\ -x-1=x+3 \end{array} \right.} \end{array} \right. \iff $$

$$ \iff \left[ \begin{array}{cc} {\emptyset}\\ {\left\{ \begin{array}{c} x<-1 \\ -x-x=3+1 \end{array} \right.} \end{array} \right. \iff \left[ \begin{array}{cc} {x<-1}\\ {-2x=4} \end{array} \right. \iff \left[ \begin{array}{cc} {x<-1}\\ {x=-2} \end{array} \right. \iff x=-2 $$

Проверка:

$$|-2+1|=-2+3 \implies |-1|=1\implies 1 \equiv 1$$

Ответ: x = -2

Пример 8. При каком значении a уравнение 5ax + 18 = 3 будет иметь корень x = -3?

Решение:

Подставляем x=-3 в уравнение и решаем его относительно параметра a:

5a $\cdot$ (-3) + 18 = 3 $\iff$ -15a = 3 — 18 $\iff$ -15a = -15 $\iff$ a = -15:(-15)=1

a=1

Ответ: a = 1

Уравнение и его корни — САМОСТОЯТЕЛЬНЫЕ РАБОТЫ

Вариант 1

А1. Какое из чисел является корнем уравнения 3x² = 5x + 12?

1) 1

2) 2

3) 3

4) 4

А2. Корнем какого уравнения является число -1?

1) x(x + 5)(x — 2) = 0

2) x(x + 5)(x — 2) = 12

3) х — 1 = 0

4) |x| = -1

А3. Выясните, какие из следующих уравнений равносильны:

A. х² =25,

B. x — 5 = 0,

C. (x — 5)(x + 5) = 0.

1) В и С

2) А и В

3) А, В и С

4) А и С

В1. Сколько корней имеет уравнение |x| = 4?

С1. Составьте уравнение, корнем которого является число -7.

Вариант 2

А1. Какое из чисел является корнем уравнения 4х² = 6x + 4?

1) 1

2) 2

3) 3

4) 4

А2. Корнем какого уравнения является число -3?

1) x(x + 5)(x — 2) = 0

2) x — 3 = 0

3) x(x + 5)(x — 2) = 30

4) |x| = -3

А3. Выясните, какие из следующих уравнений равносильны:

A. x = 6,

B. x² = 36,

С. (x — 6)(x + 6) = 0.

1) В и С

2) А и В

3) А, В и С

4) А и С

В1. Сколько корней имеет уравнение |x| = -5?

С1. Составьте уравнение, корнем которого является число -8.

Вариант 3

А1. Какое из чисел является корнем уравнения 5x² = 7x — 2?

1) 1

2) 2

3) 3

4) 4

А2. Корнем какого уравнения является число -4?

1) x(x + 5)(x — 2) = 0

2) |x| =-4

3) x — 4 = 0

4) x(x + 5)(x — 2) = 24

А3. Выясните, какие из следующих уравнений равносильны:

A. (x — 4)(x + 4) = 0,

B. x² = 16,

C. x = 4.

1) В и С

2) А и В

3) А, В и С

4) А и С

В1. Сколько различных корней имеет уравнение |x| = 0?

С1. Составьте уравнение, корнем которого является число -9.

Вариант 4

А1. Какое из чисел является корнем уравнения 2x² = 9x — 4?

1) 1

2) 2

3) 3

4) 4

А2. Корнем какого уравнения является число -2?

1) x(x + 5)(x — 3) = 30

2) x(x + 5)(x — 2) = 0

3) x — 2 = 0

4) |x| = -2

А3. Выясните, какие из следующих уравнений равносильны:

A. (x — 3)(x + 3) = 0,

B. x — 3 = 0,

C. x² =9.

1) А, В и С

2) А и В

3) А и С

4) В и С

В1. Сколько корней имеет уравнение |x| = 1?

С1. Составьте уравнение, корнем которого является число -6.

§10. Уравнение — Ответы (ГДЗ) рабочая тетрадь (Мерзляк Полонский Якир) 5 класс часть 1

ПОВТОРЯЕМ ТЕОРИЮ

111. Заполните пропуски.

1) Корнем (решением) уравнения называют числовое значение переменной, которое превращает уравнение в верное числовое равенство.
2) Решить уравнение — значит найти все его корни или показать, что их нет.
3) Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное сложеное.
4) Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.
5) Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность.

РЕШАЕМ ЗАДАЧИ

112. Какое из чисел 6, 13, 18 является корнем уравнения: 1) 2х-12=24; 2) 18-3х=0?

Решение:

1. 1) 2*6-12 = 12-12 = 0
Следовательно, число 6 не является корнем уравнения.
2) 2*13-12 = 14.
Следовательно, число 13 не является корнем уравнения.
3) 2*18-12 = 24.
Следовательно, число 18 является корнем уравнения.

2. 1) 18-3*6 = 0
Следовательно, число 6 является корнем уравнения.

113. Проверьте, верно ли решено уравнение. Если оно решено неверно, что приведите верное решение.

114. Решите уравнение.

115. Решите с помощью уравнения задачу.

На участке росло 68 кустов смородины. Потом с этого участка часть кустов пересадили на другой, а на этому участке высадили 14 новых кустов. После этого на первом участке стало 52 куста смородины. Сколько кустов смородины пересадили на другой участок.

Решение:
Пусть на второй участок пересадили х кустоа смородны.
Тогда получится уравнение:
(68-х)+14=52
68-х=52-14
68-х=38
68-38=х
х=30 (кустов)

Ответ: 30 кустов смородины пересадили на другой участок.

116. Какое число надо подставить вместо а, чтобы корнем уравнения (х-а)-14=8 являлось число 32?

Решение:
Чтобы число 32 было корнем уравнения, должно выполняться равенство
(32-а)-14=8
32-а=8+14
32-а=22
32-22=а
а=10

Ответ: а=10

Тест по алгебре с ответами

Страница 1 из 3Страница 2 из 3Страница 3 из 31. При каком, выраженном через а и b, значении m выражение будет полным квадратом?

1. 4/9a²b²
2. ±3/2ab
3. 9/4a²b²
4. Правильный ответ не приведен

2. Решите неравенство:

1. х = 9
2. 9 ≤ х
3. х ≤ 8
4. х ≤ 9

3. Составьте квадратное уравнение, корни которого обратны корням уравнения х² — 20х + 96 = 0.

1. 96х² + 20х + 1 = 0
2. 96х² — 20х + 1 = 0
3. 96х² — 20х — 1 = 0
4. 96х² + 20х — 1 = 0

4. При каких значениях х верно равенство |x² — 49| = 49 — х²?

1. -7 ≤ х ≤ 7
2. х ≥ 7
3. х ≤ -7
4. х ≤ 7

5. Найдите сумму всех коэффициентов приведенного квадратного уравнения, корни которого равны 4+√5 и 4-√5.

6. Один из корней квадратного уравнения х² + 11х + q = 0 равен 8. Найдите второй корень.

7. Найдите значение x₁x²₂ + x²₁x₂, если x₁ и х₂ — корни квадратного уравнения х² — 8х + 11 = 0.

8. Найдите значение x₂ + x₂x₁ + x₁, если x₁ и х₂ — корни квадратного уравнения 2х² + 5х — 11 = 0.

9. Найдите значение x₂ + x₂x₁ + x₁, если x₁ и х₂ — корни квадратного уравнения 2х² + 3х — 7 = 0.

10. Найдите значение x₂ + x₂x₁ + x₁, если x₁ и х₂ — корни квадратного уравнения 2х² + 7х — 3 = 0.

11. Найдите значение x₂ + x₂x₁ + x₁, если x₁ и х₂ — корни квадратного уравнения 2х² — 5х + 3 = 0.

12. Один из корней квадратного уравнения х² — 11х + q = 0 равен 8. Найдите второй корень.

13. Найдите сумму всех коэффициентов приведенного квадратного уравнения, корни которого равны 5+√3 и 5-√3.

14. Один из корней квадратного уравнения х² + 13х + q = 0 равен 7. Найдите второй корень.

15. Найдите сумму всех коэффициентов приведенного квадратного уравнения, корни которого равны 6+√2 и 6-√2.

16. Найдите сумму всех коэффициентов приведенного квадратного уравнения, корни которого равны 3+√5 и 3-√5.

17. Найдите сумму всех коэффициентов приведенного квадратного уравнения, корни которого равны 4+√3 и 4-√3.

18. Составьте квадратное уравнение, корни которого равны 6+√3 и 6-√3.

1. х² + 12х — 33 = 0
2. х² — 12х — 33 = 0
3. х² + 12х + 33 = 0
4. х² — 12х + 33 = 0

19. Составьте квадратное уравнение, корни которого равны 4+√5 и 4-√5.

1. х² — 8х — 11 = 0
2. х² + 8х — 11 = 0
3. х² — 8х + 11 = 0
4. х² + 8х + 11 = 0

20. Составьте квадратное уравнение, корни которого равны 3+√2 и 3-√2.

1. х² — 6х — 7 = 0
2. х² + 6х + 7 = 0
3. х² — 6х + 7 = 0
4. х² + 6х — 7 = 0

21. Составьте квадратное уравнение, корни которого равны 2+√5 и 2-√5.

1. х² + 4х — 1 = 0
2. х² — 4х — 1 = 0
3. х² + 4х + 1 = 0
4. х² — 4х + 1 = 0

22. Найдите значение x₂ + x₂x₁ + x₁, если x₁ и х₂ — корни квадратного уравнения 2х² + 5х — 3 = 0.

23. Найдите значение x₁x²₂ + x²₁x₂, если x₁ и х₂ — корни квадратного уравнения х² — 10х + 22 = 0.

1. -120
2. 220
3. 280
4. -220

24. Один из корней квадратного уравнения х² — 13х + q = 0 равен 7. Найдите второй корень.

25. Один из корней квадратного уравнения х² — 7х + q = 0 равен 11. Найдите второй корень.

26. Найдите значение x₁x²₂ + x²₁x₂, если x₁ и х₂ — корни квадратного уравнения х² — 8х + 13 = 0.

1. 104
2. 94
3. -152
4. -104

27. Найдите значение x₁x²₂ + x²₁x₂, если x₁ и х₂ — корни квадратного уравнения х² — 6х + 7 = 0.

28. Найдите значение x₁x²₂ + x²₁x₂, если x₁ и х₂ — корни квадратного уравнения х² — 8х + 14 = 0.

1. -112
2. 112
3. -144
4. -92

29. Составьте квадратное уравнение, корни которого равны 2+√3 и 2-√3.

1. х² + 4х + 1 = 0
2. х² + 4х — 1 = 0
3. х² — 4х — 1 = 0
4. х² — 4х + 1 = 0

30. Найдите наименьшее целое значение k, при котором уравнение х² — 2(k + 2)х + 11 + k² = 0 имеет два различных действительных корня.

31. Найдите сумму корней уравнения:

32. При каких значениях t уравнение х² + (t — 2)х + 4 = 0 имеет два различных отрицательных корня?

1. t ≤ 1
2. t > 6
3. t
4. t

33. Корни уравнения х² + рх + q = 0 вдвое больше корней уравнения х² — 3х + 2 = 0. Чему равно р + q?

34. Найдите сумму корней уравнения:

35. Найдите разность наибольшего и наименьшего корней уравнения х⁴ — 10х² + 9 = 0.

36. Зная, что x₁ и х₂ — корни уравнения х² + х — 1 = 0, найдите х³₁+х³₂.

37. Найдите наибольшее целое значение k, при котором уравнение kz² + 2(k — 12)z + 6/5 = 0 не имеет действительных корней.

38. Сколько целых решений имеет уравнение |x² — 3х| = 3х — х²?

39. Зная, что x₁ и х₂ — корни уравнения х² — х + q = 0. Найдите q, если x³₁ + х³₂ = 19.

40. Найдите сумму корней уравнения |х| = х² — х — 4.

1. 1 — 2√5
2. 2 — √5
3. —1 + √5
4. 1 + √5

41. x₁ и х₂ — корни уравнения x² + mx + n = 0. Если каждый корень этого уравнения увеличить на 4 и из полученных чисел составить новое уравнение, то свободный член нового уравнения будет равен n — 32 (n — свободный член исходного уравнения). Чему будет равно m?

42. Найдите наибольшее значение выражения , если .

43. Вычислите x₁/х₂ + x₂/х₁, если x₁ и х₂ — корни уравнения 3х² — 8х — 15 = 0.

1. -3 19/45
2. -3 1/45
3. 5
4. -8/3

44. При каких значениях а уравнение ах² — (а + 1)х + 2а + 2 = 0 имеет один корень?

1. 0; -1
2. -1; 0; 1/7
3. 1; -1/7
4. -1; 1/7

45. Чему равна сумма всех натуральных чисел, являющихся корнями уравнения |х² — 8х + 7| = -7 + 8х — х²?

46. При каких значениях k уравнение х² – 2k(х + 1) – k2 + 6k = 0 имеет отличное от нуля два совпадающих корня?

47. z₁ и z₂ — корни уравнения z² + pz + q = 0. Если каждый корень этого уравнения увеличить на 4 и из полученных чисел составить новое уравнение, то свободный его член будет равен q + 68. Найдите р.

48. Найдите k в уравнении х² + 3х + k + 8 = 0, если его корни x₁ и х₂ удовлетворяют условию x₁/х₂ = -1/4.

49. Найдите произведение корней уравнения .

50. Найдите произведение корней уравнения 4|х — 2| = 3 + (х — 2)².

Страница 1 из 3Страница 2 из 3Страница 3 из 3

Уравнения / math5school.ru

Немного теории

При решении и исследовании олимпиадных уравнений, помимо обычных школьных методов:

подстановки,

замены переменкой,

разложения на множители и других преобразований,

иногда используются соображения монотонности:

если функция у = f (x) – строго возрастает или строго убывает, то уравнения

f (p (x)) = f ( q (x)) и p (x) = q (x)

равносильны.

При решении уравнений и систем уравнений иногда бывают полезны:

геометрическая интерпретация,

учёт области допустимых значений переменной или области значений функций, входящих в уравнение,

соображения симметрии,

идеи цикличности,

выход на линейную комбинацию между переменными и др.

Задачи с решениями

1. Решить уравнение:

а) (1 + х + х²) (1 + х + х² + . . . + х¹⁰) = (1 + х + х² + . . . + х⁶)².

б) (x² – x + 1)⁴ – 10x²(x² – x + 1)² + 9x⁴ = 0.

в) (x + 1)⁶³ + (x + 1)⁶²(x – 1) + (x + 1)⁶¹(x – 1)² + . . . + (x – 1)⁶³ = 0.

Решение

а) Так как х = 1 – не корень, то умножим обе части уравнения на (х – 1)². Получим:

(х³ – 1) (х¹¹ – 1) = (х⁷ – 1)²,

х¹¹ – 2х⁷ + х³ = 0,

х³(х⁴ – 1)² = 0,

х₁ = 0,

х₂ = –1,

х₃ = +1 – посторонний корень, возникший в результате умножения на (х – 1)².

Ответ: 0 и –1.

б) Пусть y = (x² – x + 1)², тогда y² – 10x²y + 9x⁴ = 0. Решив это уравнение относительно y, получим:

y₁ = 9x², y₂ = x².

Итак, данное уравнение свелось к двум следующим:

(x² – x + 1)² = 9x² и (x² – x + 1)² = x²,

то есть к четырём квадратным уравнениям:

x² – x + 1 = 3x, x² – x + 1 = – 3x, x² – x + 1 = x, x² – x + 1 = – x,

решить которые не представляет труда.

Ответ: –1, 1, 2 – √3, 2 + √3.

в) Умножив обе части уравнения на

(x + 1) – (x – 1) = 2,

получим

(x + 1)⁶⁴ – (x – 1)⁶⁴ = 0.

Отсюда

(x + 1) = ± (x – 1),

то есть x = 0.

Ответ: x = 0.

2. Решить уравнение:

sin x = х² + х + 1.

Решение

Если х₀ не принадлежит числовому промежутку [–1; 0], то х₀² + х₀ + 1 > 1 > sin х₀.

Если же х₀ принадлежит промежутку [–1; 0], то х₀² + х₀ + 1 > 0, а sin х₀

Значит, для любого действительного значения х₀ имеет место sin х₀0² + х₀ + 1, и исходное уравнение не имеет решений.

Ответ: решений нет.

3. Сколько корней имеет уравнение:

(7√10 + 5√11) х² – (10√10 + 13√11) х + 4√10 + 7√11 = 0?

Решение

Рассмотрим функцию

f (x) = (7√10 + 5√11) х² – (10√10 + 13√11) х + 4√10 + 7√11.

Это квадратичная функция, графиком которой есть парабола, направленная ветвями вверх. Так как

f (1) = √10 – √11

то парабола пересекает ось х в двух точках, а уравнение f (x) = 0 имеет два корня.

Ответ: два корня.

4. Известно, что уравнение ax⁵ + bx⁴ + c = 0 имеет три различных корня. Докажите, что и уравнение cx⁵ + bx + a = 0 также имеет три различных корня.

Решение

Число x = 0 не может быть корнем уравнения

ax⁵ + bx⁴ + c = 0,

так как иначе c = 0, и уравнение имеет не более двух различных корней, что противоречит условию. Разделив обе части этого уравнения на x⁵, получаем, что

a + ^b/_x + ^c/_x⁵ = 0.

Следовательно, если x₁, x₂ и x₃ – различные корни уравнения ax⁵ + bx⁴ + c = 0, то ¹/_x₁, ¹/_x₂ и ¹/_x₃ – различные корни уравнения

cx⁵ + bx + a = 0.

5. При каком положительном значении p уравнения 3x² – 4px + 9 = 0 и x² – 2px + 5 = 0 имеют общий корень?

Решение

Общий корень указанных уравнений должен быть и корнем уравнения

(3x² – 4px + 9) – 3(x² – 2px + 5) = 0,

равносильного уравнению

2px – 6 = 0.

Значит, х = ³/_p. Подставив это значение х, например, во второе уравнение, получим ⁹/_p² = 1, откуда p = 3.

Ответ: 3.

6. Решить уравнение:

5^х + 12^х = 13^х.

Решение

Способ 1.

Легко заметить, что, по крайней мере, одно решение это уравнение имеет, это х = 2. Докажем, что других решений нет. Запишем данное уравнение в виде:

(⁵/₁₃)^x + (¹²/₁₃)^x = 1.

Если x

(⁵/₁₃)^х > (⁵/₁₃)², (¹²/₁₃)^х > (¹²/₁₃)²

и, следовательно,

(⁵/₁₃)^x + (¹²/₁₃)^x > (⁵/₁₃)² + (¹²/₁₃)² = 1.

Аналогично, если x > 2, то

(⁵/₁₃)^x + (¹²/₁₃)^x5/₁₃)² + (¹²/₁₃)² = 1.

Итак, х = 2 – единственный корень.

Способ 2.

Записав уравнение в виде

(⁵/₁₃)^x + (¹²/₁₃)^x = 1,

видим, что имеет единственное решение х = 2. Действительно, число х = 2 удовлетворяет уравнению. С другой стороны, функция

f (х) = (⁵/₁₃)^x + (¹²/₁₃)^x

является строго убывающей, потому что является суммой двух строго убывающих функций, и, следовательно, значение 1 принимает только один раз при х = 2.

Способ 3.

Можно ввести обозначения:

⁵/₁₃= sin α, ¹²/₁₃ = cos α.

Тогда уравнение

(⁵/₁₃)^x + (¹²/₁₃)^x = 1,

равносильное исходному, примет следующий вид:

(sin α)^x + (cos α)^x = 1,

а это уравнение имеет единственное решение х = 2.

Ответ: 2.

7. Решить уравнение:

а) 8^х(3х + 1) = 4.

б) 4 ^{lg x}– 32 + x ^{lg 4}= 0.

Решение

а) Число х = ¹/₃ является решением данного уравнения. Докажем, что других решений нет.

При х > – ¹/₃ функции

у₁(х) = 8^х и у₂(х) = 3х + 1

принимают положительные значения и возрастают, следовательно, их произведение (левая часть уравнения) также является возрастающей функцией.

Поэтому на промежутке (– ¹/₃; + ∞) уравнение не может иметь более одного решения.

Далее, при х – ¹/₃ имеем у₁(х) > 0, у₂(х) 0, а значит, у₁(х) · у₂(х) 0.

Поэтому на промежутке (– ∞; – ¹/₃] уравнение не имеет решений. Таким образом, получаем единственное решение: ¹/₃.

Ответ: ¹/₃.

б) Область допустимых значений х является х > 0 и х ≠ ±1. Имеет место

4 ^{lg x}= x ^lg⁴ .

Для доказательства этого равенства достаточно прологарифмировать обе части равенства по основанию 10. В таком случае

4 ^{lg x}– 32 + 4 ^{lg x}= 0,

4 ^{lg x} = 16,

4 ^{lg x} = 4²,

lg x = 2,

х = 100.

Ответ: 100.

8. Докажите, что уравнение :

а) х¹⁰ – х⁷ + х² – х + 1 = 0 не имеет действительных корней;

б) (x – a)(x – b) + (x – b)(x – c) + (x – c)(x – a) = 0 для любых действительных значений a, b, c имеет хотя бы одно решение;

в) х⁴ + 5х³ + 6х² – 4х – 16 = 0 имеет ровно два решения.

Решение

а) Рассмотрим функцию

f (х) = х¹⁰ – х⁷ + х² – х + 1.

При х₀∈ (– ∞; 0] имеем f (х₀) > 0.

При х₀∈ (0; 1) имеем f (х₀) = (1 – х₀) + (х₀² – х₀⁷) + х₀¹⁰ > 0.

При х₀∈ [1; + ∞) имеем f (х₀) = (х₀¹⁰ – х₀⁷) + (х₀² – х₀) + 1 > 0.

Значит для любого действительного х₀ верно, что f (х₀) > 0 и, следовательно, исходное уравнение не имеет решений.

б) Обозначим

f (x) = (x – a)(x – b) + (x – b)(x – c) + (x – c)(x – a).

Без ограничения общности можно считать, что а b с.

Если а = b или b = с, то f (b) = (b – c)(b – a) = 0.

Если же а 0.

Так как функция f(x) непрерывна, то существует такое число х₀ из промежутка (а; b), что

f(x₀) = 0,

что и требовалось доказать.

Замечание. Это уравнение можно встретить в задаче с несколько иной формулировкой на странице Квадратный трёхчлен.

в) Докажем, что функция

f (x) = х⁴ + 5х³ + 6х² – 4х – 16

принимает значение 0 ровно в двух точках. Для этого исследуем производную этой функции

f′(x) = 4х³ + 15х² + 12х – 4 = (x + 2)²(4х – 1).

При х 1/₄ имеет место неравенство f′(x)

при х > ¹/₄ – неравенство f′(x) > 0. Поэтому функция f(x) убывает па интервале (– ∞; ¹/₄) и возрастает на интервале (¹/₄; + ∞).

Поскольку

f (–10) > 0, f (10) > 0 и f (¹/₄)

то на каждом из двух указанных интервалов функция f (х) однажды принимает значение 0, а уравнение f (х) = 0 имеет ровно два решения, что и требовалось доказать.

9. Сколько корней на отрезке [0, 1] имеет уравнение 8x (1 – 2x²) (8x⁴ – 8x² + 1) = 1?

Решение

Заметим, что

8x⁴ – 8x² + 1 = 2(2x² – 1)² – 1.

Сделав замену x = cos φ, исходное уравнение перепишем в виде:

8 cos φ cos 2φ cos 4φ = – 1.

Умножая обе части на sin φ, получим

sin 8φ = – sin φ,

8φ = – φ + 2kπ или 8φ = π + φ + 2kπ,

то есть

x = cos ^2kπ/₉ или x = cos (^π/₇ + ^2kπ/₇).

На отрезке [0, 1] лежат четыре корня уравнения:

cos ^2π/₉, cos ^4π/₉, cos ^π/₇ и cos ^3π/₇

(корень x = 1 – посторонний, он возник при умножении на sin φ).

Замечание: Всего указанное уравнение 7-й степени имеет 7 корней: к указанным в решении добавляются еще

cos ^2π/₃ = – ½, cos ^8π/₉ = – cos ^π/₉ и cos ^5π/₇ = – cos ^2π/₇.

Ответ: Четыре корня.

10. Решить уравнение:

а) х⁴ + 8х³ + 18х² + 11х + 2 = 0:

б) х⁴ – 4х³ – 1 = 0.

Решение

а) Разложим левую часть уравнения на множители. Для этого представим её в виде:

х⁴ + 8х³ + 18х² + 11х + 2 = (х² + ах + b) (х² + cх + d),

где a, b, c, d подберём методом неопределённых коэффициентов. Имеем:

х⁴ + 8х³ + 18х² + 11х + 2 = х⁴ + (a + c) x³ + (b + d + ac) x² + (ad + bc) x + bd.

Одно из решений системы

a + c = 8,

b + d + ac = 18,

ad + bc = 11,

bd = 2;

подбираем методом подбора:

a = 5, b = 2, c = 3, d = 1,

(находить все её решения не обязательно). Значит,

х⁴ + 8х³ + 18х² + 11х + 2 = (х² + 5х + 2) (х² + 3х + 1),

а исходное уравнение равносильно совокупности уравнений:

х² + 5х + 2 = 0 и х² + 3х + 1 = 0,

решение которых элементарно.

Ответ: х_1,2 = ^–5^±^√17/₂, х_3,4 = ^–3^±^√5/₂.

б) Введём новую переменную

t = x – 1, x = t + 1,

и получим

(t + 1)⁴ – 4(t + 1)³ – 1 = 0,

t⁴ – 6t² – 8t – 4 = 0.

Разложим левую часть уравнения на множители. Для этого представим её в виде:

t⁴ – 6t² – 8t – 4 = (t² + а)² – (bt + c)²,

где a, b, c подберём методом неопределённых коэффициентов. Имеем:

t⁴ – 6t² – 8t – 4 = t⁴ + (2a + b²) t² – 2bc t + a² – c².

Найдём одно из решений системы

2a – b² = –6,

bc = 4,

a² – c² = –4.

Решая эту систему находим:

а = –2, b = √2, с = 2√2 .

Значит,

t⁴ – 6t² – 8t – 4 = (t² – 2)² – (√2t + 2√2)² = (t² – √2t – 2√2 – 2) (t² + √2t + 2√2 – 2) = 0,

а уравнение

t⁴ – 6t² – 8t – 4 = 0

равносильно совокупности уравнений:

t² – √2t – 2√2 – 2 = 0 и t² + √2t + 2√2 – 2 = 0,

первое из которых имеет корни:

t_1,2= ^√2^±^{√10 + 8√2}/₂ ,

а второе корней не имеет.

И, наконец, x_1,2 = t_1,2+ 1 = ^√2^±^{√10 + 8√2}/₂ + 1 = ^{2 + √2}^±^{√10 + 8√2}/₂.

Ответ: x_1,2 = ^{2 + √2}^±^{√10 + 8√2}/₂.

Задачи без решений

1. Решить уравнение 2 sin х = 5х² + 2х + 3.

2. Решить уравнение x³ + x² + x + ¹/₃ = 0.

3. Решить уравнение ⁴√1 – x + ⁴√1 + x = 4.

4. Сколько действительных корней имеет уравнение х¹³ = а (1 + х¹⁴) для каждого действительного а?

5. Доказать, что уравнение x – а sin x – b = 0 при 0

квадратный корень из 12 — Как найти квадратный корень из 12?

Квадратный корень из 12 выражается как √12 в радикальной форме и как (12) ^½ или (12) ^0,5 в экспоненциальной форме.
Квадратный корень из 12, округленный до 5 знаков после запятой, равен 3,46410.
Это положительное решение уравнения x ² = 12.
Мы можем выразить квадратный корень из 12 в его низшей радикальной форме как 2 √3.

Квадратный корень 12: 3.4641016151377544
Квадратный корень из 12 в экспоненциальной форме: (12) ^½ или (12) ^0,5
Квадратный корень из 12 в радикальной форме: √12 или 2 √3

Что такое квадратный корень из 12?

Корень квадратный из 12 в радикальной форме выражается как √ 12, а в экспоненциальной форме — как 12 ^1/2. Квадратный корень из 12 с округлением до 5 знаков после запятой равен 3.46410. Мы также можем выразить квадратный корень из 12 в его низшей радикальной форме как 2 √ 3. Числа, у которых есть радикальный символ в самой нижней форме, называются сурдами.

Является ли квадратный корень из 12 рациональным или иррациональным?

Число, которое нельзя выразить как отношение двух целых чисел, является иррациональным числом. Десятичная форма иррационального числа будет нескончаемой (т. Е. Никогда не заканчивается) и неповторяющейся (т. Е. Десятичная часть числа никогда не повторяет шаблон).

Теперь давайте посмотрим на квадратный корень из 12.

√ 12 = 3,464 1016151

Как вы думаете, десятичная часть останавливается после 3,4641016151? Нет, он бесконечен, и вы не можете увидеть узор в десятичной части. Таким образом, √ 12 — иррациональное число.

Как найти квадратный корень из 12?

Давайте проследим шаги, чтобы найти квадратный корень из 12 путем деления в столбик.

Шаг 1: Составьте пару цифр (поместив над ней полосу) с места единицы, так как наше число — 12.

Изобразим его внутри символа деления.

Шаг 2: Найдите такое число, что при умножении его на само полученное произведение будет меньше или равно 12

Мы знаем, что 3 × 3 = 9 и 9 меньше 12. Теперь разделим 12 на 3.

Шаг 3: Поставим рядом десятичную точку и пару нулей и продолжим наше деление.

Теперь умножим частное на 2, и произведение станет начальной цифрой нашего следующего делителя.

Шаг 4: Выберите число на месте единицы для нового делителя так, чтобы его произведение с числом было меньше или равно 300.

Мы знаем, что 6 находится в разряде десятков, и наше произведение должно быть 300, а ближайшее умножение будет 64 × 4 = 256

Шаг 5: Введите следующую пару нулей и умножьте частное 34 (игнорируя десятичную дробь) на 2, то есть 68, и начальную цифру нового делителя.

Шаг 6: Выберите число на месте единицы для нового делителя так, чтобы его произведение с числом было меньше или равно 4400.

Шаг 7: Добавьте еще пары нулей и повторите процесс поиска нового делителя и произведения, как на шаге 2.

Обратите внимание, что квадратный корень из 12 является иррациональным числом, т. Е. Бесконечным. Следовательно, мы можем остановить процесс после 4 или 5 итераций, и вы получите квадратный корень из 12 методом длинного деления.

Исследуйте квадратные корни с помощью иллюстраций и интерактивных примеров

Важные примечания:

Корень квадратный из 12 в радикальной форме выражается как √ 12
В экспоненциальной форме квадратный корень из 12 выражается как √ 12 = 12 ^1/2.
Настоящие корни для √ 12: 3,464 …

Сложные вопросы:

Какое значение имеет √√√√ 12
Упростить (( √ 12) ^1/2) ^1/2)

Пример 1 : Тим говорит, что значение — ( √ 12) такое же, как ( √- 12). Как вы думаете?
Решение
Отрицательный квадратный корень не может иметь действительных корней.
— ( √ 12) имеет действительные корни, но ( √- 12) имеет только мнимые корни.
Следовательно, они не совпадают. ( √- 12) не то же самое, что (- √ 12).
Пример 2 : Помогите Райану упростить квадратный корень из 12 до его младшего радикала.
Решение
Нам нужно выразить 12 как произведение его простых множителей.
12 = 3 × 2 × 2
Следовательно, √ 12 = √ {3 × 2 × 2} = 2 √ 3
Таким образом, 2 √ 3 находится в форме младшего радикала.
Пример: Если площадь круга равна 12π в ². Найдите радиус круга.
Решение:
Пусть ‘r’ будет радиусом круга.
⇒ Площадь круга = πr ² = 12π дюйм ²
⇒ r = ± √12 в
Поскольку радиус не может быть отрицательным,
⇒ г = √12
Квадратный корень из 12 равен 3,464.
⇒ г = 3.464 в

перейти к слайду перейти к слайду

Отличное обучение в старшей школе по простым подсказкам

Занимаясь заучиванием наизусть, вы, вероятно, забудете концепции. С Cuemath вы будете учиться наглядно и будете удивлены результатами.

Забронируйте бесплатную пробную версию Класс

Часто задаваемые вопросы о квадратном корне из 12

Что такое квадратный корень из 12?

Квадратный корень из 12 равен 3.4641.

Почему квадратный корень из 12 — иррациональное число?

После разложения на простые множители 12, т. Е. 2 ² × 3 ¹, 3 находится в нечетной степени. Следовательно, квадратный корень из 12 иррационален.

Что такое квадратный корень 8 из 12?

Квадратный корень из 12 равен 3,464. Следовательно, 8 √12 = 8 × 3,464 = 27,713.

Что такое квадрат квадратного корня из 12?

Квадрат квадратного корня из 12 — это само число 12 i.е. (√12) ² = (12) ^2/2 = 12.

Число 12 — это идеальный квадрат?

Разложение на простые множители числа 12 = 2 ² × 3 ¹. Здесь простого множителя 3 нет в паре. Следовательно, 12 — не идеальный квадрат.

Вычислить 2 плюс 15 квадратный корень 12

Данное выражение равно 2 + 15 √12. Мы знаем, что квадратный корень из 12 равен 3,464. Следовательно, 2 + 15 √12 = 2 + 15 × 3,464 = 2 + 51,962 = 53,962

квадратный корень из 12 — Как найти квадратный корень из 12?

Квадратный корень из 12 выражается как √12 в радикальной форме и как (12) ^½ или (12) ^0.5 в экспоненциальной форме.
Квадратный корень из 12, округленный до 5 знаков после запятой, равен 3,46410.
Это положительное решение уравнения x ² = 12.
Мы можем выразить квадратный корень из 12 в его низшей радикальной форме как 2 √3.

Квадратный корень из 12: 3,4641016151377544
Квадратный корень из 12 в экспоненциальной форме: (12) ^½ или (12) ^0,5
Квадратный корень из 12 в радикальной форме: √12 или 2 √3

Что такое квадратный корень из 12?

Корень квадратный из 12 в радикальной форме выражается как √ 12, а в экспоненциальной форме — как 12 ^1/2.Квадратный корень из 12 с округлением до 5 знаков после запятой равен 3,46410. Мы также можем выразить квадратный корень из 12 в его низшей радикальной форме как 2 √ 3. Числа, у которых есть радикальный символ в самой нижней форме, называются сурдами.

Является ли квадратный корень из 12 рациональным или иррациональным?

Число, которое нельзя выразить как отношение двух целых чисел, является иррациональным числом. Десятичная форма иррационального числа будет непрерывной (т. Е. Никогда не заканчивается) и неповторяющейся (т.е. десятичная часть числа никогда не повторяет шаблон).

Теперь давайте посмотрим на квадратный корень из 12.

√ 12 = 3,464 1016151

Как найти квадратный корень из 12?

Давайте проследим шаги, чтобы найти квадратный корень из 12 путем деления в столбик.

Шаг 1: Составьте пару цифр (поместив над ней полосу) с места единицы, так как наше число — 12.

Изобразим его внутри символа деления.

Шаг 2: Найдите такое число, что при умножении его на само полученное произведение будет меньше или равно 12

Мы знаем, что 3 × 3 = 9 и 9 меньше 12. Теперь разделим 12 на 3.

Шаг 3: Поставим рядом десятичную точку и пару нулей и продолжим наше деление.

Теперь умножим частное на 2, и произведение станет начальной цифрой нашего следующего делителя.

Шаг 7: Добавьте еще пары нулей и повторите процесс поиска нового делителя и произведения, как на шаге 2.

Исследуйте квадратные корни с помощью иллюстраций и интерактивных примеров

Важные примечания:

Корень квадратный из 12 в радикальной форме выражается как √ 12
В экспоненциальной форме квадратный корень из 12 выражается как √ 12 = 12 ^1/2.
Настоящие корни для √ 12: 3,464 …

Сложные вопросы:

Какое значение имеет √√√√ 12
Упростить (( √ 12) ^1/2) ^1/2)

Пример 1 : Тим говорит, что значение — ( √ 12) такое же, как ( √- 12). Как вы думаете?
Решение
Отрицательный квадратный корень не может иметь действительных корней.
— ( √ 12) имеет действительные корни, но ( √- 12) имеет только мнимые корни.
Следовательно, они не совпадают. ( √- 12) не то же самое, что (- √ 12).
Пример 2 : Помогите Райану упростить квадратный корень из 12 до его младшего радикала.
Решение
Нам нужно выразить 12 как произведение его простых множителей.
12 = 3 × 2 × 2
Следовательно, √ 12 = √ {3 × 2 × 2} = 2 √ 3
Таким образом, 2 √ 3 находится в форме младшего радикала.
Пример: Если площадь круга равна 12π в ². Найдите радиус круга.
Решение:
Пусть ‘r’ будет радиусом круга.
⇒ Площадь круга = πr ² = 12π дюйм ²
⇒ r = ± √12 в
Поскольку радиус не может быть отрицательным,
⇒ г = √12
Квадратный корень из 12 равен 3,464.
⇒ г = 3.464 в

перейти к слайду перейти к слайду

Отличное обучение в старшей школе по простым подсказкам

Забронируйте бесплатную пробную версию Класс

Часто задаваемые вопросы о квадратном корне из 12

Что такое квадратный корень из 12?

Квадратный корень из 12 равен 3.4641.

Почему квадратный корень из 12 — иррациональное число?

Что такое квадратный корень 8 из 12?

Квадратный корень из 12 равен 3,464. Следовательно, 8 √12 = 8 × 3,464 = 27,713.

Что такое квадрат квадратного корня из 12?

Квадрат квадратного корня из 12 — это само число 12 i.е. (√12) ² = (12) ^2/2 = 12.

Число 12 — это идеальный квадрат?

Вычислить 2 плюс 15 квадратный корень 12

квадратный корень из 12 — Как найти квадратный корень из 12?

Квадратный корень из 12: 3,4641016151377544
Квадратный корень из 12 в экспоненциальной форме: (12) ^½ или (12) ^0,5
Квадратный корень из 12 в радикальной форме: √12 или 2 √3

Что такое квадратный корень из 12?

Является ли квадратный корень из 12 рациональным или иррациональным?

Теперь давайте посмотрим на квадратный корень из 12.

√ 12 = 3,464 1016151

Как найти квадратный корень из 12?

Давайте проследим шаги, чтобы найти квадратный корень из 12 путем деления в столбик.

Шаг 1: Составьте пару цифр (поместив над ней полосу) с места единицы, так как наше число — 12.

Изобразим его внутри символа деления.

Шаг 2: Найдите такое число, что при умножении его на само полученное произведение будет меньше или равно 12

Мы знаем, что 3 × 3 = 9 и 9 меньше 12. Теперь разделим 12 на 3.

Шаг 3: Поставим рядом десятичную точку и пару нулей и продолжим наше деление.

Теперь умножим частное на 2, и произведение станет начальной цифрой нашего следующего делителя.

Шаг 7: Добавьте еще пары нулей и повторите процесс поиска нового делителя и произведения, как на шаге 2.

Исследуйте квадратные корни с помощью иллюстраций и интерактивных примеров

Важные примечания:

Корень квадратный из 12 в радикальной форме выражается как √ 12
В экспоненциальной форме квадратный корень из 12 выражается как √ 12 = 12 ^1/2.
Настоящие корни для √ 12: 3,464 …

Сложные вопросы:

Какое значение имеет √√√√ 12
Упростить (( √ 12) ^1/2) ^1/2)

Пример 1 : Тим говорит, что значение — ( √ 12) такое же, как ( √- 12). Как вы думаете?
Решение
Отрицательный квадратный корень не может иметь действительных корней.
— ( √ 12) имеет действительные корни, но ( √- 12) имеет только мнимые корни.
Следовательно, они не совпадают. ( √- 12) не то же самое, что (- √ 12).
Пример 2 : Помогите Райану упростить квадратный корень из 12 до его младшего радикала.
Решение
Нам нужно выразить 12 как произведение его простых множителей.
12 = 3 × 2 × 2
Следовательно, √ 12 = √ {3 × 2 × 2} = 2 √ 3
Таким образом, 2 √ 3 находится в форме младшего радикала.
Пример: Если площадь круга равна 12π в ². Найдите радиус круга.
Решение:
Пусть ‘r’ будет радиусом круга.
⇒ Площадь круга = πr ² = 12π дюйм ²
⇒ r = ± √12 в
Поскольку радиус не может быть отрицательным,
⇒ г = √12
Квадратный корень из 12 равен 3,464.
⇒ г = 3.464 в

перейти к слайду перейти к слайду

Отличное обучение в старшей школе по простым подсказкам

Забронируйте бесплатную пробную версию Класс

Часто задаваемые вопросы о квадратном корне из 12

Что такое квадратный корень из 12?

Квадратный корень из 12 равен 3.4641.

Почему квадратный корень из 12 — иррациональное число?

Что такое квадратный корень 8 из 12?

Квадратный корень из 12 равен 3,464. Следовательно, 8 √12 = 8 × 3,464 = 27,713.

Что такое квадрат квадратного корня из 12?

Квадрат квадратного корня из 12 — это само число 12 i.е. (√12) ² = (12) ^2/2 = 12.

Число 12 — это идеальный квадрат?

Вычислить 2 плюс 15 квадратный корень 12

9.1 Решите квадратные уравнения, используя свойство квадратного корня — промежуточная алгебра 2e

Цели обучения

К концу этого раздела вы сможете:

Решите квадратные уравнения вида ax2 = kax2 = k, используя свойство квадратного корня
Решите квадратные уравнения вида a (x – h) 2 = ka (x – h) 2 = k, используя свойство квадратного корня

Будьте готовы 9,1

Прежде чем начать, пройдите тест на готовность.

Упростить: 128.128.
Если вы пропустили эту проблему, просмотрите Пример 8.13.

Будьте готовы 9.2

Упростить: 325325.
Если вы пропустили эту проблему, просмотрите Пример 8.50.

Будьте готовы 9,3

Фактор: 9×2−12x + 49×2−12x + 4.
Если вы пропустили эту проблему, просмотрите Пример 6.23.

Квадратное уравнение — это уравнение вида ax ² + bx + c = 0, где a ≠ 0a ≠ 0. Квадратные уравнения отличаются от линейных уравнений тем, что включают квадратичный член с переменной, возведенной во вторую степень, в форме ax ².Мы используем другие методы для решения квадратных уравнений, чем линейные, потому что простое сложение, вычитание, умножение и деление членов не приведет к выделению переменной.

Мы видели, что некоторые квадратные уравнения могут быть решены путем факторизации. В этой главе мы узнаем три других метода, которые можно использовать в случае, если квадратное уравнение не может быть разложено на множители.

Решите квадратные уравнения вида ax2 = kax2 = k, используя свойство квадратного корня

Мы уже решили некоторые квадратные уравнения с помощью факторизации.Давайте рассмотрим, как мы использовали факторизацию для решения квадратного уравнения x ² = 9.

	x2 = 9×2 = 9
Приведите уравнение в стандартную форму.	x2−9 = 0x2−9 = 0
Фактор разницы квадратов.	(x − 3) (x + 3) = 0 (x − 3) (x + 3) = 0
Использовать свойство нулевого произведения.	х-3 = 0х-3 = 0х-3 = 0х-3 = 0
Решите каждое уравнение.	х = 3х = -3х = 3х = -3

Мы можем легко использовать факторизацию, чтобы найти решения подобных уравнений, например, x ² = 16 и x ² = 25, потому что 16 и 25 являются точными квадратами.В каждом случае мы получим два решения: x = 4, x = −4x = 4, x = −4 и x = 5, x = −5. X = 5, x = −5.

Но что произойдет, если у нас есть уравнение типа x ² = 7? Поскольку 7 не является полным квадратом, мы не можем решить уравнение факторизацией.

Ранее мы узнали, что, поскольку 169 — это квадрат 13, мы также можем сказать, что 13 — это квадратный корень из 169. Кроме того, (−13) ² = 169, поэтому −13 также является квадратным корнем из 169. Следовательно, и 13, и −13 являются квадратными корнями из 169.Итак, каждое положительное число имеет два квадратных корня — положительный и отрицательный. Ранее мы определили квадратный корень из числа таким образом:

Если n2 = m, то есть квадратный корень из m. Еслиn2 = m, то есть квадратный корень из m.

Поскольку все эти уравнения имеют форму x ² = k , определение квадратного корня говорит нам, что решениями являются два квадратных корня из k . Это приводит к свойству квадратного корня.

Свойство квадратного корня

Если x ² = k , то

x = korx = −korx = ± k.x = korx = −korx = ± k.

Обратите внимание, что свойство квадратного корня дает два решения уравнения в форме x ² = k , главный квадратный корень из kk и его противоположность. Мы также могли бы записать решение в виде x = ± k.x = ± k. Мы читаем это так, как x равно положительному или отрицательному квадратному корню из k .

Теперь мы снова решим уравнение x ² = 9, на этот раз используя свойство квадратного корня.

	x2 = 9×2 = 9
Используйте свойство квадратного корня.	х = ± 9х = ± 9
	х = ± 3х = ± 3
	Sox = 3 или x = −3. Sox = 3 или x = −3.

Что происходит, если константа не является точным квадратом? Давайте воспользуемся свойством квадратного корня для решения уравнения x ² = 7.

	x2 = 7×2 = 7
Используйте свойство квадратного корня.	х = 7, х = −7x = 7, х = −7

Мы не можем упростить 77, поэтому оставим ответ радикальным.

Пример 9.1

Как решить квадратное уравнение в форме

ax ² = k Использование свойства квадратного корня

Решить: x2−50 = 0. x2−50 = 0.

Попробуйте 9,1

Решите: x2−48 = 0.x2−48 = 0.

Попробуй 9,2

Решите: y2−27 = 0. y2−27 = 0.

Шаги, которые необходимо предпринять, чтобы использовать свойство квадратного корня для решения квадратного уравнения, перечислены здесь.

How To

Решите квадратное уравнение, используя свойство квадратного корня.

Шаг 1. Выделите квадратичный член и сделайте его коэффициент равным единице.
Шаг 2. Используйте свойство квадратного корня.
Шаг 3. Упростим радикал.
Шаг 4. Проверьте решения.

Чтобы использовать свойство квадратного корня, коэффициент члена переменной должен быть равен единице. В следующем примере мы должны разделить обе части уравнения на коэффициент 3, прежде чем использовать свойство квадратного корня.

Пример 9.2

Решение

	3z2 = 1083z2 = 108
Квадратичный член изолирован. Разделите на 3, чтобы получить коэффициент 1.	3z23 = 10833z23 = 1083
Упростить.	z2 = 36z2 = 36
Используйте свойство квадратного корня.	z = ± 36z = ± 36
Упростим радикал.	z = ± 6z = ± 6
Перепишите, чтобы показать два решения.	z = 6, z = −6z = 6, z = −6
Проверьте решения:

Свойство квадратного корня гласит: «Если x2 = kx2 = k,» что произойдет, если k <0? K <0? Так будет в следующем примере.

Пример 9.3

Решение

	x2 + 72 = 0x2 + 72 = 0
Выделите квадратичный член.	x2 = −72×2 = −72
Используйте свойство квадратного корня.	х = ± -72х = ± -72
Упростите, используя комплексные числа.	x = ± 72ix = ± 72i
Упростим радикал.	x = ± 62ix = ± 62i
Перепишите, чтобы показать два решения.	x = 62i, x = −62ix = 62i, x = −62i
Проверьте решения:

Наш метод также работает, когда в уравнении встречаются дроби, мы решаем как любое уравнение с дробями. В следующем примере мы сначала выделяем квадратичный член, а затем делаем коэффициент равным единице.

Пример 9.4

Решите: 23u2 + 5 = 17.23u2 + 5 = 17.

Попробовать 9,7

Решить: 12×2 + 4 = 24,12×2 + 4 = 24.

Попробуйте 9,8

Решите: 34y2−3 = 18.34y2−3 = 18.

Решения некоторых уравнений могут иметь дроби внутри радикалов. Когда это происходит, мы должны рационализировать знаменатель.

Пример 9,5

Решите: 2×2−8 = 41,2×2−8 = 41.

Попробуйте 9.9

Решите: 5r2−2 = 34,5r2−2 = 34.

Попробуйте 9.10

Решите: 3t2 + 6 = 70,3t2 + 6 = 70.

Решите квадратные уравнения вида

a ( x — h ) ² = k Используя свойство квадратного корня

Мы можем использовать свойство квадратного корня для решения уравнения вида a ( x — h ) ² = k .Обратите внимание, что квадратный член x в исходной форме ax ² = k заменяется на ( x — h ).

Первый шаг, как и раньше, — выделить термин, в котором переменная возведена в квадрат. В этом случае возводится двучлен. После выделения бинома путем деления каждой стороны на коэффициент на свойство квадратного корня можно использовать для ( x — h ) ².

Пример 9,6

Решите: 4 (y − 7) 2 = 48,4 (y − 7) 2 = 48.

Решение

	4 (y − 7) 2 = 484 (y − 7) 2 = 48
Разделим обе части на коэффициент 4.	(y − 7) 2 = 12 (y − 7) 2 = 12
Используйте свойство квадратного корня для бинома	y − 7 = ± 12y − 7 = ± 12
Упростим радикал.	y − 7 = ± 23y − 7 = ± 23
Решить относительно y.у.	у = 7 ± 23у = 7 ± 23
Перепишите, чтобы показать два решения.	y = 7 + 23, y = 7 + 23, y = 7−23y = 7−23
Чек:

Попробуйте 9.11

Решите: 3 (a − 3) 2 = 54,3 (a − 3) 2 = 54.

Попробуйте 9.12

Решите: 2 (b + 2) 2 = 80,2 (b + 2) 2 = 80.

Помните, когда мы извлекаем квадратный корень из дроби, мы можем извлекать квадратный корень из числителя и знаменателя отдельно.

Пример 9.7

Решите: (x − 13) 2 = 59. (X − 13) 2 = 59.

Решение

	(x − 13) 2 = 59 (x − 13) 2 = 59
Используйте свойство квадратного корня.	x − 13 = ± 59x − 13 = ± 59
Записываем радикал как долю квадратных корней.	x − 13 = ± 59x − 13 = ± 59
Упростим радикал.	x − 13 = ± 53x − 13 = ± 53
Решите для xx.	х = 13 ± 53х = 13 ± 53
Перепишите, чтобы показать два решения.	x = 13 + 53, x = 13−53x = 13 + 53, x = 13−53
Чек: Мы оставляем вам чек.

Попробуйте 9,13

Решите: (x − 12) 2 = 54. (X − 12) 2 = 54.

Попробуйте 9,14

Решите: (y + 34) 2 = 716. (Y + 34) 2 = 716.

Мы начнем решение следующего примера с выделения биномиального члена.

Пример 9.8

Решите: 2 (x − 2) 2 + 3 = 57,2 (x − 2) 2 + 3 = 57.

Решение

	2 (x − 2) 2 + 3 = 572 (x − 2) 2 + 3 = 57
Вычтите 3 с обеих сторон, чтобы выделить биномиальный член.	2 (x − 2) 2 = 542 (x − 2) 2 = 54
Разделите обе стороны на 2.	(x − 2) 2 = 27 (x − 2) 2 = 27
Используйте свойство квадратного корня.	х − 2 = ± 27x − 2 = ± 27
Упростим радикал.	x − 2 = ± 33x − 2 = ± 33
Решите для xx.	х = 2 ± 33х = 2 ± 33
Перепишите, чтобы показать два решения.	х = 2 + 33, х = 2-33 х = 2 + 33, х = 2-33
Чек: Мы оставляем вам чек.

Попробуйте 9,15

Решите: 5 (a − 5) 2 + 4 = 104,5 (a − 5) 2 + 4 = 104.

Попробуйте 9,16

Решите: 3 (b + 3) 2−8 = 88,3 (b + 3) 2−8 = 88.

Иногда решениями являются комплексные числа.

Пример 9.9

Решите: (2x − 3) 2 = −12. (2x − 3) 2 = −12.

Решение

	(2x − 3) 2 = −12 (2x − 3) 2 = −12
Используйте свойство квадратного корня.	2x − 3 = ± −122x − 3 = ± −12
Упростим радикал.	2x − 3 = ± 23i2x − 3 = ± 23i
Добавьте 3 с обеих сторон.	2x = 3 ± 23i2x = 3 ± 23i
Разделите обе стороны на 2.	х = 3 ± 23i2x = 3 ± 23i2
Перепишите в стандартной форме.	х = 32 ± 23i2x = 32 ± 23i2
Упростить.	x = 32 ± 3ix = 32 ± 3i
Перепишите, чтобы показать два решения.	x = 32 + 3i, x = 32−3ix = 32 + 3i, x = 32−3i
Чек: Мы оставляем вам чек.

Попробуйте 9,17

Решите: (3r + 4) 2 = −8. (3r + 4) 2 = −8.

Попробуйте 9.18

Решите: (2t − 8) 2 = −10. (2t − 8) 2 = −10.

Левая часть уравнений в следующих двух примерах не имеет формы a ( x — h ) ². Но они представляют собой идеальные квадратные трехчлены, поэтому мы будем множить их в нужную нам форму.

Пример 9.10

Решить: 4n2 + 4n + 1 = 16.4n2 + 4n + 1 = 16.

Решение

Мы замечаем, что левая часть уравнения представляет собой трехчлен в виде полного квадрата. Мы учтем это в первую очередь.

	4n2 + 4n + 1 = 164n2 + 4n + 1 = 16
Разложите на множители полный квадрат трехчлена.	(2n + 1) 2 = 16 (2n + 1) 2 = 16
Используйте свойство квадратного корня.	2n + 1 = ± 162n + 1 = ± 16
Упростим радикал.	2n + 1 = ± 42n + 1 = ± 4
Решите для nn.	2n = -1 ± 42n = -1 ± 4
Разделите каждую сторону на 2.	2n2 = -1 ± 422n2 = -1 ± 42 п = -1 ± 42 п = -1 ± 42
Перепишите, чтобы показать два решения.	п = -1 + 42n = -1 + 42, п = -1-42n = -1-42
Упростите каждое уравнение.	п = 32 п = 32, п = -52 п = -52
Чек:

Попробуйте 9,19

Решите: 9m2−12m + 4 = 25.9m2−12m + 4 = 25.

Попробуй 9.20

Решите: 16n2 + 40n + 25 = 4,16n2 + 40n + 25 = 4.

Раздел 9.1 Упражнения

Практика ведет к совершенству

Решите квадратные уравнения вида ax ² = k Используя свойство квадратного корня

В следующих упражнениях решите каждое уравнение.

16.

23y2−8 = −223y2−8 = −2

Решите квадратные уравнения вида a ( x — h ) ² = k Использование свойства квадратного корня

В следующих упражнениях решите каждое уравнение.

30.

(t − 56) 2 = 1125 (t − 56) 2 = 1125

31.

(а-7) 2 + 5 = 55 (а-7) 2 + 5 = 55

32.

(b − 1) 2−9 = 39 (b − 1) 2−9 = 39

33.

4 (x + 3) 2−5 = 274 (x + 3) 2−5 = 27

34.

5 (x + 3) 2−7 = 685 (x + 3) 2−7 = 68

35.

(5c + 1) 2 = −27 (5c + 1) 2 = −27

36.

(8d − 6) 2 = −24 (8d − 6) 2 = −24

37.

(4x − 3) 2 + 11 = −17 (4x − 3) 2 + 11 = −17

38.

(2y + 1) 2−5 = −23 (2y + 1) 2−5 = −23

43.

25×2−30x + 9 = 3625×2−30x + 9 = 36

45.

36×2−24x + 4 = 8136×2−24x + 4 = 81

46.

64×2 + 144x + 81 = 2564×2 + 144x + 81 = 25

Смешанная практика

В следующих упражнениях решите, используя свойство квадратного корня.

51.

9w2−24w + 16 = 19w2−24w + 16 = 1

59.

u2−14u + 49 = 72u2−14u + 49 = 72

61.

(м − 4) 2 + 3 = 15 (м − 4) 2 + 3 = 15

62.

(n − 7) 2−8 = 64 (n − 7) 2−8 = 64

68.

(y − 4) 2 + 10 = 9 (y − 4) 2 + 10 = 9

Письменные упражнения

69.

Объясните своими словами свойство квадратного корня.

70.

Объясните своими словами, как использовать свойство квадратного корня для решения квадратного уравнения (x + 2) 2 = 16 (x + 2) 2 = 16.

Самопроверка

ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.

Выберите, как вы отреагируете на утверждение: «Я могу решить квадратные уравнения вида, умноженного на квадрат x минус h, равный k, используя свойство квадратного корня». «Уверенно», «с некоторой помощью» или «Нет, я не понимаю.”

ⓑ Если большая часть ваших чеков была:

… уверенно. Поздравляем! Вы достигли целей в этом разделе. Поразмышляйте над своими учебными навыками, чтобы вы могли продолжать их использовать. Что вы сделали, чтобы убедиться в своей способности делать эти вещи? Быть конкретным.

… с некоторой помощью. Эту проблему нужно решать быстро, потому что темы, которые вы не осваиваете, становятся ухабами на вашем пути к успеху. В математике каждая тема основывается на предыдущей работе.Прежде чем двигаться дальше, важно убедиться, что у вас есть прочный фундамент. К кому вы можете обратиться за помощью? Ваши одноклассники и инструктор — хорошие помощники. Есть ли в кампусе место, где доступны репетиторы по математике? Можно ли улучшить свои учебные навыки?

… нет, не понимаю! Это предупреждающий знак, игнорировать его нельзя. Вам следует немедленно обратиться за помощью, иначе вы быстро не справитесь. Как можно скорее обратитесь к своему инструктору, чтобы обсудить вашу ситуацию. Вместе вы сможете составить план оказания вам необходимой помощи.

мнимых и комплексных чисел

Мнимые числа

В конце концов, вы столкнетесь с ситуацией, когда вам придется иметь дело с квадратным
корни отрицательных чисел. Как это может быть сделано ? В конце концов, положительное число в квадрате или
отрицательное число в квадрате всегда будет положительным числом.

Математики выделили особый
число i, которое равно квадратному корню из минус 1.Тогда i ² =
-1. Чтобы определить квадратный корень из отрицательного числа (например, -16), возьмите
квадратный корень из абсолютного значения числа (квадратный корень из 16 = 4), а затем умножьте его на
‘я’. Итак, квадратный корень из -16 равен 4i.
В качестве двойной проверки мы можем возвести в квадрат 4i (4 * 4 = 16 и
i * i = -1), что дает -16.
Все отрицательные квадратные корни называются
«мнимые числа» (теперь вы знаете, откуда взялась буква «i»).

Комплексные числа

Когда число имеет форму a + bi (действительное число плюс мнимое число), оно называется числом.
«комплексное число».Как комплексные числа «возникают» в математике? Хорошим примером может служить
корни квадратного уравнения x ² -6x + 25 = 0, где 2 корня равны 3 + 4i и
3 — 4i. Можем ли мы быть уверены, что это корни уравнения?
В качестве двойной проверки, используя эти корни, мы можем «перестроить» исходное уравнение,

(X — 3 -4i) * (X — 3 + 4i) = X ² -3x + 4Xi -3X +9 -12i -4Xi + 12i — (4i) ²

Это сокращается до: X ² -3x -3X +9 — (16) * i ²

Поскольку i ² = -1, то — (16) * i ² становится — (- 16) = 16 и поэтому:
Х ² -6Х +25 = 0

Умножение комплексных чисел

Сложение и вычитание комплексных чисел в значительной степени следуют правилам базовой арифметики и
поэтому мы не будем это обсуждать.Умножение становится немного сложнее. Рассмотрим:
(5 + 6i) * (7 + 8i)
Это равно 35 + 40i + 42i + 48i ²
Как мы видели выше, i ² = -1, поэтому 48i ² = -48
Итак, ответ = -13 + 82i

Дивизион комплексных чисел

Вам было интересно — деление сложнее умножения? Уверенный. Сначала мы должны определить
новый термин — конъюгат , при этом конъюгат a + bi = a-bi.
Пример — сопряжение (3 + 4i) есть (3 — 4i).
Главный принцип, который следует помнить при делении комплексных чисел, заключается в следующем:
умножаем «верхнюю» и «нижнюю» дроби на сопряжение знаменателя .
Время для примера: разделим (9 + 3i) на (7 + 5i) (9 + 3i)
—————
(7 + 5i)

Знаменатель (7 + 5i), а его сопряжение (7-5i)

Умножая верх и низ на конъюгат:

((9 + 3i) * (7 — 5i))
——————————
((7 + 5i) * (7 — 5i)), что равно
(78 — 24 i)
——— ——
74 Что равняется
78 24i
—— минус ——
74 74 Что равняется
Ответ = 1,054054054054054 & -0.32432432432432434 я

Квадратный корень комплексного числа

Теперь переходим к еще большей сложности.
Пора определить еще один термин — модуль , в соответствии с которым модуль комплексного числа a + bi равен квадратному корню из
(а ² + б ²).
Модуль комплексного числа обычно обозначается буквой ‘r’, поэтому:
r = квадратный корень (a ² + b ²)
Далее мы определим эти две величины:
y = квадратный корень ((ra) / 2)
x = b / 2y
Наконец, два квадратных корня комплексного числа равны:
корень ₁ = x + yi
root ₂ = -x — yi
Пример должен сделать эту процедуру более понятной.
Найдите квадратный корень из 12 + 16i
r = Квадратный корень (12 ² + 16 ²)
r = квадратный корень (144 + 256) = 20
y = квадратный корень ((20-12) / 2) = 2
x = 16 / (2 * 2) = 4
корень ₁ = 4 + 2i
корень ₂ = -4 — 2i

Даже если у вас есть калькулятор, который может выполнять эти расчеты для
вы, теперь вы знаете процедуры арифметики комплексных чисел.

Вернуться к калькулятору

Вернуться на главную страницу

1728 Программные системы

Сложение и вычитание квадратного корня

Мы можем складывать или вычитать радикальные выражения только тогда, когда они имеют одно и то же подкоренное выражение и когда они имеют один и тот же радикальный тип, например квадратные корни.Например, сумма [latex] \ sqrt {2} [/ latex] и [latex] 3 \ sqrt {2} [/ latex] равна [latex] 4 \ sqrt {2} [/ latex]. Однако часто можно упростить радикальные выражения, и это может изменить подкоренное выражение. Радикальное выражение [latex] \ sqrt {18} [/ latex] может быть записано с помощью [latex] 2 [/ latex] в подкоренной строке, как [latex] 3 \ sqrt {2} [/ latex], поэтому [latex ] \ sqrt {2} + \ sqrt {18} = \ sqrt {2} +3 \ sqrt {2} = 4 \ sqrt {2} [/ latex].

Практическое руководство. Решите радикальное выражение, требующее сложения или вычитания квадратных корней.

Упростите каждое радикальное выражение.
Сложить или вычесть выражения с одинаковыми подкоренными выражениями.

Пример 6: Добавление квадратного корня

Добавьте [латекс] 5 \ sqrt {12} +2 \ sqrt {3} \\ [/ latex].

Решение

Мы можем переписать [latex] 5 \ sqrt {12} [/ latex] как [latex] 5 \ sqrt {4 \ cdot 3} [/ latex]. Согласно правилу продукта это становится [латекс] 5 \ sqrt {4} \ sqrt {3} [/ latex]. Квадратный корень из [latex] \ sqrt {4} [/ latex] равен 2, поэтому выражение становится [latex] 5 \ left (2 \ right) \ sqrt {3} [/ latex], то есть [latex] 10. \ sqrt {3} [/ латекс].{2} \) само по себе. Шаг 2 : Используйте свойство квадратного корня. Не забудьте написать символ \ (\ pm \). \ (х = \ pm \ sqrt {50} \) Шаг 3 : Упростите корень. Перепишите, чтобы показать два решения. \ (\ begin {array} {l} {x = \ pm \ sqrt {25} \ cdot \ sqrt {2}} \\ {x = \ pm 5 \ sqrt {2}} \\ {} x = 5 \ sqrt {2}, \: x = -5 \ sqrt {2} \ end {array} \) Шаг 4 : Проверьте решения.{2} -27 = 0 \).

Ответ: \ (y = 3 \ sqrt {3}, y = -3 \ sqrt {3} \)

Шаги, которые необходимо предпринять для использования свойства квадратного корня для решения квадратного уравнения, перечислены здесь.

Решите квадратное уравнение, используя свойство квадратного корня

Выделите квадратичный член и сделайте его коэффициент равным единице.
Использовать свойство квадратного корня.
Упростите радикал.
Проверьте решения.{2} = 36 \) Используйте свойство квадратного корня. \ (z = \ pm \ sqrt {36} \) Упростим радикал. \ (z = \ pm 6 \) Перепишите, чтобы показать два решения. \ (z = 6, \ quad z = -6 \)
Проверьте решения:
Рисунок 9.1.1 Таблица 9.{2} = — 72 \) Используйте свойство квадратного корня. \ (x = \ pm \ sqrt {-72} \) Упростите, используя комплексные числа. \ (х = \ pm \ sqrt {72} i \) Упростим радикал. \ (x = \ pm 6 \ sqrt {2} i \) Перепишите, чтобы показать два решения
Проверьте решения:
Рисунок 9.{2} = 12 \) Используйте свойство квадратного корня для бинома. \ (y-7 = \ pm \ sqrt {12} \) Упростим радикал. \ (y-7 = \ pm 2 \ sqrt {3} \) Решите относительно \ (y \). \ (y = 7 \ pm 2 \ sqrt {3} \) Перепишите, чтобы показать два решения. \ (y = 7 + 2 \ sqrt {3} \)
\ (y = 7-2 \ sqrt {3} \)
Чек:
Рисунок 9.{2} = \ frac {5} {9} \)
Используйте свойство квадратного корня.
\ (x- \ frac {1} {3} = \ pm \ sqrt {\ frac {5} {9}} \)
Записываем радикал как долю квадратных корней.
\ (x- \ frac {1} {3} = \ pm \ frac {\ sqrt {5}} {\ sqrt {9}} \)
Упростите радикал.
\ (x- \ frac {1} {3} = \ pm \ frac {\ sqrt {5}} {3} \)
Решите относительно \ (x \).
\ (x = \ frac {1} {3} \ pm \ frac {\ sqrt {5}} {3} \)
Перепишите, чтобы показать два решения.
\ (x = \ frac {1} {3} + \ frac {\ sqrt {5}} {3}, x = \ frac {1} {3} — \ frac {\ sqrt {5}} {3} \)
Чек:
Оставляем вам чек.{2} = — 12 \)
Используйте свойство квадратного корня.
\ (2 x-3 = \ pm \ sqrt {-12} \)
Упростите радикал.
\ (2 x-3 = \ pm 2 \ sqrt {3} i \)
Добавьте \ (3 \) к обеим сторонам.
\ (2 x = 3 \ pm 2 \ sqrt {3} i \)
Разделите обе части на \ (2 \).
\ (x = \ frac {3 \ pm 2 \ sqrt {3 i}} {2} \)
Перепишите в стандартной форме.
\ (x = \ frac {3} {2} \ pm \ frac {2 \ sqrt {3} i} {2} \)
Упростить.
\ (x = \ frac {3} {2} \ pm \ sqrt {3} i \)
Перепишите, чтобы показать два решения.{2} = 16 \) Используйте свойство квадратного корня. \ (2 n + 1 = \ pm \ sqrt {16} \) Упростим радикал. \ (2 n + 1 = \ pm 4 \) Решите относительно \ (n \). Разделите каждую сторону на \ (2 \). Перепишите, чтобы показать два решения. \ (n = \ frac {-1 + 4} {2}, n = \ frac {-1-4} {2} \) Упростите каждое уравнение.{2} +40 п + 25 = 4 \).
Ответ
\ (n = — \ frac {3} {4}, \ quad n = — \ frac {7} {4} \)
Получите доступ к этому онлайн-ресурсу для получения дополнительных инструкций и практики использования свойства квадратного корня для решения квадратных уравнений.