Содержание
Урок 14. статика. равновесие абсолютно твердых тел — Физика — 10 класс
Физика, 10 класс
Урок 14. Статика. Равновесие абсолютно твёрдых тел
Перечень вопросов, рассматриваемых на уроке:
1.Условия равновесия тела
2.Момент силы
3.Плечо силы
4. Центр тяжести
Глоссарий по теме
Статика – раздел механики, в котором изучается равновесие абсолютно твердых тел, называется статикой
Абсолютно твердое тело – модельное понятие классической механики, обозначающее совокупность точек, расстояния между текущими положениями которых не изменяются.
Центр тяжести – центром тяжести тела называют точку, через которую при любом положении тела в пространстве проходит равнодействующая сил тяжести, действующих на все частицы тела.
Плечо силы — это длина перпендикуляра, опущенного от оси вращения на линию действия силы.
Момент силы — это физическая величина, равная произведению модуля силы на ее плечо.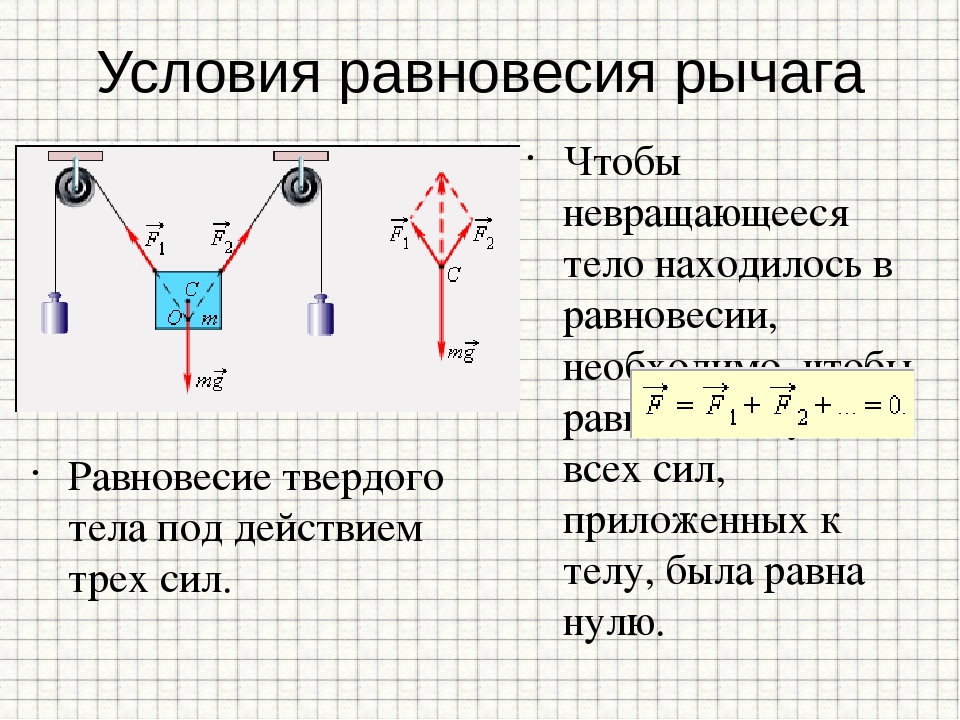
Устойчивое равновесие — это равновесие, при котором тело, выведенное из состояния устойчивого равновесия, стремится вернуться в начальное положение.
Неустойчивое равновесие — это равновесие, при котором тело, выведенное из положения равновесия и предоставленное самому себе, будет еще больше отклоняться от положения равновесия.
Безразличное равновесие системы — равновесие, при котором после устранения причин, вызвавших малые отклонения, система остается в покое в этом отклоненном состоянии
Основная и дополнительная литература по теме урока:
Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017.– С. 165 – 169.
Рымкевич А.П. Сборник задач по физике. 10-11 класс. — М.: Дрофа, 2009.
Степанова Г.Н. Сборник задач по физике. 10-11 класс. — М.: Просвещение. 1999 г. С.48- 50.
Теоретический материал для самостоятельного изучения
Равновесие – это состояние покоя, т.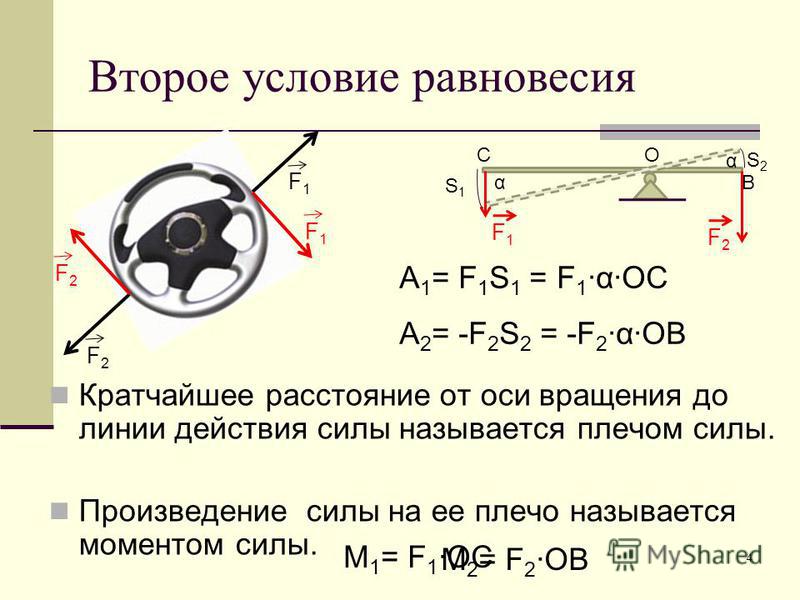 е. если тело покоится относительно инерциальной системы отсчета, то говорят, что оно находится в равновесии. Вопросы равновесия интересуют строителей, альпинистов, артистов цирка и многих-многих других людей. Любому человеку приходилось сталкиваться с проблемой сохранения равновесия. Почему одни тела, выведенные из состояния равновесия, падают, а другие – нет? Выясним, при каком условии тело будет находиться в состоянии равновесия.
е. если тело покоится относительно инерциальной системы отсчета, то говорят, что оно находится в равновесии. Вопросы равновесия интересуют строителей, альпинистов, артистов цирка и многих-многих других людей. Любому человеку приходилось сталкиваться с проблемой сохранения равновесия. Почему одни тела, выведенные из состояния равновесия, падают, а другие – нет? Выясним, при каком условии тело будет находиться в состоянии равновесия.
Раздел механики, в котором изучается равновесие абсолютно твердых тел, называется статикой. Статика является частным случаем динамики. В статике твердое тело рассматривается как абсолютно твердое, т.е. недеформируемое тело. Это означает, что деформация так мала, что её можно не учитывать.
Центр тяжести существует у любого тела. Эта точка может находиться и вне тела. Как же подвесить или подпереть тело, чтобы оно находилось в равновесии.
Подобную задачу в свое время решил Архимед. Им же были введены понятие плеча силы и момента силы.
Плечо силы — это длина перпендикуляра, опущенного от оси вращения на линию действия силы.
Момент силы — это физическая величина, равная произведению модуля силы на ее плечо.
После своих исследований Архимед сформулировал условие равновесия рычага и вывел формулу:
Это правило является следствием 2-го закона Ньютона.
Первое условие равновесия
Для равновесия тела необходимо, чтобы сумма всех сил, приложенных к телу была равна нулю.
формула должна быть в векторном виде и стоять знак суммы
Второе условие равновесия
При равновесии твердого тела сумма моментов вcех внешних сил, действующих на него относительно любой оси, равна нулю.
Не менее важен случай, когда тело имеет площадь опоры. Тело, имеющее площадь опоры, находится в равновесии, когда вертикальная прямая, проходящая через центр тяжести тела, не выходит за пределы площади опоры этого тела. Известно, что в городе Пизе в Италии существует наклонная башня. Несмотря на то, что башня наклонена, она не опрокидывается, хотя ее часто называют падающей. Очевидно, что при том наклоне, которого башня достигла к настоящему времени, вертикаль, проведенная из центра тяжести башни, все еще проходит внутри ее площади опоры.
Очевидно, что при том наклоне, которого башня достигла к настоящему времени, вертикаль, проведенная из центра тяжести башни, все еще проходит внутри ее площади опоры.
В практике большую роль играет не только выполнение условия равновесия тел, но и качественная характеристика равновесия, называемая устойчивостью.
Различают 3 вида равновесия: устойчивое, неустойчивое, безразличное.
Если при отклонении тела от положения равновесия, возникают силы или моменты сил, стремящиеся вернуть тело в положение равновесия, то такое равновесие называется устойчивым.
Неустойчивое равновесие — это противоположный случай. При отклонении тела от положения равновесия, возникают силы или моменты сил, которые стремятся увеличить это отклонение.
Наконец, если при малом отклонении от положения равновесия тело все равно остается в равновесии, то такое равновесие называется безразличным.
Чаще всего необходимо, чтобы равновесие было устойчивым. Когда равновесие нарушается, то сооружение становится опасным, если его размеры велики.
Примеры и разбор решения заданий
1. Чему равен момент силы тяжести груза массой 40 кг, подвешенного на кронштейне АВС, относительно оси, проходящей через точку В, если АВ=0,5 м и угол α=450
Решение:
Момент силы – это величина равная произведению модуля силы на её плечо.
Сначала найдём плечо силы, для этого нам надо опустить перпендикуляр из точки опоры на линию действия силы. Плечо силы тяжести равно расстоянию АС. Так как угол равен 45°, то мы видим, что АС=АВ
Модуль силы тяжести находим по формуле:
После подстановки числовых значений величин мы получим:
F=40×9,8 =400 Н, М= 400 ×0,5=200 Н м.
Ответ: М=200 Н м.
2. Приложив вертикальную силу F, груз массой М — 100 кг удерживают на месте с помощью рычага (см. рис.). Рычаг состоит из шарнира без трения и однородного массивного стержня длиной L=8 м. Расстояние от оси шарнира до точки подвеса груза равно b=2 м. Чему равен модуль силы F, если масса рычага равна 40 кг.
Решение:
По условию задачи рычаг находится в равновесии. Напишем второе условие равновесия для рычага:
.
После подстановки числовых значений величин получим
F= (100×9,8 ×2 + 0,5×40×9,8×8)/8=450 Н
Ответ: 450 Н.
Условия равновесия: первое, второе. Виды равновесия: устойчивое, неустойчивое, безразличное, опрокидывание. Формулы, примеры
Тестирование онлайн
Равновесие
Состояние тела, которое не изменяется со временем. Например, тело длительно находится в покое или движется равномерно, или длительно вращается.
Первое условие равновесия
Векторная сумма всех действующих на тело сил равна нулю.
Рассмотрим на примере первое условие равновесия
Предмет будет находиться в равновесии, если векторная сумма всех сил (Fтр1, Fтр2, N1, N2, mg) равна нулю. То есть
Второе условие равновесия
Векторная сумма моментов сил равна нулю
Точку О выберем в точке пересечения Fтр2 и N2. Плечи этих сил равны нулю, значит и моменты этих сил равны нулю.
Плечи этих сил равны нулю, значит и моменты этих сил равны нулю.
Определяем плечи сил Fтр1, N1 и mg и направление моментов сил (положительное или отрицательное).
Равновесие бывает устойчивым (тело возвращается в свое первоначальное положение), неустойчивым (тело не возвращается в свое первоначальное состояние), безразличное (тело остается в равновесии, несмотря на то, что на него подействовали (например переложили книгу из одного места на столе в другое). Тело стремится занять такое состояние, при котором его потенциальная энергия будет минимальной, центр масс стремиться быть ниже.
1 — безразличное равновесие, 2 — неустойчивое равновесие, 3 — устойчивое равновесие
На рисунке изображено условие опрокидывания тела.
Тело слева возвращается в исходное состояние. Тело справа опрокидывается.
Тело, имеющее площадь опоры, находится в состоянии устойчивого равновесия, если вертикаль, проведенная через центр масс этого тела, не выходит за рамки контура, ограниченного точками соприкосновения тела с опорой. Если же эта вертикаль проходит вне указанного контура, тело опрокидывается.
Если же эта вертикаль проходит вне указанного контура, тело опрокидывается.
Условие равновесия тела, теория и онлайн калькуляторы
Задание: Балка массой $m$, имеющая длину $l$ лежит на двух опорах (рис.2). Какая сила давления действует на каждую из опор? Считать, что расстояние $l_1$ известно.
Решение: Рассмотрим рис.2. Обозначим силы, которые действуют на балку. Это сила тяжести ($m\overline{g}$), силы реакции опор ${\overline{N}}_1$ и ${\overline{N}}_2$. Балка находится в состоянии равновесия, следовательно, из первого условия равновесия имеем:
\[m\overline{g}+{\overline{N}}_1+{\overline{N}}_2=0\ \left(1.1\right).\]
В проекции на ось Y уравнение (1.1):
\[N_1+N_2-mg=0\ \left(1.2\right).\]
Для записи второго условия равновесия балки выберем в качестве оси вращения, ось, проходящую через первую опору. Моменты сил проектируем на ось X, перпендикулярную плоскости рисунка (рис.2). Тогда моменты сил равны:
\[{\overline{M}}_1={\overline{r}}_1\times {\overline{N}}_1=0\ \left(1. 3\right),\]
3\right),\]
так как расстояние от точки вращения до точки приложения силы ($\left|{\overline{r}}_1\right|=0$) равно нулю.
\[{\overline{M}}_2={\overline{r}}_2\times {\overline{N}}_2;;\ M_{x2}=\left(l-l_1\right)N_{2\ }\left(1.4\right),\]
где угол между ${\overline{r}}_2и\ {\overline{N}}_2$ равен 900; $\left|{\overline{r}}_2\right|=l-l_1$.
Сила тяжести приложена к центру тяжести балки, если она однородна, то цент тяжести находится на середине длины балки, получаем:
\[{\overline{M}}_3={\overline{r}}_3\times m\overline{g};;\ M_{x3}=-mg\left(\frac{l}{2}-l_1\right)\left(1.5\right),\]
Моменты сил направлены вдоль оси X. По второму условию равновесия имеем:
\[M_{x2}+M_{x3}=0\to \left(l-l_1\right)N_{2\ }-mg\left(\frac{l}{2}-l_1\right)=0\ \left(1.6\right).\]
Из выражения (1.6) найдем $N_{2\ }$:
\[N_{2\ }=\frac{mg\left(l-2l_1\right)}{2\left(l-l_1\right)}\left(1.7\right).\]
Подставим (1.7) в формулу (1.2), выразим $N_{1\ }$:
\[N_1+\frac{mg\left(l-2l_1\right)}{2\left(l-l_1\right)}-mg=0\to N_1=\frac{mgl}{2\left(l-l_1\right)}.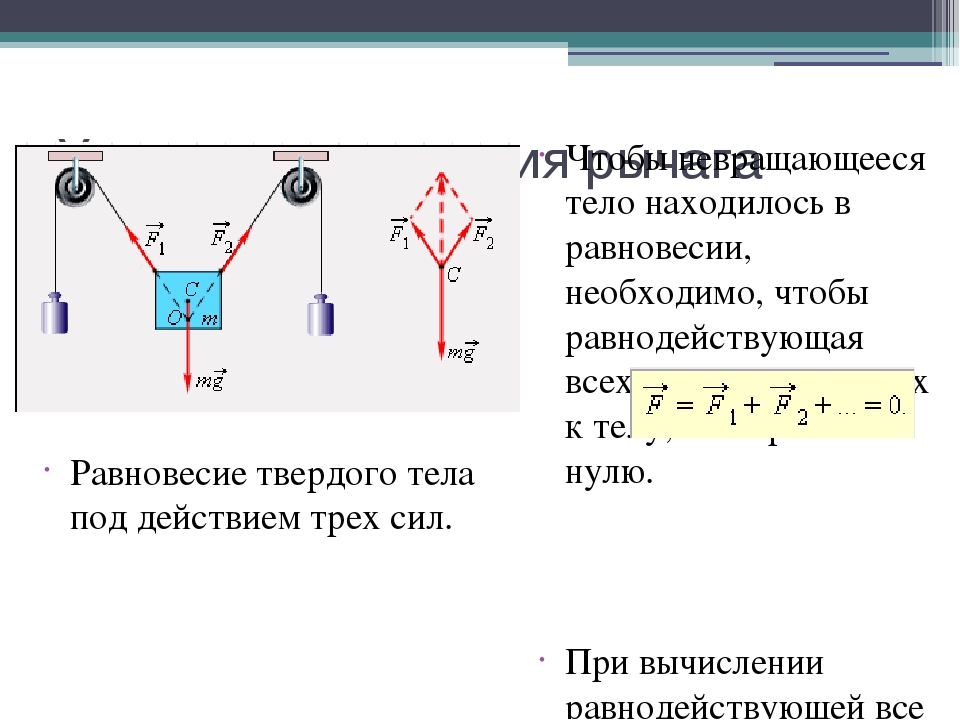 \]
\]
По третьему закону Ньютона силы давления на опоры равны по величине реакциям соответствующих опор:
\[F_1=N_1=\frac{mgl}{2\left(l-l_1\right)};;\ F_2=N_2=\frac{mg\left(l-2l_1\right)}{2\left(l-l_1\right)}.\]
Ответ: $F_1=\frac{mgl}{2\left(l-l_1\right)};;\ F_2=\frac{mg\left(l-2l_1\right)}{2\left(l-l_1\right)}$
Задачи
Задачи к уроку 50/14
1. Космическая ракета при старте с Земли движется вертикально вверх с ускорением a = 25 м/с2. Определите вес космонавта массой m = 100 кг. Ускорение свободного падения считать равным 10 м/с2.
2. Парашютист, достигнув в затяжном прыжке скорости υ1 = 60 м/с, раскрыл парашют, после чего его скорость за t = 2 с уменьшилась до υ2 = 10 м/с. Чему равен вес парашютиста массой m = 70 кг во время торможения? Ускорение свободного падения считать равным 10 м/с2.
3. Самолет, двигаясь с постоянной скоростью 720 км/ч, совершает фигуру высшего пилотажа – «мертвую петлю» – радиусом 1000 м. Чему равна перегрузка летчика в верхней точке петли? (g = 10 м/с2).
Чему равна перегрузка летчика в верхней точке петли? (g = 10 м/с2).
Задачи д/з к уроку 48/12
1. Во сколько раз изменится сила Всемирного тяготения, если массу одного тела увеличить в 3 раза, а другого уменьшить в 9 раз?
2. Во сколько раз изменится сила Всемирного тяготения, если расстояние между телами уменьшить в 5 раз?
3. С каким ускорением всплывает тело массой 25 кг, если на него действует сила Архимеда 300 Н?
Задачи д/з к уроку 60
1. Почему невозможно, из положения сидя прямо на стуле, встать на ноги, не наклонившись предварительно вперед?
2. Почему однородный прямоугольный кирпич можно положить на край стола, только если с края стола свисает не более половины длины кирпича?
3. Почему вы вынуждены отклоняться назад, когда несете в руках тяжелый груз?
Задачи д/з к уроку 58/7
1. Какова средняя сила давления F на плечо при стрельбе из автомата, если масса пули m = 10 г, а скорость пули при вылете из канала ствола v = 300 м/с? Автомат делает 300 выстрелов в минуту.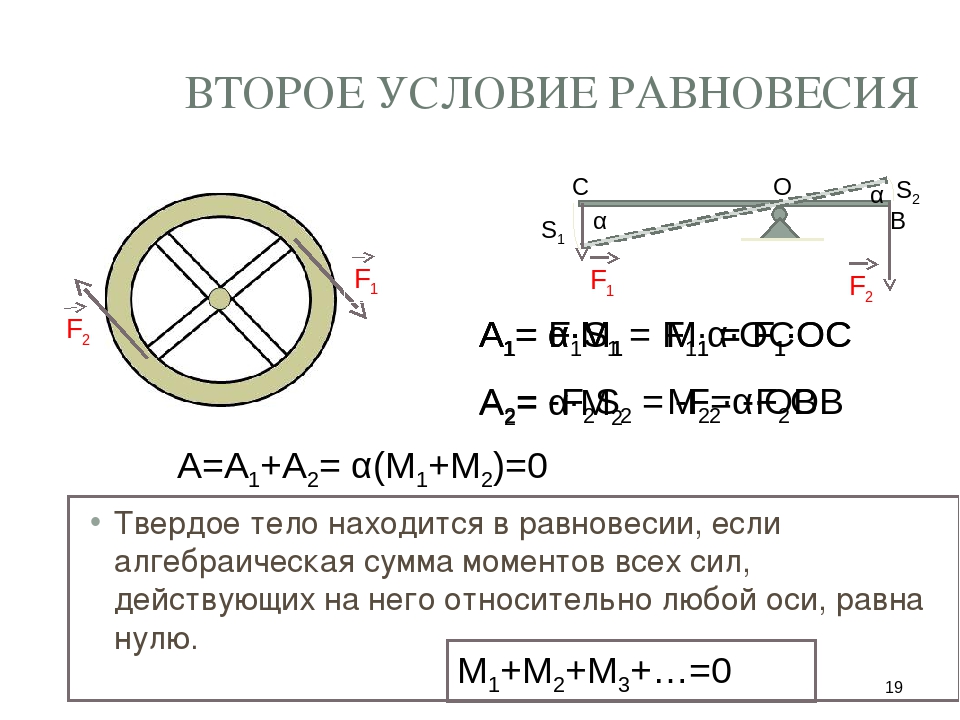
2. Для проведения огневых испытаний жидкостный ракетный двигатель закрепили на стенде. С какой силой он действует на стенд, если скорость истечения продуктов сгорания из сопла 150 м/с, а расход топлива за 5 секунд составил 30 кг?
3. Ракета массой 1000 кг неподвижно зависла над поверхностью земли. Сколько топлива в единицу времени сжигает ракета, если скорость истечения продуктов сгорания из ракеты равна 2 км/с?
Условия равновесия тел
Равновесие тела
Тело находится в состоянии покоя (или движется равномерно и прямолинейно), если векторная сумма всех сил, действующих на него, равна нулю. Говорят, что силы уравновешивают друг друга. Когда мы имеем дело с телом определенной геометрической формы, при вычислении равнодействующей силы можно все силы прикладывать к центру масс тела.
Условие равновесия тел
Чтобы тело, которое не вращается, находилось в равновесии, необходимо, чтобы равнодействующая всех сил, действующий на него, была равна нулю.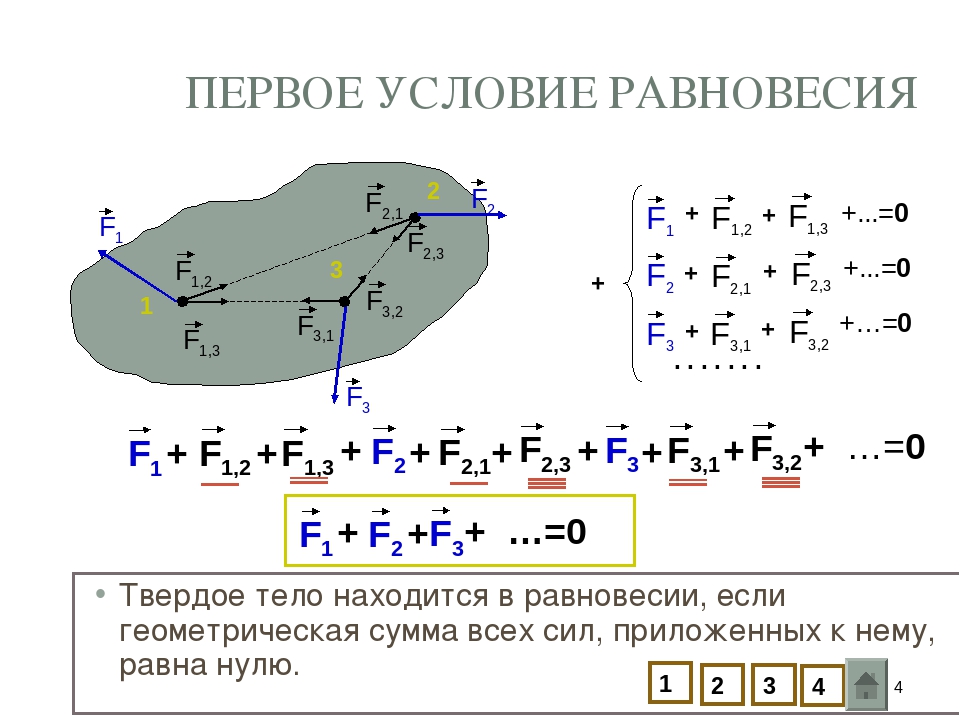
F→=F1→+F2→+..+Fn→=0.
На рисунке выше изображено равновесие твердого тела. Брусок находится в состоянии равновесия под действием трех действующих не него сил. Линии действия сил F1→ и F2→ пересекаются в точке O. Точка приложения силы тяжести — центр масс тела C. Данные точки лежат на одной прямой, и при вычислении равнодействующей силы F1→, F2→ и mg→ приводятся к точке C.
Равновесие вращающегося тела. Правило моментов
Условия равенства нулю равнодействующей всех сил недостаточно, если тело может вращаться вокруг некоторой оси.
Плечом силы d называется длина перпендикуляра, проведенного от линии действия силы к точке ее приложения. Момент силы M — произведение плеча силы на ее модуль.
M=d·F.
Момент силы стремится повернуть тело вокруг оси. Те моменты, которые поворачивают тело против часовой стрелки, считаются положительными. Единица измерения момента силы в международной системе CИ — 1 Ньютонметр.
Определение. Правило моментов
Если алгебраическая сумма всех моментов, приложенных к телу относительно неподвижной оси вращения, равна нулю, то тело находится в состоянии равновесия.
M1+M2+..+Mn=0
Важно!
В общем случае для равновесия тел необходимо выполнение двух условий: равенство нулю равнодействующей силы и соблюдение правила моментов.
Безразличное, устойчивое и неустойчивое равновесие
В механике есть разные виды равновесия. Так, различают устойчивое и неустойчивое, а также безразличное равновесие.
Типичный пример безразличного равновесия — катящееся колесо (или шар), которое, если остановить его в любой точке, окажется в состоянии равновесия.
Устойчивое равновесие — такое равновесие тела, когда при его малых отклонениях возникают силы или моменты сил, которые стремятся вернуть тело в равновесное состояние.
Неустойчивое равновесие — состояние равновесия, при малом отклонении от которого силы и моменты сил стремятся вывести тело из равновесия еще больше.
На рисунке выше положение шара (1) — безразличное равновесие, (2) — неустойчивое равновесие, (3) — устойчивое равновесие.
Тело с неподвижной осью вращения может находится в любом из описанных положений равновесия.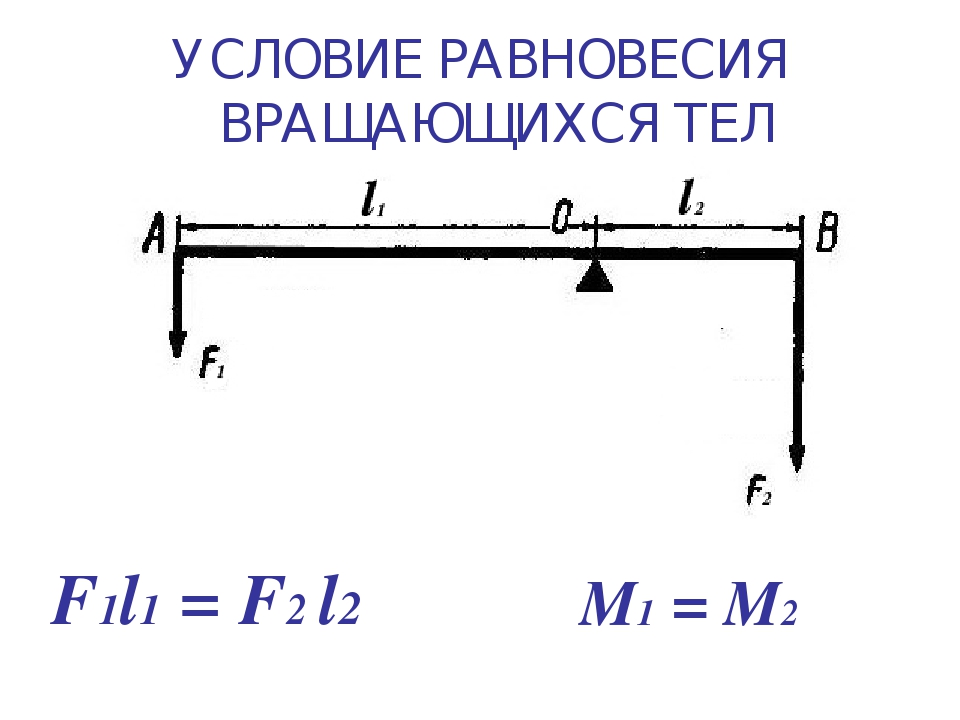 Если ось вращения проходит через центр масс, возникает безразличное равновесие. При устойчивом и неустойчивом равновесии центр масс располагается на вертикальной прямой, которая проходит через ось вращения. Когда центр масс находится ниже оси вращения, равновесие является устойчивым. Иначе — наоборот.
Если ось вращения проходит через центр масс, возникает безразличное равновесие. При устойчивом и неустойчивом равновесии центр масс располагается на вертикальной прямой, которая проходит через ось вращения. Когда центр масс находится ниже оси вращения, равновесие является устойчивым. Иначе — наоборот.
Особый случай равновесия — равновесие тела на опоре. При этом упругая сила распределяется по всему основанию тела, а не проходит через одну точку. Тело покоится в равновесии, когда вертикальная линия, проведенная через центр масс, пересекает площадь опоры. Иначе, если линия из центра масс не попадает в контур, образованный линиями, соединяющими точки опоры, тело опрокидывается.
Пример равновесия тела на опоре — знаменитая Пизанская башня. По легенде с нее сбрасывал шары Галилео Галилей, когда проводил свои опыты по изучению свободного падения тел.
Линия, проведенная из центра масс башни пересекает основание приблизительно в 2,3 м от его центра.
Условия равновесия твердого тела и системы сил
Термины «равновесие тела» и «равновесие системы сил»
Здесь мы рассматриваем условия, при которых твердое тело находится в состоянии равновесия.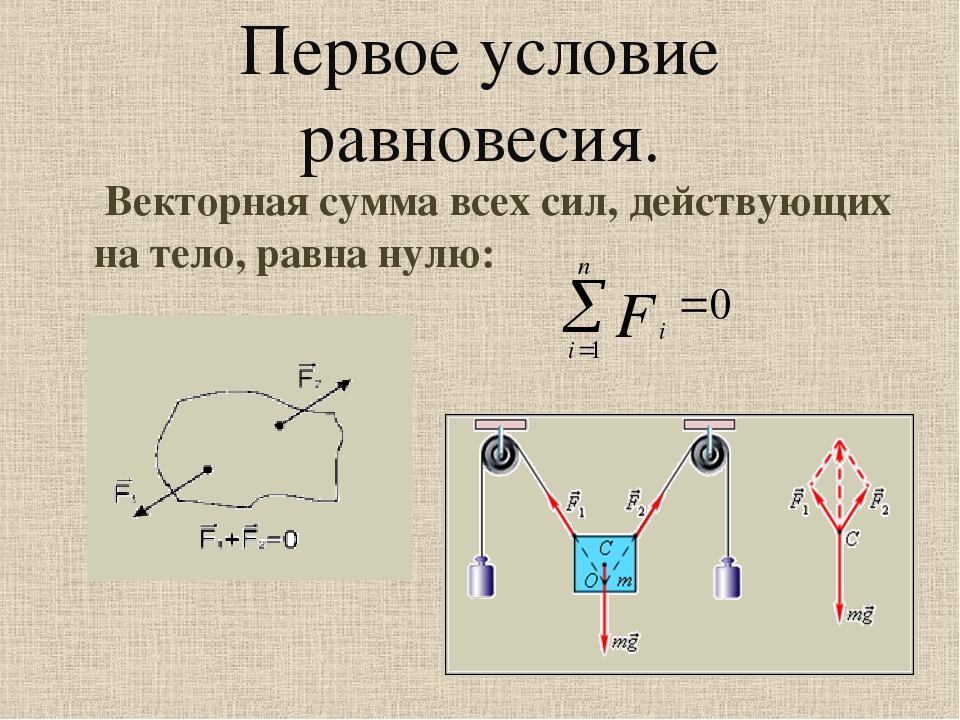 Под этим мы подразумеваем, что если тело в некоторый момент времени покоилось, то оно будет покоится и в последующие моменты времени, относительно некоторой инерциальной системы отсчета.
Под этим мы подразумеваем, что если тело в некоторый момент времени покоилось, то оно будет покоится и в последующие моменты времени, относительно некоторой инерциальной системы отсчета.
Об этом также говорят как об условиях равновесия системы сил. Под системой сил в статике всегда подразумеваются силы, действующие на абсолютно твердое тело, или на систему, которую, в соответствии с принципом затвердевания, можно считать единым твердым телом. Все законы преобразования сил относятся только к силам, действующим на одно тело. Под равновесием системы сил подразумевается уравновешенная система, которую эквивалентными преобразованиями можно свести к отсутствию сил, то есть к их взаимному уничтожению. Тогда если система сил находится в равновесии, то она эквивалентна отсутствию сил. Такая система не оказывает никакого влияния на движение тела. И если оно вначале покоилось, то будет покоиться и в последующие моменты времени.
Термин равновесие системы сил несколько отличается от термина равновесие твердого тела.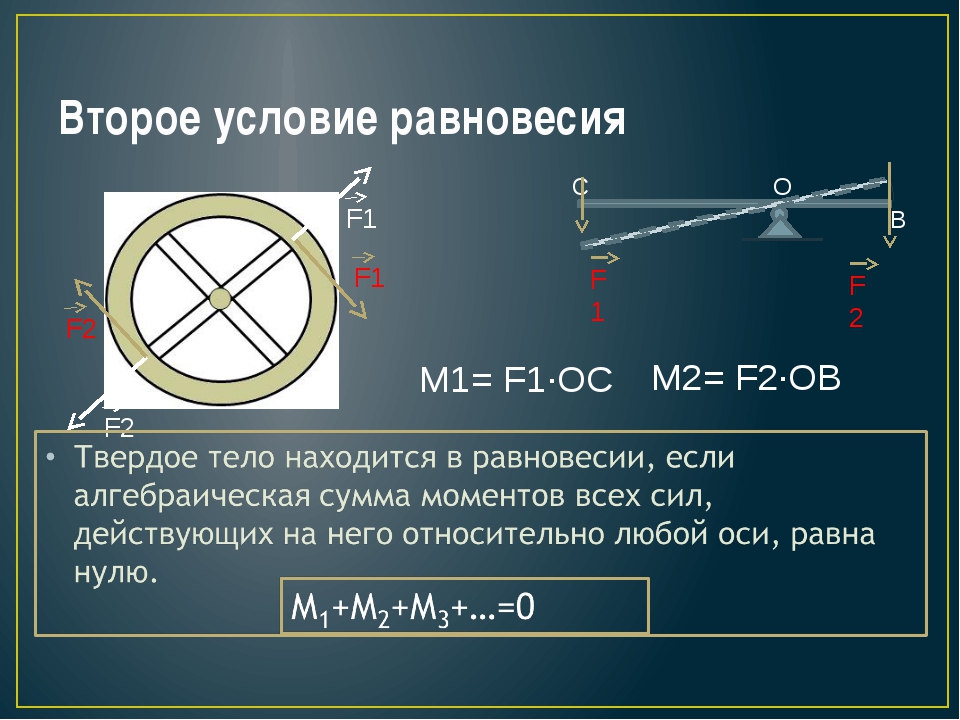 Различие связано с тем, что силы, действующие на тело можно разбить на несколько систем. Некоторые из этих систем могут находиться в равновесии, и не оказывать влияния на движение. Их можно исключить. В тоже время могут существовать неравновесные системы, приводящие к изменению скорости движения центра масс и момента импульса тела.
Различие связано с тем, что силы, действующие на тело можно разбить на несколько систем. Некоторые из этих систем могут находиться в равновесии, и не оказывать влияния на движение. Их можно исключить. В тоже время могут существовать неравновесные системы, приводящие к изменению скорости движения центра масс и момента импульса тела.
Однако, если в систему сил включены все внешние силы, то эти понятия совпадают. Далее мы будем говорить об условиях равновесия твердого тела. Эти условия есть то же самое, что условия равновесия системы сил, если под системой сил подразумевать все внешние силы, действующие на тело.
Основная форма условий равновесия
Для равновесия твердого тела необходимо и достаточно, чтобы векторная сумма внешних сил, действующих на тело равнялась нулю, и чтобы векторная сумма моментов этих сил, относительно произвольно выбранного центра C, равнялась нулю:
(1.1) ;
(1.2) .
Доказательство ⇓
Здесь внешние силы приложены к телу в точках .
Если мы выберем прямоугольную систему координат Cxyz с центром в точке C, то условия (1.1) и (1.2) можно выразить через проекции сил и моментов на оси этой системы. Тогда мы получим шесть уравнений:
; ; ;
; ; .
Из этих уравнений можно определить шесть неизвестных величин, определяющих реакции опор тела.
Также мы можем произвольным образом выбрать три вектора, не лежащие в одной плоскости, и спроектировать уравнения (1.1) и (1.2) на их направления. В результате мы также получим систему из шести уравнений.
Вторая форма условий равновесия
Условия равновесия можно записать и в других формах, которые могут оказаться более удобными при решении некоторых задач. Вот вторая форма условий равновесия.
Для равновесия твердого тела необходимо и достаточно, чтобы векторная сумма моментов внешних сил, действующих на тело, относительно произвольным образом выбранных точек и равнялась нулю, и чтобы сумма проекций сил на произвольное направление, не перпендикулярное направлению , равнялась нулю:
(2. 1) ;
1) ;
(2.2) ;
(2.3) .
Доказательство ⇓
Если спроектировать условия (2.1) и (2.2) на оси координат, то получим три уравнения (2.1), три уравнения (2.2) и одно уравнение (2.3). Всего получается семь уравнений. Однако, как показано ниже, между шестью уравнениями (2.1) и (2.2) существует одна линейная зависимость (см. «Линейная зависимость моментов относительно двух точек ⇓»). Таким образом, в условиях (2.1-3) имеется 7-1=6 линейно независимых уравнений, из которых можно определить шесть неизвестных величин.
Третья форма условий равновесия
И наконец, имеется третья форма условий равновесия.
Для равновесия твердого тела необходимо и достаточно, чтобы векторная сумма моментов внешних сил, действующих на тело, относительно произвольным образом выбранных точек и , не лежащих на одной прямой, равнялась нулю:
(3.1) ;
(3.2) ;
(3.3) ;
(3.4) .
Доказательство ⇓
Если спроектировать условия (3.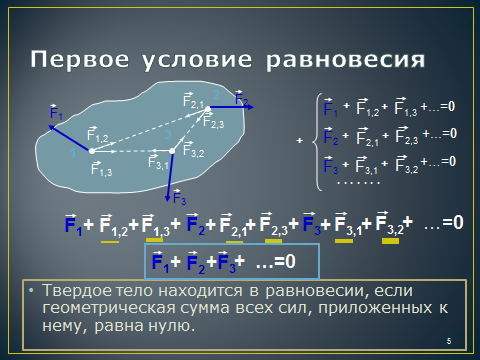 1), (3.2) и (3.3) на оси координат, то получим три уравнения (3.1), три уравнения (3.2) и три уравнения (3.3) – всего девять уравнений. Как показано ниже, между шестью уравнениями (3.1) и (3.2) существует одна линейная зависимость (см. «Линейная зависимость моментов относительно двух точек ⇓»). Аналогичным образом, между шестью уравнениями (3.1) и (3.3) существует еще одна линейная зависимость. И наконец, между шестью уравнениями (3.2) и (3.3) существует третья линейная зависимость. То есть, в условиях (3.1-3) имеется три линейных зависимости. Тогда число линейно независимых уравнений равно 9–3=6. Также, как и в предыдущих формах, из этих уравнений можно определить шесть неизвестных величин.
1), (3.2) и (3.3) на оси координат, то получим три уравнения (3.1), три уравнения (3.2) и три уравнения (3.3) – всего девять уравнений. Как показано ниже, между шестью уравнениями (3.1) и (3.2) существует одна линейная зависимость (см. «Линейная зависимость моментов относительно двух точек ⇓»). Аналогичным образом, между шестью уравнениями (3.1) и (3.3) существует еще одна линейная зависимость. И наконец, между шестью уравнениями (3.2) и (3.3) существует третья линейная зависимость. То есть, в условиях (3.1-3) имеется три линейных зависимости. Тогда число линейно независимых уравнений равно 9–3=6. Также, как и в предыдущих формах, из этих уравнений можно определить шесть неизвестных величин.
Условия равновесия плоского тела
Теперь рассмотрим плоскую систему, в которой тело может совершать движение только вдоль одной плоскости. При этом силы также направлены в этой плоскости. В этом случае мы выбираем систему отсчета так, чтобы оси x и y лежали в рассматриваемой плоскости, а ось z была ей перпендикулярна.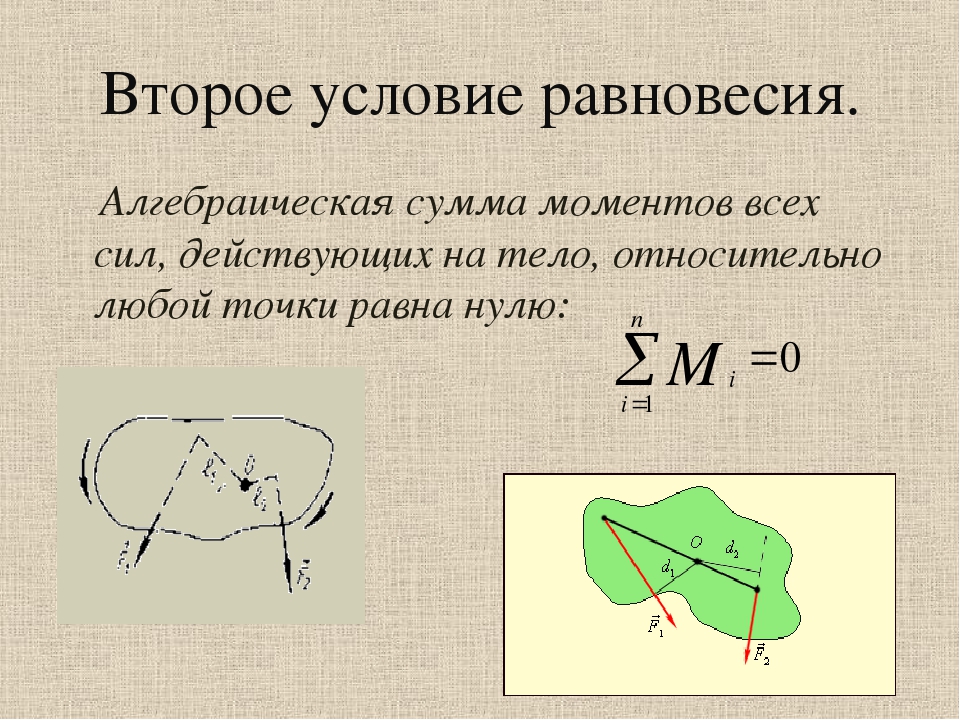 Тогда приведенные выше формы условий равновесия сохраняют свой вид. При этом z – компоненты всех сил равны нулю: , а у моментов сил отлична от нулю только z – компонента: .
Тогда приведенные выше формы условий равновесия сохраняют свой вид. При этом z – компоненты всех сил равны нулю: , а у моментов сил отлична от нулю только z – компонента: .
Выпишем условия равновесия для плоской системы, расписав их по компонентам.
Основная форма условий равновесия
;
;
.
Вторая форма условий равновесия
;
;
.
Третья форма условий равновесия
;
;
;
.
Здесь во всех формах имеется по три уравнения, из которых можно определить три неизвестных величины.
Доказательство условий равновесия
Основная форма условий равновесия
Все формы ⇑ Для равновесия твердого тела необходимо и достаточно, чтобы векторная сумма внешних сил, действующих на тело равнялась нулю, и чтобы векторная сумма моментов этих сил, относительно произвольно выбранного центра C, равнялась нулю:
(1.1)
(1.2)
Доказательство
Для доказательства воспользуемся законами движения твердого тела. Они описываются уравнениями:
Они описываются уравнениями:
(1.3) ;
(1.4) .
Здесь – ускорение центра масс тела; M – его масса; – момент импульса тела относительно произвольно выбранного центра C; – внешние силы, действующие на тело, приложенные в точках .
Необходимость.
Пусть тело находится в состоянии покоя относительно выбранной инерциальной системы координат. Тогда, в этой системе координат, скорость всех точек равна нулю. Отсюда
, .
Подставляя в (1.3) и (1.4), получаем (1.1) и (1.2).
Необходимость доказана.
Достаточность.
Пусть выполняются условия равновесия (1.1) и (1.2). Подставляя их в уравнения движения (1.3) и (1.4), получаем:
;
.
Отсюда получаем, что скорость движения центра масс и момент импульса постоянны, не меняются со временем. Пусть теперь в начальный момент времени тело покоилось. Тогда скорость движения его центра масс и момент импульса равны нулю. А поскольку они не меняются со временем, то они равны нулю и в последующие моменты времени. То есть тело остается в состоянии покоя во все моменты времени.
То есть тело остается в состоянии покоя во все моменты времени.
Свойство доказано.
Вторая форма условий равновесия
Все формы ⇑ Для равновесия твердого тела необходимо и достаточно, чтобы векторная сумма моментов внешних сил, действующих на тело, относительно произвольным образом выбранных точек и равнялась нулю, и чтобы сумма проекций сил на произвольное направление, не перпендикулярное направлению , равнялась нулю:
(2.1)
(2.2)
(2.3)
Доказательство
Необходимость.
Пусть тело находится в состоянии равновесия. Возьмем произвольные точки и и выберем произвольный вектор , не перпендикулярный прямой : . Как уже было доказано при выводе основной формы условий равновесия ⇑, выполняются условия (1.1) и(1.2):
(1.1) :
(1.2) .
Поскольку здесь C – произвольная точка, то в качестве нее возьмем точку . В результате получим (2.1):
(2.1) .
Далее, в качестве C возьмем точку . Получим (2.2):
Получим (2.2):
(2.2) .
Теперь спроектируем уравнение (1.1) на направление вектора . Получим (2.3):
(2.3) .
Это уравнение выполняется для любых векторов . В том числе и для тех, направление которых не перпендикулярно : .
Необходимость доказана.
Достаточность.
Пусть выполняются условия (2.1), (2.2) и (2.3). Докажем, что тогда тело будет находиться в состоянии равновесия. Воспользуемся векторным уравнением:
(2.4) .
Подставим его в (2.1):
.
Поскольку из (2.2), , то .
Отсюда
(2.5) ,
где λ – произвольная постоянная. Умножим это уравнение скалярно на и применим (2.3):
(2.6) .
По условию, . Поэтому .
Тогда, чтобы выполнялось (2.6) нужно положить . В результате из (2.5) получаем уравнение (1.1):
.
Условие (1.2) также выполняется, если положить . Таким образом мы получили, что если выполняются условия (2.1), (2.2) и (2.3), то выполняются условия (1.1) и (1.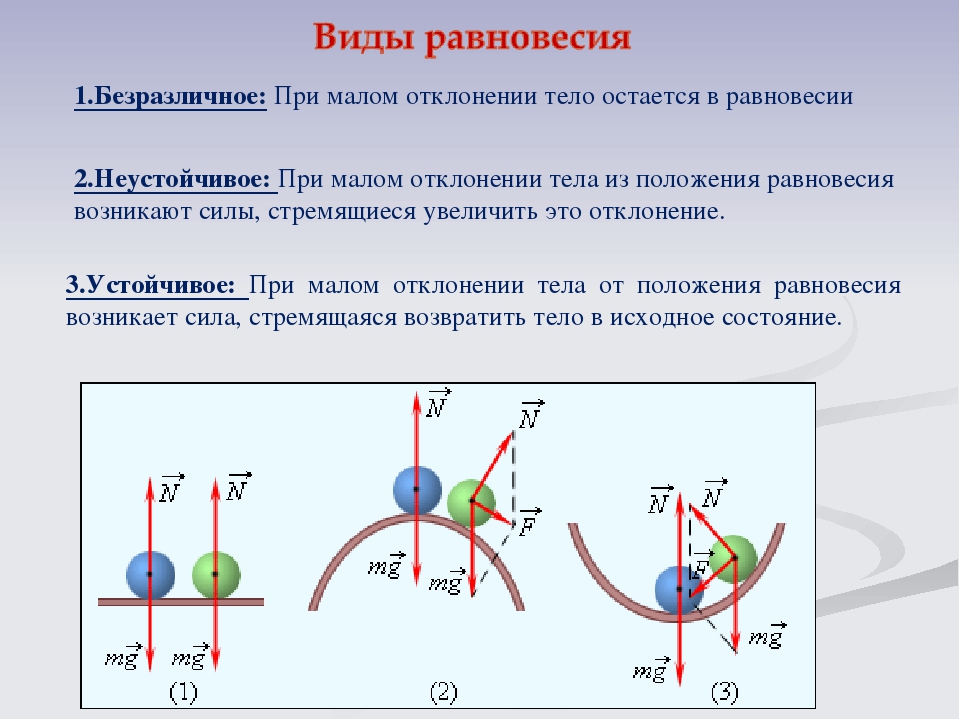 2):
2):
(1.1) ;
(1.2) .
Как мы уже доказали при выводе основной формы условий равновесия ⇑, это означает, что тело находится в равновесии.
Свойство доказано.
Линейная зависимость моментов относительно двух точек
Докажем, что уравнения (2.1) и (2.2) линейно зависимы. Для этого из (2.1) вычтем (2.2) и воспользуемся (2.4):
.
Здесь мы ввели обозначение . Умножим это уравнение скалярно на :
.
В правой части стоит смешанное произведение векторов, в которое входит два одинаковых вектора . Поэтому оно равно нулю. В результате получаем линейную зависимость между уравнениями (2.1) и (2.2):
.
Третья форма условий равновесия
Все формы ⇑ Для равновесия твердого тела необходимо и достаточно, чтобы векторная сумма моментов внешних сил, действующих на тело, относительно произвольным образом выбранных точек и , не лежащих на одной прямой, равнялась нулю:
(3.1) ;
(3.2) ;
(3. 3) ;
3) ;
(3.4) .
Доказательство
Необходимость.
Пусть тело находится в состоянии равновесия. Как уже было доказано при выводе основной формы условий равновесия ⇑, при этом выполняется условие (1.2):
(1.2) .
Возьмем произвольные точки , и , не лежащие на одной прямой. Поскольку в (1.2) C – произвольная точка, то в качестве нее возьмем последовательно точки , и . В результате получим уравнения (3.1), (3.2) и (3.3):
(3.1) ;
(3.2) ;
(3.3) .
Эти уравнения выполняются для любых точек , и . В том числе и для тех, которые не лежат на одной прямой:
(3.4) .
Необходимость доказана.
Достаточность.
Пусть выполняются условия (3.1), (3.2), (3.3) и (3.4). Докажем, что тело будет находиться в состоянии равновесия. Как и при доказательстве второй формы, воспользуемся векторным уравнением:
(3.5) .
Подставим его в (3.1):
.
Поскольку из (3.2), , то .
Отсюда
(3.6) ,
где – произвольная постоянная.
Выполняя те же действия с точками и , найдем:
(3.7) ,
где – также произвольная постоянная. Сравнивая (3.6) и (3.7) имеем:
(3.8) .
Поскольку векторы и не параллельны, то уравнение (3.8) может выполняться только при . Тогда из (3.6) следует, что .
Для доказательства того, что , достаточно умножить скалярно уравнение (3.8) на вектор, перпендикулярный и вектор, перпендикулярный .
Если обозначить точку как C, то (3.1) примет вид:
.
Итак, мы получили, что если выполняются условия (3.1), (3.2) и (3.3), то выполняются условия (1.1) и (1.2):
(1.1) ;
(1.2) .
Как мы уже доказали при выводе основной формы условий равновесия ⇑, это означает, что тело находится в равновесии.
Свойство доказано.
Автор: Олег Одинцов. Опубликовано:
Условия равновесия твердых тел
На прошлом уроке мы уже
выяснили, что для равновесия необходимо, чтобы сумма всех внешних и внутренних
сил, приложенных к телу, была равна нулю.
Но сумма всех внутренних
сил любого тела равна нулю, исходя из третьего закона Ньютона. Поэтому, первое
условие равновесия таково: сумма всех внешних сил, действующих на тело, должна
быть равна нулю:
Самой очевидной внешней
силой является сила тяжести, которая действует на все тела, находящиеся на
Земле. Но эту силу, как мы помним, могут уравновешивать другие внешние силы. В
этих случаях, возникает равновесие твердых тел.
Однако, даже если сумма
всех внешних сил, действующих на тело, равна нулю — этого еще не достаточно,
чтобы утверждать, что тело находится в равновесии. Дело в том, что тело может вращаться.
Скажем, вы можете приложить к противоположным краям линейки силы, равные по
модулю и противоположные по направлению. В этом случае, равнодействующая этих
сил будет равна нулю. Несмотря на это, линейка начнет вращаться.
Значит, нужно найти еще
одно условие, равновесия тела. Проведем простой опыт: попытайтесь положить
линейку на ластик, так, чтоб ни один из краёв линейки не касался стола. Вам
удастся сделать это только тогда, когда ластик будет точно посередине линейки.
Теперь, давайте разберемся, почему так происходит. На каждый конец линейки
действует сила тяжести. Кроме того, на ту часть линейки, которая соприкасается
с ластиком, действует реакция опоры. Очевидно, что сила тяжести, действующая на
оба конца линейки, не меняется из-за того, что вы двигаете линейку.
Значит, играет роль
расстояние от каждого из концов до точки приложения силы реакции опоры.
Рассмотрим случай очень
маленького отклонения линейки от положения равновесия. В этом случае, линейка
повернётся на очень малый угол α.
Если линейка пришла в
движение, значит, увеличилась её кинетическая энергия. А для того, чтобы
изменить кинетическую энергию, необходимо совершить работу. Давайте подсчитаем
работу сил:
Работа силы, как мы
помним, равна произведению модулей силы, перемещения, и косинуса угла между их
направлениями:
Формально, в описанной
ситуации концы линейки будут двигаться криволинейно. Но мы оговорили в самом
начале, что угол поворота очень маленький, поэтому, перемещения концов линейки
можно считать прямолинейными. В этом случае:
Очевидно, что ось
вращения проходит через середину линейки. Плечо силы — это кратчайшее
расстояние от оси вращения до линии действия силы. Произведения силы на
её плечо, называется моментом силы.
Исходя из этого, мы можем
сформулировать второе условие равновесия тел: сумма моментов внешних сил,
действующих на тело относительно оси вращения, должна быть равна нулю:
Условимся считать момент
силы положительным, если эта сила стремится повернуть тело против часовой
стрелки. И наоборот, момент силы будем считать отрицательным, если эта сила
стремится повернуть тело по часовой стрелке.
Итак, для того, чтобы
твердое тело находилось в равновесии, сумма внешних сил должна быть равна нулю
и сумма моментов внешних сил должна быть равна нулю:
Например, качаясь
на качелях, можно найти положение равновесия. Если оба человека обладают одной
и той же массой, то самое простое — это сесть обоим на самый край. Если же
массы не равны, то человек с наименьшей массой должен сесть на самый край, а
второй человек должен подсаживаться все ближе и ближе к оси вращения (то есть к
середине качели).
В какой-то момент,
расстояние от второго человека до середины качели будет меньше, чем расстояние
от первого человека до середины качели, ровно во столько раз, во сколько масса
второго человека, больше, чем масса первого человека. Это и будет означать, что
сумма моментов внешних сил равна нулю, поэтому, качели окажутся в равновесии.
Вы знаете, что качаясь на
таких качелях, нужно постоянно отталкиваться от земли.
Давайте разберемся, что
происходит в этот момент. Обозначим на рисунке силы, действующие на каждого
человека. Будем считать, что и тот, и другой человек сидит на краю качели, то
есть расстояние от каждого из них до середины качели одинаково. Итак,
представим, что один край качели, на котором сидит человек, обладающий большей
массой, только что опустился. Качели не сдвинутся с места до тех пор, пока
человек не оттолкнется от земли. Дело в том, что момент М1
> M2.
Действительно, поскольку расстояние d1
= d2,
момент силы будет больше при большей силе. Чтобы начать качаться, нужно сделать
так, чтобы момент M1
стал меньше M2.
То есть, в нашем случае, нужно сделать силу F1
меньше, чем F2.
На первый взгляд, это
кажется невозможным, поскольку изменить силу тяжести можно только изменив
массу. Но, мы имеем дело не с силой тяжести, а с весом. Вспомните, ведь именно
вес определяется как сила, действующая на опору. До тех пор, пока человек не
предпринимает никаких действий, сила тяжести уравновешивается реакцией опоры. То
есть, в данном случае, вес равен силе тяжести. Рассмотрим теперь, что
произойдет, если человек, оттолкнётся от земли. Мышцы ног приложат некоторую
силу, направленную вертикально вниз, к поверхности земли. При этом по третьему
закону Ньютона, поверхность земли подействует на человека с силой, равной по
модулю, но противоположной по направлению. То есть, эта сила будет направлена
вертикально вверх. Тогда, по второму закону Ньютона, сила тяжести будет равна
сумме силы реакции опоры и силы, с которой человек оттолкнётся от земли. Таким
образом, вес человека (равный реакции опоры N1) будет равен
разности между силой тяжести и силой F.
Теперь, если выражение F1
– F2
меньше, чем F2,
то качели начнут двигаться. Как правило, достаточно приложить сравнительно
небольшую силу, поскольку чаще всего, на таких качелях качаются люди с
приблизительно одинаковой массой. Однако, очевидно, что человек, обладающий
меньшей массой, должен будет прикладывать бо́льшую силу, чтобы нормально
качаться. Или же, человек, обладающий большей массой, должен будет
пододвинуться поближе к середине качели.
Все выше сказанное,
скорее всего, знал каждый из вас. Теперь же, вы можете описать это с точки
зрения физики и объяснить, почему так происходит.
Пример решения задачи.
Задача. На
двух веревках подвешен груз, так, как показано на рисунке. Если масса груза 20
кг,
то каковы силы натяжения веревок?
12.1 Условия статического равновесия
Цели обучения
К концу этого раздела вы сможете:
- Определите физические условия статического равновесия.
- Нарисуйте диаграмму свободного тела для твердого тела, на которое действуют силы.
- Объясните, как условия равновесия позволяют нам решать задачи статики.
Мы говорим, что твердое тело находится в состоянии равновесия , когда его линейное и угловое ускорение равны нулю относительно инерциальной системы отсчета.Это означает, что тело в состоянии равновесия может двигаться, но в этом случае его линейная и угловая скорости должны быть постоянными. Мы говорим, что твердое тело находится в состоянии статического равновесия , когда оно находится в состоянии покоя в нашей выбранной системе координат . Обратите внимание, что различие между состоянием покоя и состоянием равномерного движения является искусственным — то есть объект может находиться в состоянии покоя в выбранной нами системе отсчета, но для наблюдателя, движущегося с постоянной скоростью относительно нашей системы координат, тот же объект кажется, находится в равномерном движении с постоянной скоростью.Поскольку движение составляет относительно , то, что для нас находится в статическом равновесии, находится в динамическом равновесии для движущегося наблюдателя, и наоборот. Поскольку законы физики идентичны для всех инерциальных систем отсчета, в инерциальной системе отсчета нет различия между статическим равновесием и равновесием.
Согласно второму закону движения Ньютона, линейное ускорение твердого тела вызывается действующей на него чистой силой, или
[латекс] \ sum _ {k} {\ overset {\ to} {F}} _ {k} = m {\ overset {\ to} {a}} _ {\ text {CM}}.[/ латекс]
Здесь сумма всех внешних сил, действующих на тело, где м — это его масса, а [latex] {\ overset {\ to} {a}} _ {\ text {CM}} [/ latex] — линейное ускорение его центра масс (концепция, которую мы обсуждали в статьях «Линейный импульс и столкновения по импульсу и столкновениям»). В состоянии равновесия линейное ускорение равно нулю. Если установить нулевое ускорение на (Рисунок), мы получим следующее уравнение:
Первое условие равновесия
Первое условие равновесия для статического равновесия твердого тела выражает поступательное равновесие:
[латекс] \ sum _ {k} {\ overset {\ to} {F}} _ {k} = \ overset {\ to} {0}.[/ латекс]
Первое условие равновесия (рисунок) — это условие равновесия сил, с которым мы столкнулись при изучении приложений законов Ньютона.
Это векторное уравнение эквивалентно следующим трем скалярным уравнениям для компонентов чистой силы:
[латекс] \ sum _ {k} {F} _ {kx} = 0, \ quad \ sum _ {k} {F} _ {ky} = 0, \ quad \ sum _ {k} {F} _ {kz} = 0. [/ латекс]
Аналогично (рисунок), мы можем утверждать, что вращательное ускорение [латекс] \ overset {\ to} {\ alpha} [/ latex] твердого тела вокруг фиксированной оси вращения вызывается чистым крутящим моментом, действующим на body, или
[латекс] \ sum _ {k} {\ overset {\ to} {\ tau}} _ {k} = I \ overset {\ to} {\ alpha}.[/ латекс]
Здесь [латекс] I [/ латекс] — это инерция вращения тела при вращении вокруг этой оси, а сумма составляет более всех крутящих моментов [латекс] {\ overset {\ to} {\ tau}} _ {k} [/ latex] внешних сил в (Рисунок). В состоянии равновесия ускорение вращения равно нулю. Обнуляя правую часть (рисунок), мы получаем второе условие равновесия:
Второе состояние равновесия
Второе условие равновесия для статического равновесия твердого тела выражает вращательное равновесие:
[латекс] \ sum _ {k} {\ overset {\ to} {\ tau}} _ {k} = \ overset {\ to} {0}.[/ латекс]
Второе условие равновесия (рисунок) — это условие равновесия для крутящих моментов, с которым мы столкнулись при изучении динамики вращения. Стоит отметить, что это уравнение равновесия обычно справедливо для вращательного равновесия вокруг любой оси вращения (фиксированной или иной). Опять же, это векторное уравнение эквивалентно трем скалярным уравнениям для векторных компонентов чистого крутящего момента:
[латекс] \ sum _ {k} {\ tau} _ {kx} = 0, \ quad \ sum _ {k} {\ tau} _ {ky} = 0, \ quad \ sum _ {k} {\ тау} _ {kz} = 0.[/ латекс]
Второе условие равновесия означает, что в равновесии нет чистого внешнего крутящего момента, вызывающего вращение вокруг любой оси.
Первое и второе условия равновесия указаны в конкретной системе отсчета. Первое условие включает только силы и поэтому не зависит от источника системы отсчета. Однако второе условие включает крутящий момент, который определяется как перекрестное произведение, [латекс] {\ overset {\ to} {\ tau}} _ {k} = {\ overset {\ to} {r}} _ {k } \, × \, {\ overset {\ to} {F}} _ {k}, [/ latex], где вектор положения [latex] {\ overset {\ to} {r}} _ {k} [/ латекс] относительно оси вращения точки приложения силы входит в уравнение.Следовательно, крутящий момент зависит от положения оси в системе отсчета. Однако, когда условия вращательного и поступательного равновесия выполняются одновременно в одной системе отсчета, они также сохраняются в любой другой инерциальной системе отсчета, так что чистый крутящий момент вокруг любой оси вращения по-прежнему равен нулю. Объяснение этому довольно простое.
Предположим, что вектор [latex] \ overset {\ to} {R} [/ latex] — это позиция начала координат новой инерциальной системы отсчета [latex] S \ prime [/ latex] в старой инерциальной системе отсчета S .{\ prime}} _ {k} \, × \, {\ overset {\ to} {F}} _ {k} = \ sum _ {k} ({\ overset {\ to} {r}} _ { k} — \ overset {\ to} {R}) \, × \, {\ overset {\ to} {F}} _ {k} = \ sum _ {k} {\ overset {\ to} {r} } _ {k} \, × \, {\ overset {\ to} {F}} _ {k} — \ sum _ {k} \ overset {\ to} {R} \, × \, {\ overset { \ to} {F}} _ {k} = \ sum _ {k} {\ overset {\ to} {\ tau}} _ {k} — \ overset {\ to} {R} \, × \, \ сумма _ {k} {\ overset {\ to} {F}} _ {k} = \ overset {\ to} {0}. [/ латекс]
На последнем этапе этой цепочки рассуждений мы использовали тот факт, что в равновесии в старой системе отсчета, S , первый член исчезает из-за (Рисунок), а второй член исчезает из-за (Рисунок).Следовательно, мы видим, что чистый крутящий момент в любой инерциальной системе отсчета [латекс] S \ prime [/ latex] равен нулю, при условии, что оба условия равновесия выполняются в инерциальной системе отсчета S .
Практическое значение этого состоит в том, что при применении условий равновесия для твердого тела мы можем выбрать любую точку в качестве начала отсчета системы отсчета. Наш выбор системы отсчета продиктован физическими особенностями решаемой проблемы. В одной системе координат математическая форма условий равновесия может быть довольно сложной, тогда как в другой системе координат те же условия могут иметь более простую математическую форму, которую легко решить.Начало выбранной системы отсчета называется точкой поворота .
В самом общем случае условия равновесия выражаются шестью скалярными уравнениями ((Рисунок) и (Рисунок)). Для плоских задач равновесия с вращением вокруг фиксированной оси, которые мы рассматриваем в этой главе, мы можем сократить количество уравнений до трех. Стандартная процедура заключается в принятии системы отсчета, в которой ось z является осью вращения. При таком выборе оси чистый крутящий момент имеет только компонент z , все силы, которые имеют ненулевые крутящие моменты, лежат в плоскости xy , и, следовательно, вклад в чистый крутящий момент поступает только от x — и y — составляющие внешних сил.Таким образом, для плоских задач с осью вращения, перпендикулярной плоскости xy , мы имеем следующие три условия равновесия для сил и моментов:
[латекс] {F} _ {1x} + {F} _ {2x} + \ text {⋯} + {F} _ {Nx} = 0 [/ латекс]
[латекс] {F} _ {1y} + {F} _ {2y} + \ text {⋯} + {F} _ {Ny} = 0 [/ латекс]
[латекс] {\ tau} _ {1} + {\ tau} _ {2} + \ text {⋯} + {\ tau} _ {N} = 0 [/ латекс]
, где суммирование ведется по всем внешним силам N , действующим на тело, и их крутящим моментам.На (Рисунок) мы упростили обозначения, опустив индекс z , но мы понимаем, что здесь суммирование ведется по всем вкладам вдоль оси z , которая является осью вращения. На (Рисунок) z -компонент крутящего момента [латекс] {\ overset {\ to} {\ tau}} _ {k} [/ latex] от силы [латекс] {\ overset {\ to} { F}} _ {k} [/ latex] —
[латекс] {\ tau} _ {k} = {r} _ {k} {F} _ {k} \ text {sin} \, \ theta [/ latex]
где [латекс] {r} _ {k} [/ latex] — длина плеча рычага силы, а [latex] {F} _ {k} [/ latex] — величина силы (как вы пила в режиме вращения с фиксированной осью).Угол [latex] \ theta [/ latex] — это угол между векторами [latex] {\ overset {\ to} {r}} _ {k} [/ latex] и [latex] {\ overset {\ to} { F}} _ {k}, [/ latex] измерение от вектора [latex] {\ overset {\ to} {r}} _ {k} [/ latex] до вектора [latex] {\ overset { \ to} {F}} _ {k} [/ latex] в направлении против часовой стрелки ((рисунок)). При использовании (Рисунок) мы часто вычисляем величину крутящего момента и назначаем его значение либо положительным [латекс] (+) [/ латекс], либо отрицательным [латекс] (-), [/ латекс] в зависимости от направления вращения, вызванного только этим крутящим моментом.На (Рисунок) чистый крутящий момент представляет собой сумму членов, каждый член вычисляется из (Рисунок), и каждый член должен иметь правильное значение . Точно так же на (Рисунок) мы назначаем знак [latex] + [/ latex] компонентам в направлении [latex] + [/ latex] x и знак [latex] — [/ latex] компонентам. в направлении [латекс] — [/ латекс] x . Это же правило должно последовательно соблюдаться на (Рисунок) при вычислении составляющих силы по оси y .
Рисунок 12.2 Крутящий момент силы: (a) Когда крутящий момент силы вызывает вращение против часовой стрелки вокруг оси вращения, мы говорим, что его направление положительное, что означает, что вектор крутящего момента параллелен оси вращения. (b) Когда крутящий момент силы вызывает вращение вокруг оси по часовой стрелке, мы говорим, что его направление отрицательное, что означает, что вектор крутящего момента антипараллелен оси вращения.
Во многих ситуациях равновесия одной из сил, действующих на тело, является его вес.На диаграммах свободного тела вектор веса привязан к центру тяжести тела. Для всех практических целей центр тяжести идентичен центру масс, как вы узнали из статей «Линейный импульс» и «Столкновения» о линейном импульсе и столкновениях. Только в тех случаях, когда тело имеет большую пространственную протяженность, так что гравитационное поле неоднородно по всему его объему, центр тяжести и центр масс расположены в разных точках. Однако на практике даже такие большие объекты, как здания или круизные лайнеры, находятся в однородном гравитационном поле на поверхности Земли, где ускорение свободного падения имеет постоянную величину [латекс] g = 9.{2}. [/ latex] В этих ситуациях центр тяжести идентичен центру масс. Поэтому на протяжении всей главы мы используем центр масс (CM) как точку, к которой прикреплен вектор веса. Напомним, что ЦМ имеет особый физический смысл: когда внешняя сила приложена к телу точно в его ЦМ, тело в целом совершает поступательное движение, и такая сила не вызывает вращения.
Когда ЦМ расположен вне оси вращения, на объекте возникает чистый гравитационный момент .Гравитационный момент — это крутящий момент, вызванный весом. Этот гравитационный момент может вращать объект, если нет опоры для его балансировки. Величина гравитационного момента зависит от того, как далеко от оси находится ЦМ. Например, в случае самосвала ((Рисунок)) ось поворота расположена на линии, где шины соприкасаются с поверхностью дороги. Если CM расположен высоко над поверхностью дороги, гравитационный момент может быть достаточно большим, чтобы перевернуть грузовик.Легковые автомобили с низко расположенной КМ, близкой к тротуару, более устойчивы к опрокидыванию, чем грузовики.
Рисунок 12.3 Распределение массы влияет на положение центра масс (CM), к которому прикреплен вектор веса [latex] \ overset {\ to} {w} [/ latex]. Если центр тяжести находится в зоне опоры, погрузчик возвращается в исходное положение после опрокидывания [см. Левую панель в (b)]. Но если центр тяжести находится за пределами зоны опоры, грузовик перевернется [см. Правую панель в (b)].Оба транспортных средства в (b) находятся вне равновесия. Обратите внимание, что автомобиль на (а) находится в равновесии: низкое расположение центра тяжести затрудняет опрокидывание.
Пример
Центр тяжести автомобиля
Легковой автомобиль с колесной базой 2,5 м имеет 52% веса на передние колеса на ровной поверхности, как показано на (Рисунок). Где находится ЦМ этого автомобиля по отношению к задней оси?
Рисунок 12.4 Распределение веса между осями автомобиля.Где находится центр тяжести?
Стратегия
Вес автомобиля w нам неизвестен. Все, что мы знаем, это то, что когда автомобиль стоит на ровной поверхности, 0,52 w давит на поверхность в точках контакта передних колес, а 0,48 w толкает вниз на поверхность в точках контакта задних колес. Также точки контакта отделены друг от друга расстоянием [латекс] d = 2,5 \, \ text {m}. [/ latex] В этих точках контакта автомобиль испытывает нормальные силы реакции с величиной [латекс] {F} _ {\ text {F}} = 0.52 Вт [/ латекс] и [латекс] {F} _ {\ text {R}} = 0,48 Вт [/ латекс] на передней и задней осях соответственно. Мы также знаем, что автомобиль является примером твердого тела, находящегося в равновесии, весь вес которого w действует на его ЦМ. CM находится где-то между точками, где действуют нормальные силы реакции, где-то на расстоянии x от точки, где действует [латекс] {F} _ {R} [/ латекс]. Наша задача найти х . Таким образом, мы идентифицируем три силы, действующие на тело (автомобиль), и можем нарисовать диаграмму свободного тела для расширенного твердого тела, как показано на (Рисунок).
Рисунок 12.5 Диаграмма свободного тела для автомобиля четко указывает векторы сил, действующих на автомобиль, и расстояния до центра масс (CM). Когда CM выбран в качестве точки поворота, эти расстояния представляют собой плечи рычага нормальных сил реакции. Обратите внимание, что величины векторов и рычаги не нужно рисовать в масштабе, но все релевантные величины должны быть четко обозначены.
Мы почти готовы записать условия равновесия (рисунок) — (рисунок) для автомобиля, но сначала мы должны определиться с системой отсчета.Предположим, мы выбрали ось x по длине кабины, ось y — вертикальную, а ось z — перпендикулярно этой плоскости xy . При таком выборе нам нужно только написать (рисунок) и (рисунок), потому что все компоненты y тождественно равны нулю. Теперь нам нужно определиться с расположением точки поворота. Мы можем выбрать любую точку в качестве местоположения оси вращения ( z -ось). Предположим, мы разместили ось вращения на CM, как показано на схеме свободного тела для автомобиля.На этом этапе мы готовы написать условия равновесия для автомобиля.
Решение
Каждое условие равновесия содержит только три члена, потому что на автомобиль действуют силы [latex] N = 3 [/ latex]. Первое условие равновесия (рисунок) читается как
.
[латекс] + {F} _ {\ text {F}} — w + {F} _ {\ text {R}} = 0. [/ латекс]
Это условие тривиально выполняется, потому что, когда мы подставляем данные, (рисунок) становится [латекс] + 0,52w-w + 0,48w = 0. [/ latex] Второе условие равновесия (рисунок) читается как
.
[латекс] {\ tau} _ {\ text {F}} + {\ tau} _ {w} + {\ tau} _ {\ text {R}} = 0 [/ латекс]
где [латекс] {\ tau} _ {\ text {F}} [/ latex] — это крутящий момент силы [латекс] {F} _ {\ text {F}}, \, {\ tau} _ {w } [/ latex] — это гравитационный момент силы w , а [latex] {\ tau} _ {\ text {R}} [/ latex] — это крутящий момент силы [latex] {F} _ {\ text {Р}}.[/ latex] Когда ось расположена в CM, гравитационный момент идентично нулю, потому что плечо рычага веса относительно оси, которая проходит через CM, равно нулю. Линии действия обеих нормальных сил реакции перпендикулярны плечам их рычагов, поэтому на (Рисунок) мы имеем [latex] | \, \ text {sin} \, \ theta | = 1 [/ latex] для обеих сил. Из диаграммы свободного тела мы читаем, что крутящий момент [латекс] {\ tau} _ {\ text {F}} [/ latex] вызывает вращение по часовой стрелке вокруг оси в CM, поэтому его смысл отрицательный; и крутящий момент [latex] {\ tau} _ {\ text {R}} [/ latex] вызывает вращение против часовой стрелки вокруг оси в CM, поэтому его смысл положительный.Имея эту информацию, запишем второе условие равновесия как
[латекс] \ text {-} {r} _ {\ text {F}} {F} _ {\ text {F}} + {r} _ {\ text {R}} {F} _ {\ text {R}} = 0. [/ латекс]
С помощью диаграммы свободного тела мы определяем величины силы [латекс] {F} _ {\ text {R}} = 0,48w [/ латекс] и [латекс] {F} _ {\ text {F }} = 0,52w, [/ latex] и соответствующие им рычаги [латекс] {r} _ {\ text {R}} = x [/ latex] и [latex] {r} _ {\ text {F}} = dx. [/ latex] Теперь мы можем записать второе условие равновесия (рисунок) в явном виде в терминах неизвестного расстояния x :
[латекс] -0.52 (г-х) ш + 0,48 х ш = 0. [/ латекс]
Здесь вес w отменяется, и мы можем решить уравнение для неизвестного положения x CM. Ответ: [латекс] x = 0,52d = 0,52 (2,5 \, \ text {m}) = 1,3 \, \ text {m} \ text {.} [/ Latex]
Решение
Выбор шарнира в положении передней оси не меняет результата. Схема свободного тела для этого места поворота представлена на (Рисунок). Для этого выбора точки поворота второе условие равновесия равно
.
[латекс] \ text {-} {r} _ {w} w + {r} _ {\ text {R}} {F} _ {\ text {R}} = 0.[/ латекс]
Когда мы подставляем числа, указанные на диаграмме, получаем
[латекс] \ text {-} (d-x) w + 0,48dw = 0. [/ латекс]
Ответ, полученный путем решения (рисунок), опять же, [латекс] x = 0,52d = 1,3 \, \ text {m}. [/ латекс]
Рисунок 12.6 Эквивалентная диаграмма свободного тела для автомобиля; точка поворота четко обозначена.
Значение
Этот пример показывает, что при решении задач статического равновесия мы можем выбрать точку поворота.Для различных вариантов выбора точки поворота у нас есть разные наборы условий равновесия, которые необходимо решить. Однако любой выбор приводит к одному и тому же решению проблемы.
Проверьте свое понимание
Решите (рисунок), выбрав шарнир в месте расположения задней оси.
Показать решение
[латекс] x = 1,3 \, \ text {m} [/ латекс]
Проверьте свое понимание
Объясните, какая из следующих ситуаций удовлетворяет обоим условиям равновесия: (а) теннисный мяч, который не вращается при движении в воздухе; (б) пеликан, который парит в воздухе с постоянной скоростью на одной высоте; или (c) коленчатый вал двигателя припаркованного автомобиля.
Особый случай статического равновесия возникает, когда все внешние силы на объект действуют на оси вращения или вдоль нее, или когда пространственное протяжение объекта можно не принимать во внимание. В таком случае объект можно эффективно рассматривать как точечную массу. В этом частном случае нам не нужно беспокоиться о втором условии равновесия (рисунок), потому что все крутящие моменты тождественно равны нулю, а первое условие равновесия (для сил) является единственным условием, которое должно выполняться. Диаграмма свободного тела и стратегия решения проблем для этого особого случая были изложены в «Законах Ньютона» и «Приложениях законов Ньютона».В следующем примере вы увидите типичную ситуацию равновесия, включающую только первое условие равновесия.
Пример
Разрывное напряжение
Маленькая кастрюля массой 42,0 г поддерживается двумя струнами, как показано на (Рисунок). Максимальное натяжение, которое может выдержать струна, составляет 2,80 Н. Масса постепенно добавляется к чаше, пока одна из струн не сломается. Какая это струна? Какую массу нужно добавить, чтобы это произошло?
Рисунок 12.7 Масса постепенно добавляется к кастрюле, пока одна из струн не лопнет.
Стратегия
Эта механическая система, состоящая из струн, масс и сковороды, находится в статическом равновесии. В частности, узел, который привязывает струны к кастрюле, находится в статическом равновесии. Узел можно рассматривать как точку; следовательно, нам нужно только первое условие равновесия. Три силы, тянущие к узлу: натяжение [латекс] {\ overset {\ to} {T}} _ {1} [/ latex] в 5,0-сантиметровой струне, натяжение [латекс] {\ overset {\ to } {T}} _ {2} [/ latex] в веревке длиной 10,0 см и вес [латекс] \ overset {\ to} {w} [/ latex] сковороды, удерживающей гири.Мы принимаем прямоугольную систему координат с осью y , направленной противоположно направлению силы тяжести, и рисуем диаграмму свободного тела для узла (см. (Рисунок)). Чтобы найти компоненты натяжения, мы должны определить углы направления [латекс] {\ alpha} _ {1} [/ latex] и [latex] {\ alpha} _ {2} [/ latex], которые образуют струны с горизонтальным направление оси x . Как вы можете видеть на (Рисунок), струны составляют две стороны прямоугольного треугольника. Мы можем использовать теорему Пифагора, чтобы решить этот треугольник, показанный на (Рисунок), и найти синус и косинус углов [латекс] {\ alpha} _ {1} [/ latex] и [latex] {\ alpha} _ {2}.[/ latex] Затем мы можем разложить натяжения на их прямоугольные составляющие, подставить в первое условие равновесия ((Рисунок) и (Рисунок)) и найти натяжения в струнах. Первой порвется струна с большим натяжением.
Рисунок 12.8 Схема свободного тела для узла на (Рисунок).
Решение
Вес w , натягивающий узел, обусловлен массой M кастрюли и массой m , добавленной к кастрюле, или [латекс] w = (M + m) g.[/ latex] С помощью диаграммы свободного тела на (Рисунок) мы можем установить условия равновесия для узла:
[латекс] \ begin {array} {ccccc} \ text {в направлении} \, x \ text {-direction,} \ hfill & & \ hfill \ text {-} {T} _ {1x} + {T} _ {2x} & = \ hfill & 0 \ hfill \\ \ text {в направлении} \, y \ text {,} \ hfill & & \ hfill \ text {+} {T} _ {1y} + { T} _ {2y} -w & = \ hfill & 0. \ hfill \ end {array} [/ latex]
Из диаграммы свободного тела, величины компонентов в этих уравнениях равны
.
[латекс] \ begin {array} {ccc} {T} _ {1x} = {T} _ {1} \ text {cos} \, {\ alpha} _ {1} = {T} _ {1} \ text {/} \ sqrt {5}, \ hfill & & {T} _ {1y} = {T} _ {1} \ text {sin} \, {\ alpha} _ {1} = 2 {T} _ {1} \ text {/} \ sqrt {5} \ hfill \\ {T} _ {2x} = {T} _ {2} \ text {cos} \, {\ alpha} _ {2} = 2 {T} _ {2} \ text {/} \ sqrt {5}, \ hfill & & {T} _ {2y} = {T} _ {2} \ text {sin} \, {\ alpha} _ { 2} = {T} _ {2} \ text {/} \ sqrt {5}.\ hfill \ end {array} [/ latex]
Подставляем эти компоненты в условия равновесия и упрощаем. Затем мы получаем два уравнения равновесия для натяжений:
[латекс] \ begin {array} {ccccc} \ text {in} \, x \ text {-direction,} \ hfill & & \ hfill {T} _ {1} & = \ hfill & 2 {T} _ {2} \ hfill \\ \ text {in} \, y \ text {-direction,} \ hfill & & \ hfill \ frac {2 {T} _ {1}} {\ sqrt {5}} + \ frac {{T} _ {2}} {\ sqrt {5}} & = \ hfill & (M + m) g. \ Hfill \ end {array} [/ latex]
Уравнение равновесия для направления x говорит нам, что натяжение [латекс] {T} _ {1} [/ латекс] в 5.0-сантиметровая струна вдвое превышает натяжение [латекс] {T} _ {2} [/ latex] в 10-сантиметровой струне. Таким образом, более короткая струна порвется. Когда мы используем первое уравнение, чтобы исключить [латекс] {T} _ {2} [/ latex] из второго уравнения, мы получаем соотношение между массой [латекс] м [/ латекс] на сковороде и натяжением [латекс ] {T} _ {1} [/ latex] в более короткой строке:
[латекс] 2,5 {T} _ {1} \ text {/} \ sqrt {5} = (M + m) г. [/ латекс]
Струна разрывается, когда натяжение достигает критического значения [латекс] {T} _ {1} = 2.{2}} — 0,042 \, \ text {kg} = 0,277 \, \ text {kg} = 277,0 \, \ text {g.} [/ Latex]
Значение
Предположим, что механическая система, рассматриваемая в этом примере, прикреплена к потолку внутри лифта, поднимающегося вверх. Пока лифт движется вверх с постоянной скоростью, результат остается неизменным, потому что вес [латекс] w [/ латекс] не меняется. Если лифт движется вверх с ускорением, критическая масса меньше, потому что вес [латекса] M + m [/ латекса] становится больше на кажущийся вес из-за ускорения лифта.Тем не менее, во всех случаях более короткая струна рвется первой.
Сводка
- Тело находится в равновесии, когда оно остается либо в равномерном движении (поступательном и вращательном), либо в состоянии покоя. Когда тело в выбранной инерциальной системе отсчета не вращается и не движется в поступательном движении, мы говорим, что тело находится в статическом равновесии в этой системе отсчета.
- Условия равновесия требуют, чтобы сумма всех внешних сил, действующих на тело, была равна нулю (первое условие равновесия), а сумма всех внешних моментов от внешних сил была равна нулю (второе условие равновесия).Эти два условия должны одновременно выполняться в состоянии равновесия. Если один из них не удовлетворен, тело не находится в равновесии.
- Диаграмма свободного тела для тела — полезный инструмент, который позволяет нам правильно подсчитать все вклады от всех внешних сил и моментов, действующих на тело. Диаграммы свободного тела для равновесия вытянутого твердого тела должны указывать точку поворота и плечи рычага действующих сил по отношению к оси вращения.
Концептуальные вопросы
Что вы можете сказать о скорости движущегося тела, находящегося в динамическом равновесии?
При каких условиях вращающееся тело может находиться в равновесии? Привести пример.
Какие три фактора влияют на крутящий момент, создаваемый силой относительно определенной точки поворота?
Показать решение
величина и направление силы, а ее плечо рычага
Механики иногда кладут кусок трубы на рукоятку гаечного ключа, когда пытаются открутить очень тугой болт. Как это помогает?
Для следующих четырех задач оцените утверждение как истинное или ложное и объясните свой ответ.
Если на объект действует только одна внешняя сила (или крутящий момент), он не может находиться в равновесии.
Показать решение
Верно, поскольку в этом случае сумма сил не может быть равна нулю, если сама сила не равна нулю.
Если объект находится в равновесии, на него должно действовать четное число сил.
Если на объект действует нечетное количество сил, объект не может находиться в равновесии.
Показать решение
Ложь, если силы складываются в ноль как векторы, тогда равновесие может быть достигнуто.
Тело, движущееся по окружности с постоянной скоростью, находится в равновесии вращения.
Для чего нужен длинный и гибкий шест, который переносят канатоходцы?
Показать решение
Помогает канатоходцу сохранять равновесие.
Проблемы
При затяжке болта вы нажимаете гаечный ключ перпендикулярно с усилием 165 Н на расстоянии 0,140 м от центра болта. Какой крутящий момент вы прикладываете относительно центра болта?
При открытии двери вы нажимаете на нее перпендикулярно с силой 55.0 Н на расстоянии 0,850 м от петель. Какой крутящий момент вы прикладываете относительно петель?
Показать решение
[латекс] 46,8 \, \ text {N} · \ text {m} [/ латекс]
Найдите величину натяжения каждого поддерживающего троса, показанного ниже. В каждом случае вес подвешенного тела составляет 100,0 Н, а массой кабелей можно пренебречь.
Какая сила должна быть приложена в точке P , чтобы удерживать показанную конструкцию в равновесии? Вес конструкции незначительный.
Можно ли приложить силу к P , чтобы удерживать в равновесии показанную конструкцию? Вес конструкции незначительный.
Двое детей толкают противоположные стороны двери во время игры. Оба толкаются горизонтально и перпендикулярно двери. Один ребенок толкает с силой 17,5 Н на расстоянии 0,600 м от петель, а второй ребенок толкает на расстоянии 0,450 м. Какую силу должен приложить второй ребенок, чтобы дверь не двигалась? Предположим, трение незначительно.
Небольшой внедорожник массой 1000 кг имеет колесную базу 3,0 м. Если 60%, если его вес приходится на передние колеса, как далеко за передними колесами находится центр масс фургона?
Унифицированные качели сбалансированы в центре масс, как показано ниже. Маленький мальчик справа имеет массу 40,0 кг. Какая масса у его друга?
Глоссарий
- центр тяжести
- точка, к которой прикреплен вектор весов
- равновесие
- находится в равновесии, когда его линейное и угловое ускорения равны нулю относительно инерциальной системы отсчета
Тело
- первое условие равновесия
- выражает поступательное равновесие; все внешние силы, действующие на тело, уравновешиваются и их векторная сумма равна нулю
- гравитационный момент
- крутящий момент на корпусе, вызванный его весом; возникает, когда центр тяжести тела не расположен на оси вращения
- второе состояние равновесия
- выражает вращательное равновесие; все крутящие моменты от внешних сил, действующих на тело, уравновешиваются и их векторная сумма равна нулю
- статическое равновесие
- Тело находится в статическом равновесии, когда оно покоится в нашей выбранной инерциальной системе отсчета
ньютоновская механика — Условия статического равновесия твердого тела
ньютоновская механика — Условия статического равновесия твердого тела — Physics Stack Exchange
Сеть обмена стеком
Сеть Stack Exchange состоит из 176 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.
Посетить Stack Exchange
0
+0
- Авторизоваться
Зарегистрироваться
Physics Stack Exchange — это сайт вопросов и ответов для активных исследователей, ученых и студентов-физиков.Регистрация займет всего минуту.
Зарегистрируйтесь, чтобы присоединиться к этому сообществу
Кто угодно может задать вопрос
Кто угодно может ответить
Лучшие ответы голосуются и поднимаются наверх
Спросил
Просмотрено
520 раз
$ \ begingroup $
На этот вопрос уже есть ответы :
Закрыт 2 года назад.
Когда на твердое тело действуют силы, два условия, которые должны быть выполнены для того, чтобы тело находилось в статическом равновесии:
1. Сумма всех сил должна быть равна нулю (поступательное равновесие):
$$ \ sum_i F_i = 0 $$
2. Сумма всех моментов относительно любой точки должна быть равна нулю (вращательное равновесие):
$$ \ sum_i \ tau_i = 0 $$
Почему крутящий момент должен быть нулевым относительно любой точки ? Насколько я понимаю, до тех пор, пока крутящий момент равен нулю относительно оси поворота , , тело не будет находиться во вращательном движении.Что это значит, когда вы говорите о крутящем моменте без привязки к оси вращения?
Кроме того, как вы можете убедиться, что крутящий момент равен нулю относительно любой точки? Вы учитываете все возможные моменты?
Создан 13 июн.
$ \ endgroup $
3
$ \ begingroup $
Когда выполняется условие (1), то условие (2) эквивалентно нулевому крутящему моменту через шарнир (что может быть не совсем точно определено для твердого тела, которое может двигаться без ограничений).Справедлива следующая теорема:
При условии, что сумма действующих сил равна нулю, крутящий момент равен нулю относительно всех точек тогда и только тогда, когда он равен нулю относительно одной точки.
Доказательство выполняется путем вычисления изменения крутящего момента при изменении базовой точки (так что $ \ vec r \ mapsto \ vec r ‘= \ vec d + \ vec r $):
\ begin {align *}
\ sum_i \ vec \ tau’_i & = \ sum_i \ vec r’_i \ times \ vec F_i = \ sum_i (\ vec r_i + \ vec d) \ times \ vec F_i \\
& = \ sum_i \ vec r_i \ times \ vec F_i + \ vec d \ times \ underbrace {\ left (\ sum_i \ vec F_i \ right)} _ {\ vec F_T} \\
& = \ sum_i \ vec \ tau_i + \ vec d \ times \ left (\ sum_i \ vec F_i \ right).\ end {выровнять *}
Таким образом, имеет место еще более сильное утверждение, что сумма крутящих моментов изменяется на $ \ vec d \ times \ vec F_T $ при изменении точки отсчета. Если сумма сил, действующих на тело, равна нулю, это означает, что общий крутящий момент не изменяется при изменении опорной точки.
Создан 13 июн.
Себастьян РизеСебастьян Ризе
8,29222 золотых знака2525 серебряных знаков4242 бронзовых знака
$ \ endgroup $
Physics Stack Exchange лучше всего работает с включенным JavaScript
Ваша конфиденциальность
Нажимая «Принять все файлы cookie», вы соглашаетесь с тем, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie.
Принимать все файлы cookie
Настроить параметры
12.1 Условия статического равновесия — University Physics Volume 1
Цели обучения
К концу этого раздела вы сможете:
- Определите физические условия статического равновесия.
- Нарисуйте диаграмму свободного тела для твердого тела, на которое действуют силы.
- Объясните, как условия равновесия позволяют нам решать задачи статики.
Мы говорим, что твердое тело находится в состоянии равновесия , когда его линейное и угловое ускорение равны нулю относительно инерциальной системы отсчета. Это означает, что тело в состоянии равновесия может двигаться, но в этом случае его линейная и угловая скорости должны быть постоянными. Мы говорим, что твердое тело находится в состоянии статического равновесия , когда оно находится в состоянии покоя в нашей выбранной системе координат .Обратите внимание, что различие между состоянием покоя и состоянием равномерного движения является искусственным — то есть объект может находиться в состоянии покоя в выбранной нами системе отсчета, но для наблюдателя, движущегося с постоянной скоростью относительно нашей системы координат, тот же объект кажется, находится в равномерном движении с постоянной скоростью. Поскольку движение составляет относительно , то, что для нас находится в статическом равновесии, находится в динамическом равновесии для движущегося наблюдателя, и наоборот. Поскольку законы физики идентичны для всех инерциальных систем отсчета, в инерциальной системе отсчета нет различия между статическим равновесием и равновесием.
Согласно второму закону движения Ньютона, линейное ускорение твердого тела вызывается действующей на него чистой силой, или
[латекс] \ sum _ {k} {\ mathbf {\ overset {\ to} {F}}} _ {k} = m {\ mathbf {\ overset {\ to} {a}}} _ {\ text {CM}}. [/ Латекс]
Здесь сумма всех внешних сил, действующих на тело, где м — его масса и [латекс] {\ mathbf {\ overset {\ to} {a}}} _ {\ text {CM}} [ / latex] — это линейное ускорение его центра масс (концепция, которую мы обсуждали в статьях «Линейный импульс и столкновения с линейным импульсом и столкновениями»).В состоянии равновесия линейное ускорение равно нулю. Если мы установим ускорение на ноль на рисунке, мы получим следующее уравнение:
Первое условие равновесия
Первое условие равновесия для статического равновесия твердого тела выражает поступательное равновесие:
[латекс] \ sum _ {k} {\ mathbf {\ overset {\ to} {F}}} _ {k} = \ mathbf {\ overset {\ to} {0}}. [/ Latex]
Первое условие равновесия, рисунок, является условием равновесия сил, с которым мы столкнулись при изучении приложений законов Ньютона.
Это векторное уравнение эквивалентно следующим трем скалярным уравнениям для компонентов чистой силы:
[латекс] \ sum _ {k} {F} _ {kx} = 0, \ quad \ sum _ {k} {F} _ {ky} = 0, \ quad \ sum _ {k} {F} _ {kz} = 0. [/ latex]
Аналогично рисунку, мы можем утверждать, что вращательное ускорение [latex] \ mathbf {\ overset {\ to} {\ alpha}} [/ latex] твердого тела вокруг фиксированной оси вращения вызывается действующим чистым крутящим моментом на корпусе, или
[латекс] \ sum _ {k} {\ mathbf {\ overset {\ to} {\ tau}}} _ {k} = I \ mathbf {\ overset {\ to} {\ alpha}}.[/ латекс]
Здесь [латекс] I [/ latex] — это инерция вращения тела при вращении вокруг этой оси, а сумма составляет более всех моментов [латекс] {\ mathbf {\ overset {\ to} {\ tau}}} _ {k} [/ latex] внешних сил на рис. В состоянии равновесия ускорение вращения равно нулю. Обнуляя правую часть рисунка, мы получаем второе условие равновесия:
Второе состояние равновесия
Второе условие равновесия для статического равновесия твердого тела выражает вращательное равновесие:
[латекс] \ sum _ {k} {\ mathbf {\ overset {\ to} {\ tau}}} _ {k} = \ mathbf {\ overset {\ to} {0}}.[/ латекс]
Второе условие равновесия, рисунок, является условием равновесия для крутящих моментов, с которым мы столкнулись при изучении динамики вращения. Стоит отметить, что это уравнение равновесия обычно справедливо для вращательного равновесия вокруг любой оси вращения (фиксированной или иной). Опять же, это векторное уравнение эквивалентно трем скалярным уравнениям для векторных компонентов чистого крутящего момента:
[латекс] \ sum _ {k} {\ tau} _ {kx} = 0, \ quad \ sum _ {k} {\ tau} _ {ky} = 0, \ quad \ sum _ {k} {\ тау} _ {kz} = 0.[/ латекс]
Второе условие равновесия означает, что в равновесии нет чистого внешнего крутящего момента, вызывающего вращение вокруг любой оси.
Первое и второе условия равновесия указаны в конкретной системе отсчета. Первое условие включает только силы и поэтому не зависит от источника системы отсчета. Однако второе условие включает крутящий момент, который определяется как перекрестное произведение, [латекс] {\ mathbf {\ overset {\ to} {\ tau}}} _ {k} = {\ mathbf {\ overset {\ to} {r}}} _ {k} \ times {\ mathbf {\ overset {\ to} {F}}} _ {k}, [/ latex] где вектор положения [latex] {\ mathbf {\ overset {\ to} {r}}} _ {k} [/ latex] относительно оси вращения точки приложения силы входит в уравнение.Следовательно, крутящий момент зависит от положения оси в системе отсчета. Однако, когда условия вращательного и поступательного равновесия выполняются одновременно в одной системе отсчета, они также сохраняются в любой другой инерциальной системе отсчета, так что чистый крутящий момент вокруг любой оси вращения по-прежнему равен нулю. Объяснение этому довольно простое.
Предположим, что вектор [latex] \ mathbf {\ overset {\ to} {R}} [/ latex] — это позиция начала координат новой инерциальной системы отсчета [latex] S \ prime [/ latex] в старом инерциальном Система отсчета S .{\ prime}} _ {k} \ times {\ mathbf {\ overset {\ to} {F}}} _ {k} = \ sum _ {k} ({\ mathbf {\ overset {\ to} {r }}} _ {k} — \ mathbf {\ overset {\ to} {R}}) \ times {\ mathbf {\ overset {\ to} {F}}} _ {k} = \ sum _ {k} {\ mathbf {\ overset {\ to} {r}}} _ {k} \ times {\ mathbf {\ overset {\ to} {F}}} _ {k} — \ sum _ {k} \ mathbf { \ overset {\ to} {R}} \ times {\ mathbf {\ overset {\ to} {F}}} _ {k} = \ sum _ {k} {\ mathbf {\ overset {\ to} {\ tau}}} _ {k} — \ mathbf {\ overset {\ to} {R}} \ times \ sum _ {k} {\ mathbf {\ overset {\ to} {F}}} _ {k} = \ mathbf {\ overset {\ to} {0}}. [/ latex]
На последнем этапе этой цепочки рассуждений мы использовали тот факт, что в равновесии в старой системе отсчета S первый член исчезает из-за рисунка, а второй член исчезает из-за рисунка.Следовательно, мы видим, что чистый крутящий момент в любой инерциальной системе отсчета [латекс] S \ prime [/ latex] равен нулю, при условии, что оба условия равновесия выполняются в инерциальной системе отсчета S .
Практическое значение этого состоит в том, что при применении условий равновесия для твердого тела мы можем выбрать любую точку в качестве начала отсчета системы отсчета. Наш выбор системы отсчета продиктован физическими особенностями решаемой проблемы. В одной системе координат математическая форма условий равновесия может быть довольно сложной, тогда как в другой системе координат те же условия могут иметь более простую математическую форму, которую легко решить.Начало выбранной системы отсчета называется точкой поворота .
В самом общем случае условия равновесия выражаются шестью скалярными уравнениями (рисунок и рисунок). Для плоских задач равновесия с вращением вокруг фиксированной оси, которые мы рассматриваем в этой главе, мы можем сократить количество уравнений до трех. Стандартная процедура заключается в принятии системы отсчета, в которой ось z является осью вращения. При таком выборе оси чистый крутящий момент имеет только компонент z , все силы, которые имеют ненулевые крутящие моменты, лежат в плоскости xy , и, следовательно, вклад в чистый крутящий момент поступает только от x — и y — составляющие внешних сил.Таким образом, для плоских задач с осью вращения, перпендикулярной плоскости xy , мы имеем следующие три условия равновесия для сил и моментов:
[латекс] {F} _ {1x} + {F} _ {2x} + \ cdots + {F} _ {Nx} = 0 [/ латекс]
[латекс] {F} _ {1y} + {F} _ {2y} + \ cdots + {F} _ {Ny} = 0 [/ latex]
[латекс] {\ tau} _ {1} + {\ tau} _ {2} + \ cdots + {\ tau} _ {N} = 0 [/ латекс]
, где суммирование ведется по всем внешним силам N , действующим на тело, и их крутящим моментам. На рисунке мы упростили обозначения, опустив нижний индекс z , но мы понимаем, что здесь суммирование ведется по всем вкладам вдоль оси z , которая является осью вращения.На рисунке z -компонент крутящего момента [латекс] {\ mathbf {\ overset {\ to} {\ tau}}} _ {k} [/ latex] от силы [латекс] {\ mathbf {\ overset {\ to} {F}}} _ {k} [/ latex] —
[латекс] {\ tau} _ {k} = {r} _ {k} {F} _ {k} \ text {sin} \, \ theta [/ latex]
где [латекс] {r} _ {k} [/ latex] — длина плеча рычага силы, а [latex] {F} _ {k} [/ latex] — величина силы (как вы пила в режиме вращения с фиксированной осью). Угол [latex] \ theta [/ latex] — это угол между векторами [latex] {\ mathbf {\ overset {\ to} {r}}} _ {k} [/ latex] и [latex] {\ mathbf { \ overset {\ to} {F}}} _ {k}, [/ latex] измерение от вектора [латекс] {\ mathbf {\ overset {\ to} {r}}} _ {k} [/ latex ] в вектор [латекс] {\ mathbf {\ overset {\ to} {F}}} _ {k} [/ latex] в направлении против часовой стрелки (рисунок).При использовании рисунка мы часто вычисляем величину крутящего момента и назначаем его значение либо как положительное [латекс] (+) [/ латекс], либо как отрицательное [латекс] (-), [/ латекс], в зависимости от направления вращения, вызванного этим. только крутящий момент. На рисунке чистый крутящий момент представляет собой сумму членов, каждый член вычисляется по рисунку, и каждый член должен иметь правильное значение . Точно так же на рисунке мы назначаем знак [latex] + [/ latex] компонентам в направлении [latex] + [/ latex] x и знак [latex] — [/ latex] компонентам в [латекс] — [/ латекс] х -направление.Это же правило должно последовательно соблюдаться на рисунке при вычислении компонентов силы по оси y .
Рисунок 12.2 Крутящий момент силы: (a) Когда крутящий момент силы вызывает вращение против часовой стрелки вокруг оси вращения, мы говорим, что его направление положительное, что означает, что вектор крутящего момента параллелен оси вращения. (b) Когда крутящий момент силы вызывает вращение вокруг оси по часовой стрелке, мы говорим, что его направление отрицательное, что означает, что вектор крутящего момента антипараллелен оси вращения.
Во многих ситуациях равновесия одной из сил, действующих на тело, является его вес. На диаграммах свободного тела вектор веса привязан к центру тяжести тела. Для всех практических целей центр тяжести идентичен центру масс, как вы узнали из статей «Линейный импульс» и «Столкновения» о линейном импульсе и столкновениях. Только в тех случаях, когда тело имеет большую пространственную протяженность, так что гравитационное поле неоднородно по всему его объему, центр тяжести и центр масс расположены в разных точках.{2}. [/ Latex] В этих ситуациях центр тяжести идентичен центру масс. Поэтому на протяжении всей главы мы используем центр масс (CM) как точку, к которой прикреплен вектор веса. Напомним, что ЦМ имеет особый физический смысл: когда внешняя сила приложена к телу точно в его ЦМ, тело в целом совершает поступательное движение, и такая сила не вызывает вращения.
Когда ЦМ расположен вне оси вращения, на объекте возникает чистый гравитационный момент .Гравитационный момент — это крутящий момент, вызванный весом. Этот гравитационный момент может вращать объект, если нет опоры для его балансировки. Величина гравитационного момента зависит от того, как далеко от оси находится ЦМ. Например, в случае самосвала (рисунок) ось поворота расположена на линии, где шины соприкасаются с поверхностью дороги. Если CM расположен высоко над поверхностью дороги, гравитационный момент может быть достаточно большим, чтобы перевернуть грузовик.Легковые автомобили с низко расположенной КМ, близкой к тротуару, более устойчивы к опрокидыванию, чем грузовики.
Рис. 12.3 Распределение массы влияет на положение центра масс (CM), к которому прикреплен вектор веса [latex] \ mathbf {\ overset {\ to} {w}} [/ latex]. Если центр тяжести находится в зоне опоры, погрузчик возвращается в исходное положение после опрокидывания [см. Левую панель в (b)]. Но если центр тяжести находится за пределами зоны опоры, грузовик перевернется [см. Правую панель в (b)].Оба транспортных средства в (b) находятся вне равновесия. Обратите внимание, что автомобиль на (а) находится в равновесии: низкое расположение центра тяжести затрудняет опрокидывание.
Пример
Центр тяжести автомобиля
Легковой автомобиль с колесной базой 2,5 м имеет 52% веса на передних колесах на ровной поверхности, как показано на рисунке. Где находится ЦМ этого автомобиля по отношению к задней оси?
Рисунок 12.4 Распределение веса между осями автомобиля.Где находится центр тяжести?
Стратегия
Вес автомобиля w нам неизвестен. Все, что мы знаем, это то, что когда автомобиль стоит на ровной поверхности, 0,52 w давит на поверхность в точках контакта передних колес, а 0,48 w толкает вниз на поверхность в точках контакта задних колес. Кроме того, точки контакта отделены друг от друга расстоянием [латекс] d = 2,5 \, \ text {m}. [/ Latex] В этих точках контакта автомобиль испытывает нормальные силы реакции величиной [латекс] {F} _ {\ text {F}} = 0.52 Вт [/ латекс] и [латекс] {F} _ {\ text {R}} = 0,48 Вт [/ латекс] на передней и задней осях соответственно. Мы также знаем, что автомобиль является примером твердого тела, находящегося в равновесии, весь вес которого w действует на его ЦМ. CM находится где-то между точками, где действуют нормальные силы реакции, где-то на расстоянии x от точки, где действует [латекс] {F} _ {R} [/ латекс]. Наша задача найти х . Таким образом, мы идентифицируем три силы, действующие на кузов (автомобиль), и можем нарисовать диаграмму свободного тела для расширенного твердого тела, как показано на рисунке.
Рис. 12.5. Диаграмма свободного тела для автомобиля четко указывает векторы сил, действующих на автомобиль, и расстояния до центра масс (CM). Когда CM выбран в качестве точки поворота, эти расстояния представляют собой плечи рычага нормальных сил реакции. Обратите внимание, что величины векторов и рычаги не нужно рисовать в масштабе, но все релевантные величины должны быть четко обозначены.
Мы почти готовы записать условия равновесия с рисунка по рисунок для автомобиля, но сначала мы должны определиться с системой отсчета.Предположим, мы выбрали ось x по длине кабины, ось y — вертикальную, а ось z — перпендикулярно этой плоскости xy . При таком выборе нам нужно только написать Figure и Figure, потому что все компоненты y идентичны нулю. Теперь нам нужно определиться с расположением точки поворота. Мы можем выбрать любую точку в качестве местоположения оси вращения ( z -ось). Предположим, мы разместили ось вращения на CM, как показано на схеме свободного тела для автомобиля.На этом этапе мы готовы написать условия равновесия для автомобиля.
Решение
Каждое условие равновесия содержит только три члена, потому что на автомобиль действуют силы [latex] N = 3 [/ latex]. Первое условие равновесия, рисунок, читается как
.
[латекс] + {F} _ {\ text {F}} — w + {F} _ {\ text {R}} = 0. [/ Latex]
Это условие тривиально выполняется, потому что, когда мы подставляем данные, Figure становится [latex] + 0,52w-w + 0,48w = 0. [/ Latex] Второе условие равновесия, Figure, читается как
[латекс] {\ tau} _ {\ text {F}} + {\ tau} _ {w} + {\ tau} _ {\ text {R}} = 0 [/ латекс]
где [латекс] {\ tau} _ {\ text {F}} [/ latex] — это крутящий момент силы [латекс] {F} _ {\ text {F}}, \, {\ tau} _ {w } [/ latex] — это гравитационный момент силы w , а [latex] {\ tau} _ {\ text {R}} [/ latex] — это крутящий момент силы [latex] {F} _ {\ text {Р}}.[/ latex] Когда ось расположена в CM, гравитационный момент идентично нулю, потому что плечо рычага веса относительно оси, которая проходит через CM, равно нулю. Линии действия обеих нормальных сил реакции перпендикулярны плечам их рычагов, поэтому на рисунке мы имеем [latex] | \, \ text {sin} \, \ theta | = 1 [/ latex] для обеих сил. Из диаграммы свободного тела мы читаем, что крутящий момент [латекс] {\ tau} _ {\ text {F}} [/ latex] вызывает вращение по часовой стрелке вокруг оси в CM, поэтому его смысл отрицательный; и крутящий момент [latex] {\ tau} _ {\ text {R}} [/ latex] вызывает вращение против часовой стрелки вокруг оси в CM, поэтому его смысл положительный.Имея эту информацию, запишем второе условие равновесия как
[латекс] \ text {-} {r} _ {\ text {F}} {F} _ {\ text {F}} + {r} _ {\ text {R}} {F} _ {\ text {R}} = 0. [/ Latex]
С помощью диаграммы свободного тела мы определяем величины силы [латекс] {F} _ {\ text {R}} = 0,48w [/ латекс] и [латекс] {F} _ {\ text {F }} = 0,52w, [/ latex] и соответствующие им плечи [латекс] {r} _ {\ text {R}} = x [/ latex] и [latex] {r} _ {\ text {F}} = dx. [/ latex] Теперь мы можем записать второе условие равновесия, рисунок, явно в терминах неизвестного расстояния x :
[латекс] -0.52 (d-x) w + 0,48xw = 0. [/ Латекс]
Здесь вес w отменяется, и мы можем решить уравнение для неизвестного положения x CM. Ответ: [латекс] x = 0,52d = 0,52 (2,5 \, \ text {m}) = 1,3 \, \ text {m} \ text {.} [/ Latex]
Решение
Выбор шарнира в положении передней оси не меняет результата. Схема свободного тела для этой точки поворота представлена на рисунке. Для этого выбора точки поворота второе условие равновесия равно
.
[латекс] \ text {-} {r} _ {w} w + {r} _ {\ text {R}} {F} _ {\ text {R}} = 0.[/ латекс]
Когда мы подставляем числа, указанные на диаграмме, получаем
[латекс] \ text {-} (d-x) w + 0,48dw = 0. [/ Latex]
Ответ, полученный при решении рисунка, опять же, [латекс] x = 0,52d = 1,3 \, \ text {m}. [/ Latex]
Рисунок 12.6 Эквивалентная диаграмма свободного тела для автомобиля; точка поворота четко обозначена.
Значение
Этот пример показывает, что при решении задач статического равновесия мы можем выбрать точку поворота.Для различных вариантов выбора точки поворота у нас есть разные наборы условий равновесия, которые необходимо решить. Однако любой выбор приводит к одному и тому же решению проблемы.
Проверьте свое понимание
Решите фигуру, выбрав шарнир в месте расположения задней оси.
Показать решение
[латекс] x = 1,3 \, \ text {m} [/ latex]
Проверьте свое понимание
Объясните, какая из следующих ситуаций удовлетворяет обоим условиям равновесия: (а) теннисный мяч, который не вращается при движении в воздухе; (б) пеликан, который парит в воздухе с постоянной скоростью на одной высоте; или (c) коленчатый вал двигателя припаркованного автомобиля.
Особый случай статического равновесия возникает, когда все внешние силы на объект действуют на оси вращения или вдоль нее, или когда пространственное протяжение объекта можно не принимать во внимание. В таком случае объект можно эффективно рассматривать как точечную массу. В этом частном случае нам не нужно беспокоиться о втором условии равновесия, рис., Потому что все крутящие моменты тождественно равны нулю, а первое условие равновесия (для сил) является единственным условием, которое должно выполняться. Диаграмма свободного тела и стратегия решения проблем для этого особого случая были изложены в «Законах Ньютона» и «Приложениях законов Ньютона».В следующем примере вы увидите типичную ситуацию равновесия, включающую только первое условие равновесия.
Пример
Разрывное напряжение
Маленькая кастрюля массой 42,0 г поддерживается двумя струнами, как показано на рисунке. Максимальное натяжение, которое может выдержать струна, составляет 2,80 Н. Масса постепенно добавляется к чаше, пока одна из струн не сломается. Какая это струна? Какую массу нужно добавить, чтобы это произошло?
Рисунок 12.7 Масса добавляется в кастрюлю постепенно, пока одна из струн не лопнет.
Стратегия
Эта механическая система, состоящая из струн, масс и сковороды, находится в статическом равновесии. В частности, узел, который привязывает струны к кастрюле, находится в статическом равновесии. Узел можно рассматривать как точку; следовательно, нам нужно только первое условие равновесия. Три силы, тянущие к узлу, — это натяжение [латекс] {\ mathbf {\ overset {\ to} {T}}} _ {1} [/ latex] в 5,0-сантиметровой струне, натяжение [латекс] {\ mathbf {\ overset {\ to} {T}}} _ {2} [/ latex] в строке длиной 10,0 см и вес [латекс] \ mathbf {\ overset {\ to} {w}} [/ latex ] сковороды, удерживающей массы.Мы принимаем прямоугольную систему координат с осью y , направленной противоположно направлению силы тяжести, и рисуем диаграмму свободного тела для узла (см. Рисунок). Чтобы найти компоненты натяжения, мы должны определить углы направления [латекс] {\ alpha} _ {1} [/ latex] и [latex] {\ alpha} _ {2} [/ latex], которые образуют струны с горизонтальным направление оси x . Как вы можете видеть на рисунке, струны составляют две стороны прямоугольного треугольника. Мы можем использовать теорему Пифагора, чтобы решить этот треугольник, показанный на рисунке, и найти синус и косинус углов [latex] {\ alpha} _ {1} [/ latex] и [latex] {\ alpha} _ {2 }.[/ latex] Затем мы можем разложить натяжения на их прямоугольные составляющие, подставить в первое условие равновесия (рисунок и рисунок) и найти натяжения в струнах. Первой порвется струна с большим натяжением.
Рисунок 12.8 Схема свободного тела узла на рисунке.
Решение
Вес w , натягивающий узел, обусловлен массой M кастрюли и массой m , добавленной к кастрюле, или [латекс] w = (M + m) g.[/ latex] С помощью диаграммы свободного тела на рисунке, мы можем установить условия равновесия для узла:
[латекс] \ begin {array} {ccccc} \ text {в направлении} \, x \ text {-direction,} \ hfill & & \ hfill \ text {-} {T} _ {1x} + {T} _ {2x} & = \ hfill & 0 \ hfill \\ \ text {в направлении} \, y \ text {,} \ hfill & & \ hfill \ text {+} {T} _ {1y} + { T} _ {2y} -w & = \ hfill & 0. \ hfill \ end {array} [/ latex]
Из диаграммы свободного тела, величины компонентов в этих уравнениях равны
.
[латекс] \ begin {array} {ccc} {T} _ {1x} = {T} _ {1} \ text {cos} \, {\ alpha} _ {1} = {T} _ {1} \ text {/} \ sqrt {5}, \ hfill & & {T} _ {1y} = {T} _ {1} \ text {sin} \, {\ alpha} _ {1} = 2 {T} _ {1} \ text {/} \ sqrt {5} \ hfill \\ {T} _ {2x} = {T} _ {2} \ text {cos} \, {\ alpha} _ {2} = 2 {T} _ {2} \ text {/} \ sqrt {5}, \ hfill & & {T} _ {2y} = {T} _ {2} \ text {sin} \, {\ alpha} _ { 2} = {T} _ {2} \ text {/} \ sqrt {5}.\ hfill \ end {array} [/ latex]
Подставляем эти компоненты в условия равновесия и упрощаем. Затем мы получаем два уравнения равновесия для натяжений:
[латекс] \ begin {array} {ccccc} \ text {in} \, x \ text {-direction,} \ hfill & & \ hfill {T} _ {1} & = \ hfill & 2 {T} _ {2} \ hfill \\ \ text {in} \, y \ text {-direction,} \ hfill & & \ hfill \ frac {2 {T} _ {1}} {\ sqrt {5}} + \ frac {{T} _ {2}} {\ sqrt {5}} & = \ hfill & (M + m) g. \ Hfill \ end {array} [/ latex]
Уравнение равновесия для направления x говорит нам, что натяжение [латекс] {T} _ {1} [/ латекс] в 5.0-сантиметровая струна вдвое превышает натяжение [латекс] {T} _ {2} [/ latex] в 10-сантиметровой струне. Таким образом, более короткая струна порвется. Когда мы используем первое уравнение, чтобы исключить [латекс] {T} _ {2} [/ latex] из второго уравнения, мы получаем соотношение между массой [латекс] м [/ латекс] на противне и натяжением [латекс ] {T} _ {1} [/ latex] в более короткой строке:
[латекс] 2,5 {T} _ {1} \ text {/} \ sqrt {5} = (M + m) г. [/ латекс]
Струна разрывается, когда натяжение достигает критического значения [латекс] {T} _ {1} = 2.{2}} — 0,042 \, \ text {kg} = 0,277 \, \ text {kg} = 277,0 \, \ text {g.} [/ Latex]
Значение
Предположим, что механическая система, рассматриваемая в этом примере, прикреплена к потолку внутри лифта, поднимающегося вверх. Пока лифт движется вверх с постоянной скоростью, результат остается неизменным, потому что вес [латекс] w [/ латекс] не меняется. Если лифт движется вверх с ускорением, критическая масса меньше, потому что вес [латекса] M + m [/ latex] становится больше на кажущийся вес из-за ускорения лифта.Тем не менее, во всех случаях более короткая струна рвется первой.
Сводка
- Тело находится в равновесии, когда оно остается либо в равномерном движении (поступательном и вращательном), либо в состоянии покоя. Когда тело в выбранной инерциальной системе отсчета не вращается и не движется в поступательном движении, мы говорим, что тело находится в статическом равновесии в этой системе отсчета.
- Условия равновесия требуют, чтобы сумма всех внешних сил, действующих на тело, была равна нулю (первое условие равновесия), а сумма всех внешних моментов от внешних сил была равна нулю (второе условие равновесия).Эти два условия должны одновременно выполняться в состоянии равновесия. Если один из них не удовлетворен, тело не находится в равновесии.
- Диаграмма свободного тела для тела — полезный инструмент, который позволяет нам правильно подсчитать все вклады от всех внешних сил и моментов, действующих на тело. Диаграммы свободного тела для равновесия вытянутого твердого тела должны указывать точку поворота и плечи рычага действующих сил по отношению к оси вращения.
Концептуальные вопросы
Что вы можете сказать о скорости движущегося тела, находящегося в динамическом равновесии?
При каких условиях вращающееся тело может находиться в равновесии? Привести пример.
Какие три фактора влияют на крутящий момент, создаваемый силой относительно определенной точки поворота?
Показать решение
Величина и направление силы и ее плечо рычага
Механики иногда кладут кусок трубы на рукоятку гаечного ключа, когда пытаются открутить очень тугой болт. Как это помогает?
Для следующих четырех задач оцените утверждение как истинное или ложное и объясните свой ответ.
Если на объект действует только одна внешняя сила (или крутящий момент), он не может находиться в равновесии.
Показать решение
Верно, поскольку в этом случае сумма сил не может быть равна нулю, если сама сила не равна нулю.
Если объект находится в равновесии, на него должно действовать четное число сил.
Если на объект действует нечетное количество сил, объект не может находиться в равновесии.
Показать решение
Неверно, если силы добавляются к нулю как векторы, тогда равновесие может быть достигнуто.
Тело, движущееся по окружности с постоянной скоростью, находится в равновесии вращения.
Для чего нужен длинный и гибкий шест, который переносят канатоходцы?
Показать решение
Помогает канатоходцу сохранять равновесие.
Проблемы
При затяжке болта вы нажимаете гаечный ключ перпендикулярно с усилием 165 Н на расстоянии 0,140 м от центра болта. Какой крутящий момент вы прикладываете относительно центра болта?
При открытии двери вы нажимаете на нее перпендикулярно с силой 55.0 Н на расстоянии 0,850 м от петель. Какой крутящий момент вы прикладываете относительно петель?
Показать решение
[латекс] 46.8 \, \ text {N} \ cdot \ text {m} [/ latex]
Найдите величину натяжения каждого поддерживающего троса, показанного ниже. В каждом случае вес подвешенного тела составляет 100,0 Н, а массой кабелей можно пренебречь.
Какая сила должна быть приложена в точке P , чтобы удерживать показанную конструкцию в равновесии? Вес конструкции незначительный.
Можно ли приложить силу к P , чтобы удерживать в равновесии показанную конструкцию? Вес конструкции незначительный.
Двое детей толкают противоположные стороны двери во время игры. Оба толкаются горизонтально и перпендикулярно двери. Один ребенок толкает с силой 17,5 Н на расстоянии 0,600 м от петель, а второй ребенок толкает на расстоянии 0,450 м. Какую силу должен приложить второй ребенок, чтобы дверь не двигалась? Предположим, трение незначительно.
Небольшой внедорожник массой 1000 кг имеет колесную базу 3,0 м. Если 60%, если его вес приходится на передние колеса, как далеко за передними колесами находится центр масс фургона?
Унифицированные качели сбалансированы в центре масс, как показано ниже. Маленький мальчик справа имеет массу 40,0 кг. Какая масса у его друга?
Глоссарий
- центр тяжести
- точка, к которой прикреплен вектор весов
- равновесие
- находится в равновесии, когда его линейное и угловое ускорения равны нулю относительно инерциальной системы отсчета
Тело
- первое условие равновесия
- выражает поступательное равновесие; все внешние силы, действующие на тело, уравновешиваются и их векторная сумма равна нулю
- гравитационный момент
- крутящий момент на корпусе, вызванный его весом; возникает, когда центр тяжести тела не расположен на оси вращения
- второе состояние равновесия
- выражает вращательное равновесие; все крутящие моменты от внешних сил, действующих на тело, уравновешиваются и их векторная сумма равна нулю
- статическое равновесие
- Тело находится в статическом равновесии, когда оно покоится в нашей выбранной инерциальной системе отсчета
Объяснитель урока: Равновесие твердого тела под действием параллельных сил
В этом объяснителе мы узнаем, как решать задачи о равновесии тела под действием параллельных копланарных сил.
Если тело жесткое, силы, действующие на него, не могут вызвать деформацию. Силы имеют только два возможных воздействия на организм.
Эти эффекты — линейное ускорение тела и вращение тела вокруг точки.
Если силы, действующие на твердое тело, не вызывают чистого линейного ускорения тела,
тогда тело находится в поступательном равновесии. Для этого сумма сил на теле должна быть равна нулю.
Если силы, действующие на твердое тело, не производят чистого вращения тела, то тело находится в равновесии вращения.Сумма моментов на теле должна быть равна нулю, чтобы это применимо.
Если сумма сил и сумма моментов твердого тела равны нулю, тело находится в равновесии.
Определим условия равновесия твердого тела.
Определение: Условия равновесия твердого тела
Твердое тело находится в равновесии, если сумма сил и сумма моментов на теле равны нулю.
Давайте также определим момент от силы.
Определение: момент силы
Момент силы относительно точки 𝑃 — это расстояние
𝑑 от 𝑃 до точки, где
сила действует, умноженная на составляющую силы, перпендикулярную направлению
прямая, пересекающая 𝑃 и точку, где действует сила. Это можно записать как
𝜏 = 𝐹⋅𝑑𝜃, грех
где 𝐹 — сила, а 𝜃 — угол между направлением силы и
направление линии, пересекающей 𝑃 и точку, в которой действует сила.
В этом пояснении конкретно рассматриваются примеры, в которых силы, действующие на твердое тело, параллельны и компланарны.
Чтобы твердое тело находилось в равновесии при действии на него параллельных сил, должно выполняться одно из двух условий.
Первое условие — это тривиальное условие, что линии действия всех сил параллельны длине
тело и пересечение центра масс тела. Линия действия таких сил показана на следующем рисунке.
Ни одна из сил в любой точке по длине тела, действующих вдоль этой линии, не создает момента.
Второе условие — линии действия всех сил должны быть перпендикулярны длине тела.
Возможная линия действия таких сил показана на следующем рисунке.
Угол 𝜃 для сил вдоль этой линии действия или для любой линии, параллельной этой линии, должен быть
90∘.
Как
грех (90) = 1,
расчет моментов в этих примерах требует только использования формулы
𝜏 = 𝐹⋅𝑑.
Давайте посмотрим на такой пример.
Пример 1: Определение реакций опор стержня в состоянии равновесия
Однородный стержень, имеющий вес
35 Н опирается горизонтально на две опоры 𝐴 и
𝐵 на концах,
где расстояние между опорами 48 см.
Если груз величиной 24 Н подвешен на
точка, находящаяся на расстоянии 38 см от
𝐴, определите реакции двух опор 𝑅 и 𝑅.
Ответ
Есть две неизвестные силы реакции. Стержень покоится, поэтому сумма этих сил должна равняться сумме веса.
штанги и груза, подвешенного к штанге; следовательно,
𝑅 + 𝑅 = 35 + 24 = 59.NNN
Можно определить моменты, действующие относительно about или. Возьмем моменты о 𝐵.
Стержень находится в равновесии, поэтому моменты по и против часовой стрелки равны.
На следующем рисунке показаны силы, действующие на шток.Стержень однородный, поэтому его вес приходится на его середину.
Расстояния в сантиметрах конвертируются в расстояния.
в метрах.
Единственный момент по часовой стрелке относительно 𝐵 связан с 𝑅.
Моменты против часовой стрелки около 𝐵 обусловлены весом стержня и весом, подвешенным на стержне.
Приравнивание моментов около дает
(0,24 × 35) + ((0,48−0,38) × 24) = 0,48 × 𝑅.
Это можно упростить следующим образом:
𝑅 = (0,24 × 35) + ((0.48−0,38) × 24) 0,48𝑅 = 8,4 + 2,40,48 = 22,5.N
Как было сказано ранее,
𝑅 + 𝑅 = 35 + 24 = 59, NNN
и поэтому 𝑅 задается формулой
𝑅 = 59 − 𝑅𝑅 = 36,5.N
Давайте посмотрим на другой такой пример, на этот раз с неоднородным телом.
Пример 2: Нахождение точки, в которой вес действует на неоднородный стержень, путем определения результирующих сил и измерения моментов
Неоднородный стержень 𝐴𝐵, имеющий вес 40 Н и длину
80 см подвешивается вертикально от
его середина с помощью легкой струны, и он становится в равновесии в горизонтальном положении, когда груз величиной
29 с.ш.
подвешивается к его концу 𝐴.Определите расстояние 𝑥 между точкой, в которой
вес стержня действует и заканчивается 𝐴.
После снятия груза в точке определите величину вертикальной силы, которая потребуется для удержания стержня в
равновесие в горизонтальном положении, когда оно действует в конце 𝐵.
Ответ
В этом примере неизвестна только вертикально направленная вверх сила, оказываемая струной.
Струна легкая, что означает, что она имеет незначительный вес, поэтому сила, направленная вниз из-за веса струны, незначительна.
Направляющая вверх сила, действующая на стержень, равна сумме направленных вниз сил. Следовательно, натяжение струны определяется выражением
𝑇 = 40 + 29 = 69.NNN
Стержень неоднороден, поэтому положение центра масс стержня неизвестно, кроме того, что он не находится в средней точке стержня.
Когда груз подвешен к стержню в точке 𝐴, стержень находится в равновесии.
Если моменты по часовой стрелке и против часовой стрелки взяты относительно точки 𝑃,
там, где струна подвешивает стержень, сила, создаваемая струной, создает нулевой момент около.Единственные моменты на штанге около 𝑃 возникают из-за веса, подвешенного на
и вес стержня, действующий в центре масс стержня.
Поскольку стержень находится в равновесии, эти моменты должны быть равны.
Нам дана длина стержня 80 см, поэтому расстояние
от 𝑃 до 𝐴
составляет 40 см. Следовательно, моменты относительно даются формулами
29 × 40 = 40𝑑,
где 𝑑 — расстояние от 𝑃 до центра масс стержня. Решение уравнения для дает
𝑑 = 29 × 4040 = 29.см
Центр масс находится в 29 см от середины стержня.
Средняя точка находится в 40 см от 𝐴, поэтому расстояние от
к центру масс стержня находится
29 + 40 = 69.см
Когда груз, подвешенный на, снимается, стержень перестает находиться в равновесии до тех пор, пока не появится вертикальная сила
⃑𝐹
действует в 𝐵.
Снова принимая моменты около 𝑃, отметим, что момент, обусловленный весом стержня, который находится справа от
𝑃 действует по часовой стрелке.Сила, действующая в, находится правее,
поэтому сила, действующая в 𝐵, должна действовать в направлении, противоположном весу стержня.
Моменты по поводу 𝑃 теперь дает
40 × 29 = 𝐹 × 40.Ncmcm
Решение уравнения для 𝐹 дает
𝐹 = 40 × 2940 = 29.N
Интересно отметить, что в предыдущем примере не было необходимости рассматривать условия поступательного равновесия
для стержня, чтобы определить неизвестные значения, которые необходимо найти, только условия вращательного равновесия для стержня.
Давайте посмотрим на другой пример, связанный с натяжением струн, поддерживающих тело.
Этот пример включает большее количество сил, действующих на стержень, чем в предыдущих примерах, но решается таким же образом.
Пример 3: Нахождение напряжений в задаче равновесия
Равномерный стержень 𝐴𝐵 весит
70 Н и имеет длину
95 см.
Он подвешен на концах двумя вертикальными струнами, где 𝑇
натяжение струны при 𝐴
и 𝑇 — натяжение струны в точке 𝐵.Вес 100 Н
подвешивается к штанге, 30 см
вдали от 𝐴,
и массой 93 Н
подвешивается к штанге, 20 см
вдали от 𝐵. Определите значения 𝑇 и 𝑇.
Ответ
Есть две неизвестные силы натяжения. Стержень покоится, поэтому сумма этих сил
должен равняться сумме веса штанги и двух грузов, подвешенных к штанге; следовательно,
𝑇 + 𝑇 = 70 + 100 + 93 = 263.NNNN
Моменты, действующие на 𝐴 или 𝐵
можно определить. Возьмем моменты о 𝐴.
Стержень находится в равновесии, поэтому моменты по часовой стрелке и против часовой стрелки примерно
𝐴 равны.
Поскольку 𝑇 действует на 𝐴, он создает нулевые моменты около 𝐴.
𝑇 действует вверх, а все остальные силы на стержень действуют вниз, поэтому момент, обусловленный
𝑇 равно сумме оставшихся моментов,
95 × 𝑇 = (30 × 100) + 952 × 70 + ((95−20) × 93) 95 × 𝑇 = 3000 + 3325 + 6975 = 13300𝑇 = 1330095 = 140.N
Как указывалось ранее,
𝑇 + 𝑇 = 263, N
так
𝑇 = 263−140 = 123.N
Некоторые силы, действующие на тела, обычно не считаются переменными.
Например, обычно не считается, что вес тела меняется. Технически, если тело переместилось на значительный
на расстоянии от Земли, тогда он будет различаться по весу. Также, если тело фрагментировано, то вес фрагментов
удаленная из тела будет вычтена из веса тела.Подобные ситуации не рассматриваются в данном пояснительном механизме.
Однако, когда на удлиненное твердое тело действуют множественные силы реакции или силы натяжения,
величины этих сил могут изменяться только из-за положения точки на теле, где на нее действует приложенная сила.
Рассмотрим силы, действующие на однородное тело на следующем рисунке.
На тело действуют две силы реакции. Чтобы тело находилось в поступательном равновесии, сумма сил реакции должна быть суммой
вес тела 𝑊 и приложенная вниз сила ⃑𝐹.Это должно быть верно везде, откуда действует ⃑𝐹.
Для того, чтобы тело находилось в вращательном равновесии, если ⃑𝐹
действует в центре масс тела, ⃑𝑅
должно быть не равно ⃑𝑅.
Если изменить точку, в которой действует, то ⃑𝑅
и ⃑𝑅 будут различаться. Чем больше расстояние ⃑𝐹
от 𝐴, тем меньше величина ⃑𝑅
должно быть, и чем больше должна быть величина ⃑𝑅, чтобы тело находилось во вращательном равновесии.
Изменяя положение точки, в которой сила действует на тело, и сравнивая моменты относительно точки на
тело, когда на него действует сила в разных точках, можно определить положение точки
на которую действует вес тела, а также величина веса.
Давайте теперь посмотрим на пример, где приложенная сила к телу действует в разных точках.
Пример 4: Уравновешенные моменты
𝐴𝐵 — неоднородный стержень, имеющий длину
77 см в горизонтальном положении на одной опоре,
который находится на расстоянии 26 см от конца
𝐴. Равновесие поддерживается за счет приостановки
вес 16 Н на его конце 𝐴 и вес
2 Н на конце 𝐵. Если расстояние
между опорой и концом 𝐴 изменяется на 23 см,
стержень будет сохранен
в равновесии, подвешивая груз весом 18 Н только на конце 𝐴.Найдите величину
веса стержня 𝑊 и расстояния 𝑥 между линией его действия и точкой.
Округлите ответы до двух ближайших десятичных знаков.
Ответ
То, что описывается в вопросе, можно кратко представить с помощью следующего рисунка,
который показывает два расположения стержня. В обоих положениях стержень находится в равновесии.
В точке действия силы реакции реакция определяется выражением
𝑅 = 18 + 𝑊,
но неизвестно, как и Эти две неизвестные не могут быть однозначно определены
рассматривая любое из расположений стержня изолированно, только сравнивая оба расположения.
Для обеих схем стержень находится в равновесии, поэтому чистый момент относительно любой точки на стержне равен нулю для обеих схем.
Рассмотрим чистый момент около для обоих расположений.
Для конструкции с силами, действующими как в 𝐴, так и в 𝐵, моменты относительно задаются выражением
(26 (18 + 𝑊)) — 𝑥𝑊 − 2 (77) = 0.
Это можно изменить как
468 + 26𝑊 = 𝑥𝑊 + 154314 = 𝑥𝑊 − 26𝑊.
Для конструкции с силой, действующей только на, моменты около равны
(23 (18 + 𝑊)) — 𝑥𝑊 = 0.
Это можно изменить как
414 = 𝑥𝑊 − 23𝑊.
Поскольку чистые моменты около для обеих схем равны нулю, они также должны быть равны друг другу, поэтому
314 + 26𝑊 − 𝑥𝑊 = 414 + 23𝑊 − 𝑥𝑊.
Это можно изменить, чтобы сделать 𝑊 объектом уравнения следующим образом.
Вычтем − из обеих частей уравнения, чтобы получить
314 + 26𝑊 = 414 + 23𝑊.
Вычтем 314 из обеих частей уравнения, чтобы получить
26𝑊 = 100 + 23𝑊.
Вычтем 23𝑊 из обеих частей уравнения, чтобы получить
3𝑊 = 100𝑊 = 1003.N
С точностью до двух десятичных знаков,
𝑊 = 33.33.N
Вопрос гласит, что для конструкции с силой, действующей только на.
Расстояние между местом действия веса стержня и концом 𝐴 равно 𝑥.
в обеих конфигурациях.
Чтобы определить 𝑥, можно взять моменты относительно точки, в которой действует сила реакции.
Расстояние между этой точкой и точкой, в которой действует вес стержня, равно 𝑑, что определяется выражением
(23 × 18) = 𝑑1003414 = 𝑑10034143100 = 𝑑 = 12.42.см
Расстояние от 𝐴 до точки, в которой действует вес стержня, определяется по формуле
𝑥 = 23 + 12,42 = 35,42 см
Ключевые моменты
- Параллельные силы, действующие на твердое тело в равновесии, должны действовать либо параллельно его длине, либо
пересекая его центр масс, или действовать перпендикулярно этому направлению. - Чистая сила и чистый момент из-за параллельных сил должны быть равны нулю, чтобы тело находилось в равновесии.
- Значения множественных сил натяжения или реакции, действующих на твердое тело в равновесии, являются зависимыми.
на их соответствующих расстояниях от центра масс тела.
Механическая карта — Анализ равновесия для твердого тела
Для твердого тела в статическом равновесии, то есть недеформируемого тела, в котором силы не совпадают, сумма как сил , так и моментов , действующих на тело, должна быть равна нулю. Добавление моментов (в отличие от частиц, где мы рассматривали только силы) добавляет еще один набор возможных уравнений равновесия, позволяя нам решать больше неизвестных по сравнению с проблемами частиц.
Моменты, как и силы, являются векторами. Это означает, что наше векторное уравнение необходимо разбить на скалярные компоненты, прежде чем мы сможем решить уравнения равновесия. В двумерной задаче тело может вращаться только по часовой стрелке или против часовой стрелки (что соответствует вращению вокруг оси z). Это означает, что твердое тело в двумерной задаче имеет три возможных уравнения равновесия; то есть сумма составляющих силы в направлениях x и y и моментов вокруг оси z.Сумма каждого из них будет равна нулю.
Для двумерной задачи мы разбиваем одно векторное уравнение силы на два уравнения скалярных компонентов.
| \ [\ sum \ vec {F} = 0 \] | |
| \ [\ sum F_x = 0 \] | \ [\ sum F_y = 0 \] |
Уравнение вектора одного момента становится скалярным уравнением одного момента.
| \ [\ sum \ vec {M} = 0 \] |
| \ [\ sum M_z = 0 \] |
Если мы посмотрим на трехмерную задачу, мы увеличим количество возможных уравнений равновесия до шести.Существует три уравнения равновесия для силы, в которых сумма компонентов в направлениях x, y и z должна быть равна нулю. Тело также может иметь моменты относительно каждой из трех осей. Второй набор из трех уравнений равновесия утверждает, что сумма составляющих момента вокруг осей x, y и z также должна быть равна нулю.
Мы разбиваем силы на три составляющих уравнения
| \ [\ sum \ vec {F} = 0 \] | ||
| \ [\ sum F_x = 0 \] | \ [\ sum F_y = 0 \] | \ [\ sum F_z = 0 \] |
Мы разбиваем моменты на три составляющих уравнения
| \ [\ sum \ vec {M} = 0 \] | ||
| \ [\ sum M_x = 0 \] | \ [\ sum M_y = 0 \] | \ [\ sum M_z = 0 \] |
Поиск уравнений равновесия:
Как и в случае с частицами, первым шагом в нахождении уравнений равновесия является построение диаграммы свободного тела анализируемого тела.На этой диаграмме должны быть показаны все векторы сил, действующих на тело. На схеме свободного тела укажите значения для любых известных величин, направлений и точек приложения векторов силы и укажите имена переменных для любых неизвестных (величин, направлений или расстояний).
Далее вам нужно будет выбрать оси x, y, z. Эти оси должны быть перпендикулярны друг другу, но они не обязательно должны быть горизонтальными или вертикальными. Если вы выберете оси координат, которые совпадают с некоторыми из ваших векторов силы, вы упростите последующий анализ.
После того, как вы выбрали оси, вам нужно разбить все векторы сил на компоненты по направлениям x, y и z (см. Страницу векторов на странице Приложения 1 для получения более подробной информации об этом процессе). Ваше первое уравнение будет представлять собой сумму величин компонентов в направлении x, равных нулю, второе уравнение будет представлять собой сумму величин компонентов в направлении y, равных нулю, а третье (если вы есть трехмерная задача) будет сумма величин в направлении z, равная нулю.
Затем вам нужно будет составить уравнения моментов. Для этого вам нужно будет выбрать точку, о которой вы будете рассказывать. Любая точка должна работать, но обычно лучше выбрать точку, которая уменьшит количество неизвестных в уравнении. Помните, что любой вектор силы, проходящий через данную точку, не будет оказывать никакого воздействия на эту точку. Чтобы записать уравнения моментов, просто просуммируйте моменты, действующие от каждой силы (добавляя чистые моменты, показанные на диаграмме) относительно данной точки и данной оси (x, y или z), и установите эту сумму равной нулю.Все моменты будут относиться к оси z для двумерных задач, хотя моменты могут быть около осей x, y и z для трехмерных задач.
Когда у вас есть уравнения равновесия, вы можете решать эти формулы для неизвестных. Количество неизвестных, которые вы сможете решить, снова будет числом или уравнениями, которые у вас есть.
Равновесие твердых тел
Равновесие
твердых тел
Статический
равновесие для твердого тела: Тело (или любая его часть), которое в настоящее время
стационарный останется стационарным, если равнодействующая сила и равнодействующий момент
равны нулю для всех приложенных сил и пар
в теме.
Ньютон с 3 rd закон: Каждое действие имеет реакцию, равную по величине
и противоположное по направлению. Этот закон предусматривает метод, используемый для одного тела (или
часть тела) для взаимодействия с другим телом (или другой частью тела).
Свободное тело
Схема: Схема
тела (или его части), которая показывает все силы и пары, приложенные к
он, и в котором есть все силы и пары, предназначенные для использования в растворе
проблема называется диаграммой свободного тела. Выполните следующие действия, чтобы нарисовать
диаграмма свободного тела.
1.
Выберите тело (или часть тела), которое вы хотите
проанализировать и нарисовать.
2.
Определите все силы и пары, которые
нанесите на тело и нарисуйте их на теле. Поместите каждую силу и пару в
Дело в том, что это применяется.
3.
Обозначьте все свои силы и пары уникальным
этикетки для использования в процессе решения.
4.
Добавьте любые подходящие размеры на свою картинку.
Композитные тела
и внутренние силы: Силы и пары, которые
результат взаимодействия одной части объекта с другой его частью
не будет отображаться на диаграмме свободного тела всего объекта.Это связано с законом Ньютона 3 rd . В
два корпуса в следующем примере свариваются в точке A. Когда две части
если рассматривать как единое тело, внутренние силы и пары складываются вместе,
и в результате третий закон Ньютона аннулируется.
Силы и
пары на диаграмме свободного тела: Каждая сила или пара, которые вы положили на диаграмму свободного тела
представляет собой модель того, как на тело на диаграмме свободного тела влияет его окружение.При выборе сил и
пары, которые должны быть нанесены на диаграмму свободного тела, выполните следующие действия:
1.
Определите все
силы, возникающие при взаимодействии одного тела с другим. Многие из
общие опоры и их эффекты показаны в Табл. 5-1 на стр. 184. Помните
что для каждого способа, которым опора ограничивает свободное движение тела,
к телу должна быть приложена сила или момент, чтобы наложить ограничение на
движение.
2.
Применить груз
тела к его центру тяжести (если он однородный, то примените его к центроиду).
3.
Помните, что
струны и тросы можно тянуть только за объект.
4.
Помните, что
внутренние нагрузки компенсируются и не должны наноситься на диаграмму свободного тела.
5.
Помните, что если
вы выбрали направление сил или пары взаимодействия на одном
тело, затем Ньютон s 3 rd Закон гласит, что вы должны применять силы
или пары в противоположном направлении на другом теле.
Решение для
неизвестных: Вы
может написать один набор уравнений равновесия для каждой нарисованной вами диаграммы свободного тела. Что нужно запомнить:
1.
В 2-D проблемы
уравнения равновесия приводят к трем независимым скалярным уравнениям (две компоненты силы и
одна составляющая момента). Следовательно, вы можете решить только три скалярных
неизвестные.
2.
Попробуйте выбрать
укажите, вы берете моменты так, чтобы линия действий хотя бы одного
неизвестная сила проходит через эту точку. Это устранит одно неизвестное из
ваше уравнение моментов и приведет к более простым уравнениям для работы. Этот
шаг не является существенным, но значительно упростит алгебру, используемую в
решение вашей системы уравнений.
3.
Можно
иногда берут моменты о двух или трех разных моментах в проблеме.Выбирать
каждую точку, чтобы вы исключили одно или несколько неизвестных из результирующего момента
уравнение. Помните, что генерируемые таким образом дополнительные уравнения
не независимы от исходных уравнений, и, следовательно, у вас останется только три независимых уравнения в 2-D
проблемы по диаграмме свободного тела и вы можете
решайте только три неизвестных на диаграмму свободного тела.
4.
Для композита
тело, если вы нарисовали диаграмму свободного тела и написали равновесие
уравнения для каждого из его подразделов, вы не получите дополнительной информации
если вы нарисуете диаграмму свободного тела всего составного тела и напишете ее
уравнения равновесия.
5.
В 3-D проблемы
уравнения равновесия приводят к шести независимых скалярных уравнениям (три компоненты силы
и три составляющие момента). Таким образом, вы можете найти до шести скалярных
неизвестные по диаграмме свободного тела.
Двухсиловая
участник: A
тело, у которого есть силы
наносится на него только в двух точках, и никакие пары не накладываются на
это и вовсе называется двусиловым членом.Двухсиловой элемент может быть только в
равновесие, если линия действия равнодействующей сил в каждой точке
проходит через другую точку, и каждая равнодействующая сила равна по величине
но противоположно по направлению равнодействующей сил, приложенных к другому
точка.
А трехступенчатый
участник: Тело
у которого есть силы
нанесен на него только в трех точках, и никакие пары не наложены на
это вообще называется трехсиловым членом.Трехсиловой член может находиться только в
равновесие, если направления действия равнодействующих сил на каждом
точки пересекаются в одной точке.
Мехрдад Негахбан и Университет Небраски, 1996–2000 годы.
Все права защищены
Бесплатное копирование и распространение только для личного использования
Кафедра инженерной механики, Университет
Небраски, Линкольн,
NE68588-0526
Общие системы сил, равновесие твердого тела
- Дитмар Гросс
- Вернер Хаугер
- Йорг Шредер
- Вольфганг А.Стена
- Нимал Раджапаксе
Аннотация
Цели: В этой главе рассматриваются общие системы сил, то есть силы, линии действия которых не пересекаются в одной точке. Для анализа необходимо ввести понятие момент . Студенты должны узнать, как можно уменьшить компланарные или пространственные системы сил и при каких условиях они находятся в равновесии. Им также следует научиться применять метод сечений для получения диаграммы свободного тела.Правильная диаграмма свободного тела и соответствующее применение условий равновесия являются ключом к решению компланарной или пространственной задачи.
Ключевые слова
Контактное усилие жесткого тела Уравнение момента результирующей силы общей системы
Эти ключевые слова были добавлены машиной, а не авторами. Это экспериментальный процесс, и ключевые слова могут обновляться по мере улучшения алгоритма обучения.
Это предварительный просмотр содержимого подписки,
войдите в
, чтобы проверить доступ.
Предварительный просмотр
Невозможно отобразить предварительный просмотр. Скачать превью PDF.
Информация об авторских правах
© Springer-Verlag Berlin Heidelberg 2013
Авторы и аффилированные лица
- Дитмар Гросс Автор электронной почты
- Вернер Хаугер
- Йорг Шредер
- Вольфганг1478 Механоси
- Posted in Разное
