Содержание
Теорема Фалеса
Пользователи также искали:
обобщенная теорема фалеса,
обратная теорема фалеса,
теорема фалеса 8 класс,
теорема фалеса доказательство,
теорема фалеса это,
теорема фалеса формулировка,
теорема фалеса в треугольнике,
теорема фалеса — задачи,
Фалеса,
теорема,
фалеса,
Теорема,
Теорема Фалеса,
обратная теорема фалеса,
обобщенная теорема фалеса,
теорема фалеса в треугольнике,
теорема фалеса класс,
теорема фалеса это,
класс,
треугольнике,
доказательство,
формулировка,
обратная,
обобщенная,
задачи,
теорема фалеса формулировка,
теорема фалеса — задачи,
теорема фалеса доказательство,
теорема фалеса 8 класс,
теорема фалеса,
теоремы планиметрии. теорема фалеса,
теорема фалеса,
…
Разработка открытого урока по геометрии по теме «Теорема Пифагора». 8-й класс
Тип урока: изучение и первичное закрепление новых знаний и способов деятельности с помощью практико-ориентированного проекта.
Цели урока:
Образовательные:
- ознакомить и обеспечить овладение учащимися основными алгоритмическими приемами при нахождении сторон прямоугольного треугольника при помощи теоремы Пифагора;
- показать практическое применение теоремы Пифагора в жизни.
Воспитательные:
- формирование культуры поведения при фронтальной, групповой и индивидуальной работе.
Формировать УУД:
Личностные: способность к самооценке на основе критерия успешности учебной деятельности.
Регулятивные: оценивать результаты деятельности, анализировать собственную работу, планировать своё действие в соответствии с поставленной задачей, уметь ориентироваться в информации, уметь составлять алгоритм действия.
Коммуникативные: определять цель учебной деятельности, оформлять свои мысли в устной форме; слушать и понимать речь других; совместно договариваться о правилах поведения и общения в школе и следовать им.
Познавательные: ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя; добывать новые знания: находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке.
Планируемые результаты обучения, в том числе и формирование УУД:
Предметные:
- Понимать, что такое «теорема Пифагора». Знать, как найти неизвестную сторону прямоугольного треугольника при помощи теоремы Пифагора.
Личностные:
- Уметь проводить самооценку на основе критерия успешности учебной деятельности.
Метапредметные:
- Уметь оценивать результаты деятельности, анализировать собственную работу, планировать своё действие в соответствии с поставленной задачей, уметь ориентироваться в учебнике, уметь составлять алгоритм действия.
Основные понятия: Теорема Пифагора.
Межпредметные связи: математика, история.
Ресурсы:
- учебник для общеобразовательных учреждений: «Геометрия 7-9 класс» Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др;
презентация к уроку; - смартфоны без доступа в сеть интернет и без сим-карт для осуществления голосовых вызовов с предустановленными приложением «Пифагория»;
- ноутбук с выходом в интернет для использования сайта «Математические этюды»;
- раздаточный печатный материал.
Ход урока
1) Оранизационный момент, приветствие, запись в тетради даты урока и наименование работы: Классная работа
Эпиграф к уроку:
2) Формулировка проблемной задачи
Обсуждение задачи, постановка гипотез, практическое решение задачи в тетради с использованием карандаша и линейки.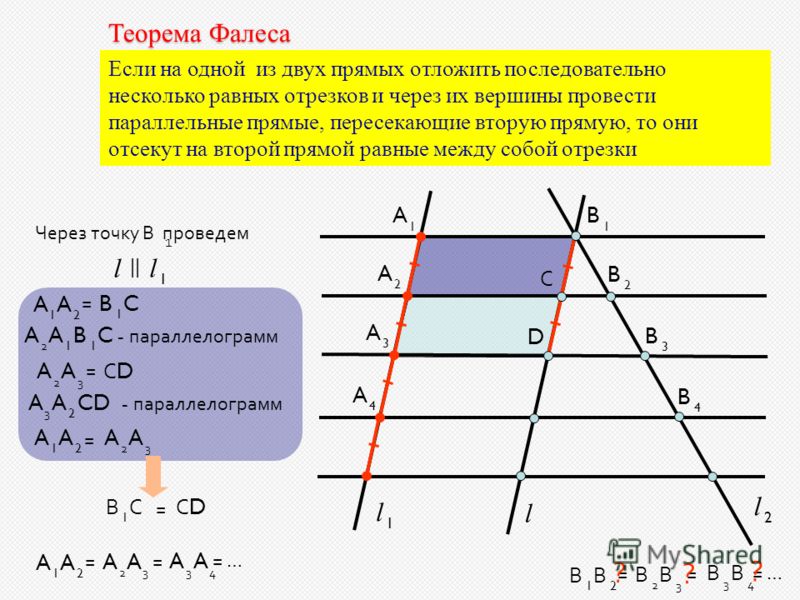 Чертёж выполняем в масштабе.
Чертёж выполняем в масштабе.
3) Чтобы ответить на этот вопрос точно и математически грамотно, нам придётся отправиться в путешествие
(работа в малых группах по 4 человека, раздаточный материал: посадочные талоны на самолёт, чтобы не скучать в пути — кроссворд, после разгадывания которого будет ясна ТЕМА УРОКА)
Две пары работают в мультимедийном приложении на смартфоне «Пифагория» в теме «Прямые углы. Прямоугольные треугольники».
Ответ на кроссворд: ПИФАГОР.
4) Формулировка обучающимися ТЕМЫ УРОКА, озвучивание учителем целей и задач урока
5) Историческая справка о Пифагоре
О Пифагоре
О жизни Пифагора известно немного. Он родился в 580 г. до н.э. в Древней Греции на острове Самос, который находится в Эгейском море у берегов Малой Азии, в семье резчика по камню.
Он родился в 580 г. до н.э. в Древней Греции на острове Самос, который находится в Эгейском море у берегов Малой Азии, в семье резчика по камню.
Ещё в детстве он проявлял незаурядные способности, и когда подрос, неугомонному воображению юноши стало тесно на маленьком острове.
Пифагор перебрался в город Милеет и стал учеником Фалеса, которому в то время шёл восьмой десяток. Мудрый учёный посоветовал юноше отправиться в Египет, где сам, когда-то изучал науки.
Перед Пифагором открылась неизвестная страна. Его поразило то, что в родной Греции боги были в образе людей, а египетские боги – в образе полулюдей-полуживотных. Знания были сосредоточены в храмах, доступ в которые был ограничен. Пифагору потребовались годы, чтобы глубоко изучить египетскую культуру прежде, чем, ему было разрешено познакомиться с многовековыми достижениями египетской науки.
Когда Пифагор постиг науку египетских жрецов, то засобирался домой, чтобы там создать свою школу. Жрецы, не желавшие распространения своих знаний за пределы храмов, не хотели его отпускать.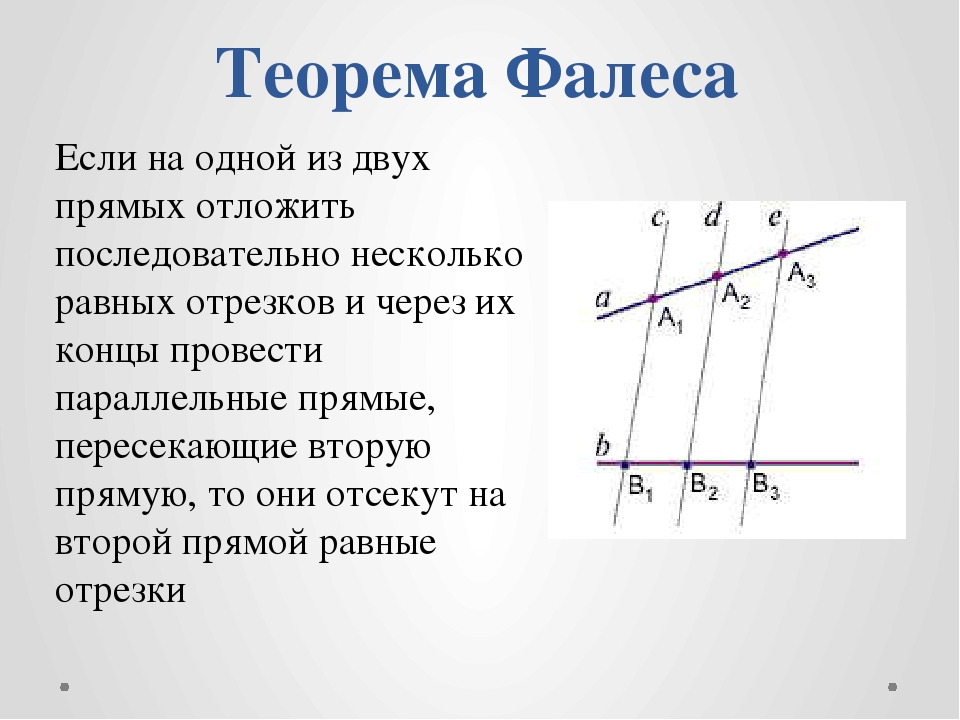 С большим трудом ему удалось преодолеть эту преграду.
С большим трудом ему удалось преодолеть эту преграду.
Однако по дороге домой, Пифагор попал в плен и оказался в Вавилоне. Вавилоняне ценили умных людей, поэтому он нашёл своё место среди вавилонских мудрецов. Наука Вавилона была более развитой, нежели египетская. Наиболее поразительными были успехи алгебры. Вавилоняне изобрели и применяли при счёте позиционную систему счисления, умели решать линейные, квадратные и некоторые виды кубических уравнений.
Пифагор прожил в Вавилоне около десяти лет и в сорокалетнем возрасте вернулся на родину. Но на острове Самос он оставался недолго. В знак протеста против тирана Поликрата, который тогда правил островом, поселился в одной из греческих колоний Южной Италии в городе Крóтоне.
Там Пифагор организовал тайный союз молодёжи из представителей аристократии. В этот союз принимались с большими церемониями после долгих испытаний. Каждый вступающий отрекался от своего имущества и давал клятву хранить в тайне учения основателя. Пифагорейцы, как их позднее стали называть, занимались математикой, философией, естественными науками.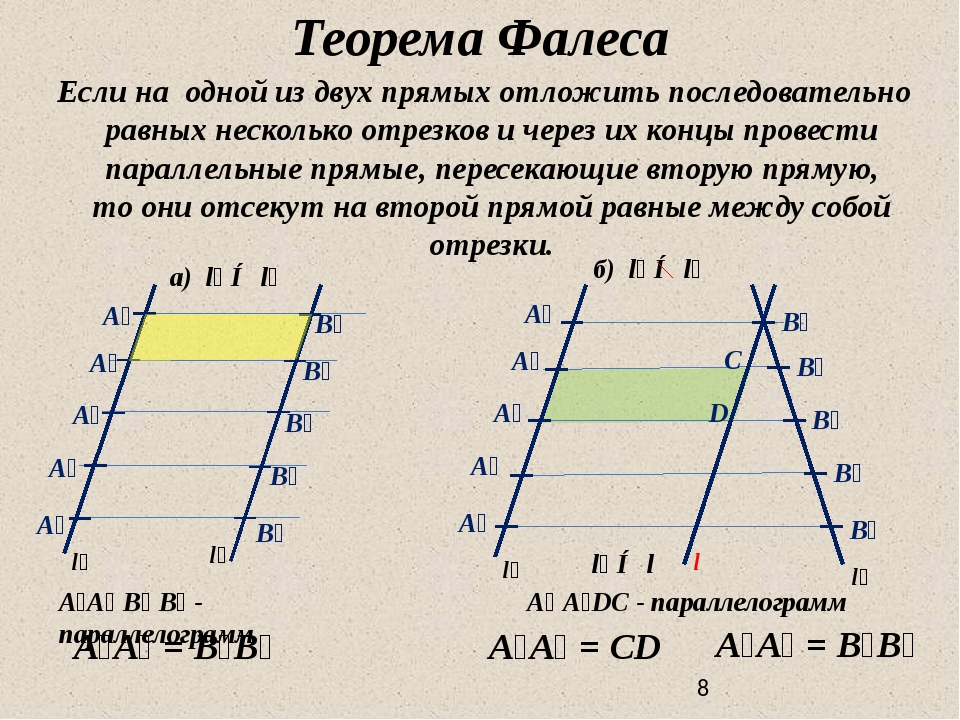 В школе существовал декрет, по которому авторство всех математических работ приписывалось учителю.
В школе существовал декрет, по которому авторство всех математических работ приписывалось учителю.
Пифагорейцами было сделано много важных открытий в арифметике и геометрии, в том числе:
- теорема о сумме внутренних углов треугольника;
- построение правильных многоугольников и деление плоскости на некоторые из них;
- геометрические способы решения квадратных уравнений;
- деление чисел на чётные и нечётные, простые и составные; введение фигурных, совершенных и дружественных чисел;
- доказательство того, что не является рациональным числом;
- создание математической теории музыки и учения об арифметических, геометрических и гармонических пропорциях и многое другое.
Известно также, что кроме духовного и нравственного развития учеников Пифагора заботило их физическое развитие. Он не только сам участвовал в Олимпийских играх и два раза побеждал в кулачных боях, но и воспитал плеяду великих олимпийцев.
Около сорока лет учёный посвятил созданной им школе и, по одной из версий, в возрасте восьмидесяти лет Пифагор был убит в уличной схватке во время народного восстания.
После его смерти ученики окружили имя своего учителя множеством легенд.
10 фактов о теореме Пифагора
Пифагоровы штаны – на все стороны равны.
Чтобы это доказать, нужно снять и показать.
Этот стишок известен всем со средней школы, с тех самых пор, когда на уроке геометрии мы изучали знаменитую теорему Пифагора: квадрат длины гипотенузы прямоугольного треугольника равен сумме квадратов катетов. А вот вам 10 фактов о знаменитой теореме.
1. Происхождение штанов понятно: построенные на сторонах треугольника и расходящиеся в разные стороны квадраты напоминали школьникам покрой мужских штанов. Правда, это как посмотреть: средневековые школяры называли эту теорему «pons asinorum», что означает «ослиный мост».
2. Книга рекордов Гиннесса называет теорему Пифагора теоремой с максимальным числом доказательств. И поясняет в 1940 году была опубликована книга, которая содержала триста семьдесят доказательств теоремы Пифагора, включая одно предложенное президентом США Джеймсом Абрамом Гарфилдом.
3. Теорему Пифагора доказывали через подобные треугольники, методом площадей и даже через дифференциальные уравнения – это сделал английский математик начала двадцатого века Годфри Харди. Известны доказательства теоремы Пифагора, предложенные Евклидом и Леонардо Да Винчи. А Электроник – мальчик из чемоданчика в книге Евгения Велтистова знал целых двенадцать способов, а среди них «метод укладки паркета» и «стул невесты».
4. Только одно доказательство теоремы Пифагора нам не известно: доказательство самого Пифагора. Долгое время считалось, что доказательство Евклида и есть доказательство Пифагора, но теперь считают, что это доказательство принадлежит Евклиду.
5. К настоящему моменту историки математики обнаружили, что теорема Пифагора не была открыта Пифагором – ее знали в разных странах задолго до древнегреческого философа и математика родом с острова Самос, жившего в VI веке до н.э.
6. Крупнейший историк математики Мориц Кантор разглядел папирус из Берлинского музея и обнаружил, что равенство три в квадрате плюс четыре в квадрате равно пяти в квадрате было известно уже египтянам около 2300 года до нашей эры во времена царя Аменемхета I.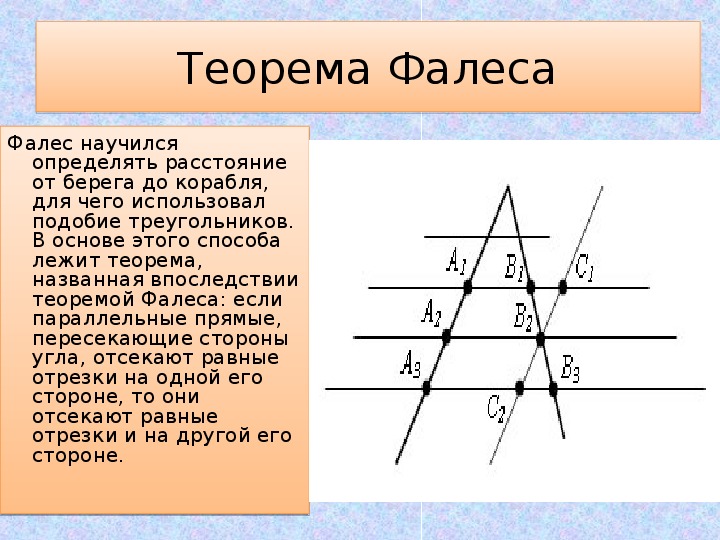
7. Приближенное вычисление гипотенузы прямоугольного треугольника обнаруживается в вавилонских текстах времен правления царя Хаммурапи, то есть за два тысячелетия до нашей эры. Весьма вероятно, что теорема о квадрате гипотенузы была известна в Индии уже около VIII века до нашей эры.
8. Голландский математик Бартель Ван дер Варден сделал важный вывод: «Заслугой первых греческих математиков, таких как Пифагор, является не открытие математики, но ее систематизация и обоснование. В их руках вычислительные рецепты, основанные на смутных представлениях, превратились в точную науку».
9. «В день, когда Пифагор открыл свой чертёж знаменитый,
Славную он за него жертву быками воздвиг».
Со слов неизвестного древнего стихотворца легенда о гекатомбе – жертвоприношении ста быков пошла гулять по умам и страницам изданий. Остряки шутят, что с тех самых пор все скоты боятся нового.
10. Сам Пифагор никогда не носил штанов – в те времена греки их не знали.
6) Формулировка теоремы Пифагора
Выполнение чертежа в тетради и математическая запись теоремы.
7) Показ отрывка из фильма «Приключения электроника» (30 сек)
Вопрос для обучающихся и статистика ответов с помощью сервиса Plickers.
Верный ответ: примерно 400.
8) Физкультминутка (посвящение в Пифагорейцы)
Все встали около парт и поочерёдно каждой рукой в воздухе «пишут» тайный знак Пифагорейской школы (пентаграмму)
9) Доказательство Теоремы Пифагора (практический способ)
Одна из формулировок теоремы Пифагора:
Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на катетах».
Два человека за компьютером на сайте «Математические этюды»,
http://www.etudes.ru/ru/etudes/pythagorean-theorem/
остальные: работа в парах, раздаточный материал.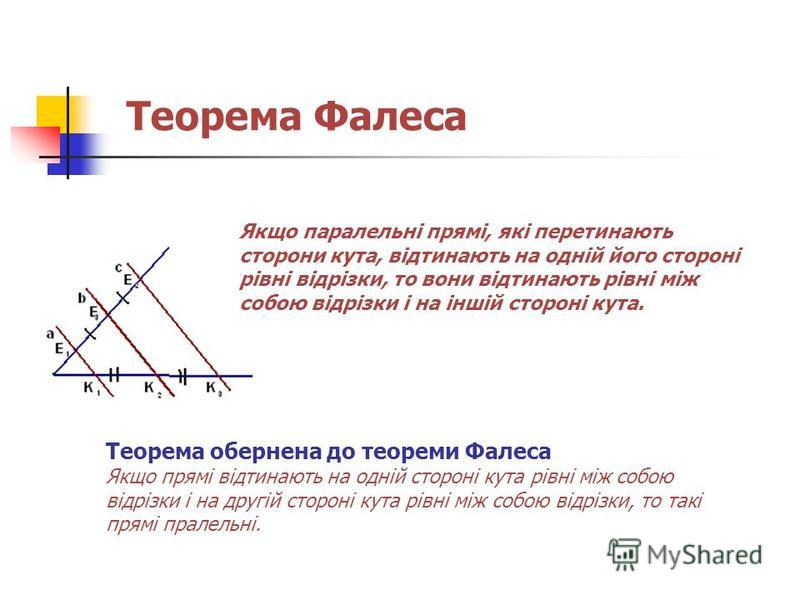
10) Решение опорных задач, оформление их в рабочей тетради
Задачи.
1. Катеты прямоугольного треугольника равны 3 и 4. Найти гипотенузу.
2. Гипотенуза прямоугольного треугольника равна 13, а один из катетов равен 12. Найти второй катет.
3. Один из катетов прямоугольного треугольника равен 4, а угол, прилежащий к этому катету, равен 60°. Найти квадрат второго катета.
4. Разбор задачи про дальнобойщиков (см.начало урока).
5. Как с помощью верёвки изобразить прямой угол?
Домашнее задание:
- параграф 3, пункт 55, теорема+доказательство
- выполнить № 483(а,в), 486(а,б)
11) Рефлексия
В тетрадях по пятибалльной шкале обучающиеся оценивают урок, отвечая на вопросы:
- Понравился ли в целом вам урок?
- Приобрели ли вы новые знания?
- Всё ли вам было понятно?
- Сможете ли вы теперь объяснить своим товарищам тему «Теорема Пифагора» и рассказать о её практическом применении?
12) Заключение
Все обучающиеся получают сертификат об успешном изучении темы «Теорема Пифагора».
Теорема Пифагора 8 класс онлайн-подготовка на Ростелеком Лицей
Теорема Пифагора
Древнегреческому учёному Пифагору приписывают открытие и доказательство следующей теоремы:
Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах.
В истории математики находим утверждения, что эту теорему знали за много лет до Пифагора, – например, древние египтяне знали о том, что треугольник со сторонами 3, 4 и 5 является прямоугольным.
В наше время теорема звучит так (подразумевая не только площади, но и длины сторон прямоугольного треугольника):
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов: c2 = a2+b2.
Известны очень многие доказательства теоремы разными математическими методами, но одна из самых наглядных связана с площадями.
-
Построим квадрат, сторона которого равна сумме катетов данного треугольника: a+b. Площадь квадрата равна (a+b)2:
-
Проведем внутри четыре гипотенузы с так, чтобы образовалось четыре прямоугольных треугольника, равных данному (имеющих длины сторон a, b, c).
-
В центре образовался новый четырехугольник. Его стороны равны c, а углы — прямые, так как острые углы прямоугольного треугольника в сумме дают 90°, то угол четырёхугольника также равен 90°, потому что вместе все три угла дают 180°.
Следовательно, площадь квадрата состоит из четырёх площадей равных прямоугольных треугольников и площади квадрата, образованного гипотенузами.
Площадь маленького квадрата равна с2, площади равных треугольников равны ab2. Значит, площадь большого квадрата равна c2+4∙ab2=c2+2ab. С другой стороны, из пункта 1 мы знаем, что эта площадь равна (a+b)2. Приравняем полученные выражения:
С другой стороны, из пункта 1 мы знаем, что эта площадь равна (a+b)2. Приравняем полученные выражения:
c2+2ab=(a+b)2
c2+2ab=a2+2ab+b2
c2=a2+b2
Теорема доказана.
Это доказательство – не единственное доказательство теоремы Пифагора. У нее очень много доказательств.
Если требуется найти длину гипотенузы c, то выполняем сложение квадратов длин катетов a и b и определяем квадратный корень:
c=a2+b2.
Если требуется найти длину одного катета, то выполняем вычитание длины квадрата другого катета из квадрата длины гипотенузы и определяем квадратный корень:
a=c2-b2.
Обратная теорема используется как признак прямоугольного треугольника.
Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник является прямоугольным.
Конспект уроку теорема фалеса 8 клас
Скачать конспект уроку теорема фалеса 8 клас fb2
УРОК ГЕОМЕТРИИ В 8 КЛАССЕ Тема: Теорема Фалеса Цель урока: сформулировать и доказать теорему Фалеса; научить учащихся делить отрезок на заданное число равных частей.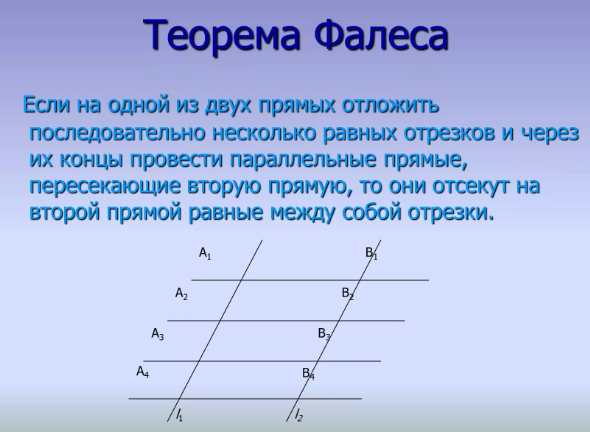 Тип урока: усвоение новых знаний. Оборудование: набор чертежных инструментов. Ход урока1)Организационный момент Учитель: Сегодня на уроке геометрии мы проведем экскурсию по необычному музею — музею математики.
Тип урока: усвоение новых знаний. Оборудование: набор чертежных инструментов. Ход урока1)Организационный момент Учитель: Сегодня на уроке геометрии мы проведем экскурсию по необычному музею — музею математики.
Тема нашей экскурсии — «Теорема Фалеса». 2) Формулирование целей и задач урока.Первый зал«Биография» Фалес Милетский, Фалес из Милета, жил в VI веке до н.э. Крупнейший мыслитель древней Греции. В молодые годы Фалес жил в Ег. Упражнения по теме «Теорема Фалеса. Теорема о пропорциональных отрезках». Материал для составления самостоятельных проверочных работ.
Раздел состоит из трёх однотипных вариантов задач по проверяемой теме. Теорема Фалеса. На сторонах А В и ВС треугольника АВС отметили точки М и N соответственно. Отрезки AN и СМ пересекаются в точке О. В каком отношении точка О делит отрезок СМ, если AM: МВ = 5: 3 и CN: NB = 9: 16? Вы смотрели: Геометрия 8 класс (УМК Мерзляк, Полонский, Якир). Упражнения по теме «Теорема Фалеса. Теорема о пропорциональных отрезках». Материал в первую очередь предназначен для составления самостоятельных проверочных работ.
Материал в первую очередь предназначен для составления самостоятельных проверочных работ.
ГЕОМЕТРИЯ Уроки для 8 классов. Урок № Тема. Теорема Фалеса. Цель: формировать у учащихся осознанное понимание содержания теоремы Фалеса и способа ее доказательства; формировать умение воспроизводить формулировки теоремы Фалеса; применять ее для решения задач на нахождение длин отрезков на сторонах отсекаются параллельными прямыми; решать задачи на деление отрезка на п равные отрезки или в данном отношении.
Тип урока: усвоение новых знаний. Наглядность и оборудование: конспект «Теорема Фалеса». Ход урока. I. Организационный этап. 8 класс. Урок 5. Теорема Фалеса. Назад Вперёд. Урок Конспект Дополнительные материалы. Начнём урок. Основная часть. Тренировочные задания. Доказанная выше теорема является частным случаем общей теоремы Фалеса, так как равные отрезки пропорциональны с коэффициентом, равным единице.
Для теоремы Фалеса верно обратное утверждение: Если прямые, пересекающие две другие прямые (параллельные или нет), отсекают на обеих из них равные (или пропорциональные) отрезки, начиная от вершины, то такие прямые параллельны.
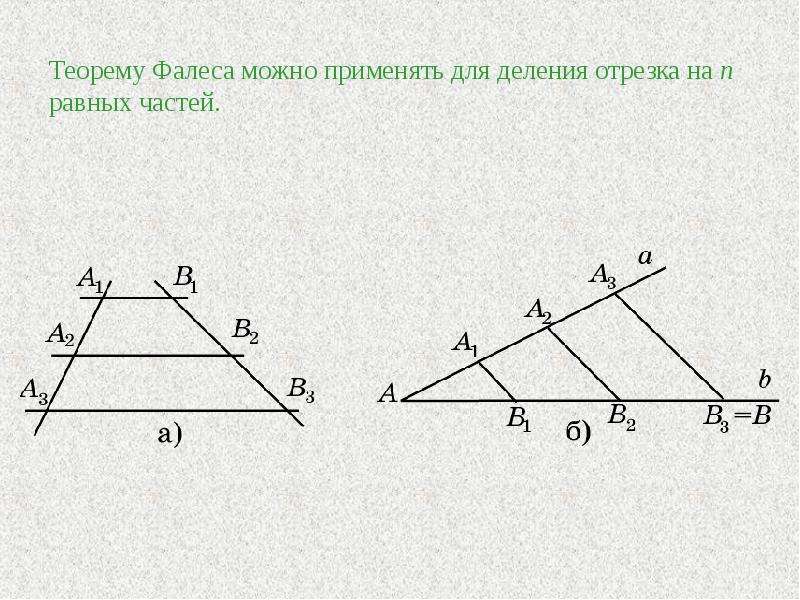
В этой теореме важно, что равные отрезки начинаются от вершины. С помощью теоремы Фалеса можно разделить данный отрезок на n равных частей. Презентация к уроку геометрии в 8 классе по теме: «Теорема Фалеса» представлена в рамках иллюстрации реализации системно-деятельностного подхода при реализации ФГОС СОО.
Автор: Борисова Светлана Александровна. Работа: Получить программу конференций. Получить программу конференций. Быстрые ссылки. Создать диплом/свидетельство Оплатить созданный диплом Опубликовать статью.
Самостоятельная работа «Теорема Фалеса. Теорема о пропорциональных отрезках». 1. 2. Категория: РАБОЧИЕ МАТЕРИАЛЫ К УРОКАМ ГЕОМЕТРИИ. 8 КЛАСС | Добавил: tineydgers (). Просмотров: | Теги: | Рейтинг: /0. Поиск. Узнаем формулировку теоремы Фалеса, смоем применять ее на практике. Ссылка на страницу с видео: Ссылка HTML на страницу с видео Теорема Піфагора Найпростіша задача 2 — Геоме Добавлено: 5 год. uklasicomua 5 год.
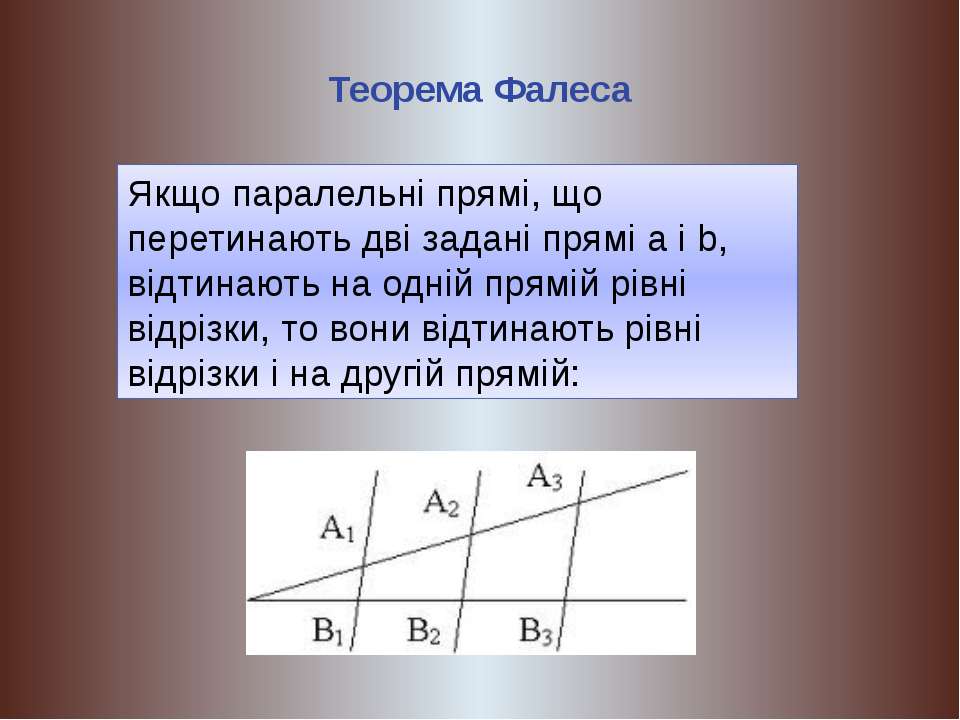
11 класс, 40 урок, Угол между касательной и х. Урок по теме Теорема Фалеса. Теоретические материалы и задания Геометрия, 8 класс. ЯКласс — онлайн-школа нового поколения. 3. Теорема Фалеса. Теория: Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.
Урок по теме Теорема Фалеса. Теоретические материалы и задания Геометрия, 8 класс. ЯКласс — онлайн-школа нового поколения. 3. Теорема Фалеса. Теория: Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.
Теорему Фалеса используют, чтобы разделить отрезок на несколько равных частей. Необходимо разделить отрезок \(AB\) на \(7\) равных частей. Нарисуем угол, на одной стороне которого лежит отрезок \(AB\).
fb2, rtf, rtf, rtf
Похожее:
Презентація до уроку фізики 7 клас
Гдз англійська мова 6 клас алла 2014 нова програма
Українська мова 8 клас підручник глазова скачать
Болото природне угруповання презентація 4 клас
Підручник українська мова 2 клас хорошковська охота
Теорема Пифагора [Love Soft]
Среднее пропорциональное (геометрическое) чисел
Среднее пропорциональное (или среднее геометрическое) чисел $a$ и $b$ — это такое число $x$, что
$a:x = x:b$. 2 = ab$.
2 = ab$.
Отсюда $x = \sqrt{ab}$ — корень из произведения двух чисел.
Другими словами, средним геометрическим нескольких положительных вещественных чисел называется такое число, которым можно заменить каждое из этих чисел так, чтобы их произведение не изменилось.
Метрические соотношения в прямоугольном треугольнике
Лемма. Высота, проведенная из вершины прямого угла, разбивает прямоугольный треугольник на два подобных треугольника. Каждый из этих треугольников подобен исходному. (доказать самостоятельно)
Теорема. В прямоугольном треугольнике
высота, проведенная к гипотенузе, является средним пропорциональным проекций катетов на гипотенузу.
катет — среднее пропорциональное между гипотенузой и его проекцией на гипотенузу.
Следствие 1. Проекции катетов на гипотенузу относятся как квадраты катетов.
Следствие 2. Теорема Пифагора.
$$AC^2 + BC^2 = AB \cdot AC’ + AB \cdot BC’ = AB \cdot (AC’+BC’) = AB^2$$
Следствие 3.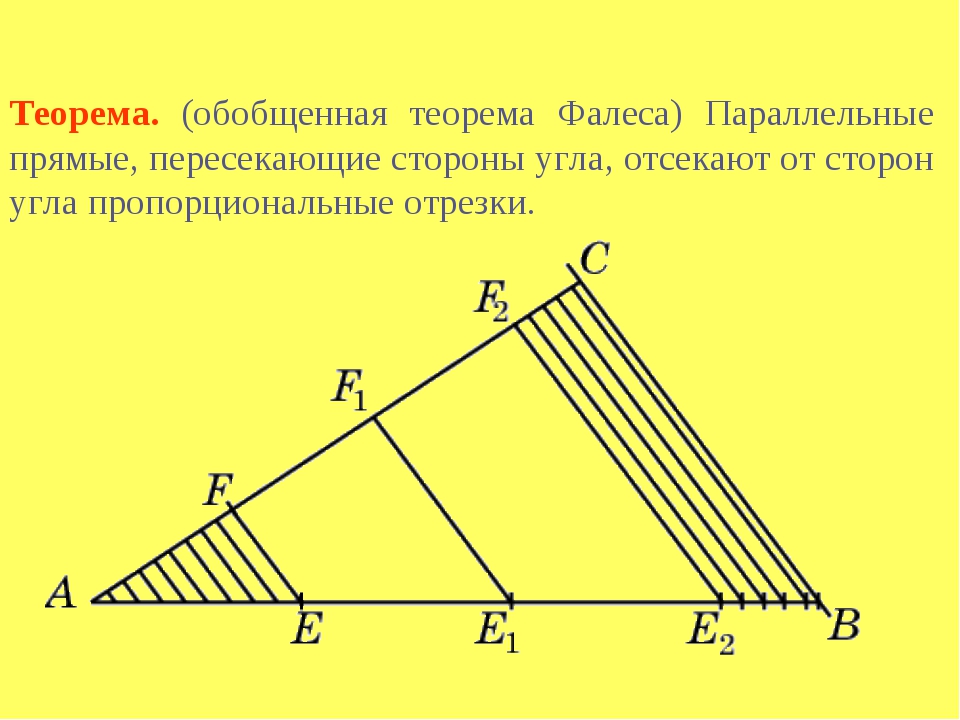 Проекция и перпендикуляр короче наклонной (разумеется, проведенные из одной и той же точки к некоторой прямой).
Проекция и перпендикуляр короче наклонной (разумеется, проведенные из одной и той же точки к некоторой прямой).
Следствие 4. Формула Герона для вычисления площади треугольника.
Теорема Пифагора
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Пифагоровы штаны на все стороны равны!
Без преувеличения можно сказать, что это самая известная теорема геометрии, ибо о ней знает подавляющее большинство населения планеты.
Сумма площадей квадратов, построенных на катетах, равна площади квадрата, построенного на гипотенузе.
Физическое доказательство (точнее, показательство) теоремы Пифагора — видео
Еще одно физическое доказательство теоремы Пифагора. Берёте ножницы и бумагу. Вырезаете квадраты в соответствии с формулировкой теоремы и взвешиваете. Правда, в физическом доказательстве неминуемо появится погрешность измерения веса.
На данный момент в научной литературе зафиксировано 367 доказательств данной теоремы.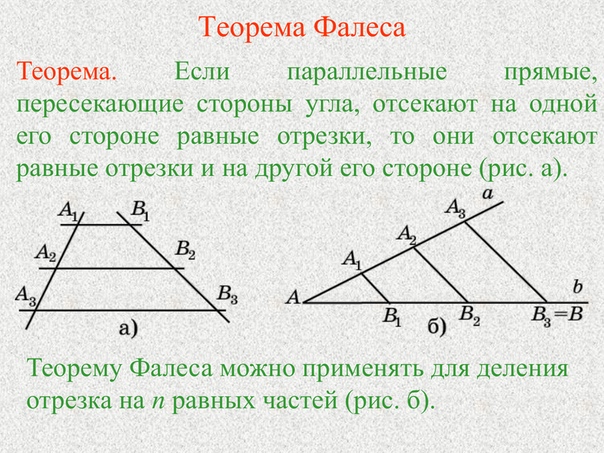 Такое многообразие можно объяснить лишь фундаментальным значением теоремы для геометрии.
Такое многообразие можно объяснить лишь фундаментальным значением теоремы для геометрии.
В Древнем Египте геометрию не только знали, но и использовали при разработке строительных шедевров (пирамид) и при ежегодной разметке полей, на которых вода при наводнении уничтожала все межи. Даже была особая служба землемеров, которая восстанавливала границы полей, когда вода спадала. И это за 1500 лет до Пифагора.
Неудивительно, что теорему Пифагора, которая широко использовалась в прикладных науках, древние греки называли «мостом ослов».
Теорема Пифагора примечательна еще и тем, что сама по себе она вовсе неочевидна. Например, свойства равнобедренного треугольника можно видеть непосредственно на рисунке. Но сколько ни гляди на прямоугольный треугольник, никак не увидишь, что между его сторонами есть такое простое соотношение.
С помощью теоремы Пифагора вычисляют расстояние между точками на координатной плоскости.
Доказательство Евклида
Площадь розового квадрата равна площади розового прямоугольника, площадь голубого квадрата равна площади голубого прямоугольника.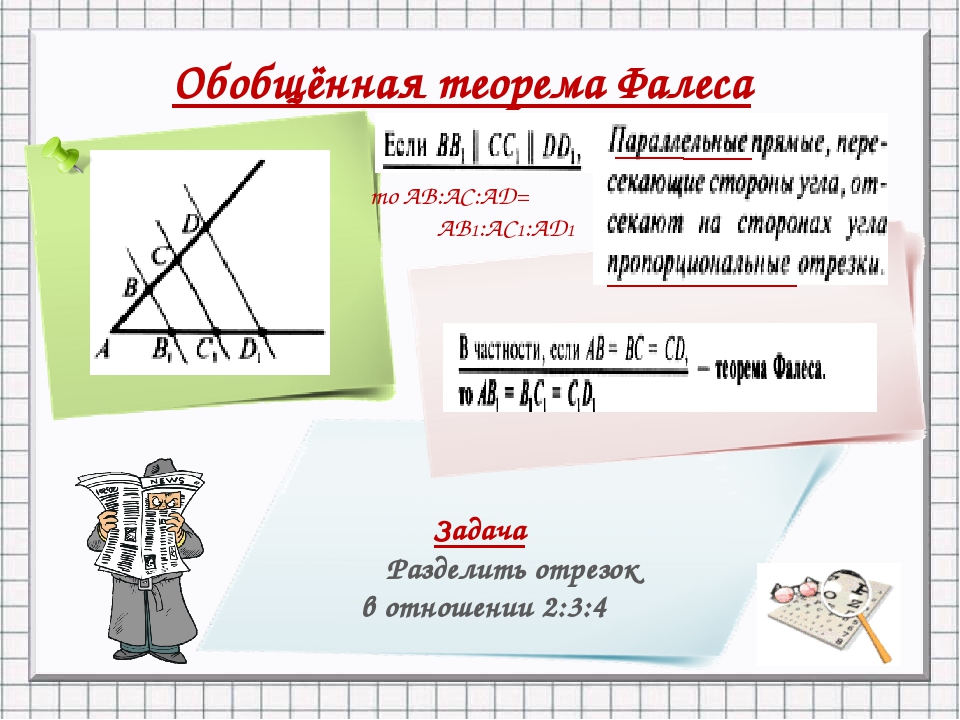
Доказательство
For the formal proof, we require four elementary lemmata:
If two triangles have two sides of the one equal to two sides of the other, each to each, and the angles included by those sides equal, then the triangles are congruent. (Side — Angle — Side Theorem)
The area of a triangle is half the area of any parallelogram on the same base and having the same altitude.
The area of any square is equal to the product of two of its sides.
The area of any rectangle is equal to the product of two adjacent sides (follows from Lemma 3).
The intuitive idea behind this proof, which can make it easier to follow, is that the top squares are morphed into parallelograms with the same size, then turned and morphed into the left and right rectangles in the lower square, again at constant area.
The proof is as follows:
Let ACB be a right-angled triangle with right angle CAB.
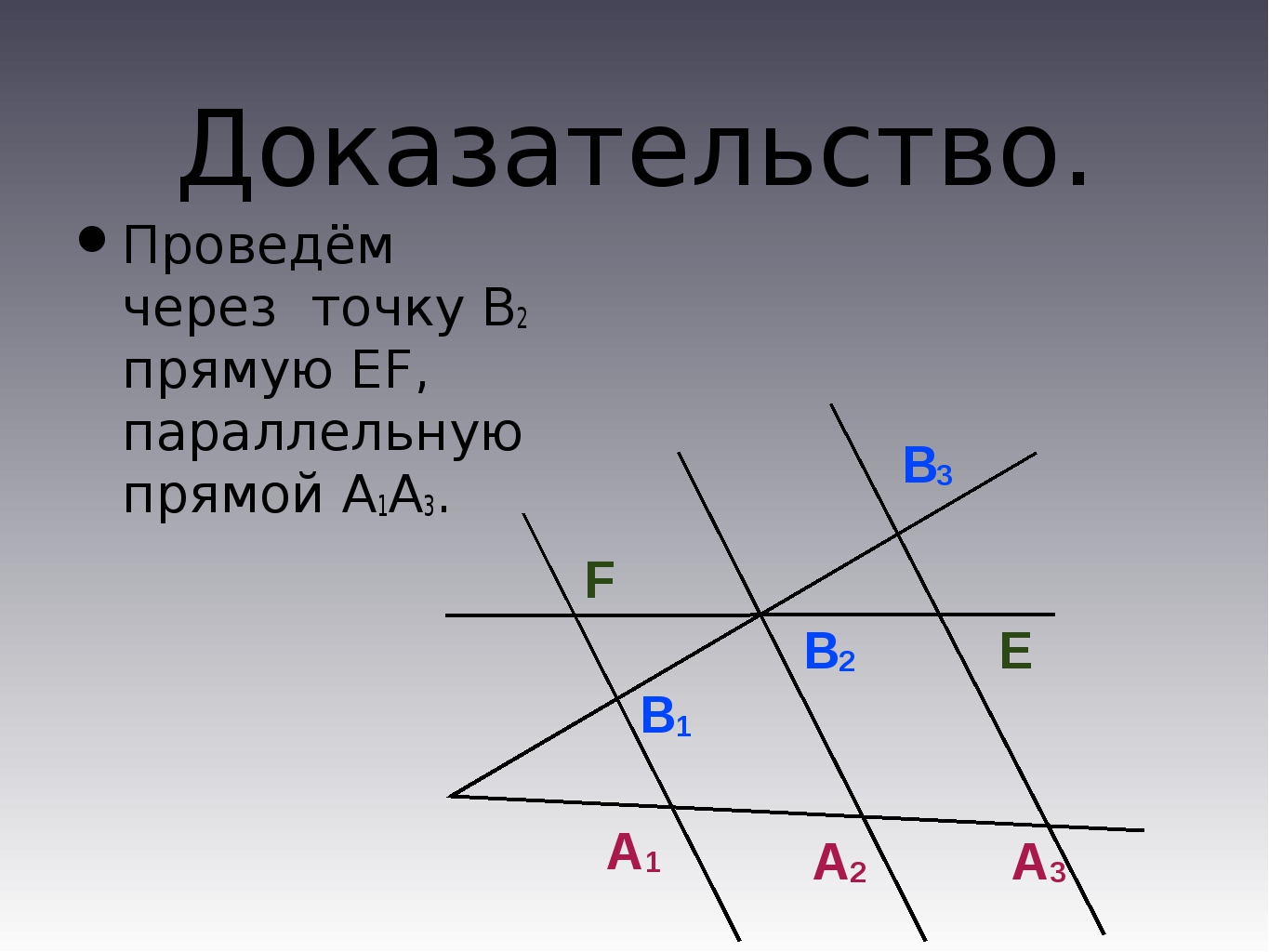
On each of the sides BC, AB, and CA, squares are drawn, CBDE, BAGF, and ACIH, in that order.
From A, draw a line parallel to BD and CE. It will perpendicularly intersect BC and DE at K and L, respectively.
Join CF and AD, to form the triangles BCF and BDA.
Angles CAB and BAG are both right angles; therefore C, A, and G are collinear. Similarly for B, A, and H.
Angles CBD and FBA are both right angles; therefore angle ABD equals angle FBC, since both are the sum of a right angle and angle ABC.
Since AB and BD are equal to FB and BC, respectively, triangle ABD must be equal to triangle FBC.
Since A is collinear with K and L, rectangle BDLK must be twice in area to triangle ABD.
Since C is collinear with A and G, square BAGF must be twice in area to triangle FBC.
Therefore rectangle BDLK must have the same area as square BAGF = AB2.

Similarly, it can be shown that rectangle CKLE must have the same area as square ACIH = AC2.
Adding these two results, AB2 + AC2 = BD × BK + KL × KC
Since BD = KL, BD* BK + KL × KC = BD(BK + KC) = BD × BC
Therefore AB2 + AC2 = BC2, since CBDE is a square.
This proof appears in Euclid’s Elements as that of Proposition 1.47.
Три домика
Домики подобны. Крыши синего и красного домиков в сумме составляют крышу черного, поэтому то же самое верно для площадей квадратных стен.
Задача
[ДПА] На рисунке изображены треугольники ABC и ACD такие, что ∠ABC = ∠ACD = 90°. Какова длина отрезка x (длины отрезков на рисунке приведены в см)?
А) $\sqrt5$ см
Б) $\sqrt7$ см
В) $3$ см
Г) $2$ см
Теорема, обратная теореме Пифагора
Если сумма квадратов двух сторон
треугольника равна квадрату третьей стороны, то такой треугольник прямоугольный.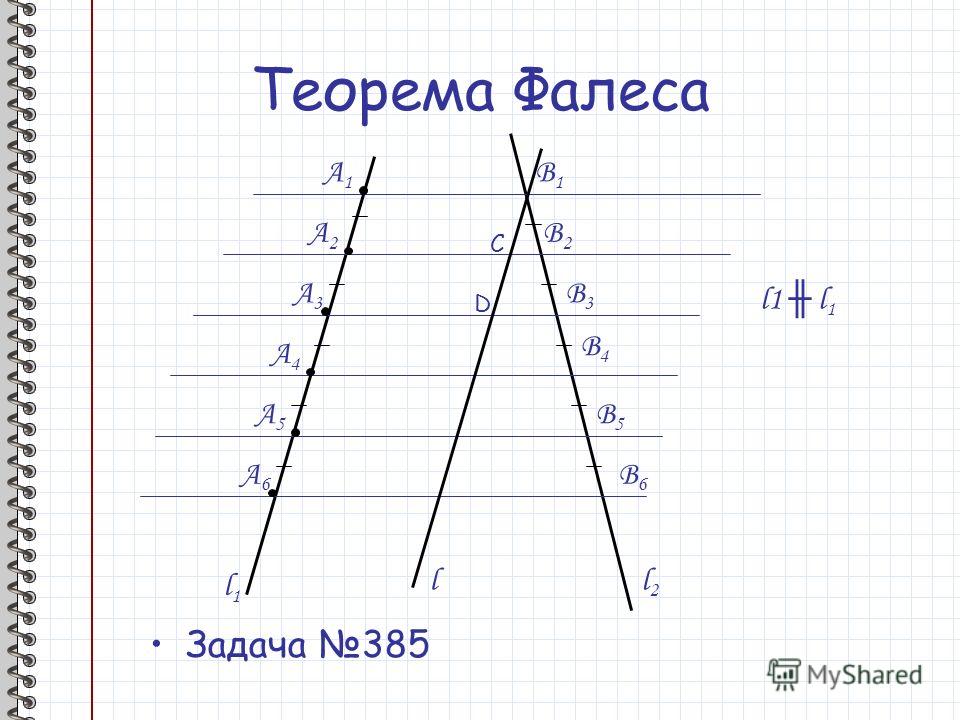 n$
n$
не имеет решений в целых ненулевых числах a, b и c.
Другими словами, задача нахождения пифагоровых троек для степени более 2 не имеет решения.
Фильм Математик и чёрт, СССР, 1972. Фильм снят по мотивам рассказа «Саймон Флэгг и дьявол» американского писателя-фантаста Артура Порджеса. Профессор математики обращается за доказательством теоремы к дьяволу…
Доказательство теоремы искали многие математики более трёхсот лет. Окончательно доказана в 1995 году Эндрю Уайлсом.
Ссылки по теме
Обобщения
Теорема Пифагора верна только в евклидовой геометрии. Ни в геометрии Лобачевского, ни в других неевклидовых геометриях она не имеет места, как и нет аналога теоремы Пифагора на сфере.
Вместо квадратов на сторонах прямоугольного треугольника можно строить любые подобные между собой фигуры (равносторонние треугольники, полукруги и т.д.). При этом площадь фигуры, построенной на гипотенузе, равна сумме площадей фигур, построенных на катетах.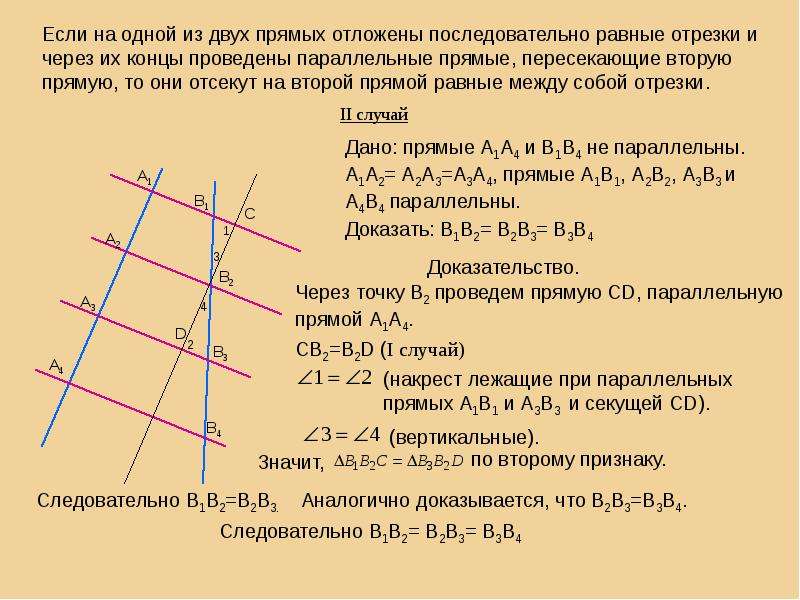
Живая модель — полукруги
Другое обобщение связано с переходом от плоскости к пространству. Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений (длины, ширины и высоты). Аналогичная теорема верна и в многомерном и даже в бесконечномерном случае.
Теорема Пифагора — это частный случай более общей теоремы косинусов, которая связывает длины сторон в произвольном треугольнике.
picture-proof of the Law of Cosines
mat/geom/triangle/pifagor.txt · Последние изменения: 2019/07/23 22:40 — kc
Геометрический сайт
Статьи:
И. Ф. Шарыгин. Избранные статьи djvu. Статьи Игоря Фёдоровича в «Кванте» ссылка.
В. Протасов, В. Тихомиров. Геометрические шедевры Шарыгина (pdf) «Квант», №1, 2006 г.
Классика
Этот раздел предназначен, в первую очередь, школьникам 8-10 классов, которые уверенно справляются с задачами из учебника и решили
узнать чуть больше.
И. Ф. Шарыгин. Вокруг биссектрисы «Квант», №8, 1983 г."В этой статье собраны некоторые геометрические факты, прямо или
косвенно связанные с биссектрисой треугольника."
И. Ф. Шарыгин, А. Ягубьянц Окружность девяти точек и прямая Эйлера «Квант» №8, 1981 г. К этой статье рекомендуем такую серию задач.
И. А. Кушнир Золотой ключ Леонарда Эйлера (pdf) «Математика в школах Украины», №13-15, 2012 г. Рассказывается о приложениях окружности девяти точек для доказательства классических задач.
А.Д. Блинков, Ю.А. Блинков. Вневписанная окружность. (pdf) «Квант», №2, 2009 г.
В статье излагаются классические факты о вневписанной окружности, обсуждаются задачи, в которых вневписанная окружность возникает
самым неожиданным образом.
Г. Б. Филипповский. Параллелограмм Вариньона решает задачи
Г. Б. Филипповский.О двух параллелограммах в треугольнике. (pdf) «Квант», №4, 2008 г.
Б. Филипповский.О двух параллелограммах в треугольнике. (pdf) «Квант», №4, 2008 г.
Г. Б. Филипповский.Замечательная прямая треугольника. (pdf) «Квант», №4, 2007 г.
К статье рекомендуем подборку задач о вписанной окружности.
Конструкции
В.Ю. Протасов. О двух велосипедистах и вешнёвой косточке (pdf) «Квант», №3, 2008 г.
"Попробуем подвести некоторые итоги. Две задачи международных олимпиад,
задача о бабочке, два десятка геометрических задач, которые мы сформулировали
в виде упражнений (некоторые из них появлялись на математических олимпиадах,
в Задачнике , и в различных сборниках задач). Список далеко не полный.
И все это выросло из задачи 1, совсем простенькой и неинтересной, которую мы
вначале и решать-то не хотели."
А. Д. Блинков, Ю. А. Блинков. Две окружности в треугольнике, три окружности в треугольнике…
(pdf) «Квант», №2, 2012 г.
Г. Б. Филипповский О точке на стороне
Б. Филипповский О точке на стороне
и двух параллельных
(pdf) «Математика в школах Украины», №4, 2011 г.
А. Полянский. Воробьями по пушкам (pdf) «Квант», №2, 2012 г. Решения упражнений "В этой статье мы пользуясь двумя простыми и элегантными фактами, решим две достаточно сложные задачи."
Теорема Фейербаха и точка Фейербаха
В.Ю. Протасов. Касающиеся окружноти: от Тебо до Фейербаха. (pdf) «Квант», №4, 2008 г.
В статье обсуждаются сразу две жемчужины: теорема Тебо и теорема Фейербаха. Оказывается, что одна из теорем является следствием другой!
П.А. Кожевников. Ещё раз о точке Фейербаха. (pdf) Математическое просвещение, Выпуск 15, 2012 г.
"В этой заметке предлагается геометрическое доказательство
теоремы Фейербаха, которое дает возможность описать точку Фейербаха
и, в частности, получить отличное от авторского геометрическое решение
задачи 8 из задачного раздела «Математического просвещения», вып. 14,
14,
2010 г."
J.L. Ayme. Красивое доказательство теоремы Фейербаха. (pdf)
Очень красивое доказательство теоремы Фейербаха, найдённое не так давно.
Оригинал статьи можно посмотреть на странице автора.
Фольклор. Доказательство теоремы Фейербаха по И. Ф. Шарыгину. (pdf)
Nguyen Minh Ha and Nguyen Pham Dat.Synthetic Proofs of Two Theorems Related to
the Feuerbach Point.(pdf) Forum Geometricorum
Volume 12 (2012) 39–46. В статье излагаются геометрические доказательства двух замечательных теорем, связанных с точкой Фейербаха.
Кроме цитированной статьи J. Vonk, рекомендуем
заглянуть в статью Куланина Е. Д., в которой теорема Емельянова доказывается с помощью коник.
Jan Vonk. The Feuerbach point and reflections of the Euler line. (pdf) Forum Geometricorum, 9 (2009) 47—55. Рассматриваются интересные свойства точки Фейербаха.
Куланин Е. Д., Шихова Н.А. Прямые Эйлера и точки Фейербаха.(pdf)
Д., Шихова Н.А. Прямые Эйлера и точки Фейербаха.(pdf)
Математическое образование, №2, 2012.
Кожевников П. А.(по статье Д. Гринберга) Обобщение теоремы Фейербаха. (pdf)
Куланин Е. Д. Об описанных окружностях чевианных и педальных треугольников и некоторых кривых, связанных с треугольником.
(pdf)
Ежегодник «Математическое просвещение», №9, М., 2005. Доказательство теоремы Фейербаха через коники! В статье указывается целое семейство окружностей, проходящих через точку Фейербаха(например,
окружность, проходящая через основания биссектрис, проходит через точку Фейербаха). Для понимания статьи необходим некоторый опыт работы с
кониками, который можно получить, почитав замечательную книгу А. Акопяна, А. Заславского (pdf).
Построения
А. Д. Блинков Геометрические построения с помощью треугольника-шаблона (pdf) «Квантик», №3-4, 2012 г.
Е. Д. Куланин Еще раз о трисекции угла
Д. Куланин Еще раз о трисекции угла
(pdf) «Математика в
школах Украины», №4, 2012 г.
Гомотетия
Рекомендуем такие интересные серии задач на гомотетию:
Ортоцентр, середина стороны, точка пересечения касательных и … еще одна точка! (pdf)
Прямая Нагеля (pdf)
Лемма о вписанной окружности
Поворотная гомотетия
Полувписанная окружность, окружности Тебо
А. Гирич Несколько задач о треугольниках и окружностях текст
«Квант», №11, 1990 г.
В.Ю. Протасов. Касающиеся окружноти: от Тебо до Фейербаха. (pdf) «Квант», №4, 2008 г. Рекомендуем серию задач про полувписанную окружность:
полувписанная окружность
Изогональное сопряжение
Для первого знакомства с темой рекомендуем книжку В. В. Прасолова.
А. В. Акопян, А. А. Заславский Разные взгляды на изогональное сопряжение (pdf) Математическое просвещение, сер. 3, вып. 11, 2007.
3, вып. 11, 2007.
Dimitar Belev Some Properties of the Brocard Points of a Cyclic Quadrilateral (pdf), Journal of Classical Geometry, volume 2, 2013
Д. Гринберг Isogonal conjugation with respect to a triangle (zip)
Комбинаторная геометрия
В. Ю. Протасов Теорема Хелли и вокруг неё (pdf) «Квант», №3, 2009 г.
Н. Б. Васильев Формула Пика «Квант», №12, 1974 г.
Для дальнейшего знакомства с этим сюжетом рекомендуем книжку Вавилова и Устинова "Многоугольники
на решетках"(pdf).
Н. Б. Васильев Сложение фигур «Квант», №4, 1976 г.
А. Спивак, М. Смуров Покрытие полосками (часть-1) и (часть-2) «Квант», №4-5, 1998 г.
С. Табачников, В. Тиморин Прямая Сильвестра(pdf) «Квант», №5, 2009 г.
Геометрические неравенства
В. Протасов, В. Тихомиров Пространство Lp и замечательные точки треугольника (pdf) «Квант», №2, 2012 г.
Claudi Alsina, Roger B. Nelsen. Геометрическое доказательство неравенства Эрдеша-Морделла.(pdf)
Forum Geometricorum, 7 (2007) 99-102. В статье излагается одно из самых красивых доказательств известного неравенства.
Замечательные кривые
Акопян А. В. Кардиоида. «Квант» №3, 2012 год.
Акопян А. В. Лемниската Бернулли «Квант» №3, 2009 год.
Трисекция. Теорема Морлея
Штейнгарц Л. Снова о теореме Морлея «Квант» №5, 2009 год.
Тоноян Г., Яглом И. Теорема Морлея «Квант» №8, 1978 год.
Е. Д. Куланин Еще раз о трисекции угла
(pdf) «Математика в
школах Украины», №4, 2012 г.
Алгебра и геометрия
Г. Б. Филипповский Рене Декарт (1596–1650).
Декартова система координат
(pdf) «Математика в школах Украины», №35-36, 2011 г.
А.И. Сгибнев. «Геометрия помогает алгебре» (ps, 2M), (ps-zip, 400K), (pdf, 190K)
Тетраэдр
В. Дубровский, В. Матизен. Из геометрии тетраэдра «Квант» №9, 1988 год.
Дубровский, В. Матизен. Из геометрии тетраэдра «Квант» №9, 1988 год.
А. Заславский. Описанная и вписанные сферы тетраэдра «Квант» №1, 2004 год.
А. Заславский, Д. Косов. Изогонально сопряжение в тетраэдре и его гранях «Квант» №3, 2004 год.
Миниатюры:
М. Петкова Салфетки «Кванта» и теорема Пифагора (pdf) «Квант» №3, 2012 год.
П. А. Кожевников Задача M2100 (pdf)
Фольклор Задача Ф. Ивлева. (pdf) В заметке решение трудной и красивой задачи разбито на несколько подзадач, что позволяет использовать материал на кружке.
Решения многих задач и различные обобщения можно найти в статье.
Л. А. Емельянов Задача 7.8. (pdf)
Теорема Пифагора: формулы, пример задачи
Теорема Пифагора – одна из самых известных геометрических теорем, которая устанавливает, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Большинство ученых считают, что теорема Пифагора была доказана древнегреческим математиком и философом Пифагором (или Питагором). Однако есть версия, что теорему знали и до его рождения. Доказательством этого является то, что в Древнем Египте знали, что треугольник, у которого стороны имеют 3 см, 4 см и 5 см, является прямоугольным. А о других теоремах можно узнать в учебнике по геометрии за 8 класс А.Г. Мерзляка.
История теоремы Пифагора
Еще в детстве Пифагор отличился интересом к точным наукам. Впоследствии он переехал жить на остров Лесбос, где познакомился с Фалесом Милетским – древнегреческим философом и математиком, который доказал теоремы о трех точках на окружности и пропорциональных отрезках. За время, когда Пифагор учился в Милетской школе, он изучал астрологию, медицину, прогнозы затмений и другие важные в то время науки. Лекции Фалеса и его ученика Анаксимандра сыграли важную роль для Пифагора.
После обучения в Египте, плена в Вавилоне, в 60 лет Пифагор решает вернуться домой, чтобы поделиться своими знаниями с народом. Впоследствии он открыл собственную школу, в которой геометрия впервые выступает как самостоятельная наука.
Впоследствии он открыл собственную школу, в которой геометрия впервые выступает как самостоятельная наука.
О том, что квадрат гипотенузы равен сумме квадратов катетов, знали задолго до рождения Пифагора. Но именно он считается первым ученым, который доказал соотношение сторон треугольника.
Формулы
В теореме Пифагора говорится, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Пусть ВС = а; АС = b; АВ = с.
Тогда имеем такую формулу, которая применяется при нахождении неизвестной стороны в прямоугольном треугольнике, когда две другие – известны:
с — гипотенуза, a и b — катеты
Когда мы определили квадрат гипотенузы, нужно найти квадратный корень. Такую же формулу мы можем применить к неизвестному катету:
с — гипотенуза, a и b — катеты
А больше рисунков и формул можно увидеть в онлайн уроке за 8 класс по геометрии на тему «Метрические соотношения в прямоугольном треугольнике.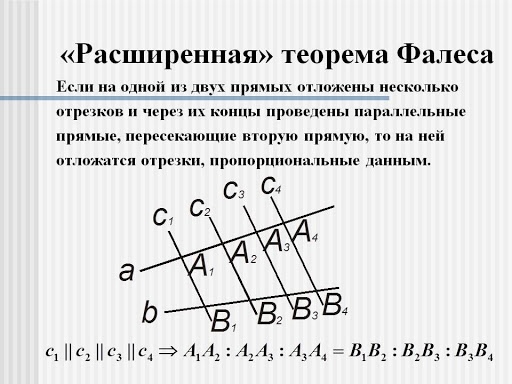 Теорема Пифагора».
Теорема Пифагора».
Доказательство теоремы Пифагора
1. Алгебраическое доказательство
Самый популярный и самый простой метод доказательства теоремы связан с площадями фигуры.
Нужно расположить одинаковые прямоугольные треугольники так, чтобы внутри образовался квадрат. Каждая сторона внешнего квадрата должна состоять из суммы катетов прямоугольного треугольника a + b.
Квадраты, которые образуются из равных прямоугольных треугольников, где c — стороны внутреннего квадрата, а и b — внешнего
Площадь этого квадрата можно будет найти благодаря формуле:
Площадь внешнего квадрата, где a и b — катеты прямоугольного треугольника, из которых состоит сторона квадрата
Внутренний четырехугольник можно считать квадратом, ведь, если добавить два острые углы прямоугольного треугольника, то получится 90°. Следует считать, что площадь внешнего квадрата состоит из площади внутреннего квадрата и четырех площадей одинаковых прямоугольных треугольников. Итак, в заключении:
Итак, в заключении:
С одной стороны — площадь внешнего квадрата, с другой — сумма площадей внутреннего квадрата и четырех одинаковых прямоугольных треугольников
Итак, теорема Пифагора доказана.
2. Доказательство Евклида
Доказательство Евклида также называется «Пифагоровы штаны». Ее так назвали, потому что сумма площади квадратов, образованных с использованием катетов прямоугольного треугольника равна площади квадрата, который построен на гипотенузе этого же треугольника. Квадраты напоминали ученикам мужские штаны.
На примере приведенных картинок ниже можно увидеть, как оригинально передали суть доказательства Евклида.
«Пифагоровы штаны — на все стороны равны они» — это придумали ученики средних веков, которые изучали теорему. Источник: senogrif.com
Оригинальное представление доказательства Евклида. Источник: senogrif.com
В вашем учебнике не было таких доказательств? Вы можете найти другой в разделе «Учебники по геометрии за 8 класс».
Пример задачи на применение теоремы Пифагора
Условия задачи. В треугольнике ABC дано: ∠C = 90 °, BC = 20 см, AC = 15 см. Найти сторону AB.
Прямоугольный треугольник
Решение. Поскольку в треугольнике АВС ∠С = 90°, следовательно, по теореме Пифагора имеем:
АВ² = BС² + АС²; AВ² = 20² + 15², AВ² = 625, AB = √625| AB = 25 см.
Если вам нужно решить задачу с помощью теоремы Пифагора, а вы сомневаетесь в конечном ответе, тогда можете проверить свои знания благодаря разделу «ГДЗ и решебники по геометрии за 8 класс».
А если вы хотите крепче закрепить знания по другим темам по геометрии, то можете просматривать видео в разделе «Онлайн уроки за 8 класс по геометрии». Узнайте больше о перпендикуляре и наклонной, сумме углов выпуклого треугольника, площадь квадрата и прямоугольника, решение задач методом площадей и тому подобное.
Подпишись на Telegram-канал и посмотри, что будет дальше!
Решения
NCERT для математики класса 10 Глава 6
Страница № 122:
Вопрос 1:
Заполните пропуски, используя правильное слово, указанное в скобках: —
(i) Все круги __________.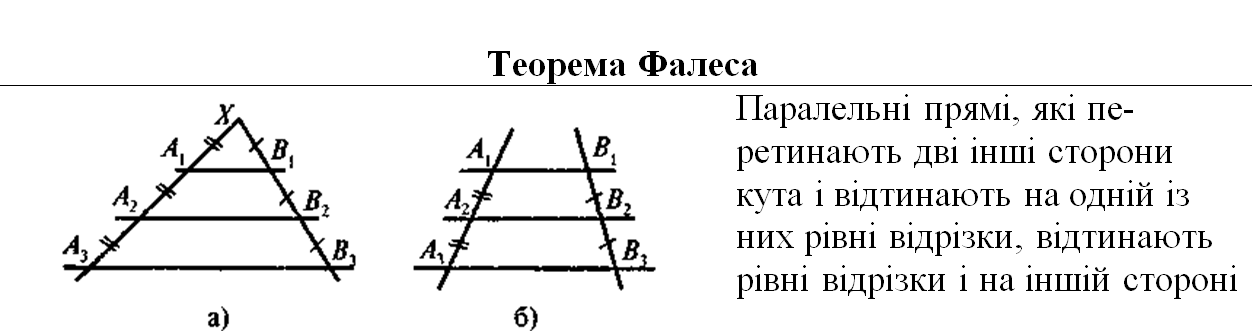 (конгруэнтно, аналогично)
(конгруэнтно, аналогично)
(ii) Все квадраты __________. (похожие, совпадающие)
(iii) Все __________ треугольники похожи. (равнобедренный, равносторонний)
(iv) Два многоугольника с одинаковым количеством сторон подобны, если (a) их соответствующие углы равны __________ и (b) их соответствующие стороны равны __________.(равный, пропорциональный)
Ответ:
(i) Аналогичный
(ii) Аналогичное
(iii) Равносторонний
(iv) (a) Равно
(б) Пропорциональная
Видео решение для треугольников (Страница: 122, Q.No .: 1)
Решение NCERT для математики класса 10 — треугольники 122, вопрос 1
Страница № 122:
Вопрос 2:
Приведите два разных примера пары
(i) Аналогичные цифры
(ii) Не похожие цифры
Ответ:
(i) Два равносторонних треугольника со сторонами 1 см и 2 см
Два квадрата со стороной 1 см и 2 см
(ii) Трапеция и квадрат
Треугольник и параллелограмм
Видео решение для треугольников (Страница: 122, В.
 №: 2)
№: 2)
Решение NCERT для математики класса 10 — треугольники 122, вопрос 2
Страница № 122:
Вопрос 3:
Укажите, похожи ли следующие четырехугольники:
Ответ:
Четырехугольник PQRS и ABCD не похожи, поскольку их соответствующие стороны пропорциональны, т.е.е. 1: 2, но их соответствующие углы не равны.
Видео решение для треугольников (Страница: 122, Q.No .: 3)
Решение NCERT для математики класса 10 — треугольники 122, вопрос 3
Страница № 128:
Вопрос 1:
На рисунке 6.17. (i) и (ii), DE || ДО Н.Э. Найдите EC в (i) и AD в (ii).
(я)
(ii)
Ответ:
(я)
Пусть EC = x см
Приведено, что DE || ДО Н.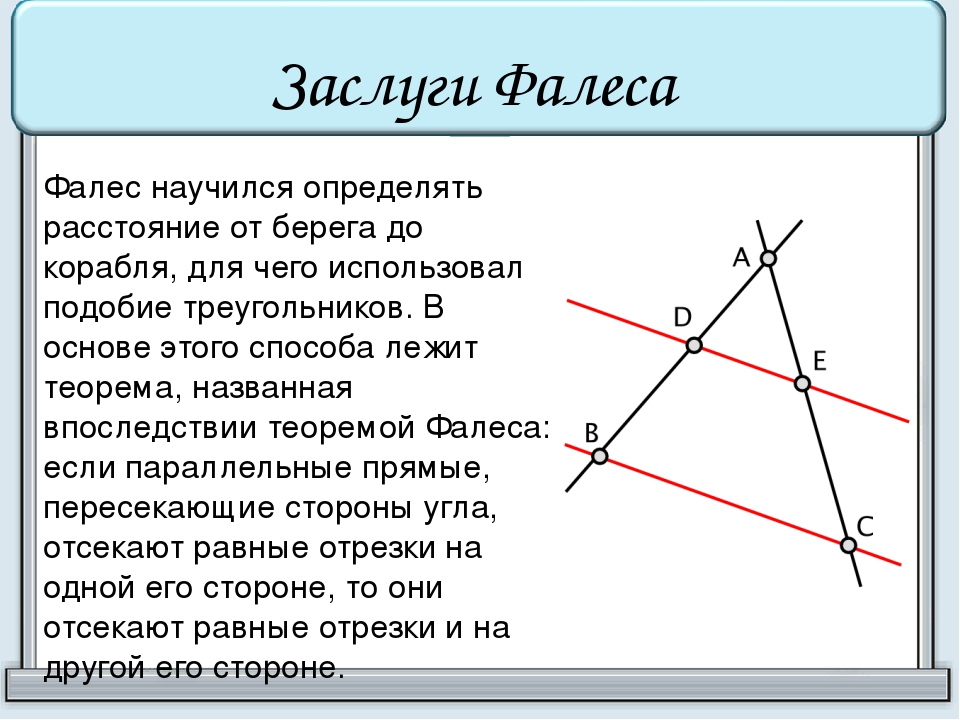 Э.
Э.
Используя основную теорему пропорциональности, получаем
(ii)
Пусть AD = x см
Приведено, что DE || ДО Н.Э.
Используя основную теорему пропорциональности, получаем
Видео решение для треугольников (Страница: 128, Q.No: 1)
Решение NCERT для математики класса 10 — треугольники 128, вопрос 1
Страница № 128:
Вопрос 2:
E и F — точки на сторонах PQ и PR соответственно ΔPQR.Для каждого из следующих случаев укажите, является ли EF || QR.
(i) PE = 3,9 см, EQ = 3 см, PF = 3,6 см и FR = 2,4 см
(ii) PE = 4 см, QE = 4,5 см, PF = 8 см и RF = 9 см
(iii) PQ = 1,28 см, PR = 2,56 см, PE = 0,18 см и PF = 0,63 см
Ответ:
(я)
Учитывая, что PE = 3,9 см, EQ = 3 см, PF = 3,6 см, FR = 2,4 см
(ii)
PE = 4 см, QE = 4. 5 см, PF = 8 см, RF = 9 см
5 см, PF = 8 см, RF = 9 см
(iii)
PQ = 1,28 см, PR = 2,56 см, PE = 0,18 см, PF = 0,36 см
Видео решение для треугольников (Страница: 128, Q.No: 2)
Решение NCERT для математики класса 10 — треугольники 128, вопрос 2
Страница № 128:
Вопрос 3:
На следующем рисунке, если LM || CB и LN || CD, докажите, что
Ответ:
На данном рисунке LM || CB
Используя основную теорему пропорциональности, получаем
Видео решение для треугольников (Страница: 128, Q.№: 3)
Решение NCERT для математики класса 10 — треугольники 128, вопрос 3
Страница № 128:
Вопрос 4:
На следующем рисунке DE || AC и DF || AE. Докажите, что
Докажите, что
Ответ:
In ΔABC, DE || AC
Видео решение для треугольников (Страница: 128, Q.№: 4)
Решение NCERT для математики класса 10 — треугольники 128, вопрос 4
Страница № 129:
Вопрос 5:
На следующем рисунке DE || OQ и DF || ИЛИ, покажите, что EF || QR.
Ответ:
In Δ POQ, DE || OQ
Видео решение для треугольников (Стр .: 129, В.№: 5)
Решение NCERT для математики класса 10 — треугольники 129, вопрос 5
Страница № 129:
Вопрос 6:
На следующем рисунке A, B и C — это точки на OP, OQ и OR соответственно, такие что AB || PQ и AC || PR. Покажи, что BC || QR.
Покажи, что BC || QR.
Ответ:
In Δ POQ, AB || PQ
Видео решение для треугольников (Стр .: 129, В.№: 6)
Решение NCERT для математики класса 10 — треугольники 129, вопрос 6
Страница № 129:
Вопрос 7:
Используя Основную теорему пропорциональности, докажите, что линия, проведенная через средние точки одной стороны треугольника, параллельной другой стороне, делит третью сторону пополам. (Напомним, что вы доказали это в классе IX).
Ответ:
Рассмотрим данный рисунок, на котором l — это линия, проведенная через среднюю точку P отрезка AB, пересекающего AC в точке Q, так что.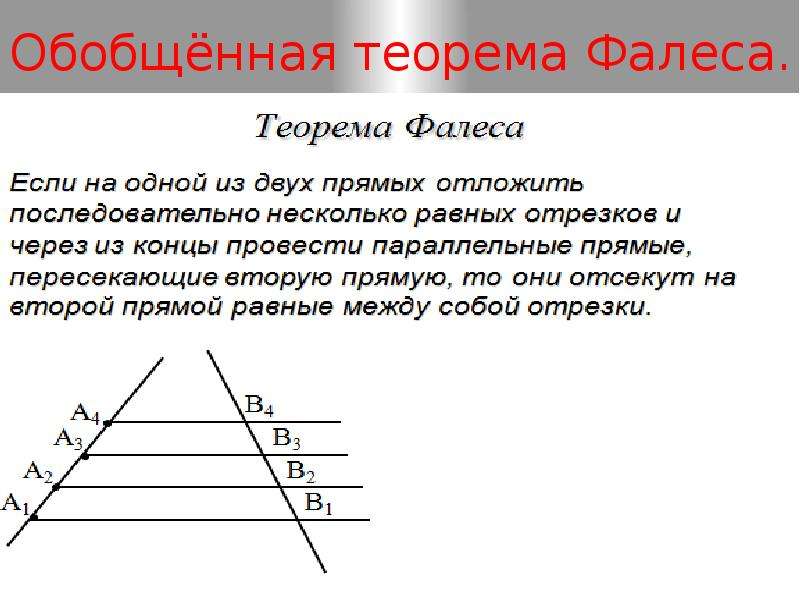
Или, Q — средняя точка переменного тока.
Видео решение для треугольников (Страница: 129, Q.No: 7)
Решение NCERT для математики класса 10 — треугольники 129, вопрос 7
Страница № 129:
Вопрос 8:
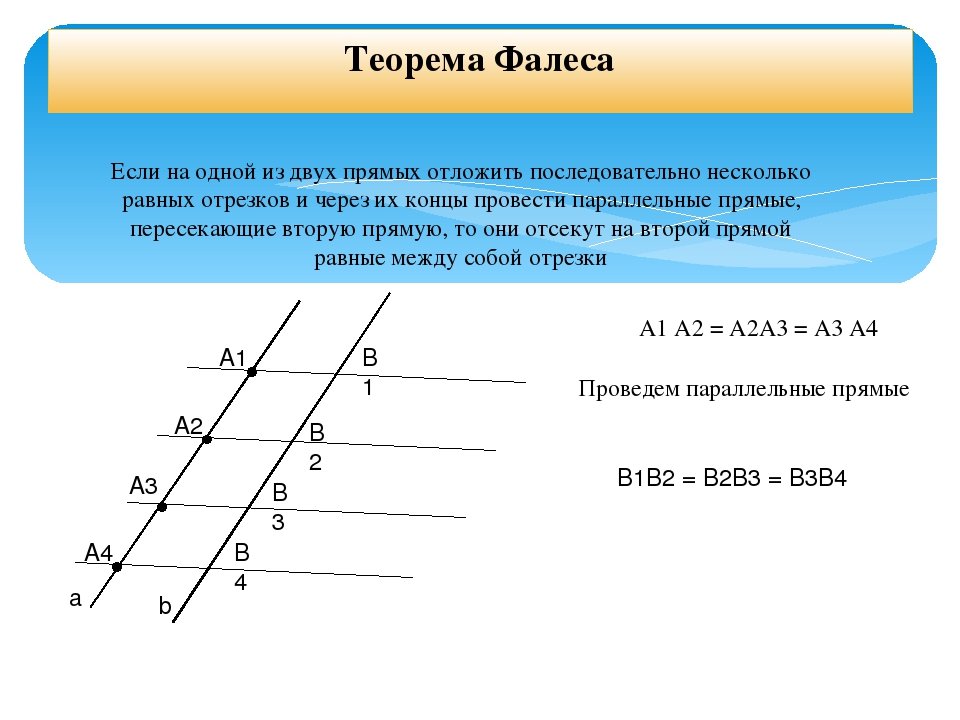
Используя Обратную теорему о пропорциональности, докажите, что прямая, соединяющая середины любых двух сторон треугольника, параллельна третьей стороне.(Напомним, что вы делали это в IX классе).
Ответ:
Рассмотрим данный рисунок, на котором PQ — это отрезок прямой, соединяющий средние точки P и Q прямых AB и AC соответственно.
то есть AP = PB и AQ = QC
Можно заметить, что
Следовательно, используя основную теорему пропорциональности, получаем
Видео решение для треугольников (Стр .
 : 129, В.№: 8)
: 129, В.№: 8)
Решение NCERT для математики класса 10 — треугольники 129, вопрос 8
Страница № 129:
Вопрос 9:
ABCD представляет собой трапецию, в которой AB || DC и его диагонали пересекаются в точке O. Покажите, что
Ответ:
Проведите линию EF через точку O так, чтобы
В ΔADC,
Используя основную теорему пропорциональности, получаем
В ΔABD,
Итак, используя основную теорему пропорциональности, получаем
Из уравнений (1) и (2) получаем
Видео решение для треугольников (Стр .: 129, В.№: 9)
Решение NCERT для математики класса 10 — треугольники 129, вопрос 9
Страница № 129:
Вопрос 10:
Диагонали четырехугольника ABCD пересекаются друг с другом в точке O, так что Покажите, что ABCD — трапеция.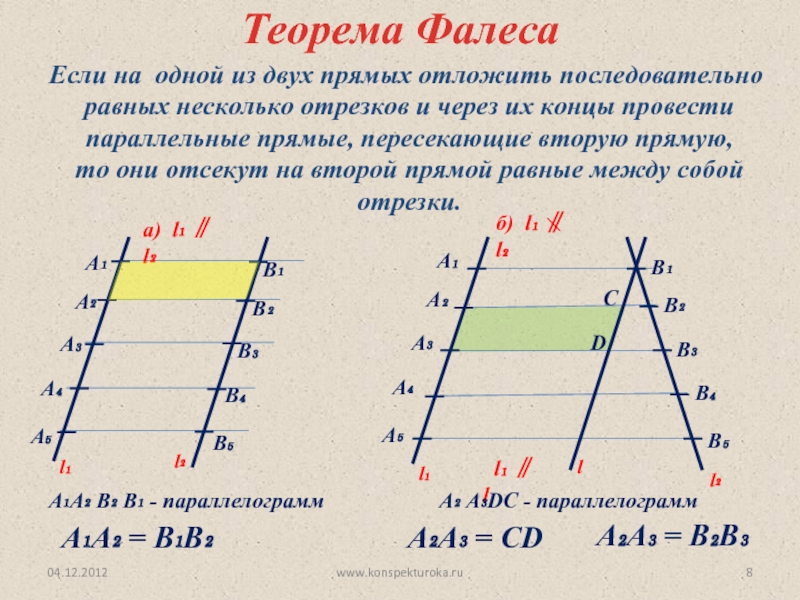
Ответ:
Рассмотрим следующий рисунок для данного вопроса.
Нарисуйте линию OE || AB
In ΔABD, OE || AB
Используя основную теорему пропорциональности, получаем
Однако указано, что
⇒ EO || DC [Обратное к основной теореме пропорциональности]
⇒ AB || OE || DC
⇒ AB || CD
∴ ABCD — трапеция.
Видео решение для треугольников (Стр .: 129, В.№: 10)
Решение NCERT для математики класса 10 — треугольники 129, вопрос 10
Страница № 138:
Вопрос 1:
Укажите, какие пары треугольников на следующем рисунке похожи? Напишите критерий подобия, который вы использовали для ответа на вопрос, а также напишите пары похожих треугольников в символической форме:
(я)
(ii)
(iii)
(iv)
(в)
(vi)
Ответ:
(я) ∠A = ∠P = 60 °
∠B = ∠Q = 80 °
∠C = ∠R = 40 °
Следовательно, ΔABC ∼ ΔPQR [По критерию сходства AAA]
(ii)
(iii) Данные треугольники не похожи, так как соответствующие стороны не пропорциональны.
(iv) В ∆ MNL и ∆ QPR мы видим, что
MNQP = MLQR = 12∠M = ∠Q = 70 ° ∴∆MNL ~ ∆QPR По критерию подобия SAS
(v) Данные треугольники не похожи друг на друга, так как соответствующие стороны не пропорциональны.
(vi) В ΔDEF,
∠D + ∠E + ∠F = 180º
(Сумма углов треугольника 180º.)
70º + 80º + ∠F = 180º
∠F = 30º
Аналогично, в ΔPQR,
∠P + ∠Q + ∠R = 180º
(Сумма углов треугольника 180º.)
∠P + 80º + 30º = 180º
∠P = 70º
В ΔDEF и ΔPQR,
∠D = ∠P (каждые 70 °)
∠E = ∠Q (каждые 80 °)
∠F = ∠R (каждые 30 °)
∴ ΔDEF ∼ ΔPQR [По критерию сходства AAA]
Видео решение для треугольников (Страница: 138, Q.No: 1)
Решение NCERT для математики класса 10 — треугольники 138, вопрос 1
Страница № 139:
Вопрос 2:
На следующем рисунке ΔODC ∼ ΔOBA, BOC = 125 ° и ∠CDO = 70 °. Найдите ∠DOC, ∠DCO и ∠OAB
Найдите ∠DOC, ∠DCO и ∠OAB
.
Ответ:
DOB — прямая линия.
∴ DOC + ∠COB = 180 °
⇒ ∠DOC = 180 ° — 125 °
= 55 °
В ΔDOC,
∠DCO + ∠CDO + ∠DOC = 180 °
(Сумма углов треугольника 180º.)
⇒ ∠DCO + 70º + 55º = 180 °
⇒ ∠DCO = 55 °
Задано, что ΔODC ∼ ΔOBA.
∴ ∠OAB = ∠ OCD [Соответствующие углы в подобных треугольниках равны.]
⇒ ∠OAB = 55 °
Видео решение для треугольников (Страница: 139, Q.No: 2)
Решение NCERT для математики класса 10 — треугольники 139, вопрос 2
Страница № 139:
Вопрос 3:
Диагонали AC и BD трапеции ABCD с AB || DC пересекаются друг с другом в точке O.Используя критерий подобия для двух треугольников, покажите, что
Ответ:
In ΔDOC и ΔBOA,
∠CDO = ∠ABO [Альтернативные внутренние углы как AB || CD]
∠DCO = ∠BAO [Альтернативные внутренние углы как AB || CD]
∠DOC = ∠BOA [Вертикально противоположные углы]
∴ ΔDOC ∼ ΔBOA [критерий сходства AAA]
Видео решение для треугольников (Стр .
 : 139, В.№: 3)
: 139, В.№: 3)
Решение NCERT для математики класса 10 — треугольники 139, вопрос 3
Страница № 140:
Вопрос 4:
На следующем рисунке покажите, что
Ответ:
В ΔPQR, ∠PQR = ∠PRQ
∴ PQ = PR (i)
Дано,
Видео решение для треугольников (Страница: 140, В.№: 4)
Решение NCERT для математики класса 10 — треугольники 140, вопрос 4
Страница № 140:
Вопрос 5:
S и T — точки на сторонах PR и QR ΔPQR, такие что ∠P = ∠RTS. Покажите, что ΔRPQ ∼ ΔRTS.
Ответ:
В ΔRPQ и ΔRST,
∠RTS = ∠QPS (дано)
∠R = ∠R (Общий угол)
∴ ΔRPQ ∼ ΔRTS (по критерию сходства AA)
Видео решение для треугольников (Страница: 140, В.
 №: 5)
№: 5)
Решение NCERT для математики класса 10 — треугольники 140, вопрос 5
Страница № 140:
Вопрос 6:
На следующем рисунке, если ΔABE ≅ ΔACD, покажите, что ΔADE ∼ ΔABC.
Ответ:
Принято, что ΔABE ≅ ΔACD.
∴ AB = AC [По CPCT] (1)
А, AD = AE [по CPCT] (2)
В ΔADE и ΔABC,
[Разделив уравнение (2) на (1)]
∠A = ∠A [Общий угол]
∴ ΔADE ∼ ΔABC [По критерию подобия SAS]
Видео решение для треугольников (Страница: 140, В.№: 6)
Решение NCERT для математики класса 10 — треугольники 140, вопрос 6
Страница № 140:
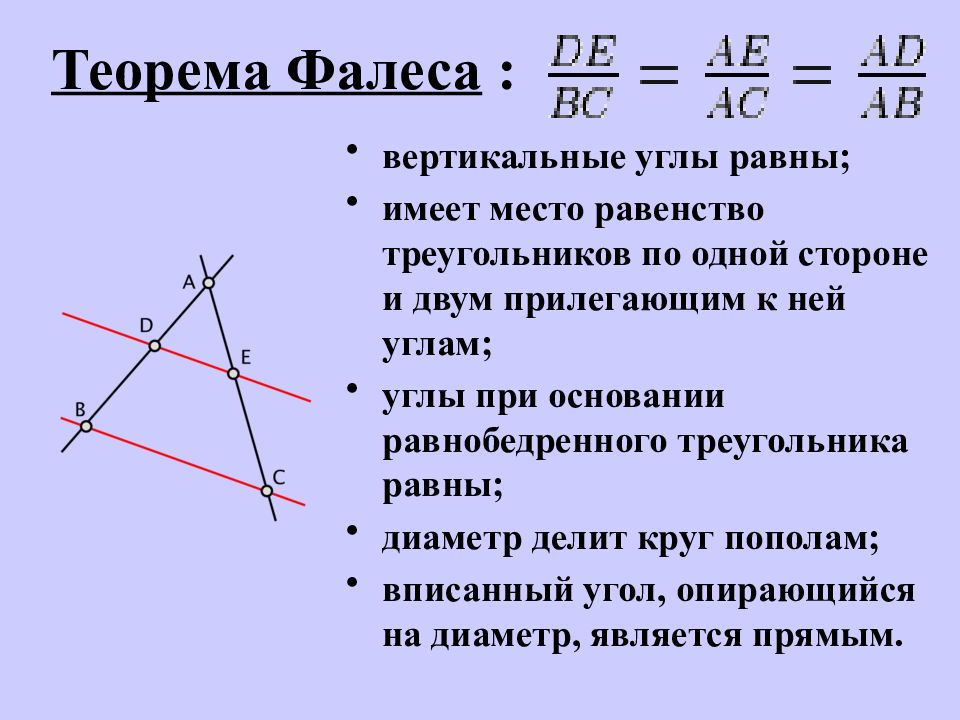
Вопрос 7:
На следующем рисунке высоты AD и CE ΔABC пересекаются друг с другом в точке P. Покажите, что:
Покажите, что:
(i) ΔAEP ∼ ΔCDP
(ii) ΔABD ∼ ΔCBE
(iii) ΔAEP ∼ ΔADB
(в) ΔPDC ∼ ΔBEC
Ответ:
(я)
В ΔAEP и ΔCDP,
∠AEP = ∠CDP (каждый 90 °)
∠APE = ∠CPD (вертикально противоположные углы)
Следовательно, используя критерий сходства AA,
ΔAEP ∼ ΔCDP
(ii)
В ΔABD и ΔCBE,
∠ADB = ∠CEB (каждый 90 °)
∠ABD = ∠CBE (общий)
Следовательно, используя критерий сходства AA,
ΔABD ∼ ΔCBE
(iii)
В ΔAEP и ΔADB,
∠AEP = ∠ADB (каждые 90 °)
∠PAE = ∠DAB (общий)
Следовательно, используя критерий сходства AA,
ΔAEP ∼ ΔADB
(iv)
In ΔPDC и ΔBEC,
∠PDC = ∠BEC (каждый 90 °)
∠PCD = ∠BCE (Общий угол)
Следовательно, используя критерий сходства AA,
ΔPDC ∼ ΔBEC
Видео решение для треугольников (Страница: 140, В.
 №: 7)
№: 7)
Решение NCERT для математики класса 10 — треугольники 140, вопрос 7
Страница № 140:
Вопрос 8:
E — точка на стороне AD, образованная параллелограммом ABCD, и BE пересекает CD в точке F. Покажите, что ΔABE ∼ ΔCFB
Ответ:
В ΔABE и ΔCFB,
∠A = ∠C (Противоположные углы параллелограмма)
∠AEB = ∠CBF (Альтернативные внутренние углы как AE || BC)
∴ ΔABE ∼ ΔCFB (по критерию сходства AA)
Видео решение для треугольников (Страница: 140, В.№: 8)
Решение NCERT для математики класса 10 — треугольники 140, вопрос 8
Страница № 140:
Вопрос 9:
На следующем рисунке ABC и AMP представляют собой два прямоугольных треугольника, расположенных под прямым углом в точках B и M соответственно, что доказывает, что:
(i) ΔABC ∼ ΔAMP
(ii)
Ответ:
In ΔABC и ΔAMP,
∠ABC = ∠AMP (каждый 90 °)
∠A = ∠A (общий)
∴ ΔABC ∼ ΔAMP (по критерию сходства AA)
Видео решение для треугольников (Страница: 140, В.
 №: 9)
№: 9)
Решение NCERT для математики класса 10 — треугольники 140, вопрос 9
Страница № 140:
Вопрос 10:
CD и GH являются биссектрисами ofACB и EGF соответственно, так что D и H лежат на сторонах AB и FE ΔABC и ΔEFG соответственно. Если ΔABC ∼ ΔFEG, Покажите, что:
(я)
(ii) ΔDCB ∼ ΔHGE
(iii) ΔDCA ∼ ΔHGF
Ответ:
Принято, что ΔABC ∼ ΔFEG.
∴ ∠A = ∠F, ∠B = ∠E и ∠ACB = ∠FGE
∠ACB = ∠FGE
∴ ∠ACD = ∠FGH (Биссектриса угла)
А, DCB = ∠HGE (Биссектриса угла)
In ΔACD и ΔFGH,
∠A = ∠F (Доказано выше)
∠ACD = ∠FGH (Доказано выше)
∴ ΔACD ∼ ΔFGH (по критерию сходства AA)
В ΔDCB и ΔHGE,
∠DCB = ∠HGE (Доказано выше)
∠B = ∠E (Доказано выше)
∴ ΔDCB ∼ ΔHGE (по критерию сходства AA)
В ΔDCA и ΔHGF,
∠ACD = ∠FGH (Доказано выше)
∠A = ∠F (Доказано выше)
∴ ΔDCA ∼ ΔHGF (по критерию сходства AA)
Видео решение для треугольников (Страница: 140, В.
 №: 10)
№: 10)
Решение NCERT для математики класса 10 — треугольники 140, вопрос 10
Страница № 141:
Вопрос 11:
На следующем рисунке E — точка на стороне CB, образованная равнобедренным треугольником ABC с AB = AC. Если AD ⊥ BC и EF ⊥ AC, докажите, что ΔABD ∼ ΔECF
Ответ:
Принято, что ABC — равнобедренный треугольник.
∴ AB = AC
⇒ ABD = ∠ECF
В ΔABD и ΔECF,
∠ADB = ∠EFC (каждый 90 °)
∠ABD = ∠ECF (Доказано выше)
∴ ΔABD ∼ ΔECF (по критерию сходства AA)
Видео решение для треугольников (Страница: 141, Q.No .: 11)
Решение NCERT для математики класса 10 — треугольники 141, вопрос 11
Страница № 141:
Вопрос 12:
Стороны AB и BC и медиана AD треугольника ABC соответственно пропорциональны сторонам PQ и QR и медиане PM ΔPQR (см. Данный рисунок).Покажите, что ΔABC ∼ ΔPQR.
Данный рисунок).Покажите, что ΔABC ∼ ΔPQR.
Ответ:
Медиана разделяет противоположную сторону.
∴
Учитывая это,
В ΔABD и ΔPQM,
(доказано)
∴ ΔABD ∼ ΔPQM (по критерию подобия SSS)
⇒ ABD = ∠PQM (Соответствующие углы подобных треугольников)
В ΔABC и ΔPQR,
∠ABD = ∠PQM (Доказано выше)
∴ ΔABC ∼ ΔPQR (по критерию подобия SAS)
Видео решение для треугольников (Стр .: 141, В.№: 12)
Решение NCERT для математики класса 10 — треугольники 141, вопрос 12
Страница № 141:
Вопрос 13:
D — точка на стороне BC треугольника ABC такая, что ∠ADC = ∠BAC. Покажи, что
Ответ:
In ΔADC и ΔBAC,
∠ADC = ∠BAC (дано)
∠ACD = ∠BCA (общий угол)
∴ ΔADC ∼ ΔBAC (по критерию сходства AA)
Мы знаем, что соответствующие стороны одинаковых треугольников пропорциональны.
Видео решение для треугольников (Страница: 141, Q.No .: 13)
Решение NCERT для математики класса 10 — треугольники 141, вопрос 13
Страница № 141:
Вопрос 14:
Стороны AB и AC и медиана AD треугольника ABC соответственно пропорциональны сторонам PQ и PR и медиане PM другого треугольника PQR.Покажи, что
Ответ:
Учитывая это,
Продолжим AD и PM до точек E и L соответственно, так что AD = DE и PM = ML. Затем соедините B с E, C с E, Q с L и R с L.
Мы знаем, что медианы делят противоположные стороны.
Следовательно, BD = DC и QM = MR
Также AD = DE (По конструкции)
А, ПМ = МЛ (По конструкции)
В четырехугольнике ABEC диагонали AE и BC делят друг друга пополам в точке D.
Следовательно, четырехугольник ABEC — параллелограмм.
∴ AC = BE и AB = EC (противоположные стороны параллелограмма равны)
Аналогичным образом можно доказать, что четырехугольник PQLR является параллелограммом и PR = QL, PQ = LR
Было дано, что
∴ ΔABE ∼ ΔPQL (по критерию подобия SSS)
Мы знаем, что соответствующие углы одинаковых треугольников равны.
∴ ∠BAE = ∠QPL… (1)
Аналогично можно доказать, что ΔAEC ∼ ΔPLR и
∠CAE = ∠RPL… (2)
Складывая уравнения (1) и (2), получаем
BAE + ∠CAE = ∠QPL + ∠RPL
⇒ ∠CAB = ∠RPQ… (3)
В ΔABC и ΔPQR,
(дано)
∠CAB = ∠RPQ [Используя уравнение (3)]
∴ ΔABC ∼ ΔPQR (по критерию подобия SAS)
Видео решение для треугольников (Стр .: 141, В.№: 14)
Решение NCERT для математики класса 10 — треугольники 141, вопрос 14
Страница № 141:
Вопрос 15:
Вертикальный столб длиной 6 м отбрасывает тень длиной 4 м на землю, и в то же время башня отбрасывает тень длиной 28 м. Найдите высоту башни.
Найдите высоту башни.
Ответ:
Пусть AB и CD — башня и столб соответственно.
Пусть тень BE и DF будет тенью AB и CD соответственно.
В то же время световые лучи от солнца будут падать на башню и столб под одним и тем же углом.
Следовательно, ∠DCF = ∠BAE
А, ∠DFC = ∠BEA
∠CDF = ∠ABE (Башня и столб вертикальны к земле)
∴ ΔABE ∼ ΔCDF (критерий сходства AAA)
Следовательно, высота башни составит 42 метра.
Видео решение для треугольников (Стр .: 141, В.№: 15)
Решение NCERT для математики класса 10 — треугольники 141, вопрос 15
Страница № 141:
Вопрос 16:
Если AD и PM — медианы треугольников ABC и PQR, соответственно, где
Ответ:
Принято, что ΔABC ∼ ΔPQR
Мы знаем, что соответствующие стороны одинаковых треугольников пропорциональны.
∴… (1)
Также ∠A = ∠P, ∠B = ∠Q, ∠C = ∠R… (2)
Поскольку AD и PM — медианы, они будут делить свои противоположные стороны.
∴… (3)
Из уравнений (1) и (3) получаем
… (4)
В ΔABD и ΔPQM,
∠B = ∠Q [Используя уравнение (2)]
[Используя уравнение (4)]
∴ ΔABD ∼ ΔPQM (по критерию подобия SAS)
⇒
.
Видео решение для треугольников (Стр .: 141, В.№: 16)
Решение NCERT для математики класса 10 — треугольники 141, вопрос 16
Страница № 143:
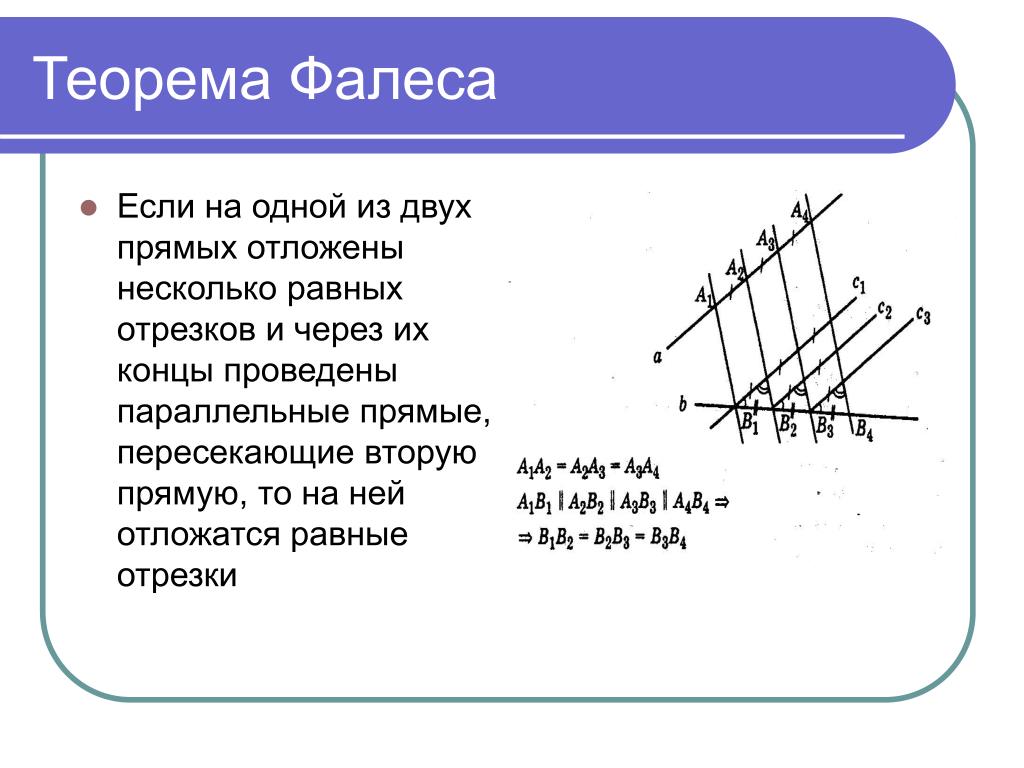
Вопрос 1:
Пусть и их площади будут соответственно 64 см 2 и 121 см 2 . Если EF = 15,4 см, найдите BC.
Ответ:
Видео решение для треугольников (Стр .
 : 143, В.№: 1)
: 143, В.№: 1)
Решение NCERT для математики класса 10 — треугольники 143, вопрос 1
Страница № 143:
Вопрос 2:
Диагонали трапеции ABCD с AB || DC пересекаются друг с другом в точке O. Если AB = 2CD, найти отношение площадей треугольников AOB и COD.
Ответ:
Начиная с AB || CD,
∴ ∠OAB = ∠OCD и ∠OBA = ∠ODC (альтернативные внутренние углы)
In ΔAOB и ΔCOD,
∠AOB = ∠COD (вертикально противоположные углы)
∠OAB = ∠OCD (Альтернативные внутренние углы)
∠OBA = ∠ODC (альтернативные внутренние углы)
∴ ΔAOB ∼ ΔCOD (по критерию сходства AAA)
Видео решение для треугольников (Стр .: 143, В.№: 2)
Решение NCERT для математики класса 10 — треугольники 143, вопрос 2
Страница № 144:
Вопрос 3:
На следующем рисунке ABC и DBC — это два треугольника на одном основании BC. Если AD пересекает BC в точке O, покажите, что
Если AD пересекает BC в точке O, покажите, что
Ответ:
Нарисуем два перпендикуляра AP и DM на линии BC.
Мы знаем, что площадь треугольника =
.
В ΔAPO и ΔDMO,
∠APO = ∠DMO (каждый = 90 °)
∠AOP = ∠DOM (вертикально противоположные углы)
∴ ΔAPO ∼ ΔDMO (по критерию сходства AA)
Видео решение для треугольников (Страница: 144, Q.No .: 3)
Решение NCERT для математики класса 10 — треугольники 144, вопрос 3
Страница № 144:
Вопрос 4:
Если площади двух одинаковых треугольников равны, докажите, что они равны.
Ответ:
Предположим, что два подобных треугольника обозначены ΔABC ∼ ΔPQR.
Видео решение для треугольников (Страница: 144, Q.No: 4)
Решение NCERT для математики класса 10 — треугольники 144, вопрос 4
Страница № 144:
Вопрос 5:
D, E и F — это середины сторон AB, BC и CA отрезка ΔABC, соответственно.Найдите соотношение площадей ΔDEF и ΔABC.
Ответ:
D и E — средние точки ΔABC.
Видео решение для треугольников (Страница: 144, Q.No: 5)
Решение NCERT для математики класса 10 — треугольники 144, вопрос 5
Страница № 144:
Вопрос 6:
Докажите, что отношение площадей двух одинаковых треугольников равно квадрату
отношения их соответствующих медиан.
Ответ:
Предположим, что два подобных треугольника обозначены ΔABC ∼ ΔPQR. Пусть AD и PS — медианы этих треугольников.
ΔABC ∼ ΔPQR
… (1)
∠A = ∠P, ∠B = ∠Q, ∠C = ∠R… (2)
Поскольку AD и PS — медианы,
∴ BD = DC =
А, QS = SR =
Уравнение (1) становится
… (3)
В ΔABD и ΔPQS,
∠B = ∠Q [Используя уравнение (2)]
And, [Используя уравнение (3)]
∴ ΔABD ∼ ΔPQS (критерий SAS-подобия)
Следовательно, можно сказать, что
… (4)
Из уравнений (1) и (4) мы можем найти, что
И, следовательно,
Видео решение для треугольников (Страница: 144, В.№: 6)
Решение NCERT для математики класса 10 — треугольники 144, вопрос 6
Страница № 144:
Вопрос 7:
Докажите, что площадь равностороннего треугольника, описанного на одной стороне квадрата, равна половине площади равностороннего треугольника, описанного на одной из его диагоналей.
Ответ:
Пусть ABCD — квадрат со стороной a.
Следовательно, его диагональ
Два желаемых равносторонних треугольника образуются как ΔABE и ΔDBF.
Сторона равностороннего треугольника ΔABE, описанная на одной из его сторон = a
Сторона равностороннего треугольника ΔDBF, описанная на одной из его диагоналей
Мы знаем, что все равносторонние треугольники имеют углы 60º и все стороны одинаковой длины. Следовательно, все равносторонние треугольники похожи друг на друга. Следовательно, отношение площадей этих треугольников будет равно квадрату отношения сторон этих треугольников.
Видео решение для треугольников (Страница: 144, Q.No: 7)
Решение NCERT для математики класса 10 — треугольники 144, вопрос 7
Страница № 144:
Вопрос 8:
ABC и BDE — два равносторонних треугольника, D — середина BC. Соотношение площадей треугольников ABC и BDE составляет
Соотношение площадей треугольников ABC и BDE составляет
.
(А) 2: 1
(В) 1: 2
(К) 4: 1
(Д) 1: 4
Ответ:
Мы знаем, что все равносторонние треугольники имеют углы 60º и все стороны одинаковой длины.Следовательно, все равносторонние треугольники похожи друг на друга. Следовательно, отношение площадей этих треугольников будет равно квадрату отношения сторон этих треугольников.
Пусть сторона ΔABC = x
Следовательно, сторона
Следовательно, правильный ответ (C).
Видео решение для треугольников (Страница: 144, Q.No: 8)
Решение NCERT для математики класса 10 — треугольники 144, вопрос 8
Страница № 144:
Вопрос 9:
Стороны двух одинаковых треугольников находятся в соотношении 4: 9. Площади этих треугольников находятся в соотношении
Площади этих треугольников находятся в соотношении
.
(А) 2: 3
(В) 4: 9
(К) 81: 16
(D) 16: 81
Ответ:
Если два треугольника подобны друг другу, то отношение площадей этих треугольников будет равно квадрату отношения соответствующих сторон этих треугольников.
При этом соотношение сторон 4: 9.
Следовательно, отношение площадей этих треугольников =
.
Следовательно, правильный ответ (D).
Видео решение для треугольников (Страница: 144, Q.No: 9)
Решение NCERT для математики класса 10 — треугольники 144, вопрос 9
Страница № 150:
Вопрос 1:
Стороны треугольников указаны ниже. Определите, какие из них являются прямыми треугольниками? В случае прямоугольного треугольника запишите длину его гипотенузы.
(i) 7 см, 24 см, 25 см
(ii) 3 см, 8 см, 6 см
(iii) 50 см, 80 см, 100 см
(iv) 13 см, 12 см, 5 см
Ответ:
(i) Дано, что стороны треугольника равны 7 см, 24 см и 25 см.
Возведя в квадрат длины этих сторон, мы получим 49, 576 и 625.
49 + 576 = 625
Или,
Стороны данного треугольника удовлетворяют теореме Пифагора.
Следовательно, это прямоугольный треугольник.
Мы знаем, что самая длинная сторона прямоугольного треугольника — гипотенуза.
Следовательно, длина гипотенузы этого треугольника равна 25 см.
(ii) Дано, что стороны треугольника равны 3 см, 8 см и 6 см.
Возведя в квадрат длины этих сторон, мы получим 9, 64 и 36.
Однако 9 + 36 ≠ 64
Или, 3 2 + 6 2 ≠ 8 2
Ясно, что сумма квадратов длин двух сторон не равна квадрату длины третьей стороны.
Следовательно, данный треугольник не удовлетворяет теореме Пифагора.
Следовательно, это не прямоугольный треугольник.
(iii) Учитывая, что стороны составляют 50 см, 80 см и 100 см.
Возведя в квадрат длины этих сторон, мы получим 2500, 6400 и 10000.
Однако 2500 + 6400 ≠ 10000
Или, 50 2 + 80 2 ≠ 100 2
Ясно, что сумма квадратов длин двух сторон не равна квадрату длины третьей стороны.
Следовательно, данный треугольник не удовлетворяет теореме Пифагора.
Следовательно, это не прямоугольный треугольник.
(iv) Учитывая, что стороны равны 13 см, 12 см и 5 см.
Возведя в квадрат длины этих сторон, мы получим 169, 144 и 25.
Очевидно, 144 +25 = 169
Или,
Стороны данного треугольника удовлетворяют теореме Пифагора.
Следовательно, это прямоугольный треугольник.
Мы знаем, что самая длинная сторона прямоугольного треугольника — гипотенуза.
Следовательно, длина гипотенузы этого треугольника составляет 13 см.
Видео решение для треугольников (Страница: 150, Q.No: 1)
Решение NCERT для математики класса 10 — треугольники 150, вопрос 1
Страница № 150:
Вопрос 2:
PQR — это треугольник, расположенный под прямым углом в точке P, а M — точка на QR, такая, что PM ⊥ QR.Покажите, что PM 2 = QM × MR.
Ответ:
Видео решение для треугольников (Страница: 150, Q.No: 2)
Решение NCERT для математики класса 10 — треугольники 150, вопрос 2
Страница № 150:
Вопрос 3:
На следующем рисунке ABD представляет собой треугольник, расположенный под прямым углом к A и AC ⊥ BD. Покажи, что
Покажи, что
(i) AB 2 = BC × BD
(ii) AC 2 = BC × DC
(iii) AD 2 = BD × CD
Ответ:
(i) В,
∴ (критерий сходства AA)
(ii)
(iii)
∠DCA = ∠ DAB (каждые 90º)
∠CDA = ∠ ADB (общий угол)
Видео решение для треугольников (Страница: 150, В.№: 3)
Решение NCERT для математики класса 10 — треугольники 150, вопрос 3
Страница № 150:
Вопрос 4:
ABC — это равнобедренный треугольник, расположенный под прямым углом к C. Докажите, что AB 2 = 2 AC 2 .
Ответ:
Учитывая, что ΔABC — равнобедренный треугольник.
∴ AC = CB
Применяя теорему Пифагора в ΔABC (т. Е. Под прямым углом в точке C), получаем
Видео решение для треугольников (Страница: 150, Q.No: 4)
Решение NCERT для математики класса 10 — треугольники 150, вопрос 4
Страница № 150:
Вопрос 5:
ABC — равнобедренный треугольник с AC = BC.Если AB 2 = 2 AC 2 , докажите, что ABC — прямоугольный треугольник.
Ответ:
Учитывая это,
Видео решение для треугольников (Страница: 150, Q.No: 5)
Решение NCERT для математики класса 10 — треугольники 150, вопрос 5
Страница № 150:
Вопрос 6:
ABC — равносторонний треугольник со стороной 2 на . Найдите каждую из его высот.
Найдите каждую из его высот.
Ответ:
Пусть AD будет высотой в данном равностороннем треугольнике, ΔABC.
Мы знаем, что высота делит противоположную сторону пополам.
∴ BD = DC = a
В равностороннем треугольнике все высоты равны по длине.
Следовательно, длина каждой высоты будет.
Видео решение для треугольников (Страница: 150, В.№: 6)
Решение NCERT для математики класса 10 — треугольники 150, вопрос 6
Страница № 150:
Вопрос 7:
Докажите, что сумма квадратов сторон ромба равна сумме квадратов его диагоналей.
Ответ:
In ΔAOB, ΔBOC, ΔCOD, ΔAOD,
Применяя теорему Пифагора, получаем
Видео решение для треугольников (Страница: 150, В.
 №: 7)
№: 7)
Решение NCERT для математики класса 10 — треугольники 150, вопрос 7
Стр. № 151:
Вопрос 8:
На следующем рисунке O — точка внутри треугольника ABC, OD ⊥ BC, OE ⊥ AC и OF ⊥ AB. Покажи, что
(i) OA 2 + OB 2 + OC 2 — OD 2 — OE 2 — OF 2 = AF 2 + BD 2 + CE 2
(ii) AF 2 + BD 2 + CE 2 = AE 2 + CD 2 + BF 2
Ответ:
Присоединитесь к OA, OB и OC.
(i) Применяя теорему Пифагора в ΔAOF, получаем
Аналогично, в ΔBOD,
Аналогично, в ΔCOE,
(ii) Из приведенного выше результата
Видео решение для треугольников (Страница: 151, Q.
 No .: 8)
No .: 8)
Решение NCERT для математики класса 10 — треугольники 151, вопрос 8
Стр. № 151:
Вопрос 9:
Лестница длиной 10 м ведет к окну на высоте 8 м над землей.Найдите расстояние от основания лестницы до основания стены.
Ответ:
Пусть OA — стена, а AB — лестница.
Следовательно, по теореме Пифагора,
Следовательно, расстояние подошвы лестницы от основания стены составляет 6 м.
Видео решение для треугольников (Страница: 151, Q.No .: 9)
Решение NCERT для математики класса 10 — треугольники 151, вопрос 9
Стр. № 151:
Вопрос 10:
Растяжка, прикрепленная к вертикальной опоре высотой 18 м, имеет длину 24 м, на другом конце которой прикреплен столб.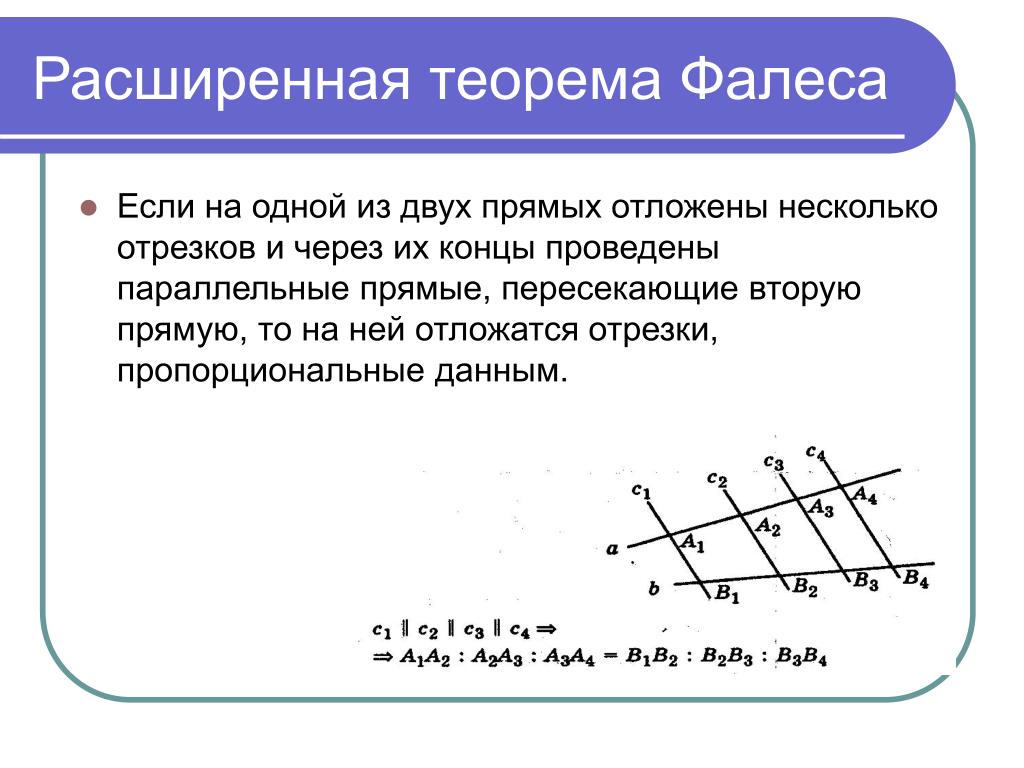 Как далеко от основания шеста следует забивать кол, чтобы проволока была натянута?
Как далеко от основания шеста следует забивать кол, чтобы проволока была натянута?
Ответ:
Пусть OB — полюс, а AB — провод.
По теореме Пифагора,
Следовательно, расстояние от базы равно m.
Видео решение для треугольников (Страница: 151, Q.No .: 10)
Решение NCERT для математики класса 10 — треугольники 151, вопрос 10
Стр. № 151:
Вопрос 11:
Самолет вылетает из аэропорта и летит на север со скоростью 1 000 км в час.В то же время другой самолет вылетает из того же аэропорта и летит строго на запад со скоростью 1200 км в час. Как далеко будут друг от друга два самолета в нерабочее время?
Ответ:
Расстояние, пройденное самолетом, летящим на север в
Аналогично, расстояние, пройденное самолетом, летящим на запад, в
Пусть эти расстояния представлены OA и OB соответственно.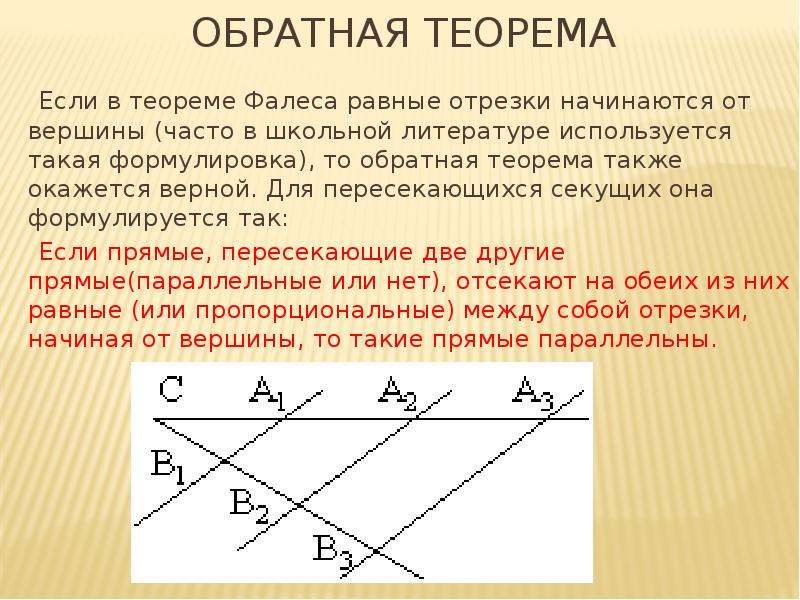
Применение теоремы Пифагора,
Расстояние между этими плоскостями после, AB =
Следовательно, расстояние между этими самолетами будет км позже.
Видео решение для треугольников (Страница: 151, Q.No .: 11)
Решение NCERT для математики класса 10 — треугольники 151, вопрос 11
Стр. № 151:
Вопрос 12:
Две опоры высотой 6 м и 11 м стоят на ровной поверхности. Если расстояние между ножками шестов 12 м, найдите расстояние между их вершинами.
Ответ:
Пусть CD и AB — опоры высотой 11 м и 6 м.
Следовательно, CP = 11-6 = 5 м
Из рисунка видно, что AP = 12 м
Применяя теорему Пифагора для ΔAPC, получаем
Следовательно, расстояние между их вершинами 13 м.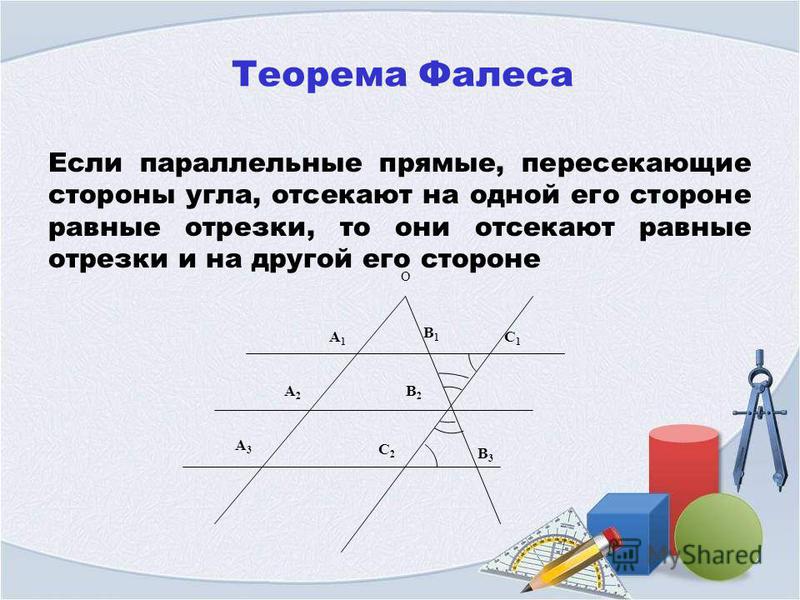
Видео решение для треугольников (Стр .: 151, В.№: 12)
Решение NCERT для математики класса 10 — треугольники 151, вопрос 12
Стр. № 151:
Вопрос 13:
D и E — точки на сторонах CA и CB соответственно треугольника ABC, расположенного под прямым углом к C. Докажите, что AE 2 + BD 2 = AB 2 + DE 2
Ответ:
Применяя теорему Пифагора в ΔACE, получаем
Видео решение для треугольников (Стр .: 151, В.№: 13)
Решение NCERT для математики класса 10 — треугольники 151, вопрос 13
Стр. № 151:
Вопрос 14:
Перпендикуляр из A на стороне BC ΔABC пересекает BC в точке D, так что DB = 3 CD. Докажите, что 2 AB 2 = 2 AC 2 + BC 2
Докажите, что 2 AB 2 = 2 AC 2 + BC 2
Ответ:
Применяя теорему Пифагора для ΔACD, получаем
Применяя теорему Пифагора в ΔABD, получаем
Видео решение для треугольников (Стр .: 151, В.№: 14)
Решение NCERT для математики класса 10 — треугольники 151, вопрос 14
Стр. № 151:
Вопрос 15:
В равностороннем треугольнике ABC точка D на стороне BC такая, что BD = BC. Докажите, что 9 AD 2 = 7 AB 2 .
Ответ:
Пусть сторона равностороннего треугольника будет a , а AE будет высотой ΔABC.
∴ BE = EC = =
А, АЕ =
Учитывая это, BD = BC
∴ BD =
DE = BE — BD =
Применяя теорему Пифагора в ΔADE, получаем
AD 2 = AE 2 + DE 2
⇒ 9 г.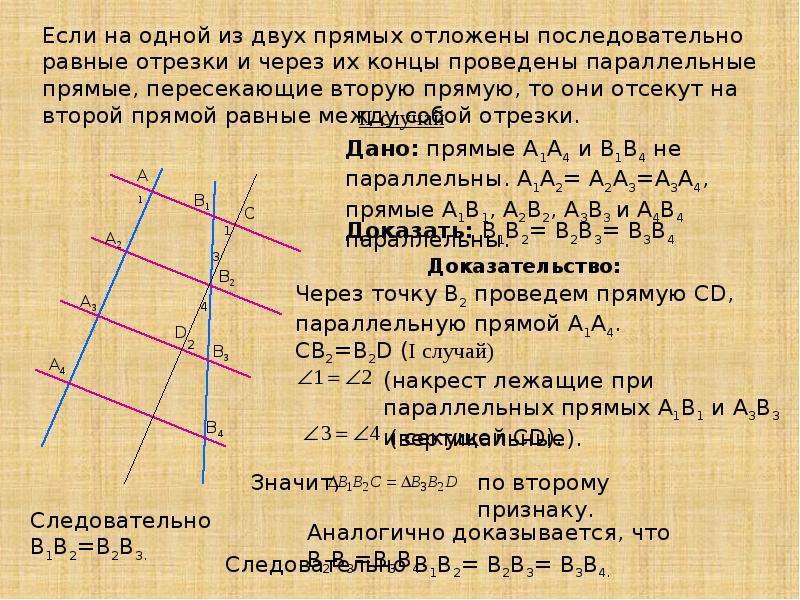 н.э. 2 = 7 AB 2
н.э. 2 = 7 AB 2
Видео решение для треугольников (Страница: 151, Q.No .: 15)
Решение NCERT для математики класса 10 — треугольники 151, вопрос 15
Стр. № 151:
Вопрос 16:
Докажите, что в равностороннем треугольнике квадрат одной стороны, умноженный на три, равен квадрату одной из его высот в четыре раза.
Ответ:
Пусть сторона равностороннего треугольника будет a , а AE будет высотой ΔABC.
∴ BE = EC = =
Применяя теорему Пифагора в ΔABE, получаем
AB 2 = AE 2 + BE 2
4AE 2 = 3 a 2
⇒ 4 × (квадрат высоты) = 3 × (квадрат одной стороны)
Видео решение для треугольников (Стр .
 : 151, В.№: 16)
: 151, В.№: 16)
Решение NCERT для математики класса 10 — треугольники 151, вопрос 16
Стр. № 151:
Вопрос 17:
Отметьте правильный ответ и обоснуйте: В ΔABC, AB = см, AC = 12 см и BC = 6 см.
Угол B составляет:
(А) 120 ° (В) 60 °
(С) 90 ° (Г) 45 °
Ответ:
Учитывая, что AB = см, AC = 12 см и BC = 6 см
Можно заметить, что
AB 2 = 108
ВС 2 = 144
А, ВС 2 = 36
AB 2 + BC 2 = AC 2
Данный треугольник ΔABC удовлетворяет теореме Пифагора.
Следовательно, треугольник представляет собой прямоугольный треугольник, расположенный под прямым углом в точке B.
∴ ∠B = 90 °
Следовательно, правильный ответ (C).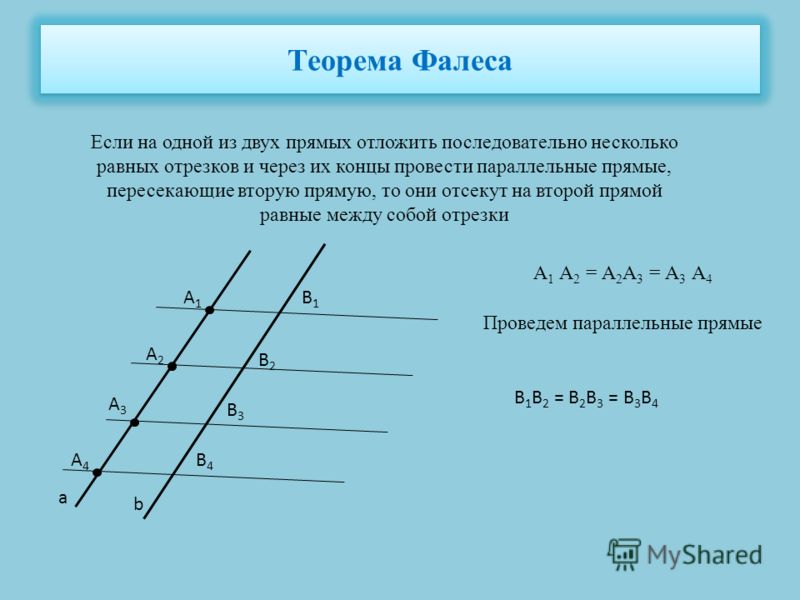
Видео решение для треугольников (Страница: 151, Q.No .: 17)
Решение NCERT для математики класса 10 — треугольники 151, вопрос 17
Страница № 152:
Вопрос 1:
На данном рисунке PS — биссектриса ∠QPR ΔPQR.Докажи это .
Ответ:
Нарисуем отрезок RT, параллельный SP, который пересекает удлиненный отрезок QP в точке T.
При этом PS — это биссектриса угла ∠QPR.
∠QPS = ∠SPR… (1)
По строительству,
∠SPR = ∠PRT (As PS || TR)… (2)
∠QPS = ∠QTR (As PS || TR)… (3)
Используя эти уравнения, получаем
∠PRT = ∠QTR
∴ PT = PR
По строительству,
PS || TR
Используя основную теорему пропорциональности для ΔQTR,
QSSR = QPPT
⇒QSSR = PQPR ∵PT = PR
Видео решение для треугольников (Страница: 152, В.
 №: 1)
№: 1)
Решение NCERT для математики класса 10 — треугольники 152, вопрос 1
Страница № 152:
Вопрос 2:
На данном рисунке D — точка на гипотенузе AC для ΔABC, DM ⊥ BC и DN ⊥ AB. Докажите, что:
(i) DM 2 = DN.MC
(ii) DN 2 = DM.AN
Ответ:
(i) Присоединяемся к БД.
Имеем, DN || CB, DM || AB, а ∠B = 90 °
∴ DMBN представляет собой прямоугольник.
∴ DN = MB и DM = NB
Условие, которое необходимо доказать, — это случай, когда D является основанием перпендикуляра, проведенного из B в AC.
∴ ∠CDB = 90 °
⇒ ∠2 + ∠3 = 90 °… (1)
В ΔCDM,
∠1 + ∠2 + ∠DMC = 180 °
⇒ ∠1 + ∠2 = 90 °… (2)
дюйм ΔDMB,
∠3 + ∠DMB + ∠4 = 180 °
⇒ ∠3 + ∠4 = 90 °… (3)
Из уравнений (1) и (2) получаем
∠1 = ∠3
Из уравнений (1) и (3) получаем
∠2 = ∠4
В ΔDCM и ΔBDM,
∠1 = ∠3 (Доказано выше)
∠2 = ∠4 (Доказано выше)
∴ ΔDCM ∼ ΔBDM (критерий сходства AA)
⇒ DM 2 = DN × MC
(ii) В прямоугольном треугольнике DBN,
∠5 + ∠7 = 90 °… (4)
В прямоугольном треугольнике ДАН,
∠6 + ∠8 = 90 °… (5)
D — основание перпендикуляра, проведенного от B к AC.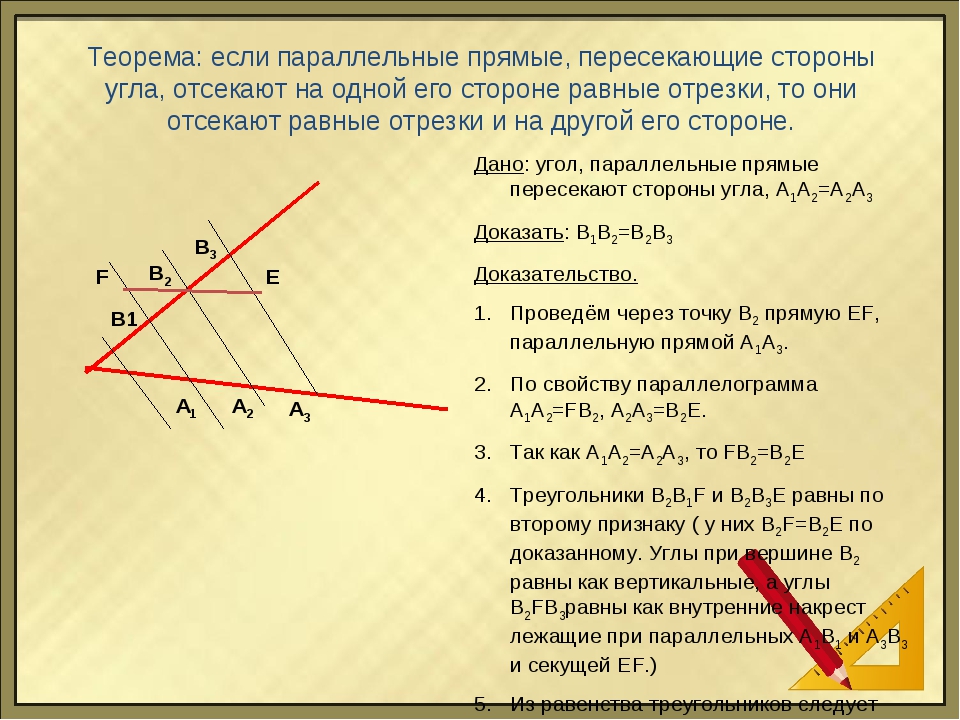
∴ ∠ADB = 90 °
⇒ ∠5 + ∠6 = 90 °… (6)
Из уравнений (4) и (6) получаем
∠6 = ∠7
Из уравнений (5) и (6) получаем
∠8 = ∠5
В ΔDNA и ΔBND,
∠6 = ∠7 (Доказано выше)
∠8 = ∠5 (Доказано выше)
∴ ΔDNA ∼ ΔBND (критерий сходства AA)
⇒ DN 2 = AN × NB
⇒ DN 2 = AN × DM (As NB = DM)
Видео решение для треугольников (Страница: 152, В.№: 2)
Решение NCERT для математики класса 10 — треугольники 152, вопрос 2
Страница № 152:
Вопрос 3:
На данном рисунке ABC представляет собой треугольник, в котором образовано ∠ABC> 90 ° и AD ⊥ CB. Докажите, что AC 2 = AB 2 + BC 2 + 2BC.BD.
Ответ:
Применяя теорему Пифагора в ΔADB, получаем
AB 2 = AD 2 + DB 2 … (1)
Применяя теорему Пифагора в ΔACD, получаем
AC 2 = AD 2 + DC 2
AC 2 = AD 2 + (DB + BC) 2
AC 2 = AD 2 + DB 2 + BC 2 + 2DB × BC
AC 2 = AB 2 + BC 2 + 2DB × BC [Используя уравнение (1)]
Видео решение для треугольников (Страница: 152, В.
 №: 3)
№: 3)
Решение NCERT для математики класса 10 — треугольники 152, вопрос 3
Страница № 152:
Вопрос 4:
На данном рисунке ABC представляет собой треугольник, в котором ∠ABC <90 ° и AD ⊥ BC. Докажите, что AC 2 = AB 2 + BC 2 — 2BC.BD.
Ответ:
Применяя теорему Пифагора в ΔADB, получаем
AD 2 + DB 2 = AB 2
⇒ AD 2 = AB 2 — DB 2 … (1)
Применяя теорему Пифагора в ΔADC, получаем
AD 2 + DC 2 = AC 2
AB 2 — BD 2 + DC 2 = AC 2 [Используя уравнение (1)]
AB 2 — BD 2 + (BC — BD) 2 = AC 2
AC 2 = AB 2 — BD 2 + BC 2 + BD 2 −2BC × BD
= AB 2 + BC 2 — 2BC × BD
Видео решение для треугольников (Страница: 152, В.
 №: 4)
№: 4)
Решение NCERT для математики класса 10 — треугольники 152, вопрос 4
Страница № 152:
Вопрос 5:
На данном рисунке AD — это медиана треугольника ABC и AM ⊥ BC. Докажите, что:
(я)
(ii)
(iii)
Ответ:
(i) Применяя теорему Пифагора в ΔAMD, получаем
AM 2 + MD 2 = AD 2 … (1)
Применяя теорему Пифагора в ΔAMC, получаем
AM 2 + MC 2 = AC 2
AM 2 + (MD + DC) 2 = AC 2
(AM 2 + MD 2 ) + DC 2 + 2MD.Постоянный ток = переменный ток 2
AD 2 + DC 2 + 2MD.DC = AC 2 [Используя уравнение (1)]
Используя результат, получаем
(ii) Применяя теорему Пифагора в ΔABM, получаем
AB 2 = AM 2 + MB 2
= (AD 2 — DM 2 ) + MB 2
= (AD 2 — DM 2 ) + (BD — MD) 2
= AD 2 — DM 2 + BD 2 + MD 2 — 2BD × MD
= AD 2 + BD 2 — 2BD × MD
(iii) Применяя теорему Пифагора в ΔABM, получаем
AM 2 + MB 2 = AB 2 … (1)
Применяя теорему Пифагора в ΔAMC, получаем
AM 2 + MC 2 = AC 2 … (2)
Складывая уравнения (1) и (2), получаем
2AM 2 + MB 2 + MC 2 = AB 2 + AC 2
2AM 2 + (BD — DM) 2 + (MD + DC) 2 = AB 2 + AC 2
2AM 2 + BD 2 + DM 2 — 2BD. DM + MD 2 + DC 2 + 2MD.DC = AB 2 + AC 2
DM + MD 2 + DC 2 + 2MD.DC = AB 2 + AC 2
2AM 2 + 2MD 2 + BD 2 + DC 2 + 2MD (- BD + DC) = AB 2 + AC 2
Видео решение для треугольников (Страница: 152, Q.No: 5)
Решение NCERT для математики класса 10 — треугольники 152, вопрос 5
Стр. № 153:
Вопрос 6:
Докажите, что сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.
Ответ:
Пусть ABCD — параллелограмм.
Нарисуем перпендикуляр DE на вытянутой стороне AB, а AF на стороне DC.
Применяя теорему Пифагора в ΔDEA, получаем
DE 2 + EA 2 = DA 2 … ( i )
Применяя теорему Пифагора в ΔDEB, получаем
DE 2 + EB 2 = DB 2
DE 2 + (EA + AB) 2 = DB 2
(DE 2 + EA 2 ) + AB 2 + 2EA × AB = DB 2
DA 2 + AB 2 + 2EA × AB = DB 2 … ( ii )
Применяя теорему Пифагора в ΔADF, получаем
AD 2 = AF 2 + FD 2
Применяя теорему Пифагора в ΔAFC, получаем
AC 2 = AF 2 + FC 2
= AF 2 + (DC — FD) 2
= AF 2 + DC 2 + FD 2 — 2DC × FD
= (AF 2 + FD 2 ) + DC 2 — 2DC × FD
AC 2 = AD 2 + DC 2 — 2DC × FD… ( iii )
Поскольку ABCD — параллелограмм,
AB = CD… ( iv )
А, BC = AD… ( v )
In ΔDEA и ΔADF,
∠DEA = ∠AFD (оба 90 °)
∠EAD = ∠ADF (EA || DF)
н. э. = н.э. (общий)
э. = н.э. (общий)
∴ ΔEAD ΔFDA (критерий конгруэнтности AAS)
⇒ EA = DF… (vi)
Складывая уравнения ( i ) и ( iii ), получаем
DA 2 + AB 2 + 2EA × AB + AD 2 + DC 2 — 2DC × FD = DB 2 + AC 2
DA 2 + AB 2 + AD 2 + DC 2 + 2EA × AB — 2DC × FD = DB 2 + AC 2
BC 2 + AB 2 + AD 2 + DC 2 + 2EA × AB — 2AB × EA = DB 2 + AC 2
[Используя уравнения ( iv ) и ( vi )]
AB 2 + BC 2 + CD 2 + DA 2 = AC 2 + BD 2
Видео решение для треугольников (Стр .: 153, В.№: 6)
Решение NCERT для математики класса 10 — треугольники 153, вопрос 6
Стр.
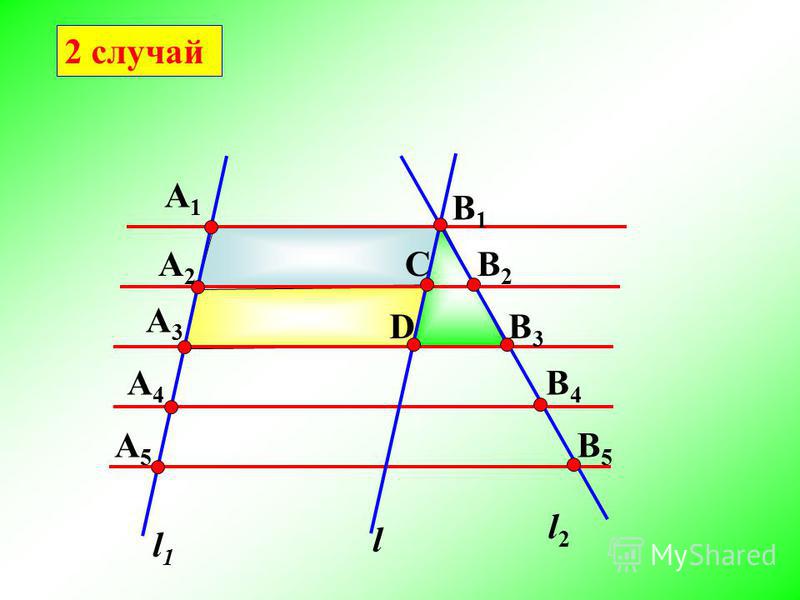 № 153:
№ 153:
Вопрос 7:
На данном рисунке две хорды AB и CD пересекаются друг с другом в точке P. Доказывают, что:
(i) ΔAPC ∼ ΔDPB
(ii) AP.BP = CP.DP
Ответ:
Присоединяемся к CB.
(i) В ΔAPC и ΔDPB,
∠APC = ∠DPB (вертикально противоположные углы)
∠CAP = ∠BDP (Углы в одном сегменте для хорды CB)
ΔAPC ∼ ΔDPB (по критерию сходства AA)
(ii) Мы уже доказали, что
ΔAPC ∼ ΔDPB
Мы знаем, что соответствующие стороны подобных треугольников пропорциональны.
∴ AP. PB = ПК. ДП
Видео решение для треугольников (Стр .: 153, В.№: 7)
Решение NCERT для математики класса 10 — треугольники 153, вопрос 7
Стр.
 № 153:
№ 153:
Вопрос 8:
На данном рисунке две хорды AB и CD окружности пересекаются друг с другом в точке P (если она образована) вне окружности. Докажите, что
(i) ΔPAC ∼ ΔPDB
(ii) PA.PB = PC.PD
Ответ:
(i) В ΔPAC и ΔPDB,
∠P = ∠P (общий)
∠PAC = ∠PDB (Внешний угол вписанного четырехугольника ∠PCA = ∠PBD равен противоположному внутреннему углу)
∴ ΔPAC ∼ ΔPDB
(ii) Мы знаем, что соответствующие стороны подобных треугольников пропорциональны.
∴ PA.PB = PC.PD
Видео решение для треугольников (Страница: 153, Q.No .: 8)
Решение NCERT для математики класса 10 — треугольники 153, вопрос 8
Стр. № 153:
Вопрос 9:
На данном рисунке D — точка на стороне BC отрезка ΔABC такая, что.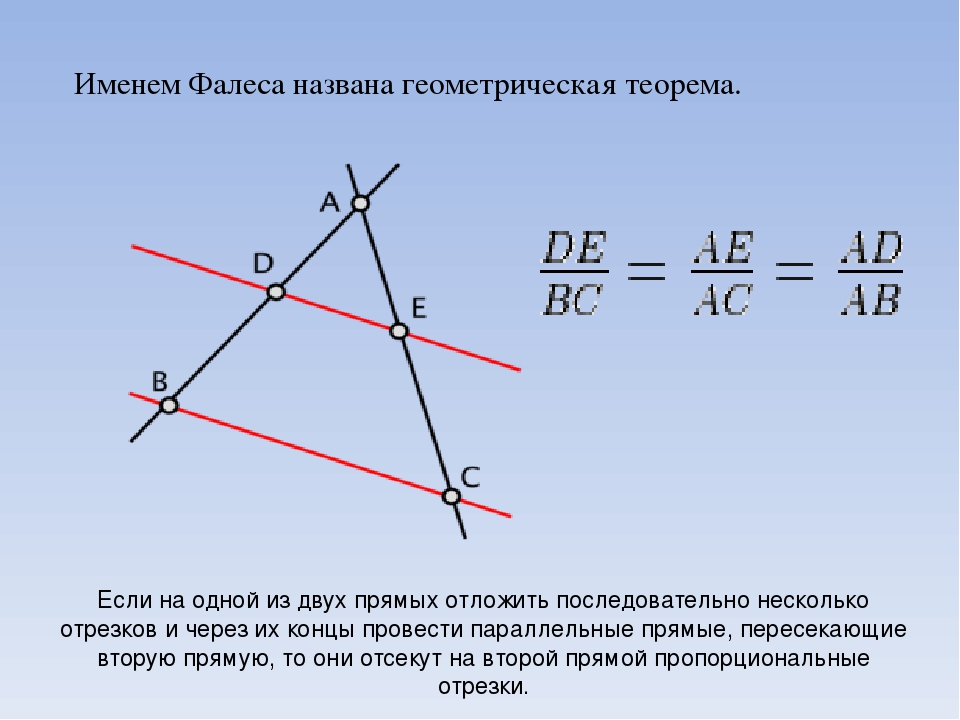 Докажите, что AD — биссектриса BAC.
Докажите, что AD — биссектриса BAC.
Ответ:
Продолжим BA до P так, что AP = AC. Присоединяйтесь к ПК.
Принято, что,
Используя обратную теорему о пропорциональности, получаем
г. н.э. || PC
⇒ ∠BAD = ∠APC (Соответствующие углы)… (1)
А, ∠DAC = ∠ACP (Альтернативные внутренние углы)… (2)
По построению имеем
AP = AC
⇒ APC = ∠ACP… (3)
Сравнивая уравнения (1), (2) и (3), получаем
∠BAD = ∠APC
⇒ AD — биссектриса угла BAC.
Видео решение для треугольников (Страница: 153, Q.No .: 9)
Решение NCERT для математики класса 10 — треугольники 153, вопрос 9
Стр. № 153:
Вопрос 10:
Назима ловит рыбу нахлыстом в ручье. Кончик ее удочки находится на высоте 1,8 м над поверхностью воды, а мушка на конце веревки опирается на воду 3.На расстоянии 6 м и 2,4 м от точки непосредственно под концом удилища. Если предположить, что ее тетива (от кончика удочки до мухи) натянута, сколько у нее тетивы (см. Рис. 6.64)? Если она натягивает веревку со скоростью 5 см в секунду, какое расстояние по горизонтали будет от нее до мухи через 12 секунд?
Кончик ее удочки находится на высоте 1,8 м над поверхностью воды, а мушка на конце веревки опирается на воду 3.На расстоянии 6 м и 2,4 м от точки непосредственно под концом удилища. Если предположить, что ее тетива (от кончика удочки до мухи) натянута, сколько у нее тетивы (см. Рис. 6.64)? Если она натягивает веревку со скоростью 5 см в секунду, какое расстояние по горизонтали будет от нее до мухи через 12 секунд?
Ответ:
Пусть AB будет высотой кончика удочки от поверхности воды.Пусть BC будет горизонтальным расстоянием от мухи до кончика удочки.
Тогда AC — длина строки.
AC можно найти, применив теорему Пифагора в ΔABC.
AC 2 = AB 2 + BC 2
AB 2 = (1,8 м) 2 + (2,4 м) 2
AB 2 = (3,24 + 5,76) м 2
AB 2 = 9,00 м 2
Таким образом, длина струны на выходе составляет 3 метра.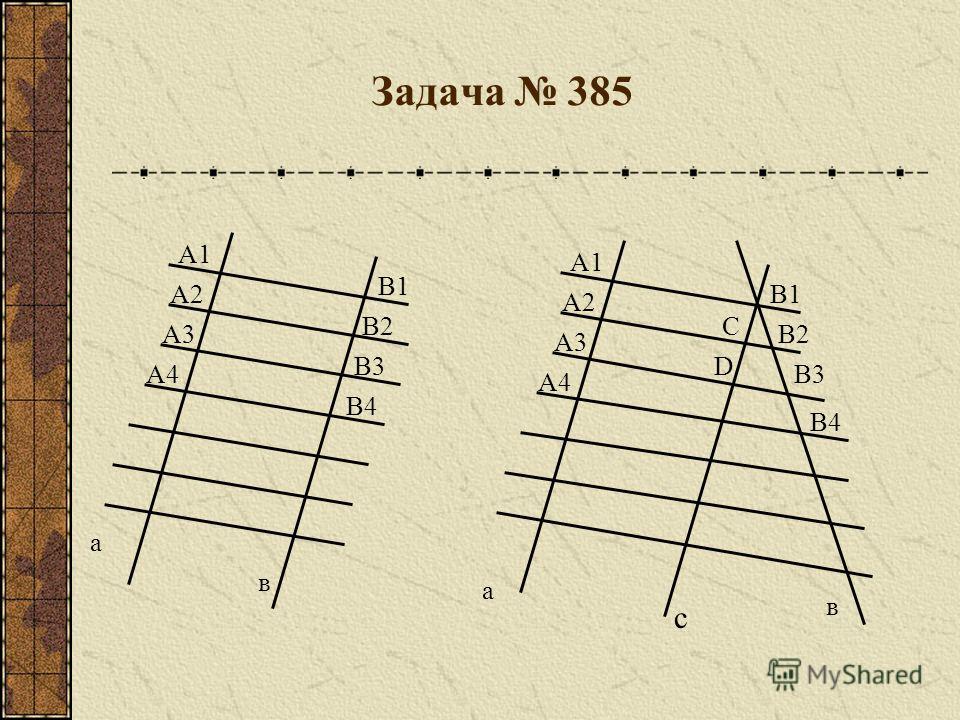
Она тянет за веревку со скоростью 5 см в секунду.
Следовательно, натянуть тетиву за 12 секунд = 12 × 5 = 60 см = 0,6 м
Дайте мухе добраться до точки D через 12 секунд.
Длина строки через 12 секунд — AD.
AD = AC — Назима натянула нитку за 12 секунд
= (3,00 — 0,6) м
= 2,4 м
В ΔADB,
AB 2 + BD 2 = AD 2
(1.8 м) 2 + BD 2 = (2,4 м) 2
BD 2 = (5,76 — 3,24) м 2 = 2,52 м 2
BD = 1,587 м
Горизонтальное расстояние полета = BD + 1,2 м
= (1,587 + 1,2) м
= 2,787 м
= 2,79 м
Видео решение для треугольников (Страница: 153, Q.No .: 10)
Решение NCERT для математики класса 10 — треугольники 153, вопрос 10
Просмотреть решения NCERT для всех глав класса 10
Решения
NCERT для математики класса 10 Глава 6 Треугольники в PDF 2021-22
Математика класса 10 Глава 6 Решение треугольников
10-я математика Глава 6 Упражнение 6.
 1
110-я математическая глава 6 Упражнение 6.2
10-я математическая глава 6 Упражнение 6.3
10-я математическая глава 6 Упражнение 6.4
9296 9296 929 929 929 929
10-я математика Глава 6 Упражнение 6.6
| Класс: 10 | Математика (английский и хинди средний) | |
| Глава 6: | Глава 6: | Глава |
Конгруэнтное | Похожие | |
Уголки | Соответствующие углы такие же. | Соответствующие углы такие же. |
Стороны | Соответствующие стороны такие же. | Соответствующие стороны пропорциональны. |
Пример | ||
Пояснение | Оба квадрата имеют одинаковые углы и одну и ту же сторону. | Оба квадрата имеют одинаковые углы, но разные стороны. |
Условные обозначения |
Приведенное выше объяснение показывает, что если две фигуры совпадают, то они также будут подобны, но необязательно, что если две фигуры подобны, то они также будут конгруэнтными.
Подобие треугольников
В треугольниках мы также будем использовать то же условие, что два треугольника будут одинаковыми, если —
Два вышеуказанных треугольника ∆ABC и ∆DEF аналогичны-
.
Если соответствующие углы двух треугольников совпадают, то они называются равноугольными треугольниками.
Основная теорема пропорциональности (теорема Фалеса)
Согласно теореме Фалеса , если в данном Треугольнике линия проводится параллельно любой из сторон Треугольника так, что две другие стороны пересекаются в некоторой отдельной точке, то она делит две стороны в одинаковом соотношении.
В ∆KMN, если PQ║MN и пересекает KM в точке P и KN в точке Q, то
Обращение к основной теореме о пропорциональности
Это противоположность основной теоремы пропорциональности, которая гласит, что если в данном Треугольнике прямая линия делит две стороны Треугольника в одинаковом соотношении, то эта прямая линия параллельна третьей стороне Треугольника.
Критерии подобия треугольников
По сути, есть три критерия, чтобы найти сходство двух Треугольников.
1. Критерии сходства AAA (угол-угол-угол)
Если в двух данных Треугольниках все соответствующие углы равны, то их соответствующие стороны также будут пропорциональны.
Это показывает, что все соответствующие углы в ∆ABC и ∆PQR одинаковы, поэтому их соответствующие стороны пропорциональны, поэтому два треугольника похожи.
Следовательно, ∆ABC ~ ∆PQR
Замечание : Если два соответствующих угла двух Треугольников равны, то, согласно сумме углов Треугольника, третий угол также будет равен. Таким образом, два треугольника будут подобны, если их два угла равны двум углам другого треугольника. Это известно как критерий AA (угол-угол) .
2. Критерии сходства SSS (Side-Side-Side)
Если в двух Треугольниках все стороны одного Треугольника находятся в таком же соотношении с соответствующими сторонами другого Треугольника, то их соответствующие углы будут равны.Следовательно, два треугольника похожи.
In ∆ABC и ∆DEF
Следовательно, ∆ABC ~ ∆DEF
Замечание : Приведенные выше два критерия показывают, что если один из двух критериев удовлетворяет, то другой подразумевается. Таким образом, нам не нужно проверять оба условия, чтобы найти сходство двух треугольников. Если все углы равны, тогда все стороны будут пропорциональны, и наоборот.
3. Критерии подобия SAS (Side-Angle-Side)
Если в двух Треугольниках две стороны находятся в том же соотношении с двумя сторонами другого Треугольника и угол, включающий эти стороны, равен, то эти два Треугольника будут подобны.
In ∆ABC и ∆KLM
Следовательно, ∆ABC ~ ∆KLM
Области подобных треугольников
Если даны два одинаковых Треугольника, то квадрат отношения их соответствующих сторон будет равен отношению их площади.
Если ∆ABC ~ ∆PQR, то
Теорема Пифагора (теорема Баудхаяна)
Теорема Пифагора гласит, что в прямоугольном треугольнике квадрат гипотенузы i.е. сторона, противоположная прямому углу, равна сумме квадратов двух других сторон Треугольника.
Если один угол равен 90 °, то a 2 + b 2 = c 2
Пример
Найдите гипотенузу в прямоугольном треугольнике.
Раствор
AB и BC — две стороны прямоугольного треугольника.
BC = 12 см и AB = 5 см
Из теоремы Пифагора имеем:
CA 2 = AB 2 + BC 2
= (5) 2 + (12) 2
= 25 + 144
Итак, АС 2 = 169
AC = 13 см
Обращение к теореме Пифагора
В Треугольнике, если сумма квадратов двух сторон равна квадрату третьей стороны, тогда данный Треугольник является Треугольником с прямым углом.
Если a 2 + b 2 = c 2 , то один угол равен 90 °.
Сходство двух прямоугольных треугольников Треугольник
В прямоугольном Треугольнике, если мы проведем перпендикуляр от прямого угла к гипотенузе Треугольника, то оба новых Треугольника будут похожи на весь Треугольник.
В приведенном выше правом углу треугольник CP является вершиной гипотенузы, поэтому
∆ACP ~ ∆ACB
∆PCB ~ ∆ACB
∆PCB ~ ∆ACP
Законы синусов и косинусов в треугольнике
Законы синусов и косинусов используются для нахождения неизвестной стороны или угла наклонного треугольника.Олигогий треугольник — это треугольник, который не является треугольником с прямым углом.
1. Закон синусов
Показывает соотношение между углом и сторонами треугольника.
Используется, когда
i) Дано два угла и одна сторона (AAS или ASA)
ii) Две стороны и угол без включения (SSA)
Закон синусов показывает, что стороны треугольника пропорциональны синусам противоположных углов.
2. Закон косинуса
Используется, когда
i) Даны две стороны и включенный угол (SAS)
ii) Даны три стороны (SSS)
Когда мы можем использовать такие законы?
Теорема Фалеса | Блестящая вики по математике и науке
Есть много способов доказать эту теорему. Одно из самых классических доказательств выглядит следующим образом:
Мы знаем, что AO = BO = COAO = BO = COAO = BO = CO, поскольку все они являются радиусами круга.\ circ. \ _ \ квадрат
\ end {выровнен} ∠ABC + ∠BCA + ∠CAB∠OAB + (∠OBA + ∠OBC) + ∠OCBα + (α + β) + βα + β∠ABC = 180∘ = 180∘ = 180∘ = 90∘ = 90∘ . □
Есть другой способ доказать это, основанный на другой теореме, называемой теоремой об альтернативном сегменте, которая утверждает, что
Теорема об альтернативном сегменте:
Угол, образованный хордой (или двумя радиусами) в центре круга, в два раза больше угла, образованного им на оставшейся части круга. □ _ \ квадрат □
Попробуем теперь доказать теорему Фалеса с помощью указанной выше теоремы.\ circ 90∘
АБАБАБ — диаметр полукруга.
CCC — точка на окружности.
Что такое угол ACB? ACB? ACB?
Самая длинная хорда в круге — это его диаметр.
Пусть окружность с центром ООО имеет хорду АБАБАБ. Присоединитесь к OAOAOA и OBOBOB, и пусть PPP будет точкой на ABABAB, такой что OP⊥ABOP \ perp ABOP⊥AB.
Мы знаем, что перпендикуляр от центра окружности к хорде делит хорду пополам. Тогда PA = PB = 12ABPA = PB = \ dfrac12 ABPA = PB = 21 AB.Пусть радиус равен rr r, длина хорды ABABAB равна ccc, а расстояние по перпендикуляру между центром и хордой ABABAB равно xxx.
Теперь по теореме Пифагора в △ OPA \ треугольнике OPA △ OPA
OA2 = OP2 + AP2r2 = x2 + (c2) 2⇒c = 2r2 − x2.2} = 2r = 2 \ times \ text {(радиус)} = \ text {(диаметр)}. \ _ \ Squarec = 2r2−02 = 2r2 = 2r = 2 × (радиус) = (диаметр). □
Верно или нет?
Длина наибольшего возможного хорды в окружности всегда равна удвоенному радиусу.
#CelebrateWithDE — День теоремы Пифагора
августа 2017 г. — STEM в мозгу. За несколько дней до полного солнечного затмения математики повсюду будут отмечать День теоремы Пифагора, 15 августа 2017 года, одну из редких дат, совпадающих с теоремой. Дата иллюстрирует теорему, которая гласит, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадрата длин двух других сторон треугольника.Это отличный день, чтобы подумать о вкладе Пифагора и геометрии в целом. Discovery Education имеет множество ресурсов различного типа. Вы и ваши ученики можете сложить эти ресурсы вместе, чтобы получить много отличного обучения!
Не забудьте опубликовать уравнение на доске: 8² + 15² = 17²
Рекомендуемый ресурс
Геометрические доказательства: коллекция материалов
Discovery Education Streaming
Классы K-2, 3-5, 6-8, 9-12, разные ресурсы
Древнегреческие математики, такие как Евклид и Пифагор, применили дедуктивное мышление к математическому мышлению и разработали первую теорему, составляющую основу геометрических доказательств.Примените эти теоремы для решения реальных проблем.
Базовые знания о создании
Треугольники
(канадская версия)
Discovery Education Streaming, Science Techbook, Math Techbook, Social Studies Techbook
3-5, 6-8, 9-12 классы, сегмент видео
Базовый обзор треугольников, включая определения различных типов треугольников. Обзор углов, длины, гипотенузы, площади и теоремы Пифагора.
Pythagoras
(канадская версия)
Discovery Education Streaming, Science Techbook, Math Techbook, Social Studies Techbook
6-8, 9-12 классы, сегмент видео
Описывает вклад греческого философа и математика Пифагора в области философии, нумерологии, теории чисел и геометрии.
Доказательство теоремы Пифагора Евклидом
(канадская версия)
Discovery Education Streaming, Math Techbook, Social Studies Techbook
6–8, 9–12 классы, видеосегмент
Объясняется доказательство Евклида теоремы Пифагора.
Практика
Культура и математика: математика и греки
(канадская версия)
Discovery Education Streaming, Social Studies Techbook
6-8, 9-12 классы, игры
Помогите Пифагору выбраться из храмового лабиринта, доказав теорему Пифагора.Изучите свойства треугольников и доказательство Евклида теоремы Пифагора, чтобы выбраться из лабиринта и не быть съеденным Минотавром.
Теорема Пифагора
Math Techbook
6–8 классы, анимация
Длина кабеля на мосту может быть найдена с помощью теоремы Пифагора. Обратное к теореме Пифагора используется для определения того, совпадают ли стороны треугольника со сторонами прямоугольного треугольника.
Теорема Пифагора
(канадская версия)
Discovery Education Streaming
6–8, 9–12 классы, Skill Builder
Доказывает теорему Пифагора и исследует использование формулы в реальных задачах.Включает ссылки на глоссарий и викторину.
Стратегия SOS
В центре внимания стратегии: бумажный слайд
(канадская версия)
Все услуги
Классы K-2, 3-5, 6-8, 9-12, учебная стратегия
Эта стратегия обучения требует от студентов пересказа истории или концепции, сосредоточив внимание на ключевых моментах и подтверждающих деталях или доказательствах. Студенты создают видеоролики с логической последовательностью основных моментов.

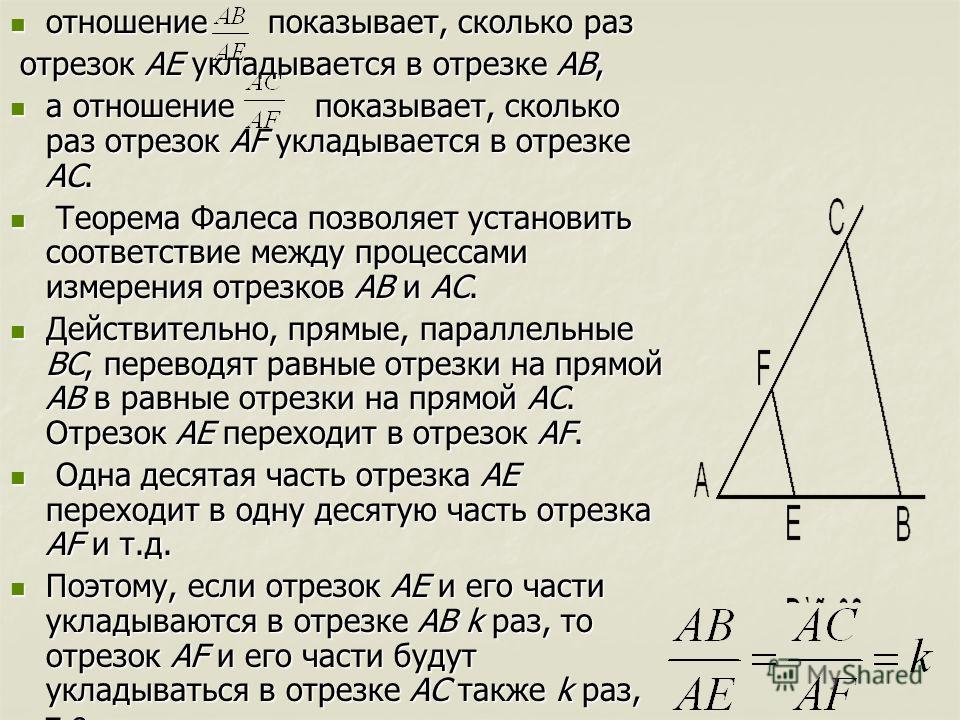 2 Решения в видео
2 Решения в видео 3 Объяснение Математика класса 10 Глава 6 Упражнение 6.3 Решение
3 Объяснение Математика класса 10 Глава 6 Упражнение 6.3 Решение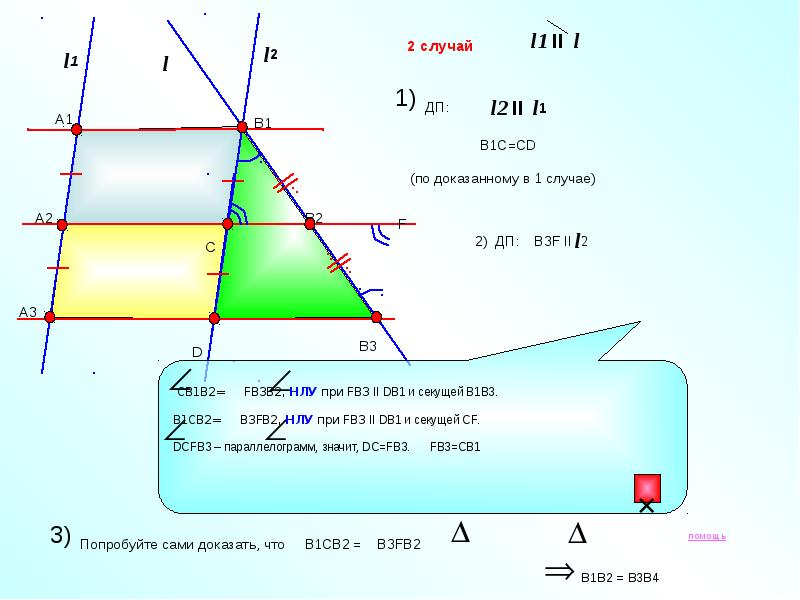 4 Решение
4 Решение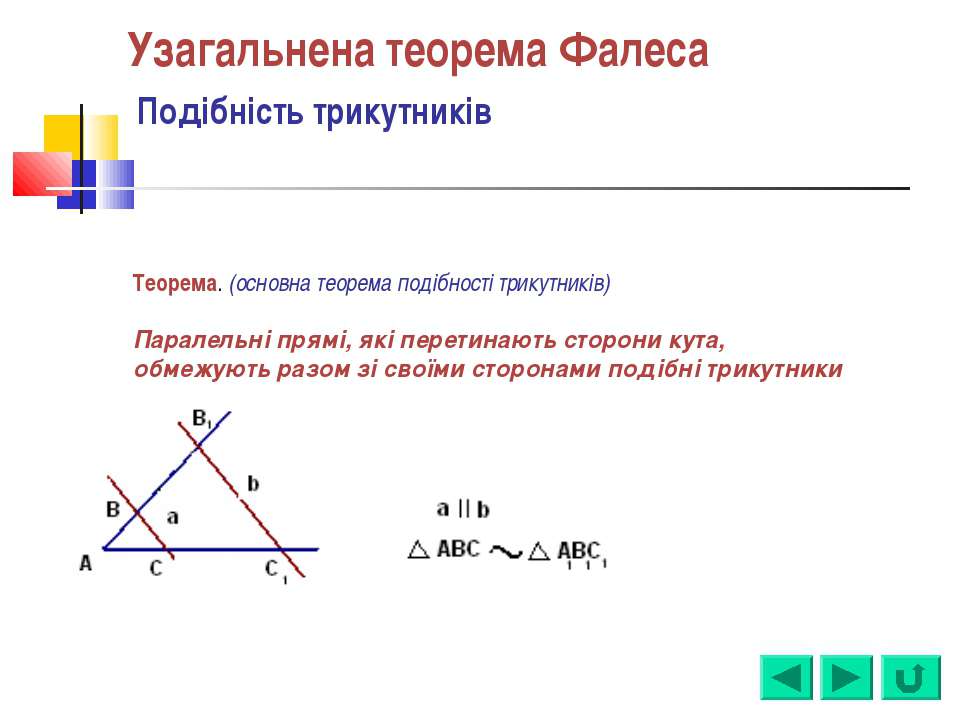 Сходство в геометрическом преобразовании одной фигуры в другую фигуру, при которой размеры всех линейных элементов одной фигуры пропорциональны соответствующим линейным элементам другой фигуры.Два треугольника (или любые многоугольники с одинаковым числом сторон) подобны, если (i) их соответствующие углы равны и (ii) их соответствующие стороны находятся в одинаковом соотношении (или пропорции). Все совпадающие числа похожи, но подобные числа не обязательно должны совпадать.
Сходство в геометрическом преобразовании одной фигуры в другую фигуру, при которой размеры всех линейных элементов одной фигуры пропорциональны соответствующим линейным элементам другой фигуры.Два треугольника (или любые многоугольники с одинаковым числом сторон) подобны, если (i) их соответствующие углы равны и (ii) их соответствующие стороны находятся в одинаковом соотношении (или пропорции). Все совпадающие числа похожи, но подобные числа не обязательно должны совпадать.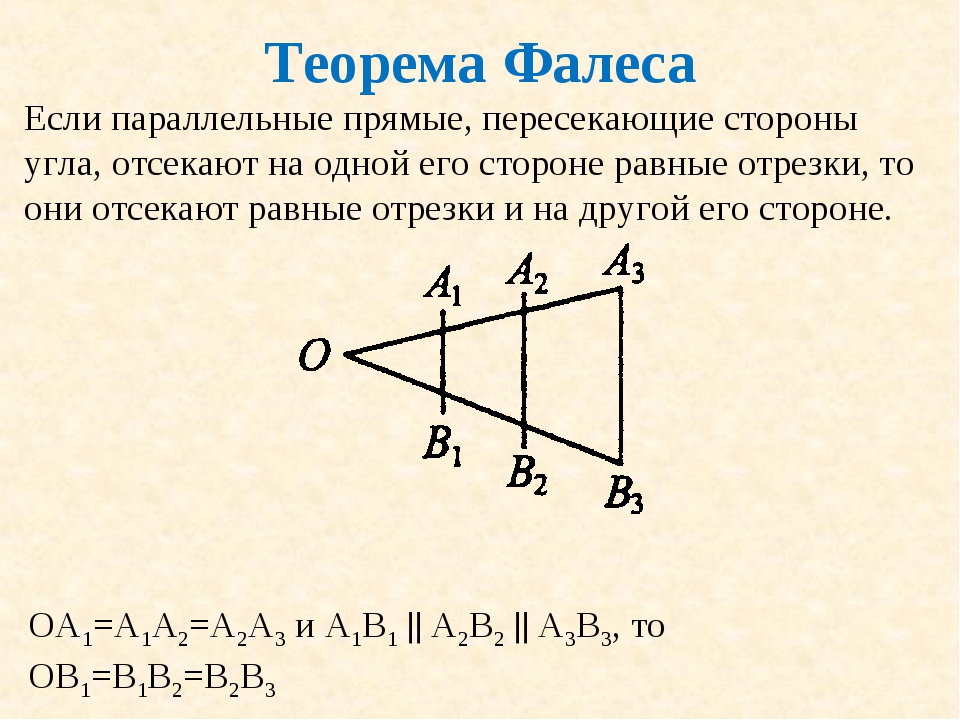 Согласно теореме, в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов двух других сторон. Утверждение должно быть заучено студентам, так как оно также просили написать на экзамене.
Согласно теореме, в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов двух других сторон. Утверждение должно быть заучено студентам, так как оно также просили написать на экзамене. AAA, SSS и SAS.
AAA, SSS и SAS. Или, если два угла одного треугольника равны двум углам другого треугольника, то эти два треугольника подобны. Загрузите документы по экзаменам совета CBSE для вопросов, основанных на BPT на экзаменах совета директоров.
Или, если два угла одного треугольника равны двум углам другого треугольника, то эти два треугольника подобны. Загрузите документы по экзаменам совета CBSE для вопросов, основанных на BPT на экзаменах совета директоров. Высота пирамид также может быть определена с помощью приложений тригонометрии.
Высота пирамид также может быть определена с помощью приложений тригонометрии.