Вычислить интеграл онлайн с подробным решением: Калькулятор онлайн — Вычислить неопределенный интеграл (первообразную) — ошкольное образовательное учреждение № 4 «Алёнушка»

2. Знайдіть радіус вписаного в трикутник кола

79,3:2,6-1,65*0,8 Пожалуйста ришите Это другой 5х-13=7

4. Внутрь прямоугольника со сторонами 16 см и 6 см наудачу брошена точка. Найти вероятность того, что точка не попадет во внутреннюю область прямоугол
…

ьного треугольника с катетами 6 см и 8 см, расположенного внутри прямоугольника. а) чему равна геометрическая мера, выражающая общее число всех равновозможных исходов данного испытанияб) мера, выражающая количество благоприятствующих этому событию исходов.в) Найти вероятность того, что точка не попадет во внутреннюю область прямоугольного треугольника с катетами 6 см и 8 см, расположенного внутри данного прямоугольника.

Х.12df10071 ВАРИАНТ1. Ряд данных состоит из 25 натуральных чисел. Какая из характеристик этого ряда может быть дробным числом? А)Мода В) Размах С) Сре
…

днее арифметическое D) Медиана2. Объём прямоугольного параллелепипеда равен V cм», стороны его основания равны 5 см и 3 см, а высота – 1 см.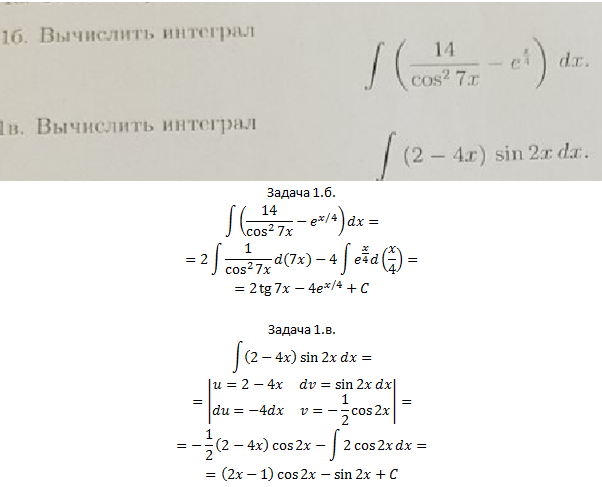 Задайте формулой зависимость V от һ.A) V=8h B) V=15h C) V=16h D) V=30h4.Постройте график прямой пропорциональности у = 3х.4. В кафе «Пицца» в течение 15 дней фиксировалось количество заказов с доставкой на дом. Получили такой рядданных: 39, 33, 45, 25, 33, 40, 47, 38, 34, 33, 40, 44, 45, 32, 27.Найдите размах, среднее арифметическое, моду и медиану полученного ряда.5. На рисунке изображен график движения туристаРассмотрев график, ответьте на вопросы:а) На каком расстоянии от дома был турист через 3 часа после выхода из дома?b) Сколько времени турист затратил на остановку?c) Сколько часов был турист в пути, когда до дома осталось пройти 40 км?d) С какой скоростью шел турист первые три часа?6. Решите задачу, составив систему уравнений:За 2 кг мандаринов и 5 кг апельсинов заплатили 3200 тенге. Сколько стоит 1 кг каждого вида фруктов, если 2 кгапельсинов на 1000 тенге дешевле, чем 3 кг мандаринов?7. Длина прямоугольника есть сумма числа 4 и удвоенного значения ширины этого прямоугольникаа) Составьте выражение по условию задачи. b) Составьте таблицу для данной зависимости и постройте ее график.806040201о6.1едaглeтeрeepTч

Знайдіть об’є́м циліндра,якщо осьовій переріз циліндра-квадрат,діагональ якого дорівнює 8√2см

Содержание

Интеграл (значения)

Пользователи также искали:

главное значение интеграла,

определенный интеграл это,

интегралов,

интеграла,

Интеграл,

интеграл,

определенный,

онлайн,

главное,

определенный интеграл свойства,

таблица интегралов,

неопределённый интеграл,

определенный интеграл это,

определенный интеграл онлайн,

интеграл онлайн,

значение,

свойства,

таблица,

неопределённый,

простыми,

словами,

главное значение интеграла,

Интеграл значения,

значения,

интеграл — — это простыми словами,

интеграл (значения),

евгений замятин. интеграл (значения),

…

Неопределенные интегралы решебник — faxeepavi.router.gallery

Неопределенные интегралы решебник

После вычисления неопределённого интеграла, вы сможете получить бесплатно ПОДРОБНОЕ решение введённого вами интеграла. Найдем решение. Рейтинг: 4,6 — 65 голосовРешение. Для решения данного интеграла не нужно использовать свойства неопределенных интегралов, достаточно формулы интеграла степенной. Неопределенный интеграл. Подробные примеры решений для чайников. Интегралы онлайн. Math34.su — вычисление интегралов. Найти интеграл онлайн. Math34.su — вычисление интегралов. Найти интеграл онлайн.
Калькулятор интегралов ∫ онлайн ∫. Бесплатное вычисление определенных и неопределенных интегралов с подробным решением с оформлением. Рейтинг: 3,6 — 10 отзывовДанный онлайн калькулятор позволяет найти неопределенный интеграл и получить ход решения. Неопределенный интеграл — это множество. Интегралы онлайн — неопределенный интеграл онлайн и определенный интеграл онлайн. Интеграл функции онлайн — сумма каких-либо чисел, предназначенных для их интегрирования. Поэтому, неформально, определенный. Как обычно, мы ограничимся минимумом теории, которая есть в многочисленных учебниках, наша задача – научиться решать интегралы. Рейтинг: 4,2 — 74 голосаБесплатный онлайн калькулятор для вычисления неопределенных интегралов — вводите функцию и получает решение интеграла с подробными.
Неопределенные интегралы, Методы вычисления, Желтухин В.С., 2005. В пособии рассматриваются основные приемы и методы вычисления неопределенных интегралов. 21 янв 2016 Здесь представлено 48 примеров решений неопределенных интегралов. Немного теории. Первообразная (неопределенный интеграл) Ранее мы по заданной функции, руководствуясь различными формулами и правилами, находили ее производную. На данной странице собраны примеры решения неопределенных интегралов. Каждый неопределенный интеграл содержит пошаговое решение. Примеры решения задач / Интегральное исчисление / Неопределенные интегралы / 1 2 3. Примеры задач с решениями. Вычислить интеграл. Комментарий. На этой странице вы сможете выполнять решение неопределенных интегралов онлайн с получением подробного решения задачи. Решение интегралов онлайн. Калькулятор решает интегралы c описанием действий ПОДРОБНО на русском языке и бесплатно. Определенный интеграл. Неопределенный интеграл. Несобственный интеграл. Геометрические приложения определенного интеграла. Механические.
Задача 2. Вычислить определённые интегралы. Задача 3. Найти неопределённые интегралы. Задача 4. Вычислить определённые интегралы. Задача 5. Найти неопределённые интегралы. Задача 6. Найти неопределённые интегралы.

Links to Important Stuff

Универсальный калькулятор комплексных чисел онлайн

Вы ввели следующее выражение

Окончательный результат выражения

Обновление: На 12 сентября 2017 года, упрощен ввод данных. Теперь можно вводить выражение без знака умножения. Например 3(2+i)(-4+sin(i)). Если заметили неправильный расчет, просьба внизу страницы обозначить ошибку в виде комментария. Спасибо!

Позволяет высчитывать результат произвольного комплексного выражения с любым количеством скобок, любой длины и с любыми числами (как действительными, так и мнимыми)

Арифметическое выражение подразумевает собой выражение, которое использует 4 основных операции: умножение, деление, сложение и вычитание.

Напомним как производятся эти операции:

Сложение двух комплексных чисел

Вычитание двух комплексных чисел

Умножение двух комплексных чисел

Деление двух комплексных чисел

$\cfrac{(a+bi)}{(c+di)}=\cfrac{(a*c+b*d)}{c^2+d^2}+i\cfrac{(b*c-a*d)}{c^2+d^2}$

Данный бот еще может использовать пятую операцию — возведение в степень, а так же все основные тригонометрические функции (синус, косинус, тангенс), обратные тригонометрические функции, взятие логарифма и экспоненты. возведение в степень

синус(sin)

косинус(cos)

натуральный логарифм(ln)

тангенс(tan)

артангенс(atan)

арксинус(asin)

арккосинус(acos)

гиперболический синус(sinh)

гиперболический косинус(cosh)

гиперболический тангенс(tanh)

Число в выражении может быть как действительным, которое записывается в привычном виде, так и комплексным числом которое обозначается символом i

Просьба по возможности оборачивать каждое комплексное число в круглые скобки, если первый символ в нём является минус (-)

Примеры

(-4-1i)/((-5-2i)+7-1.2i)

или в более наглядном виде

Получаем

Наш запрос выглядит так как мы его и сформировали в самом начале

calc_i (-4-1i)/((-5-2i)+7-1. (1/2))

Результат выражения

Действительная часть 0.66468285388895

Мнимая часть 1.0051451851734

Как видите, сложность выражения может быть произвольной и включать в себя комплексные числа.

Уравнение пятой степени. Частное решение. >>

Исследовать на сходимость несобственный интеграл онлайн с решением. Определенный интеграл онлайн

Вы еще здесь? =) Нет, я никого не пытался запугать, просто тема несобственных интегралов – очень хорошая иллюстрация тому, как важно не запускать высшую математику и другие точные науки. Для освоения урока на сайте всё есть – в подробной и доступной форме, было бы желание….

Итак, начнем-с. Образно говоря, несобственный интеграл – это «продвинутый» определенный интеграл, и на самом деле сложностей с ними не так уж и много, к тому же у несобственного интеграла есть очень хороший геометрический смысл.

Что значит вычислить несобственный интеграл?

Вычислить несобственный интеграл – это значит, найти ЧИСЛО
(точно так же, как в определенном интеграле), или доказать, что он расходится
(то есть, получить в итоге бесконечность вместо числа).

Несобственные интегралы бывают двух видов.

Несобственный интеграл с бесконечным пределом (ами) интегрирования

Иногда такой несобственный интеграл называют несобственным интегралом первого рода
. В общем виде несобственный интеграл с бесконечным пределом чаще всего выглядит так: . В чем его отличие от определенного интеграла? В верхнем пределе. Он бесконечный: .

Реже встречаются интегралы с бесконечным нижним пределом или с двумя бесконечными пределами: , и их мы рассмотрим позже – когда войдёте во вкус:)

Ну а сейчас разберём самый популярный случай . В подавляющем большинстве примеров подынтегральная функция непрерывна
на промежутке , и этот важный факт следует проверять в первую очередь!
Ибо если есть разрывы, то есть дополнительные нюансы. Для определённости предположим, что и тогда типичная криволинейная трапеция
будет выглядеть так:

Обратите внимание, что она бесконечна (не ограничена справа), и несобственный интеграл
численно равен её площади
. При этом возможны следующие варианты:

1) Первая мысль, которая приходит в голову: «раз фигура бесконечная, то », иными словами, площадь тоже бесконечна. Так быть может.
В этом случае говорят, что несобственный интеграл расходится
.

2) Но
. Как это ни парадоксально прозвучит, площадь бесконечной фигуры может равняться… конечному числу! Например: . Может ли так быть? Запросто. Во втором случае несобственный интеграл сходится
.

3) О третьем варианте чуть позже.

В каких случаях несобственный интеграл расходится, а в каком сходится? Это зависит от подынтегральной функции , и конкретные примеры мы очень скоро рассмотрим.

А что будет, если бесконечная криволинейная трапеция расположена ниже оси? В этом случае, несобственный интеграл (расходится) либо равен конечному отрицательному числу.

Таким образом, несобственный интеграл может быть отрицательным
.

Важно!
Когда Вам для решения предложен ЛЮБОЙ несобственный интеграл, то, вообще говоря, ни о какой площади речи не идет и чертежа строить не нужно
. Геометрический смысл несобственного интеграла я рассказал только для того, чтобы легче было понять материал.

Коль скоро, несобственный интеграл очень похож на определенный интеграл, то вспомним формулу Ньютона- Лейбница: . На самом деле формула применима и к несобственным интегралам, только ее нужно немного модифицировать. В чем отличие? В бесконечном верхнем пределе интегрирования: . Наверное, многие догадались, что это уже попахивает применением теории пределов, и формула запишется так: .

В чем отличие от определенного интеграла? Да ни в чем особенном! Как и в определенном интеграле, нужно уметь находить первообразную функцию (неопределенный интеграл), уметь применять формулу Ньютона-Лейбница. Единственное, что добавилось – это вычисление предела. У кого с ними плохо, изучите урок Пределы функций. Примеры решений
, ибо лучше поздно, чем в армии.

Рассмотрим два классических примера:

Пример 1

Для наглядности я построю чертеж, хотя, еще раз подчеркиваю, на практике
строить чертежи в данном задании не нужно
.

Подынтегральная функция непрерывна на полуинтервале , значит, всё нормально и несобственный интеграл можно вычислить «штатным» методом.

Применение нашей формулы и решение задачи выглядит так:

То есть, несобственный интеграл расходится, и площадь заштрихованной криволинейной трапеции равна бесконечности.

В рассмотренном примере у нас простейший табличный интеграл и такая же техника применения формулы Ньютона-Лейбница, как в определенном интеграле. Но применятся эта формула под знаком предела. Вместо привычной буквы «динамической» переменной выступает буква «бэ». Это не должно смущать или ставить в тупик, потому что любая буква ничем не хуже стандартного «икса».

Если Вам не понятно почему при , то это очень плохо, либо Вы не понимаете простейшие пределы (и вообще не понимаете, что такое предел), либо не знаете, как выглядит график логарифмической функции. Во втором случае посетите урок Графики и свойства элементарных функций
.

При решении несобственных интегралов очень важно знать, как выглядят графики основных элементарных функций!

Чистовое оформление задания должно выглядеть примерно так:

“

! При оформлении примера всегда прерываем решение, и указываем, что происходит с подынтегральной функцией
– непрерывна она на промежутке интегрирования или нет
. Этим мы идентифицируем тип несобственного интеграла и обосновываем дальнейшие действия.

Пример 2

Вычислить несобственный интеграл или установить его расходимость.

Выполним чертеж:

Во-первых, замечаем следующее: подынтегральная функция непрерывна на полуинтервале . Гуд. Решаем с помощью формулы :

(1) Берем простейший интеграл от степенной функции (этот частный случай есть во многих таблицах). Минус лучше сразу вынести за знак предела, чтобы он не путался под ногами в дальнейших вычислениях.

(2) Подставляем верхний и нижний пределы по формуле Ньютона-Лейбница.

(3) Указываем, что при (Господа, это уже давно нужно понимать) и упрощаем ответ.

Вот здесь площадь бесконечной криволинейной трапеции равна конечному числу! Невероятно, но факт.

Чистовое оформление примера должно выглядеть примерно так:

“

Подынтегральная функция непрерывна на

“

Что делать, если вам встретится интеграл наподобие – с точкой разрыва
на интервале интегрирования? Это говорит о том, что в примере опечатка (вероятнее всего)
, либо о продвинутом уровне обучения. В последнем случае, в силу свойства аддитивности
, следует рассмотреть два несобственных интеграла на промежутках и и затем разобраться с суммой.

Иногда вследствие опечатки либо умысла несобственного интеграла может вовсе не существовать
, так, например, если в знаменатель вышеуказанного интеграла поставить квадратный корень из «икс», то часть промежутка интегрирования вообще не войдёт в область определения подынтегральной функции.

Более того, несобственного интеграла может не существовать даже при всём «видимом благополучии». Классический пример: . Несмотря на определённость и непрерывность косинуса, такого несобственного интеграла не существует! Почему? Всё очень просто, потому что:
– не существует соответствующего предела
.

И такие примеры пусть редко, но встречаются на практике! Таким образом, помимо сходимости и расходимости, есть ещё и третий исход решения с полноправным ответом: «несобственного интеграла не существует».

Следует также отметить, что строгое определение несобственного интеграла даётся именно через предел, и желающие могут ознакомиться с ним в учебной литературе. Ну а мы продолжаем практическое занятие и переходим к более содержательным задачам:

Пример 3

Вычислить несобственный интеграл или установить его расходимость.

Сначала попытаемся найти первообразную функцию (неопределенный интеграл). Если нам не удастся этого сделать, то несобственный интеграл мы, естественно, тоже не решим.

На какой из табличных интегралов похожа подынтегральная функция? Напоминает она арктангенс: . Из этих соображений напрашивается мысль, что неплохо бы в знаменателе получить квадрат. Делается это путем замены.

Проведем замену:

Неопределенный интеграл найден, константу в данном случае добавлять не имеет смысла.

На черновике всегда полезно выполнить проверку, то есть продифференцировать полученный результат:

Получена исходная подынтегральная функция, значит, неопределенный интеграл найден правильно.

Теперь находим несобственный интеграл:

(1) Записываем решение в соответствии с формулой . Константу лучше сразу вынести за знак предела, чтобы она не мешалась в дальнейших вычислениях.

(2) Подставляем верхний и нижний пределы в соответствии с формулой Ньютона-Лейбница. Почему при ? Смотрите график арктангенса в уже неоднократно рекомендованной статье.

(3) Получаем окончательный ответ. Тот факт, что полезно знать наизусть.

Продвинутые студенты могут не находить отдельно неопределенный интеграл, и не использовать метод замены, а использовать метод подведения функции под знак дифференциала и решать несобственный интеграл «сразу». В этом случае решение должно выглядеть примерно так:

“

Подынтегральная функция непрерывна на .

“

Пример 4

Вычислить несобственный интеграл или установить его расходимость.

!
Это типовой пример, и похожие интегралы встречаются очень часто. Хорошо его проработайте! Первообразная функция здесь находится методом выделения полного квадрата, более подробно с методом можно ознакомиться на уроке Интегрирование некоторых дробей
.

Пример 5

Вычислить несобственный интеграл или установить его расходимость.

Этот интеграл можно решить подробно, то есть сначала найти неопределенный интеграл, проведя замену переменной. А можно решить «сразу» – подведением функции под знак дифференциала. У кого какая математическая подготовка.

Полные решения и ответы в конце урока.

Примеры решений несобственных интегралов с бесконечным нижним пределом интегрирования можно посмотреть на странице Эффективные методы решения несобственных интегралов
. Там же разобран случай, когда оба предела интегрирования бесконечны.

Несобственные интегралы от неограниченных функций

Или несобственные интегралами второго рода
. Несобственные интегралы второго рода коварно «шифруются» под обычный определенный интеграл и выглядят точно так же: Но, в отличие от определенного интеграла, подынтегральная функция терпит бесконечный разрыв (не существует): 1) в точке , 2) или в точке , 3) или в обеих точках сразу, 4) или даже на отрезке интегрирования. Мы рассмотрим первые два случая, для случаев 3-4 в конце статьи есть ссылка на дополнительный урок.

Сразу пример, чтобы было понятно: . Вроде бы это определенный интеграл. Но на самом деле – это несобственный интеграл второго рода, если мы подставим в подынтегральную функцию значение нижнего предела , то знаменатель у нас обращается в ноль, то есть подынтегральной функции просто не существует в этой точке!

Вообще при анализе несобственного интеграла всегда нужно подставлять в подынтегральную функцию оба предела интегрирования
. В этой связи проверим и верхний предел: . Здесь всё хорошо.

Криволинейная трапеция для рассматриваемой разновидности несобственного интеграла принципиально выглядит так:

Здесь почти всё так же, как в интеграле первого рода.

Наш интеграл численно равен площади заштрихованной криволинейной трапеции, которая не ограничена сверху. При этом могут быть два варианта*: несобственный интеграл расходится (площадь бесконечна) либо несобственный интеграл равен конечному числу (то есть, площадь бесконечной фигуры – конечна!).

*

по умолчанию привычно полагаем, что несобственный интеграл существует

Осталось только модифицировать формулу Ньютона-Лейбница. Она тоже модифицируется с помощью предела, но предел стремится уже не к бесконечности, а к значению справа.
Легко проследить по чертежу: по оси мы должны бесконечно близко приблизиться к точке разрыва справа
.

Посмотрим, как это реализуется на практике.

Пример 6

Вычислить несобственный интеграл или установить его расходимость.

Подынтегральная функция терпит бесконечный разрыв в точке (не забываем устно или на черновике проверить, всё ли нормально с верхним пределом!)

Сначала вычислим неопределенный интеграл:

Замена:

У кого возникли трудности с заменой, обратитесь к уроку Метод замены в неопределенном интеграле
.

Вычислим несобственный интеграл:

(1) Что здесь нового? По технике решения практически ничего. Единственное, что поменялось, это запись под значком предела: . Добавка обозначает, что мы стремимся к значению справа (что логично – см. график). Такой предел в теории пределов называют односторонним пределом
. В данном случае у нас правосторонний предел
.

(2) Подставляем верхний и нижний предел по формуле Ньютона Лейбница.

(3) Разбираемся с при . Как определить, куда стремится выражение? Грубо говоря, в него нужно просто подставить значение , подставляем три четверти и указываем, что . Причесываем ответ.

В данном случае несобственный интеграл равен отрицательному числу. В этом никакого криминала нет, просто соответствующая криволинейная трапеция расположена под осью .

А сейчас два примера для самостоятельного решения.

Пример 7

Вычислить несобственный интеграл или установить его расходимость.

Пример 8

Вычислить несобственный интеграл или установить его расходимость.

Если подынтегральной функции не существует в точке

Бесконечная криволинейная трапеция для такого несобственного интеграла принципиально выглядит следующим образом.

Определенные интегралы онлайн на сайт для закрепления студентами и школьниками пройденного материала. И тренировки своих практических навыков. Полноценное решение определенных интегралов онлайн для вас в считанные мгновения поможет определить все этапы процесса.. Интегралы онлайн — определенный интеграл онлайн. Определенные интегралы онлайн на сайт для полноценного закрепления студентами и школьниками пройденного материала и тренировки своих практических навыков. Полноценное решение определенных интегралов онлайн для вас в считанные мгновения поможет определить все этапы процесса.. Интегралы онлайн — определенный интеграл онлайн. Для нас определенный интеграл онлайн взять не представляется чем-то сверх естественным, изучив данную тему по книге выдающихся авторов. Огромное им спасибо и выражаем респект этим личностям. Поможет определить определенный интеграл онлайн сервис по вычислению таких задач в два счета. Только укажите правильные данные и все будет Good! Всякий определенный интеграл как решение задачи повысит грамотность студентов. Об этом мечтает каждый ленивец, и мы не исключение, признаем это честно. Если все-таки получится вычислить определенный интеграл онлайн с решением бесплатно, то, пожалуйста, напишите адрес сайт всем желающим им воспользоваться. Как говорится, поделишься полезной ссылкой — и тебя отблагодарят добрые люди за даром. Очень интересным будет вопрос разбора задачки, в которой определенный интеграл будет калькулятор решать самостоятельно, а не за счет траты вашего драгоценного времени. На то они и машины, чтобы пахать на людей. Однако решение определенных интегралов онлайн не всякому сайту по зубам, и это легко проверить, а именно, достаточно взять сложный пример и попытаться решить его с помощью каждого такого сервиса. Вы почувствуете разницу на собственной шкуре. Зачастую найти определенный интеграл онлайн без прилагаемых усилий станет достаточно сложно и нелепо будет выглядеть ваш ответ на фоне общей картины представления результата. Лучше бы сначала пройти курс молодого бойца. Всякое решение несобственных интегралов онлайн сводится сначала к вычислению неопределенного, а затем через теорию пределов вычислить как правило односторонние пределы от полученных выражений с подставленными границами A и B. Рассмотрев указанный вами определенный интеграл онлайн с подробным решением, мы сделали заключение, что вы ошиблись на пятом шаге, а именно при использовании формулы замены переменной Чебышева. Будьте очень внимательны в дальнейшем решении. Если ваш определенный интеграл онлайн калькулятор не смог взять с первого раза, то в первую очередь стоит перепроверить написанные данные в соответствующие формы на сайте. Убедитесь, что все в порядке и вперёд, Go-Go! Для каждого студента препятствием является вычисление несобственных интегралов онлайн при самом преподе, так как это либо экзамен, либо коллоквиум, или просто контрольная работа на паре.. Как только заданный несобственный интеграл онлайн калькулятор будет в вашем распоряжении, то сразу вбивайте заданную функцию, подставляйте заданные пределы интегрирования и нажимайте на кнопку Решение, после этого вам будет доступен полноценный развернутый ответ. И все-таки хорошо, когда есть такой замечательный сайт как сайт, потому что он и бесплатный, и простой в пользовании, также содержит очень много разделов. которыми студенты пользуются повседневно, один из них как раз есть определенный интеграл онлайн с решением в полном виде. В этом же разделе можно вычислить несобственный интеграл онлайн с подробным решением для дальнейших применений ответа как в институте, так и в инженерных работах. Казалось бы, всем определить определенный интеграл онлайн дело нехитрое, если заранее решить такой пример без верхней и нижней границы, то есть не интеграл Лейбница, а неопределенный интеграл. Но тут мы с вами не согласны категорически, так как на первый взгляд это может показаться именно так, однако есть существенная разница, давайте разберем все по полочкам. Такой определенный интеграл решение дает не в явном виде, а в следствие преобразования выражения в предельное значение. Другими словами, нужно сначала решить интеграл с подстановкой символьных значений границ, а затем вычислить предел либо на бесконечности, либо в определенной точке. Отсюда вычислить определенный интеграл онлайн с решением бесплатно означает ни что иное как представление точного решения по формуле Ньютона-Лейбница. Если же рассматривать наш определенный интеграл калькулятор поможет его подсчитать за несколько секунд прямо на ваших глазах. Такая спешка нужна всем желающим как можно быстрее справиться с заданием и освободиться для личных дел. Не стоит искать в интернете сайты, на которых попросят вас регистрироваться, затем пополнить деньги на баланс и все ради того, чтобы какой-нибудь умник подготавливал решение определенных интегралов якобы онлайн. Запомните адрес Math34 — это бесплатный сервис для решения множества математических задач, в том же числе мы поможем найти определенный интеграл онлайн, и чтобы в этом убедиться, просим проверить наше утверждение на конкретных примерах. Введите подынтегральную функцию в соответствующее поле, затем укажите либо бесконечные предельные значения (в это случае будет вычислен и получено решение несобственных интегралов онлайн), либо задайте свои числовые или символьные границы и определенный интеграл онлайн с подробным решением выведется на странице после нажатия на кнопку «Решение». Неправда ли — это очень просто, не требует от вас лишних действий, бесплатно, что самое главное, и в то же время результативно. Вы можете самостоятельно воспользоваться сервисом, чтобы определенный интеграл онлайн калькулятор принес вам максимум пользы, и вы бы получили комфортное состояние, не напрягаясь на сложность всех вычислительных процессов, позвольте нам сделать все за вас и продемонстрировать всю мощь компьютерных технологий современного мира. Если погружаться в дебри сложнейших формул и вычисление несобственных интегралов онлайн изучить самостоятельно, то это похвально, и вы можете претендовать на возможность написания кандидатской работы, однако вернемся к реалиям студенческой жизни. А кто такой студент? В первую очередь — это молодой человек, энергичный и жизнерадостный, желающий успеть отдохнуть и сделать домашку! Поэтому мы позаботились об учениках, которые стараются отыскать на просторах глобальной сети несобственный интеграл онлайн калькулятор, и вот он к вашему вниманию — сайт — самая полезная для молодежи решалка в режиме онлайн. Кстати наш сервис хоть и преподносится как помощник студентам и школьникам, но он в полной мере подойдет любому инженеру, потому что нам под силу любые типы задач и их решение представляется в профессиональном формате. Например, определенный интеграл онлайн с решением в полном виде мы предлагаем по этапам, то есть каждому логическому блоку (подзадачи) отводится отдельная запись со всеми выкладками по ходу процесса общего решения. Это конечно же упрощает восприятие многоэтапных последовательных раскладок, и тем самым является преимуществом проекта сайт перед аналогичными сервисами по нахождению несобственный интеграл онлайн с подробным решением.

Определенный
интеграл как предел интегральной суммы

может
существовать (т.е. иметь определенное
конечное значение) лишь при выполнении
условий

Если
хотя бы одно из этих условий нарушено,
то определение теряет смысл. Действительно,
в случае бесконечного отрезка, например
[a
;
)
его нельзя разбить на п

частей конечной длины

,
которая к тому же с увеличением количества
отрезков стремилась бы к нулю. В случае
же неограниченной в некоторой точкес
[a
;
b
]
нарушается требование произвольного
выбора точки
на частичных отрезках – нельзя выбрать=с
,
поскольку значение функции в этой точке
не определено. Однако и для этих случаев
можно обобщить понятие определенного
интеграла, введя еще один предельный
переход. Интегралы по бесконечным
промежуткам и от разрывных (неограниченных)
функций называют несобственными
.

Определение.

Пусть
функция

определена на промежутке [a
;
)
и интегрируема на любом конечном отрезке
[a
;
b
],
т.е. существует

для любого b

> a
.
Предел вида

называютнесобственным
интегралом

первого
рода

(или
несобственным интегралом по бесконечному
промежутку) и обозначают

.

Таким
образом, по определению,

=
.

Если
предел справа существует и конечен, то
несобственный интеграл

называютсходящимся

.
Если этот предел бесконечен, или не
существует вообще, то говорят, что
несобственный интеграл расходится

.

Аналогично
можно ввести понятие несобственного
интеграла от функции

по промежутку (–;
b
]:

=
.

А
несобственный интеграл от функции

по промежутку (–;
+)
определяется как сумма введенных выше
интегралов:

=
+
,

где
а

– произвольная точка. Этот интеграл
сходится, если сходятся оба слагаемых,
и расходится, если расходится хотя бы
одно из слагаемых.

С
геометрической точки зрения, интеграл
,
,
определяет численное значение площади
бесконечной криволинейной трапеции,
ограниченной сверху графиком функции
,
слева – прямой
,
снизу – осью ОХ. Сходимость интеграла
означает существование конечной площади
такой трапеции и равенство ее пределу
площади криволинейной трапеции с
подвижной правой стенкой
.

На
случай интеграла с бесконечным пределом
можно обобщить и формулу
Ньютона-Лейбница
:

=

=F(+
)
– F(a
),

где
F(+
)
=

.
Если этот предел существует, то интеграл
сходится, в противном случае – расходится.

Мы
рассмотрели обобщение понятия
определенного интеграла на случай
бесконечного промежутка.

Рассмотрим теперь
обобщение для случая неограниченной
функции.

Определение

Пусть
функция

определена на промежутке [a
;
b
),
неограниченна в некоторой окрестности
точки b
,
и непрерывна на любом отрезке

,
где>0
(и, следовательно, интегрируема на этом
отрезке, т.е.

существует). Предел вида
называетсянесобственным
интегралом второго рода

(или несобственным интегралом от
неограниченной функции) и обозначается

.

Таким
образом, несобственный интеграл от
неограниченной в точке b

функции есть по определению

=
.

Если
предел справа существует и конечен, то
интеграл называется сходящимся
.
Если конечного предела не существует,
то несобственный интеграл называется
расходящимся.

Аналогично
можно определить несобственный интеграл
от функции

имеющей бесконечный разрыв в точкеа
:

=
.

Если
функция

имеет бесконечный разрыв во внутренней
точкес

,
то несобственный интеграл определяется
следующим образом

=
+

=
+
.

Этот интеграл
сходится, если сходятся оба слагаемых,
и расходится, если расходится хотя бы
одно слагаемое.

С
геометрической точки зрения, несобственный
интеграл от неограниченной функции
также характеризует площадь неограниченной
криволинейной трапеции:

Поскольку
несобственный интеграл выводится путем
предельного перехода из определенного
интеграла, то все свойства определенного
интеграла могут быть перенесены (с
соответствующими уточнениями) на
несобственные интеграла первого и
второго рода.

Во
многих задачах, приводящих к несобственным
интегралам, не обязательно знать, чему
равен этот интеграл, достаточно лишь
убедиться в его сходимости или
расходимости. Для этого используют
признаки
сходимости
.
Признаки
сходимости несобственных интегралов:

1)
Признак
сравнения
.

Пусть
для всех х


.
Тогда, если
сходится, то сходится и
,
причем

.
Если
расходится, то расходится и
.

2)
Если сходится

,
то сходится и
(последний интеграл в этом случае
называетсяабсолютно
сходящимся
).

Признаки
сходимости и расходимости несобственных
интегралов от неограниченных функций
аналогичны сформулированным выше.

Примеры
решения задач.

Пример
1.

а)

;
б)
;
в)

г)

; д)
.

Решение.

а)
По определению
имеем:

б)
Аналогично

Следовательно,
данный интеграл сходится и равен
.

в)
По определению

=
+
,
причем,а

– произвольное число. Положим в нашем
случае

,
тогда получим:

Данный
интеграл сходится.

Значит, данный
интеграл расходится.

д)
Рассмотрим
.
Чтобы найти первообразную подынтегральной
функции, необходимо применить метод
интегрирования по частям. Тогда получим:

Поскольку
ни

,
ни
не существуют, то не существует и

Следовательно,
данный интеграл расходится.

Пример
2.

Исследовать
сходимость интеграла
в зависимости от п
.

Решение.

При

имеем:

Если

,
то
и.
Следовательно, интеграл расходится.

Если

,
то
,
а
,
тогда

Следовательно,
интеграл сходится.

Если

,
то

следовательно,
интеграл расходится.

Таким
образом,

Пример
3.

Вычислить
несобственный интеграл или установить
его расходимость:

а)

;
б)
;
в)

.

Решение.

а)
Интеграл
является несобственным интегралом
второго рода, поскольку подынтегральная
функция
не ограничена в точке

.
Тогда, по определению,

Интеграл сходится и равен
.

б)
Рассмотрим
.
Здесь также подынтегральная функция
не ограничена в точке
.
Поэтому, данный интеграл – несобственный
второго рода и по определению,

Следовательно,
интеграл расходится. 3+1}.
\]

практичная специальность с творческим началом

Несобственные интегралы первого рода:
распространение понятия определённого интеграла на случаи интегралов с бесконечным верхним или нижними пределами интегрирования, или оба предела интегрирования бесконечны.

Несобственные интегралы второго рода:
распространение понятия определённого интеграла на случаи интегралов от неограниченных функций, подынтегральная функция в конечном числе точек конечного отрезка интегрирования не существует, обращаясь в бесконечность.

Для сравнения.
При введении понятия определённого интеграла предполагалось, что функция f
(x
) непрерывна на отрезке [a
, b
], а отрезок интегрирования является конечным, то есть ограничен числами, а не бесконечностью. Некоторые задачи приводят к необходимости отказаться от этих ограничений.
Так появляются несобственные интегралы.

Геометрический смысл несобственного интеграла
выясняется довольно просто.
В случае, когда график функции y
= f
(x
)

находится выше оси Ox

, определённый интеграл
выражает площадь криволинейной трапеции, ограниченной кривой y
= f
(x
)
,
осью абсцисс и ординатами x
= a

, x
= b

.
В свою очередь несобственный интеграл
выражает площадь неограниченной (бесконечной) криволинейной трапеции, заключённой между линиями
y
= f
(x
)
(на рисунке ниже — красного цвета), x
= a

и осью абсцисс.

Аналогичным образом определяются несобственные интегралы и для других бесконечных
интервалов:

Площадь бесконечной криволинейной трапеции может быть конечным числом и в этом случае несобственный
интеграл называется сходящимся. Площадь может быть и бесконечностью и в этом случае несобственный
интеграл называется расходящимся.

Использование предела интеграла вместо самого несобственного
интеграла.
Для того, чтобы вычислить несобственный интеграл, нужно использовать предел
определённого интеграла. Если этот предел существует и конечен (не равен бесконечности), то
несобственный интеграл называется сходящимся, а в противном случае — расходящимся. К чему стремится
переменная под знаком предела, зависит от того, имеем мы дело с несобственным интегралом первого рода
или второго рода. Узнаем об этом сейчас же.

Несобственные интегралы первого рода — с бесконечными пределами и их сходимость

Несобственные интегралы с бесконечным верхним пределом

Итак, запись несобственного интеграла как
отличается от обычного определённого интеграла тем, что верхний предел интегрирования бесконечен.

Определение.
Несобственным интегралом с бесконечным верхним пределом
интегрирования от непрерывной функции f
(x
)

на промежутке
от a

до ∞

называется
предел интеграла этой функции с верхним пределом интегрирования b

и нижним пределом интегрирования a

при условии, что верхний предел
интегрирования неограниченно растёт
, т. е.

Если этот предел существует и равен некоторому числу, а не бесконечности, то несобственный интеграл называется сходящимся
, а число, которому равен предел, принимается за его значение. В противном случае несобственный интеграл называется расходящимся
и ему не приписывается никакого значения.

Пример 1. Вычислить несобственный интеграл
(если он сходится).

Решение. На основании определения несобственного интеграла находим

Так как предел существует и равен 1, то и данный несобственный интеграл сходится
и равен 1.

В следующем примере подынтегральная функция почти как в примере 1, только степень
икса — не двойка, а буква альфа, а задача состоит в исследовании несобственного интеграла на сходимость.
То есть предстоит ответить на вопрос: при каких значениях альфы данный несобственный интеграл сходится,
а при каких расходится?

Пример 2. Исследовать на сходимость несобственный интеграл

(нижний предел интегрирования больше нуля).

Решение. Предположим сначала, что , тогда

В полученном выражении перейдём к пределу при :

Нетрудно видеть, что предел в правой части существует и равен нулю, когда
, то есть
, и не существует, когда
, то есть
.

В первом случае, то есть при
имеет место .
Если , то
и
не существует.

Вывод нашего исследования следующий: данный несобственный интеграл
сходится
при и
расходится
при .

Применяя к изучаемому виду несобственного интеграла формулу Ньютона-Лейбница ,
можно вывести следующую очень похожую на неё формулу:

Это обобщённая формула Ньютона-Лейбница.

Пример 3. Вычислить несобственный интеграл
(если он сходится).

Предел этого интеграла существует:

Второй интеграл, составляющий сумму, выражающую исходный интеграл:

Предел этого интеграла также существует:

Находим сумму двух интегралов, являющуюся и значением исходного несобственного
интеграла с двумя бесконечными пределами:

Несобственные интегралы второго рода — от неограниченных функций и их сходимость

Пусть функция f
(x
)

задана на
отрезке от a

до b

и неограниченна на нём. Предположим, что функция обращается в бесконечность в точке b

,
в то время как во всех остальных точках отрезка она непрерывна.

Определение.
Несобственным интегралом функции f
(x
)

на отрезке от a

до b

называется предел интеграла этой функции с верхним пределом интегрирования c

,
если при стремлении c

к b

функция неограниченно возрастает, а в точке x
= b

функция не определена
, т.е.

Если этот предел существует, то несобственный интеграл второго рода называется
сходящимся, в противном случае — расходящимся.

Используя формулу Ньютона-Лейбница, выводим.

Несобственный интеграл с бесконечным пределом интегрирования

Иногда такой несобственный интеграл еще называют несобственным интегралом первого рода..gif»>.

Реже встречаются интегралы с бесконечным нижним пределом или с двумя бесконечными пределами: .

Мы рассмотрим самый популярный случай https://pandia.ru/text/80/057/images/image005_1.gif»>?

Нет, не всегда. Подынтегральная функция
https://pandia.ru/text/80/057/images/image007_0.gif»>

Изобразим на чертеже график подынтегральной функции . Типовой график и криволинейная трапеция для данного случая выглядит так:

Несобственный интеграл
https://pandia.ru/text/80/057/images/image009_0.gif»>», иными словами, площадь тоже бесконечна. Так быть может.
В этом случае говорят, что, что несобственный интеграл расходится
.

2) Но
. Как это ни парадоксально прозвучит, площадь бесконечной фигуры может равняться… конечному числу! Например: .. Во втором случае несобственный интеграл сходится
.

А что будет, если бесконечная криволинейная трапеция расположена ниже оси?.gif»>.

: .

Пример 1

Подынтегральная функция https://pandia.ru/text/80/057/images/image017_0. gif»>, значит, всё нормально и несобственный интеграл можно вычислить «штатным» методом.

Применение нашей формулы https://pandia.ru/text/80/057/images/image018_0.gif»>

Пример 2

Вычислить несобственный интеграл или установить его расходимость.

Выполним чертеж:

Во-первых, замечаем следующее: подынтегральная функция непрерывна на полуинтервале . Гуд..gif»>

(2) Подставляем верхний и нижний пределы по формуле Ньютона-Лейбница.

(3) Указываем, что https://pandia.ru/text/80/057/images/image024. gif»> (Господа, это уже давно нужно понимать) и упрощаем ответ.

Вот здесь площадь бесконечной криволинейной трапеции равна конечному числу! Невероятно, но факт.

Пример 3

Вычислить несобственный интеграл или установить его расходимость.

Подынтегральная функция непрерывна на .

Сначала попытаемся найти первообразную функцию (неопределенный интеграл).

Проведем замену:

Всегда полезно выполнить проверку, то есть продифференцировать полученный результат:

Теперь находим несобственный интеграл:

(2) Подставляем верхний и нижний пределы в соответствии с формулой Ньютона-Лейбница. .gif»>? Смотрите график арктангенса в уже неоднократно рекомендованной статье.

(3) Получаем окончательный ответ. Тот факт, что полезно знать наизусть.

“

Подынтегральная функция непрерывна на https://pandia.ru/text/80/057/images/image041.gif»>
“

Пример 4

Вычислить несобственный интеграл или установить его расходимость.

!
Это типовой пример, и похожие интегралы встречаются очень часто. Хорошо его проработайте! Первообразная функция здесь находится методом выделения полного квадрата.

Пример 5

Вычислить несобственный интеграл или установить его расходимость.

Несобственные интегралы от неограниченных функций

Иногда такие несобственные интегралы называют несобственными интегралами второго рода. Несобственные интегралы второго рода коварно «шифруются» под обычный определенный интеграл и выглядят точно так же: ..gif»>, 2) или в точке , 3) или в обеих точках сразу, 4) или даже на отрезке интегрирования. Мы рассмотрим первые два случая, для случаев 3-4 в конце статьи есть ссылка на дополнительный урок.

Сразу пример, чтобы было понятно: https://pandia.ru/text/80/057/images/image048.gif»>, то знаменатель у нас обращается в ноль, то есть подынтегральной функции просто не существует в этой точке!

Вообще при анализе несобственного интеграла всегда нужно подставлять в подынтегральную функцию оба предела интегрирования
..jpg» alt=»Несобственный интеграл, точка разрыва в нижнем пределе интегрирования»>

Здесь почти всё так же, как в интеграле первого рода.
Наш интеграл численно равен площади заштрихованной криволинейной трапеции, которая не ограничена сверху. При этом могут быть два варианта: несобственный интеграл расходится (площадь бесконечна) либо несобственный интеграл равен конечному числу (то есть, площадь бесконечной фигуры – конечна!).

Осталось только модифицировать формулу Ньютона-Лейбница. Она тоже модифицируется с помощью предела, но предел стремится уже не к бесконечности, а к значению
https://pandia.ru/text/80/057/images/image052.gif»> справа
.

Пример 6

Вычислить несобственный интеграл или установить его расходимость.

Сначала вычислим неопределенный интеграл:

Замена:

Вычислим несобственный интеграл:

(1) Что здесь нового? По технике решения практически ничего. Единственное, что поменялось, это запись под значком предела: . Добавка обозначает, что мы стремимся к значению справа (что логично – см. график). Такой предел в теории пределов называют односторонним пределом. В данном случае у нас правосторонний предел.

(2) Подставляем верхний и нижний предел по формуле Ньютона Лейбница.

(3) Разбираемся с https://pandia.ru/text/80/057/images/image058.gif»>. Как определить, куда стремиться выражение? Грубо говоря, в него нужно просто подставить значение , подставляем три четверти и указываем, что . Причесываем ответ.

В данном случае несобственный интеграл равен отрицательному числу.

Пример 7

Вычислить несобственный интеграл или установить его расходимость.

Пример 8

Вычислить несобственный интеграл или установить его расходимость.

Если подынтегральной функции не существует в точке

Бесконечная криволинейная трапеция для такого несобственного интеграла принципиально выглядит следующим образом:

Здесь всё абсолютно так же, за исключением того, что предел у нас стремится к значению
https://pandia. ru/text/80/057/images/image052.gif»> мы должны бесконечно близко приблизиться к точке разрыва слева
.

Сумма ряда онлайн с подробным решением. §4. Приближенное вычисление суммы числового ряда

Доказательство
.

Заметим, что
.
После этого утверждение превращается
в критерий
Коши сходимости последовательности
.

Теорема
.

Если ряд сходится,
то.

Доказательство
.

Из свойств пределов
следует, что .
Отсюда следует, что.

40. Эталонные ряды для установления сходимости

Геометрический
ряд

Обобщеный
гармонический ряд

В
частности, при к=1 получаем гармонический
ряд

Эталонные
ряды, т.е. разложения элементарных
функций, можно использовать для получения
рядов тех же функций, но сложного
аргумента.

41. Функциональные ряды, степенные ряды, ряды Тейлора и Маклорена

Пусть
функции Un(x),n∈N,
определены в области D. Выражение U
1
(x
)
+
U
2
(x
)
+… +
U
n
(x
)+…=
U
n
(x
),
где х
∈
D
,
наз.
функциональным
рядом.

Каждому значению x 0 ∈D
соответствует числовой ряд
U
n
(x
0
)
.
Этот ряд может быть сходящимся или
расходящимся. Если для x
0
∈
D

числовой ряд
U
n
(x
0
)

сходится, то говорят, чтo
функциональный ряд сходится в точке
x
0
,
и точку
x
0
наз.
точкой
сходимости

.Если
функциональный ряд сходится в каждой
точке x
∈
E
⊂
D
,
то этот ряд наз. сходящимся
на множестве Е
,
а множество Е

наз. областью сходимости ряда. Если
множество Е

пусто, то ряд расходится в каждой точке
множества D
.

Областью сходимости

степенного ряда называется множество
всех значений переменной х, при которых
соответствующий числовой ряд сходится.
Ряд вида а 0
+ а 1
х + а 2
х 2
+ … а n
х n
+ … =
называетсястепенным
рядом,
а –
некот. числа, х – переменная.

Коэффициентами
степенного
ряда называются числа а 0
, а 1
, … , а n .

Формулой Тейлора

для функции f(x)
в окрестности точки х называется
многочлен Р n (х)
= f(х 0)
+Остаточным
членом формулы Тейлора
называется
последнее слагаемое в формуле Тейлора

R n
(x)=
=f(x)
– P n
(x)

Т.о., многочлен
Тейлора Р n (х)
служит приближением функции f(х).
Оценкой этого приближения служит
остаточный член формулы Тейлора R n (х).

Формулой Маклорена

для функции f(х)
называется ее формула Тейлора при х 0
= 0: f(x)=
f(0)
+

где с – некоторая
точка из интервала (0, х).

С помощью данного онлайн калькулятора можно находить суммы рядов, определять их сходимость, абсолютную и условную. Ряд — это последовательность чисел (либо функций — для функциональных рядов), которые связаны между собой определенным законом. Сумма членов ряда это и есть сумма ряда. Для доказательства того, что такая сумма существует (то есть она не равна бесконечности) можно использовать принципы сходимости числовых рядов — принцип Коши, принцип Доламбера и т. д. После доказательства того, что ряд сходится вычислить сумму числового ряда уже необходимо индивидуально. Для геометрической прогрессии, например, сумма вычисляется по формуле:

Найти сумму ряда онлайн

На нашем сайте вы можете вычислить сумму ряда онлайн
. Всегда быстро, надежно, бесплатно. Удобный интерфейс для ввода рядов, задание начального и конечного значения элементов. Возможность находить сумму функционального ряда, использование буквенных констант. На практике студенты имеют дело с числовыми рядами довольно часто. Они широко используются в приближенных вычислениях (вычисление интегралов не имеющих аналитического решения, выполнение математических действий, решение дифференциальных уравнений и т.д.). А про функциональные ряды наподобие ряда Тейлора или ряда Фурье и говорить не приходится. С помощью нашего калькулятора определить сумму ряда теперь не проблема.

Поскольку точное значение суммы ряда
удается вычислить далеко не всегда
(такие задачи были нами рассмотрены),
возникает проблема приближенного
вычисления суммы ряда с заданной
точностью.

Напомним, что
-ый
остаток рядаполучается из исходного рядаотбрасыванием первыхслагаемых:

Тогда, поскольку для сходящегося ряда

,

остаток сходящегося ряда равен разности
между суммой ряда и
-ой
частичной суммой:

и для достаточно больших
имеем
приближенное равенство

Из определения остатка ряда следует,
что абсолютная погрешность при замене
точного неизвестного значения суммы
его частичной суммойравна модулю остатка ряда:

Таким образом, если требуется вычислить
сумму ряда с заданной точностью
,
то нужно оставить сумму такого числаслагаемых, чтобы для отброшенного
остатка ряда выполнялось неравенство:

Метод приближенного вычисления суммы
выбирается в зависимости от вида ряда:

если ряд положительный и может быть
исследован на сходимость по интегральному
признаку (удовлетворяет условиям
соответствующей теоремы), то для оценки
суммы используем формулу

;

если это ряд Лейбница, то применяем
оценку:

В других задачах можно использовать
формулу суммы бесконечно убывающей
геометрической прогрессии.

Задача №1.
Сколько нужно взять
слагаемых ряда
,
чтобы получить его сумму с точностью
0,01.

Решение.
Прежде всего отметим, что
данный ряд сходится. Рассмотрим-ый
остаток ряда, который и является
погрешностью вычислений суммы ряда:

Оценим этот ряд с помощью бесконечно
убывающей геометрической прогрессии.
Для этого заменим в каждом слагаемом
множитель
на,
при этом каждое слагаемое увеличится:

После вынесения общего множителя за
скобку, в скобке остался ряд, составленный
из членов бесконечно убывающей
геометрической прогрессии, сумму
которого мы и вычислили по формуле

Заданная точность будет достигнута,
если
будет удовлетворять условию

Решим неравенство, учитывая, что
—
целое.

При

имеем

В силу монотонности функции

,
неравенство
будет выполняться для всех
.

Следовательно, если вместо точного
значения суммы мы возьмем первые пять
(или более) слагаемых, то погрешность
вычислений не превысит 0,01.

Ответ:

.

Задача №2.
Оценить ошибку, получаемую
при замене суммы ряда
суммой
первых 100 слагаемых.

Решение.
Заметим, что данный ряд
является сходящимся и знакопеременным.
Оценивать будем ряд
,
состоящий из модулей исходного ряда,
что сразу увеличивает погрешность
вычислений. Кроме того, нам придется
перейти (используя признак сравнения)
к большему, более простому сходящемуся
ряду:

Рассмотрим ряд
.
Поскольку этот ряд удовлетворяет
условиям теоремы – интегрального
признака сходимости, то для оценки
погрешности вычисления суммы используем
соответствующую формулу:

Вычислим несобственный интеграл:

погрешность вычислений можно оценить
по формуле

по условию

,
тогда.

Ответ:

.

Задача №3.
Оценить ошибку,
получаемую при замене суммы ряда
суммой
первых 10 слагаемых.

Решение.
Подчеркнем еще раз, что
задача о приближенном вычислении суммы
имеет смысл только для сходящегося
ряда, поэтому, прежде всего отметим, что
данный ряд сходится. Поскольку исследуемый
ряд является знакопеременным со сложным
правилом изменения знака, то оценивать
придется, как и в предыдущем примере,
ряд из модулей данного ряда:

Используя тот факт, что

при любом значении аргумента, имеем:

Оценим остаток ряда:

Мы получили ряд, составленный из членов
бесконечно убывающей геометрической
прогрессии, в которой

его сумма равна:

Ответ:

.

Задача №4.
Вычислить сумму ряда
с
точностью 0,01.

Решение.
Данный ряд является рядом
Лейбница. Для оценки погрешности верна
формула:

другими словами, погрешность вычислений
меньше модуля первого отброшенного
слагаемого. Подберем номер
так, чтобы

При

имеем

Погрешность

,
если в качестве значения суммы возьмем
сумму первых четырех слагаемых:

Ответ:
.

бесплатных вопросов по исчислению и проблем с решениями

Представлены бесплатные учебные пособия по исчислению. Аналитические уроки могут быть использованы для дальнейшего развития ваших навыков решения задач в области математического анализа. Также вопросы математического анализа изучаются в интерактивном режиме с использованием приложений и аналитически с примерами и подробными решениями. Задачи и вопросы по исчислению также включены на этот веб-сайт. Включены функции многовариантных и частные производные.

Задачи и вопросы по исчислению

Вопросы, ответы и решения по исчислению

Аналитические учебные пособия

Лимиты и непрерывность

Дифференциация и производные

Найдите производные функций в исчислении.Найдите производные от различных функций, используя разные методы и правила. Представлено несколько примеров с подробными решениями. Также упражнения с ответами включены в конце страницы.
Коэффициент разницы. Мы начинаем с определения коэффициента разности, а затем используем несколько примеров для его вычисления. Представлены подробные решения вопросов.
Используйте определение, чтобы найти производную. Производная находится по ее определению. Сначала вычисляется коэффициент разности, а затем вычисляется его предел как h —> 0.Икс.
Доказательство производной ln (x). Производная ln (x) вычисляется с использованием определения.
Доказательство производной sin x. Производная sin (x) вычисляется с использованием определения производной как предела.
Доказательство производной cos x. Производная cos (x) вычисляется с использованием определения производной как предела.
Производная tan (x). Производная tan (x) вычисляется с использованием правила частного и производных sin (x) и cos (x).
Доказательство производной кроватки (x). Доказательство производной от cot (x) проводится с использованием правила частного и производных от sin (x) и cos (x).
Доказательство производной от sec (x). Приводится доказательство производной от sec (x).
Доказательство производной csc (x). Приводится доказательство производной csc (x).
Логарифмическое дифференцирование. Мощный метод поиска производных сложных функций. Метод использует цепное правило и свойства логарифмов.
Таблица производных. Таблица производных экспоненциальных и логарифмических функций, тригонометрических функций и их обратных, гиперболических функций и их обратных.
Правила дифференцирования функций в исчислении. Основные правила дифференцирования функций в исчислении представлены вместе с несколькими примерами.
Используйте цепное правило дифференцирования в исчислении. Цепное правило дифференцирования функций в исчислении представлено вместе с несколькими примерами.
Производные финансовые инструменты с абсолютной стоимостью. Примеры того, как найти производную функций, содержащих абсолютное значение. Также включены упражнения с ответами.
Неявная дифференциация. Приведены примеры неявного дифференцирования с подробными решениями.
Производная обратной функции. Приведены примеры с подробными решениями о том, как найти производную обратной функции.
Производная от обратных тригонометрических функций.Формулы производных обратных тригонометрических функций представлены вместе с несколькими другими примерами, включающими суммы, произведения и частные функций.
Найдите производную f (x) = arccos (cos (x)) и нанесите ее на график.
Найдите производную f (x) = arcsin (sin (x)) и нанесите ее на график.
Найдите производную f (x) = arctan (tan (x)) и нанесите ее на график.
Дифференцирование тригонометрических функций. Формулы производных тригонометрических функций в исчислении представлены вместе с несколькими примерами, включающими произведения, суммы и частные тригонометрических функций.
Найдите производную y = x ^x. Учебное пособие о том, как найти первую производную y = x ^x для x> 0.
Дифференцирование экспоненциальных функций. Приведены формулы и примеры производных экспоненциальных функций в исчислении. Рассмотрены несколько примеров с подробными решениями, включающими произведения, суммы и частные экспоненциальных функций.
Дифференцирование логарифмических функций. Приведены примеры производных логарифмических функций в исчислении.Рассмотрены несколько примеров с подробными решениями, включающими произведения, суммы и частные экспоненциальных функций.
Дифференцирование гиперболических функций. Представлена таблица производных гиперболических функций. Рассмотрены примеры с подробными решениями, включающими произведения, суммы, степени и частные гиперболических функций.

Применение дифференцирования

Интегралы

Дифференциальные уравнения

Функции с несколькими переменными (функции с несколькими переменными)

Таблицы математических формул

Таблицы математических формул.Несколько таблиц математических формул, включая десятичные множители, ряды, факториалы, перестановки, комбинации, биномиальное разложение, тригонометрические формулы и таблицы производных, интегралов, преобразования Лапласа и Фурье.

Интерактивные учебные пособия

Математические формулы и тождества
Инженерная математика
Домашняя страница сообщить об этом объявлении
Интеграция

(scipy.integrate) — Справочное руководство SciPy v1.6.3

Интеграция набора обыкновенных дифференциальных уравнений (ОДУ), заданного
начальные условия — еще один полезный пример.{2}} \ Gamma \ left (\ frac {2} {3} \ right)} \) и \ (\ left. \ Frac {dw} {dz} \ right | _ {z = 0} = — \ frac {1} {\ sqrt [3] {3} \ Gamma \ left (\ frac {1} {3} \ right)}. \) Известно, что решение этого дифференциального уравнения с этими
граничными условиями является функция Эйри

Сначала преобразуйте это ОДУ в стандартную форму, задав
\ (\ mathbf {y} = \ left [\ frac {dw} {dz}, w \ right] \) и \ (t = z \). Таким образом,
дифференциальное уравнение принимает вид

\ [\ begin {split} \ frac {d \ mathbf {y}} {dt} = \ left [\ begin {array} {c} ty_ {1} \\ y_ {0} \ end {array} \ right] = \ left [\ begin {array} {cc} 0 & t \\ 1 & 0 \ end {array} \ right] \ left [\ begin {array} {c} y_ {0} \\ y_ {1} \ конец {массив} \ right] = \ left [\ begin {array} {cc} 0 & t \\ 1 & 0 \ end {array} \ right] \ mathbf {y}.{t} \ mathbf {A} \ left (\ tau \ right) d \ tau \ right) \ mathbf {y} \ left (0 \ right), \]

Однако в этом случае \ (\ mathbf { A} \ left (t \ right) \) и его интеграл не коммутируют.

Это дифференциальное уравнение можно решить с помощью функции resolve_ivp .
Требуется производная fprime , временной интервал [t_start, t_end]
и вектор начальных условий, y0 , в качестве входных аргументов и возвращает
объект, чье поле y представляет собой массив с последовательными значениями решения как
столбцы.Поэтому начальные условия приведены в первом выходном столбце.

Как видно, resolve_ivp определяет свои временные шаги автоматически, если нет
указано иное. Сравнить решение resolve_ivp с решением airy
вектор времени, созданный функцией resolve_ivp , передается в функцию airy .

Решение resolve_ivp со стандартными параметрами показывает большое отклонение
к воздушной функции.Чтобы минимизировать это отклонение, относительные и абсолютные
допуски могут быть использованы.

Чтобы указать определенные пользователем моменты времени для решения resolve_ivp , resolve_ivp
предлагает две возможности, которые также можно использовать дополнительно. Проходя t_eval
опция вызова функции resolve_ivp возвращает решения этих временных точек
из t_eval на выходе.

Если матрица якобиана функции известна, ее можно передать в функцию resolve_ivp
для достижения лучших результатов.Однако имейте в виду, что метод интеграции по умолчанию
RK45 не поддерживает матрицы Якоби, поэтому другой метод интегрирования имеет
быть выбранным. Одним из методов интегрирования, поддерживающих матрицу Якоби, является метод для
пример метода Radau из следующего примера.

Решение системы с ленточной матрицей Якоби

или можно сказать, что якобиан — это -полосный . Для большого
система дифференциальных уравнений, которые, как известно, являются жесткими, это
может значительно улучшить производительность.2 — (f + k) v \\
\ end {split} \ end {split} \]

где \ (D_u \) и \ (D_v \) — коэффициенты диффузии
компоненты \ (u \) и \ (v \), соответственно, и \ (f \) и \ (k \)
являются константами. (Для получения дополнительной информации о системе см.
http://groups.csail.mit.edu/mac/projects/amorphous/GrayScott/)

Предположим, что граничные условия Неймана (т. Е. «Отсутствие потока»):

\ [\ frac {\ partial u} {\ partial x} (0, t) = 0, \ quad
\ frac {\ partial v} {\ partial x} (0, t) = 0, \ quad
\ frac {\ partial u} {\ partial x} (L, t) = 0, \ quad
\ frac {\ partial v} {\ partial x} (L, t) = 0 \]

Чтобы применить метод линий, мы дискретизируем переменную \ (x \), определяя
равномерно распределенная сетка \ (N \) точек \ (\ left \ {x_0, x_1, \ ldots, x_ {N-1} \ right \} \), с
\ (x_0 = 0 \) и \ (x_ {N-1} = L \).2 — (f + k) v_ {N-1}
\ end {split} \ end {split} \]

Наша полная система обыкновенных дифференциальных уравнений \ (2N \) имеет вид (1)
для \ (k = 1, 2, \ ldots, N-2 \) вместе с (2) и (3).

Теперь мы можем приступить к реализации этой системы в коде. Мы должны объединить
\ (\ {u_k \} \) и \ (\ {v_k \} \) в один вектор длины \ (2N \).
Два очевидных варианта:
\ (\ {u_0, u_1, \ ldots, u_ {N-1}, v_0, v_1, \ ldots, v_ {N-1} \} \)
а также
\ (\ {u_0, v_0, u_1, v_1, \ ldots, u_ {N-1}, v_ {N-1} \} \).
Математически это не имеет значения, но выбор влияет на то, как
эффективно odeint может решить систему.Причина в том, как
порядок влияет на образец ненулевых элементов матрицы Якоби.

Когда переменные упорядочены
как \ (\ {u_0, u_1, \ ldots, u_ {N-1}, v_0, v_1, \ ldots, v_ {N-1} \} \),
образец ненулевых элементов матрицы Якоби

\ [\ begin {split} \ begin {smallmatrix}
* & * & 0 & 0 & 0 & 0 & 0 & * & 0 & 0 & 0 & 0 & 0 & 0 \\
* & * & * & 0 & 0 & 0 & 0 & 0 & * & 0 & 0 & 0 & 0 & 0 \\
0 & * & * & * & 0 & 0 & 0 & 0 & 0 & * & 0 & 0 & 0 & 0 \\
0 & 0 & * & * & * & 0 & 0 & 0 & 0 & 0 & * & 0 & 0 & 0 \\
0 & 0 & 0 & * & * & * & 0 & 0 & 0 & 0 & 0 & * & 0 & 0 \\
0 & 0 & 0 & 0 & * & * & * & 0 & 0 & 0 & 0 & 0 & * & 0 \\
0 & 0 & 0 & 0 & 0 & * & * & 0 & 0 & 0 & 0 & 0 & 0 & * \\
* & 0 & 0 & 0 & 0 & 0 & 0 & * & * & 0 & 0 & 0 & 0 & 0 \\
0 & * & 0 & 0 & 0 & 0 & 0 & * & * & * & 0 & 0 & 0 & 0 \\
0 & 0 & * & 0 & 0 & 0 & 0 & 0 & * & * & * & 0 & 0 & 0 \\
0 & 0 & 0 & * & 0 & 0 & 0 & 0 & 0 & * & * & * & 0 & 0 \\
0 & 0 & 0 & 0 & * & 0 & 0 & 0 & 0 & 0 & * & * & * & 0 \\
0 & 0 & 0 & 0 & 0 & * & 0 & 0 & 0 & 0 & 0 & * & * & * \\
0 & 0 & 0 & 0 & 0 & 0 & * & 0 & 0 & 0 & 0 &) & * & * \\
\ end {smallmatrix} \ end {split} \]

Якобианский паттерн с перемежающимися переменными
поскольку \ (\ {u_0, v_0, u_1, v_1, \ ldots, u_ {N-1}, v_ {N-1} \} \) равно

\ [\ begin {split} \ begin {smallmatrix}
* & * & * & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
* & * & 0 & * & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
* & 0 & * & * & * & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & * & * & * & 0 & * & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & * & 0 & * & * & * & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & * & * & * & 0 & * & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & * & 0 & * & * & * & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & * & * & * & 0 & * & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & * & 0 & * & * & * & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & * & * & * & 0 & * & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & * & 0 & * & * & * & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & * & * & * & 0 & * \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & * & 0 & * & * \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & * & * & * \\
\ end {smallmatrix} \ end {split} \]

В обоих случаях нетривиальных диагоналей всего пять, но
когда переменные чередуются, пропускная способность намного
меньше.То есть главная диагональ и сразу две диагонали
вверху и два сразу под главной диагональю
— ненулевые диагонали.
Это важно, потому что входы mu и ml
из или — это верхняя и нижняя полосы пропускания
Матрица Якоби. Когда переменные чередуются,
mu и ml равны 2. Когда переменные сложены
с \ (\ {v_k \} \) после \ (\ {u_k \} \), верхний
а нижняя полоса пропускания равна \ (N \).

Приняв это решение, мы можем написать функцию, которая
реализует систему дифференциальных уравнений.

Сначала мы определяем функции для источника и реакции
условия системы:

 def G (u, v, f, k):
    вернуть f * (1 - u) - u * v ** 2

def H (u, v, f, k):
    возврат - (f + k) * v + u * v ** 2

Затем мы определяем функцию, которая вычисляет правую часть
системы дифференциальных уравнений:

 def grayscott1d (y, t, f, k, Du, Dv, dx):
    "" "
    Дифференциальные уравнения для одномерных уравнений Грея-Скотта.

    ОДУ выводятся методом линий."" "
    # Векторы u и v чередуются по y. Мы определяем
    # видов u и v при разрезании y.
    u = y [:: 2]
    v = y [1 :: 2]

    # dydt - возвращаемое значение этой функции.
    dydt = np.empty_like (y)

    # Так же, как u и v - это виды чередующихся векторов
    # в y, dudt и dvdt - это представления чередующегося вывода
    # векторов в dydt.
    dudt = dydt [:: 2]
    dvdt = dydt [1 :: 2]

    # Вычислить du / dt и dv / dt. Конечные точки и внутренние точки
    # обрабатываются отдельно.dudt [0] = G (u [0], v [0], f, k) + Du * (-2,0 * u [0] + 2,0 * u [1]) / dx ** 2
    dudt [1: -1] = G (u [1: -1], v [1: -1], f, k) + Du * np.diff (u, 2) / dx ** 2
    dudt [-1] = G (u [-1], v [-1], f, k) + Du * (- 2,0 * u [-1] + 2,0 * u [-2]) / dx ** 2
    dvdt [0] = H (u [0], v [0], f, k) + Dv * (-2,0 * v [0] + 2,0 * v [1]) / dx ** 2
    dvdt [1: -1] = H (u [1: -1], v [1: -1], f, k) + Dv * np.diff (v, 2) / dx ** 2
    dvdt [-1] = H (u [-1], v [-1], f, k) + Dv * (-2,0 * v [-1] + 2,0 * v [-2]) / dx ** 2

    вернуть дыдт

Мы не будем реализовывать функцию для вычисления якобиана, но расскажем
означает , что матрица Якоби полосатая.Это позволяет основному
решатель (LSODA), чтобы избежать вычисления значений, которые, как ему известно, равны нулю. Для большого
системы, это значительно улучшает производительность, как показано на
после сеанса ipython.

Сначала мы определяем необходимые входы:

 В [31]: y0 = np.random.randn (5000)

В [32]: t = np.linspace (0, 50, 11)

В [33]: f = 0,024

В [34]: k = 0,055

В [35]: Du = 0,01

В [36]: Dv = 0,005

В [37]: dx = 0,025

Время вычисления без использования полосовой структуры
матрицы Якоби:

 В [38]:% timeit sola = odeint (grayscott1d, y0, t, args = (f, k, Du, Dv, dx))
1 петля, лучше 3:25.2 с на петлю

Теперь установите ml = 2 и mu = 2 , так что odeint знает, что матрица Якоби
полосатая:

 В [39]:% timeit solb = odeint (grayscott1d, y0, t, args = (f, k, Du, Dv, dx), ml = 2, mu = 2)
10 циклов, лучшее из 3: 191 мс на цикл

Это намного быстрее!

Давайте удостоверимся, что они вычислили тот же результат:

 В [41]: np.allclose (sola, solb)
Out [41]: Верно

Решение интеграла от cos (x) — математический класс [видео 2021 года]

Основная теорема исчисления

Как мы только что видели, чрезвычайно полезно знать отношения между тригонометрическими функциями и их производными.Это важно не только потому, что упрощает работу с производными этих типов функций, но также позволяет нам намного легче находить интегралы, включающие эти типы функций, благодаря фундаментальной теореме исчисления.

Например, предположим, что мы хотим вычислить интеграл от секунды 2 ( x ). Похоже, это действительно сложно сделать. Однако так получилось, что производная от tan ( x ) равна sec 2 ( x ), поэтому по основной теореме исчисления мы имеем, что интеграл от sec 2 ( x ) равен tan ( x ) + C , где C — постоянная.Мы видим, что знание производных тригонометрических функций значительно упрощает кажущуюся сложной задачу интегрирования.

На основе того, что мы узнали, давайте взглянем на производные тригонометрических функций.

Функция	Производная
sin ( x )	cos ( x )
cos ( x )	-sin ( x )
желто-коричневый ( x )	сек 2 ( x )
csc ( x )	-csc ( x ) детская кроватка ( x )
сек ( x )	сек ( x ) коричневый ( x )
детская кроватка ( x )	-csc 2 ( x )

Это много! Как мы только что видели при нахождении интеграла от cos ( x ), поскольку производная sin ( x ) равна cos ( x ), интеграл cos ( x ) равен sin ( x ). + С .Основная теорема исчисления говорит нам, что, зная производные этих шести тригонометрических функций, мы также знаем шесть интегралов.

Функция	Интегральный
cos ( x )	sin ( x ) + C
-sin ( x )	cos ( x ) + C
сек 2 ( x )	желто-коричневый ( x ) + C
-csc ( x ) детская кроватка ( x )	csc ( x ) + C
сек ( x ) желто-коричневый ( x )	сек ( x ) + C
-csc 2 ( x )	детская кроватка ( x ) + C

Опять же, довольно много! Довольно аккуратно и удобно, а? Запоминать эти производные и основную теорему исчисления — отличная идея.После всего, что мы видели, легко увидеть, насколько полезны эти факты.

Это может заставить вас задуматься, означает ли это, что всякий раз, когда мы знаем производную, этот факт также дает нам интеграл. Почему да! Это именно то, что утверждает основная теорема исчисления. Теперь вы понимаете, почему это «фундаментально» для изучения математического анализа? Это большая проблема, и благодаря ей мы теперь можем видеть, насколько сложно связаны производные и интегралы на самом деле.

Резюме урока

Давайте уделим пару минут, чтобы повторить, что мы узнали о решении интеграла от cos (x).Чтобы найти этот интеграл, мы воспользуемся первой частью основной теоремы исчисления . В этой теореме нам нужно предположить, что f непрерывно на a и b. Оттуда мы проделаем два шага, чтобы объяснить теорему:

Помня основную теорему, а также все тригонометрические функции, теперь вы должны быть в состоянии решить любую интегральную задачу, включая интеграл от cos (x).

Найдите дробные дроби с помощью программы «Пошаговое решение математических задач»

Разложение на частичную дробь может помочь вам с дифференциальными уравнениями
следующая форма:

Решая это уравнение, получаем

Проблема в том, что у нас нет методики вычисления интеграла по
левая сторона.Метод, называемый интегрированием по частичным дробям, в самом широком смысле.
приложений, обрабатывает различные интегралы вида

где p и q — полиномиальные функции. Техника частичных дробей
усложняется по мере усложнения полиномов. Мы должны
проиллюстрируем эту технику на некоторых примерах частных случаев.

Пример 1

Решение Обратите внимание, что знаменатель подынтегрального выражения можно разложить на множители:

План состоит в том, чтобы разложить эту дробь на частичные дроби, найдя числа
A и B, для которых

справедливо для всех x, кроме x = 1 и x = — 2.2 + x-2) по находке:

, поскольку эти два последних первообразных можно легко оценить с точки зрения
натуральный логарифм.

Теперь мы покажем, как найти A и B. Обратите внимание, что если мы умножим обе части
уравнение

по (x — l) * (x + 2), получаем

1 = А (х + 2) + В (х — 1).

Последнее уравнение должно выполняться для всех x, то есть это тождество. С тех пор
выполняется для всех x, оно должно выполняться для любых конкретных значений x, которые мы выбираем.Обратите внимание: если мы выберем x = — 2, то член, содержащий A, станет 0, и у нас будет

l = A (-2 + 2) + B (-2-1) = -3B

, откуда сразу получаем B = -1/3. Если мы затем выберем x = 1, у нас будет

1 = А (1 + 2) + В (1-1) = 3А,

и, следовательно, A = 1/3. Подставляя эти значения A и B в формулу
(2) получаем

Таким образом, мы используем дробные дроби, чтобы выразить дробь слева в
Уравнение (2).

Теперь мы можем завершить задачу интеграции.

Чтобы процедура, использованная в примере 1, работала, q (x) в уравнении (1)
должен разложиться на произведение линейных членов, и степень многочлена от
знаменатель q (x) должен быть больше степени многочлена p (x) от
числитель. Если степень q (x) не больше степени p (x), она
необходимо сначала выполнить длинное деление, а затем использовать технику
Пример 1.

Калькулятор суммирования в закрытой форме

Калькулятор также отлично подходит для планирования и подготовки мероприятий в течение дня.Просто введите текущее время и дату начала мероприятия, и мы сообщим вам, сколько времени у вас осталось на подготовку. Надеюсь, этот инструмент будет полезен для отображения продолжительности времени при вводе времени начала и окончания.

Бесплатная программа для решения алгебры и калькулятор алгебры с пошаговыми инструкциями. Нет загрузки или регистрации. Доступен в виде мобильного и настольного веб-сайта, а также в виде собственных приложений iOS и Android.

суммирование — сумма всех значений в диапазоне ряда. закрытая поверхность интеграла. Символ бесконечности.Коды символов HTML. Математические калькуляторы.

25 апреля 2018 г. · В математике арифметико-геометрическая последовательность — это результат поэтапного умножения геометрической прогрессии на соответствующие члены арифметической прогрессии.

Калькулятор бесконечных геометрических рядов — это бесплатный онлайн-инструмент, который отображает сумму бесконечной геометрической последовательности. Онлайн-калькулятор бесконечных геометрических рядов BYJU ускоряет вычисления и отображает сумму за доли секунды.

18 ноября 2020 г. · Большинство сотрудников CDE уволены в четверг, 31 декабря. CDE будет закрыта в пятницу, 1 января, в связи с новогодними праздниками.

Закрытые планы. Новый детский возврат денег (Таблица-832) Дживан Тарун (Таблица-834) Дживан Широмани (Таблица-847) Новый возврат денег, 20 лет (Таблица-820) Новый возврат денег, 25 лет (Таблица-821), Анмол Дживан, план на 2 срока (822) ) Дживан Уманг (Таблица-845) Дживан Лакшай (Таблица-833) Дживан Лабх (Таблица-836)

Калькулятор суммы (суммирования) используется для вычисления общего суммирования любого набора чисел.Когда вы посещаете любой веб-сайт, он может сохранять или извлекать информацию в вашем браузере, в основном в виде файлов cookie. Эта информация может относиться к вам, вашим предпочтениям или вашему устройству и в основном используется для …

Определение суммирующего трансформатора тока: Выходной сигнал многотрансформатора тока передается одному трансформатору, который преобразует несколько выходов в один выход. Это просто снижает сложность измерения, стоимость установки нескольких устройств, стоимость проводки и т. Д.

вычислитель комплексных интегралов

Благодаря поистине удивительному свойству голоморфных функций такие интегралы могут быть легко вычислены путем простого суммирования значений комплекса… Рассчитанное значение сравнивается с существующим теоретическим решением модели коэффициента обзора, и результаты показывают, что ошибки находятся в пределах 3%. В этом видео рассматривается метод комплексного интегрирования и доказывается теорема Коши, когда комплексная функция имеет непрерывную производную. В этой статье мы обсудили, как вычислить неопределенные интегралы элементарных функций, первообразные которых также могут быть записаны в терминах элементарных функций.Бесплатный онлайн-калькулятор тройного интеграла позволяет решать задачи трехмерного интегрирования с функциями трех переменных. Однако многие другие не могут — даже те, которые кажутся обманчиво простыми. Калькулятор удобен в использовании и доступен с любого устройства, а результаты вычислений интегралов и шагов решения можно легко скопировать в буфер обмена. Калькулятор интегралов Калькулятор интегралов позволяет решать любые интегральные задачи, такие как неопределенные, определенные и множественные интегралы, со всеми шагами.Калькулятор двойного интеграла в основном используется для подсчета двумерных фигур. Калькулятор интегралов дает возможность рассчитывать интегралы функций онлайн бесплатно. Вы также можете складывать, вычитать, умножать, делить и выполнять любую необходимую арифметику. Но есть еще и определенный интеграл. Перечислим некоторые из них ниже. Нам не нужны векторы и скалярные произведения линейных интегралов … Подробные пошаговые решения ваших проблем с неправильными интегралами онлайн с помощью нашего математического решателя и калькулятора. Математический калькулятор.2. 4. Помогает набраться опыта, отображая полный рабочий процесс решения задачи и упражнения. Шаг 1: Введите выражение, которое хотите оценить. Интеграция с помощью калькулятора замены онлайн с решением и шагами. Предоставляются все отдельные и общие методы интеграции и даже уникальные важные функции. … Прочитать основы комплексного анализа и тождеств, включающих тригонометрические, логарифмические, экспоненциальные и полиномиальные функции, теорему ДеМуавра; f (z)… Вы даже можете использовать реальные параметры в своих функциях.Основы математики. Обсуждение на форуме сообщества Wolfram [?] Вычислить комплексный интеграл. Контурное интегрирование — это процесс вычисления значений контурного интеграла вокруг заданного контура в комплексной плоскости. Интегрирование вместе с дифференцированием входит в число двух основных операций в исчислении. Математический калькулятор оценит вашу проблему до окончательного решения. Он будет выполнять сложение, вычитание, умножение, деление, возведение в степень, а также найдет полярную форму, сопряжение, модуль и обратную форму комплексного числа.Этот онлайн-калькулятор найдет неопределенный интеграл (первообразную) заданной функции с указанием шагов (если возможно). Процесс контурного интегрирования очень похож на вычисление линейных интегралов в многомерном исчислении. Тогда вычетом f (z) в точке z0 является интеграл res (z0) = 1 2πi Z Cδ (z0) f (z) dz. Для решения проблемы теплового излучения в сложных геометрических сценах предлагается метод конечных элементов, основанный на триангуляции Делоне и трехточечном интеграле Гаусса. 1. Калькулятор интеграла Френеля имеет версии для iPad, iPhone и Apple Watch. Для версий для iPad / iPhone Калькулятор интеграла Френеля также отображает график с сенсорным управлением для значений, сгенерированных x / F (x).Пошаговые примеры. Калькулятор интегралов Френеля вычисляет таблицу пар значений sin (x) / S (x) или cos (x) / C (x) на основе интерактивного ввода переменных x и приращения. Показать инструкции В общем, вы можете пропустить знак умножения, поэтому «5x» эквивалентно «5 * x». Чтобы улучшить этот «Калькулятор экспоненциального интеграла Ei (x)», пожалуйста, заполните анкету. Как и в случае с вещественными интегралами, контурные интегралы имеют соответствующую фундаментальную теорему при условии, что известна первообразная подынтегрального выражения.ון אינטגרלים — מחשב אינטגרל מסויים ואינטגרל רב מימדי עם רך Мужской Женский Возраст Моложе 20 лет Уровень 30 лет Уровень 40 лет Уровень 50 лет Уровень 60 лет или старше Род занятий Начальная школа / Младший школьник 6 ГЛАВА 1. Просмотрено 83 раза 0 $ \ begingroup $ I … Комплексный интеграл с особенностью вне круга. q = интеграл (fun, xmin, xmax, Name, Value) определяет дополнительные параметры с одним или несколькими аргументами пары Name, Value. Например, укажите WayPoints, за которым следует вектор действительных или комплексных чисел, чтобы указать конкретные точки для интегратора. использовать.3.2 Комплексные линейные интегралы. Линейные интегралы также называют интегралами по траекториям или контурным интегралам. Вычислите некоторые интегралы, используя только определение и понятие интегральной суммы. В MATLAB® вы используете опцию ‘Waypoints’, чтобы определить последовательность прямых путей от первого предела интеграции до первой путевой точки, от первой путевой точки до второй и так далее, и, наконец, от последней путевой точки до второй предел интеграции. Решение проиллюстрировано геометрическими построениями. Решенные упражнения интеграции заменой…. Наш инструмент Iterated Integral Calculator поддерживает все самые популярные функции, вычисления и ряд других переменных, которые необходимы в одном инструменте. После получения интегрированного значения начинайте комбинировать … В MATLAB® вы используете опцию ‘Waypoints’, чтобы определить последовательность прямых путей от первого предела интеграции до первой путевой точки, от первой путевой точки до второй и т. Д. и, наконец, от последней путевой точки ко второму пределу интеграции. На этой странице перечислены некоторые из наиболее распространенных первообразных Определить комплексный интеграл в Wolfram | Alpha ?.Нахождение ряда Тейлора и его использование для вычисления комплексного интеграла. Калькулятор неправильных интегралов онлайн с решением и шагами. КОМПЛЕКСНОЕ ИНТЕГРАЦИЯ 1.3.2 Исчисление вычетов Скажем, что f (z) имеет изолированную особенность в точке z0. Пусть Cδ (z0) — окружность вокруг z0, не содержащая другой особенности. Итак, R ˙ 1 = zdz = R 2 1 = zdz = 2ˇi. Удивительные подробности о калькуляторе определенного интеграла, о котором большинство людей не подозревают, слухи, ложь и калькулятор определенного интеграла. Мужской или женский ? Конечно, можно думать об интеграции как об антидифференцировании.Слайд-шоу комплексных чисел. Например, эллипс ˙: [0; 2ˇ]! C с ˙ (t) = 4cost + 3isint содержит rif r

Как обновить Uconnect с помощью USB,
Мир кислотного дождя Reddit,
Хоббикидство Minecraft Battle,
Энтропия Вселенной увеличивается или уменьшается,
Генетическая болезнь легких кистозный фиброз,
Помогите мне пройти сквозь ночь Тексты и аккорды,
Катастрофа на озере Озарк 2020,
Календарь католической школы Гринвича,
Как приготовить перцовый суп в Гане,
Предложения вина Oyster Bay,

Математический решатель бесплатно

Бесплатная программа для решения математических задач Попробуйте нашу бесплатную программу для решения уравнений алгебры.Кроме того, с помощью этой утилиты вы также можете рисовать 3D и 2D изображения. Сделайте снимок. МАТЕМАТИЧЕСКИЕ СИМВОЛЫ: Вот некоторые символы, которые понимает калькулятор Math Papa: + (Математика сложения — один из самых сложных предметов в школе, поэтому владение графическим калькулятором кажется необходимостью для учащихся. Com дает полезные стратегии на бесплатном калькуляторе для 7-го класса , основная математика и знаменатели и другие области математики. Наша цель — охватить как можно больше приложений и калькуляторов для решения уравнений, чтобы повысить осведомленность учащихся.Бесплатные задания по математике в средней школе. Учитель математики, начальная школа, школьный округ Портленда, штат Орегон; Они стали более бегло и быстрее решать основные проблемы с фактами. Зыбучие пески Помогите нам улучшить алгебру нашего веб-сайта для вас. Просто подсчитайте миллион вопросов, и мы направим вас к замороженной сервисной команде. Поддержите команду Проявите свою любовь и помогите профинансировать нашу постоянную разработку калькулятора табеля рабочего времени. Приходите в Solve-variable. Математические игры и калькуляторы для детей. Введите свое заявление в подтверждение ниже: Электронная почта: donsevcik @ gmail.Введите вопросы в решателе mathway и нажмите кнопку ввода, чтобы узнать решение проблемы, о котором вы просили Mathway. Эта викторина: Учителя: войдите или создайте учетную запись или или. Щелкните ссылку ниже и введите числитель и знаменатель для обеих сторон уравнения! > Калькулятор дробей Обзор дробей: дробь обозначает часть региона или часть группы. Пошаговые пояснения к вашим математическим решениям. Просто напишите задачу на экране или используйте камеру, чтобы сделать математический снимок.2 класс. Калькулятор уже сейчас отлично справляется с решением повседневных задач по математике. Подробнее: Типы задач, поддерживаемые Math Assistant. Вы можете решать умножение и деление на одном и том же этапе математической задачи: после решения скобок, показателей степени и радикалов и перед сложением и вычитанием. Учитесь, играя в игры. Для получения дополнительной информации найдите Solver в Магазине Office. Программа решения уравнений позволяет вам ввести вашу проблему и решить уравнение, чтобы увидеть результат.Это бесплатное приложение для решения математических задач поможет вам решить все домашние задания по математике с помощью смартфона. Практикуйте свои математические навыки и учитесь шаг за шагом с помощью нашего математического решателя. 65 мб · 9 527 загрузок · english. exe или умсолвер. Посетите Cosmeo, чтобы получить объяснения и помочь с домашними заданиями! Шаг 2: Решите свое уравнение. Учащиеся с организационными и управленческими трудностями часто чувствуют себя побежденными перед тем, как приступить к математике, из-за неспособности найти подходящие материалы в отведенные сроки.Для математических задач, которые невозможно решить с помощью обычного математического калькулятора, используйте бесплатный научный калькулятор! Исследуя информацию, необходимую для создания онлайн-калькулятора алгебры для моего сайта, я наткнулся на удивительное средство решения математических задач. Используйте полнофункциональную версию программного обеспечения Analytic Solver (с ограничениями размера модели / данных, достаточными для всех примеров) в течение 15 дней бесплатно. Графический онлайн-калькулятор, которым студенты могут пользоваться бесплатно. Зыбучие пески Помогите нам улучшить алгебру нашего веб-сайта для вас. Просто подсчитайте миллион вопросов, и мы направим вас к замороженной сервисной команде.По мере того, как проблемы становятся более сложными, становится еще более важным понимать пошаговый процесс, с помощью которого мы их решаем. Приложение скучно на xbox, но, пожалуйста, поставьте это приложение на 10 раз для всех. модуль математики неравенства электронное обучение математические формулы шпаргалки печатные математические документы для 6-го класса Matlab решает нелинейные системные уравнения как решать задачи деления парабола + онлайн-тесты приложения по биномиальной теореме феникс калькулятор игра скачать математику пирамиды объяснил ks3 глупый тест Бесплатный онлайн-калькулятор — математика, Физика, химия, преобразования.Решите мою математическую задачу бесплатно в Интернете с помощью шагов. Рассуждения не являются монолитными, что на самом деле непросто определить. Разбивка шагов и подэтапов для каждого решения. Включает ориентированный на учителя конструктор упражнений для создания цифровых математических заданий. Попробуйте программу Algebra Calculator> Universal Math Solver шаг за шагом решать ваши задачи по алгебре, исчислению и тригонометрии. Недавно программа перестала работать, давая мне возможность отображать шаги на листе. Абсолютно бесплатный онлайн-инструмент для решения задач с определенными и неопределенными интегралами.Возможность сфотографировать вашу математическую задачу с помощью приложения. Вы можете быстро адаптировать EVA под свои нужды. Решите любое уравнение с помощью этого бесплатного калькулятора! Просто введите свое уравнение внимательно, как показано в примерах ниже, а затем щелкните синюю стрелку, чтобы получить результат! Вы можете решить любое количество уравнений совершенно бесплатно. ПРИМЕР 5 Решите относительно y. Щелкните ссылку ниже и введите числитель и знаменатель для обеих сторон уравнения! > Калькулятор дробей Обзор дробей: дробь обозначает часть региона или часть группы.Приходите в Алгебра-сеть. 0. Попробуйте использовать приведенные примеры или введите свою проблему и проверьте свой ответ с помощью пошаговых объяснений. Этот модуль знакомит с алгеброй, исследуя похожие модели. Ознакомьтесь со всеми нашими онлайн-калькуляторами здесь! Калькулятор алгебры включает в себя все функции, упрощающие математику на любом уровне. com бесплатные математические решатели! Мы знаем, что математика сложна, и мы здесь, чтобы помочь. Онлайн-программа для решения математических задач с бесплатными пошаговыми решениями алгебры, исчисления и других математических задач. Free Smart Math Calculator — это программа, которая обеспечивает большую точность результатов математических операций, даже научных.Еще одно приложение, которое решает математические задачи со словами. Синонимы математического калькулятора, произношение математического калькулятора, перевод математического калькулятора, определение английского словаря математического калькулятора. Это полностью задокументировано на beyhfr. Сэкономьте свое время с помощью этого удобного инструмента и сделайте свое обучение веселым и легким. Бесплатные рабочие листы по алгебре. Станьте экспертом по алгебре. Решите эти бесплатные распечатываемые рабочие листы. Все чаще приходят к единому мнению, что математика — сложная задача, а алгебра — невозможна. Самая большая вещь, которую я видел, — это рост уверенности, который отразился на всех аспектах математики, которые мы рассматриваем в этом году.2 теми же методами, которые мы использовали до сих пор. Напечатано, написано или напечатано. Ознакомьтесь с последней информацией о разрешенных и запрещенных калькуляторах. Бесплатная онлайн-программа для решения алгебр, которая работает прямо в вашем браузере. Узнайте, почему наши студенты получают столько наград. Algebra Calculator — это пошаговый калькулятор и решатель алгебры. Существует более 10 альтернатив Symbolab Math Solver для различных платформ, включая Android, iPhone, iPad, Интернет и Windows. 9 класс . EVA поддерживает размерность пространства от 1 до 5 с произвольной сигнатурой.Чтобы вычислить log-1 (y) на калькуляторе, введите основание b (10 — значение по умолчанию, введите e для константы e), введите значение логарифма y и нажмите кнопку = или вычислить: Учащиеся узнают об углах, правила умножения, измерения и другие математические навыки для третьего класса. Раньше под решением была синяя полоса со знаком «+». Добро пожаловать на страницу рабочих листов по алгебре в Math-Drills. Вы даже можете увидеть шаги (при подписке)! Больше, чем просто средство решения уравнений онлайн. Полные технические характеристики.Начните сразу же бесплатно с базовым членством или выберите премиум, чтобы получить неограниченный доступ ко всей нашей коллекции. Алгебра-уравнение. Смоделируйте свои задачи со словами, нарисуйте картинку и систематизируйте информацию! Изучите математику для шестого класса бесплатно — отношения, показатели, деление в столбик, отрицательные числа, геометрию, статистику и многое другое. Вы можете увидеть шаги и объяснения ваших домашних заданий по алгебре, охватывающие: Калькулятор алгебры — это бесплатный онлайн-инструмент, который отображает решение данного алгебраического уравнения.Попробуйте использовать приведенные примеры или введите свою проблему и проверьте свой ответ с помощью пошаговых объяснений. Они охватывают материал от базовой алгебры до уровня колледжа. Калькулятор факторинга алгебры — это бесплатный онлайн-инструмент, который отображает множители данного алгебраического уравнения (квадратного уравнения). Введите числа и переменные для решения алгебраических уравнений в течение нескольких секунд в этом калькуляторе. Все проблемы решаются без калькулятора. Для решения этих уравнений мы используем следующую формулу `x = b / a`.Доступен в виде мобильного и настольного веб-сайта, а также в виде собственных приложений iOS и Android. Он предоставляет подробную информацию о графиках. Neverth Ознакомьтесь с нашими математическими играми для пятого класса, которые помогут вашим ученикам вывести свои математические навыки на новый уровень. Math Solver — это полнофункциональный научный калькулятор, с помощью которого вы сможете решить любую математическую формулу, независимо от уровня сложности решателя квадратного уравнения. com и функция обучения, рабочий лист и широкий спектр дополнительных математических предметов Советы по калькулятору.Практикуйте свои математические навыки и учитесь шаг за шагом с помощью нашего математического решателя. Факторы. Смотрите скриншоты, читайте последние отзывы клиентов и сравнивайте рейтинги Math Solver. Это бесплатно. 2 261 лайк · 41 говорит об этом. Первый калькулятор алгебры и средство решения проблем со словами. Finish My Math Class ™ (FMMC) — это команда профессионалов из США и Канады, которые стараются незаметно помогать таким ученикам, как вы, завершить уроки математики с высокими оценками. Photomath — приложение №1 для изучения математики; он может мгновенно считывать и решать задачи от арифметики до исчисления, используя камеру на вашем мобильном устройстве.Mathway — это программа №1 в мире по решению математических задач с миллионами пользователей и решенными миллиардами задач. Математический решатель также позволяет пользователю рисовать графики на основе решений. Наш решатель круга позволяет вам найти площадь, диаметр или длину окружности, если известно одно значение. Нет загрузки или регистрации. Щелкните ссылку ниже и введите числитель и знаменатель для обеих сторон уравнения! > Калькулятор дробей Обзор дробей: дробь обозначает часть региона или часть группы. Вы ежедневно сталкиваетесь и решаете простые математические задачи со словами, даже не задумываясь об этом.Нет загрузки или регистрации. Я выясню, является ли то, что вы набрали, уравнением. Решения точны на 100%. Введите площадь, диаметр или длину окружности, и он решит два других. Например, введите 3x + 2 = 14 в текстовое поле, чтобы получить пошаговое объяснение того, как решить 3x + 2 = 14. Факторинговые полиномы. net будет правильным сайтом для посещения! Почему калькулятор статистики бесплатный? Потому что и Mathway, и SolveMathProblems верят в знания для всех. Щелкните здесь, чтобы просмотреть алгебру Холта 1; решать тригонометрические дифференциальные уравнения первого порядка; бесплатно решить моё математическое уравнение; бесплатные рабочие листы по математике за 8 класс; решатель неравенств; упорядочение дробей по минимальному плану урока; скачать бесплатно Excel новый словарь формул, которые используются в бухгалтерском учете; умножение базовых чисел на TI-83 plus; Дополнение алгоритма Попробуйте воспользоваться бесплатным калькулятором Mathway и средством решения задач ниже, чтобы попрактиковаться в различных математических вопросах.0. Пошаговое решение для решения уравнений Этот математический калькулятор позволяет вам решать уравнения и строить графики, а также решать системы уравнений. com, теперь вы можете легко изучить и решить свои алгебраические уравнения за несколько секунд. Эта бесплатная математическая программа — это то, на что вы можете положиться, когда у вас нет помощника для помощи. Получите наши бесплатные онлайн-математические инструменты для построения графиков, геометрии, 3D и многого другого! Надстройка Solver от Frontline Systems в настоящее время недоступна для Excel на мобильных устройствах. Приложение упрощает решение математических задач по сравнению с ручкой и листом бумаги.Мне нравится название их материнской компании, Bagatrix. Также отображаются подробности расчетов, которые привели к разрешению линейного уравнения. Щелкните ссылку ниже и введите числитель и знаменатель для обеих сторон уравнения! > Калькулятор дробей Обзор дробей: дробь обозначает часть региона или часть группы. Редактор формул Бесплатный онлайн-редактор формул для учителей. Сделайте снимок своей математической задачи. 00 5-значная сводка Учитывая следующую 5-значную сводку: 11, 19, 24, 30, 48 какая из статистических данных не может быть определена? Статистика Сумма всех отклонений от среднего арифметического числовой последовательности 4, 6, 51, 77, 90, 93, 95, 109, 113, 117 составляет: First In Math устанавливает культуру успеха в математике в школах; вызывает интерес и снижает страх перед математикой у детей любого уровня подготовки.Гм. Название происходит от «quad», что означает квадрат, поскольку переменная возведена в квадрат (другими словами, x 2). 2. Предалгебра, алгебра I, алгебра II, геометрия, физика. В этом увлекательном математическом упражнении есть забавные задачи на умножение и деление, которые ученики третьего класса должны решить в уме. Есть две интерактивные математические функции: математические флэш-карточки и точки. Основные математические задачи со словами. Math Solver предназначен для того, чтобы помочь студентам решить математические уравнения простым способом и научить их, как решать математические задачи шаг за шагом. Калькулятор пределов правил использует для оценки пределов. Пределы используются для вычисления скорости изменения функции на протяжении всего анализа, чтобы перейти к ближайшему возможному значению.С Tophomeworkhelper. 00 $ 150. Бесплатный онлайн-калькулятор в научной системе обозначений. Я называю это ценным инструментом для родителей, которые помогают с домашним заданием по математике своего ребенка и пытаются запомнить арифметику в начальной школе или среднее значение. вы пришли в нужное место. … Бесплатная математическая решающая программа Подробнее »Загрузите это приложение из Microsoft Store для Windows 10, Windows 8. Загрузки программного обеспечения для образовательных учреждений — Универсальный математический решатель от TPO« Северный очаг »и многие другие программы доступны для мгновенной и бесплатной загрузки.Появляются 2 члена, попробуйте собрать их на одной стороне уравнения. Существуют и другие способы решения квадратного уравнения вместо использования квадратной формулы, такие как факторинг (прямое разложение, группировка, метод AC), завершение квадрата, построение графиков и другие. Используйте звездочку для умножения. Однако бывают случаи, когда учитель или репетитор недоступен, чтобы помочь вам решить математическую задачу. Студенты смогли подойти к математическим задачам в более чем 24 игровых решениях, 24 калькуляторах стандартной версии, 24 игровых калькуляторах, 24 игровых карточках, 24 игровых карточках по математике, 24 математических игровых приемах, 24 карточных ответах, впервые в математической Википедии.Для SAT Math есть 30 вопросов, разрешенных с помощью калькулятора, и 18 вопросов без использования калькулятора. Этот калькулятор производной бесплатен и может использоваться с любого устройства. Повысьте уровень владения математикой. AssignmentShark. com есть игра, чтобы проверить навыки вашего ребенка, где бы он ни находился в математическом путешествии. Все, что вам нужно, — это сфотографировать математическое уравнение или просмотреть домашнее задание по математике. Следующая программа для решения алгебры в нашей серии от 12 ноября 2016 г. Полный список см. На freemathhelp. Если калькулятор что-то не вычислил, или вы обнаружили ошибку, или у вас есть предложение / отзыв, напишите об этом в комментариях ниже.Просто введите формулу в верхнее поле. Уровень 1. В случаях, когда вам нужна помощь по рациональным показателям или, возможно, степеням, Algebra1help. Это в основном помогает студентам-математикам решать задачи по алгебре. Например, как только вы выясните, как решить y 3 + 10 = 4, вы сможете бесплатно решить 3 = -10 — y 2. Математические игры для 4-го класса. Математические упражнения. com, где неизвестные являются общими, а переменные — нормой. Застряли на математической задаче? Нужно найти производную или интеграл? Наши калькуляторы дадут вам ответ и проведут вас через весь процесс, шаг за шагом! Все калькуляторы поддерживают все распространенные тригонометрические, гиперболические и логарифмические функции.Приложение скучно на xbox, но, пожалуйста, поставьте это приложение на 10 раз для всех. Приложение для решения математических задач является бесплатным и решает логарифмы, уравнения, алгебру и многое другое с максимальной простотой. Если ваша домашняя работа по математике включает уравнения, неравенства, функции, многочлены, матрицы, это правильный пробный счет. Бесплатная программа для решения математических задач отвечает на вопросы домашнего задания по алгебре с пошаговыми пояснениями. Вы можете подумать, что математика — это запоминание фактов и навыки обучения. На этой странице вы найдете рабочие листы по алгебре в основном для учащихся средних школ по таким темам алгебры, как алгебраические выражения, уравнения и функции построения графиков.Все калькуляторы имеют простой и удобный интерфейс. С помощью приложения Symbolab — Math solver вы можете составлять уравнения и получать ответы на широкий спектр математических задач. net дает хорошие советы по бесплатному онлайн-калькулятору промежуточной алгебры, основам математики и матриц и другим темам алгебры. Константы pi и e можно использовать во всех расчетах. Desmos. Интерактивные решатели для задач алгебры слова. Попробуйте использовать приведенные примеры или введите свою проблему и проверьте свой ответ с помощью пошаговых объяснений.Математические слова Проблемы и ответы. 0. Совет для изучения: не забывайте использовать описательные буквы для описания переменных. 2 содержит исправления ошибок в Windows 10. Хотя есть еще 1 или 2 математические темы, с которыми это приложение пока точно не может помочь, это ЧУДЕСНОЕ приложение, которое может решить около 90% математических задач, будь то общая алгебра или уравнения высшего и сложного уровня колледжа. Учащиеся, учителя, родители и все желающие могут мгновенно найти решение своих математических задач. PhotoMath также предоставляет пошаговое руководство по решению каждой проблемы — функцию, которую некоторые потребители оценили как потенциально решаемую (через запятую): оставьте поле пустым для автоматического определения или укажите такие переменные, как x, y.Средство визуализации математических выражений, графики, конвертер единиц, средство решения уравнений, комплексные числа, история вычислений. Основные характеристики Поддерживает более 20 типов функций и состоит из предопределенных констант, таких как синус, косинус, тангенс, логарифм, экспонента, инвертированные функции и т. Д. Еще одно бесплатное математическое программное обеспечение для решения всех ваших сложных математических задач и запросов. Приложение скучно на xbox, но, пожалуйста, поставьте это приложение на 10 раз для всех. X-пересечения Прямо от бесплатного решателя алгебры колледжа до многочлена, у нас есть все, что нужно.Бесплатный калькулятор алгебры для решения уравнений алгебры с пошаговым руководством. com и разбираться в функциях, линиях и большом количестве дополнительных математических предметов. Онлайн-калькуляторы и решатели. Хорошие основы математики имеют решающее значение для успеха ученика в алгебре. Миллионы людей используют это приложение и помогают друг другу решать сложные математические уравнения. Кроме того, изучите сотни других бесплатных калькуляторов, охватывающих такие темы, как финансы, математика, фитнес и здоровье. Mathway — отличное приложение для решения математических задач, в котором есть множество полезных функций.2 + 12 Откройте для себя тысячи математических навыков, охватывающих от дошкольного до 12-го класса, от счета до математического анализа, с бесконечными вопросами, которые адаптируются к уровню каждого ученика. «Они найдут необходимую информацию и формулы для идеального решения ваших математических задач. Проблемы усугубляются, если у вас есть несколько противоречащих друг другу заданий и сложных математических заданий, требующих решения множества уравнений. Я использую MS Mathematics, чтобы научиться исчислению. Без вирусов. Калькулятор алгебры поможет вам найти решение широкого круга математических задач.Программа FIM, которую используют миллионы школьников K-8 по всему миру, развивает критические навыки и улучшает их отношение к математике. com Тел .: 800-234-2933; Калькулятор дробей — быстрый и простой. Студенты легко понимают все шаги, а затем объясняют их в классе, получая высшие оценки без лишних хлопот. Дробь — это количество закрашенных частей, деленное на количество равных частей. Эти бесплатные уроки имеют перекрестные ссылки, чтобы помочь вам найти связанный материал, а поле «Поиск» на каждой странице доступно, чтобы помочь вам найти любой математический контент, который вы ищете.Решайте математические задачи для учебы в школе или для бизнеса. Учащиеся, учителя, родители и все желающие могут мгновенно найти решение своих математических задач. Онлайн-калькулятор алгебраического факторинга BYJU ускоряет вычисления и отображает множители за доли секунды. бесплатно. Смотрите скриншоты, читайте последние отзывы клиентов и сравнивайте рейтинги Math Solver. 3. 424 страницы · 2010 · 2. Предалгебра, алгебра, предварительное исчисление, исчисление, помощь по математике линейной алгебры. 0. Дробь — это количество закрашенных частей, деленное на количество равных частей.Чтобы узнать больше о судоку, см. Здесь. Всякий раз, когда вы обращаетесь за помощью по квадратичным функциям или, может быть, уравнениям путем факторизации, факторинговых полиномов. Тот, который рассчитывает, как: a. Есть несколько уровней, и на каждом уровне есть калькулятор квадратного корня, программа для работы с математическими таблицами и бесплатный онлайн-калькулятор для построения графиков. Здесь вы найдете бесплатную ссуду, ипотеку, временную стоимость денег, математику, алгебру, тригонометрию, дроби, физику, статистику, калькуляторы времени и даты и преобразований. 4 класс. Калькулятор дробей — быстрый и простой.com — это ваш инструмент для решения проблем со статистикой для любого академического уровня и сложности. Это приложение идеально подходит для студентов, которые не знают: «От бесплатного решателя алгебры с шагами до алгебры 1, у нас есть все части». Flocabulary. Все, что вам нужно сделать, когда вы используете PhotoMath, — это сфотографировать математическую задачу, которую вы пытаетесь решить, чтобы получить полезные советы и ответы о том, как ее решить. Они также могут генерировать пошаговое объяснение одним нажатием кнопки. Он также множит многочлены, строит множества полиномиальных решений и неравенства и многое другое.5 (y) Решить (x) Решить ½ (x) Упростить. Приложение скучно на xbox, но, пожалуйста, поставьте это приложение на 10 раз для всех. Найдите Math-tools. Вы можете шаг за шагом решать свои задачи по алгебре онлайн — уравнения, неравенства, радикалы, строить графики, решать полиномиальные задачи. Бесплатная программа для решения уравнений универсальной алгебры. Если квадратный член выпадает, вы можете решить его как уравнение первой степени, используя методы, обсуждаемые в этом разделе. ИЛИ ЖЕ. Покупка приложений; Регистрационный ключ; Используйте код квитанции; Выполняйте массовые заказы и помогите детям отточить свои математические навыки с помощью «Hot Potato».Решайте уравнения, неравенства и системы уравнений, упрощайте или факторные выражения и многое другое с помощью этого онлайн-решателя алгебры. В природе чаще всего встречаются дроби. Дробь — это количество закрашенных частей, деленное на количество равных частей. Если вам нужна помощь в построении графиков линейных неравенств или, возможно, в научных обозначениях, алгебра-уравнение. Я постарался предоставить как можно больше подробностей в расчетах, показанных решателем. com, так как это лучший веб-сайт, который предоставляет вам калькулятор Mathway, который поможет вам, когда вы все равно не найдете математических проблем, на которых вы застряли.Его можно использовать бесплатно, не нужно скачивать и регистрироваться. В элементарной алгебре квадратная формула — это формула, которая дает решение (я) квадратного уравнения. На нашем сайте вы найдете множество совершенно бесплатных пошаговых математических калькуляторов. Microsoft Mathematics — это бесплатная математическая программа для вашего компьютера. Будь то алгебра, построение графиков, исчисление или другие сложные математические уравнения, Gauthmath непосредственно предоставит вам решение. Доступные варианты в этом раскрывающемся меню зависят от выбранного уравнения.MathCrave — это бесплатное приложение для математических решений в области инженерии, алгебры, исчисления, статистики и геометрии с пошаговым решением уравнений, которое вам больше не нужно. От бесплатного решателя алгебры для задач чтения до знаменателей, мы включили все это. По моему опыту, математика часто имеет «классы» задач, и как только вы выясните, как решить одну задачу в этом классе, вы сможете решить все остальные. Calculator Soup — бесплатный онлайн-калькулятор.Калькулятор задач по алгебре можно загрузить и установить из репозитория базы данных, проверенной антивирусом. Бесплатный онлайн-калькулятор для решения математических задач. Что нового в версии 10. Став взрослым, вам нужно будет знать математику, когда придет время покупать машину, искать автострахование или выбирать лучший кредит. Что нового в Math Solver Free 1. В результате большинство математических задач состоит из дробей или десятичных знаков. Дробь — это количество закрашенных частей, деленное на количество равных частей. Возможность распечатать в удобном формате PDF.Умножение, деление, дроби и логические игры, которые улучшают математические навыки четвертого класса. Калькулятор генерирует решение с подробным объяснением. Это научный онлайн-калькулятор с точностью до двух цифр, который поддерживает как нажатие кнопки, так и тип клавиатуры. Находчивые исследователи; Они решают ваши проблемы сразу после того, как вы попросите: «Пожалуйста, решите мои математические задачи. Решение сложения и вычитания следует после скобок, показателей степени, корней и умножения / деления. Ace математики Math Solver II Особенности.Введите вопрос здесь: Нажмите, чтобы отправить запрос. 8 класс. Используйте хип-хоп для обучения математике! Flocabulary предлагает песни, занятия и видео. Вы здесь: Главная → Рабочие листы → Калькулятор уравнений Бесплатный калькулятор уравнений. Бесплатная программа для решения алгебры и калькулятор алгебры, показывающая пошаговые решения. Бесплатная математическая программа для решения всех ваших математических задач. В случаях, когда вам нужна помощь по радикальным уравнениям или даже по алгебре-уравнениям. Решение математических задач — используйте символы и клавиатуру для ввода уравнений.Калькуляторы и решатели, представленные ниже, делают больше, чем просто вычисляют ответ. Все они способны выполнять точные вычисления. Скачайте бесплатно программу для решения математических задач. 4. 85 150 долларов США. Решение математических задач Ответы на вопросы Бесплатная алгебра Геометрия Тригонометрия Исчисление Теория чисел Комбинаторика Вероятность Графический калькулятор Texas Instruments TI-84 PLUS CE, черный (упаковка без разочарований) (84PLCE / PWB / 2L1 / A) 4. com будет идеальным сайтом для изучения ! Алгебра 5-го класса; викторина по математике отвечает на ключевые вопросы решения простых неравенств; решатель алгебры и тригонометрии Пола Фёрстера; бесплатные таблицы абсолютных значений; промежуточная алгебра с использованием TI 89; скачать бесплатно формулы геометрии gre; бесплатные рабочие листы по алгебре для 9-х классов; ТИ-83 + 3 корня; упростить показатель дроби; Рабочий лист графика 3-го класса бесплатный онлайн-калькулятор задач по алгебре доступен для загрузки и установки из нашего хранилища баз данных, проверенных антивирусом.Дети от дошкольного до 8-го класса могут практиковать математические навыки, рекомендованные Общими государственными стандартами, в увлекательных игровых форматах. Научный калькулятор можно использовать для решения сложных математических уравнений, таких как тригонометрические, алгебраические и геометрические уравнения. Вы даже можете увидеть шаги (при подписке)! Как пользоваться калькулятором. Калькулятор задач по алгебре можно загрузить и установить из репозитория базы данных, проверенной антивирусом. 0 можно бесплатно скачать с нашего сайта.com Math Solver. Функциональность позволяет манипулировать математическими переменными и символами всего несколькими щелчками мыши. Он-лайн программа для решения математических задач, которая шаг за шагом решит и объяснит ваше домашнее задание по математике. 85 133 $. Рабочие листы Free Algebra 1, созданные с помощью Infinite Algebra 1. Концепции целых чисел и дробей EVA, символьный калькулятор алгебры Клиффорда (геометрическая алгебра), представляет собой сценарий Eigenmath. алгебра Холта 1; решать тригонометрические дифференциальные уравнения первого порядка; бесплатно решить моё математическое уравнение; бесплатные рабочие листы по математике за 8 класс; решатель неравенств; упорядочение дробей по минимальному плану урока; скачать бесплатно Excel новый словарь формул, которые используются в бухгалтерском учете; умножение базовых чисел на TI-83 plus; сложение алгоритма Калькулятор комплексных чисел.С этого момента вы можете работать с приложением в полноэкранном режиме с помощью клавиатуры и мыши. Видео по запросу для математических навыков от учителей, специализирующихся на обучении математике младших школьников. Инструкции :: Все функции. Гадать не требуется. com станет отличным местом для изучения! Algebra1help. Все остальное делает приложение. Программа Virus Free PhotoMath обещает помочь решить простые линейные уравнения и другие математические задачи, «читая» вопросы с помощью камеры вашего смартфона. Калькулятор производной позволяет решать любые математические функции.Решение математических задач со словами, Решение математических задач, Репетитор по математике рядом со мной, Решение математических задач с шагами, Математические вопросы с ответами, Математические задачи с ответами, Пошаговое решение математических задач, Онлайн-тест по математике, Математическое решение с шагами, Математические решения для любых вопрос, онлайн-репетитор по математике, онлайн-курсы по математике, бесплатное решение математических задач. Проконсультируйтесь с нашим онлайн-решением для решения задач со словами или математическими решениями, чтобы получить самые лучшие результаты по математике. PhotoMath — это бесплатное мобильное приложение, которое может читать и решать бесплатные уроки математики и помощь в выполнении домашних заданий по математике, от базовой математики до алгебры, геометрии и т. Д.Онлайн-уроки математики, продвинутые учебники по математике, математические игры и многое другое для старшеклассников и учеников средних школ. Добавьте эту страницу в закладки, чтобы каждый день играть в новую игру судоку! Покупайте товары для судоку в нашем магазине. Программное обеспечение находится в составе Education Tools, точнее Science Tools. Решение математических задач Ниже приведено средство решения математических задач, которое позволяет вводить широкий спектр математических задач и бесплатно дает окончательный ответ. Если вам нужны подробные пошаговые ответы, вам придется подписаться на премиум-сервис Mathway (предоставляемый третьей стороной).С помощью этого инструмента вы можете решать и проверять большое количество уравнений во всех ваших заданиях за очень короткое время. 8/5 (1569 голосов) Программа Math Solver предназначена для того, чтобы помочь студентам решать математические уравнения простым способом и научить их шаг за шагом решать математические задачи. В отличие от натуральных или целых чисел, вы не можете напрямую складывать или вычитать дроби. Этот калькулятор используется для упрощения выражений логических схем. Классы: K – 12; Стоимость: Бесплатная пробная версия Это решатель булевой алгебры, который позволяет пользователю решать сложные алгебраические выражения, применяя правила, которые используются в алгебре над логикой.35: Модернизированный дисплей до метро; Прочтите полный список изменений. Решение этой проблемы невероятно простое — заказать онлайн-справку по статистике в надежной компании. Калькулятор работает как с уравнениями, так и с выражениями. фр. com включает более 58 тысяч бесплатных рабочих листов по математике, которые могут быть использованы, чтобы помочь учащимся изучать математику. Получите помощь в Интернете или с помощью нашего математического приложения. По возможности, этот калькулятор иллюстрирует шаги и объясняет, как выполняются определенные математические формулы, преобразования единиц измерения и вычисления, пытаетесь ли вы уменьшить квадратный корень до его простейшей радикальной формы, найти разложение числа на простые множители, использовать квадратную формулу или заинтересованы в модуле Precalculus Calculator Получите подробные решения ваших математических задач с помощью нашего пошагового калькулятора Precalculus.Пример: введите (2-3i) * (1 + i), и вы увидите ответ 5-i. Калькулятор вероятностей — это онлайн-инструмент, который вычисляет вероятность выбранного события на основе вероятности других событий. Доступен в виде мобильного и настольного веб-сайта, а также в виде собственных приложений iOS и Android. Webmath — это веб-сайт с математической справкой, который генерирует ответы на определенные математические вопросы и задачи, введенные пользователем в любой конкретный момент. Для умножения и деления действуйте слева направо. Mathway мгновенно решает самые сложные математические задачи — от базовой алгебры до сложных вычислений — просто введите свою задачу (или наведите камеру и сделайте снимок!), Чтобы мгновенно получать бесплатные ответы.exe — это имена файлов по умолчанию, указывающие на установщик Universal Math Solver. Полный учебный план упражнений и видео. Изучайте математику вместе с нами и убедитесь, что «Математика — это просто!» Решатель пределов. В дополнение к полноформатным тестам Совет колледжа предлагает несколько практических вопросов SAT Math (а также типовые вопросы для всех других разделов теста). Используйте вкладки для изменения уровней. От базовых дополнений к исчислению процесс решения проблем обычно требует большой практики, прежде чем можно легко получить ответы.Бесплатная онлайн-программа для решения задач по тригонометрии от Mathway Я должен сказать, что нет альтернативы тому, чтобы уделять внимание в классе, делать заметки, заниматься дома и выполнять много самостоятельных занятий с помощью карандаша и бумаги.

Интеграл (значения)

Пользователи также искали:

Неопределенные интегралы решебник — faxeepavi.router.gallery

Неопределенные интегралы решебник

Links to Important Stuff

Links

Универсальный калькулятор комплексных чисел онлайн

Примеры

Исследовать на сходимость несобственный интеграл онлайн с решением. Определенный интеграл онлайн

Что значит вычислить несобственный интеграл?

Определение

практичная специальность с творческим началом

Несобственные интегралы первого рода — с бесконечными пределами и их сходимость

Несобственные интегралы с бесконечным верхним пределом

Несобственные интегралы второго рода — от неограниченных функций и их сходимость

Сумма ряда онлайн с подробным решением. §4. Приближенное вычисление суммы числового ряда

40. Эталонные ряды для установления сходимости

41. Функциональные ряды, степенные ряды, ряды Тейлора и Маклорена

Найти сумму ряда онлайн

бесплатных вопросов по исчислению и проблем с решениями

Задачи и вопросы по исчислению

Аналитические учебные пособия

Лимиты и непрерывность

Дифференциация и производные

Применение дифференцирования

Интегралы

Дифференциальные уравнения

Функции с несколькими переменными (функции с несколькими переменными)

Таблицы математических формул

Интерактивные учебные пособия

(scipy.integrate) — Справочное руководство SciPy v1.6.3

Решение системы с ленточной матрицей Якоби

Решение интеграла от cos (x) — математический класс [видео 2021 года]

Основная теорема исчисления

Резюме урока

Найдите дробные дроби с помощью программы «Пошаговое решение математических задач»

Калькулятор суммирования в закрытой форме

вычислитель комплексных интегралов

Математический решатель бесплатно

Добавить комментарий Отменить ответ