Содержание
Контрольная работа на тему «Площади»
Просмотр содержимого документа
«Контрольная работа на тему «Площади»»
Вариант – 1
1. Найдите площадь квадрата, если сторона равна
2. Сколько потребуется кафельных плиток квадратной формы со стороной 15 см, чтобы облицевать ими стену, имеющую форму прямоугольника со сторонами 3 м и 2,7 м.
3. Найдите стороны прямоугольника, если площадь равна 250см2 а одна сторона в 2,5 раза больше другой.
4. Смежные стороны параллелограмма равны 12 см и 14 см, а его острый угол равен 300. Найдите площадь параллелограмма.
5. Найдите площадь прямоугольного треугольника, если катеты равны 4 см и 11 см.
6. Вычислите площадь ромба, если его диагонали равны 3,2 дм и 14 см
7. Найдите высоту равностороннего треугольника, если его сторона равна 6 см.
8. Найдите площадь треугольника со сторонами 15 см,20 см и 25 см.
9. Найдите площадь трапеции АBCD с основаниями АВ и CD, если АВ=10 см, ВС=AD=13 см., CD=20 см.
10. Выясните, является ли треугольник прямоугольным со сторонами 9 см, 12 см и 15 см.
Вариант – 2
1. Найдите площадь квадрата, если сторона равна
2. Сколько потребуется потолочных плиток квадратной формы со стороной 50 см, чтобы облицевать ими потолок, имеющую форму прямоугольника со сторонами 3,2 м и 2,8 м.
3. Найдите стороны прямоугольника, если площадь равна 9м2 а периметр равен 12 м.
4. Смежные стороны параллелограмма равны 15 см и 10 см, а его острый угол равен 600. Найдите площадь параллелограмма.
Найдите площадь параллелограмма.
5. Найдите площадь прямоугольного треугольника, если катеты равны 8 см и 13 см.
6. Вычислите площадь ромба, если его диагонали равны 4,6 дм и 20 см
7. Найдите высоту равностороннего треугольника, если его сторона равна 8 см.
8. Найдите площадь треугольника со сторонами 14 см, 15 см и 13 см.
9. Найдите площадь трапеции АBCD с основаниями АВ и CD, если АВ=13 см, ВС=AD=10 см., CD=25 см.
10. Выясните, является ли треугольник прямоугольным со сторонами 10 см, 24 см и 26 см.
Тренажер по теме «Площади фигур»
Муниципальное автономное образовательное учреждение
вечерняя сменная общеобразовательное учреждение
г. Березники Пермского края
ТРЕНАЖЕР ПО ТЕМЕ
«ПЛОЩАДИ ФИГУР»
Составила
учитель математики
Хватынец Валентина Юрьевна
г. Березники, 2017 год
Березники, 2017 год
СОДЕРЖАНИЕ
Предисловие…………………………………………………….
§1. Знание теоретического материала……………………………….
§2. Задачи по теме «Прямоугольник» ……………………………………………………….
§3. Задачи по теме «Параллелограмм» ……………………………………………………….
§4. Задачи по теме «Треугольник» ……………………………………………………………
§5. Задачи по теме «Трапеция» …………………………………………
§6. Задачи по теме «Площадь фигур, заданных координатами» ……
§7. Задачи по теме «Площадь фигур на сетке» …………………………………
§8. Задачи по теме «Площадь заштрихованной фигуры» ……………….
§9. Ответы.
Справочный материал.
Список использованной литературы.
Предисловие
Цель данного пособия – помочь учащимся и учителям 9-х классов систематизировать знания по теме «Площадь фигур», закрепить знания теоретического материала и применение их на практике. Задачи:
выработать умение применять формулу для нахождения площади фигур;
совершенствовать навыки чтения математических чертежей; — развивать способность выбирать оптимальный путь решения задачи. Развитие вычислительной грамотности, пространственного воображения. Пособие предназначено для работы на уроке, для выполнения домашних заданий, а также для подготовки к итоговой аттестации. Рекомендовано для учащихся обучающихся по форме самообразования (экстернат). Пособие включает в себя справочные материалы, представленные в таблицах. Тренировочные упражнения помогают запомнить изученный материал, закрепить знания теоретического материала на практических заданиях. Каждую тему завершают контрольные диагностические наборы или тесты формата ОГЭ. Тренировочный материал пособия апробирован на уроках математики в Вечерней сменной школе г. Березники.
Развитие вычислительной грамотности, пространственного воображения. Пособие предназначено для работы на уроке, для выполнения домашних заданий, а также для подготовки к итоговой аттестации. Рекомендовано для учащихся обучающихся по форме самообразования (экстернат). Пособие включает в себя справочные материалы, представленные в таблицах. Тренировочные упражнения помогают запомнить изученный материал, закрепить знания теоретического материала на практических заданиях. Каждую тему завершают контрольные диагностические наборы или тесты формата ОГЭ. Тренировочный материал пособия апробирован на уроках математики в Вечерней сменной школе г. Березники.
§1. Знание теоретического материала.
№ п/п | Текст задания | Ответы |
1. | По данным величинам запишите формулу площади данной фигуры. | |
2 | По данным величинам запишите формулу площади данной фигуры. | |
3 | По данным величинам запишите формулу площади данной фигуры. | |
4 | По данным величинам запишите формулу площади данной фигуры. | |
5 | По данным величинам запишите формулу площади данной фигуры. | |
6 | По данным величинам запишите формулу площади данной фигуры. | |
7 | По данным величинам запишите формулу площади данной фигуры. | |
8 | По данным величинам запишите формулу площади данной фигуры. | |
9 | По данным величинам запишите формулу площади данной фигуры. | |
10 | По данным величинам запишите формулу площади данной фигуры. |
§2. Задачи по теме «Прямоугольник»
№ | Текст задания | Ответы | ||
А | В | С | ||
1. | В прямоугольнике одна сторона равна 20, другая сторона равна 24. Найдите площадь прямоугольника. | 88 | 480 | 68 |
2. | Найдите площадь прямоугольника, по стороне и диагонали. | 1440 | 98 | 196 |
3. | В прямоугольнике периметр равен 72, а одна из его сторон равна 16. Найдите площадь прямоугольника. | 88 | 320 | 896 |
4. | В прямоугольнике диагональ равна 32, а угол между ней и одной из сторон равен 60°. Найдите площадь прямоугольника, деленную на √3. | 640 | 256 | 1920 |
5. | Найдите площадь прямоугольника, если его периметр равен 68 и одна сторона на 4 больше другой. | 285 | 272 | 1156 |
6. | Площадь прямоугольника равна 18. Найдите его большую сторону, если она в 2 раза больше меньшей стороны. | 9 | 6 | 3 |
7 | Одна из сторон прямоугольника равна 30, а площадь равна 480. Найдите диагональ этого прямоугольника. | 34 | 16 | 510 |
8. | Найдите площадь прямоугольника, изображенного на рисунке. | 350 | 780 | 39 |
9. | Найдите площадь прямоугольника, изображенного на рисунке.
| 180 | 580 | 420 |
10. | Сторона квадрата равна 21. Найдите площадь квадрата. | 42 | 84 | 441 |
11. | Как изменится площадь прямоугольника, если каждую сторону увеличить в два раза? | В 4 раза | В 2 раза | Не измен. |
12. | Пол комнаты, имеющей форму прямоугольника со сторонами 5,5 м и 6 м, нужно покрыть паркетом прямоугольной формы. Длина каждой дощечки паркета равна 30 см, а ширина – 5 см. Сколько потребуется таких дощечек для покрытия пола? | 2200 | 220 | 22 |
13. | Сколько потребуется кафельных плиток квадратной формы со стороной 15 см, чтобы облицевать ими стену, имеющую форму прямоугольника со сторонами 3 м и 2,7 м? | 36 | 360 | 400 |
Проверочная работа.
А
В
1. Укажите неверную формулу площади.
a) SABCD = AB · AD
б) SABCD = AB · BC
D
С
в) S∆ABC = AB · BC
2. Как изменится площадь прямоугольника, если одну его сторону увеличить в 2 раза, а другую – в 4 раза?
3. Площадь прямоугольника со сторонами 8см и 2 дм равна:
а) 56 см б) 16 см2 в) 160см2
4. Сколько потребуется досок для настила пол в зале, длина которого равна 20 м, а ширина 10 м, если длина доски 4 м, а ширина 25 см?
а) 125 шт. б) 200 шт. в) 180 шт.
§3. Задачи по теме «Параллелограмм»
№ | Текст задания | Ответы | ||
А | В | С | ||
1. | Одна из сторон параллелограмма равна 31, а опущенная на нее высота равна 7. Найдите площадь параллелограмма. | 38 | 217 | 76 |
2 | Одна из сторон параллелограмма равна 13, другая равна 20, а один из углов – 45°. Найдите площадь параллелограмма, умноженную на √2. | 260 | 130 | 57 |
3. | Стороны параллелограмма равны 9 и 10. Высота, опущенная на первую сторону, равна 14.Найдите высоту, опущенную на вторую сторону параллелограмма. | 266 | 12,6 | 33 |
4. | Площадь параллелограмма равна 65, две его стороны равны 5 и 10. | 6,5 | 13 | 5 |
5. | Площадь параллелограмма равна 205, две его высоты равны 5 и 17. Найдите большую сторону этого параллелограмма. | 41 | 12 | 9 |
6. | Найдите площадь параллелограмма, изображенного на рисунке. | 42 | 24 | 70 |
7. | Смежные стороны параллелограмма равны 12 см и 14 см, а его острый угол равен 30°. Найдите площадь параллелограмма. | 168 | 56 | 84 |
8. | Периметр параллелограмма равен 20 см. Вычислите его площадь, если один из его углов равен 150°, а длина одной из его сторон равна 8 см. | 15 | 8 | 12 |
9 | Стороны параллелограмма 6см и 9 см. Длина большей высоты параллелограмма 8 см. Найдите его площадь. | 48 | 72 | 54 |
10. | Площадь параллелограмма равна 25 см2. Стороны параллелограмма равны 2а + 3; 3а + 4 см, тогда меньшая высота этого параллелограмма равна: | 25: (3а + 4) | 25: (2а + 3) | (2а + 3) (3а + 4) |
Проверочная работа.
1. Стороны параллелограмма равны 8см и 14 см, а угол между ними 30°. Найдите площадь параллелограмма.
Найдите площадь параллелограмма.
2. Стороны параллелограмма равны 4 см и 8 см. Высота, опущенная на первую из этих сторон, равна 6 см. Найдите высоту, опущенную на вторую сторону параллелограмма.
3. Площадь параллелограмма равна 24 см2, каждая из его сторон равна 6 см. Найдите расстояние между противоположными сторонами параллелограмма.
4. Укажите формулу для вычисления площади параллелограмма:
а) S = ½ a·ha
b
б) S = 2 a ·ha
hb
ha
в) S = a ha
а
§4. Задачи по теме «Ромб»
№ п/п | Текст задания | Ответы | ||
А | В | С | ||
1. | Найдите площадь ромба, если его диагонали равны 8 и 12. | 96 | 48 | 40 |
2. | Периметр ромба равен 72, а один из углов равен 45°. Найдите площадь ромба, деленную на √2. | 162 | 117 | 27 |
3. | Найдите сторону ромба, если его площадь равна 72, а острый угол 30°. | 24 | 12 | 216 |
4. | Площадь ромба равна 26. Одна из диагоналей равна 4. Найдите другую диагональ. | 6,5 | 13 | 65 |
5. | Найдите высоту ромба, если его площадь равна 54, а сторона равна 4. | 13,4 | 216 | 58 |
6. | Сторона ромба равна 25, а диагональ – 48. Найдите площадь ромба. | 1200 | 73 | 336 |
7. | Найдите площадь ромба, изображенного на рисунке. | 14 | 20 | 24 |
8. | Найдите площадь ромба, изображенного на рисунке. | 90 | 60 | 21 |
9. | Найдите площадь ромба, если его высота равна 12, а острый угол 30°. | 288 | 360 | 42 |
10. | Сторона ромба 8 см, а острый угол 30°. Найдите площадь ромба. | 32 | 240 | 64 |
Самостоятельная работа.
Укажите неверное утверждение:
а) площадь ромба равна произведению диагоналей;
б) площадь ромба равна произведению его стороны на высоту;
в) диагонали ромба разбивают его на 4 равновеликих треугольника.
Найдите высоту ромба, сторона которого равна 6, 5 см, а площадь – 26 см2.
Сторона ромба 6 см, а острый угол 30°. Найдите площадь ромба.
Периметр ромба равен 40 см, а высота равна 8 см. Вычислите площадь ромба.
§5. Задачи по теме «Треугольник»
№ п/п | Текст заданий | Ответы | ||
А | В | С | ||
1. | Найдите площадь треугольника, изображенного на рисунке. | 42 | 70 | 300 |
2. | В прямоугольном треугольнике один из катетов равен 8, а угол, лежащий против него, равен 30°. Найдите площадь треугольника. В ответе напишите площадь, деленную на √3. | 32 | 240 | 38√3 |
3. | В прямоугольном треугольнике один из катетов равен 5, а острый угол, прилежащий к нему, равен 30°. Найдите площадь треугольника. В ответе запишите площадь, умноженную на √3. | 150 | 12,5 | 50 |
4. | В прямоугольном треугольнике один из катетов равен 12, а угол, лежащий напротив него, равен 45°. Найдите площадь треугольника. | 72 | 144 | 57 |
5. | Периметр равностороннего треугольника равен 84. Найдите его площадь, деленную на √3. | 28 | 84√3 | 196 |
6. | Найдите площадь равностороннего треугольника, высота которого равна 4. | 16 | 4√3 | 12 |
7. | Периметр равнобедренного треугольника равен 36, а боковая сторона – 13. Найдите площадь треугольника. | 43 | 60 | 468 |
8. | Периметр равнобедренного треугольника равен 100, а основание – 18. Найдите площадь треугольника. | 118 | 820 | 180 |
9. | У треугольника со сторонами 14 и 21 проведены высоты к этим. Высота, проведенная к меньшей стороне, равна 6. Чему равна высота, проведенная к большей стороне? | 4 | 5,8 | 49 |
10. | Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 90°. Найдите боковую сторону треугольника, если его площадь равен 450. | 540 | 5 | 30 |
11. | Найдите площадь треугольника, изображенного на рисунке. | 132 | 264 | 62 |
12. | Найдите площадь треугольника, изображенного на рисунке. | 40 | 120 | 60 |
13. | Найдите площадь прямоугольного треугольника, изображенного на рисунке. | 52 | 315 | 24,5 |
14. | Найдите площадь равнобедренного треугольника, изображенного на рисунке. | 168 | 98 | 200 |
15. | Найдите площадь равнобедренного треугольника, изображенного на рисунке. | 60 | 42 | 84 |
Проверочная работа.
Катеты прямоугольного треугольника равны 4 см и 3 см. Вычислите площадь данного треугольника.
а) 7см; в) 6 см; с) 12 см
2. В треугольнике одна из сторон 12, другая 8, а синус угла между ними равен 0,2. Найдите площадь треугольника. a) 9, 6 в) 4, 8 с) 48
3. Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1см х 1см. Ответ дайте в квадратных сантиметрах
а) 21 в) 13см с) 30 см
4. Найдите площадь прямоугольного треугольника, если один из его катетов равен 8 см, а гипотенуза равна 10 см.
Найдите площадь прямоугольного треугольника, если один из его катетов равен 8 см, а гипотенуза равна 10 см.
а) 80см2 в) 24см2 с) 48см2
§6. Задачи по теме «Трапеция»
№ п/п | Тексты заданий | Ответы | ||
А | В | С | ||
1. | Основания трапеции равны 17 и 22, площадь трапеции равен 390. Найдите высоту трапеции. | 10 | 20 | 5 |
2. | Одно из оснований трапеции равно 12, высота равна 6, а площадь трапеции равна 96. Найдите второе основание трапеции. | 16 | 4 | 20 |
3. | Основания равнобедренной трапеции равны 8 и 29, площадь равна 333. Найдите ее высоту. | 18 | 9 | 15 |
4. | Основание трапеции равно 23, высота равна 5, а площадь равна 150. Найдите второе основание трапеции. | 7 | 8,3 | 5 |
5. | Основания равнобедренной трапеции равны 7 и 13, а ее периметр равен 30. Найдите площадь трапеции. | 30 | 40 | 600 |
6. | Найдите большее основание прямоугольной трапеции, площадь которой равна 48, высота равна 6 и большая боковая сторона составляет с основанием угол 45°. | 11 | 8 | 42 |
7. | В равнобокой трапеции основания равны 10 см и 20 см, боковая сторона равна 25 см. Найдите площадь трапеции, деленную на √5. | 200 | 500 | 40 |
8. | Тупой угол равнобедренной трапеции равен 135°, а высота, проведенная из вершины этого угла, делит большее основание на отрезки 1,4 см и 3,4 см. Найдите площадь трапеции. | 13,98 | 4,76 | 87 |
9. | Найдите площадь прямоугольной трапеции, у которой две меньшие стороны равны 6 см, а больший угол равен 135°. | 36 | 54 | 129 |
10. | Основания равнобедренной трапеции равны 6 см и 10 см. Ее острый угол равен 45°. Найдите площадь трапеции. | 16 | 60 | 30 |
Проверочная работа
1. Основания равнобедренной трапеции равны 14 и 20, а высота равна 5. Найдите площадь трапеции.
а) 68 б) 34 в) 85
2.Укажите верную формулу для вычисления площади трапеции
a
а) S =
h
б) S = (a + b) h
b
в) S =
3. Найдите площадь прямоугольной трапеции, у которой две меньшие стороны равны 6 см, а больший угол 135°.
а) 36 см2 б) 54 см2 в) 18 см2
4. Параллельные стороны трапеции равны 2 см и 5 см, а расстояние между ними равно 4 см. Площадь трапеции равна:
а) 40 см2 б) 14 см2 в) 2,5 см2
§7. Задачи по теме «Площадь фигур, заданных координатами».
Задачи по теме «Площадь фигур, заданных координатами».
№ п/п | Текст задания | Ответы | ||
А | В | С | ||
1. | Найдите площадь треугольника, вершины которого имеют координаты (1; 0), (11; 7), (8;10). | 31 | 27 | 15 |
2. | Найдите площадь прямоугольника, вершины которого имеют координаты (1; 0), (10; 0), (1; 10), (10; 10) | 90 | 38 | 19 |
3. | Найдите площадь трапеции, вершины которой имеют координаты (-4; -2), (4; -2), (3; 5), (0; 5). | 77 | 38,5 | 56 |
4. | Найдите площадь параллелограмма, вершины которого имеют координаты (-2; -1), (4; -1), (2; 4), (-4; 4). | 30 | 22 | 11 |
§8. Задачи по теме «Площадь фигур на сетке»
№ п/п | Тексты заданий | Ответы | ||
А | В | С | ||
1 | Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1см х 1см. Ответ дайте в квадратных сантиметрах. | 7,5 | 8 | 11 |
2 | Найдите площадь прямоугольника, изображенного на клетчатой бумаге с размером клетки 1см х 1см. Ответ дайте в квадратных сантиметрах. | 12 | 18 | 9 |
3 | Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1см х 1см. Ответ дайте в квадратных сантиметрах. | 8 | 13 | 10 |
4 | Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1см х 1см. Ответ дайте в квадратных сантиметрах. | 6 | 12 | 10 |
5 | Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1см х 1см. | 8 | 10 | 12 |
6 | Найдите площадь параллелограмма, изображенного на клетчатой бумаге с размером клетки 1см х 1см. Ответ дайте в квадратных сантиметрах. | 17 | 12 | 10 |
7 | Найдите площадь фигуры, изображенного на клетчатой бумаге с размером клетки 1см х 1см. Ответ дайте в квадратных сантиметрах. | 13 | 21 | 20 |
§9. Задачи по теме «Площадь заштрихованной фигуры»
№ п/п | Тексты заданий | Ответы | ||
А | В | С | ||
1 | Выполните необходимые измерения и вычислите площадь заштрихованной фигуры. | 22 | 42 | 25 |
2 | Выполните необходимые измерения и вычислите площадь заштрихованной фигуры. | 22 | 34 | 25 |
3 | Выполните необходимые измерения и вычислите площадь заштрихованной фигуры. | 29,5 | 20,5 | 25 |
4 | Выполните необходимые измерения и вычислите площадь заштрихованной фигуры. | 18 | 30 | 25 |
5 | Выполните необходимые измерения и вычислите площадь заштрихованной фигуры. | 16,5 | 25,5 | 25 |
6 | Вычислите площадь заштрихованной фигуры, если R = 6; r1 = 3; r2 = 1 | 81,64 | 15 | 100 |
7. | Вычислите площадь заштрихованной фигуры, если AB = AC = BC =6. | 21,6 | 3,79 | 37,9 |
8 | АВСD – прямоугольник | 18,58 | 1,858 | 185,8 |
9. | АВСD – квадрат, АВ = 6 см. | 77,4 | 7,74 | 0,774 |
Контрольная работа по теме «Площади»
Найдите площадь фигуры, изображенного на клетчатой бумаге с размером клетки 1см х 1см. Ответ дайте в квадратных сантиметрах.
Ответ дайте в квадратных сантиметрах.
Ответы.
§1. Знание теоретического материала
S = a b
S = a h
S = a b sin α
S = ½ a b sin α
S =
S =
S ==
S =
S = π R2
10.S = √ p (p-a) (p-b) (p-c), где p =
тема «Прямоугольник» | тема «Параллелограмм | тема «Ромб» | тема «Треугольник |
1-В | 1-В | 1-В | 1-В |
2-А | 2-А | 2-А | 2-А |
3-В | 3-В | 3-В | 3-В |
4-В | 4-В | 4-В | 4-А |
5-А | 5-А | 5-А | 5-С |
6-С | 6-А | 6-С | 6-А |
7-А | 7-С | 7-С | 7-В |
8-А | 8-В | 8-А | 8-В |
9-С | 9 — А | 9-А | 9-А |
10-С | 10 — В | 10-А | 10-С |
11-А | 11-А | ||
12-А | 12-С | ||
13-В | 13-С | ||
14-А | |||
15-А |
тема «Трапеция» | тема «Площадь фигур, заданных координатами» | Тема «Площадь фигур на сетке» | Площадь заштрихованной фигуры |
1-В | 1-В | 1-А | 1-А |
2-С | 2-А | 2-В | 2-А |
3-А | 3-В | 3-А | 3-В |
4-А | 4-А | 4-А | 4-А |
5-В | 5-А | 5-А | |
6-А | 6-В | 6-А | |
7-А | 7-А | 7-В | |
8-В | 8-А | ||
9-В | 9-В | ||
10 — А |
Ответы на проверочные и самостоятельные работы.
Прямоугольник | Параллелограмм | Ромб | Треугольник | Трапеция |
1 – в | 1 -56 см2 | 1 – а | 1 – в | 1 – в |
2 – в 8 раз | 2 – 3 см | 2 – 4 см | 2 – а | 2 – в |
3 – в | 3 – 4 см | 3 – 18 см2 | 3 — а | 3 — б |
4 — б | 4 — в | 4 – 80см2 | 4 — в | 4 — в |
Справочный материал
функция | 30° | 45° | 60° |
sin α | |||
cos α | |||
tg α | 1 | √3 |
Список использованной литературы.
А.В. Погорелов. Геометрия 7-9 классы. Учебник для общеобразовательных организаций, М.: Просвещение, 2014.
Л. С. Атанасян. Геометрия 7-9 классы. Учебник для общеобразовательных организаций, М.: Просвещение, 2011.
Математика. 9 класс. ОГЭ-2017. Тренажер по новому плану экзамена. Легион, 2016.
А. П. Ершова. Самостоятельные и контрольные работы по геометрии для 8 класса. М.: ИЛЕКСА, 2015.
А.М.Лукашенок. Тесты по геометрии для поурочного контроля. 8 класс. М., Белый ветер.
Сканави. Планиметрия. Задачи 101 – 150 с ответами и решениями
Сканави М.И.
Задачи по планиметрии с ответами и решениями
перейти к содержанию
Группа А. Задачи 101 — 150 (с ответами и решениями)
В прямоугольный треугольник с катетами а и b вписан квадрат, имеющий с треугольником общий прямой угол. Найти периметр квадрата. Ответ: Решение
В правильный треугольник вписан квадрат, сторона которого равна m.
 Найти сторону треугольника. Ответ: Решение
Найти сторону треугольника. Ответ: РешениеНайти площадь квадрата, вписанного в правильный треугольник со стороной а. Ответ: Решение
Сторона правильного треугольника, вписанного в окружность, равна а. Вычислить площадь квадрата, вписанного в ту же окружность. Ответ: Решение
На сторонах квадрата вне его построены правильные треугольники, и их вершины последовательно соединены. Определить отношение периметра полученного четырехугольника к периметру данного квадрата. Ответ: Решение
В квадрате, сторона которого а, середины двух смежных сторон соединены между собой и с противоположной вершиной квадрата. Найти площадь полученного треугольника. Ответ: Решение
В равнобедренный треугольник вписан квадрат единичной площади, одна сторона которого лежит на основании треугольника. Найти площадь треугольника, если известно, что центры масс треугольника и квадрата совпадают (центр масс треугольника лежит на пересечении его медиан).
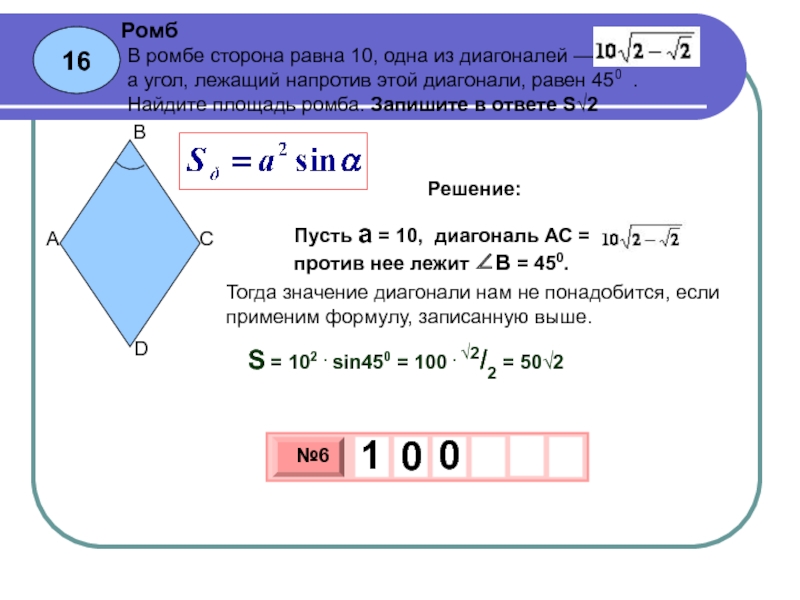 Ответ: 9/4 Решение
Ответ: 9/4 Решение- Площадь равнобедренного треугольника равна 1/3 площади квадрата, построенного на основании данного треугольника. Длины боковых сторон треугольника короче длины его основания на 1 см. Найти длины сторон и высоты треугольника, проведенной к основанию. Ответ: 4; 6 Решение
- Найти площадь правильного треугольника, вписанного в квадрат со стороной а при условии, что одна из вершин треугольника совпадает с вершиной квадрата. Ответ: Решение
- На сторонах равнобедренного прямоугольного треугольника с гипотенузой с вне этого треугольника построены квадраты. Центры этих квадратов соединены между собой. Найти площадь полученного треугольника. Ответ: Решение
- В квадрате со стороной а середины двух смежных сторон соединены между собой и с противоположной вершиной квадрата. Определить площадь внутреннего треугольника. Ответ: Решение
- В квадрат вписан другой квадрат, вершины которого лежат на сторонах первого, а стороны составляют со сторонами первого квадрата углы в 60°.
 Какую часть площади данного квадрата составляет площадь вписанного? Ответ: Решение
Какую часть площади данного квадрата составляет площадь вписанного? Ответ: Решение - Дан квадрат, две вершины которого лежат на окружности радиуса R, две другие — на касательной к этой окружности. Найти длину диагонали квадрата. Ответ: Решение
- Около квадрата со стороной а описана окружность. В один из образовавшихся сегментов вписан квадрат. Определить площадь этого квадрата. Ответ: Решение
- В сегмент, дуга которого равна 60°, вписан квадрат. Вычислить площадь квадрата, если радиус круга равен . Ответ: 1 Решение
- Сторона квадрата, вписанного в окружность, отсекает сегмент, площадь которого равна см2. Найти площадь квадрата. Ответ: 16 Решение
- Площадь прямоугольника равна 9 см2, а величина одного из углов, образованного диагоналями, равна 120°. Найти стороны прямоугольника. Ответ: Решение
- В круг радиуса R вписан прямоугольник, площадь которого вдвое меньше площади круга. Определить стороны прямоугольника.
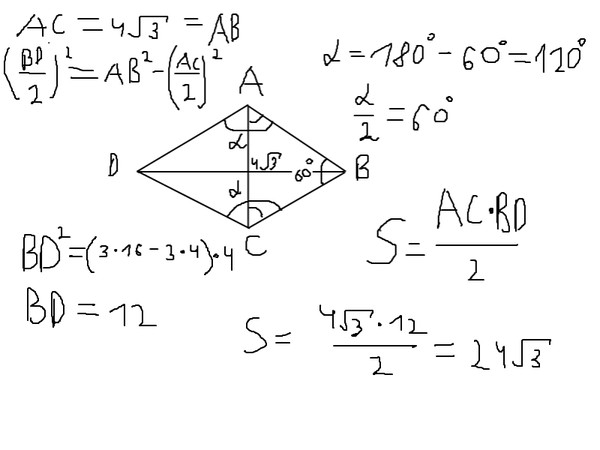 Ответ: Решение
Ответ: Решение - В прямоугольнике проведены биссектрисы двух углов, прилежащих к большей стороне. Определить, на какие части делится площадь прямоугольника этими биссектрисами, если стороны прямоугольника равны 2 и 4 м. Ответ: 2,2; 4 Решение
- В прямоугольный треугольник с углом 60° вписан ромб со стороной, равной 6 см, так, что угол в 60° у них общий и все вершины ромба лежат на сторонах треугольника. Найти стороны треугольника. Ответ: Решение
- В треугольник вписан ромб так, что один угол у них общий, а противоположная вершина делит сторону треугольника в отношении 2 : 3. Диагонали ромба равны n и m. Найти стороны треугольника, содержащие стороны ромба. Ответ: Решение
- Сумма длин диагоналей ромба равна m, а его площадь равна S. Найти сторону ромба. Ответ: Решение
- В ромб с острым углом 30° вписан круг, площадь которого равна Q. Найти площадь ромба. Ответ: Решение
- Периметр ромба равен 2 м, длины его диагоналей относятся как 3 : 4.
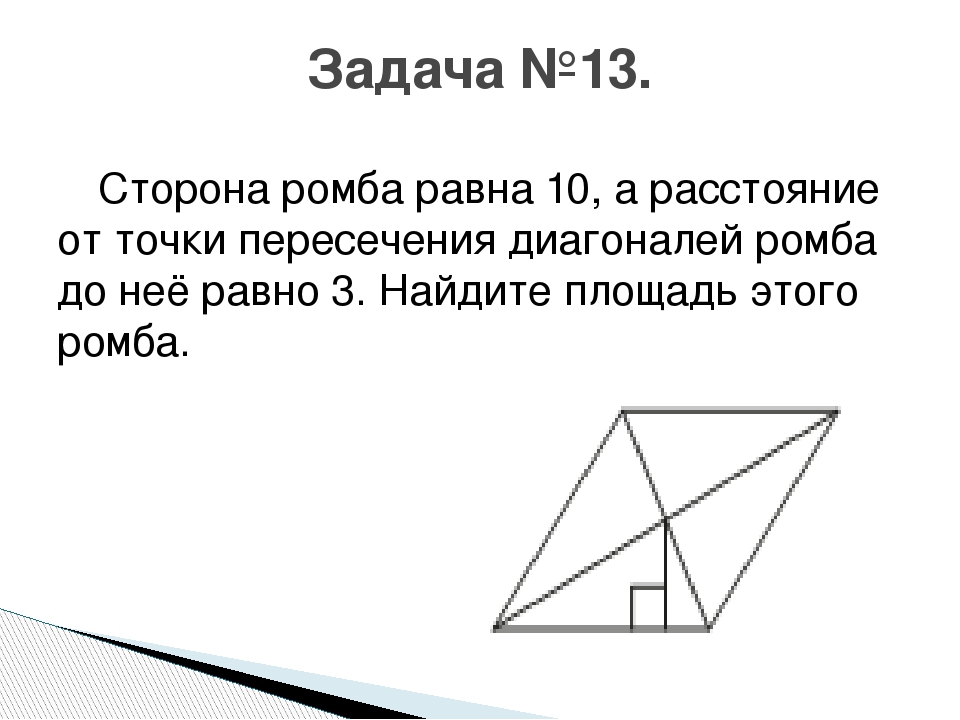 Найти площадь ромба. Ответ: 0,24 Решение
Найти площадь ромба. Ответ: 0,24 Решение - Определить сторону ромба, зная, что площадь его равна S, а длины диагоналей относятся как m : n. Ответ: Решение
- Периметр ромба равен 2р, а длины диагоналей относятся как m : n. Вычислить площадь ромба. Ответ: Решение
- Высота ромба равна 12 см, а одна из его диагоналей равна 15 см. Найти площадь ромба. Ответ: 150 Решение
- Высота ромба, проведенная из вершины тупого угла, делит его сторону на отрезки длиной m и n (m считать от вершины острого угла). Определить диагонали ромба. Ответ: Решение
- Ромб, у которого сторона равна меньшей диагонали, равновелик кругу радиуса R. Определить сторону ромба. Ответ: Решение
В ромб с острым углом 30° вписан круг, а в круг — квадрат. Найти отношение площади ромба к площади квадрата. Ответ: 4 Решение
- В пересечение двух равных кругов вписан ромб с диагоналями 12 и 6 см. Найти радиус окружностей. Ответ: 7,5 Решение
- В ромб, который делится своей диагональю на два равносторонних треугольника, вписана окружность радиуса 2.
 Найти сторону ромба. Ответ: Решение
Найти сторону ромба. Ответ: Решение - Доказать, что если в четырехугольнике диагонали лежат на биссектрисах его углов, то такой четырехугольник есть ромб.
- На сторонах ромба как на диаметрах описаны полуокружности, обращенные внутрь ромба. Определить площадь полученной розетки, если диагонали ромба равны а и b. Ответ: Решение
- Периметр параллелограмма равен 90 см, а острый угол содержит 60°. Диагональ параллелограмма делит его тупой угол на части в отношении 1:3. Найти стороны параллелограмма. Ответ: 15; 30 Решение
- Величина одного из углов параллелограмма равна 60°, а меньшая диагональ см. Длина перпендикуляра, проведенного из точки пересечения диагоналей к большей стороне, равна см. Найти длины сторон и большей диагонали параллелограмма. Ответ: Решение
- Перпендикуляр, проведенный из вершины параллелограмма к его диагонали, делит эту диагональ на отрезки длиной 6 и 15 см. Разность длин сторон параллелограмма равна 7 см. Найти длины сторон параллелограмма и его диагоналей.
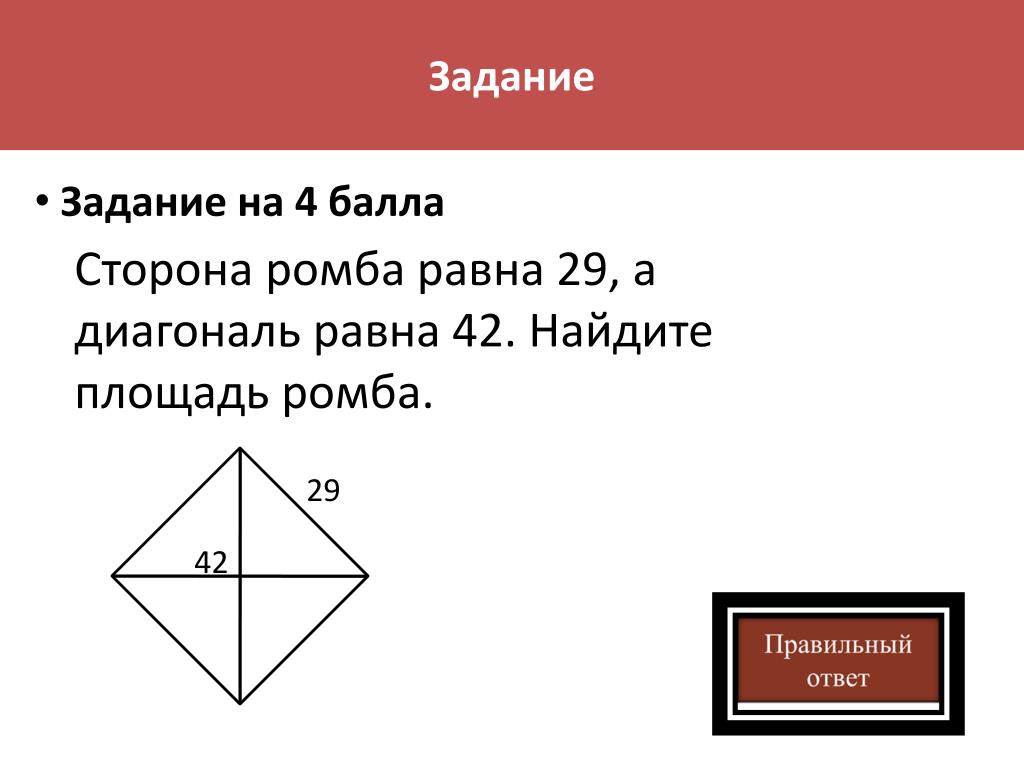 Ответ: 10, 17, 21, Решение
Ответ: 10, 17, 21, Решение - В параллелограмме с периметром 32 см проведены диагонали. Разность между периметрами двух смежных треугольников равна 8 см. Найти длины сторон параллелограмма. Ответ: 4; 12 Решение
- В параллелограмме ABCD высота, проведенная из вершины В тупого угла на сторону DA, делит ее в отношении 5 : 3, считая от вершины D. Найти отношение AC : BD, если AD : AB = 2. Ответ: 2:1 Решение
- Через точки R и E, принадлежащие сторонам АВ и AD параллелограмма ABCD и такие, что AR = 2 АВ /3, АЕ = AD/3, проведена прямая. Найти отношение площади параллелограмма к площади полученного треугольника. Ответ: 9 Решение
- Доказать, что в параллелограмме ABCD расстояния от любой точки диагонали АС до прямых ВС и CD обратно пропорциональны длинам этих сторон.
- Доказать, что если через вершины четырехугольника провести прямые, параллельные его диагоналям, то площадь параллелограмма, определяемою этими прямыми, в 2 раза больше площади данного четырехугольника.
- Две окружности радиуса R с центрами О1 и О2 касаются друг друга. Их пересекает прямая в точках А, В, С и D так, что АВ = ВС = CD. Найти площадь четырехугольника O1ADO2. Ответ: Решение
- В точках пересечения двух окружностей с радиусами 4 и 8 см касательные к ним взаимно перпендикулярны. Вычислить площадь фигуры О1АВО2, где АВ — общая касательная к окружностям, а О1 и О2 — их центры. Ответ: Решение
- Большее основание трапеции имеет длину 24 см. Найти длину ее меньшего основания, если известно, что расстояние между серединами диагоналей трапеции равно 4 см. Ответ: 16 Решение
- Один из углов трапеции равен 30°, а прямые, содержащие боковые стороны трапеции, пересекаются под прямым углом. Найти длину меньшей боковой стороны трапеции, если ее средняя линия равна 10 см, а одно из оснований 8 см. Ответ: 2 Решение
- Вычислить площадь трапеции, параллельные стороны которой содержат 16 и 44 см, а непараллельные — 17 и 25 см.
 Ответ: 450 Решение
Ответ: 450 Решение - Длины параллельных сторон трапеции равны 25 и 4 см, а длины непараллельных сторон — 20 и 13 см. Найти высоту трапеции. Ответ: 12 Решение
- Основания трапеции равны а и b, углы при большем основании равны и . Найти площадь трапеции. Ответ: Решение
- Вычислить площадь трапеции ABCD (AD параллельно BC), если длины ее оснований относятся как 5 : 3 и площадь треугольника ADM равна 50 см2, где М — точка пересечения прямых АВ и CD. Ответ: 32 Решение
Метки Сканави. Смотреть запись.
Меню
Многогранники: Тела вращения: Вспомогательные материалы: |
Задания » Ромб ABCD-ромб, сумма диагоналей 14см, периметр=20см. Найти площадь ромба. Диагонали ромба равны 12 см и 16 см. Точка М находится в не плоскости ромба и отдалена от всех сторон ромба на 8 см. Найдите расстояние от точки М до плоскости ромба. У ромбі зі стороною 10 коренів з трьох см і кутом 60 градусів через вершину гострого кута проведено площину на відстані 9 см від усіх точок його меншої діагоналі. |
Разработка проблемного модуля «Четырехугольники» — геометрия, разное
Конструирование проблемного модуля по теме «Четырехугольники» школьного курса математики
Проблемный модуль «Четырехугольники» в процессе обучения может применяться для представления учебного материала в сжатом виде; основным дидактическим материалом при проведении уроков с применением проблемно-модульной технологии; для обобщающего повторения темы «Четырехугольники»; как справочный материал для учащихся.
У каждого учебного элемента есть свое краткое обозначение (оно записывается в левом верхнем углу блока, например, ТБ-1) и название.
Условные обозначения блоков проблемного модуля: БВ – блок входа, БА – блок актуализации, ИБ – исторический блок, ПБ – проблемный блок, ТБ – теоретический блок, БП – блок применения, БО – блок обобщения, БГ – блок генерализации, БУ – блок углубления, БС – блок стыковки, ТТ – текущий тест, БВ – блок выхода.
Иногда в одном учебном элементе могут содержаться материалы нескольких блоков. В таком случае краткие обозначения блоков соединяются знаком «+». Например, запись «ТБ-1 + БП-1» означает, что в учебном элементе объединены теоретический блок-1 и блок применения-1 .
Далее опишем блоки проблемного модуля «Четырехугольники».
Блок актуализации
Дидактическая цель:
-
актуализировать прежние знания, навыки и умения непосредственно связанные с темой «Четырехугольники» (многоугольники, диагональ, периметр, сумма углов выпуклого многоугольника, виды и свойства углов, образованных при пересечении двух параллельных прямых третьей, свойство прямоугольного треугольника с углом 30°).
Блок входа.
Входная контрольная работа.
Дидактическая цель:
-
оценить уровень готовности учащихся к изучению проблемного модуля «Четырехугольники»; -
проверить знания учащихся по темам «Многоугольники» и «Параллельные прямые», выявить пробелы в знаниях.
Входная контрольная работа представлена в двух вариантах и состоит из 6 заданий. Первые два вопроса – в форме теста, остальные четыре вопроса требуют развернутого ответа.
Входная контрольная работа проводится с целью оценки уровня готовности учащихся к изучению проблемного модуля «Четырехугольники». Если при выполнении заданий у учащихся возникают трудности или ошибки, то они вместе с учителем заново повторяют материал, представленный в блоке актуализации. А если проблем с контрольной работой не будет, то учащийся приступает к изучению модуля «Четырехугольники».
А если проблем с контрольной работой не будет, то учащийся приступает к изучению модуля «Четырехугольники».
Исторический блок
Дидактическая цель:
-
сделать краткий обзор в историю четырехугольников; -
выявить успехи и ошибки в изучении четырехугольников в древние времена.
В этом блоке проводится краткий экскурс в историю четырехугольников. Этот материал будет полезным для учащихся, интересующихся математикой.
Проблемный блок
Дидактическая цель:
-
мотивировать учащихся к изучению четырехугольников.
В этом блоке ставится проблемный вопрос в форме сказки о выборе царя четырехугольников. Ответ на этот вопрос учащиеся будут искать на протяжении всего модуля, а в конце модуля в блоке стыковки они будут сравнивать свои ответы с правильным ответом.
Ответ на этот вопрос учащиеся будут искать на протяжении всего модуля, а в конце модуля в блоке стыковки они будут сравнивать свои ответы с правильным ответом.
Теоретический блок-1 и блок применения-1
Четырехугольники
Дидактическая цель:
-
изучить выпуклые и невыпуклые четырехугольники и их элементы, теорему о сумме углов выпуклого четырехугольника; -
применять теоретические знания на практике при решении задач.
В этом блоке рассматриваются выпуклые и невыпуклые четырехугольники и их элементы, теорема о сумме углов выпуклого четырехугольника, предлагаются задачи на применение полученных знаний.
Теоретический блок-2 и блок применения-2
Параллелограмм
Дидактическая цель:
-
изучить определение параллелограмма; -
изучить свойства параллелограмма; -
изучить признаки параллелограмма; -
применять теоретические знания на практике при решении задач.
В этом блоке дается определение параллелограмму, рассматриваются его свойства и признаки, предлагаются задачи на применение полученных знаний.
Теоретический блок-3 и блок применения-3
Трапеция
Дидактическая цель:
-
изучить определение трапеции; -
рассмотреть виды трапеций; -
изучить теорему о средней линии трапеции; -
применять теоретические знания на практике при решении задач.
В этом блоке дается определение трапеции, рассматриваются равнобедренные и прямоугольные трапеции, средняя линия трапеции и предлагаются задачи на применение полученных знаний.
Теоретический блок-4 и блок применения-4
Прямоугольник
Дидактическая цель:
-
изучить определение прямоугольника;
-
изучить свойства прямоугольника; -
изучить признак прямоугольника; -
применять теоретические знания на практике при решении задач.
В этом блоке дается определение прямоугольнику, рассматриваются его свойства и признак, предлагаются задачи на применение полученных знаний.
Теоретический блок-5 и блок применения-5
Ромб
Дидактическая цель:
-
изучить определение ромба;
-
изучить свойства ромба; -
применять теоретические знания на практике при решении задач.
В этом блоке дается определение ромбу, рассматриваются его свойства, предлагаются задачи на применение полученных знаний.
Теоретический блок-6 и блок применения-6
Квадрат
Дидактическая цель:
-
изучить определение квадрата;
-
изучить свойства квадрата; -
применять теоретические знания на практике при решении задач.
В этом блоке дается определение квадрату, рассматриваются его свойства, предлагаются задачи на применение полученных знаний.
Текущий тест
Текущая контрольная работа.
Дидактическая цель:
-
проверить уровень приобретенных знаний учащимися об основных видах четырехугольников (параллелограмм, трапеция, прямоугольник, ромб, квадрат), их свойствах и признаках; -
выявить пробелы и недостатки в знаниях учащихся об основных видах четырехугольников (параллелограмм, трапеция, прямоугольник, ромб, квадрат), их свойствах и признаках.
Текущая контрольная работа представлена в двух вариантах и состоит из 12 заданий. Задания даны в форме теста. Эта контрольное тестирование проводится после изучения темы «Четырехугольники» (первые шесть теоретических блоков), но до начала изучения темы «Площадь четырехугольников». Учащиеся, которые выполняют тест без затруднений и ошибок, продолжают изучение модуля. А у кого возникают трудности, они выполняют работу над ошибками.
Теоретический блок-7 и блок применения-7
Площадь квадрата и прямоугольника
Дидактическая цель:
-
изучить правило и формулу нахождения площади квадрата; -
изучить правило и формулу нахождения площади прямоугольника; -
применять теоретические знания на практике при решении задач.
В этом блоке даются формулы вычисления площадей квадрата и прямоугольника, предлагаются задачи на применение полученных знаний.
Теоретический блок-8 и блок применения-8
Площадь параллелограмма и трапеции
Дидактическая цель:
-
рассмотреть основание параллелограмма и высоту, опущенную на это основание; -
рассмотреть основание трапеции и высоту, опущенную на это основание; -
изучить правило и формулу нахождения площади параллелограмма; -
изучить правило и формулу нахождения площади трапеции; -
применять теоретические знания на практике при решении задач.
В этом блоке даются формулы вычисления площадей параллелограмма и трапеции, предлагаются задачи на применение полученных знаний.
Теоретический блок-9 и блок применения-9
Площадь ромба
Дидактическая цель:
-
изучить два правила и формулы нахождения площади ромба; -
применять теоретические знания на практике при решении задач.
В этом блоке даются формулы вычисления площади ромба, предлагаются задачи на применение полученных знаний.
Блок обобщения
«Дерево» видов четырехугольников
Дидактическая цель:
-
обобщить знания по четырехугольникам; -
рассмотреть взаимосвязь четырехугольников; -
повторить свойства и признаки четырехугольников.
В этом блоке обобщаются знания по классификации четырехугольников, рассматривается взаимосвязь четырехугольников.
Блок генерализации
Параллелограмм, трапеция, прямоугольник, квадрат, ромб и их свойства и признаки. Формулы вычисления площадей.
Дидактическая цель:
-
закрепить знания о параллелограмме, его свойствах и признаках; -
закрепить знания о трапеции, равнобедренной и прямоугольной трапеции; -
закрепить знания о прямоугольнике, его свойствах и признаке; -
закрепить знания о ромбе, его свойствах; -
закрепить знания о квадрате, его свойствах; -
отличать параллелограмм, трапецию, прямоугольник, ромб, квадрат друг от друга; -
повторить формулы нахождения площадей параллелограмма, трапеции, прямоугольника, ромба, квадрата.
В этом блоке обобщается весь теоретический материал, изученный в проблемном модуле «Четырехугольники».
Блок углубления и блок применения-10
Дидактическая цель:
-
изучить правило и формулу нахождения площади любого выпуклого четырехугольника, у которого известны все стороны и диагонали.
В этом блоке рассматривается правило и формула Бертшнайдера нахождения площади любого выпуклого четырехугольника, у которого известны все стороны и диагонали. Предлагаются две задачи на применение данной формулы. Материал, представленный в этом блоке, будет полезен учащимся, заинтересованных математикой.
Блок стыковки
Дидактическая цель:
-
поиск ответа на вопрос, поставленный в проблемном блоке.
В этом блоке, опираясь на материал, изученный в модуле «Четырехугольники», дается ответ на вопрос, поставленный в проблемном блоке.
Блок выхода
Итоговая контрольная работа.
Дидактическая цель:
-
проверить уровень приобретенных знаний учащимися по модулю «Четырехугольники»; -
выявить пробелы и проблемы учащихся по изученному модулю.
Итоговая контрольная работа представлена в четырех вариантах, каждый вариант состоит из четырех задач. Во всех задачах нужно найти площади четырехугольников, но для этого также надо знать их свойства и признаки.
Эта контрольная работа является выходной. Если учащийся выполняет эту работу без затруднений и ошибок, то считается, что он изучил модуль очень хорошо и может приступать к изучению нового модуля. Если наоборот, возникли трудности и ошибки, учащийся должен повторить модуль вместе с учителем, акцентируя внимание на тех местах, где у него возникли проблемы и выполнить работу над ошибками.
Блок генерализации проблемного модуля «Четырехугольники»
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Блок углубления и блок применения-10 проблемного модуля «Четырехугольники»
|
|
| ||||||
|
| |||||||
Блок стыковки проблемного модуля «Четырехугольники»
|
|
| ||
|
| |||
Блок выхода проблемного модуля «Четырехугольники»
|
|
| ||||||||||
|
| |||||||||||
Список использованной литературы
1. Чошанов, М.А. Инженерия обучающих технологий / М.А.Чошанов. – 3-е изд. – М.:БИНОМ. Лаборатория знаний, 2015. – 239 с. : ил.
2. Атанасян, Л.С. Геометрия. 7-9 классы: Учебник для общеобразовательных учреждений / Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др. – 2-е изд. – М.: Просвещение, 2014 – 383 с. : ил.
3. Погорелов, А.В. Геометрия. 7-9 классы.: Учебник для общеобразовательных учреждений / А.В.Погорелов – 2-е изд. – М.: Просвещение, 2014 – 240 с. : ил.
4. Шарыгин, И.Ф. Геометрия. 7-9 классы: Учебник для общеобразовательных учреждений / И.Ф.Шарыгин – М.:Дрофа, 2012 – 462 с. : ил.
5. Атанасян, Л.С. Изучение геометрии в 7-9 классах: Пособие для учителей / Л.С.Атанасян, В.Ф.Бутузов, Ю.А.Глазков и др. – 7-е изд. – М.: Просвещение, 2009 – 255 с. : ил.
7. Атанасян, Л.С. Геометрия. Рабочая тетрадь. 8 класс: Пособие для учащихся общеобразовательных учреждений / Л.С.Атанасян, В.Ф.Бутузов, Ю.А.Глазков, И.И.Юдина – 14-е изд. – М.: Просвещение, 2014 – 65 с.
8. Баянова Л. А. Технология модульного обучения в школе [Текст] // Педагогика: традиции и инновации: материалы Междунар. науч. конф. (г. Челябинск, октябрь 2011 г.) .Т. I. – Челябинск: Два комсомольца, 2011. – С. 107-109.
Подборка задач по теме « Площади» ОГЭ /зачёт 2/ 8класс
1.Найдите площадь трапеции, изображённой на рисунке.
2..В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна1. Найдите площадь трапеции.
3.Площадь параллелограмма ABCD равна 56. Точка E — середина стороны CD. Найдите площадь трапеции AECB.
Площадь параллелограмма ABCD равна 176. Точка E — середина стороны AD. Найдите площадь трапеции AECB.
5.Боковая сторона трапеции равна 4, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 2 и 7.
6.Найдите площадь трапеции, изображённой на рисунке.
7.В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна6. Найдите площадь трапеции.
8.Пол комнаты, имеющей форму прямоугольника со сторонами 5 м и 8 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 5 см и 40 см. Сколько потребуется таких дощечек?
9.Пол комнаты, имеющей форму прямоугольника со сторонами 7 м и 8 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 10 см и 40 см. Сколько потребуется таких дощечек?
10.Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=12, а расстояние от точки K до стороны AB равно 9.
11.Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=2, а расстояние от точки K до стороны AB равно 8.
12.Два катета прямоугольного треугольника равны 6 и 7. Найдите площадь этого треугольника.
13Два катета прямоугольного треугольника равны 14 и 5. Найдите площадь этого треугольника.
14.Периметр равнобедренного треугольника равен 234, а основание — 104. Найдите площадь треугольника.
15.Периметр равнобедренного треугольника равен 342, а основание — 152. Найдите площадь треугольника.
16.Площадь прямоугольного земельного участка равна 18 га, ширина участка равна 240 м. Найдите длину этого участка в метрах.
17.Площадь прямоугольного земельного участка равна 14 га, ширина участка равна 250 м. Найдите длину этого участка в метрах.
1. Найдите диагональ квадрата, если его площадь равна 4,5.
2. Найдите сторону квадрата, площадь которого равна площади прямоугольника со сторонами 0,5 и 2.
3. Найдите сторону квадрата, площадь которого равна площади прямоугольника со сторонами 13 и 52.
4. Найдите площадь параллелограмма, если две его стороны равны 40 и 10, угол между ними равен 30o.
5. Найдите площадь ромба, если его стороны равны 6, а один из углов равен 150o.
6. Найдите площадь ромба, если его стороны равны 5, а один из углов равен 150o.
7. Площадь прямоугольного треугольника равна 224. Один из его катетов равен 28. Найдите другой катет.
8. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 150o. Боковая сторона треугольника равна 2. Найдите площадь этого треугольника.
9. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 150o. Боковая сторона треугольника равна 34. Найдите площадь этого треугольника.
10. Найдите площадь треугольника, две стороны которого равны 44 и 8, а угол между ними равен 30o.
11. Площадь треугольника АВС равна 12. DE — средняя линия. Найдите площадь треугольника CDE.
12. Площадь треугольника АВС равна 70. DE — средняя линия. Найдите площадь треугольника CDE.
13. Основания трапеции равны 8 и 2, высота равна 4. Найдите площадь трапеции
14. Основания трапеции равны 24 и 18, высота равна 4. Найдите площадь трапеции
15. Периметры двух подобных многоугольников относятся как 1 : 10. Площадь меньшего многоугольника равна 9. Найдите площадь большего многоугольника.
16. Периметры двух подобных многоугольников относятся как 1 : 3. Площадь меньшего многоугольника равна 3. Найдите площадь большего многоугольника.
17. Площадь круга равна 25π. Найдите длину его окружности.
18. Площадь круга равна 121π. Найдите длину его окружности.
19. Найдите площадь сектора круга радиуса 10π, центральный угол которого равен 90o.
20. Найдите площадь сектора круга радиуса 16, длина дуги которого равна 1.
21. Найдите площадь прямоугольника, если его периметр равен 20 и одна сторона на 8 больше другой.
22. Найдите площадь прямоугольника, если его периметр равен 52, а отношение соседних сторон равно 3 : 10.
23. Найдите периметр прямоугольника, если его площадь равна 624, а отношение соседних сторон равно 4 : 39.
24. Периметр прямоугольника равен 30, а диагональ равна 14. Найдите площадь этого прямоугольника.
25. Сторона прямоугольника относится к его диагонали как 15 : 17, а другая сторона равна 16. Найдите площадь прямоугольника.
26. Стороны параллелограмма равны 44 и 88. Высота, опущенная на первую сторону, равна 66. Найдите высоту, опущенную на вторую сторону параллелограмма.
27. Стороны параллелограмма равны 10 и 85. Высота, опущенная на первую сторону, равна 51. Найдите высоту, опущенную на вторую сторону параллелограмма.
28. Найдите площадь ромба, если его высота равна 5, а острый угол равен 30o.
29. Найдите площадь ромба, если его диагонали равны 13 и 6.
30. Найдите площадь ромба, если его диагонали равны 315 и 2.
31. Площадь ромба равна 507. Одна из его диагоналей в 6 раз больше другой. Найдите меньшую диагональ.
32. Площадь прямоугольного треугольника равна 65. Один из его катетов на 3 больше другого. Найдите меньший катет.
перейти к содержанию задачника
Ответы
1. 3
2. 1
3. 26
4. 200
5. 18
6. 12,5
7. 16
8. 1
9. 289
10. 88
11. 3
12. 17,5
13. 20
14. 84
15. 900
16. 27
17. 10
18. 22
19. 25
20. 8
21. 9
22. 120
23. 172
24. 14,5
25. 480
26. 33
27. 6
28. 50
29. 39
30. 315
31. 13
32. 10
| 1в | 2в | 3в | 4в |
| Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 15 и 17 см. | Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 12 и 13 см. | Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 16 и 20 см. | Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 100 и 28см. |
| Найдите площадь квадрата, если его диагональ равна 20. | Найдите площадь ромба, если его диагонали 20 и 10. | Найдите площадь квадрата, если его диагональ равна 50. | Найдите площадь ромба, если его диагонали 30 и 70. |
| Сторона ромба равна 50, а диагональ равна 80. Найдите площадь ромба. | Сторона ромба равна 29, а диагональ равна 42. Найдите площадь ромба. | Сторона ромба равна 65, а диагональ равна 104. Найдите площадь ромба. | Сторона ромба равна 10, а диагональ равна 12. Найдите площадь ромба. |
| Боковая сторона равнобедренного треугольника равна 34, а основание равно 60. Найдите площадь. | Боковая сторона равнобедренного треугольника равна 25, а основание равно 48. Найдите площадь. | Боковая сторона равнобедренного треугольника равна 25, а основание равно 30. Найдите площадь. | Боковая сторона равнобедренного треугольника равна 50, а основание равно 60. Найдите площадь. |
| В прямоугольном треугольнике гипотенуза равна 70, а один из острых углов равен 45∘. Найдите площадь треугольника. | В прямоугольном треугольнике гипотенуза равна 82, а один из острых углов равен 45∘. Найдите площадь треугольника. | В прямоугольном треугольнике гипотенуза равна 8, а один из острых углов равен 45∘. Найдите площадь треугольника | В прямоугольном треугольнике гипотенуза равна 18, а один из острых углов равен 45∘. Найдите площадь треугольника |
| В треугольнике со сторонами 16 и 2 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 1. Чему равна высота, проведённая ко второй стороне? | В треугольнике со сторонами 15 и 3 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 1. Чему равна высота, проведённая ко второй стороне? | В треугольнике со сторонами 2 и 4 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 2. Чему равна высота, проведённая ко второй стороне? | В треугольнике со сторонами 12 и 8 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 4. Чему равна высота, проведённая ко второй стороне? |
Вычислите площадь заданной фигуры:
1. Гипотенуза равна 12, катет 8.
2. Стороны треугольника равны 12, 14, 10.
3. Сторона ромба равна 12, один из углов 45 .
4. Боковая сторона равнобедренного треугольника 10, основание 12.
5. Диагонали параллелограмма 12 и 14 , угол между ними 30 .
6. Сторона равностороннего треугольника равна 8 .
7. Диагонали ромба равны 20 и 12.
8. Стороны треугольника равны 10 и 6 , угол между ними 30
9. Диагональ квадрата равна 16.
10. В прямоугольном треугольнике меньший катет равен 6, один из углов 30 .
11. Стороны параллелограмма равны 10 и 6, угол между ними 60 .
12. Стороны треугольника 10, 8, 6.
13. Стороны параллелограмма равны 12 и 8, меньшая высота его равна 5.
14. Сторона равностороннего треугольника равна 12.
15. Основание равнобедренного треугольника равно 8, боковая сторона равна 12.
16. Диагонали выпуклого четырёхугольника взаимно перпендикулярны и равны 6 и 8.
17. Гипотенуза треугольника равна 5, один из катетов равен 3.
18. Стороны параллелограмма равны 12 и 18, один из углов равен 150 .
19. Диагонали ромба 6 и 8.
20. Стороны треугольника равны 24 и 20, угол между ними 30 .
21. Высота треугольника, проведённая к гипотенузе, делит её на отрезки, равные 4 и 9.
22. Гипотенуза равнобедренного треугольника 16 .
23. Диагонали параллелограмма равны 12 и 16, угол между ними 30 .
24. Стороны треугольника равны 16 и 9, угол между ними 60 .
25. Диагонали ромба равны 10 и 12.
26. Боковая сторона равнобедренного треугольника равна 15, высота, проведённая к основанию, равна 9.
27. Стороны параллелограмма равны 16 и 4, угол между ними 60 .
28. Гипотенуза треугольника равна 4 , один из его катетов равен 10.
29. Средняя линия трапеции равна 12, высота составляет длины средней линии.
30. Один из углов ромба 120 , меньшая диагональ равна 2 .
31. Основания равнобедренной трапеции равны 7 и 11, один из углов равен 60 .
32. Один из катетов равен 12, другой составляет первого.
33. Одна диагональ ромба в 6 раз больше другой. Найдите меньшую диагональ, если площадь ромба равна 108.
34. Площадь треугольника равна 270, сторона 5. Найти высоту, проведённую к данной стороне.
35. Площадь трапеции равна 75, её высота равна 5. найти среднюю линию трапеции.
36. В равнобедренной трапеции боковая сторона равна , основания трапеции равны 16 и 12. Вычислите площадь.
1.Вычислите | 2.Вычислите | 3. Вычислите | 4. Вычислите |
5. Вычислите | 6. Вычислите | 7. Вычислите | 8. Вычислите |
9. Вычислите | 10. Площадь | 11. Вычислите | 12. Вычислите |
13. Вычислите | 14. Вычислите | 15.Вычислите | 16.Средняя линия |
17. Вычислите | 18.Вычислите | 19.Одна из | 20. Площадь |
21.В | 22. Вычислите | 23. Вычислите | 24. |
Площадь ромба с углом 60 °
Если мы знаем длину стороны ромба с углом 60 °, мы можем определить его площадь разными способами. Мы будем использовать разные свойства параллелограммов, ромбов или равносторонних треугольников. Здесь мы опишем несколько из этих методов.
Задача
Ромб с длиной стороны 10 единиц имеет угол 60 °. Найдите его область.
Стратегия
Начнем с самого простого метода решения этой проблемы.Ромб — это особый вид параллелограмма. Мы знаем, что площадь любого параллелограмма определяется формулой A = l · h, где l — длина одной стороны параллелограмма, а h — высота этой стороны с противоположной стороны. Итак, давайте нарисуем эту высоту:
В параллелограмме противоположные углы совпадают, поэтому m∠ABE = 60 °. Это делает ΔABE треугольником 30-60-90. Мы знаем гипотенузу этого треугольника 30-60-90 — это 10-, поскольку все стороны ромба равны. Длинный катет треугольника 30-60-90, AE, равен половине времени гипотенузы √3, поэтому это 5√3.
AE — высота ромба, а площадь ромба l · h, или 10 · 5√3 = 50√3
Теперь попробуем по-другому:
В ромбе диагонали делятся пополам. углы и перпендикулярны друг другу:
Это создает 4 прямоугольных треугольника. Все они совпадают с использованием постулата «сторона-угол-сторона»: все они имеют одинаковую длину гипотенузы, все имеют общую сторону и все имеют угол 30 °.
Каждый из этих треугольников представляет собой треугольник 30-60-90 с гипотенузой 10.Их высота равна 5√3, а их основание — 5. Таким образом, площадь каждого треугольника равна (5 · 5√3) / 2. Площадь ромба состоит из 4 таких треугольников, поэтому его площадь равна 4 · (5 · 5√3) / 2, или 50√3.
Еще один способ решить эту проблему:
Наконец, мы можем представить себе этот ромб как состоящий из двух равносторонних треугольников:
Один из углов равен 60 °, обе стороны равны, поэтому треугольник равнобедренный, и поэтому каждый из базовых углов составляет (180 ° -60 °) / 2 = 60 °.
Мы уже вывели общую формулу для площади равностороннего треугольника, используя длину его стороны: Площадь ΔРавносторонний = (s 2 * √3) / 4
Таким образом, каждый из этих треугольников имеет площадь (10 2 * √3) / 4 или 25√3, и у нас есть два таких треугольника, что составляет площадь ромба 50√3.
Площадь ромба
Ромб — это четырехугольник, у которого на всех сторонах неравные диагонали, пересекающие друг друга пополам.
Примечание : Если квадрат нажать с двух противоположных углов, образуется ромб.
Пусть $$ ABCD $$ — ромб, тогда его площадь можно оценить двумя способами.
(1) Если указаны одна сторона и включенный угол:
Пусть одна сторона будет равна $$ a $$ с углом $$ \ theta $$.2} \ sin \ theta $$.
(2) Если указаны две диагонали:
Пусть $$ d $$ и $$ d ’$$ будут длиной диагоналей $$ AC $$ и $$ BD $$ соответственно, а поскольку ромб разделен на четыре равных треугольника, следовательно,
Площадь ромба $$ = 4 \ times \ frac {1} {2} \ times \ frac {{BD}} {2} \ times \ frac {{CA}} {2} = 4 \ times \ frac {{BD \ times CA}} {8} = \ frac {{BD \ times CA}} {2} $$.
Площадь ромба $$ = \ frac {{AC \ times BD}} {2} = \ frac {{d \ times d ’}} {2} $$.\ circ = 120 \ times 120 \ times 0,866 = 12470,4 $$ кв. см.
Пример :
Диагонали ромба составляют 40 м и 30 м. Найдите его область.
Решение :
Учитывая, что диагонали равны $$ d = 40 $$ м и $$ d ’= 30 $$ м,
площадь ромба $$ = \ frac {{d \ times d ’}} {2} = \ frac {{40 \ times 30}} {2} = 600 $$ кв. М.
Как найти площадь ромба
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно
или несколько ваших авторских прав, сообщите нам об этом, отправив письменное уведомление («Уведомление о нарушении»), содержащее
то
информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Как найти длину диагонали ромба
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно
или несколько ваших авторских прав, сообщите нам об этом, отправив письменное уведомление («Уведомление о нарушении»), содержащее
то
информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Если длина каждой стороны ромба 8 см, и класс 8 по математике CBSE
Подсказка : Ромб — это плоская форма с 4 прямыми сторонами, параллельными друг другу.Ромб напоминает алмаз. По весу борта у всех одинаковые. Противоположные стороны параллельны (это параллелограмм), а противоположные углы аналогичны. Высота — это разница между двумя сторонами под прямым углом.
Мы будем использовать здесь тригонометрические отношения, чтобы найти стороны треугольников, а затем, наконец, используем теорему Пифогора, чтобы определить длину диагоналей.
Полный пошаговый ответ :
Учитывая, что четырехугольник — ромб, его сторона равна 8 см, а угол — 60 градусов.\ circ = \ dfrac {{DO}} {{AD}} \\
\ Rightarrow \ dfrac {{\ sqrt 3}} {2} = \ dfrac {{DO}} {8} \\
\ Rightarrow DO = 4 \ sqrt 3 \;
$
Так же, как в ромбе диагонали делят друг друга пополам,
Следовательно, $ AD = 4 \ sqrt 3 \ times 2 = 8 \ sqrt 3 $.
Итак, длина второй диагонали $ 8 \ sqrt 3 $ см.
Итак, правильный ответ: «8 см и $ 8 \ sqrt 3 $ см. ».
Примечание : Ниже приведены некоторые из основных свойств ромба:
1. Все стороны ромба равны.
2. Противоположные стороны ромба параллельны.
3. Противоположные углы равны ромбу.
4. Диагонали пересекают друг друга под прямым углом в виде ромба.
5. Углы ромба разделены диагоналями пополам.
6. Два соседних угла в сумме равны 180 градусам.
Площадь параллелограмма с учетом сторон и угла Калькулятор
- Цель использования
- Викторина по геометрии.
- Комментарий / запрос
- Не могли бы вы рассказать, как вы получили решение?
[1] 2020/03/24 03:52 Женский / Моложе 20 лет / Высшая школа / Университет / аспирант / Немного /
- Цель использования
- Рассчитать площадь параллелограмма, необходимую для построения рисунка для деревянного художественного проекта .
[2] 2019/07/14 23:58 Женщина / Уровень 40 лет / Самостоятельно занятые люди / Полезно /
- Цель использования
- Домашнее задание Precalc
- Комментарий / Запрос
- Пошаговый процесс, показывающий пользователям, как перейти от цифр к ответам.
[3] 2019/04/18 11:24 Женский / До 20 лет / Старшая школа / Университет / аспирант / Немного /
- Цель использования
- решение математической задачи, дал мне ответ, но никаких шагов для его решения нет
[4] 2018/12/06 01:45 Мужчина / До 20 лет / Другое / Немного /
- Цель использования
- Для выполнения домашнего задания по математике
- Комментарий / Запрос
- это сработало хорошо
[5] 2018/11/22 12:22 Мужчина / Моложе 20 лет / Начальная школа / Младший школьник / Очень /
- Цель использования
- Программа
[6] 2018/04/12 13:28 Мужчина / Моложе 20 лет / Средняя школа / Университет / аспирант / Очень /
- Цель использования
- для ответа на мои неизвестные вопросы
- Комментарий / запрос
- I не может видеть процесс, который он делает
Вы добавляете кнопку ниже, по крайней мере, для студентов, которые хотят изучать 9023 2
[ 7] 2018/01/18 21:09 Мужчина / Моложе 20 лет / Средняя школа / Университет / Аспирант / Совсем нет /
- Цель использования
- На карте участка, представляющем собой идеальный параллелограмм, проверьте квадрат футов (и посевных площадей).
- Комментарий / запрос
- Для нематематических основных единиц измерения и синтаксиса символов всегда неприятно. Было бы здорово ввести угол в десятичной системе или в градусах-минутах-секундах (преобразовать несложно, но требуются дополнительные шаги). Также неплохо было бы иметь формулу Excel. В Excel функция Sin требует ввода в радианах, поэтому side1 * side2 * sin (pi () / 180)
[8] 2017/06/13 10:13 Мужчина / 60 лет и старше / Самостоятельно занятые люди / Очень /
- Цель использования
- Математическая версия
- Комментарий / запрос
- как вы получили площадь с заданными сторонами и углом? Какой был метод?
- from Keisan
- Площадь параллелограмма = основание * высота = a * (b * sinθ)
[9] 26.03.2017 19:00 Женщина / Моложе 20 лет / Средняя школа / Университет / аспирант / Полезно /
- Цель использования
- Знать площадь параллелограмма с учетом сторон и угла
- Комментарий / запрос
- Это очень просто и быстро.
[10] 10.10.2015 11:45 Женщина / 30-летний уровень / Учитель / Исследователь / Very /
наклонных треугольников
наклонных треугольников
Наклонный треугольник — это любой треугольник, не являющийся прямоугольным. Это может быть острый треугольник (все три угла треугольника меньше прямых углов) или тупой треугольник (один из трех углов больше прямого). На самом деле, для целей тригонометрии класс «наклонных треугольников» с таким же успехом мог бы включать и прямоугольные треугольники. Тогда изучение косых треугольников — это действительно изучение всех треугольников.
Давайте согласимся с соглашением для обозначения частей наклонных треугольников, обобщающим соглашение для прямоугольных треугольников.Обозначим углы A, B, и C, , а противоположные стороны обозначим a, b, и c, соответственно.
Решение косых треугольников
Тригонометрия наклонных треугольников не так проста, как тригонометрия прямоугольных треугольников, но есть две теоремы геометрии, которые дают полезные законы тригонометрии. Это называется «законом косинусов» и «законом синусов». Раньше использовались и другие «законы», но для обычного использования калькуляторов этих двух законов достаточно.
Закон косинусов
Это просто формулировка уравнения:
Похоже на теорему Пифагора, за исключением последнего члена, и если C оказывается прямым углом, последний член исчезает (поскольку косинус 90 ° равен 0), поэтому закон косинусов на самом деле является обобщением Теорема Пифагора.
Обратите внимание, что каждый треугольник дает три уравнения для закона косинусов, поскольку вы можете переставлять буквы по своему усмотрению.Остальные две версии затем
a 2 = b 2 + c 2 -2 bc cos A, и
b 2 = c 2 + a 2 -2 ca cos B.
Закон косинусов связывает три стороны треугольника с одним из углов. Вы можете использовать его несколькими способами.
Во-первых, если вы знаете один угол и две смежные стороны, вы можете определить противоположную сторону.Например, если угол C = 60 °, сторона a = 5 и сторона b = 8, то закон косинусов говорит, что c 2 = 25 + 64 — 80 cos 60 °. Поскольку косинус 60 ° равен 1/2, это уравнение упрощается до c 2 = 49, поэтому c = 7.
Во-вторых, если вы знаете все три стороны треугольника, вы можете использовать его, чтобы найти любой угол. Например, если три стороны равны a = 5, b = 6 и c = 7, то закон косинусов говорит, что 49 = 25 + 36-60 cos C, , поэтому cos C = 12/60 = 0.2, а с помощью калькулятора C = 1,3734 радиана = 78,69 °.
Примечание: Когда треугольник тупой, cos C отрицательный. Предположим, что три стороны равны a = 5, b = 6 и c = 10. Тогда закон косинусов гласит: 100 = 25 + 36 — 60 cos C, , поэтому cos C = — 49 / 60 = — 0,81667. Как вы можете видеть на графиках на предыдущей странице, косинус тупого угла отрицателен. Это нормально, и ваш калькулятор правильно вычислит арккосинус.Вы получите C = 2,2556 радиан = 129,237 °.
Закон синусов
Закон синусов — это также просто сформулированное уравнение
Обратите внимание, что закон синусов гласит, что три отношения равны. Подобно закону косинусов, вы можете использовать закон синусов двумя способами.
Во-первых, если вы знаете два угла и сторону, противоположную одному из них, то вы можете определить сторону, противоположную другому из них. Например, если угол A = 30 °, угол B = 45 ° и сторона a = 16, тогда закон синусов говорит (sin 30 °) / 16 = (sin 45 °) / b . Решение относительно b дает b = 16 (sin 45 °) / (sin 30 °) = 22,6274.
Во-вторых, если вы знаете две стороны и угол, противоположный одной из них, то вы почти можете определить угол, противоположный другой из них. Например, если сторона a = 25, сторона b = 15 и угол A = 40 °, то закон синусов говорит (sin 40 °) / 25 = (sin B ) / 15. Решение относительно sin B дает sin B = 15 (sin 40 °) / 25 = 0.38567. Теперь arcsin 0,38567 = 22,686 °.
Предупреждение: возможно, у вас нет правильного ответа. Есть два угла от 0 до 180 ° с заданным синусом; второй — дополнение к первому. Итак, в данном случае второй — тупой угол 180 — 22,686 = 157,314 °. Эта ситуация неопределенная. Зная две стороны и угол, противоположный одной из них, не всегда достаточно для определения треугольника. В геометрии нет детерминированной теоремы о конгруэнтности «сторона-сторона-угол».
Проблемы
553. AB — линия длиной 652 фута на одном берегу ручья, а C — точка на противоположном берегу. A = 53 ° 18 ‘и B = 48 ° 36′. Найдите ширину потока от C до AB.
557. В треугольнике ABC, a = 700 футов, B = 73 ° 48 ‘и C = 37 ° 21′. Если M — средняя точка BC , найдите длину AM, и углы BAM и MAC.
561. Три окружности радиуса 3, 4 и 5 касаются друг друга снаружи. Найдите углы треугольника, образованного соединением их центров.
563. A и B — точки на противоположных сторонах реки. На одном берегу отмерена линия AC 650 футов. Угол A, = 73 ° 40 ‘, а C, = 52 ° 38′. Найдите AB.
570. P и Q — две недоступные точки.Чтобы найти расстояние между ними, в полученном QP берется точка A и измеряется линия AB длиной 1200 футов, составляющая угол PAB = 26 ° 35 ‘. Угол ABP = 48 ° 12 ‘и ABQ = 106 ° 42′. Как долго PQ ?
579. Стороны параллелограмма равны AB = 209,16 и AD = 347,25, а диагональ AC = 351,47. Найдите углы и другую диагональ.
580. В параллелограмме ABCD, диагональ AC = 521,16, чем угол ABC = 110 ° 48 ’12 дюймов, и BAC = 27 ° 19′ 36 дюймов. Найдите длины сторон и другой диагонали.
586. Диагонали параллелограмма равны 374,14 и 427,21, а угол наклона составляет 70 ° 12 ’38 дюймов. Найдите стороны.
590. Порядковые стороны четырехугольника равны 763.83, 721,75, 547,12 и 593,21, а угол между первыми двумя сторонами составляет 53 ° 13 ’12 дюймов. Найдите три других угла.
593. A и B — две точки на противоположных сторонах водоема, и замеры должны проводиться по линии AB в точках одной четверти, одной половины и трех четвертей длины. расстояние от A до B. На берегу измеряется линия AC длиной 1200 футов, а углы BAC = 63 ° 19 ‘и ACB = 78 ° 43′.Какие углы должны быть отклонены от CA на C , чтобы выровнять лодку, с которой проводятся измерения, в нужных точках на AB ?
608. На одной стороне линий потока PA = 586,3 фута, PB = 751,6 фута — это размеры, угол APB составляет 167 ° 36 ‘. Q — точка на противоположной стороне ручья. Угол PAQ = 63 ° 18 ‘и PBQ = 49 ° 24′. Найдите PQ.
612. Чтобы найти расстояние между двумя недоступными точками P и Q, откладывается линия AB длиной 763,4 фута, так что произведенный AB пересекает PQ снаружи [то есть два отрезки AB и PQ не пересекаются]. Углы PAB = 98 ° 47 ‘, QAB = 41 ° 36′, PBA = 37 ° 16 ‘и QBA = 94 ° 12′. Найдите длину PQ.
Подсказки
553. Вы можете использовать закон синусов, чтобы определить любую из длин: AB, или BC. Вопрос в том, чтобы найти расстояние от C до AB. Это означает, что вы опускаете перпендикуляр от C к этой линии и определяете его длину. Вы можете использовать угол A и линию AC , чтобы найти его, или вы можете использовать угол B и линию BC , чтобы найти его.
557. Тот же намек, что и 553.
561. Окружности касаются друг друга, поэтому линия от одного центра до другого представляет собой сумму радиусов одной окружности и другой. У вас есть треугольник со сторонами 7, 8 и 9. Вы можете использовать закон косинусов, чтобы найти углы.
563. Здесь хорошо работает закон синусов.
570. Нарисуйте фигуру. Чтобы найти PQ, сначала найдите AP и AQ. Вы можете найти AP , используя закон синусов на треугольнике ABP, , и вы можете найти AQ , используя закон синусов на треугольнике ABQ.
579. Вам известны стороны треугольников ABC, и ADC, , поэтому вы можете определить их углы. В треугольнике ABD вы знаете угол и две смежные стороны, поэтому вы можете найти противоположную сторону BD.
580. Сначала решите треугольник ABC. Далее в треугольнике ABD вы знаете две стороны и легко можете определить угол BAD.
586. «Включенный угол» — это один из двух углов между двумя диагоналями. Другой включенный угол — это его дополнение 180 ° — 70 ° 12 ’38 «. Пусть P будет точкой, где встречаются две диагонали. Это середина каждой диагонали, так что вы знаете расстояние между P и любой вершиной.Используйте закон косинусов для двух треугольников с вершинами P и двух вершин параллелограмма.
590. Вы знаете стороны четырехугольника ABCD и угол B. Вы можете решить треугольник ABC. Тогда вы знаете все стороны треугольника ACD, и можете найти его углы.
593. Сначала определите расстояние AB по закону синусов.Тогда для каждого из правильных положений лодки P, вы знаете две стороны и включенный угол треугольника PAC, , так что вы можете определить необходимый угол, используя закон косинусов.
608. Сначала решите треугольник APB. Тогда у вас будет достаточно информации, чтобы решить треугольник AQB.
612. Есть несколько способов решить эту проблему. Вот один способ. Определите PA , используя закон синусов для треугольника PAB, и определите QA , используя закон синусов для треугольника QAB. Затем используйте закон косинусов для треугольника PAQ.
ответы
553. 345,43 футов.
557. 490,83 футов.
561. 48 ° 11 ’24 «, 58 ° 24′ 42», 73 ° 23 ’54 «.
563. 640 футов 10 дюймов.
570. 651,9 футов.
579. 106 ° 18 ’46 дюймов, 73 ° 41′ 14 дюймов, 452,92.
580. 255,93, 372,11, 369,22.
586. 231,94, 328,93.
590. 125 ° 6 ’12 «, 70 ° 57′ 54», 110 ° 42 ’42 «.
593. 23 ° 27 ‘, 47 ° 58, 66 ° 34’.





 Найдите большую высоту этого параллелограмма.
Найдите большую высоту этого параллелограмма.




 В ответе запишите площадь, умноженную на √3.
В ответе запишите площадь, умноженную на √3.


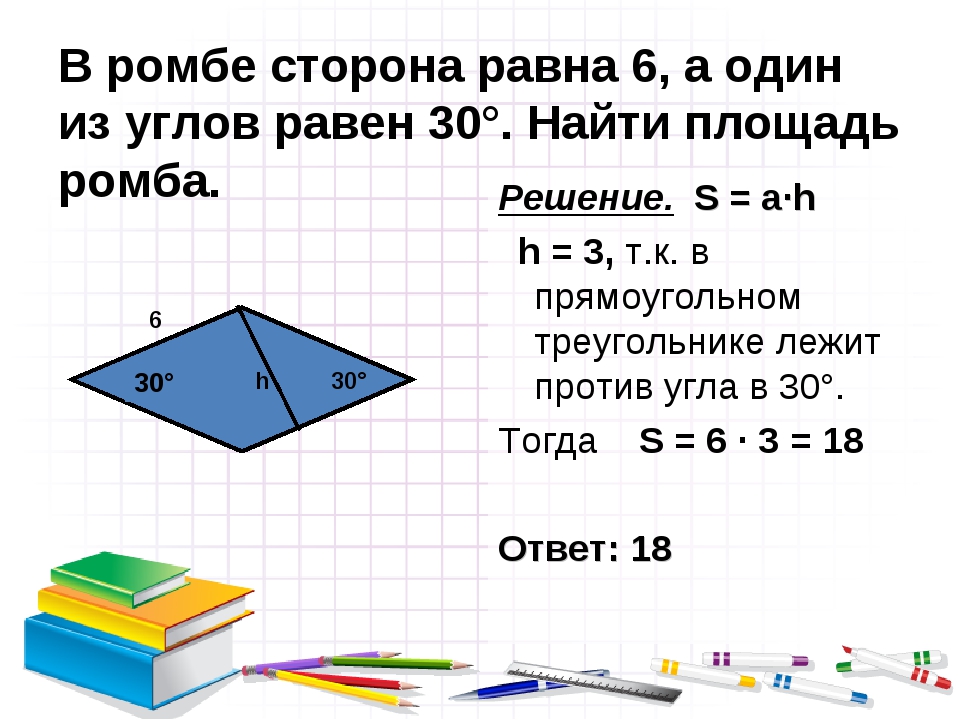

 Ответ дайте в квадратных сантиметрах.
Ответ дайте в квадратных сантиметрах.
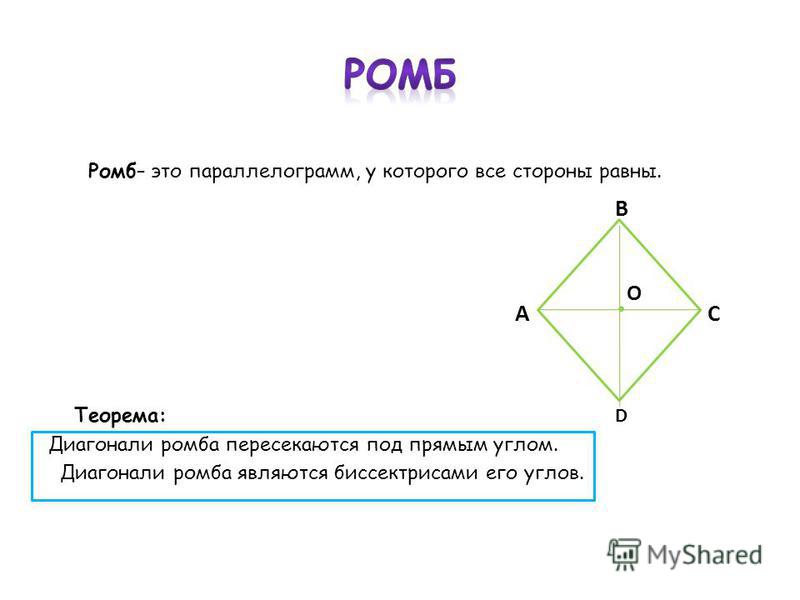

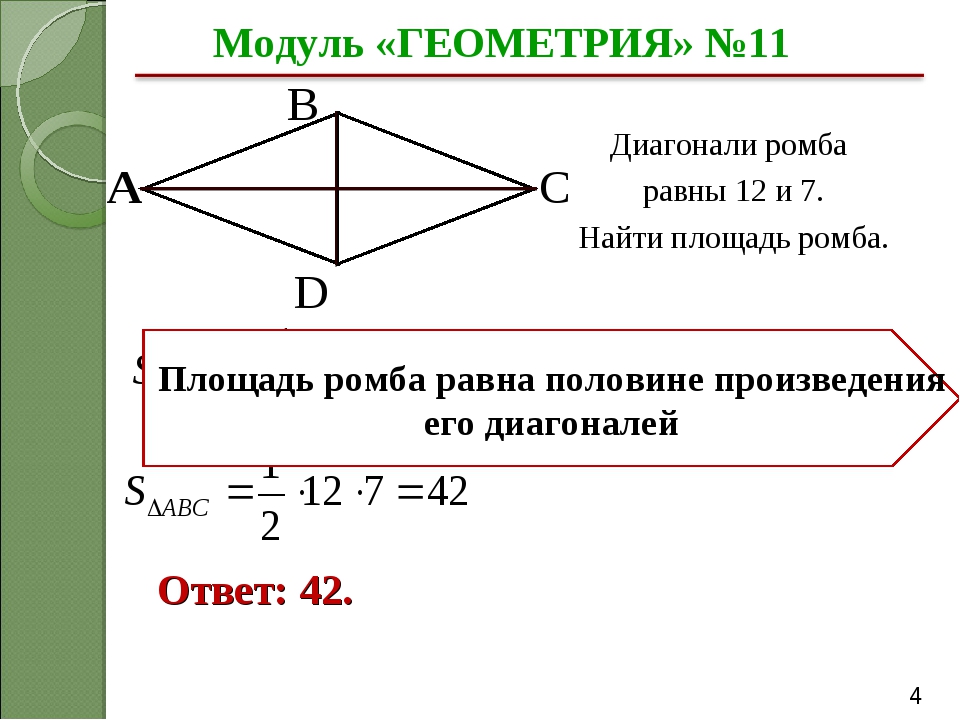 Знайдіть проекції діагоналей ромба на цю площину. Основание прямой призмы-ромб со стороной 5 см и тупым углом 120 градусов, боковая поверхность призмы имеет площадь равную 240 см. Найдите площадь сечения призмы, проходящее через боковое ребро и меньшую диагональ основания.Основание прямого параллелепипеда является ромб с диагоналями 10 и 24 см. Меньшая диагональ параллелепипеда образует с плоскостью основания угол в 45 градусов. Найти площадь полной поверхностиНайдите sin, cos, tg острого угла ромба, если Р= 52 см, S=120смОснование прямого параллелепипеда — ромб с диагоналями 10 и 24 см. Меньшая диоганаль параллепипеда образует с плоскостью оснований угол 45 градусов. Найдите площадь полной поверхности параллепипеда.Сторона АВ ромба ABCD равна a, а один из его углов равен 60гр. Через сторону АВ проведена плоскость альфа на расстоянии а2 от точки D. А)Найти расстояние от точки С до плоскости альфа. Б)Показать на рисунке линейный угол двугранного угла DABM, M принадлежит пл. Альфа.
Знайдіть проекції діагоналей ромба на цю площину. Основание прямой призмы-ромб со стороной 5 см и тупым углом 120 градусов, боковая поверхность призмы имеет площадь равную 240 см. Найдите площадь сечения призмы, проходящее через боковое ребро и меньшую диагональ основания.Основание прямого параллелепипеда является ромб с диагоналями 10 и 24 см. Меньшая диагональ параллелепипеда образует с плоскостью основания угол в 45 градусов. Найти площадь полной поверхностиНайдите sin, cos, tg острого угла ромба, если Р= 52 см, S=120смОснование прямого параллелепипеда — ромб с диагоналями 10 и 24 см. Меньшая диоганаль параллепипеда образует с плоскостью оснований угол 45 градусов. Найдите площадь полной поверхности параллепипеда.Сторона АВ ромба ABCD равна a, а один из его углов равен 60гр. Через сторону АВ проведена плоскость альфа на расстоянии а2 от точки D. А)Найти расстояние от точки С до плоскости альфа. Б)Показать на рисунке линейный угол двугранного угла DABM, M принадлежит пл. Альфа. В)НайОснованием прямого параллелепипеда ABCDA1B1C1D1 является ромб ABCD, сторона которого равна а и угол равен 60. Плоскость AD1C1 составляет с плоскостью основания угол 60. Найдите: а)высоту ромба б)высоту параллелепипеда в)площадь боковой поверхности параллелепипеда г)площадь поверхности параллелепипедОснованием пирамиды служит ромб, сторонаи которого равна а, а острый угол 60⁰. Боковые грани наклонены к основанию под углом 45⁰. Найдите высоту пирамиды и площадь ее боковой поверхности.Диагонали ромба «abcd» пересекаются в точке «о». Докажите, что прямая «bd» касается окружности с центром «а» и радиусом, равным «ос».Сторона ромбы равна 50 см, А ОДНА ИЗ ДИАГОНАЛЕЙ-60СМ. НАЙДИТЕ РАДИУС ОКРУЖНОСТИ, ВПИСАННЫЙ В РОМБ.Диагонали ромба АВСD пересекаются в точке О. Докажите, что прямая BD касается окружности с центром А и радиусом, равным ОС. Нужно решениеДан робм. Периметр ромба равен 24 см. Его вы высота равна 4 см. Найти площадь?Сторона ромба равна 8см, а его острый угол 60 градусам.
В)НайОснованием прямого параллелепипеда ABCDA1B1C1D1 является ромб ABCD, сторона которого равна а и угол равен 60. Плоскость AD1C1 составляет с плоскостью основания угол 60. Найдите: а)высоту ромба б)высоту параллелепипеда в)площадь боковой поверхности параллелепипеда г)площадь поверхности параллелепипедОснованием пирамиды служит ромб, сторонаи которого равна а, а острый угол 60⁰. Боковые грани наклонены к основанию под углом 45⁰. Найдите высоту пирамиды и площадь ее боковой поверхности.Диагонали ромба «abcd» пересекаются в точке «о». Докажите, что прямая «bd» касается окружности с центром «а» и радиусом, равным «ос».Сторона ромбы равна 50 см, А ОДНА ИЗ ДИАГОНАЛЕЙ-60СМ. НАЙДИТЕ РАДИУС ОКРУЖНОСТИ, ВПИСАННЫЙ В РОМБ.Диагонали ромба АВСD пересекаются в точке О. Докажите, что прямая BD касается окружности с центром А и радиусом, равным ОС. Нужно решениеДан робм. Периметр ромба равен 24 см. Его вы высота равна 4 см. Найти площадь?Сторона ромба равна 8см, а его острый угол 60 градусам.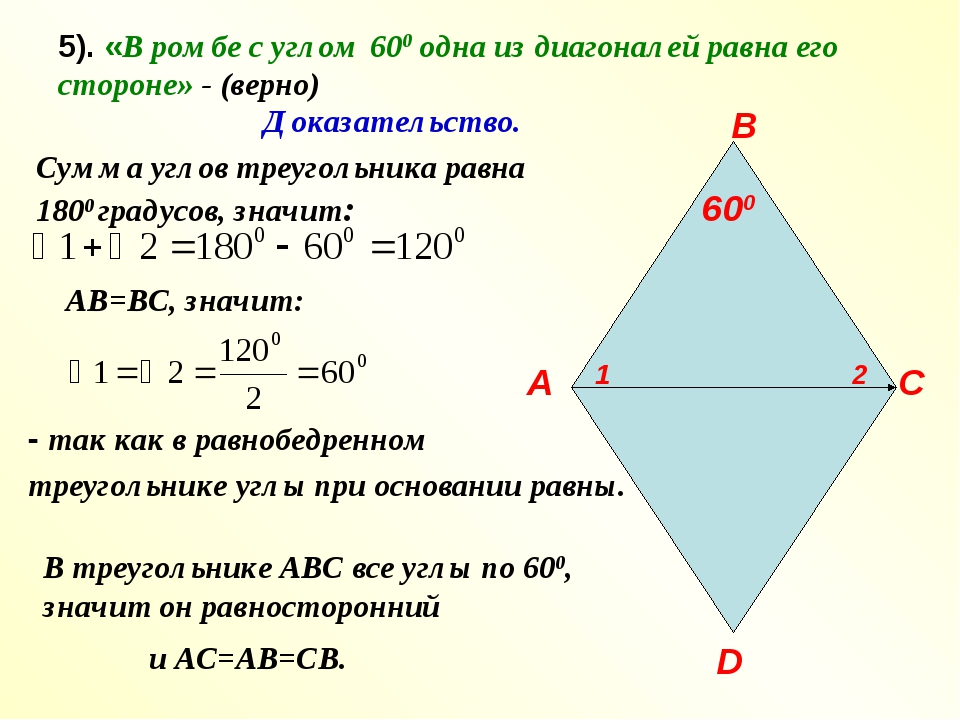 Найдите площадь ромба.Одна из диагоналей ромба на 4 см больше другой, а площадь равна 96 см квадратных. Найти стороны ромба.Найти углы ромба, если его диагонали равны 2корней из 3 и 2.Диагонали ромба равны 30см и 40см. Найдите радиус окружности, вписано в ромб Основанием пирамиды является ромб, стороны которого равны 5 см, а одна из диагоналей равна 8 см. Найдите боковые рёбра пирамиды, если высота её проходит через точку пересечения диагоналей и равна 7 см.Диагональ ромба образует с одной из его сторон угол 20. Найти углы ромбаВычислить длину меньшей диагональной прямой призмы в основании, которой ромб со стороной=6м, острый угол 60, высота призмы 8м.Найдите сторону и площадь ромба, если его диагонали равны 10 см. И 24 см.В ромбе высота, проведенная из вершины тупого угла, делит его сторону пополам. Найдите: а)углы ромба б)его периметр, если меньшая диагональ равна 3,5смВ ромбе АВСD угол А = 60 0, сторона ромба равна 4 см. Прямая АЕ перпендикулярна плоскости ромба. Расстояние от точки Е до прямой DС равно 4 см.
Найдите площадь ромба.Одна из диагоналей ромба на 4 см больше другой, а площадь равна 96 см квадратных. Найти стороны ромба.Найти углы ромба, если его диагонали равны 2корней из 3 и 2.Диагонали ромба равны 30см и 40см. Найдите радиус окружности, вписано в ромб Основанием пирамиды является ромб, стороны которого равны 5 см, а одна из диагоналей равна 8 см. Найдите боковые рёбра пирамиды, если высота её проходит через точку пересечения диагоналей и равна 7 см.Диагональ ромба образует с одной из его сторон угол 20. Найти углы ромбаВычислить длину меньшей диагональной прямой призмы в основании, которой ромб со стороной=6м, острый угол 60, высота призмы 8м.Найдите сторону и площадь ромба, если его диагонали равны 10 см. И 24 см.В ромбе высота, проведенная из вершины тупого угла, делит его сторону пополам. Найдите: а)углы ромба б)его периметр, если меньшая диагональ равна 3,5смВ ромбе АВСD угол А = 60 0, сторона ромба равна 4 см. Прямая АЕ перпендикулярна плоскости ромба. Расстояние от точки Е до прямой DС равно 4 см.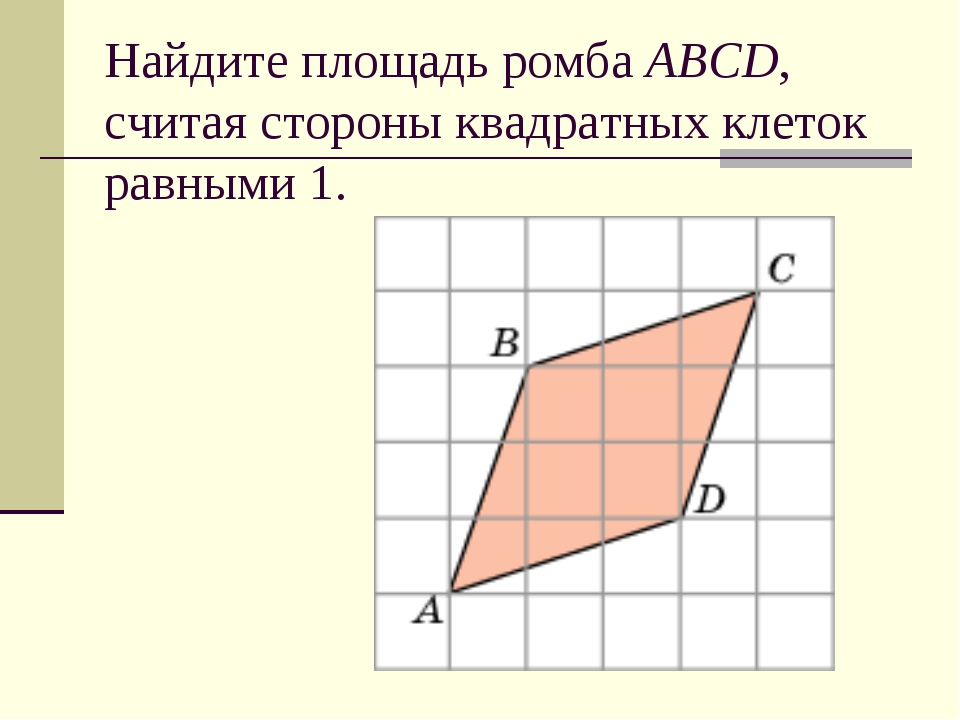 Найдите расстояние от точки Е до плоскости ромба.Большая диагональ ромба равна 12 см а один из его углов равен 60. Найдите длину вписанной в него окружностиМенша діагональ ромба = 10 см, а висота 8 см, Знайдіть сторону ромбаБоковая сторона ромба ровна 25см, а разница диагоналей составляет 10см. Найдите площадь ромба.Сторона ромба 13 см, а одна із діагоналей 24 см. Знайдіть другу діагональ ромба. )Найдите площадь ромба если его сторона 15 см, а сумма диагоналей 42.Из точки данной окружности проведены две хорды, равные радиусу. Найдите угол между ними
Найдите расстояние от точки Е до плоскости ромба.Большая диагональ ромба равна 12 см а один из его углов равен 60. Найдите длину вписанной в него окружностиМенша діагональ ромба = 10 см, а висота 8 см, Знайдіть сторону ромбаБоковая сторона ромба ровна 25см, а разница диагоналей составляет 10см. Найдите площадь ромба.Сторона ромба 13 см, а одна із діагоналей 24 см. Знайдіть другу діагональ ромба. )Найдите площадь ромба если его сторона 15 см, а сумма диагоналей 42.Из точки данной окружности проведены две хорды, равные радиусу. Найдите угол между ними