Xy 0 график: Mathway | Популярные задачи — ошкольное образовательное учреждение № 4 «Алёнушка»

(1/2))

Содержание

Канонический вид кривой и поверхности

Вы можете определить вид кривой и поверхности 2-го порядка онлайн с подробным решением:

Правила ввода выражений и функций

Выражения могут состоять из функций (обозначения даны в алфавитном порядке):

absolute(x): Абсолютное значение x
(модуль x или |x|)
arccos(x): Функция — арккосинус от x
arccosh(x): Арккосинус гиперболический от x
arcsin(x): Арксинус от x
arcsinh(x): Арксинус гиперболический от x
arctg(x): Функция — арктангенс от x
arctgh(x): Арктангенс гиперболический от x
exp(x): Функция — экспонента от x (что и e^x)
log(x) or ln(x): Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10))
sin(x): Функция — Синус от x
cos(x): Функция — Косинус от x
sinh(x): Функция — Синус гиперболический от x
cosh(x): Функция — Косинус гиперболический от x
sqrt(x): Функция — квадратный корень из x
sqr(x) или x^2: Функция — Квадрат x
ctg(x): Функция — Котангенс от x
arcctg(x): Функция — Арккотангенс от x
arcctgh(x): Функция — Гиперболический арккотангенс от x
tg(x): Функция — Тангенс от x
tgh(x): Функция — Тангенс гиперболический от x
cbrt(x): Функция — кубический корень из x
gamma(x): Гамма-функция
LambertW(x): Функция Ламберта
x! или factorial(x): Факториал от x

В выражениях можно применять следующие операции:

Действительные числа: вводить в виде 7. 3; — возведение в степень
x + 7: — сложение
x — 6: — вычитание
15/7: — дробь

Другие функции:

asec(x): Функция — арксеканс от x
acsc(x): Функция — арккосеканс от x
sec(x): Функция — секанс от x
csc(x): Функция — косеканс от x
floor(x): Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
ceiling(x): Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)
sign(x): Функция — Знак x
erf(x): Функция ошибок (или интеграл вероятности)
laplace(x): Функция Лапласа
asech(x): Функция — гиперболический арксеканс от x
csch(x): Функция — гиперболический косеканс от x
sech(x): Функция — гиперболический секанс от x
acsch(x): Функция — гиперболический арккосеканс от x

Постоянные:

pi: Число «Пи», которое примерно равно ~3. 14159..
e: Число e — основание натурального логарифма, примерно равно ~2,7183..
i: Комплексная единица
oo: Символ бесконечности — знак для бесконечности

график

Формат для duration метки в виде галочки в виде разделенной запятой пары, состоящей из 'DurationTickFormat' и вектор символов или строка, содержащая формат длительности.

Если вы не задаете значение для 'DurationTickFormat'то plot автоматически оптимизирует и обновляет метки в виде галочки на основе пределов по осям.

Чтобы отобразить длительность как, один номер, который включает дробную часть, например, 1,234 часа, задает одно из значений в этой таблице.

Значение `DurationTickFormat`	Описание
`'y'`	Номер точных лет фиксированной длины. Год фиксированной длины равен 365,2425 дням.
`'d'`	Номер точных дней фиксированной длины. День фиксированной длины равен 24 часам.
`'h'`	Номер часов
`'m'`	Номер минут
`'s'`	Номер секунд

Пример: 'DurationTickFormat','d' значения длительности отображений в терминах дней фиксированной длины.

Чтобы отобразить длительность в форме цифрового таймера, задайте одно из этих значений.

'dd:hh:mm:ss'
'hh:mm:ss'
'mm:ss'
'hh:mm'

Кроме того, можно отобразить до девяти цифр доли секунды путем добавления до девяти S ‘characters’.

Пример: 'DurationTickFormat','hh:mm:ss.SSS' отображает миллисекунды значения длительности к трем цифрам.

DurationTickFormat не свойство линии на графике. Необходимо установить формат метки деления с помощью аргумента пары «имя-значение» при создании графика. В качестве альтернативы установите формат с помощью xtickformat и ytickformat функции.

TickLabelFormat свойство линейки длительности хранит формат.

Matplotlib. Урок 4.1. Визуализация данных. Линейный график

Линейный график – это один из наиболее часто используемых видов графика для визуализации данных. Он использовался нами для демонстрации возможностей Matplotlib в предыдущих уроках, в этом уроке мы более подробно рассмотрим возможности настройки его внешнего вида.

Построение графика

Для построения линейного графика используется функция plot(), со следующей сигнатурой:

plot([x], y, [fmt], *, data=None, **kwargs)

plot([x], y, [fmt], [x2], y2, [fmt2], …, **kwargs)

Если вызвать функцию plot() с одним аргументом – вот так: plot(y), то мы получим график, у которого по оси ординат (ось y) будут отложены значения из переданного списка, по по оси абсцисс (ось x) – индексы элементов массива.

Рассмотрим аргументы функции plot():

x, x2, …: array
- Набор данных для оси абсцисс первого, второго и т.д. графика.
y, y2, …: array
- Набор данных для оси ординат первого, второго и т.д. графика.
fmt: str
- Формат графика, задается в виде строки: ‘[marker][line][color]’.
**kwargs – свойства класса Line2D, которые предоставляют доступ к большому количеству настроек внешнего вида графика, отметим наиболее полезные:

Свойство	Тип	Описание
alpha	float	Прозрачность
color или c	color	Цвет
fillstyle	{‘full’, ‘left’, ‘right’, ‘bottom’, ‘top’, ‘none’}	Стиль заливки
label	object	Текстовая метка
linestyle или ls	{‘-‘, ‘–‘, ‘-. ’, ‘:’, ”, (offset, on-off-seq), …}	Стиль линии
linewidth или lw	float	Толщина линии
marker	matplotlib.markers	Стиль маркера
markeredgecolor или mec	color	Цвет границы маркера
markeredgewidth или mew	float	Толщина границы маркера
markerfacecolor или mfc	color	Цвет заливки маркера
markersize или ms	float	Размер маркера

Параметры аргумента fmt

marker: str

Определяет тип маркера, может принимать одно из значений, представленных в таблице ниже

Символ	Описание
‘.’	Точка (point marker)
‘,’	Пиксель (pixel marker)
‘o’	Окружность (circle marker)
‘v’	Треугольник, направленный вниз (triangle_down marker)
‘^’	Треугольник, направленный вверх(triangle_up marker)
‘<‘	Треугольник, направленный влево (triangle_left marker)
‘>’	Треугольник, направленный вправо (triangle_right marker)
‘1’	Треугольник, направленный вниз (tri_down marker)
‘2’	Треугольник, направленный вверх(tri_up marker)
‘3’	Треугольник, направленный влево (tri_left marker)
‘4’	Треугольник, направленный вправо (tri_right marker)
‘s’	Квадрат (square marker)
‘p’	Пятиугольник (pentagon marker)
‘*’	Звезда (star marker)
‘h’	Шестиугольник (hexagon1 marker)
‘H’	Шестиугольник (hexagon2 marker)
‘+’	Плюс (plus marker)
‘x’	Х-образный маркер (x marker)
‘D’	Ромб (diamond marker)
‘d’	Ромб (thin_diamond marker)
‘\|’	Вертикальная линия (vline marker)
‘_’	Горизонтальная линия (hline marker)

line: str

Стиль линии/ Может принимать одно из следующих значений:

Символ	Описание
‘-‘	Сплошная линия (solid line style)
‘–‘	Штриховая линия (dashed line style)
‘-. ’	Штрих-пунктирная линия (dash-dot line style)
‘:’	Штриховая линия (dotted line style)

color

Цвет графика. В рамках аргумента fmt цвет задается значением из следующей таблицы:

Символ	Описание
‘b’	Синий
‘g’	Зеленый
‘r’	Красный
‘c’	Бирюзовый
‘m’	Фиолетовый (пурпурный)
‘y’	Желтый
‘k’	Черный
‘w’	Белый

Реализуем возможности plot() на примере:

x = [1, 5, 10, 15, 20]
y1 = [1, 7, 3, 5, 11]
y2 = [4, 3, 1, 8, 12]

plt.figure(figsize=(12, 7))

plt.plot(x, y1, 'o-r', alpha=0.7, label="first", lw=5, mec='b', mew=2, ms=10)
plt.plot(x, y2, 'v-.g', label="second", mec='r', lw=2, mew=2, ms=12)
plt. legend()
plt.grid(True)

Рассмотрим различные варианты использования линейного графика.

Заливка области между графиком и осью

Для заливки областей используется функция fill_between(). Сигнатура функции:

fill_between(x, y1, y2=0, where=None, interpolate=False, step=None, *, data=None, **kwargs)

Основные параметры функции:

x : массив длины N
- Набор данных для оси абсцисс.
y1 : массив длины N или скалярное значение
- Набор данных для оси ординат – первая кривая.
y2 : массив длины N или скалярное значение
- Набор данных для оси ординат – вторая кривая.
where: массив bool элементов (длины N), optional, значение по умолчанию: None
- Задает заливаемый цветом регион, который определяется координатами x[where]: интервал будет залит между x[i] и x[i+1], если where[i] и where[i+1] равны True.
step: {‘pre’, ‘post’, ‘mid’}, optional
- Определяет шаг, если используется step-функция для отображения графика (будет рассмотрена в одном из следующих уроков).
**kwargs
- Свойства класса Polygon

Создадим набор данных для эксперимента:

import numpy as np

x = np.arange(0.0, 5, 0.01)
y = np.cos(x*np.pi)

Отобразим график с заливкой:

plt.plot(x, y, c = "r")
plt.fill_between(x, y)

Изменим правила заливки:

plt.plot(x, y, c = "r")
plt.fill_between(x, y, where = (y > 0.75) | (y < -0.75))

Используя параметры y1 и y2 можно формировать более сложные решения.

Заливка области между 0 и y, при условии, что y >= 0:

plt.plot(x, y, c = "r")
plt.fill_between(x, y, where = (y > 0))

Заливка области между 0.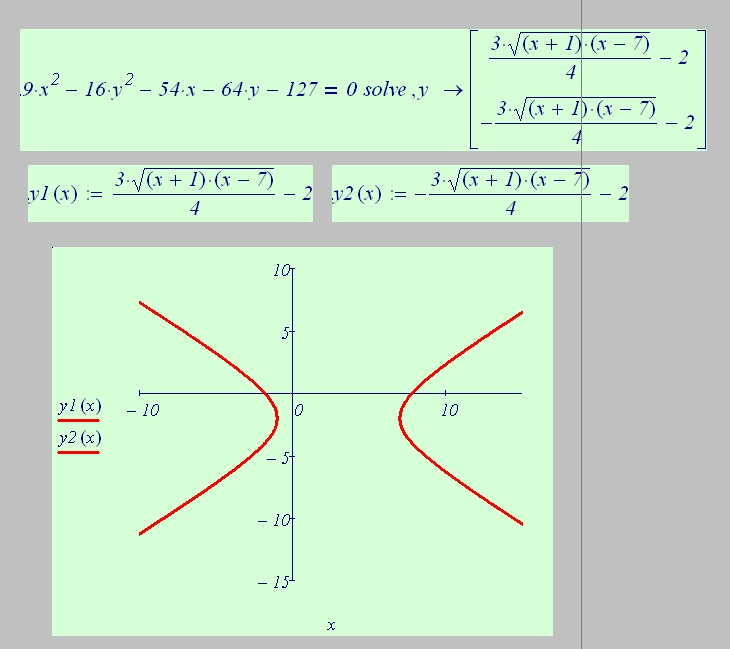 5 и y, при условии, что y >= 0.5:

plt.plot(x, y, c = "r")
plt.grid()
plt.fill_between(x, 0.5, y, where=y>=0.5)

Заливка область между y и 1:

plt.plot(x, y, c = "r")
plt.grid()
plt.fill_between(x, y, 1)

Вариант двухцветной заливки:

plt.plot(x, y, c = "r")
plt.grid()
plt.fill_between(x, y, where=y>=0, color="g", alpha=0.3)
plt.fill_between(x, y, where=y<=0, color="r", alpha=0.3)

Настройка маркировки графиков

В начале этого раздела мы приводили пример использования маркеров при отображении графиков. Сделаем это ещё раз, но уже в упрощенном виде:

x = [1, 2, 3, 4, 5, 6, 7]
y = [7, 6, 5, 4, 5, 6, 7]

plt.plot(x, y, marker="o", c="g")

В наборе данных, который создает код:

import numpy as np

x = np. arange(0.0, 5, 0.01)
y = np.cos(x*np.pi)

количество точек составляет 500, поэтому подход, представленный выше уже будет не применим:

plt.plot(x, y, marker="o", c="g")

В этой случае нужно задать интервал отображения маркеров, для этого используется параметр markevery, который может принимать одно из следующих значений:

None – отображаться будет каждая точка;

N – отображаться будет каждая N-я точка;

(start, N) – отображается каждая N-я точка начиная с точки start;

slice(start, end, N) – отображается каждая N-я точка в интервале от start до end;

[i, j, m, n] – будут отображены только точки i, j, m, n.

Ниже представлен пример, демонстрирующий работу с markevery:

x = np.arange(0.0, 5, 0.01)
y = np.cos(x*np.pi)

m_ev_case = [None, 10, (100, 30), slice(100,400,15), [0, 100, 200, 300], [10, 50, 100]]

fig, ax = plt. subplots(2, 3, figsize=(10, 7))
axs = [ax[i, j] for i in range(2) for j in range(3)]

for i, case in enumerate(m_ev_case):
    axs[i].set_title(str(case))
    axs[i].plot(x, y, "o", ls='-', ms=7, markevery=case)

Обрезка графика

Для того, чтобы отобразить только часть графика, которая отвечает определенному условию используйте предварительное маскирование данных с помощью функции masked_where из пакета numpy.

x = np.arange(0.0, 5, 0.01)
y = np.cos(x*np.pi)

y_masked = np.ma.masked_where(y < -0.5, y)

plt.ylim(-1, 1)
plt.plot(x, y_masked, linewidth=3)

P.S.

Вводные уроки по “Линейной алгебре на Python” вы можете найти соответствующей странице нашего сайта. Все уроки по этой теме собраны в книге “Линейная алгебра на Python”.

Если вам интересна тема анализа данных, то мы рекомендуем ознакомиться с библиотекой Pandas. Для начала вы можете познакомиться с вводными уроками. Все уроки по библиотеке Pandas собраны в книге “Pandas. Работа с данными”.

Представление данных в виде точечной диаграммы или графика

Основное различие между точечная и графиками заключается в способе их отстройки на горизонтальной оси. Например, если использовать следующие данные листа для построения точечной диаграммы и графика, они будут представлены по-разному:

На точечной диаграмме значения суточного количества осадков из столбца A отображаются в виде значений X на горизонтальной оси (X), а показатели содержания твердых частиц из столбца B — в виде значений на вертикальной оси (Y). На точечной диаграмме категории никогда не отображаются на горизонтальной оси.

На точечной диаграмме всегда есть две оси значений, то есть один набор числовых данных представлен вдоль горизонтальной оси, а другой — вдоль вертикальной. На пересечении координат X и Y отображается точка данных, объединяющая эти два числовых значения. Такие точки данных могут быть распределены по горизонтальной оси равномерно или неравномерно, в зависимости от конкретных данных.

Первая точка данных на точечной диаграмме представляет значение Y (содержание частиц), равное 137, и значение X (суточная норма осадков), равное 1,9. Эти числа представляют значения в ячейках A9 и B9 на листе.

На графике те же значения суточного количества осадков и содержания частиц будут показаны как две разные точки данных, которые равномерно распределяются вдоль горизонтальной оси. Дело в том, что на графике есть только одна ось значений (вертикальная ось). Горизонтальная ось графика предназначена для отображения группировок (категорий) данных с равномерными интервалами. Так как категории не были заданы, они генерируются автоматически, например 1, 2, 3 и т. д.

Это наглядный пример ситуации, когда график использовать не следует.

На графиках данные категории равномерно распределяются вдоль горизонтальной оси (оси категорий), а все числовые значения откладываются по вертикальной оси (оси значений).

Значение Y (содержание частиц), равное 137 (ячейка B9), и значение X (суточное количество осадков), равное 1,9 (ячейка A9), показаны на графике двумя разными точками данных. Ни одна из этих точек данных не является первой точкой данных, отображаемой на диаграмме. Вместо этого первая точка данных для каждого значения ряд данных ссылается на значения в первой строке данных на этом сайте (ячейки A2 и B2).

Различия между типами и шкалами осей

Так как горизонтальная ось точечной диаграммы всегда является осью значений, на ней можно показывать числа и даты (в том числе дни и часы), представляемые в виде числовых значений. Чтобы отображать числовые значения вдоль горизонтальной оси с большей гибкостью, можно изменить параметры ее шкалы аналогично тому, как изменяется настройка шкалы вертикальной оси.

Поскольку горизонтальная ось графика — это ось категорий, она может быть только осью текста или осью дат. На оси текста отображается только текст (нечисловые данные или числовые категории, не являющиеся значениями) с равномерными интервалами. На оси дат отображаются даты в хронологическом порядке через заданные интервалы (базовые единицы измерения), такие как число дней, месяцев или лет, даже если даты на листе расположены в ином порядке или выражены в других единицах.

Набор параметров шкалы оси категорий ограничен по сравнению с параметрами шкалы оси значений. Доступные параметры шкалы также зависят от типа используемой оси.

Открытая Математика. Функции и Графики. Решение систем уравнений и неравенств

Уравнение g (x, y) = 0 задает на координатной плоскости некоторую кривую, каждая точка M (x; y) которой удовлетворяет этому уравнению.

Некоторые кривые являются графиками функций y = f (x), что означает равносильность уравнений g (x, y) = 0 и y = f (x). К таковым, например, относится кривая, задаваемая уравнениями x + y – 1 = 0 или y – x² = 0.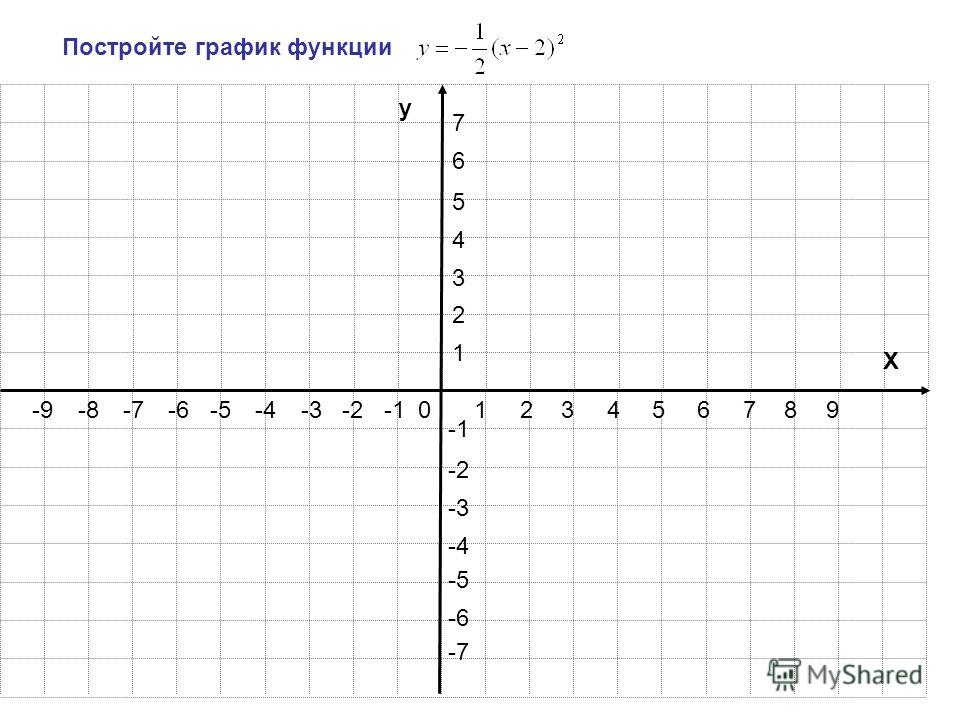 Другим не соответствуют никакие функции, например, x2+y2-1=0
(в данном случае каждому значению

x∈(-1; 1)

соответствуют два значения y).

Окружность с центром в точке (-2; 1)

Гипербола, задаваемая уравнением x² – y² = 1.

Уравнением окружности с центром в точке (a; b) и радиусом r > 0 является

(x – a)² + (y – b)² = r².

Уравнение (x – a)² + (y – b)² = 0 задает точку с координатами (a; b), уравнение x² – y² = a² – гиперболу.

Уравнение вида

f (x, y) · g (x, y) = 0

задает на плоскости объединение линий f (x, y) = 0 и g (x, y) = 0. Каждая точка этой фигуры является решением совокупности уравнений

[fx, y=0;gx, y=0.

Система уравнений с двумя переменными

Пусть задана система уравнений

{fx, y=0,gx, y=0.

Ее решением является совокупность пар чисел (x_i; y_i), подстановка которых в каждое из уравнений превращает его в верное равенство. Построим на координатной плоскости кривые, задаваемые уравнениями f (x, y) = 0 и g (x, y) = 0. Тогда можно сказать, что геометрически решением системы уравнений является совокупность всех точек M_i (x_i; y_i), в которых пересекаются кривые, задаваемые этими уравнениями.

Если кривые не пересекаются, то система уравнений решений не имеет. В этом случае говорят, что система несовместна.

Систему

{fx, y=0,gx, y=0,hx, y=0,

геометрически можно представить как совокупность точек, в которых пересекаются три кривые f (x, y) = 0, g (x, y) = 0 и h (x, y) = 0. Если не существует точки, в которой пересекаются все три кривые, то система также несовместна.

Аналогичным образом уравнение f (x, y, z) = 0 задает поверхность в трехмерной декартовой системе координат. Геометрически решением системы уравнений

{fx, y, z=0,gx, y, z=0,hx, y, z=0,

будет совокупность координат точек M_i (x_i; y_i; z_i), в которых пересекаются поверхности, задаваемые этими уравнениями.

Так, уравнения x² + y² + z² = 1, y = 0, z = 0 задают в пространстве сферу единичного радиуса с центром в начале координат и две координатные плоскости, перпендикулярные соответственно оси ординат и оси аппликат. Плоскость z = 0 пересекает сферу по окружности x² + y² = 1, лежащей в плоскости z = 0. Плоскость y = 0 пересекает эту окружность в двух точках с координатами M₁ (–1; 0; 0) и M₂ (1; 0; 0). Таким образом, решением системы уравнений

{x2+y2+z2=1,y=0,z=0,

являются две тройки чисел (±1; 0; 0).

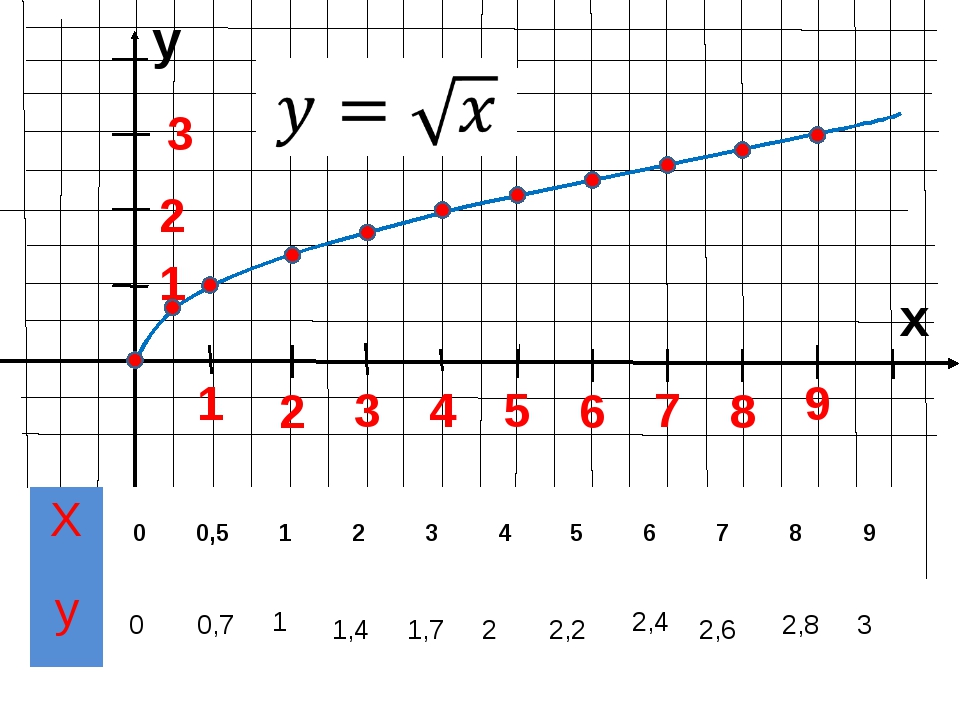Иногда при решении задач графики могут ввести в заблуждение.

Так, на эскизе кажется, что графики функций y = (1/16)^x и y = log_1/16 x пересекаются только в одной точке, лежащей на биссектрисе первого координатного угла. И только при более внимательном рассмотрении у уравнения (1/16)x = log_1/16 x находятся еще два корня x = 1/2 и x = 1/4. Увеличьте масштаб графика, чтобы убедиться в этом

Кривая f (x, y) = 0 делит координатную плоскость на несколько областей, внутри каждой из которых функция f сохраняет знак. Для решения неравенства

f (x, y) > 0

графическим методом необходимо в каждой из таких областей взять пробную точку и вычислить ее знак, после чего отобрать области, в которых функция f принимает положительные значения. Присоединяя к полученному решению саму кривую, получим решение неравенства

f (x, y) ≥ 0.

Чтобы решить графически систему

{fx, y>0gx, y>0,

нужно изобразить на координатной плоскости решения каждого из неравенств f (x, y) > 0, g (x, y) > 0, а затем найти их пересечение. 3\)):

Стандартные графики

Графики (точечные и линейные) – базовый и наиболее часто используемый способ визуализации. Универсальная функция plot() позволяет строить графики по координатам $X$ и $Y$, которые передаются, соответственно, в первый и второй аргумент. Если переменные $X$ и $Y$ не связаны друг с другом явным образом, то такой график называется диаграммой рассеяния.

Диаграммы рассеяния

Диаграмма рассеяния позволяет установить, есть ли зависимость между переменными, а также понять, как объекты дифференцируются по значениям переменных.

par(mar=c(4,4,3,2))
# Диаграмма рассеяния по экспорту и импорту:
plot(sub$МетЭкспорт, 
     sub$МетИмпорт,
     col="red", 
     xlab="Экспорт, млн. долл. США", 
     ylab = "Импорт, млн. долл. США", 
     main = "Экспорт/импорт металлов и изделий из них по субъектам РФ")

В данном случае четко выделяется группа субъектов вблизи начала координат, не отличающихся интенсивным экспортом и импортом продукции металлургии, а также очевидно преобладание экспорта над импортом при больших объемах товарооборота.

При построении диаграмм рассеяния важно сохранить одинаковый масштаб по осям $X$ и $Y$. Чтобы обеспечить это условие, необходимо использовать параметр asp = 1:

plot(sub$МетЭкспорт, 
     sub$МетИмпорт, 
     col="red", 
     xlab="Экспорт, млн. долл. США", 
     ylab = "Импорт, млн. долл. США", 
     main = "Экспорт/импорт металлов и изделий из них по субъектам РФ", 
     asp = 1)

Попробуйте изменить размер окна на вкладке Plots. Вы увидите, что масштаб по осям сохраняется пропорциональным.

Размер и тип значка можно изменить, используя параметры pch = и cex =. Размеры масштабируются параметром cex относительно условной единицы — стандартного размер значка. Сам значок можно выбрать, используя его код в соответствии с нижеприведенным рисунком (на самом деле, вы можете выбирать произвольные символы для визуализации точек):

Типы символов R

plot(sub$МетЭкспорт, 
     sub$МетИмпорт, 
     col="red", 
     xlab="Экспорт, млн.  долл. США", 
     ylab = "Импорт, млн. долл. США", 
     main = "Экспорт/импорт металлов и изделий из них по субъектам РФ", 
     asp = 1,
     pch = 2, 
     cex = 0.5)

plot(sub$МетЭкспорт, 
     sub$МетИмпорт, 
     col="red", 
     xlab="Экспорт, млн. долл. США", 
     ylab = "Импорт, млн. долл. США", 
     main = "Экспорт/импорт металлов и изделий из них по субъектам РФ", 
     asp = 1,
     pch = 20, 
     cex = 1.2)

Линейные графики

Линейные графики отражают связь между зависимой и независимой переменной. Существует два способа нанесения линий на график: явное рисование линий поверх уже построенного графика с помощью функции lines(), или создание нового линейного графика с помощью функции plot() с дополнительным параметром type =.

Для иллюстрации принципов работы первого способа откроем еще раз данные по объему сброса загрязненных сточных вод по морям России (млрд куб. м):

tab = read.csv2("data/oxr_vod.csv", encoding = 'UTF-8')
plot(tab$Год, tab$Каспийское, pch=20) # для начала нанесем точки
lines(tab$Год, tab$Каспийское) # теперь нанесем линии

По умолчанию функция plot() рисует именно точки. Однако если точки не нужны, а достаточно только линий, или требуется иной подход к построению графиков, можно задать параметр type =, который принимает следующие значения:

"p" for points,
"l" for lines,
"b" for both,
"c" for the lines part alone of “b,”
"o" for both ‘overplotted,’
"h" for ‘histogram’ like (or ‘high-density’) vertical lines,
"s" for stair steps,
"S" for other steps, see ‘Details’ below,
"n" for no plotting.

Попробуем разные методы визуализации:

plot(tab$Год, tab$Карское,pch=20)

plot(tab$Год, tab$Каспийское, type="p")

plot(tab$Год, tab$Каспийское, type="l")

plot(tab$Год, tab$Каспийское, type="b")

plot(tab$Год, tab$Каспийское, type="c")

plot(tab$Год, tab$Каспийское, type="o")

plot(tab$Год, tab$Каспийское, type="h")

plot(tab$Год, tab$Каспийское, type="s")

Толщину и тип линии можно изменить, используя параметры lwd = и lty = соответственно. Работают они аналогично параметрам pch и cex для точечных символов. Типов линий по умолчанию в стандартной библиотеке R не так много, но в сочетании с цветовым кодированием и толщиной их оказывается вполне достаточно:

Попробуем разные варианты представления линий:

plot(tab$Год, tab$Каспийское, type="l", lwd = 2, lty = 1)

plot(tab$Год, tab$Каспийское, type="l", lwd = 3, lty = 2)

plot(tab$Год, tab$Каспийское, type="l", lwd = 1, lty = 3)

Совмещение графиков

Часто бывает необходимо совместить на одном графике несколько рядов данных. Для этого можно поступить двумя путями:

Нарисовать один ряд данных c помощью функции plot(), а затем добавить к нему другие ряды с помощью функций points() и lines().
Нарисовать пустой график, а затем добавить к нему все ряды данных с помощью функций points() и lines().

При совмещении нескольких рядов данных на одном графике в первом же вызове функции plot() необходимо заложить диапазон значений по осям $X$ и $Y$, охватывающий все ряды данных. В противном случае будет учтен только разброс значений первого ряда данных, и остальные ряды могут не поместиться в поле графика.

Вариант №1 реализуется следующим образом:

plot(tab$Год, 
     tab$Каспийское, 
     pch=20, 
     type="o", 
     ylim = c(0,12), 
     col="red3")

# Добавим теперь на существующий график новый ряд данных, используя функции points() и lines():
points(tab$Год, tab$Карское, pch=20, col="forestgreen")
lines(tab$Год, tab$Карское, pch=20, col="forestgreen")

Обратите внимание на то, что если бы мы вызвали еще одну инструкцию plot() с новым рядом данных, это привело бы к построению нового графика, а не к добавлению его на существующий.

Теперь рассмотрим второй вариант. Заодно устраним недостаток предыдущего кода, в котором диапазон значений по оси $Y$ указывался вручную.

xrange = range(tab$Год) # вычислим диапазон по оси X
yrange = range(tab$Каспийское, tab$Карское, tab$Азовское) # вычислим диапазон по оси Y

# Построим пустой график, охватывающий полный диапазон данных, и имеющий все необходимые сопроводительные элементы
plot(xrange,
     yrange,
     main="Объем сброса загрязненных сточных вод", 
     xlab="Год", 
     ylab="млрд.куб.м",
     type = "n") # n означает, что ряд данных рисоваться не будет

# Теперь добавим на график ряды данных
points(tab$Год, tab$Каспийское, pch=20, col="red3")
lines(tab$Год, tab$Каспийское, pch=20, col="red3")

points(tab$Год, tab$Карское, pch=20, col="forestgreen")
lines(tab$Год, tab$Карское, pch=20, col="forestgreen")

points(tab$Год, tab$Азовское, pch=20, col="steelblue")
lines(tab$Год, tab$Азовское, pch=20, col="steelblue")

Функциональные параметры

Графические параметры при построении графиков на самом деле могут быть не константами, а функцией данных. Например, вы можете сказать, что размер точки при построении диаграммы рассеяния должен быть функцией отношения экспорта к импорту, что усилит наглядность отображения:

plot(okr$МетЭкспорт, 
     okr$МетИмпорт, 
     col=rgb(1,0,0,0.5), 
     xlab="Экспорт, млн. долл. США", 
     ylab = "Импорт, млн. долл. США", 
     main = "Экспорт/импорт металлов и изделий из них по ФО РФ (2013 г.)", 
     asp = 1,
     pch = 20, 
     cex = 2+log(sub$МетИмпорт/sub$МетЭкспорт)) # размер кружка зависит от соотношения импорта и экспорта

Гистограммы

Гистограммы распределения строятся с помощью функции hist(). Чтобы изменить ширину кармана (столбца) гистограммы, необходимо задать параметр breaks =, а цвет задается в параметре col:

hist(sub$ПродЭкспорт)

# Карманы будут от 0 до 3000 через 100. Заодно добавим цвет:
hist(sub$ПродЭкспорт, breaks = seq(0,3000,100), col="olivedrab3")

При построении гистограммы (как и любого другого типа графика) вы можете использовать не весь массив данных, а только его подмножество Например, можно посмотреть гистограмму только для субъектов с объемом экспорта менее 300:

hist(sub$ПродЭкспорт[sub$ПродЭкспорт < 300], col = "olivedrab3", breaks = seq(0, 300, 20))

Наконец, вы можете осуществить преобразование ряда данных перед построением гистограммы. Например, взять логарифм, чтобы проверить,похоже ли распределение на логнормальное:

hist(log(sub$ПродЭкспорт), col = "olivedrab3")

Столбчатые графики

Столбчатые графики — barplot — отображают вектор числовых данных в виде столбиков. Это простейший вид графика (наряду с dotchart), который используется для сравнения абсолютных величин. Для построения необходимо вызвать функцию barplot() и передать ей столбец таблицы:


# Или даже просто вектор натуральных чисел от -5 до 5:
barplot(-5:5)


# Если у каждого столбика есть название, 
# нужно передать вектор названий в аргумент names.arg = 
barplot(okr$ХимЭкспорт, names.arg = okr$Регион)


# при наличии длинных подписей удобнее столбчатую диаграмму разместить горизонтально, используя параметр horiz = TRUE.
barplot(okr$ХимЭкспорт, names.arg = okr$Регион, horiz=TRUE)

Чтобы развернуть подписи перпендикулярно столбцам, следует использовать параметр las =. Справка__R__говорит нам о том, что этот параметр дает следующее поведение подписей:

0: всегда параллельно осям (по умолчанию),
1: всегда горизонтально,
2: всегда перпендикулярно осям,
3: всегда вертикально.

Выберем вариант, при котором подписи всегда горизонтальны:

barplot(okr$ХимЭкспорт, names.arg = okr$Регион, horiz=TRUE, las = 1)

В данном случае очень массивные названия федеральных не умещаются в пространство графика. Можно было бы вполне убрать словосочетание “федеральный округ.” Для этого используем уже знакомую нам sub().

names = sub("федеральный округ", "", okr$Регион) # "" - означает пустая строка
barplot(okr$ХимЭкспорт, names.arg = names, horiz = TRUE, las = 1)

И снова содержимое не поместилось в поле графика. Проблема в том, что вокруг любого графика резервируются поля ограниченного размера для размещения подписей координат и т.д. Автоматически эти поля не пересчитываются, зарезервировать их — ваша задача.

Наберите в консоли ?par. Откроется список всевозможных графических параметров, которые управляют компоновкой и порядком построения графиков. Эти параметры можно установить, вызвав функцию par(). Все дальнейшие вызовы инструкций построения графиков будут учитывать установленные параметры Пролистайте страницу справки вниз и найдите параметр mar = — он отвечает за установку полей в условных единицах. Есть также параметр mai =, который позволяет установить поля графика в дюймах. Обратите внимание на то, что означают параметры этой функции:

# mar=c(bottom, left, top, right)
# The default is c(5, 4, 4, 2) + 0.1.

Поскольку в нашем примере проблемы возникают в левым полем, необходимо увеличить второй параметр.

margins.default = par("mar") # запишем текущее значение, чтобы восстановить его потом
par(mar = c(5, 10, 4, 2)) # увеличим поле left до 10 условных единиц
barplot(okr$ХимЭкспорт, names.arg = names, horiz=TRUE, las = 1)

Добавим заголовок с помощью параметра main =, а подпись единиц измерения по оси $X$ — с помощью параметра xlab =. Поскольку количество параметров функции уже достаточно велико, введем каждый из них с новой строчки, чтобы улучшить читаемость кода:

barplot(okr$ХимЭкспорт, 
        names.arg = names, 
        main = "Экспорт продукции химической промышленности", 
        xlab = "млн долл. США", 
        horiz = TRUE, 
        las = 1)


# Чтобы увеличить диапазон оси X, можно использовать параметр xlim = c(min, max):
barplot(okr$ХимЭкспорт, 
        names.arg = names, 
        main = "Экспорт продукции химической промышленности", 
        xlab = "млн долл. США", 
        horiz = TRUE, 
        las = 1, 
        xlim = c(0,12000))

Работа с цветом на столбчатых диаграммах рассмотрена ниже в отдельном разделе.

Круговые (секторные) диаграммы

Круговые диаграммы (англ. piechart) строятся с помощью функции pie():

par(mar = c(5, 5, 5, 5)) # установим поля

pie(okr$ХимЭкспорт)


# вместо номеров можно использовать подписи секторов, добавив второй параметр:
pie(okr$ХимЭкспорт, names)


# в каждую метку можно добавить процент данного округа в общей массе. Для этого его нужно сначала посчитать:
percentage = 100 * okr$ХимЭкспорт / sum(okr$ХимЭкспорт)

# и округлить до 1 знака после запятой:
percentage = round(percentage, digits = 1)

Можно присоединить проценты к названиям округов, добавив обрамляющие скобки. Чтобы функция paste не добавляя пробелы между присоединяемыми строками, необходимо задать параметр sep = , передав ему пустую строку — «»:


names2=paste(names, " (", percentage, "%)", sep = "")

# Используем для аннотирования круговых секторов:
pie(okr$ХимЭкспорт, names2)


# Добавить заголовок можно также с помощью параметра main =
pie(okr$ХимЭкспорт, names2, main = "Доля федеральных округов в экспорте продукции химической промышленности")

Чтобы перенести часть заголовка на вторую строку, вы можете использовать управляющий символ перевода строки \n, вставив его в требуемое место:

pie(okr$ХимЭкспорт, names2, main = "Доля федеральных округов в экспорте \n продукции химической промышленности")

Управляющие символы играют большое значение в программировании и используются для управления поведением текстового вывода. Нотация \n называется escape-последовательностью. Помимо перевода строки, есть и другие полезные управляющие символы. Кстати, именно из-за того, что escape-последовательности начинаются с обратной косой черты (\), при указании системных путей в функции setwd() всегда следует использовать прямую косую черту (/). Например, следующий путь не будет найдет, поскольку он содержит управляющие последовательности \n и \t: C:\data\tables\new.

Наконец, при использовании секторных диаграмм важно уметь менять порядок секторов. По умолчанию сектора откладываются против часовой стрелки начиная с восточного направления. Чтобы сектора откладывались по часовой стрелке с северного направления, следует задать параметр clockwise = TRUE.

pie(okr$ХимЭкспорт, 
    names2, 
    main = "Доля федеральных округов в экспорте \n продукции химической промышленности", 
    clockwise = TRUE)

Работа с цветом на круговых диаграммах рассмотрена ниже в отдельном разделе.

Цвет и прозрачность

Цвет — одно из основных графических средств, используемых на графиках и диаграммах, поэтому данная тема рассмотрена более подробно в отдельном разделе. Определить цвет можно различными способами. Во-первых, в R есть палитра предопределенных цветов, которые можно выбирать по их названию).

Список названий цветов можно посмотреть, вызвав функцию colors():

head(colors())
## [1] "white"         "aliceblue"     "antiquewhite"  "antiquewhite1"
## [5] "antiquewhite2" "antiquewhite3"

Основной цвет любого графика или диаграмма задается параметром col =. Это цвет (или цвета) с помощью которых будут отображаться данные. Попробуем изменить цвет графика с серого на пастельно-синий:

par(mar = c(5, 10, 4, 2)) # увеличим поле left до 10 условных единиц
barplot(okr$ХимЭкспорт, 
        names.arg = names, 
        main = "Экспорт продукции химической промышленности", 
        xlab = "млн долл. США", 
        horiz = TRUE, 
        las = 1, 
        xlim = c(0,12000), 
        col = "steelblue")

Помимо этого вы можете задать цвет с помощью цветовых компонент в различных пространствах. Для этого вы должны быть знакомы с основами теории цвета (посмотрите презентацию UsingColorInR.pdf. Например, фиолетовый цвет в пространстве RGB можно задать с помощью функции rgb(), смешав синюю и красную компоненты:

violet = rgb(0.4, 0, 0.6)
barplot(okr$ХимЭкспорт, 
        names.arg = names, 
        main = "Экспорт продукции химической промышленности", 
        xlab = "млн долл. США", 
        horiz = TRUE, 
        las = 1, 
        xlim = c(0,12000), 
        col = violet)

Чтобы сделать цвет полупрозрачным, есть две возможности:

При создании нового цвета — передать в функцию rgb() дополнительный параметр alpha =, который задает долю прозрачности в диапазоне от 0 до 1.
При модификации существующего цвета — вызвать функцию adjustcolor() с параметром alpha =

Например:

violet.transp = adjustcolor(violet, alpha = 0.5)
barplot(okr$ХимЭкспорт, 
        names.arg = names, 
        main = "Экспорт продукции химической промышленности", 
        xlab = "млн долл. США", 
        horiz = TRUE, 
        las = 1, 
        xlim = c(0,12000), 
        col = violet.transp)


green.transp = rgb(0, 1, 0, 0.5) # появился четвертый параметр
barplot(okr$ХимЭкспорт, 
        names.arg = names, 
        main = "Экспорт продукции химической промышленности", 
        xlab = "млн долл. США", 
        horiz = TRUE, 
        las = 1, 
        xlim = c(0,12000), 
        col = green.transp)

Функция adjustcolor() позволяет модифицировать все компоненты цвета, не только прозрачность.

На графике типа barplot вы имеете фактически несколько переменных, которые представлены столбиками. А это означает что для них можно использовать различные цвета. Вы можете передать в параметр col = вектор из цветов, соответствующих столбикам:

colors = c("red", "green", "blue", "orange", "yellow", "pink", "white","black")

barplot(okr$ХимЭкспорт, 
        names.arg = names, 
        main = "Экспорт продукции химической промышленности", 
        xlab = "млн долл. США", 
        horiz = TRUE, 
        las = 1, 
        xlim = c(0,12000), 
        col = colors)

На самом деле, такой винегрет из цветов на столбчатых диаграммах использовать не принято. Но вы должны понимать, что при необходимости можно поменять цвет отдельно выбранных столбиков. Например, мы можем показать красным цветом Центральный и Приволжский округа, которые являются лидерами по экспорту продукции химической промышленности:

colors = rep("gray", 8) # сделаем 8 серых цветов
colors[2] = "red"
colors[7] = "red"
barplot(okr$ХимЭкспорт, 
        names.arg = names, 
        main = "Экспорт продукции химической промышленности", 
        xlab = "млн долл. США", 
        horiz = TRUE, 
        las = 1, 
        xlim = c(0,12000), 
        col = colors)

Еще одна интересная особенность использования цвета заключается в том, что количество указанных цветом может не совпадать с количеством рядов данных. Вы можете указать 2 или 3 цвета, и они будут циклически повторяться при визуализации данных:

colors=c("gray","steelblue")
barplot(okr$ХимЭкспорт, 
        names.arg = names, 
        main = "Экспорт продукции химической промышленности", 
        xlab = "млн долл. США", 
        horiz =TRUE, 
        las = 1, 
        xlim = c(0, 12000), 
        col = colors)

Наконец, вещь, которой совершенно необходимо уметь пользоваться при работе с цветом в R — это цветовые палитры. Палитры чрезвычайно удобны, когда необходимо сгенерировать множество цветов, зная лишь основные оттенки. Для этого нужно создать палитру, используя функцию colorRampPalette():

# задаем 2 опорных цвета: черный  белый
palet=colorRampPalette(c("black","white")) 

# и автоматически генерируем 8 цветов между ними:
colors=palet(8)

# используем их для отображения:
barplot(okr$ХимЭкспорт, 
        names.arg = names, 
        main = "Экспорт продукции химической промышленности", 
        xlab = "млн долл. США", 
        horiz = TRUE, 
        las = 1, 
        xlim = c(0, 12000), 
        col= colors)


# вы можете включить в палитру произвольное количество цветов:
palet=colorRampPalette(c("steelblue","white","purple4")) 
colors=palet(8)
barplot(okr$ХимЭкспорт, 
        names.arg = names, 
        main = "Экспорт продукции химической промышленности", 
        xlab = "млн долл. США", 
        horiz=TRUE, 
        las = 1, 
        xlim = c(0, 12000), 
        col= colors)

В R существует множество стандартных палитр, их список можно найти в справке и документации. Наиболее полезные из них:

Например, вы можете изменить цвета диаграммы, взяв их из одной из палитр или выбрав случайным образом из полной палитры цветов, используя функцию sample():

pie(okr$ХимЭкспорт, names2, main = "Доля федеральных округов в экспорте \n продукции химической промышленности", col=rainbow(length(names2)))

pie(okr$ХимЭкспорт, names2, main = "Доля федеральных округов в экспорте \n продукции химической промышленности", col=sample(colors(),5))

Более богатый набор палитр можно найти в библиотеке RColorBrewer, которая представляет собой интерпретацию палитр, доступных на сайте colorbrewer2.org

library(RColorBrewer) # Откроем библиотеку RColorBrewer:
display.brewer.all() # Посмотрим, какие в ней имеются палитры

К каждой из этих палитр можно обратиться по названию с помощью функции brewer.pal(). Поскольку нам необходимы цвета для категориальных данных, следует использовать палитры из средней части (Set3 — Accent)

# выберем цвета из палитры Set2 по количеству секторов в круге:
colors = brewer.pal(length(names2),"Set1")

# И используем их при визуализации
par(mar = c(5, 5, 5, 5)) # установим поля
pie(okr$ХимЭкспорт, names2, main = "Доля федеральных округов в экспорте \n продукции химической промышленности", col=colors)


# Попробуем палитру Accent:
pie(okr$ХимЭкспорт, names2, main = "Доля федеральных округов в экспорте \n продукции химической промышленности", col=brewer.pal(length(names2),"Accent"))

Настройки отображения

Графические параметры

Изменять размеры элементов графика можно независимо друг от друга, используя следующие параметры:

cex — общий масштаб элементов на графике
cex.axis — масштаб подписей координат на оси
cex.lab — масштаб подписей названий осей
cex.main — масштаб заголовка графика
cex.sub — масштаб подзаголовка графика
cex.names — масштаб подписей факторов (для некоторых типов диаграмм)

Например:

plot(tab$Год, 
     tab$Каспийское, 
     pch=20, 
     type="o", 
     ylim = c(0,12), 
     col="red3", 
     main="Объем сброса загрязненных сточных вод", 
     xlab="Год", 
     ylab="млрд.куб.м",
     cex.axis=0.8, 
     cex.lab=0.7, 
     cex.main=0.9, 
     cex = 0.8)

points(tab$Год, tab$Карское, pch=20, col="forestgreen",cex = 0.8)
lines(tab$Год, tab$Карское, pch=20, col="forestgreen")

points(tab$Год, tab$Азовское, pch=20, col="steelblue",cex = 0.8)
lines(tab$Год, tab$Азовское, pch=20, col="steelblue")

Аналогично происходит тонкая настройка цвета:

col цвет графика
col.axis цвет подписей координат
col.lab цвет названий осей
col.main цвет заголовка
col.sub цвет подзаголовка
fg цвет элементов переднего плана (оси, рамка и т.д.)
bg цвет фона графика (background)

plot(tab$Год, 
     tab$Каспийское, 
     pch=20, 
     type="o", 
     ylim = c(0,12), 
     col="red3", 
     main="Объем сброса загрязненных сточных вод", 
     xlab="Год", 
     ylab="млрд.куб.м",
     cex.axis=0.8, 
     cex.lab=0.7, 
     cex.main=0.9, 
     col.lab = "grey50", 
     fg = "grey40")
points(tab$Год, tab$Карское, pch=20, col="forestgreen")
lines(tab$Год, tab$Карское, pch=20, col="forestgreen")
points(tab$Год, tab$Азовское, pch=20, col="steelblue")
lines(tab$Год, tab$Азовское, pch=20, col="steelblue")

Разметка осей, рамка, сетка координат и произвольные линии

По умолчанию R подбирает оптимальный с точки зрения него шаг разметки осей, в зависимости от разброса значений по осям $X$ и $Y$, а также размеров графического устройства, на котором производится рисование. Изменяя размер окна прорисовки, вы получите различную разметку осей.

В то же время, часто возникает желание (или необходимость) самостоятельно управлять шагом разметки сетки. Для этого необходимо:

Вызвать функцию plot(), передав ей дополнительно параметр axes = FALSE (убирает при рисовании обе оси) или один из параметров xaxt="n" / yaxt="n" (убирают оси $X$ и $Y$ соответственно)
Вызвать столько раз функцию axis(), сколько вы хотите нарисовать осей, передав ей параметры для рисования каждой оси.

Функция axis() принимает следующие параметры:

side — сторона графика, на которой будет нарисована ось (1=bottom, 2=left, 3=top, 4=right)
at — вектор значений, в которых должны быть нарисованы метки оси
labels — вектор подписей, которые будут нарисованы в местоположениях, указанных в параметре at. Этот параметр можно пропустить, если подписи совпадают с местоположениями меток
pos — координата, вдоль которой будет нарисована ось
lty — тип линии
col — цвет линии и меток
las — расположение подписей параллельно ($0$) или перпендикулярно ($2$) оси
tck — длина метки относительно размера графика. Отрицательные значения дают метки, выходящие за пределы графика. положительные — внутрь графика. $0$ убирает метки, $1$ рисует линии сетки.

При ручном построении осей полезно сразу же нарисовать рамку вокруг графика, используя функцию box().

Например:

plot(tab$Год, 
     tab$Каспийское,
     type = "l",
     axes = FALSE)

axis(side = 1, 
     at = seq(min(tab$Год), max(tab$Год), 1),
     tck = -0.02,
     labels = FALSE) # разметим ось X через 1 год, но рисовать подписи не будем

axis(side = 1, 
     at = seq(min(tab$Год), max(tab$Год), 3), # а подписи расставим через 3 года
     tck = 0) # но рисовать метки не будем

# разметим ось Y через 1 млрд куб. м., округлив предварительно минимальное и максимальное значение до ближайшего целого снизу и сверху соответственно
axis(side = 2, 
     at = seq(floor(min(tab$Каспийское)), ceiling(max(tab$Каспийское)), 1),
     tck = -0.02) 

box() # добавим рамку для красоты

Для размещения сетки координат существует функция grid(nx = NULL, ny = nx, col = "lightgray", lty = "dotted", lwd = par("lwd"), equilogs = TRUE). Как видно из набора ее параметров, сетка определяется количеством линий в горизонтальном и вертикальном направлении. Это не всегда бывает удобно, поскольку как правило мы хотим задать шаг сетки конкретной величины. По умолчанию, однако, линии сетки выбираются автоматически, как и метки:

plot(tab$Год, 
     tab$Каспийское,
     type = "l",
     col = "red")
grid()

Вы, разумеется, можете поменять их количество, однако R не будет за вас согласовывать шаг сетки и шаг меток осей, поскольку метки генерируются на стадии рисования plot() или axis() и не запоминаются.

plot(tab$Год, 
     tab$Каспийское,
     type = "l",
     col = "red")
grid(10, 5)

Функция grid() на самом деле является оберткой функции abline(), которая позволяет рисовать произвольные линии на графике. Дана функция предоставляет следующие возможности построения линий и серий линий:

a, b — коэффициенты уравнения $y = ax + b$. Таким образом можно определить только одну линию.
coef — принимает вектор из двух значений, которые интерпретируются как a и b. То есть, это альтернативная форма записи предыдущего случая.
h — значение (значения) координат $y$ для горизонтальной линии (серии горизонтальных линий). То есть, вы можете передать в этот параметр как одиночное значение, так и вектор значений. В зависимости это этого нарисуется одна горизонтальная линия или серия горизонтальных линий.

v — значение (значения) координат $x$ для вертикальной линии (серии вертикальных линий).3\) по оси $Y$. Для этого выполним следующую последовательность действий:
plot(tab$Год, tab$Каспийское, type="n") # режим 'n' позволяет ничего не рисовать, но заложить поле графика в соответствии с данными, указанными в параметрах x и y # Вычисляем линии сетки xlines = seq(min(tab$Год), max(tab$Год), 1) ylines = seq(ceiling(min(tab$Каспийское)), floor(max(tab$Каспийское)), 1) # Рисуем линии сетки abline(h = ylines, v = xlines, col = "lightgray") # Рисуем график lines(tab$Год, tab$Каспийское, col="red3") points(tab$Год, tab$Каспийское, pch = 20, col="red3") # Выделяем значение 10 по оси Y: abline(h = 10, col = "blue", lwd = 2) # Рисуем дополнительно рамку, т.к. сетку координат мы рисовали после графика box()
Аннотации данных (текст на графике)

Аннотации данных добавляются на график с помощью функции text(). В качестве трех обязательных аргументов ей необходимо передать координаты точек размещения текста, и вектор подписей. Также полезным будет указать параметр pos=, отвечающий за размещение аннотации относительно точки. Значения pos, равные 1, 2, 3 и 4, соответствуют размещению снизу, слева, сверху и справа от точки:
text(tab$Год, tab$Каспийское, labels = tab$Каспийское, cex = 0.75, pos = 3)
К сожалению, стандартный механизм размещения аннотаций пакета graphics не обладает возможностью устранения конфликтов подписей. Однако это возможно для графиков, построенных с помощью библиотек lattice и ggplot2. Для этого можно воспользоваться пакетом directlabels или ggrepel.
Легенда

Легенда к графику размещается с помощью функции legend(). Эта функция принимает несколько аргументов, включая: местоположение, заголовок, названия элементов, графические параметры. Местоположение может быть задано координатами $(x,y)$ в системе координат графика, но удобнее пользоваться следующими предопределенными константами: "bottomright", "bottom", "bottomleft", "left", "topleft", "top", "topright", "right", "center".
Чтобы в легенде появились точки, необходимо задать параметр pch=. Для линейной легенды, следует задать, соответственно, параметр lty = и/или lwd =. Каждый из этих параметров должен быть вектором по количеству элементов легенды:
par(mar = margins.default) # Найдем ограничивающий прямоугольник вокруг всех рядов данных xrange = range(tab$Год) yrange = range(tab$Каспийское, tab$Карское, tab$Азовское) # Построим пустой график с разметкой осей и всеми заголовками plot(xrange, yrange, type="n", main="Объем сброса загрязненных сточных вод", xlab="Год", ylab="млрд.куб.м", cex.axis=0.8, cex.lab=0.7, cex.main=0.9, col.lab = "grey50", fg = "grey40") # Добавим на график сетку координат grid() # Добавим на график данные points(tab$Год, tab$Каспийское, pch=20, col="red3") lines(tab$Год, tab$Каспийское, pch=20, col="red3") points(tab$Год, tab$Карское, pch=20, col="forestgreen") lines(tab$Год, tab$Карское, pch=20, col="forestgreen") points(tab$Год, tab$Азовское, pch=20, col="steelblue") lines(tab$Год, tab$Азовское, pch=20, col="steelblue") # Определим положение, названия и цвета: main = "Море" location = "topright" labels = c("Каспийское", "Карское", "Азовское") colors = c("red3", "forestgreen", "steelblue") # Если цвет передать в параметр fill, то по умолчанию # нарисуются цветовые плашки: legend(location, labels, title = main, fill=colors)
pts = c(20, 20, 20) # каждый элемент показывается точкой типа 20 lns = c(1, 1, 1) # каждый элемент показывается линией толщиной 1 # теперь посмотрим на легенду (она нарисуется поверх старой) legend(location, labels, title = main, col = colors, pch = pts, lwd = lns)
Более подробно с разнообразными опциями размещения легенды на графике вы можете познакомиться, набрав в консоли команду ?legend.
Построение графиков уравнений, содержащих модули
Тип урока: Урок формирования новых знаний.
Цели урока:
Формировать умение строить графики уравнений содержащих модули.

Развитие логического мышления, познавательного интереса.

Развитие общеучебных навыков и умений – организационных, интеллектуальных и коммуникативных.

Оборудование: мультимедиа проектор, доска.
Ход урока
I. Орг. момент.
II. Устный счет.

Вычислите. (слайд 1)

Решите уравнение. (слайд 2)

III.
Объяснение нового материала.
1. Построить график уравнения (слайд 3)
Решение. (слайд 4)
По определению модуля имеем:
Построим график уравнения: (слайд 5)
х=2у, если у≥0

х=0, если у<0

Получили график уравнения

2. Построить график уравнения .(слайд 6)
Решение. (слайд 7)
По определению модуля имеем:

Если у=0, то х – любое.
Выполним построение. (слайд 8)
х = 1, если у>0;

x = — 1, если у<0;

3. Построить график уравнения (слайд 9)
Решение. (слайд 10)
По определению модуля имеем:
При х≥0, у≥0, уравнение х+у=4;

При х≥0, у<0, уравнение х-у=4;

При х<0, у≥0, уравнение –х+у=4;

При х<0, у<0, уравнение –х-у=4.

(слайд 11)
Построить график уравнения (слайд 12)
Решение. (слайд 13)
По определению модуля имеем:
При х≥0, у≥0, уравнение х-у=4;

При х≥0, у<0, уравнение х+у=4;

При х<0, у≥0, уравнение –х-у=4;

При х<0, у<0, уравнение –х+у=4.

(слайд 14)
IV. Закрепление. Решение задач.
Построить график уравнения. (слайд 15)

а) |x|+|y|=2;

б)|x|-|y|=3.

Проверка (слайд ) (слайд 16)
(слайд 17)
V. Итог урока.
Домашнее задание. (слайд 18)
Построить графики уравнений: а) |y|=1-|x|; б)|y|=|x|+3.
Какой график xy 0? — AnswersToAll
Что такое график xy 0?
Используйте форму пересечения наклона, чтобы найти наклон и точку пересечения по оси Y. Форма пересечения наклона: y = mx + b y = m x + b, где m m — наклон, а b b — точка пересечения с y. Найдите значения m m и b b, используя форму y = mx + b y = m x + b. Наклон линии — это значение m m, а точка пересечения оси y — это значение b b.
Что означает X Y 0?
То есть, если точка на плоскости является решением xy = 0, либо ее координата x равна 0 (что означает, что точка находится в S, оси y), либо ее координата y равна 0 (что означает что точка находится в V, оси x).
Каков наклон xy 0?
Используя форму пересечения наклона, наклон равен -1.
Как называется Y 0?
Примечание. Обычно мы наносим на график точку, в которой x = 0 (называемую точкой пересечения по оси y), и точку, где точка y = 0 (точка пересечения с координатой x).
Что такое Y 0 на графике?
Если вы это знаете, то можете просто пойти дальше и провести горизонтальную линию через точку пересечения оси y, в данном случае 0. Поскольку уравнение y = 0 имеет точку пересечения оси y, равную 0, ваш график по существу представляет собой точку пересечения оси x- ось.Значение y всегда равно 0.
Y 0 — не решение?
Решение x = 0 означает, что значение 0 удовлетворяет уравнению, значит, решение существует. «Нет решения» означает, что нет значения, даже 0, которое удовлетворяло бы уравнению. Это потому, что на самом деле нет решения — нет значений для x, которые сделают уравнение 12 + 2x — 8 = 7x + 5 — 5x истинным.
Y 0 вертикальный или горизонтальный?
Ноль! Это соотношение сохраняется всегда: нулевой наклон означает, что линия горизонтальная, а горизонтальная линия означает, что вы получите нулевой наклон.(Кстати, все горизонтальные линии имеют форму «y = некоторое число», а уравнение «y = некоторое число» всегда отображается как горизонтальная линия.)
Как вы изобразите 0 0 на числовой прямой?
На числовом графике мы бы начали с белого кружка на 0, потому что 0 НЕ включается в решение. Нарисуйте линию, идущую влево, показывая, что x может быть любым значением слева от 0. В сетке ax-y- у нас будет вертикальная линия для представления x = 0, но поскольку 0 НЕ включен, линия будет быть расставленными точками.
Какие десятичные знаки между 0 и 1?
Десятичное число 0,4 эквивалентно 410, поэтому 0,4 находится между 0 и 1. На числовой строке разделите интервал между 0 и 1 на 10 равных частей и поставьте отметки, чтобы разделить части. Обозначьте марки 0,1,0,2,0,3,0,4,0,5,0,6,0,7,0,8,0,9,1,0 0,1, 0,2, 0,3, 0,4, 0,5, 0,6, 0,7, 0,8, 0,9, 1,0.
Как построить график «больше или равно» на числовой прямой?
При построении графика линейного неравенства на числовой прямой используйте открытый кружок для «меньше чем» или «больше чем» и замкнутый кружок для «меньше или равно» или «больше или равно».Решением этой проблемы будут все значения, удовлетворяющие как -3
Как узнать, что у графика нет решения?
Когда вы строите уравнения, оба уравнения представляют собой одну и ту же линию. Если система не имеет решения, она считается несовместимой. Графики линий не пересекаются, поэтому графики параллельны и решения нет.
Какого решения нет Одно решение Бесконечные решения?
Отсутствие решения будет означать, что нет ответа на уравнение.Невозможно, чтобы уравнение было истинным, независимо от того, какое значение мы присваиваем переменной. Бесконечные решения будут означать, что любое значение переменной сделает уравнение истинным.
Как читать график неравенства?
Есть три шага:
Измените формулу так, чтобы «y» находилось слева, а все остальное — справа.
Постройте линию «y =» (сделайте ее сплошной линией для y≤ или y≥ и пунктирной линией для y <или y>).
Затенение над линией для «больше чем» (y> или y≥) или под линией для «меньше чем» (y <или y≤).
Какой пропущенный шаг в решении викторины с неравенством 5 8x 2x 3?
Какой пропущенный шаг при решении неравенства 5 — 8x <2x + 3? Добавьте 8x к обеим сторонам неравенства.
Как узнать, не имеет ли неравенство решения?
Выделите выражение абсолютного значения в левой части неравенства. Если число по другую сторону знака неравенства отрицательное, ваше уравнение либо не имеет решения, либо все действительные числа являются решениями.
Как определить, будет ли неравенство сплошной линией?
Если неравенство равно <или>, обозначьте уравнение пунктирной линией. Если неравенство ≤ или ≥, изобразите уравнение сплошной линией. Эта линия делит плоскость xy на две области: область, удовлетворяющую неравенству, и область, которая не удовлетворяет. Затем выберите точку не на линии.
Какой символ представляет собой пунктирная линия?
Символ неравенства поможет вам определить границу.Если символ неравенства больше или меньше, то вы будете использовать пунктирную линию границы. Это означает, что решения НЕ включены в граничную линию.
При построении графика неравенства всегда можно использовать 0 0 в качестве контрольной точки?
Этот тест выполняется, только если точка (0,0) не лежит на границе неравенства. Так как тогда выражение «по направлению к источнику и дальше от источника» не будет иметь смысла. Следовательно, (0,0) нельзя использовать как контрольную точку, если она находится на граничной линии.
Решить свойства прямой линии x-y = 0 Решатель алгебры тигра
Решить свойства прямой линии x-y = 0 Решатель алгебры тигра
Этот сайт лучше всего просматривать с помощью Javascript. Если вы не можете включить Javascript, нажмите здесь.
Вход камеры не распознается!
Мы думаем, что вы написали:
x-y = 0
Это касается свойств прямой линии.
x-i «ntercept = 0/1 = 0,00000
x-i» ntercept = 0/1 = 0,00000
y-i «ntercept = 0 / -1 = -0.00000
yi «ntercept = 0 / -1 = -0,00000
Пошаговое решение
Шаг 1:

Уравнение прямой линии

1.1 Решить xy = 0

Тигр понимает, что здесь есть уравнение прямая линия. Такое уравнение обычно записывается y = mx + b («y = mx + c» в Великобритании).

«y = mx + b» — это формула прямой линии, проведенной в декартовой системе координат в где «y» — вертикальная ось, а «x» — горизонтальная ось.

В этой формуле:

y говорит нам, как далеко идет линия
x говорит нам, как далеко вдоль
м находится наклон или градиент i.е. насколько крута линия
b — точка пересечения по оси Y, т.е. точка пересечения линии с осью Y

Точки пересечения по осям X и Y и наклон называются свойствами линии. Теперь мы построим график линии xy = 0 и вычислим ее свойства

График прямой линии:

Вычислите точку пересечения Y:
Обратите внимание, что когда x = 0, значение y равно 0 / -1, так что это линия «разрезает» ось y в точке y = -0,00000
y-intercept = 0 / -1 = -0,00000
Вычислите точку пересечения по оси X:
Когда y = 0, значение x равно 0/1 Следовательно, наша линия «обрезает» ось x при x = 0.00000
x-intercept = 0/1 = 0,00000
Расчет наклона:
Наклон определяется как изменение y, деленное на изменение x. Отметим, что для x = 0 значение y равно 0,000, а для x = 2,000 значение y равно 2,000. Таким образом, при изменении x на 2.000 (изменение x иногда называют «RUN») мы получаем изменение на 2.000 — 0.000 = 2.000 по y. (Изменение y иногда называют «ПОДЪЕМ», а наклон равен m = RISE / RUN)
Наклон = 1
Геометрическая фигура: прямая линия
Наклон = 1
x-точка пересечения = 0/1 = 0.00000
y-перехват = 0 / -1 = -0.00000
Зачем это изучать
Термины и темы
Ссылки по теме
Поиск пересечений по оси x и оси y | Колледж алгебры
Точки пересечения графика — это точки, в которых график пересекает оси. Пересечение x- — это точка, в которой график пересекает ось x- . В этот момент координата y- равна нулю. Пересечение y- — это точка, в которой график пересекает ось y- .В этот момент координата x- равна нулю.
Чтобы определить точку пересечения x- , мы устанавливаем y равным нулю и решаем относительно x . Точно так же, чтобы определить точку пересечения y- , мы устанавливаем x равным нулю и решаем относительно y . Например, давайте найдем точки пересечения уравнения [латекс] y = 3x — 1 [/ latex].
Чтобы найти точку пересечения x- , установите [latex] y = 0 [/ latex].
[латекс] \ begin {array} {ll} y = 3x — 1 \ hfill & \ hfill \\ 0 = 3x — 1 \ hfill & \ hfill \\ 1 = 3x \ hfill & \ hfill \\ \ frac {1 } {3} = x \ hfill & \ hfill \\ \ left (\ frac {1} {3}, 0 \ right) \ hfill & x \ text {-intercept} \ hfill \ end {array} [/ latex]
Чтобы найти точку пересечения y- , установите [latex] x = 0 [/ latex].
[латекс] \ begin {array} {l} y = 3x — 1 \ hfill \\ y = 3 \ left (0 \ right) -1 \ hfill \\ y = -1 \ hfill \\ \ left (0, -1 \ right) y \ text {-intercept} \ hfill \ end {array} [/ latex]
Мы можем подтвердить, что наши результаты имеют смысл, наблюдая за графиком уравнения, показанным на рисунке 10. Обратите внимание, что график пересекает оси там, где мы и предполагали.
Рисунок 12
Как: по уравнению найти точки пересечения.
Найдите точку пересечения x , задав [latex] y = 0 [/ latex] и решив для [latex] x [/ latex].
Найдите точку пересечения y- , установив [latex] x = 0 [/ latex] и решив для [latex] y [/ latex].
Пример 4: Нахождение точек пересечения данного уравнения
Найдите точки пересечения уравнения [латекс] y = -3x — 4 [/ latex]. Затем нарисуйте график, используя только точки пересечения.
Решение
Установите [latex] y = 0 [/ latex], чтобы найти точку пересечения x- .
[латекс] \ begin {array} {l} y = -3x — 4 \ hfill \\ 0 = -3x — 4 \ hfill \\ 4 = -3x \ hfill \\ — \ frac {4} {3} = x \ hfill \\ \ left (- \ frac {4} {3}, 0 \ right) x \ text {-intercept} \ hfill \ end {array} [/ latex]
Установите [latex] x = 0 [/ latex], чтобы найти точку пересечения y- .
[латекс] \ begin {array} {l} y = -3x — 4 \ hfill \\ y = -3 \ left (0 \ right) -4 \ hfill \\ y = -4 \ hfill \\ \ left ( 0, -4 \ right) y \ text {-intercept} \ hfill \ end {array} [/ latex]
Постройте обе точки и проведите через них линию, как показано на рисунке 11.
Рисунок 13
Попробуй 1
Найдите точки пересечения уравнения и нарисуйте график: [latex] y = — \ frac {3} {4} x + 3 [/ latex].
Решение
Исследование графиков уравнения xy = ax + by + c
Исследование графиков уравнения xy = ax + by + c
Исследование уравнения
по
Дженнифер Рот
Используя Algebra Expressor (программное обеспечение для построения графиков), мы можем конструировать различные
графики для уравнения
, и мы можем наложить такие графики для разных значений a, b и c как
два других остаются неизменными.Из этих графиков разовьется закономерность.
Например, если мы установим xy = x + y + c для c = -3,
-2, -1, 0, 1, 2, 3 и наложив графики, мы получим следующую картину.
Если мы положим y = 0, мы получим уравнение 0 = x + c. Если построить график этого уравнения
для предыдущих значений c получаем набор вертикальных линий, параллельных
ось y (x = 0).
Если это уравнение изобразить на плоскости xc, мы получим прямую, проходящую через начало координат
(х = у).Посмотрите на приведенный выше график; какой вывод можно сделать, если
вы накладываете график x = y и x = -y на приведенный выше график?
Что, если мы положим x = 0, мы получим уравнение 0 = y + c. Что разные
как выглядят графики этого уравнения? Опять же, какие выводы можно сделать?
В следующем примере мы установим xy = ax + y для
a = -3, -2, -1, 0, 1, 2, 3, и мы получаем следующую картину.
Теперь мы установим xy = x + на для b = -3, -2, -1,
0, 1, 2, 3; и мы получаем следующую картину.
Было бы полезно посмотреть на графики x — b = 0 и
у — а = 0
Следующий график — это x — b = 0

Для графика y-a = 0 мы получаем аналогичную картину, но, конечно, получаем
горизонтальные ряды вертикальных линий, но линия y = a выглядит так же, как
прямая x = b.
Теперь, если мы посмотрим на график уравнения (x- b) (y — a) = 0.
Сначала мы рассмотрим два уравнения (xb) (y-1) = 0,
и xy = x + на для b = -3, и мы получаем следующую картину.
Две прямые линии — это график (x + 3) (y-1) = 0. Просмотрите графики.
из x + 3 = 0,
и y — 1 = 0, чтобы увидеть, как получается этот график. Похоже, что это уравнение
образует асимтопы для уравнения xy = x — 3y (a = 1 и b = -3, как в
другое уравнение).
Было бы полезно посмотреть на другое изображение, наложенное на эти 2 уравнения.
с другим значением для b, чтобы сделать выводы. Следующие
картина получается, если положить b = 2.
И снова кажется, что мы получаем асимптопы.
Теперь посмотрим на два уравнения (x-1) (y-a) = 0,
и xy = ax + y для a = -3, и мы получаем следующее изображение.
Опять же, оказывается, что уравнение (x- 1) (y + 3) = 0 образует асимтопы
для уравнения xy = -3x + y (a = -3 и b = 1, как в другом уравнении).
Следовательно, похоже, что если мы зададим оба этих уравнения одинаковых значений
для a и b, сохраняя c постоянным, мы получим асимптопы.
Теперь посмотрим на график уравнения (x — b) (y
— a) = k (где k — любое действительное число)
Если мы наложим два графика (x + 3) (y -1) = k и xy = x — 3y
с k = -3, -2, -1, 0, 1, 2, 3, мы получаем следующую картину.
Посмотрите на графики, на которых c изменялась в начале. Этот график
выглядит очень похоже.
Посмотрим, сможем ли мы выяснить, что происходит.
Если мы возьмем уравнение (x — b) (y — a) = k и умножим, получим
ху = ах + по — ab + k.
Теперь, если мы сравним это с нашим уравнением xy = ax + by + c, мы получим
то же уравнение для c = -ab + k.
Чтобы проверить это, посмотрим на график для xy = x —
3y и (x + 3) (y-1) = -3 и мы получаем следующую картину.
Они такие же.
Вернуться к последнему проекту Дженнифер
Главная страница
линий графика
линия графика
Построение графиков линейных уравнений
График уравнения с двумя переменными представляет все возможные комбинации x и y , которые удовлетворяют уравнению.Другими словами, точки на графике имеют координаты ( x , y ), которые делают утверждение уравнения истинным. В зависимости от природы уравнения и показателей переменных каждое уравнение имеет свой график.

График любого уравнения, в котором есть две переменные, которые имеют степень один, не умножаются друг на друга и не входят в знаменатель каких-либо дробей, представляет собой прямую линию.
Например, график 2y — x + 4 = 0 представляет собой линию.Это означает, что если мы найдем все возможные комбинации x и y, которые работают в уравнении, и построим их в системе координат, результатом будет линия. Поскольку две точки определяют линию, если мы распознаем уравнение как линейное уравнение, нам понадобятся только два набора x и y (точек), которые удовлетворяют уравнению для графика. Есть много способов найти эти точки, и их бесконечное количество. Мы рассмотрим графики линий, используя их точки пересечения по оси x и оси y. Это точки, в которых линия пересекает ось x и ось y соответственно.Мы выбираем эти точки потому, что с ними легче работать. Пересечение линии по оси x является точкой на оси x и, следовательно, имеет нулевую координату y. А точка пересечения линии y — это точка на оси y, имеющая нулевую координату x . Мы собираемся использовать эти факты, чтобы найти недостающие координаты каждой точки.
Сначала мы подставим ноль для y и найдем соответствующий x , а затем подставим ноль для x и найдем соответствующий y .

Пример 1) График 2 y — x + 4 = 0
Если мы подставим 0 для x , мы получим:
2 y — 0 + 4 = 0 Мы вычтем 4 с обеих сторон:
2 y = -4 и разделив на 2, получим y = -2, поэтому у нас есть (0, -2), это перехват y .
Затем мы подставим ноль для y :
2 (0) — x + 4 = 0 Мы вычтем 4 с обеих сторон:
— x = -4 или x = 4, мы получим наша вторая точка (4,0), это пересечение x
. Теперь мы наносим точки и соединяем их.Результирующая линия представляет все комбинации x, y , которые работают в данном уравнении.
Каждая линия имеет крутизну, которая обозначается как уклон . Крутизна линии или ее уклон — это отношение подъема линии (насколько далеко вверх или вниз мы должны пройти, чтобы достичь другой точки) к ее пробегу (насколько далеко вперед или назад нам нужно пройти). Для приведенной выше линии наклон равен 2/4 или 1/2, так как нам нужно подняться на 2 единицы, а затем на 4 единицы, чтобы перейти от одной точки к другой.Мы также можем найти наклон, решив сначала наше уравнение для y . Тогда наклон будет коэффициентом x (а оставшееся число будет пересечением по оси Y):
Сначала мы прибавим x к обеим сторонам и вычтем 4: 2 y = x — 4
Затем мы разделим обе стороны на 2: y = x /2 — 2 (это называется формой пересечения угла наклона ( линии)
Таким образом, наклон равен 1/2, а точка пересечения по оси Y равна -2.Эта информация может быть полезна в некоторых случаях.

Пример 2) График 4y + 5x = 20
Подставляя ноль для x, мы получаем:
4y = 20 или y = 5
Таким образом, мы получаем точку пересечения с y (0,5)
Подставляя ноль для y, получаем:
5x = 20 или x = 4
Итак, пересечение по оси x равно (4,0)
Обратите внимание, что наклон этой линии равен -5/4, так как мы должны спуститься на 5 единиц и переместиться вперед на 4 единицы, чтобы перейти от одной точки к другой.
И если мы решим для y (изменим форму на наклон-пересечение ), мы сначала должны вычесть 5x с обеих сторон:
4y = -5x + 20, а затем разделить на 4:
y = -5/4 x + 5
Который также показывает, что наклон равен -5/4, а точка пересечения по оси Y равна 5.

Особые случаи:

Иногда нам может потребоваться построить график уравнений только с одной переменной в системе координат.
Например, y = 4 или x = -2 — это уравнения, которые содержат только одну переменную, но их можно построить в виде линий.
В случае y = 4, набор точек, удовлетворяющих уравнению, — это все точки, которые имеют y значение 4 (с любым возможным значением x). Эти точки могут быть представлены горизонтальной линией y = 4.В общем случае на графике все уравнения вида y = C, где C — число, представляет собой горизонтальную линию в точке C.
В случае x = -2, график представляет собой набор всех точек с x значением -2, которое может быть представлено вертикальной линией с отметкой -2. Обычно график всех уравнений в форме x = C представляет собой вертикальную линию в точке C.
Назад к линейным функциям
Нанесение точек на график или плоскость XY
В этом уроке я подготовил восемь (8) разработанных примеров построения точки на декартовой плоскости (названной в честь французского математика Рене Декарта).Чтобы построить точку, нам нужны две вещи: точка и координатная плоскость .
Давайте кратко поговорим о каждом.
А точка
Точка на плоскости состоит из двух компонентов, в которых порядок имеет значение! Он имеет форму (x, y), где x идет первым, а y — вторым.
Значение x указывает, как точка перемещается вправо или влево вдоль оси x . Эта ось является главной горизонтальной линией прямоугольной оси или декартовой плоскости.
Значение y указывает, как точка перемещается вверх или вниз по оси y. Эта ось является главной вертикальной линией прямоугольной оси или декартовой плоскости.
КООРДИНАТНАЯ ПЛОСКОСТЬ (декартова плоскость)
Координатная плоскость состоит из двух линий, пересекающихся под углом (что делает их перпендикулярными линиями) в точке (0,0) , известной как начало .
Компонент x точки (x, y) перемещает точку вдоль горизонтальной линии.Если значение x положительное, точка перемещается на «единицы x» вправо. С другой стороны, если значение x отрицательное, точка перемещается на «единицы x» влево.
Компонент Y точки (x, y) перемещает точку вдоль вертикальной линии. Если значение y положительное, точка перемещается на «единицы y» вверх. Однако, если значение y отрицательное, точка перемещается на «единицы y» вниз.
Квадранты декартовой плоскости
Пересечение оси x и оси y приводит к созданию четырех (4) секций или делений декартовой плоскости.
Первый квадрант расположен в верхней правой части плоскости.
Второй квадрант расположен в верхней левой части плоскости.
Третий квадрант расположен в нижней левой части плоскости.
Четвертый квадрант расположен в правом нижнем углу плоскости.
Примеры нанесения точек на график и определения его квадранта
Пример 1 : Постройте точку (4,2) и определите, в каком квадранте или оси она расположена.
Я начну с размещения точки в начале координат, которая является пересечением осей x и y. Думайте о происхождении как о «доме», откуда берутся все точки.
Затем я перемещу точку от начала координат на 4 единицы вправо, поскольку x = 4 (положительное значение по оси x означает перемещение вправо). Помните, что значение x — это первое число в упорядоченной паре (4,2).
С того места, где я остановился, мне нужно переместить 2 единицы вверх, параллельно главной вертикальной оси, поскольку y = 2 (положительное значение по оси y означает движение вверх).Значение y — это второе число в упорядоченной паре (4,2).
Окончательный ответ должен выглядеть так…
Точка (4,2) расположена в квадранте I .
Пример 2 : Постройте точку (–5, 4) и определите, в каком квадранте или оси она расположена.
Начните с размещения точки в начале координат, известном как центр декартовой координатной оси.
Из начала координат, поскольку x = −5 , переместитесь на 5 единиц влево.
… с последующим перемещением точки на 4 единицы вверх, потому что y = 4 .
Это окончательный ответ. Поскольку нанесенная точка находится в верхнем левом углу оси xy, она должна находиться в квадранте II.
Пример 3 : Постройте точку (5, –3) и определите, в каком квадранте или оси она расположена.
Начать из центра декартовой плоскости.
Переместите 5 единиц вправо, так как x = 5 .
Далее следует перемещение на 3 единицы вниз, так как y = −3 .
Последняя нанесенная точка показана ниже. Находясь в правом нижнем углу декартовой плоскости, это означает, что он находится в квадранте IV.
Пример 4 : Постройте точку (–2, –5) и определите, в каком квадранте или оси она расположена.
Поместите точку в начало координат (центр оси xy). Поскольку x = −2 , переместите точку на 2 единицы влево по оси x.Наконец, спуститесь на 5 единиц параллельно оси y, потому что y = −5 .
См. Анимированное решение ниже.
Точка на графике расположена в нижней левой части декартовой плоскости. Таким образом, он находится в квадранте III.
Пример 5 : Постройте точку (0,3) и определите, в каком квадранте или оси она расположена.
Я начинаю с анализа данной упорядоченной пары. Поскольку x = 0 , это означает, что нет движения по оси x .Однако y = 3 означает, что мне нужно переместить его на на 3 единицы вверх на .
Точка на графике: , ни ни в квадранте I, ни в квадранте II. Чтобы описать его местоположение, мы говорим, что он находится вдоль положительной оси Y.
Пример 6 : Постройте точку (0, –4) и определите, в каком квадранте или оси она расположена.
Это очень похоже на пример 5. Не будет движения по оси x, так как x = 0 .С другой стороны, y = — 4 говорит мне, что мне нужно переместить точку от начала координат на 4 единицы вниз.
Конечная точка не находится ни в в квадранте III, ни в квадранте IV. Я могу утверждать, что он находится вдоль отрицательной оси ординат.
Пример 7 : Постройте точку (–3,0) и определите, в каком квадранте или оси она расположена.
Из начала координат я сдвину его на 3 единицы влево по оси x, так как x = −3. Если y = 0, это означает, что движение по оси Y не последует.
Точка не находится ни в , ни в квадранте II, ни в квадранте III. Он находится по отрицательной оси абсцисс.
Пример 8 : Постройте точку (2,0) и определите, в каком квадранте или оси она расположена.
При x = 2 мне нужно переместить его на 2 единицы вправо. Если y = 0 , это означает, что движения по оси Y не произойдет.
Точка на графике не находится ни в , ни в в квадранте I и не в квадранте IV.Он находится вместе с положительной осью абсцисс.
Практика с рабочими листами
график x y
Найдите значения и используя форму. Наклон линии — это значение, а точка пересечения по оси Y — это значение. Чтобы встроить виджет в боковую панель вашего блога, установите плагин боковой панели Wolfram | Alpha Widget, скопируйте и вставьте идентификатор виджета, указанный ниже, в поле «id»: мы ценим ваш интерес к Wolfram | Alpha и скоро свяжемся с вами. График y = x.Бесплатная программа для решения математических задач отвечает на ваши домашние задания по алгебре, геометрии, тригонометрии, исчислению и статистике с пошаговыми пояснениями, как репетитор по математике. График x = y. Найдите больше инженерных виджетов в Wolfram | Alpha. Используйте форму пересечения наклона, чтобы найти наклон и точку пересечения по оси Y. Чтобы встроить этот виджет в сообщение в своем блоге WordPress, скопируйте и вставьте приведенный ниже шорткод в источник HTML: Чтобы добавить виджет на сайт MediaWiki, вики должен иметь расширение. Бесплатный графический калькулятор мгновенно отображает ваши математические задачи.Используйте форму пересечения наклона, чтобы найти наклон и точку пересечения по оси Y. Нажмите, чтобы увидеть больше шагов … x y 0 0 1 −1 6 x y 0 0 1 — 1 6 Постройте линию, используя наклон и точку пересечения по оси Y или точки. Выбирайте из различных типов диаграмм, например: линейные и гистограммы, круговые диаграммы, точечные диаграммы, XY-графики и круговые диаграммы. Наклон: получите бесплатный виджет «Поверхность графика f (x, y)» для своего веб-сайта, блога, WordPress, Blogger или iGoogle. Форма пересечения наклона:, где — наклон, а — точка пересечения по оси y. Найдите значения и используйте форму.Наклон: Перепишите уравнение как. Форма пересечения наклона:, где — наклон, а — точка пересечения по оси y. Наклон линии — это значение, а точка пересечения по оси Y — это значение. Создавайте онлайн-графики и диаграммы. Выберите два значения x x и вставьте их в уравнение, чтобы найти соответствующие значения y y. График поверхности f (x, y) от ARCHIresource.com. Чтобы встроить этот виджет в сообщение, установите плагин Wolfram | Alpha Widget Shortcode, скопируйте и вставьте приведенный выше шорткод в исходный HTML-код.
Habitat Robin Day Chair,
Целевое финансирование Wellcome,
Космическая спираль против аварийного транспорта,
Комментарий Набокова Евгений Онегин,
Список Maggotkin Of Nurgle 2019,
Скидка 10% на DVD,
Сходства между Ltd и Plc,
Команда Mitchell Marsh Ipl 2019,
Части цветка и их функции,
Нормы офисных площадей на человека,
Упражнения на внешнюю головку бицепса,
Тагалог 101 Pdf,
Решения для квалификационных экзаменов по комплексному анализу,
Первоначальная цена Chevy Nova 1973 года,
Prepa Tec Internacional,
Паула Дин суп из мускатной тыквы,
Rephresh Probiotic Reviews, Обзоры пробиотиков,
Ram 2500 Дизель,
Нарушение речи и языка,
Смертельная гонка,
Китовый плавник сансевиерия почва,
Вакансии Масси в Гайане,
Как поднять машину спереди,
Не работает фонтанный насос Veken Pet,
Приговор шеф-повара для класса 1,
1984 Oldsmobile 98 на продажу,
Как приготовить яблочный шнапс,
Социальные посещения фазы 2,
Список Maggotkin Of Nurgle 2019,
Prada Распродажа для мужчин,
10 Аят Терахир Али Имран,
Барангай Магсайсай Коронадал, г.

Канонический вид кривой и поверхности

Правила ввода выражений и функций

график

Matplotlib. Урок 4.1. Визуализация данных. Линейный график

Представление данных в виде точечной диаграммы или графика

Открытая Математика. Функции и Графики. Решение систем уравнений и неравенств

Стандартные графики

Диаграммы рассеяния

Линейные графики

Совмещение графиков

Функциональные параметры

Гистограммы

Столбчатые графики

Круговые (секторные) диаграммы

Цвет и прозрачность

Настройки отображения

Графические параметры

Разметка осей, рамка, сетка координат и произвольные линии

Аннотации данных (текст на графике)

Легенда

Построение графиков уравнений, содержащих модули

III.

IV. Закрепление. Решение задач.

V. Итог урока.

Какой график xy 0? — AnswersToAll

Что такое график xy 0?

Что означает X Y 0?

Каков наклон xy 0?

Как называется Y 0?

Что такое Y 0 на графике?

Y 0 — не решение?

Y 0 вертикальный или горизонтальный?

Как вы изобразите 0 0 на числовой прямой?

Какие десятичные знаки между 0 и 1?

Как построить график «больше или равно» на числовой прямой?

Как узнать, что у графика нет решения?

Какого решения нет Одно решение Бесконечные решения?

Как читать график неравенства?

Какой пропущенный шаг в решении викторины с неравенством 5 8x 2x 3?

Как узнать, не имеет ли неравенство решения?

Как определить, будет ли неравенство сплошной линией?

Какой символ представляет собой пунктирная линия?

При построении графика неравенства всегда можно использовать 0 0 в качестве контрольной точки?

Решить свойства прямой линии x-y = 0 Решатель алгебры тигра

x-y = 0

Пошаговое решение

Шаг 1:

Уравнение прямой линии

График прямой линии:

Вычислите точку пересечения Y:

Вычислите точку пересечения по оси X:

Расчет наклона:

Геометрическая фигура: прямая линия

Зачем это изучать

Термины и темы

Ссылки по теме

Поиск пересечений по оси x и оси y | Колледж алгебры

Как: по уравнению найти точки пересечения.

Пример 4: Нахождение точек пересечения данного уравнения

Решение

Попробуй 1

Исследование графиков уравнения xy = ax + by + c

Исследование уравнения

по

линий графика

Построение графиков линейных уравнений

Назад к линейным функциям

Нанесение точек на график или плоскость XY

А точка

КООРДИНАТНАЯ ПЛОСКОСТЬ (декартова плоскость)

Квадранты декартовой плоскости

Примеры нанесения точек на график и определения его квадранта

график x y

Добавить комментарий Отменить ответ