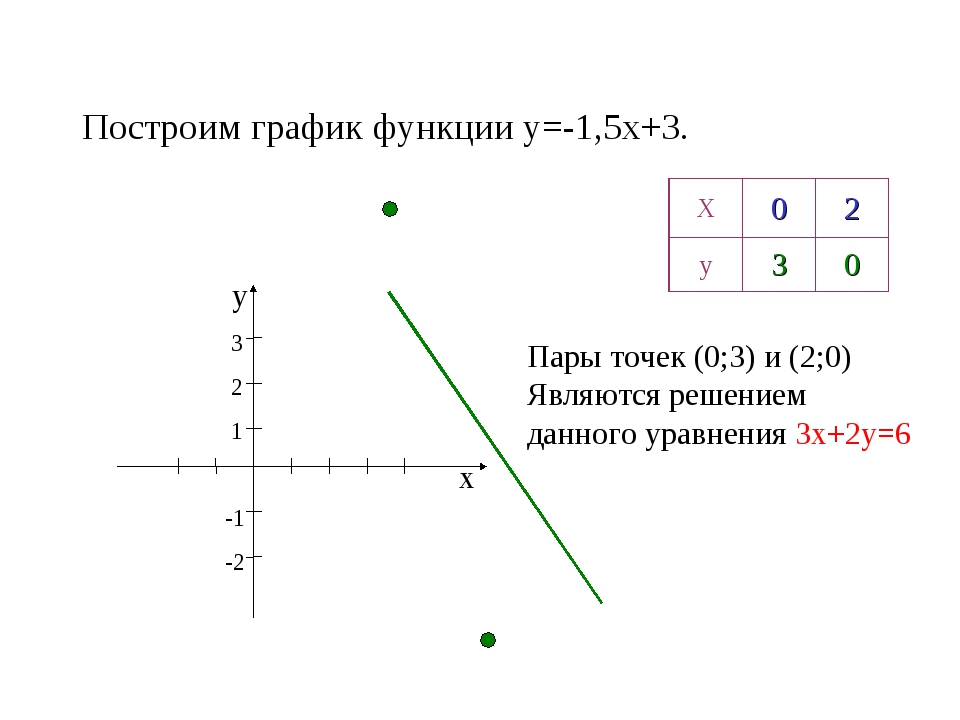
2/ab-3a-2b/bЕсли не понятно смотри картинку
Дана система уравнений: {6a+b=210 a−b=0 Вычисли значение переменной a.
Суммативное оценивание за раздел.Задание 1. 1) Сравните тексты с точки зрения целевойаудитории, стиля.1Великая Отечественная война — всенародная война
…
, в которой взначительной мере стёрлись грани между фронтом и тылом. Этаособенность ярко проявилась в массовом участии трудящихся воборонительных мероприятиях. Усилия народа привели к тому,что объем выпуска военной продукции резко возрос. Массовоепроизводство новейшей по тем временам военной техники ивооружений позволило уже в конце 1942 — начале 1943 годапревзойти врага не только в количестве, но и в качестве военнойтехники. Вместе с рабочим классом самоотверженную помощьфронту оказало колхозное крестьянство. Огромный вклад вперестройку народного хозяйства на военный лад оказали учёныеи научные учреждения. Образец героизма явили в эти суровыегоды женщины и молодёжь,N 2Великая Отечественная война 1941-1945 — война СоюзаСоветских Социалистических Республик против вторгшихся насоветскую территорию нацистской Германии и её европейскихсоюзников (Венгрии, Италии, Румынии, Словакии, Финляндии,Хорватии).
2/ab-3a-2b/b
Если не понятно смотри картинку
СОКРАТИТЬ ДРОБЬ !! ДАЮ 40 БАЛЛОВ
Найдите область определения функций: y в корни (3-x)(2x-5)
Содержание
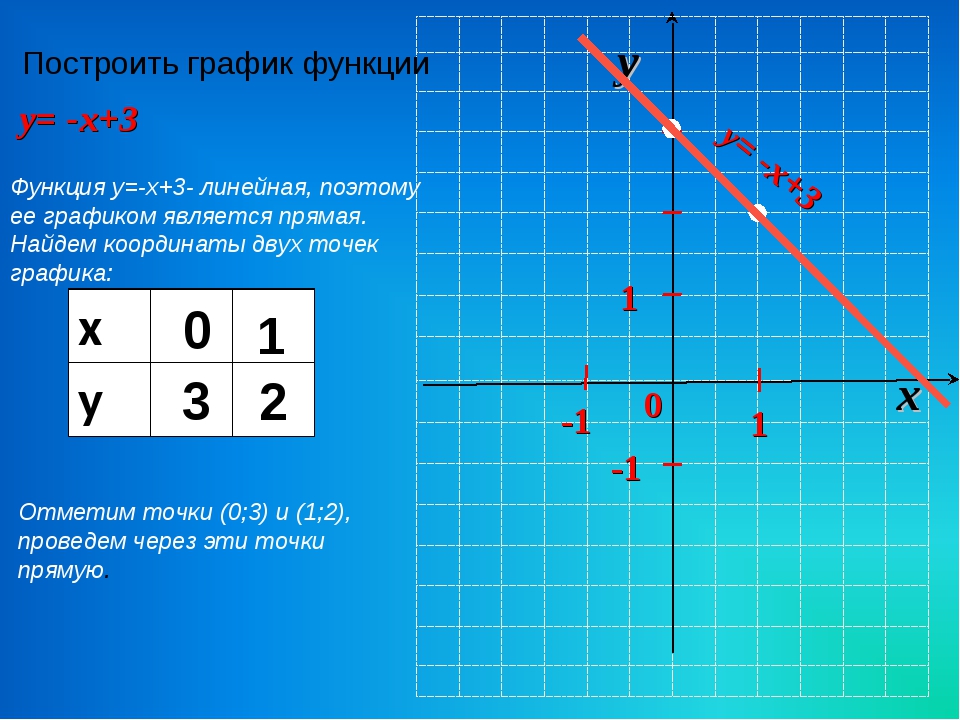
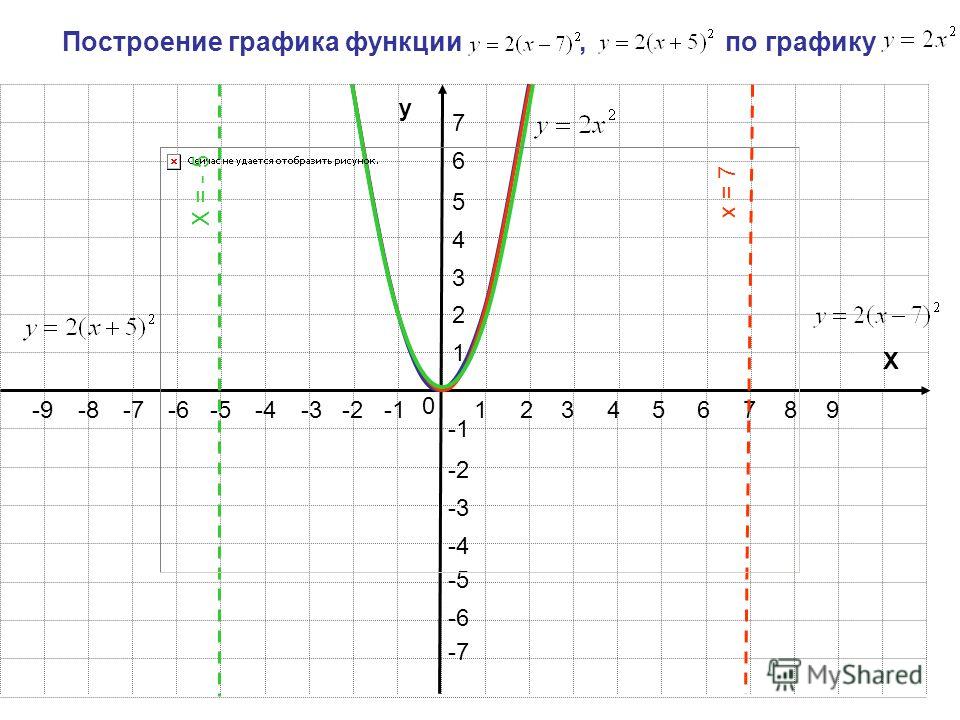
Построить график y 3x 2. Квадратичная и кубическая функции
Разберем как строить график с модулем.
Найдем точки при переходе которых знак модулей меняется.
Каждое выражения, которое под модулем приравниваем к 0. У нас их два x-3 и x+3.
x-3=0 и x+3=0
x=3 и x=-3
У нас числовая прямая разделится на три интервала (-∞;-3)U(-3;3)U(3;+∞). На каждом интервале нужно определить знак под модульных выражений.
1. Это сделать очень просто, рассмотрим первый интервал (-∞;-3). Возьмем с этого отрезка любое значение, например, -4 и подставим в каждое под модульное уравнение вместо значения х.
х=-4
x-3=-4-3=-7 и x+3=-4+3=-1
У обоих выражений знаки отрицательный, значит перед знаком модуля в уравнении ставим минус, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (-∞;-3).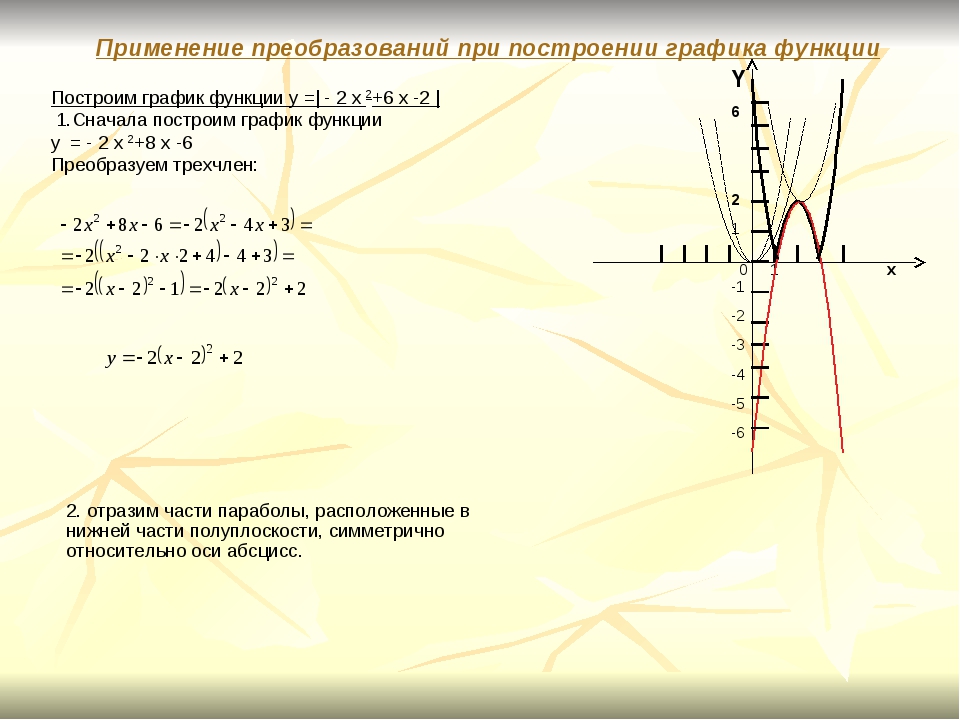
y=—
(x-3)-(—
(x+3))=-х+3+х+3=6
На интервале (-∞;-3) получился график линейной функции (прямой) у=6
2. Рассмотрим второй интервал (-3;3). Найдем как будет выглядеть уравнение графика на этом отрезке. Возьмем любое число от -3 до 3, например, 0. Подставим вместо значения х значение 0.
х=0
x-3=0-3=-3 и x+3=0+3=3
У первого выражения x-3 знак отрицательный получился, а у второго выражения x+3 положительный. Следовательно, перед выражением x-3 запишем знак минус, а перед вторым выражением знак плюс.
y=—
(x-3)-(+
(x+3))=-х+3-х-3=-2x
На интервале (-3;3) получился график линейной функции (прямой) у=-2х
3.Рассмотрим третий интервал (3;+∞). Возьмем с этого отрезка любое значение, например 5, и подставим в каждое под модульное уравнение вместо значения х.
х=5
x-3=5-3=2 и x+3=5+3=8
У обоих выражений знаки получились положительными, значит перед знаком модуля в уравнении ставим плюс, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (3;+∞).
y=+
(x-3)-(+
(x+3))=х-3-х-3=-6
На интервале (3;+∞) получился график линейной функции (прямой) у=-6
4. Теперь подведем итог.Постоим график y=|x-3|-|x+3|.
На интервале (-∞;-3) строим график линейной функции (прямой) у=6.
На интервале (-3;3) строим график линейной функции (прямой) у=-2х.
Чтобы построить график у=-2х подберем несколько точек.
x=-3 y=-2*(-3)=6 получилась точка (-3;6)
x=0 y=-2*0=0 получилась точка (0;0)
x=3 y=-2*(3)=-6 получилась точка (3;-6)
На интервале (3;+∞) строим график линейной функции (прямой) у=-6.
5. Теперь проанализируем результат и ответим на вопрос задания найдем значение k, при которых прямая y=kx имеет с графиком y=|x-3|-|x+3| данной функции ровно одну общую точку.
Прямая y=kx при любом значении k всегда будет проходить через точку (0;0). Поэтому мы можем изменить только наклон данной прямой y=kx, а за наклон у нас отвечает коэффициент k.
Если k будет любое положительное число, то будет одно пересечение прямой y=kx с графиком y=|x-3|-|x+3|.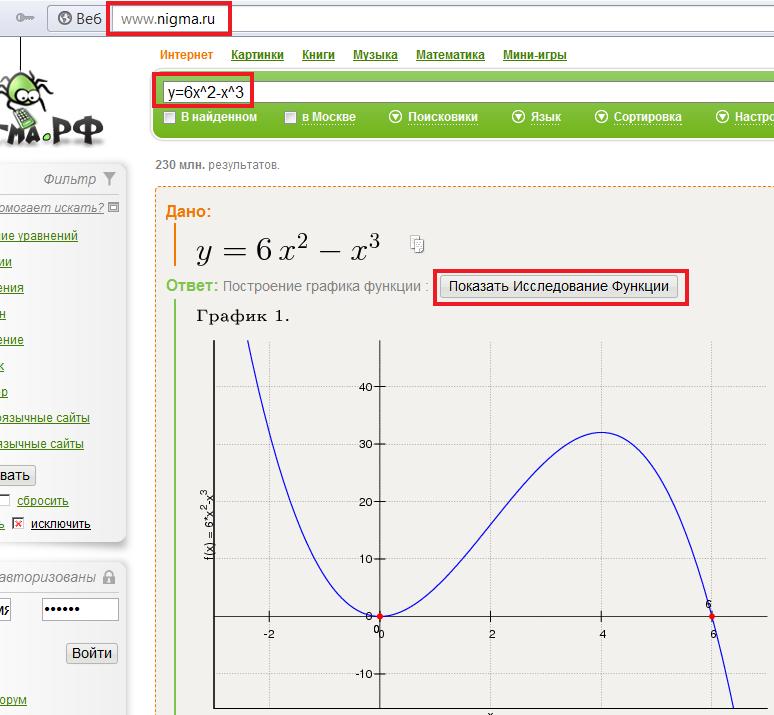
Этот вариант нам подходит.
Если k будет принимать значение (-2;0), то пересечений прямой y=kx с графиком y=|x-3|-|x+3| будет три.Этот вариант нам не подходит.
Если k=-2, решений будет множество [-2;2], потому что прямая y=kx будет совпадать с графиком y=|x-3|-|x+3| на данном участке. Этот вариант нам не подходит.
Если k будет меньше -2, то прямая y=kx с графиком y=|x-3|-|x+3| будет иметь одно пересечение.Этот вариант нам подходит.
Если k=0, то пересечений прямой y=kx с графиком y=|x-3|-|x+3| также будет одно.Этот вариант нам подходит.
Ответ: при k принадлежащей интервалу (-∞;-2)U и возрастает на промежутке }
График показательной функции, область определения и область значений функции — Алгебра 11 класс — Osvita.name
1. Функция y=3x−1 образована от показательной функции y=3x (показательной функцией называется функция, которая записана в виде y=ax, где (a>0, a≠1). Чтобы построить график этой функции, необходимо составить следующую таблицу с произвольно выбранными значениями аргумента x:
| x | −2 | −1 | 0 | 1 | 2 |
| y |
2.
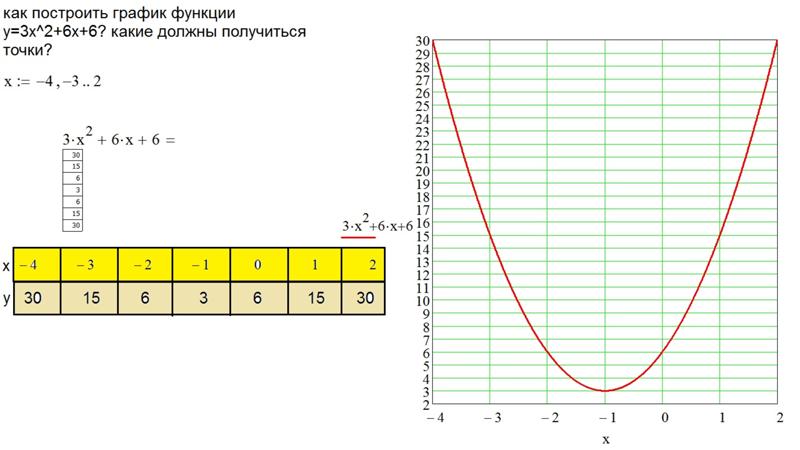Чтобы вычислить соответствующие значения функции, необходимо подставить соответствующие значения аргумента x в формулу функции y=3x:
a) y=3−2=132=19
б) y=3−1=131=13
в) y=30=1
г) y=31=3
д) y=32=9
3. Вычисленные значения функции записываем в таблицу:
x | -2 | -1 | 0 | 1 | 2 |
y | 19 | 13 | 1 | 3 | 9 |
4.
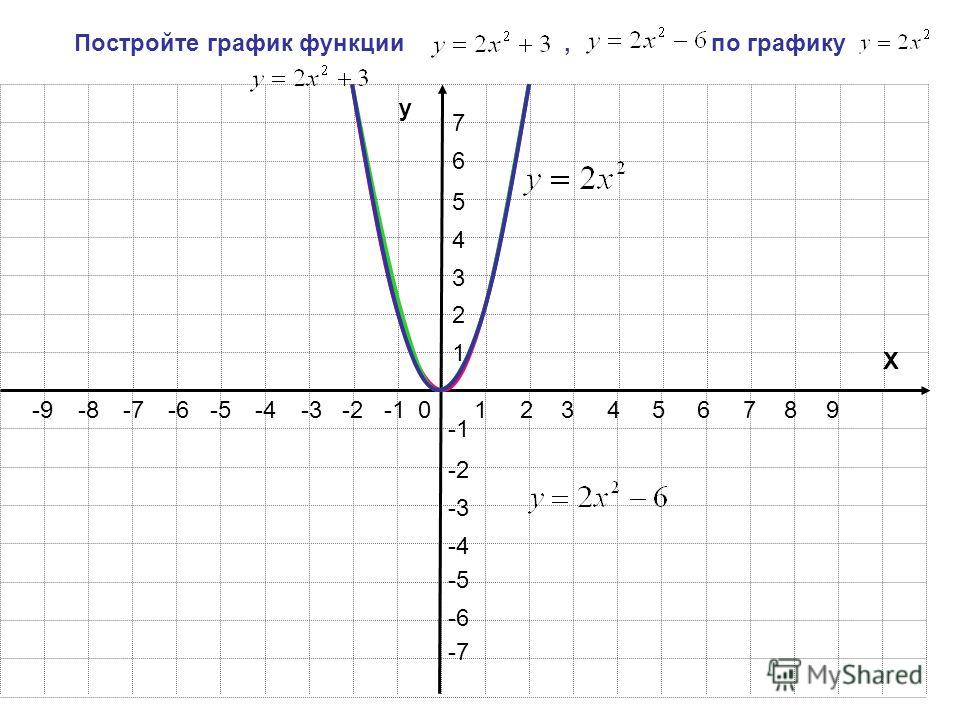Используя таблицу, строим график функции y=3x:
5. Функцию y=3x−1 можно записать в виде y=f(x)+a, где a≠0.
* Если a>0, то график функции y=f(x) переместится вдоль оси Oy на a единиц вверх.
* Если a<0, то график функции y=f(x) переместится вдоль оси Oy
Графики уравнений, содержащих знак модуля
Цель:
- закрепить методы построения графика линейной функции,
- закрепить умение учащихся задавать уравнением функцию, заданную при помощи графика,
- познакомить учащихся с тем, каким образом влияет знак модуля на отображение графика линейной функции
Оборудование: презентация (приложение 1)
Ход урока №1
При решении многих математических задач
необходимо быстро и точно строить графики любых
функций, изучаемых в школьном курсе алгебры.
Т.к. на уроке предстоит много построений,
начинаем, вспоминая, как строить график линейной
функции y = kx + b на основе анализа
углового коэффициента и коэффициента смещения
(слайд 2)
Сопоставляем уравнения и графики (слайд 3):
Построим в тетрадях в одной системе координат графики функций (y = —x; y = —x -4; y = -1/3 x – 2; y = 2x + 5; y = x + 1), проверяя себя при помощи слайда 4
Вспомним определение модуля числа x (слайд 5)
Рассматриваем, как можно построить график функции y = |x| на основании определения модуля, отбрасывая части прямых, не лежащих в полуплоскостях x < 0 и x> 0 (слайд 6)
Аналогично рассматриваем способ построения графика функции y = |x + 1| (слайд 7)
Сравнивая графики и уравнения функций (слайд 8-9),
делаем вывод о том, как можно построить график функции y = |x + a| — b смещением графика функции y = |x| (слайд 10-11)
Строим в тетрадях графики функций y = |x-3| + 3, y = |x – 3| — 2, y = |x+2| — 5, y = |x + 3| + 2 и проверяем себя при помощи слайда 12
Далее учащиеся должны на основе рисунка, представленного на слайде 13, задать функцию уравнением:
При построении графиков очень важно научить
ребят анализировать область определения и
множество значений функции и “переносить”
указанные множества на координатную плоскость.
Заполняем таблицу (слайд 12):
D(y)
E (y)
y = |x|
y = |x – 3|
y = |x – 3| +2
y = — |x|
y = |x + 2| -5
y = — |x +2| -5
И рассматриваем, как множества значений можно определить на основе графиков (слайд 15)
Учащимся предлагается определить D (y) и E(y) по рисунку (слайд 16):
Ученики самостоятельно придумывают уравнение функции по заданным D(y) и E(y) (слайд 17):
Анализируя графики и уравнения (слайд
18), ученики делают вывод о том, как влияет знак
минуса перед модульными скобками на график.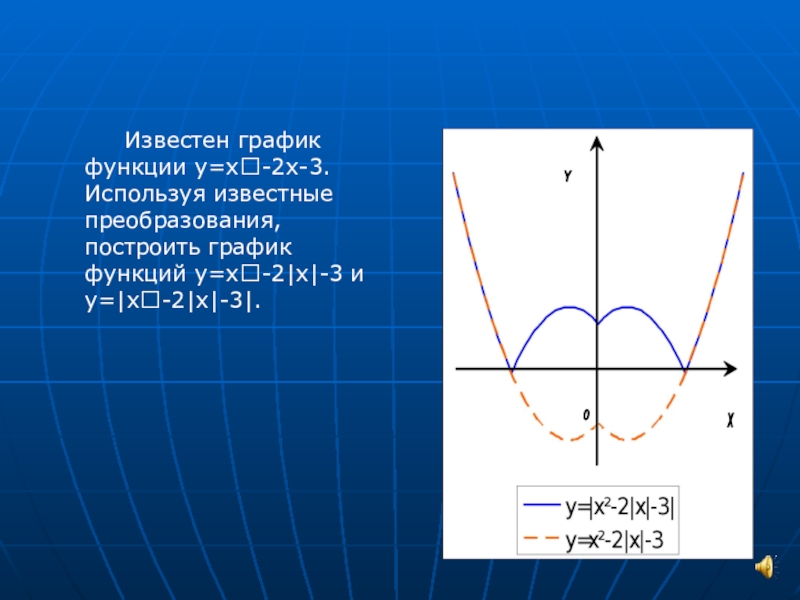
И
самостоятельно задают уравнение по графикам,
представленным на слайде 19.
Ход урока № 2
Устно проговариваем уравнения функций по графикам (слайд 20):
Аналогично схеме предыдущего урока (слайд 21-27) ученики знакомятся с тем, каким образом влияет коэффициент перед аргументом функции на график. В результате они должны научиться описывать уравнением следующие графики:
Для закрепления полученных знаний, в тетрадях в одной системе координат ребята строят следующие графики:
y = |0,5x| при -3 < x< 3;
y = 3 при -1 < x< 1;
y = -|x + 3| + 6 при -4 < x < -2;
y = -|x — 3| + 6 при 2 < x < 4;
y = |x + 3| + 4 при -4 < x < -2;
y = |x — 3| + 4 при 2 < x ? 4;
y = -|0,5x – 1,5| + 7 при -5 < x < -1;
y = -|0,5x + 1,5| + 7 при 1 < x < 5.
Проверяют себя по слайду 29:
Домашнее задание: придумать картину, состоящую из отрезков прямых, и описать ее при помощи уравнений функций.
Ход урока № 3
Построим графики функций y = |3x| — 3 и y = |3x – 3|. Как в каждом случае связаны y(x) и y(-x)?
Наличие условия y(x) = y(-x) означает симметрию относительно …?
Приведите примеры уравнений функции, графики которых будут симметричны относительно оси ординат
Если в модульные скобки заключается переменная y, то мы получаем условие |y| = |-y|. Какую симметрию задает это условие?
На слайде 34 последовательно рассматриваем цепочку построения графиков:
y = 3x – 3, |y| = 3x – 3, |y| = |3x| — 3, |y|
= |3x – 3| путем преобразований симметрии.
Выводим и запоминаем три правила:
Распределите, к какому типу из трех (y = f(|x|, |y| = f(x), y = |f(x)|), можно отнести каждое уравнение:
|y| = 2 – x, y = |3x — 4|, |x| + |y| = 2, |y| = 3x – 4, y = |3|x| — 4|, y = |3x| — 4, |y| = |3|x| — 4|, |y| = |3x – 4|.
Проверяем себя (слайд 35)
Строим последовательную цепочку графиков (тонкими линиями в тетрадях):
1) y = 3x – 4, y = |3x – 4|, y = |3|x| - 4|, |y| = |3|x| — 4|
2) y = 3x – 4, y = 3|x| — 4, y = |3|x| — 4|
Рассматриваем способ построения графика соответствия |x| + |y| = 2.
Самостоятельно строим график |x| — |y| = 2 и
проверяем себя по слайду 39.
Домашнее задание: придумать пять уравнений соответствий с модулем, в которых встречаются все случаи, рассмотренные на уроке, и построить графики.
Электронные домашние задания по математике с 02-09.02.2016 для групп 1-ТО и 1-ТЭР преподаватель Семенихина Е.А. | Учебно-методический материал на тему:
Электронные домашние задания по математике с 02-09.02.2016 для групп 1-ТО и 1-ТЭР
Преподаватель Семенихина Е.А.
Задание № 23. Определить промежутки монотонности функций.
Монотонность функции – это возрастание и убывание функции:
Пример :Определить промежутки монотонности функции:
у = х3 – 2х2 – 5х + 3
- Найдем область определения функции:
D(у) = R
- Находим производную функции и приравниваем ее к нулю:
у′ = 3х2 – 4х – 5 у′ =0
3х2 – 4х – 5 = 0
3)Решаем полученное уравнение: 4) Выставляем полученные значения
D = 16 + 20 • 3 = 76 икса на ось х:
х1 ≈ (4-8,4)/6 ≈ -4,4/6 ≈ — 0,8 у1 + — +
х2 (4+8,4)/6 = 12,4/6 ≈ 2,6 у -0,8 2,6
Определяем знак производной на каждом из участков , для этого любое число с участка подставляем в производную.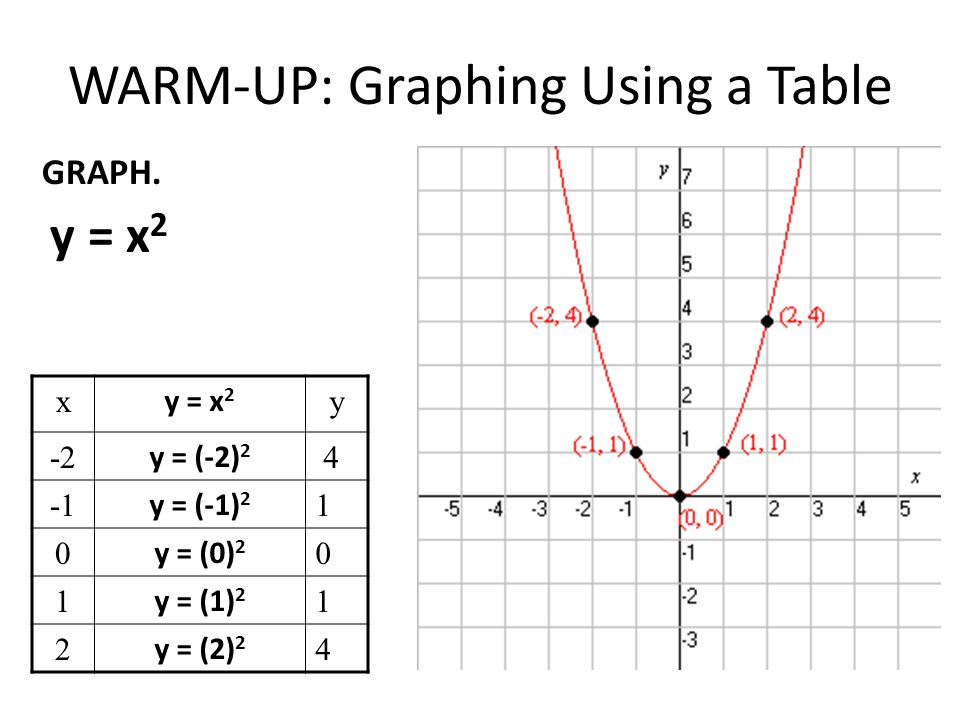
Если производная на участке имеет знак «+», то функция возрастает, а если «-», то функция убывает.
Ответ: у↑ при х ∈ ( -∞; -0,8) U ( 2,6; + ∞)
у↓ при х ∈ (- 0,8; 2,6 )
Варианты:
- a) y = (x-3) (x-2) b) y = x4 –8×2 –9
c) y = 1/3 x3 – 2×2 –5
- a) y = x3 – 3×2 + 2 b) y = x5 –x3 + x + 2
c) y = 8×3 – 4×2 + 3
- a) y = (x2 +x) (x-2) b) y = 1/5 x5 –4×2 c) y = 6×3 – 2x –41
- a) y = x5 – x2 + 8 b) y = x5 –x3 + x + 2 c) y = — 2×3 + x – 4
- a) y = 3×2 – 6x + 5 b) y = 3×4 + 4×3 + 1 c) y = 3×2 – 4x + 5
- a) y = 4×4 – 2×2 + 3 b) y = 2×3 + 3×2 – 12x + 1 c) y = 8×3 – x2 + 7x – 2
- a) y = x4 – 10×2 + 9 b) y = x5 –x3 + x + 2 c) y = — 7×3 + x2 – 3x – 1
- a) y = x4 – 4×3 – 8×2 + 3 b) y = 3×3 –9×2 + 2 c) y = x3 – 4×2 + 3x + 1
- a) y = x5 – x2 + 8 b) y = x3/3 + 2×2 – 5x + 4 c) y = -5×3 + 6×2 – 3
- a) y = x3 – 3×2 + 2 b) y = x5 –x3 + x + 2 c) y = 8×3 – 4×2 + 3
- a) y = x3 – 3x + 2 b) y = 2×3 + 3×2 – 1 c) y = 6×3 – 8x + 21
- a) y = x (x2 + 3x + 2) b) y = x4/4 –2×2 – 9/4 c) y = 2×3 – 4x + 7
13.
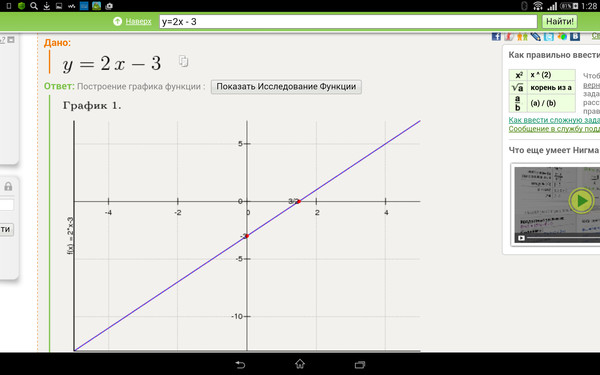a) y = 1/15 x3 – 9/20 x2 – 1/2 x b) y = x3 –3×2 + 2 c) y = 7×3 – 2×2 + 3x – 1
14.а) y = x3 – 3×2 + 2 b) y = x5 –x3 + x + 2 c) y = 8×3 – 4×2 + 3
15.а) y = (x2 +x) (x-2) b) y = 1/5 x5 –4×2 c) y = 6×3 – 2x –41
16. а)y = x4 – 4×3 – 8×2 + 3 b) y = 2×3 + 3×2 – 12x + 30 c) y = 6×3 – 2×2 + x – 5
17.a) y = x3 – 3×2 + 2 b) y = 2×3 + 3×2 – 1 c) y = 6×3 – 8x + 21
18.a) y = x3 – 4×2 – 3x + 12 b) y = 0,5×4 – 4×2 c) y = 8×2 – 3x — 2
19.
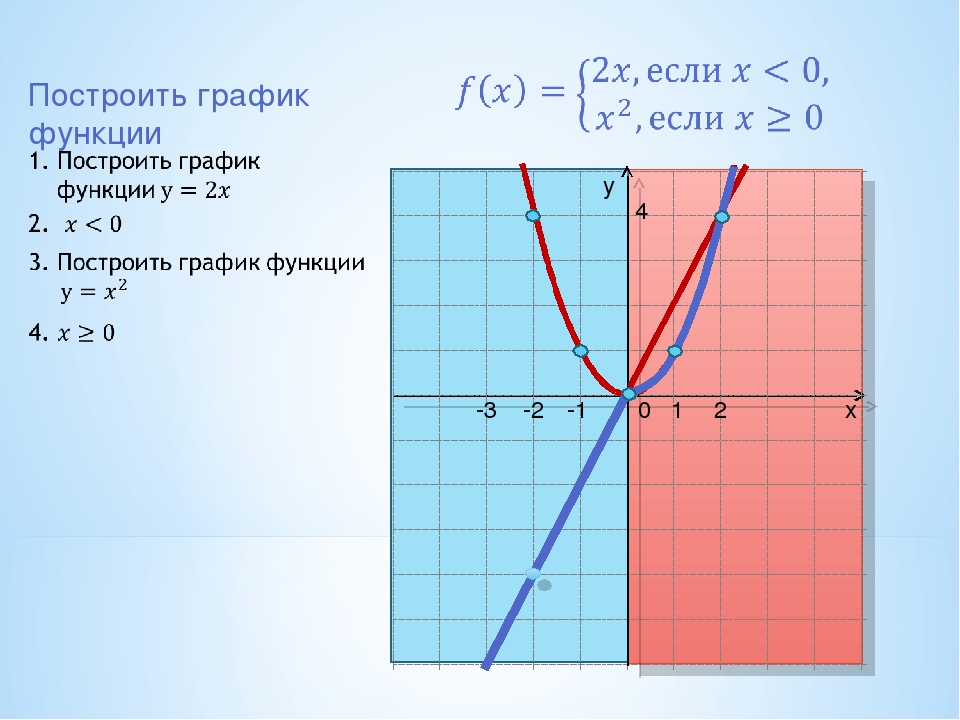a) y = x3 – 3×2 + 2 b) y = 2×3 + 3×2 – 1 c) y = 6×3 – 8x + 21
20.a) y = x3 – 3×2 + 2 b) y = x5 — x3 +x + 2 c) y = 8×3 – 4x + 3
21.a) y = 3×2 – 6x + 5 b) y = 3×4 + 4×3 + 1 c) y = — 3×2 – 4x + 5
22.a) y = x5 – x2 + 8 b) y = x3/3 + 2×2 – 5x + 4 c) y = -5×3 + 6×2 – 3
23.a) y = 1/5 x5 –4×2 b) y = x5 –x3 + x + 2 c) y = — 2×3 + x – 4
24.a) y = (x-3) (x-2) b) y = x4 –8×2 –9 c) y = 1/3 x3 – 2×2 –5
25.a) y = x4 – 10×2 + 9 b) y = x3 – 3×2 + x + 5 c) y = — 7×3 + x2 – 3x – 1
26.
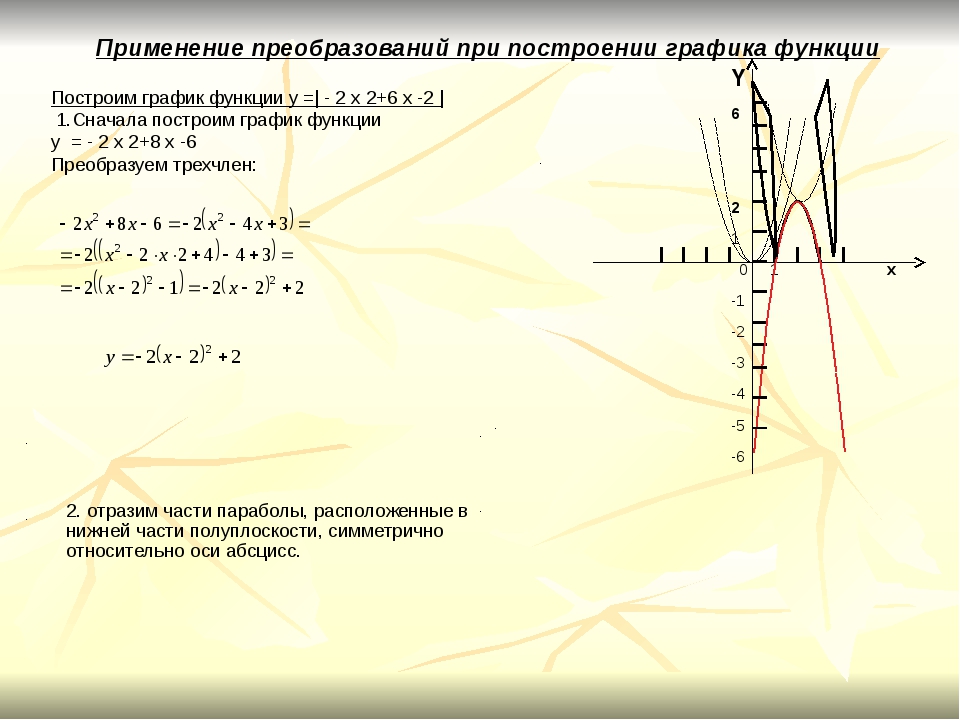a) y = 3×4 – 4×3 b) y = x2 (2x – 3) – 12 (3x – 2) c) y = 5×3 — 3×2 + x – 1
27.a) y = 4×4 – 2×2 + 3 b) y = 2×3 + 3×2 – 12x + 1 c) y = 8×3 – x2 + 7x – 2
28.a) y = x4 – 4×3 – 8×2 + 3 b) y = 2×3 + 3×2 – 12x + 30 c) y = 6×3 – 2×2 + x – 5
29.a) y = x (x2 + 3x + 2) b) y = x4/4 –2×2 – 9/4 c) y = 2×3 – 4x + 7
30.a) y = 2×3 – 6×2 – 18x + 7 b) y = 2×3 – 9×2 + 12x c) y = x2 – 5x + 6
Задание № 24. Найти точки экстремума функций.
Экстремумом функции называется значение функции в точках максимума и минимума.
Пример: y = x3 – 2×2 + x – 5
Д (y) = R
y1 = 3×2 – 4x + 1 y1 + — +
y1 = 0 y 1/3 1
3×2 – 4x + 1 = 0
Д = 4 x1 = 1/3 x2 = 1
Если производная при переходе через точку меняет знак с «+» на «-», то в этой точке максимум, а если производная меняет знак с «-» на «+», то эта точка минимума функции.
X max = 1/3 X min = 1
Находим экстремумы:
y max = (1/3)3 — 2(1/3)2 + 1/3 – 5 = 1/27 — 2/9 + 1/3 – 5 = 4/27 – 5 = 4 23/27
y min = 13 – 2 · 12 + 1 – 5 = -5
Варианты:
1. a) y = x4 – 4×3 – 8×2 + 3
b) y = 3×3 –9×2 + 2 c) y = x3 – 4×2 + 3x + 1
2. а) y = (x2 +x) (x-2)
b) y = 1/5 x5 –4×2 c) y = 6×3 – 2x –41
3. a) y = x3 – 3x + 2
b) y = 2×3 + 3×2 – 1 c) y = 6×3 – 8x + 21
4. a) y = (x-3) (x-2)
b) y = x4 –8×2 –9 c) y = 1/3 x3 – 2×2 –5
5. a) y = x (x2 + 3x + 2)
b) y = x4/4 –2×2 – 9/4 c) y = 2×3 – 4x + 7
6. а) y = x3 – 3×2 + 2
b) y = x5 –x3 + x + 2 c) y = 8×3 – 4×2 + 3
7. a) y = x3 – 4×2 – 3x + 12
b) y = 0,5×4 – 4×2 c) y = 8×2 – 3x — 2
8. a) y = 1/5 x5 –4×2
b) y = x5 –x3 + x + 2 c) y = — 2×3 + x – 4
9.
a) y = x3 – 3×2 + 2
b) y = x5 — x3 +x + 2 c) y = 8×3 – 4x + 3
10. a) y = 1/15 x3 – 9/20 x2 – 1/2 x
b) y = x3 –3×2 + 2 c) y = 7×3 – 2×2 + 3x – 1
11. a) y = 3×4 – 4×3
b) y = x2 (2x – 3) – 12 (3x – 2) c) y = 5×3 — 3×2 + x – 1
12. a) y = x3 – 3×2 + 2
b) y = 2×3 + 3×2 – 1 c) y = 6×3 – 8x + 21
13. a) y = 3×2 – 6x + 5
b) y = 3×4 + 4×3 + 1 c) y = 3×2 – 4x + 5
14. a) y = x3 – 3×2 + 2
b) y = 2×3 + 3×2 – 1 c) y = 6×3 – 8x + 21
15. a) y = (x-3) (x-2)
b) y = x4 –8×2 –9 c) y = 1/3 x3 – 2×2 –5
16. a) y = x4 – 4×3 – 8×2 + 3
b) y = 2×3 + 3×2 – 12x + 30 c) y = 6×3 – 2×2 + x – 5
17. a) y = 4×4 – 2×2 + 3
b) y = 2×3 + 3×2 – 12x + 1 c) y = 8×3 – x2 + 7x – 2
18. a) y = x4 – 10×2 + 9
b) y = x3 – 3×2 + x + 5 c) y = — 7×3 + x2 – 3x – 1
19.
a) y = x3 – 3×2 + 2
b) y = x5 –x3 + x + 2 c) y = 8×3 – 4×2 + 3
20. a) y = 2×3 – 6×2 – 18x + 7
b) y = 2×3 – 9×2 + 12x c) y = x2 – 5x + 6
21. a) y = 1/5 x5 –4×2
b) y = x5 –x3 + x + 2 c) y = — 2×3 + x – 4
22. a) y = x5 – x2 + 8
b) y = x3/3 + 2×2 – 5x + 4 c) y = -5×3 + 6×2 – 3
23. а)y = x4 – 4×3 – 8×2 + 3
b) y = 2×3 + 3×2 – 12x + 30 c) y = 6×3 – 2×2 + x – 5
24. a) y = x5 – x2 + 8
b) y = x3/3 + 2×2 – 5x + 4 c) y = -5×3 + 6×2 – 3
25. a) y = 4×4 – 2×2 + 3
b) y = 2×3 + 3×2 – 12x + 1 c) y = 8×3 – x2 + 7x – 2
26. a) y = 3×2 – 6x + 5
b) y = 3×4 + 4×3 + 1 c) y = — 3×2 – 4x + 5
27. a) y = x3 – 3×2 + 2
b) y = x5 –x3 + x + 2 c) y = 8×3 – 4×2 + 3
28. a) y = x4 – 10×2 + 9
b) y = x5 –x3 + x + 2 c) y = — 7×3 + x2 – 3x – 1
29.
a) y = x (x2 + 3x + 2)
b) y = x4/4 –2×2 – 9/4 c) y = 2×3 – 4x + 7
30. a) y = x3 – 3x + 2
b) y = 2×3 + 3×2 – 1 c) y = 6×3 – 8x + 21
Задание № 25.Исследовать функцию и построить эскиз графика.
Исследование функции провести по следующей схеме:
- Область определения
- Точки пересечения с осями
- Промежутки монотонности
- Экстремумы функции
- Эскиз графика
Пример: у = 3х2 – х – 2
1) Д(у) = R
2) х = 0; у = -2
у = 0 3х2 – х – 2 = 0
Д = 25 х1 = 1 х2 = — 2/3
3) у1 = 6х – 1 у1 = 0 6х – 1 = 0 х = 1/6
у1 — +
у 1/6
у↑ при х Є (1/6; +∞)
у↓ при х Є (-∞; 1/6)
4) х min = 1/6
x min = 3(1/6)2 — 1/6 – 2 = 1/12 — 1/6 – 2 = -21/12
5) у
0
-2/3 1/6 1 х
-21/12
Варианты:
1.
Исследовать функцию и построить эскиз графика:
y = x3 – 3×2 + 2
2. Исследовать функцию и построить эскиз графика:
y = 4×4 – 2×2 + 3
3. Исследовать функцию и построить эскиз графика:
y = 1/15 x3 – 9/20 x2 – 1/2 x
4. Исследовать функцию и построить эскиз графика:
y = x3 – 3×2 + 2
5. Исследовать функцию и построить эскиз графика:
y = 2×3 – 6×2 – 18x + 7
6. Исследовать функцию и построить эскиз графика:
y = 1/5 x5 –4×2
7. Исследовать функцию и построить эскиз графика:
y = 3×4 – 4×3
8. Исследовать функцию и построить эскиз графика:
y = (x2 +x) (x-2)
9. Исследовать функцию и построить эскиз графика:
y = x3 – 3×2 + 2
10. Исследовать функцию и построить эскиз графика:
y = 4×4 – 2×2 + 3
11. Исследовать функцию и построить эскиз графика:
y = x4 – 10×2 + 9
12. Исследовать функцию и построить эскиз графика:
y = x4 – 4×3 – 8×2 + 3
13.
Исследовать функцию и построить эскиз графика:
y = (x-3) (x-2)
14. Исследовать функцию и построить эскиз графика:
y = x (x2 + 3x + 2)
15. Исследовать функцию и построить эскиз графика:
y = (x2 +x) (x-2)
16. Исследовать функцию и построить эскиз графика:
y = x5 – x2 + 8
17. Исследовать функцию и построить эскиз графика:
y = x3 – 3×2 + 2
18. Исследовать функцию и построить эскиз графика:
y = (x-3) (x-2)
19. Исследовать функцию и построить эскиз графика:
y = x4 – 4×3 – 8×2 + 3
20. Исследовать функцию и построить эскиз графика:
y = x3 – 3x + 2
21. Исследовать функцию и построить эскиз графика:
y = x3 – 4×2 – 3x + 12
22. Исследовать функцию и построить эскиз графика:
y = x (x2 + 3x + 2)
23. Исследовать функцию и построить эскиз графика:
y = 3×2 – 6x + 5
24. Исследовать функцию и построить эскиз графика:
y = x3 – 3×2 + 2
25.
Исследовать функцию и построить эскиз графика:
y = 1/5 x5 –4×2
26. Исследовать функцию и построить эскиз графика:
y = x4 – 10×2 + 9
27. Исследовать функцию и построить эскиз графика:
y = x4 – 4×3 – 8×2 + 3
28. Исследовать функцию и построить эскиз графика:
y = x3 – 3×2 + 2
29. Исследовать функцию и построить эскиз графика:
y = 3×2 – 6x + 5
30. Исследовать функцию и построить эскиз графика:
y = x5 – x2 + 8
к графику функции в данной точке.
Уравнение касательной к графику функции в данной точки х0 имеет вид:
у – у0 = у1 (х0) · (х – х0)
Пример: Написать уравнение касательной в точке х0 = 1 к графику функции:
у = 3х2 – 5х – 1
у0 = 3 · (1)2 – 5 · 1 – 1 = -3
у1(х0) = 3 · 2х – 5 = 3 · 2 · 1 – 5 = 1
у + 3 = 1 (х – 1)
у = х – 1 – 3
у = х – 4
Варианты:
1. Найдите уравнение касательной к графику функции в точке
x0 = 2 y = 8×3 – 4x + 3
2.
Найдите уравнение касательной к графику функции в точке
x0 = 1 y = 8×3 – x2 + 7x – 2
3. Найдите уравнение касательной к графику функции в точке
x0 = 2 y = 7×3 – 2×2 + 3x – 1
4. Найдите уравнение касательной к графику функции в точке
x0 =-1 y = 6×3 – 8x + 21
5. Найдите уравнение касательной к графику функции в точке
x0 = 3 y = x2 – 5x + 6
6. Найдите уравнение касательной к графику функции в точке
x0 = 3 y = — 2×3 + x – 4
7. Найдите уравнение касательной к графику функции в точке
x0 = -1 y = 5×3 — 3×2 + x – 1
8. Найдите уравнение касательной к графику функции в точке
x0 = 1 y = 6×3 – 2x –41
9. Найдите уравнение касательной к графику функции в точке
x0 =-1 y = 6×3 – 8x + 21
10.
Найдите уравнение касательной к графику функции в точке
x0 = 1 y = 8×3 – x2 + 7x – 2
11. Найдите уравнение касательной к графику функции в точке
x0 = 2 y = — 7×3 + x2 – 3x – 1
12. Найдите уравнение касательной к графику функции в точке
x0 = 1 y = 6×3 – 2×2 + x – 5
13. Найдите уравнение касательной к графику функции в точке
x0 = 3 y = 1/3 x3 – 2×2 –5
14. Найдите уравнение касательной к графику функции в точке
x0 =-1 y = 2×3 – 4x + 7
15. Найдите уравнение касательной к графику функции в точке
x0 = 1 y = 6×3 – 2x –41
16. Найдите уравнение касательной к графику функции в точке
x0 = -1 y = -5×3 + 6×2 – 3
17. Найдите уравнение касательной к графику функции в точке
x0 = 2 y = 8×3 – 4×2 + 3
18.
Найдите уравнение касательной к графику функции в точке
x0 = 3 y = 1/3 x3 – 2×2 –5
19. Найдите уравнение касательной к графику функции в точке
x0 = 1 y = x3 – 4×2 + 3x + 1
20. Найдите уравнение касательной к графику функции в точке
x0 = 1 y = 6×3 – 8x + 21
21. Найдите уравнение касательной к графику функции в точке
x0 = -2 y = 8×2 – 3x — 2
22. Найдите уравнение касательной к графику функции в точке
x0 =-1 y = 2×3 – 4x + 7
23. Найдите уравнение касательной к графику функции в точке
x0 =-2 y = — 3×2 – 4x + 5
24. Найдите уравнение касательной к графику функции в точке
x0 = 2 y = 8×3 – 4×2 + 3
25. Найдите уравнение касательной к графику функции в точке
x0 = 3 y = — 2×3 + x – 4
26.
Найдите уравнение касательной к графику функции в точке
x0 = 2 y = — 7×3 + x2 – 3x – 1
27. Найдите уравнение касательной к графику функции в точке
x0 = 1 y = 6×3 – 2×2 + x – 5
28. Найдите уравнение касательной к графику функции в точке
x0 = 2 y = 8×3 – 4×2 + 3
29. Найдите уравнение касательной к графику функции в точке
x0 = -2 y = 3×2 – 4x + 5
30. Найдите уравнение касательной к графику функции в точке
x0 = -1 y = -5×3 + 6×2 – 3
значение функции на отрезке.
Пример: Найти наибольшее и наименьшее значение функции:
y = 5×3 – x2 – x + 1 на отрезке [-1; 1]
- Подставим концы отрезка в функцию и найдем два игрека.
y(-1) = 5(-1)3 – (-1)2 – (-1) + 1 = -5-1+1+1 = -4
y(1) = 5 · 13 – 12 – 1 + 1 = 4
- Найдем производную функции и приравняем ее к нулю.
Решаем полученное уравнение:
Решаем полученное уравнение:y1 = 5 · 3×2 – 2x – 1 = 0
15×2 – 2x – 1 = 0
Д = 4 + 4 · 15 = 64
x1 = 2-8/30 = -1/5 x2 = 2+8/30 = 1/3
Так как полученные числа входят в отрезок [-1; 1], то им находим игреки:
y(-1/5) = 5(-1/5)3 — (-1/5)2 — (-1/5) + 1 = 1 23/25
y(1/3) = 5(1/3)3 — (1/3)2 — (1/3) + 1 = 20/27
Из всех полученных игреков выбираем самый большой и самый маленький.
Ответ: у наиб. = у(1) = 4 у наим. = у(-1) = -4
[-1;1] [-1;1]
Варианты:
1. Найдите наибольшее и наименьшее значение функции на отрезке:
[-1;1] y = x5 –x3 + x + 2
2. Найдите наибольшее и наименьшее значение функции на отрезке:
[-2;2] y = 2×3 + 3×2 — 1
3. Найдите наибольшее и наименьшее значение функции на отрезке:
[-3;3] y = 2×3 + 3×2 – 12x + 30
4.
Найдите наибольшее и наименьшее значение функции на отрезке:
[-2;0] y = x3/3 + 2×2 – 5x + 4
5. Найдите наибольшее и наименьшее значение функции на отрезке:
[-2;0] y = 2×3 + 3×2 — 1
6. Найдите наибольшее и наименьшее значение функции на отрезке:
[-2;2] y = x3/3 + 2×2 – 5x + 4
7. Найдите наибольшее и наименьшее значение функции на отрезке:
[-1;1] y = x5 –x3 + x + 2
8. Найдите наибольшее и наименьшее значение функции на отрезке:
[-3;0] y = 2×3 + 3×2 – 12x + 30
9. Найдите наибольшее и наименьшее значение функции на отрезке:
[0;3] y = 2×3 – 9×2 + 12x
10. Найдите наибольшее и наименьшее значение функции на отрезке:
[-1;3] y = x4/4 –2×2 – 9/4
11. Найдите наибольшее и наименьшее значение функции на отрезке:
[-1;1] y = x4 –8×2 -9
12.
Найдите наибольшее и наименьшее значение функции на отрезке:
[-2;1] y = 3×4 + 4×3 + 1
13. Найдите наибольшее и наименьшее значение функции на отрезке:
[-3;6] y = x2 (2x – 3) – 12 (3x – 2)
14. Найдите наибольшее и наименьшее значение функции на отрезке:
[0;3] y = 1/5 x5 –4×2
15. Найдите наибольшее и наименьшее значение функции на отрезке:
[0;3] y = x5 –x3 + x + 2
16. Найдите наибольшее и наименьшее значение функции на отрезке:
[-2;1] y = 3×4 + 4×3 + 1
17. Найдите наибольшее и наименьшее значение функции на отрезке:
[-1;5] y = 2×3 + 3×2 – 12x + 1
18. Найдите наибольшее и наименьшее значение функции на отрезке:
[-1;1] y = x5 –x3 + x + 2
19. Найдите наибольшее и наименьшее значение функции на отрезке:
[-1;3] y = x4/4 –2×2 – 9/4
20.
Найдите наибольшее и наименьшее значение функции на отрезке:
[-1;1] y = x5 –x3 + x + 2
21. Найдите наибольшее и наименьшее значение функции на отрезке:
[-2;2] y = 2×3 + 3×2 – 1
22. Найдите наибольшее и наименьшее значение функции на отрезке:
[0;3] y = 1/5 x5 –4×2
23. Найдите наибольшее и наименьшее значение функции на отрезке:
[0;3] y = x3 – 3×2 + x + 5
24. Найдите наибольшее и наименьшее значение функции на отрезке:
[-1;1] y = x5 –x3 + x + 2
25. Найдите наибольшее и наименьшее значение функции на отрезке:
[-1;1] y = x4 –8×2 -9
26. Найдите наибольшее и наименьшее значение функции на отрезке:
[-2;2] y = x3 –3×2 + 2
27. Найдите наибольшее и наименьшее значение функции на отрезке:
[-1;4] y = 3×3 –9×2 + 2
28.
Найдите наибольшее и наименьшее значение функции на отрезке:
[0;3] y = 0,5×4 – 4×2
29. Найдите наибольшее и наименьшее значение функции на отрезке:
[-2;2] y = x3 –3×2 + 2
30. Найдите наибольшее и наименьшее значение функции на отрезке:
[-1;5] y = 2×3 + 3×2 – 12x + 1
Как строить функцию в Excel — Построение в Excel графиков математических и тригонометрических функций
Графика функций. Построение графиков функций в среде МS Excel
- Войнова Татьяна Олеговна, учитель математики
- Гусев Александр Николаевич, учитель информатики и ИКТ
Разделы: Математика
В настоящее время компьютеры используются во всех сферах деятельности человека. Внедрение информационных технологий в учебный процесс сегодня актуально. С целью повышения эффективности обучения учитель-предметник должен уметь использовать компьютерные технологии на своих уроках.
Одним из популярных программных средств, используемых на уроках математики, является MS Excel. Excel позволяет выполнять сложные вычислительные процедуры, автоматизировать рутинные вычисления, строить диаграммы, гистограммы и графики различной сложности.
Известно, что одним из способов задания функции является графический. Графиком функции y=f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению. Графический способ задания обладает очень важным преимуществом: он самый наглядный из всех. Графики часто используются в физике и технике, так как иногда они являются единственно возможными.
Учащимся 8-го класса известны следующие виды функций:
- y=kx+b;
- y=;
- y=|x|;
- y=kx2 (y=ax2+bx+c);
- y= ,
а также способы построения графиков функций y=f(x+l), y=f(x)+m, если известен график функции y=f(x) и элементарные методы исследования.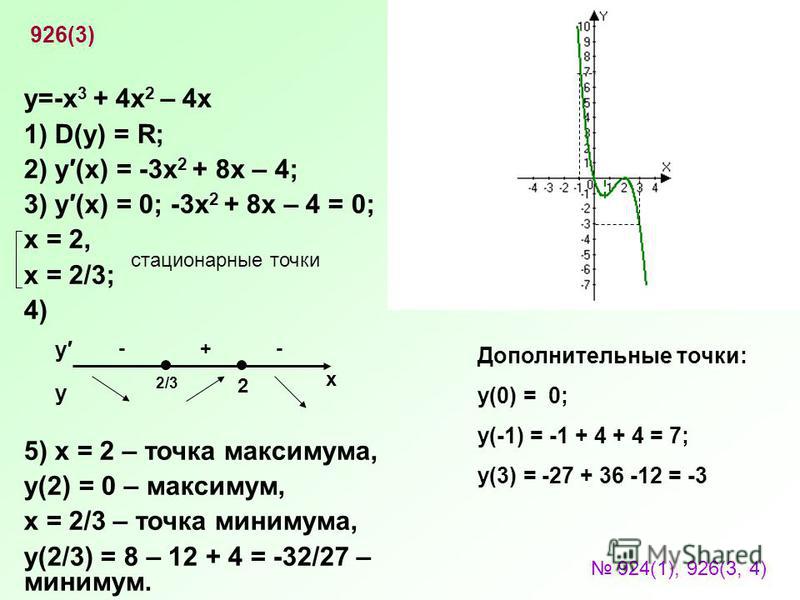
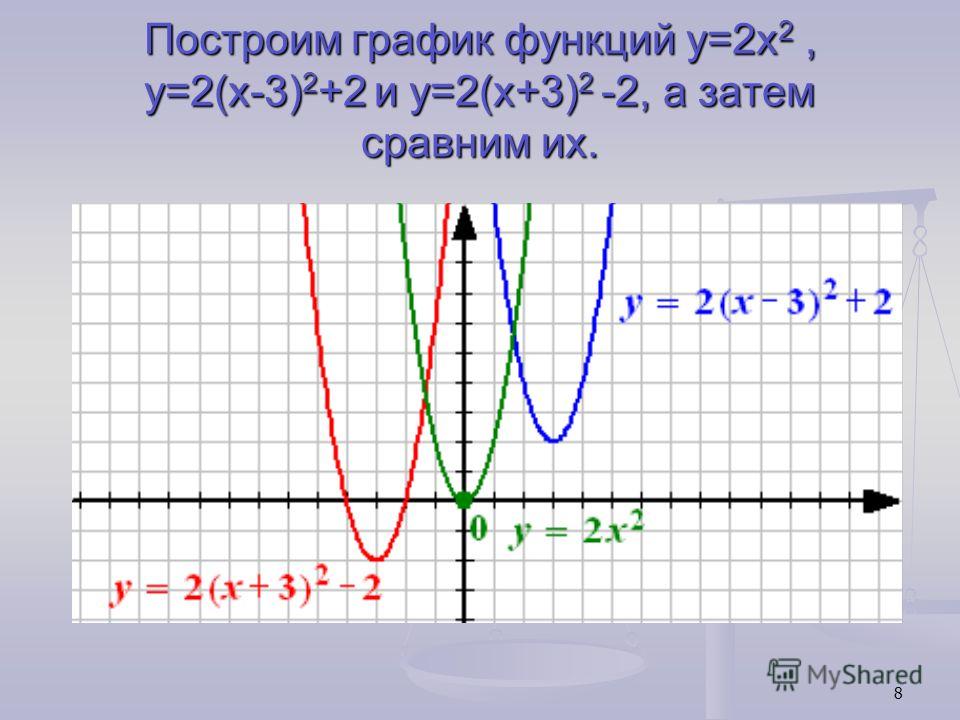
По каждому из указанных видов функций учащимся в качестве домашнего задания было предложено построить несколько графиков в одной и той системе координат для каждой группы, чтобы наглядно продемонстрировать их отличия. На уроке графики тех же функций дети построили в среде MS Excel и провели их исследование. В качестве групп функций были предложены следующие:
1-я группа
- y=3x+5;
- y=x+5;
- y=3x+5;
- y=3x-1;
- y=-3x+5;
- y=-x+5;
2-я группа
3-я группа
- y=x2;
- y=x2-1;
- y=(x-1)2;
- y=x2-5x+4;
- y=-x2-1;
- y=-(x-1)2;
4-я группа
5-я группа
Работу учащихся опишем на примере построения графика функции y=:
- Определим промежуток построения графика функции. Пусть х1=-2, х2=2.
- В ячейке А3 электронной таблицы введем начальное значение промежутка (-2).
- Разобьем промежуток на равные отрезки с учетом желаемой точности. Допустим, шаг разбиения равен 0,1. Для этого в ячейке А4 введем формулу =A3+0,1 и скопируем эту формулу в ячейки с А5 по А43.
Пусть х1=-2, х2=2.Рис. 1. В ячейке А4 вводим формулу =A3+0,1
- Вычислим значение функции в начальной точке отрезка (в точке −2). Для этого в ячейку В3 введем формулу: =(A3+1)/(F3-1) (1).
Рис. 2. Вычислим значение функции в начальной точке отрезка
- Вычислим значения функции в каждой точке промежутка разбиения. Для этого скопируем формулу (1)в ячейки В4 — В43.
- Построим график функции. Для этого выделим числовой блок
Рис. 3. Построим график функции
ячейки А3 — В43, откроем вкладку «Вставка», выберем тип графика «Точечная» и вид «С гладкими кривыми». График функции y=построен.
При желании на график можно наложить цвет, вертикальную сетку, сделать пояснительные записи. Для этого используется инструментарий вкладки «Макет».
Рис. 4. Построим график функции
Таким образом, учащиеся не только смогли получить навыки построения графиков функций в среде MS Excel, но и наглядно продемонстрировать отличительные характеристики каждой из функций в отдельно взятой группе.
Постройте график функции y 3x 2 6x. Постройте график функции y=
Построение графиков функций, содержащих модули, обычно вызывает немалые затруднения у школьников. Однако, все не так плохо. Достаточно запомнить несколько алгоритмов решения таких задач, и вы сможете без труда построить график даже самой на вид сложной функции. Давайте разберемся, что же это за алгоритмы.
1. Построение графика функции y = |f(x)|
Заметим, что множество значений функций y = |f(x)| : y ≥ 0.
Таким образом, графики таких функций всегда расположены полностью в верхней полуплоскости.
Построение графика функции y = |f(x)| состоит из следующих простых четырех этапов.
1) Построить аккуратно и внимательно график функции y = f(x).
2) Оставить без изменения все точки графика, которые находятся выше оси 0x или на ней.
3) Часть графика, которая лежит ниже оси 0x, отобразить симметрично относительно оси 0x.
Пример 1. Изобразить график функции y = |x 2 – 4x + 3|
1) Строим график функции y = x 2 – 4x + 3. Очевидно, что график данной функции – парабола. Найдем координаты всех точек пересечения параболы с осями координат и координаты вершины параболы.
x 2 – 4x + 3 = 0.
x 1 = 3, x 2 = 1.
Следовательно, парабола пересекает ось 0x в точках (3, 0) и (1, 0).
y = 0 2 – 4 · 0 + 3 = 3.
Следовательно, парабола пересекает ось 0y в точке (0, 3).
Координаты вершины параболы:
x в = -(-4/2) = 2, y в = 2 2 – 4 · 2 + 3 = -1.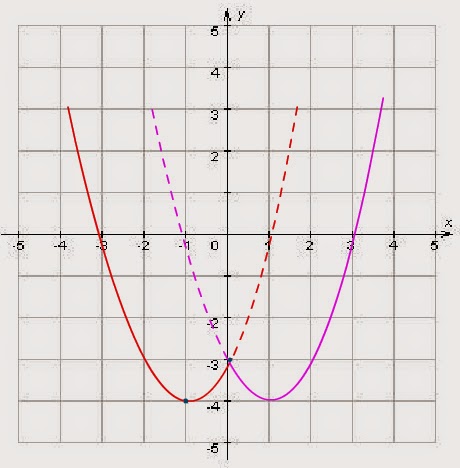
Следовательно, точка (2, -1) является вершиной данной параболы.
Рисуем параболу, используя полученные данные (рис. 1)
2) Часть графика, лежащую ниже оси 0x, отображаем симметрично относительно оси 0x.
3) Получаем график исходной функции (рис. 2
, изображен пунктиром).
2.
Построение графика функции y = f(|x|)
Заметим, что функции вида y = f(|x|) являются четными:
y(-x) = f(|-x|) = f(|x|) = y(x). Значит, графики таких функций симметричны относительно оси 0y.
Построение графика функции y = f(|x|) состоит из следующей несложной цепочки действий.
1) Построить график функции y = f(x).
2) Оставить ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.
3) Отобразить указанную в пункте (2) часть графика симметрично оси 0y.
4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).
Пример 2.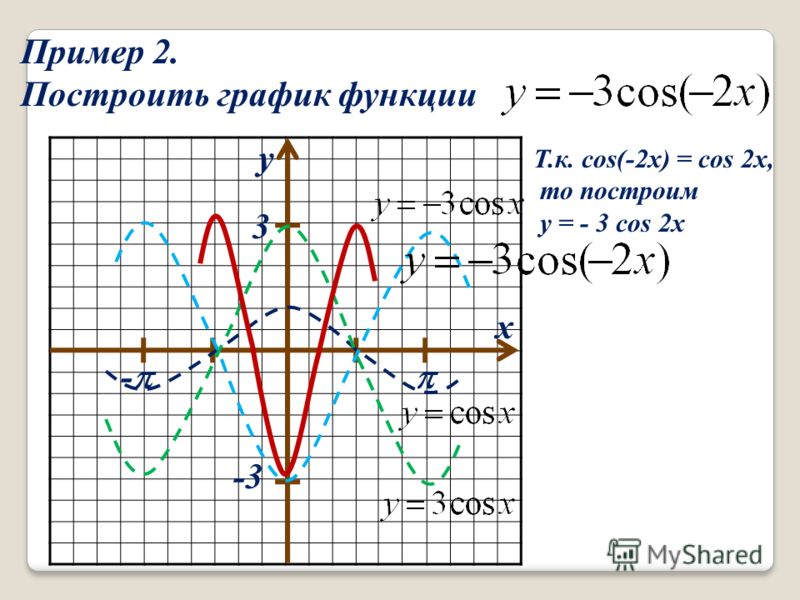
Изобразить график функции y = x 2 – 4 · |x| + 3
Так как x 2 = |x| 2 , то исходную функцию можно переписать в следующем виде: y = |x| 2 – 4 · |x| + 3. А теперь можем применять предложенный выше алгоритм.
1) Строим аккуратно и внимательно график функции y = x 2 – 4 · x + 3 (см. также рис. 1
).
2) Оставляем ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.
3) Отображаем правую часть графика симметрично оси 0y.
(рис. 3)
.
Пример 3. Изобразить график функции y = log 2 |x|
Применяем схему, данную выше.
1) Строим график функции y = log 2 x (рис. 4)
.
3. Построение графика функции y = |f(|x|)|
Заметим, что функции вида y = |f(|x|)| тоже являются четными. Действительно, y(-x) = y = |f(|-x|)| = y = |f(|x|)| = y(x), и поэтому, их графики симметричны относительно оси 0y. Множество значений таких функций: y ≥
0. Значит, графики таких функций расположены полностью в верхней полуплоскости.
Чтобы построить график функции y = |f(|x|)|, необходимо:
1) Построить аккуратно график функции y = f(|x|).
2) Оставить без изменений ту часть графика, которая находится выше оси 0x или на ней.
3) Часть графика, расположенную ниже оси 0x, отобразить симметрично относительно оси 0x.
4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).
Пример 4. Изобразить график функции y = |-x 2 + 2|x| – 1|.
1) Заметим, что x 2 = |x| 2 . Значит, вместо исходной функции y = -x 2 + 2|x| – 1
можно использовать функцию y = -|x| 2 + 2|x| – 1, так как их графики совпадают.
Строим график y = -|x| 2 + 2|x| – 1. Для этого применяем алгоритм 2.
a) Строим график функции y = -x 2 + 2x – 1 (рис. 6)
.
b) Оставляем ту часть графика, которая расположена в правой полуплоскости.
c) Отображаем полученную часть графика симметрично оси 0y.
d) Полученный график изображен на рисунке пунктиром (рис.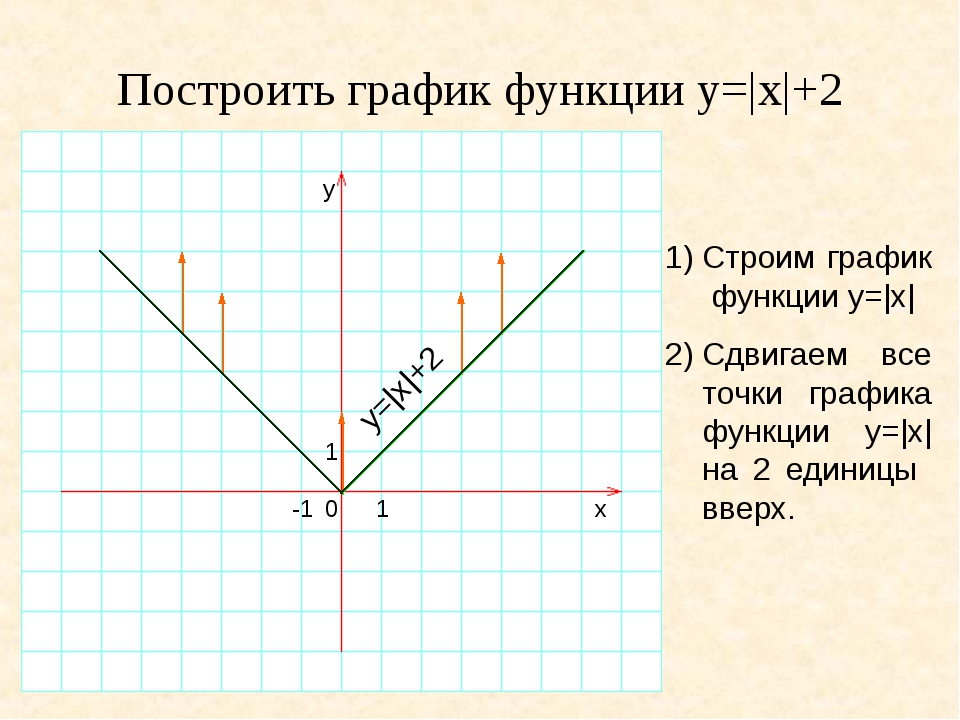
7)
.
2) Выше оси 0х точек нет, точки на оси 0х оставляем без изменения.
3) Часть графика, расположенную ниже оси 0x, отображаем симметрично относительно 0x.
4) Полученный график изображен на рисунке пунктиром (рис. 8)
.
Пример 5. Построить график функции y = |(2|x| – 4) / (|x| + 3)|
1) Сначала необходимо построить график функции y = (2|x| – 4) / (|x| + 3). Для этого возвращаемся к алгоритму 2.
a) Аккуратно строим график функции y = (2x – 4) / (x + 3) (рис. 9)
.
Заметим, что данная функция является дробно-линейной и ее график есть гипербола. Для построения кривой сначала необходимо найти асимптоты графика. Горизонтальная – y = 2/1 (отношение коэффициентов при x в числителе и знаменателе дроби), вертикальная – x = -3.
2) Ту часть графика, которая находится выше оси 0x или на ней, оставим без изменений.
3) Часть графика, расположенную ниже оси 0x, отобразим симметрично относительно 0x.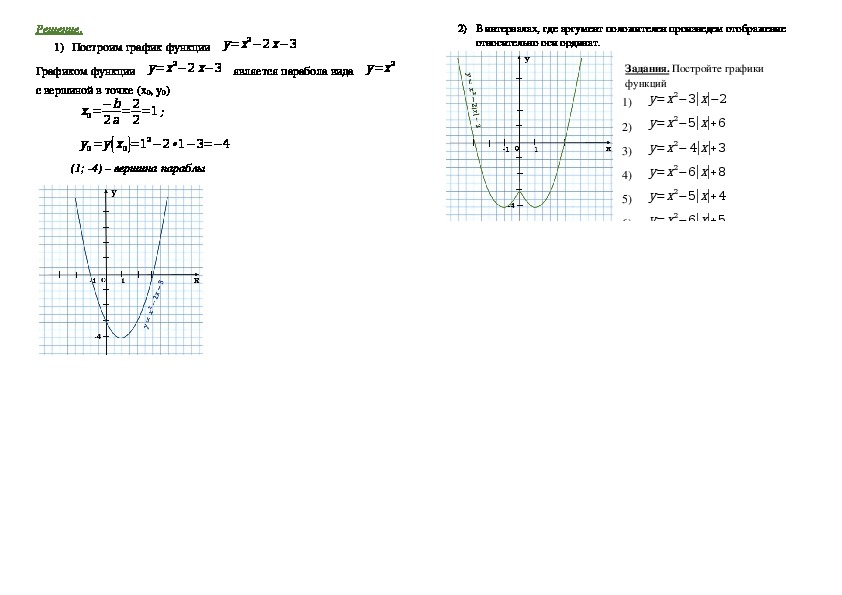
4) Окончательный график изображен на рисунке (рис. 11)
.
сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Разберем как строить график с модулем.
Найдем точки при переходе которых знак модулей меняется.
Каждое выражения, которое под модулем приравниваем к 0. У нас их два x-3 и x+3.
x-3=0 и x+3=0
x=3 и x=-3
У нас числовая прямая разделится на три интервала (-∞;-3)U(-3;3)U(3;+∞). На каждом интервале нужно определить знак под модульных выражений.
1. Это сделать очень просто, рассмотрим первый интервал (-∞;-3). Возьмем с этого отрезка любое значение, например, -4 и подставим в каждое под модульное уравнение вместо значения х.
х=-4
x-3=-4-3=-7 и x+3=-4+3=-1
У обоих выражений знаки отрицательный, значит перед знаком модуля в уравнении ставим минус, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (-∞;-3).
y=—
(x-3)-(—
(x+3))=-х+3+х+3=6
На интервале (-∞;-3) получился график линейной функции (прямой) у=6
2.
Рассмотрим второй интервал (-3;3). Найдем как будет выглядеть уравнение графика на этом отрезке. Возьмем любое число от -3 до 3, например, 0. Подставим вместо значения х значение 0.
х=0
x-3=0-3=-3 и x+3=0+3=3
У первого выражения x-3 знак отрицательный получился, а у второго выражения x+3 положительный. Следовательно, перед выражением x-3 запишем знак минус, а перед вторым выражением знак плюс.
y=—
(x-3)-(+
(x+3))=-х+3-х-3=-2x
На интервале (-3;3) получился график линейной функции (прямой) у=-2х
3.Рассмотрим третий интервал (3;+∞). Возьмем с этого отрезка любое значение, например 5, и подставим в каждое под модульное уравнение вместо значения х.
х=5
x-3=5-3=2 и x+3=5+3=8
У обоих выражений знаки получились положительными, значит перед знаком модуля в уравнении ставим плюс, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (3;+∞).
y=+
(x-3)-(+
(x+3))=х-3-х-3=-6
На интервале (3;+∞) получился график линейной функции (прямой) у=-6
4.
Теперь подведем итог.Постоим график y=|x-3|-|x+3|.
На интервале (-∞;-3) строим график линейной функции (прямой) у=6.
На интервале (-3;3) строим график линейной функции (прямой) у=-2х.
Чтобы построить график у=-2х подберем несколько точек.
x=-3 y=-2*(-3)=6 получилась точка (-3;6)
x=0 y=-2*0=0 получилась точка (0;0)
x=3 y=-2*(3)=-6 получилась точка (3;-6)
На интервале (3;+∞) строим график линейной функции (прямой) у=-6.
5. Теперь проанализируем результат и ответим на вопрос задания найдем значение k, при которых прямая y=kx имеет с графиком y=|x-3|-|x+3| данной функции ровно одну общую точку.
Прямая y=kx при любом значении k всегда будет проходить через точку (0;0). Поэтому мы можем изменить только наклон данной прямой y=kx, а за наклон у нас отвечает коэффициент k.
Если k будет любое положительное число, то будет одно пересечение прямой y=kx с графиком y=|x-3|-|x+3|. Этот вариант нам подходит.
Если k будет принимать значение (-2;0), то пересечений прямой y=kx с графиком y=|x-3|-|x+3| будет три.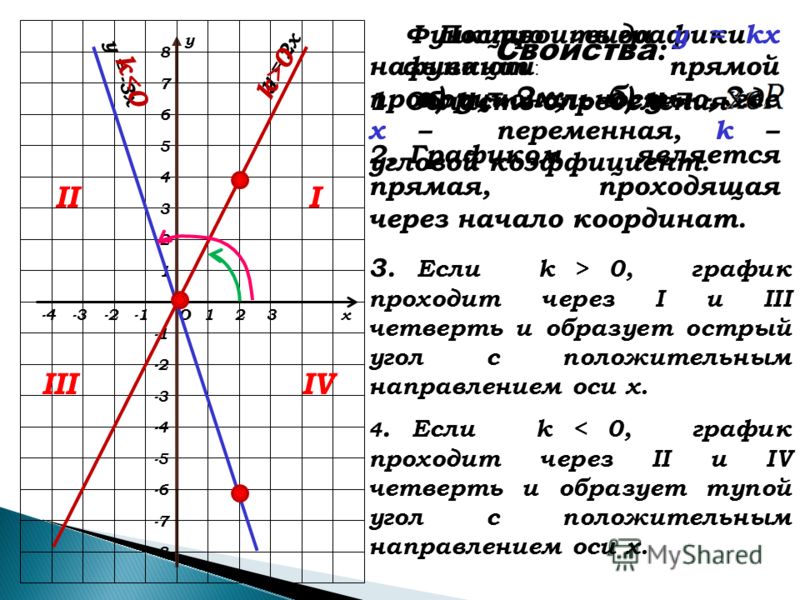
Этот вариант нам не подходит.
Если k=-2, решений будет множество [-2;2], потому что прямая y=kx будет совпадать с графиком y=|x-3|-|x+3| на данном участке. Этот вариант нам не подходит.
Если k будет меньше -2, то прямая y=kx с графиком y=|x-3|-|x+3| будет иметь одно пересечение.Этот вариант нам подходит.
Если k=0, то пересечений прямой y=kx с графиком y=|x-3|-|x+3| также будет одно.Этот вариант нам подходит.
Ответ: при k принадлежащей интервалу (-∞;-2)U и возрастает на промежутке }
Линейные уравнения и функции — Функции и их графики
Функции и их графики
Функция, функция, какова ваша функция? Вы личный тренер, известный шпион, ограничитель дверей или что-то совсем другое? Думаем, последний.
Функция принимает некоторые входные данные, обычно называемые x , в уравнение f ( x ). Затем x проходит через уравнение, и в конце мы получаем некоторый результат, обычно известный как y .
Обратите внимание, что y и f ( x ) на самом деле одно и то же. Может быть, y — знаменитый шпион?
Мы называем x независимой переменной , а y — зависимой переменной . Итак, x неплохо работает, а y все еще живет дома. Все возможные значения x- — это область , а все возможные значения y- — это диапазон .
Пример задачи
Найдите область и диапазон y = 3 x — 4, где 0 ≤ x <4.
Если бы нам просто дали уравнение y = 3 x — 4, не говоря больше ничего, мы бы сказали, что домен — это все действительные числа. При этом не учитываются воображаемые, фальшивые, бредовые и позерские числа.
Однако в данном случае мы не можем выбрать любой размер x , который нам нравится под солнцем. Проблема говорит, что 0 ≤ x <4.
Это означает, что наш домен ограничен всеми действительными числами от 0 до 4, включая 0, но не 4 (из-за линии под голодным ртом Пакмана).
А теперь ассортимент. Диапазон всех возможных y -значений. В нашем уравнении y = 3 x -4, значения y- — это то, что мы получаем, когда вставляем известные нам значения x- . Давайте составим таблицу, чтобы уточнить диапазон.
Диапазон этой функции: -4 ≤ y <8. Обратите внимание, что y меньше 8, потому что x не может равняться 4, поэтому y также никогда не может быть точно равно 8.
В этом случае диапазон легкий; мы могли бы посмотреть на наименьшее и наибольшее значения x , и они дают нам наименьшее и наибольшее значения y .Что, если бы у нас было что-то вроде y = — x 2 , с -2 < x <2?
Здесь, если мы просто подключим x = -2 и 2, мы получим y = -4 для них обоих.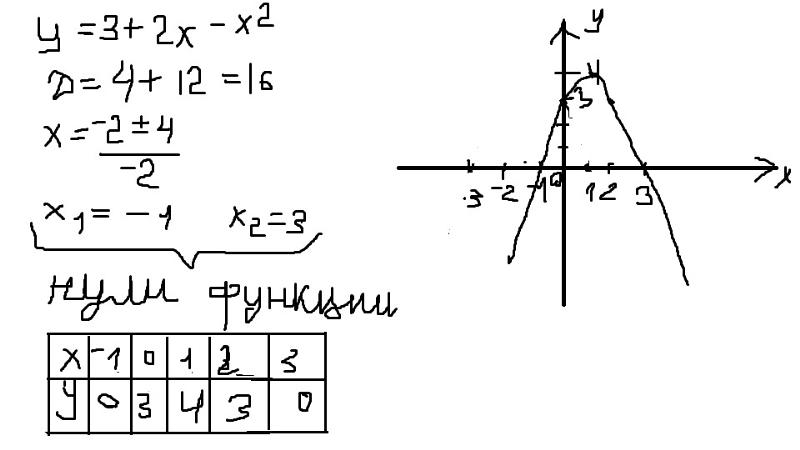
Однако мы знаем, что y не просто все время остаются на -4. Мы должны проверить x = 0, чтобы найти, что y = 0, что дает нам диапазон -4 < y <0. Каждый раз, когда график может качаться или опускаться, проверьте различные числа, чтобы найти правильный диапазон.
Теперь поговорим на секунду о функциях построения графиков. Собственно, давайте поговорим и построим график одновременно. Только не проси нас тоже жевать жвачку.
Пример задачи
График y = 3 x — 4, где 0 ≤ x <4.
О, это снова вы. Вы собираетесь повторять вещь , не так ли?
Ничего страшного, потому что это означает, что мы уже проделали большую работу. Мы знаем домен и диапазон, и мы отметили несколько моментов.
Начните с рисования координатной плоскости . x -ось замерзает на спине, лежа, в то время как y -ось стоит по стойке «смирно».
Они встречаются посередине в исходной точке . Не пытайтесь слишком сильно визуализировать это; на самом деле это не так больно, как кажется. Мы надеемся.
Мы используем числа на осях, чтобы построить точки и линию. Мы делаем заказанных пар , которые выглядят так: ( x , y ).А x всегда вызывает дробовик, поэтому y никогда не будет первым.
Начиная с начала координат (0, 0), положительные значения x перемещаются вправо, а положительные значения y перемещаются вверх. Переместите оба числа вместе, чтобы построить каждую точку из нашей таблицы.
Видите, как красиво они выстраиваются? Почему они не могли так красиво выглядеть на школьных фотографиях? Что ж, проведем через них черту, пока они сидят неподвижно.
У нас здесь ограниченная область, поэтому мы рисуем только линию, где функция действительно существует.Несуществующие линии на удивление легко рисовать, так что будьте начеку.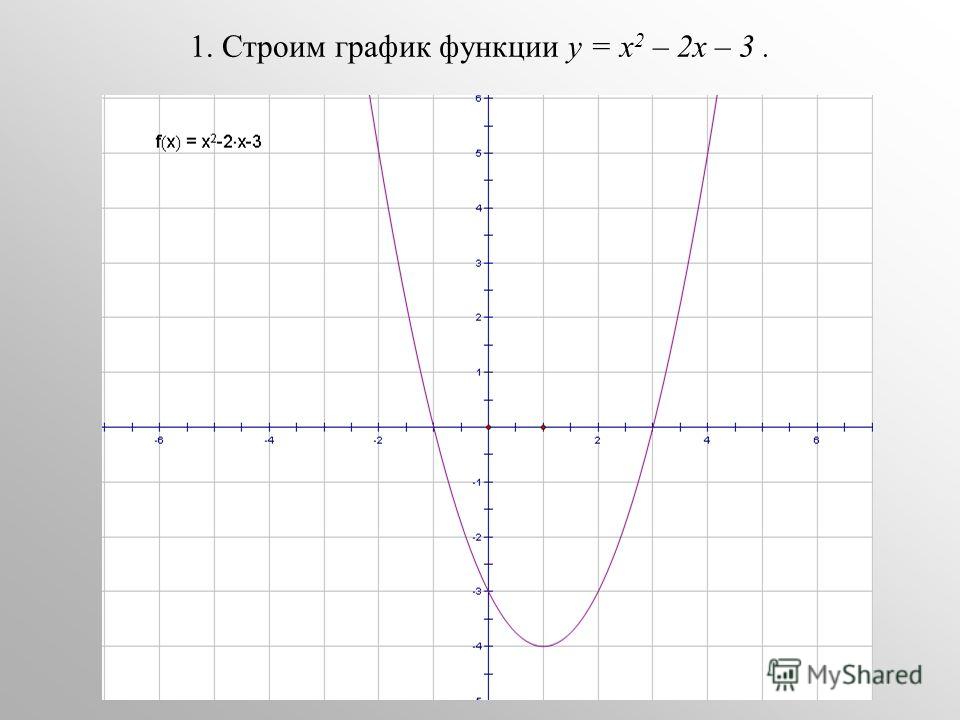
Вертикальность
В функциях есть кое-что очень важное. Фактически, это настолько важно, что мы собираемся поместить его в отдельную строку:
На каждые x есть только один y . Другими словами, каждый вход имеет только один выход. Один x входит, один y уходит.
Если уравнение нарушает этот принцип, это не функция.К счастью, нам не нужно подключаться и проверять каждое значение x- , чтобы увидеть, не имеет ли какое-либо из них значение y- . Это было бы утомительно и ужасно. Вместо этого мы можем использовать тест вертикальной линии . Какое имя, а?
Возьмем, к примеру, эти графики. Это именно то, на что похоже: рисование вертикальных линий поверх графика. Если какая-либо вертикальная линия может проходить через график более одного раза, то уравнение — это , а не как функция.
См.? Мы можем сразу сказать, что является функцией, а что нет.
И обратите внимание, что второй график посередине имеет одинаковое значение y- для двух разных значений x- (например, при y = 0). Это полностью разрешено. Мы просто не можем иметь одно и то же значение x- для более чем одного значения y- , как на первом и третьем графиках.
С этого момента мы будем иметь дело с линейными уравнениями, которые легко классифицировать как линейные функции (ох, заголовок). Это вертикальная линия? Если нет, то да, Вирджиния, это функция.
Графики и функции АбстрактныеЭтот урок разработан, чтобы познакомить студентов с функциями построения графиков. ЦелиПо завершении этого урока студенты:
Стандарты Задания и обсуждения в этом уроке касаются следующих Алгебра Понять закономерности, отношения и функции
Представляйте и анализируйте математические ситуации и структуры с помощью алгебраических символов.
использовать математические модели для представления и понимания количественных соотношений
Анализируйте изменения в различных контекстах
Необходимые условия для учащихся
Подготовка учителейСтудентам понадобится:
Ключевые терминыЭтот урок знакомит студентов со следующими терминами посредством включенных обсуждений: Содержание урока Эти задания можно выполнять индивидуально или в группах по четыре человека.Выделите 2-3 часа классного времени на весь урок, если все части
работать с предыдущим действием, построив те же функции с помощью Инструмент Graph Sketcher Tool. форма y = _____ x + ____ с использованиемИнструмент Graph Sketcher для определения какие функции поступают из этой формы и что меняет каждый константа выполняет функцию. Убедитесь, что они следят за тем, что они попробуйте записать их гипотезы и наблюдения.2 + ____ .
Альтернативные контурыЭтот урок можно перестроить по-разному.
Предлагаемое последующее наблюдение После этих обсуждений и занятий у студентов будет больше опыта. Что из следующего представляет собой уравнение для этого графика? 4+ a) y = -3 cos (3x … |
| куб.см | Вертикальный след для x = cx = c |
|---|---|
| −π4 − π4 | z = −2cosy2z = −2cosy2 |
| 00 | z = 0z = 0 |
| π4π4 | z = 2cosy2z = 2cosy2 |
Таблица 4.1 Вертикальные трассы, параллельные плоскости xz, xz для функции f (x, y) = sinxcosyf (x, y) = sinxcosy
Аналогичным образом мы можем подставить значения y в уравнение f (x, y) f (x, y), чтобы получить трассы в плоскости yz, плоскости yz, как указано в следующей таблице. .
| dd | Вертикальный след для y = dy = d |
|---|---|
| −π4 − π4 | z = 2sinx2z = 2sinx2 |
| 00 | z = sinxz = sinx |
| π4π4 | z = 2sinx2z = 2sinx2 |
Таблица 4.2 Вертикальные трассы, параллельные плоскости yz-Planeyz для функции f (x, y) = sinxcosyf (x, y) = sinxcosy
Три трассы в плоскости xz-planexz являются косинусоидальными функциями; три следа в плоскости yz-planeyz являются синусоидальными функциями.Эти кривые появляются на пересечениях поверхности с плоскостями x = −π4, x = 0, x = π4x = −π4, x = 0, x = π4 и y = −π4, y = 0, y = π4y = — π4, y = 0, y = π4, как показано на следующем рисунке.
Рис. 4.11 Вертикальные кривые функции f (x, y) f (x, y) — это косинусоидальные кривые в плоскостях xz, плоскостях xz (a) и синусоидальные кривые в плоскостях yz, плоскостях yz (b).
КПП 4.3
Определите уравнение вертикального следа функции g (x, y) = — x2 − y2 + 2x + 4y − 1g (x, y) = — x2 − y2 + 2x + 4y − 1, соответствующего y = 3, y = 3, и описать его график.
Функции двух переменных могут создавать поразительные поверхности. На следующем рисунке показаны два примера.
Рисунок 4.12 Примеры поверхностей, представляющих функции двух переменных: (a) комбинация степенной функции и синусоидальной функции и (b) комбинация тригонометрических, экспоненциальных и логарифмических функций.
Функции более двух переменных
До сих пор мы рассматривали только функции двух переменных. Однако полезно кратко рассмотреть функции более чем двух переменных.Два таких примера:
f (x, y, z) = x2−2xy + y2 + 3yz − z2 + 4x − 2y + 3x − 6 (многочлен от трех переменных) f (x, y, z) = x2−2xy + y2 + 3yz− z2 + 4x − 2y + 3x − 6 (многочлен от трех переменных)
и
g (x, y, t) = (x2−4xy + y2) sint− (3x + 5y) cost. g (x, y, t) = (x2−4xy + y2) sint− (3x + 5y) cost.
В первой функции (x, y, z) (x, y, z) представляет точку в пространстве, а функция ff сопоставляет каждую точку в пространстве с четвертой величиной, такой как температура или скорость ветра. Во второй функции (x, y) (x, y) может представлять точку на плоскости, а tt может представлять время.Функция может сопоставлять точку на плоскости с третьей величиной (например, давлением) в данный момент времени t.t. Метод поиска области определения функции более двух переменных аналогичен методу для функций одной или двух переменных.
Пример 4.6
Домены для функций трех переменных
Найдите домен каждой из следующих функций:
- f (x, y, z) = 3x − 4y + 2z9 − x2 − y2 − z2f (x, y, z) = 3x − 4y + 2z9 − x2 − y2 − z2
- г (x, y, t) = 2t − 4×2 − y2g (x, y, t) = 2t − 4×2 − y2
Решение
- Для определения функции f (x, y, z) = 3x − 4y + 2z9 − x2 − y2 − z2f (x, y, z) = 3x − 4y + 2z9 − x2 − y2 − z2 (и реальное значение) должны выполняться два условия:
- Знаменатель не может быть нулевым.
- Подкоренное выражение не может быть отрицательным.
Комбинирование этих условий приводит к неравенству
9 − x2 − y2 − z2> 0,9 − x2 − y2 − z2> 0.
Перемещение переменных на другую сторону и обращение неравенства дает домен как
область (f) = {(x, y, z) ∈ℝ3 | x2 + y2 + z2 <9}, область (f) = {(x, y, z) ∈ℝ3 | x2 + y2 + z2 <9},
который описывает шар радиуса 33 с центром в начале координат. ( Примечание : Поверхность шара не включена в этот домен.) - Чтобы функция g (x, y, t) = 2t − 4×2 − y2g (x, y, t) = 2t − 4×2 − y2 была определена (и была действительным значением), должны выполняться два условия:
- Подкоренное выражение не может быть отрицательным.
- Знаменатель не может быть нулевым.
Поскольку подкоренное выражение не может быть отрицательным, отсюда следует 2t − 4≥0,2t − 4≥0 и, следовательно, t≥2.t≥2. Поскольку знаменатель не может быть равен нулю, x2 − y2 ≠ 0, x2 − y2 ≠ 0 или x2 ≠ y2, x2 ≠ y2, которые можно переписать как y ≠ ± xy ≠ ± x, которые являются уравнениями двух прямых, проходящих через Происхождение. Следовательно, домен gg равен
область (g) = {(x, y, t) | y ≠ ± x, t≥2}. область (g) = {(x, y, t) | y ≠ ± x, t≥2}.
КПП 4.4
Найти область определения функции h (x, y, t) = (3t − 6) y − 4×2 + 4.ч (х, у, т) знак равно (3т-6) у-4х2 + 4.
Функции двух переменных имеют кривые уровня, которые показаны как кривые на плоскости xy-plane.xy-plane. Однако, когда функция имеет три переменных, кривые становятся поверхностями, поэтому мы можем определить поверхности уровня для функций трех переменных.
Определение
Для данной функции f (x, y, z) f (x, y, z) и числа cc в диапазоне f, f поверхность уровня функции трех переменных определяется как набор точек, удовлетворяющих уравнение f (x, y, z) = c.е (х, у, г) = с.
Пример 4.7
Поиск ровной поверхности
Найдите поверхность уровня для функции f (x, y, z) = 4×2 + 9y2 − z2f (x, y, z) = 4×2 + 9y2 − z2, соответствующей c = 1.c = 1.
Решение
Поверхность уровня определяется уравнением 4×2 + 9y2 − z2 = 1,4×2 + 9y2 − z2 = 1. Это уравнение описывает гиперболоид из одного листа, как показано на следующем рисунке.
Рис. 4.13. Гиперболоид из одного листа с некоторыми его плоскими поверхностями.
Контрольно-пропускной пункт 4.5
Найдите уравнение поверхности уровня функции
g (x, y, z) = x2 + y2 + z2−2x + 4y − 6zg (x, y, z) = x2 + y2 + z2−2x + 4y − 6z.
, что соответствует c = 2, c = 2, и, если возможно, опишите поверхность.
Раздел 4.1. Упражнения
В следующих упражнениях оцените каждую функцию по указанным значениям.
1.
W (x, y) = 4×2 + y2.W (x, y) = 4×2 + y2. Найдите W (2, −1), W (2, −1), W (−3,6) .W (−3,6).
2.
W (x, y) = 4×2 + y2.W (x, y) = 4×2 + y2. Найдите W (2 + h, 3 + h). W (2 + h, 3 + h).
3.
Объем правого кругового цилиндра вычисляется функцией двух переменных: V (x, y) = πx2y, V (x, y) = πx2y, где xx — радиус правого кругового цилиндра, а yy — высота. цилиндра. Оцените V (2,5) V (2,5) и объясните, что это означает.
4.
Кислородный баллон состоит из правого цилиндра высотой yy и радиуса xx с двумя полусферами радиуса xx, установленными сверху и снизу баллона. Выразите объем резервуара как функцию двух переменных, xandy, xandy, найдите V (10,2), V (10,2) и объясните, что это означает.
Для следующих упражнений найдите домен функции.
5.
V (x, y) = 4×2 + y2V (x, y) = 4×2 + y2
6.
f (x, y) = x2 + y2−4f (x, y) = x2 + y2−4
7.
f (x, y) = 4ln (y2 − x) f (x, y) = 4ln (y2 − x)
.
8.
г (x, y) = 16−4×2 − y2g (x, y) = 16−4×2 − y2
9.
г (х, у) = у2-х2z (х, у) = у2-х2
Найдите диапазон функций.
11.
г (x, y) = 16−4×2 − y2g (x, y) = 16−4×2 − y2
12.
V (x, y) = 4×2 + y2V (x, y) = 4×2 + y2
Для следующих упражнений найдите кривые уровня каждой функции при указанном значении cc, чтобы визуализировать данную функцию.
14.
z (x, y) = y2 − x2, z (x, y) = y2 − x2, c = 1c = 1
15.
z (x, y) = y2 − x2, z (x, y) = y2 − x2, c = 4c = 4
16.
g (x, y) = x2 + y2; c = 4, c = 9g (x, y) = x2 + y2; c = 4, c = 9
17.
г (х, у) = 4-х-у; с = 0,4 г (х, у) = 4-х-у; с = 0,4
18.
f (x, y) = xy; c = 1; c = −1f (x, y) = xy; c = 1; c = −1
19.
h (x, y) = 2x − y; c = 0, −2,2 h (x, y) = 2x − y; c = 0, −2,2
20.
f (x, y) = x2 − y; c = 1,2 f (x, y) = x2 − y; c = 1,2
21.
г (х, у) = хх + у; с = -1,0,2 г (х, у) = хх + у; с = -1,0,2
22.
г (х, у) = х3-у; с = -1,0,2 г (х, у) = х3-у; с = -1,0,2
23.
г (x, y) = exy; c = 12,3g (x, y) = exy; c = 12,3
24.
f (x, y) = x2; c = 4,9 f (x, y) = x2; c = 4,9
25.
f (x, y) = xy − x; c = −2,0,2 f (x, y) = xy − x; c = −2,0,2
26.
h (x, y) = ln (x2 + y2); c = −1,0,1 h (x, y) = ln (x2 + y2); c = −1,0,1
27.
г (x, y) = ln (yx2); c = −2,0,2g (x, y) = ln (yx2); c = −2,0,2
28.
z = f (x, y) = x2 + y2, z = f (x, y) = x2 + y2, c = 3c = 3
29.
f (x, y) = y + 2×2, f (x, y) = y + 2×2, c = c = любая константа
Для следующих упражнений найдите вертикальные кривые функций при указанных значениях xx и y и постройте кривые.
30.
z = 4 − x − y; x = 2z = 4 − x − y; x = 2
31.
f (x, y) = 3x + y3, x = 1 f (x, y) = 3x + y3, x = 1
32.
z = cosx2 + y2z = cosx2 + y2 x = 1x = 1
Найдите домен следующих функций.
33.
z = 100−4×2−25y2z = 100−4×2−25y2
35.
f (x, y, z) = 136−4×2−9y2 − z2f (x, y, z) = 136−4×2−9y2 − z2
36.
f (x, y, z) = 49 − x2 − y2 − z2f (x, y, z) = 49 − x2 − y2 − z2
.
37.
f (x, y, z) = 16 − x2 − y2 − z23f (x, y, z) = 16 − x2 − y2 − z23
.
38.
f (x, y) = cosx2 + y2f (x, y) = cosx2 + y2
Для следующих упражнений постройте график функции.
39.
z = f (x, y) = x2 + y2z = f (x, y) = x2 + y2
41.
Используйте технологию для построения графика z = x2y.z = x2y.
Нарисуйте следующее, найдя кривые уровня. Проверить график, используя технологию.
42.
f (x, y) = 4 − x2 − y2f (x, y) = 4 − x2 − y2
43.
f (x, y) = 2 − x2 + y2f (x, y) = 2 − x2 + y2
44.
г = 1 + е-х2-у2z = 1 + е-х2-у2
47.
Опишите изолинии для нескольких значений cc для z = x2 + y2−2x − 2y.z = x2 + y2−2x − 2y.
Найдите поверхность уровня для функций трех переменных и опишите ее.
48.
w (x, y, z) = x − 2y + z, c = 4w (x, y, z) = x − 2y + z, c = 4
49.
w (x, y, z) = x2 + y2 + z2, c = 9w (x, y, z) = x2 + y2 + z2, c = 9
50.
w (x, y, z) = x2 + y2 − z2, c = −4w (x, y, z) = x2 + y2 − z2, c = −4
51.
w (x, y, z) = x2 + y2 − z2, c = 4w (x, y, z) = x2 + y2 − z2, c = 4
52.
w (x, y, z) = 9×2−4y2 + 36z2, c = 0w (x, y, z) = 9×2−4y2 + 36z2, c = 0
Для следующих упражнений найдите уравнение кривой уровня ff, которое содержит точку P.P.
53.
f (x, y) = 1−4×2 − y2, P (0,1) f (x, y) = 1−4×2 − y2, P (0,1)
.
54.
г (x, y) = y2arctanx, P (1,2) g (x, y) = y2arctanx, P (1,2)
55.
g (x, y) = exy (x2 + y2), P (1,0) g (x, y) = exy (x2 + y2), P (1,0)
56.
Напряженность EE электрического поля в точке (x, y, z) (x, y, z), возникающего из-за бесконечно длинного заряженного провода, лежащего вдоль оси y, определяется как E (x, y, z) = k / x2 + y2, E (x, y, z) = k / x2 + y2, где kk — положительная постоянная. Для простоты положим k = 1k = 1 и найдем уравнения поверхностей уровня для E = 10 и E = 100, E = 10 и E = 100.
57.
Тонкая пластина из железа расположена в плоскости xy.xy-плоскость. Температура TT в градусах Цельсия в точке P (x, y) P (x, y) обратно пропорциональна квадрату ее расстояния от начала координат. Выразите TT как функцию от xandy.xandy.
58.
Обратитесь к предыдущей проблеме. Используя найденную там температурную функцию, определите константу пропорциональности, если температура в точке P (1,2) составляет 50 ° C, P (1,2) составляет 50 ° C. Используйте эту константу, чтобы определить температуру в точке Q (3,4) .Q (3,4).
59.
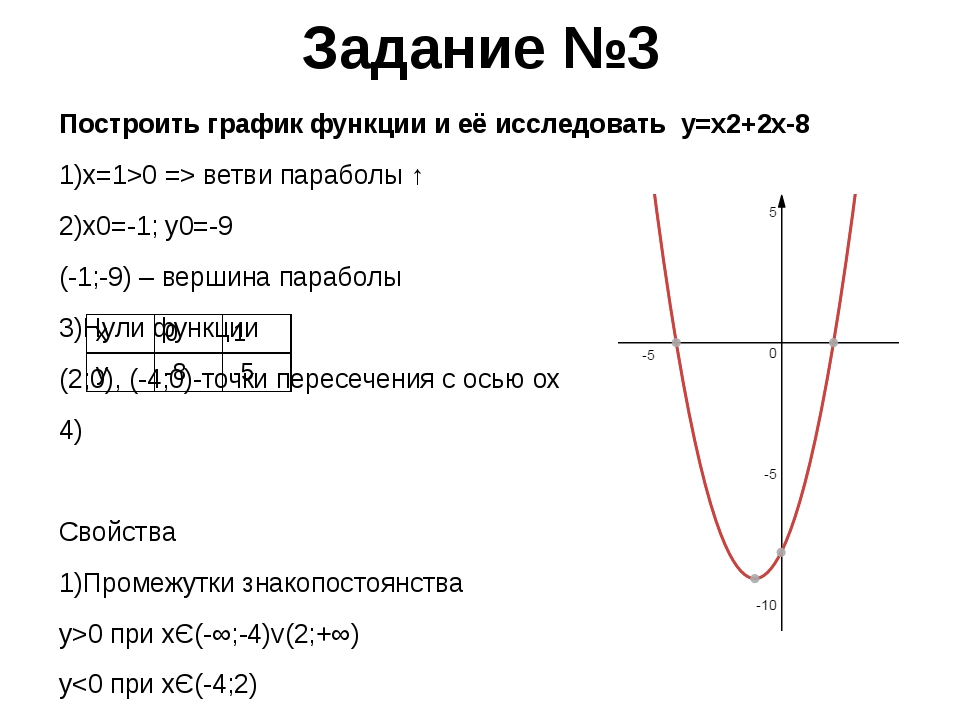
Обратитесь к предыдущей проблеме.2 + 6x-8
3) y = 3 x 2 + 6 x — 8
Сравните его со стандартной формой уравнения параболы y = ax 2 + bx + c
Ось симметрии x = — b /2 a = -6/6 = -1. 2 + 6 (-1) -8 = -11
Вершина = (-1, -11)
Составьте таблицу значений, чтобы найти упорядоченные пары, удовлетворяющие уравнению.
Выберите значения для y и найдите соответствующие значения для x .
х | y = 3 x 2 + 6 x — 8 | ( x, y ) |
1 | y = 3 (1) 2 + 6 (1) — 8 = 1 | (1,1) |
-1 | y = 3 (-1) 2 + 6 (-1) — 8 = -11 | (-1, -11) |
-2 | y = 3 (-2) 2 + 6 (-2) — 8 = -8 | (1, -2) |
0 | y = 3 (0) 2 + 6 (0) — 8 = -8 | (0, -8) |
-3 | y = 3 (-3) 2 + 6 (-3) — 8 = 1 | (-3,1) |
График
1.Нарисуйте координатную плоскость.
2. Постройте координатные точки, найденные в таблице, и ось симметрии.
3. Затем нарисуйте график, соединив точки плавной кривой.
Ось симметрии x = -1
Вершина параболы (-1, -11).
Графические логарифмические функции
Функция
y
знак равно
бревно
б
Икс
является обратной функцией
экспоненциальная функция
y
знак равно
б
Икс
.
Рассмотрим функцию
y
знак равно
3
Икс
.
Это можно изобразить как:
График обратной функции любой функции — это отражение графика функции относительно линии
y
знак равно
Икс
.
Итак, график логарифмической функции
y
знак равно
бревно
3
(
Икс
)
которая является обратной функцией
y
знак равно
3
Икс
является отражением приведенного выше графика относительно линии
y
знак равно
Икс
.
Икс
1
9
1
3
1
3
9
27
81 год
y
знак равно
бревно
3
Икс
—
2
—
1
0
1
2
3
4
Область определения функции — это набор всех положительных действительных чисел.
Если база не записана, предположим, что журнал является базовым.
10
.
Икс
1
1000
1
100
1
10
1
10
100
1000
y
знак равно
бревно
Икс
—
3
—
2
—
1
0
1
2
3
Логарифмическая функция,
y
знак равно
бревно
б
(
Икс
)
,
можно сдвинуть
k
единиц по вертикали и
час
единиц по горизонтали с уравнением
y
знак равно
бревно
б
(
Икс
+
час
)
+
k
.
Вертикальный сдвиг
Если
k
>
0
, график сдвинется вверх.
Если
k
< 0 , график сместится вниз.
Горизонтальный сдвиг
Если
час
>
0
, график сдвинется влево.
Если
час
< 0 , график сдвинется вправо.
Рассмотрим логарифмическую функцию
y
знак равно
[
бревно
2
(
Икс
+
1
)
—
3
]
.
Это можно получить, переведя родительский граф
y
знак равно
бревно
2
(
Икс
)
Пару раз.
Рассмотрим график функции
y
знак равно
бревно
2
(
Икс
)
.
С
час
знак равно
1
,
y
знак равно
[
бревно
2
(
Икс
+
1
)
]
перевод
y
знак равно
бревно
2
(
Икс
)
на одну единицу влево.
Сейчас,
k
знак равно
—
3
.График
y
знак равно
[
бревно
2
(
Икс
+
1
)
]
будет перемещен
3
единицы вниз, чтобы получить
y
знак равно
[
бревно
2
(
Икс
+
1
)
]
—
3
.
Вы можете вспомнить, что логарифмические функции определены только для положительных действительных чисел.Это связано с тем, что для отрицательных значений соответствующее экспоненциальное уравнение не имеет решения. Например,
3
Икс
знак равно
—
1
не имеет реального решения, поэтому
бревно
3
(
—
1
)
не определено.
Итак, как насчет такой функции, как
y
знак равно
бревно
4
(
—
Икс
)
?
Это определено только для отрицательных значений
Икс
.
Найдите значения функции для нескольких отрицательных значений
Икс
. Для упрощения расчета вы можете использовать экспоненциальную форму уравнения,
4
y
знак равно
—
Икс
.
Икс
—
1
—
2
—
4
—
8
—
16
—
32
y
знак равно
бревно
4
(
—
Икс
)
или же
4
y
знак равно
—
Икс
0
1
2
1
1
1
2
2
2
1
2
Постройте точки и соедините их плавной кривой.
Вы можете видеть, что график является отражением графика функции
y
знак равно
бревно
4
(
Икс
)
о
y
-ось.
Math on the Mind Постройте график y = 3x + 2 из данной таблицы значений. xy ppt скачать
Презентация на тему: «Математика в уме Постройте график y = 3x + 2 из данной таблицы значений.xy -2-4 02 15 28 »- стенограмма презентации:
ins [data-ad-slot = «4502451947»] {display: none! important;}}
@media (max-width: 800px) {# place_14> ins: not ([data-ad-slot = «4502451947»]) {display: none! important;}}
@media (max-width: 800px) {# place_14 {width: 250px;}}
@media (max-width: 500 пикселей) {# place_14 {width: 120px;}}
]]>
1
Математика в уме Постройте график y = 3x + 2 из данной таблицы значений.ху -2-4 02 15 28
2
3
4
5
6
7
Математика в уме Постройте график y = 3x + 2 из данной таблицы значений.ху -2-4 02 15 28
8
Создание таблицы значений алгебры Задание 5, Урок 2
9
10
11
Построим график y = 3x — 2 Составим таблицу значений 2 1 0 –1 –2 yx y = 3 (–2) — 2 = –8 y = 3 (–1) — 2 = –5 y = 3 (0) — 2 = –2 y = 3 (2) — 2 = 4 y = 3 (1) — 2 = 1 –8 –5 –2 1 4 www.chaoticgolf.com/pptlessons/graphinglinearequations.ppt
12
Быстрая проверка
13
В игре с мячом они берут 2 доллара за хот-дог. Функция C (h) = 2h описывает стоимость h хот-догов. Используйте точки для каждого входного значения. hC (h) = 2h (h, C (h)) 1C (1) = 2 (1) (1, 2) 2C (2) = 2 (2) (2, 4) 3C (3) = 2 (3 ) (3, 6) 4C (4) = 2 (4) (4, 8)
14
В местном видеомагазине вы можете взять напрокат видеоигру за 3 доллара.Использование проигрывателя для видеоигр стоит 5 долларов в месяц. Общая ежемесячная стоимость C (v) зависит от количества видеоигр v, которые вы арендуете. Используйте правило функции C (v) = 5 + 3v, чтобы создать таблицу значений и график. vC (v) = 5 + 3 v (v, C (v)) 0C (0) = 5 + 3 (0) (0, 5) 1C (1) = 5 + 3 (1) (1, 8) 2C ( 2) = 5 + 3 (2) (2, 11)
15
Напомним: https://www.