Содержание
Логарифмическая функция
Основные сведения
Логарифмической функцией называется функция вида y = logax, где a > 0 и a ≠ 1.
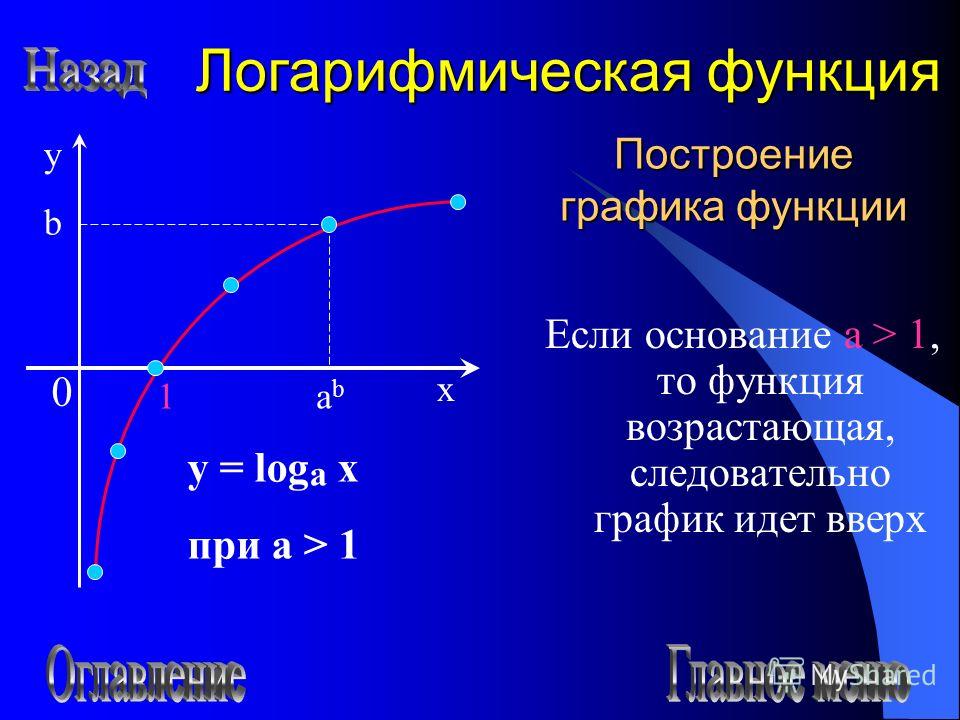
График функции имеет следующий вид:
Рассмотрим свойства функции:
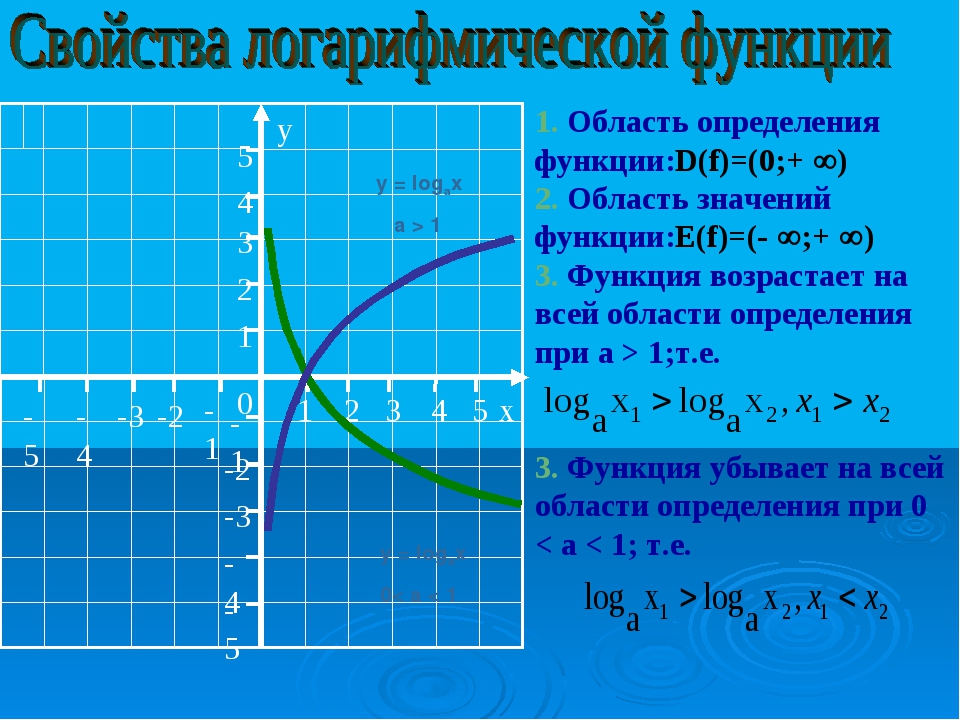
- Областью определения функции является множество всех положительных чисел D(y) = (0; +∞).
- Множеством значений функции являются все действительные числа R.
- Наименьшего и наибольшего значений функция не имеет.
- Функция не является ни нечетной, ни четной. Имеет общий вид.
- Функция непереодическая.
- Нули функции: функция пересекает координатную ось Ox в точке (1; 0).
- При a > 1 функция возрастает, при 0 < a < 1 функция убывает.
Примеры решения задач
Задание 1.
В одной координатной плоскости построить графики функций:
- y = log2x
- y = log3x
- y = log5x
- y = log10x
Решение.
Для начала построим график функции y = log2x. Для этого найдем значения функции при x = , , , 1, 2, 4, 8.
| x | 1 | 2 | 4 | 8 | |||
| y(x) | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
Отметим полученные точки на координатной плоскости, соединив их плавной линией.
Большему значению аргумента х соответствует и большее значение функции у. Функция y = log2x возрастает на всей области определения D(y)=R+, так как основание функции 2 > 1.
Подобным образом построим графики остальных функций.
Переменная х может принимать только положительные значения (D(y) = R+), при этом значение у может быть любым (E(y) = R).
Графики всех данных функций пересекают ось Оx в точке (0; 1), так как логарифм по любому основанию от единицы равен нулю.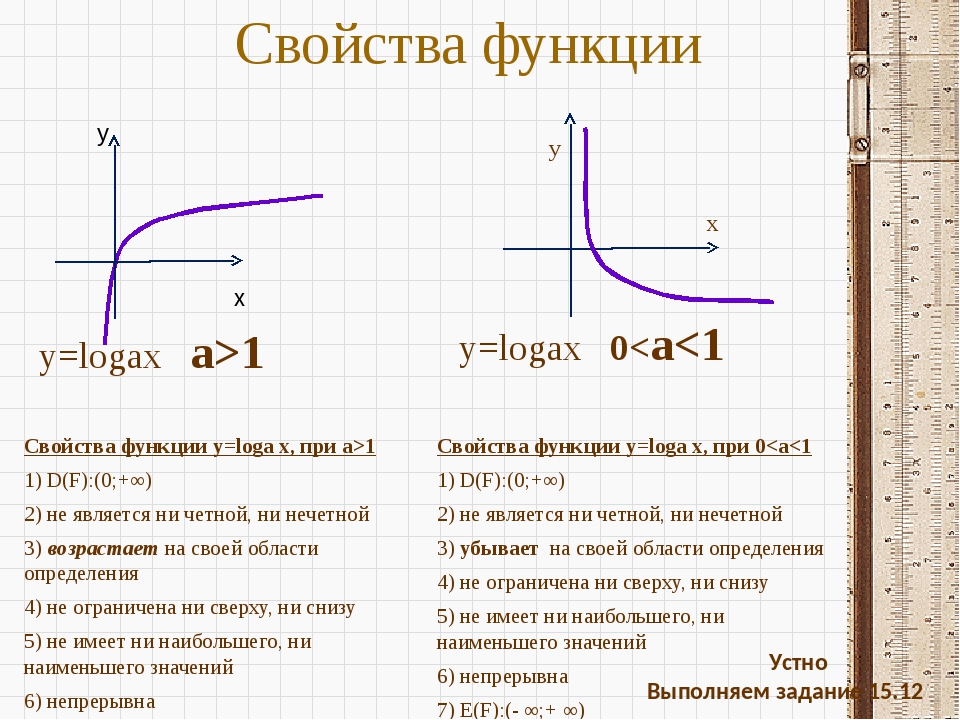 C осью Оy графики не пересекаются, так как логарифм по положительному основанию не может быть равен нулю.
C осью Оy графики не пересекаются, так как логарифм по положительному основанию не может быть равен нулю.
Чем больше основание a (если a > 1) логарифмической функции y = logax, тем ближе расположена кривая к оси Оx.
Все данные функции являются возрастающими, так как большему значению аргумента соответствует и большее значение функции.
Задание 2.
В одной координатной плоскости построить графики функций:
Решение.
Для начала построим график функции. Для этого найдем значения функции при x = , , , 1, 2, 4, 8.
| x | 1 | 2 | 4 | 8 | |||
| y(x) | 3 | 2 | 1 | 0 | -1 | -2 | -3 |
Отметим полученные точки на координатной плоскости, соединив их плавной линией.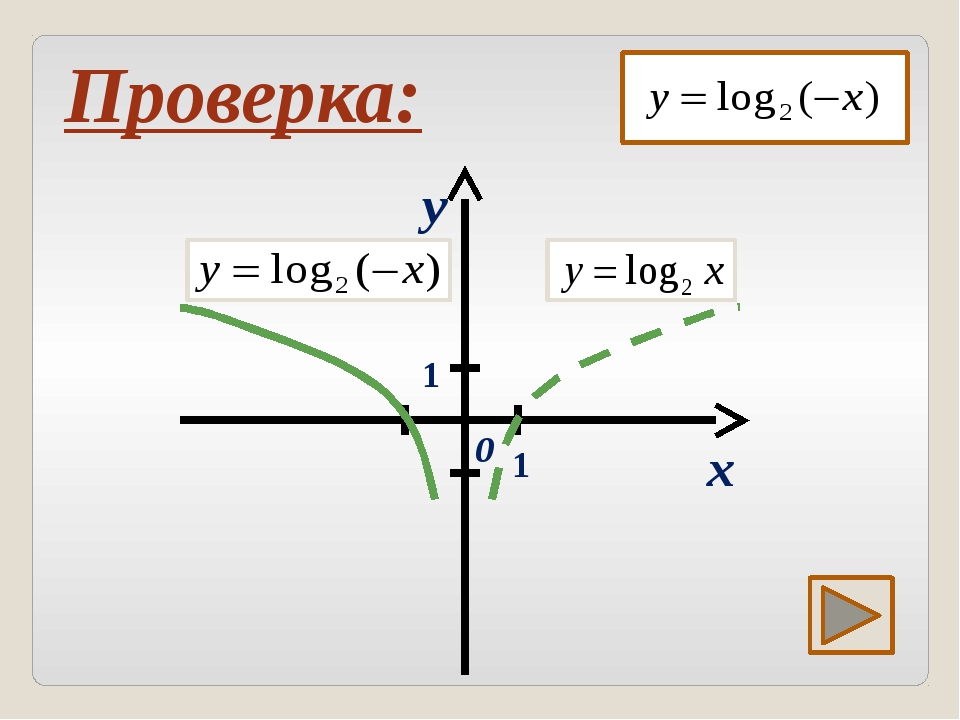
Большему значению аргумента х соответствует меньшее значение функции y. Функция убывает на всей своей области определения: D(y) = R, так как основание функции 0 < < 1.
Подобным образом построим графики остальных функций.
Переменная х может принимать только положительные значения (D(y) = R+), при этом значение у может быть любым (E(y) = R).
Графики всех данных функций пересекают ось Оx в точке (0; 1), так как логарифм по любому основанию от единицы равен нулю. С осью Оy графики не пересекаются, так как логарифм по положительному основанию не может быть равен нулю.
Чем меньше основание a (если 0 < a < 1) логарифмической функции y = logax, тем ближе расположена кривая к оси Оx.
Все данные функции являются убывающими, так как большему значению аргумента соответствует меньшее значение функции.
Задание 3.
Найти обасть определеления функции:
- y = logπ(2x-4)
- y = log2((x-1)(x+5))
Решение
1. y = logπ(2x-4).
y = logπ(2x-4).
Область определения данной функции задается следующим неравенством:
2x-4 > 0
Решим это линейное неравенство:
2x > 4 → x > 2
Ответ: D(y): (2; +∞).
2. y = log2((x-1)(x+5)).
Логарифм определен, если подлогарифмическая функция является положительной, то есть искомая область определения: D(y): (x-1)(x+5) > 0.
Решим полученное уравнение методом интервалов. Для этого найдем нули каждого из сомножителей:
x-1 = 0 → x = 1
x+5 = 0 → x = -5
Наносим их на координатную прямую и определяем знак неравенства на каждом из полученных промежутков.
Поскольку решаем неравенство со знаком «>», то оставляем промежутки со знаком «+», т. е D(y): (-∞; -5)U(1; +∞).
Ответ: D(y): (-∞; -5)U(1; +∞).
Функция y = loga x, её свойства и график.
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Рабочая программа по алгебре и началам математического анализа в 11 классе разработана на основе федерального компонента Государственного образовательного стандарта, утвержденного
Подробнее
Дифференциальное исчисление
Дифференциальное исчисление Основные понятия и формулы Определение 1 Производной функции в точке называется предел отношения приращения функции к приращению аргумента, при условии, что приращение аргумента
Подробнее
Пояснительная записка.
Пояснительная записка. Рабочая программа учебного курса алгебры для 9-го класса составлена на основе программы для общеобразовательных учреждений составитель: Мордкович А.Г., И.И.Зубарева, «Алгебра 9»,
Подробнее
Математическая индустрия моды
Краевая научно-практическая конференция учебно-исследовательских и проектных работ учащихся 6-11 классов «Прикладные и фундаментальные вопросы математики» прикладные вопросы математики Математическая индустрия
Подробнее
Содержание темы учебного курса
Содержание темы учебного курса п/п Наименование разделов, тем уроков Кол-во часов Содержание учебной темы Требование к знаниям и умениям Формы и виды контроля Глава. Рациональные неравенства 5-3 Линейные
Подробнее
присутствие функций арксинуса вида arcsin f x
Практическая работа Полное исследование функции и построение графика Цель: закрепить навыки исследования функций и построения графиков Оборудование (приборы, материалы, дидактическое обеспечение): методические
Подробнее
Тема 9 «Функция.
 Свойства функций»
Свойства функций»
Тема 9 «Функция. Свойства функций» Пусть X некоторое непустое множество действительных чисел. И пусть указан закон f, по которому каждому числу х ϵ X ставится в соответствие единственное число y ϵ Y, обозначаемое
Подробнее
Содержание рабочей программы
Содержание рабочей программы Пояснительная записка Планируемые результаты освоения учебного предмета «Алгебра и начала анализа» Содержание учебного предмета 5 4 Тематическое планирование с указанием количества
Подробнее
Тема 1.4 Функции, их свойства и графики
Тема.4 Функции, их свойства и графики Автор: Переверзьева Н.С. Преподаватель математики Лицей 6 Цели урока: Ознакомиться с понятием «функция», закрепить его на примерах Усвоить новые термины Узнать методы
Подробнее
Пояснительная записка.

Пояснительная записка. Рабочая программа по алгебре и началам анализа 0 класса составлена на основе примерной программы министерства образования Российской Федерации с учетом федерального компонента государственного
Подробнее
4. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ В результате изучения данной темы студент должен: уметь применять таблицу производных и правила дифференцирования для вычисления производных элементарных функций находить производные
Подробнее
Построение графиков функций
Построение графиков функций 1. План исследования функции при построении графика 1. Найти область определения функции. Часто полезно учесть множество значений функции. Исследовать специальные свойства функции:
Подробнее
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Тематическое планирование составлено к УМК А.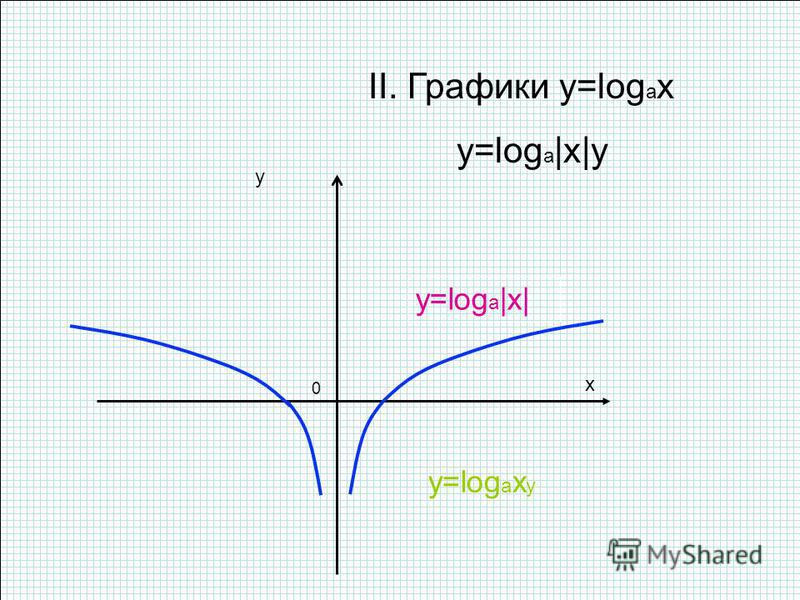 Г. Мордковича и др. «Алгебра и начала анализа», 10-11 класс, М. «Мнемозина», 2009 года на основе федерального компонента государственного
Г. Мордковича и др. «Алгебра и начала анализа», 10-11 класс, М. «Мнемозина», 2009 года на основе федерального компонента государственного
Подробнее
Алгоритм решения квадратных неравенств
Алгоритм решения квадратных неравенств 1) Привести неравенство к стандартному виду : 2) Решить квадратное уравнение (т.е. найти точки пересечения параболы с осью Ох):,, если D > 0, то (две точки пересечения
Подробнее
Математический анализ
Математический анализ Понятие функции. Основные свойства функций Математический анализ (лекция 2) 28 / 64 Понятие функции. Основные свойства функций Если каждому элементу (значению) x множества X поставлен
Подробнее
x 4 ; x log 6 — логарифмические неравенства
Вопрос. Неравенства, система линейных неравенств Рассмотрим выражения, которые содержат знак неравенства и переменную:. >, — +х -это линейные неравенств с одной переменной х.. 0 — квадратное неравенство.
>, — +х -это линейные неравенств с одной переменной х.. 0 — квадратное неравенство.
Подробнее
Функция y = cos x. Ее свойства и график
Функция y = cos x Ее свойства и график 1 Сегодня мы рассмотрим Построение графика функции y = cos x; Свойства функции y = cos x; Изменение графика функции y = cos x в зависимости от изменения функции и
Подробнее
Алгебра. Программа. 9 класс
Алгебра. Программа. 9 класс Пояснительная записка. Изучение математики на ступени основного общего образования направлено на достижение следующих целей: овладение системой математических знаний и умений,
Подробнее
10 класс, Математика (профиль) уч.год Тема модуля 1 «Корни, степени, логарифмы»
0 класс, Математика (профиль) 0-08 учгод Тема модуля «Корни, степени, логарифмы» Знать Понятия действительного числа, множества чисел, свойства действительных чисел, делимость целых чисел****, свойства
Подробнее
Примерные практические задания:
Банк заданий по теме «ПРОИЗВОДНАЯ» МАТЕМАТИКА 11 класс (база) Учащиеся должны знать/понимать: Понятие производной. Определение производной. Теоремы и правила нахождения производных суммы, разности, произведения
Определение производной. Теоремы и правила нахождения производных суммы, разности, произведения
Подробнее
16.2.Н. Производная.
6..Н. Производная 6..Н. Производная. Оглавление 6..0.Н. Производная Введение…. 6..0.Н. Производная сложной функции…. 5 6..0.Н. Производные от функций с модулями…. 7 6..0.Н. Возрастание и убывание
Подробнее
Содержание первой четверти
класс I четверть Тузова Валентина Андреевна учитель математики, e-mail [email protected] Расписание консультаций: Вторник 5:00-7:00, среда 5:00-6:00, четверг 5:00-7:00 Критерии оценивания учащихся
Подробнее
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Уровень рочей программы базовый. Примерная программа по алгебре и началам анализа составлена на основе федерального компонента государственного стандарта среднего (полного) общего
Подробнее
Алгебра и начала анализа, ХI
Алгебра и начала анализа, ХI АЛГЕБРА И НАЧАЛА АНАЛИЗА По Положению о государственной (итоговой) аттестации выпускников XI(XII) классов общеобразовательных учреждений Российской Федерации учащиеся сдают
Подробнее
Содержание курса Алгебраические дроби
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Данная рабочая программа по алгебре для 8 класса составлена в соответствии с федеральным компонентом государственного образовательного стандарта основного общего образования и на
Подробнее
Пояснительная записка.
 Цели обучения
Цели обучения
Пояснительная записка. Рабочая программа по алгебре для 11 класса составлена на основе примерной программы среднего общего образования по математике (базовый уровень) и в соответствии с Федеральным компонентом
Подробнее
Логарифмическая функция: основные свойства и графики
Функцию вида y = loga(x), где a любое положительное число не равное единице, называют логарифмической функцией с основанием а. Здесь и далее для обозначения логарифма мы будем использовать следующую нотацию: loga(b) — данная запись будет обозначать логарифм b по основанию а.
Основные свойства логарифмической функции:
1. Областью определения логарифмической функции будет являться все множество положительных вещественных чисел. Для краткости его еще обозначают R+. Очевидное свойство, так как каждое положительное число имеет логарифм по основанию а.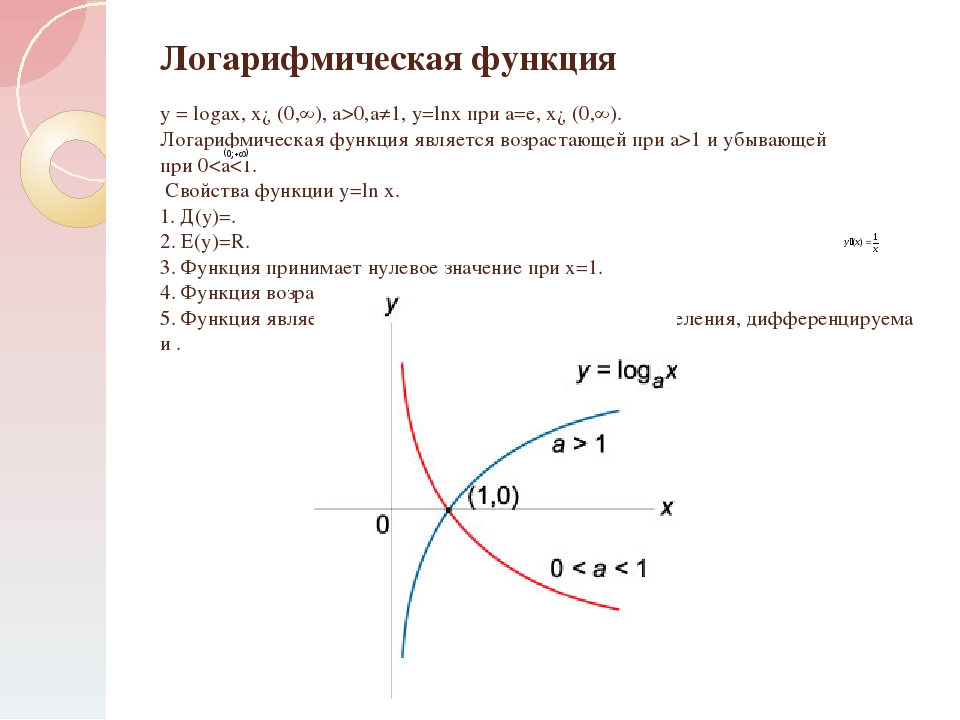
2. Областью значения логарифмической функции будет являться все множество вещественных чисел.
3. Если основание логарифмической функции a>1, то на всей области определения функции возрастает. Если для основания логарифмической функции выполняется следующее неравенство 0<a
4. График логарифмической функции всегда проходит через точку (1;0).
5. Возрастающая логарифмическая функция, будет положительной при x>1, и отрицательной при 0<х<1.
6. Убывающая логарифмическая функция, будет отрицательной при х>1, и положительной при 0<x<1:
На следующем рисунке представлен график убывающей логарифмической функции — (0<a<1):
7. Функция не является четной или нечетной. Логарифмическая функция – функция общего вид.
8. Функция не имеет точек максимума и минимума.
Если построить в одной оси координат показательную и логарифмическую функции с одинаковыми основаниями, то графики этих функций будут симметричны относительно прямой y = x. Данное утверждение показано на следующем рисунке.
Данное утверждение показано на следующем рисунке.
Изложенное выше утверждение будет справедливо, как для возрастающих, так и для убывающих логарифмических и показательных функций. Рассмотрим пример: найти область определения логарифмической функции f(x) = log8(4 — 5*x).
Исходя из свойств логарифмической функции, областью определения является все множество положительных вещественных чисел R+. Тогда заданная функция будет определена для таких х, при которых 4 — 5*x>0. Решаем это неравенство и получаем x<0.8.
Таким образом, получается, что областью определения функции f(x) = log8(4 — 5*x) будет являться промежуток (-∞;0.8)
Нужна помощь в учебе?
Предыдущая тема: Логарифмы и их свойства: определение и алгоритм решения
Следующая тема:   Понятие об обратной функции: график функции и теорема
Калькулятор онлайн — Решение логарифмических уравнений
Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.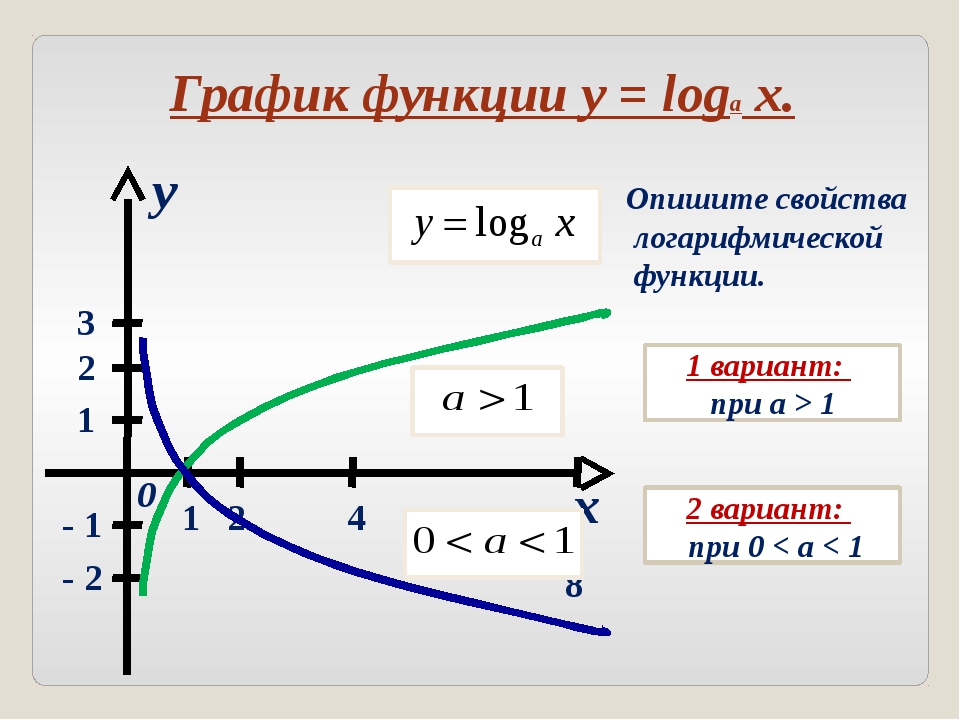
Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.
Логарифмическая функция. Логарифмы
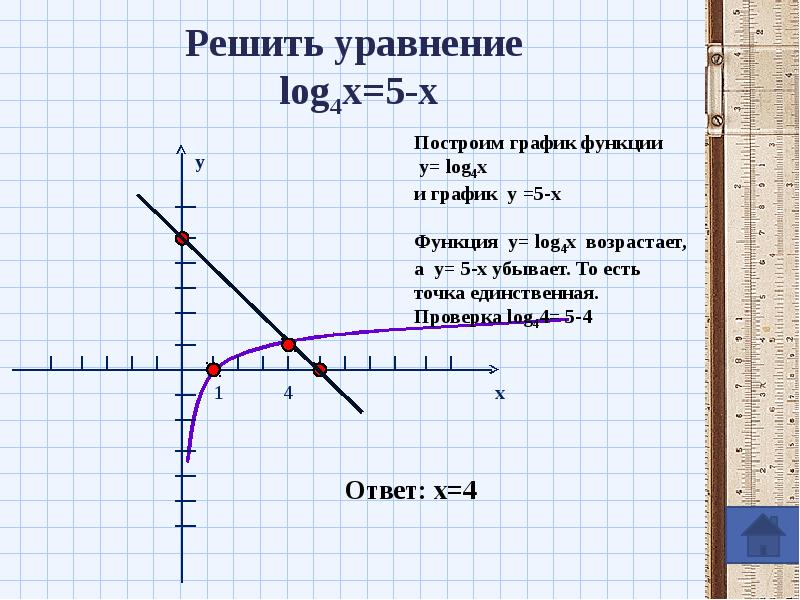
Задача 1. Найти положительный корень уравнения x4 = 81
По определению арифметического корня имеем \( x = \sqrt[4]{81} = 3 \)
Задача 2. Решить уравнение 3x = 81
Запишем данное уравнение так: 3x = 34, откуда x = 4
В задаче 1 неизвестным является основание степени, а в задаче 2 — показатель степени. Способ решения задачи 2 состоял в том,
что левую и правую части уравнения удалось представить в виде степени с одним и тем же основанием 3.
Но уже, например, уравнение 3x = 80 таким способом решить не удаётся. Однако это уравнение имеет корень.
Чтобы уметь решать такие уравнения, вводится понятие логарифма числа.
Уравнение ax = b, где a > 0, \( a \neq 1 \), b > 0, имеет единственный корень.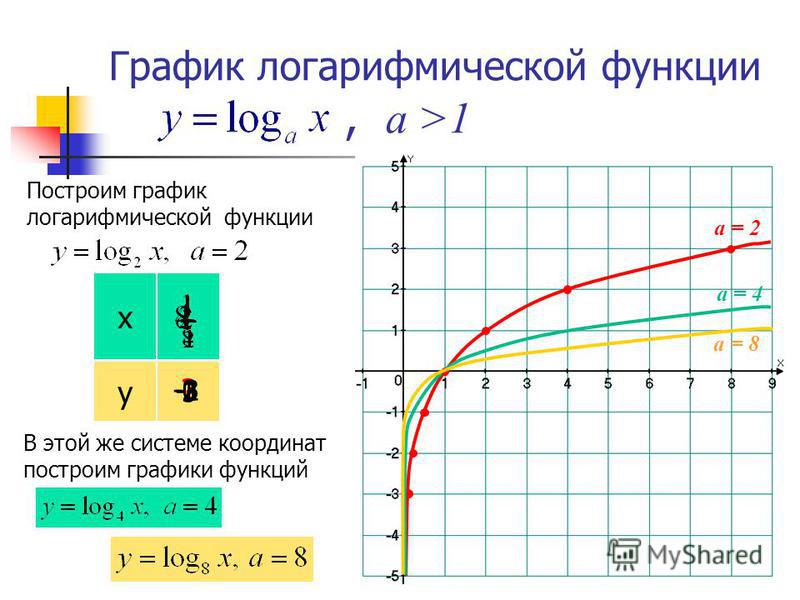 {-2} = \frac{1}{25}$$
{-2} = \frac{1}{25}$$
Решить уравнение log3(1-x) = 2
По определению логарифма 32 = 1 — x, откуда x = -8
Свойства логарифмов
При выполнении преобразований выражений, содержащих логарифмы, при вычислениях и при решении уравнений часто используются
различные свойства логарифмов. Рассмотрим основные из них.
Пусть а > 0, \( a \neq 1 \), b > 0, c > 0, r — любое действительное число. Тогда справедливы формулы:
1) loga(bc) = logab + logac
2) \( \log_a \frac{b}{c} = \log_a b — \log_a c \)
3) logabr = r logab
Десятичные и натуральные логарифмы
Для логарифмов чисел составлены специальные таблицы (таблицы логарифмов). Логарифмы вычисляют также с помощью микрокалькулятора.
И в том и в другом случае находятся только десятичные или натуральные логарифмы.
Определение.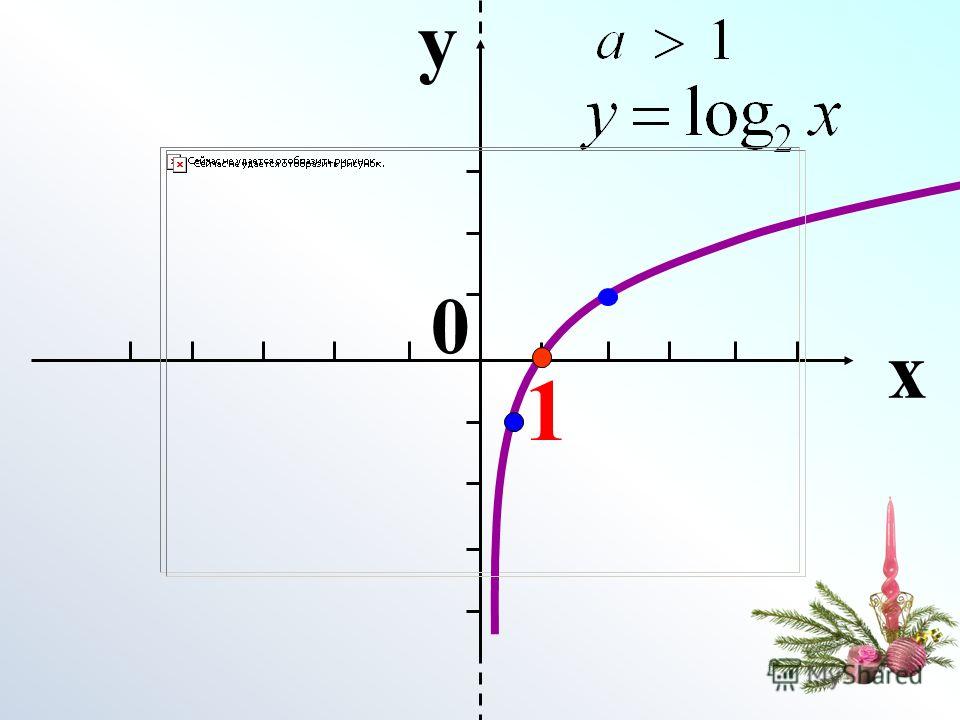 {\infty} \frac{1}{n!} $$
{\infty} \frac{1}{n!} $$
$$ e \approx 2,7182818284 $$
Оказывается, что достаточно знать значения только десятичных или только натуральных логарифмов чисел, чтобы находить логарифмы
чисел по любому основанию.
Для этого используется формула замены основания логарифма:
$$ \log_a b = \frac{\log_c b}{\log_c a} $$
где b > 0, a > 0, \( a \neq 1 \), c > 0, \( c \neq 1 \)
Следствия из формулы замены основания логарифма.
При c = 10 и c = e получаются формулы перехода к десятичным и натуральным логарифмам:
$$ \log_a b = \frac{\lg b}{\lg a} , \;\; \log_a b = \frac{\ln b}{\ln a} $$
Логарифмическая функция, её свойства и график
В математике и её приложениях часто встречается логарифмическая функция
y = logax
где а — заданное число, a > 0, \( a \neq 1 \)
Логарифмическая функция обладает свойствами:
1) Область определения логарифмической функции — множество всех положительных чисел.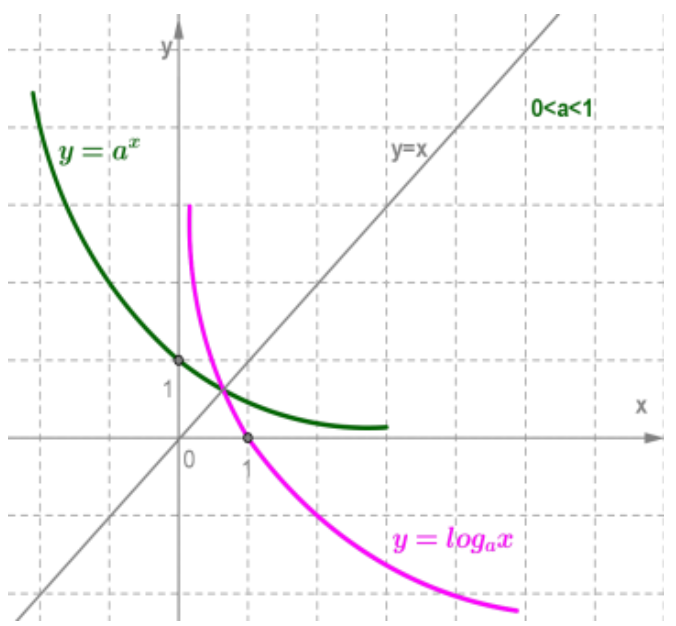
2) Множество значений логарифмической функции — множество всех действительных чисел.
3) Логарифмическая функция не является ограниченной.
4) Логарифмическая функция y = logax является возрастающей на промежутке \( (0; +\infty) \), если a > 1,
и убывающей, если 0
5) Если a > 1, то функция y = logax принимает положительные значения при х > 1,
отрицательные при 0
Если 0 ax принимает положительные значения при 0
отрицательные при х > 1.
Ось Oy является вертикальной асимптотой графика функции y = logax
Отметим, что график любой логарифмической функции y = logax проходит через точку (1; 0).
При решении уравнений часто используется следующая теорема:
Теорема. Если logax1 = logax2 где a > 0, \( a \neq 1 \),
x1 > 0, x2 > 0, то x1 = x2
Логарифмическая функция y = logax и показательная функция y = ax, где a > 0, \( a \neq 1 \), взаимно обратны.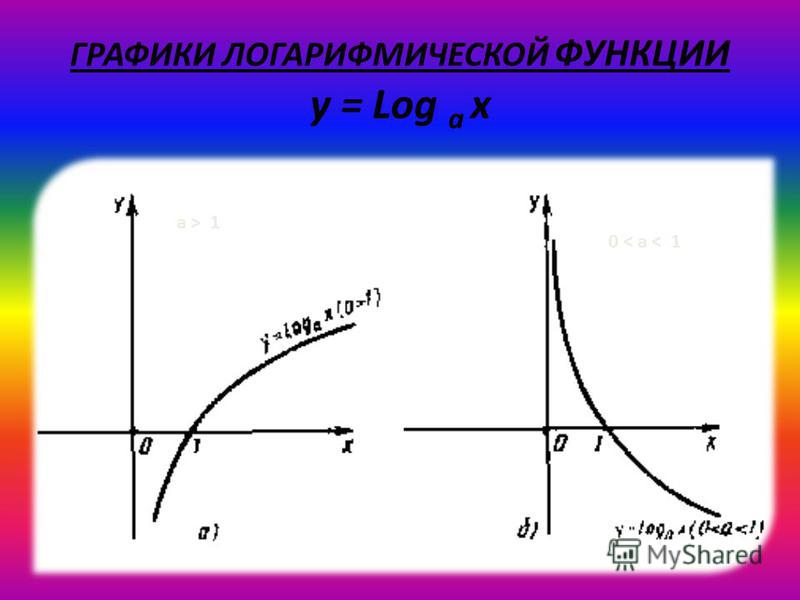
Логарифмические уравнения
Решить уравнение log2(x+1) + log2(x+3) = 3
Предположим, что х — такое число, при котором равенство является верным, т.е. х — корень уравнения. Тогда по свойству логарифма
верно равенство
log2((x+1)(x+3)) = 3
Из этого равенства по определению логарифма получаем
(x+1)(x+3) = 8
х2 + 4х + 3 = 8, т.е. х2 + 4x — 5 = 0, откуда x1 = 1, х2 = -5
Так как квадратное уравнение является следствием исходного уравнения, то необходима проверка.
Проверим, являются ли числа 1 и -5 корнями исходного уравнения.
Подставляя в левую часть исходного уравнения х = 1, получаем
log2(1+1) + log2(1+3) = log22 + log24 = 1 + 2 = 3, т.е. х = 1 — корень уравнения.
При х = -5 числа х + 1 и х + 3 отрицательны, и поэтому левая часть уравнения не имеет смысла, т. е. х = -5 не является корнем этого
е. х = -5 не является корнем этого
уравнения.
Ответ x = 1
Решить уравнение lg(2x2 — 4x + 12) = lg x + lg(x+3)
По свойству логарифмов
lg(2x2 — 4x + 12) = lg(x2 + 3x)
откуда
2x2 — 4x + 12 = x2 + 3x
x2 — 7x + 12 = 0
x1 = 3, х2 = 4
Проверка показывает, что оба значения х являются корнями исходного уравнения.
Ответ x1 = 3, х2 = 4
Решить уравнение log4(2x — 1) • log4x = 2 log4(2x — 1)
Преобразуем данное уравнение:
log4(2x — 1) • log4x — 2 log4(2x — 1) = 0
log4(2х — 1) • (log4 x — 2) = 0
Приравнивая каждый из множителей левой части уравнения к нулю, получаем:
1) log4 (2х — 1) = 0, откуда 2х — 1 = 1, х1 = 1
2) log4 х — 2 = 0, откуда log4 = 2, х2 = 16
Проверка показывает, что оба значения х являются корнями исходного уравнения.
Ответ x1 = 1, х2 = 16
Логарифмическая функция y loga x
ИНЖЕНЕРНО-ПЕДАГОГИЧЕСКИЙ КОЛЛЕДЖ
ГОСУДАРСТВЕННОГО БЮДЖЕТНОГО ОБРАЗОВАТЕЛЬНОГО УЧРЕЖДЕНИЯ
ВЫСШЕГО ОБРАЗОВАНИЯ РЕСПУБЛИКИ КРЫМ
«КРЫМСКИЙ ИНЖЕНЕРНО-ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ»
ПЛАН-КОНСПЕКТ
открытого урока
по предмету:
Математика: алгебра и начало математического анализа
Специальность: 44.02.01 «Дошкольное образование»
ТЕМА:«Логарифмическая функцияy = logax»
ПРЕПОДАВАТЕЛЬ:
Усеинова Акиме Мусретовна
Симферополь, 2016 г.
ПЛАН-КОНСПЕКТ
Тема урока: Логарифмическая функцияy = logax
1 курс, группа ДО-15
Тип урока: урок изучения нового материала.
Цель урока: Ввести определение логарифмической функции.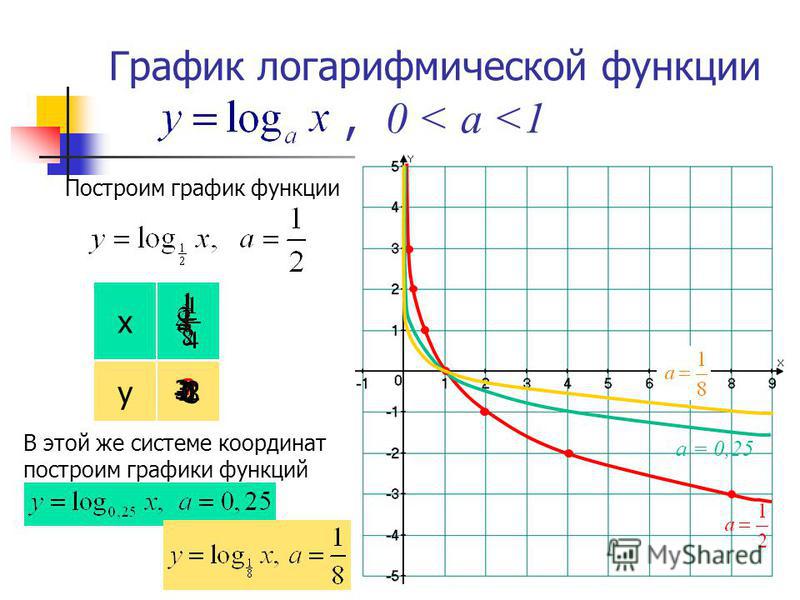 Формировать умение строить график логарифмической функции. Научить выявлять свойства логарифмической функции по графику.
Формировать умение строить график логарифмической функции. Научить выявлять свойства логарифмической функции по графику.
Задачи урока:
Образовательная: повторить определение логарифма, план исследования свойств функции, вспомнить график и свойства показательной функции; сформировать умение строить график логарифмической функции, изучит свойства логарифмической функции; осуществить контроль знаний с помощью проверочного задания и теста.
Развивающая: способствовать развитию внимания, развитию логического мышления, математической интуиции, умению анализировать, применять знания в нестандартных ситуациях,
Воспитательная: воспитывать информационную культуру, выработать навыки работы в группе и индивидуально.
Методы обучения: словесные, наглядные, практические, методы стимулирования к обучению и побуждение к поиску альтернативных решений.
Формы работы на уроке: фронтальная, групповая, работа в парах, индивидуальная.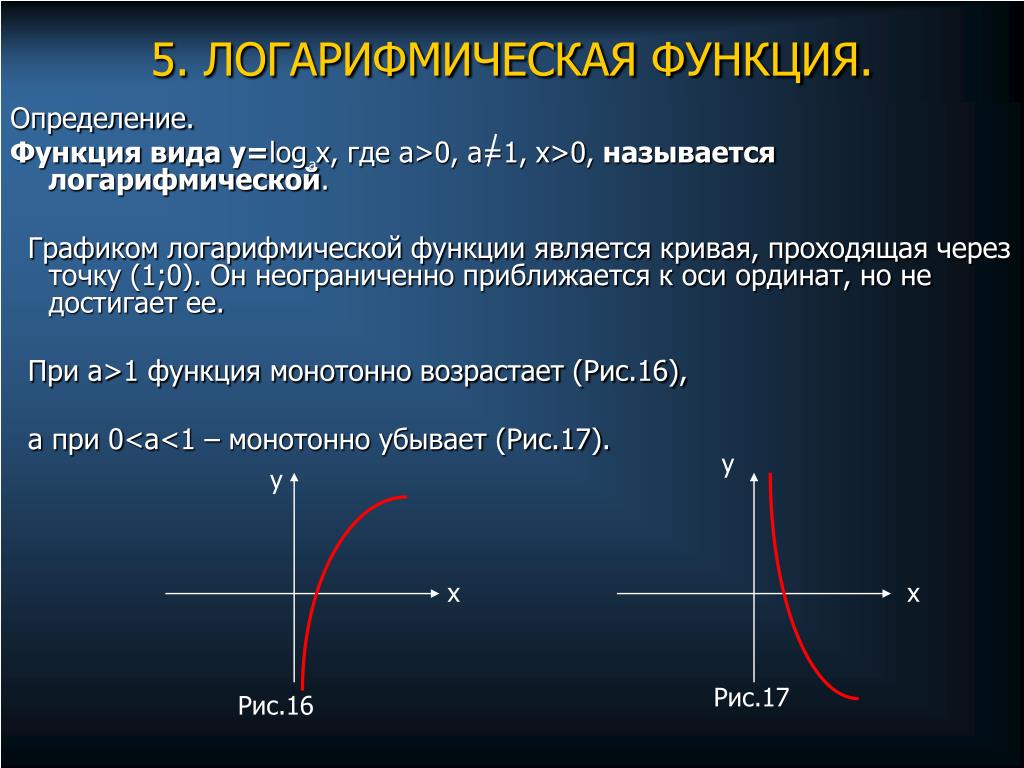
Оборудование: мультимедийный проектор, компьютер, презентация PowerPoint «Логарифмическая функция y = logax», учебник «Алгебра и начала математического анализа 10-11» издательство Просвещение.
План урока
Организационный момент
Актуализация познавательного интереса к изучаемой теме
Актуализация темы урока, создание проблемной ситуации.
Динамическая пауза или разрядка для глаз.
Закрепление изученного материала.
Подведение итогов и результатов работы на уроке (рефлексия).
Домашнее задание.
Ход урока (2 часа)
1.Организационный момент
Учитель приветствует учащихся и рассказывает о цели урока.
Учитель: Мы с Вами продолжаем изучение 7 – ой главы. Сегодня познакомимся с новой функцией – логарифмической, построим её график и изучим свойства.
2. Актуализация познавательного интереса к изучаемой теме
Актуализация познавательного интереса к изучаемой теме
Учитель предлагает решить учащимся задания устной разминки. Называя координаты ячейки и открывая её, считаем логарифмы. В некоторых ячейках есть буквы. После решения всех заданий из этих букв выстраивается фамилия Непер – математик, изобретатель логарифмов (слайд 2,3).
На слайде показывается его портрет и краткая справка о нём.
Вторая часть устной разминки – прочитать и назвать график функции, изображённый на рисунке. Можно воспользоваться подсказкой – «План» или проверить, все ли свойства отражены в ответе. Ученики узнают на рисунке график показательной функции при a > 1. Далееучащимся надо ответить на вопрос: какими свойствами обладает эта функция при 0 < a <1? (сдайд4).
На следующем слайде появляется портрет великого математика – Леонарда Эйлера и краткая справка о нём. Учитель задаёт вопрос: Как вы думаете в связи с чем появился портрет этого учёного? Учитель выслушивает варианты ответов и, или подтверждает правильный ответ, или сообщает, что определение логарифмической функции – это заслуга Леонарда Эйлера.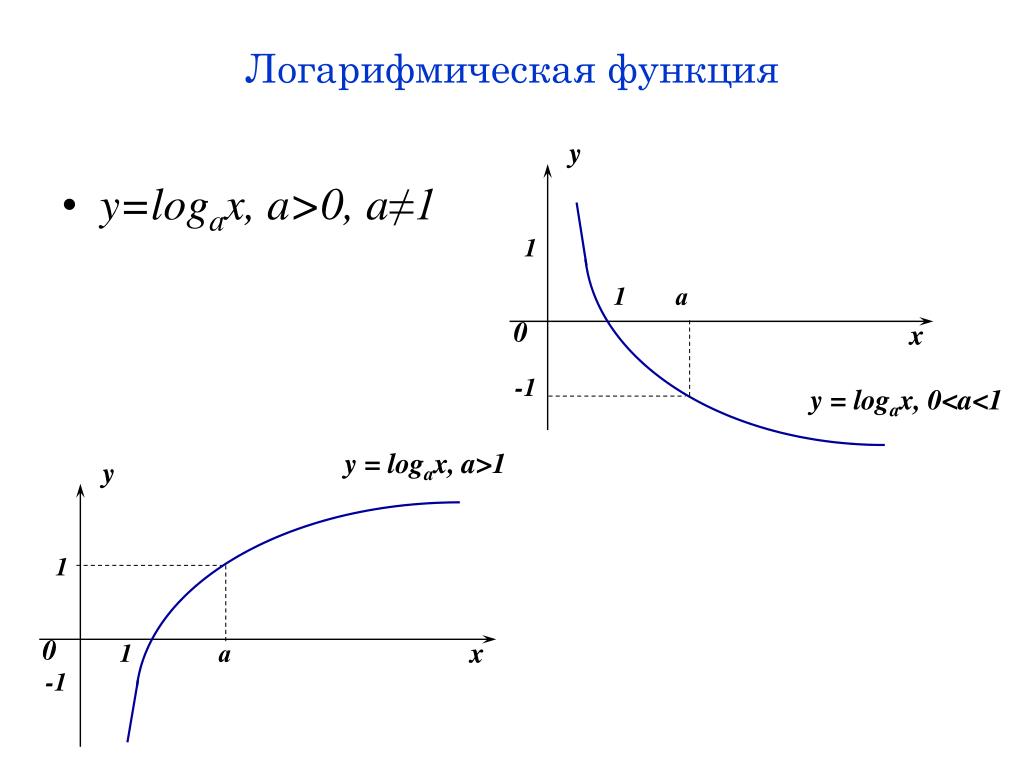 Итак, мы сегодня будем изучать логарифмическую функцию (слайд 6).
Итак, мы сегодня будем изучать логарифмическую функцию (слайд 6).
3.Актуализация темы урока, создание проблемной ситуации.
Учитель просит дать определение показательной функции и самостоятельно сформулировать определение логарифмической функции. В координатной плоскости построить точку с координатами (b;c) и, предположить, что она принадлежит графику показательной функции. Значит . Попробуйте переписать эту запись на «языке логарифмов». Т.е. . Что можно сказать про точку с координатами (b;c)? Ответ: они симметричны относительно прямой у = х (слайд 7).
Сделайте вывод: график логарифмической функции симметричен графику показательной функции относительно прямой у = х. Учащимся предлагается сделать эскизы графиков при a > 1(1 вариант) и при 0 < a <1 (2 вариант). Правильность эскизов проверяется с помощью слайдов 8,9.
После проверки, учитель даёт задание: построить графики функций (1 вариант) и (2вариант). Правильность табличных результатов и графиков проверяется с помощью слайдов 10,11.
Учащимся предлагается сделать эскиз графика функции и описать его свойства при a > 1(1 вариант) и при 0 < a <1 (2 вариант). Проверка – слайд 13,14.
После проверки свойств графиков функций, учитель просит учащихся сделать вывод о свойствах логарифмической функции (слайд 15).
4. Динамическая пауза или разрядка для глаз.
(исходное положение — сидя, каждое упражнение повторяется 3-4 раза):
1.Откинувшись назад, сделать глубокий вдох, затем, наклонившись вперед, выдох.
2.Откинувшись на спинку стула, прикрыть веки, крепко зажмурить глаза, не открывая век.
3.Руки вдоль туловища, круговые движения плечами назад и вперёд.
4.Гимнастика для глаз с помощью тренажёра.
5. Закрепление изученного материала.
Учитель демонстрирует задания на слайдах презентации. Учащиеся устно решают первое задание.
Задание 1. Найдите наименьшее и наибольшее значения функций на данном промежутке: а) б)
Правильность ответа проверяется с помощью презентации (слайд 16).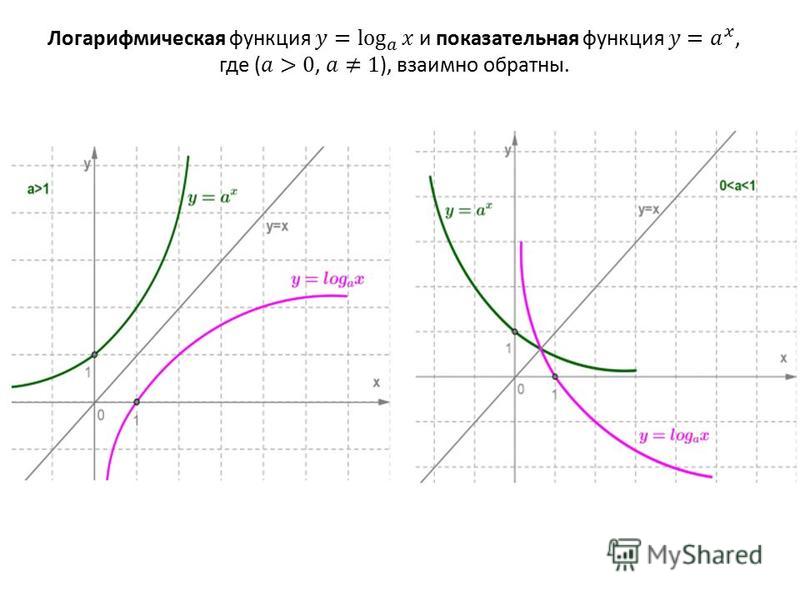
Аналогично решается второе задание (слайд 17).
Похожее задание решаю самостоятельно, записывая только ответы в тетрадь (слайд 18).
Третье задание на построение графика функции разбирает весь класс с помощью учителя. Далее самостоятельно строят графики функций в тетради с последующей проверкой (слайды 19 — 21).
6. Подведение итогов и результатов работы на уроке (рефлексия).
Учитель предлагает учащимся блиц — опрос, чтобы проверить себя, на сколько каждый понял изученный материал (слайд 22 – 24). Необходимо ответить только «да» или «нет». Проверяется сразу.
Вопросы:
Ось у является вертикальной асимптотой графика логарифмической функции.
Графики показательной и логарифмической функций симметричны относительно прямой у = х.
Область определения логарифмической функции – вся числовая прямая, а область значений этой функции – промежуток
Монотонность логарифмической функции зависит от основания логарифма.
Не каждый график логарифмической функции проходит через точку с координатами (1; 0).
Логарифмическая кривая это та же экспонента, только по-другому расположенная в координатной плоскости.
Выпуклость логарифмической функции не зависит от основания логарифма.
Логарифмическая функция не является ни чётной, ни нечётной.
Логарифмическая функция имеет наибольшее значение и не имеет наименьшего значения при а > 1 и наоборот при 0 < a < 1.
Проверка: да, да, нет, да, нет, да, нет, да, нет.
Учитель задаёт вопрос: Каковы результаты? Есть ли учащиеся, которые на все вопросы ответили правильно? У кого только одна или две ошибки? Если есть ученики, у которых больше четырёх ошибок, то не стоит отчаиваться, потому что есть возможность ещё раз дома просмотреть этот материал и найти правильные ответы на вопросы теста.
Учитель выводит на экран домашнее задание, делает соответствующие пояснения о том, какие результаты по его выполнению будут необходимы на следующем уроке. Учащиеся записывают задание.
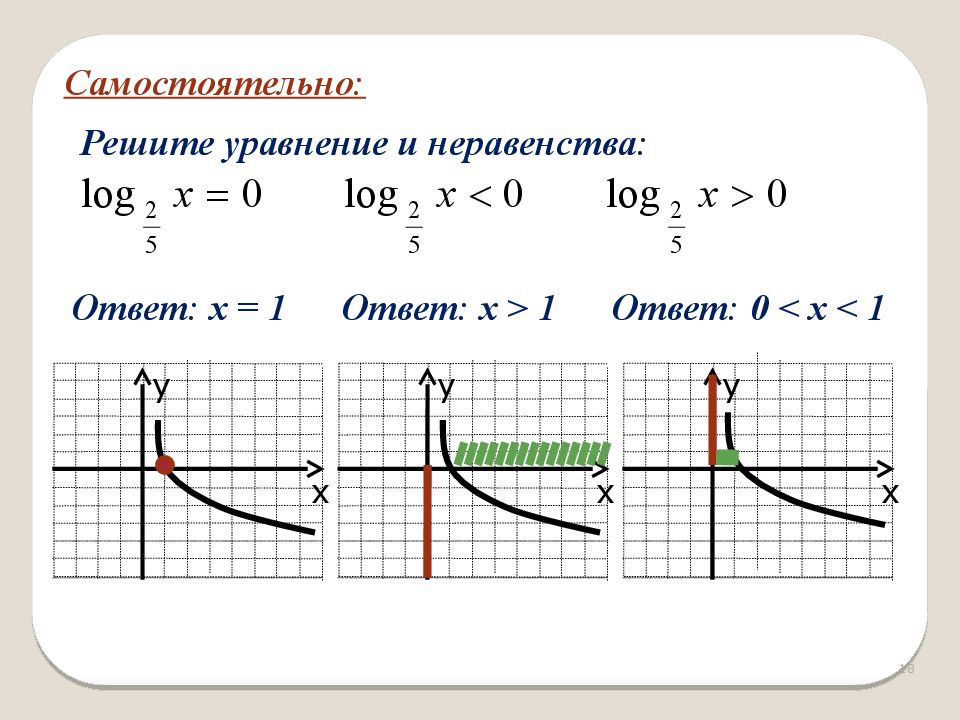
7. Домашнее задание: № 1460, 1463, 1467, 1480 по вариантам.
8. Список использованных источников
1. Алгебра и начала анализа. 10 – 11 кл.: Контрольные работы для общеобразоват. учреждений: учеб. пособие / А.Г. Мордковича, Е.Е. Тульчинская. – 5-е изд. – М.: Мнемозина, 2014. – 62 с.
2. Алгебра и начала математического анализа. 10 класс. Контрольные работы для учащихся общеобразовательных учреждений (базовый уровень) / В.И. Глизбург; под ред. А.Г. Мордковича. – М.: Мнемозина, 2009. – 39 с.
3. Алгебра и начала анализа. 10 – 11 кл.: Тематические тесты и зачеты для общеобразоват. учреждений / Л.О. Денищева, Т.А Корешкова; под ред. А.Г. Мордковича. – 2-е изд., испр. и доп. – М.: Мнемозина, 2014. – 102 с.
4. Геометрии. 10 кл: учебник для общеобразоват. организаций: углубленный уровень / А. Д. Александров, А. Л. Вернер, В. И. Рыжик. – М.: Просвещение, 2014. – 271 с.
5. Геометрия 10 – 11классы: учебник для общеобразоват. организаций: базовый и углублен. уровни / Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др. – М.: Просвещение, 2014. – 255 с.
Зам. директора по УВР_________С.И.Исмаилова
Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/447837-tema-uroka-logarifmicheskaja-funkcija-y—log
Область определения функции | Онлайн калькулятор
Данный калькулятор позволит найти область определения функции онлайн.
Область определения функции y=f(x) – это множество всех значений аргумента x, на котором задана функция. Другими словами, это все x, для которых могут существовать значения y. На графике областью определения функции является промежуток, на котором есть график функции.
Область определения функции f(x), как правило, обозначается как D(f). Принадлежность к определенному множеству обозначается символом ∈, а X – область определения функции. Таким образом, формула x∈X означает, что множество всех значений x принадлежит к области определения функции f(x).
Приведем примеры определения основных элементарных функций. Областью определения постоянной функции y=f(x)=C является множество всех действительных чисел. Когда речь идет о степенной функции y=f(x)=xa, область определения зависит от показателя степени данной функции. При нахождении области определения функции y=f(x)= √(n&x) (корень n-ой степени) следует обращать внимание на четность или нечетность n.
Областью определения логарифмической функции являются все положительные действительные числа, и она не зависит от основания логарифма. Областью определения показательной функции, также как и у постоянной функции, является множество всех действительных чисел.
Областью определения сложных функций y=f1(f2(x)) является пересечение двух множеств: x∈D(f2) и множества всех x, для которых f2(x) ∈ D(f1). Следовательно, для того чтобы найти область определения сложной функции, необходимо решить систему неравенства.
Преимуществом онлайн калькулятора является то, что Вам нет необходимости знать и понимать, как находить область определения функции.4)
Логарифм — свойства, формулы, график
Определение логарифма
- Логарифм с основанием a
- – это функция y(x) = loga x, обратная к показательной функции с основанием a: x(y) = a y.
В дальнейшем будем считать, что основание логарифма a положительное, не равное единице число: .
- Десятичный логарифм
- – это логарифм по основанию числа 10: lg x ≡ log10 x.
- Натуральный логарифм
- – это логарифм по основанию числа e: ln x ≡ loge x.
2,718281828459045…;
.
Графики логарифма
Графики логарифма y = loga x при различных значениях основания a.
График логарифма получается из графика показательной функции зеркальным отражением относительно прямой y = x. Слева изображены графики функции y = loga x для четырех значений основания логарифма: a = 2, a = 8, a = 1/2 и a = 1/8. На графике видно, что при a > 1 логарифм монотонно возрастает. С увеличением x рост существенно замедляется. При 0 < a < 1 логарифм монотонно убывает.
Свойства логарифма
См. также «Определение и доказательство свойств логарифма».
Область определения, множество значений, возрастание, убывание
Логарифм является монотонной функцией, поэтому экстремумов не имеет. Основные свойства логарифма представлены в таблице.
| Область определения | 0 < x < + ∞ | 0 < x < + ∞ |
| Область значений | – ∞ < y < + ∞ | – ∞ < y < + ∞ |
| Монотонность | монотонно возрастает | монотонно убывает |
| Нули, y = 0 | x = 1 | x = 1 |
| Точки пересечения с осью ординат, x = 0 | нет | нет |
| + ∞ | – ∞ | |
| – ∞ | + ∞ |
Частные значения
Логарифм по основанию 10 называется десятичным логарифмом и обозначается так:
Логарифм по основанию e называется натуральным логарифмом:
Основные формулы логарифмов
Свойства логарифма, вытекающие из определения обратной функции:
Основное свойство логарифмов и его следствия
Формула замены основания
- Логарифмирование
- – это математическая операция взятия логарифма. При логарифмировании, произведения сомножителей преобразуются в суммы членов.
- Потенцирование
- – это математическая операция обратная логарифмированию. При потенцировании заданное основание возводится в степень выражения, над которым выполняется потенцирование. При этом суммы членов преобразуются в произведения сомножителей.
Доказательство основных формул логарифмов
Формулы, связанные с логарифмами вытекают из формул для показательных функций и из определения обратной функции.
Рассмотрим свойство показательной функции
.
Тогда
.
Применим свойство показательной функции
:
.
Докажем формулу замены основания.
;
.
Полагая c = b, имеем:
Обратная функция
Обратной для логарифма по основанию a является показательная функция с показателем степени a.
Если , то
Если , то
Производная логарифма
Производная логарифма от модуля x:
.
Производная n-го порядка:
.
Вывод формул > > >
Для нахождения производной логарифма, его нужно привести к основанию e.
;
.
Интеграл
Интеграл от логарифма вычисляется интегрированием по частям: .
Итак,
Выражения через комплексные числа
Рассмотрим функцию комплексного числа z:
.
Выразим комплексное число z через модуль r и аргумент φ:
.
Тогда, используя свойства логарифма, имеем:
.
Или
Однако, аргумент φ определен не однозначно. Если положить
, где n — целое,
то будет одним и тем же числом при различных n.
Поэтому логарифм, как функция от комплексного переменного, является не однозначной функцией.
Разложение в степенной ряд
При имеет место разложение:
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009. {n} \ right) = n \, \ text {log} _ {a} x.{x} \ right) = x \, \ text {log} _ {a} c,
и поэтому
x = \ frac {\ text {log} _ {a} b} {\ text {log} _ {a} c},
завершая доказательство.)
Теорема об изменении основания позволяет нам выразить логарифмы любого основания через логарифмы любого другого основания. Поэтому часто имеет смысл выбрать одну конкретную основу и придерживаться ее. Обычно мы выбираем e = 2.71828 \ text {…}
Логарифм по основанию e называется натуральным логарифмом и записывается как \ ln.{x}
тогда
е = \ ln \, y.
На рисунке 1 показан график натурального логарифма в виде толстой черной линии вместе с логарифмами по основанию 2 и 3 (тонкие синие и тонкие красные линии соответственно).
Рисунок 1: графики натурального логарифма y = \, \ ln \, x (толстая черная линия), y = \ text {log} _ {2} x (тонкая синяя линия), y = \ text {log} _ { 3} x (тонкая красная линия).
Логарифмические функции и их графики
4.2 — Логарифмические функции и их графики
Функция, обратная экспоненциальной
В разделе об экспоненциальных функциях мы заявили, что
экспоненциальные функции взаимно однозначны.Один к одному
функции обладали особым свойством: они имеют обратные
это тоже функции. И, как многие из вас говорили в классе,
и я так рад, что вы помните, функции «один-к-одному» могут
применяться к обеим сторонам уравнения. Они также проходят
горизонтальная линия тест.
Этот раздел посвящен обратной экспоненциальной
функция. Обратной к экспоненциальной функции является
логарифмическая функция. Помните, что обратное
Функция получается переключением координат x и y.Это отражает
график относительно прямой y = x. Как видно из графика справа,
логарифмическая кривая является отражением экспоненциальной кривой.
В таблице ниже показано, как значения x и y точек экспоненты
кривую можно переключить, чтобы найти координаты точек на логарифмической
изгиб.
| Точка на экспоненциальной кривой | Соответствующая точка на логарифмической кривой |
|---|---|
| (-3, 1/8) | (1/8, -3) |
| (-2, 1/4) | (1/4, -2) |
| (-1, 1/2) | (1/2, -1) |
| (0, 1) | (1, 0) |
| (1, 2) | (2, 1) |
| (2, 4) | (4, 2) |
| (3, 8) | (8, 3) |
Сравнение экспоненциальных и логарифмических функций
Давайте посмотрим на некоторые свойства
из двух функций.
Стандартная форма логарифмической функции: y = log a x
Обратите внимание: если «a» в приведенном выше выражении не является нижним индексом (ниже, чем
«журнал»),
тогда вам нужно обновить
веб-браузер.
Рабочее определение логарифма
В экспоненциальной функции x был показателем.Назначение обратной функции —
чтобы сообщить вам, какое значение x использовалось, когда вы уже знаете значение y. Итак, цель
логарифм должен сказать вам показатель степени.
Таким образом, наше простое определение логарифма состоит в том, что это показатель степени.
Другой способ взглянуть на выражение «log a x» — это «до какой степени (экспоненты) нужно возвести
получить х? «
Эквивалентные формы
Логарифмическая форма уравнения y = log a x эквивалентна экспоненциальной форме x = a y .
Чтобы переписать одну форму в другую, оставьте основу такой же и поменяйте сторону с двумя другими
значения.
Свойства логарифмов
- журнал a 1 = 0, потому что 0 =
1 - Неважно, каково основание, если оно допустимо, логарифм 1 всегда равен 0.
Это потому что
логарифмические кривые всегда проходят через (1,0) - журнал a a = 1, потому что a 1 = a
- Любое значение, возведенное в первую степень, означает, что
такое же значение. - журнал a a x = x
- Логарифмическое основание x и степень x являются обратными функциями. Всякий раз, когда обратный
функции применяются друг к другу, они инвертируются, и вы остаетесь с
то
аргумент, в данном случае x. - log a x = log a y означает, что x = y
- Если два бревна с одинаковым основанием равны, то
аргументы должны быть равны. - журнал a x = log b x означает, что a = b
- Если два логарифма с одним и тем же аргументом
равны, то основания должны быть равны.
Обычные бревна и натуральные бревна
На вашем калькуляторе есть две кнопки логарифма. Один помечен как «журнал» и
другой отмечен
«пер». Ни в одном из них нет записанной базы. Базу можно определить,
однако, глядя на обратную функцию, которая написана над ключом и
доступ осуществляется клавишей 2 nd .
Десятичный логарифм (основание 10)
Когда вы видите записанный «журнал» без базы, предположите, что база равна 10.
То есть: журнал x = журнал 10 x.
Некоторые приложения, в которых используются десятичные логарифмы, относятся к pH (для измерения кислотности), децибелам.
(интенсивность звука), шкала Рихтера (землетрясения).
Интересное (возможно) примечание о pH. «Глава 50: Канализация» деревни
Кодекса Форсайта запрещает сброс отходов с pH ниже
5,5 или выше 10,5
(раздел 50.07).
Общие журналы служат и для другой цели. Каждое увеличение десятичного логарифма на единицу
является результатом 10-кратного аргумента.То есть землетрясение силой 6,3 балла имеет 10
раз больше
5.3 землетрясение. Уровень децибел громкой рок-музыки или бензопилы (115 децибел
= 11,5 бел) в 10 раз
громче, чем цыплята внутри здания (105 децибел = 10,5 бел)
Натуральные логарифмы (основание е)
Помните тот номер e , который у нас был из предыдущего раздела? Вы знаете, тот, который был
приблизительно 2,718281828 (но не повторяется и не прерывается). Это основа для естественного
логарифм.
Когда вы видите написанное «ln», это означает, что основание — e .
То есть: ln x = log e x
Модели экспоненциального роста и спада — это одно приложение, в котором используются натуральные логарифмы. Этот
включает непрерывное соединение, радиоактивный распад (период полураспада), рост населения. Обычно
приложения, в которых процесс происходит постоянно. Теперь эти приложения были первыми
упомянутые в экспоненциальном разделе, но вы сможете решить для других переменных
задействованы (после раздела 4) с использованием логарифмов.
В математике более высокого уровня натуральный логарифм — это логарифм выбора. Есть несколько
специальные свойства функции натурального логарифма и ее обратной функции, которые делают жизнь очень
проще в исчислении.
Поскольку «ln x» и « e x » являются обратными функциями друг друга, каждый раз, когда «ln» и «e» появляются справа
рядом друг с другом, между ними абсолютно ничего нет (то есть, когда они
составлены друг с другом), затем они инвертируются, и вы остаетесь с
Аргумент.
Логарифмические и экспоненциальные графики
Экспоненциальные функции
y = a x
Обычная экспоненциальная функция всегда имеет точки
(0, 1), (1, основание) и (-1, 1 / основание)
поскольку
a 0 = 1, a 1 = a и a -1 = 1 / a
Ось x — это асимптота, график никогда не пересекает ось x.
Когда база больше 1
А когда база меньше 1
Пример
Чтобы вычислить значения y, возведите x в степень основания.
y = 2 x
Таблица значений
Обычная функция журнала всегда имеет точки
(1, 0) и (основание, 1)
с
log a 1 = 0 и loga a = 1
Ось y — это асимптота, график никогда не пересекает ось y.
Пример
Для вычисления значений y,
Если y = a x
x = журнал a y
Сдвиг графиков журнала влево и вправо
Возьмем график y = logx
Здесь база равна 10.
Найдите точки (1,0) и (10,1)
Теперь возьмем графики y = log (x + 2) и y = log (x-2)
Обратите внимание, как они меняют направление!
Переключение вверх и вниз
Опять же, база 10.
Найдите точки (1,0) и (10,1)
(1,0) переместился в (1, 2), а (10,1) переместился в (10,3)
(1,0) переместился в (1, -2), а (10,1) переместился в (10, -1)
Собираем все вместе
График ниже имеет уравнение y = log (x + a) + b.
Найдите значения целых чисел a и b.
Запишите уравнение графика.
Во-первых, обратите внимание на асимптоту при x = -3.
График сместился на три места влево.
Это означает, что a должно быть 3.
, поэтому y = log (x + 3) + b.
База 10, так как в журнале нет нижнего индекса.
Это означает, что точка (10,1) обычно существует.
Однако это переместилось на три позиции влево, поэтому
ожидаем точку (7,1)
На графике, когда x = 7, y = -1.
Это означает, что график сдвинулся на два деления вниз.
b должно быть равно -2.
, поэтому a = 3, b = -2
и y = log (x + 3) –2
© Александр Форрест
Справочник логарифмических функций
Это логарифмическая функция:
f (x) = журнал a (x)
a — любое значение больше 0, кроме 1
Свойства зависят от значения «а»
- Когда a = 1 , график не определен
- Кроме того, есть два случая, на которые стоит обратить внимание:
a от 0 до 1 | a выше 1 | |
Пример: f (x) = log ½ (x) | Пример: f (x) = log 2 (x) | |
Для a от 0 до 1 | Для и и выше 1: |
Постройте график здесь (используйте ползунок «a»)
В общем, логарифмическая функция:
- всегда находится на положительной стороне (и никогда не пересекает) оси y
- всегда пересекает ось x при x = 1… другими словами он проходит через (1,0)
- равно 1 , когда x = a , другими словами, он проходит через (a, 1)
- — это инъективная (однозначная) функция
Его домен — положительные действительные числа: (0, + ∞)
Его диапазон — действительные числа:
Обратный
Таким образом, логарифмическая функция может быть «обращена» экспоненциальной функцией.
Функция натурального логарифма
Это «натуральный» Логарифм Функция:
f (x) = журнал e (x)
Где e — «число Эйлера» = 2.718281828459 … и т. Д.
Но чаще пишут так:
f (x) = ln (x)
«ln» означает «журнал, натуральный»
Итак, когда вы видите ln (x), просто помните, что это логарифмическая функция с основанием e : log e (x).
График f (x) = ln (x)
В точке (e, 1) наклон линии равен 1 / e , и прямая касается кривой.
Решение логарифмических функций — объяснение и примеры
В этой статье мы узнаем, как вычислять и решать логарифмические функции с неизвестными переменными.
Логарифмы и экспоненты — две тесно связанные друг с другом темы в математике. Поэтому полезно сделать краткий обзор показателей степени.
Показатель степени — это форма записи многократного умножения числа на само себя. Показательная функция имеет вид f (x) = b y , где b> 0 Например, , 32 = 2 × 2 × 2 × 2 × 2 = 2 2 . Показательная функция 2 2 читается как « два в возведении в степень пяти », или « два в степени пять, » или « два в пятой степени. ” С другой стороны, логарифмическая функция определяется как функция, обратная возведению в степень. Снова рассмотрим экспоненциальную функцию f (x) = b y , где b> 0 y = log b x Тогда логарифмическая функция имеет вид; f (x) = log b x = y, где b — основание, y — показатель степени, а x — аргумент. Функция f (x) = log b x читается как «log base b of x». Логарифмы полезны в математике, потому что они позволяют нам выполнять вычисления с очень большими числами. Для решения логарифмических функций важно использовать экспоненциальные функции в данном выражении.Натуральное бревно или ln — это обратное значение e . Это означает, что один может отменить другой, т.е. ln (e x ) = x e ln x = x Чтобы решить уравнение с логарифмом (ами), важно знать их свойства. Свойства логарифмических функций — это просто правила для упрощения логарифмов, когда входные данные имеют форму деления, умножения или экспоненты логарифмических значений. Некоторые из объектов недвижимости перечислены ниже. Правило произведения логарифма гласит, что логарифм произведения двух чисел, имеющих общее основание, равен сумме отдельных логарифмов. ⟹ log a (p q) = log a p + log a q. Правило частного логарифмов утверждает, что логарифм отношения двух чисел с одинаковыми основаниями равен разности каждого логарифма. ⟹ log a (p / q) = log a p — log a q Правило логарифма степени утверждает, что логарифм числа с рациональной степенью равен произведению экспоненты и его логарифм. ⟹ log a (p q ) = q log a p ⟹ log a p = log x p ⋅ log a x ⟹ log q p = log x p / log x q ⟹ log p 1 = 0. Другие свойства логарифмических функций включают: log a a = 1 log a 1 = 0 Всякий раз, когда вы видите логарифмы в уравнении, вы всегда думаете о том, как отменить логарифм, чтобы решить уравнение. Для этого вы используете экспоненциальную функцию . Обе эти функции взаимозаменяемы. В следующей таблице показан способ записи и замены экспоненциальных функций и логарифмических функций . В третьем столбце рассказывается о том, как читать обе логарифмические функции. Давайте воспользуемся этими свойствами для решения пары задач, связанных с логарифмическими функциями. Пример 1 Перепишите экспоненциальную функцию 7 2 = 49 в ее эквивалентную логарифмическую функцию. Решение Дано 7 2 = 64. Здесь основание = 7, показатель степени = 2 и аргумент = 49. Следовательно, 7 2 = 64 в логарифмической функции; ⟹ log 7 49 = 2 Пример 2 Запишите логарифмический эквивалент 5 3 = 125. Решение База = 5; показатель степени = 3; и аргумент = 125 5 3 = 125 ⟹ log 5 125 = 3 Пример 3 Решить для x в журнале 3 x = 2 Решение 9 log 3 x = 2 Пример 4 Если 2 log x = 4 log 3, найдите значение ‘x’. Решение 2 log x = 4 log 3 Разделите каждую сторону на 2. log x = (4 log 3) / 2 log x = 2 log 3 log x = log 3 2 log x = log 9 x = 9 Пример 5 Найдите логарифм 1024 по основанию 2. Решение 1024 = 2 10 Как решать логарифмические функции?
Свойства логарифмических функций
Сравнение экспоненциальной функции и логарифмической функции
Экспоненциальная функция Логарифмическая функция Считывается как 8 2 = 64 log 8 64 = 2 логарифм с основанием 8 из 64 10 3 = 1000 log 1000 = 3 log base 10 из 1000 10 0 = 1 log 1 = 0 log base 10 из 1 25 2 = 625 журнал 25 625 = 2 бревенчатая база 25 из 625 12 2 = 144 лог 12 144 = 2 лог-база 12 из 144
3 2 = x
⟹ x = 9
log 2 1024 = 10
Пример 6
Найдите значение x в журнале 2 ( x ) = 4
Решение
Перепишите логарифмическую функцию log 2 x ) = 4 в экспоненциальной форме.
2 4 = x
16 = x
Пример 7
Решите относительно x в следующей логарифмической функции log 2 (x — 1) = 5. 9907
Решение
Запишите логарифм в экспоненциальной форме как;
log 2 (x — 1) = 5 ⟹ x — 1 = 2 5
Теперь решите относительно x в алгебраическом уравнении.
⟹ x — 1 = 32
x = 33
Пример 8
Найдите значение x в логарифме x 900 = 2.
Решение
Запишите логарифм в экспоненциальной форме как;
x 2 = 900
Найдите квадратный корень из обеих частей уравнения, чтобы получить;
x = -30 и 30
Но поскольку основание логарифмов никогда не может быть отрицательным или 1, правильный ответ равен 30.
Пример 9
Решите относительно данного x, log x = log 2 + log 5
Решение
Используя правило продукта Log b (mn) = log b m + log b n получаем;
⟹ журнал 2 + журнал 5 = журнал (2 * 5) = журнал (10).
Следовательно, x = 10.
Пример 10
Логарифм решения x (4x — 3) = 2
Решение
Перепишите логарифм в экспоненциальной форме, чтобы получить;
x 2 = 4x — 3
Теперь решите квадратное уравнение.
x 2 = 4x — 3
x 2 — 4x + 3 = 0
(x -1) (x — 3) = 0
x = 1 или 3
Поскольку основание логарифма никогда не может быть 1, тогда единственное решение — 3.
Практические вопросы
1. Выразите следующие логарифмы в экспоненциальной форме.
а. 1ог 2 6
б. журнал 9 3
c. журнал 4 1
д. журнал 6 6
д. журнал 8 25
ф. log 3 (-9)
2. Найдите x в каждом из следующих логарифмов
a. журнал 3 (x + 1) = 2
b. журнал 5 (3x — 8) = 2
c.журнал (x + 2) + журнал (x — 1) = 1
d. log x 4 — log 3 = log (3x 2 )
3. Найдите значение y в каждом из следующих логарифмов.
а. журнал 2 8 = y
b. журнал 5 1 = y
c. журнал 4 1/8 = y
d. log y = 100000
4. Решите относительно xif log x (9/25) = 2.
5. Решите log 2 3 — log 2 24
6. Найдите значение x в следующий логарифм log 5 (125x) = 4
7.Учитывая, что Log 10 2 = 0,30103, Log 10 3 = 0,47712 и Log 10 7 = 0,84510, решите следующие логарифмы:
a. журнал 6
б. журнал 21
c. журнал 14
Предыдущий урок | Главная страница | Следующий урок
Обратная логарифмическая функция — ChiliMath
Найти обратную функцию журнала так же просто, как выполнить следующие шаги. Позже вы поймете, увидев несколько примеров, что большая часть работы сводится к решению уравнения.Ключевые шаги включают выделение логарифмического выражения, а затем переписывание логарифмического уравнения в экспоненциальное уравнение. Вы поймете, что я имею в виду, когда ознакомитесь с приведенными ниже примерами.
Шаги, чтобы найти обратный логарифм
ШАГ 1. Замените обозначение функции f \ left (x \ right) на y.
от f \ влево (x \ вправо) \ до y
ШАГ 2: Поменяйте роли x и y.
х \ к
у \ к х
ШАГ 3: Выделите логарифмическое выражение на одной стороне (левой или правой) уравнения.{- 1}} \ left (x \ right), чтобы получить обратное. Часть приведенного ниже решения включает в себя переписывание логарифмического уравнения в экспоненциальное уравнение. Вот снова формула, которая используется в процессе преобразования.
Обратите внимание, как основание 2 логарифмического выражения становится основанием с показателем x. Материал внутри скобок остается на своем исходном месте.
Когда логарифмическое выражение исчезнет, преобразовав его в экспоненциальное выражение, мы можем закончить это, вычтя обе части на 3.{- 1}} \ left (x \ right) конец.
Один из способов проверить, правильно ли получен обратный результат, — это построить график логарифмического уравнения и обратной функции на одной оси xy. Если их графики симметричны вдоль линии \ large {\ color {green} y = x}, то мы можем быть уверены, что наш ответ действительно правильный.
Пример 2: Найдите обратное значение функции журнала
f \ left (x \ right) = {\ log _5} \ left ({2x — 1} \ right) — 7
Давайте добавим сложности к этой задаче.Уравнение имеет логарифмическое выражение, вычитаемое на 7. Я надеюсь, что вы понимаете, что эта проблема чрезвычайно разрешима. Решение будет немного запутанным, но определенно управляемым.
Итак, я начинаю с изменения f \ left (x \ right) на y и меняя местами \ color {red} x и \ color {red} y.
Теперь мы можем найти y. Сложите обе части уравнения на 7, чтобы выделить логарифмическое выражение в правой части.
Успешно выделив логарифмическое выражение справа, мы готовы преобразовать его в экспоненциальное уравнение.Обратите внимание, что основание логарифмического выражения, равное 6, становится основанием экспоненциального выражения с левой стороны. Выражение 2y-1 внутри скобок справа теперь само по себе без операции журнала.
После этого перейдите к решению для \ color {red} y, чтобы получить требуемую обратную функцию. Сделайте это, сложив обе стороны на 1, а затем разделив обе стороны на коэффициент \ color {red} y, равный 2.
Давайте нарисуем графики логарифмической и обратной функций в одной декартовой плоскости, чтобы убедиться, что они действительно симметричны вдоль линии \ large {\ color {green} y = x}.
Пример 3: Найдите обратную функцию журнала
Итак, это немного интереснее, чем первые две задачи. Обратите внимание, что основание логарифмического выражения отсутствует. Если вы столкнетесь с чем-то подобным, предполагается, что мы работаем с логарифмическим выражением с основанием 10. Всегда помните об этой концепции, чтобы помочь вам обойти проблемы с той же настройкой.
Надеюсь, вы уже освоились с процедурами. Мы начинаем снова, делая f \ left (x \ right) как y, а затем переключая переменные \ color {red} x и \ color {red} y в уравнении.
Наша следующая цель — выделить логарифмическое выражение. Мы можем сделать это, вычтя обе части на 1, а затем разделив обе стороны на -3.
Логическое выражение теперь само по себе. Помните, что «отсутствующее» основание в логарифмическом выражении подразумевает основание 10. Преобразуйте это в экспоненциальное уравнение и начните решать относительно y.
Обратите внимание, что все выражение в левой части уравнения становится показателем степени 10, который является подразумеваемым основанием, как указывалось ранее.
Продолжите решение относительно y, вычтя обе части на 1 и разделив на -4.{- 1}} \ left (x \ right)}. Сделанный!
Построение графика исходной функции и ее обратной на одной оси xy показывает, что они симметричны относительно линии \ large {\ color {green} y = x}.
Возможно, вас заинтересует:
Инверсия матрицы 2 × 2
Функция, обратная абсолютному значению
Функция, обратная постоянной
Обратная экспоненциальная функция
Функция, обратная линейной
Обратная квадратичная функция
Обратная рациональная функция
Функция, обратная квадратному корню
Нахождение логарифмических функций Найдите функцию вида y = log a x, график которой дан.53.
Поиск перехватов В упражнениях 1–4 найдите перехватчики. y = x3x4
Исчисление: ранние трансцендентные функции
Найдите не менее 10 частичных сумм ряда. Изобразите как последовательность членов, так и последовательность частичных сумм …
Исчисление: ранние трансцендентальные методы
В Упражнениях 14 заполните данные таблицы. Экспоненциальная форма 102 = 100 43 = 64 44 = 256 0,450 = 1 81/2 = 22 43 = 164 Логари …
Прикладное исчисление
Найдите наклон прямой, проходящей через P и Q.10. P (1, 4), Q (6, 0)
Исчисление с одной переменной: ранние трансцендентальные методы, том I
Последовательность терминов определяется как a1 = 1an = (5n) an1 Вычислить n = 1an.
Многопараметрическое исчисление
Преобразуйте каждое выражение из упражнений 25–50 в его технологический эквивалент формулы, как в таблице в тексте. …
Конечная математика и прикладное исчисление (список курсов MindTap)
Поиск области и диапазона функции В упражнении 1316 найдите область определения и диапазон функции.Использование в …
Исчисление: прикладной подход (Список курсов MindTap)
SOC Семьи среднего класса более склонны, чем семьи рабочего класса, поддерживать контакты с родственниками? Напишите пар …
Основы статистики
Для следующего набора оценок найдите значение каждого выражения: a. Х б. (X) 2 с. X2 г. (X +3)
Основы статистики для поведенческих наук (список курсов MindTap)
Вычислите поверхностный интеграл. sFdS, где F (x, y, z) = x2i + xyj + zk, а S — часть параболоида z = x2 + y2 belo…
Исчисление (список курсов MindTap)
Найдите границы z-значений, которые разделяют нормальное распределение, как описано в каждом из следующих пунктов. Средне …
Статистика для поведенческих наук (список курсов MindTap)
Производитель имеет фиксированную ежемесячную стоимость 100 000 и производственные затраты 14 на каждую произведенную единицу. Продукт …
Прикладное исчисление для управленческих, жизненных и социальных наук: краткий подход
Используйте преобразования, чтобы нарисовать график функции.16. f (x) = {1 + xifx01 + x2ifx0
Исчисление с одной переменной
Стабильность веб-сайта Джон Огаган рассматривает возможность обновления оборудования веб-сервера на OHaganBooks.com из-за f …
Конечная математика
Статистическая грамотность Учитывать проверка гипотезы о разнице пропорций для двух независимых популяций. S …
Основные сведения о статистике
Мысли словами Объясните своими словами разницу между рефлексивным свойством равенства и…
Промежуточная алгебра
Был выбран образец из 20 стеклянных бутылок определенного типа, и внутреннее давление каждой бутылки …
Вероятность и статистика для инженерии и науки
Используйте индуктивные рассуждения и данные в таблице время-расстояние в наклонной плоскости, показанной выше, упражнение 17 предсказать …
Математические экскурсии (список курсов MindTap)
65. Отскок мяча Мяч падает с высоты 128 футов.Если он отскакивает от высоты, с которой он …
Математические приложения для менеджмента, жизни и социальных наук
С помощью угловых мер, как указано, определите: a) соотношение между y и z, чтобы ABDC. б) соотношение …
Элементарная геометрия для студентов колледжа, 7e
Тест на делимость на 2: 1367
Элементарная техническая математика
Используя обычные проценты, вычислите недостающую информацию для следующих простых заметок о скидках.21. $ 875,00 …
Современная математика для бизнеса и потребителей
Вычислите интеграл. 13. x29x3dx
Исчисление с одной переменной: ранние трансцендентальные методы
Нахождение линии регрессии методом наименьших квадратов В упражнениях 21-24 (a) найдите линию регрессии наименьших квадратов и (b …
Исчисление: ранние трансцендентальные функции (курс MindTap) List)
Сложные проценты. В упражнениях 45-48 найдите основную сумму P, которая должна быть инвестирована по ставке r, начисляемой ежемесячно…
Исчисление одной переменной
Отметьте каждое из следующих утверждений как истинное или ложное. Наименьшая верхняя граница непустого множества S равна un …
Элементы современной алгебры
Задачи 45 и 46 относятся к рисунку 10, который представляет собой схему рамы велосипеда Colnago Dream Plus. Кадр может b …
Тригонометрия (Список курсов MindTap)
Число c, которое удовлетворяет теореме о среднем значении для f (x) = x3 на [1, 4], равно: a) 7 b) 12 c) 63 d) 63
Учебное пособие по исчислению с одной переменной Стюарта: ранние трансцендентальные методы, 8-е
Если yc (x) — общее решение ay ″ + by ′ + cy = 0, а yp (x) — частное решение ay ″ + by ′ + cy = G…
Учебное пособие по многомерному исчислению Стюарта, 8-е
УДАЛЕНИЕ ФОНДОВ Руководство ассоциации кондоминиумов ожидает капитальных затрат в размере 120 000 за 2 года …
Конечная математика для управленческих, жизненных и социальных наук
Заданный круг P и точки RPT, так что R и T находятся на внешней стороне круга P, предположим, что касательные являются cons …
Элементарная геометрия для студентов колледжа
В примере 7.32 исследуются данные об осадках для MinneapolisSt.Павел. Преобразование квадратного корня было использовано для получения …
Введение в статистику и анализ данных
Площадь В упражнениях 29 и 30 используйте двойной интеграл, чтобы найти площадь заштрихованной области.
Исчисление (Список курсов MindTap)
Формула Стирлинга Для больших значений n, n! = 1234 (n1) n может быть аппроксимировано формулой Стирлинга, n! (N3) n2n В примере …
Исчисление
Настройка Тройной интеграл В упражнениях 13-18 установите тройной интеграл для объема твердого тела.Не уходить …
Многопараметрическое исчисление
В упражнениях 29 и 30 найдите количество перестановок букв в каждом слове. а. ВЛИЯНИЕ b. EFFECT
Математика: практическая одиссея
Опишите основную проблему, связанную с измерением надежности между экспертами, и объясните, как каппа Коэна решает эту проблему …
Методы исследования поведенческих наук (список курсов MindTap)
Определите основные разделы исследовательской статьи в стиле APA, знайте, чего ожидать в каждом разделе, и подведите итоги…
Методы исследования поведенческих наук (Список курсов MindTap)
Эксперимент с тремя результатами был повторен 50 раз, и было выяснено, что E1 повторялся 20 раз, E2 …
Статистика для бизнеса и экономики, Пересмотрено (Список курсов MindTap)
Определите функции следующих углов. Округлите ответы до 4 знаков после запятой. sin 7,43
Математика для машинной техники
Russell 1000 — это индекс фондового рынка, состоящий из крупнейших U.С. компании. Индустриальный проспект Доу-Джонса …
СТАТИСТИКА F / БИЗНЕС + ЭКОНОМИКА-ТЕКСТ
Найдите требуемый член в каждом биномиальном разложении. (а + б) 17; 5-й семестр
Колледж по алгебре (Список курсов MindTap)
Пусть X = {a, b, c}. Напомним, что P (X) — это набор степеней X. Определите отношение S P (X) следующим образом: Для всех наборов A и B …
Дискретная математика с приложениями
Следуют данные из упражнения 2.
Вычислите среднеквадратичную ошибку, используя уравнение (14.15).
Вычислите стандартную эр …
Основы статистики для бизнеса и экономики
Наблюдение за Землей: астронавты, смотрящие на Землю с космического корабля, могут видеть только часть ее поверхности. См. Рисунок …
Функции и изменения: подход к моделированию алгебры колледжа (список курсов MindTap)
2. Пересмотрите наблюдаемые частоты в упражнении 1
а. Вычислите долю выборки для каждой генеральной совокупности.
б. u …
Современная бизнес-статистика с помощью Microsoft Office Excel (с печатной картой доступа XLSTAT Education Edition) (Список курсов MindTap)
В задачах 1926 решите данное дифференциальное уравнение.19. (y2 + 1) dx = y sec2 x dy
Первый курс по дифференциальным уравнениям с приложениями моделирования (список курсов MindTap)
Для следующих упражнений используйте график f (x) = x2, чтобы отобразить каждое преобразованное функция g. 91. g (x) = x1
Calculus Volume 1
Предположим, что [a, b} можно разделить на подинтервалы a = a0a1a2 .
