Задача эйлера: Проект Эйлера. Задача #15. Как решить правильно? — Хабр Q&A — ошкольное образовательное учреждение № 4 «Алёнушка»

Содержание

задачи, которые может решить только настоящий программист

Разработчику практически всегда нужно решать разнообразные задачи и нет ничего лучше, чем практика. В Проекте Эйлер есть огромное количество различных заданий, которые помогут держать свой мозг в тонусе.

Особенности платформы:

Задачи можно решить на любом языке программирования, и они показывают, как хорошо вы знаете базовые операции выбранного языка.
Вы научитесь писать надёжный, стандартный, классический код. Никаких библиотек, так что опираться на чужой код не получится.
Вам придётся думать о том, как хранить данные в памяти и получать к ним доступ.
Вам предстоит оптимизировать скорость обработки и хорошо подумать над используемыми алгоритмами.

Однако сначала несколько слов о самом проекте.

Проект Эйлер

Это некоммерческая площадка с набором задач по математике и программированию, которая позволяет (и зачастую требует) расширить свои знания в различных областях и просто пораскинуть мозгами.

Есть задачи разного уровня сложности, поэтому каждый, если постарается, найдёт ту, с которой сможет справиться. Сложность можно приблизительно оценить по количеству пользователей, решивших задачу. Не возбраняется пользоваться поисковиками, однако авторы предупреждают, что между поиском нужной информации и копипастой чужого решения есть тонкая грань, за которую не стоит заступать — ведь в чём тогда ваше достижение?

Вот пример простой задачи, самой первой в списке:

Если выписать все натуральные числа меньше 10, кратные 3 или 5, то получим 3, 5, 6 и 9. Сумма этих чисел равна 23.
Найдите сумму всех чисел меньше 1000, кратных 3 или 5.

А вот сложная задача, которую решило всего 157 участников:

Пусть G(a, b) — наименьшее неотрицательное целое число n, для которого НОД(n³ + b, (n + a)³ + b) имеет наибольшее возможное значение.
Например, G(1, 1) = 5, так как НОД(n³ + 1, (n + 1)³ + 1) достигает максимального значения 7 при n = 5 и имеет меньшие значения при 0 ≤ n < 5.
Пусть H(m, n) = Σ G(a, b) для 1 ≤ a ≤ m, 1 ≤ b ≤ n.
Известно, что H(5, 5) = 128878 и H(10, 10) = 32936544.
Найдите H(18, 1900).

Прим. перев. На платформе задачи представлены на английском языке. Впрочем, на этом сайте можно посмотреть переводы для большинства из них.

Процесс отправки решения довольно простой. Вам не нужно загружать код или делать ещё что-то в таком духе — просто введите ответ и код подтверждения, после чего вы мгновенно узнаете, правы ли вы. Такой подход позволяет участникам не привязываться к конкретному языку программирования, а использовать любой.

У некоторых задач есть разбор, который становится доступен после отправки ответа. В нём вы можете посмотреть на общий подход к решению, а также почерпнуть новые идеи из оптимизированных вариантов. Кроме того, после успешного выполнения открывается доступ к индивидуальному для каждой задачи форуму, где можно посмотреть на решения других участников на различных языках и обсудить задачу.

Для любителей визуального отражения успехов на платформе предусмотрена система достижений.

Всё начинается с основ

Любое соревнование по программированию проверяет ваше умение использовать переменные, условные конструкции, циклы, структуры данных и прочие особенности языков программирования. Однако Проект Эйлер — ещё более тщательная проверка понимания и владения основами. Вам придётся комбинировать базовые инструменты разными способами для решения задач.

Если вы писали веб-приложения, игры или ещё что-нибудь, то скорее всего привыкли работать с разными библиотеками, решающими типичные задачи. Проект Эйлер заставляет забыть про эти библиотеки и проверяет вашу способность размышлять над простыми логическими задачами и самостоятельно писать простой код для их решения.

Развиваем шестое чувство

Есть причина, по которой каждая специальность в университете, связанная с Computer Science, содержит в своей программе изучение алгоритмов и структур данных, и по которой так много компаний проверяют алгоритмическое мышление при приёме на работу. По сути, написание хорошего кода заключается в поиске лучшего алгоритма для рассматриваемой логической задачи. Сложность заключается в том, чтобы понять, когда нужно тратить время на оптимизацию, а когда лучше обойтись простым решением.

Интуитивное решение, которое другим людям легче всего понять, часто является лучшим.

Первые несколько задач помогут вам усвоить эту мысль. Они включают в себя простые вычисления с относительно низким порогом вхождения. Компьютеры работают быстро, поэтому не нужно создавать себе лишнюю работу, пытаясь оптимизировать ваши первые решения. Со временем опытные разработчики развивают шестое чувство для реализации решений, близких к оптимальным. Эта интуиция появится у вас с опытом, а дальнейшие задачи Проекта Эйлер ясно дадут понять, что значит чувствовать эффективность.

Улучшаем навыки программирования

Решение даже нескольких задач сотворит чудо с вашей уверенностью в используемом языке. Также это отличный способ освежить в памяти детали языка или изучить новый.

Учимся документировать и впечатляем работодателя

Если вы хотите добавить в своё портфолио что-нибудь впечатляющее, создайте репозиторий на GitHub и сохраняйте в него решения задач.

Прим. перев. В портфолио следует включать исключительно архивные задачи; по правилам свежие задачи можно только обсуждать на форуме после их решения, да и в целом распространение готовых решений не приветствуется.

После написания решения проверьте, что имена переменных и функций понятны, уберите весь ненужный код и красиво всё отформатируйте.

Затем добавьте комментарии в код, объясняющие принятые вами решения. Умение писать хорошие комментарии — это навык. Помните, любой хороший разработчик поймёт, что делает код, поэтому комментарии должны объяснять, почему он делает именно так.

Помните, что пытливый ум — залог успеха профессионального разработчика. Чем больше разнообразных задач вы решаете, тем быстрее и лучше вы сможете справиться с преобразованием бизнес-тасков в код.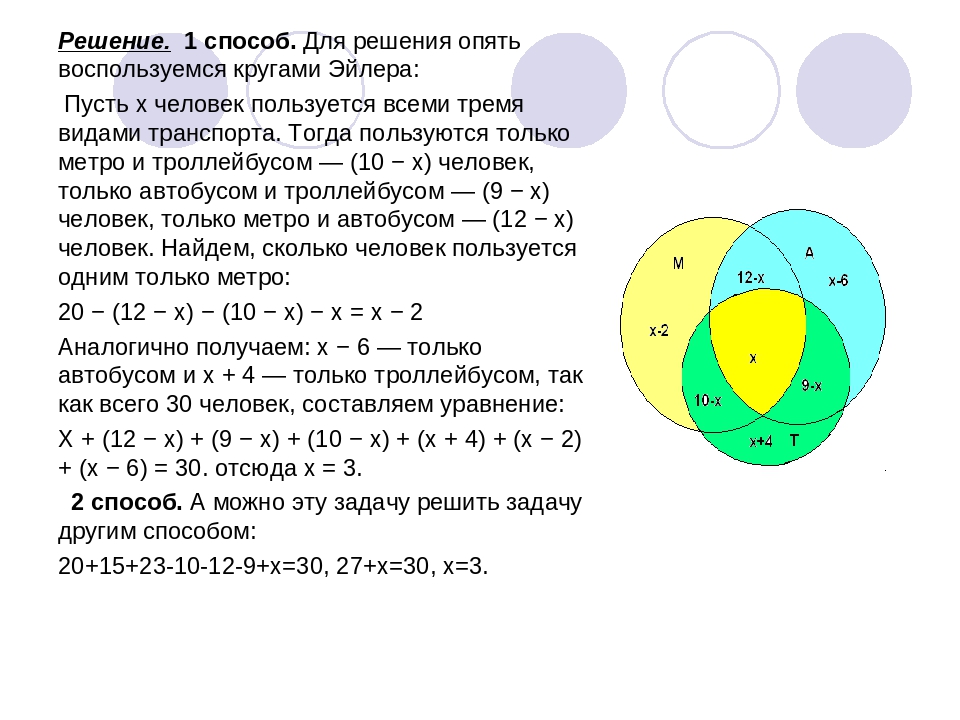 А это, как вы понимаете, послужит вам огромным плюсом при устройстве на работу или попытках увеличения зарплаты.

Смотрите также: Задачи для программистов

На основе статьи «Consider Yourself a Developer? You Should Solve the Project Euler Problems»

круги Эйлера — Основы логики и логические основы компьютера

В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети интернет.Какое количество страниц (в тысячах) будет найдено по запросу Крейсер & Линкор?Считается, что все вопросы выполняются практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

При помощи кругов Эйлера изобразим условия задачи. При этом цифры 1, 2 и 3 используем, чтобы обозначить полученные в итоге области.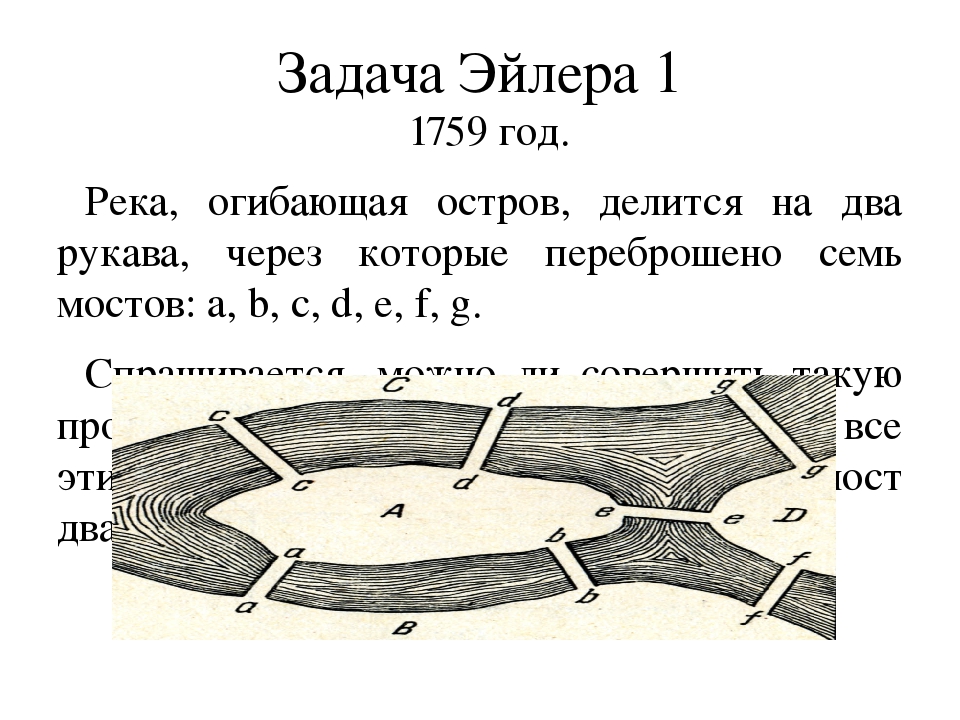

Опираясь на условия задачи, составим уравнения:

Чтобы найти Крейсер & Линкор (обозначенный на чертеже как область 2), подставим уравнение (2) в уравнение (1) и выясним, что:

4800 + 3 = 7000, откуда получаем 3 = 2200.

Теперь этот результат мы можем подставить в уравнение (3) и выяснить, что:

2 + 2200 = 4500, откуда 2 = 2300.

Ответ: 2300 — количество страниц, найденных по запросу Крейсер & Линкор.

Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение

Для решения задачи отобразим множества Тортов и Пирогов в виде кругов Эйлера.

Обозначим каждый сектор отдельной буквой (А, Б, В).

Из условия задачи следует:

Торты │Пироги = А+Б+В = 12000

Торты & Пироги = Б = 6500

Пироги = Б+В = 7700

Чтобы найти количество Тортов (Торты = А+Б), надо найти сектор А, для этого из общего множества (Торты│Пироги) отнимем множество Пироги.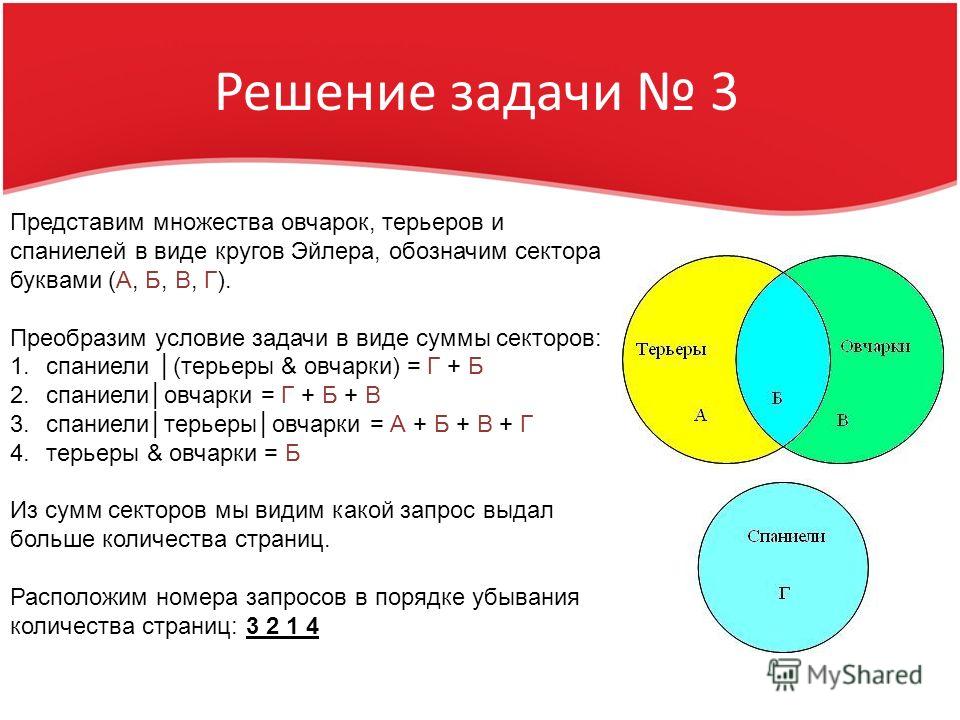

Торты│Пироги – Пироги = А+Б+В-(Б+В) = А = 1200 – 7700 = 4300

Сектор А равен 4300, следовательно

Торты = А+Б = 4300+6500 = 10800

Задача 3

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Запрос	Найдено страниц (в тысячах)
Пироженое & Выпечка	5100
Пироженое	9700
Пироженое \| Выпечка	14200

Какое количество страниц (в тысячах) будет найдено по запросуВыпечка?

Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.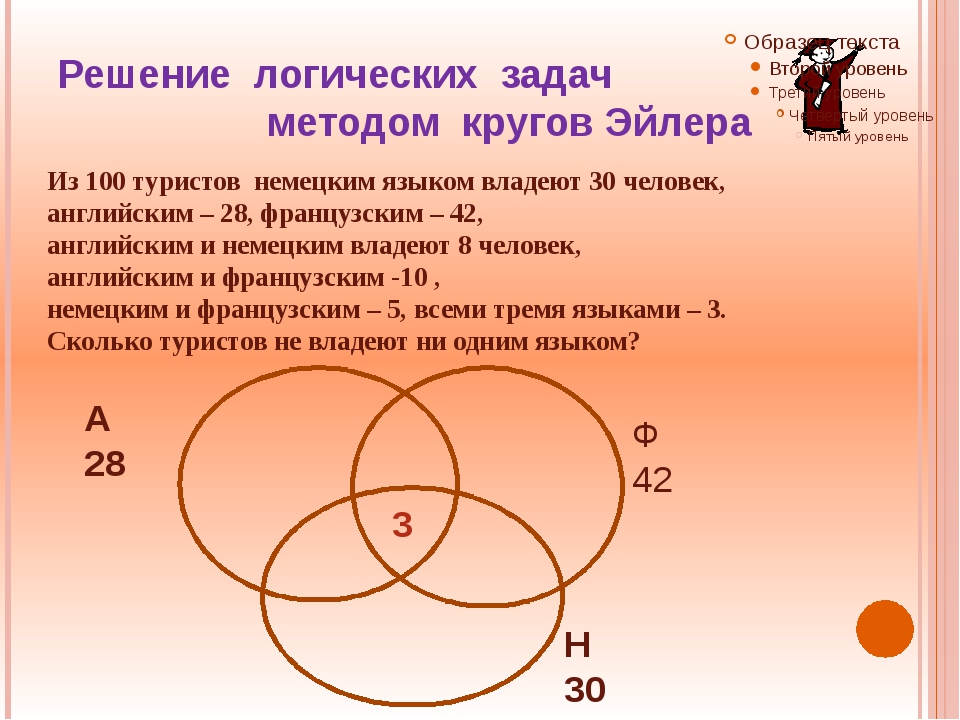 Решение

Для решения задачи отобразим множестваПироженых и Выпечек в виде кругов Эйлера.

Обозначим каждый сектор отдельной буквой (А, Б, В).

Из условия задачи следует:

Пироженое & Выпечка = Б = 5100

Пироженое = А+Б = 9700

Пироженое │ Выпечка = А+Б+В = 14200

Чтобы найти количество Выпечки (Выпечка = Б+В), надо найти секторВ, для этого из общего множества (Пироженое │ Выпечка ) отнимем множество Пироженое.

Пироженое │ Выпечка – Пироженное = А+Б+В-(А+Б) = В = 14200–9700 = 4500

Сектор В равен 4500, следовательно Выпечка = Б + В = 4500+5100 =9600

Задача 4
В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке убывания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».

1	спаниели \| (терьеры & овчарки)
2	спаниели \| овчарки
3	спаниели \| терьеры \| овчарки
4	терьеры & овчарки

Решение

Представим множества овчарок, терьеров и спаниелей в виде кругов Эйлера, обозначим сектора буквами (А, Б, В, Г).

Преобразим условие задачи в виде суммы секторов:

спаниели │(терьеры & овчарки) = Г + Б

спаниели│овчарки = Г + Б + В

спаниели│терьеры│овчарки = А + Б + В + Г

терьеры & овчарки = Б

Из сумм секторов мы видим какой запрос выдал больше количества страниц.

Расположим номера запросов в порядке убывания количества страниц: 3 2 1 4

Задача 5

В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».

1	барокко \| классицизм \| ампир
2	барокко \| (классицизм & ампир)
3	классицизм & ампир
4	барокко \| классицизм

Решение

Представим множества классицизм, ампир и классицизм в виде кругов Эйлера, обозначим сектора буквами (А, Б, В, Г).

Преобразим условие задачи в виде суммы секторов:

барокко│ классицизм │ампир = А + Б + В + Г
барокко │(классицизм & ампир) = Г + Б
классицизм & ампир = Б
барокко│ классицизм = Г + Б + А

Из сумм секторов мы видим какой запрос выдал больше количества страниц.

Расположим номера запросов в порядке возрастания количества страниц: 3 2 4 1

Задача 6
В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».

1	канарейки \| щеглы \| содержание
2	канарейки & содержание
3	канарейки & щеглы & содержание
4	разведение & содержание & канарейки & щеглы

Решение

Для решения задачи представим запросы в виде кругов Эйлера.

K — канарейки,

Щ – щеглы,

С – содержание,

Р – разведение.

Далее будем закрашивать красным цветом сектора согласно запросам, наибольший по величине сектор даст большее количество страниц на запрос.

канарейки \| терьеры \| содержание	канарейки & содержание	канарейки & щеглы & содержание	разведение & содержание & канарейки & щеглы

Самая большая область закрашенных секторов у первого запроса, затем у второго, затем у третьего, а у четвертого запроса самый маленький.

В порядке возрастания по количеству страниц запросы будут представлены в следующем порядке: 4 3 2 1

Обратите внимание что в первом запросе закрашенные сектора кругов Эйлера содержат в себе закрашенные сектора второго запроса, а закрашенные сектора второго запроса содержат закрашенные сектора третьего запроса, закрашенные сектора третьего запроса содержат закрашенный сектор четвертого запроса.

Только при таких условиях мы можем быть уверены, что правильно решили задачу.

Задача 7 (ЕГЭ 2013)

В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&».

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Запрос	Найдено страниц (в тысячах)
Фрегат \| Эсминец	3400
Фрегат & Эсминец	900
Фрегат	2100

Какое количество страниц (в тысячах) будет найдено по запросу Эсминец?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Ответ: 2200

Решение: Запрос «Фрегат» обозначим символом «Ф», «Эсминец» — символом «Э».

Э=(Ф|Э)-Ф+(Ф&Э)=3400-2100+900=2200.

Разбор задачи B12 (демо ЕГЭ 2012)

Время выполнения-2 мин, уровень сложности-повышенный

В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Запрос	Найдено страниц (в тысячах)
Шахматы \| Теннис	7770
Теннис	5500
Шахматы & Теннис	1000

Какое количество страниц (в тысячах) будет найдено по запросу Шахматы?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Ответ: 3270

Решение: Изобразим запросы в виде диаграмм Эйлера-Венна.

Запрос «Шахматы» обозначим символом «Ш», «Теннис» — символом «Т».

Ш=(Ш|Т)-Т+(Ш&Т)=7770-5500+1000=3270.

Задачи для самостоятельного решения

Задача 1

1	принтеры & сканеры & продажа
2	принтеры & продажа
3	принтеры \| продажа
4	принтеры \| сканеры \| продажа

Задача 2

1	физкультура
2	физкультура & подтягивания & отжимания
3	физкультура & подтягивания
4	физкультура \| фитнесс

Круги Эйлера в информатике

Сегодня разберём задачи на круги Эйлера в информатике.

Леонард Эйлер — швейцарский, немецкий и российский математик и механик, сыгравший огромную роль в развитии этих наук.

Задача (Простая)

В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Запрос	Найдено страниц (в тысячах)
Пушкин	3500
Лермонтов	2000
Пушкин \| Лермонтов	4500

Какое количество страниц (в тысячах) будет найдено по запросу Пушкин & Лермонтов? Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение:

Видим, что по запросу «Пушкин» в поисковике нашлось 3500 страниц. По запросу «Лермонтов» — 2000 страниц.

Запрос «Пушкин | Лермонтов» обозначает, что поисковик выдаст страницы, где есть слова про «Пушкина», и страницы, где есть слова про «Лермонтова», а так же могут быть страницы, где написано и про «Пушкина», и про «Лермонтова» одновременно.

Если сложить страницы, в которых написано про «Пушкина» и про «Лермонтова» получается 3500 + 2000 = 5500 страниц. Но почему же при запросе «Пушкин | Лермонтов» получается меньше страниц, всего 4500 ?

Этот факт обозначает то, что когда мы подсчитывали страницы про «Пушкина» (3500 страниц), мы подсчитали и те страницы, где было написано и про «Пушкина», и про «Лермонтова» одновременно.

Тоже самое и для количества страниц, где написано про «Лермонтова» (2000 страниц). В этом числе находятся и те, в которых одновременно упоминается и про «Пушкина», и про «Лермонтова».

В вопросе спрашивается, сколько страниц будет по запросу «Пушкин & Лермонтов«. Это обозначает, что как раз нужно найти количество страниц, где будет одновременно написано и про «Пушкина», и про «Лермонтова».

Отсюда получается:

Пушкин & Лермонтов = (3500 + 2000) — 4500 = 5500 — 4500 = 1000 страниц.

Это и будет ответ!

Теперь решим эту задачу с помощью Кругов Эйлера!

У нас всего есть две сущности: «Пушкин» и «Лермонтов».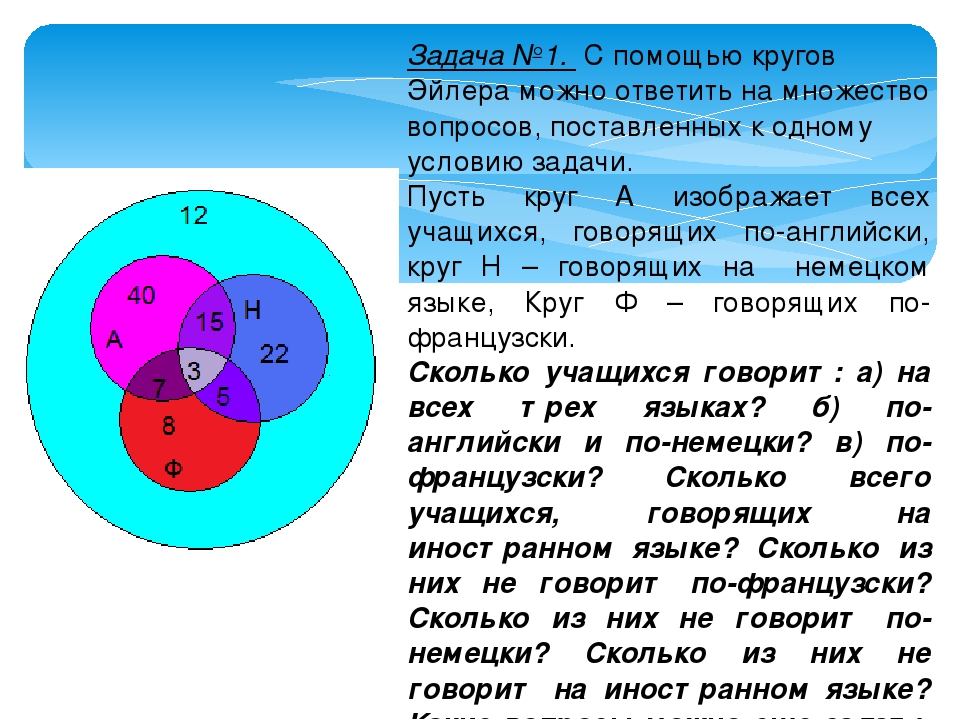 Поэтому рисуем два пересекающихся круга, желательно разными цветами.

Объединение двух кругов в общую фигуру (показано фиолетовым цветом), показывает операцию «Пушкин | Лермонтов». Эта операция всегда стремится увеличить площадь, объединить площади других фигур!

Обратите внимание, что круги пересекаются, из-за этого сумма площадей двух кругов по отдельности (3500 + 2000 = 5500) больше чем у фигуры, которая характеризует логическую операцию «ИЛИ» «Пушкин | Лермонтов» (4500).

Нужно найти площадь фигуры Пушкин & Лермонтов, которая закрашена золотистым цветом. Данная логическая операция «И» стремится уменьшить площадь. Она обозначает общую площадь других фигур.

Найдём сначала заштрихованную часть синего круга. Она равна: площадь фиолетовой фигуры (4500) минус площадь красного круга (3500).

Теперь легко найти площадь золотистой фигуры. Для этого нужно от площади синего круга вычесть площадь заштрихованной части. Получается:

Пушкин & Лермонтов (Количество страниц) = 2000 — 1000 = 1000

Получается, что по запросу Пушкин & Лермонтов будет найдено 1000 страниц.

Ответ: 1000

Рассмотрим ещё одну не сложную разминочную задачу.

Задача (Разминочная)

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Запрос	Найдено страниц (в тысячах)
Кокос \| Ананас	3400
Кокос & Ананас	900
Кокос	2100

Какое количество страниц (в тысячах) будет найдено по запросу Ананас?

Решение:

У нас две сущности: Кокос и Ананас. Нарисуем два круга Эйлера, которые пересекаются между собой. Так же отменим все имеющееся данные.

Найдём заштрихованную часть красного круга.

Весь красный круг 2100. Золотистая область равна 900. Заштрихованная часть равна 2100 — 900 = 1200.

После того, как нашли заштрихованную часть (такой полумесяц), можно найти уже площадь синего круга. Для этого нужно от площади фиолетовой фигуры отнять площадь заштрихованной части!

Ананас (Количество страниц) = 3400 — 1200 = 2200

Ответ: 2200

Разберём классическую задачу из информатики по кругам Эйлера.

Задача (Классическая)

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Запрос	Найдено страниц (в тысячах)
(Космос & Звезда) \| (Космос & Планета)	1100
Космос & Планета	600
Космос & Планета & Звезда	50

Какое количество страниц (в тыс. ) будет найдено по запросу Космос & Звезда?

Решение:

В этой задаче у нас три сущности: Космос, Планета, Звезда. Поэтому рисуем три круга Эйлера, которые пересекаются между собой.

Могут ли круги не пересекаться ? Могут! Если мы докажем, что площади по отдельности двух кругов в сумме дают площадь фигуры, которая получается при применении операции логического «ИЛИ».

Теперь отметим на нашем рисунке запрос (Космос & Звезда) | (Космос & Планета).

Сначала отменим для себя то, что находится в скобках. Первое Космос & Звезда

Теперь отметим вторую скобку Космос & Планета.

В выражении (Космос & Звезда) | (Космос & Планета) две скобки соединяет знак логического «ИЛИ». Значит, эти две области нужно объединить! Область (Космос & Звезда) | (Космос & Планета) отмечена фиолетовым цветом!

Отметим Космос & Планета ещё раз, т. к. для этого выражения известно количество страниц.

Площадь фигуры для выражения Космос & Планета & Звезда будет очень маленькая. Это общая часть для всех трёх кругов. Отметим её оранжевым цветом! Каждая точка этой фигуры должна одновременно быть в трёх кругах!

Найти нужно Космос & Звезда. Отменим на рисунке чёрным цветом ту область, которую нужно найти. Мы эту область уже отмечали салатовым цветом.

Теперь у нас есть все компоненты, чтобы решить эту задачу.

Найдём заштрихованную область.

Вся область Космос & Планета равна 600. А заштрихованная часть равна: область Космос & Планета (600) минус оранжевая область (50).

Количество страниц в заштрихованной части = 600 — 50 = 550

Тогда черная область легко находится: фиолетовая область (1100) минус заштрихованная область (550).

Количество страниц (при запросе Космос & Звезда) = 1100 — 550 = 550

Ответ: 550

Закрепляем материал по задачам на Круги Эйлера.

Задача (На закрепление)

В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» – символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Запрос	Найдено страниц (в тысячах)
Море & Солнце	290
Море & Пляж	355
Море & (Пляж \| Солнце)	465

Какое количество страниц (в тысячах) будет найдено по запросу Море & Пляж & Солнце? Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение:

В задаче используются три сущности: Море, Пляж, Солнце. Поэтому нарисуем три пересекающихся круга Эйлера.

Отметим все области для которых нам даны количество страниц.

В начале отметим Море & (Пляж | Солнце). Для начало нарисуем область, которая в скобках (Пляж | Солнце)

Теперь нужно очертить общую часть фиолетовой области и зелёного круга и получится Море & (Пляж | Солнце). Отметим оранжевым цветом.

Теперь отметим Море & Пляж.

Теперь отметим Море & Солнце.

Найти нужно ту область, которая получается в результате выделения общей части для всех трёх кругов! Обозначим её чёрным цветом!

Найдём заштрихованную область!

Количество страниц (в заштрихованной области) =
= Количество страниц (В оранжевой области) — Море & Солнце =

= 465 — 290 = 175

Чтобы найти искомую чёрную область, нужно из Море & Пляж (355) вычесть заштрихованную область (175).

Количество страниц (Море & Пляж & Солнце) =

= Море & Пляж (355) — Количество страниц (в заштрихованной области) 175 =

= 355 — 175 = 180

Ответ: 180

Решим ещё одну тренировочную задачу из информатики на Круги Эйлера.

Задача (с 4 сущностями)

В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» – символ «&».

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.

Запрос	Найдено страниц (в тысячах)
Англия & (Уэльс & Шотландия \| Ирландия)	450
Англия & Уэльс & Шотландия	213
Англия & Уэльс & Шотландия & Ирландия	87

Какое количество страниц (в тысячах) будет найдено по запросу

Англия & Ирландия?

Решение:

Нужно нарисовать 4 пересекающихся круга. Сначала нарисуем три круга, как обычно, оставив немного места для четвёртого круга.

Четвёртый круг для Ирландии нужно нарисовать так, чтобы он проходил через область (Англия & Уэльс & Шотландия). Это нам подсказывает сама таблица, где есть количество страниц для Англия & Уэльс & Шотландия, а так же для Англия & Уэльс & Шотландия & Ирландия.

Нужно отметить на рисунке Англия & (Уэльс & Шотландия | Ирландия). Это будем делать, как всегда поэтапно.

Область Уэльс & Шотландия выглядит так:

Добавим к этой области Ирландию через логическое «ИЛИ». Получается область (Уэльс & Шотландия | Ирландия). Произошло объединение серой области и жёлтого круга!

Теперь нужно сделать операцию логического «И» получившийся области с «Англией». Тогда область Англия & (Уэльс & Шотландия | Ирландия) примет вид:

Т.е. это общее между предыдущем серым контуром и красным кругом!

Отметим Англия & Уэльс & Шотландия — это общая территория трёх кругов: Красного, Синего и Зелёного. Отмечено оранжевым цветом.

Отметим Англия & Уэльс & Шотландия & Ирландия — это общая территория четырёх кругов. Область получается ещё меньше. Если взять точку в этой области, то мы будем находится сразу в четырёх кругах одновременно. Отмечено фиолетовым цветом.

Отметим то, что нужно найти Англия & Ирландия чёрным цветом.

Искомую чёрную область легко найти, если из серой области вычесть кусочек, окрашенный в бирюзовый цвет!

Найдём, сколько страниц приходится на бирюзовый кусочек:

Количество страниц (для бирюзового кусочка) =

= Англия & Уэльс & Шотландия (213) — Англия & Уэльс & Шотландия & Ирландия (87) =

= 213 — 87 = 126

Найдём искомую чёрную область.

Количество станиц (для чёрной области) =

= Англия & (Уэльс & Шотландия | Ирландия) (450) — Количество (для бирюзового кусочка) =

450 — 126 = 324

Это и будет ответ!

Ответ: 324.

Разберём задачу из реального экзамена по информатике, которая была в 2019 году в Москве! (Сейчас в 2021 задачи не встречаются на Круги Эйлера)

Задача (ЕГЭ по информатике, 2019, Москва)

В таблице приведены запросы и количество страниц, которые нашёл поисковый сервер по этим запросам в некоторым сегменте Интернета:

Запрос	Найдено страниц (в тысячах)
Суфле	450
Корзина	200
Эклер	490
Суфле & Корзина	70
Суфле & Эклер	160
Корзина & Эклер	0

Сколько страниц (в тысячах) будет найдено по запросу

Суфле | Корзина | Эклер

Решение:

Видим, что у нас три поисковых разных слова, поэтому будет три разных круга Эйлера!

Так же видим, что логическое «И» между словами Корзина и Эклер даёт 0 страниц. Это значит, что эти круги не пересекаются! Так же круги бы не пересекались, если бы операция логического «ИЛИ» совпадала бы с суммой этих кругов.

Видим, что Суфле имеет с двумя кругами пересечения, а Корзина и Эклер не пересекаются.

Отметим всё, что нам дано в условии.

Жёлтым цветом отмечено Суфле | Корзина | Эклер . Объединение всех трёх кругов. Это то, что нужно найти.

Искомая жёлтая фигура складывается из заштрихованных областей и красного круга! Площадь красного круга мы знаем. Нужно найти площади заштрихованных частей.

Левая заштрихованная область находится просто:

Количество страниц (лев. заштрих. область) =

= Эклер (490) — Суфле & Эклер (160) = 330

Так же найдём площадь правой заштрихованной области:

Количество страниц (прав. заштрих. область) =

= Корзина (200) — Суфле & Корзина (70) = 130

Теперь можно найти искомую жёлтую область

Количество страниц (Суфле | Корзина | Эклер) =

= Красный круг (450) + лев. заштрих. область (310) + прав. заштрих. область (130) =

= 450 + 330 + 130 = 910

Задача решена, можно писать ответ.

Ответ: 910

Разберём ещё одну задачу из реального ЕГЭ уже 2020 года

Задача (ЕГЭ по информатике, 2020, Москва)

Запрос	Найдено страниц (в тысячах)
Аврора	50
Крейсер	45
Заря	23
Аврора & Заря	9
Заря & Крейсер	0
Заря \| Крейсер \| Аврора	93

Сколько страниц (в тысячах) будет найдено по запросу

Аврора & Крейсер

Решение:

Количество страниц при запросе Заря & Крейсер равно нулю. Значит, эти два круга не будут пересекаться.

Нарисуем все данные на рисунке.

Нужно найти для начала заштрихованную правую часть.

Количество страниц (для двух заштрих. частей) =
З | К | А (93) — Красный круг (50) = 43

Левую заштрихованную область легко найти.

Количество страниц (для левой заштрих. части) =

Синий круг (23) — А & З (9) = 14

Тогда для правой заштрихованной области получается:

Колич. страниц (для правой заштрих. части) =

Колич. страниц (для двух заштрих. частей) (43) — Колич. страниц (для лев. заштрих. части) (14) =

= 43 — 14 = 29

Тогда искомую область легко найти:

Колич. страниц (А & K) =

Зелёный круг (45) — Колич. страниц (для правой заштрих. части) (29) =

45 — 29 = 16

Ответ: 16

На этом всё! Надеюсь, вы теперь будете с удовольствием решать задачи по информатике с помощью Кругов Эйлера.

Задача о кёнигсбергских мостах

Рис. 1. Карта Кёнигсберга

Однажды великому математику Леонарду Эйлеру был задан вопрос: можно ли обойти все семь мостов, стоявших тогда в городе Кёнигсберге (современный Калининград, Россия), побывав на каждом по одному разу? Перед вами план Кёнигсберга – можете попробовать!

Рис. 2. Кенигсбергские мосты

Рассмотрев эту задачу, в 1736 году Эйлер доказал, что это невозможно, причем он рассмотрел более общую задачу: какие местности, разделенные рукавами рек и соединенные мостами, возможно обойти, побывав на каждом мосту ровно один раз, а какие невозможно.

Рис. 3. Граф кенигсбергских мостов

Несколько модифицируем задачу. Каждую из рассматриваемых местностей, разделенных рекой, обозначим точкой, а соединяющие их мосты – отрезком линии (не обязательно прямой). Тогда вместо плана будем работать просто с некой фигурой, составленной из отрезков кривых и прямых. Такие фигуры в современной математике называются графами, отрезки – ребрами, а точки, которые соединяют ребра – вершинами. Тогда исходная задача эквивалентна следующей: можно ли начертить данный граф, не отрывая карандаша от бумаги, то есть таким образом, чтобы каждое его ребро пройти ровно один раз.

Такие графы, которые можно начертить, не отрывая карандаша от бумаги, называются уникурсальными (от латинского unus cursus – один путь), или эйлеровыми. Итак, задача ставится таким образом: при каких условиях граф уникурсален?
Ясно, что уникурсальный граф не перестанет быть уникурсальным, если изменить длину или форму его ребер, а также изменить расположение вершин – лишь бы не менялось соединение вершин ребрами (в том смысле, что если две вершины соединены, они должны оставаться соединенными, а если разъединены – то разъединенными).

Рис. 4. Топологически эквивалентные графы

Если граф уникурсален, то и топологически эквивалентный ему граф тоже будет уникурсальным. Уникурсальность, таким образом, является топологическим свойством графа.

Во-первых, надо отличать связные графы от несвязных. Связными называются такие фигуры, что любые две точки можно соединить каким-нибудь путем, принадлежащим этой фигуре. Например, большая часть букв русского алфавита связны, но вот буква Ы – нет: невозможно перейти с ее левой половинки на правую по точкам, принадлежащим этой букве. Связность – это топологическое свойство: оно не меняется при преобразованиях фигуры без разрывов и склеек. Понятно, что если граф уникурсален, то он обязан быть связным.

Во-вторых, рассмотрим вершины графа. Будем называть индексом вершины число ребер, встречающихся в этой вершине. Теперь зададимся вопросом: чему могут равняться индексы вершин уникурсального графа.

Здесь может быть два случая: линия, вычерчивающая граф, может начинаться и заканчиваться в одной и той же точке (назовем ее «замкнутый путь»), а может в разных (назовем ее «незамкнутый путь»). Попробуйте сами нарисовать такие линии – с какими хотите самопересечениями – двойными, тройными и т. д. (для наглядности лучше, чтобы ребер было не больше 15).

Нетрудно видеть, что в замкнутом пути все вершины имеют четный индекс, а в незамкнутом – ровно две имеют нечетный (это начало и конец пути). Дело в том, что, если вершина не является начальной или конечной, то, придя в нее, надо затем из нее выйти – таким образом, сколько ребер входят в нее, столько же выходят из нее, а всего число входящих и исходящих ребер будет четным. Если начальная вершина совпадает с конечной, то ее индекс также четен: сколько ребер из нее вышло, столько же и вошло. А если начальная точка не совпадает с конечной, то их индексы нечетные: из начальной точки нужно один раз выйти, а затем, если в нее и вернемся, то выйти снова, если еще раз вернемся – опять выйти, и т. д.; а в конечную нужно придти, а если из нее потом и выходим, то опять нужно вернуться, и т. д.

Итак, чтобы граф был уникурсальным, необходимо, чтобы все его вершины имели четный индекс либо чтобы число вершин с нечетным индексом равнялось двум.

Теперь посмотрите еще раз на граф задачи о кенигсбергских мостах.

Рис. 5. Граф кенигсбергских мостов

Посчитайте индексы его вершин и убедитесь, что он никак не может быть уникурсальным. Вот поэтому-то у вас ничего не получалось, когда вы хотели обойти все мосты…

Возникает вопрос: а если в связном графе нет вершин с нечетным индексом либо таких вершин ровно две, то обязательно ли граф уникурсален? Можно строго доказать, что да! Таким образом, уникурсальность однозначно связана с числом вершин с нечетным индексом.

Упражнение: постройте на схеме кенигсбергских мостов еще один мост – там, где захотите – чтобы полученные мосты можно было бы обойти, побывав на каждом ровно по разу; реально проделайте такой путь.

Вот вам еще несколько графов – посчитайте сами индексы вершин и, если это возможно, попробуйте обойти их «не отрывая карандаша от бумаги».

Модель 1. Уникурсальные графы

Теперь еще один интересный факт: оказывается, любую систему местностей, соединенных мостами, можно обойти, если необходимо побывать на каждом мосту ровно два раза! Попробуйте это доказать самостоятельно.

Рис. 6. Граф кенигсбергских мостов с удвоенным количеством мостов уникурсален

Ответ

Дело все в том, что любой мост, на котором надо побывать два раза, можно заменить на два моста, имеющих общее начало и конец, и тогда задача сведется к предыдущей, причем индекс всех вершин получаемого графа удвоится, а значит, станет четным.

Рисунок с кенигсбергскими мостами, у каждого из которых появляется рядом мост-близнец; рисуется также эквивалентный граф, у всех вершин пишется их новый индекс, выделенная точка зримо обходит этой граф и – синхронно – схему плана Кёнигсберга, при этом получаемый путь постепенно закрашивается; когда вернулась в исходную точку, обходит все снова, при этом весь путь постепенно перекрашивается в новый цвет, и так далее.

Занятие 3. Задача Эйлера

Леонард Эйлер (1707-1783) – швейцарец по происхождению – обрёл в России вторую родину. Он проработал в Петербургской академии наук более 30 лет. Исторически теория графов зародилась при решении Леонардом Эйлером головоломки о Кёнигсбергских мостах.

Река Прегель, протекающая через Кёнигсберг (Калининград), омывает два острова. Берега реки с островами были во времена Эйлера связаны мостами так, как показано на рисунке.

Жители Кёнигсберга любили говорить, что никто не может осмотреть центр города, пройдя при этом по каждому из семи мостов лишь по одному разу, а начало и конец пути при этом должны совпадать. Эйлер начертил схематическую карту города, обозначив его четыре части, отделённые друг от друга водой, точками и буквами A, B, C, D и соединив их рёбрами – мостами.

Пользуясь полученным графом, Эйлер доказал, что маршрута, который бы отвечал условиям задачи, не существует, и разработал теорию решения такого рода головоломок.

Эйлеровым путём в графе называется путь, содержащий все рёбра графа. Иными словами, граф обладает эйлеровым путём, если его можно начертить, не отрывая карандаш от бумаги и не проводя дважды по одному и тому же ребру.

Эйлеровым циклом в графе называется цикл, содержащий все рёбра графа. Иными словами, если граф можно начертить не отрывая карандаш от бумаги и не проводя дважды по одному и тому же ребру, при этом начало и конец нашего пути совпадут, то граф обладает эйлеровым циклом.

1. Попробуй нарисовать графы не отрывая карандаш от бумаги, обводя каждое ребро в точности один раз.

Какие графы нельзя нарисовать так, чтобы линия удовлетворяла условиям?

Какие графы получилось нарисовать, но начало и конец не совпадают?

2. На озере семь островов, которые соединены между собой мостами. На какой остров катер должэен доставить путешественников, чтобы они могли пройти по каждому мосту и только один раз? С какого острова катер должен снять этих людей?

3. На реке 8 островов, которые соединены между собой мостами. Могут ли путешественники пройти по всем эти мостам? Могут ли они пройти по всем мостам и вернуться на тот остров, с которого они начнут свой маршрут?

б)

в)

4. Инженер разработал проект соединения островов мостами. Могут ли путешественники пройти все мосты и вернуться на остров, с которого начали путь?

Как, убрав всего один мост, сделать так, чтобы путешественники прошли по всем мостам и вернулись на остров, с которого начали свой путь?

Как, добавив два моста, сделать так, чтобы путешественники прошли по всем мостам и вернулись на остров, с которого начали путь?

5. На рисунке изображена схема зоопарка (вершины графа – вход, выход, перекрестки, повороты, тупики; рёбра – дорожки, вдоль которых расположены клетки). Найдите маршрут, по которому экскурсовод мог бы провести посетителей, показав им всех зверей и не проходя более одного раза ни одного участка пути.

6. Придумана игра: шарик катится по дорожкам и закатывается в отверстия. На графе дорожки изображены рёбрами, а отверстия – вершинами графа. Может ли шарик прокатиться по всем дорожкам, но не более одного раза?

Как, добавив одно ребро (одну дорожку в игре), сделать так, чтобы шарик мог прокатиться по всем дорожкам (при этом начало и конец пути не совпадают)?

Как, добавив два ребра, сделать так, чтобы шарик мог прокатиться по всем дорожкам (при этом начало и конец пути совпадают)?

7. Придумай для своего товарища фигуры (графы), которые он должен начертить , не отрывая карандаш от бумаги.

Определение критической силы. Задача Эйлера

Содержание:

Определение критической силы. Задача Эйлера

Определение критической прочности. Работа Эйлера Задача определения критической силы Fcr была впервые решена Л. Эйлером в 1744 году. Сила сжатия важна. Чтобы проверить изгиб, используйте дифференциальное уравнение (5.44) оси изгиба стержня. d2y / dx2 = МДж (El). (5,53) Рисунок 5.30 Изгиб происходит в плоскости с наименьшей жесткостью. Сечение вращается вокруг своей оси с минимальным моментом инерции /.

Изгибающий момент MI при абсолютном значении всех сечений равен fcr Y *, где Y ~~ — отклонение сечения. Отклонение y и его вторая производная d2 y / dx2 имеют вид Если есть противоположный знак, уравнение (5.53) выражается как: d2y / dx2 = −Fcr y / (E1). (5,54) Ввод обозначений k2 = Fcr / (EI) y (5,55) Выражение (5.54) выражается в формате y + k2y = 0. Это линейное дифференциальное уравнение второго порядка. y = Csmkx + Dcoskx. (5,56)

Чтобы определить константы интегрирования C и D, мы используем известные граничные условия, то есть условия монтажа на конце стержня: x = 0 и x = / нет прогиба, т.е. y = 0.
Людмила Фирмаль

Подставляя в уравнение (5.56) >> = 0 (при x = 0), мы видим, что D-0, а стержень изгибается вдоль синусоиды y = Сsinbс. Для второго граничного условия (y = 0, если x = 1), C sin kl = 0. Если C = Oli sin kl = 0, результирующая связь действительна. Это не согласуется с исходным предположением, потому что не все поперечные сечения по длине стержня х существуют. Выражение sin kl = 0 действительно, когда /: / = ll. Где n — любое целое число (n = 0, 1, 2, …). Подставляя значение k = kn / 1 в уравнение (5.55), оно становится следующим. Fcr = k2EI = n2n2 EI / l2. Чтобы сохранить изогнутую форму стержня, сила отлична от нуля, то есть pf0. С практической точки зрения минимальная критическая сила представляет собой минимум под действием кривизны оси стержня, потери устойчивости. Если n = 1, получите минимальную критическую силу.

Fcr = k2E I / l2. Используя функцию эластичной проволоки, полученное решение может быть распространено на другие случаи крепления стержня. Таким образом, если стержень на одном конце защемлен, а другой конец пуст (рис. 5.30, б), эластичная линия стержня просто вызывается зеркальным отображением уплотнения относительно эластичной линии шарика.

Неподвижный стержень Нирно (рис. 5.30, а). Очевидно, что критическая сила стержня с такой длиной фиксации l равна критической силе шарнирно закрепленного стержня длины 21. Общее представление о критической силе общего вида стержня сжатия принимает следующий вид с учетом его типа фиксации. Fcr = n1El / (vl) 2 (5,57) Здесь v — коэффициент уменьшения длины стержня (коэффициент Яшинского), то есть числовое значение, указывающее, сколько раз необходимо изменить длину стержня, повернутого с обоих концов (рис. 5.31, б).

Его критическая прочность равна критической прочности стержня при определенных фиксированных условиях. В большинстве случаев конец сжимаемого стержня фиксируется одним из четырех способов, показанных на рисунке. 5,31. Коэффициент уменьшения длины показан в фиксированной схеме. Застежка, показанная на рисунке 5.31, наиболее чувствительна к изгибу, а застежка, показанная на рисунке 5.31, наименее чувствительная. 5.31, д. Отметим, что использование уравнения (5.57) справедливо только в том случае, если деформация стержня сжатия в момент потери исходного равновесия является упругой. F F F V * 0,7 V * 2 против / 7P7ShTP г TP7GSh ////////// a tgsht Рисунок 5.31 б

Смотрите также:

Решение задач по прикладной механике

Если вам потребуется помощь по прикладной механике вы всегда можете написать мне в whatsapp.

Урок и презентация «Задача Эйлера»

Цель урока: Познакомить с математическим понятием граф.

Задачи урока:

Образовательные:

— ввести понятие нового термина «граф» ;

— научить строить графы;

Развивающие:

— развивать практические умения;

— развивать интеллектуальные и коммуникативные общеучебные умения;

— развивать память, внимание, математические исследовательские способности;

— развивать навыки рефлексии.

Воспитательные:

— воспитывать организованность, умение работать в группах;

— прививать интерес к предмету.

Тип урока: открытие нового знания

Методы обучения:

— словесные методы: объяснение, беседа, работа с карточками;

— наглядные методы: наблюдение;

— практические методы: поисковый, практическая работа индивидуальная и в группах.

Оборудование – мультимедиа проектор, экран, компьютер, индивидуальный раздаточный материал: карточки.

Ход урока:

Сегодня на уроке у нас две темы и первая из них «Порядок и хаос». С вашей точки зрения, что такое хаос? (нарушение порядка), а порядок? Хаос – это хорошо или плохо? (плохо) Хорошо запомним это и пойдём дальше. У нас урок математики. Как вы думаете математика это мир порядка или хаоса? (порядка) Почему?

Устный счёт (слайд 2)

На прошлом уроке вы познакомились с правилами раскрытия скобок. Продолжите запись. (слайд 3) Молодцы. Как вы думаете записанные правила это порядок или хаос? (порядок) А теперь нарушим этот порядок, поменяем местами части утверждений. И проверим сохранится ли истина утверждений? Да. Таким образом мы нарушили порядок и в результате опять получили порядок. Так может хаос всё таки не так и плохо?

У вас на столах лежат файлы, возьмите каждый свой. Выполним первое задание. У каждого из вас есть по одному примеру, его нужно выполнить и выбрать нужную букву. Теперь переверните листочки там номер места вашей буквы в слове. Составьте слова и назовите. (семь, мост, Эйлер).

Если слова семь и мост вам знакомы, то слово Эйлер нет.

Леонард Эйлер жил в 18 веке, (слайд 5) родился в Швейцарии, но большую часть своей жизни он прожил в России, в Санкт – Петербурге. Это один из немногих математиков, который при жизни был признан первым математиком мира. Именно Леонард Эйлер ввёл понятие скобки и впервые записал их.

Вернёмся к нашим словам. Так что же их объединяет? А объединяет их знаменитая задача Эйлера о семи мостах. Посмотрите на экран. (слайд 6)

Леонард Эйлер гулял в городе Кёнигсберг по берегам реки Прегель. Жители города задали ему вопрос: «Можно ли совершить прогулку по семи мостам, так чтобы не проходить по каждому мосту дважды?»

Что сделал Эйлер? Он изобразил острова в виде точек, мосты в виде линий и построил схему. (слайд 7). Впоследствии такие схемы он назовёт ГРАФ. Позже мы вернёмся к этой задаче и вы сами дадите мне ответ. А сейчас познакомимся понятием граф?(слайд 8)

Граф – это набор точек некоторые из которых соединены линиями. Точки называются вершинами, а соединяющие их линии – рёбрами. Обращаю ваше внимание, я не сказала отрезки это линии. Давайте посчитаем сколько в этом графе вершин, а сколько ребёр? (3 и 3) Ещё один граф (6 и 6)

(слайд 9) Число рёбер выходящих и любой вершины называется степень вершины. Если из из вершины нечётное число рёбер, то она называется нечётной. Если чётное число рёбер, то чётной. Назовите степень каждой вершины на слайде? ( А – 1, В – 3, С — 2, D – 2)

(слайд 10) Следующий граф (А – 1, В – 3, С – 1, D – 1, Е – 2, О — 4)

Ребята, скажите, как связаны количество ребёр и сумма степеней вершин? (рёбер в 2 раза меньше суммы степеней вершин) Молодцы. Итак, чтобы найти количество рёбер графа нужно суммировать степени вершин и поделить на 2.

Возьмите листы со 2 — м заданием, постройте граф который у вас слева. ( на листе даны все определения). Что определяем в первую очередь?

А – 2, В – 1, С – 3, D – 4, Е – 2

Граф справа А – 1, В – 3, С – 2. Опредяляем количество рёбер (2, 5). Можно ли его построить? (нет) Сделайте вывод. (Если сумма степеней вершин графа четная его можно построить, а если нечётная нельзя)

Теперь я попрошу вспомнить пытались ли вы когда – нибудь рисовать домик не отрывая карандаша от бумаги? (да). Вы строили уникурсальный граф. Построение графа не отрывая карандаша от бумаги.

Возьмите листы с заданием №3 и выясните, какую фигуру можно построить, а какую нет.

Ребята, как вы думаете , почему графы 1, 3, 5, 6 сразу получилось построить, а 2 и 4 нет? Не знаете? Давайте подсчитаем степени вершин.

Возвращаемся к нашей задаче. «Можно ли совершить прогулку по семи мостам, так чтобы не проходить по каждому мосту дважды?» Т. е. можно ли нарисовать граф не отрывая карандаша от бумаги?(НЕТ) все его вершины его нечётные.

Давайте вернёмся в начало урока. Вы сказали, что хаос – это плохо. Я внесла хаос в планирование вашего учителя. Это плохо, но вы узнали много нового и это по — моему хорошо. Ведь мы проводили урок математики в кабинете английского языка, а это не порядок, т. е. хаос.

В конце урока мне хотелось, чтобы вы ответили «Не говори чему учили, а скажи, что узнал»

Д/з

У вас остались листы с заданием №4 выполнив его вы узнаете номер домашнего задания.

Спасибо за урок!

О компании — Project Euler

О проекте Euler

Что такое проект Эйлер?

Project Euler — это серия сложных задач математического / компьютерного программирования, для решения которых потребуется нечто большее, чем просто математическое понимание. Хотя математика поможет вам найти элегантные и эффективные методы, для решения большинства задач потребуется использование компьютера и навыков программирования.

Мотивация к запуску проекта «Эйлер» и его продолжения состоит в том, чтобы предоставить пытливому уму платформу, чтобы вникнуть в незнакомые области и изучить новые концепции в развлекательном и развлекательном контексте.

На кого нацелены проблемы?

Целевая аудитория включает студентов, для которых базовая учебная программа не утоляет их жажду учиться, взрослых, чье образование не было в первую очередь математикой, но интересовалось математикой, и профессионалов, которые хотят, чтобы их решение задач и математика оставались на переднем крае.

В настоящее время у нас есть
1035776 зарегистрированных участников, которые решили хотя бы одну проблему, представляя 220 населенных пунктов по всему миру и совместно использующие 108 разных языков программирования для решения проблем.

Может кто решит проблемы?

Задачи различаются по сложности, и для многих это индуктивное цепное обучение. То есть, решив одну проблему, вы познакомитесь с новой концепцией, которая позволит вам взяться за ранее недоступную проблему. Таким образом, целеустремленный участник будет медленно, но верно решать каждую проблему.

Что дальше?

Чтобы отслеживать ваш прогресс, необходимо настроить учетную запись и включить файлы cookie.

Если у вас уже есть учетная запись, войдите в систему. В противном случае, пожалуйста, зарегистрируйтесь — это совершенно бесплатно!

Однако, поскольку проблемы являются сложными, вы можете просмотреть Проблемы перед регистрацией.

«Проект Эйлер существует для поощрения, развития и развития навыков и удовольствия всех, кто интересуется увлекательным миром математики».

Проект Эйлера: проблема 1 с Javascript | Джаред Натт

, кратное 3 и 5

Решение проекта Эйлера, умноженное на 3 и 5

Вот и мы, пытаемся решить проблемы программирования Dark Souls.Сегодня мы начнем с довольно простого: получить числа, кратные 3 и 5.

Если мы перечислим все натуральные числа меньше 10, которые кратны 3 или 5, мы получим 3, 5, 6 и 9. Сумма чисел это кратное 23.

Найдите сумму всех кратных 3 или 5 ниже заданного значения параметра число .

Если вам нравится смотреть, а не читать, посмотрите видео, которое сопровождает эту статью. Если нет, продолжайте читать!

На первый взгляд это кажется более сложным, чем есть на самом деле.В целях обучения я буду как можно более подробным, а потом проведу рефакторинг.

Важно разбить все элементы проблемы, чтобы мы полностью понимали, что пытаемся сделать.

положительные целые числа (целые числа) 1, 2, 3 и т. Д., А иногда и ноль.

Когда мы говорим,

«6 кратно 3?»

мы спрашиваем,

«это 6 число, которое можно вычислить, умножив 3 на число (в нашем случае целые числа)»

В этом случае да, 3 x 2 = 6 .

Теперь, когда мы понимаем нашу проблему, давайте сделаем несколько логических утверждений.

Если задано число, проверьте, кратно ли оно 3
Если это правда, добавьте его к общему числу
Если дано число, посмотрите, кратно ли оно 5
Если верно, добавьте его к общему числу номер

Разберем его в коде. Опять же, это очень многословно.

 function multiplesOf3and5 (number) {
 // установить глобальную сумму и установить начальное значение на 0 
 let total = 0 
 // перебрать все значения от 0 до заданного числа 
 for (let i = 0; i <= number ; i ++) {
 // Получить остаток от i и 3 
 let restderFor3 = i% 3; 
 // Получить остаток от i и 5 
 let stayderFor5 = i% 5; // проверяем, является ли остаток 3 или 5 
 if (elsederFor3 == 0 || остатокFor5 == 0) {
 // Если true, это означает, что i кратно 3 
 // прибавляем к итоговому результату 
 total = total + i 
} 
} 
 // вернуть наше общее число 
 вернуть общее 
}

Эта строка здесь делает кое-что интересное:

 i% 3

Оператор в середине называется модулем.Возвращает остаток от двух чисел. Мы можем использовать его, чтобы узнать, кратно ли одно число другому.

Мы можем значительно сократить код, не теряя контекста того, что мы пытаемся сделать. Вот мое окончательное решение.

 функция multiplesOf3and5 (число) {
 let total = 0; 
 for (let i = 0; i <= number; i ++) {
 if (i% 3 == 0 || i% 5 == 0) {
 total + = i; 
} 
} 
 итого возврата; 
}

Всегда есть возможности для улучшения, однако мне нравится, как это устроено.Это просто и не слишком абстрагируется от того, чего мы пытаемся достичь. Я уверен, что если я вернусь к этому через два года, я все равно буду знать, что происходит.

Если вы хотите увидеть код, посмотрите мое репозиторий Github с проблемами, которые я уже решил.

DarthOstrich / projectEuler

Ознакомьтесь с моим решением проблемы 2 здесь:

Знакомство с проблемой # ProjectEuler100: «Темные души» достижений кодирования

11. Метод Эйлера — численное решение дифференциальных уравнений

Почему численные решения?

Для многих дифференциальных уравнений, которые нам нужно решить в реальном мире, не существует «хороших» алгебраических решений.То есть мы не можем решить эту проблему, используя методы, с которыми мы познакомились в этой главе (разделение переменных, интегрируемые комбинации или использование интегрирующего фактора), или другие подобные средства.

В результате приходится прибегать к численным методам решения таких ДУ. Эта концепция аналогична численным подходам, которые мы видели в предыдущей главе об интегрировании (правило трапеции, правило Симпсона и суммы Римана).

Даже если мы сможем решить некоторые дифференциальные уравнения алгебраически, решения могут быть довольно сложными и поэтому не очень полезными.В таких случаях численный подход дает нам хорошее приближенное решение.

Общая проблема начальной стоимости

Мы пытаемся решить проблемы, которые представлены следующим образом:

`dy / dx = f (x, y)`; а также
`y (a)` (начальное значение) известно,

где `f (x, y)` — некоторая функция переменных `x` и` y`, которые участвуют в задаче. 2-10y) / 3`

`y (0) = 0`

Обратите внимание, что правая часть является функцией «x» и «y» в каждом случае.(«iv») (x)) / (4!) `+ …`

Это дает нам достаточно хорошее приближение, если мы возьмем много членов и если значение `h` будет достаточно маленьким.

Для метода Эйлера мы берем только первые 2 члена.

`y (x + h)` ~~ y (x) + h y ‘(x) `

Последний член просто равен h, умноженному на наше выражение dy / dx, поэтому мы можем записать метод Эйлера следующим образом:

`y (x + h)` ~~ y (x) + h f (x, y) `

Как мы используем эту формулу?

Мы начинаем с некоторого известного значения для `y`, которое мы могли бы назвать` y_0`.Он имеет это значение, когда `x = x_0`. (Мы используем начальное значение `(x_0, y_0)`.)

Результатом использования этой формулы является значение для `y`, на один шаг` h` вправо от текущего значения. Назовем его `y_1`. Итак, имеем:

`y_1« ~~ y_0 + h f (x_0, y_0) `

где

`y_1` — следующее оценочное значение решения;
y_0 — текущее значение;
h — интервал между шагами; и
`f (x_0, y_0)` — значение производной в начальной точке, `(x_0, y_0)`.

Следующее значение: Чтобы получить следующее значение y_2, мы должны использовать значение, которое мы только что нашли для y_1, следующим образом:

`y_2« ~~ y_1 + h f (x_1, y_1) `

где

`y_2` — следующее оценочное значение решения;
`y_1` — текущее значение;
h — интервал между шагами;
`x_1 = x_0 + h`; и
`f (x_1, y_1)` — значение производной в текущей точке `(x_1, y_1)`.

Продолжаем этот процесс столько шагов, сколько потребуется.

Что происходит?

Правая часть приведенной выше формулы означает: «начните с известного значения« y », затем переместите на один шаг« h »вправо в направлении наклона в этой точке,
что есть `dy / dx = f (x, y)`. Мы достигнем хорошего приближения к значению кривой y в этой новой точке ».

Мы сделаем это для каждой из подпунктов, кроме `h`, от некоторого начального значения` x = a` до некоторого конечного значения `x = b`, как показано на графике ниже.

Посмотрим, как это работает на примере.

Пример: метод Эйлера

Решим пример (б) сверху. У нас была проблема с начальным значением:

`dy / dx = (y ln y) / x`
`y (2) = e`

Шаг 1

Мы начнем с точки `(x_0, y_0) = (2, e)` и используем размер шага `h = 0,1` и проделаем 10 шагов. То есть мы аппроксимируем решение от «t = 2» до «t = 3» для нашего дифференциального уравнения. Мы закончим с набором точек, которые представляют решение в числовом виде.

Мы уже знаем первое значение, когда `x_0 = 2`, то есть` y_0 = e` (начальное значение).

Теперь мы вычисляем значение производной в этой начальной точке. (Это говорит нам направление движения.)

`dy / dx = f (2, e)` `= (e ln e) / 2« = e / 2 ~~ 1.35
`

Это означает, что наклон линии от «t = 2» до «t = 2,1» приблизительно равен «1,35

».

Шаг 2

Теперь для второго шага (поскольку `h = 0.1`, следующая точка будет` x + h = 2 + 0.1 = 2,1`), подставляем то, что знаем, в формулу метода Эйлера, и получаем:

`y (x + h)` ~~ y (x) + h f (x, y) `
`y_1 = y (2.1)` ~~ e + 0.1 (e / 2) `= 2.8541959`

Это означает, что приблизительное значение решения при x = 2,1 равно 2,8540959.

Посмотрим, что мы сделали на графике.

На этом этапе нам понадобится новый склон, так что мы будем знать, куда двигаться дальше.

`dy / dx = f (2.1,2.8541959)` = (2.8541959 дюйм 2,8541959) / 2,1 «= 1,4254536`

Это означает, что наклон линии аппроксимации от «x = 2,1» до «x = 2,2» равен «1,4254536». Так что он немного круче, чем первый найденный нами склон.

Шаг 3

Теперь мы пытаемся найти значение решения, когда x = 2.2. Подставляем наши известные значения:

`y (x + h)` ~~ y (x) + h f (x, y) `
` y (2,2) ~~ `2,8540959 + 0,1 (1,4254536)` = 2,99664126`

С этим новым значением наш график теперь:

На этом этапе нам понадобится новый склон, так что мы будем знать, куда двигаться дальше.

`f (2.2,2.99664126)` = (2.99664126 ln 2.99664126) / 2.2` = 1.494
`

Это означает, что наклон линии аппроксимации от «x = 2,2» до «x = 2,3» равен «1,494

». Так что он немного круче, чем первые 2 найденных нами склона.

Шаг 4

Теперь мы пытаемся найти значение решения, когда x = 2.3. Подставляем наши известные значения:

`y (x + h)` ~~ y (x) + h f (x, y) `
у (2.3) ~~ `2.99664126 + 0.1 (1.494
) ‘= 3.1461317`

С этим новым значением наш график теперь:

Последующие шаги

Мы представляем все значения до «x = 3» в следующей таблице.

Конечно, большую часть времени мы будем использовать компьютеры, чтобы найти эти приближения. Я использовал электронную таблицу, чтобы получить следующие значения. Не используйте калькулятор для решения этих задач — это очень утомительно и подвержено ошибкам. Вы можете использовать онлайн-калькулятор или поиск в Google.

`x`	`г`	`dy / dx`
2.0	e = 2,7182818285	( e ln e ) / 2 = 1,35 142
2,1	e +0,1 ( e /2) = 2,8541959199	(2.8541959199 дюйм 2.8541959199) / 2 = 1.4254536226
2,2	2.9967412821	1.4949999323
2,3	3,1462412754	1,5679341197
2.4	3,3030346873	1.6444180873
2,5	3,4674764961	1,7246216904
2,6	3.6399386651	1,8087230858
2,7	3.8208109737	1,896
2,8	4,0 105018841	1.9893756448
2.9	4.2094394486	2,08632809
3,0	4,4180722576

(Нет окончательного значения dy / dx, потому что оно нам не нужно. Мы нашли все требуемые значения y.)

Вот график наших расчетных значений решения от «x = 2» до «x = 3».

Насколько это хорошо?

Этот конкретный вопрос на самом деле легко решить алгебраически, и мы сделали это еще в разделе «Разделение переменных».(x «/» 2) `пурпурного (розоватого) цвета. Мы видим, что они очень близки.

В этом случае график решения лишь слегка изогнут, поэтому для метода Эйлера «легко» получить довольно близкий результат.

Фактически, при `x = 3` фактическое решение -` y = 4.48168

`, и мы получили приближение `y = 4.4180722576`, поэтому ошибка составляет всего:

‘(4,48168
— 4,4180722576) / 4,48168
‘ ‘= 1,42%’.

Упражнение

Следующий вопрос не может быть решен с помощью алгебраических методов, которые мы изучили ранее в этой главе, поэтому единственный способ решить его — численно.0,1`

`= -1.8103864498`

Еще раз, мы заменяем нашу текущую точку и производную, которую мы только что нашли, чтобы получить следующую точку.

`y (x + h) ~~ y (x) + hf (x, y)`

` y (0,2) ~~ 3,82431975047 + `0,1 (-1,8103864498)`

`~~ 3.64328110549`

Проделываем необходимое количество шагов и получаем такие значения:

`x`	`г`	`dy / dx`
0	4	-1.7568024953
0,1	3.8243197505	-1,8103864498
0,2	3.6432811055	-1,866	57
0,3	3,4565 9	-1,926815173
0,4	3,263
-1,92334
0.5	3,0648371723	-2,0594421065
0,6	2,8588929616	-2,1341215746
0,7	2,6454808042	-2,2162311734
0,8	2,4238576868	-2,3077132045
0,9	2,1930863664	-2.4111158431
1	1.9519747821

Вот график этого решения.

В следующем разделе мы увидим более сложный метод численного решения дифференциальных уравнений, называемый методом Рунге-Кутта .

Решение Леонарда Эйлера проблемы Кенигсбергского моста — проблема Эйлера и моста

Проблема Эйлера и моста

Зачем Эйлеру заниматься проблемой, не имеющей отношения к области математики? Зачем такому великому математику тратить много времени на такую тривиальную задачу, как проблема Кенигсбергского моста? Эйлер, очевидно, был занятым человеком, опубликовав за свою жизнь более 500 книг и статей.Только в 1775 году он писал в среднем одну математическую работу в неделю, и в течение своей жизни он писал на множество тем, помимо математики, включая механику, оптику, астрономию, навигацию и гидродинамику. Неудивительно, что Эйлер счел эту проблему тривиальной, заявив в письме 1736 года Карлу Леонхарду Готтлибу Элеру, мэру Данцига, который просил его решить проблему [цитата из Hopkins, 2]:

. . . Таким образом, вы видите, благороднейший сэр, как этот тип решения имеет мало отношения к математике, и я не понимаю, почему вы ожидаете, что математик произведет его, а не кто-либо другой, поскольку решение основано только на разуме, а его открытие не зависит от какого-либо математического принципа.Из-за этого я не знаю, почему даже вопросы, которые так мало связаны с математикой, математики решают быстрее, чем другие.

Хотя Эйлер счел задачу тривиальной, она все равно заинтриговала его. В письме, написанном в том же году итальянскому математику и инженеру Джованни Маринони, Эйлер сказал: «Этот вопрос настолько банален, но мне показался достойным внимания в этой [ни] геометрии, ни в алгебре, ни даже в искусстве счета. было достаточно, чтобы решить эту проблему.»[цитируется у Хопкинса, 2] Эйлер считал, что эта проблема связана с темой, которую Готфрид Вильгельм Лейбниц когда-то обсуждал и с которой хотел работать, что Лейбниц называл geometria situs , или геометрией положения. Это так называемая геометрия позиции — это то, что сейчас называется теорией графов, которую Эйлер вводит и использует при решении этой знаменитой проблемы.
Решение Эйлера

Базельской проблемы | MathAdam

Все четные коэффициенты равны 0.Коэффициенты с нечетными номерами меняют знаки. А коэффициент принимает форму, обратную факториалу порядкового номера коэффициента.

Резюме:

Ур. 6

Для решения Базельской задачи нам нужен только коэффициент x ³:

Ур. 7

Факторизация Weirstrass

Следующим инструментом в арсенале Эйлера была факторизация Weirstrass. Этот метод еще не получил строгой проверки. Однако, когда Эйлер применил его к проблеме Базеля, он получил захватывающие результаты.

Мы можем определить полиномиальную функцию в терминах ее нулей (корней) и коэффициента масштабирования. Например, любую квадратичную можно записать так:

Eq. 8

Здесь R₁ и R₂ — корни. Если значения и положительны, парабола откроется вверх; если отрицательный, то вниз. Расположение вершины однозначно определяется номерами и .

Проделаем то же самое с функцией sin x . Все его нули имеют одинаковую форму:

Eq. 9

Таким образом:

Ур.10.

Как умножить бесконечное произведение?

Очень осторожно.

Но сначала нам нужно определить константу a .

Ур. 11

Теперь мы воспользуемся следующим пределом:

Ур. 12

Затем мы вычисляем вторую часть выражения как x = 0 .

Ур. 13

Еще один бесконечный продукт? Без проблем! Мы делим каждый из множителей и на множители sin x :

Ур. 14

Мы будем расширять это, добавляя по одному множителю за раз.Это даст многочлен только с нечетными показателями. Мы хотим знать коэффициент при члене x³.

Ур. 15

Подбросьте в 4-м множителе. Тщательно перемешайте:

экв. 16

Утомительная работа. Но мы почти закончили. Смесь фактора №5.

Ур. 17

Подождите!

Прежде чем мы утонем в терминах, помните: мы ищем только коэффициент x ³. При каждом умножении мы добавляем один член. Вы видите, что будет дальше?

Вот наш коэффициент x ³:

Ур.18

Коэффициент x³ из разложения Маклаурина равен 6. Приравняем их друг к другу и немного перемешаем:

Eq. 19

И… готово.

Но Эйлер на этом не остановился. Он разработал общее решение для всех равнодействующих.

Вы можете следовать описанной здесь процедуре, чтобы найти сумму обратных четвертых степеней. Вам нужно выделить коэффициент x ⁵.

Что касается нечетных обратных величин — это пока загадка. Помимо серии Harmonic, мы все еще ждем, чтобы кто-нибудь расколол этот орешек.

Может быть, вы, будете тем кем.

Метод Эйлера А.С.

Подраздел 7.3.1 Метод Эйлера

Предварительный просмотр Задание 7.3.1 демонстрирует алгоритм, известный как метод Эйлера ¹, который генерирует численное приближение к решению задачи начального значения. В этом алгоритме мы аппроксимируем решение, выполняя горизонтальные шаги фиксированного размера, которые мы обозначим как \ (\ Delta t \ text {.} \)

«Эйлер» произносится как «Ой-лер.Среди прочего, Эйлер — математик, которому приписывают знаменитое число \ (e \ text {;} \), если вы неправильно произнесете его имя «Ю-лер», вы не сможете оценить его гений и наследие.

Прежде чем подробно объяснять алгоритм, давайте вспомним, как мы вычисляем наклон линии: наклон — это отношение вертикального изменения к горизонтальному изменению, как показано на рисунке 7.3.2.

Другими словами, \ (m = \ frac {\ Delta y} {\ Delta t} \ text {.} \) Решая для \ (\ Delta y \ text {,} \), мы видим, что вертикальное изменение произведение наклона и горизонтального изменения, или

\ begin {уравнение *}
\ Delta y = m \ Delta t \ text {.{-t} \ text {.} \) Но вместо этого мы заинтересованы в генерации приближенного решения путем создания последовательности точек \ ((t_i, y_i) \ text {,} \), где \ (y_i \ приблизительно y (t_i ) \ text {.} \) В этом первом примере мы выбираем \ (\ Delta t = 0.2 \ text {.} \)

Поскольку мы знаем, что \ (y (0) = 1 \ text {,} \), мы возьмем начальную точку как \ ((t_0, y_0) = (0,1) \) и переместим горизонтально на \ (\ Дельта t = 0,2 \) до точки \ ((t_1, y_1) \ text {.} \) Таким образом, \ (t_1 = t_0 + \ Delta t = 0,2 \ text {.} \) Теперь дифференциальное уравнение говорит нам, что наклон касательной в этой точке

\ begin {уравнение *}
m = \ frac {dy} {dt} \ bigg \ vert _ {(0,1)} = 0-1 = -1 \ text {,}
\ end {уравнение *}

, чтобы переместиться по касательной, сделав шаг по горизонтали размером \ (\ Delta t = 0.2 \ text {,} \) мы также должны двигаться по вертикали на

\ begin {уравнение *}
\ Delta y = m \ Delta t = -1 \ cdot 0,2 = -0,2 \ text {.}
\ end {уравнение *}

Затем у нас есть приближение \ (y (0,2) \ приблизительно y_1 = y_0 + \ Delta y = 1 — 0,2 = 0,8 \ text {.} \) На этом этапе мы выполнили один шаг метода Эйлера, как показано графически. на рисунке 7.3.3.

Рисунок 7.3.3. Один шаг метода Эйлера.

Теперь мы повторяем этот процесс: при \ ((t_1, y_1) = (0.2,0.8) \ text {,} \) дифференциальное уравнение сообщает нам, что наклон равен

\ begin {уравнение *}
m = \ frac {dy} {dt} \ bigg \ vert _ {(0.2,0,8)} = 0,2-0,8 = -0,6 \ текст {.}
\ end {уравнение *}

Если мы переместимся вперед по горизонтали на \ (\ Delta t \) к \ (t_2 = t_1 + \ Delta = 0.4 \ text {,} \), мы должны переместиться по вертикали на

\ begin {уравнение *}
\ Delta y = -0.6 \ cdot0.2 = -0.12 \ text {.}
\ end {уравнение *}

Следовательно, мы приходим к \ (y_2 = y_1 + \ Delta y = 0,8-0,12 = 0,68 \ text {,} \), что дает \ (y (0,2) \ приблизительно 0,68 \ text {.} \). Теперь мы завершили вторую шаг метода Эйлера, как показано на рисунке 7.3.4.

Рисунок 7.3.4.Два шага метода Эйлера.

Если мы продолжим таким образом, мы можем сгенерировать точки \ ((t_i, y_i) \), показанные на рисунке 7.3.5. Поскольку мы можем найти формулу для фактического решения \ (y (t) \) этого дифференциального уравнения, мы можем построить график \ (y (t) \) и сравнить его с точками, полученными методом Эйлера, как показано на рисунке 7.3. .6.

Рисунок 7.3.5. Точки и кусочно-линейное приближенное решение, порожденное методом Эйлера.
Рисунок 7.3.6. Приблизительное решение по сравнению с точным решением (показано синим цветом).

Поскольку нам нужно сгенерировать большое количество точек \ ((t_i, y_i) \ text {,} \), удобно организовать реализацию метода Эйлера в таблице, как показано. Начнем с приведенных исходных данных.

\ (т_и \)	\ (y_i \)	\ (dy / dt \)	\ (\ Дельта у \)
\ (0,0000 \)	\ (1.0000 \)

Отсюда мы вычисляем наклон касательной \ (m = dy / dt \), используя формулу для \ (dy / dt \) из дифференциального уравнения, а затем находим \ (\ Delta y \ text {, } \) изменение \ (y \ text {,} \) с использованием правила \ (\ Delta y = m \ Delta t \ text {.} \)

\ (т_и \)	\ (y_i \)	\ (dy / dt \)	\ (\ Дельта у \)
\ (0,0000 \)	\ (1.0000 \)	\ (- 1.0000 \)	\ (- 0,2000 \)

Затем мы увеличиваем \ (t_i \) на \ (\ Delta t \) и \ (y_i \) на \ (\ Delta y \), чтобы получить

\ (т_и \)	\ (y_i \)	\ (dy / dt \)	\ (\ Дельта у \)
\ (0,0000 \)	\ (1.0000 \)	\ (- 1.0000 \)	\ (- 0,2000 \)
\ (0,2000 \)	\ (0,8000 \)

Мы продолжаем процесс, сколько бы этапов ни выбрали, в конечном итоге создавая таблицу, подобную Таблице 7.3.7.

Таблица 7.3.7. Метод Эйлера для 6 шагов с \ (\ Delta t = 0.2 \ text {.} \)

\ (t_i \)	\ (y_i \)	\ (dy / dt \)	\ (\ Дельта у \)
\ (0,0000 \)	\ (1.0000 \)	\ (- 1.0000 \)	\ (- 0,2000 \)
\ (0,2000 \)	\ (0,8000 \)	\ (- 0,6000 \)	\ (- 0,1200 \)
\ (0,4000 \)	\ (0,6800 \)	\ (- 0,2800 \)	\ (- 0,0560 \)
\ (0,6000 \)	\ (0,6240 \)	\ (- 0,0240 \)	\ (- 0,0048 \)
\ (0,8000 \)	\ (0,6192 \)	\ (0,1808 \)	\ (0.0362 \)
\ (1.0000 \)	\ (0,6554 \)	\ (0,3446 \)	\ (0,0689 \)
\ (1.2000 \)	\ (0,7243 \)	\ (0,4757 \)	\ (0,0951 \)

Мероприятие 7.3.2.

Рассмотрим задачу начального значения

\ begin {уравнение *}
\ frac {dy} {dt} = 2t-1, \ y (0) = 0
\ end {уравнение *}

Используйте метод Эйлера с \ (\ Delta t = 0,2 \), чтобы аппроксимировать решение при \ (t_i = 0.2, 0.4, 0.6, 0.8 \ text {,} \) и \ (1.0 \ text {.} \) Запишите свою работу в следующую таблицу и нарисуйте точки \ ((t_i, y_i) \) на предоставленных осях. .
Таблица 7.3.8. Таблица для записи результатов метода Эйлера.
\ (т_и \) \ (y_i \) \ (dy / dt \) \ (\ Дельта у \)
\ (0,0000 \) \ (0,0000 \)
\ (0,2000 \)
\ (0,4000 \)
\ (0.6000 \)
\ (0,8000 \)
\ (1.0000 \)
Рисунок 7.3.9. Сетка для построения точек, построенных методом Эйлера.

Найдите точное решение исходной проблемы с начальным значением и используйте эту функцию, чтобы найти ошибку в вашем приближении в каждой из точек \ (t_i \ text {. 1 (2t-1) ~ dt \ text {.2 \ text {.} \)

Изобразите поле уклона для этого дифференциального уравнения по осям, представленным на рисунке 7.3.10.
Рисунок 7.3.10. Сетка для построения поля наклонов данного дифференциального уравнения.
Определите любые равновесные решения и определите, являются ли они стабильными или нестабильными.
Каково долгосрочное поведение решения, которое удовлетворяет начальному значению \ (y (0) = 1 \ text {?} \)
Используя начальное значение \ (y (0) = 1 \ text {,} \), используйте метод Эйлера с \ (\ Delta t = 0.2 \) для аппроксимации решения в \ (t_i = 0.2, 0.4, 0.6, 0.8 \ text {,} \) и \ (1.0 \ text {.} \) Запишите свои результаты в Таблицу 7.3.11 и нарисуйте соответствующие точки. \ ((t_i, y_i) \) по осям, представленным на рисунке 7.3.12. Обратите внимание на различный горизонтальный масштаб по осям на рисунке 7.3.12 по сравнению с рисунком 7.3.10.
Таблица 7.3.11. Таблица для записи результатов метода Эйлера с \ (\ Delta t = 0.2 \ text {.} \)
\ (t_i \) \ (y_i \) \ (dy / dt \) \ (\ Дельта у \)
\ (0.0 \) \ (1.0000 \)
\ (0,2 \)
\ (0,4 \)
\ (0,6 \)
\ (0,8 \)
\ (1.0 \)
Рисунок 7.3.12. Оси для построения результатов метода Эйлера.
Что произойдет, если мы применим метод Эйлера для аппроксимации решения с помощью \ (y (0) = 6 \ text {?} \)

Подраздел 7.3.2 Ошибка метода Эйлера

Поскольку мы аппроксимируем решения задачи начального значения с помощью касательных, следует ожидать, что ошибка аппроксимации будет меньше, когда размер шага меньше. t \ text {.} \) Теперь применим метод Эйлера для аппроксимации \ (y (1) = e \) с использованием нескольких значений \ (\ Delta t \ text {.} \). Эти приближения будут обозначаться \ (E _ {\ Delta t} \ text {,} \), и мы воспользуемся ими, чтобы увидеть, насколько точен метод Эйлера.

Для начала применим метод Эйлера с размером шага \ (\ Delta t =
0.2 \ text {.} \) В этом случае мы обнаруживаем, что \ (y (1) \ приблизительно E_ {0.2} = 2.4883 \ text {.} \) Следовательно, ошибка составляет

\ begin {уравнение *}
y (1) — E_ {0,2} = e — 2,4883 \ приблизительно 0,2300 \ text {.}
\ end {уравнение *}

Многократное уменьшение вдвое \ (\ Delta t \) дает следующие результаты, выраженные как в табличной, так и в графической форме.

Таблица 7.3.13. Ошибки, соответствующие разным значениям \ (\ Delta t \).

\ (\ Delta t \)	\ (E _ {\ Delta t} \)	Ошибка
\ (0.200 \)	\ (2.4883 \)	\ (0,2300 \)
\ (0,100 \)	\ (2,5937 \)	\ (0,1245 \)
\ (0,050 \)	\ (2.6533 \)	\ (0,0650 \)
\ (0,025 \)	\ (2.6851 \)	\ (0.0332 \)

Рисунок 7.3.14. График ошибки как функции \ (\ Delta t \ text {.} \)

Обратите внимание, как численно, так и графически, что ошибка уменьшается примерно вдвое, когда \ (\ Delta t \) уменьшается вдвое. Этот пример иллюстрирует следующий общий принцип.

Если метод Эйлера используется для аппроксимации решения задачи начального значения в точке \ (\ overline {t} \ text {,} \), то ошибка пропорциональна \ (\ Delta t \ text {.} \) То есть

\ begin {уравнение *}
y (\ overline {t}) — E _ {\ Delta t} \ приблизительно K \ Delta t
\ end {уравнение *}

для некоторой константы пропорциональности \ (K \ text {.} \)

Упражнения 7.3.4 Упражнения

1. Несколько шагов метода Эйлера.

2. Использование метода Эйлера для решения задачи \ (y ‘= 4y \).

3. Использование метода Эйлера с разными временными шагами.

4.

Закон охлаждения Ньютона гласит, что скорость, с которой объект, например чашка кофе, охлаждается, пропорциональна разнице между температурой объекта и комнатной температурой. Если \ (T (t) \) — температура объекта, а \ (T_r \) — комнатная температура, этот закон выражается как

\ begin {уравнение *}
\ frac {dT} {dt} = -k (T-T_r) \ text {,}
\ end {уравнение *}

где \ (k \) — постоянная пропорциональности.\ circ \ text {.} \) Дифференциальное уравнение для Алисы имеет константу пропорциональности \ (k = 0,5 \ text {,} \), в то время как константа пропорциональности для Боба равна \ (k = 0,1 \ text {.} \ ) Какова начальная скорость изменения кофе Алисы? Какова начальная скорость изменения кофе Боба?

Какая особенность чашек кофе Алисы и Боба может объяснить эту разницу?
По мере включения и выключения отопительного агрегата в помещении температура в помещении
\ begin {уравнение *}
Т_р = 70 + 10 \ грех т \ текст {.}
\ end {уравнение *}
Реализуйте метод Эйлера с размером шага \ (\ Delta t = 0,1 \), чтобы приблизительно определить температуру кофе Алисы за временной интервал \ (0 \ leq t \ leq
50 \ text {.} \) Проще всего это сделать с помощью электронной таблицы, такой как Excel . Постройте график температуры ее кофе и комнатной температуры за этот интервал.
Таким же образом реализуйте метод Эйлера, чтобы приблизительно определить температуру кофе Боба за тот же интервал времени.Постройте график температуры его кофе и комнатной температуры за интервал.
Объясните сходства и различия, которые вы видите в поведении чашек кофе Алисы и Боба.

5.

Мы видели, что ошибка аппроксимации решения задачи с начальным значением пропорциональна \ (\ Delta t \ text {.} \), То есть если \ (E _ {\ Delta t} \) является приближением метода Эйлера. к решению задачи начального значения в \ (\ overline {t} \ text {,} \), затем

\ begin {уравнение *}
y (\ overline {t}) — E _ {\ Delta t} \ приблизительно K \ Delta t
\ end {уравнение *}

для некоторой константы пропорциональности \ (K \ text {.} \)

В этой задаче мы увидим, как использовать этот факт для улучшения наших оценок, используя идею под названием ускоренная сходимость .

Мы создадим новое приближение, предполагая, что ошибка точно пропорциональна \ (\ Delta t \ text {,} \) в соответствии с формулой
.
\ begin {уравнение *}
y (\ overline {t}) — E _ {\ Delta t} = K \ Delta t \ text {.}
\ end {уравнение *}
Используя наши более ранние результаты из задачи начального значения \ (dy / dt = y \) и \ (y (0) = 1 \) с \ (\ Delta t = 0.2 \) и \ (\ Delta t = 0.1 \ text {,} \) имеем
\ begin {align *}
у (1) — 2.4883 = \ mathstrut \ amp 0.2K \\
y (1) — 2.5937 = \ mathstrut \ amp 0.1K \ text {.}
\ end {выровнять *}
Это система двух линейных уравнений относительно неизвестных \ (y (1) \) и \ (K \ text {.} \). Решите эту систему, чтобы найти новое приближение для \ (y (1) \ text {. } \) (Вы можете помнить, что точное значение \ (y (1) = e =
2.71828 \ ldots \ text {.} \))
Используйте другие данные, \ (E_ {0,05} = 2,6533 \) и \ (E_ {0,025} = 2.6851 \), чтобы проделать ту же работу, что и в (а), чтобы получить другое приближение. Что дает лучшее приближение? Как вы думаете, почему это так?
Давайте теперь изучим проблему начального значения
\ begin {уравнение *}
\ frac {dy} {dt} = t-y, \ y (0) = 0 \ text {.}
\ end {уравнение *}
Приближаем \ (y (0.3) \), применяя метод Эйлера для нахождения приближений \ (E_ {0.1} \) и \ (E_ {0.05} \ text {.} \). Теперь используйте идею ускоренной сходимости, чтобы получить лучшую приближение. (Для сравнения вы хотите отметить, что фактическое значение равно \ (y (0.3) =
0,0408 \ text {.} \))

6.

В этой задаче мы модифицируем метод Эйлера, чтобы получить лучшие приближения к решениям задач с начальным значением. Этот метод называется улучшенным методом Эйлера .

В методе Эйлера мы проходим интервал шириной \ (\ Delta t \), используя наклон, полученный из дифференциального уравнения в левой конечной точке интервала. Конечно, наклон решения, скорее всего, изменится в течение этого интервала.Мы можем улучшить наше приближение, пытаясь учесть изменение наклона за интервал.

Давайте снова рассмотрим задачу начального значения \ (dy / dt = y \) и \ (y (0) = 1 \ text {,} \), которую мы аппроксимируем, используя шаги ширины \ (\ Delta t = 0.2 \ text {.} \) Таким образом, наш первый интервал равен \ (0 \ leq t \ leq 0.2 \ text {.} \) При \ (t = 0 \ text {,} \) дифференциальное уравнение сообщает нам, что наклон равен 1, и приближение, которое мы получаем из метода Эйлера, таково, что \ (y (0.2) \ приблизительно y_1 = 1+ 1 (0.2) = 1.2 \ text {.} \)

Это дает нам некоторое представление о том, как наклон изменился за интервал \ (0 \ leq t \ leq 0.2 \ text {.} \). Мы знаем, что наклон в \ (t = 0 \) равен 1, а наклон в \ (t = 0,2 \) равно 1,2, если полагаться на приближение метода Эйлера. Поэтому мы уточним нашу оценку начального наклона до среднего значения этих двух наклонов; то есть, мы оценим наклон как \ ((1 + 1.2) / 2 = 1.1 \ text {.} \) Это дает новое приближение \ (y (1) = y_1 = 1 + 1.1 (0.2) = 1.22 \ text {.} \)

Первые несколько шагов выглядят так, как показано в таблице 7.3.15.

Таблица 7.3.15. Первые несколько шагов улучшенного метода Эйлера

\ (t_i \)	\ (y_i \)	Наклон в точке \ ((t_ {i + 1}, y_ {i + 1}) \)	Средний уклон
\ (0,0 \)	\ (1.0000 \)	\ (1,2000 \)	\ (1.1000 \)
\ (0,2 \)	\ (1,2200 \)	\ (1.4640 \)	\ (1,3420 \)
\ (0,4 \)	\ (1.4884 \)	\ (1.7861 \)	\ (1,6372 \)
\ (\ vdots \)	\ (\ vdots \)	\ (\ vdots \)	\ (\ vdots \)

Продолжайте использовать этот метод, чтобы получить приближение для \ (y (1) = e \ text {.} \)
Повторите этот метод с \ (\ Delta t = 0.1 \), чтобы получить лучшее приближение для \ (y (1) \ text {.} \)
Мы видели, что ошибка в методе Эйлера пропорциональна \ (\ Delta t \ text {.} \). Используя ваши результаты из частей (a) и (b), какая степень \ (\ Delta t \) кажется быть пропорциональным ошибке в улучшенном методе Эйлера?

«Темные души» достижений в кодировании

Меня часто спрашивают: «Как мне попасть в соревновательное программирование?»

Мой ответ всегда был прост: отработайте как можно больше проблем с алгоритмами и структурами данных.

Но сегодня у меня для вас есть кое-что более конкретное. Задача, которая расширит ваши знания в области информатики и математики — и при этом даст вам массу практических навыков программирования.

Он называется # ProjectEuler100. И многие люди уже публично приняли вызов.

Задача названа в честь Леонарда Эйлера, одного из самых плодовитых математиков в истории.

Леонард Эйлер — швейцарский математик XVI века, в честь которого назван этот вызов.

Представляет обучение в сложном режиме.Выполнение этой задачи потребует творчества и навыков решения проблем, о которых вы даже не подозревали. Это превратит вас в невероятно находчивого разработчика. Это придаст вам уверенности в выполнении самых амбициозных проектов.

Короче говоря, задача # ProjectEuler100 станет тиглем, в котором выковывается ваше супер-сайянское «я», готовое раскрыть свой скрытый инженерный гений в мире.

Гоку становится супер сайян.

Что такое проект Эйлер?

Project Euler — это веб-сайт, созданный еще в 2001 году.В нем собрано около 600 различных задач алгоритмов, которые становятся все сложнее, вплоть до того, что даже люди с докторской степенью математики все еще борются с ними.

При этом первые 100 проблем полностью решаются новым разработчиком. Тысячи людей выполнили первые 100 задач Project Euler за эти годы.

Это просто ужасно сложно. Вроде … Dark Souls тяжело.

Dark Souls — видеоигра, известная своей невероятной сложностью. Но с последовательной практикой это становится намного проще — точно так же, как эти проблемы алгоритмов.

Мне нравятся задачи Project Euler. Я активно использовал их, когда только учился программировать. Мне это так нравится, что мы добавили эти задачи Project Euler в раздел «Подготовка к собеседованию» freeCodeCamp.

Это действительно потрясет ваш мозг. Но они будут вознаграждены. Они тяжелые, но справедливые. И если вы готовы проглотить свою гордость и пройти несколько кроличьих нор в Википедии, вы тоже можете решить их.

Так что ты думаешь. Готовы ли вы решить первые 100 проблем Project Euler? Вот правила.

Правила конкурса # ProjectEuler100

Я свел все к этим 6 простым правилам, которым должны следовать все участники.

Разместите в Твиттере фотографию, на которой вы показываете большой палец вверх и объявляете, что принимаете участие в испытании # ProjectEuler100.
Создайте репозиторий GitHub.
Каждый раз, когда вы выполняете задачу, добавляйте свое решение в репозиторий GitHub и публикуйте ссылку на него в Твиттере с хэштегом # ProjectEuler100.
Затем прокрутите хэштег # ProjectEuler100 и дайте положительный отзыв как минимум на 2 твита от других разработчиков.
Переходите к следующему испытанию Project Euler. Вы не можете пропустить вперед. Вы должны выполнить все 100 задач по порядку. Но вы можете использовать любой язык программирования для решения этих проблем.
После того, как вы закончите все 100 из них, разместите в Твиттере праздничное фото себя с ноутбуком, открытым в репозитории GitHub.

Где мне писать код?

Вы можете использовать сам веб-сайт Project Euler, которому уже 20 лет.

Или вы можете использовать версию freeCodeCamp.org, которая позволяет писать код прямо в браузере и имеет встроенные тесты.

Или, если вы чувствуете себя пикантно, вы можете создать свой собственный веб-сайт для решения этих задач. (Все проблемы Project Euler лицензированы Creative Commons и бесплатны для некоммерческого использования.)

Почему мне нужно размещать свои решения на GitHub?

Размещение ваших решений в GitHub (или GitLab, или BitBucket) позволяет добиться нескольких целей:

Это дает вам хороший публичный отчет о вашем прогрессе, которым вы можете поделиться с другими людьми.
Это сделает ваш профиль GitHub очень активным для любых работодателей / клиентов, которые хотят вас нанять.
Это дает вам то, что вы можете показать своим внукам.

Могу я посмотреть на решения других людей?

Вы можете посмотреть на решения других проблем, которые вы сами уже решили.

Каждую задачу можно решить разными способами, некоторые из которых более элегантны, чем другие. И вы можете похвалить других людей за их подходы.

Таким образом, наступил 2020 год. Реальность такова, что решения этих проблем уже найдены в Интернете.Вы можете случайно наткнуться на решение, если ищете подсказки.

Если вам предстоит решить задачу, которую вы еще не выполнили самостоятельно, вам ни в коем случае не следует использовать код, который вы там видите. Вам нужно самостоятельно придумывать кодовые решения для каждой из этих проблем.

Могу ли я транслировать свои попытки в прямом эфире?

Да. Во всех смыслах. Как я уже сказал, решения этих проблем уже есть во всем Интернете. И многие из людей, которые настроились бы на Twitch или YouTube, не будут выполнять эту задачу — они просто будут наслаждаться просмотром программных потоков в целом.

Так что не беспокойтесь о том, чтобы что-то «испортили» во время ваших прямых трансляций.

Мы будем транслировать # ProjectEuler100 в прямом эфире на YouTube-канале freeCodeCamp.

При этом, если вы создаете видео-руководства или статьи, которые люди будут использовать в качестве справочника по этим проблемам, я рекомендую вам включить предупреждения о спойлерах. Людям нужны подсказки, а не полные решения.

Как быстро мне нужно решить эти проблемы?

Процитирую великого человека:

«Неважно, как медленно вы идете, пока вы не останавливаетесь.»- Леонард Эйлер

(ОК, эту цитату обычно приписывают Конфуцию. Но все виды цитат ошибочно приписывают Конфуцию, поэтому я ошибочно приписываю эту цитату моему мальчику Эйлеру?)

Первые несколько проблем — это относительно легко. Но они быстро увеличиваются с трудом. К тому времени, когда вы дойдете до последних 20 или 30, вы, возможно, потратите дни на решение одной проблемы.

Так что не делайте ошибки, говоря «Я собираюсь закончить это за 100 дней »или что-то в этом роде.Просто продолжайте работать над этим понемногу каждый день. Вокруг вас целое сообщество, которое поможет вам преодолеть финишную черту.

Мы все вместе. Мы сгрудились вокруг хэштега # ProjectEuler100 в Твиттере. Это заложено прямо в правилах соревнований. («Правило № 4: пролистайте хэштег # ProjectEuler100 и дайте положительный отзыв по крайней мере о двух твитах от других разработчиков».)

Вы будете поддерживать других разработчиков, приступающих к решению этой задачи. И они будут рядом, чтобы поддержать вас.

Я также призываю вас присоединиться к нашей чат-комнате в Discord # ProjectEuler100, где вы можете поговорить о проблеме и получить помощь.

И вы можете подписаться на наш Twitter-бот # ProjectEuler100.

Итак, если вы готовы, сделайте первый шаг. Разместите в Твиттере фотографию, на которой вы поднимаете палец вверх и объявляете, что принимаете участие в испытании # ProjectEuler100.

Вот это у вас есть.

1	спаниели \| (терьеры & овчарки)
2	спаниели \| овчарки
3	спаниели \| терьеры \| овчарки
4	терьеры & овчарки

1	барокко \| классицизм \| ампир
2	барокко \| (классицизм & ампир)
3	классицизм & ампир
4	барокко \| классицизм

задачи, которые может решить только настоящий программист

Проект Эйлер

Всё начинается с основ

Развиваем шестое чувство

Улучшаем навыки программирования

Учимся документировать и впечатляем работодателя

круги Эйлера — Основы логики и логические основы компьютера

Разбор задачи B12 (демо ЕГЭ 2012)

Круги Эйлера в информатике

Теперь решим эту задачу с помощью Кругов Эйлера!

Задача о кёнигсбергских мостах

Занятие 3. Задача Эйлера

Определение критической силы. Задача Эйлера

Содержание:

Определение критической силы. Задача Эйлера

Урок и презентация «Задача Эйлера»

О компании — Project Euler

О проекте Euler

Что такое проект Эйлер?

На кого нацелены проблемы?

Может кто решит проблемы?

Что дальше?

Проект Эйлера: проблема 1 с Javascript | Джаред Натт

11. Метод Эйлера — численное решение дифференциальных уравнений

Почему численные решения?

Общая проблема начальной стоимости

Как мы используем эту формулу?

Что происходит?

Пример: метод Эйлера

Шаг 1

Шаг 2

Шаг 3

Шаг 4

Последующие шаги

Насколько это хорошо?

Упражнение

Решение Леонарда Эйлера проблемы Кенигсбергского моста — проблема Эйлера и моста

Проблема Эйлера и моста

Базельской проблемы | MathAdam

Факторизация Weirstrass

Метод Эйлера А.С.

Подраздел 7.3.1 Метод Эйлера

Мероприятие 7.3.2.

Подраздел 7.3.2 Ошибка метода Эйлера

Упражнения 7.3.4 Упражнения

1. Несколько шагов метода Эйлера.

2. Использование метода Эйлера для решения задачи \ (y ‘= 4y \).

3. Использование метода Эйлера с разными временными шагами.

4.

5.

6.

«Темные души» достижений в кодировании

Что такое проект Эйлер?

Правила конкурса # ProjectEuler100

Где мне писать код?

Почему мне нужно размещать свои решения на GitHub?

Могу я посмотреть на решения других людей?

Могу ли я транслировать свои попытки в прямом эфире?

Как быстро мне нужно решить эти проблемы?

Добавить комментарий Отменить ответ