Геометрия трапеция задачи 8 класс. | Геометрия

Геометрия трапеция задачи 8 класс. | Геометрия — просто!

      Добрый день, дорогие друзья!

      Сегодня мы продолжим тему геометрия трапеция задачи 8 класс.
И я подобрал на сегодня несколько необычные задачи.
Чем же они необычны?
Дело в том, что они из самого первого сборника под редакцией М.И. Сканави «Сборник задач по математике для конкурсных экзаменов во ВТУЗы».
Этот сборник вышел в далёком 1969 году, а задачи, которые в нём напечатаны, я даю своим ученикам, начиная с 8 класса.
ВТУЗ — это высшее техническое учебное заведение (институт), которое готовило инженеров, т.е. людей с математическим складом ума.  Итак:

Задача 1.  Большее основание трапеции равно 24 см. Найдите её меньшее основание, если расстояние между серединами её диагоналей равно 4 см.

Решение: По условию задачи AD=24 см, KP=4 см.
Если KP — расстояние между серединами диагоналей, то КР лежит на средней линии MN трапеции.
А это значит, что средняя линия трапеции включает в себя среднюю линию MP треугольника ABD.
А мы знаем, что средняя линия треугольника параллельна  основанию и равна его половине.
Т.е. MP равно половине от 24 см, или 12 см.
Итого имеем MK+KP = 12 см  или MK+4=12 см. Отсюда MK = 12-4 = 8 см.
Но МК является средней линией для треугольника АВС, параллельно основанию ВС и равна его половине.
Поскольку средняя линия равна 8 см, то основание будет в 2 раза больше, или 16 см.
Ответ: Меньшее основание трапеции ВС равно 16 см.

Задача 2. Боковые стороны равнобедренной трапеции  при их продолжении пересекаются под прямым углом. Найти все стороны трапеции, если её площадь равна 12 см², а высота равна 2 см.

Решение: Поскольку угол М равен 90º, а трапеция равнобедренная, то и треугольник  AMD будет равнобедренный и прямоугольный.
А мы знаем, что острые углы в таком треугольнике равны 45°.
Поскольку BN и СР — высоты трапеции, они образуют прямые углы.
Значит, треугольники  ABN  и DCP — прямоугольные.
Но у них есть по одному острому углу, равному 45°.
А мы знаем, что сумма острых углов в прямоугольном треугольнике равна 90°, следовательно, углы в этих треугольниках при вершинах В и С будут так же по 45°.
А это значит, что данные треугольники будут также прямоугольные и равнобедренные.
Отсюда BN=AN=2 см, CP=DP=2 см. И мы можем составить уравнение для площади трапеции.
Площадь трапеции равна произведению полу-суммы оснований на высоту.
(2+х+2+х) / 2  * 2 = 12   2х+4 = 12   2х = 8     х = 4см.
Верхнее основание ВС = 4 см.
Нижнее основание AD= 2+4+2 = 8 см.
Боковые стороны AB и CD находим из прямоугольных треугольников по теореме Пифагора.
Оба катета в треугольниках равны по 2 см, значит, гипотенуза в них будет 2√2 см.
Ответ: 4 см, 8 см, 2√2 см,  2√2 см.

Задача 3.  Один из углов трапеции равен 30°, а боковые стороны при продолжении пересекаются под прямым углом.

Найти меньшую сторону трапеции, если её средняя линия равна 10 см, а одно из оснований равно 8 см.
Решение: В трапеции ABCD средняя линия равна 10 см.
Значит, по определению средней линии трапеции получаем сумму оснований трапеции, равной 10*2 = 20см.
Одно из оснований равно 8 см, значит, второе основание будет 20-8 = 12 см.
Получается, что AD=12 см, ВС=8 см.
Из треугольника AKD, где К — прямой угол, имеем: АК лежит против угла в 30°, значит АК равно половине гипотенузы треугольника, или половине AD. т.е. 12:2 = 6 см.
Теперь рассмотрим треугольник ВКС.
Этот треугольник подобен треугольнику AKD, поскольку они оба прямоугольные, а углы ВСК и ADK равны, как соответственные при параллельных прямых ВС и AD и секущей CD.
Значит, угол ВСК тоже равен 30°.
Отсюда имеем, что ВК равно половине ВС, или 8:2 = 4 см.
Тогда АВ = АК — ВК = 6 — 4 = 2 см.
А точно ли она меньшая?
Из двух прямоугольных треугольников АВМ и CND ВМ=CN. Угол D=30°, угол А=60°.
АВ=ВМ:sin 60° ≈1.15 ВМ, а CD = ВМ:sin30° = 2ВМ.
Получается, АВ меньшая сторона.
Ответ: Меньшая боковая сторона трапеции равна 2 см.

Задача 4. Длины параллельных сторон трапеции AD и BC равны соответственно 25 см и 4 см, а длины непараллельных сторон АВ и CD — 13 см и 20 см. Найти площадь трапеции.

Решение: площадь трапеции равна произведению полу-суммы оснований на высоту.
Основания нам известны, значит, осталось найти высоту.
Сделаем дополнительные построения — проведём высоты трапеции ВМ и CN из точек В и С.
И рассмотрим два прямоугольных треугольника АВМ и CND.
По теореме Пифагора выразим в каждом из них квадрат высоты трапеции и приравняем друг к другу.
Примем  АМ за Х, тогда MN будет равно 4, а ND = 21-Х.
Из первого треугольника имеем ВМ² = 13² — Х².
Из второго треугольника имеем CN² = 20² — (21 — Х)².
Поскольку ВМ=CN, приравняем два выражения.
13² — Х² = 20² — (21 — Х)²
169 — Х² = 400 — 441 + 42Х — Х²
42Х = 169 — 400 + 441
42Х = 210     Х = 5
Из треугольника АВМ при гипотенузе 13 см и катете 5 см находим второй катет:
ВМ = √13² — 5² = √169 — 25 = √144 = 12.
Высота трапеции равна 12 см.
Отсюда, площадь трапеции считаем: (25+4)/2 * 12 = 174см².
Ответ: площадь трапеции равна 174 см².

На сегодня всё. В следующий раз мы продолжим решение задач  на тему геометрия трапеция 8 класс.

Успехов!

Вам так же будет интересно:

Оставить комментарий

Параллелограмм. Свойства параллелограмма. Трапеция. Геометрия, 8 класс: уроки, тесты, задания.

1.	Вопросы по свойствам и признакам параллелограмма Сложность: лёгкое	2
2.	Углы параллелограмма (проверка) Сложность: лёгкое	2
3.	Углы параллелограмма (вычисление) Сложность: лёгкое	2
4.	Углы трапеции Сложность: лёгкое	2
5.	Углы равнобедренной трапеции Сложность: лёгкое	1,5
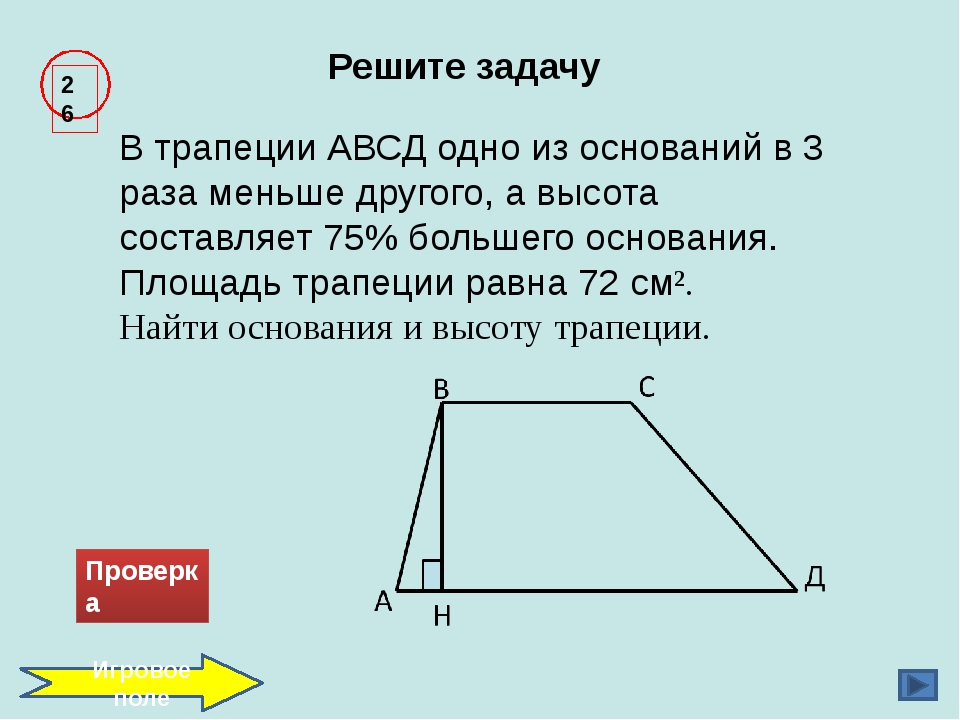
6.	Средняя линия трапеции Сложность: лёгкое	1
7.	Углы параллелограмма (уравнение) Сложность: среднее	3
8.	Углы параллелограмма, даны углы между стороной и диагональю Сложность: среднее	4
9.	Тупой угол параллелограмма Сложность: среднее	3
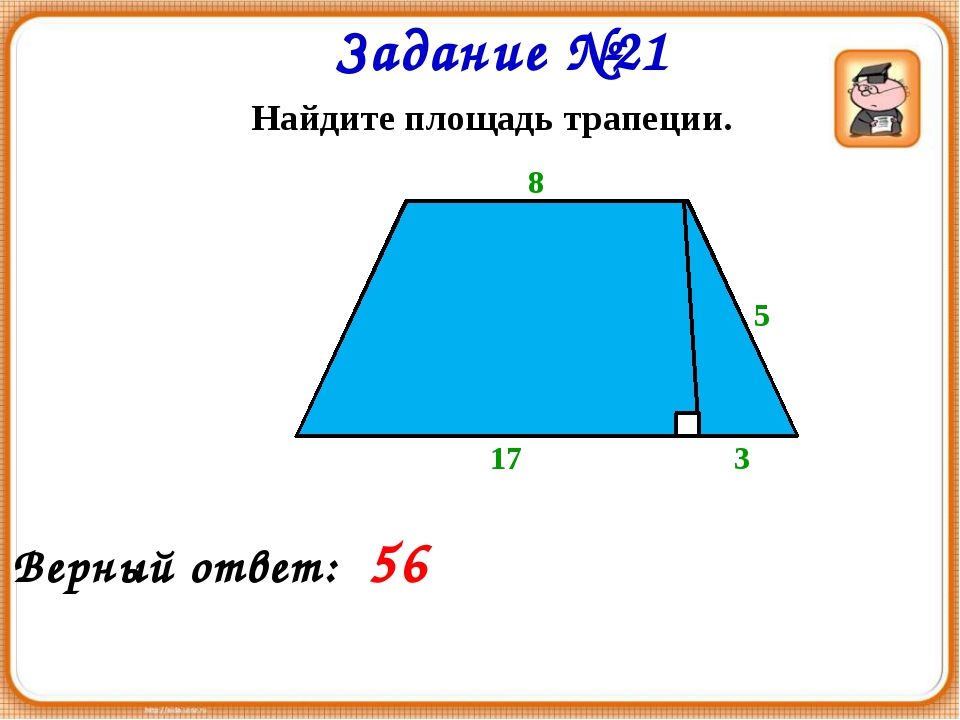
10.	Вычисление сторон параллелограмма, дан периметр Сложность: среднее	3
11.	Периметр параллелограмма Сложность: среднее	3
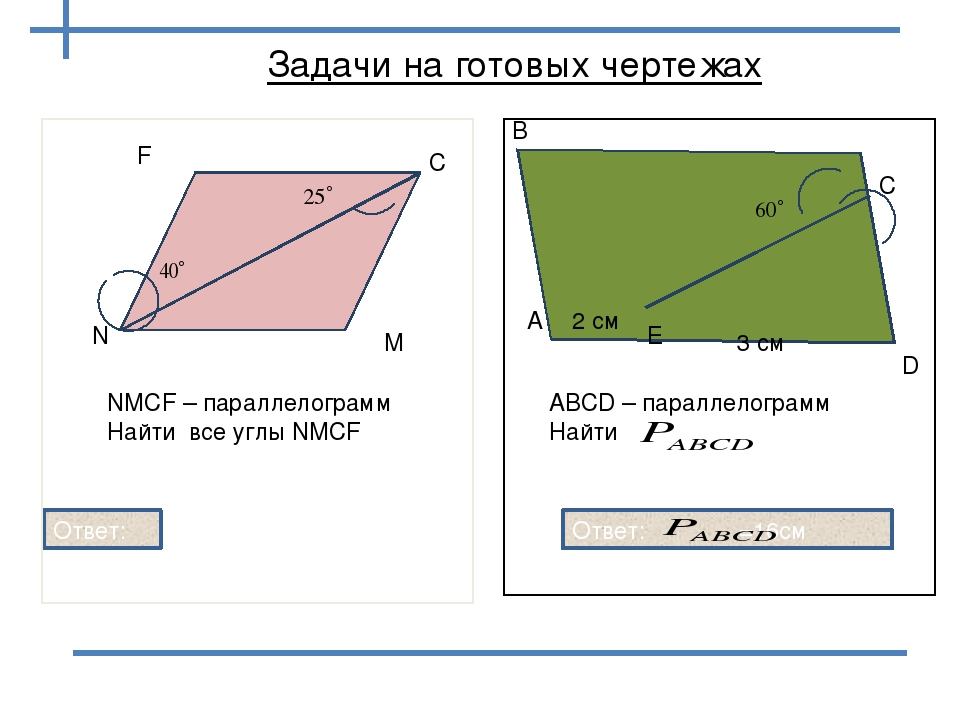
12.	Стороны параллелограмма (разница сторон) Сложность: среднее	4
13.	Стороны параллелограмма (соотношение сторон) Сложность: среднее	4
14.	Стороны трапеции Сложность: среднее	3
15.	Основание прямоугольной трапеции Сложность: среднее	3
16.	Высота трапеции Сложность: среднее	2
17.	Стороны равнобедренной трапеции Сложность: сложное	3
18.	Периметр равнобедренной трапеции Сложность: сложное	4
19.	Прикладная задача на использование свойства средней линии трапеции Сложность: сложное	4
20.	Расстояние от точки до прямой Сложность: сложное	4

Геометрия 8 класс. Урок — практикум по теме : Параллелограмм и трапеция.

УРОК 5 (практикум)

ПО ТЕМЕ: «Параллелограмм и трапеция».

ЦЕЛИ:

Образовательные

1. Формировать умения и навыки при решении задач по теме «Параллелограмм и трапеция».

2. Добиться усвоения учащимися свойств и признаков параллелограмма и трапеции.

Развивающие

1. Способствовать обучению школьников умению выделять условие и вопрос задачи.

2. Развивать у учащихся умение выдвигать гипотезу о способе решения задачи и обосновывать логику доказательства своего предложения в ходе решения задач.

3. Развивать у школьников умение комментировать решение задачи.

Воспитательные

1. Воспитать у учащихся добросовестное отношение к труду, положительное отношение к знаниям.

2. Воспитывать у школьников самостоятельность в работе, умение отстаивать свою точку зрения, дисциплинированность.

3. Воспитывать коммуникативные навыки у учащихся.

ХОД УРОКА:

I. Оргмомент.

II. Программированный опрос по теме: «Параллелограмм и трапеция».

Цель программированного опроса – проверить как учащиеся усвоили тему. Задания высвечиваются с помощью кодоскопа. Учащиеся пишут ответ на листочках под копировку. Один листочек сдают учителю, второй остается у них. Работа по двум вариантам.

На рисунке изображены параллелограммы

1. Противоположные стороны параллелограмма:

1)АВ и СD; 2)АС и ВС 1)NM и ML; 2)MN и ML;

3)АD и АВ; 4)BD и AB 3)NK и MK; 4)KL и MK;

2.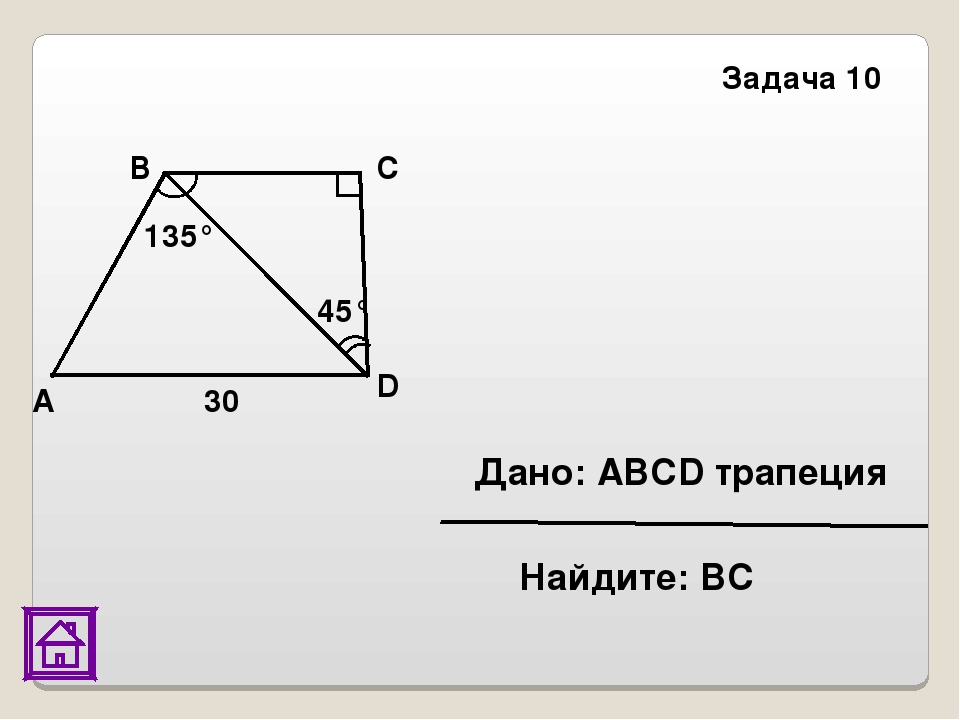 Диагонали параллелограмма

1)АВ и АС; 2)АD и ВС; 1)MN и LK; 2)KN и KL;

3)ВD и АС; 4)СD и ВD; 3)MK и NK; 4)MK и MN;

3. Точка пересечения диагоналей параллелограмма

1) А; 2) В; 3) Е; 4) С. 1) K; 2) M; 3) Q; 4) L.

На рисунке изображена трапеция

4. Данная трапеция является

1) прямоугольной 1) равнобедренной

2) равносторонней 2) равносторонней

3) равнобедренной 3) прямоугольной

5. Основания трапеции

1)MN и LK; 2)KN и LM; 1)АВ и ВС; 2)ВС и АD;

3)KL и KM; 4)NM и NK; 3)АD и АВ; 4)АС и ВС.

После проведения такого опроса ученики сдают свои листочки с ответами, а по копиям сверяют ответы высвечиваемые с помощью кодоскопа. Все оценки за эту работу выставляются в журнал.

III. Решение задач по теме: «Параллелограмм и трапеция».

На этом этапе ученики решают задачи на нахождение элементов параллелограмма и трапеции. В ходе решения требуется вспомнить некоторые сведения. В связи с этим ученикам предлагается ответить на следующие вопросы:

1) Что называется биссектрисой угла?

2) Что такое высота параллелограмма (трапеции)?

3) Что такое диагональ параллелограмма (многоугольника)?

4) Как вычислить периметр параллелограмма (трапеции)?

Задачи 1 и 2 решает один ученик у доски (с комментариями) все остальные в тетрадях.

Задача 1. Стороны параллелограмма равны 5 см. и 8 см. На какие отрезки делят большую сторону биссектриса острого угла параллелограмма.

В Е С Дано: АВСD – параллелограмм

3 АВ = 5см., ВС = 8см.

1 АЕ — биссектрисаА

2 АЕ∩ВС = Е

А D Найти: ВЕ, ЕС

Решение:

По условию АЕ – биссектриса угла А, поэтому  1 =  2,

 2 =  3 – накрест лежащие при ВС ║ АD и секущей АЕ.

∆АВС – равнобедренный, т.к. 1 = 3 =>ВЕ=АВ=5см., тогда ЕС=ВС–ВЕ=>

ЕС = 8 – 5 = 3 (см)

Ответ: 5см, 3см. (средний ученик)

Задача 2 В параллелограмме из вершины тупого угла, равного 150º, проведены высоты h₁ и h₂, сумма их длин равна 10 см. Вычислить периметр параллелограмма.

В С Дано: АВСD – параллелограмм

h₂ ВН₁АD; ВН₂DС;

h₁H₂ ВН₁ = h₁; ВН₂ = h₂;В =150º

h₁ + h₂ = 10см.

А Н₁D Найти: Р_АВСD

Решение:

ЕслиВ = 150º, то А = 180º-В; А =180º-150º=30º.

Из прямоугольного АВН₁ по свойству катета, лежащего против угла в 30º, следует, что АВ = 2h₁. Аналогично с = 30^о; из прямоугольного ВСН₂ по этому же свойству следует, что ВС = 2h₂. Следовательно Р_АВСD= 2(АВ+ВС)=2(2h₁+2h₂)=4(h₁+h₂)=40(см).

Ответ: 40см.

Задача 3 (Эту задачу решают на листочках средние и слабые ученики (групповая работа. Тест задачи 3 и 4проектируется через кодоскоп ). Работа проверяется после урока)Диагональ равнобедренной трапеции является биссектрисой острого угла, а основания относятся как 1:2. периметр трапеции равен 90см. Вычислите стороны трапеции.

В С Дано: АВСD – равнобедренная трапеция,

АС – биссектриса А, ВС:АD=1:2,

Р_АВСD=90.

А D Найти: АВ, ВС, АD.

Решение:

По условию 1=2;2=3 – накрест лежащие углы при АD║ВС и секущей АС 1=3;АВС – равнобедренный (по признаку равнобедренного треугольника)  АВ=ВС.

По условию АD=2ВС. Пусть АВ=х, тогда АВ=ВС=СD=х.; ВС=2х;

х+х+х+2х=90

5х=90

х=90/5

х=18(см)

АВ=ВС=СD=18см. ; ВС=18*2=36см.

Ответ: 18, 18, 18, 36.

Задача 4 (Для более подготовленных учащихся) на листочках.

В равнобедренной трапеции диагонали взаимно перпендикулярны. Докажите что высота трапеции равна полусумме оснований.

В М С Дано: АВСD – равнобедренная трапеция.

АСВD

O Доказать: MN=½(AD + ВС).

Доказательство:

АВD=АСD (АD – общая, АВ=СD по

А ND условию, А=D (по свойству равнобедренной трапеции)ВОС,АОD – прямоугольные – равнобедренные и углы при основаниях равны 45. ВАОDОN=AD=DN; ON=½AD. Аналогично OM=BM=MC  OM=½BC.

MN=MO+ON=½AD+½BC=½(AD+BC), MN=½(AD+BC). Ч.т.д.

Эту задачу проверяют на уроке по готовому решению учителя.

IV. Итог урока

1. Чем мы сегодня занимались на уроке?

2. На какие теоретические понятия опирались при решении задач?

V. Домашние задание: п.42, 43, 44 №390, №383. Дополнительная задача №432 (для сильных учащихся).

Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/104169-geometrija-8-klass-urokpraktikum-po-temepar

Решение задач на трапецию по геометрии стр 1

2812	Площадь параллелограмма ABCD равна 28. Точка E — середина стороны AD. Найдите площадь трапеции BCDE Решение	Площадь параллелограмма ABCD равна 28 ! 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 27 Задание 6
2808	Основания равнобедренной трапеции равны 24 и 10. Радиус описанной окружности равен 13. Центр окружности лежит внутри трапеции. Найдите высоту трапеции Решение	Основания равнобедренной трапеции равны 24 и 10 ! 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 26 Задание 6
2688	В равнобедренной трапеции боковая сторона равна меньшему основанию, диагональ перпендикулярна боковой стороне. @) с основаниями AD=12 и ВС=8 бóльшая диагональ BD=20. Диагонали АС и BD пересекаются в точке М. а) Докажите, что треугольники BMC и DMA подобны. б) Найдите длину высоты МН треугольника AMD Решение	В прямоугольной трапеции ABCD (/_BAD = 90) с основаниями AD=12 и ВС=8 бóльшая диагональ BD=20 ! Задание 4 Диагностической работы по геометрии Статград 09-12-2020 Вариант МА2090403 # Для обучающихся по учебнику А.В. Погорелова
2627	Окружность проходит через вершины A, B и D параллелограмма ABCD, пересекает сторону BC в точках B и M, а так же пересекает продолжение стороны CD за точку D в точке N. а) Докажите, что AM=AN. б) Найдите отношение CD:DN, если AB:BC=1:3, a cos /_BAD=0,4 Решение	Окружность проходит через вершины A, B и D параллелограмма ABCD ! 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 13 Задание 16
2575	В окружность, радиус которой равен 2sqrt7, вписана трапеция ABCD, причем ее основание AD – диаметр окружности, а /_BAD = 60^@.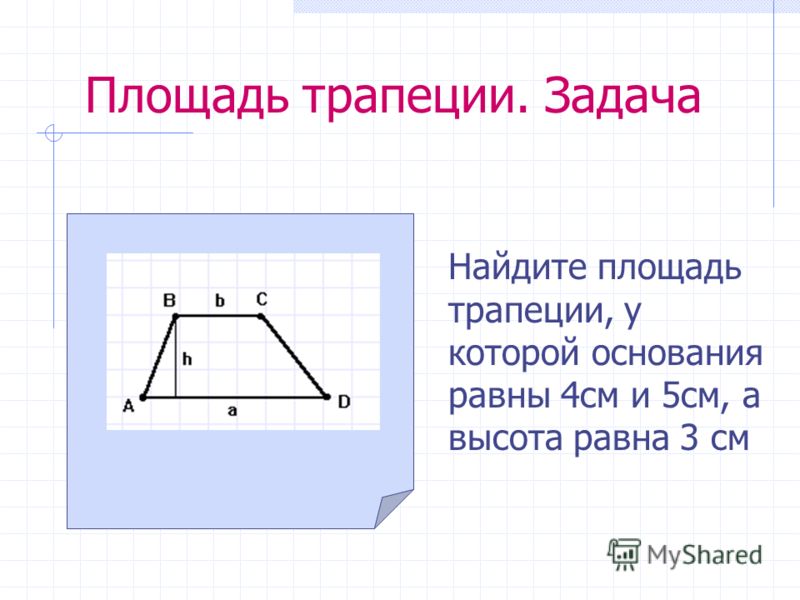 Хорда СЕ пересекает диаметр AD в точке Р такой, что AP : PD = 1 : 3. а) Докажите, что Р – cередина отрезка АО. б) Найдите площадь треугольника BPE Решение	В окружность, радиус которой равен 2 корня из 7, вписана трапеция ABCD ! Тренировочный вариант 328 от Ларина Задание 16 # Решение — Елены Ильиничны Хажинской
2569	В равнобедренную трапецию вписана окружность. Известно, что боковая сторона трапеции точкой касания делится на отрезки длиной 4 и 1. Найдите площадь трапеции Решение	Известно, что боковая сторона трапеции точкой касания делится на отрезки ! Тренировочный вариант 328 от Ларина Задание 6
2550	В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 сторона основания AB равна 4, а боковое ребро AA1 равно 5sqrt3. На ребре DD1 отмечена точка M так, что DM:MD1=3:2. Плоскость alpha параллельна прямой A1F1 и проходит через точки M и E. а) Докажите, что сечение призмы ABCDEFA1B1C1D1E1F1 плоскостью alpha — равнобедренная трапеция. б) Найдите объём пирамиды, вершиной которой является точка F, а основанием — сечение призмы ABCDEFA1B1C1D1E1F1 плоскостью alpha Решение	В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 сторона основания AB равна 4 ! 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 5 Задание 14
2523	Равнобокая трапеция ABCD разбивается диагональю АС на два равнобедренных треугольника. Определите, чему равен больший угол трапеции. Ответ дайте в градусах Решение	Равнобокая трапеция ABCD разбивается диагональю АС на два равнобедренных треугольника ! Тренировочный вариант 325 от Ларина Задание 6
2505	Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=24 и BF=10 Решение	Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F ! 257 вариант Ларина ОГЭ (уровень 1) Задание 23

Карточки-задания по геометрии на тему «Параллелограмм и трапеция», 8 класс

Решение задач по теме «Параллелограмм и трапеция»
1. Высота параллелограмма составляет со стороной угол 32°. Найдите углы параллелограмма.
2. Найдите боковые стороны равнобедренной трапеции, основания которой равны 14 см и 8 см, а один из 
углов равен 120°.
3. Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 4 : 3, 
считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр 
равен 88 см.
4. Стороны параллелограмма равны 10см и 3 см. Биссектрисы двух углов, прилегающих к большей стороне, 
делят противоположную сторону на три отрезка.  Найдите эти отрезки.
5. Найдите меньшее основание равнобедренной трапеции, если ее большее основание равно 16 см, боковая 
сторона – 10 см, а один из углов равен 60°.
6. Диагональ АС равнобедренной трапеции АВСD делит пополам угол ВАD. Найти периметр трапеции, если 
основание АD равно 12 см, а угол АDС равен 60°.
7. Один угол параллелограмма больше другого на 70°. Найдите больший угол. 
8. Периметр параллелограмма равен 46 см. Одна сторона параллелограмма на 3см больше другой. 
Найдите меньшую сторону параллелограмм
Решение задач по теме «Параллелограмм и трапеция»
1. Высота параллелограмма составляет со стороной угол 32°. Найдите углы параллелограмма.
2. Найдите боковые стороны равнобедренной трапеции, основания которой равны 14 см и 8 см, а один из углов 
равен 120°.
3. Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 4 : 3, 
считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр равен 
88 см.
4. Стороны параллелограмма равны 10см и 3 см. Биссектрисы двух углов, прилегающих к большей стороне, 
делят противоположную сторону на три отрезка. Найдите эти отрезки.
5. Найдите меньшее основание равнобедренной трапеции, если ее большее основание равно 16 см, боковая 
сторона – 10 см, а один из углов равен 60°.
6. Диагональ АС равнобедренной трапеции АВСD делит пополам угол ВАD. Найти периметр трапеции, если 
основание АD равно 12 см, а угол АDС равен 60°.
7. Один угол параллелограмма больше другого на 70°. Найдите больший угол. 
8. Периметр параллелограмма равен 46 см. Одна сторона параллелограмма на 3см больше другой. 
Найдите меньшую сторону параллелограмм
Решение задач по теме «Параллелограмм и трапеция»
1. Высота параллелограмма составляет со стороной угол 32°. Найдите углы параллелограмма.
2. Найдите боковые стороны равнобедренной трапеции, основания которой равны 14 см и 8 см, а один из углов 
равен 120°.
3. Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 4 : 3, 
считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр равен 
88 см.
4. Стороны параллелограмма равны 10см и 3 см. Биссектрисы двух углов, прилегающих к большей стороне, 
делят противоположную сторону на три отрезка. Найдите эти отрезки.
5. Найдите меньшее основание равнобедренной трапеции, если ее большее основание равно 16 см, боковая 
сторона – 10 см, а один из углов равен 60°. 6. Диагональ АС равнобедренной трапеции АВСD делит пополам угол ВАD. Найти периметр трапеции, если 
основание АD равно 12 см, а угол АDС равен 60°.
7. Один угол параллелограмма больше другого на 70°. Найдите больший угол. 
8. Периметр параллелограмма равен 46 см. Одна сторона параллелограмма на 3см больше другой. 
Найдите меньшую сторону параллелограмм
9. Стороны параллелограмма равны 
. Биссектрисы двух углов, прилегающих к большей сто­
роне, делят противоположную сторону на три отрезка. Найдите эти отрезки.
Дано: 
 – параллелограмм; 
 – биссектрисы.
Найти: 
Решение:
Если воспользоваться решением примера 1, можно сразу сделать вывод, что треугольники 
равнобедренные (так как 
). Получаем, что
, 
. Тогда: 
 – 
.
Ответ: 
.
10. Найдите боковые стороны равнобедренной трапеции, основания которой равны 14 см и 8 см, а один из 
углов равен 120°.
 
СD = 2ND = 6 см.
11. Найдите меньшее основание равнобедренной трапеции, если ее большее основание равно 16 см, боковая 
сторона – 10 см, а один из углов равен 60°.
 ND = CD = 5 см.
12.Диагональ АС равнобедренной трапеции АВСD делит пополам угол ВАD. Найти периметр трапеции, если 
основание АD равно 12 см, а угол АDС равен 60°. СD = АD = 6 см. ВС = 6 см.
Задачи по теме «Параллелограмм»
1.
Периметр параллелограмма равен 46. Одна сторона параллелограмма на 3 больше другой. 
Найдите меньшую сторону параллелограмм
2.
Две стороны параллелограмма относятся как 3 : 4, а периметр его равен 70. Найдите 
большую сторону параллелограмма
3.
 Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 
4 : 3, считая от вершины острого угла. Найдите большую сторону параллелограмма, если его
периметр равен 88
4.
Точка пересечения  биссектрис двух углов параллелограмма, прилежащих к одной стороне, 
принадлежит противоположной стороне. Меньшая сторона параллелограмма равна 5. 
Найдите периметр параллелограмма.
5.
Один угол параллелограмма больше другого на 70. Найдите больший угол. 
6.
Найдите угол между биссектрисами углов параллелограмма, прилежащих к одной стороне
7.
В параллелограмме АВСD диагонали пересекаются в точке К и АВ=16,
АD=7, ВD=21.  Найдите 1) периметр параллелограмма,2) АС
8.
Высота параллелограмма составляет со стороной угол 32. Найдите углы параллелограмма.

Планиметрия в тезисах и решениях. 9 класс

При решении задач на трапецию нужно помнить следующие положения:

1)

где а, b – длины оснований, h – высота трапеции;

2) Если около трапеции ABCD можно описать окружность, то она равнобокая. Если при этом требуется найти радиус этой окружности, то он совпадает с радиусом окружности, описанной около любого из треугольников: ABC, ABD, ACD, BCD.

3) Если в трапецию ABCD вписана окружность, то AB + CD = BC + AD.

4) Трапецию принято изображать как на рис. 143.

Рис. 143.

При нижнем основании оба угла – острые, но она может выглядеть и как на рис. 144.

Рис. 144.

Поэтому, например, задача «Одно из оснований трапеции равно 6, боковые стороны трапеции равны ?5 и ?13. Высота трапеции равна 2. Найдите площадь трапеции» имеет 4 решения:16, 14, 10 и 8.

Примеры решения задач

37. В равнобокой трапеции ABCD высоты ВК и CL отсекают на основании AD отрезки АК и LD. Найдите длины этих отрезков, если AD = 19, ВС = 7 (рис. 145). (1)

Рис. 145.

Решение. Так как трапеция равнобокая, то треугольники АВК и CLD равны. В самом деле, АВ = CD по условию, ВК = CL как высоты трапеции. Значит, прямоугольные треугольники АВК и CLD равны по гипотенузе и катету. Так как KBCL – прямоугольник, то KL = ВС = 7; АК + LD = AD – KL = 19 – 7 = 12; AK = LD = 6.

Ответ: 6; 6.

38. Углы при основании трапеции равны 60° и 45°, высота трапеции равна 6 см. Найдите боковые стороны трапеции (рис. 146). (1)

Рис. 146.

Решение. Построим трапецию ABCD и проведём высоты ВК и СМ. Из прямоугольного ?АВК находим:

Из прямоугольного ?CMD получаем:

Ответ: 4?3 см; 6?2 см.

39. Средняя линия трапеции равна 10 и делит площадь трапеции в отношении 3:5. Найдите длины оснований этой трапеции. (2)

Рис. 147.

Решение. Рассмотрим трапеции EBCF и AEFD (рис. 147). Введем обозначения: AD = х, ВС = у; высоты трапеций EBCF и AEFD обозначим через h. Так как площадь трапеции равна произведению полусуммы оснований на высоту трапеции, то

Отсюда

Из свойства средней линии трапеции:

Таким образом, получаем систему уравнений:

Ответ: 5; 15.

40. В равнобедренной трапеции даны основания а = 21, b = 9 и высота h = 8. Найдите длину описанной около трапеции окружности (рис. 148; окружность на рисунке не показана). (2)

Рис. 148.

Решение. Проведём высоты трапеции ВК и СМ. Так как АВ = CD, то

Из ?АВК по теореме Пифагора получаем:

тогда

KD = KM + MD = 9 + 6 = 15. Так как окружность, описанная около трапеции, совпадает с окружностью, описанной около треугольника ABD, то по теореме синусов имеем:

Отсюда

или

Длина окружности

Ответ: 85?/4.

41. В выпуклом четырёхугольнике MNLQ углы при вершинах N и L – прямые, а величина угла при вершине М равна arctg2/3. Найти длину диагонали NQ, если известно, что длина стороны LQ вдвое меньше длины стороны MN и на 2 м больше длины стороны LN (рис. 149). (2)

Рис. 149.

Решение: Из условия задачи следует, что угол NMQ острый. Пусть QK – высота треугольника MNQ. По условию LN ? MN и LN ? LQ, следовательно, MN||LQ и LN||QK, т. е. четырёхугольник KNLQ – параллелограмм. Тогда QK = LN и NK = LQ. Имеем, пользуясь условием задачи: QK = LN = LQ – 2, КМ = NM – NK = 2LQ – LQ = LQ. В прямоугольном треугольнике QKM отрезки QK и КМ являются катетами, следовательно,

и, значит, LQ – 2 = 2/3 LQ, откуда LQ = 6 и LN = 4. Из прямоугольного треугольника NLQ, наконец, по теореме Пифагора находим:

Ответ:

42. В трапеции ABCD отрезки АВ и DC являются основаниями. Диагонали трапеции пересекаются в точке Е. Найти площадь треугольника, ВСЕ, если АВ = 30 см, DC = 24 см, AD = 3 см и ?DAB = ?/3. (рис. 150). (3)

Рис. 150.

Решение. Обозначим через h длину высоты треугольника ABC, опущенной из вершины В на продолжение стороны АС. Так как этот отрезок одновременно является и высотой в треугольнике ВСЕ, то имеем:

Из полученных равенств находим:

В треугольниках ABE и CED равны величины соответствующих углов (?АЕВ = ?CED, ?ABE = ?CDE). Значит, эти треугольники подобны и

Теперь из (1) и (2) находим, что

Треугольники ABC и ABD имеют общее основание АВ. Поскольку АВ||CD, то их высоты, опущенные соответственно из вершин С и D, имеют равную величину. Поэтому

Ответ:

Задачи для самостоятельного решения

43. Найдите площадь равнобокой трапеции, если ее основания равны 12 и 4 см, а боковая сторона образует с одним из оснований угол в 45°. (1)

44. Меньшее основание равнобедренной трапеции равно высоте и равно h. Острый угол трапеции равен 30°. Найдите периметр трапеции. (1)

45. Длины параллельных сторон трапеции равны 25 и 4, а длины боковых сторон равны 20 и 13. Найдите высоту трапеции. (2)

46. Основания трапеции равны а и b, боковые стороны равны с. Найдите длину диагонали трапеции. (2)

47. Определите длину высоты трапеции, если её основания равны 28 и 16 см, а боковые стороны равны 25 и 17 см. (2)

48. Найдите площадь равнобедренной трапеции, у которой высота равна 10, а диагонали взаимно перпендикулярны. (2)

49. В трапецию ABCD с основаниями AD и ВС и с боковыми сторонами АВ и CD вписана окружность с центром О. Найти площадь трапеции, если угол DAB прямой, ОС = 2 и OD = 4. (3)

Практикум «Решение задач по теме трапеция»

Площадь трапеции — Измерение | Математика 8 класса

Измерение — это раздел математики, который занимается изучением геометрических форм, их площади, объема и других связанных параметров. Четырехсторонняя замкнутая фигура, в которой одна пара параллельных сторон, противоположных друг другу, и другая непара непараллельных сторон, называется трапецией.

Свойства трапеции

• Это четырехгранная замкнутая фигура с суммой внутренних углов 360 °.
• Одна пара параллельных сторон, которые должны быть противоположны друг другу.
• Одна пара непараллельных сторон.
• Сумма углов смежных сторон 180 °.
• Диагонали трапеции делят друг друга пополам на пересечении.

Основная терминология трапеции

Основание трапеции: Пара параллельных сторон, противоположных друг другу, называется основанием. Вы можете коллировать как b1, так и b2 соответственно.

Высота трапеции: Перпендикулярное расстояние между двумя параллельными линиями называется высотой трапеции.

Формула для площади трапеции

Если даны основание и высота трапеции, то площадь трапеции можно рассчитать по формуле:

Площадь трапеции = 1/2 x (сумма оснований) x (высота трапеции)

Расчет площади трапеции

Площадь трапеции равна сумме площадей двух треугольников и площади прямоугольника. Ниже приводится вывод для вычисления площади трапеции:

Поскольку мы знаем, что:

Площадь трапеции = Площадь треугольника 1 + площадь прямоугольника + Площадь треугольника 2

Предположим, что основание треугольник 1 равен B1, а основание треугольника 2 равно B2, а высота обоих треугольников равна h.А для прямоугольника предположим, что его ширина и высота равны b1 и h.

Это означает, что

A = (B1 xh / 2) + b1h + (B2 xh / 2)

A = (B1 xh + 2b1h + B2 xh) / 2

Упрощение уравнение, переставляя члены и получая результат разложения на множители:

A = h / 2 [b1 + (B1 + b1 + B2]…. (i)

Если мы предположим, что более длинное основание трапеции равно b2, то

b2 = B1 + b1 + B2… .. (ii)

Подставляя (ii) в уравнение (i),

A = h / 2 (b1 + b2)

Следовательно, площадь a трапеция с основаниями b1, b2 и высотой h составляет;

A = h / 2 (b1 + b2)

, что также может быть записано ниже:

Площадь трапеции = 1/2 x (сумма баз) x (Высота трапеции)

= 1/2 x (b1 + b2) xh

Примеры задач на основе формулы

Задача 1: Рассчитайте площадь трапеции, в которой значение оснований 10 и 5 соответственно, а высота трапеции 2 м. 2, одно основание составляет 6 м, а другое основание — 4 м.Рассчитайте высоту трапеции.

Решение:

Площадь трапеции = 1/2 x (сумма оснований) x (Высота трапеции)

Пусть значение высоты будет h.

Подставив все указанные значения в приведенную выше формулу, мы получили

220 = 1/2 x (4 + 6) xh

220 = 10 xh

22 = h

h = 22m

NCERT Solutions for Class 8 Math Глава 18

Страница № 207:

Вопрос 1:

Найдите площадь трапеции с параллельными сторонами 24 см и 20 см и расстоянием между ними 15 см.

Ответ:

Площадь трапеции = 12 × Сумма параллельных сторон × Расстояние между ними

= 12 × 24 + 20 × 15 см2 = 12 × 44 × 15 см2 = 22 × 15 см2 = 330 см2

Следовательно, площадь трапеция 330 см2.

Страница № 207:

Вопрос 2:

Найдите площадь трапеции, параллельные стороны которой равны 38,7 см и 22.3 см, а расстояние между ними — 16 см.

Ответ:

Площадь трапеции = 12 × Сумма параллельных сторон × Расстояние между ними

= 12 × 38,7 + 22,3 × 16 см2 = 12 × 61 × 16 см2 = 61 × 8 см2 = 488 см2

Следовательно, площадь трапеция 488 см2.

Страница № 207:

Вопрос 3:

Форма верхней поверхности стола — трапеция.Его параллельные стороны составляют 1 м и 1,4 м, а расстояние по перпендикуляру между ними составляет 0,9 м. Найдите его область.

Ответ:

Площадь трапеции = 12 × Сумма параллельных сторон × Расстояние между ними
= 12 × 1 + 1,4 × 0,9 м2 = 12 × 2,4 × 0,9 м2 = 1,2 × 0,9 м2 = 1,08 м2
Следовательно, площадь верхней поверхности площади стола 1,08 м2.

Страница № 207:

Вопрос 4:

Площадь трапеции 1080 см ² .Если длины его параллельных сторон равны 55 см и 35 см, найдите расстояние между ними.

Ответ:

Пусть расстояние между параллельными сторонами равно x. Теперь Площадь трапеции = 12 × 55 + 35 × x см2

= 12 × 90 × x см2 = 45x см2
Площадь трапеции = 1080 см2 Учитывая 45x = 1080⇒x = 108045⇒x = 24 см Следовательно, расстояние между параллельными сторонами — 24 см.

Страница № 207:

Вопрос 5:

Поле в форме трапеции.Его площадь составляет 1586 м 2 ² , а расстояние между параллельными сторонами 26 м. Если одна из параллельных сторон равна 84 м, найдите другую.

Ответ:

Пусть длина требуемой стороны будет x см. Теперь Площадь трапеции = 12 × 84 + x × 26 м2

= 1092 + 13x м2

Площадь трапеции = 1586 м2 Дано 1092 + 13x = 1586⇒13x = 1586-1092⇒13x = 494⇒x = 49413⇒x = 38 м. Следовательно, длина другой стороны равна 38 м.

Страница № 207:

Вопрос 6:

Площадь трапеции 405 см ² . Его параллельные стороны в соотношении 4: 5, а расстояние между ними 18 см. Найдите длину каждой из параллельных сторон.

Ответ:

Пусть длины параллельных сторон трапеции равны 4x см и 5x см соответственно. Теперь Площадь трапеции = 12 × 4x + 5x × 18 см2
= 12 × 9x × 18 см2 = 81x см2
Площадь трапеции = 405 см2 Дано ∴81x = 405⇒x = 40581⇒x = 5 см Длина одной стороны = 4 × 5 см = 20 см Длина другой стороны = 5 × 5 см = 25 см

Страница № 207:

Вопрос 7:

Площадь трапеции 180 см ² , высота 9 см.Если одна из параллельных сторон длиннее другой на 6 см, найдите две параллельные стороны.

Ответ:

Пусть длины параллельных сторон равны x см и x + 6 см. Теперь площадь трапеции = 12 × x + x + 6 × 9 см2
= 12 × 2x + 6 × 9 см2 = 4,52x + 6 см2 = 9x + 27 см2

Площадь трапеции = 180 см2 Учитывая 9x + 27 = 180⇒9x = 180-27⇒9x = 153⇒x = 1539⇒x = 17 Следовательно, длины параллельных сторон равны 17 см и 23 см. , То есть 17 + 6 см.

Страница № 207:

Вопрос 8:

В поле формы трапеции одна из параллельных сторон вдвое больше другой. Если площадь поля составляет 9450 м ² , а расстояние по перпендикуляру между двумя параллельными сторонами равно 84 м, найдите длину большей из параллельных сторон.

Ответ:

Пусть длины параллельных сторон равны x см и 2x см.Площадь трапеции = 12 × x + 2x × 84 м2
= 12 × 3x × 84 м2 = 42 × 3x м2 = 126x м2

Площадь трапеции = 9450 м2 Дано 126x = 9450⇒x = 9450126⇒x = 75 Таким образом , Длина параллельных сторон составляет 75 м и 150 м, то есть 2 × 75 м, а длина более длинной стороны — 150 м.

Страница № 207:

Вопрос 9:

Длина ограждения трапециевидного поля ABCD составляет 130 м, а сторона AB перпендикулярна каждой из параллельных сторон AD и BC .Если BC = 54 м, CD = 19 м и AD = 42 м, найдите площадь поля.

Ответ:

Длина стороны AB = 130-54 + 19 + 42 м
= 15 м
Площадь трапециевидного поля = 12 × AD + BC × AB
= 12 × 42 + 54 × 15 м2 = 12 × 96 × 15 м2 = 48 × 15 м2 = 720 м2

Следовательно, площадь поля 720 м2.

Страница № 207:

Вопрос 10:

На данном рисунке ABCD представляет собой трапецию, в которой AD || BC, ∠ABC = 90 °, AD = 16 см, AC = 41 см и BC = 40 см.Найдите площадь трапеции.

Ответ:

∠ABC = 90 ° Справа от ∆ABC имеем: AB2 = AC2-BC2⇒AB2 = 412-402⇒AB2 = 1681-1600⇒AB2 = 81⇒AB = 81⇒AB = 9 см∴ Длина AB = 9 см Теперь площадь трапеции = 12 × AD + BC × AB
= 12 × 16 + 40 × 9 см2 = 12 × 56 × 9 см2 = 28 × 9 см2 = 252 см2
Следовательно, площадь трапеции составляет 252 см2. .

Страница № 207:

Вопрос 11:

Параллельные стороны трапеции 20 см и 10 см.Обе его непараллельные стороны равны по 13 см каждая. Найдите площадь трапеции.

Ответ:

Пусть ABCD будет заданной трапецией, в которой AB∥DC, AB = 20 см, DC = 10 см и AD = BC = 13 см. Нарисуйте CL⊥AB и CM∥DA, пересекающиеся с AB в точках L и M, соответственно. AMCD — это параллелограмм. Теперь AM = DC = 10 см. MB = AB-AM = 20-10 см = 10 см. Также CM = DA = 13 см. Следовательно, ∆CMB — равнобедренный треугольник, а CL⊥MB.L — середина точки B. .⇒ML = LB = 12 × MB
= 12 × 10 см = 5 см

Справа ∆CLM, имеем: CL2 = CM2-ML2 см2⇒CL2 = 132-52 см2⇒CL2 = 109-25 см2⇒CL2 = 144 см2⇒CL = 144 см⇒CL = 12 см∴ Длина CL = 12 см Площадь трапеции = 12 × AB + DC × CL
= 12 × 20 + 10 × 12 см2 = 12 × 30 × 12 см2 = 15 × 12 см2 = 180 см2
Следовательно, площадь трапеции составляет 180 см2.

Страница № 207:

Вопрос 12:

Параллельные стороны трапеции равны 25 см и 11 см, а ее непараллельные стороны — 15 см и 13 см. Найдите площадь трапеции.

Ответ:

Пусть ABCD будет трапецией, в которой AB∥DC, AB = 25 см, CD = 11 см, AD = 13 см и BC = 15 см. Нарисуйте CL⊥AB и CM∥DA, пересекающиеся с AB в точках L и M соответственно. .Ясно, что AMCD — это параллелограмм. Теперь MC = AD = 13 см AM = DC = 11 см⇒MB = AB-AM
= 25-11 см = 14 см

Таким образом, в ∆CMB имеем: CM = 13 смMB = 14 см BC = 15 см∴ s = 1213 + 14 + 15 см = 1242 см = 21 см-a = 21-13 см = 8 см-b = 21-14 см = 7 см-c = 21-15 см = 6 см∴ Площадь ∆CMB = ss-as-bs-c
= 21 × 8 × 7 × 6 см2 = 84 см2

∴ 12 × MB × CL = 84 см2⇒12 × 14 × CL = 84 см2
⇒CL = 847⇒CL = 12 см
Площадь трапеции = 12 × AB + DC × CL
= 12 × 25 + 11 × 12 см2 = 12 × 36 × 12 см2 = 18 × 12 см2 = 216 см2

Следовательно, площадь трапеции 216 см2.

Страница № 210:

Вопрос 1:

На данном рисунке ABCD представляет собой четырехугольник, в котором AC = 24 см, B L ⊥ AC и DM ⊥ AC , так что BL = 8 см и DM = 7 см. Найдите площадь квадрата. ABCD .

Ответ:

Площадь четырехугольника ABCD = Площадь ∆ADC + Площадь ∆ACB
= 12 × AC × DM + 12 × AC × BL = 12 × 24 × 7 + 12 × 24 × 8 см2 = 84 + 96 см2 = 180 см2

Следовательно, площадь четырехугольника 180 см2.

Страница № 210:

Вопрос 2:

На данном рисунке ABCD представляет собой поле четырехугольной формы, в котором диагональ BD составляет 36 м, AL ⊥ BD и CM ⊥ BD , так что AL = 19 м и CM = 11 м. Найдите площадь поля.

Ответ:

Площадь четырехугольника ABCD = Площадь ∆ABD + Площадь ∆BCD
= 12 × BD × AL + 12 × BD × CM
= 12 × 36 × 19 + 12 × 36 × 11 м2 = 342 + 198 м2 = 540 м2

Таким образом, площадь поля 540 м2.

Страница № 210:

Вопрос 3:

Найдите площадь пятиугольника ABCDE , в которой BL ⊥ AC , DM ⊥ AC и EN ⊥ AC , так что AC = 18 см, AM = 14 см, AN = 6 см, BL = 4 см, DM = 12 см и EN = 9 см.

Ответ:

Площадь пятиугольника ABCDE = Площадь ∆AEN + Площадь трапеции EDMN + Площадь ∆DMC + Площадь ∆ACB
= 12 × AN × EN + 12 × EN + DM × NM + 12 × MC × DM + 12 × AC × BL = 12 × AN × EN + 12 × EN + DM × AM-AN + 12 × AC-AM × DM + 12 × AC × BL = 12 × 6 × 9 + 12 × 9 + 12 × 14-6 + 12 × 18-14 × 12 + 12 × 18 × 4 см2 = 27 + 84 + 24 + 36 см2 = 171 см2

Следовательно, площадь данного пятиугольника составляет 171 см2.

Страница № 210:

Вопрос 4:

Найдите площадь шестигранника ABCDEF , в котором BL ⊥ AD , CM ⊥ AD , EN ⊥ AD и FP ⊥ AD таким образом, что см AP , PL = 2 см, LN = 8 см, NM = 2 см, MD = 3 см, FP = 8 см, EN = 12 см, BL = 8 см и CM = 6 см.

Ответ:

Площадь шестиугольника ABCDEF = Площадь ∆AFP + Площадь трапеции FENP + Площадь ∆END + Площадь ∆CMD + Площадь трапеции BCML + Площадь ∆ALB

= 12 × AP × FP + 12 × FP + EN × PN + 12 × ND × EN + 12 × MD × CM + 12 × CM + BL × LM + 12 × AL × BL = 12 × AP × FP + 12 × FP + EN × PL + LN + 12 × NM + MD × EN + 12 × MD × CM + 12 × CM + BL × LN + NM + 12 × AP + PL × BL = 12 × 6 × 8 + 12 × 8 + 12 × 2 + 8 + 12 × 2 + 3 × 12 + 12 × 3 × 6 + 12 × 6 + 8 × 8 + 2 + 12 × 6 + 2 × 8 см2 = 24 + 100 + 30 + 9 + 70 + 32 см2 = 265 см2

Следовательно, площадь шестиугольника равна 265 см2.

Страница № 210:

Вопрос 5:

Найдите площадь пятиугольника ABCDE , в которой BL ⊥ AC , CM ⊥ AD и EN ⊥ AD , так что AC = 10 см, AD = 12 см, BL = 3 см, CM = 7 см и EN = 5 см.

Ответ:

Площадь пятиугольника ABCDE = Площадь ∆ABC + Площадь ∆ACD + Площадь ∆ADE
= 12 × AC × BL + 12 × AD × CM + 12 × AD × EM = 12 × 10 × 3 + 12 × 12 × 7 + 12 × 12 × 5 см2 = 15 + 42 + 30 см2 = 87 см2

Следовательно, площадь пятиугольника составляет 87 см2.

Страница № 210:

Вопрос 6:

Найдите площадь, ограниченную данным рисунком ABCDEF в соответствии с размерами, указанными здесь.

Ответ:

Площадь, ограниченная данным рисунком = Площадь трапеции FEDC + Площадь квадрата ABCF
= 12 × 6 + 20 × 8 + 20 × 20 см2 = 104 + 400 см2 = 504 см2

Следовательно, площадь, ограниченная рисунком, составляет 504 см2 .

Страница № 211:

Вопрос 7:

Найдите площадь данного рисунка ABCDEFGH в соответствии с указанными в нем размерами.

Ответ:

Найдем длину AC. Из прямоугольных треугольников ABC и HGF имеем: AC2 = HF2 = 52-42 см
= 25-16см = 9 см

AC = HF = 9 см = 3 см
Площадь данной фигуры ABCDEFGH = Площадь прямоугольника ADEH + Площадь ∆ABC + Площадь ∆HGF
= Площадь прямоугольника ADEH + 2 Площадь ∆ABC = AD × DE + 2 Площадь ∆ABC = AC + CD × DE + 212 × BC × AC = 3 + 4 × 8 + 212 × 4 × 3 см2 = 56 + 12 см = 68 см2
Следовательно, площадь данного рисунка составляет 68 см2.

Страница № 211:

Вопрос 8:

Найдите площадь правильного шестиугольника ABCDEF , каждая сторона которого составляет 13 см, а высота — 23 см, как показано на данном рисунке.

Ответ:

Пусть AL = DM = x см LM = BC = 13 см∴ x + 13 + x = 23⇒2x + 13 = 23⇒2x = 23-13⇒2x = 10⇒x = 5∴ AL = 5 см справа ∆ AFL, имеем: FL2 = AF2-AL2⇒FL2 = 132-52⇒FL2 = 169-25⇒FL2 = 144⇒FL = 144⇒FL = 12 см∴ FL = BL = 12 см Площадь правильного шестиугольника = Площадь трапеция ADEF + Площадь трапеции ABCD
= 2 Площадь трапеции ADEF = 212 × AD + EF × FL = 212 × 23 + 13 × 12 см2 = 212 × 36 × 12 см2 = 432 см2
Следовательно, площадь данного правильного шестиугольника равна 432 см2.

Страница № 211:

Вопрос 1:

Отметьте (✓) правильный ответ:
Длина параллельных сторон трапеции составляет 14 см и 18 см, а расстояние между ними составляет 9 см. Площадь трапеции
(а) 96 см ²
(б) 144 см ²
(в) 189 см ²
(г) 207 см ²

Ответ:

(б) 144 см ²
Площадь трапеции = 12 × 14 + 18 × 9 см2
= 12 × 32 × 9 см2 = 144 см2

Страница № 211:

Вопрос 2:

Отметьте (✓) правильный ответ:
Длина параллельных сторон трапеции составляет 19 см и 13 см, а ее площадь составляет 128 см ² .Расстояние между параллельными сторонами
(а) 9 см
(б) 7 см
(в) 8 см
(г) 12,5 см

Ответ:

(c) 8 см

Пусть расстояние между параллельными сторонами равно x см. Тогда площадь трапеции = 12 × 19 + 13 × x см2
= 12 × 32 × x см2 = 16x см2
Но это дано что площадь трапеции 128 см2.
∴ 16x = 128⇒x = 12816⇒x = 8 см

Страница № 211:

Вопрос 3:

Отметьте (✓) правильный ответ:
Параллельные стороны трапеции находятся в соотношении 3: 4, а расстояние между ними по перпендикуляру составляет 12 см.Если площадь трапеции 630 см ² , то ее меньшая из параллельных сторон будет
(а) 45 см
(б) 42 см
(в) 60 см
(г) 36 см

Ответ:

(a) 45 см

Пусть длина параллельных сторон равна 3x см и 4x см соответственно. Тогда площадь трапеции = 12 × 3x + 4x × 12 см2
= 12 × 7x × 12 см2 = 42 x см2

Но при условии, что площадь трапеции 630 см2.

∴ 42x = 630⇒x = 63042⇒x = 15 см
Длина параллельных сторон = 3 × 15 см = 45 см 4 × 15 см = 60 см Следовательно, более короткая из параллельных сторон составляет 45 см.

Страница № 211:

Вопрос 4:

Отметьте (✓) правильный ответ:
Площадь трапеции составляет 180 см ² , а ее высота — 9 см. Если одна из параллельных сторон длиннее другой на 6 см, длина большей из параллельных сторон составляет
(a) 17 см
(b) 23 см
(c) 18 см
(d) 24 см

Ответ:

(b) 23 см

Пусть длина параллельных сторон равна x см и x + 6 см соответственно.Тогда площадь трапеции = 12 × x + x + 6 × 9 см2
= 12 × 2x + 6 × 9 см2 = 4,52x + 6 см2 = 9x + 27 см2
Но при условии, что площадь трапеции равна 180 см2. 9x + 27 = 180⇒9x = 180-27⇒9x = 153⇒x = 1539⇒x = 17 Следовательно, длина параллельных сторон составляет 17 см и 17 + 6 см, что равно 23 см. Следовательно, длина более длинной параллельной стороны составляет 23 см.

Страница № 211:

Вопрос 5:

Отметьте (✓) правильный ответ:
На данном рисунке AB || DC и D A ⊥ AB .Если DC = 7 см, BC = 10 см, AB = 13 см и CL ⊥ AB , площадь ловушки. ABCD is
(а) 84 см ²
(б) 72 см ²
(в) 80 см ²
(г) 91 см ²

Ответ:

(c) 80 см ²

Из данной трапеции находим: DC = AL = 7 см, так как DA⊥AB и CL⊥AB Из правого ∆CBL имеем: CL2 = CB2-LB2⇒CL2 = 102 -62⇒CL2 = 100-36⇒CL2 = 64⇒CL = 64⇒CL = 8 см Площадь трапеции = 12 × 7 + 13 × 8 см2
= 12 × 20 × 8 см2 = 80 см2

Страница № 212:

Вопрос 1:

Основание треугольного поля в три раза больше его высоты, а его площадь составляет 1350 м. ² .Найдите основание и высоту поля.

Ответ:

Пусть основание треугольного поля составляет 3x см, а его высота — x см. Тогда площадь треугольника = 12 × 3x × x м2
= 3×22 м2
Но при условии, что площадь треугольного поля составляет 1350 м2 .
∴ 3×22 = 1350⇒x2 = 1350 × 23⇒x2 = 900⇒x = 900⇒x = 30 м
Следовательно, высота поля 30 м. Его основание = 3 × 30 м = 90 м

Страница № 212:

Вопрос 2:

Найдите площадь равностороннего треугольника со стороной 6 см.

Ответ:

Площадь равностороннего треугольника = 34 × 2 квадратных единицы = 34 × 6 × 6 см2
= 34 × 36 см2 = 93 см2
Следовательно, площадь равностороннего треугольника равна 93 см2.

Страница № 212:

Вопрос 3:

Периметр ромба — 180 см, одна из диагоналей — 72 см.Найдите длину другой диагонали и площадь ромба.

Ответ:

Пусть ABCD — ромб, диагонали которого AC и BD пересекаются в точке O. Пусть длина диагонали AC равна 72 см, а сторона ромба — x см. Периметр ромба = 4x см. периметр ромба 180 см. 4x = 180 ⇒x = 1804⇒x = 45 Следовательно, длина стороны ромба составляет 45 см. Мы знаем, что диагонали ромба делят друг друга пополам под прямым углом.∴ AO = 12AC⇒AO = 12 × 72 см⇒AO = 36 см. Справа ∆AOB, имеем: BO2 = AB2-AO2⇒BO2 = 452-362⇒BO2 = 2025-1296⇒BO2 = 729⇒BO = 729⇒BO = 27 см∴ BD = 2 × BOBD = 2 × 27 смBD = 54 см Следовательно, длина другой диагонали равна 54 см. Площадь ромба = 12 × 72 × 54 см2
= 1944 см2

Страница № 212:

Вопрос 4:

Площадь трапеции 216 м ² , высота 12 м. Если одна из параллельных сторон на 14 м меньше другой, найдите длину каждой из параллельных сторон.

Ответ:

Пусть длина параллельных сторон будет x м и x-14 м. Тогда площадь трапеции = 12 × x + x-14 × 12 м2
= 62x-14м2 = 12x-84м2
Но при условии, что площадь трапеции составляет 216 м2. 12x-84 = 216⇒ 12x = 216 + 84⇒ 12x = 300⇒ x = 30012⇒ x = 25 Следовательно, длина параллельных сторон 25 м и 25-14 м, что равно до 11 мес.

Страница № 212:

Вопрос 5:

Найдите площадь четырехугольника, одна из диагоналей которого равна 40 см, а длины перпендикуляров, проведенных из противоположных вершин диагонали, равны 16 см и 12 см.

Ответ:

Пусть ABCD — четырехугольник. Диагональ, AC = 40 смBL⊥AC, такая, что BL = 16 смDM⊥AC, такое, что DM = 12 см. Площадь четырехугольника = Площадь ∆DAC + Площадь ∆ACB

= 12 × AC × DM + 12 × AC × BL см2 = 12 × 40 × 12 + 12 × 40 × 16 см2 = 240 + 320 см2 = 560 см2

Следовательно, площадь четырехугольника равна 560 см2.

Страница № 212:

Вопрос 6:

Поле имеет форму прямоугольного треугольника с гипотенузой 50 м и одной стороной 30 м.Найдите площадь поля.

Ответ:

Пусть другая сторона треугольного поля равна x m. ∴ x2 = 502-302⇒x2 = 2500-900⇒x2 = 1600⇒x = 1600⇒x = 40∴ Площадь поля = 12 × 30 × 40 м2

= 600 м2

Страница № 212:

Вопрос 7:

Отметьте (✓) напротив правильного ответа:
Основание треугольника 14 см, а его высота 8 см.Площадь треугольника
(а) 112 см ²
(б) 56 см ²
(в) 122 см ²
(г) 66 см ²

Ответ:

(б) 56 см ²
Площадь треугольника = 12 × 14 × 8 см2
= 56 см2

Страница № 212:

Вопрос 8:

Отметьте (✓) напротив правильного ответа:
Основание треугольника в четыре раза больше его высоты, а его площадь составляет 50 м ² .Длина его основания
(а) 10 м
(б) 15 м
(в) 20 м
(г) 25 м

Ответ:

(c) 20 м

Пусть высота треугольника будет x м, а его основание — 4x м соответственно. Тогда площадь треугольника = 12 × 4x × x м2
= 2×2 м2
Но площадь треугольника составляет 50 м2. 2×2 = 50⇒x2 = 502⇒x2 = 25⇒x = 25⇒x = 5∴ Длина его основания = 4 × 5 м = 20 м

Страница № 212:

Вопрос 9:

Отметьте (✓) напротив правильного ответа:
Длина диагонали четырехугольника составляет 20 см, а длина перпендикуляров на нем от противоположных вершин равна 8.5 см и 11,5 см. Площадь четырехугольника
(а) 400 см ²
(б) 200 см ²
(в) 300 см ²
(г) 240 см ²

Ответ:

(б) 200 см ²

Пусть ABCD — четырехугольник. Диагональ, AC = 20 смBL⊥AC, такая что BL = 8,5 смDM⊥AC, такая, что DM = 11,5 см Площадь четырехугольника = Площадь ∆DAC + Площадь ∆ACB
= 12 × AC × DM + 12 × AC × BL см2 = 12 × 20 × 11.5 + 12 × 20 × 8,5 см2 = 85 + 115 см2 = 200 см2

Страница № 212:

Вопрос 10:

Отметьте (✓) напротив правильного ответа:
Каждая сторона ромба составляет 15 см, а длина одной из его диагоналей — 24 см. Площадь ромба
(а) 432 см ²
(б) 216 см ²
(в) 180 см ²
(г) 144 см ²

Ответ:

(б) 216 см ²

Пусть ABCD — ромб, диагонали которого AC и BD пересекаются в точке O.Пусть длина диагонали AC равна 24 см, а сторона ромба — 15 см. Мы знаем, что диагонали ромба делят друг друга пополам под прямым углом. ∴ AO = 12AC⇒AO = 12 × 24 см⇒AO = 12 см. Справа ∆AOB, имеем: BO2 = AB2-AO2⇒BO2 = 152-122⇒BO2 = 225-144⇒BO2 = 81⇒BO = 81⇒BO = 9 см∴BD = 2 × BOBD = 2 × 9 смBD = 18 см Следовательно, длина другой диагонали составляет 18 см. Площадь ромба = 12 × 24 × 18 см2

= 216 см2

Страница № 212:

Вопрос 11:

Отметьте (✓) напротив правильного ответа:
Площадь ромба 120 см ² , а одна из диагоналей 24 см.Каждая сторона ромба
(а) 10 см
(б) 13 см
(в) 12 см
(г) 15 см

Ответ:

(b) 13 см

Пусть ABCD — ромб, диагонали которого AC и BD пересекаются в точке O. Пусть длина диагонали AC равна 24 см. Площадь ромба = 12 × AC × BD см2 Но площадь ромбуса составляет 120 см2 (дано) ∴12 × AC × BD = 120 или 12 × 24 × BD = 120 или 12 × BD = 120 или BD = 12012 = 10 см OB = BD2 = 102 = 5 см

И OA = AC2 = 242 = 12 см. Теперь в прямоугольном треугольнике AOB: AB2 = OA2 + OB2 или AB2 = 122 + 52 = 144 + 25 = 169 или AB = 169 = 13 см. Таким образом, каждая сторона ромба составляет 13 см.

Страница № 212:

Вопрос 12:

Отметьте (✓) напротив правильного ответа:
Параллельные стороны трапеции равны 54 см и 26 см, а расстояние между ними — 15 см. Площадь трапеции
(а) 702 см ²
(б) 810 см ²
(в) 405 см ²
(г) 600 см ²

Ответ:

(г) 600 см ²

Площадь трапеции = 12 × 54 + 26 × 15 см ²
= 12 × 80 × 15 см2
= 600 см ²

Страница № 212:

Вопрос 13:

Отметьте (✓) напротив правильного ответа:
Площадь трапеции 384 см ² .Его параллельные стороны в соотношении 5: 3, расстояние между ними 12 см. Более длинная из параллельных сторон
(а) 24 см
(б) 40 см
(в) 32 см
(г) 36 см

Ответ:

(б) 40 см

Пусть длина параллельных сторон равна 5x см и 3x см соответственно. Площадь трапеции = 12 × 5x + 3x × 12 см ²
= 12 × 8x × 12 см ² = 48x см ²

Но площадь трапеции составляет 384 см2.48x = 384⇒x = 38448 = 8 Более длинная сторона = 5x = 5 × 8 = 40 см

Страница № 212:

Вопрос 14:

Заполните пустые поля.
(i) Площадь треугольника = 12 × (………) × (………).
(ii) Площадь || gm = 12 × (………) × (………).
(iii) Площадь трапеции = 12 × (………) × (………).
(iv) Параллельные стороны трапеции равны 14 см и 18 см, а расстояние между ними — 8 см.Площадь трапеции ……… см ² .

Ответ:

i Площадь треугольника = 12 × Основание × Высота Площадь ∥gm = Основание × Высота Площадь трапеции = 12 × Сумма параллельных сторон × Расстояние между ними Площадь трапеции = 12 × 14 + 18 × 8 см2
= 12 × 32 × 8 см2 = 128 см2

Просмотреть решения NCERT для всех глав класса 8

Периметр формулы трапеции | Формула площади трапеции

Периметр трапеции — это просто сумма длин ее сторон.

$ периметр = AB + BC + CD + DA $

Чтобы найти площадь трапеции, мы разбиваем ее на параллелограмм и треугольник, как показано на схеме.

\ [площадь \ влево ({трапеция \, ABCD} \ вправо) = площадь \ влево ({{\ text {треугольник}} \, ADE} \ вправо) + площадь \ влево ({{\ text {параллелограмм }} \, ABCE} \ right) \]

\ [= \ frac {1} {2} \ times DE \ times h + EC \ times h \]

Поскольку противоположные стороны параллелограмма равны равно, $ EC = AB = {b_1} $

$ DE = DC — EC = {b_2} — {b_1} $

\ [\ Rightarrow area \ left ({trapezium \, ABCD} \ right ) = \ frac {h} {2} \ times \ left ({DE + 2EC} \ right) = \ frac {h} {2} \ times \ left ({{b_2} — {b_1} + 2 {b_1} } \ right) = \ frac {h} {2} \ left ({{b_1} + {b_2}} \ right) \]

Давайте рассмотрим пример, чтобы увидеть, как использовать эти формулы.2} $. Если его высота 4 см, а непараллельные стороны 6 см и 5 см, оцените его периметр.

Варианты:

(а) $ 21 \, см $

(б) $ 25 \, см $

(в) $ 27 \, см $

(г) ни один из этих

Ответ: (а)

Решение:

$ {\ text {area}} = \ frac {h} {2} \ left ({{b_1} + {b_2}} \ right) \ Rightarrow 20 = \ frac {4} {2 } \ times \ left ({{b_1} + {b_2}} \ right) \ Rightarrow {b_1} + {b_2} = 10 \, см $

$ {\ text {perimeter}} = 6 + 5 + {b_1 } + {b_2} = 11 + 10 = 21 \, см $

Eureka Math 5 класс Модуль 5 Урок 16 Ключевые ответы — CCSS Math Answers

Engage NY Eureka Math 5-й класс Модуль 5 Урок 16 Ответы на вопросы

Eureka Math 5 класс Модуль 5 Урок 16 Набор задач Ключ с ответами

Вопрос 1.
Нарисуйте пару параллельных линий в каждом квадрате. Затем с помощью параллельных линий нарисуйте трапецию со следующим:
a. Никаких прямых углов.
г. Всего 1 тупой угол.
г. 2 тупых угла.
г. Минимум 1 прямой угол.
Ответ:

Вопрос 2.
Используйте нарисованные вами трапеции для выполнения следующих задач.
а. Измерьте углы трапеции с помощью транспортира и запишите измерения на фигурах.
г. С помощью маркера или мелка обведите пары углов внутри каждой трапеции с суммой, равной 180 °.Используйте разные цвета для каждой пары.
Ответ:

Вопрос 3.
Перечислите свойства, общие для всех трапеций, с которыми вы работали сегодня.
Ответ:

Недвижимость:

Это четырехугольники.

Имеют разную длину сторон и угол наклона.

У них есть по крайней мере одна пара параллельных сторон.

Вопрос 4.
Когда четырехугольник еще можно назвать трапецией?
Ответ:

Если у четырехугольника есть хотя бы одна пара противоположных параллельных сторон, то четырехугольник также называется трапецией.

Вопрос 5.
Следуйте инструкциям, чтобы нарисовать последнюю трапецию.
а. Нарисуйте отрезок \ (\ overline {A B} \), параллельный нижней части этой страницы, длиной 5 см.
г. Нарисуйте два угла 55 ° с вершинами в точках A и B так, чтобы образовался равнобедренный треугольник с основанием \ (\ overline {A B} \).
г. Обозначьте верхнюю вершину треугольника C.
d. С помощью установленного квадрата нарисуйте линию, параллельную \ (\ overline {A B} \), которая пересекает как \ (\ overline {A C} \), так и \ (\ overline {B C} \).
у.е. Заштрихуйте нарисованную трапецию.
Ответ:

Eureka Math 5 класс Модуль 5 Урок 16 Ключ ответа на входной билет

а. Используйте линейку и квадрат, чтобы нарисовать трапецию.
г. Какой атрибут должен присутствовать, чтобы четырехугольник также был трапецией?
Ответ:

г.

Основным признаком того, что четырехугольник также является трапецией, является пара параллельных противоположных сторон.

Эврика Математика 5 класс Модуль 5 Урок 16 Домашнее задание Ответы

Вопрос 1.
С помощью линейки и сетки нарисуйте:
a. Трапеция ровно с двумя прямыми углами.

Ответ:

г. Трапеция без прямых углов.

Ответ:

Вопрос 2.
Каплан неправильно отсортировал некоторые четырехугольники на трапеции и нетрапеции, как показано ниже.
а. Обведите фигуры, которые находятся в неправильной группе, и объясните, почему они неправильно отсортированы.

Ответ:

г.Объясните, какие инструменты необходимо использовать для проверки размещения всех трапеций.
Ответ:

Для проверки размещения всех трапеций,

Прямая голова и треугольник 45 градусов для проверки на параллельность линий

Вопрос 3.
а. С помощью линейки нарисуйте равнобедренную трапецию на сетке.

Ответ:

г. Почему эта форма называется равнобедренной трапецией?
Ответ:

Форма называется равнобедренной трапецией, потому что,

Две противоположные стороны параллельны.

Две другие стороны равны по длине.

Диагонали также равны по длине.

Как найти периметр трапеции — стенограмма видео и урока

Определение периметра трапеции: задача со словами

В этом упражнении вы проверите свои знания о том, как найти периметр трапеции.

Проезд

Для этого задания распечатайте или скопируйте эту страницу на чистый лист бумаги. Затем внимательно прочтите данное слово «проблемы» и предложите решение.

1.) Ваша гостиная имеет форму трапеции с периметром двадцать восемь футов и имеет три стороны размером семь, восемь и четыре фута, которые все полностью заняты вещами. Вы планируете поставить диван на оставшееся место с четвертой стороны, которое удерживает двухфутовый вход. Какого размера будет ваш диван?

2.) Вы хотите повесить светодиодные полосы по краям, где стены и потолок встречаются в вашей трапециевидной спальне. Будет ли достаточно трех комплектов светодиодных лент длиной двадцать четыре дюйма для вашей комнаты, у которой две стороны имеют длину три фута, а другие стороны — четыре и два фута соответственно?

3.) Полянку в лесу планируется обустроить под летний лагерь. У поляны трапециевидной формы равные непараллельные стороны, каждая размером по сто пятьдесят ярдов. Самая короткая сторона составляет девяносто ярдов, а самая длинная — сто восемьдесят ярдов. Для защиты от диких животных вокруг кемпинга установят забор. Какой длины будет забор?

Ключ ответа

1.) P = 28, a = 7, b = 8, c = 4, d =?

P — (a + b + c) = d

28–19 = 9

Четвертая сторона — 9 футов в длину.Прихожая составляет 2 фута.

9 — 2 = 7

Кушетка может быть длиной 7 футов.

2.) 3 + 3 + 4 + 2 = 12 футов

Комната имеет периметр 12 футов.

24 x 3 = 72 дюйма

Общая длина светодиодных лент составляет 72 дюйма.

1 фут = 12 дюймов

72/12 = 6 футов

Светодиодные ленты покрывают только половину периметра вашей спальни. Вам нужно будет купить больше.

3.) 150 + 150 + 90 + 180 = 570

Забор будет 570 ярдов в длину.

Иллюстративная математика 6 класс, Раздел 4.5 — Учителя

Сосредоточьте обсуждение всего класса на последних двух вопросах, особенно на том, как визуальное представление помогает нам рассуждать о точках зрения Джады и Диего, а также на связи между вербальным и числовым представлением ситуации.

Выберите двух ранее указанных учеников, чтобы объяснить, почему Диего или Джада правы. Покажите наглядное представление «сколько ромбов в трапеции?» для всеобщего обозрения (как показано здесь) или воспользуйтесь апплетом по адресу https: // ggbm.в / VmEqZvke для иллюстрации.

Развернуть изображение

Чтобы выделить количество групп и размер одной группы в задаче, обсудите такие вопросы, как:

• «Это вопрос типа« сколько всего этого в этом? ». Что в данном случае составляет 1 группу? » (Один ромб.)
• «Как узнать, сравнивать ли остаток с ромбом или трапецией?» (Поскольку ромб составляет 1 группу, нам нужно сравнить остаток с ромбом.)

Если учащимся сложно сравнить остаток с ромбом, спросите: «Сколько треугольников в трапеции?» и укажите, что ответ — «3 треугольника.Вот ответ на вопрос «сколько ромбов в трапеции?» будет «(некоторое количество) ромбов».

Тот факт, что нужно отслеживать два целых числа 1, может быть источником путаницы (трапеция представляет величину 1, а ромб представляет 1 группу). У студентов будет возможность более четко различать эти два целых в предстоящих занятиях.

Говорение, слушание: Поддерживает обсуждение MLR8. Используйте эту процедуру для поддержки обсуждения всего класса.После того, как учащийся поделится своими соображениями относительно того, согласны ли они с Диего или Джадой, попросите учащихся переформулировать услышанное, используя точный математический язык. Спросите первоначального оратора, смог ли его коллега правильно изложить свое мнение. Обращайте внимание студентов на любые слова или фразы, которые помогли прояснить исходное утверждение. Это дает большему количеству студентов возможность использовать язык, интерпретируя рассуждения других.
Принцип (ы) дизайна: Поддержка смысла

Иди по математике, 8 класс. Ключ ответов на вопросы Глава 9 Преобразования и конгруэнтность — Иди по математике. Ключ ответов

Fins несколько способов решения математических задач.Выберите лучший и простой способ решить свои математические задачи, представленные в Go Math Text Book. Каждый ученик в первую очередь отдает предпочтение математике в 8-м классе. Перейти к математике 8 класс Глава 9 Преобразования и ключ ответа на соответствие вместе с различными объяснениями упрощают и упрощают практику учащихся по математике. Обратитесь к разделу «Иди по математике» для 8-го класса, чтобы выучить математику.

Иди по математике 8 класс. Ключевой ответ Глава 9 Преобразования и сравнение

Как много способов решения задач доступно в Go Math 8 класс Глава 9 Преобразования и Конгруэнтный ключ решения, учащиеся могут выбрать простой метод решения и изучить метод решения математических задач.Кроме того, изображения включены для лучшего понимания учащегося. Таким образом, учащиеся, которые хотят получить хорошие оценки на экзамене, должны практиковаться с помощью Go Math 8 класс. Ключевые ответы Глава 9 Преобразования и конгруэнтность.

Урок 1: Свойства переводов

Урок 2: Свойства отражений

Урок 3: Алгебраические представления преобразований

Урок 4: Конгруэнтные числа

Тест модели

Смешанный обзор

Практическое руководство — Свойства переводов — Стр.282

Вопрос 1.
Словарь A __________________ — это изменение положения, размера или формы фигуры.
____________

Ответ: преобразование

Пояснение:
Преобразование — это изменение положения, размера или формы фигуры.

Вопрос 2.
Словарь Когда вы выполняете преобразование фигуры на координатной плоскости, вход преобразования называется ________________, а выход преобразования называется _________________.
Тип ниже:
____________

Ответ:
изображений
изображений

Пояснение:
Когда вы выполняете преобразование фигуры на координатной плоскости, вход преобразования называется прообразом, а выход преобразования называется изображением.

Вопрос 3.
Джони переводит прямоугольный треугольник на 2 единицы вниз и на 4 единицы вправо. Как ориентация изображения треугольника соотносится с ориентацией прообраза?
Ориентация: _______

Ответ:
Ориентация такая же

Пояснение:
Поскольку перенос не изменяет форму и размер геометрической фигуры, два треугольника идентичны по форме и размеру, поэтому они совпадают и ориентация одинакова.

Вопрос 4.
Рашид нарисовал прямоугольник PQRS на координатной плоскости. Затем он перевел прямоугольник на 3 единицы вверх и на 3 единицы влево и пометил изображение P ‘Q‘ R ‘S‘. Как соотносятся прямоугольник PQRS и прямоугольник P ‘Q‘ R ‘S‘?
Это: _______

Ответ:
соответствует

Пояснение:
Поскольку перемещение не меняет форму и размер геометрической фигуры, два прямоугольника идентичны по форме и размеру, поэтому они совпадают.

Вопрос 5.
На рисунке изображена трапеция WXYZ.Постройте изображение трапеции после перемещения на 4 единицы вверх и на 2 единицы влево.

Тип ниже:
____________

Ответ:
После перевода:
W ‘(- 4, 3)
X’ (2, 3)
Y ‘(1, 1)
Z’ (- 3, 1)

ОБЯЗАТЕЛЬНЫЕ ВОПРОСЫ РЕГИСТРАЦИЯ

Вопрос 6.
Каковы свойства переводов?
Тип ниже:
____________

Ответ:
-> перевод — это геометрическое преобразование, которое перемещает каждую точку фигуры или пространства на одинаковую величину в заданном направлении.
-> Значит, цифры идентичны и совпадают.

9.1 Независимая практика — Свойства переводов — Стр. № 283

Вопрос 7.
На рисунке изображен треугольник DEF.

а. Постройте график изображения треугольника после перевода, который сопоставляет точку D с точкой D ‘.
Тип ниже:
____________

Ответ:
2 слева и 4 вниз

Вопрос 7.
б. Как бы вы описали перевод?
Тип ниже:
____________

Ответ:
Он имеет такой же размер, форму.и ориентация, но в другом месте

Вопрос 7.
c. Как изображение треугольника DEF соотносится с прообразом?
____________

Ответ:
соответствует

Вопрос 8.
а. Изобразите четырехугольник KLMN с вершинами K (-3, 2), L (2, 2), M (0, -3) и N (-4, 0) на координатной сетке.

Тип ниже:
____________

Вопрос 8.
б. На той же координатной сетке нарисуйте изображение четырехугольника KLMN после перемещения на 3 единицы вправо и на 4 единицы вверх.
Тип ниже:
____________

Ответ:

Вопрос 8.
c. Какая сторона изображения соответствует стороне \ (\ overline {LM} \)?
___________
Назовите три другие пары совпадающих сторон.
___________
Тип ниже:
____________

Ответ:
Линия LM соответствует линии L! M!
Линия KL равна K’L ’
Линия MN равна M’N’
Линия KN равна K’N ’

Рисуйте изображение фигуры после каждого перевода.

Вопрос 9.
4 единицы слева и 2 единицы вниз

Тип ниже:
____________

Ответ:
После перевода
P ‘(- 3, 1)
Q’ (0, 2)
R ‘(0, -1)
S’ (- 3, -3)

Вопрос 10.
5 единиц справа и 3 единицы вверх

Тип внизу:
____________

Ответ:
После перевода
A ‘(0, 4)
B’ (3, 5)
C ‘(3, 1)
D’ (0, 0)

Свойства переводов — стр. № 284

Вопрос 11.
На рисунке показан подъем воздушного шара. Как бы вы описали перевод?

Тип ниже:
____________

Ответ:
4 единицы по положительной оси X и 5 единиц по положительной оси Y

Пояснение:
Начальная координата балуна = (-2, -4)
Конечные координаты балуна = (2,1)
Смещение по оси x = 2 — (-2)
= 4 единицы по положительному направлению x
Смещение по оси y = 1 — (- 4)
= 5 единиц вдоль положительного направления y

Вопрос 12.
Критическое мышление Возможно ли, что ориентация фигуры может измениться после ее перевода? Объяснять.
_________

Ответ:
Нет, просто переводом поменять ориентацию нельзя. Как перевод означает преобразование, при котором фигура перемещается в другое место без каких-либо изменений в размере или ориентации.

ФОКУС НА МЫШЛЕНИЕ ВЫСШЕГО ПОРЯДКА

Вопрос 13.
а. Многоступенчатый графический треугольник XYZ с вершинами X (-2, -5), Y (2, -2) и Z (4, -4) на координатной сетке.

Вопрос 13.
б. На той же координатной сетке, графике и обозначении треугольника X’Y’Z ’, изображение треугольника XYZ после перемещения на 3 единицы влево и на 6 единиц вверх.

Вопрос 13.
c. Теперь изобразите и обозначьте треугольник X ”Y” Z ”, изображение треугольника X’Y’Z’ после перемещения на 1 единицу влево и 2 единицы вниз.
Тип ниже:
____________

Ответ:

Вопрос 13.
г. Анализируйте взаимосвязи Как бы вы описали перевод, который отображает треугольник XYZ на треугольник X ”Y” Z ”?
Тип ниже:
____________

Ответ:
Треугольник XYZ переместился на 4 единицы вверх и на 4 единицы влево

Вопрос 14.
Критическое мышление На рисунке показан прямоугольник P’Q’R’S ’, изображение прямоугольника PQRS после сдвига на 5 единиц вправо и на 7 единиц вверх. Постройте график и обозначьте прообраз PQRS.

Тип ниже:
____________

Ответ:

Вопрос 15.
Сообщайте математические идеи Объясните, почему изображение фигуры после перевода совпадает с ее прообразом.
Тип ниже:
____________

Ответ:
Перевод — это геометрическое преобразование, которое перемещает каждую точку фигуры или пространства на одинаковую величину в заданном направлении.Таким образом, 2 фигуры идентичны, а переведенная фигура соответствует ее прообразу.

Управляемая практика — Свойства отражений — Стр. № 288

Вопрос 1.
Словарь Отражение — это преобразование, при котором фигура переворачивается по линии, называемой __________.
____________

Ответ:
Ось отражения

Пояснение:
Отражение — это преобразование, при котором фигура переворачивается по линии, называемой осью отражения.

Вопрос 2.
На рисунке изображена трапеция ABCD.

а. Постройте изображение трапеции после отражения по оси абсцисс. Обозначьте вершины изображения.
Тип ниже:
____________

Ответ:
A ‘(- 3, -4)
B’ (1, -4)
C ‘(3, -1)
D’ (- 3, -1)

Вопрос 2.
б. Как соотносятся трапеция ABCD и трапеция A’B’C’D ’?
____________

Ответ:
соответствует

Пояснение:
трапеция ABCD и трапеция A’B’C’D ’совпадают

Вопрос 2.
г. Что, если? Предположим, вы отразили трапецию ABCD поперек оси y. Как ориентация изображения трапеции будет сравниваться с ориентацией прообраза?
Тип ниже:
____________

Ответ:
Ориентация была бы обратной по горизонтали.

ОБЯЗАТЕЛЬНЫЕ ВОПРОСЫ РЕГИСТРАЦИЯ

Вопрос 3.
Каковы свойства отражений?
Тип ниже:
____________

Ответ:
свойств отражений
-> размер остается прежним
-> форма остается прежней
-> ориентация НЕ остается прежней

9.2 Независимая практика — Свойства отражений — Стр. № 289

На графике показаны четыре прямоугольных треугольника. Используйте график для упражнений 4-7.

Вопрос 4.
Какие два треугольника отражают друг друга по оси x?
Тип ниже:
____________

Ответ:
Треугольники A и C являются отражениями друг друга по оси x.

Вопрос 5.
Для каких двух треугольников линия отражения является осью y?
Тип ниже:
____________

Ответ:
Для треугольников C и D линия отражения представляет собой ось y.

Вопрос 6.
Какой треугольник является переводом треугольника C? Как бы вы описали перевод?
Тип ниже:
____________

Ответ:
Треугольник B является переносом треугольника C.
Давайте возьмем любую точку треугольника = (-2, -6)
Давайте возьмем соответствующую сторону треугольника B = (4,2)
Перенос по оси x = 4 — (- 2) = 6 единиц
Смещение по оси y = 2 — (- 6) = 8 единиц

Вопрос 7.
Какие треугольники конгруэнтны? Откуда вы знаете?
Тип ниже:
____________

Ответ:
Все 4 треугольника A, B, C, D равны.
Длина основания и высота всех четырех треугольников составляют 3 единицы, 4 единицы соответственно.

Пояснение:
Все 4 треугольника A, B, C, D совпадают.
Если основание и высота равны, то гипотенуза также должна быть одинаковой. Таким образом, все три стороны треугольников A, B, C, D равны. Таким образом, эти треугольники совпадают,
Длина основания и высота всех четырех треугольников составляют 3 единицы, 4 единицы соответственно.

Вопрос 8.
а. Постройте четырехугольник WXYZ с вершинами W (-2, -2), X (3, 1), Y (5, -1) и Z (4, -6) на координатной сетке.
Тип ниже:
____________

Вопрос 8.
б. На той же координатной сетке постройте четырехугольник W’X’Y’Z ’, изображение четырехугольника WXYZ после отражения относительно оси x.
Тип ниже:
____________

Ответ:

Вопрос 8.
c. Какая сторона изображения соответствует стороне \ (\ overline {YZ} \)?
_______________
Назовите три другие пары совпадающих сторон.
_______________
Тип ниже:
____________

Ответ:
Линия YZ = Линия Y’Z ’
Линия WX = Линия W’X’
Линия XY = Линия X’Y ’
Линия WZ = Линия W’Z’

Вопрос 8.
г. Какой угол изображения соответствует ∠X?
_______________
Назовите три другие пары совпадающих углов.
_______________
Тип ниже:
____________

Ответ:
Угол X ’
Угол W и Угол W’
Угол Y и Угол Y ’
Угол Z и Угол Z’

Свойства отражений — стр. № 290

Вопрос 9.
Критическое мышление Возможно ли, что изображение точки после отражения может быть той же точкой, что и прообраз? Объяснять.
________

Ответ:
Да

Пояснение:
Возможно, что изображение точки после отражения может быть той же точкой, что и прообраз

ФОКУС НА МЫШЛЕНИЕ ВЫСШЕГО ПОРЯДКА

Вопрос 10.
а. Постройте изображение фигуры, показанной после отражения, по оси ординат.

Тип ниже:
____________

Ответ:

Вопрос 10.
б. На той же координатной сетке нарисуйте изображение фигуры, которую вы нарисовали в части a, после отражения по оси x.
Тип ниже:
____________

Ответ:

Вопрос 10.
c. Сделайте предположение. Какая другая последовательность преобразований даст такое же окончательное изображение из исходного прообраза? Проверьте свой ответ, выполнив преобразования. Затем сделайте предположение, обобщающее ваши выводы.
Тип ниже:
____________

Ответ:
То же изображение может быть получено путем отражения сначала по оси x, а затем по оси y.
Отражение фигуры сначала по оси Y, а затем по оси X дает тот же результат.отражаясь сначала по оси x, а затем по оси y.

Вопрос 11.
а. Построить треугольник DEF с вершинами D (2, 6), E (5, 6) и F (5, 1) на координатной сетке.

Вопрос 11.
б. Следующий график — треугольник D ′ E ′ F ′, изображение треугольника DEF после отражения поперек оси y.
Тип ниже:
____________

Вопрос 11.
c. На той же координатной сетке графически изображен треугольник D ′ ′ E ′ ′ F ′ ′, изображение треугольника D ′ E ′ F ′ после перемещения на 7 единиц вниз и на 2 единицы вправо.
Тип ниже:
____________

Ответ:

Вопрос 11.
d. Анализ взаимосвязей Найдите другую последовательность преобразований, которая преобразует треугольник DEF в треугольник D ′ ′ E ′ ′ F ′ ′.
Тип ниже:
____________

Ответ:
Переведите треугольник DEF на 7 единиц вниз и на 2 единицы влево. Затем отразите изображение по оси ординат.

Управляемая практика — Свойства отражений — Стр. № 294

Вопрос 1.
Словарь Вращение — это преобразование, которое поворачивает фигуру вокруг заданного _____, называемого центром вращения.
____________

Ответ:
баллов

Пояснение:
Вращение — это преобразование, которое поворачивает фигуру вокруг заданной точки, называемой центром вращения.

Шивон поворачивает прямоугольный треугольник на 90 ° против часовой стрелки вокруг начала координат.

Вопрос 2.
Как ориентация изображения треугольника соотносится с ориентацией прообраза?
Тип ниже:
____________

Ответ:
Каждая нога в прообразе перпендикулярна соответствующей ноге на изображении.

Вопрос 3.
Совпадает ли изображение треугольника с прообразом?
______

Ответ:
Да

Пояснение:
Изображение треугольника совпадает с прообразом

Нарисуйте изображение фигуры после заданного поворота вокруг начала координат.

Вопрос 4.
90 ° против часовой стрелки

Тип ниже:
____________

Ответ:

Вопрос 5.
180 °

Тип ниже:
____________

Ответ:
После поворота на 180 °
A ‘(- 2, -3)
B’ (- 4, -1)
C ‘(- 2, 0)
D’ (0, -1)

ОБЯЗАТЕЛЬНЫЕ ВОПРОСЫ РЕГИСТРАЦИЯ

Вопрос 6.
Каковы свойства поворотов?
Тип ниже:
____________

Ответ:
При повороте сохраняются размер и форма, но изменяется ориентация.

9.3 Независимая практика — Свойства отражений — Стр. № 295

Вопрос 7.
На рисунке показан треугольник ABC и поворот треугольника вокруг начала координат.

а. Как бы вы описали ротацию?
____________

Ответ:
ABC был повернут на 90º против часовой стрелки относительно начала координат

Вопрос 7.
г. Каковы координаты изображения?
Тип ниже:
____________

Ответ:
A ‘(3, 1)
B’ (2, 3)
C ‘(- 1, 4)

Вопрос 8.
На графике показана фигура и ее изображение после преобразования.

а. Как бы вы описали это как ротацию?
____________

Ответ:
Фигура была повернута на 180 ° относительно начала координат.

Вопрос 8.
б. Можете ли вы описать это как преобразование, отличное от вращения? Объяснять.
____________

Ответ:
Да

Пояснение:
Это также можно описать как отражение по оси y.

Вопрос 9.
Какой тип поворота сохранит ориентацию H-образной фигуры в сетке?

____________

Ответ:
Поворот на 180 ° относительно начала координат сохранит ориентацию H-образной фигуры в сетке.

Вопрос 10.
Точка с координатами (-2, -3) поворачивается на 90 ° по часовой стрелке относительно начала координат.Каковы координаты его изображения?
(_______, _______)

Ответ:
(-3, 2)

Пояснение:
Новые координаты (-3, 2)

Дополните стол поворотом на 180 ° или 90 °. Включите направление вращения для поворотов на 90 °.

Вопрос 11.

Тип ниже:
____________

Ответ:

Свойства отражений — стр. № 296

Нарисуйте изображение фигуры после заданного поворота вокруг начала координат.

Вопрос 14.
180 °

Тип ниже:
____________

Ответ:
После 180 °
A ‘(4, 0)
B’ (2, -1)
C ‘(0, 0)
D’ (2, 1)

Вопрос 15.
270 ° против часовой стрелки

Тип ниже:
____________

Ответ:
После поворота на 270º против часовой стрелки
A ‘(1, 2)
B’ (2, -1)
C ‘(4, 2)

Вопрос 16.
Есть ли поворот, при котором ориентация изображения всегда совпадает с ориентацией прообраза? Если так, то?
______

Ответ:
Да

Пояснение:
Поворот на 360 ° всегда будет таким же, как у исходного изображения

ФОКУС НА МЫШЛЕНИЕ ВЫСШЕГО ПОРЯДКА

Вопрос 17.
Решение проблем Лукас играет в игру, в которой он должен повернуть фигуру, чтобы она поместилась на открытом пространстве. Каждый раз, когда он нажимает кнопку, фигурка поворачивается на 90 градусов по часовой стрелке. Сколько раз ему нужно нажимать кнопку, чтобы каждая фигура вернулась в исходную ориентацию?
Рисунок A ____________
Рисунок B ____________
Рисунок C ____________

Рисунок A: _________ время (с)
Рисунок B: _________ время (с)
Рисунок C: _________ время (с)

Ответ:
Рисунок A: 2 раза (с)
Рисунок B: 1 раз (с)
Рисунок C: 4 раза (с)

Пояснение:
2 раза для возврата к исходной ориентации
1 раз для возврата к исходной ориентации
4 раза для возврата к исходной ориентации

Вопрос 18.
Построение гипотезы Треугольник ABC отражается поперек оси y, образуя изображение A’B’C ‘. Затем треугольник A’B’C ‘отражается поперек оси x, образуя изображение A ″ B ″ C ″. Какой тип вращения можно использовать для описания взаимосвязи между треугольником A ″ B ″ C ″ и треугольником ABC?
Тип ниже:
____________

Ответ:
Треугольник A’B’C ‘- это поворот на 90 ° треугольника ABC.
Треугольник A «B» C «- поворот на 90 ° треугольника A’B’C’
Следовательно, треугольник A» B «C» — это Поворот на 180º треугольника ABC

Вопрос 19.
Сообщайте математические идеи Точка A находится на оси y. Опишите все возможные положения изображения A ‘для поворота на 90 °, 180 ° и 270 °. Включите источник в качестве возможного местоположения для A.
Тип ниже:
____________

Ответ:
Если точка A находится на оси y, точка A ‘будет на оси x при поворотах на 190 ° и 270 ° и на оси y при повороте на 180 °
Если точка A находится в начале координат,
A ‘находится в начале координат для любого поворота вокруг начала координат.

Управляемая практика — Алгебраические представления преобразований — Стр.300

Вопрос 1.
Треугольник XYZ имеет вершины X (-3, -2), Y (-1, 0) и Z (1, -6). Найдите вершины треугольника X′Y′Z ′ после сдвига вправо на 6 единиц. Затем нарисуйте треугольник и его изображение.

Тип ниже:
____________

Ответ:
После перевода вправо на 6 единиц:
X ‘(3, -2)
Y’ (5, 0)
Z ‘(7, -6)

Вопрос 2.
Опишите, что происходит с координатами x и y после того, как точка отражается поперек оси x.
Тип ниже:
____________

Ответ:
Координата x остается прежней, а знак координаты y меняется

Вопрос 3.
Используйте правило (x, y) → (y, -x) для построения графика изображения треугольника справа. Затем опишите трансформацию.

Тип ниже:
____________

Ответ:
Треугольник повернут на 90º по часовой стрелке вокруг начала координат

ОБЯЗАТЕЛЬНЫЕ ВОПРОСЫ РЕГИСТРАЦИЯ

Вопрос 4.
Как меняются координаты x и y при переводе фигуры вправо на a единиц и вниз на b единиц?
Тип ниже:
____________

Ответ:
Координаты x увеличиваются на a, а координаты y уменьшаются на b

9.4 Независимая практика — Алгебраические представления преобразований — Стр. № 301

Напишите алгебраическое правило для описания каждого преобразования. Затем опишите преобразование.

Вопрос 5.

Тип ниже:
____________

Ответ:
алгебраическое правило
(x, y) -> (x-2, y-5)
преобразование
перемещение на 2 единицы влево и 5 единиц вниз
новые координаты
M ‘(- 4, -2)
N ‘(- 2, -2)
O’ (- 1, -4)
P ‘(- 4, -4)

Вопрос 6.

Тип ниже:
____________

Ответ:
алгебраическое правило
(x, y) -> (-x, -y)
преобразование
поворот на 180º
новые координаты
A ‘(0, 0)
B’ (0, -3)
C ‘ (2, -3)
D ‘(2, 0)

Вопрос 7.
Треугольник XYZ имеет вершины X (6, -2,3), Y (7,5, 5) и Z (8, 4). При переводе X ′ имеет координаты (2,8, -1,3). Напишите правило, описывающее это преобразование. Затем найдите координаты Y ′ и Z ′.
Тип ниже:
____________

Ответ:
алгебраическое правило
(x, y) -> (x-3.2, y + 1)
новых координат
Y ‘(4.3, 6)
Z’ (4.8, 5)

Вопрос 8.
Точка L имеет координаты (3, -5). Координаты точки L ′ после отражения равны (-3, -5). Без графического представления укажите, поперек какой точки оси L отражалась. Поясните свой ответ.
____________

Ответ:
Точка L отразилась на оси ординат.
Когда вы отражаете точку поперек оси y, знак координаты x изменяется, а знак координаты y остается прежним

Вопрос 9.
Используйте правило (x, y) → (x — 2, y — 4) для построения графика изображения прямоугольника. Затем опишите трансформацию.

Тип ниже:
____________

Ответ:
Прямоугольник сдвинут на 2 единицы влево и на 4 единицы вниз

Вопрос 10.
Параллелограмм ABCD имеет вершины A (−2, −5 \ (\ frac {1} {2} \)), B (−4, −5 \ (\ frac {1} {2} \)) , С (-3, -2) и D (-1, -2). Найдите вершины параллелограмма A′B′C′D ′ после сдвига на 2 \ (\ frac {1} {2} \) единиц вниз.
Тип ниже:
__________

Ответ:
после перевода 2 \ (\ frac {1} {2} \) единиц
A ‘(- 2, -8)
B’ (- 4, -8)
C ‘(- 3, — 4 \ (\ frac {1} {2} \))
D ‘(- 1, -4 \ (\ frac {1} {2} \))

Алгебраические представления преобразований — стр.302

Вопрос 11.
Александра нарисовала логотип на миллиметровой бумаге толщиной в полдюйма. Напишите правило, описывающее перевод, который использовала Александра для создания тени на букве A.

Введите ниже:
__________

Ответ:
(x, y) -> (x + 1, y-0,5)
(x + 1, y-0,5) -> (x + 0,5, y-0,25)

Пояснение:
преобразование в единицах
(x, y) -> (x + 1, y-0.5)
На этом шаге правило преобразования преобразуется в единицы измерения в правило перевода в дюймах. (Разделите на 2, так как миллиметровая бумага — это полдюймовая бумага.
(x + 1, y-0,5) -> (x + 0,5, y-0,25)

Вопрос 12.
Воздушный змей KLMN имеет вершины в точках K (1, 3), L (2, 4), M (3, 3) и N (2, 0). После поворота воздушного змея K ‘имеет координаты (-3, 1). Опишите поворот и включите в описание правило. Затем найдите координаты L ′, M ′ и N ′.
Тип ниже:
__________

Ответ:
вращение
90 против часовой стрелки
правило
(x, y) -> (-y, x)
новые координаты
L ‘(- 4, 2)
M’ (- 3, 3)
N ‘(0 , 2)

ФОКУС НА МЫШЛЕНИЕ ВЫСШЕГО ПОРЯДКА

Вопрос 13.
Постройте гипотезу Изобразите треугольник с вершинами (-3, 4), (3, 4) и (-5, -5). Используйте преобразование (y, x), чтобы построить график его изображения.
а. Какая вершина изображения имеет те же координаты, что и вершина исходной фигуры? Объясните, почему это правда.

Тип ниже:
__________

Ответ:
(-5, 5) имеет те же координаты

Вопрос 13.
б. Каково уравнение прямой, проходящей через начало координат и эту точку?
Тип ниже:
__________

Ответ:
x и y равны, поэтому переключение x и y не влияет на координаты

Вопрос 13.
г. Опишите преобразование треугольника.
Тип ниже:
__________

Ответ:
x и y равны, поэтому переключение x и y не влияет на координаты

Вопрос 14.
Критическое мышление Митчелл говорит, что точка (0, 0) не изменяется при отражении по оси x или y или при вращении вокруг начала координат. Вы согласны с Митчеллом? Объясните, почему да или почему нет.
_______

Ответ:
Да, согласен с Mitchell

Пояснение:
Отражение поперек оси x или оси y меняет знак y или координаты x 0 не может менять знаки.
Вращение вокруг исходной точки не меняет исходную точку (0, 0)

Вопрос 15.
Анализ взаимосвязей Треугольник ABC с вершинами A (-2, -2), B (-3, 1) и C (1, 1) переводится как (x, y) → (x — 1, y + 3). Затем изображение, треугольник A′B′C ′, переводится как (x, y) → (x + 4, y — 1), в результате получается A ″ B ″ C ″.
а. Найдите координаты вершин треугольника A ″ B ″ C ″.
Тип ниже:
__________

Ответ:
A ”(- 2-1 + 4, -2 + 3-1) = A” (1, 0)
B ”(- 3-1 + 4, 1 + 3-1) = B” ( 0, 3)
C ”(1-1 + 4, 1 + 3-1) = C” (4, 3)

Вопрос 15.
г. Напишите правило для одного перевода, который отображает треугольник ABC в треугольник A ″ B ″ C ″.
Тип ниже:
__________

Ответ:
(x, y) -> (x-1 + 4, y + 3-1)
(x, y) -> (x + 3, y + 2)

Практика под руководством — Конгруэнтные числа — Стр. № 306

Вопрос 1.
Примените указанную серию преобразований к прямоугольнику. Каждое преобразование применяется к изображению предыдущего преобразования, а не к исходной фигуре. Обозначьте каждое изображение буквой примененного преобразования.

A. Отражение по оси y
B. Поворот на 90 ° по часовой стрелке вокруг исходной точки
C. (x, y) → (x — 2, y)
D. Поворот на 90 ° против часовой стрелки вокруг исходной точки
E. ( x, y) → (x — 7, y — 2)
Тип ниже:
__________

Ответ:
A. После преобразования
(1, 3)
(1, 4)
(4, 4)
(4, 3)
B. После преобразования
(3, -1)
(4, -1 )
(4, -4)
(3, -4)
C. После преобразования
(1, -1)
(2, -1)
(2, -4)
(1, -4)
D .После преобразования
(1, 1)
(1, 2)
(4, 2)
(4, 1)
E. После преобразования
(-6, -1)
(-6, 0)
(-3 , 0)
(-3, -1)

Определите последовательность преобразований, которые превратят фигуру A в фигуру C.

Вопрос 2.
Какое преобразование используется для преобразования фигуры A в фигуру B?
Тип ниже:
__________

Ответ:
Отражение по оси Y

Пояснение:
Отражение по оси Y используется для преобразования фигуры A в фигуру B

Вопрос 3.
Какое преобразование используется для преобразования фигуры B в фигуру C?
Тип ниже:
__________

Ответ:
Перевод 3 единицы вправо и 4 единицы вниз

Пояснение:
Преобразование на 3 единицы вправо и на 4 единицы вниз используется для преобразования рисунка B в рисунок C

Вопрос 4.
Какая последовательность преобразований используется для преобразования фигуры A в фигуру C? Выразите преобразования алгебраически.
Тип ниже:
__________

Ответ:
Отражение по оси Y используется для преобразования фигуры A в фигуру B
Преобразование на 3 единицы вправо и 4 единицы вниз используется для преобразования фигуры B в фигуру C
Алгебраически:
(x, y) -> (- х, у)
(х, у) -> (х +3, у-4)

Вопрос 5.
Словарь Что значит совпадение двух фигур?
Тип ниже:
__________

Ответ:
Две фигуры совпадают, если фигуры имеют одинаковый размер и форму.

ОБЯЗАТЕЛЬНЫЕ ВОПРОСЫ РЕГИСТРАЦИЯ

Вопрос 6.
Что верно в отношении первой и последней фигур после последовательности перемещений, отражений и вращений?
Тип ниже:
__________

Ответ:
После последовательности перемещений, отражений и вращений первая и последняя фигуры имеют одинаковый размер и форму.(Они совпадают)

9.5 Независимая практика — Конгруэнтные цифры — Стр. № 307

Для каждого заданного рисунка A графические рисунки B и C используют заданную последовательность преобразований. Укажите, одинаковую или разную ориентацию фигур A и C.

Вопрос 7.

Рисунок B: перемещение на 1 единицу вправо и на 3 единицы вверх
Рисунок C: поворот на 90 ° по часовой стрелке вокруг исходной точки
Тип ниже:
__________

Ответ:
Другая ориентация

Пояснение:

Другая ориентация

Вопрос 8.

Рисунок B: отражение поперек оси y
Рисунок C: поворот на 180 ° вокруг исходной точки
Тип ниже:
__________

Ответ:
Другая ориентация

Пояснение:

Другая ориентация

Вопрос 9.

Рисунок B: отражение поперек оси y
Рисунок C: перемещение на 2 единицы вниз
Тип ниже:
__________

Ответ:
Другая ориентация

Пояснение:

Другая ориентация

Вопрос 10.

Рисунок B: сдвиг на 2 единицы вверх
Рисунок C: поворот на 180 ° вокруг исходной точки
Тип ниже:
__________

Ответ:
Другая ориентация

Пояснение:

Другая ориентация

Конгруэнтные цифры — Стр. № 308

Вопрос 11.
Представляют проблемы реального мира Градостроитель хотел разместить новую городскую библиотеку на участке А. Мэр подумал, что будет лучше на участке Б. Какие преобразования были применены к зданию на участке А, чтобы переместить здание на сайт B? Мэр изменил размер или ориентацию библиотеки?

Тип ниже:
__________

Ответ:
От сайта A к сайту B: перевод 2 единицы вправо и 4 единицы вниз
Размер НЕ изменился
Ориентация изменилась

Вопрос 12.
Упорство в решении проблем Найдите последовательность из трех преобразований, которые можно использовать для получения фигуры D из рисунка A. Постройте график фигур B и C, созданных преобразованиями.

Тип ниже:
__________

Ответ:
От рисунка A до D:
Отражение по оси x (-1, -5) (-1, -6) (2, -5) (4, -6)
Поворот на 90 ° по часовой стрелке (4, -1) (5, -1) (5, -4) (4, -6)
перевод 6 единиц осталось (4, -1) (5, -1) (5, -4) (4, -6)

ФОКУС НА МЫШЛЕНИЕ ВЫСШЕГО ПОРЯДКА

Вопрос 13.
Контрпримеры Коммутативные свойства для сложения и умножения утверждают, что порядок сложения или умножения двух чисел не меняет сумму или произведение. Коммутативны ли переводы и повороты? Если нет, приведите контрпример.
________

Ответ:
Нет, сдвиг и повороты не коммутативны

Пояснение:
Точка (2, 2) становится (2, -4) при перемещении на 2 единицы вправо, а затем повороте на 90 вокруг начала координат.
Точка (2, 2) становится (4, -2) при повороте на 90 вокруг начала координат и смещении на 2 единицы вправо.
Два вышеуказанных пункта не совпадают.

Вопрос 14.
Множественные представления Для каждого представления опишите возможную последовательность преобразований.
а. (x, y) → (-x — 2, y + 1)
Тип ниже:
____________

Ответ:
смещение 2 единицы вправо и 1 единица вверх Отражение
по оси Y

Вопрос 14.
б. (x, y) → (y, -x — 3)
Тип ниже:
____________

Ответ:
поворот на 90º по часовой стрелке вокруг исходной точки
перемещение на 3 единицы вниз

Готовы к работе? — Модель викторины — Номер страницы.309

9.1–9.3 Свойства сдвигов, отражений и поворотов

Вопрос 1.
Постройте график изображения треугольника ABC после сдвига на 6 единиц вправо и на 4 единицы вниз. Обозначьте вершины изображения A ’, B’ и C ’.

Тип ниже:
____________

Ответ:
После перевода:
A ‘(2, 1)
B’ (2, -1)
C ‘(5, -1)

Вопрос 2.
На той же координатной сетке нанесите на график изображение треугольника ABC после отражения по оси x.Обозначьте вершины изображения A ”, B” и C ”.
Тип ниже:
____________

Ответ:
После размышлений:
A ”(- 4, -5)
B” (- 4, -3)
C ”(- 1, -3)

Вопрос 3.
Постройте график изображения HIJK после его поворота на 180 ° относительно начала координат. Обозначьте вершины изображения H’I’J’K ’.

Тип ниже:
____________

Ответ:
После вращения:
H ‘(0, -4)
I’ (0, -1)
J ‘(2, -2)
K’ (2, -3)

9.4 Алгебраические представления преобразований

Вопрос 4.
Треугольник имеет вершины в точках (2, 3), (−2, 2) и (−3, 5). Каковы координаты вершин изображения после перевода (x, y) → (x + 4, y — 3)?
Тип ниже:
____________

Ответ:
После перевода:
(6, 0)
(2, -1)
(1, 2)

9,5 Конгруэнтные числа

Вопрос 5.
Словарь Переводы, отражения и вращения производят фигуру, которая _____ к исходной фигуре.
Тип ниже:
____________

Ответ:
соответствует

Explanation:
Словарь При переводе, отражении и повороте получается фигура, соответствующая исходной фигуре.

Вопрос 6.
Используйте координатную сетку для упражнения 3. Отразите H’I’J’K ’над осью y, затем поверните его на 180 ° относительно начала координат. Обозначьте новую цифру H ″ I ″ J ″ K ″.
Тип ниже:
____________

Ответ:
после отражения
H ‘(0, -4)
I’ (0, -1)
J ‘(- 2, -2)
K’ (- 2, -3)
после поворота
H » (0, 4)
I ”(0, 1)
J” (2, 2)
K ”(2, 3)

ОСНОВНОЙ ВОПРОС

Вопрос 7.
Как можно использовать преобразования для решения реальных проблем?
Тип ниже:
____________

Ответ:
Трансформационные свойства позволяют систематически перемещать конгруэнтные фигуры, сохраняя или регулируя их ориентацию.

Выбранный ответ — Смешанный обзор — Стр. № 310

Вопрос 1.
Какой была бы ориентация фигуры L после перемещения на 8 единиц вправо и на 3 единицы вверх?

Опции:
а. А
б. B
c. C
г. D

Ответ:
c. C

Пояснение:
После перемещения на 8 единиц вправо и на 3 единицы вверх ориентация рисунка L остается прежней.

Вопрос 2.
Рисунок A отражается по оси Y и затем опускается на 6 единиц.Какая последовательность описывает эти преобразования?
Опции:
а. (x, y) -> (x, -y) и (x, y) -> (x, y — 6)
б. (x, y) -> (-x, y) и (x, y) -> (x, y — 6)
c. (x, y) -> (x, -y) и (x, y) -> (x — 6, y)
d. (x, y) -> (-x, y) и (x, y) -> (x — 6, y)

Ответ:
б. (x, y) -> (-x, y) и (x, y) -> (x, y — 6)

Пояснение:
отражение по оси Y:
(x, y) -> (-x, y)
Смещение на 6 единиц вниз
(x, y) -> (x, y-6)

Вопрос 3.
В каком квадранте оказался бы треугольник после поворота на 90 ° против часовой стрелки относительно начала координат?

Опции:
а. Я
б. II
г. III
г. IV

Ответ:
г. IV

Пояснение:
После поворота на 90 ° против часовой стрелки вокруг начала координат треугольник будет в QIV

.

Вопрос 4.
Какое рациональное число больше −3 \ (\ frac {1} {3} \), но меньше — \ (\ frac {4} {5} \)?
Опции:
а. −0,4
б. — \ (\ frac {9} {7} \)
с.−0,19
г. — \ (\ frac {22} {5} \)

Ответ:
б. — \ (\ frac {9} {7} \)

Вопрос 5.
Что из следующего не верно для трапеции, отраженной поперек оси x?
Опции:
а. Новая трапеция такого же размера, как и исходная трапеция.
г. Новая трапеция имеет ту же форму, что и исходная трапеция.
г. Новая трапеция имеет ту же ориентацию, что и исходная трапеция.
г. Координаты x новой трапеции такие же, как координаты x исходной трапеции.

Ответ:
г. Координаты x новой трапеции такие же, как координаты x исходной трапеции.

Пояснение:
Координаты x новой трапеции такие же, как координаты x исходной трапеции.

Вопрос 6.
Треугольник с координатами (6, 4), (2, −1) и (−3, 5) перемещается на 4 единицы влево и поворачивается на 180 ° относительно начала координат. Каковы координаты его изображения?
Опции:
а. (2, 4), (-2, -1), (-7, 5)
б.(4, 6), (-1, 2), (5, -3)
с. (4, -2), (-1, 2), (5, 7)
д. (-2, -4), (2, 1), (7, -5)

Ответ:
г. (-2, -4), (2, 1), (7, -5)

Вопрос 7.
Прямоугольник с вершинами (3, -2), (3, -4), (7, -2), (7, -4) отражается поперек оси x и затем поворачивается на 90 ° против часовой стрелки.
а. В каком квадранте лежит изображение?
____________

Ответ:
После отражения и поворота изображение лежит в QII

Вопрос 7.
б. Каковы вершины изображения?
Тип ниже:
____________

Ответ:
вершин изображения
(-2, 3)
(-4, 3)
(-2, 7)
(-4, 7)

Вопрос 7.
г. Какие еще преобразования дают такое же изображение?
Тип ниже:
____________

Ответ:
Отражение поперек оси y и вращение на 90º по часовой стрелке даст тот же результат.