Содержание
Какие задачи использует репетитор по математике на параллелограмм в 8 классе
Предлагаю Вашему вниманию страницы своей коллекции задач по геометрии для 8 класса. Это авторские номера, составлены мной собственноручно к рядовому уроку со средним (но способным) учеником. Репетитору по математике для разработки индивидуального урока.
Задачи репетитора на параллелограмм и свойство угла в 30 градусов.
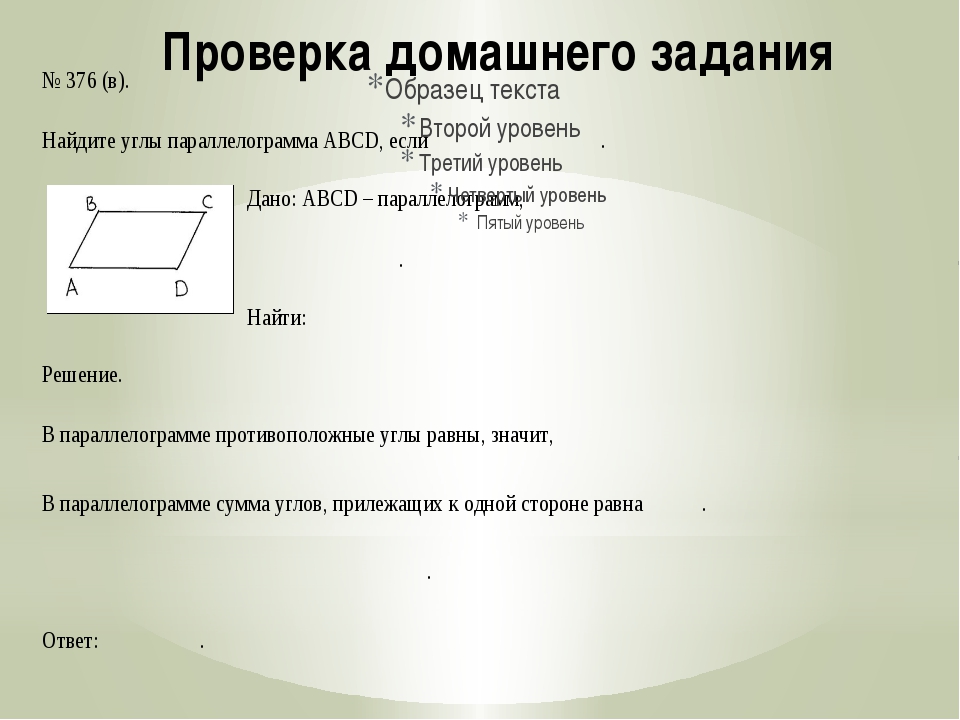
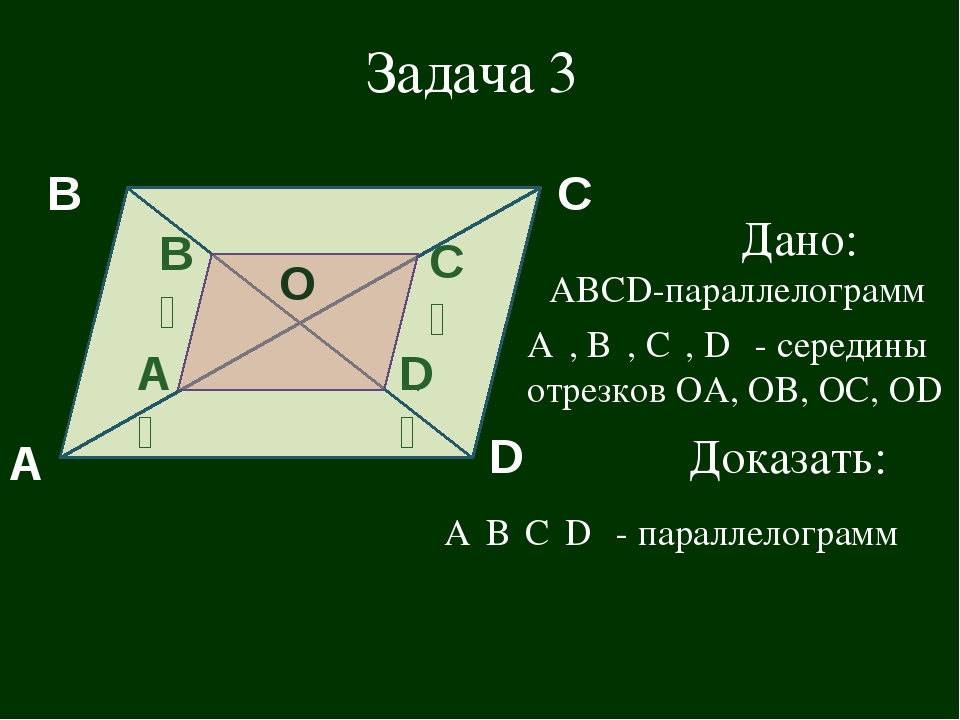
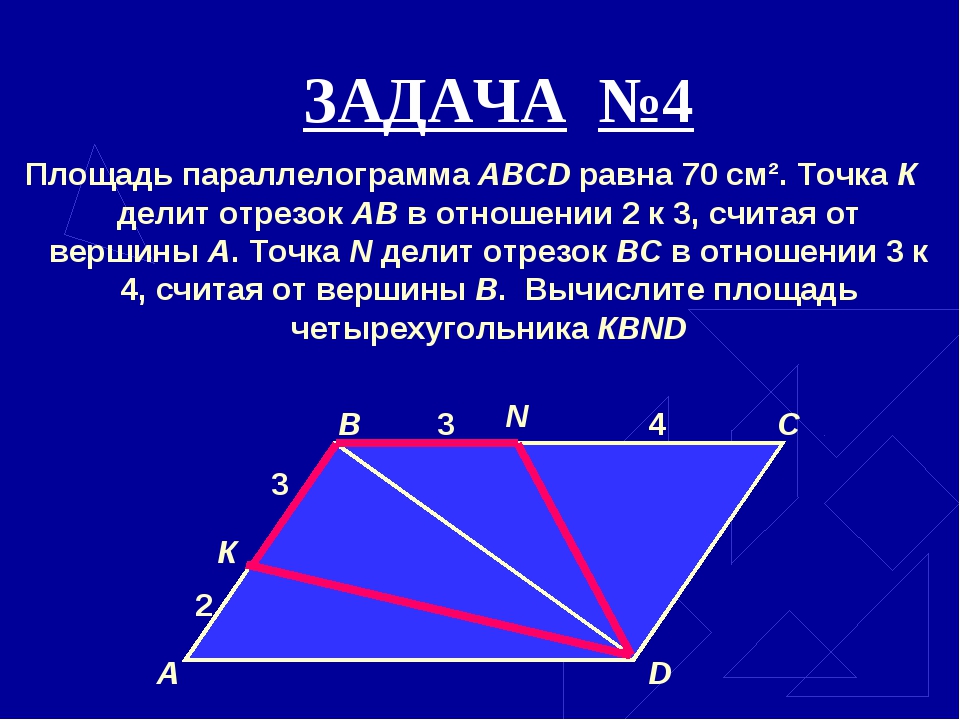
1) На стороне AB параллелограмма ABCD отмечена середина M. Найдите расстояние от M до AD, если и MC=10 см.
2) Точка P — середина стороны AD параллелограмма ABCD. Известно, что PC=8 см, . Найдите расстояние от P до стороны AB. Задача на дом.
Задачи на биссектрисы углов:
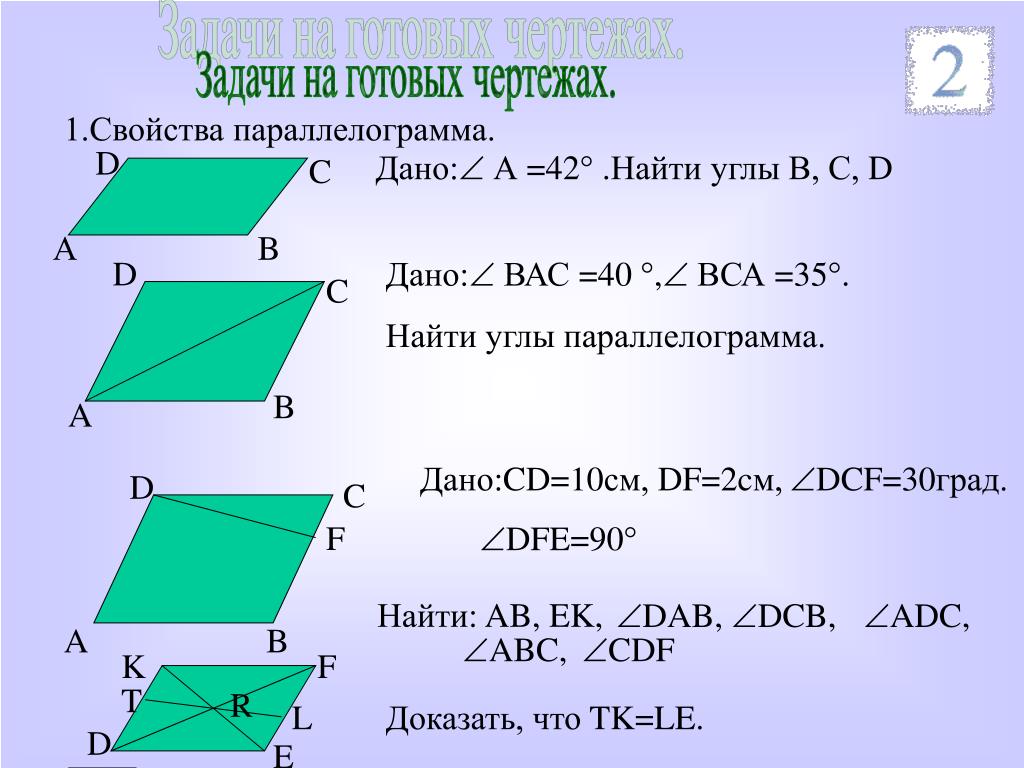
Точка М середина стороны BC параллелограмма ABCD, причем AM и DM — биссектрисы углов BAD и ADC. Найдите DM, если и BC=6 см.
2) На стороне AD параллелограмма ABCD отмечена точка N так, что BN и CN — биссектрисы его углов B и C. Известно, что BN=4 и AD=8см.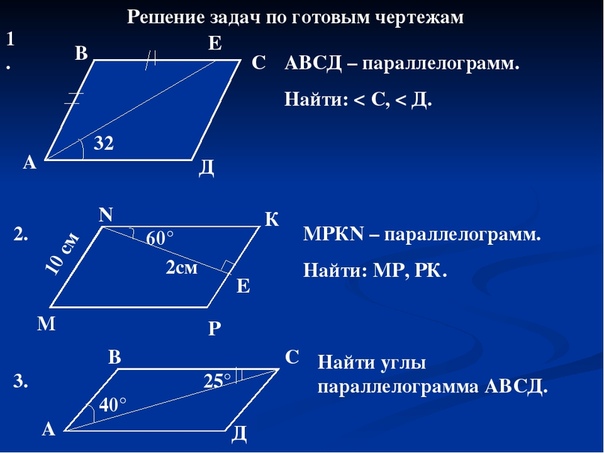 Найдите градусную меру угла А. (Обратная задача, составленная репетитором на биссектрисы ). Для домашней работы ученика.
Найдите градусную меру угла А. (Обратная задача, составленная репетитором на биссектрисы ). Для домашней работы ученика.
Репетитору по математике в копилку красивых задач на параллелограмм
На сторонах параллелограмма ABCD построены равносторонние треугольники BKC и AND. Докажите, что BKDN — параллелограмм.
Школьная математика (особенно геометрия) сильно ограничивает репетитора в варьировании простейшими объектами для составления с их участием комбинированных задач под конкретную учебную ситуацию. В начале 8 класса список пройденных теорем и понятий весьма невелик. Поэтому репетитор по математике всегда испытывает определенный недостаток в материале узкого назначения. Простые задачи — однотипные, а сложных не так много. Первые не дают развития, а последние доступны далеко не всем учащимся. Найди что-то интересное посередине — отличительная черта хорошего репетитора по математике. Недавно летом я попал ситуацию, когда со средним учеником 8 класса были перерешены все виды типовых номеров учебника и дидактических материалов (я не беру задачи — клоны).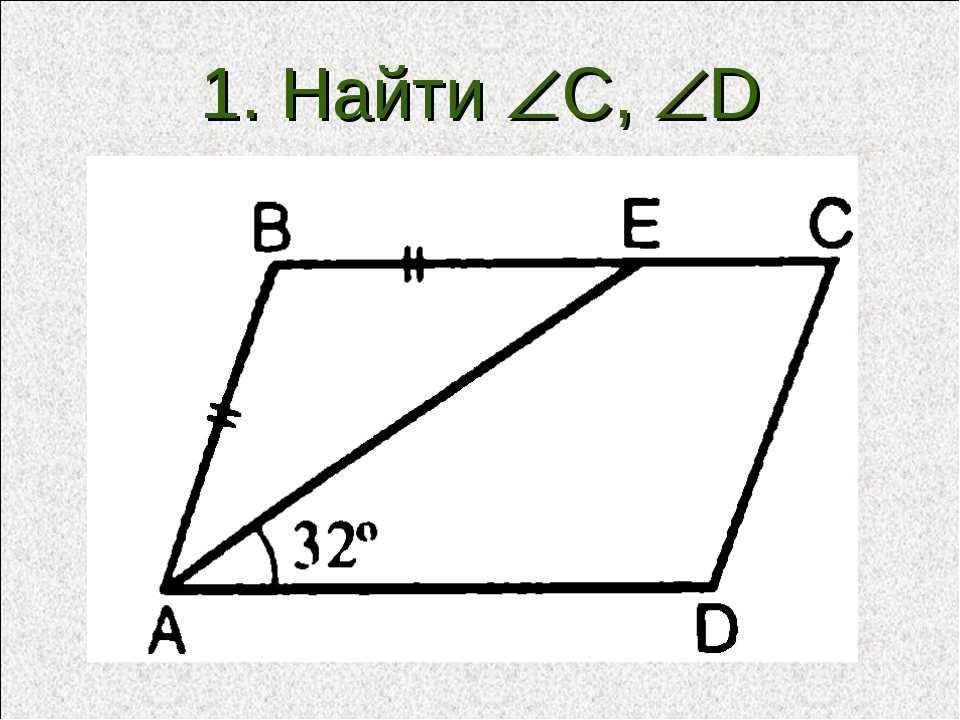 Пришлось составлять оригинальные упражнения. Причем к их подбору я всегда подхожу методически аккуратно и выдерживаю главное правило любого комплекта упражнений: если репетитор по математике разбирает на уроке какую-либо задачу, то аналогичная ей обязательно должна задаваться на дом.
Пришлось составлять оригинальные упражнения. Причем к их подбору я всегда подхожу методически аккуратно и выдерживаю главное правило любого комплекта упражнений: если репетитор по математике разбирает на уроке какую-либо задачу, то аналогичная ей обязательно должна задаваться на дом.
Задача, которая была представлена выше явилась результатом таких поисков. Для того, чтобы получить правильную домашнюю задачу на параллелограмм и треугольники репетитору по математике достаточно симметрично отобразить эти треугольники относительно сторон BC и AD. Вы видите их на рисунке справа. Нужно доказать, что BPDK — параллелограмм.
Как репетитор по математике растягивает задачи?
Как правило, любую задачу можно «дожать» или «растянуть», оптимизируя ее под конкретные цели повторения тех или иных теорем и формул. Я ругулярно комплектую задачи по геометрии несколькими пунктами в графе «докажите». В каждый номер с равносторонними треугольниками репетитору по математике можно посоветовать включить еще один пункт: докажите, что
Вы можете изучить рабочий листочек (план на урок) с этими задачами, который я обычно готовлю каждому ученику. Кликните на него и он откроется в отдельном окне. В него включены еще две задачи на биссектрисы внутренних и внешних углов параллелограмма.
Кликните на него и он откроется в отдельном окне. В него включены еще две задачи на биссектрисы внутренних и внешних углов параллелограмма.
Надеюсь, что репетиторам по базовой математике 8 класса пригодятся предоставленные материалы для работы со средним и даже сильным учеником. Удачного плана на урок!
Репетитор по математике в Москве ( м. Строгино ). А.Н. Колпаков
Решение задач по теме параллелограмм 8 класс
На прошлом уроке мы изучили параллелограмм. Вы узнали свойства и признаки параллелограмма. Сегодня мы обобщим наши знания по этой теме, отработаем навыки и умения решать задачи.
2
Вначале для успешной работы освежим в памяти наши знания. Какую фигуру называют параллелограммом?
Сколько параллелограммов изображено на рисунке? / 9 /
3
Вспомним свойства параллелограмма. Также вспомним графическую иллюстрацию данных свойств.
4
Устно решить по готовым чертежам. Первое задание найти периметр
а) 20
б) 14
5
Второе задание. Найти углы параллелограмма
а) 110 и 70
б) 110 и 70
6
Чему равен полупериметр? /10/
Вспоминаем неравенство треугольника: /каждая сторона треугольника меньше суммы длин других сторон/
значит /9/
7
Следующую задачу оформим в тетрадях. Запишите №1, сделайте чертёж.
Что неопределенно в этой задаче?
Как поступить в этом случае?
8
Проверяем ответы / 70 и 50 /
9
Задача вторая… Чертёж выполняем самостоятельно.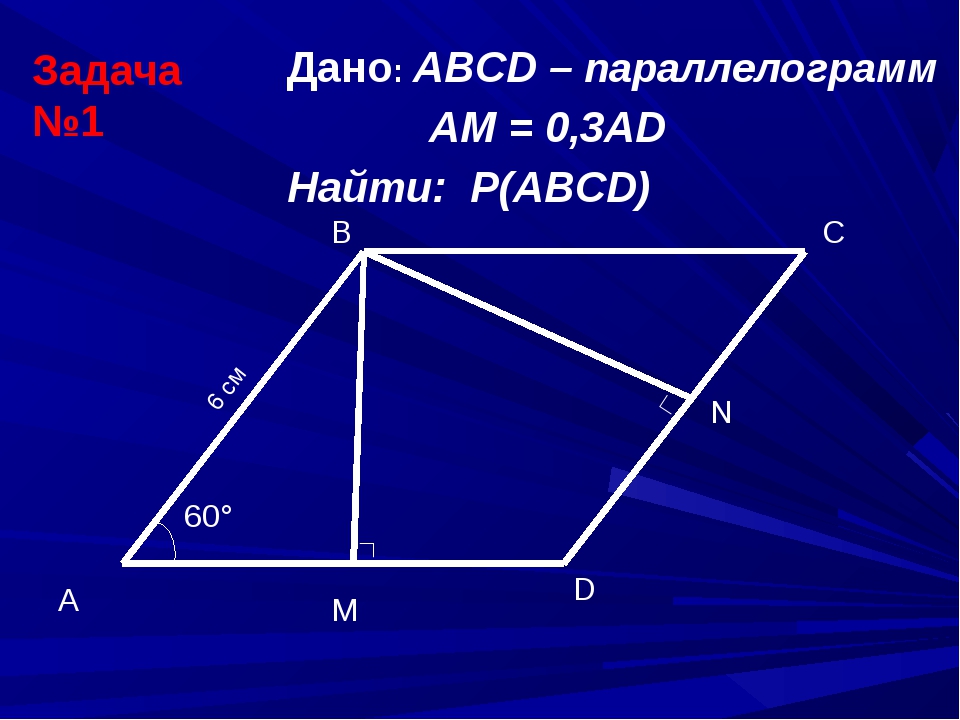
Давайте подумаем, может и здесь тоже несколько случаев?
Какой ещё чертёж можно начертить, следуя условиям задачи?
Решаем оба случая
В каком случае задача не имеет решения?
Почему? / Значит задача имеет одно решение / 3, 2, 3 /
Итак, как мы видим, при решении задач по геометрии необходимо разбирать все случаи.
10
Теперь вспомним признаки параллелограмма. По каким критериям можно сказать, что четырёхугольник является параллелограммом?
11
Устно доказать, что фигура параллелограмм и почему?
12
Ученики проговаривают решение устно, затем самостоятельно оформляют решение в тетради.
/ Проверка см. слайд 17/
13
И, наконец, обобщим наши знания признаков параллелограмма. №4. Сначала сформулируйте, условие задачи
№4. Сначала сформулируйте, условие задачи
Докажем, что четырёхугольник – параллелограмм разными способами:
по определению,
используя тот факт, что две стороны равны и параллельны,
противоположные стороны попарно равны.
1 способ: проговаривают, оформляют в тетради, проверка на экране
2 и 3 способы:
АВС = СDА по стороне и двум прилежащим углам
далее самостоятельно 1 вариант – по 1 признаку, 2 вариант – по 2 признаку; самопроверка в парах 2 минуты
14
№5 Вам предлагается выбрать два способа из четырёх предложенных и полностью самостоятельно оформить доказательство данной задачи двумя способами.
15
Подведём итоги:
Что нового узнали на уроке?
16
Задание на дом: п.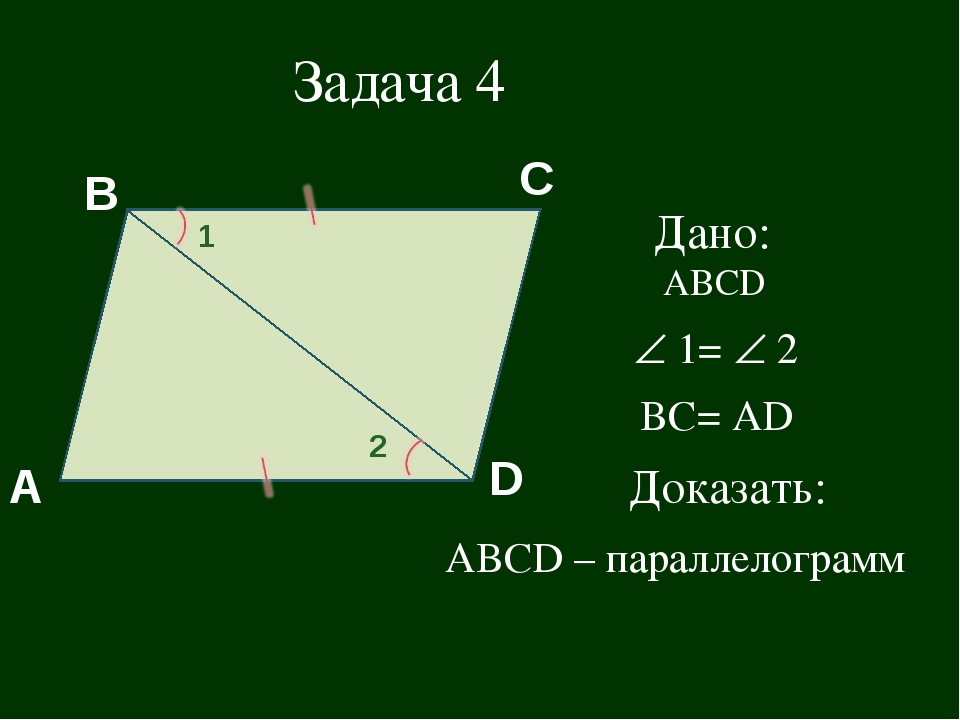 43 – 44 повторить теорию; № 376(д), 425, 429.
43 – 44 повторить теорию; № 376(д), 425, 429.
Задачи по геометрии параллелограмм. | Геометрия
Задачи по геометрии параллелограмм. | Геометрия — просто!
Добрый день, дорогие друзья!
Сегодня мы продолжим решение задач из сборника под редакцией М.И. Сканави.
И на этот раз мы будем решать задачи по геометрии параллелограмма.
Понятно, что прежде, чем приступать к решению таких задач, надо понимать, что такое параллелограмм и какие у него есть свойства.
Параллелограмм — выпуклый четырёхугольник, у которого противоположные стороны попарно параллельны.
У параллелограмма противоположные стороны и противоположные углы равны;
диагонали его делят параллелограмм на 2 равных треугольника,
а сами диагонали точкой пересечения делятся пополам.
И сумма углов, прилежащих к одной стороне параллелограмма, равна 180°.
Вот в основном те свойства, которые в первую очередь необходимы для понимания и решения задач по геометрии параллелограмма.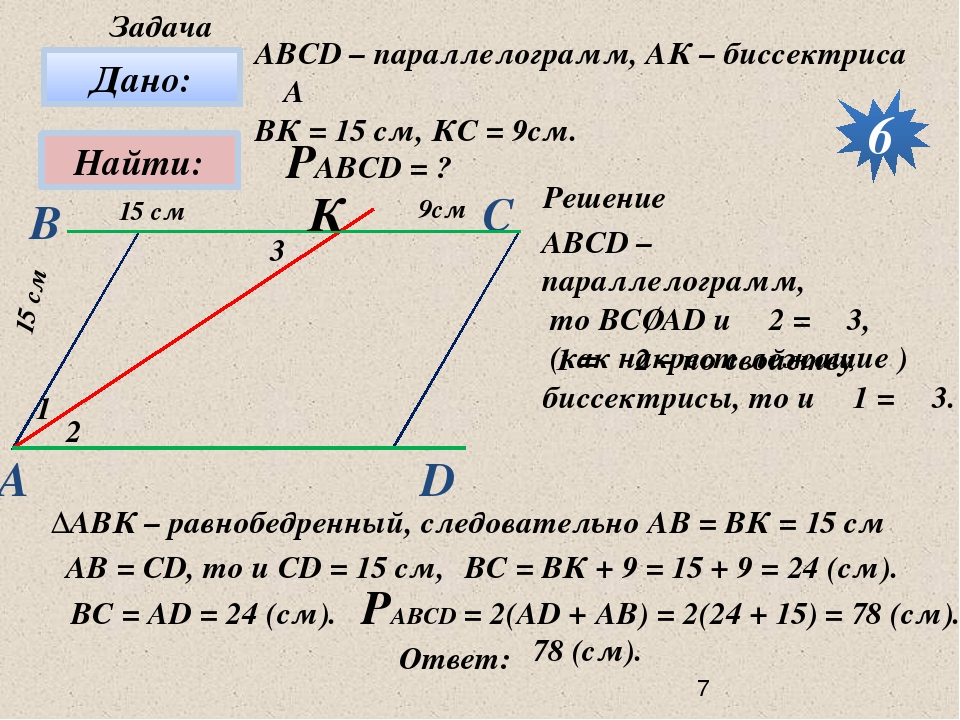 А теперь задачи.
А теперь задачи.
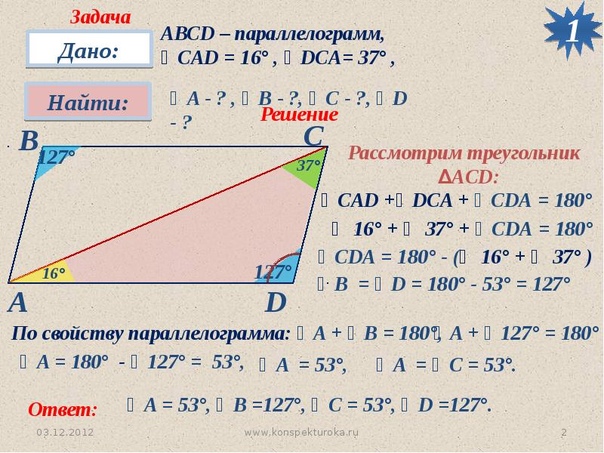
Задача 1. Периметр параллелограмма равен 90 см, а его острый угол равен 60°.
Диагональ параллелограмма делит его тупой угол на части в отношении 1:3. Найти стороны параллелограмма.
Решение: Если угол А равен 60°, то угол В, лежащий рядом с ним , будет равен 180-60=120°.
Но диагональ BD делит его в соотношении 1:3, или на 4 равные части.
Получается, что одной части принадлежит 120:4 = 30°.
Следовательно, диагональ BD делит угол В на 2 угла 30° и 90°.
По рисунку угол 1 — прямой. Треугольник ABD — прямоугольный.
И угол 2 в треугольнике равен 30º, как накрест лежащий при параллельных прямых AB и CD и секущей BD.
А мы знаем, что катет, лежащий против угла в 30°, равен половине гипотенузы. Получается, что АВ=1/2 AD.
Теперь составляем уравнение для периметра.
AB+BC+CD+AD=90
1/2AD+AD+1/2AD+AD= 90
3AD=90 AD=30 AB=1/2*30 = 15.
Ответ: стороны параллелограмма равны 30 см и 15 см.
Задача 2. Биссектриса острого угла параллелограмма делит его диагональ на отрезки длиной 3,2 см и 8,8 см.
Найти стороны параллелограмма, если его периметр равен 30 см.
Решение: Мы знаем, что биссектриса угла треугольника делит его противоположную сторону на отрезки, пропорциональные сторонам угла.
А именно, AB:AD = BO:OD, но BO и OD равны соответственно 3,2 см и 8,8 см.
Поэтому, можно принять, что АВ = 3,2х, а AD равно 8,8х.
Противоположные стороны параллелограмма равны.
Периметр это есть сумма всех сторон параллелограмма.
Составляем уравнение: 3,2х+8,8х+3,2х+8,8х = 30 24х = 30 х = 30/24 = 5/4.
Мы нашли коэффициент пропорциональности Х=5/4.
Отсюда, сторона АВ = 3,2х = 3,2 * 5/4 = 4 см.
Сторона AD равна 8,8х = 8,8 * 5/4 = 11 см.
Ответ: стороны параллелограмма равны 4 см, 4 см, 11 см, 11 см.
Задача 3. Параллелограмм с периметром 44 см разделён диагоналями на 4 треугольника.
Разность между периметрами двух смежных треугольников равна 6 см.
Найти стороны параллелограмма.
Решение: Рассмотрим два треугольника, лежащих выше диагонали d.
Периметр первого равен b+c+d.
Периметр второго равен a+c+d.
Разность периметров двух треугольников равна 6 см.
Составляем уравнение:
a+c+d — (b+c+d) = a+c+d-b-c-d = a-b = 6.
Получилось, что разность двух сторон параллелограмма равна 6 см.
Второе уравнение составляем из свойства периметра параллелограмма:
a+b+a+b = 44
2a+2b=44
a+b=22.
Получили систему двух уравнений с двумя неизвестными:
a — b = 6
a + b = 22 Решим её методом сложения. Сложим левые и правые части уравнений. Получим:
a — b + a + b = 6 + 22 2a = 28 a = 14.
a — b = 6 b = a — 6 = 14 — 6 = 8.
Ответ: Стороны параллелограмма равны 14 см, 14 см, 8 см, 8 см.
Задача 4. Перпендикуляр, опущенный из вершины параллелограмма на его диагональ, делит эту диагональ на отрезки АМ и МС длиной 6 см и 15 см соответственно.
Разность сторон параллелограмма равна 7 см.
Найти длины сторон и диагонали параллелограмма.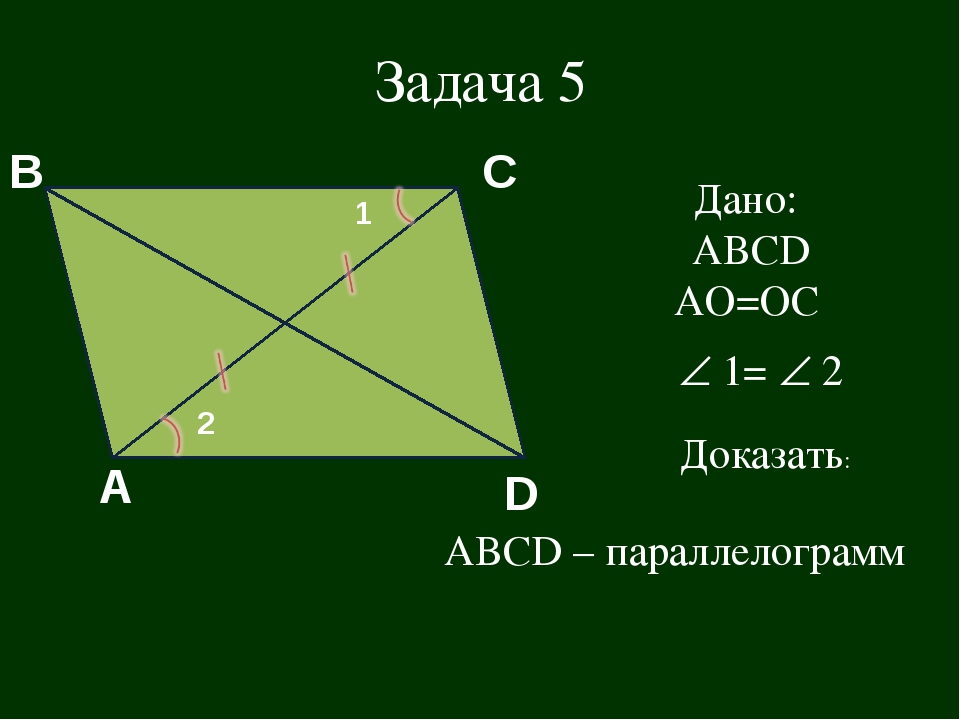
Решение: Примем сторону AB за a, сторону BC за b.
Из двух прямоугольных треугольников АВМ и ВМС выразим равный для них катет ВМ по теореме Пифагора.
АВ² — АМ² = ВС² — МС².
Подставляем вместо сторон известные выражения:
а² — 6² = b² — 15² или 15² — 6² = b² — а² (b — а) (b + а) = (15 — 6) (15 + 6),
но b — а = 7
7 (b + а) = 9 * 21 b + a = 9 * 3 = 27.
Имеем систему двух уравнений с двумя неизвестными, как в задаче 3.
b + a = 27
b — а = 7 Отсюда получаем 2b = 34 b = 17, a = 27 — 17 = 10.
Теперь, зная стороны параллелограмма, мы можем найти высоту ВМ.
ВМ² = 10² — 6² = 64. Отсюда ВМ = 8 см.
А теперь, из прямоугольного треугольника ВМО находим ВО.
ВМ = 8 см,
МО = АО — АМ = АС/2 — АМ = (6+15)/2 — 6 = 21/2 — 6 = 10,5 — 6 = 4,5 см.
По теореме Пифагора находим ВО.
ВО² = 8² + 4,5² = 64 + (9/2)² = 64 + 81/4 = 337/4. Или ВО = √337/2.
Поскольку BD в 2 раза больше, чем ВО, то её длина будет равна √337.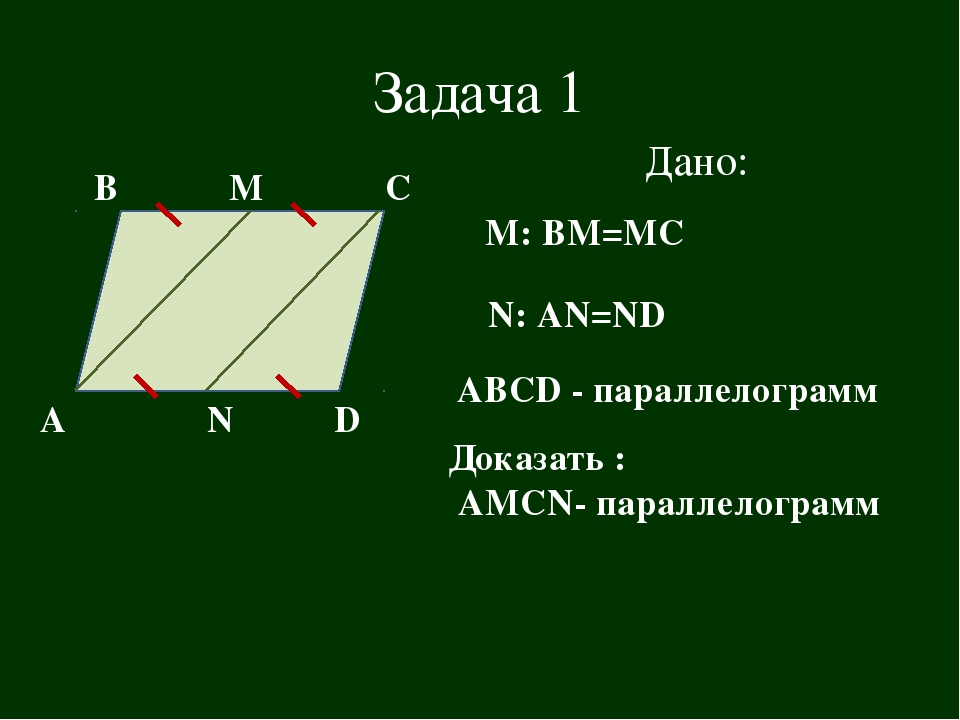
Ответ: Длины сторон параллелограмма 17 см, 17 см, 10 см, 10 см. Длина диагонали √337.
На сегодня всё. В следующий раз мы продолжим решение задач по геометрии из «Сборника для поступающих во ВТУЗы». Успехов!
Вам так же будет интересно:
Оставить комментарий
Самостоятельная работа по теме «Параллелограмм», ФГОС, УМК А. В. Погорелова
Самостоятельная работа по теме: «Параллелограмм»
Технологическая карта контрольно-измерительных материалов
Класс | 8 |
Предмет | Геометрия |
Учебник, по которому ведется преподавание | Геометрия. 2-е изд. — М.: Просвещение, 2014 |
Тема контроля | «Параллелограмм» |
Вид контроля | Текущий |
Форма и методы контроля | 1) по степени индивидуализации: индивидуальный; 2) по манере исполнения: письменный; 3) по способу подачи контролирующих заданий: самостоятельная работа. |
Тип контроля | Внешний |
Время контроля | 30 -35 минут |
Цель контроля | Проверить умения учащихся находить градусные меры углов параллелограмма, длину его сторон и периметр, используя при этом соответствующие свойства. |
Содержание контроля | Вид деятельности: Самостоятельная работа содержит 2 одноуровневых варианта. В каждом варианте 4 задачи на нахождение углов или сторон параллелограмма. Она направлена на проверку достижения уровня базовой подготовки учащихся, повторение и анализ основных фактов. С помощью этих заданий проверяется умение учащихся применять знания и умения при решении задач. Любой из вариантом можно использовать в качестве тренировочного. Тип деятельности: контролирующая работа. Форма деятельности: индивидуальная. |
Критерии оценивания | Для оценивания результатов выполнения работ учащихся применяется традиционная отметка («2», «3», «4» и «5»). Оценка знаний и умений учащихся: «5» -если верно выполнены 4 задания; «4»- если верно выполнены любые 3 задания; «3» — если верно выполнено любое 2 задания. |
Вариант 1
1.Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 50°. Найдите меньший угол параллелограмма.
2. В четырехугольнике ABCD ABǁ CD, BCǁ AD, AC=16см, BD=20см, AB=15см. Найдите периметр треугольника COD.
3. Периметр параллелограмма равен 60 дм, одна из сторон на 4 дм больше другой. Найдите эти стороны.
4. Из вершины D параллелограмма ABCD с острым углом А проведен перпендикуляр DН на прямую ВС; DН=С D:2. Найдите величины углов А,В.
Вариант 2
1.Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 50° и 85°. Найдите меньший угол параллелограмма.
2. В четырехугольнике ABCD ABǁ CD, BCǁ AD, периметр треугольника АОD равен 31дм, AC=14дм, BD=22дм. Найдите периметр треугольника BС.
3.Периметр параллелограмма равен 48 см, одна из сторон в 5 раза больше другой. Найдите эти стороны.
Найдите эти стороны.
4. Из вершины В параллелограмма ABCD с острым углом А проведен перпендикуляр ВК на прямую AD; АК=ВК. Найдите величины углов С, D.
Ответы
Вариант1 | Вариант2 | |
1 | 650 | 350 |
2 | 33см | 5дм |
3 | 13 дм, 17 дм | 4см, 20см |
4 | 300, 1500 | 450 ; 1350 |
Методическая разработка интегрированного урока геометрия+информатика по теме «Параллелограмм и его свойства»
Цель: открытие учащимися свойств параллелограмма в ходе эксперимента при работе в виртуальной среде «Живая математика»; применение свойств параллелограмма в ходе решения задач.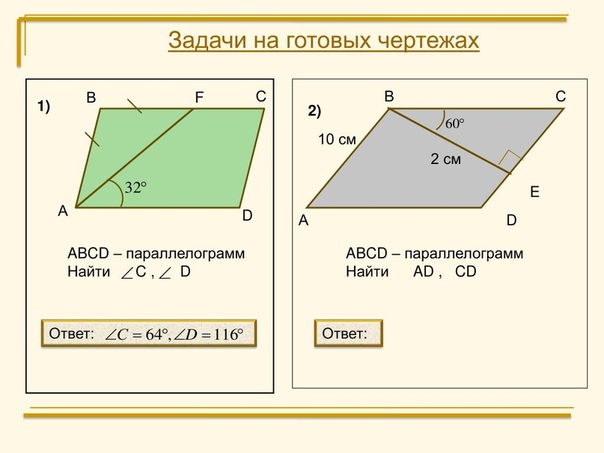
Оборудование:
- компьютер учителя;
- нетбуки для учащихся;
- мультимедийный проектор, экран;
- документ-камера,
- тетради на печатной основе по геометрии для 8 класса (у каждого учащегося).
Структура урока:
- Организационный момент.
- Постановка цели урока.
- Актуализация знаний учащихся в ходе проверки домашней работы.
- Решение задач на готовых чертежах с целью подготовки к изучению нового материала (устно).
- Изучение нового материала, экспериментальная работа.
- Закрепление изученного материала в ходе решения задач в рабочих тетрадях на печатной основе.
- Постановка домашнего задания.
- Подведение итогов урока.
Ход урока
1. Организационный момент
Проверяется подготовленность классного помещения и готовность учащихся к уроку.
2. Постановка целей урока
Данный урок является уроком изучения нового материала по теме «Параллелограмм и его свойства».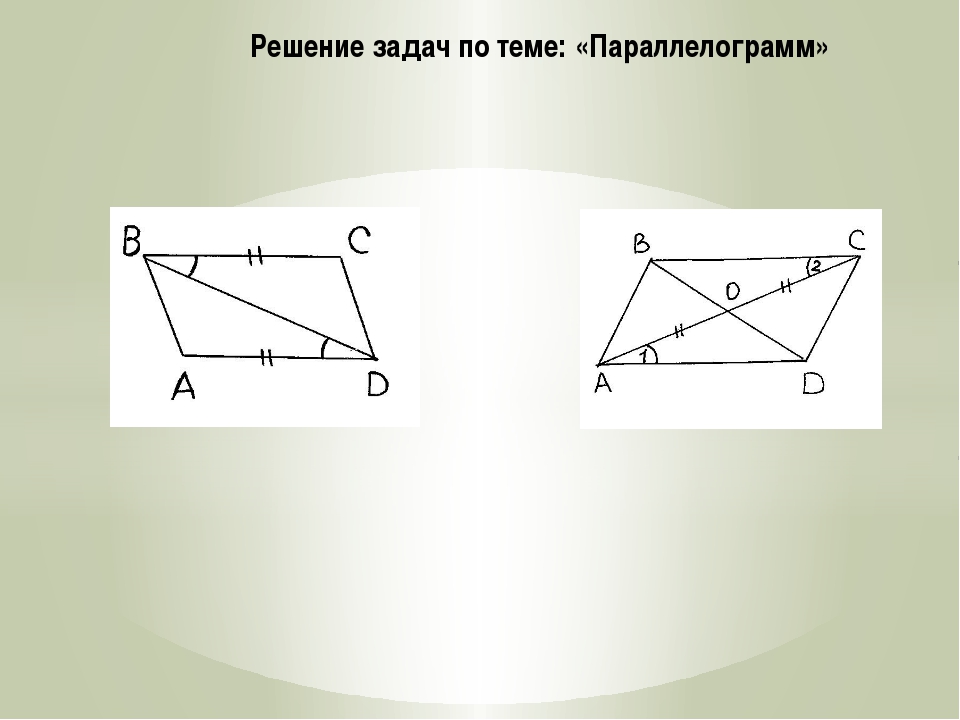 На уроке в ходе исследовательской работы в виртуальной среде «Живая математика» учащиеся экспериментально выводят свойства параллелограмма. А также приобретают практические навыки применения знаний по теме в стандартных условиях в ходе решения задач в рабочих тетрадях на печатной основе.
На уроке в ходе исследовательской работы в виртуальной среде «Живая математика» учащиеся экспериментально выводят свойства параллелограмма. А также приобретают практические навыки применения знаний по теме в стандартных условиях в ходе решения задач в рабочих тетрадях на печатной основе.
3. Актуализация знаний учащихся в ходе проверки домашней работы
Решение задач домашней работы проверяется с помощью документ-камеры.
4. Решение задач на готовых чертежах с целью подготовки к изучению нового материала (устно)
Учащиеся решают устно задачи на готовых чертежах (чертежи заранее заготовлены на доске).
Работа проводится с целью подготовки к изучению нового материала. Учащимся дается 1-2 минуты на обдумывание задачи, а затем заслушиваются различные варианты решений, обсуждается, какое из решений наиболее верное, рациональное.
Задачи
- Дано: АВ || CD, BC || AD (рисунок 1)
Доказать: ВС = АD, - Дано АВ || CD, AB = CD (рисунок 2)
Доказать: О – середина AC и BD.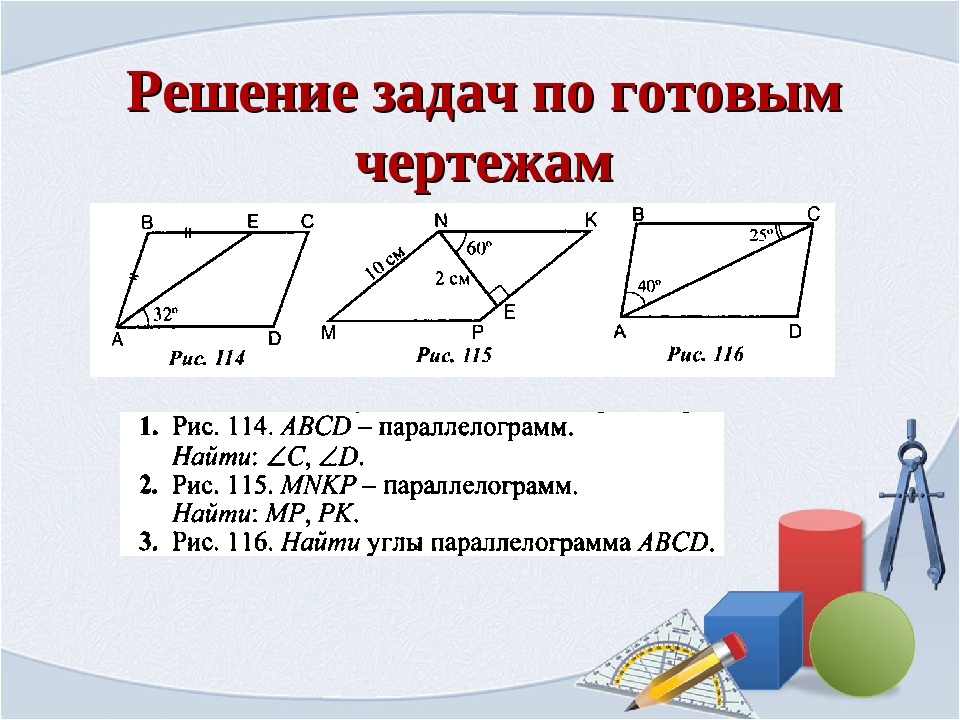
5. Изучение нового материала, экспериментальная работа
Учащиеся работают с нетбуками в виртуальной среде «Живая математика».
- Вводится понятие параллелограмма.
- Исследовательская работа в виртуальной среде «Живая математика», в ходе которой учащиеся экспериментально выводят свойства параллелограмма. Они производят измерения отрезков и углов с помощью инструментария программы «Живая математика». Учащиеся сопровождают решение каждой задачи анализом того, насколько формулируемые ими положения выдерживают вариации исходных элементов чертежей, полученных из исходных, с помощью команды Анимация.
- Первый этап: учащиеся измеряют стороны фигуры с помощью выбора вкладки Измерения горизонтального меню.
- Второй этап: воспользовавшись командой Анимация (меню Вид) учащиеся наблюдают, анализируют и делают выводы, каким образом меняются измеренные ими величины. Учитель контролирует правильность умозаключений и формулировок свойств параллелограмма, предложенных учащимися.
- Далее учащиеся работают в виртуальной среде «Живая математика», следуя четко инструкции, записанной справа на каждом слайде презентации в программе под руководством учителя (выполняя первый и второй этапы). Смотри Приложение 1.
6. Закрепление изученного материала в ходе решения задач в рабочих тетрадях на печатной основе.
Задачи № 8, 9, 10 учащиеся решают самостоятельно, затем один из учащихся читает свое решение, остальные проверяют свое решение, исправляют ошибки отвечающего.
Задача № 8
В параллелограмме ABCD найдите: а) стороны, если ВС на 8 см больше стороны АВ, а периметр равен 64 см; б) углы, если
Решение.
а) По свойству параллелограмма АВ = CD, ВС = АD и . По условию РABCD = 64 см, следовательно, 2 (АВ + ВС) = 64 см, откуда АВ + ВС = 32 см, но ВС на 8 см больше АВ, поэтому АВ + АВ + 8 см = 32 см, откуда АВ = 12 см, ВС = 12 см + 8 см = 20 см.
б) По условию , а так как , то
Задача № 9
В параллелограмме АВСD диагональ АС, равная 24 см, образует со стороной АD угол в 30о, о – точка пересечения диагоналей АС и ВD, . Найдите длину отрезка ОЕ.
Решение.
Диагонали параллелограмма точкой пересечения делятся пополам, поэтому АО = ОС = 12 см. Треугольник AOE – прямоугольный с гипотенузой АО и острым углом А, равным 30°. Поэтому катет ОЕ, лежащий против угла в 30о, равен ½ АО, т.е. ОЕ = ½ * 12 см = 6 см.
Ответ: 6 см.
Задача №10.
Биссектриса угла АВ параллелограмма АВСD пересекает сторону ВС в точке Р, причем ВР = РС. Найдите стороны параллелограмма, если его периметр равен 54 см.
Решение.
- , так как луч АР – биссектриса угла А, , так как эти углы накрест лежащие при пересечении параллельных прямых AD и ВС секущей АР.
 Следовательно, .
Следовательно, . - Треугольник АВР – равнобедренный, так как его углы 1 и 3 равны, поэтому АВ = ВР.
- По условию ВР = РС, следовательно, ВС = 2 * ВР = 2 * АВ.
Итак, Р ABCD = 2(АВ + 2 * АВ) = 6 * АВ.
Так как периметр параллелограмма равен 54 см, то 6 * АВ = 54 см, откуда АВ = 9 см и ВС = 18 см.
Ответ: АВ = DC = 9 см.
ВС = AD = 18 см.
7. Постановка домашнего задания
Домашнее задание находится на столах учащихся на листах с напечатанными на них готовыми чертежами (смотри Приложение 2).
8. Подведение итогов урока
Учитель: «Итак, изучением какой темы мы с вами занимались на сегодняшнем уроке? А чем конкретно мы занимались, и что нам дал этот урок?»
Сообщаются оценки учащимся, отвечавшим на уроке.
Решение задач по теме «Параллелограмм».
 8-й класс
8-й класс
Тип урока: урок обобщения и систематизации.
Цели.
Предметные: систематизировать знания
параллелограмме.
Личностные: развивать навыки
самостоятельной работы, эмоциональной сферы,
анализа своей работы.
Метапредметные: умение самостоятельно
определять цели своего обучения, ставить и
формулировать для себя новые задачи в учёбе и
познавательной деятельности.
Планируемые результаты: учащийся научится
решать задачи разного уровня сложности на
применение свойств и признаков параллелограмма
из материалов ГИА.
Основные понятия: параллелограмм, его
определение, свойства и признаки.
Организационная структура урока
| Этапы проведения урока | Форма организации УД | Задания для учащихся,
выполнение которых приведёт к достижению запланированных результатов | ||
| Презентация | Приложения | Учебник | ||
1. Организационный этап Организационный этап | ||||
| 2. Постановка цели и
задач урока. Мотивация учебной деятельности учащихся | ||||
| 3. Актуализация знаний | ф | Слайд 1 | Повторение свойств и признаков
параллелограмма | |
| 4. Проверка домашнего задания | Ф | Слайды 2 и 3 | Приложение 1. | №372(в), № 376(в) |
| 5. Контроль и коррекция знаний | И | Слайд 4 (ответы) | Приложение 2. (текст) (текст) | Тест |
| 6. Повторение | Ф | Слайды 5 и 6 | Приложение 3. | |
| В группах | Слайды 7, 8, 9 | Приложение 3. | ||
| 7. Рефлексия учебной
деятельности на уроке | Я сегодня научился решать
задачи на применение свойств и признаков параллелограмма | |||
| 8. Информация о домашнем
задании | Слайд 10 | № 375, № 376(б) | ||
Приложение 1
Приложение 2
Приложение 3
Литература
- Атанасян Л.
 С., Бутузов В.Ф. и др. Геометрия.
С., Бутузов В.Ф. и др. Геометрия.
Учебник для 7-9 классов. М.: Просвещение, 2012 г. - Атанасян Л.С., Бутузов В.Ф. и др. Рабочая тетрадь
по геометрии для 8 класса. М.: Просвещение, 2013 г. - Ершова А.П., Голобородько В.В. Устные проверочные
и зачётные работы по геометрии для 7-9 классов. М.:
Илекса, 2004 г. - Контрольно-измерительные материалы. Геометрия:
8 класс / Сост. Н.Ф. Гаврилова. М.: ВАКО, 2011 г. - Ольховская Л.С., Коннова Е.Г., Резникова Н.М.
Геометрия. 8-й класс. Рабочая тетрадь:
учебно-методическое пособие. Под редакцией
Ф.Ф.Лысенко, С.Ю.Кулубухова. Ростов-на-Дону:
Легион, 2012. (ГИА-9) - Рабинович Е.М. Задачи и упражнения на готовых
чертежах. 7-9 классы. Геометрия. – М.: Илекса, 1999 г. - Семёнов А.Л. ГИА: 3000 задач с ответами по
математике. Все задачи части 1. – М.: Издательство
“Экзамен”, 2013 г.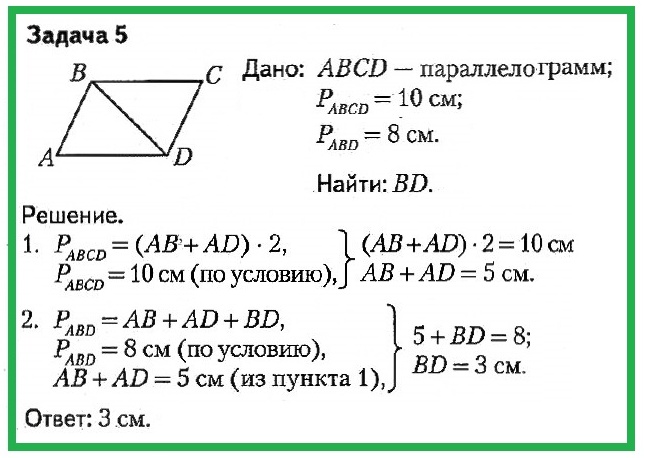
- Варианты ОГЭ по математике 2014 года.
- Материалы конкурса “Открытый урок”
издательского дома “Первое сентября”.
Четырехугольники. Параллелограмм. Геометрия 8 класс
30.11.2012
www.konspekturoka.ru
1
– четырехугольник,
у которого противоположные
стороны попарно параллельны.
В
С
А
30.11.2012
D
www.konspekturoka.ru
2
Если в задаче дано, что
четырехугольник –
параллелограмм,
то можно использовать
свойства параллелограмма.
Если в задаче нужно доказать,
что четырехугольник является
параллелограммом,
то применяют один из признаков
параллелограмма.
В
1
С
А
D
В параллелограмме противоположные
стороны равны и противоположные
углы равны.
30.11.2012
www.konspekturoka.ru
5
В
2
С
О
А
D
Диагонали параллелограмма делятся
точкой пересечения пополам.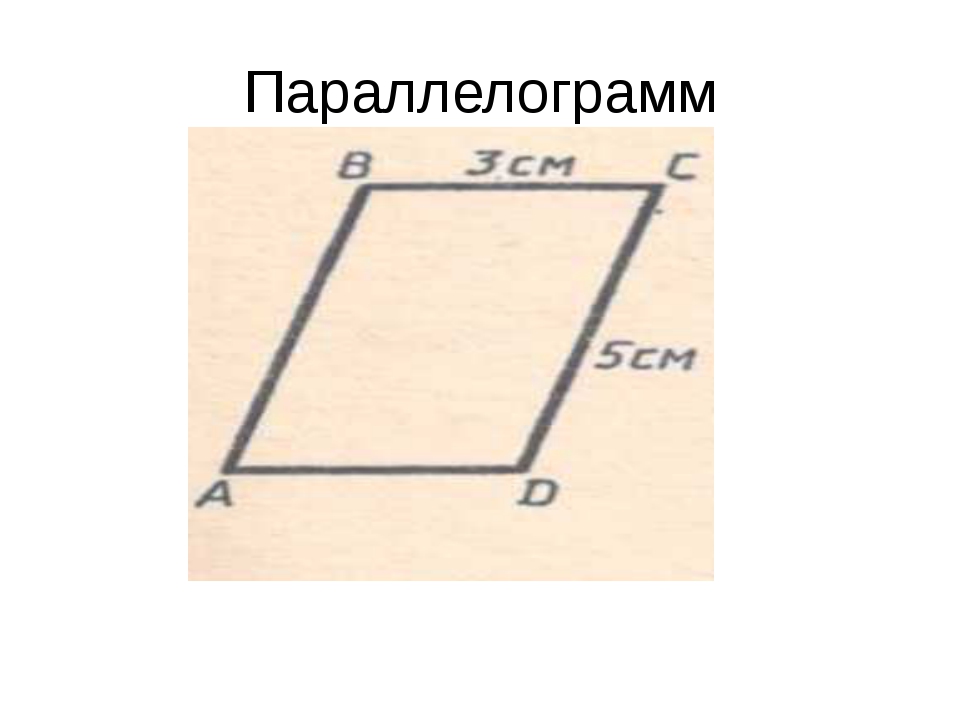
30.11.2012
www.konspekturoka.ru
6
В
С
3
А
D
В параллелограмме сумма углов, прилежащих
к одной стороне, равна 180°.
30.11.2012
www.konspekturoka.ru
7
Свойства параллелограмма
В
А
F
N
К
С
D
4. Сумма смежных углов равна
5.Биссектриса угла отсекает от него равнобедренный
треугольник.
перпендикулярны.
6.Биссектрисы соседних углов
7.Биссектрисы противоположных углов параллельны или
совпадают.
1
Признаки параллелограмма
Если в четырехугольнике две стороны равны и
параллельны, то этот четырехугольник
параллелограмм.
Если в четырехугольнике противоположные
стороны попарно равны, то этот четырехугольник
— параллелограмм.
3
Если в четырехугольнике диагонали пересекаются
и точкой пересечения делятся пополам, то этот
четырехугольник параллелограмм.
9
Параллелограмм –
это
четырехугольник
многоугольник
у которого
противоположные
стороны попарно
параллельны.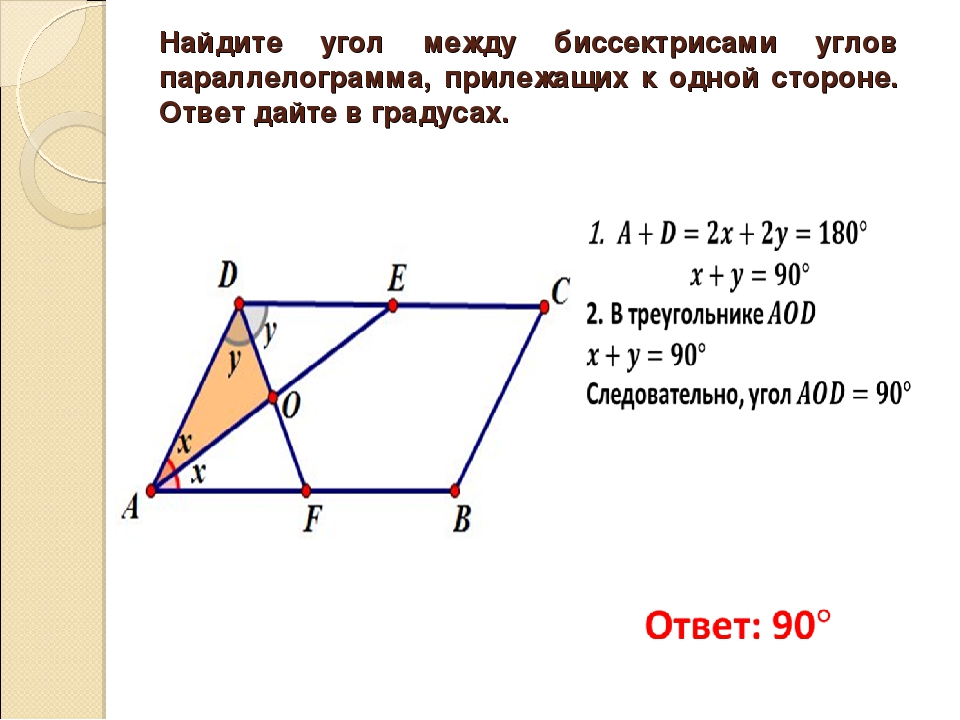
равны.
11. Задача 1
Дано: ABCD –
параллелограмм
Найти: CBА
Задача 1
B
C
4
1
2
A
75°
3
D
К
12. Задача 2
Дано: ABCD –
параллелограмм
Найти: C и D
Задача 2
Е
B
30°
A
D
C
13. Задача 3
Дано: ABCD –
параллелограмм
Найти: АD и DС
Задача 3
B
C
60°
2 см
Е
A
D
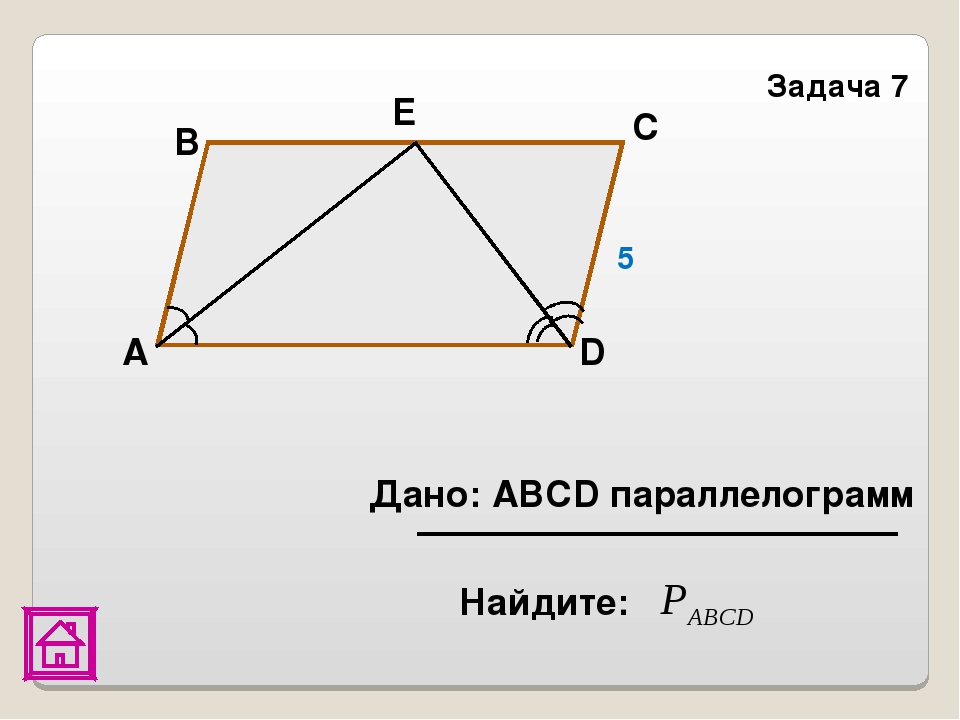
14. Задача 4
B
Дано: ABCD –
параллелограмм
Найти: РАВСD
Е
C
5 см
A
D
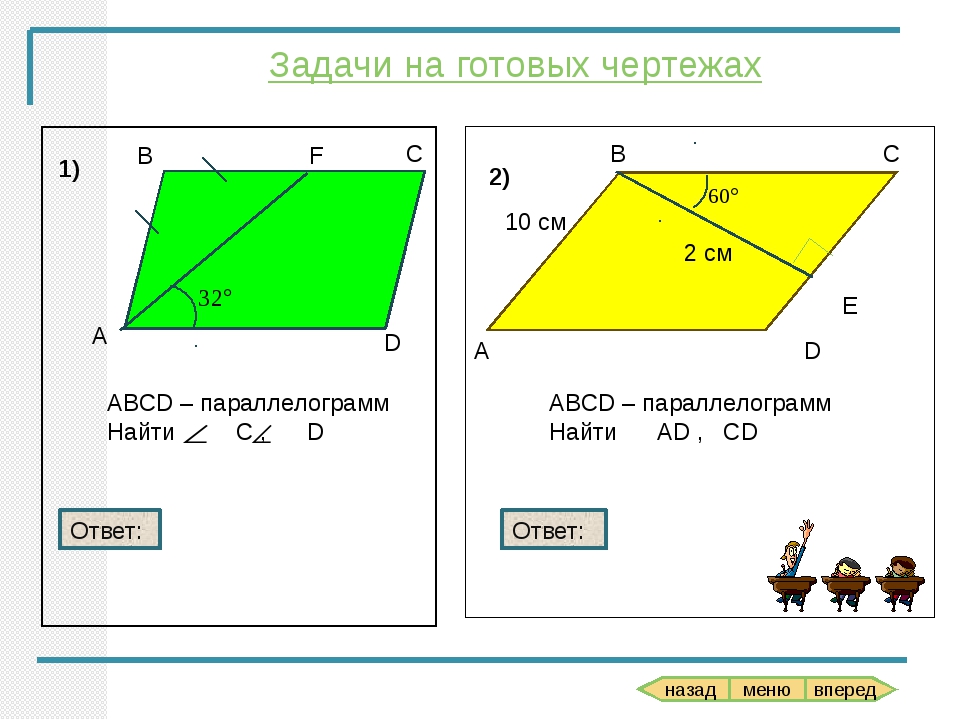
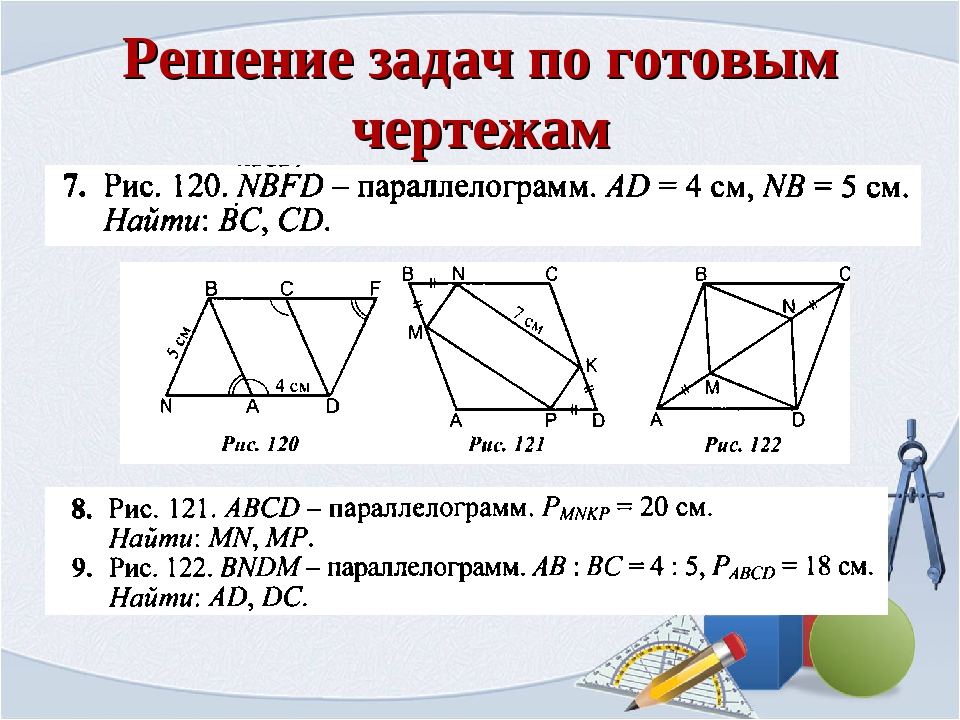
Задачи на готовых чертежах
В
1)
С
F
В
2)
С
60
10 см
2 см
32
А
E
D
ABCD – параллелограмм
Найти C , D
Ответ:
А
D
ABCD – параллелограмм
Найти
AD , CD
Ответ:
Задачи на готовых чертежах
В
F
С
25
60
С
40
N
А
2 см
M
E
3 см
D
NMCF – параллелограмм
Найти все углы NMCF
ABCD – параллелограмм
Найти PABCD
Ответ:
Ответ:
Задачи на готовых чертежах
В
С
F
В
С
E
60
M
5 см
F
N
А
4 см
M
NBCM – параллелограмм
Найти BF, FM
Ответ:
А
K
ABCD – параллелограмм
PABCD
= 20 cм
Найти ME, MK
Ответ:
D
Восьмиугольник в параллелограмме.
 Сможете ли вы решить эту задачу о геометрии для 8-го класса из России? — Помните о своих решениях
Сможете ли вы решить эту задачу о геометрии для 8-го класса из России? — Помните о своих решениях
Из каждого угла параллелограмма нарисуйте два отрезка линии, чтобы соединить угол с серединами противоположных сторон. Эти восемь отрезков линии ограничивают восьмиугольник. Каково отношение площади восьмиугольника к площади параллелограмма?
Эта задача была дана восьмиклассникам в России для поступления в отборную среднюю школу, но я признаю, что она поставила меня в тупик! Проблема также была представлена только текстом.Но для начала приведу следующую цифру.
Сможете разобраться? Попробуйте решить проблему, а когда будете готовы, посмотрите видео, чтобы найти решение.
Я благодарю Майкла К. за отправку проблемы и решение, представленное в видео.
Сможете ли вы решить эту ТРУДНУЮ задачу о геометрии для 8-го класса из России? Октагон в параллелограмме
Или продолжайте читать.
.
.
«Все будет хорошо, если вы будете использовать свой разум для принятия решений, и думать только о своих решениях. «С 2007 года я посвятил свою жизнь тому, чтобы делиться радостью теории игр и математики. MindYourDecisions теперь имеет более 1000 бесплатных статей без рекламы благодаря поддержке сообщества! Помогите и получите ранний доступ к сообщениям с обещанием на Patreon.
«С 2007 года я посвятил свою жизнь тому, чтобы делиться радостью теории игр и математики. MindYourDecisions теперь имеет более 1000 бесплатных статей без рекламы благодаря поддержке сообщества! Помогите и получите ранний доступ к сообщениям с обещанием на Patreon.
.
.
.
.
.
.
M
I
N
D
.
Y
O
U
R
.
D
E
C
I
S
I
O
N
S
P
U
Z
Z
L
E
.
.
.
.
Ответ восьмиугольника в параллелограмме
Есть много способов подойти к проблеме. Один из подходов, связанных с высшей математикой, выглядит следующим образом.
Примените аффинное преобразование (линейное преобразование плюс возможное смещение вектора), чтобы преобразовать всю фигуру так, чтобы параллелограмм стал единичным квадратом в начале координат. Отношение площадей инвариантно относительно аффинных преобразований, поэтому мы можем найти соотношение восьмиугольника в единичном квадрате, и это будет тот же ответ, что и исходная задача.
Существует несколько методов решения восьмиугольника в квадрате в CAS Musings.
Это самое простое решение, которое я нашел: Google отображает восьмиугольник в квадрате.
Есть также несколько методов для решения проблемы в Cut The Knot, но большинство из них зависит от следующего факта: центроид треугольника (где пересекаются медианы) делит каждую медиану в соотношении 2: 1.
Но восьмиклассник определенно не знает об аффинных преобразованиях и может не знать о медианах и центроидах (в Америке геометрию обычно преподают в 9 или 10 классах).
Итак, как восьмикласснику решить эту задачу? Майкл К. придумал замечательное решение, которое зависит только от схожих форм и знания площади треугольника (или трапеции). Этим концепциям обязательно учат в 8-м классе.
Ключ в том, чтобы увидеть узор похожих форм.
Решение
Проблема была отправлена мне по электронной почте Майклом К., который также разработал решение.
Пусть p будет площадью параллелограмма, а x будет площадью восьмиугольника.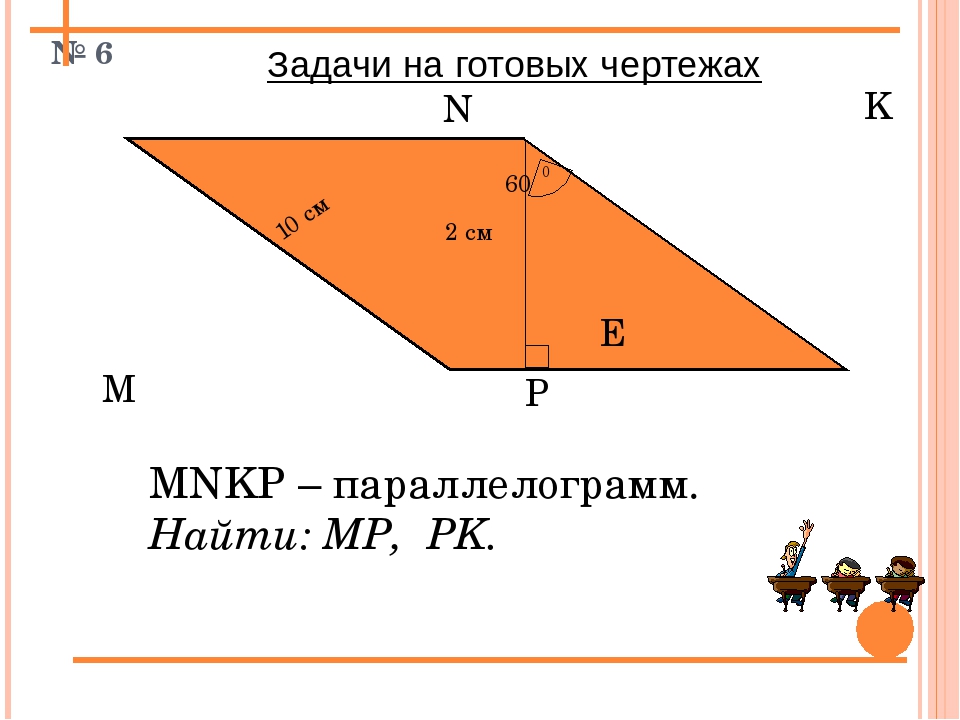 Мы хотим найти x / p .
Мы хотим найти x / p .
Соедините середины противоположных сторон параллелограмма. Это делит восьмиугольник на 4 области равной площади ( x /4), а также параллелограмм на 4 меньших параллелограмма с площадью p /4.
Повторите шаги в правом верхнем параллелограмме еще раз: соедините середины противоположных сторон. Затем повторите для левого нижнего маленького параллелограмма: соедините середины противоположных сторон.
(Для лучшей графики, пожалуйста, посмотрите видео, в котором я также делаю анимацию, чтобы показать «масштабирование» в меньшие области: Октагон в задаче параллелограмма )
В итоге мы разделим четверть восьмиугольника на четыре области
— небольшой параллелограмм площадью p /64 (мы увеличили в три раза 1/4)
— две области с трапециями, которые имеют площадь (3/4) ( p /64) (трапеция площадь малого параллелограмма за вычетом треугольника площадью 1/4 малого параллелограмма)
— одна область, которая является увеличенной копией четверти восьмиугольника! Эта область масштабируется на 1/4 два раза, поэтому ее площадь составляет (1/4) (1/4) ( x /4) = x /64.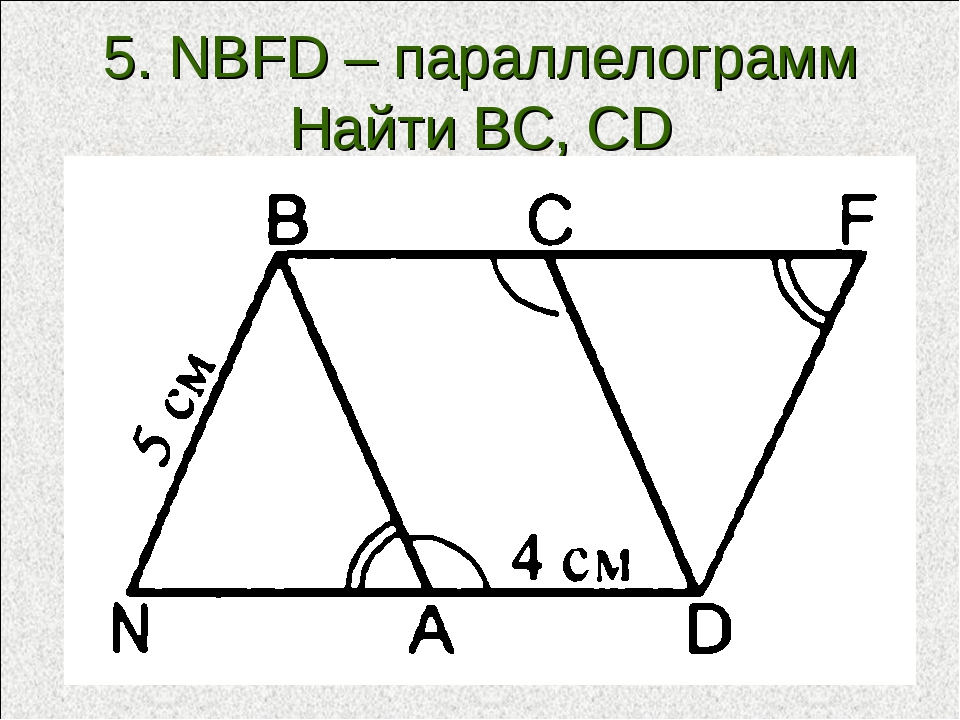 (Для строгости вы можете доказать подобие четверти восьмиугольника (фигура в форме воздушного змея). Один из способов — соединить нижний левый угол с верхним правым углом, чтобы разделить фигуру на треугольники, и вы можете доказать, что треугольники малого и большого воздушного змея похожи.)
(Для строгости вы можете доказать подобие четверти восьмиугольника (фигура в форме воздушного змея). Один из способов — соединить нижний левый угол с верхним правым углом, чтобы разделить фигуру на треугольники, и вы можете доказать, что треугольники малого и большого воздушного змея похожи.)
Мы можем сложить эти площади, чтобы найти площадь четверти восьмиугольника. И мы также знаем, что площадь составляет x /4. Таким образом, мы приравниваем выражения, чтобы получить:
x /4 = p /64 + 2 (3/4) p /64 + x /64
Мы можем решить это, чтобы найти:
x / p = 1/6
Удивительно! Площадь восьмиугольника составляет 1/6 площади параллелограмма.
Как мы решили для параллелограмма, тот же результат применим для любого параллелограмма (включая ромбы, прямоугольники и квадраты).
Другое решение, использующее симметрию
Я получил очень хорошую рецензию Боба Корнса, в которой используется симметрия форм, доступная в Документах Google:
https://docs. google.com/document/d/1tututTqcCr -VEkAieAyQPX5-tTIlSaD5kit8zo7KFpY / edit? Usp = sharing
google.com/document/d/1tututTqcCr -VEkAieAyQPX5-tTIlSaD5kit8zo7KFpY / edit? Usp = sharing
Еще одно очень простое решение
Я также получил это видео решение от Реувена Бар Йехуды, которое очень хорошо объяснено:
https: // youtu.be / OUC5u7neHQs
Источники и решения для восьмиугольника в квадрате
Cut The Knot (1): * Диаграммы находятся в апплете (заблокированы большинством браузеров), поэтому трудно найти решения, но осторожно читатель может пройти через это!
https://www.cut-the-knot.org/Curriculum/Geometry/OctagonInParallelogram.shtml
Cut The Knot (2): * Диаграммы находятся в апплете (заблокированы большинством браузеров), поэтому их сложно понять есть решения, но внимательный читатель сможет с этим справиться!
https: // www.cut-the-knot.org/Curriculum/Geometry/OctagonByOverlap.shtml
Math StackExchange восьмиугольник в квадрате
https://math.stackexchange.com/questions/978384/area-of-octagon-constructed-in-a-square
Восьмиугольник CAS Musings в квадрате, компиляция
https://casmusings.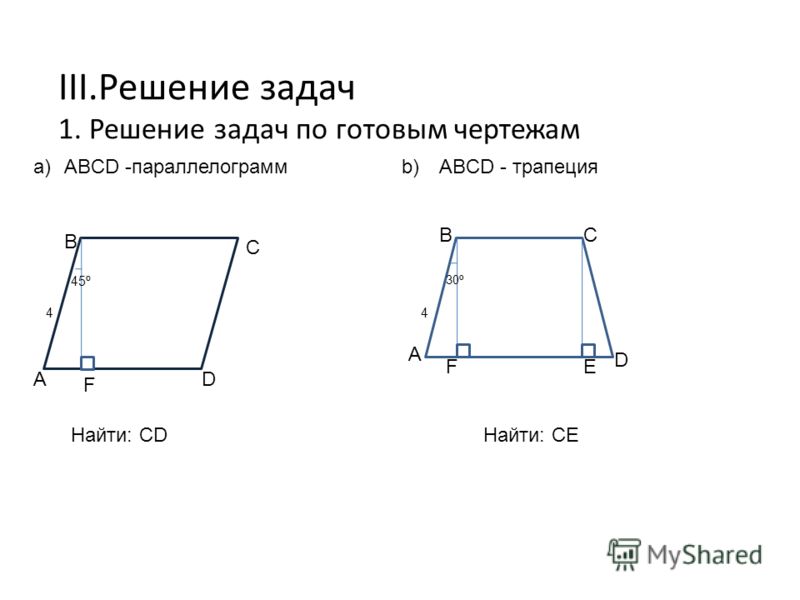 wordpress.com/2014/11/13/squares-and-octagons-a-compilation/
wordpress.com/2014/11/13/squares-and-octagons-a-compilation/
Восьмиугольник CAS Musings в квадратном тригонометрическом решении
https: // casmusings .wordpress.com / 2014/11/08 / squares-and-octagons /
Восьмиугольник FiveTriangles в квадратном решении 1
https: // docs.google.com/document/d/1AvrWFOf1TeUhaJPFDJLh3BNCKu2QLSIsorjngJ6JoB0/edit#heading=h.kmcbdznv9nix
FiveTriangles восьмиугольника в квадратном растворе 2
https://docs.google.com/document/d/1MHSp0RFVHBUQLPmLpXeSvd_jiJKF3-EdTJxIaxlnJBo/edit#heading=h. 5k5c3iq9cfjy
Восьмиугольник Дэвида Рэдклиффа в квадратном решении
http://gotmath.com/doc/octagon.pdf
Восьмиугольник Майка Лоулера в квадратном решении
https://twitter.com/mikeandallie/status/531765555754446848/photo/1
Восьмиугольник CoMaC в квадратных аналогичных треугольниках
http: // apfstatic.s3.ap-south-1.amazonaws.com/s3fs-public/14-comac_alternate-solution-octagon-problem.pdf
МОИ КНИГИ
Если вы совершите покупку по этим ссылкам, я могу получить компенсацию за покупки, сделанные на Amazon.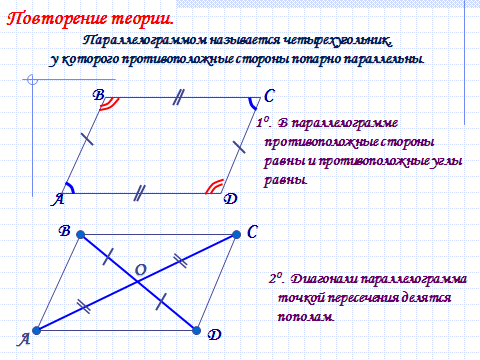 Как партнер Amazon я зарабатываю на соответствующих покупках. Это не влияет на цену, которую вы платите.
Как партнер Amazon я зарабатываю на соответствующих покупках. Это не влияет на цену, которую вы платите.
(ссылки для США и других стран)
https://mindyourdecisions.com/blog/my-books
Mind Your Decisions — это сборник из 5 книг:
(1) The Joy of Game Theory: An Introduction to Strategic Мышление
(2) 40 парадоксов в теории логики, вероятностей и игр
(3) Иллюзия иррациональности: как принимать разумные решения и преодолевать предвзятость
(4) Лучшие уловки мысленной математики
(5) Умножать числа, рисуя линии
Радость теории игр показывает, как можно использовать математику, чтобы перехитрить своих конкурентов.(рейтинг 4,2 / 5 звезд в 194 отзывах)
40 Парадоксов в логике, вероятности и теории игр содержит наводящие на размышления и противоречащие интуиции результаты. (рейтинг 4/5 звезд в 29 обзорах)
Иллюзия иррациональности: как принимать разумные решения и преодолевать предвзятость — это руководство, в котором объясняются многие способы предвзятого отношения к принятию решений и предлагаются методы принятия разумных решений. (рейтинг 3.9 / 5 звезд в 16 отзывах)
(рейтинг 3.9 / 5 звезд в 16 отзывах)
Лучшие уловки в области умственной математики учит, как можно выглядеть математическим гением, решая задачи в уме (оценка 4.2/5 звезд в 54 обзорах)
Умножение чисел на рисование линий Эта книга представляет собой справочное руководство для моего видео, которое набрало более 1 миллиона просмотров о геометрическом методе умножения чисел. (рейтинг 4,1 / 5 звезд в 22 обзорах)
Mind Your Puzzles представляет собой сборник из трех книг «Математические головоломки», тома 1, 2 и 3. Темы головоломок включают математические предметы, включая геометрию, вероятность и т. д. логика и теория игр.
Math Puzzles Volume 1 содержит классические головоломки и загадки с полными решениями задач счета, геометрии, вероятности и теории игр.Том 1 получил оценку 4,4 / 5 звезд в 72 отзывах.
Math Puzzles Volume 2 — это продолжение книги с более серьезными задачами. (рейтинг 4,2 / 5 звезд в 20 отзывах)
Math Puzzles Volume 3 — третий в серии.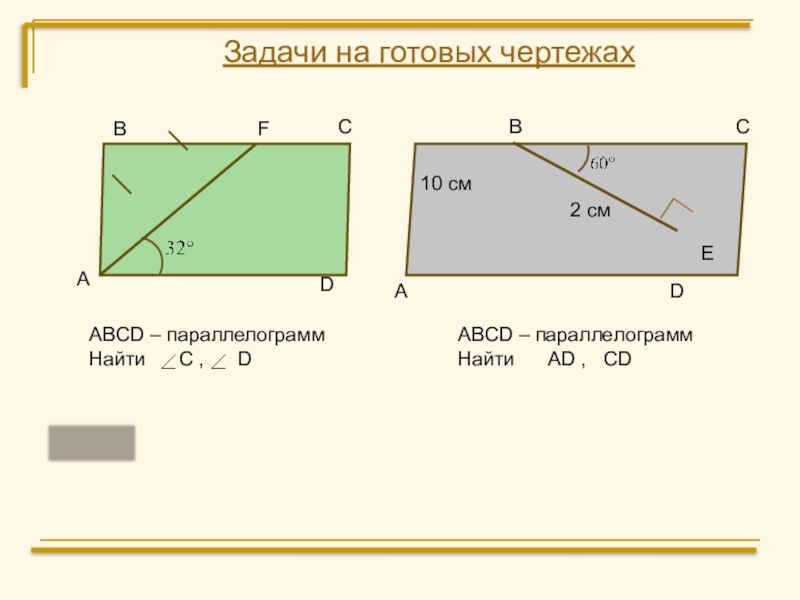 (рейтинг 4,2 / 5 звезд по 16 отзывам)
(рейтинг 4,2 / 5 звезд по 16 отзывам)
KINDLE UNLIMITED
Учителя и студенты со всего мира часто пишут мне о книгах. Поскольку образование может иметь такое огромное влияние, я стараюсь сделать электронные книги доступными как можно шире по как можно более низкой цене.
В настоящее время вы можете читать большинство моих электронных книг с помощью программы Amazon Kindle Unlimited. Включив подписку, вы получите доступ к миллионам электронных книг. Вам не нужно устройство Kindle: вы можете установить приложение Kindle на любой смартфон / планшет / компьютер и т. Д. Ниже я собрал ссылки на программы в некоторых странах. Пожалуйста, проверьте свой местный веб-сайт Amazon, чтобы узнать о доступности и условиях программы.
США, список моих книг (США)
Великобритания, список моих книг (Великобритания)
Канада, результаты книги (CA)
Германия, список моих книг (DE)
Франция, список моих книг (FR)
Индия , список моих книг (IN)
Австралия, результаты книги (AU)
Италия, список моих книг (IT)
Испания, список моих книг (ES)
Япония, список моих книг (JP)
Бразилия, книга results (BR)
Mexico, book results (MX)
MERCHANDISE
Купите кружку, футболку и многое другое на официальном сайте товаров: Mind Your Decisions at Teespring .
Параллелограмм
(переход к области параллелограмма или периметру параллелограмма)
Параллелограмм — это плоская форма, противоположные стороны которой параллельны и равны по длине.
| и || показать равные стороны
| Противоположные стороны параллельны | |
Противоположные стороны равны по длине | |
| Противоположные углы равны (углы «а» совпадают, а углы «б» такие же) | |
| Углы «a» и «b» в сумме составляют 180 °, поэтому они являются дополнительными углами. |
Играть с параллелограммом:
ПРИМЕЧАНИЕ. Квадраты, прямоугольники и ромбы — это все
Параллелограммы!
Пример:
Параллелограмм , в котором все углы прямые — это прямоугольник !
Площадь
параллелограмма
Площадь равна основанию , умноженному на высоту : Площадь = b × h ( h находится под прямым углом к b ) |
Пример: параллелограмм с основанием 6 м и высотой 3 м.
 Какова его площадь?
Какова его площадь?
Площадь = 6 м × 3 м = 18 м 2
Периметр параллелограмма
Периметр — это расстояние по краям.
Периметр составляет в 2 раза больше (основание + длина стороны) : Периметр = 2 (ш + с) |
Пример: у параллелограмма основание 12 см и длина стороны 6 см. Каков его периметр?
Периметр = 2 × (12 см + 6 см) = 2 × 18 см = 36 см
Диагонали параллелограмма
Диагонали параллелограмма делят друг друга пополам.
Другими словами, диагонали пересекаются на полпути.
Внутри любой четырехугольник
А в любом четырехугольнике есть параллелограмм.
Что такое параллелограмм? [Определение, факты и пример]
Что такое параллелограмм?
Параллелограмм — это особый тип четырехугольника, у которого равные и параллельные противоположные стороны.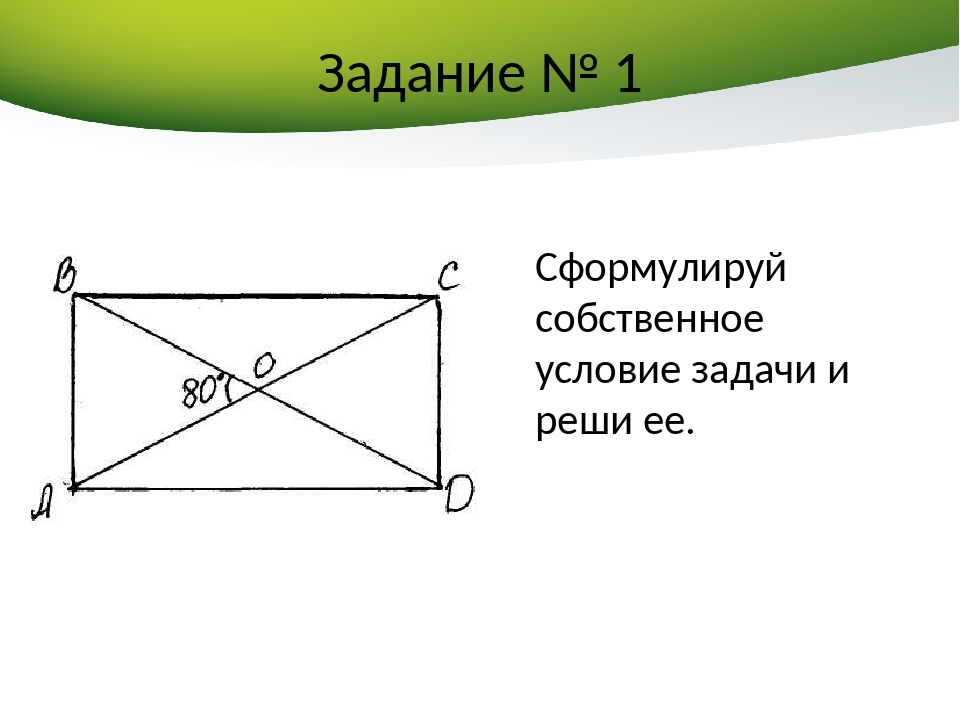
На данном рисунке показан параллелограмм ABCD, который как AB параллелен CD, а AD параллелен BC.
Также AD = BC и AB = CD.
Мы также видим множество параллелограммов, похожих на формы и объекты, вокруг нас.
Свойства параллелограмма
Противоположные стороны параллелограмма параллельны друг другу. Здесь AB ∥ CD и AD ∥ BC | |
Противоположные стороны параллелограмма равны по длине. Здесь AB = CD и AD = BC | |
Противоположные углы параллелограмма равны по меру. Здесь угол A = угол C и Угол B = Угол D. | |
Смежные углы параллелограмма в сумме составляют 180 ° Здесь угол A + угол B = 180 ° Угол B + Угол C = 180 ° Угол C + Угол D = 180 ° Угол D + Угол A = 180 ° | |
Диагонали параллелограмма делят друг друга пополам. Здесь AC и BD пересекают друг друга пополам. |
Виды параллелограмма
Есть три особых типа параллелограмма.
1. Ромб : параллелограмм, у которого все стороны равны.
Здесь AB = BC = CD = DA. ABCD — ромб.
2. Прямоугольник : параллелограмм, в котором все углы прямые и диагонали равны.
Здесь все углы прямые. Диагонали PN и OM равны.
3. Квадрат : параллелограмм со всеми равными сторонами и всеми углами, равными 90 градусам. Диагонали квадрата также равны.
Здесь все стороны равны и все углы прямые.
Диагонали AC и BD равны.
Интересные факты
|
Параллелограммы — математика для старших классов
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно
или несколько ваших авторских прав, сообщите нам об этом, отправив письменное уведомление («Уведомление о нарушении»), содержащее
то
информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как
в виде
ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т.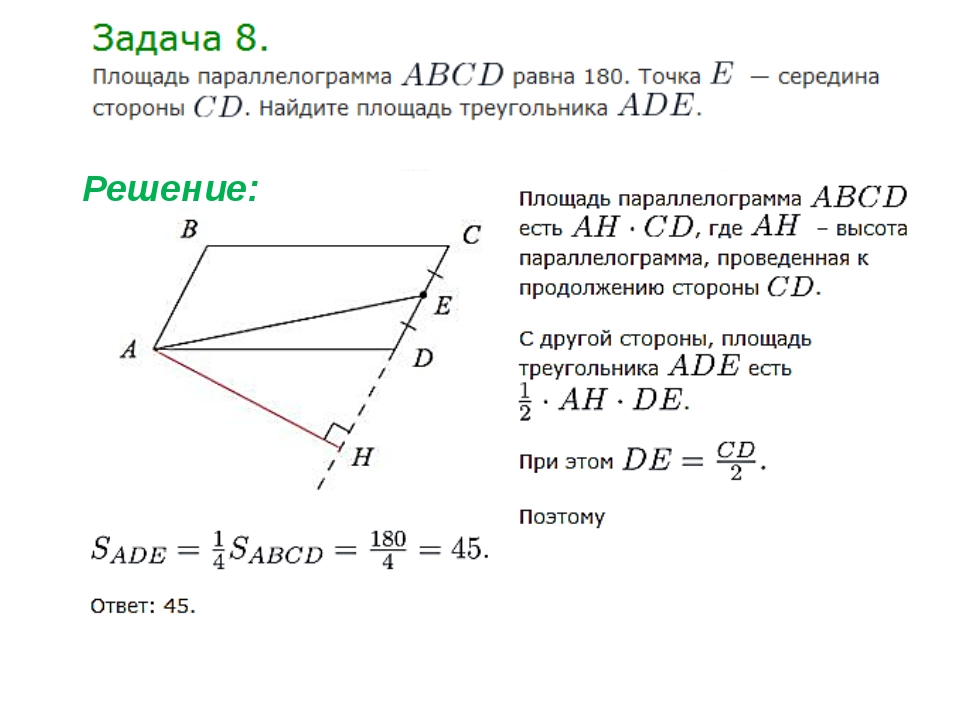 д. — относится ваша жалоба;
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
типов четырехугольников — прямоугольник, квадрат, ромб, параллелограмм | Class 8 Maths
Типы четырехугольников — прямоугольник, квадрат, ромб, параллелограмм | Математика класса 8
Четырехугольники можно определить как типов многоугольников , у которых четыре стороны, четыре вершины , и четыре угла вместе с парой диагоналей. Сумма внутренних углов четырехугольника равна 360 ° . Есть разные виды четырехугольников. Как следует из названия, это слово представляет собой комбинацию двух латинских слов « Quadri » означает вариант из четырех, а « latus » означает сторону.
Сумма внутренних углов четырехугольника равна 360 ° . Есть разные виды четырехугольников. Как следует из названия, это слово представляет собой комбинацию двух латинских слов « Quadri » означает вариант из четырех, а « latus » означает сторону.
Виды четырехугольников
Четырехугольники в зависимости от их свойств могут быть подразделены на другие группы, и основное подразделение четырехугольников находится между выпуклыми и вогнутыми четырехугольниками.Эти вогнутые и выпуклые четырехугольники можно разделить на их подразделения.
Вогнутые четырехугольники
Четырехугольники, у которых один из внутренних углов больше 180 °, а одна диагональ лежит за пределами четырехугольника, называются выпуклыми четырехугольниками.
Одним из примеров вогнутого четырехугольника является дротик Dart . Это четырехугольник с двусторонней симметрией, как у воздушного змея, но с внутренним углом отражения.
Выпуклые четырехугольники
Четырехугольники, у которых все четыре внутренних угла меньше 180 °, называются вогнутыми четырехугольниками. Существуют различные типы выпуклых четырехугольников:
- Трапеция
- Воздушный змей
- Параллелограмм
- Прямоугольник
- Ромб
- Квадрат
Трапеция
Пара противоположных сторон трапеции является параллельной парой четырехугольников. У правильной трапеции непараллельные стороны равны и углы ее основания равны.
Воздушный змей
Воздушный змей имеет две пары равных смежных сторон и одну пару равных противоположных углов. Диагонали воздушного змея пересекаются перпендикулярно. Самая длинная диагональ кайта делит пополам меньшую.
Параллелограмм
Четырехугольник, противоположные стороны которого равны и параллельны, называется параллелограммом. Противоположные углы параллелограмма равны, а его диагонали делят друг друга пополам.
Прямоугольник
Четырехугольник, противоположные стороны которого равны и параллельны, а все внутренние углы равны 90 °, определяется как Прямоугольник.Диагонали прямоугольника делят друг друга пополам. Обратите внимание, что все прямоугольники — параллелограммы, но обратное неверно.
Ромб
Четырехугольник, у которого все стороны равны, а противоположные стороны параллельны, называется ромбом. Противоположные углы ромба равны, а диагонали ромба делят друг друга пополам перпендикулярно. Обратите внимание, что все ромбы — параллелограммы, но обратное неверно.
Квадрат
Четырехугольник, у которого все стороны равны, а противоположные стороны параллельны, а все внутренние углы равны 90 °, называется Квадратом.Диагонали квадрата пересекают друг друга перпендикулярно. Обратите внимание, что все квадраты ромбические, но не наоборот.
Примеры задач на четырехугольниках
Теперь рассмотрим некоторые задачи, основанные на четырехугольниках:
Задача 1: Периметр четырехугольника ABCD равен 46 единицам. AB = x + 7, BC = 2x + 3, CD = 3x — 8 и DA = 4x — 6. Найдите длину самой короткой стороны четырехугольника.
AB = x + 7, BC = 2x + 3, CD = 3x — 8 и DA = 4x — 6. Найдите длину самой короткой стороны четырехугольника.
Решение :
Периметр = Сумма всех сторон
=> 46 = 10x — 4 или [x = 5]
Это дает AB = 12 единиц, BC = 13 единиц, CD = 7 единиц, DC = 14 единиц
Следовательно, длина самой короткой стороны составляет 7 единиц (т.е.е. CD).
Задача 2: Дана трапеция ABCD (AB || DC) с медианным EF. AB = 3x — 5, CD = 2x -1 и EF = 2x + 1. Найдите значение EF.
Решение :
Мы знаем, что медиана трапеции составляет половину суммы ее оснований.
=> EF = (AB + CD) / 2
=> 4x + 2 = 5x — 6 или [x = 8]
Следовательно, EF = 2x + 1 = 2 (8) + 1 => EF = 17 шт.
Задача 3: В параллелограмме смежные углы находятся в соотношении 1: 2. Найдите размеры всех углов этого параллелограмма.
Найдите размеры всех углов этого параллелограмма.
Решение :
Пусть смежный угол равен x и 2x.
Мы знаем, что в параллелограмме смежные углы являются дополнительными .
=> x + 2x = 180 ° или [x = 60 °]
Кроме того, противоположных угла равны в параллелограмме .
Следовательно, размеры каждого угла равны 60 °, 120 °, 60 °, 120 °.
Задача 4: Периметр ромба составляет 52 единицы, а длина одной из его диагоналей — 24 единицы.Найдите длину другой диагонали.
Решение:
Дано: Периметр = 52 единицы.
Длина диагонали (например, переменного тока) = 24 единицы.
Мы знаем, что у ромба все четыре стороны равны .
=> AB + BC + CD + DA = 52.
=> 4. (AB) = 52 => AB = 13 единиц.
Также диагонали ромба делят друг друга пополам перпендикулярно .
Следовательно, на данном рисунке AE = EC, BE = ED и ∠AEB = 90 °.
Применение теоремы Пифагора в ∆AEB, (∠AEB = 90 °)
=> (AB) ² = (AE) ² + (EB) ²
=> (13) ² = (12) ² + (EB) ²
=> (EB) ² = 169 — 144 = 25
=> EB = 5 единиц.
Так как AC = 2 * EB = 10 ед.
Следовательно, необходимая длина другой диагонали ромба составляет 10 единиц .
% PDF-1.6
%
391 0 объект>
эндобдж
xref
391 82
0000000016 00000 н.
0000002767 00000 н.
0000002951 00000 н.
0000003002 00000 п.
0000003130 00000 н.
0000003386 00000 н.
0000003666 00000 н.
0000004844 00000 н.
0000004973 00000 н.
0000005058 00000 н.
0000005241 00000 п.
0000006415 00000 н.
0000007593 00000 н.
0000008778 00000 н.
0000008996 00000 н.
0000010174 00000 п.
0000010395 00000 п.
0000011566 00000 п.
0000012747 00000 п.
0000012958 00000 п.
0000013035 00000 п.
0000013163 00000 п.
0000014348 00000 п.
0000014424 00000 п.
0000014622 00000 п.
0000014841 00000 п.
0000015050 00000 п.
0000020990 00000 н.
0000021198 00000 п.
0000022146 00000 п.
0000023337 00000 п.
0000023621 00000 п.
0000030893 00000 п.
0000031081 00000 п.
0000031175 00000 п.
0000031869 00000 п.
0000033039 00000 п.
0000033225 00000 п.
0000033318 00000 п.
0000042628 00000 п.
0000043044 00000 п.
0000043172 00000 п.
0000043292 00000 п.
0000044004 00000 п.
0000045169 00000 п.
0000046335 00000 п.
0000052129 00000 п.
0000052315 00000 п.
0000052407 00000 п.
0000052593 00000 п.
0000052678 00000 п.
0000061603 00000 п.
0000062448 00000 п.
0000062576 00000 п.
0000063220 00000 н.
0000063948 00000 п.
0000064619 00000 п.
0000064849 00000 п.
0000064907 00000 н.
0000067349 00000 п.
0000079537 00000 п.
0000094339 00000 п.
0000106893 00000 п.
0000107230 00000 н.
0000107460 00000 п.
0000122103 00000 п.
0000125771 00000 н.
0000125841 00000 н.
0000126060 00000 н.
0000126498 00000 н.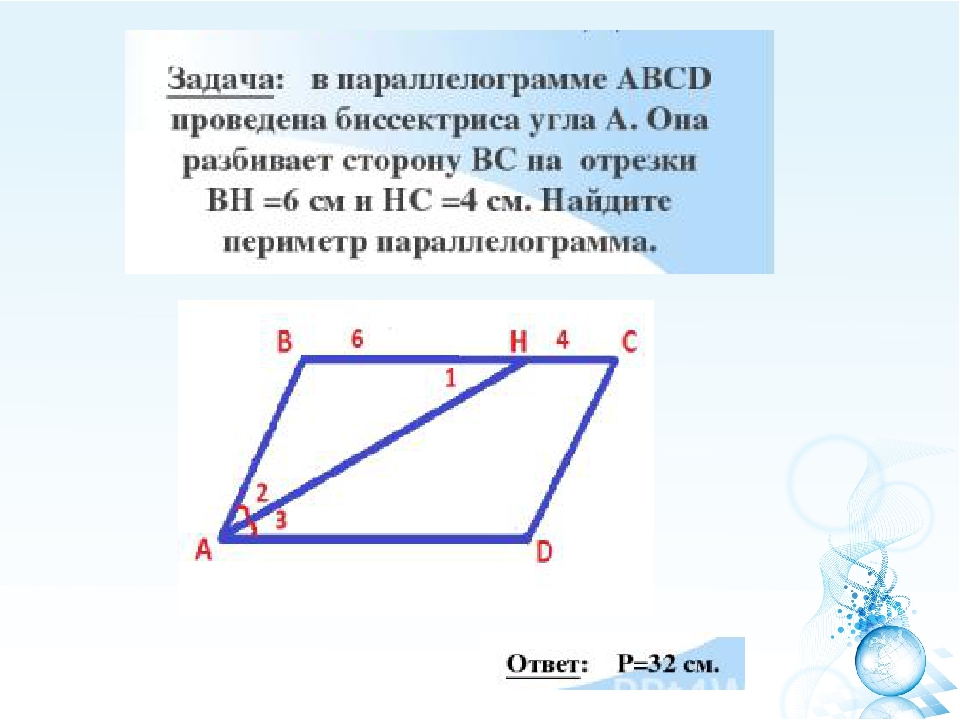
0000139913 00000 н.
0000142354 00000 п.
0000155381 00000 п.
0000155439 00000 н.
0000155773 00000 н.
0000169664 00000 н.
0000170207 00000 н.
0000170270 00000 н.
0000170494 00000 п.
0000170704 00000 н.
0000170760 00000 н.
0000001936 00000 н.
трейлер
] >>
startxref
0
%% EOF
472 0 obj> поток
xb«e`f«gb @
Параллелограммы — 3-й класс по математике
Узнайте о параллелограммах
На последних двух уроках вы узнали все о трехсторонних многоугольниках, называемых треугольниками.
В следующих нескольких уроках вы узнаете о четырехсторонних многоугольниках. Их называют четырехугольниками .
Четырехугольники
Четырехугольники — это четырехугольники.
Совет: Многоугольники — это замкнутые двухмерные фигуры с прямыми сторонами.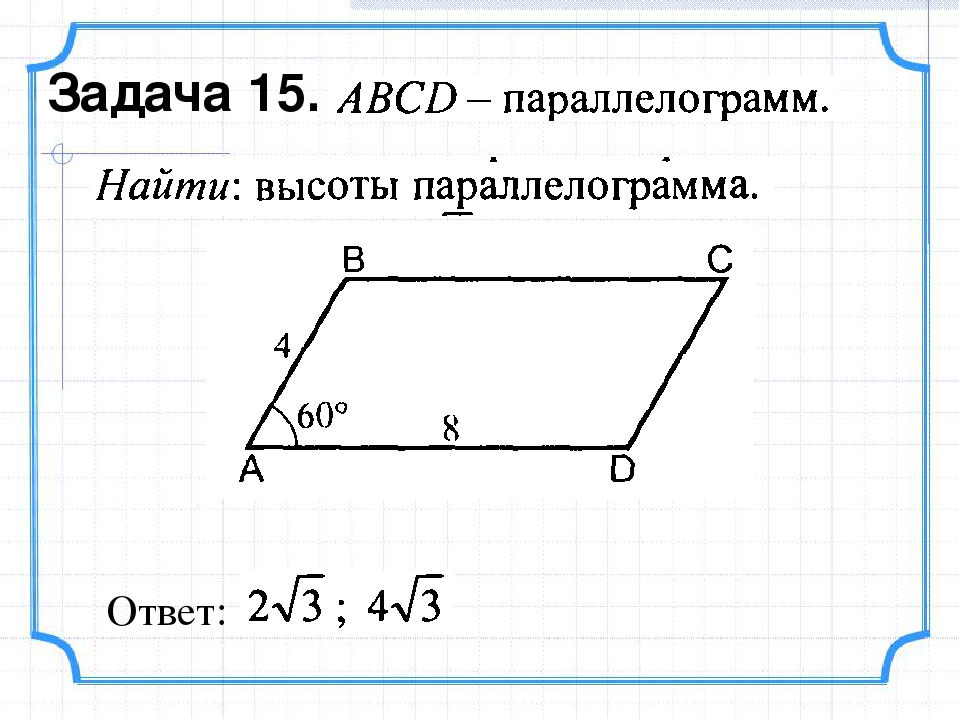
Вы помните, как узнали о прямоугольниках и квадратах? 🤔
Прямоугольники, квадраты, ромбы и трапеции — все это четырехугольники !
Давайте узнаем о новом типе четырехугольника: параллелограмме.
Параллелограммы
Ранее вы узнали о параллельных прямых.
Параллельные прямые — это прямые, которые никогда не пересекаются и не пересекаются.
Параллельные граммы — это четырехугольники с двумя наборами параллельных сторон.
Взгляните!
Это все параллелограммы!
Вы что-нибудь замечаете в слове параллелограмм? 🤔
В нем есть слово «параллель»!
Параллельно означает, что две или более линий расположены бок о бок, не касаясь друг друга.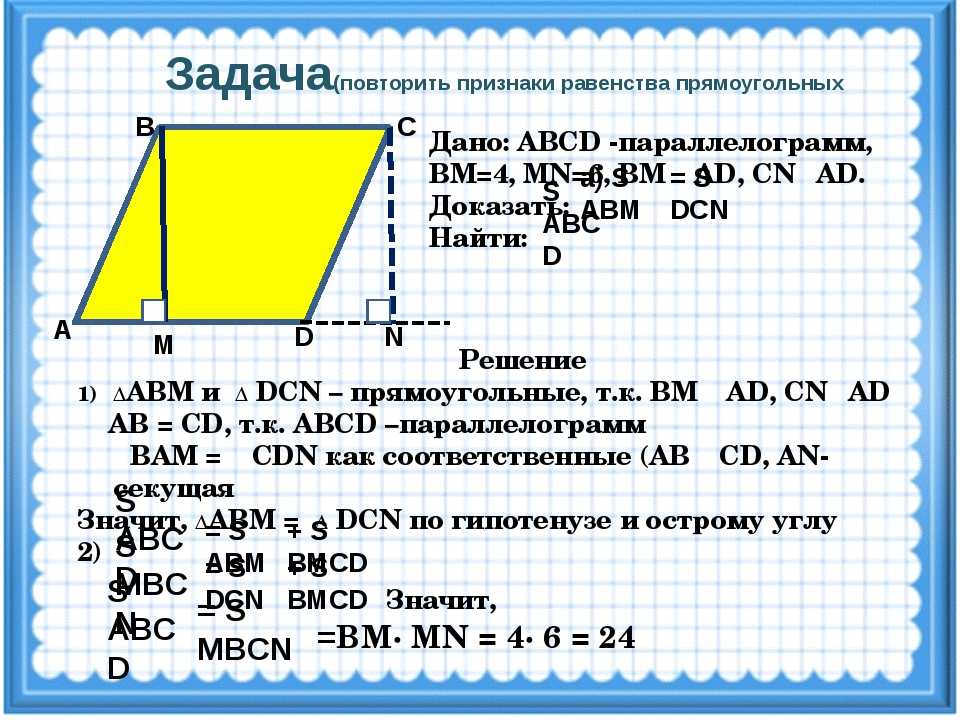
Итак, у параллелограмма будет как минимум две стороны, параллельные друг другу.
Вы знаете, что некоторые формы представляют собой параллелограммы!
Верно! Квадраты и прямоугольники — параллелограммы. ✅
Противоположные стороны
Прежде чем мы рассмотрим еще несколько форм, давайте поговорим о противоположных сторонах.
Противоположные стороны — это две стороны, не имеющие общей вершины.
Посмотрите:
Эти две стороны противоположны!
Теперь, когда вы знаете, каковы противоположные стороны, давайте попробуем определить параллелограммы!
Определение параллелограммов
Эта форма — параллелограмм?
Да! 🤗 Это так! Противоположные стороны параллельны друг другу:
Давай попробуем еще раз! 💪
Эта форма — параллелограмм?
Нет, это не так! ❎ Ни одна из его противоположных сторон не параллельна друг другу.

 Учебник для 7-9 классов. Погорелов А.В.
Учебник для 7-9 классов. Погорелов А.В.