Математический портал. Высшая математика. Математический анализ.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Зная координаты точек $M_1(x_1, y_1, z_1)$ и $M_2(x_2, y_2, z_2)$ и отношение $\lambda,$ в котором точка $M$ делит направленный отрезок $\overline{M_1M_2},$ найдем координаты точки $M.$

Пусть $O -$ начало координат. Обозначим $\overline{OM_1}=r_1,$ $\overline{OM_2}=r_2,$ $\overline{OM}=r.$ Так как, $$\overline{M_1M}=r-r_1, \overline{MM_2}=r_2-r,$$ то $r-r_1=\lambda(r_2-r),$ откуда (так как $\lambda\neq -1$) $$r=\frac{r_1+\lambda r_2}{1+\lambda}.$$ Полученная форма и дает решение задачи в векторной форме. Переходя в этой формуле к координатам, получим $$x=\frac{x_1+\lambda x_2}{1+\lambda}, y=\frac{y_1+\lambda y_2}{1+\lambda}, z=\frac{z_1+\lambda z_2}{1+\lambda}.$$

Примеры.

2.57. Отрезок с концами в точках $A(3, -2)$ и $B(6, 4)$ разделен на три равные части. Найти координаты точек деления.

Решение.

Пусть $C(x_C, y_C)$ и $D(x_D, y_D) -$ точки, которые делят отрезок $AB$ на три равные части. Тогда $$\lambda_1=\frac{AC}{CB}=\frac{1}{2};$$ $$x_C=\frac{x_A+\lambda_1x_B}{1+\lambda_1}=\frac{3+\frac{1}{2}\cdot 6}{1+\frac{1}{2}}=4;$$ 

$$y_C=\frac{y_A+\lambda_1y_B}{1+\lambda_1}=\frac{-2+\frac{1}{2}\cdot 4}{1+\frac{1}{2}}=0.$$ 

Далее находим координаты точки $D:$

$$\lambda_2=\frac{AD}{DB}=\frac{2}{1}=2;$$ $$x_D=\frac{x_A+\lambda_2x_B}{1+\lambda_2}=\frac{3+2\cdot 6}{1+2}=5;$$ 

$$y_D=\frac{y_A+\lambda_2y_B}{1+\lambda_2}=\frac{-2+2\cdot 4}{1+2}=2.$$ 

Ответ: $(4, 0)$ и $(5, 2).$

2.58.Определить координаты концов отрезка, который точками $C(2, 0, 2)$ и $D(5, -2, 0)$ разделен на три равные части.

Решение.

Пусть $A(x_A, y_A, z_A)$ и $B(x_B, y_B, z_B) -$ концы заданного отрезка.

Выпишем формулы для нахождения координат точки $C$ и подставим известные координаты:

$$\lambda_1=\frac{AC}{CB}=\frac{1}{2};$$ $$x_C=\frac{x_A+\lambda_1x_B}{1+\lambda_1}\Rightarrow 2=\frac{x_A+\frac{1}{2}\cdot x_B}{1+\frac{1}{2}}=2\frac{x_A+\frac{1}{2}\cdot x_B}{3}\Rightarrow $$ $$\Rightarrow 3=x_A+\frac{1}{2}\cdot x_B;$$ 

$$y_C=\frac{y_A+\lambda_1y_B}{1+\lambda_1}\Rightarrow 0=\frac{y_A+\frac{1}{2}\cdot y_B}{1+\frac{1}{2}}\Rightarrow 0=y_A+\frac{1}{2}\cdot y_B;$$

$$z_C=\frac{z_A+\lambda_1z_B}{1+\lambda_1}\Rightarrow 2=\frac{z_A+\frac{1}{2}\cdot z_B}{1+\frac{1}{2}}=2\frac{z_A+\frac{1}{2}\cdot z_B}{3}\Rightarrow$$ $$\Rightarrow 3=z_A+\frac{1}{2}\cdot z_B. $$ 

Аналогичные равенства запишем для точки $D:$

$$\lambda_2=\frac{AD}{DB}=\frac{2}{1}=2;$$ $$x_D=\frac{x_A+\lambda_2x_B}{1+\lambda_2}\Rightarrow 5=\frac{x_A+2\cdot x_B}{1+2}=\frac{x_A+2\cdot x_B}{3}\Rightarrow $$ $$\Rightarrow 15=x_A+2\cdot x_B;$$ 

$$y_D=\frac{y_A+\lambda_2y_B}{1+\lambda_2}\Rightarrow -2=\frac{y_A+2\cdot y_B}{1+2}\Rightarrow -6=y_A+2\cdot y_B;$$

$$z_D=\frac{z_A+\lambda_2z_B}{1+\lambda_2}\Rightarrow 0=\frac{z_A+2\cdot z_B}{1+2}\Rightarrow 0=z_A+2\cdot z_B.$$

Далее запишем полученные уравнения относительно $x_A, x_B;$ $y_A, y_B$  и $z_A, z_B$ попарно в виде систем и решим их:

$$\left\{\begin{array}{lcl}x_A+\frac{1}{2}x_B=3\\x_A+2x_B=15\end{array}\right.\Rightarrow\left\{\begin{array}{lcl}x_A=3-0,5x_B\\3-0,5x_B+2x_B=15\end{array}\right.\Rightarrow$$ $$\Rightarrow\left\{\begin{array}{lcl}x_A=3-0,5\cdot8=-1\\x_B=\frac{12}{1,5}=8\end{array}\right.$$

$$\left\{\begin{array}{lcl}y_A+\frac{1}{2}y_B=0\\y_A+2y_B=-6\end{array}\right. \Rightarrow\left\{\begin{array}{lcl}y_B=-2y_A\\y_A-4y_A=-6\end{array}\right.\Rightarrow$$ $$\Rightarrow\left\{\begin{array}{lcl}y_B=-4\\y_A=2\end{array}\right.$$

$$\left\{\begin{array}{lcl}z_A+\frac{1}{2}z_B=3\\z_A+2z_B=0\end{array}\right.\Rightarrow\left\{\begin{array}{lcl}-2z_B+0,5z_B=3\\z_A=-2z_B\end{array}\right.\Rightarrow$$ $$\Rightarrow\left\{\begin{array}{lcl}z_B=-2\\z_A=4\end{array}\right.$$

Таким образом, получили координаты концов отрезка $A(-1, 2, 4)$ и $B(8, -4, -2).$ 

Ответ: $A(-1, 2, 4),$ $B(8, -4, -2).$ 

Как найти Координаты Точки? Примеры

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты вашей квартиры тоже можно записать числами — они помогут понять, где именно находится тот дом, где вы живете. С точками на плоскости та же история.

Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.

Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.

Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.

Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.

Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.

• Координатные оси — это прямые, образующие систему координат.
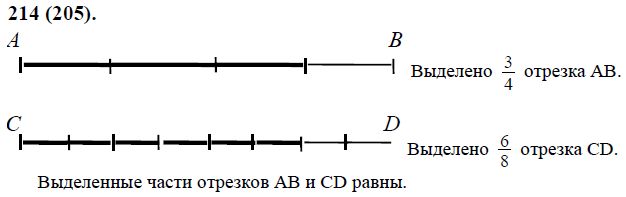
• Ось абсцисс Ox — горизонтальная ось.
• Ось ординат Oy — вертикальная ось.
• Координатная плоскость — плоскость, в которой находится система координат. Обозначается так: x0y.
• Единичный отрезок — величина, которая принимается за единицу при геометрических построениях. В декартовой системе координат единичный отрезок отмечается на каждой из осей. Длина отрезка показывает сколько раз единичный отрезок и его части укладываются в данном отрезке.

Оси координат делят плоскость на четыре угла — четыре координатные четверти.

У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:

• верхний правый угол — первая четверть I;
• верхний левый угол — вторая четверть II;
• нижний левый угол — третья четверть III;
• нижний правый угол — четвертая четверть IV;

Правила координат:

• Если обе координаты положительны, то точка находится в первой четверти координатной плоскости.
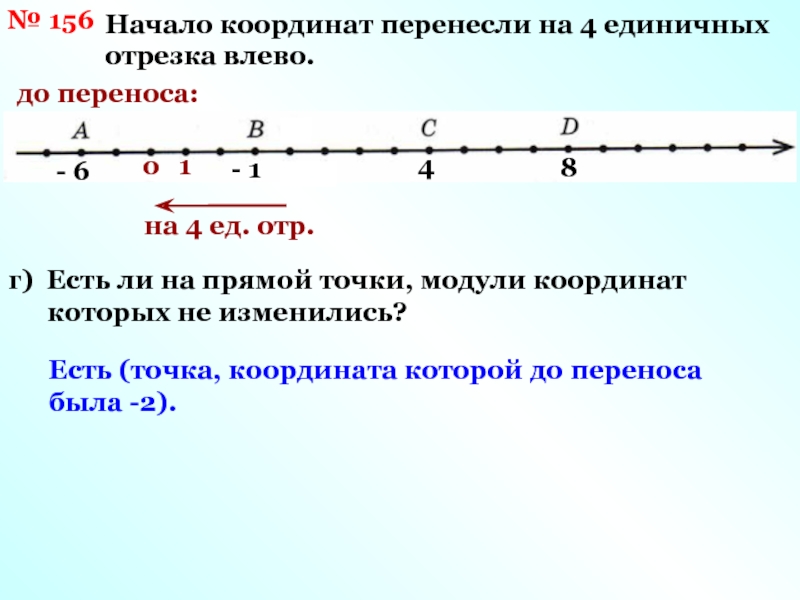
• Если координата х отрицательная, а координата у положительная, то точка находится во второй четверти.
• Если обе координаты отрицательны, то число находится в третьей четверти.
• Если координата х положительная, а координата у отрицательная, то точка лежит в четвертой четверти.

Определение координат точки

Каждой точке координатной плоскости соответствуют две координаты.

Точка пересечения с осью Ох называется абсциссой точки А, а с осью Оу называется ординатой точки А.

Чтобы узнать координаты точки на плоскости, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра.

Координаты точки на плоскости записывают в скобках, первая по оси Ох, вторая по оси Оу.

Смотрим на график и фиксируем: A (1; 2) и B (2; 3).

Особые случаи расположения точек

В геометрии есть несколько особых случаев расположения точек. Лучше их запомнить, чтобы без запинки решать задачки. Вот они:

1. Если точка лежит на оси Oy, то ее абсцисса равна 0. Например,
   точка С (0, 2).
2. Если точка лежит на оси Ox, то ее ордината равна 0. Например,
   точка F (3, 0).
3. Начало координат — точка O. Ее координаты равны нулю: O (0,0).
4. Точки любой прямой, которая перпендикулярна оси абсцисс, имеют одинаковые абсциссы.
5. Точки любой прямой, которая перпендикулярна оси ординат, имеют одинаковые ординаты.
6. Если точка лежит на оси абсцисс, то ее координаты будут иметь вид: (x, 0).
7. Если точка лежит на оси ординат, то ее координаты будут иметь вид: (0, y).

Способы нахождения точки по её координатам

Чтобы узнать, как найти точку в системе координат, можно использовать один из двух способов.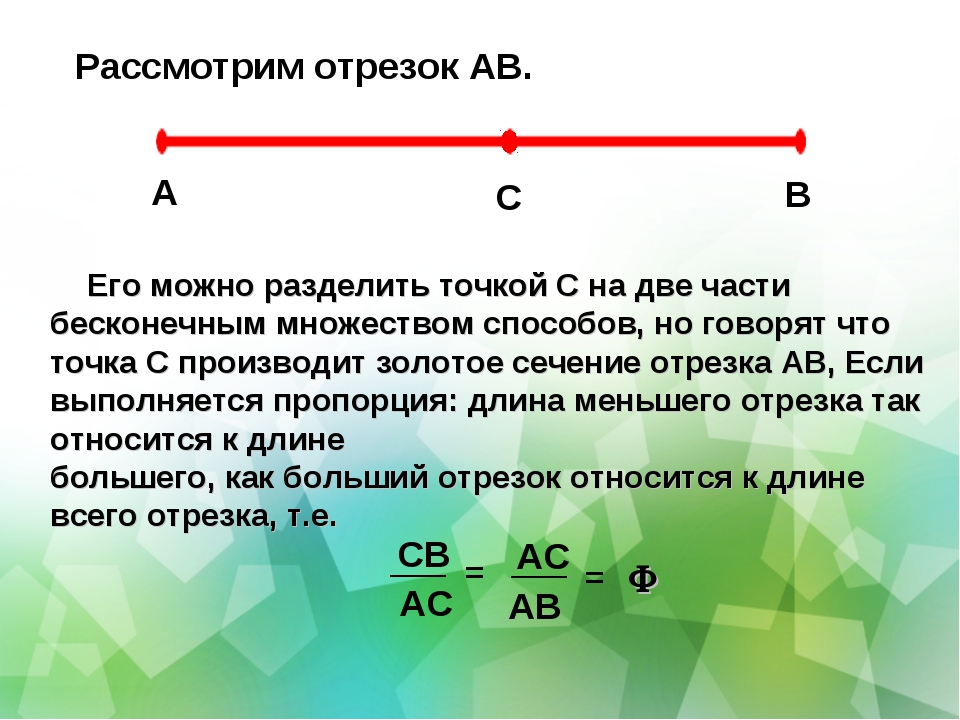

Способ первый. Как определить положение точки D по её координатам (-4, 2):

1. Отметить на оси Ox, точку с координатой -4, и провести через нее прямую перпендикулярную оси Ox.
2. Отметить на оси Oy, точку с координатой 2, и провести через нее прямую перпендикулярную оси Oy.
3. Точка пересечения перпендикуляров и есть искомая точка D. Ее абсцисса равна -4, а ордината — 2.

Способ второй. Как определить положение точки D (-4, 2):

1. Сместить прямую по оси Ox влево на 4 единицы, так как у нас
   перед 4 стоит знак минус.
2. Подняться из этой точки параллельно оси Oy вверх на 2 единицы, так как у нас перед 2 стоит знак плюс.

Чтобы легко и быстро находить координаты точек или строить точки по координатам, скачайте готовую систему координат и храните ее в учебнике:

Координаты и векторы. Исчерпывающий гид (ЕГЭ — 2021)

Нам нужно найти угол между прямыми \( \displaystyle SB\) и \( \displaystyle CD\).

Таким образом, наша задача сводится к поиску координат точек: \( \displaystyle S,B,C,D\).

Координаты последних трех мы найдем по маленькому рисунку, а коодинату вершины \( \displaystyle S\) найдем через координату точки \( \displaystyle O\).

Работы навалом, но надо к ней приступать!

a) Координата \( \displaystyle D\): ясно, что ее аппликата и ордината равны нулю.

Найдем абсциссу. Для этого рассмотрим прямоугольный треугольник \( \displaystyle EDP\). Увы, в нем нам известна только гипотенуза, которая равна \( \displaystyle 1\). Катет \( \displaystyle DP\) мы будем стараться отыскать (ибо ясно, что удвоенная длина катета \( \displaystyle DP\) даст нам абсциссу точки \( \displaystyle D\)).

Как же нам ее искать?

Давай вспомним, что за фигура у нас лежит в основании пирамиды? Это правильный шестиугольник.

А что это значит? Это значит, что у него все стороны и все углы равны. Надо бы найти один такой угол. Есть идеи?

Идей масса, но есть формула:

Сумма углов правильного n-угольника равна \( \left( n-2 \right)\cdot 180{}^\circ \). \circ \)

Опять-таки, при решении этой задачи я не использовал никаких изошренных приемов, кроме формулы суммы углов правильного n-угольника, а также определения косинуса и синуса прямоугольного треугольника.

3. Поскольку нам опять не даны длины ребер в пирамиде, то я буду считать их равными единице.

Таким образом, поскольку ВСЕ ребра, а не только боковые, равны между собой, то в основании пирамиды и меня лежит квадрат, а боковые грани – правильные треугольники.

Изобразим такую пирамиду, а также ее основание на плоскости, отметив все данные, приведенные в тексте задачи:

Найти координаты середины вектора. Формулы деления отрезка в данном отношении. Формулы координат середины отрезка. Формула нахождения координаты середины отрезка

Не составляет никакого труда. Для их расчета существует простое выражение, которое легко запомнить. Например, если координаты концов какого-либо отрезка соответственно равняются (х1; у1) и (х2; у2) соответственно, то координаты его середины рассчитываются как среднее арифметическое этих координат, то есть:

Вот и вся сложность.
Рассмотрим расчет координат центра одного из отрезков на конкретном примере, как Вы и просили.

Задача.

Найти координаты некоей точки М, если она является серединой (центром) отрезка КР, концов которого имеют такие координаты: (—3; 7) и (13; 21) соответственно.

Решение.

Используем рассмотренную выше формулу:

Ответ
. М (5; 14).

С помощью данной формулы можно также найти не только координаты середины какого-либо отрезка, но и его концов. Рассмотрим пример.

Задача.

Даны координаты двух точек (7; 19) и (8; 27). Найти координаты одного из концов отрезка, если предыдущие две точки являются его концом и серединой.

Решение.

Обозначим концы отрезка К и Р, а его середину S. Перепишем формулу с учетом новых названий:

Подставим известные координаты и вычислим отдельные координаты:

Очень часто в задаче C2 требуется работать с точками, которые делят отрезок пополам. Координаты таких точек легко считаются, если известны координаты концов отрезка.

Итак, пусть отрезок задан своими концами — точками A = (x a ; y a ; z a) и B = (x b ; y b ; z b). Тогда координаты середины отрезка — обозначим ее точкой H — можно найти по формуле:

Другими словами, координаты середины отрезка — это среднее арифметическое координат его концов.

· Задача

. Единичный куб ABCDA 1 B 1 C 1 D 1 помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD и AA 1 соответственно, а начало координат совпадает с точкой A. Точка K — середина ребра A 1 B 1 . Найдите координаты этой точки.

Решение
. Поскольку точка K — середина отрезка A 1 B 1 , ее координаты равных среднему арифметическому координат концов. Запишем координаты концов: A 1 = (0; 0; 1) и B 1 = (1; 0; 1). Теперь найдем координаты точки K:

Ответ
: K = (0,5; 0; 1)

· Задача

. Единичный куб ABCDA 1 B 1 C 1 D 1 помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD и AA 1 соответственно, а начало координат совпадает с точкой A. Найдите координаты точки L, в которой пересекаются диагонали квадрата A 1 B 1 C 1 D 1 .

Решение
. Из курса планиметрии известно, что точка пересечения диагоналей квадрата равноудалена от всех его вершин. В частности, A 1 L = C 1 L, т.е. точка L — это середина отрезка A 1 C 1 . Но A 1 = (0; 0; 1), C 1 = (1; 1; 1), поэтому имеем:

Ответ
: L = (0,5; 0,5; 1)

Простейшие задачи аналитической геометрии.

Действия с векторами в координатах

Задания, которые будут рассмотрены, крайне желательно научиться решать на полном автомате, а формулы запомнить наизусть
, даже специально не запоминать, сами запомнятся =) Это весьма важно, поскольку на простейших элементарных примерах базируются другие задачи аналитической геометрии, и будет досадно тратить дополнительное время на поедание пешек. Не нужно застёгивать верхние пуговицы на рубашке, многие вещи знакомы вам со школы.

Изложение материала пойдет параллельным курсом – и для плоскости, и для пространства.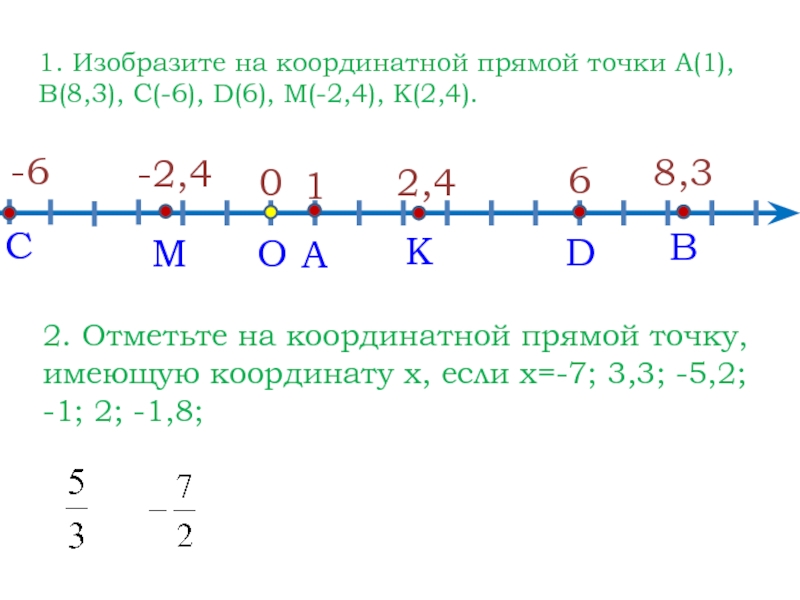 По той причине, что все формулы… сами увидите.

Начальные геометрические сведения

Понятие отрезка, как и понятие точки, прямой, луча и угла, относится к начальным геометрическим сведениям. С перечисленных понятий начинается изучение геометрии.

Под «начальными сведениями» обычно понимают нечто элементарное и простое. В понимании, возможно, это так и есть. Тем не менее, такие простые понятия часто встречаются и оказываются необходимыми не только в нашей повседневной жизни, но и в производстве, строительстве и прочих сферах нашей жизнедеятельности.

Начнём с определений.

Определение 1

Отрезок — часть прямой, ограниченная двумя точками (концами).

Если концы отрезка являются точками $A$ и $B$, то образованный отрезок записывают как $AB$ или $BA$. Такому отрезку принадлежат точки $A$ и $B$, а также все точки прямой, лежащие между этими точками.

Определение 2

Середина отрезка — точка отрезка, которая делит его пополам на два равных отрезка.

Если это точка $C$, то $AC=CB$.

Измерение отрезка происходит сравнением с определённым отрезком, принятым за единицу измерения. Чаще всего используют сантиметр. Если в заданном отрезке сантиметр укладывается ровно четыре раза, то это означает, что длина данного отрезка равна $4$ см.

Введём простое наблюдение. Если точка делит отрезок на два отрезка, то длина всего отрезка равна сумме длин этих отрезков.

Формула нахождения координаты середины отрезка

Формула нахождения координаты середины отрезка относится к курсу аналитической геометрии на плоскости.

Дадим определение координатам.

Определение 3

Координаты — это определённые (или упорядоченные) числа, которые показывают положение точки на плоскости, на поверхности или в пространстве.

В нашем случае, координаты отмечаются на плоскости, определённой координатными осями.

Рисунок 3. Координатная плоскость. Автор24 — интернет-биржа студенческих работ

Опишем рисунок. На плоскости выбрана точка, называемая началом координат. Её обозначают буквой $O$. Через начало координат проведены две прямые (координатные оси), пересекающиеся под прямым углом, причём одна из них строго горизонтальная, а другая — вертикальная. Такое положение считается обычным. Горизонтальная прямая называется осью абсцисс и обозначается $OX$, вертикальная — осью ординат $OY$.

Таким образом, оси определяют плоскость $XOY$.

Координаты точек в такой системе определяются двумя числами.

Существуют разные формулы (уравнения), определяющие те или иные координаты. Обычно в курсе аналитической геометрии изучают разные формулы прямых, углов, длины отрезка и прочие.

Перейдём сразу к формуле координаты середины отрезка.

Определение 4

Если координаты точки $E(x,y)$ — это середина отрезка $M_1M_2$, то:

Рисунок 4. Формула нахождения координаты середины отрезка. Автор24 — интернет-биржа студенческих работ

Практическая часть

Примеры из школьного курса геометрии достаточно просты. Рассмотрим несколько основных.

Для лучшего понимания, рассмотрим для начала элементарный наглядный пример.

Пример 1

Имеем рисунок:

На рисунке отрезки $AC, CD, DE, EB$ равны.

1. Серединой каких отрезков является точка $D$?
2. Какая точка является серединой отрезка $DB$?

1. точка $D$ является серединой отрезков $AB$ и $CE$;
2. точка $E$.

Рассмотрим другой простой пример, в котором нужно вычислить длину.

Пример 2

Точка $B$ — середина отрезка $AC$. $AB = 9$ см. Какая длина $AC$?

Так как т. $B$ делит $AC$ пополам, то $AB = BC= 9$ см. Значит, $AC = 9+9=18$ см.

Ответ: 18 см.

Прочие подобные примеры обычно идентичны и ориентированы на умение сопоставлять значения длин и их представление с алгебраическими действиями. Нередко в задачах встречаются случаи, когда сантиметр не укладывается ровное количество раз в отрезок. Тогда единицу измерения делят на равные части. В нашем случае сантиметр делится на 10 миллиметров.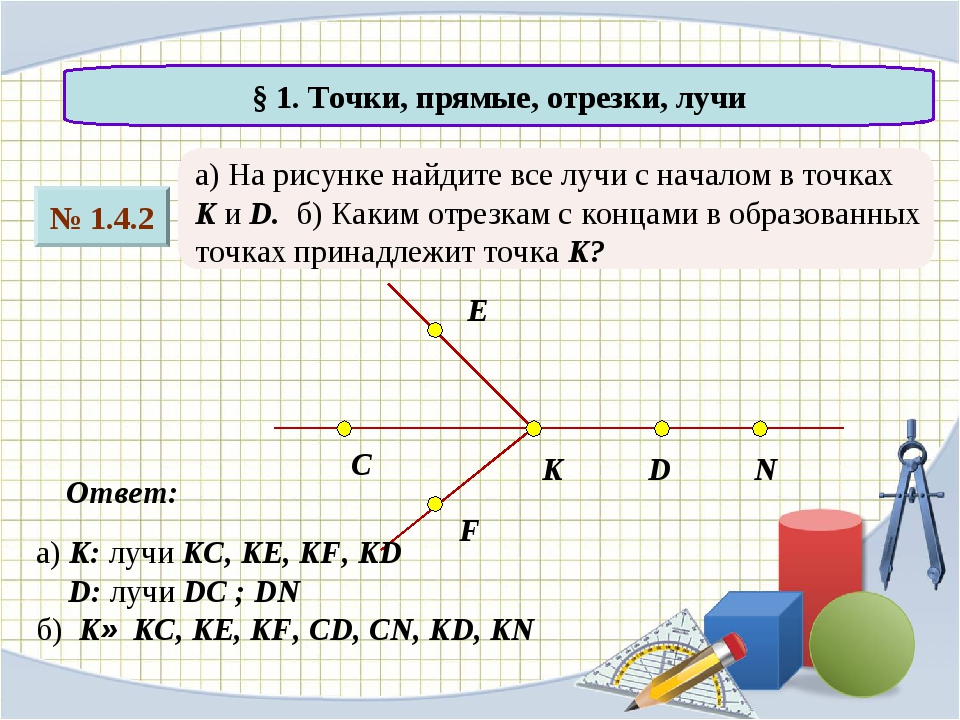 Отдельно измеряют остаток, сравнивая с миллиметром. Приведём пример, демонстрирующий такой случай.

После кропотливого труда я вдруг заметил, что размеры веб страниц достаточно велики, и если так пойдёт дальше, то можно тихо мирно озвереть =) Поэтому предлагаю вашему вниманию небольшое эссе, посвященное очень распространённой геометрической задаче – о делении отрезка в данном отношении
, и, как частный случай, о делении отрезка пополам
.

Данная задача по тем или иным причинам не вписалась в другие уроки, но зато сейчас есть прекрасная возможность рассмотреть её подробно и неторопливо. Приятная новость состоит в том, что мы немного отдохнём от векторов и сконцентрируем внимание на точках и отрезках.

Формулы деления отрезка в данном отношении

Понятие деления отрезка в данном отношении

Нередко обещанного вовсе ждать не приходится, сразу рассмотрим пару точек и, очевидное невероятное – отрезок :

Рассматриваемая задача справедлива, как для отрезков плоскости, так и для отрезков пространства. То есть, демонстрационный отрезок можно как угодно разместить на плоскости или в пространстве. Для удобства объяснений я нарисовал его горизонтально.

Что будем делать с данным отрезком? На этот раз пилить. Кто-то пилит бюджет, кто-то пилит супруга, кто-то пилит дрова, а мы начнём пилить отрезок на две части. Отрезок делится на две части с помощью некоторой точки , которая, понятно, расположена прямо на нём:

В данном примере точка делит отрезок ТАКИМ образом, что отрезок в два раза короче отрезка . ЕЩЁ можно сказать, что точка делит отрезок в отношении («один к двум»), считая от вершины .

На сухом математическом языке этот факт записывают следующим образом: , или чаще в виде привычной пропорции: . Отношение отрезков принято стандартно обозначать греческой буквой «лямбда», в данном случае: .

Пропорцию несложно составить и в другом порядке: – сия запись означает, что отрезок в два раза длиннее отрезка , но какого-то принципиального значения для решения задач это не имеет. Можно так, а можно так.

Разумеется, отрезок легко разделить в каком-нибудь другом отношении, и в качестве закрепления понятия второй пример:

Здесь справедливо соотношение: . Если составить пропорцию наоборот, тогда получаем: .

После того, как мы разобрались, что значит разделить отрезок в данном отношении, перейдём к рассмотрению практических задач.

Если известны две точки плоскости , то координаты точки , которая делит отрезок в отношении , выражаются формулами:

Откуда взялись данные формулы? В курсе аналитической геометрии эти формулы строго выводятся с помощью векторов (куда ж без них? =)). Кроме того, они справедливы не только для декартовой системы координат, но и для произвольной аффинной системы координат (см. урок Линейная (не) зависимость векторов. Базис векторов
). Такая вот универсальная задача.

Пример 1

Найти координаты точки , делящей отрезок в отношении , если известны точки

Решение
: В данной задаче . По формулам деления отрезка в данном отношении, найдём точку :

Ответ
:

Обратите внимание на технику вычислений: сначала нужно отдельно вычислить числитель и отдельно знаменатель. В результате часто (но далеко не всегда) получается трёх- или четырёхэтажная дробь. После этого избавляемся от многоэтажности дроби и проводим окончательные упрощения.

В задаче не требуется строить чертежа, но его всегда полезно выполнить на черновике:

Действительно, соотношение выполняется, то есть отрезок в три раза короче отрезка . Если пропорция не очевидна, то отрезки всегда можно тупо измерить обычной линейкой.

Равноценен второй способ решения
: в нём отсчёт начинается с точки и справедливым является отношение: (человеческими словами, отрезок в три раза длиннее отрезка ). По формулам деления отрезка в данном отношении:

Ответ
:

Заметьте, что в формулах необходимо переместить координаты точки на первое место, поскольку маленький триллер начинался именно с неё.

Также видно, что второй способ рациональнее ввиду более простых вычислений. Но всё-таки данную задачу чаще решают в «традиционном» порядке. Например, если по условию дан отрезок , то предполагается, что вы составите пропорцию , если дан отрезок , то «негласно» подразумевается пропорция .

А 2-ой способ я привёл по той причине, что частенько условие задачи пытаются намеренно подзапутать. Именно поэтому очень важно выполнять черновой чертёж чтобы, во-первых, правильно проанализировать условие, а, во-вторых, в целях проверки. Обидно допускать ошибки в такой простой задаче.

Пример 2

Даны точки . Найти:

а) точку , делящую отрезок в отношении ;
б) точку , делящую отрезок в отношении .

Это пример для самостоятельного решения. Полное решение и ответ в конце урока.

Иногда встречаются задачи, где неизвестен один из концов отрезка:

Пример 3

Точка принадлежит отрезку . Известно, что отрезок в два раза длиннее отрезка . Найти точку , если .

Решение
: Из условия следует, что точка делит отрезок в отношении , считая от вершины , то есть, справедлива пропорция: . По формулам деления отрезка в данном отношении:

Сейчас нам неизвестны координаты точки : , но это не является особой проблемой, так как их легко выразить из вышеприведённых формул. В общем виде выражать ничего не стОит, гораздо проще подставить конкретные числа и аккуратно разобраться с вычислениями:

Ответ
:

Для проверки можно взять концы отрезка и, пользуясь формулами в прямом порядке, убедиться, что при соотношении действительно получится точка . И, конечно же, конечно же, не лишним будет чертёж. А чтобы окончательно убедить вас в пользе клетчатой тетради, простого карандаша да линейки, предлагаю хитрую задачу для самостоятельного решения:

Пример 4

Точка . Отрезок в полтора раза короче отрезка . Найти точку , если известны координат точек .

Решение в конце урока. Оно, кстати, не единственное, если пойдёте отличным от образца путём, то это не будет ошибкой, главное, чтобы совпали ответы.

Для пространственных отрезков всё будет точно так же, только добавится ещё одна координата.

Если известны две точки пространства , то координаты точки , которая делит отрезок в отношении , выражаются формулами:
.

Пример 5

Даны точки . Найти координаты точки , принадлежащей отрезку , если известно, что .

Решение
: Из условия следует отношение: . Данный пример взят из реальной контрольной работы, и его автор позволил себе небольшую шалость (вдруг кто споткнётся) – пропорцию в условии рациональнее было записать так: .

По формулам координат середины отрезка:

Ответ
:

Трёхмерные чертежи в целях проверки выполнять значительно сложнее. Однако всегда можно сделать схематический рисунок, чтобы разобраться хотя бы в условии – какие отрезки необходимо соотносить.

Что касается дробей в ответе, не удивляйтесь, обычное дело. Много раз говорил, но повторюсь: в высшей математике принято орудовать обыкновенными правильными и неправильными дробями. Ответ в виде пойдёт, но вариант с неправильными дробями более стандартен.

Разминочная задача для самостоятельного решения:

Пример 6

Даны точки . Найти координаты точки , если известно, что она делит отрезок в отношении .

Решение и ответ в конце урока. Если трудно сориентироваться в пропорциях, выполните схематический чертёж.

В самостоятельных и контрольных работах рассмотренные примеры встречаются как сами по себе, так и составной частью более крупных задач. В этом смысле типична задача нахождения центра тяжести треугольника.

Разновидность задания, где неизвестен один из концов отрезка, разбирать не вижу особого смысла, так как всё будет похоже на плоский случай, разве что вычислений чуть больше. Лучше вспомним годы школьные:

Формулы координат середины отрезка

Даже неподготовленные читатели могут помнить, как разделить отрезок пополам. Задача деления отрезка на две равные части – это частный случай деления отрезка в данном отношении. Двуручная пила работает самым демократичным образом, и каждому соседу за партой достаётся по одинаковой палке:

В этот торжественный час стучат барабаны, приветствуя знаменательную пропорцию . И общие формулы чудесным образом преображаются в нечто знакомое и простое:

Удобным моментом является тот факт, что координаты концов отрезка можно безболезненно переставить:

В общих формулах такой роскошный номер, как понимаете, не проходит. Да и здесь в нём нет особой надобности, так, приятная мелочь.

Для пространственного случая справедлива очевидная аналогия. Если даны концы отрезка , то координаты его середины выражаются формулами:

Пример 7

Параллелограмм задан координатами своих вершин . Найти точку пересечения его диагоналей.

Решение
: Желающие могут выполнить чертёж. Граффити особенно рекомендую тем, кто капитально забыл школьный курс геометрии.

По известному свойству, диагонали параллелограмма своей точкой пересечения делятся пополам, поэтому задачу можно решить двумя способами.

Способ первый
: Рассмотрим противоположные вершины . По формулам деления отрезка пополам найдём середину диагонали :

Как найти координаты середины отрезка

Для начала разберемся, что такое середина отрезка.
Серединой отрезка считают точку, которая принадлежит данному отрезку и отстоит на одинаковое расстояние от его концов.

Координаты такой точки несложно найти, если известны координаты концов этого отрезка. В таком случае координаты середины отрезка будут равны половине суммы соответствующих координат концов отрезка.
Координаты середины отрезка часто находят, решая задачи на медиану, среднюю линию и т.п.
Рассмотрим вычисление координат середины отрезка для двух случаев: когда отрезок задан на плоскости и задан в пространстве.
Пусть отрезок на плоскости задан двумя точками с координатами и . Тогда координаты середины отрезка РН рассчитываются по формуле:

Пусть отрезок задан в пространстве двумя точками с координатами и . Тогда координаты середины отрезка РН рассчитываются по формуле:

Пример.

Найти координаты точки К — середины МО, если М (—1; 6) и О (8; 5).

Решение.

Поскольку точки имеют две координаты, значит, отрезок задан на плоскости. Используем соответствующие формулы:

Следовательно, середина МО будет иметь координаты К (3,5; 5,5).

Ответ.
К (3,5; 5,5).

Урок 2. равномерное прямолинейное движение материальной точки — Физика — 10 класс

Физика, 10 класс

Урок 2. Равномерное прямолинейное движение материальной точки

Перечень вопросов, рассматриваемых в теме: 1) основная задача механики; 2) относительность механического движения; 3) система отсчёта, материальная точка, перемещение, траектория, скорость; 4) кинематическое уравнение.

Глоссарий по теме:

Раздел механики, в котором изучается движение тел без выяснения причин, вызывающих данное движение, называют кинематикой.

Механическим движением тела называется изменение положения тела в пространстве относительно других тел с течением времени.

Материальной точкой называют тело, размерами и формой которого в условиях рассматриваемой задачи можно пренебречь. Тело, относительно которого рассматривается движение, называется телом отсчета. Совокупность тела отсчета, связанной с ним системы координат и часов называют системой отсчета.

Траектория — линия, по которой движется точка в пространстве.

Длину траектории, по которой двигалось тело в течение какого-то промежутка времени, называют путем, пройденным за этот промежуток времени.

Перемещением тела (материальной точки) называется вектор, соединяющий начальное положение тела с его последующим положением.

Равномерное прямолинейное движение – это движение, при котором за любые равные промежутки времени тело совершает равные перемещения.

Скорость равномерного прямолинейного движения точки – величина, равная отношению перемещения к промежутку времени, в течение которого это перемещение произошло.

Относительность механического движения – это зависимость траектории движения тела, пройденного пути, перемещения и скорости от выбора системы отсчёта

Основная и дополнительная литература по теме урока:

Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н.. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2016.– С.10-30.

Рымкевич А.П. Сборник задач по физике. 10-11 класс.-М.:Дрофа,2009.

Открытые электронные ресурсы по теме урока:

http://kvant.mccme.ru/1974/12/byvaet_li_ravnomernoe_dvizheni.htm.

Теоретический материал для самостоятельного изучения

Основная задача классической механики — определить положение тела в пространстве в любой момент времени. По характеру решаемых задач классическую механику делят на кинематику, динамику и статику. В кинематике описывают движение тел без выяснения причин, вызывающих данное движение. Раздел механики, в котором изучаются причины движения, называют динамикой. Статика — раздел механики, в котором изучаются условия равновесия абсолютно твердых тел. Законы сохранения импульса и энергии являются следствиями законов Ньютонов.

Механическим движением тела называется изменение положения тела в пространстве относительно других тел с течением времени. Сформулируем закон относительности движения: характер движения тела зависит от того, относительно каких тел мы рассматриваем движение. Нет абсолютно неподвижных тел.

Рассмотрим самое простое движение – прямолинейное равномерное движение. Описать движение тела – это значит, указать способ определения его положения в пространстве в любой момент времени.

Для описания движения нужно ввести некоторые понятия: материальная точка, траектория, путь, перемещение, координата, момент времени, промежуток времени, скорость. Материальной точкой называют тело, размерами которого в условиях рассматриваемой задачи можно пренебречь. Это первая физическая модель реальных тел. Практически всякое тело можно рассматривать как материальную точку в тех случаях, когда расстояния, проходимые точками тела, очень велики по сравнению с его размерами. Например, материальными точками считают Землю и другие планеты при изучении их движения вокруг Солнца. В данном случае различия в движении разных точек любой планеты, вызванные её суточным вращением, не влияют на величины, описывающие годовое движение. Но при решении задач, связанных с суточным вращением планет (например, при определении времени восхода солнца в разных местах поверхности земного шара), считать планету материальной точкой нельзя, так как результат задачи зависит от размеров этой планеты и скорости движения точек её поверхности.

Тело, движущееся поступательно, можно принимать за материальную точку даже в том случае, если его размеры соизмеримы с проходимыми им расстояниями. Поступательным называется такое движение абсолютно твердого тела, при котором любой отрезок, соединяющий любые две точки тела, остается параллельным самому себе.

Что нужно знать для того, чтобы в любой момент времени указать положение тела? Надо, во-первых, знать, где оно было в начальный момент времени; во-вторых, каков вектор перемещения в любой момент времени. Мы уже знаем, что движение любого тела относительно. Поэтому, изучая движение тела, мы обязательно указываем, относительно какого тела это движение рассматривается. Тело, относительно которого рассматривается движение, называется телом отсчета. Чтобы рассчитать положение материальной точки относительно выбранной точки отсчета, надо связать с ним систему координат и измерить время. Совокупность тела отсчета, связанной с ним системы координат и часов называют системой отсчета.

Рассмотрим два наиболее часто применяемых способа описания движения тел: координатный и векторный. В координатном способе положение тела в пространстве задается координатами, которые с течением времени меняются.

Рассмотрим движение материальной точки М с координатами (х, y, z) в момент времени t.

Математически это принято записывать в виде:

Количество координат зависит от условия задачи: на прямой – одна, в плоскости – две, в пространстве – три.

В векторном способе используется радиус-вектор. Радиус-вектор – это направленный отрезок, проведенный из начала координат в данную точку. Закон (или уравнение) движения в векторной форме — зависимость радиуса-вектора от времени:

Итак, для задания закона движения материальной точки необходимо указать либо вид функциональной зависимости всех трех ее координат от времени, либо зависимость от времени радиус-вектора этой точки.

Три скалярных уравнения или эквивалентное им одно векторное уравнение называются кинематическими уравнениями движения материальной точки.

Двигаясь, материальная точка занимает различные положения в пространстве относительно выбранной системы отсчета. При этом она «описывает» в пространстве какую-то линию. Линия, по которой движется точка в пространстве, называется траекторией. По форме траектории все движения делятся на прямолинейные и криволинейные. Траектория движения указывает все положения, которые занимала точка, но, зная траекторию, ничего нельзя сказать о том, быстро или медленно проходила точка отдельные участки траектории. Длину траектории, по которой двигалось тело в течение какого-то промежутка времени, называют путём, пройденным за этот промежуток времени, его обозначают буквой S. Путь – скалярная величина.

Для описания движения тела нужно указать, как меняется положение точек с течением времени. Если участки криволинейные, то изменение координат тела описывают с помощью такого понятия как перемещение. Перемещением тела (материальной точки) называется вектор, соединяющий начальное положение тела с его последующим положением. Обозначается на чертежах как направленный отрезок, соединяющий начальное и конечное положение тела в пространстве:

Путь и модуль перемещения могут совпадать по значению, только в том случае, если тело движется вдоль одной прямой в одном направлении.

Важной величиной, характеризующей движение тела, является его скорость. Скорость – векторная величина. Она считается заданной, если известен ее модуль и направление. Скорость равномерного прямолинейного движения точки – векторная величина, равная отношению перемещения к промежутку времени, в течение которого это перемещение произошло. Пусть радиус-вектор задает положение точки в начальный момент времени t₀, а радиус-вектор- в момент времени t. Тогда промежуток времени:

,

и перемещение:

.

Подставляя выражение для скорости, получим:

Если начальный момент времени t₀ принять равным нулю, то скорость равна:

Выразим отсюда радиус-вектор :

Это и есть уравнение равномерного прямолинейного движения точки, записанное в векторной форме. Оно позволяет найти радиус-вектор точки при этом движении в любой момент времени, если известны скорость точки и радиус-вектор, задающий ее положение в начальный момент времени. В проекциях на ось ОХ уравнение можно записать в виде:

х=х₀+v_хt.

Это уравнение есть уравнение равномерного прямолинейного движения точки, записанное в координатной форме. Оно позволяет найти координату х тела при этом движении в любой момент времени, если известны проекция его скорости на ось ОX и его начальная координата х₀.

Путь S, пройденный точкой при движении вдоль оси ОХ, равен модулю изменения ее координаты:

Его можно найти, зная модуль скорости

Строго говоря, равномерного прямолинейного движения не существует. Но приближенно на протяжении не слишком большого промежутка времени движение автомобиля можно считать равномерным и прямолинейным с достаточной для практических целей точностью. Таково одно из упрощений действительности, позволяющее без больших усилий описывать многие движения.

Полученные результаты можно изобразить наглядно с помощью графиков. Для прямолинейного равномерного движения график зависимости проекции скорости от времени очень прост. Это прямая, параллельная оси времени.

Как мы уже знаем, зависимость координаты тела от времени описывается формулой х=х₀+𝞾_хt. График движения представляет собой прямую линию:

Из второго рисунка видим, что углы наклона прямых разные. Угол наклона второй прямой больше угол наклона первой прямой , т.е за одно и тоже время тело, движущееся со скоростью , проходит большее расстояние, чем при движении со скоростью А значит А что же в случае 3, когда угол α < 0? В случае 3 тело движется в сторону, противоположную оси ОХ. Проекция скорости в случае 3 имеет отрицательное значение и график проходит ниже оси ОХ. Проекция скорости определяет угол наклона прямой х(t) к оси t и численно равна тангенсу угла

Относительность механического движения – это зависимость траектории движения тела, пройденного пути, перемещения и скорости от выбора системы отсчёта. В рамках классической механики время есть величина абсолютная, то есть протекающее во всех системах отсчета одинаково.

Примеры и разбор решения заданий

1. Тело движется равномерно и прямолинейно в положительном направлении оси ОХ. Координата тела в начальный момент времени равна x_о = -10м. Найдите координату тела через 5с, если модуль её скорости равен ʋ=2 м/с. Какой путь проделало тело за это время?

Дано: x_о = — 10 м, t = 5 c, ʋ = 2 м/с. Найти s, х.

Решение: координату точки найдем по формуле:

х = х₀ + 𝞾_х t

Так как направление вектора скорости совпадает с направлением оси координат, проекция вектора скорости положительна и равна ʋ_x=ʋ; тогда вычисляем:

х = — 10 + 2· 5 = 0 (м).

Пройденный путь найдем s = ʋ t; s = 2·5 = 10 м.

2. Равномерно друг за другом движутся два поезда. Скорость первого равна 72 км/ч, а скорость второго — 54 км/ч. Определите скорость первого поезда относительно второго.

Дано:

Найти .

Решение: Из условия задачи ясно, что векторы скоростей поездов направлены в одну сторону. По закону сложения скоростей запишем:

,

где — искомая величина.

Находим проекцию скоростей на ось ОХ и записываем, чему равен модуль искомой величины

Ответ: .

Разделение сегмента в заданном соотношении

Предположим, у вас есть отрезок PQ ¯ на координатной плоскости, и вам нужно найти точку на отрезке 13 пути от P до Q.

Давайте сначала рассмотрим простой случай, когда P находится в начале координат, а отрезок прямой — горизонтальный.

Длина линии составляет 6 единиц, а точка на отрезке 13 пути от P до Q будет на 2 единицы от P и на 4 единицы от Q
и будет в (2,0).

Рассмотрим случай, когда сегмент не является горизонтальной или вертикальной линией.

Компоненты направленного отрезка PQ¯ равны 〈6,3〉, и нам нужно найти точку, скажем X, на отрезке 13 пути от P до Q.

Тогда компоненты отрезка PX¯ равны 〈(13) (6), (13) (3)〉 = 〈2,1〉.

Поскольку начальная точка сегмента находится в начале координат, координаты точки X задаются выражением (0 + 2,0 + 1) = (2,1).

Теперь давайте займемся более сложной задачей, когда ни P, ни Q не находятся в начале координат.

Используйте конечные точки сегмента PQ¯, чтобы записать компоненты направленного сегмента.

〈(x2 − x1), (y2 − y1)〉 = 〈(7−1), (2−6)〉 = 〈6, −4〉

Теперь аналогично компоненты отрезка PX¯, где X — точка на отрезке 13 пути от P до Q, 〈(13) (6), (13) (- 4)〉 = 〈2, −1,25〉.

Чтобы найти координаты точки X, сложите компоненты отрезка PX¯ с координатами начальной точки P.

Итак, координаты точки X равны (1 + 2,6−1,25) = (3,4,75).

Обратите внимание, что результирующие сегменты PX¯ и XQ¯ имеют длину в соотношении 1: 2.

В общем: что, если вам нужно найти точку на отрезке линии, которая делит его на два отрезка с длиной в соотношении a: b?

Рассмотрим направленный отрезок XY¯ с координатами концов как X (x1, y1) и Y (x2, y2).

Предположим, что точка Z делит отрезок в соотношении a: b, тогда точка представляет собой aa + b пути от X до Y.

Итак, обобщая имеющийся у нас метод, компоненты отрезка XZ¯ равны 〈(aa + b (x2 − x1)), (aa + b (y2 − y1))〉.

Тогда координата X точки Z равна

.

x1 + aa + b (x2 − x1) = x1 (a + b) + a (x2 − x1) a + b = bx1 + ax2a + b.

Аналогично, координата Y равна

.

y1 + aa + b (y2 − y1) = y1 (a + b) + a (y2 − y1) a + b = by1 + ay2a + b.

Следовательно, координаты точки Z равны (bx1 + ax2a + b, by1 + ay2a + b).

Пример 1:

Найдите координаты точки, которая разделяет направленный отрезок MN¯ с координатами конечных точек в точках M (−4,0) и M (0,4) в соотношении 3: 1?

Пусть L — точка, которая делит MN¯ в соотношении 3: 1.

Здесь (x1, y1) = (- 4,0), (x2, y2) = (0,4) и a: b = 3: 1.

Подставить в формулу. Координаты L:

(1 (−4) +3 (0) 3 + 1,1 (0) +3 (4) 3 + 1).

Упростить.

(−4 + 04,0 + 124) = (- 1,3)

Следовательно, точка L (−1,3) делит MN¯ в соотношении 3: 1.

Пример 2:

Каковы координаты точки, разделяющей направленный отрезок AB¯ в соотношении 2: 3?

Пусть C будет точкой, которая делит AB¯ в соотношении 2: 3.

Здесь (x1, y1) = (- 4,4), (x2, y2) = (6, −5) и a: b = 2: 3.

Подставить в формулу. Координаты C:

(3 (−4) +2 (6) 5,3 (4) +2 (−5) 5).

Упростить.

(−12 + 125,12−105) = (0,25) = (0,0.4)

Следовательно, точка C (0,0.4) делит AB¯ в соотношении 2: 3.

Вы можете заметить, что формула средней точки является частным случаем этой формулы, когда a = b = 1.

Видео-вопрос: поиск координат точек, разделяющих отрезок прямой на три равные части

Стенограмма видео

Учитывая точку 𝐴 отрицательные пять, девять и точку 𝐵 семь, отрицательные три, какие точки 𝐶 и 𝐷 делят отрезок прямой 𝐴𝐵 на три части равной длины?

Итак, первое, что мы сделали, это нарисовали эскиз для нашего отрезка линии 𝐴𝐵. И мы сделали это, построив точку 𝐴 минус пять, девять и точку 𝐵 семь, минус три.Итак, мы просто смоделировали ситуацию с помощью горизонтальной линии. Итак, у нас есть отрезок 𝐴𝐵. Затем у нас есть две точки, которые делят его на три равные части. Итак, у нас есть треть длины, треть длины и треть длины. Таким образом, из этой диаграммы мы можем видеть, что точка 𝐶 будет составлять треть пути вдоль линии. А точка 𝐷 будет составлять две трети длины линии.

Теперь у нас есть два разных способа решить эту проблему.Первый способ, которым мы воспользуемся, — это взглянуть на координатную сетку. Итак, во-первых, если мы посчитаем, на сколько единиц он упал с 𝐴 до 𝐵, то есть в направлении, мы увидим, что это 12. И если мы сделаем то же самое в направлении, мы увидим, сколько единиц вдоль от 𝐴 до 𝐵 равно 12. Ну, если мы начнем с точки 𝐶, то мы знаем, что точка 𝐶 составляет треть расстояния вдоль линии от 𝐴 до 𝐵. Таким образом, мы можем найти треть пути от 𝐴 до 𝐵, что будет на четыре квадрата вниз, потому что треть от 12 равна четырем.И то же самое по оси, потому что это будет четыре единицы, потому что это треть от 12, что, опять же, равно четырем.

Итак, теперь мы можем пойти на четыре вниз от 𝐴 и на четыре вниз от. А затем мы выясняем, где это встречается. Что ж, точка, где они встречаются, — это точка 𝐶, которая имеет отрицательные координаты один, пять. Что ж, теперь, если мы посмотрим на точку what, мы увидим точку, которая составляет две трети от 𝐴 до 𝐵. Итак, я снова отмечу это на диаграмме, чтобы у нас было две трети.Итак, восемь единиц вниз и восемь единиц пересекаются. Итак, они встречаются в точке, которую мы назовем 𝐷, которая является точкой три, один. Итак, теперь отлично! Мы обнаружили две точки 𝐶 и 𝐷, которые делят отрезок 𝐴𝐵 на три части равной длины.

Итак, мы сказали, что можем использовать несколько методов. Итак, мы рассмотрим другой метод. И в этом методе мы фактически формализуем процесс с помощью формулы. Итак, формула, которая у нас есть, состоит в том, что если мы хотим найти точку line, 𝑦 на отрезке прямой, то она равна 𝑥 sub one плюс one, умноженному на sub two минус 𝑥 sub one.И это для координаты. И для-координаты у нас есть суб-один плюс 𝑘, умноженный на суб-два минус 𝑦 суб-один. И здесь 𝑥 sub one, 𝑦 sub one и 𝑥 sub two, 𝑦 sub two — координаты двух точек линейного сегмента, и в данном случае это будут 𝐴 и 𝐵. А 𝑘 — это доля или доля расстояния или длины этого сегмента линии до точки, которую вы ищете.

Хорошо, теперь давайте подставим наши значения в нашу формулу. Итак, первое, что мы сделали, это пометили полученные координаты.Итак, у нас есть под-один, 𝑦 под-один и and под-два, 𝑦 под-два. Итак, теперь мы посмотрим на точку 𝐶, которая составляет треть пути по нашей линии. Итак, когда мы сделаем это для координаты 𝑥, мы получим отрицательные пять плюс треть, умноженные на семь минус отрицательные пять. Тогда для координаты 𝑦 у нас будет девять плюс треть, умноженная на минус три минус девять.

И, как мы уже говорили, это просто формализация того, что мы сделали с предыдущим методом, потому что в скобках слева мы только что получили изменение 𝑥-координат.Это означает, что нам нужна треть пути к этому изменению. И в правой части скобок у нас есть изменение в 𝑦-координатах, поэтому нам нужна треть пути от этого изменения. Итак, когда мы вычисляем эти значения, у нас будут отрицательные пять плюс четыре, девять минус четыре, что даст нам отрицательные координаты один, пять, что соответствует тому, что мы получили с помощью первого метода.

Итак, перейдем к делу point. Что ж, для точки 𝐷 все будет точно так же, за исключением того, что на этот раз у нас две трети — это наша 𝑘, потому что это две трети пути вдоль отрезка линии 𝐴𝐵.Итак, мы получили отрицательные пять плюс две трети, умноженные на семь минус отрицательные пять для 𝑥-координаты и девять плюс две трети, умноженные на отрицательные три минус девять для 𝑦-координаты, которые при вычислении дадут нам координаты три, один. , что аналогично первому способу.

Итак, мы нашли точки 𝐶 и 𝐷, которые делят отрезок прямой 𝐴𝐵 на три равные части, и они отрицательны: единица, пять и три, единица соответственно.

Разделение отрезков линии на равные части: геометрическое построение — Видео и стенограмма урока

Количество частей

Этот метод будет работать, если вы разделите отрезок линии , линию, соединяющую две точки, на две части, три части или более.Обычно задача подскажет, сколько равных частей ей нужно.

В реальном мире дизайнеры и архитекторы могут выбрать лучшее число, которое приведет к наиболее устойчивому зданию. Как и в случае с железнодорожными путями, стержни расположены на определенном расстоянии, чтобы обеспечить максимальную прочность и устойчивость путей.

Процесс

Для метода, который я собираюсь показать вам для разделения отрезков линии, вам понадобятся всего два инструмента. Первый инструмент, который вам понадобится, — это линейка, похожая на край куска картона.Второй инструмент — компас. Вы можете взять линейку и компас, чтобы вы могли следовать за ним. Я собираюсь показать вам процесс разделения данного отрезка линии на 5 равных частей. Вы можете использовать этот процесс для любого количества равных частей, изменив ширину на шаге 3.

1. Шаг первый — нарисовать линейный сегмент. Используйте линейку, чтобы нарисовать отрезок линии. Отметьте начальную точку как A, а конечную точку как B. Мы будем ссылаться на эти точки в дальнейшем. Буквы обозначают этот конкретный отрезок линии как отрезок AB.

2. Возьмите линейку и нарисуйте еще один отрезок линии, начинающийся из точки A, и наклоните эту линию вверх и в сторону от точки B. В итоге вы получите то, что выглядит как символ гигантского угла. Хотя не имеет значения, какой длины будет эта новая линия, я бы нарисовал эту линию такой же длины или чуть больше, чем отрезок AB.

3.Теперь возьмите циркуль и установите его ширину примерно на 1/5 длины новой линии. Мы делим на 5, потому что хотим 5 равных частей. Это не обязательно должно быть точно, так что вы можете это увидеть. Используйте ширину, чтобы разделить новую линию на 5 равных частей. Начните с того, что поместите кончик циркуля в точку A, а затем проведите дугу через новую линию свободным концом. Это создает пересечение между только что нарисованной дугой и новой линией. Затем переместите циркуль к вновь созданному перекрестку и проведите еще одну дугу через новую линию дальше по ней.Продолжайте делать это, пока не отметите пять равных частей на новой линии. Отметьте это последнее пересечение как точку C.

4. Поместите кончик компаса в точку B и установите ширину компаса так, чтобы другой конец касался точки C. Переместите компас так, чтобы кончик компаса находился в точке A, а затем нарисуйте дугу прямо под точкой. А.

5.Затем переместите кончик компаса в точку A и установите ширину так, чтобы другой кончик компаса достиг точки C. Затем переместите кончик компаса в точку B и нарисуйте дугу, которая пересекается с дугой, нарисованной на шаге 4. Обозначьте эту точку пересечения D.

6. Соедините точки D и B с помощью линейки.

7.Используя ту же ширину циркуля, что и на шаге 3, начиная с точки D, сделайте то же, что и на шаге 3, и разделите линейный сегмент DB на пять равных частей.

8. В конце возьмите линейку и соединив соответствующие пересечения вдоль отрезков AC и DB. Теперь вы должны смотреть на исходный отрезок линии, разделенный на пять равных частей.

Резюме урока

Таким образом, разделенный отрезок линии представляет собой прямую линию, соединяющую две точки, разделенную на несколько равных частей.Отрезок — это прямая линия, соединяющая две точки. Чтобы разделить отрезок AB на несколько равных частей, вам понадобится линейка и циркуль. Вы используете их, чтобы нарисовать две новые линии, одну от точки A, а другую от точки B. Эти две линии отмечены с помощью циркуля количеством желаемых равных частей. Итак, если вам нужны 3 равные части, вы бы разметили две новые линии на 3 равные части; если вам нужно 6 равных частей, вы бы разметили две новые линии на 6 равных частей.Затем вы завершаете, соединяя пересечения на двух новых линиях друг с другом, чтобы разделить исходную линию на желаемое количество равных частей.

Результаты обучения

После этого видеоурока вы должны уметь:

• Определить разделенный отрезок линии
• Определите инструменты, необходимые для разделения линейного сегмента на равные части
• Объясните, как разделить линейный сегмент на равные части с помощью этих инструментов

куб боулдер должностных инструкций

Используйте шаблон «Соглашение о компенсации сверхурочной работы для двойного найма сотрудников CU Boulder», чтобы задокументировать право на сверхурочную работу для каждого назначения и то, как сверхурочная работа будет управляться и отслеживаться.описания курсов по боулдерингу, документ с описаниями курсов по боулдерингу, загрузите на свой компьютер все описания курсов по боулдерингу. Самые горячие порнозвезды и мамочки с большими сиськами Перечисленные здесь курсы включены в каталог кампуса Боулдера в течение 2019–20 учебного года. База данных руководств, доступная в Национальном информационном центре руководств, и рекомендации Целевой группы США по профилактическим услугам особенно полезны. Предварительный опыт или образование не требуются или не требуются.Квалифицированные кандидаты получат вознаграждение за трудоустройство независимо от расы, цвета кожи, религии, пола, национального происхождения, сексуальной ориентации, гендерной идентичности, инвалидности или защищенного статуса ветерана. Положение AD&D предоставляет льготу в размере до и в дополнение к сумме основного срока жизни в случае вашей смерти в результате несчастного случая. Садитесь в коричневатый поезд справа, чтобы убрать другой поезд с дороги. Этот термин чаще всего относится к персонажам-магам, которые могут наносить огромный урон, но легко умирают, но он может относиться и к другим типам персонажей.Менеджеры и руководители несут ответственность за распределение работы, определение работы, прием на работу и оценку производительности, определение рабочего времени, определение должностей, которые необходимо создать или упразднить, и назначение сотрудников на должности. Конфиденциальность • Юридическая информация и товарные знаки • Карта кампуса. Закончите работу, также запрыгнув в верхний шлейф. Агентство, основанное в 2012 году, насчитывает более 300 сотрудников и предоставляет услуги контент-маркетинга, электронного маркетинга, PPC, SEO, маркетинга в социальных сетях, веб-дизайна и PR. Группы Google доступны для преподавателей, сотрудников и студентов, которым предоставлены учетные записи Google.Эта позиция будет иметь решающее значение для организации и управления лабораторией, как описано ниже. Компетентные органы могут рассмотреть этот вариант в тех случаях, когда сотрудники, проходящие испытательный срок, продемонстрировали образцовые способности при выполнении своей работы, а ранняя аттестация приносит пользу организации. Согласно закону PERA, классифицированные сотрудники должны быть зарегистрированы в PERA во время приема на работу. Работа, как правило, выполняется в рамках курса обучения студента на уровне старших курсов или магистратуры. Свяжитесь с вашим консультантом по управлению персоналом / вознаграждениям (PMC) для получения дополнительной информации о преобразовании должности из секретной в университетский штат.Неполучение разрешения до начала работы по совместительству может привести к исправительным или дисциплинарным мерам. , Должности и требования определяются системой и кампусами Университета Колорадо. Персонал основных служб, который постоянно не соответствует заявленным ожиданиям в связи с этим назначением, может быть подвергнут дисциплинарным взысканиям или лишен статуса основных служб. Классифицированные сотрудники, которые получают зарплату в рамках ежемесячного цикла оплаты труда университета и назначены на регулярную (временную) должность с правом выплаты пособия 50% или выше, имеют право на участие в программе медицинского страхования CU.Gl — Удачи. Губернатор установил партнерские отношения с некоторыми классифицированными сотрудниками. Роль консультанта по вопросам управления / вознаграждения (PMC) в Боулдере, создание, пересмотр или заполнение кадровой должности, определение должности в качестве основных услуг, правила и административные процедуры Совета по персоналу штата Колорадо, Департамент персонала и администрации, HR Консультант по управлению должностями / вознаграждениям (PMC), классифицированный / Сравнительная таблица сотрудников университета, Соглашение о компенсации сверхурочных за двойную работу сотрудников CU Boulder, Форма запроса на привлечение сторонней работы, Форма запроса о смене дифференциального назначения, Исключения специалистов из государственной кадровой системы FAQ, секретные vs.Таблица сравнения сотрудников университета, классифицированные должности, имеющие право на преобразование из секретного в университетский персонал, диаграмма рабочего процесса анализа управления должностями, когда вам нужно создать, изменить или заполнить классифицированную или штатную должность в университете, пожалуйста, свяжитесь с вашим отделом кадрового управления / компенсаций (PMC) в Боулдере консультант как можно скорее. Временная занятость не может превышать 9 месяцев из 12-месячного скользящего периода. Цикл выступления длится с 1 апреля по 31 марта каждого года. Требуется предварительный опыт, образование или специальные навыки.Присоединяйтесь к динамичному, творческому и интересному городу. Во многих отношениях кампус CU Boulder — это отдельный город. Да, перераспределение будет обработано в секретной системе в соответствии со стандартными процессами. HR-рекрутер не может начать процесс размещения вакансий или найма до тех пор, пока название должности и уровень заработной платы не будут оценены и утверждены консультантом PMC. Все бесплатное порно, которое вы хотите, здесь! Прием на работу в университет регулируется законодательством и политиками Регентского университета Колорадо. Некоторые вакансии могут не выходить за пределы этого уровня.Руководитель несет ответственность за распределение работ, однако контроль за ходом работы осуществляется в меньшей степени, а данные инструкции носят более общий характер. Классифицированные сотрудники, которым выплачивается ежемесячный платежный цикл университета с регулярным (временным) назначением менее 50 процентов, имеют право на участие в планах медицинского страхования CU. Государственные кадровые правила предоставляют компетентному органу право по своему усмотрению сертифицировать государственного служащего до окончания 12-месячного испытательного срока. Любая корректировка заработной платы будет рекомендована деканом или главой отдела и утверждена соответствующим старшим должностным лицом университетского городка и канцлером, как правило, 1 июля каждого года.Компетентные органы определяют, какие должности в их соответствующих областях должны быть определены в качестве основных служб и при каких условиях конкретные лица должны будут работать. Как насчет влияния на другие мои льготы, если я перейду на штатную должность в университете? Ранее ENGL 4523. Эта система позволяет вам создать профиль, отправить новую вакансию для публикации, внести изменения в существующее объявление о вакансии и удалить ваше объявление о вакансии, когда должность будет заполнена. Наем в секретной системе регулируется Правилами и административными процедурами Совета по персоналу штата Колорадо.Консультант PMC гарантирует, что содержание описания должности направлено в группу утверждения центра кадрового обслуживания для ввода и утверждения в HCM, а также создание номера должности, если это применимо. После получения служебной записки в отдел кадров, она будет отправлена ​​соответствующему консультанту, который быстро рассмотрит документ и при необходимости запросит дополнительную информацию у компетентного органа. Этот подход рассматривает общество через ориентацию на макроуровне, которая представляет собой широкий акцент на социальных структурах, формирующих общество в целом, и полагает, что общество развивалось как организмы.Ваш консультант проконсультирует вас по структуре должности и предоставит рекомендации по заполнению или обновлению описания должности. Если ваша избирательная форма не будет получена к указанному сроку, будет считаться, что вы безоговорочно избраны для участия в PERA. Классифицированные сотрудники получают ежегодный отпуск, основанный на полных полных месяцах государственной службы в государственной кадровой системе или вне ее ( за исключением временных командировок). Чтобы получить полную диаграмму, сравнивающую эти две группы занятости, ознакомьтесь с C.Точно нет. Назначение основных услуг требует одобрения проректора кампуса или вице-канцлера. Родительский отпуск действует одновременно с семейным отпуском по болезни. 47 лайков, 1 комментарий — Университет Центрального Арканзаса (@ucabears) в Instagram: «Ваш подарок предоставляет студентам УЦА стипендии, программы, неоценимые возможности обучения и…» План Basic Term Life приносит выгоду вашим получателям в случае вашей смерти пока покрывается политикой. Сертифицированные классифицированные сотрудники имеют право на прогрессивную дисциплину, и все классифицированные сотрудники, занимающие обычные (не временные) должности, могут использовать процессы рассмотрения жалоб и апелляций штата.Если не будет предпринято никаких действий для регистрации / отказа или изменения льгот, сотрудник может быть переведен в план или лишен права изменить страховое покрытие на оставшуюся часть льготного года. В статуте говорится, что эквивалентный специализированный опыт может заменить образование или подготовку, отвечающую требованиям степени бакалавра или более высокой степени. Сотрудникам следует обращаться к своим руководителям, если у них есть вопросы о том, считаются ли они персоналом «основных служб». Помимо инноваций, город Боулдер способствует гражданской активности через консультативные комитеты, общественные собрания и волонтерство.Соискатели работы также могут контролировать получение текстовых SMS-сообщений через настройки своей учетной записи соискателя, связавшись с Клиентом, к которому относится текстовое сообщение, или отправив уведомление в службу поддержки по адресу [email protected]. Просмотрите наши списки, чтобы найти работу в Германии для эмигрантов, в том числе работу для англоговорящих или тех, кто на вашем родном языке. «Теперь каждый год 6000 новых студентов узнают о своих сильных сторонах и о том, как их продуктивно использовать для улучшения самочувствия и вовлеченности. Текущие классифицированные сотрудники не обязаны переходить на штатную должность в университете, даже если их должности теперь соответствуют критериям освобождения.Показатели служебной аттестации могут повлиять на ежегодное повышение заработной платы для обеих групп занятости. Если будет утверждено повышение заслуг, вы будете включены в цикл корректировки заработной платы за этот год. Я должен оставаться в ПЕРА? Если вы решите перейти на новую должность штатного сотрудника университета в соответствии с критериями исключения, вы не имеете права быть переведенным обратно на классифицированную должность, даже если она является вакантной. Это означает, что по мере создания или освобождения новых освобожденных от налогообложения должностей они будут освобождаться от государственной кадровой системы и создаваться как штатные должности университета.Рабочие задания могут включать использование специального оборудования, программных приложений или инструментов в установленном порядке. Сотрудник может подписаться на льготы в течение следующего открытого периода регистрации с покрытием льгот, начиная с начала года нового плана льгот. Например, если я занимаю должность General Professional I, могу ли я получить повышение до General Professional II? Эта должность обеспечивает интенсивную индивидуальную помощь студентам из групп риска. Консультант по управлению персоналом по управлению персоналом организует встречу по стратегии или позвонит, чтобы обсудить должность, вашу организацию и бизнес-потребности отдела.Должности сотрудников OEP / университета регулируются всеми другими применимыми федеральными законами и законами и постановлениями штата, а также законами и политиками, установленными Советом регентов Университета Колорадо и другими политиками университетов и кампусов Боулдера. Работа требует умеренных независимых суждений, анализа и навыков принятия решений. Вы также можете подать заявку на другие должности сотрудников университета, которые могут привести к повышению по службе. Помимо FML, сотрудники университета имеют право на получение отпуска по уходу за ребенком сроком до шести месяцев после рождения или усыновления ребенка.Это оставит достаточно места в диапазоне оплаты для увеличения заслуг и продолжительности жизни в том случае, если сотрудник продолжит выполнять ту же работу с течением времени.

Формула раздела — Внутреннее и внешнее деление | Координатная геометрия

Предположим, что точка делит линейный сегмент на две части, которые могут быть равными или нет, с помощью формулы сечения мы можем найти эту точку, если заданы координаты линейного сегмента, и мы также можем найти соотношение, в котором точка делит данный отрезок линии, если заданы координаты этой точки.

Когда точка C делит отрезок AB в соотношении m: n, мы используем формулу сечения, чтобы найти координаты этой точки. Формула сечения бывает двух видов. Эти типы зависят от точки C, которая может находиться между точками или вне отрезка линии.

Эти два типа:

1. Формула внутреннего сечения
2. Формула внешнего сечения

Формула внутреннего сечения

Когда точка делит линейный сегмент в соотношении m: n внутри точки C, тогда эта точка находится между координаты отрезка, то мы можем использовать эту формулу.Его еще называют внутренним делением.

Если координаты A и B равны (x1, y1) и (x2, y2) соответственно, то формула внутреннего сечения задается как:

Вывод формулы

Пусть A (x1, y1) и B (x2, y2) — конечные точки данного отрезка AB, а C (x, y) — точка, которая делит AB в соотношении m: n.

Тогда AC / CB = m / n

Мы хотим найти координаты (x, y) точки C.

Теперь нарисуйте перпендикуляры A, C, B, параллельные координате Y, соединяющиеся в точках P, Q и R на оси X.

Если посмотреть на диаграмму выше,

AM = PQ = OQ — OP = (x — x1)

CN = QR = OR — OQ = (x2 — x)

CM = CQ — MQ = (y — y1)

BN = BR — NR = (y2 — y)

Очевидно, мы можем видеть, что ∆AMC и ∆CNB подобны и, следовательно, их стороны пропорциональны правилу сравнения AA.

AC / CB = AM / CN = CM / BN

Теперь подставляем значения в указанное выше соотношение

=> m / n = [x — x1 / x2 -x] = [y — y1 / y2 — y]

=> m / n = [x — x1 / x2 -x] и m / n = [y — y1 / y2 — y]

Решая 1-е условие,

=> m (x2 — x ) = n (x — x1)

=> (m + n) x = (mx2 + nx1)

=> x = (mx2 + nx1) / (m + n)

Решая 1-е условие,

=> m (y2 — y) = n (y — y1)

=> (m + n) y = (my2 + ny1)

=> y = (my2 + ny1) / (m + n)

Следовательно, координаты C (x, y) равны

{(m × x ₂ + n × x ₁ ) / (m + n), (m × y ₂ + n × y ₁ ) / (m + n)}

Формула внешнего сечения

Когда точка, разделяющая линейный сегмент, делится снаружи в соотношении m: n, находится за пределами линейного сегмента i.е, когда мы удлиняем линию, она совпадает с точкой, тогда мы можем использовать эту формулу. Его также называют внешним делением.

Если координаты A и B равны (x1, y1) и (x2, y2) соответственно, то формула внешнего сечения задается как

Вывод формулы

Для получения внутреннего сечения мы взяли линию отрезок и точка C (x, y) внутри линии, но в случае формулы внешнего сечения мы должны взять эту точку C (x, y) за пределы отрезка линии.

Пусть A (x1, y1) и B (x2, y2) — конечные точки данного отрезка AB, а C (x, y) — точка, которая делит AB во внешнем отношении m: n.

Нам нужно найти координаты (x, y) точки C. Для этого нарисуйте перпендикуляры A, B, C, параллельные координате Y, соединяющиеся в точках P, Q и R на оси X.

Если посмотреть на диаграмму выше,

AM = PR = OR — OP = (x — x1)

BN = QR = OR — OQ = (x — x2)

аналогично,

CM = RC — MR = (y — y1)

CN = CR — NR = (y — y2)

Очевидно, мы можем видеть, что треугольник AMC и треугольник BNC подобны, и, следовательно, их стороны пропорциональны правилу сравнения AA

AC / BC = AM / BN = CM / CN

Теперь подставляем значения в приведенном выше соотношении

=> m / n = [x — x1 / x — x2] = [y — y1 / y — y2]

=> m / n = [x — x1 / x — x2] и m / n = [y — y1 / y — y2]

Решая 1-е условие,

=> m (x — x2) = n (x — x1)

=> (m — n) x = (mx2 — nx1)

=> x = (mx2 — nx1) / (m — n)

Решая 2-е условие,

=> m (y — y2) = n (y — y1)

=> (m — n) y = (my2 — ny1)

=> y = (my2 — ny1) / (m — n)

Следовательно, -координаты C (x, y) равны

{(m × x ₂ — n × x ₁ ) / (m — n), (m × y ₂ — n × y ₁ ) / (m — n)}

Задачи по формуле сечения

Задача 1: Найдите координаты точки C (x, y), где она делит отрезок прямой, соединяющий (4, — 1) и (4, 3) в соотношение 3: 1 внутри?

Решение:

Заданные координаты: A (4, -3) и B (8, 5)

Пусть C (x, y) будет точкой, которая делит отрезок линии в соотношении 3 : 1 я.em: n = 3: 1

Теперь, используя формулу C (x, y) = {(m × x2 + n × x1) / (m + n), (m × y2 + n × y1) / (m + n)} , поскольку C делит внутри.

=> C (x, y) = {(3 * 4 + 1 * 4) / (3 + 1), (3 * 3 + 1 * (- 1)) / (3 + 1)}

= > C (x, y) = {16/4, 8/4}

=> C (x, y) = {4, 2}

Следовательно, координаты равны (4, 2).

Задача 2: Если точка P (k, 7) делит отрезок прямой, соединяющий A (8, 9) и B (1, 2) в соотношении m: n, то найдите значения m и n.

Решение:

Не упоминается, что точка разделяет линейный сегмент внутри или снаружи. Итак, в то время мы будем рассматривать внутреннюю секцию по умолчанию.

Заданные координаты: A (8, 9) и B (1, 2)

Пусть заданная точка P (k, 7) делит отрезок прямой в соотношении m: 1

Теперь используем сечение формула, находящая только координату x,

=> k = (m × x2 + n × x1) / (m + n)

=> k = (m × 1 + 1 × 8) / (m +1)

=> k = (m + 8) / (m + 1)

=> km + k = m + 8 …….(1)

Снова используя формулу сечения для координаты y.

=> 7 = (m × y2 + n × y1) / (m + n)

=> 7 = (m × 2 + 1 × 9) / (m + 1)

=> 7 = (2m + 9) / (m +1)

=> 7m + 7 = 2m +9

=> 5m = 2

=> m = 5/2

Таким образом, требуемое соотношение составляет 5: 2

Следовательно, значение m равно 5, а значение n равно 2

Задача 3: A (4, 5) и B (7, -1) — две заданные точки, а точка C делит линейный сегмент AB снаружи в соотношение 4: 3.Найдите координаты C.

Решение:

Заданные координаты: A (4, 5) и B (7, -1)

Пусть C (x, y) будет точкой, которая разделяет линию сегмент снаружи в соотношении 4: 3, т.е. m: n = 4: 3

Теперь используя формулу C (x, y) = {(m × x2 — n × x1) / (m — n), (m × y2 — n × y1) / (m — n)} , поскольку C делит внутри.

значение x = (mx2 — nx1) / (m — n)

=> (4 * 7-3 * 4) / (4-3)

=> 16

значение y = (my2 — ny1) / (m — n)

=> (4 * (-1) — 3 * 5) / (4 — 3)

=> -19

Следовательно, координаты (16 , -19).

Задача 4: Линия 2x + y − 4 = 0 делит отрезок прямой, соединяющий точки A (2, −2) и B (3,7). Найдите соотношение отрезка линии, в котором линия делится?

Решение:

Заданы координаты A (2, -2) и B (3, 7).

Линия с уравнением 2x + y — 4 = 0 делит отрезок прямой в точке C (x, y)

Предположим, данная линия разрезает отрезок прямой в соотношении 1: n.

По формуле сечения,

=> x = (m * x2 + n * x1) / (m + n)

=> x = (3 + 2n) / (1 + n) ………..1

Аналогично

=> y = (m * y2 + n * y1) / (m + n)

=> y = (7 — 2n) / (1 + n) ……… .2

Теперь подставляем уравнения 1 и 2 в данное уравнение прямой.

=> 2x + y — 4 = 0

=> 2 [(3 + 2n) / (1 + n)] + [(7 — 2n) / (1 + n)] — 4 = 0

= > 6 + 4n + 7 — 2n — 4 (1 + n) = 0

=> 13 + 2n — 4 — 4n = 0

=> 9 — 2n = 0

=> n = 2/9

Следовательно, соотношение, при котором линия делится, составляет 9: 2.Мы также можем найти значения x и y, подставив значение n в уравнения 1 и 2.

Задача 5: A (2, 7) и B (–4, –8) являются координатами отрезок AB. Есть две точки, которые делят сегмент пополам. Найдите их координаты.

Решение:

Две точки пересекали отрезок прямой, что означает, что отрезок делится на 3 равные части.

AS = ST = TB ………… 1

=> AS / SB

=> AS / ST + TB

=> AS / (AS + AS) из уравнения 1

=> AS / 2 AS

=> 1/2

Итак, S делит отрезок AB в соотношении 1: 2

Теперь применяя формулу сечения, чтобы найти координаты точки S

=> x1 = (1 × (-4 ) + 2 × 2) / (1 + 2)

=> x1 = (-4 + 4) / 3

=> x1 = 0

Аналогично для координаты y

=> y1 = (1 × (-8) + 2 × 7) / (1 + 2)

=> y1 = (14-8) / 3

=> y1 = 2

Также.

=> AT / TB

=> (AS + ST) / TB

=> 2 ТБ / ТБ из уравнения 1

=> 2/1

Итак, T делит отрезок AB в соотношении 2: 1

Теперь применив формулу сечения, чтобы найти координаты точки T

=> x2 = (2 × (-4) + 1 × 2) / (2 + 1)

=> x2 = (-8 + 2) / 3

=> x2 = -2

Аналогично, для координаты y

=> y2 = (2 × (-8) + 1 × 7) / (2 + 1)

=> y2 = ( -16 + 7) / 3

=> y2 = -3

Таким образом, координаты:

S (x1, y1) = (0, 2)

T (x2, y2) = (-2, -3)

геометрия — Как найти середину (1/2), 1/3, 1/4 и т. Д. Линии?

geometry — Как найти середину (1/2), 1/3, 1/4 и т. Д. Линии? — Обмен математическими стеками

Сеть обмена стеков

Сеть Stack Exchange состоит из 177 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.

Посетить Stack Exchange

2. 0

3. +0

6. Авторизоваться
   Зарегистрироваться

Mathematics Stack Exchange — это сайт вопросов и ответов для людей, изучающих математику на любом уровне, и профессионалов в смежных областях.Регистрация займет всего минуту.

Зарегистрируйтесь, чтобы присоединиться к этому сообществу

Кто угодно может задать вопрос

Кто угодно может ответить

Лучшие ответы голосуются и поднимаются наверх

Спросил
7 лет, 7 мес. Назад

Просмотрено
53k раз

$ \ begingroup $

Аналогично этому вопросу: Как рассчитать середину строки? где объясняется, как найти середину линии (x, y), так что это половина линии 1/2, но мне также нужно найти одну треть линии, одну четвертую и так далее.

Я попытался разделить на 4 вместо 2, чтобы получить 1/4, но это не сработало:

1/2 (работает):

$ x = \ dfrac {x_1 + x_2} {2} $ $ y = \ dfrac {y_1 + y_2} {2}

долл. США

1/4 (не работает):

$ x = \ dfrac {x_1 + x_2} {4} $ $ y = \ dfrac {y_1 + y_2} {4}

долл. США

Создан 12 ноя.

01AutoMonkey01AutoMonkey

24511 золотой знак44 серебряных знака99 бронзовых знаков

$ \ endgroup $

$ \ begingroup $

Подумайте о формуле для средней точки линии как
$$ x = \ frac {1} {2} x_ {1} + \ frac {1} {2} x_ {2}.$$
Мы находим середину, беря равные вклады с обоих концов линии.

Если мы хотим найти точку, которая находится на одной трети длины линии, мы должны использовать следующий
$$ x = \ frac {2} {3} x_ {1} + \ frac {1} {3} x_ {2} $$
где мы берем неравные вклады от двух конечных точек.

Точку в четверти длины линии можно найти с помощью
$$ x = \ frac {3} {4} x_ {1} + \ frac {1} {4} x_ {2}. $$

Координаты Y находятся аналогичным образом.

Создан 12 ноя.

$ \ endgroup $

$ \ begingroup $

Разделите ваш сегмент на равные части.

Из последней точки видно, что
$$
x_2 = x_1 + n \ Delta \ подразумевает \ Delta = \ frac {x_2 — x_1} n
$$
Вам нужно найти вторую точку в этом дивизионе, поэтому
$$
x ‘= x_1 + \ Delta = x_1 + \ frac {x_2-x_1} n = \ frac {n-1} n x_1 + \ frac 1n x_2
$$
Итак, предположим, вы хотите разделить свой сегмент на 2 равные части, тогда $ n = 2 $ и
$$
x ‘= \ frac {x_1} 2 + \ frac {x_2} 2
$$
Если $ n = 3 $ (3 четных части)
$$
x ‘= \ frac 23 x_1 + \ frac 13 x_2
$$
$ n = 4 $ (4 четных части)
$$
x ‘= \ frac 34 x_1 + \ frac 14 x_2

$

Создан 12 ноя.

КастерКастер

9,4222 золотых знака2020 серебряных знаков3131 бронзовый знак

$ \ endgroup $

$ \ begingroup $

Считать $ x_1 $ смещением, а $ x_2-x_1 $ — расстоянием, на котором требуется секционирование: $$ x = x_1 + \ frac {x_2-x_1} n \ quad, \ quad y = y_1 + \ frac {y_2-y_1} n \ quad, \ quad z = z_1 + \ frac {z_2-z_1} n $$ Для $ x_1 = y_1 = z_1 = 0 $ результат становится очевидным.

Создан 12 ноя.

ЛучианЛусиан

45.9k11 золотых знаков7373 серебряных знака145145 бронзовых знаков

$ \ endgroup $

$ \ begingroup $

Пусть $ P $ и $ Q $ — две разные точки и определяют функцию (линейки).
$ f: \ mathbb R \ to \ overleftrightarrow {PQ} $, из набора действительных чисел в строку $ \ overleftrightarrow {PQ} $ на $ f (t) = (1-t) P + tQ $.Эта функция накладывает линейку на прямую $ \ overleftrightarrow {PQ} $ так, что ордината $ P $ равна $ 0 $ ($ f (0) = P $), а ордината $ Q $ равна $ 1 $ $ (f ( 1) = Q) $. Так, например, точка $ \ dfrac34 $ пути от $ P $ до $ Q $ равна $ f \ left (\ dfrac 34 \ right) = \ dfrac 14 P + \ dfrac 34 Q $.

Создан 24 июн.

Стивен Грегористевен Грегори

24.4k44 золотых знака3838 серебряных знаков7777 бронзовых знаков

$ \ endgroup $

Mathematics Stack Exchange лучше всего работает с включенным JavaScript

Ваша конфиденциальность

Нажимая «Принять все файлы cookie», вы соглашаетесь с тем, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в ​​отношении файлов cookie.

Принимать все файлы cookie

Настроить параметры

Координатная геометрия Внутреннее деление | Решенные примеры | Геометрия

Мы уже встречались с концепцией внутреннего деления линейного сегмента в более ранних классах.Рассмотрим отрезок AB:

Предположим, вам нужно найти точку C на AB, которая делит AB в соотношении 2: 1. Это означает, что \ ({\ rm {AC: CB = 2: 1}} \), как показано на следующем рисунке:

Как нам найти C? Прежде чем мы продолжим, обратите внимание на огромную разницу в между следующими двумя утверждениями:

Разница в том, что в первом случае отношение AC к BC составляет 2: 1, а во втором случае отношение BC к AC составляет 2: 1.Таким образом, расположение C в обоих случаях будет совершенно другим.

Теперь вернемся к проблеме того, как определить местонахождение C. Мы воспользуемся основной теоремой пропорциональности. Через A проведите любой луч AX и обрежьте на нем 3 равных интервала с помощью циркуля, как показано:

Теперь соедините R с B и через Q нарисуйте \ ({\ rm {QZ || RB}} \). Точка пересечения QZ с AB — это точка C:

.

Почему это работает? Поскольку \ ({\ rm {QC || RB}} \), мы имеем (используя BPT):

AC: CB = AQ: QR

Но \ ({\ rm {AQ: QR}} \), очевидно, 2: 1, потому что мы отсекли равные интервалы на AX.Таким образом,

AC: CB = 2: 1

Теперь давайте вернемся к этой проблеме внутреннего деления с точки зрения координат. Предположим, вам даны координаты двух точек A и B на плоскости. Как найти координаты точки C, которая делит AB внутри в заданном соотношении? Обратите внимание, что мы хотим найти координаты C, то есть нам нужен алгебраический ответ в терминах координат A и B.

Предположим, что координаты A и B:

\ [\ begin {array} {l} A \ Equiv \ left ({{x_1}, \; {y_1}} \ right) \\ B \ Equiv \ left ({{x_2}, \; {y_2}} \ right) \ end {array} \]

Мы хотим найти точку C, которая делит AB внутри в соотношении m : n .Пусть C — точка

\ [C \ Equiv \ left ({h, \; k} \ right) \]

Рассмотрим следующий рисунок:

Наша задача — найти координаты C через координаты A и B и параметры m и n . Завершим прямоугольный треугольник APB и AQC, как показано ниже:

Обратите внимание, что AQ и AP параллельны оси x , а BP и CQ параллельны оси y , и поэтому:

\ [\ begin {array} {l} P \ Equiv \ left ({{x_2}, \; {y_1}} \ right) \\ Q \ Equiv \ left ({h, \; {y_1}} \ right ) \ end {array} \]

Теперь мы сделаем следующие наблюдения:

\ [\ begin {align} & AP = {x_2} — {x_1}, \; BP = {y_2} — {y_1} \\ & AQ = h — {x_1}, \; CQ = k — {y_1} \ end {align} \]

Поскольку \ (\ Delta AQC {\ rm {}} \ sim {\ rm {}} \ Delta APB \), мы имеем:

\ [\ frac {{AQ}} {{AP}} = \ frac {{CQ}} {{BP}} = \ frac {{AC}} {{AB}} \; \; \; \; \ ; \; \; \; \; \; \; \; \; \ ;… ({\ rm {1}}) \]

А теперь самое важное. У нас уже есть выражения для членов первых двух соотношений выше, но как насчет третьего отношения? Какое значение имеет \ ({\ rm {AC: AB}} \)? Поскольку C делит AB внутри в соотношении m : n , мы имеем:

\ [\ begin {align} & \ frac {{AC}} {{CB}} = \ frac {m} {n} \\ & \ Rightarrow \ frac {{AC}} {{AB}} = \ frac {m} {{m + n}} \ end {align} \]

Убедитесь, что вы понимаете, как это получается. Используя это значение для \ ({\ rm {AC: AB}} \) в (1), мы имеем:

\ [\ begin {align} & \ frac {{AQ}} {{AP}} = \ frac {{CQ}} {{BP}} = \ frac {m} {{m + n}} \\ \ Стрелка вправо и \ frac {{h — {x_1}}} {{{x_2} — {x_1}}} = \ frac {{k — {y_1}}} {{{y_2} — {y_1}}} = \ frac {m} {{m + n}} \\ \ Rightarrow & \ left \ {\ begin {gather} \ frac {{h — {x_1}}} {{{x_2} — {x_1}}} = \ frac { m} {{m + n}} \\\ frac {{k — {y_1}}} {{{y_2} — {y_1}}} = \ frac {m} {{m + n}} \ end {собрано } \верно.\\ \ Rightarrow & \ left \ {\ begin {gather} h — {x_1} = \ left ({\ frac {m} {{m + n}}} \ right) \ left ({{x_2} — {x_1 }} \ right) \\ k — {y_1} = \ left ({\ frac {m} {{m + n}}} \ right) \ left ({{y_2} — {y_1}} \ right) \ end {собрано} \ right. \\ \ Rightarrow & \ left \ {\ begin {gather} h = {x_1} + \ left ({\ frac {m} {{m + n}}} \ right) \ left ({ {x_2} — {x_1}} \ right) \\ k = {y_1} + \ left ({\ frac {m} {{m + n}}} \ right) \ left ({{y_2} — {y_1} } \ right) \ end {собран} \ right. \\ \ Rightarrow & \ left \ {\ begin {gather} h = \ frac {{m {x_1} + n {x_1} + m {x_2} — m {x_1 }}} {{m + n}} \\ k = \ frac {{m {y_1} + n {y_1} + m {y_2} — m {y_1}}} {{m + n}} \ end {в собранном виде } \верно.\ end {align} \]

\ (\ Rightarrow \) \ (\ fbox {$ \ displaystyle {{h \, \, \, = \ frac {{m {x_2} + n {x_1}}} {{m + n}}, \; k = \ frac {{m {y_2} + n {y_1}}} {{m + n}}}} $} \)

Это называется формулой сечения , и она дает нам координаты C в терминах координат A и B, а также параметры m и n . Применим эту формулу к некоторым примерам.

Пример-1: Примите во внимание следующие два момента:

\ [A = \ left ({- 1, \; 2} \ right), \; B = \ left ({2, \; — 3} \ right) \]

Найдите точку, которая делит AB внутри в соотношении:

Решение: Let

\ [C = \ left ({{x_C}, \; {y_C}} \ right), \; D = \ left ({{x_D}, \; {y_D}} \ right) \]

— это точки, которые делят AB внутри в соотношении 1: 3 и 3: 1 соответственно.Теперь воспользуемся формулой сечения.

Координаты C

\ [\ begin {align} & {x_C} = \ frac {{\ underbrace {1 \ times 2} _ {m {x_2}} + \ underbrace {3 \ times — 1} _ {n {x_1}}}} } {{\ underbrace {1 \ times 3} _ {m + n}}} \; = \ frac {{2 — 3}} {4} = — \ frac {1} {4} \\ & {y_C} = \ frac {{\ underbrace {1 \ times — 3} _ {m {y_2}} + \ underbrace {3 \ times 2} _ {n {y_1}}}} {{\ underbrace {1 \ times 3} _ {m + n}}} = \ frac {{- 3 + 6}} {4} = \ frac {3} {4} \\ & \ Rightarrow \; \; \; \; C = \ left ({{x_C}, \; {y_C}} \ right) = \ left ({- \ frac { 1} {4}, \; \ frac {3} {4}} \ right) \ end {align} \]

Координаты D

\ [\ begin {align} & {x_D} = \ frac {{\ underbrace {3 \ times 2} _ {m {x_2}} + \ underbrace {1 \ times — 1} _ {n {x_1}}}} } {{\ underbrace {3 \ times 1} _ {m + n}}} = \ frac {{6 — 1}} {4} = \ frac {5} {4} \\ & {y_D} \, = \ frac {{\ underbrace {3 \ times — 3} _ {m {y_2}} + \ underbrace {1 \ times 2} _ {n {y_1}}}} {{\ underbrace {3 + 1} _ {m + n}}} \; = \ frac {{- 9 + 2}} {4} = — \ frac {7} {4} \\ & \ Rightarrow \; \; \; \; D = \ left ({{x_D}, \; { y_D}} \ right) = \ left ({\ frac {5} {4}, \; — \ frac {7} {4}} \ right) \ end {align} \]

Эти две точки нанесены на AB на рисунке ниже:

.